Geometry
Geometry
Jump to year
Paper 1, Section I, F
Let be a smooth function and let (assumed not empty). Show that if the differential for all , then is a smooth surface in .
Is a smooth surface? Is every surface of the form for some smooth ? Justify your answers.
Paper 1, Section II, F
Let be an oriented surface. Define the Gauss map and show that the differential of the Gauss map at any point is a self-adjoint linear map. Define the Gauss curvature and compute in a given parametrisation.
A point is called umbilic if has a repeated eigenvalue. Let be a surface such that every point is umbilic and there is a parametrisation such that . Prove that is part of a plane or part of a sphere. Hint: consider the symmetry of the mixed partial derivatives , where for
Paper 2, Section II, E
Define , the upper half plane model for the hyperbolic plane, and show that acts on by isometries, and that these isometries preserve the orientation of .
Show that every orientation preserving isometry of is in , and hence the full group of isometries of is , where .
Let be a hyperbolic line. Define the reflection in . Now let be two hyperbolic lines which meet at a point at an angle . What are the possibilities for the group generated by and ? Carefully justify your answer.
Paper 3, Section I, E
State the local Gauss-Bonnet theorem for geodesic triangles on a surface. Deduce the Gauss-Bonnet theorem for closed surfaces. [Existence of a geodesic triangulation can be assumed.]
Let denote the sphere with radius centred at the origin. Show that the Gauss curvature of is . An octant is any of the eight regions in bounded by arcs of great circles arising from the planes . Verify directly that the local Gauss-Bonnet theorem holds for an octant. [You may assume that the great circles on are geodesics.]
Paper 3, Section II, E
Let be an embedded smooth surface and a parameterised smooth curve on . What is the energy of ? By applying the Euler-Lagrange equations for stationary curves to the energy function, determine the differential equations for geodesics on explicitly in terms of a parameterisation of .
If contains a straight line , prove from first principles that each segment (with some parameterisation) is a geodesic on .
Let be the hyperboloid defined by the equation and let . By considering appropriate isometries, or otherwise, display explicitly three distinct (as subsets of ) geodesics through in the case when and four distinct geodesics through in the case when . Justify your answer.
Let be a geodesic, with coordinates . Clairaut's relation asserts is constant, where and is the angle between and the plane through the point and the -axis. Deduce from Clairaut's relation that there exist infinitely many geodesics on which stay in the half-space for all .
[You may assume that if satisfies the geodesic equations on then is defined for all and the Euclidean norm is constant. If you use a version of the geodesic equations for a surface of revolution, then that should be proved.]
Paper 4, Section II, F
Define an abstract smooth surface and explain what it means for the surface to be orientable. Given two smooth surfaces and and a map , explain what it means for to be smooth
For the cylinder
let be the orientation reversing diffeomorphism . Let be the quotient of by the equivalence relation and let be the canonical projection map. Show that can be made into an abstract smooth surface so that is smooth. Is orientable? Justify your answer.
Paper 1, Section I, E
Define the Gauss map of a smooth embedded surface. Consider the surface of revolution with points
for . Let be the Gauss map of . Describe on the cross-section of , and use this to write down an explicit formula for .
Let be the upper hemisphere of the 2 -sphere , and the Gauss curvature of . Calculate .
Paper 1, Section II, E
Let be the curve in the -plane defined by the equation
Sketch , taking care with inflection points.
Let be the surface of revolution in given by spinning about the -axis. Write down an equation defining . Stating any result you use, show that is a smooth embedded surface.
Let be the radial coordinate on the -plane. Show that the Gauss curvature of vanishes when . Are these the only points at which the Gauss curvature of vanishes? Briefly justify your answer.
Paper 2, Section II, F
Let be the hyperbolic half-plane with the metric . Define the length of a continuously differentiable curve in with respect to .
What are the hyperbolic lines in ? Show that for any two distinct points in , the infimum of the lengths (with respect to ) of curves from to is attained by the segment of the hyperbolic line with an appropriate parameterisation.
The 'hyperbolic Pythagoras theorem' asserts that if a hyperbolic triangle has angle at then
where are the lengths of the sides , respectively.
Let and be two hyperbolic lines in such that
Prove that the distance is attained by the points of intersection with a hyperbolic line that meets each of orthogonally. Give an example of two hyperbolic lines and such that the infimum of is not attained by any .
[You may assume that every Möbius transformation that maps H onto itself is an isometry of
Paper 1, Section I, E
Describe the Poincaré disc model for the hyperbolic plane by giving the appropriate Riemannian metric.
Calculate the distance between two points . You should carefully state any results about isometries of that you use.
Paper 2, Section II, E
Define a smooth embedded surface in . Sketch the surface given by
and find a smooth parametrisation for it. Use this to calculate the Gaussian curvature of at every point.
Hence or otherwise, determine which points of the embedded surface
have Gaussian curvature zero. [Hint: consider a transformation of .]
[You should carefully state any result that you use.]
Paper 3, Section I, E
State a formula for the area of a spherical triangle with angles .
Let . What is the area of a convex spherical -gon with interior angles ? Justify your answer.
Find the range of possible values for the interior angle of a regular convex spherical
Paper 3, Section II, E
Define a geodesic triangulation of an abstract closed smooth surface. Define the Euler number of a triangulation, and state the Gauss-Bonnet theorem for closed smooth surfaces. Given a vertex in a triangulation, its valency is defined to be the number of edges incident at that vertex.
(a) Given a triangulation of the torus, show that the average valency of a vertex of the triangulation is 6 .
(b) Consider a triangulation of the sphere.
(i) Show that the average valency of a vertex is strictly less than 6 .
(ii) A triangulation can be subdivided by replacing one triangle with three sub-triangles, each one with vertices two of the original ones, and a fixed interior point of .

Using this, or otherwise, show that there exist triangulations of the sphere with average vertex valency arbitrarily close to 6 .
(c) Suppose is a closed abstract smooth surface of everywhere negative curvature. Show that the average vertex valency of a triangulation of is bounded above and below.
Paper 4, Section II, E
Let be the upper-half plane with hyperbolic metric . Define the group , and show that it acts by isometries on . [If you use a generation statement you must carefully state it.]
(a) Prove that acts transitively on the collection of pairs , where is a hyperbolic line in and .
(b) Let be the imaginary half-axis. Find the isometries of which fix pointwise. Hence or otherwise find all isometries of .
(c) Describe without proof the collection of all hyperbolic lines which meet with (signed) angle . Explain why there exists a hyperbolic triangle with angles and whenever .
(d) Is this triangle unique up to isometry? Justify your answer. [You may use without proof the fact that Möbius maps preserve angles.]
Paper 1, Section I, G
(a) State the Gauss-Bonnet theorem for spherical triangles.
(b) Prove that any geodesic triangulation of the sphere has Euler number equal to
(c) Prove that there is no geodesic triangulation of the sphere in which every vertex is adjacent to exactly 6 triangles.
Paper 2, Section II, G
For any matrix
the corresponding Möbius transformation is
which acts on the upper half-plane , equipped with the hyperbolic metric .
(a) Assuming that , prove that is conjugate in to a diagonal matrix . Determine the relationship between and .
(b) For a diagonal matrix with , prove that
for all not on the imaginary axis.
(c) Assume now that . Prove that fixes a point in .
(d) Give an example of a matrix in that does not preserve any point or hyperbolic line in . Justify your answer.
Paper 3, Section I, G
Consider a quadrilateral in the hyperbolic plane whose sides are hyperbolic line segments. Suppose angles and are right-angles. Prove that is longer than .
[You may use without proof the distance formula in the upper-half-plane model
Paper 3, Section II, G
Let be an open subset of the plane , and let be a smooth parametrization of a surface . A coordinate curve is an arc either of the form
for some constant and , or of the form
for some constant and . A coordinate rectangle is a rectangle in whose sides are coordinate curves.
Prove that all coordinate rectangles in have opposite sides of the same length if and only if at all points of , where and are the usual components of the first fundamental form, and are coordinates in .
Paper 4, Section II, G
A Möbius strip in is parametrized by
for , where . Show that the Gaussian curvature is
at
Paper 1, Section I, G
Give the definition for the area of a hyperbolic triangle with interior angles .
Let . Show that the area of a convex hyperbolic -gon with interior angles is .
Show that for every and for every with there exists a regular hyperbolic -gon with area .
Paper 2, Section II, G
Let be a hyperplane in , where is a unit vector and is a constant. Show that the reflection map
is an isometry of which fixes pointwise.
Let be distinct points in . Show that there is a unique reflection mapping to , and that if and only if and are equidistant from the origin.
Show that every isometry of can be written as a product of at most reflections. Give an example of an isometry of which cannot be written as a product of fewer than 3 reflections.
Paper 3, Section I, G
Let
be stereographic projection from the unit sphere in to the Riemann sphere . Show that if is a rotation of , then is a Möbius transformation of which can be represented by an element of . (You may assume without proof any result about generation of by a particular set of rotations, but should state it carefully.)
Paper 3, Section II, G
Let be a parametrised surface, where is an open set.
(a) Explain what are the first and second fundamental forms of the surface, and what is its Gaussian curvature. Compute the Gaussian curvature of the hyperboloid .
(b) Let and be parametrised curves in , and assume that
Find a formula for the first fundamental form, and show that the Gaussian curvature vanishes if and only if
Paper 4, Section II, G
What is a hyperbolic line in (a) the disc model (b) the upper half-plane model of the hyperbolic plane? What is the hyperbolic distance between two points in the hyperbolic plane? Show that if is any continuously differentiable curve with endpoints and then its length is at least , with equality if and only if is a monotonic reparametrisation of the hyperbolic line segment joining and .
What does it mean to say that two hyperbolic lines are (a) parallel (b) ultraparallel? Show that and are ultraparallel if and only if they have a common perpendicular, and if so, then it is unique.
A horocycle is a curve in the hyperbolic plane which in the disc model is a Euclidean circle with exactly one point on the boundary of the disc. Describe the horocycles in the upper half-plane model. Show that for any pair of horocycles there exists a hyperbolic line which meets both orthogonally. For which pairs of horocycles is this line unique?
Paper 1, Section I, F
(a) Describe the Poincaré disc model for the hyperbolic plane by giving the appropriate Riemannian metric.
(b) Let be some point. Write down an isometry with .
(c) Using the Poincaré disc model, calculate the distance from 0 to re with
(d) Using the Poincaré disc model, calculate the area of a disc centred at a point and of hyperbolic radius .
Paper 2, Section II, F
(a) Let be a hyperbolic triangle, with the angle at at least . Show that the side has maximal length amongst the three sides of .
[You may use the hyperbolic cosine formula without proof. This states that if and are the lengths of , and respectively, and and are the angles of the triangle at and respectively, then
(b) Given points in the hyperbolic plane, let be any point on the hyperbolic line segment joining to , and let be any point not on the hyperbolic line passing through . Show that
where denotes hyperbolic distance.
(c) The diameter of a hyperbolic triangle is defined to be
Show that the diameter of is equal to the length of its longest side.
Paper 3, Section I,
(a) State Euler's formula for a triangulation of a sphere.
(b) A sphere is decomposed into hexagons and pentagons with precisely three edges at each vertex. Determine the number of pentagons.
Paper 3, Section II, F
(a) Define the cross-ratio of four distinct points . Show that the cross-ratio is invariant under Möbius transformations. Express in terms of .
(b) Show that is real if and only if lie on a line or circle in .
(c) Let lie on a circle in , given in anti-clockwise order as depicted.
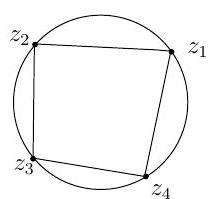
Show that is a negative real number, and that is a positive real number greater than 1 . Show that . Use this to deduce Ptolemy's relation on lengths of edges and diagonals of the inscribed 4-gon:
Paper 4, Section II, F
Let be a simple curve in parameterised by arc length with for all , and consider the surface of revolution in defined by the parameterisation
(a) Calculate the first and second fundamental forms for . Show that the Gaussian curvature of is given by
(b) Now take . What is the integral of the Gaussian curvature over the surface of revolution determined by and ?
[You may use the Gauss-Bonnet theorem without proof.]
(c) Now suppose has constant curvature , and suppose there are two points such that is a smooth closed embedded surface. Show that is a unit sphere, minus two antipodal points.
[Do not attempt to integrate an expression of the form when . Study the behaviour of the surface at the largest and smallest possible values of .]
Paper 1, Section I, F
(i) Give a model for the hyperbolic plane. In this choice of model, describe hyperbolic lines.
Show that if are two hyperbolic lines and are points, then there exists an isometry of the hyperbolic plane such that and .
(ii) Let be a triangle in the hyperbolic plane with angles and . What is the area of ?
Paper 2, Section II, F
(a) For each of the following subsets of , explain briefly why it is a smooth embedded surface or why it is not.
(b) Let be given by
and let . You may assume that is a smooth embedded surface.
Find the first fundamental form of this surface.
Find the second fundamental form of this surface.
Compute the Gaussian curvature of this surface.
Paper 3, Section , F
State the sine rule for spherical triangles.
Let be a spherical triangle with vertices , and , with angles and at the respective vertices. Let , and be the lengths of the edges and respectively. Show that if and only if . [You may use the cosine rule for spherical triangles.] Show that this holds if and only if there exists a reflection such that and .
Are there equilateral triangles on the sphere? Justify your answer.
Paper 3, Section II, F
Let be a Möbius transformation on the Riemann sphere .
(i) Show that has either one or two fixed points.
(ii) Show that if is a Möbius transformation corresponding to (under stereographic projection) a rotation of through some fixed non-zero angle, then has two fixed points, , with .
(iii) Suppose has two fixed points with . Show that either corresponds to a rotation as in (ii), or one of the fixed points, say , is attractive, i.e. as for any .
Paper 4, Section II, F
Let be a curve in parameterized by arc length, and consider the surface of revolution in defined by the parameterization
In what follows, you may use that a curve in , with , is a geodesic if and only if
(i) Write down the first fundamental form for , and use this to write down a formula which is equivalent to being a unit speed curve.
(ii) Show that for a given , the circle on determined by is a geodesic if and only if .
(iii) Let be a curve in such that parameterizes a unit speed curve that is a geodesic in . For a given time , let denote the angle between the curve and the circle on determined by . Derive Clairault's relation that
is independent of .
Paper 1, Section I, F
Determine the second fundamental form of a surface in defined by the parametrisation
for , with some fixed . Show that the Gaussian curvature of this surface takes both positive and negative values.
Paper 2, Section II, F
Let be the upper half-plane with a hyperbolic metric . Prove that every hyperbolic circle in is also a Euclidean circle. Is the centre of as a hyperbolic circle always the same point as the centre of as a Euclidean circle? Give a proof or counterexample as appropriate.
Let and be two hyperbolic triangles and denote the hyperbolic lengths of their sides by and , respectively. Show that if and , then there is a hyperbolic isometry taking to . Is there always such an isometry if instead the triangles have one angle the same and Justify your answer.
[Standard results on hyperbolic isometries may be assumed, provided they are clearly stated.]
Paper 3, Section I, F
Let be an isometry , where is an matrix and . What are the possible values of ?
Let denote the identity matrix. Show that if and , but , then has a fixed point. Must have a fixed point if and , but Justify your answer.
Paper 3, Section II, F
Let be a decomposition of the two-dimensional sphere into polygonal domains, with every polygon having at least three edges. Let , and denote the numbers of vertices, edges and faces of , respectively. State Euler's formula. Prove that .
Suppose that at least three edges meet at every vertex of . Let be the number of faces of that have exactly edges and let be the number of vertices at which exactly edges meet . Is it possible for to have ? Justify your answer.
By expressing in terms of the , or otherwise, show that has at least four faces that are triangles, quadrilaterals and/or pentagons.
Paper 4, Section II, F
Define an embedded parametrised surface in . What is the Riemannian metric induced by a parametrisation? State, in terms of the Riemannian metric, the equations defining a geodesic curve , assuming that is parametrised by arc-length.
Let be a conical surface
Using an appropriate smooth parametrisation, or otherwise, prove that is locally isometric to the Euclidean plane. Show that any two points on can be joined by a geodesic. Is this geodesic always unique (up to a reparametrisation)? Justify your answer.
[The expression for the Euclidean metric in polar coordinates on may be used without proof.]
Paper 1, Section I, F
Let and be ultraparallel geodesics in the hyperbolic plane. Prove that the have a unique common perpendicular.
Suppose now are pairwise ultraparallel geodesics in the hyperbolic plane. Can the three common perpendiculars be pairwise disjoint? Must they be pairwise disjoint? Briefly justify your answers.
Paper 2, Section II, F
Let and be disjoint circles in . Prove that there is a Möbius transformation which takes and to two concentric circles.
A collection of circles , for which
is tangent to and , where indices are ;
the circles are disjoint away from tangency points;
is called a constellation on . Prove that for any there is some pair and a constellation on made up of precisely circles. Draw a picture illustrating your answer.
Given a constellation on , prove that the tangency points for all lie on a circle. Moreover, prove that if we take any other circle tangent to and , and then construct for inductively so that is tangent to and , then we will have , i.e. the chain of circles will again close up to form a constellation.
Paper 3, Section I, F
Let be a surface with Riemannian metric having first fundamental form . State a formula for the Gauss curvature of .
Suppose that is flat, so vanishes identically, and that is a geodesic on when parametrised by arc-length. Using the geodesic equations, or otherwise, prove that , i.e. is locally isometric to a plane.
Paper 3, Section II, F
Show that the set of all straight lines in admits the structure of an abstract smooth surface . Show that is an open Möbius band (i.e. the Möbius band without its boundary circle), and deduce that admits a Riemannian metric with vanishing Gauss curvature.
Show that there is no metric , in the sense of metric spaces, which
induces the locally Euclidean topology on constructed above;
is invariant under the natural action on of the group of translations of .
Show that the set of great circles on the two-dimensional sphere admits the structure of a smooth surface . Is homeomorphic to ? Does admit a Riemannian metric with vanishing Gauss curvature? Briefly justify your answers.
Paper 4, Section II, F
Let be a smooth curve in the -plane , with for every and . Let be the surface obtained by rotating around the -axis. Find the first fundamental form of .
State the equations for a curve parametrised by arc-length to be a geodesic.
A parallel on is the closed circle swept out by rotating a single point of . Prove that for every there is some for which exactly parallels are geodesics. Sketch possible such surfaces in the cases and .
If every parallel is a geodesic, what can you deduce about ? Briefly justify your answer.
Paper 1, Section I, G
Describe a collection of charts which cover a circular cylinder of radius . Compute the first fundamental form, and deduce that the cylinder is locally isometric to the plane.
Paper 2, Section II, G
Let be a closed surface, equipped with a triangulation. Define the Euler characteristic of . How does depend on the triangulation?
Let and denote the number of vertices, edges and faces of the triangulation. Show that .
Suppose now the triangulation is tidy, meaning that it has the property that no two vertices are joined by more than one edge. Deduce that satisfies
Hence compute the minimal number of vertices of a tidy triangulation of the real projective plane. [Hint: it may be helpful to consider the icosahedron as a triangulation of the sphere
Paper 3, Section I,
State a formula for the area of a hyperbolic triangle.
Hence, or otherwise, prove that if and are disjoint geodesics in the hyperbolic plane, there is at most one geodesic which is perpendicular to both and .
Paper 3, Section II, G
Define the first and second fundamental forms of a smooth surface , and explain their geometrical significance.
Write down the geodesic equations for a smooth curve . Prove that is a geodesic if and only if the derivative of the tangent vector to is always orthogonal to .
A plane cuts in a smooth curve , in such a way that reflection in the plane is an isometry of (in particular, preserves ). Prove that is a geodesic.
Paper 4, Section II, G
Let be a smooth closed surface. Define the principal curvatures and at a point . Prove that the Gauss curvature at is the product of the two principal curvatures.
A point is called a parabolic point if at least one of the two principal curvatures vanishes. Suppose is a plane and is tangent to along a smooth closed curve . Show that is composed of parabolic points.
Can both principal curvatures vanish at a point of ? Briefly justify your answer.
Paper 1, Section I, F
Suppose that is the upper half-plane, . Using the Riemannian metric , define the length of a curve and the area of a region in .
Find the area of
Paper 2, Section II, F
Suppose that is stereographic projection. Show that, via , every rotation of corresponds to a Möbius transformation in .
Paper 3, Section I, F
Let denote anti-clockwise rotation of the Euclidean plane through an angle about a point .
Show that is a composite of two reflexions.
Assume . Show that the composite is also a rotation . Find and .
Paper 3, Section II, F
Suppose that is a unit speed curve in . Show that the corresponding surface of revolution obtained by rotating this curve about the -axis has Gaussian curvature .
Paper 4, Section II, F
Suppose that is a point on a Riemannian surface . Explain the notion of geodesic polar co-ordinates on in a neighbourhood of , and prove that if is a geodesic circle centred at of small positive radius, then the geodesics through meet at right angles.
Paper 1, Section I, F
(i) Define the notion of curvature for surfaces embedded in .
(ii) Prove that the unit sphere in has curvature at all points.
Paper 2, Section II, F
Suppose that and that is the half-cone defined by , . By using an explicit smooth parametrization of , calculate the curvature of .
Describe the geodesics on . Show that for , no geodesic intersects itself, while for some geodesic does so.
Paper 3, Section I, F
(i) Write down the Poincaré metric on the unit disc model of the hyperbolic plane. Compute the hyperbolic distance from to , with .
(ii) Given a point in and a hyperbolic line in with not on , describe how the minimum distance from to is calculated. Justify your answer.
Paper 3, Section II, F
Describe the hyperbolic metric on the upper half-plane . Show that any Möbius transformation that preserves is an isometry of this metric.
Suppose that are distinct and that the hyperbolic line through and meets the real axis at . Show that the hyperbolic distance between and is given by , where is the cross-ratio of the four points , taken in an appropriate order.
Paper 4, Section II, F
Suppose that is the unit disc, with Riemannian metric
[Note that this is not a multiple of the Poincaré metric.] Show that the diameters of are, with appropriate parametrization, geodesics.
Show that distances between points in are bounded, but areas of regions in are unbounded.
Paper 1, Section I, G
What is an ideal hyperbolic triangle? State a formula for its area.
Compute the area of a hyperbolic disk of hyperbolic radius . Hence, or otherwise, show that no hyperbolic triangle completely contains a hyperbolic circle of hyperbolic radius
Paper 2, Section II, G
What is meant by stereographic projection from the unit sphere in to the complex plane? Briefly explain why a spherical triangle cannot map to a Euclidean triangle under stereographic projection.
Derive an explicit formula for stereographic projection. Hence, or otherwise, prove that if a Möbius map corresponds via stereographic projection to a rotation of the sphere, it has two fixed points and which satisfy . Give, with justification:
(i) a Möbius transformation which fixes a pair of points satisfying but which does not arise from a rotation of the sphere;
(ii) an isometry of the sphere (for the spherical metric) which does not correspond to any Möbius transformation under stereographic projection.
Paper 3, Section I, G
Write down the equations for geodesic curves on a surface. Use these to describe all the geodesics on a circular cylinder, and draw a picture illustrating your answer.
Paper 3, Section II, G
Consider a tessellation of the two-dimensional sphere, that is to say a decomposition of the sphere into polygons each of which has at least three sides. Let and denote the numbers of edges, vertices and faces in the tessellation, respectively. State Euler's formula. Prove that . Deduce that not all the vertices of the tessellation have valence .
By considering the plane , or otherwise, deduce the following: if is a finite set of straight lines in the plane with the property that every intersection point of two lines is an intersection point of at least three, then all the lines in meet at a single point.
Paper 4, Section II, G
Let be an open set. Let be a surface locally given as the graph of an infinitely-differentiable function . Compute the Gaussian curvature of in terms of .
Deduce that if is a compact surface without boundary, its Gaussian curvature is not everywhere negative.
Give, with brief justification, a compact surface without boundary whose Gaussian curvature must change sign.
1.I.2G
Show that any element of is a rotation, and that it can be written as the product of two reflections.
2.II.12G
Show that the area of a spherical triangle with angles is . Hence derive the formula for the area of a convex spherical -gon.
Deduce Euler's formula for a decomposition of a sphere into convex polygons with a total of edges and vertices.
A sphere is decomposed into convex polygons, comprising quadrilaterals, pentagons and hexagons, in such a way that at each vertex precisely three edges meet. Show that there are at most 7 possibilities for the pair , and that at least 3 of these do occur.
3.I.2G
A smooth surface in has parametrization
Show that a unit normal vector at the point is
and that the curvature is .
3.II.12G
Let be the unit disc model of the hyperbolic plane, with metric
(i) Show that the group of Möbius transformations mapping to itself is the group of transformations
where and .
(ii) Assuming that the transformations in (i) are isometries of , show that any hyperbolic circle in is a Euclidean circle.
(iii) Let and be points on the unit circle with . Show that the hyperbolic distance from to the hyperbolic line is given by
(iv) Deduce that if then no hyperbolic open disc of radius is contained in a hyperbolic triangle.
4.II.12G
Let be a curve on a smoothly embedded surface . Define the energy of . Show that if is a stationary point for the energy for proper variations of , then satisfies the geodesic equations
where in terms of a smooth parametrization for , with first fundamental form .
Now suppose that for every the curves are geodesics.
(i) Show that and .
(ii) Suppose moreover that the angle between the curves is independent of and . Show that .
1.I.2A
State the Gauss-Bonnet theorem for spherical triangles, and deduce from it that for each convex polyhedron with faces, edges, and vertices, .
2.II.12A
(i) The spherical circle with centre and radius , is the set of all points on the unit sphere at spherical distance from . Find the circumference of a spherical circle with spherical radius . Compare, for small , with the formula for a Euclidean circle and comment on the result.
(ii) The cross ratio of four distinct points in is
Show that the cross-ratio is a real number if and only if lie on a circle or a line.
[You may assume that Möbius transformations preserve the cross-ratio.]
3.I
Let be a line in the Euclidean plane and a point on . Denote by the reflection in and by the rotation through an angle about . Describe, in terms of , and , a line fixed by the composition and show that is a reflection.
3.II.12A
For a parameterized smooth embedded surface , where is an open domain in , define the first fundamental form, the second fundamental form, and the Gaussian curvature . State the Gauss-Bonnet formula for a compact embedded surface having Euler number .
Let denote a surface defined by rotating a curve
about the -axis. Here are positive constants, such that and . By considering a smooth parameterization, find the first fundamental form and the second fundamental form of .
4.II.12A
Write down the Riemannian metric for the upper half-plane model of the hyperbolic plane. Describe, without proof, the group of isometries of and the hyperbolic lines (i.e. the geodesics) on .
Show that for any two hyperbolic lines , there is an isometry of which maps onto .
Suppose that is a composition of two reflections in hyperbolic lines which are ultraparallel (i.e. do not meet either in the hyperbolic plane or at its boundary). Show that cannot be an element of finite order in the group of isometries of .
[Existence of a common perpendicular to two ultraparallel hyperbolic lines may be assumed. You might like to choose carefully which hyperbolic line to consider as a common perpendicular.]
1.I
Define the hyperbolic metric in the upper half-plane model of the hyperbolic plane. How does one define the hyperbolic area of a region in ? State the Gauss-Bonnet theorem for hyperbolic triangles.
Let be the region in defined by
Calculate the hyperbolic area of .
2.II.12H
Let denote a parametrized smooth embedded surface, where is an open ball in with coordinates . Explain briefly the geometric meaning of the second fundamental form
where , with denoting the unit normal vector to the surface .
Prove that if the second fundamental form is identically zero, then as vector-valued functions on , and hence that is a constant vector. Deduce that is then contained in a plane given by constant.
3.I.2H
Show that the Gaussian curvature at an arbitrary point of the hyperboloid , as an embedded surface in , is given by the formula
3.II.12H
Describe the stereographic projection map from the sphere to the extended complex plane , positioned equatorially. Prove that correspond to antipodal points on if and only if . State, without proof, a result which relates the rotations of to a certain group of Möbius transformations on .
Show that any circle in the complex plane corresponds, under stereographic projection, to a circle on . Let denote any circle in the complex plane other than the unit circle; show that corresponds to a great circle on if and only if its intersection with the unit circle consists of two points, one of which is the negative of the other.
[You may assume the result that a Möbius transformation on the complex plane sends circles and straight lines to circles and straight lines.]
4.II.12H
Describe the hyperbolic lines in both the disc and upper half-plane models of the hyperbolic plane. Given a hyperbolic line and a point , we define
where denotes the hyperbolic distance. Show that , where is the unique point of for which the hyperbolic line segment is perpendicular to .
Suppose now that is the positive imaginary axis in the upper half-plane model of the hyperbolic plane, and is the semicircle with centre on the real line, and radius , where . For any , show that the hyperbolic line through which is perpendicular to is a semicircle centred on the origin of radius , and prove that
For arbitrary hyperbolic lines in the hyperbolic plane, we define
If and are ultraparallel (i.e. hyperbolic lines which do not meet, either inside the hyperbolic plane or at its boundary), prove that is strictly positive.
[The equivalence of the disc and upper half-plane models of the hyperbolic plane, and standard facts about the metric and isometries of these models, may be quoted without proof.]
1.I
Let be the map defined by
where . Describe briefly the image . Let denote the open subset of given by ; prove that the restriction defines a smooth parametrization of a certain open subset (which you should specify) of . Hence, or otherwise, prove that is a smooth embedded surface in .
[You may assume that the image under of any open set is open in .]
2.II.12A
Let be an open subset of equipped with a Riemannian metric. For a smooth curve, define what is meant by its length and energy. Prove that length , with equality if and only if has constant norm with respect to the metric.
Suppose now is the upper half plane model of the hyperbolic plane, and are points on the positive imaginary axis. Show that a smooth curve joining and represents an absolute minimum of the length of such curves if and only if , with a smooth monotonic real function.
Suppose that a smooth curve joining the above points and represents a stationary point for the energy under proper variations; deduce from an appropriate form of the Euler-Lagrange equations that must be of the above form, with constant.
3.I.2A
Write down the Riemannian metric on the disc model of the hyperbolic plane. Given that the length minimizing curves passing through the origin correspond to diameters, show that the hyperbolic circle of radius centred on the origin is just the Euclidean circle centred on the origin with Euclidean . Prove that the hyperbolic area is .
State the Gauss-Bonnet theorem for the area of a hyperbolic triangle. Given a hyperbolic triangle and an interior point , show that the distance from to the nearest side is at most .
3.II.12A
Describe geometrically the stereographic projection map from the unit sphere to the extended complex plane , positioned equatorially, and find a formula for .
Show that any Möbius transformation on has one or two fixed points. Show that the Möbius transformation corresponding (under the stereographic projection map) to a rotation of through a non-zero angle has exactly two fixed points and , where . If now is a Möbius transformation with two fixed points and satisfying , prove that either corresponds to a rotation of , or one of the fixed points, say , is an attractive fixed point, i.e. for as .
[You may assume the fact that any rotation of corresponds to some Möbius transformation of under the stereographic projection map.]
4.II.12A
Given a parametrized smooth embedded surface , where is an open subset of with coordinates , and a point , define what is meant by the tangent space at , the unit normal at , and the first fundamental form
[You need not show that your definitions are independent of the parametrization.]
The second fundamental form is defined to be
where and . Prove that the partial derivatives of (considered as a vector-valued function of ) are of the form , , where
Explain briefly the significance of the determinant .
1.I.3G
Using the Riemannian metric
define the length of a curve and the area of a region in the upper half-plane .
Find the hyperbolic area of the region .
1.II.14G
Show that for every hyperbolic line in the hyperbolic plane there is an isometry of which is the identity on but not on all of . Call it the reflection .
Show that every isometry of is a composition of reflections.
3.I.3G
State Euler's formula for a convex polyhedron with faces, edges, and vertices.
Show that any regular polyhedron whose faces are pentagons has the same number of vertices, edges and faces as the dodecahedron.
3.II.15G
Let be the lengths of a right-angled triangle in spherical geometry, where is the hypotenuse. Prove the Pythagorean theorem for spherical geometry in the form
Now consider such a spherical triangle with the sides replaced by for a positive number . Show that the above formula approaches the usual Pythagorean theorem as approaches zero.
1.I.4F
Describe the geodesics (that is, hyperbolic straight lines) in either the disc model or the half-plane model of the hyperbolic plane. Explain what is meant by the statements that two hyperbolic lines are parallel, and that they are ultraparallel.
Show that two hyperbolic lines and have a unique common perpendicular if and only if they are ultraparallel.
[You may assume standard results about the group of isometries of whichever model of the hyperbolic plane you use.]
1.II.13F
Write down the Riemannian metric in the half-plane model of the hyperbolic plane. Show that Möbius transformations mapping the upper half-plane to itself are isometries of this model.
Calculate the hyperbolic distance from to , where and are positive real numbers. Assuming that the hyperbolic circle with centre and radius is a Euclidean circle, find its Euclidean centre and radius.
Suppose that and are positive real numbers for which the points and of the upper half-plane are such that the hyperbolic distance between them coincides with the Euclidean distance. Obtain an expression for as a function of . Hence show that, for any with , there is a unique positive value of such that the hyperbolic distance between and coincides with the Euclidean distance.
3.I.4F
Show that any isometry of Euclidean 3 -space which fixes the origin can be written as a composite of at most three reflections in planes through the origin, and give (with justification) an example of an isometry for which three reflections are necessary.
3.II.14F
State and prove the Gauss-Bonnet formula for the area of a spherical triangle. Deduce a formula for the area of a spherical -gon with angles . For what range of values of does there exist a (convex) regular spherical -gon with angle ?
Let be a spherical triangle with angles and where are integers, and let be the group of isometries of the sphere generated by reflections in the three sides of . List the possible values of , and in each case calculate the order of the corresponding group . If , show how to construct a regular dodecahedron whose group of symmetries is .
[You may assume that the images of under the elements of form a tessellation of the sphere.]
1.I.4E
Show that any finite group of orientation-preserving isometries of the Euclidean plane is cyclic.
Show that any finite group of orientation-preserving isometries of the hyperbolic plane is cyclic.
[You may assume that given any non-empty finite set in the hyperbolic plane, or the Euclidean plane, there is a unique smallest closed disc that contains E. You may also use any general fact about the hyperbolic plane without proof providing that it is stated carefully.]
1.II.13E
Let , and let have the hyperbolic metric derived from the line element . Let be the group of Möbius maps of the form , where and are real and . Show that every in is an isometry of the metric space . For and in , let
Show that for every in . By considering , where , and , or otherwise, show that for all and in ,
By considering points , where and , where , or otherwise, derive Pythagoras' Theorem for hyperbolic geometry in the form , where and are the lengths of sides of a right-angled triangle whose hypotenuse has length .
3.I.4E
State Euler's formula for a graph with faces, edges and vertices on the surface of a sphere.
Suppose that every face in has at least three edges, and that at least three edges meet at every vertex of . Let be the number of faces of that have exactly edges , and let be the number of vertices at which exactly edges meet . By expressing in terms of the , or otherwise, show that every convex polyhedron has at least four faces each of which is a triangle, a quadrilateral or a pentagon.
3.II.14E
Show that every isometry of Euclidean space is a composition of reflections in planes
What is the smallest integer such that every isometry of with can be expressed as the composition of at most reflections? Give an example of an isometry that needs this number of reflections and justify your answer.
Describe (geometrically) all twelve orientation-reversing isometries of a regular tetrahedron.
1.I.4B
Write down the Riemannian metric on the disc model of the hyperbolic plane. What are the geodesics passing through the origin? Show that the hyperbolic circle of radius centred on the origin is just the Euclidean circle centred on the origin with Euclidean radius .
Write down an isometry between the upper half-plane model of the hyperbolic plane and the disc model , under which corresponds to . Show that the hyperbolic circle of radius centred on in is a Euclidean circle with centre and of radius .
1.II.13B
Describe geometrically the stereographic projection map from the unit sphere to the extended complex plane , and find a formula for . Show that any rotation of about the -axis corresponds to a Möbius transformation of . You are given that the rotation of defined by the matrix
corresponds under to a Möbius transformation of ; deduce that any rotation of about the -axis also corresponds to a Möbius transformation.
Suppose now that correspond under to distinct points , and let denote the angular distance from to on . Show that is the cross-ratio of the points , taken in some order (which you should specify). [You may assume that the cross-ratio is invariant under Möbius transformations.]
3.I.4B
State and prove the Gauss-Bonnet theorem for the area of a spherical triangle.
Suppose is a regular dodecahedron, with centre the origin. Explain how each face of gives rise to a spherical pentagon on the 2 -sphere . For each such spherical pentagon, calculate its angles and area.
3.II.14B
Describe the hyperbolic lines in the upper half-plane model of the hyperbolic plane. The group acts on via Möbius transformations, which you may assume are isometries of . Show that acts transitively on the hyperbolic lines. Find explicit formulae for the reflection in the hyperbolic line in the cases (i) is a vertical line , and (ii) is the unit semi-circle with centre the origin. Verify that the composite of a reflection of type (ii) followed afterwards by one of type (i) is given by .
Suppose now that and are distinct hyperbolic lines in the hyperbolic plane, with denoting the corresponding reflections. By considering different models of the hyperbolic plane, or otherwise, show that
(a) has infinite order if and are parallel or ultraparallel, and
(b) has finite order if and only if and meet at an angle which is a rational multiple of .