Part IB, 2008

Analysis II

• $3 . \mathrm{I} . 3 \mathrm{~F} \quad$

  Analysis II | Part IB, 2008

  Explain what it means for a function $f(x, y)$ of two variables to be differentiable at a point $\left(x_{0}, y_{0}\right)$. If $f$ is differentiable at $\left(x_{0}, y_{0}\right)$, show that for any $\alpha$ the function $g_{\alpha}$ defined by

  $$g_{\alpha}(t)=f\left(x_{0}+t \cos \alpha, y_{0}+t \sin \alpha\right)$$

  is differentiable at $t=0$, and find its derivative in terms of the partial derivatives of $f$ at $\left(x_{0}, y_{0}\right)$.

  Consider the function $f$ defined by

  

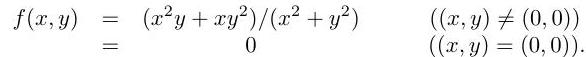
  Is $f$ differentiable at $(0,0)$ ? Justify your answer.

  comment

• 1.II.11F

  Analysis II | Part IB, 2008

  State and prove the Contraction Mapping Theorem.

  Let $(X, d)$ be a nonempty complete metric space and $f: X \rightarrow X$ a mapping such that, for some $k>0$, the $k$ th iterate $f^{k}$ of $f$ (that is, $f$ composed with itself $k$ times) is a contraction mapping. Show that $f$ has a unique fixed point.

  Now let $X$ be the space of all continuous real-valued functions on $[0,1]$, equipped with the uniform norm $\|h\|_{\infty}=\sup \{|h(t)|: t \in[0,1]\}$, and let $\phi: \mathbb{R} \times[0,1] \rightarrow \mathbb{R}$ be a continuous function satisfying the Lipschitz condition

  $$|\phi(x, t)-\phi(y, t)| \leqslant M|x-y|$$

  for all $t \in[0,1]$ and all $x, y \in \mathbb{R}$, where $M$ is a constant. Let $F: X \rightarrow X$ be defined by

  $$F(h)(t)=g(t)+\int_{0}^{t} \phi(h(s), s) d s$$

  where $g$ is a fixed continuous function on $[0,1]$. Show by induction on $n$ that

  $$\left|F^{n}(h)(t)-F^{n}(k)(t)\right| \leqslant \frac{M^{n} t^{n}}{n !}\|h-k\|_{\infty}$$

  for all $h, k \in X$ and all $t \in[0,1]$. Deduce that the integral equation

  $$f(t)=g(t)+\int_{0}^{t} \phi(f(s), s) d s$$

  has a unique continuous solution $f$ on $[0,1]$.

  comment

• 2.I.3F

  Analysis II | Part IB, 2008

  Explain what is meant by the statement that a sequence $\left(f_{n}\right)$ of functions defined on an interval $[a, b]$ converges uniformly to a function $f$. If $\left(f_{n}\right)$ converges uniformly to $f$, and each $f_{n}$ is continuous on $[a, b]$, prove that $f$ is continuous on $[a, b]$.

  Now suppose additionally that $\left(x_{n}\right)$ is a sequence of points of $[a, b]$ converging to a limit $x$. Prove that $f_{n}\left(x_{n}\right) \rightarrow f(x)$.

  comment

• 2.II.13F

  Analysis II | Part IB, 2008

  Let $\left(u_{n}(x): n=0,1,2, \ldots\right)$ be a sequence of real-valued functions defined on a subset $E$ of $\mathbb{R}$. Suppose that for all $n$ and all $x \in E$ we have $\left|u_{n}(x)\right| \leqslant M_{n}$, where $\sum_{n=0}^{\infty} M_{n}$ converges. Prove that $\sum_{n=0}^{\infty} u_{n}(x)$ converges uniformly on $E$.

  Now let $E=\mathbb{R} \backslash \mathbb{Z}$, and consider the series $\sum_{n=0}^{\infty} u_{n}(x)$, where $u_{0}(x)=1 / x^{2}$ and

  $$u_{n}(x)=1 /(x-n)^{2}+1 /(x+n)^{2}$$

  for $n>0$. Show that the series converges uniformly on $E_{R}=\{x \in E:|x|<R\}$ for any real number $R$. Deduce that $f(x)=\sum_{n=0}^{\infty} u_{n}(x)$ is a continuous function on $E$. Does the series converge uniformly on $E$ ? Justify your answer.

  comment

• 3.II.13F

  Analysis II | Part IB, 2008

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be a function, and $\left(x_{0}, y_{0}\right)$ a point of $\mathbb{R}^{2}$. Prove that if the partial derivatives of $f$ exist in some open disc around $\left(x_{0}, y_{0}\right)$ and are continuous at $\left(x_{0}, y_{0}\right)$, then $f$ is differentiable at $\left(x_{0}, y_{0}\right)$.

  Now let $X$ denote the vector space of all $(n \times n)$ real matrices, and let $f: X \rightarrow \mathbb{R}$ be the function assigning to each matrix its determinant. Show that $f$ is differentiable at the identity matrix $I$, and that $\left.D f\right|_{I}$ is the linear map $H \mapsto \operatorname{tr} H$. Deduce that $f$ is differentiable at any invertible matrix $A$, and that $\left.D f\right|_{A}$ is the linear map $H \mapsto \operatorname{det} A \operatorname{tr}\left(A^{-1} H\right) .$

  Show also that if $K$ is a matrix with $\|K\|<1$, then $(I+K)$ is invertible. Deduce that $f$ is twice differentiable at $I$, and find $\left.D^{2} f\right|_{I}$ as a bilinear map $X \times X \rightarrow \mathbb{R}$.

  [You may assume that the norm $\|-\|$ on $X$ is complete, and that it satisfies the inequality $\|A B\| \leqslant\|A\| \cdot\|B\|$ for any two matrices $A$ and $B .]$

  comment

• 4.I.3F

  Analysis II | Part IB, 2008

  Let $X$ be the vector space of all continuous real-valued functions on the unit interval $[0,1]$. Show that the functions

  $$\|f\|_{1}=\int_{0}^{1}|f(t)| d t \quad \text { and } \quad\|f\|_{\infty}=\sup \{|f(t)|: 0 \leqslant t \leqslant 1\}$$

  both define norms on $X$.

  Consider the sequence $\left(f_{n}\right)$ defined by $f_{n}(t)=n t^{n}(1-t)$. Does $\left(f_{n}\right)$ converge in the norm $\|-\|_{1}$ ? Does it converge in the norm $\|-\|_{\infty}$ ? Justify your answers.

  comment

• 4.II.13F

  Analysis II | Part IB, 2008

  Explain what it means for two norms on a real vector space to be Lipschitz equivalent. Show that if two norms are Lipschitz equivalent, then one is complete if and only if the other is.

  Let $\|-\|$ be an arbitrary norm on the finite-dimensional space $\mathbb{R}^{n}$, and let $\|-\|_{2}$ denote the standard (Euclidean) norm. Show that for every $\mathbf{x} \in \mathbb{R}^{n}$ with $\|\mathbf{x}\|_{2}=1$, we have

  $$\|\mathbf{x}\| \leqslant\left\|\mathbf{e}_{1}\right\|+\left\|\mathbf{e}_{2}\right\|+\cdots+\left\|\mathbf{e}_{n}\right\|$$

  where $\left(\mathbf{e}_{1}, \mathbf{e}_{2}, \ldots, \mathbf{e}_{n}\right)$ is the standard basis for $\mathbb{R}^{n}$, and deduce that the function $\|-\|$ is continuous with respect to $\|-\|_{2}$. Hence show that there exists a constant $m>0$ such that $\|\mathbf{x}\| \geqslant m$ for all $\mathbf{x}$ with $\|\mathbf{x}\|_{2}=1$, and deduce that $\|-\|$ and $\|-\|_{2}$ are Lipschitz equivalent.

  [You may assume the Bolzano-Weierstrass Theorem.]

  comment

Complex Analysis

• 3.II.14E

  Complex Analysis | Part IB, 2008

  State and prove Rouché's theorem, and use it to count the number of zeros of $3 z^{9}+8 z^{6}+z^{5}+2 z^{3}+1$ inside the annulus $\{z: 1<|z|<2\}$.

  Let $\left(p_{n}\right)_{n=1}^{\infty}$ be a sequence of polynomials of degree at most $d$ with the property that $p_{n}(z)$ converges uniformly on compact subsets of $\mathbb{C}$ as $n \rightarrow \infty$. Prove that there is a polynomial $p$ of degree at most $d$ such that $p_{n} \rightarrow p$ uniformly on compact subsets of $\mathbb{C}$. [If you use any results about uniform convergence of analytic functions, you should prove them.]

  Suppose that $p$ has $d$ distinct roots $z_{1}, \ldots, z_{d}$. Using Rouché's theorem, or otherwise, show that for each $i$ there is a sequence $\left(z_{i, n}\right)_{n=1}^{\infty}$ such that $p_{n}\left(z_{i, n}\right)=0$ and $z_{i, n} \rightarrow z_{i}$ as $n \rightarrow \infty$.

  comment

• 4.I.4E

  Complex Analysis | Part IB, 2008

  Suppose that $f$ and $g$ are two functions which are analytic on the whole complex plane $\mathbb{C}$. Suppose that there is a sequence of distinct points $z_{1}, z_{2}, \ldots$ with $\left|z_{i}\right| \leqslant 1$ such that $f\left(z_{i}\right)=g\left(z_{i}\right)$. Show that $f(z)=g(z)$ for all $z \in \mathbb{C}$. [You may assume any results on Taylor expansions you need, provided they are clearly stated.]

  What happens if the assumption that $\left|z_{i}\right| \leqslant 1$ is dropped?

  comment

Complex Analysis or Complex Methods

• 1.I.3C

  Complex Analysis or Complex Methods | Part IB, 2008

  Given that $f(z)$ is an analytic function, show that the mapping $w=f(z)$

  (a) preserves angles between smooth curves intersecting at $z$ if $f^{\prime}(z) \neq 0$;

  (b) has Jacobian given by $\left|f^{\prime}(z)\right|^{2}$.

  comment

• 1.II.13C

  Complex Analysis or Complex Methods | Part IB, 2008

  By a suitable choice of contour show the following:

  (a)

  $$\int_{0}^{\infty} \frac{x^{1 / n}}{1+x^{2}} d x=\frac{\pi}{2 \cos (\pi / 2 n)}$$

  where $n>1$,

  (b)

  $$\int_{0}^{\infty} \frac{x^{1 / 2} \log x}{1+x^{2}} d x=\frac{\pi^{2}}{2 \sqrt{2}}$$

  comment

• 2.II.14C

  Complex Analysis or Complex Methods | Part IB, 2008

  Let $f(z)=1 /\left(e^{z}-1\right)$. Find the first three terms in the Laurent expansion for $f(z)$ valid for $0<|z|<2 \pi$.

  Now let $n$ be a positive integer, and define

  $$\begin{aligned} &f_{1}(z)=\frac{1}{z}+\sum_{r=1}^{n} \frac{2 z}{z^{2}+4 \pi^{2} r^{2}} \\ &f_{2}(z)=f(z)-f_{1}(z) \end{aligned}$$

  Show that the singularities of $f_{2}$ in $\{z:|z|<2(n+1) \pi\}$ are all removable. By expanding $f_{1}$ as a Laurent series valid for $|z|>2 n \pi$, and $f_{2}$ as a Taylor series valid for $|z|<2(n+1) \pi$, find the coefficients of $z^{j}$ for $-1 \leq j \leq 1$ in the Laurent series for $f$ valid for $2 n \pi<|z|<2(n+1) \pi$.

  By estimating an appropriate integral around the contour $|z|=(2 n+1) \pi$, show that

  $$\sum_{r=1}^{\infty} \frac{1}{r^{2}}=\frac{\pi^{2}}{6}$$

  comment

Complex Methods

• 3.I.5C

  Complex Methods | Part IB, 2008

  Using the contour integration formula for the inversion of Laplace transforms find the inverse Laplace transforms of the following functions: (a) $\frac{s}{s^{2}+a^{2}} \quad(a$ real and non-zero $)$, (b) $\frac{1}{\sqrt{s}}$.

  [You may use the fact that $\int_{-\infty}^{\infty} e^{-b x^{2}} d x=\sqrt{\pi / b}$.]

  comment

• 4.II.15C

  Complex Methods | Part IB, 2008

  Let $H$ be the domain $\mathbb{C}-\{x+i y: x \leq 0, y=0\}$ (i.e., $\mathbb{C}$ cut along the negative $x$-axis). Show, by a suitable choice of branch, that the mapping

  $$z \mapsto w=-i \log z$$

  maps $H$ onto the strip $S=\{z=x+i y,-\pi<x<\pi\}$.

  How would a different choice of branch change the result?

  Let $G$ be the domain $\{z \in \mathbb{C}:|z|<1,|z+i|>\sqrt{2}\}$. Find an analytic transformation that maps $G$ to $S$, where $S$ is the strip defined above.

  comment

Electromagnetism

• 1.II.16B

  Electromagnetism | Part IB, 2008

  Suppose that the current density $\mathbf{J}(\mathbf{r})$ is constant in time but the charge density $\rho(\mathbf{r}, t)$ is not.

  (i) Show that $\rho$ is a linear function of time:

  $$\rho(\mathbf{r}, t)=\rho(\mathbf{r}, 0)+\dot{\rho}(\mathbf{r}, 0) t$$

  where $\dot{\rho}(\mathbf{r}, 0)$ is the time derivative of $\rho$ at time $t=0$.

  (ii) The magnetic induction due to a current density $\mathbf{J}(\mathbf{r})$ can be written as

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d V^{\prime}$$

  Show that this can also be written as

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \nabla \times \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d V^{\prime}$$

  (iii) Assuming that $\mathbf{J}$ vanishes at infinity, show that the curl of the magnetic field in (1) can be written as

  $$\nabla \times \mathbf{B}(\mathbf{r})=\mu_{0} \mathbf{J}(\mathbf{r})+\frac{\mu_{0}}{4 \pi} \nabla \int \frac{\nabla^{\prime} \cdot \mathbf{J}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d V^{\prime}$$

  [You may find useful the identities $\nabla \times(\nabla \times \mathbf{A})=\nabla(\nabla \cdot \mathbf{A})-\nabla^{2} \mathbf{A}$ and also $\left.\nabla^{2}\left(1 /\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\right)=-4 \pi \delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right) .\right]$

  (iv) Show that the second term on the right hand side of (2) can be expressed in terms of the time derivative of the electric field in such a way that $\mathbf{B}$ itself obeys Ampère's law with Maxwell's displacement current term, i.e. $\nabla \times \mathbf{B}=\mu_{0} \mathbf{J}+\mu_{0} \epsilon_{0} \partial \mathbf{E} / \partial t$.

  comment

• 2.I.6B

  Electromagnetism | Part IB, 2008

  Given the electric potential of a dipole

  $$\phi(r, \theta)=\frac{p \cos \theta}{4 \pi \epsilon_{0} r^{2}},$$

  where $p$ is the magnitude of the dipole moment, calculate the corresponding electric field and show that it can be written as

  $$\mathbf{E}(\mathbf{r})=\frac{1}{4 \pi \epsilon_{0}} \frac{1}{r^{3}}\left[3\left(\mathbf{p} \cdot \hat{\mathbf{e}}_{r}\right) \hat{\mathbf{e}}_{r}-\mathbf{p}\right]$$

  where $\hat{\mathbf{e}}_{r}$ is the unit vector in the radial direction.

  comment

• 2.II.17B

  Electromagnetism | Part IB, 2008

  Two perfectly conducting rails are placed on the $x y$-plane, one coincident with the $x$-axis, starting at $(0,0)$, the other parallel to the first rail a distance $\ell$ apart, starting at $(0, \ell)$. A resistor $R$ is connected across the rails between $(0,0)$ and $(0, \ell)$, and a uniform magnetic field $\mathbf{B}=B \hat{\mathbf{e}}_{z}$, where $\hat{\mathbf{e}}_{z}$ is the unit vector along the $z$-axis and $B>0$, fills the entire region of space. A metal bar of negligible resistance and mass $m$ slides without friction on the two rails, lying perpendicular to both of them in such a way that it closes the circuit formed by the rails and the resistor. The bar moves with speed $v$ to the right such that the area of the loop becomes larger with time.

  (i) Calculate the current in the resistor and indicate its direction of flow in a diagram of the system.

  (ii) Show that the magnetic force on the bar is

  $$\mathbf{F}=-\frac{B^{2} \ell^{2} v}{R} \hat{\mathbf{e}}_{x}$$

  (iii) Assume that the bar starts moving with initial speed $v_{0}$ at time $t=0$, and is then left to slide freely. Using your result from part (ii) and Newton's laws show that its velocity at the time $t$ is

  $$v(t)=v_{0} e^{-\left(B^{2} \ell^{2} / m R\right) t} .$$

  (iv) By calculating the total energy delivered to the resistor, verify that energy is conserved.

  comment

• 3.II.17B

  Electromagnetism | Part IB, 2008

  (i) From Maxwell's equations in vacuum,

  $$\begin{array}{ll} \nabla \cdot \mathbf{E}=0 & \nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t} \\ \nabla \cdot \mathbf{B}=0 & \nabla \times \mathbf{B}=\mu_{0} \epsilon_{0} \frac{\partial \mathbf{E}}{\partial t} \end{array}$$

  obtain the wave equation for the electric field E. [You may find the following identity useful: $\left.\nabla \times(\nabla \times \mathbf{A})=\nabla(\nabla \cdot \mathbf{A})-\nabla^{2} \mathbf{A} .\right]$

  (ii) If the electric and magnetic fields of a monochromatic plane wave in vacuum are

  $$\mathbf{E}(z, t)=\mathbf{E}_{0} \mathrm{e}^{i(k z-\omega t)} \text { and } \mathbf{B}(z, t)=\mathbf{B}_{0} \mathrm{e}^{i(k z-\omega t)}$$

  show that the corresponding electromagnetic waves are transverse (that is, both fields have no component in the direction of propagation).

  (iii) Use Faraday's law for these fields to show that

  $$\mathbf{B}_{0}=\frac{k}{\omega}\left(\hat{\mathbf{e}}_{z} \times \mathbf{E}_{0}\right)$$

  (iv) Explain with symmetry arguments how these results generalise to

  $$\mathbf{E}(\mathbf{r}, t)=E_{0} \mathrm{e}^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)} \hat{\mathbf{n}} \quad \text { and } \quad \mathbf{B}(\mathbf{r}, t)=\frac{1}{c} E_{0} \mathrm{e}^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}(\hat{\mathbf{k}} \times \hat{\mathbf{n}})$$

  where $\hat{\mathbf{n}}$ is the polarisation vector, i.e., the unit vector perpendicular to the direction of motion and along the direction of the electric field, and $\hat{\mathbf{k}}$ is the unit vector in the direction of propagation of the wave.

  (v) Using Maxwell's equations in vacuum prove that:

  $$\oint_{\mathcal{A}}\left(1 / \mu_{0}\right)(\mathbf{E} \times \mathbf{B}) \cdot d \mathcal{A}=-\frac{\partial}{\partial t} \int_{\mathcal{V}}\left(\frac{\epsilon_{0} E^{2}}{2}+\frac{B^{2}}{2 \mu_{0}}\right) d V$$

  where $\mathcal{V}$ is the closed volume and $\mathcal{A}$ is the bounding surface. Comment on the differing time dependencies of the left-hand-side of (1) for the case of (a) linearly-polarized and (b) circularly-polarized monochromatic plane waves.

  comment

• 4.I.7B

  Electromagnetism | Part IB, 2008

  The energy stored in a static electric field $\mathbf{E}$ is

  $$U=\frac{1}{2} \int \rho \phi d V,$$

  where $\phi$ is the associated electric potential, $\mathbf{E}=-\nabla \phi$, and $\rho$ is the volume charge density.

  (i) Assuming that the energy is calculated over all space and that $\mathbf{E}$ vanishes at infinity, show that the energy can be written as

  $$U=\frac{\epsilon_{0}}{2} \int|\mathbf{E}|^{2} d V$$

  (ii) Find the electric field produced by a spherical shell with total charge $Q$ and radius $R$, assuming it to vanish inside the shell. Find the energy stored in the electric field.

  comment

Fluid Dynamics

• 1.I.5B

  Fluid Dynamics | Part IB, 2008

  Verify that the two-dimensional flow given in Cartesian coordinates by

  $$\mathbf{u}=\left(\mathrm{e}^{y} \sinh x,-\mathrm{e}^{y} \cosh x\right)$$

  satisfies $\nabla \cdot \mathbf{u}=0$. Find the stream function $\psi(x, y)$. Sketch the streamlines.

  comment

• 1.II.17B

  Fluid Dynamics | Part IB, 2008

  Two incompressible fluids flow in infinite horizontal streams, the plane of contact being $z=0$, with $z$ positive upwards. The flow is given by

  $$\mathbf{U}(\mathbf{r})= \begin{cases}U_{2} \hat{\mathbf{e}}_{x}, & z>0 \\ U_{1} \hat{\mathbf{e}}_{x}, & z<0\end{cases}$$

  where $\hat{\mathbf{e}}_{x}$ is the unit vector in the positive $x$ direction. The upper fluid has density $\rho_{2}$ and pressure $p_{0}-g \rho_{2} z$, the lower has density $\rho_{1}$ and pressure $p_{0}-g \rho_{1} z$, where $p_{0}$ is a constant and $g$ is the acceleration due to gravity.

  (i) Consider a perturbation to the flat surface $z=0$ of the form

  $$z \equiv \zeta(x, y, t)=\zeta_{0} e^{i(k x+\ell y)+s t} .$$

  State the kinematic boundary conditions on the velocity potentials $\phi_{i}$ that hold on the interface in the two domains, and show by linearising in $\zeta$ that they reduce to

  $$\frac{\partial \phi_{i}}{\partial z}=\frac{\partial \zeta}{\partial t}+U_{i} \frac{\partial \zeta}{\partial x} \quad(z=0, i=1,2) .$$

  (ii) State the dynamic boundary condition on the perturbed interface, and show by linearising in $\zeta$ that it reduces to

  $$\rho_{1}\left(U_{1} \frac{\partial \phi_{1}}{\partial x}+\frac{\partial \phi_{1}}{\partial t}+g \zeta\right)=\rho_{2}\left(U_{2} \frac{\partial \phi_{2}}{\partial x}+\frac{\partial \phi_{2}}{\partial t}+g \zeta\right) \quad(z=0)$$

  (iii) Use the velocity potentials

  $$\phi_{1}=U_{1} x+A_{1} e^{q z} e^{i(k x+\ell y)+s t}, \quad \phi_{2}=U_{2} x+A_{2} e^{-q z} e^{i(k x+\ell y)+s t},$$

  where $q=\sqrt{k^{2}+\ell^{2}}$, and the conditions in (i) and (ii) to perform a stability analysis. Show that the relation between $s, k$ and $\ell$ is

  $$s=-i k \frac{\rho_{1} U_{1}+\rho_{2} U_{2}}{\rho_{1}+\rho_{2}} \pm\left[\frac{k^{2} \rho_{1} \rho_{2}\left(U_{1}-U_{2}\right)^{2}}{\left(\rho_{1}+\rho_{2}\right)^{2}}-\frac{q g\left(\rho_{1}-\rho_{2}\right)}{\rho_{1}+\rho_{2}}\right]^{1 / 2} .$$

  Find the criterion for instability.

  comment

• 2.I.8B

  Fluid Dynamics | Part IB, 2008

  (i) Show that for a two-dimensional incompressible flow $(u(x, y), v(x, y), 0)$, the vorticity is given by $\boldsymbol{\omega} \equiv \omega_{z} \hat{\mathbf{e}}_{z}=\left(0,0,-\nabla^{2} \psi\right)$ where $\psi$ is the stream function.

  (ii) Express the $z$-component of the vorticity equation

  $$\frac{\partial \boldsymbol{\omega}}{\partial t}+(\mathbf{u} \cdot \nabla) \boldsymbol{\omega}=(\boldsymbol{\omega} \cdot \nabla) \mathbf{u}$$

  in terms of the stream function $\psi$.

  comment

• 3.II.18B

  Fluid Dynamics | Part IB, 2008

  An ideal liquid contained within a closed circular cylinder of radius $a$ rotates about the axis of the cylinder (assume this axis to be in the vertical $z$-direction).

  (i) Prove that the equation of continuity and the boundary conditions are satisfied by the velocity $\mathbf{v}=\boldsymbol{\Omega} \times \mathbf{r}$, where $\boldsymbol{\Omega}=\Omega \hat{\mathbf{e}}_{z}$ is the angular velocity, with $\hat{\mathbf{e}}_{z}$ the unit vector in the $z$-direction, which depends only on time, and $\mathbf{r}$ is the position vector measured from a point on the axis of rotation.

  (ii) Calculate the angular momentum $\mathbf{M}=\rho \int(\mathbf{r} \times \mathbf{v}) d V$ per unit length of the cylinder.

  (iii) Suppose the the liquid starts from rest and flows under the action of an external force per unit mass $\mathbf{f}=(\alpha x+\beta y, \gamma x+\delta y, 0)$. By taking the curl of the Euler equation, prove that

  $$\frac{d \Omega}{d t}=\frac{1}{2}(\gamma-\beta)$$

  (iv) Find the pressure.

  comment

• 4.II.18B

  Fluid Dynamics | Part IB, 2008

  (i) Starting from Euler's equation for an incompressible fluid show that for potential flow with $\mathbf{u}=\nabla \phi$,

  $$\frac{\partial \phi}{\partial t}+\frac{1}{2} u^{2}+\chi=f(t)$$

  where $u=|\mathbf{u}|, \chi=p / \rho+V$, the body force per unit mass is $-\nabla V$ and $f(t)$ is an arbitrary function of time.

  (ii) Hence show that, for the steady flow of a liquid of density $\rho$ through a pipe of varying cross-section that is subject to a pressure difference $\Delta p=p_{1}-p_{2}$ between its two ends, the mass flow through the pipe per unit time is given by

  $$m \equiv \frac{d M}{d t}=S_{1} S_{2} \sqrt{\frac{2 \rho \Delta p}{S_{1}^{2}-S_{2}^{2}}}$$

  where $S_{1}$ and $S_{2}$ are the cross-sectional areas of the two ends.

  comment

Geometry

• 1.I.2G

  Geometry | Part IB, 2008

  Show that any element of $S O(3, \mathbb{R})$ is a rotation, and that it can be written as the product of two reflections.

  comment

• 2.II.12G

  Geometry | Part IB, 2008

  Show that the area of a spherical triangle with angles $\alpha, \beta, \gamma$ is $\alpha+\beta+\gamma-\pi$. Hence derive the formula for the area of a convex spherical $n$-gon.

  Deduce Euler's formula $F-E+V=2$ for a decomposition of a sphere into $F$ convex polygons with a total of $E$ edges and $V$ vertices.

  A sphere is decomposed into convex polygons, comprising $m$ quadrilaterals, $n$ pentagons and $p$ hexagons, in such a way that at each vertex precisely three edges meet. Show that there are at most 7 possibilities for the pair $(m, n)$, and that at least 3 of these do occur.

  comment

• 3.I.2G

  Geometry | Part IB, 2008

  A smooth surface in $\mathbb{R}^{3}$ has parametrization

  $$\sigma(u, v)=\left(u-\frac{u^{3}}{3}+u v^{2}, v-\frac{v^{3}}{3}+u^{2} v, u^{2}-v^{2}\right) .$$

  Show that a unit normal vector at the point $\sigma(u, v)$ is

  $$\left(\frac{-2 u}{1+u^{2}+v^{2}}, \frac{2 v}{1+u^{2}+v^{2}}, \frac{1-u^{2}-v^{2}}{1+u^{2}+v^{2}}\right)$$

  and that the curvature is $\frac{-4}{\left(1+u^{2}+v^{2}\right)^{4}}$.

  comment

• 3.II.12G

  Geometry | Part IB, 2008

  Let $D$ be the unit disc model of the hyperbolic plane, with metric

  $$\frac{4|d \zeta|^{2}}{\left(1-|\zeta|^{2}\right)^{2}}$$

  (i) Show that the group of Möbius transformations mapping $D$ to itself is the group of transformations

  $$\zeta \mapsto \omega \frac{\zeta-\lambda}{\bar{\lambda} \zeta-1},$$

  where $|\lambda|<1$ and $|\omega|=1$.

  (ii) Assuming that the transformations in (i) are isometries of $D$, show that any hyperbolic circle in $D$ is a Euclidean circle.

  (iii) Let $P$ and $Q$ be points on the unit circle with $\angle P O Q=2 \alpha$. Show that the hyperbolic distance from $O$ to the hyperbolic line $P Q$ is given by

  $$2 \tanh ^{-1}\left(\frac{1-\sin \alpha}{\cos \alpha}\right)$$

  (iv) Deduce that if $a>2 \tanh ^{-1}(2-\sqrt{3})$ then no hyperbolic open disc of radius $a$ is contained in a hyperbolic triangle.

  comment

• 4.II.12G

  Geometry | Part IB, 2008

  Let $\gamma:[a, b] \rightarrow S$ be a curve on a smoothly embedded surface $S \subset \mathbf{R}^{3}$. Define the energy of $\gamma$. Show that if $\gamma$ is a stationary point for the energy for proper variations of $\gamma$, then $\gamma$ satisfies the geodesic equations

  $$\begin{aligned} \frac{d}{d t}\left(E \dot{\gamma}_{1}+F \dot{\gamma}_{2}\right) &=\frac{1}{2}\left(E_{u} \dot{\gamma}_{1}^{2}+2 F_{u} \dot{\gamma}_{1} \dot{\gamma}_{2}+G_{u} \dot{\gamma}_{2}^{2}\right) \\ \frac{d}{d t}\left(F \dot{\gamma}_{1}+G \dot{\gamma}_{2}\right) &=\frac{1}{2}\left(E_{v} \dot{\gamma}_{1}^{2}+2 F_{v} \dot{\gamma}_{1} \dot{\gamma}_{2}+G_{v} \dot{\gamma}_{2}^{2}\right) \end{aligned}$$

  where $\gamma=\left(\gamma_{1}, \gamma_{2}\right)$ in terms of a smooth parametrization $(u, v)$ for $S$, with first fundamental form $E d u^{2}+2 F d u d v+G d v^{2}$.

  Now suppose that for every $c, d$ the curves $u=c, v=d$ are geodesics.

  (i) Show that $(F / \sqrt{G})_{v}=(\sqrt{G})_{u}$ and $(F / \sqrt{E})_{u}=(\sqrt{E})_{v}$.

  (ii) Suppose moreover that the angle between the curves $u=c, v=d$ is independent of $c$ and $d$. Show that $E_{v}=0=G_{u}$.

  comment

Groups, Rings and Modules

• $3 . \mathrm{II} . 11 \mathrm{G}$

  Groups, Rings and Modules | Part IB, 2008

  What is a Euclidean domain? Show that a Euclidean domain is a principal ideal domain.

  Show that $\mathbb{Z}[\sqrt{-7}]$ is not a Euclidean domain (for any choice of norm), but that the ring

  $$\mathbb{Z}\left[\frac{1+\sqrt{-7}}{2}\right]$$

  is Euclidean for the norm function $N(z)=z \bar{z}$.

  comment

• 1.II.10G

  Groups, Rings and Modules | Part IB, 2008

  (i) Show that $A_{4}$ is not simple.

  (ii) Show that the group Rot $(D)$ of rotational symmetries of a regular dodecahedron is a simple group of order 60 .

  (iii) Show that $\operatorname{Rot}(D)$ is isomorphic to $A_{5}$.

  comment

• 2.I.2G

  Groups, Rings and Modules | Part IB, 2008

  What does it means to say that a complex number $\alpha$ is algebraic over $\mathbb{Q}$ ? Define the minimal polynomial of $\alpha$.

  Suppose that $\alpha$ satisfies a nonconstant polynomial $f \in \mathbb{Z}[X]$ which is irreducible over $\mathbb{Z}$. Show that there is an isomorphism $\mathbb{Z}[X] /(f) \cong \mathbb{Z}[\alpha]$.

  [You may assume standard results about unique factorisation, including Gauss's lemma.]

  comment

• 2.II.11G

  Groups, Rings and Modules | Part IB, 2008

  Let $F$ be a field. Prove that every ideal of the ring $F\left[X_{1}, \ldots, X_{n}\right]$ is finitely generated.

  Consider the set

  $$R=\left\{p(X, Y)=\sum c_{i j} X^{i} Y^{j} \in F[X, Y] \mid c_{0 j}=c_{j 0}=0 \text { whenever } j>0\right\}$$

  Show that $R$ is a subring of $F[X, Y]$ which is not Noetherian.

  comment

• 3.I.1G

  Groups, Rings and Modules | Part IB, 2008

  Let $G$ be the abelian group generated by elements $a, b, c, d$ subject to the relations

  $$4 a-2 b+2 c+12 d=0, \quad-2 b+2 c=0, \quad 2 b+2 c=0, \quad 8 a+4 c+24 d=0$$

  Express $G$ as a product of cyclic groups, and find the number of elements of $G$ of order 2 .

  comment

• 4.I.2G

  Groups, Rings and Modules | Part IB, 2008

  Let $n \geq 2$ be an integer. Show that the polynomial $\left(X^{n}-1\right) /(X-1)$ is irreducible over $\mathbb{Z}$ if and only if $n$ is prime.

  [You may use Eisenstein's criterion without proof.]

  comment

• 4.II.11G

  Groups, Rings and Modules | Part IB, 2008

  Let $R$ be a ring and $M$ an $R$-module. What does it mean to say that $M$ is a free $R$-module? Show that $M$ is free if there exists a submodule $N \subseteq M$ such that both $N$ and $M / N$ are free.

  Let $M$ and $M^{\prime}$ be $R$-modules, and $N \subseteq M, N^{\prime} \subseteq M^{\prime}$ submodules. Suppose that $N \cong N^{\prime}$ and $M / N \cong M^{\prime} / N^{\prime}$. Determine (by proof or counterexample) which of the following statements holds:

  (1) If $N$ is free then $M \cong M^{\prime}$.

  (2) If $M / N$ is free then $M \cong M^{\prime}$.

  comment

Linear Algebra

• 1.I.1E

  Linear Algebra | Part IB, 2008

  Let $A$ be an $n \times n$ matrix over $\mathbb{C}$. What does it mean to say that $\lambda$ is an eigenvalue of $A$ ? Show that $A$ has at least one eigenvalue. For each of the following statements, provide a proof or a counterexample as appropriate.

  (i) If $A$ is Hermitian, all eigenvalues of $A$ are real.

  (ii) If all eigenvalues of $A$ are real, $A$ is Hermitian.

  (iii) If all entries of $A$ are real and positive, all eigenvalues of $A$ have positive real part.

  (iv) If $A$ and $B$ have the same trace and determinant then they have the same eigenvalues.

  comment

• 1.II.9E

  Linear Algebra | Part IB, 2008

  Let $A$ be an $m \times n$ matrix of real numbers. Define the row rank and column rank of $A$ and show that they are equal.

  Show that if a matrix $A^{\prime}$ is obtained from $A$ by elementary row and column operations then $\operatorname{rank}\left(A^{\prime}\right)=\operatorname{rank}(A)$.

  Let $P, Q$ and $R$ be $n \times n$ matrices. Show that the $2 n \times 2 n$ matrices $\left(\begin{array}{cc}P Q & 0 \\ Q & Q R\end{array}\right)$ and $\left(\begin{array}{cc}0 & P Q R \\ Q & 0\end{array}\right)$ have the same rank.

  Hence, or otherwise, prove that

  $$\operatorname{rank}(P Q)+\operatorname{rank}(Q R) \leqslant \operatorname{rank}(Q)+\operatorname{rank}(P Q R)$$

  comment

• 2.I.1E

  Linear Algebra | Part IB, 2008

  Suppose that $V$ and $W$ are finite-dimensional vector spaces over $\mathbb{R}$. What does it mean to say that $\psi: V \rightarrow W$ is a linear map? State the rank-nullity formula. Using it, or otherwise, prove that a linear map $\psi: V \rightarrow V$ is surjective if, and only if, it is injective.

  Suppose that $\psi: V \rightarrow V$ is a linear map which has a right inverse, that is to say there is a linear map $\phi: V \rightarrow V$ such that $\psi \phi=\mathrm{id}_{V}$, the identity map. Show that $\phi \psi=\mathrm{id}_{V}$.

  Suppose that $A$ and $B$ are two $n \times n$ matrices over $\mathbb{R}$ such that $A B=I$. Prove that $B A=I$.

  comment

• 2.II.10E

  Linear Algebra | Part IB, 2008

  Define the determinant $\operatorname{det}(A)$ of an $n \times n$ square matrix $A$ over the complex numbers. If $A$ and $B$ are two such matrices, show that $\operatorname{det}(A B)=\operatorname{det}(A) \operatorname{det}(B)$.

  Write $p_{M}(\lambda)=\operatorname{det}(M-\lambda I)$ for the characteristic polynomial of a matrix $M$. Let $A, B, C$ be $n \times n$ matrices and suppose that $C$ is nonsingular. Show that $p_{B C}=p_{C B}$. Taking $C=A+t I$ for appropriate values of $t$, or otherwise, deduce that $p_{B A}=p_{A B}$.

  Show that if $p_{A}=p_{B}$ then $\operatorname{tr}(A)=\operatorname{tr}(B)$. Which of the following statements is true for all $n \times n$ matrices $A, B, C$ ? Justify your answers.

  (i) $p_{A B C}=p_{A C B}$;

  (ii) $p_{A B C}=p_{B C A}$.

  comment

• 3.II.10E

  Linear Algebra | Part IB, 2008

  Let $k=\mathbb{R}$ or $\mathbb{C}$. What is meant by a quadratic form $q: k^{n} \rightarrow k$ ? Show that there is a basis $\left\{v_{1}, \ldots, v_{n}\right\}$ for $k^{n}$ such that, writing $x=x_{1} v_{1}+\ldots+x_{n} v_{n}$, we have $q(x)=a_{1} x_{1}^{2}+\ldots+a_{n} x_{n}^{2}$ for some scalars $a_{1}, \ldots, a_{n} \in\{-1,0,1\} .$

  Suppose that $k=\mathbb{R}$. Define the rank and signature of $q$ and compute these quantities for the form $q: \mathbb{R}^{3} \rightarrow \mathbb{R}$ given by $q(x)=-3 x_{1}^{2}+x_{2}^{2}+2 x_{1} x_{2}-2 x_{1} x_{3}+2 x_{2} x_{3}$.

  Suppose now that $k=\mathbb{C}$ and that $q_{1}, \ldots, q_{d}: \mathbb{C}^{n} \rightarrow \mathbb{C}$ are quadratic forms. If $n \geqslant 2^{d}$, show that there is some nonzero $x \in \mathbb{C}^{n}$ such that $q_{1}(x)=\ldots=q_{d}(x)=0$.

  comment

• 4.I.1E

  Linear Algebra | Part IB, 2008

  Describe (without proof) what it means to put an $n \times n$ matrix of complex numbers into Jordan normal form. Explain (without proof) the sense in which the Jordan normal form is unique.

  Put the following matrix in Jordan normal form:

  $$\left(\begin{array}{ccc} -7 & 3 & -5 \\ 7 & -1 & 5 \\ 17 & -6 & 12 \end{array}\right)$$

  comment

• 4.II.10E

  Linear Algebra | Part IB, 2008

  What is meant by a Hermitian matrix? Show that if $A$ is Hermitian then all its eigenvalues are real and that there is an orthonormal basis for $\mathbb{C}^{n}$ consisting of eigenvectors of $A$.

  A Hermitian matrix is said to be positive definite if $\langle A x, x\rangle>0$ for all $x \neq 0$. We write $A>0$ in this case. Show that $A$ is positive definite if, and only if, all of its eigenvalues are positive. Show that if $A>0$ then $A$ has a unique positive definite square root $\sqrt{A}$.

  Let $A, B$ be two positive definite Hermitian matrices with $A-B>0$. Writing $C=\sqrt{A}$ and $X=\sqrt{A}-\sqrt{B}$, show that $C X+X C>0$. By considering eigenvalues of $X$, or otherwise, show that $X>0$.

  comment

Markov Chains

• 1.II.19H

  Markov Chains | Part IB, 2008

  The village green is ringed by a fence with $N$ fenceposts, labelled $0,1, \ldots, N-1$. The village idiot is given a pot of paint and a brush, and started at post 0 with instructions to paint all the posts. He paints post 0 , and then chooses one of the two nearest neighbours, 1 or $N-1$, with equal probability, moving to the chosen post and painting it. After painting a post, he chooses with equal probability one of the two nearest neighbours, moves there and paints it (regardless of whether it is already painted). Find the distribution of the last post unpainted.

  comment

• 2.II.20H

  Markov Chains | Part IB, 2008

  A Markov chain with state-space $I=\mathbb{Z}^{+}$has non-zero transition probabilities $p_{00}=q_{0}$ and

  $$p_{i, i+1}=p_{i}, \quad p_{i+1, i}=q_{i+1} \quad(i \in I) .$$

  Prove that this chain is recurrent if and only if

  $$\sum_{n \geqslant 1} \prod_{r=1}^{n} \frac{q_{r}}{p_{r}}=\infty$$

  Prove that this chain is positive-recurrent if and only if

  $$\sum_{n \geqslant 1} \prod_{r=1}^{n} \frac{p_{r-1}}{q_{r}}<\infty$$

  comment

• 3.I.9H

  Markov Chains | Part IB, 2008

  What does it mean to say that a Markov chain is recurrent?

  Stating clearly any general results to which you appeal, prove that the symmetric simple random walk on $\mathbb{Z}$ is recurrent.

  comment

• 4.I.9H

  Markov Chains | Part IB, 2008

  A Markov chain on the state-space $I=\{1,2,3,4,5,6,7\}$ has transition matrix

  $$P=\left(\begin{array}{ccccccc} 0 & 1 / 2 & 1 / 4 & 0 & 1 / 4 & 0 & 0 \\ 1 / 3 & 0 & 1 / 2 & 0 & 0 & 1 / 6 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 / 2 & 0 & 1 / 2 \end{array}\right)$$

  Classify the chain into its communicating classes, deciding for each what the period is, and whether the class is recurrent.

  For each $i, j \in I$ say whether the $\operatorname{limit}^{-1} \lim _{n \rightarrow \infty} p_{i j}^{(n)}$ exists, and evaluate the limit when it does exist.

  comment

Methods

• $2 . \mathrm{I} . 5 \mathrm{D} \quad$

  Methods | Part IB, 2008

  Describe briefly the method of Lagrange multipliers for finding the stationary values of a function $f(x, y)$ subject to a constraint $g(x, y)=0$.

  Use the method to find the largest possible volume of a circular cylinder that has surface area $A$ (including both ends).

  comment

• 1.II.14D

  Methods | Part IB, 2008

  Write down the Euler-Lagrange equation for the variational problem for $y(x)$ that extremizes the integral $I$ defined as

  $$I=\int_{x_{1}}^{x_{2}} f\left(x, y, y^{\prime}\right) d x$$

  with boundary conditions $y\left(x_{1}\right)=y_{1}, y\left(x_{2}\right)=y_{2}$, where $y_{1}$ and $y_{2}$ are positive constants such that $y_{2}>y_{1}$, with $x_{2}>x_{1}$. Find a first integral of the equation when $f$ is independent of $y$, i.e. $f=f\left(x, y^{\prime}\right)$.

  A light ray moves in the $(x, y)$ plane from $\left(x_{1}, y_{1}\right)$ to $\left(x_{2}, y_{2}\right)$ with speed $c(x)$ taking a time $T$. Show that the equation of the path that makes $T$ an extremum satisfies

  $$\frac{d y}{d x}=\frac{c(x)}{\sqrt{k^{2}-c^{2}(x)}}$$

  where $k$ is a constant and write down an integral relating $k, x_{1}, x_{2}, y_{1}$ and $y_{2}$.

  When $c(x)=a x$ where $a$ is a constant and $k=a x_{2}$, show that the path is given by

  $$\left(y_{2}-y\right)^{2}=x_{2}^{2}-x^{2} .$$

  comment

• 2.II.15D

  Methods | Part IB, 2008

  (a) Legendre's equation may be written in the form

  $$\frac{d}{d x}\left(\left(1-x^{2}\right) \frac{d y}{d x}\right)+\lambda y=0$$

  Show that there is a series solution for $y$ of the form

  $$y=\sum_{k=0}^{\infty} a_{k} x^{k},$$

  where the $a_{k}$ satisfy the recurrence relation

  $$\frac{a_{k+2}}{a_{k}}=-\frac{(\lambda-k(k+1))}{(k+1)(k+2)} .$$

  Hence deduce that there are solutions for $y(x)=P_{n}(x)$ that are polynomials of degree $n$, provided that $\lambda=n(n+1)$. Given that $a_{0}$ is then chosen so that $P_{n}(1)=1$, find the explicit form for $P_{2}(x)$.

  (b) Laplace's equation for $\Phi(r, \theta)$ in spherical polar coordinates $(r, \theta, \phi)$ may be written in the axisymmetric case as

  $$\frac{\partial^{2} \Phi}{\partial r^{2}}+\frac{2}{r} \frac{\partial \Phi}{\partial r}+\frac{1}{r^{2}} \frac{\partial}{\partial x}\left(\left(1-x^{2}\right) \frac{\partial \Phi}{\partial x}\right)=0$$

  where $x=\cos \theta$.

  Write down without proof the general form of the solution obtained by the method of separation of variables. Use it to find the form of $\Phi$ exterior to the sphere $r=a$ that satisfies the boundary conditions, $\Phi(a, x)=1+x^{2}$, and $\lim _{r \rightarrow \infty} \Phi(r, x)=0$.

  comment

• 3.I.6D

  Methods | Part IB, 2008

  Let $\mathcal{L}$ be the operator

  $$\mathcal{L} y=\frac{d^{2} y}{d x^{2}}-k^{2} y$$

  on functions $y(x)$ satisfying $\lim _{x \rightarrow-\infty} \quad y(x)=0$ and $\lim _{x \rightarrow \infty} y(x)=0$.

  Given that the Green's function $G(x ; \xi)$ for $\mathcal{L}$ satisfies

  $$\mathcal{L} G=\delta(x-\xi)$$

  show that a solution of

  $$\mathcal{L} y=S(x)$$

  for a given function $S(x)$, is given by

  $$y(x)=\int_{-\infty}^{\infty} G(x ; \xi) S(\xi) d \xi$$

  Indicate why this solution is unique.

  Show further that the Green's function is given by

  $$G(x ; \xi)=-\frac{1}{2|k|} \exp (-|k||x-\xi|)$$

  comment

• 3.II.15D

  Methods | Part IB, 2008

  Let $\lambda_{1}<\lambda_{2}<\ldots \lambda_{n} \ldots$ and $y_{1}(x), y_{2}(x), \ldots y_{n}(x) \ldots$ be the eigenvalues and corresponding eigenfunctions for the Sturm-Liouville system

  $$\mathcal{L} y_{n}=\lambda_{n} w(x) y_{n},$$

  where

  $$\mathcal{L} y \equiv \frac{d}{d x}\left(-p(x) \frac{d y}{d x}\right)+q(x) y,$$

  with $p(x)>0$ and $w(x)>0$. The boundary conditions on $y$ are that $y(0)=y(1)=0$.

  Show that two distinct eigenfunctions are orthogonal in the sense that

  $$\int_{0}^{1} w y_{n} y_{m} d x=\delta_{n m} \int_{0}^{1} w y_{n}^{2} d x .$$

  Show also that if $y$ has the form

  $$y=\sum_{n=1}^{\infty} a_{n} y_{n},$$

  with $a_{n}$ being independent of $x$, then

  $$\frac{\int_{0}^{1} y \mathcal{L} y d x}{\int_{0}^{1} w y^{2} d x} \geq \lambda_{1}$$

  Assuming that the eigenfunctions are complete, deduce that a solution of the diffusion equation,

  $$\frac{\partial y}{\partial t}=-\frac{1}{w} \mathcal{L} y$$

  that satisfies the boundary conditions given above is such that

  $$\frac{1}{2} \frac{d}{d t}\left(\int_{0}^{1} w y^{2} d x\right) \leq-\lambda_{1} \int_{0}^{1} w y^{2} d x .$$

  comment

• 4.I.5A

  Methods | Part IB, 2008

  Find the half-range Fourier cosine series for $f(x)=x^{2}, 0<x<1$. Hence show that

  $$\sum_{n=1}^{\infty} \frac{1}{n^{2}}=\frac{\pi^{2}}{6} .$$

  comment

• 4.II.16A

  Methods | Part IB, 2008

  Assume $F(x)$ satisfies

  $$\int_{-\infty}^{\infty}|F(x)| d x<\infty$$

  and that the series

  $$g(\tau)=\sum_{n=-\infty}^{\infty} F(2 n \pi+\tau)$$

  converges uniformly in $[0 \leqslant \tau \leqslant 2 \pi]$.

  If $\tilde{F}$ is the Fourier transform of $F$, prove that

  $$g(\tau)=\frac{1}{2 \pi} \sum_{n=-\infty}^{\infty} \tilde{F}(n) e^{i n \tau}$$

  [Hint: prove that $g$ is periodic and express its Fourier expansion coefficients in terms of $\tilde{F}]$.

  In the case that $F(x)=e^{-|x|}$, evaluate the sum

  $$\sum_{n=-\infty}^{\infty} \frac{1}{1+n^{2}} .$$

  comment

Metric and Topological Spaces

• $3 . \mathrm{I} . 4 \mathrm{~F} \quad$

  Metric and Topological Spaces | Part IB, 2008

  Explain what it means for a topological space to be connected.

  Are the following subspaces of the unit square $[0,1] \times[0,1]$ connected? Justify your answers.

  (a) $\{(x, y): x \neq 0, y \neq 0$, and $x / y \in \mathbb{Q}\}$.

  (b) $\{(x, y):(x=0)$ or $(x \neq 0$ and $y \in \mathbb{Q})\}$.

  comment

• 1.II.12F

  Metric and Topological Spaces | Part IB, 2008

  Write down the definition of a topology on a set $X$.

  For each of the following families $\mathcal{T}$ of subsets of $\mathbb{Z}$, determine whether $\mathcal{T}$ is a topology on $\mathbb{Z}$. In the cases where the answer is 'yes', determine also whether $(\mathbb{Z}, \mathcal{T})$ is a Hausdorff space and whether it is compact.

  (a) $\mathcal{T}=\{U \subseteq \mathbb{Z}$ : either $U$ is finite or $0 \in U\}$.

  (b) $\mathcal{T}=\{U \subseteq \mathbb{Z}$ : either $\mathbb{Z} \backslash U$ is finite or $0 \notin U\}$.

  (c) $\mathcal{T}=\{U \subseteq \mathbb{Z}$ : there exists $k>0$ such that, for all $n, n \in U \Leftrightarrow n+k \in U\}$.

  (d) $\mathcal{T}=\{U \subseteq \mathbb{Z}$ : for all $n \in U$, there exists $k>0$ such that $\{n+k m: m \in \mathbb{Z}\} \subseteq U\}$.

  comment

• 2.I.4F

  Metric and Topological Spaces | Part IB, 2008

  Stating carefully any results on compactness which you use, show that if $X$ is a compact space, $Y$ is a Hausdorff space and $f: X \rightarrow Y$ is bijective and continuous, then $f$ is a homeomorphism.

  Hence or otherwise show that the unit circle $S=\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2}=1\right\}$ is homeomorphic to the quotient space $[0,1] / \sim$, where $\sim$ is the equivalence relation defined by

  $$x \sim y \Leftrightarrow \text { either } x=y \text { or }\{x, y\}=\{0,1\} .$$

  comment

• 4.II.14F

  Metric and Topological Spaces | Part IB, 2008

  Explain what is meant by a base for a topology. Illustrate your definition by describing bases for the topology induced by a metric on a set, and for the product topology on the cartesian product of two topological spaces.

  A topological space $(X, \mathcal{T})$ is said to be separable if there is a countable subset $C \subseteq X$ which is dense, i.e. such that $C \cap U \neq \emptyset$ for every nonempty $U \in \mathcal{T}$. Show that a product of two separable spaces is separable. Show also that a metric space is separable if and only if its topology has a countable base, and deduce that every subspace of a separable metric space is separable.

  Now let $X=\mathbb{R}$ with the topology $\mathcal{T}$ having as a base the set of all half-open intervals

  $$[a, b)=\{x \in \mathbb{R}: a \leqslant x<b\}$$

  with $a<b$. Show that $X$ is separable, but that the subspace $Y=\{(x,-x): x \in \mathbb{R}\}$ of $X \times X$ is not separable.

  [You may assume standard results on countability.]

  comment

Numerical Analysis

• 1.I.6D

  Numerical Analysis | Part IB, 2008

  Show that if $A=L D L^{T}$, where $L \in \mathbb{R}^{m \times m}$ is a lower triangular matrix with all elements on the main diagonal being unity and $D \in \mathbb{R}^{m \times m}$ is a diagonal matrix with positive elements, then $A$ is positive definite. Find $L$ and the corresponding $D$ when

  $$A=\left[\begin{array}{rrr} 1 & -1 & 2 \\ -1 & 3 & 1 \\ 2 & 1 & 3 \end{array}\right]$$

  comment

• 2.II.18D

  Numerical Analysis | Part IB, 2008

  (a) A Householder transformation (reflection) is given by

  $$H=I-\frac{2 u u^{T}}{\|u\|^{2}},$$

  where $H \in \mathbb{R}^{m \times m}, u \in \mathbb{R}^{m}$, and $I$ is the $m \times m$ unit matrix and $u$ is a non-zero vector which has norm $\|u\|=\left(\sum_{i=1}^{m} u_{i}^{2}\right)^{1 / 2}$. Show that $H$ is orthogonal.

  (b) Suppose that $A \in \mathbb{R}^{m \times n}, x \in \mathbb{R}^{n}$ and $b \in \mathbb{R}^{m}$ with $n<m$. Show that if $x$ minimises $\|A x-b\|^{2}$ then it also minimises $\|Q A x-Q b\|^{2}$, where $Q$ is an arbitrary $m \times m$ orthogonal matrix.

  (c) Using Householder reflection, find the $x$ that minimises $\|A x-b\|^{2}$ when

  $$A=\left[\begin{array}{ll} 1 & 2 \\ 0 & 4 \\ 0 & 2 \\ 0 & 4 \end{array}\right] \quad b=\left[\begin{array}{r} 1 \\ 1 \\ 2 \\ -1 \end{array}\right]$$

  comment

• 3.II.19D

  Numerical Analysis | Part IB, 2008

  Starting from the Taylor formula for $f(x) \in C^{k+1}[a, b]$ with an integral remainder term, show that the error of an approximant $L(f)$ can be written in the form (Peano kernel theorem)

  $$L(f)=\frac{1}{k !} \int_{a}^{b} K(\theta) f^{(k+1)}(\theta) d \theta,$$

  when $L(f)$, which is identically zero if $f(x)$ is a polynomial of degree $k$, satisfies conditions that you should specify. Give an expression for $K(\theta)$.

  Hence determine the minimum value of $c$ in the inequality

  $$|L(f)| \leq c\left\|f^{\prime \prime \prime}\right\|_{\infty}$$

  when

  $$L(f)=f^{\prime}(1)-\frac{1}{2}(f(2)-f(0)) \text { for } f(x) \in C^{3}[0,2]$$

  comment

• 4.I.8D

  Numerical Analysis | Part IB, 2008

  Show that the Chebyshev polynomials, $T_{n}(x)=\cos \left(n \cos ^{-1} x\right), n=0,1,2, \ldots$ obey the orthogonality relation

  $$\int_{-1}^{1} \frac{T_{n}(x) T_{m}(x)}{\sqrt{1-x^{2}}} d x=\frac{\pi}{2} \delta_{n, m}\left(1+\delta_{n, 0}\right)$$

  State briefly how an optimal choice of the parameters $a_{k}, x_{k}, k=1,2 \ldots n$ is made in the Gaussian quadrature formula

  $$\int_{-1}^{1} \frac{f(x)}{\sqrt{1-x^{2}}} d x \sim \sum_{k=1}^{n} a_{k} f\left(x_{k}\right)$$

  Find these parameters for the case $n=3$.

  comment

Optimization

• 1.I.8H

  Optimization | Part IB, 2008

  State the Lagrangian Sufficiency Theorem for the maximization over $x$ of $f(x)$ subject to the constraint $g(x)=b$.

  For each $p>0$, solve

  $$\max \sum_{i=1}^{d} x_{i}^{p} \quad \text { subject to } \sum_{i=1}^{d} x_{i}=1, \quad x_{i} \geqslant 0 .$$

  comment

• 2.I.9H

  Optimization | Part IB, 2008

  Goods from three warehouses have to be delivered to five shops, the cost of transporting one unit of good from warehouse $i$ to shop $j$ being $c_{i j}$, where

  $$C=\left(\begin{array}{ccccc} 2 & 3 & 6 & 6 & 4 \\ 7 & 6 & 1 & 1 & 5 \\ 3 & 6 & 6 & 2 & 1 \end{array}\right)$$

  The requirements of the five shops are respectively $9,6,12,5$ and 10 units of the good, and each warehouse holds a stock of 15 units. Find a minimal-cost allocation of goods from warehouses to shops and its associated cost.

  comment

• 3.II.20H

  Optimization | Part IB, 2008

  Use the simplex algorithm to solve the problem

  $$\max x_{1}+2 x_{2}-6 x_{3}$$

  subject to $x_{1}, x_{2} \geqslant 0,\left|x_{3}\right| \leqslant 5$, and

  $$\begin{array}{r} x_{1}+x_{2}+x_{3} \leqslant 7 \\ 2 x_{2}+x_{3} \geqslant 1 \end{array}$$

  comment

• 4.II.20H

  Optimization | Part IB, 2008

  (i) Suppose that $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$, and $g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ are continuously differentiable. Suppose that the problem

  $\max f(x)$ subject to $g(x)=b$

  is solved by a unique $\bar{x}=\bar{x}(b)$ for each $b \in \mathbb{R}^{m}$, and that there exists a unique $\lambda(b) \in \mathbb{R}^{m}$ such that

  $$\varphi(b) \equiv f(\bar{x}(b))=\sup _{x}\left\{f(x)+\lambda(b)^{T}(b-g(x))\right\}$$

  Assuming that $\bar{x}$ and $\lambda$ are continuously differentiable, prove that

  $$\frac{\partial \varphi}{\partial b_{i}}(b)=\lambda_{i}(b)$$

  (ii) The output of a firm is a function of the capital $K$ deployed, and the amount $L$ of labour employed, given by

  $$f(K, L)=K^{\alpha} L^{\beta}$$

  where $\alpha, \beta \in(0,1)$. The firm's manager has to optimize the output subject to the budget constraint

  $$K+w L=b,$$

  where $w>0$ is the wage rate and $b>0$ is the available budget. By casting the problem in Lagrangian form, find the optimal solution and verify the relation $(*)$.

  comment

Quantum Mechanics

• 1.II.15A

  Quantum Mechanics | Part IB, 2008

  The radial wavefunction $g(r)$ for the hydrogen atom satisfies the equation

  $$-\frac{\hbar^{2}}{2 m r^{2}} \frac{d}{d r}\left(r^{2} \frac{d g(r)}{d r}\right)-\frac{e^{2} g(r)}{4 \pi \epsilon_{0} r}+\hbar^{2} \frac{\ell(\ell+1)}{2 m r^{2}} g(r)=E g(r)$$

  With reference to the general form for the time-independent Schrödinger equation, explain the origin of each term. What are the allowed values of $\ell$ ?

  The lowest-energy bound-state solution of $(*)$, for given $\ell$, has the form $r^{\alpha} e^{-\beta r}$. Find $\alpha$ and $\beta$ and the corresponding energy $E$ in terms of $\ell$.

  A hydrogen atom makes a transition between two such states corresponding to $\ell+1$ and $\ell$. What is the frequency of the emitted photon?

  comment

• 2.II.16A

  Quantum Mechanics | Part IB, 2008

  Give the physical interpretation of the expression

  $$\langle A\rangle_{\psi}=\int \psi(x)^{*} \hat{A} \psi(x) d x$$

  for an observable $A$, where $\hat{A}$ is a Hermitian operator and $\psi$ is normalised. By considering the norm of the state $(A+i \lambda B) \psi$ for two observables $A$ and $B$, and real values of $\lambda$, show that

  $$\left\langle A^{2}\right\rangle_{\psi}\left\langle B^{2}\right\rangle_{\psi} \geqslant \frac{1}{4}\left|\langle[A, B]\rangle_{\psi}\right|^{2} .$$

  Deduce the uncertainty relation

  $$\Delta A \Delta B \geqslant \frac{1}{2}\left|\langle[A, B]\rangle_{\psi}\right|,$$

  where $\Delta A$ is the uncertainty of $A$.

  A particle of mass $m$ moves in one dimension under the influence of potential $\frac{1}{2} m \omega^{2} x^{2}$. By considering the commutator $[x, p]$, show that the expectation value of the Hamiltonian satisfies

  $$\langle H\rangle_{\psi} \geqslant \frac{1}{2} \hbar \omega .$$

  comment

• 3.I.7A

  Quantum Mechanics | Part IB, 2008

  Write down a formula for the orbital angular momentum operator $\hat{\mathbf{L}}$. Show that its components satisfy

  $$\left[L_{i}, L_{j}\right]=i \hbar \epsilon_{i j k} L_{k} .$$

  If $L_{3} \psi=0$, show that $\left(L_{1} \pm i L_{2}\right) \psi$ are also eigenvectors of $L_{3}$, and find their eigenvalues.

  comment

• 3.II.16A

  Quantum Mechanics | Part IB, 2008

  What is the probability current for a particle of mass $m$, wavefunction $\psi$, moving in one dimension?

  A particle of energy $E$ is incident from $x<0$ on a barrier given by

  $$V(x)=\left\{\begin{array}{cc} 0 & x \leqslant 0 \\ V_{1} & 0<x<a \\ V_{0} & x \geqslant a \end{array}\right.$$

  where $V_{1}>V_{0}>0$. What are the conditions satisfied by $\psi$ at $x=0$ and $x=a$ ? Write down the form taken by the wavefunction in the regions $x \leqslant 0$ and $x \geqslant a$ distinguishing between the cases $E>V_{0}$ and $E<V_{0}$. For both cases, use your expressions for $\psi$ to calculate the probability currents in these two regions.

  Define the reflection and transmission coefficients, $R$ and $T$. Using current conservation, show that the expressions you have derived satisfy $R+T=1$. Show that $T=0$ if $0<E<V_{0}$.

  comment

• 4.I.6A

  Quantum Mechanics | Part IB, 2008

  What is meant by a stationary state? What form does the wavefunction take in such a state? A particle has wavefunction $\psi(x, t)$, such that

  $$\psi(x, 0)=\sqrt{\frac{1}{2}}\left(\chi_{1}(x)+\chi_{2}(x)\right)$$

  where $\chi_{1}$ and $\chi_{2}$ are normalised eigenstates of the Hamiltonian with energies $E_{1}$ and $E_{2}$. Write down $\psi(x, t)$ at time $t$. Show that the expectation value of $A$ at time $t$ is

  $$\langle A\rangle_{\psi}=\frac{1}{2} \int_{-\infty}^{\infty}\left(\chi_{1}^{*} \hat{A} \chi_{1}+\chi_{2}^{*} \hat{A} \chi_{2}\right) d x+\operatorname{Re}\left(e^{i\left(E_{1}-E_{2}\right) t / \hbar} \int_{-\infty}^{\infty} \chi_{1}^{*} \hat{A} \chi_{2} d x\right)$$

  comment

Special Relativity

• 1.I.4C

  Special Relativity | Part IB, 2008

  In an inertial frame $S$ a photon of energy $E$ is observed to travel at an angle $\theta$ relative to the $x$-axis. The inertial frame $S^{\prime}$ moves relative to $S$ at velocity $v$ in the $x$ direction and the $x^{\prime}$-axis of $S^{\prime}$ is taken parallel to the $x$-axis of $S$. Observed in $S^{\prime}$, the photon has energy $E^{\prime}$ and travels at an angle $\theta^{\prime}$ relative to the $x^{\prime}$-axis. Show that

  $$E^{\prime}=\frac{E(1-\beta \cos \theta)}{\sqrt{1-\beta^{2}}}, \quad \cos \theta^{\prime}=\frac{\cos \theta-\beta}{1-\beta \cos \theta},$$

  where $\beta=v / c$.

  comment

• 2.I.7C

  Special Relativity | Part IB, 2008

  A photon of energy $E$ collides with a particle of rest mass $m$, which is at rest. The final state consists of a photon and a particle of rest mass $M, M>m$. Show that the minimum value of $E$ for which it is possible for this reaction to take place is

  $$E_{\min }=\frac{M^{2}-m^{2}}{2 m} c^{2}$$

  comment

• 4.II.17C

  Special Relativity | Part IB, 2008

  Write down the formulae for the one-dimensional Lorentz transformation $(x, t) \rightarrow$ $\left(x^{\prime}, t^{\prime}\right)$ for frames moving with relative velocity $v$ along the $x$-direction. Derive the relativistic formula for the addition of velocities $v$ and $u$.

  A train, of proper length $L$, travels past a station at velocity $v>0$. The origin of the inertial frame $S$, with coordinates $(x, t)$, in which the train is stationary, is located at the mid-point of the train. The origin of the inertial frame $S^{\prime}$, with coordinates $\left(x^{\prime}, t^{\prime}\right)$, in which the station is stationary, is located at the mid-point of the platform. Coordinates are chosen such that when the origins coincide then $t=t^{\prime}=0$.

  Observers A and B, stationary in $S$, are located, respectively, at the front and rear of the train. Observer C, stationary in $S^{\prime}$, is located at the origin of $S^{\prime}$. At $t^{\prime}=0$, C sends two signals, which both travel at speed $u$, where $v<u \leq c$, one directed towards $\mathrm{A}$ and the other towards $\mathrm{B}$, who receive the signals at respective times $t_{A}$ and $t_{B}$. $\mathrm{C}$ observes these events to occur, respectively, at times $t_{A}^{\prime}$ and $t_{B}^{\prime}$. At $t^{\prime}=0, \mathrm{C}$ also observes that the two ends of the platform coincide with the positions of $A$ and $B$.

  (a) Draw two space-time diagrams, one for $S$ and the other for $S^{\prime}$, showing the trajectories of the observers and the events that take place.

  (b) What is the length of the platform in terms of $L$ ? Briefly illustrate your answer by reference to the space-time diagrams.

  (c) Calculate the time differences $t_{B}-t_{A}$ and $t_{B}^{\prime}-t_{A}^{\prime}$.

  (d) Setting $u=c$, use this example to discuss briefly the fact that two events observed to be simultaneous in one frame need not be observed to be simultaneous in another.

  comment

Statistics

• $1 . \mathrm{I} . 7 \mathrm{H} \quad$

  Statistics | Part IB, 2008

  A Bayesian statistician observes a random sample $X_{1}, \ldots, X_{n}$ drawn from a $N\left(\mu, \tau^{-1}\right)$ distribution. He has a prior density for the unknown parameters $\mu, \tau$ of the form

  $$\pi_{0}(\mu, \tau) \propto \tau^{\alpha_{0}-1} \exp \left(-\frac{1}{2} K_{0} \tau\left(\mu-\mu_{0}\right)^{2}-\beta_{0} \tau\right) \sqrt{\tau},$$

  where $\alpha_{0}, \beta_{0}, \mu_{0}$ and $K_{0}$ are constants which he chooses. Show that after observing $X_{1}, \ldots, X_{n}$ his posterior density $\pi_{n}(\mu, \tau)$ is again of the form

  $$\pi_{n}(\mu, \tau) \propto \tau^{\alpha_{n}-1} \exp \left(-\frac{1}{2} K_{n} \tau\left(\mu-\mu_{n}\right)^{2}-\beta_{n} \tau\right) \sqrt{\tau}$$

  where you should find explicitly the form of $\alpha_{n}, \beta_{n}, \mu_{n}$ and $K_{n}$.

  comment

• $3 . \mathrm{I} . 8 \mathrm{H} \quad$

  Statistics | Part IB, 2008

  If $X_{1}, \ldots, X_{n}$ is a sample from a density $f(\cdot \mid \theta)$ with $\theta$ unknown, what is a $95 \%$ confidence set for $\theta$ ?

  In the case where the $X_{i}$ are independent $N\left(\mu, \sigma^{2}\right)$ random variables with $\sigma^{2}$ known, $\mu$ unknown, find (in terms of $\sigma^{2}$ ) how large the size $n$ of the sample must be in order for there to exist a $95 \%$ confidence interval for $\mu$ of length no more than some given $\varepsilon>0$.

  [Hint: If $Z \sim N(0,1)$ then $P(Z>1.960)=0.025 .]$

  comment

• 1.II.18H

  Statistics | Part IB, 2008

  Suppose that $X_{1}, \ldots, X_{n}$ is a sample of size $n$ with common $N\left(\mu_{X}, 1\right)$ distribution, and $Y_{1}, \ldots, Y_{n}$ is an independent sample of size $n$ from a $N\left(\mu_{Y}, 1\right)$ distribution.

  (i) Find (with careful justification) the form of the size- $\alpha$ likelihood-ratio test of the null hypothesis $H_{0}: \mu_{Y}=0$ against alternative $H_{1}:\left(\mu_{X}, \mu_{Y}\right)$ unrestricted.

  (ii) Find the form of the size- $\alpha$ likelihood-ratio test of the hypothesis

  $$H_{0}: \mu_{X} \geqslant A, \mu_{Y}=0$$

  against $H_{1}:\left(\mu_{X}, \mu_{Y}\right)$ unrestricted, where $A$ is a given constant.

  Compare the critical regions you obtain in (i) and (ii) and comment briefly.

  comment

• 2.II.19H

  Statistics | Part IB, 2008

  Suppose that the joint distribution of random variables $X, Y$ taking values in $\mathbb{Z}^{+}=\{0,1,2, \ldots\}$ is given by the joint probability generating function

  $$\varphi(s, t) \equiv E\left[s^{X} t^{Y}\right]=\frac{1-\alpha-\beta}{1-\alpha s-\beta t}$$

  where the unknown parameters $\alpha$ and $\beta$ are positive, and satisfy the inequality $\alpha+\beta<1$. Find $E(X)$. Prove that the probability mass function of $(X, Y)$ is

  $$f(x, y \mid \alpha, \beta)=(1-\alpha-\beta)\left(\begin{array}{c} x+y \\ x \end{array}\right) \alpha^{x} \beta^{y} \quad\left(x, y \in \mathbb{Z}^{+}\right)$$

  and prove that the maximum-likelihood estimators of $\alpha$ and $\beta$ based on a sample of size $n$ drawn from the distribution are

  $$\hat{\alpha}=\frac{\bar{X}}{1+\bar{X}+\bar{Y}}, \quad \hat{\beta}=\frac{\bar{Y}}{1+\bar{X}+\bar{Y}},$$

  where $\bar{X}$ (respectively, $\bar{Y}$ ) is the sample mean of $X_{1}, \ldots, X_{n}$ (respectively, $Y_{1}, \ldots, Y_{n}$ ).

  By considering $\hat{\alpha}+\hat{\beta}$ or otherwise, prove that the maximum-likelihood estimator is biased. Stating clearly any results to which you appeal, prove that as $n \rightarrow \infty, \hat{\alpha} \rightarrow \alpha$, making clear the sense in which this convergence happens.

  comment

• 4.II.19H

  Statistics | Part IB, 2008

  (i) Consider the linear model

  $$Y_{i}=\alpha+\beta x_{i}+\varepsilon_{i}$$

  where observations $Y_{i}, i=1, \ldots, n$, depend on known explanatory variables $x_{i}$, $i=1, \ldots, n$, and independent $N\left(0, \sigma^{2}\right)$ random variables $\varepsilon_{i}, i=1, \ldots, n$.

  Derive the maximum-likelihood estimators of $\alpha, \beta$ and $\sigma^{2}$.

  Stating clearly any results you require about the distribution of the maximum-likelihood estimators of $\alpha, \beta$ and $\sigma^{2}$, explain how to construct a test of the hypothesis that $\alpha=0$ against an unrestricted alternative.

  (ii) A simple ballistic theory predicts that the range of a gun fired at angle of elevation $\theta$ should be given by the formula

  $$Y=\frac{V^{2}}{g} \sin 2 \theta$$

  where $V$ is the muzzle velocity, and $g$ is the gravitational acceleration. Shells are fired at 9 different elevations, and the ranges observed are as follows:

  $\begin{array}{cccccccccc}\theta \text { (degrees) } & 5 & 15 & 25 & 35 & 45 & 55 & 65 & 75 & 85 \\ \sin 2 \theta & 0.1736 & 0.5 & 0.7660 & 0.9397 & 1 & 0.9397 & 0.7660 & 0.5 & 0.1736 \\ Y(\mathrm{~m}) & 4322 & 11898 & 17485 & 20664 & 21296 & 19491 & 15572 & 10027 & 3458\end{array}$

  The model

  $$Y_{i}=\alpha+\beta \sin 2 \theta_{i}+\varepsilon_{i}$$

  is proposed. Using the theory of part (i) above, find expressions for the maximumlikelihood estimators of $\alpha$ and $\beta$.

  The $t$-test of the null hypothesis that $\alpha=0$ against an unrestricted alternative does not reject the null hypothesis. Would you be willing to accept the model $(*)$ ? Briefly explain your answer.

  [You may need the following summary statistics of the data. If $x_{i}=\sin 2 \theta_{i}$, then $\bar{x} \equiv n^{-1} \sum x_{i}=0.63986, \bar{Y}=13802, S_{x x} \equiv \sum\left(x_{i}-\bar{x}\right)^{2}=0.81517, S_{x y}=\sum Y_{i}\left(x_{i}-\bar{x}\right)=$ 17186. ]

  comment