Part IB, 2017

Analysis II

• Paper 1, Section II, G

  Analysis II | Part IB, 2017

  What does it mean to say that a real-valued function on a metric space is uniformly continuous? Show that a continuous function on a closed interval in $\mathbb{R}$ is uniformly continuous.

  What does it mean to say that a real-valued function on a metric space is Lipschitz? Show that if a function is Lipschitz then it is uniformly continuous.

  Which of the following statements concerning continuous functions $f: \mathbb{R} \rightarrow \mathbb{R}$ are true and which are false? Justify your answers.

  (i) If $f$ is bounded then $f$ is uniformly continuous.

  (ii) If $f$ is differentiable and $f^{\prime}$ is bounded, then $f$ is uniformly continuous.

  (iii) There exists a sequence of uniformly continuous functions converging pointwise to $f$.

  comment

• Paper 2, Section I, G

  Analysis II | Part IB, 2017

  Let $X \subset \mathbb{R}$. What does it mean to say that a sequence of real-valued functions on $X$ is uniformly convergent?

  Let $f, f_{n}(n \geqslant 1): \mathbb{R} \rightarrow \mathbb{R}$ be functions.

  (a) Show that if each $f_{n}$ is continuous, and $\left(f_{n}\right)$ converges uniformly on $\mathbb{R}$ to $f$, then $f$ is also continuous.

  (b) Suppose that, for every $M>0,\left(f_{n}\right)$ converges uniformly on $[-M, M]$. Need $\left(f_{n}\right)$ converge uniformly on $\mathbb{R}$ ? Justify your answer.

  comment

• Paper 2, Section II, G

  Analysis II | Part IB, 2017

  Let $V$ be a real vector space. What is a norm on $V$ ? Show that if $\|-\|$ is a norm on $V$, then the maps $T_{v}: x \mapsto x+v\left(\right.$ for $v \in V$ ) and $m_{a}: x \mapsto a x$ (for $a \in \mathbb{R}$ ) are continuous with respect to the norm.

  Let $B \subset V$ be a subset containing 0 . Show that there exists at most one norm on $V$ for which $B$ is the open unit ball.

  Suppose that $B$ satisfies the following two properties:

  • if $v \in V$ is a nonzero vector, then the line $\mathbb{R} v \subset V$ meets $B$ in a set of the form $\{t v:-\lambda<t<\lambda\}$ for some $\lambda>0$;

  • if $x, y \in B$ and $s, t>0$ then $(s+t)^{-1}(s x+t y) \in B$.

  Show that there exists a norm $\|-\|_{B}$ for which $B$ is the open unit ball.

  Identify $\|-\|_{B}$ in the following two cases:

  (i) $V=\mathbb{R}^{n}, B=\left\{\left(x_{1}, \ldots, x_{n}\right) \in \mathbb{R}^{n}:-1<x_{i}<1\right.$ for all $\left.i\right\}$.

  (ii) $V=\mathbb{R}^{2}, B$ the interior of the square with vertices $(\pm 1,0),(0, \pm 1)$.

  Let $C \subset \mathbb{R}^{2}$ be the set

  $$C=\left\{\left(x_{1}, x_{2}\right) \in \mathbb{R}^{2}:\left|x_{1}\right|<1,\left|x_{2}\right|<1, \text { and }\left(\left|x_{1}\right|-1\right)^{2}+\left(\left|x_{2}\right|-1\right)^{2}>1\right\}$$

  Is there a norm on $\mathbb{R}^{2}$ for which $C$ is the open unit ball? Justify your answer.

  comment

• Paper 3, Section I, G

  Analysis II | Part IB, 2017

  What does it mean to say that a metric space is complete? Which of the following metric spaces are complete? Briefly justify your answers.

  (i) $[0,1]$ with the Euclidean metric.

  (ii) $\mathbb{Q}$ with the Euclidean metric.

  (iii) The subset

  $$\{(0,0)\} \cup\{(x, \sin (1 / x)) \mid x>0\} \subset \mathbb{R}^{2}$$

  with the metric induced from the Euclidean metric on $\mathbb{R}^{2}$.

  Write down a metric on $\mathbb{R}$ with respect to which $\mathbb{R}$ is not complete, justifying your answer.

  [You may assume throughout that $\mathbb{R}$ is complete with respect to the Euclidean metric.

  comment

• Paper 3, Section II, G

  Analysis II | Part IB, 2017

  What is a contraction map on a metric space $X$ ? State and prove the contraction mapping theorem.

  Let $(X, d)$ be a complete non-empty metric space. Show that if $f: X \rightarrow X$ is a map for which some iterate $f^{k}(k \geqslant 1)$ is a contraction map, then $f$ has a unique fixed point. Show that $f$ itself need not be a contraction map.

  Let $f:[0, \infty) \rightarrow[0, \infty)$ be the function

  $$f(x)=\frac{1}{3}\left(x+\sin x+\frac{1}{x+1}\right)$$

  Show that $f$ has a unique fixed point.

  comment

• Paper 4, Section I, G

  Analysis II | Part IB, 2017

  State the chain rule for the composition of two differentiable functions $f: \mathbb{R}^{m} \rightarrow \mathbb{R}^{n}$ and $g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{p}$.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be differentiable. For $c \in \mathbb{R}$, let $g(x)=f(x, c-x)$. Compute the derivative of $g$. Show that if $\partial f / \partial x=\partial f / \partial y$ throughout $\mathbb{R}^{2}$, then $f(x, y)=h(x+y)$ for some function $h: \mathbb{R} \rightarrow \mathbb{R}$.

  comment

• Paper 4, Section II, G

  Analysis II | Part IB, 2017

  Let $U \subset \mathbb{R}^{m}$ be a nonempty open set. What does it mean to say that a function $f: U \rightarrow \mathbb{R}^{n}$ is differentiable?

  Let $f: U \rightarrow \mathbb{R}$ be a function, where $U \subset \mathbb{R}^{2}$ is open. Show that if the first partial derivatives of $f$ exist and are continuous on $U$, then $f$ is differentiable on $U$.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be the function

  $$f(x, y)= \begin{cases}0 & (x, y)=(0,0) \\ \frac{x^{3}+2 y^{4}}{x^{2}+y^{2}} & (x, y) \neq(0,0)\end{cases}$$

  Determine, with proof, where $f$ is differentiable.

  comment

Complex Analysis

• Paper 3, Section II, F

  Complex Analysis | Part IB, 2017

  Let $f$ be an entire function. Prove Taylor's theorem, that there exist complex numbers $c_{0}, c_{1}, \ldots$ such that $f(z)=\sum_{n=0}^{\infty} c_{n} z^{n}$ for all $z$. [You may assume Cauchy's Integral Formula.]

  For a positive real $r$, let $M_{r}=\sup \{|f(z)|:|z|=r\}$. Explain why we have

  $$\left|c_{n}\right| \leqslant \frac{M_{r}}{r^{n}}$$

  for all $n$.

  Now let $n$ and $r$ be fixed. For which entire functions $f$ do we have $\left|c_{n}\right|=\frac{M_{r}}{r^{n}} ?$

  comment

• Paper 4, Section I, 4F

  Complex Analysis | Part IB, 2017

  Let $D$ be a star-domain, and let $f$ be a continuous complex-valued function on $D$. Suppose that for every triangle $T$ contained in $D$ we have

  $$\int_{\partial T} f(z) d z=0$$

  Show that $f$ has an antiderivative on $D$.

  If we assume instead that $D$ is a domain (not necessarily a star-domain), does this conclusion still hold? Briefly justify your answer.

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, A

  Complex Analysis or Complex Methods | Part IB, 2017

  Let $F(z)=u(x, y)+i v(x, y)$ where $z=x+i y$. Suppose $F(z)$ is an analytic function of $z$ in a domain $\mathcal{D}$ of the complex plane.

  Derive the Cauchy-Riemann equations satisfied by $u$ and $v$.

  For $u=\frac{x}{x^{2}+y^{2}}$ find a suitable function $v$ and domain $\mathcal{D}$ such that $F=u+i v$ is analytic in $\mathcal{D}$.

  comment

• Paper 1, Section II, A

  Complex Analysis or Complex Methods | Part IB, 2017

  (a) Let $f(z)$ be defined on the complex plane such that $z f(z) \rightarrow 0$ as $|z| \rightarrow \infty$ and $f(z)$ is analytic on an open set containing $\operatorname{Im}(z) \geqslant-c$, where $c$ is a positive real constant.

  Let $C_{1}$ be the horizontal contour running from $-\infty-i c$ to $+\infty-i c$ and let

  $$F(\lambda)=\frac{1}{2 \pi i} \int_{C_{1}} \frac{f(z)}{z-\lambda} d z$$

  By evaluating the integral, show that $F(\lambda)$ is analytic for $\operatorname{Im}(\lambda)>-c$.

  (b) Let $g(z)$ be defined on the complex plane such that $z g(z) \rightarrow 0$ as $|z| \rightarrow \infty$ with $\operatorname{Im}(z) \geqslant-c$. Suppose $g(z)$ is analytic at all points except $z=\alpha_{+}$and $z=\alpha_{-}$which are simple poles with $\operatorname{Im}\left(\alpha_{+}\right)>c$ and $\operatorname{Im}\left(\alpha_{-}\right)<-c$.

  Let $C_{2}$ be the horizontal contour running from $-\infty+i c$ to $+\infty+i c$, and let

  $$\begin{gathered} H(\lambda)=\frac{1}{2 \pi i} \int_{C_{1}} \frac{g(z)}{z-\lambda} d z \\ J(\lambda)=-\frac{1}{2 \pi i} \int_{C_{2}} \frac{g(z)}{z-\lambda} d z . \end{gathered}$$

  (i) Show that $H(\lambda)$ is analytic for $\operatorname{Im}(\lambda)>-c$.

  (ii) Show that $J(\lambda)$ is analytic for $\operatorname{Im}(\lambda)<c$.

  (iii) Show that if $-c<\operatorname{Im}(\lambda)<c$ then $H(\lambda)+J(\lambda)=g(\lambda)$.

  [You should be careful to make sure you consider all points in the required regions.]

  comment

• Paper 2, Section II, 13A

  Complex Analysis or Complex Methods | Part IB, 2017

  State the residue theorem.

  By considering

  $$\oint_{C} \frac{z^{1 / 2} \log z}{1+z^{2}} d z$$

  with $C$ a suitably chosen contour in the upper half plane or otherwise, evaluate the real integrals

  $$\int_{0}^{\infty} \frac{x^{1 / 2} \log x}{1+x^{2}} d x$$

  and

  $$\int_{0}^{\infty} \frac{x^{1 / 2}}{1+x^{2}} d x$$

  where $x^{1 / 2}$ is taken to be the positive square root.

  comment

Complex Methods

• Paper 3, Section I, A

  Complex Methods | Part IB, 2017

  By using the Laplace transform, show that the solution to

  $$y^{\prime \prime}-4 y^{\prime}+3 y=t e^{-3 t},$$

  subject to the conditions $y(0)=0$ and $y^{\prime}(0)=1$, is given by

  $$y(t)=\frac{37}{72} e^{3 t}-\frac{17}{32} e^{t}+\left(\frac{5}{288}+\frac{1}{24} t\right) e^{-3 t}$$

  when $t \geqslant 0$.

  comment

• Paper 4, Section II, A

  Complex Methods | Part IB, 2017

  By using Fourier transforms and a conformal mapping

  $$w=\sin \left(\frac{\pi z}{a}\right)$$

  with $z=x+i y$ and $w=\xi+i \eta$, and a suitable real constant $a$, show that the solution to

  $$\begin{array}{rlrl} \nabla^{2} \phi & =0 & -2 \pi \leqslant x \leqslant 2 \pi, y \geqslant 0 \\ \phi(x, 0) & =f(x) & -2 \pi \leqslant x \leqslant 2 \pi \\ \phi(\pm 2 \pi, y) & =0 & y>0, \\ \phi(x, y) & \rightarrow 0 & y \rightarrow \infty,-2 \pi \leqslant x \leqslant 2 \pi \end{array}$$

  is given by

  $$\phi(\xi, \eta)=\frac{\eta}{\pi} \int_{-1}^{1} \frac{F\left(\xi^{\prime}\right)}{\eta^{2}+\left(\xi-\xi^{\prime}\right)^{2}} d \xi^{\prime}$$

  where $F\left(\xi^{\prime}\right)$ is to be determined.

  In the case of $f(x)=\sin \left(\frac{x}{4}\right)$, give $F\left(\xi^{\prime}\right)$ explicitly as a function of $\xi^{\prime}$. [You need not evaluate the integral.]

  comment

Electromagnetism

• Paper 1, Section II, C

  Electromagnetism | Part IB, 2017

  Write down Maxwell's equations for the electric field $\mathbf{E}(\mathbf{x}, t)$ and the magnetic field $\mathbf{B}(\mathbf{x}, t)$ in a vacuum. Deduce that both $\mathbf{E}$ and $\mathbf{B}$ satisfy a wave equation, and relate the wave speed $c$ to the physical constants $\epsilon_{0}$ and $\mu_{0}$.

  Verify that there exist plane-wave solutions of the form

  $$\begin{aligned} &\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{e} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right] \\ &\mathbf{B}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{b} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right] \end{aligned}$$

  where $\mathbf{e}$ and $\mathbf{b}$ are constant complex vectors, $\mathbf{k}$ is a constant real vector and $\omega$ is a real constant. Derive the dispersion relation that relates the angular frequency $\omega$ of the wave to the wavevector $\mathbf{k}$, and give the algebraic relations between the vectors $\mathbf{e}, \mathbf{b}$ and $\mathbf{k}$ implied by Maxwell's equations.

  Let $\mathbf{n}$ be a constant real unit vector. Suppose that a perfect conductor occupies the region $\mathbf{n} \cdot \mathbf{x}<0$ with a plane boundary $\mathbf{n} \cdot \mathbf{x}=0$. In the vacuum region $\mathbf{n} \cdot \mathbf{x}>0$, a plane electromagnetic wave of the above form, with $\mathbf{k} \cdot \mathbf{n}<0$, is incident on the plane boundary. Write down the boundary conditions on $\mathbf{E}$ and $\mathbf{B}$ at the surface of the conductor. Show that Maxwell's equations and the boundary conditions are satisfied if the solution in the vacuum region is the sum of the incident wave given above and a reflected wave of the form

  $$\begin{aligned} &\mathbf{E}^{\prime}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{e}^{\prime} e^{i\left(\mathbf{k}^{\prime} \cdot \mathbf{x}-\omega t\right)}\right] \\ &\mathbf{B}^{\prime}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{b}^{\prime} e^{i\left(\mathbf{k}^{\prime} \cdot \mathbf{x}-\omega t\right)}\right] \end{aligned}$$

  where

  $$\begin{aligned} &\mathbf{e}^{\prime}=-\mathbf{e}+2(\mathbf{n} \cdot \mathbf{e}) \mathbf{n} \\ &\mathbf{b}^{\prime}=\mathbf{b}-2(\mathbf{n} \cdot \mathbf{b}) \mathbf{n} \\ &\mathbf{k}^{\prime}=\mathbf{k}-2(\mathbf{n} \cdot \mathbf{k}) \mathbf{n} \end{aligned}$$

  comment

• Paper 2, Section I, $\mathbf{6 C}$

  Electromagnetism | Part IB, 2017

  State Gauss's Law in the context of electrostatics.

  A spherically symmetric capacitor consists of two conductors in the form of concentric spherical shells of radii $a$ and $b$, with $b>a$. The inner sphere carries a charge $Q$ and the outer sphere carries a charge $-Q$. Determine the electric field $\mathbf{E}$ and the electrostatic potential $\phi$ in the regions $r<a, a<r<b$ and $r>b$. Show that the capacitance is

  $$C=\frac{4 \pi \epsilon_{0} a b}{b-a}$$

  and calculate the electrostatic energy of the system in terms of $Q$ and $C$.

  comment

• Paper 2, Section II, C

  Electromagnetism | Part IB, 2017

  In special relativity, the electromagnetic fields can be derived from a 4-vector potential $A^{\mu}=(\phi / c, \mathbf{A})$. Using the Minkowski metric tensor $\eta_{\mu \nu}$ and its inverse $\eta^{\mu \nu}$, state how the electromagnetic tensor $F_{\mu \nu}$ is related to the 4-potential, and write out explicitly the components of both $F_{\mu \nu}$ and $F^{\mu \nu}$ in terms of those of $\mathbf{E}$ and $\mathbf{B}$.

  If $x^{\prime \mu}=\Lambda_{\nu}^{\mu} x^{\nu}$ is a Lorentz transformation of the spacetime coordinates from one inertial frame $\mathcal{S}$ to another inertial frame $\mathcal{S}^{\prime}$, state how $F^{\prime \mu \nu}$ is related to $F^{\mu \nu}$.

  Write down the Lorentz transformation matrix for a boost in standard configuration, such that frame $\mathcal{S}^{\prime}$ moves relative to frame $\mathcal{S}$ with speed $v$ in the $+x$ direction. Deduce the transformation laws

  $$\begin{aligned} E_{x}^{\prime} &=E_{x} \\ E_{y}^{\prime} &=\gamma\left(E_{y}-v B_{z}\right) \\ E_{z}^{\prime} &=\gamma\left(E_{z}+v B_{y}\right) \\ B_{x}^{\prime} &=B_{x} \\ B_{y}^{\prime} &=\gamma\left(B_{y}+\frac{v}{c^{2}} E_{z}\right) \\ B_{z}^{\prime} &=\gamma\left(B_{z}-\frac{v}{c^{2}} E_{y}\right) \end{aligned}$$

  where $\gamma=\left(1-\frac{v^{2}}{c^{2}}\right)^{-1 / 2}$

  In frame $\mathcal{S}$, an infinitely long wire of negligible thickness lies along the $x$ axis. The wire carries $n$ positive charges $+q$ per unit length, which travel at speed $u$ in the $+x$ direction, and $n$ negative charges $-q$ per unit length, which travel at speed $u$ in the $-x$ direction. There are no other sources of the electromagnetic field. Write down the electric and magnetic fields in $\mathcal{S}$ in terms of Cartesian coordinates. Calculate the electric field in frame $\mathcal{S}^{\prime}$, which is related to $\mathcal{S}$ by a boost by speed $v$ as described above. Give an explanation of the physical origin of your expression.

  comment

• Paper 3, Section II, C

  Electromagnetism | Part IB, 2017

  (i) Two point charges, of opposite sign and unequal magnitude, are placed at two different locations. Show that the combined electrostatic potential vanishes on a sphere that encloses only the charge of smaller magnitude.

  (ii) A grounded, conducting sphere of radius $a$ is centred at the origin. A point charge $q$ is located outside the sphere at position vector $\mathbf{p}$. Formulate the differential equation and boundary conditions for the electrostatic potential outside the sphere. Using the result of part (i) or otherwise, show that the electric field outside the sphere is identical to that generated (in the absence of any conductors) by the point charge $q$ and an image charge $q^{\prime}$ located inside the sphere at position vector $\mathbf{p}^{\prime}$, provided that $\mathbf{p}^{\prime}$ and $q^{\prime}$ are chosen correctly.

  Calculate the magnitude and direction of the force experienced by the charge $q$.

  comment

• Paper 4 , Section I, $7 \mathrm{C}$

  Electromagnetism | Part IB, 2017

  A thin wire, in the form of a closed curve $C$, carries a constant current $I$. Using either the Biot-Savart law or the magnetic vector potential, show that the magnetic field far from the loop is of the approximate form

  $$\mathbf{B}(\mathbf{r}) \approx \frac{\mu_{0}}{4 \pi}\left[\frac{3(\mathbf{m} \cdot \mathbf{r}) \mathbf{r}-\mathbf{m}|\mathbf{r}|^{2}}{|\mathbf{r}|^{5}}\right]$$

  where $\mathbf{m}$ is the magnetic dipole moment of the loop. Derive an expression for $\mathbf{m}$ in terms of $I$ and the vector area spanned by the curve $C$.

  comment

Fluid Dynamics

• Paper 1, Section I, D

  Fluid Dynamics | Part IB, 2017

  For each of the flows

  (i) $\mathbf{u}=\left(2 x y, x^{2}+y^{2}\right)$

  (ii) $\mathbf{u}=(-2 y,-2 x)$

  determine whether or not the flow is incompressible and/or irrotational. Find the associated velocity potential and/or stream function when appropriate. For either one of the flows, sketch the streamlines of the flow, indicating the direction of the flow.

  comment

• Paper 1, Section II, D

  Fluid Dynamics | Part IB, 2017

  A layer of thickness $h$ of fluid of density $\rho$ and dynamic viscosity $\mu$ flows steadily down and parallel to a rigid plane inclined at angle $\alpha$ to the horizontal. Wind blows over the surface of the fluid and exerts a stress $S$ on the surface of the fluid in the upslope direction.

  (a) Draw a diagram of this situation, including indications of the applied stresses and body forces, a suitable coordinate system and a representation of the expected velocity profile.

  (b) Write down the equations and boundary conditions governing the flow, with a brief description of each, paying careful attention to signs. Solve these equations to determine the pressure and velocity fields.

  (c) Determine the volume flux and show that there is no net flux if

  $$S=\frac{2}{3} \rho g h \sin \alpha$$

  Draw a sketch of the corresponding velocity profile.

  (d) Determine the value of $S$ for which the shear stress on the rigid plane is zero and draw a sketch of the corresponding velocity profile.

  comment

• Paper 2, Section I, $7 \mathrm{D}$

  Fluid Dynamics | Part IB, 2017

  From Euler's equations describing steady inviscid fluid flow under the action of a conservative force, derive Bernoulli's equation for the pressure along a streamline of the flow, defining all variables that you introduce.

  Water fills an inverted, open, circular cone (radius increasing upwards) of half angle $\pi / 4$ to a height $h_{0}$ above its apex. At time $t=0$, the tip of the cone is removed to leave a small hole of radius $\epsilon \ll h_{0}$. Assuming that the flow is approximately steady while the depth of water $h(t)$ is much larger than $\epsilon$, show that the time taken for the water to drain is approximately

  $$\left(\frac{2}{25} \frac{h_{0}^{5}}{\epsilon^{4} g}\right)^{1 / 2}$$

  comment

• Paper 3, Section II, D

  Fluid Dynamics | Part IB, 2017

  Use Euler's equations to derive the vorticity equation

  $$\frac{D \boldsymbol{\omega}}{D t}=\boldsymbol{\omega} \cdot \nabla \mathbf{u}$$

  where $\mathbf{u}$ is the fluid velocity and $\boldsymbol{\omega}$ is the vorticity.

  Consider axisymmetric, incompressible, inviscid flow between two rigid plates at $z=h(t)$ and $z=-h(t)$ in cylindrical polar coordinates $(r, \theta, z)$, where $t$ is time. Using mass conservation, or otherwise, find the complete flow field whose radial component is independent of $z$.

  Now suppose that the flow has angular velocity $\boldsymbol{\Omega}=\Omega(t) \mathbf{e}_{z}$ and that $\Omega=\Omega_{0}$ when $h=h_{0}$. Use the vorticity equation to determine the angular velocity for subsequent times as a function of $h$. What physical principle does your result illustrate?

  comment

• Paper 4, Section II, D

  Fluid Dynamics | Part IB, 2017

  The linearised equations governing the horizontal components of flow $\mathbf{u}(x, y, t)$ in a rapidly rotating shallow layer of depth $h=h_{0}+\eta(x, y, t)$, where $\eta \ll h_{0}$, are

  $$\begin{gathered} \frac{\partial \mathbf{u}}{\partial t}+\mathbf{f} \times \mathbf{u}=-g \nabla \eta \\ \frac{\partial \eta}{\partial t}+h_{0} \nabla \cdot \mathbf{u}=0 \end{gathered}$$

  where $\mathbf{f}=f \mathbf{e}_{z}$ is the constant Coriolis parameter, and $\mathbf{e}_{z}$ is the unit vector in the vertical direction.

  Use these equations, either in vector form or using Cartesian components, to show that the potential vorticity

  $$\mathbf{Q}=\zeta-\frac{\eta}{h_{0}} \mathbf{f}$$

  is independent of time, where $\zeta=\nabla \times \mathbf{u}$ is the relative vorticity.

  Derive the equation

  $$\frac{\partial^{2} \eta}{\partial t^{2}}-g h_{0} \nabla^{2} \eta+f^{2} \eta=-h_{0} \mathbf{f} \cdot \mathbf{Q}$$

  In the case that $\mathbf{Q} \equiv 0$, determine and sketch the dispersion relation $\omega(k)$ for plane waves with $\eta=A e^{i(k x+\omega t)}$, where $A$ is constant. Discuss the nature of the waves qualitatively: do long waves propagate faster or slower than short waves; how does the phase speed depend on wavelength; does rotation have more effect on long waves or short waves; how dispersive are the waves?

  comment

Geometry

• Paper 1, Section I, G

  Geometry | Part IB, 2017

  Give the definition for the area of a hyperbolic triangle with interior angles $\alpha, \beta, \gamma$.

  Let $n \geqslant 3$. Show that the area of a convex hyperbolic $n$-gon with interior angles $\alpha_{1}, \ldots, \alpha_{n}$ is $(n-2) \pi-\sum \alpha_{i}$.

  Show that for every $n \geqslant 3$ and for every $A$ with $0<A<(n-2) \pi$ there exists a regular hyperbolic $n$-gon with area $A$.

  comment

• Paper 2, Section II, G

  Geometry | Part IB, 2017

  Let $H=\left\{\mathbf{x} \in \mathbb{R}^{n} \mid \mathbf{u} \cdot \mathbf{x}=c\right\}$ be a hyperplane in $\mathbb{R}^{n}$, where $\mathbf{u}$ is a unit vector and $c$ is a constant. Show that the reflection map

  $$\mathbf{x} \mapsto \mathbf{x}-2(\mathbf{u} \cdot \mathbf{x}-c) \mathbf{u}$$

  is an isometry of $\mathbb{R}^{n}$ which fixes $H$ pointwise.

  Let $\mathbf{p}, \mathbf{q}$ be distinct points in $\mathbb{R}^{n}$. Show that there is a unique reflection $R$ mapping $\mathbf{p}$ to $\mathbf{q}$, and that $R \in O(n)$ if and only if $\mathbf{p}$ and $\mathbf{q}$ are equidistant from the origin.

  Show that every isometry of $\mathbb{R}^{n}$ can be written as a product of at most $n+1$ reflections. Give an example of an isometry of $\mathbb{R}^{2}$ which cannot be written as a product of fewer than 3 reflections.

  comment

• Paper 3, Section I, G

  Geometry | Part IB, 2017

  Let

  $$\pi(x, y, z)=\frac{x+i y}{1-z}$$

  be stereographic projection from the unit sphere $S^{2}$ in $\mathbb{R}^{3}$ to the Riemann sphere $\mathbb{C}_{\infty}$. Show that if $r$ is a rotation of $S^{2}$, then $\pi r \pi^{-1}$ is a Möbius transformation of $\mathbb{C}_{\infty}$ which can be represented by an element of $S U(2)$. (You may assume without proof any result about generation of $S O(3)$ by a particular set of rotations, but should state it carefully.)

  comment

• Paper 3, Section II, G

  Geometry | Part IB, 2017

  Let $\sigma: U \rightarrow \mathbb{R}^{3}$ be a parametrised surface, where $U \subset \mathbb{R}^{2}$ is an open set.

  (a) Explain what are the first and second fundamental forms of the surface, and what is its Gaussian curvature. Compute the Gaussian curvature of the hyperboloid $\sigma(x, y)=(x, y, x y)$.

  (b) Let $\mathbf{a}(x)$ and $\mathbf{b}(x)$ be parametrised curves in $\mathbb{R}^{3}$, and assume that

  $$\sigma(x, y)=\mathbf{a}(x)+y \mathbf{b}(x)$$

  Find a formula for the first fundamental form, and show that the Gaussian curvature vanishes if and only if

  $$\mathbf{a}^{\prime} \cdot\left(\mathbf{b} \times \mathbf{b}^{\prime}\right)=0$$

  comment

• Paper 4, Section II, G

  Geometry | Part IB, 2017

  What is a hyperbolic line in (a) the disc model (b) the upper half-plane model of the hyperbolic plane? What is the hyperbolic distance $d(P, Q)$ between two points $P, Q$ in the hyperbolic plane? Show that if $\gamma$ is any continuously differentiable curve with endpoints $P$ and $Q$ then its length is at least $d(P, Q)$, with equality if and only if $\gamma$ is a monotonic reparametrisation of the hyperbolic line segment joining $P$ and $Q$.

  What does it mean to say that two hyperbolic lines $L, L^{\prime}$ are (a) parallel (b) ultraparallel? Show that $L$ and $L^{\prime}$ are ultraparallel if and only if they have a common perpendicular, and if so, then it is unique.

  A horocycle is a curve in the hyperbolic plane which in the disc model is a Euclidean circle with exactly one point on the boundary of the disc. Describe the horocycles in the upper half-plane model. Show that for any pair of horocycles there exists a hyperbolic line which meets both orthogonally. For which pairs of horocycles is this line unique?

  comment

Groups, Rings and Modules

• Paper 1, Section II, 10E

  Groups, Rings and Modules | Part IB, 2017

  (a) State Sylow's theorem.

  (b) Let $G$ be a finite simple non-abelian group. Let $p$ be a prime number. Show that if $p$ divides $|G|$, then $|G|$ divides $n_{p} ! / 2$ where $n_{p}$ is the number of Sylow $p$-subgroups of $G$.

  (c) Let $G$ be a group of order 48 . Show that $G$ is not simple. Find an example of $G$ which has no normal Sylow 2-subgroup.

  comment

• Paper 2, Section I, E

  Groups, Rings and Modules | Part IB, 2017

  (a) Define what is meant by a unique factorisation domain and by a principal ideal domain. State Gauss's lemma and Eisenstein's criterion, without proof.

  (b) Find an example, with justification, of a ring $R$ and a subring $S$ such that

  (i) $R$ is a principal ideal domain, and

  (ii) $S$ is a unique factorisation domain but not a principal ideal domain.

  comment

• Paper 2, Section II, E

  Groups, Rings and Modules | Part IB, 2017

  Let $R$ be a commutative ring.

  (a) Let $N$ be the set of nilpotent elements of $R$, that is,

  $$N=\left\{r \in R \mid r^{n}=0 \text { for some } n \in \mathbb{N}\right\}$$

  Show that $N$ is an ideal of $R$.

  (b) Assume $R$ is Noetherian and assume $S \subset R$ is a non-empty subset such that if $s, t \in S$, then $s t \in S$. Let $I$ be an ideal of $R$ disjoint from $S$. Show that there is a prime ideal $P$ of $R$ containing $I$ and disjoint from $S$.

  (c) Again assume $R$ is Noetherian and let $N$ be as in part (a). Let $\mathcal{P}$ be the set of all prime ideals of $R$. Show that

  $$N=\bigcap_{P \in \mathcal{P}} P$$

  comment

• Paper 3, Section I, E

  Groups, Rings and Modules | Part IB, 2017

  Let $R$ be a commutative ring and let $M$ be an $R$-module. Show that $M$ is a finitely generated $R$-module if and only if there exists a surjective $R$-module homomorphism $R^{n} \rightarrow M$ for some $n$.

  Find an example of a $\mathbb{Z}$-module $M$ such that there is no surjective $\mathbb{Z}$-module homomorphism $\mathbb{Z} \rightarrow M$ but there is a surjective $\mathbb{Z}$-module homomorphism $\mathbb{Z}^{2} \rightarrow M$ which is not an isomorphism. Justify your answer.

  comment

• Paper 3, Section II, E

  Groups, Rings and Modules | Part IB, 2017

  (a) Define what is meant by a Euclidean domain. Show that every Euclidean domain is a principal ideal domain.

  (b) Let $p \in \mathbb{Z}$ be a prime number and let $f \in \mathbb{Z}[x]$ be a monic polynomial of positive degree. Show that the quotient ring $\mathbb{Z}[x] /(p, f)$ is finite.

  (c) Let $\alpha \in \mathbb{Z}[\sqrt{-1}]$ and let $P$ be a non-zero prime ideal of $\mathbb{Z}[\alpha]$. Show that the quotient $\mathbb{Z}[\alpha] / P$ is a finite ring.

  comment

• Paper 4, Section I, $2 E$

  Groups, Rings and Modules | Part IB, 2017

  Let $G$ be a non-trivial finite $p$-group and let $Z(G)$ be its centre. Show that $|Z(G)|>1$. Show that if $|G|=p^{3}$ and if $G$ is not abelian, then $|Z(G)|=p$.

  comment

• Paper 4, Section II, E

  Groups, Rings and Modules | Part IB, 2017

  (a) State (without proof) the classification theorem for finitely generated modules over a Euclidean domain. Give the statement and the proof of the rational canonical form theorem.

  (b) Let $R$ be a principal ideal domain and let $M$ be an $R$-submodule of $R^{n}$. Show that $M$ is a free $R$-module.

  comment

Linear Algebra

• Paper 1, Section I, F

  Linear Algebra | Part IB, 2017

  State and prove the Steinitz Exchange Lemma.

  Deduce that, for a subset $S$ of $\mathbb{R}^{n}$, any two of the following imply the third:

  (i) $S$ is linearly independent

  (ii) $S$ is spanning

  (iii) $S$ has exactly $n$ elements

  Let $e_{1}, e_{2}$ be a basis of $\mathbb{R}^{2}$. For which values of $\lambda$ do $\lambda e_{1}+e_{2}, e_{1}+\lambda e_{2}$ form a basis of $\mathbb{R}^{2} ?$

  comment

• Paper 1, Section II, F

  Linear Algebra | Part IB, 2017

  Let $U$ and $V$ be finite-dimensional real vector spaces, and let $\alpha: U \rightarrow V$ be a surjective linear map. Which of the following are always true and which can be false? Give proofs or counterexamples as appropriate.

  (i) There is a linear map $\beta: V \rightarrow U$ such that $\beta \alpha$ is the identity map on $U$.

  (ii) There is a linear map $\beta: V \rightarrow U$ such that $\alpha \beta$ is the identity map on $V$.

  (iii) There is a subspace $W$ of $U$ such that the restriction of $\alpha$ to $W$ is an isomorphism from $W$ to $V$.

  (iv) If $X$ and $Y$ are subspaces of $U$ with $U=X \oplus Y$ then $V=\alpha(X) \oplus \alpha(Y)$.

  (v) If $X$ and $Y$ are subspaces of $U$ with $V=\alpha(X) \oplus \alpha(Y)$ then $U=X \oplus Y$.

  comment

• Paper 2, Section I, F

  Linear Algebra | Part IB, 2017

  State and prove the Rank-Nullity theorem.

  Let $\alpha$ be a linear map from $\mathbb{R}^{3}$ to $\mathbb{R}^{3}$ of rank 2 . Give an example to show that $\mathbb{R}^{3}$ may be the direct sum of the kernel of $\alpha$ and the image of $\alpha$, and also an example where this is not the case.

  comment

• Paper 2, Section II, F

  Linear Algebra | Part IB, 2017

  Let $\alpha: U \rightarrow V$ and $\beta: V \rightarrow W$ be linear maps between finite-dimensional real vector spaces.

  Show that the rank $r(\beta \alpha)$ satisfies $r(\beta \alpha) \leqslant \min (r(\beta), r(\alpha))$. Show also that $r(\beta \alpha) \geqslant r(\alpha)+r(\beta)-\operatorname{dim} V$. For each of these two inequalities, give examples to show that we may or may not have equality.

  Now let $V$ have dimension $2 n$ and let $\alpha: V \rightarrow V$ be a linear map of rank $2 n-2$ such that $\alpha^{n}=0$. Find the rank of $\alpha^{k}$ for each $1 \leqslant k \leqslant n-1$.

  comment

• Paper 3, Section II, F

  Linear Algebra | Part IB, 2017

  Let $f$ be a quadratic form on a finite-dimensional real vector space $V$. Prove that there exists a diagonal basis for $f$, meaning a basis with respect to which the matrix of $f$ is diagonal.

  Define the rank $r$ and signature $s$ of $f$ in terms of this matrix. Prove that $r$ and $s$ are independent of the choice of diagonal basis.

  In terms of $r, s$, and the dimension $n$ of $V$, what is the greatest dimension of a subspace on which $f$ is zero?

  Now let $f$ be the quadratic form on $\mathbb{R}^{3}$ given by $f(x, y, z)=x^{2}-y^{2}$. For which points $v$ in $\mathbb{R}^{3}$ is it the case that there is some diagonal basis for $f$ containing $v$ ?

  comment

• Paper 4, Section I, F

  Linear Algebra | Part IB, 2017

  Briefly explain the Gram-Schmidt orthogonalisation process in a real finite-dimensional inner product space $V$.

  For a subspace $U$ of $V$, define $U^{\perp}$, and show that $V=U \oplus U^{\perp}$.

  For which positive integers $n$ does

  $$(f, g)=f(1) g(1)+f(2) g(2)+f(3) g(3)$$

  define an inner product on the space of all real polynomials of degree at most $n$ ?

  comment

• Paper 4, Section II, F

  Linear Algebra | Part IB, 2017

  What is the dual $X^{*}$ of a finite-dimensional real vector space $X$ ? If $X$ has a basis $e_{1}, \ldots, e_{n}$, define the dual basis, and prove that it is indeed a basis of $X^{*}$.

  [No results on the dimension of duals may be assumed without proof.]

  Write down (without making a choice of basis) an isomorphism from $X$ to $X^{* *}$. Prove that your map is indeed an isomorphism.

  Does every basis of $X^{*}$ arise as the dual basis of some basis of $X ?$ Justify your answer.

  A subspace $W$ of $X^{*}$ is called separating if for every non-zero $x \in X$ there is a $T \in W$ with $T(x) \neq 0$. Show that the only separating subspace of $X^{*}$ is $X^{*}$ itself.

  Now let $X$ be the (infinite-dimensional) space of all real polynomials. Explain briefly how we may identify $X^{*}$ with the space of all real sequences. Give an example of a proper subspace of $X^{*}$ that is separating.

  comment

Markov Chains

• Paper 1, Section II, H

  Markov Chains | Part IB, 2017

  A rich and generous man possesses $n$ pounds. Some poor cousins arrive at his mansion. Being generous he decides to give them money. On day 1 , he chooses uniformly at random an integer between $n-1$ and 1 inclusive and gives it to the first cousin. Then he is left with $x$ pounds. On day 2 , he chooses uniformly at random an integer between $x-1$ and 1 inclusive and gives it to the second cousin and so on. If $x=1$ then he does not give the next cousin any money. His choices of the uniform numbers are independent. Let $X_{i}$ be his fortune at the end of day $i$.

  Show that $X$ is a Markov chain and find its transition probabilities.

  Let $\tau$ be the first time he has 1 pound left, i.e. $\tau=\min \left\{i \geqslant 1: X_{i}=1\right\}$. Show that

  $$\mathbb{E}[\tau]=\sum_{i=1}^{n-1} \frac{1}{i}$$

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2017

  Let $Y_{1}, Y_{2}, \ldots$ be i.i.d. random variables with values in $\{1,2, \ldots\}$ and $\mathbb{E}\left[Y_{1}\right]=\mu<\infty$. Moreover, suppose that the greatest common divisor of $\left\{n: \mathbb{P}\left(Y_{1}=n\right)>0\right\}$ is 1 . Consider the following process

  $$X_{n}=\inf \left\{m \geqslant n: Y_{1}+\ldots+Y_{k}=m, \text { for some } k \geqslant 0\right\}-n .$$

  (a) Show that $X$ is a Markov chain and find its transition probabilities.

  (b) Let $T_{0}=\inf \left\{n \geqslant 1: X_{n}=0\right\}$. Find $\mathbb{E}_{0}\left[T_{0}\right]$.

  (c) Find the limit as $n \rightarrow \infty$ of $\mathbb{P}\left(X_{n}=0\right)$. State carefully any theorems from the course that you are using.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2017

  (a) What does it mean to say that a Markov chain is reversible?

  (b) Let $G$ be a finite connected graph on $n$ vertices. What does it mean to say that $X$ is a simple random walk on $G$ ?

  Find the unique invariant distribution $\pi$ of $X$.

  Show that $X$ is reversible when $X_{0} \sim \pi$.

  [You may use, without proof, results about detailed balance equations, but you should state them clearly.]

  comment

• Paper 4, Section I, $\mathbf{9 H}$

  Markov Chains | Part IB, 2017

  Prove that the simple symmetric random walk on $\mathbb{Z}^{3}$ is transient.

  [Any combinatorial inequality can be used without proof.]

  comment

Methods

• Paper 1, Section II, 14B

  Methods | Part IB, 2017

  (a)

  (i) Compute the Fourier transform $\tilde{h}(k)$ of $h(x)=e^{-a|x|}$, where $a$ is a real positive constant.

  (ii) Consider the boundary value problem

  $$-\frac{d^{2} u}{d x^{2}}+\omega^{2} u=e^{-|x|} \quad \text { on }-\infty<x<\infty$$

  with real constant $\omega \neq \pm 1$ and boundary condition $u(x) \rightarrow 0$ as $|x| \rightarrow \infty$.

  Find the Fourier transform $\tilde{u}(k)$ of $u(x)$ and hence solve the boundary value problem. You should clearly state any properties of the Fourier transform that you use.

  (b) Consider the wave equation

  $$v_{t t}=v_{x x} \quad \text { on } \quad-\infty<x<\infty \text { and } t>0$$

  with initial conditions

  $$v(x, 0)=f(x) \quad v_{t}(x, 0)=g(x) .$$

  Show that the Fourier transform $\tilde{v}(k, t)$ of the solution $v(x, t)$ with respect to the variable $x$ is given by

  $$\tilde{v}(k, t)=\tilde{f}(k) \cos k t+\frac{\tilde{g}(k)}{k} \sin k t$$

  where $\tilde{f}(k)$ and $\tilde{g}(k)$ are the Fourier transforms of the initial conditions. Starting from $\tilde{v}(k, t)$ derive d'Alembert's solution for the wave equation:

  $$v(x, t)=\frac{1}{2}(f(x-t)+f(x+t))+\frac{1}{2} \int_{x-t}^{x+t} g(\xi) d \xi$$

  You should state clearly any properties of the Fourier transform that you use.

  comment

• Paper 2, Section I, B

  Methods | Part IB, 2017

  Expand $f(x)=x$ as a Fourier series on $-\pi<x<\pi$.

  By integrating the series show that $x^{2}$ on $-\pi<x<\pi$ can be written as

  $$x^{2}=\frac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos n x$$

  where $a_{n}, n=1,2, \ldots$, should be determined and

  $$a_{0}=8 \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}} .$$

  By evaluating $a_{0}$ another way show that

  $$\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}=\frac{\pi^{2}}{12}$$

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2017

  Laplace's equation for $\phi$ in cylindrical coordinates $(r, \theta, z)$, is

  $$\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} \phi}{\partial \theta^{2}}+\frac{\partial^{2} \phi}{\partial z^{2}}=0$$

  Use separation of variables to find an expression for the general solution to Laplace's equation in cylindrical coordinates that is $2 \pi$-periodic in $\theta$.

  Find the bounded solution $\phi(r, \theta, z)$ that satisfies

  $$\begin{aligned} \nabla^{2} \phi &=0 \quad z \geqslant 0, \quad 0 \leqslant r \leqslant 1 \\ \phi(1, \theta, z) &=e^{-4 z}(\cos \theta+\sin 2 \theta)+2 e^{-z} \sin 2 \theta \end{aligned}$$

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2017

  Using the substitution $u(x, y)=v(x, y) e^{-x^{2}}$, find $u(x, y)$ that satisfies

  $$u_{x}+x u_{y}+2 x u=e^{-x^{2}}$$

  with boundary data $u(0, y)=y e^{-y^{2}}$.

  comment

• Paper 3, Section II, A

  Methods | Part IB, 2017

  Let $\mathcal{L}$ be the linear differential operator

  $$\mathcal{L} y=y^{\prime \prime \prime}-y^{\prime \prime}-2 y^{\prime}$$

  where $^{\prime}$ denotes differentiation with respect to $x$.

  Find the Green's function, $G(x ; \xi)$, for $\mathcal{L}$ satisfying the homogeneous boundary conditions $G(0 ; \xi)=0, G^{\prime}(0 ; \xi)=0, G^{\prime \prime}(0 ; \xi)=0$.

  Using the Green's function, solve

  $$\mathcal{L} y=e^{x} \Theta(x-1)$$

  with boundary conditions $y(0)=1, y^{\prime}(0)=-1, y^{\prime \prime}(0)=0$. Here $\Theta(x)$ is the Heaviside step function having value 0 for $x<0$ and 1 for $x>0$.

  comment

• Paper 4, Section I, A

  Methods | Part IB, 2017

  The Legendre polynomials, $P_{n}(x)$ for integers $n \geqslant 0$, satisfy the Sturm-Liouville equation

  $$\frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d}{d x} P_{n}(x)\right]+n(n+1) P_{n}(x)=0$$

  and the recursion formula

  $$(n+1) P_{n+1}(x)=(2 n+1) x P_{n}(x)-n P_{n-1}(x), \quad P_{0}(x)=1, \quad P_{1}(x)=x$$

  (i) For all $n \geqslant 0$, show that $P_{n}(x)$ is a polynomial of degree $n$ with $P_{n}(1)=1$.

  (ii) For all $m, n \geqslant 0$, show that $P_{n}(x)$ and $P_{m}(x)$ are orthogonal over the range $x \in[-1,1]$ when $m \neq n$.

  (iii) For each $n \geqslant 0$ let

  $$R_{n}(x)=\frac{d^{n}}{d x^{n}}\left[\left(x^{2}-1\right)^{n}\right]$$

  Assume that for each $n$ there is a constant $\alpha_{n}$ such that $P_{n}(x)=\alpha_{n} R_{n}(x)$ for all $x$. Determine $\alpha_{n}$ for each $n$.

  comment

• Paper 4, Section II, B

  Methods | Part IB, 2017

  (a)

  (i) For the diffusion equation

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=0 \quad \text { on }-\infty<x<\infty \text { and } t \geqslant 0$$

  with diffusion constant $K$, state the properties (in terms of the Dirac delta function) that define the fundamental solution $F(x, t)$ and the Green's function $G(x, t ; y, \tau)$.

  You are not required to give expressions for these functions.

  (ii) Consider the initial value problem for the homogeneous equation:

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=0, \quad \phi\left(x, t_{0}\right)=\alpha(x) \quad \text { on }-\infty<x<\infty \text { and } t \geqslant t_{0}$$

  and the forced equation with homogeneous initial condition (and given forcing term $h(x, t))$ :

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=h(x, t), \quad \phi(x, 0)=0 \quad \text { on }-\infty<x<\infty \text { and } t \geqslant 0$$

  Given that $F$ and $G$ in part (i) are related by

  $$G(x, t ; y, \tau)=\Theta(t-\tau) F(x-y, t-\tau)$$

  (where $\Theta(t)$ is the Heaviside step function having value 0 for $t<0$ and 1 for $t>0$, show how the solution of (B) can be expressed in terms of solutions of (A) with suitable initial conditions. Briefly interpret your expression.

  (b) A semi-infinite conducting plate lies in the $\left(x_{1}, x_{2}\right)$ plane in the region $x_{1} \geqslant 0$. The boundary along the $x_{2}$ axis is perfectly insulated. Let $(r, \theta)$ denote standard polar coordinates on the plane. At time $t=0$ the entire plate is at temperature zero except for the region defined by $-\pi / 4<\theta<\pi / 4$ and $1<r<2$ which has constant initial temperature $T_{0}>0$. Subsequently the temperature of the plate obeys the two-dimensional heat equation with diffusion constant $K$. Given that the fundamental solution of the twodimensional heat equation on $\mathbb{R}^{2}$ is

  $$F\left(x_{1}, x_{2}, t\right)=\frac{1}{4 \pi K t} e^{-\left(x_{1}^{2}+x_{2}^{2}\right) /(4 K t)}$$

  show that the origin $(0,0)$ on the plate reaches its maximum temperature at time $t=3 /(8 K \log 2)$.

  comment

Metric and Topological Spaces

• Paper 1, Section II, E

  Metric and Topological Spaces | Part IB, 2017

  Consider $\mathbb{R}$ and $\mathbb{R}^{2}$ with their usual Euclidean topologies.

  (a) Show that a non-empty subset of $\mathbb{R}$ is connected if and only if it is an interval. Find a compact subset $K \subset \mathbb{R}$ for which $\mathbb{R} \backslash K$ has infinitely many connected components.

  (b) Let $T$ be a countable subset of $\mathbb{R}^{2}$. Show that $\mathbb{R}^{2} \backslash T$ is path-connected. Deduce that $\mathbb{R}^{2}$ is not homeomorphic to $\mathbb{R}$.

  comment

• Paper 2, Section I, E

  Metric and Topological Spaces | Part IB, 2017

  Let $f:(X, d) \rightarrow(Y, e)$ be a function between metric spaces.

  (a) Give the $\epsilon-\delta$ definition for $f$ to be continuous. Show that $f$ is continuous if and only if $f^{-1}(U)$ is an open subset of $X$ for each open subset $U$ of $Y$.

  (b) Give an example of $f$ such that $f$ is not continuous but $f(V)$ is an open subset of $Y$ for every open subset $V$ of $X$.

  comment

• Paper 3, Section I, $3 E$

  Metric and Topological Spaces | Part IB, 2017

  Let $X$ and $Y$ be topological spaces.

  (a) Define what is meant by the product topology on $X \times Y$. Define the projection maps $p: X \times Y \rightarrow X$ and $q: X \times Y \rightarrow Y$ and show they are continuous.

  (b) Consider $\Delta=\{(x, x) \mid x \in X\}$ in $X \times X$. Show that $X$ is Hausdorff if and only if $\Delta$ is a closed subset of $X \times X$ in the product topology.

  comment

• Paper 4, Section II, E

  Metric and Topological Spaces | Part IB, 2017

  Let $f: X \rightarrow Y$ be a continuous map between topological spaces.

  (a) Assume $X$ is compact and that $Z \subseteq X$ is a closed subset. Prove that $Z$ and $f(Z)$ are both compact.

  (b) Suppose that

  (i) $f^{-1}(\{y\})$ is compact for each $y \in Y$, and

  (ii) if $A$ is any closed subset of $X$, then $f(A)$ is a closed subset of $Y$.

  Show that if $K \subseteq Y$ is compact, then $f^{-1}(K)$ is compact.

  $\left[\right.$ Hint: Given an open cover $f^{-1}(K) \subseteq \bigcup_{i \in I} U_{i}$, find a finite subcover, say $f^{-1}(\{y\}) \subseteq$ $\bigcup_{i \in I_{y}} U_{i}$, for each $y \in K$; use closedness of $X \backslash \bigcup_{i \in I_{y}} U_{i}$ and property (ii) to produce an open cover of $K$.]

  comment

Numerical Analysis

• Paper 1, Section I, C

  Numerical Analysis | Part IB, 2017

  Given $n+1$ real points $x_{0}<x_{1}<\cdots<x_{n}$, define the Lagrange cardinal polynomials $\ell_{i}(x), i=0,1, \ldots, n$. Let $p(x)$ be the polynomial of degree $n$ that interpolates the function $f \in C^{n}\left[x_{0}, x_{n}\right]$ at these points. Express $p(x)$ in terms of the values $f_{i}=f\left(x_{i}\right)$, $i=0,1, \ldots, n$ and the Lagrange cardinal polynomials.

  Define the divided difference $f\left[x_{0}, x_{1}, \ldots, x_{n}\right]$ and give an expression for it in terms of $f_{0}, f_{1}, \ldots, f_{n}$ and $x_{0}, x_{1}, \ldots, x_{n}$. Prove that

  $$f\left[x_{0}, x_{1}, \ldots, x_{n}\right]=\frac{1}{n !} f^{(n)}(\xi)$$

  for some number $\xi \in\left[x_{0}, x_{n}\right]$.

  comment

• Paper 1, Section II, C

  Numerical Analysis | Part IB, 2017

  A three-stage explicit Runge-Kutta method for solving the autonomous ordinary differential equation

  $$\frac{d y}{d t}=f(y)$$

  is given by

  $$y_{n+1}=y_{n}+h\left(b_{1} k_{1}+b_{2} k_{2}+b_{3} k_{3}\right),$$

  where

  $$\begin{aligned} &k_{1}=f\left(y_{n}\right) \\ &k_{2}=f\left(y_{n}+h a_{1} k_{1}\right) \\ &k_{3}=f\left(y_{n}+h\left(a_{2} k_{1}+a_{3} k_{2}\right)\right) \end{aligned}$$

  and $h>0$ is the time-step. Derive sufficient conditions on the coefficients $b_{1}, b_{2}, b_{3}, a_{1}$, $a_{2}$ and $a_{3}$ for the method to be of third order.

  Assuming that these conditions hold, verify that $-\frac{5}{2}$ belongs to the linear stability domain of the method.

  comment

• Paper 2, Section II, C

  Numerical Analysis | Part IB, 2017

  Define the linear least-squares problem for the equation $A \mathbf{x}=\mathbf{b}$, where $A$ is an $m \times n$ matrix with $m>n, \mathbf{b} \in \mathbb{R}^{m}$ is a given vector and $\mathbf{x} \in \mathbb{R}^{n}$ is an unknown vector.

  If $A=Q R$, where $Q$ is an orthogonal matrix and $R$ is an upper triangular matrix in standard form, explain why the least-squares problem is solved by minimizing the Euclidean norm $\left\|R \mathbf{x}-Q^{\top} \mathbf{b}\right\|$.

  Using the method of Householder reflections, find a QR factorization of the matrix

  $$A=\left[\begin{array}{rrr} 1 & 3 & 3 \\ 1 & 3 & 1 \\ 1 & 1 & 1 \\ 1 & 1 & -1 \end{array}\right]$$

  Hence find the solution of the least-squares problem in the case

  $$\mathbf{b}=\left[\begin{array}{r} 1 \\ 1 \\ 3 \\ -1 \end{array}\right]$$

  comment

• Paper 3, Section II, C

  Numerical Analysis | Part IB, 2017

  Let $p_{n} \in \mathbb{P}_{n}$ be the $n$th monic orthogonal polynomial with respect to the inner product

  $$\langle f, g\rangle=\int_{a}^{b} w(x) f(x) g(x) d x$$

  on $C[a, b]$, where $w$ is a positive weight function.

  Prove that, for $n \geqslant 1, p_{n}$ has $n$ distinct zeros in the interval $(a, b)$.

  Let $c_{1}, c_{2}, \ldots, c_{n} \in[a, b]$ be $n$ distinct points. Show that the quadrature formula

  $$\int_{a}^{b} w(x) f(x) d x \approx \sum_{i=1}^{n} b_{i} f\left(c_{i}\right)$$

  is exact for all $f \in \mathbb{P}_{n-1}$ if the weights $b_{i}$ are chosen to be

  $$b_{i}=\int_{a}^{b} w(x) \prod_{\substack{j=1 \\ j \neq i}}^{n} \frac{x-c_{j}}{c_{i}-c_{j}} d x$$

  Show further that the quadrature formula is exact for all $f \in \mathbb{P}_{2 n-1}$ if the nodes $c_{i}$ are chosen to be the zeros of $p_{n}$ (Gaussian quadrature). [Hint: Write $f$ as $q p_{n}+r$, where $q, r \in \mathbb{P}_{n-1}$.]

  Use the Peano kernel theorem to write an integral expression for the approximation error of Gaussian quadrature for sufficiently differentiable functions. (You should give a formal expression for the Peano kernel but are not required to evaluate it.)

  comment

• Paper 4, Section I, C

  Numerical Analysis | Part IB, 2017

  For the matrix

  $$A=\left[\begin{array}{rrrr} 1 & 1 & 1 & 1 \\ 1 & 5 & 5 & 5 \\ 1 & 5 & 14 & 14 \\ 1 & 5 & 14 & \lambda \end{array}\right]$$

  find a factorization of the form

  $$A=L D L^{\top} \text {, }$$

  where $D$ is diagonal and $L$ is lower triangular with ones on its diagonal.

  For what values of $\lambda$ is $A$ positive definite?

  In the case $\lambda=30$ find the Cholesky factorization of $A$.

  comment

Optimization

• Paper 1, Section I, H

  Optimization | Part IB, 2017

  Solve the following linear programming problem using the simplex method:

  $$\begin{array}{r} \max \left(x_{1}+2 x_{2}+x_{3}\right) \\ \text { subject to } \quad x_{1}, x_{2}, x_{3} \geqslant 0 \\ x_{1}+x_{2}+2 x_{3} \leqslant 10 \\ 2 x_{1}+x_{2}+3 x_{3} \leqslant 15 \end{array}$$

  Suppose we now subtract $\Delta \in[0,10]$ from the right hand side of the last two constraints. Find the new optimal value.

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2017

  Consider the following optimization problem

  $$\mathrm{P}: \quad \min f(x) \quad \text { subject to } \quad g(x)=b, x \in X .$$

  (a) Write down the Lagrangian for this problem. State the Lagrange sufficiency theorem.

  (b) Formulate the dual problem. State and prove the weak duality property.

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2017

  (a) Explain what is meant by a two-person zero-sum game with payoff matrix $A=\left(a_{i j}: 1 \leqslant i \leqslant m, 1 \leqslant j \leqslant n\right)$ and define what is an optimal strategy (also known as a maximin strategy) for each player.

  (b) Suppose the payoff matrix $A$ is antisymmetric, i.e. $m=n$ and $a_{i j}=-a_{j i}$ for all $i, j$. What is the value of the game? Justify your answer.

  (c) Consider the following two-person zero-sum game. Let $n \geqslant 3$. Both players simultaneously call out one of the numbers $\{1, \ldots, n\}$. If the numbers differ by one, the player with the higher number wins $£ 1$ from the other player. If the players' choices differ by 2 or more, the player with the higher number pays $£ 2$ to the other player. In the event of a tie, no money changes hands.

  Write down the payoff matrix.

  For the case when $n=3$ find the value of the game and an optimal strategy for each player.

  Find the value of the game and an optimal strategy for each player for all $n$.

  [You may use results from the course provided you state them clearly.]

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2017

  (a) Let $G$ be a flow network with capacities $c_{i j}$ on the edges. Explain the maximum flow problem on this network defining all the notation you need.

  (b) Describe the Ford-Fulkerson algorithm for finding a maximum flow and state the max-flow min-cut theorem.

  (c) Apply the Ford-Fulkerson algorithm to find a maximum flow and a minimum cut of the following network:

  

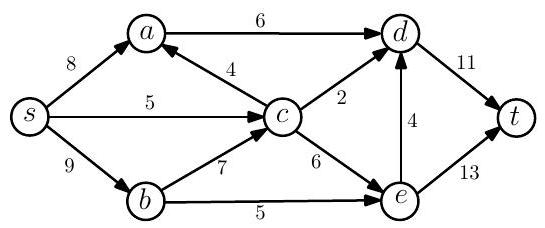
  (d) Suppose that we add $\varepsilon>0$ to each capacity of a flow network. Is it true that the maximum flow will always increase by $\varepsilon$ ? Justify your answer.

  comment

Quantum Mechanics

• Paper 1, Section II, B

  Quantum Mechanics | Part IB, 2017

  Consider the time-independent Schrödinger equation in one dimension for a particle of mass $m$ with potential $V(x)$.

  (a) Show that if the potential is an even function then any non-degenerate stationary state has definite parity.

  (b) A particle of mass $m$ is subject to the potential $V(x)$ given by

  $$V(x)=-\lambda(\delta(x-a)+\delta(x+a))$$

  where $\lambda$ and $a$ are real positive constants and $\delta(x)$ is the Dirac delta function.

  Derive the conditions satisfied by the wavefunction $\psi(x)$ around the points $x=\pm a$.

  Show (using a graphical method or otherwise) that there is a bound state of even parity for any $\lambda>0$, and that there is an odd parity bound state only if $\lambda>\hbar^{2} /(2 m a)$. [Hint: You may assume without proof that the functions $x \tanh x$ and $x \operatorname{coth} x$ are monotonically increasing for $x>0$.]

  comment

• Paper 2, Section II, B

  Quantum Mechanics | Part IB, 2017

  (a) The potential for the one-dimensional harmonic oscillator is $V(x)=\frac{1}{2} m \omega^{2} x^{2}$. By considering the associated time-independent Schrödinger equation for the wavefunction $\psi(x)$ with substitutions

  $$\xi=\left(\frac{m \omega}{\hbar}\right)^{1 / 2} x \quad \text { and } \quad \psi(x)=f(\xi) e^{-\xi^{2} / 2}$$

  show that the allowed energy levels are given by $E_{n}=\left(n+\frac{1}{2}\right) \hbar \omega$ for $n=0,1,2, \ldots$ [You may assume without proof that $f$ must be a polynomial for $\psi$ to be normalisable.]

  (b) Consider a particle with charge $q$ and mass $m=1$ subject to the one-dimensional harmonic oscillator potential $U_{0}(x)=x^{2} / 2$. You may assume that the normalised ground state of this potential is

  $$\psi_{0}(x)=\left(\frac{1}{\pi \hbar}\right)^{1 / 4} e^{-x^{2} /(2 \hbar)}$$

  The particle is in the stationary state corresponding to $\psi_{0}(x)$ when at time $t=t_{0}$, an electric field of constant strength $E$ is turned on, adding an extra term $U_{1}(x)=-q E x$ to the harmonic potential.

  (i) Using the result of part (a) or otherwise, find the energy levels of the new potential.

  (ii) Show that the probability of finding the particle in the ground state immediately after $t_{0}$ is given by $e^{-q^{2} E^{2} /(2 \hbar)}$. [You may assume that $\int_{-\infty}^{\infty} e^{-x^{2}+2 A x} d x=$ $\sqrt{\pi} e^{A^{2}}$.]

  comment

• Paper 3, Section I, B

  Quantum Mechanics | Part IB, 2017

  A particle of mass $m$ is confined to a one-dimensional box $0 \leqslant x \leqslant a$. The potential $V(x)$ is zero inside the box and infinite outside.

  (a) Find the allowed energies of the particle and the normalised energy eigenstates.

  (b) At time $t=0$ the particle has wavefunction $\psi_{0}$ that is uniform in the left half of the box i.e. $\psi_{0}(x)=\sqrt{\frac{2}{a}}$ for $0<x<a / 2$ and $\psi_{0}(x)=0$ for $a / 2<x<a$. Find the probability that a measurement of energy at time $t=0$ will yield a value less than $5 \hbar^{2} \pi^{2} /\left(2 m a^{2}\right)$.

  comment

• Paper 3, Section II, B

  Quantum Mechanics | Part IB, 2017

  (a) Given the position and momentum operators $\hat{x}_{i}=x_{i}$ and $\hat{p}_{i}=-i \hbar \partial / \partial x_{i}$ (for $i=1,2,3)$ in three dimensions, define the angular momentum operators $\hat{L}_{i}$ and the total angular momentum $\hat{L}^{2}$.

  Show that $\hat{L}_{3}$ is Hermitian.

  (b) Derive the generalised uncertainty relation for the observables $\hat{L}_{3}$ and $\hat{x}_{1}$ in the form

  $$\Delta_{\psi} \hat{L}_{3} \Delta_{\psi} \hat{x}_{1} \geqslant M$$

  for any state $\psi$ and a suitable expression $M$ that you should determine. [Hint: It may be useful to consider the operator $\hat{L}_{3}+i \lambda \hat{x}_{1}$.]

  (c) Consider a particle with wavefunction

  $$\psi=K\left(x_{1}+x_{2}+2 x_{3}\right) e^{-\alpha r}$$

  where $r=\sqrt{x_{1}^{2}+x_{2}^{2}+x_{3}^{2}}$ and $K$ and $\alpha$ are real positive constants.

  Show that $\psi$ is an eigenstate of total angular momentum $\hat{L}^{2}$ and find the corresponding angular momentum quantum number $l$. Find also the expectation value of a measurement of $\hat{L}_{3}$ on the state $\psi$.

  comment

• Paper 4, Section I, B

  Quantum Mechanics | Part IB, 2017

  (a) Give a physical interpretation of the wavefunction $\phi(x, t)=A e^{i k x} e^{-i E t / \hbar}$ (where $A, k$ and $E$ are real constants).

  (b) A particle of mass $m$ and energy $E>0$ is incident from the left on the potential step

  $$V(x)=\left\{\begin{array}{cl} 0 & \text { for }-\infty<x<a \\ V_{0} & \text { for } a<x<\infty \end{array}\right.$$

  with $V_{0}>0$.

  State the conditions satisfied by a stationary state at the point $x=a$.

  Compute the probability that the particle is reflected as a function of $E$, and compare your result with the classical case.

  comment

Statistics

• Paper 1, Section I, H

  Statistics | Part IB, 2017

  (a) State and prove the Rao-Blackwell theorem.

  (b) Let $X_{1}, \ldots, X_{n}$ be an independent sample from $\operatorname{Poisson}(\lambda)$ with $\theta=e^{-\lambda}$ to be estimated. Show that $Y=1_{\{0\}}\left(X_{1}\right)$ is an unbiased estimator of $\theta$ and that $T=\sum_{i} X_{i}$ is a sufficient statistic.

  What is $\mathbb{E}[Y \mid T] ?$

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2017

  (a) Give the definitions of a sufficient and a minimal sufficient statistic $T$ for an unknown parameter $\theta$.

  Let $X_{1}, X_{2}, \ldots, X_{n}$ be an independent sample from the geometric distribution with success probability $1 / \theta$ and mean $\theta>1$, i.e. with probability mass function

  $$p(m)=\frac{1}{\theta}\left(1-\frac{1}{\theta}\right)^{m-1} \text { for } m=1,2, \ldots$$

  Find a minimal sufficient statistic for $\theta$. Is your statistic a biased estimator of $\theta ?$

  [You may use results from the course provided you state them clearly.]

  (b) Define the bias of an estimator. What does it mean for an estimator to be unbiased?

  Suppose that $Y$ has the truncated Poisson distribution with probability mass function

  $$p(y)=\left(e^{\theta}-1\right)^{-1} \cdot \frac{\theta^{y}}{y !} \quad \text { for } y=1,2, \ldots$$

  Show that the only unbiased estimator $T$ of $1-e^{-\theta}$ based on $Y$ is obtained by taking $T=0$ if $Y$ is odd and $T=2$ if $Y$ is even.

  Is this a useful estimator? Justify your answer.

  comment

• Paper 2, Section I, 8H

  Statistics | Part IB, 2017

  (a) Define a $100 \gamma \%$ confidence interval for an unknown parameter $\theta$.

  (b) Let $X_{1}, \ldots, X_{n}$ be i.i.d. random variables with distribution $N(\mu, 1)$ with $\mu$ unknown. Find a $95 \%$ confidence interval for $\mu$.

  [You may use the fact that $\Phi(1.96) \simeq 0.975 .]$

  (c) Let $U_{1}, U_{2}$ be independent $U[\theta-1, \theta+1]$ with $\theta$ to be estimated. Find a $50 \%$ confidence interval for $\theta$.

  Suppose that we have two observations $u_{1}=10$ and $u_{2}=11.5$. What might be a better interval to report in this case?

  comment

• Paper 3, Section II, $\mathbf{2 0 H}$

  Statistics | Part IB, 2017

  Consider the general linear model

  $$\boldsymbol{Y}=X \boldsymbol{\beta}+\varepsilon$$

  where $X$ is a known $n \times p$ matrix of full rank $p<n, \varepsilon \sim \mathcal{N}_{n}\left(0, \sigma^{2} I\right)$ with $\sigma^{2}$ known and $\boldsymbol{\beta} \in \mathbb{R}^{p}$ is an unknown vector.

  (a) State without proof the Gauss-Markov theorem.

  Find the maximum likelihood estimator $\widehat{\boldsymbol{\beta}}$ for $\boldsymbol{\beta}$. Is it unbiased?

  Let $\boldsymbol{\beta}^{*}$ be any unbiased estimator for $\boldsymbol{\beta}$ which is linear in $\left(Y_{i}\right)$. Show that

  $$\operatorname{var}\left(\boldsymbol{t}^{T} \widehat{\boldsymbol{\beta}}\right) \leqslant \operatorname{var}\left(\boldsymbol{t}^{T} \boldsymbol{\beta}^{*}\right)$$

  for all $\boldsymbol{t} \in \mathbb{R}^{p}$.

  (b) Suppose now that $p=1$ and that $\boldsymbol{\beta}$ and $\sigma^{2}$ are both unknown. Find the maximum likelihood estimator for $\sigma^{2}$. What is the joint distribution of $\widehat{\boldsymbol{\beta}}$ and $\widehat{\sigma}^{2}$ in this case? Justify your answer.

  comment

• Paper 4, Section II, H

  Statistics | Part IB, 2017

  (a) State and prove the Neyman-Pearson lemma.

  (b) Let $X$ be a real random variable with density $f(x)=(2 \theta x+1-\theta) 1_{[0,1]}(x)$ with $-1 \leqslant \theta \leqslant 1 .$

  Find a most powerful test of size $\alpha$ of $H_{0}: \theta=0$ versus $H_{1}: \theta=1$.

  Find a uniformly most powerful test of size $\alpha$ of $H_{0}: \theta=0$ versus $H_{1}: \theta>0$.

  comment

Variational Principles

• Paper 1, Section I, D

  Variational Principles | Part IB, 2017

  Derive the Euler-Lagrange equation for the function $u(x, y)$ that gives a stationary value of

  $$I[u]=\int_{\mathcal{D}} L\left(x, y, u, \frac{\partial u}{\partial x}, \frac{\partial u}{\partial y}\right) d x d y$$

  where $\mathcal{D}$ is a bounded domain in the $(x, y)$-plane and $u$ is fixed on the boundary $\partial \mathcal{D}$.

  Find the equation satisfied by the function $u$ that gives a stationary value of

  $$I=\int_{\mathcal{D}}\left[\left(\frac{\partial u}{\partial x}\right)^{2}+\left(\frac{\partial u}{\partial y}\right)^{2}+k^{2} u^{2}\right] d x d y$$

  where $k$ is a constant and $u$ is prescribed on $\partial \mathcal{D}$.

  comment

• Paper 2, Section II, D

  Variational Principles | Part IB, 2017

  A proto-planet of mass $m$ in a uniform galactic dust cloud has kinetic and potential energies

  $$T=\frac{1}{2} m \dot{r}^{2}+\frac{1}{2} m r^{2} \dot{\phi}^{2}, \quad V=k m r^{2}$$

  where $k$ is constant. State Hamilton's principle and use it to determine the equations of motion for the proto-planet.

  Write down two conserved quantities of the motion and state why their existence illustrates Noether's theorem.

  Determine the Hamiltonian $H(\mathbf{p}, \mathbf{x})$ of this system, where $\mathbf{p}=\left(p_{r}, p_{\phi}\right), \mathbf{x}=(r, \phi)$ and $\left(p_{r}, p_{\phi}\right)$ are the conjugate momenta corresponding to $(r, \phi)$.

  Write down Hamilton's equations for this system and use them to show that

  $$m \ddot{r}=-V_{\text {eff }}^{\prime}(r), \quad \text { where } \quad V_{\text {eff }}(r)=m\left(\frac{h^{2}}{2 m^{2} r^{2}}+k r^{2}\right)$$

  and $h$ is a constant. With the aid of a diagram, explain why there is a stable circular orbit.

  comment

• Paper 3, Section $I$, D

  Variational Principles | Part IB, 2017

  (a) A Pringle crisp can be defined as the surface

  $$z=x y \quad \text { with } \quad x^{2}+y^{2} \leqslant 1$$

  Use the method of Lagrange multipliers to find the minimum and maximum values of $z$ on the boundary of the Pringle crisp and the $(x, y)$ positions where these occur.

  (b) A farmer wishes to construct a grain silo in the form of a hollow vertical cylinder of radius $r$ and height $h$ with a hollow hemispherical cap of radius $r$ on top of the cylinder. The walls of the cylinder cost $£ x$ per unit area to construct and the surface of the cap costs $£ 2 x$ per unit area to construct. Given that a total volume $V$ is desired for the silo, what values of $r$ and $h$ should be chosen to minimise the cost?

  comment

• Paper 4, Section II, $16 \mathrm{D}$

  Variational Principles | Part IB, 2017

  Consider the functional

  $$F[y]=\int_{\alpha}^{\beta} f\left(y, y^{\prime}, x\right) d x$$

  of a function $y(x)$ defined for $x \in[\alpha, \beta]$, with $y$ having fixed values at $x=\alpha$ and $x=\beta$.

  By considering $F[y+\epsilon \xi]$, where $\xi(x)$ is an arbitrary function with $\xi(\alpha)=\xi(\beta)=0$ and $\epsilon \ll 1$, determine that the second variation of $F$ is

  $$\delta^{2} F[y, \xi]=\int_{\alpha}^{\beta}\left\{\xi^{2}\left[\frac{\partial^{2} f}{\partial y^{2}}-\frac{d}{d x}\left(\frac{\partial^{2} f}{\partial y \partial y^{\prime}}\right)\right]+\xi^{\prime 2} \frac{\partial^{2} f}{\partial y^{\prime 2}}\right\} d x$$

  The surface area of an axisymmetric soap film joining two parallel, co-axial, circular rings of radius a distance $2 L$ apart can be expressed by the functional

  $$F[y]=\int_{-L}^{L} 2 \pi y \sqrt{1+y^{\prime 2}} d x$$

  where $x$ is distance in the axial direction and $y$ is radial distance from the axis. Show that the surface area is stationary when

  $$y=E \cosh \frac{x}{E},$$

  where $E$ is a constant that need not be determined, and that the stationary area is a local minimum if

  $$\int_{-L / E}^{L / E}\left(\xi^{\prime 2}-\xi^{2}\right) \operatorname{sech}^{2} z d z>0$$

  for all functions $\xi(z)$ that vanish at $z=\pm L / E$, where $z=x / E$.

  comment