Part IB, 2012

Analysis II

• Paper 1, Section II, E

  Analysis II | Part IB, 2012

  State the inverse function theorem for a function $F: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$. Suppose $F$ is a differentiable bijection with $F^{-1}$ also differentiable. Show that the derivative of $F$ at any point in $\mathbb{R}^{n}$ is a linear isomorphism.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be a function such that the partial derivatives $\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}$ exist and are continuous. Assume there is a point $(a, b) \in \mathbb{R}^{2}$ for which $f(a, b)=0$ and $\frac{\partial f}{\partial x}(a, b) \neq 0$. Prove that there exist open sets $U \subset \mathbb{R}^{2}$ and $W \subset \mathbb{R}$ containing $(a, b)$ and $b$, respectively, such that for every $y \in W$ there exists a unique $x$ such that $(x, y) \in U$ and $f(x, y)=0$. Moreover, if we define $g: W \rightarrow \mathbb{R}$ by $g(y)=x$, prove that $g$ is differentiable with continuous derivative. Find the derivative of $g$ at $b$ in terms of $\frac{\partial f}{\partial x}(a, b)$ and $\frac{\partial f}{\partial y}(a, b)$.

  comment

• Paper 2, Section I, E

  Analysis II | Part IB, 2012

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be a function. What does it mean to say that $f$ is differentiable at a point $(x, y) \in \mathbb{R}^{2} ?$ Prove directly from this definition, that if $f$ is differentiable at $(x, y)$, then $f$ is continuous at $(x, y)$.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be the function:

  $$f(x, y)= \begin{cases}x^{2}+y^{2} & \text { if } x \text { and } y \text { are rational } \\ 0 & \text { otherwise. }\end{cases}$$

  For which points $(x, y) \in \mathbb{R}^{2}$ is $f$ differentiable? Justify your answer.

  comment

• Paper 2, Section II, E

  Analysis II | Part IB, 2012

  Let $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ be a mapping. Fix $a \in \mathbb{R}^{n}$ and prove that the following two statements are equivalent:

  (i) Given $\varepsilon>0$ there is $\delta>0$ such that $\|f(x)-f(a)\|<\varepsilon$ whenever $\|x-a\|<\delta$ (we use the standard norm in Euclidean space).

  (ii) $f\left(x_{n}\right) \rightarrow f(a)$ for any sequence $x_{n} \rightarrow a$.

  We say that $f$ is continuous if (i) (or equivalently (ii)) holds for every $a \in \mathbb{R}^{n}$.

  Let $E$ and $F$ be subsets of $\mathbb{R}^{n}$ and $\mathbb{R}^{m}$ respectively. For $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ as above, determine which of the following statements are always true and which may be false, giving a proof or a counterexample as appropriate.

  (a) If $f^{-1}(F)$ is closed whenever $F$ is closed, then $f$ is continuous.

  (b) If $f$ is continuous, then $f^{-1}(F)$ is closed whenever $F$ is closed.

  (c) If $f$ is continuous, then $f(E)$ is open whenever $E$ is open.

  (d) If $f$ is continuous, then $f(E)$ is bounded whenever $E$ is bounded.

  (e) If $f$ is continuous and $f^{-1}(F)$ is bounded whenever $F$ is bounded, then $f(E)$ is closed whenever $E$ is closed.

  comment

• Paper 3, Section I, $2 \mathbf{E}$

  Analysis II | Part IB, 2012

  Let $C[0,1]$ be the set of continuous real-valued functions on $[0,1]$ with the uniform norm. Suppose $T: C[0,1] \rightarrow C[0,1]$ is defined by

  $$T(f)(x)=\int_{0}^{x} f\left(t^{3}\right) d t$$

  for all $x \in[0,1]$ and $f \in C[0,1]$. Is $T$ a contraction mapping? Does $T$ have a unique fixed point? Justify your answers.

  comment

• Paper 3, Section II, E

  Analysis II | Part IB, 2012

  Let $f_{n}$ be a sequence of continuous functions on the interval $[0,1]$ such that $f_{n}(x) \rightarrow f(x)$ for each $x$. For the three statements:

  (a) $f_{n} \rightarrow f$ uniformly on $[0,1]$;

  (b) $f$ is a continuous function;

  (c) $\int_{0}^{1} f_{n}(x) d x \rightarrow \int_{0}^{1} f(x) d x$ as $n \rightarrow \infty ;$

  say which of the six possible implications $(a) \Rightarrow(b),(a) \Rightarrow(c),(b) \Rightarrow(a),(b) \Rightarrow(c)$, $(c) \Rightarrow(a),(c) \Rightarrow(b)$ are true and which false, giving in each case a proof or counterexample.

  comment

• Paper 4, Section I, E

  Analysis II | Part IB, 2012

  Let $f: \mathbb{R}^{n} \times \mathbb{R}^{m} \rightarrow \mathbb{R}$ be a bilinear function. Show that $f$ is differentiable at any point in $\mathbb{R}^{n} \times \mathbb{R}^{m}$ and find its derivative.

  comment

• Paper 4, Section II, E

  Analysis II | Part IB, 2012

  State and prove the Bolzano-Weierstrass theorem in $\mathbb{R}^{n}$. [You may assume the Bolzano-Weierstrass theorem in $\mathbb{R}$.]

  Let $X \subset \mathbb{R}^{n}$ be a subset and let $f: X \rightarrow X$ be a mapping such that $d(f(x), f(y))=d(x, y)$ for all $x, y \in X$, where $d$ is the Euclidean distance in $\mathbb{R}^{n}$. Prove that if $X$ is closed and bounded, then $f$ is a bijection. Is this result still true if we drop the boundedness assumption on $X$ ? Justify your answer.

  comment

Complex Analysis

• Paper 3, Section II, E

  Complex Analysis | Part IB, 2012

  Let $D(a, R)$ denote the disc $|z-a|<R$ and let $f: D(a, R) \rightarrow \mathbb{C}$ be a holomorphic function. Using Cauchy's integral formula show that for every $r \in(0, R)$

  $$f(a)=\int_{0}^{1} f\left(a+r e^{2 \pi i t}\right) d t$$

  Deduce that if for every $z \in D(a, R),|f(z)| \leqslant|f(a)|$, then $f$ is constant.

  Let $f: D(0,1) \rightarrow D(0,1)$ be holomorphic with $f(0)=0$. Show that $|f(z)| \leqslant|z|$ for all $z \in D(0,1)$. Moreover, show that if $|f(w)|=|w|$ for some $w \neq 0$, then there exists $\lambda$ with $|\lambda|=1$ such that $f(z)=\lambda z$ for all $z \in D(0,1)$.

  comment

• Paper 4, Section I, $4 \mathrm{E}$

  Complex Analysis | Part IB, 2012

  Let $h: \mathbb{C} \rightarrow \mathbb{C}$ be a holomorphic function with $h(i) \neq h(-i)$. Does there exist a holomorphic function $f$ defined in $|z|<1$ for which $f^{\prime}(z)=\frac{h(z)}{1+z^{2}}$ ? Does there exist a holomorphic function $f$ defined in $|z|>1$ for which $f^{\prime}(z)=\frac{h(z)}{1+z^{2}}$ ? Justify your answers.

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, A

  Complex Analysis or Complex Methods | Part IB, 2012

  Find a conformal transformation $\zeta=\zeta(z)$ that maps the domain $D, 0<\arg z<\frac{3 \pi}{2}$, on to the strip $0<\operatorname{Im}(\zeta)<1$.

  Hence find a bounded harmonic function $\phi$ on $D$ subject to the boundary conditions $\phi=0, A$ on $\arg z=0, \frac{3 \pi}{2}$, respectively, where $A$ is a real constant.

  comment

• Paper 1, Section II, 13A

  Complex Analysis or Complex Methods | Part IB, 2012

  Using Cauchy's integral theorem, write down the value of a holomorphic function $f(z)$ where $|z|<1$ in terms of a contour integral around the unit circle, $\zeta=e^{i \theta} .$

  By considering the point $1 / \bar{z}$, or otherwise, show that

  $$f(z)=\frac{1}{2 \pi} \int_{0}^{2 \pi} f(\zeta) \frac{1-|z|^{2}}{|\zeta-z|^{2}} \mathrm{~d} \theta$$

  By setting $z=r e^{i \alpha}$, show that for any harmonic function $u(r, \alpha)$,

  $$u(r, \alpha)=\frac{1}{2 \pi} \int_{0}^{2 \pi} u(1, \theta) \frac{1-r^{2}}{1-2 r \cos (\alpha-\theta)+r^{2}} \mathrm{~d} \theta$$

  if $r<1$.

  Assuming that the function $v(r, \alpha)$, which is the conjugate harmonic function to $u(r, \alpha)$, can be written as

  $$v(r, \alpha)=v(0)+\frac{1}{\pi} \int_{0}^{2 \pi} u(1, \theta) \frac{r \sin (\alpha-\theta)}{1-2 r \cos (\alpha-\theta)+r^{2}} \mathrm{~d} \theta$$

  deduce that

  $$f(z)=i v(0)+\frac{1}{2 \pi} \int_{0}^{2 \pi} u(1, \theta) \frac{\zeta+z}{\zeta-z} \mathrm{~d} \theta$$

  [You may use the fact that on the unit circle, $\zeta=1 / \bar{\zeta}$, and hence

  $$\left.\frac{\zeta}{\zeta-1 / \bar{z}}=-\frac{\bar{z}}{\bar{\zeta}-\bar{z}} \cdot\right]$$

  comment

• Paper 2, Section II, A

  Complex Analysis or Complex Methods | Part IB, 2012

  By a suitable choice of contour show that, for $-1<\alpha<1$,

  $$\int_{0}^{\infty} \frac{x^{\alpha}}{1+x^{2}} \mathrm{~d} x=\frac{\pi}{2 \cos (\alpha \pi / 2)}$$

  comment

Complex Methods

• Paper 3, Section I, A

  Complex Methods | Part IB, 2012

  State the formula for the Laplace transform of a function $f(t)$, defined for $t \geqslant 0$.

  Let $f(t)$ be periodic with period $T$ (i.e. $f(t+T)=f(t)$ ). If $g(t)$ is defined to be equal to $f(t)$ in $[0, T]$ and zero elsewhere and its Laplace transform is $G(s)$, show that the Laplace transform of $f(t)$ is given by

  $$F(s)=\frac{G(s)}{1-e^{-s T}}$$

  Hence, or otherwise, find the inverse Laplace transform of

  $$F(s)=\frac{1}{s} \frac{1-e^{-s T / 2}}{1-e^{-s T}}$$

  comment

• Paper 4, Section II, A

  Complex Methods | Part IB, 2012

  State the convolution theorem for Fourier transforms.

  The function $\phi(x, y)$ satisfies

  $$\nabla^{2} \phi=0$$

  on the half-plane $y \geqslant 0$, subject to the boundary conditions

  $$\begin{gathered} \phi \rightarrow 0 \text { as } y \rightarrow \infty \text { for all } x \\ \phi(x, 0)= \begin{cases}1, & |x| \leqslant 1 \\ 0, & |x|>1\end{cases} \end{gathered}$$

  Using Fourier transforms, show that

  $$\phi(x, y)=\frac{y}{\pi} \int_{-1}^{1} \frac{1}{y^{2}+(x-t)^{2}} \mathrm{~d} t$$

  and hence that

  $$\phi(x, y)=\frac{1}{\pi}\left[\tan ^{-1}\left(\frac{1-x}{y}\right)+\tan ^{-1}\left(\frac{1+x}{y}\right)\right]$$

  comment

Electromagnetism

• Paper 1, Section II, B

  Electromagnetism | Part IB, 2012

  A sphere of radius a carries an electric charge $Q$ uniformly distributed over its surface. Calculate the electric field outside and inside the sphere. Also calculate the electrostatic potential outside and inside the sphere, assuming it vanishes at infinity. State the integral formula for the energy $U$ of the electric field and use it to evaluate $U$ as a function of $Q$

  Relate $\frac{d U}{d Q}$ to the potential on the surface of the sphere and explain briefly the physical interpretation of the relation.

  comment

• Paper 2, Section I, B

  Electromagnetism | Part IB, 2012

  Write down the expressions for a general, time-dependent electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$ in terms of a vector potential $\mathbf{A}$ and scalar potential $\phi$. What is meant by a gauge transformation of $\mathbf{A}$ and $\phi$ ? Show that $\mathbf{E}$ and $\mathbf{B}$ are unchanged under a gauge transformation.

  A plane electromagnetic wave has vector and scalar potentials

  $$\begin{aligned} \mathbf{A}(\mathbf{x}, t) &=\mathbf{A}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)} \\ \phi(\mathbf{x}, t) &=\phi_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)} \end{aligned}$$

  where $\mathbf{A}_{0}$ and $\phi_{0}$ are constants. Show that $\left(\mathbf{A}_{0}, \phi_{0}\right)$ can be modified to $\left(\mathbf{A}_{0}+\mu \mathbf{k}, \phi_{0}+\mu \omega\right)$ by a gauge transformation. What choice of $\mu$ leads to the modified $\mathbf{A}(\mathbf{x}, t)$ satisfying the Coulomb gauge condition $\boldsymbol{\nabla} \cdot \mathbf{A}=0$ ?

  comment

• Paper 2, Section II, B

  Electromagnetism | Part IB, 2012

  A straight wire has $n$ mobile, charged particles per unit length, each of charge $q$. Assuming the charges all move with velocity $v$ along the wire, show that the current is $I=n q v$.

  Using the Lorentz force law, show that if such a current-carrying wire is placed in a uniform magnetic field of strength $B$ perpendicular to the wire, then the force on the wire, per unit length, is $B I$.

  Consider two infinite parallel wires, with separation $L$, carrying (in the same sense of direction) positive currents $I_{1}$ and $I_{2}$, respectively. Find the force per unit length on each wire, determining both its magnitude and direction.

  comment

• Paper 3, Section II, B

  Electromagnetism | Part IB, 2012

  Using the Maxwell equations

  $$\begin{gathered} \nabla \cdot \mathbf{E}=\frac{\rho}{\epsilon_{0}}, \quad \nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t} \\ \nabla \cdot \mathbf{B}=0, \quad \boldsymbol{\nabla} \times \mathbf{B}-\epsilon_{0} \mu_{0} \frac{\partial \mathbf{E}}{\partial t}=\mu_{0} \mathbf{j} \end{gathered}$$

  show that in vacuum, E satisfies the wave equation

  $$\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}-\nabla^{2} \mathbf{E}=0$$

  where $c^{2}=\left(\epsilon_{0} \mu_{0}\right)^{-1}$, as well as $\nabla \cdot \mathbf{E}=0$. Also show that at a planar boundary between two media, $\mathbf{E}_{t}$ (the tangential component of $\mathbf{E}$ ) is continuous. Deduce that if one medium is of negligible resistance, $\mathbf{E}_{t}=0$.

  Consider an empty cubic box with walls of negligible resistance on the planes $x=0$, $x=a, y=0, y=a, z=0, z=a$, where $a>0$. Show that an electric field in the interior of the form

  $$\begin{aligned} &E_{x}=f(x) \sin \left(\frac{m \pi y}{a}\right) \sin \left(\frac{n \pi z}{a}\right) e^{-i \omega t} \\ &E_{y}=g(y) \sin \left(\frac{l \pi x}{a}\right) \sin \left(\frac{n \pi z}{a}\right) e^{-i \omega t} \\ &E_{z}=h(z) \sin \left(\frac{l \pi x}{a}\right) \sin \left(\frac{m \pi y}{a}\right) e^{-i \omega t} \end{aligned}$$

  with $l, m$ and $n$ positive integers, satisfies the boundary conditions on all six walls. Now suppose that

  $$f(x)=f_{0} \cos \left(\frac{l \pi x}{a}\right), \quad g(y)=g_{0} \cos \left(\frac{m \pi y}{a}\right), \quad h(z)=h_{0} \cos \left(\frac{n \pi z}{a}\right)$$

  where $f_{0}, g_{0}$ and $h_{0}$ are constants. Show that the wave equation $(*)$ is satisfied, and determine the frequency $\omega$. Find the further constraint on $f_{0}, g_{0}$ and $h_{0}$ ?

  comment

• Paper 4, Section I, B

  Electromagnetism | Part IB, 2012

  Define the notions of magnetic flux, electromotive force and resistance, in the context of a single closed loop of wire. Use the Maxwell equation

  $$\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$$

  to derive Faraday's law of induction for the loop, assuming the loop is at rest.

  Suppose now that the magnetic field is $\mathbf{B}=(0,0, B \tanh t)$ where $B$ is a constant, and that the loop of wire, with resistance $R$, is a circle of radius a lying in the $(x, y)$ plane. Calculate the current in the wire as a function of time.

  Explain briefly why, even in a time-independent magnetic field, an electromotive force may be produced in a loop of wire that moves through the field, and state the law of induction in this situation.

  comment

Fluid Dynamics

• Paper 1, Section I, A

  Fluid Dynamics | Part IB, 2012

  Viscous fluid, with viscosity $\mu$ and density $\rho$ flows along a straight circular pipe of radius $R$. The average velocity of the flow is $U$. Define a Reynolds number for the flow.

  The flow is driven by a constant pressure gradient $-G>0$ along the pipe and the velocity is parallel to the axis of the pipe with magnitude $u(r)$ that satisfies

  $$\frac{\mu}{r} \frac{\mathrm{d}}{\mathrm{d} r}\left(r \frac{\mathrm{d} u}{\mathrm{~d} r}\right)=-G,$$

  where $r$ is the radial distance from the axis.

  State the boundary conditions on $u$ and find the velocity as a function of $r$ assuming that it is finite on the axis $r=0$. Hence, show that the shear stress $\tau$ at the pipe wall is independent of the viscosity. Why is this the case?

  comment

• Paper 1, Section II, A

  Fluid Dynamics | Part IB, 2012

  Consider inviscid, incompressible fluid flow confined to the $(x, y)$ plane. The fluid has density $\rho$, and gravity can be neglected. Using the conservation of volume flux, determine the velocity potential $\phi(r)$ of a point source of strength $m$, in terms of the distance $r$ from the source.

  Two point sources each of strength $m$ are located at $\boldsymbol{x}_{+}=(0, a)$ and $\boldsymbol{x}_{-}=(0,-a)$. Find the velocity potential of the flow.

  Show that the flow in the region $y \geqslant 0$ is equivalent to the flow due to a source at $\boldsymbol{x}_{+}$and a fixed boundary at $y=0 .$

  Find the pressure on the boundary $y=0$ and hence determine the force on the boundary.

  [Hint: you may find the substitution $x=a \tan \theta$ useful for the calculation of the pressure.]

  comment

• Paper 2, Section I, A

  Fluid Dynamics | Part IB, 2012

  Starting from Euler's equation for the motion of an inviscid fluid, derive the vorticity equation in the form

  $$\frac{D \boldsymbol{\omega}}{D t}=\boldsymbol{\omega} \cdot \nabla \boldsymbol{u}$$

  Deduce that an initially irrotational flow remains irrotational.

  Consider a plane flow that at time $t=0$ is described by the streamfunction

  $$\psi=x^{2}+y^{2} .$$

  Calculate the vorticity everywhere at times $t>0$.

  comment

• Paper 3, Section II, A

  Fluid Dynamics | Part IB, 2012

  A rigid circular cylinder of radius $a$ executes small amplitude oscillations with velocity $U(t)$ in a direction perpendicular to its axis, while immersed in an inviscid fluid of density $\rho$ contained within a larger concentric fixed cylinder of radius $b$. Gravity is negligible. Neglecting terms quadratic in the amplitude, determine the boundary condition on the velocity on the inner cylinder, and calculate the velocity potential of the induced flow.

  With the same approximations show that the difference in pressures on the surfaces of the two cylinders has magnitude

  $$\rho \frac{\mathrm{d} U}{\mathrm{~d} t} \frac{a(b-a)}{b+a} \cos \theta$$

  where $\theta$ is the azimuthal angle measured from the direction of $U$.

  comment

• Paper 4, Section II, A

  Fluid Dynamics | Part IB, 2012

  The equations governing the flow of a shallow layer of inviscid liquid of uniform depth $H$ rotating with angular velocity $\frac{1}{2} f$ about the vertical $z$-axis are

  $$\begin{aligned} \frac{\partial u}{\partial t}-f v &=-g \frac{\partial \eta}{\partial x} \\ \frac{\partial v}{\partial t}+f u &=-g \frac{\partial \eta}{\partial y} \\ \frac{\partial \eta}{t}+H\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) &=0 \end{aligned}$$

  where $u, v$ are the $x$ - and $y$-components of velocity, respectively, and $\eta$ is the elevation of the free surface. Show that these equations imply that

  $$\frac{\partial q}{\partial t}=0, \quad \text { where } \quad q=\omega-\frac{f \eta}{H} \text { and } \omega=\frac{\partial v}{\partial x}-\frac{\partial u}{\partial y}$$

  Consider an initial state where there is flow in the $y$-direction given by

  $$\begin{aligned} u &=\eta=0, \quad-\infty<x<\infty \\ v &= \begin{cases}\frac{g}{2 f} e^{2 x}, & x<0 \\ -\frac{g}{2 f} e^{-2 x}, & x>0\end{cases} \end{aligned}$$

  Find the initial potential vorticity.

  Show that when this initial state adjusts, there is a final steady state independent of $y$ in which $\eta$ satisfies

  $$\frac{\partial^{2} \eta}{\partial x^{2}}-\frac{\eta}{a^{2}}= \begin{cases}e^{2 x}, & x<0 \\ e^{-2 x}, & x>0\end{cases}$$

  where $a^{2}=g H / f^{2}$.

  In the case $a=1$, find the final free surface elevation that is finite at large $|x|$ and which is continuous and has continuous slope at $x=0$, and show that it is negative for all $x$.

  comment

Geometry

• Paper 1, Section I, G

  Geometry | Part IB, 2012

  Describe a collection of charts which cover a circular cylinder of radius $R$. Compute the first fundamental form, and deduce that the cylinder is locally isometric to the plane.

  comment

• Paper 2, Section II, G

  Geometry | Part IB, 2012

  Let $S$ be a closed surface, equipped with a triangulation. Define the Euler characteristic $\chi(S)$ of $S$. How does $\chi(S)$ depend on the triangulation?

  Let $V, E$ and $F$ denote the number of vertices, edges and faces of the triangulation. Show that $2 E=3 F$.

  Suppose now the triangulation is tidy, meaning that it has the property that no two vertices are joined by more than one edge. Deduce that $V$ satisfies

  $$V \geqslant \frac{7+\sqrt{49-24 \chi(S)}}{2} .$$

  Hence compute the minimal number of vertices of a tidy triangulation of the real projective plane. [Hint: it may be helpful to consider the icosahedron as a triangulation of the sphere $\left.S^{2} .\right]$

  comment

• Paper 3, Section I, $5 G$

  Geometry | Part IB, 2012

  State a formula for the area of a hyperbolic triangle.

  Hence, or otherwise, prove that if $l_{1}$ and $l_{2}$ are disjoint geodesics in the hyperbolic plane, there is at most one geodesic which is perpendicular to both $l_{1}$ and $l_{2}$.

  comment

• Paper 3, Section II, G

  Geometry | Part IB, 2012

  Define the first and second fundamental forms of a smooth surface $\Sigma \subset \mathbb{R}^{3}$, and explain their geometrical significance.

  Write down the geodesic equations for a smooth curve $\gamma:[0,1] \rightarrow \Sigma$. Prove that $\gamma$ is a geodesic if and only if the derivative of the tangent vector to $\gamma$ is always orthogonal to $\Sigma$.

  A plane $\Pi \subset \mathbb{R}^{3}$ cuts $\Sigma$ in a smooth curve $C \subset \Sigma$, in such a way that reflection in the plane $\Pi$ is an isometry of $\Sigma$ (in particular, preserves $\Sigma$ ). Prove that $C$ is a geodesic.

  comment

• Paper 4, Section II, G

  Geometry | Part IB, 2012

  Let $\Sigma \subset \mathbb{R}^{3}$ be a smooth closed surface. Define the principal curvatures $\kappa_{\max }$ and $\kappa_{\min }$ at a point $p \in \Sigma$. Prove that the Gauss curvature at $p$ is the product of the two principal curvatures.

  A point $p \in \Sigma$ is called a parabolic point if at least one of the two principal curvatures vanishes. Suppose $\Pi \subset \mathbb{R}^{3}$ is a plane and $\Sigma$ is tangent to $\Pi$ along a smooth closed curve $C=\Pi \cap \Sigma \subset \Sigma$. Show that $C$ is composed of parabolic points.

  Can both principal curvatures vanish at a point of $C$ ? Briefly justify your answer.

  comment

Groups, Rings and Modules

• Paper 1, Section II, G

  Groups, Rings and Modules | Part IB, 2012

  Let $G$ be a finite group. What is a Sylow $p$-subgroup of $G$ ?

  Assuming that a Sylow $p$-subgroup $H$ exists, and that the number of conjugates of $H$ is congruent to $1 \bmod p$, prove that all Sylow $p$-subgroups are conjugate. If $n_{p}$ denotes the number of Sylow $p$-subgroups, deduce that

  $$n_{p} \equiv 1 \quad \bmod p \quad \text { and } \quad n_{p}|| G \mid$$

  If furthermore $G$ is simple prove that either $G=H$ or

  $$|G| \mid n_{p} \text { ! }$$

  Deduce that a group of order $1,000,000$ cannot be simple.

  comment

• Paper 2, Section I, $2 G$

  Groups, Rings and Modules | Part IB, 2012

  What does it mean to say that the finite group $G$ acts on the set $\Omega$ ?

  By considering an action of the symmetry group of a regular tetrahedron on a set of pairs of edges, show there is a surjective homomorphism $S_{4} \rightarrow S_{3}$.

  [You may assume that the symmetric group $S_{n}$ is generated by transpositions.]

  comment

• Paper 2, Section II, G

  Groups, Rings and Modules | Part IB, 2012

  State Gauss's Lemma. State Eisenstein's irreducibility criterion.

  (i) By considering a suitable substitution, show that the polynomial $1+X^{3}+X^{6}$ is irreducible over $\mathbb{Q}$.

  (ii) By working in $\mathbb{Z}_{2}[X]$, show that the polynomial $1-X^{2}+X^{5}$ is irreducible over $\mathbb{Q}$.

  comment

• Paper 3, Section I, $1 \mathbf{G}$

  Groups, Rings and Modules | Part IB, 2012

  What is a Euclidean domain?

  Giving careful statements of any general results you use, show that in the ring $\mathbb{Z}[\sqrt{-3}], 2$ is irreducible but not prime.

  comment

• Paper 3, Section II, G

  Groups, Rings and Modules | Part IB, 2012

  For each of the following assertions, provide either a proof or a counterexample as appropriate:

  (i) The ring $\mathbb{Z}_{2}[X] /\left\langle X^{2}+X+1\right\rangle$ is a field.

  (ii) The ring $\mathbb{Z}_{3}[X] /\left\langle X^{2}+X+1\right\rangle$ is a field.

  (iii) If $F$ is a finite field, the ring $F[X]$ contains irreducible polynomials of arbitrarily large degree.

  (iv) If $R$ is the ring $C[0,1]$ of continuous real-valued functions on the interval $[0,1]$, and the non-zero elements $f, g \in R$ satisfy $f \mid g$ and $g \mid f$, then there is some unit $u \in R$ with $f=u \cdot g$.

  comment

• Paper 4, Section I, $2 G$

  Groups, Rings and Modules | Part IB, 2012

  An idempotent element of a ring $R$ is an element $e$ satisfying $e^{2}=e$. A nilpotent element is an element e satisfying $e^{N}=0$ for some $N \geqslant 0$.

  Let $r \in R$ be non-zero. In the ring $R[X]$, can the polynomial $1+r X$ be (i) an idempotent, (ii) a nilpotent? Can $1+r X$ satisfy the equation $(1+r X)^{3}=(1+r X)$ ? Justify your answers.

  comment

• Paper 4, Section II, G

  Groups, Rings and Modules | Part IB, 2012

  Let $R$ be a commutative ring with unit 1. Prove that an $R$-module is finitely generated if and only if it is a quotient of a free module $R^{n}$, for some $n>0$.

  Let $M$ be a finitely generated $R$-module. Suppose now $I$ is an ideal of $R$, and $\phi$ is an $R$-homomorphism from $M$ to $M$ with the property that

  $$\phi(M) \subset I \cdot M=\left\{m \in M \mid m=r m^{\prime} \quad \text { with } \quad r \in I, m^{\prime} \in M\right\}$$

  Prove that $\phi$ satisfies an equation

  $$\phi^{n}+a_{n-1} \phi^{n-1}+\cdots+a_{1} \phi+a_{0}=0$$

  where each $a_{j} \in I$. [You may assume that if $T$ is a matrix over $R$, then $\operatorname{adj}(T) T=$ $\operatorname{det} T$ (id), with id the identity matrix.]

  Deduce that if $M$ satisfies $I \cdot M=M$, then there is some $a \in R$ satisfying

  $$a-1 \in I \quad \text { and } \quad a M=0 .$$

  Give an example of a finitely generated $\mathbb{Z}$-module $M$ and a proper ideal $I$ of $\mathbb{Z}$ satisfying the hypothesis $I \cdot M=M$, and for your example, give an explicit such element $a$.

  comment

Linear Algebra

• Paper 1, Section I, F

  Linear Algebra | Part IB, 2012

  Define the notions of basis and dimension of a vector space. Prove that two finitedimensional real vector spaces with the same dimension are isomorphic.

  In each case below, determine whether the set $S$ is a basis of the real vector space $V:$

  (i) $V=\mathbb{C}$ is the complex numbers; $S=\{1, i\}$.

  (ii) $V=\mathbb{R}[x]$ is the vector space of all polynomials in $x$ with real coefficients; $S=\{1,(x-1),(x-1)(x-2),(x-1)(x-2)(x-3), \ldots\} .$

  (iii) $V=\{f:[0,1] \rightarrow \mathbb{R}\} ; S=\left\{\chi_{p} \mid p \in[0,1]\right\}$, where

  $$\chi_{p}(x)= \begin{cases}1 & x=p \\ 0 & x \neq p\end{cases}$$

  comment

• Paper 1, Section II, F

  Linear Algebra | Part IB, 2012

  Define what it means for two $n \times n$ matrices to be similar to each other. Show that if two $n \times n$ matrices are similar, then the linear transformations they define have isomorphic kernels and images.

  If $A$ and $B$ are $n \times n$ real matrices, we define $[A, B]=A B-B A$. Let

  $$\begin{aligned} K_{A} &=\left\{X \in M_{n \times n}(\mathbb{R}) \mid[A, X]=0\right\} \\ L_{A} &=\left\{[A, X] \mid X \in M_{n \times n}(\mathbb{R})\right\} \end{aligned}$$

  Show that $K_{A}$ and $L_{A}$ are linear subspaces of $M_{n \times n}(\mathbb{R})$. If $A$ and $B$ are similar, show that $K_{A} \cong K_{B}$ and $L_{A} \cong L_{B}$.

  Suppose that $A$ is diagonalizable and has characteristic polynomial

  $$\left(x-\lambda_{1}\right)^{m_{1}}\left(x-\lambda_{2}\right)^{m_{2}}$$

  where $\lambda_{1} \neq \lambda_{2}$. What are $\operatorname{dim} K_{A}$ and $\operatorname{dim} L_{A} ?$

  comment

• Paper 2, Section I, $1 F$

  Linear Algebra | Part IB, 2012

  Define the determinant $\operatorname{det} A$ of an $n \times n$ real matrix $A$. Suppose that $X$ is a matrix with block form

  $$X=\left(\begin{array}{cc} A & B \\ 0 & C \end{array}\right) \text {, }$$

  where $A, B$ and $C$ are matrices of dimensions $n \times n, n \times m$ and $m \times m$ respectively. Show that $\operatorname{det} X=(\operatorname{det} A)(\operatorname{det} C)$.

  comment

• Paper 2, Section II, F

  Linear Algebra | Part IB, 2012

  (i) Define the transpose of a matrix. If $V$ and $W$ are finite-dimensional real vector spaces, define the dual of a linear map $T: V \rightarrow W$. How are these two notions related?

  Now suppose $V$ and $W$ are finite-dimensional inner product spaces. Use the inner product on $V$ to define a linear map $V \rightarrow V^{*}$ and show that it is an isomorphism. Define the adjoint of a linear map $T: V \rightarrow W$. How are the adjoint of $T$ and its dual related? If $A$ is a matrix representing $T$, under what conditions is the adjoint of $T$ represented by the transpose of $A$ ?

  (ii) Let $V=C[0,1]$ be the vector space of continuous real-valued functions on $[0,1]$, equipped with the inner product

  $$\langle f, g\rangle=\int_{0}^{1} f(t) g(t) d t$$

  Let $T: V \rightarrow V$ be the linear map

  $$T f(t)=\int_{0}^{t} f(s) d s$$

  What is the adjoint of $T ?$

  comment

• Paper 3, Section II, F

  Linear Algebra | Part IB, 2012

  What is meant by the Jordan normal form of an $n \times n$ complex matrix?

  Find the Jordan normal forms of the following matrices:

  $$\left(\begin{array}{llll} 1 & 1 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ 0 & 0 & 1 & 1 \\ 0 & 0 & 0 & 1 \end{array}\right), \quad\left(\begin{array}{cccc} -1 & -1 & 1 & 0 \\ 0 & -1 & 0 & 1 \\ 0 & 0 & -1 & 1 \\ 0 & 0 & 0 & -1 \end{array}\right), \quad\left(\begin{array}{cccc} 3 & 0 & 0 & 0 \\ 3 & 3 & 0 & 0 \\ 9 & 6 & 3 & 0 \\ 15 & 12 & 9 & 3 \end{array}\right)$$

  Suppose $A$ is an invertible $n \times n$ complex matrix. Explain how to derive the characteristic and minimal polynomials of $A^{n}$ from the characteristic and minimal polynomials of $A$. Justify your answer. [Hint: write each polynomial as a product of linear factors.]

  comment

• Paper 4, Section I, F

  Linear Algebra | Part IB, 2012

  Let $V$ be a complex vector space with basis $\left\{e_{1}, \ldots, e_{n}\right\}$. Define $T: V \rightarrow V$ by $T\left(e_{i}\right)=e_{i}-e_{i+1}$ for $i<n$ and $T\left(e_{n}\right)=e_{n}-e_{1}$. Show that $T$ is diagonalizable and find its eigenvalues. [You may use any theorems you wish, as long as you state them clearly.]

  comment

• Paper 4, Section II, F

  Linear Algebra | Part IB, 2012

  Let $V$ be a finite-dimensional real vector space of dimension $n$. A bilinear form $B: V \times V \rightarrow \mathbb{R}$ is nondegenerate if for all $\mathbf{v} \neq 0$ in $V$, there is some $\mathbf{w} \in V$ with $B(\mathbf{v}, \mathbf{w}) \neq 0$. For $\mathbf{v} \in V$, define $\langle\mathbf{v}\rangle^{\perp}=\{\mathbf{w} \in V \mid B(\mathbf{v}, \mathbf{w})=0\}$. Assuming $B$ is nondegenerate, show that $V=\langle\mathbf{v}\rangle \oplus\langle\mathbf{v}\rangle^{\perp}$ whenever $B(\mathbf{v}, \mathbf{v}) \neq 0$.

  Suppose that $B$ is a nondegenerate, symmetric bilinear form on $V$. Prove that there is a basis $\left\{\mathbf{v}_{1}, \ldots, \mathbf{v}_{n}\right\}$ of $V$ with $B\left(\mathbf{v}_{i}, \mathbf{v}_{j}\right)=0$ for $i \neq j$. [If you use the fact that symmetric matrices are diagonalizable, you must prove it.]

  Define the signature of a quadratic form. Explain how to determine the signature of the quadratic form associated to $B$ from the basis you constructed above.

  A linear subspace $V^{\prime} \subset V$ is said to be isotropic if $B(\mathbf{v}, \mathbf{w})=0$ for all $\mathbf{v}, \mathbf{w} \in V^{\prime}$. Show that if $B$ is nondegenerate, the maximal dimension of an isotropic subspace of $V$ is $(n-|\sigma|) / 2$, where $\sigma$ is the signature of the quadratic form associated to $B$.

  comment

Markov Chains

• Paper 1, Section II, 20H

  Markov Chains | Part IB, 2012

  A Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ has as its state space the integers, with

  $$p_{i, i+1}=p, \quad p_{i, i-1}=q=1-p$$

  and $p_{i j}=0$ otherwise. Assume $p>q$.

  Let $T_{j}=\inf \left\{n \geqslant 1: X_{n}=j\right\}$ if this is finite, and $T_{j}=\infty$ otherwise. Let $V_{0}$ be the total number of hits on 0 , and let $V_{0}(n)$ be the total number of hits on 0 within times $0, \ldots, n-1$. Let

  $$\begin{aligned} h_{i} &=P\left(V_{0}>0 \mid X_{0}=i\right) \\ r_{i}(n) &=E\left[V_{0}(n) \mid X_{0}=i\right] \\ r_{i} &=E\left[V_{0} \mid X_{0}=i\right] \end{aligned}$$

  (i) Quoting an appropriate theorem, find, for every $i$, the value of $h_{i}$.

  (ii) Show that if $\left(x_{i}, i \in \mathbb{Z}\right)$ is any non-negative solution to the system of equations

  $$\begin{aligned} x_{0} &=1+q x_{1}+p x_{-1}, \\ x_{i} &=q x_{i-1}+p x_{i+1}, \quad \text { for all } i \neq 0 \end{aligned}$$

  then $x_{i} \geqslant r_{i}(n)$ for all $i$ and $n$.

  (iii) Show that $P\left(V_{0}\left(T_{1}\right) \geqslant k \mid X_{0}=1\right)=q^{k}$ and $E\left[V_{0}\left(T_{1}\right) \mid X_{0}=1\right]=q / p$.

  (iv) Explain why $r_{i+1}=(q / p) r_{i}$ for $i>0$.

  (v) Find $r_{i}$ for all $i$.

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2012

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be the symmetric random walk on vertices of a connected graph. At each step this walk jumps from the current vertex to a neighbouring vertex, choosing uniformly amongst them. Let $T_{i}=\inf \left\{n \geqslant 1: X_{n}=i\right\}$. For each $i \neq j$ let $q_{i j}=P\left(T_{j}<T_{i} \mid X_{0}=i\right)$ and $m_{i j}=E\left(T_{j} \mid X_{0}=i\right)$. Stating any theorems that you use:

  (i) Prove that the invariant distribution $\pi$ satisfies detailed balance.

  (ii) Use reversibility to explain why $\pi_{i} q_{i j}=\pi_{j} q_{j i}$ for all $i, j$.

  Consider a symmetric random walk on the graph shown below.

  

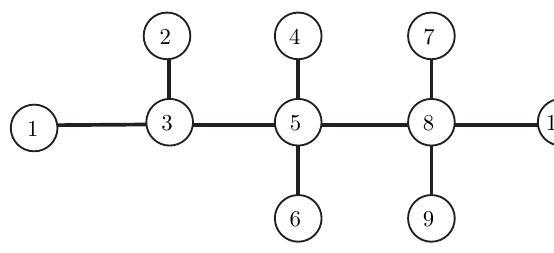
  (iii) Find $m_{33}$.

  (iv) The removal of any edge $(i, j)$ leaves two disjoint components, one which includes $i$ and one which includes $j$. Prove that $m_{i j}=1+2 e_{i j}(i)$, where $e_{i j}(i)$ is the number of edges in the component that contains $i$.

  (v) Show that $m_{i j}+m_{j i} \in\{18,36,54,72\}$ for all $i \neq j$.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2012

  A runner owns $k$ pairs of running shoes and runs twice a day. In the morning she leaves her house by the front door, and in the evening she leaves by the back door. On starting each run she looks for shoes by the door through which she exits, and runs barefoot if none are there. At the end of each run she is equally likely to return through the front or back doors. She removes her shoes (if any) and places them by the door. In the morning of day 1 all shoes are by the back door so she must run barefoot.

  Let $p_{00}^{(n)}$ be the probability that she runs barefoot on the morning of day $n+1$. What conditions are satisfied in this problem which ensure $\lim _{n \rightarrow \infty} p_{00}^{(n)}$ exists? Show that its value is $1 / 2 k$.

  Find the expected number of days that will pass until the first morning that she finds all $k$ pairs of shoes at her front door.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2012

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be an irreducible Markov chain with $p_{i j}^{(n)}=P\left(X_{n}=j \mid X_{0}=i\right)$. Define the meaning of the statements:

  (i) state $i$ is transient,

  (ii) state $i$ is aperiodic.

  Give a criterion for transience that can be expressed in terms of the probabilities $\left(p_{i i}^{(n)}, n=0,1, \ldots\right)$.

  Prove that if a state $i$ is transient then all states are transient.

  Prove that if a state $i$ is aperiodic then all states are aperiodic.

  Suppose that $p_{i i}^{(n)}=0$ unless $n$ is divisible by 3 . Given any other state $j$, prove that $p_{j j}^{(n)}=0$ unless $n$ is divisible by 3 .

  comment

Methods

• Paper 1, Section II, C

  Methods | Part IB, 2012

  Consider the regular Sturm-Liouville (S-L) system

  $$(\mathcal{L} y)(x)-\lambda \omega(x) y(x)=0, \quad a \leqslant x \leqslant b$$

  where

  $$(\mathcal{L} y)(x):=-\left[p(x) y^{\prime}(x)\right]^{\prime}+q(x) y(x)$$

  with $\omega(x)>0$ and $p(x)>0$ for all $x$ in $[a, b]$, and the boundary conditions on $y$ are

  $$\left\{\begin{array}{l} A_{1} y(a)+A_{2} y^{\prime}(a)=0 \\ B_{1} y(b)+B_{2} y^{\prime}(b)=0 \end{array}\right.$$

  Show that with these boundary conditions, $\mathcal{L}$ is self-adjoint. By considering $y \mathcal{L} y$, or otherwise, show that the eigenvalue $\lambda$ can be written as

  $$\lambda=\frac{\int_{a}^{b}\left(p y^{\prime 2}+q y^{2}\right) d x-\left[p y y^{\prime}\right]_{a}^{b}}{\int_{a}^{b} \omega y^{2} d x}$$

  Now suppose that $a=0$ and $b=\ell$, that $p(x)=1, q(x) \geqslant 0$ and $\omega(x)=1$ for all $x \in[0, \ell]$, and that $A_{1}=1, A_{2}=0, B_{1}=k \in \mathbb{R}^{+}$and $B_{2}=1$. Show that the eigenvalues of this regular S-L system are strictly positive. Assuming further that $q(x)=0$, solve the system explicitly, and with the aid of a graph, show that there exist infinitely many eigenvalues $\lambda_{1}<\lambda_{2}<\cdots<\lambda_{n}<\cdots$. Describe the behaviour of $\lambda_{n}$ as $n \rightarrow \infty$.

  comment

• Paper 2, Section I, C

  Methods | Part IB, 2012

  Using the method of characteristics, obtain a solution to the equation

  $$u_{x}+2 x u_{y}=y$$

  subject to the Cauchy data $u(0, y)=1+y^{2}$ for $-\frac{1}{2}<y<\frac{1}{2}$.

  Sketch the characteristics and specify the greatest region of the plane in which a unique solution exists.

  comment

• Paper 2, Section II, C

  Methods | Part IB, 2012

  Consider the linear differential operator $\mathcal{L}$ defined by

  $$\mathcal{L} y:=-\frac{d^{2} y}{d x^{2}}+y$$

  on the interval $0 \leqslant x<\infty$. Given the boundary conditions $y(0)=0$ and $\lim _{x \rightarrow \infty} y(x)=0$, find the Green's function $G(x, \xi)$ for $\mathcal{L}$ with these boundary conditions. Hence, or otherwise, obtain the solution of

  $$\mathcal{L} y= \begin{cases}1, & 0 \leqslant x \leqslant \mu \\ 0, & \mu<x<\infty\end{cases}$$

  subject to the above boundary conditions, where $\mu$ is a positive constant. Show that your piecewise solution is continuous at $x=\mu$ and has the value

  $$y(\mu)=\frac{1}{2}\left(1+e^{-2 \mu}-2 e^{-\mu}\right) .$$

  comment

• Paper 3, Section I, D

  Methods | Part IB, 2012

  For the step-function

  $$F(x)= \begin{cases}1, & |x| \leqslant 1 / 2 \\ 0, & \text { otherwise }\end{cases}$$

  its convolution with itself is the hat-function

  $$G(x)=[F * F](x)= \begin{cases}1-|x|, & |x| \leqslant 1 \\ 0, & \text { otherwise }\end{cases}$$

  Find the Fourier transforms of $F$ and $G$, and hence find the values of the integrals

  $$I_{1}=\int_{-\infty}^{\infty} \frac{\sin ^{2} y}{y^{2}} d y, \quad I_{2}=\int_{-\infty}^{\infty} \frac{\sin ^{4} y}{y^{4}} d y$$

  comment

• Paper 3, Section II, D

  Methods | Part IB, 2012

  Consider Legendre's equation

  $$\left(1-x^{2}\right) y^{\prime \prime}-2 x y^{\prime}+\lambda y=0 .$$

  Show that if $\lambda=n(n+1)$, with $n$ a non-negative integer, this equation has a solution $y=P_{n}(x)$, a polynomial of degree $n$. Find $P_{0}, P_{1}$ and $P_{2}$ explicitly, subject to the condition $P_{n}(1)=1$.

  The general solution of Laplace's equation $\nabla^{2} \psi=0$ in spherical polar coordinates, in the axisymmetric case, has the form

  $$\psi(r, \theta)=\sum_{n=0}^{\infty}\left(A_{n} r^{n}+B_{n} r^{-(n+1)}\right) P_{n}(\cos \theta)$$

  Hence, find the solution of Laplace's equation in the region $a \leqslant r \leqslant b$ satisfying the boundary conditions

  $$\begin{cases}\psi(r, \theta)=1, & r=a \\ \psi(r, \theta)=3 \cos ^{2} \theta, & r=b\end{cases}$$

  comment

• Paper 4, Section I, D

  Methods | Part IB, 2012

  Show that the general solution of the wave equation

  $$\frac{1}{c^{2}} \frac{\partial^{2} y}{\partial t^{2}}-\frac{\partial^{2} y}{\partial x^{2}}=0$$

  can be written in the form

  $$y(x, t)=f(x-c t)+g(x+c t)$$

  Hence derive the solution $y(x, t)$ subject to the initial conditions

  $$y(x, 0)=0, \quad \frac{\partial y}{\partial t}(x, 0)=\psi(x)$$

  comment

• Paper 4, Section II, D

  Methods | Part IB, 2012

  Let $D \subset \mathbb{R}^{2}$ be a two-dimensional domain with boundary $S=\partial D$, and let

  $$G_{2}=G_{2}\left(\mathbf{r}, \mathbf{r}_{0}\right)=\frac{1}{2 \pi} \log \left|\mathbf{r}-\mathbf{r}_{0}\right|$$

  where $\mathbf{r}_{0}$ is a point in the interior of $D$. From Green's second identity,

  $$\int_{S}\left(\phi \frac{\partial \psi}{\partial n}-\psi \frac{\partial \phi}{\partial n}\right) d \ell=\int_{D}\left(\phi \nabla^{2} \psi-\psi \nabla^{2} \phi\right) d a$$

  derive Green's third identity

  $$u\left(\mathbf{r}_{0}\right)=\int_{D} G_{2} \nabla^{2} u d a+\int_{S}\left(u \frac{\partial G_{2}}{\partial n}-G_{2} \frac{\partial u}{\partial n}\right) d \ell$$

  [Here $\frac{\partial}{\partial n}$ denotes the normal derivative on $S$.]

  Consider the Dirichlet problem on the unit $\operatorname{disc} D_{1}=\left\{\mathbf{r} \in \mathbb{R}^{2}:|\mathbf{r}| \leqslant 1\right\}$ :

  $$\begin{aligned} \nabla^{2} u=0, & \mathbf{r} \in D_{1} \\ u(\mathbf{r})=f(\mathbf{r}), & \mathbf{r} \in S_{1}=\partial D_{1} \end{aligned}$$

  Show that, with an appropriate function $G\left(\mathbf{r}, \mathbf{r}_{0}\right)$, the solution can be obtained by the formula

  $$u\left(\mathbf{r}_{0}\right)=\int_{S_{1}} f(\mathbf{r}) \frac{\partial}{\partial n} G\left(\mathbf{r}, \mathbf{r}_{0}\right) d \ell$$

  State the boundary conditions on $G$ and explain how $G$ is related to $G_{2}$.

  For $\mathbf{r}, \mathbf{r}_{0} \in \mathbb{R}^{2}$, prove the identity

  $$\left|\frac{\mathbf{r}}{|\mathbf{r}|}-\mathbf{r}_{0}\right| \mathbf{r}||=\left|\frac{\mathbf{r}_{0}}{\left|\mathbf{r}_{0}\right|}-\mathbf{r}\right| \mathbf{r}_{0}|| \text {, }$$

  and deduce that if the point $\mathbf{r}$ lies on the unit circle, then

  $$\left|\mathbf{r}-\mathbf{r}_{0}\right|=\left|\mathbf{r}_{0}\right|\left|\mathbf{r}-\mathbf{r}_{0}^{*}\right|, \text { where } \mathbf{r}_{0}^{*}=\frac{\mathbf{r}_{0}}{\left|\mathbf{r}_{0}\right|^{2}}$$

  Hence, using the method of images, or otherwise, find an expression for the function $G\left(\mathbf{r}, \mathbf{r}_{0}\right)$. [An expression for $\frac{\partial}{\partial n} G$ is not required.]

  comment

Metric and Topological Spaces

• Paper 1, Section II, F

  Metric and Topological Spaces | Part IB, 2012

  A topological space $X$ is said to be normal if each point of $X$ is a closed subset of $X$ and for each pair of closed sets $C_{1}, C_{2} \subset X$ with $C_{1} \cap C_{2}=\emptyset$ there are open sets $U_{1}, U_{2} \subset X$ so that $C_{i} \subset U_{i}$ and $U_{1} \cap U_{2}=\emptyset$. In this case we say that the $U_{i}$ separate the $C_{i}$.

  Show that a compact Hausdorff space is normal. [Hint: first consider the case where $C_{2}$ is a point.]

  For $C \subset X$ we define an equivalence relation $\sim_{C}$ on $X$ by $x \sim_{C} y$ for all $x, y \in C$, $x \sim_{C} x$ for $x \notin C$. If $C, C_{1}$ and $C_{2}$ are pairwise disjoint closed subsets of a normal space $X$, show that $C_{1}$ and $C_{2}$ may be separated by open subsets $U_{1}$ and $U_{2}$ such that $U_{i} \cap C=\emptyset$. Deduce that the quotient space $X / \sim_{C}$ is also normal.

  comment

• Paper 2, Section I,

  Metric and Topological Spaces | Part IB, 2012

  For each case below, determine whether the given metrics $d_{1}$ and $d_{2}$ induce the same topology on $X$. Justify your answers.

  $$\begin{gathered} \text { (i) } X=\mathbb{R}^{2}, d_{1}\left(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)\right)=\sup \left\{\left|x_{1}-x_{2}\right|,\left|y_{1}-y_{2}\right|\right\} \\ d_{2}\left(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)\right)=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right| . \\ \text { (ii) } X=C[0,1], d_{1}(f, g)=\sup _{t \in[0,1]}|f(t)-g(t)| \\ d_{2}(f, g)=\int_{0}^{1}|f(t)-g(t)| d t . \end{gathered}$$

  comment

• Paper 3, Section I, $3 F$

  Metric and Topological Spaces | Part IB, 2012

  Define the notion of a connected component of a space $X$.

  If $A_{\alpha} \subset X$ are connected subsets of $X$ such that $\bigcap_{\alpha} A_{\alpha} \neq \emptyset$, show that $\bigcup_{\alpha} A_{\alpha}$ is connected.

  Prove that any point $x \in X$ is contained in a unique connected component.

  Let $X \subset \mathbb{R}$ consist of the points $0,1, \frac{1}{2}, \frac{1}{3}, \ldots, \frac{1}{n}, \ldots$. What are the connected components of $X$ ?

  comment

• Paper 4, Section II, F

  Metric and Topological Spaces | Part IB, 2012

  Suppose $A_{1}$ and $A_{2}$ are topological spaces. Define the product topology on $A_{1} \times A_{2}$. Let $\pi_{i}: A_{1} \times A_{2} \rightarrow A_{i}$ be the projection. Show that a map $F: X \rightarrow A_{1} \times A_{2}$ is continuous if and only if $\pi_{1} \circ F$ and $\pi_{2} \circ F$ are continuous.

  Prove that if $A_{1}$ and $A_{2}$ are connected, then $A_{1} \times A_{2}$ is connected.

  Let $X$ be the topological space whose underlying set is $\mathbb{R}$, and whose open sets are of the form $(a, \infty)$ for $a \in \mathbb{R}$, along with the empty set and the whole space. Describe the open sets in $X \times X$. Are the maps $f, g: X \times X \rightarrow X$ defined by $f(x, y)=x+y$ and $g(x, y)=x y$ continuous? Justify your answers.

  comment

Numerical Analysis

• Paper 1, Section I, D

  Numerical Analysis | Part IB, 2012

  $$A=\left[\begin{array}{cccc} 1 & a & a^{2} & a^{3} \\ a^{3} & 1 & a & a^{2} \\ a^{2} & a^{3} & 1 & a \\ a & a^{2} & a^{3} & 1 \end{array}\right], \quad b=\left[\begin{array}{l} \gamma \\ 0 \\ 0 \\ 0 \end{array}\right], \quad \gamma=1-a^{4} \neq 0$$

  Find the LU factorization of the matrix $A$ and use it to solve the system $A x=b$ via forward and backward substitution. [Other methods of solution are not acceptable.]

  comment

• Paper 1, Section II, D

  Numerical Analysis | Part IB, 2012

  For a numerical method for solving $y^{\prime}=f(t, y)$, define the linear stability domain, and state when such a method is A-stable.

  Determine all values of the real parameter $a$ for which the Runge-Kutta method

  $$\begin{aligned} k_{1} &=f\left(t_{n}+\left(\frac{1}{2}-a\right) h, y_{n}+\left(\frac{1}{4} h k_{1}+\left(\frac{1}{4}-a\right) h k_{2}\right)\right) \\ k_{2} &=f\left(t_{n}+\left(\frac{1}{2}+a\right) h, y_{n}+\left(\left(\frac{1}{4}+a\right) h k_{1}+\frac{1}{4} h k_{2}\right)\right) \\ y_{n+1} &=y_{n}+\frac{1}{2} h\left(k_{1}+k_{2}\right) \end{aligned}$$

  is A-stable.

  comment

• Paper 2, Section II, D

  Numerical Analysis | Part IB, 2012

  Let $\left\{P_{n}\right\}_{n=0}^{\infty}$ be the sequence of monic polynomials of degree $n$ orthogonal on the interval $[-1,1]$ with respect to the weight function $w$.

  Prove that each $P_{n}$ has $n$ distinct zeros in the interval $(-1,1)$.

  Let $P_{0}(x)=1, P_{1}(x)=x-a_{1}$, and let $P_{n}$ satisfy the following three-term recurrence relation:

  $$P_{n}(x)=\left(x-a_{n}\right) P_{n-1}(x)-b_{n}^{2} P_{n-2}(x), \quad n \geqslant 2$$

  Set

  $$A_{n}=\left[\begin{array}{ccccc} a_{1} & b_{2} & 0 & \cdots & 0 \\ b_{2} & a_{2} & b_{3} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0 \\ \vdots & \ddots & b_{n-1} & a_{n-1} & b_{n} \\ 0 & \cdots & 0 & b_{n} & a_{n} \end{array}\right]$$

  Prove that $P_{n}(x)=\operatorname{det}\left(x I-A_{n}\right), n \geqslant 1$, and deduce that all the eigenvalues of $A_{n}$ are distinct and reside in $(-1,1)$.

  comment

• Paper 3, Section II, D

  Numerical Analysis | Part IB, 2012

  Define the QR factorization of an $m \times n$ matrix $A$ and explain how it can be used to solve the least squares problem of finding the vector $x^{*} \in \mathbb{R}^{n}$ which minimises $\left\|A x^{*}-b\right\|$, where $b \in \mathbb{R}^{m}, m>n$, and the norm is the Euclidean one.

  Define a Householder transformation $H$ and show that it is an orthogonal matrix.

  Using a Householder transformation, solve the least squares problem for

  $$A=\left[\begin{array}{rrr} 1 & -1 & 5 \\ 0 & 1 & 5 \\ 0 & 0 & 3 \\ 0 & 0 & 4 \end{array}\right], \quad b=\left[\begin{array}{r} 1 \\ 2 \\ -1 \\ 2 \end{array}\right]$$

  giving both $x^{*}$ and $\left\|A x^{*}-b\right\|$.

  comment

• Paper 4, Section I, D

  Numerical Analysis | Part IB, 2012

  State the Dahlquist equivalence theorem regarding convergence of a multistep method.

  The multistep method, with a real parameter $a$,

  $$y_{n+3}+(2 a-3)\left(y_{n+2}-y_{n+1}\right)-y_{n}=h a\left(f_{n+2}-f_{n+1}\right)$$

  is of order 2 for any $a$, and also of order 3 for $a=6$. Determine all values of $a$ for which the method is convergent, and find the order of convergence.

  comment

Optimization

• Paper 1, Section I, 8H

  Optimization | Part IB, 2012

  State the Lagrangian sufficiency theorem.

  Use Lagrange multipliers to find the optimal values of $x_{1}$ and $x_{2}$ in the problem: maximize $x_{1}^{2}+x_{2} \quad$ subject to $\quad x_{1}^{2}+\frac{1}{2} x_{2}^{2} \leqslant b_{1}, \quad x_{1} \geqslant b_{2}$ and $x_{1}, x_{2} \geqslant 0$ for all values of $b_{1}, b_{2}$ such that $b_{1}-b_{2}^{2} \geqslant 0$.

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2012

  Consider the two-player zero-sum game with payoff matrix

  $$A=\left(\begin{array}{rrr} 2 & 0 & -2 \\ 3 & 4 & 5 \\ 6 & 0 & 6 \end{array}\right)$$

  Express the problem of finding the column player's optimal strategy as a linear programming problem in which $x_{1}+x_{2}+x_{3}$ is to be maximized subject to some constraints.

  Solve this problem using the simplex algorithm and find the optimal strategy for the column player.

  Find also, from the final tableau you obtain, both the value of the game and the row player's optimal strategy.

  comment

• Paper 3, Section II, 21H

  Optimization | Part IB, 2012

  For given positive real numbers $\left(c_{i j}: i, j \in\{1,2,3\}\right)$, consider the linear program

  $$P: \operatorname{minimize} \sum_{i=1}^{3} \sum_{j=1}^{3} c_{i j} x_{i j},$$

  subject to $\sum_{i=1}^{3} x_{i j} \leqslant 1$ for all $j, \quad \sum_{j=1}^{3} x_{i j} \geqslant 1$ for all $i$,

  and $x_{i j} \geqslant 0$ for all $i, j$.

  (i) Consider the feasible solution $x$ in which $x_{11}=x_{12}=x_{22}=x_{23}=x_{31}=x_{33}=1 / 2$ and $x_{i j}=0$ otherwise. Write down two basic feasible solutions of $P$, one of which you can be sure is at least as good as $x$. Are either of these basic feasible solutions of $P$ degenerate?

  (ii) Starting from a general definition of a Lagrangian dual problem show that the dual of $P$ can be written as

  $$D: \operatorname{maximize}_{\lambda_{i} \geqslant 0, \mu_{i} \geqslant 0} \sum_{i=1}^{3}\left(\lambda_{i}-\mu_{i}\right) \quad \text { subject to } \lambda_{i}-\mu_{j} \leqslant c_{i j} \text { for all } i, j .$$

  What happens to the optimal value of this problem if the constraints $\lambda_{i} \geqslant 0$ and $\mu_{i} \geqslant 0$ are removed?

  Prove that $x_{11}=x_{22}=x_{33}=1$ is an optimal solution to $P$ if and only if there exist $\lambda_{1}, \lambda_{2}, \lambda_{3}$ such that

  $$\lambda_{i}-\lambda_{j} \leqslant c_{i j}-c_{j j}, \quad \text { for all } i, j$$

  [You may use any facts that you know from the general theory of linear programming provided that you state them.]

  comment

• Paper 4, Section II, 20H

  Optimization | Part IB, 2012

  Describe the Ford-Fulkerson algorithm.

  State conditions under which the algorithm is guaranteed to terminate in a finite number of steps. Explain why it does so, and show that it finds a maximum flow. [You may assume that the value of a flow never exceeds the value of any cut.]

  In a football league of $n$ teams the season is partly finished. Team $i$ has already won $w_{i}$ matches. Teams $i$ and $j$ are to meet in $m_{i j}$ further matches. Thus the total number of remaining matches is $M=\sum_{i<j} m_{i j}$. Assume there will be no drawn matches. We wish to determine whether it is possible for the outcomes of the remaining matches to occur in such a way that at the end of the season the numbers of wins by the teams are $\left(x_{1}, \ldots, x_{n}\right)$.

  Invent a network flow problem in which the maximum flow from source to sink equals $M$ if and only if $\left(x_{1}, \ldots, x_{n}\right)$ is a feasible vector of final wins.

  Illustrate your idea by answering the question of whether or not $x=(7,5,6,6)$ is a possible profile of total end-of-season wins when $n=4, w=(1,2,3,4)$, and $M=14$ with

  $$\left(m_{i j}\right)=\left(\begin{array}{cccc} - & 2 & 2 & 2 \\ 2 & - & 1 & 1 \\ 2 & 1 & - & 6 \\ 2 & 1 & 6 & - \end{array}\right)$$

  comment

Quantum Mechanics

• Paper 1, Section II, C

  Quantum Mechanics | Part IB, 2012

  Show that if the energy levels are discrete, the general solution of the Schrödinger equation

  $$i \hbar \frac{\partial \psi}{\partial t}=-\frac{\hbar^{2}}{2 m} \nabla^{2} \psi+V(\mathbf{x}) \psi$$

  is a linear superposition of stationary states

  $$\psi(\mathbf{x}, t)=\sum_{n=1}^{\infty} a_{n} \chi_{n}(\mathbf{x}) \exp \left(-i E_{n} t / \hbar\right)$$

  where $\chi_{n}(\mathbf{x})$ is a solution of the time-independent Schrödinger equation and $a_{n}$ are complex coefficients. Can this general solution be considered to be a stationary state? Justify your answer.

  A linear operator $\hat{O}$ acts on the orthonormal energy eigenfunctions $\chi_{n}$ as follows:

  $$\begin{aligned} &\hat{O} \chi_{1}=\chi_{1}+\chi_{2} \\ &\hat{O} \chi_{2}=\chi_{1}+\chi_{2} \\ &\hat{O} \chi_{n}=0, \quad n \geqslant 3 \end{aligned}$$

  Obtain the eigenvalues of $\hat{O}$. Hence, find the normalised eigenfunctions of $\hat{O}$. In an experiment a measurement is made of $\hat{O}$ at $t=0$ yielding an eigenvalue of 2 . What is the probability that a measurement at some later time $t$ will yield an eigenvalue of 2 ?

  comment

• Paper 2, Section II, C

  Quantum Mechanics | Part IB, 2012

  Consider a quantum mechanical particle in a one-dimensional potential $V(x)$, for which $V(x)=V(-x)$. Prove that when the energy eigenvalue $E$ is non-degenerate, the energy eigenfunction $\chi(x)$ has definite parity.

  Now assume the particle is in the double potential well

  $$V(x)= \begin{cases}U, & 0 \leqslant|x| \leqslant l_{1} \\ 0, & l_{1}<|x| \leqslant l_{2} \\ \infty, & l_{2}<|x|\end{cases}$$

  where $0<l_{1}<l_{2}$ and $0<E<U$ (U being large and positive). Obtain general expressions for the even parity energy eigenfunctions $\chi^{+}(x)$ in terms of trigonometric and hyperbolic functions. Show that

  $$-\tan \left[k\left(l_{2}-l_{1}\right)\right]=\frac{k}{\kappa} \operatorname{coth}\left(\kappa l_{1}\right)$$

  where $k^{2}=\frac{2 m E}{\hbar^{2}}$ and $\kappa^{2}=\frac{2 m(U-E)}{\hbar^{2}}$.

  comment

• Paper 3, Section I, C

  Quantum Mechanics | Part IB, 2012

  A one-dimensional quantum mechanical particle has normalised bound state energy eigenfunctions $\chi_{n}(x)$ and corresponding non-degenerate energy eigenvalues $E_{n}$. At $t=0$ the normalised wavefunction $\psi(x, t)$ is given by

  $$\psi(x, 0)=\sqrt{\frac{5}{6}} e^{i k_{1}} \chi_{1}(x)+\sqrt{\frac{1}{6}} e^{i k_{2}} \chi_{2}(x)$$

  where $k_{1}$ and $k_{2}$ are real constants. Write down the expression for $\psi(x, t)$ at a later time $t$ and give the probability that a measurement of the particle's energy will yield a value of $E_{2}$.

  Show that the expectation value of $x$ at time $t$ is given by

  $$\langle x\rangle=\frac{5}{6}\langle x\rangle_{11}+\frac{1}{6}\langle x\rangle_{22}+\frac{\sqrt{5}}{3} \operatorname{Re}\left[\langle x\rangle_{12} e^{i\left(k_{2}-k_{1}\right)-i\left(E_{2}-E_{1}\right) t / \hbar}\right]$$

  where $\langle x\rangle_{i j}=\int_{-\infty}^{\infty} \chi_{i}^{*}(x) x \chi_{j}(x) d x$.

  comment

• Paper 3, Section II, C

  Quantum Mechanics | Part IB, 2012

  State the condition for a linear operator $\hat{O}$ to be Hermitian.

  Given the position and momentum operators $\hat{x}_{i}$ and $\hat{p}_{i}=-i \hbar \frac{\partial}{\partial x_{i}}$, define the angular momentum operators $\hat{L}_{i}$. Establish the commutation relations

  $$\left[\hat{L}_{i}, \hat{L}_{j}\right]=i \hbar \epsilon_{i j k} \hat{L}_{k}$$

  and use these relations to show that $\hat{L}_{3}$ is Hermitian assuming $\hat{L}_{1}$ and $\hat{L}_{2}$ are.

  Consider a wavefunction of the form

  $$\chi(\mathbf{x})=x_{3}\left(x_{1}+k x_{2}\right) e^{-r}$$

  where $r=|\mathbf{x}|$ and $k$ is some constant. Show that $\chi(\mathbf{x})$ is an eigenstate of the total angular momentum operator $\hat{\mathbf{L}}^{2}$ for all $k$, and calculate the corresponding eigenvalue. For what values of $k$ is $\chi(\mathbf{x})$ an eigenstate of $\hat{L}_{3}$ ? What are the corresponding eigenvalues?

  comment

• Paper 4, Section I, $\mathbf{6 C}$

  Quantum Mechanics | Part IB, 2012

  In terms of quantum states, what is meant by energy degeneracy?

  A particle of mass $m$ is confined within the box $0<x<a, 0<y<a$ and $0<z<c$. The potential vanishes inside the box and is infinite outside. Find the allowed energies by considering a stationary state wavefunction of the form

  $$\chi(x, y, z)=X(x) Y(y) Z(z)$$

  Write down the normalised ground state wavefunction. Assuming that $c<a<\sqrt{2} c$, give the energies of the first three excited states.

  comment

Statistics

• Paper 1, Section I, H

  Statistics | Part IB, 2012

  Describe the generalised likelihood ratio test and the type of statistical question for which it is useful.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent and identically distributed random variables with the Gamma $(2, \lambda)$ distribution, having density function $\lambda^{2} x \exp (-\lambda x), x \geqslant 0$. Similarly, $Y_{1}, \ldots, Y_{n}$ are independent and identically distributed with the Gamma $(2, \mu)$ distribution. It is desired to test the hypothesis $H_{0}: \lambda=\mu$ against $H_{1}: \lambda \neq \mu$. Derive the generalised likelihood ratio test and express it in terms of $R=\sum_{i} X_{i} / \sum_{i} Y_{i}$.

  Let $F_{\nu_{1}, \nu_{2}}^{(1-\alpha)}$ denote the value that a random variable having the $F_{\nu_{1}, \nu_{2}}$ distribution exceeds with probability $\alpha$. Explain how to decide the outcome of a size $0.05$ test when $n=5$ by knowing only the value of $R$ and the value $F_{\nu_{1}, \nu_{2}}^{(1-\alpha)}$, for some $\nu_{1}, \nu_{2}$ and $\alpha$, which you should specify.

  [You may use the fact that the $\chi_{k}^{2}$ distribution is equivalent to the $\operatorname{Gamma}(k / 2,1 / 2)$ distribution.]

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2012

  State and prove the Neyman-Pearson lemma.

  A sample of two independent observations, $\left(x_{1}, x_{2}\right)$, is taken from a distribution with density $f(x ; \theta)=\theta x^{\theta-1}, 0 \leqslant x \leqslant 1$. It is desired to test $H_{0}: \theta=1$ against $H_{1}: \theta=2$. Show that the best test of size $\alpha$ can be expressed using the number $c$ such that

  $$1-c+c \log c=\alpha .$$

  Is this the uniformly most powerful test of size $\alpha$ for testing $H_{0}$ against $H_{1}: \theta>1 ?$

  Suppose that the prior distribution of $\theta$ is $P(\theta=1)=4 \gamma /(1+4 \gamma), P(\theta=2)=$ $1 /(1+4 \gamma)$, where $1>\gamma>0$. Find the test of $H_{0}$ against $H_{1}$ that minimizes the probability of error.

  Let $w(\theta)$ denote the power function of this test at $\theta(\geqslant 1)$. Show that

  $$w(\theta)=1-\gamma^{\theta}+\gamma^{\theta} \log \gamma^{\theta}$$

  comment

• Paper 2, Section I, H

  Statistics | Part IB, 2012

  Let the sample $x=\left(x_{1}, \ldots, x_{n}\right)$ have likelihood function $f(x ; \theta)$. What does it mean to say $T(x)$ is a sufficient statistic for $\theta$ ?

  Show that if a certain factorization criterion is satisfied then $T$ is sufficient for $\theta$.

  Suppose that $T$ is sufficient for $\theta$ and there exist two samples, $x$ and $y$, for which $T(x) \neq T(y)$ and $f(x ; \theta) / f(y ; \theta)$ does not depend on $\theta$. Let

  $$T_{1}(z)= \begin{cases}T(z) & z \neq y \\ T(x) & z=y\end{cases}$$

  Show that $T_{1}$ is also sufficient for $\theta$.

  Explain why $T$ is not minimally sufficient for $\theta$.

  comment

• Paper 3, Section II, H

  Statistics | Part IB, 2012

  Suppose that $X$ is a single observation drawn from the uniform distribution on the interval $[\theta-10, \theta+10]$, where $\theta$ is unknown and might be any real number. Given $\theta_{0} \neq 20$ we wish to test $H_{0}: \theta=\theta_{0}$ against $H_{1}: \theta=20$. Let $\phi\left(\theta_{0}\right)$ be the test which accepts $H_{0}$ if and only if $X \in A\left(\theta_{0}\right)$, where

  $$A\left(\theta_{0}\right)= \begin{cases}{\left[\theta_{0}-8, \infty\right),} & \theta_{0}>20 \\ \left(-\infty, \theta_{0}+8\right], & \theta_{0}<20\end{cases}$$

  Show that this test has size $\alpha=0.10$.

  Now consider

  $$\begin{aligned} &C_{1}(X)=\{\theta: X \in A(\theta)\} \\ &C_{2}(X)=\{\theta: X-9 \leqslant \theta \leqslant X+9\} \end{aligned}$$

  Prove that both $C_{1}(X)$ and $C_{2}(X)$ specify $90 \%$ confidence intervals for $\theta$. Find the confidence interval specified by $C_{1}(X)$ when $X=0$.

  Let $L_{i}(X)$ be the length of the confidence interval specified by $C_{i}(X)$. Let $\beta\left(\theta_{0}\right)$ be the probability of the Type II error of $\phi\left(\theta_{0}\right)$. Show that

  $$E\left[L_{1}(X) \mid \theta=20\right]=E\left[\int_{-\infty}^{\infty} 1_{\left\{\theta_{0} \in C_{1}(X)\right\}} d \theta_{0} \mid \theta=20\right]=\int_{-\infty}^{\infty} \beta\left(\theta_{0}\right) d \theta_{0}$$

  Here $1_{\{B\}}$ is an indicator variable for event $B$. The expectation is over $X$. [Orders of integration and expectation can be interchanged.]

  Use what you know about constructing best tests to explain which of the two confidence intervals has the smaller expected length when $\theta=20$.

  comment

• Paper 4, Section II, H

  Statistics | Part IB, 2012

  From each of 3 populations, $n$ data points are sampled and these are believed to obey

  $$y_{i j}=\alpha_{i}+\beta_{i}\left(x_{i j}-\bar{x}_{i}\right)+\epsilon_{i j}, \quad j \in\{1, \ldots, n\}, i \in\{1,2,3\},$$

  where $\bar{x}_{i}=(1 / n) \sum_{j} x_{i j}$, the $\epsilon_{i j}$ are independent and identically distributed as $N\left(0, \sigma^{2}\right)$, and $\sigma^{2}$ is unknown. Let $\bar{y}_{i}=(1 / n) \sum_{j} y_{i j}$.

  (i) Find expressions for $\hat{\alpha}_{i}$ and $\hat{\beta}_{i}$, the least squares estimates of $\alpha_{i}$ and $\beta_{i}$.

  (ii) What are the distributions of $\hat{\alpha}_{i}$ and $\hat{\beta}_{i}$ ?

  (iii) Show that the residual sum of squares, $R_{1}$, is given by

  $$R_{1}=\sum_{i=1}^{3}\left[\sum_{j=1}^{n}\left(y_{i j}-\bar{y}_{i}\right)^{2}-\hat{\beta}_{i}^{2} \sum_{j=1}^{n}\left(x_{i j}-\bar{x}_{i}\right)^{2}\right]$$

  Calculate $R_{1}$ when $n=9,\left\{\hat{\alpha}_{i}\right\}_{i=1}^{3}=\{1.6,0.6,0.8\},\left\{\hat{\beta}_{i}\right\}_{i=1}^{3}=\{2,1,1\}$,

  $$\left\{\sum_{j=1}^{9}\left(y_{i j}-\bar{y}_{i}\right)^{2}\right\}_{i=1}^{3}=\{138,82,63\}, \quad\left\{\sum_{j=1}^{9}\left(x_{i j}-\bar{x}_{i}\right)^{2}\right\}_{i=1}^{3}=\{30,60,40\}$$

  (iv) $H_{0}$ is the hypothesis that $\alpha_{1}=\alpha_{2}=\alpha_{3}$. Find an expression for the maximum likelihood estimator of $\alpha_{1}$ under the assumption that $H_{0}$ is true. Calculate its value for the above data.

  (v) Explain (stating without proof any relevant theory) the rationale for a statistic which can be referred to an $F$ distribution to test $H_{0}$ against the alternative that it is not true. What should be the degrees of freedom of this $F$ distribution? What would be the outcome of a size $0.05$ test of $H_{0}$ with the above data?

  comment

Variational Principles

• Paper 1, Section I, B

  Variational Principles | Part IB, 2012

  State how to find the stationary points of a $C^{1}$ function $f(x, y)$ restricted to the circle $x^{2}+y^{2}=1$, using the method of Lagrange multipliers. Explain why, in general, the method of Lagrange multipliers works, in the case where there is just one constraint.

  Find the stationary points of $x^{4}+2 y^{3}$ restricted to the circle $x^{2}+y^{2}=1$.

  comment

• Paper 2, Section II, B

  Variational Principles | Part IB, 2012

  (i) A two-dimensional oscillator has action

  $$S=\int_{t_{0}}^{t_{1}}\left\{\frac{1}{2} \dot{x}^{2}+\frac{1}{2} \dot{y}^{2}-\frac{1}{2} \omega^{2} x^{2}-\frac{1}{2} \omega^{2} y^{2}\right\} d t$$

  Find the equations of motion as the Euler-Lagrange equations associated to $S$, and use them to show that

  $$J=\dot{x} y-\dot{y} x$$

  is conserved. Write down the general solution of the equations of motion in terms of sin $\omega t$ and $\cos \omega t$, and evaluate $J$ in terms of the coefficients which arise in the general solution.

  (ii) Another kind of oscillator has action

  $$\widetilde{S}=\int_{t_{0}}^{t_{1}}\left\{\frac{1}{2} \dot{x}^{2}+\frac{1}{2} \dot{y}^{2}-\frac{1}{4} \alpha x^{4}-\frac{1}{2} \beta x^{2} y^{2}-\frac{1}{4} \alpha y^{4}\right\} d t$$

  where $\alpha$ and $\beta$ are real constants. Find the equations of motion and use these to show that in general $J=\dot{x} y-\dot{y} x$ is not conserved. Find the special value of the ratio $\beta / \alpha$ for which $J$ is conserved. Explain what is special about the action $\widetilde{S}$in this case, and state the interpretation of $J$.

  comment

• Paper 3, Section I, B

  Variational Principles | Part IB, 2012

  For a particle of unit mass moving freely on a unit sphere, the Lagrangian in polar coordinates is

  $$L=\frac{1}{2} \dot{\theta}^{2}+\frac{1}{2} \sin ^{2} \theta \dot{\phi}^{2} .$$

  Find the equations of motion. Show that $l=\sin ^{2} \theta \dot{\phi}$ is a conserved quantity, and use this result to simplify the equation of motion for $\theta$. Deduce that

  $$h=\dot{\theta}^{2}+\frac{l^{2}}{\sin ^{2} \theta}$$

  is a conserved quantity. What is the interpretation of $h$ ?

  comment

• Paper 4, Section II, B

  Variational Principles | Part IB, 2012

  Consider a functional

  $$I=\int_{a}^{b} F\left(x, y, y^{\prime}\right) d x$$

  where $F$ is smooth in all its arguments, $y(x)$ is a $C^{1}$ function and $y^{\prime}=\frac{d y}{d x}$. Consider the function $y(x)+h(x)$ where $h(x)$ is a small $C^{1}$ function which vanishes at $a$ and $b$. Obtain formulae for the first and second variations of $I$ about the function $y(x)$. Derive the Euler-Lagrange equation from the first variation, and state its variational interpretation.

  Suppose now that

  $$I=\int_{0}^{1}\left(y^{\prime 2}-1\right)^{2} d x$$

  where $y(0)=0$ and $y(1)=\beta$. Find the Euler-Lagrange equation and the formula for the second variation of $I$. Show that the function $y(x)=\beta x$ makes $I$ stationary, and that it is a (local) minimizer if $\beta>\frac{1}{\sqrt{3}}$.

  Show that when $\beta=0$, the function $y(x)=0$ is not a minimizer of $I$.

  comment