Part IB, 2018

Analysis II

• Paper 1, Section II, F

  Analysis II | Part IB, 2018

  Let $U \subset \mathbb{R}^{n}$ be a non-empty open set and let $f: U \rightarrow \mathbb{R}^{n}$.

  (a) What does it mean to say that $f$ is differentiable? What does it mean to say that $f$ is a $C^{1}$ function?

  If $f$ is differentiable, show that $f$ is continuous.

  State the inverse function theorem.

  (b) Suppose that $U$ is convex, $f$ is $C^{1}$ and that its derivative $D f(a)$ at a satisfies $\|D f(a)-I\|<1$ for all $a \in U$, where $I: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is the identity map and $\|\cdot\|$ denotes the operator norm. Show that $f$ is injective.

  Explain why $f(U)$ is an open subset of $\mathbb{R}^{n}$.

  Must it be true that $f(U)=\mathbb{R}^{n}$ ? What if $U=\mathbb{R}^{n}$ ? Give proofs or counter-examples as appropriate.

  (c) Find the largest set $U \subset \mathbb{R}^{2}$ such that the map $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ given by $f(x, y)=\left(x^{2}-y^{2}, 2 x y\right)$ satisfies $\|D f(a)-I\|<1$ for every $a \in U$.

  comment

• Paper 2, Section I, F

  Analysis II | Part IB, 2018

  Show that $\|f\|_{1}=\int_{0}^{1}|f(x)| d x$ defines a norm on the space $C([0,1])$ of continuous functions $f:[0,1] \rightarrow \mathbb{R}$.

  Let $\mathcal{S}$ be the set of continuous functions $g:[0,1] \rightarrow \mathbb{R}$ with $g(0)=g(1)=0$. Show that for each continuous function $f:[0,1] \rightarrow \mathbb{R}$, there is a sequence $g_{n} \in \mathcal{S}$ with $\sup _{x \in[0,1]}\left|g_{n}(x)\right| \leqslant \sup _{x \in[0,1]}|f(x)|$ such that $\left\|f-g_{n}\right\|_{1} \rightarrow 0$ as $n \rightarrow \infty$

  Show that if $f:[0,1] \rightarrow \mathbb{R}$ is continuous and $\int_{0}^{1} f(x) g(x) d x=0$ for every $g \in \mathcal{S}$ then $f=0$.

  comment

• Paper 2, Section II, F

  Analysis II | Part IB, 2018

  (a) Let $(X, d)$ be a metric space, $A$ a non-empty subset of $X$ and $f: A \rightarrow \mathbb{R}$. Define what it means for $f$ to be Lipschitz. If $f$ is Lipschitz with Lipschitz constant $L$ and if

  $$F(x)=\inf _{y \in A}(f(y)+L d(x, y))$$

  for each $x \in X$, show that $F(x)=f(x)$ for each $x \in A$ and that $F: X \rightarrow \mathbb{R}$ is Lipschitz with Lipschitz constant $L$. (Be sure to justify that $F(x) \in \mathbb{R}$, i.e. that the infimum is finite for every $x \in X$.)

  (b) What does it mean to say that two norms on a vector space are Lipschitz equivalent?

  Let $V$ be an $n$-dimensional real vector space equipped with a norm $\|$. Let $\left\{e_{1}, e_{2}, \ldots, e_{n}\right\}$ be a basis for $V$. Show that the map $g: \mathbb{R}^{n} \rightarrow \mathbb{R}$ defined by $g\left(x_{1}, x_{2}, \ldots, x_{n}\right)=\left\|x_{1} e_{1}+x_{2} e_{2}+\ldots+x_{n} e_{n}\right\|$ is continuous. Deduce that any two norms on $V$ are Lipschitz equivalent.

  (c) Prove that for each positive integer $n$ and each $a \in(0,1]$, there is a constant $C>0$ with the following property: for every polynomial $p$ of degree $\leqslant n$, there is a point $y \in[0, a]$ such that

  $$\sup _{x \in[0,1]}\left|p^{\prime}(x)\right| \leqslant C|p(y)|$$

  where $p^{\prime}$ is the derivative of $p$.

  comment

• Paper 3, Section I, $2 F$

  Analysis II | Part IB, 2018

  For a continuous function $f=\left(f_{1}, f_{2}, \ldots, f_{m}\right):[0,1] \rightarrow \mathbb{R}^{m}$, define

  $$\int_{0}^{1} f(t) d t=\left(\int_{0}^{1} f_{1}(t) d t, \int_{0}^{1} f_{2}(t) d t, \ldots, \int_{0}^{1} f_{m}(t) d t\right)$$

  Show that

  $$\left\|\int_{0}^{1} f(t) d t\right\|_{2} \leqslant \int_{0}^{1}\|f(t)\|_{2} d t$$

  for every continuous function $f:[0,1] \rightarrow \mathbb{R}^{m}$, where $\|\cdot\|_{2}$ denotes the Euclidean norm on $\mathbb{R}^{m}$.

  Find all continuous functions $f:[0,1] \rightarrow \mathbb{R}^{m}$ with the property that

  $$\left\|\int_{0}^{1} f(t) d t\right\|=\int_{0}^{1}\|f(t)\| d t$$

  regardless of the norm $\|\cdot\|$ on $\mathbb{R}^{m}$.

  [Hint: start by analysing the case when $\|\cdot\|$ is the Euclidean norm $\|\cdot\|_{2}$.]

  comment

• Paper 3, Section II, F

  Analysis II | Part IB, 2018

  (a) Let $A \subset \mathbb{R}^{m}$ and let $f, f_{n}: A \rightarrow \mathbb{R}$ be functions for $n=1,2,3, \ldots$ What does it mean to say that the sequence $\left(f_{n}\right)$ converges uniformly to $f$ on $A$ ? What does it mean to say that $f$ is uniformly continuous?

  (b) Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a uniformly continuous function. Determine whether each of the following statements is true or false. Give reasons for your answers.

  (i) If $f_{n}(x)=f(x+1 / n)$ for each $n=1,2,3, \ldots$ and each $x \in \mathbb{R}$, then $f_{n} \rightarrow f$ uniformly on $\mathbb{R}$.

  (ii) If $g_{n}(x)=(f(x+1 / n))^{2}$ for each $n=1,2,3, \ldots$ and each $x \in \mathbb{R}$, then $g_{n} \rightarrow(f)^{2}$ uniformly on $\mathbb{R}$.

  (c) Let $A$ be a closed, bounded subset of $\mathbb{R}^{m}$. For each $n=1,2,3, \ldots$, let $g_{n}: A \rightarrow \mathbb{R}$ be a continuous function such that $\left(g_{n}(x)\right)$ is a decreasing sequence for each $x \in A$. If $\delta \in \mathbb{R}$ is such that for each $n$ there is $x_{n} \in A$ with $g_{n}\left(x_{n}\right) \geqslant \delta$, show that there is $x_{0} \in A$ such that $\lim _{n \rightarrow \infty} g_{n}\left(x_{0}\right) \geqslant \delta$.

  Deduce the following: If $f_{n}: A \rightarrow \mathbb{R}$ is a continuous function for each $n=1,2,3, \ldots$ such that $\left(f_{n}(x)\right)$ is a decreasing sequence for each $x \in A$, and if the pointwise limit of $\left(f_{n}\right)$ is a continuous function $f: A \rightarrow \mathbb{R}$, then $f_{n} \rightarrow f$ uniformly on $A$.

  comment

• Paper 4, Section I, F

  Analysis II | Part IB, 2018

  State the Bolzano-Weierstrass theorem in $\mathbb{R}$. Use it to deduce the BolzanoWeierstrass theorem in $\mathbb{R}^{n}$.

  Let $D$ be a closed, bounded subset of $\mathbb{R}^{n}$, and let $f: D \rightarrow \mathbb{R}$ be a function. Let $\mathcal{S}$ be the set of points in $D$ where $f$ is discontinuous. For $\rho>0$ and $z \in \mathbb{R}^{n}$, let $B_{\rho}(z)$ denote the ball $\left\{x \in \mathbb{R}^{n}:\|x-z\|<\rho\right\}$. Prove that for every $\epsilon>0$, there exists $\delta>0$ such that $|f(x)-f(y)|<\epsilon$ whenever $x \in D, y \in D \backslash \cup_{z \in \mathcal{S}} B_{\epsilon}(z)$ and $\|x-y\|<\delta$.

  (If you use the fact that a continuous function on a compact metric space is uniformly continuous, you must prove it.)

  comment

• Paper 4, Section II, F

  Analysis II | Part IB, 2018

  (a) Define what it means for a metric space $(X, d)$ to be complete. Give a metric $d$ on the interval $I=(0,1]$ such that $(I, d)$ is complete and such that a subset of $I$ is open with respect to $d$ if and only if it is open with respect to the Euclidean metric on $I$. Be sure to prove that $d$ has the required properties.

  (b) Let $(X, d)$ be a complete metric space.

  (i) If $Y \subset X$, show that $Y$ taken with the subspace metric is complete if and only if $Y$ is closed in $X$.

  (ii) Let $f: X \rightarrow X$ and suppose that there is a number $\lambda \in(0,1)$ such that $d(f(x), f(y)) \leqslant \lambda d(x, y)$ for every $x, y \in X$. Show that there is a unique point $x_{0} \in X$ such that $f\left(x_{0}\right)=x_{0}$.

  Deduce that if $\left(a_{n}\right)$ is a sequence of points in $X$ converging to a point $a \neq x_{0}$, then there are integers $\ell$ and $m \geqslant \ell$ such that $f\left(a_{m}\right) \neq a_{n}$ for every $n \geqslant \ell$.

  comment

Complex Analysis

• Paper 3, Section II, F

  Complex Analysis | Part IB, 2018

  Let $D=\{z \in \mathbb{C}:|z|<1\}$ and let $f: D \rightarrow \mathbb{C}$ be analytic.

  (a) If there is a point $a \in D$ such that $|f(z)| \leqslant|f(a)|$ for all $z \in D$, prove that $f$ is constant.

  (b) If $f(0)=0$ and $|f(z)| \leqslant 1$ for all $z \in D$, prove that $|f(z)| \leqslant|z|$ for all $z \in D$.

  (c) Show that there is a constant $C$ independent of $f$ such that if $f(0)=1$ and $f(z) \notin(-\infty, 0]$ for all $z \in D$ then $|f(z)| \leqslant C$ whenever $|z| \leqslant 1 / 2 .$

  [Hint: you may find it useful to consider the principal branch of the map $z \mapsto z^{1 / 2}$.]

  (d) Does the conclusion in (c) hold if we replace the hypothesis $f(z) \notin(-\infty, 0]$ for $z \in D$ with the hypothesis $f(z) \neq 0$ for $z \in D$, and keep all other hypotheses? Justify your answer.

  comment

• Paper 4, Section I, F

  Complex Analysis | Part IB, 2018

  (a) Let $\Omega \subset \mathbb{C}$ be open, $a \in \Omega$ and suppose that $D_{\rho}(a)=\{z \in \mathbb{C}:|z-a| \leqslant \rho\} \subset \Omega$. Let $f: \Omega \rightarrow \mathbb{C}$ be analytic.

  State the Cauchy integral formula expressing $f(a)$ as a contour integral over $C=\partial D_{\rho}(a)$. Give, without proof, a similar expression for $f^{\prime}(a)$.

  If additionally $\Omega=\mathbb{C}$ and $f$ is bounded, deduce that $f$ must be constant.

  (b) If $g=u+i v: \mathbb{C} \rightarrow \mathbb{C}$ is analytic where $u, v$ are real, and if $u^{2}(z)-u(z) \geqslant v^{2}(z)$ for all $z \in \mathbb{C}$, show that $g$ is constant.

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, A

  Complex Analysis or Complex Methods | Part IB, 2018

  (a) Show that

  $$w=\log (z)$$

  is a conformal mapping from the right half $z$-plane, $\operatorname{Re}(z)>0$, to the strip

  $$S=\left\{w:-\frac{\pi}{2}<\operatorname{Im}(w)<\frac{\pi}{2}\right\}$$

  for a suitably chosen branch of $\log (z)$ that you should specify.

  (b) Show that

  $$w=\frac{z-1}{z+1}$$

  is a conformal mapping from the right half $z$-plane, $\operatorname{Re}(z)>0$, to the unit disc

  $$D=\{w:|w|<1\}$$

  (c) Deduce a conformal mapping from the strip $S$ to the disc $D$.

  comment

• Paper 1, Section II, A

  Complex Analysis or Complex Methods | Part IB, 2018

  (a) Let $C$ be a rectangular contour with vertices at $\pm R+\pi i$ and $\pm R-\pi i$ for some $R>0$ taken in the anticlockwise direction. By considering

  $$\lim _{R \rightarrow \infty} \oint_{C} \frac{e^{i z^{2} / 4 \pi}}{e^{z / 2}-e^{-z / 2}} d z$$

  show that

  $$\lim _{R \rightarrow \infty} \int_{-R}^{R} e^{i x^{2} / 4 \pi} d x=2 \pi e^{\pi i / 4}$$

  (b) By using a semi-circular contour in the upper half plane, calculate

  $$\int_{0}^{\infty} \frac{x \sin (\pi x)}{x^{2}+a^{2}} d x$$

  for $a>0$.

  [You may use Jordan's Lemma without proof.]

  comment

• Paper 2, Section II, A

  Complex Analysis or Complex Methods | Part IB, 2018

  (a) Let $f(z)$ be a complex function. Define the Laurent series of $f(z)$ about $z=z_{0}$, and give suitable formulae in terms of integrals for calculating the coefficients of the series.

  (b) Calculate, by any means, the first 3 terms in the Laurent series about $z=0$ for

  $$f(z)=\frac{1}{e^{2 z}-1}$$

  Indicate the range of values of $|z|$ for which your series is valid.

  (c) Let

  $$g(z)=\frac{1}{2 z}+\sum_{k=1}^{m} \frac{z}{z^{2}+\pi^{2} k^{2}}$$

  Classify the singularities of $F(z)=f(z)-g(z)$ for $|z|<(m+1) \pi$.

  (d) By considering

  $$\oint_{C_{R}} \frac{F(z)}{z^{2}} d z$$

  where $C_{R}=\{|z|=R\}$ for some suitably chosen $R>0$, show that

  $$\sum_{k=1}^{\infty} \frac{1}{k^{2}}=\frac{\pi^{2}}{6}$$

  comment

Complex Methods

• Paper 3, Section I, A

  Complex Methods | Part IB, 2018

  (a) Let $f(z)=\left(z^{2}-1\right)^{1 / 2}$. Define the branch cut of $f(z)$ as $[-1,1]$ such that

  $$f(x)=+\sqrt{x^{2}-1} \quad x>1$$

  Show that $f(z)$ is an odd function.

  (b) Let $g(z)=\left[(z-2)\left(z^{2}-1\right)\right]^{1 / 2}$.

  (i) Show that $z=\infty$ is a branch point of $g(z)$.

  (ii) Define the branch cuts of $g(z)$ as $[-1,1] \cup[2, \infty)$ such that

  $$g(x)=e^{\pi i / 2} \sqrt{|x-2|\left|x^{2}-1\right|} \quad x \in(1,2) .$$

  Find $g\left(0_{\pm}\right)$, where $0_{+}$denotes $z=0$ just above the branch cut, and $0_{-}$denotes $z=0$ just below the branch cut.

  comment

• Paper 4, Section II, A

  Complex Methods | Part IB, 2018

  (a) Find the Laplace transform of

  $$y(t)=\frac{e^{-a^{2} / 4 t}}{\sqrt{\pi t}}$$

  for $a \in \mathbb{R}, a \neq 0$.

  [You may use without proof that

  $$\left.\int_{0}^{\infty} \exp \left(-c^{2} x^{2}-\frac{c^{2}}{x^{2}}\right) d x=\frac{\sqrt{\pi}}{2|c|} e^{-2 c^{2}} .\right]$$

  (b) By using the Laplace transform, show that the solution to

  $$\begin{aligned} \frac{\partial^{2} u}{\partial x^{2}} &=\frac{\partial u}{\partial t} \quad-\infty<x<\infty, \quad t>0 \\ u(x, 0) &=f(x) \\ u(x, t) \quad \text { bounded, } \end{aligned}$$

  can be written as

  $$u(x, t)=\int_{-\infty}^{\infty} K(|x-\xi|, t) f(\xi) d \xi$$

  for some $K(|x-\xi|, t)$ to be determined.

  [You may use without proof that a particular solution to

  $$y^{\prime \prime}(x)-s y(x)+f(x)=0$$

  is given by

  $$\left.y(x)=\frac{e^{-\sqrt{s} x}}{2 \sqrt{s}} \int_{0}^{x} e^{\sqrt{s} \xi} f(\xi) d \xi-\frac{e^{\sqrt{s} x}}{2 \sqrt{s}} \int_{0}^{x} e^{-\sqrt{s} \xi} f(\xi) d \xi .\right]$$

  comment

Electromagnetism

• Paper 1, Section II, C

  Electromagnetism | Part IB, 2018

  Starting from the Lorentz force law acting on a current distribution $\mathbf{J}$ obeying $\boldsymbol{\nabla} \cdot \mathbf{J}=0$, show that the energy of a magnetic dipole $\mathbf{m}$ in the presence of a time independent magnetic field $\mathbf{B}$ is

  $$U=-\mathbf{m} \cdot \mathbf{B}$$

  State clearly any approximations you make.

  [You may use without proof the fact that

  $$\int(\mathbf{a} \cdot \mathbf{r}) \mathbf{J}(\mathbf{r}) \mathrm{d} V=-\frac{1}{2} \mathbf{a} \times \int(\mathbf{r} \times \mathbf{J}(\mathbf{r})) \mathrm{d} V$$

  for any constant vector $\mathbf{a}$, and the identity

  $$(\mathbf{b} \times \boldsymbol{\nabla}) \times \mathbf{c}=\boldsymbol{\nabla}(\mathbf{b} \cdot \mathbf{c})-\mathbf{b}(\boldsymbol{\nabla} \cdot \mathbf{c})$$

  which holds when $\mathbf{b}$ is constant.]

  A beam of slowly moving, randomly oriented magnetic dipoles enters a region where the magnetic field is

  $$\mathbf{B}=\hat{\mathbf{z}} B_{0}+(y \hat{\mathbf{x}}+x \hat{\mathbf{y}}) B_{1},$$

  with $B_{0}$ and $B_{1}$ constants. By considering their energy, briefly describe what happens to those dipoles that are parallel to, and those that are anti-parallel to the direction of $\mathbf{B}$.

  comment

• Paper 2, Section I, $\mathbf{6 C}$

  Electromagnetism | Part IB, 2018

  Derive the Biot-Savart law

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int_{V} \frac{\mathbf{j}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} \mathrm{~d} V$$

  from Maxwell's equations, where the time-independent current $\mathbf{j}(\mathbf{r})$ vanishes outside $V$. [You may assume that the vector potential can be chosen to be divergence-free.]

  comment

• Paper 2, Section II, C

  Electromagnetism | Part IB, 2018

  A plane with unit normal $\mathbf{n}$ supports a charge density and a current density that are each time-independent. Show that the tangential components of the electric field and the normal component of the magnetic field are continuous across the plane.

  Albert moves with constant velocity $\mathbf{v}=v \mathbf{n}$ relative to the plane. Find the boundary conditions at the plane on the normal component of the magnetic field and the tangential components of the electric field as seen in Albert's frame.

  comment

• Paper 3, Section II, C

  Electromagnetism | Part IB, 2018

  Use Maxwell's equations to show that

  $$\frac{d}{d t} \int_{\Omega}\left(\frac{\epsilon_{0}}{2} \mathbf{E} \cdot \mathbf{E}+\frac{1}{2 \mu_{0}} \mathbf{B} \cdot \mathbf{B}\right) d V+\int_{\Omega} \mathbf{J} \cdot \mathbf{E} d V=-\frac{1}{\mu_{0}} \int_{\partial \Omega}(\mathbf{E} \times \mathbf{B}) \cdot \mathbf{n} d S$$

  where $\Omega \subset \mathbb{R}^{3}$ is a bounded region, $\partial \Omega$ its boundary and $\mathbf{n}$ its outward-pointing normal. Give an interpretation for each of the terms in this equation.

  A certain capacitor consists of two conducting, circular discs, each of large area $A$, separated by a small distance along their common axis. Initially, the plates carry charges $q_{0}$ and $-q_{0}$. At time $t=0$ the plates are connected by a resistive wire, causing the charge on the plates to decay slowly as $q(t)=q_{0} \mathrm{e}^{-\lambda t}$ for some constant $\lambda$. Construct the Poynting vector and show that energy flows radially out of the capacitor as it discharges.

  comment

• Paper 4, Section I, $7 \mathrm{C}$

  Electromagnetism | Part IB, 2018

  Show that Maxwell's equations imply the conservation of charge.

  A conducting medium has $\mathbf{J}=\sigma \mathbf{E}$ where $\sigma$ is a constant. Show that any charge density decays exponentially in time, at a rate to be determined.

  comment

Fluid Dynamics

• Paper 1, Section I, D

  Fluid Dynamics | Part IB, 2018

  Show that the flow with velocity potential

  $$\phi=\frac{q}{2 \pi} \ln r$$

  in two-dimensional, plane-polar coordinates $(r, \theta)$ is incompressible in $r>0$. Determine the flux of fluid across a closed contour $C$ that encloses the origin. What does this flow represent?

  Show that the flow with velocity potential

  $$\phi=\frac{q}{4 \pi} \ln \left(x^{2}+(y-a)^{2}\right)+\frac{q}{4 \pi} \ln \left(x^{2}+(y+a)^{2}\right)$$

  has no normal flow across the line $y=0$. What fluid flow does this represent in the unbounded plane? What flow does it represent for fluid occupying the domain $y>0$ ?

  comment

• Paper 1, Section II, D

  Fluid Dynamics | Part IB, 2018

  A layer of fluid of dynamic viscosity $\mu$, density $\rho$ and uniform thickness $h$ flows down a rigid vertical plane. The adjacent air has uniform pressure $p_{0}$ and exerts a tangential stress on the fluid that is proportional to the surface velocity and opposes the flow, with constant of proportionality $k$. The acceleration due to gravity is $g$.

  (a) Draw a diagram of this situation, including indications of the applied stresses and body forces, a suitable coordinate system and a representation of the expected velocity profile.

  (b) Write down the equations and boundary conditions governing the flow, with a brief description of each, paying careful attention to signs. Solve these equations to determine the pressure and velocity fields in terms of the parameters given above.

  (c) Show that the surface velocity of the fluid layer is $\frac{\rho g h^{2}}{2 \mu}\left(1+\frac{k h}{\mu}\right)^{-1}$.

  (d) Determine the volume flux per unit width of the plane for general values of $k$ and its limiting values when $k \rightarrow 0$ and $k \rightarrow \infty$.

  comment

• Paper 2, Section I, D

  Fluid Dynamics | Part IB, 2018

  The Euler equations for steady fluid flow $\mathbf{u}$ in a rapidly rotating system can be written

  $$\rho \mathbf{f} \times \mathbf{u}=-\nabla p+\rho \mathbf{g},$$

  where $\rho$ is the density of the fluid, $p$ is its pressure, $\mathbf{g}$ is the acceleration due to gravity and $\mathbf{f}=(0,0, f)$ is the constant Coriolis parameter in a Cartesian frame of reference $(x, y, z)$, with $z$ pointing vertically upwards.

  Fluid occupies a layer of slowly-varying height $h(x, y)$. Given that the pressure $p=p_{0}$ is constant at $z=h$ and that the flow is approximately horizontal with components $\mathbf{u}=(u, v, 0)$, show that the contours of $h$ are streamlines of the horizontal flow. What is the leading-order horizontal volume flux of fluid between two locations at which $h=h_{0}$ and $h=h_{0}+\Delta h$, where $\Delta h \ll h_{0}$ ?

  Identify the dimensions of all the quantities involved in your expression for the volume flux and show that your expression is dimensionally consistent.

  comment

• Paper 3, Section II, D

  Fluid Dynamics | Part IB, 2018

  A soap bubble of radius $a(t)$ is attached to the end of a long, narrow straw of internal radius $\epsilon$ and length $L$, the other end of which is open to the atmosphere. The pressure difference between the inside and outside of the bubble is $2 \gamma / a$, where $\gamma$ is the surface tension of the soap bubble. At time $t=0, a=a_{0}$ and the air in the straw is at rest. Assume that the flow of air through the straw is irrotational and consider the pressure drop along the straw to show that subsequently

  $$a^{3} \ddot{a}+2 a^{2} \dot{a}^{2}=-\frac{\gamma \epsilon^{2}}{2 \rho L},$$

  where $\rho$ is the density of air.

  By multiplying the equation by $2 a \dot{a}$ and integrating, or otherwise, determine an implicit equation for $a(t)$ and show that the bubble disappears in a time

  $$t=\frac{\pi}{2} \frac{a_{0}^{2}}{\epsilon}\left(\frac{\rho L}{2 \gamma}\right)^{1 / 2}$$

  [Hint: The substitution $a=a_{0} \sin \theta$ can be used.]

  comment

• Paper 4, Section II, D

  Fluid Dynamics | Part IB, 2018

  A deep layer of inviscid fluid is initially confined to the region $0<x<a, 0<y<a$, $z<0$ in Cartesian coordinates, with $z$ directed vertically upwards. An irrotational disturbance is caused to the fluid so that its upper surface takes position $z=\eta(x, y, t)$. Determine the linear normal modes of the system and the dispersion relation between the frequencies of the normal modes and their wavenumbers.

  If the interface is initially displaced to position $z=\epsilon \cos \frac{3 \pi x}{a} \cos \frac{4 \pi y}{a}$ and released from rest, where $\epsilon$ is a small constant, determine its position for subsequent times. How far below the surface will the velocity have decayed to $1 / e$ times its surface value?

  comment

Geometry

• Paper 1, Section I, G

  Geometry | Part IB, 2018

  (a) State the Gauss-Bonnet theorem for spherical triangles.

  (b) Prove that any geodesic triangulation of the sphere has Euler number equal to $2 .$

  (c) Prove that there is no geodesic triangulation of the sphere in which every vertex is adjacent to exactly 6 triangles.

  comment

• Paper 2, Section II, G

  Geometry | Part IB, 2018

  For any matrix

  $$A=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \in S L(2, \mathbb{R})$$

  the corresponding Möbius transformation is

  $$z \mapsto A z=\frac{a z+b}{c z+d},$$

  which acts on the upper half-plane $\mathbb{H}$, equipped with the hyperbolic metric $\rho$.

  (a) Assuming that $|\operatorname{tr} A|>2$, prove that $A$ is conjugate in $S L(2, \mathbb{R})$ to a diagonal matrix $B$. Determine the relationship between $|\operatorname{tr} A|$ and $\rho(i, B i)$.

  (b) For a diagonal matrix $B$ with $|\operatorname{tr} B|>2$, prove that

  $$\rho(x, B x)>\rho(i, B i)$$

  for all $x \in \mathbb{H}$ not on the imaginary axis.

  (c) Assume now that $|\operatorname{tr} A|<2$. Prove that $A$ fixes a point in $\mathbb{H}$.

  (d) Give an example of a matrix $A$ in $S L(2, \mathbb{R})$ that does not preserve any point or hyperbolic line in $\mathbb{H}$. Justify your answer.

  comment

• Paper 3, Section I, G

  Geometry | Part IB, 2018

  Consider a quadrilateral $A B C D$ in the hyperbolic plane whose sides are hyperbolic line segments. Suppose angles $A B C, B C D$ and $C D A$ are right-angles. Prove that $A D$ is longer than $B C$.

  [You may use without proof the distance formula in the upper-half-plane model

  $$\left.\rho\left(z_{1}, z_{2}\right)=2 \tanh ^{-1}\left|\frac{z_{1}-z_{2}}{z_{1}-\bar{z}_{2}}\right| \cdot\right]$$

  comment

• Paper 3, Section II, G

  Geometry | Part IB, 2018

  Let $U$ be an open subset of the plane $\mathbb{R}^{2}$, and let $\sigma: U \rightarrow S$ be a smooth parametrization of a surface $S$. A coordinate curve is an arc either of the form

  $$\alpha_{v_{0}}(t)=\sigma\left(t, v_{0}\right)$$

  for some constant $v_{0}$ and $t \in\left[u_{1}, u_{2}\right]$, or of the form

  $$\beta_{u_{0}}(t)=\sigma\left(u_{0}, t\right)$$

  for some constant $u_{0}$ and $t \in\left[v_{1}, v_{2}\right]$. A coordinate rectangle is a rectangle in $S$ whose sides are coordinate curves.

  Prove that all coordinate rectangles in $S$ have opposite sides of the same length if and only if $\frac{\partial E}{\partial v}=\frac{\partial G}{\partial u}=0$ at all points of $S$, where $E$ and $G$ are the usual components of the first fundamental form, and $(u, v)$ are coordinates in $U$.

  comment

• Paper 4, Section II, G

  Geometry | Part IB, 2018

  A Möbius strip in $\mathbb{R}^{3}$ is parametrized by

  $$\sigma(u, v)=(Q(u, v) \sin u, Q(u, v) \cos u, v \cos (u / 2))$$

  for $(u, v) \in U=(0,2 \pi) \times \mathbb{R}$, where $Q \equiv Q(u, v)=2-v \sin (u / 2)$. Show that the Gaussian curvature is

  $$K=\frac{-1}{\left(v^{2} / 4+Q^{2}\right)^{2}}$$

  at $(u, v) \in U$

  comment

Groups, Rings and Modules

• Paper 1, Section II, G

  Groups, Rings and Modules | Part IB, 2018

  (a) State Sylow's theorems.

  (b) Prove Sylow's first theorem.

  (c) Let $G$ be a group of order 12. Prove that either $G$ has a unique Sylow 3-subgroup or $G \cong A_{4}$.

  comment

• Paper 2, Section $I$, $2 G$

  Groups, Rings and Modules | Part IB, 2018

  Let $R$ be a principal ideal domain and $x$ a non-zero element of $R$. We define a new $\operatorname{ring} R^{\prime}$ as follows. We define an equivalence relation $\sim$ on $R \times\left\{x^{n} \mid n \in \mathbb{Z}_{\geqslant 0}\right\}$ by

  $$\left(r, x^{n}\right) \sim\left(r^{\prime}, x^{n^{\prime}}\right)$$

  if and only if $x^{n^{\prime}} r=x^{n} r^{\prime}$. The underlying set of $R^{\prime}$ is the set of $\sim$-equivalence classes. We define addition on $R^{\prime}$ by

  $$\left[\left(r, x^{n}\right)\right]+\left[\left(r^{\prime}, x^{n^{\prime}}\right)\right]=\left[\left(x^{n^{\prime}} r+x^{n} r^{\prime}, x^{n+n^{\prime}}\right)\right]$$

  and multiplication by $\left[\left(r, x^{n}\right)\right]\left[\left(r^{\prime}, x^{n^{\prime}}\right)\right]=\left[\left(r r^{\prime}, x^{n+n^{\prime}}\right)\right]$.

  (a) Show that $R^{\prime}$ is a well defined ring.

  (b) Prove that $R^{\prime}$ is a principal ideal domain.

  comment

• Paper 2, Section II, G

  Groups, Rings and Modules | Part IB, 2018

  (a) Prove that every principal ideal domain is a unique factorization domain.

  (b) Consider the ring $R=\{f(X) \in \mathbb{Q}[X] \mid f(0) \in \mathbb{Z}\}$.

  (i) What are the units in $R$ ?

  (ii) Let $f(X) \in R$ be irreducible. Prove that either $f(X)=\pm p$, for $p \in \mathbb{Z}$ a prime, or $\operatorname{deg}(f) \geqslant 1$ and $f(0)=\pm 1$.

  (iii) Prove that $f(X)=X$ is not expressible as a product of irreducibles.

  comment

• Paper 3, Section I, $1 G$

  Groups, Rings and Modules | Part IB, 2018

  (a) Find all integer solutions to $x^{2}+5 y^{2}=9$.

  (b) Find all the irreducibles in $\mathbb{Z}[\sqrt{-5}]$ of norm 9 .

  comment

• Paper 3, Section II, G

  Groups, Rings and Modules | Part IB, 2018

  (a) State Gauss's Lemma.

  (b) State and prove Eisenstein's criterion for the irreducibility of a polynomial.

  (c) Determine whether or not the polynomial

  $$f(X)=2 X^{3}+19 X^{2}-54 X+3$$

  is irreducible over $\mathbb{Q}$.

  comment

• Paper 4, Section I, G

  Groups, Rings and Modules | Part IB, 2018

  (a) Show that every automorphism $\alpha$ of the dihedral group $D_{6}$ is equal to conjugation by an element of $D_{6}$; that is, there is an $h \in D_{6}$ such that

  $$\alpha(g)=h g h^{-1}$$

  for all $g \in D_{6}$.

  (b) Give an example of a non-abelian group $G$ with an automorphism which is not equal to conjugation by an element of $G$.

  comment

• Paper 4, Section II, G

  Groups, Rings and Modules | Part IB, 2018

  (a) State the classification theorem for finitely generated modules over a Euclidean domain.

  (b) Deduce the existence of the rational canonical form for an $n \times n$ matrix $A$ over a field $F$.

  (c) Compute the rational canonical form of the matrix

  $$A=\left(\begin{array}{ccc} 3 / 2 & 1 & 0 \\ -1 & -1 / 2 & 0 \\ 2 & 2 & 1 / 2 \end{array}\right)$$

  comment

Linear Algebra

• Paper 1, Section I, E

  Linear Algebra | Part IB, 2018

  State the Rank-Nullity Theorem.

  If $\alpha: V \rightarrow W$ and $\beta: W \rightarrow X$ are linear maps and $W$ is finite dimensional, show that

  $$\operatorname{dim} \operatorname{Im}(\alpha)=\operatorname{dim} \operatorname{Im}(\beta \alpha)+\operatorname{dim}(\operatorname{Im}(\alpha) \cap \operatorname{Ker}(\beta))$$

  If $\gamma: U \rightarrow V$ is another linear map, show that

  $$\operatorname{dim} \operatorname{Im}(\beta \alpha)+\operatorname{dim} \operatorname{Im}(\alpha \gamma) \leqslant \operatorname{dim} \operatorname{Im}(\alpha)+\operatorname{dim} \operatorname{Im}(\beta \alpha \gamma)$$

  comment

• Paper 1, Section II, E

  Linear Algebra | Part IB, 2018

  Define a Jordan block $J_{m}(\lambda)$. What does it mean for a complex $n \times n$ matrix to be in Jordan normal form?

  If $A$ is a matrix in Jordan normal form for an endomorphism $\alpha: V \rightarrow V$, prove that

  $$\operatorname{dim} \operatorname{Ker}\left((\alpha-\lambda I)^{r}\right)-\operatorname{dim} \operatorname{Ker}\left((\alpha-\lambda I)^{r-1}\right)$$

  is the number of Jordan blocks $J_{m}(\lambda)$ of $A$ with $m \geqslant r$.

  Find a matrix in Jordan normal form for $J_{m}(\lambda)^{2}$. [Consider all possible values of $\lambda$.]

  Find a matrix in Jordan normal form for the complex matrix

  $$\left[\begin{array}{cccc} 0 & 0 & 0 & a_{1} \\ 0 & 0 & a_{2} & 0 \\ 0 & a_{3} & 0 & 0 \\ a_{4} & 0 & 0 & 0 \end{array}\right]$$

  assuming it is invertible.

  comment

• Paper 2, Section I, E

  Linear Algebra | Part IB, 2018

  Let $V$ be a real vector space. Define the dual vector space $V^{*}$ of $V$. If $U$ is a subspace of $V$, define the annihilator $U^{0}$ of $U$. If $x_{1}, x_{2}, \ldots, x_{n}$ is a basis for $V$, define its dual $x_{1}^{*}, x_{2}^{*}, \ldots, x_{n}^{*}$ and prove that it is a basis for $V^{*}$.

  If $V$ has basis $x_{1}, x_{2}, x_{3}, x_{4}$ and $U$ is the subspace spanned by

  $$x_{1}+2 x_{2}+3 x_{3}+4 x_{4} \quad \text { and } \quad 5 x_{1}+6 x_{2}+7 x_{3}+8 x_{4},$$

  give a basis for $U^{0}$ in terms of the dual basis $x_{1}^{*}, x_{2}^{*}, x_{3}^{*}, x_{4}^{*}$.

  comment

• Paper 2, Section II, E

  Linear Algebra | Part IB, 2018

  If $X$ is an $n \times m$ matrix over a field, show that there are invertible matrices $P$ and $Q$ such that

  $$Q^{-1} X P=\left[\begin{array}{cc} I_{r} & 0 \\ 0 & 0 \end{array}\right]$$

  for some $0 \leqslant r \leqslant \min (m, n)$, where $I_{r}$ is the identity matrix of dimension $r$.

  For a square matrix of the form $A=\left[\begin{array}{cc}B & D \\ 0 & C\end{array}\right]$ with $B$ and $C$ square matrices, prove that $\operatorname{det}(A)=\operatorname{det}(B) \operatorname{det}(C)$.

  If $A \in M_{n \times n}(\mathbb{C})$ and $B \in M_{m \times m}(\mathbb{C})$ have no common eigenvalue, show that the linear map

  $$\begin{aligned} L: M_{n \times m}(\mathbb{C}) & \longrightarrow M_{n \times m}(\mathbb{C}) \\ X & \longmapsto A X-X B \end{aligned}$$

  is injective.

  comment

• Paper 3, Section II, E

  Linear Algebra | Part IB, 2018

  State and prove the Cayley-Hamilton Theorem.

  Let $A$ be an $n \times n$ complex matrix. Using division of polynomials, show that if $p(x)$ is a polynomial then there is another polynomial $r(x)$ of degree at most $(n-1)$ such that $p(\lambda)=r(\lambda)$ for each eigenvalue $\lambda$ of $A$ and such that $p(A)=r(A)$.

  Hence compute the $(1,1)$ entry of the matrix $A^{1000}$ when

  $$A=\left[\begin{array}{ccc} 2 & -1 & 0 \\ 1 & -1 & 1 \\ -1 & -1 & 1 \end{array}\right]$$

  comment

• Paper 4, Section I, E

  Linear Algebra | Part IB, 2018

  Define a quadratic form on a finite dimensional real vector space. What does it mean for a quadratic form to be positive definite?

  Find a basis with respect to which the quadratic form

  $$x^{2}+2 x y+2 y^{2}+2 y z+3 z^{2}$$

  is diagonal. Is this quadratic form positive definite?

  comment

• Paper 4, Section II, E

  Linear Algebra | Part IB, 2018

  Let $V$ be a finite dimensional inner-product space over $\mathbb{C}$. What does it mean to say that an endomorphism of $V$ is self-adjoint? Prove that a self-adjoint endomorphism has real eigenvalues and may be diagonalised.

  An endomorphism $\alpha: V \rightarrow V$ is called positive definite if it is self-adjoint and satisfies $\langle\alpha(x), x\rangle>0$ for all non-zero $x \in V$; it is called negative definite if $-\alpha$ is positive definite. Characterise the property of being positive definite in terms of eigenvalues, and show that the sum of two positive definite endomorphisms is positive definite.

  Show that a self-adjoint endomorphism $\alpha: V \rightarrow V$ has all eigenvalues in the interval $[a, b]$ if and only if $\alpha-\lambda I$ is positive definite for all $\lambda<a$ and negative definite for all $\lambda>b$.

  Let $\alpha, \beta: V \rightarrow V$ be self-adjoint endomorphisms whose eigenvalues lie in the intervals $[a, b]$ and $[c, d]$ respectively. Show that all of the eigenvalues of $\alpha+\beta$ lie in the interval $[a+c, b+d]$.

  comment

Markov Chains

• Paper 1, Section II, H

  Markov Chains | Part IB, 2018

  A coin-tossing game is played by two players, $A_{1}$ and $A_{2}$. Each player has a coin and the probability that the coin tossed by player $A_{i}$ comes up heads is $p_{i}$, where $0<p_{i}<1, i=1,2$. The players toss their coins according to the following scheme: $A_{1}$ tosses first and then after each head, $A_{2}$ pays $A_{1}$ one pound and $A_{1}$ has the next toss, while after each tail, $A_{1}$ pays $A_{2}$ one pound and $A_{2}$ has the next toss.

  Define a Markov chain to describe the state of the game. Find the probability that the game ever returns to a state where neither player has lost money.

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2018

  For a finite irreducible Markov chain, what is the relationship between the invariant probability distribution and the mean recurrence times of states?

  A particle moves on the $2^{n}$ vertices of the hypercube, $\{0,1\}^{n}$, in the following way: at each step the particle is equally likely to move to each of the $n$ adjacent vertices, independently of its past motion. (Two vertices are adjacent if the Euclidean distance between them is one.) The initial vertex occupied by the particle is $(0,0, \ldots, 0)$. Calculate the expected number of steps until the particle

  (i) first returns to $(0,0, \ldots, 0)$,

  (ii) first visits $(0,0, \ldots, 0,1)$,

  (iii) first visits $(0,0, \ldots, 0,1,1)$.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2018

  The mathematics course at the University of Barchester is a three-year one. After the end-of-year examinations there are three possibilities:

  (i) failing and leaving (probability $p$ );

  (ii) taking that year again (probability $q$ );

  (iii) going on to the next year (or graduating, if the current year is the third one) (probability $r$ ).

  Thus there are five states for a student $\left(1^{\text {st }}\right.$ year, $2^{\text {nd }}$year, $3^{\text {rd }}$year, left without a degree, graduated).

  Write down the $5 \times 5$ transition matrix. Classify the states, assuming $p, q, r \in(0,1)$. Find the probability that a student will eventually graduate.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2018

  Let $P=\left(p_{i j}\right)_{i, j \in S}$ be the transition matrix for an irreducible Markov chain on the finite state space $S$.

  (a) What does it mean to say that a distribution $\pi$ is the invariant distribution for the chain?

  (b) What does it mean to say that the chain is in detailed balance with respect to a distribution $\pi$ ? Show that if the chain is in detailed balance with respect to a distribution $\pi$ then $\pi$ is the invariant distribution for the chain.

  (c) A symmetric random walk on a connected finite graph is the Markov chain whose state space is the set of vertices of the graph and whose transition probabilities are

  $$p_{i j}= \begin{cases}1 / D_{i} & \text { if } j \text { is adjacent to } i \\ 0 & \text { otherwise }\end{cases}$$

  where $D_{i}$ is the number of vertices adjacent to vertex $i$. Show that the random walk is in detailed balance with respect to its invariant distribution.

  comment

Methods

• Paper 1, Section II, 14C

  Methods | Part IB, 2018

  Define the convolution $f * g$ of two functions $f$ and $g$. Defining the Fourier transform $\tilde{f}$ of $f$ by

  $$\tilde{f}(k)=\int_{-\infty}^{\infty} \mathrm{e}^{-\mathrm{i} k x} f(x) \mathrm{d} x$$

  show that

  $$\widehat{f * g}(k)=\tilde{f}(k) \tilde{g}(k) .$$

  Given that the Fourier transform of $f(x)=1 / x$ is

  $$\tilde{f}(k)=-\mathrm{i} \pi \operatorname{sgn}(k),$$

  find the Fourier transform of $\sin (x) / x^{2}$.

  comment

• Paper 2, Section I, $5 \mathrm{C}$

  Methods | Part IB, 2018

  Show that

  $$a(x, y)\left(\frac{d y}{d s}\right)^{2}-2 b(x, y) \frac{d x}{d s} \frac{d y}{d s}+c(x, y)\left(\frac{d x}{d s}\right)^{2}=0$$

  along a characteristic curve $(x(s), y(s))$ of the $2^{\text {nd }}$-order pde

  $$a(x, y) u_{x x}+2 b(x, y) u_{x y}+c(x, y) u_{y y}=f(x, y)$$

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2018

  (a) Let $f(x)$ be a $2 \pi$-periodic function (i.e. $f(x)=f(x+2 \pi)$ for all $x$ ) defined on $[-\pi, \pi]$ by

  $$f(x)=\left\{\begin{array}{cl} x & x \in[0, \pi] \\ -x & x \in[-\pi, 0] \end{array}\right.$$

  Find the Fourier series of $f(x)$ in the form

  $$f(x)=\frac{1}{2} a_{0}+\sum_{n=1}^{\infty} a_{n} \cos (n x)+\sum_{n=1}^{\infty} b_{n} \sin (n x)$$

  (b) Find the general solution to

  $$y^{\prime \prime}+2 y^{\prime}+y=f(x)$$

  where $f(x)$ is as given in part (a) and $y(x)$ is $2 \pi$-periodic.

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2018

  (a) Determine the Green's function $G(x ; \xi)$ satisfying

  $$G^{\prime \prime}-4 G^{\prime}+4 G=\delta(x-\xi),$$

  with $G(0 ; \xi)=G(1 ; \xi)=0$. Here ' denotes differentiation with respect to $x$.

  (b) Using the Green's function, solve

  $$y^{\prime \prime}-4 y^{\prime}+4 y=e^{2 x}$$

  with $y(0)=y(1)=0$.

  comment

• Paper 3, Section II, A

  Methods | Part IB, 2018

  Consider the Dirac delta function, $\delta(x)$, defined by the sampling property

  $$\int_{-\infty}^{\infty} f(x) \delta\left(x-x_{0}\right) d x=f\left(x_{0}\right)$$

  for any suitable function $f(x)$ and real constant $x_{0}$.

  (a) Show that $\delta(\alpha x)=|\alpha|^{-1} \delta(x)$ for any non-zero $\alpha \in \mathbb{R}$.

  (b) Show that $x \delta^{\prime}(x)=-\delta(x)$, where ${ }^{\prime}$ denotes differentiation with respect to $x$.

  (c) Calculate

  $$\int_{-\infty}^{\infty} f(x) \delta^{(m)}(x) d x$$

  where $\delta^{(m)}(x)$ is the $m^{\text {th }}$derivative of the delta function.

  (d) For

  $$\gamma_{n}(x)=\frac{1}{\pi} \frac{n}{(n x)^{2}+1}$$

  show that $\lim _{n \rightarrow \infty} \gamma_{n}(x)=\delta(x)$.

  (e) Find expressions in terms of the delta function and its derivatives for

  (i)

  $$\lim _{n \rightarrow \infty} n^{3} x e^{-x^{2} n^{2}}$$

  (ii)

  $$\lim _{n \rightarrow \infty} \frac{1}{\pi} \int_{0}^{n} \cos (k x) d k .$$

  (f) Hence deduce that

  $$\lim _{n \rightarrow \infty} \frac{1}{2 \pi} \int_{-n}^{n} e^{i k x} d k=\delta(x)$$

  [You may assume that

  $$\left.\int_{-\infty}^{\infty} e^{-y^{2}} d y=\sqrt{\pi} \quad \text { and } \quad \int_{-\infty}^{\infty} \frac{\sin y}{y} d y=\pi .\right]$$

  comment

• Paper 4, Section I, A

  Methods | Part IB, 2018

  By using separation of variables, solve Laplace's equation

  $$\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}=0 \quad 0<x<1, \quad 0<y<1$$

  subject to

  $$\begin{array}{ll} u(0, y)=0 & 0 \leqslant y \leqslant 1 \\ u(1, y)=0 & 0 \leqslant y \leqslant 1 \\ u(x, 0)=0 & 0 \leqslant x \leqslant 1 \\ u(x, 1)=2 \sin (3 \pi x) & 0 \leqslant x \leqslant 1 \end{array}$$

  comment

• Paper 4, Section II, 17C

  Methods | Part IB, 2018

  Let $\Omega$ be a bounded region in the plane, with smooth boundary $\partial \Omega$. Green's second identity states that for any smooth functions $u, v$ on $\Omega$

  $$\int_{\Omega}\left(u \nabla^{2} v-v \nabla^{2} u\right) \mathrm{d} x \mathrm{~d} y=\oint_{\partial \Omega} u(\mathbf{n} \cdot \nabla v)-v(\mathbf{n} \cdot \nabla u) \mathrm{d} s$$

  where $\mathbf{n}$ is the outward pointing normal to $\partial \Omega$. Using this identity with $v$ replaced by

  $$G_{0}\left(\mathbf{x} ; \mathbf{x}_{0}\right)=\frac{1}{2 \pi} \ln \left(\left\|\mathbf{x}-\mathbf{x}_{0}\right\|\right)=\frac{1}{4 \pi} \ln \left(\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}\right)$$

  and taking care of the singular point $(x, y)=\left(x_{0}, y_{0}\right)$, show that if $u$ solves the Poisson equation $\nabla^{2} u=-\rho$ then

  $$\begin{aligned} u(\mathbf{x})=-\int_{\Omega} G_{0}\left(\mathbf{x} ; \mathbf{x}_{0}\right) \rho\left(\mathbf{x}_{0}\right) \mathrm{d} x_{0} \mathrm{~d} y_{0} \\ &+\oint_{\partial \Omega}\left(u\left(\mathbf{x}_{0}\right) \mathbf{n} \cdot \nabla G_{0}\left(\mathbf{x} ; \mathbf{x}_{0}\right)-G_{0}\left(\mathbf{x} ; \mathbf{x}_{0}\right) \mathbf{n} \cdot \nabla u\left(\mathbf{x}_{0}\right)\right) \mathrm{d} s \end{aligned}$$

  at any $\mathbf{x}=(x, y) \in \Omega$, where all derivatives are taken with respect to $\mathbf{x}_{0}=\left(x_{0}, y_{0}\right)$.

  In the case that $\Omega$ is the unit disc $\|\mathbf{x}\| \leqslant 1$, use the method of images to show that the solution to Laplace's equation $\nabla^{2} u=0$ inside $\Omega$, subject to the boundary condition

  $$u(1, \theta)=\delta(\theta-\alpha),$$

  is

  $$u(r, \theta)=\frac{1}{2 \pi} \frac{1-r^{2}}{1+r^{2}-2 r \cos (\theta-\alpha)}$$

  where $(r, \theta)$ are polar coordinates in the disc and $\alpha$ is a constant.

  [Hint: The image of a point $\mathbf{x}_{0} \in \Omega$ is the point $\mathbf{y}_{0}=\mathbf{x}_{0} /\left\|\mathbf{x}_{0}\right\|^{2}$, and then

  $$\left\|\mathbf{x}-\mathbf{x}_{0}\right\|=\left\|\mathbf{x}_{0}\right\|\left\|\mathbf{x}-\mathbf{y}_{0}\right\|$$

  for all $\mathbf{x} \in \partial \Omega .]$

  comment

Metric and Topological Spaces

• Paper 1, Section II, E

  Metric and Topological Spaces | Part IB, 2018

  What does it mean to say that a topological space is compact? Prove directly from the definition that $[0,1]$ is compact. Hence show that the unit circle $S^{1} \subset \mathbb{R}^{2}$ is compact, proving any results that you use. [You may use without proof the continuity of standard functions.]

  The set $\mathbb{R}^{2}$ has a topology $\mathcal{T}$ for which the closed sets are the empty set and the finite unions of vector subspaces. Let $X$ denote the set $\mathbb{R}^{2} \backslash\{0\}$ with the subspace topology induced by $\mathcal{T}$. By considering the subspace topology on $S^{1} \subset \mathbb{R}^{2}$, or otherwise, show that $X$ is compact.

  comment

• Paper 2, Section I, E

  Metric and Topological Spaces | Part IB, 2018

  What does it mean to say that $d$ is a metric on a set $X$ ? What does it mean to say that a subset of $X$ is open with respect to the metric $d$ ? Show that the collection of subsets of $X$ that are open with respect to $d$ satisfies the axioms of a topology.

  For $X=C[0,1]$, the set of continuous functions $f:[0,1] \rightarrow \mathbb{R}$, show that the metrics

  $$\begin{aligned} &d_{1}(f, g)=\int_{0}^{1}|f(x)-g(x)| \mathrm{d} x \\ &d_{2}(f, g)=\left[\int_{0}^{1}|f(x)-g(x)|^{2} \mathrm{~d} x\right]^{1 / 2} \end{aligned}$$

  give different topologies.

  comment

• Paper 3, Section I, $3 E$

  Metric and Topological Spaces | Part IB, 2018

  What does it mean to say that a topological space is connected? If $X$ is a topological space and $x \in X$, show that there is a connected subspace $K_{x}$ of $X$ so that if $S$ is any other connected subspace containing $x$ then $S \subseteq K_{x}$.

  Show that the sets $K_{x}$ partition $X$.

  comment

• Paper 4, Section II, E

  Metric and Topological Spaces | Part IB, 2018

  Let $X=\{2,3,4,5,6,7,8, \ldots\}$ and for each $n \in X$ let

  $$U_{n}=\{d \in X \mid d \text { divides } n\} .$$

  Prove that the set of unions of the sets $U_{n}$ forms a topology on $X$.

  Prove or disprove each of the following:

  (i) $X$ is Hausdorff;

  (ii) $X$ is compact.

  If $Y$ and $Z$ are topological spaces, $Y$ is the union of closed subspaces $A$ and $B$, and $f: Y \rightarrow Z$ is a function such that both $\left.f\right|_{A}: A \rightarrow Z$ and $\left.f\right|_{B}: B \rightarrow Z$ are continuous, show that $f$ is continuous. Hence show that $X$ is path-connected.

  comment

Numerical Analysis

• Paper 1, Section I, D

  Numerical Analysis | Part IB, 2018

  The Trapezoidal Rule for solving the differential equation

  $$y^{\prime}(t)=f(t, y), \quad t \in[0, T], \quad y(0)=y_{0}$$

  is defined by

  $$y_{n+1}=y_{n}+\frac{1}{2} h\left[f\left(t_{n}, y_{n}\right)+f\left(t_{n+1}, y_{n+1}\right)\right]$$

  where $h=t_{n+1}-t_{n}$.

  Determine the minimum order of convergence $k$ of this rule for general functions $f$ that are sufficiently differentiable. Show with an explicit example that there is a function $f$ for which the local truncation error is $A h^{k+1}$ for some constant $A$.

  comment

• Paper 1, Section II, D

  Numerical Analysis | Part IB, 2018

  Show that if $\mathbf{u} \in \mathbb{R}^{m} \backslash\{\mathbf{0}\}$ then the $m \times m$ matrix transformation

  $$H_{\mathbf{u}}=I-2 \frac{\mathbf{u} \mathbf{u}^{\top}}{\|\mathbf{u}\|^{2}}$$

  is orthogonal. Show further that, for any two vectors $\mathbf{a}, \mathbf{b} \in \mathbb{R}^{m}$ of equal length,

  $$H_{\mathbf{a}-\mathbf{b}} \mathbf{a}=\mathbf{b} .$$

  Explain how to use such transformations to convert an $m \times n$ matrix $A$ with $m \geqslant n$ into the form $A=Q R$, where $Q$ is an orthogonal matrix and $R$ is an upper-triangular matrix, and illustrate the method using the matrix

  $$A=\left[\begin{array}{rrr} 1 & -1 & 4 \\ 1 & 4 & -2 \\ 1 & 4 & 2 \\ 1 & -1 & 0 \end{array}\right]$$

  comment

• Paper 2, Section II, D

  Numerical Analysis | Part IB, 2018

  Show that the recurrence relation

  $$\begin{aligned} p_{0}(x) &=1 \\ p_{n+1}(x) &=q_{n+1}(x)-\sum_{k=0}^{n} \frac{\left\langle q_{n+1}, p_{k}\right\rangle}{\left\langle p_{k}, p_{k}\right\rangle} p_{k}(x) \end{aligned}$$

  where $\langle\cdot, \cdot\rangle$ is an inner product on real polynomials, produces a sequence of orthogonal, monic, real polynomials $p_{n}(x)$ of degree exactly $n$ of the real variable $x$, provided that $q_{n}$ is a monic, real polynomial of degree exactly $n$.

  Show that the choice $q_{n+1}(x)=x p_{n}(x)$ leads to a three-term recurrence relation of the form

  $$\begin{aligned} p_{0}(x) &=1 \\ p_{1}(x) &=x-\alpha_{0} \\ p_{n+1}(x) &=\left(x-\alpha_{n}\right) p_{n}(x)-\beta_{n} p_{n-1}(x) \end{aligned}$$

  where $\alpha_{n}$ and $\beta_{n}$ are constants that should be determined in terms of the inner products $\left\langle p_{n}, p_{n}\right\rangle,\left\langle p_{n-1}, p_{n-1}\right\rangle$ and $\left\langle p_{n}, x p_{n}\right\rangle$.

  Use this recurrence relation to find the first four monic Legendre polynomials, which correspond to the inner product defined by

  $$\langle p, q\rangle \equiv \int_{-1}^{1} p(x) q(x) d x$$

  comment

• Paper 3, Section II, D

  Numerical Analysis | Part IB, 2018

  Taylor's theorem for functions $f \in C^{k+1}[a, b]$ is given in the form

  $$f(x)=f(a)+(x-a) f^{\prime}(a)+\cdots+\frac{(x-a)^{k}}{k !} f^{(k)}(a)+R(x) .$$

  Use integration by parts to show that

  $$R(x)=\frac{1}{k !} \int_{a}^{x}(x-\theta)^{k} f^{(k+1)}(\theta) d \theta$$

  Let $\lambda_{k}$ be a linear functional on $C^{k+1}[a, b]$ such that $\lambda_{k}[p]=0$ for $p \in \mathbb{P}_{k}$. Show that

  $$\lambda_{k}[f]=\frac{1}{k !} \int_{a}^{b} K(\theta) f^{(k+1)}(\theta) d \theta$$

  where the Peano kernel function $K(\theta)=\lambda_{k}\left[(x-\theta)_{+}^{k}\right] . \quad[$ You may assume that the functional commutes with integration over a fixed interval.]

  The error in the mid-point rule for numerical quadrature on $[0,1]$ is given by

  $$e[f]=\int_{0}^{1} f(x) d x-f\left(\frac{1}{2}\right)$$

  Show that $e[p]=0$ if $p$ is a linear polynomial. Find the Peano kernel function corresponding to $e$ explicitly and verify the formula ( $\dagger$ ) in the case $f(x)=x^{2}$.

  comment

• Paper 4 , Section I, D

  Numerical Analysis | Part IB, 2018

  $$A=\left[\begin{array}{cccc} 1 & 2 & 1 & 2 \\ 2 & 5 & 5 & 6 \\ 1 & 5 & 13 & 14 \\ 2 & 6 & 14 & \lambda \end{array}\right], \quad b=\left[\begin{array}{l} 1 \\ 3 \\ 7 \\ \mu \end{array}\right]$$

  where $\lambda$ and $\mu$ are real parameters. Find the $L U$ factorisation of the matrix $A$. For what values of $\lambda$ does the equation $A x=b$ have a unique solution for $x$ ?

  For $\lambda=20$, use the $L U$ decomposition with forward and backward substitution to determine a value for $\mu$ for which a solution to $A x=b$ exists. Find the most general solution to the equation in this case.

  comment

Optimization

• Paper 1, Section I, 8H

  Optimization | Part IB, 2018

  What is meant by a transportation problem? Illustrate the transportation algorithm by solving the problem with three sources and three destinations described by the table

  

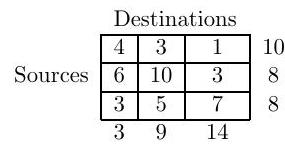
  where the figures in the boxes denote transportation costs, the right-hand column denotes supplies, and the bottom row denotes requirements.

  comment

• Paper 2, Section $I$, H

  Optimization | Part IB, 2018

  What does it mean to state that $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$ is a convex function?

  Suppose that $f, g: \mathbb{R}^{n} \rightarrow \mathbb{R}$ are convex functions, and for $b \in \mathbb{R}$ let

  $$\phi(b)=\inf \{f(x): g(x) \leqslant b\}$$

  Assuming $\phi(b)$ is finite for all $b \in \mathbb{R}$, prove that the function $\phi$ is convex.

  comment

• Paper 3, Section II, 21H

  Optimization | Part IB, 2018

  State and prove the Lagrangian Sufficiency Theorem.

  The manufacturers, $A$ and $B$, of two competing soap powders must plan how to allocate their advertising resources ( $X$ and $Y$ pounds respectively) among $n$ distinct geographical regions. If $x_{i} \geqslant 0$ and $y_{i} \geqslant 0$ denote, respectively, the resources allocated to area $i$ by $A$ and $B$ then the number of packets sold by $A$ and $B$ in area $i$ are

  $$\frac{x_{i} u_{i}}{x_{i}+y_{i}}, \quad \frac{y_{i} u_{i}}{x_{i}+y_{i}}$$

  respectively, where $u_{i}$ is the total market in area $i$, and $u_{1}, u_{2}, \ldots, u_{n}$ are known constants. The difference between the amount sold by $A$ and $B$ is then

  $$\sum_{i=1}^{n} \frac{x_{i}-y_{i}}{x_{i}+y_{i}} u_{i}$$

  $A$ seeks to maximize this quantity, while $B$ seeks to minimize it.

  (i) If $A$ knows $B$ 's allocation, how should $A$ choose $x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ ?

  (ii) Determine the best strategies for $A$ and $B$ if each assumes the other will know its strategy and react optimally.

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2018

  Given a network with a source $A$, a sink $B$, and capacities on directed edges, define a cut. What is meant by the capacity of a cut? State the max-flow min-cut theorem. If the capacities of edges are integral, what can be said about the maximum flow?

  Consider an $m \times n$ matrix $A$ in which each entry is either 0 or 1 . We say that a set of lines (rows or columns of the matrix) covers the matrix if each 1 belongs to some line of the set. We say that a set of 1 's is independent if no pair of 1 's of the set lie in the same line. Use the max-flow min-cut theorem to show that the maximal number of independent 1's equals the minimum number of lines that cover the matrix.

  comment

Quantum Mechanics

• Paper 1, Section II, B

  Quantum Mechanics | Part IB, 2018

  The relative motion of a neutron and proton is described by the Schrödinger equation for a single particle of mass $m$ under the influence of the central potential

  $$V(r)=\left\{\begin{array}{rr} -U & r<a \\ 0 & r>a \end{array}\right.$$

  where $U$ and $a$ are positive constants. Solve this equation for a spherically symmetric state of the deuteron, which is a bound state of a proton and a neutron, giving the condition on $U$ for this state to exist.

  [If $\psi$ is spherically symmetric then $\nabla^{2} \psi=\frac{1}{r} \frac{d^{2}}{d r^{2}}(r \psi)$.]

  comment

• Paper 2, Section II, B

  Quantum Mechanics | Part IB, 2018

  For an electron in a hydrogen atom, the stationary-state wavefunctions are of the form $\psi(r, \theta, \phi)=R(r) Y_{l m}(\theta, \phi)$, where in suitable units $R$ obeys the radial equation

  $$\frac{d^{2} R}{d r^{2}}+\frac{2}{r} \frac{d R}{d r}-\frac{l(l+1)}{r^{2}} R+2\left(E+\frac{1}{r}\right) R=0$$

  Explain briefly how the terms in this equation arise.

  This radial equation has bound-state solutions of energy $E=E_{n}$, where $E_{n}=-\frac{1}{2 n^{2}}(n=1,2,3, \ldots)$. Show that when $l=n-1$, there is a solution of the form $R(r)=r^{\alpha} e^{-r / n}$, and determine $\alpha$. Find the expectation value $\langle r\rangle$ in this state.

  Determine the total degeneracy of the energy level with energy $E_{n}$.

  comment

• Paper 3, Section I, B

  Quantum Mechanics | Part IB, 2018

  What is meant by the statement that an operator is Hermitian?

  Consider a particle of mass $m$ in a real potential $V(x)$ in one dimension. Show that the Hamiltonian of the system is Hermitian.

  Starting from the time-dependent Schrödinger equation, show that

  $$\frac{d}{d t}\langle\hat{x}\rangle=\frac{1}{m}\langle\hat{p}\rangle, \quad \frac{d}{d t}\langle\hat{p}\rangle=-\left\langle V^{\prime}(\hat{x})\right\rangle$$

  where $\hat{p}$ is the momentum operator and $\langle\hat{A}\rangle$ denotes the expectation value of the operator $\hat{A}$.

  comment

• Paper 3, Section II, B

  Quantum Mechanics | Part IB, 2018

  What is the physical significance of the expectation value

  $$\langle Q\rangle=\int \psi^{*}(x) Q \psi(x) d x$$

  of an observable $Q$ in the normalised state $\psi(x)$ ? Let $P$ and $Q$ be two observables. By considering the norm of $(Q+i \lambda P) \psi$ for real values of $\lambda$, show that

  $$\left\langle Q^{2}\right\rangle\left\langle P^{2}\right\rangle \geqslant \frac{1}{4}|\langle[Q, P]\rangle|^{2} .$$

  Deduce the generalised uncertainty relation

  $$\Delta Q \Delta P \geqslant \frac{1}{2}|\langle[Q, P]\rangle|,$$

  where the uncertainty $\Delta Q$ in the state $\psi(x)$ is defined by

  $$(\Delta Q)^{2}=\left\langle(Q-\langle Q\rangle)^{2}\right\rangle$$

  A particle of mass $m$ moves in one dimension under the influence of the potential $\frac{1}{2} m \omega^{2} x^{2}$. By considering the commutator $[x, p]$, show that every energy eigenvalue $E$ satisfies

  $$E \geqslant \frac{1}{2} \hbar \omega$$

  comment

• Paper 4, Section I, B

  Quantum Mechanics | Part IB, 2018

  A particle moving in one space dimension with wavefunction $\Psi(x, t)$ obeys the timedependent Schrödinger equation. Write down the probability density $\rho$ and current density $j$ in terms of the wavefunction and show that they obey the equation

  $$\frac{\partial j}{\partial x}+\frac{\partial \rho}{\partial t}=0$$

  Evaluate $j(x, t)$ in the case that

  $$\Psi(x, t)=\left(A e^{i k x}+B e^{-i k x}\right) e^{-i E t / \hbar}$$

  where $E=\hbar^{2} k^{2} / 2 m$, and $A$ and $B$ are constants, which may be complex.

  comment

Statistics

• Paper 1, Section I, H

  Statistics | Part IB, 2018

  $X_{1}, X_{2}, \ldots, X_{n}$ form a random sample from a distribution whose probability density function is

  $$f(x ; \theta)=\left\{\begin{array}{cc} \frac{2 x}{\theta^{2}} & 0 \leqslant x \leqslant \theta \\ 0 & \text { otherwise } \end{array}\right.$$

  where the value of the positive parameter $\theta$ is unknown. Determine the maximum likelihood estimator of the median of this distribution.

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2018

  (a) Consider the general linear model $Y=X \theta+\varepsilon$ where $X$ is a known $n \times p$ matrix, $\theta$ is an unknown $p \times 1$ vector of parameters, and $\varepsilon$ is an $n \times 1$ vector of independent $N\left(0, \sigma^{2}\right)$ random variables with unknown variances $\sigma^{2}$. Show that, provided the matrix $X$ is of rank $p$, the least squares estimate of $\theta$ is

  $$\hat{\theta}=\left(X^{\mathrm{T}} X\right)^{-1} X^{\mathrm{T}} Y$$

  Let

  $$\hat{\varepsilon}=Y-X \hat{\theta}$$

  What is the distribution of $\hat{\varepsilon}^{\mathrm{T}} \hat{\varepsilon}$ ? Write down, in terms of $\hat{\varepsilon}^{\mathrm{T}} \hat{\varepsilon}$, an unbiased estimator of $\sigma^{2}$.

  (b) Four points on the ground form the vertices of a plane quadrilateral with interior angles $\theta_{1}, \theta_{2}, \theta_{3}, \theta_{4}$, so that $\theta_{1}+\theta_{2}+\theta_{3}+\theta_{4}=2 \pi$. Aerial observations $Z_{1}, Z_{2}, Z_{3}, Z_{4}$ are made of these angles, where the observations are subject to independent errors distributed as $N\left(0, \sigma^{2}\right)$ random variables.

  (i) Represent the preceding model as a general linear model with observations $\left(Z_{1}, Z_{2}, Z_{3}, Z_{4}-2 \pi\right)$ and unknown parameters $\left(\theta_{1}, \theta_{2}, \theta_{3}\right)$.

  (ii) Find the least squares estimates $\hat{\theta}_{1}, \hat{\theta}_{2}, \hat{\theta}_{3}$.

  (iii) Determine an unbiased estimator of $\sigma^{2}$. What is its distribution?

  comment

• Paper 2, Section I, $8 \mathrm{H}$

  Statistics | Part IB, 2018

  Define a simple hypothesis. Define the terms size and power for a test of one simple hypothesis against another. State the Neyman-Pearson lemma.

  There is a single observation of a random variable $X$ which has a probability density function $f(x)$. Construct a best test of size $0.05$ for the null hypothesis

  $$H_{0}: \quad f(x)=\frac{1}{2}, \quad-1 \leqslant x \leqslant 1,$$

  against the alternative hypothesis

  $$H_{1}: \quad f(x)=\frac{3}{4}\left(1-x^{2}\right), \quad-1 \leqslant x \leqslant 1 .$$

  Calculate the power of your test.

  comment

• Paper 3, Section II, H

  Statistics | Part IB, 2018

  A treatment is suggested for a particular illness. The results of treating a number of patients chosen at random from those in a hospital suffering from the illness are shown in the following table, in which the entries $a, b, c, d$ are numbers of patients.

  $\begin{array}{lcc} & \text { Recovery } & \text { Non-recovery } \\ \text { Untreated } & a & b \\ \text { Treated } & c & d\end{array}$

  Describe the use of Pearson's $\chi^{2}$ statistic in testing whether the treatment affects recovery, and outline a justification derived from the generalised likelihood ratio statistic. Show that

  $$\chi^{2}=\frac{(a d-b c)^{2}(a+b+c+d)}{(a+b)(c+d)(a+c)(b+d)}$$

  [Hint: You may find it helpful to observe that $a(a+b+c+d)-(a+b)(a+c)=a d-b c .]$

  Comment on the use of this statistical technique when

  $$a=50, \quad b=10, \quad c=15, \quad d=5 .$$

  comment

• Paper 4, Section II, H

  Statistics | Part IB, 2018

  There is widespread agreement amongst the managers of the Reliable Motor Company that the number $X$ of faulty cars produced in a month has a binomial distribution

  $$P(X=s)=\left(\begin{array}{c} n \\ s \end{array}\right) p^{s}(1-p)^{n-s} \quad(s=0,1, \ldots, n ; \quad 0 \leqslant p \leqslant 1)$$

  where $n$ is the total number of cars produced in a month. There is, however, some dispute about the parameter $p$. The general manager has a prior distribution for $p$ which is uniform, while the more pessimistic production manager has a prior distribution with density $2 p$, both on the interval $[0,1]$.

  In a particular month, $s$ faulty cars are produced. Show that if the general manager's loss function is $(\hat{p}-p)^{2}$, where $\hat{p}$ is her estimate and $p$ the true value, then her best estimate of $p$ is

  $$\hat{p}=\frac{s+1}{n+2}$$

  The production manager has responsibilities different from those of the general manager, and a different loss function given by $(1-p)(\hat{p}-p)^{2}$. Find his best estimate of $p$ and show that it is greater than that of the general manager unless $s \geqslant \frac{1}{2} n$.

  [You may use the fact that for non-negative integers $\alpha, \beta$,

  $$\left.\int_{0}^{1} p^{\alpha}(1-p)^{\beta} d p=\frac{\alpha ! \beta !}{(\alpha+\beta+1) !}\right]$$

  comment

Variational Principles

• Paper 1, Section I, B

  Variational Principles | Part IB, 2018

  Find, using a Lagrange multiplier, the four stationary points in $\mathbb{R}^{3}$ of the function $x^{2}+y^{2}+z^{2}$ subject to the constraint $x^{2}+2 y^{2}-z^{2}=1$. By sketching sections of the constraint surface in each of the coordinate planes, or otherwise, identify the nature of the constrained stationary points.

  How would the location of the stationary points differ if, instead, the function $x^{2}+2 y^{2}-z^{2}$ were subject to the constraint $x^{2}+y^{2}+z^{2}=1 ?$

  comment

• Paper 2, Section II, B

  Variational Principles | Part IB, 2018

  Derive the Euler-Lagrange equation for the integral

  $$I[y]=\int_{x_{0}}^{x_{1}} f\left(y, y^{\prime}, y^{\prime \prime}, x\right) d x$$

  when $y(x)$ and $y^{\prime}(x)$ take given values at the fixed endpoints.

  Show that the only function $y(x)$ with $y(0)=1, y^{\prime}(0)=2$ and $y(x) \rightarrow 0$ as $x \rightarrow \infty$ for which the integral

  $$I[y]=\int_{0}^{\infty}\left(y^{2}+\left(y^{\prime}\right)^{2}+\left(y^{\prime}+y^{\prime \prime}\right)^{2}\right) d x$$

  is stationary is $(3 x+1) e^{-x}$.

  comment

• Paper 3, Section I, B

  Variational Principles | Part IB, 2018

  For a particle of unit mass moving freely on a unit sphere, the Lagrangian in polar coordinates is

  $$L=\frac{1}{2} \dot{\theta}^{2}+\frac{1}{2} \sin ^{2} \theta \dot{\phi}^{2}$$

  Determine the equations of motion. Show that $l=\sin ^{2} \theta \dot{\phi}$ is a conserved quantity, and use this result to simplify the equation of motion for $\theta$. Deduce that

  $$h=\dot{\theta}^{2}+\frac{l^{2}}{\sin ^{2} \theta}$$

  is a conserved quantity. What is the interpretation of $h$ ?

  comment

• Paper 4, Section II, B

  Variational Principles | Part IB, 2018

  (a) A two-dimensional oscillator has action

  $$S=\int_{t_{0}}^{t_{1}}\left\{\frac{1}{2} \dot{x}^{2}+\frac{1}{2} \dot{y}^{2}-\frac{1}{2} \omega^{2} x^{2}-\frac{1}{2} \omega^{2} y^{2}\right\} d t$$

  Find the equations of motion as the Euler-Lagrange equations associated with $S$, and use them to show that

  $$J=\dot{x} y-\dot{y} x$$

  is conserved. Write down the general solution of the equations of motion in terms of $\sin \omega t$ and $\cos \omega t$, and evaluate $J$ in terms of the coefficients that arise in the general solution.

  (b) Another kind of oscillator has action

  $$\widetilde{S}=\int_{t_{0}}^{t_{1}}\left\{\frac{1}{2} \dot{x}^{2}+\frac{1}{2} \dot{y}^{2}-\frac{1}{4} \alpha x^{4}-\frac{1}{2} \beta x^{2} y^{2}-\frac{1}{4} \alpha y^{4}\right\} d t$$

  where $\alpha$ and $\beta$ are real constants. Find the equations of motion and use these to show that in general $J=\dot{x} y-\dot{y} x$ is not conserved. Find the special value of the ratio $\beta / \alpha$ for which $J$ is conserved. Explain what is special about the action $\widetilde{S}$in this case, and state the interpretation of $J$.

  comment