Part IB, 2009

Analysis II

• Paper 1, Section II, E

  Analysis II | Part IB, 2009

  Define a function $f: \mathbb{R} \rightarrow \mathbb{R}$ by

  $$f(x)=\sum_{n=1}^{\infty} 2^{-n}\left\|2^{n} x\right\|$$

  where $\|t\|$ is the distance from $t$ to the nearest integer. Prove that $f$ is continuous. [Results about uniform convergence may not be used unless they are clearly stated and proved.]

  Suppose now that $g: \mathbb{R} \rightarrow \mathbb{R}$ is a function which is differentiable at some point $x$, and let $\left(u_{n}\right)_{n=1}^{\infty},\left(v_{n}\right)_{n=1}^{\infty}$ be two sequences of real numbers with $u_{n} \leqslant x \leqslant v_{n}$ for all $n$, $u_{n} \neq v_{n}$ and $u_{n}, v_{n} \rightarrow x$ as $n \rightarrow \infty$. Prove that

  $$\lim _{n \rightarrow \infty} \frac{g\left(v_{n}\right)-g\left(u_{n}\right)}{v_{n}-u_{n}}$$

  exists.

  By considering appropriate sequences of rationals with denominator $2^{-n}$, or otherwise, show that $f$ is nowhere differentiable.

  comment

• Paper 2, Section I, E

  Analysis II | Part IB, 2009

  State and prove the contraction mapping theorem. Let $f(x)=e^{-x}$. By considering $f(f(x))$ and using the contraction mapping theorem, show that there is a unique real number $x$ such that $x=e^{-x}$.

  comment

• Paper 2, Section II, E

  Analysis II | Part IB, 2009

  Let $U \subseteq \mathbb{R}^{n}$ be a set. What does it mean to say that $U$ is open? Show that if $U$ is open and if $f: U \rightarrow\{0,1\}$ is a continuous function then $f$ is also differentiable, and that its derivative is zero.

  Suppose that $g: U \rightarrow \mathbb{R}$ is differentiable and that $\left\|\left.(D g)\right|_{x}\right\| \leqslant M$ for all $x$, where $\left.(D g)\right|_{x}$ denotes the derivative of $g$ at $x$ and $\|\cdot\|$ is the operator norm. Suppose that $\mathbf{a}, \mathbf{b} \in \mathbb{R}^{n}$ and that the line segment $[\mathbf{a}, \mathbf{b}]=\{\lambda \mathbf{a}+(1-\lambda) \mathbf{b}: \lambda \in[0,1]\}$ lies wholly in $U$. Prove that $|g(\mathbf{a})-g(\mathbf{b})| \leqslant M\|\mathbf{a}-\mathbf{b}\|$.

  Let $\ell_{1}, \ldots, \ell_{k}$ be (infinite) lines in $\mathbb{R}^{3}$, and write $V=\mathbb{R}^{3} \backslash\left(\ell_{1} \cup \cdots \cup \ell_{k}\right)$. If $\mathbf{a}, \mathbf{b} \in V$, show that there is some $\mathbf{c} \in V$ such that the line segments $[\mathbf{a}, \mathbf{c}]$ and $[\mathbf{c}, \mathbf{b}]$ both lie inside V. [You may assume without proof that $\mathbb{R}^{3}$ may not be written as the union of finitely many planes.]

  Show that if $V \rightarrow\{0,1\}$ is a continuous function then $f$ is constant on $V$.

  comment

• Paper 3, Section I, E

  Analysis II | Part IB, 2009

  What is meant by a norm on $\mathbb{R}^{n}$ ? For $\mathbf{x} \in \mathbb{R}^{n}$ write

  $$\begin{gathered} \|\mathbf{x}\|_{1}=\left|x_{1}\right|+\left|x_{2}\right|+\cdots+\left|x_{n}\right| \\ \|\mathbf{x}\|_{2}=\sqrt{\left|x_{1}\right|^{2}+\left|x_{2}\right|^{2}+\cdots+\left|x_{n}\right|^{2}} \end{gathered}$$

  Prove that $\|\cdot\|_{1}$ and $\|\cdot\|_{2}$ are norms. [You may assume the Cauchy-Schwarz inequality.]

  Find the smallest constant $C_{n}$ such that $\|x\|_{1} \leqslant C_{n}\|x\|_{2}$ for all $x \in \mathbb{R}^{n}$, and also the smallest constant $C_{n}^{\prime}$ such that $\|x\|_{2} \leqslant C_{n}^{\prime}\|x\|_{1}$ for all $x \in \mathbb{R}^{n}$.

  comment

• Paper 3, Section II, E

  Analysis II | Part IB, 2009

  What does it mean for a function $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ of several variables to be differentiable at a point $x$ ? State and prove the chain rule for functions of several variables. For each of the following two functions from $\mathbb{R}^{2}$ to $\mathbb{R}$, give with proof the set of points at which it is differentiable:

  $$\begin{aligned} &g_{1}(x, y)= \begin{cases}\left(x^{2}-y^{2}\right) \sin \frac{1}{x^{2}-y^{2}} & \text { if } x \neq \pm y \\ 0 & \text { otherwise; }\end{cases} \\ &g_{2}(x, y)= \begin{cases}\left(x^{2}+y^{2}\right) \sin \frac{1}{x^{2}+y^{2}} & \text { if at least one of } x, y \text { is not } 0 \\ 0 & \text { if } x=y=0\end{cases} \end{aligned}$$

  comment

• Paper 4, Section I, E

  Analysis II | Part IB, 2009

  Let $\left(s_{n}\right)_{n=1}^{\infty}$ be a sequence of continuous functions from $\mathbb{R}$ to $\mathbb{R}$ and let $s: \mathbb{R} \rightarrow \mathbb{R}$ be another continuous function. What does it mean to say that $s_{n} \rightarrow s$ uniformly? Give examples (without proof) of a sequence $\left(s_{n}\right)$ of nonzero functions which converges to 0 uniformly, and of a sequence which converges to 0 pointwise but not uniformly. Show that if $s_{n} \rightarrow s$ uniformly then

  $$\int_{-1}^{1} s_{n}(x) d x \rightarrow \int_{-1}^{1} s(x) d x$$

  Give an example of a continuous function $s: \mathbb{R} \rightarrow \mathbb{R}$ with $s(x) \geqslant 0$ for all $x, s(x) \rightarrow 0$ as $|x| \rightarrow \infty$ but for which $\int_{-\infty}^{\infty} s(x) d x$ does not converge. For each positive integer $n$ define $s_{n}(x)$ to be equal to $s(x)$ if $|x| \leqslant n$, and to be $s(n) \min \left(1,|| x|-n|^{-2}\right)$ for $|x|>n$. Show that the functions $s_{n}$ are continuous, tend uniformly to $s$, and furthermore that $\int_{-\infty}^{\infty} s_{n}(x) d x$ exists and is finite for all $n$.

  comment

• Paper 4, Section II, E

  Analysis II | Part IB, 2009

  Let $(X, d)$ be a metric space with at least two points. If $f: X \rightarrow \mathbb{R}$ is a function, write

  $$\operatorname{Lip}(f)=\sup _{x \neq y} \frac{|f(x)-f(y)|}{d(x, y)}+\sup _{z}|f(z)|$$

  provided that this supremum is finite. $\operatorname{Let} \operatorname{Lip}(X)=\{f: \operatorname{Lip}(f)$ is defined $\}$. Show that $\operatorname{Lip}(X)$ is a vector space over $\mathbb{R}$, and that Lip is a norm on it.

  Now let $X=\mathbb{R}$. Suppose that $\left(f_{i}\right)_{i=1}^{\infty}$ is a sequence of functions with $\operatorname{Lip}\left(f_{i}\right) \leqslant 1$ and with the property that the sequence $f_{i}(q)$ converges as $i \rightarrow \infty$ for every rational number $q$. Show that the $f_{i}$ converge pointwise to a function $f$ satisfying $\operatorname{Lip}(f) \leqslant 1$.

  Suppose now that $\left(f_{i}\right)_{i=1}^{\infty}$ are any functions with $\operatorname{Lip}\left(f_{i}\right) \leqslant 1$. Show that there is a subsequence $f_{i_{1}}, f_{i_{2}}, \ldots$ which converges pointwise to a function $f$ with $\operatorname{Lip}(f) \leqslant 1$.

  comment

Complex Analysis

• Paper 3, Section II, E

  Complex Analysis | Part IB, 2009

  For each positive real number $R$ write $B_{R}=\{z \in \mathbb{C}:|z| \leqslant R\}$. If $F$ is holomorphic on some open set containing $B_{R}$, we define

  $$J(F, R)=\frac{1}{2 \pi} \int_{0}^{2 \pi} \log \left|F\left(R e^{i \theta}\right)\right| d \theta$$

  1. If $F_{1}, F_{2}$ are both holomorphic on some open set containing $B_{R}$, show that $J\left(F_{1} F_{2}, R\right)=$ $J\left(F_{1}, R\right)+J\left(F_{2}, R\right) .$

  2. Suppose that $F(0)=1$ and that $F$ does not vanish on some open set containing $B_{R}$. By showing that there is a holomorphic branch of logarithm of $F$ and then considering $z^{-1} \log F(z)$, prove that $J(F, R)=0$.

  3. Suppose that $|w|<R$. Prove that the function $\psi_{W, R}(z)=R(z-w) /\left(R^{2}-\bar{w} z\right)$ has modulus 1 on $|z|=R$ and hence that it satisfies $J\left(\psi_{W, R}, R\right)=0$.

  Suppose now that $F: \mathbb{C} \rightarrow \mathbb{C}$ is holomorphic and not identically zero, and let $R$ be such that no zeros of $F$ satisfy $|z|=R$. Briefly explain why there are only finitely many zeros of $F$ in $B_{R}$ and, assuming these are listed with the correct multiplicity, derive a formula for $J(F, R)$ in terms of the zeros, $R$, and $F(0)$.

  Suppose that $F$ has a zero at every lattice point (point with integer coordinates) except for $(0,0)$. Show that there is a constant $c>0$ such that $\left|F\left(z_{i}\right)\right|>e^{c\left|z_{i}\right|^{2}}$ for a sequence $z_{1}, z_{2}, \ldots$ of complex numbers tending to infinity.

  comment

• Paper 4, Section I, E

  Complex Analysis | Part IB, 2009

  State Rouché's Theorem. How many complex numbers $z$ are there with $|z| \leqslant 1$ and $2 z=\sin z ?$

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, D

  Complex Analysis or Complex Methods | Part IB, 2009

  Let $f(z)=u(x, y)+i v(x, y)$, where $z=x+i y$, be an analytic function of $z$ in a domain $D$ of the complex plane. Derive the Cauchy-Riemann equations relating the partial derivatives of $u$ and $v$.

  For $u=e^{-x} \cos y$, find $v$ and hence $f(z)$.

  comment

• Paper 1, Section II, D

  Complex Analysis or Complex Methods | Part IB, 2009

  Consider the real function $f(t)$ of a real variable $t$ defined by the following contour integral in the complex $s$-plane:

  $$f(t)=\frac{1}{2 \pi i} \int_{\Gamma} \frac{e^{s t}}{\left(s^{2}+1\right) s^{1 / 2}} d s,$$

  where the contour $\Gamma$ is the line $s=\gamma+i y,-\infty<y<\infty$, for constant $\gamma>0$. By closing the contour appropriately, show that

  $$f(t)=\sin (t-\pi / 4)+\frac{1}{\pi} \int_{0}^{\infty} \frac{e^{-r t} d r}{\left(r^{2}+1\right) r^{1 / 2}}$$

  when $t>0$ and is zero when $t<0$. You should justify your evaluation of the inversion integral over all parts of the contour.

  By expanding $\left(r^{2}+1\right)^{-1} r^{-1 / 2}$ as a power series in $r$, and assuming that you may integrate the series term by term, show that the two leading terms, as $t \rightarrow \infty$, are

  $$f(t) \sim \sin (t-\pi / 4)+\frac{1}{(\pi t)^{1 / 2}}+\cdots$$

  [You may assume that $\int_{0}^{\infty} x^{-1 / 2} e^{-x} d x=\pi^{1 / 2}$.]

  comment

• Paper 2, Section II, D

  Complex Analysis or Complex Methods | Part IB, 2009

  Show that both the following transformations from the $z$-plane to the $\zeta$-plane are conformal, except at certain critical points which should be identified in both planes, and in each case find a domain in the $z$-plane that is mapped onto the upper half $\zeta$-plane:

  $$\begin{aligned} &\text { (i) } \zeta=z+\frac{b^{2}}{z} \\ &\text { (ii) } \zeta=\cosh \frac{\pi z}{b} \end{aligned}$$

  where $b$ is real and positive.

  comment

Complex Methods

• Paper 3, Section I, $5 \mathrm{D}$

  Complex Methods | Part IB, 2009

  Use the residue calculus to evaluate (i) $\oint_{C} z e^{1 / z} d z$ and (ii) $\oint_{C} \frac{z d z}{1-4 z^{2}}$,

  where $C$ is the circle $|z|=1$.

  comment

• Paper 4, Section II, D

  Complex Methods | Part IB, 2009

  The function $u(x, y)$ satisfies Laplace's equation in the half-space $y \geqslant 0$, together with boundary conditions

  $$\begin{gathered} u(x, y) \rightarrow 0 \text { as } y \rightarrow \infty \text { for all } x \\ u(x, 0)=u_{0}(x), \text { where } x u_{0}(x) \rightarrow 0 \text { as }|x| \rightarrow \infty \end{gathered}$$

  Using Fourier transforms, show that

  $$u(x, y)=\int_{-\infty}^{\infty} u_{0}(t) v(x-t, y) d t$$

  where

  $$v(x, y)=\frac{y}{\pi\left(x^{2}+y^{2}\right)}$$

  Suppose that $u_{0}(x)=\left(x^{2}+a^{2}\right)^{-1}$. Using contour integration and the convolution theorem, or otherwise, show that

  $$u(x, y)=\frac{y+a}{a\left[x^{2}+(y+a)^{2}\right]}$$

  [You may assume the convolution theorem of Fourier transforms, i.e. that if $\tilde{f}(k), \tilde{g}(k)$ are the Fourier transforms of two functions $f(x), g(x)$, then $\tilde{f}(k) \tilde{g}(k)$ is the Fourier transform of $\int_{-\infty}^{\infty} f(t) g(x-t) d t$.]

  comment

Electromagnetism

• Paper 1, Section II, A

  Electromagnetism | Part IB, 2009

  Suppose the region $z<0$ is occupied by an earthed ideal conductor.

  (a) Derive the boundary conditions on the tangential electric field $\mathbf{E}$ that hold on the surface $z=0$.

  (b) A point charge $q$, with mass $m$, is held above the conductor at $(0,0, d)$. Show that the boundary conditions on the electric field are satisfied if we remove the conductor and instead place a second charge $-q$ at $(0,0,-d)$.

  (c) The original point charge is now released with zero initial velocity. Ignoring gravity, determine how long it will take for the charge to hit the plane.

  comment

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2009

  For a volume $V$ with surface $S$, state Gauss's Law relating the flux of $\mathbf{E}$ across $S$ to the total charge within $V$.

  A uniformly charged sphere of radius $R$ has total charge $Q$.

  (a) Find the electric field inside the sphere.

  (b) Using the differential relation $d \mathbf{F}=\mathbf{E} d q$ between the force $d \mathbf{F}$ on a small charge $d q$ in an electric field $\mathbf{E}$, find the force on the top half of the sphere due to its bottom half. Express your answer in terms of $R$ and $Q$.

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2009

  Starting from Maxwell's equations in vacuo, show that the cartesian components of $\mathbf{E}$ and $\mathbf{B}$ each satisfy

  $$\nabla^{2} f=\frac{1}{c^{2}} \frac{\partial^{2} f}{\partial t^{2}}$$

  Consider now a rectangular waveguide with its axis along $z$, width $a$ along $x$ and $b$ along $y$, with $a \geqslant b$. State and explain the boundary conditions on the fields $\mathbf{E}$ and $\mathbf{B}$ at the interior waveguide surfaces.

  One particular type of propagating wave has

  $$\mathbf{B}(x, y, z, t)=B_{0}(x, y) \hat{\mathbf{z}} e^{i(k z-\omega t)}$$

  Show that

  $$B_{x}=\frac{i}{(\omega / c)^{2}-k^{2}}\left(k \frac{\partial B_{z}}{\partial x}-\frac{\omega}{c^{2}} \frac{\partial E_{z}}{\partial y}\right)$$

  and derive an equivalent expression for $B_{y}$.

  Assume now that $E_{z}=0$. Write down the equation satisfied by $B_{z}$, find separable solutions, and show that the above implies Neumann boundary conditions on $B_{z}$. Find the "cutoff frequency" below which travelling waves do not propagate. For higher frequencies, find the wave velocity and the group velocity and explain the significance of your results.

  comment

• Paper 3, Section II, A

  Electromagnetism | Part IB, 2009

  Two long thin concentric perfectly conducting cylindrical shells of radii $a$ and $b$ $(a<b)$ are connected together at one end by a resistor of resistance $R$, and at the other by a battery that establishes a potential difference $V$. Thus, a current $I=V / R$ flows in opposite directions along each of the cylinders.

  (a) Using Ampère's law, find the magnetic field $\mathbf{B}$ in between the cylinders.

  (b) Using Gauss's law and the integral relationship between the potential and the electric field, or otherwise, show that the charge per unit length on the inner cylinder is

  $$\lambda=\frac{2 \pi \epsilon_{0} V}{\ln (b / a)}$$

  and also calculate the radial electric field.

  (c) Calculate the Poynting vector and by suitable integration verify that the power delivered by the system is $V^{2} / R$.

  comment

• Paper 4, Section I, A

  Electromagnetism | Part IB, 2009

  State the relationship between the induced EMF $V$ in a loop and the flux $\Phi$ through it. State the force law for a current-carrying wire in a magnetic field $\mathbf{B}$.

  A rectangular loop of wire with mass $m$, width $w$, vertical length $l$, and resistance $R$ falls out of a magnetic field under the influence of gravity. The magnetic field is $\mathbf{B}=B \hat{\mathbf{x}}$ for $z \geqslant 0$ and $\mathbf{B}=0$ for $z<0$, where $B$ is constant. Suppose the loop lies in the $(y, z)$ plane, with its top initially at $z=z_{0}<l$. Find the equation of motion for the loop and its terminal velocity, assuming that the loop continues to intersect the plane $z=0$.

  comment

Fluid Dynamics

• Paper 1, Section I, D

  Fluid Dynamics | Part IB, 2009

  A steady velocity field $\mathbf{u}=\left(u_{r}, u_{\theta}, u_{z}\right)$ is given in cylindrical polar coordinates $(r, \theta, z)$ by

  $$u_{r}=-\alpha r, \quad u_{\theta}=\frac{\gamma}{r}\left(1-e^{-\beta r^{2}}\right), \quad u_{z}=2 \alpha z$$

  where $\alpha, \beta, \gamma$ are positive constants.

  Show that this represents a possible flow of an incompressible fluid, and find the vorticity $\omega$.

  Show further that

  $$\operatorname{curl}(\mathbf{u} \wedge \boldsymbol{\omega})=-\nu \nabla^{2} \boldsymbol{\omega}$$

  for a constant $\nu$ which should be calculated.

  [The divergence and curl operators in cylindrical polars are given by

  $$\begin{aligned} \operatorname{div} \mathbf{u} &=\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{r}\right)+\frac{1}{r} \frac{\partial u_{\theta}}{\partial \theta}+\frac{\partial u_{z}}{\partial z} \\ \operatorname{curl} \mathbf{u} &=\left(\frac{1}{r} \frac{\partial u_{z}}{\partial \theta}-\frac{\partial u_{\theta}}{\partial z}, \frac{\partial u_{r}}{\partial z}-\frac{\partial u_{z}}{\partial r}, \frac{1}{r} \frac{\partial}{\partial r}\left(r u_{\theta}\right)-\frac{1}{r} \frac{\partial u_{r}}{\partial \theta}\right) \\ \text { and ,when } \boldsymbol{\omega} &=[0,0, \omega(r, z)], \\ \nabla^{2} \boldsymbol{\omega} &\left.=\left[0,0, \frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \omega}{\partial r}\right)+\frac{\partial^{2} \omega}{\partial z^{2}}\right] .\right] \end{aligned}$$

  comment

• Paper 1, Section II, D

  Fluid Dynamics | Part IB, 2009

  A canal has uniform width and a bottom that is horizontal apart from a localised slowly-varying hump of height $D(x)$ whose maximum value is $D_{\text {max }}$. Far upstream the water has depth $h_{1}$ and velocity $u_{1}$. Show that the depth $h(x)$ of the water satisfies the following equation:

  $$\frac{D(x)}{h_{1}}=1-\frac{h}{h_{1}}-\frac{F}{2}\left(\frac{h_{1}^{2}}{h^{2}}-1\right)$$

  where $F=u_{1}^{2} / g h_{1}$.

  Describe qualitatively how $h(x)$ varies as the flow passes over the hump in the three cases

  $$\begin{array}{ll} \text { (i) } F<1 & \text { and } D_{\max }<D^{*} \\ \text { (ii) } F>1 & \text { and } D_{\max }<D^{*} \\ \text { (iii) } \quad D_{\max } & =D^{*}, \end{array}$$

  where $D^{*}=h_{1}\left(1-\frac{3}{2} F^{1 / 3}+\frac{1}{2} F\right)$.

  Calculate the water depth far downstream in case (iii) when $F<1$.

  comment

• Paper 2, Section I, D

  Fluid Dynamics | Part IB, 2009

  A fireman's hose full of water has cross-sectional area $A_{0}$, apart from a smooth contraction to the outlet nozzle which has cross-sectional area $A_{1}<A_{0}$. The volume flow rate of water through the hose is $Q$.

  Use Bernoulli's equation to calculate the pressure in the main part of the tube (relative to atmospheric pressure). Then use the integral momentum equation in the direction of the flow to show that the force $F$ that the fireman has to exert on the nozzle to keep it still is given by

  $$F=\frac{\rho Q^{2}}{2 A_{0}}\left(\frac{A_{0}}{A_{1}}-1\right)^{2}$$

  where $\rho$ is the density of water.

  comment

• Paper 3, Section II, D

  Fluid Dynamics | Part IB, 2009

  Starting from Euler's equations for an inviscid incompressible fluid of density $\rho$ with no body force, undergoing irrotational motion, show that the pressure $p$ is given by

  $$\frac{p}{\rho}+\frac{\partial \phi}{\partial t}+\frac{1}{2}(\nabla \phi)^{2}=F(t)$$

  for some function $F(t)$, where $\phi$ is the velocity potential.

  The fluid occupies an infinite domain and contains a spherical gas bubble of radius $R(t)$ in which the pressure is $p_{g}$. The pressure in the fluid at infinity is $p_{\infty}$.

  Show that

  $$\ddot{R} R+\frac{3}{2} \dot{R}^{2}=\frac{p_{g}-p_{\infty}}{\rho}$$

  The bubble contains a fixed mass $M$ of gas in which

  $$p_{g}=C\left(M / R^{3}\right)^{2}$$

  for a constant $C$. At time $t=0, R=R_{0}, \dot{R}=0$ and $p_{g}=p_{\infty} / 2$. Show that

  $$\dot{R}^{2} R^{3}=\frac{p_{\infty}}{\rho}\left[R_{0}^{3}-\frac{R_{0}^{6}}{3 R^{3}}-\frac{2}{3} R^{3}\right]$$

  and deduce that the bubble radius oscillates between $R_{0}$ and $R_{0} / 2^{1 / 3}$.

  comment

• Paper 4, Section II, D

  Fluid Dynamics | Part IB, 2009

  An inviscid incompressible fluid occupies a rectangular tank with vertical sides at $x=0, a$ and $y=0, b$ and a horizontal bottom at $z=-h$. The undisturbed free surface is at $z=0$.

  (i) Write down the equations and boundary conditions governing small amplitude free oscillations of the fluid, neglecting surface tension, and show that the frequencies $\omega$ of such oscillations are given by

  $$\frac{\omega^{2}}{g}=k \tanh k h, \text { where } k^{2}=\pi^{2}\left(\frac{m^{2}}{a^{2}}+\frac{n^{2}}{b^{2}}\right)$$

  for non-negative integers $m, n$, which cannot both be zero.

  (ii) The free surface is now acted on by a small external pressure

  $$p=\epsilon \rho g h \sin \Omega t \cos \frac{m \pi x}{a} \cos \frac{n \pi y}{b},$$

  where $\epsilon \ll 1$. Calculate the corresponding oscillation of the free surface when $\Omega$ is not equal to the quantity $\omega$ given by (1).

  Why does your solution break down as $\Omega \rightarrow \omega ?$

  comment

Geometry

• Paper 1, Section I, G

  Geometry | Part IB, 2009

  What is an ideal hyperbolic triangle? State a formula for its area.

  Compute the area of a hyperbolic disk of hyperbolic radius $\rho$. Hence, or otherwise, show that no hyperbolic triangle completely contains a hyperbolic circle of hyperbolic radius $2 .$

  comment

• Paper 2, Section II, G

  Geometry | Part IB, 2009

  What is meant by stereographic projection from the unit sphere in $\mathbb{R}^{3}$ to the complex plane? Briefly explain why a spherical triangle cannot map to a Euclidean triangle under stereographic projection.

  Derive an explicit formula for stereographic projection. Hence, or otherwise, prove that if a Möbius map corresponds via stereographic projection to a rotation of the sphere, it has two fixed points $p$ and $q$ which satisfy $p \bar{q}=-1$. Give, with justification:

  (i) a Möbius transformation which fixes a pair of points $p, q \in \mathbb{C}$ satisfying $p \bar{q}=-1$ but which does not arise from a rotation of the sphere;

  (ii) an isometry of the sphere (for the spherical metric) which does not correspond to any Möbius transformation under stereographic projection.

  comment

• Paper 3, Section I, G

  Geometry | Part IB, 2009

  Write down the equations for geodesic curves on a surface. Use these to describe all the geodesics on a circular cylinder, and draw a picture illustrating your answer.

  comment

• Paper 3, Section II, G

  Geometry | Part IB, 2009

  Consider a tessellation of the two-dimensional sphere, that is to say a decomposition of the sphere into polygons each of which has at least three sides. Let $E, V$ and $F$ denote the numbers of edges, vertices and faces in the tessellation, respectively. State Euler's formula. Prove that $2 E \geqslant 3 F$. Deduce that not all the vertices of the tessellation have valence $\geqslant 6$.

  By considering the plane $\{z=1\} \subset \mathbb{R}^{3}$, or otherwise, deduce the following: if $\Sigma$ is a finite set of straight lines in the plane $\mathbb{R}^{2}$ with the property that every intersection point of two lines is an intersection point of at least three, then all the lines in $\Sigma$ meet at a single point.

  comment

• Paper 4, Section II, G

  Geometry | Part IB, 2009

  Let $U \subset \mathbb{R}^{2}$ be an open set. Let $\Sigma \subset \mathbb{R}^{3}$ be a surface locally given as the graph of an infinitely-differentiable function $f: U \rightarrow \mathbb{R}$. Compute the Gaussian curvature of $\Sigma$ in terms of $f$.

  Deduce that if $\widehat{\Sigma} \subset \mathbb{R}^{3}$ is a compact surface without boundary, its Gaussian curvature is not everywhere negative.

  Give, with brief justification, a compact surface $\widehat{\Sigma} \subset \mathbb{R}^{3}$ without boundary whose Gaussian curvature must change sign.

  comment

Groups, Rings and Modules

• Paper 1, Section II, F

  Groups, Rings and Modules | Part IB, 2009

  Prove that a principal ideal domain is a unique factorization domain.

  Give, with justification, an example of an element of $\mathbb{Z}[\sqrt{-3}]$ which does not have a unique factorization as a product of irreducibles. Show how $\mathbb{Z}[\sqrt{-3}]$ may be embedded as a subring of index 2 in a ring $R$ (that is, such that the additive quotient group $R / \mathbb{Z}[\sqrt{-3}]$ has order 2) which is a principal ideal domain. [You should explain why $R$ is a principal ideal domain, but detailed proofs are not required.]

  comment

• Paper 2, Section $\mathbf{I}$, $2 F$

  Groups, Rings and Modules | Part IB, 2009

  State Sylow's theorems. Use them to show that a group of order 56 must have either a normal subgroup of order 7 or a normal subgroup of order 8 .

  comment

• Paper 2, Section II, F

  Groups, Rings and Modules | Part IB, 2009

  Define the centre of a group, and prove that a group of prime-power order has a nontrivial centre. Show also that if the quotient group $G / Z(G)$ is cyclic, where $Z(G)$ is the centre of $G$, then it is trivial. Deduce that a non-abelian group of order $p^{3}$, where $p$ is prime, has centre of order $p$.

  Let $F$ be the field of $p$ elements, and let $G$ be the group of $3 \times 3$ matrices over $F$ of the form

  $$\left(\begin{array}{lll} 1 & a & b \\ 0 & 1 & c \\ 0 & 0 & 1 \end{array}\right)$$

  Identify the centre of $G$.

  comment

• Paper 3, Section I, F

  Groups, Rings and Modules | Part IB, 2009

  Let $F$ be a field. Show that the polynomial ring $F[X]$ is a principal ideal domain. Give, with justification, an example of an ideal in $F[X, Y]$ which is not principal.

  comment

• Paper 3, Section II, F

  Groups, Rings and Modules | Part IB, 2009

  Let $S$ be a multiplicatively closed subset of a ring $R$, and let $I$ be an ideal of $R$ which is maximal among ideals disjoint from $S$. Show that $I$ is prime.

  If $R$ is an integral domain, explain briefly how one may construct a field $F$ together with an injective ring homomorphism $R \rightarrow F$.

  Deduce that if $R$ is an arbitrary ring, $I$ an ideal of $R$, and $S$ a multiplicatively closed subset disjoint from $I$, then there exists a ring homomorphism $f: R \rightarrow F$, where $F$ is a field, such that $f(x)=0$ for all $x \in I$ and $f(y) \neq 0$ for all $y \in S$.

  [You may assume that if $T$ is a multiplicatively closed subset of a ring, and $0 \notin T$, then there exists an ideal which is maximal among ideals disjoint from $T$.]

  comment

• Paper 4, Section I, F

  Groups, Rings and Modules | Part IB, 2009

  Let $M$ be a module over an integral domain $R$. An element $m \in M$ is said to be torsion if there exists a nonzero $r \in R$ with $\mathrm{rm}=0 ; M$ is said to be torsion-free if its only torsion element is 0 . Show that there exists a unique submodule $N$ of $M$ such that (a) all elements of $N$ are torsion and (b) the quotient module $M / N$ is torsion-free.

  comment

• Paper 4, Section II, F

  Groups, Rings and Modules | Part IB, 2009

  Let $R$ be a principal ideal domain. Prove that any submodule of a finitely-generated free module over $R$ is free.

  An $R$-module $P$ is said to be projective if, whenever we have module homomorphisms $f: M \rightarrow N$ and $g: P \rightarrow N$ with $f$ surjective, there exists a homomorphism $h: P \rightarrow M$ with $f \circ h=g$. Show that any free module (over an arbitrary ring) is projective. Show also that a finitely-generated projective module over a principal ideal domain is free.

  comment

Linear Algebra

• Paper 1, Section I, G

  Linear Algebra | Part IB, 2009

  (1) Let $V$ be a finite-dimensional vector space and let $T: V \rightarrow V$ be a non-zero endomorphism of $V$. If $\operatorname{ker}(T)=\operatorname{im}(T)$ show that the dimension of $V$ is an even integer. Find the minimal polynomial of $T$. [You may assume the rank-nullity theorem.]

  (2) Let $A_{i}, 1 \leqslant i \leqslant 3$, be non-zero subspaces of a vector space $V$ with the property that

  $$V=A_{1} \oplus A_{2}=A_{2} \oplus A_{3}=A_{1} \oplus A_{3} .$$

  Show that there is a 2-dimensional subspace $W \subset V$ for which all the $W \cap A_{i}$ are one-dimensional.

  comment

• Paper 1, Section II, G

  Linear Algebra | Part IB, 2009

  Define the dual of a vector space $V$. State and prove a formula for its dimension.

  Let $V$ be the vector space of real polynomials of degree at most $n$. If $\left\{a_{0}, \ldots, a_{n}\right\}$ are distinct real numbers, prove that there are unique real numbers $\left\{\lambda_{0}, \ldots, \lambda_{n}\right\}$ with

  $$\frac{d p}{d x}(0)=\sum_{j=0}^{n} \lambda_{j} p\left(a_{j}\right)$$

  for every $p(x) \in V$.

  comment

• Paper 2, Section I, $1 \mathbf{G}$

  Linear Algebra | Part IB, 2009

  Let $V$ denote the vector space of polynomials $f(x, y)$ in two variables of total degree at most $n$. Find the dimension of $V$.

  If $S: V \rightarrow V$ is defined by

  $$(S f)(x, y)=x^{2} \frac{\partial^{2} f}{\partial x^{2}}+y^{2} \frac{\partial^{2} f}{\partial y^{2}}$$

  find the kernel of $S$ and the image of $S$. Compute the trace of $S$ for each $n$ with $1 \leqslant n \leqslant 4$.

  comment

• Paper 2, Section II, G

  Linear Algebra | Part IB, 2009

  Let $V$ be a finite-dimensional vector space and let $T: V \rightarrow V$ be an endomorphism of $V$. Show that there is a positive integer $l$ such that $V=\operatorname{ker}\left(T^{l}\right) \oplus \operatorname{im}\left(T^{l}\right)$. Hence, or otherwise, show that if $T$ has zero determinant there is some non-zero endomorphism $S$ with $T S=0=S T$.

  Suppose $T_{1}$ and $T_{2}$ are endomorphisms of $V$ for which $T_{i}^{2}=T_{i}, i=1,2$. Show that $T_{1}$ is similar to $T_{2}$ if and only if they have the same rank.

  comment

• Paper 3, Section II, G

  Linear Algebra | Part IB, 2009

  For each of the following, provide a proof or counterexample.

  (1) If $A, B$ are complex $n \times n$ matrices and $A B=B A$, then $A$ and $B$ have a common eigenvector.

  (2) If $A, B$ are complex $n \times n$ matrices and $A B=B A$, then $A$ and $B$ have a common eigenvalue.

  (3) If $A, B$ are complex $n \times n$ matrices and $(A B)^{n}=0$ then $(B A)^{n}=0$.

  (4) If $T: V \rightarrow V$ is an endomorphism of a finite-dimensional vector space $V$ and $\lambda$ is an eigenvalue of $T$, then the dimension of $\{v \in V \mid(T-\lambda I) v=0\}$ equals the multiplicity of $\lambda$ as a root of the minimal polynomial of $T$.

  (5) If $T: V \rightarrow V$ is an endomorphism of a finite-dimensional complex vector space $V$, $\lambda$ is an eigenvalue of $T$, and $W_{i}=\left\{v \in V \mid(T-\lambda I)^{i}(v)=0\right\}$, then $W_{c}=W_{c+1}$ where $c$ is the multiplicity of $\lambda$ as a root of the minimal polynomial of $T$.

  comment

• Paper 4, Section I, G

  Linear Algebra | Part IB, 2009

  Show that every endomorphism of a finite-dimensional vector space satisfies some polynomial, and define the minimal polynomial of such an endomorphism.

  Give a linear transformation of an eight-dimensional complex vector space which has minimal polynomial $x^{2}(x-1)^{3}$.

  comment

• Paper 4, Section II, G

  Linear Algebra | Part IB, 2009

  What does it mean to say two real symmetric bilinear forms $A$ and $B$ on a vector space $V$ are congruent ?

  State and prove Sylvester's law of inertia, and deduce that the rank and signature determine the congruence class of a real symmetric bilinear form. [You may use without proof a result on diagonalisability of real symmetric matrices, provided it is clearly stated.]

  How many congruence classes of symmetric bilinear forms on a real $n$-dimensional vector space are there? Such a form $\psi$ defines a family of subsets $\left\{x \in \mathbb{R}^{n} \mid \psi(x, x)=t\right\}$, for $t \in \mathbb{R}$. For how many of the congruence classes are these associated subsets all bounded subsets of $\mathbb{R}^{n}$ ? Is the quadric surface

  $$\left\{3 x^{2}+6 y^{2}+5 z^{2}+4 x y+2 x z+8 y z=1\right\}$$

  a bounded or unbounded subset of $\mathbb{R}^{3}$ ? Justify your answers.

  comment

Markov Chains

• Paper 1, Section II, H

  Markov Chains | Part IB, 2009

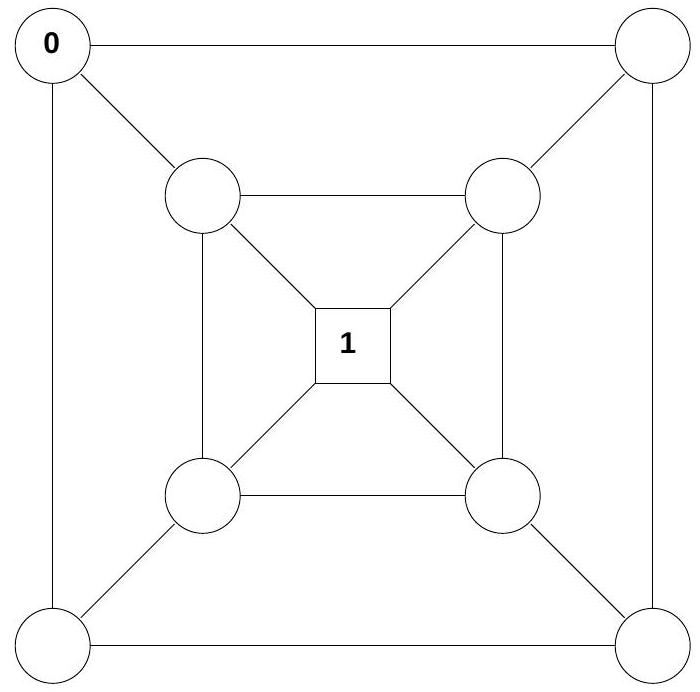
  A gerbil is introduced into a maze at the node labelled 0 in the diagram. It roams at random through the maze until it reaches the node labelled 1. At each vertex, it chooses to move to one of the neighbouring nodes with equal probability, independently of all other choices. Find the mean number of moves required for the gerbil to reach node 1 .

  Suppose now that the gerbil is intelligent, in that when it reaches a node it will not immediately return to the node from which it has just come, choosing with equal probability from all other neighbouring nodes. Express the movement of the gerbil in terms of a Markov chain whose states and transition probabilities you should specify. Find the mean number of moves until the intelligent gerbil reaches node 1 . Compare with your answer to the first part, and comment briefly.

  

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2009

  Suppose that $B$ is a non-empty subset of the statespace $I$ of a Markov chain $X$ with transition matrix $P$, and let $\tau \equiv \inf \left\{n \geqslant 0: X_{n} \in B\right\}$, with the convention that inf $\emptyset=\infty$. If $h_{i}=P\left(\tau<\infty \mid X_{0}=i\right)$, show that the equations

  (a)

  $$g_{i} \geqslant(P g)_{i} \equiv \sum_{j \in I} p_{i j} g_{j} \geqslant 0 \quad \forall i$$

  $$g_{i}=1 \quad \forall i \in B$$

  are satisfied by $g=h$.

  If $g$ satisfies (a), prove that $g$ also satisfies

  $(c)$

  $$g_{i} \geqslant(\tilde{P} g)_{i} \quad \forall i,$$

  where

  $$\tilde{p}_{i j}=\left\{\begin{array}{cl} p_{i j} & (i \notin B), \\ \delta_{i j} & (i \in B) \end{array}\right.$$

  By interpreting the transition matrix $\tilde{P}$, prove that $h$ is the minimal solution to the equations (a), (b).

  Now suppose that $P$ is irreducible. Prove that $P$ is recurrent if and only if the only solutions to (a) are constant functions.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2009

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple random walk on the integers: the random variables $\xi_{n} \equiv X_{n}-X_{n-1}$ are independent, with distribution

  $$P(\xi=1)=p, \quad P(\xi=-1)=q$$

  where $0<p<1$, and $q=1-p$. Consider the hitting time $\tau=\inf \left\{n: X_{n}=0\right.$ or $\left.X_{n}=N\right\}$, where $N>1$ is a given integer. For fixed $s \in(0,1)$ define $\xi_{k}=E\left[s^{\tau}: X_{\tau}=0 \mid X_{0}=k\right]$ for $k=0, \ldots, N$. Show that the $\xi_{k}$ satisfy a second-order difference equation, and hence find them.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2009

  In chess, a bishop is allowed to move only in straight diagonal lines. Thus if the bishop stands on the square marked $\mathrm{A}$ in the diagram, it is able in one move to reach any of the squares marked with an asterisk. Suppose that the bishop moves at random around the chess board, choosing at each move with equal probability from the squares it can reach, the square chosen being independent of all previous choices. The bishop starts at the bottom left-hand corner of the board.

  If $X_{n}$ is the position of the bishop at time $n$, show that $\left(X_{n}\right)_{n \geqslant 0}$ is a reversible Markov chain, whose statespace you should specify. Find the invariant distribution of this Markov chain.

  What is the expected number of moves the bishop will make before first returning to its starting square?

  

  comment

Methods

• Paper 1, Section II, B

  Methods | Part IB, 2009

  Find a power series solution about $x=0$ of the equation

  $$x y^{\prime \prime}+(1-x) y^{\prime}+\lambda y=0,$$

  with $y(0)=1$, and show that $y$ is a polynomial if and only if $\lambda$ is a non-negative integer $n$. Let $y_{n}$ be the solution for $\lambda=n$. Establish an orthogonality relation between $y_{m}$ and $y_{n}(m \neq n)$.

  Show that $y_{m} y_{n}$ is a polynomial of degree $m+n$, and hence that

  $$y_{m} y_{n}=\sum_{p=0}^{m+n} a_{p} y_{p}$$

  for appropriate choices of the coefficients $a_{p}$ and with $a_{m+n} \neq 0$.

  For given $n>0$, show that the functions

  $$\left\{y_{m}, y_{m} y_{n}: m=0,1,2, \ldots, n-1\right\}$$

  are linearly independent.

  Let $f(x)$ be a polynomial of degree 3. Explain why the expansion

  $$f(x)=a_{0} y_{0}(x)+a_{1} y_{1}(x)+a_{2} y_{2}(x)+a_{3} y_{1}(x) y_{2}(x)$$

  holds for appropriate choices of $a_{p}, p=0,1,2,3$. Hence show that

  $$\int_{0}^{\infty} e^{-x} f(x) d x=w_{1} f\left(\alpha_{1}\right)+w_{2} f\left(\alpha_{2}\right)$$

  where

  $$w_{1}=\frac{y_{1}\left(\alpha_{2}\right)}{y_{1}\left(\alpha_{2}\right)-y_{1}\left(\alpha_{1}\right)}, \quad w_{2}=\frac{-y_{1}\left(\alpha_{1}\right)}{y_{1}\left(\alpha_{2}\right)-y_{1}\left(\alpha_{1}\right)},$$

  and $\alpha_{1}, \alpha_{2}$ are the zeros of $y_{2}$. You need not construct the polynomials $y_{1}(x), y_{2}(x)$ explicitly.

  comment

• Paper 2, Section I, B

  Methods | Part IB, 2009

  Expand $f(x)=x, 0<x<\pi$, as a half-range sine series.

  By integrating the series show that a Fourier cosine series for $x^{2}, 0<x<\pi$, can be written as

  $$x^{2}=\frac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos n x$$

  where $a_{n}, n=1,2, \ldots$, should be determined and

  $$a_{0}=8 \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}$$

  By evaluating $a_{0}$ another way show that

  $$\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}=\frac{\pi^{2}}{12}$$

  comment

• Paper 2, Section II, B

  Methods | Part IB, 2009

  A string of uniform density $\rho$ is stretched under tension along the $x$-axis and undergoes small transverse oscillations in the $(x, y)$ plane with amplitude $y(x, t)$. Given that waves in the string travel at velocity $c$, write down the equation of motion satisfied by $y(x, t)$.

  The string is now fixed at $x=0$ and $x=L$. Derive the general separable solution for the amplitude $y(x, t)$.

  For $t<0$ the string is at rest. At time $t=0$ the string is struck by a hammer in the interval $[l-a / 2, l+a / 2]$, distance being measured from one end. The effect of the hammer is to impart a constant velocity $v$ to the string inside the interval and zero velocity outside it. Calculate the proportion of the total energy given to the string in each mode.

  If $l=L / 3$ and $a=L / 10$, find all the modes of the string which are not excited in the motion.

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2009

  The Fourier transform $\tilde{f}(\omega)$ of a suitable function $f(t)$ is defined as $\tilde{f}(\omega)=$ $\int_{-\infty}^{\infty} f(t) e^{-i \omega t} d t$. Consider the function $h(t)=e^{\alpha t}$ for $t>0$, and zero otherwise. Show that

  $$\tilde{h}(\omega)=\frac{1}{i \omega-\alpha},$$

  provided $\Re(\alpha)<0$.

  The angle $\theta(t)$ of a forced, damped pendulum satisfies

  $$\ddot{\theta}+2 \dot{\theta}+5 \theta=e^{-4 t},$$

  with initial conditions $\theta(0)=\dot{\theta}(0)=0$. Show that the transfer function for this system is

  $$\tilde{R}(\omega)=\frac{1}{4 i}\left[\frac{1}{(i \omega+1-2 i)}-\frac{1}{(i \omega+1+2 i)}\right]$$

  comment

• Paper 3, Section II, 15A

  Methods | Part IB, 2009

  A function $g(r)$ is chosen to make the integral

  $$\int_{a}^{b} f\left(r, g, g^{\prime}\right) d r$$

  stationary, subject to given values of $g(a)$ and $g(b)$. Find the Euler-Lagrange equation for $g(r) .$

  In a certain three-dimensional electrostatics problem the potential $\phi$ depends only on the radial coordinate $r$, and the energy functional of $\phi$ is

  $$\mathcal{E}[\phi]=2 \pi \int_{R_{1}}^{R_{2}}\left[\frac{1}{2}\left(\frac{d \phi}{d r}\right)^{2}+\frac{1}{2 \lambda^{2}} \phi^{2}\right] r^{2} d r$$

  where $\lambda$ is a parameter. Show that the Euler-Lagrange equation associated with minimizing the energy $\mathcal{E}$ is equivalent to

  $$\frac{1}{r} \frac{d^{2}(r \phi)}{d r^{2}}-\frac{1}{\lambda^{2}} \phi=0$$

  Find the general solution of this equation, and the solution for the region $R_{1} \leqslant r \leqslant R_{2}$ which satisfies $\phi\left(R_{1}\right)=\phi_{1}$ and $\phi\left(R_{2}\right)=0$.

  Consider an annular region in two dimensions, where the potential is a function of the radial coordinate $r$ only. Write down the equivalent expression for the energy functional $\mathcal{E}$ above, in cylindrical polar coordinates, and derive the equivalent of (1).

  comment

• Paper 4, Section I, B

  Methods | Part IB, 2009

  Describe briefly the method of Lagrange multipliers for finding the stationary points of a function $f(x, y)$ subject to the constraint $g(x, y)=0$.

  Show that at a stationary point $(a, b)$

  $$\left|\begin{array}{ll} \frac{\partial f}{\partial x}(a, b) & \frac{\partial g}{\partial x}(a, b) \\ \frac{\partial f}{\partial y}(a, b) & \frac{\partial g}{\partial y}(a, b) \end{array}\right|=0$$

  Find the maximum distance from the origin to the curve

  $$x^{2}+y^{2}+x y-4=0 .$$

  comment

• Paper 4, Section II, A

  Methods | Part IB, 2009

  Suppose that $y_{1}(x)$ and $y_{2}(x)$ are linearly independent solutions of

  $$\frac{d^{2} y}{d x^{2}}+b(x) \frac{d y}{d x}+c(x) y=0$$

  with $y_{1}(0)=0$ and $y_{2}(1)=0$. Show that the Green's function $G(x, \xi)$ for the interval $0 \leqslant x, \xi \leqslant 1$ and with $G(0, \xi)=G(1, \xi)=0$ can be written in the form

  $$G(x, \xi)= \begin{cases}y_{1}(x) y_{2}(\xi) / W(\xi) ; & 0<x<\xi \\ y_{2}(x) y_{1}(\xi) / W(\xi) ; & \xi<x<1\end{cases}$$

  where $W(x)=W\left[y_{1}(x), y_{2}(x)\right]$ is the Wronskian of $y_{1}(x)$ and $y_{2}(x)$.

  Use this result to find the Green's function $G(x, \xi)$ that satisfies

  $$\frac{d^{2} G}{d x^{2}}+3 \frac{d G}{d x}+2 G=\delta(x-\xi)$$

  in the interval $0 \leqslant x, \xi \leqslant 1$ and with $G(0, \xi)=G(1, \xi)=0$. Hence obtain an integral expression for the solution of

  $$\frac{d^{2} y}{d x^{2}}+3 \frac{d y}{d x}+2 y= \begin{cases}0 ; & 0<x<x_{0} \\ 2 ; & x_{0}<x<1\end{cases}$$

  for the case $x<x_{0}$.

  comment

Metric and Topological Spaces

• Paper 1, Section II, F

  Metric and Topological Spaces | Part IB, 2009

  Given a function $f: X \rightarrow Y$ between metric spaces, we write $\Gamma_{f}$ for the subset $\{(x, f(x)) \mid x \in X\}$ of $X \times Y .$

  (i) If $f$ is continuous, show that $\Gamma_{f}$ is closed in $X \times Y$.

  (ii) If $Y$ is compact and $\Gamma_{f}$ is closed in $X \times Y$, show that $f$ is continuous.

  (iii) Give an example of a function $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $\Gamma_{f}$ is closed but $f$ is not continuous.

  comment

• Paper 2, Section I, $4 F$

  Metric and Topological Spaces | Part IB, 2009

  Explain what is meant by a Hausdorff (topological) space, and prove that every compact subset of a Hausdorff space is closed.

  Let $X$ be an uncountable set, and consider the topology $\mathcal{T}$ on $X$ defined by

  $$U \in \mathcal{T} \Leftrightarrow \text { either } U=\emptyset \text { or } X \backslash U \text { is countable. }$$

  Is $(X, \mathcal{T})$ Hausdorff? Is every compact subset of $X$ closed? Justify your answers.

  comment

• Paper 3, Section I, F

  Metric and Topological Spaces | Part IB, 2009

  Are the following statements true or false? Give brief justifications for your answers.

  (i) If $X$ is a connected open subset of $\mathbb{R}^{n}$ for some $n$, then $X$ is path-connected.

  (ii) A cartesian product of two connected spaces is connected.

  (iii) If $X$ is a Hausdorff space and the only connected subsets of $X$ are singletons $\{x\}$, then $X$ is discrete.

  comment

• Paper 4, Section II, F

  Metric and Topological Spaces | Part IB, 2009

  A nonempty subset $A$ of a topological space $X$ is called irreducible if, whenever we have open sets $U$ and $V$ such that $U \cap A$ and $V \cap A$ are nonempty, then we also have $U \cap V \cap A \neq \emptyset$. Show that the closure of an irreducible set is irreducible, and deduce that the closure of any singleton set $\{x\}$ is irreducible.

  $X$ is said to be a sober topological space if, for any irreducible closed $A \subseteq X$, there is a unique $x \in X$ such that $A=\overline{\{x\}}$. Show that any Hausdorff space is sober, but that an infinite set with the cofinite topology is not sober.

  Given an arbitrary topological space $(X, \mathcal{T})$, let $\widehat{X}$denote the set of all irreducible closed subsets of $X$, and for each $U \in \mathcal{T}$ let

  $$\widehat{U}=\{A \in \widehat{X} \mid U \cap A \neq \emptyset\}$$

  Show that the sets $\{\widehat{U} \mid U \in \mathcal{T}\}$ form a topology $\widehat{\mathcal{T}}$on $\widehat{X}$, and that the mapping $U \mapsto \widehat{U}$is a bijection from $\mathcal{T}$ to $\widehat{\mathcal{T}}$. Deduce that $(\widehat{X}, \widehat{\mathcal{T}}$) is sober. [Hint: consider the complement of an irreducible closed subset of $\widehat{X}$.]

  comment

Numerical Analysis

• Paper 1, Section I, C

  Numerical Analysis | Part IB, 2009

  The real non-singular matrix $A \in \mathbb{R}^{m \times m}$ is written in the form $A=A_{D}+A_{U}+A_{L}$, where the matrices $A_{D}, A_{U}, A_{L} \in \mathbb{R}^{m \times m}$ are diagonal and non-singular, strictly uppertriangular and strictly lower-triangular respectively.

  Given $b \in \mathbb{R}^{m}$, the Jacobi iteration for solving $A x=b$ is

  $$A_{D} x_{n}=-\left(A_{U}+A_{L}\right) x_{n-1}+b, \quad n=1,2 \ldots$$

  where the $n$th iterate is $x_{n} \in \mathbb{R}^{m}$. Show that the iteration converges to the solution $x$ of $A x=b$, independent of the starting choice $x_{0}$, if and only if the spectral radius $\rho(H)$ of the matrix $H=-A_{D}^{-1}\left(A_{U}+A_{L}\right)$ is less than 1 .

  Hence find the range of values of the real number $\mu$ for which the iteration will converge when

  $$A=\left[\begin{array}{rrr} 1 & 0 & -\mu \\ -\mu & 3 & -\mu \\ -4 \mu & 0 & 4 \end{array}\right]$$

  comment

• Paper 2, Section II, C

  Numerical Analysis | Part IB, 2009

  The real orthogonal matrix $\Omega^{[p, q]} \in \mathbb{R}^{m \times m}$ with $1 \leqslant p<q \leqslant m$ is a Givens rotation with rotation angle $\theta$. Write down the form of $\Omega^{[p, q]}$.

  Show that for any matrix $A \in \mathbb{R}^{m \times m}$ it is possible to choose $\theta$ such that the matrix $\Omega^{[p, q]} A$ satisfies $\left(\Omega^{[p, q]} A\right)_{q, j}=0$ for any $j$, where $1 \leqslant j \leqslant m$.

  Let

  $$A=\left[\begin{array}{ccc} 1 & 3 & 2 \\ 1 & 4 & 4 \\ \sqrt{2} & 7 / \sqrt{2} & 4 \sqrt{2} \end{array}\right]$$

  By applying a sequence of Givens rotations of the form $\Omega^{[1,3]} \Omega^{[1,2]}$, chosen to reduce the elements in the first column below the main diagonal to zero, find a factorisation of the matrix $A \in \mathbb{R}^{3 \times 3}$ of the form $A=Q R$, where $Q \in \mathbb{R}^{3 \times 3}$ is an orthogonal matrix and $R \in \mathbb{R}^{3 \times 3}$ is an upper-triangular matrix for which the leading non-zero element in each row is positive.

  comment

• Paper 3, Section II, C

  Numerical Analysis | Part IB, 2009

  Starting from Taylor's theorem with integral form of the remainder, prove the Peano kernel theorem: the error of an approximant $L(f)$ applied to $f(x) \in C^{k+1}[a, b]$ can be written in the form

  $$L(f)=\frac{1}{k !} \int_{a}^{b} K(\theta) f^{(k+1)}(\theta) d \theta$$

  You should specify the form of $K(\theta)$. Here it is assumed that $L(f)$ is identically zero when $f(x)$ is a polynomial of degree $k$. State any other necessary conditions.

  Setting $a=0$ and $b=2$, find $K(\theta)$ and show that it is negative for $0<\theta<2$ when

  $$L(f)=\int_{0}^{2} f(x) d x-\frac{1}{3}(f(0)+4 f(1)+f(2)) \quad \text { for } \quad f(x) \in C^{4}[0,2] .$$

  Hence determine the minimum value of $\rho$ for which

  $$|L(f)| \leqslant \rho\left\|f^{(4)}\right\|_{\infty}$$

  holds for all $f(x) \in C^{4}[0,2]$.

  comment

• Paper 4, Section I, C

  Numerical Analysis | Part IB, 2009

  Suppose that $w(x)>0$ for all $x \in(a, b)$. The weights $b_{1}, \ldots, b_{n}$ and nodes $x_{1}, \ldots, x_{n}$ are chosen so that the Gaussian quadrature formula

  $$\int_{a}^{b} w(x) f(x) d x \sim \sum_{k=1}^{n} b_{k} f\left(x_{k}\right)$$

  is exact for every polynomial of degree $2 n-1$. Show that the $b_{i}, i=1, \ldots, n$ are all positive.

  When $w(x)=1+x^{2}, a=-1$ and $b=1$, the first three underlying orthogonal polynomials are $p_{0}(x)=1, p_{1}(x)=x$, and $p_{2}(x)=x^{2}-2 / 5$. Find $x_{1}, x_{2}$ and $b_{1}, b_{2}$ when $n=2$.

  comment

Optimization

• Paper 1, Section I, H

  Optimization | Part IB, 2009

  Find an optimal solution to the linear programming problem

  $$\max 3 x_{1}+2 x_{2}+2 x_{3}$$

  in $x \geqslant 0$ subject to

  $$\begin{gathered} 7 x_{1}+3 x_{2}+5 x_{3} \leqslant 44 \\ x_{1}+2 x_{2}+x_{3} \leqslant 10 \\ x_{1}+x_{2}+x_{3} \geqslant 8 \end{gathered}$$

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2009

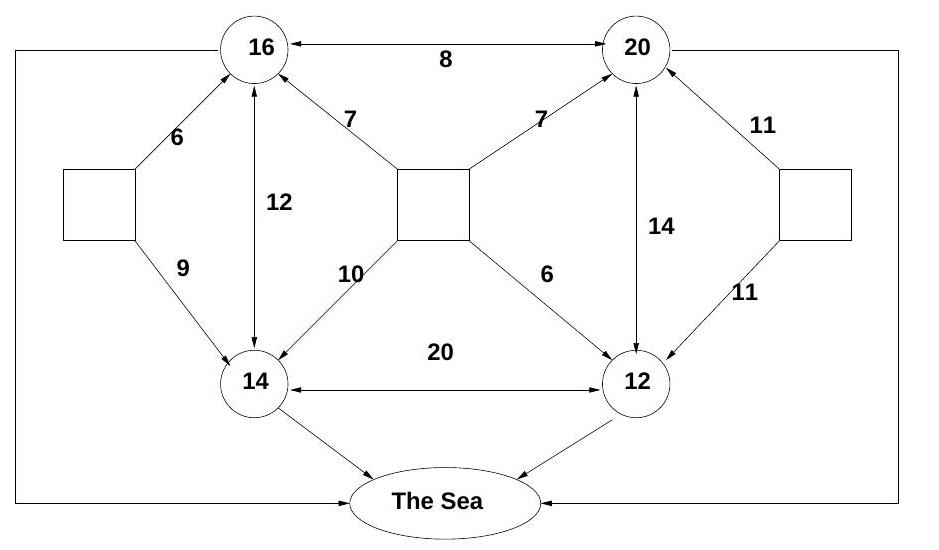
  The diagram shows a network of sewage treatment plants, shown as circles, connected by pipes. Some pipes (indicated by a line with an arrowhead at one end only) allow sewage to flow in one direction only, others (indicated by a line with an arrowhead at both ends) allow sewage to flow in either direction. The capacities of the pipes are shown. The system serves three towns, shown in the diagram as squares.

  Each sewage treatment plant can treat a limited amount of sewage, indicated by the number in the circle, and this may not be exceeded for fear of environmental damage. Treated sewage is pumped into the sea, but at any treatment plant incoming untreated sewage may be immediately pumped to another plant for treatment there.

  Find the maximum amount of sewage which can be handled by the system, and how this is assigned to each of the three towns.

  

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2009

  Four factories supply stuff to four shops. The production capacities of the factories are $7,12,8$ and 9 units per week, and the requirements of the shops are 8 units per week each. If the costs of transporting a unit of stuff from factory $i$ to shop $j$ is the $(i, j)$ th element in the matrix

  $$\left(\begin{array}{cccc} 6 & 10 & 3 & 5 \\ 4 & 8 & 6 & 12 \\ 3 & 4 & 9 & 2 \\ 5 & 7 & 2 & 6 \end{array}\right)$$

  find a minimal-cost allocation of the outputs of the factories to the shops.

  Suppose that the cost of producing one unit of stuff varies across the factories, being $3,2,4,5$ respectively. Explain how you would modify the original problem to minimise the total cost of production and of transportation, and find an optimal solution for the modified problem.

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2009

  In a pure exchange economy, there are $J$ agents, and $d$ goods. Agent $j$ initially holds an endowment $x_{j} \in \mathbb{R}^{d}$ of the $d$ different goods, $j=1, \ldots, J$. Agent $j$ has preferences given by a concave utility function $U_{j}: \mathbb{R}^{d} \rightarrow \mathbb{R}$ which is strictly increasing in each of its arguments, and is twice continuously differentiable. Thus agent $j$ prefers $y \in \mathbb{R}^{d}$ to $x \in \mathbb{R}^{d}$ if and only if $U_{j}(y) \geqslant U_{j}(x)$.

  The agents meet and engage in mutually beneficial trades. Thus if agent $i$ holding $z_{i}$ meets agent $j$ holding $z_{j}$, then the amounts $z_{i}^{\prime}$ held by agent $i$ and $z_{j}^{\prime}$ held by agent $j$ after trading must satisfy $U_{i}\left(z_{i}^{\prime}\right) \geqslant U_{i}\left(z_{i}\right), U_{j}\left(z_{j}^{\prime}\right) \geqslant U_{j}\left(z_{j}\right)$, and $z_{i}^{\prime}+z_{j}^{\prime}=z_{i}+z_{j}$. Meeting and trading continues until, finally, agent $j$ holds $y_{j} \in \mathbb{R}^{d}$, where

  $$\sum_{j} x_{j}=\sum_{j} y_{j}$$

  and there are no further mutually beneficial trades available to any pair of agents. Prove that there must exist a vector $v \in \mathbb{R}^{d}$ and positive scalars $\lambda_{1}, \ldots, \lambda_{J}$ such that

  $$\nabla U_{j}\left(y_{j}\right)=\lambda_{j} v$$

  for all $j$. Show that for some positive $a_{1}, \ldots, a_{J}$ the final allocations $y_{j}$ are what would be achieved by a social planner, whose objective is to obtain

  $$\max \sum_{j} a_{j} U_{j}\left(y_{j}\right) \quad \text { subject to } \sum_{j} y_{j}=\sum_{j} x_{j}$$

  comment

Quantum Mechanics

• Paper 1, Section II, B

  Quantum Mechanics | Part IB, 2009

  A particle of mass $m$ moves in one dimension in a potential $V(x)$ which satisfies $V(x)=V(-x)$. Show that the eigenstates of the Hamiltonian $H$ can be chosen so that they are also eigenstates of the parity operator $P$. For eigenstates with odd parity $\psi^{\text {odd }}(x)$, show that $\psi^{o d d}(0)=0$.

  A potential $V(x)$ is given by

  $$V(x)= \begin{cases}\kappa \delta(x) & |x|<a \\ \infty & |x|>a\end{cases}$$

  State the boundary conditions satisfied by $\psi(x)$ at $|x|=a$, and show also that

  $$\frac{\hbar^{2}}{2 m} \lim _{\epsilon \rightarrow 0}\left[\left.\frac{d \psi}{d x}\right|_{\epsilon}-\left.\frac{d \psi}{d x}\right|_{-\epsilon}\right]=\kappa \psi(0)$$

  Let the energy eigenstates of even parity be given by

  $$\psi^{\text {even }}(x)=\left\{\begin{array}{lc} A \cos \lambda x+B \sin \lambda x & -a<x<0 \\ A \cos \lambda x-B \sin \lambda x & 0<x<a \\ 0 & \text { otherwise } \end{array}\right.$$

  Verify that $\psi^{\text {even }}(x)$ satisfies

  $$P \psi^{\text {even }}(x)=\psi^{\text {even }}(x)$$

  By demanding that $\psi^{e v e n}(x)$ satisfy the relevant boundary conditions show that

  $$\tan \lambda a=-\frac{\hbar^{2}}{m} \frac{\lambda}{\kappa}$$

  For $\kappa>0$ show that the energy eigenvalues $E_{n}^{\text {even }}, n=0,1,2, \ldots$, with $E_{n}^{\text {even }}<E_{n+1}^{\text {even }}$, satisfy

  $$\eta_{n}=E_{n}^{e v e n}-\frac{1}{2 m}\left[\frac{(2 n+1) \hbar \pi}{2 a}\right]^{2}>0$$

  Show also that

  $$\lim _{n \rightarrow \infty} \eta_{n}=0,$$

  and give a physical explanation of this result.

  Show that the energy eigenstates with odd parity and their energy eigenvalues do not depend on $\kappa$.

  comment

• Paper 2, Section II, B

  Quantum Mechanics | Part IB, 2009

  Write down the expressions for the probability density $\rho$ and the associated current density $j$ for a particle with wavefunction $\psi(x, t)$ moving in one dimension. If $\psi(x, t)$ obeys the time-dependent Schrödinger equation show that $\rho$ and $j$ satisfy

  $$\frac{\partial j}{\partial x}+\frac{\partial \rho}{\partial t}=0$$

  Give an interpretation of $\psi(x, t)$ in the case that

  $$\psi(x, t)=\left(e^{i k x}+R e^{-i k x}\right) e^{-i E t / \hbar}$$

  and show that $E=\frac{\hbar^{2} k^{2}}{2 m}$ and $\frac{\partial \rho}{\partial t}=0$.

  A particle of mass $m$ and energy $E>0$ moving in one dimension is incident from the left on a potential $V(x)$ given by

  $$V(x)=\left\{\begin{array}{rl} -V_{0} & 0<x<a \\ 0 & x<0, x>a \quad, \end{array}\right.$$

  where $V_{0}$ is a positive constant. What conditions must be imposed on the wavefunction at $x=0$ and $x=a$ ? Show that when $3 E=V_{0}$ the probability of transmission is

  $$\left[1+\frac{9}{16} \sin ^{2} \frac{a \sqrt{8 m E}}{\hbar}\right]^{-1}$$

  For what values of $a$ does this agree with the classical result?

  comment

• Paper 3, Section I, B

  Quantum Mechanics | Part IB, 2009

  The motion of a particle in one dimension is described by the time-independent hermitian Hamiltonian operator $H$ whose normalized eigenstates $\psi_{n}(x), n=0,1,2, \ldots$, satisfy the Schrödinger equation

  $$H \psi_{n}=E_{n} \psi_{n},$$

  with $E_{0}<E_{1}<E_{2}<\cdots<E_{n}<\cdots$. Show that

  $$\int_{-\infty}^{\infty} \psi_{m}^{*} \psi_{n} d x=\delta_{m n}$$

  The particle is in a state represented by the wavefunction $\Psi(x, t)$ which, at time $t=0$, is given by

  $$\Psi(x, 0)=\sum_{n=0}^{\infty}\left(\frac{1}{\sqrt{2}}\right)^{n+1} \psi_{n}(x) .$$

  Write down an expression for $\Psi(x, t)$ and show that it is normalized to unity.

  Derive an expression for the expectation value of the energy for this state and show that it is independent of time.

  Calculate the probability that the particle has energy $E_{m}$ for a given integer $m \geqslant 0$, and show that this also is time-independent.

  comment

• Paper 3, Section II, B

  Quantum Mechanics | Part IB, 2009

  If $A, B$, and $C$ are operators establish the identity

  $$[A B, C]=A[B, C]+[A, C] B$$

  A particle moves in a two-dimensional harmonic oscillator potential with Hamiltonian

  $$H=\frac{1}{2}\left(p_{x}^{2}+p_{y}^{2}\right)+\frac{1}{2}\left(x^{2}+y^{2}\right) .$$

  The angular momentum operator is defined by

  $$L=x p_{y}-y p_{x}$$

  Show that $L$ is hermitian and hence that its eigenvalues are real. Establish the commutation relation $[L, H]=0$. Why does this ensure that eigenstates of $H$ can also be chosen to be eigenstates of $L$ ?

  Let $\phi_{0}(x, y)=e^{-\left(x^{2}+y^{2}\right) / 2 \hbar}$, and show that $\phi_{0}, \quad \phi_{x}=x \phi_{0}$ and $\phi_{y}=y \phi_{0}$ are all eigenstates of $H$, and find their respective eigenvalues. Show that

  $$L \phi_{0}=0, \quad L \phi_{x}=i \hbar \phi_{y}, \quad L \phi_{y}=-i \hbar \phi_{x}$$

  and hence, by taking suitable linear combinations of $\phi_{x}$ and $\phi_{y}$, find two states, $\psi_{1}$ and $\psi_{2}$, satisfying

  $$L \psi_{j}=\lambda_{j} \psi_{j}, \quad H \psi_{j}=E_{j} \psi_{j} \quad j=1,2 .$$

  Show that $\psi_{1}$ and $\psi_{2}$ are orthogonal, and find $\lambda_{1}, \lambda_{2}, E_{1}$ and $E_{2}$.

  The particle has charge $e$, and an electric field of strength $\mathcal{E}$ is applied in the $x$ direction so that the Hamiltonian is now $H^{\prime}$, where

  $$H^{\prime}=H-e \mathcal{E} x$$

  Show that $\left[L, H^{\prime}\right]=-i \hbar e \mathcal{E} y$. Why does this mean that $L$ and $H^{\prime}$ cannot have simultaneous eigenstates?

  By making the change of coordinates $x^{\prime}=x-e \mathcal{E}, y^{\prime}=y$, show that $\psi_{1}\left(x^{\prime}, y^{\prime}\right)$ and $\psi_{2}\left(x^{\prime}, y^{\prime}\right)$ are eigenstates of $H^{\prime}$ and write down the corresponding energy eigenvalues.

  Find a modified angular momentum operator $L^{\prime}$ for which $\psi_{1}\left(x^{\prime}, y^{\prime}\right)$ and $\psi_{2}\left(x^{\prime}, y^{\prime}\right)$ are also eigenstates.

  comment

• Paper 4, Section I, B

  Quantum Mechanics | Part IB, 2009

  The wavefunction of a Gaussian wavepacket for a particle of mass $m$ moving in one dimension is

  $$\psi(x, t)=\frac{1}{\pi^{1 / 4}} \sqrt{\frac{1}{1+i \hbar t / m}} \exp \left(-\frac{x^{2}}{2(1+i \hbar t / m)}\right)$$

  Show that $\psi(x, t)$ satisfies the appropriate time-dependent Schrödinger equation.

  Show that $\psi(x, t)$ is normalized to unity and calculate the uncertainty in measurement of the particle position, $\Delta x=\sqrt{\left\langle x^{2}\right\rangle-\langle x\rangle^{2}}$.

  Is $\psi(x, t)$ a stationary state? Give a reason for your answer.

  $\left[\right.$ You may assume that $\left.\int_{-\infty}^{\infty} e^{-\lambda x^{2}} d x=\sqrt{\frac{\pi}{\lambda}} \cdot\right]$

  comment

Special Relativity

• Paper 1, Section I, C

  Special Relativity | Part IB, 2009

  Write down the components of the position four-vector $x_{\mu}$. Hence find the components of the four-momentum $p_{\mu}=M U_{\mu}$ of a particle of mass $M$, where $U_{\mu}=d x_{\mu} / d \tau$, with $\tau$ being the proper time.

  The particle, viewed in a frame in which it is initially at rest, disintegrates leaving a particle of mass $m$ moving with constant velocity together with other remnants which have a total three-momentum $\mathbf{p}$ and energy $E$. Show that

  $$m=\sqrt{\left(M-\frac{E}{c^{2}}\right)^{2}-\frac{|\mathbf{p}|^{2}}{c^{2}}}$$

  comment

• Paper 2, Section I, C

  Special Relativity | Part IB, 2009

  Show that the two-dimensional Lorentz transformation relating $\left(c t^{\prime}, x^{\prime}\right)$ in frame $S^{\prime}$ to $(c t, x)$ in frame $S$, where $S^{\prime}$ moves relative to $S$ with speed $v$, can be written in the form

  $$\begin{gathered} x^{\prime}=x \cosh \phi-c t \sinh \phi \\ c t^{\prime}=-x \sinh \phi+c t \cosh \phi \end{gathered}$$

  where the hyperbolic angle $\phi$ associated with the transformation is given by $\tanh \phi=v / c$. Deduce that

  $$\begin{aligned} &x^{\prime}+c t^{\prime}=e^{-\phi}(x+c t) \\ &x^{\prime}-c t^{\prime}=e^{\phi}(x-c t) \end{aligned}$$

  Hence show that if the frame $S^{\prime \prime}$ moves with speed $v^{\prime}$ relative to $S^{\prime}$ and $\tanh \phi^{\prime}=v^{\prime} / c$, then the hyperbolic angle associated with the Lorentz transformation connecting $S^{\prime \prime}$ and $S$ is given by

  $$\phi^{\prime \prime}=\phi^{\prime}+\phi$$

  Hence find an expression for the speed of $S^{\prime \prime}$ as seen from $S$.

  comment

• Paper 4, Section II, C

  Special Relativity | Part IB, 2009

  A star moves with speed $v$ in the $x$-direction in a reference frame $S$. When viewed in its rest frame $S^{\prime}$ it emits a photon of frequency $\nu^{\prime}$ which propagates along a line making an angle $\theta^{\prime}$ with the $x^{\prime}$-axis. Write down the components of the four-momentum of the photon in $S^{\prime}$. As seen in $S$, the photon moves along a line that makes an angle $\theta$ with the $x$-axis and has frequency $\nu$. Using a Lorentz transformation, write down the relationship between the components of the four-momentum of the photon in $S^{\prime}$ to those in $S$ and show that

  $$\cos \theta=\frac{\cos \theta^{\prime}+v / c}{1+v \cos \theta^{\prime} / c}$$

  As viewed in $S^{\prime}$, the star emits two photons with frequency $\nu^{\prime}$ in opposite directions with $\theta^{\prime}=\pi / 2$ and $\theta^{\prime}=-\pi / 2$, respectively. Show that an observer in $S$ records them as having a combined momentum $p$ directed along the $x$-axis, where

  $$p=\frac{E v}{c^{2} \sqrt{1-v^{2} / c^{2}}}$$

  and where $E$ is the combined energy of the photons as seen in $S^{\prime}$. How is this momentum loss from the star consistent with its maintaining a constant speed as viewed in $S ?$

  comment

Statistics

• Paper 1, Section I, $\mathbf{7 H} \quad$

  Statistics | Part IB, 2009

  What does it mean to say that an estimator $\hat{\theta}$ of a parameter $\theta$ is unbiased?

  An $n$-vector $Y$ of observations is believed to be explained by the model

  $$Y=X \beta+\varepsilon$$

  where $X$ is a known $n \times p$ matrix, $\beta$ is an unknown $p$-vector of parameters, $p<n$, and $\varepsilon$ is an $n$-vector of independent $N\left(0, \sigma^{2}\right)$ random variables. Find the maximum-likelihood estimator $\hat{\beta}$ of $\beta$, and show that it is unbiased.

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2009

  What is the critical region $C$ of a test of the null hypothesis $H_{0}: \theta \in \Theta_{0}$ against the alternative $H_{1}: \theta \in \Theta_{1}$ ? What is the size of a test with critical region $C ?$ What is the power function of a test with critical region $C$ ?

  State and prove the Neyman-Pearson Lemma.

  If $X_{1}, \ldots, X_{n}$ are independent with $\operatorname{common} \operatorname{Exp}(\lambda)$ distribution, and $0<\lambda_{0}<\lambda_{1}$, find the form of the most powerful size- $\alpha$ test of $H_{0}: \lambda=\lambda_{0}$ against $H_{1}: \lambda=\lambda_{1}$. Find the power function as explicitly as you can, and prove that it is increasing in $\lambda$. Deduce that the test you have constructed is a size- $\alpha$ test of $H_{0}: \lambda \leqslant \lambda_{0}$ against $H_{1}: \lambda=\lambda_{1}$.

  comment

• Paper 2, Section II, H

  Statistics | Part IB, 2009

  What does it mean to say that the random $d$-vector $X$ has a multivariate normal distribution with mean $\mu$ and covariance matrix $\Sigma$ ?

  Suppose that $X \sim N_{d}\left(0, \sigma^{2} I_{d}\right)$, and that for each $j=1, \ldots, J, A_{j}$ is a $d_{j} \times d$ matrix. Suppose further that

  $$A_{j} A_{i}^{T}=0$$

  for $j \neq i$. Prove that the random vectors $Y_{j} \equiv A_{j} X$ are independent, and that $Y \equiv\left(Y_{1}^{T}, \ldots, Y_{J}^{T}\right)^{T}$ has a multivariate normal distribution.

  [Hint: Random vectors are independent if their joint $M G F$ is the product of their individual MGFs.]

  If $Z_{1}, \ldots, Z_{n}$ is an independent sample from a univariate $N\left(\mu, \sigma^{2}\right)$ distribution, prove that the sample variance $S_{Z Z} \equiv(n-1)^{-1} \sum_{i=1}^{n}\left(Z_{i}-\bar{Z}\right)^{2}$ and the sample mean $\bar{Z} \equiv$ $n^{-1} \sum_{i=1}^{n} Z_{i}$ are independent.

  comment

• Paper 3, Section $\mathbf{I}$, H

  Statistics | Part IB, 2009

  In a demographic study, researchers gather data on the gender of children in families with more than two children. For each of the four possible outcomes $G G, G B, B G, B B$ of the first two children in the family, they find 50 families which started with that pair, and record the gender of the third child of the family. This produces the following table of counts:

  First two children Third child $B$ Third child $G$

  $\begin{array}{ccc}G G & 16 & 34 \\ G B & 28 & 22 \\ B G & 25 & 25 \\ B B & 31 & 19\end{array}$

  In view of this, is the hypothesis that the gender of the third child is independent of the genders of the first two children rejected at the $5 \%$ level?

  [Hint: the $95 \%$ point of a $\chi_{3}^{2}$ distribution is $7.8147$, and the $95 \%$ point of a $\chi_{4}^{2}$ distribution is $9.4877 .]$

  comment

• Paper 4, Section II, H

  Statistics | Part IB, 2009

  What is a sufficient statistic? State the factorization criterion for a statistic to be sufficient.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent random variables uniformly distributed over $[a, b]$, where the parameters $a<b$ are not known, and $n \geqslant 2$. Find a sufficient statistic for the parameter $\theta \equiv(a, b)$ based on the sample $X_{1}, \ldots, X_{n}$. Based on your sufficient statistic, derive an unbiased estimator of $\theta$.

  comment