Part IB, 2019

Analysis II

• Paper 1, Section II, E

  Analysis II | Part IB, 2019

  Let $A \subset \mathbb{R}^{n}$ be an open subset. State what it means for a function $f: A \rightarrow \mathbb{R}^{m}$ to be differentiable at a point $p \in A$, and define its derivative $D f(p)$.

  State and prove the chain rule for the derivative of $g \circ f$, where $g: \mathbb{R}^{m} \rightarrow \mathbb{R}^{r}$ is a differentiable function.

  Let $M=M_{n}(\mathbb{R})$ be the vector space of $n \times n$ real-valued matrices, and $V \subset M$ the open subset consisting of all invertible ones. Let $f: V \rightarrow V$ be given by $f(A)=A^{-1}$.

  (a) Show that $f$ is differentiable at the identity matrix, and calculate its derivative.

  (b) For $C \in V$, let $l_{C}, r_{C}: M \rightarrow M$ be given by $l_{C}(A)=C A$ and $r_{C}(A)=A C$. Show that $r_{C} \circ f \circ l_{C}=f$ on $V$. Hence or otherwise, show that $f$ is differentiable at any point of $V$, and calculate $D f(C)(h)$ for $h \in M$.

  comment

• Paper 2, Section I, E

  Analysis II | Part IB, 2019

  Consider the map $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ given by

  $$f(x, y)=\left(x^{1 / 3}+y^{2}, y^{5}\right)$$

  where $x^{1 / 3}$ denotes the unique real cube root of $x \in \mathbb{R}$.

  (a) At what points is $f$ continuously differentiable? Calculate its derivative there.

  (b) Show that $f$ has a local differentiable inverse near any $(x, y)$ with $x y \neq 0$.

  You should justify your answers, stating accurately any results that you require.

  comment

• Paper 2, Section II, 12E

  Analysis II | Part IB, 2019

  (a) (i) Define what it means for two norms on a vector space to be Lipschitz equivalent.

  (ii) Show that any two norms on a finite-dimensional vector space are Lipschitz equivalent.

  (iii) Show that if two norms $\|\cdot\|,\|\cdot\|^{\prime}$ on a vector space $V$ are Lipschitz equivalent then the following holds: for any sequence $\left(v_{n}\right)$ in $V,\left(v_{n}\right)$ is Cauchy with respect to $\|\cdot\|$ if and only if it is Cauchy with respect to $\|\cdot\|^{\prime}$.

  (b) Let $V$ be the vector space of real sequences $x=\left(x_{i}\right)$ such that $\sum\left|x_{i}\right|<\infty$. Let

  $$\|x\|_{\infty}=\sup \left\{\left|x_{i}\right|: i \in \mathbb{N}\right\},$$

  and for $1 \leqslant p<\infty$, let

  $$\|x\|_{p}=\left(\sum\left|x_{i}\right|^{p}\right)^{1 / p}$$

  You may assume that $\|\cdot\|_{\infty}$ and $\|\cdot\|_{p}$ are well-defined norms on $V$.

  (i) Show that $\|\cdot\|_{p}$ is not Lipschitz equivalent to $\|\cdot\|_{\infty}$ for any $1 \leqslant p<\infty$.

  (ii) Are there any $p, q$ with $1 \leqslant p<q<\infty$ such that $\|\cdot\|_{p}$ and $\|\cdot\|_{q}$ are Lipschitz equivalent? Justify your answer.

  comment

• Paper 3, Section I, $2 E$

  Analysis II | Part IB, 2019

  (a) Let $A \subset \mathbb{R}$. What does it mean for a function $f: A \rightarrow \mathbb{R}$ to be uniformly continuous?

  (b) Which of the following functions are uniformly continuous? Briefly justify your answers.

  (i) $f(x)=x^{2}$ on $\mathbb{R}$.

  (ii) $f(x)=\sqrt{x}$ on $[0, \infty)$.

  (iii) $f(x)=\cos (1 / x)$ on $[1, \infty)$.

  comment

• Paper 3, Section II, E

  Analysis II | Part IB, 2019

  (a) Carefully state the Picard-Lindelöf theorem on solutions to ordinary differential equations.

  (b) Let $X=C\left([1, b], \mathbb{R}^{n}\right)$ be the set of continuous functions from a closed interval $[1, b]$ to $\mathbb{R}^{n}$, and let $\|\cdot\|$ be a norm on $\mathbb{R}^{n}$.

  (i) Let $f \in X$. Show that for any $c \in[0, \infty)$ the norm

  $$\|f\|_{c}=\sup _{t \in[1, b]}\left\|f(t) t^{-c}\right\|$$

  is Lipschitz equivalent to the usual sup norm on $X$.

  (ii) Assume that $F:[1, b] \times \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is continuous and Lipschitz in the second variable, i.e. there exists $M>0$ such that

  $$\|F(t, x)-F(t, y)\| \leqslant M\|x-y\|$$

  for all $t \in[1, b]$ and all $x, y \in \mathbb{R}^{n}$. Define $\varphi: X \rightarrow X$ by

  $$\varphi(f)(t)=\int_{1}^{t} F(l, f(l)) d l$$

  for $t \in[1, b]$.

  Show that there is a choice of $c$ such that $\varphi$ is a contraction on $\left(X,\|\cdot\|_{c}\right)$. Deduce that for any $y_{0} \in \mathbb{R}^{n}$, the differential equation

  $$D f(t)=F(t, f(t))$$

  has a unique solution on $[1, b]$ with $f(1)=y_{0}$.

  comment

• Paper 4, Section I, E

  Analysis II | Part IB, 2019

  Let $A \subset \mathbb{R}$. What does it mean to say that a sequence of real-valued functions on $A$ is uniformly convergent?

  (i) If a sequence $\left(f_{n}\right)$ of real-valued functions on $A$ converges uniformly to $f$, and each $f_{n}$ is continuous, must $f$ also be continuous?

  (ii) Let $f_{n}(x)=e^{-n x}$. Does the sequence $\left(f_{n}\right)$ converge uniformly on $[0,1]$ ?

  (iii) If a sequence $\left(f_{n}\right)$ of real-valued functions on $[-1,1]$ converges uniformly to $f$, and each $f_{n}$ is differentiable, must $f$ also be differentiable?

  Give a proof or counterexample in each case.

  comment

• Paper 4, Section II, E

  Analysis II | Part IB, 2019

  (a) (i) Show that a compact metric space must be complete.

  (ii) If a metric space is complete and bounded, must it be compact? Give a proof or counterexample.

  (b) A metric space $(X, d)$ is said to be totally bounded if for all $\epsilon>0$, there exists $N \in \mathbb{N}$ and $\left\{x_{1}, \ldots, x_{N}\right\} \subset X$ such that $X=\bigcup_{i=1}^{N} B_{\epsilon}\left(x_{i}\right) .$

  (i) Show that a compact metric space is totally bounded.

  (ii) Show that a complete, totally bounded metric space is compact.

  [Hint: If $\left(x_{n}\right)$ is Cauchy, then there is a subsequence $\left(x_{n_{j}}\right)$ such that

  $$\left.\sum_{j} d\left(x_{n_{j+1}}, x_{n_{j}}\right)<\infty .\right]$$

  (iii) Consider the space $C[0,1]$ of continuous functions $f:[0,1] \rightarrow \mathbb{R}$, with the metric

  $$d(f, g)=\min \left\{\int_{0}^{1}|f(t)-g(t)| d t, 1\right\} .$$

  Is this space compact? Justify your answer.

  comment

Complex Analysis

• Paper 3, Section II, F

  Complex Analysis | Part IB, 2019

  Define the winding number $n(\gamma, w)$ of a closed path $\gamma:[a, b] \rightarrow \mathbb{C}$ around a point $w \in \mathbb{C}$ which does not lie on the image of $\gamma$. [You do not need to justify its existence.]

  If $f$ is a meromorphic function, define the order of a zero $z_{0}$ of $f$ and of a pole $w_{0}$ of $f$. State the Argument Principle, and explain how it can be deduced from the Residue Theorem.

  How many roots of the polynomial

  $$z^{4}+10 z^{3}+4 z^{2}+10 z+5$$

  lie in the right-hand half plane?

  comment

• Paper 4, Section I, $4 \mathbf{F}$

  Complex Analysis | Part IB, 2019

  State the Cauchy Integral Formula for a disc. If $f: D\left(z_{0} ; r\right) \rightarrow \mathbb{C}$ is a holomorphic function such that $|f(z)| \leqslant\left|f\left(z_{0}\right)\right|$ for all $z \in D\left(z_{0} ; r\right)$, show using the Cauchy Integral Formula that $f$ is constant.

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, F

  Complex Analysis or Complex Methods | Part IB, 2019

  What is the Laurent series for a function $f$ defined in an annulus $A$ ? Find the Laurent series for $f(z)=\frac{10}{(z+2)\left(z^{2}+1\right)}$ on the annuli

  $$\begin{aligned} &A_{1}=\{z \in \mathbb{C}|0<| z \mid<1\} \quad \text { and } \\ &A_{2}=\{z \in \mathbb{C}|1<| z \mid<2\} \end{aligned}$$

  comment

• Paper 1, Section II, F

  Complex Analysis or Complex Methods | Part IB, 2019

  State and prove Jordan's lemma.

  What is the residue of a function $f$ at an isolated singularity $a$ ? If $f(z)=\frac{g(z)}{(z-a)^{k}}$ with $k$ a positive integer, $g$ analytic, and $g(a) \neq 0$, derive a formula for the residue of $f$ at $a$ in terms of derivatives of $g$.

  Evaluate

  $$\int_{-\infty}^{\infty} \frac{x^{3} \sin x}{\left(1+x^{2}\right)^{2}} d x$$

  comment

• Paper 2, Section II, D

  Complex Analysis or Complex Methods | Part IB, 2019

  Let $C_{1}$ and $C_{2}$ be smooth curves in the complex plane, intersecting at some point $p$. Show that if the map $f: \mathbb{C} \rightarrow \mathbb{C}$ is complex differentiable, then it preserves the angle between $C_{1}$ and $C_{2}$ at $p$, provided $f^{\prime}(p) \neq 0$. Give an example that illustrates why the condition $f^{\prime}(p) \neq 0$ is important.

  Show that $f(z)=z+1 / z$ is a one-to-one conformal map on each of the two regions $|z|>1$ and $0<|z|<1$, and find the image of each region.

  Hence construct a one-to-one conformal map from the unit disc to the complex plane with the intervals $(-\infty,-1 / 2]$ and $[1 / 2, \infty)$ removed.

  comment

Complex Methods

• Paper 3, Section I, D

  Complex Methods | Part IB, 2019

  By considering the transformation $w=i(1-z) /(1+z)$, find a solution to Laplace's equation $\nabla^{2} \phi=0$ inside the unit disc $D \subset \mathbb{C}$, subject to the boundary conditions

  $$\left.\phi\right|_{|z|=1}= \begin{cases}\phi_{0} & \text { for } \arg (z) \in(0, \pi) \\ -\phi_{0} & \text { for } \arg (z) \in(\pi, 2 \pi)\end{cases}$$

  where $\phi_{0}$ is constant. Give your answer in terms of $(x, y)=(\operatorname{Re} z, \operatorname{Im} z)$.

  comment

• Paper 4, Section II, D

  Complex Methods | Part IB, 2019

  (a) Using the Bromwich contour integral, find the inverse Laplace transform of $1 / s^{2}$.

  The temperature $u(r, t)$ of mercury in a spherical thermometer bulb $r \leqslant a$ obeys the radial heat equation

  $$\frac{\partial u}{\partial t}=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r u)$$

  with unit diffusion constant. At $t=0$ the mercury is at a uniform temperature $u_{0}$ equal to that of the surrounding air. For $t>0$ the surrounding air temperature lowers such that at the edge of the thermometer bulb

  $$\left.\frac{1}{k} \frac{\partial u}{\partial r}\right|_{r=a}=u_{0}-u(a, t)-t$$

  where $k$ is a constant.

  (b) Find an explicit expression for $U(r, s)=\int_{0}^{\infty} e^{-s t} u(r, t) d t$.

  (c) Show that the temperature of the mercury at the centre of the thermometer bulb at late times is

  $$u(0, t) \approx u_{0}-t+\frac{a}{3 k}+\frac{a^{2}}{6}$$

  [You may assume that the late time behaviour of $u(r, t)$ is determined by the singular part of $U(r, s)$ at $s=0 .]$

  comment

Electromagnetism

• Paper 1, Section II, A

  Electromagnetism | Part IB, 2019

  Let $\mathbf{E}(\mathbf{x})$ be the electric field and $\varphi(\mathbf{x})$ the scalar potential due to a static charge density $\rho(\mathbf{x})$, with all quantities vanishing as $r=|\mathbf{x}|$ becomes large. The electrostatic energy of the configuration is given by

  $$U=\frac{\varepsilon_{0}}{2} \int|\mathbf{E}|^{2} d V=\frac{1}{2} \int \rho \varphi d V$$

  with the integrals taken over all space. Verify that these integral expressions agree.

  Suppose that a total charge $Q$ is distributed uniformly in the region $a \leqslant r \leqslant b$ and that $\rho=0$ otherwise. Use the integral form of Gauss's Law to determine $\mathbf{E}(\mathbf{x})$ at all points in space and, without further calculation, sketch graphs to indicate how $|\mathbf{E}|$ and $\varphi$ depend on position.

  Consider the limit $b \rightarrow a$ with $Q$ fixed. Comment on the continuity of $\mathbf{E}$ and $\varphi$. Verify directly from each of the integrals in $(*)$ that $U=Q \varphi(a) / 2$ in this limit.

  Now consider a small change $\delta Q$ in the total charge $Q$. Show that the first-order change in the energy is $\delta U=\delta Q \varphi(a)$ and interpret this result.

  comment

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2019

  Write down the solution for the scalar potential $\varphi(\mathbf{x})$ that satisfies

  $$\nabla^{2} \varphi=-\frac{1}{\varepsilon_{0}} \rho,$$

  with $\varphi(\mathbf{x}) \rightarrow 0$ as $r=|\mathbf{x}| \rightarrow \infty$. You may assume that the charge distribution $\rho(\mathbf{x})$ vanishes for $r>R$, for some constant $R$. In an expansion of $\varphi(\mathbf{x})$ for $r \gg R$, show that the terms of order $1 / r$ and $1 / r^{2}$ can be expressed in terms of the total charge $Q$ and the electric dipole moment $\mathbf{p}$, which you should define.

  Write down the analogous solution for the vector potential $\mathbf{A}(\mathbf{x})$ that satisfies

  $$\nabla^{2} \mathbf{A}=-\mu_{0} \mathbf{J}$$

  with $\mathbf{A}(\mathbf{x}) \rightarrow \mathbf{0}$ as $r \rightarrow \infty$. You may assume that the current $\mathbf{J}(\mathbf{x})$ vanishes for $r>R$ and that it obeys $\nabla \cdot \mathbf{J}=0$ everywhere. In an expansion of $\mathbf{A}(\mathbf{x})$ for $r \gg R$, show that the term of order $1 / r$ vanishes.

  $\left[\right.$ Hint: $\left.\frac{\partial}{\partial x_{j}}\left(x_{i} J_{j}\right)=J_{i}+x_{i} \frac{\partial J_{j}}{\partial x_{j}} .\right]$

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2019

  Consider a conductor in the shape of a closed curve $C$ moving in the presence of a magnetic field B. State Faraday's Law of Induction, defining any quantities that you introduce.

  Suppose $C$ is a square horizontal loop that is allowed to move only vertically. The location of the loop is specified by a coordinate $z$, measured vertically upwards, and the edges of the loop are defined by $x=\pm a,-a \leqslant y \leqslant a$ and $y=\pm a,-a \leqslant x \leqslant a$. If the magnetic field is

  $$\mathbf{B}=b(x, y,-2 z),$$

  where $b$ is a constant, find the induced current $I$, given that the total resistance of the loop is $R$.

  Calculate the resulting electromagnetic force on the edge of the loop $x=a$, and show that this force acts at an angle $\tan ^{-1}(2 z / a)$ to the vertical. Find the total electromagnetic force on the loop and comment on its direction.

  Now suppose that the loop has mass $m$ and that gravity is the only other force acting on it. Show that it is possible for the loop to fall with a constant downward velocity $R m g /\left(8 b a^{2}\right)^{2}$.

  comment

• Paper 3, Section II, A

  Electromagnetism | Part IB, 2019

  The electric and magnetic fields $\mathbf{E}, \mathbf{B}$ in an inertial frame $\mathcal{S}$ are related to the fields $\mathbf{E}^{\prime}, \mathbf{B}^{\prime}$ in a frame $\mathcal{S}^{\prime}$ by a Lorentz transformation. Given that $\mathcal{S}^{\prime}$ moves in the $x$-direction with speed $v$ relative to $\mathcal{S}$, and that

  $$E_{y}^{\prime}=\gamma\left(E_{y}-v B_{z}\right), \quad B_{z}^{\prime}=\gamma\left(B_{z}-\left(v / c^{2}\right) E_{y}\right),$$

  write down equations relating the remaining field components and define $\gamma$. Use your answers to show directly that $\mathbf{E}^{\prime} \cdot \mathbf{B}^{\prime}=\mathbf{E} \cdot \mathbf{B}$.

  Give an expression for an additional, independent, Lorentz-invariant function of the fields, and check that it is invariant for the special case when $E_{y}=E$ and $B_{y}=B$ are the only non-zero components in the frame $\mathcal{S}$.

  Now suppose in addition that $c B=\lambda E$ with $\lambda$ a non-zero constant. Show that the angle $\theta$ between the electric and magnetic fields in $\mathcal{S}^{\prime}$ is given by

  $$\cos \theta=f(\beta)=\frac{\lambda\left(1-\beta^{2}\right)}{\left\{\left(1+\lambda^{2} \beta^{2}\right)\left(\lambda^{2}+\beta^{2}\right)\right\}^{1 / 2}}$$

  where $\beta=v / c$. By considering the behaviour of $f(\beta)$ as $\beta$ approaches its limiting values, show that the relative velocity of the frames can be chosen so that the angle takes any value in one of the ranges $0 \leqslant \theta<\pi / 2$ or $\pi / 2<\theta \leqslant \pi$, depending on the sign of $\lambda$.

  comment

• Paper 4, Section I, A

  Electromagnetism | Part IB, 2019

  Write down Maxwell's Equations for electric and magnetic fields $\mathbf{E}(\mathbf{x}, t)$ and $\mathbf{B}(\mathbf{x}, t)$ in the absence of charges and currents. Show that there are solutions of the form

  $$\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left\{\mathbf{E}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right\}, \quad \mathbf{B}(\mathbf{x}, t)=\operatorname{Re}\left\{\mathbf{B}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right\}$$

  if $\mathbf{E}_{0}$ and $\mathbf{k}$ satisfy a constraint and if $\mathbf{B}_{0}$ and $\omega$ are then chosen appropriately.

  Find the solution with $\mathbf{E}_{0}=E(1, i, 0)$, where $E$ is real, and $\mathbf{k}=k(0,0,1)$. Compute the Poynting vector and state its physical significance.

  comment

Fluid Dynamics

• Paper 1, Section I, C

  Fluid Dynamics | Part IB, 2019

  A viscous fluid flows steadily down a plane that is inclined at an angle $\alpha$ to the horizontal. The fluid layer is of uniform thickness and has a free upper surface. Determine the velocity profile in the direction perpendicular to the plane and also the volume flux (per unit width), in terms of the gravitational acceleration $g$, the angle $\alpha$, the kinematic viscosity $\nu$ and the thickness $h$ of the fluid layer.

  Show that the volume flux is reduced if the free upper surface is replaced by a stationary plane boundary, and give a physical explanation for this.

  comment

• Paper 1, Section II, C

  Fluid Dynamics | Part IB, 2019

  Explain why the irrotational flow of an incompressible fluid can be expressed in terms of a velocity potential $\phi$ that satisfies Laplace's equation.

  The axis of a stationary cylinder of radius $a$ coincides with the $z$-axis of a Cartesian coordinate system $(x, y, z)$ with unit vectors $\left(\mathbf{e}_{x}, \mathbf{e}_{y}, \mathbf{e}_{z}\right)$. A fluid of density $\rho$ flows steadily past the cylinder such that the velocity field $\mathbf{u}$ is independent of $z$ and has no component in the $z$-direction. The flow is irrotational but there is a constant non-zero circulation

  $$\oint \mathbf{u} \cdot d \mathbf{r}=\kappa$$

  around every closed curve that encloses the cylinder once in a positive sense. Far from the cylinder, the velocity field tends towards the uniform flow $\mathbf{u}=U \mathbf{e}_{x}$, where $U$ is a constant.

  State the boundary conditions on the velocity potential, in terms of polar coordinates $(r, \theta)$ in the $(x, y)$-plane. Explain why the velocity potential is not required to be a single-valued function of position. Hence obtain the appropriate solution $\phi(r, \theta)$, in terms of $a, U$ and $\kappa$.

  Neglecting gravity, show that the net force on the cylinder, per unit length in the $z$-direction, is

  $$-\rho \kappa U \mathbf{e}_{y}$$

  Determine the number and location of stagnation points in the flow as a function of the dimensionless parameter

  $$\lambda=\frac{\kappa}{4 \pi U a}$$

  comment

• Paper 2, Section I, C

  Fluid Dynamics | Part IB, 2019

  Consider the steady flow

  $$u_{x}=\sin x \cos y, \quad u_{y}=-\cos x \sin y, \quad u_{z}=0$$

  where $(x, y, z)$ are Cartesian coordinates. Show that $\boldsymbol{\nabla} \cdot \mathbf{u}=0$ and determine the streamfunction. Calculate the vorticity and verify that the vorticity equation is satisfied in the absence of viscosity. Sketch the streamlines in the region $0<x<2 \pi, 0<y<2 \pi$.

  comment

• Paper 3, Section II, C

  Fluid Dynamics | Part IB, 2019

  A cubic box of side $2 h$, enclosing the region $0<x<2 h, 0<y<2 h,-h<z<h$, contains equal volumes of two incompressible fluids that remain distinct. The system is initially at rest, with the fluid of density $\rho_{1}$ occupying the region $0<z<h$ and the fluid of density $\rho_{2}$ occupying the region $-h<z<0$, and with gravity $(0,0,-g)$. The interface between the fluids is then slightly perturbed. Derive the linearized equations and boundary conditions governing small disturbances to the initial state.

  In the case $\rho_{2}>\rho_{1}$, show that the angular frequencies $\omega$ of the normal modes are given by

  $$\omega^{2}=\left(\frac{\rho_{2}-\rho_{1}}{\rho_{1}+\rho_{2}}\right) g k \tanh (k h)$$

  and express the allowable values of the wavenumber $k$ in terms of $h$. Identify the lowestfrequency non-trivial mode $(\mathrm{s})$. Comment on the limit $\rho_{1} \ll \rho_{2}$. What physical behaviour is expected in the case $\rho_{1}>\rho_{2}$ ?

  comment

• Paper 4, Section II, C

  Fluid Dynamics | Part IB, 2019

  The linear shallow-water equations governing the motion of a fluid layer in the neighbourhood of a point on the Earth's surface in the northern hemisphere are

  $$\begin{aligned} \frac{\partial u}{\partial t}-f v &=-g \frac{\partial \eta}{\partial x} \\ \frac{\partial v}{\partial t}+f u &=-g \frac{\partial \eta}{\partial y} \\ \frac{\partial \eta}{\partial t} &=-h\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right) \end{aligned}$$

  where $u(x, y, t)$ and $v(x, y, t)$ are the horizontal velocity components and $\eta(x, y, t)$ is the perturbation of the height of the free surface.

  (a) Explain the meaning of the three positive constants $f, g$ and $h$ appearing in the equations above and outline the assumptions made in deriving these equations.

  (b) Show that $\zeta$, the $z$-component of vorticity, satisfies

  $$\frac{\partial \zeta}{\partial t}=-f\left(\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}\right)$$

  and deduce that the potential vorticity

  $$q=\zeta-\frac{f}{h} \eta$$

  satisfies

  $$\frac{\partial q}{\partial t}=0$$

  (c) Consider a steady geostrophic flow that is uniform in the latitudinal $(y)$ direction. Show that

  $$\frac{d^{2} \eta}{d x^{2}}-\frac{f^{2}}{g h} \eta=\frac{f}{g} q .$$

  Given that the potential vorticity has the piecewise constant profile

  $$q= \begin{cases}q_{1}, & x<0 \\ q_{2}, & x>0\end{cases}$$

  where $q_{1}$ and $q_{2}$ are constants, and that $v \rightarrow 0$ as $x \rightarrow \pm \infty$, solve for $\eta(x)$ and $v(x)$ in terms of the Rossby radius $R=\sqrt{g h} / f$. Sketch the functions $\eta(x)$ and $v(x)$ in the case $q_{1}>q_{2}$.

  comment

Geometry

• Paper 1, Section I, E

  Geometry | Part IB, 2019

  Describe the Poincaré disc model $D$ for the hyperbolic plane by giving the appropriate Riemannian metric.

  Calculate the distance between two points $z_{1}, z_{2} \in D$. You should carefully state any results about isometries of $D$ that you use.

  comment

• Paper 2, Section II, E

  Geometry | Part IB, 2019

  Define a smooth embedded surface in $\mathbb{R}^{3}$. Sketch the surface $C$ given by

  $$\left(\sqrt{2 x^{2}+2 y^{2}}-4\right)^{2}+2 z^{2}=2$$

  and find a smooth parametrisation for it. Use this to calculate the Gaussian curvature of $C$ at every point.

  Hence or otherwise, determine which points of the embedded surface

  $$\left(\sqrt{x^{2}+2 x z+z^{2}+2 y^{2}}-4\right)^{2}+(z-x)^{2}=2$$

  have Gaussian curvature zero. [Hint: consider a transformation of $\mathbb{R}^{3}$.]

  [You should carefully state any result that you use.]

  comment

• Paper 3, Section I, E

  Geometry | Part IB, 2019

  State a formula for the area of a spherical triangle with angles $\alpha, \beta, \gamma$.

  Let $n \geqslant 3$. What is the area of a convex spherical $n$-gon with interior angles $\alpha_{1}, \ldots, \alpha_{n}$ ? Justify your answer.

  Find the range of possible values for the interior angle of a regular convex spherical $n-g \mathrm{gn}$

  comment

• Paper 3, Section II, E

  Geometry | Part IB, 2019

  Define a geodesic triangulation of an abstract closed smooth surface. Define the Euler number of a triangulation, and state the Gauss-Bonnet theorem for closed smooth surfaces. Given a vertex in a triangulation, its valency is defined to be the number of edges incident at that vertex.

  (a) Given a triangulation of the torus, show that the average valency of a vertex of the triangulation is 6 .

  (b) Consider a triangulation of the sphere.

  (i) Show that the average valency of a vertex is strictly less than 6 .

  (ii) A triangulation can be subdivided by replacing one triangle $\Delta$ with three sub-triangles, each one with vertices two of the original ones, and a fixed interior point of $\Delta$.

  Using this, or otherwise, show that there exist triangulations of the sphere with average vertex valency arbitrarily close to 6 .

  (c) Suppose $S$ is a closed abstract smooth surface of everywhere negative curvature. Show that the average vertex valency of a triangulation of $S$ is bounded above and below.

  comment

• Paper 4, Section II, E

  Geometry | Part IB, 2019

  Let $H=\{x+i y \mid x, y \in \mathbb{R}, y>0\}$ be the upper-half plane with hyperbolic metric $\frac{d x^{2}+d y^{2}}{y^{2}}$. Define the group $P S L(2, \mathbb{R})$, and show that it acts by isometries on $H$. [If you use a generation statement you must carefully state it.]

  (a) Prove that $P S L(2, \mathbb{R})$ acts transitively on the collection of pairs $(l, P)$, where $l$ is a hyperbolic line in $H$ and $P \in l$.

  (b) Let $l^{+} \subset H$ be the imaginary half-axis. Find the isometries of $H$ which fix $l^{+}$ pointwise. Hence or otherwise find all isometries of $H$.

  (c) Describe without proof the collection of all hyperbolic lines which meet $l^{+}$with (signed) angle $\alpha, 0<\alpha<\pi$. Explain why there exists a hyperbolic triangle with angles $\alpha, \beta$ and $\gamma$ whenever $\alpha+\beta+\gamma<\pi$.

  (d) Is this triangle unique up to isometry? Justify your answer. [You may use without proof the fact that Möbius maps preserve angles.]

  comment

Groups, Rings and Modules

• Paper 1, Section II, G

  Groups, Rings and Modules | Part IB, 2019

  (a) Let $G$ be a group of order $p^{4}$, for $p$ a prime. Prove that $G$ is not simple.

  (b) State Sylow's theorems.

  (c) Let $G$ be a group of order $p^{2} q^{2}$, where $p, q$ are distinct odd primes. Prove that $G$ is not simple.

  comment

• Paper 2, Section I, G

  Groups, Rings and Modules | Part IB, 2019

  Let $R$ be an integral domain. A module $M$ over $R$ is torsion-free if, for any $r \in R$ and $m \in M, r m=0$ only if $r=0$ or $m=0$.

  Let $M$ be a module over $R$. Prove that there is a quotient

  $$q: M \rightarrow M_{0}$$

  with $M_{0}$ torsion-free and with the following property: whenever $N$ is a torsion-free module and $f: M \rightarrow N$ is a homomorphism of modules, there is a homomorphism $f_{0}: M_{0} \rightarrow N$ such that $f=f_{0} \circ q$.

  comment

• Paper 2, Section II, G

  Groups, Rings and Modules | Part IB, 2019

  (a) Let $k$ be a field and let $f(X)$ be an irreducible polynomial of degree $d>0$ over $k$. Prove that there exists a field $F$ containing $k$ as a subfield such that

  $$f(X)=(X-\alpha) g(X)$$

  where $\alpha \in F$ and $g(X) \in F[X]$. State carefully any results that you use.

  (b) Let $k$ be a field and let $f(X)$ be a monic polynomial of degree $d>0$ over $k$, which is not necessarily irreducible. Prove that there exists a field $F$ containing $k$ as a subfield such that

  $$f(X)=\prod_{i=1}^{d}\left(X-\alpha_{i}\right)$$

  where $\alpha_{i} \in F$.

  (c) Let $k=\mathbb{Z} /(p)$ for $p$ a prime, and let $f(X)=X^{p^{n}}-X$ for $n \geqslant 1$ an integer. For $F$ as in part (b), let $K$ be the set of roots of $f(X)$ in $F$. Prove that $K$ is a field.

  comment

• Paper 3, Section I, $1 G$

  Groups, Rings and Modules | Part IB, 2019

  Prove that the ideal $(2,1+\sqrt{-13})$ in $\mathbb{Z}[\sqrt{-13}]$ is not principal.

  comment

• Paper 3, Section II, G

  Groups, Rings and Modules | Part IB, 2019

  Let $\omega=\frac{1}{2}(-1+\sqrt{-3})$.

  (a) Prove that $\mathbb{Z}[\omega]$ is a Euclidean domain.

  (b) Deduce that $\mathbb{Z}[\omega]$ is a unique factorisation domain, stating carefully any results from the course that you use.

  (c) By working in $\mathbb{Z}[\omega]$, show that whenever $x, y \in \mathbb{Z}$ satisfy

  $$x^{2}-x+1=y^{3}$$

  then $x$ is not congruent to 2 modulo 3 .

  comment

• Paper 4, Section I, G

  Groups, Rings and Modules | Part IB, 2019

  Let $G$ be a group and $P$ a subgroup.

  (a) Define the normaliser $N_{G}(P)$.

  (b) Suppose that $K \triangleleft G$ and $P$ is a Sylow $p$-subgroup of $K$. Using Sylow's second theorem, prove that $G=N_{G}(P) K$.

  comment

• Paper 4, Section II, G

  Groups, Rings and Modules | Part IB, 2019

  (a) Define the Smith Normal Form of a matrix. When is it guaranteed to exist?

  (b) Deduce the classification of finitely generated abelian groups.

  (c) How many conjugacy classes of matrices are there in $G L_{10}(\mathbb{Q})$ with minimal polynomial $X^{7}-4 X^{3} ?$

  comment

Linear Algebra

• Paper 1, Section I, F

  Linear Algebra | Part IB, 2019

  Define a basis of a vector space $V$.

  If $V$ has a finite basis $\mathcal{B}$, show using only the definition that any other basis $\mathcal{B}^{\prime}$ has the same cardinality as $\mathcal{B}$.

  comment

• Paper 1, Section II, F

  Linear Algebra | Part IB, 2019

  What is the adjugate adj $(A)$ of an $n \times n$ matrix $A$ ? How is it related to $\operatorname{det}(A) ?$

  (a) Define matrices $B_{0}, B_{1}, \ldots, B_{n-1}$ by

  $$\operatorname{adj}(t I-A)=\sum_{i=0}^{n-1} B_{i} t^{n-1-i}$$

  and scalars $c_{0}, c_{1}, \ldots, c_{n}$ by

  $$\operatorname{det}(t I-A)=\sum_{j=0}^{n} c_{j} t^{n-j}$$

  Find a recursion for the matrices $B_{i}$ in terms of $A$ and the $c_{j}$ 's.

  (b) By considering the partial derivatives of the multivariable polynomial

  $$p\left(t_{1}, t_{2}, \ldots, t_{n}\right)=\operatorname{det}\left(\left(\begin{array}{cccc} t_{1} & 0 & \cdots & 0 \\ 0 & t_{2} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots \\ 0 & 0 & \cdots & t_{n} \end{array}\right)-A\right)$$

  show that

  $$\frac{d}{d t}(\operatorname{det}(t I-A))=\operatorname{Tr}(\operatorname{adj}(t I-A))$$

  (c) Hence show that the $c_{j}$ 's may be expressed in terms of $\operatorname{Tr}(A), \operatorname{Tr}\left(A^{2}\right), \ldots, \operatorname{Tr}\left(A^{n}\right)$.

  comment

• Paper 2, Section I, F

  Linear Algebra | Part IB, 2019

  If $U$ and $W$ are finite-dimensional subspaces of a vector space $V$, prove that

  $$\operatorname{dim}(U+W)=\operatorname{dim}(U)+\operatorname{dim}(W)-\operatorname{dim}(U \cap W)$$

  Let

  $$\begin{aligned} U &=\left\{\mathbf{x} \in \mathbb{R}^{4} \mid x_{1}=7 x_{3}+8 x_{4}, x_{2}+5 x_{3}+6 x_{4}=0\right\} \\ W &=\left\{\mathbf{x} \in \mathbb{R}^{4} \mid x_{1}+2 x_{2}+3 x_{3}=0, x_{4}=0\right\} . \end{aligned}$$

  Show that $U+W$ is 3 -dimensional and find a linear map $\ell: \mathbb{R}^{4} \rightarrow \mathbb{R}$ such that

  $$U+W=\left\{\mathbf{x} \in \mathbb{R}^{4} \mid \ell(\mathbf{x})=0\right\}$$

  comment

• Paper 2, Section II, F

  Linear Algebra | Part IB, 2019

  Let $A$ and $B$ be $n \times n$ matrices over $\mathbb{C}$.

  (a) Assuming that $A$ is invertible, show that $A B$ and $B A$ have the same characteristic polynomial.

  (b) By considering the matrices $A-s I$, show that $A B$ and $B A$ have the same characteristic polynomial even when $A$ is singular.

  (c) Give an example to show that the minimal polynomials $m_{A B}(t)$ and $m_{B A}(t)$ of $A B$ and $B A$ may be different.

  (d) Show that $m_{A B}(t)$ and $m_{B A}(t)$ differ at most by a factor of $t$. Stating carefully any results which you use, deduce that if $A B$ is diagonalisable then so is $(B A)^{2}$.

  comment

• Paper 3, Section II, F

  Linear Algebra | Part IB, 2019

  If $q$ is a quadratic form on a finite-dimensional real vector space $V$, what is the associated symmetric bilinear form $\varphi(\cdot, \cdot)$ ? Prove that there is a basis for $V$ with respect to which the matrix for $\varphi$ is diagonal. What is the signature of $q$ ?

  If $R \leqslant V$ is a subspace such that $\varphi(r, v)=0$ for all $r \in R$ and all $v \in V$, show that $q^{\prime}(v+R)=q(v)$ defines a quadratic form on the quotient vector space $V / R$. Show that the signature of $q^{\prime}$ is the same as that of $q$.

  If $e, f \in V$ are vectors such that $\varphi(e, e)=0$ and $\varphi(e, f)=1$, show that there is a direct sum decomposition $V=\operatorname{span}(e, f) \oplus U$ such that the signature of $\left.q\right|_{U}$ is the same as that of $q$.

  comment

• Paper 4, Section I, F

  Linear Algebra | Part IB, 2019

  What is an eigenvalue of a matrix $A$ ? What is the eigenspace corresponding to an eigenvalue $\lambda$ of $A$ ?

  Consider the matrix

  $$A=\left(\begin{array}{cccc} a a & a b & a c & a d \\ b a & b b & b c & b d \\ c a & c b & c c & c d \\ d a & d b & d c & d d \end{array}\right)$$

  for $(a, b, c, d) \in \mathbb{R}^{4}$ a non-zero vector. Show that $A$ has rank 1 . Find the eigenvalues of $A$ and describe the corresponding eigenspaces. Is $A$ diagonalisable?

  comment

• Paper 4, Section II, F

  Linear Algebra | Part IB, 2019

  If $U$ is a finite-dimensional real vector space with inner product $\langle\cdot, \cdot\rangle$, prove that the linear map $\phi: U \rightarrow U^{*}$ given by $\phi(u)\left(u^{\prime}\right)=\left\langle u, u^{\prime}\right\rangle$ is an isomorphism. [You do not need to show that it is linear.]

  If $V$ and $W$ are inner product spaces and $\alpha: V \rightarrow W$ is a linear map, what is meant by the adjoint $\alpha^{*}$ of $\alpha$ ? If $\left\{e_{1}, e_{2}, \ldots, e_{n}\right\}$ is an orthonormal basis for $V,\left\{f_{1}, f_{2}, \ldots, f_{m}\right\}$ is an orthonormal basis for $W$, and $A$ is the matrix representing $\alpha$ in these bases, derive a formula for the matrix representing $\alpha^{*}$ in these bases.

  Prove that $\operatorname{Im}(\alpha)=\operatorname{Ker}\left(\alpha^{*}\right)^{\perp}$.

  If $w_{0} \notin \operatorname{Im}(\alpha)$ then the linear equation $\alpha(v)=w_{0}$ has no solution, but we may instead search for a $v_{0} \in V$ minimising $\left\|\alpha(v)-w_{0}\right\|^{2}$, known as a least-squares solution. Show that $v_{0}$ is such a least-squares solution if and only if it satisfies $\alpha^{*} \alpha\left(v_{0}\right)=\alpha^{*}\left(w_{0}\right)$. Hence find a least-squares solution to the linear equation

  $$\left(\begin{array}{ll} 1 & 0 \\ 1 & 1 \\ 0 & 1 \end{array}\right)\left(\begin{array}{l} x \\ y \end{array}\right)=\left(\begin{array}{l} 1 \\ 2 \\ 3 \end{array}\right)$$

  comment

Markov Chains

• Paper 1, Section II, H

  Markov Chains | Part IB, 2019

  Let $P$ be a transition matrix for a Markov chain $\left(X_{n}\right)$ on a state space with $N$ elements with $N<\infty$. Assume that the Markov chain is aperiodic and irreducible and let $\pi$ be its unique invariant distribution. Assume that $X_{0} \sim \pi$.

  (a) Let $P^{*}(x, y)=\mathbb{P}\left[X_{0}=y \mid X_{1}=x\right]$. Show that $P^{*}(x, y)=\pi(y) P(y, x) / \pi(x)$.

  (b) Let $T=\min \left\{n \geqslant 1: X_{n}=X_{0}\right\}$. Compute $\mathbb{E}[T]$ in terms of an explicit function of $N$.

  (c) Suppose that a cop and a robber start from a common state chosen from $\pi$. The robber then takes one step according to $P^{*}$ and stops. The cop then moves according to $P$ independently of the robber until the cop catches the robber (i.e., the cop visits the state occupied by the robber). Compute the expected amount of time for the cop to catch the robber.

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2019

  Fix $n \geqslant 1$ and let $G$ be the graph consisting of a copy of $\{0, \ldots, n\}$ joining vertices $A$ and $B$, a copy of $\{0, \ldots, n\}$ joining vertices $B$ and $C$, and a copy of $\{0, \ldots, n\}$ joining vertices $B$ and $D$. Let $E$ be the vertex adjacent to $B$ on the segment from $B$ to $C$. Shown below is an illustration of $G$ in the case $n=5$. The vertices are solid squares and edges are indicated by straight lines.

  

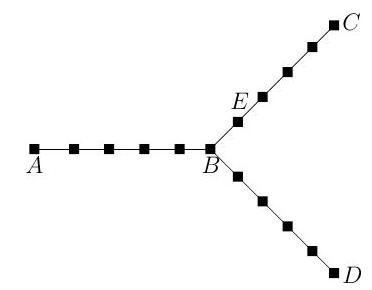
  Let $\left(X_{k}\right)$ be a simple random walk on $G$. In other words, in each time step, $X$ moves to one of its neighbours with equal probability. Assume that $X_{0}=A$.

  (a) Compute the expected amount of time for $X$ to hit $B$.

  (b) Compute the expected amount of time for $X$ to hit $E$. [Hint: first show that the expected amount of time $x$ for $X$ to go from $B$ to $E$ satisfies $x=\frac{1}{3}+\frac{2}{3}(L+x)$ where $L$ is the expected return time of $X$ to $B$ when starting from $B$.]

  (c) Compute the expected amount of time for $X$ to hit $C$. [Hint: for each $i$, let $v_{i}$ be the vertex which is $i$ places to the right of $B$ on the segment from $B$ to $C$. Derive an equation for the expected amount of time $x_{i}$ for $X$ to go from $v_{i}$ to $v_{i+1}$.]

  Justify all of your answers.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2019

  Suppose that $\left(X_{n}\right)$ is a Markov chain with state space $S$.

  (a) Give the definition of a communicating class.

  (b) Give the definition of the period of a state $a \in S$.

  (c) Show that if two states communicate then they have the same period.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2019

  For a Markov chain $X$ on a state space $S$ with $u, v \in S$, we let $p_{u v}(n)$ for $n \in\{0,1, \ldots\}$ be the probability that $X_{n}=v$ when $X_{0}=u$.

  (a) Let $X$ be a Markov chain. Prove that if $X$ is recurrent at a state $v$, then $\sum_{n=0}^{\infty} p_{v v}(n)=\infty$. [You may use without proof that the number of returns of a Markov chain to a state $v$ when starting from $v$ has the geometric distribution.]

  (b) Let $X$ and $Y$ be independent simple symmetric random walks on $\mathbb{Z}^{2}$ starting from the origin 0 . Let $Z=\sum_{n=0}^{\infty} \mathbf{1}_{\left\{X_{n}=Y_{n}\right\}}$. Prove that $\mathbb{E}[Z]=\sum_{n=0}^{\infty} p_{00}(2 n)$ and deduce that $\mathbb{E}[Z]=\infty$. [You may use without proof that $p_{x y}(n)=p_{y x}(n)$ for all $x, y \in \mathbb{Z}^{2}$ and $n \in \mathbb{N}$, and that $X$ is recurrent at 0.]

  comment

Methods

• Paper 1, Section II, B

  Methods | Part IB, 2019

  The Bessel functions $J_{n}(r)(n \geqslant 0)$ can be defined by the expansion

  $$e^{i r \cos \theta}=J_{0}(r)+2 \sum_{n=1}^{\infty} i^{n} J_{n}(r) \cos n \theta$$

  By using Cartesian coordinates $x=r \cos \theta, y=r \sin \theta$, or otherwise, show that

  $$\left(\nabla^{2}+1\right) e^{i r \cos \theta}=0$$

  Deduce that $J_{n}(r)$ satisfies Bessel's equation

  $$\left(r^{2} \frac{d^{2}}{d r^{2}}+r \frac{d}{d r}-\left(n^{2}-r^{2}\right)\right) J_{n}(r)=0$$

  By expanding the left-hand side of $(*)$ up to cubic order in $r$, derive the series expansions of $J_{0}(r), J_{1}(r), J_{2}(r)$ and $J_{3}(r)$ up to this order.

  comment

• Paper 2, Section I, B

  Methods | Part IB, 2019

  Let $r, \theta, \phi$ be spherical polar coordinates, and let $P_{n}$ denote the $n$th Legendre polynomial. Write down the most general solution for $r>0$ of Laplace's equation $\nabla^{2} \Phi=0$ that takes the form $\Phi(r, \theta, \phi)=f(r) P_{n}(\cos \theta)$.

  Solve Laplace's equation in the spherical shell $1 \leqslant r \leqslant 2$ subject to the boundary conditions

  $$\begin{aligned} &\Phi=3 \cos 2 \theta \text { at } r=1 \\ &\Phi=0 \quad \text { at } r=2 \end{aligned}$$

  [The first three Legendre polynomials are

  $$\left.P_{0}(x)=1, \quad P_{1}(x)=x \quad \text { and } \quad P_{2}(x)=\frac{3}{2} x^{2}-\frac{1}{2} .\right]$$

  comment

• Paper 2, Section II, D

  Methods | Part IB, 2019

  For $n=0,1,2, \ldots$, the degree $n$ polynomial $C_{n}^{\alpha}(x)$ satisfies the differential equation

  $$\left(1-x^{2}\right) y^{\prime \prime}-(2 \alpha+1) x y^{\prime}+n(n+2 \alpha) y=0$$

  where $\alpha$ is a real, positive parameter. Show that, when $m \neq n$,

  $$\int_{a}^{b} C_{m}^{\alpha}(x) C_{n}^{\alpha}(x) w(x) d x=0$$

  for a weight function $w(x)$ and values $a<b$ that you should determine.

  Suppose that the roots of $C_{n}^{\alpha}(x)$ that lie inside the domain $(a, b)$ are $\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}$, with $k \leqslant n$. By considering the integral

  $$\int_{a}^{b} C_{n}^{\alpha}(x) \prod_{i=1}^{k}\left(x-x_{i}\right) w(x) d x$$

  show that in fact all $n$ roots of $C_{n}^{\alpha}(x)$ lie in $(a, b)$.

  comment

• Paper 3, Section I, D

  Methods | Part IB, 2019

  Define the discrete Fourier transform of a sequence $\left\{x_{0}, x_{1}, \ldots, x_{N-1}\right\}$ of $N$ complex numbers.

  Compute the discrete Fourier transform of the sequence

  $$x_{n}=\frac{1}{N}\left(1+e^{2 \pi i n / N}\right)^{N-1} \quad \text { for } n=0, \ldots, N-1 .$$

  comment

• Paper 3, Section II, D

  Methods | Part IB, 2019

  By differentiating the expression $\psi(t)=H(t) \sin (\alpha t) / \alpha$, where $\alpha$ is a constant and $H(t)$ is the Heaviside step function, show that

  $$\frac{d^{2} \psi}{d t^{2}}+\alpha^{2} \psi=\delta(t)$$

  where $\delta(t)$ is the Dirac $\delta$-function.

  Hence, by taking a Fourier transform with respect to the spatial variables only, derive the retarded Green's function for the wave operator $\partial_{t}^{2}-c^{2} \nabla^{2}$ in three spatial dimensions.

  [You may use that

  $$\frac{1}{2 \pi} \int_{\mathbb{R}^{3}} e^{i \mathbf{k} \cdot(\mathbf{x}-\mathbf{y})} \frac{\sin (k c t)}{k c} d^{3} k=-\frac{i}{c|\mathbf{x}-\mathbf{y}|} \int_{-\infty}^{\infty} e^{i k|\mathbf{x}-\mathbf{y}|} \sin (k c t) d k$$

  without proof.]

  Thus show that the solution to the homogeneous wave equation $\partial_{t}^{2} u-c^{2} \nabla^{2} u=0$, subject to the initial conditions $u(\mathbf{x}, 0)=0$ and $\partial_{t} u(\mathbf{x}, 0)=f(\mathbf{x})$, may be expressed as

  $$u(\mathbf{x}, t)=\langle f\rangle t$$

  where $\langle f\rangle$ is the average value of $f$ on a sphere of radius $c t$ centred on $\mathbf{x}$. Interpret this result.

  comment

• Paper 4, Section I, D

  Methods | Part IB, 2019

  Let

  $$g_{\epsilon}(x)=\frac{-2 \epsilon x}{\pi\left(\epsilon^{2}+x^{2}\right)^{2}} .$$

  By considering the integral $\int_{-\infty}^{\infty} \phi(x) g_{\epsilon}(x) d x$, where $\phi$ is a smooth, bounded function that vanishes sufficiently rapidly as $|x| \rightarrow \infty$, identify $\lim _{\epsilon \rightarrow 0} g_{\epsilon}(x)$ in terms of a generalized function.

  comment

• Paper 4, Section II, B

  Methods | Part IB, 2019

  (a) Show that the operator

  $$\frac{d^{4}}{d x^{4}}+p \frac{d^{2}}{d x^{2}}+q \frac{d}{d x}+r$$

  where $p(x), q(x)$ and $r(x)$ are real functions, is self-adjoint (for suitable boundary conditions which you need not state) if and only if

  $$q=\frac{d p}{d x}$$

  (b) Consider the eigenvalue problem

  $$\frac{d^{4} y}{d x^{4}}+p \frac{d^{2} y}{d x^{2}}+\frac{d p}{d x} \frac{d y}{d x}=\lambda y$$

  on the interval $[a, b]$ with boundary conditions

  $$y(a)=\frac{d y}{d x}(a)=y(b)=\frac{d y}{d x}(b)=0$$

  Assuming that $p(x)$ is everywhere negative, show that all eigenvalues $\lambda$ are positive.

  (c) Assume now that $p \equiv 0$ and that the eigenvalue problem (*) is on the interval $[-c, c]$ with $c>0$. Show that $\lambda=1$ is an eigenvalue provided that

  $$\cos c \sinh c \pm \sin c \cosh c=0$$

  and show graphically that this condition has just one solution in the range $0<c<\pi$.

  [You may assume that all eigenfunctions are either symmetric or antisymmetric about $x=0 .]$

  comment

Metric and Topological Spaces

• Paper 1, Section II, G

  Metric and Topological Spaces | Part IB, 2019

  Consider the set of sequences of integers

  $$X=\left\{\left(x_{1}, x_{2}, \ldots\right) \mid x_{n} \in \mathbb{Z} \text { for all } n\right\}$$

  Define

  $$n_{\min }\left(\left(x_{n}\right),\left(y_{n}\right)\right)= \begin{cases}\infty & x_{n}=y_{n} \text { for all } n \\ \min \left\{n \mid x_{n} \neq y_{n}\right\} & \text { otherwise }\end{cases}$$

  for two sequences $\left(x_{n}\right),\left(y_{n}\right) \in X$. Let

  $$d\left(\left(x_{n}\right),\left(y_{n}\right)\right)=2^{-n_{\min }\left(\left(x_{n}\right),\left(y_{n}\right)\right)}$$

  where, as usual, we adopt the convention that $2^{-\infty}=0$.

  (a) Prove that $d$ defines a metric on $X$.

  (b) What does it mean for a metric space to be complete? Prove that $(X, d)$ is complete.

  (c) Is $(X, d)$ path connected? Justify your answer.

  comment

• Paper 2, Section I, G

  Metric and Topological Spaces | Part IB, 2019

  (a) Let $f: X \rightarrow Y$ be a continuous surjection of topological spaces. Prove that, if $X$ is connected, then $Y$ is also connected.

  (b) Let $g:[0,1] \rightarrow[0,1]$ be a continuous map. Deduce from part (a) that, for every $y$ between $g(0)$ and $g(1)$, there is $x \in[0,1]$ such that $g(x)=y$. [You may not assume the Intermediate Value Theorem, but you may use the fact that suprema exist in $\mathbb{R}$.]

  comment

• Paper 3, Section I, $3 G$

  Metric and Topological Spaces | Part IB, 2019

  Let $X$ be a metric space.

  (a) What does it mean for $X$ to be compact? What does it mean for $X$ to be sequentially compact?

  (b) Prove that if $X$ is compact then $X$ is sequentially compact.

  comment

• Paper 4, Section II, G

  Metric and Topological Spaces | Part IB, 2019

  (a) Define the subspace, quotient and product topologies.

  (b) Let $X$ be a compact topological space and $Y$ a Hausdorff topological space. Prove that a continuous bijection $f: X \rightarrow Y$ is a homeomorphism.

  (c) Let $S=[0,1] \times[0,1]$, equipped with the product topology. Let $\sim$ be the smallest equivalence relation on $S$ such that $(s, 0) \sim(s, 1)$ and $(0, t) \sim(1, t)$, for all $s, t \in[0,1]$. Let

  $$T=\left\{(x, y, z) \in \mathbb{R}^{3} \mid\left(\sqrt{x^{2}+y^{2}}-2\right)^{2}+z^{2}=1\right\}$$

  equipped with the subspace topology from $\mathbb{R}^{3}$. Prove that $S / \sim$ and $T$ are homeomorphic.

  [You may assume without proof that $S$ is compact.]

  comment

Numerical Analysis

• Paper 1, Section I, C

  Numerical Analysis | Part IB, 2019

  Let $[a, b]$ be the smallest interval that contains the $n+1$ distinct real numbers $x_{0}, x_{1}, \ldots, x_{n}$, and let $f$ be a continuous function on that interval.

  Define the divided difference $f\left[x_{0}, x_{1}, \ldots, x_{m}\right]$ of degree $m \leqslant n$.

  Prove that the polynomial of degree $n$ that interpolates the function $f$ at the points $x_{0}, x_{1}, \ldots, x_{n}$ is equal to the Newton polynomial

  $$p_{n}(x)=f\left[x_{0}\right]+f\left[x_{0}, x_{1}\right]\left(x-x_{0}\right)+\cdots+f\left[x_{0}, x_{1}, \ldots, x_{n}\right] \prod_{i=0}^{n-1}\left(x-x_{i}\right)$$

  Prove the recursive formula

  $$f\left[x_{0}, x_{1}, \ldots, x_{m}\right]=\frac{f\left[x_{1}, x_{2}, \ldots, x_{m}\right]-f\left[x_{0}, x_{1}, \ldots, x_{m-1}\right]}{x_{m}-x_{0}}$$

  for $1 \leqslant m \leqslant n .$

  comment

• Paper 1, Section II, C

  Numerical Analysis | Part IB, 2019

  (a) An $s$-step method for solving the ordinary differential equation

  $$\frac{d \mathbf{y}}{d t}=\mathbf{f}(t, \mathbf{y})$$

  is given by

  $$\sum_{l=0}^{s} \rho_{l} \mathbf{y}_{n+l}=h \sum_{l=0}^{s} \sigma_{l} \mathbf{f}\left(t_{n+l}, \mathbf{y}_{n+l}\right), \quad n=0,1, \ldots$$

  where $\rho_{l}$ and $\sigma_{l}(l=0,1, \ldots, s)$ are constant coefficients, with $\rho_{s}=1$, and $h$ is the time-step. Prove that the method is of order $p \geqslant 1$ if and only if

  $$\rho\left(e^{z}\right)-z \sigma\left(e^{z}\right)=O\left(z^{p+1}\right)$$

  as $z \rightarrow 0$, where

  $$\rho(w)=\sum_{l=0}^{s} \rho_{l} w^{l}, \quad \sigma(w)=\sum_{l=0}^{s} \sigma_{l} w^{l}$$

  (b) Show that the Adams-Moulton method

  $$\mathbf{y}_{n+2}=\mathbf{y}_{n+1}+\frac{h}{12}\left(5 \mathbf{f}\left(t_{n+2}, \mathbf{y}_{n+2}\right)+8 \mathbf{f}\left(t_{n+1}, \mathbf{y}_{n+1}\right)-\mathbf{f}\left(t_{n}, \mathbf{y}_{n}\right)\right)$$

  is of third order and convergent.

  [You may assume the Dahlquist equivalence theorem if you state it clearly.]

  comment

• Paper 2, Section II, C

  Numerical Analysis | Part IB, 2019

  Define the linear least squares problem for the equation

  $$A \mathbf{x}=\mathbf{b}$$

  where $A$ is a given $m \times n$ matrix with $m>n, \mathbf{b} \in \mathbb{R}^{m}$ is a given vector and $\mathbf{x} \in \mathbb{R}^{n}$ is an unknown vector.

  Explain how the linear least squares problem can be solved by obtaining a $Q R$ factorization of the matrix $A$, where $Q$ is an orthogonal $m \times m$ matrix and $R$ is an uppertriangular $m \times n$ matrix in standard form.

  Use the Gram-Schmidt method to obtain a $Q R$ factorization of the matrix

  $$A=\left(\begin{array}{lll} 1 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0 \\ 1 & 0 & 0 \end{array}\right)$$

  and use it to solve the linear least squares problem in the case

  $$\mathbf{b}=\left(\begin{array}{l} 1 \\ 2 \\ 3 \\ 6 \end{array}\right)$$

  comment

• Paper 3, Section II, C

  Numerical Analysis | Part IB, 2019

  (a) Let $w(x)$ be a positive weight function on the interval $[a, b]$. Show that

  $$\langle f, g\rangle=\int_{a}^{b} f(x) g(x) w(x) d x$$

  defines an inner product on $C[a, b]$.

  (b) Consider the sequence of polynomials $p_{n}(x)$ defined by the three-term recurrence relation

  $$p_{n+1}(x)=\left(x-\alpha_{n}\right) p_{n}(x)-\beta_{n} p_{n-1}(x), \quad n=1,2, \ldots$$

  where

  $$p_{0}(x)=1, \quad p_{1}(x)=x-\alpha_{0},$$

  and the coefficients $\alpha_{n}$ (for $\left.n \geqslant 0\right)$ and $\beta_{n}$ (for $\left.n \geqslant 1\right)$ are given by

  $$\alpha_{n}=\frac{\left\langle p_{n}, x p_{n}\right\rangle}{\left\langle p_{n}, p_{n}\right\rangle}, \quad \beta_{n}=\frac{\left\langle p_{n}, p_{n}\right\rangle}{\left\langle p_{n-1}, p_{n-1}\right\rangle}$$

  Prove that this defines a sequence of monic orthogonal polynomials on $[a, b]$.

  (c) The Hermite polynomials $H e_{n}(x)$ are orthogonal on the interval $(-\infty, \infty)$ with weight function $e^{-x^{2} / 2}$. Given that

  $$H e_{n}(x)=(-1)^{n} e^{x^{2} / 2} \frac{d^{n}}{d x^{n}}\left(e^{-x^{2} / 2}\right)$$

  deduce that the Hermite polynomials satisfy a relation of the form $(*)$ with $\alpha_{n}=0$ and $\beta_{n}=n$. Show that $\left\langle H e_{n}, H e_{n}\right\rangle=n ! \sqrt{2 \pi}$.

  (d) State, without proof, how the properties of the Hermite polynomial $\operatorname{He}_{N}(x)$, for some positive integer $N$, can be used to estimate the integral

  $$\int_{-\infty}^{\infty} f(x) e^{-x^{2} / 2} d x$$

  where $f(x)$ is a given function, by the method of Gaussian quadrature. For which polynomials is the quadrature formula exact?

  comment

• Paper 4, Section I, C

  Numerical Analysis | Part IB, 2019

  Calculate the $L U$ factorization of the matrix

  $$A=\left(\begin{array}{rrrr} 3 & 2 & -3 & -3 \\ 6 & 3 & -7 & -8 \\ 3 & 1 & -6 & -4 \\ -6 & -3 & 9 & 6 \end{array}\right)$$

  Use this to evaluate $\operatorname{det}(A)$ and to solve the equation

  $$A \mathbf{x}=\mathbf{b}$$

  with

  $$\mathbf{b}=\left(\begin{array}{r} 3 \\ 3 \\ -1 \\ -3 \end{array}\right)$$

  comment

Optimization

• Paper 1, Section I, H

  Optimization | Part IB, 2019

  Suppose that $f$ is an infinitely differentiable function on $\mathbb{R}$. Assume that there exist constants $0<C_{1}, C_{2}<\infty$ so that $\left|f^{\prime \prime}(x)\right| \geqslant C_{1}$ and $\left|f^{\prime \prime \prime}(x)\right| \leqslant C_{2}$ for all $x \in \mathbb{R}$. Fix $x_{0} \in \mathbb{R}$ and for each $n \in \mathbb{N}$ set

  $$x_{n}=x_{n-1}-\frac{f^{\prime}\left(x_{n-1}\right)}{f^{\prime \prime}\left(x_{n-1}\right)} .$$

  Let $x^{*}$ be the unique value of $x$ where $f$ attains its minimum. Prove that

  $$\left|x^{*}-x_{n+1}\right| \leqslant \frac{C_{2}}{2 C_{1}}\left|x^{*}-x_{n}\right|^{2} \quad \text { for all } n \in \mathbb{N} .$$

  [Hint: Express $f^{\prime}\left(x^{*}\right)$ in terms of the Taylor series for $f^{\prime}$ at $x_{n}$ using the Lagrange form of the remainder: $f^{\prime}\left(x^{*}\right)=f^{\prime}\left(x_{n}\right)+f^{\prime \prime}\left(x_{n}\right)\left(x^{*}-x_{n}\right)+\frac{1}{2} f^{\prime \prime \prime}\left(y_{n}\right)\left(x^{*}-x_{n}\right)^{2}$ where $y_{n}$ is between $x_{n}$ and $\left.x^{*} .\right]$

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2019

  State the Lagrange sufficiency theorem.

  Find the maximum of $\log (x y z)$ over $x, y, z>0$ subject to the constraint

  $$x^{2}+y^{2}+z^{2}=1$$

  using Lagrange multipliers. Carefully justify why your solution is in fact the maximum.

  Find the maximum of $\log (x y z)$ over $x, y, z>0$ subject to the constraint

  $$x^{2}+y^{2}+z^{2} \leqslant 1$$

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2019

  (a) Suppose that $A \in \mathbb{R}^{m \times n}$ and $b \in \mathbb{R}^{m}$, with $n \geqslant m$. What does it mean for $x \in \mathbb{R}^{n}$ to be a basic feasible solution of the equation $A x=b ?$

  Assume that the $m$ rows of $A$ are linearly independent, every set of $m$ columns is linearly independent, and every basic solution has exactly $m$ non-zero entries. Prove that the extreme points of $\mathcal{X}(b)=\{x \geqslant 0: A x=b\}$ are the basic feasible solutions of $A x=b$. [Here, $x \geqslant 0$ means that each of the coordinates of $x$ are at least 0 .]

  (b) Use the simplex method to solve the linear program

  $$\begin{array}{cl} \max & 4 x_{1}+3 x_{2}+7 x_{3} \\ \text { s.t. } & x_{1}+3 x_{2}+x_{3} \leqslant 14 \\ & 4 x_{1}+3 x_{2}+2 x_{3} \leqslant 5 \\ & -x_{1}+x_{2}-x_{3} \geqslant-2 \\ & x_{1}, x_{2}, x_{3} \geqslant 0 \end{array}$$

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2019

  (a) State and prove the max-flow min-cut theorem.

  (b) (i) Apply the Ford-Fulkerson algorithm to find the maximum flow of the network illustrated below, where $S$ is the source and $T$ is the sink.

  

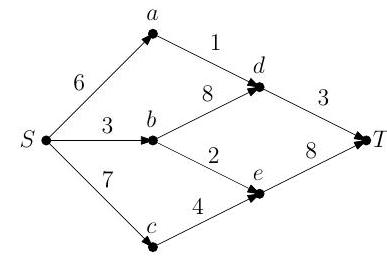
  (ii) Verify the optimality of your solution using the max-flow min-cut theorem.

  (iii) Is there a unique flow which attains the maximum? Explain your answer.

  (c) Prove that the Ford-Fulkerson algorithm always terminates when the network is finite, the capacities are integers, and the algorithm is initialised where the initial flow is 0 across all edges. Prove also in this case that the flow across each edge is an integer.

  comment

Quantum Mechanics

• Paper 1, Section II, B

  Quantum Mechanics | Part IB, 2019

  Starting from the time-dependent Schrödinger equation, show that a stationary state $\psi(x)$ of a particle of mass $m$ in a harmonic oscillator potential in one dimension with frequency $\omega$ satisfies

  $$-\frac{\hbar^{2}}{2 m} \frac{d^{2} \psi}{d x^{2}}+\frac{1}{2} m \omega^{2} x^{2} \psi=E \psi .$$

  Find a rescaling of variables that leads to the simplified equation

  $$-\frac{d^{2} \psi}{d y^{2}}+y^{2} \psi=\varepsilon \psi$$

  Setting $\psi=f(y) e^{-\frac{1}{2} y^{2}}$, find the equation satisfied by $f(y)$.

  Assume now that $f$ is a polynomial

  $$f(y)=y^{N}+a_{N-1} y^{N-1}+a_{N-2} y^{N-2}+\ldots+a_{0}$$

  Determine the value of $\varepsilon$ and deduce the corresponding energy level $E$ of the harmonic oscillator. Show that if $N$ is even then the stationary state $\psi(x)$ has even parity.

  comment

• Paper 2, Section II, B

  Quantum Mechanics | Part IB, 2019

  Let $x, y, z$ be Cartesian coordinates in $\mathbb{R}^{3}$. The angular momentum operators satisfy the commutation relation

  $$\left[L_{x}, L_{y}\right]=i \hbar L_{z}$$

  and its cyclic permutations. Define the total angular momentum operator $\mathbf{L}^{2}$ and show that $\left[L_{z}, \mathbf{L}^{2}\right]=0$. Write down the explicit form of $L_{z}$.

  Show that a function of the form $(x+i y)^{m} z^{n} f(r)$, where $r^{2}=x^{2}+y^{2}+z^{2}$, is an eigenfunction of $L_{z}$ and find the eigenvalue. State the analogous result for $(x-i y)^{m} z^{n} f(r)$.

  There is an energy level for a particle in a certain spherically symmetric potential well that is 6-fold degenerate. A basis for the (unnormalized) energy eigenstates is of the form

  $$\left(x^{2}-1\right) f(r),\left(y^{2}-1\right) f(r),\left(z^{2}-1\right) f(r), x y f(r), x z f(r), y z f(r) \text {. }$$

  Find a new basis that consists of simultaneous eigenstates of $L_{z}$ and $\mathbf{L}^{2}$ and identify their eigenvalues.

  [You may quote the range of $L_{z}$ eigenvalues associated with a particular eigenvalue of $\mathbf{L}^{2}$.]

  comment

• Paper 3, Section $I$, B

  Quantum Mechanics | Part IB, 2019

  Consider a quantum mechanical particle moving in two dimensions with Cartesian coordinates $x, y$. Show that, for wavefunctions with suitable decay as $x^{2}+y^{2} \rightarrow \infty$, the operators

  $$x \quad \text { and } \quad-i \hbar \frac{\partial}{\partial x}$$

  are Hermitian, and similarly

  $$y \text { and }-i \hbar \frac{\partial}{\partial y}$$

  are Hermitian.

  Show that if $F$ and $G$ are Hermitian operators, then

  $$\frac{1}{2}(F G+G F)$$

  is Hermitian. Deduce that

  $$L=-i \hbar\left(x \frac{\partial}{\partial y}-y \frac{\partial}{\partial x}\right) \quad \text { and } \quad D=-i \hbar\left(x \frac{\partial}{\partial x}+y \frac{\partial}{\partial y}+1\right)$$

  are Hermitian. Show that

  $$[L, D]=0 .$$

  comment

• Paper 3, Section II, B

  Quantum Mechanics | Part IB, 2019

  Consider a particle of unit mass in a one-dimensional square well potential

  $$V(x)=0 \text { for } 0 \leqslant x \leqslant \pi,$$

  with $V$ infinite outside. Find all the stationary states $\psi_{n}(x)$ and their energies $E_{n}$, and write down the general normalized solution of the time-dependent Schrödinger equation in terms of these.

  The particle is initially constrained by a barrier to be in the ground state in the narrower square well potential

  $$V(x)=0 \quad \text { for } \quad 0 \leqslant x \leqslant \frac{\pi}{2}$$

  with $V$ infinite outside. The barrier is removed at time $t=0$, and the wavefunction is instantaneously unchanged. Show that the particle is now in a superposition of stationary states of the original potential well, and calculate the probability that an energy measurement will yield the result $E_{n}$.

  comment

• Paper 4, Section I, B

  Quantum Mechanics | Part IB, 2019

  (a) Define the probability density $\rho$ and probability current $j$ for the wavefunction $\Psi(x, t)$ of a particle of mass $m$. Show that

  $$\frac{\partial \rho}{\partial t}+\frac{\partial j}{\partial x}=0$$

  and deduce that $j=0$ for a normalizable, stationary state wavefunction. Give an example of a non-normalizable, stationary state wavefunction for which $j$ is non-zero, and calculate the value of $j$.

  (b) A particle has the instantaneous, normalized wavefunction

  $$\Psi(x, 0)=\left(\frac{2 \alpha}{\pi}\right)^{1 / 4} e^{-\alpha x^{2}+i k x}$$

  where $\alpha$ is positive and $k$ is real. Calculate the expectation value of the momentum for this wavefunction.

  comment

Statistics

• Paper 1, Section I, H

  Statistics | Part IB, 2019

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. $N\left(\mu, \sigma^{2}\right)$ random variables.

  (a) Compute the MLEs $\widehat{\mu}, \widehat{\sigma}^{2}$ for the unknown parameters $\mu, \sigma^{2}$.

  (b) Give the definition of an unbiased estimator. Determine whether $\widehat{\mu}, \widehat{\sigma}^{2}$ are unbiased estimators for $\mu, \sigma^{2}$.

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2019

  State and prove the Neyman-Pearson lemma.

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. $\exp (\lambda)$ random variables where $\lambda$ is an unknown parameter. We wish to test the hypothesis $H_{0}: \lambda=\lambda_{0}$ against the hypothesis $H_{1}: \lambda=\lambda_{1}$ where $\lambda_{1}<\lambda_{0}$.

  (a) Find the critical region of the likelihood ratio test of size $\alpha$ in terms of the sample mean $\bar{X}$.

  (b) Define the power function of a hypothesis test and identify the power function in the setting described above in terms of the $\Gamma(n, \lambda)$ probability distribution function. [You may use without proof that $X_{1}+\cdots+X_{n}$ is distributed as a $\Gamma(n, \lambda)$ random variable.]

  (c) Define what it means for a hypothesis test to be uniformly most powerful. Determine whether the likelihood ratio test considered above is uniformly most powerful for testing $H_{0}: \lambda=\lambda_{0}$ against $\widetilde{H}_{1}: \lambda<\lambda_{0}$.

  comment

• Paper 2, Section I, H

  Statistics | Part IB, 2019

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. coin tosses with probability $\theta$ of obtaining a head.

  (a) Compute the posterior distribution of $\theta$ given the observations $X_{1}, \ldots, X_{n}$ in the case of a uniform prior on $[0,1]$.

  (b) Give the definition of the quadratic error loss function.

  (c) Determine the value $\widehat{\theta}$of $\theta$ which minimizes the quadratic error loss function. Justify your answer. Calculate $\mathbb{E}[\hat{\theta}]$.

  [You may use that the $\beta(a, b), a, b>0$, distribution has density function on $[0,1]$ given by

  $$c_{a, b} x^{a-1}(1-x)^{b-1}$$

  where $c_{a, b}$ is a normalizing constant. You may also use without proof that the mean of a $\beta(a, b)$ random variable is $a /(a+b) .]$

  comment

• Paper 3, Section II, H

  Statistics | Part IB, 2019

  Suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. $N\left(\mu, \sigma^{2}\right)$. Let

  $$\bar{X}=\frac{1}{n} \sum_{i=1}^{n} X_{i} \quad \text { and } \quad S_{X X}=\sum_{i=1}^{n}\left(X_{i}-\bar{X}\right)^{2}$$

  (a) Compute the distributions of $\bar{X}$ and $S_{X X}$ and show that $\bar{X}$ and $S_{X X}$ are independent.

  (b) Write down the distribution of $\sqrt{n}(\bar{X}-\mu) / \sqrt{S_{X X} /(n-1)}$.

  (c) For $\alpha \in(0,1)$, find a $100(1-\alpha) \%$ confidence interval in each of the following situations: (i) for $\mu$ when $\sigma^{2}$ is known; (ii) for $\mu$ when $\sigma^{2}$ is not known; (iii) for $\sigma^{2}$ when $\mu$ is not known.

  (d) Suppose that $\widetilde{X}_{1}, \ldots, \widetilde{X}_{\widetilde{n}}$ are i.i.d. $N\left(\widetilde{\mu}, \widetilde{\sigma}^{2}\right)$. Explain how you would use the $F$ test to test the hypothesis $H_{1}: \sigma^{2}>\tilde{\sigma}^{2}$ against the hypothesis $H_{0}: \sigma^{2}=\tilde{\sigma}^{2}$. Does the $F$ test depend on whether $\mu, \widetilde{\mu}$ are known?

  comment

• Paper 4, Section II, 19H

  Statistics | Part IB, 2019

  Consider the linear model

  $$Y_{i}=\beta x_{i}+\epsilon_{i} \quad \text { for } \quad i=1, \ldots, n$$

  where $x_{1}, \ldots, x_{n}$ are known and $\epsilon_{1}, \ldots, \epsilon_{n}$ are i.i.d. $N\left(0, \sigma^{2}\right)$. We assume that the parameters $\beta$ and $\sigma^{2}$ are unknown.

  (a) Find the MLE $\widehat{\beta}$ of $\beta$. Explain why $\widehat{\beta}$ is the same as the least squares estimator of $\beta$.

  (b) State and prove the Gauss-Markov theorem for this model.

  (c) For each value of $\theta \in \mathbb{R}$ with $\theta \neq 0$, determine the unbiased linear estimator $\tilde{\beta}$ of $\beta$ which minimizes

  $$\mathbb{E}_{\beta, \sigma^{2}}[\exp (\theta(\tilde{\beta}-\beta))]$$

  comment

Variational Principles

• Paper 1, Section I, A

  Variational Principles | Part IB, 2019

  A function $\phi=x y-y z$ is defined on the surface $x^{2}+2 y^{2}+z^{2}=1$. Find the location $(x, y, z)$ of every stationary point of this function.

  comment

• Paper 2, Section II, A

  Variational Principles | Part IB, 2019

  Write down the Euler-Lagrange (EL) equations for a functional

  $$\int_{a}^{b} f\left(u, w, u^{\prime}, w^{\prime}, x\right) d x$$

  where $u(x)$ and $w(x)$ each take specified values at $x=a$ and $x=b$. Show that the EL equations imply that

  $$\kappa=f-u^{\prime} \frac{\partial f}{\partial u^{\prime}}-w^{\prime} \frac{\partial f}{\partial w^{\prime}}$$

  is independent of $x$ provided $f$ satisfies a certain condition, to be specified. State conditions under which there exist additional first integrals of the $\mathrm{EL}$ equations.

  Consider

  $$f=\left(1-\frac{m}{u}\right) w^{\prime 2}-\left(1-\frac{m}{u}\right)^{-1} u^{\prime 2}$$

  where $m$ is a positive constant. Show that solutions of the EL equations satisfy

  $$u^{\prime 2}=\lambda^{2}+\kappa\left(1-\frac{m}{u}\right)$$

  for some constant $\lambda$. Assuming that $\kappa=-\lambda^{2}$, find $d w / d u$ and hence determine the most general solution for $w$ as a function of $u$ subject to the conditions $u>m$ and $w \rightarrow-\infty$ as $u \rightarrow \infty$. Show that, for any such solution, $w \rightarrow \infty$ as $u \rightarrow m$.

  [Hint:

  $$\left.\frac{d}{d z}\left\{\log \left(\frac{z^{1 / 2}-1}{z^{1 / 2}+1}\right)\right\}=\frac{1}{z^{1 / 2}(z-1)} . \quad\right]$$

  comment

• Paper 3, Section I, A

  Variational Principles | Part IB, 2019

  The function $f$ with domain $x>0$ is defined by $f(x)=\frac{1}{a} x^{a}$, where $a>1$. Verify that $f$ is convex, using an appropriate sufficient condition.

  Determine the Legendre transform $f^{*}$ of $f$, specifying clearly its domain of definition, and find $\left(f^{*}\right)^{*}$.

  Show that

  $$\frac{x^{r}}{r}+\frac{y^{s}}{s} \geqslant x y$$

  where $x, y>0$ and $r$ and $s$ are positive real numbers such that $\frac{1}{r}+\frac{1}{s}=1$.

  comment

• Paper 4, Section II, A

  Variational Principles | Part IB, 2019

  Consider the functional

  $$I[y]=\int_{-\infty}^{\infty}\left(\frac{1}{2} y^{\prime 2}+\frac{1}{2} U(y)^{2}\right) d x$$

  where $y(x)$ is subject to boundary conditions $y(x) \rightarrow a_{\pm}$as $x \rightarrow \pm \infty$ with $U\left(a_{\pm}\right)=0$. [You may assume the integral converges.]

  (a) Find expressions for the first-order and second-order variations $\delta I$ and $\delta^{2} I$ resulting from a variation $\delta y$ that respects the boundary conditions.

  (b) If $a_{\pm}=a$, show that $I[y]=0$ if and only if $y(x)=a$ for all $x$. Explain briefly how this is consistent with your results for $\delta I$ and $\delta^{2} I$ in part (a).

  (c) Now suppose that $U(y)=c^{2}-y^{2}$ with $a_{\pm}=\pm c(c>0)$. By considering an integral of $U(y) y^{\prime}$, show that

  $$I[y] \geqslant \frac{4 c^{3}}{3},$$

  with equality if and only if $y$ satisfies a first-order differential equation. Deduce that global minima of $I[y]$ with the specified boundary conditions occur precisely for

  $$y(x)=c \tanh \left\{c\left(x-x_{0}\right)\right\}$$

  where $x_{0}$ is a constant. How is the first-order differential equation that appears in this case related to your general result for $\delta I$ in part (a)?

  comment