Analysis Ii
Analysis Ii
Jump to year
Paper 1, Section II, E
Let be an open subset. State what it means for a function to be differentiable at a point , and define its derivative .
State and prove the chain rule for the derivative of , where is a differentiable function.
Let be the vector space of real-valued matrices, and the open subset consisting of all invertible ones. Let be given by .
(a) Show that is differentiable at the identity matrix, and calculate its derivative.
(b) For , let be given by and . Show that on . Hence or otherwise, show that is differentiable at any point of , and calculate for .
Paper 2, Section I, E
Consider the map given by
where denotes the unique real cube root of .
(a) At what points is continuously differentiable? Calculate its derivative there.
(b) Show that has a local differentiable inverse near any with .
You should justify your answers, stating accurately any results that you require.
Paper 2, Section II, 12E
(a) (i) Define what it means for two norms on a vector space to be Lipschitz equivalent.
(ii) Show that any two norms on a finite-dimensional vector space are Lipschitz equivalent.
(iii) Show that if two norms on a vector space are Lipschitz equivalent then the following holds: for any sequence in is Cauchy with respect to if and only if it is Cauchy with respect to .
(b) Let be the vector space of real sequences such that . Let
and for , let
You may assume that and are well-defined norms on .
(i) Show that is not Lipschitz equivalent to for any .
(ii) Are there any with such that and are Lipschitz equivalent? Justify your answer.
Paper 3, Section I,
(a) Let . What does it mean for a function to be uniformly continuous?
(b) Which of the following functions are uniformly continuous? Briefly justify your answers.
(i) on .
(ii) on .
(iii) on .
Paper 3, Section II, E
(a) Carefully state the Picard-Lindelöf theorem on solutions to ordinary differential equations.
(b) Let be the set of continuous functions from a closed interval to , and let be a norm on .
(i) Let . Show that for any the norm
is Lipschitz equivalent to the usual sup norm on .
(ii) Assume that is continuous and Lipschitz in the second variable, i.e. there exists such that
for all and all . Define by
for .
Show that there is a choice of such that is a contraction on . Deduce that for any , the differential equation
has a unique solution on with .
Paper 4, Section I, E
Let . What does it mean to say that a sequence of real-valued functions on is uniformly convergent?
(i) If a sequence of real-valued functions on converges uniformly to , and each is continuous, must also be continuous?
(ii) Let . Does the sequence converge uniformly on ?
(iii) If a sequence of real-valued functions on converges uniformly to , and each is differentiable, must also be differentiable?
Give a proof or counterexample in each case.
Paper 4, Section II, E
(a) (i) Show that a compact metric space must be complete.
(ii) If a metric space is complete and bounded, must it be compact? Give a proof or counterexample.
(b) A metric space is said to be totally bounded if for all , there exists and such that
(i) Show that a compact metric space is totally bounded.
(ii) Show that a complete, totally bounded metric space is compact.
[Hint: If is Cauchy, then there is a subsequence such that
(iii) Consider the space of continuous functions , with the metric
Is this space compact? Justify your answer.
Paper 1, Section II, F
Let be a non-empty open set and let .
(a) What does it mean to say that is differentiable? What does it mean to say that is a function?
If is differentiable, show that is continuous.
State the inverse function theorem.
(b) Suppose that is convex, is and that its derivative at a satisfies for all , where is the identity map and denotes the operator norm. Show that is injective.
Explain why is an open subset of .
Must it be true that ? What if ? Give proofs or counter-examples as appropriate.
(c) Find the largest set such that the map given by satisfies for every .
Paper 2, Section I, F
Show that defines a norm on the space of continuous functions .
Let be the set of continuous functions with . Show that for each continuous function , there is a sequence with such that as
Show that if is continuous and for every then .
Paper 2, Section II, F
(a) Let be a metric space, a non-empty subset of and . Define what it means for to be Lipschitz. If is Lipschitz with Lipschitz constant and if
for each , show that for each and that is Lipschitz with Lipschitz constant . (Be sure to justify that , i.e. that the infimum is finite for every .)
(b) What does it mean to say that two norms on a vector space are Lipschitz equivalent?
Let be an -dimensional real vector space equipped with a norm . Let be a basis for . Show that the map defined by is continuous. Deduce that any two norms on are Lipschitz equivalent.
(c) Prove that for each positive integer and each , there is a constant with the following property: for every polynomial of degree , there is a point such that
where is the derivative of .
Paper 3, Section I,
For a continuous function , define
Show that
for every continuous function , where denotes the Euclidean norm on .
Find all continuous functions with the property that
regardless of the norm on .
[Hint: start by analysing the case when is the Euclidean norm .]
Paper 3, Section II, F
(a) Let and let be functions for What does it mean to say that the sequence converges uniformly to on ? What does it mean to say that is uniformly continuous?
(b) Let be a uniformly continuous function. Determine whether each of the following statements is true or false. Give reasons for your answers.
(i) If for each and each , then uniformly on .
(ii) If for each and each , then uniformly on .
(c) Let be a closed, bounded subset of . For each , let be a continuous function such that is a decreasing sequence for each . If is such that for each there is with , show that there is such that .
Deduce the following: If is a continuous function for each such that is a decreasing sequence for each , and if the pointwise limit of is a continuous function , then uniformly on .
Paper 4, Section I, F
State the Bolzano-Weierstrass theorem in . Use it to deduce the BolzanoWeierstrass theorem in .
Let be a closed, bounded subset of , and let be a function. Let be the set of points in where is discontinuous. For and , let denote the ball . Prove that for every , there exists such that whenever and .
(If you use the fact that a continuous function on a compact metric space is uniformly continuous, you must prove it.)
Paper 4, Section II, F
(a) Define what it means for a metric space to be complete. Give a metric on the interval such that is complete and such that a subset of is open with respect to if and only if it is open with respect to the Euclidean metric on . Be sure to prove that has the required properties.
(b) Let be a complete metric space.
(i) If , show that taken with the subspace metric is complete if and only if is closed in .
(ii) Let and suppose that there is a number such that for every . Show that there is a unique point such that .
Deduce that if is a sequence of points in converging to a point , then there are integers and such that for every .
Paper 1, Section II, G
What does it mean to say that a real-valued function on a metric space is uniformly continuous? Show that a continuous function on a closed interval in is uniformly continuous.
What does it mean to say that a real-valued function on a metric space is Lipschitz? Show that if a function is Lipschitz then it is uniformly continuous.
Which of the following statements concerning continuous functions are true and which are false? Justify your answers.
(i) If is bounded then is uniformly continuous.
(ii) If is differentiable and is bounded, then is uniformly continuous.
(iii) There exists a sequence of uniformly continuous functions converging pointwise to .
Paper 2, Section I, G
Let . What does it mean to say that a sequence of real-valued functions on is uniformly convergent?
Let be functions.
(a) Show that if each is continuous, and converges uniformly on to , then is also continuous.
(b) Suppose that, for every converges uniformly on . Need converge uniformly on ? Justify your answer.
Paper 2, Section II, G
Let be a real vector space. What is a norm on ? Show that if is a norm on , then the maps for ) and (for ) are continuous with respect to the norm.
Let be a subset containing 0 . Show that there exists at most one norm on for which is the open unit ball.
Suppose that satisfies the following two properties:
if is a nonzero vector, then the line meets in a set of the form for some ;
if and then .
Show that there exists a norm for which is the open unit ball.
Identify in the following two cases:
(i) for all .
(ii) the interior of the square with vertices .
Let be the set
Is there a norm on for which is the open unit ball? Justify your answer.
Paper 3, Section I, G
What does it mean to say that a metric space is complete? Which of the following metric spaces are complete? Briefly justify your answers.
(i) with the Euclidean metric.
(ii) with the Euclidean metric.
(iii) The subset
with the metric induced from the Euclidean metric on .
Write down a metric on with respect to which is not complete, justifying your answer.
[You may assume throughout that is complete with respect to the Euclidean metric.
Paper 3, Section II, G
What is a contraction map on a metric space ? State and prove the contraction mapping theorem.
Let be a complete non-empty metric space. Show that if is a map for which some iterate is a contraction map, then has a unique fixed point. Show that itself need not be a contraction map.
Let be the function
Show that has a unique fixed point.
Paper 4, Section I, G
State the chain rule for the composition of two differentiable functions and .
Let be differentiable. For , let . Compute the derivative of . Show that if throughout , then for some function .
Paper 4, Section II, G
Let be a nonempty open set. What does it mean to say that a function is differentiable?
Let be a function, where is open. Show that if the first partial derivatives of exist and are continuous on , then is differentiable on .
Let be the function
Determine, with proof, where is differentiable.
Paper 1, Section II, G
Let be a metric space.
(a) What does it mean to say that is a Cauchy sequence in ? Show that if is a Cauchy sequence, then it converges if it contains a convergent subsequence.
(b) Let be a Cauchy sequence in .
(i) Show that for every , the sequence converges to some .
(ii) Show that as .
(iii) Let be a subsequence of . If are such that , show that as .
(iv) Show also that for every and ,
(v) Deduce that has a subsequence such that for every and ,
and
(c) Suppose that every closed subset of has the property that every contraction mapping has a fixed point. Prove that is complete.
Paper 2, Section I, G
(a) What does it mean to say that the function is differentiable at the point ? Show from your definition that if is differentiable at , then is continuous at .
(b) Suppose that there are functions such that for every ,
Show that is differentiable at if and only if each is differentiable at .
(c) Let be given by
Determine at which points the function is differentiable.
Paper 2, Section II, G
(a) What is a norm on a real vector space?
(b) Let be the space of linear maps from to . Show that
defines a norm on , and that if then .
(c) Let be the space of real matrices, identified with in the usual way. Let be the subset
Show that is an open subset of which contains the set .
(d) Let be the map . Show carefully that the series converges on to . Hence or otherwise, show that is twice differentiable at 0 , and compute its first and second derivatives there.
Paper 3, Section I, G
(a) Let be a subset of . What does it mean to say that a sequence of functions is uniformly convergent?
(b) Which of the following sequences of functions are uniformly convergent? Justify your answers.
(i)
(ii) .
(iii) , .
(iv) .
Paper 3, Section II, G
Let be a metric space.
(a) What does it mean to say that a function is uniformly continuous? What does it mean to say that is Lipschitz? Show that if is Lipschitz then it is uniformly continuous. Show also that if is a Cauchy sequence in , and is uniformly continuous, then the sequence is convergent.
(b) Let be continuous, and be sequentially compact. Show that is uniformly continuous. Is necessarily Lipschitz? Justify your answer.
(c) Let be a dense subset of , and let be a continuous function. Show that there exists at most one continuous function such that for all , . Prove that if is uniformly continuous, then such a function exists, and is uniformly continuous.
[A subset is dense if for any nonempty open subset , the intersection is nonempty.]
Paper 4, Section I, G
(a) What does it mean to say that a mapping from a metric space to itself is a contraction?
(b) State carefully the contraction mapping theorem.
(c) Let . By considering the metric space with
or otherwise, show that there exists a unique solution of the system of equations
Paper 4, Section II, G
(a) Let be a real vector space. What does it mean to say that two norms on are Lipschitz equivalent? Prove that every norm on is Lipschitz equivalent to the Euclidean norm. Hence or otherwise, show that any linear map from to is continuous.
(b) Let be a linear map between normed real vector spaces. We say that is bounded if there exists a constant such that for all . Show that is bounded if and only if is continuous.
(c) Let denote the space of sequences of real numbers such that is convergent, with the norm . Let be the sequence with and if . Let be the sequence . Show that the subset is linearly independent. Let be the subspace it spans, and consider the linear map defined by
Is continuous? Justify your answer.
Paper 1, Section II, G
Define what it means for a sequence of functions to converge uniformly on to a function .
Let , where are positive constants. Determine all the values of for which converges pointwise on . Determine all the values of for which converges uniformly on .
Let now . Determine whether or not converges uniformly on .
Let be a continuous function. Show that the sequence is uniformly convergent on if and only if .
[If you use any theorems about uniform convergence, you should prove these.]
Paper 2, Section I, G
Show that the map given by
is differentiable everywhere and find its derivative.
Stating accurately any theorem that you require, show that has a differentiable local inverse at a point if and only if
Paper 2, Section II, G
Let be normed spaces with norms . Show that for a map and , the following two statements are equivalent:
(i) For every given there exists such that whenever
(ii) for each sequence .
We say that is continuous at if (i), or equivalently (ii), holds.
Let now be a normed space. Let be a non-empty closed subset and define . Show that
In the case when with the standard Euclidean norm, show that there exists such that .
Let be two disjoint closed sets in . Must there exist disjoint open sets such that and ? Must there exist and such that for all and ? For each answer, give a proof or counterexample as appropriate.
Paper 3, Section I, G
Define what is meant by a uniformly continuous function on a subset of a metric space. Show that every continuous function on a closed, bounded interval is uniformly continuous. [You may assume the Bolzano-Weierstrass theorem.]
Suppose that a function is continuous and tends to a finite limit at . Is necessarily uniformly continuous on Give a proof or a counterexample as appropriate.
Paper 3, Section II, G
Define what it means for a function to be differentiable at with derivative .
State and prove the chain rule for the derivative of , where is a differentiable function.
Now let be a differentiable function and let where is a constant. Show that is differentiable and find its derivative in terms of the partial derivatives of . Show that if holds everywhere in , then for some differentiable function
Paper 4, Section I, G
Define what is meant for two norms on a vector space to be Lipschitz equivalent.
Let denote the vector space of continuous functions with continuous first derivatives and such that for in some neighbourhood of the end-points and 1 . Which of the following four functions define norms on (give a brief explanation)?
Among those that define norms, which pairs are Lipschitz equivalent? Justify your answer.
Paper 4, Section II, G
Consider the space of bounded real sequences with the norm . Show that for every bounded sequence in there is a subsequence which converges in every coordinate, i.e. the sequence of real numbers converges for each . Does every bounded sequence in have a convergent subsequence? Justify your answer.
Let be the subspace of real sequences such that converges. Is complete in the norm (restricted from to ? Justify your answer.
Suppose that is a real sequence such that, for every , the series converges. Show that
Suppose now that is a real sequence such that, for every , the series converges. Show that
Paper 1, Section II, F
Define what it means for two norms on a real vector space to be Lipschitz equivalent. Show that if two norms on are Lipschitz equivalent and , then is closed in one norm if and only if is closed in the other norm.
Show that if is finite-dimensional, then any two norms on are Lipschitz equivalent.
Show that is a norm on the space of continuous realvalued functions on . Is the set closed in the norm ?
Determine whether or not the norm is Lipschitz equivalent to the uniform on .
[You may assume the Bolzano-Weierstrass theorem for sequences in .]
Paper 2, Section I, F
Define what is meant by a uniformly continuous function on a set .
If and are uniformly continuous functions on , is the (pointwise) product necessarily uniformly continuous on ?
Is a uniformly continuous function on necessarily bounded?
Is uniformly continuous on
Justify your answers.
Paper 2, Section II,
Let be subsets of and define . For each of the following statements give a proof or a counterexample (with justification) as appropriate.
(i) If each of is bounded and closed, then is bounded and closed.
(ii) If is bounded and closed and is closed, then is closed.
(iii) If are both closed, then is closed.
(iv) If is open and is closed, then is open.
[The Bolzano-Weierstrass theorem in may be assumed without proof.]
Paper 3, Section I, F
Let be an open set and let be a differentiable function on such that for some constant and all , where denotes the operator norm of the linear map . Let be a straight-line segment contained in . Prove that , where denotes the Euclidean norm on .
Prove that if is an open ball and for each , then is constant on .
Paper 3, Section II, F
Let , be continuous functions on an open interval . Prove that if the sequence converges to uniformly on then the function is continuous on .
If instead is only known to converge pointwise to and is continuous, must be uniformly convergent? Justify your answer.
Suppose that a function has a continuous derivative on and let
Stating clearly any standard results that you require, show that the functions converge uniformly to on each interval .
Paper 4, Section I, F
Define a contraction mapping and state the contraction mapping theorem.
Let be the space of continuous real-valued functions on endowed with the uniform norm. Show that the map defined by
is not a contraction mapping, but that is.
Paper 4, Section II, F
Let be an open set. Define what it means for a function to be differentiable at a point .
Prove that if the partial derivatives and exist on and are continuous at , then is differentiable at .
If is differentiable on must be continuous at Give a proof or counterexample as appropriate.
The function is defined by
Determine all the points at which is differentiable.
Paper 1, Section II, F
Define what it means for a sequence of functions , to converge uniformly on an interval .
By considering the functions , or otherwise, show that uniform convergence of a sequence of differentiable functions does not imply uniform convergence of their derivatives.
Now suppose is continuously differentiable on for each , that converges as for some , and moreover that the derivatives converge uniformly on . Prove that converges to a continuously differentiable function on , and that
Hence, or otherwise, prove that the function
is continuously differentiable on .
Paper 2, Section I, F
Let denote the vector space of continuous real-valued functions on the interval , and let denote the subspace of continuously differentiable functions.
Show that defines a norm on . Show furthermore that the map takes the closed unit ball to a bounded subset of .
If instead we had used the norm restricted from to , would take the closed unit ball to a bounded subset of ? Justify your answer.
Paper 2, Section II, F
Let be continuous on an open set . Suppose that on the partial derivatives and exist and are continuous. Prove that on .
If is infinitely differentiable, and , what is the maximum number of distinct -th order partial derivatives that may have on ?
Let be defined by
Let be defined by
For each of and , determine whether they are (i) differentiable, (ii) infinitely differentiable at the origin. Briefly justify your answers.
Paper 3, Section I,
For each of the following sequences of functions on , indexed by , determine whether or not the sequence has a pointwise limit, and if so, determine whether or not the convergence to the pointwise limit is uniform.
Paper 3, Section II, F
For each of the following statements, provide a proof or justify a counterexample.
The norms and on are Lipschitz equivalent.
The norms and on the vector space of sequences with are Lipschitz equivalent.
Given a linear function between normed real vector spaces, there is some for which for every with .
Given a linear function between normed real vector spaces for which there is some for which for every with , then is continuous.
The uniform norm is complete on the vector space of continuous real-valued functions on for which for sufficiently large.
The uniform norm is complete on the vector space of continuous real-valued functions on which are bounded.
Paper 4, Section I,
State and prove the chain rule for differentiable mappings and .
Suppose now has image lying on the unit circle in . Prove that the determinant vanishes for every .
Paper 4, Section II, F
State the contraction mapping theorem.
A metric space is bounded if is a bounded subset of . Suppose is complete and bounded. Let denote the set of continuous from to itself. For , let
Prove that is a complete metric space. Is the subspace of contraction mappings a complete subspace?
Let be the map which associates to any contraction its fixed point. Prove that is continuous.
Paper 1, Section II, E
State the inverse function theorem for a function . Suppose is a differentiable bijection with also differentiable. Show that the derivative of at any point in is a linear isomorphism.
Let be a function such that the partial derivatives exist and are continuous. Assume there is a point for which and . Prove that there exist open sets and containing and , respectively, such that for every there exists a unique such that and . Moreover, if we define by , prove that is differentiable with continuous derivative. Find the derivative of at in terms of and .
Paper 2, Section I, E
Let be a function. What does it mean to say that is differentiable at a point Prove directly from this definition, that if is differentiable at , then is continuous at .
Let be the function:
For which points is differentiable? Justify your answer.
Paper 2, Section II, E
Let be a mapping. Fix and prove that the following two statements are equivalent:
(i) Given there is such that whenever (we use the standard norm in Euclidean space).
(ii) for any sequence .
We say that is continuous if (i) (or equivalently (ii)) holds for every .
Let and be subsets of and respectively. For as above, determine which of the following statements are always true and which may be false, giving a proof or a counterexample as appropriate.
(a) If is closed whenever is closed, then is continuous.
(b) If is continuous, then is closed whenever is closed.
(c) If is continuous, then is open whenever is open.
(d) If is continuous, then is bounded whenever is bounded.
(e) If is continuous and is bounded whenever is bounded, then is closed whenever is closed.
Paper 3, Section I,
Let be the set of continuous real-valued functions on with the uniform norm. Suppose is defined by
for all and . Is a contraction mapping? Does have a unique fixed point? Justify your answers.
Paper 3, Section II, E
Let be a sequence of continuous functions on the interval such that for each . For the three statements:
(a) uniformly on ;
(b) is a continuous function;
(c) as
say which of the six possible implications , are true and which false, giving in each case a proof or counterexample.
Paper 4, Section I, E
Let be a bilinear function. Show that is differentiable at any point in and find its derivative.
Paper 4, Section II, E
State and prove the Bolzano-Weierstrass theorem in . [You may assume the Bolzano-Weierstrass theorem in .]
Let be a subset and let be a mapping such that for all , where is the Euclidean distance in . Prove that if is closed and bounded, then is a bijection. Is this result still true if we drop the boundedness assumption on ? Justify your answer.
Paper 1, Section II, E
What is meant by saying that a sequence of functions converges uniformly to a function ?
Let be a sequence of differentiable functions on with continuous and such that converges for some point . Assume in addition that converges uniformly on . Prove that converges uniformly to a differentiable function on and for all . [You may assume that the uniform limit of continuous functions is continuous.]
Show that the series
converges for and is uniformly convergent on for any . Show that is differentiable on and
[You may use the Weierstrass -test provided it is clearly stated.]
Paper 2, Section I, E
Define differentiability of a function . Let be a constant. For which points is
differentiable? Justify your answer.
Paper 2, Section II, E
What is meant by saying that two norms on a real vector space are Lipschitz equivalent?
Show that any two norms on are Lipschitz equivalent. [You may assume that a continuous function on a closed bounded set in has closed bounded image.]
Show that defines a norm on the space of continuous real-valued functions on . Is it Lipschitz equivalent to the uniform norm? Justify your answer. Prove that the normed space is not complete.
Paper 3, Section I,
Suppose is a uniformly continuous mapping from a metric space to a metric space . Prove that is a Cauchy sequence in for every Cauchy sequence in .
Let be a continuous mapping between metric spaces and suppose that has the property that is a Cauchy sequence whenever is a Cauchy sequence. Is it true that must be uniformly continuous? Justify your answer.
Paper 3, Section II, E
Consider a map .
Assume is differentiable at and let denote the derivative of at . Show that
for any .
Assume now that is such that for some fixed and for every the limit
exists. Is it true that is differentiable at Justify your answer.
Let denote the set of all real matrices which is identified with . Consider the function given by . Explain why is differentiable. Show that the derivative of at the matrix is given by
for any matrix . State carefully the inverse function theorem and use it to prove that there exist open sets and containing the identity matrix such that given there exists a unique such that .
Paper 4, Section I, E
Let denote the set of bounded real-valued functions on . A distance on is defined by
Given that is a metric space, show that it is complete. Show that the subset of continuous functions is a closed set.
Paper 4, Section II, E
Define a contraction mapping and state the contraction mapping theorem.
Let be a non-empty complete metric space and let be a map. Set and . Assume that for some integer is a contraction mapping. Show that has a unique fixed point and that any has the property that as .
Let be the set of continuous real-valued functions on with the uniform norm. Suppose is defined by
for all and . Show that is not a contraction mapping but that is.
Paper 1, Section II, G
State and prove the contraction mapping theorem. Demonstrate its use by showing that the differential equation , with boundary condition , has a unique solution on , with one-sided derivative at zero.
Paper 2, Section I, G
Let be a real number, and let be the space of sequences of real numbers with convergent. Show that defines a norm on .
Let denote the space of sequences a with bounded; show that . If , show that the norms on given by restricting to the norms on and on are not Lipschitz equivalent.
By considering sequences of the form in , for an appropriate real number, or otherwise, show that (equipped with the norm ) is not complete.
Paper 2, Section II, G
Suppose the functions are defined on the open interval and that tends uniformly on to a function . If the are continuous, show that is continuous. If the are differentiable, show by example that need not be differentiable.
Assume now that each is differentiable and the derivatives converge uniformly on . For any given , we define functions by
Show that each is continuous. Using the general principle of uniform convergence (the Cauchy criterion) and the Mean Value Theorem, or otherwise, prove that the functions converge uniformly to a continuous function on , where
Deduce that is differentiable on .
Paper 3, Section I, G
Consider the map given by
Show that is differentiable everywhere and find its derivative.
Stating carefully any theorem that you quote, show that is locally invertible near a point unless .
Paper 3, Section II, G
Let be a map on an open subset . Explain what it means for to be differentiable on . If is a differentiable map on an open subset with , state and prove the Chain Rule for the derivative of the composite .
Suppose now is a differentiable function for which the partial derivatives for all . By considering the function given by
or otherwise, show that there exists a differentiable function with at all points of
Paper 4, Section I, G
Let denote the set of continuous real-valued functions on the interval . For , set
Show that both and define metrics on . Does the identity map on define a continuous map of metric spaces Does the identity map define a continuous map of metric spaces ?
Paper 4, Section II, G
What does it mean to say that a function on an interval in is uniformly continuous? Assuming the Bolzano-Weierstrass theorem, show that any continuous function on a finite closed interval is uniformly continuous.
Suppose that is a continuous function on the real line, and that tends to finite limits as ; show that is uniformly continuous.
If is a uniformly continuous function on , show that is bounded as . If is a continuous function on for which as , determine whether is necessarily uniformly continuous, giving proof or counterexample as appropriate.
Paper 1, Section II, E
Define a function by
where is the distance from to the nearest integer. Prove that is continuous. [Results about uniform convergence may not be used unless they are clearly stated and proved.]
Suppose now that is a function which is differentiable at some point , and let be two sequences of real numbers with for all , and as . Prove that
exists.
By considering appropriate sequences of rationals with denominator , or otherwise, show that is nowhere differentiable.
Paper 2, Section I, E
State and prove the contraction mapping theorem. Let . By considering and using the contraction mapping theorem, show that there is a unique real number such that .
Paper 2, Section II, E
Let be a set. What does it mean to say that is open? Show that if is open and if is a continuous function then is also differentiable, and that its derivative is zero.
Suppose that is differentiable and that for all , where denotes the derivative of at and is the operator norm. Suppose that and that the line segment lies wholly in . Prove that .
Let be (infinite) lines in , and write . If , show that there is some such that the line segments and both lie inside V. [You may assume without proof that may not be written as the union of finitely many planes.]
Show that if is a continuous function then is constant on .
Paper 3, Section I, E
What is meant by a norm on ? For write
Prove that and are norms. [You may assume the Cauchy-Schwarz inequality.]
Find the smallest constant such that for all , and also the smallest constant such that for all .
Paper 3, Section II, E
What does it mean for a function of several variables to be differentiable at a point ? State and prove the chain rule for functions of several variables. For each of the following two functions from to , give with proof the set of points at which it is differentiable:
Paper 4, Section I, E
Let be a sequence of continuous functions from to and let be another continuous function. What does it mean to say that uniformly? Give examples (without proof) of a sequence of nonzero functions which converges to 0 uniformly, and of a sequence which converges to 0 pointwise but not uniformly. Show that if uniformly then
Give an example of a continuous function with for all as but for which does not converge. For each positive integer define to be equal to if , and to be for . Show that the functions are continuous, tend uniformly to , and furthermore that exists and is finite for all .
Paper 4, Section II, E
Let be a metric space with at least two points. If is a function, write
provided that this supremum is finite. is defined . Show that is a vector space over , and that Lip is a norm on it.
Now let . Suppose that is a sequence of functions with and with the property that the sequence converges as for every rational number . Show that the converge pointwise to a function satisfying .
Suppose now that are any functions with . Show that there is a subsequence which converges pointwise to a function with .
Explain what it means for a function of two variables to be differentiable at a point . If is differentiable at , show that for any the function defined by
is differentiable at , and find its derivative in terms of the partial derivatives of at .
Consider the function defined by
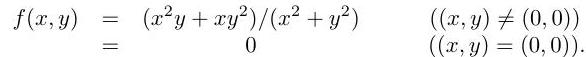
Is differentiable at ? Justify your answer.
1.II.11F
State and prove the Contraction Mapping Theorem.
Let be a nonempty complete metric space and a mapping such that, for some , the th iterate of (that is, composed with itself times) is a contraction mapping. Show that has a unique fixed point.
Now let be the space of all continuous real-valued functions on , equipped with the uniform norm , and let be a continuous function satisfying the Lipschitz condition
for all and all , where is a constant. Let be defined by
where is a fixed continuous function on . Show by induction on that
for all and all . Deduce that the integral equation
has a unique continuous solution on .
2.I.3F
Explain what is meant by the statement that a sequence of functions defined on an interval converges uniformly to a function . If converges uniformly to , and each is continuous on , prove that is continuous on .
Now suppose additionally that is a sequence of points of converging to a limit . Prove that .
2.II.13F
Let be a sequence of real-valued functions defined on a subset of . Suppose that for all and all we have , where converges. Prove that converges uniformly on .
Now let , and consider the series , where and
for . Show that the series converges uniformly on for any real number . Deduce that is a continuous function on . Does the series converge uniformly on ? Justify your answer.
3.II.13F
Let be a function, and a point of . Prove that if the partial derivatives of exist in some open disc around and are continuous at , then is differentiable at .
Now let denote the vector space of all real matrices, and let be the function assigning to each matrix its determinant. Show that is differentiable at the identity matrix , and that is the linear map . Deduce that is differentiable at any invertible matrix , and that is the linear map
Show also that if is a matrix with , then is invertible. Deduce that is twice differentiable at , and find as a bilinear map .
[You may assume that the norm on is complete, and that it satisfies the inequality for any two matrices and
4.I.3F
Let be the vector space of all continuous real-valued functions on the unit interval . Show that the functions
both define norms on .
Consider the sequence defined by . Does converge in the norm ? Does it converge in the norm ? Justify your answers.
4.II.13F
Explain what it means for two norms on a real vector space to be Lipschitz equivalent. Show that if two norms are Lipschitz equivalent, then one is complete if and only if the other is.
Let be an arbitrary norm on the finite-dimensional space , and let denote the standard (Euclidean) norm. Show that for every with , we have
where is the standard basis for , and deduce that the function is continuous with respect to . Hence show that there exists a constant such that for all with , and deduce that and are Lipschitz equivalent.
[You may assume the Bolzano-Weierstrass Theorem.]
For integers and , define to be 0 if , or if and is the largest non-negative integer such that is a multiple of . Show that is a metric on the integers .
Does the sequence converge in this metric?
Let be the real vector space of continuous functions . Show that defining
makes a normed vector space.
Define for positive integers . Is the sequence convergent to some element of ? Is a Cauchy sequence in ? Justify your answers.
Define uniform continuity for a real-valued function on an interval in the real line. Is a uniformly continuous function on the real line necessarily bounded?
Which of the following functions are uniformly continuous on the real line?
(i) ,
(ii) .
Justify your answers.
1.II.11H
Define what it means for a function to be differentiable at a point with derivative a linear map
State the Chain Rule for differentiable maps and . Prove the Chain Rule.
Let denote the standard Euclidean norm of . Find the partial derivatives of the function where they exist.
2.II.13H
Show that the limit of a uniformly convergent sequence of real valued continuous functions on is continuous on .
Let be a sequence of continuous functions on which converge point-wise to a continuous function. Suppose also that the integrals converge to . Must the functions converge uniformly to Prove or give a counterexample.
Let be a sequence of continuous functions on which converge point-wise to a function . Suppose that is integrable and that the integrals converge to . Is the limit necessarily continuous? Prove or give a counterexample.
4.I.3H
Define uniform convergence for a sequence of real-valued functions on the interval .
For each of the following sequences of functions on , find the pointwise limit function. Which of these sequences converge uniformly on ?
(i) ,
(ii) .
Justify your answers.
4.II.13H
State and prove the Contraction Mapping Theorem.
Find numbers and , with , such that the mapping defined by
is a contraction, in the sup norm on . Deduce that the differential equation
has a unique solution in some interval containing 0 .
Define what it means for a function to be differentiable at a point . If the partial derivatives and are defined and continuous on a neighbourhood of , show that is differentiable at .
1.II.11F
Let and be sequences of real numbers for such that and for all , for some constants and . Show that the series
converges uniformly to a continuous function on the real line. Show that is periodic in the sense that .
Now suppose that and for all , for some constants and . Show that is differentiable on the real line, with derivative
[You may assume the convergence of standard series.]
2.I.3F
Define uniform convergence for a sequence of real-valued functions on an interval in . If is a sequence of continuous functions converging uniformly to a (necessarily continuous) function on a closed interval , show that
as .
Which of the following sequences of functions converges uniformly on the open interval ? Justify your answers.
(i) ;
(ii) .
2.II.13F
For a smooth mapping , the Jacobian at a point is defined as the determinant of the derivative , viewed as a linear map . Suppose that maps into a curve in the plane, in the sense that is a composition of two smooth mappings . Show that the Jacobian of is identically zero.
Conversely, let be a smooth mapping whose Jacobian is identically zero. Write . Suppose that . Show that on some open neighbourhood of and that on
for some smooth function defined on . Now suppose that is a smooth curve of the form such that is constant. Write down a differential equation satisfied by . Apply an existence theorem for differential equations to show that there is a neighbourhood of such that every point in lies on a curve on which is constant.
[A function is said to be smooth when it is infinitely differentiable. Detailed justification of the smoothness of the functions in question is not expected.]
3.II.13F
State precisely the inverse function theorem for a smooth map from an open subset of to
Define by
Determine the open subset of on which is locally invertible.
Let be the curve . Show that is the union of the two subsets and . Show that for each there is a unique such that . Show that is locally invertible at all points of , and deduce that is a smooth function of .
[A function is said to be smooth when it is infinitely differentiable.]
4.I.3F
Let be the vector space of all sequences of real numbers such that converges to zero. Show that the function
defines a norm on .
Is the sequence
convergent in Justify your answer.
4.II.13F
State precisely the contraction mapping theorem.
An ancient way to approximate the square root of a positive number is to start with a guess and then hope that the average of and gives a better guess. We can then repeat the procedure using the new guess. Justify this procedure as follows. First, show that all the guesses after the first one are greater than or equal to . Then apply the properties of contraction mappings to the interval to show that the procedure always converges to .
Once the above procedure is close enough to , estimate how many more steps of the procedure are needed to get one more decimal digit of accuracy in computing .
1.II.11B
Let be a sequence of continuous real-valued functions defined on a set . Suppose that the functions converge uniformly to a function . Prove that is continuous on .
Show that the series defines a continuous function on the half-open interval .
[Hint: You may assume the convergence of standard series.]
2.I.3B
Define uniform continuity for a real-valued function defined on an interval in .
Is a uniformly continuous function on the interval necessarily bounded?
Is uniformly continuous on ?
Is uniformly continuous on ?
Justify your answers.
2.II.13B
Use the standard metric on in this question.
(i) Let be a nonempty closed subset of and a point in . Show that there is a point which minimizes the distance to , in the sense that for all .
(ii) Suppose that the set in part (i) is convex, meaning that contains the line segment between any two of its points. Show that point described in part (i) is unique.
3.I.3B
Let be a function. What does it mean to say that is differentiable at a point in ? Show that if is differentiable at , then is continuous at .
For each of the following functions, determine whether or not it is differentiable at . Justify your answers.
(i)
(ii)
3.II.13B
Let be a real-valued differentiable function on an open subset of . Assume that and that for all and is also in . Suppose that is homogeneous of degree , in the sense that for all and . By means of the Chain Rule or otherwise, show that
for all . (Here denotes the derivative of at , viewed as a linear map .)
Conversely, show that any differentiable function on with for all must be homogeneous of degree .
4.I 3 B
Let be the vector space of continuous real-valued functions on . Show that the function
defines a norm on .
For , let . Is a convergent sequence in the space with this norm? Justify your answer.
4.II.13B
Let be a continuous function. Let be the maximum value of . Suppose there is a constant such that
for all and . Let . Show that there is a unique function such that
and
[Hint: First show that the differential equation with its initial condition is equivalent to the integral equation
State and prove the contraction mapping theorem.
Let be a positive real number, and take . Prove that the function
is a contraction from to . Find the unique fixed point of .
1.I.4G
Define what it means for a sequence of functions , where , to converge uniformly to a function .
For each of the following sequences of functions on , find the pointwise limit function. Which of these sequences converge uniformly? Justify your answers.
(i)
(ii)
(iii)
1.II.15G
State the axioms for a norm on a vector space. Show that the usual Euclidean norm on ,
satisfies these axioms.
Let be any bounded convex open subset of that contains 0 and such that if then . Show that there is a norm on , satisfying the axioms, for which is the set of points in of norm less than 1 .
2.I.3G
Consider a sequence of continuous functions . Suppose that the functions converge uniformly to some continuous function . Show that the integrals converge to .
Give an example to show that, even if the functions and are differentiable, the derivatives need not converge to .
2.II.14G
Let be a non-empty complete metric space. Give an example to show that the intersection of a descending sequence of non-empty closed subsets of , can be empty. Show that if we also assume that
then the intersection is not empty. Here the diameter is defined as the supremum of the distances between any two points of a set .
We say that a subset of is dense if it has nonempty intersection with every nonempty open subset of . Let be any sequence of dense open subsets of . Show that the intersection is not empty.
[Hint: Look for a descending sequence of subsets , with , such that the previous part of this problem applies.]
3.I.4F
Let and be metric spaces with metrics and . If and are any two points of , prove that the formula
defines a metric on . If , prove that the diagonal of is closed in .
4.I.3F
Let be open sets in , respectively, and let be a map. What does it mean for to be differentiable at a point of ?
Let be the map given by
Prove that is differentiable at all points with .
4.II.13F
State the inverse function theorem for maps , where is a non-empty open subset of .
Let be the function defined by
Find a non-empty open subset of such that is locally invertible on , and compute the derivative of the local inverse.
Let be the set of all points in satisfying
Prove that is locally invertible at all points of except and . Deduce that, for each point in except and , there exist open intervals containing , respectively, such that for each in , there is a unique point in with in .
State and prove the Contraction Mapping Theorem.
Let be a bounded metric space, and let denote the set of all continuous maps . Let be the function
Show that is a metric on , and that is complete if is complete. [You may assume that a uniform limit of continuous functions is continuous.]
Now suppose that is complete. Let be the set of contraction mappings, and let be the function which sends a contraction mapping to its unique fixed point. Show that is continuous. [Hint: fix and consider , where is close to .]
1.I.1F
Let be a subset of . Prove that the following conditions on are equivalent:
(i) is closed and bounded.
(ii) has the Bolzano-Weierstrass property (i.e., every sequence in has a subsequence convergent to a point of ).
(iii) Every continuous real-valued function on is bounded.
[The Bolzano-Weierstrass property for bounded closed intervals in may be assumed.]
1.II.10F
Explain briefly what is meant by a metric space, and by a Cauchy sequence in a metric space.
A function is called a pseudometric on if it satisfies all the conditions for a metric except the requirement that implies . If is a pseudometric on , show that the binary relation on defined by is an equivalence relation, and that the function induces a metric on the set of equivalence classes.
Now let be a metric space. If and are Cauchy sequences in , show that the sequence whose th term is is a Cauchy sequence of real numbers. Deduce that the function defined by
is a pseudometric on the set of all Cauchy sequences in . Show also that there is an isometric embedding (that is, a distance-preserving mapping) , where is the equivalence relation on induced by the pseudometric as in the previous paragraph. Under what conditions on is bijective? Justify your answer.
2.I.1F
Explain what it means for a function to be differentiable at a point . Show that if the partial derivatives and exist in a neighbourhood of and are continuous at then is differentiable at .
Let
and . Do the partial derivatives of exist at Is differentiable at Justify your answers.
2.II.10F
Let be the space of real matrices. Show that the function
(where denotes the usual Euclidean norm on ) defines a norm on . Show also that this norm satisfies for all and , and that if then all entries of have absolute value less than . Deduce that any function such that is a polynomial in the entries of is continuously differentiable.
Now let be the mapping sending a matrix to its determinant. By considering as a polynomial in the entries of , show that the derivative is the function . Deduce that, for any is the mapping , where is the adjugate of , i.e. the matrix of its cofactors.
[Hint: consider first the case when is invertible. You may assume the results that the set of invertible matrices is open in and that its closure is the whole of , and the identity .]
3.I.1F
Let be the vector space of continuous real-valued functions on . Show that the function
defines a norm on .
Let . Show that is a Cauchy sequence in . Is convergent? Justify your answer.
4.I.1F
Explain what it means for a sequence of functions to converge uniformly to a function on an interval. If is a sequence of continuous functions converging uniformly to on a finite interval , show that
Let . Does uniformly on Does ? Justify your answers.
4.II.10F
Let be a sequence of continuous complex-valued functions defined on a set , and converging uniformly on to a function . Prove that is continuous on .
State the Weierstrass -test for uniform convergence of a series of complex-valued functions on a set .
Now let , where
Prove carefully that is continuous on .
[You may assume the inequality
Show that if and are non-negative numbers, and , then
Deduce that if is a metric space, then is a metric on .
Let and . Let be the class of continuous complex-valued functions on and, for and in , define
where . Show that the series for converges, and that is a metric on .
For , let and . Show that for . By considering the sums for and separately, show that for each ,
and deduce that as .
1.I.1E
Suppose that for each , the function is uniformly continuous on .
(a) If pointwise on is necessarily continuous on ?
(b) If uniformly on is necessarily continuous on ?
In each case, give a proof or a counter-example (with justification).
1.II.10E
Suppose that is a metric space that has the Bolzano-Weierstrass property (that is, any sequence has a convergent subsequence). Let be any metric space, and suppose that is a continuous map of onto . Show that also has the Bolzano-Weierstrass property.
Show also that if is a bijection of onto , then is continuous.
By considering the map defined on the real interval , or otherwise, show that there exists a continuous choice of arg for the complex number lying in the right half-plane .
2.I.1E
Define what is meant by (i) a complete metric space, and (ii) a totally bounded metric space.
Give an example of a metric space that is complete but not totally bounded. Give an example of a metric space that is totally bounded but not complete.
Give an example of a continuous function that maps a complete metric space onto a metric space that is not complete. Give an example of a continuous function that maps a totally bounded metric space onto a metric space that is not totally bounded.
[You need not justify your examples.]
2.II.10E
(a) Let be a map of a complete metric space into itself, and suppose that there exists some in , and some positive integer , such that for all distinct and in , where is the th iterate of . Show that has a unique fixed point in .
(b) Let be a map of a compact metric space into itself such that for all distinct and in . By considering the function , or otherwise, show that has a unique fixed point in .
(c) Suppose that satisfies for every distinct and in . Suppose that for some , the orbit is bounded. Show that maps the closure of into itself, and deduce that has a unique fixed point in .
[The Contraction Mapping Theorem may be used without proof providing that it is correctly stated.]
3.I.1E
Let be defined by , where and are defined by and, for and . Show that is differentiable on .
Show that for any real non-zero , where we regard as the vector in .
4.I.1E
(a) Let be a metric space containing the point , and let
Is necessarily the largest open subset of ? Is necessarily the smallest closed set that contains ? Justify your answers.
(b) Let be a normed space with norm , and let
Is necessarily the largest open subset of ? Is necessarily the smallest closed set that contains ? Justify your answers.
4.II.10E
(a) Let be a finite-dimensional real vector space, and let and be two norms on . Show that a function is differentiable at a point in with respect to if and only if it is differentiable at with respect to , and that if this is so then the derivative of is independent of the norm used. [You may assume that all norms on a finite-dimensional vector space are equivalent.]
(b) Let and be finite-dimensional normed real vector spaces with having norm , and let be a continuous bilinear mapping. Show that is differentiable at any point in , and that [You may assume that is a norm on , and that is compact.]
1.I.1A
Define uniform continuity for functions defined on a (bounded or unbounded) interval in .
Is it true that a real function defined and uniformly continuous on is necessarily bounded?
Is it true that a real function defined and with a bounded derivative on is necessarily uniformly continuous there?
Which of the following functions are uniformly continuous on :
(i) ;
(ii) ;
(iii) ?
Justify your answers.
1.II.10A
Show that each of the functions below is a metric on the set of functions :
Is the space complete in the metric? Justify your answer.
Show that the set of functions
is a Cauchy sequence with respect to the metric on , yet does not tend to a limit in the metric in this space. Hence, deduce that this space is not complete in the metric.
2.I.1A
State and prove the contraction mapping theorem.
Let , let be the discrete metric on , and let be the metric given by: is symmetric and
Verify that is a metric, and that it is Lipschitz equivalent to .
Define an appropriate function such that is a contraction in the metric, but not in the metric.
2.II.10A
Define total boundedness for metric spaces.
Prove that a metric space has the Bolzano-Weierstrass property if and only if it is complete and totally bounded.
3.I.1A
Define what is meant by a norm on a real vector space.
(a) Prove that two norms on a vector space (not necessarily finite-dimensional) give rise to equivalent metrics if and only if they are Lipschitz equivalent.
(b) Prove that if the vector space has an inner product, then for all ,
in the induced norm.
Hence show that the norm on defined by , where , cannot be induced by an inner product.
3.II.11A
Prove that if all the partial derivatives of (with ) exist in an open set containing and are continuous at this point, then is differentiable at .
Let
and
At which points of the plane is the partial derivative continuous?
At which points is the function differentiable? Justify your answers.
4.I.1A
Let be a mapping of a metric space into itself such that for all distinct in .
Show that and are continuous functions of .
Now suppose that is compact and let
Show that we cannot have .
[You may assume that a continuous function on a compact metric space is bounded and attains its bounds.]
Deduce that possesses a fixed point, and that it is unique.
4.II.10A
Let be a pointwise convergent sequence of real-valued functions on a closed interval . Prove that, if for every , the sequence is monotonic in , and if all the functions , and are continuous, then uniformly on .
By considering a suitable sequence of functions on , show that if the interval is not closed but all other conditions hold, the conclusion of the theorem may fail.