Methods

2021

• Paper 1, Section II, C

  Methods | Part IB, 2021

  (a) By introducing the variables $\xi=x+c t$ and $\eta=x-c t$ (where $c$ is a constant), derive d'Alembert's solution of the initial value problem for the wave equation:

  $$u_{t t}-c^{2} u_{x x}=0, \quad u(x, 0)=\phi(x), \quad u_{t}(x, 0)=\psi(x)$$

  where $-\infty<x<\infty, t \geqslant 0$ and $\phi$ and $\psi$ are given functions (and subscripts denote partial derivatives).

  (b) Consider the forced wave equation with homogeneous initial conditions:

  $$u_{t t}-c^{2} u_{x x}=f(x, t), \quad u(x, 0)=0, \quad u_{t}(x, 0)=0$$

  where $-\infty<x<\infty, t \geqslant 0$ and $f$ is a given function. You may assume that the solution is given by

  $$u(x, t)=\frac{1}{2 c} \int_{0}^{t} \int_{x-c(t-s)}^{x+c(t-s)} f(y, s) d y d s$$

  For the forced wave equation $u_{t t}-c^{2} u_{x x}=f(x, t)$, now in the half space $x \geqslant 0$ (and with $t \geqslant 0$ as before), find (in terms of $f$ ) the solution for $u(x, t)$ that satisfies the (inhomogeneous) initial conditions

  $$u(x, 0)=\sin x, \quad u_{t}(x, 0)=0, \quad \text { for } x \geqslant 0$$

  and the boundary condition $u(0, t)=0$ for $t \geqslant 0$.

  comment

• Paper 2, Section I, C

  Methods | Part IB, 2021

  Consider the differential operator

  $$\mathcal{L} y=\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}$$

  acting on real functions $y(x)$ with $0 \leqslant x \leqslant 1$.

  (i) Recast the eigenvalue equation $\mathcal{L} y=-\lambda y$ in Sturm-Liouville form $\tilde{\mathcal{L}} y=-\lambda w y$, identifying $\tilde{\mathcal{L}}$ and $w$.

  (ii) If boundary conditions $y(0)=y(1)=0$ are imposed, show that the eigenvalues form an infinite discrete set $\lambda_{1}<\lambda_{2}<\ldots$ and find the corresponding eigenfunctions $y_{n}(x)$ for $n=1,2, \ldots$. If $f(x)=x-x^{2}$ on $0 \leqslant x \leqslant 1$ is expanded in terms of your eigenfunctions i.e. $f(x)=\sum_{n=1}^{\infty} A_{n} y_{n}(x)$, give an expression for $A_{n}$. The expression can be given in terms of integrals that you need not evaluate.

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2021

  The Fourier transform $\tilde{f}(k)$ of a function $f(x)$ and its inverse are given by

  $$\tilde{f}(k)=\int_{-\infty}^{\infty} f(x) e^{-i k x} d x, \quad f(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \tilde{f}(k) e^{i k x} d k$$

  (a) Calculate the Fourier transform of the function $f(x)$ defined by:

  $$f(x)= \begin{cases}1 & \text { for } 0<x<1 \\ -1 & \text { for }-1<x<0 \\ 0 & \text { otherwise }\end{cases}$$

  (b) Show that the inverse Fourier transform of $\tilde{g}(k)=e^{-\lambda|k|}$, for $\lambda$ a positive real constant, is given by

  $$g(x)=\frac{\lambda}{\pi\left(x^{2}+\lambda^{2}\right)}$$

  (c) Consider the problem in the quarter plane $0 \leqslant x, 0 \leqslant y$ :

  $$\begin{aligned} \frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}} &=0 ; \\ u(x, 0) &= \begin{cases}1 & \text { for } 0<x<1, \\ 0 & \text { otherwise; }\end{cases} \\ u(0, y)=\lim _{x \rightarrow \infty} u(x, y)=\lim _{y \rightarrow \infty} u(x, y) &=0 . \end{aligned}$$

  Use the answers from parts (a) and (b) to show that

  $$u(x, y)=\frac{4 x y}{\pi} \int_{0}^{1} \frac{v d v}{\left[(x-v)^{2}+y^{2}\right]\left[(x+v)^{2}+y^{2}\right]}$$

  (d) Hence solve the problem in the quarter plane $0 \leqslant x, 0 \leqslant y$ :

  $$\begin{aligned} \frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}} &=0 ; \\ w(x, 0) &= \begin{cases}1 & \text { for } 0<x<1 \\ 0 & \text { otherwise }\end{cases} \\ w(0, y) &= \begin{cases}1 & \text { for } 0<y<1 \\ 0 & \text { otherwise }\end{cases} \\ \lim _{x \rightarrow \infty} w(x, y)=\lim _{y \rightarrow \infty} w(x, y) &=0 \end{aligned}$$

  [You may quote without proof any property of Fourier transforms.]

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2021

  Let $f(\theta)$ be a $2 \pi$-periodic function with Fourier expansion

  $$f(\theta)=\frac{1}{2} a_{0}+\sum_{n=1}^{\infty}\left(a_{n} \cos n \theta+b_{n} \sin n \theta\right)$$

  Find the Fourier coefficients $a_{n}$ and $b_{n}$ for

  $$f(\theta)=\left\{\begin{aligned} 1, & 0<\theta<\pi \\ -1, & \pi<\theta<2 \pi \end{aligned}\right.$$

  Hence, or otherwise, find the Fourier coefficients $A_{n}$ and $B_{n}$ for the $2 \pi$-periodic function $F$ defined by

  $$F(\theta)=\left\{\begin{array}{cc} \theta, & 0<\theta<\pi \\ 2 \pi-\theta, & \pi<\theta<2 \pi \end{array}\right.$$

  Use your answers to evaluate

  $$\sum_{r=0}^{\infty} \frac{(-1)^{r}}{2 r+1} \quad \text { and } \quad \sum_{r=0}^{\infty} \frac{1}{(2 r+1)^{2}}$$

  comment

• Paper 3, Section II, A

  Methods | Part IB, 2021

  Let $P(x)$ be a solution of Legendre's equation with eigenvalue $\lambda$,

  $$\left(1-x^{2}\right) \frac{d^{2} P}{d x^{2}}-2 x \frac{d P}{d x}+\lambda P=0$$

  such that $P$ and its derivatives $P^{(k)}(x)=d^{k} P / d x^{k}, k=0,1,2, \ldots$, are regular at all points $x$ with $-1 \leqslant x \leqslant 1$.

  (a) Show by induction that

  $$\left(1-x^{2}\right) \frac{d^{2}}{d x^{2}}\left[P^{(k)}\right]-2(k+1) x \frac{d}{d x}\left[P^{(k)}\right]+\lambda_{k} P^{(k)}=0$$

  for some constant $\lambda_{k}$. Find $\lambda_{k}$ explicitly and show that its value is negative when $k$ is sufficiently large, for a fixed value of $\lambda$.

  (b) Write the equation for $P^{(k)}(x)$ in part (a) in self-adjoint form. Hence deduce that if $P^{(k)}(x)$ is not identically zero, then $\lambda_{k} \geqslant 0$.

  [Hint: Establish a relation between integrals of the form $\int_{-1}^{1}\left[P^{(k+1)}(x)\right]^{2} f(x) d x$ and $\int_{-1}^{1}\left[P^{(k)}(x)\right]^{2} g(x) d x$ for certain functions $f(x)$ and $\left.g(x) .\right]$

  (c) Use the results of parts (a) and (b) to show that if $P(x)$ is a non-zero, regular solution of Legendre's equation on $-1 \leqslant x \leqslant 1$, then $P(x)$ is a polynomial of degree $n$ and $\lambda=n(n+1)$ for some integer $n=0,1,2, \ldots$

  comment

• Paper 4, Section II, C

  Methods | Part IB, 2021

  The function $\theta(x, t)$ obeys the diffusion equation

  $$\frac{\partial \theta}{\partial t}=D \frac{\partial^{2} \theta}{\partial x^{2}}$$

  Verify that

  $$\theta(x, t)=\frac{1}{\sqrt{t}} e^{-x^{2} / 4 D t}$$

  is a solution of $(*)$, and by considering $\int_{-\infty}^{\infty} \theta(x, t) d x$, find the solution having the initial form $\theta(x, 0)=\delta(x)$ at $t=0$.

  Find, in terms of the error function, the solution of $(*)$ having the initial form

  $$\theta(x, 0)= \begin{cases}1, & |x| \leqslant 1 \\ 0, & |x|>1\end{cases}$$

  Sketch a graph of this solution at various times $t \geqslant 0$.

  [The error function is

  $$\left.\operatorname{Erf}(x)=\frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{-y^{2}} d y .\right]$$

  comment

2020

• Paper 1, Section II, B

  Methods | Part IB, 2020

  Consider the equation

  $$\nabla^{2} \phi=\delta(x) g(y)$$

  on the two-dimensional strip $-\infty<x<\infty, 0 \leqslant y \leqslant a$, where $\delta(x)$ is the delta function and $g(y)$ is a smooth function satisfying $g(0)=g(a)=0 . \phi(x, y)$ satisfies the boundary conditions $\phi(x, 0)=\phi(x, a)=0$ and $\lim _{x \rightarrow \pm \infty} \phi(x, y)=0$. By using solutions of Laplace's equation for $x<0$ and $x>0$, matched suitably at $x=0$, find the solution of $(*)$ in terms of Fourier coefficients of $g(y)$.

  Find the solution of $(*)$ in the limiting case $g(y)=\delta(y-c)$, where $0<c<a$, and hence determine the Green's function $\phi(x, y)$ in the strip, satisfying

  $$\nabla^{2} \phi=\delta(x-b) \delta(y-c)$$

  and the same boundary conditions as before.

  comment

• Paper 2, Section I, B

  Methods | Part IB, 2020

  Find the Fourier transform of the function

  $$f(x)= \begin{cases}A, & |x| \leqslant 1 \\ 0, & |x|>1\end{cases}$$

  Determine the convolution of the function $f(x)$ with itself.

  State the convolution theorem for Fourier transforms. Using it, or otherwise, determine the Fourier transform of the function

  $$g(x)= \begin{cases}B(2-|x|), & |x| \leqslant 2 \\ 0, & |x|>2\end{cases}$$

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2020

  (i) The solution to the equation

  $$\frac{d}{d x}\left(x \frac{d F}{d x}\right)+\alpha^{2} x F=0$$

  that is regular at the origin is $F(x)=C J_{0}(\alpha x)$, where $\alpha$ is a real, positive parameter, $J_{0}$ is a Bessel function, and $C$ is an arbitrary constant. The Bessel function has infinitely many zeros: $J_{0}\left(\gamma_{k}\right)=0$ with $\gamma_{k}>0$, for $k=1,2, \ldots$. Show that

  $$\int_{0}^{1} J_{0}(\alpha x) J_{0}(\beta x) x d x=\frac{\beta J_{0}(\alpha) J_{0}^{\prime}(\beta)-\alpha J_{0}(\beta) J_{0}^{\prime}(\alpha)}{\alpha^{2}-\beta^{2}}, \quad \alpha \neq \beta$$

  (where $\alpha$ and $\beta$ are real and positive) and deduce that

  $$\int_{0}^{1} J_{0}\left(\gamma_{k} x\right) J_{0}\left(\gamma_{\ell} x\right) x d x=0, \quad k \neq \ell ; \quad \int_{0}^{1}\left(J_{0}\left(\gamma_{k} x\right)\right)^{2} x d x=\frac{1}{2}\left(J_{0}^{\prime}\left(\gamma_{k}\right)\right)^{2}$$

  [Hint: For the second identity, consider $\alpha=\gamma_{k}$ and $\beta=\gamma_{k}+\epsilon$ with $\epsilon$ small.]

  (ii) The displacement $z(r, t)$ of the membrane of a circular drum of unit radius obeys

  $$\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial z}{\partial r}\right)=\frac{\partial^{2} z}{\partial t^{2}}, \quad z(1, t)=0$$

  where $r$ is the radial coordinate on the membrane surface, $t$ is time (in certain units), and the displacement is assumed to have no angular dependence. At $t=0$ the drum is struck, so that

  $$z(r, 0)=0, \quad \frac{\partial z}{\partial t}(r, 0)=\left\{\begin{array}{cc} U, & r<b \\ 0, & r>b \end{array}\right.$$

  where $U$ and $b<1$ are constants. Show that the subsequent motion is given by

  $$z(r, t)=\sum_{k=1}^{\infty} C_{k} J_{0}\left(\gamma_{k} r\right) \sin \left(\gamma_{k} t\right) \quad \text { where } \quad C_{k}=-2 b U \frac{J_{0}^{\prime}\left(\gamma_{k} b\right)}{\gamma_{k}^{2}\left(J_{0}^{\prime}\left(\gamma_{k}\right)\right)^{2}}$$

  comment

2019

• Paper 1, Section II, B

  Methods | Part IB, 2019

  The Bessel functions $J_{n}(r)(n \geqslant 0)$ can be defined by the expansion

  $$e^{i r \cos \theta}=J_{0}(r)+2 \sum_{n=1}^{\infty} i^{n} J_{n}(r) \cos n \theta$$

  By using Cartesian coordinates $x=r \cos \theta, y=r \sin \theta$, or otherwise, show that

  $$\left(\nabla^{2}+1\right) e^{i r \cos \theta}=0$$

  Deduce that $J_{n}(r)$ satisfies Bessel's equation

  $$\left(r^{2} \frac{d^{2}}{d r^{2}}+r \frac{d}{d r}-\left(n^{2}-r^{2}\right)\right) J_{n}(r)=0$$

  By expanding the left-hand side of $(*)$ up to cubic order in $r$, derive the series expansions of $J_{0}(r), J_{1}(r), J_{2}(r)$ and $J_{3}(r)$ up to this order.

  comment

• Paper 2, Section I, B

  Methods | Part IB, 2019

  Let $r, \theta, \phi$ be spherical polar coordinates, and let $P_{n}$ denote the $n$th Legendre polynomial. Write down the most general solution for $r>0$ of Laplace's equation $\nabla^{2} \Phi=0$ that takes the form $\Phi(r, \theta, \phi)=f(r) P_{n}(\cos \theta)$.

  Solve Laplace's equation in the spherical shell $1 \leqslant r \leqslant 2$ subject to the boundary conditions

  $$\begin{aligned} &\Phi=3 \cos 2 \theta \text { at } r=1 \\ &\Phi=0 \quad \text { at } r=2 \end{aligned}$$

  [The first three Legendre polynomials are

  $$\left.P_{0}(x)=1, \quad P_{1}(x)=x \quad \text { and } \quad P_{2}(x)=\frac{3}{2} x^{2}-\frac{1}{2} .\right]$$

  comment

• Paper 2, Section II, D

  Methods | Part IB, 2019

  For $n=0,1,2, \ldots$, the degree $n$ polynomial $C_{n}^{\alpha}(x)$ satisfies the differential equation

  $$\left(1-x^{2}\right) y^{\prime \prime}-(2 \alpha+1) x y^{\prime}+n(n+2 \alpha) y=0$$

  where $\alpha$ is a real, positive parameter. Show that, when $m \neq n$,

  $$\int_{a}^{b} C_{m}^{\alpha}(x) C_{n}^{\alpha}(x) w(x) d x=0$$

  for a weight function $w(x)$ and values $a<b$ that you should determine.

  Suppose that the roots of $C_{n}^{\alpha}(x)$ that lie inside the domain $(a, b)$ are $\left\{x_{1}, x_{2}, \ldots, x_{k}\right\}$, with $k \leqslant n$. By considering the integral

  $$\int_{a}^{b} C_{n}^{\alpha}(x) \prod_{i=1}^{k}\left(x-x_{i}\right) w(x) d x$$

  show that in fact all $n$ roots of $C_{n}^{\alpha}(x)$ lie in $(a, b)$.

  comment

• Paper 3, Section I, D

  Methods | Part IB, 2019

  Define the discrete Fourier transform of a sequence $\left\{x_{0}, x_{1}, \ldots, x_{N-1}\right\}$ of $N$ complex numbers.

  Compute the discrete Fourier transform of the sequence

  $$x_{n}=\frac{1}{N}\left(1+e^{2 \pi i n / N}\right)^{N-1} \quad \text { for } n=0, \ldots, N-1 .$$

  comment

• Paper 3, Section II, D

  Methods | Part IB, 2019

  By differentiating the expression $\psi(t)=H(t) \sin (\alpha t) / \alpha$, where $\alpha$ is a constant and $H(t)$ is the Heaviside step function, show that

  $$\frac{d^{2} \psi}{d t^{2}}+\alpha^{2} \psi=\delta(t)$$

  where $\delta(t)$ is the Dirac $\delta$-function.

  Hence, by taking a Fourier transform with respect to the spatial variables only, derive the retarded Green's function for the wave operator $\partial_{t}^{2}-c^{2} \nabla^{2}$ in three spatial dimensions.

  [You may use that

  $$\frac{1}{2 \pi} \int_{\mathbb{R}^{3}} e^{i \mathbf{k} \cdot(\mathbf{x}-\mathbf{y})} \frac{\sin (k c t)}{k c} d^{3} k=-\frac{i}{c|\mathbf{x}-\mathbf{y}|} \int_{-\infty}^{\infty} e^{i k|\mathbf{x}-\mathbf{y}|} \sin (k c t) d k$$

  without proof.]

  Thus show that the solution to the homogeneous wave equation $\partial_{t}^{2} u-c^{2} \nabla^{2} u=0$, subject to the initial conditions $u(\mathbf{x}, 0)=0$ and $\partial_{t} u(\mathbf{x}, 0)=f(\mathbf{x})$, may be expressed as

  $$u(\mathbf{x}, t)=\langle f\rangle t$$

  where $\langle f\rangle$ is the average value of $f$ on a sphere of radius $c t$ centred on $\mathbf{x}$. Interpret this result.

  comment

• Paper 4, Section I, D

  Methods | Part IB, 2019

  Let

  $$g_{\epsilon}(x)=\frac{-2 \epsilon x}{\pi\left(\epsilon^{2}+x^{2}\right)^{2}} .$$

  By considering the integral $\int_{-\infty}^{\infty} \phi(x) g_{\epsilon}(x) d x$, where $\phi$ is a smooth, bounded function that vanishes sufficiently rapidly as $|x| \rightarrow \infty$, identify $\lim _{\epsilon \rightarrow 0} g_{\epsilon}(x)$ in terms of a generalized function.

  comment

• Paper 4, Section II, B

  Methods | Part IB, 2019

  (a) Show that the operator

  $$\frac{d^{4}}{d x^{4}}+p \frac{d^{2}}{d x^{2}}+q \frac{d}{d x}+r$$

  where $p(x), q(x)$ and $r(x)$ are real functions, is self-adjoint (for suitable boundary conditions which you need not state) if and only if

  $$q=\frac{d p}{d x}$$

  (b) Consider the eigenvalue problem

  $$\frac{d^{4} y}{d x^{4}}+p \frac{d^{2} y}{d x^{2}}+\frac{d p}{d x} \frac{d y}{d x}=\lambda y$$

  on the interval $[a, b]$ with boundary conditions

  $$y(a)=\frac{d y}{d x}(a)=y(b)=\frac{d y}{d x}(b)=0$$

  Assuming that $p(x)$ is everywhere negative, show that all eigenvalues $\lambda$ are positive.

  (c) Assume now that $p \equiv 0$ and that the eigenvalue problem (*) is on the interval $[-c, c]$ with $c>0$. Show that $\lambda=1$ is an eigenvalue provided that

  $$\cos c \sinh c \pm \sin c \cosh c=0$$

  and show graphically that this condition has just one solution in the range $0<c<\pi$.

  [You may assume that all eigenfunctions are either symmetric or antisymmetric about $x=0 .]$

  comment

2018

• Paper 1, Section II, 14C

  Methods | Part IB, 2018

  Define the convolution $f * g$ of two functions $f$ and $g$. Defining the Fourier transform $\tilde{f}$ of $f$ by

  $$\tilde{f}(k)=\int_{-\infty}^{\infty} \mathrm{e}^{-\mathrm{i} k x} f(x) \mathrm{d} x$$

  show that

  $$\widehat{f * g}(k)=\tilde{f}(k) \tilde{g}(k) .$$

  Given that the Fourier transform of $f(x)=1 / x$ is

  $$\tilde{f}(k)=-\mathrm{i} \pi \operatorname{sgn}(k),$$

  find the Fourier transform of $\sin (x) / x^{2}$.

  comment

• Paper 2, Section I, $5 \mathrm{C}$

  Methods | Part IB, 2018

  Show that

  $$a(x, y)\left(\frac{d y}{d s}\right)^{2}-2 b(x, y) \frac{d x}{d s} \frac{d y}{d s}+c(x, y)\left(\frac{d x}{d s}\right)^{2}=0$$

  along a characteristic curve $(x(s), y(s))$ of the $2^{\text {nd }}$-order pde

  $$a(x, y) u_{x x}+2 b(x, y) u_{x y}+c(x, y) u_{y y}=f(x, y)$$

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2018

  (a) Let $f(x)$ be a $2 \pi$-periodic function (i.e. $f(x)=f(x+2 \pi)$ for all $x$ ) defined on $[-\pi, \pi]$ by

  $$f(x)=\left\{\begin{array}{cl} x & x \in[0, \pi] \\ -x & x \in[-\pi, 0] \end{array}\right.$$

  Find the Fourier series of $f(x)$ in the form

  $$f(x)=\frac{1}{2} a_{0}+\sum_{n=1}^{\infty} a_{n} \cos (n x)+\sum_{n=1}^{\infty} b_{n} \sin (n x)$$

  (b) Find the general solution to

  $$y^{\prime \prime}+2 y^{\prime}+y=f(x)$$

  where $f(x)$ is as given in part (a) and $y(x)$ is $2 \pi$-periodic.

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2018

  (a) Determine the Green's function $G(x ; \xi)$ satisfying

  $$G^{\prime \prime}-4 G^{\prime}+4 G=\delta(x-\xi),$$

  with $G(0 ; \xi)=G(1 ; \xi)=0$. Here ' denotes differentiation with respect to $x$.

  (b) Using the Green's function, solve

  $$y^{\prime \prime}-4 y^{\prime}+4 y=e^{2 x}$$

  with $y(0)=y(1)=0$.

  comment

• Paper 3, Section II, A

  Methods | Part IB, 2018

  Consider the Dirac delta function, $\delta(x)$, defined by the sampling property

  $$\int_{-\infty}^{\infty} f(x) \delta\left(x-x_{0}\right) d x=f\left(x_{0}\right)$$

  for any suitable function $f(x)$ and real constant $x_{0}$.

  (a) Show that $\delta(\alpha x)=|\alpha|^{-1} \delta(x)$ for any non-zero $\alpha \in \mathbb{R}$.

  (b) Show that $x \delta^{\prime}(x)=-\delta(x)$, where ${ }^{\prime}$ denotes differentiation with respect to $x$.

  (c) Calculate

  $$\int_{-\infty}^{\infty} f(x) \delta^{(m)}(x) d x$$

  where $\delta^{(m)}(x)$ is the $m^{\text {th }}$derivative of the delta function.

  (d) For

  $$\gamma_{n}(x)=\frac{1}{\pi} \frac{n}{(n x)^{2}+1}$$

  show that $\lim _{n \rightarrow \infty} \gamma_{n}(x)=\delta(x)$.

  (e) Find expressions in terms of the delta function and its derivatives for

  (i)

  $$\lim _{n \rightarrow \infty} n^{3} x e^{-x^{2} n^{2}}$$

  (ii)

  $$\lim _{n \rightarrow \infty} \frac{1}{\pi} \int_{0}^{n} \cos (k x) d k .$$

  (f) Hence deduce that

  $$\lim _{n \rightarrow \infty} \frac{1}{2 \pi} \int_{-n}^{n} e^{i k x} d k=\delta(x)$$

  [You may assume that

  $$\left.\int_{-\infty}^{\infty} e^{-y^{2}} d y=\sqrt{\pi} \quad \text { and } \quad \int_{-\infty}^{\infty} \frac{\sin y}{y} d y=\pi .\right]$$

  comment

• Paper 4, Section I, A

  Methods | Part IB, 2018

  By using separation of variables, solve Laplace's equation

  $$\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}=0 \quad 0<x<1, \quad 0<y<1$$

  subject to

  $$\begin{array}{ll} u(0, y)=0 & 0 \leqslant y \leqslant 1 \\ u(1, y)=0 & 0 \leqslant y \leqslant 1 \\ u(x, 0)=0 & 0 \leqslant x \leqslant 1 \\ u(x, 1)=2 \sin (3 \pi x) & 0 \leqslant x \leqslant 1 \end{array}$$

  comment

• Paper 4, Section II, 17C

  Methods | Part IB, 2018

  Let $\Omega$ be a bounded region in the plane, with smooth boundary $\partial \Omega$. Green's second identity states that for any smooth functions $u, v$ on $\Omega$

  $$\int_{\Omega}\left(u \nabla^{2} v-v \nabla^{2} u\right) \mathrm{d} x \mathrm{~d} y=\oint_{\partial \Omega} u(\mathbf{n} \cdot \nabla v)-v(\mathbf{n} \cdot \nabla u) \mathrm{d} s$$

  where $\mathbf{n}$ is the outward pointing normal to $\partial \Omega$. Using this identity with $v$ replaced by

  $$G_{0}\left(\mathbf{x} ; \mathbf{x}_{0}\right)=\frac{1}{2 \pi} \ln \left(\left\|\mathbf{x}-\mathbf{x}_{0}\right\|\right)=\frac{1}{4 \pi} \ln \left(\left(x-x_{0}\right)^{2}+\left(y-y_{0}\right)^{2}\right)$$

  and taking care of the singular point $(x, y)=\left(x_{0}, y_{0}\right)$, show that if $u$ solves the Poisson equation $\nabla^{2} u=-\rho$ then

  $$\begin{aligned} u(\mathbf{x})=-\int_{\Omega} G_{0}\left(\mathbf{x} ; \mathbf{x}_{0}\right) \rho\left(\mathbf{x}_{0}\right) \mathrm{d} x_{0} \mathrm{~d} y_{0} \\ &+\oint_{\partial \Omega}\left(u\left(\mathbf{x}_{0}\right) \mathbf{n} \cdot \nabla G_{0}\left(\mathbf{x} ; \mathbf{x}_{0}\right)-G_{0}\left(\mathbf{x} ; \mathbf{x}_{0}\right) \mathbf{n} \cdot \nabla u\left(\mathbf{x}_{0}\right)\right) \mathrm{d} s \end{aligned}$$

  at any $\mathbf{x}=(x, y) \in \Omega$, where all derivatives are taken with respect to $\mathbf{x}_{0}=\left(x_{0}, y_{0}\right)$.

  In the case that $\Omega$ is the unit disc $\|\mathbf{x}\| \leqslant 1$, use the method of images to show that the solution to Laplace's equation $\nabla^{2} u=0$ inside $\Omega$, subject to the boundary condition

  $$u(1, \theta)=\delta(\theta-\alpha),$$

  is

  $$u(r, \theta)=\frac{1}{2 \pi} \frac{1-r^{2}}{1+r^{2}-2 r \cos (\theta-\alpha)}$$

  where $(r, \theta)$ are polar coordinates in the disc and $\alpha$ is a constant.

  [Hint: The image of a point $\mathbf{x}_{0} \in \Omega$ is the point $\mathbf{y}_{0}=\mathbf{x}_{0} /\left\|\mathbf{x}_{0}\right\|^{2}$, and then

  $$\left\|\mathbf{x}-\mathbf{x}_{0}\right\|=\left\|\mathbf{x}_{0}\right\|\left\|\mathbf{x}-\mathbf{y}_{0}\right\|$$

  for all $\mathbf{x} \in \partial \Omega .]$

  comment

2017

• Paper 1, Section II, 14B

  Methods | Part IB, 2017

  (a)

  (i) Compute the Fourier transform $\tilde{h}(k)$ of $h(x)=e^{-a|x|}$, where $a$ is a real positive constant.

  (ii) Consider the boundary value problem

  $$-\frac{d^{2} u}{d x^{2}}+\omega^{2} u=e^{-|x|} \quad \text { on }-\infty<x<\infty$$

  with real constant $\omega \neq \pm 1$ and boundary condition $u(x) \rightarrow 0$ as $|x| \rightarrow \infty$.

  Find the Fourier transform $\tilde{u}(k)$ of $u(x)$ and hence solve the boundary value problem. You should clearly state any properties of the Fourier transform that you use.

  (b) Consider the wave equation

  $$v_{t t}=v_{x x} \quad \text { on } \quad-\infty<x<\infty \text { and } t>0$$

  with initial conditions

  $$v(x, 0)=f(x) \quad v_{t}(x, 0)=g(x) .$$

  Show that the Fourier transform $\tilde{v}(k, t)$ of the solution $v(x, t)$ with respect to the variable $x$ is given by

  $$\tilde{v}(k, t)=\tilde{f}(k) \cos k t+\frac{\tilde{g}(k)}{k} \sin k t$$

  where $\tilde{f}(k)$ and $\tilde{g}(k)$ are the Fourier transforms of the initial conditions. Starting from $\tilde{v}(k, t)$ derive d'Alembert's solution for the wave equation:

  $$v(x, t)=\frac{1}{2}(f(x-t)+f(x+t))+\frac{1}{2} \int_{x-t}^{x+t} g(\xi) d \xi$$

  You should state clearly any properties of the Fourier transform that you use.

  comment

• Paper 2, Section I, B

  Methods | Part IB, 2017

  Expand $f(x)=x$ as a Fourier series on $-\pi<x<\pi$.

  By integrating the series show that $x^{2}$ on $-\pi<x<\pi$ can be written as

  $$x^{2}=\frac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos n x$$

  where $a_{n}, n=1,2, \ldots$, should be determined and

  $$a_{0}=8 \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}} .$$

  By evaluating $a_{0}$ another way show that

  $$\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}=\frac{\pi^{2}}{12}$$

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2017

  Laplace's equation for $\phi$ in cylindrical coordinates $(r, \theta, z)$, is

  $$\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} \phi}{\partial \theta^{2}}+\frac{\partial^{2} \phi}{\partial z^{2}}=0$$

  Use separation of variables to find an expression for the general solution to Laplace's equation in cylindrical coordinates that is $2 \pi$-periodic in $\theta$.

  Find the bounded solution $\phi(r, \theta, z)$ that satisfies

  $$\begin{aligned} \nabla^{2} \phi &=0 \quad z \geqslant 0, \quad 0 \leqslant r \leqslant 1 \\ \phi(1, \theta, z) &=e^{-4 z}(\cos \theta+\sin 2 \theta)+2 e^{-z} \sin 2 \theta \end{aligned}$$

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2017

  Using the substitution $u(x, y)=v(x, y) e^{-x^{2}}$, find $u(x, y)$ that satisfies

  $$u_{x}+x u_{y}+2 x u=e^{-x^{2}}$$

  with boundary data $u(0, y)=y e^{-y^{2}}$.

  comment

• Paper 3, Section II, A

  Methods | Part IB, 2017

  Let $\mathcal{L}$ be the linear differential operator

  $$\mathcal{L} y=y^{\prime \prime \prime}-y^{\prime \prime}-2 y^{\prime}$$

  where $^{\prime}$ denotes differentiation with respect to $x$.

  Find the Green's function, $G(x ; \xi)$, for $\mathcal{L}$ satisfying the homogeneous boundary conditions $G(0 ; \xi)=0, G^{\prime}(0 ; \xi)=0, G^{\prime \prime}(0 ; \xi)=0$.

  Using the Green's function, solve

  $$\mathcal{L} y=e^{x} \Theta(x-1)$$

  with boundary conditions $y(0)=1, y^{\prime}(0)=-1, y^{\prime \prime}(0)=0$. Here $\Theta(x)$ is the Heaviside step function having value 0 for $x<0$ and 1 for $x>0$.

  comment

• Paper 4, Section I, A

  Methods | Part IB, 2017

  The Legendre polynomials, $P_{n}(x)$ for integers $n \geqslant 0$, satisfy the Sturm-Liouville equation

  $$\frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d}{d x} P_{n}(x)\right]+n(n+1) P_{n}(x)=0$$

  and the recursion formula

  $$(n+1) P_{n+1}(x)=(2 n+1) x P_{n}(x)-n P_{n-1}(x), \quad P_{0}(x)=1, \quad P_{1}(x)=x$$

  (i) For all $n \geqslant 0$, show that $P_{n}(x)$ is a polynomial of degree $n$ with $P_{n}(1)=1$.

  (ii) For all $m, n \geqslant 0$, show that $P_{n}(x)$ and $P_{m}(x)$ are orthogonal over the range $x \in[-1,1]$ when $m \neq n$.

  (iii) For each $n \geqslant 0$ let

  $$R_{n}(x)=\frac{d^{n}}{d x^{n}}\left[\left(x^{2}-1\right)^{n}\right]$$

  Assume that for each $n$ there is a constant $\alpha_{n}$ such that $P_{n}(x)=\alpha_{n} R_{n}(x)$ for all $x$. Determine $\alpha_{n}$ for each $n$.

  comment

• Paper 4, Section II, B

  Methods | Part IB, 2017

  (a)

  (i) For the diffusion equation

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=0 \quad \text { on }-\infty<x<\infty \text { and } t \geqslant 0$$

  with diffusion constant $K$, state the properties (in terms of the Dirac delta function) that define the fundamental solution $F(x, t)$ and the Green's function $G(x, t ; y, \tau)$.

  You are not required to give expressions for these functions.

  (ii) Consider the initial value problem for the homogeneous equation:

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=0, \quad \phi\left(x, t_{0}\right)=\alpha(x) \quad \text { on }-\infty<x<\infty \text { and } t \geqslant t_{0}$$

  and the forced equation with homogeneous initial condition (and given forcing term $h(x, t))$ :

  $$\frac{\partial \phi}{\partial t}-K \frac{\partial^{2} \phi}{\partial x^{2}}=h(x, t), \quad \phi(x, 0)=0 \quad \text { on }-\infty<x<\infty \text { and } t \geqslant 0$$

  Given that $F$ and $G$ in part (i) are related by

  $$G(x, t ; y, \tau)=\Theta(t-\tau) F(x-y, t-\tau)$$

  (where $\Theta(t)$ is the Heaviside step function having value 0 for $t<0$ and 1 for $t>0$, show how the solution of (B) can be expressed in terms of solutions of (A) with suitable initial conditions. Briefly interpret your expression.

  (b) A semi-infinite conducting plate lies in the $\left(x_{1}, x_{2}\right)$ plane in the region $x_{1} \geqslant 0$. The boundary along the $x_{2}$ axis is perfectly insulated. Let $(r, \theta)$ denote standard polar coordinates on the plane. At time $t=0$ the entire plate is at temperature zero except for the region defined by $-\pi / 4<\theta<\pi / 4$ and $1<r<2$ which has constant initial temperature $T_{0}>0$. Subsequently the temperature of the plate obeys the two-dimensional heat equation with diffusion constant $K$. Given that the fundamental solution of the twodimensional heat equation on $\mathbb{R}^{2}$ is

  $$F\left(x_{1}, x_{2}, t\right)=\frac{1}{4 \pi K t} e^{-\left(x_{1}^{2}+x_{2}^{2}\right) /(4 K t)}$$

  show that the origin $(0,0)$ on the plate reaches its maximum temperature at time $t=3 /(8 K \log 2)$.

  comment

2016

• Paper 1, Section II, A

  Methods | Part IB, 2016

  (a) Consider the general self-adjoint problem for $y(x)$ on $[a, b]$ :

  $$-\frac{d}{d x}\left[p(x) \frac{d}{d x} y\right]+q(x) y=\lambda w(x) y ; \quad y(a)=y(b)=0$$

  where $\lambda$ is the eigenvalue, and $w(x)>0$. Prove that eigenfunctions associated with distinct eigenvalues are orthogonal with respect to a particular inner product which you should define carefully.

  (b) Consider the problem for $y(x)$ given by

  $$x y^{\prime \prime}+3 y^{\prime}+\left(\frac{1+\lambda}{x}\right) y=0 ; \quad y(1)=y(e)=0 .$$

  (i) Recast this problem into self-adjoint form.

  (ii) Calculate the complete set of eigenfunctions and associated eigenvalues for this problem. [Hint: You may find it useful to make the substitution $\left.x=e^{s} .\right]$

  (iii) Verify that the eigenfunctions associated with distinct eigenvalues are indeed orthogonal.

  comment

• Paper 2, Section I, A

  Methods | Part IB, 2016

  Use the method of characteristics to find $u(x, y)$ in the first quadrant $x \geqslant 0, y \geqslant 0$, where $u(x, y)$ satisfies

  $$\frac{\partial u}{\partial x}-2 x \frac{\partial u}{\partial y}=\cos x$$

  with boundary data $u(x, 0)=\cos x$.

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2016

  Consider a bar of length $\pi$ with free ends, subject to longitudinal vibrations. You may assume that the longitudinal displacement $y(x, t)$ of the bar satisfies the wave equation with some wave speed $c$ :

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}$$

  for $x \in(0, \pi)$ and $t>0$ with boundary conditions:

  $$\frac{\partial y}{\partial x}(0, t)=\frac{\partial y}{\partial x}(\pi, t)=0$$

  for $t>0$. The bar is initially at rest so that

  $$\frac{\partial y}{\partial t}(x, 0)=0$$

  for $x \in(0, \pi)$, with a spatially varying initial longitudinal displacement given by

  $$y(x, 0)=b x$$

  for $x \in(0, \pi)$, where $b$ is a real constant.

  (a) Using separation of variables, show that

  $$y(x, t)=\frac{b \pi}{2}-\frac{4 b}{\pi} \sum_{n=1}^{\infty} \frac{\cos [(2 n-1) x] \cos [(2 n-1) c t]}{(2 n-1)^{2}}$$

  (b) Determine a periodic function $P(x)$ such that this solution may be expressed as

  $$y(x, t)=\frac{1}{2}[P(x+c t)+P(x-c t)]$$

  comment

• Paper 3, Section $\mathbf{I}$, A

  Methods | Part IB, 2016

  Calculate the Green's function $G(x ; \xi)$ given by the solution to

  $$\frac{d^{2} G}{d x^{2}}=\delta(x-\xi) ; \quad G(0 ; \xi)=\frac{d G}{d x}(1 ; \xi)=0$$

  where $\xi \in(0,1), x \in(0,1)$ and $\delta(x)$ is the Dirac $\delta$-function. Use this Green's function to calculate an explicit solution $y(x)$ to the boundary value problem

  $$\frac{d^{2} y}{d x^{2}}=x e^{-x}$$

  where $x \in(0,1)$, and $y(0)=y^{\prime}(1)=0$.

  comment

• Paper 3, Section II, B

  Methods | Part IB, 2016

  (a) Show that the Fourier transform of $f(x)=e^{-a^{2} x^{2}}$, for $a>0$, is

  $$\tilde{f}(k)=\frac{\sqrt{\pi}}{a} e^{-\frac{k^{2}}{4 a^{2}}},$$

  stating clearly any properties of the Fourier transform that you use.

  [Hint: You may assume that $\int_{0}^{\infty} e^{-t^{2}} d t=\sqrt{\pi} / 2$.]

  (b) Consider now the Cauchy problem for the diffusion equation in one space dimension, i.e. solving for $\theta(x, t)$ satisfying:

  $$\frac{\partial \theta}{\partial t}=D \frac{\partial^{2} \theta}{\partial x^{2}} \quad \text { with } \theta(x, 0)=g(x)$$

  where $D$ is a positive constant and $g(x)$ is specified. Consider the following property of a solution:

  Property P: If the initial data $g(x)$ is positive and it is non-zero only within a bounded region (i.e. there is a constant $\alpha$ such that $\theta(x, 0)=0$ for all $|x|>\alpha)$, then for any $\epsilon>0$ (however small) and $\beta$ (however large) the solution $\theta(\beta, \epsilon)$ can be non-zero, i.e. the solution can become non-zero arbitrarily far away after an arbitrarily short time.

  Does Property P hold for solutions of the diffusion equation? Justify your answer (deriving any expression for the solution $\theta(x, t)$ that you use).

  (c) Consider now the wave equation in one space dimension:

  $$\frac{\partial^{2} u}{\partial t^{2}}=c^{2} \frac{\partial^{2} u}{\partial x^{2}}$$

  with given initial data $u(x, 0)=\phi(x)$ and $\frac{\partial u}{\partial t}(x, 0)=0$ (and $c$ is a constant).

  Does Property $\mathrm{P}$ (with $g(x)$ and $\theta(\beta, \epsilon)$ now replaced by $\phi(x)$ and $u(\beta, \epsilon)$ respectively) hold for solutions of the wave equation? Justify your answer again as above.

  comment

• Paper 4, Section I, A

  Methods | Part IB, 2016

  Consider the function $f(x)$ defined by

  $$f(x)=x^{2}, \text { for }-\pi<x<\pi$$

  Calculate the Fourier series representation for the $2 \pi$-periodic extension of this function. Hence establish that

  $$\frac{\pi^{2}}{6}=\sum_{n=1}^{\infty} \frac{1}{n^{2}}$$

  and that

  $$\frac{\pi^{2}}{12}=\sum_{n=1}^{\infty} \frac{(-1)^{n+1}}{n^{2}}$$

  comment

• Paper 4, Section II, B

  Methods | Part IB, 2016

  Let $\mathcal{D}$ be a 2-dimensional region in $\mathbb{R}^{2}$ with boundary $\partial \mathcal{D}$. In this question you may assume Green's second identity:

  $$\int_{\mathcal{D}}\left(f \nabla^{2} g-g \nabla^{2} f\right) d A=\int_{\partial \mathcal{D}}\left(f \frac{\partial g}{\partial n}-g \frac{\partial f}{\partial n}\right) d l$$

  where $\frac{\partial}{\partial n}$ denotes the outward normal derivative on $\partial \mathcal{D}$, and $f$ and $g$ are suitably regular functions that include the free space Green's function in two dimensions. You may also assume that the free space Green's function for the Laplace equation in two dimensions is given by

  $$G_{0}\left(\boldsymbol{r}, \boldsymbol{r}_{0}\right)=\frac{1}{2 \pi} \log \left|\boldsymbol{r}-\boldsymbol{r}_{0}\right|$$

  (a) State the conditions required on a function $G\left(\boldsymbol{r}, \boldsymbol{r}_{\mathbf{0}}\right)$ for it to be a Dirichlet Green's function for the Laplace operator on $\mathcal{D}$. Suppose that $\nabla^{2} \psi=0$ on $\mathcal{D}$. Show that if $G$ is a Dirichlet Green's function for $\mathcal{D}$ then

  $$\psi\left(\boldsymbol{r}_{\mathbf{0}}\right)=\int_{\partial \mathcal{D}} \psi(\boldsymbol{r}) \frac{\partial}{\partial n} G\left(\boldsymbol{r}, \boldsymbol{r}_{\mathbf{0}}\right) d l \quad \text { for } \boldsymbol{r}_{\mathbf{0}} \in \mathcal{D}$$

  (b) Consider the Laplace equation $\nabla^{2} \phi=0$ in the quarter space

  $$\mathcal{D}=\{(x, y): x \geqslant 0 \text { and } y \geqslant 0\}$$

  with boundary conditions

  $$\phi(x, 0)=e^{-x^{2}}, \phi(0, y)=e^{-y^{2}} \text { and } \phi(x, y) \rightarrow 0 \text { as } \sqrt{x^{2}+y^{2}} \rightarrow \infty$$

  Using the method of images, show that the solution is given by

  $$\phi\left(x_{0}, y_{0}\right)=F\left(x_{0}, y_{0}\right)+F\left(y_{0}, x_{0}\right),$$

  where

  $$F\left(x_{0}, y_{0}\right)=\frac{4 x_{0} y_{0}}{\pi} \int_{0}^{\infty} \frac{t e^{-t^{2}}}{\left[\left(t-x_{0}\right)^{2}+y_{0}^{2}\right]\left[\left(t+x_{0}\right)^{2}+y_{0}^{2}\right]} d t$$

  comment

2015

• Paper 1, Section II, C

  Methods | Part IB, 2015

  (i) Briefly describe the Sturm-Liouville form of an eigenfunction equation for real valued functions with a linear, second-order ordinary differential operator. Briefly summarize the properties of the solutions.

  (ii) Derive the condition for self-adjointness of the differential operator in (i) in terms of the boundary conditions of solutions $y_{1}, y_{2}$ to the Sturm-Liouville equation. Give at least three types of boundary conditions for which the condition for self-adjointness is satisfied.

  (iii) Consider the inhomogeneous Sturm-Liouville equation with weighted linear term

  $$\frac{1}{w(x)} \frac{d}{d x}\left(p(x) \frac{d y}{d x}\right)-\frac{q(x)}{w(x)} y-\lambda y=f(x),$$

  on the interval $a \leqslant x \leqslant b$, where $p$ and $q$ are real functions on $[a, b]$ and $w$ is the weighting function. Let $G(x, \xi)$ be a Green's function satisfying

  $$\frac{d}{d x}\left(p(x) \frac{d G}{d x}\right)-q(x) G(x, \xi)=\delta(x-\xi)$$

  Let solutions $y$ and the Green's function $G$ satisfy the same boundary conditions of the form $\alpha y^{\prime}+\beta y=0$ at $x=a, \mu y^{\prime}+\nu y=0$ at $x=b(\alpha, \beta$ are not both zero and $\mu, \nu$ are not both zero) and likewise for $G$ for the same constants $\alpha, \beta, \mu$ and $\nu$. Show that the Sturm-Liouville equation can be written as a so-called Fredholm integral equation of the form

  $$\psi(\xi)=U(\xi)+\lambda \int_{a}^{b} K(x, \xi) \psi(x) d x$$

  where $K(x, \xi)=\sqrt{w(\xi) w(x)} G(x, \xi), \psi=\sqrt{w} y$ and $U$ depends on $K, w$ and the forcing term $f$. Write down $U$ in terms of an integral involving $f, K$ and $w$.

  (iv) Derive the Fredholm integral equation for the Sturm-Liouville equation on the interval $[0,1]$

  $$\frac{d^{2} y}{d x^{2}}-\lambda y=0,$$

  with $y(0)=y(1)=0$.

  comment

• Paper 2, Section I, C

  Methods | Part IB, 2015

  (i) Write down the trigonometric form for the Fourier series and its coefficients for a function $f:[-L, L) \rightarrow \mathbb{R}$ extended to a $2 L$-periodic function on $\mathbb{R}$.

  (ii) Calculate the Fourier series on $[-\pi, \pi)$ of the function $f(x)=\sin (\lambda x)$ where $\lambda$ is a real constant. Take the limit $\lambda \rightarrow k$ with $k \in \mathbb{Z}$ in the coefficients of this series and briefly interpret the resulting expression.

  comment

• Paper 2, Section II, C

  Methods | Part IB, 2015

  (i) The Laplace operator in spherical coordinates is

  $$\vec{\nabla}^{2}=\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial}{\partial \theta}\right)+\frac{1}{r^{2} \sin ^{2} \theta} \frac{\partial^{2}}{\partial \phi^{2}}$$

  Show that general, regular axisymmetric solutions $\psi(r, \theta)$ to the equation $\vec{\nabla}^{2} \psi=0$ are given by

  $$\psi(r, \theta)=\sum_{n=0}^{\infty}\left(A_{n} r^{n}+B_{n} r^{-(n+1)}\right) P_{n}(\cos \theta)$$

  where $A_{n}, B_{n}$ are constants and $P_{n}$ are the Legendre polynomials. [You may use without proof that regular solutions to Legendre's equation $-\frac{d}{d x}\left[\left(1-x^{2}\right) \frac{d}{d x} y(x)\right]=\lambda y(x)$ are given by $P_{n}(x)$ with $\lambda=n(n+1)$ and non-negative integer $n$.]

  (ii) Consider a uniformly charged wire in the form of a ring of infinitesimal width with radius $r_{0}=1$ and a constant charge per unit length $\sigma$. By Coulomb's law, the electric potential due to a point charge $q$ at a point a distance $d$ from the charge is

  $$U=\frac{q}{4 \pi \epsilon_{0} d}$$

  where $\epsilon_{0}$ is a constant. Let the $z$-axis be perpendicular to the circle and pass through the circle's centre (see figure). Show that the potential due to the charged ring at a point on the $z$-axis at location $z$ is given by

  

  $$V=\frac{\sigma}{2 \epsilon_{0} \sqrt{1+z^{2}}} .$$

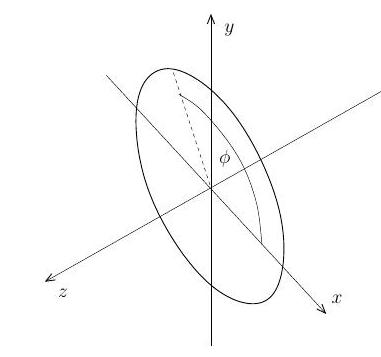
  (iii) The potential $V$ generated by the charged ring of (ii) at arbitrary points (excluding points directly on the ring which can be ignored for this question) is determined by Laplace's equation $\vec{\nabla}^{2} V=0$. Calculate this potential with the boundary condition $\lim _{r \rightarrow \infty} V=0$, where $r=\sqrt{x^{2}+y^{2}+z^{2}}$. [You may use without proof that

  $$\frac{1}{\sqrt{1+x^{2}}}=\sum_{m=0}^{\infty} x^{2 m}(-1)^{m} \frac{(2 m) !}{2^{2 m}(m !)^{2}}$$

  for $|x|<1$. Furthermore, the Legendre polynomials are normalized such that $\left.P_{n}(1)=1 .\right]$

  comment

• Paper 3, Section I, $7 \mathrm{C}$

  Methods | Part IB, 2015

  (a) From the defining property of the $\delta$ function,

  $$\int_{-\infty}^{\infty} \delta(x) f(x) d x=f(0)$$

  for any function $f$, prove that

  (i) $\delta(-x)=\delta(x)$

  (ii) $\delta(a x)=|a|^{-1} \delta(x)$ for $a \in \mathbb{R}, a \neq 0$,

  (iii) If $g: \mathbb{R} \rightarrow \mathbb{R}, x \mapsto g(x)$ is smooth and has isolated zeros $x_{i}$ where the derivative $g^{\prime}\left(x_{i}\right) \neq 0$, then

  $$\delta[g(x)]=\sum_{i} \frac{\delta\left(x-x_{i}\right)}{\left|g^{\prime}\left(x_{i}\right)\right|}$$

  (b) Show that the function $\gamma(x)$ defined by

  $$\gamma(x)=\lim _{s \rightarrow 0} \frac{e^{x / s}}{s\left(1+e^{x / s}\right)^{2}}$$

  is the $\delta(x)$ function.

  comment

• Paper 3, Section II, C

  Methods | Part IB, 2015

  (i) Consider the Poisson equation $\nabla^{2} \psi(\mathbf{r})=f(\mathbf{r})$ with forcing term $f$ on the infinite domain $\mathbb{R}^{3}$ with $\lim _{|\mathbf{r}| \rightarrow \infty} \psi=0$. Derive the Green's function $G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=-1 /\left(4 \pi\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\right)$ for this equation using the divergence theorem. [You may assume without proof that the divergence theorem is valid for the Green's function.]

  (ii) Consider the Helmholtz equation

  $$\tag{†} \nabla^{2} \psi(\mathbf{r})+k^{2} \psi(\mathbf{r})=f(\mathbf{r})$$

  where $k$ is a real constant. A Green's function $g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)$ for this equation can be constructed from $G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)$ of (i) by assuming $g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=U(r) G\left(\mathbf{r}, \mathbf{r}^{\prime}\right)$ where $r=\left|\mathbf{r}-\mathbf{r}^{\prime}\right|$ and $U(r)$ is a regular function. Show that $\lim _{r \rightarrow 0} U(r)=1$ and that $U$ satisfies the equation

  $$\tag{‡} \frac{d^{2} U}{d r^{2}}+k^{2} U(r)=0$$

  (iii) Take the Green's function with the specific solution $U(r)=e^{i k r}$ to Eq. ($‡$) and consider the Helmholtz equation $(†)$ on the semi-infinite domain $z>0, x, y \in \mathbb{R}$. Use the method of images to construct a Green's function for this problem that satisfies the boundary conditions

  $$\frac{\partial g}{\partial z^{\prime}}=0 \text { on } z^{\prime}=0 \quad \text { and } \quad \lim _{|\mathbf{r}| \rightarrow \infty} g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)=0$$

  (iv) A solution to the Helmholtz equation on a bounded domain can be constructed in complete analogy to that of the Poisson equation using the Green's function in Green's 3rd identity

  $$\psi(\mathbf{r})=\int_{\partial V}\left[\psi\left(\mathbf{r}^{\prime}\right) \frac{\partial g\left(\mathbf{r}, \mathbf{r}^{\prime}\right)}{\partial n^{\prime}}-g\left(\mathbf{r}, \mathbf{r}^{\prime}\right) \frac{\partial \psi\left(\mathbf{r}^{\prime}\right)}{\partial n^{\prime}}\right] d S^{\prime}+\int_{V} f\left(\mathbf{r}^{\prime}\right) g\left(\mathbf{r}, \mathbf{r}^{\prime}\right) d V^{\prime},$$

  where $V$ denotes the volume of the domain, $\partial V$ its boundary and $\partial / \partial n^{\prime}$ the outgoing normal derivative on the boundary. Now consider the homogeneous Helmholtz equation $\nabla^{2} \psi(\mathbf{r})+k^{2} \psi(\mathbf{r})=0$ on the domain $z>0, x, y \in \mathbb{R}$ with boundary conditions $\psi(\mathbf{r})=0$ at $|\mathbf{r}| \rightarrow \infty$ and

  $$\left.\frac{\partial \psi}{\partial z}\right|_{z=0}= \begin{cases}0 & \text { for } \rho>a \\ A & \text { for } \rho \leqslant a\end{cases}$$

  where $\rho=\sqrt{x^{2}+y^{2}}$ and $A$ and $a$ are real constants. Construct a solution in integral form to this equation using cylindrical coordinates $(z, \rho, \varphi)$ with $x=\rho \cos \varphi, y=\rho \sin \varphi$.

  comment

• Paper 4, Section I, 5C

  Methods | Part IB, 2015

  (a) The convolution $f * g$ of two functions $f, g: \mathbb{R} \rightarrow \mathbb{C}$ is related to their Fourier transforms $\tilde{f}, \tilde{g}$ by

  $$\frac{1}{2 \pi} \int_{-\infty}^{\infty} \tilde{f}(k) \tilde{g}(k) e^{i k x} d k=\int_{-\infty}^{\infty} f(u) g(x-u) d u$$

  Derive Parseval's theorem for Fourier transforms from this relation.

  (b) Let $a>0$ and

  $$f(x)= \begin{cases}\cos x & \text { for } x \in[-a, a] \\ 0 & \text { elsewhere }\end{cases}$$

  (i) Calculate the Fourier transform $\tilde{f}(k)$ of $f(x)$.

  (ii) Determine how the behaviour of $\tilde{f}(k)$ in the limit $|k| \rightarrow \infty$ depends on the value of $a$. Briefly interpret the result.

  comment

• Paper 4, Section II, 17C

  Methods | Part IB, 2015

  Describe the method of characteristics to construct solutions for 1st-order, homogeneous, linear partial differential equations

  $$\alpha(x, y) \frac{\partial u}{\partial x}+\beta(x, y) \frac{\partial u}{\partial y}=0$$

  with initial data prescribed on a curve $x_{0}(\sigma), y_{0}(\sigma): u\left(x_{0}(\sigma), y_{0}(\sigma)\right)=h(\sigma)$.

  Consider the partial differential equation (here the two independent variables are time $t$ and spatial direction $x$ )

  $$\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=0$$

  with initial data $u(t=0, x)=e^{-x^{2}}$.

  (i) Calculate the characteristic curves of this equation and show that $u$ remains constant along these curves. Qualitatively sketch the characteristics in the $(x, t)$ diagram, i.e. the $x$ axis is the horizontal and the $t$ axis is the vertical axis.

  (ii) Let $\tilde{x}_{0}$ denote the $x$ value of a characteristic at time $t=0$ and thus label the characteristic curves. Let $\tilde{x}$ denote the $x$ value at time $t$ of a characteristic with given $\tilde{x}_{0}$. Show that $\partial \tilde{x} / \partial \tilde{x}_{0}$ becomes a non-monotonic function of $\tilde{x}_{0}$ (at fixed $t$ ) at times $t>\sqrt{e / 2}$, i.e. $\tilde{x}\left(\tilde{x}_{0}\right)$ has a local minimum or maximum. Qualitatively sketch snapshots of the solution $u(t, x)$ for a few fixed values of $t \in[0, \sqrt{e / 2}]$ and briefly interpret the onset of the non-monotonic behaviour of $\tilde{x}\left(\tilde{x}_{0}\right)$ at $t=\sqrt{e / 2}$.

  comment

2014

• Paper 1, Section II, D

  Methods | Part IB, 2014

  (a) Legendre's differential equation may be written

  $$\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-2 x \frac{d y}{d x}+n(n+1) y=0, \quad y(1)=1$$

  Show that for non-negative integer $n$, this equation has a solution $P_{n}(x)$ that is a polynomial of degree $n$. Find $P_{0}, P_{1}$ and $P_{2}$ explicitly.

  (b) Laplace's equation in spherical coordinates for an axisymmetric function $U(r, \theta)$ (i.e. no $\phi$ dependence) is given by

  $$\frac{1}{r^{2}} \frac{\partial}{\partial r}\left(r^{2} \frac{\partial U}{\partial r}\right)+\frac{1}{r^{2} \sin \theta} \frac{\partial}{\partial \theta}\left(\sin \theta \frac{\partial U}{\partial \theta}\right)=0$$

  Use separation of variables to find the general solution for $U(r, \theta)$.

  Find the solution $U(r, \theta)$ that satisfies the boundary conditions

  $$\begin{aligned} &U(r, \theta) \rightarrow v_{0} r \cos \theta \quad \text { as } r \rightarrow \infty \\ &\frac{\partial U}{\partial r}=0 \quad \text { at } r=r_{0} \end{aligned}$$

  where $v_{0}$ and $r_{0}$ are constants.

  comment

• Paper 2, Section I, D

  Methods | Part IB, 2014

  (i) Calculate the Fourier series for the periodic extension on $\mathbb{R}$ of the function

  $$f(x)=x(1-x)$$

  defined on the interval $[0,1)$.

  (ii) Explain why the Fourier series for the periodic extension of $f^{\prime}(x)$ can be obtained by term-by-term differentiation of the series for $f(x)$.

  (iii) Let $G(x)$ be the Fourier series for the periodic extension of $f^{\prime}(x)$. Determine the value of $G(0)$ and explain briefly how it is related to the values of $f^{\prime}$.

  comment

• Paper 2, Section II, 16D

  Methods | Part IB, 2014

  The Fourier transform $\tilde{f}$ of a function $f$ is defined as

  $$\tilde{f}(k)=\int_{-\infty}^{\infty} f(x) e^{-i k x} d x, \quad \text { so that } f(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \tilde{f}(k) e^{i k x} d k$$

  A Green's function $G\left(t, t^{\prime}, x, x^{\prime}\right)$ for the diffusion equation in one spatial dimension satisfies

  $$\frac{\partial G}{\partial t}-D \frac{\partial^{2} G}{\partial x^{2}}=\delta\left(t-t^{\prime}\right) \delta\left(x-x^{\prime}\right)$$

  (a) By applying a Fourier transform, show that the Fourier transform $\tilde{G}$ of this Green's function and the Green's function $G$ are

  $$\begin{aligned} \tilde{G}\left(t, t^{\prime}, k, x^{\prime}\right) &=H\left(t-t^{\prime}\right) e^{-i k x^{\prime}} e^{-D k^{2}\left(t-t^{\prime}\right)} \\ G\left(t, t^{\prime}, x, x^{\prime}\right) &=\frac{H\left(t-t^{\prime}\right)}{\sqrt{4 \pi D\left(t-t^{\prime}\right)}} e^{-\frac{\left(x-x^{\prime}\right)^{2}}{4 D\left(t-t^{\prime}\right)}} \end{aligned}$$

  where $H$ is the Heaviside function. [Hint: The Fourier transform $\tilde{F}$ of a Gaussian $F(x)=\frac{1}{\sqrt{4 \pi a}} e^{-\frac{x^{2}}{4 a}}, a=\mathrm{const}$, is given by $\left.\tilde{F}(k)=e^{-a k^{2}} .\right]$

  (b) The analogous result for the Green's function for the diffusion equation in two spatial dimensions is

  $$G\left(t, t^{\prime}, x, x^{\prime}, y, y^{\prime}\right)=\frac{H\left(t-t^{\prime}\right)}{4 \pi D\left(t-t^{\prime}\right)} e^{-\frac{1}{4 D\left(t-t^{\prime}\right)}\left[\left(x-x^{\prime}\right)^{2}+\left(y-y^{\prime}\right)^{2}\right]}$$

  Use this Green's function to construct a solution for $t \geqslant 0$ to the diffusion equation

  $$\frac{\partial \Psi}{\partial t}-D\left(\frac{\partial^{2} \Psi}{\partial x^{2}}+\frac{\partial^{2} \Psi}{\partial y^{2}}\right)=p(t) \delta(x) \delta(y)$$

  with the initial condition $\Psi(0, x, y)=0$.

  Now set

  $$p(t)= \begin{cases}p_{0}=\mathrm{const} & \text { for } \quad 0 \leqslant t \leqslant t_{0} \\ 0 & \text { for } \quad t>t_{0}\end{cases}$$

  Find the solution $\Psi(t, x, y)$ for $t>t_{0}$ in terms of the exponential integral defined by

  $$E i(-\eta)=-\int_{\eta}^{\infty} \frac{e^{-\lambda}}{\lambda} d \lambda$$

  Use the approximation $E i(-\eta) \approx \ln \eta+C$, valid for $\eta \ll 1$, to simplify this solution $\Psi(t, x, y)$. Here $C \approx 0.577$ is Euler's constant.

  comment

• Paper 3, Section I, D

  Methods | Part IB, 2014

  Using the method of characteristics, solve the differential equation

  $$-y \frac{\partial u}{\partial x}+x \frac{\partial u}{\partial y}=0$$

  where $x, y \in \mathbb{R}$ and $u=\cos y^{2}$ on $x=0, y \geqslant 0$.

  comment

• Paper 3, Section II, 15D

  Methods | Part IB, 2014

  Let $\mathcal{L}$ be a linear second-order differential operator on the interval $[0, \pi / 2]$. Consider the problem

  $$\mathcal{L} y(x)=f(x) ; \quad y(0)=y(\pi / 2)=0$$

  with $f(x)$ bounded in $[0, \pi / 2]$.

  (i) How is a Green's function for this problem defined?

  (ii) How is a solution $y(x)$ for this problem constructed from the Green's function?

  (iii) Describe the continuity and jump conditions used in the construction of the Green's function.

  (iv) Use the continuity and jump conditions to construct the Green's function for the differential equation

  $$\frac{d^{2} y}{d x^{2}}-\frac{d y}{d x}+\frac{5}{4} y=f(x)$$

  on the interval $[0, \pi / 2]$ with the boundary conditions $y(0)=0, y(\pi / 2)=0$ and an arbitrary bounded function $f(x)$. Use the Green's function to construct a solution $y(x)$ for the particular case $f(x)=e^{x / 2}$.

  comment

• Paper 4, Section I, D

  Methods | Part IB, 2014

  Consider the ordinary differential equation

  $$\frac{d^{2} \psi}{d z^{2}}-\left[\frac{15 k^{2}}{4(k|z|+1)^{2}}-3 k \delta(z)\right] \psi=0$$

  where $k$ is a positive constant and $\delta$ denotes the Dirac delta function. Physically relevant solutions for $\psi$ are bounded over the entire range $z \in \mathbb{R}$.

  (i) Find piecewise bounded solutions to this differential equations in the ranges $z>0$ and $z<0$, respectively. [Hint: The equation $\frac{d^{2} y}{d x^{2}}-\frac{c}{x^{2}} y=0$ for a constant $c$ may be solved using the Ansatz $y=x^{\alpha}$.]

  (ii) Derive a matching condition at $z=0$ by integrating ( $\dagger$ ) over the interval $(-\epsilon, \epsilon)$ with $\epsilon \rightarrow 0$ and use this condition together with the requirement that $\psi$ be continuous at $z=0$ to determine the solution over the entire range $z \in \mathbb{R}$.

  comment

• Paper 4, Section II, D

  Methods | Part IB, 2014

  Let $f(x)$ be a complex-valued function defined on the interval $[-L, L]$ and periodically extended to $x \in \mathbb{R}$.

  (i) Express $f(x)$ as a complex Fourier series with coefficients $c_{n}, n \in \mathbb{Z}$. How are the coefficients $c_{n}$ obtained from $f(x)$ ?

  (ii) State Parseval's theorem for complex Fourier series.

  (iii) Consider the function $f(x)=\cos (\alpha x)$ on the interval $[-\pi, \pi]$ and periodically extended to $x \in \mathbb{R}$ for a complex but non-integer constant $\alpha$. Calculate the complex Fourier series of $f(x)$.

  (iv) Prove the formula

  $$\sum_{n=1}^{\infty} \frac{1}{n^{2}-\alpha^{2}}=\frac{1}{2 \alpha^{2}}-\frac{\pi}{2 \alpha \tan (\alpha \pi)}$$

  (v) Now consider the case where $\alpha$ is a real, non-integer constant. Use Parseval's theorem to obtain a formula for

  $$\sum_{n=-\infty}^{\infty} \frac{1}{\left(n^{2}-\alpha^{2}\right)^{2}}$$

  What value do you obtain for this series for $\alpha=5 / 2 ?$

  comment

2013

• Paper 1, Section II, B

  Methods | Part IB, 2013

  (i) Let $f(x)=x, 0<x \leqslant \pi$. Obtain the Fourier sine series and sketch the odd and even periodic extensions of $f(x)$ over the interval $-2 \pi \leqslant x \leqslant 2 \pi$. Deduce that

  $$\sum_{n=1}^{\infty} \frac{1}{n^{2}}=\frac{\pi^{2}}{6}$$

  (ii) Consider the eigenvalue problem

  $$\mathcal{L} y=-\frac{d^{2} y}{d x^{2}}-2 \frac{d y}{d x}=\lambda y, \quad \lambda \in \mathbb{R}$$

  with boundary conditions $y(0)=y(\pi)=0$. Find the eigenvalues and corresponding eigenfunctions. Recast $\mathcal{L}$ in Sturm-Liouville form and give the orthogonality condition for the eigenfunctions. Using the Fourier sine series obtained in part (i), or otherwise, and assuming completeness of the eigenfunctions, find a series for $y$ that satisfies

  $$\mathcal{L} y=x e^{-x}$$

  for the given boundary conditions.

  comment

• Paper 2, Section I, B

  Methods | Part IB, 2013

  Consider the equation

  $$x u_{x}+(x+y) u_{y}=1$$

  subject to the Cauchy data $u(1, y)=y$. Using the method of characteristics, obtain a solution to this equation.

  comment

• Paper 2, Section II, B

  Methods | Part IB, 2013

  The steady-state temperature distribution $u(x)$ in a uniform rod of finite length satisfies the boundary value problem

  $$\begin{gathered} -D \frac{d^{2}}{d x^{2}} u(x)=f(x), \quad 0<x<l \\ u(0)=0, \quad u(l)=0 \end{gathered}$$

  where $D>0$ is the (constant) diffusion coefficient. Determine the Green's function $G(x, \xi)$ for this problem. Now replace the above homogeneous boundary conditions with the inhomogeneous boundary conditions $u(0)=\alpha, \quad u(l)=\beta$ and give a solution to the new boundary value problem. Hence, obtain the steady-state solution for the following problem with the specified boundary conditions:

  $$\begin{aligned} &-D \frac{\partial^{2}}{\partial x^{2}} u(x, t)+\frac{\partial}{\partial t} u(x, t)=x, \quad 0<x<1 \\ &u(0, t)=1 / D, \quad u(1, t)=2 / D, \quad t>0 \end{aligned}$$

  [You may assume that a steady-state solution exists.]

  comment

• Paper 3, Section I, C

  Methods | Part IB, 2013

  The solution to the Dirichlet problem on the half-space $D=\{\mathbf{x}=(x, y, z): z>0\}$ :

  $$\nabla^{2} u(\mathbf{x})=0, \quad \mathbf{x} \in D, \quad u(\mathbf{x}) \rightarrow 0 \quad \text { as } \quad|\mathbf{x}| \rightarrow \infty, \quad u(x, y, 0)=h(x, y)$$

  is given by the formula

  $$u\left(\mathbf{x}_{0}\right)=u\left(x_{0}, y_{0}, z_{0}\right)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} h(x, y) \frac{\partial}{\partial n} G\left(\mathbf{x}, \mathbf{x}_{0}\right) d x d y$$

  where $n$ is the outward normal to $\partial D$.

  State the boundary conditions on $G$ and explain how $G$ is related to $G_{3}$, where

  $$G_{3}\left(\mathbf{x}, \mathbf{x}_{0}\right)=-\frac{1}{4 \pi} \frac{1}{\left|\mathbf{x}-\mathbf{x}_{0}\right|}$$

  is the fundamental solution to the Laplace equation in three dimensions.

  Using the method of images find an explicit expression for the function $\frac{\partial}{\partial n} G\left(\mathbf{x}, \mathbf{x}_{0}\right)$ in the formula.

  comment

• Paper 3, Section II, C

  Methods | Part IB, 2013

  The Laplace equation in plane polar coordinates has the form

  $$\nabla^{2} \phi=\left[\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial \theta^{2}}\right] \phi(r, \theta)=0 .$$

  Using separation of variables, derive the general solution to the equation that is singlevalued in the domain $1<r<2$.

  For

  $$f(\theta)=\sum_{n=1}^{\infty} A_{n} \sin n \theta$$

  solve the Laplace equation in the annulus with the boundary conditions:

  $$\nabla^{2} \phi=0, \quad 1<r<2, \quad \phi(r, \theta)= \begin{cases}f(\theta), & r=1 \\ f(\theta)+1, & r=2\end{cases}$$

  comment

• Paper 4, Section I, C

  Methods | Part IB, 2013

  Show that the general solution of the wave equation

  $$\frac{1}{c^{2}} \frac{\partial^{2} y}{\partial t^{2}}-\frac{\partial^{2} y}{\partial x^{2}}=0$$

  can be written in the form

  $$y(x, t)=f(c t-x)+g(c t+x) .$$

  For the boundary conditions

  $$y(0, t)=y(L, t)=0, \quad t>0,$$

  find the relation between $f$ and $g$ and show that they are $2 L$-periodic. Hence show that

  $$E(t)=\frac{1}{2} \int_{0}^{L}\left(\frac{1}{c^{2}}\left(\frac{\partial y}{\partial t}\right)^{2}+\left(\frac{\partial y}{\partial x}\right)^{2}\right) d x$$

  is independent of $t$.

  comment

• Paper 4, Section II, C

  Methods | Part IB, 2013

  Find the inverse Fourier transform $G(x)$ of the function

  $$g(k)=e^{-a|k|}, \quad a>0, \quad-\infty<k<\infty .$$

  Assuming that appropriate Fourier transforms exist, determine the solution $\psi(x, y)$ of

  $$\nabla^{2} \psi=0, \quad-\infty<x<\infty, \quad 0<y<1$$

  with the following boundary conditions

  $$\psi(x, 0)=\delta(x), \quad \psi(x, 1)=\frac{1}{\pi} \frac{1}{x^{2}+1}$$

  Here $\delta(x)$ is the Dirac delta-function.

  comment

2012

• Paper 1, Section II, C

  Methods | Part IB, 2012

  Consider the regular Sturm-Liouville (S-L) system

  $$(\mathcal{L} y)(x)-\lambda \omega(x) y(x)=0, \quad a \leqslant x \leqslant b$$

  where

  $$(\mathcal{L} y)(x):=-\left[p(x) y^{\prime}(x)\right]^{\prime}+q(x) y(x)$$

  with $\omega(x)>0$ and $p(x)>0$ for all $x$ in $[a, b]$, and the boundary conditions on $y$ are

  $$\left\{\begin{array}{l} A_{1} y(a)+A_{2} y^{\prime}(a)=0 \\ B_{1} y(b)+B_{2} y^{\prime}(b)=0 \end{array}\right.$$

  Show that with these boundary conditions, $\mathcal{L}$ is self-adjoint. By considering $y \mathcal{L} y$, or otherwise, show that the eigenvalue $\lambda$ can be written as

  $$\lambda=\frac{\int_{a}^{b}\left(p y^{\prime 2}+q y^{2}\right) d x-\left[p y y^{\prime}\right]_{a}^{b}}{\int_{a}^{b} \omega y^{2} d x}$$

  Now suppose that $a=0$ and $b=\ell$, that $p(x)=1, q(x) \geqslant 0$ and $\omega(x)=1$ for all $x \in[0, \ell]$, and that $A_{1}=1, A_{2}=0, B_{1}=k \in \mathbb{R}^{+}$and $B_{2}=1$. Show that the eigenvalues of this regular S-L system are strictly positive. Assuming further that $q(x)=0$, solve the system explicitly, and with the aid of a graph, show that there exist infinitely many eigenvalues $\lambda_{1}<\lambda_{2}<\cdots<\lambda_{n}<\cdots$. Describe the behaviour of $\lambda_{n}$ as $n \rightarrow \infty$.

  comment

• Paper 2, Section I, C

  Methods | Part IB, 2012

  Using the method of characteristics, obtain a solution to the equation

  $$u_{x}+2 x u_{y}=y$$

  subject to the Cauchy data $u(0, y)=1+y^{2}$ for $-\frac{1}{2}<y<\frac{1}{2}$.

  Sketch the characteristics and specify the greatest region of the plane in which a unique solution exists.

  comment

• Paper 2, Section II, C

  Methods | Part IB, 2012

  Consider the linear differential operator $\mathcal{L}$ defined by

  $$\mathcal{L} y:=-\frac{d^{2} y}{d x^{2}}+y$$

  on the interval $0 \leqslant x<\infty$. Given the boundary conditions $y(0)=0$ and $\lim _{x \rightarrow \infty} y(x)=0$, find the Green's function $G(x, \xi)$ for $\mathcal{L}$ with these boundary conditions. Hence, or otherwise, obtain the solution of

  $$\mathcal{L} y= \begin{cases}1, & 0 \leqslant x \leqslant \mu \\ 0, & \mu<x<\infty\end{cases}$$

  subject to the above boundary conditions, where $\mu$ is a positive constant. Show that your piecewise solution is continuous at $x=\mu$ and has the value

  $$y(\mu)=\frac{1}{2}\left(1+e^{-2 \mu}-2 e^{-\mu}\right) .$$

  comment

• Paper 3, Section I, D

  Methods | Part IB, 2012

  For the step-function

  $$F(x)= \begin{cases}1, & |x| \leqslant 1 / 2 \\ 0, & \text { otherwise }\end{cases}$$

  its convolution with itself is the hat-function

  $$G(x)=[F * F](x)= \begin{cases}1-|x|, & |x| \leqslant 1 \\ 0, & \text { otherwise }\end{cases}$$

  Find the Fourier transforms of $F$ and $G$, and hence find the values of the integrals

  $$I_{1}=\int_{-\infty}^{\infty} \frac{\sin ^{2} y}{y^{2}} d y, \quad I_{2}=\int_{-\infty}^{\infty} \frac{\sin ^{4} y}{y^{4}} d y$$

  comment

• Paper 3, Section II, D

  Methods | Part IB, 2012

  Consider Legendre's equation

  $$\left(1-x^{2}\right) y^{\prime \prime}-2 x y^{\prime}+\lambda y=0 .$$

  Show that if $\lambda=n(n+1)$, with $n$ a non-negative integer, this equation has a solution $y=P_{n}(x)$, a polynomial of degree $n$. Find $P_{0}, P_{1}$ and $P_{2}$ explicitly, subject to the condition $P_{n}(1)=1$.

  The general solution of Laplace's equation $\nabla^{2} \psi=0$ in spherical polar coordinates, in the axisymmetric case, has the form

  $$\psi(r, \theta)=\sum_{n=0}^{\infty}\left(A_{n} r^{n}+B_{n} r^{-(n+1)}\right) P_{n}(\cos \theta)$$

  Hence, find the solution of Laplace's equation in the region $a \leqslant r \leqslant b$ satisfying the boundary conditions

  $$\begin{cases}\psi(r, \theta)=1, & r=a \\ \psi(r, \theta)=3 \cos ^{2} \theta, & r=b\end{cases}$$

  comment

• Paper 4, Section I, D

  Methods | Part IB, 2012

  Show that the general solution of the wave equation

  $$\frac{1}{c^{2}} \frac{\partial^{2} y}{\partial t^{2}}-\frac{\partial^{2} y}{\partial x^{2}}=0$$

  can be written in the form

  $$y(x, t)=f(x-c t)+g(x+c t)$$

  Hence derive the solution $y(x, t)$ subject to the initial conditions

  $$y(x, 0)=0, \quad \frac{\partial y}{\partial t}(x, 0)=\psi(x)$$

  comment

• Paper 4, Section II, D

  Methods | Part IB, 2012

  Let $D \subset \mathbb{R}^{2}$ be a two-dimensional domain with boundary $S=\partial D$, and let

  $$G_{2}=G_{2}\left(\mathbf{r}, \mathbf{r}_{0}\right)=\frac{1}{2 \pi} \log \left|\mathbf{r}-\mathbf{r}_{0}\right|$$

  where $\mathbf{r}_{0}$ is a point in the interior of $D$. From Green's second identity,

  $$\int_{S}\left(\phi \frac{\partial \psi}{\partial n}-\psi \frac{\partial \phi}{\partial n}\right) d \ell=\int_{D}\left(\phi \nabla^{2} \psi-\psi \nabla^{2} \phi\right) d a$$

  derive Green's third identity

  $$u\left(\mathbf{r}_{0}\right)=\int_{D} G_{2} \nabla^{2} u d a+\int_{S}\left(u \frac{\partial G_{2}}{\partial n}-G_{2} \frac{\partial u}{\partial n}\right) d \ell$$

  [Here $\frac{\partial}{\partial n}$ denotes the normal derivative on $S$.]

  Consider the Dirichlet problem on the unit $\operatorname{disc} D_{1}=\left\{\mathbf{r} \in \mathbb{R}^{2}:|\mathbf{r}| \leqslant 1\right\}$ :

  $$\begin{aligned} \nabla^{2} u=0, & \mathbf{r} \in D_{1} \\ u(\mathbf{r})=f(\mathbf{r}), & \mathbf{r} \in S_{1}=\partial D_{1} \end{aligned}$$

  Show that, with an appropriate function $G\left(\mathbf{r}, \mathbf{r}_{0}\right)$, the solution can be obtained by the formula

  $$u\left(\mathbf{r}_{0}\right)=\int_{S_{1}} f(\mathbf{r}) \frac{\partial}{\partial n} G\left(\mathbf{r}, \mathbf{r}_{0}\right) d \ell$$

  State the boundary conditions on $G$ and explain how $G$ is related to $G_{2}$.

  For $\mathbf{r}, \mathbf{r}_{0} \in \mathbb{R}^{2}$, prove the identity

  $$\left|\frac{\mathbf{r}}{|\mathbf{r}|}-\mathbf{r}_{0}\right| \mathbf{r}||=\left|\frac{\mathbf{r}_{0}}{\left|\mathbf{r}_{0}\right|}-\mathbf{r}\right| \mathbf{r}_{0}|| \text {, }$$

  and deduce that if the point $\mathbf{r}$ lies on the unit circle, then

  $$\left|\mathbf{r}-\mathbf{r}_{0}\right|=\left|\mathbf{r}_{0}\right|\left|\mathbf{r}-\mathbf{r}_{0}^{*}\right|, \text { where } \mathbf{r}_{0}^{*}=\frac{\mathbf{r}_{0}}{\left|\mathbf{r}_{0}\right|^{2}}$$

  Hence, using the method of images, or otherwise, find an expression for the function $G\left(\mathbf{r}, \mathbf{r}_{0}\right)$. [An expression for $\frac{\partial}{\partial n} G$ is not required.]

  comment

2011

• Paper 1, Section II, A

  Methods | Part IB, 2011

  Let $f(t)$ be a real function defined on an interval $(-T, T)$ with Fourier series

  $$f(t)=\frac{a_{0}}{2}+\sum_{n=1}^{\infty}\left(a_{n} \cos \frac{n \pi t}{T}+b_{n} \sin \frac{n \pi t}{T}\right)$$

  State and prove Parseval's theorem for $f(t)$ and its Fourier series. Write down the formulae for $a_{0}, a_{n}$ and $b_{n}$ in terms of $f(t), \cos \frac{n \pi t}{T}$ and $\sin \frac{n \pi t}{T}$.

  Find the Fourier series of the square wave function defined on $(-\pi, \pi)$ by

  $$g(t)=\left\{\begin{array}{lr} 0 & -\pi<t \leqslant 0 \\ 1 & 0<t<\pi \end{array}\right.$$

  Hence evaluate

  $$\sum_{k=0}^{\infty} \frac{(-1)^{k}}{(2 k+1)}$$

  Using some of the above results evaluate

  $$\sum_{k=0}^{\infty} \frac{1}{(2 k+1)^{2}}$$

  What is the sum of the Fourier series for $g(t)$ at $t=0$ ? Comment on your answer.

  comment

• Paper 2, Section I, A

  Methods | Part IB, 2011

  The Legendre equation is

  $$\left(1-x^{2}\right) \frac{d^{2} y}{d x^{2}}-2 x \frac{d y}{d x}+n(n+1) y=0$$

  for $-1 \leqslant x \leqslant 1$ and non-negative integers $n$.

  Write the Legendre equation as an eigenvalue equation for an operator $L$ in SturmLiouville form. Show that $L$ is self-adjoint and find the orthogonality relation between the eigenfunctions.

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2011

  Use a Green's function to find an integral expression for the solution of the equation

  $$\frac{d^{2} \theta}{d t^{2}}+4 \frac{d \theta}{d t}+29 \theta=f(t)$$

  for $t \geqslant 0$ subject to the initial conditions

  $$\theta(0)=0 \quad \text { and } \quad \frac{d \theta}{d t}(0)=0$$

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2011

  The Fourier transform $\tilde{h}(k)$ of the function $h(x)$ is defined by

  $$\tilde{h}(k)=\int_{-\infty}^{\infty} h(x) e^{-i k x} d x$$

  (i) State the inverse Fourier transform formula expressing $h(x)$ in terms of $\widetilde{h}(k)$.

  (ii) State the convolution theorem for Fourier transforms.

  (iii) Find the Fourier transform of the function $f(x)=e^{-|x|}$. Hence show that the convolution of the function $f(x)=e^{-|x|}$ with itself is given by the integral expression

  $$\frac{2}{\pi} \int_{-\infty}^{\infty} \frac{e^{i k x}}{\left(1+k^{2}\right)^{2}} d k$$

  comment

• Paper 3, Section II, A

  Methods | Part IB, 2011

  A uniform stretched string of length $L$, density per unit length $\mu$ and tension $T=\mu c^{2}$ is fixed at both ends. Its transverse displacement is given by $y(x, t)$ for $0 \leqslant x \leqslant L$. The motion of the string is resisted by the surrounding medium with a resistive force per unit length of $-2 k \mu \frac{\partial y}{\partial t}$.

  (i) Show that the equation of motion of the string is

  $$\frac{\partial^{2} y}{\partial t^{2}}+2 k \frac{\partial y}{\partial t}-c^{2} \frac{\partial^{2} y}{\partial x^{2}}=0$$

  provided that the transverse motion can be regarded as small.

  (ii) Suppose now that $k=\frac{\pi c}{L}$. Find the displacement of the string for $t \geqslant 0$ given the initial conditions

  $$y(x, 0)=A \sin \left(\frac{\pi x}{L}\right) \quad \text { and } \quad \frac{\partial y}{\partial t}(x, 0)=0$$

  (iii) Sketch the transverse displacement at $x=\frac{L}{2}$ as a function of time for $t \geqslant 0$.

  comment

• Paper 4, Section I, A

  Methods | Part IB, 2011

  Use the method of characteristics to find a continuous solution $u(x, y)$ of the equation

  $$y \frac{\partial u}{\partial x}+x \frac{\partial u}{\partial y}=0$$

  subject to the condition $u(0, y)=y^{4}$.

  In which region of the plane is the solution uniquely determined?

  comment

• Paper 4, Section II, A

  Methods | Part IB, 2011

  Let $D$ be a two dimensional domain with boundary $\partial D$. Establish Green's second identity

  $$\int_{D}\left(\phi \nabla^{2} \psi-\psi \nabla^{2} \phi\right) d A=\int_{\partial D}\left(\phi \frac{\partial \psi}{\partial n}-\psi \frac{\partial \phi}{\partial n}\right) d s$$

  where $\frac{\partial}{\partial n}$ denotes the outward normal derivative on $\partial D$.

  State the differential equation and boundary conditions which are satisfied by a Dirichlet Green's function $G\left(\mathbf{r}, \mathbf{r}_{0}\right)$ for the Laplace operator on the domain $D$, where $\mathbf{r}_{0}$ is a fixed point in the interior of $D$.

  Suppose that $\nabla^{2} \psi=0$ on $D$. Show that

  $$\psi\left(\mathbf{r}_{0}\right)=\int_{\partial D} \psi(\mathbf{r}) \frac{\partial}{\partial n} G\left(\mathbf{r}, \mathbf{r}_{\mathbf{0}}\right) d s$$

  Consider Laplace's equation in the upper half plane,

  $$\nabla^{2} \psi(x, y)=0, \quad-\infty<x<\infty \quad \text { and } \quad y>0$$

  with boundary conditions $\psi(x, 0)=f(x)$ where $f(x) \rightarrow 0$ as $|x| \rightarrow \infty$, and $\psi(x, y) \rightarrow 0$ as $\sqrt{x^{2}+y^{2}} \rightarrow \infty$. Show that the solution is given by the integral formula

  $$\psi\left(x_{0}, y_{0}\right)=\frac{y_{0}}{\pi} \int_{-\infty}^{\infty} \frac{f(x)}{\left(x-x_{0}\right)^{2}+y_{0}^{2}} d x$$

  [ Hint: It might be useful to consider

  $$G\left(\mathbf{r}, \mathbf{r}_{0}\right)=\frac{1}{2 \pi}\left(\log \left|\mathbf{r}-\mathbf{r}_{0}\right|-\log \left|\mathbf{r}-\tilde{\mathbf{r}}_{0}\right|\right)$$

  for suitable $\tilde{\mathbf{r}}_{\mathbf{0}}$. You may assume $\nabla^{2} \log \left|\mathbf{r}-\mathbf{r}_{0}\right|=2 \pi \delta\left(\mathbf{r}-\mathbf{r}_{0}\right)$. ]

  comment

2010

• Paper 1, Section II, A

  Methods | Part IB, 2010

  (a) A function $f(t)$ is periodic with period $2 \pi$ and has continuous derivatives up to and including the $k$ th derivative. Show by integrating by parts that the Fourier coefficients of $f(t)$

  $$\begin{aligned} &a_{n}=\frac{1}{\pi} \int_{0}^{2 \pi} f(t) \cos n t d t \\ &b_{n}=\frac{1}{\pi} \int_{0}^{2 \pi} f(t) \sin n t d t \end{aligned}$$

  decay at least as fast as $1 / n^{k}$ as $n \rightarrow \infty$

  (b) Calculate the Fourier series of $f(t)=|\sin t|$ on $[0,2 \pi]$.

  (c) Comment on the decay rate of your Fourier series.

  comment

• Paper 2, Section I, A

  Methods | Part IB, 2010

  Consider the initial value problem

  $$\mathcal{L} x(t)=f(t), \quad x(0)=0, \quad \dot{x}(0)=0, \quad t \geqslant 0,$$

  where $\mathcal{L}$ is a second-order linear operator involving differentiation with respect to $t$. Explain briefly how to solve this by using a Green's function.

  Now consider

  $$\ddot{x}(t)= \begin{cases}a & 0 \leqslant t \leqslant T \\ 0 & T<t<\infty\end{cases}$$

  where $a$ is a constant, subject to the same initial conditions. Solve this using the Green's function, and explain how your answer is related to a problem in Newtonian dynamics.

  comment

• Paper 2, Section II, B

  Methods | Part IB, 2010

  Explain briefly the use of the method of characteristics to solve linear first-order partial differential equations.

  Use the method to solve the problem

  $$(x-y) \frac{\partial u}{\partial x}+(x+y) \frac{\partial u}{\partial y}=\alpha u$$

  where $\alpha$ is a constant, with initial condition $u(x, 0)=x^{2}, x \geqslant 0$.

  By considering your solution explain:

  (i) why initial conditions cannot be specified on the whole $x$-axis;

  (ii) why a single-valued solution in the entire plane is not possible if $\alpha \neq 2$.

  comment

• Paper 3, Section I, B

  Methods | Part IB, 2010

  Show that Laplace's equation $\nabla^{2} \phi=0$ in polar coordinates $(r, \theta)$ has solutions proportional to $r^{\pm \alpha} \sin \alpha \theta, r^{\pm \alpha} \cos \alpha \theta$ for any constant $\alpha$.

  Find the function $\phi$ satisfying Laplace's equation in the region $a<r<b, 0<\theta<\pi$, where $\phi(a, \theta)=\sin ^{3} \theta, \phi(b, \theta)=\phi(r, 0)=\phi(r, \pi)=0$.

  [The Laplacian $\nabla^{2}$ in polar coordinates is

  $$\left.\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial \theta^{2}}\right]$$

  comment

• Paper 3, Section II, A

  Methods | Part IB, 2010

  (a) Put the equation

  $$x \frac{d^{2} u}{d x^{2}}+\frac{d u}{d x}+\lambda x u=0, \quad 0 \leqslant x \leqslant 1$$

  into Sturm-Liouville form.

  (b) Suppose $u_{n}(x)$ are eigenfunctions such that $u_{n}(x)$ are bounded as $x$ tends to zero and

  $$x \frac{d^{2} u_{n}}{d x^{2}}+\frac{d u_{n}}{d x}+\lambda_{n} x u_{n}=0, \quad 0 \leqslant x \leqslant 1$$

  Identify the weight function $w(x)$ and the most general boundary conditions on $u_{n}(x)$ which give the orthogonality relation

  $$\left(\lambda_{m}-\lambda_{n}\right) \int_{0}^{1} u_{m}(x) w(x) u_{n}(x) d x=0$$

  (c) The equation

  $$x \frac{d^{2} y}{d x^{2}}+\frac{d y}{d x}+x y=0, \quad x>0$$

  has a solution $J_{0}(x)$ and a second solution which is not bounded at the origin. The zeros of $J_{0}(x)$ arranged in ascending order are $j_{n}, n=1,2, \ldots$. Given that $u_{n}(1)=0$, show that the eigenvalues of the Sturm-Liouville problem in (b) are $\lambda=j_{n}^{2}, n=1,2, \ldots$

  (d) Using the differential equations for $J_{0}(\alpha x)$ and $J_{0}(\beta x)$ and integration by parts, show that

  $$\int_{0}^{1} J_{0}(\alpha x) J_{0}(\beta x) x d x=\frac{\beta J_{0}(\alpha) J_{0}^{\prime}(\beta)-\alpha J_{0}(\beta) J_{0}^{\prime}(\alpha)}{\alpha^{2}-\beta^{2}} \quad(\alpha \neq \beta)$$

  comment

• Paper 4, Section I, A

  Methods | Part IB, 2010

  (a) By considering strictly monotonic differentiable functions $\varphi(x)$, such that the zeros satisfy $\varphi(c)=0$ but $\varphi^{\prime}(c) \neq 0$, establish the formula

  $$\int_{-\infty}^{\infty} f(x) \delta(\varphi(x)) d x=\frac{f(c)}{\left|\varphi^{\prime}(c)\right|}$$

  Hence show that for a general differentiable function with only such zeros, labelled by $c$,

  $$\int_{-\infty}^{\infty} f(x) \delta(\varphi(x)) d x=\sum_{c} \frac{f(c)}{\left|\varphi^{\prime}(c)\right|}$$

  (b) Hence by changing to plane polar coordinates, or otherwise, evaluate,

  $$I=\int_{0}^{\infty} \int_{0}^{\infty}\left(x^{3}+y^{2} x\right) \delta\left(x^{2}+y^{2}-1\right) d y d x$$

  comment

• Paper 4, Section II, B

  Methods | Part IB, 2010

  Defining the function $G_{f_{3}}\left(\mathbf{r} ; \mathbf{r}_{0}\right)=-1 /\left(4 \pi\left|\mathbf{r}-\mathbf{r}_{0}\right|\right)$, prove Green's third identity for functions $u(\mathbf{r})$ satisfying Laplace's equation in a volume $V$ with surface $S$, namely

  $$u\left(\mathbf{r}_{0}\right)=\int_{S}\left(u \frac{\partial G_{f_{3}}}{\partial n}-\frac{\partial u}{\partial n} G_{f_{3}}\right) d S$$

  A solution is sought to the Neumann problem for $\nabla^{2} u=0$ in the half plane $z>0$ :

  $$u=O\left(|\mathbf{x}|^{-a}\right), \quad \frac{\partial u}{\partial r}=O\left(|\mathbf{x}|^{-a-1}\right) \text { as }|\mathbf{x}| \rightarrow \infty, \quad \frac{\partial u}{\partial z}=p(x, y) \text { on } z=0$$

  where $a>0$. It is assumed that $\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x, y) d x d y=0$. Explain why this condition is necessary.

  Construct an appropriate Green's function $G\left(\mathbf{r} ; \mathbf{r}_{0}\right)$ satisfying $\partial G / \partial z=0$ at $z=0$, using the method of images or otherwise. Hence find the solution in the form

  $$u\left(x_{0}, y_{0}, z_{0}\right)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} p(x, y) f\left(x-x_{0}, y-y_{0}, z_{0}\right) d x d y$$

  where $f$ is to be determined.

  Now let

  $$p(x, y)= \begin{cases}x & |x|,|y|<a \\ 0 & \text { otherwise }\end{cases}$$

  By expanding $f$ in inverse powers of $z_{0}$, show that

  $$u \rightarrow \frac{-2 a^{4} x_{0}}{3 \pi z_{0}^{3}} \quad \text { as } \quad z_{0} \rightarrow \infty .$$

  comment

2009

• Paper 1, Section II, B

  Methods | Part IB, 2009

  Find a power series solution about $x=0$ of the equation

  $$x y^{\prime \prime}+(1-x) y^{\prime}+\lambda y=0,$$

  with $y(0)=1$, and show that $y$ is a polynomial if and only if $\lambda$ is a non-negative integer $n$. Let $y_{n}$ be the solution for $\lambda=n$. Establish an orthogonality relation between $y_{m}$ and $y_{n}(m \neq n)$.

  Show that $y_{m} y_{n}$ is a polynomial of degree $m+n$, and hence that

  $$y_{m} y_{n}=\sum_{p=0}^{m+n} a_{p} y_{p}$$

  for appropriate choices of the coefficients $a_{p}$ and with $a_{m+n} \neq 0$.

  For given $n>0$, show that the functions

  $$\left\{y_{m}, y_{m} y_{n}: m=0,1,2, \ldots, n-1\right\}$$

  are linearly independent.

  Let $f(x)$ be a polynomial of degree 3. Explain why the expansion

  $$f(x)=a_{0} y_{0}(x)+a_{1} y_{1}(x)+a_{2} y_{2}(x)+a_{3} y_{1}(x) y_{2}(x)$$

  holds for appropriate choices of $a_{p}, p=0,1,2,3$. Hence show that

  $$\int_{0}^{\infty} e^{-x} f(x) d x=w_{1} f\left(\alpha_{1}\right)+w_{2} f\left(\alpha_{2}\right)$$

  where

  $$w_{1}=\frac{y_{1}\left(\alpha_{2}\right)}{y_{1}\left(\alpha_{2}\right)-y_{1}\left(\alpha_{1}\right)}, \quad w_{2}=\frac{-y_{1}\left(\alpha_{1}\right)}{y_{1}\left(\alpha_{2}\right)-y_{1}\left(\alpha_{1}\right)},$$

  and $\alpha_{1}, \alpha_{2}$ are the zeros of $y_{2}$. You need not construct the polynomials $y_{1}(x), y_{2}(x)$ explicitly.

  comment

• Paper 2, Section I, B

  Methods | Part IB, 2009

  Expand $f(x)=x, 0<x<\pi$, as a half-range sine series.

  By integrating the series show that a Fourier cosine series for $x^{2}, 0<x<\pi$, can be written as

  $$x^{2}=\frac{a_{0}}{2}+\sum_{n=1}^{\infty} a_{n} \cos n x$$

  where $a_{n}, n=1,2, \ldots$, should be determined and

  $$a_{0}=8 \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}$$

  By evaluating $a_{0}$ another way show that

  $$\sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{2}}=\frac{\pi^{2}}{12}$$

  comment

• Paper 2, Section II, B

  Methods | Part IB, 2009

  A string of uniform density $\rho$ is stretched under tension along the $x$-axis and undergoes small transverse oscillations in the $(x, y)$ plane with amplitude $y(x, t)$. Given that waves in the string travel at velocity $c$, write down the equation of motion satisfied by $y(x, t)$.

  The string is now fixed at $x=0$ and $x=L$. Derive the general separable solution for the amplitude $y(x, t)$.

  For $t<0$ the string is at rest. At time $t=0$ the string is struck by a hammer in the interval $[l-a / 2, l+a / 2]$, distance being measured from one end. The effect of the hammer is to impart a constant velocity $v$ to the string inside the interval and zero velocity outside it. Calculate the proportion of the total energy given to the string in each mode.

  If $l=L / 3$ and $a=L / 10$, find all the modes of the string which are not excited in the motion.

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2009

  The Fourier transform $\tilde{f}(\omega)$ of a suitable function $f(t)$ is defined as $\tilde{f}(\omega)=$ $\int_{-\infty}^{\infty} f(t) e^{-i \omega t} d t$. Consider the function $h(t)=e^{\alpha t}$ for $t>0$, and zero otherwise. Show that

  $$\tilde{h}(\omega)=\frac{1}{i \omega-\alpha},$$

  provided $\Re(\alpha)<0$.

  The angle $\theta(t)$ of a forced, damped pendulum satisfies

  $$\ddot{\theta}+2 \dot{\theta}+5 \theta=e^{-4 t},$$

  with initial conditions $\theta(0)=\dot{\theta}(0)=0$. Show that the transfer function for this system is

  $$\tilde{R}(\omega)=\frac{1}{4 i}\left[\frac{1}{(i \omega+1-2 i)}-\frac{1}{(i \omega+1+2 i)}\right]$$

  comment

• Paper 3, Section II, 15A

  Methods | Part IB, 2009

  A function $g(r)$ is chosen to make the integral

  $$\int_{a}^{b} f\left(r, g, g^{\prime}\right) d r$$

  stationary, subject to given values of $g(a)$ and $g(b)$. Find the Euler-Lagrange equation for $g(r) .$

  In a certain three-dimensional electrostatics problem the potential $\phi$ depends only on the radial coordinate $r$, and the energy functional of $\phi$ is

  $$\mathcal{E}[\phi]=2 \pi \int_{R_{1}}^{R_{2}}\left[\frac{1}{2}\left(\frac{d \phi}{d r}\right)^{2}+\frac{1}{2 \lambda^{2}} \phi^{2}\right] r^{2} d r$$

  where $\lambda$ is a parameter. Show that the Euler-Lagrange equation associated with minimizing the energy $\mathcal{E}$ is equivalent to

  $$\frac{1}{r} \frac{d^{2}(r \phi)}{d r^{2}}-\frac{1}{\lambda^{2}} \phi=0$$

  Find the general solution of this equation, and the solution for the region $R_{1} \leqslant r \leqslant R_{2}$ which satisfies $\phi\left(R_{1}\right)=\phi_{1}$ and $\phi\left(R_{2}\right)=0$.

  Consider an annular region in two dimensions, where the potential is a function of the radial coordinate $r$ only. Write down the equivalent expression for the energy functional $\mathcal{E}$ above, in cylindrical polar coordinates, and derive the equivalent of (1).

  comment

• Paper 4, Section I, B

  Methods | Part IB, 2009

  Describe briefly the method of Lagrange multipliers for finding the stationary points of a function $f(x, y)$ subject to the constraint $g(x, y)=0$.

  Show that at a stationary point $(a, b)$

  $$\left|\begin{array}{ll} \frac{\partial f}{\partial x}(a, b) & \frac{\partial g}{\partial x}(a, b) \\ \frac{\partial f}{\partial y}(a, b) & \frac{\partial g}{\partial y}(a, b) \end{array}\right|=0$$

  Find the maximum distance from the origin to the curve

  $$x^{2}+y^{2}+x y-4=0 .$$

  comment

• Paper 4, Section II, A

  Methods | Part IB, 2009

  Suppose that $y_{1}(x)$ and $y_{2}(x)$ are linearly independent solutions of

  $$\frac{d^{2} y}{d x^{2}}+b(x) \frac{d y}{d x}+c(x) y=0$$

  with $y_{1}(0)=0$ and $y_{2}(1)=0$. Show that the Green's function $G(x, \xi)$ for the interval $0 \leqslant x, \xi \leqslant 1$ and with $G(0, \xi)=G(1, \xi)=0$ can be written in the form

  $$G(x, \xi)= \begin{cases}y_{1}(x) y_{2}(\xi) / W(\xi) ; & 0<x<\xi \\ y_{2}(x) y_{1}(\xi) / W(\xi) ; & \xi<x<1\end{cases}$$

  where $W(x)=W\left[y_{1}(x), y_{2}(x)\right]$ is the Wronskian of $y_{1}(x)$ and $y_{2}(x)$.

  Use this result to find the Green's function $G(x, \xi)$ that satisfies

  $$\frac{d^{2} G}{d x^{2}}+3 \frac{d G}{d x}+2 G=\delta(x-\xi)$$

  in the interval $0 \leqslant x, \xi \leqslant 1$ and with $G(0, \xi)=G(1, \xi)=0$. Hence obtain an integral expression for the solution of

  $$\frac{d^{2} y}{d x^{2}}+3 \frac{d y}{d x}+2 y= \begin{cases}0 ; & 0<x<x_{0} \\ 2 ; & x_{0}<x<1\end{cases}$$

  for the case $x<x_{0}$.

  comment

2008

• $2 . \mathrm{I} . 5 \mathrm{D} \quad$

  Methods | Part IB, 2008

  Describe briefly the method of Lagrange multipliers for finding the stationary values of a function $f(x, y)$ subject to a constraint $g(x, y)=0$.

  Use the method to find the largest possible volume of a circular cylinder that has surface area $A$ (including both ends).

  comment

• 1.II.14D

  Methods | Part IB, 2008

  Write down the Euler-Lagrange equation for the variational problem for $y(x)$ that extremizes the integral $I$ defined as

  $$I=\int_{x_{1}}^{x_{2}} f\left(x, y, y^{\prime}\right) d x$$

  with boundary conditions $y\left(x_{1}\right)=y_{1}, y\left(x_{2}\right)=y_{2}$, where $y_{1}$ and $y_{2}$ are positive constants such that $y_{2}>y_{1}$, with $x_{2}>x_{1}$. Find a first integral of the equation when $f$ is independent of $y$, i.e. $f=f\left(x, y^{\prime}\right)$.

  A light ray moves in the $(x, y)$ plane from $\left(x_{1}, y_{1}\right)$ to $\left(x_{2}, y_{2}\right)$ with speed $c(x)$ taking a time $T$. Show that the equation of the path that makes $T$ an extremum satisfies

  $$\frac{d y}{d x}=\frac{c(x)}{\sqrt{k^{2}-c^{2}(x)}}$$

  where $k$ is a constant and write down an integral relating $k, x_{1}, x_{2}, y_{1}$ and $y_{2}$.

  When $c(x)=a x$ where $a$ is a constant and $k=a x_{2}$, show that the path is given by

  $$\left(y_{2}-y\right)^{2}=x_{2}^{2}-x^{2} .$$

  comment

• 2.II.15D

  Methods | Part IB, 2008

  (a) Legendre's equation may be written in the form

  $$\frac{d}{d x}\left(\left(1-x^{2}\right) \frac{d y}{d x}\right)+\lambda y=0$$

  Show that there is a series solution for $y$ of the form

  $$y=\sum_{k=0}^{\infty} a_{k} x^{k},$$

  where the $a_{k}$ satisfy the recurrence relation

  $$\frac{a_{k+2}}{a_{k}}=-\frac{(\lambda-k(k+1))}{(k+1)(k+2)} .$$

  Hence deduce that there are solutions for $y(x)=P_{n}(x)$ that are polynomials of degree $n$, provided that $\lambda=n(n+1)$. Given that $a_{0}$ is then chosen so that $P_{n}(1)=1$, find the explicit form for $P_{2}(x)$.

  (b) Laplace's equation for $\Phi(r, \theta)$ in spherical polar coordinates $(r, \theta, \phi)$ may be written in the axisymmetric case as

  $$\frac{\partial^{2} \Phi}{\partial r^{2}}+\frac{2}{r} \frac{\partial \Phi}{\partial r}+\frac{1}{r^{2}} \frac{\partial}{\partial x}\left(\left(1-x^{2}\right) \frac{\partial \Phi}{\partial x}\right)=0$$

  where $x=\cos \theta$.

  Write down without proof the general form of the solution obtained by the method of separation of variables. Use it to find the form of $\Phi$ exterior to the sphere $r=a$ that satisfies the boundary conditions, $\Phi(a, x)=1+x^{2}$, and $\lim _{r \rightarrow \infty} \Phi(r, x)=0$.

  comment

• 3.I.6D

  Methods | Part IB, 2008

  Let $\mathcal{L}$ be the operator

  $$\mathcal{L} y=\frac{d^{2} y}{d x^{2}}-k^{2} y$$

  on functions $y(x)$ satisfying $\lim _{x \rightarrow-\infty} \quad y(x)=0$ and $\lim _{x \rightarrow \infty} y(x)=0$.

  Given that the Green's function $G(x ; \xi)$ for $\mathcal{L}$ satisfies

  $$\mathcal{L} G=\delta(x-\xi)$$

  show that a solution of

  $$\mathcal{L} y=S(x)$$

  for a given function $S(x)$, is given by

  $$y(x)=\int_{-\infty}^{\infty} G(x ; \xi) S(\xi) d \xi$$

  Indicate why this solution is unique.

  Show further that the Green's function is given by

  $$G(x ; \xi)=-\frac{1}{2|k|} \exp (-|k||x-\xi|)$$

  comment

• 3.II.15D

  Methods | Part IB, 2008

  Let $\lambda_{1}<\lambda_{2}<\ldots \lambda_{n} \ldots$ and $y_{1}(x), y_{2}(x), \ldots y_{n}(x) \ldots$ be the eigenvalues and corresponding eigenfunctions for the Sturm-Liouville system

  $$\mathcal{L} y_{n}=\lambda_{n} w(x) y_{n},$$

  where

  $$\mathcal{L} y \equiv \frac{d}{d x}\left(-p(x) \frac{d y}{d x}\right)+q(x) y,$$

  with $p(x)>0$ and $w(x)>0$. The boundary conditions on $y$ are that $y(0)=y(1)=0$.

  Show that two distinct eigenfunctions are orthogonal in the sense that

  $$\int_{0}^{1} w y_{n} y_{m} d x=\delta_{n m} \int_{0}^{1} w y_{n}^{2} d x .$$

  Show also that if $y$ has the form

  $$y=\sum_{n=1}^{\infty} a_{n} y_{n},$$

  with $a_{n}$ being independent of $x$, then

  $$\frac{\int_{0}^{1} y \mathcal{L} y d x}{\int_{0}^{1} w y^{2} d x} \geq \lambda_{1}$$

  Assuming that the eigenfunctions are complete, deduce that a solution of the diffusion equation,

  $$\frac{\partial y}{\partial t}=-\frac{1}{w} \mathcal{L} y$$

  that satisfies the boundary conditions given above is such that

  $$\frac{1}{2} \frac{d}{d t}\left(\int_{0}^{1} w y^{2} d x\right) \leq-\lambda_{1} \int_{0}^{1} w y^{2} d x .$$

  comment

• 4.I.5A

  Methods | Part IB, 2008

  Find the half-range Fourier cosine series for $f(x)=x^{2}, 0<x<1$. Hence show that

  $$\sum_{n=1}^{\infty} \frac{1}{n^{2}}=\frac{\pi^{2}}{6} .$$

  comment

• 4.II.16A

  Methods | Part IB, 2008

  Assume $F(x)$ satisfies

  $$\int_{-\infty}^{\infty}|F(x)| d x<\infty$$

  and that the series

  $$g(\tau)=\sum_{n=-\infty}^{\infty} F(2 n \pi+\tau)$$

  converges uniformly in $[0 \leqslant \tau \leqslant 2 \pi]$.

  If $\tilde{F}$ is the Fourier transform of $F$, prove that

  $$g(\tau)=\frac{1}{2 \pi} \sum_{n=-\infty}^{\infty} \tilde{F}(n) e^{i n \tau}$$

  [Hint: prove that $g$ is periodic and express its Fourier expansion coefficients in terms of $\tilde{F}]$.

  In the case that $F(x)=e^{-|x|}$, evaluate the sum

  $$\sum_{n=-\infty}^{\infty} \frac{1}{1+n^{2}} .$$

  comment

2007

• $2 . \mathrm{I} . 5 \mathrm{D}$

  Methods | Part IB, 2007

  Show that a smooth function $y(x)$ that satisfies $y(0)=y^{\prime}(1)=0$ can be written as a Fourier series of the form

  $$y(x)=\sum_{n=0}^{\infty} a_{n} \sin \lambda_{n} x, \quad 0 \leqslant x \leqslant 1$$

  where the $\lambda_{n}$ should be specified. Write down an integral expression for $a_{n}$.

  Hence solve the following differential equation

  $$y^{\prime \prime}-\alpha^{2} y=x \cos \pi x$$

  with boundary conditions $y(0)=y^{\prime}(1)=0$, in the form of an infinite series.

  $$\begin{aligned} & \text { (i) } f(x)=e^{-a|x|} \text {, } \\ & \text { and }(i i) \quad g(x)= \begin{cases}1, & |x| \leqslant b \\ 0, & |x|>b .\end{cases} \end{aligned}$$

  comment

• $3 . \mathrm{I} . 6 \mathrm{E} \quad$

  Methods | Part IB, 2007

  Describe the method of Lagrange multipliers for finding extrema of a function $f(x, y, z)$ subject to the constraint that $g(x, y, z)=c$.

  Illustrate the method by finding the maximum and minimum values of $x y$ for points $(x, y, z)$ lying on the ellipsoid

  $$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1$$

  with $a, b$ and $c$ all positive.

  comment

• 1.II.14D

  Methods | Part IB, 2007

  Define the Fourier transform $\tilde{f}(k)$ of a function $f(x)$ that tends to zero as $|x| \rightarrow \infty$, and state the inversion theorem. State and prove the convolution theorem.

  Calculate the Fourier transforms of

  Hence show that

  $$\int_{-\infty}^{\infty} \frac{\sin (b k) e^{i k x}}{k\left(a^{2}+k^{2}\right)} d k=\frac{\pi \sinh (a b)}{a^{2}} e^{-a x} \quad \text { for } \quad x>b$$

  and evaluate this integral for all other (real) values of $x$.

  comment

• 2.II.15D

  Methods | Part IB, 2007

  Let $y_{0}(x)$ be a non-zero solution of the Sturm-Liouville equation

  $$L\left(y_{0} ; \lambda_{0}\right) \equiv \frac{d}{d x}\left(p(x) \frac{d y_{0}}{d x}\right)+\left(q(x)+\lambda_{0} w(x)\right) y_{0}=0$$

  with boundary conditions $y_{0}(0)=y_{0}(1)=0$. Show that, if $y(x)$ and $f(x)$ are related by

  $$L\left(y ; \lambda_{0}\right)=f$$

  with $y(x)$ satisfying the same boundary conditions as $y_{0}(x)$, then

  $$\int_{0}^{1} y_{0} f d x=0$$

  Suppose that $y_{0}$ is normalised so that

  $$\int_{0}^{1} w y_{0}^{2} d x=1$$

  and consider the problem

  $$L(y ; \lambda)=y^{3} ; \quad y(0)=y(1)=0$$

  By choosing $f$ appropriately in $(*)$ deduce that, if

  $$\lambda-\lambda_{0}=\epsilon^{2} \mu[\mu=O(1), \epsilon \ll 1], \quad \text { and } \quad y(x)=\epsilon y_{0}(x)+\epsilon^{2} y_{1}(x)$$

  then

  $$\mu=\int_{0}^{1} y_{0}^{4} d x+O(\epsilon)$$

  comment

• 3.II.15E

  Methods | Part IB, 2007

  Legendre's equation may be written

  $$\left(1-x^{2}\right) y^{\prime \prime}-2 x y^{\prime}+n(n+1) y=0 \quad \text { with } \quad y(1)=1$$

  Show that if $n$ is a positive integer, this equation has a solution $y=P_{n}(x)$ that is a polynomial of degree $n$. Find $P_{0}, P_{1}$ and $P_{2}$ explicitly.

  Write down a general separable solution of Laplace's equation, $\nabla^{2} \phi=0$, in spherical polar coordinates $(r, \theta)$. (A derivation of this result is not required.)

  Hence or otherwise find $\phi$ when

  $$\nabla^{2} \phi=0, \quad a<r<b$$

  with $\phi=\sin ^{2} \theta$ both when $r=a$ and when $r=b$.

  comment

• 4.I.5B

  Methods | Part IB, 2007

  Show that the general solution of the wave equation

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}$$

  where $c$ is a constant, is

  $$y=f(x+c t)+g(x-c t),$$

  where $f$ and $g$ are twice differentiable functions. Briefly discuss the physical interpretation of this solution.

  Calculate $y(x, t)$ subject to the initial conditions

  $$y(x, 0)=0 \quad \text { and } \quad \frac{\partial y}{\partial t}(x, 0)=\psi(x)$$

  comment

• 4.II.16E

  Methods | Part IB, 2007

  Write down the Euler-Lagrange equation for extrema of the functional

  $$I=\int_{a}^{b} F\left(y, y^{\prime}\right) d x$$

  Show that a first integral of this equation is given by

  $$F-y^{\prime} \frac{\partial F}{\partial y^{\prime}}=C$$

  A road is built between two points $A$ and $B$ in the plane $z=0$ whose polar coordinates are $r=a, \theta=0$ and $r=a, \theta=\pi / 2$ respectively. Owing to congestion, the traffic speed at points along the road is $k r^{2}$ with $k$ a positive constant. If the equation describing the road is $r=r(\theta)$, obtain an integral expression for the total travel time $T$ from $A$ to $B$.

  [Arc length in polar coordinates is given by $d s^{2}=d r^{2}+r^{2} d \theta^{2}$.]

  Calculate $T$ for the circular road $r=a$.

  Find the equation for the road that minimises $T$ and determine this minimum value.

  comment

2006

• 1.II.14A

  Methods | Part IB, 2006

  Define a second rank tensor. Show from your definition that if $M_{i j}$ is a second rank tensor then $M_{i i}$ is a scalar.

  A rigid body consists of a thin flat plate of material having density $\rho(\mathbf{x})$ per unit area, where $\mathbf{x}$ is the position vector. The body occupies a region $D$ of the $(x, y)$-plane; its thickness in the $z$-direction is negligible. The moment of inertia tensor of the body is given as

  $$M_{i j}=\int_{D}\left(x_{k} x_{k} \delta_{i j}-x_{i} x_{j}\right) \rho d S$$

  Show that the $z$-direction is an eigenvector of $M_{i j}$ and write down an integral expression for the corresponding eigenvalue $M_{\perp}$.

  Hence or otherwise show that if the remaining eigenvalues of $M_{i j}$ are $M_{1}$ and $M_{2}$ then

  $$M_{\perp}=M_{1}+M_{2} .$$

  Find $M_{i j}$ for a circular disc of radius $a$ and uniform density having its centre at the origin.

  comment

• 2.I.5A

  Methods | Part IB, 2006

  Describe briefly the method of Lagrange multipliers for finding the stationary values of a function $f(x, y)$ subject to a constraint $g(x, y)=0$.

  Use the method to find the smallest possible surface area (including both ends) of a circular cylinder that has volume $V$.

  comment

• 2.II.15G

  Methods | Part IB, 2006

  Verify that $y=e^{-x}$ is a solution of the differential equation

  $$(x+2) y^{\prime \prime}+(x+1) y^{\prime}-y=0,$$

  and find a second solution of the form $a x+b$.

  Let $L$ be the operator

  $$L[y]=y^{\prime \prime}+\frac{(x+1)}{(x+2)} y^{\prime}-\frac{1}{(x+2)} y$$

  on functions $y(x)$ satisfying

  $$y^{\prime}(0)=y(0) \quad \text { and } \quad \lim _{x \rightarrow \infty} y(x)=0 .$$

  The Green's function $G(x, \xi)$ for $L$ satisfies

  $$L[G]=\delta(x-\xi)$$

  with $\xi>0$. Show that

  $$G(x, \xi)=-\frac{(\xi+1)}{(\xi+2)} e^{\xi-x}$$

  for $x>\xi$, and find $G(x, \xi)$ for $x<\xi$.

  Hence or otherwise find the solution of

  $$L[y]=-(x+2) e^{-x},$$

  for $x \geqslant 0$, with $y(x)$ satisfying the boundary conditions above.

  comment

• 3.I.6A

  Methods | Part IB, 2006

  If $T_{i j}$ is a second rank tensor such that $b_{i} T_{i j} c_{j}=0$ for every vector $\mathbf{b}$ and every vector c, show that $T_{i j}=0$.

  Let $S$ be a closed surface with outward normal $\mathbf{n}$ that encloses a three-dimensional region having volume $V$. The position vector is $\mathbf{x}$. Use the divergence theorem to find

  $$\int_{S}(\mathbf{b} \cdot \mathbf{x})(\mathbf{c} \cdot \mathbf{n}) d S$$

  for constant vectors $\mathbf{b}$ and $\mathbf{c}$. Hence find

  $$\int_{S} x_{i} n_{j} d S$$

  and deduce the values of

  $$\int_{S} \mathbf{x} \cdot \mathbf{n} d S \text { and } \int_{S} \mathbf{x} \times \mathbf{n} d S$$

  comment

• 3.II.15G

  Methods | Part IB, 2006

  (a) Find the Fourier sine series of the function

  $$f(x)=x$$

  for $0 \leqslant x \leqslant 1$.

  (b) The differential operator $L$ acting on $y$ is given by

  $$L[y]=y^{\prime \prime}+y^{\prime}$$

  Show that the eigenvalues $\lambda$ in the eigenvalue problem

  $$L[y]=\lambda y, \quad y(0)=y(1)=0$$

  are given by $\lambda=-n^{2} \pi^{2}-\frac{1}{4}, \quad n=1,2, \ldots$, and find the corresponding eigenfunctions $y_{n}(x)$.

  By expressing the equation $L[y]=\lambda y$ in Sturm-Liouville form or otherwise, write down the orthogonality relation for the $y_{n}$. Assuming the completeness of the eigenfunctions and using the result of part (a), find, in the form of a series, a function $y(x)$ which satisfies

  $$L[y]=x e^{-x / 2}$$

  and $y(0)=y(1)=0$.

  comment

• 4.I.5G

  Methods | Part IB, 2006

  A finite-valued function $f(r, \theta, \phi)$, where $r, \theta, \phi$ are spherical polar coordinates, satisfies Laplace's equation in the regions $r<1$ and $r>1$, and $f \rightarrow 0$ as $r \rightarrow \infty$. At $r=1, f$ is continuous and its derivative with respect to $r$ is discontinuous by $A \sin ^{2} \theta$, where $A$ is a constant. Write down the general axisymmetric solution for $f$ in the two regions and use the boundary conditions to find $f$.

  $$\left[\text { Hint }: \quad P_{2}(\cos \theta)=\frac{1}{2}\left(3 \cos ^{2} \theta-1\right) \cdot\right]$$

  comment

• 4.II.16B

  Methods | Part IB, 2006

  The integral

  $$I=\int_{a}^{b} F\left(y(x), y^{\prime}(x)\right) d x,$$

  where $F$ is some functional, is defined for the class of functions $y(x)$ for which $y(a)=y_{0}$, with the value $y(b)$ at the upper endpoint unconstrained. Suppose that $y(x)$ extremises the integral among the functions in this class. By considering perturbed paths of the form $y(x)+\epsilon \eta(x)$, with $\epsilon \ll 1$, show that

  $$\frac{d}{d x}\left(\frac{\partial F}{\partial y^{\prime}}\right)-\frac{\partial F}{\partial y}=0$$

  and that

  $$\left.\frac{\partial F}{\partial y^{\prime}}\right|_{x=b}=0 .$$

  Show further that

  $$F-y^{\prime} \frac{\partial F}{\partial y^{\prime}}=k$$

  for some constant $k$.

  A bead slides along a frictionless wire under gravity. The wire lies in a vertical plane with coordinates $(x, y)$ and connects the point $A$ with coordinates $(0,0)$ to the point $B$ with coordinates $\left(x_{0}, y\left(x_{0}\right)\right)$, where $x_{0}$ is given and $y\left(x_{0}\right)$ can take any value less than zero. The bead is released from rest at $A$ and slides to $B$ in a time $T$. For a prescribed $x_{0}$ find both the shape of the wire, and the value of $y\left(x_{0}\right)$, for which $T$ is as small as possible.

  comment

2005

• 1.II.14E

  Methods | Part IB, 2005

  Find the Fourier Series of the function

  $$f(\theta)= \begin{cases}1 & 0 \leq \theta<\pi \\ -1 & \pi \leq \theta<2 \pi\end{cases}$$

  Find the solution $\phi(r, \theta)$ of the Poisson equation in two dimensions inside the unit disk $r \leq 1$

  $$\nabla^{2} \phi=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} \phi}{\partial \theta^{2}}=f(\theta)$$

  subject to the boundary condition $\phi(1, \theta)=0$.

  [Hint: The general solution of $r^{2} R^{\prime \prime}+r R^{\prime}-n^{2} R=r^{2}$ is $R=a r^{n}+b r^{-n}-r^{2} /\left(n^{2}-4\right) .$ ]

  From the solution, show that

  $$\int_{r \leq 1} f \phi d A=-\frac{4}{\pi} \sum_{n \text { odd }} \frac{1}{n^{2}(n+2)^{2}}$$

  comment

• 2.I.5E

  Methods | Part IB, 2005

  Consider the differential equation for $x(t)$ in $t>0$

  $$\ddot{x}-k^{2} x=f(t),$$

  subject to boundary conditions $x(0)=0$, and $\dot{x}(0)=0$. Find the Green function $G\left(t, t^{\prime}\right)$ such that the solution for $x(t)$ is given by

  $$x(t)=\int_{0}^{t} G\left(t, t^{\prime}\right) f\left(t^{\prime}\right) d t^{\prime} .$$

  comment

• 2.II.15E

  Methods | Part IB, 2005

  Write down the Euler-Lagrange equation for the variational problem for $r(z)$

  $$\delta \int_{-h}^{h} F\left(z, r, r^{\prime}\right) d z=0$$

  with boundary conditions $r(-h)=r(h)=R$, where $R$ is a given positive constant. Show that if $F$ does not depend explicitly on $z$, i.e. $F=F\left(r, r^{\prime}\right)$, then the equation has a first integral

  $$F-r^{\prime} \frac{\partial F}{\partial r^{\prime}}=\frac{1}{k},$$

  where $k$ is a constant.

  An axisymmetric soap film $r(z)$ is formed between two circular rings $r=R$ at $z=\pm H$. Find the equation governing the shape which minimizes the surface area. Show that the shape takes the form

  $$r(z)=k^{-1} \cosh k z .$$

  Show that there exist no solution if $R / H<\sinh A$, where $A$ is the unique positive solution of $A=\operatorname{coth} A$.

  comment

• 3.I.6E

  Methods | Part IB, 2005

  Describe briefly the method of Lagrangian multipliers for finding the stationary points of a function $f(x, y)$ subject to a constraint $g(x, y)=0$.

  Use the method to find the stationary values of $x y$ subject to the constraint $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 .$

  comment

• 3.II.15H

  Methods | Part IB, 2005

  Obtain the power series solution about $t=0$ of

  $$\left(1-t^{2}\right) \frac{\mathrm{d}^{2}}{\mathrm{~d} t^{2}} y-2 t \frac{\mathrm{d}}{\mathrm{d} t} y+\lambda y=0$$

  and show that regular solutions $y(t)=P_{n}(t)$, which are polynomials of degree $n$, are obtained only if $\lambda=n(n+1), n=0,1,2, \ldots$ Show that the polynomial must be even or odd according to the value of $n$.

  Show that

  $$\int_{-1}^{1} P_{n}(t) P_{m}(t) \mathrm{d} t=k_{n} \delta_{n m}$$

  for some $k_{n}>0$.

  Using the identity

  $$\left(x \frac{\partial^{2}}{\partial x^{2}} x+\frac{\partial}{\partial t}\left(1-t^{2}\right) \frac{\partial}{\partial t}\right) \frac{1}{\left(1-2 x t+x^{2}\right)^{\frac{1}{2}}}=0,$$

  and considering an expansion $\sum_{n} a_{n}(x) P_{n}(t)$ show that

  $$\frac{1}{\left(1-2 x t+x^{2}\right)^{\frac{1}{2}}}=\sum_{n=0}^{\infty} x^{n} P_{n}(t), \quad 0<x<1$$

  if we assume $P_{n}(1)=1$.

  By considering

  $$\int_{-1}^{1} \frac{1}{1-2 x t+x^{2}} d t$$

  determine the coefficient $k_{n}$.

  comment

• 4.I.5H

  Methods | Part IB, 2005

  Show how the general solution of the wave equation for $y(x, t)$,

  $$\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}} y(x, t)-\frac{\partial^{2}}{\partial x^{2}} y(x, t)=0$$

  can be expressed as

  $$y(x, t)=f(c t-x)+g(c t+x) .$$

  Show that the boundary conditions $y(0, t)=y(L, t)=0$ relate the functions $f$ and $g$ and require them to be periodic with period $2 L$.

  Show that, with these boundary conditions,

  $$\frac{1}{2} \int_{0}^{L}\left(\frac{1}{c^{2}}\left(\frac{\partial y}{\partial t}\right)^{2}+\left(\frac{\partial y}{\partial x}\right)^{2}\right) \mathrm{d} x=\int_{-L}^{L} g^{\prime}(c t+x)^{2} \mathrm{~d} x$$

  and that this is a constant independent of $t$.

  comment

• 4.II.16H

  Methods | Part IB, 2005

  Define an isotropic tensor and show that $\delta_{i j}, \epsilon_{i j k}$ are isotropic tensors.

  For $\hat{\mathbf{x}}$ a unit vector and $\mathrm{d} S(\hat{\mathbf{x}})$ the area element on the unit sphere show that

  $$\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i_{1}} \ldots \hat{x}_{i_{n}}$$

  is an isotropic tensor for any $n$. Hence show that

  $$\begin{aligned} &\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j}=a \delta_{i j}, \quad \int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j} \hat{x}_{k}=0 \\ &\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j} \hat{x}_{k} \hat{x}_{l}=b\left(\delta_{i j} \delta_{k l}+\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right) \end{aligned}$$

  for some $a, b$ which should be determined.

  Explain why

  $$\int_{V} \mathrm{~d}^{3} x\left(x_{1}+\sqrt{-1} x_{2}\right)^{n} f(|\mathbf{x}|)=0, \quad n=2,3,4$$

  where $V$ is the region inside the unit sphere.

  [The general isotropic tensor of rank 4 has the form $a \delta_{i j} \delta_{k l}+b \delta_{i k} \delta_{j l}+c \delta_{i l} \delta_{j k} .$ ]

  comment

2004

• 1.I.6B

  Methods | Part IB, 2004

  Write down the general isotropic tensors of rank 2 and 3 .

  According to a theory of magnetostriction, the mechanical stress described by a second-rank symmetric tensor $\sigma_{i j}$ is induced by the magnetic field vector $B_{i}$. The stress is linear in the magnetic field,

  $$\sigma_{i j}=A_{i j k} B_{k},$$

  where $A_{i j k}$ is a third-rank tensor which depends only on the material. Show that $\sigma_{i j}$ can be non-zero only in anisotropic materials.

  comment

• 1.II.17B

  Methods | Part IB, 2004

  The equation governing small amplitude waves on a string can be written as

  $$\frac{\partial^{2} y}{\partial t^{2}}=\frac{\partial^{2} y}{\partial x^{2}}$$

  The end points $x=0$ and $x=1$ are fixed at $y=0$. At $t=0$, the string is held stationary in the waveform,

  $$y(x, 0)=x(1-x) \quad \text { in } \quad 0 \leq x \leq 1 .$$

  The string is then released. Find $y(x, t)$ in the subsequent motion.

  Given that the energy

  $$\int_{0}^{1}\left[\left(\frac{\partial y}{\partial t}\right)^{2}+\left(\frac{\partial y}{\partial x}\right)^{2}\right] d x$$

  is constant in time, show that

  $$\sum_{\substack{n \text { odd } \\ n \geqslant 1}} \frac{1}{n^{4}}=\frac{\pi^{4}}{96}$$

  comment

• 2.I.6B

  Methods | Part IB, 2004

  Write down the general form of the solution in polar coordinates $(r, \theta)$ to Laplace's equation in two dimensions.

  Solve Laplace's equation for $\phi(r, \theta)$ in $0<r<1$ and in $1<r<\infty$, subject to the conditions

  $$\begin{gathered} \phi \rightarrow 0 \quad \text { as } \quad r \rightarrow 0 \text { and } r \rightarrow \infty \\ \left.\phi\right|_{r=1+}=\left.\phi\right|_{r=1-} \quad \text { and }\left.\quad \frac{\partial \phi}{\partial r}\right|_{r=1+}-\left.\frac{\partial \phi}{\partial r}\right|_{r=1-}=\cos 2 \theta+\cos 4 \theta . \end{gathered}$$

  comment

• 2.II.17B

  Methods | Part IB, 2004

  Let $I_{i j}(P)$ be the moment-of-inertia tensor of a rigid body relative to the point $P$. If $G$ is the centre of mass of the body and the vector $G P$ has components $X_{i}$, show that

  $$I_{i j}(P)=I_{i j}(G)+M\left(X_{k} X_{k} \delta_{i j}-X_{i} X_{j}\right),$$

  where $M$ is the mass of the body.

  Consider a cube of uniform density and side $2 a$, with centre at the origin. Find the inertia tensor about the centre of mass, and thence about the corner $P=(a, a, a)$.

  Find the eigenvectors and eigenvalues of $I_{i j}(P)$.

  comment

• 3.I.6D

  Methods | Part IB, 2004

  Let

  $$S[x]=\int_{0}^{T} \frac{1}{2}\left(\dot{x}^{2}-\omega^{2} x^{2}\right) \mathrm{d} t, \quad x(0)=a, \quad x(T)=b .$$

  For any variation $\delta x(t)$ with $\delta x(0)=\delta x(T)=0$, show that $\delta S=0$ when $x=x_{c}$ with

  $$x_{c}(t)=\frac{1}{\sin \omega T}[a \sin \omega(T-t)+b \sin \omega t] .$$

  By using integration by parts, show that

  $$S\left[x_{c}\right]=\left[\frac{1}{2} x_{c} \dot{x}_{c}\right]_{0}^{T}=\frac{\omega}{2 \sin \omega T}\left[\left(a^{2}+b^{2}\right) \cos \omega T-2 a b\right]$$

  comment

• 3.II.18D

  Methods | Part IB, 2004

  Starting from the Euler-Lagrange equations, show that the condition for the variation of the integral $\int I\left(y, y^{\prime}\right) \mathrm{d} x$ to be stationary is

  $$I-y^{\prime} \frac{\partial I}{\partial y^{\prime}}=\text { constant }$$

  In a medium with speed of light $c(y)$ the ray path taken by a light signal between two points satisfies the condition that the time taken is stationary. Consider the region $0<y<\infty$ and suppose $c(y)=e^{\lambda y}$. Derive the equation for the light ray path $y(x)$. Obtain the solution of this equation and show that the light ray between $(-a, 0)$ and $(a, 0)$ is given by

  $$e^{\lambda y}=\frac{\cos \lambda x}{\cos \lambda a},$$

  if $\lambda a<\frac{\pi}{2}$.

  Sketch the path for $\lambda a$ close to $\frac{\pi}{2}$ and evaluate the time taken for a light signal between these points.

  [The substitution $u=k e^{\lambda y}$, for some constant $k$, should prove useful in solving the differential equation.]

  comment

• 4.I.6C

  Methods | Part IB, 2004

  Chebyshev polynomials $T_{n}(x)$ satisfy the differential equation

  $$\left(1-x^{2}\right) y^{\prime \prime}-x y^{\prime}+n^{2} y=0 \quad \text { on } \quad[-1,1],$$

  where $n$ is an integer.

  Recast this equation into Sturm-Liouville form and hence write down the orthogonality relationship between $T_{n}(x)$ and $T_{m}(x)$ for $n \neq m$.

  By writing $x=\cos \theta$, or otherwise, show that the polynomial solutions of ( $\dagger$ ) are proportional to $\cos \left(n \cos ^{-1} x\right)$.

  comment

• 4.II.16C

  Methods | Part IB, 2004

  Obtain the Green function $G(x, \xi)$ satisfying

  $$G^{\prime \prime}+\frac{2}{x} G^{\prime}+k^{2} G=\delta(x-\xi),$$

  where $k$ is real, subject to the boundary conditions

  $$\begin{array}{rll} G \text { is finite } & \text { at } & x=0, \\ G=0 & \text { at } & x=1 . \end{array}$$

  [Hint: You may find the substitution $G=H / x$ helpful.]

  Use the Green function to determine that the solution of the differential equation

  $$y^{\prime \prime}+\frac{2}{x} y^{\prime}+k^{2} y=1,$$

  subject to the boundary conditions

  $$\begin{array}{rll} y \text { is finite } & \text { at } & x=0, \\ y=0 & \text { at } & x=1, \end{array}$$

  is

  $$y=\frac{1}{k^{2}}\left[1-\frac{\sin k x}{x \sin k}\right]$$

  comment

2003

• 1.I.2D

  Methods | Part IB, 2003

  Fermat's principle of optics states that the path of a light ray connecting two points will be such that the travel time $t$ is a minimum. If the speed of light varies continuously in a medium and is a function $c(y)$ of the distance from the boundary $y=0$, show that the path of a light ray is given by the solution to

  $$c(y) y^{\prime \prime}+c^{\prime}(y)\left(1+y^{\prime 2}\right)=0$$

  where $y^{\prime}=\frac{d y}{d x}$, etc. Show that the path of a light ray in a medium where the speed of light $c$ is a constant is a straight line. Also find the path from $(0,0)$ to $(1,0)$ if $c(y)=y$, and sketch it.

  comment

• 1.II.11D

  Methods | Part IB, 2003

  (a) Determine the Green's function $G(x, \xi)$ for the operator $\frac{d^{2}}{d x^{2}}+k^{2}$ on $[0, \pi]$ with Dirichlet boundary conditions by solving the boundary value problem

  $$\frac{d^{2} G}{d x^{2}}+k^{2} G=\delta(x-\xi), \quad G(0)=0, G(\pi)=0$$

  when $k$ is not an integer.

  (b) Use the method of Green's functions to solve the boundary value problem

  $$\frac{d^{2} y}{d x^{2}}+k^{2} y=f(x), \quad y(0)=a, y(\pi)=b$$

  when $k$ is not an integer.

  comment

• 2.I.2C

  Methods | Part IB, 2003

  Explain briefly why the second-rank tensor

  $$\int_{S} x_{i} x_{j} d S(\mathbf{x})$$

  is isotropic, where $S$ is the surface of the unit sphere centred on the origin.

  A second-rank tensor is defined by

  $$T_{i j}(\mathbf{y})=\int_{S}\left(y_{i}-x_{i}\right)\left(y_{j}-x_{j}\right) d S(\mathbf{x})$$

  where $S$ is the surface of the unit sphere centred on the origin. Calculate $T(\mathbf{y})$ in the form

  $$T_{i j}=\lambda \delta_{i j}+\mu y_{i} y_{j}$$

  where $\lambda$ and $\mu$ are to be determined.

  By considering the action of $T$ on $\mathbf{y}$ and on vectors perpendicular to $\mathbf{y}$, determine the eigenvalues and associated eigenvectors of $T$.

  comment

• 2.II.11C

  Methods | Part IB, 2003

  State the transformation law for an $n$ th-rank tensor $T_{i j \cdots k}$.

  Show that the fourth-rank tensor

  $$c_{i j k l}=\alpha \delta_{i j} \delta_{k l}+\beta \delta_{i k} \delta_{j l}+\gamma \delta_{i l} \delta_{j k}$$

  is isotropic for arbitrary scalars $\alpha, \beta$ and $\gamma$.

  The stress $\sigma_{i j}$ and strain $e_{i j}$ in a linear elastic medium are related by

  $$\sigma_{i j}=c_{i j k l} e_{k l} .$$

  Given that $e_{i j}$ is symmetric and that the medium is isotropic, show that the stress-strain relationship can be written in the form

  $$\sigma_{i j}=\lambda e_{k k} \delta_{i j}+2 \mu e_{i j}$$

  Show that $e_{i j}$ can be written in the form $e_{i j}=p \delta_{i j}+d_{i j}$, where $d_{i j}$ is a traceless tensor and $p$ is a scalar to be determined. Show also that necessary and sufficient conditions for the stored elastic energy density $E=\frac{1}{2} \sigma_{i j} e_{i j}$ to be non-negative for any deformation of the solid are that

  $$\mu \geq 0 \quad \text { and } \quad \lambda \geq-\frac{2}{3} \mu .$$

  comment

• 3.I.2D

  Methods | Part IB, 2003

  Consider the path between two arbitrary points on a cone of interior angle $2 \alpha$. Show that the arc-length of the path $r(\theta)$ is given by

  $$\int\left(r^{2}+r^{\prime 2} \operatorname{cosec}^{2} \alpha\right)^{1 / 2} d \theta$$

  where $r^{\prime}=\frac{d r}{d \theta}$. By minimizing the total arc-length between the points, determine the equation for the shortest path connecting them.

  comment

• 3.II.12D

  Methods | Part IB, 2003

  The transverse displacement $y(x, t)$ of a stretched string clamped at its ends $x=0, l$ satisfies the equation

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}-2 k \frac{\partial y}{\partial t}, \quad y(x, 0)=0, \frac{\partial y}{\partial t}(x, 0)=\delta(x-a)$$

  where $c>0$ is the wave velocity, and $k>0$ is the damping coefficient. The initial conditions correspond to a sharp blow at $x=a$ at time $t=0$.

  (a) Show that the subsequent motion of the string is given by

  $$y(x, t)=\frac{1}{\sqrt{\alpha_{n}^{2}-k^{2}}} \sum_{n} 2 e^{-k t} \sin \frac{\alpha_{n} a}{c} \sin \frac{\alpha_{n} x}{c} \sin /\left(\sqrt{\alpha_{n}^{2}-k^{2}} t\right)$$

  where $\alpha_{n}=\pi c n / l$.

  (b) Describe what happens in the limits of small and large damping. What critical parameter separates the two cases?

  comment

• 4.I.2D

  Methods | Part IB, 2003

  Consider the wave equation in a spherically symmetric coordinate system

  $$\frac{\partial^{2} u(r, t)}{\partial t^{2}}=c^{2} \Delta u(r, t)$$

  where $\Delta u=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r u)$ is the spherically symmetric Laplacian operator.

  (a) Show that the general solution to the equation above is

  $$u(r, t)=\frac{1}{r}[f(r+c t)+g(r-c t)]$$

  where $f(x), g(x)$ are arbitrary functions.

  (b) Using separation of variables, determine the wave field $u(r, t)$ in response to a pulsating source at the origin $u(0, t)=A \sin \omega t$.

  comment

• 4.II.11D

  Methods | Part IB, 2003

  The velocity potential $\phi(r, \theta)$ for inviscid flow in two dimensions satisfies the Laplace equation

  $$\Delta \phi=\left[\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial \theta^{2}}\right] \phi(r, \theta)=0$$

  (a) Using separation of variables, derive the general solution to the equation above that is single-valued and finite in each of the domains (i) $0 \leqslant r \leqslant a$; (ii) $a \leqslant r<\infty$.

  (b) Assuming $\phi$ is single-valued, solve the Laplace equation subject to the boundary conditions $\frac{\partial \phi}{\partial r}=0$ at $r=a$, and $\frac{\partial \phi}{\partial r} \rightarrow U \cos \theta$ as $r \rightarrow \infty$. Sketch the lines of constant potential.

  comment

2002

• 1.I.2A

  Methods | Part IB, 2002

  Find the Fourier sine series for $f(x)=x$, on $0 \leqslant x<L$. To which value does the series converge at $x=\frac{3}{2} L$ ?

  Now consider the corresponding cosine series for $f(x)=x$, on $0 \leqslant x<L$. Sketch the cosine series between $x=-2 L$ and $x=2 L$. To which value does the series converge at $x=\frac{3}{2} L$ ? [You do not need to determine the cosine series explicitly.]

  comment

• 1.II.11A

  Methods | Part IB, 2002

  The potential $\Phi(r, \vartheta)$, satisfies Laplace's equation everywhere except on a sphere of unit radius and $\Phi \rightarrow 0$ as $r \rightarrow \infty$. The potential is continuous at $r=1$, but the derivative of the potential satisfies

  $$\lim _{r \rightarrow 1^{+}} \frac{\partial \Phi}{\partial r}-\lim _{r \rightarrow 1^{-}} \frac{\partial \Phi}{\partial r}=V \cos ^{2} \vartheta$$

  where $V$ is a constant. Use the method of separation of variables to find $\Phi$ for both $r>1$ and $r<1$.

  [The Laplacian in spherical polar coordinates for axisymmetric systems is

  $$\nabla^{2} \equiv \frac{1}{r^{2}}\left(\frac{\partial}{\partial r} r^{2} \frac{\partial}{\partial r}\right)+\frac{1}{r^{2} \sin \vartheta}\left(\frac{\partial}{\partial \vartheta} \sin \vartheta \frac{\partial}{\partial \vartheta}\right)$$

  You may assume that the equation

  $$\left(\left(1-x^{2}\right) y^{\prime}\right)^{\prime}+\lambda y=0$$

  has polynomial solutions of degree $n$, which are regular at $x=\pm 1$, if and only if $\lambda=n(n+1) .]$

  comment

• 2.I.2C

  Methods | Part IB, 2002

  Write down the transformation law for the components of a second-rank tensor $A_{i j}$ explaining the meaning of the symbols that you use.

  A tensor is said to have cubic symmetry if its components are unchanged by rotations of $\pi / 2$ about each of the three co-ordinate axes. Find the most general secondrank tensor having cubic symmetry.

  comment

• 2.II.11C

  Methods | Part IB, 2002

  If $\mathbf{B}$ is a vector, and

  $$T_{i j}=\alpha B_{i} B_{j}+\beta B_{k} B_{k} \delta_{i j}$$

  show for arbitrary scalars $\alpha$ and $\beta$ that $T_{i j}$ is a symmetric second-rank tensor.

  Find the eigenvalues and eigenvectors of $T_{i j}$.

  Suppose now that $\mathbf{B}$ depends upon position $\mathbf{x}$ and that $\nabla \cdot \mathbf{B}=0$. Find constants $\alpha$ and $\beta$ such that

  $$\frac{\partial}{\partial x_{j}} T_{i j}=[(\nabla \times \mathbf{B}) \times \mathbf{B}]_{i} .$$

  Hence or otherwise show that if $\mathbf{B}$ vanishes everywhere on a surface $S$ that encloses a volume $V$ then

  $$\int_{V}(\nabla \times \mathbf{B}) \times \mathbf{B} d V=0$$

  comment

• 3.I.2A

  Methods | Part IB, 2002

  Write down the wave equation for the displacement $y(x, t)$ of a stretched string with constant mass density and tension. Obtain the general solution in the form

  $$y(x, t)=f(x+c t)+g(x-c t)$$

  where $c$ is the wave velocity. For a solution in the region $0 \leqslant x<\infty$, with $y(0, t)=0$ and $y \rightarrow 0$ as $x \rightarrow \infty$, show that

  $$E=\int_{0}^{\infty}\left[\frac{1}{2}\left(\frac{\partial y}{\partial t}\right)^{2}+\frac{1}{2} c^{2}\left(\frac{\partial y}{\partial x}\right)^{2}\right] d x$$

  is constant in time. Express $E$ in terms of the general solution in this case.

  comment

• 3.II.12A

  Methods | Part IB, 2002

  Consider the real Sturm-Liouville problem

  $$\mathcal{L} y(x)=-\left(p(x) y^{\prime}\right)^{\prime}+q(x) y=\lambda r(x) y,$$

  with the boundary conditions $y(a)=y(b)=0$, where $p, q$ and $r$ are continuous and positive on $[a, b]$. Show that, with suitable choices of inner product and normalisation, the eigenfunctions $y_{n}(x), \quad n=1,2,3 \ldots$, form an orthonormal set.

  Hence show that the corresponding Green's function $G(x, \xi)$ satisfying

  $$(\mathcal{L}-\mu r(x)) G(x, \xi)=\delta(x-\xi),$$

  where $\mu$ is not an eigenvalue, is

  $$G(x, \xi)=\sum_{n=1}^{\infty} \frac{y_{n}(x) y_{n}(\xi)}{\lambda_{n}-\mu}$$

  where $\lambda_{n}$ is the eigenvalue corresponding to $y_{n}$.

  Find the Green's function in the case where

  $$\mathcal{L} y \equiv y^{\prime \prime},$$

  with boundary conditions $y(0)=y(\pi)=0$, and deduce, by suitable choice of $\mu$, that

  $$\sum_{n=0}^{\infty} \frac{1}{(2 n+1)^{2}}=\frac{\pi^{2}}{8} .$$

  comment

• 4.I.2A

  Methods | Part IB, 2002

  Use the method of Lagrange multipliers to find the largest volume of a rectangular parallelepiped that can be inscribed in the ellipsoid

  $$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1 .$$

  comment

• 4.II.11A

  Methods | Part IB, 2002

  A function $y(x)$ is chosen to make the integral

  $$I=\int_{a}^{b} f\left(x, y, y^{\prime}, y^{\prime \prime}\right) d x$$

  stationary, subject to given values of $y(a), y^{\prime}(a), y(b)$ and $y^{\prime}(b)$. Derive an analogue of the Euler-Lagrange equation for $y(x)$.

  Solve this equation for the case where

  $$f=x^{4} y^{\prime \prime 2}+4 y^{2} y^{\prime}$$

  in the interval $[0,1]$ and

  $$x^{2} y(x) \rightarrow 0, \quad x y(x) \rightarrow 1$$

  as $x \rightarrow 0$, whilst

  $$y(1)=2, \quad y^{\prime}(1)=0$$

  comment

2001

• 1.I.2H

  Methods | Part IB, 2001

  The even function $f(x)$ has the Fourier cosine series

  $$f(x)=\frac{1}{2} a_{0}+\sum_{n=1}^{\infty} a_{n} \cos n x$$

  in the interval $-\pi \leqslant x \leqslant \pi$. Show that

  $$\frac{1}{\pi} \int_{-\pi}^{\pi}(f(x))^{2} d x=\frac{1}{2} a_{0}^{2}+\sum_{n=1}^{\infty} a_{n}^{2}$$

  Find the Fourier cosine series of $x^{2}$ in the same interval, and show that

  $$\sum_{n=1}^{\infty} \frac{1}{n^{4}}=\frac{\pi^{4}}{90}$$

  comment

• 1.II.11H

  Methods | Part IB, 2001

  Use the substitution $y=x^{p}$ to find the general solution of

  $$\mathcal{L}_{x} y \equiv \frac{d^{2} y}{d x^{2}}-\frac{2}{x^{2}} y=0$$

  Find the Green's function $G(x, \xi), 0<\xi<\infty$, which satisfies

  $$\mathcal{L}_{x} G(x, \xi)=\delta(x-\xi)$$

  for $x>0$, subject to the boundary conditions $G(x, \xi) \rightarrow 0$ as $x \rightarrow 0$ and as $x \rightarrow \infty$, for each fixed $\xi$.

  Hence, find the solution of the equation

  $$\mathcal{L}_{x} y= \begin{cases}1, & 0 \leqslant x<1, \\ 0, & x>1\end{cases}$$

  subject to the same boundary conditions.

  Verify that both forms of your solution satisfy the appropriate equation and boundary conditions, and match at $x=1$.

  comment

• 2.I.2G

  Methods | Part IB, 2001

  Show that the symmetric and antisymmetric parts of a second-rank tensor are themselves tensors, and that the decomposition of a tensor into symmetric and antisymmetric parts is unique.

  For the tensor $A$ having components

  $$A=\left(\begin{array}{lll} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 1 & 2 & 3 \end{array}\right)$$

  find the scalar $a$, vector $\mathbf{p}$ and symmetric traceless tensor $B$ such that

  $$A \mathbf{x}=a \mathbf{x}+\mathbf{p} \wedge \mathbf{x}+B \mathbf{x}$$

  for every vector $\mathbf{x}$.

  comment

• 2.II.11G

  Methods | Part IB, 2001

  Explain what is meant by an isotropic tensor.

  Show that the fourth-rank tensor

  $$A_{i j k l}=\alpha \delta_{i j} \delta_{k l}+\beta \delta_{i k} \delta_{j l}+\gamma \delta_{i l} \delta_{j k}$$

  is isotropic for arbitrary scalars $\alpha, \beta$ and $\gamma$.

  Assuming that the most general isotropic tensor of rank 4 has the form $(*)$, or otherwise, evaluate

  $$B_{i j k l}=\int_{r<a} x_{i} x_{j} \frac{\partial^{2}}{\partial x_{k} \partial x_{l}}\left(\frac{1}{r}\right) d V$$

  where $\mathbf{x}$ is the position vector and $r=|\mathbf{x}|$.

  comment

• 3.I.2G

  Methods | Part IB, 2001

  Laplace's equation in the plane is given in terms of plane polar coordinates $r$ and $\theta$ in the form

  $$\nabla^{2} \phi \equiv \frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} \phi}{\partial \theta^{2}}=0$$

  In each of the cases

  $$\text { (i) } 0 \leqslant r \leqslant 1, \text { and (ii) } 1 \leqslant r<\infty \text {, }$$

  find the general solution of Laplace's equation which is single-valued and finite.

  Solve also Laplace's equation in the annulus $a \leqslant r \leqslant b$ with the boundary conditions

  $$\begin{aligned} &\phi=1 \quad \text { on } \quad r=a \text { for all } \theta \\ &\phi=2 \quad \text { on } \quad r=b \text { for all } \theta . \end{aligned}$$

  comment

• 3.II.12H

  Methods | Part IB, 2001

  Find the Fourier sine series representation on the interval $0 \leqslant x \leqslant l$ of the function

  $$f(x)= \begin{cases}0, & 0 \leqslant x<a \\ 1, & a \leqslant x \leqslant b \\ 0, & b<x \leqslant l\end{cases}$$

  The motion of a struck string is governed by the equation

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}, \quad \text { for } \quad 0 \leqslant x \leqslant l \quad \text { and } \quad t \geqslant 0$$

  subject to boundary conditions $y=0$ at $x=0$ and $x=l$ for $t \geqslant 0$, and to the initial conditions $y=0$ and $\frac{\partial y}{\partial t}=\delta\left(x-\frac{1}{4} l\right)$ at $t=0$.

  Obtain the solution $y(x, t)$ for this motion. Evaluate $y(x, t)$ for $t=\frac{1}{2} l / c$, and sketch it clearly.

  comment

• 4.I.2H

  Methods | Part IB, 2001

  The Legendre polynomial $P_{n}(x)$ satisfies

  $$\left(1-x^{2}\right) P_{n}^{\prime \prime}-2 x P_{n}^{\prime}+n(n+1) P_{n}=0, \quad n=0,1, \ldots,-1 \leqslant x \leqslant 1 .$$

  Show that $R_{n}(x)=P_{n}^{\prime}(x)$ obeys an equation which can be recast in Sturm-Liouville form and has the eigenvalue $(n-1)(n+2)$. What is the orthogonality relation for $R_{n}(x), R_{m}(x)$ for $n \neq m$ ?

  comment

• 4.II.11H

  Methods | Part IB, 2001

  A curve $y(x)$ in the $x y$-plane connects the points $(\pm a, 0)$ and has a fixed length $l, 2 a<l<\pi a$. Find an expression for the area $A$ of the surface of the revolution obtained by rotating $y(x)$ about the $x$-axis.

  Show that the area $A$ has a stationary value for

  $$y=\frac{1}{k}(\cosh k x-\cosh k a),$$

  where $k$ is a constant such that

  $$l k=2 \sinh k a .$$

  Show that the latter equation admits a unique positive solution for $k$.

  comment