Representation Theory
Representation Theory
Jump to year
Paper 1, Section II, I
(a) What does it mean to say that a representation of a group is completely reducible? State Maschke's theorem for representations of finite groups over fields of characteristic 0 . State and prove Schur's lemma. Deduce that if there exists a faithful irreducible complex representation of , then is cyclic.
(b) If is any finite group, show that the regular representation is faithful. Show further that for every finite simple group , there exists a faithful irreducible complex representation of .
(c) Which of the following groups have a faithful irreducible representation? Give brief justification of your answers.
(i) the cyclic groups a positive integer ;
(ii) the dihedral group ;
(iii) the direct product .
Paper 2, Section II, I
Let be a finite group and work over .
(a) Let be a faithful character of , and suppose that takes precisely different values as varies over all the elements of . Show that every irreducible character of is a constituent of one of the powers . [Standard properties of the Vandermonde matrix may be assumed if stated correctly.]
(b) Assuming that the number of irreducible characters of is equal to the number of conjugacy classes of , show that the irreducible characters of form a basis of the complex vector space of all class functions on . Deduce that are conjugate if and only if for all characters of .
(c) Let be a character of which is not faithful. Show that there is some irreducible character of such that for all integers .
Paper 3, Section II, I
In this question we work over .
(a) (i) Let be a subgroup of a finite group . Given an -space , define the complex vector space . Define, with justification, the -action on .
(ii) Write for the conjugacy class of . Suppose that breaks up into conjugacy classes of with representatives . If is a character of , write down, without proof, a formula for the induced character as a certain sum of character values .
(b) Define permutations by and let be the subgroup of . It is given that the elements of are all of the form for and that has order 21 .
(i) Find the orders of the centralisers and . Hence show that there are five conjugacy classes of .
(ii) Find all characters of degree 1 of by lifting from a suitable quotient group.
(iii) Let . By first inducing linear characters of using the formula stated in part (a)(ii), find the remaining irreducible characters of .
Paper 4, Section II, I
(a) Define the group . Sketch a proof of the classification of the irreducible continuous representations of . Show directly that the characters obey an orthogonality relation.
(b) Define the group .
(i) Show that there is a bijection between the conjugacy classes in and the subset of the real line. [If you use facts about a maximal torus , you should prove them.]
(ii) Write for the conjugacy class indexed by an element , where . Show that is homeomorphic to . [Hint: First show that is in bijection with .
(iii) Let be the parametrisation of conjugacy classes from part (i). Determine the representation of whose character is the function .
Paper 1, Section II, F
State and prove Maschke's theorem.
Let be the group of isometries of . Recall that is generated by the elements where and for .
Show that every non-faithful finite-dimensional complex representation of is a direct sum of subrepresentations of dimension at most two.
Write down a finite-dimensional complex representation of the group that is not a direct sum of one-dimensional subrepresentations. Hence, or otherwise, find a finitedimensional complex representation of that is not a direct sum of subrepresentations of dimension at most two. Briefly justify your answer.
[Hint: You may assume that any non-trivial normal subgroup of contains an element of the form for some .]
Paper 2, Section II, F
Let be the unique non-abelian group of order 21 up to isomorphism. Compute the character table of .
[You may find it helpful to think of as the group of matrices of the form with and . You may use any standard results from the course provided you state them clearly.]
Paper 3, Section II, F
State Mackey's restriction formula and Frobenius reciprocity for characters. Deduce Mackey's irreducibility criterion for an induced representation.
For show that if is the subgroup of consisting of the elements that fix , and is a complex representation of , then is not irreducible.
Paper 4, Section II, F
(a) State and prove Burnside's lemma. Deduce that if a finite group acts 2transitively on a set then the corresponding permutation character has precisely two (distinct) irreducible summands.
(b) Suppose that is a field with elements. Write down a list of conjugacy class representatives for . Consider the natural action of on the set of lines through the origin in . What values does the corresponding permutation character take on each conjugacy class representative in your list? Decompose this permutation character into irreducible characters.
Paper 1, Section II, I
(a) State and prove Schur's lemma over .
In the remainder of this question we work over .
(b) Let be the cyclic group of order 3 .
(i) Write the regular -module as a direct sum of irreducible submodules.
(ii) Find all the intertwining homomorphisms between the irreducible -modules. Deduce that the conclusion of Schur's lemma is false if we replace by .
(c) Henceforth let be a cyclic group of order . Show that
(i) if is even, the regular -module is a direct sum of two (non-isomorphic) 1dimensional irreducible submodules and (non-isomorphic) 2-dimensional irreducible submodules;
(ii) if is odd, the regular -module is a direct sum of one 1-dimensional irreducible submodule and (non-isomorphic) 2-dimensional irreducible submodules.
Paper 2, Section II, I
(a) For any finite group , let be a complete set of non-isomorphic complex irreducible representations of , with dimensions , respectively. Show that
(b) Let be the matrices
and let . Write .
(i) Prove that the derived subgroup .
(ii) Show that for all , and deduce that is a 2-group of order at most 32 .
(iii) Prove that the given representation of of degree 4 is irreducible.
(iv) Prove that has order 32 , and find all the irreducible representations of .
Paper 3, Section II, I
In this question all representations are complex and is a finite group.
(a) State and prove Mackey's theorem. State the Frobenius reciprocity theorem.
(b) Let be a finite -set and let be the corresponding permutation representation. Pick any orbit of on : it is isomorphic as a -set to for some subgroup of . Write down the character of .
(i) Let be the trivial representation of . Show that may be written as a direct sum
for some representation .
(ii) Using the results of (a) compute the character inner product in terms of the number of double cosets.
(iii) Now suppose that , so that . By writing as a direct sum of irreducible representations, deduce from (ii) that the representation is irreducible if and only if acts 2 -transitively. In that case, show that is not the trivial representation.
Paper 4, Section II, I
(a) What is meant by a compact topological group? Explain why is an example of such a group.
[In the following the existence of a Haar measure for any compact Hausdorff topological group may be assumed, if required.]
(b) Let be any compact Hausdorff topological group. Show that there is a continuous group homomorphism if and only if has an -dimensional representation over . [Here denotes the subgroup of preserving the standard (positive-definite) symmetric bilinear form.]
(c) Explicitly construct such a representation by showing that acts on the following vector space of matrices,
by conjugation.
Show that
(i) this subspace is isomorphic to ;
(ii) the trace map induces an invariant positive definite symmetric bilinear form;
(iii) is surjective with kernel . [You may assume, without proof, that is connected.]
Paper 1, Section II, I
(a) Define the derived subgroup, , of a finite group . Show that if is a linear character of , then ker . Prove that the linear characters of are precisely the lifts to of the irreducible characters of . [You should state clearly any additional results that you require.]
(b) For , you may take as given that the group
has order .
(i) Let . Show that if is any -th root of unity in , then there is a representation of over which sends
(ii) Find all the irreducible representations of .
(iii) Find the character table of .
Paper 2, Section II, I
(a) Suppose is a subgroup of a finite group is an irreducible character of and are the irreducible characters of . Show that in the restriction , the multiplicities satisfy
Determine necessary and sufficient conditions under which the inequality in ( ) is actually an equality.
(b) Henceforth suppose that is a (normal) subgroup of index 2 in , and that is an irreducible character of .
Lift the non-trivial linear character of to obtain a linear character of which satisfies
(i) Show that the following are equivalent:
(1) is irreducible;
(2) for some with ;
(3) the characters and of are not equal.
(ii) Suppose now that is irreducible. Show that if is an irreducible character of which satisfies
then either or
(iii) Suppose that is the sum of two irreducible characters of , say . If is an irreducible character of such that has or as a constituent, show that .
(c) Suppose that is a finite group with a subgroup of index 3 , and let be an irreducible character of . Prove that
Give examples to show that each possibility can occur, giving brief justification in each case.
Paper 3, Section II, I
State the row orthogonality relations. Prove that if is an irreducible character of the finite group , then divides the order of .
Stating clearly any additional results you use, deduce the following statements:
(i) Groups of order , where is prime, are abelian.
(ii) If is a group of order , where is prime, then either the degrees of the irreducible characters of are all 1 , or they are
(iii) No simple group has an irreducible character of degree 2 .
(iv) Let and be prime numbers with , and let be a non-abelian group of order . Then divides and has conjugacy classes.
Paper 4, Section II, I
Define and write down a complete list
of its continuous finite-dimensional irreducible representations. You should define all the terms you use but proofs are not required. Find the character of . State the Clebsch-Gordan formula.
(a) Stating clearly any properties of symmetric powers that you need, decompose the following spaces into irreducible representations of :
(i) ;
(ii) (with multiplicands);
(iii) .
(b) Let act on the space of complex matrices by
where is the block matrix . Show that this gives a representation of and decompose it into irreducible summands.
Paper 1, Section II, G
(a) Prove that if there exists a faithful irreducible complex representation of a finite group , then the centre is cyclic.
(b) Define the permutations by
and let .
(i) Using the relations and , prove that has order 18 .
(ii) Suppose that and are complex cube roots of unity. Prove that there is a (matrix) representation of over such that
(iii) For which values of is faithful? For which values of is irreducible?
(c) Note that is a normal subgroup of which is isomorphic to . By inducing linear characters of this subgroup, or otherwise, obtain the character table of .
Deduce that has the property that is cyclic but has no faithful irreducible representation over .
Paper 2, Section II, G
In this question you may assume the following result. Let be a character of a finite group and let . If is a rational number, then is an integer.
(a) If and are positive integers, we denote their highest common factor by . Let be an element of order in the finite group . Suppose that is conjugate to for all with and . Prove that is an integer for all characters of .
[You may use the following result without proof. Let be an th root of unity. Then
is an integer.]
Deduce that all the character values of symmetric groups are integers.
(b) Let be a group of odd order.
Let be an irreducible character of with . Prove that
where is an algebraic integer. Deduce that .
Paper 3, Section II, G
(a) State Burnside's theorem.
(b) Let be a non-trivial group of prime power order. Show that if is a non-trivial normal subgroup of , then .
Deduce that a non-abelian simple group cannot have an abelian subgroup of prime power index.
(c) Let be a representation of the finite group over . Show that is a linear character of . Assume that for some . Show that has a normal subgroup of index 2 .
Now let be a group of order , where is an odd integer. By considering the regular representation of , or otherwise, show that has a normal subgroup of index
Deduce that if is a non-abelian simple group of order less than 80 , then has order 60 .
Paper 4, Section II, G
Let and let be the vector space of complex homogeneous polynomials of degree in two variables.
(a) Prove that has the structure of an irreducible representation for .
(b) State and prove the Clebsch-Gordan theorem.
(c) Quoting without proof any properties of symmetric and exterior powers which you need, decompose and into irreducible -spaces.
Paper 1, Section II, I
Let be a normal subgroup of the finite group . Explain how a (complex) representation of gives rise to an associated representation of , and briefly describe which representations of arise this way.
Let be the group of order 54 which is given by
Find the conjugacy classes of . By observing that and are normal in , or otherwise, construct the character table of .
Paper 2, Section II, I
Show that the 1-dimensional (complex) characters of a finite group form a group under pointwise multiplication. Denote this group by . Show that if , the map from to is a character of , hence an element of . What is the kernel of the ?
Show that if is abelian the map is an isomorphism. Deduce, from the structure theorem for finite abelian groups, that the groups and are isomorphic as abstract groups.
Paper 3, Section II, I
(a) Let the finite group act on a finite set and let be the permutation character. If is 2 -transitive on , show that , where is an irreducible character of .
(b) Let , and let be the symmetric group acting naturally on the set . For any integer , write for the set of all -element subsets of , and let be the permutation character of the action of on . Compute the degree of . If , compute the character inner product .
Let if is even, and if is odd. Deduce that has distinct irreducible characters such that for all ,
(c) Let be the set of all ordered pairs with and . Let act on in the obvious way. Write for the permutation character of in this action. By considering inner products, or otherwise, prove that
where is an irreducible character. Calculate the degree of , and calculate its value on the elements and of .
Paper 4, Section II, I
Let be a proper normal subgroup of a finite group and let be an irreducible complex representation of . Show that either restricted to is a sum of copies of a single irreducible representation of , or else is induced from an irreducible representation of some proper subgroup of .
Recall that a -group is a group whose order is a power of the prime number . Deduce, by induction on the order of the group, or otherwise, that every irreducible complex representation of a -group is induced from a 1-dimensional representation of some subgroup.
[You may assume that a non-abelian -group has an abelian normal subgroup which is not contained in the centre of .]
Paper 1, Section II, F
(a) Let be a finite group and let be a representation of . Suppose that there are elements in such that the matrices and do not commute. Use Maschke's theorem to prove that is irreducible.
(b) Let be a positive integer. You are given that the dicyclic group
has order .
(i) Show that if is any th root of unity in , then there is a representation of over which sends
(ii) Find all the irreducible representations of .
(iii) Find the character table of .
[Hint: You may find it helpful to consider the cases odd and even separately.]
Paper 2, Section II,
Let be a finite group. Suppose that is a finite-dimensional complex representation of dimension . Let be arbitrary.
(i) Define the th symmetric power and the th exterior power and write down their respective dimensions.
Let and let be the eigenvalues of on . What are the eigenvalues of on and on ?
(ii) Let be an indeterminate. For any , define the characteristic polynomial of on by . What is the relationship between the coefficients of and the character of the exterior power?
Find a relation between the character of the symmetric power and the polynomial .
Paper 3, Section II, F
(a) State Mackey's theorem, defining carefully all the terms used in the statement.
(b) Let be a finite group and suppose that acts on the set .
If , we say that the action of on is -transitive if has at least elements and for every pair of -tuples and such that the are distinct elements of and the are distinct elements of , there exists with for every .
(i) Let have at least elements, where and let . Show that acts -transitively on if and only if acts transitively on and the stabiliser acts -transitively on .
(ii) Show that the permutation module can be decomposed as
where is the trivial module and is some -module.
(iii) Assume that , so that . Prove that is irreducible if and only if acts 2-transitively on . In that case show also that is not the trivial representation. [Hint: Pick any orbit of on ; it is isomorphic as a -set to for some subgroup . Consider the induced character
Paper 4, Section II, F
(a) Let be the circle group. Assuming any required facts about continuous functions from real analysis, show that every 1-dimensional continuous representation of is of the form
for some .
(b) Let , and let be a continuous representation of on a finitedimensional vector space .
(i) Define the character of , and show that .
(ii) Show that .
(iii) Let be the irreducible 4-dimensional representation of . Decompose into irreducible representations. Hence decompose the exterior square into irreducible representations.
Paper 1, Section II, H
(i) Let be any field and let . Let be the Jordan block
Compute for each .
(ii) Let be a cyclic group of order , and let be an algebraically closed field of characteristic . Determine all the representations of on vector spaces over , up to equivalence. Which are irreducible? Which do not split as a direct sum , with and
Paper 2, Section II, H
In this question work over . Let be a subgroup of . State Mackey's restriction formula, defining all the terms you use. Deduce Mackey's irreducibility criterion.
Let (the dihedral group of order ) and let (the cyclic subgroup of of order ). Write down the inequivalent irreducible characters of . Determine the values of for which the induced character is irreducible.
Paper 3, Section II, H
(i) State Frobenius' theorem for transitive permutation groups acting on a finite set. Define Frobenius group and show that any finite Frobenius group (with an appropriate action) satisfies the hypotheses of Frobenius' theorem.
(ii) Consider the group
where is prime, divides ( not necessarily prime), and has multiplicative order modulo (such elements exist since divides . Let be the subgroup of consisting of the powers of , so that . Write , and let be coset representatives for in .
(a) Show that has conjugacy classes and that a complete list of the classes comprises and .
(b) By observing that the derived subgroup , find 1-dimensional characters of . [Appropriate results may be quoted without proof.]
(c) Let . For denote by the character of defined by . By inducing these characters to , or otherwise, find distinct irreducible characters of degree .
Paper 4, Section II, H
Let .
(i) Sketch a proof that there is an isomorphism of topological groups
(ii) Let be the irreducible complex representation of of dimension 3. Compute the character of the (symmetric power) representation of for any . Show that the dimension of the space of invariants , meaning the subspace of where acts trivially, is 1 for even and 0 for odd. [Hint: You may find it helpful to restrict to the unit circle subgroup . The irreducible characters of may be quoted without proof.]
Using the fact that yields the standard 3-dimensional representation of , show that . Deduce that the ring of complex polynomials in three variables which are invariant under the action of is a polynomial ring in one generator. Find a generator for this polynomial ring.
Paper 1, Section II, 19G
State and prove Maschke's Theorem for complex representations of finite groups.
Without using character theory, show that every irreducible complex representation of the dihedral group of order , has dimension at most two. List the irreducible complex representations of up to isomorphism.
Let be the set of vertices of a regular pentagon with the usual action of . Explicitly decompose the permutation representation into a direct sum of irreducible subrepresentations.
Paper 2, Section II, G
Recall that a regular icosahedron has 20 faces, 30 edges and 12 vertices. Let be the group of rotational symmetries of a regular icosahedron.
Compute the conjugacy classes of . Hence, or otherwise, construct the character table of . Using the character table explain why must be a simple group.
[You may use any general theorems provided that you state them clearly.]
Paper 3, Section II, G
Suppose that and are complex representations of the finite groups and respectively. Use and to construct a representation of on and show that its character satisfies
for each .
Prove that if and are irreducible then is irreducible as a representation of . Moreover, show that every irreducible complex representation of arises in this way.
Is it true that every complex representation of is of the form with a complex representation of for Justify your answer.
Paper 4, Section II, G
State and prove Burnside's -theorem.
Paper 1, Section II, 19H
Write down the character table of .
Suppose that is a group of order 60 containing 24 elements of order 5,20 elements of order 3 and 15 elements of order 2 . Calculate the character table of , justifying your answer.
[You may assume the formula for induction of characters, provided you state it clearly.]
Paper 2, Section II, H
Suppose that is a finite group. Define the inner product of two complex-valued class functions on . Prove that the characters of the irreducible representations of form an orthonormal basis for the space of complex-valued class functions.
Suppose that is a prime and is the field of elements. Let . List the conjugacy classes of .
Let act naturally on the set of lines in the space . Compute the corresponding permutation character and show that it is reducible. Decompose this character as a sum of two irreducible characters.
Paper 3, Section II, H
Show that every complex representation of a finite group is equivalent to a unitary representation. Let be a character of some finite group and let . Explain why there are roots of unity such that
for all integers .
For the rest of the question let be the symmetric group on some finite set. Explain why whenever is coprime to the order of .
Prove that .
State without proof a formula for when is irreducible. Is there an irreducible character of degree at least 2 with for all ? Explain your answer.
[You may assume basic facts about the symmetric group, and about algebraic integers, without proof. You may also use without proof the fact that for any th root of unity
Paper 4, Section II, H
Write an essay on the finite-dimensional representations of , including a proof of their complete reducibility, and a description of the irreducible representations and the decomposition of their tensor products.
Paper 1, Section II, I
Let be a finite group and its centre. Suppose that has order and has order . Suppose that is a complex irreducible representation of degree
(i) For , show that is a scalar multiple of the identity.
(ii) Deduce that .
(iii) Show that, if is faithful, then is cyclic.
[Standard results may be quoted without proof, provided they are stated clearly.]
Now let be a group of order 18 containing an elementary abelian subgroup of order 9 and an element of order 2 with for each . By considering the action of on an irreducible -module prove that has no faithful irreducible complex representation.
Paper 2, Section II, I
State Maschke's Theorem for finite-dimensional complex representations of the finite group . Show by means of an example that the requirement that be finite is indispensable.
Now let be a (possibly infinite) group and let be a normal subgroup of finite index in . Let be representatives of the cosets of in . Suppose that is a finite-dimensional completely reducible -module. Show that
(i) if is a -submodule of and , then the set is a -submodule of ;
(ii) if is a -submodule of , then is a -submodule of ;
(iii) is completely reducible regarded as a -module.
Hence deduce that if is an irreducible character of the finite group then all the constituents of have the same degree.
Paper 3, Section II, I
Define the character of a finite group which is induced by a character of a subgroup of .
State and prove the Frobenius reciprocity formula for the characters of and of .
Now suppose that has index 2 in . An irreducible character of and an irreducible character of are said to be 'related' if
Show that each of degree is either 'monogamous' in the sense that it is related to one (of degree ), or 'bigamous' in the sense that it is related to precisely two distinct characters (of degree . Show that each is related to one bigamous , or to two monogamous characters (of the same degree).
Write down the degrees of the complex irreducible characters of the alternating group . Find the degrees of the irreducible characters of a group containing as a subgroup of index 2 , distinguishing two possible cases.
Paper 4, Section II, I
Define the groups and .
Show that acts on the vector space of complex matrices of the form
by conjugation. Denote the corresponding representation of on by .
Prove the following assertions about this action:
(i) The subspace is isomorphic to .
(ii) The pairing defines a positive definite non-degenerate invariant bilinear form.
(iii) The representation maps into . [You may assume that for any compact group , and any , there is a continuous group homomorphism if and only if has an -dimensional representation over .]
Write down an orthonormal basis for and use it to show that is surjective with kernel .
Use the isomorphism to write down a list of irreducible representations of in terms of irreducibles for . [Detailed explanations are not required.]
Paper 1, Section II, F
(i) Let be a normal subgroup of the finite group . Without giving detailed proofs, define the process of lifting characters from to . State also the orthogonality relations for .
(ii) Let be the following two permutations in ,
and let , a subgroup of . Prove that is a group of order 12 and list the conjugacy classes of . By identifying a normal subgroup of of index 4 and lifting irreducible characters, calculate all the linear characters of . Calculate the complete character table of . By considering 6 th roots of unity, find explicit matrix representations affording the non-linear characters of .
Paper 2, Section II, F
Define the concepts of induction and restriction of characters. State and prove the Frobenius Reciprocity Theorem.
Let be a subgroup of and let . We write for the conjugacy class of in , and write for the centraliser of in . Suppose that breaks up into conjugacy classes of , with representatives .
Let be a character of . Writing for the induced character, prove that
(i) if no element of lies in , then ,
(ii) if some element of lies in , then
Let and let , where and dihedral group and write down its character table. Restrict each -conjugacy class to and calculate the -conjugacy classes contained in each restriction. Given a character of , express Ind in terms of , where runs through a set of conjugacy classes of . Use your calculation to find the values of all the irreducible characters of induced to .
Paper 3, Section II, F
Show that the degree of a complex irreducible character of a finite group is a factor of the order of the group.
State and prove Burnside's theorem. You should quote clearly any results you use.
Prove that for any group of odd order having precisely conjugacy classes, the integer is divisible by 16 .
Paper 4, Section II, F
Define the circle group . Give a complete list of the irreducible representations of
Define the spin group , and explain briefly why it is homeomorphic to the unit 3-sphere in . Identify the conjugacy classes of and describe the classification of the irreducible representations of . Identify the characters afforded by the irreducible representations. You need not give detailed proofs but you should define all the terms you use.
Let act on the space of complex matrices by conjugation, where acts by
in which denotes the block diagonal matrix . Show that this gives a representation of and decompose it into irreducibles.
Paper 1, Section II, F
Let be a finite group, and suppose acts on the finite sets . Define the permutation representation corresponding to the action of on , and compute its character . State and prove "Burnside's Lemma".
Let act on via the usual diagonal action. Prove that the character inner product is equal to the number of -orbits on .
Hence, or otherwise, show that the general linear group of invertible matrices over the finite field of elements has an irreducible complex representation of dimension equal to .
Let be the symmetric group acting on the set . Denote by the set of all 2-element subsets of elements of , with the natural action of . If , decompose into irreducible complex representations, and determine the dimension of each irreducible constituent. What can you say when ?
Paper 2, Section II, 19F
(i) Let be a finite group. Show that
(1) If is an irreducible character of then so is its conjugate .
(2) The product of any two characters of is again a character of .
(3) If and are irreducible characters of then
(ii) If is a character of the finite group , define and . For prove that
(iii) A certain group of order 24 has precisely seven conjugacy classes with representatives ; further, has a character with values as follows:
where .
It is given that are conjugate to respectively.
Determine and , and show that both are irreducible.
Paper 3, Section II, F
Let . Let be the complex vector space of homogeneous polynomials of degree in two variables . Define the usual left action of on and denote by the representation induced by this action. Describe the character afforded by .
Quoting carefully any results you need, show that
(i) The representation has dimension and is irreducible for ;
(ii) Every finite-dimensional continuous irreducible representation of is one of the ;
(iii) is isomorphic to its dual .
Paper 4, Section II, F
Let be finite groups.
(a) Let be a representation of affording the character . Define the restriction, of to .
Suppose is irreducible and suppose affords the character . Let be the irreducible characters of . Prove that , where the nonnegative integers satisfy the inequality
Prove that there is equality in (1) if and only if for all elements of which lie outside .
(b) Let be a class function of . Define the induced class function, .
State the Frobenius reciprocity theorem for class functions and deduce that if is a character of then is a character of .
Assuming is a character, identify a -space affording the character . Briefly justify your answer.
(c) Let be the irreducible characters of and let be an irreducible character of . Show that the integers , which are given by , satisfy
1.II.19G
For a complex representation of a finite group , define the action of on the dual representation . If denotes the character of , compute the character of .
[Your formula should express just in terms of the character .]
Using your formula, how can you tell from the character whether a given representation is self-dual, that is, isomorphic to the dual representation?
Let be an irreducible representation of . Show that the trivial representation occurs as a summand of with multiplicity either 0 or 1 . Show that it occurs once if and only if is self-dual.
For a self-dual irreducible representation , show that either has a nondegenerate -invariant symmetric bilinear form or a nondegenerate -invariant alternating bilinear form, but not both.
If is an irreducible self-dual representation of odd dimension , show that the corresponding homomorphism is conjugate to a homomorphism into the orthogonal group . Here means the subgroup of that preserves a nondegenerate symmetric bilinear form on .
2.II.19G
A finite group of order 360 has conjugacy classes of sizes . The values of four of its irreducible characters are given in the following table.
Complete the character table.
[Hint: it will not suffice just to use orthogonality of characters.]
Deduce that the group is simple.
3.II.19G
Let denote the irreducible representation of ; thus has dimension 3. Compute the character of the representation of for any . Compute the dimension of the invariants , meaning the subspace of where acts trivially.
Hence, or otherwise, show that the ring of complex polynomials in three variables which are invariant under the action of is a polynomial ring. Find a generator for this polynomial ring.
4.II.19G
(a) Let be a normal subgroup of a finite group , and let be an irreducible representation of . Show that either restricted to is isotypic (a sum of copies of one irreducible representation of , or else is induced from an irreducible representation of some proper subgroup of .
(b) Using (a), show that every (complex) irreducible representation of a -group is induced from a 1-dimensional representation of some subgroup.
[You may assume that a nonabelian -group has an abelian normal subgroup which is not contained in the centre of .]
1.II.19H
A finite group has seven conjugacy classes and the values of five of its irreducible characters are given in the following table.
Calculate the number of elements in the various conjugacy classes and complete the character table.
[You may not identify with any known group, unless you justify doing so.]
2.II.19H
Let be a finite group and let be its centre. Show that if is a complex irreducible representation of , assumed to be faithful (that is, the kernel of is trivial), then is cyclic.
Now assume that is a p-group (that is, the order of is a power of the prime , and assume that is cyclic. If is a faithful representation of , show that some irreducible component of is faithful.
[You may use without proof the fact that, since is a p-group, is non-trivial and any non-trivial normal subgroup of intersects non-trivially.]
Deduce that a finite -group has a faithful irreducible representation if and only if its centre is cyclic.
3.II.19H
Let be a finite group with a permutation action on the set . Describe the corresponding permutation character . Show that the multiplicity in of the principal character equals the number of orbits of on .
Assume that is transitive on , with . Show that contains an element which is fixed-point-free on , that is, for all in .
Assume that , with an irreducible character of , for some natural number . Show that .
[You may use without proof any facts about algebraic integers, provided you state them correctly.]
Explain how the action of on induces an action of on . Assume that has orbits on . If now
with distinct irreducible characters of , and natural numbers, show that . Deduce that, if , then and .
4.II.19H
Write an essay on the representation theory of .
Your answer should include a description of each irreducible representation and an explanation of how to decompose arbitrary representations into a direct sum of these.
1.II.19F
(a) Let be a finite group and a finite set on which acts. Define the permutation representation and compute its character.
(b) Let and be the following subgroups of , where is a prime,
(i) Decompose into irreducible representations.
(ii) Let be a non-trivial, one-dimensional representation. Determine the character of the induced representation , and decompose into irreducible representations.
(iii) List all of the irreducible representations of and show that your list is complete.
2.II.19F
(a) Let be , the symmetric group on four letters. Determine the character table of .
[Begin by listing the conjugacy classes and their orders.]
(b) For each irreducible representation of , decompose into irreducible representations. You must justify your answer.
3.II.19F
(a) Let , and let be the space of homogeneous polynomials of degree in the variables and . Thus . Define the action of on and show that is an irreducible representation of .
(b) Decompose into irreducible representations. Decompose and into irreducible representations.
(c) Given any representation of a group , define the dual representation . Show that is isomorphic to as a representation of .
[You may use any results from the lectures provided that you state them clearly.]
4.II.19F
In this question, all vector spaces will be complex.
(a) Let be a finite abelian group.
(i) Show directly from the definitions that any irreducible representation must be one-dimensional.
(ii) Show that has a faithful one-dimensional representation if and only if is cyclic.
(b) Now let be an arbitrary finite group and suppose that the centre of is nontrivial. Write for this centre.
(i) Let be an irreducible representation of . Show that , where is an irreducible representation of .
(ii) Show that every irreducible representation of occurs in this way.
(iii) Suppose that is not a cyclic group. Show that there does not exist an irreducible representation of such that every irreducible representation occurs as a summand of for some .
1.II.19G
Let the finite group act on finite sets and , and denote by the associated permutation representations on the spaces of complex functions on and . Call their characters and .
(i) Show that the inner product is the number of orbits for the diagonal action of on .
(ii) Assume that , and let be the subspace of those functions whose values sum to zero. By considering , show that is irreducible if and only if the -action on is doubly transitive: this means that for any two pairs and of points in with and , there exists some with and .
(iii) Let now acting on the set . Call the set of 2element subsets of , with the natural action of . If , show that decomposes under into three irreducible representations, one of which is the trivial representation and another of which is . What happens when ?
[Hint: Consider and .]
2.II.19G
Let be a finite group and the set of its irreducible characters. Also choose representatives for the conjugacy classes, and denote by their centralisers.
(i) State the orthogonality and completeness relations for the .
(ii) Using Part (i), or otherwise, show that
(iii) Let be the matrix with . Prove that
(iv) Show that is either real or purely imaginary, explaining when each situation occurs.
[Hint for (iv): Consider the effect of complex conjugation on the rows of the matrix A.]
3.II.19G
Let be the group with 21 elements generated by and , subject to the relations and
(i) Find the conjugacy classes of .
(ii) Find three non-isomorphic one-dimensional representations of .
(iii) For a subgroup of a finite group , write down (without proof) the formula for the character of the -representation induced from a representation of .
(iv) By applying Part (iii) to the case when is the subgroup of , find the remaining irreducible characters of .
4.II.19G
(i) State and prove the Weyl integration formula for .
(ii) Determine the characters of the symmetric powers of the standard 2-dimensional representation of and prove that they are irreducible.
[Any general theorems from the course may be used.]
B1.6
(a) Show that every irreducible complex representation of an abelian group is onedimensional.
(b) Show, by example, that the analogue of (a) fails for real representations.
(c) Let the cyclic group of order act on by cyclic permutation of the standard basis vectors. Decompose this representation explicitly into irreducibles.
B2.6
Let be a group with three generators and relations , and where is a prime number.
(a) Show that . Show that the conjugacy classes of are the singletons and the sets , as range from 0 to , but .
(b) Find 1-dimensional representations of .
(c) Let be a th root of unity. Show that the following defines an irreducible representation of on :
where the are the standard basis vectors of .
(d) Show that (b) and (c) cover all irreducible isomorphism classes.
B3.5
Compute the character table for the group of even permutations of five elements. You may wish to follow the steps below.
(a) List the conjugacy classes in and their orders.
(b) acts on by permuting the standard basis vectors. Show that splits as , where is the trivial 1-dimensional representation and is irreducible.
(c) By using the formula for the character of the symmetric square ,
decompose to produce a 5-dimensional, irreducible representation, and find its character.
(d) Show that the exterior square decomposes into two distinct irreducibles and compute their characters, to complete the character table of .
[Hint: You can save yourself some computational effort if you can explain why the automorphism of , defined by conjugation by a transposition in , must swap the two summands of .]
B4.2
Write an essay on the finite-dimensional representations of , including a proof of their complete reducibility, and a description of the irreducible representations and the decomposition of their tensor products.
B1.6
Define the inner product of two class functions from the finite group into the complex numbers. Prove that characters of the irreducible representations of form an orthonormal basis for the space of class functions.
Consider the representation of the symmetric group by permutation matrices. Show that splits as a direct sum where 1 denotes the trivial representation. Is the -dimensional representation irreducible?
B2.6
Let be the space of homogeneous polynomials of degree in two variables and . Define a left action of on the space of polynomials by setting
where and .
Show that
(a) the representations are irreducible,
(b) the representations exhaust the irreducible representations of , and
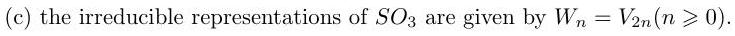
B3.5
If and are representations of the finite groups and respectively, define the tensor product as a representation of the group and show that its character is given by
Prove that
(a) if and are irreducible, then is an irreducible representation of ;
(b) each irreducible representation of is equivalent to a representation where each is irreducible
Is every representation of the tensor product of a representation of and a representation of ?
B4.2
Assume that the group of matrices of determinant 1 with entries from the field has presentation
Show that the subgroup generated by is central and that the quotient group can be identified with the alternating group . Assuming further that has seven conjugacy classes find the character table.
Is it true that every irreducible character is induced up from the character of a 1-dimensional representation of some subgroup?
[Hint: You may find it useful to note that may be regarded as a subgroup of , providing a faithful 2-dimensional representation; the subgroup generated by and is the quaternion group of order 8 , acting irreducibly.]
B1.6
Construct the character table of the symmetric group , explaining the steps in your construction.
Use the character table to show that the alternating group is the only non-trivial normal subgroup of .
B2.6
State and prove Schur's Lemma. Deduce that the centre of a finite group with a faithful irreducible complex representation is cyclic and that consists of scalar transformations.
Let be the subgroup of order 18 of the symmetric group given by
Show that has a normal subgroup of order 9 and four normal subgroups of order 3 . By considering quotients, show that has two representations of dimension 1 and four inequivalent irreducible representations of degree 2 . Deduce that has no faithful irreducible complex representations.
Show finally that if is a finite group with trivial centre and is a subgroup of with non-trivial centre, then any faithful representation of is reducible on restriction to .
B3.5
Let be a finite group acting on a finite set . Define the permutation representation of and compute its character . Prove that equals the number of orbits of on . If acts also on the finite set , with character , show that equals the number of orbits of on .
Now let be the symmetric group acting naturally on the set , and let be the set of all -element subsets of . Let be the permutation character of on . Prove that
Deduce that the class functions
are irreducible characters of , for .
B4.2
Write an essay on the representation theory of .
B1.6
Compute the character table of (begin by listing the conjugacy classes and their orders).
[It is not enough to write down the result; you must justify your answer.]
B2.6
(i) Let be a group, and and finite -sets. Define the permutation representation and compute its character. Show that
is equal to the number of -orbits in .
(ii) Let , and
be the set of 2 -element subsets of . Decompose into irreducibles, and determine the dimension of each irreducible constituent.
B3.5
Let , and be the vector space of homogeneous polynomials of degree in the variables and .
(i) Define the action of on , and prove that is an irreducible representation of .
(ii) Decompose into irreducible representations of . Briefly justify your answer.
(iii) acts on the vector space of complex matrices via
Decompose this representation into irreducible representations.
B4.2
Let be the Heisenberg group of order . This is the subgroup
of matrices over the finite field ( prime). Let be the subgroup of of such matrices with .
(i) Find all one dimensional representations of .
[You may assume without proof that is equal to the set of matrices in with
(ii) Let be a non-trivial one dimensional representation of , and define a one dimensional representation of by
Show that is irreducible.
(iii) List all the irreducible representations of and explain why your list is complete.