Part II, 2003

Algebraic Curves

• B2.10

  Algebraic Curves | Part II, 2003

  (a) For which polynomials $f(x)$ of degree $d>0$ does the equation $y^{2}=f(x)$ define a smooth affine curve?

  (b) Now let $C$ be the completion of the curve defined in (a) to a projective curve. For which polynomials $f(x)$ of degree $d>0$ is $C$ a smooth projective curve?

  (c) Suppose that $C$, defined in (b), is a smooth projective curve. Consider a map $p: C \rightarrow \mathbb{P}^{1}$, given by $p(x, y)=x$. Find the degree and the ramification points of $p$.

  comment

• B3.10

  Algebraic Curves | Part II, 2003

  (a) Let $X \subseteq \mathbb{A}^{n}$ be an affine algebraic variety. Define the tangent space $T_{p} X$ for $p \in X$. Show that the set

  $$\left\{p \in X \mid \operatorname{dim} T_{p} X \geqslant d\right\}$$

  is closed, for every $d \geqslant 0$.

  (b) Let $C$ be an irreducible projective curve, $p \in C$, and $f: C \backslash\{p\} \rightarrow \mathbb{P}^{n}$ a rational map. Show, carefully quoting any theorems that you use, that if $C$ is smooth at $p$ then $f$ extends to a regular map at $p$.

  comment

• B4.9

  Algebraic Curves | Part II, 2003

  Let $X$ be a smooth curve of genus 0 over an algebraically closed field $k$. Show that $k(X)=k\left(\mathbb{P}^{1}\right) .$

  Now let $C$ be a plane projective curve defined by an irreducible homogeneous cubic polynomial.

  (a) Show that if $C$ is smooth then $C$ is not isomorphic to $\mathbb{P}^{1}$. Standard results on the canonical class may be assumed without proof, provided these are clearly stated.

  (b) Show that if $C$ has a singularity then there exists a non-constant morphism from $\mathbb{P}^{1}$ to $C$.

  comment

Algebraic Topology

• B2.8

  Algebraic Topology | Part II, 2003

  Define the fundamental group of a topological space and explain briefly why a continuous map gives rise to a homomorphism between fundamental groups.

  Let $X$ be a subspace of the Euclidean space $\mathbb{R}^{3}$ which contains all of the points $(x, y, 0)$ with $(x, y) \neq(0,0)$, and which does not contain any of the points $(0,0, z)$. Show that $X$ has an infinite fundamental group.

  comment

• B3.7

  Algebraic Topology | Part II, 2003

  Define a covering map. Prove that any covering map induces an injective homomorphisms of fundamental groups.

  Show that there is a non-trivial covering map of the real projective plane. Explain how to use this to find the fundamental group of the real projective plane.

  comment

• B4.5

  Algebraic Topology | Part II, 2003

  State the Mayer-Vietoris theorem. You should give the definition of all the homomorphisms involved.

  Compute the homology groups of the union of the 2 -sphere with the line segment from the North pole to the South pole.

  comment

Algorithms and Networks

• A2.10

  Algorithms and Networks | Part II, 2003

  (i) Consider a network with node set $N$ and set of directed arcs $A$ equipped with functions $d^{+}: A \rightarrow \mathbb{Z}$ and $d^{-}: A \rightarrow \mathbb{Z}$ with $d^{-} \leqslant d^{+}$. Given $u: N \rightarrow \mathbb{R}$ we define the differential $\Delta u: A \rightarrow \mathbb{R}$ by $\Delta u(j)=u\left(i^{\prime}\right)-u(i)$ for $j=\left(i, i^{\prime}\right) \in A$. We say that $\Delta u$ is a feasible differential if

  $$d^{-}(j) \leqslant \Delta u(j) \leqslant d^{+}(j) \text { for all } j \in A$$

  Write down a necessary and sufficient condition on $d^{+}, d^{-}$for the existence of a feasible differential and prove its necessity.

  Assuming Minty's Lemma, describe an algorithm to construct a feasible differential and outline how this algorithm establishes the sufficiency of the condition you have given.

  (ii) Let $E \subseteq S \times T$, where $S, T$ are finite sets. A matching in $E$ is a subset $M \subseteq E$ such that, for all $s, s^{\prime} \in S$ and $t, t^{\prime} \in T$,

  $$\begin{array}{lll} (s, t),\left(s^{\prime}, t\right) \in M & \text { implies } & s=s^{\prime} \\ (s, t),\left(s, t^{\prime}\right) \in M & \text { implies } & t=t^{\prime} \end{array}$$

  A matching $M$ is maximal if for any other matching $M^{\prime}$ with $M \subseteq M^{\prime}$ we must have $M=M^{\prime}$. Formulate the problem of finding a maximal matching in $E$ in terms of an optimal distribution problem on a suitably defined network, and hence in terms of a standard linear optimization problem.

  [You may assume that the optimal distribution subject to integer constraints is integervalued.]

  comment

• A3.10

  Algorithms and Networks | Part II, 2003

  (i) Consider the problem

  $$\begin{aligned} \operatorname{minimize} & f(x) \\ \text { subject to } & h(x)=b, \quad x \in X, \end{aligned}$$

  where $f: \mathbb{R}^{n} \rightarrow \mathbb{R}, h: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}, X \subseteq \mathbb{R}^{n}$ and $b \in \mathbb{R}^{m}$. State and prove the Lagrangian sufficiency theorem.

  In each of the following cases, where $n=2, m=1$ and $X=\{(x, y): x, y \geqslant 0\}$, determine whether the Lagrangian sufficiency theorem can be applied to solve the problem:

  (ii) Consider the problem in $\mathbb{R}^{n}$

  $$\begin{aligned} \operatorname{minimize} & \frac{1}{2} x^{T} Q x+c^{T} x \\ \text { subject to } & A x=b \end{aligned}$$

  where $Q$ is a positive-definite symmetric $n \times n$ matrix, $A$ is an $m \times n$ matrix, $c \in \mathbb{R}^{n}$ and $b \in \mathbb{R}^{m}$. Explain how to reduce this problem to the solution of simultaneous linear equations.

  Consider now the problem

  $$\begin{aligned} \operatorname{minimize} & \frac{1}{2} x^{T} Q x+c^{T} x \\ \text { subject to } & A x \geqslant b \end{aligned}$$

  Describe the active set method for its solution.

  Consider the problem

  $$\begin{aligned} \operatorname{minimize} &(x-a)^{2}+(y-b)^{2}+x y \\ \text { subject to } & 0 \leqslant x \leqslant 1 \text { and } 0 \leqslant y \leqslant 1 \end{aligned}$$

  where $a, b \in \mathbb{R}$. Draw a diagram partitioning the $(a, b)$-plane into regions according to which constraints are active at the minimum.

  $$\begin{aligned} & \text { (a) } \quad f(x, y)=-x, \quad h(x, y)=x^{2}+y^{2}, \quad b=1 \text {; } \\ & \text { (b) } \quad f(x, y)=e^{-x y}, \quad h(x)=x, \quad b=0 \text {. } \end{aligned}$$

  comment

• A4.11

  Algorithms and Networks | Part II, 2003

  Define the optimal distribution problem. State what it means for a circuit $P$ to be flow-augmenting, and what it means for $P$ to be unbalanced. State the optimality theorem for flows. Describe the simplex-on-a-graph algorithm, giving a brief justification of its stopping rules.

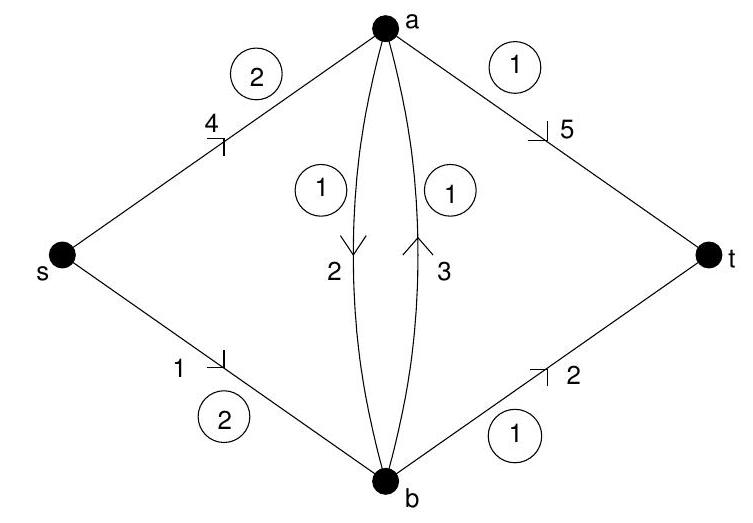
  Consider the problem of finding, in the network shown below, a minimum-cost flow from $s$ to $t$ of value 2 . Here the circled numbers are the upper arc capacities, the lower arc capacities all being zero, and the uncircled numbers are costs. Apply the simplex-on-agraph algorithm to solve this problem, taking as initial flow the superposition of a unit flow along the path $s,(s, a), a,(a, t), t$ and a unit flow along the path $s,(s, a), a,(a, b), b,(b, t), t$.

  

  Part II 2003

  comment

Applications of Quantum Mechanics

• B1.23

  Applications of Quantum Mechanics | Part II, 2003

  Define the differential cross section $\frac{d \sigma}{d \Omega}$. Show how it may be related to a scattering amplitude $f$ defined in terms of the behaviour of a wave function $\psi$ satisfying suitable boundary conditions as $r=|\mathbf{r}| \rightarrow \infty$.

  For a particle scattering off a potential $V(r)$ show how $f(\theta)$, where $\theta$ is the scattering angle, may be expanded, for energy $E=\hbar^{2} k^{2} / 2 m$, as

  $$f(\theta)=\sum_{\ell=0}^{\infty} f_{\ell}(k) P_{\ell}(\cos \theta),$$

  and find $f_{\ell}(k)$ in terms of the phase shift $\delta_{\ell}(k)$. Obtain the optical theorem relating $\sigma_{\text {total }}$ and $f(0)$.

  Suppose that

  $$e^{2 i \delta_{1}}=\frac{E-E_{0}-\frac{1}{2} i \Gamma}{E-E_{0}+\frac{1}{2} i \Gamma}$$

  Why for $E \approx E_{0}$ may $f_{1}(k)$ be dominant, and what is the expected behaviour of $\frac{d \sigma}{d \Omega}$ for $E \approx E_{0}$ ?

  [For large $r$

  $$e^{i k r \cos \theta} \sim \frac{1}{2 i k r} \sum_{\ell=0}^{\infty}(2 \ell+1)\left((-1)^{\ell+1} e^{-i k r}+e^{i k r}\right) P_{\ell}(\cos \theta)$$

  Legendre polynomials satisfy

  $$\left.\int_{-1}^{1} P_{\ell}(t) P_{\ell^{\prime}}(t) d t=\frac{2}{2 \ell+1} \delta_{\ell \ell^{\prime}} \cdot\right]$$

  comment

• B2.22

  Applications of Quantum Mechanics | Part II, 2003

  The Hamiltonian $H_{0}$ for a single electron atom has energy eigenstates $\left|\psi_{n}\right\rangle$ with energy eigenvalues $E_{n}$. There is an interaction with an electromagnetic wave of the form

  $$H_{1}=-e \mathbf{r} \cdot \boldsymbol{\epsilon} \cos (\mathbf{k} \cdot \mathbf{r}-\omega t), \quad \omega=|\mathbf{k}| c,$$

  where $\boldsymbol{\epsilon}$ is the polarisation vector. At $t=0$ the atom is in the state $\left|\psi_{0}\right\rangle$. Find a formula for the probability amplitude, to first order in $e$, to find the atom in the state $\left|\psi_{1}\right\rangle$ at time $t$. If the atom has a size $a$ and $|\mathbf{k}| a \ll 1$ what are the selection rules which are relevant? For $t$ large, under what circumstances will the transition rate be approximately constant?

  [You may use the result

  $$\left.\int_{-\infty}^{\infty} \frac{\sin ^{2} \lambda t}{\lambda^{2}} d \lambda=\pi|t| . \quad\right]$$

  comment

• B3.23

  Applications of Quantum Mechanics | Part II, 2003

  Consider the two Hamiltonians

  $$\begin{aligned} &H_{1}=\frac{\mathbf{p}^{2}}{2 m}+V(|\mathbf{r}|), \\ &H_{2}=\frac{\mathbf{p}^{2}}{2 m}+\sum_{n_{i} \in \mathbb{Z}} V\left(\left|\mathbf{r}-n_{1} \mathbf{a}_{1}-n_{2} \mathbf{a}_{2}-n_{3} \mathbf{a}_{3}\right|\right), \end{aligned}$$

  where $\mathbf{a}_{i}$ are three linearly independent vectors. For each of the Hamiltonians $H=H_{1}$ and $H=H_{2}$, what are the symmetries of $H$ and what unitary operators $U$ are there such that $U H U^{-1}=H$ ?

  For $\mathrm{H}_{2}$ derive Bloch's theorem. Suppose that $H_{1}$ has energy eigenfunction $\psi_{0}(\mathbf{r})$ with energy $E_{0}$ where $\psi_{0}(\mathbf{r}) \sim N e^{-K r}$ for large $r=|\mathbf{r}|$. Assume that $K\left|\mathbf{a}_{i}\right| \gg 1$ for each $i$. In a suitable approximation derive the energy eigenvalues for $H_{2}$ when $E \approx E_{0}$. Verify that the energy eigenfunctions and energy eigenvalues satisfy Bloch's theorem. What happens if $K\left|\mathbf{a}_{i}\right| \rightarrow \infty$ ?

  comment

• B4.24

  Applications of Quantum Mechanics | Part II, 2003

  Atoms of mass $m$ in an infinite one-dimensional periodic array, with interatomic spacing $a$, have perturbed positions $x_{n}=n a+y_{n}$, for integer $n$. The potential between neighbouring atoms is

  $$\frac{1}{2} \lambda\left(x_{n+1}-x_{n}-a\right)^{2}$$

  for positive constant $\lambda$. Write down the Lagrangian for the variables $y_{n}$. Find the frequency $\omega(k)$ of a normal mode of wavenumber $k$. Define the Brillouin zone and explain why $k$ may be restricted to lie within it.

  Assume now that the array is periodically-identified, so that there are effectively only $N$ atoms in the array and the atomic displacements $y_{n}$ satisfy the periodic boundary conditions $y_{n+N}=y_{n}$. Determine the allowed values of $k$ within the Brillouin zone. Show, for allowed wavenumbers $k$ and $k^{\prime}$, that

  $$\sum_{n=0}^{N-1} e^{i n\left(k-k^{\prime}\right) a}=N \delta_{k, k^{\prime}}$$

  By writing $y_{n}$ as

  $$y_{n}=\frac{1}{\sqrt{N}} \sum_{k} q_{k} e^{i n k a}$$

  where the sum is over allowed values of $k$, find the Lagrangian for the variables $q_{k}$, and hence the Hamiltonian $H$ as a function of $q_{k}$ and the conjugate momenta $p_{k}$. Show that the Hamiltonian operator $\hat{H}$ of the quantum theory can be written in the form

  $$\hat{H}=E_{0}+\sum_{k} \hbar \omega(k) a_{k}^{\dagger} a_{k}$$

  where $E_{0}$ is a constant and $a_{k}, a_{k}^{\dagger}$ are harmonic oscillator annihilation and creation operators. What is the physical interpretation of $a_{k}$ and $a_{k}^{\dagger}$ ? How does this show that phonons have quantized energies?

  comment

Applied Probability

• B2.13

  Applied Probability | Part II, 2003

  Let $S_{k}$ be the sum of $k$ independent exponential random variables of rate $k \mu$. Compute the moment generating function of $S_{k}$.

  Consider, for each fixed $k$ and for $0<\lambda<\mu$, an $M / G / 1$ queue with arrival rate $\lambda$ and with service times distributed as $S_{k}$. Assume that the queue is empty at time 0 and write $T_{k}$ for the earliest time at which a customer departs leaving the queue empty. Show that, as $k \rightarrow \infty, T_{k}$ converges in distribution to a random variable $T$ whose moment generating function $M_{T}(\theta)$ satisfies

  $$\log \left(1-\frac{\theta}{\lambda}\right)+\log M_{T}(\theta)=\left(\frac{\theta-\lambda}{\mu}\right)\left(1-M_{T}(\theta)\right)$$

  Hence obtain the mean value of $T$.

  For what service-time distribution would the empty-to-empty time correspond exactly to $T$ ?

  comment

• B3.13

  Applied Probability | Part II, 2003

  State the product theorem for Poisson random measures.

  Consider a system of $n$ queues, each with infinitely many servers, in which, for $i=1, \ldots, n-1$, customers leaving the $i$ th queue immediately arrive at the $(i+1)$ th queue. Arrivals to the first queue form a Poisson process of rate $\lambda$. Service times at the $i$ th queue are all independent with distribution $F$, and independent of service times at other queues, for all $i$. Assume that initially the system is empty and write $V_{i}(t)$ for the number of customers at queue $i$ at time $t \geqslant 0$. Show that $V_{1}(t), \ldots, V_{n}(t)$ are independent Poisson random variables.

  In the case $F(t)=1-e^{-\mu t}$ show that

  $$\mathbb{E}\left(V_{i}(t)\right)=\frac{\lambda}{\mu} \mathbb{P}\left(N_{t} \geqslant i\right), \quad t \geqslant 0, \quad i=1, \ldots, n,$$

  where $\left(N_{t}\right)_{t \geqslant 0}$ is a Poisson process of rate $\mu$.

  Suppose now that arrivals to the first queue stop at time $T$. Determine the mean number of customers at the $i$ th queue at each time $t \geqslant T$.

  comment

• B4.12

  Applied Probability | Part II, 2003

  Explain what is meant by a renewal process and by a renewal-reward process.

  State and prove the law of large numbers for renewal-reward processes.

  A component used in a manufacturing process has a maximum lifetime of 2 years and is equally likely to fail at any time during that period. If the component fails whilst in use, it is replaced immediately by a similar component, at a cost of $£ 1000$. The factory owner may alternatively replace the component before failure, at a time of his choosing, at a cost of $£ 200$. What should the factory owner do?

  comment

Coding and Cryptography

• A1.10

  Coding and Cryptography | Part II, 2003

  (i) We work over the field of two elements. Define what is meant by a linear code of length $n$. What is meant by a generator matrix for a linear code?

  Define what is meant by a parity check code of length $n$. Show that a code is linear if and only if it is a parity check code.

  Give the original Hamming code in terms of parity checks and then find a generator matrix for it.

  [You may use results from the theory of vector spaces provided that you quote them correctly.]

  (ii) Suppose that $1 / 4>\delta>0$ and let $\alpha(n, n \delta)$ be the largest information rate of any binary error correcting code of length $n$ which can correct $[n \delta]$ errors.

  Show that

  $$1-H(2 \delta) \leqslant \liminf _{n \rightarrow \infty} \alpha(n, n \delta) \leqslant 1-H(\delta)$$

  where

  $$H(\eta)=-\eta \log _{2} \eta-(1-\eta) \log _{2}(1-\eta)$$

  [You may assume any form of Stirling's theorem provided that you quote it correctly.]

  comment

• A2.9

  Coding and Cryptography | Part II, 2003

  (i) Answer the following questions briefly but clearly.

  (a) How does coding theory apply when the error rate $p>1 / 2$ ?

  (b) Give an example of a code which is not a linear code.

  (c) Give an example of a linear code which is not a cyclic code.

  (d) Give an example of a general feedback register with output $k_{j}$, and initial fill $\left(k_{0}, k_{1}, \ldots, k_{N}\right)$, such that

  $$\left(k_{n}, k_{n+1}, \ldots, k_{n+N}\right) \neq\left(k_{0}, k_{1}, \ldots, k_{N}\right)$$

  for all $n \geqslant 1$.

  (e) Explain why the original Hamming code can not always correct two errors.

  (ii) Describe the Rabin-Williams scheme for coding a message $x$ as $x^{2}$ modulo a certain $N$. Show that, if $N$ is chosen appropriately, breaking this code is equivalent to factorising the product of two primes.

  comment

Combinatorics

• B1.5

  Combinatorics | Part II, 2003

  Let $G$ be a graph of order $n \geqslant 4$. Prove that if $G$ has $t_{2}(n)+1$ edges then it contains two triangles with a common edge. Here, $t_{2}(n)=\left\lfloor n^{2} / 4\right\rfloor$ is the Turán number.

  Suppose instead that $G$ has exactly one triangle. Show that $G$ has at most $t_{2}(n-1)+2$ edges, and that this number can be attained.

  comment

• B2.5

  Combinatorics | Part II, 2003

  Prove Ramsey's theorem in its usual infinite form, namely, that if $\mathbb{N}^{(r)}$ is finitely coloured then there is an infinite subset $M \subset \mathbb{N}$ such that $M^{(r)}$ is monochromatic.

  Now let the graph $\mathbb{N}^{(2)}$ be coloured with an infinite number of colours in such a way that there is no infinite $M \subset \mathbb{N}$ with $M^{(2)}$ monochromatic. By considering a suitable 2-colouring of the set $\mathbb{N}^{(4)}$ of 4 -sets, show that there is an infinite $M \subset \mathbb{N}$ with the property that any two edges of $M^{(2)}$ of the form $a d, b c$ with $a<b<c<d$ have different colours.

  By considering two further 2-colourings of $\mathbb{N}^{(4)}$, show that there is an infinite $M \subset \mathbb{N}$ such that any two non-incident edges of $M^{(2)}$ have different colours.

  comment

• B4.1

  Combinatorics | Part II, 2003

  Write an essay on the Kruskal-Katona theorem. As well as stating the theorem and giving a detailed sketch of a proof, you should describe some further results that may be derived from it.

  comment

Computational Statistics and Statistical Modelling

• A1.13

  Computational Statistics and Statistical Modelling | Part II, 2003

  (i) Suppose $Y_{i}, 1 \leqslant i \leqslant n$, are independent binomial observations, with $Y_{i} \sim B i\left(t_{i}, \pi_{i}\right)$, $1 \leqslant i \leqslant n$, where $t_{1}, \ldots, t_{n}$ are known, and we wish to fit the model

  $$\omega: \log \frac{\pi_{i}}{1-\pi_{i}}=\mu+\beta^{T} x_{i} \quad \text { for each } i$$

  where $x_{1}, \ldots, x_{n}$ are given covariates, each of dimension $p$. Let $\hat{\mu}, \hat{\beta}$ be the maximum likelihood estimators of $\mu, \beta$. Derive equations for $\hat{\mu}, \hat{\beta}$ and state without proof the form of the approximate distribution of $\hat{\beta}$.

  (ii) In 1975 , data were collected on the 3-year survival status of patients suffering from a type of cancer, yielding the following table

  \begin{tabular}{ccrr} & & \multicolumn{2}{c}{ survive? } \ age in years & malignant & yes & no \ under 50 & no & 77 & 10 \ under 50 & yes & 51 & 13 \ $50-69$ & no & 51 & 11 \ $50-69$ & yes & 38 & 20 \ $70+$ & no & 7 & 3 \ $70+$ & yes & 6 & 3 \end{tabular}

  Here the second column represents whether the initial tumour was not malignant or was malignant.

  Let $Y_{i j}$ be the number surviving, for age group $i$ and malignancy status $j$, for $i=1,2,3$ and $j=1,2$, and let $t_{i j}$ be the corresponding total number. Thus $Y_{11}=77$, $t_{11}=87$. Assume $Y_{i j} \sim B i\left(t_{i j}, \pi_{i j}\right), 1 \leqslant i \leqslant 3,1 \leqslant j \leqslant 2$. The results from fitting the model

  $$\log \left(\pi_{i j} /\left(1-\pi_{i j}\right)\right)=\mu+\alpha_{i}+\beta_{j}$$

  with $\alpha_{1}=0, \beta_{1}=0$ give $\hat{\beta}_{2}=-0.7328(\mathrm{se}=0.2985)$, and deviance $=0.4941$. What do you conclude?

  Why do we take $\alpha_{1}=0, \beta_{1}=0$ in the model?

  What "residuals" should you compute, and to which distribution would you refer them?

  comment

• A2.12

  Computational Statistics and Statistical Modelling | Part II, 2003

  (i) Suppose $Y_{1}, \ldots, Y_{n}$ are independent Poisson variables, and

  $$\mathbb{E}\left(Y_{i}\right)=\mu_{i}, \quad \log \mu_{i}=\alpha+\beta t_{i}, \quad \text { for } \quad i=1, \ldots, n,$$

  where $\alpha, \beta$ are two unknown parameters, and $t_{1}, \ldots, t_{n}$ are given covariates, each of dimension 1. Find equations for $\hat{\alpha}, \hat{\beta}$, the maximum likelihood estimators of $\alpha, \beta$, and show how an estimate of $\operatorname{var}(\hat{\beta})$ may be derived, quoting any standard theorems you may need.

  (ii) By 31 December 2001, the number of new vCJD patients, classified by reported calendar year of onset, were

  $$8,10,11,14,17,29,23$$

  for the years

  $$1994, \ldots, 2000 \text { respectively }$$

  Discuss carefully the (slightly edited) $R$ output for these data given below, quoting any standard theorems you may need.

  year

  year

  [1] 1994199519961997199819992000

  $>$ tot

  [1] $\begin{array}{lllllll}8 & 10 & 11 & 14 & 17 & 29 & 23\end{array}$

  first.glm - glm(tot year, family = poisson)

  $>\operatorname{summary}$ (first.glm)

  Call:

  glm(formula $=$ tot year, family $=$ poisson $)$

  Coefficients

  Estimate Std. Error z value $\operatorname{Pr}(>|z|)$

  (Intercept) $-407.8128599 .35366-4.1054 .05 \mathrm{e}-05$

  year $\quad 0.20556 \quad 0.04973 \quad 4.1333 .57 e-05$

  (Dispersion parameter for poisson family taken to be 1)

  Null deviance: $20.7753$ on 6 degrees of freedom

  Residual deviance: $2.7931$ on 5 degrees of freedom

  Number of Fisher Scoring iterations: 3

  Part II 2003

  comment

• A4.14

  Computational Statistics and Statistical Modelling | Part II, 2003

  The nave height $x$, and the nave length $y$ for 16 Gothic-style cathedrals and 9 Romanesque-style cathedrals, all in England, have been recorded, and the corresponding $R$ output (slightly edited) is given below.

  

  You may assume that $x, y$ are in suitable units, and that "style" has been set up as a factor with levels 1,2 corresponding to Gothic, Romanesque respectively.

  (a) Explain carefully, with suitable graph(s) if necessary, the results of this analysis.

  (b) Using the general model $Y=X \beta+\epsilon$ (in the conventional notation) explain carefully the theory needed for (a).

  [Standard theorems need not be proved.]

  comment

Differentiable Manifolds

• B1.8

  Differentiable Manifolds | Part II, 2003

  State the Implicit Function Theorem and outline how it produces submanifolds of Euclidean spaces.

  Show that the unitary group $U(n) \subset G L(n, \mathbb{C})$ is a smooth manifold and find its dimension.

  Identify the tangent space to $U(n)$ at the identity matrix as a subspace of the space of $n \times n$ complex matrices.

  comment

• B2.7

  Differentiable Manifolds | Part II, 2003

  Let $M$ and $N$ be smooth manifolds. If $\pi: M \times N \rightarrow M$ is the projection onto the first factor and $\pi^{*}$ is the map in cohomology induced by the pull-back map on differential forms, show that $\pi^{*}\left(H^{k}(M)\right)$ is a direct summand of $H^{k}(M \times N)$ for each $k \geqslant 0$.

  Taking $H^{k}(M)$ to be zero for $k<0$ and $k>\operatorname{dim} M$, show that for $n \geqslant 1$ and all $k$

  $$H^{k}\left(M \times S^{n}\right) \cong H^{k}(M) \oplus H^{k-n}(M)$$

  [You might like to use induction in n.]

  comment

• B4.4

  Differentiable Manifolds | Part II, 2003

  Define the 'pull-back' homomorphism of differential forms determined by the smooth map $f: M \rightarrow N$ and state its main properties.

  If $\theta: W \rightarrow V$ is a diffeomorphism between open subsets of $\mathbb{R}^{m}$ with coordinates $x_{i}$ on $V$ and $y_{j}$ on $W$ and the $m$-form $\omega$ is equal to $f d x_{1} \wedge \ldots \wedge d x_{m}$ on $V$, state and prove the expression for $\theta^{*}(\omega)$ as a multiple of $d y_{1} \wedge \ldots \wedge d y_{m}$.

  Define the integral of an $m$-form $\omega$ over an oriented $m$-manifold $M$ and prove that it is well-defined.

  Show that the inclusion map $f: N \hookrightarrow M$, of an oriented $n$-submanifold $N$ (without boundary) into $M$, determines an element $\nu$ of $H_{n}(M) \cong \operatorname{Hom}\left(H^{n}(M), \mathbb{R}\right)$. If $M=N \times P$ and $f(x)=(x, p)$, for $x \in N$ and $p$ fixed in $P$, what is the relation between $\nu$ and $\pi^{*}\left(\left[\omega_{N}\right]\right)$, where $\left[\omega_{N}\right]$ is the fundamental cohomology class of $N$ and $\pi$ is the projection onto the first factor?

  comment

Dynamical Systems

• B1.17

  Dynamical Systems | Part II, 2003

  Consider the one-dimensional map $f: \mathbb{R} \rightarrow \mathbb{R}$, where $f(x)=\mu x^{2}(1-x)$ with $\mu$ a real parameter. Find the range of values of $\mu$ for which the open interval $(0,1)$ is mapped into itself and contains at least one fixed point. Describe the bifurcation at $\mu=4$ and find the parameter value for which there is a period-doubling bifurcation. Determine whether the fixed point is an attractor at this bifurcation point.

  comment

• B3.17

  Dynamical Systems | Part II, 2003

  Let $f: I \rightarrow I$ be a continuous one-dimensional map of the interval $I \subset \mathbb{R}$. Explain what is meant by saying (a) that the map $f$ is topologically transitive, and (b) that the map $f$ has a horseshoe.

  Consider the tent map defined on the interval $[0,1]$ by

  $$f(x)= \begin{cases}\mu x & 0 \leqslant x<\frac{1}{2} \\ \mu(1-x) & \frac{1}{2} \leqslant x \leqslant 1\end{cases}$$

  for $1<\mu \leqslant 2$. Show that if $\mu>\sqrt{2}$ then this map is topologically transitive, and also that $f^{2}$ has a horseshoe.

  comment

• B4.17

  Dynamical Systems | Part II, 2003

  Let $f: S^{1} \rightarrow S^{1}$ be an orientation-preserving invertible map of the circle onto itself, with a lift $F: \mathbb{R} \rightarrow \mathbb{R}$. Define the rotation numbers $\rho_{0}(F)$ and $\rho(f)$.

  Suppose that $\rho_{0}(F)=p / q$, where $p$ and $q$ are coprime integers. Prove that the map $f$ has periodic points of least period $q$, and no periodic points with any least period not equal to $q$.

  Now suppose that $\rho_{0}(F)$ is irrational. Explain the distinction between wandering and non-wandering points under $f$. Let $\Omega(x)$ be the set of limit points of the sequence $\left\{x, f(x), f^{2}(x), \ldots\right\}$. Prove

  (a) that the set $\Omega(x)=\Omega$ is independent of $x$ and is the smallest closed, non-empty, $f$-invariant subset of $S^{1}$;

  (b) that $\Omega$ is the set of non-wandering points of $S^{1}$;

  (c) that $\Omega$ is either the whole of $S^{1}$ or a Cantor set in $S^{1}$.

  comment

Dynamics of Differential Equations

• A1.6

  Dynamics of Differential Equations | Part II, 2003

  (i) State and prove Dulac's Criterion for the non-existence of periodic orbits in $\mathbb{R}^{2}$. Hence show (choosing a weighting factor of the form $x^{\alpha} y^{\beta}$ ) that there are no periodic orbits of the equations

  $$\dot{x}=x\left(2-6 x^{2}-5 y^{2}\right), \quad \dot{y}=y\left(-3+10 x^{2}+3 y^{2}\right)$$

  (ii) State the Poincaré-Bendixson Theorem. A model of a chemical reaction (the Brusselator) is defined by the second order system

  $$\dot{x}=a-x(1+b)+x^{2} y, \quad \dot{y}=b x-x^{2} y$$

  where $a, b$ are positive parameters. Show that there is a unique fixed point. Show that, for a suitable choice of $p>0$, trajectories enter the closed region bounded by $x=p, y=b / p$, $x+y=a+b / p$ and $y=0$. Deduce that when $b>1+a^{2}$, the system has a periodic orbit.

  comment

• A2.6 B2.4

  Dynamics of Differential Equations | Part II, 2003

  (i) What is a Liapunov function?

  Consider the second order ODE

  $$\dot{x}=y, \quad \dot{y}=-y-\sin ^{3} x$$

  By finding a suitable Liapunov function of the form $V(x, y)=f(x)+g(y)$, where $f$ and $g$ are to be determined, show that the origin is asymptotically stable. Using your form of $V$, find the greatest value of $y_{0}$ such that a trajectory through $\left(0, y_{0}\right)$ is guaranteed to tend to the origin as $t \rightarrow \infty$.

  [Any theorems you use need not be proved but should be clearly stated.]

  (ii) Explain the use of the stroboscopic method for investigating the dynamics of equations of the form $\ddot{x}+x=\epsilon f(x, \dot{x}, t)$, when $|\epsilon| \ll 1$. In particular, for $x=R \cos (t+\theta)$, $\dot{x}=-R \sin (t+\theta)$ derive the equations, correct to order $\epsilon$,

  $$\dot{R}=-\epsilon\langle f \sin (t+\theta)\rangle, \quad R \dot{\theta}=-\epsilon\langle f \cos (t+\theta)\rangle$$

  where the brackets denote an average over the period of the unperturbed oscillator.

  Find the form of the right hand sides of these equations explicitly when $f=$ $\Gamma x^{2} \cos t-3 q x$, where $\Gamma>0, q \neq 0$. Show that apart from the origin there is another fixed point of $(*)$, and determine its stability. Sketch the trajectories in $(R, \theta)$ space in the case $q>0$. What do you deduce about the dynamics of the full equation?

  [You may assume that $\left\langle\cos ^{2} t\right\rangle=\frac{1}{2},\left\langle\cos ^{4} t\right\rangle=\frac{3}{8},\left\langle\cos ^{2} t \sin ^{2} t\right\rangle=\frac{1}{8}$.]

  comment

• A3.6 B3.4

  Dynamics of Differential Equations | Part II, 2003

  (i) Define the Poincaré index of a curve $\mathcal{C}$ for a vector field $\mathbf{f}(\mathbf{x}), \mathbf{x} \in \mathbb{R}^{2}$. Explain why the index is uniquely given by the sum of the indices for small curves around each fixed point within $\mathcal{C}$. Write down the indices for a saddle point and for a focus (spiral) or node, and show that the index of a periodic solution of $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ has index unity.

  A particular system has a periodic orbit containing five fixed points, and two further periodic orbits. Sketch the possible arrangements of these orbits, assuming there are no degeneracies.

  (ii) A dynamical system in $\mathbb{R}^{2}$ depending on a parameter $\mu$ has a homoclinic orbit when $\mu=\mu_{0}$. Explain how to determine the stability of this orbit, and sketch the different behaviours for $\mu<\mu_{0}$ and $\mu>\mu_{0}$ in the case that the orbit is stable.

  Now consider the system

  $$\dot{x}=y, \quad \dot{y}=x-x^{2}+y(\alpha+\beta x)$$

  where $\alpha, \beta$ are constants. Show that the origin is a saddle point, and that if there is an orbit homoclinic to the origin then $\alpha, \beta$ are related by

  $$\oint y^{2}(\alpha+\beta x) d t=0$$

  where the integral is taken round the orbit. Evaluate this integral for small $\alpha, \beta$ by approximating $y$ by its form when $\alpha=\beta=0$. Hence give conditions on (small) $\alpha, \beta$ that lead to a stable homoclinic orbit at the origin. [Note that $y d t=d x$.]

  comment

• A4.6

  Dynamics of Differential Equations | Part II, 2003

  Explain what is meant by a steady-state bifurcation of a fixed point $\mathbf{x}_{0}(\mu)$ of an ODE $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x}, \mu)$, in $\mathbb{R}^{n}$, where $\mu$ is a real parameter. Give examples for $n=1$ of equations exhibiting saddle-node, transcritical and pitchfork bifurcations.

  Consider the system in $\mathbb{R}^{2}$, with $\mu>0$,

  $$\dot{x}=x\left(1-y-4 x^{2}\right), \quad \dot{y}=y\left(\mu-y-x^{2}\right) .$$

  Show that the fixed point $(0, \mu)$ has a bifurcation when $\mu=1$, while the fixed points $\left(\pm \frac{1}{2}, 0\right)$ have a bifurcation when $\mu=\frac{1}{4}$. By finding the first approximation to the extended centre manifold, construct the normal form at the bifurcation point in each case, and determine the respective bifurcation types. Deduce that for $\mu$ just greater than $\frac{1}{4}$, and for $\mu$ just less than 1 , there is a stable pair of "mixed-mode" solutions with $x^{2}>0, y>0$.

  comment

Electrodynamics

• B1.21

  Electrodynamics | Part II, 2003

  A particle of charge $q$ and mass $m$ moves non-relativistically with 4 -velocity $u^{a}(t)$ along a trajectory $x^{a}(t)$. Its electromagnetic field is determined by the Liénard-Wiechert potential

  $$A^{a}\left(\mathbf{x}^{\prime}, t^{\prime}\right)=\frac{q}{4 \pi \epsilon_{0}} \frac{u^{a}(t)}{u_{b}(t)\left(x^{\prime}-x(t)\right)^{b}}$$

  where $t^{\prime}=t+\left|\mathbf{x}-\mathbf{x}^{\prime}\right|$ and $\mathbf{x}$ denotes the spatial part of the 4 -vector $x^{a}$.

  Derive a formula for the Poynting vector at very large distances from the particle. Hence deduce Larmor's formula for the rate of loss of energy due to electromagnetic radiation by the particle.

  A particle moves in the $(x, y)$ plane in a constant magnetic field $\mathbf{B}=(0,0, B)$. Initially it has kinetic energy $E_{0}$; derive a formula for the kinetic energy of this particle as a function of time.

  comment

• B2.20

  Electrodynamics | Part II, 2003

  A plane electromagnetic wave of frequency $\omega$ and wavevector $\mathbf{k}$ has an electromagnetic potential given by

  $$A^{a}=A \epsilon^{a} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}$$

  where $A$ is the amplitude of the wave and $\epsilon^{a}$ is the polarization vector. Explain carefully why there are two independent polarization states for such a wave, and why $|\mathbf{k}|^{2}=\omega^{2}$.

  A wave travels in the positive $z$-direction with polarization vector $\epsilon^{a}=(0,1, i, 0)$. It is incident at $z=0$ on a plane surface which conducts perfectly in the $x$-direction, but not at all in the $y$-direction. Find an expression for the electromagnetic potential of the radiation that is reflected from this surface.

  comment

• B4.21

  Electrodynamics | Part II, 2003

  Describe the physical meaning of the various components of the stress-energy tensor $T^{a b}$ of the electromagnetic field.

  Suppose that one is given an electric field $\mathbf{E}(\mathbf{x})$ and a magnetic field $\mathbf{B}(\mathbf{x})$. Show that the angular momentum about the origin of these fields is

  $$\mathbf{J}=\frac{1}{\mu_{0}} \int \mathbf{x} \times(\mathbf{E} \times \mathbf{B}) d^{3} \mathbf{x}$$

  where the integral is taken over all space.

  A point electric charge $Q$ is at the origin, and has electric field

  $$\mathbf{E}=\frac{Q}{4 \pi \epsilon_{0}} \frac{\mathbf{x}}{|\mathbf{x}|^{3}}$$

  A point magnetic monopole of strength $P$ is at $\mathbf{y}$ and has magnetic field

  $$\mathbf{B}=\frac{\mu_{0} P}{4 \pi} \frac{\mathbf{x}-\mathbf{y}}{|\mathbf{x}-\mathbf{y}|^{3}}$$

  Find the component, along the axis between the electric charge and the magnetic monopole, of the angular momentum of the electromagnetic field about the origin.

  [Hint: You may find it helpful to express both $\mathbf{E}$ and $\mathbf{B}$ as gradients of scalar potentials.]

  comment

Electromagnetism

• A $1 . 5 \quad$ B $1 . 4 \quad$

  Electromagnetism | Part II, 2003

  (i) Using Maxwell's equations as they apply to magnetostatics, show that the magnetic field $\mathbf{B}$ can be described in terms of a vector potential $\mathbf{A}$ on which the condition $\nabla \cdot \mathbf{A}=0$ may be imposed. Hence derive an expression, valid at any point in space, for the vector potential due to a steady current distribution of density $\mathbf{j}$ that is non-zero only within a finite domain.

  (ii) Verify that the vector potential $\mathbf{A}$ that you found in Part (i) satisfies $\nabla \cdot \mathbf{A}=0$, and use it to obtain the Biot-Savart law expression for $\mathbf{B}$. What is the corresponding result for a steady surface current distribution of density $\mathbf{s}$ ?

  In cylindrical polar coordinates $(\rho, \phi, z)$ (oriented so that $\mathbf{e}_{\rho} \times \mathbf{e}_{\phi}=\mathbf{e}_{z}$ ) a surface current

  $$\mathbf{s}=s(\rho) \mathbf{e}_{\phi}$$

  flows in the plane $z=0$. Given that

  $$s(\rho)= \begin{cases}4 I\left(1+\frac{a^{2}}{\rho^{2}}\right)^{\frac{1}{2}} & a \leqslant \rho \leqslant 3 a \\ 0 & \text { otherwise }\end{cases}$$

  show that the magnetic field at the point $\mathbf{r}=a \mathbf{e}_{z}$ has $z$-component

  $$B_{z}=\mu_{0} I \log 5 .$$

  State, with justification, the full result for $\mathbf{B}$ at the point $\mathbf{r}=a \mathbf{e}_{z}$.

  comment

• A2 $. 5 \quad$

  Electromagnetism | Part II, 2003

  (i) A plane electromagnetic wave has electric and magnetic fields

  $$\mathbf{E}=\mathbf{E}_{0} e^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}, \quad \mathbf{B}=\mathbf{B}_{0} e^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}$$

  for constant vectors $\mathbf{E}_{0}, \mathbf{B}_{0}$, constant positive angular frequency $\omega$ and constant wavevector $\mathbf{k}$. Write down the vacuum Maxwell equations and show that they imply

  $$\mathbf{k} \cdot \mathbf{E}_{0}=0, \quad \mathbf{k} \cdot \mathbf{B}_{0}=0, \quad \omega \mathbf{B}_{0}=\mathbf{k} \times \mathbf{E}_{0}$$

  Show also that $|\mathbf{k}|=\omega / c$, where $c$ is the speed of light.

  (ii) State the boundary conditions on $\mathbf{E}$ and $\mathbf{B}$ at the surface $S$ of a perfect conductor. Let $\sigma$ be the surface charge density and s the surface current density on $S$. How are $\sigma$ and $\mathbf{s}$ related to $\mathbf{E}$ and $\mathbf{B}$ ?

  A plane electromagnetic wave is incident from the half-space $x<0$ upon the surface $x=0$ of a perfectly conducting medium in $x>0$. Given that the electric and magnetic fields of the incident wave take the form $(*)$ with

  $$\mathbf{k}=k(\cos \theta, \sin \theta, 0) \quad(0<\theta<\pi / 2)$$

  and

  $$\mathbf{E}_{0}=\lambda(-\sin \theta, \cos \theta, 0),$$

  find $\mathbf{B}_{0}$.

  Reflection of the incident wave at $x=0$ produces a reflected wave with electric field

  $$\mathbf{E}_{0}^{\prime} e^{i\left(\mathbf{k}^{\prime} \cdot \mathbf{r}-\omega t\right)}$$

  with

  $$\mathbf{k}^{\prime}=k(-\cos \theta, \sin \theta, 0)$$

  By considering the boundary conditions at $x=0$ on the total electric field, show that

  $$\mathbf{E}_{0}^{\prime}=-\lambda(\sin \theta, \cos \theta, 0)$$

  Show further that the electric charge density on the surface $x=0$ takes the form

  $$\sigma=\sigma_{0} e^{i k(y \sin \theta-c t)}$$

  for a constant $\sigma_{0}$ that you should determine. Find the magnetic field of the reflected wave and hence the surface current density $\mathbf{s}$ on the surface $x=0$.

  comment

• A3.5 B3.3

  Electromagnetism | Part II, 2003

  (i) Given the electric field (in cartesian components)

  $$\mathbf{E}(\mathbf{r}, t)=\left(0, x / t^{2}, 0\right)$$

  use the Maxwell equation

  $$\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$$

  to find $\mathbf{B}$ subject to the boundary condition that $|\mathbf{B}| \rightarrow 0$ as $t \rightarrow \infty$.

  Let $S$ be the planar rectangular surface in the $x y$-plane with corners at

  $$(0,0,0), \quad(L, 0,0), \quad(L, a, 0), \quad(0, a, 0)$$

  where $a$ is a constant and $L=L(t)$ is some function of time. The magnetic flux through $S$ is given by the surface integral

  $$\Phi=\int_{S} \mathbf{B} \cdot d \mathbf{S}$$

  Compute $\Phi$ as a function of $t$.

  Let $\mathcal{C}$ be the closed rectangular curve that bounds the surface $S$, taken anticlockwise in the $x y$-plane, and let $\mathbf{v}$ be its velocity (which depends, in this case, on the segment of $\mathcal{C}$ being considered). Compute the line integral

  $$\oint_{\mathcal{C}}(\mathbf{E}+\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{r}$$

  Hence verify that

  $$\oint_{\mathcal{C}}(\mathbf{E}+\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{r}=-\frac{d \Phi}{d t}$$

  (ii) A surface $S$ is bounded by a time-dependent closed curve $\mathcal{C}(t)$ such that in time $\delta t$ it sweeps out a volume $\delta V$. By considering the volume integral

  $$\int_{\delta V} \nabla \cdot \mathbf{B} d \tau$$

  and using the divergence theorem, show that the Maxwell equation $\nabla \cdot \mathbf{B}=0$ implies that

  $$\frac{d \Phi}{d t}=\int_{S} \frac{\partial \mathbf{B}}{\partial t} \cdot d \mathbf{S}-\oint_{\mathcal{C}}(\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{r}$$

  where $\Phi$ is the magnetic flux through $S$ as given in Part (i). Hence show, using (1) and Stokes' theorem, that (2) is a consequence of Maxwell's equations.

  comment

• A4.5

  Electromagnetism | Part II, 2003

  Let $\mathbf{E}(\mathbf{r})$ be the electric field due to a continuous static charge distribution $\rho(\mathbf{r})$ for which $|\mathbf{E}| \rightarrow 0$ as $|\mathbf{r}| \rightarrow \infty$. Starting from consideration of a finite system of point charges, deduce that the electrostatic energy of the charge distribution $\rho$ is

  $$W=\frac{1}{2} \varepsilon_{0} \int|\mathbf{E}|^{2} d \tau$$

  where the volume integral is taken over all space.

  A sheet of perfectly conducting material in the form of a surface $S$, with unit normal $\mathbf{n}$, carries a surface charge density $\sigma$. Let $E_{\pm}=\mathbf{n} \cdot \mathbf{E}_{\pm}$denote the normal components of the electric field $\mathbf{E}$ on either side of $S$. Show that

  $$\frac{1}{\varepsilon_{0}} \sigma=E_{+}-E_{-} .$$

  Three concentric spherical shells of perfectly conducting material have radii $a, b, c$ with $a<b<c$. The innermost and outermost shells are held at zero electric potential. The other shell is held at potential $V$. Find the potentials $\phi_{1}(r)$ in $a<r<b$ and $\phi_{2}(r)$ in $b<r<c$. Compute the surface charge density $\sigma$ on the shell of radius $b$. Use the formula $(*)$ to compute the electrostatic energy of the system.

  comment

Fluid Dynamics II

• B1.25

  Fluid Dynamics II | Part II, 2003

  Consider a two-dimensional horizontal vortex sheet of strength $U$ at height $h$ above a horizontal rigid boundary at $y=0$, so that the inviscid fluid velocity is

  $$\mathbf{u}= \begin{cases}(U, 0) & 0<y<h \\ (0,0) & y>h\end{cases}$$

  Examine the temporal linear instabililty of the sheet and determine the relevant dispersion relationship.

  For what wavelengths is the sheet unstable?

  Evaluate the temporal growth rate and the wave propagation speed in the limit of both short and long waves. Comment briefly on the significance of your results.

  comment

• B2 24

  Fluid Dynamics II | Part II, 2003

  A plate is drawn vertically out of a bath and the resultant liquid drains off the plate as a thin film. Using lubrication theory, show that the governing equation for the thickness of the film, $h(x, t)$ is

  $$\frac{\partial h}{\partial t}+\left(\frac{g h^{2}}{\nu}\right) \frac{\partial h}{\partial x}=0$$

  where $t$ is time and $x$ is the distance down the plate measured from the top.

  Verify that

  $$h(x, t)=F\left(x-\frac{g h^{2}}{\nu} t\right)$$

  satisfies $(*)$ and identify the function $F(x)$. Using this relationship or otherwise, determine an explicit expression for the thickness of the film assuming that it was initially of uniform thickness $h_{0}$.

  comment

• B3.24

  Fluid Dynamics II | Part II, 2003

  A steady two-dimensional jet is generated in an infinite, incompressible fluid of density $\rho$ and kinematic viscosity $\nu$ by a point source of momentum with momentum flux in the $x$ direction $F$ per unit length located at the origin.

  Using boundary layer theory, analyse the motion in the jet and show that the $x$-component of the velocity is given by

  $$u=U(x) f^{\prime}(\eta)$$

  where

  $$\eta=y / \delta(x), \quad \delta(x)=\left(\rho \nu^{2} x^{2} / F\right)^{1 / 3} \text { and } U(x)=\left(F^{2} / \rho^{2} \nu x\right)^{1 / 3}$$

  Show that $f$ satisfies the differential equation

  $$f^{\prime \prime \prime}+\frac{1}{3}\left(f f^{\prime \prime}+f^{\prime^{2}}\right)=0 .$$

  Write down the appropriate boundary conditions for this equation. [You need not solve the equation.]

  comment

• B4.26

  Fluid Dynamics II | Part II, 2003

  Show that the complex potential in the complex $\zeta$ plane,

  $$w=(U-i V) \zeta+(U+i V) \frac{c^{2}}{\zeta}-\frac{i \kappa}{2 \pi} \log \zeta$$

  describes irrotational, inviscid flow past the rigid cylinder $|\zeta|=c$, placed in a uniform flow $(U, V)$ with circulation $\kappa$.

  Show that the transformation

  $$z=\zeta+\frac{c^{2}}{\zeta}$$

  maps the circle $|\zeta|=c$ in the $\zeta$ plane onto the flat plate airfoil $-2 c<x<2 c, y=0$ in the $z$ plane $(z=x+i y)$. Hence, write down an expression for the complex potential, $w_{p}$, of uniform flow past the flat plate, with circulation $\kappa$. Indicate very briefly how the value of $\kappa$ might be chosen to yield a physical solution.

  Calculate the turning moment, $M$, exerted on the flat plate by the flow.

  (You are given that

  $$M=-\frac{1}{2} \rho \operatorname{Re}\left\{\oint\left[\frac{\left(\frac{d w}{d \zeta}\right)^{2}}{\frac{d z}{d \zeta}}\right] z(\zeta) d \zeta\right\} \text {, }$$

  where $\rho$ is the fluid density and the integral is to be completed around a contour enclosing the circle $|\zeta|=c$ ).

  comment

Foundations of Quantum Mechanics

• A2.13 B2.21

  Foundations of Quantum Mechanics | Part II, 2003

  (i) Define the Heisenberg picture of quantum mechanics in relation to the Schrödinger picture. Explain how the two pictures provide equivalent descriptions of observable results.

  Derive the equation of motion for an operator in the Heisenberg picture.

  (ii) For a particle moving in one dimension, the Hamiltonian is

  $$\hat{H}=\frac{\hat{p}^{2}}{2 m}+V(\hat{x}),$$

  where $\hat{x}$ and $\hat{p}$ are the position and momentum operators, and the state vector is $|\Psi\rangle$.

  Eigenstates of $\hat{x}$ and $\hat{p}$ satisfy

  $$\langle x \mid p\rangle=\left(\frac{1}{2 \pi \hbar}\right)^{1 / 2} e^{i p x / \hbar}, \quad\left\langle x \mid x^{\prime}\right\rangle=\delta\left(x-x^{\prime}\right), \quad\left\langle p \mid p^{\prime}\right\rangle=\delta\left(p-p^{\prime}\right) .$$

  Use standard methods in the Dirac formalism to show that

  $$\begin{aligned} &\left\langle x|\hat{p}| x^{\prime}\right\rangle=-i \hbar \frac{\partial}{\partial x} \delta\left(x-x^{\prime}\right) \\ &\left\langle p|\hat{x}| p^{\prime}\right\rangle=i \hbar \frac{\partial}{\partial p} \delta\left(p-p^{\prime}\right) \end{aligned}$$

  Calculate $\left\langle x|\hat{H}| x^{\prime}\right\rangle$ and express $\langle x|\hat{p}| \Psi\rangle,\langle x|\hat{H}| \Psi\rangle$ in terms of the position space wave function $\Psi(x)$.

  Compute the momentum space Hamiltonian for the harmonic oscillator with potential $V(\hat{x})=\frac{1}{2} m \omega^{2} \hat{x}^{2}$.

  comment

• A3.13 B3.21

  Foundations of Quantum Mechanics | Part II, 2003

  (i) What are the commutation relations satisfied by the components of an angular momentum vector $\mathbf{J}$ ? State the possible eigenvalues of the component $J_{3}$ when $\mathbf{J}^{2}$ has eigenvalue $j(j+1) \hbar^{2}$.

  Describe how the Pauli matrices

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  are used to construct the components of the angular momentum vector $\mathbf{S}$ for a spin $\frac{1}{2}$ system. Show that they obey the required commutation relations.

  Show that $S_{1}, S_{2}$ and $S_{3}$ each have eigenvalues $\pm \frac{1}{2} \hbar$. Verify that $\mathbf{S}^{2}$ has eigenvalue $\frac{3}{4} \hbar^{2} .$

  (ii) Let $\mathbf{J}$ and $|j m\rangle$ denote the standard operators and state vectors of angular momentum theory. Assume units where $\hbar=1$. Consider the operator

  $$U(\theta)=e^{-i \theta J_{2}}$$

  Show that

  $$\begin{aligned} &U(\theta) J_{1} U(\theta)^{-1}=\cos \theta J_{1}-\sin \theta J_{3} \\ &U(\theta) J_{3} U(\theta)^{-1}=\sin \theta J_{1}+\cos \theta J_{3} \end{aligned}$$

  Show that the state vectors $U\left(\frac{\pi}{2}\right)|j m\rangle$ are eigenvectors of $J_{1}$. Suppose that $J_{1}$ is measured for a system in the state $|j m\rangle$; show that the probability that the result is $m^{\prime}$ equals

  $$\left|\left\langle j m^{\prime}\left|e^{i \frac{\pi}{2} J_{2}}\right| j m\right\rangle\right|^{2}$$

  Consider the case $j=m=\frac{1}{2}$. Evaluate the probability that the measurement of $J_{1}$ will result in $m^{\prime}=-\frac{1}{2}$.

  comment

• A4.15 B4.22

  Foundations of Quantum Mechanics | Part II, 2003

  Discuss the quantum mechanics of the one-dimensional harmonic oscillator using creation and annihilation operators, showing how the energy levels are calculated.

  A quantum mechanical system consists of two interacting harmonic oscillators and has the Hamiltonian

  $$H=\frac{1}{2} \hat{p}_{1}^{2}+\frac{1}{2} \hat{x}_{1}^{2}+\frac{1}{2} \hat{p}_{2}^{2}+\frac{1}{2} \hat{x}_{2}^{2}+\lambda \hat{x}_{1} \hat{x}_{2}$$

  For $\lambda=0$, what are the degeneracies of the three lowest energy levels? For $\lambda \neq 0$ compute, to lowest non-trivial order in perturbation theory, the energies of the ground state and first excited state.

  [Standard results for perturbation theory may be stated without proof.]

  comment

Functional Analysis

• A1.3

  Functional Analysis | Part II, 2003

  (i) Let $T: H_{1} \rightarrow H_{2}$ be a continuous linear map between two Hilbert spaces $H_{1}, H_{2}$. Define the adjoint $T^{*}$ of $T$. Explain what it means to say that $T$ is Hermitian or unitary.

  Let $\phi: \mathbb{R} \rightarrow \mathbb{C}$ be a bounded continuous function. Show that the map

  $$T: L^{2}(\mathbb{R}) \rightarrow L^{2}(\mathbb{R})$$

  with $T f(x)=\phi(x) f(x+1)$ is a continuous linear map and find its adjoint. When is $T$ Hermitian? When is it unitary?

  (ii) Let $C$ be a closed, non-empty, convex subset of a real Hilbert space $H$. Show that there exists a unique point $x_{o} \in C$ with minimal norm. Show that $x_{o}$ is characterised by the property

  $$\left\langle x_{o}-x, x_{o}\right\rangle \leqslant 0 \quad \text { for all } x \in C .$$

  Does this result still hold when $C$ is not closed or when $C$ is not convex? Justify your answers.

  comment

• A2.3 B2.2

  Functional Analysis | Part II, 2003

  (i) Define the dual of a normed vector space $(E,\|\cdot\|)$. Show that the dual is always a complete normed space.

  Prove that the vector space $\ell_{1}$, consisting of those real sequences $\left(x_{n}\right)_{n=1}^{\infty}$ for which the norm

  $$\left\|\left(x_{n}\right)\right\|_{1}=\sum_{n=1}^{\infty}\left|x_{n}\right|$$

  is finite, has the vector space $\ell_{\infty}$ of all bounded sequences as its dual.

  (ii) State the Stone-Weierstrass approximation theorem.

  Let $K$ be a compact subset of $\mathbb{R}^{n}$. Show that every $f \in C_{\mathbb{R}}(K)$ can be uniformly approximated by a sequence of polynomials in $n$ variables.

  Let $f$ be a continuous function on $[0,1] \times[0,1]$. Deduce that

  $$\int_{0}^{1}\left(\int_{0}^{1} f(x, y) d x\right) d y=\int_{0}^{1}\left(\int_{0}^{1} f(x, y) d y\right) d x$$

  comment

• A3.3 B3.2

  Functional Analysis | Part II, 2003

  (i) Let $p$ be a point of the compact interval $I=[a, b] \subset \mathbb{R}$ and let $\delta_{p}: C(I) \rightarrow \mathbb{R}$ be defined by $\delta_{p}(f)=f(p)$. Show that

  $$\delta_{p}:\left(C(I),\|\cdot\|_{\infty}\right) \rightarrow \mathbb{R}$$

  is a continuous, linear map but that

  $$\delta_{p}:\left(C(I),\|\cdot\|_{1}\right) \rightarrow \mathbb{R}$$

  is not continuous.

  (ii) Consider the space $C^{(n)}(I)$ of $n$-times continuously differentiable functions on the interval $I$. Write

  $$\|f\|_{\infty}^{(n)}=\sum_{k=0}^{n}\left\|f^{(k)}\right\|_{\infty} \quad \text { and } \quad\|f\|_{1}^{(n)}=\sum_{r=0}^{n}\left\|f^{(k)}\right\|_{1}$$

  for $f \in C^{(n)}(I)$. Show that $\left(C^{(n)}(I),\left\|^{\prime} \cdot\right\|_{\infty}^{(n)}\right)$ is a complete normed space. Is the space $\left(C^{(n)}(I),\|\cdot\|_{1}^{(n)}\right)$ also complete?

  Let $f: I \rightarrow I$ be an $n$-times continuously differentiable map and define

  $$\mu_{f}: C^{(n)}(I) \rightarrow C^{(n)}(I) \quad \text { by } \quad g \mapsto g \circ f .$$

  Show that $\mu_{f}$ is a continuous linear map when $C^{(n)}(I)$ is equipped with the norm $\|\cdot\|_{\infty}^{(n)}$.

  comment

• A4.3

  Functional Analysis | Part II, 2003

  (i) State the Monotone Convergence Theorem and explain briefly how to prove it.

  (ii) For which real values of $\alpha$ is $x^{-\alpha} \log x \in L^{1}((1, \infty))$ ?

  Let $p>0$. Using the Monotone Convergence Theorem and the identity

  $$\frac{1}{x^{p}(x-1)}=\sum_{n=0}^{\infty} \frac{1}{x^{p+n+1}}$$

  prove carefully that

  $$\int_{1}^{\infty} \frac{\log x}{x^{p}(x-1)} d x=\sum_{n=0}^{\infty} \frac{1}{(n+p)^{2}}$$

  comment

Galois Theory

• B1.7

  Galois Theory | Part II, 2003

  What does it mean to say that a field is algebraically closed? Show that a field $M$ is algebraically closed if and only if, for any finite extension $L / K$ and every homomorphism $\sigma: K \hookrightarrow M$, there exists a homomorphism $L \hookrightarrow M$ whose restriction to $K$ is $\sigma$.

  Let $K$ be a field of characteristic zero, and $M / K$ an algebraic extension such that every nonconstant polynomial over $K$ has at least one root in $M$. Prove that $M$ is algebraically closed.

  comment

• B3.6

  Galois Theory | Part II, 2003

  Let $f$ be a separable polynomial of degree $n \geqslant 1$ over a field $K$. Explain what is meant by the Galois group $\operatorname{Gal}(f / K)$ of $f$ over $K$. Explain how $\operatorname{Gal}(f / K)$ can be identified with a subgroup of the symmetric group $S_{n}$. Show that as a permutation group, $\operatorname{Gal}(f / K)$ is transitive if and only if $f$ is irreducible over $K$.

  Show that the Galois group of $f(X)=X^{5}+20 X^{2}-2$ over $\mathbb{Q}$ is $S_{5}$, stating clearly any general results you use.

  Now let $K / \mathbb{Q}$ be a finite extension of prime degree $p>5$. By considering the degrees of the splitting fields of $f$ over $K$ and $\mathbb{Q}$, show that $\operatorname{Gal}(f / K)=S_{5}$ also.

  comment

• B4.3

  Galois Theory | Part II, 2003

  Write an essay on finite fields and their Galois theory.

  comment

General Relativity

• A1.15 B1.24

  General Relativity | Part II, 2003

  (i) The worldline $x^{a}(\lambda)$ of a massive particle moving in a spacetime with metric $g_{a b}$ obeys the geodesic equation

  $$\frac{d^{2} x^{a}}{d \tau^{2}}+\Gamma^a_{bc} \frac{d x^{b}}{d \tau} \frac{d x^{c}}{d \tau}=0$$

  where $\tau$ is the particle's proper time and $\Gamma^a_{bc}$ are the Christoffel symbols; these are the equations of motion for the Lagrangian

  $$L_{1}=-m \sqrt{-g_{a b} \dot{x}^{a} \dot{x}^{b}}$$

  where $m$ is the particle's mass, and $\dot{x}^{a}=d x^{a} / d \lambda$. Why is the choice of worldline parameter $\lambda$ irrelevant? Among all possible worldlines passing through points $A$ and $B$, why is $x^{a}(\lambda)$ the one that extremizes the proper time elapsed between $A$ and $B$ ?

  Explain how the equations of motion for a massive particle may be obtained from the alternative Lagrangian

  $$L_{2}=\frac{1}{2} g_{a b} \dot{x}^{a} \dot{x}^{b} .$$

  What can you conclude from the fact that $L_{2}$ has no explicit dependence on $\lambda$ ? How are the equations of motion for a massless particle obtained from $L_{2}$ ?

  (ii) A photon moves in the Schwarzschild metric

  $$d s^{2}=\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)-\left(1-\frac{2 M}{r}\right) d t^{2}$$

  Given that the motion is confined to the plane $\theta=\pi / 2$, obtain the radial equation

  $$\left(\frac{d r}{d \lambda}\right)^{2}=E^{2}-\frac{h^{2}}{r^{2}}\left(1-\frac{2 M}{r}\right)$$

  where $E$ and $h$ are constants, the physical meaning of which should be stated.

  Setting $u=1 / r$, obtain the equation

  $$\frac{d^{2} u}{d \phi^{2}}+u=3 M u^{2}$$

  Using the approximate solution

  $$u=\frac{1}{b} \sin \phi+\frac{M}{2 b^{2}}(3+\cos 2 \phi)+\ldots$$

  obtain the standard formula for the deflection of light passing far from a body of mass $M$ with impact parameter $b$. Reinstate factors of $G$ and $c$ to give your result in physical units.

  comment

• A2.15 B2.23

  General Relativity | Part II, 2003

  (i) What is a "stationary" metric? What distinguishes a stationary metric from a "static" metric?

  A Killing vector field $K^{a}$ of a metric $g_{a b}$ satisfies

  $$K_{a ; b}+K_{b ; a}=0$$

  Show that this is equivalent to

  $$g_{a b, c} K^{c}+g_{a c} K_{, b}^{c}+g_{c b} K_{, a}^{c}=0$$

  Hence show that a constant vector field $K^{a}$ with one non-zero component, $K^{4}$ say, is a Killing vector field if $g_{a b}$ is independent of $x^{4}$.

  (ii) Given that $K^{a}$ is a Killing vector field, show that $K_{a} u^{a}$ is constant along the geodesic worldline of a massive particle with 4-velocity $u^{a}$. Hence find the energy $\varepsilon$ of a particle of unit mass moving in a static spacetime with metric

  $$d s^{2}=h_{i j} d x^{i} d x^{j}-e^{2 U} d t^{2}$$

  where $h_{i j}$ and $U$ are functions only of the space coordinates $x^{i}$. By considering a particle with speed small compared with that of light, and given that $U \ll 1$, show that $h_{i j}=\delta_{i j}$ to lowest order in the Newtonian approximation, and that $U$ is the Newtonian potential.

  A metric admits an antisymmetric tensor $Y_{a b}$ satisfying

  $$Y_{a b ; c}+Y_{a c ; b}=0$$

  Given a geodesic $x^{a}(\lambda)$, let $s_{a}=Y_{a b} \dot{x}^{b}$. Show that $s_{a}$ is parallelly propagated along the geodesic, and that it is orthogonal to the tangent vector of the geodesic. Hence show that the scalar

  $$\phi=s^{a} s_{a}$$

  is constant along the geodesic.

  comment

• A4.17 B4.25

  General Relativity | Part II, 2003

  What are "inertial coordinates" and what is their physical significance? [A proof of the existence of inertial coordinates is not required.] Let $O$ be the origin of inertial coordinates and let $\left.R_{a b c d}\right|_{O}$ be the curvature tensor at $O$ (with all indices lowered). Show that $\left.R_{a b c d}\right|_{O}$ can be expressed entirely in terms of second partial derivatives of the metric $g_{a b}$, evaluated at $O$. Use this expression to deduce that (a) $R_{a b c d}=-R_{b a c d}$ (b) $R_{a b c d}=R_{c d a b}$ (c) $R_{a[b c d]}=0$.

  Starting from the expression for $R_{b c d}^{a}$ in terms of the Christoffel symbols, show (again by using inertial coordinates) that

  $$R_{a b[c d ; e]}=0$$

  Obtain the contracted Bianchi identities and explain why the Einstein equations take the form

  $$R_{a b}-\frac{1}{2} R g_{a b}=8 \pi T_{a b}-\Lambda g_{a b},$$

  where $T_{a b}$ is the energy-momentum tensor of the matter and $\Lambda$ is an arbitrary constant.

  comment

Geometry of Surfaces

• A2.7

  Geometry of Surfaces | Part II, 2003

  (i) What are geodesic polar coordinates at a point $P$ on a surface $M$ with a Riemannian metric $d s^{2}$ ?

  Assume that

  $$d s^{2}=d r^{2}+H(r, \theta)^{2} d \theta^{2}$$

  for geodesic polar coordinates $r, \theta$ and some function $H$. What can you say about $H$ and $d H / d r$ at $r=0$ ?

  (ii) Given that the Gaussian curvature $K$ may be computed by the formula $K=-H^{-1} \partial^{2} H / \partial r^{2}$, show that for small $R$ the area of the geodesic disc of radius $R$ centred at $P$ is

  $$\pi R^{2}-(\pi / 12) K R^{4}+a(R),$$

  where $a(R)$ is a function satisfying $\lim _{R \rightarrow 0} a(R) / R^{4}=0$.

  comment

• A3.7

  Geometry of Surfaces | Part II, 2003

  (i) Suppose that $C$ is a curve in the Euclidean $(\xi, \eta)$-plane and that $C$ is parameterized by its arc length $\sigma$. Suppose that $S$ in Euclidean $\mathbb{R}^{3}$ is the surface of revolution obtained by rotating $C$ about the $\xi$-axis. Take $\sigma, \theta$ as coordinates on $S$, where $\theta$ is the angle of rotation.

  Show that the Riemannian metric on $S$ induced from the Euclidean metric on $\mathbb{R}^{3}$ is

  $$d s^{2}=d \sigma^{2}+\eta(\sigma)^{2} d \theta^{2}$$

  (ii) For the surface $S$ described in Part (i), let $e_{\sigma}=\partial / \partial \sigma$ and $e_{\theta}=\partial / \partial \theta$. Show that, along any geodesic $\gamma$ on $S$, the quantity $g\left(\dot{\gamma}, e_{\theta}\right)$ is constant. Here $g$ is the metric tensor on $S$.

  [You may wish to compute $\left[X, e_{\theta}\right]=X e_{\theta}-e_{\theta} X$ for any vector field $X=A e_{\sigma}+B e_{\theta}$, where $A, B$ are functions of $\sigma, \theta$. Then use symmetry to compute $D_{\dot{\gamma}}\left(g\left(\dot{\gamma}, e_{\theta}\right)\right)$, which is the rate of change of $g\left(\dot{\gamma}, e_{\theta}\right)$ along $\gamma$.]

  comment

• A4.7

  Geometry of Surfaces | Part II, 2003

  Write an essay on the Theorema Egregium for surfaces in $\mathbb{R}^{3}$.

  comment

Graph Theory

• A $2 . 8$,

  Graph Theory | Part II, 2003

  (i) State and prove a result of Euler relating the number of vertices, edges and faces of a plane graph. Use this result to exhibit a non-planar graph.

  (ii) State the vertex form of Menger's Theorem and explain how it follows from an appropriate version of the Max-flow-min-cut Theorem. Let $k \geqslant 2$. Show that every $k$-connected graph of order at least $2 k$ contains a cycle of length at least $2 k$.

  comment

• A1.8

  Graph Theory | Part II, 2003

  (i) State Brooks' Theorem, and prove it in the case of a 3 -connected graph.

  (ii) Let $G$ be a bipartite graph, with vertex classes $X$ and $Y$, each of order $n$. If $G$ contains no cycle of length 4 show that

  $$e(G) \leqslant \frac{n}{2}(1+\sqrt{4 n-3})$$

  For which integers $n \leq 12$ are there examples where equality holds?

  comment

• A4.9

  Graph Theory | Part II, 2003

  Write an essay on the vertex-colouring of graphs drawn on compact surfaces other than the sphere. You should include a proof of Heawood's bound, and an example of a surface for which this bound is not attained.

  comment

Groups, Rings and Fields

• A1.4

  Groups, Rings and Fields | Part II, 2003

  (i) Let $p$ be a prime number. Show that a group $G$ of order $p^{n}(n \geqslant 2)$ has a nontrivial normal subgroup, that is, $G$ is not a simple group.

  (ii) Let $p$ and $q$ be primes, $p>q$. Show that a group $G$ of order $p q$ has a normal Sylow $p$-subgroup. If $G$ has also a normal Sylow $q$-subgroup, show that $G$ is cyclic. Give a necessary and sufficient condition on $p$ and $q$ for the existence of a non-abelian group of order $p q$. Justify your answer.

  comment

• A2.4 B2.3

  Groups, Rings and Fields | Part II, 2003

  (i) In each of the following two cases, determine a highest common factor in $\mathbb{Z}[i]$ :

  (a) $3+4 i, 4-3 i$;

  (b) $3+4 i, 1+2 i$.

  (ii) State and prove the Eisenstein criterion for irreducibility of polynomials with integer coefficients. Show that, if $p$ is prime, the polynomial

  $$1+x+\cdots+x^{p-1}$$

  is irreducible over $\mathbb{Z}$.

  comment

• A3.4

  Groups, Rings and Fields | Part II, 2003

  (i) Let $K$ be the splitting field of the polynomial $f=X^{3}-2$ over the rationals. Find the Galois group $G$ of $K / \mathbb{Q}$ and describe its action on the roots of $f$.

  (ii) Let $K$ be the splitting field of the polynomial $X^{4}+a X^{2}+b$ (where $a, b \in \mathbb{Q}$ ) over the rationals. Assuming that the polynomial is irreducible, prove that the Galois group $G$ of the extension $K / \mathbb{Q}$ is either $C_{4}$, or $C_{2} \times C_{2}$, or the dihedral group $D_{8}$.

  comment

• A4.4

  Groups, Rings and Fields | Part II, 2003

  Write an essay on the theory of invariants. Your essay should discuss the theorem on the finite generation of the ring of invariants, the theorem on elementary symmetric functions, and some examples of calculation of rings of invariants.

  comment

• B1.3

  Groups, Rings and Fields | Part II, 2003

  (i) Let $p$ be a prime number. Show that a group $G$ of order $p^{n}(n \geqslant 2)$ has a nontrivial normal subgroup, that is, $G$ is not a simple group.

  (ii) Let $p$ and $q$ be primes, $p>q$. Show that a group $G$ of order $p q$ has a normal Sylow $p$-subgroup. If $G$ has also a normal Sylow $q$-subgroup, show that $G$ is cyclic. Give a necessary and sufficient condition on $p$ and $q$ for the existence of a non-abelian group of order $p q$. Justify your answer.

  comment

Hilbert Spaces

• B1.10

  Hilbert Spaces | Part II, 2003

  Let $H$ be a Hilbert space and let $T \in \mathcal{B}(H)$.

  (a) Define what it means for $T$ to be (i) invertible, and (ii) bounded below. Prove that $T$ is invertible if and only if both $T$ and $T^{*}$ are bounded below.

  (b) Define what it means for $T$ to be normal. Prove that $T$ is normal if and only if $\|T x\|=\left\|T^{*} x\right\|$ for all $x \in H$. Deduce that, if $T$ is normal, then every point of Sp $T$ is an approximate eigenvalue of $T$.

  (c) Let $S \in \mathcal{B}(H)$ be a self-adjoint operator, and let $\left(x_{n}\right)$ be a sequence in $H$ such that $\left\|x_{n}\right\|=1$ for all $n$ and $\left\|S x_{n}\right\| \rightarrow\|S\|$ as $n \rightarrow \infty$. Show, by direct calculation, that

  $$\left\|\left(S^{2}-\|S\|^{2}\right) x_{n}\right\|^{2} \rightarrow 0 \quad \text { as } n \rightarrow \infty$$

  and deduce that at least one of $\pm\|S\|$ is an approximate eigenvalue of $S$.

  (d) Deduce that, with $S$ as in (c),

  $$r(S)=\|S\|=\sup \{|\langle S x, x\rangle|: x \in H,\|x\|=1\}$$

  comment

• B3.8

  Hilbert Spaces | Part II, 2003

  Let $\mathcal{H}$ be the space of all functions on the real line $\mathbb{R}$ of the form $p(x) e^{-x^{2} / 2}$, where $p$ is a polynomial with complex coefficients. Make $\mathcal{H}$ into an inner-product space, in the usual way, by defining the inner product to be

  $$\langle f, g\rangle=\int_{-\infty}^{\infty} f(t) \overline{g(t)} d t, \quad f, g \in \mathcal{H}$$

  You should assume, without proof, that this equation does define an inner product on $\mathcal{H}$. Define the norm by $\|f\|_{2}=\langle f, f\rangle^{1 / 2}$ for $f \in \mathcal{H}$. Now define a sequence of functions $\left(F_{n}\right)_{n \geqslant 0}$ on $\mathbb{R}$ by

  $$F_{n}(x)=(-1)^{n} e^{x^{2} / 2} \frac{d^{n}}{d x^{n}} e^{-x^{2}}$$

  Prove that $\left(F_{n}\right)$ is an orthogonal sequence in $\mathcal{H}$ and that it spans $\mathcal{H}$.

  For every $f \in \mathcal{H}$ define the Fourier transform $\widehat{f}$ of $f$ by

  $$\widehat{f}(t)=\frac{1}{\sqrt{2 \pi}} \int_{-\infty}^{\infty} f(x) e^{-i t x} d x, \quad t \in \mathbb{R}$$

  Show that

  (a) $\widehat{F}_{n}=(-i)^{n} F_{n}$ for $n=0,1,2, \ldots$;

  (b) for all $f \in \mathcal{H}$ and $x \in \mathbb{R}$,

  $$\widehat{\widehat{f}}(x)=f(-x)$$

  (c) $\|\widehat{f}\|_{2}=\|f\|_{2}$ for all $f \in \mathcal{H}$.

  comment

• B4.7

  Hilbert Spaces | Part II, 2003

  Let $H$ be a Hilbert space and let $T \in \mathcal{B}(H)$.

  (a) Show that if $\|I-T\|<1$ then $T$ is invertible.

  (b) Prove that if $T$ is invertible and if $S \in \mathcal{B}(H)$ satisfies $\|S-T\|<\left\|T^{-1}\right\|^{-1}$, then $S$ is invertible.

  (c) Define what it means for $T$ to be compact. Prove that the set of compact operators on $H$ is a closed subset of $\mathcal{B}(H)$.

  (d) Prove that $T$ is compact if and only if there is a sequence $\left(F_{n}\right)$ in $\mathcal{B}(H)$, where each operator $F_{n}$ has finite rank, such that $\left\|F_{n}-T\right\| \rightarrow 0$ as $n \rightarrow \infty$.

  (e) Suppose that $T=A+K$, where $A$ is invertible and $K$ is compact. Prove that then, also, $T=B+F$, where $B$ is invertible and $F$ has finite rank.

  comment

Information Theory

• B1.14

  Information Theory | Part II, 2003

  A binary Huffman code is used for encoding symbols $1, \ldots, m$ occurring with probabilities $p_{1} \geqslant \ldots \geqslant p_{m}>0$ where $\sum_{1 \leqslant j \leqslant m} p_{j}=1$. Let $s_{1}$ be the length of a shortest codeword and $s_{m}$ of a longest codeword. Determine the maximal and minimal values of $s_{1}$ and $s_{m}$, and find binary trees for which they are attained.

  comment

• B2.14

  Information Theory | Part II, 2003

  Let $\mathcal{X}$ be a binary linear code of length $n$, rank $k$ and distance $d$. Let $x=$ $\left(x_{1}, \ldots, x_{n}\right) \in \mathcal{X}$ be a codeword with exactly $d$ non-zero digits.

  (a) Prove that $n \geqslant d+k-1$ (the Singleton bound).

  (b) Prove that truncating $\mathcal{X}$ on the non-zero digits of $x$ produces a code $\mathcal{X}^{\prime}$ of length $n-d$, rank $k-1$ and distance $d^{\prime}$ for some $d^{\prime} \geqslant\left\lceil\frac{d}{2}\right\rceil$. Here $\lceil a\rceil$ is the integer satisfying $a \leqslant\lceil a\rceil<a+1, a \in \mathbb{R}$.

  [Hint: Assume the opposite. Then, given $y \in \mathcal{X}$ and its truncation $y^{\prime} \in \mathcal{X}^{\prime}$, consider the coordinates where $x$ and $y$ have 1 in common (i.e. $x_{j}=y_{j}=1$ ) and where they differ $\left(\right.$ e.g. $x_{j}=1$ and $\left.y_{j}=0\right)$.]

  (c) Deduce that $n \geqslant d+\sum_{1 \leqslant \ell \leqslant k-1}\left\lceil\frac{d}{2^{\ell}}\right\rceil$ (an improved Singleton bound).

  comment

• B4.13

  Information Theory | Part II, 2003

  State and prove the Fano and generalized Fano inequalities.

  comment

Logic, Computation and Set Theory

• A $1 . 7 \quad$ B1.12

  Logic, Computation and Set Theory | Part II, 2003

  (i) State Zorn's Lemma. Use Zorn's Lemma to prove that every real vector space has a basis.

  (ii) State the Bourbaki-Witt Theorem, and use it to prove Zorn's Lemma, making clear where in the argument you appeal to the Axiom of Choice.

  Conversely, deduce the Bourbaki-Witt Theorem from Zorn's Lemma.

  If $X$ is a non-empty poset in which every chain has an upper bound, must $X$ be chain-complete?

  comment

• A3.8 B3.11

  Logic, Computation and Set Theory | Part II, 2003

  (i) What does it mean for a function from $\mathbb{N}^{k}$ to $\mathbb{N}$ to be recursive? Write down a function that is not recursive. You should include a proof that your example is not recursive.

  (ii) What does it mean for a subset of $\mathbb{N}^{k}$ to be recursive, and what does it mean for it to be recursively enumerable? Give, with proof, an example of a set that is recursively enumerable but not recursive. Prove that a set is recursive if and only if both it and its complement are recursively enumerable. If a set is recursively enumerable, must its complement be recursively enumerable?

  [You may assume the existence of any universal recursive functions or universal register machine programs that you wish.]

  comment

• A4.8 B4.10

  Logic, Computation and Set Theory | Part II, 2003

  Write an essay on propositional logic. You should include all relevant definitions, and should cover the Completeness Theorem, as well as the Compactness Theorem and the Decidability Theorem.

  [You may assume that the set of primitive propositions is countable. You do not need to give proofs of simple examples of syntactic implication, such as the fact that $p \Rightarrow p$ is a theorem or that $p \Rightarrow q$ and $q \Rightarrow r$ syntactically imply $p \Rightarrow r$.]

  comment

• B2.11

  Logic, Computation and Set Theory | Part II, 2003

  State the Axiom of Replacement.

  Show that for any set $x$ there is a transitive set $y$ that contains $x$, indicating where in your argument you have used the Axiom of Replacement. No form of recursion theorem may be assumed without proof.

  Which of the following are true and which are false? Give proofs or counterexamples as appropriate. You may assume standard properties of ordinals.

  (a) If $x$ is a transitive set then $x$ is an ordinal.

  (b) If each member of a set $x$ is an ordinal then $x$ is an ordinal.

  (c) If $x$ is a transitive set and each member of $x$ is an ordinal then $x$ is an ordinal.

  comment

Markov Chains

• A1.1 B1.1

  Markov Chains | Part II, 2003

  (i) Let $\left(X_{n}, Y_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk in $\mathbb{Z}^{2}$, starting from $(0,0)$, and set $T=\inf \left\{n \geqslant 0: \max \left\{\left|X_{n}\right|,\left|Y_{n}\right|\right\}=2\right\}$. Determine the quantities $\mathbb{E}(T)$ and $\mathbb{P}\left(X_{T}=2\right.$ and $\left.Y_{T}=0\right)$.

  (ii) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a discrete-time Markov chain with state-space $I$ and transition matrix $P$. What does it mean to say that a state $i \in I$ is recurrent? Prove that $i$ is recurrent if and only if $\sum_{n=0}^{\infty} p_{i i}^{(n)}=\infty$, where $p_{i i}^{(n)}$ denotes the $(i, i)$ entry in $P^{n}$.

  Show that the simple symmetric random walk in $\mathbb{Z}^{2}$ is recurrent.

  comment

• A2.1

  Markov Chains | Part II, 2003

  (i) What is meant by a Poisson process of rate $\lambda$ ? Show that if $\left(X_{t}\right)_{t \geqslant 0}$ and $\left(Y_{t}\right)_{t \geqslant 0}$ are independent Poisson processes of rates $\lambda$ and $\mu$ respectively, then $\left(X_{t}+Y_{t}\right)_{t \geqslant 0}$ is also a Poisson process, and determine its rate.

  (ii) A Poisson process of rate $\lambda$ is observed by someone who believes that the first holding time is longer than all subsequent holding times. How long on average will it take before the observer is proved wrong?

  comment

• A3.1 B3.1

  Markov Chains | Part II, 2003

  (i) Consider the continuous-time Markov chain $\left(X_{t}\right)_{t \geqslant 0}$ with state-space $\{1,2,3,4\}$ and $Q$-matrix

  $$Q=\left(\begin{array}{rrrr} -2 & 0 & 0 & 2 \\ 1 & -3 & 2 & 0 \\ 0 & 2 & -2 & 0 \\ 1 & 5 & 2 & -8 \end{array}\right)$$

  Set

  $$Y_{t}= \begin{cases}X_{t} & \text { if } X_{t} \in\{1,2,3\} \\ 2 & \text { if } X_{t}=4\end{cases}$$

  and

  $$Z_{t}= \begin{cases}X_{t} & \text { if } X_{t} \in\{1,2,3\} \\ 1 & \text { if } X_{t}=4\end{cases}$$

  Determine which, if any, of the processes $\left(Y_{t}\right)_{t \geqslant 0}$ and $\left(Z_{t}\right)_{t \geqslant 0}$ are Markov chains.

  (ii) Find an invariant distribution for the chain $\left(X_{t}\right)_{t \geqslant 0}$ given in Part (i). Suppose $X_{0}=1$. Find, for all $t \geqslant 0$, the probability that $X_{t}=1$.

  comment

• A4.1

  Markov Chains | Part II, 2003

  Consider a pack of cards labelled $1, \ldots, 52$. We repeatedly take the top card and insert it uniformly at random in one of the 52 possible places, that is, either on the top or on the bottom or in one of the 50 places inside the pack. How long on average will it take for the bottom card to reach the top?

  Let $p_{n}$ denote the probability that after $n$ iterations the cards are found in increasing order. Show that, irrespective of the initial ordering, $p_{n}$ converges as $n \rightarrow \infty$, and determine the limit $p$. You should give precise statements of any general results to which you appeal.

  Show that, at least until the bottom card reaches the top, the ordering of cards inserted beneath it is uniformly random. Hence or otherwise show that, for all $n$,

  $$\left|p_{n}-p\right| \leqslant 52(1+\log 52) / n$$

  comment

Mathematical Methods

• A2.17

  Mathematical Methods | Part II, 2003

  (i) Explain how to solve the Fredholm integral equation of the second kind,

  $$f(x)=\mu \int_{a}^{b} K(x, t) f(t) d t+g(x)$$

  in the case where $K(x, t)$ is of the separable (degenerate) form

  $$K(x, t)=a_{1}(x) b_{1}(t)+a_{2}(x) b_{2}(t)$$

  (ii) For what values of the real constants $\lambda$ and $A$ does the equation

  $$u(x)=\lambda \sin x+A \int_{0}^{\pi}(\cos x \cos t+\cos 2 x \cos 2 t) u(t) d t$$

  have (a) a unique solution, (b) no solution?

  comment

• A3.17

  Mathematical Methods | Part II, 2003

  (i) Explain what is meant by the assertion: "the series $\sum_{0}^{\infty} b_{n} x^{n}$ is asymptotic to $f(x)$ as $x \rightarrow 0 "$.

  Consider the integral

  $$I(\lambda)=\int_{0}^{A} e^{-\lambda x} g(x) d x$$

  where $A>0, \lambda$ is real and $g$ has the asymptotic expansion

  $$g(x) \sim a_{0} x^{\alpha}+a_{1} x^{\alpha+1}+a_{2} x^{\alpha+2}+\ldots$$

  as $x \rightarrow+0$, with $\alpha>-1$. State Watson's lemma describing the asymptotic behaviour of $I(\lambda)$ as $\lambda \rightarrow \infty$, and determine an expression for the general term in the asymptotic series.

  (ii) Let

  $$h(t)=\pi^{-1 / 2} \int_{0}^{\infty} \frac{e^{-x}}{x^{1 / 2}(1+2 x t)} d x$$

  for $t \geqslant 0$. Show that

  $$h(t) \sim \sum_{k=0}^{\infty}(-1)^{k} 1.3 . \cdots \cdot(2 k-1) t^{k}$$

  as $t \rightarrow+0$.

  Suggest, for the case that $t$ is smaller than unity, the point at which this asymptotic series should be truncated so as to produce optimal numerical accuracy.

  comment

• A4.21

  Mathematical Methods | Part II, 2003

  Let $y(x, \lambda)$ denote the solution for $0 \leqslant x<\infty$ of

  $$\frac{d^{2} y}{d x^{2}}-\left(x+\lambda^{2}\right) y=0$$

  subject to the conditions that $y(0, \lambda)=a$ and $y(x, \lambda) \rightarrow 0$ as $x \rightarrow \infty$, where $a>0$; it may be assumed that $y(x, \lambda)>0$ for $x>0$. Write $y(x, \lambda)$ in the form

  $$y(x, \lambda)=\exp (z(x, \lambda))$$

  and consider an asymptotic expansion of the form

  $$z(x, \lambda) \sim \sum_{n=0}^{\infty} \lambda^{1-n} \phi_{n}(x),$$

  valid in the limit $\lambda \rightarrow \infty$ with $x=O(1)$. Find $\phi_{0}(x), \phi_{1}(x), \phi_{2}(x)$ and $\phi_{3}(x)$.

  It is known that the solution $y(x, \lambda)$ is of the form

  $$y(x, \lambda)=c Y(X)$$

  where

  $$X=x+\lambda^{2}$$

  and the constant factor $c$ depends on $\lambda$. By letting $Y(X)=\exp (Z(X))$, show that the expression

  $$Z(X)=-\frac{2}{3} X^{3 / 2}-\frac{1}{4} \ln X$$

  satisfies the relevant differential equation with an error of $O\left(1 / X^{3 / 2}\right)$ as $X \rightarrow \infty$. Comment on the relationship between your answers for $z(x, \lambda)$ and $Z(X)$.

  comment

Methods of Mathematical Physics

• B1.19

  Methods of Mathematical Physics | Part II, 2003

  By considering the integral

  $$\int_{C}\left(\frac{t}{1-t}\right)^{i} d t$$

  where $C$ is a large circle centred on the origin, show that

  $$B(1+i, 1-i)=\pi \operatorname{cosech} \pi$$

  where

  $$B(p, q)=\int_{0}^{1} t^{p-1}(1-t)^{q-1} d t, \operatorname{Re}(p)>0, \operatorname{Re}(q)>0$$

  By using $B(p, q)=\frac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}$, deduce that $\Gamma(i) \Gamma(-i)=\pi \operatorname{cosech} \pi$.

  comment

• B2.18

  Methods of Mathematical Physics | Part II, 2003

  Let $\widehat{y}(p)$ be the Laplace transform of $y(t)$, where $y(t)$ satisfies

  $$y^{\prime}(t)=y(\pi-t)$$

  and

  $$y(0)=1 ; \quad y(\pi)=k ; \quad y(t)=0 \text { for } t<0 \text { and for } t>\pi$$

  Show that

  $$p \widehat{y}(p)+k e^{-\pi p}-1=e^{-\pi p} \widehat{y}(-p)$$

  and hence deduce that

  $$\widehat{y}(p)=\frac{(k+p)-(1+p k) e^{-\pi p}}{1+p^{2}}$$

  Use the inversion formula for Laplace transforms to find $y(t)$ for $t>\pi$ and deduce that a solution of the above boundary value problem exists only if $k=-1$. Hence find $y(t)$ for $0 \leqslant t \leqslant \pi$.

  comment

• B3.19

  Methods of Mathematical Physics | Part II, 2003

  Let

  $$f(\lambda)=\int_{\gamma} e^{\lambda\left(t-t^{3} / 3\right)} d t, \quad \lambda \text { real and positive }$$

  where $\gamma$ is a path beginning at $\infty e^{-2 i \pi / 3}$ and ending at $+\infty$ (on the real axis). Identify the saddle points and sketch the paths of constant phase through these points.

  Hence show that $f(\lambda) \sim e^{2 \lambda / 3} \sqrt{\pi / \lambda}$ as $\lambda \rightarrow \infty$.

  comment

• B4.19

  Methods of Mathematical Physics | Part II, 2003

  By setting $w(z)=\int_{\gamma} f(t) e^{-z t} d t$, where $\gamma$ and $f(t)$ are to be suitably chosen, explain how to find integral representations of the solutions of the equation

  $$z w^{\prime \prime}-k w=0$$

  where $k$ is a non-zero real constant and $z$ is complex. Discuss $\gamma$ in the particular case that $z$ is restricted to be real and positive and distinguish the different cases that arise according to the $\operatorname{sign}$ of $k$.

  Show that in this particular case, by choosing $\gamma$ as a closed contour around the origin, it is possible to express a solution in the form

  $$w(z)=A \sum_{n=0}^{\infty} \frac{(z k)^{n+1}}{n !(n+1) !}$$

  where $A$ is a constant.

  Show also that for $k>0$ there are solutions that satisfy

  $$w(z) \sim B z^{1 / 4} e^{-2 \sqrt{k z}} \quad \text { as } z \rightarrow \infty$$

  where $B$ is a constant.

  comment

Nonlinear Waves and Integrable Systems

• A2.18

  Nonlinear Waves and Integrable Systems | Part II, 2003

  (i) Write down the shock condition associated with the equation

  $$\rho_{t}+q_{x}=0$$

  where $q=q(\rho)$. Discuss briefly two possible heuristic approaches to justifying this shock condition.

  (ii) According to shallow water theory, waves on a uniformly sloping beach are described by the equations

  $$\begin{aligned} &\frac{\partial h}{\partial t}+\frac{\partial}{\partial x}(h u)=0, \\ &\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}+g \frac{\partial \eta}{\partial x}=0, \quad h=\alpha x+\eta, \end{aligned}$$

  where $\alpha$ is the constant slope of the beach, $g$ is the gravitational acceleration, $u(x, t)$ is the fluid velocity, and $\eta(x, t)$ is the elevation of the fluid surface above the undisturbed level.

  Find the characteristic velocities and the characteristic form of the equations.

  What are the Riemann variables and how do they vary with $t$ on the characteristics?

  comment

• A3.18

  Nonlinear Waves and Integrable Systems | Part II, 2003

  (i) Write down a Lax pair for the equation

  $$i q_{t}+q_{x x}=0 .$$

  Discuss briefly, without giving mathematical details, how this pair can be used to solve the Cauchy problem on the infinite line for this equation. Discuss how this approach can be used to solve the analogous problem for the nonlinear Schrödinger equation.

  (ii) Let $q(\zeta, \eta), \tilde{q}(\zeta, \eta)$ satisfy the equations

  $$\begin{aligned} &\tilde{q}_{\zeta}=q_{\zeta}+2 \lambda \sin \frac{\tilde{q}+q}{2} \\ &\tilde{q}_{\eta}=-q_{\eta}+\frac{2}{\lambda} \sin \frac{\tilde{q}-q}{2} \end{aligned}$$

  where $\lambda$ is a constant.

  (a) Show that the above equations are compatible provided that $q, \tilde{q}$ both satisfy the Sine-Gordon equation

  $$q_{\zeta \eta}=\sin q$$

  (b) Use the above result together with the fact that

  $$\int \frac{d x}{\sin x}=\ln \left(\tan \frac{x}{2}\right)+\text { constant }$$

  to show that the one-soliton solution of the Sine-Gordon equation is given by

  $$\tan \frac{q}{4}=c \exp \left(\lambda \zeta+\frac{\eta}{\lambda}\right)$$

  where $c$ is a constant.

  comment

• A4.22

  Nonlinear Waves and Integrable Systems | Part II, 2003

  Let $\Phi^{+}(t), \Phi^{-}(t)$ denote the boundary values of functions which are analytic inside and outside a disc of radius $\frac{1}{2}$ centred at the origin. Let $C$ denote the boundary of this disc.

  Suppose that $\Phi^{+}, \Phi^{-}$satisfy the jump condition

  $$\Phi^{+}(t)=\frac{t}{t^{2}-1} \Phi^{-}(t)+\frac{t^{3}-t^{2}+1}{t^{2}-t}, \quad t \in C .$$

  (a) Show that the associated index is 1 .

  (b) Find the canonical solution of the homogeneous problem, i.e. the solution satisfying

  $$X(z) \sim z^{-1}, \quad z \rightarrow \infty$$

  (c) Find the general solution of the Riemann-Hilbert problem satisfying the above jump condition as well as

  $$\Phi(z)=O\left(z^{-1}\right), \quad z \rightarrow \infty$$

  (d) Use the above result to solve the linear singular integral problem

  $$\left(t^{2}+t-1\right) \phi(t)+\frac{t^{2}-t-1}{\pi i} \oint_{C} \frac{\phi(\tau)}{\tau-t} d \tau=\frac{2\left(t^{3}-t^{2}+1\right)(t+1)}{t}, \quad t \in C .$$

  comment

Number Fields

• B1.9

  Number Fields | Part II, 2003

  Let $K=\mathbb{Q}(\alpha)$, where $\alpha=\sqrt[3]{10}$, and let $\mathcal{O}_{K}$ be the ring of algebraic integers of $K$. Show that the field polynomial of $r+s \alpha$, with $r$ and $s$ rational, is $(x-r)^{3}-10 s^{3}$.

  Let $\beta=\frac{1}{3}\left(\alpha^{2}+\alpha+1\right)$. By verifying that $\beta=3 /(\alpha-1)$ and determining the field polynomial, or otherwise, show that $\beta$ is in $\mathcal{O}_{K}$.

  By computing the traces of $\theta, \alpha \theta, \alpha^{2} \theta$, show that the elements of $\mathcal{O}_{K}$ have the form

  $$\theta=\frac{1}{3}\left(l+\frac{1}{10} m \alpha+\frac{1}{10} n \alpha^{2}\right)$$

  where $l, m, n$ are integers. By further computing the norm of $\frac{1}{10} \alpha(m+n \alpha)$, show that $\theta$ can be expressed as $\frac{1}{3}(u+v \alpha)+w \beta$ with $u, v, w$ integers. Deduce that $1, \alpha, \beta$ form an integral basis for $K$.

  comment

• B2.9

  Number Fields | Part II, 2003

  By Dedekind's theorem, or otherwise, factorise $2,3,5$ and 7 into prime ideals in the field $K=\mathbb{Q}(\sqrt{-34})$. Show that the ideal equations

  $$[\omega]=[5, \omega][7, \omega], \quad[\omega+3]=[2, \omega+3][5, \omega+3]^{2}$$

  hold in $K$, where $\omega=1+\sqrt{-34}$. Hence, prove that the ideal class group of $K$ is cyclic of order $4 .$

  [It may be assumed that the Minkowski constant for $K$ is $2 / \pi$.]

  comment

• B4.6

  Number Fields | Part II, 2003

  Write an essay on the Dirichlet unit theorem with particular reference to quadratic fields.

  comment

Number Theory

• A1.9

  Number Theory | Part II, 2003

  (i) Let $p$ be an odd prime and $k$ a strictly positive integer. Prove that the multiplicative group of relatively prime residue classes modulo $p^{k}$ is cyclic.

  [You may assume that the result is true for $k=1$.]

  (ii) Let $n=p_{1} p_{2} \ldots p_{r}$, where $r \geqslant 2$ and $p_{1}, p_{2}, \ldots, p_{r}$ are distinct odd primes. Let $B$ denote the set of all integers which are relatively prime to $n$. We recall that $n$ is said to be an Euler pseudo-prime to the base $b \in B$ if

  $$b^{(n-1) / 2} \equiv\left(\frac{b}{n}\right) \bmod n .$$

  If $n$ is an Euler pseudo-prime to the base $b_{1} \in B$, but is not an Euler pseudo-prime to the base $b_{2} \in B$, prove that $n$ is not an Euler pseudo-prime to the base $b_{1} b_{2}$. Let $p$ denote any of the primes $p_{1}, p_{2}, \ldots, p_{r}$. Prove that there exists a $b \in B$ such that

  $$\left(\frac{b}{p}\right)=-1 \quad \text { and } \quad b \equiv 1 \bmod n / p$$

  and deduce that $n$ is not an Euler pseudo-prime to this base $b$. Hence prove that $n$ is not an Euler pseudo-prime to the base $b$ for at least half of all the relatively prime residue classes $b \bmod n$.

  comment

• A3.9

  Number Theory | Part II, 2003

  (i) Let $x \geqslant 2$ be a real number and let $P(x)=\prod_{p \leqslant x}\left(1-\frac{1}{p}\right)^{-1}$, where the product is taken over all primes $p \leqslant x$. Prove that $P(x)>\log x$.

  (ii) Define the continued fraction of any positive irrational real number $x$. Illustrate your definition by computing the continued fraction of $1+\sqrt{3}$.

  Suppose that $a, b, c$ are positive integers with $b=a c$ and that $x$ has the periodic continued fraction $[b, a, b, a, \ldots]$. Prove that $x=\frac{1}{2}\left(b+\sqrt{b^{2}+4 c}\right)$.

  comment

• A4.10

  Number Theory | Part II, 2003

  Write an essay describing the factor base method for factorising a large odd positive integer $n$. Your essay should include a detailed explanation of how the continued fraction of $\sqrt{n}$ can be used to find a suitable factor base.

  comment

Numerical Analysis

• A1.20 B1.20

  Numerical Analysis | Part II, 2003

  (i) The linear algebraic equations $A \mathbf{u}=\mathbf{b}$, where $A$ is symmetric and positive-definite, are solved with the Gauss-Seidel method. Prove that the iteration always converges.

  (ii) The Poisson equation $\nabla^{2} u=f$ is given in the bounded, simply connected domain $\Omega \subseteq \mathbb{R}^{2}$, with zero Dirichlet boundary conditions on $\partial \Omega$. It is approximated by the fivepoint formula

  $$U_{m-1, n}+U_{m, n-1}+U_{m+1, n}+U_{m, n+1}-4 U_{m, n}=(\Delta x)^{2} f_{m, n}$$

  where $U_{m, n} \approx u(m \Delta x, n \Delta x), \quad f_{m, n}=f(m \Delta x, n \Delta x)$, and $(m \Delta x, n \Delta x)$ is in the interior of $\Omega$.

  Assume for the sake of simplicity that the intersection of $\partial \Omega$ with the grid consists only of grid points, so that no special arrangements are required near the boundary. Prove that the method can be written in a vector notation, $A \mathbf{u}=\mathbf{b}$ with a negative-definite matrix $A$.

  comment

• A2.19 B2.19

  Numerical Analysis | Part II, 2003

  (i) Explain briefly what is meant by the convergence of a numerical method for ordinary differential equations.

  (ii) Suppose the sufficiently-smooth function $f: \mathbb{R} \times \mathbb{R}^{d} \rightarrow \mathbb{R}^{d}$ obeys the Lipschitz condition: there exists $\lambda>0$ such that

  $$\|\mathbf{f}(t, \mathbf{x})-\mathbf{f}(t, \mathbf{y})\| \leqslant \lambda\|\mathbf{x}-\mathbf{y}\|, \quad \mathbf{x}, \mathbf{y} \in \mathbb{R}^{d}, t \geqslant 0$$

  Prove from first principles, without using the Dahlquist equivalence theorem, that the trapezoidal rule

  $$\mathbf{y}_{n+1}=\mathbf{y}_{n}+\frac{1}{2} h\left[\mathbf{f}\left(t_{n}, \mathbf{y}_{n}\right)+\mathbf{f}\left(t_{n+1}, \mathbf{y}_{n+1}\right)\right]$$

  for the solution of the ordinary differential equation

  $$\mathbf{y}^{\prime}=\mathbf{f}(t, \mathbf{y}), \quad t \geqslant 0, \quad \mathbf{y}(0)=\mathbf{y}_{0},$$

  converges.

  comment

• A3.19 B3.20

  Numerical Analysis | Part II, 2003

  (i) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial}{\partial x}\left(a(x) \frac{\partial u}{\partial x}\right), \quad 0 \leqslant x \leqslant 1, \quad t \geqslant 0$$

  with the initial condition $u(x, 0)=\phi(x), 0 \leqslant x \leqslant 1$ and zero boundary conditions at $x=0$ and $x=1$, is solved by the finite-difference method

  $$\begin{gathered} u_{m}^{n+1}=u_{m}^{n}+\mu\left[a_{m-\frac{1}{2}} u_{m-1}^{n}-\left(a_{m-\frac{1}{2}}+a_{m+\frac{1}{2}}\right) u_{m}^{n}+a_{m+\frac{1}{2}} u_{m+1}^{n}\right] \\ m=1,2, \ldots, N \end{gathered}$$

  where $\mu=\Delta t /(\Delta x)^{2}, \quad \Delta x=\frac{1}{N+1}$ and $u_{m}^{n} \approx u(m \Delta x, n \Delta t), a_{\alpha}=a(\alpha \Delta x)$.

  Assuming sufficient smoothness of the function $a$, and that $\mu$ remains constant as $\Delta x>0$ and $\Delta t>0$ become small, prove that the exact solution satisfies the numerical scheme with error $O\left((\Delta x)^{3}\right)$.

  (ii) For the problem defined in Part (i), assume that there exist $0<a_{-}<a_{+}<\infty$ such that $a_{-} \leqslant a(x) \leqslant a_{+}, \quad 0 \leqslant x \leqslant 1$. Prove that the method is stable for $0<\mu \leqslant 1 /\left(2 a_{+}\right)$.

  [Hint: You may use without proof the Gerschgorin theorem: All the eigenvalues of the matrix $A=\left(a_{k, l}\right)_{k, l=1, \ldots, M}$ are contained in $\bigcup_{k=1}^{m} \mathbb{S}_{k}$, where

  $$\left.\mathbb{S}_{k}=\left\{z \in \mathbb{C}:\left|z-a_{k, k}\right| \leqslant \sum_{\substack{l=1 \\ l \neq k}}^{m}\left|a_{k, l}\right|\right\}, \quad k=1,2, \ldots, m . \quad\right]$$

  comment

• A4.23 B4.20

  Numerical Analysis | Part II, 2003

  Write an essay on the conjugate gradient method. Your essay should include:

  (a) a statement of the method and a sketch of its derivation;

  (b) discussion, without detailed proofs, but with precise statements of relevant theorems, of the conjugacy of the search directions;

  (c) a description of the standard form of the algorithm;

  (d) discussion of the connection of the method with Krylov subspaces.

  comment

Optimization and Control

• B2.15

  Optimization and Control | Part II, 2003

  The owner of a put option may exercise it on any one of the days $1, \ldots, h$, or not at all. If he exercises it on day $t$, when the share price is $x_{t}$, his profit will be $p-x_{t}$. Suppose the share price obeys $x_{t+1}=x_{t}+\epsilon_{t}$, where $\epsilon_{1}, \epsilon_{2}, \ldots$ are i.i.d. random variables for which $E\left|\epsilon_{t}\right|<\infty$. Let $F_{s}(x)$ be the maximal expected profit the owner can obtain when there are $s$ further days to go and the share price is $x$. Show that

  (a) $F_{s}(x)$ is non-decreasing in $s$,

  (b) $F_{s}(x)+x$ is non-decreasing in $x$, and

  (c) $F_{s}(x)$ is continuous in $x$.

  Deduce that there exists a non-decreasing sequence, $a_{1}, \ldots, a_{h}$, such that expected profit is maximized by exercising the option the first day that $x_{t} \leqslant a_{t}$.

  Now suppose that the option never expires, so effectively $h=\infty$. Show by examples that there may or may not exist an optimal policy of the form 'exercise the option the first day that $x_{t} \leqslant a$.

  comment

• B3.14

  Optimization and Control | Part II, 2003

  State Pontryagin's Maximum Principle (PMP).

  In a given lake the tonnage of fish, $x$, obeys

  $$d x / d t=0.001(50-x) x-u, \quad 0<x \leqslant 50$$

  where $u$ is the rate at which fish are extracted. It is desired to maximize

  $$\int_{0}^{\infty} u(t) e^{-0.03 t} d t$$

  choosing $u(t)$ under the constraints $0 \leqslant u(t) \leqslant 1.4$, and $u(t)=0$ if $x(t)=0$. Assume the PMP with an appropriate Hamiltonian $H(x, u, t, \lambda)$. Now define $G(x, u, t, \eta)=$ $e^{0.03 t} H(x, u, t, \lambda)$ and $\eta(t)=e^{0.03 t} \lambda(t)$. Show that there exists $\eta(t), 0 \leqslant t$ such that on the optimal trajectory $u$ maximizes

  $$G(x, u, t, \eta)=\eta[0.001(50-x) x-u]+u$$

  and

  $$d \eta / d t=0.002(x-10) \eta$$

  Suppose that $x(0)=20$ and that under an optimal policy it is not optimal to extract all the fish. Argue that $\eta(0) \geqslant 1$ is impossible and describe qualitatively what must happen under the optimal policy.

  comment

• B4.14

  Optimization and Control | Part II, 2003

  The scalars $x_{t}, y_{t}, u_{t}$, are related by the equations

  $$x_{t}=x_{t-1}+u_{t-1}, \quad y_{t}=x_{t-1}+\eta_{t-1}, \quad t=1, \ldots, T,$$

  where $\left\{\eta_{t}\right\}$ is a sequence of uncorrelated random variables with means of 0 and variances of 1. Given that $\hat{x}_{0}$ is an unbiased estimate of $x_{0}$ of variance 1 , the control variable $u_{t}$ is to be chosen at time $t$ on the basis of the information $W_{t}$, where $W_{0}=\left(\hat{x}_{0}\right)$ and $W_{t}=\left(\hat{x}_{0}, u_{0}, \ldots, u_{t-1}, y_{1}, \ldots, y_{t}\right), t=1,2, \ldots, T-1$. Let $\hat{x}_{1}, \ldots, \hat{x}_{T}$ be the Kalman filter estimates of $x_{1}, \ldots, x_{T}$ computed from

  $$\hat{x}_{t}=\hat{x}_{t-1}+u_{t-1}+h_{t}\left(y_{t}-\hat{x}_{t-1}\right)$$

  by appropriate choices of $h_{1}, \ldots, h_{T}$. Show that the variance of $\hat{x}_{t}$ is $V_{t}=1 /(1+t)$.

  Define $F\left(W_{T}\right)=E\left[x_{T}^{2} \mid W_{T}\right]$ and

  $$F\left(W_{t}\right)=\inf _{u_{t}, \ldots, u_{T-1}} E\left[\sum_{\tau=t}^{T-1} u_{\tau}^{2}+x_{T}^{2} \mid W_{t}\right], \quad t=0, \ldots, T-1$$

  Show that $F\left(W_{t}\right)=\hat{x}_{t}^{2} P_{t}+d_{t}$, where $P_{t}=1 /(T-t+1), d_{T}=1 /(1+T)$ and $d_{t-1}=V_{t-1} V_{t} P_{t}+d_{t} .$

  How would the expression for $F\left(W_{0}\right)$ differ if $\hat{x}_{0}$ had a variance different from $1 ?$

  comment

Partial Differential Equations

• B1.18

  Partial Differential Equations | Part II, 2003

  (a) Define characteristic hypersurfaces and state a local existence and uniqueness theorem for a quasilinear partial differential equation with data on a non-characteristic hypersurface.

  (b) Consider the initial value problem

  $$3 u_{x}+u_{y}=-y u, \quad u(x, 0)=f(x),$$

  for a function $u: \mathbb{R}^{2} \rightarrow \mathbb{R}$ with $C^{1}$ initial data $f$ given for $y=0$. Obtain a formula for the solution by the method of characteristics and deduce that a $C^{1}$ solution exists for all $(x, y) \in \mathbb{R}^{2}$.

  Derive the following (well-posedness) property for solutions $u(x, y)$ and $v(x, y)$ corresponding to data $u(x, 0)=f(x)$ and $v(x, 0)=g(x)$ respectively:

  $$\sup _{x}|u(x, y)-v(x, y)| \leqslant \sup _{x}|f(x)-g(x)| \quad \text { for all } y .$$

  (c) Consider the initial value problem

  $$3 u_{x}+u_{y}=u^{2}, \quad u(x, 0)=f(x),$$

  for a function $u: \mathbb{R}^{2} \rightarrow \mathbb{R}$ with $C^{1}$ initial data $f$ given for $y=0$. Obtain a formula for the solution by the method of characteristics and hence show that if $f(x)<0$ for all $x$, then the solution exists for all $y>0$. Show also that if there exists $x_{0}$ with $f\left(x_{0}\right)>0$, then the solution does not exist for all $y>0$.

  comment

• B2.17

  Partial Differential Equations | Part II, 2003

  (a) If $f$ is a radial function on $\mathbb{R}^{n}$ (i.e. $f(x)=\phi(r)$ with $r=|x|$ for $x \in \mathbb{R}^{n}$ ), and $n>2$, then show that $f$ is harmonic on $\mathbb{R}^{n}-\{0\}$ if and only if

  $$\phi(r)=a+b r^{2-n}$$

  for $a, b \in \mathbb{R}$.

  (b) State the mean value theorem for harmonic functions and prove it for $n>2$.

  (c) Generalise the statement and the proof of the mean value theorem to the case of a subharmonic function, i.e. a $C^{2}$ function such that $\Delta u \leqslant 0$.

  comment

• B3.18

  Partial Differential Equations | Part II, 2003

  Consider the initial value problem

  $$\frac{\partial^{2} u}{\partial t^{2}}-\Delta u=0$$

  to be solved for $u: \mathbb{R} \times \mathbb{R}^{n} \rightarrow \mathbb{R}$, subject to the initial conditions

  $$u(0, x)=f(x), \quad \frac{\partial u}{\partial t}(0, x)=0$$

  for $f$ in the Schwarz space $\mathcal{S}\left(\mathbb{R}^{n}\right)$. Use the Fourier transform in $x$ to obtain a representation for the solution in the form

  $$u(t, x)=\int e^{i x \cdot \xi} A(t, \xi) \widehat{f}(\xi) d^{n} \xi$$

  where $A$ should be determined explicitly. Explain carefully why your formula gives a smooth solution to (1) and why it satisfies the initial conditions (2), referring to the required properties of the Fourier transform as necessary.

  Next consider the case $n=1$. Find a tempered distribution $T$ (depending on $t, x$ ) such that (3) can be written

  $$u=<T, \widehat{f}>$$

  and (using the definition of Fourier transform of tempered distributions) show that the formula reduces to

  $$u(t, x)=\frac{1}{2}[f(x-t)+f(x+t)]$$

  State and prove the Duhamel principle relating to the solution of the $n$-dimensional inhomogeneous wave equation

  $$\frac{\partial^{2} u}{\partial t^{2}}-\Delta u=h$$

  to be solved for $u: \mathbb{R} \times \mathbb{R}^{n} \rightarrow \mathbb{R}$, subject to the initial conditions

  $$u(0, x)=0, \quad \frac{\partial u}{\partial t}(0, x)=0$$

  for $h$ a $C^{\infty}$ function. State clearly assumptions used on the solvability of the homogeneous problem.

  [Hint: it may be useful to consider the Fourier transform of the tempered distribution defined by the function $\xi \mapsto e^{i \xi \cdot a}$.]

  comment

• B4.18

  Partial Differential Equations | Part II, 2003

  Discuss the basic properties of the Fourier transform and how it is used in the study of partial differential equations.

  The essay should include: definition and basic properties, inversion theorem, applications to establishing well-posedness of evolution partial differential equations with constant coefficients.

  comment

Principles of Dynamics

• A1.2 B1.2

  Principles of Dynamics | Part II, 2003

  (i) Consider $N$ particles moving in 3 dimensions. The Cartesian coordinates of these particles are $x^{A}(t), A=1, \ldots, 3 N$. Now consider an invertible change of coordinates to coordinates $q^{a}\left(x^{A}, t\right), \quad a=1, \ldots, 3 N$, so that one may express $x^{A}$ as $x^{A}\left(q^{a}, t\right)$. Show that the velocity of the system in Cartesian coordinates $\dot{x}^{A}(t)$ is given by the following expression:

  $$\dot{x}^{A}\left(\dot{q}^{a}, q^{a}, t\right)=\sum_{b=1}^{3 N} \dot{q}^{b} \frac{\partial x^{A}}{\partial q^{b}}\left(q^{a}, t\right)+\frac{\partial x^{A}}{\partial t}\left(q^{a}, t\right)$$

  Furthermore, show that Lagrange's equations in the two coordinate systems are related via

  $$\frac{\partial L}{\partial q^{a}}-\frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}^{a}}\right)=\sum_{A=1}^{3 N} \frac{\partial x^{A}}{\partial q^{a}}\left(\frac{\partial L}{\partial x^{A}}-\frac{d}{d t} \frac{\partial L}{\partial \dot{x}^{A}}\right)$$

  (ii) Now consider the case where there are $p<3 N$ constraints applied, $f^{\ell}\left(x^{A}, t\right)=$ $0, \ell=1, \ldots, p$. By considering the $f^{\ell}, \ell=1, \ldots, p$, and a set of independent coordinates $q^{a}, a=1, \ldots, 3 N-p$, as a set of $3 N$ new coordinates, show that the Lagrange equations of the constrained system, i.e.

  $$\begin{gathered} \frac{\partial L}{\partial x^{A}}-\frac{d}{d t}\left(\frac{\partial L}{\partial \dot{x}^{A}}\right)+\sum_{\ell=1}^{p} \lambda^{\ell} \frac{\partial f^{\ell}}{\partial x^{A}}=0, \quad A=1, \ldots, 3 N \\ f^{\ell}=0, \quad \ell=1, \ldots, p \end{gathered}$$

  (where the $\lambda^{\ell}$ are Lagrange multipliers) imply Lagrange's equations for the unconstrained coordinates, i.e.

  $$\frac{\partial L}{\partial q^{a}}-\frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}^{a}}\right)=0, \quad a=1, \ldots, 3 N-p .$$

  comment

• A2.2 B2.1

  Principles of Dynamics | Part II, 2003

  (i) The trajectory $\mathbf{x}(t)$ of a non-relativistic particle of mass $m$ and charge $q$ moving in an electromagnetic field obeys the Lorentz equation

  $$m \ddot{\mathbf{x}}=q\left(\mathbf{E}+\frac{\dot{\mathbf{x}}}{c} \wedge \mathbf{B}\right) .$$

  Show that this equation follows from the Lagrangian

  $$L=\frac{1}{2} m \dot{\mathbf{x}}^{2}-q\left(\phi-\frac{\dot{\mathbf{x}} \cdot \mathbf{A}}{c}\right)$$

  where $\phi(\mathbf{x}, t)$ is the electromagnetic scalar potential and $\mathbf{A}(\mathbf{x}, t)$ the vector potential, so that

  $$\mathbf{E}=-\frac{1}{c} \dot{\mathbf{A}}-\nabla \phi \text { and } \mathbf{B}=\nabla \wedge \mathbf{A}$$

  (ii) Let $\mathbf{E}=0$. Consider a particle moving in a constant magnetic field which points in the $z$ direction. Show that the particle moves in a helix about an axis pointing in the $z$ direction. Evaluate the radius of the helix.

  comment

• A3.2

  Principles of Dynamics | Part II, 2003

  (i) An axisymmetric bowling ball of mass $M$ has the shape of a sphere of radius $a$. However, it is biased so that the centre of mass is located a distance $a / 2$ away from the centre, along the symmetry axis.

  The three principal moments of inertia about the centre of mass are $(A, A, C)$. The ball starts out in a stable equilibrium at rest on a perfectly frictionless flat surface with the symmetry axis vertical. The symmetry axis is then tilted through $\theta_{0}$, the ball is spun about this axis with an angular velocity $n$, and the ball is released.

  Explain why the centre of mass of the ball moves only in the vertical direction during the subsequent motion. Write down the Lagrangian for the ball in terms of the usual Euler angles $\theta, \phi$ and $\psi$.

  (ii) Show that there are three independent constants of the motion. Eliminate two of the angles from the Lagrangian and find the effective Lagrangian for the coordinate $\theta$.

  Find the maximum and minimum values of $\theta$ in the motion of the ball when the quantity $\frac{C^{2} n^{2}}{A M g a}$ is (a) very small and (b) very large.

  comment

• A4.2

  Principles of Dynamics | Part II, 2003

  The action $S$ of a Hamiltonian system may be regarded as a function of the final coordinates $q^{a}, a=1, \ldots, N$, and the final time $t$ by setting

  $$S\left(q^{a}, t\right)=\int_{\left(q_{i}^{a}, t_{i}\right)}^{\left(q^{a}, t\right)} d t^{\prime}\left[p^{a}\left(t^{\prime}\right) \dot{q}^{a}\left(t^{\prime}\right)-H\left(p^{a}\left(t^{\prime}\right), q^{a}\left(t^{\prime}\right), t^{\prime}\right)\right]$$

  where the initial coordinates $q_{i}^{a}$ and time $t_{i}$ are held fixed, and $p^{a}\left(t^{\prime}\right), q^{a}\left(t^{\prime}\right)$ are the solutions to Hamilton's equations with Hamiltonian $H$, satisfying $q^{a}(t)=q^{a}, q^{a}\left(t_{i}\right)=q_{i}^{a}$.

  (a) Show that under an infinitesimal change of the final coordinates $\delta q^{a}$ and time $\delta t$, the change in $S$ is

  $$\delta S=p_{a}(t) \delta q_{a}-H\left(p^{a}(t), q^{a}(t), t\right) \delta t$$

  (b) Hence derive the Hamilton-Jacobi equation

  $$\frac{\partial S}{\partial t}\left(q^{a}, t\right)+H\left(\frac{\partial S}{\partial q^{a}}\left(q^{a}, t\right), q^{a}, t\right)=0$$

  (c) If we can find a solution to $(*)$,

  $$S=S\left(q^{a}, t ; P^{a}\right),$$

  where $P^{a}$ are $N$ integration constants, then we can use $S$ as a generating function of type $I I$, where

  $$p^{a}=\frac{\partial S}{\partial q^{a}} \quad, \quad Q^{a}=-\frac{\partial S}{\partial P^{a}}$$

  Show that the Hamiltonian $K$ in the new coordinates $Q^{a}, P^{a}$ vanishes.

  (d) Write down and solve the Hamilton-Jacobi equation for the one-dimensional simple harmonic oscillator, where $H=\frac{1}{2}\left(p^{2}+q^{2}\right)$. Show the solution takes the form $S(q, t ; E)=W(q, E)-E t$. Using this as a generating function $F_{I I}(q, t, P)$ show that the new coordinates $Q, P$ are constants of the motion and give their physical interpretation.

  comment

Principles of Statistics

• A1.12 B1.15

  Principles of Statistics | Part II, 2003

  (i) A public health official is seeking a rational policy of vaccination against a relatively mild ailment which causes absence from work. Surveys suggest that $60 \%$ of the population are already immune, but accurate tests to detect vulnerability in any individual are too costly for mass screening. A simple skin test has been developed, but is not completely reliable. A person who is immune to the ailment will have a negligible reaction to the skin test with probability $0.4$, a moderate reaction with probability $0.5$ and a strong reaction with probability 0.1. For a person who is vulnerable to the ailment the corresponding probabilities are $0.1,0.4$ and $0.5$. It is estimated that the money-equivalent of workhours lost from failing to vaccinate a vulnerable person is 20 , that the unnecessary cost of vaccinating an immune person is 8 , and that there is no cost associated with vaccinating a vulnerable person or failing to vaccinate an immune person. On the basis of the skin test, it must be decided whether to vaccinate or not. What is the Bayes decision rule that the health official should adopt?

  (ii) A collection of $I$ students each sit $J$ exams. The ability of the $i$ th student is represented by $\theta_{i}$ and the performance of the $i$ th student on the $j$ th exam is measured by $X_{i j}$. Assume that, given $\boldsymbol{\theta}=\left(\theta_{1}, \ldots, \theta_{I}\right)$, an appropriate model is that the variables $\left\{X_{i j}, 1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J\right\}$ are independent, and

  $$X_{i j} \sim N\left(\theta_{i}, \tau^{-1}\right),$$

  for a known positive constant $\tau$. It is reasonable to assume, a priori, that the $\theta_{i}$ are independent with

  $$\theta_{i} \sim N\left(\mu, \zeta^{-1}\right),$$

  where $\mu$ and $\zeta$ are population parameters, known from experience with previous cohorts of students.

  Compute the posterior distribution of $\boldsymbol{\theta}$ given the observed exam marks vector $\mathbf{X}=\left\{X_{i j}, 1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J\right\} .$

  Suppose now that $\tau$ is also unknown, but assumed to have a $\operatorname{Gamma}\left(\alpha_{0}, \beta_{0}\right)$ distribution, for known $\alpha_{0}, \beta_{0}$. Compute the posterior distribution of $\tau$ given $\boldsymbol{\theta}$ and $\mathbf{X}$ Find, up to a normalisation constant, the form of the marginal density of $\boldsymbol{\theta}$ given $\mathbf{X}$.

  comment

• A2.11 B2.16

  Principles of Statistics | Part II, 2003

  (i) Outline briefly the Bayesian approach to hypothesis testing based on Bayes factors.

  (ii) Let $Y_{1}, Y_{2}$ be independent random variables, both uniformly distributed on $\left(\theta-\frac{1}{2}, \theta+\frac{1}{2}\right)$. Find a minimal sufficient statistic for $\theta$. Let $Y_{(1)}=\min \left\{Y_{1}, Y_{2}\right\}$, $Y_{(2)}=\max \left\{Y_{1}, Y_{2}\right\}$. Show that $R=Y_{(2)}-Y_{(1)}$ is ancilliary and explain why the Conditionality Principle would lead to inference about $\theta$ being drawn from the conditional distribution of $\frac{1}{2}\left\{Y_{(1)}+Y_{(2)}\right\}$ given $R$. Find the form of this conditional distribution.

  comment

• A3.12 B3.15

  Principles of Statistics | Part II, 2003

  (i) Let $X_{1}, \ldots, X_{n}$ be independent, identically distributed random variables, with the exponential density $f(x ; \theta)=\theta e^{-\theta x}, x>0$.

  Obtain the maximum likelihood estimator $\hat{\theta}$ of $\theta$. What is the asymptotic distribution of $\sqrt{n}(\hat{\theta}-\theta)$ ?

  What is the minimum variance unbiased estimator of $\theta ?$ Justify your answer carefully.

  (ii) Explain briefly what is meant by the profile log-likelihood for a scalar parameter of interest $\gamma$, in the presence of a nuisance parameter $\xi$. Describe how you would test a null hypothesis of the form $H_{0}: \gamma=\gamma_{0}$ using the profile log-likelihood ratio statistic.

  In a reliability study, lifetimes $T_{1}, \ldots, T_{n}$ are independent and exponentially distributed, with means of the form $E\left(T_{i}\right)=\exp \left(\beta+\xi z_{i}\right)$ where $\beta, \xi$ are unknown and $z_{1}, \ldots, z_{n}$ are known constants. Inference is required for the mean lifetime, $\exp \left(\beta+\xi z_{0}\right)$, for covariate value $z_{0}$.

  Find, as explicitly as possible, the profile log-likelihood for $\gamma \equiv \beta+\xi z_{0}$, with nuisance parameter $\xi$.

  Show that, under $H_{0}: \gamma=\gamma_{0}$, the profile $\log -$ likelihood ratio statistic has a distribution which does not depend on the value of $\xi$. How might the parametric bootstrap be used to obtain a test of $H_{0}$ of exact size $\alpha$ ?

  [Hint: if $Y$ is exponentially distributed with mean 1 , then $\mu Y$ is exponentially distributed with mean $\mu$.]

  comment

• A4.13 B4.15

  Principles of Statistics | Part II, 2003

  Write an account, with appropriate examples, of inference in multiparameter exponential families. Your account should include a discussion of natural statistics and their properties and of various conditional tests on natural parameters.

  comment

Probability and Measure

• B1.13

  Probability and Measure | Part II, 2003

  State and prove the first Borel-Cantelli Lemma.

  Suppose that $\left(F_{n}\right)$ is a sequence of events in a common probability space such that $\mathbb{P}\left(F_{i} \cap F_{j}\right) \leqslant \mathbb{P}\left(F_{i}\right) \cdot \mathbb{P}\left(F_{j}\right)$ whenever $i \neq j$ and that $\sum_{n} \mathbb{P}\left(F_{n}\right)=\infty$.

  Let $1_{F_{n}}$ be the indicator function of $F_{n}$ and let

  $$S_{n}=\sum_{k \leqslant n} 1_{F_{k}} ; \mu_{n}=\mathbb{E}\left(S_{n}\right)$$

  Use Chebyshev's inequality to show that

  $$\mathbb{P}\left(S_{n}<\frac{1}{2} \mu_{n}\right) \leqslant \mathbb{P}\left(\left|S_{n}-\mu_{n}\right|>\frac{1}{2} \mu_{n}\right) \leqslant \frac{4}{\mu_{n}}$$

  Deduce, using the first Borel-Cantelli Lemma, that $\mathbb{P}\left(F_{n}\right.$ infinitely often $)=1$.

  comment

• B2.12

  Probability and Measure | Part II, 2003

  Let $H$ be a Hilbert space and let $V$ be a closed subspace of $H$. Let $x \in H$. Show that there is a unique decomposition $x=u+v$ such that $v \in V$ and $u \in V^{\perp}$.

  Now suppose $(\Omega, \mathcal{F}, \mathbb{P})$ is a probability space and let $X \in L^{2}(\Omega, \mathcal{F}, \mathbb{P})$. Suppose $\mathcal{G}$ is a sub- $\sigma$-algebra of $\mathcal{F}$. Define $\mathbb{E}(X \mid \mathcal{G})$ using a decomposition of the above type. Show that $\mathbb{E}\left(\mathbb{E}(X \mid \mathcal{G}) .1_{A}\right)=\mathbb{E}\left(X .1_{A}\right)$ for each set $A \in \mathcal{G}$.

  Let $\mathcal{G}_{1} \subseteq \mathcal{G}_{2}$ be two sub- $\sigma$-algebras of $\mathcal{F}$. Show that (a) $\mathbb{E}\left(\mathbb{E}\left(X \mid \mathcal{G}_{1}\right) \mid \mathcal{G}_{2}\right)=\mathbb{E}\left(X \mid \mathcal{G}_{1}\right)$; (b) $\mathbb{E}\left(\mathbb{E}\left(X \mid \mathcal{G}_{2}\right) \mid \mathcal{G}_{1}\right)=\mathbb{E}\left(X \mid \mathcal{G}_{1}\right)$.

  No general theorems about projections on Hilbert spaces may be quoted without proof.

  comment

• B3.12

  Probability and Measure | Part II, 2003

  Explain what is meant by the characteristic function $\phi$ of a real-valued random variable and prove that $|\phi|^{2}$ is also a characteristic function of some random variable.

  Let us say that a characteristic function $\phi$ is infinitely divisible when, for each $n \geqslant 1$, we can write $\phi=\left(\phi_{n}\right)^{n}$ for some characteristic function $\phi_{n}$. Prove that, in this case, the limit

  $$\psi(t)=\lim _{n \rightarrow \infty}\left|\phi_{2 n}(t)\right|^{2}$$

  exists for all real $t$ and is continuous at $t=0$.

  Using Lévy's continuity theorem for characteristic functions, which you should state carefully, deduce that $\psi$ is a characteristic function. Hence show that, if $\phi$ is infinitely divisible, then $\phi(t)$ cannot vanish for any real $t$.

  comment

• B4.11

  Probability and Measure | Part II, 2003

  Let $f:[a, b] \rightarrow \mathbb{R}$ be integrable with respect to Lebesgue measure $\mu$ on $[a, b]$. Prove that, if

  $$\int_{J} f d \mu=0$$

  for every sub-interval $J$ of $[a, b]$, then $f=0$ almost everywhere on $[a, b]$.

  Now define

  $$F(x)=\int_{a}^{x} f d \mu .$$

  Prove that $F$ is continuous on $[a, b]$. Show that, if $F$ is zero on $[a, b]$, then $f$ is zero almost everywhere on $[a, b]$.

  Suppose now that $f$ is bounded and Lebesgue integrable on $[a, b]$. By applying the Dominated Convergence Theorem to

  $$F_{n}(x)=\frac{F\left(x+\frac{1}{n}\right)-F(x)}{\frac{1}{n}},$$

  or otherwise, show that, if $F$ is differentiable on $[a, b]$, then $F^{\prime}=f$ almost everywhere on $[a, b]$.

  The functions $f_{n}:[a, b] \rightarrow \mathbb{R}$ have the properties:

  (a) $f_{n}$ converges pointwise to a differentiable function $g$ on $[a, b]$,

  (b) each $f_{n}$ has a continuous derivative $f_{n}^{\prime}$ with $\left|f_{n}^{\prime}(x)\right| \leqslant 1$ on $[a, b]$,

  (c) $f_{n}^{\prime}$ converges pointwise to some function $h$ on $[a, b]$.

  Deduce that

  $$h(x)=\lim _{n \rightarrow \infty}\left(\frac{d f_{n}(x)}{d x}\right)=\frac{d}{d x}\left(\lim _{n \rightarrow \infty} f_{n}(x)\right)=g^{\prime}(x)$$

  almost everywhere on $[a, b]$.

  comment

Quantum Physics

• A1.14

  Quantum Physics | Part II, 2003

  (i) An electron of mass $m$ and spin $\frac{1}{2}$ moves freely inside a cubical box of side $L$. Verify that the energy eigenstates of the system are $\phi_{l m n}(\mathbf{r}) \chi_{\pm}$where the spatial wavefunction is given by

  $$\phi_{l m n}(\mathbf{r})=\left(\frac{2}{L}\right)^{3 / 2} \sin \left(\frac{l \pi x}{L}\right) \sin \left(\frac{m \pi y}{L}\right) \sin \left(\frac{n \pi z}{L}\right)$$

  and

  $$\chi_{+}=\left(\begin{array}{l} 1 \\ 0 \end{array}\right), \quad \chi_{-}=\left(\begin{array}{l} 0 \\ 1 \end{array}\right)$$

  Give the corresponding energy eigenvalues.

  A second electron is inserted into the box. Explain how the Pauli principle determines the structure of the wavefunctions associated with the lowest energy level and the first excited energy level. What are the values of the energy in these two levels and what are the corresponding degeneracies?

  (ii) When the side of the box, $L$, is large, the number of eigenstates available to the electron with energy in the range $E \rightarrow E+d E$ is $\rho(E) d E$. Show that

  $$\rho(E)=\frac{L^{3}}{\pi^{2} \hbar^{3}} \sqrt{2 m^{3} E}$$

  A large number, $N$, of electrons are inserted into the box. Explain how the ground state is constructed and define the Fermi energy, $E_{F}$. Show that in the ground state

  $$N=\frac{2}{3} \frac{L^{3}}{\pi^{2} \hbar^{3}} \sqrt{2 m^{3}}\left(E_{F}\right)^{3 / 2}$$

  When a magnetic field $H$ in the $z$-direction is applied to the system, an electron with spin up acquires an additional energy $+\mu H$ and an electron with spin down an energy $-\mu H$, where $-\mu$ is the magnetic moment of the electron and $\mu>0$. Describe, for the case $E_{F}>\mu H$, the structure of the ground state of the system of $N$ electrons in the box and show that

  $$N=\frac{1}{3} \frac{L^{3}}{\pi^{2} \hbar^{3}} \sqrt{2 m^{3}}\left(\left(E_{F}+\mu H\right)^{3 / 2}+\left(E_{F}-\mu H\right)^{3 / 2}\right) \text {. }$$

  Calculate the induced magnetic moment, $M$, of the ground state of the system and show that for a weak magnetic field the magnetic moment is given by

  $$M \approx \frac{3}{2} N \frac{\mu^{2} H}{E_{F}}$$

  comment

• A2.14

  Quantum Physics | Part II, 2003

  (i) A system of $N$ distinguishable non-interacting particles has energy levels $E_{i}$ with degeneracy $g_{i}, 1 \leqslant i<\infty$, for each particle. Show that in thermal equilibrium the number of particles $N_{i}$ with energy $E_{i}$ is given by

  $$N_{i}=g_{i} e^{-\beta\left(E_{i}-\mu\right)}$$

  where $\beta$ and $\mu$ are parameters whose physical significance should be briefly explained.

  A gas comprises a set of atoms with non-degenerate energy levels $E_{i}, 1 \leqslant i<\infty$. Assume that the gas is dilute and the motion of the atoms can be neglected. For such a gas the atoms can be treated as distinguishable. Show that when the system is at temperature $T$, the number of atoms $N_{i}$ at level $i$ and the number $N_{j}$ at level $j$ satisfy

  $$\frac{N_{i}}{N_{j}}=e^{-\left(E_{i}-E_{j}\right) / k T}$$

  where $k$ is Boltzmann's constant.

  (ii) A system of bosons has a set of energy levels $W_{a}$ with degeneracy $f_{a}, 1 \leqslant a<\infty$, for each particle. In thermal equilibrium at temperature $T$ the number $n_{a}$ of particles in level $a$ is

  $$n_{a}=\frac{f_{a}}{e^{\left(W_{a}-\mu\right) / k T}-1} \text {. }$$

  What is the value of $\mu$ when the particles are photons?

  Given that the density of states $\rho(\omega)$ for photons of frequency $\omega$ in a cubical box of side $L$ is

  $$\rho(\omega)=L^{3} \frac{\omega^{2}}{\pi^{2} c^{3}}$$

  where $c$ is the speed of light, show that at temperature $T$ the density of photons in the frequency range $\omega \rightarrow \omega+d \omega$ is $n(\omega) d \omega$ where

  $$n(\omega)=\frac{\omega^{2}}{\pi^{2} c^{3}} \frac{1}{e^{\hbar \omega / k T}-1}$$

  Deduce the energy density, $\epsilon(\omega)$, for photons of frequency $\omega$.

  The cubical box is occupied by the gas of atoms described in Part (i) in the presence of photons at temperature $T$. Consider the two atomic levels $i$ and $j$ where $E_{i}>E_{j}$ and $E_{i}-E_{j}=\hbar \omega$. The rate of spontaneous photon emission for the transition $i \rightarrow j$ is $A_{i j}$. The rate of absorption is $B_{j i} \epsilon(\omega)$ and the rate of stimulated emission is $B_{i j} \epsilon(\omega)$. Show that the requirement that these processes maintain the atoms and photons in thermal equilibrium yields the relations

  $$B_{i j}=B_{j i}$$

  and

  $$A_{i j}=\left(\frac{\hbar \omega^{3}}{\pi^{2} c^{3}}\right) B_{i j}$$

  comment

• A4.16

  Quantum Physics | Part II, 2003

  Describe the energy band structure available to electrons moving in crystalline materials. How can it be used to explain the properties of crystalline materials that are conductors, insulators and semiconductors?

  Where does the Fermi energy lie in an intrinsic semiconductor? Describe the process of doping of semiconductors and explain the difference between $n$-type and $p$-type doping. What is the effect of the doping on the position of the Fermi energy in the two cases?

  Why is there a potential difference across a junction of $n$-type and $p$-type semiconductors?

  Derive the relation

  $$I=I_{0}\left(1-e^{-q V / k T}\right)$$

  between the current, $I$, and the voltage, $V$, across an $n p$ junction, where $I_{0}$ is the total minority current in the semiconductor and $q$ is the charge on the electron, $T$ is the temperature and $k$ is Boltzmann's constant. Your derivation should include an explanation of the terms majority current and minority current.

  Why can the $n p$ junction act as a rectifier?

  comment

Representation Theory

• B1.6

  Representation Theory | Part II, 2003

  Define the inner product $\langle\varphi, \psi\rangle$ of two class functions from the finite group $G$ into the complex numbers. Prove that characters of the irreducible representations of $G$ form an orthonormal basis for the space of class functions.

  Consider the representation $\pi: S_{n} \rightarrow G L_{n}(\mathbb{C})$ of the symmetric group $S_{n}$ by permutation matrices. Show that $\pi$ splits as a direct sum $1 \oplus \rho$ where 1 denotes the trivial representation. Is the $(n-1)$-dimensional representation $\rho$ irreducible?

  comment

• B2.6

  Representation Theory | Part II, 2003

  Let $V_{n}$ be the space of homogeneous polynomials of degree $n$ in two variables $z_{1}$ and $z_{2}$. Define a left action of $G=S U_{2}$ on the space of polynomials by setting

  $$(g P) z=P(z g),$$

  where $P \in \mathbb{C}\left[z_{1}, z_{2}\right], \quad g=\left(\begin{array}{cc}a & b \\ c & d\end{array}\right), \quad z=\left(z_{1}, z_{2}\right) \quad$ and $\quad z g=\left(a z_{1}+c z_{2}, b z_{1}+d z_{2}\right)$.

  Show that

  (a) the representations $V_{n}$ are irreducible,

  (b) the representations $V_{n}$ exhaust the irreducible representations of $S U_{2}$, and

  

  comment

• B3.5

  Representation Theory | Part II, 2003

  If $\rho_{1}: G_{1} \rightarrow G L\left(V_{1}\right)$ and $\rho_{2}: G_{2} \rightarrow G L\left(V_{2}\right)$ are representations of the finite groups $G_{1}$ and $G_{2}$ respectively, define the tensor product $\rho_{1} \otimes \rho_{2}$ as a representation of the group $G_{1} \times G_{2}$ and show that its character is given by

  $$\chi_{\rho_{1} \otimes \rho_{2}}\left(g_{1}, g_{2}\right)=\chi_{\rho_{1}}\left(g_{1}\right) \chi_{\rho_{2}}\left(g_{2}\right)$$

  Prove that

  (a) if $\rho_{1}$ and $\rho_{2}$ are irreducible, then $\rho_{1} \otimes \rho_{2}$ is an irreducible representation of $G_{1} \times G_{2}$;

  (b) each irreducible representation of $G_{1} \times G_{2}$ is equivalent to a representation $\rho_{1} \otimes \rho_{2}$ where each $\rho_{i}$ is irreducible $(i=1,2) .$

  Is every representation of $G_{1} \times G_{2}$ the tensor product of a representation of $G_{1}$ and a representation of $G_{2}$ ?

  comment

• B4.2

  Representation Theory | Part II, 2003

  Assume that the group $S L_{2}\left(\mathbb{F}_{3}\right)$ of $2 \times 2$ matrices of determinant 1 with entries from the field $\mathbb{F}_{3}$ has presentation

  $$\left\langle X, P, Q: X^{3}=P^{4}=1, P^{2}=Q^{2}, P Q P^{-1}=Q^{-1}, X P X^{-1}=Q, X Q X^{-1}=P Q\right\rangle$$

  Show that the subgroup generated by $P^{2}$ is central and that the quotient group can be identified with the alternating group $A_{4}$. Assuming further that $S L_{2}\left(\mathbb{F}_{3}\right)$ has seven conjugacy classes find the character table.

  Is it true that every irreducible character is induced up from the character of a 1-dimensional representation of some subgroup?

  [Hint: You may find it useful to note that $S L_{2}\left(\mathbb{F}_{3}\right)$ may be regarded as a subgroup of $S U_{2}$, providing a faithful 2-dimensional representation; the subgroup generated by $P$ and $Q$ is the quaternion group of order 8 , acting irreducibly.]

  comment

Riemann Surfaces

• B1.11

  Riemann Surfaces | Part II, 2003

  Prove that a holomorphic map from $\mathbb{P}^{1}$ to itself is either constant or a rational function. Prove that a holomorphic map of degree 1 from $\mathbb{P}^{1}$ to itself is a Möbius transformation.

  Show that, for every finite set of distinct points $z_{1}, z_{2}, \ldots, z_{N}$ in $\mathbb{P}^{1}$ and any values $w_{1}, w_{2}, \ldots, w_{N} \in \mathbb{P}^{1}$, there is a holomorphic function $f: \mathbb{P}^{1} \rightarrow \mathbb{P}^{1}$ with $f\left(z_{n}\right)=w_{n}$ for $n=1,2, \ldots, N$.

  comment

• B3.9

  Riemann Surfaces | Part II, 2003

  Let $L$ be the lattice $\mathbb{Z} \omega_{1}+\mathbb{Z} \omega_{2}$ for two non-zero complex numbers $\omega_{1}, \omega_{2}$ whose ratio is not real. Recall that the Weierstrass function $\wp$ is given by the series

  $$\wp(u)=\frac{1}{u^{2}}+\sum_{\omega \in L-\{0\}}\left(\frac{1}{(u-\omega)^{2}}-\frac{1}{\omega^{2}}\right)$$

  the function $\zeta$ is the (unique) odd anti-derivative of $-\wp$; and $\sigma$ is defined by the conditions

  $$\sigma^{\prime}(u)=\zeta(u) \sigma(u) \quad \text { and } \quad \sigma^{\prime}(0)=1$$

  (a) By writing a differential equation for $\sigma(-u)$, or otherwise, show that $\sigma$ is an odd function.

  (b) Show that $\sigma\left(u+\omega_{i}\right)=-\sigma(u) \exp \left(a_{i}\left(u+b_{i}\right)\right)$ for some constants $a_{i}, b_{i}$. Use (a) to express $b_{i}$ in terms of $\omega_{i}$. [Do not attempt to express $a_{i}$ in terms of $\omega_{i}$.]

  (c) Show that the function $f(u)=\sigma(2 u) / \sigma(u)^{4}$ is periodic with respect to the lattice $L$ and deduce that $f(u)=-\wp^{\prime}(u)$.

  comment

• B4.8

  Riemann Surfaces | Part II, 2003

  (a) Define the degree $\operatorname{deg} f$ of a meromorphic function on the Riemann sphere $\mathbb{P}^{1}$. State the Riemann-Hurwitz theorem.

  Let $f$ and $g$ be two rational functions on the sphere $\mathbb{P}^{1}$. Show that

  $$\operatorname{deg}(f+g) \leqslant \operatorname{deg} f+\operatorname{deg} g$$

  Deduce that

  $$|\operatorname{deg} f-\operatorname{deg} g| \leqslant \operatorname{deg}(f+g) \leqslant \operatorname{deg} f+\operatorname{deg} g .$$

  (b) Describe the topological type of the Riemann surface defined by the equation $w^{2}+2 w=z^{5}$ in $\mathbb{C}^{2}$. [You should analyse carefully the behaviour as $w$ and $z$ approach $\infty$.]

  comment

Statistical Physics

• B1.22

  Statistical Physics | Part II, 2003

  A gas in equilibrium at temperature $T$ and pressure $P$ has quantum stationary states $i$ with energies $E_{i}(V)$ in volume $V$. What does it mean to say that a change in volume from $V$ to $V+d V$ is reversible?

  Write down an expression for the probability that the gas is in state $i$. How is the entropy $S$ defined in terms of these probabilities? Write down an expression for the energy $E$ of the gas, and establish the relation

  $$d E=T d S-P d V$$

  for reversible changes.

  By considering the quantity $F=E-T S$, derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  A gas obeys the equation of state

  $$P V=R T+\frac{B(T)}{V}$$

  where $R$ is a constant and $B(T)$ is a function of $T$ only. The gas is expanded isothermally, at temperature $T$, from volume $V_{0}$ to volume $2 V_{0}$. Find the work $\Delta W$ done on the gas. Show that the heat $\Delta Q$ absorbed by the gas is given by

  $$\Delta Q=R T \log 2+\frac{T}{2 V_{0}} \frac{d B}{d T}$$

  comment

• B3.22

  Statistical Physics | Part II, 2003

  A diatomic molecule, free to move in two space dimensions, has classical Hamiltonian

  $$H=\frac{1}{2 m}|\mathbf{p}|^{2}+\frac{1}{2 I} J^{2}$$

  where $\mathbf{p}=\left(p_{1}, p_{2}\right)$ is the particle's momentum and $J$ is its angular momentum. Write down the classical partition function $Z$ for an ideal gas of $N$ such molecules in thermal equilibrium at temperature $T$. Show that it can be written in the form

  $$Z=\left(z_{t} z_{r o t}\right)^{N}$$

  where $z_{t}$ and $z_{\text {rot }}$ are the one-molecule partition functions associated with the translational and rotational degrees of freedom, respectively. Compute $z_{t}$ and $z_{r o t}$ and hence show that the energy $E$ of the gas is given by

  $$E=\frac{3}{2} N k T$$

  where $k$ is Boltzmann's constant. How does this result illustrate the principle of equipartition of energy?

  In an improved model of the two-dimensional gas of diatomic molecules, the angular momentum $J$ is quantized in integer multiples of $\hbar$ :

  $$J=j \hbar, \quad j=0, \pm 1, \pm 2, \ldots$$

  Write down an expression for $z_{\text {rot }}$ in this case. Given that $k T \ll\left(\hbar^{2} / 2 I\right)$, obtain an expression for the energy $E$ in the form

  $$E \approx A T+B e^{-\hbar^{2} / 2 I k T}$$

  where $A$ and $B$ are constants that should be computed. How is this result compatible with the principle of equipartition of energy? Find $C_{v}$, the specific heat at constant volume, for $k T \ll\left(\hbar^{2} / 2 I\right)$.

  Why can the sum over $j$ in $z_{\text {rot }}$ be approximated by an integral when $k T \gg\left(\hbar^{2} / 2 I\right)$ ? Deduce that $E \approx \frac{3}{2} N k T$ in this limit.

  comment

• B4.23

  Statistical Physics | Part II, 2003

  A gas of non-interacting identical bosons in volume $V$, with one-particle energy levels $\epsilon_{r}, r=1,2, \ldots, \infty$, is in equilibrium at temperature $T$ and chemical potential $\mu$. Let $n_{r}$ be the number of particles in the $r$ th one-particle state. Write down an expression for the grand partition function $\mathcal{Z}$. Write down an expression for the probability of finding a given set of occupation numbers $n_{r}$ of the one-particle states. Hence determine the mean occupation numbers $\bar{n}_{r}$ (the Bose-Einstein distribution). Write down expressions, in terms of the mean occupation numbers, for the total energy $E$ and total number of particles $N$.

  Write down an expression for the grand potential $\Omega$ in terms of $\mathcal{Z}$. Given that

  $$S=-\left(\frac{\partial \Omega}{\partial T}\right)_{V, \mu}$$

  show that $S$ can be written in the form

  $$S=k \sum_{r} f\left(\bar{n}_{r}\right)$$

  for some function $f$, which you should determine. Hence show that $d S=0$ for any change of the gas that leaves the mean occupation numbers unchanged. Consider a (quasi-static) change of $V$ with this property. Using the formula

  $$P=-\left(\frac{\partial E}{\partial V}\right)_{N, S}$$

  and given that $\epsilon_{r} \propto V^{-\sigma}(\sigma>0)$ for each $r$, show that

  $$P=\sigma(E / V)$$

  What is the value of $\sigma$ for photons?

  Let $\mu=0$, so that $E$ is a function only of $T$ and $V$. Why does the energy density $\varepsilon=E / V$ depend only on $T ?$ Using the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  and the first law of thermodynamics for reversible changes, show that

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=T\left(\frac{\partial P}{\partial T}\right)_{V}-P$$

  and hence that

  $$\varepsilon(T) \propto T^{\gamma}$$

  for some power $\gamma$ that you should determine. Show further that

  $$S \propto\left(T V^{\sigma}\right)^{\frac{1}{\sigma}} .$$

  Hence verify, given $\mu=0$, that $\bar{n}_{r}$ is left unchanged by a change of $V$ at constant $S$.

  comment

Statistical Physics and Cosmology

• A1.16

  Statistical Physics and Cosmology | Part II, 2003

  (i) Explain briefly how the relative motion of galaxies in a homogeneous and isotropic universe is described in terms of the scale factor $a(t)$ (where $t$ is time). In particular, show that the relative velocity $\mathbf{v}(t)$ of two galaxies is given in terms of their relative displacement $\mathbf{r}(t)$ by the formula $\mathbf{v}(t)=H(t) \mathbf{r}(t)$, where $H(t)$ is a function that you should determine in terms of $a(t)$. Given that $a(0)=0$, obtain a formula for the distance $R(t)$ to the cosmological horizon at time $t$. Given further that $a(t)=\left(t / t_{0}\right)^{\alpha}$, for $0<\alpha<1$ and constant $t_{0}$, compute $R(t)$. Hence show that $R(t) / a(t) \rightarrow 0$ as $t \rightarrow 0$.

  (ii) A homogeneous and isotropic model universe has energy density $\rho(t) c^{2}$ and pressure $P(t)$, where $c$ is the speed of light. The evolution of its scale factor $a(t)$ is governed by the Friedmann equation

  $$\dot{a}^{2}=\frac{8 \pi G}{3} \rho a^{2}-k c^{2}$$

  where the overdot indicates differentiation with respect to $t$. Use the "Fluid" equation

  $$\dot{\rho}=-3\left(\rho+\frac{P}{c^{2}}\right)\left(\frac{\dot{a}}{a}\right)$$

  to obtain an equation for the acceleration $\ddot{a}(t)$. Assuming $\rho>0$ and $P \geqslant 0$, show that $\rho a^{3}$ cannot increase with time as long as $\dot{a}>0$, nor decrease if $\dot{a}<0$. Hence determine the late time behaviour of $a(t)$ for $k<0$. For $k>0$ show that an initially expanding universe must collapse to a "big crunch" at which $a \rightarrow 0$. How does $\dot{a}$ behave as $a \rightarrow 0$ ? Given that $P=0$, determine the form of $a(t)$ near the big crunch. Discuss the qualitative late time behaviour for $k=0$.

  Cosmological models are often assumed to have an equation of state of the form $P=\sigma \rho c^{2}$ for constant $\sigma$. What physical principle requires $\sigma \leqslant 1$ ? Matter with $P=\rho c^{2}$ $(\sigma=1)$ is called "stiff matter" by cosmologists. Given that $k=0$, determine $a(t)$ for a universe that contains only stiff matter. In our Universe, why would you expect stiff matter to be negligible now even if it were significant in the early Universe?

  comment

• A3.14

  Statistical Physics and Cosmology | Part II, 2003

  (i) The pressure $P(r)$ and mass density $\rho(r)$, at distance $r$ from the centre of a spherically-symmetric star, obey the pressure-support equation

  $$P^{\prime}=-\frac{G m \rho}{r^{2}}$$

  where $m^{\prime}=4 \pi r^{2} \rho(r)$, and the prime indicates differentiation with respect to $r$. Let $V$ be the total volume of the star, and $\langle P\rangle$ its average pressure. Use the pressure-support equation to derive the "virial theorem"

  $$\langle P\rangle V=-\frac{1}{3} E_{g r a v}$$

  where $E_{g r a v}$ is the total gravitational potential energy [Hint: multiply by $4 \pi r^{3}$ ]. If a star is assumed to be a self-gravitating ball of a non-relativistic ideal gas then it can be shown that

  $$\langle P\rangle V=\frac{2}{3} E_{k i n}$$

  where $E_{k i n}$ is the total kinetic energy. Use this result to show that the total energy $U=E_{\text {grav }}+E_{k i n}$ is negative. When nuclear reactions have converted the hydrogen in a star's core to helium the core contracts until the helium is converted to heavier elements, thereby increasing the total energy $U$ of the star. Explain briefly why this converts the star into a "Red Giant". (ii) Write down the first law of thermodynamics for the change in energy $E$ of a system at temperature $T$, pressure $P$ and chemical potential $\mu$ as a result of small changes in the entropy $S$, volume $V$ and particle number $N$. Use this to show that

  $$P=-\left(\frac{\partial E}{\partial V}\right)_{N, S}$$

  The microcanonical ensemble is the set of all accessible microstates of a system at fixed $E, V, N$. Define the canonical and grand-canonical ensembles. Why are the properties of a macroscopic system independent of the choice of thermodynamic ensemble?

  The Gibbs "grand potential" $\mathcal{G}(T, V, \mu)$ can be defined as

  $$\mathcal{G}=E-T S-\mu N$$

  Use the first law to find expressions for $S, P, N$ as partial derivatives of $\mathcal{G}$. A system with variable particle number $n$ has non-degenerate energy eigenstates labeled by $r^{(n)}$, for each $n$, with energy eigenvalues $E_{r}^{(n)}$. If the system is in equilibrium at temperature $T$ and chemical potential $\mu$ then the probability $p\left(r^{(n)}\right)$ that it will be found in a particular $n$-particle state $r^{(n)}$ is given by the Gibbs probability distribution

  $$p\left(r^{(n)}\right)=\mathcal{Z}^{-1} e^{\left(\mu n-E_{r}^{(n)}\right) / k T}$$

  where $k$ is Boltzmann's constant. Deduce an expression for the normalization factor $\mathcal{Z}$ as a function of $\mu$ and $\beta=1 / k T$, and hence find expressions for the partial derivatives

  $$\frac{\partial \log \mathcal{Z}}{\partial \mu}, \quad \frac{\partial \log \mathcal{Z}}{\partial \beta}$$

  in terms of $N, E, \mu, \beta$.

  Why does $\mathcal{Z}$ also depend on the volume $V$ ? Given that a change in $V$ at fixed $N, S$ leaves unchanged the Gibbs probability distribution, deduce that

  $$\left(\frac{\partial \log \mathcal{Z}}{\partial V}\right)_{\mu, \beta}=\beta P$$

  Use your results to show that

  $$\mathcal{G}=-k T \log \left(\mathcal{Z} / \mathcal{Z}_{0}\right)$$

  for some constant $\mathcal{Z}_{0}$.

  comment

• A4.18

  Statistical Physics and Cosmology | Part II, 2003

  Let $g(p)$ be the density of states of a particle in volume $V$ as a function of the magnitude $p$ of the particle's momentum. Explain why $g(p) \propto V p^{2} / h^{3}$, where $h$ is Planck's constant. Write down the Bose-Einstein and Fermi-Dirac distributions for the (average) number $\bar{n}(p)$ of particles of an ideal gas with momentum $p$. Hence write down integrals for the (average) total number $N$ of particles and the (average) total energy $E$ as functions of temperature $T$ and chemical potential $\mu$. Why do $N$ and $E$ also depend on the volume $V ?$

  Electromagnetic radiation in thermal equilibrium can be regarded as a gas of photons. Why are photons "ultra-relativistic" and how is photon momentum $p$ related to the frequency $\nu$ of the radiation? Why does a photon gas have zero chemical potential? Use your formula for $\bar{n}(p)$ to express the energy density $\varepsilon_{\gamma}$ of electromagnetic radiation in the form

  $$\varepsilon_{\gamma}=\int_{0}^{\infty} \epsilon(\nu) d \nu$$

  where $\epsilon(\nu)$ is a function of $\nu$ that you should determine up to a dimensionless multiplicative constant. Show that $\epsilon(\nu)$ is independent of $h$ when $k T \gg h \nu$, where $k$ is Boltzmann's constant. Let $\nu_{\text {peak }}$ be the value of $\nu$ at the maximum of the function $\epsilon(\nu)$; how does $\nu_{\text {peak }}$ depend on $T$ ?

  Let $n_{\gamma}$ be the photon number density at temperature $T$. Show that $n_{\gamma} \propto T^{q}$ for some power $q$, which you should determine. Why is $n_{\gamma}$ unchanged as the volume $V$ is increased quasi-statically? How does $T$ depend on $V$ under these circumstances? Applying your result to the Cosmic Microwave Background Radiation (CMBR), deduce how the temperature $T_{\gamma}$ of the CMBR depends on the scale factor $a$ of the Universe. At a time when $T_{\gamma} \sim 3000 K$, the Universe underwent a transition from an earlier time at which it was opaque to a later time at which it was transparent. Explain briefly the reason for this transition and its relevance to the CMBR.

  An ideal gas of fermions $f$ of mass $m$ is in equilibrium at temperature $T$ and chemical potential $\mu_{f}$ with a gas of its own anti-particles $\bar{f}$ and photons $(\gamma)$. Assuming that chemical equilibrium is maintained by the reaction

  $$f+\bar{f} \leftrightarrow \gamma$$

  determine the chemical potential $\mu_{\bar{f}}$ of the antiparticles. Let $n_{f}$ and $n_{\bar{f}}$ be the number densities of $f$ and $\bar{f}$, respectively. What will their values be for $k T \ll m c^{2}$ if $\mu_{f}=0$ ? Given that $\mu_{f}>0$, but $\mu_{f} \ll k T$, show that

  $$n_{f} \approx n_{0}(T)\left[1+\frac{\mu_{f}}{k T} F\left(m c^{2} / k T\right)\right]$$

  where $n_{0}(T)$ is the fermion number density at zero chemical potential and $F$ is a positive function of the dimensionless ratio $m c^{2} / k T$. What is $F$ when $k T \ll m c^{2}$ ?

  Given that $\mu_{f} \ll k T$, obtain an expression for the ratio $\left(n_{f}-n_{\bar{f}}\right) / n_{0}$ in terms of $\mu, T$ and the function $F$. Supposing that $f$ is either a proton or neutron, why should you expect the ratio $\left(n_{f}-n_{\bar{f}}\right) / n_{\gamma}$ to remain constant as the Universe expands?

  comment

Stochastic Financial Models

• A1.11 B1.16

  Stochastic Financial Models | Part II, 2003

  (i) In the context of a single-period financial market with $d$ traded assets, what is an arbitrage? What is an equivalent martingale measure?

  A simple single-period financial market contains two assets, $S^{0}$ (a bond), and $S^{1}$ (a share). The period can be good, bad, or indifferent, with probabilities $1 / 3$ each. At the beginning of the period, time 0 , both assets are worth 1 , i.e.

  $$S_{0}^{0}=1=S_{0}^{1}$$

  and at the end of the period, time 1 , the share is worth

  $$S_{1}^{1}= \begin{cases}a & \text { if the period was bad, } \\ b & \text { if the period was indifferent } \\ c & \text { if the period was good }\end{cases}$$

  where $a<b<c$. The bond is always worth 1 at the end of the period. Show that there is no arbitrage in this market if and only if $a<1<c$.

  (ii) An agent with $C^{2}$ strictly increasing strictly concave utility $U$ has wealth $w_{0}$ at time 0 , and wishes to invest his wealth in shares and bonds so as to maximise his expected utility of wealth at time 1 . Explain how the solution to his optimisation problem generates an equivalent martingale measure.

  Assume now that $a=3 / 4, b=1$, and $c=3 / 2$. Characterise all equivalent martingale measures for this problem. Characterise all equivalent martingale measures which arise as solutions of an agent's optimisation problem.

  Calculate the largest and smallest possible prices for a European call option with strike 1 and expiry 1, as the pricing measure ranges over all equivalent martingale measures. Calculate the corresponding bounds when the pricing measure is restricted to the set arising from expected-utility-maximising agents' optimisation problems.

  comment

• A3.11 B3.16

  Stochastic Financial Models | Part II, 2003

  (i) What does it mean to say that the process $\left(W_{t}\right)_{t \geqslant 0}$ is a Brownian motion? What does it mean to say that the process $\left(M_{t}\right)_{t \geqslant 0}$ is a martingale?

  Suppose that $\left(W_{t}\right)_{t \geqslant 0}$ is a Brownian motion and the process $\left(X_{t}\right)_{t \geqslant 0}$ is given in terms of $W$ as

  $$X_{t}=x_{0}+\sigma W_{t}+\mu t$$

  for constants $\sigma, \mu$. For what values of $\theta$ is the process

  $$M_{t}=\exp \left(\theta X_{t}-\lambda t\right)$$

  a martingale? (Here, $\lambda$ is a positive constant.)

  (ii) In a standard Black-Scholes model, the price at time $t$ of a share is represented as $S_{t}=\exp \left(X_{t}\right)$. You hold a perpetual American put option on this share, with strike $K$; you may exercise at any stopping time $\tau$, and upon exercise you receive $\max \left\{0, K-S_{\tau}\right\}$. Let $0<a<\log K$. Suppose you plan to use the exercise policy: 'Exercise as soon as the price falls to $e^{a}$ or lower.' Calculate what the option would be worth if you were to follow this policy. (Assume that the riskless rate of interest is constant and equal to $r>0$.) For what choice of $a$ is this value maximised?

  comment

• A4.12 B4.16

  Stochastic Financial Models | Part II, 2003

  A single-period market contains $d$ risky assets, $S^{1}, S^{2}, \ldots, S^{d}$, initially worth $\left(S_{0}^{1}, S_{0}^{2}, \ldots, S_{0}^{d}\right)$, and at time 1 worth random amounts $\left(S_{1}^{1}, S_{1}^{2}, \ldots, S_{1}^{d}\right)$ whose first two moments are given by

  $$\mu=E S_{1}, \quad V=\operatorname{cov}\left(S_{1}\right) \equiv E\left[\left(S_{1}-E S_{1}\right)\left(S_{1}-E S_{1}\right)^{T}\right]$$

  An agent with given initial wealth $w_{0}$ is considering how to invest in the available assets, and has asked for your advice. Develop the theory of the mean-variance efficient frontier far enough to exhibit explicitly the minimum-variance portfolio achieving a required mean return, assuming that $V$ is non-singular. How does your analysis change if a riskless asset $S^{0}$ is added to the market? Under what (sufficient) conditions would an agent maximising expected utility actually choose a portfolio on the mean-variance efficient frontier?

  comment

Symmetries and Groups in Physics

• A1.17

  Symmetries and Groups in Physics | Part II, 2003

  (i) Define the character $\chi$ of a representation $D$ of a finite group $G$. Show that $<\chi \mid \chi>=1$ if and only if $D$ is irreducible, where

  $$<\chi \mid \chi>=\frac{1}{|G|} \sum_{g \in G} \chi(g) \chi\left(g^{-1}\right)$$

  If $|G|=8$ and $<\chi \mid \chi>=2$, what are the possible dimensions of the representation $D ?$

  (ii) State and prove Schur's first and second lemmas.

  comment

• A3.15

  Symmetries and Groups in Physics | Part II, 2003

  (i) Given that the character of an $S U(2)$ transformation in the $(2 l+1)$-dimensional irreducible representation $d_{l}$ is given by

  $$\chi_{l}(\theta)=\frac{\sin \left(l+\frac{1}{2}\right) \theta}{\sin \frac{\theta}{2}}$$

  show how the direct product representation $d_{l_{1}} \otimes d_{l_{2}}$ decomposes into irreducible $S U(2)$ representations.

  (ii) Find the decomposition of the direct product representation $3 \otimes \overline{3}$ of $S U(3)$ into irreducible $S U(3)$ representations.

  Mesons consist of one quark and one antiquark. The scalar Meson Octet consists of the following particles: $K^{\pm}\left(Y=\pm 1, I_{3}=\pm \frac{1}{2}\right), K^{0}\left(Y=1, I_{3}=-\frac{1}{2}\right), \bar{K}^{0}(Y=-1$, $\left.I_{3}=\frac{1}{2}\right), \pi^{\pm}\left(Y=0, I_{3}=\pm 1\right), \pi^{0}\left(Y=0, I_{3}=0\right)$ and $\eta\left(Y=0, I_{3}=0\right)^{2}$.

  Use the direct product representation $3 \otimes \overline{3}$ of $S U(3)$ to identify the quark-type of the particles in the scalar Meson Octet. Deduce the quark-type of the $S U(3)$ singlet state $\eta^{\prime}$ contained in $3 \otimes \overline{3}$.

  comment

Theoretical Geophysics

• A1.19

  Theoretical Geophysics | Part II, 2003

  (i) Explain the concepts of: traction on an element of surface; the stress tensor; the strain tensor in an elastic medium. Derive a relationship between the two tensors for a linear isotropic elastic medium, stating clearly any assumption you need to make.

  (ii) State what is meant by an $\mathrm{SH}$ wave in a homogeneous isotropic elastic medium. An SH wave in a medium with shear modulus $\mu$ and density $\rho$ is incident at angle $\theta$ on an interface with a medium with shear modulus $\mu^{\prime}$ and density $\rho^{\prime}$. Evaluate the form and amplitude of the reflected wave and transmitted wave. Comment on the case $c^{\prime} \sin \theta / c>1$, where $c^{2}=\mu / \rho$ and $\left(c^{\prime}\right)^{2}=\mu^{\prime} / \rho^{\prime}$.

  comment

• A2.16

  Theoretical Geophysics | Part II, 2003

  (i) Explain briefly what is meant by the concepts of hydrostatic equilibrium and the buoyancy frequency. Evaluate an expression for the buoyancy frequency in an incompressible inviscid fluid with stable density profile $\rho(z)$.

  (ii) Explain briefly what is meant by the Boussinesq approximation.

  Write down the equations describing motions of small amplitude in an incompressible, stratified, Boussinesq fluid of constant buoyancy frequency.

  Derive the resulting dispersion relationship for plane wave motion. Show that there is a maximum frequency for the waves and explain briefly why this is the case.

  What would be the response to a solid body oscillating at a frequency in excess of the maximum?

  comment

• A4.20

  Theoretical Geophysics | Part II, 2003

  Define the Rossby number. Under what conditions will a fluid flow be at (a) high and (b) low values of the Rossby number? Briefly describe both an oceanographic and a meteorological example of each type of flow.

  Explain the concept of quasi-geostrophy for a thin layer of homogeneous fluid in a rapidly rotating system. Write down the quasi-geostrophic approximation for the vorticity in terms of the pressure, the fluid density and the rate of rotation. Define the potential vorticity and state the associated conservation law.

  A broad current flows directly eastwards ( $+x$ direction) with uniform velocity $U$ across a flat ocean basin of depth $H$. The current encounters a low, two-dimensional ridge of width $L$ and height $H h(x)(0<x<L)$, whose axis is aligned in the north-south $(y)$ direction. Neglecting any effects of stratification and assuming a constant vertical rate of rotation $\frac{1}{2} f$, such that the Rossby number is small, determine the effect of the ridge on the current. Show that the direction of the current after it leaves the ridge is dependent on the cross-sectional area of the ridge, but not on the explicit form of $h(x)$.

  comment

Transport Processes

• A1.18

  Transport Processes | Part II, 2003

  (i) A solute occupying a domain $V_{0}$ has concentration $C(\boldsymbol{x}, t)$ and is created at a rate $S(\boldsymbol{x}, t)$ per unit volume; $\boldsymbol{J}(\boldsymbol{x}, t)$ is the flux of solute per unit area; $\boldsymbol{x}, t$ are position and time. Derive the transport equation

  $$C_{t}+\nabla \cdot \boldsymbol{J}=S$$

  State Fick's Law of diffusion and hence write down the diffusion equation for $C(\boldsymbol{x}, t)$ for a case in which the solute flux occurs solely by diffusion, with diffusivity $D(\boldsymbol{x})$.

  In a finite domain $0 \leqslant x \leqslant L, D, S$ and the steady-state distribution of $C$ depend only on $x ; C$ is equal to $C_{0}$ at $x=0$ and $C_{1} \neq C_{0}$ at $x=L$. Find $C(x)$ in the following two cases: (a) $D=D_{0}, S=0$, (b) $D=D_{1} x^{1 / 2}, S=0$,

  where $D_{0}$ and $D_{1}$ are positive constants.

  Show that there is no steady solution satisfying the boundary conditions if $D=$ $D_{1} x, S=0 .$

  (ii) For the problem of Part (i), consider the case $D=D_{0}, S=k C$, where $D_{0}$ and $k$ are positive constants. Calculate the steady-state solution, $C=C_{s}(x)$, assuming that $\sqrt{k / D_{0}} \neq n \pi / L$ for any integer $n$.

  Now let

  $$C(x, 0)=C_{0} \frac{\sin \alpha(L-x)}{\sin \alpha L}$$

  where $\alpha=\sqrt{k / D_{0}}$. Find the equations, boundary and initial conditions satisfied by $C^{\prime}(x, t)=C(x, t)-C_{s}(x)$. Solve the problem using separation of variables and show that

  $$C^{\prime}(x, t)=\sum_{n=1}^{\infty} A_{n} \sin \frac{n \pi x}{L} \exp \left[\left(\alpha^{2}-\frac{n^{2} \pi^{2}}{L^{2}}\right) D_{0} t\right]$$

  for some constants $A_{n}$. Write down an integral expression for $A_{n}$, show that

  $$A_{1}=-\frac{2 \pi C_{1}}{\alpha^{2} L^{2}-\pi^{2}},$$

  and comment on the behaviour of the solution for large times in the two cases $\alpha L<\pi$ and $\alpha L>\pi$.

  comment

• A3.16

  Transport Processes | Part II, 2003

  (i) When a solid crystal grows into a supercooled infinite melt, latent heat must be removed from the interface by diffusion into the melt. Write down the equation and boundary conditions satisfied by the temperature $\theta(\boldsymbol{x}, t)$ in the melt, where $\boldsymbol{x}$ is position and $t$ time, in terms of the following material properties: solid density $\rho_{s}$, specific heat capacity $C_{p}$, coefficient of latent heat per unit mass $L$, thermal conductivity $k$, melting temperature $\theta_{m}$. You may assume that the densities of the melt and the solid are the same and that temperature in the melt far from the interface is $\theta_{m}-\Delta \theta$, where $\Delta \theta$ is a positive constant.

  A spherical crystal of radius $a(t)$ grows into such a melt with $a(0)=0$. Use dimensional analysis to show that $a(t)$ is proportional to $t^{1 / 2}$.

  (ii) Show that the above problem should have a similarity solution of the form

  $$\theta=\theta_{m}-\Delta \theta(1-F(\xi))$$

  where $\xi=r(\kappa t)^{-1 / 2}, r$ is the radial coordinate in spherical polars and $\kappa=k / \rho_{s} C_{p}$ is the thermal diffusivity. Recalling that, for spherically symmetric $\theta, \nabla^{2} \theta=\frac{1}{r^{2}}\left(r^{2} \theta_{r}\right)_{r}$, write down the equation and boundary conditions to be satisfied by $F(\xi)$. Hence show that the radius of the crystal is given by $a(t)=\lambda(\kappa t)^{1 / 2}$, where $\lambda$ satisfies the equation

  $$\int_{\lambda}^{\infty} \frac{e^{-\frac{1}{4} u^{2}}}{u^{2}} d u=\frac{2}{S \lambda^{3}} e^{-\frac{1}{4} \lambda^{2}}$$

  and $S=L / C_{p} \Delta \theta$.

  Integrate the left hand side of this equation by parts, to give

  $$\frac{\sqrt{\pi}}{2} \lambda e^{\frac{1}{4} \lambda^{2}} \operatorname{erfc}\left(\frac{1}{2} \lambda\right)=1-\frac{2}{S \lambda^{2}} .$$

  Hence show that a solution with $\lambda$ small must have $\lambda \approx(2 / S)^{\frac{1}{2}}$, which is self-consistent if $S$ is large.

  comment

• A4.19

  Transport Processes | Part II, 2003

  A shallow layer of fluid of viscosity $\mu$, density $\rho$ and depth $h(x, t)$ lies on a rigid horizontal plane $y=0$ and is bounded by impermeable barriers at $x=-L$ and $x=L$ $(L \gg h)$. Gravity acts vertically and a wind above the layer causes a shear stress $\tau(x)$ to be exerted on the upper surface in the $+x$ direction. Surface tension is negligible compared to gravity.

  (a) Assuming that the steady flow in the layer can be analysed using lubrication theory, show that the horizontal pressure gradient $p_{x}$ is given by $p_{x}=\rho g h_{x}$ and hence that

  $$h h_{x}=\frac{3}{2} \frac{\tau}{\rho g} .$$

  Show also that the fluid velocity at the surface $y=h$ is equal to $\tau h / 4 \mu$, and sketch the velocity profile for $0 \leqslant y \leqslant h$.

  (b) In the case in which $\tau$ is a constant, $\tau_{0}$, and assuming that the difference between $h$ and its average value $h_{0}$ remains small compared with $h_{0}$, show that

  $$h \approx h_{0}\left(1+\frac{3 \tau_{0} x}{2 \rho g h_{0}^{2}}\right)$$

  provided that

  $$\frac{\tau_{0} L}{\rho g h_{0}^{2}} \ll 1$$

  (c) Surfactant at surface concentration $\Gamma(x)$ is added to the surface, so that now

  $$\tau=\tau_{0}-A \Gamma_{x},$$

  where $A$ is a positive constant. The surfactant is advected by the surface fluid velocity and also experiences a surface diffusion with diffusivity $D$. Write down the equation for conservation of surfactant, and hence show that

  $$\left(\tau_{0}-A \Gamma_{x}\right) h \Gamma=4 \mu D \Gamma_{x}$$

  From equations (1), (2) and (3) deduce that

  $$\frac{\Gamma}{\Gamma_{0}}=\exp \left[\frac{\rho g}{18 \mu D}\left(h^{3}-h_{0}^{3}\right)\right]$$

  where $\Gamma_{0}$ is a constant. Assuming once more that $h_{1} \equiv h-h_{0} \ll h_{0}$, and that $h=h_{0}$ at $x=0$, show further that

  $$h_{1} \approx \frac{3 \tau_{0} x}{2 \rho g h_{0}}\left[1+\frac{A \Gamma_{0} h_{0}}{4 \mu D}\right]^{-1}$$

  provided that

  $$\frac{\tau_{0} h_{0} L}{\mu D} \ll 1 \quad \text { as well as } \quad \frac{\tau_{0} L}{\rho g h_{0}^{2}} \ll 1$$

  comment

Waves in Fluid and Solid Media

• B1.26

  Waves in Fluid and Solid Media | Part II, 2003

  Consider the equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}+\alpha^{2} \frac{\partial^{4} \phi}{\partial x^{4}}+\beta^{2} \phi=0$$

  with $\alpha$ and $\beta$ real constants. Find the dispersion relation for waves of frequency $\omega$ and wavenumber $k$. Find the phase velocity $c(k)$ and the group velocity $c_{g}(k)$, and sketch the graphs of these functions.

  By multiplying $(*)$ by $\partial \phi / \partial t$, obtain an energy equation in the form

  $$\frac{\partial E}{\partial t}+\frac{\partial F}{\partial x}=0$$

  where $E$ represents the energy density and $F$ the energy flux.

  Now let $\phi(x, t)=A \cos (k x-\omega t)$, where $A$ is a real constant. Evaluate the average values of $E$ and $F$ over a period of the wave to show that

  $$\langle F\rangle=c_{g}\langle E\rangle$$

  Comment on the physical meaning of this result.

  comment

• B2.25

  Waves in Fluid and Solid Media | Part II, 2003

  Starting from the equations for the one-dimensional unsteady flow of a perfect gas of uniform entropy, derive the Riemann invariants

  $$u \pm \frac{2}{\gamma-1} c=\text { constant }$$

  on characteristics

  $$C_{\pm}: \frac{d x}{d t}=u \pm c$$

  A piston moves smoothly down a long tube, with position $x=X(t)$. Gas occupies the tube ahead of the piston, $x>X(t)$. Initially the gas and the piston are at rest, and the speed of sound in the gas is $c_{0}$. For $t>0$, show that the $C_{+}$characteristics are straight lines, provided that a shock-wave has not formed. Hence find a parametric representation of the solution for the velocity $u(x, t)$ of the gas.

  comment

• B3.25

  Waves in Fluid and Solid Media | Part II, 2003

  Derive the wave equation governing the velocity potential for linearised sound in a perfect gas. How is the pressure disturbance related to the velocity potential? Write down the spherically symmetric solution to the wave equation with time dependence $e^{i \omega t}$, which is regular at the origin.

  A high pressure gas is contained, at density $\rho_{0}$, within a thin metal spherical shell which makes small amplitude spherically symmetric vibrations. Ignore the low pressure gas outside. Let the metal shell have radius $a$, mass $m$ per unit surface area, and elastic stiffness which tries to restore the radius to its equilibrium value $a_{0}$ with a force $-\kappa\left(a-a_{0}\right)$ per unit surface area. Show that the frequency of these vibrations is given by

  $$\omega^{2}\left(m+\frac{\rho_{0} a_{0}}{\theta \cot \theta-1}\right)=\kappa \quad \text { where } \theta=\omega a_{0} / c_{0}$$

  comment

• B4.27

  Waves in Fluid and Solid Media | Part II, 2003

  Show that the equations governing isotropic linear elasticity have plane-wave solutions, identifying them as $\mathrm{P}, \mathrm{SV}$ or $\mathrm{SH}$ waves.

  A semi-infinite elastic medium in $y<0$ (where $y$ is the vertical coordinate) with density $\rho$ and Lamé moduli $\lambda$ and $\mu$ is overlaid by a layer of thickness $h$ (in $0<y<h$ ) of a second elastic medium with density $\rho^{\prime}$ and Lamé moduli $\lambda^{\prime}$ and $\mu^{\prime}$. The top surface at $y=h$ is free, i.e. the surface tractions vanish there. The speed of S-waves is lower in the layer, i.e. $c_{S}^{\prime}{ }^{2}=\mu^{\prime} / \rho^{\prime}<\mu / \rho=c_{S}^{2}$. For a time-harmonic SH-wave with horizontal wavenumber $k$ and frequency $\omega$, which oscillates in the slow top layer and decays exponentially into the fast semi-infinite medium, derive the dispersion relation for the apparent wave speed $c(k)=\omega / k$,

  $$\tan \left(k h \sqrt{\frac{c^{2}}{c_{S}^{2}}-1}\right)=\frac{\mu \sqrt{1-\frac{c^{2}}{c_{S}^{2}}}}{\mu^{\prime} \sqrt{\frac{c^{2}}{c_{S}^{\prime}}-1}} .$$

  Show graphically that there is always one root, and at least one higher mode if $\sqrt{c_{S}^{2} / c_{S}^{\prime 2}-1}>\pi / k h$.

  comment