Part II, 2001

Algebraic Curves

• B2.10

  Algebraic Curves | Part II, 2001

  Let $f: \mathbb{P}^{2} \rightarrow \mathbb{P}^{2}$ be the rational map given by $f\left(X_{0}: X_{1}: X_{2}\right)=\left(X_{1} X_{2}: X_{0} X_{2}\right.$ : $\left.X_{0} X_{1}\right)$. Determine whether $f$ is defined at the following points: $(1: 1: 1),(0: 1: 1),(0:$ $0: 1)$.

  Let $C \subset \mathbb{P}^{2}$ be the curve defined by $X_{1}^{2} X_{2}-X_{0}^{3}=0$. Define a bijective morphism $\alpha: \mathbb{P}^{1} \rightarrow C$. Prove that $\alpha$ is not an isomorphism.

  comment

• B3.10

  Algebraic Curves | Part II, 2001

  Let $C$ be the projective curve (over an algebraically closed field $k$ of characteristic zero) defined by the affine equation

  $$x^{5}+y^{5}=1$$

  Determine the points at infinity of $C$ and show that $C$ is smooth.

  Determine the divisors of the rational functions $x, y \in k(C)$.

  Show that $\omega=d x / y^{4}$ is a regular differential on $C$.

  Compute the divisor of $\omega$. What is the genus of $C$ ?

  comment

• B4.9

  Algebraic Curves | Part II, 2001

  Write an essay on curves of genus one (over an algebraically closed field $k$ of characteristic zero). Legendre's normal form should not be discussed.

  comment

Algebraic Topology

• B2.8

  Algebraic Topology | Part II, 2001

  Show that the fundamental group of the 2-torus $S^{1} \times S^{1}$ is isomorphic to $\mathbf{Z} \times \mathbf{Z}$.

  Show that an injective continuous map from the circle $S^{1}$ to itself induces multiplication by $\pm 1$ on the fundamental group.

  Show that there is no retraction from the solid torus $S^{1} \times D^{2}$ to its boundary.

  comment

• B3.7

  Algebraic Topology | Part II, 2001

  Write down the Mayer-Vietoris sequence and describe all the maps involved.

  Use the Mayer-Vietoris sequence to compute the homology of the $n$-sphere $S^{n}$ for all $n$.

  comment

• B4.5

  Algebraic Topology | Part II, 2001

  Write an essay on the definition of simplicial homology groups. The essay should include a discussion of orientations, of the action of a simplicial map and a proof of $\partial^{2}=0$.

  comment

Algorithms and Networks

• A2.10

  Algorithms and Networks | Part II, 2001

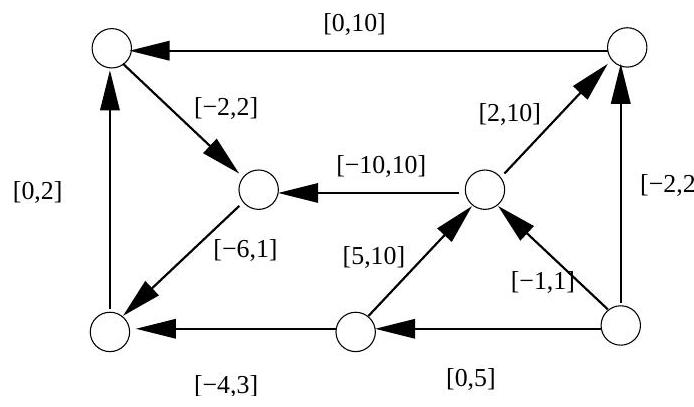
  (i) Let $G$ be a directed network with nodes $N$ and $\operatorname{arcs} A$. Let $S \subset N$ be a subset of the nodes, $x$ be a flow on $G$, and $y$ be the divergence of $x$. Describe carefully what is meant by a cut $Q=[S, N \backslash S]$. Define the arc-cut incidence $e_{Q}$, and the flux of $x$ across $Q$. Define also the divergence $y(S)$ of $S$. Show that $y(S)=x \cdot e_{Q}$.

  Now suppose that capacity constraints are specified on each of the arcs. Define the upper cut capacity $c^{+}(Q)$ of $Q$. State the feasible distribution problem for a specified divergence $b$, and show that the problem only has a solution if $b(N)=0$ and $b(S) \leqslant c^{+}(Q)$ for all cuts $Q=[S, N \backslash S]$.

  (ii) Describe an algorithm to find a feasible distribution given a specified divergence $b$ and capacity constraints on each arc. Explain what happens when no feasible distribution exists.

  Illustrate the algorithm by either finding a feasible circulation, or demonstrating that one does not exist, in the network given below. Arcs are labelled with capacity constraint intervals.

  

  Part II

  comment

• A3.10

  Algorithms and Networks | Part II, 2001

  (i) Let $P$ be the problem

  $$\text { minimize } f(x) \quad \text { subject to } h(x)=b, \quad x \in X \text {. }$$

  Explain carefully what it means for the problem $P$ to be Strong Lagrangian.

  Outline the main steps in a proof that a quadratic programming problem

  $$\operatorname{minimize} \frac{1}{2} x^{T} Q x+c^{T} x \quad \text { subject to } A x \geqslant b$$

  where $Q$ is a symmetric positive semi-definite matrix, is Strong Lagrangian.

  [You should carefully state the results you need, but should not prove them.]

  (ii) Consider the quadratic programming problem:

  $$\begin{aligned} \operatorname{minimize} & x_{1}^{2}+2 x_{1} x_{2}+2 x_{2}^{2}+x_{1}-4 x_{2} \\ \text { subject to } 3 x_{1}+2 x_{2} \leqslant 6, \quad x_{1}+x_{2} \geqslant 1 . \end{aligned}$$

  State necessary and sufficient conditions for $\left(x_{1}, x_{2}\right)$ to be optimal, and use the activeset algorithm (explaining your steps briefly) to solve the problem starting with initial condition $(2,0)$. Demonstrate that the solution you have found is optimal by showing that it satisfies the necessary and sufficient conditions stated previously.

  comment

• A4.11

  Algorithms and Networks | Part II, 2001

  State the optimal distribution problem. Carefully describe the simplex-on-a-graph algorithm for solving optimal distribution problems when the flow in each arc in the network is constrained to lie in the interval $[0, \infty)$. Explain how the algorithm can be initialised if there is no obvious feasible solution with which to begin. Describe the adjustments that are needed for the algorithm to cope with more general capacity constraints $x(j) \in\left[c^{-}(j), c^{+}(j)\right]$ for each arc $j$ (where $c^{\pm}(j)$ may be finite or infinite).

  Part II

  comment

Applications of Quantum Mechanics

• B1.23

  Applications of Quantum Mechanics | Part II, 2001

  A steady beam of particles, having wavenumber $k$ and moving in the $z$ direction, scatters on a spherically-symmetric potential. Write down the asymptotic form of the wave function at large $r$.

  The incoming wave is written as a partial-wave series

  $$\sum_{\ell=0}^{\infty} \chi_{\ell}(k r) P_{\ell}(\cos \theta)$$

  Show that for large $r$

  $$\chi_{\ell}(k r) \sim \frac{\ell+\frac{1}{2}}{i k r}\left(e^{i k r}-(-1)^{\ell} e^{-i k r}\right)$$

  and calculate $\chi_{0}(k r)$ and $\chi_{1}(k r)$ for all $r$.

  Write down the second-order differential equation satisfied by the $\chi_{\ell}(k r)$. Construct a second linearly-independent solution for each $\ell$ that is singular at $r=0$ and, when it is suitably normalised, has large- $r$ behaviour

  $$\frac{\ell+\frac{1}{2}}{i k r}\left(e^{i k r}+(-1)^{\ell} e^{-i k r}\right)$$

  comment

• B2.22

  Applications of Quantum Mechanics | Part II, 2001

  A particle of charge $e$ moves freely within a cubical box of side $a$. Its initial wavefunction is

  $$(2 / a)^{-\frac{3}{2}} \sin (\pi x / a) \sin (\pi y / a) \sin (\pi z / a) .$$

  A uniform electric field $\mathcal{E}$ in the $x$ direction is switched on for a time $T$. Derive from first principles the probability, correct to order $\mathcal{E}^{2}$, that after the field has been switched off the wave function will be found to be

  $$(2 / a)^{-\frac{3}{2}} \sin (2 \pi x / a) \sin (\pi y / a) \sin (\pi z / a) .$$

  comment

• B3.23

  Applications of Quantum Mechanics | Part II, 2001

  Write down the commutation relations satisfied by the cartesian components of the total angular momentum operator $\mathbf{J}$.

  In quantum mechanics an operator $\mathbf{V}$ is said to be a vector operator if, under rotations, its components transform in the same way as those of the coordinate operator r. Show from first principles that this implies that its cartesian components satisfy the commutation relations

  $$\left[J_{j}, V_{k}\right]=i \epsilon_{j k l} V_{l}$$

  Hence calculate the total angular momentum of the nonvanishing states $V_{j}|0\rangle$, where $|0\rangle$ is the vacuum state.

  comment

• B4.24

  Applications of Quantum Mechanics | Part II, 2001

  Derive the Bloch form of the wave function $\psi(x)$ of an electron moving in a onedimensional crystal lattice.

  The potential in such an $N$-atom lattice is modelled by

  $$V(x)=\sum_{n}\left(-\frac{\hbar^{2} U}{2 m} \delta(x-n L)\right)$$

  Assuming that $\psi(x)$ is continuous across each lattice site, and applying periodic boundary conditions, derive an equation for the allowed electron energy levels. Show that for suitable values of $U L$ they have a band structure, and calculate the number of levels in each band when $U L>2$. Verify that when $U L \gg 1$ the levels are very close to those corresponding to a solitary atom.

  Describe briefly how the band structure in a real 3-dimensional crystal differs from that of this simple model.

  comment

Applied Probability

• B2.13

  Applied Probability | Part II, 2001

  Let $M$ be a Poisson random measure on $E=\mathbb{R} \times[0, \pi)$ with constant intensity $\lambda$. For $(x, \theta) \in E$, denote by $l(x, \theta)$ the line in $\mathbb{R}^{2}$ obtained by rotating the line $\{(x, y): y \in \mathbb{R}\}$ through an angle $\theta$ about the origin.

  Consider the line process $L=M \circ l^{-1}$.

  (i) What is the distribution of the number of lines intersecting the disc $\left\{z \in \mathbb{R}^{2}:|z| \leqslant a\right\}$ ?

  (ii) What is the distribution of the distance from the origin to the nearest line?

  (iii) What is the distribution of the distance from the origin to the $k$ th nearest line?

  comment

• B3.13

  Applied Probability | Part II, 2001

  Consider an $M / G / 1$ queue with arrival rate $\lambda$ and traffic intensity less

  than 1. Prove that the moment-generating function of a typical busy period, $M_{B}(\theta)$, satisfies

  $$M_{B}(\theta)=M_{S}\left(\theta-\lambda+\lambda M_{B}(\theta)\right),$$

  where $M_{S}(\theta)$ is the moment-generating function of a typical service time.

  If service times are exponentially distributed with parameter $\mu>\lambda$, show that

  $$M_{B}(\theta)=\frac{\lambda+\mu-\theta-\left\{(\lambda+\mu-\theta)^{2}-4 \lambda \mu\right\}^{1 / 2}}{2 \lambda}$$

  for all sufficiently small but positive values of $\theta$.

  comment

• B4.12

  Applied Probability | Part II, 2001

  Define a renewal process and a renewal reward process.

  State and prove the strong law of large numbers for these processes.

  [You may assume the strong law of large numbers for independent, identically-distributed random variables.

  State and prove Little's formula.

  Customers arrive according to a Poisson process with rate $\nu$ at a single server, but a restricted waiting room causes those who arrive when $n$ customers are already present to be lost. Accepted customers have service times which are independent and identicallydistributed with mean $\alpha$ and independent of the arrival process. Let $P_{j}$ be the equilibrium probability that an arriving customer finds $j$ customers already present.

  Using Little's formula, or otherwise, determine a relationship between $P_{0}, P_{n}, \nu$ and

  Part II

  comment

Coding and Cryptography

• A1.10

  Coding and Cryptography | Part II, 2001

  (i) Explain briefly how and why a signature scheme is used. Describe the el Gamal scheme,

  (ii) Define a cyclic code. Define the generator of a cyclic code and show that it exists. Prove a necessary and sufficient condition for a polynomial to be the generator of a cyclic code of length $n$.

  What is the $\mathrm{BCH}$ code? Show that the $\mathrm{BCH}$ code associated with $\left\{\beta, \beta^{2}\right\}$, where $\beta$ is a root of $X^{3}+X+1$ in an appropriate field, is Hamming's original code.

  comment

• A2.9

  Coding and Cryptography | Part II, 2001

  (i) Give brief answers to the following questions.

  (a) What is a stream cypher?

  (b) Explain briefly why a one-time pad is safe if used only once but becomes unsafe if used many times.

  (c) What is a feedback register of length $d$ ? What is a linear feedback register of length $d ?$

  (d) A cypher stream is given by a linear feedback register of known length $d$. Show that, given plain text and cyphered text of length $2 d$, we can find the complete cypher stream.

  (e) State and prove a similar result for a general feedback register.

  (ii) Describe the construction of a Reed-Muller code. Establish its information rate and its weight

  comment

Combinatorics

• B1.5

  Combinatorics | Part II, 2001

  Let $\mathcal{A} \subset[n]^{(r)}$ where $r \leqslant n / 2$. Prove that, if $\mathcal{A}$ is 1-intersecting, then $|\mathcal{A}| \leqslant\left(\begin{array}{l}n-1 \\ r-1\end{array}\right)$. State an upper bound on $|\mathcal{A}|$ that is valid if $\mathcal{A}$ is $t$-intersecting and $n$ is large compared to $r$ and $t$.

  Let $\mathcal{B} \subset \mathcal{P}([n])$ be maximal 1-intersecting; that is, $\mathcal{B}$ is 1-intersecting but if $\mathcal{B} \subset \mathcal{C} \subset \mathcal{P}([n])$ and $\mathcal{B} \neq \mathcal{C}$ then $\mathcal{C}$ is not 1-intersecting. Show that $|\mathcal{B}|=2^{n-1}$.

  Let $\mathcal{B} \subset \mathcal{P}([n])$ be 2 -intersecting. Show that $|\mathcal{B}| \geqslant 2^{n-2}$ is possible. Can the inequality be strict?

  comment

• B2.5

  Combinatorics | Part II, 2001

  As usual, $R_{k}^{(r)}(m)$ denotes the smallest integer $n$ such that every $k$-colouring of $[n]^{(r)}$ yields a monochromatic $m$-subset $M \in[n]^{(m)}$. Prove that $R_{2}^{(2)}(m)>2^{m / 2}$ for $m \geqslant 3$.

  Let $\mathcal{P}([n])$ have the colex order, and for $a, b \in \mathcal{P}([n])$ let $\delta(a, b)=\max a \triangle b$; thus $a<b$ means $\delta(a, b) \in b$. Show that if $a<b<c$ then $\delta(a, b) \neq \delta(b, c)$, and that $\delta(a, c)=\max \{\delta(a, b), \delta(b, c)\} .$

  Given a red-blue colouring of $[n]^{(2)}$, the 4 -colouring

  $$\chi: \mathcal{P}([n])^{(3)} \rightarrow\{\text { red, blue }\} \times\{0,1\}$$

  is defined as follows:

  $$\chi(\{a, b, c\})= \begin{cases}(\text { red, } 0) & \text { if }\{\delta(a, b), \delta(b, c)\} \text { is red and } \delta(a, b)<\delta(b, c) \\ (\text { red }, 1) & \text { if }\{\delta(a, b), \delta(b, c)\} \text { is red and } \delta(a, b)>\delta(b, c) \\ (\text { blue, } 0) & \text { if }\{\delta(a, b), \delta(b, c)\} \text { is blue and } \delta(a, b)<\delta(b, c) \\ \text { (blue, } 1) & \text { if }\{\delta(a, b), \delta(b, c)\} \text { is blue and } \delta(a, b)>\delta(b, c)\end{cases}$$

  where $a<b<c$. Show that if $M=\left\{a_{0}, a_{1}, \ldots, a_{m}\right\} \in \mathcal{P}([n])^{(m+1)}$ is monochromatic then $\left\{\delta_{1}, \ldots, \delta_{m}\right\} \in[n]^{(m)}$ is monochromatic, where $\delta_{i}=\delta\left(a_{i-1}, a_{i}\right)$ and $a_{0}<a_{1}<\cdots<a_{m}$.

  Deduce that $R_{4}^{(3)}(m+1)>2^{2^{m / 2}}$ for $m \geqslant 3$.

  comment

• B4.1

  Combinatorics | Part II, 2001

  Write an essay on extremal graph theory. You should give proofs of at least two major theorems and you should also include a description of alternative proofs or further results.

  comment

Computational Statistics and Statistical Modelling

• A1.13

  Computational Statistics and Statistical Modelling | Part II, 2001

  (i) Assume that the $n$-dimensional observation vector $Y$ may be written as

  $$Y=X \beta+\epsilon$$

  where $X$ is a given $n \times p$ matrix of $\operatorname{rank} p, \beta$ is an unknown vector, and

  $$\epsilon \sim N_{n}\left(0, \sigma^{2} I\right)$$

  Let $Q(\beta)=(Y-X \beta)^{T}(Y-X \beta)$. Find $\widehat{\beta}$, the least-squares estimator of $\beta$, and show that

  $$Q(\widehat{\beta})=Y^{T}(I-H) Y$$

  where $H$ is a matrix that you should define.

  (ii) Show that $\sum_{i} H_{i i}=p$. Show further for the special case of

  $$Y_{i}=\beta_{1}+\beta_{2} x_{i}+\beta_{3} z_{i}+\epsilon_{i}, \quad 1 \leqslant i \leqslant n$$

  where $\Sigma x_{i}=0, \Sigma z_{i}=0$, that

  $$H=\frac{1}{n} \mathbf{1 1}{ }^{T}+a x x^{T}+b\left(x z^{T}+z x^{T}\right)+c z z^{T} ;$$

  here, $\mathbf{1}$ is a vector of which every element is one, and $a, b, c$, are constants that you should derive.

  Hence show that, if $\widehat{Y}=X \widehat{\beta}$ is the vector of fitted values, then

  $$\frac{1}{\sigma^{2}} \operatorname{var}\left(\widehat{Y}_{i}\right)=\frac{1}{n}+a x_{i}^{2}+2 b x_{i} z_{i}+c z_{i}^{2}, \quad 1 \leqslant i \leqslant n .$$

  comment

• A2.12

  Computational Statistics and Statistical Modelling | Part II, 2001

  (i) Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and that $Y_{i}$ has probability density function

  $$f\left(y_{i} \mid \theta_{i}, \phi\right)=\exp \left[\left(y_{i} \theta_{i}-b\left(\theta_{i}\right)\right) / \phi+c\left(y_{i}, \phi\right)\right]$$

  Assume that $E\left(Y_{i}\right)=\mu_{i}$, and that $g\left(\mu_{i}\right)=\beta^{T} x_{i}$, where $g(\cdot)$ is a known 'link' function, $x_{1}, \ldots, x_{n}$ are known covariates, and $\beta$ is an unknown vector. Show that

  $$\mathbb{E}\left(Y_{i}\right)=b^{\prime}\left(\theta_{i}\right), \operatorname{var}\left(Y_{i}\right)=\phi b^{\prime \prime}\left(\theta_{i}\right)=V_{i} \text {, say, }$$

  and hence

  $$\frac{\partial l}{\partial \beta}=\sum_{i=1}^{n} \frac{\left(y_{i}-\mu_{i}\right) x_{i}}{g^{\prime}\left(\mu_{i}\right) V_{i}}, \text { where } l=l(\beta, \phi) \text { is the log-likelihood. }$$

  (ii) The table below shows the number of train miles (in millions) and the number of collisions involving British Rail passenger trains between 1970 and 1984 . Give a detailed interpretation of the $R$ output that is shown under this table:

  $\begin{array}{llll} & \text { year } & \text { collisions } & \text { miles } \\ 1 & 1970 & 3 & 281 \\ 2 & 1971 & 6 & 276 \\ 3 & 1972 & 4 & 268 \\ 4 & 1973 & 7 & 269 \\ 5 & 1974 & 6 & 281 \\ 6 & 1975 & 2 & 271 \\ 7 & 1976 & 2 & 265 \\ 8 & 1977 & 4 & 264 \\ 9 & 1978 & 1 & 267 \\ 10 & 1979 & 7 & 265 \\ 11 & 1980 & 3 & 267 \\ 12 & 1981 & 5 & 260 \\ 13 & 1982 & 6 & 231 \\ 14 & 1983 & 1 & 249\end{array}$

  Call:

  glm(formula $=$ collisions $\sim$ year $+\log ($ miles $)$, family $=$ poisson)

  Coefficients:

  $\begin{array}{lrrrr} & \text { Estimate } & \text { Std. Error } & \text { z value } & \operatorname{Pr}(>|z|) \\ \text { (Intercept) } & 127.14453 & 121.37796 & 1.048 & 0.295 \\ \text { year } & -0.05398 & 0.05175 & -1.043 & 0.297 \\ \log \text { (miles) } & -3.41654 & 4.18616 & -0.816 & 0.414\end{array}$

  (Dispersion parameter for poisson family taken to be 1)

  Null deviance: $15.937$ on 13 degrees of freedom

  Residual deviance: $14.843$ on 11 degrees of freedom

  Number of Fisher Scoring iterations: 4

  Part II

  comment

• A4.14

  Computational Statistics and Statistical Modelling | Part II, 2001

  (i) Assume that independent observations $Y_{1}, \ldots, Y_{n}$ are such that

  $$Y_{i} \sim \operatorname{Binomial}\left(t_{i}, \pi_{i}\right), \log \frac{\pi_{i}}{1-\pi_{i}}=\beta^{T} x_{i} \quad \text { for } 1 \leqslant i \leqslant n$$

  where $x_{1}, \ldots, x_{n}$ are given covariates. Discuss carefully how to estimate $\beta$, and how to test that the model fits.

  (ii) Carmichael et al. (1989) collected data on the numbers of 5 -year old children with "dmft", i.e. with 5 or more decayed, missing or filled teeth, classified by social class, and by whether or not their tap water was fluoridated or non-fluoridated. The numbers of such children with dmft, and the total numbers, are given in the table below:

  \begin{tabular}{l|ll} Social Class & Fluoridated & Non-fluoridated \ \hline I & $12 / 117$ & $12 / 56$ \ II & $26 / 170$ & $48 / 146$ \ III & $11 / 52$ & $29 / 64$ \ Unclassified & $24 / 118$ & $49 / 104$ \end{tabular}

  A (slightly edited) version of the $R$ output is given below. Explain carefully what model is being fitted, whether it does actually fit, and what the parameter estimates and Std. Errors are telling you. (You may assume that the factors SClass (social class) and Fl (with/without) have been correctly set up.)

  

  $\begin{array}{lrrrr} & \text { Estimate } & \text { Std. } & \text { Error } & \text { z value } \\ \text { (Intercept) } & -2.2716 & 0.2396 & -9.480 \\ \text { SClassII } & 0.5099 & 0.2628 & 1.940 \\ \text { SClassIII } & 0.9857 & 0.3021 & 3.262 \\ \text { SClassUnc } & 1.0020 & 0.2684 & 3.734 \\ \text { Flwithout } & 1.0813 & 0.1694 & 6.383\end{array}$

  

  Here 'Yes' is the vector of numbers with dmft, taking values $12,12, \ldots, 24,49$, 'Total' is the vector of Total in each category, taking values $117,56, \ldots, 118,104$, and SClass, Fl are the factors corresponding to Social class and Fluoride status, defined in the obvious way.

  comment

Differentiable Manifolds

• B1.8

  Differentiable Manifolds | Part II, 2001

  Define an immersion and an embedding of one manifold in another. State a necessary and sufficient condition for an immersion to be an embedding and prove its necessity.

  Assuming the existence of "bump functions" on Euclidean spaces, state and prove a version of Whitney's embedding theorem.

  Deduce that $\mathbb{R}^{n}$ embeds in $\mathbb{R}^{(n+1)^{2}}$.

  comment

• B2.7

  Differentiable Manifolds | Part II, 2001

  State Stokes' Theorem.

  Prove that, if $M^{m}$ is a compact connected manifold and $\Phi: U \rightarrow \mathbb{R}^{m}$ is a surjective chart on $M$, then for any $\omega \in \Omega^{m}(M)$ there is $\eta \in \Omega^{m-1}(M)$ such that $\operatorname{supp}(\omega+d \eta) \subseteq \Phi^{-1}\left(\mathbf{B}^{m}\right)$, where $\mathbf{B}^{m}$ is the unit ball in $\mathbb{R}^{m}$.

  [You may assume that, if $\omega \in \Omega^{m}\left(\mathbb{R}^{m}\right)$ with $\operatorname{supp}(\omega) \subseteq \mathbf{B}^{m}$ and $\int_{\mathbb{R}^{m}} \omega=0$, then $\exists \eta \in \Omega^{m-1}\left(\mathbb{R}^{m}\right)$ with $\operatorname{supp}(\eta) \subseteq \mathbf{B}^{m}$ such that $\left.d \eta=\omega .\right]$

  By considering the $m$-form

  $$\omega=x_{1} d x_{2} \wedge \ldots \wedge d x_{m+1}+\cdots+x_{m+1} d x_{1} \wedge \ldots \wedge d x_{m}$$

  on $\mathbb{R}^{m+1}$, or otherwise, deduce that $H^{m}\left(S^{m}\right) \cong \mathbb{R}$.

  comment

• B4.4

  Differentiable Manifolds | Part II, 2001

  Describe the Mayer-Vietoris exact sequence for forms on a manifold $M$ and show how to derive from it the Mayer-Vietoris exact sequence for the de Rham cohomology.

  Calculate $H^{*}\left(\mathbb{R} \mathbb{P}^{n}\right)$.

  comment

Dynamical Systems

• B1.17

  Dynamical Systems | Part II, 2001

  Define topological conjugacy and $C^{1}$-conjugacy.

  Let $a, b$ be real numbers with $a>b>0$ and let $F_{a}, F_{b}$ be the maps of $(0, \infty)$ to itself given by $F_{a}(x)=a x, F_{b}(x)=b x$. For which pairs $a, b$ are $F_{a}$ and $F_{b}$ topologically conjugate? Would the answer be the same for $C^{1}$-conjugacy? Justify your statements.

  comment

• B3.17

  Dynamical Systems | Part II, 2001

  If $A=\left(\begin{array}{ll}0 & 1 \\ 1 & 1\end{array}\right)$ show that $A^{n+2}=A^{n+1}+A^{n}$ for all $n \geqslant 0$. Show that $A^{5}$ has trace 11 and deduce that the subshift map defined by $A$ has just two cycles of exact period 5. What are they?

  comment

• B4.17

  Dynamical Systems | Part II, 2001

  Define the rotation number $\rho(f)$ of an orientation-preserving circle map $f$ and the rotation number $\rho(F)$ of a lift $F$ of $f$. Prove that $\rho(f)$ and $\rho(F)$ are well-defined. Prove also that $\rho(F)$ is a continuous function of $F$.

  State without proof the main consequence of $\rho(f)$ being rational.

  comment

Dynamics of Differential Equations

• A1.6

  Dynamics of Differential Equations | Part II, 2001

  (i) Given a differential equation $\dot{x}=f(x)$ for $x \in \mathbb{R}^{n}$, explain what it means to say that the solution is given by a flow $\phi: \mathbb{R} \times \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$. Define the orbit, $o(x)$, through a point $x$ and the $\omega$-limit set, $\omega(x)$, of $x$. Define also a homoclinic orbit to a fixed point $x_{0}$. Sketch a flow in $\mathbb{R}^{2}$ with a homoclinic orbit, and identify (without detailed justification) the $\omega$-limit sets $\omega(x)$ for each point $x$ in your diagram.

  (ii) Consider the differential equations

  $$\dot{x}=z y, \quad \dot{y}=-z x, \quad \dot{z}=-z^{2} .$$

  Transform the equations to polar coordinates $(r, \theta)$ in the $(x, y)$ plane. Solve the equation for $z$ to find $z(t)$, and hence find $\theta(t)$. Hence, or otherwise, determine (with justification) the $\omega$-limit set for all points $\left(x_{0}, y_{0}, z_{0}\right) \in \mathbb{R}^{3}$.

  comment

• A2.6 B2.4

  Dynamics of Differential Equations | Part II, 2001

  (i) Define a Liapounov function for a flow $\phi$ on $\mathbb{R}^{n}$. Explain what it means for a fixed point of the flow to be Liapounov stable. State and prove Liapounov's first stability theorem.

  (ii) Consider the damped pendulum

  $$\ddot{\theta}+k \dot{\theta}+\sin \theta=0,$$

  where $k>0$. Show that there are just two fixed points (considering the phase space as an infinite cylinder), and that one of these is the origin and is Liapounov stable. Show further that the origin is asymptotically stable, and that the the $\omega$-limit set of each point in the phase space is one or other of the two fixed points, justifying your answer carefully.

  [You should state carefully any theorems you use in your answer, but you need not prove them.]

  comment

• A3.6 B3.4

  Dynamics of Differential Equations | Part II, 2001

  (i) Define a hyperbolic fixed point $x_{0}$ of a flow determined by a differential equation $\dot{x}=f(x)$ where $x \in R^{n}$ and $f$ is $C^{1}$ (i.e. differentiable). State the Hartman-Grobman Theorem for flow near a hyperbolic fixed point. For nonlinear flows in $R^{2}$ with a hyperbolic fixed point $x_{0}$, does the theorem necessarily allow us to distinguish, on the basis of the linearized flow near $x_{0}$ between (a) a stable focus and a stable node; and (b) a saddle and a stable node? Justify your answers briefly.

  (ii) Show that the system:

  $$\begin{aligned} &\dot{x}=-(\mu+1)+(\mu-3) x-y+6 x^{2}+12 x y+5 y^{2}-2 x^{3}-6 x^{2} y-5 x y^{2} \\ &\dot{y}=2-2 x+(\mu-5) y+4 x y+6 y^{2}-2 x^{2} y-6 x y^{2}-5 y^{3} \end{aligned}$$

  has a fixed point $\left(x_{0}, 0\right)$ on the $x$-axis. Show that there is a bifurcation at $\mu=0$ and determine the stability of the fixed point for $\mu>0$ and for $\mu<0$.

  Make a linear change of variables of the form $u=x-x_{0}+\alpha y, v=x-x_{0}+\beta y$, where $\alpha$ and $\beta$ are constants to be determined, to bring the system into the form:

  $$\begin{aligned} &\dot{u}=v+u\left[\mu-\left(u^{2}+v^{2}\right)\right] \\ &\dot{v}=-u+v\left[\mu-\left(u^{2}+v^{2}\right)\right] \end{aligned}$$

  and hence determine whether the periodic orbit produced in the bifurcation is stable or unstable, and whether it exists in $\mu<0$ or $\mu>0$.

  comment

• A4.6

  Dynamics of Differential Equations | Part II, 2001

  Write a short essay about periodic orbits in flows in two dimensions. Your essay should include criteria for the existence and non-existence of periodic orbits, and should mention (with sketches) at least two bifurcations that create or destroy periodic orbits in flows as a parameter is altered (though a detailed analysis of any bifurcation is not required).

  comment

Electrodynamics

• B1.21

  Electrodynamics | Part II, 2001

  Explain the multipole expansion in electrostatics, and devise formulae for the total charge, dipole moments and quadrupole moments given by a static charge distribution $\rho(\mathbf{r})$.

  A nucleus is modelled as a uniform distribution of charge inside the ellipsoid

  $$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{a^{2}}+\frac{z^{2}}{c^{2}}=1$$

  The total charge of the nucleus is $Q$. What are the dipole moments and quadrupole moments of this distribution?

  Describe qualitatively what happens if the nucleus starts to oscillate.

  comment

• B2.20

  Electrodynamics | Part II, 2001

  In a superconductor, there are superconducting charge carriers with number density $n$, mass $m$ and charge $q$. Starting from the quantum mechanical wavefunction $\Psi=R e^{i \Phi}$ (with real $R$ and $\Phi$ ), construct a formula for the electric current and explain carefully why your result is gauge invariant.

  Now show that inside a superconductor a static magnetic field obeys the equation

  $$\nabla^{2} \mathbf{B}=\frac{\mu_{0} n q^{2}}{m} \mathbf{B}$$

  A superconductor occupies the region $z>0$, while for $z<0$ there is a vacuum with a constant magnetic field in the $x$ direction. Show that the magnetic field cannot penetrate deep into the superconductor.

  comment

• B4.21

  Electrodynamics | Part II, 2001

  The Liénard-Wiechert potential for a particle of charge $q$, assumed to be moving non-relativistically along the trajectory $y^{\mu}(\tau), \tau$ being the proper time along the trajectory,

  $$A^{\mu}(x, t)=\left.\frac{\mu_{0} q}{4 \pi} \frac{d y^{\mu} / d \tau}{(x-y(\tau))_{\nu} d y^{\nu} / d \tau}\right|_{\tau=\tau_{0}} .$$

  Explain how to calculate $\tau_{0}$ given $x^{\mu}=(x, t)$ and $y^{\mu}=\left(y, t^{\prime}\right)$.

  Derive Larmor's formula for the rate at which electromagnetic energy is radiated from a particle of charge $q$ undergoing an acceleration $a$.

  Suppose that one considers the classical non-relativistic hydrogen atom with an electron of mass $m$ and charge $-e$ orbiting a fixed proton of charge $+e$, in a circular orbit of radius $r_{0}$. What is the total energy of the electron? As the electron is accelerated towards the proton it will radiate, thereby losing energy and causing the orbit to decay. Derive a formula for the lifetime of the orbit.

  Part II

  comment

Electromagnetism

• A $1 . 5 \quad$ B $1 . 4 \quad$

  Electromagnetism | Part II, 2001

  (i) Write down the two Maxwell equations that govern steady magnetic fields. Show that the boundary conditions satisfied by the magnetic field on either side of a current sheet, $\mathbf{J}$, with unit normal to the sheet $\mathbf{n}$, are

  $$\mathbf{n} \wedge \mathbf{B}_{2}-\mathbf{n} \wedge \mathbf{B}_{1}=\mu_{0} \mathbf{J}$$

  State without proof the force per unit area on $\mathbf{J}$.

  (ii) Conducting gas occupies the infinite slab $0 \leqslant x \leqslant a$. It carries a steady current $\mathbf{j}=(0,0, j)$ and a magnetic field $\mathbf{B}=(0, B, 0)$ where $\mathbf{j}$, $\mathbf{B}$ depend only on $x$. The pressure is $p(x)$. The equation of hydrostatic equilibrium is $\nabla p=\mathbf{j} \wedge \mathbf{B}$. Write down the equations to be solved in this case. Show that $p+\left(1 / 2 \mu_{0}\right) B^{2}$ is independent of $x$. Using the suffixes 1,2 to denote values at $x=0, a$, respectively, verify that your results are in agreement with those of Part (i) in the case of $a \rightarrow 0$.

  Suppose that

  $$j(x)=\frac{\pi j_{0}}{2 a} \sin \left(\frac{\pi x}{a}\right), \quad B_{1}=0, \quad p_{2}=0$$

  Find $B(x)$ everywhere in the slab.

  comment

• A2.5

  Electromagnetism | Part II, 2001

  (i) Write down the expression for the electrostatic potential $\phi(\mathbf{r})$ due to a distribution of charge $\rho(\mathbf{r})$ contained in a volume $V$. Perform the multipole expansion of $\phi(\mathbf{r})$ taken only as far as the dipole term.

  (ii) If the volume $V$ is the sphere $|\mathbf{r}| \leqslant a$ and the charge distribution is given by

  $$\rho(\mathbf{r})= \begin{cases}r^{2} \cos \theta & r \leqslant a \\ 0 & r>a\end{cases}$$

  where $r, \theta$ are spherical polar coordinates, calculate the charge and dipole moment. Hence deduce $\phi$ as far as the dipole term.

  Obtain an exact solution for $r>a$ by solving the boundary value problem using trial solutions of the forms

  $$\phi=\frac{A \cos \theta}{r^{2}} \text { for } r>a,$$

  and

  $$\phi=B r \cos \theta+C r^{4} \cos \theta \text { for } r<a .$$

  Show that the solution obtained from the multipole expansion is in fact exact for $r>a$.

  [You may use without proof the result

  $$\left.\nabla^{2}\left(r^{k} \cos \theta\right)=(k+2)(k-1) r^{k-2} \cos \theta, \quad k \in \mathbb{N} .\right]$$

  comment

• A3.5 B3.3

  Electromagnetism | Part II, 2001

  (i) Develop the theory of electromagnetic waves starting from Maxwell equations in vacuum. You should relate the wave-speed $c$ to $\epsilon_{0}$ and $\mu_{0}$ and establish the existence of plane, plane-polarized waves in which $\mathbf{E}$ takes the form

  $$\mathbf{E}=\left(E_{0} \cos (k z-\omega t), 0,0\right) .$$

  You should give the form of the magnetic field $\mathbf{B}$ in this case.

  (ii) Starting from Maxwell's equation, establish Poynting's theorem.

  $$-\mathbf{j} \cdot \mathbf{E}=\frac{\partial W}{\partial t}+\nabla \cdot \mathbf{S},$$

  where $W=\frac{\epsilon_{0}}{2} \mathbf{E}^{2}+\frac{1}{2 \mu_{0}} \mathbf{B}^{2}$ and $\mathbf{S}=\frac{1}{\mu_{0}} \mathbf{E} \wedge \mathbf{B}$. Give physical interpretations of $W, S$ and the theorem.

  Compute the averages over space and time of $W$ and $\mathbf{S}$ for the plane wave described in (i) and relate them. Comment on the result.

  comment

• A4.5 $\quad$

  Electromagnetism | Part II, 2001

  Write down the form of Ohm's Law that applies to a conductor if at a point $\mathbf{r}$ it is moving with velocity $\mathbf{v}(\mathbf{r})$.

  Use two of Maxwell's equations to prove that

  $$\int_{C}(\mathbf{E}+\mathbf{v} \wedge \mathbf{B}) \cdot d \mathbf{r}=-\frac{d}{d t} \int_{S} \mathbf{B} \cdot d \mathbf{S}$$

  where $C(t)$ is a moving closed loop, $\mathbf{v}$ is the velocity at the point $\mathbf{r}$ on $C$, and $S$ is a surface spanning $C$. The time derivative on the right hand side accounts for changes in both $C$ and B. Explain briefly the physical importance of this result.

  Find and sketch the magnetic field $\mathbf{B}$ described in the vector potential

  $$\mathbf{A}(r, \theta, z)=\left(0, \frac{1}{2} b r z, 0\right)$$

  in cylindrical polar coordinates $(r, \theta, z)$, where $b>0$ is constant.

  A conducting circular loop of radius $a$ and resistance $R$ lies in the plane $z=h(t)$ with its centre on the $z$-axis.

  Find the magnitude and direction of the current induced in the loop as $h(t)$ changes with time, neglecting self-inductance.

  At time $t=0$ the loop is at rest at $z=0$. For time $t>0$ the loop moves with constant velocity $d h / d t=v>0$. Ignoring the inertia of the loop, use energy considerations to find the force $F(t)$ necessary to maintain this motion.

  [ In cylindrical polar coordinates

  $$\left.\operatorname{curl} \mathbf{A}=\left(\frac{1}{r} \frac{\partial A_{z}}{\partial \theta}-\frac{\partial A_{\theta}}{\partial z}, \frac{\partial A_{r}}{\partial z}-\frac{\partial A_{z}}{\partial r}, \frac{1}{r} \frac{\partial}{\partial r}\left(r A_{\theta}\right)-\frac{1}{r} \frac{\partial A_{r}}{\partial \theta}\right)\right]$$

  Part II

  comment

Fluid Dynamics II

• B1.25

  Fluid Dynamics II | Part II, 2001

  The energy equation for the motion of a viscous, incompressible fluid states that

  $$\frac{d}{d t} \int_{V(t)} \frac{1}{2} \rho u^{2} d V=\int_{S(t)} u_{i} \sigma_{i j} n_{j} d S-2 \mu \int_{V(t)} e_{i j} e_{i j} d V$$

  Interpret each term in this equation and explain the meaning of the symbols used.

  For steady rectilinear flow in a (not necessarily circular) pipe having rigid stationary walls, deduce a relation between the viscous dissipation per unit length of the pipe, the pressure gradient $G$, and the volume flux $Q$.

  Starting from the Navier-Stokes equations, calculate the velocity field for steady rectilinear flow in a circular pipe of radius $a$. Using the relationship derived above, or otherwise, find in terms of $G$ the viscous dissipation per unit length for this flow.

  [In cylindrical polar coordinates,

  $$\left.\nabla^{2} w(r)=\frac{1}{r} \frac{d}{d r}\left(r \frac{d w}{d r}\right) .\right]$$

  comment

• B2.24

  Fluid Dynamics II | Part II, 2001

  Explain what is meant by a Stokes flow and show that, in such a flow, in the absence of body forces, $\partial \sigma_{i j} / \partial x_{j}=0$, where $\sigma_{i j}$ is the stress tensor.

  State and prove the reciprocal theorem for Stokes flow.

  When a rigid sphere of radius $a$ translates with velocity $\mathbf{U}$ through unbounded fluid at rest at infinity, it may be shown that the traction per unit area, $\boldsymbol{\sigma} \cdot \mathbf{n}$, exerted by the sphere on the fluid, has the uniform value $3 \mu \mathbf{U} / 2 a$ over the sphere surface. Find the drag on the sphere.

  Suppose that the same sphere is free of external forces and is placed with its centre at the origin in an unbounded Stokes flow given in the absence of the sphere as $\mathbf{u}_{s}(\mathbf{x})$. By applying the reciprocal theorem to the perturbation to the flow generated by the presence of the sphere, and assuming this to tend to zero sufficiently rapidly at infinity, show that the instantaneous velocity of the centre of the sphere is

  $$\mathbf{V}=\frac{1}{4 \pi a^{2}} \int_{r=a} \mathbf{u}_{s}(\mathbf{x}) d S$$

  Part II

  comment

• B3.24

  Fluid Dynamics II | Part II, 2001

  A planar flow of an inviscid, incompressible fluid is everywhere in the $x$-direction and has velocity profile

  $$u=\left\{\begin{array}{cc} U & y>0, \\ 0 & y<0 . \end{array}\right.$$

  By examining linear perturbations to the vortex sheet at $y=0$ that have the form $e^{i k x-i \omega t}$, show that

  $$\omega=\frac{1}{2} k U(1 \pm i)$$

  and deduce the temporal stability of the sheet to disturbances of wave number $k$.

  Use this result to determine also the spatial growth rate and propagation speed of disturbances of frequency $\omega$ introduced at a fixed spatial position.

  comment

• B4.26

  Fluid Dynamics II | Part II, 2001

  Starting from the steady planar vorticity equation

  $$\mathbf{u} \cdot \nabla \omega=\nu \nabla^{2} \omega,$$

  outline briefly the derivation of the boundary layer equation

  $$u u_{x}+v u_{y}=U d U / d x+\nu u_{y y},$$

  explaining the significance of the symbols used.

  Viscous fluid occupies the region $y>0$ with rigid stationary walls along $y=0$ for $x>0$ and $x<0$. There is a line sink at the origin of strength $\pi Q, Q>0$, with $Q / \nu \gg 1$. Assuming that vorticity is confined to boundary layers along the rigid walls:

  (a) Find the flow outside the boundary layers.

  (b) Explain why the boundary layer thickness $\delta$ along the wall $x>0$ is proportional to $x$, and deduce that

  $$\delta=\left(\frac{\nu}{Q}\right)^{\frac{1}{2}} x$$

  (c) Show that the boundary layer equation admits a solution having stream function

  $$\psi=(\nu Q)^{1 / 2} f(\eta) \quad \text { with } \quad \eta=y / \delta$$

  Find the equation and boundary conditions satisfied by $f$.

  (d) Verify that a solution is

  $$f^{\prime}=\frac{6}{1+\cosh (\eta \sqrt{2}+c)}-1$$

  provided that $c$ has one of two values to be determined. Should the positive or negative value be chosen?

  comment

Foundations of Quantum Mechanics

• A2.13 B2.21

  Foundations of Quantum Mechanics | Part II, 2001

  (i) Hermitian operators $\hat{x}, \hat{p}$, satisfy $[\hat{x}, \hat{p}]=i \hbar$. The eigenvectors $|p\rangle$, satisfy $\hat{p}|p\rangle=p|p\rangle$ and $\left\langle p^{\prime} \mid p\right\rangle=\delta\left(p^{\prime}-p\right)$. By differentiating with respect to $b$ verify that

  $$e^{-i b \hat{x} / \hbar} \hat{p} e^{i b \hat{x} / \hbar}=\hat{p}+b$$

  and hence show that

  $$e^{i b \hat{x} / \hbar}|p\rangle=|p+b\rangle$$

  Show that

  $$\langle p|\hat{x}| \psi\rangle=i \hbar \frac{\partial}{\partial p}\langle p \mid \psi\rangle$$

  and

  $$\langle p|\hat{p}| \psi\rangle=p\langle p \mid \psi\rangle .$$

  (ii) A quantum system has Hamiltonian $H=H_{0}+H_{1}$, where $H_{1}$ is a small perturbation. The eigenvalues of $H_{0}$ are $\epsilon_{n}$. Give (without derivation) the formulae for the first order and second order perturbations in the energy level of a non-degenerate state. Suppose that the $r$ th energy level of $H_{0}$ has $j$ degenerate states. Explain how to determine the eigenvalues of $H$ corresponding to these states to first order in $H_{1}$.

  In a particular quantum system an orthonormal basis of states is given by $\left|n_{1}, n_{2}\right\rangle$, where $n_{i}$ are integers. The Hamiltonian is given by

  $$H=\sum_{n_{1}, n_{2}}\left(n_{1}^{2}+n_{2}^{2}\right)\left|n_{1}, n_{2}\right\rangle\left\langle n_{1}, n_{2}\left|+\sum_{n_{1}, n_{2}, n_{1}^{\prime}, n_{2}^{\prime}} \lambda_{\left|n_{1}-n_{1}^{\prime}\right|,\left|n_{2}-n_{2}^{\prime}\right|}\right| n_{1}, n_{2}\right\rangle\left\langle n_{1}^{\prime}, n_{2}^{\prime}\right|,$$

  where $\lambda_{r, s}=\lambda_{s, r}, \lambda_{0,0}=0$ and $\lambda_{r, s}=0$ unless $r$ and $s$ are both even.

  Obtain an expression for the ground state energy to second order in the perturbation, $\lambda_{r, s}$. Find the energy eigenvalues of the first excited state to first order in the perturbation. Determine a matrix (which depends on two independent parameters) whose eigenvalues give the first order energy shift of the second excited state.

  comment

• A3.13 B3.21

  Foundations of Quantum Mechanics | Part II, 2001

  (i) Write the Hamiltonian for the harmonic oscillator,

  $$H=\frac{p^{2}}{2 m}+\frac{1}{2} m \omega^{2} x^{2}$$

  in terms of creation and annihilation operators, defined by

  $$a^{\dagger}=\left(\frac{m \omega}{2 \hbar}\right)^{\frac{1}{2}}\left(x-i \frac{p}{m \omega}\right), \quad a=\left(\frac{m \omega}{2 \hbar}\right)^{\frac{1}{2}}\left(x+i \frac{p}{m \omega}\right)$$

  Obtain an expression for $\left[a^{\dagger}, a\right]$ by using the usual commutation relation between $p$ and $x$. Deduce the quantized energy levels for this system.

  (ii) Define the number operator, $N$, in terms of creation and annihilation operators, $a^{\dagger}$ and $a$. The normalized eigenvector of $N$ with eigenvalue $n$ is $|n\rangle$. Show that $n \geq 0$.

  Determine $a|n\rangle$ and $a^{\dagger}|n\rangle$ in the basis defined by $\{|n\rangle\}$.

  Show that

  $$a^{\dagger m} a^{m}|n\rangle=\left\{\begin{aligned} \frac{n !}{(n-m) !}|n\rangle, & m \leq n \\ 0, & m>n \end{aligned}\right.$$

  Verify the relation

  $$|0\rangle\langle 0|=\sum_{m=0} \frac{1}{m !}(-1)^{m} a^{\dagger m} a^{m}$$

  by considering the action of both sides of the equation on an arbitrary basis vector.

  comment

• A4.15 B4.22

  Foundations of Quantum Mechanics | Part II, 2001

  (i) The two states of a spin- $\frac{1}{2}$ particle corresponding to spin pointing along the $z$ axis are denoted by $|\uparrow\rangle$ and $|\downarrow\rangle$. Explain why the states

  $$|\uparrow, \theta\rangle=\cos \frac{\theta}{2}|\uparrow\rangle+\sin \frac{\theta}{2}|\downarrow\rangle, \quad \quad|\downarrow, \theta\rangle=-\sin \frac{\theta}{2}|\uparrow\rangle+\cos \frac{\theta}{2}|\downarrow\rangle$$

  correspond to the spins being aligned along a direction at an angle $\theta$ to the $z$ direction.

  The spin- 0 state of two spin- $\frac{1}{2}$ particles is

  $$|0\rangle=\frac{1}{\sqrt{2}}\left(|\uparrow\rangle_{1}|\downarrow\rangle_{2}-|\downarrow\rangle_{1}|\uparrow\rangle_{2}\right)$$

  Show that this is independent of the direction chosen to define $|\uparrow\rangle_{1,2},|\downarrow\rangle_{1,2}$. If the spin of particle 1 along some direction is measured to be $\frac{1}{2} \hbar$ show that the spin of particle 2 along the same direction is determined, giving its value.

  [The Pauli matrices are given by

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  (ii) Starting from the commutation relation for angular momentum in the form

  $$\left[J_{3}, J_{\pm}\right]=\pm \hbar J_{\pm}, \quad\left[J_{+}, J_{-}\right]=2 \hbar J_{3},$$

  obtain the possible values of $j, m$, where $m \hbar$ are the eigenvalues of $J_{3}$ and $j(j+1) \hbar^{2}$ are the eigenvalues of $\mathbf{J}^{2}=\frac{1}{2}\left(J_{+} J_{-}+J_{-} J_{+}\right)+J_{3}^{2}$. Show that the corresponding normalized eigenvectors, $|j, m\rangle$, satisfy

  $$J_{\pm}|j, m\rangle=\hbar((j \mp m)(j \pm m+1))^{1 / 2}|j, m \pm 1\rangle,$$

  and that

  $$\frac{1}{n !} J_{-}^{n}|j, j\rangle=\hbar^{n}\left(\frac{(2 j) !}{n !(2 j-n) !}\right)^{1 / 2}|j, j-n\rangle, \quad n \leq 2 j$$

  The state $|w\rangle$ is defined by

  $$|w\rangle=e^{w J_{-} / \hbar}|j, j\rangle$$

  for any complex $w$. By expanding the exponential show that $\langle w \mid w\rangle=\left(1+|w|^{2}\right)^{2 j}$. Verify that

  $$e^{-w J_{-} / \hbar} J_{3} e^{w J_{-} / \hbar}=J_{3}-w J_{-}$$

  and hence show that

  $$J_{3}|w\rangle=\hbar\left(j-w \frac{\partial}{\partial w}\right)|w\rangle$$

  If $H=\alpha J_{3}$ verify that $\left|e^{i \alpha t}\right\rangle e^{-i j \alpha t}$ is a solution of the time-dependent Schrödinger equation.

  comment

Functional Analysis

• A1 $. 3 \quad$

  Functional Analysis | Part II, 2001

  (i) Define the adjoint of a bounded, linear map $u: H \rightarrow H$ on the Hilbert space $H$. Find the adjoint of the map

  $$u: H \rightarrow H ; \quad x \mapsto \phi(x) a$$

  where $a, b \in H$ and $\phi \in H^{*}$ is the linear map $x \mapsto\langle b, x\rangle$.

  Now let $J$ be an incomplete inner product space and $u: J \rightarrow J$ a bounded, linear map. Is it always true that there is an adjoint $u^{*}: J \rightarrow J$ ?

  (ii) Let $\mathcal{H}$ be the space of analytic functions $f: \mathbb{D} \rightarrow \mathbb{C}$ on the unit disc $\mathbb{D}$ for which

  $$\iint_{\mathbb{D}}|f(z)|^{2} d x d y<\infty \quad(z=x+i y)$$

  You may assume that this is a Hilbert space for the inner product:

  $$\langle f, g\rangle=\iint_{\mathbb{D}} \overline{f(z)} g(z) d x d y .$$

  Show that the functions $u_{k}: z \mapsto \alpha_{k} z^{k}(k=0,1,2, \ldots)$ form an orthonormal sequence in $\mathcal{H}$ when the constants $\alpha_{k}$ are chosen appropriately.

  Prove carefully that every function $f \in \mathcal{H}$ can be written as the sum of a convergent series $\sum_{k=0}^{\infty} f_{k} u_{k}$ in $\mathcal{H}$ with $f_{k} \in \mathbb{C}$.

  For each smooth curve $\gamma$ in the disc $\mathbb{D}$ starting from 0 , prove that

  $$\phi: \mathcal{H} \rightarrow \mathbb{C} ; \quad f \mapsto \int_{\gamma} f(z) d z$$

  is a continuous, linear map. Show that the norm of $\phi$ satisfies

  $$\|\phi\|^{2}=\frac{1}{\pi} \log \left(\frac{1}{1-|w|^{2}}\right)$$

  where $w$ is the endpoint of $\gamma$.

  comment

• A2.3 B2.2

  Functional Analysis | Part II, 2001

  (i) State the Stone-Weierstrass theorem for complex-valued functions. Use it to show that the trigonometric polynomials are dense in the space $C(\mathbb{T})$ of continuous, complexvalued functions on the unit circle $\mathbb{T}$ with the uniform norm.

  Show further that, for $f \in C(\mathbb{T})$, the $n$th Fourier coefficient

  $$\widehat{f}(n)=\frac{1}{2 \pi} \int_{0}^{2 \pi} f\left(e^{i \theta}\right) e^{-i n \theta} d \theta$$

  tends to 0 as $|n|$ tends to infinity.

  (ii) (a) Let $X$ be a normed space with the property that the series $\sum_{n=1}^{\infty} x_{n}$ converges whenever $\left(x_{n}\right)$ is a sequence in $X$ with $\sum_{n=1}^{\infty}\left\|x_{n}\right\|$ convergent. Show that $X$ is a Banach space.

  (b) Let $K$ be a compact metric space and $L$ a closed subset of $K$. Let $R: C(K) \rightarrow$ $C(L)$ be the map sending $f \in C(K)$ to its restriction $R(f)=f \mid L$ to $L$. Show that $R$ is a bounded, linear map and that its image is a subalgebra of $C(L)$ separating the points of

  Show further that, for each function $g$ in the image of $R$, there is a function $f \in C(K)$ with $R(f)=g$ and $\|f\|_{\infty}=\|g\|_{\infty}$. Deduce that every continuous, complexvalued function on $L$ can be extended to a continuous function on all of $K$.

  comment

• A3.3 B3.2

  Functional Analysis | Part II, 2001

  (i) Define the notion of a measurable function between measurable spaces. Show that a continuous function $\mathbb{R}^{2} \rightarrow \mathbb{R}$ is measurable with respect to the Borel $\sigma$-fields on $\mathbb{R}^{2}$ and $\mathbb{R}$.

  By using this, or otherwise, show that, when $f, g: X \rightarrow \mathbb{R}$ are measurable with respect to some $\sigma$-field $\mathcal{F}$ on $X$ and the Borel $\sigma$-field on $\mathbb{R}$, then $f+g$ is also measurable.

  (ii) State the Monotone Convergence Theorem for $[0, \infty]$-valued functions. Prove the Dominated Convergence Theorem.

  [You may assume the Monotone Convergence Theorem but any other results about integration that you use will need to be stated carefully and proved.]

  Let $X$ be the real Banach space of continuous real-valued functions on $[0,1]$ with the uniform norm. Fix $u \in X$ and define

  $$T: X \rightarrow \mathbb{R} ; \quad f \mapsto \int_{0}^{1} f(t) u(t) d t$$

  Show that $T$ is a bounded, linear map with norm

  $$\|T\|=\int_{0}^{1}|u(t)| d t$$

  Is it true, for every choice of $u$, that there is function $f \in X$ with $\|f\|=1$ and $\|T(f)\|=\|T\|$ ?

  comment

• A4.3

  Functional Analysis | Part II, 2001

  Write an account of the classical sequence spaces: $\ell_{p}(1 \leqslant p \leqslant \infty)$ and $c_{0}$. You should define them, prove that they are Banach spaces, and discuss their properties, including their dual spaces. Show that $\ell_{\infty}$ is inseparable but that $c_{0}$ and $\ell_{p}$ for $1 \leqslant p<\infty$ are separable.

  Prove that, if $T: X \rightarrow Y$ is an isomorphism between two Banach spaces, then

  $$T^{*}: Y^{*} \rightarrow X^{*} ; \quad f \mapsto f \circ T$$

  is an isomorphism between their duals.

  Hence, or otherwise, show that no two of the spaces $c_{0}, \ell_{1}, \ell_{2}, \ell_{\infty}$ are isomorphic.

  comment

Galois Theory

• B1.7

  Galois Theory | Part II, 2001

  Prove that the Galois group $G$ of the polynomial $X^{6}+3$ over $\mathbf{Q}$ is of order 6 . By explicitly describing the elements of $G$, show that they have orders 1,2 or 3 . Hence deduce that $G$ is isomorphic to $S_{3}$.

  Why does it follow that $X^{6}+3$ is reducible over the finite field $\mathbf{F}_{p}$, for all primes $p ?$

  comment

• B3.6

  Galois Theory | Part II, 2001

  Let $\mathbf{F}_{p}$ be the finite field with $p$ elements ( $p$ a prime), and let $k$ be a finite extension of $\mathbf{F}_{p}$. Define the Frobenius automorphism $\sigma: k \longrightarrow k$, verifying that it is an $\mathbf{F}_{p^{-}}$ automorphism of $k$.

  Suppose $f=X^{p+1}+X^{p}+1 \in \mathbf{F}_{p}[X]$ and that $K$ is its splitting field over $\mathbf{F}_{p}$. Why are the zeros of $f$ distinct? If $\alpha$ is any zero of $f$ in $K$, show that $\sigma(\alpha)=-\frac{1}{\alpha+1}$. Prove that $f$ has at most two zeros in $\mathbf{F}_{p}$ and that $\sigma^{3}=i d$. Deduce that the Galois group of $f$ over $\mathbf{F}_{p}$ is a cyclic group of order three.

  comment

• B4.3

  Galois Theory | Part II, 2001

  Define the concept of separability and normality for algebraic field extensions. Suppose $K=k(\alpha)$ is a simple algebraic extension of $k$, and that $\operatorname{Aut}(K / k)$ denotes the group of $k$-automorphisms of $K$. Prove that $|\operatorname{Aut}(K / k)| \leqslant[K: k]$, with equality if and only if $K / k$ is normal and separable.

  [You may assume that the splitting field of a separable polynomial $f \in k[X]$ is normal and separable over $k$.]

  Suppose now that $G$ is a finite group of automorphisms of a field $F$, and $E=F^{G}$ is the fixed subfield. Prove:

  (i) $F / E$ is separable.

  (ii) $G=\operatorname{Aut}(F / E)$ and $[F: E]=|G|$.

  (iii) $F / E$ is normal.

  [The Primitive Element Theorem for finite separable extensions may be used without proof.]

  comment

General Relativity

• A1.15 B1.24

  General Relativity | Part II, 2001

  (i) The metric of any two-dimensional curved space, rotationally symmetric about a point $P$, can by suitable choice of coordinates be written locally in the form

  $$d s^{2}=e^{2 \phi(r)}\left(d r^{2}+r^{2} d \theta^{2}\right),$$

  where $r=0$ at $P, r>0$ away from $P$, and $0 \leqslant \theta<2 \pi$. Labelling the coordinates as $\left(x^{1}, x^{2}\right)=(r, \theta)$, show that the Christoffel symbols $\Gamma_{12}^{1}, \Gamma_{11}^{2}$ and $\Gamma_{22}^{2}$ are each zero, and compute the non-zero Christoffel symbols $\Gamma_{11}^{1}, \Gamma_{22}^{1}$ and $\Gamma_{12}^{2}=\Gamma_{21}^{2}$.

  The Ricci tensor $R_{a b}(a, b=1,2)$ is defined by

  $$R_{a b}=\Gamma_{a b, c}^{c}-\Gamma_{a c, b}^{c}+\Gamma_{c d}^{c} \Gamma_{a b}^{d}-\Gamma_{a c}^{d} \Gamma_{b d}^{c},$$

  where a comma denotes a partial derivative. Show that $R_{12}=0$ and that

  $$R_{11}=-\phi^{\prime \prime}-r^{-1} \phi^{\prime}, \quad R_{22}=r^{2} R_{11}$$

  (ii) Suppose further that, in a neighbourhood of $P$, the Ricci scalar $R$ takes the constant value $-2$. Find a second order differential equation, which you should denote by $(*)$, for $\phi(r)$.

  This space of constant Ricci scalar can, by a suitable coordinate transformation $r \rightarrow \chi(r)$, leaving $\theta$ invariant, be written locally as

  $$d s^{2}=d \chi^{2}+\sinh ^{2} \chi d \theta^{2}$$

  By studying this coordinate transformation, or otherwise, find $\cosh \chi$ and $\sinh \chi$ in terms of $r$ (up to a constant of integration). Deduce that

  $$e^{\phi(r)}=\frac{2 A}{\left(1-A^{2} r^{2}\right)} \quad, \quad(0 \leqslant A r<1)$$

  where $\mathrm{A}$ is a positive constant and verify that your equation $(*)$ for $\phi$ holds.

  [Note that

  $$\left.\int \frac{d \chi}{\sinh \chi}=\text { const. }+\frac{1}{2} \log (\cosh \chi-1)-\frac{1}{2} \log (\cosh \chi+1) .\right]$$

  Part II

  comment

• A2.15 B2.23

  General Relativity | Part II, 2001

  (i) Show that the geodesic equation follows from a variational principle with Lagrangian

  $$L=g_{a b} \dot{x}^{a} \dot{x}^{b}$$

  where the path of the particle is $x^{a}(\lambda)$, and $\lambda$ is an affine parameter along that path.

  (ii) The Schwarzschild metric is given by

  $$d s^{2}=d r^{2}\left(1-\frac{2 M}{r}\right)^{-1}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)-\left(1-\frac{2 M}{r}\right) d t^{2}$$

  Consider a photon which moves within the equatorial plane $\theta=\frac{\pi}{2}$. Using the above Lagrangian, or otherwise, show that

  $$\left(1-\frac{2 M}{r}\right)\left(\frac{d t}{d \lambda}\right)=E, \text { and } r^{2}\left(\frac{d \phi}{d \lambda}\right)=h$$

  for constants $E$ and $h$. Deduce that

  $$\left(\frac{d r}{d \lambda}\right)^{2}=E^{2}-\frac{h^{2}}{r^{2}}\left(1-\frac{2 M}{r}\right)$$

  Assume further that the photon approaches from infinity. Show that the impact parameter $b$ is given by

  $$b=\frac{h}{E}$$

  By considering the equation $(*)$, or otherwise

  (a) show that, if $b^{2}>27 M^{2}$, the photon is deflected but not captured by the black hole;

  (b) show that, if $b^{2}<27 M^{2}$, the photon is captured;

  (c) describe, with justification, the qualitative form of the photon's orbit in the case $b^{2}=27 M^{2}$.

  comment

• A4.17 B4.25

  General Relativity | Part II, 2001

  Discuss how Einstein's theory of gravitation reduces to Newton's in the limit of weak fields. Your answer should include discussion of: (a) the field equations; (b) the motion of a point particle; (c) the motion of a pressureless fluid.

  [The metric in a weak gravitational field, with Newtonian potential $\phi$, may be taken as

  $$d s^{2}=d x^{2}+d y^{2}+d z^{2}-(1+2 \phi) d t^{2} .$$

  The Riemann tensor is

  $$\left.R_{b c d}^{a}=\Gamma_{b d, c}^{a}-\Gamma_{b c, d}^{a}+\Gamma_{c f}^{a} \Gamma_{b d}^{f}-\Gamma_{d f}^{a} \Gamma_{b c}^{f}\right]$$

  comment

Geometry of Surfaces

• A $4 . 7 \quad$

  Geometry of Surfaces | Part II, 2001

  Write an essay on the Gauss-Bonnet theorem. Make sure that your essay contains a precise statement of the theorem, in its local form, and a discussion of some of its applications, including the global Gauss-Bonnet theorem.

  comment

• A2.7

  Geometry of Surfaces | Part II, 2001

  (i) Give the definition of the curvature $\kappa(t)$ of a plane curve $\gamma:[a, b] \longrightarrow \mathbf{R}^{2}$. Show that, if $\gamma:[a, b] \longrightarrow \mathbf{R}^{2}$ is a simple closed curve, then

  $$\int_{a}^{b} \kappa(t)\|\dot{\gamma}(t)\| d t=2 \pi$$

  (ii) Give the definition of a geodesic on a parametrized surface in $\mathbf{R}^{3}$. Derive the differential equations characterizing geodesics. Show that a great circle on the unit sphere is a geodesic.

  comment

• A3.7

  Geometry of Surfaces | Part II, 2001

  (i) Give the definition of the surface area of a parametrized surface in $\mathbf{R}^{3}$ and show that it does not depend on the parametrization.

  (ii) Let $\varphi(u)>0$ be a differentiable function of $u$. Consider the surface of revolution:

  $$\left(\begin{array}{l} u \\ v \end{array}\right) \mapsto f(u, v)=\left(\begin{array}{c} \varphi(u) \cos (v) \\ \varphi(u) \sin (v) \\ u \end{array}\right)$$

  Find a formula for each of the following: (a) The first fundamental form. (b) The unit normal. (c) The second fundamental form. (d) The Gaussian curvature.

  comment

Graph Theory

• A1.8

  Graph Theory | Part II, 2001

  (i) Show that any graph $G$ with minimal degree $\delta$ contains a cycle of length at least $\delta+1$. Give examples to show that, for each possible value of $\delta$, there is a graph with minimal degree $\delta$ but no cycle of length greater than $\delta+1$.

  (ii) Let $K_{N}$ be the complete graph with $N$ vertices labelled $v_{1}, v_{2}, \ldots, v_{N}$. Prove, from first principles, that there are $N^{N-2}$ different spanning trees in $K_{N}$. In how many of these spanning trees does the vertex $v_{1}$ have degree 1 ?

  A spanning tree in $K_{N}$ is chosen at random, with each of the $N^{N-2}$ trees being equally likely. Show that the average number of vertices of degree 1 in the random tree is approximately $N / e$ when $N$ is large.

  Find the average degree of vertices in the random tree.

  comment

• A2.8

  Graph Theory | Part II, 2001

  (i) Prove that any graph $G$ drawn on a compact surface $S$ with negative Euler characteristic $E(S)$ has a vertex colouring that uses at most

  $$h=\left\lfloor\frac{1}{2}(7+\sqrt{49-24 E(S)})\right\rfloor$$

  colours.

  Briefly discuss whether the result is still true when $E(S) \geqslant 0$.

  (ii) Prove that a graph $G$ is $k$ edge-connected if and only if the removal of no set of less than $k$ edges from $G$ disconnects $G$.

  [If you use any form of Menger's theorem, you must prove it.]

  Let $G$ be a minimal example of a graph that requires $k+1$ colours for a vertex colouring. Show that $G$ must be $k$ edge-connected.

  comment

• A4.9

  Graph Theory | Part II, 2001

  Write an essay on extremal graph theory. Your essay should include proofs of at least two major results and a discussion of variations on these results or their proofs.

  comment

Groups, Rings and Fields

• A1.4 B1.3

  Groups, Rings and Fields | Part II, 2001

  (i) Define the notion of a Sylow $p$-subgroup of a finite group $G$, and state a theorem concerning the number of them and the relation between them.

  (ii) Show that any group of order 30 has a non-trivial normal subgroup. Is it true that every group of order 30 is commutative?

  comment

• A2.4 B2.3

  Groups, Rings and Fields | Part II, 2001

  (i) Show that the ring $k=\mathbf{F}_{2}[X] /\left(X^{2}+X+1\right)$ is a field. How many elements does it have?

  (ii) Let $k$ be as in (i). By considering what happens to a chosen basis of the vector space $k^{2}$, or otherwise, find the order of the groups $G L_{2}(k)$ and $S L_{2}(k)$.

  By considering the set of lines in $k^{2}$, or otherwise, show that $S L_{2}(k)$ is a subgroup of the symmetric group $S_{5}$, and identify this subgroup.

  comment

• A3.4

  Groups, Rings and Fields | Part II, 2001

  (i) Let $G$ be the cyclic subgroup of $G L_{2}(\mathbf{C})$ generated by the matrix $\left(\begin{array}{cc}1 & 2 \\ 0 & -1\end{array}\right)$, acting on the polynomial ring $\mathbf{C}[X, Y]$. Determine the ring of invariants $\mathbf{C}[X, Y]^{G}$.

  (ii) Determine $\mathbf{C}[X, Y]^{G}$ when $G$ is the cyclic group generated by $\left(\begin{array}{cc}0 & -1 \\ 1 & -1\end{array}\right)$.

  [Hint: consider the eigenvectors.]

  comment

• A4.4

  Groups, Rings and Fields | Part II, 2001

  Show that the ring $\mathbf{Z}[\omega]$ is Euclidean, where $\omega=\exp (2 \pi i / 3)$.

  Show that a prime number $p \neq 3$ is reducible in $\mathbf{Z}[\omega]$ if and only if $p \equiv 1(\bmod 3)$.

  Which prime numbers $p$ can be written in the form $p=a^{2}+a b+b^{2}$ with $a, b \in \mathbf{Z}$ (and why)?

  comment

Hilbert Spaces

• B1.10

  Hilbert Spaces | Part II, 2001

  State and prove the Riesz representation theorem for bounded linear functionals on a Hilbert space $H$.

  [You may assume, without proof, that $H=E \oplus E^{\perp}$, for every closed subspace $E$ of $H$.]

  Prove that, for every $T \in \mathcal{B}(H)$, there is a unique $T^{*} \in \mathcal{B}(H)$ such that $\langle T x, y\rangle=\left\langle x, T^{*} y\right\rangle$ for every $x, y \in H$. Prove that $\left\|T^{*} T\right\|=\|T\|^{2}$ for every $T \in \mathcal{B}(H)$.

  Define a normal operator $T \in \mathcal{B}(H)$. Prove that $T$ is normal if and only if $\|T x\|=\left\|T^{*} x\right\|$ for every $x \in H$. Deduce that every point in the spectrum of a normal operator $T$ is an approximate eigenvalue of $T$.

  [You may assume, without proof, any general criterion for the invertibility of a bounded linear operator on $H$.]

  comment

• B3.8

  Hilbert Spaces | Part II, 2001

  Let $T$ be a bounded linear operator on a Hilbert space $H$. Define what it means to say that $T$ is (i) compact, and (ii) Fredholm. What is the index, ind $(T)$, of a Fredholm operator $T$ ?

  Let $S, T$ be bounded linear operators on $H$. Prove that $S$ and $T$ are Fredholm if and only if both $S T$ and $T S$ are Fredholm. Prove also that if $S$ is invertible and $T$ is Fredholm then $\operatorname{ind}(S T)=\operatorname{ind}(T S)=\operatorname{ind}(T)$.

  Let $K$ be a compact linear operator on $H$. Prove that $I+K$ is Fredholm with index zero.

  comment

• B4.7

  Hilbert Spaces | Part II, 2001

  Write an essay on the use of Hermite functions in the elementary theory of the Fourier transform on $L^{2}(\mathbb{R})$.

  [You should assume, without proof, any results that you need concerning the approximation of functions by Hermite functions.]

  comment

Information Theory

• B1.14

  Information Theory | Part II, 2001

  Let $p_{1}, \ldots, p_{n}$ be a probability distribution, with $p^{*}=\max _{i}\left[p_{i}\right]$. Prove that

  $$\begin{aligned} &(i)-\sum_{i} p_{i} \log p_{i} \geqslant-p^{*} \log p^{*}-\left(1-p^{*}\right) \log \left(1-p^{*}\right) \\ &(\text { ii })-\sum_{i} p_{i} \log p_{i} \geqslant \log \left(1 / p^{*}\right) ; \text { and } \\ &(\text { iii })-\sum_{i} p_{i} \log p_{i} \geqslant 2\left(1-p^{*}\right) \end{aligned}$$

  All logarithms are to base 2 .

  [Hint: To prove (iii), it is convenient to use (i) for $p^{*} \geqslant \frac{1}{2}$ and (ii) for $p^{*} \leqslant \frac{1}{2}$.]

  Random variables $X$ and $Y$ with values $x$ and $y$ from finite 'alphabets' $I$ and $J$ represent the input and output of a transmission channel, with the conditional probability $p(x \mid y)=\mathbb{P}(X=x \mid Y=y)$. Let $h(p(\cdot \mid y))$ denote the entropy of the conditional distribution $p(\cdot \mid y), y \in J$, and $h(X \mid Y)$ denote the conditional entropy of $X$ given $Y$. Define the ideal observer decoding rule as a map $f: J \rightarrow I$ such that $p(f(y) \mid y)=\max _{x \in I} p(x \mid y)$ for all $y \in J$. Show that under this rule the error probability

  $$\pi_{\mathrm{er}}(y)=\sum_{\substack{x \in I \\ x \neq f(y)}} p(x \mid y)$$

  satisfies $\pi_{\mathrm{er}}(y) \leqslant \frac{1}{2} h(p(\cdot \mid y))$, and the expected value satisfies

  $$\mathbb{E} \pi_{\mathrm{er}}(Y) \leqslant \frac{1}{2} h(X \mid Y)$$

  comment

• B2.14

  Information Theory | Part II, 2001

  A subset $\mathcal{C}$ of the Hamming space $\{0,1\}^{n}$ of cardinality $|\mathcal{C}|=r$ and with the minimal (Hamming) distance $\min \left[d\left(x, x^{\prime}\right): x, x^{\prime} \in \mathcal{C}, x \neq x^{\prime}\right]=\delta$ is called an $[n, r, \delta]$-code (not necessarily linear). An $[n, r, \delta]$-code is called maximal if it is not contained in any $[n, r+1, \delta]$-code. Prove that an $[n, r, \delta]$-code is maximal if and only if for any $y \in\{0,1\}^{n}$ there exists $x \in \mathcal{C}$ such that $d(x, y)<\delta$. Conclude that if there are $\delta$ or more changes made in a codeword then the new word is closer to some other codeword than to the original one.

  Suppose that a maximal $[n, r, \delta]$-code is used for transmitting information via a binary memoryless channel with the error probability $p$, and the receiver uses the maximum likelihood decoder. Prove that the probability of erroneous decoding, $\pi_{\mathrm{err}}^{\mathrm{ml}}$, obeys the bounds

  $$1-b(n, \delta-1) \leqslant \pi_{\mathrm{err}}^{\mathrm{ml}} \leqslant 1-b(n,[(\delta-1) / 2])$$

  where

  $$b(n, m)=\sum_{0 \leqslant k \leqslant m}\left(\begin{array}{l} n \\ k \end{array}\right) p^{k}(1-p)^{n-k}$$

  is a partial binomial sum and $[\cdot]$ is the integer part.

  comment

• B4.13

  Information Theory | Part II, 2001

  State the Kraft inequality. Prove that it gives a necessary and sufficient condition for the existence of a prefix-free code with given codeword lengths.

  comment

Logic, Computation and Set Theory

• A $1 . 7 \quad$ B1.12

  Logic, Computation and Set Theory | Part II, 2001

  (i) What is the Halting Problem? What is an unsolvable problem?

  (ii) Prove that the Halting Problem is unsolvable. Is it decidable whether or not a machine halts with input zero?

  comment

• A3.8 B3.11

  Logic, Computation and Set Theory | Part II, 2001

  (i) Write down a set of axioms for the theory of dense linear order with a bottom element but no top element.

  (ii) Prove that this theory has, up to isomorphism, precisely one countable model.

  comment

• A4.8 B4.10

  Logic, Computation and Set Theory | Part II, 2001

  What is a wellfounded relation, and how does wellfoundedness underpin wellfounded induction?

  A formula $\phi(x, y)$ with two free variables defines an $\in$-automorphism if for all $x$ there is a unique $y$, the function $f$, defined by $y=f(x)$ if and only if $\phi(x, y)$, is a permutation of the universe, and we have $(\forall x y)(x \in y \leftrightarrow f(x) \in f(y))$.

  Use wellfounded induction over $\in$ to prove that all formulæ defining $\in$-automorphisms are equivalent to $x=y$.

  comment

• B2.11

  Logic, Computation and Set Theory | Part II, 2001

  Let $U$ be an arbitrary set, and $\mathcal{P}(U)$ the power set of $U$. For $X$ a subset of $\mathcal{P}(U)$, the dual $X^{\vee}$ of $X$ is the set $\{y \subseteq U:(\forall x \in X)(y \cap x \neq \emptyset)\}$.

  (i) Show that $X \subseteq Y \rightarrow Y^{\vee} \subseteq X^{\vee}$.

  Show that for $\left\{X_{i}: i \in I\right\}$ a family of subsets of $\mathcal{P}(U)$

  $$\left(\bigcup\left\{X_{i}: i \in I\right\}\right)^{\vee}=\bigcap\left\{X_{i}^{\vee}: i \in I\right\}$$

  (ii) Consider $S=\left\{X \subseteq \mathcal{P}(U): X \subseteq X^{\vee}\right\}$. Show that $S$, $\subseteq$ is a chain-complete poset.

  State Zorn's lemma and use it to deduce that there exists $X$ with $X=X^{\vee}$.

  Show that if $X=X^{\vee}$ then the following hold:

  $X$ is closed under superset; for all $U^{\prime} \subseteq U, X$ contains either $U^{\prime}$ or $U \backslash U^{\prime}$.

  comment

Markov Chains

• A1.1 B1.1

  Markov Chains | Part II, 2001

  (i) Let $X=\left(X_{n}: 0 \leqslant n \leqslant N\right)$ be an irreducible Markov chain on the finite state space $S$ with transition matrix $P=\left(p_{i j}\right)$ and invariant distribution $\pi$. What does it mean to say that $X$ is reversible in equilibrium?

  Show that $X$ is reversible in equilibrium if and only if $\pi_{i} p_{i j}=\pi_{j} p_{j i}$ for all $i, j \in S$.

  (ii) A finite connected graph $G$ has vertex set $V$ and edge set $E$, and has neither loops nor multiple edges. A particle performs a random walk on $V$, moving at each step to a randomly chosen neighbour of the current position, each such neighbour being picked with equal probability, independently of all previous moves. Show that the unique invariant distribution is given by $\pi_{v}=d_{v} /(2|E|)$ where $d_{v}$ is the degree of vertex $v$.

  A rook performs a random walk on a chessboard; at each step, it is equally likely to make any of the moves which are legal for a rook. What is the mean recurrence time of a corner square. (You should give a clear statement of any general theorem used.)

  [A chessboard is an $8 \times 8$ square grid. A legal move is one of any length parallel to the axes.]

  comment

• A2.1

  Markov Chains | Part II, 2001

  (i) The fire alarm in Mill Lane is set off at random times. The probability of an alarm during the time-interval $(u, u+h)$ is $\lambda(u) h+o(h)$ where the 'intensity function' $\lambda(u)$ may vary with the time $u$. Let $N(t)$ be the number of alarms by time $t$, and set $N(0)=0$. Show, subject to reasonable extra assumptions to be stated clearly, that $p_{i}(t)=P(N(t)=i)$ satisfies

  $$p_{0}^{\prime}(t)=-\lambda(t) p_{0}(t), \quad p_{i}^{\prime}(t)=\lambda(t)\left\{p_{i-1}(t)-p_{i}(t)\right\}, \quad i \geqslant 1 .$$

  Deduce that $N(t)$ has the Poisson distribution with parameter $\Lambda(t)=\int_{0}^{t} \lambda(u) d u$.

  (ii) The fire alarm in Clarkson Road is different. The number $M(t)$ of alarms by time $t$ is such that

  $$P(M(t+h)=m+1 \mid M(t)=m)=\lambda_{m} h+o(h),$$

  where $\lambda_{m}=\alpha m+\beta, m \geqslant 0$, and $\alpha, \beta>0$. Show, subject to suitable extra conditions, that $p_{m}(t)=P(M(t)=m)$ satisfies a set of differential-difference equations to be specified. Deduce without solving these equations in their entirety that $M(t)$ has mean $\beta\left(e^{\alpha t}-1\right) / \alpha$, and find the variance of $M(t)$.

  comment

• A3.1 B3.1

  Markov Chains | Part II, 2001

  (i) Explain what is meant by the transition semigroup $\left\{P_{t}\right\}$ of a Markov chain $X$ in continuous time. If the state space is finite, show under assumptions to be stated clearly, that $P_{t}^{\prime}=G P_{t}$ for some matrix $G$. Show that a distribution $\pi$ satisfies $\pi G=0$ if and only if $\pi P_{t}=\pi$ for all $t \geqslant 0$, and explain the importance of such $\pi$.

  (ii) Let $X$ be a continuous-time Markov chain on the state space $S=\{1,2\}$ with generator

  $$G=\left(\begin{array}{cc} -\beta & \beta \\ \gamma & -\gamma \end{array}\right), \quad \text { where } \beta, \gamma>0 .$$

  Show that the transition semigroup $P_{t}=\exp (t G)$ is given by

  $$(\beta+\gamma) P_{t}=\left(\begin{array}{cc} \gamma+\beta h(t) & \beta(1-h(t)) \\ \gamma(1-h(t)) & \beta+\gamma h(t) \end{array}\right),$$

  where $h(t)=e^{-t(\beta+\gamma)}$.

  For $0<\alpha<1$, let

  $$H(\alpha)=\left(\begin{array}{cc} \alpha & 1-\alpha \\ 1-\alpha & \alpha \end{array}\right)$$

  For a continuous-time chain $X$, let $M$ be a matrix with $(i, j)$ entry

  $P(X(1)=j \mid X(0)=i)$, for $i, j \in S$. Show that there is a chain $X$ with $M=H(\alpha)$ if and only if $\alpha>\frac{1}{2}$.

  comment

• A4.1

  Markov Chains | Part II, 2001

  Write an essay on the convergence to equilibrium of a discrete-time Markov chain on a countable state-space. You should include a discussion of the existence of invariant distributions, and of the limit theorem in the non-null recurrent case.

  comment

Mathematical Methods

• A2.17

  Mathematical Methods | Part II, 2001

  (i) A certain physical quantity $q(x)$ can be represented by the series $\sum_{n=0}^{\infty} c_{n} x^{n}$ in $0 \leqslant x<x_{0}$, but the series diverges for $x>x_{0}$. Describe the Euler transformation to a new series which may enable $q(x)$ to be computed for $x>x_{0}$. Give the first four terms of the new series.

  Describe briefly the disadvantages of the method.

  (ii) The series $\sum_{1}^{\infty} c_{r}$ has partial sums $S_{n}=\sum_{1}^{n} c_{r}$. Describe Shanks' method to approximate $S_{n}$ by

  $$S_{n}=A+B C^{n}$$

  giving expressions for $A, B$ and $C$.

  Denote by $B_{N}$ and $C_{N}$ the values of $B$ and $C$ respectively derived from these expressions using $S_{N-1}, S_{N}$ and $S_{N+1}$ for some fixed $N$. Now let $A^{(n)}$ be the value of $A$ obtained from $(*)$ with $B=B_{N}, C=C_{N}$. Show that, if $\left|C_{N}\right|<1$,

  $$\sum_{1}^{\infty} c_{r}=\lim _{n \rightarrow \infty} A^{(n)}$$

  If, in fact, the partial sums satisfy

  $$S_{n}=a+\alpha c^{n}+\beta d^{n}$$

  with $1>|c|>|d|$, show that

  $$A^{(n)}=A+\gamma d^{n}+o\left(d^{n}\right)$$

  where $\gamma$ is to be found.

  comment

• A3.17

  Mathematical Methods | Part II, 2001

  (i) The function $y(x)$ satisfies the differential equation

  $$y^{\prime \prime}+b y^{\prime}+c y=0, \quad 0<x<1,$$

  where $b$ and $c$ are constants, with boundary conditions $y(0)=0, y^{\prime}(0)=1$. By integrating this equation or otherwise, show that $y$ must also satisfy the integral equation

  $$y(x)=g(x)+\int_{0}^{1} K(x, t) y(t) d t$$

  and find the functions $g(x)$ and $K(x, t)$.

  (ii) Solve the integral equation

  $$\varphi(x)=1+\lambda^{2} \int_{0}^{x}(x-t) \varphi(t) d t, \quad x>0, \quad \lambda \text { real }$$

  by finding an ordinary differential equation satisfied by $\varphi(x)$ together with boundary conditions.

  Now solve the integral equation by the method of successive approximations and show that the solutions are the same.

  comment

• A4.21

  Mathematical Methods | Part II, 2001

  The equation

  $$\mathbf{A x}=\lambda \mathbf{x}$$

  where $\mathbf{A}$ is a real square matrix and $\mathbf{x}$ a column vector, has a simple eigenvalue $\lambda=\mu$ with corresponding right-eigenvector $\mathbf{x}=\mathbf{X}$. Show how to find expressions for the perturbed eigenvalue and right-eigenvector solutions of

  $$\mathbf{A} \mathbf{x}+\epsilon \mathbf{b}(\mathbf{x})=\lambda \mathbf{x}, \quad|\epsilon| \ll 1$$

  to first order in $\epsilon$, where $\mathbf{b}$ is a vector function of $\mathbf{x}$. State clearly any assumptions you make.

  If $\mathbf{A}$ is $(n \times n)$ and has a complete set of right-eigenvectors $\mathbf{X}^{(j)}, j=1,2, \ldots n$, which span $\mathbb{R}^{n}$ and correspond to separate eigenvalues $\mu^{(j)}, j=1,2, \ldots n$, find an expression for the first-order perturbation to $\mathbf{X}^{(1)}$ in terms of the $\left\{\mathbf{X}^{(j)}\right\}$ and the corresponding lefteigenvectors of $\mathbf{A}$.

  Find the normalised eigenfunctions and eigenvalues of the equation

  $$\frac{d^{2} y}{d x^{2}}+\lambda y=0,0<x<1$$

  with $y(0)=y(1)=0$. Let these be the zeroth order approximations to the eigenfunctions of

  $$\frac{d^{2} y}{d x^{2}}+\lambda y+\epsilon b(y)=0,0<x<1$$

  with $y(0)=y(1)=0$ and where $b$ is a function of $y$. Show that the first-order perturbations of the eigenvalues are given by

  $$\lambda_{n}^{(1)}=-\epsilon \sqrt{2} \int_{0}^{1} \sin (n \pi x) \quad b(\sqrt{2} \sin n \pi x) d x$$

  Part II

  comment

Methods of Mathematical Physics

• B1.19

  Methods of Mathematical Physics | Part II, 2001

  State and prove the convolution theorem for Laplace transforms.

  Use the convolution theorem to prove that the Beta function

  $$B(p, q)=\int_{0}^{1}(1-\tau)^{p-1} \tau^{q-1} d \tau$$

  may be written in terms of the Gamma function as

  $$B(p, q)=\frac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}$$

  comment

• B2.18

  Methods of Mathematical Physics | Part II, 2001

  The Bessel function $J_{\nu}(z)$ is defined, for $|\arg z|<\pi / 2$, by

  $$J_{\nu}(z)=\frac{1}{2 \pi i} \int_{-\infty}^{\left(0^{+}\right)} \mathrm{e}^{\left(t-t^{-1}\right) z / 2} t^{-\nu-1} d t,$$

  where the path of integration is the Hankel contour and $t^{-\nu-1}$ is the principal branch.

  Use the method of steepest descent to show that, as $z \rightarrow+\infty$,

  $$J_{\nu}(z) \sim(2 / \pi z)^{\frac{1}{2}} \cos (z-\pi \nu / 2-\pi / 4) .$$

  You should give a rough sketch of the steepest descent paths.

  comment

• B3.19

  Methods of Mathematical Physics | Part II, 2001

  Consider the integral

  $$\int_{0}^{\infty} \frac{t^{z} \mathrm{e}^{-a t}}{1+t} d t$$

  where $t^{z}$ is the principal branch and $a$ is a positive constant. State the region of the complex $z$-plane in which the integral defines a holomorphic function.

  Show how the analytic continuation of this function can be obtained by means of an alternative integral representation using the Hankel contour.

  Hence show that the analytic continuation is holomorphic except for simple poles at $z=-1,-2, \ldots$, and that the residue at $z=-n$ is

  $$(-1)^{n-1} \sum_{r=0}^{n-1} \frac{a^{r}}{r !}$$

  Part II

  comment

• B4.19

  Methods of Mathematical Physics | Part II, 2001

  Show that $\int_{0}^{\pi} \mathrm{e}^{i x \cos t} d t$ satisfies the differential equation

  $$x y^{\prime \prime}+y^{\prime}+x y=0$$

  and find a second solution, in the form of an integral, for $x>0$.

  Show, by finding the asymptotic behaviour as $x \rightarrow+\infty$, that your two solutions are linearly independent.

  comment

Nonlinear Waves

• A2.18

  Nonlinear Waves | Part II, 2001

  (i) Establish two conservation laws for the $\mathrm{MKdV}$ equation

  $$\frac{\partial u}{\partial t}+u^{2} \frac{\partial u}{\partial x}+\frac{\partial^{3} u}{\partial x^{3}}=0$$

  State sufficient boundary conditions that $u$ should satisfy for the conservation laws to be valid.

  (ii) The equation

  $$\frac{\partial \rho}{\partial t}+\frac{\partial}{\partial x}(\rho V)=0$$

  models traffic flow on a single-lane road, where $\rho(x, t)$ represents the density of cars, and $V$ is a given function of $\rho$. By considering the rate of change of the integral

  $$\int_{a}^{b} \rho d x,$$

  show that $V$ represents the velocity of the cars.

  Suppose now that $V=1-\rho$ (in suitable units), and that $0 \leqslant \rho \leqslant 1$ everywhere. Assume that a queue is building up at a traffic light at $x=1$, so that, when the light turns green at $t=0$,

  $$\rho(x, 0)=\left\{\begin{array}{l} 0 \text { for } x<0 \text { and } x>1 \\ x \text { for } 0 \leqslant x<1 . \end{array}\right.$$

  For this problem, find and sketch the characteristics in the $(x, t)$ plane, for $t>0$, paying particular attention to those emerging from the point $(1,0)$. Show that a shock forms at $t=\frac{1}{2}$. Find the density of cars $\rho(x, t)$ for $0<t<\frac{1}{2}$, and all $x$.

  comment

• A3.18

  Nonlinear Waves | Part II, 2001

  (i) The so-called breather solution of the sine-Gordon equation is

  $$\phi(x, t)=4 \tan ^{-1}\left(\frac{\left(1-\lambda^{2}\right)^{\frac{1}{2}}}{\lambda} \frac{\sin \lambda t}{\cosh \left(1-\lambda^{2}\right)^{\frac{1}{2}} x}\right), \quad 0<\lambda<1$$

  Describe qualitatively the behaviour of $\phi(x, t)$, for $\lambda \ll 1$, when $|x| \gg \ln (2 / \lambda)$, when $|x| \ll 1$, and when $\cosh x \approx \frac{1}{\lambda}|\sin \lambda t|$. Explain how this solution can be interpreted in terms of motion of a kink and an antikink. Estimate the greatest separation of the kink and antikink.

  (ii) The field $\psi(x, t)$ obeys the nonlinear wave equation

  $$\frac{\partial^{2} \psi}{\partial t^{2}}-\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{d U}{d \psi}=0$$

  where the potential $U$ has the form

  $$U(\psi)=\frac{1}{2}\left(\psi-\psi^{3}\right)^{2} .$$

  Show that $\psi=0$ and $\psi=1$ are stable constant solutions.

  Find a steady wave solution $\psi=f(x-v t)$ satisfying the boundary conditions $\psi \rightarrow 0$ as $x \rightarrow-\infty, \psi \rightarrow 1$ as $x \rightarrow \infty$. What constraint is there on the velocity $v ?$

  comment

Number Fields

• B1.9

  Number Fields | Part II, 2001

  Let $K=\mathbf{Q}(\alpha)$ be a number field, where $\alpha \in \mathcal{O}_{K}$. Let $f$ be the (normalized) minimal polynomial of $\alpha$ over $Q$. Show that the discriminant $\operatorname{disc}(f)$ of $f$ is equal to $\left(\mathcal{O}_{K}: \mathbf{Z}[\alpha]\right)^{2} D_{K}$.

  Show that $f(x)=x^{3}+5 x^{2}-19$ is irreducible over Q. Determine $\operatorname{disc}(f)$ and the ring of algebraic integers $\mathcal{O}_{K}$ of $K=\mathbf{Q}(\alpha)$, where $\alpha \in \mathbf{C}$ is a root of $f$.

  comment

• B2.9

  Number Fields | Part II, 2001

  Determine the ideal class group of $\mathbf{Q}(\sqrt{-11})$.

  Find all solutions of the diophantine equation

  $$y^{2}+11=x^{3} \quad(x, y \in \mathbf{Z})$$

  [Minkowski's bound is $n ! n^{-n}(4 / \pi)^{r_{2}}\left|D_{k}\right|^{1 / 2}$.]

  comment

• B4.6

  Number Fields | Part II, 2001

  For a prime number $p>2$, set $\zeta=e^{2 \pi i / p}, K=\mathbf{Q}(\zeta)$ and $K^{+}=\mathbf{Q}\left(\zeta+\zeta^{-1}\right)$.

  (a) Show that the (normalized) minimal polynomial of $\zeta-1$ over $\mathbf{Q}$ is equal to

  $$f(x)=\frac{(x+1)^{p}-1}{x} .$$

  (b) Determine the degrees $[K: \mathbf{Q}]$ and $\left[K^{+}: \mathbf{Q}\right]$.

  (c) Show that

  $$\prod_{j=1}^{p-1}\left(1-\zeta^{j}\right)=p$$

  (d) Show that $\operatorname{disc}(f)=(-1)^{\frac{p-1}{2}} p^{p-2}$.

  (e) Show that $K$ contains $\mathbf{Q}\left(\sqrt{p^{*}}\right)$, where $p^{*}=(-1)^{\frac{p-1}{2}} p$.

  (f) If $j, k \in \mathbf{Z}$ are not divisible by $p$, show that $\frac{1-\zeta^{j}}{1-\zeta^{k}}$ lies in $\mathcal{O}_{K}^{*}$.

  (g) Show that the ideal $(p)=p \mathcal{O}_{K}$ is equal to $(1-\zeta)^{p-1}$.

  comment

Number Theory

• A1.9

  Number Theory | Part II, 2001

  (i) Describe Euclid's algorithm.

  Find, in the RSA algorithm, the deciphering key corresponding to the enciphering key 7,527 .

  (ii) Explain what is meant by a primitive root modulo an odd prime $p$.

  Show that, if $g$ is a primitive root modulo $p$, then all primitive roots modulo $p$ are given by $g^{m}$, where $1 \leqslant m<p$ and $(m, p-1)=1$.

  Verify, by Euler's criterion, that 3 is a primitive root modulo 17 . Hence find all primitive roots modulo 17 .

  comment

• A3.9

  Number Theory | Part II, 2001

  (i) State the law of quadratic reciprocity.

  Prove that 5 is a quadratic residue modulo primes $p \equiv \pm 1 \quad(\bmod 10)$ and a quadratic non-residue modulo primes $p \equiv \pm 3 \quad(\bmod 10)$.

  Determine whether 5 is a quadratic residue or non-residue modulo 119 and modulo $539 .$

  (ii) Explain what is meant by the continued fraction of a real number $\theta$. Define the convergents to $\theta$ and write down the recurrence relations satisfied by their numerators and denominators.

  Use the continued fraction method to find two solutions in positive integers $x, y$ of the equation $x^{2}-15 y^{2}=1$.

  comment

• A4.10

  Number Theory | Part II, 2001

  Attempt one of the following:

  (i) Discuss pseudoprimes and primality testing. Find all bases for which 57 is a Fermat pseudoprime. Determine whether 57 is also an Euler pseudoprime for these bases.

  (ii) Write a brief account of various methods for factoring large numbers. Use Fermat factorization to find the factors of 10033. Would Pollard's $p-1$ method also be practical in this instance?

  (iii) Show that $\sum 1 / p_{n}$ is divergent, where $p_{n}$ denotes the $n$-th prime.

  Write a brief account of basic properties of the Riemann zeta-function.

  State the prime number theorem. Show that it implies that for all sufficiently large positive integers $n$ there is a prime $p$ satisfying $n<p \leqslant 2 n$.

  comment

Numerical Analysis

• A1.20 B1.20

  Numerical Analysis | Part II, 2001

  (i) Let $A$ be a symmetric $n \times n$ matrix such that

  $$A_{k, k}>\sum_{\substack{l=1 \\ l \neq k}}^{n}\left|A_{k, l}\right| \quad 1 \leqslant k \leqslant n .$$

  Prove that it is positive definite.

  (ii) Prove that both Jacobi and Gauss-Seidel methods for the solution of the linear system $A \mathrm{x}=\mathbf{b}$, where the matrix $A$ obeys the conditions of (i), converge.

  [You may quote the Householder-John theorem without proof.]

  comment

• A2.19 B2.19

  Numerical Analysis | Part II, 2001

  (i) Define $m$-step BDF (backward differential formula) methods for the numerical solution of ordinary differential equations and derive explicitly their coefficients.

  (ii) Prove that the linear stability domain of the two-step BDF method includes the interval $(-\infty, 0)$.

  comment

• A3.19 B3.20

  Numerical Analysis | Part II, 2001

  (i) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}$$

  is discretized by the finite-difference method

  $$u_{m}^{n+1}-\frac{1}{2}(\mu-\alpha)\left(u_{m-1}^{n+1}-2 u_{m}^{n+1}+u_{m+1}^{n+1}\right)=u_{m}^{n}+\frac{1}{2}(\mu+\alpha)\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right)$$

  where $u_{m}^{n} \approx u(m \Delta x, n \Delta t), \mu=\Delta t /(\Delta x)^{2}$ and $\alpha$ is a constant. Derive the order of magnitude (as a power of $\Delta x$ ) of the local error for different choices of $\alpha$.

  (ii) Investigate the stability of the above finite-difference method for different values of $\alpha$ by the Fourier technique.

  comment

• A4.22 B4.20

  Numerical Analysis | Part II, 2001

  Write an essay on the computation of eigenvalues and eigenvectors of matrices.

  comment

Optimization and Control

• B2.15

  Optimization and Control | Part II, 2001

  A street trader wishes to dispose of $k$ counterfeit Swiss watches. If he offers one for sale at price $u$ he will sell it with probability $a e^{-u}$. Here $a$ is known and less than 1 . Subsequent to each attempted sale (successful or not) there is a probability $1-\beta$ that he will be arrested and can make no more sales. His aim is to choose the prices at which he offers the watches so as to maximize the expected values of his sales up until the time he is arrested or has sold all $k$ watches.

  Let $V(k)$ be the maximum expected amount he can obtain when he has $k$ watches remaining and has not yet been arrested. Explain why $V(k)$ is the solution to

  $$V(k)=\max _{u>0}\left\{a e^{-u}[u+\beta V(k-1)]+\left(1-a e^{-u}\right) \beta V(k)\right\}$$

  Denote the optimal price by $u_{k}$ and show that

  $$u_{k}=1+\beta V(k)-\beta V(k-1)$$

  and that

  $$V(k)=a e^{-u_{k}} /(1-\beta)$$

  Show inductively that $V(k)$ is a nondecreasing and concave function of $k$.

  comment

• B3.14

  Optimization and Control | Part II, 2001

  A file of $X \mathrm{Mb}$ is to be transmitted over a communications link. At each time $t$ the sender can choose a transmission rate, $u(t)$, within the range $[0,1]$ Mb per second. The charge for transmitting at rate $u(t)$ at time $t$ is $u(t) p(t)$. The function $p$ is fully known at time 0. If it takes a total time $T$ to transmit the file then there is a delay cost of $\gamma T^{2}$, $\gamma>0$. Thus $u$ and $T$ are to be chosen to minimize

  $$\int_{0}^{T} u(t) p(t) d t+\gamma T^{2}$$

  where $u(t) \in[0,1], d x(t) / d t=-u(t), x(0)=X$ and $x(T)=0$. Quoting and applying appropriate results of Pontryagin's maximum principle show that a property of the optimal policy is that there exists $p^{*}$ such that $u(t)=1$ if $p(t)<p^{*}$ and $u(t)=0$ if $p(t)>p^{*}$.

  Show that the optimal $p^{*}$ and $T$ are related by $p^{*}=p(T)+2 \gamma T$.

  Suppose $p(t)=t+1 / t$ and $X=1$. For what value of $\gamma$ is it optimal to transmit at a constant rate 1 between times $1 / 2$ and $3 / 2$ ?

  comment

• B4.14

  Optimization and Control | Part II, 2001

  Consider the scalar system with plant equation $x_{t+1}=x_{t}+u_{t}, t=0,1, \ldots$ and cost

  $$C_{s}\left(x_{0}, u_{0}, u_{1}, \ldots\right)=\sum_{t=0}^{s}\left[u_{t}^{2}+\frac{4}{3} x_{t}^{2}\right]$$

  Show from first principles that $\min _{u_{0}, u_{1}, \ldots} C_{s}=V_{s} x_{0}^{2}$, where $V_{0}=4 / 3$ and for $s=0,1, \ldots$

  $$V_{s+1}=4 / 3+V_{s} /\left(1+V_{s}\right)$$

  Show that $V_{s} \rightarrow 2$ as $s \rightarrow \infty$.

  Prove that $C_{\infty}$ is minimized by the stationary control, $u_{t}=-2 x_{t} / 3$ for all $t$.

  Consider the stationary policy $\pi_{0}$ that has $u_{t}=-x_{t}$ for all $t$. What is the value of $C_{\infty}$ under this policy?

  Consider the following algorithm, in which steps 1 and 2 are repeated as many times as desired.

  1. For a given stationary policy $\pi_{n}$, for which $u_{t}=k_{n} x_{t}$ for all $t$, determine the value of $C_{\infty}$ under this policy as $V^{\pi_{n}} x_{0}^{2}$ by solving for $V^{\pi_{n}}$ in

  $$V^{\pi_{n}}=k_{n}^{2}+4 / 3+\left(1+k_{n}\right)^{2} V^{\pi_{n}}$$

  2. Now find $k_{n+1}$ as the minimizer of

  $$k_{n+1}^{2}+4 / 3+\left(1+k_{n+1}\right)^{2} V^{\pi_{n}}$$

  and define $\pi_{n+1}$ as the policy for which $u_{t}=k_{n+1} x_{t}$ for all $t$.

  Explain why $\pi_{n+1}$ is guaranteed to be a better policy than $\pi_{n}$.

  Let $\pi_{0}$ be the stationary policy with $u_{t}=-x_{t}$. Determine $\pi_{1}$ and verify that it minimizes $C_{\infty}$ to within $0.2 \%$ of its optimum.

  comment

Partial Differential Equations

• B1.18

  Partial Differential Equations | Part II, 2001

  (a) Solve the equation

  $$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=u^{2}$$

  together with the boundary condition on the $x$-axis:

  $$u(x, 0)=f(x)$$

  where $f$ is a smooth function. You should discuss the domain on which the solution is smooth. For which functions $f$ can the solution be extended to give a smooth solution on the upper half plane $\{y>0\}$ ?

  (b) Solve the equation

  $$x \frac{\partial u}{\partial x}+y \frac{\partial u}{\partial y}=0$$

  together with the boundary condition on the unit circle:

  $$u(x, y)=x \quad \text { when } \quad x^{2}+y^{2}=1$$

  comment

• B2.17

  Partial Differential Equations | Part II, 2001

  Define the Schwartz space $\mathcal{S}(\mathbb{R})$ and the corresponding space of tempered distributions $\mathcal{S}^{\prime}(\mathbb{R})$.

  Use the Fourier transform to give an integral formula for the solution of the equation

  $$-\frac{d^{2} u}{d x^{2}}+\frac{d u}{d x}+u=f$$

  for $f \in \mathcal{S}(\mathbb{R})$. Prove that your solution lies in $\mathcal{S}(\mathbb{R})$. Is your formula the unique solution to $(*)$ in the Schwartz space?

  Deduce from this formula an integral expression for the fundamental solution of the operator $P=-\frac{d^{2}}{d x^{2}}+\frac{d}{d x}+1$.

  Let $K$ be the function:

  $$K(x)= \begin{cases}\frac{1}{\sqrt{5}} e^{-(\sqrt{5}-1) x / 2} & \text { for } x \geqslant 0 \\ \frac{1}{\sqrt{5}} e^{(\sqrt{5}+1) x / 2} & \text { for } x \leqslant 0\end{cases}$$

  Using the definition of distributional derivatives verify that this function is a fundamental solution for $P$.

  comment

• B3.18

  Partial Differential Equations | Part II, 2001

  Write down a formula for the solution $u=u(t, x)$, for $t>0$ and $x \in \mathbb{R}^{n}$, of the initial value problem for the heat equation:

  $$\frac{\partial u}{\partial t}-\Delta u=0 \quad u(0, x)=f(x)$$

  for $f$ a bounded continuous function $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$. State (without proof) a theorem which ensures that this formula is the unique solution in some class of functions (which should be explicitly described).

  By writing $u=e^{t} v$, or otherwise, solve the initial value problem

  $$\tag{†} \frac{\partial v}{\partial t}+v-\Delta v=0, \quad v(0, x)=g(x)$$

  for $g$ a bounded continuous function $g: \mathbb{R}^{n} \rightarrow \mathbb{R}$ and give a class of functions in which your solution is the unique one.

  Hence, or otherwise, prove that for all $t>0$ :

  $$\sup _{x \in \mathbb{R}^{n}} v(t, x) \leqslant \sup _{x \in \mathbb{R}^{n}} g(x)$$

  and deduce that the solutions $v_{1}(t, x)$ and $v_{2}(t, x)$ of $(†)$ corresponding to initial values $g_{1}(x)$ and $g_{2}(x)$ satisfy, for $t>0$,

  $$\sup _{x \in \mathbb{R}^{n}}\left|v_{1}(t, x)-v_{2}(t, x)\right| \leqslant \sup _{x \in \mathbb{R}^{n}}\left|g_{1}(x)-g_{2}(x)\right| .$$

  comment

• B4.18

  Partial Differential Equations | Part II, 2001

  Write an essay on one of the following two topics:

  (a) The notion of well-posedness for initial and boundary value problems for differential equations. Your answer should include a definition and give examples and state precise theorems for some specific problems.

  (b) The concepts of distribution and tempered distribution and their use in the study of partial differential equations.

  comment

Principles of Dynamics

• A1.2 B1.2

  Principles of Dynamics | Part II, 2001

  (i) Show that Newton's equations in Cartesian coordinates, for a system of $N$ particles at positions $\mathbf{x}_{i}(t), i=1,2 \ldots N$, in a potential $V(\mathbf{x}, t)$, imply Lagrange's equations in a generalised coordinate system

  $$q_{j}=q_{j}\left(\mathbf{x}_{i}, t\right) \quad, \quad j=1,2 \ldots 3 N$$

  that is,

  $$\frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}_{j}}\right)=\frac{\partial L}{\partial q_{j}} \quad, \quad j=1,2 \ldots 3 N$$

  where $L=T-V, T(q, \dot{q}, t)$ being the total kinetic energy and $V(q, t)$ the total potential energy.

  (ii) Consider a light rod of length $L$, free to rotate in a vertical plane (the $x z$ plane), but with one end $P$ forced to move in the $x$-direction. The other end of the rod is attached to a heavy mass $M$ upon which gravity acts in the negative $z$ direction.

  (a) Write down the Lagrangian for the system.

  (b) Show that, if $P$ is stationary, the rod has two equilibrium positions, one stable and the other unstable.

  (c) The end at $P$ is now forced to move with constant acceleration, $\ddot{x}=A$. Show that, once more, there is one stable equilibrium value of the angle the rod makes with the vertical, and find it.

  comment

• A2.2 B2.1

  Principles of Dynamics | Part II, 2001

  (i) An axially symmetric top rotates freely about a fixed point $O$ on its axis. The principal moments of inertia are $A, A, C$ and the centre of gravity $G$ is a distance $h$ from $O .$

  Define the three Euler angles $\theta, \phi$ and $\psi$, specifying the orientation of the top. Use Lagrange's equations to show that there are three conserved quantities in the motion. Interpret them physically.

  (ii) Initially the top is spinning with angular speed $n$ about $O G$, with $O G$ vertical, before it is slightly disturbed.

  Show that, in the subsequent motion, $\theta$ stays close to zero if $C^{2} n^{2}>4 m g h A$, but if this condition fails then $\theta$ attains a maximum value given approximately by

  $$\cos \theta \approx \frac{C^{2} n^{2}}{2 m g h A}-1$$

  Why is this only an approximation?

  comment

• A3.2

  Principles of Dynamics | Part II, 2001

  (i) (a) Write down Hamilton's equations for a dynamical system. Under what condition is the Hamiltonian a constant of the motion? What is the condition for one of the momenta to be a constant of the motion?

  (b) Explain the notion of an adiabatic invariant. Give an expression, in terms of Hamiltonian variables, for one such invariant.

  (ii) A mass $m$ is attached to one end of a straight spring with potential energy $\frac{1}{2} k r^{2}$, where $k$ is a constant and $r$ is the length. The other end is fixed at a point $O$. Neglecting gravity, consider a general motion of the mass in a plane containing $O$. Show that the Hamiltonian is given by

  $$H=\frac{1}{2} \frac{p_{\theta}^{2}}{m r^{2}}+\frac{1}{2} \frac{p_{r}^{2}}{m}+\frac{1}{2} k r^{2},$$

  where $\theta$ is the angle made by the spring relative to a fixed direction, and $p_{\theta}, p_{r}$ are the generalised momenta. Show that $p_{\theta}$ and the energy $E$ are constants of the motion, using Hamilton's equations.

  If the mass moves in a non-circular orbit, and the spring constant $k$ is slowly varied, the orbit gradually changes. Write down the appropriate adiabatic invariant $J\left(E, p_{\theta}, k, m\right)$. Show that $J$ is proportional to

  $$\sqrt{m k}\left(r_{+}-r_{-}\right)^{2},$$

  where

  $$r_{\pm}^{2}=\frac{E}{k} \pm \sqrt{\left(\frac{E}{k}\right)^{2}-\frac{p_{\theta}^{2}}{m k}}$$

  Consider an orbit for which $p_{\theta}$ is zero. Show that, as $k$ is slowly varied, the energy $E \propto k^{\alpha}$, for a constant $\alpha$ which should be found.

  [You may assume without proof that

  $$\left.\int_{r_{-}}^{r_{+}} d r \sqrt{\left(1-\frac{r^{2}}{r_{+}^{2}}\right)\left(1-\frac{r_{-}^{2}}{r^{2}}\right)}=\frac{\pi}{4 r_{+}}\left(r_{+}-r_{-}\right)^{2} \cdot\right]$$

  comment

• A4.2

  Principles of Dynamics | Part II, 2001

  (i) Consider a particle of charge $q$ and mass $m$, moving in a stationary magnetic field B. Show that Lagrange's equations applied to the Lagrangian

  $$L=\frac{1}{2} m \dot{\mathbf{r}}^{2}+q \dot{\mathbf{r}} \cdot \mathbf{A}(\mathbf{r})$$

  where $\mathbf{A}$ is the vector potential such that $\mathbf{B}=\operatorname{curl} \mathbf{A}$, lead to the correct Lorentz force law. Compute the canonical momentum $\mathbf{p}$, and show that the Hamiltonian is $H=\frac{1}{2} m \dot{\mathbf{r}}^{2}$.

  (ii) Expressing the velocity components $\dot{r}_{i}$ in terms of the canonical momenta and co-ordinates for the above system, derive the following formulae for Poisson brackets: (b) $\left\{m \dot{r}_{i}, m \dot{r}_{j}\right\}=q \epsilon_{i j k} B_{k}$; (c) $\left\{m \dot{r}_{i}, r_{j}\right\}=-\delta_{i j}$; (d) $\left\{m \dot{r}_{i}, f\left(r_{j}\right)\right\}=-\frac{\partial}{\partial r_{i}} f\left(r_{j}\right)$.

  (a) $\{F G, H\}=F\{G, H\}+\{F, H\} G$, for any functions $F, G, H$;

  Now consider a particle moving in the field of a magnetic monopole,

  $$B_{i}=g \frac{r_{i}}{r^{3}} .$$

  Show that $\{H, \mathbf{J}\}=0$, where $\mathbf{J}=m \mathbf{r} \wedge \dot{\mathbf{r}}-g q \hat{\mathbf{r}}$. Explain why this means that $\mathbf{J}$ is conserved.

  Show that, if $g=0$, conservation of $\mathbf{J}$ implies that the particle moves in a plane perpendicular to $\mathbf{J}$. What type of surface does the particle move on if $g \neq 0$ ?

  comment

Principles of Statistics

• A1.12 B1.15

  Principles of Statistics | Part II, 2001

  (i) What are the main approaches by which prior distributions are specified in Bayesian inference?

  Define the risk function of a decision rule $d$. Given a prior distribution, define what is meant by a Bayes decision rule and explain how this is obtained from the posterior distribution.

  (ii) Dashing late into King's Cross, I discover that Harry must have already boarded the Hogwarts Express. I must therefore make my own way onto platform nine and threequarters. Unusually, there are two guards on duty, and I will ask one of them for directions. It is safe to assume that one guard is a Wizard, who will certainly be able to direct me, and the other a Muggle, who will certainly not. But which is which? Before choosing one of them to ask for directions to platform nine and three-quarters, I have just enough time to ask one of them "Are you a Wizard?", and on the basis of their answer I must make my choice of which guard to ask for directions. I know that a Wizard will answer this question truthfully, but that a Muggle will, with probability $\frac{1}{3}$, answer it untruthfully.

  Failure to catch the Hogwarts Express results in a loss which I measure as 1000 galleons, there being no loss associated with catching up with Harry on the train.

  Write down an exhaustive set of non-randomised decision rules for my problem and, by drawing the associated risk set, determine my minimax decision rule.

  My prior probability is $\frac{2}{3}$ that the guard I ask "Are you a Wizard?" is indeed a Wizard. What is my Bayes decision rule?

  comment

• A2.11 B2.16

  Principles of Statistics | Part II, 2001

  (i) Let $X_{1}, \ldots, X_{n}$ be independent, identically-distributed $N\left(\mu, \mu^{2}\right)$ random variables, $\mu>0$.

  Find a minimal sufficient statistic for $\mu$.

  Let $T_{1}=n^{-1} \sum_{i=1}^{n} X_{i}$ and $T_{2}=\sqrt{n^{-1} \sum_{i=1}^{n} X_{i}^{2}}$. Write down the distribution of $X_{i} / \mu$, and hence show that $Z=T_{1} / T_{2}$ is ancillary. Explain briefly why the Conditionality Principle would lead to inference about $\mu$ being drawn from the conditional distribution of $T_{2}$ given $Z$.

  What is the maximum likelihood estimator of $\mu$ ?

  (ii) Describe briefly the Bayesian approach to predictive inference,

  Let $Z_{1}, \ldots, Z_{n}$ be independent, identically-distributed $N\left(\mu, \sigma^{2}\right)$ random variables, with $\mu, \sigma^{2}$ both unknown. Derive the maximum likelihood estimators $\widehat{\mu}, \widehat{\sigma}^{2}$ of $\mu, \sigma^{2}$ based on $Z_{1}, \ldots, Z_{n}$, and state, without proof, their joint distribution.

  Suppose that it is required to construct a prediction interval

  $I_{1-\alpha} \equiv I_{1-\alpha}\left(Z_{1}, \ldots, Z_{n}\right)$ for a future, independent, random variable $Z_{0}$ with the same $N\left(\mu, \sigma^{2}\right)$ distribution, such that

  $$P\left(Z_{0} \in I_{1-\alpha}\right)=1-\alpha$$

  with the probability over the joint distribution of $Z_{0}, Z_{1}, \ldots, Z_{n}$. Let

  $$I_{1-\alpha}\left(Z_{1}, \ldots, Z_{n} ; \sigma^{2}\right)=\left[\bar{Z}_{n}-z_{\alpha / 2} \sigma \sqrt{1+1 / n}, \bar{Z}_{n}+z_{\alpha / 2} \sigma \sqrt{1+1 / n}\right]$$

  where $\bar{Z}_{n}=n^{-1} \sum_{i=1}^{n} Z_{i}$, and $\Phi\left(z_{\beta}\right)=1-\beta$, with $\Phi$ the distribution function of $N(0,1)$.

  Show that $P\left(Z_{0} \in I_{1-\alpha}\left(Z_{1}, \ldots, Z_{n} ; \sigma^{2}\right)\right)=1-\alpha$.

  By considering the distribution of $\left(Z_{0}-\bar{Z}_{n}\right) /\left(\widehat{\sigma} \sqrt{\frac{n+1}{n-1}}\right)$, or otherwise, show that

  $$P\left(Z_{0} \in I_{1-\alpha}\left(Z_{1}, \ldots, Z_{n} ; \widehat{\sigma}^{2}\right)\right)<1-\alpha,$$

  and show how to construct an interval $I_{1-\gamma}\left(Z_{1}, \ldots, Z_{n} ; \widehat{\sigma}^{2}\right)$ with

  $$P\left(Z_{0} \in I_{1-\gamma}\left(Z_{1}, \ldots, Z_{n} ; \widehat{\sigma}^{2}\right)\right)=1-\alpha .$$

  [Hint: if $Y$ has the $t$-distribution with $m$ degrees of freedom and $t_{\beta}^{(m)}$ is defined by $P\left(Y<t_{\beta}^{(m)}\right)=1-\beta$ then $t_{\beta}>z_{\beta}$ for $\beta<\frac{1}{2}$.]

  comment

• A3.12 B3.15

  Principles of Statistics | Part II, 2001

  (i) Explain what is meant by a uniformly most powerful unbiased test of a null hypothesis against an alternative.

  Let $Y_{1}, \ldots, Y_{n}$ be independent, identically distributed $N\left(\mu, \sigma^{2}\right)$ random variables, with $\sigma^{2}$ known. Explain how to construct a uniformly most powerful unbiased size $\alpha$ test of the null hypothesis that $\mu=0$ against the alternative that $\mu \neq 0$.

  (ii) Outline briefly the Bayesian approach to hypothesis testing based on Bayes factors.

  Let the distribution of $Y_{1}, \ldots, Y_{n}$ be as in (i) above, and suppose we wish to test, as in (i), $\mu=0$ against the alternative $\mu \neq 0$. Suppose we assume a $N\left(0, \tau^{2}\right)$ prior for $\mu$ under the alternative. Find the form of the Bayes factor $B$, and show that, for fixed $n, B$ $\rightarrow \infty$ as $\tau \rightarrow \infty$.

  comment

• A4.13 B4.15

  Principles of Statistics | Part II, 2001

  Write an account, with appropriate examples, of one of the following:

  (a) Inference in multi-parameter exponential families;

  (b) Asymptotic properties of maximum-likelihood estimators and their use in hypothesis testing;

  (c) Bootstrap inference.

  comment

Probability and Measure

• B1.13

  Probability and Measure | Part II, 2001

  State and prove Hölder's Inequality.

  [Jensen's inequality, and other standard results, may be assumed.]

  Let $\left(X_{n}\right)$ be a sequence of random variables bounded in $L_{p}$ for some $p>1$. Prove that $\left(X_{n}\right)$ is uniformly integrable.

  Suppose that $X \in L_{p}(\Omega, \mathcal{F}, \mathbb{P})$ for some probability space $(\Omega, \mathcal{F}, \mathbb{P})$ and some $p \in(1, \infty)$. Show that $X \in L_{r}(\Omega, \mathcal{F}, \mathbb{P})$ for all $1 \leqslant r<p$ and that $\|X\|_{r}$ is an increasing function of $r$ on $[1, p]$.

  Show further that $\lim _{r \rightarrow 1^{+}}\|X\|_{r}=\|X\|_{1}$.

  comment

• B2.12

  Probability and Measure | Part II, 2001

  (a) Let $\Omega=(0,1), \mathcal{F}=\mathcal{B}((0,1))$ be the Borel $\sigma$-field and let $\mathbb{P}$ be Lebesgue measure on $(\Omega, \mathcal{F})$. What is the distribution of the random variable $Z$, where $Z(\omega)=2 \omega-1$ ?

  Let $\omega=\sum_{n=1}^{\infty} 2^{-n} R_{n}(\omega)$ be the binary expansion of the point $\omega \in \Omega$ and set $U(\omega)=\sum_{n \text { odd }} 2^{-n} Q_{n}(\omega)$, where $Q_{n}(\omega)=2 R_{n}(\omega)-1$. Find a random variable $V$ independent of $U$ such that $U$ and $V$ are identically distributed and $U+\frac{1}{2} V$ is uniformly distributed on $(-1,1)$.

  (b) Now suppose that on some probability triple $X$ and $Y$ are independent, identicallydistributed random variables such that $X+\frac{1}{2} Y$ is uniformly distributed on $(-1,1)$.

  Let $\phi$ be the characteristic function of $X$. Calculate $\phi(t) / \phi(t / 4)$. Show that the distribution of $X$ must be the same as the distribution of the random variable $U$ in (a).

  comment

• B3.12

  Probability and Measure | Part II, 2001

  State and prove Birkhoff's almost-everywhere ergodic theorem.

  [You need not prove convergence in $L_{p}$ and the maximal ergodic lemma may be assumed provided that it is clearly stated.]

  Let $\Omega=[0,1), \mathcal{F}=\mathcal{B}([0,1))$ be the Borel $\sigma$-field and let $\mathbb{P}$ be Lebesgue measure on $(\Omega, \mathcal{F})$. Give an example of an ergodic measure-preserving map $\theta: \Omega \rightarrow \Omega$ (you need not prove it is ergodic).

  Let $f(x)=x$ for $x \in[0,1)$. Find (at least for all $x$ outside a set of measure zero)

  $$\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{i=1}^{n}\left(f \circ \theta^{i-1}\right)(x) .$$

  Briefly justify your answer.

  comment

• B4.11

  Probability and Measure | Part II, 2001

  State the first and second Borel-Cantelli Lemmas and the Kolmogorov 0-1 law.

  Let $\left(X_{n}\right)_{n \geqslant 1}$ be a sequence of independent random variables with distribution given

  by

  $$\mathbb{P}\left(X_{n}=n\right)=\frac{1}{n}=1-\mathbb{P}\left(X_{n}=0\right)$$

  and set $S_{n}=\sum_{i=1}^{n} X_{i}$.

  (a) Show that there exist constants $0 \leqslant c_{1} \leqslant c_{2} \leqslant \infty$ such that $\lim \inf _{n}\left(S_{n} / n\right)=c_{1}$, almost surely and $\lim \sup _{n}\left(S_{n} / n\right)=c_{2}$ almost surely.

  (b) Let $Y_{k}=\sum_{i=k+1}^{2 k} X_{i}$ and $\tilde{Y}_{k}=\sum_{i=1}^{k} Z_{i}^{(k)}$, where $\left(Z_{i}^{(k)}\right)_{i=1}^{k}$ are independent with

  $$\mathbb{P}\left(Z_{i}^{(k)}=k\right)=\frac{1}{2 k}=1-\mathbb{P}\left(Z_{i}^{(k)}=0\right), \quad 1 \leqslant i \leqslant k,$$

  and suppose that $\alpha \in \mathbb{Z}^{+}$.

  Use the fact that $\mathbb{P}\left(Y_{k} \geqslant \alpha k\right) \geqslant \mathbb{P}\left(\tilde{Y}_{k} \geqslant \alpha k\right)$ to show that there exists $p_{\alpha}>0$ such that $\mathbb{P}\left(Y_{k} \geqslant \alpha k\right) \geqslant p_{\alpha}$ for all sufficiently large $k$.

  [You may use the Poisson approximation to the binomial distribution without proof.]

  By considering a suitable subsequence of $\left(Y_{k}\right)$, or otherwise, show that $c_{2}=\infty$.

  (c) Show that $c_{1} \leqslant 1$. Consider an appropriately chosen sequence of random times $T_{i}$, with $2 T_{i} \leqslant T_{i+1}$, for which $\left(S_{T_{i}} / T_{i}\right) \leqslant 3 c_{1} / 2$. Using the fact that the random variables $\left(Y_{T_{i}}\right)$ are independent, and by considering the events $\left\{Y_{T_{i}}=0\right\}$, or otherwise, show that $c_{1}=0$.

  comment

Quantum Physics

• A1.14

  Quantum Physics | Part II, 2001

  (i) A spinless quantum mechanical particle of mass $m$ moving in two dimensions is confined to a square box with sides of length $L$. Write down the energy eigenfunctions for the particle and the associated energies.

  Show that, for large $L$, the number of states in the energy range $E \rightarrow E+d E$ is $\rho(E) d E$, where

  $$\rho(E)=\frac{m L^{2}}{2 \pi \hbar^{2}}$$

  (ii) If, instead, the particle is an electron with magnetic moment $\mu$ moving in an external magnetic field, $H$, show that

  $$\begin{array}{rlr} \rho(E) & =\frac{m L^{2}}{2 \pi \hbar^{2}}, & -\mu H<E<\mu H \\ & =\frac{m L^{2}}{\pi \hbar^{2}}, & \mu H<E \end{array}$$

  Let there be $N$ electrons in the box. Explain briefly how to construct the ground state of the system. Let $E_{F}$ be the Fermi energy. Show that when $E_{F}>\mu H$,

  $$N=\frac{m L^{2}}{\pi \hbar^{2}} E_{F}$$

  Show also that the magnetic moment, $M$, of the system in the ground state is

  $$M=\frac{\mu^{2} m L^{2}}{\pi \hbar^{2}} H$$

  and that the ground state energy is

  $$\frac{1}{2} \frac{\pi \hbar^{2}}{m L^{2}} N^{2}-\frac{1}{2} M H$$

  Part II

  comment

• A2.14

  Quantum Physics | Part II, 2001

  (i) Each particle in a system of $N$ identical fermions has a set of energy levels, $E_{i}$, with degeneracy $g_{i}$, where $1 \leq i<\infty$. Explain why, in thermal equilibrium, the average number of particles with energy $E_{i}$ is

  $$N_{i}=\frac{g_{i}}{e^{\beta\left(E_{i}-\mu\right)}+1} .$$

  The physical significance of the parameters $\beta$ and $\mu$ should be made clear.

  (ii) A simple model of a crystal consists of a linear array of sites with separation $a$. At the $n$th site an electron may occupy either of two states with probability amplitudes $b_{n}$ and $c_{n}$, respectively. The time-dependent Schrödinger equation governing the amplitudes gives

  $$\begin{aligned} &i \hbar \dot{b}_{n}=E_{0} b_{n}-A\left(b_{n+1}+b_{n-1}+c_{n+1}+c_{n-1}\right), \\ &i \hbar \dot{c}_{n}=E_{1} c_{n}-A\left(b_{n+1}+b_{n-1}+c_{n+1}+c_{n-1}\right) \end{aligned}$$

  where $A>0$.

  By examining solutions of the form

  $$\left(\begin{array}{l} b_{n} \\ c_{n} \end{array}\right)=\left(\begin{array}{l} B \\ C \end{array}\right) e^{i(k n a-E t / \hbar)},$$

  show that the energies of the electron fall into two bands given by

  $$E=\frac{1}{2}\left(E_{0}+E_{1}-4 A \cos k a\right) \pm \frac{1}{2} \sqrt{\left(E_{0}-E_{1}\right)^{2}+16 A^{2} \cos ^{2} k a}$$

  Describe briefly how the energy band structure for electrons in real crystalline materials can be used to explain why they are insulators, conductors or semiconductors.

  comment

• A4.16

  Quantum Physics | Part II, 2001

  A harmonic oscillator of frequency $\omega$ is in thermal equilibrium with a heat bath at temperature $T$. Show that the mean number of quanta $n$ in the oscillator is

  $$n=\frac{1}{e^{\hbar \omega / k T}-1} .$$

  Use this result to show that the density of photons of frequency $\omega$ for cavity radiation at temperature $T$ is

  $$n(\omega)=\frac{\omega^{2}}{\pi^{2} c^{3}} \frac{1}{e^{\hbar \omega / k T}-1}$$

  By considering this system in thermal equilibrium with a set of distinguishable atoms, derive formulae for the Einstein $A$ and $B$ coefficients.

  Give a brief description of the operation of a laser.

  comment

Representation Theory

• B1.6

  Representation Theory | Part II, 2001

  Compute the character table of $A_{5}$ (begin by listing the conjugacy classes and their orders).

  [It is not enough to write down the result; you must justify your answer.]

  comment

• B2.6

  Representation Theory | Part II, 2001

  (i) Let $G$ be a group, and $X$ and $Y$ finite $G$-sets. Define the permutation representation $\mathbf{C}[X]$ and compute its character. Show that

  $$\operatorname{dim}_{\operatorname{Hom}_{G}}(\mathbf{C}[X], \mathbf{C}[Y])$$

  is equal to the number of $G$-orbits in $X \times Y$.

  (ii) Let $G=S_{n}(n \geqslant 4), X=\{1, \ldots, n\}$, and

  $$Z=\{\{i, j\} \subseteq X \mid i \neq j\}$$

  be the set of 2 -element subsets of $X$. Decompose $\mathbf{C}[Z]$ into irreducibles, and determine the dimension of each irreducible constituent.

  comment

• B3.5

  Representation Theory | Part II, 2001

  Let $G=S U_{2}$, and $V_{n}$ be the vector space of homogeneous polynomials of degree $n$ in the variables $x$ and $y$.

  (i) Define the action of $G$ on $V_{n}$, and prove that $V_{n}$ is an irreducible representation of $G$.

  (ii) Decompose $V_{4} \otimes V_{3}$ into irreducible representations of $S U_{2}$. Briefly justify your answer.

  (iii) $S U_{2}$ acts on the vector space $M_{3}(\mathbf{C})$ of complex $3 \times 3$ matrices via

  $$\rho\left(\begin{array}{ll} a & b \\ c & d \end{array}\right) \cdot X=\left(\begin{array}{lll} a & b & 0 \\ c & d & 0 \\ 0 & 0 & 1 \end{array}\right) X\left(\begin{array}{lll} a & b & 0 \\ c & d & 0 \\ 0 & 0 & 1 \end{array}\right)^{-1}, \quad X \in M_{3}(\mathbf{C}) .$$

  Decompose this representation into irreducible representations.

  comment

• B4.2

  Representation Theory | Part II, 2001

  Let $G$ be the Heisenberg group of order $p^{3}$. This is the subgroup

  $$G=\left\{\left(\begin{array}{ccc} 1 & a & x \\ 0 & 1 & b \\ 0 & 0 & 1 \end{array}\right) \mid a, b, x \in \mathbf{F}_{p}\right\}$$

  of $3 \times 3$ matrices over the finite field $\mathbf{F}_{p}$ ( $p$ prime). Let $H$ be the subgroup of $G$ of such matrices with $a=0$.

  (i) Find all one dimensional representations of $G$.

  [You may assume without proof that $[G, G]$ is equal to the set of matrices in $G$ with $a=b=0 .]$

  (ii) Let $\psi: \mathbf{F}_{p}=\mathbf{Z} / p \mathbf{Z} \longrightarrow \mathbf{C}^{*}$ be a non-trivial one dimensional representation of $\mathbf{F}_{p}$, and define a one dimensional representation $\rho$ of $H$ by

  $$\rho\left(\begin{array}{lll} 1 & 0 & x \\ 0 & 1 & b \\ 0 & 0 & 1 \end{array}\right)=\psi(x)$$

  Show that $V_{\psi}=\operatorname{Ind}_{H}^{G}(\rho)$ is irreducible.

  (iii) List all the irreducible representations of $G$ and explain why your list is complete.

  comment

Riemann Surfaces

• B1.11

  Riemann Surfaces | Part II, 2001

  Recall that an automorphism of a Riemann surface is a bijective analytic map onto itself, and that the inverse map is then guaranteed to be analytic.

  Let $\Delta$ denote the $\operatorname{disc}\{z \in \mathbb{C}|| z \mid<1\}$, and let $\Delta^{*}=\Delta-\{0\}$.

  (a) Prove that an automorphism $\phi: \Delta \rightarrow \Delta$ with $\phi(0)=0$ is a Euclidian rotation.

  [Hint: Apply the maximum modulus principle to the functions $\phi(z) / z$ and $\phi^{-1}(z) / z$.]

  (b) Prove that a holomorphic map $\phi: \Delta^{*} \rightarrow \Delta$ extends to the entire disc, and use this to conclude that any automorphism of $\Delta^{*}$ is a Euclidean rotation.

  [You may use the result stated in part (a).]

  (c) Define an analytic map between Riemann surfaces. Show that a continuous map between Riemann surfaces, known to be analytic everywhere except perhaps at a single point $P$, is, in fact, analytic everywhere.

  comment

• B3.9

  Riemann Surfaces | Part II, 2001

  Let $f: X \rightarrow Y$ be a nonconstant holomorphic map between compact connected Riemann surfaces. Define the valency of $f$ at a point, and the degree of $f$.

  Define the genus of a compact connected Riemann surface $X$ (assuming the existence of a triangulation).

  State the Riemann-Hurwitz theorem. Show that a holomorphic non-constant selfmap of a compact Riemann surface of genus $g>1$ is bijective, with holomorphic inverse. Verify that the Riemann surface in $\mathbb{C}^{2}$ described in the equation $w^{4}=z^{4}-1$ is non-singular, and describe its topological type.

  [Note: The description can be in the form of a picture or in words. If you apply RiemannHurwitz, explain first how you compactify the surface.]

  comment

• B4.8

  Riemann Surfaces | Part II, 2001

  Let $\lambda$ and $\mu$ be fixed, non-zero complex numbers, with $\lambda / \mu \notin \mathbb{R}$, and let $\Lambda=\mathbb{Z} \mu+\mathbb{Z} \lambda$ be the lattice they generate in $\mathbb{C}$. The series

  $$\wp(z)=\frac{1}{z^{2}}+\sum_{m, n}\left[\frac{1}{(z-m \lambda-n \mu)^{2}}-\frac{1}{(m \lambda+n \mu)^{2}}\right]$$

  with the sum taken over all pairs $(m, n) \in \mathbb{Z} \times \mathbb{Z}$ other than $(0,0)$, is known to converge to an elliptic function, meaning a meromorphic function $\wp: \mathbb{C} \rightarrow \mathbb{C} \cup\{\infty\}$ satisfying $\wp(z)=\wp(z+\mu)=\wp(z+\lambda)$ for all $z \in \mathbb{C}$. ( $\wp$ is called the Weierstrass function.)

  (a) Find the three zeros of $\wp^{\prime}$ modulo $\Lambda$, explaining why there are no others.

  (b) Show that, for any number $a \in \mathbb{C}$, other than the three values $\wp(\lambda / 2), \wp(\mu / 2)$ and $\wp((\lambda+\mu) / 2)$, the equation $\wp(z)=a$ has exactly two solutions, modulo $\Lambda$; whereas, for each of the specified values, it has a single solution.

  [In (a) and (b), you may use, without proof, any known results about valencies and degrees of holomorphic maps between compact Riemann surfaces, provided you state them correctly.]

  (c) Prove that every even elliptic function $\phi(z)$ is a rational function of $\wp(z)$; that is, there exists a rational function $R$ for which $\phi(z)=R(\wp(z))$.

  comment

Statistical Physics

• B1.22

  Statistical Physics | Part II, 2001

  Write down the first law of thermodynamics in differential form for an infinitesimal reversible change in terms of the increments $d E, d S$ and $d V$, where $E, S$ and $V$ are to be defined. Briefly give an interpretation of each term and deduce that

  $$P=-\left(\frac{\partial E}{\partial V}\right)_{S}, \quad T=\left(\frac{\partial E}{\partial S}\right)_{V}$$

  Define the specific heat at constant volume $C_{V}$ and show that for an adiabatic change

  $$C_{V} d T+\left(\left(\frac{\partial E}{\partial V}\right)_{T}+P\right) d V=0$$

  Derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  where $T$ is temperature and hence show that

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=-P+T\left(\frac{\partial P}{\partial T}\right)_{V}$$

  An imperfect gas of volume $V$ obeys the van der Waals equation of state

  $$\left(P+\frac{a}{V^{2}}\right)(V-b)=R T$$

  where $a$ and $b$ are non-negative constants. Show that

  $$\left(\frac{\partial C_{V}}{\partial V}\right)_{T}=0,$$

  and deduce that $C_{V}$ is a function of $T$ only. It can further be shown that in this case $C_{V}$ is independent of $T$. Hence show that

  $$T(V-b)^{R / C_{V}}$$

  is constant on adiabatic curves.

  comment

• B3.22

  Statistical Physics | Part II, 2001

  A system consists of $N$ weakly interacting non-relativistic fermions, each of mass $m$, in a three-dimensional volume, $V$. Derive the Fermi-Dirac distribution

  $$n(\epsilon)=K V g \frac{\epsilon^{1 / 2}}{\exp ((\epsilon-\mu) / k T)+1}$$

  where $n(\epsilon) d \epsilon$ is the number of particles with energy in $(\epsilon, \epsilon+d \epsilon)$ and $K=2 \pi(2 m)^{3 / 2} / h^{3}$. Explain the physical significance of $g$.

  Explain how the constant $\mu$ is determined by the number of particles $N$ and write down expressions for $N$ and the internal energy $E$ in terms of $n(\epsilon)$.

  Show that, in the limit $\kappa \equiv e^{-\mu / k T} \gg 1$,

  $$N=\frac{V}{A \kappa}\left(1-\frac{1}{2 \sqrt{2} \kappa}+O\left(\frac{1}{\kappa^{2}}\right)\right)$$

  where $A=h^{3} / g(2 \pi m k T)^{3 / 2}$.

  Show also that in this limit

  $$E=\frac{3}{2} N k T\left(1+\frac{1}{4 \sqrt{2} \kappa}+O\left(\frac{1}{\kappa^{2}}\right)\right) \text {. }$$

  Deduce that the condition $\kappa \gg 1$ implies that $A N / V \ll 1$. Discuss briefly whether or not this latter condition is satisfied in a white dwarf star and in a dilute electron gas at room temperature.

  $\left[\right.$ Note that $\left.\int_{0}^{\infty} d u e^{-u^{2} a}=\frac{1}{2} \sqrt{\frac{\pi}{a}}\right]$.

  comment

• B4.23

  Statistical Physics | Part II, 2001

  Given that the free energy $F$ can be written in terms of the partition function $Z$ as $F=-k T \log Z$ show that the entropy $S$ and internal energy $E$ are given by

  $$S=k \frac{\partial(T \log Z)}{\partial T}, \quad E=k T^{2} \frac{\partial \log Z}{\partial T}$$

  A system of particles has Hamiltonian $H(\mathbf{p}, \mathbf{q})$ where $\mathbf{p}$ is the set of particle momenta and $\mathbf{q}$ the set of particle coordinates. Write down the expression for the classical partition function $Z_{C}$ for this system in equilibrium at temperature $T$. In a particular case $H$ is given by

  $$H(\mathbf{p}, \mathbf{q})=p_{\alpha} A_{\alpha \beta}(\mathbf{q}) p_{\beta}+q_{\alpha} B_{\alpha \beta}(\mathbf{q}) q_{\beta}$$

  Let $H$ be a homogeneous function in all the $p_{\alpha}, 1 \leq \alpha \leq N$, and in a subset of the $q_{\alpha}, 1 \leq \alpha \leq M(M \leq N)$. Derive the principle of equipartition for this system.

  A system consists of $N$ weakly interacting harmonic oscillators each with Hamiltonian

  $$h(p, q)=\frac{1}{2} p^{2}+\frac{1}{2} \omega^{2} q^{2} .$$

  Using equipartition calculate the classical specific heat of the system, $C_{C}(T)$. Also calculate the classical entropy $S_{C}(T)$.

  Write down the expression for the quantum partition function of the system and derive expressions for the specific heat $C(T)$ and the entropy $S(T)$ in terms of $N$ and the parameter $\theta=\hbar \omega / k T$. Show for $\theta \ll 1$ that

  $$C(T)=C_{C}(T)+O(\theta), \quad S(T)=S_{C}(T)+S_{0}+O(\theta)$$

  where $S_{0}$ should be calculated. Comment briefly on the physical significance of the constant $S_{0}$ and why it is non-zero.

  comment

Statistical Physics and Cosmology

• A1.16

  Statistical Physics and Cosmology | Part II, 2001

  (i) Introducing the concept of a co-moving distance co-ordinate, explain briefly how the velocity of a galaxy in an isotropic and homogeneous universe is determined by the scale factor $a(t)$. How is the scale factor related to the Hubble constant $H_{0}$ ?

  A homogeneous and isotropic universe has an energy density $\rho(t) c^{2}$ and a pressure $P(t)$. Use the relation $d E=-P d V$ to derive the "fluid equation"

  $$\dot{\rho}=-3\left(\rho+\frac{P}{c^{2}}\right)\left(\frac{\dot{a}}{a}\right)$$

  where the overdot indicates differentiation with respect to time, $t$. Given that $a(t)$ satisfies the "acceleration equation"

  $$\ddot{a}=-\frac{4 \pi G}{3} a\left(\rho+\frac{3 P}{c^{2}}\right)$$

  show that the quantity

  $$k=c^{-2}\left(\frac{8 \pi G}{3} \rho a^{2}-\dot{a}^{2}\right)$$

  is time-independent.

  The pressure $P$ is related to $\rho$ by the "equation of state"

  $$P=\sigma \rho c^{2}, \quad|\sigma|<1 .$$

  Given that $a\left(t_{0}\right)=1$, find $a(t)$ for $k=0$, and hence show that $a(0)=0$.

  (ii) What is meant by the expression "the Hubble time"?

  Assuming that $a(0)=0$ and $a\left(t_{0}\right)=1$, where $t_{0}$ is the time now (of the current cosmological era), obtain a formula for the radius $R_{0}$ of the observable universe.

  Given that

  $$a(t)=\left(\frac{t}{t_{0}}\right)^{\alpha}$$

  for constant $\alpha$, find the values of $\alpha$ for which $R_{0}$ is finite. Given that $R_{0}$ is finite, show that the age of the universe is less than the Hubble time. Explain briefly, and qualitatively, why this result is to be expected as long as

  $$\rho+3 \frac{P}{c^{2}}>0 .$$

  Part II

  comment

• A3.14

  Statistical Physics and Cosmology | Part II, 2001

  (i) A spherically symmetric star has pressure $P(r)$ and mass density $\rho(r)$, where $r$ is distance from the star's centre. Stating without proof any theorems you may need, show that mechanical equilibrium implies the Newtonian pressure support equation

  $$P^{\prime}=-\frac{G m \rho}{r^{2}},$$

  where $m(r)$ is the mass within radius $r$ and $P^{\prime}=d P / d r$.

  Write down an integral expression for the total gravitational potential energy, $E_{g r}$. Use this to derive the "virial theorem"

  $$E_{g r}=-3\langle P\rangle V$$

  when $\langle P\rangle$ is the average pressure.

  (ii) Given that the total kinetic energy, $E_{k i n}$, of a spherically symmetric star is related to its average pressure by the formula

  $$E_{k i n}=\alpha\langle P\rangle V$$

  for constant $\alpha$, use the virial theorem (stated in part (i)) to determine the condition on $\alpha$ needed for gravitational binding. State the relation between pressure $P$ and "internal energy" $U$ for an ideal gas of non-relativistic particles. What is the corresponding relation for ultra-relativistic particles? Hence show that the formula $(*)$ applies in these cases, and determine the values of $\alpha$.

  Why does your result imply a maximum mass for any star, whatever the source of its pressure? What is the maximum mass, approximately, for stars supported by

  (a) thermal pressure,

  (b) electron degeneracy pressure (White Dwarf),

  (c) neutron degeneracy pressure (Neutron Star).

  A White Dwarf can accrete matter from a companion star until its mass exceeds the Chandrasekar limit. Explain briefly the process by which it then evolves into a neutron star.

  comment

• A4.18

  Statistical Physics and Cosmology | Part II, 2001

  (i) Given that $g(p) d p$ is the number of eigenstates of a gas particle with momentum between $p$ and $p+d p$, write down the Bose-Einstein distribution $\bar{n}(p)$ for the average number of particles with momentum between $p$ and $p+d p$, as a function of temperature $T$ and chemical potential $\mu$.

  Given that $\mu=0$ and $g(p)=8 \pi \frac{V p^{2}}{h^{3}}$ for a gas of photons, obtain a formula for the energy density $\rho_{T}$ at temperature $T$ in the form

  $$\rho_{T}=\int_{0}^{\infty} \epsilon_{T}(\nu) d \nu,$$

  where $\epsilon_{T}(\nu)$ is a function of the photon frequency $\nu$ that you should determine. Hence show that the value $\nu_{\text {peak }}$ of $\nu$ at the maximum of $\epsilon_{T}(\nu)$ is proportional to $T$.

  A thermally isolated photon gas undergoes a slow change of its volume $V$. Why is $\bar{n}(p)$ unaffected by this change? Use this fact to show that $V T^{3}$ remains constant.

  (ii) According to the "Hot Big Bang" theory, the Universe evolved by expansion from an earlier state in which it was filled with a gas of electrons, protons and photons (with $n_{e}=n_{p}$ ) at thermal equilibrium at a temperature $T$ such that

  $$2 m_{e} c^{2} \gg k T \gg B$$

  where $m_{e}$ is the electron mass and $B$ is the binding energy of a hydrogen atom. Why must the composition have been different when $k T \gg 2 m_{e} c^{2}$ ? Why must it change as the temperature falls to $k T \ll B$ ? Why does this lead to a thermal decoupling of radiation from matter?

  The baryon number of the Universe can be taken to be the number of protons, either as free particles or as hydrogen atom nuclei. Let $n_{b}$ be the baryon number density and $n_{\gamma}$ the photon number density. Why is the ratio $\eta=n_{b} / n_{\gamma}$ unchanged by the expansion of the universe? Given that $\eta \ll 1$, obtain an estimate of the temperature $T_{D}$ at which decoupling occurs, as a function of $\eta$ and $B$. How does this decoupling lead to the concept of a "surface of last scattering" and a prediction of a Cosmic Microwave Background Radiation (CMBR)?

  Part II

  comment

Stochastic Financial Models

• A1.11 B1.16

  Stochastic Financial Models | Part II, 2001

  (i) The price of the stock in the binomial model at time $r, 1 \leqslant r \leqslant n$, is $S_{r}=S_{0} \prod_{j=1}^{r} Y_{j}$, where $Y_{1}, Y_{2}, \ldots, Y_{n}$ are independent, identically-distributed random variables with $\mathbb{P}\left(Y_{1}=u\right)=p=1-\mathbb{P}\left(Y_{1}=d\right)$ and the initial price $S_{0}$ is a constant. Denote the fixed interest rate on the bank account by $\rho$, where $u>1+\rho>d>0$, and let the discount factor $\alpha=1 /(1+\rho)$. Determine the unique value $p=\bar{p}$ for which the sequence $\left\{\alpha^{r} S_{r}, 0 \leqslant r \leqslant n\right\}$ is a martingale.

  Explain briefly the significance of $\bar{p}$ for the pricing of contingent claims in the model.

  (ii) Let $T_{a}$ denote the first time that a standard Brownian motion reaches the level $a>0$. Prove that for $t>0$,

  $$\mathbb{P}\left(T_{a} \leqslant t\right)=2[1-\Phi(a / \sqrt{t})],$$

  where $\Phi$ is the standard normal distribution function.

  Suppose that $A_{t}$ and $B_{t}$ represent the prices at time $t$ of two different stocks with initial prices 1 and 2 , respectively; the prices evolve so that they may be represented as $A_{t}=e^{\sigma_{1} X_{t}+\mu t}$ and $B_{t}=2 e^{\sigma_{2} Y_{t}+\mu t}$, respectively, where $\left\{X_{t}\right\}_{t \geqslant 0}$ and $\left\{Y_{t}\right\}_{t \geqslant 0}$ are independent standard Brownian motions and $\sigma_{1}, \sigma_{2}$ and $\mu$ are constants. Let $T$ denote the first time, if ever, that the prices of the two stocks are the same. Determine $\mathbb{P}(T \leqslant t)$, for $t>0$.

  comment

• A3.11 B3.16

  Stochastic Financial Models | Part II, 2001

  (i) Suppose that $Z$ is a random variable having the normal distribution with $\mathbb{E} Z=\beta$ and $\operatorname{Var} Z=\tau^{2}$.

  For positive constants $a, c$ show that

  $$\mathbb{E}\left(a e^{Z}-c\right)_{+}=a e^{\left(\beta+\tau^{2} / 2\right)} \Phi\left(\frac{\log (a / c)+\beta}{\tau}+\tau\right)-c \Phi\left(\frac{\log (a / c)+\beta}{\tau}\right)$$

  where $\Phi$ is the standard normal distribution function.

  In the context of the Black-Scholes model, derive the formula for the price at time 0 of a European call option on the stock at strike price $c$ and maturity time $t_{0}$ when the interest rate is $\rho$ and the volatility of the stock is $\sigma$.

  (ii) Let $p$ denote the price of the call option in the Black-Scholes model specified in (i). Show that $\frac{\partial p}{\partial \rho}>0$ and sketch carefully the dependence of $p$ on the volatility $\sigma$ (when the other parameters in the model are held fixed).

  Now suppose that it is observed that the interest rate lies in the range $0<\rho<\rho_{0}$ and when it changes it is linked to the volatility by the formula $\sigma=\ln \left(\rho_{0} / \rho\right)$. Consider a call option at strike price $c=S_{0}$, where $S_{0}$ is the stock price at time 0 . There is a small increase $\Delta \rho$ in the interest rate; will the price of the option increase or decrease (assuming that the stock price is unaffected)? Justify your answer carefully.

  [You may assume that the function $\phi(x) / \Phi(x)$ is decreasing in $x,-\infty<x<\infty$, and increases to $+\infty$ as $x \rightarrow-\infty$, where $\Phi$ is the standard-normal distribution function and $\phi=\Phi^{\prime}$.]

  comment

• A4.12 B4.16

  Stochastic Financial Models | Part II, 2001

  Write an essay on the mean-variance approach to portfolio selection in a one-period model. Your essay should contrast the solution in the case when all the assets are risky with that for the case when there is a riskless asset.

  comment

Symmetries and Groups in Physics

• A1.17

  Symmetries and Groups in Physics | Part II, 2001

  (i) Let $h: G \rightarrow G^{\prime}$ be a surjective homomorphism between two groups, $G$ and $G^{\prime}$. If $D^{\prime}: G^{\prime} \rightarrow G L\left(\mathbb{C}^{n}\right)$ is a representation of $G^{\prime}$, show that $D(g)=D^{\prime}(h(g))$ for $g \in G$ is a representation of $G$ and, if $D^{\prime}$ is irreducible, show that $D$ is also irreducible. Show further that $\widetilde{D}(\widetilde{g})=D^{\prime}(\widetilde{h}(\widetilde{g}))$ is a representation of $G / \operatorname{ker}(h)$, where $\tilde{h}(\widetilde{g})=h(g)$ for $g \in G$ and $\widetilde{g} \in G / \operatorname{ker}(h)$ (with $g \in \widetilde{g}$ ). Deduce that the characters $\chi, \widetilde{\chi}, \chi^{\prime}$ of $D, \widetilde{D}, D^{\prime}$, respectively, satisfy

  $$\chi(g)=\tilde{\chi}(\widetilde{g})=\chi^{\prime}(h(g))$$

  (ii) $D_{4}$ is the symmetry group of rotations and reflections of a square. If $c$ is a rotation by $\pi / 2$ about the centre of the square and $b$ is a reflection in one of its symmetry axes, then $D_{4}=\left\{e, c, c^{2}, c^{3}, b, b c, b c^{2}, b c^{3}\right\}$. Given that the conjugacy classes are $\{e\}\left\{c^{2}\right\},\left\{c, c^{3}\right\}$ $\left\{b, b c^{2}\right\}$ and $\left\{b c, b c^{3}\right\}$ derive the character table of $D_{4}$.

  Let $H_{0}$ be the Hamiltonian of a particle moving in a central potential. The $S O(3)$ symmetry ensures that the energy eigenvalues of $H_{0}$ are the same for all the angular momentum eigenstates in a given irreducible $S O(3)$ representation. Therefore, the energy eigenvalues of $H_{0}$ are labelled $E_{n l}$ with $n \in \mathbb{N}$ and $l \in \mathbb{N}_{0}, l<n$. Assume now that in a crystal the symmetry is reduced to a $D_{4}$ symmetry by an additional term $H_{1}$ of the total Hamiltonian, $H=H_{0}+H_{1}$. Find how the $H_{0}$ eigenstates in the $S O(3)$ irreducible representation with $l=2$ (the D-wave orbital) decompose into irreducible representations of $H$. You may assume that the character, $g(\theta)$, of a group element of $S O(3)$, in a representation labelled by $l$ is given by

  $$\chi\left(g_{\theta}\right)=1+2 \cos \theta+2 \cos (2 \theta)+\ldots+2 \cos (l \theta)$$

  where $\theta$ is a rotation angle and $l(l+1)$ is the eigenvalue of the total angular momentum, $\mathbf{L}^{2}$.

  comment

• A3.15

  Symmetries and Groups in Physics | Part II, 2001

  (i) The pions form an isospin triplet with $\pi^{+}=|1,1\rangle, \pi^{0}=|1,0\rangle$ and $\pi^{-}=|1,-1\rangle$, whilst the nucleons form an isospin doublet with $p=\left|\frac{1}{2}, \frac{1}{2}\right\rangle$ and $n=\left|\frac{1}{2},-\frac{1}{2}\right\rangle$. Consider the isospin representation of two-particle states spanned by the basis

  $$T=\left\{\left|\pi^{+} p\right\rangle,\left|\pi^{+} n\right\rangle,\left|\pi^{0} p\right\rangle,\left|\pi^{0} n\right\rangle,\left|\pi^{-} p\right\rangle,\left|\pi^{-} n\right\rangle\right\}$$

  State which irreducible representations are contained in this representation and explain why $\left|\pi^{+} p\right\rangle$ is an isospin eigenstate.

  Using

  $$I_{-}|j, m\rangle=\sqrt{(j-m+1)(j+m)}|j, m-1\rangle,$$

  where $I_{-}$is the isospin ladder operator, write the isospin eigenstates in terms of the basis, $T$.

  (ii) The Lie algebra $s u(2)$ of generators of $S U(2)$ is spanned by the operators $\left\{J_{+}, J_{-}, J_{3}\right\}$ satisfying the commutator algebra $\left[J_{+}, J_{-}\right]=2 J_{3}$ and $\left[J_{3}, J_{\pm}\right]=\pm J_{\pm}$. Let $\Psi_{j}$ be an eigenvector of $J_{3}: J_{3}\left(\Psi_{j}\right)=j \Psi_{j}$ such that $J_{+} \Psi_{j}=0$. The vector space $V_{j}=\operatorname{span}\left\{J_{-}^{n} \Psi_{j}: n \in \mathbb{N}_{0}\right\}$ together with the action of an arbitrary su(2) operator $A$ on $V_{j}$ defined by

  $$J_{-}\left(J_{-}^{n} \Psi_{j}\right)=J_{-}^{n+1} \Psi_{j}, \quad A\left(J_{-}^{n} \Psi_{j}\right)=\left[A, J_{-}\right]\left(J_{-}^{n-1} \Psi_{j}\right)+J_{-}\left(A\left(J_{-}^{n-1} \Psi_{j}\right)\right)$$

  forms a representation (not necessarily reducible) of $s u(2)$. Show that if $J_{-}^{n} \Psi_{j}$ is nontrivial then it is an eigenvector of $J_{3}$ and find its eigenvalue. Given that $\left[J_{+}, J_{-}^{n}\right]=$ $\alpha_{n} J_{-}^{n-1} J_{3}+\beta_{n} J_{-}^{n-1}$ show that $\alpha_{n}$ and $\beta_{n}$ satisfy

  $$\alpha_{n}=\alpha_{n-1}+2, \quad \beta_{n}=\beta_{n-1}-\alpha_{n-1}$$

  By solving these equations evaluate $\left[J_{+}, J_{-}^{n}\right]$. Show that $J_{+} J_{-}^{2 j+1} \Psi_{j}=0$. Hence show that $J_{-}^{2 j+1} \Psi_{j}$ is contained in a proper sub-representation of $V_{j}$.

  comment

Theoretical Geophysics

• A1.19

  Theoretical Geophysics | Part II, 2001

  (i) From the surface of a flat Earth, an explosive source emits P-waves downward into a horizontal homogeneous elastic layer of uniform thickness $h$ and P-wave speed $\alpha_{1}$ overlying a lower layer of infinite depth and P-wave speed $\alpha_{2}$, where $\alpha_{2}>\alpha_{1}$. A line of seismometers on the surface records the travel time $t$ as a function of distance $x$ from the source for the various arrivals along different ray paths.

  Sketch the ray paths associated with the direct, reflected and head waves arriving at a given position. Calculate the travel times $t(x)$ of the direct and reflected waves, and sketch the corresponding travel-time curves. Hence explain how to estimate $\alpha_{1}$ and $h$ from the recorded arrival times. Explain briefly why head waves are only observed beyond a minimum distance $x_{c}$ from the source and why they have a travel-time curve of the form $t=t_{c}+\left(x-x_{c}\right) / \alpha_{2}$ for $x>x_{c}$.

  [You need not calculate $x_{c}$ or $t_{c}$.]

  (ii) A plane $\mathrm{SH}$-wave in a homogeneous elastic solid has displacement proportional to $\exp [i(k x+m z-\omega t)]$. Express the slowness vector $\mathbf{s}$ in terms of the wavevector $\mathbf{k}=(k, 0, m)$ and $\omega$. Deduce an equation for $m$ in terms of $k, \omega$ and the S-wave speed $\beta$.

  A homogeneous elastic layer of uniform thickness $h$, S-wave speed $\beta_{1}$ and shear modulus $\mu_{1}$ has a stress-free surface $z=0$ and overlies a lower layer of infinite depth, S-wave speed $\beta_{2}\left(>\beta_{1}\right)$ and shear modulus $\mu_{2}$. Find the vertical structure of Love waves with displacement proportional to $\exp [i(k x-\omega t)]$, and show that the horizontal phase speed $c$ obeys

  $$\tan \left[\left(\frac{1}{\beta_{1}^{2}}-\frac{1}{c^{2}}\right)^{1 / 2} \omega h\right]=\frac{\mu_{2}}{\mu_{1}}\left(\frac{1 / c^{2}-1 / \beta_{2}^{2}}{1 / \beta_{1}^{2}-1 / c^{2}}\right)^{1 / 2}$$

  By sketching both sides of the equation as a function of $c$ in $\beta_{1} \leqslant c \leqslant \beta_{2}$ show that at least one mode exists for every value of $\omega$.

  comment

• A2.16

  Theoretical Geophysics | Part II, 2001

  (i) In a reference frame rotating with constant angular velocity $\boldsymbol{\Omega}$ the equations of motion for an inviscid, incompressible fluid of density $\rho$ in a gravitational field $g=-\nabla \Phi$ are

  $$\rho \frac{D \mathbf{u}}{D t}+2 \rho \boldsymbol{\Omega} \wedge \mathbf{u}=-\nabla p+\rho \mathbf{g}, \quad \nabla \cdot \mathbf{u}=0$$

  Define the Rossby number and explain what is meant by geostrophic flow.

  Derive the vorticity equation

  $$\frac{D \boldsymbol{\omega}}{D t}=(\boldsymbol{\omega}+2 \boldsymbol{\Omega}) \cdot \nabla \mathbf{u}+\frac{\nabla \rho \wedge \nabla p}{\rho^{2}}$$

  $\left[\right.$ Recall that $\mathbf{u} \cdot \nabla \mathbf{u}=\nabla\left(\frac{1}{2} \mathbf{u}^{2}\right)-\mathbf{u} \wedge(\nabla \wedge \mathbf{u})$.]

  Give a physical interpretation for the term $(\boldsymbol{\omega}+2 \boldsymbol{\Omega}) \cdot \nabla \mathbf{u}$.

  (ii) Consider the rotating fluid of part (i), but now let $\rho$ be constant and absorb the effects of gravity into a modified pressure $P=p-\rho \mathbf{g} \cdot \mathbf{x}$. State the linearized equations of motion and the linearized vorticity equation for small-amplitude motions (inertial waves).

  Use the linearized equations of motion to show that

  $$\nabla^{2} P=2 \rho \boldsymbol{\Omega} \cdot \boldsymbol{\omega} .$$

  Calculate the time derivative of the curl of the linearized vorticity equation. Hence show that

  $$\frac{\partial^{2}}{\partial t^{2}}\left(\nabla^{2} \mathbf{u}\right)=-(2 \mathbf{\Omega} \cdot \nabla)^{2} \mathbf{u}$$

  Deduce the dispersion relation for waves proportional to $\exp [i(\mathbf{k} \cdot \mathbf{x}-n t)]$. Show that $|n| \leq 2 \Omega$. Show further that if $n=2 \Omega$ then $P=0$.

  comment

• A4.20

  Theoretical Geophysics | Part II, 2001

  Write down expressions for the phase speed $c$ and group velocity $c_{g}$ in one dimension for general waves of the form $A \exp [i(k x-\omega t)]$ with dispersion relation $\omega(k)$. Briefly indicate the physical significance of $c$ and $c_{g}$ for a wavetrain of finite size.

  The dispersion relation for internal gravity waves with wavenumber $\mathbf{k}=(k, 0, m)$ in an incompressible stratified fluid with constant buoyancy frequency $N$ is

  $$\omega=\frac{\pm N k}{\left(k^{2}+m^{2}\right)^{1 / 2}} .$$

  Calculate the group velocity $\mathbf{c}_{g}$ and show that it is perpendicular to $\mathbf{k}$. Show further that the horizontal components of $\mathbf{k} / \omega$ and $\mathbf{c}_{g}$ have the same sign and that the vertical components have the opposite sign.

  The vertical velocity $w$ of small-amplitude internal gravity waves is governed by

  $$\frac{\partial^{2}}{\partial t^{2}}\left(\nabla^{2} w\right)+N^{2} \nabla_{h}^{2} w=0$$

  where $\nabla_{h}^{2}$ is the horizontal part of the Laplacian and $N$ is constant.

  Find separable solutions to $(*)$ of the form $w(x, z, t)=X(x-U t) Z(z)$ corresponding to waves with constant horizontal phase speed $U>0$. Comment on the nature of these solutions for $0<k<N / U$ and for $k>N / U$.

  A semi-infinite stratified fluid occupies the region $z>h(x, t)$ above a moving lower boundary $z=h(x, t)$. Construct the solution to $(*)$ for the case $h=\epsilon \sin [k(x-U t)]$, where $\epsilon$ and $k$ are constants and $\epsilon \ll 1$.

  Sketch the orientation of the wavecrests, the propagation direction and the group velocity for the case $0<k<N / U$.

  Part II

  comment

Transport Processes

• A1.18

  Transport Processes | Part II, 2001

  (i) The diffusion equation for a spherically-symmetric concentration field $C(r, t)$ is

  $$C_{t}=\frac{D}{r^{2}}\left(r^{2} C_{r}\right)_{r},$$

  where $r$ is the radial coordinate. Find and sketch the similarity solution to (1) which satisfies $C \rightarrow 0$ as $r \rightarrow \infty$ and $\int_{0}^{\infty} 4 \pi r^{2} C(r, t) d r=M=$ constant, assuming it to be of the form

  $$C=\frac{M}{(D t)^{a}} F(\eta), \quad \eta=\frac{r}{(D t)^{b}},$$

  where $a$ and $b$ are numbers to be found.

  (ii) A two-dimensional piece of heat-conducting material occupies the region $a \leqslant r \leqslant$ $b,-\pi / 2 \leqslant \theta \leqslant \pi / 2$ (in plane polar coordinates). The surfaces $r=a, \theta=-\pi / 2, \theta=\pi / 2$ are maintained at a constant temperature $T_{1}$; at the surface $r=b$ the boundary condition on temperature $T(r, \theta)$ is

  $$T_{r}+\beta T=0,$$

  where $\beta>0$ is a constant. Show that the temperature, which satisfies the steady heat conduction equation

  $$T_{r r}+\frac{1}{r} T_{r}+\frac{1}{r^{2}} T_{\theta \theta}=0,$$

  is given by a Fourier series of the form

  $$\frac{T}{T_{1}}=K+\sum_{n=0}^{\infty} \cos \left(\alpha_{n} \theta\right)\left[A_{n}\left(\frac{r}{a}\right)^{2 n+1}+B_{n}\left(\frac{a}{r}\right)^{2 n+1}\right]$$

  where $K, \alpha_{n}, A_{n}, B_{n}$ are to be found.

  In the limits $a / b \ll 1$ and $\beta b \ll 1$, show that

  $$\int_{-\pi / 2}^{\pi / 2} T_{r} r d \theta \approx-\pi \beta b T_{1}$$

  given that

  $$\sum_{n=0}^{\infty} \frac{1}{(2 n+1)^{2}}=\frac{\pi^{2}}{8} .$$

  Explain how, in these limits, you could have obtained this result much more simply.

  comment

• A3.16

  Transport Processes | Part II, 2001

  (i) Incompressible fluid of kinematic viscosity $\nu$ occupies a parallel-sided channel $0 \leqslant y \leqslant h_{0},-\infty<x<\infty$. The wall $y=0$ is moving parallel to itself, in the $x$ direction, with velocity $\operatorname{Re}\left\{U e^{i \omega t}\right\}$, where $t$ is time and $U, \omega$ are real constants. The fluid velocity $u(y, t)$ satisfies the equation

  $$u_{t}=\nu u_{y y}$$

  write down the boundary conditions satisfied by $u$.

  Assuming that

  $$u=\operatorname{Re}\left\{a \sinh [b(1-\eta)] e^{i \omega t}\right\}$$

  where $\eta=y / h_{0}$, find the complex constants $a, b$. Calculate the velocity (in real, not complex, form) in the limit $h_{0}(\omega / \nu)^{1 / 2} \rightarrow 0$.

  (ii) Incompressible fluid of viscosity $\mu$ fills the narrow gap between the rigid plane $y=0$, which moves parallel to itself in the $x$-direction with constant speed $U$, and the rigid wavy wall $y=h(x)$, which is at rest. The length-scale, $L$, over which $h$ varies is much larger than a typical value, $h_{0}$, of $h$.

  Assume that inertia is negligible, and therefore that the governing equations for the velocity field $(u, v)$ and the pressure $p$ are

  $$u_{x}+v_{y}=0, p_{x}=\mu\left(u_{x x}+u_{y y}\right), p_{y}=\mu\left(v_{x x}+v_{y y}\right)$$

  Use scaling arguments to show that these equations reduce approximately to

  $$p_{x}=\mu u_{y y}, \quad p_{y}=0$$

  Hence calculate the velocity $u(x, y)$, the flow rate

  $$Q=\int_{0}^{h} u d y$$

  and the viscous shear stress exerted by the fluid on the plane wall,

  $$\tau=-\left.\mu u_{y}\right|_{y=0}$$

  in terms of $p_{x}, h, U$ and $\mu$.

  Now assume that $h=h_{0}(1+\epsilon \sin k x)$, where $\epsilon \ll 1$ and $k h_{0} \ll 1$, and that $p$ is periodic in $x$ with wavelength $2 \pi / k$. Show that

  $$Q=\frac{h_{0} U}{2}\left(1-\frac{3}{2} \epsilon^{2}+O\left(\epsilon^{4}\right)\right)$$

  and calculate $\tau$ correct to $O\left(\epsilon^{2}\right)$. Does increasing the amplitude $\epsilon$ of the corrugation cause an increase or a decrease in the force required to move the plane $y=0$ at the chosen speed $U ?$

  comment

• A4.19

  Transport Processes | Part II, 2001

  Fluid flows in the $x$-direction past the infinite plane $y=0$ with uniform but timedependent velocity $U(t)=U_{0} G\left(t / t_{0}\right)$, where $G$ is a positive function with timescale $t_{0}$. A long region of the plane, $0<x<L$, is heated and has temperature $T_{0}\left(1+\gamma(x / L)^{n}\right)$, where $T_{0}, \gamma, n$ are constants $[\gamma=O(1)]$; the remainder of the plane is insulating $\left(T_{y}=0\right)$. The fluid temperature far from the heated region is $T_{0}$. A thermal boundary layer is formed over the heated region. The full advection-diffusion equation for temperature $T(x, y, t)$ is

  $$T_{t}+U(t) T_{x}=D\left(T_{y y}+T_{x x}\right),$$

  where $D$ is the thermal diffusivity. By considering the steady case $(G \equiv 1)$, derive a scale for the thickness of the boundary layer, and explain why the term $T_{x x}$ in (1) can be neglected if $U_{0} L / D \gg 1$.

  Neglecting $T_{x x}$, use the change of variables

  $$\tau=\frac{t}{t_{0}}, \quad \xi=\frac{x}{L}, \quad \eta=y\left[\frac{U(t)}{D x}\right]^{1 / 2}, \quad \frac{T-T_{0}}{T_{0}}=\gamma\left(\frac{x}{L}\right)^{n} f(\xi, \eta, \tau)$$

  to transform the governing equation to

  $$f_{\eta \eta}+\frac{1}{2} \eta f_{\eta}-n f=\xi f_{\xi}+\frac{L \xi}{t_{0} U_{0}}\left(\frac{G_{\tau}}{2 G^{2}} \eta f_{\eta}+\frac{1}{G} f_{\tau}\right)$$

  Write down the boundary conditions to be satisfied by $f$ in the region $0<\xi<1$.

  In the case in which $U$ is slowly-varying, so $\epsilon=\frac{L}{t_{0} U_{0}} \ll 1$, consider a solution for $f$ in the form

  $$f=f_{0}(\eta)+\epsilon f_{1}(\xi, \eta, \tau)+O\left(\epsilon^{2}\right) .$$

  Explain why $f_{0}$ is independent of $\xi$ and $\tau$.

  Henceforth take $n=\frac{1}{2}$. Calculate $f_{0}(\eta)$ and show that

  $$f_{1}=\frac{G_{\tau} \xi}{G^{2}} g(\eta)$$

  where $g$ satisfies the ordinary differential equation

  $$g^{\prime \prime}+\frac{1}{2} \eta g^{\prime}-\frac{3}{2} g=\frac{-\eta}{4} \int_{\eta}^{\infty} e^{-u^{2} / 4} d u .$$

  State the boundary conditions on $g(\eta)$.

  The heat transfer per unit length of the heated region is $-\left.D T_{y}\right|_{y=0}$. Use the above results to show that the total rate of heat transfer is

  $$T_{0}[D L U(t)]^{1 / 2} \frac{\gamma}{2}\left\{\sqrt{\pi}-\frac{\epsilon G_{\tau}}{G^{2}} g^{\prime}(0)+O\left(\epsilon^{2}\right)\right\}$$

  comment

Waves in Fluid and Solid Media

• B1.26

  Waves in Fluid and Solid Media | Part II, 2001

  Derive Riemann's equations for finite amplitude, one-dimensional sound waves in a perfect gas with ratio of specific heats $\gamma$.

  At time $t=0$ the gas is at rest and has uniform density $\rho_{0}$, pressure $p_{0}$ and sound speed $c_{0}$. A piston initially at $x=0$ starts moving backwards at time $t=0$ with displacement $x=-a \sin \omega t$, where $a$ and $\omega$ are positive constants. Explain briefly how to find the resulting disturbance using a graphical construction in the $x t$-plane, and show that prior to any shock forming $c=c_{0}+\frac{1}{2}(\gamma-1) u$.

  For small amplitude $a$, show that the excess pressure $\Delta p=p-p_{0}$ and the excess sound speed $\Delta c=c-c_{0}$ are related by

  $$\frac{\Delta p}{p_{0}}=\frac{2 \gamma}{\gamma-1} \frac{\Delta c}{c_{0}}+\frac{\gamma(\gamma+1)}{(\gamma-1)^{2}}\left(\frac{\Delta c}{c_{0}}\right)^{2}+O\left(\left(\frac{\Delta c}{c_{0}}\right)^{3}\right)$$

  Deduce that the time-averaged pressure on the face of the piston exceeds $p_{0}$ by

  $$\frac{1}{8} \rho_{0} a^{2} \omega^{2}(\gamma+1)+O\left(a^{3}\right)$$

  comment

• B2.25

  Waves in Fluid and Solid Media | Part II, 2001

  A semi-infinite elastic medium with shear modulus $\mu_{1}$ and shear-wave speed $c_{1}$ lies in $y<0$. Above it there is a layer $0 \leq y \leqslant h$ of a second elastic medium with shear modulus $\mu_{2}$ and shear-wave speed $c_{2}\left(<c_{1}\right)$. The top boundary $y=h$ is stress-free. Consider a monochromatic shear wave propagating at speed $c$ with wavenumber $k$ in the $x$-direction and with displacements only in the $z$-direction.

  Obtain the dispersion relation

  $$\tan k h \theta=\frac{\mu_{1} c_{2}}{\mu_{2} c_{1}} \frac{1}{\theta}\left(\frac{c_{1}^{2}}{c_{2}^{2}}-1-\theta^{2}\right)^{1 / 2}, \quad \text { where } \quad \theta=\sqrt{\frac{c^{2}}{c_{2}^{2}}-1} .$$

  Deduce that the modes have a cut-off frequency $\pi n c_{1} c_{2} / h \sqrt{c_{1}^{2}-c_{2}^{2}}$ where they propagate at speed $c=c_{1}$.

  comment

• B3.25

  Waves in Fluid and Solid Media | Part II, 2001

  Consider the equation

  $$\phi_{t t}+\alpha^{2} \phi_{x x x x}+\beta^{2} \phi=0,$$

  where $\alpha$ and $\beta$ are real constants. Find the dispersion relation for waves of frequency $\omega$ and wavenumber $k$. Find the phase velocity $c(k)$ and the group velocity $c_{g}(k)$ and sketch graphs of these functions.

  Multiplying equation $(*)$ by $\phi_{t}$, obtain an equation of the form

  $$\frac{\partial A}{\partial t}+\frac{\partial B}{\partial x}=0$$

  where $A$ and $B$ are expressions involving $\phi$ and its derivatives. Give a physical interpretation of this equation.

  Evaluate the time-averaged energy $\langle E\rangle$ and energy flux $\langle I\rangle$ of a monochromatic wave $\phi=\cos (k x-w t)$, and show that

  $$\langle I\rangle=c_{g}\langle E\rangle .$$

  comment

• B4.27

  Waves in Fluid and Solid Media | Part II, 2001

  Derive the ray-tracing equations governing the evolution of a wave packet $\phi(\mathbf{x}, t)=$ $A(\mathbf{x}, t) \exp \{i \psi(\mathbf{x}, t)\}$ in a slowly varying medium, stating the conditions under which the equations are valid.

  Consider now a stationary obstacle in a steadily moving homogeneous two-dimensional medium which has the dispersion relation

  $$\omega\left(k_{1}, k_{2}\right)=\alpha\left(k_{1}^{2}+k_{2}^{2}\right)^{1 / 4}-V k_{1}$$

  where $(V, 0)$ is the velocity of the medium. The obstacle generates a steady wave system. Writing $\left(k_{1}, k_{2}\right)=\kappa(\cos \phi, \sin \phi)$, show that the wave satisfies

  $$\kappa=\frac{\alpha^{2}}{V^{2} \cos ^{2} \phi}$$

  Show that the group velocity of these waves can be expressed as

  $$\mathbf{c}_{g}=V\left(\frac{1}{2} \cos ^{2} \phi-1, \frac{1}{2} \cos \phi \sin \phi\right) .$$

  Deduce that the waves occupy a wedge of semi-angle $\sin ^{-1} \frac{1}{3}$ about the negative $x_{1}$-axis.

  comment