Part II, 2011

Algebraic Geometry

• Paper 1, Section II, H

  Algebraic Geometry | Part II, 2011

  (i) Let $X$ be an affine variety over an algebraically closed field. Define what it means for $X$ to be irreducible, and show that if $U$ is a non-empty open subset of an irreducible $X$, then $U$ is dense in $X$.

  (ii) Show that $n \times n$ matrices with distinct eigenvalues form an affine variety, and are a Zariski open subvariety of affine space $\mathbb{A}^{n^{2}}$ over an algebraically closed field.

  (iii) Let $\operatorname{char}_{A}(x)=\operatorname{det}(x I-A)$ be the characteristic polynomial of $A$. Show that the $n \times n$ matrices $A$ such that $\operatorname{char}_{A}(A)=0$ form a Zariski closed subvariety of $\mathbb{A}^{n^{2}}$. Hence conclude that this subvariety is all of $\mathbb{A}^{n^{2}}$.

  comment

• Paper 2, Section II, H

  Algebraic Geometry | Part II, 2011

  (i) Let $k$ be an algebraically closed field, and let $I$ be an ideal in $k\left[x_{0}, \ldots, x_{n}\right]$. Define what it means for $I$ to be homogeneous.

  Now let $Z \subseteq \mathbb{A}^{n+1}$ be a Zariski closed subvariety invariant under $k^{*}=k-\{0\}$; that is, if $z \in Z$ and $\lambda \in k^{*}$, then $\lambda z \in Z$. Show that $I(Z)$ is a homogeneous ideal.

  (ii) Let $f \in k\left[x_{1}, \ldots, x_{n-1}\right]$, and let $\Gamma=\left\{(x, f(x)) \mid x \in \mathbb{A}^{n-1}\right\} \subseteq \mathbb{A}^{n}$ be the graph of $f$.

  Let $\bar{\Gamma}$ be the closure of $\Gamma$ in $\mathbb{P}^{n}$.

  Write, in terms of $f$, the homogeneous equations defining $\bar{\Gamma}$.

  Assume that $k$ is an algebraically closed field of characteristic zero. Now suppose $n=3$ and $f(x, y)=y^{3}-x^{2} \in k[x, y]$. Find the singular points of the projective surface $\bar{\Gamma}$.

  comment

• Paper 3, Section II, H

  Algebraic Geometry | Part II, 2011

  Let $X$ be a smooth projective curve over an algebraically closed field $k$ of characteristic 0 .

  (i) Let $D$ be a divisor on $X$.

  Define $\mathcal{L}(D)$, and show $\operatorname{dim} \mathcal{L}(D) \leqslant \operatorname{deg} D+1$.

  (ii) Define the space of rational differentials $\Omega_{k(X) / k}^{1}$.

  If $p$ is a point on $X$, and $t$ a local parameter at $p$, show that $\Omega_{k(X) / k}^{1}=k(X) d t$.

  Use that equality to give a definition of $v_{p}(\omega) \in \mathbb{Z}$, for $\omega \in \Omega_{k(X) / k}^{1}, p \in X$. [You need not show that your definition is independent of the choice of local parameter.]

  comment

• Paper 4, Section II, H

  Algebraic Geometry | Part II, 2011

  Let $X$ be a smooth projective curve over an algebraically closed field $k$.

  State the Riemann-Roch theorem, briefly defining all the terms that appear.

  Now suppose $X$ has genus 1 , and let $P_{\infty} \in X$.

  Compute $\mathcal{L}\left(n P_{\infty}\right)$ for $n \leqslant 6$. Show that $\phi_{3 P_{\infty}}$ defines an isomorphism of $X$ with a smooth plane curve in $\mathbb{P}^{2}$ which is defined by a polynomial of degree 3 .

  comment

Algebraic Topology

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2011

  Are the following statements true or false? Justify your answers.

  (i) If $x$ and $y$ lie in the same path-component of $X$, then $\Pi_{1}(X, x) \cong \Pi_{1}(X, y)$.

  (ii) If $x$ and $y$ are two points of the Klein bottle $K$, and $u$ and $v$ are two paths from $x$ to $y$, then $u$ and $v$ induce the same isomorphism from $\Pi_{1}(K, x)$ to $\Pi_{1}(K, y)$.

  (iii) $\Pi_{1}(X \times Y,(x, y))$ is isomorphic to $\Pi_{1}(X, x) \times \Pi_{1}(Y, y)$ for any two spaces $X$ and $Y$.

  (iv) If $X$ and $Y$ are connected polyhedra and $H_{1}(X) \cong H_{1}(Y)$, then $\Pi_{1}(X) \cong \Pi_{1}(Y)$.

  comment

• Paper 2, Section II, H

  Algebraic Topology | Part II, 2011

  Explain what is meant by a covering projection. State and prove the pathlifting property for covering projections, and indicate briefly how it generalizes to a lifting property for homotopies between paths. [You may assume the Lebesgue Covering Theorem.]

  Let $X$ be a simply connected space, and let $G$ be a subgroup of the group of all homeomorphisms $X \rightarrow X$. Suppose that, for each $x \in X$, there exists an open neighbourhood $U$ of $x$ such that $U \cap g[U]=\emptyset$ for each $g \in G$ other than the identity. Show that the projection $p: X \rightarrow X / G$ is a covering projection, and deduce that $\Pi_{1}(X / G) \cong G$.

  By regarding $S^{3}$ as the set of all quaternions of modulus 1 , or otherwise, show that there is a quotient space of $S^{3}$ whose fundamental group is a non-abelian group of order $8 .$

  comment

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2011

  Let $K$ and $L$ be (finite) simplicial complexes. Explain carefully what is meant by a simplicial approximation to a continuous map $f:|K| \rightarrow|L|$. Indicate briefly how the cartesian product $|K| \times|L|$ may be triangulated.

  Two simplicial maps $g, h: K \rightarrow L$ are said to be contiguous if, for each simplex $\sigma$ of $K$, there exists a simplex $\sigma *$ of $L$ such that both $g(\sigma)$ and $h(\sigma)$ are faces of $\sigma *$. Show that:

  (i) any two simplicial approximations to a given map $f:|K| \rightarrow|L|$ are contiguous;

  (ii) if $g$ and $h$ are contiguous, then they induce homotopic maps $|K| \rightarrow|L|$;

  (iii) if $f$ and $g$ are homotopic maps $|K| \rightarrow|L|$, then for some subdivision $K^{(n)}$ of $K$ there exists a sequence $\left(h_{1}, h_{2}, \ldots, h_{m}\right)$ of simplicial maps $K^{(n)} \rightarrow L$ such that $h_{1}$ is a simplicial approximation to $f, h_{m}$ is a simplicial approximation to $g$ and each pair $\left(h_{i}, h_{i+1}\right)$ is contiguous.

  comment

• Paper 4, Section II, H

  Algebraic Topology | Part II, 2011

  State the Mayer-Vietoris theorem, and use it to calculate, for each integer $q>1$, the homology group of the space $X_{q}$ obtained from the unit disc $B^{2} \subseteq \mathbb{C}$ by identifying pairs of points $\left(z_{1}, z_{2}\right)$ on its boundary whenever $z_{1}^{q}=z_{2}^{q}$. [You should construct an explicit triangulation of $X_{q}$.]

  Show also how the theorem may be used to calculate the homology groups of the suspension $S K$ of a connected simplicial complex $K$ in terms of the homology groups of $K$, and of the wedge union $X \vee Y$ of two connected polyhedra. Hence show that, for any finite sequence $\left(G_{1}, G_{2}, \ldots, G_{n}\right)$ of finitely-generated abelian groups, there exists a polyhedron $X$ such that $H_{0}(X) \cong \mathbb{Z}, H_{i}(X) \cong G_{i}$ for $1 \leqslant i \leqslant n$ and $H_{i}(X)=0$ for $i>n$. [You may assume the structure theorem which asserts that any finitely-generated abelian group is isomorphic to a finite direct sum of (finite or infinite) cyclic groups.]

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, E

  Applications of Quantum Mechanics | Part II, 2011

  In one dimension a particle of mass $m$ and momentum $\hbar k, k>0$, is scattered by a potential $V(x)$ where $V(x) \rightarrow 0$ as $|x| \rightarrow \infty$. Incoming and outgoing plane waves of positive $(+)$ and negative $(-)$ parity are given, respectively, by

  $$\begin{array}{ll} I_{+}(k, x)=e^{-i k|x|}, & I_{-}(k, x)=\operatorname{sgn}(x) e^{-i k|x|} \\ O_{+}(k, x)=e^{i k|x|}, & O_{-}(k, x)=-\operatorname{sgn}(x) e^{i k|x|} \end{array}$$

  The scattering solutions to the time-independent Schrödinger equation with positive and negative parity incoming waves are $\psi_{+}(x)$ and $\psi_{-}(x)$, respectively. State how the asymptotic behaviour of $\psi_{+}$and $\psi_{-}$can be expressed in terms of $I_{+}, I_{-}, O_{+}, O_{-}$and the S-matrix denoted by

  $$\boldsymbol{S}=\left(\begin{array}{cc} S_{++} & S_{+-} \\ S_{-+} & S_{--} \end{array}\right)$$

  In the case where $V(x)=V(-x)$ explain briefly why you expect $S_{+-}=S_{-+}=0$.

  The potential $V(x)$ is given by

  $$V(x)=V_{0}[\delta(x-a)+\delta(x+a)]$$

  where $V_{0}$ is a constant. In this case, show that

  $$S_{--}(k)=e^{-2 i k a}\left[\frac{\left(2 k-i U_{0}\right) e^{i k a}+i U_{0} e^{-i k a}}{\left(2 k+i U_{0}\right) e^{-i k a}-i U_{0} e^{i k a}}\right]$$

  where $U_{0}=2 m V_{0} / \hbar^{2}$. Verify that $\left|S_{--}\right|^{2}=1$ and explain briefly the physical meaning of this result.

  For $V_{0}<0$, by considering the poles or zeros of $S_{--}(k)$ show that there exists one bound state of negative parity in this potential if $U_{0} a<-1$.

  For $V_{0}>0$ and $U_{0} a \gg 1$, show that $S_{--}(k)$ has a pole at

  $$k a=\pi+\alpha-i \gamma$$

  where, to leading order in $1 /\left(U_{0} a\right)$,

  $$\alpha=-\frac{\pi}{U_{0} a}, \quad \gamma=\left(\frac{\pi}{U_{0} a}\right)^{2}$$

  Explain briefy the physical meaning of this result, and why you expect that $\gamma>0$.

  comment

• Paper 2, Section II, E

  Applications of Quantum Mechanics | Part II, 2011

  A beam of particles of mass $m$ and momentum $p=\hbar k$, incident along the $z$-axis, is scattered by a spherically symmetric potential $V(r)$, where $V(r)=0$ for large $r$. State the boundary conditions on the wavefunction as $r \rightarrow \infty$ and hence define the scattering amplitude $f(\theta)$, where $\theta$ is the scattering angle.

  Given that, for large $r$,

  $$e^{i k r \cos \theta}=\frac{1}{2 i k r} \sum_{l=0}^{\infty}(2 l+1)\left(e^{i k r}-(-1)^{l} e^{-i k r}\right) P_{l}(\cos \theta)$$

  explain how the partial-wave expansion can be used to define the phase shifts $\delta_{l}(k)(l=$ $0,1,2, \ldots)$. Furthermore, given that $d \sigma / d \Omega=|f(\theta)|^{2}$, derive expressions for $f(\theta)$ and the total cross-section $\sigma$ in terms of the $\delta_{l}$.

  In a particular case $V(r)$ is given by

  $$V(r)=\left\{\begin{array}{cl} \infty, & r<a \\ -V_{0}, & a<r<2 a \\ 0, & r>2 a \end{array}\right.$$

  where $V_{0}>0$. Show that the $\mathrm{S}$-wave phase shift $\delta_{0}$ satisfies

  $$\tan \left(\delta_{0}\right)=\frac{k \cos (2 k a)-\kappa \cot (\kappa a) \sin (2 k a)}{k \sin (2 k a)+\kappa \cot (\kappa a) \cos (2 k a)},$$

  where $\kappa^{2}=2 m V_{0} / \hbar^{2}+k^{2}$.

  Derive an expression for the scattering length $a_{s}$ in terms of $\kappa$. Find the values of $\kappa$ for which $\left|a_{s}\right|$ diverges and briefly explain their physical significance.

  comment

• Paper 3, Section II, E

  Applications of Quantum Mechanics | Part II, 2011

  An electron of mass $m$ moves in a $D$-dimensional periodic potential that satisfies the periodicity condition

  $$V(\boldsymbol{r}+\boldsymbol{l})=V(\boldsymbol{r}) \quad \forall l \in \Lambda,$$

  where $\Lambda$ is a D-dimensional Bravais lattice. State Bloch's theorem for the energy eigenfunctions of the electron.

  For a one-dimensional potential $V(x)$ such that $V(x+a)=V(x)$, give a full account of how the "nearly free electron model" leads to a band structure for the energy levels.

  Explain briefly the idea of a Fermi surface and its rôle in explaining the existence of conductors and insulators.

  comment

• Paper 4, Section II, E

  Applications of Quantum Mechanics | Part II, 2011

  A particle of charge $-e$ and mass $m$ moves in a magnetic field $\boldsymbol{B}(\boldsymbol{x}, t)$ and in an electric potential $\phi(\boldsymbol{x}, t)$. The time-dependent Schrödinger equation for the particle's wavefunction $\Psi(\boldsymbol{x}, t)$ is

  $$i \hbar\left(\frac{\partial}{\partial t}-\frac{i e}{\hbar} \phi\right) \Psi=-\frac{\hbar^{2}}{2 m}\left(\nabla+\frac{i e}{\hbar} \boldsymbol{A}\right)^{2} \Psi$$

  where $\boldsymbol{A}$ is the vector potential with $\boldsymbol{B}=\boldsymbol{\nabla} \wedge \boldsymbol{A}$. Show that this equation is invariant under the gauge transformations

  $$\begin{array}{ll} \boldsymbol{A}(\boldsymbol{x}, t) & \rightarrow \boldsymbol{A}(\boldsymbol{x}, t)+\boldsymbol{\nabla} f(\boldsymbol{x}, t) \\ \phi(\boldsymbol{x}, t) & \rightarrow \quad \phi(\boldsymbol{x}, t)-\frac{\partial}{\partial t} f(\boldsymbol{x}, t) \end{array}$$

  where $f$ is an arbitrary function, together with a suitable transformation for $\Psi$ which should be stated.

  Assume now that $\partial \Psi / \partial z=0$, so that the particle motion is only in the $x$ and $y$ directions. Let $\boldsymbol{B}$ be the constant field $\boldsymbol{B}=(0,0, B)$ and let $\phi=0$. In the gauge where $\boldsymbol{A}=(-B y, 0,0)$ show that the stationary states are given by

  $$\Psi_{k}(\boldsymbol{x}, t)=\psi_{k}(\boldsymbol{x}) e^{-i E t / \hbar}$$

  with

  $$\psi_{k}(\boldsymbol{x})=e^{i k x} \chi_{k}(y)$$

  Show that $\chi_{k}(y)$ is the wavefunction for a simple one-dimensional harmonic oscillator centred at position $y_{0}=\hbar k / e B$. Deduce that the stationary states lie in infinitely degenerate levels (Landau levels) labelled by the integer $n \geqslant 0$, with energy

  $$E_{n}=(2 n+1) \frac{\hbar e B}{2 m}$$

  A uniform electric field $\mathcal{E}$ is applied in the $y$-direction so that $\phi=-\mathcal{E} y$. Show that the stationary states are given by $(*)$, where $\chi_{k}(y)$ is a harmonic oscillator wavefunction centred now at

  $$y_{0}=\frac{1}{e B}\left(\hbar k-m \frac{\mathcal{E}}{B}\right)$$

  Show also that the eigen-energies are given by

  $$E_{n, k}=(2 n+1) \frac{\hbar e B}{2 m}+e \mathcal{E} y_{0}+\frac{m \mathcal{E}^{2}}{2 B^{2}} .$$

  Why does this mean that the Landau energy levels are no longer degenerate in two dimensions?

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2011

  (i) Let $X$ be a Markov chain with finitely many states. Define a stopping time and state the strong Markov property.

  (ii) Let $X$ be a Markov chain with state-space $\{-1,0,1\}$ and Q-matrix

  $$Q=\left(\begin{array}{ccc} -(q+\lambda) & \lambda & q \\ 0 & 0 & 0 \\ q & \lambda & -(q+\lambda) \end{array}\right), \text { where } q, \lambda>0$$

  Consider the integral $\int_{0}^{t} X(s) \mathrm{d} s$, the signed difference between the times spent by the chain at states $+1$ and $-1$ by time $t$, and let

  $$\begin{aligned} Y &=\sup \left[\int_{0}^{t} X(s) \mathrm{d} s: t>0\right] \\ \psi_{\pm}(c) &=\mathbb{P}\left(Y>c \mid X_{0}=\pm 1\right), \quad c>0 \end{aligned}$$

  Derive the equation

  $$\psi_{-}(c)=\int_{0}^{\infty} q e^{-(\lambda+q) u_{+}} \psi_{+}(c+u) \mathrm{d} u$$

  (iii) Obtain another equation relating $\psi_{+}$to $\psi_{-}$.

  (iv) Assuming that $\psi_{+}(c)=e^{-c A}, c>0$, where $A$ is a non-negative constant, calculate $A$.

  (v) Give an intuitive explanation why the function $\psi_{+}$must have the exponential form $\psi_{+}(c)=e^{-c A}$ for some $A$.

  comment

• Paper 2, Section II, J

  Applied Probability | Part II, 2011

  (i) Explain briefly what is meant by saying that a continuous-time Markov chain $X(t)$ is a birth-and-death process with birth rates $\lambda_{i}>0, i \geqslant 0$, and death rates $\mu_{i}>0$, $i \geqslant 1$.

  (ii) In the case where $X(t)$ is recurrent, find a sufficient condition on the birth and death parameters to ensure that

  $$\lim _{t \rightarrow \infty} \mathbb{P}(X(t)=j)=\pi_{j}>0, \quad j \geqslant 0$$

  and express $\pi_{j}$ in terms of these parameters. State the reversibility property of $X(t)$.

  Jobs arrive according to a Poisson process of rate $\lambda>0$. They are processed individually, by a single server, the processing times being independent random variables, each with the exponential distribution of rate $\nu>0$. After processing, the job either leaves the system, with probability $p, 0<p<1$, or, with probability $1-p$, it splits into two separate jobs which are both sent to join the queue for processing again. Let $X(t)$ denote the number of jobs in the system at time $t$.

  (iii) In the case $1+\lambda / \nu<2 p$, evaluate $\lim _{t \rightarrow \infty} \mathbb{P}(X(t)=j), j=0,1, \ldots$, and find the expected time that the processor is busy between two successive idle periods.

  (iv) What happens if $1+\lambda / \nu \geqslant 2 p$ ?

  comment

• Paper 3, Section II, J

  Applied Probability | Part II, 2011

  (i) Define an inhomogeneous Poisson process with rate function $\lambda(u)$.

  (ii) Show that the number of arrivals in an inhomogeneous Poisson process during the interval $(0, t)$ has the Poisson distribution with mean

  $$\int_{0}^{t} \lambda(u) \mathrm{d} u$$

  (iii) Suppose that $\Lambda=\{\Lambda(t), t \geqslant 0\}$ is a non-negative real-valued random process. Conditional on $\Lambda$, let $N=\{N(t), t \geqslant 0\}$ be an inhomogeneous Poisson process with rate function $\Lambda(u)$. Such a process $N$ is called a doubly-stochastic Poisson process. Show that the variance of $N(t)$ cannot be less than its mean.

  (iv) Now consider the process $M(t)$ obtained by deleting every odd-numbered point in an ordinary Poisson process of rate $\lambda$. Check that

  $$\mathbb{E} M(t)=\frac{2 \lambda t+e^{-2 \lambda t}-1}{4}, \quad \operatorname{Var} M(t)=\frac{4 \lambda t-8 \lambda t e^{-2 \lambda t}-e^{-4 \lambda t}+1}{16}$$

  Deduce that $M(t)$ is not a doubly-stochastic Poisson process.

  comment

• Paper 4, Section II, J

  Applied Probability | Part II, 2011

  At an $\mathrm{M} / \mathrm{G} / 1$ queue, the arrival times form a Poisson process of rate $\lambda$ while service times $S_{1}, S_{2}, \ldots$ are independent of each other and of the arrival times and have a common distribution $G$ with mean $\mathbb{E} S_{1}<+\infty$.

  (i) Show that the random variables $Q_{n}$ giving the number of customers left in the queue at departure times form a Markov chain.

  (ii) Specify the transition probabilities of this chain as integrals in $\mathrm{d} G(t)$ involving parameter $\lambda$. [No proofs are needed.]

  (iii) Assuming that $\rho=\lambda \mathbb{E} S_{1}<1$ and the chain $\left(Q_{n}\right)$ is positive recurrent, show that its stationary distribution $\left(\pi_{k}, k \geqslant 0\right)$ has the generating function given by

  $$\sum_{k \geqslant 0} \pi_{k} s^{k}=\frac{(1-\rho)(s-1) g(s)}{s-g(s)},|s| \leqslant 1$$

  for an appropriate function $g$, to be specified.

  (iv) Deduce that, in equilibrium, $Q_{n}$ has the mean value

  $$\rho+\frac{\lambda^{2} \mathbb{E} S_{1}^{2}}{2(1-\rho)}$$

  comment

Asymptotic Methods

• Paper 1, Section II, A

  Asymptotic Methods | Part II, 2011

  A function $f(n)$, defined for positive integer $n$, has an asymptotic expansion for large $n$ of the following form:

  $$f(n) \sim \sum_{k=0}^{\infty} a_{k} \frac{1}{n^{2 k}}, \quad n \rightarrow \infty$$

  What precisely does this mean?

  Show that the integral

  $$I(n)=\int_{0}^{2 \pi} \frac{\cos n t}{1+t^{2}} d t$$

  has an asymptotic expansion of the form $(*)$. [The Riemann-Lebesgue lemma may be used without proof.] Evaluate the coefficients $a_{0}, a_{1}$ and $a_{2}$.

  comment

• Paper 3, Section II, A

  Asymptotic Methods | Part II, 2011

  Let

  $$I_{0}=\int_{C_{0}} e^{x \phi(z)} d z \text {, }$$

  where $\phi(z)$ is a complex analytic function and $C_{0}$ is a steepest descent contour from a simple saddle point of $\phi(z)$ at $z_{0}$. Establish the following leading asymptotic approximation, for large real $x$ :

  $$I_{0} \sim i \sqrt{\frac{\pi}{2 \phi^{\prime \prime}\left(z_{0}\right) x}} e^{x \phi\left(z_{0}\right)}$$

  Let $n$ be a positive integer, and let

  $$I=\int_{C} e^{-t^{2}-2 n \ln t} d t$$

  where $C$ is a contour in the upper half $t$-plane connecting $t=-\infty$ to $t=\infty$, and $\ln t$ is real on the positive $t$-axis with a branch cut along the negative $t$-axis. Using the method of steepest descent, find the leading asymptotic approximation to $I$ for large $n$.

  comment

• Paper 4, Section II, A

  Asymptotic Methods | Part II, 2011

  Determine the range of the integer $n$ for which the equation

  $$\frac{d^{2} y}{d z^{2}}=z^{n} y$$

  has an essential singularity at $z=\infty$.

  Use the Liouville-Green method to find the leading asymptotic approximation to two independent solutions of

  $$\frac{d^{2} y}{d z^{2}}=z^{3} y$$

  for large $|z|$. Find the Stokes lines for these approximate solutions. For what range of $\arg z$ is the approximate solution which decays exponentially along the positive $z$-axis an asymptotic approximation to an exact solution with this exponential decay?

  comment

Classical Dynamics

• Paper 1, Section I, C

  Classical Dynamics | Part II, 2011

  (i) A particle of mass $m$ and charge $q$, at position $\mathbf{x}$, moves in an electromagnetic field with scalar potential $\phi(\mathbf{x}, t)$ and vector potential $\mathbf{A}(\mathbf{x}, t)$. Verify that the Lagrangian

  $$L=\frac{1}{2} m \dot{\mathbf{x}}^{2}-q(\phi-\dot{\mathbf{x}} \cdot \mathbf{A})$$

  gives the correct equations of motion.

  [Note that $\mathbf{E}=-\nabla \phi-\dot{\mathbf{A}}$ and $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}$.]

  (ii) Consider the case of a constant uniform magnetic field, with $\mathbf{E}=\mathbf{0}$, given by $\phi=0$, $\mathbf{A}=(0, x B, 0)$, where $(x, y, z)$ are Cartesian coordinates and $B$ is a constant. Find the motion of the particle, and describe it carefully.

  comment

• Paper 2, Section I, C

  Classical Dynamics | Part II, 2011

  Three particles, each of mass $m$, move along a straight line. Their positions on the line containing the origin, $O$, are $x_{1}, x_{2}$ and $x_{3}$. They are subject to forces derived from the potential energy function

  $$V=\frac{1}{2} m \Omega^{2}\left[\left(x_{1}-x_{2}\right)^{2}+\left(x_{2}-x_{3}\right)^{2}+\left(x_{3}-x_{1}\right)^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right]$$

  Obtain Lagrange's equations for the system, and show that the frequency, $\omega$, of a normal mode satisfies

  $$f^{3}-9 f^{2}+24 f-16=0$$

  where $f=\left(\omega^{2} / \Omega^{2}\right)$. Find a complete set of normal modes for the system, and draw a diagram indicating the nature of the corresponding motions.

  comment

• Paper 2, Section II, C

  Classical Dynamics | Part II, 2011

  Derive Euler's equations governing the torque-free and force-free motion of a rigid body with principal moments of inertia $I_{1}, I_{2}$ and $I_{3}$, where $I_{1}<I_{2}<I_{3}$. Identify two constants of the motion. Hence, or otherwise, find the equilibrium configurations such that the angular-momentum vector, as measured with respect to axes fixed in the body, remains constant. Discuss the stability of these configurations.

  A spacecraft may be regarded as moving in a torque-free and force-free environment. Nevertheless, flexing of various parts of the frame can cause significant dissipation of energy. How does the angular-momentum vector ultimately align itself within the body?

  comment

• Paper 3, Section I, $\mathbf{9 C}$

  Classical Dynamics | Part II, 2011

  The Lagrangian for a heavy symmetric top is

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  State Noether's Theorem. Hence, or otherwise, find two conserved quantities linear in momenta, and a third conserved quantity quadratic in momenta.

  Writing $\mu=\cos \theta$, deduce that $\mu$ obeys an equation of the form

  $$\dot{\mu}^{2}=F(\mu)$$

  where $F(\mu)$ is cubic in $\mu$. [You need not determine the explicit form of $F(\mu) .$ ]

  comment

• Paper 4, Section I, C

  Classical Dynamics | Part II, 2011

  (i) A dynamical system is described by the Hamiltonian $H\left(q_{i}, p_{i}\right)$. Define the Poisson bracket $\{f, g\}$ of two functions $f\left(q_{i}, p_{i}, t\right), g\left(q_{i}, p_{i}, t\right)$. Assuming the Hamiltonian equations of motion, find an expression for $d f / d t$ in terms of the Poisson bracket.

  (ii) A one-dimensional system has the Hamiltonian

  $$H=p^{2}+\frac{1}{q^{2}}$$

  Show that $u=p q-2 H t$ is a constant of the motion. Deduce the form of $(q(t), p(t))$ along a classical path, in terms of the constants $u$ and $H$.

  comment

• Paper 4, Section II, C

  Classical Dynamics | Part II, 2011

  Given a Hamiltonian system with variables $\left(q_{i}, p_{i}\right), i=1, \ldots, n$, state the definition of a canonical transformation

  $$\left(q_{i}, p_{i}\right) \rightarrow\left(Q_{i}, P_{i}\right),$$

  where $\mathbf{Q}=\mathbf{Q}(\mathbf{q}, \mathbf{p}, t)$ and $\mathbf{P}=\mathbf{P}(\mathbf{q}, \mathbf{p}, t)$. Write down a matrix equation that is equivalent to the condition that the transformation is canonical.

  Consider a harmonic oscillator of unit mass, with Hamiltonian

  $$H=\frac{1}{2}\left(p^{2}+\omega^{2} q^{2}\right) .$$

  Write down the Hamilton-Jacobi equation for Hamilton's principal function $S(q, E, t)$, and deduce the Hamilton-Jacobi equation

  $$\frac{1}{2}\left[\left(\frac{\partial W}{\partial q}\right)^{2}+\omega^{2} q^{2}\right]=E$$

  for Hamilton's characteristic function $W(q, E)$.

  Solve (1) to obtain an integral expression for $W$, and deduce that, at energy $E$,

  $$S=\sqrt{2 E} \int d q \sqrt{\left(1-\frac{\omega^{2} q^{2}}{2 E}\right)}-E t$$

  Let $\alpha=E$, and define the angular coordinate

  $$\beta=\left(\frac{\partial S}{\partial E}\right)_{q, t}$$

  You may assume that (2) implies

  $$t+\beta=\left(\frac{1}{\omega}\right) \arcsin \left(\frac{\omega q}{\sqrt{2 E}}\right)$$

  Deduce that

  $$p=\frac{\partial S}{\partial q}=\frac{\partial W}{\partial q}=\sqrt{\left(2 E-\omega^{2} q^{2}\right)}$$

  from which

  $$p=\sqrt{2 E} \cos [\omega(t+\beta)] .$$

  Hence, or otherwise, show that the transformation from variables $(q, p)$ to $(\alpha, \beta)$ is canonical.

  comment

Coding and Cryptography

• Paper 1, Section I, G

  Coding and Cryptography | Part II, 2011

  I think of an integer $n$ with $1 \leqslant n \leqslant 10^{6}$. Explain how to find $n$ using twenty questions (or less) of the form 'Is it true that $n \geqslant m$ ?' to which I answer yes or no.

  I have watched a horse race with 15 horses. Is it possible to discover the order in which the horses finished by asking me twenty questions to which I answer yes or no?

  Roughly how many questions of the yes/no type are required to discover the order in which $n$ horses finished if $n$ is large?

  [You may assume that I answer honestly.]

  comment

• Paper 1, Section II, $12 G$

  Coding and Cryptography | Part II, 2011

  Describe the Rabin-Williams coding scheme. Show that any method for breaking it will enable us to factorise the product of two primes.

  Explain how the Rabin-Williams scheme can be used for bit sharing (that is to say 'tossing coins by phone').

  comment

• Paper 2, Section I, G

  Coding and Cryptography | Part II, 2011

  I happen to know that an apparently fair coin actually has probability $p$ of heads with $1>p>1 / 2$. I play a very long sequence of games of heads and tails in which my opponent pays me back twice my stake if the coin comes down heads and takes my stake if the coin comes down tails. I decide to bet a proportion $\alpha$ of my fortune at the end of the $n$th game in the $(n+1)$ st game. Determine, giving justification, the value $\alpha_{0}$ maximizing the expected logarithm of my fortune in the long term, assuming I use the same $\alpha_{0}$ at each game. Can it be actually disadvantageous for me to choose an $\alpha<\alpha_{0}$ (in the sense that I would be better off not playing)? Can it be actually disadvantageous for me to choose an $\alpha>\alpha_{0}$ ?

  [Moral issues should be ignored.]

  comment

• Paper 2, Section II, G

  Coding and Cryptography | Part II, 2011

  Define a cyclic code. Show that there is a bijection between the cyclic codes of length $n$ and the factors of $X^{n}-1$ over the field $\mathbb{F}_{2}$ of order 2 .

  What is meant by saying that $\alpha$ is a primitive $n$th root of unity in a finite field extension $K$ of $\mathbb{F}_{2}$ ? What is meant by saying that $C$ is a BCH code of length $n$ with defining set $\left\{\alpha, \alpha^{2}, \ldots, \alpha^{\delta-1}\right\}$ ? Show that such a code has minimum distance at least $\delta$.

  Suppose that $K$ is a finite field extension of $\mathbb{F}_{2}$ in which $X^{7}-1$ factorises into linear factors. Show that if $\beta$ is a root of $X^{3}+X^{2}+1$ then $\beta$ is a primitive 7 th root of unity and $\beta^{2}$ is also a root of $X^{3}+X^{2}+1$. Quoting any further results that you need show that the $\mathrm{BCH}$ code of length 7 with defining set $\left\{\beta, \beta^{2}\right\}$ is the Hamming code.

  [Results on the Vandermonde determinant may be used without proof provided they are quoted correctly.]

  comment

• Paper 3, Section I, G

  Coding and Cryptography | Part II, 2011

  What is the rank of a binary linear code $C ?$ What is the weight enumeration polynomial $W_{C}$ of $C ?$

  Show that $W_{C}(1,1)=2^{r}$ where $r$ is the rank of $C$. Show that $W_{C}(s, t)=W_{C}(t, s)$ for all $s$ and $t$ if and only if $W_{C}(1,0)=1$.

  Find, with reasons, the weight enumeration polynomial of the repetition code of length $n$, and of the simple parity check code of length $n$.

  comment

• Paper 4, Section I, G

  Coding and Cryptography | Part II, 2011

  Describe a scheme for sending messages based on quantum theory which is not vulnerable to eavesdropping. You may ignore engineering problems.

  comment

Cosmology

• Paper 1, Section I, E

  Cosmology | Part II, 2011

  Light of wavelength $\lambda_{e}$ emitted by a distant object is observed by us to have wavelength $\lambda_{0}$. The redshift $z$ of the object is defined by

  $$1+z=\frac{\lambda_{0}}{\lambda_{e}}$$

  Assuming that the object is at a fixed comoving distance from us in a homogeneous and isotropic universe with scale factor $a(t)$, show that

  $$1+z=\frac{a\left(t_{0}\right)}{a\left(t_{e}\right)}$$

  where $t_{e}$ is the time of emission and $t_{0}$ the time of observation (i.e. today).

  [You may assume the non-relativistic Doppler shift formula $\Delta \lambda / \lambda=(v / c) \cos \theta$ for the shift $\Delta \lambda$ in the wavelength of light emitted by a nearby object travelling with velocity $v$ at angle $\theta$ to the line of sight.]

  Given that the object radiates energy $L$ per unit time, explain why the rate at which energy passes through a sphere centred on the object and intersecting the Earth is $L /(1+z)^{2}$.

  comment

• Paper 1, Section II, E

  Cosmology | Part II, 2011

  A homogeneous and isotropic universe, with scale factor $a$, curvature parameter $k$, energy density $\rho$ and pressure $P$, satisfies the Friedmann and energy conservation equations

  $$\begin{aligned} &H^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho \\ &\dot{\rho}+3 H\left(\rho+P / c^{2}\right)=0 \end{aligned}$$

  where $H=\dot{a} / a$, and the dot indicates a derivative with respect to cosmological time $t$.

  (i) Derive the acceleration equation

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)$$

  Given that the strong energy condition $\rho c^{2}+3 P \geqslant 0$ is satisfied, show that $(a H)^{2}$ is a decreasing function of $t$ in an expanding universe. Show also that the density parameter $\Omega=8 \pi G \rho /\left(3 H^{2}\right)$ satisfies

  $$\Omega-1=\frac{k c^{2}}{a^{2} H^{2}}$$

  Hence explain, briefly, the flatness problem of standard big bang cosmology.

  (ii) A flat $(k=0)$ homogeneous and isotropic universe is filled with a radiation fluid $\left(w_{R}=1 / 3\right)$ and a dark energy fluid $\left(w_{\Lambda}=-1\right)$, each with an equation of state of the form $P_{i}=w_{i} \rho_{i} c^{2}$ and density parameters today equal to $\Omega_{R 0}$ and $\Omega_{\Lambda 0}$ respectively. Given that each fluid independently obeys the energy conservation equation, show that the total energy density $\left(\rho_{R}+\rho_{\Lambda}\right) c^{2}$ equals $\rho c^{2}$, where

  $$\rho(t)=\frac{3 H_{0}^{2}}{8 \pi G} \frac{\Omega_{R 0}}{a^{4}}\left(1+\frac{1-\Omega_{R 0}}{\Omega_{R 0}} a^{4}\right)$$

  with $H_{0}$ being the value of the Hubble parameter today. Hence solve the Friedmann equation to get

  $$a(t)=\alpha(\sinh \beta t)^{1 / 2}$$

  where $\alpha$ and $\beta$ should be expressed in terms $\Omega_{R 0}$ and $\Omega_{\Lambda 0}$. Show that this result agrees with the expected asymptotic solutions at both early $(t \rightarrow 0)$ and late $(t \rightarrow \infty)$ times.

  [Hint: $\int d x / \sqrt{x^{2}+1}=\operatorname{arcsinh} x$.]

  comment

• Paper 2, Section I, E

  Cosmology | Part II, 2011

  A spherically symmetric star in hydrostatic equilibrium has density $\rho(r)$ and pressure $P(r)$, which satisfy the pressure support equation,

  $$\frac{d P}{d r}=-\frac{G m \rho}{r^{2}}$$

  where $m(r)$ is the mass within a radius $r$. Show that this implies

  $$\frac{d}{d r}\left(\frac{r^{2}}{\rho} \frac{d P}{d r}\right)=-4 \pi G r^{2} \rho .$$

  Provide a justification for choosing the boundary conditions $d P / d r=0$ at the centre of the $\operatorname{star}(r=0)$ and $P=0$ at its outer radius $(r=R)$.

  Use the pressure support equation $(*)$ to derive the virial theorem for a star,

  $$\langle P\rangle V=-\frac{1}{3} E_{\mathrm{grav}}$$

  where $\langle P\rangle$ is the average pressure, $V$ is the total volume of the star and $E_{\text {grav }}$ is its total gravitational potential energy.

  comment

• Paper 3, Section I, E

  Cosmology | Part II, 2011

  For an ideal gas of fermions of mass $m$ in volume $V$, and at temperature $T$ and chemical potential $\mu$, the number density $n$ and kinetic energy $E$ are given by

  $$n=\frac{4 \pi g_{s}}{h^{3}} \int_{0}^{\infty} \bar{n}(p) p^{2} d p, \quad E=\frac{4 \pi g_{s}}{h^{3}} V \int_{0}^{\infty} \bar{n}(p) \epsilon(p) p^{2} d p$$

  where $g_{s}$ is the spin-degeneracy factor, $h$ is Planck's constant, $\epsilon(p)=c \sqrt{p^{2}+m^{2} c^{2}}$ is the single-particle energy as a function of the momentum $p$, and

  $$\bar{n}(p)=\left[\exp \left(\frac{\epsilon(p)-\mu}{k T}\right)+1\right]^{-1}$$

  where $k$ is Boltzmann's constant.

  (i) Sketch the function $\bar{n}(p)$ at zero temperature, explaining why $\bar{n}(p)=0$ for $p>p_{F}$ (the Fermi momentum). Find an expression for $n$ at zero temperature as a function of $p F$.

  Assuming that a typical fermion is ultra-relativistic $\left(p c \gg m c^{2}\right)$ even at zero temperature, obtain an estimate of the energy density $E / V$ as a function of $p_{F}$, and hence show that

  $$E \sim h c n^{4 / 3} V$$

  in the ultra-relativistic limit at zero temperature.

  (ii) A white dwarf star of radius $R$ has total mass $M=\frac{4 \pi}{3} m_{p} n_{p} R^{3}$, where $m_{p}$ is the proton mass and $n_{p}$ the average proton number density. On the assumption that the star's degenerate electrons are ultra-relativistic, so that $(*)$ applies with $n$ replaced by the average electron number density $n_{e}$, deduce the following estimate for the star's internal kinetic energy:

  $$E_{\mathrm{kin}} \sim h c\left(\frac{M}{m_{p}}\right)^{4 / 3} \frac{1}{R} .$$

  By comparing this with the total gravitational potential energy, briefly discuss the consequences for white dwarf stability.

  comment

• Paper 3, Section II, E

  Cosmology | Part II, 2011

  An expanding universe with scale factor $a(t)$ is filled with (pressure-free) cold dark matter (CDM) of average mass density $\bar{\rho}(t)$. In the Zel'dovich approximation to gravitational clumping, the perturbed position $\mathbf{r}(\mathbf{q}, t)$ of a CDM particle with unperturbed comoving position $\mathbf{q}$ is given by

  $$\mathbf{r}(\mathbf{q}, t)=a(t)[\mathbf{q}+\boldsymbol{\psi}(\mathbf{q}, t)]$$

  where $\psi$ is the comoving displacement.

  (i) Explain why the conservation of CDM particles implies that

  $$\rho(\mathbf{r}, t) d^{3} r=a^{3} \bar{\rho}(t) d^{3} q,$$

  where $\rho(\mathbf{r}, t)$ is the CDM mass density. Use (1) to verify that $d^{3} q=a^{-3}\left[1-\nabla_{\mathbf{q}} \cdot \psi\right] d^{3} r$, and hence deduce that the fractional density perturbation is, to first order,

  $$\delta \equiv \frac{\rho-\bar{\rho}}{\bar{\rho}}=-\nabla_{\mathbf{q}} \cdot \psi \text {. }$$

  Use this result to integrate the Poisson equation $\nabla^{2} \Phi=4 \pi G \bar{\rho}$ for the gravitational potential $\Phi$. Then use the particle equation of motion $\ddot{\mathbf{r}}=-\nabla \Phi$ to deduce a second-order differential equation for $\psi$, and hence that

  $$\ddot{\delta}+2\left(\frac{\dot{a}}{a}\right) \dot{\delta}-4 \pi G \bar{\rho} \delta=0 .$$

  [You may assume that $\nabla^{2} \Phi=4 \pi G \bar{\rho}$ implies $\nabla \Phi=(4 \pi G / 3) \bar{\rho} \mathbf{r}$ and that the pressure-free acceleration equation is $\ddot{a}=-(4 \pi G / 3) \bar{\rho} a .]$

  (ii) A flat matter-dominated universe with background density $\bar{\rho}=\left(6 \pi G t^{2}\right)^{-1}$ has scale factor $a(t)=\left(t / t_{0}\right)^{2 / 3}$. The universe is filled with a pressure-free homogeneous (non-clumping) fluid of mass density $\rho_{H}(t)$, as well as cold dark matter of mass density $\rho_{C}(\mathbf{r}, t)$.

  Assuming that the Zel'dovich perturbation equation in this case is as in (2) but with $\bar{\rho}$ replaced by $\bar{\rho}_{C}$, i.e. that

  $$\ddot{\delta}+2\left(\frac{\dot{a}}{a}\right) \dot{\delta}-4 \pi G \bar{\rho}_{C} \delta=0,$$

  seek power-law solutions $\delta \propto t^{\alpha}$ to find growing and decaying modes with

  $$\alpha=\frac{1}{6}\left(-1 \pm \sqrt{25-24 \Omega_{H}}\right)$$

  where $\Omega_{H}=\rho_{H} / \bar{\rho}$.

  Given that matter domination starts $\left(t=t_{\text {eq }}\right)$ at a redshift $z \approx 10^{5}$, and given an initial perturbation $\delta\left(t_{\mathrm{eq}}\right) \approx 10^{-5}$, show that $\Omega_{H}=2 / 3$ yields a model that is not compatible with the large-scale structure observed today.

  comment

• Paper 4, Section I, 10E

  Cosmology | Part II, 2011

  The equilibrium number density of fermions at temperature $T$ is

  $$n=\frac{4 \pi g_{s}}{h^{3}} \int_{0}^{\infty} \frac{p^{2} d p}{\exp [(\epsilon(p)-\mu) / k T]+1}$$

  where $g_{s}$ is the spin degeneracy and $\epsilon(p)=c \sqrt{p^{2}+m^{2} c^{2}}$. For a non-relativistic gas with $p c \ll m c^{2}$ and $k T \ll m c^{2}-\mu$, show that the number density becomes

  $$n=g_{s}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} \exp \left[\left(\mu-m c^{2}\right) / k T\right]$$

  [You may assume that $\int_{0}^{\infty} d x x^{2} e^{-x^{2} / \alpha}=(\sqrt{\pi} / 4) \alpha^{3 / 2}$ for $\alpha>0$.]

  Before recombination, equilibrium is maintained between neutral hydrogen, free electrons, protons and photons through the interaction

  $$p+e^{-} \leftrightarrow H+\gamma$$

  Using the non-relativistic number density $(*)$, deduce Saha's equation relating the electron and hydrogen number densities,

  $$\frac{n_{e}^{2}}{n_{H}} \approx\left(\frac{2 \pi m_{e} k T}{h^{2}}\right)^{3 / 2} \exp (-I / k T)$$

  where $I=\left(m_{p}+m_{e}-m_{H}\right) c^{2}$ is the ionization energy of hydrogen. State clearly any assumptions you have made.

  comment

Differential Geometry

• Paper 1, Section II, I

  Differential Geometry | Part II, 2011

  Let $X$ and $Y$ be manifolds and $f: X \rightarrow Y$ a smooth map. Define the notions critical point, critical value, regular value of $f$. Prove that if $y$ is a regular value of $f$, then $f^{-1}(y)$ (if non-empty) is a smooth manifold of $\operatorname{dimension} \operatorname{dim} X-\operatorname{dim} Y$.

  [The Inverse Function Theorem may be assumed without proof if accurately stated.]

  Let $M_{n}(\mathbb{R})$ be the set of all real $n \times n$ matrices and $\operatorname{SO}(n) \subset M_{n}(\mathbb{R})$ the group of all orthogonal matrices with determinant 1 . Show that $\mathrm{SO}(n)$ is a smooth manifold and find its dimension.

  Show further that $\mathrm{SO}(n)$ is compact and that its tangent space at $A \in \operatorname{SO}(n)$ is given by all matrices $H$ such that $A H^{t}+H A^{t}=0$.

  comment

• Paper 2, Section II, I

  Differential Geometry | Part II, 2011

  Let $\alpha: I \rightarrow \mathbb{R}^{3}$ be a smooth curve parametrized by arc-length, with $\alpha^{\prime \prime}(s) \neq 0$ for all $s \in I$. Define what is meant by the Frenet frame $t(s), n(s), b(s)$, the curvature and torsion of $\alpha$. State and prove the Frenet formulae.

  By considering $\langle\alpha, t \times n\rangle$, or otherwise, show that, if for each $s \in I$ the vectors $\alpha(s)$, $t(s)$ and $n(s)$ are linearly dependent, then $\alpha(s)$ is a plane curve.

  State and prove the isoperimetric inequality for $C^{1}$ regular plane curves.

  [You may assume Wirtinger's inequality, provided you state it accurately.]

  comment

• Paper 3, Section II, I

  Differential Geometry | Part II, 2011

  For an oriented surface $S$ in $\mathbb{R}^{3}$, define the Gauss map, the second fundamental form and the normal curvature in the direction $w \in T_{p} S$ at a point $p \in S$.

  Let $\tilde{k}_{1}, \ldots, \tilde{k}_{m}$ be normal curvatures at $p$ in the directions $v_{1}, \ldots, v_{m}$, such that the angle between $v_{i}$ and $v_{i+1}$ is $\pi / m$ for each $i=1, \ldots, m-1(m \geqslant 2)$. Show that

  $$\tilde{k}_{1}+\ldots+\tilde{k}_{m}=m H$$

  where $H$ is the mean curvature of $S$ at $p$.

  What is a minimal surface? Show that if $S$ is a minimal surface, then its Gauss $\operatorname{map} N$ at each point $p \in S$ satisfies

  $$\left\langle d N_{p}\left(w_{1}\right), d N_{p}\left(w_{2}\right)\right\rangle=\mu(p)\left\langle w_{1}, w_{2}\right\rangle, \quad \text { for all } w_{1}, w_{2} \in T_{p} S,$$

  where $\mu(p) \in \mathbb{R}$ depends only on $p$. Conversely, if the identity $(*)$ holds at each point in $S$, must $S$ be minimal? Justify your answer.

  comment

• Paper 4, Section II, I

  Differential Geometry | Part II, 2011

  Define what is meant by a geodesic. Let $S \subset \mathbb{R}^{3}$ be an oriented surface. Define the geodesic curvature $k_{g}$ of a smooth curve $\gamma: I \rightarrow S$ parametrized by arc-length.

  Explain without detailed proofs what are the exponential map $\exp _{p}$ and the geodesic polar coordinates $(r, \theta)$ at $p \in S$. Determine the derivative $d\left(\exp _{p}\right)_{0}$. Prove that the coefficients of the first fundamental form of $S$ in the geodesic polar coordinates satisfy

  $$E=1, \quad F=0, \quad G(0, \theta)=0, \quad(\sqrt{G})_{r}(0, \theta)=1$$

  State the global Gauss-Bonnet formula for compact surfaces with boundary. [You should identify all terms in the formula.]

  Suppose that $S$ is homeomorphic to a cylinder $S^{1} \times \mathbb{R}$ and has negative Gaussian curvature at each point. Prove that $S$ has at most one simple (i.e. without selfintersections) closed geodesic.

  [Basic properties of geodesics may be assumed, if accurately stated.]

  comment

Dynamical Systems

• Paper 1, Section I, C

  Dynamical Systems | Part II, 2011

  Find the fixed points of the dynamical system (with $\mu \neq 0$ )

  $$\begin{aligned} &\dot{x}=\mu^{2} x-x y \\ &\dot{y}=-y+x^{2} \end{aligned}$$

  and determine their type as a function of $\mu$.

  Find the stable and unstable manifolds of the origin correct to order $4 .$

  comment

• Paper 2, Section I, C

  Dynamical Systems | Part II, 2011

  State the Poincaré-Bendixson theorem for two-dimensional dynamical systems.

  A dynamical system can be written in polar coordinates $(r, \theta)$ as

  $$\begin{aligned} &\dot{r}=r-r^{3}(1+\alpha \cos \theta) \\ &\dot{\theta}=1-r^{2} \beta \cos \theta \end{aligned}$$

  where $\alpha$ and $\beta$ are constants with $0<\alpha<1$.

  Show that trajectories enter the annulus $(1+\alpha)^{-1 / 2}<r<(1-\alpha)^{-1 / 2}$.

  Show that if there is a fixed point $\left(r_{0}, \theta_{0}\right)$ inside the annulus then $r_{0}^{2}=(\beta-\alpha) / \beta$ and $\cos \theta_{0}=1 /(\beta-\alpha)$.

  Use the Poincaré-Bendixson theorem to derive conditions on $\beta$ that guarantee the existence of a periodic orbit.

  comment

• Paper 3, Section I, C

  Dynamical Systems | Part II, 2011

  For the map $x_{n+1}=\lambda x_{n}\left(1-x_{n}^{2}\right)$, with $\lambda>0$, show the following:

  (i) If $\lambda<1$, then the origin is the only fixed point and is stable.

  (ii) If $\lambda>1$, then the origin is unstable. There are two further fixed points which are stable for $1<\lambda<2$ and unstable for $\lambda>2$.

  (iii) If $\lambda<3 \sqrt{3} / 2$, then $x_{n}$ has the same sign as the starting value $x_{0}$ if $\left|x_{0}\right|<1$.

  (iv) If $\lambda<3$, then $\left|x_{n+1}\right|<2 \sqrt{3} / 3$ when $\left|x_{n}\right|<2 \sqrt{3} / 3$. Deduce that iterates starting sufficiently close to the origin remain bounded, though they may change sign.

  [Hint: For (iii) and (iv) a graphical representation may be helpful.]

  comment

• Paper 3, Section II, C

  Dynamical Systems | Part II, 2011

  Explain what is meant by a steady-state bifurcation of a fixed point $\mathbf{x}_{0}(\mu)$ of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x}, \mu)$ in $\mathbb{R}^{n}$, where $\mu$ is a real parameter.

  Consider the system in $x \geqslant 0, y \geqslant 0$, with $\mu>0$,

  $$\begin{aligned} \dot{x} &=x\left(1-y^{2}-x^{2}\right), \\ \dot{y} &=y\left(\mu-y-x^{2}\right) . \end{aligned}$$

  (i) Show that both the fixed point $(0, \mu)$ and the fixed point $(1,0)$ have a steady-state bifurcation when $\mu=1$.

  (ii) By finding the first approximation to the extended centre manifold, construct the normal form near the bifurcation point $(1,0)$ when $\mu$ is close to unity, and show that there is a transcritical bifurcation there. Explain why the symmetries of the equations mean that the bifurcation at $(0,1)$ must be of pitchfork type.

  (iii) Show that two fixed points with $x, y>0$ exist in the range $1<\mu<5 / 4$. Show that the solution with $y<1 / 2$ is stable. Identify the bifurcation that occurs at $\mu=5 / 4$.

  (iv) Draw a sketch of the values of $y$ at the fixed points as functions of $\mu$, indicating the bifurcation points and the regions where each branch is stable. [Detailed calculations are not required.]

  comment

• Paper 4, Section I, $7 \mathrm{C}$

  Dynamical Systems | Part II, 2011

  (i) Explain the use of the energy balance method for describing approximately the behaviour of nearly Hamiltonian systems.

  (ii) Consider the nearly Hamiltonian dynamical system

  $$\ddot{x}+\epsilon \dot{x}\left(-1+\alpha x^{2}-\beta x^{4}\right)+x=0, \quad 0<\epsilon \ll 1$$

  where $\alpha$ and $\beta$ are positive constants. Show that, for sufficiently small $\epsilon$, the system has periodic orbits if $\alpha^{2}>8 \beta$, and no periodic orbits if $\alpha^{2}<8 \beta$. Show that in the first case there are two periodic orbits, and determine their approximate size and their stability.

  What can you say about the existence of periodic orbits when $\alpha^{2}=8 \beta ?$

  [You may assume that

  $$\left.\int_{0}^{2 \pi} \sin ^{2} t d t=\pi, \quad \int_{0}^{2 \pi} \sin ^{2} t \cos ^{2} t d t=\frac{\pi}{4}, \quad \int_{0}^{2 \pi} \sin ^{2} t \cos ^{4} t d t=\frac{\pi}{8}\right]$$

  comment

• Paper 4, Section II, C

  Dynamical Systems | Part II, 2011

  (i) State and prove Lyapunov's First Theorem, and state (without proof) La Salle's Invariance Principle. Show by example how the latter result can be used to prove asymptotic stability of a fixed point even when a strict Lyapunov function does not exist.

  (ii) Consider the system

  $$\begin{aligned} &\dot{x}=-x+2 y+x^{3}+2 x^{2} y+2 x y^{2}+2 y^{3}, \\ &\dot{y}=-y-x-2 x^{3}+\frac{1}{2} x^{2} y-3 x y^{2}+y^{3} \end{aligned}$$

  Show that the origin is asymptotically stable and that the basin of attraction of the origin includes the region $x^{2}+2 y^{2}<2 / 3$.

  comment

Electrodynamics

• Paper 1, Section II, C

  Electrodynamics | Part II, 2011

  In the Landau-Ginzburg model of superconductivity, the energy of the system is given, for constants $\alpha$ and $\beta$, by

  $$E=\int\left\{\frac{1}{2 \mu_{0}} \mathbf{B}^{2}+\frac{1}{2 m}\left[(i \hbar \nabla-q \mathbf{A}) \psi^{*} \cdot(-i \hbar \nabla-q \mathbf{A}) \psi\right]+\alpha \psi^{*} \psi+\beta\left(\psi^{*} \psi\right)^{2}\right\} d^{3} \mathbf{x},$$

  where $\mathbf{B}$ is the time-independent magnetic field derived from the vector potential $\mathbf{A}$, and $\psi$ is the wavefunction of the charge carriers, which have mass $m$ and charge $q$.

  Describe the physical meaning of each of the terms in the integral.

  Explain why in a superconductor one must choose $\alpha<0$ and $\beta>0$. Find an expression for the number density $n$ of the charge carriers in terms of $\alpha$ and $\beta$.

  Show that the energy is invariant under the gauge transformations

  $$\mathbf{A} \rightarrow \mathbf{A}+\nabla \Lambda, \quad \psi \rightarrow \psi e^{i q \Lambda / \hbar}$$

  Assuming that the number density $n$ is uniform, show that, if $E$ is a minimum under variations of $\mathbf{A}$, then

  $$\operatorname{curl} \mathbf{B}=-\frac{\mu_{0} q^{2} n}{m}\left(\mathbf{A}-\frac{\hbar}{q} \nabla \phi\right)$$

  where $\phi=\arg \psi$.

  Find a formula for $\nabla^{2} \mathbf{B}$ and use it to explain why there cannot be a magnetic field inside the bulk of a superconductor.

  comment

• Paper 3, Section II, C

  Electrodynamics | Part II, 2011

  Explain how time-dependent distributions of electric charge $\rho(\mathbf{x}, t)$ and current $\mathbf{j}(\mathbf{x}, t)$ can be combined into a four-vector $j^{a}(x)$ that obeys $\partial_{a} j^{a}=0$.

  This current generates a four-vector potential $A^{a}(x)$. Explain how to find $A^{a}$ in the gauge $\partial_{a} A^{a}=0$.

  A small circular loop of wire of radius $r$ is centred at the origin. The unit vector normal to the plane of the loop is $\mathbf{n}$. A current $I_{o} \sin \omega t$ flows in the loop. Find the three-vector potential $\mathbf{A}(\mathbf{x}, t)$ to leading order in $r /|\mathbf{x}|$.

  comment

• Paper 4, Section II, C

  Electrodynamics | Part II, 2011

  Suppose that there is a distribution of electric charge given by the charge density $\rho(\mathbf{x})$. Develop the multipole expansion, up to quadrupole terms, for the electrostatic potential $\phi$ and define the dipole and quadrupole moments of the charge distribution.

  A tetrahedron has a vertex at $(1,1,1)$ where there is a point charge of strength $3 q$. At each of the other vertices located at $(1,-1,-1),(-1,1,-1)$ and $(-1,-1,1)$ there is a point charge of strength $-q$.

  What is the dipole moment of this charge distribution?

  What is the quadrupole moment?

  comment

Fluid Dynamics II

• Paper 1, Section II, B

  Fluid Dynamics II | Part II, 2011

  The steady two-dimensional boundary-layer equations for flow primarily in the $x$ direction are

  $$\begin{gathered} \rho\left(u \frac{\partial u}{\partial x}+v \frac{\partial u}{\partial y}\right)=-\frac{d P}{d x}+\mu \frac{\partial^{2} u}{\partial y^{2}} \\ \frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0 \end{gathered}$$

  A thin, steady, two-dimensional jet emerges from a point at the origin and flows along the $x$-axis in a fluid at rest far from the $x$-axis. Show that the momentum flux

  $$F=\int_{-\infty}^{\infty} \rho u^{2} d y$$

  is independent of position $x$ along the jet. Deduce that the thickness $\delta(x)$ of the jet increases along the jet as $x^{2 / 3}$, while the centre-line velocity $U(x)$ decreases as $x^{-1 / 3}$.

  A similarity solution for the jet is sought with a streamfunction $\psi$ of the form

  $$\psi(x, y)=U(x) \delta(x) f(\eta) \quad \text { with } \quad \eta=y / \delta(x) .$$

  Derive the nonlinear third-order non-dimensional differential equation governing $f$, and write down the boundary and normalisation conditions which must be applied.

  comment

• Paper 2, Section II, B

  Fluid Dynamics II | Part II, 2011

  The energy equation for the motion of a viscous, incompressible fluid states that

  $$\frac{d}{d t} \int_{V} \frac{1}{2} \rho u^{2} d V+\int_{S} \frac{1}{2} \rho u^{2} u_{i} n_{i} d S=\int_{S} u_{i} \sigma_{i j} n_{j} d S-2 \mu \int_{V} e_{i j} e_{i j} d V$$

  Interpret each term in this equation and explain the meaning of the symbols used.

  Consider steady rectilinear flow in a (not necessarily circular) pipe having rigid stationary walls. Deduce a relation between the viscous dissipation per unit length of the pipe, the pressure gradient $G$, and the volume flux $Q$.

  Starting from the Navier-Stokes equations, calculate the velocity field for steady rectilinear flow in a circular pipe of radius $a$. Using the relationship derived above, or otherwise, find the viscous dissipation per unit length of this flow in terms of $G$.

  [Hint: In cylindrical polar coordinates,

  $$\nabla^{2} w(r)=\frac{1}{r} \frac{d}{d r}\left(r \frac{d w}{d r}\right)$$

  comment

• Paper 3, Section II, B

  Fluid Dynamics II | Part II, 2011

  If $A_{i}\left(x_{j}\right)$ is harmonic, i.e. if $\nabla^{2} A_{i}=0$, show that

  $$u_{i}=A_{i}-x_{k} \frac{\partial A_{k}}{\partial x_{i}}, \quad \text { with } \quad p=-2 \mu \frac{\partial A_{n}}{\partial x_{n}},$$

  satisfies the incompressibility condition and the Stokes equation. Show that the stress tensor is

  $$\sigma_{i j}=2 \mu\left(\delta_{i j} \frac{\partial A_{n}}{\partial x_{n}}-x_{k} \frac{\partial^{2} A_{k}}{\partial x_{i} \partial x_{j}}\right)$$

  Consider the Stokes flow corresponding to

  $$A_{i}=V_{i}\left(1-\frac{a}{2 r}\right),$$

  where $V_{i}$ are the components of a constant vector $\mathbf{V}$. Show that on the sphere $r=a$ the normal component of velocity vanishes and the surface traction $\sigma_{i j} x_{j} / a$ is in the normal direction. Hence deduce that the drag force on the sphere is given by

  $$\mathbf{F}=4 \pi \mu a \mathbf{V}$$

  comment

• Paper 4, Section II, B

  Fluid Dynamics II | Part II, 2011

  A viscous fluid flows along a slowly varying thin channel between no-slip surfaces at $y=0$ and $y=h(x, t)$ under the action of a pressure gradient $d p / d x$. After explaining the approximations and assumptions of lubrication theory, including a comment on the reduced Reynolds number, derive the expression for the volume flux

  $$q=\int_{0}^{h} u d y=-\frac{h^{3}}{12 \mu} \frac{d p}{d x}$$

  as well as the equation

  $$\frac{\partial h}{\partial t}+\frac{\partial q}{\partial x}=0$$

  In peristaltic pumping, the surface $h(x, t)$ has a periodic form in space which propagates at a constant speed $c$, i.e. $h(x-c t)$, and no net pressure gradient is applied, i.e. the pressure gradient averaged over a period vanishes. Show that the average flux along the channel is given by

  $$\langle q\rangle=c\left(\langle h\rangle-\frac{\left\langle h^{-2}\right\rangle}{\left\langle h^{-3}\right\rangle}\right)$$

  where $\langle\cdot\rangle$ denotes an average over one period.

  comment

Further Complex Methods

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2011

  Show that the following integral is well defined:

  $$I(a, b)=\int_{0}^{\infty}\left(\frac{e^{-b x}}{e^{i a} e^{x}-1}-\frac{e^{b x}}{e^{-i a} e^{x}-1}\right) d x, \quad 0<a<\infty, a \neq 2 n \pi, n \in \mathbb{Z}, 0<b<1$$

  Express $I(a, b)$ in terms of a combination of hypergeometric functions.

  [You may assume without proof that the hypergeometric function $F(a, b ; c ; z)$ can be expressed in the form

  $$F(a, b ; c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  for appropriate restrictions on $c, b, z$. Furthermore,

  $$\Gamma(z+1)=z \Gamma(z) \cdot]$$

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2011

  (i) By assuming the validity of the Fourier transform pair, prove the validity of the following transform pair:

  $$\begin{gathered} \hat{q}(k)=\int_{0}^{\infty} e^{-i k x} q(x) d x, \quad \operatorname{Im} k \leqslant 0, \\ q(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i k x} \hat{q}(k) d k+\frac{c}{2 \pi} \int_{L} e^{i k x} \hat{q}(-k) d k, \quad 0<x<\infty, \end{gathered}$$

  where $c$ is an arbitrary complex constant and $L$ is the union of the two rays arg $k=\frac{\pi}{2}$ and $\arg k=0$ with the orientation shown in the figure below:

  

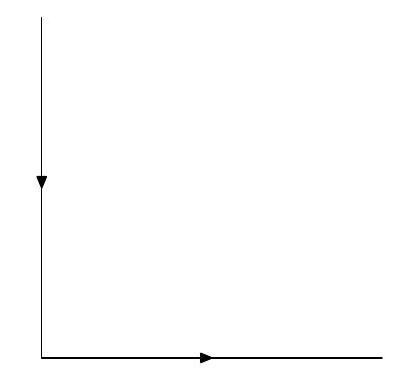
  The contour $L$.

  (ii) Verify that the partial differential equation

  $$i q_{t}+q_{x x}=0, \quad 0<x<\infty, t>0,$$

  can be rewritten in the following form:

  $$\left(e^{-i k x+i k^{2} t} q\right)_{t}-\left[e^{-i k x+i k^{2} t}\left(-k q+i q_{x}\right)\right]_{x}=0, \quad k \in \mathbb{C} .$$

  Consider equation (2) supplemented with the conditions

  $$\begin{aligned} &q(x, 0)=q_{0}(x), \quad 0<x<\infty \\ &q(x, t) \text { vanishes sufficiently fast for all } t \text { as } x \rightarrow \infty \end{aligned}$$

  By using equations (1a) and (3), show that

  $$\hat{q}(k, t)=e^{-i k^{2} t} \hat{q}_{0}(k)+e^{-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)-i \tilde{g}_{1}\left(k^{2}, t\right)\right], \operatorname{Im} k \leqslant 0$$

  where

  $$\hat{q}_{0}(k)=\int_{0}^{\infty} e^{-i k x} q_{0}(x) d x, \quad \operatorname{Im} k \leqslant 0$$

  Part II, $2011 \quad$ List of Questions

  [TURN OVER

  $$\tilde{g}_{0}(k, t)=\int_{0}^{t} e^{i k \tau} q(0, \tau) d \tau, \quad \tilde{g}_{1}(k, t)=\int_{0}^{t} e^{i k \tau} q_{x}(0, \tau) d \tau, k \in \mathbb{C}, t>0 .$$

  Use (1b) to invert equation (5) and furthermore show that

  $$\int_{-\infty}^{\infty} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)+i \tilde{g}_{1}\left(k^{2}, t\right)\right] d k=\int_{L} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)+i \tilde{g}_{1}\left(k^{2}, t\right)\right] d k, t>0, x>0$$

  Hence determine the constant $c$ so that the solution of equation (2), with the conditions (4) and with the condition that either $q(0, t)$ or $q_{x}(0, t)$ is given, can be expressed in terms of an integral involving $\hat{q}_{0}(k)$ and either $\tilde{g}_{0}$ or $\tilde{g}_{1}$.

  comment

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2011

  Find the two complex-valued functions $F^{+}(z)$ and $F^{-}(z)$ such that all of the following hold:

  (i) $F^{+}(z)$ and $F^{-}(z)$ are analytic for $\operatorname{Im} z>0$ and $\operatorname{Im} z<0$ respectively, where $z=x+i y, x, y \in \mathbb{R}$.

  (ii) $F^{+}(x)-F^{-}(x)=\frac{1}{x^{4}+1}, \quad x \in \mathbb{R}$.

  (iii) $F^{\pm}(z)=O\left(\frac{1}{z}\right), \quad z \rightarrow \infty, \quad \operatorname{Im} z \neq 0$.

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2011

  Consider the following sum related to Riemann's zeta function:

  $$S:=\sum_{m=1}^{\left[\frac{a}{2 \pi}\right]} m^{s-1}, \quad s=\sigma+i t, \sigma, t \in \mathbb{R}, \quad a>2 \pi, a \neq 2 \pi N, N \in \mathbb{Z}^{+},$$

  where $[a / 2 \pi]$ denotes the integer part of $a / 2 \pi$.

  (i) By using an appropriate branch cut, show that

  $$S=\frac{e^{-\frac{i \pi s}{2}}}{(2 \pi)^{s}} \int_{L} f(z, s) d z, \quad f(z, s)=\frac{e^{-z}}{1-e^{-z}} z^{s-1}$$

  where $L$ is the circle in the complex $z$-plane centred at $i(a+b) / 2$ with radius $(a-b) / 2$, $0<b<2 \pi$.

  (ii) Use the above representation to show that, for $a>2 \pi$ and $0<b<2 \pi$,

  $$\sum_{m=1}^{\left[\frac{a}{2 \pi}\right]} m^{s-1}=\frac{1}{(2 \pi)^{s}}\left[e^{-\frac{i \pi s}{2}} \int_{C_{b}^{a}} f(z, s) d z-e^{\frac{i \pi s}{2}} \int_{C_{-a}^{-b}} f(z, s) d z+\frac{a^{s}}{s}-\frac{b^{s}}{s}\right]$$

  where $f(z, s)$ is defined in (i) and the curves $C_{b}^{a}, C_{-a}^{-b}$ are the following semi-circles in the right half complex $z$-plane:

  

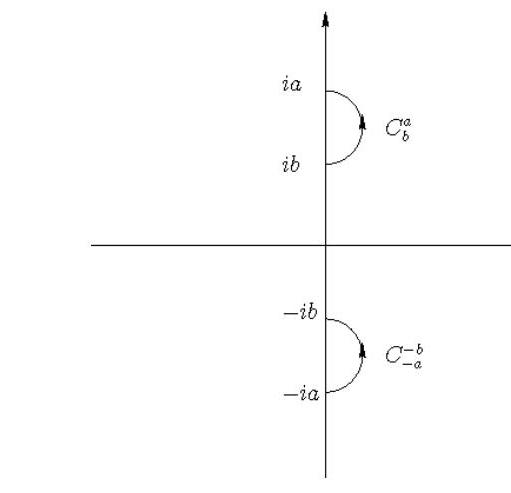
  The curves $C_{b}^{a}$ and $C_{-a}^{-b}$.

  $$\begin{aligned} C_{b}^{a} &=\left\{\frac{i(a+b)}{2}+\frac{(a-b)}{2} e^{i \theta}, \quad-\frac{\pi}{2}<\theta<\frac{\pi}{2}\right\} \\ C_{-a}^{-b} &=\left\{\frac{-i(a+b)}{2}+\frac{(a-b)}{2} e^{i \theta}, \quad-\frac{\pi}{2}<\theta<\frac{\pi}{2}\right\} \end{aligned}$$

  Part II, 2011 List of Questions

  [TURN OVER

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2011

  Explain the meaning of $z_{j}$ in the Weierstrass canonical product formula

  $$f(z)=f(0) \exp \left[\frac{f^{\prime}(0)}{f(0)} z\right] \prod_{j=1}^{\infty}\left\{\left(1-\frac{z}{z_{j}}\right) e^{\frac{z}{z_{j}}}\right\}$$

  Show that

  $$\frac{\sin (\pi z)}{\pi z}=\prod_{n=1}^{\infty}\left(1-\frac{z^{2}}{n^{2}}\right)$$

  Deduce that

  $$\pi \cot (\pi z)=\frac{1}{z}+2 \sum_{n=1}^{\infty} \frac{z}{z^{2}-n^{2}}$$

  comment

• Paper 4, Section $I$, E

  Further Complex Methods | Part II, 2011

  Let $F(z)$ be defined by

  $$F(z)=\int_{0}^{\infty} \frac{e^{-z t}}{1+t^{2}} d t, \quad|\arg z|<\frac{\pi}{2}$$

  Let $\tilde{F}(z)$ be defined by

  $$\tilde{F}(z)=\mathcal{P} \int_{0}^{\infty e^{-\frac{i \pi}{2}}} \frac{e^{-z \zeta}}{1+\zeta^{2}} d \zeta, \quad 0<\arg z<\pi$$

  where $\mathcal{P}$ denotes principal value integral and the contour is the negative imaginary axis.

  By computing $F(z)-\tilde{F}(z)$, obtain a formula for the analytic continuation of $F(z)$ for $\frac{\pi}{2} \leqslant \arg z<\pi$.

  comment

Galois Theory

• Paper 1, Section II, 18H

  Galois Theory | Part II, 2011

  Let $K$ be a field.

  (i) Let $F$ and $F^{\prime}$ be two finite extensions of $K$. When the degrees of these two extensions are equal, show that every $K$-homomorphism $F \rightarrow F^{\prime}$ is an isomorphism. Give an example, with justification, of two finite extensions $F$ and $F^{\prime}$ of $K$, which have the same degrees but are not isomorphic over $K$.

  (ii) Let $L$ be a finite extension of $K$. Let $F$ and $F^{\prime}$ be two finite extensions of $L$. Show that if $F$ and $F^{\prime}$ are isomorphic as extensions of $L$ then they are isomorphic as extensions of $K$. Prove or disprove the converse.

  comment

• Paper 2, Section II, H

  Galois Theory | Part II, 2011

  Let $F=\mathbb{C}(x, y)$ be the function field in two variables $x, y$. Let $n \geqslant 1$, and $K=\mathbb{C}\left(x^{n}+y^{n}, x y\right)$ be the subfield of $F$ of all rational functions in $x^{n}+y^{n}$ and $x y .$

  (i) Let $K^{\prime}=K\left(x^{n}\right)$, which is a subfield of $F$. Show that $K^{\prime} / K$ is a quadratic extension.

  (ii) Show that $F / K^{\prime}$ is cyclic of order $n$, and $F / K$ is Galois. Determine the Galois $\operatorname{group} \operatorname{Gal}(F / K)$.

  comment

• Paper 3, Section II, H

  Galois Theory | Part II, 2011

  Let $n \geqslant 1$ and $K=\mathbb{Q}\left(\boldsymbol{\mu}_{n}\right)$ be the cyclotomic field generated by the $n$th roots of unity. Let $a \in \mathbb{Q}$ with $a \neq 0$, and consider $F=K(\sqrt[n]{a})$.

  (i) State, without proof, the theorem which determines $\operatorname{Gal}(K / \mathbb{Q})$.

  (ii) Show that $F / \mathbb{Q}$ is a Galois extension and that $\operatorname{Gal}(F / \mathbb{Q})$ is soluble. [When using facts about general Galois extensions and their generators, you should state them clearly.]

  (iii) When $n=p$ is prime, list all possible degrees $[F: \mathbb{Q}]$, with justification.

  comment

• Paper 4, Section II, H

  Galois Theory | Part II, 2011

  Let $K$ be a field of characteristic 0 , and let $P(X)=X^{4}+b X^{2}+c X+d$ be an irreducible quartic polynomial over $K$. Let $\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}$ be its roots in an algebraic closure of $K$, and consider the Galois group $\operatorname{Gal}(P)$ (the group $\operatorname{Gal}(F / K)$ for a splitting field $F$ of $P$ over $K$ ) as a subgroup of $S_{4}$ (the group of permutations of $\left.\alpha_{1}, \alpha_{2}, \alpha_{3}, \alpha_{4}\right)$.

  Suppose that $\operatorname{Gal}(P)$ contains $V_{4}=\{1,(12)(34),(13)(24),(14)(23)\}$.

  (i) List all possible $\operatorname{Gal}(P)$ up to isomorphism. [Hint: there are 4 cases, with orders 4 , 8,12 and 24.]

  (ii) Let $Q(X)$ be the resolvent cubic of $P$, i.e. a cubic in $K[X]$ whose roots are $-\left(\alpha_{1}+\alpha_{2}\right)\left(\alpha_{3}+\alpha_{4}\right),-\left(\alpha_{1}+\alpha_{3}\right)\left(\alpha_{2}+\alpha_{4}\right)$ and $-\left(\alpha_{1}+\alpha_{4}\right)\left(\alpha_{2}+\alpha_{3}\right)$. Construct a natural surjection $\operatorname{Gal}(P) \rightarrow \operatorname{Gal}(Q)$, and find $\operatorname{Gal}(Q)$ in each of the four cases found in (i).

  (iii) Let $\Delta \in K$ be the discriminant of $Q$. Give a criterion to determine $\operatorname{Gal}(P)$ in terms of $\Delta$ and the factorisation of $Q$ in $K[X]$.

  (iv) Give a specific example of $P$ where $\operatorname{Gal}(P)$ is abelian.

  comment

General Relativity

• Paper 1, Section II, 37D

  General Relativity | Part II, 2011

  Consider a metric of the form

  $$d s^{2}=-2 d u d v+d x^{2}+d y^{2}-2 H(u, x, y) d u^{2} .$$

  Let $x^{a}(\lambda)$ describe an affinely-parametrised geodesic, where $x^{a} \equiv\left(x^{1}, x^{2}, x^{3}, x^{4}\right)=$ $(u, v, x, y)$. Write down explicitly the Lagrangian

  $$L=g_{a b} \dot{x}^{a} \dot{x}^{b},$$

  with $\dot{x}^{a}=d x^{a} / d \lambda$, using the given metric. Hence derive the four geodesic equations. In particular, show that

  $$\ddot{v}+2\left(\frac{\partial H}{\partial x} \dot{x}+\frac{\partial H}{\partial y} \dot{y}\right) \dot{u}+\frac{\partial H}{\partial u} \dot{u}^{2}=0$$

  By comparing these equations with the standard form of the geodesic equation, show that $\Gamma_{13}^{2}=\partial H / \partial x$ and derive the other Christoffel symbols.

  The Ricci tensor, $R_{a b}$, is defined by

  $$R_{a b}=\Gamma_{a b, d}^{d}-\Gamma_{a d, b}^{d}+\Gamma_{d f}^{d} \Gamma_{b a}^{f}-\Gamma_{b f}^{d} \Gamma_{d a}^{f}$$

  By considering the case $a=1, b=1$, show that the vacuum Einstein field equations imply

  $$\frac{\partial^{2} H}{\partial x^{2}}+\frac{\partial^{2} H}{\partial y^{2}}=0$$

  comment

• Paper 2, Section II, 36D

  General Relativity | Part II, 2011

  The curvature tensor $R_{b c d}^{a}$ satisfies

  $$V_{a ; b c}-V_{a ; c b}=V_{e} R_{a b c}^{e}$$

  for any covariant vector field $V_{a}$. Hence express $R_{a b c}^{e}$ in terms of the Christoffel symbols and their derivatives. Show that

  $$R_{a b c}^{e}=-R_{a c b}^{e}$$

  Further, by setting $V_{a}=\partial \phi / \partial x^{a}$, deduce that

  $$R_{a b c}^{e}+R_{c a b}^{e}+R_{b c a}^{e}=0 .$$

  Using local inertial coordinates or otherwise, obtain the Bianchi identities.

  Define the Ricci tensor in terms of the curvature tensor and show that it is symmetric. [You may assume that $R_{a b c d}=-R_{b a c d}$.] Write down the contracted Bianchi identities.

  In certain spacetimes of dimension $n \geqslant 2, R_{a b c d}$ takes the form

  $$R_{a b c d}=K\left(g_{a c} g_{b d}-g_{a d} g_{b c}\right)$$

  Obtain the Ricci tensor and curvature scalar. Deduce, under some restriction on $n$ which should be stated, that $K$ is a constant.

  comment

• Paper 4, Section II, D

  General Relativity | Part II, 2011

  The metric of the Schwarzschild solution is

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\frac{1}{\left(1-\frac{2 M}{r}\right)} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right) .$$

  Show that, for an incoming radial light ray, the quantity

  $$v=t+r+2 M \log \left|\frac{r}{2 M}-1\right|$$

  is constant.

  Express $d s^{2}$ in terms of $r, v, \theta$ and $\phi$. Determine the light-cone structure in these coordinates, and use this to discuss the nature of the apparent singularity at $r=2 M$.

  An observer is falling radially inwards in the region $r<2 M$. Assuming that the metric for $r<2 M$ is again given by $(*)$, obtain a bound for $d \tau$, where $\tau$ is the proper time of the observer, in terms of $d r$. Hence, or otherwise, determine the maximum proper time that can elapse between the events at which the observer crosses $r=2 M$ and is torn apart at $r=0$.

  comment

Geometry and Groups

• Paper 1, Section I, G

  Geometry and Groups | Part II, 2011

  Let $G$ be a finite subgroup of $\mathrm{SO}(3)$ and let $\Omega$ be the set of unit vectors that are fixed by some non-identity element of $G$. Show that the group $G$ permutes the unit vectors in $\Omega$ and that $\Omega$ has at most three orbits. Describe these orbits when $G$ is the group of orientation-preserving symmetries of a regular dodecahedron.

  comment

• Paper 1, Section II, G

  Geometry and Groups | Part II, 2011

  Prove that a group of Möbius transformations is discrete if, and only if, it acts discontinuously on hyperbolic 3 -space.

  Let $G$ be the set of Möbius transformations $z \mapsto \frac{a z+b}{c z+d}$ with

  $$a, b, c, d \in \mathbb{Z}[i]=\{u+i v: u, v \in \mathbb{Z}\} \quad \text { and } \quad a d-b c=1$$

  Show that $G$ is a group and that it acts discontinuously on hyperbolic 3-space. Show that $G$ contains transformations that are elliptic, parabolic, hyperbolic and loxodromic.

  comment

• Paper 2, Section $I$, $3 \mathrm{G}$

  Geometry and Groups | Part II, 2011

  Let $A$ and $B$ be two rotations of the Euclidean plane $\mathbb{E}^{2}$ about centres $a$ and $b$ respectively. Show that the conjugate $A B A^{-1}$ is also a rotation and find its fixed point. When do $A$ and $B$ commute? Show that the commutator $A B A^{-1} B^{-1}$ is a translation.

  Deduce that any group of orientation-preserving isometries of the Euclidean plane either fixes a point or is infinite.

  comment

• Paper 3, Section I, $3 G$

  Geometry and Groups | Part II, 2011

  Define a Kleinian group.

  Give an example of a Kleinian group that is a free group on two generators and explain why it has this property.

  comment

• Paper 4, Section I, G

  Geometry and Groups | Part II, 2011

  Define inversion in a circle $\Gamma$ on the Riemann sphere. You should show from your definition that inversion in $\Gamma$ exists and is unique.

  Prove that the composition of an even number of inversions is a Möbius transformation of the Riemann sphere and that every Möbius transformation is the composition of an even number of inversions.

  comment

• Paper 4, Section II, G

  Geometry and Groups | Part II, 2011

  Define a lattice in $\mathbb{R}^{2}$ and the rank of such a lattice.

  Let $\Lambda$ be a rank 2 lattice in $\mathbb{R}^{2}$. Choose a vector $\boldsymbol{w}_{1} \in \Lambda \backslash\{\boldsymbol{0}\}$ with $\left\|\boldsymbol{w}_{1}\right\|$ as small as possible. Then choose $\boldsymbol{w}_{2} \in \Lambda \backslash \mathbb{Z} \boldsymbol{w}_{1}$ with $\left\|\boldsymbol{w}_{2}\right\|$ as small as possible. Show that $\Lambda=\mathbb{Z} \boldsymbol{w}_{1}+\mathbb{Z} \boldsymbol{w}_{2}$.

  Suppose that $\boldsymbol{w}_{1}$ is the unit vector $\left(\begin{array}{l}1 \\ 0\end{array}\right)$. Draw the region of possible values for $\boldsymbol{w}_{2}$. Suppose that $\Lambda$ also equals $\mathbb{Z} \boldsymbol{v}_{1}+\mathbb{Z} \boldsymbol{v}_{2}$. Prove that

  $$\boldsymbol{v}_{1}=a \boldsymbol{w}_{1}+b \boldsymbol{w}_{2} \quad \text { and } \quad \boldsymbol{v}_{2}=c \boldsymbol{w}_{1}+d \boldsymbol{w}_{2}$$

  for some integers $a, b, c, d$ with $a d-b c=\pm 1$.

  comment

Graph Theory

• Paper 1, Section II, F

  Graph Theory | Part II, 2011

  Let $G$ be a bipartite graph with vertex classes $X$ and $Y$. What is a matching from $X$ to $Y$ ?

  Show that if $|\Gamma(A)| \geqslant|A|$ for all $A \subset X$ then $G$ contains a matching from $X$ to $Y$.

  Let $d$ be a positive integer. Show that if $|\Gamma(A)| \geqslant|A|-d$ for all $A \subset X$ then $G$ contains a set of $|X|-d$ independent edges.

  Show that if 0 is not an eigenvalue of $G$ then $G$ contains a matching from $X$ to $Y$.

  Suppose now that $|X|=|Y| \geqslant 1$ and that $G$ does contain a matching from $X$ to $Y$. Must it be the case that 0 is not an eigenvalue of $G$ ? Justify your answer.

  comment

• Paper 2, Section II, F

  Graph Theory | Part II, 2011

  What does it mean to say that a graph $G$ is $k$-colourable? Define the chromatic number $\chi(G)$ of a graph $G$, and the chromatic number $\chi(S)$ of a closed surface $S$.

  State the Euler-Poincaré formula relating the numbers of vertices, edges and faces in a drawing of a graph $G$ on a closed surface $S$ of Euler characteristic $E$. Show that if $E \leqslant 0$ then

  $$\chi(S) \leqslant\left[\frac{7+\sqrt{49-24 E}}{2}\right\rfloor$$

  Find, with justification, the chromatic number of the Klein bottle $N_{2}$. Show that if $G$ is a triangle-free graph which can be drawn on the Klein bottle then $\chi(G) \leqslant 4$.

  [You may assume that the Klein bottle has Euler characteristic 0 , and that $K_{6}$ can be drawn on the Klein bottle but $K_{7}$ cannot. You may use Brooks's theorem.]

  comment

• Paper 3, Section II, $17 \mathrm{~F}$

  Graph Theory | Part II, 2011

  Define the Turán graph $T_{r}(n)$. State and prove Turán's theorem. Hence, or otherwise, find $\operatorname{ex}\left(K_{3} ; n\right)$.

  Let $G$ be a bipartite graph with $n$ vertices in each class. Let $k$ be an integer, $1 \leqslant k \leqslant n$, and assume $e(G)>(k-1) n$. Show that $G$ contains a set of $k$ independent edges.

  [Hint: Suppose $G$ contains a set $D$ of a independent edges but no set of a $+1$ independent edges. Let $U$ be the set of vertices of the edges in $D$ and let $F$ be the set of edges in $G$ with precisely one vertex in $U$; consider $|F| .]$

  Hence, or otherwise, show that if $H$ is a triangle-free tripartite graph with $n$ vertices in each class then $e(H) \leqslant 2 n^{2}$.

  comment

• Paper 4, Section II, F

  Graph Theory | Part II, 2011

  (i) Given a positive integer $k$, show that there exists a positive integer $n$ such that, whenever the edges of the complete graph $K_{n}$ are coloured with $k$ colours, there exists a monochromatic triangle.

  Denote the least such $n$ by $f(k)$. Show that $f(k) \leqslant 3 \cdot k !$ for all $k$.

  (ii) You may now assume that $f(2)=6$ and $f(3)=17$.

  Let $H$ denote the graph of order 4 consisting of a triangle together with one extra edge. Given a positive integer $k$, let $g(k)$ denote the least positive integer $n$ such that, whenever the edges of the complete graph $K_{n}$ are coloured with $k$ colours, there exists a monochromatic copy of $H$. By considering the edges from one vertex of a monochromatic triangle in $K_{7}$, or otherwise, show that $g(2) \leqslant 7$. By exhibiting a blue-yellow colouring of the edges of $K_{6}$ with no monochromatic copy of $H$, show that in fact $g(2)=7$.

  What is $g(3) ?$ Justify your answer.

  comment

Integrable Systems

• Paper 1, Section II, A

  Integrable Systems | Part II, 2011

  Define a finite-dimensional integrable system and state the Arnold-Liouville theorem.

  Consider a four-dimensional phase space with coordinates $\left(q_{1}, q_{2}, p_{1}, p_{2}\right)$, where $q_{2}>0$ and $q_{1}$ is periodic with period $2 \pi$. Let the Hamiltonian be

  $$H=\frac{\left(p_{1}\right)^{2}}{2\left(q_{2}\right)^{2}}+\frac{\left(p_{2}\right)^{2}}{2}-\frac{k}{q_{2}}, \quad \text { where } k>0$$

  Show that the corresponding Hamilton equations form an integrable system.

  Determine the sign of the constant $E$ so that the motion is periodic on the surface $H=E$. Demonstrate that in this case, the action variables are given by

  $$I_{1}=p_{1}, \quad I_{2}=\gamma \int_{\alpha}^{\beta} \frac{\sqrt{\left(q_{2}-\alpha\right)\left(\beta-q_{2}\right)}}{q_{2}} d q_{2},$$

  where $\alpha, \beta, \gamma$ are positive constants which you should determine.

  comment

• Paper 2, Section II, A

  Integrable Systems | Part II, 2011

  Consider the Poisson structure

  $$\{F, G\}=\int_{\mathbb{R}} \frac{\delta F}{\delta u(x)} \frac{\partial}{\partial x} \frac{\delta G}{\delta u(x)} d x$$

  where $F, G$ are polynomial functionals of $u, u_{x}, u_{x x}, \ldots$. Assume that $u, u_{x}, u_{x x}, \ldots$ tend to zero as $|x| \rightarrow \infty$.

  (i) Show that $\{F, G\}=-\{G, F\}$.

  (ii) Write down Hamilton's equations for $u=u(x, t)$ corresponding to the following Hamiltonians:

  $$H_{0}[u]=\int_{\mathbb{R}} \frac{1}{2} u^{2} d x, \quad H[u]=\int_{\mathbb{R}}\left(\frac{1}{2} u_{x}^{2}+u^{3}+u u_{x}\right) d x$$

  (iii) Calculate the Poisson bracket $\left\{H_{0}, H\right\}$, and hence or otherwise deduce that the following overdetermined system of partial differential equations for $u=u\left(x, t_{0}, t\right)$ is compatible:

  $$\begin{gathered} u_{t_{0}}=u_{x} \\ u_{t}=6 u u_{x}-u_{x x x} \end{gathered}$$

  [You may assume that the Jacobi identity holds for (1).]

  (iv) Find a symmetry of (3) generated by $X=\partial / \partial u+\alpha t \partial / \partial x$ for some constant $\alpha \in \mathbb{R}$ which should be determined. Construct a vector field $Y$ corresponding to the one parameter group

  $$x \rightarrow \beta x, \quad t \rightarrow \gamma t, \quad u \rightarrow \delta u,$$

  where $(\beta, \gamma, \delta)$ should be determined from the symmetry requirement. Find the Lie algebra generated by the vector fields $(X, Y)$.

  comment

• Paper 3, Section II, A

  Integrable Systems | Part II, 2011

  Let $U(\rho, \tau, \lambda)$ and $V(\rho, \tau, \lambda)$ be matrix-valued functions. Consider the following system of overdetermined linear partial differential equations:

  $$\frac{\partial}{\partial \rho} \psi=U \psi, \quad \frac{\partial}{\partial \tau} \psi=V \psi$$

  where $\psi$ is a column vector whose components depend on $(\rho, \tau, \lambda)$. Using the consistency condition of this system, derive the associated zero curvature representation (ZCR)

  $$\frac{\partial}{\partial \tau} U-\frac{\partial}{\partial \rho} V+[U, V]=0,$$

  where $[\cdot, \cdot]$ denotes the usual matrix commutator.

  (i) Let

  $$U=\frac{i}{2}\left(\begin{array}{cc} 2 \lambda & \partial_{\rho} \phi \\ \partial_{\rho} \phi & -2 \lambda \end{array}\right), \quad V=\frac{1}{4 i \lambda}\left(\begin{array}{cc} \cos \phi & -i \sin \phi \\ i \sin \phi & -\cos \phi \end{array}\right)$$

  Find a partial differential equation for $\phi=\phi(\rho, \tau)$ which is equivalent to the $\mathrm{ZCR}(*)$.

  (ii) Assuming that $U$ and $V$ in $(*)$ do not depend on $t:=\rho-\tau$, show that the trace of $(U-V)^{p}$ does not depend on $x:=\rho+\tau$, where $p$ is any positive integer. Use this fact to construct a first integral of the ordinary differential equation

  $$\phi^{\prime \prime}=\sin \phi, \quad \text { where } \quad \phi=\phi(x) .$$

  comment

Linear Analysis

• Paper 1, Section II, G

  Linear Analysis | Part II, 2011

  State a version of the Stone-Weierstrass Theorem for real-valued functions on a compact metric space.

  Suppose that $K:[0,1]^{2} \rightarrow \mathbb{R}$ is a continuous function. Show that $K(x, y)$ may be uniformly approximated by functions of the form $\sum_{i=1}^{n} f_{i}(x) g_{i}(y)$ with $f_{i}, g_{i}:[0,1] \rightarrow \mathbb{R}$ continuous.

  Let $X, Y$ be Banach spaces and suppose that $T: X \rightarrow Y$ is a bounded linear operator. What does it mean to say that $T$ is finite-rank? What does it mean to say that $T$ is compact? Give an example of a bounded linear operator from $C[0,1]$ to itself which is not compact.

  Suppose that $\left(T_{n}\right)_{n=1}^{\infty}$ is a sequence of finite-rank operators and that $T_{n} \rightarrow T$ in the operator norm. Briefly explain why the $T_{n}$ are compact. Show that $T$ is compact.

  Hence, show that the integral operator $T: C[0,1] \rightarrow C[0,1]$ defined by

  $$T f(x)=\int_{0}^{1} f(y) K(x, y) d y$$

  is compact.

  comment

• Paper 2, Section II, G

  Linear Analysis | Part II, 2011

  State and prove the Baire Category Theorem. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function. For $x \in \mathbb{R}$, define

  $$\omega_{f}(x)=\inf _{\delta>0} \sup _{\substack{|y-x| \leqslant \delta \\\left|y^{\prime}-x\right| \leqslant \delta}}\left|f(y)-f\left(y^{\prime}\right)\right|$$

  Show that $f$ is continuous at $x$ if and only if $\omega_{f}(x)=0$.

  Show that for any $\epsilon>0$ the set $\left\{x \in \mathbb{R}: \omega_{f}(x)<\epsilon\right\}$ is open.

  Hence show that the set of points at which $f$ is continuous cannot be precisely the set $\mathbb{Q}$ of rationals.

  comment

• Paper 3, Section II, G

  Linear Analysis | Part II, 2011

  Let $H$ be a complex Hilbert space with orthonormal basis $\left(e_{n}\right)_{n=-\infty}^{\infty}$ Let $T: H \rightarrow H$ be a bounded linear operator. What is meant by the spectrum $\sigma(T)$ of $T$ ?

  Define $T$ by setting $T\left(e_{n}\right)=e_{n-1}+e_{n+1}$ for $n \in \mathbb{Z}$. Show that $T$ has a unique extension to a bounded, self-adjoint linear operator on $H$. Determine the norm $\|T\|$. Exhibit, with proof, an element of $\sigma(T)$.

  Show that $T$ has no eigenvectors. Is $T$ compact?

  [General results from spectral theory may be used without proof. You may also use the fact that if a sequence $\left(x_{n}\right)$ satisfies a linear recurrence $\lambda x_{n}=x_{n-1}+x_{n+1}$ with $\lambda \in \mathbb{R}$, $|\lambda| \leqslant 2, \lambda \neq 0$, then it has the form $x_{n}=A \alpha^{n} \sin \left(\theta_{1} n+\theta_{2}\right)$ or $x_{n}=(A+n B) \alpha^{n}$, where $A, B, \alpha \in \mathbb{R}$ and $0 \leqslant \theta_{1}<\pi,\left|\theta_{2}\right| \leqslant \pi / 2$.]

  comment

• Paper 4, Section II, G

  Linear Analysis | Part II, 2011

  State Urysohn's Lemma. State and prove the Tietze Extension Theorem.

  Let $X, Y$ be two topological spaces. We say that the extension property holds if, whenever $S \subseteq X$ is a closed subset and $f: S \rightarrow Y$ is a continuous map, there is a continuous function $\tilde{f}: X \rightarrow Y$ with $\left.\tilde{f}\right|_{S}=f$.

  For each of the following three statements, say whether it is true or false. Briefly justify your answers.

  1. If $X$ is a metric space and $Y=[-1,1]$ then the extension property holds.

  2. If $X$ is a compact Hausdorff space and $Y=\mathbb{R}$ then the extension property holds.

  3. If $X$ is an arbitrary topological space and $Y=[-1,1]$ then the extension property holds.

  comment

Logic and Set Theory

• Paper 1, Section II, H

  Logic and Set Theory | Part II, 2011

  Give the inductive and synthetic definitions of ordinal addition, and prove that they are equivalent.

  Which of the following assertions about ordinals $\alpha, \beta$ and $\gamma$ are always true, and which can be false? Give proofs or counterexamples as appropriate.

  (i) $\alpha \beta=\beta \alpha$.

  (ii) $\alpha(\beta+\gamma)=\alpha \beta+\alpha \gamma$.

  (iii) If $\alpha \geqslant \omega^{2}$ then $\alpha+\omega^{2}=\omega^{2}+\alpha$.

  (iv) If $\alpha \geqslant \omega_{1}$ then $\alpha \omega_{1}=\omega_{1} \alpha$.

  comment

• Paper 2, Section II, H

  Logic and Set Theory | Part II, 2011

  State and prove Zorn's Lemma. [You may assume Hartogs' Lemma.] Where in your argument have you made use of the Axiom of Choice?

  Show that every real vector space has a basis.

  Let $V$ be a real vector space having a basis of cardinality $\aleph_{1}$. What is the cardinality of $V$ ? Justify your answer.

  comment

• Paper 3, Section II, H

  Logic and Set Theory | Part II, 2011

  State and prove the Upward Löwenheim-Skolem Theorem.

  [You may assume the Compactness Theorem, provided that you state it clearly.]

  A total ordering $(X,<)$ is called dense if for any $x<y$ there exists $z$ with $x<z<y$. Show that a dense total ordering (on more than one point) cannot be a well-ordering.

  For each of the following theories, either give axioms, in the language of posets, for the theory or prove carefully that the theory is not axiomatisable in the language of posets.

  (i) The theory of dense total orderings.

  (ii) The theory of countable dense total orderings.

  (iii) The theory of uncountable dense total orderings.

  (iv) The theory of well-orderings.

  comment

• Paper 4, Section II, H

  Logic and Set Theory | Part II, 2011

  Define the sets $V_{\alpha}$ for ordinals $\alpha$. Show that each $V_{\alpha}$ is transitive. Show also that $V_{\alpha} \subseteq V_{\beta}$ whenever $\alpha \leqslant \beta$. Prove that every set $x$ is a member of some $V_{\alpha}$.

  For which ordinals $\alpha$ does there exist a set $x$ such that the power-set of $x$ has rank $\alpha$ ? [You may assume standard properties of rank.]

  comment

Mathematical Biology

• Paper 1, Section I, B

  Mathematical Biology | Part II, 2011

  A proposed model of insect dispersal is given by the equation

  $$\frac{\partial n}{\partial t}=D \frac{\partial}{\partial x}\left[\left(\frac{n_{0}}{n}\right) \frac{\partial n}{\partial x}\right]$$

  where $n(x, t)$ is the density of insects and $D$ and $n_{0}$ are constants.

  Interpret the term on the right-hand side.

  Explain why a solution of the form

  $$n(x, t)=n_{0}(D t)^{-\beta} g\left(x /(D t)^{\beta}\right),$$

  where $\beta$ is a positive constant, can potentially represent the dispersal of a fixed number $n_{0}$ of insects initially localised at the origin.

  Show that the equation (1) can be satisfied by a solution of the form (2) if $\beta=1$ and find the corresponding function $g$.

  comment

• Paper 2, Section I, B

  Mathematical Biology | Part II, 2011

  A population with variable growth and harvesting is modelled by the equation

  $$u_{t+1}=\max \left(\frac{r u_{t}^{2}}{1+u_{t}^{2}}-E u_{t}, 0\right)$$

  where $r$ and $E$ are positive constants.

  Given that $r>1$, show that a non-zero steady state exists if $0<E<E_{m}(r)$, where $E_{m}(r)$ is to be determined.

  Show using a cobweb diagram that, if $E<E_{m}(r)$, a non-zero steady state may be attained only if the initial population $u_{0}$ satisfies $\alpha<u_{0}<\beta$, where $\alpha$ should be determined explicitly and $\beta$ should be specified as a root of an algebraic equation.

  With reference to the cobweb diagram, give an additional criterion that implies that $\alpha<u_{0}<\beta$ is a sufficient condition, as well as a necessary condition, for convergence to a non-zero steady state.

  comment

• Paper 2, Section II, B

  Mathematical Biology | Part II, 2011

  Consider a population subject to the following birth-death process. When the number of individuals in the population is $n$, the probability of an increase from $n$ to $n+1$ in unit time is $\beta n+\gamma$ and the probability of a decrease from $n$ to $n-1$ is $\alpha n(n-1)$, where $\alpha, \beta$ and $\gamma$ are constants.

  Show that the master equation for $P(n, t)$, the probability that at time $t$ the population has $n$ members, is

  $$\frac{\partial P}{\partial t}=\alpha n(n+1) P(n+1, t)-\alpha n(n-1) P(n, t)+(\beta n-\beta+\gamma) P(n-1, t)-(\beta n+\gamma) P(n, t) .$$

  Show that $\langle n\rangle$, the mean number of individuals in the population, satisfies

  $$\frac{d\langle n\rangle}{d t}=-\alpha\left\langle n^{2}\right\rangle+(\alpha+\beta)\langle n\rangle+\gamma$$

  Deduce that, in a steady state,

  $$\langle n\rangle=\frac{\alpha+\beta}{2 \alpha} \pm \sqrt{\frac{(\alpha+\beta)^{2}}{4 \alpha^{2}}+\frac{\gamma}{\alpha}-(\Delta n)^{2}}$$

  where $\Delta n$ is the standard deviation of $n$. When is the minus sign admissable?

  Show how a Fokker-Planck equation of the form

  $$\frac{\partial P}{\partial t}=\frac{\partial}{\partial n}[g(n) P(n, t)]+\frac{1}{2} \frac{\partial^{2}}{\partial n^{2}}[h(n) P(n, t)]$$

  may be derived under conditions to be explained, where the functions $g(n)$ and $h(n)$ should be evaluated.

  In the case $\alpha \ll \gamma$ and $\beta=0$, find the leading-order approximation to $n_{*}$ such that $g\left(n_{*}\right)=0$. Defining the new variable $x=n-n_{*}$, where $g\left(n_{*}\right)=0$, approximate $g(n)$ by $g^{\prime}\left(n_{*}\right) x$ and $h(n)$ by $h\left(n_{*}\right)$. Solve $(*)$ for $P(x)$ in the steady-state limit and deduce leading-order estimates for $\langle n\rangle$ and $(\Delta n)^{2}$.

  comment

• Paper 3, Section I, B

  Mathematical Biology | Part II, 2011

  The dynamics of a directly transmitted microparasite can be modelled by the system

  $$\begin{aligned} \frac{d X}{d t} &=b N-\beta X Y-b X \\ \frac{d Y}{d t} &=\beta X Y-(b+r) Y \\ \frac{d Z}{d t} &=r Y-b Z \end{aligned}$$

  where $b, \beta$ and $r$ are positive constants and $X, Y$ and $Z$ are respectively the numbers of susceptible, infected and immune (i.e. infected by the parasite, but showing no further symptoms of infection) individuals in a population of size $N$, independent of $t$, where $N=X+Y+Z$.

  Consider the possible steady states of these equations. Show that there is a threshold population size $N_{c}$ such that if $N<N_{c}$ there is no steady state with the parasite maintained in the population. Show that in this case the number of infected and immune individuals decreases to zero for all possible initial conditions.

  Show that for $N>N_{c}$ there is a possible steady state with $X=X_{s}<N$ and $Y=Y_{s}>0$, and find expressions for $X_{s}$ and $Y_{s}$.

  By linearising the equations for $d X / d t$ and $d Y / d t$ about the steady state $X=X_{s}$ and $Y=Y_{s}$, derive a quadratic equation for the possible growth or decay rate in terms of $X_{s}$ and $Y_{s}$ and hence show that the steady state is stable.

  comment

• Paper 3, Section II, B

  Mathematical Biology | Part II, 2011

  The number density of a population of amoebae is $n(\mathbf{x}, t)$. The amoebae exhibit chemotaxis and are attracted to high concentrations of a chemical which has concentration $a(\mathbf{x}, t)$. The equations governing $n$ and $a$ are

  $$\begin{aligned} &\frac{\partial n}{\partial t}=\alpha n\left(n_{0}^{2}-n^{2}\right)+\nabla^{2} n-\nabla \cdot(\chi(n) n \nabla a) \\ &\frac{\partial a}{\partial t}=\beta n-\gamma a+D \nabla^{2} a \end{aligned}$$

  where the constants $n_{0}, \alpha, \beta, \gamma$ and $D$ are all positive.

  (i) Give a biological interpretation of each term in these equations and discuss the sign of $\chi(n)$.

  (ii) Show that there is a non-trivial (i.e. $a \neq 0, n \neq 0$ ) steady-state solution for $n$ and $a$, independent of $\mathbf{x}$, and show further that it is stable to small disturbances that are also independent of $\mathbf{x}$.

  (iii) Consider small spatially varying disturbances to the steady state, with spatial structure such that $\nabla^{2} \psi=-k^{2} \psi$, where $\psi$ is any disturbance quantity. Show that if such disturbances also satisfy $\partial \psi / \partial t=p \psi$, where $p$ is a constant, then $p$ satisfies a quadratic equation, to be derived. By considering the conditions required for $p=0$ to be a possible solution of this quadratic equation, or otherwise, deduce that instability is possible if

  $$\beta \chi_{0} n_{0}>2 \alpha n_{0}^{2} D+\gamma+2\left(2 D \alpha n_{0}^{2} \gamma\right)^{1 / 2}$$

  where $\chi_{0}=\chi\left(n_{0}\right)$.

  (iv) Explain briefly how your conclusions might change if an additional geometric constraint implied that $k^{2}>k_{0}^{2}$, where $k_{0}$ is a given constant.

  comment

• Paper 4, Section I, B

  Mathematical Biology | Part II, 2011

  A neglected flower garden contains $M_{n}$ marigolds in the summer of year $n$. On average each marigold produces $\gamma$ seeds through the summer. Seeds may germinate after one or two winters. After three winters or more they will not germinate. Each winter a fraction $1-\alpha$ of all seeds in the garden are eaten by birds (with no preference to the age of the seed). In spring a fraction $\mu$ of seeds that have survived one winter and a fraction $\nu$ of seeds that have survived two winters germinate. Finite resources of water mean that the number of marigolds growing to maturity from $S$ germinating seeds is $\mathcal{N}(S)$, where $\mathcal{N}(S)$ is an increasing function such that $\mathcal{N}(0)=0, \mathcal{N}^{\prime}(0)=1, \mathcal{N}^{\prime}(S)$ is a decreasing function of $S$ and $\mathcal{N}(S) \rightarrow N_{\max }$ as $S \rightarrow \infty$

  Show that $M_{n}$ satisfies the equation

  $$M_{n+1}=\mathcal{N}\left(\alpha \mu \gamma M_{n}+\nu \gamma \alpha^{2}(1-\mu) M_{n-1}\right)$$

  Write down an equation for the number $M_{*}$ of marigolds in a steady state. Show graphically that there are two solutions, one with $M_{*}=0$ and the other with $M_{*}>0$ if

  $$\alpha \mu \gamma+\nu \gamma \alpha^{2}(1-\mu)>1$$

  Show that the $M_{*}=0$ steady-state solution is unstable to small perturbations in this case.

  comment

Number Fields

• Paper 1, Section II, F

  Number Fields | Part II, 2011

  Calculate the class group for the field $K=\mathbb{Q}(\sqrt{-17})$.

  [You may use any general theorem, provided that you state it accurately.]

  Find all solutions in $\mathbb{Z}$ of the equation $y^{2}=x^{5}-17$.

  comment

• Paper 2, Section II, F

  Number Fields | Part II, 2011

  (i) Suppose that $d>1$ is a square-free integer. Describe, with justification, the ring of integers in the field $K=\mathbb{Q}(\sqrt{d})$.

  (ii) Show that $\mathbb{Q}\left(2^{1 / 3}\right)=\mathbb{Q}\left(4^{1 / 3}\right)$ and that $\mathbb{Z}\left[4^{1 / 3}\right]$ is not the ring of integers in this field.

  comment

• Paper 4, Section II, F

  Number Fields | Part II, 2011

  (i) Prove that the ring of integers $\mathcal{O}_{K}$ in a real quadratic field $K$ contains a non-trivial unit. Any general results about lattices and convex bodies may be assumed.

  (ii) State the general version of Dirichlet's unit theorem.

  (iii) Show that for $K=\mathbb{Q}(\sqrt{7}), 8+3 \sqrt{7}$ is a fundamental unit in $\mathcal{O}_{K}$.

  [You may not use results about continued fractions unless you prove them.]

  comment

Number Theory

• Paper 1, Section I, I

  Number Theory | Part II, 2011

  Prove that, under the action of $\mathrm{SL}_{2}(\mathbb{Z})$, every positive definite binary quadratic form of discriminant $-163$, with integer coefficients, is equivalent to

  $$x^{2}+x y+41 y^{2} .$$

  comment

• Paper 2, Section I, I

  Number Theory | Part II, 2011

  (i) Find a primitive root modulo $17 .$

  (ii) Let $p$ be a prime of the form $2^{m}+1$ for some integer $m \geqslant 1$. Prove that every quadratic non-residue modulo $p$ is a primitive root modulo $p$.

  comment

• Paper 3, Section I, I

  Number Theory | Part II, 2011

  (i) State Lagrange's Theorem, and prove that, if $p$ is an odd prime,

  $$(p-1) ! \equiv-1 \quad \bmod p$$

  (ii) Still assuming $p$ is an odd prime, prove that

  $$3^{2} \cdot 5^{2} \cdots(p-2)^{2} \equiv(-1)^{\frac{p+1}{2}} \bmod p$$

  comment

• Paper 3, Section II, I

  Number Theory | Part II, 2011

  Let $\zeta(s)$ be the Riemann zeta function, and put $s=\sigma+i t$ with $\sigma, t \in \mathbb{R}$.

  (i) If $\sigma>1$, prove that

  $$\zeta(s)=\prod_{p}\left(1-p^{-s}\right)^{-1}$$

  where the product is taken over all primes $p$.

  (ii) Assuming that, for $\sigma>1$, we have

  $$\zeta(s)=\sum_{n=1}^{\infty} n\left(n^{-s}-(n+1)^{-s}\right)$$

  prove that $\zeta(s)-\frac{1}{s-1}$ has an analytic continuation to the half plane $\sigma>0$.

  comment

• Paper 4, Section $I$, I

  Number Theory | Part II, 2011

  (i) Prove that there are infinitely many primes.

  (ii) Prove that arbitrarily large gaps can occur between consecutive primes.

  comment

• Paper 4, Section II, I

  Number Theory | Part II, 2011

  (i) Prove the law of reciprocity for the Jacobi symbol. You may assume the law of reciprocity for the Legendre symbol.

  (ii) Let $n$ be an odd positive integer which is not a square. Prove that there exists an odd prime $p$ with $\left(\frac{n}{p}\right)=-1$.

  comment

Numerical Analysis

• Paper 1, Section II, A

  Numerical Analysis | Part II, 2011

  The nine-point method for the Poisson equation $\nabla^{2} u=f$ (with zero Dirichlet boundary conditions) in a square, reads

  $$\begin{array}{r} \frac{2}{3}\left(u_{i-1, j}+u_{i+1, j}+u_{i, j-1}+u_{i, j+1}\right)+\frac{1}{6}\left(u_{i-1, j-1}+u_{i-1, j+1}+u_{i+1, j-1}+u_{i+1, j+1}\right) \\ -\frac{10}{3} u_{i, j}=h^{2} f_{i, j}, \quad i, j=1, \ldots, m, \end{array}$$

  where $u_{0, j}=u_{m+1, j}=u_{i, 0}=u_{i, m+1}=0$, for all $i, j=0, \ldots, m+1$.

  (i) By arranging the two-dimensional arrays $\left\{u_{i, j}\right\}_{i, j=1, \ldots, m}$ and $\left\{f_{i, j}\right\}_{i, j=1, \ldots, m}$ into column vectors $u \in \mathbb{R}^{m^{2}}$ and $b \in \mathbb{R}^{m^{2}}$ respectively, the linear system above takes the matrix form $A u=b$. Prove that, regardless of the ordering of the points on the grid, the matrix $A$ is symmetric and negative definite.

  (ii) Formulate the Jacobi method with relaxation for solving the above linear system.

  (iii) Prove that the iteration converges if the relaxation parameter $\omega$ is equal to $1 .$

  [You may quote without proof any relevant result about convergence of iterative methods.]

  comment

• Paper 2, Section II, A

  Numerical Analysis | Part II, 2011

  Let $A \in \mathbb{R}^{n \times n}$ be a real matrix with $n$ linearly independent eigenvectors. The eigenvalues of $A$ can be calculated from the sequence $x^{(k)}, k=0,1, \ldots$, which is generated by the power method

  $$x^{(k+1)}=\frac{A x^{(k)}}{\left\|A x^{(k)}\right\|},$$

  where $x^{(0)}$ is a real nonzero vector.

  (i) Describe the asymptotic properties of the sequence $x^{(k)}$ in the case that the eigenvalues $\lambda_{i}$ of $A$ satisfy $\left|\lambda_{i}\right|<\left|\lambda_{n}\right|, i=1, \ldots, n-1$, and the eigenvectors are of unit length.

  (ii) Present the implementation details for the power method for the setting in (i) and define the Rayleigh quotient.

  (iii) Let $A$ be the $3 \times 3$ matrix

  $$A=\lambda I+P, \quad P=\left(\begin{array}{lll} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right)$$

  where $\lambda$ is real and nonzero. Find an explicit expression for $A^{k}, k=1,2,3, \ldots$

  Let the sequence $x^{(k)}$ be generated by the power method as above. Deduce from your expression for $A^{k}$ that the first and second components of $x^{(k+1)}$ tend to zero as $k \rightarrow \infty$. Further show that this implies $A x^{(k+1)}-\lambda x^{(k+1)} \rightarrow 0$ as $k \rightarrow \infty$.

  comment

• Paper 3, Section II, A

  Numerical Analysis | Part II, 2011

  (i) The difference equation

  $$u_{i}^{n+1}=u_{i}^{n}+\frac{3}{2} \mu\left(u_{i-1}^{n}-2 u_{i}^{n}+u_{i+1}^{n}\right)-\frac{1}{2} \mu\left(u_{i-1}^{n-1}-2 u_{i}^{n-1}+u_{i+1}^{n-1}\right)$$

  where $\mu=\Delta t /(\Delta x)^{2}$, is the basic equation used in the second-order AdamsBashforth method and can be employed to approximate a solution of the diffusion equation $u_{t}=u_{x x}$. Prove that, as $\Delta t \rightarrow 0$ with constant $\mu$, the local error of the method is $O(\Delta t)^{2}$.

  (ii) By applying the Fourier stability test, show that the above method is stable if and only if $\mu \leqslant 1 / 4$.

  (iii) Define the leapfrog scheme to approximate the diffusion equation and prove that it is unstable for every choice of $\mu>0$.

  comment

• Paper 4, Section II, A

  Numerical Analysis | Part II, 2011

  (i) Consider the Poisson equation

  $$\nabla^{2} u=f, \quad-1 \leqslant x, y \leqslant 1$$

  with the periodic boundary conditions

  and the normalization condition

  $$\int_{-1}^{1} \int_{-1}^{1} u(x, y) d x d y=0$$

  Moreover, $f$ is analytic and obeys the periodic boundary conditions $f(-1, y)=$ $f(1, y), f(x,-1)=f(x, 1),-1 \leqslant x, y \leqslant 1 .$

  Derive an explicit expression of the approximation of a solution $u$ by means of a spectral method. Explain the term convergence with spectral speed and state its validity for the approximation of $u$.

  (ii) Consider the second-order linear elliptic partial differential equation

  $$\nabla \cdot(a \nabla u)=f, \quad-1 \leqslant x, y \leqslant 1$$

  with the periodic boundary conditions and normalization condition specified in (i). Moreover, $a$ and $f$ are given by

  $$a(x, y)=\cos (\pi x)+\cos (\pi y)+3, \quad f(x, y)=\sin (\pi x)+\sin (\pi y)$$

  [Note that $a$ is a positive analytic periodic function.]

  Construct explicitly the linear algebraic system that arises from the implementation of a spectral method to the above equation.

  $$\begin{aligned} & u(-1, y)=u(1, y), \quad u_{x}(-1, y)=u_{x}(1, y), \quad-1 \leqslant y \leqslant 1, \\ & u(x,-1)=u(x, 1), \quad u_{y}(x,-1)=u_{y}(x, 1), \quad-1 \leqslant x \leqslant 1 \end{aligned}$$

  comment

Optimization and Control

• Paper 2, Section II, K

  Optimization and Control | Part II, 2011

  Consider an optimal stopping problem in which the optimality equation takes the form

  $$F_{t}(x)=\max \left\{r(x), E\left[F_{t+1}\left(x_{t+1}\right)\right]\right\}, \quad t=1, \ldots, N-1,$$

  $F_{N}(x)=r(x)$, and where $r(x)>0$ for all $x$. Let $S$ denote the stopping set of the onestep-look-ahead rule. Show that if $S$ is closed (in a sense you should explain) then the one-step-look-ahead rule is optimal.

  $N$ biased coins are to be tossed successively. The probability that the $i$ th coin toss will show a head is known to be $p_{i}\left(0<p_{i}<1\right)$. At most once, after observing a head, and before tossing the next coin, you may guess that you have just seen the last head (i.e. that all subsequent tosses will show tails). If your guess turns out to be correct then you win $£ 1$.

  Suppose that you have not yet guessed 'last head', and the $i$ th toss is a head. Show that it cannot be optimal to guess that this is the last head if

  $$\frac{p_{i+1}}{q_{i+1}}+\cdots+\frac{p_{N}}{q_{N}}>1$$

  where $q_{j}=1-p_{j}$.

  Suppose that $p_{i}=1 / i$. Show that it is optimal to guess that the last head is the first head (if any) to occur after having tossed at least $i^{*}$ coins, where $i^{*} \approx N / e$ when $N$ is large.

  comment

• Paper 3, Section II, 28K

  Optimization and Control | Part II, 2011

  An observable scalar state variable evolves as $x_{t+1}=x_{t}+u_{t}, t=0,1, \ldots$ Let controls $u_{0}, u_{1}, \ldots$ be determined by a policy $\pi$ and define

  $$C_{s}\left(\pi, x_{0}\right)=\sum_{t=0}^{s-1}\left(x_{t}^{2}+2 x_{t} u_{t}+7 u_{t}^{2}\right) \quad \text { and } \quad C_{s}\left(x_{0}\right)=\inf _{\pi} C_{s}\left(\pi, x_{0}\right)$$

  Show that it is possible to express $C_{s}\left(x_{0}\right)$ in terms of $\Pi_{s}$, which satisfies the recurrence

  $$\Pi_{s}=\frac{6\left(1+\Pi_{s-1}\right)}{7+\Pi_{s-1}}, \quad s=1,2, \ldots$$

  with $\Pi_{0}=0$.

  Deduce that $C_{\infty}\left(x_{0}\right) \geqslant 2 x_{0}^{2} .\left[C_{\infty}\left(x_{0}\right)\right.$ is defined as $\left.\lim _{s \rightarrow \infty} C_{s}\left(x_{0}\right) .\right]$

  By considering the policy $\pi^{*}$ which takes $u_{t}=-(1 / 3)(2 / 3)^{t} x_{0}, t=0,1, \ldots$, show that $C_{\infty}\left(x_{0}\right)=2 x_{0}^{2}$.

  Give an alternative description of $\pi^{*}$ in closed-loop form.

  comment

• Paper 4, Section II, K

  Optimization and Control | Part II, 2011

  Describe the type of optimal control problem that is amenable to analysis using Pontryagin's Maximum Principle.

  A firm has the right to extract oil from a well over the interval $[0, T]$. The oil can be sold at price $£ p$ per unit. To extract oil at rate $u$ when the remaining quantity of oil in the well is $x$ incurs cost at rate $£ u^{2} / x$. Thus the problem is one of maximizing

  $$\int_{0}^{T}\left[p u(t)-\frac{u(t)^{2}}{x(t)}\right] d t$$

  subject to $d x(t) / d t=-u(t), u(t) \geqslant 0, x(t) \geqslant 0$. Formulate the Hamiltonian for this problem.

  Explain why $\lambda(t)$, the adjoint variable, has a boundary condition $\lambda(T)=0$.

  Use Pontryagin's Maximum Principle to show that under optimal control

  $$\lambda(t)=p-\frac{1}{1 / p+(T-t) / 4}$$

  and

  $$\frac{d x(t)}{d t}=-\frac{2 p x(t)}{4+p(T-t)}$$

  Find the oil remaining in the well at time $T$, as a function of $x(0), p$, and $T$,

  comment

Partial Differential Equations

• Paper 1, Section II, A

  Partial Differential Equations | Part II, 2011

  Let $H=H(x, v), x, v \in \mathbb{R}^{n}$, be a smooth real-valued function which maps $\mathbb{R}^{2 n}$ into $\mathbb{R}$. Consider the initial value problem for the equation

  $$\begin{aligned} &f_{t}+\nabla_{v} H \cdot \nabla_{x} f-\nabla_{x} H \cdot \nabla_{v} f=0, \quad x, v \in \mathbb{R}^{n}, t>0 \\ &f(x, v, t=0)=f_{I}(x, v), \quad x, v \in \mathbb{R}^{n} \end{aligned}$$

  for the unknown function $f=f(x, v, t)$.

  (i) Use the method of characteristics to solve the initial value problem, locally in time.

  (ii) Let $f_{I} \geqslant 0$ on $\mathbb{R}^{2 n}$. Use the method of characteristics to prove that $f$ remains non-negative (as long as it exists).

  (iii) Let $F: \mathbb{R} \rightarrow \mathbb{R}$ be smooth. Prove that

  $$\int_{\mathbb{R}^{2 n}} F(f(x, v, t)) d x d v=\int_{\mathbb{R}^{2 n}} F\left(f_{I}(x, v)\right) d x d v$$

  as long as the solution exists.

  (iv) Let $H$ be independent of $x$, namely $H(x, v)=a(v)$, where $a$ is smooth and realvalued. Give the explicit solution of the initial value problem.

  comment

• Paper 2, Section II, A

  Partial Differential Equations | Part II, 2011

  Consider the Schrödinger equation

  $$\begin{aligned} i \partial_{t} \psi(t, x) &=-\frac{1}{2} \Delta \psi(t, x)+V(x) \psi(t, x), \quad x \in \mathbb{R}^{n}, t>0 \\ \psi(t=0, x) &=\psi_{I}(x), \quad x \in \mathbb{R}^{n} \end{aligned}$$

  where $V$ is a smooth real-valued function.

  Prove that, for smooth solutions, the following equations are valid for all $t>0$ :

  (i)

  $$\int_{\mathbb{R}^{n}}|\psi(t, x)|^{2} d x=\int_{\mathbb{R}^{n}}\left|\psi_{I}(x)\right|^{2} d x$$

  (ii)

  $$\begin{aligned} &\int_{\mathbb{R}^{n}} \frac{1}{2}|\nabla \psi(t, x)|^{2} d x+\int_{\mathbb{R}^{n}} V(x)|\psi(t, x)|^{2} d x \\ &=\int_{\mathbb{R}^{n}} \frac{1}{2}\left|\nabla \psi_{I}(x)\right|^{2} d x+\int_{\mathbb{R}^{n}} V(x)\left|\psi_{I}(x)\right|^{2} d x \end{aligned}$$

  comment

• Paper 3, Section II, A

  Partial Differential Equations | Part II, 2011

  (a) State the local existence theorem of a classical solution of the Cauchy problem

  $$\begin{aligned} &a\left(x_{1}, x_{2}, u\right) \frac{\partial u}{\partial x_{1}}+b\left(x_{1}, x_{2}, u\right) \frac{\partial u}{\partial x_{2}}=c\left(x_{1}, x_{2}, u\right) \\ &\left.u\right|_{\Gamma}=u_{0} \end{aligned}$$

  where $\Gamma$ is a smooth curve in $\mathbb{R}^{2}$.

  (b) Solve, by using the method of characteristics,

  $$\begin{aligned} &2 x_{1} \frac{\partial u}{\partial x_{1}}+4 x_{2} \frac{\partial u}{\partial x_{2}}=u^{2} \\ &u\left(x_{1}, 2\right)=h \end{aligned}$$

  where $h>0$ is a constant. What is the maximal domain of existence in which $u$ is a solution of the Cauchy problem?

  comment

• Paper 4, Section II, A

  Partial Differential Equations | Part II, 2011

  Consider the functional

  $$E(u)=\frac{1}{2} \int_{\Omega}|\nabla u|^{2} d x+\int_{\Omega} F(u, x) d x$$

  where $\Omega$ is a bounded domain in $\mathbb{R}^{n}$ with smooth boundary and $F: \mathbb{R} \times \Omega \rightarrow \mathbb{R}$ is smooth. Assume that $F(u, x)$ is convex in $u$ for all $x \in \Omega$ and that there is a $K>0$ such that

  $$-K \leqslant F(v, x) \leqslant K\left(|v|^{2}+1\right) \quad \forall v \in \mathbb{R}, x \in \Omega$$

  (i) Prove that $E$ is well-defined on $H_{0}^{1}(\Omega)$, bounded from below and strictly convex. Assume without proof that $E$ is weakly lower-semicontinuous. State this property. Conclude the existence of a unique minimizer of $E$.

  (ii) Which elliptic boundary value problem does the minimizer solve?

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, D

  Principles of Quantum Mechanics | Part II, 2011

  Two individual angular momentum states $\left|j_{1}, m_{1}\right\rangle,\left|j_{2}, m_{2}\right\rangle$, acted on by $\mathbf{J}^{(1)}$ and $\mathbf{J}^{(2)}$ respectively, can be combined to form a combined state $|J, M\rangle$. What is the combined angular momentum operator $\mathbf{J}$ in terms of $\mathbf{J}^{(1)}$ and $\mathbf{J}^{(2)}$ ? [Units in which $\hbar=1$ are to be used throughout.]

  Defining raising and lowering operators $J_{\pm}^{(i)}$, where $i \in\{1,2\}$, find an expression for $\mathbf{J}^{2}$ in terms of $\mathbf{J}^{(i)^{2}}, J_{\pm}^{(i)}$ and $J_{3}^{(i)}$. Show that this implies

  $$\left[\mathbf{J}^{2}, J_{3}\right]=0$$

  Write down the state with $J=j_{1}+j_{2}$ and with $J_{3}$ eigenvalue $M=-j_{1}-j_{2}$ in terms of the individual angular momentum states. From this starting point, calculate the combined state with eigenvalues $J=j_{1}+j_{2}-1$ and $M=-j_{1}-j_{2}+1$ in terms of the individual angular momentum states.

  If $j_{1}=3$ and $j_{2}=1$ and the combined system is in the state $|3,-3\rangle$, what is the probability of measuring the $J_{3}^{(i)}$ eigenvalues of individual angular momentum states to be $-3$ and 0 , respectively?

  [You may assume without proof that standard angular momentum states $|j, m\rangle$ are joint eigenstates of $\mathbf{J}^{2}$ and $J_{3}$, obeying

  $$J_{\pm}|j, m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j, m+1\rangle,$$

  and that

  $$\left.\left[J_{\pm}, J_{3}\right]=\pm J_{\pm} \cdot\right]$$

  comment

• Paper 2, Section II, D

  Principles of Quantum Mechanics | Part II, 2011

  A quantum system has energy eigenstates $|n\rangle$ with eigenvalues $E_{n}=n \hbar, n \in$ $\{1,2,3, \ldots\}$. An observable $Q$ is such that $Q|n\rangle=q_{n}|n\rangle$.

  (a) What is the commutator of $Q$ with the Hamiltonian $H$ ?

  (b) Given $q_{n}=\frac{1}{n}$, consider the state

  $$|\psi\rangle \propto \sum_{n=1}^{N} \sqrt{n}|n\rangle$$

  Determine:

  (i) The probability of measuring $Q$ to be $1 / N$.

  (ii) The probability of measuring energy $\hbar$ followed by another immediate measurement of energy $2 \hbar$.

  (iii) The average of many separate measurements of $Q$, each measurement being on a state $|\psi\rangle$, as $N \rightarrow \infty$.

  (c) Given $q_{1}=1$ and $q_{n}=-1$ for $n>1$, consider the state

  $$|\psi\rangle \propto \sum_{n=1}^{\infty} \alpha^{n / 2}|n\rangle,$$

  where $0<\alpha<1$.

  (i) Show that the probability of measuring an eigenvalue $q=-1$ of $|\psi\rangle$ is

  $$A+B \alpha$$

  where $A$ and $B$ are integers that you should find.

  (ii) Show that $\langle Q\rangle_{\psi}$ is $C+D \alpha$, where $C$ and $D$ are integers that you should find.

  (iii) Given that $Q$ is measured to be $-1$ at time $t=0$, write down the state after a time $t$ has passed. What is then the subsequent probability at time $t$ of measuring the energy to be $2 \hbar$ ?

  comment

• Paper 3, Section II, D

  Principles of Quantum Mechanics | Part II, 2011

  The Pauli matrices $\boldsymbol{\sigma}=\left(\sigma_{x}, \sigma_{y}, \sigma_{z}\right)=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$, with

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  are used to represent angular momentum operators with respect to basis states $|\uparrow\rangle$ and $|\downarrow\rangle$ corresponding to spin up and spin down along the $z$-axis. They satisfy

  $$\sigma_{i} \sigma_{j}=\delta_{i j}+i \epsilon_{i j k} \sigma_{k}$$

  (i) How are $|\uparrow\rangle$ and $|\downarrow\rangle$ represented? How is the spin operator s related to $\sigma$ and $\hbar$ ? Check that the commutation relations between the spin operators are as desired. Check that $\mathbf{s}^{2}$ acting on a spin one-half state has the correct eigenvalue.

  What are the states obtained by applying $s_{x}, s_{y}$ to the eigenstates $|\uparrow\rangle$ and $|\downarrow\rangle$ of $s_{z}$ ?

  (ii) Let $V$ be the space of states for a spin one-half system. Consider a combination of three such systems with states belonging to $V^{(1)} \otimes V^{(2)} \otimes V^{(3)}$ and spin operators acting on each subsystem denoted by $s_{x}^{(i)}, s_{y}^{(i)}$ with $i=1,2,3$. Find the eigenvalues of the operators

  $$s_{x}^{(1)} s_{y}^{(2)} s_{y}^{(3)}, \quad s_{y}^{(1)} s_{x}^{(2)} s_{y}^{(3)}, \quad s_{y}^{(1)} s_{y}^{(2)} s_{x}^{(3)} \quad \text { and } \quad s_{x}^{(1)} s_{x}^{(2)} s_{x}^{(3)}$$

  of the state

  $$|\Psi\rangle=\frac{1}{\sqrt{2}}\left[|\uparrow\rangle_{1}|\uparrow\rangle_{2}|\uparrow\rangle_{3}-|\downarrow\rangle_{1}|\downarrow\rangle_{2}|\downarrow\rangle_{3}\right]$$

  (iii) Consider now whether these outcomes for measurements of particular combinations of the operators $s_{x}^{(i)}, s_{y}^{(i)}$ in the state $|\Psi\rangle$ could be reproduced by replacing the spin operators with classical variables $\tilde{s}_{x}^{(i)}, \tilde{s}_{y}^{(i)}$ which take values $\pm \hbar / 2$ according to some probabilities. Assume that these variables are identical to the quantum measurements of $s_{x}^{(1)} s_{y}^{(2)} s_{y}^{(3)}, s_{y}^{(1)} s_{x}^{(2)} s_{y}^{(3)}, s_{y}^{(1)} s_{y}^{(2)} s_{x}^{(3)}$ on $|\Psi\rangle$. Show that classically this implies a unique possibility for

  $$\tilde{s}_{x}^{(1)} \tilde{s}_{x}^{(2)} \tilde{s}_{x}^{(3)},$$

  and find its value.

  State briefly how this result could be used to experimentally test quantum mechanics.

  comment

• Paper 4, Section II, D

  Principles of Quantum Mechanics | Part II, 2011

  The quantum-mechanical observable $Q$ has just two orthonormal eigenstates $|1\rangle$ and $|2\rangle$ with eigenvalues $-1$ and 1 , respectively. The operator $Q^{\prime}$ is defined by $Q^{\prime}=Q+\epsilon T$, where

  $$T=\left(\begin{array}{cc} 0 & i \\ -i & 0 \end{array}\right)$$

  Defining orthonormal eigenstates of $Q^{\prime}$ to be $\left|1^{\prime}\right\rangle$ and $\left|2^{\prime}\right\rangle$ with eigenvalues $q_{1}^{\prime}$, $q_{2}^{\prime}$, respectively, consider a perturbation to first order in $\epsilon \in \mathbb{R}$ for the states

  $$\left|1^{\prime}\right\rangle=a_{1}|1\rangle+a_{2} \epsilon|2\rangle, \quad\left|2^{\prime}\right\rangle=b_{1}|2\rangle+b_{2} \epsilon|1\rangle,$$

  where $a_{1}, a_{2}, b_{1}, b_{2}$ are complex coefficients. The real eigenvalues are also expanded to first order in $\epsilon$ :

  $$q_{1}^{\prime}=-1+c_{1} \epsilon, \quad q_{2}^{\prime}=1+c_{2} \epsilon$$

  From first principles, find $a_{1}, a_{2}, b_{1}, b_{2}, c_{1}, c_{2}$.

  Working exactly to all orders, find the real eigenvalues $q_{1}^{\prime}, q_{2}^{\prime}$ directly. Show that the exact eigenvectors of $Q^{\prime}$ may be taken to be of the form

  $$A_{j}(\epsilon)\left(\begin{array}{c} 1 \\ -i\left(1+B q_{j}^{\prime}\right) / \epsilon \end{array}\right)$$

  finding $A_{j}(\epsilon)$ and the real numerical coefficient $B$ in the process.

  By expanding the exact expressions, again find $a_{1}, a_{2}, b_{1}, b_{2}, c_{1}, c_{2}$, verifying the perturbation theory results above.

  comment

Principles of Statistics

• Paper 1, Section II, K

  Principles of Statistics | Part II, 2011

  Define admissible, Bayes, minimax decision rules.

  A random vector $X=\left(X_{1}, X_{2}, X_{3}\right)^{\mathrm{T}}$ has independent components, where $X_{i}$ has the normal distribution $\mathcal{N}\left(\theta_{i}, 1\right)$ when the parameter vector $\Theta$ takes the value $\theta=\left(\theta_{1}, \theta_{2}, \theta_{3}\right)^{\mathrm{T}}$. It is required to estimate $\Theta$ by a point $a \in \mathbb{R}^{3}$, with loss function $L(\theta, a)=\|a-\theta\|^{2}$. What is the risk function of the maximum-likelihood estimator $\widehat{\Theta}:=X ?$ Show that $\widehat{\Theta}$is dominated by the estimator $\widetilde{\Theta}:=\left(1-\|X\|^{-2}\right) X$.

  comment

• Paper 2, Section II, K

  Principles of Statistics | Part II, 2011

  Random variables $X_{1}, \ldots, X_{n}$ are independent and identically distributed from the normal distribution with unknown mean $\mathrm{M}$ and unknown precision (inverse variance) $H$. Show that the likelihood function, for data $X_{1}=x_{1}, \ldots, X_{n}=x_{n}$, is

  $$L_{n}(\mu, h) \propto h^{n / 2} \exp \left(-\frac{1}{2} h\left\{n(\bar{x}-\mu)^{2}+S\right\}\right)$$

  where $\bar{x}:=n^{-1} \sum_{i} x_{i}$ and $S:=\sum_{i}\left(x_{i}-\bar{x}\right)^{2}$.

  A bivariate prior distribution for $(\mathrm{M}, H)$ is specified, in terms of hyperparameters $\left(\alpha_{0}, \beta_{0}, m_{0}, \lambda_{0}\right)$, as follows. The marginal distribution of $H$ is $\Gamma\left(\alpha_{0}, \beta_{0}\right)$, with density

  $$\pi(h) \propto h^{\alpha_{0}-1} e^{-\beta_{0} h} \quad(h>0),$$

  and the conditional distribution of $\mathrm{M}$, given $H=h$, is normal with mean $m_{0}$ and precision $\lambda_{0} h$.

  Show that the conditional prior distribution of $H$, given $M=\mu$, is

  $$H \mid \mathrm{M}=\mu \quad \sim\left(\alpha_{0}+\frac{1}{2}, \beta_{0}+\frac{1}{2} \lambda_{0}\left(\mu-m_{0}\right)^{2}\right)$$

  Show that the posterior joint distribution of $(\mathrm{M}, H)$, given $X_{1}=x_{1}, \ldots, X_{n}=x_{n}$, has the same form as the prior, with updated hyperparameters $\left(\alpha_{n}, \beta_{n}, m_{n}, \lambda_{n}\right)$ which you should express in terms of the prior hyperparameters and the data.

  [You may use the identity

  $$p(t-a)^{2}+q(t-b)^{2}=(t-\delta)^{2}+p q(a-b)^{2}$$

  where $p+q=1$ and $\delta=p a+q b$.]

  Explain how you could implement Gibbs sampling to generate a random sample from the posterior joint distribution.

  comment

• Paper 3, Section II, $27 \mathrm{~K}$

  Principles of Statistics | Part II, 2011

  Random variables $X_{1}, X_{2}, \ldots$ are independent and identically distributed from the exponential distribution $\mathcal{E}(\theta)$, with density function

  $$p_{X}(x \mid \theta)=\theta e^{-\theta x} \quad(x>0),$$

  when the parameter $\Theta$ takes value $\theta>0$. The following experiment is performed. First $X_{1}$ is observed. Thereafter, if $X_{1}=x_{1}, \ldots, X_{i}=x_{i}$ have been observed $(i \geqslant 1)$, a coin having probability $\alpha\left(x_{i}\right)$ of landing heads is tossed, where $\alpha: \mathbb{R} \rightarrow(0,1)$ is a known function and the coin toss is independent of the $X$ 's and previous tosses. If it lands heads, no further observations are made; if tails, $X_{i+1}$ is observed.

  Let $N$ be the total number of $X$ 's observed, and $\mathbf{X}:=\left(X_{1}, \ldots, X_{N}\right)$. Write down the likelihood function for $\Theta$ based on data $\mathbf{X}=\left(x_{1}, \ldots, x_{n}\right)$, and identify a minimal sufficient statistic. What does the likelihood principle have to say about inference from this experiment?

  Now consider the experiment that only records $Y:=X_{N}$. Show that the density function of $Y$ has the form

  $$p_{Y}(y \mid \theta)=\exp \{a(y)-k(\theta)-\theta y\}$$

  Assuming the function $a(\cdot)$ is twice differentiable and that both $p_{Y}(y \mid \theta)$ and $\partial p_{Y}(y \mid \theta) / \partial y$ vanish at 0 and $\infty$, show that $a^{\prime}(Y)$ is an unbiased estimator of $\Theta$, and find its variance.

  Stating clearly any general results you use, deduce that

  $$-k^{\prime \prime}(\theta) \mathbb{E}_{\theta}\left\{a^{\prime \prime}(Y)\right\} \geqslant 1 .$$

  comment

• Paper 4, Section II, K

  Principles of Statistics | Part II, 2011

  What does it mean to say that a $(1 \times p)$ random vector $\xi$ has a multivariate normal distribution?

  Suppose $\xi=(X, Y)$ has the bivariate normal distribution with mean vector $\mu=\left(\mu_{X}, \mu_{Y}\right)$, and dispersion matrix

  $$\Sigma=\left(\begin{array}{cc} \sigma_{X X} & \sigma_{X Y} \\ \sigma_{X Y} & \sigma_{Y Y} \end{array}\right)$$

  Show that, with $\beta:=\sigma_{X Y} / \sigma_{X X}, Y-\beta X$ is independent of $X$, and thus that the conditional distribution of $Y$ given $X$ is normal with mean $\mu_{Y}+\beta\left(X-\mu_{X}\right)$ and variance $\sigma_{Y Y \cdot X}:=\sigma_{Y Y}-\sigma_{X Y}^{2} / \sigma_{X X}$.

  For $i=1, \ldots, n, \xi_{i}=\left(X_{i}, Y_{i}\right)$ are independent and identically distributed with the above distribution, where all elements of $\mu$ and $\Sigma$ are unknown. Let

  $$S=\left(\begin{array}{cc} S_{X X} & S_{X Y} \\ S_{X Y} & S_{Y Y} \end{array}\right):=\sum_{i=1}^{n}\left(\xi_{i}-\bar{\xi}\right)^{\mathrm{T}}\left(\xi_{i}-\bar{\xi}\right)$$

  where $\bar{\xi}:=n^{-1} \sum_{i=1}^{n} \xi_{i}$.

  The sample correlation coefficient is $r:=S_{X Y} / \sqrt{S_{X X} S_{Y Y}}$. Show that the distribution of $r$ depends only on the population correlation coefficient $\rho:=\sigma_{X Y} / \sqrt{\sigma_{X X} \sigma_{Y Y}}$.

  Student's $t$-statistic (on $n-2$ degrees of freedom) for testing the null hypothesis $H_{0}: \beta=0$ is

  $$t:=\frac{\widehat{\beta}}{\sqrt{S_{Y Y \cdot X} /(n-2) S_{X X}}},$$

  where $\widehat{\beta}:=S_{X Y} / S_{X X}$ and $S_{Y Y \cdot X}:=S_{Y Y}-S_{X Y}^{2} / S_{X X}$. Its density when $H_{0}$ is true is

  $$p(t)=C\left(1+\frac{t^{2}}{n-2}\right)^{-\frac{1}{2}(n-1)}$$

  where $C$ is a constant that need not be specified.

  Express $t$ in terms of $r$, and hence derive the density of $r$ when $\rho=0$.

  How could you use the sample correlation $r$ to test the hypothesis $\rho=0$ ?

  comment

Probability and Measure

• Paper 1, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2011

  (i) Let $(E, \mathcal{E}, \mu)$ be a measure space and let $1 \leqslant p<\infty$. For a measurable function $f$, let $\|f\|_{p}=\left(\int|f|^{p} d \mu\right)^{1 / p}$. Give the definition of the space $L^{p}$. Prove that $\left(L^{p},\|\cdot\|_{p}\right)$ forms a Banach space.

  [You may assume that $L^{p}$ is a normed vector space. You may also use in your proof any other result from the course provided that it is clearly stated.]

  (ii) Show that convergence in probability implies convergence in distribution.

  [Hint: Show the pointwise convergence of the characteristic function, using without proof the inequality $\left|e^{i y}-e^{i x}\right| \leqslant|x-y|$ for $x, y \in \mathbb{R}$.]

  (iii) Let $\left(\alpha_{j}\right)_{j \geqslant 1}$ be a given real-valued sequence such that $\sum_{j=1}^{\infty} \alpha_{j}^{2}=\sigma^{2}<\infty$. Let $\left(X_{j}\right)_{j \geqslant 1}$ be a sequence of independent standard Gaussian random variables defined on some probability space $(\Omega, \mathcal{F}, \mathbb{P})$. Let

  $$Y_{n}=\sum_{j=1}^{n} \alpha_{j} X_{j}$$

  Prove that there exists a random variable $Y$ such that $Y_{n} \rightarrow Y$ in $L^{2}$.

  (iv) Specify the distribution of the random variable $Y$ defined in part (iii), justifying carefully your answer.

  comment

• Paper 2, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2011

  (i) Define the notions of a $\pi$-system and a $d$-system. State and prove Dynkin's lemma.

  (ii) Let $\left(E_{1}, \mathcal{E}_{1}, \mu_{1}\right)$ and $\left(E_{2}, \mathcal{E}_{2}, \mu_{2}\right)$ denote two finite measure spaces. Define the $\sigma$ algebra $\mathcal{E}_{1} \otimes \mathcal{E}_{2}$ and the product measure $\mu_{1} \otimes \mu_{2}$. [You do not need to verify that such a measure exists.] State (without proof) Fubini's Theorem.

  (iii) Let $(E, \mathcal{E}, \mu)$ be a measure space, and let $f$ be a non-negative Borel-measurable function. Let $G$ be the subset of $E \times \mathbb{R}$ defined by

  $$G=\{(x, y) \in E \times \mathbb{R}: 0 \leqslant y \leqslant f(x)\}$$

  Show that $G \in \mathcal{E} \otimes \mathcal{B}(\mathbb{R})$, where $\mathcal{B}(\mathbb{R})$ denotes the Borel $\sigma$-algebra on $\mathbb{R}$. Show further that

  $$\int f d \mu=(\mu \otimes \lambda)(G)$$

  where $\lambda$ is Lebesgue measure.

  comment

• Paper 3, Section II, 25K

  Probability and Measure | Part II, 2011

  (i) State and prove Kolmogorov's zero-one law.

  (ii) Let $(E, \mathcal{E}, \mu)$ be a finite measure space and suppose that $\left(B_{n}\right)_{n \geqslant 1}$ is a sequence of events such that $B_{n+1} \subset B_{n}$ for all $n \geqslant 1$. Show carefully that $\mu\left(B_{n}\right) \rightarrow \mu(B)$, where $B=\cap_{n=1}^{\infty} B_{n}$.

  (iii) Let $\left(X_{i}\right)_{i \geqslant 1}$ be a sequence of independent and identically distributed random variables such that $\mathbb{E}\left(X_{1}^{2}\right)=\sigma^{2}<\infty$ and $\mathbb{E}\left(X_{1}\right)=0$. Let $K>0$ and consider the event $A_{n}$ defined by

  $$A_{n}=\left\{\frac{S_{n}}{\sqrt{n}} \geqslant K\right\}, \quad \text { where } \quad S_{n}=\sum_{i=1}^{n} X_{i}$$

  Prove that there exists $c>0$ such that for all $n$ large enough, $\mathbb{P}\left(A_{n}\right) \geqslant c$. Any result used in the proof must be stated clearly.

  (iv) Prove using the results above that $A_{n}$ occurs infinitely often, almost surely. Deduce that

  $$\limsup _{n \rightarrow \infty} \frac{S_{n}}{\sqrt{n}}=\infty$$

  almost surely.

  comment

• Paper 4, Section II, K

  Probability and Measure | Part II, 2011

  (i) State and prove Fatou's lemma. State and prove Lebesgue's dominated convergence theorem. [You may assume the monotone convergence theorem.]

  In the rest of the question, let $f_{n}$ be a sequence of integrable functions on some measure space $(E, \mathcal{E}, \mu)$, and assume that $f_{n} \rightarrow f$ almost everywhere, where $f$ is a given integrable function. We also assume that $\int\left|f_{n}\right| d \mu \rightarrow \int|f| d \mu$ as $n \rightarrow \infty$.

  (ii) Show that $\int f_{n}^{+} d \mu \rightarrow \int f^{+} d \mu$ and that $\int f_{n}^{-} d \mu \rightarrow \int f^{-} d \mu$, where $\phi^{+}=\max (\phi, 0)$ and $\phi^{-}=\max (-\phi, 0)$ denote the positive and negative parts of a function $\phi$.

  (iii) Here we assume also that $f_{n} \geqslant 0$. Deduce that $\int\left|f-f_{n}\right| d \mu \rightarrow 0$.

  comment

Representation Theory

• Paper 1, Section II, I

  Representation Theory | Part II, 2011

  Let $G$ be a finite group and $Z$ its centre. Suppose that $G$ has order $n$ and $Z$ has order $m$. Suppose that $\rho: G \rightarrow \mathrm{GL}(V)$ is a complex irreducible representation of degree $d .$

  (i) For $g \in Z$, show that $\rho(g)$ is a scalar multiple of the identity.

  (ii) Deduce that $d^{2} \leqslant n / m$.

  (iii) Show that, if $\rho$ is faithful, then $Z$ is cyclic.

  [Standard results may be quoted without proof, provided they are stated clearly.]

  Now let $G$ be a group of order 18 containing an elementary abelian subgroup $P$ of order 9 and an element $t$ of order 2 with $t x t^{-1}=x^{-1}$ for each $x \in P$. By considering the action of $P$ on an irreducible $\mathbb{C} G$-module prove that $G$ has no faithful irreducible complex representation.

  comment

• Paper 2, Section II, I

  Representation Theory | Part II, 2011

  State Maschke's Theorem for finite-dimensional complex representations of the finite group $G$. Show by means of an example that the requirement that $G$ be finite is indispensable.

  Now let $G$ be a (possibly infinite) group and let $H$ be a normal subgroup of finite index $r$ in $G$. Let $g_{1}, \ldots, g_{r}$ be representatives of the cosets of $H$ in $G$. Suppose that $V$ is a finite-dimensional completely reducible $\mathbb{C} G$-module. Show that

  (i) if $U$ is a $\mathbb{C} H$-submodule of $V$ and $g \in G$, then the set $g U=\{g u: u \in U\}$ is a $\mathbb{C} H$-submodule of $V$;

  (ii) if $U$ is a $\mathbb{C} H$-submodule of $V$, then $\sum_{i=1}^{r} g_{i} U$ is a $\mathbb{C} G$-submodule of $V$;

  (iii) $V$ is completely reducible regarded as a $\mathbb{C} H$-module.

  Hence deduce that if $\chi$ is an irreducible character of the finite group $G$ then all the constituents of $\chi_{H}$ have the same degree.

  comment

• Paper 3, Section II, I

  Representation Theory | Part II, 2011

  Define the character $\operatorname{Ind}_{H}^{G} \psi$ of a finite group $G$ which is induced by a character $\psi$ of a subgroup $H$ of $G$.

  State and prove the Frobenius reciprocity formula for the characters $\psi$ of $H$ and $\chi$ of $G$.

  Now suppose that $H$ has index 2 in $G$. An irreducible character $\psi$ of $H$ and an irreducible character $\chi$ of $G$ are said to be 'related' if

  $$\left\langle\operatorname{Ind}_{H}^{G} \psi, \chi\right\rangle_{G}=\left\langle\psi, \operatorname{Res}_{H}^{G} \chi\right\rangle_{H}>0$$

  Show that each $\psi$ of degree $d$ is either 'monogamous' in the sense that it is related to one $\chi$ (of degree $2 d$ ), or 'bigamous' in the sense that it is related to precisely two distinct characters $\chi_{1}, \chi_{2}$ (of degree $\left.d\right)$. Show that each $\chi$ is related to one bigamous $\psi$, or to two monogamous characters $\psi_{1}, \psi_{2}$ (of the same degree).

  Write down the degrees of the complex irreducible characters of the alternating group $A_{5}$. Find the degrees of the irreducible characters of a group $G$ containing $A_{5}$ as a subgroup of index 2 , distinguishing two possible cases.

  comment

• Paper 4, Section II, I

  Representation Theory | Part II, 2011

  Define the groups $\mathrm{SU}(2)$ and $\mathrm{SO}(3)$.

  Show that $G=\mathrm{SU}(2)$ acts on the vector space of $2 \times 2$ complex matrices of the form

  $$V=\left\{A=\left(\begin{array}{cc} a & b \\ c & -a \end{array}\right) \in \mathrm{M}_{2}(\mathbb{C}): A+\overline{A^{t}}=0\right\}$$

  by conjugation. Denote the corresponding representation of $\mathrm{SU}(2)$ on $V$ by $\rho$.

  Prove the following assertions about this action:

  (i) The subspace $V$ is isomorphic to $\mathbb{R}^{3}$.

  (ii) The pairing $(A, B) \mapsto-\operatorname{tr}(A B)$ defines a positive definite non-degenerate $\mathrm{SU}(2)$ invariant bilinear form.

  (iii) The representation $\rho$ maps $G$ into $\mathrm{SO}(3)$. [You may assume that for any compact group $H$, and any $n \in \mathbb{N}$, there is a continuous group homomorphism $H \rightarrow \mathrm{O}(n)$ if and only if $H$ has an $n$-dimensional representation over $\mathbb{R}$.]

  Write down an orthonormal basis for $V$ and use it to show that $\rho$ is surjective with kernel $\{\pm I\}$.

  Use the isomorphism $\mathrm{SO}(3) \cong G /\{\pm I\}$ to write down a list of irreducible representations of $\mathrm{SO}(3)$ in terms of irreducibles for $\mathrm{SU}(2)$. [Detailed explanations are not required.]

  comment

Riemann Surfaces

• Paper 1, Section II, 23G

  Riemann Surfaces | Part II, 2011

  Suppose that $R_{1}$ and $R_{2}$ are Riemann surfaces, and $A$ is a discrete subset of $R_{1}$. For any continuous map $\alpha: R_{1} \rightarrow R_{2}$ which restricts to an analytic map of Riemann surfaces $R_{1} \backslash A \rightarrow R_{2}$, show that $\alpha$ is an analytic map.

  Suppose that $f$ is a non-constant analytic function on a Riemann surface $R$. Show that there is a discrete subset $A \subset R$ such that, for $P \in R \backslash A, f$ defines a local chart on some neighbourhood of $P$.

  Deduce that, if $\alpha: R_{1} \rightarrow R_{2}$ is a homeomorphism of Riemann surfaces and $f$ is a non-constant analytic function on $R_{2}$ for which the composite $f \circ \alpha$ is analytic on $R_{1}$, then $\alpha$ is a conformal equivalence. Give an example of a pair of Riemann surfaces which are homeomorphic but not conformally equivalent.

  [You may assume standard results for analytic functions on domains in the complex plane.]

  comment

• Paper 2, Section II, 23G

  Riemann Surfaces | Part II, 2011

  Let $\Lambda$ be a lattice in $\mathbb{C}$ generated by 1 and $\tau$, where $\tau$ is a fixed complex number with non-zero imaginary part. Suppose that $f$ is a meromorphic function on $\mathbb{C}$ for which the poles of $f$ are precisely the points in $\Lambda$, and for which $f(z)-1 / z^{2} \rightarrow 0$ as $z \rightarrow 0$. Assume moreover that $f^{\prime}(z)$ determines a doubly periodic function with respect to $\Lambda$ with $f^{\prime}(-z)=-f^{\prime}(z)$ for all $z \in \mathbb{C} \backslash \Lambda$. Prove that:

  (i) $f(-z)=f(z)$ for all $z \in \mathbb{C} \backslash \Lambda$.

  (ii) $f$ is doubly periodic with respect to $\Lambda$.

  (iii) If it exists, $f$ is uniquely determined by the above properties.

  (iv) For some complex number $A, f$ satisfies the differential equation $f^{\prime \prime}(z)=6 f(z)^{2}+A$.

  comment

• Paper 3, Section II, G

  Riemann Surfaces | Part II, 2011

  State the Classical Monodromy Theorem for analytic continuations in subdomains of the plane.

  Let $n, r$ be positive integers with $r>1$ and set $h(z)=z^{n}-1$. By removing $n$ semi-infinite rays from $\mathbb{C}$, find a subdomain $U \subset \mathbb{C}$ on which an analytic function $h^{1 / r}$ may be defined, justifying this assertion. Describe briefly a gluing procedure which will produce the Riemann surface $R$ for the complete analytic function $h^{1 / r}$.

  Let $Z$ denote the set of $n$th roots of unity and assume that the natural analytic covering map $\pi: R \rightarrow \mathbb{C} \backslash Z$ extends to an analytic map of Riemann surfaces $\tilde{\pi}: \tilde{R} \rightarrow \mathbb{C}_{\infty}$, where $\tilde{R}$ is a compactification of $R$ and $\mathbb{C}_{\infty}$ denotes the extended complex plane. Show that $\tilde{\pi}$ has precisely $n$ branch points if and only if $r$ divides $n$.

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2011

  Let $Y_{1}, \ldots, Y_{n}$ be independent identically distributed random variables with model function $f(y, \theta), y \in \mathcal{Y}, \theta \in \Theta \subseteq \mathbb{R}$, and denote by $E_{\theta}$ and $\operatorname{Var}_{\theta}$ expectation and variance under $f(y, \theta)$, respectively. Define $U_{n}(\theta)=\sum_{i=1}^{n} \frac{\partial}{\partial \theta} \log f\left(Y_{i}, \theta\right)$. Prove that $E_{\theta} U_{n}(\theta)=0$. Show moreover that if $T=T\left(Y_{1}, \ldots, Y_{n}\right)$ is any unbiased estimator of $\theta$, then its variance satisfies $\operatorname{Var}_{\theta}(T) \geqslant\left(n \operatorname{Var}_{\theta}\left(U_{1}(\theta)\right)^{-1}\right.$. [You may use the Cauchy-Schwarz inequality without proof, and you may interchange differentiation and integration without justification if necessary.]

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2011

  The data consist of the record times in 1984 for 35 Scottish hill races. The columns list the record time in minutes, the distance in miles, and the total height gained during the route. The data are displayed in $R$ as follows (abbreviated):

  $\begin{array}{lrrr}\text { > hills } & & & \\ \text { Greenmantle } & 2.5 & 650 & 16.083 \\ \text { Carnethy } & 6.0 & 2500 & 48.350 \\ \text { Craig Dunain } & 6.0 & 900 & 33.650 \\ \text { Ben Rha } & 7.5 & 800 & 45.600 \\ \text { Ben Lomond } & 8.0 & 3070 & 62.267 \\ \text { [...] } & & & \\ \text { Cockleroi } & 4.5 & 850 & 28.100 \\ \text { Moffat Chase } & 20.0 & 5000 & 159.833\end{array}$

  Consider a simple linear regression of time on dist and climb. Write down this model mathematically, and explain any assumptions that you make. How would you instruct $R$ to fit this model and assign it to a variable hills. $\operatorname{lm} 1$ ?

  First, we test the hypothesis of no linear relationship to the variables dist and climb against the full model. $\mathrm{R}$ provides the following ANOVA summary:

  

  Using the information in this table, explain carefully how you would test this hypothesis. What do you conclude?

  The $\mathrm{R}$ command

  summary (hills. Im1)

  provides the following (slightly abbreviated) summary:

  

  Carefully explain the information that appears in each column of the table. What are your conclusions? In particular, how would you test for the significance of the variable climb in this model?

  

  Figure 1: Hills data: diagnostic plots

  Finally, we perform model diagnostics on the full model, by looking at studentised residuals versus fitted values, and the normal QQ-plot. The plots are displayed in Figure $1 .$ Comment on possible sources of model misspecification. Is it possible that the problem lies with the data? If so, what do you suggest?

  comment

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2011

  Let $f_{0}$ be a probability density function, with cumulant generating function $K$. Define what it means for a random variable $Y$ to have a model function of exponential dispersion family form, generated by $f_{0}$. Compute the cumulant generating function $K_{Y}$ of $Y$ and deduce expressions for the mean and variance of $Y$ that depend only on first and second derivatives of $K$.

  comment

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2011

  Define a generalised linear model for a sample $Y_{1}, \ldots, Y_{n}$ of independent random variables. Define further the concept of the link function. Define the binomial regression model with logistic and probit link functions. Which of these is the canonical link function?

  comment

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2011

  The numbers of ear infections observed among beach and non-beach (mostly pool) swimmers were recorded, along with explanatory variables: frequency, location, age, and sex. The data are aggregated by group, with a total of 24 groups defined by the explanatory variables.

  $$\begin{array}{ll} \text { freq } & \mathrm{F}=\text { frequent, } \mathrm{NF}=\text { infrequent } \\ \text { loc } & \mathrm{NB}=\text { non-beach, } \mathrm{B}=\text { beach } \\ \text { age } & 15-19,20-24,24-29 \\ \text { sex } & \mathrm{F}=\text { female, } \mathrm{M}=\text { male } \\ \text { count } & \text { the number of infections reported over a fixed time period } \\ \mathrm{n} & \text { the total number of swimmers } \end{array}$$

  The data look like this:

  $$\begin{array}{lrrrrrr} & \text { count } & \text { n } & \text { freq } & \text { loc } & \text { sex } & \text { age } \\ 1 & 68 & 31 & F & \text { NB } & \text { M } & 15-19 \\ 2 & 14 & 4 & F & \text { NB } & \text { F } & 15-19 \\ 3 & 35 & 12 & F & \text { NB } & \text { M } & 20-24 \\ 4 & 16 & 11 & F & \text { NB } & \text { F } & 20-24 \\ {[\ldots]} & & & & & & \\ 23 & 5 & 15 & \text { NF } & \text { B } & \text { M } & 25-29 \\ 24 & 6 & 6 & \text { NF } & \text { B } & \text { F } & 25-29 \end{array}$$

  Let $\mu_{j}$ denote the expected number of ear infections of a person in group $j$. Explain why it is reasonable to model count ${ }_{j}$ as Poisson with mean $n_{j} \mu_{j}$.

  We fit the following Poisson model:

  $$\log \left(\mathbb{E}\left(\operatorname{count}_{j}\right)\right)=\log \left(n_{j} \mu_{j}\right)=\log \left(n_{j}\right)+\mathbf{x}_{j} \beta$$

  where $\log \left(n_{j}\right)$ is an offset, i.e. an explanatory variable with known coefficient $1 .$ $\mathrm{R}$ produces the following (abbreviated) summary for the main effects model:

  

  Why are expressions freq $\mathrm{F}$, locB, age $15-19$, and sexF not listed?

  Suppose that we plan to observe a group of 20 female, non-frequent, beach swimmers, aged 20-24. Give an expression (using the coefficient estimates from the model fitted above) for the expected number of ear infections in this group.

  Now, suppose that we allow for interaction between variables age and sex. Give the $\mathrm{R}$ command for fitting this model. We test for the effect of this interaction by producing the following (abbreviated) ANOVA table:

  

  Briefly explain what test is performed, and what you would conclude from it. Does either of these models fit the data well?

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2011

  Consider the general linear model $Y=X \beta+\epsilon$, where the $n \times p$ matrix $X$ has full rank $p \leqslant n$, and where $\epsilon$ has a multivariate normal distribution with mean zero and covariance matrix $\sigma^{2} I_{n}$. Write down the likelihood function for $\beta, \sigma^{2}$ and derive the maximum likelihood estimators $\hat{\beta}, \hat{\sigma}^{2}$ of $\beta, \sigma^{2}$. Find the distribution of $\hat{\beta}$. Show further that $\hat{\beta}$ and $\hat{\sigma}^{2}$ are independent.

  comment

Statistical Physics

• Paper 1, Section II, D

  Statistical Physics | Part II, 2011

  Describe the physical relevance of the microcanonical, canonical and grand canonical ensembles. Explain briefly the circumstances under which all ensembles are equivalent.

  The Gibbs entropy for a probability distribution $p(n)$ over states is

  $$S=-k_{B} \sum_{n} p(n) \log p(n) .$$

  By imposing suitable constraints on $p(n)$, show how maximising the entropy gives rise to the probability distributions for the microcanonical and canonical ensembles.

  A system consists of $N$ non-interacting particles fixed at points in a lattice. Each particle has three states with energies $E=-\epsilon, 0,+\epsilon$. If the system is at a fixed temperature $T$, determine the average energy $E$ and the heat capacity $C$. Evaluate each in the limits $T \rightarrow \infty$ and $T \rightarrow 0$.

  Describe a configuration of the system that would have negative temperature. Does this system obey the third law of thermodynamics?

  comment

• Paper 2, Section II, D

  Statistical Physics | Part II, 2011

  Write down the partition function for a single classical non-relativistic particle of mass $m$ moving in three dimensions in a potential $U(\mathbf{x})$ and in equilibrium with a heat bath at temperature $T$.

  A system of $N$ non-interacting classical non-relativistic particles, in equilibrium at temperature $T$, is placed in a potential

  $$U(\mathbf{x})=\frac{\left(x^{2}+y^{2}+z^{2}\right)^{n}}{V^{2 n / 3}}$$

  where $n$ is a positive integer. Using the partition function, show that the free energy is

  $$F=-N k_{B} T\left(\log V+\frac{3}{2} \frac{n+1}{n} \log k_{B} T+\log I_{n}+\text { const }\right)$$

  where

  $$I_{n}=\left(\frac{m}{2 \pi \hbar^{2}}\right)^{3 / 2} \int_{0}^{\infty} 4 \pi u^{2} \exp \left(-u^{2 n}\right) d u$$

  Explain the physical relevance of the constant term in the expression $(*)$.

  Viewing $V$ as an external parameter, akin to volume, compute the conjugate pressure $p$ and show that the equation of state coincides with that of an ideal gas.

  Compute the energy $E$, heat capacity $C_{V}$ and entropy $S$ of the gas. Determine the local particle number density as a function of $|\mathbf{x}|$.

  comment

• Paper 3, Section II, D

  Statistical Physics | Part II, 2011

  A gas of non-interacting particles has energy-momentum relationship $E=A(\hbar k)^{\alpha}$ for some constants $A$ and $\alpha$. Determine the density of states $g(E) d E$ in a threedimensional volume $V$.

  Explain why the chemical potential $\mu$ satisfies $\mu<0$ for the Bose-Einstein distribution.

  Show that an ideal quantum Bose gas with the energy-momentum relationship above has

  $$p V=\frac{\alpha E}{3} .$$

  If the particles are bosons at fixed temperature $T$ and chemical potential $\mu$, write down an expression for the number of particles that do not occupy the ground state. Use this to determine the values of $\alpha$ for which there exists a Bose-Einstein condensate at sufficiently low temperatures.

  Discuss whether a gas of photons can undergo Bose-Einstein condensation.

  comment

• Paper 4, Section II, D

  Statistical Physics | Part II, 2011

  (i) Define the Gibbs free energy for a gas of $N$ particles with pressure $p$ at a temperature $T$. Explain why it is necessarily proportional to the number of particles $N$ in the system. Given volume $V$ and chemical potential $\mu$, prove that

  $$\left.\frac{\partial \mu}{\partial p}\right|_{T}=\frac{V}{N} .$$

  (ii) The van der Waals equation of state is

  $$\left(p+\frac{a N^{2}}{V^{2}}\right)(V-N b)=N k_{B} T$$

  Explain the physical significance of the terms with constants $a$ and $b$. Sketch the isotherms of the van der Waals equation. Show that the critical point lies at

  $$k_{B} T_{c}=\frac{8 a}{27 b}, \quad V_{c}=3 b N, \quad p_{c}=\frac{a}{27 b^{2}} .$$

  (iii) Describe the Maxwell construction to determine the condition for phase equilibrium. Hence sketch the regions of the van der Waals isotherm at $T<T_{c}$ that correspond to metastable and unstable states. Sketch those regions that correspond to stable liquids and stable gases.

  (iv) Show that, as the critical point is approached along the co-existence curve,

  $$V_{\text {gas }}-V_{\text {liquid }} \sim\left(T_{c}-T\right)^{1 / 2} .$$

  Show that, as the critical point is approached along an isotherm,

  $$p-p_{c} \sim\left(V-V_{c}\right)^{3} .$$

  comment

Stochastic Financial Models

• Paper 1, Section II, J

  Stochastic Financial Models | Part II, 2011

  In a one-period market, there are $n$ assets whose prices at time $t$ are given by $S_{t}=\left(S_{t}^{1}, \ldots, S_{t}^{n}\right)^{T}, t=0,1$. The prices $S_{1}$ of the assets at time 1 have a $N(\mu, V)$ distribution, with non-singular covariance $V$, and the prices $S_{0}$ at time 0 are known constants. In addition, there is a bank account giving interest $r$, so that one unit of cash invested at time 0 will be worth $(1+r)$ units of cash at time 1 .

  An agent with initial wealth $w_{0}$ chooses a portfolio $\theta=\left(\theta^{1}, \ldots, \theta^{n}\right)$ of the assets to hold, leaving him with $x=w_{0}-\theta \cdot S_{0}$ in the bank account. His objective is to maximize his expected utility

  $$E\left(-\exp \left[-\gamma\left\{x(1+r)+\theta \cdot S_{1}\right\}\right]\right) \quad(\gamma>0)$$

  Find his optimal portfolio in each of the following three situations:

  (i) $\theta$ is unrestricted;

  (ii) no investment in the bank account is allowed: $x=0$;

  (iii) the initial holdings $x$ of cash must be non-negative.

  For the third problem, show that the optimal initial holdings of cash will be zero if and only if

  $$\frac{S_{0} \cdot(\gamma V)^{-1} \mu-w_{0}}{S_{0} \cdot(\gamma V)^{-1} S_{0}} \geqslant 1+r$$

  comment

• Paper 2, Section II, J

  Stochastic Financial Models | Part II, 2011

  Consider a symmetric simple random walk $\left(Z_{n}\right)_{n \in \mathbb{Z}^{+}}$taking values in statespace $I=h \mathbb{Z}^{2} \equiv\{(i h, j h): i, j \in \mathbb{Z}\}$, where $h \equiv N^{-1}(N$ an integer $)$. Writing $Z_{n} \equiv\left(X_{n}, Y_{n}\right)$, the transition probabilities are given by

  $$P\left(\Delta Z_{n}=(h, 0)\right)=P\left(\Delta Z_{n}=(0, h)\right)=P\left(\Delta Z_{n}=(-h, 0)\right)=P\left(\Delta Z_{n}=(0,-h)\right)=\frac{1}{4},$$

  where $\Delta Z_{n} \equiv Z_{n}-Z_{n-1}$.

  What does it mean to say that $\left(M_{n}, \mathcal{F}_{n}\right)_{n \in \mathbb{Z}^{+}}$is a martingale? Find a condition on $\theta$ and $\lambda$ such that

  $$M_{n}=\exp \left(\theta X_{n}-\lambda Y_{n}\right)$$

  is a martingale. If $\theta=i \alpha$ for some real $\alpha$, show that $M$ is a martingale if

  $$e^{-\lambda h}=2-\cos (\alpha h)-\sqrt{(2-\cos (\alpha h))^{2}-1}$$

  Suppose that the random walk $Z$ starts at position $(0,1) \equiv(0, N h)$ at time 0 , and suppose that

  $$\tau=\inf \left\{n: Y_{n}=0\right\} .$$

  Stating fully any results to which you appeal, prove that

  $$E \exp \left(i \alpha X_{\tau}\right)=e^{-\lambda}$$

  where $\lambda$ is as given at $(*)$. Deduce that as $N \rightarrow \infty$

  $$E \exp \left(i \alpha X_{\tau}\right) \rightarrow e^{-|\alpha|}$$

  and comment briefly on this result.

  comment

• Paper 3, Section II, J

  Stochastic Financial Models | Part II, 2011

  First, what is a Brownian motion?

  (i) The price $S_{t}$ of an asset evolving in continuous time is represented as

  $$S_{t}=S_{0} \exp \left(\sigma W_{t}+\mu t\right)$$

  where $W$ is a standard Brownian motion, and $\sigma$ and $\mu$ are constants. If riskless investment in a bank account returns a continuously-compounded rate of interest $r$, derive a formula for the time-0 price of a European call option on the asset $S$ with strike $K$ and expiry $T$. You may use any general results, but should state them clearly.

  (ii) In the same financial market, consider now a derivative which pays

  $$Y=\left\{\exp \left(T^{-1} \int_{0}^{T} \log \left(S_{u}\right) d u\right)-K\right\}^{+}$$

  at time $T$. Find the time-0 price for this derivative. Show that it is less than the price of the European call option which you derived in (i).

  comment

• Paper 4, Section II, J

  Stochastic Financial Models | Part II, 2011

  In a two-period model, two agents enter a negotiation at time 0 . Agent $j$ knows that he will receive a random payment $X_{j}$ at time $1(j=1,2)$, where the joint distribution of $\left(X_{1}, X_{2}\right)$ is known to both agents, and $X_{1}+X_{2}>0$. At the outcome of the negotiation, there will be an agreed risk transfer random variable $Y$ which agent 1 will pay to agent 2 at time 1 . The objective of agent 1 is to maximize $E U_{1}\left(X_{1}-Y\right)$, and the objective of agent 2 is to maximize $E U_{2}\left(X_{2}+Y\right)$, where the functions $U_{j}$ are strictly increasing, strictly concave, $C^{2}$, and have the properties that

  $$\lim _{x \downarrow 0} U_{j}^{\prime}(x)=+\infty, \quad \lim _{x \uparrow \infty} U_{j}^{\prime}(x)=0$$

  Show that, unless there exists some $\lambda \in(0, \infty)$ such that

  $$\frac{U_{1}^{\prime}\left(X_{1}-Y\right)}{U_{2}^{\prime}\left(X_{2}+Y\right)}=\lambda \quad \text { almost surely }$$

  the risk transfer $Y$ could be altered to the benefit of both agents, and so would not be the conclusion of the negotiation.

  Show that, for given $\lambda>0$, the relation $(*)$ determines a unique risk transfer $Y=Y_{\lambda}$, and that $X_{2}+Y_{\lambda}$ is a function of $X_{1}+X_{2}$.

  comment

Topics in Analysis

• Paper 1, Section I, F

  Topics in Analysis | Part II, 2011

  (i) State the Baire Category Theorem for metric spaces in its closed sets version.

  (ii) Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be a complex analytic function which is not a polynomial. Prove that there exists a point $z_{0} \in \mathbb{C}$ such that each coefficient of the Taylor series of $f$ at $z_{0}$ is non-zero.

  comment

• Paper 2, Section I, F

  Topics in Analysis | Part II, 2011

  (i) Let $x_{1}, x_{2}, \ldots, x_{n} \in[-1,1]$ be any set of $n$ distinct numbers. Show that there exist numbers $A_{1}, A_{2}, \ldots, A_{n}$ such that the formula

  $$\int_{-1}^{1} p(x) d x=\sum_{j=1}^{n} A_{j} p\left(x_{j}\right)$$

  is valid for every polynomial $p$ of degree $\leqslant n-1$.

  (ii) For $n=0,1,2, \ldots$, let $p_{n}$ be the Legendre polynomial, over $[-1,1]$, of degree $n$. Suppose that $x_{1}, x_{2}, \ldots, x_{n} \in[-1,1]$ are the roots of $p_{n}$, and $A_{1}, A_{2}, \ldots, A_{n}$ are the numbers corresponding to $x_{1}, x_{2}, \ldots, x_{n}$ as in (i).

  [You may assume without proof that for $n \geqslant 1, p_{n}$ has $n$ distinct roots in $[-1,1] .$ ]

  Prove that the integration formula in (i) is now valid for any polynomial $p$ of degree $\leqslant 2 n-1$.

  (iii) Is it possible to choose $n$ distinct points $x_{1}, x_{2}, \ldots, x_{n} \in[-1,1]$ and corresponding numbers $A_{1}, A_{2}, \ldots, A_{n}$ such that the integration formula in (i) is valid for any polynomial $p$ of degree $\leqslant 2 n$ ? Justify your answer.

  comment

• Paper 2, Section II, F

  Topics in Analysis | Part II, 2011

  Let $C[0,1]$ be the space of real continuous functions on the interval $[0,1]$. A mapping $L: C[0,1] \rightarrow C[0,1]$ is said to be positive if $L(f) \geqslant 0$ for each $f \in C[0,1]$ with $f \geqslant 0$, and linear if $L(a f+b g)=a L(f)+b L(g)$ for all functions $f, g \in C[0,1]$ and constants $a, b \in \mathbb{R}$.

  (i) Let $L_{n}: C[0,1] \rightarrow C[0,1]$ be a sequence of positive, linear mappings such that $L_{n}(f) \rightarrow f$ uniformly on $[0,1]$ for the three functions $f(x)=1, x, x^{2}$. Prove that $L_{n}(f) \rightarrow f$ uniformly on $[0,1]$ for every $f \in C[0,1]$.

  (ii) Define $B_{n}: C[0,1] \rightarrow C[0,1]$ by

  $$B_{n}(f)(x)=\sum_{k=0}^{n}\left(\begin{array}{l} n \\ k \end{array}\right) f\left(\frac{k}{n}\right) x^{k}(1-x)^{n-k}$$

  where $\left(\begin{array}{l}n \\ k\end{array}\right)=\frac{n !}{k !(n-k) !}$. Using the result of part (i), or otherwise, prove that $B_{n}(f) \rightarrow f$ uniformly on $[0,1]$.

  (iii) Let $f \in C[0,1]$ and suppose that

  $$\int_{0}^{1} f(x) x^{4 n} d x=0$$

  for each $n=0,1, \ldots$ Prove that $f$ must be the zero function.

  [You should not use the Stone-Weierstrass theorem without proof.]

  comment

• Paper 3, Section I, F

  Topics in Analysis | Part II, 2011

  Let $\Gamma=\{z \in \mathbb{C}: z \neq 1,|\operatorname{Re}(z)|+|\operatorname{Im}(z)|=1\}$.

  (i) Prove that, for any $\zeta \in \mathbb{C}$ with $|\operatorname{Re}(\zeta)|+|\operatorname{Im}(\zeta)|>1$ and any $\epsilon>0$, there exists a complex polynomial $p$ such that

  $$\sup _{z \in \Gamma}\left|p(z)-(z-\zeta)^{-1}\right|<\epsilon$$

  (ii) Does there exist a sequence of polynomials $p_{n}$ such that $p_{n}(z) \rightarrow(z-1)^{-1}$ for every $z \in \Gamma ?$ Justify your answer.

  comment

• Paper 3, Section II, F

  Topics in Analysis | Part II, 2011

  Let $f:[0,1] \rightarrow \mathbb{R}$ be continuous and let $n$ be a positive integer. For $g:[0,1] \rightarrow \mathbb{R}$ a continuous function, write $\|f-g\|_{L^{\infty}}=\sup _{x \in[0,1]}|f(x)-g(x)|$.

  (i) Let $p$ be a polynomial of degree at most $n$ with the property that there are $(n+2)$ distinct points $x_{1}, x_{2}, \ldots, x_{n+2} \in[0,1]$ with $x_{1}<x_{2}<\ldots<x_{n+2}$ such that

  $$f\left(x_{j}\right)-p\left(x_{j}\right)=(-1)^{j}\|f-p\|_{L^{\infty}}$$

  for each $j=1,2, \ldots, n+2$. Prove that

  $$\|f-p\|_{L^{\infty}} \leqslant\|f-q\|_{L^{\infty}}$$

  for every polynomial $q$ of degree at most $n$.

  (ii) Prove that there exists a polynomial $p$ of degree at most $n$ such that

  $$\|f-p\|_{L^{\infty}} \leqslant\|f-q\|_{L^{\infty}}$$

  for every polynomial $q$ of degree at most $n$.

  [If you deduce this from a more general result about abstract normed spaces, you must prove that result.]

  (iii) Let $Y=\left\{y_{1}, y_{2}, \ldots, y_{n+2}\right\}$ be any set of $(n+2)$ distinct points in $[0,1]$.

  (a) For $j=1,2, \ldots, n+2$, let

  $$r_{j}(x)=\prod_{k=1, k \neq j}^{n+2} \frac{x-y_{k}}{y_{j}-y_{k}}$$

  $t(x)=\sum_{j=1}^{n+2} f\left(y_{j}\right) r_{j}(x)$ and $r(x)=\sum_{j=1}^{n+2}(-1)^{j} r_{j}(x)$. Explain why there is a unique number $\lambda \in \mathbb{R}$ such that the degree of the polynomial $t-\lambda r$ is at $\operatorname{most} n$.

  (b) Let $\|f-g\|_{L^{\infty}(Y)}=\sup _{x \in Y}|f(x)-g(x)|$. Deduce from part (a) that there exists a polynomial $p$ of degree at most $n$ such that

  $$\|f-p\|_{L^{\infty}(Y)} \leqslant\|f-q\|_{L^{\infty}(Y)}$$

  for every polynomial $q$ of degree at most $n$.

  comment

• Paper 4, Section I, $2 F$

  Topics in Analysis | Part II, 2011

  (a) Let $\gamma:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ be a continuous map such that $\gamma(0)=\gamma(1)$. Define the winding number $w(\gamma ; 0)$ of $\gamma$ about the origin. State precisely a theorem about homotopy invariance of the winding number.

  (b) Let $B=\{z \in \mathbb{C}:|z| \leqslant 1\}$ and let $f: B \rightarrow \mathbb{C}$ be a continuous map satisfying

  $$|f(z)-z| \leqslant 1$$

  for each $z \in \partial B$.

  (i) For $0 \leqslant t \leqslant 1$, let $\gamma(t)=f\left(e^{2 \pi i t}\right)$. If $\gamma(t) \neq 0$ for each $t \in[0,1]$, prove that $w(\gamma ; 0)=1$.

  [Hint: Consider a suitable homotopy between $\gamma$ and the map $\gamma_{1}(t)=e^{2 \pi i t}$, $0 \leqslant t \leqslant 1 .]$

  (ii) Deduce that $f(z)=0$ for some $z \in B$.

  comment

Waves

• Paper 1, Section II, 39B

  Waves | Part II, 2011

  An inviscid fluid with sound speed $c_{0}$ occupies the region $0<y<\pi \alpha, 0<z<\pi \beta$ enclosed by the rigid boundaries of a rectangular waveguide. Starting with the acoustic wave equation, find the dispersion relation $\omega(k)$ for the propagation of sound waves in the $x$-direction.

  Hence find the phase speed $c(k)$ and the group velocity $c_{g}(k)$ of both the dispersive modes and the nondispersive mode, and sketch the form of the results for $k, \omega>0$.

  Define the time and cross-sectional average appropriate for a mode with frequency $\omega$. For each dispersive mode, show that the average kinetic energy is equal to the average compressive energy.

  A general multimode acoustic disturbance is created within the waveguide at $t=0$ in a region around $x=0$. Explain briefly how the amplitude of the disturbance varies with time as $t \rightarrow \infty$ at the moving position $x=V t$ for each of the cases $0<V<c_{0}$, $V=c_{0}$ and $V>c_{0}$. [You may quote without proof any generic results from the method of stationary phase.]

  comment

• Paper 2, Section II, 38B

  Waves | Part II, 2011

  A uniform elastic solid with wavespeeds $c_{P}$ and $c_{S}$ occupies the region $z<0$. An $S$-wave with displacement

  $$\mathbf{u}=(\cos \theta, 0,-\sin \theta) \mathrm{e}^{\mathrm{i} k(x \sin \theta+z \cos \theta)-\mathrm{i} \omega t}$$

  is incident from $z<0$ on a rigid boundary at $z=0$. Find the form and amplitudes of the reflected waves.

  When is the reflected $P$-wave evanescent? Show that if the $P$-wave is evanescent then the amplitude of the reflected $S$-wave has the same magnitude as the incident wave, and interpret this result physically.

  comment

• Paper 3, Section II, 38B

  Waves | Part II, 2011

  The dispersion relation in a stationary medium is given by $\omega=\Omega_{0}(\mathbf{k})$, where $\Omega_{0}$ is a known function. Show that, in the frame of reference where the medium has a uniform velocity $-\mathbf{U}$, the dispersion relation is given by $\omega=\Omega_{0}(\mathbf{k})-\mathbf{U} \cdot \mathbf{k}$.

  An aircraft flies in a straight line with constant speed $M c_{0}$ through air with sound speed $c_{0}$. If $M>1$ show that, in the reference frame of the aircraft, the steady waves lie behind it on a cone of semi-angle $\sin ^{-1}(1 / M)$. Show further that the unsteady waves are confined to the interior of the cone.

  A small insect swims with constant velocity $\mathbf{U}=(U, 0)$ over the surface of a pool of water. The resultant capillary waves have dispersion relation $\omega^{2}=T|\mathbf{k}|^{3} / \rho$ on stationary water, where $T$ and $\rho$ are constants. Show that, in the reference frame of the insect, steady waves have group velocity

  $$\mathbf{c}_{g}=U\left(\frac{3}{2} \cos ^{2} \beta-1, \frac{3}{2} \cos \beta \sin \beta\right),$$

  where $\mathbf{k} \propto(\cos \beta, \sin \beta)$. Deduce that the steady wavefield extends in all directions around the insect.

  comment

• Paper 4, Section II, 38B

  Waves | Part II, 2011

  Show that, in the standard notation for one-dimensional flow of a perfect gas, the Riemann invariants $u \pm 2\left(c-c_{0}\right) /(\gamma-1)$ are constant on characteristics $C_{\pm}$given by

  $$\frac{\mathrm{d} x}{\mathrm{~d} t}=u \pm c$$

  Such a gas occupies the region $x>X(t)$ in a semi-infinite tube to the right of a piston at $x=X(t)$. At time $t=0$, the piston and the gas are at rest, $X=0$, and the gas is uniform with $c=c_{0}$. For $t>0$ the piston accelerates smoothly in the positive $x$-direction. Show that, prior to the formation of a shock, the motion of the gas is given parametrically by

  $$u(x, t)=\dot{X}(\tau) \quad \text { on } \quad x=X(\tau)+\left[c_{0}+\frac{1}{2}(\gamma+1) \dot{X}(\tau)\right](t-\tau)$$

  in a region that should be specified.

  For the case $X(t)=\frac{2}{3} c_{0} t^{3} / T^{2}$, where $T>0$ is a constant, show that a shock first forms in the gas when

  $$t=\frac{T}{\gamma+1}(3 \gamma+1)^{1 / 2}$$

  comment