Part II, 2018

Algebraic Geometry

• Paper 1, Section II, I

  Algebraic Geometry | Part II, 2018

  (a) Let $k$ be an uncountable field, $\mathcal{M} \subseteq k\left[x_{1}, \ldots, x_{n}\right]$ a maximal ideal and $A=k\left[x_{1}, \ldots, x_{n}\right] / \mathcal{M} .$

  Show that every element of $A$ is algebraic over $k$.

  (b) Now assume that $k$ is algebraically closed. Suppose that $J \subset k\left[x_{1}, \ldots, x_{n}\right]$ is an ideal, and that $f \in k\left[x_{1}, \ldots, x_{n}\right]$ vanishes on $Z(J)$. Using the result of part (a) or otherwise, show that $f^{N} \in J$ for some $N \geqslant 1$.

  (c) Let $f: X \rightarrow Y$ be a morphism of affine algebraic varieties. Show $\overline{f(X)}=Y$ if and only if the map $f^{*}: k[Y] \rightarrow k[X]$ is injective.

  Suppose now that $\overline{f(X)}=Y$, and that $X$ and $Y$ are irreducible. Define the dimension of $X, \operatorname{dim} X$, and show $\operatorname{dim} X \geqslant \operatorname{dim} Y$. [You may use whichever definition of $\operatorname{dim} X$ you find most convenient.]

  comment

• Paper 2, Section II, I

  Algebraic Geometry | Part II, 2018

  (a) Let $X \subseteq \mathbf{A}^{n}$ be an affine algebraic variety defined over the field $k$.

  Define the tangent space $T_{p} X$ for $p \in X$, and the dimension of $X$ in terms of $T_{p} X$.

  Suppose that $k$ is an algebraically closed field with char $k>0$. Show directly from your definition that if $X=Z(f)$, where $f \in k\left[x_{1}, \ldots, x_{n}\right]$ is irreducible, then $\operatorname{dim} X=n-1$.

  [Any form of the Nullstellensatz may be used if you state it clearly.]

  (b) Suppose that char $k=0$, and let $W$ be the vector space of homogeneous polynomials of degree $d$ in 3 variables over $k$. Show that

  $$U=\left\{(f, p) \in W \times k^{3} \mid Z(f-1) \text { is a smooth surface at } p\right\}$$

  is a non-empty Zariski open subset of $W \times k^{3}$.

  comment

• Paper 3, Section II, I

  Algebraic Geometry | Part II, 2018

  (a) State the Riemann-Roch theorem.

  (b) Let $E$ be a smooth projective curve of genus 1 over an algebraically closed field $k$, with char $k \neq 2,3$. Show that there exists an isomorphism from $E$ to the plane cubic in $\mathbf{P}^{2}$ defined by the equation

  $$y^{2}=\left(x-\lambda_{1}\right)\left(x-\lambda_{2}\right)\left(x-\lambda_{3}\right)$$

  for some distinct $\lambda_{1}, \lambda_{2}, \lambda_{3} \in k$.

  (c) Let $Q$ be the point at infinity on $E$. Show that the map $E \rightarrow C l^{0}(E), P \mapsto[P-Q]$ is an isomorphism.

  Describe how this defines a group structure on $E$. Denote addition by $\boxplus$. Determine all the points $P \in E$ with $P \boxplus P=Q$ in terms of the equation of the plane curve in part (b).

  comment

• Paper 4, Section II, I

  Algebraic Geometry | Part II, 2018

  State a theorem which describes the canonical divisor of a smooth plane curve $C$ in terms of the divisor of a hyperplane section. Express the degree of the canonical divisor $K_{C}$ and the genus of $C$ in terms of the degree of $C$. [You need not prove these statements.]

  From now on, we work over $\mathbb{C}$. Consider the curve in $\mathbf{A}^{2}$ defined by the equation

  $$y+x^{3}+x y^{3}=0$$

  Let $C$ be its projective completion. Show that $C$ is smooth.

  Compute the genus of $C$ by applying the Riemann-Hurwitz theorem to the morphism $C \rightarrow \mathbf{P}^{1}$ induced from the rational map $(x, y) \mapsto y$. [You may assume that the discriminant of $x^{3}+a x+b$ is $-4 a^{3}-27 b^{2}$.]

  comment

Algebraic Topology

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2018

  (a) Let $V$ be the vector space of 3-dimensional upper-triangular matrices with real entries:

  $$V=\left\{\left(\begin{array}{ccc} 1 & x & y \\ 0 & 1 & z \\ 0 & 0 & 1 \end{array}\right) \mid x, y, z \in \mathbb{R}\right\}$$

  Let $\Gamma$ be the set of elements of $V$ for which $x, y, z$ are integers. Notice that $\Gamma$ is a subgroup of $G L_{3}(\mathbb{R})$; let $\Gamma$ act on $V$ by left-multiplication and let $N=\Gamma \backslash V$. Show that the quotient $\operatorname{map} V \rightarrow N$ is a covering map.

  (b) Consider the unit circle $S^{1} \subseteq \mathbb{C}$, and let $T=S^{1} \times S^{1}$. Show that the map $f: T \rightarrow T$ defined by

  $$f(z, w)=(z w, w)$$

  is a homeomorphism.

  (c) Let $M=[0,1] \times T / \sim$, where $\sim$ is the smallest equivalence relation satisfying

  $$(1, x) \sim(0, f(x))$$

  for all $x \in T$. Prove that $N$ and $M$ are homeomorphic by exhibiting a homeomorphism $M \rightarrow N$. [You may assume without proof that $N$ is Hausdorff.]

  (d) Prove that $\pi_{1}(M) \cong \Gamma$.

  comment

• Paper 2, Section II, H

  Algebraic Topology | Part II, 2018

  (a) Define the first barycentric subdivision $K^{\prime}$ of a simplicial complex $K$. Hence define the $r^{t h}$ barycentric subdivision $K^{(r)}$. [You do not need to prove that $K^{\prime}$ is a simplicial complex.]

  (b) Define the mesh $\mu(K)$ of a simplicial complex $K$. State a result that describes the behaviour of $\mu\left(K^{(r)}\right)$ as $r \rightarrow \infty$.

  (c) Define a simplicial approximation to a continuous map of polyhedra

  $$f:|K| \rightarrow|L|$$

  Prove that, if $g$ is a simplicial approximation to $f$, then the realisation $|g|:|K| \rightarrow|L|$ is homotopic to $f$.

  (d) State and prove the simplicial approximation theorem. [You may use the Lebesgue number lemma without proof, as long as you state it clearly.]

  (e) Prove that every continuous map of spheres $S^{n} \rightarrow S^{m}$ is homotopic to a constant map when $n<m$.

  comment

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2018

  (a) State a version of the Seifert-van Kampen theorem for a cell complex $X$ written as the union of two subcomplexes $Y, Z$.

  (b) Let

  $$X_{n}=\underbrace{S^{1} \vee \ldots \vee S^{1}}_{n} \vee \mathbb{R} P^{2}$$

  for $n \geqslant 1$, and take any $x_{0} \in X_{n}$. Write down a presentation for $\pi_{1}\left(X_{n}, x_{0}\right)$.

  (c) By computing a homology group of a suitable four-sheeted covering space of $X_{n}$, prove that $X_{n}$ is not homotopy equivalent to a compact, connected surface whenever $n \geqslant 1$.

  comment

• Paper 4, Section II, H

  Algebraic Topology | Part II, 2018

  (a) State the Mayer-Vietoris theorem for a union of simplicial complexes

  $$K=M \cup N$$

  with $L=M \cap N$.

  (b) Construct the map $\partial_{*}: H_{k}(K) \rightarrow H_{k-1}(L)$ that appears in the statement of the theorem. [You do not need to prove that the map is well defined, or a homomorphism.]

  (c) Let $K$ be a simplicial complex with $|K|$ homeomorphic to the $n$-dimensional sphere $S^{n}$, for $n \geqslant 2$. Let $M \subseteq K$ be a subcomplex with $|M|$ homeomorphic to $S^{n-1} \times[-1,1]$. Suppose that $K=M \cup N$, such that $L=M \cap N$ has polyhedron $|L|$ identified with $S^{n-1} \times\{-1,1\} \subseteq S^{n-1} \times[-1,1]$. Prove that $|N|$ has two path components.

  comment

Analysis of Functions

• Paper 1, Section II, F

  Analysis of Functions | Part II, 2018

  (a) Consider a measure space $(X, \mathcal{A}, \mu)$ and a complex-valued measurable function $F$ on $X$. Prove that for any $\varphi:[0,+\infty) \rightarrow[0,+\infty)$ differentiable and increasing such that $\varphi(0)=0$, then

  $$\int_{X} \varphi(|F(x)|) \mathrm{d} \mu(x)=\int_{0}^{+\infty} \varphi^{\prime}(s) \mu(\{|F|>s\}) \mathrm{d} \lambda(s)$$

  where $\lambda$ is the Lebesgue measure.

  (b) Consider a complex-valued measurable function $f \in L^{1}\left(\mathbb{R}^{n}\right) \cap L^{\infty}\left(\mathbb{R}^{n}\right)$ and its maximal function $M f(x)=\sup _{r>0} \frac{1}{|B(x, r)|} \int_{B(x, r)}|f| \mathrm{d} \lambda$. Prove that for $p \in(1,+\infty)$ there is a constant $c_{p}>0$ such that $\|M f\|_{L^{p}\left(\mathbb{R}^{n}\right)} \leqslant c_{p}\|f\|_{L^{p}\left(\mathbb{R}^{n}\right)}$.

  [Hint: Split $f=f_{0}+f_{1}$ with $f_{0}=f \chi_{\{|f|>s / 2\}}$ and $f_{1}=f \chi_{\{|f| \leqslant s / 2\}}$ and prove that $\lambda(\{M f>s\}) \leqslant \lambda\left(\left\{M f_{0}>s / 2\right\}\right)$. Then use the maximal inequality $\lambda(\{M f>s\}) \leqslant$ $\frac{C_{1}}{s}\|f\|_{L^{1}\left(\mathbb{R}^{n}\right)}$ for some constant $\left.C_{1}>0 .\right]$

  (c) Consider $p, q \in(1,+\infty)$ with $p<q$ and $\alpha \in(0, n)$ such that $1 / q=1 / p-\alpha / n$. Define $I_{\alpha}|f|(x):=\int_{\mathbb{R}^{n}} \frac{|f(y)|}{|x-y|^{n-\alpha}} \mathrm{d} \lambda(y)$ and prove $I_{\alpha}|f|(x) \leqslant\|f\|_{L^{p}\left(\mathbb{R}^{n}\right)}^{\alpha p / n} M f(x)^{1-\alpha p / n}$.

  [Hint: Split the integral into $|x-y| \geqslant r$ and $|x-y| \in\left[2^{-k-1} r, 2^{-k} r\right)$ for all $k \geqslant 0$, given some suitable $r>0 .]$

  comment

• Paper 3, Section II, $22 F$

  Analysis of Functions | Part II, 2018

  (a) Let $(X, \mathcal{A}, \mu)$ be a measure space. Define the spaces $L^{p}(X)$ for $p \in[1, \infty]$. Prove that if $\mu(X)<\infty$ then $L^{q}(X) \subset L^{p}(X)$ for all $1 \leqslant p<q \leqslant \infty$.

  (b) Now let $X=\mathbb{R}^{n}$ endowed with Borel sets and Lebesgue measure. Describe the dual spaces of $L^{p}(X)$ for $p \in[1, \infty)$. Define reflexivity and say which $L^{p}(X)$ are reflexive. Prove that $L^{1}(X)$ is not the dual space of $L^{\infty}(X)$

  (c) Now let $X \subset \mathbb{R}^{n}$ be a Borel subset and consider the measure space $(X, \mathcal{A}, \mu)$ induced from Borel sets and Lebesgue measure on $\mathbb{R}^{n}$.

  (i) Given any $p \in[1, \infty]$, prove that any sequence $\left(f_{n}\right)$ in $L^{p}(X)$ converging in $L^{p}(X)$ to some $f \in L^{p}(X)$ admits a subsequence converging almost everywhere to $f$.

  (ii) Prove that if $L^{q}(X) \subset L^{p}(X)$ for $1 \leqslant p<q \leqslant \infty$ then $\mu(X)<\infty$. [Hint: You might want to prove first that the inclusion is continuous with the help of one of the corollaries of Baire's category theorem.]

  comment

• Paper 4, Section II, 23F

  Analysis of Functions | Part II, 2018

  Here and below, $\Phi: \mathbb{R} \rightarrow \mathbb{R}$ is smooth such that $\int_{\mathbb{R}} e^{-\Phi(x)} \mathrm{d} x=1$ and

  $$\lim _{|x| \rightarrow+\infty}\left(\frac{\left|\Phi^{\prime}(x)\right|^{2}}{4}-\frac{\Phi^{\prime \prime}(x)}{2}\right)=\ell \in(0,+\infty)$$

  $C_{c}^{1}(\mathbb{R})$ denotes the set of continuously differentiable complex-valued functions with compact support on $\mathbb{R}$.

  (a) Prove that there are constants $R_{0}>0, \lambda_{1}>0$ and $K_{1}>0$ so that for any $R \geqslant R_{0}$ and $h \in C_{c}^{1}(\mathbb{R})$ :

  $$\int_{\mathbb{R}}\left|h^{\prime}(x)\right|^{2} e^{-\Phi(x)} d x \geqslant \lambda_{1} \int_{\{|x| \geqslant R\}}|h(x)|^{2} e^{-\Phi(x)} d x-K_{1} \int_{\{|x| \leqslant R\}}|h(x)|^{2} e^{-\Phi(x)} d x$$

  [Hint: Denote $g:=h e^{-\Phi / 2}$, expand the square and integrate by parts.]

  (b) Prove that, given any $R>0$, there is a $C_{R}>0$ so that for any $h \in C^{1}([-R, R])$ with $\int_{-R}^{+R} h(x) e^{-\Phi(x)} d x=0$ :

  $$\max _{x \in[-R, R]}|h(x)|+\operatorname{sip}_{\{x, y \in[-R, R], x \neq y\}} \frac{|h(x)-h(y)|}{|x-y|^{1 / 2}} \leqslant C_{R}\left(\int_{-R}^{+R}\left|h^{\prime}(x)\right|^{2} e^{-\Phi(x)} d x\right)^{1 / 2}$$

  [Hint: Use the fundamental theorem of calculus to control the second term of the left-hand side, and then compare $h$ to its weighted mean to control the first term of the left-hand side.]

  (c) Prove that, given any $R>0$, there is a $\lambda_{R}>0$ so that for any $h \in C^{1}([-R, R])$ :

  $$\int_{-R}^{+R}\left|h^{\prime}(x)\right|^{2} e^{-\Phi(x)} d x \geqslant \lambda_{R} \int_{-R}^{+R}\left|h(x)-\frac{\int_{-R}^{+R} h(y) e^{-\Phi(y)} d y}{\int_{-R}^{+R} e^{-\Phi(y)} d y}\right|^{2} e^{-\Phi(x)} d x$$

  [Hint: Show first that one can reduce to the case $\int_{-R}^{+R} h e^{-\Phi}=0$. Then argue by contradiction with the help of the Arzelà-Ascoli theorem and part (b).]

  (d) Deduce that there is a $\lambda_{0}>0$ so that for any $h \in C_{c}^{1}(\mathbb{R})$ :

  $$\int_{\mathbb{R}}\left|h^{\prime}(x)\right|^{2} e^{-\Phi(x)} d x \geqslant \lambda_{0} \int_{\mathbb{R}}\left|h(x)-\left(\int_{\mathbb{R}} h(y) e^{-\Phi(y)} d y\right)\right|^{2} e^{-\Phi(x)} d x$$

  [Hint: Show first that one can reduce to the case $\int_{\mathbb{R}} h e^{-\Phi}=0$. Then combine the inequality (a), multiplied by a constant of the form $\epsilon=\epsilon_{0} \lambda_{R}$ (where $\epsilon_{0}>0$ is chosen so that $\epsilon$ be sufficiently small), and the inequality (c).]

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, A

  Applications of Quantum Mechanics | Part II, 2018

  A particle of mass $m$ moves in one dimension in a periodic potential $V(x)$ satisfying $V(x+a)=V(x)$. Define the Floquet matrix $F$. Show that $\operatorname{det} F=1$ and explain why Tr $F$ is real. Show that allowed bands occur for energies such that $(\operatorname{Tr} F)^{2}<4$. Consider the potential

  $$V(x)=-\frac{\hbar^{2} \lambda}{m} \sum_{n=-\infty}^{+\infty} \delta(x-n a)$$

  For states of negative energy, construct the Floquet matrix with respect to the basis of states $e^{\pm \mu x}$. Derive an inequality for the values of $\mu$ in an allowed energy band.

  For states of positive energy, construct the Floquet matrix with respect to the basis of states $e^{\pm i k x}$. Derive an inequality for the values of $k$ in an allowed energy band.

  Show that the state with zero energy lies in a forbidden region for $\lambda a>2$.

  comment

• Paper 2, Section II, A

  Applications of Quantum Mechanics | Part II, 2018

  Consider a one-dimensional chain of $2 N \gg 1$ atoms, each of mass $m$. Impose periodic boundary conditions. The forces between neighbouring atoms are modelled as springs, with alternating spring constants $\lambda$ and $\alpha \lambda$. In equilibrium, the separation between the atoms is $a$.

  Denote the position of the $n^{\text {th }}$atom as $x_{n}(t)$. Let $u_{n}(t)=x_{n}(t)-n a$ be the displacement from equilibrium. Write down the equations of motion of the system.

  Show that the longitudinal modes of vibration are labelled by a wavenumber $k$ that is restricted to lie in a Brillouin zone. Find the frequency spectrum. What is the frequency gap at the edge of the Brillouin zone? Show that the gap vanishes when $\alpha=1$. Determine approximations for the frequencies near the centre of the Brillouin zone. Plot the frequency spectrum. What is the speed of sound in this system?

  comment

• Paper 3, Section II, A

  Applications of Quantum Mechanics | Part II, 2018

  A beam of particles of mass $m$ and momentum $p=\hbar k$ is incident along the $z$-axis. The beam scatters off a spherically symmetric potential $V(r)$. Write down the asymptotic form of the wavefunction in terms of the scattering amplitude $f(\theta)$.

  The incoming plane wave and the scattering amplitude can be expanded in partial waves as,

  $$\begin{gathered} e^{i k r \cos \theta} \sim \frac{1}{2 i k r} \sum_{l=0}^{\infty}(2 l+1)\left(e^{i k r}-(-1)^{l} e^{-i k r}\right) P_{l}(\cos \theta) \\ f(\theta)=\sum_{l=0}^{\infty} \frac{2 l+1}{k} f_{l} P_{l}(\cos \theta) \end{gathered}$$

  where $P_{l}$ are Legendre polynomials. Define the $S$-matrix. Assuming that the S-matrix is unitary, explain why we can write

  $$f_{l}=e^{i \delta_{l}} \sin \delta_{l}$$

  for some real phase shifts $\delta_{l}$. Obtain an expression for the total cross-section $\sigma_{T}$ in terms of the phase shifts $\delta_{l}$.

  [Hint: You may use the orthogonality of Legendre polynomials:

  $$\left.\int_{-1}^{+1} d w P_{l}(w) P_{l^{\prime}}(w)=\frac{2}{2 l+1} \delta_{l l^{\prime}} .\right]$$

  Consider the repulsive, spherical potential

  $$V(r)=\left\{\begin{array}{cc} +V_{0} & r<a \\ 0 & r>a \end{array}\right.$$

  where $V_{0}=\hbar^{2} \gamma^{2} / 2 m$. By considering the s-wave solution to the Schrödinger equation, show that

  $$\frac{\tan \left(k a+\delta_{0}\right)}{k a}=\frac{\tanh \left(\sqrt{\gamma^{2}-k^{2}} a\right)}{\sqrt{\gamma^{2}-k^{2}} a}$$

  For low momenta, $k a \ll 1$, compute the s-wave contribution to the total cross-section. Comment on the physical interpretation of your result in the limit $\gamma a \rightarrow \infty$.

  comment

• Paper 4, Section II, A

  Applications of Quantum Mechanics | Part II, 2018

  Define a Bravais lattice $\Lambda$ in three dimensions. Define the reciprocal lattice $\Lambda^{\star}$. Define the Brillouin zone.

  An FCC lattice has a basis of primitive vectors given by

  $$\mathbf{a}_{1}=\frac{a}{2}\left(\mathbf{e}_{2}+\mathbf{e}_{3}\right), \quad \mathbf{a}_{2}=\frac{a}{2}\left(\mathbf{e}_{1}+\mathbf{e}_{3}\right), \quad \mathbf{a}_{3}=\frac{a}{2}\left(\mathbf{e}_{1}+\mathbf{e}_{2}\right),$$

  where $\mathbf{e}_{i}$ is an orthonormal basis of $\mathbb{R}^{3}$. Find a basis of reciprocal lattice vectors. What is the volume of the Brillouin zone?

  The asymptotic wavefunction for a particle, of wavevector $\mathbf{k}$, scattering off a potential $V(\mathbf{r})$ is

  $$\psi(\mathbf{r}) \sim e^{i \mathbf{k} \cdot \mathbf{r}}+f_{\mathrm{V}}\left(\mathbf{k} ; \mathbf{k}^{\prime}\right) \frac{e^{i k r}}{r}$$

  where $\mathbf{k}^{\prime}=k \hat{\mathbf{r}}$ and $f_{\mathrm{V}}\left(\mathbf{k} ; \mathbf{k}^{\prime}\right)$ is the scattering amplitude. Give a formula for the Born approximation to the scattering amplitude.

  Scattering of a particle off a single atom is modelled by a potential $V(\mathbf{r})=V_{0} \delta(r-d)$ with $\delta$-function support on a spherical shell, $r=|\mathbf{r}|=d$ centred at the origin. Calculate the Born approximation to the scattering amplitude, denoting the resulting expression as $\tilde{f}_{V}\left(\mathbf{k} ; \mathbf{k}^{\prime}\right)$.

  Scattering of a particle off a crystal consisting of atoms located at the vertices of a lattice $\Lambda$ is modelled by a potential

  $$V_{\Lambda}=\sum_{\mathbf{R} \in \Lambda} V(\mathbf{r}-\mathbf{R})$$

  where $V(\mathbf{r})=V_{0} \delta(r-d)$ as above. Calculate the Born approximation to the scattering amplitude giving your answer in terms of your approximate expression $\tilde{f}_{\mathrm{V}}$ for scattering off a single atom. Show that the resulting amplitude vanishes unless the momentum transfer $\mathbf{q}=\mathbf{k}-\mathbf{k}^{\prime}$ lies in the reciprocal lattice $\Lambda^{\star}$.

  For the particular FCC lattice considered above, show that, when $k=|\mathbf{k}|>2 \pi / a$, scattering occurs for two values of the scattering angle, $\theta_{1}$ and $\theta_{2}$, related by

  $$\frac{\sin \left(\frac{\theta_{1}}{2}\right)}{\sin \left(\frac{\theta_{2}}{2}\right)}=\frac{2}{\sqrt{3}}$$

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2018

  Let $\lambda:[0, \infty) \rightarrow(0, \infty)$ be a continuous function. Explain what is meant by an inhomogeneous Poisson process with intensity function $\lambda$.

  Let $\left(N_{t}: t \geqslant 0\right)$ be such an inhomogeneous Poisson process, and let $M_{t}=N_{g(t)}$ where $g:[0, \infty) \rightarrow[0, \infty)$ is strictly increasing, differentiable and satisfies $g(0)=0$. Show that $M$ is a homogeneous Poisson process with intensity 1 if $\Lambda(g(t))=t$ for all $t$, where $\Lambda(t)=\int_{0}^{t} \lambda(u) d u$. Deduce that $N_{t}$ has the Poisson distribution with mean $\Lambda(t)$.

  Bicycles arrive at the start of a long road in the manner of a Poisson process $N=\left(N_{t}: t \geqslant 0\right)$ with constant intensity $\lambda$. The $i$ th bicycle has constant velocity $V_{i}$, where $V_{1}, V_{2}, \ldots$ are independent, identically distributed random variables, which are independent of $N$. Cyclists can overtake one another freely. Show that the number of bicycles on the first $x$ miles of the road at time $t$ has the Poisson distribution with parameter $\lambda \mathbb{E}\left(V^{-1} \min \{x, V t\}\right)$.

  comment

• Paper 2, Section II, J

  Applied Probability | Part II, 2018

  Let $X=\left(X_{t}: t \geqslant 0\right)$ be a continuous-time Markov chain on the finite state space $S$. Define the terms generator (or Q-matrix) and invariant distribution, and derive an equation that links the generator $G$ and any invariant distribution $\pi$. Comment on the possible non-uniqueness of invariant distributions.

  Suppose $X$ is irreducible, and let $N=\left(N_{t}: t \geqslant 0\right)$ be a Poisson process with intensity $\lambda$, that is independent of $X$. Let $Y_{n}$ be the value of $X$ immediately after the $n$th arrival-time of $N$ (and $\left.Y_{0}=X_{0}\right)$. Show that $\left(Y_{n}: n=0,1, \ldots\right)$ is a discrete-time Markov chain, state its transition matrix and prove that it has the same invariant distribution as $X$.

  comment

• Paper 3, Section II, J

  Applied Probability | Part II, 2018

  Individuals arrive in a shop in the manner of a Poisson process with intensity $\lambda$, and they await service in the order of their arrival. Their service times are independent, identically distributed random variables $S_{1}, S_{2}, \ldots$. For $n \geqslant 1$, let $Q_{n}$ be the number remaining in the shop immediately after the $n$th departure. Show that

  $$Q_{n+1}=A_{n}+Q_{n}-h\left(Q_{n}\right)$$

  where $A_{n}$ is the number of arrivals during the $(n+1)$ th service period, and $h(x)=$ $\min \{1, x\}$.

  Show that

  $$\mathbb{E}\left(A_{n}\right)=\rho, \quad \mathbb{E}\left(A_{n}^{2}\right)=\rho+\lambda^{2} \mathbb{E}\left(S^{2}\right),$$

  where $S$ is a typical service period, and $\rho=\lambda \mathbb{E}(S)$ is the traffic intensity of the queue.

  Suppose $\rho<1$, and the queue is in equilibrium in the sense that $Q_{n}$ and $Q_{n+1}$ have the same distribution for all $n$. Express $\mathbb{E}\left(Q_{n}\right)$ in terms of $\lambda, \mathbb{E}(S), \mathbb{E}\left(S^{2}\right)$. Deduce that the mean waiting time (prior to service) of a typical individual is $\frac{1}{2} \lambda \mathbb{E}\left(S^{2}\right) /(1-\rho)$.

  comment

• Paper 4, Section II, J

  Applied Probability | Part II, 2018

  Let $X_{1}, X_{2}, \ldots$ be independent, identically distributed random variables with finite mean $\mu$. Explain what is meant by saying that the random variable $M$ is a stopping time with respect to the sequence $\left(X_{i}: i=1,2, \ldots\right)$.

  Let $M$ be a stopping time with finite mean $\mathbb{E}(M)$. Prove Wald's equation:

  $$\mathbb{E}\left(\sum_{i=1}^{M} X_{i}\right)=\mu \mathbb{E}(M)$$

  [Here and in the following, you may use any standard theorem about integration.]

  Suppose the $X_{i}$ are strictly positive, and let $N$ be the renewal process with interarrival times $\left(X_{i}: i=1,2, \ldots\right)$. Prove that $m(t)=\mathbb{E}\left(N_{t}\right)$ satisfies the elementary renewal theorem:

  $$\frac{1}{t} m(t) \rightarrow \frac{1}{\mu} \quad \text { as } t \rightarrow \infty .$$

  A computer keyboard contains 100 different keys, including the lower and upper case letters, the usual symbols, and the space bar. A monkey taps the keys uniformly at random. Find the mean number of keys tapped until the first appearance of the sequence 'lava' as a sequence of 4 consecutive characters.

  Find the mean number of keys tapped until the first appearance of the sequence 'aa' as a sequence of 2 consecutive characters.

  comment

Asymptotic Methods

• Paper 2, Section II, B

  Asymptotic Methods | Part II, 2018

  Given that $\int_{-\infty}^{+\infty} e^{-u^{2}} d u=\sqrt{\pi}$ obtain the value of $\lim _{R \rightarrow+\infty} \int_{-R}^{+R} e^{-i t u^{2}} d u$ for real positive $t$. Also obtain the value of $\lim _{R \rightarrow+\infty} \int_{0}^{R} e^{-i t u^{3}} d u$, for real positive $t$, in terms of $\Gamma\left(\frac{4}{3}\right)=\int_{0}^{+\infty} e^{-u^{3}} d u .$

  For $\alpha>0, x>0$, let

  $$Q_{\alpha}(x)=\frac{1}{\pi} \int_{0}^{\pi} \cos (x \sin \theta-\alpha \theta) d \theta$$

  Find the leading terms in the asymptotic expansions as $x \rightarrow+\infty$ of (i) $Q_{\alpha}(x)$ with $\alpha$ fixed, and (ii) of $Q_{x}(x)$.

  comment

• Paper 3, Section II, B

  Asymptotic Methods | Part II, 2018

  (a) Find the curves of steepest descent emanating from $t=0$ for the integral

  $$J_{x}(x)=\frac{1}{2 \pi i} \int_{C} e^{x(\sinh t-t)} d t$$

  for $x>0$ and determine the angles at which they meet at $t=0$, and their asymptotes at infinity.

  (b) An integral representation for the Bessel function $K_{\nu}(x)$ for real $x>0$ is

  $$K_{\nu}(x)=\frac{1}{2} \int_{-\infty}^{+\infty} e^{\nu h(t)} d t \quad, \quad h(t)=t-\left(\frac{x}{\nu}\right) \cosh t$$

  Show that, as $\nu \rightarrow+\infty$, with $x$ fixed,

  $$K_{\nu}(x) \sim\left(\frac{\pi}{2 \nu}\right)^{\frac{1}{2}}\left(\frac{2 \nu}{e x}\right)^{\nu}$$

  comment

• Paper 4, Section II, B

  Asymptotic Methods | Part II, 2018

  Show that

  $$I_{0}(x)=\frac{1}{\pi} \int_{0}^{\pi} e^{x \cos \theta} d \theta$$

  is a solution to the equation

  $$x y^{\prime \prime}+y^{\prime}-x y=0,$$

  and obtain the first two terms in the asymptotic expansion of $I_{0}(x)$ as $x \rightarrow+\infty$.

  For $x>0$, define a new dependent variable $w(x)=x^{\frac{1}{2}} y(x)$, and show that if $y$ solves the preceding equation then

  $$w^{\prime \prime}+\left(\frac{1}{4 x^{2}}-1\right) w=0 .$$

  Obtain the Liouville-Green approximate solutions to this equation for large positive $x$, and compare with your asymptotic expansion for $I_{0}(x)$ at the leading order.

  comment

Automata and Formal Languages

• Paper 1, Section I, G

  Automata and Formal Languages | Part II, 2018

  (a) State the pumping lemma for context-free languages (CFLs).

  (b) Which of the following are CFLs? Justify your answers.

  (i) $\left\{w w \mid w \in\{a, b, c\}^{*}\right\}$

  (ii) $\left\{a^{m} b^{n} c^{k} d^{l} \mid 3 m=4 n\right.$ and $\left.2 k=5 l\right\}$

  (iii) $\left\{a^{3^{n}} \mid n \geqslant 0\right\}$

  (c) Let $L$ be a CFL. Show that $L^{*}$ is also a CFL.

  comment

• Paper 1, Section II, G

  Automata and Formal Languages | Part II, 2018

  (a) Define the halting set $\mathbb{K}$. Prove that $\mathbb{K}$ is recursively enumerable, but not recursive.

  (b) Given $A, B \subseteq \mathbb{N}$, define a many-one reduction of $A$ to $B$. Show that if $B$ is recursively enumerable and $A \leqslant_{m} B$, then $A$ is also recursively enumerable.

  (c) Show that each of the functions $f(n)=2 n$ and $g(n)=2 n+1$ are both partial recursive and total, by building them up as partial recursive functions.

  (d) Let $X, Y \subseteq \mathbb{N}$. We define the set $X \oplus Y$ via

  $$X \oplus Y:=\{2 x \mid x \in X\} \cup\{2 y+1 \mid y \in Y\}$$

  (i) Show that both $X \leqslant_{m} X \oplus Y$ and $Y \leqslant_{m} X \oplus Y$.

  (ii) Using the above, or otherwise, give an explicit example of a subset $C$ of $\mathbb{N}$ for which neither $C$ nor $\mathbb{N} \backslash C$ are recursively enumerable.

  (iii) For every $Z \subseteq \mathbb{N}$, show that if $X \leqslant_{m} Z$ and $Y \leqslant_{m} Z$ then $X \oplus Y \leqslant_{m} Z$.

  [Note that we define $\mathbb{N}=\{0,1, \ldots\}$. Any use of Church's thesis in your answers should be explicitly stated.]

  comment

• Paper 2, Section I, G

  Automata and Formal Languages | Part II, 2018

  (a) Let $E=\left(Q_{E}, \Sigma, \delta_{E}, q_{0}, F_{E}\right)$ be a nondeterministic finite-state automaton with $\epsilon$-transitions $(\epsilon$-NFA). Define the deterministic finite-state automaton (DFA) $D=\left(Q_{D}, \Sigma, \delta_{D}, q_{D}, F_{D}\right)$ obtained from $E$ via the subset construction with $\epsilon$-transitions.

  (b) Let $E$ and $D$ be as above. By inducting on lengths of words, prove that

  $$\hat{\delta}_{E}\left(q_{0}, w\right)=\hat{\delta}_{D}\left(q_{D}, w\right) \text { for all } w \in \Sigma^{*}$$

  (c) Deduce that $\mathcal{L}(D)=\mathcal{L}(E)$.

  comment

• Paper 3, Section I, G

  Automata and Formal Languages | Part II, 2018

  (a) Define what it means for a context-free grammar (CFG) to be in Chomsky normal form ( $\mathrm{CNF})$.

  (b) Give an algorithm for converting a CFG $G$ into a corresponding CFG $G_{\text {Chom }}$ in CNF satisfying $\mathcal{L}\left(G_{\text {Chom }}\right)=\mathcal{L}(G)-\{\epsilon\}$. [You need only outline the steps, without proof.]

  (c) Convert the following $\mathrm{CFG}\ G$ :

  $$S \rightarrow A S c \mid B, \quad A \rightarrow a, \quad B \rightarrow b$$

  into a grammar in CNF.

  comment

• Paper 3, Section II, G

  Automata and Formal Languages | Part II, 2018

  (a) State and prove the pumping lemma for regular languages.

  (b) Let $D$ be a minimal deterministic finite-state automaton whose language $\mathcal{L}(D)$ is finite. Let $\Gamma_{D}$ be the transition diagram of $D$, and suppose there exists a non-empty closed path $\gamma$ in $\Gamma_{D}$ starting and ending at state $p$.

  (i) Show that there is no path in $\Gamma_{D}$ from $p$ to any accept state of $D$.

  (ii) Show that there is no path in $\Gamma_{D}$ from $p$ to any other state of $D$.

  comment

• Paper 4, Section I, 4G

  Automata and Formal Languages | Part II, 2018

  (a) State the $s-m-n$ theorem, the recursion theorem, and Rice's theorem.

  (b) Show that if $g: \mathbb{N}^{2} \rightarrow \mathbb{N}$ is partial recursive, then there is some $e \in \mathbb{N}$ such that

  $$f_{e, 1}(y)=g(e, y) \quad \forall y \in \mathbb{N}$$

  (c) By considering the partial function $g: \mathbb{N}^{2} \rightarrow \mathbb{N}$ given by

  $$g(x, y)= \begin{cases}0 & \text { if } y<x \\ \uparrow & \text { otherwise }\end{cases}$$

  show there exists some $m \in \mathbb{N}$ such that $W_{m}$ has exactly $m$ elements.

  (d) Given $n \in \mathbb{N}$, is it possible to compute whether or not $W_{n}$ has exactly 9 elements? Justify your answer.

  [Note that we define $\mathbb{N}=\{0,1, \ldots\}$. Any use of Church's thesis in your answers should be explicitly stated.]

  comment

Classical Dynamics

• Paper 1, Section I, B

  Classical Dynamics | Part II, 2018

  Derive Hamilton's equations from an action principle.

  Consider a two-dimensional phase space with the Hamiltonian $H=p^{2}+q^{-2}$. Show that $F=p q-c t H$ is the first integral for some constant $c$ which should be determined. By considering the surfaces of constant $F$ in the extended phase space, solve Hamilton's equations, and sketch the orbits in the phase space.

  comment

• Paper 2, Section I, B

  Classical Dynamics | Part II, 2018

  Let $\mathbf{x}=x \mathbf{i}+y \mathbf{j}+z \mathbf{k}$. Consider a Lagrangian

  $$\mathcal{L}=\frac{1}{2} \dot{\mathbf{x}}^{2}+y \dot{x}$$

  of a particle constrained to move on a sphere $|\mathbf{x}|=1 / c$ of radius $1 / c$. Use Lagrange multipliers to show that

  $$\ddot{\mathbf{x}}+\ddot{y} \mathbf{i}-\dot{x} \mathbf{j}+c^{2}\left(|\dot{\mathbf{x}}|^{2}+y \dot{x}-x \dot{y}\right) \mathbf{x}=0$$

  Now, consider the system $(*)$ with $c=0$, and find the particle trajectories.

  comment

• Paper 2, Section II, B

  Classical Dynamics | Part II, 2018

  Define a body frame $\mathbf{e}_{a}(t), a=1,2,3$ of a rotating rigid body, and show that there exists a vector $\boldsymbol{\omega}=\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$ such that

  $$\dot{\mathbf{e}}_{a}=\boldsymbol{\omega} \times \mathbf{e}_{a}$$

  Let $\mathbf{L}=I_{1} \omega_{1}(t) \mathbf{e}_{1}+I_{2} \omega_{2}(t) \mathbf{e}_{2}+I_{3} \omega_{3}(t) \mathbf{e}_{3}$ be the angular momentum of a free rigid body expressed in the body frame. Derive the Euler equations from the conservation of angular momentum.

  Verify that the kinetic energy $E$, and the total angular momentum $L^{2}$ are conserved. Hence show that

  $$\dot{\omega}_{3}^{2}=f\left(\omega_{3}\right),$$

  where $f\left(\omega_{3}\right)$ is a quartic polynomial which should be explicitly determined in terms of $L^{2}$ and $E$.

  comment

• Paper 3, Section I, B

  Classical Dynamics | Part II, 2018

  Three particles of unit mass move along a line in a potential

  $$V=\frac{1}{2}\left(\left(x_{1}-x_{2}\right)^{2}+\left(x_{1}-x_{3}\right)^{2}+\left(x_{3}-x_{2}\right)^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right)$$

  where $x_{i}$ is the coordinate of the $i$ th particle, $i=1,2,3$.

  Write the Lagrangian in the form

  $$\mathcal{L}=\frac{1}{2} T_{i j} \dot{x}_{i} \dot{x}_{j}-\frac{1}{2} V_{i j} x_{i} x_{j}$$

  and specify the matrices $T_{i j}$ and $V_{i j}$.

  Find the normal frequencies and normal modes for this system.

  comment

• Paper 4, Section I, B

  Classical Dynamics | Part II, 2018

  State and prove Noether's theorem in Lagrangian mechanics.

  Consider a Lagrangian

  $$\mathcal{L}=\frac{1}{2} \frac{\dot{x}^{2}+\dot{y}^{2}}{y^{2}}-V\left(\frac{x}{y}\right)$$

  for a particle moving in the upper half-plane $\left\{(x, y) \in \mathbb{R}^{2}, y>0\right\}$ in a potential $V$ which only depends on $x / y$. Find two independent first integrals.

  comment

• Paper 4, Section II, B

  Classical Dynamics | Part II, 2018

  Given a Lagrangian $\mathcal{L}\left(q_{i}, \dot{q}_{i}, t\right)$ with degrees of freedom $q_{i}$, define the Hamiltonian and show how Hamilton's equations arise from the Lagrange equations and the Legendre transform.

  Consider the Lagrangian for a symmetric top moving in constant gravity:

  $$\mathcal{L}=\frac{1}{2} A\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} B(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  where $A, B, M, g$ and $l$ are constants. Construct the corresponding Hamiltonian, and find three independent Poisson-commuting first integrals of Hamilton's equations.

  comment

Coding and Cryptography

• Paper 1, Section I, H

  Coding and Cryptography | Part II, 2018

  State and prove Shannon's noiseless coding theorem. [You may use Gibbs' and Kraft's inequalities as long as they are clearly stated.]

  comment

• Paper 1, Section II, H

  Coding and Cryptography | Part II, 2018

  Define the bar product $C_{1} \mid C_{2}$ of binary linear codes $C_{1}$ and $C_{2}$, where $C_{2}$ is a subcode of $C_{1}$. Relate the rank and minimum distance of $C_{1} \mid C_{2}$ to those of $C_{1}$ and $C_{2}$ and justify your answer.

  What is a parity check matrix for a linear code? If $C_{1}$ has parity check matrix $P_{1}$ and $C_{2}$ has parity check matrix $P_{2}$, find a parity check matrix for $C_{1} \mid C_{2}$.

  Using the bar product construction, or otherwise, define the Reed-Muller code $R M(d, r)$ for $0 \leqslant r \leqslant d$. Compute the rank of $R M(d, r)$. Show that all but two codewords in $R M(d, 1)$ have the same weight. Given $d$, for which $r$ is it true that all elements of $R M(d, r)$ have even weight? Justify your answer.

  comment

• Paper 2, Section I, H

  Coding and Cryptography | Part II, 2018

  What is the channel matrix of a binary symmetric channel with error probability $p$ ?

  State the maximum likelihood decoding rule and the minimum distance decoding rule. Prove that if $p<1 / 2$, then they agree.

  Let $C$ be the repetition code $\{000,111\}$. Suppose a codeword from $C$ is sent through a binary symmetric channel with error probability $p$. Show that, if the minimum distance decoding rule is used, then the probability of error is $3 p^{2}-2 p^{3}$.

  comment

• Paper 2, Section II, H

  Coding and Cryptography | Part II, 2018

  Describe the RSA encryption scheme with public key $(N, e)$ and private key $d$.

  Suppose $N=p q$ with $p$ and $q$ distinct odd primes and $1 \leqslant x \leqslant N$ with $x$ and $N$ coprime. Denote the order of $x$ in $\mathbb{F}_{p}^{*}$ by $\mathrm{O}_{p}(x)$. Further suppose $\Phi(N)$ divides $2^{a} b$ where $b$ is odd. If $\mathrm{O}_{p}\left(x^{b}\right) \neq \mathrm{O}_{q}\left(x^{b}\right)$ prove that there exists $0 \leqslant t<a$ such that the greatest common divisor of $x^{2^{t} b}-1$ and $N$ is a nontrivial factor of $N$. Further, prove that the number of $x$ satisfying $\mathrm{O}_{p}\left(x^{b}\right) \neq \mathrm{O}_{q}\left(x^{b}\right)$ is $\geqslant \Phi(N) / 2$.

  Hence, or otherwise, prove that finding the private key $d$ from the public key $(N, e)$ is essentially as difficult as factoring $N$.

  Suppose a message $m$ is sent using the $\mathrm{RSA}$ scheme with $e=43$ and $N=77$, and $c=5$ is the received text. What is $m$ ?

  An integer $m$ satisfying $1 \leqslant m \leqslant N-1$ is called a fixed point if it is encrypted to itself. Prove that if $m$ is a fixed point then so is $N-m$.

  comment

• Paper 3, Section $I$, H

  Coding and Cryptography | Part II, 2018

  Compute the rank and minimum distance of the cyclic code with generator polynomial $g(X)=X^{3}+X^{2}+1$ and parity check polynomial $h(X)=X^{4}+X^{3}+X^{2}+1$. Now let $\alpha$ be a root of $g(X)$ in the field with 8 elements. We receive the word $r(X)=X^{2}+X+1$ $\left(\bmod X^{7}-1\right)$. Verify that $r(\alpha)=\alpha^{4}$, and hence decode $r(X)$ using minimum-distance decoding.

  comment

• Paper 4, Section I, H

  Coding and Cryptography | Part II, 2018

  What is a linear feedback shift register? Explain the Berlekamp-Massey method for recovering a feedback polynomial of a linear feedback shift register from its output. Illustrate the method in the case when we observe output

  $010111100010 \ldots$

  comment

Cosmology

• Paper 1, Section I, B

  Cosmology | Part II, 2018

  For a homogeneous and isotropic universe filled with pressure-free matter $(P=0)$, the Friedmann and Raychaudhuri equations are, respectively,

  $$\left(\frac{\dot{a}}{a}\right)^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho \quad \text { and } \quad \frac{\ddot{a}}{a}=-\frac{4 \pi G}{3} \rho,$$

  with mass density $\rho$, curvature $k$, and where $\dot{a} \equiv d a / d t$. Using conformal time $\tau$ with $d \tau=d t / a$, show that the relative density parameter can be expressed as

  $$\Omega(t) \equiv \frac{\rho}{\rho_{\text {crit }}}=\frac{8 \pi G \rho a^{2}}{3 \mathcal{H}^{2}}$$

  where $\mathcal{H}=\frac{1}{a} \frac{d a}{d \tau}$ and $\rho_{\text {crit }}$ is the critical density of a flat $k=0$ universe (Einstein-de Sitter). Use conformal time $\tau$ again to show that the Friedmann and Raychaudhuri equations can be re-expressed as

  $$\frac{k c^{2}}{\mathcal{H}^{2}}=\Omega-1 \quad \text { and } \quad 2 \frac{d \mathcal{H}}{d \tau}+\mathcal{H}^{2}+k c^{2}=0$$

  From these derive the evolution equation for the density parameter $\Omega$ :

  $$\frac{d \Omega}{d \tau}=\mathcal{H} \Omega(\Omega-1)$$

  Plot the qualitative behaviour of $\Omega$ as a function of time relative to the expanding Einsteinde Sitter model with $\Omega=1$ (i.e., include curves initially with $\Omega>1$ and $\Omega<1$ ).

  comment

• Paper 1, Section II, B

  Cosmology | Part II, 2018

  A flat $(k=0)$ homogeneous and isotropic universe with scale factor $a(t)$ is filled with a scalar field $\phi(t)$ with potential $V(\phi)$. Its evolution satisfies the Friedmann and scalar field equations,

  $$H^{2}=\frac{1}{3 M_{\mathrm{Pl}}^{2}}\left(\frac{1}{2} \dot{\phi}^{2}+c^{2} V(\phi)\right), \quad \ddot{\phi}+3 H \dot{\phi}+c^{2} \frac{d V}{d \phi}=0$$

  where $H(t)=\frac{\dot{a}}{a}$ is the Hubble parameter, $M_{\mathrm{Pl}}$ is the reduced Planck mass, and dots denote derivatives with respect to cosmic time $t$, e.g. $\dot{\phi} \equiv d \phi / d t$.

  (a) Use these equations to derive the Raychaudhuri equation, expressed in the form:

  $$\dot{H}=-\frac{1}{2 M_{\mathrm{Pl}}^{2}} \dot{\phi}^{2}$$

  (b) Consider the following ansatz for the scalar field evolution,

  $$\phi(t)=\phi_{0} \ln \tanh (\lambda t)$$

  where $\lambda, \phi_{0}$ are constants. Find the specific cosmological solution,

  $$\begin{aligned} H(t) &=\lambda \frac{\phi_{0}^{2}}{M_{\mathrm{Pl}}^{2}} \operatorname{coth}(2 \lambda t) \\ a(t) &=a_{0}[\sinh (2 \lambda t)]^{\phi_{0}^{2} / 2 M_{\mathrm{Pl}}^{2}}, \quad a_{0} \text { constant. } \end{aligned}$$

  (c) Hence, show that the Hubble parameter can be expressed in terms of $\phi$ as

  $$H(\phi)=\lambda \frac{\phi_{0}^{2}}{M_{\mathrm{P} 1}^{2}} \cosh \left(\frac{\phi}{\phi_{0}}\right),$$

  and that the scalar field ansatz solution ( $\dagger$ ) requires the following form for the potential:

  $$V(\phi)=\frac{2 \lambda^{2} \phi_{0}^{2}}{c^{2}}\left[\left(\frac{3 \phi_{0}^{2}}{2 M_{\mathrm{Pl}}^{2}}-1\right) \cosh ^{2}\left(\frac{\phi}{\phi_{0}}\right)+1\right]$$

  (d) Assume that the given parameters in $V(\phi)$ are such that $2 / 3<\phi_{0}^{2} / M_{\mathrm{Pl}}^{2}<2$. Show that the asymptotic limit for the cosmological solution as $t \rightarrow 0$ exhibits decelerating power law evolution and that there is an accelerating solution as $t \rightarrow \infty$, that is,

  $$\begin{array}{lll} t \rightarrow 0, & \phi \rightarrow-\infty, & a(t) \sim t^{\phi_{0}^{2} / 2 M_{\mathrm{Pl}}^{2}} \\ t \rightarrow \infty, & \phi \rightarrow 0, & a(t) \sim \exp \left(\lambda \phi_{0}^{2} t / M_{\mathrm{Pl}}^{2}\right) . \end{array}$$

  Find the time $t_{\mathrm{acc}}$ at which the solution transitions from deceleration to acceleration.

  comment

• Paper 2, Section I, B

  Cosmology | Part II, 2018

  (a) Consider a homogeneous and isotropic universe with a uniform distribution of galaxies. For three galaxies at positions $\mathbf{r}_{A}, \mathbf{r}_{B}, \mathbf{r}_{C}$, show that spatial homogeneity implies that their non-relativistic velocities $\mathbf{v}(\mathbf{r})$ must satisfy

  $$\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{A}\right)=\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{C}\right)-\mathbf{v}\left(\mathbf{r}_{A}-\mathbf{r}_{C}\right)$$

  and hence that the velocity field coordinates $v_{i}$ are linearly related to the position coordinates $r_{j}$ via

  $$v_{i}=H_{i j} r_{j}$$

  where the matrix coefficients $H_{i j}$ are independent of the position. Show why isotropy then implies Hubble's law

  $$\mathbf{v}=H \mathbf{r}, \quad \text { with } H \text { independent of } \mathbf{r}$$

  Explain how the velocity of a galaxy is determined by the scale factor $a$ and express the Hubble parameter $H_{0}$ today in terms of $a$.

  (b) Define the cosmological horizon $d_{H}(t)$. For an Einstein-de Sitter universe with $a(t) \propto t^{2 / 3}$, calculate $d_{H}\left(t_{0}\right)$ at $t=t_{0}$ today in terms of $H_{0}$. Briefly describe the horizon problem of the standard cosmology.

  comment

• Paper 3, Section I, B

  Cosmology | Part II, 2018

  The energy density of a particle species is defined by

  $$\epsilon=\int_{0}^{\infty} E(p) n(p) d p$$

  where $E(p)=c \sqrt{p^{2}+m^{2} c^{2}}$ is the energy, and $n(p)$ the distribution function, of a particle with momentum $p$. Here $c$ is the speed of light and $m$ is the rest mass of the particle. If the particle species is in thermal equilibrium then the distribution function takes the form

  $$n(p)=\frac{4 \pi}{h^{3}} g \frac{p^{2}}{\exp ((E(p)-\mu) / k T) \mp 1}$$

  where $g$ is the number of degrees of freedom of the particle, $T$ is the temperature, $h$ and $k$ are constants and $-$ is for bosons and $+$ is for fermions.

  (a) Stating any assumptions you require, show that in the very early universe the energy density of a given particle species $i$ is

  $$\epsilon_{i}=\frac{4 \pi g_{i}}{(h c)^{3}}(k T)^{4} \int_{0}^{\infty} \frac{y^{3}}{e^{y} \mp 1} d y$$

  (b) Show that the total energy density in the very early universe is

  $$\epsilon=\frac{4 \pi^{5}}{15(h c)^{3}} g^{*}(k T)^{4}$$

  where $g^{*}$ is defined by

  $$g^{*} \equiv \sum_{\text {Bosons }} g_{i}+\frac{7}{8} \sum_{\text {Fermions }} g_{i}$$

  [Hint: You may use the fact that $\left.\int_{0}^{\infty} y^{3}\left(e^{y}-1\right)^{-1} d y=\pi^{4} / 15 .\right]$

  comment

• Paper 3, Section II, B

  Cosmology | Part II, 2018

  The pressure support equation for stars is

  $$\frac{1}{r^{2}} \frac{d}{d r}\left[\frac{r^{2}}{\rho} \frac{d P}{d r}\right]=-4 \pi G \rho$$

  where $\rho$ is the density, $P$ is the pressure, $r$ is the radial distance, and $G$ is Newton's constant.

  (a) What two boundary conditions should we impose on the above equation for it to describe a star?

  (b) By assuming a polytropic equation of state,

  $$P(r)=K \rho^{1+\frac{1}{n}}(r)$$

  where $K$ is a constant, derive the Lane-Emden equation

  $$\frac{1}{\xi^{2}} \frac{d}{d \xi}\left[\xi^{2} \frac{d \theta}{d \xi}\right]=-\theta^{n}$$

  where $\rho=\rho_{c} \theta^{n}$, with $\rho_{c}$ the density at the centre of the star, and $r=a \xi$, for some $a$ that you should determine.

  (c) Show that the mass of a polytropic star is

  $$M=\frac{1}{2 \sqrt{\pi}}\left(\frac{(n+1) K}{G}\right)^{\frac{3}{2}} \rho_{c}^{\frac{3-n}{2 n}} Y_{n}$$

  where $Y_{n} \equiv-\left.\xi_{1}^{2} \frac{d \theta}{d \xi}\right|_{\xi=\xi_{1}}$ and $\xi_{1}$ is the value of $\xi$ at the surface of the star.

  (d) Derive the following relation between the mass, $M$, and radius, $R$, of a polytropic star

  $$M=A_{n} K^{\frac{n}{n-1}} R^{\frac{3-n}{1-n}}$$

  where you should determine the constant $A_{n}$. What type of star does the $n=3$ polytrope represent and what is the significance of the mass being constant for this star?

  comment

• Paper 4, Section I, B

  Cosmology | Part II, 2018

  A constant overdensity is created by taking a spherical region of a flat matterdominated universe with radius $\bar{R}$ and compressing it into a region with radius $R<\bar{R}$. The evolution is governed by the parametric equations

  $$R=A R_{0}(1-\cos \theta), \quad t=B(\theta-\sin \theta)$$

  where $R_{0}$ is a constant and

  $$A=\frac{\Omega_{m, 0}}{2\left(\Omega_{m, 0}-1\right)}, \quad B=\frac{\Omega_{m, 0}}{2 H_{0}\left(\Omega_{m, 0}-1\right)^{3 / 2}}$$

  where $H_{0}$ is the Hubble constant and $\Omega_{m, 0}$ is the fractional overdensity at time $t_{0}$.

  Show that, as $t \rightarrow 0^{+}$,

  $$R(t)=R_{0} \Omega_{m, 0}^{1 / 3} a(t)\left(1-\frac{1}{20}\left(\frac{6 t}{B}\right)^{2 / 3}+\ldots\right)$$

  where the scale factor is given by $a(t)=\left(3 H_{0} t / 2\right)^{2 / 3}$.

  that, when the spherical overdensity has collapsed to zero radius, the linear perturbation has value $\delta_{\text {linear }}=\frac{3}{20}(12 \pi)^{2 / 3}$.

  comment

Differential Geometry

• Paper 1, Section II, I

  Differential Geometry | Part II, 2018

  (a) Let $X \subset \mathbb{R}^{n}$ be a manifold and $p \in X$. Define the tangent space $T_{p} X$ and show that it is a vector subspace of $\mathbb{R}^{n}$, independent of local parametrization, of dimension equal to $\operatorname{dim} X$.

  (b) Now show that $T_{p} X$ depends continuously on $p$ in the following sense: if $p_{i}$ is a sequence in $X$ such that $p_{i} \rightarrow p \in X$, and $w_{i} \in T_{p_{i}} X$ is a sequence such that $w_{i} \rightarrow w \in \mathbb{R}^{n}$, then $w \in T_{p} X$. If $\operatorname{dim} X>0$, show that all $w \in T_{p} X$ arise as such limits where $p_{i}$ is a sequence in $X \backslash p$.

  (c) Consider the set $X_{a} \subset \mathbb{R}^{4}$ defined by $X_{a}=\left\{x_{1}^{2}+2 x_{2}^{2}=a^{2}\right\} \cap\left\{x_{3}=a x_{4}\right\}$, where $a \in \mathbb{R}$. Show that, for all $a \in \mathbb{R}$, the set $X_{a}$ is a smooth manifold. Compute its dimension.

  (d) For $X_{a}$ as above, does $T_{p} X_{a}$ depend continuously on $p$ and $a$ for all $a \in \mathbb{R}$ ? In other words, let $a_{i} \in \mathbb{R}, p_{i} \in X_{a_{i}}$ be sequences with $a_{i} \rightarrow a \in \mathbb{R}, p_{i} \rightarrow p \in X_{a}$. Suppose that $w_{i} \in T_{p_{i}} X_{a_{i}}$ and $w_{i} \rightarrow w \in \mathbb{R}^{4}$. Is it necessarily the case that $w \in T_{p} X_{a}$ ? Justify your answer.

  comment

• Paper 2, Section II, I

  Differential Geometry | Part II, 2018

  Let $\gamma(t):[a, b] \rightarrow \mathbb{R}^{3}$ denote a regular curve.

  (a) Show that there exists a parametrization of $\gamma$ by arc length.

  (b) Under the assumption that the curvature is non-zero, define the torsion of $\gamma$. Give an example of two curves $\gamma_{1}$ and $\gamma_{2}$ in $\mathbb{R}^{3}$ whose curvature (as a function of arc length $s$ ) coincides and is non-vanishing, but for which the curves are not related by a rigid motion, i.e. such that $\gamma_{1}(s)$ is not identically $\rho_{(R, T)}\left(\gamma_{2}(s)\right)$ where $R \in S O(3), T \in \mathbb{R}^{3}$ and

  $$\rho_{(R, T)}(v):=T+R v$$

  (c) Give an example of a simple closed curve $\gamma$, other than a circle, which is preserved by a non-trivial rigid motion, i.e. which satisfies

  $$\rho_{(R, T)}(v) \in \gamma([a, b]) \text { for all } v \in \gamma([a, b])$$

  for some choice of $R \in S O(3), T \in \mathbb{R}^{3}$ with $(R, T) \neq(\mathrm{Id}, 0)$. Justify your answer.

  (d) Now show that a simple closed curve $\gamma$ which is preserved by a nontrivial smooth 1-parameter family of rigid motions is necessarily a circle, i.e. show the following:

  Let $(R, T):(-\epsilon, \epsilon) \rightarrow S O(3) \times \mathbb{R}^{3}$ be a regular curve. If for all $\tilde{t} \in(-\epsilon, \epsilon)$,

  $$\rho_{(R(\tilde{t}), T(\tilde{t}))}(v) \in \gamma([a, b]) \text { for all } v \in \gamma([a, b]) \text {, }$$

  then $\gamma([a, b])$ is a circle. [You may use the fact that the set of fixed points of a non-trivial rigid motion is either $\emptyset$ or a line $L \subset \mathbb{R}^{3}$.]

  comment

• Paper 3, Section II, I

  Differential Geometry | Part II, 2018

  Let $S \subset \mathbb{R}^{3}$ be a surface.

  (a) Define the Gaussian curvature $K$ of $S$ in terms of the coefficients of the first and second fundamental forms, computed with respect to a local parametrization $\phi(u, v)$ of $S$.

  Prove the Theorema Egregium, i.e. show that the Gaussian curvature can be expressed entirely in terms of the coefficients of the first fundamental form and their first and second derivatives with respect to $u$ and $v$.

  (b) State the global Gauss-Bonnet theorem for a compact orientable surface $S$.

  (c) Now assume that $S$ is non-compact and diffeomorphic to $\mathbb{S}^{2} \backslash\{(1,0,0)\}$ but that there is a point $p \in \mathbb{R}^{3}$ such that $S \cup\{p\}$ is a compact subset of $\mathbb{R}^{3}$. Is it necessarily the case that $\int_{S} K d A=4 / \pi ?$ Justify your answer.

  comment

• Paper 4, Section II, I

  Differential Geometry | Part II, 2018

  Let $S \subset \mathbb{R}^{3}$ be a surface.

  (a) Define what it means for a curve $\gamma: I \rightarrow S$ to be a geodesic, where $I=(a, b)$ and $-\infty \leqslant a<b \leqslant \infty$.

  (b) A geodesic $\gamma: I \rightarrow S$ is said to be maximal if any geodesic $\widetilde{\gamma}: \tilde{I} \rightarrow S$ with $I \subset \tilde{I}$ and $\left.\tilde{\gamma}\right|_{I}=\gamma$ satisfies $I=\tilde{I}$. A surface is said to be geodesically complete if all maximal geodesics are defined on $I=(-\infty, \infty)$, otherwise, the surface is said to be geodesically incomplete. Give an example, with justification, of a non-compact geodesically complete surface $S$ which is not a plane.

  (c) Assume that along any maximal geodesic

  $$\gamma:\left(-T_{-}, T_{+}\right) \rightarrow S$$

  the following holds:

  $$\tag{*} T_{\pm}<\infty \Longrightarrow \limsup _{s \rightarrow T_{\pm}}|K(\gamma(\pm s))|=\infty$$

  Here $K$ denotes the Gaussian curvature of $S$.

  (i) Show that $S$ is inextendible, i.e. if $\widetilde{S} \subset \mathbb{R}^{3}$ is a connected surface with $S \subset \widetilde{S}$, then $\widetilde{S}=S$.

  (ii) Give an example of a surface $S$ which is geodesically incomplete and satisfies $(*)$. Do all geodesically incomplete inextendible surfaces satisfy $(*)$ ? Justify your answer.

  [You may use facts about geodesics from the course provided they are clearly stated.]

  comment

Dynamical Systems

• Paper 1, Section II, E

  Dynamical Systems | Part II, 2018

  Consider the system

  $$\dot{x}=-2 a x+2 x y, \quad \dot{y}=1-x^{2}-y^{2}$$

  where $a$ is a constant.

  (a) Find and classify the fixed points of the system. For $a=0$ show that the linear classification of the non-hyperbolic fixed points is nonlinearly correct. For $a \neq 0$ show that there are no periodic orbits. [Standard results for periodic orbits may be quoted without proof.]

  (b) Sketch the phase plane for the cases (i) $a=0$, (ii) $a=\frac{1}{2}$, and (iii) $a=\frac{3}{2}$, showing any separatrices clearly.

  (c) For what values of a do stationary bifurcations occur? Consider the bifurcation with $a>0$. Let $y_{0}, a_{0}$ be the values of $y, a$ at which the bifurcation occurs, and define $Y=y-y_{0}, \mu=a-a_{0}$. Assuming that $\mu=O\left(x^{2}\right)$, find the extended centre manifold $Y=Y(x, \mu)$ to leading order. Further, determine the evolution equation on the centre manifold to leading order. Hence identify the type of bifurcation.

  comment

• Paper 2, Section II, 32E

  Dynamical Systems | Part II, 2018

  Consider the system

  $$\dot{x}=y, \quad \dot{y}=x-x^{3}+\epsilon\left(1-\alpha x^{2}\right) y,$$

  where $\alpha$ and $\epsilon$ are real constants, and $0 \leqslant \epsilon \ll 1$. Find and classify the fixed points.

  Show that when $\epsilon=0$ the system is Hamiltonian and find $H$. Sketch the phase plane for this case.

  Suppose now that $0<\epsilon \ll 1$. Show that the small change in $H$ following a trajectory of the perturbed system around an orbit $H=H_{0}$ of the unperturbed system is given to leading order by an equation of the form

  $$\Delta H=\epsilon \int_{x_{1}}^{x_{2}} F\left(x ; \alpha, H_{0}\right) d x$$

  where $F$ should be found explicitly, and where $x_{1}$ and $x_{2}$ are the minimum and maximum values of $x$ on the unperturbed orbit.

  Use the energy-balance method to find the value of $\alpha$, correct to leading order in $\epsilon$, for which the system has a homoclinic orbit. [Hint: The substitution $u=1-\frac{1}{2} x^{2}$ may prove useful.]

  Over what range of $\alpha$ would you expect there to be periodic solutions that enclose only one of the fixed points?

  comment

• Paper 3, Section II, 32E

  Dynamical Systems | Part II, 2018

  Consider the system

  $$\dot{x}=y, \quad \dot{y}=\mu_{1} x+\mu_{2} y-(x+y)^{3}$$

  where $\mu_{1}$ and $\mu_{2}$ are parameters.

  By considering a function of the form $V(x, y)=f(x+y)+\frac{1}{2} y^{2}$, show that when $\mu_{1}=\mu_{2}=0$ the origin is globally asymptotically stable. Sketch the phase plane for this case.

  Find the fixed points for the general case. Find the values of $\mu_{1}$ and $\mu_{2}$ for which the fixed points have (i) a stationary bifurcation and (ii) oscillatory (Hopf) bifurcations. Sketch these bifurcation values in the $\left(\mu_{1}, \mu_{2}\right)$-plane.

  For the case $\mu_{2}=-1$, find the leading-order approximation to the extended centre manifold of the bifurcation as $\mu_{1}$ varies, assuming that $\mu_{1}=O\left(x^{2}\right)$. Find also the evolution equation on the extended centre manifold to leading order. Deduce the type of bifurcation, and sketch the bifurcation diagram in the $\left(\mu_{1}, x\right)$-plane.

  comment

• Paper 4, Section II, E

  Dynamical Systems | Part II, 2018

  Let $F: I \rightarrow I$ be a continuous one-dimensional map of an interval $I \subset \mathbb{R}$. Define what it means (i) for $F$ to have a horseshoe (ii) for $F$ to be chaotic. [Glendinning's definition should be used throughout this question.]

  Prove that if $F$ has a 3 -cycle $x_{1}<x_{2}<x_{3}$ then $F$ is chaotic. [You may assume the intermediate value theorem and any corollaries of it.]

  State Sharkovsky's theorem.

  Use the above results to deduce that if $F$ has an $N$-cycle, where $N$ is any integer that is not a power of 2 , then $F$ is chaotic.

  Explain briefly why if $F$ is chaotic then $F$ has $N$-cycles for many values of $N$ that are not powers of 2. [You may assume that a map with a horseshoe acts on some set $\Lambda$ like the Bernoulli shift map acts on $[0,1)$.]

  The logistic map is not chaotic when $\mu<\mu_{\infty} \approx 3.57$ and it has 3 -cycles when $\mu>1+\sqrt{8} \approx 3.84$. What can be deduced from these statements about the values of $\mu$ for which the logistic map has a 10-cycle?

  comment

Electrodynamics

• Paper 1, Section II, D

  Electrodynamics | Part II, 2018

  Define the field strength tensor $F^{\mu \nu}(x)$ for an electromagnetic field specified by a 4-vector potential $A^{\mu}(x)$. How do the components of $F^{\mu \nu}$ change under a Lorentz transformation? Write down two independent Lorentz-invariant quantities which are quadratic in the field strength tensor.

  [Hint: The alternating tensor $\varepsilon^{\mu \nu \rho \sigma}$ takes the values $+1$ and $-1$ when $(\mu, \nu, \rho, \sigma)$ is an even or odd permutation of $(0,1,2,3)$ respectively and vanishes otherwise. You may assume this is an invariant tensor of the Lorentz group. In other words, its components are the same in all inertial frames.]

  In an inertial frame with spacetime coordinates $x^{\mu}=(c t, \mathbf{x})$, the 4-vector potential has components $A^{\mu}=(\phi / c, \mathbf{A})$ and the electric and magnetic fields are given as

  $$\begin{aligned} \mathbf{E} &=-\nabla \phi-\frac{\partial \mathbf{A}}{\partial t} \\ \mathbf{B} &=\nabla \times \mathbf{A} \end{aligned}$$

  Evaluate the components of $F^{\mu \nu}$ in terms of the components of $\mathbf{E}$ and $\mathbf{B}$. Show that the quantities

  $$S=|\mathbf{B}|^{2}-\frac{1}{c^{2}}|\mathbf{E}|^{2} \quad \text { and } \quad T=\mathbf{E} \cdot \mathbf{B}$$

  are the same in all inertial frames.

  A relativistic particle of mass $m$, charge $q$ and 4 -velocity $u^{\mu}(\tau)$ moves according to the Lorentz force law,

  $$\frac{d u^{\mu}}{d \tau}=\frac{q}{m} F_{\nu}^{\mu} u^{\nu}$$

  Here $\tau$ is the proper time. For the case of a constant, uniform field, write down a solution of $(*)$ giving $u^{\mu}(\tau)$ in terms of its initial value $u^{\mu}(0)$ as an infinite series in powers of the field strength.

  Suppose further that the fields are such that both $S$ and $T$ defined above are zero. Work in an inertial frame with coordinates $x^{\mu}=(c t, x, y, z)$ where the particle is at rest at the origin at $t=0$ and the magnetic field points in the positive $z$-direction with magnitude $|\mathbf{B}|=B$. The electric field obeys $\mathbf{E} \cdot \hat{\mathbf{y}}=0$. Show that the particle moves on the curve $y^{2}=A x^{3}$ for some constant $A$ which you should determine.

  comment

• Paper 3, Section II, D

  Electrodynamics | Part II, 2018

  Starting from the covariant form of the Maxwell equations and making a suitable choice of gauge which you should specify, show that the 4-vector potential due to an arbitrary 4-current $J^{\mu}(x)$ obeys the wave equation,

  $$\left(\nabla^{2}-\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}}\right) A^{\mu}=-\mu_{0} J^{\mu}$$

  where $x^{\mu}=(c t, \mathbf{x})$.

  Use the method of Green's functions to show that, for a localised current distribution, this equation is solved by

  $$A^{\mu}(t, \mathbf{x})=\frac{\mu_{0}}{4 \pi} \int d^{3} x^{\prime} \frac{J^{\mu}\left(t_{\mathrm{ret}}, \mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|}$$

  for some $t_{\text {ret }}$ that you should specify.

  A point particle, of charge $q$, moving along a worldline $y^{\mu}(\tau)$ parameterised by proper time $\tau$, produces a 4 -vector potential

  $$A^{\mu}(x)=\frac{\mu_{0} q c}{4 \pi} \frac{\dot{y}^{\mu}\left(\tau_{\star}\right)}{\left|R^{\nu}\left(\tau_{\star}\right) \dot{y}_{\nu}\left(\tau_{\star}\right)\right|}$$

  where $R^{\mu}(\tau)=x^{\mu}-y^{\mu}(\tau)$. Define $\tau_{\star}(x)$ and draw a spacetime diagram to illustrate its physical significance.

  Suppose the particle follows a circular trajectory,

  $$\mathbf{y}(t)=(R \cos (\omega t), R \sin (\omega t), 0)$$

  (with $y^{0}=c t$ ), in some inertial frame with coordinates $(c t, x, y, z)$. Evaluate the resulting 4 -vector potential at a point on the $z$-axis as a function of $z$ and $t$.

  comment

• Paper 4 , Section II, D

  Electrodynamics | Part II, 2018

  (a) Define the polarisation of a dielectric material and explain what is meant by the term bound charge.

  Consider a sample of material with spatially dependent polarisation $\mathbf{P}(\mathbf{x})$ occupying a region $V$ with surface $S$. Show that, in the absence of free charge, the resulting scalar potential $\phi(\mathbf{x})$ can be ascribed to bulk and surface densities of bound charge.

  Consider a sphere of radius $R$ consisting of a dielectric material with permittivity $\epsilon$ surrounded by a region of vacuum. A point-like electric charge $q$ is placed at the centre of the sphere. Determine the density of bound charge on the surface of the sphere.

  (b) Define the magnetization of a material and explain what is meant by the term bound current.

  Consider a sample of material with spatially-dependent magnetization $\mathbf{M}(\mathbf{x})$ occupying a region $V$ with surface $S$. Show that, in the absence of free currents, the resulting vector potential $\mathbf{A}(\mathbf{x})$ can be ascribed to bulk and surface densities of bound current.

  Consider an infinite cylinder of radius $r$ consisting of a material with permeability $\mu$ surrounded by a region of vacuum. A thin wire carrying current $I$ is placed along the axis of the cylinder. Determine the direction and magnitude of the resulting bound current density on the surface of the cylinder. What is the magnetization $\mathbf{M}(\mathbf{x})$ on the surface of the cylinder?

  comment

Fluid Dynamics II

• Paper 1, Section II, C

  Fluid Dynamics II | Part II, 2018

  A two-dimensional layer of very viscous fluid of uniform thickness $h(t)$ sits on a stationary, rigid surface $y=0$. It is impacted by a stream of air (which can be assumed inviscid) such that the air pressure at $y=h$ is $p_{0}-\frac{1}{2} \rho_{a} E^{2} x^{2}$, where $p_{0}$ and $E$ are constants, $\rho_{a}$ is the density of the air, and $x$ is the coordinate parallel to the surface.

  What boundary conditions apply to the velocity $\mathbf{u}=(u, v)$ and stress tensor $\sigma$ of the viscous fluid at $y=0$ and $y=h$ ?

  By assuming the form $\psi=x f(y)$ for the stream function of the flow, or otherwise, solve the Stokes equations for the velocity and pressure fields. Show that the layer thins at a rate

  $$V=-\frac{\mathrm{d} h}{\mathrm{~d} t}=\frac{1}{3} \frac{\rho_{a}}{\mu} E^{2} h^{3}$$

  comment

• Paper 2, Section II, C

  Fluid Dynamics II | Part II, 2018

  An initially unperturbed two-dimensional inviscid jet in $-h<y<h$ has uniform speed $U$ in the $x$ direction, while the surrounding fluid is stationary. The unperturbed velocity field $\mathbf{u}=(u, v)$ is therefore given by

  $$\begin{array}{ll} u=0 & \text { in } \quad y>h \\ u=U & \text { in } \quad-h<y<h \\ u=0 & \text { in } \quad y<-h \end{array}$$

  Consider separately disturbances in which the layer occupies $-h-\eta<y<h+\eta($ varicose disturbances) and disturbances in which the layer occupies $-h+\eta<y<h+\eta($ sinuous disturbances $)$, where $\eta(x, t)=\hat{\eta} e^{i k x+\sigma t}$, and determine the dispersion relation $\sigma(k)$ in each case.

  Find asymptotic expressions for the real part $\sigma_{R}$ of $\sigma$ in the limits $k \rightarrow 0$ and $k \rightarrow \infty$ and draw sketches of $\sigma_{R}(k)$ in each case.

  Compare the rates of growth of the two types of disturbance.

  comment

• Paper 3, Section II, C

  Fluid Dynamics II | Part II, 2018

  For two Stokes flows $\mathbf{u}^{(1)}(\mathbf{x})$ and $\mathbf{u}^{(2)}(\mathbf{x})$ inside the same volume $V$ with different boundary conditions on its boundary $S$, prove the reciprocal theorem

  $$\int_{S} u_{i}^{(1)} \sigma_{i j}^{(2)} n_{j} d S=\int_{S} u_{i}^{(2)} \sigma_{i j}^{(1)} n_{j} d S$$

  where $\sigma^{(1)}$ and $\sigma^{(2)}$ are the stress tensors associated with the flows.

  Stating clearly any properties of Stokes flow that you require, use the reciprocal theorem to prove that the drag $\mathbf{F}$ on a body translating with uniform velocity $\mathbf{U}$ is given by

  $$F_{i}=A_{i j} U_{j},$$

  where $\mathbf{A}$ is a symmetric second-rank tensor that depends only on the geometry of the body.

  A slender rod falls slowly through very viscous fluid with its axis inclined to the vertical. Explain why the rod does not rotate, stating any properties of Stokes flow that you use.

  When the axis of the rod is inclined at an angle $\theta$ to the vertical, the centre of mass of the rod travels at an angle $\phi$ to the vertical. Given that the rod falls twice as quickly when its axis is vertical as when its axis is horizontal, show that

  $$\tan \phi=\frac{\sin \theta \cos \theta}{1+\cos ^{2} \theta}$$

  comment

• Paper 4, Section II, C

  Fluid Dynamics II | Part II, 2018

  A cylinder of radius $a$ rotates about its axis with angular velocity $\Omega$ while its axis is fixed parallel to and at a distance $a+h_{0}$ from a rigid plane, where $h_{0} \ll a$. Fluid of kinematic viscosity $\nu$ fills the space between the cylinder and the plane. Determine the gap width $h$ between the cylinder and the plane as a function of a coordinate $x$ parallel to the surface of the wall and orthogonal to the axis of the cylinder. What is the characteristic length scale, in the $x$ direction, for changes in the gap width? Taking an appropriate approximation for $h(x)$, valid in the region where the gap width $h$ is small, use lubrication theory to determine that the volume flux between the wall and the cylinder (per unit length along the axis) has magnitude $\frac{2}{3} a \Omega h_{0}$, and state its direction.

  Evaluate the tangential shear stress $\tau$ on the surface of the cylinder. Approximating the torque on the cylinder (per unit length along the axis) in the form of an integral $T=a \int_{-\infty}^{\infty} \tau d x$, find the torque $T$ to leading order in $h_{0} / a \ll 1$.

  Explain the restriction $a^{1 / 2} \Omega h_{0}^{3 / 2} / \nu \ll 1$ for the theory to be valid.

  [You may use the facts that $\int_{-\infty}^{\infty} \frac{d x}{\left(1+x^{2}\right)^{2}}=\frac{\pi}{2}$ and $\left.\int_{-\infty}^{\infty} \frac{d x}{\left(1+x^{2}\right)^{3}}=\frac{3 \pi}{8} .\right]$

  comment

Further Complex Methods

• Paper 1, Section I, B

  Further Complex Methods | Part II, 2018

  The Beta and Gamma functions are defined by

  $$\begin{aligned} B(p, q) &=\int_{0}^{1} t^{p-1}(1-t)^{q-1} d t \\ \Gamma(p) &=\int_{0}^{\infty} e^{-t} t^{p-1} d t \end{aligned}$$

  where $\operatorname{Re} p>0, \operatorname{Re} q>0$.

  (a) By using a suitable substitution, or otherwise, prove that

  $$B(z, z)=2^{1-2 z} B\left(z, \frac{1}{2}\right)$$

  for $\operatorname{Re} z>0$. Extending $B$ by analytic continuation, for which values of $z \in \mathbb{C}$ does this result hold?

  (b) Prove that

  $$B(p, q)=\frac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}$$

  for $\operatorname{Re} p>0, \operatorname{Re} q>0$

  comment

• Paper 1, Section II, B

  Further Complex Methods | Part II, 2018

  The equation

  $$\tag{†} z w^{\prime \prime}+2 a w^{\prime}+z w=0,$$

  where $a$ is a constant with $\operatorname{Re} a>0$, has solutions of the form

  $$w(z)=\int_{\gamma} e^{z t} f(t) d t$$

  for suitably chosen contours $\gamma$ and some suitable function $f(t)$.

  (a) Find $f(t)$ and determine the condition on $\gamma$, which you should express in terms of $z, t$ and $a$.

  (b) Use the results of part (a) to show that $\gamma$ can be a finite contour and specify two possible finite contours with the help of a clearly labelled diagram. Hence, find the corresponding solution of the equation $(†)$ in the case $a=1$.

  (c) In the case $a=1$ and real $z$, show that $\gamma$ can be an infinite contour and specify two possible infinite contours with the help of a clearly labelled diagram. [Hint: Consider separately the cases $z>0$ and $z<0$.] Hence, find a second, linearly independent solution of the equation ( $\dagger$ ) in this case.

  comment

• Paper 2, Section $I$, $7 \mathrm{~B}$

  Further Complex Methods | Part II, 2018

  Show that

  $$\int_{-\infty}^{\infty} \frac{\cos n x-\cos m x}{x^{2}} d x=\pi(m-n),$$

  in the sense of Cauchy principal value, where $n$ and $m$ are positive integers. [State clearly any standard results involving contour integrals that you use.]

  comment

• Paper 2, Section II, B

  Further Complex Methods | Part II, 2018

  Consider a multi-valued function $w(z)$.

  (a) Explain what is meant by a branch point and a branch cut.

  (b) Consider $z=e^{w}$.

  (i) By writing $z=r e^{i \theta}$, where $0 \leqslant \theta<2 \pi$, and $w=u+i v$, deduce the expression for $w(z)$ in terms of $r$ and $\theta$. Hence, show that $w$ is infinitely valued and state its principal value.

  (ii) Show that $z=0$ and $z=\infty$ are the branch points of $w$. Deduce that the line $\operatorname{Im} z=0, \operatorname{Re} z>0$ is a possible choice of branch cut.

  (iii) Use the Cauchy-Riemann conditions to show that $w$ is analytic in the cut plane. Show that $\frac{d w}{d z}=\frac{1}{z}$.

  comment

• Paper 3, Section I, B

  Further Complex Methods | Part II, 2018

  Using a suitable branch cut, show that

  $$\int_{-a}^{a}\left(a^{2}-x^{2}\right)^{1 / 2} d x=\frac{a^{2} \pi}{2},$$

  where $a>0$.

  comment

• Paper 4, Section I, B

  Further Complex Methods | Part II, 2018

  State the conditions for a point $z=z_{0}$ to be a regular singular point of a linear second-order homogeneous ordinary differential equation in the complex plane.

  Find all singular points of the Bessel equation

  $$z^{2} y^{\prime \prime}(z)+z y^{\prime}(z)+\left(z^{2}-\frac{1}{4}\right) y(z)=0$$

  and determine whether they are regular or irregular.

  By writing $y(z)=f(z) / \sqrt{z}$, find two linearly independent solutions of $(*)$. Comment on the relationship of your solutions to the nature of the singular points.

  comment

Galois Theory

• Paper 1, Section II, I

  Galois Theory | Part II, 2018

  Let $f(t)=t^{4}+b t^{2}+c t+d$ be an irreducible quartic with rational coefficients. Explain briefly why it is that if the cubic $g(t)=t^{3}+2 b t^{2}+\left(b^{2}-4 d\right) t-c^{2}$ has $S_{3}$ as its Galois group then the Galois group of $f(t)$ is $S_{4}$.

  For which prime numbers $p$ is the Galois group of $t^{4}+p t+p$ a proper subgroup of $S_{4}$ ? [You may assume that the discriminant of $t^{3}+\lambda t+\mu$ is $-4 \lambda^{3}-27 \mu^{2}$.]

  comment

• Paper 2, Section II, I

  Galois Theory | Part II, 2018

  Let $K$ be a field and let $f(t)$ be a monic polynomial with coefficients in $K$. What is meant by a splitting field $L$ for $f(t)$ over $K$ ? Show that such a splitting field exists and is unique up to isomorphism.

  Now suppose that $K$ is a finite field. Prove that $L$ is a Galois extension of $K$ with cyclic Galois group. Prove also that the degree of $L$ over $K$ is equal to the least common multiple of the degrees of the irreducible factors of $f(t)$ over $K$.

  Now suppose $K$ is the field with two elements, and let

  $$\mathcal{P}_{n}=\{f(t) \in K[t] \mid f \text { has degree } n \text { and is irreducible over } K\}$$

  How many elements does the set $\mathcal{P}_{9}$ have?

  comment

• Paper 3, Section II, I

  Galois Theory | Part II, 2018

  Let $L$ be a finite field extension of a field $K$, and let $G$ be a finite group of $K$ automorphisms of $L$. Denote by $L^{G}$ the field of elements of $L$ fixed by the action of $G$.

  (a) Prove that the degree of $L$ over $L^{G}$ is equal to the order of the group $G$.

  (b) For any $\alpha \in L$ write $f(t, \alpha)=\Pi_{g \in G}(t-g(\alpha))$.

  (i) Suppose that $L=K(\alpha)$. Prove that the coefficients of $f(t, \alpha)$ generate $L^{G}$ over $K$.

  (ii) Suppose that $L=K\left(\alpha_{1}, \alpha_{2}\right)$. Prove that the coefficients of $f\left(t, \alpha_{1}\right)$ and $f\left(t, \alpha_{2}\right)$ lie in $L^{G}$. By considering the case $L=K\left(a_{1}^{1 / 2}, a_{2}^{1 / 2}\right)$ with $a_{1}$ and $a_{2}$ in $K$, or otherwise, show that they need not generate $L^{G}$ over $K$.

  comment

• Paper 4, Section II, I

  Galois Theory | Part II, 2018

  Let $K$ be a field of characteristic $p>0$ and let $L$ be the splitting field of the polynomial $f(t)=t^{p}-t+a$ over $K$, where $a \in K$. Let $\alpha \in L$ be a root of $f(t)$.

  If $L \neq K$, show that $f(t)$ is irreducible over $K$, that $L=K(\alpha)$, and that $L$ is a Galois extension of $K$. What is $\operatorname{Gal}(L / K)$ ?

  comment

General Relativity

• Paper 1, Section II, 37E

  General Relativity | Part II, 2018

  Consider the de Sitter metric

  $$d s^{2}=-d t^{2}+e^{2 H t}\left(d x^{2}+d y^{2}+d z^{2}\right)$$

  where $H>0$ is a constant.

  (a) Write down the Lagrangian governing the geodesics of this metric. Use the Euler-Lagrange equations to determine all non-vanishing Christoffel symbols.

  (b) Let $\mathcal{C}$ be a timelike geodesic parametrized by proper time $\tau$ with initial conditions at $\tau=0$,

  $$t=0, \quad x=y=z=0, \quad \dot{x}=v_{0}>0, \quad \dot{y}=\dot{z}=0,$$

  where the dot denotes differentiation with respect to $\tau$ and $v_{0}$ is a constant. Assuming both $t$ and $\tau$ to be future oriented, show that at $\tau=0$,

  $$\dot{t}=\sqrt{1+v_{0}^{2}}$$

  (c) Find a relation between $\tau$ and $t$ along the geodesic of part (b) and show that $t \rightarrow-\infty$ for a finite value of $\tau$. [You may use without proof that

  $$\left.\int \frac{1}{\sqrt{1+a e^{-b u}}} d u=\frac{1}{b} \ln \frac{\sqrt{1+a e^{-b u}}+1}{\sqrt{1+a e^{-b u}}-1}+\text { constant }, \quad a, b>0 .\right]$$

  (d) Briefly interpret this result.

  comment

• Paper 2, Section II, E

  General Relativity | Part II, 2018

  The Friedmann equations and the conservation of energy-momentum for a spatially homogeneous and isotropic universe are given by:

  $$3 \frac{\dot{a}^{2}+k}{a^{2}}-\Lambda=8 \pi \rho, \quad \frac{2 a \ddot{a}+\dot{a}^{2}+k}{a^{2}}-\Lambda=-8 \pi P, \quad \dot{\rho}=-3 \frac{\dot{a}}{a}(P+\rho),$$

  where $a$ is the scale factor, $\rho$ the energy density, $P$ the pressure, $\Lambda$ the cosmological constant and $k=+1,0,-1$.

  (a) Show that for an equation of state $P=w \rho, w=$ constant, the energy density obeys $\rho=\frac{3 \mu}{8 \pi} a^{-3(1+w)}$, for some constant $\mu$.

  (b) Consider the case of a matter dominated universe, $w=0$, with $\Lambda=0$. Write the equation of motion for the scale factor $a$ in the form of an effective potential equation,

  $$\dot{a}^{2}+V(a)=C$$

  where you should determine the constant $C$ and the potential $V(a)$. Sketch the potential $V(a)$ together with the possible values of $C$ and qualitatively discuss the long-term dynamics of an initially small and expanding universe for the cases $k=+1,0,-1$.

  (c) Repeat the analysis of part (b), again assuming $w=0$, for the cases:

  (i) $\Lambda>0, k=-1$,

  (ii) $\Lambda<0, k=0$,

  (iii) $\Lambda>0, k=1$.

  Discuss all qualitatively different possibilities for the dynamics of the universe in each case.

  comment

• Paper 3, Section II, E

  General Relativity | Part II, 2018

  The Schwarzschild metric in isotropic coordinates $\bar{x}^{\bar{\alpha}}=(\bar{t}, \bar{x}, \bar{y}, \bar{z}), \bar{\alpha}=0, \ldots, 3$, is given by:

  $$d s^{2}=\bar{g}_{\bar{\alpha} \bar{\beta}} d \bar{x}^{\bar{\alpha}} d \bar{x}^{\bar{\beta}}=-\frac{(1-A)^{2}}{(1+A)^{2}} d \bar{t}^{2}+(1+A)^{4}\left(d \bar{x}^{2}+d \bar{y}^{2}+d \bar{z}^{2}\right)$$

  where

  $$A=\frac{m}{2 \bar{r}}, \quad \bar{r}=\sqrt{\bar{x}^{2}+\bar{y}^{2}+\bar{z}^{2}}$$

  and $m$ is the mass of the black hole.

  (a) Let $x^{\mu}=(t, x, y, z), \mu=0, \ldots, 3$, denote a coordinate system related to $\bar{x}^{\bar{\alpha}}$ by

  $$\bar{t}=\gamma(t-v x), \quad \bar{x}=\gamma(x-v t), \quad \bar{y}=y, \quad \bar{z}=z,$$

  where $\gamma=1 / \sqrt{1-v^{2}}$ and $-1<v<1$. Write down the transformation matrix $\partial \bar{x}^{\bar{\alpha}} / \partial x^{\mu}$, briefly explain its physical meaning and show that the inverse transformation is of the same form, but with $v \rightarrow-v$.

  (b) Using the coordinate transformation matrix of part (a), or otherwise, show that the components $g_{\mu \nu}$ of the metric in coordinates $x^{\mu}$ are given by

  $$d s^{2}=g_{\mu \nu} d x^{\mu} d x^{\nu}=f(A)\left(-d t^{2}+d x^{2}+d y^{2}+d z^{2}\right)+\gamma^{2} g(A)(d t-v d x)^{2}$$

  where $f$ and $g$ are functions of $A$ that you should determine. You should also express $A$ in terms of the coordinates $(t, x, y, z)$.

  (c) Consider the limit $v \rightarrow 1$ with $p=m \gamma$ held constant. Show that for points $x \neq t$ the function $A \rightarrow 0$, while $\gamma^{2} A$ tends to a finite value, which you should determine. Hence determine the metric components $g_{\mu \nu}$ at points $x \neq t$ in this limit.

  comment

• Paper 4, Section II, E

  General Relativity | Part II, 2018

  (a) In the Newtonian weak-field limit, we can write the spacetime metric in the form

  $$d s^{2}=-(1+2 \Phi) d t^{2}+(1-2 \Phi) \delta_{i j} d x^{i} d x^{j},$$

  where $\delta_{i j} d x^{i} d x^{j}=d x^{2}+d y^{2}+d z^{2}$ and the potential $\Phi(t, x, y, z)$, as well as the velocity $v$ of particles moving in the gravitational field are assumed to be small, i.e.,

  $$\Phi, \partial_{t} \Phi, \partial_{x^{i}} \Phi, v^{2} \ll 1$$

  Use the geodesic equation for this metric to derive the equation of motion for a massive point particle in the Newtonian limit.

  (b) The far-field limit of the Schwarzschild metric is a special case of (*) given, in spherical coordinates, by

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1+\frac{2 M}{r}\right)\left(d r^{2}+r^{2} d \theta^{2}+r^{2} \sin ^{2} \theta d \varphi^{2}\right)$$

  where now $M / r \ll 1$. For the following questions, state your results to first order in $M / r$, i.e. neglecting terms of $\mathcal{O}\left((M / r)^{2}\right)$.

  (i) Let $r_{1}, r_{2} \gg M$. Calculate the proper length $S$ along the radial curve from $r_{1}$ to $r_{2}$ at fixed $t, \theta, \varphi$.

  (ii) Consider a massless particle moving radially from $r=r_{1}$ to $r=r_{2}$. According to an observer at rest at $r_{2}$, what time $T$ elapses during this motion?

  (iii) The effective velocity of the particle as seen by the observer at $r_{2}$ is defined as $v_{\text {eff }}:=S / T$. Evaluate $v_{\text {eff }}$ and then take the limit of this result as $r_{1} \rightarrow r_{2}$. Briefly discuss the value of $v_{\text {eff }}$ in this limit.

  comment

Graph Theory

• Paper 1, Section II, I

  Graph Theory | Part II, 2018

  (a) Define ex $(n, H)$ where $H$ is a graph with at least one edge and $n \geqslant|H|$. Show that, for any such $H$, the $\operatorname{limit}_{n \rightarrow \infty} \lim (n, H) /\left(\begin{array}{c}n \\ 2\end{array}\right)$ exists.

  [You may not assume the Erdős-Stone theorem.]

  (b) State the Erdős-Stone theorem. Use it to deduce that if $H$ is bipartite then $\lim _{n \rightarrow \infty} \operatorname{ex}(n, H) /\left(\begin{array}{l}n \\ 2\end{array}\right)=0 .$

  (c) Let $t \geqslant 2$. Show that ex $\left(n, K_{t, t}\right)=O\left(n^{2-\frac{1}{t}}\right)$.

  We say $A \subset \mathbb{Z}_{n}$ is nice if whenever $a, b, c, d \in A$ with $a+b=c+d$ then either $a=c, b=d$ or $a=d, b=c$. Let $f(n)=\max \left\{|A|: A \subset \mathbb{Z}_{n}, A\right.$ is nice $\}$. Show that $f(n)=O(\sqrt{n}) .$

  $\left[\mathbb{Z}_{n}\right.$ denotes the set of integers modulo $n$, i.e. $\mathbb{Z}_{n}=\{0,1,2, \ldots, n-1\}$ with addition modulo $n .]$

  comment

• Paper 2, Section II, I

  Graph Theory | Part II, 2018

  Let $G$ be a graph and $A, B \subset V(G)$. Show that if every $A B$-separator in $G$ has order at least $k$ then there exist $k$ vertex-disjoint $A B$-paths in $G$.

  Let $k \geqslant 3$ and assume that $G$ is $k$-connected. Show that $G$ must contain a cycle of length at least $k$.

  Assume further that $|G| \geqslant 2 k$. Must $G$ contain a cycle of length at least $2 k ?$ Justify your answer.

  What is the largest integer $n$ such that any 3-connected graph $G$ with $|G| \geqslant n$ must contain a cycle of length at least $n$ ?

  [No form of Menger's theorem or of the max-flow-min-cut theorem may be assumed without proof.]

  comment

• Paper 3, Section II, I

  Graph Theory | Part II, 2018

  What does it mean to say that a graph $G$ has a $k$-colouring? What are the chromatic number $\chi(G)$ and the independence number $\alpha(G)$ of a graph $G$ ? For each $r \geqslant 3$, give an example of a graph $G$ such that $\chi(G)>r$ but $K_{r} \not \subset G$.

  Let $g, k \geqslant 3$. Show that there exists a graph $G$ containing no cycle of length $\leqslant g$ with $\chi(G) \geqslant k$.

  Show also that if $n$ is sufficiently large then there is a triangle-free $G$ of order $n$ with $\alpha(G)<n^{0.7}$.

  comment

• Paper 4, Section II, I

  Graph Theory | Part II, 2018

  Let $s \geqslant 3$. Define the Ramsey number $R(s)$. Show that $R(s)$ exists and that $R(s) \leqslant 4^{s}$.

  Show that $R(3)=6$. Show that (up to relabelling the vertices) there is a unique way to colour the edges of the complete graph $K_{5}$ blue and yellow with no monochromatic triangle.

  What is the least positive integer $n$ such that the edges of the complete graph $K_{6}$ can be coloured blue and yellow in such a way that there are precisely $n$ monochromatic triangles?

  comment

Integrable Systems

• Paper 1, Section II, A

  Integrable Systems | Part II, 2018

  Let $M=\mathbb{R}^{2 n}=\left\{(\mathbf{q}, \mathbf{p}) \mid \mathbf{q}, \mathbf{p} \in \mathbb{R}^{n}\right\}$ be equipped with the standard symplectic form so that the Poisson bracket is given by:

  $$\{f, g\}=\frac{\partial f}{\partial q_{j}} \frac{\partial g}{\partial p_{j}}-\frac{\partial f}{\partial p_{j}} \frac{\partial g}{\partial q_{j}}$$

  for $f, g$ real-valued functions on $M$. Let $H=H(\mathbf{q}, \mathbf{p})$ be a Hamiltonian function.

  (a) Write down Hamilton's equations for $(M, H)$, define a first integral of the system and state what it means that the system is integrable.

  (b) State the Arnol'd-Liouville theorem.

  (c) Define complex coordinates $z_{j}$ by $z_{j}=q_{j}+i p_{j}$, and show that if $f, g$ are realvalued functions on $M$ then:

  $$\{f, g\}=-2 i \frac{\partial f}{\partial z_{j}} \frac{\partial g}{\partial \overline{z_{j}}}+2 i \frac{\partial g}{\partial z_{j}} \frac{\partial f}{\partial \bar{z}_{j}}$$

  (d) For an $n \times n$ anti-Hermitian matrix $A$ with components $A_{j k}$, let $I_{A}:=\frac{1}{2 i} \overline{z_{j}} A_{j k} z_{k}$. Show that:

  $$\left\{I_{A}, I_{B}\right\}=-I_{[A, B]},$$

  where $[A, B]=A B-B A$ is the usual matrix commutator.

  (e) Consider the Hamiltonian:

  $$H=\frac{1}{2} \overline{z_{j}} z_{j}$$

  Show that $(M, H)$ is integrable and describe the invariant tori.

  [In this question $j, k=1, \ldots, n$, and the summation convention is understood for these indices.]

  comment

• Paper 2, Section II, A

  Integrable Systems | Part II, 2018

  (a) Let $\mathcal{L}, \mathcal{A}$ be two families of linear operators, depending on a parameter $t$, which act on a Hilbert space $H$ with inner product $(,$, . Suppose further that for each $t, \mathcal{L}$ is self-adjoint and that $\mathcal{A}$ is anti-self-adjoint. State $L a x$ 's equation for the pair $\mathcal{L}, \mathcal{A}$, and show that if it holds then the eigenvalues of $\mathcal{L}$ are independent of $t$.

  (b) For $\psi, \phi: \mathbb{R} \rightarrow \mathbb{C}$, define the inner product:

  $$(\psi, \phi):=\int_{-\infty}^{\infty} \overline{\psi(x)} \phi(x) d x$$

  Let $L, A$ be the operators:

  $$\begin{gathered} L \psi:=i \frac{d^{3} \psi}{d x^{3}}-i\left(q \frac{d \psi}{d x}+\frac{d}{d x}(q \psi)\right)+p \psi \\ A \psi:=3 i \frac{d^{2} \psi}{d x^{2}}-4 i q \psi \end{gathered}$$

  where $p=p(x, t), q=q(x, t)$ are smooth, real-valued functions. You may assume that the normalised eigenfunctions of $L$ are smooth functions of $x, t$, which decay rapidly as $|x| \rightarrow \infty$ for all $t$.

  (i) Show that if $\psi, \phi$ are smooth and rapidly decaying towards infinity then:

  $$(L \psi, \phi)=(\psi, L \phi), \quad(A \psi, \phi)=-(\psi, A \phi)$$

  Deduce that the eigenvalues of $L$ are real.

  (ii) Show that if Lax's equation holds for $L, A$, then $q$ must satisfy the Boussinesq equation:

  $$q_{t t}=a q_{x x x x}+b\left(q^{2}\right)_{x x}$$

  where $a, b$ are constants whose values you should determine. [You may assume without proof that the identity:

  $$L A \psi=A L \psi-3 i\left(p_{x} \frac{d \psi}{d x}+\frac{d}{d x}\left(p_{x} \psi\right)\right)+\left[q_{x x x}-4\left(q^{2}\right)_{x}\right] \psi$$

  holds for smooth, rapidly decaying $\psi .]$

  comment

• Paper 3, Section II, A

  Integrable Systems | Part II, 2018

  Suppose $\psi^{s}:(x, u) \mapsto(\tilde{x}, \tilde{u})$ is a smooth one-parameter group of transformations acting on $\mathbb{R}^{2}$.

  (a) Define the generator of the transformation,

  $$V=\xi(x, u) \frac{\partial}{\partial x}+\eta(x, u) \frac{\partial}{\partial u}$$

  where you should specify $\xi$ and $\eta$ in terms of $\psi^{s}$.

  (b) Define the $n^{\text {th }}$prolongation of $V, \operatorname{Pr}^{(n)} V$ and explicitly compute $\operatorname{Pr}^{(1)} V$ in terms of $\xi, \eta$.

  Recall that if $\psi^{s}$ is a Lie point symmetry of the ordinary differential equation:

  $$\Delta\left(x, u, \frac{d u}{d x}, \ldots, \frac{d^{n} u}{d x^{n}}\right)=0$$

  then it follows that $\operatorname{Pr}^{(n)} V[\Delta]=0$ whenever $\Delta=0$.

  (c) Consider the ordinary differential equation:

  $$\frac{d u}{d x}=F(x, u),$$

  for $F$ a smooth function. Show that if $V$ generates a Lie point symmetry of this equation, then:

  $$0=\eta_{x}+\left(\eta_{u}-\xi_{x}-F \xi_{u}\right) F-\xi F_{x}-\eta F_{u}$$

  (d) Find all the Lie point symmetries of the equation:

  $$\frac{d u}{d x}=x G\left(\frac{u}{x^{2}}\right)$$

  where $G$ is an arbitrary smooth function.

  comment

Linear Analysis

• Paper 1, Section II, F

  Linear Analysis | Part II, 2018

  Let $K$ be a compact Hausdorff space.

  (a) State the Arzelà-Ascoli theorem, and state both the real and complex versions of the Stone-Weierstraß theorem. Give an example of a compact space $K$ and a bounded set of functions in $C(K)$ that is not relatively compact.

  (b) Let $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$ be continuous. Show that there exists a sequence of polynomials $\left(p_{i}\right)$ in $n$ variables such that

  $$B \subset \mathbb{R}^{n} \text { compact }\left.\left.\Rightarrow \quad p_{i}\right|_{B} \rightarrow f\right|_{B} \text { uniformly }$$

  Characterize the set of continuous functions $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$ for which there exists a sequence of polynomials $\left(p_{i}\right)$ such that $p_{i} \rightarrow f$ uniformly on $\mathbb{R}^{n}$.

  (c) Prove that if $C(K)$ is equicontinuous then $K$ is finite. Does this implication remain true if we drop the requirement that $K$ be compact? Justify your answer.

  comment

• Paper 2, Section II, F

  Linear Analysis | Part II, 2018

  Let $X, Y$ be Banach spaces and let $\mathcal{B}(X, Y)$ denote the space of bounded linear operators $T: X \rightarrow Y$.

  (a) Define what it means for a bounded linear operator $T: X \rightarrow Y$ to be compact. Let $T_{i}: X \rightarrow Y$ be linear operators with finite rank, i.e., $T_{i}(X)$ is finite-dimensional. Assume that the sequence $T_{i}$ converges to $T$ in $\mathcal{B}(X, Y)$. Show that $T$ is compact.

  (b) Let $T: X \rightarrow Y$ be compact. Show that the dual map $T^{*}: Y^{*} \rightarrow X^{*}$ is compact. [Hint: You may use the Arzelà-Ascoli theorem.]

  (c) Let $X$ be a Hilbert space and let $T: X \rightarrow X$ be a compact operator. Let $\left(\lambda_{j}\right)$ be an infinite sequence of eigenvalues of $T$ with eigenvectors $x_{j}$. Assume that the eigenvectors are orthogonal to each other. Show that $\lambda_{j} \rightarrow 0$.

  comment

• Paper 3, Section II, F

  Linear Analysis | Part II, 2018

  (a) Let $X$ be a normed vector space and let $Y$ be a Banach space. Show that the space of bounded linear operators $\mathcal{B}(X, Y)$ is a Banach space.

  (b) Let $X$ and $Y$ be Banach spaces, and let $D \subset X$ be a dense linear subspace. Prove that a bounded linear map $T: D \rightarrow Y$ can be extended uniquely to a bounded linear map $T: X \rightarrow Y$ with the same operator norm. Is the claim also true if one of $X$ and $Y$ is not complete?

  (c) Let $X$ be a normed vector space. Let $\left(x_{n}\right)$ be a sequence in $X$ such that

  $$\sum_{n=1}^{\infty}\left|f\left(x_{n}\right)\right|<\infty \quad \forall f \in X^{*}$$

  Prove that there is a constant $C$ such that

  $$\sum_{n=1}^{\infty}\left|f\left(x_{n}\right)\right| \leqslant C\|f\| \quad \forall f \in X^{*}$$

  comment

• Paper 4, Section II, F

  Linear Analysis | Part II, 2018

  (a) Let $X$ be a separable normed space. For any sequence $\left(f_{n}\right)_{n \in \mathbb{N}} \subset X^{*}$ with $\left\|f_{n}\right\| \leqslant 1$ for all $n$, show that there is $f \in X^{*}$ and a subsequence $\Lambda \subset \mathbb{N}$ such that $f_{n}(x) \rightarrow f(x)$ for all $x \in X$ as $n \in \Lambda, n \rightarrow \infty$. [You may use without proof the fact that $X^{*}$ is complete and that any bounded linear map $f: D \rightarrow \mathbb{R}$, where $D \subset X$ is a dense linear subspace, can be extended uniquely to an element $f \in X^{*}$.]

  (b) Let $H$ be a Hilbert space and $U: H \rightarrow H$ a unitary map. Let

  $$I=\{x \in H: U x=x\}, \quad W=\{U x-x: x \in H\}$$

  Prove that $I$ and $W$ are orthogonal, $H=I \oplus \bar{W}$, and that for every $x \in H$,

  $$\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{i=0}^{n-1} U^{i} x=P x$$

  where $P$ is the orthogonal projection onto the closed subspace $I$.

  (c) Let $T: C\left(S^{1}\right) \rightarrow C\left(S^{1}\right)$ be a linear map, where $S^{1}=\left\{e^{i \theta} \in \mathbb{C}: \theta \in \mathbb{R}\right\}$ is the unit circle, induced by a homeomorphism $\tau: S^{1} \rightarrow S^{1}$ by $(T f) e^{i \theta}=f\left(\tau\left(e^{i \theta}\right)\right)$. Prove that there exists $\mu \in C\left(S^{1}\right)^{*}$ with $\mu\left(1_{S^{1}}\right)=1$ such that $\mu(T f)=\mu(f)$ for all $f \in C\left(S^{1}\right)$. (Here $1_{S^{1}}$ denotes the function on $S^{1}$ which returns 1 identically.) If $T$ is not the identity map, does it follow that $\mu$ as above is necessarily unique? Justify your answer.

  comment

Logic and Set Theory

• Paper 1, Section II, G

  Logic and Set Theory | Part II, 2018

  Give the inductive definition of ordinal exponentiation. Use it to show that $\alpha^{\beta} \leqslant \alpha^{\gamma}$ whenever $\beta \leqslant \gamma$ (for $\alpha \geqslant 1$ ), and also that $\alpha^{\beta}<\alpha^{\gamma}$ whenever $\beta<\gamma($ for $\alpha \geqslant 2)$.

  Give an example of ordinals $\alpha$ and $\beta$ with $\omega<\alpha<\beta$ such that $\alpha^{\omega}=\beta^{\omega}$.

  Show that $\alpha^{\beta+\gamma}=\alpha^{\beta} \alpha^{\gamma}$, for any ordinals $\alpha, \beta, \gamma$, and give an example to show that we need not have $(\alpha \beta)^{\gamma}=\alpha^{\gamma} \beta^{\gamma}$.

  For which ordinals $\alpha$ do we have $\alpha^{\omega_{1}} \geqslant \omega_{1}$ ? And for which do we have $\alpha^{\omega_{1}} \geqslant \omega_{2}$ ? Justify your answers.

  [You may assume any standard results not concerning ordinal exponentiation.]

  comment

• Paper 2, Section II, G

  Logic and Set Theory | Part II, 2018

  State and prove the Knaster-Tarski Fixed-Point Theorem. Deduce the SchröderBernstein Theorem.

  Show that the poset $P$ of all countable subsets of $\mathbb{R}$ (ordered by inclusion) is not complete.

  Find an order-preserving function $f: P \rightarrow P$ that does not have a fixed point. [Hint: Start by well-ordering the reals.]

  comment

• Paper 3, Section II, G

  Logic and Set Theory | Part II, 2018

  State and prove the Compactness Theorem for first-order predicate logic. State and prove the Upward Löwenheim-Skolem Theorem.

  [You may assume the Completeness Theorem for first-order predicate logic.]

  For each of the following theories, either give axioms (in the specified language) for the theory or prove that the theory is not axiomatisable.

  (i) The theory of finite groups (in the language of groups).

  (ii) The theory of groups in which every non-identity element has infinite order (in the language of groups).

  (iii) The theory of total orders (in the language of posets).

  (iv) The theory of well-orderings (in the language of posets).

  If a theory is axiomatisable by a set $S$ of sentences, and also by a finite set $T$ of sentences, does it follow that the theory is axiomatisable by some finite subset of $S$ ? Justify your answer.

  comment

• Paper 4, Section II, G

  Logic and Set Theory | Part II, 2018

  State and prove the $\epsilon$-Recursion Theorem. [You may assume the Principle of $\epsilon-$ Induction.]

  What does it mean to say that a relation $r$ on a set $x$ is well-founded and extensional? State and prove Mostowski's Collapsing Theorem. [You may use any recursion theorem from the course, provided you state it precisely.]

  For which sets $x$ is it the case that every well-founded extensional relation on $x$ is isomorphic to the relation $\epsilon$ on some transitive subset of $V_{\omega}$ ?

  comment

Mathematical Biology

• Paper 1, Section I, $\mathbf{6 C}$

  Mathematical Biology | Part II, 2018

  Consider a birth-death process in which the birth and death rates in a population of size $n$ are, respectively, $B n$ and $D n$, where $B$ and $D$ are per capita birth and death rates.

  (a) Write down the master equation for the probability, $p_{n}(t)$, of the population having size $n$ at time $t$.

  (b) Obtain the differential equations for the rates of change of the mean $\mu(t)=\langle n\rangle$ and the variance $\sigma^{2}(t)=\left\langle n^{2}\right\rangle-\langle n\rangle^{2}$ in terms of $\mu, \sigma, B$ and $D$.

  (c) Compare the equations obtained above with the deterministic description of the evolution of the population size, $d n / d t=(B-D) n$. Comment on why $B$ and $D$ cannot be uniquely deduced from the deterministic model but can be deduced from the stochastic description.

  comment

• Paper 2, Section I, C

  Mathematical Biology | Part II, 2018

  Consider a model of an epidemic consisting of populations of susceptible, $S(t)$, infected, $I(t)$, and recovered, $R(t)$, individuals that obey the following differential equations

  $$\begin{aligned} \frac{d S}{d t} &=a R-b S I \\ \frac{d I}{d t} &=b S I-c I \\ \frac{d R}{d t} &=c I-a R \end{aligned}$$

  where $a, b$ and $c$ are constant. Show that the sum of susceptible, infected and recovered individuals is a constant $N$. Find the fixed points of the dynamics and deduce the condition for an endemic state with a positive number of infected individuals. Expressing $R$ in terms of $S, I$ and $N$, reduce the system of equations to two coupled differential equations and, hence, deduce the conditions for the fixed point to be a node or a focus. How do small perturbations of the populations relax to the steady state in each case?

  comment

• Paper 3, Section I, $\mathbf{6 C}$

  Mathematical Biology | Part II, 2018

  Consider a nonlinear model for the axisymmetric dispersal of a population in two spatial dimensions whose density, $n(r, t)$, obeys

  $$\frac{\partial n}{\partial t}=D \boldsymbol{\nabla} \cdot(n \boldsymbol{\nabla} n)$$

  where $D$ is a positive constant, $r$ is a radial polar coordinate, and $t$ is time.

  Show that

  $$2 \pi \int_{0}^{\infty} n(r, t) r d r=N$$

  is constant. Interpret this condition.

  Show that a similarity solution of the form

  $$n(r, t)=\left(\frac{N}{D t}\right)^{1 / 2} f\left(\frac{r}{(N D t)^{1 / 4}}\right)$$

  is valid for $t>0$ provided that the scaling function $f(x)$ satisfies

  $$\frac{d}{d x}\left(x f \frac{d f}{d x}+\frac{1}{4} x^{2} f\right)=0 .$$

  Show that there exists a value $x_{0}$ (which need not be evaluated) such that $f(x)>0$ for $x<x_{0}$ but $f(x)=0$ for $x>x_{0}$. Determine the area within which $n(r, t)>0$ at time $t$ in terms of $x_{0}$.

  [Hint: The gradient and divergence operators in cylindrical polar coordinates act on radial functions $f$ and $g$ as

  $$\left.\boldsymbol{\nabla} f(r)=\frac{\partial f}{\partial r} \hat{\boldsymbol{r}} \quad, \quad \boldsymbol{\nabla} \cdot[g(r) \hat{\boldsymbol{r}}]=\frac{1}{r} \frac{\partial}{\partial r}(r g(r)) .\right]$$

  comment

• Paper 3, Section II, C

  Mathematical Biology | Part II, 2018

  Consider fluctuations of a population described by the vector $\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{N}\right)$. The probability of the state $\mathbf{x}$ at time $t, P(\mathbf{x}, t)$, obeys the multivariate Fokker-Planck equation

  $$\frac{\partial P}{\partial t}=-\frac{\partial}{\partial x_{i}}\left(A_{i}(\mathbf{x}) P\right)+\frac{1}{2} \frac{\partial^{2}}{\partial x_{i} \partial x_{j}}\left(B_{i j}(\mathbf{x}) P\right),$$

  where $P=P(\mathbf{x}, t), A_{i}$ is a drift vector and $B_{i j}$ is a symmetric positive-definite diffusion matrix, and the summation convention is used throughout.

  (a) Show that the Fokker-Planck equation can be expressed as a continuity equation

  $$\frac{\partial P}{\partial t}+\nabla \cdot \mathbf{J}=0$$

  for some choice of probability flux $\mathbf{J}$ which you should determine explicitly. Here, $\nabla=\left(\frac{\partial}{\partial x_{1}}, \frac{\partial}{\partial x_{2}}, \ldots, \frac{\partial}{\partial x_{N}}\right)$ denotes the gradient operator.

  (b) Show that the above implies that an initially normalised probability distribution remains normalised,

  $$\int P(\mathbf{x}, t) d V=1$$

  at all times, where the volume element $d V=d x_{1} d x_{2} \ldots d x_{N}$.

  (c) Show that the first two moments of the probability distribution obey

  $$\begin{aligned} \frac{d}{d t}\left\langle x_{k}\right\rangle &=\left\langle A_{k}\right\rangle \\ \frac{d}{d t}\left\langle x_{k} x_{l}\right\rangle &=\left\langle x_{l} A_{k}+x_{k} A_{l}+B_{k l}\right\rangle \end{aligned}$$

  (d) Now consider small fluctuations with zero mean, and assume that it is possible to linearise the drift vector and the diffusion matrix as $A_{i}(\mathbf{x})=a_{i j} x_{j}$ and $B_{i j}(\mathbf{x})=b_{i j}$ where $a_{i j}$ has real negative eigenvalues and $b_{i j}$ is a symmetric positive-definite matrix. Express the probability flux in terms of the matrices $a_{i j}$ and $b_{i j}$ and assume that it vanishes in the stationary state.

  (e) Hence show that the multivariate normal distribution,

  $$P(\mathbf{x})=\frac{1}{Z} \exp \left(-\frac{1}{2} D_{i j} x_{i} x_{j}\right)$$

  where $Z$ is a normalisation and $D_{i j}$ is symmetric, is a solution of the linearised FokkerPlanck equation in the stationary state, and obtain an equation that relates $D_{i j}$ to the matrices $a_{i j}$ and $b_{i j}$.

  (f) Show that the inverse of the matrix $D_{i j}$ is the matrix of covariances $C_{i j}=\left\langle x_{i} x_{j}\right\rangle$ and obtain an equation relating $C_{i j}$ to the matrices $a_{i j}$ and $b_{i j}$.

  comment

• Paper 4, Section I, C

  Mathematical Biology | Part II, 2018

  Consider a model of a population $N_{\tau}$ in discrete time

  $$N_{\tau+1}=\frac{r N_{\tau}}{\left(1+b N_{\tau}\right)^{2}}$$

  where $r, b>0$ are constants and $\tau=1,2,3, \ldots$ Interpret the constants and show that for $r>1$ there is a stable fixed point.

  Suppose the initial condition is $N_{1}=1 / b$ and that $r>4$. Show, using a cobweb diagram, that the population $N_{\tau}$ is bounded as

  $$\frac{4 r^{2}}{(4+r)^{2} b} \leqslant N_{\tau} \leqslant \frac{r}{4 b}$$

  and attains the bounds.

  comment

• Paper 4, Section II, C

  Mathematical Biology | Part II, 2018

  An activator-inhibitor reaction diffusion system is given, in dimensionless form, by

  $$\frac{\partial u}{\partial t}=d \frac{\partial^{2} u}{\partial x^{2}}+\frac{u^{2}}{v}-2 b u, \quad \frac{\partial v}{\partial t}=\frac{\partial^{2} v}{\partial x^{2}}+u^{2}-v$$

  where $d$ and $b$ are positive constants. Which symbol represents the concentration of activator and which the inhibitor? Determine the positive steady states and show, by an examination of the eigenvalues in a linear stability analysis of the spatially uniform situation, that the reaction kinetics are stable if $b<\frac{1}{2}$.

  Determine the conditions for the steady state to be driven unstable by diffusion, and sketch the $(b, d)$ parameter space in which the diffusion-driven instability occurs. Find the critical wavenumber $k_{c}$ at the bifurcation to such a diffusion-driven instability.

  comment

Number Fields

• Paper 1, Section II, G

  Number Fields | Part II, 2018

  (a) Let $m \geqslant 2$ be an integer such that $p=4 m-1$ is prime. Suppose that the ideal class group of $L=\mathbb{Q}(\sqrt{-p})$ is trivial. Show that if $n \geqslant 0$ is an integer and $n^{2}+n+m<m^{2}$, then $n^{2}+n+m$ is prime.

  (b) Show that the ideal class group of $\mathbb{Q}(\sqrt{-163})$ is trivial.

  comment

• Paper 2, Section II, 20G

  Number Fields | Part II, 2018

  Let $p \equiv 1 \bmod 4$ be a prime, and let $\omega=e^{2 \pi i / p}$. Let $L=\mathbb{Q}(\omega)$.

  (a) Show that $[L: \mathbb{Q}]=p-1$.

  (b) Calculate $\operatorname{disc}\left(1, \omega, \omega^{2}, \ldots, \omega^{p-2}\right)$. Deduce that $\sqrt{p} \in L$.

  (c) Now suppose $p=5$. Prove that $\mathcal{O}_{L}^{\times}=\left\{\pm \omega^{a}\left(\frac{1}{2}+\frac{\sqrt{5}}{2}\right)^{b} \mid a, b \in \mathbb{Z}\right\}$. [You may use any general result without proof, provided that you state it precisely.]

  comment

• Paper 4, Section II, G

  Number Fields | Part II, 2018

  Let $m \geqslant 2$ be a square-free integer, and let $n \geqslant 2$ be an integer. Let $L=\mathbb{Q}(\sqrt[n]{m})$.

  (a) By considering the factorisation of $(m)$ into prime ideals, show that $[L: \mathbb{Q}]=n$.

  (b) Let $T: L \times L \rightarrow \mathbb{Q}$ be the bilinear form defined by $T(x, y)=\operatorname{tr}_{L / \mathbb{Q}}(x y)$. Let $\beta_{i}=\sqrt[n]{m} i, i=0, \ldots, n-1$. Calculate the dual basis $\beta_{0}^{*}, \ldots, \beta_{n-1}^{*}$ of $L$ with respect to $T$, and deduce that $\mathcal{O}_{L} \subset \frac{1}{n m} \mathbb{Z}[\sqrt[n]{m}]$.

  (c) Show that if $p$ is a prime and $n=m=p$, then $\mathcal{O}_{L}=\mathbb{Z}[\sqrt[p]{p}]$.

  comment

Number Theory

• Paper 1, Section I, G

  Number Theory | Part II, 2018

  (a) State and prove the Chinese remainder theorem.

  (b) An integer $n$ is squarefull if whenever $p$ is prime and $p \mid n$, then $p^{2} \mid n$. Show that there exist 1000 consecutive positive integers, none of which are squarefull.

  comment

• Paper 2, Section I, G

  Number Theory | Part II, 2018

  Define the Legendre symbol, and state Gauss's lemma. Show that if $p$ is an odd prime, then

  $$\left(\frac{2}{p}\right)=(-1)^{\left(p^{2}-1\right) / 8}$$

  Use the law of quadratic reciprocity to compute $\left(\frac{105}{149}\right)$.

  comment

• Paper 3, Section I, G

  Number Theory | Part II, 2018

  What is a multiplicative function? Show that if $f(n)$ is a multiplicative function, then so is $g(n)=\sum_{d \mid n} f(d)$.

  Define the Möbius function $\mu(n)$, and show that it is multiplicative. Deduce that

  $$\sum_{d \mid n} \mu(d)= \begin{cases}1 & \text { if } n=1 \\ 0 & \text { if } n>1\end{cases}$$

  and that

  $$f(n)=\sum_{e \mid n} \mu(e) g\left(\frac{n}{e}\right) .$$

  What is $g(n)$ if $f(n)=n ?$ What is $f(n)$ if $g(n)=n ?$

  comment

• Paper 3, Section II, G

  Number Theory | Part II, 2018

  What does it mean to say that a positive definite binary quadratic form is reduced? What does it mean to say that two binary quadratic forms are equivalent? Show that every positive definite binary quadratic form is equivalent to some reduced form.

  Show that the reduced positive definite binary quadratic forms of discriminant $-35$ are $f_{1}=x^{2}+x y+9 y^{2}$ and $f_{2}=3 x^{2}+x y+3 y^{2}$. Show also that a prime $p>7$ is represented by $f_{i}$ if and only if

  $$\left(\frac{p}{5}\right)=\left(\frac{p}{7}\right)= \begin{cases}+1 & (i=1) \\ -1 & (i=2)\end{cases}$$

  comment

• Paper 4, Section I, G

  Number Theory | Part II, 2018

  Show that if a continued fraction is periodic, then it represents a quadratic irrational. What number is represented by the continued fraction $[7,7,7, \ldots]$ ?

  Compute the continued fraction expansion of $\sqrt{23}$. Hence or otherwise find a solution in positive integers to the equation $x^{2}-23 y^{2}=1$.

  comment

• Paper 4, Section II, G

  Number Theory | Part II, 2018

  (a) State and prove the Fermat-Euler theorem. Let $p$ be a prime and $k$ a positive integer. Show that $b^{k} \equiv b(\bmod p)$ holds for every integer $b$ if and only if $k \equiv 1(\bmod p-1)$.

  (b) Let $N \geqslant 3$ be an odd integer and $b$ be an integer with $(b, N)=1$. What does it mean to say that $N$ is a Fermat pseudoprime to base $b$ ? What does it mean to say that $N$ is a Carmichael number?

  Show that every Carmichael number is squarefree, and that if $N$ is squarefree, then $N$ is a Carmichael number if and only if $N \equiv 1(\bmod p-1)$ for every prime divisor $p$ of $N$. Deduce that a Carmichael number is a product of at least three primes.

  (c) Let $r$ be a fixed odd prime. Show that there are only finitely many pairs of primes $p, q$ for which $N=p q r$ is a Carmichael number.

  [You may assume throughout that $\left(\mathbb{Z} / p^{n} \mathbb{Z}\right)^{*}$ is cyclic for every odd prime $p$ and every integer $n \geqslant 1 .]$

  comment

Numerical Analysis

• Paper 1, Section II, E

  Numerical Analysis | Part II, 2018

  (a) Suppose that $A$ is a real $n \times n$ matrix, and $\boldsymbol{w} \in \mathbb{R}^{n}$ and $\lambda_{1} \in \mathbb{R}$ are given so that $A \boldsymbol{w}=\lambda_{1} \boldsymbol{w}$. Further, let $S$ be a non-singular matrix such that $S \boldsymbol{w}=c e^{(1)}$, where $e^{(1)}$ is the first coordinate vector and $c \neq 0$.

  Let $\widehat{A}=S A S^{-1}$. Prove that the eigenvalues of $A$ are $\lambda_{1}$ together with the eigenvalues of the bottom right $(n-1) \times(n-1)$ submatrix of $\widehat{A}$.

  Explain briefly how, given a vector $\boldsymbol{w}$, an orthogonal matrix $S$ such that $S \boldsymbol{w}=c e^{(1)}$ can be constructed.

  (b) Suppose that $A$ is a real $n \times n$ matrix, and two linearly independent vectors $\boldsymbol{v}, \boldsymbol{w} \in \mathbb{R}^{n}$ are given such that the linear subspace $L\{\boldsymbol{v}, \boldsymbol{w}\}$ spanned by $\boldsymbol{v}$ and $\boldsymbol{w}$ is invariant under the action of $A$, i.e.,

  $$x \in L\{\boldsymbol{v}, \boldsymbol{w}\} \quad \Rightarrow \quad A x \in L\{\boldsymbol{v}, \boldsymbol{w}\}$$

  Denote by $V$ an $n \times 2$ matrix whose two columns are the vectors $\boldsymbol{v}$ and $\boldsymbol{w}$, and let $S$ be a non-singular matrix such that $R=S V$ is upper triangular:

  $$S V=S \times\left[\begin{array}{cc} v_{1} & w_{1} \\ v_{2} & w_{2} \\ v_{3} & w_{3} \\ : & : \\ v_{n} & w_{n} \end{array}\right]=\left[\begin{array}{cc} r_{11} & r_{12} \\ 0 & r_{22} \\ 0 & 0 \\ : & : \\ 0 & 0 \end{array}\right]$$

  Again, let $\widehat{A}=S A S^{-1}$. Prove that the eigenvalues of $A$ are the eigenvalues of the top left $2 \times 2$ submatrix of $\widehat{A}$together with the eigenvalues of the bottom right $(n-2) \times(n-2)$ submatrix of $\widehat{A}$.

  Explain briefly how, for given vectors $\boldsymbol{v}, \boldsymbol{w}$, an orthogonal matrix $S$ which satisfies (*) can be constructed.

  comment

• Paper 2, Section II, E

  Numerical Analysis | Part II, 2018

  The Poisson equation $\frac{d^{2} u}{d x^{2}}=f$ in the unit interval $[0,1]$, with $u(0)=u(1)=0$, is discretised with the formula

  $$u_{i-1}-2 u_{i}+u_{i+1}=h^{2} f_{i}, \quad 1 \leqslant i \leqslant n,$$

  where $u_{0}=u_{n+1}=0, h=(n+1)^{-1}$, the grid points are at $x=i h$ and $u_{i} \approx u(i h)$.

  (a) Write the above system of equations in the vector form $A \boldsymbol{u}=\boldsymbol{b}$ and describe the relaxed Jacobi method with relaxation parameter $\omega$ for solving this linear system.

  (b) For $\boldsymbol{x}^{*}$ and $\boldsymbol{x}^{(\nu)}$ being the exact and the iterated solution, respectively, let $\boldsymbol{e}^{(\nu)}:=\boldsymbol{x}^{(\nu)}-\boldsymbol{x}^{*}$ be the error and $H_{\omega}$ be the iteration matrix, so that

  $$\boldsymbol{e}^{(\nu+1)}=H_{\omega} \boldsymbol{e}^{(\nu)}$$

  Express $H_{\omega}$ in terms of the matrix $A$ and the relaxation parameter $\omega$. Using the fact that for any $n \times n$ Toeplitz symmetric tridiagonal matrix, the eigenvectors $\boldsymbol{v}_{k}(k=1, \ldots, n)$ have the form:

  $$\boldsymbol{v}_{k}=(\sin i k x)_{i=1}^{n}, \quad x=\frac{\pi}{n+1}$$

  find the eigenvalues $\lambda_{k}(A)$ of $A$. Hence deduce the eigenvalues $\lambda_{k}(\omega)$ of $H_{\omega}$.

  (c) For $A$ as above, let

  $$\boldsymbol{e}^{(\nu)}=\sum_{k=1}^{n} a_{k}^{(\nu)} \boldsymbol{v}_{k}$$

  be the expansion of the error with respect to the eigenvectors $\left(\boldsymbol{v}_{k}\right)$ of $H_{\omega}$.

  Find the range of the parameter $\omega$ which provides convergence of the method for any $n$, and prove that, for any such $\omega$, the rate of convergence $e^{(\nu)} \rightarrow 0$ is not faster than $\left(1-c / n^{2}\right)^{\nu}$ when $n$ is large.

  (d) Show that, for an appropriate range of $\omega$, the high frequency components $a_{k}^{(\nu)}$ $\left(\frac{n+1}{2} \leqslant k \leqslant n\right)$ of the error $e^{(\nu)}$ tend to zero much faster than the rate obtained in part (c). Determine the optimal parameter $\omega_{*}$ which provides the largest supression of the high frequency components per iteration, and find the corresponding attenuation factor $\mu_{*}$ assuming $n$ is large. That is, find the least $\mu_{\omega}$ such that $\left|a_{k}^{(\nu+1)}\right| \leqslant \mu_{\omega}\left|a_{k}^{(\nu)}\right|$ for $\frac{n+1}{2} \leqslant k \leqslant n$.

  comment

• Paper 3, Section II, E

  Numerical Analysis | Part II, 2018

  The diffusion equation for $u(x, t)$ :

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad x \in \mathbb{R}, \quad t \geqslant 0$$

  is solved numerically by the difference scheme

  $$u_{m}^{n+1}=u_{m}^{n}+\frac{3}{2} \mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right)-\frac{1}{2} \mu\left(u_{m-1}^{n-1}-2 u_{m}^{n-1}+u_{m+1}^{n-1}\right) .$$

  Here $\mu=\frac{k}{h^{2}}$ is the Courant number, with $k=\Delta t, h=\Delta x$, and $u_{m}^{n} \approx u(m h, n k)$.

  (a) Prove that, as $k \rightarrow 0$ with constant $\mu$, the local error of the method is $\mathcal{O}\left(k^{2}\right)$.

  (b) Applying the Fourier stability analysis, show that the method is stable if and only if $\mu \leqslant \frac{1}{4}$. [Hint: If a polynomial $p(x)=x^{2}-2 \alpha x+\beta$ has real roots, then those roots lie in $[a, b]$ if and only if $p(a) p(b) \geqslant 0$ and $\alpha \in[a, b]$.]

  (c) Prove that, for the same equation, the leapfrog scheme

  $$u_{m}^{n+1}=u_{m}^{n-1}+2 \mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right)$$

  is unstable for any choice of $\mu>0$.

  comment

• Paper 4, Section II, E

  Numerical Analysis | Part II, 2018

  The inverse discrete Fourier transform $\mathcal{F}_{n}^{-1}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is given by the formula

  $$\boldsymbol{x}=\mathcal{F}_{n}^{-1} \boldsymbol{y}, \quad \text { where } \quad x_{\ell}=\sum_{j=0}^{n-1} \omega_{n}^{j \ell} y_{j}, \quad \ell=0, \ldots, n-1$$

  Here, $\omega_{n}=\exp \frac{2 \pi i}{n}$ is the primitive root of unity of degree $n$ and $n=2^{p}, p=1,2, \ldots$

  (a) Show how to assemble $\boldsymbol{x}=\mathcal{F}_{2 m}^{-1} \boldsymbol{y}$ in a small number of operations if the Fourier transforms of the even and odd parts of $\boldsymbol{y}$,

  $$\boldsymbol{x}^{(\mathrm{E})}=\mathcal{F}_{m}^{-1} \boldsymbol{y}^{(\mathrm{E})}, \quad \boldsymbol{x}^{(\mathrm{O})}=\mathcal{F}_{m}^{-1} \boldsymbol{y}^{(\mathrm{O})}$$

  are already known.

  (b) Describe the Fast Fourier Transform (FFT) method for evaluating $\boldsymbol{x}$, and draw a diagram to illustrate the method for $n=8$.

  (c) Find the cost of the FFT method for $n=2^{p}$ (only multiplications count).

  (d) For $n=4$ use the FFT method to find $\boldsymbol{x}=\mathcal{F}_{n}^{-1} \boldsymbol{y}$ when: (i) $\boldsymbol{y}=(1,-1,1,-1)$, (ii) $\boldsymbol{y}=(1,1,-1,-1)$.

  comment

Optimisation and Control

• Paper 2, Section II, $30 K$

  Optimisation and Control | Part II, 2018

  (a) A ball may be in one of $n$ boxes. A search of the $i^{\text {th }}$box costs $c_{i}>0$ and finds the ball with probability $\alpha_{i}>0$ if the ball is in that box. We are given initial probabilities $\left(P_{i}^{1}, i=1,2, \ldots, n\right)$ that the ball is in the $i^{\text {th }}$box.

  Show that the policy which at time $t=1,2, \ldots$ searches the box with the maximal value of $\alpha_{i} P_{i}^{t} / c_{i}$ minimises the expected searching cost until the ball is found, where $P_{i}^{t}$ is the probability (given everything that has occurred up to time $t$ ) that the ball is in box $i$.

  (b) Next suppose that a reward $R_{i}>0$ is earned if the ball is found in the $i^{\text {th }}$box. Suppose also that we may decide to stop at any time. Develop the dynamic programming equation for the value function starting from the probability distribution $\left(P_{i}^{t}, i=1,2, \ldots, n\right)$.

  Show that if $\sum_{i} c_{i} /\left(\alpha_{i} R_{i}\right)<1$ then it is never optimal to stop searching until the ball is found. In this case, is the policy defined in part (a) optimal?

  comment

• Paper 3, Section II, K

  Optimisation and Control | Part II, 2018

  The scalars $x_{t}, y_{t}, u_{t}$ are related by the equations

  $$x_{t}=x_{t-1}+u_{t-1}, \quad y_{t}=x_{t-1}+\eta_{t-1}, \quad t=1,2, \ldots, T,$$

  where the initial state $x_{0}$ is normally distributed with mean $\hat{x}_{0}$ and variance 1 and $\left\{\eta_{t}\right\}$ is a sequence of independent random variables each normally distributed with mean 0 and variance 1 . The control variable $u_{t}$ is to be chosen at time $t$ on the basis of information $W_{t}$, where $W_{0}=\left(\hat{x}_{0}\right)$ and

  $$W_{t}=\left(\hat{x}_{0}, u_{0}, \ldots, u_{t-1}, y_{1}, \ldots, y_{t}\right), \quad t=1,2, \ldots, T$$

  (a) Let $\hat{x}_{1}, \hat{x}_{2}, \ldots, \hat{x}_{T}$ be the Kalman filter estimates of $x_{1}, x_{2}, \ldots, x_{T}$, i.e.

  $$\hat{x}_{t}=\hat{x}_{t-1}+u_{t-1}+h_{t}\left(y_{t}-\hat{x}_{t-1}\right)$$

  where $h_{t}$ is chosen to minimise $\mathbb{E}\left(\left(\hat{x}_{t}-x_{t}\right)^{2} \mid W_{t}\right)$. Calculate $h_{t}$ and show that, conditional on $W_{t}, x_{t}$ is normally distributed with mean $\hat{x}_{t}$ and variance $V_{t}=1 /(1+t)$.

  (b) Define

  $$\begin{aligned} &F\left(W_{T}\right)=\mathbb{E}\left(x_{T}^{2} \mid W_{T}\right), \quad \text { and } \\ &F\left(W_{t}\right)=\inf _{u_{t}, \ldots, u_{T-1}} \mathbb{E}\left(x_{T}^{2}+\sum_{j=t}^{T-1} u_{j}^{2} \mid W_{t}\right), \quad t=0, \ldots, T-1 . \end{aligned}$$

  Show that $F\left(W_{t}\right)=\hat{x}_{t}^{2} P_{t}+d_{t}$, where $P_{t}=1 /(T-t+1), d_{T}=1 /(1+T)$ and $d_{t-1}=V_{t-1} V_{t} P_{t}+d_{t}$.

  (c) Show that the minimising control $u_{t}$ can be expressed in the form $u_{t}=-K_{t} \hat{x}_{t}$ and find $K_{t}$. How would the expression for $K_{t}$ be altered if $x_{0}$ or $\left\{\eta_{t}\right\}$ had variances other than 1?

  comment

• Paper 4, Section II, $30 K$

  Optimisation and Control | Part II, 2018

  Consider the deterministic system

  $$\dot{x}_{t}=u_{t}$$

  where $x_{t}$ and $u_{t}$ are scalars. Here $x_{t}$ is the state variable and the control variable $u_{t}$ is to be chosen to minimise, for a fixed $h>0$, the cost

  $$x_{h}^{2}+\int_{0}^{h} c_{t} u_{t}^{2} \mathrm{~d} t$$

  where $c_{t}$ is known and $c_{t}>c>0$ for all $t$. Let $F(x, t)$ be the minimal cost from state $x$ and time $t$.

  (a) By writing the dynamic programming equation in infinitesimal form and taking the appropriate limit show that $F(x, t)$ satisfies

  $$\frac{\partial F}{\partial t}=-\inf _{u}\left[c_{t} u^{2}+\frac{\partial F}{\partial x} u\right], \quad t<h$$

  with boundary condition $F(x, h)=x^{2}$.

  (b) Determine the form of the optimal control in the special case where $c_{t}$ is constant, and also in general.

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, D

  Principles of Quantum Mechanics | Part II, 2018

  A one-dimensional harmonic oscillator has Hamiltonian

  $$H=\hbar \omega\left(A^{\dagger} A+\frac{1}{2}\right)$$

  where $\left[A, A^{\dagger}\right]=1$. Show that $A|n\rangle=\sqrt{n}|n-1\rangle$, where $H|n\rangle=\left(n+\frac{1}{2}\right) \hbar \omega|n\rangle$ and $\langle n \mid n\rangle=1$.

  This oscillator is perturbed by adding a new term $\lambda X^{4}$ to the Hamiltonian. Given that

  $$A=\frac{m \omega X-i P}{\sqrt{2 m \hbar \omega}}$$

  show that the ground state of the perturbed system is

  $$\left|0_{\lambda}\right\rangle=|0\rangle-\frac{\hbar \lambda}{4 m^{2} \omega^{3}}\left(3 \sqrt{2}|2\rangle+\sqrt{\frac{3}{2}}|4\rangle\right)$$

  to first order in $\lambda$. [You may use the fact that, in non-degenerate perturbation theory, a perturbation $\Delta$ causes the first-order shift

  $$\left|m^{(1)}\right\rangle=\sum_{n \neq m} \frac{\langle n|\Delta| m\rangle}{E_{m}-E_{n}}|n\rangle$$

  in the $m^{\text {th }}$energy level.]

  comment

• Paper 2, Section II, D

  Principles of Quantum Mechanics | Part II, 2018

  Explain what is meant by the intrinsic parity of a particle.

  In each of the decay processes below, parity is conserved.

  A deuteron $\left(d^{+}\right)$has intrinsic parity $\eta_{d}=+1$ and spin $s=1$. A negatively charged pion $\left(\pi^{-}\right)$has spin $s=0$. The ground state of a hydrogenic 'atom' formed from a deuteron and a pion decays to two identical neutrons $(n)$, each of spin $s=\frac{1}{2}$ and parity $\eta_{n}=+1$. Deduce the intrinsic parity of the pion.

  The $\Delta^{-}$particle has spin $s=\frac{3}{2}$ and decays as

  $$\Delta^{-} \rightarrow \pi^{-}+n .$$

  What are the allowed values of the orbital angular momentum? In the centre of mass frame, the vector $\mathbf{r}_{\pi}-\mathbf{r}_{n}$ joining the pion to the neutron makes an angle $\theta$ to the $\hat{\mathbf{z}}$-axis. The final state is an eigenstate of $J_{z}$ and the spatial probability distribution is proportional to $\cos ^{2} \theta$. Deduce the intrinsic parity of the $\Delta^{-}$.

  [Hint: You may use the fact that the first three Legendre polynomials are given by

  $$\left.P_{0}(x)=1, \quad P_{1}(x)=x, \quad P_{2}(x)=\frac{1}{2}\left(3 x^{2}-1\right) . \quad\right]$$

  comment

• Paper 3, Section II, D

  Principles of Quantum Mechanics | Part II, 2018

  A quantum system is prepared in the ground state $|0\rangle$ at time $t=0$. It is subjected to a time-varying Hamiltonian $H=H_{0}+\Delta(t)$. Show that, to first order in $\Delta(t)$, the system evolves as

  $$|\psi(t)\rangle=\sum_{k} c_{k}(t) \mathrm{e}^{-i E_{k} t / \hbar}|k\rangle$$

  where $H_{0}|k\rangle=E_{k}|k\rangle$ and

  $$c_{k}(t)=\frac{1}{i \hbar} \int_{0}^{t}\left\langle k\left|\Delta\left(t^{\prime}\right)\right| 0\right\rangle \mathrm{e}^{i\left(E_{k}-E_{0}\right) t^{\prime} / \hbar} \mathrm{d} t^{\prime}$$

  A large number of hydrogen atoms, each in the ground state, are subjected to an electric field

  $$\mathbf{E}(t)=\left\{\begin{array}{lll} 0 & \text { for } & t<0 \\ \hat{\mathbf{z}} \mathcal{E}_{0} \exp (-t / \tau) & \text { for } & t>0 \end{array}\right.$$

  where $\mathcal{E}_{0}$ is a constant. Show that the fraction of atoms found in the state $|n, \ell, m\rangle=$ $|2,1,0\rangle$ is, after a long time and to lowest non-trivial order in $\mathcal{E}_{0}$,

  $$\frac{2^{15}}{3^{10}} \frac{a_{0}^{2} e^{2} \mathcal{E}_{0}^{2}}{\hbar^{2}\left(\omega^{2}+1 / \tau^{2}\right)}$$

  where $\hbar \omega$ is the energy difference between the $|2,1,0\rangle$ and $|1,0,0\rangle$ states, and $e$ is the electron charge and $a_{0}$ the Bohr radius. What fraction of atoms lie in the $|2,0,0\rangle$ state?

  [Hint: You may assume the hydrogenic wavefunctions

  $$\langle\mathbf{r} \mid 1,0,0\rangle=\frac{2}{\sqrt{4 \pi}} \frac{1}{a_{0}^{3 / 2}} \exp \left(-\frac{r}{a_{0}}\right) \quad \text { and } \quad\langle\mathbf{r} \mid 2,1,0\rangle=\frac{1}{\sqrt{4 \pi}} \frac{1}{\left(2 a_{0}\right)^{3 / 2}} \frac{r}{a_{0}} \cos \theta \exp \left(-\frac{r}{2 a_{0}}\right)$$

  and the integral

  $$\int_{0}^{\infty} r^{m} \mathrm{e}^{-\alpha r} \mathrm{~d} r=\frac{m !}{\alpha^{m+1}}$$

  for $m$ a positive integer.]

  comment

• Paper 4, Section II, D

  Principles of Quantum Mechanics | Part II, 2018

  The spin operators obey the commutation relations $\left[S_{i}, S_{j}\right]=i \hbar \epsilon_{i j k} S_{k}$. Let $|s, \sigma\rangle$ be an eigenstate of the spin operators $S_{z}$ and $\mathbf{S}^{2}$, with $S_{z}|s, \sigma\rangle=\sigma \hbar|s, \sigma\rangle$ and $\mathbf{S}^{2}|s, \sigma\rangle=s(s+1) \hbar^{2}|s, \sigma\rangle$. Show that

  $$S_{\pm}|s, \sigma\rangle=\sqrt{s(s+1)-\sigma(\sigma \pm 1)} \hbar|s, \sigma \pm 1\rangle,$$

  where $S_{\pm}=S_{x} \pm i S_{y}$. When $s=1$, use this to derive the explicit matrix representation

  $$S_{x}=\frac{\hbar}{\sqrt{2}}\left(\begin{array}{lll} 0 & 1 & 0 \\ 1 & 0 & 1 \\ 0 & 1 & 0 \end{array}\right)$$

  in a basis in which $S_{z}$ is diagonal.

  A beam of atoms, each with spin 1 , is polarised to have spin $+\hbar$ along the direction $\mathbf{n}=(\sin \theta, 0, \cos \theta)$. This beam enters a Stern-Gerlach filter that splits the atoms according to their spin along the $\hat{\mathbf{z}}$-axis. Show that $N_{+} / N_{-}=\cot ^{4}(\theta / 2)$, where $N_{+}$(respectively, $N_{-}$) is the number of atoms emerging from the filter with spins parallel (respectively, anti-parallel) to $\hat{\mathbf{z}}$.

  comment

Principles of Statistics

• Paper 1, Section II, $29 \mathrm{~K}$

  Principles of Statistics | Part II, 2018

  A scientist wishes to estimate the proportion $\theta \in(0,1)$ of presence of a gene in a population of flies of size $n$. Every fly receives a chromosome from each of its two parents, each carrying the gene $A$ with probability $(1-\theta)$ or the gene $B$ with probability $\theta$, independently. The scientist can observe if each fly has two copies of the gene A (denoted by AA), two copies of the gene $B$ (denoted by BB) or one of each (denoted by AB). We let $n_{\mathrm{AA}}, n_{\mathrm{BB}}$, and $n_{\mathrm{AB}}$ denote the number of each observation among the $n$ flies.

  (a) Give the probability of each observation as a function of $\theta$, denoted by $f(X, \theta)$, for all three values $X=\mathrm{AA}, \mathrm{BB}$, or $\mathrm{AB}$.

  (b) For a vector $w=\left(w_{\mathrm{AA}}, w_{\mathrm{BB}}, w_{\mathrm{AB}}\right)$, we let $\hat{\theta}_{w}$ denote the estimator defined by

  $$\hat{\theta}_{w}=w_{\mathrm{AA}} \frac{n_{\mathrm{AA}}}{n}+w_{\mathrm{BB}} \frac{n_{\mathrm{BB}}}{n}+w_{\mathrm{AB}} \frac{n_{\mathrm{AB}}}{n} .$$

  Find the unique vector $w^{*}$ such that $\hat{\theta}_{w^{*}}$ is unbiased. Show that $\hat{\theta}_{w^{*}}$ is a consistent estimator of $\theta$.

  (c) Compute the maximum likelihood estimator of $\theta$ in this model, denoted by $\hat{\theta}_{M L E}$. Find the limiting distribution of $\sqrt{n}\left(\hat{\theta}_{M L E}-\theta\right)$. [You may use results from the course, provided that you state them clearly.]

  comment

• Paper 2, Section II, $28 K$

  Principles of Statistics | Part II, 2018

  We consider the model $\left\{\mathcal{N}\left(\theta, I_{p}\right), \theta \in \mathbb{R}^{p}\right\}$ of a Gaussian distribution in dimension $p \geqslant 3$, with unknown mean $\theta$ and known identity covariance matrix $I_{p}$. We estimate $\theta$ based on one observation $X \sim \mathcal{N}\left(\theta, I_{p}\right)$, under the loss function

  $$\ell(\theta, \delta)=\|\theta-\delta\|_{2}^{2}$$

  (a) Define the risk of an estimator $\hat{\theta}$. Compute the maximum likelihood estimator $\hat{\theta}_{M L E}$ of $\theta$ and its risk for any $\theta \in \mathbb{R}^{p}$.

  (b) Define what an admissible estimator is. Is $\hat{\theta}_{M L E}$ admissible?

  (c) For any $c>0$, let $\pi_{c}(\theta)$ be the prior $\mathcal{N}\left(0, c^{2} I_{p}\right)$. Find a Bayes optimal estimator $\hat{\theta}_{c}$ under this prior with the quadratic loss, and compute its Bayes risk.

  (d) Show that $\hat{\theta}_{M L E}$ is minimax.

  [You may use results from the course provided that you state them clearly.]

  comment

• Paper 3, Section II, K

  Principles of Statistics | Part II, 2018

  In the model $\left\{\mathcal{N}\left(\theta, I_{p}\right), \theta \in \mathbb{R}^{p}\right\}$ of a Gaussian distribution in dimension $p$, with unknown mean $\theta$ and known identity covariance matrix $I_{p}$, we estimate $\theta$ based on a sample of i.i.d. observations $X_{1}, \ldots, X_{n}$ drawn from $\mathcal{N}\left(\theta_{0}, I_{p}\right)$.

  (a) Define the Fisher information $I\left(\theta_{0}\right)$, and compute it in this model.

  (b) We recall that the observed Fisher information $i_{n}(\theta)$ is given by

  $$i_{n}(\theta)=\frac{1}{n} \sum_{i=1}^{n} \nabla_{\theta} \log f\left(X_{i}, \theta\right) \nabla_{\theta} \log f\left(X_{i}, \theta\right)^{\top}$$

  Find the limit of $\hat{i}_{n}=i_{n}\left(\hat{\theta}_{M L E}\right)$, where $\hat{\theta}_{M L E}$ is the maximum likelihood estimator of $\theta$ in this model.

  (c) Define the Wald statistic $W_{n}(\theta)$ and compute it. Give the limiting distribution of $W_{n}\left(\theta_{0}\right)$ and explain how it can be used to design a confidence interval for $\theta_{0}$.

  [You may use results from the course provided that you state them clearly.]

  comment

• Paper 4, Section II, $28 \mathrm{~K}$

  Principles of Statistics | Part II, 2018

  Let $g: \mathbb{R} \rightarrow \mathbb{R}$ be an unknown function, twice continuously differentiable with $\left|g^{\prime \prime}(x)\right| \leqslant M$ for all $x \in \mathbb{R}$. For some $x_{0} \in \mathbb{R}$, we know the value $g\left(x_{0}\right)$ and we wish to estimate its derivative $g^{\prime}\left(x_{0}\right)$. To do so, we have access to a pseudo-random number generator that gives $U_{1}^{*}, \ldots, U_{N}^{*}$ i.i.d. uniform over $[0,1]$, and a machine that takes input $x_{1}, \ldots, x_{N} \in \mathbb{R}$ and returns $g\left(x_{i}\right)+\varepsilon_{i}$, where the $\varepsilon_{i}$ are i.i.d. $\mathcal{N}\left(0, \sigma^{2}\right)$.

  (a) Explain how this setup allows us to generate $N$ independent $X_{i}=x_{0}+h Z_{i}$, where the $Z_{i}$ take value 1 or $-1$ with probability $1 / 2$, for any $h>0$.

  (b) We denote by $Y_{i}$ the output $g\left(X_{i}\right)+\varepsilon_{i}$. Show that for some independent $\xi_{i} \in \mathbb{R}$

  $$Y_{i}-g\left(x_{0}\right)=h Z_{i} g^{\prime}\left(x_{0}\right)+\frac{h^{2}}{2} g^{\prime \prime}\left(\xi_{i}\right)+\varepsilon_{i}$$

  (c) Using the intuition given by the least-squares estimator, justify the use of the estimator $\hat{g}_{N}$ given by

  $$\hat{g}_{N}=\frac{1}{N} \sum_{i=1}^{N} \frac{Z_{i}\left(Y_{i}-g\left(x_{0}\right)\right)}{h}$$

  (d) Show that

  $$\mathbb{E}\left[\left|\hat{g}_{N}-g^{\prime}\left(x_{0}\right)\right|^{2}\right] \leqslant \frac{h^{2} M^{2}}{4}+\frac{\sigma^{2}}{N h^{2}} .$$

  Show that for some choice $h_{N}$ of parameter $h$, this implies

  $$\mathbb{E}\left[\left|\hat{g}_{N}-g^{\prime}\left(x_{0}\right)\right|^{2}\right] \leqslant \frac{\sigma M}{\sqrt{N}}$$

  comment

Probability and Measure

• Paper 1, Section II, J

  Probability and Measure | Part II, 2018

  (a) Let $X$ be a real random variable with $\mathbb{E}\left(X^{2}\right)<\infty$. Show that the variance of $X$ is equal to $\inf _{a \in \mathbb{R}}\left(\mathbb{E}(X-a)^{2}\right)$.

  (b) Let $f(x)$ be the indicator function of the interval $[-1,1]$ on the real line. Compute the Fourier transform of $f$.

  (c) Show that

  $$\int_{0}^{+\infty}\left(\frac{\sin x}{x}\right)^{2} d x=\frac{\pi}{2}$$

  (d) Let $X$ be a real random variable and $\widehat{\mu_{X}}$ be its characteristic function.

  (i) Assume that $\left|\widehat{\mu_{X}}(u)\right|=1$ for some $u \in \mathbb{R}$. Show that there exists $\theta \in \mathbb{R}$ such that almost surely:

  $$u X \in \theta+2 \pi \mathbb{Z}$$

  (ii) Assume that $\left|\widehat{\mu_{X}}(u)\right|=\left|\widehat{\mu_{X}}(v)\right|=1$ for some real numbers $u$, $v$ not equal to 0 and such that $u / v$ is irrational. Prove that $X$ is almost surely constant. [Hint: You may wish to consider an independent copy of $X$.]

  comment

• Paper 2, Section II, J

  Probability and Measure | Part II, 2018

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space. Let $\left(X_{n}\right)_{n \geqslant 1}$ be a sequence of random variables with $\mathbb{E}\left(\left|X_{n}\right|^{2}\right) \leqslant 1$ for all $n \geqslant 1$.

  (a) Suppose $Z$ is another random variable such that $\mathbb{E}\left(|Z|^{2}\right)<\infty$. Why is $Z X_{n}$ integrable for each $n$ ?

  (b) Assume $\mathbb{E}\left(Z X_{n}\right) \underset{n \rightarrow \infty}{\longrightarrow} 0$ for every random variable $Z$ on $(\Omega, \mathcal{F}, \mathbb{P})$ such that $\mathbb{E}\left(|Z|^{2}\right)<\infty$. Show that there is a subsequence $Y_{k}:=X_{n_{k}}, k \geqslant 1$, such that

  $$\frac{1}{N} \sum_{k=1}^{N} Y_{k} \underset{N \rightarrow \infty}{\longrightarrow} 0 \text { in } \mathbb{L}^{2}$$

  (c) Assume that $X_{n} \rightarrow X$ in probability. Show that $X \in \mathbb{L}^{2}$. Show that $X_{n} \rightarrow X$ in $\mathbb{L}^{1}$. Must it converge also in $\mathbb{L}^{2} ?$ Justify your answer.

  (d) Assume that the $\left(X_{n}\right)_{n \geqslant 1}$ are independent. Give a necessary and sufficient condition on the sequence $\left(\mathbb{E}\left(X_{n}\right)_{n \geqslant 1}\right)$ for the sequence

  $$Y_{N}=\frac{1}{N} \sum_{k=1}^{N} X_{k}$$

  to converge in $\mathbb{L}^{2}$.

  comment

• Paper 3, Section II, J

  Probability and Measure | Part II, 2018

  Let $m$ be the Lebesgue measure on the real line. Recall that if $E \subseteq \mathbb{R}$ is a Borel subset, then

  $$m(E)=\inf \left\{\sum_{n \geqslant 1}\left|I_{n}\right|, E \subseteq \bigcup_{n \geqslant 1} I_{n}\right\},$$

  where the infimum is taken over all covers of $E$ by countably many intervals, and $|I|$ denotes the length of an interval $I$.

  (a) State the definition of a Borel subset of $\mathbb{R}$.

  (b) State a definition of a Lebesgue measurable subset of $\mathbb{R}$.

  (c) Explain why the following sets are Borel and compute their Lebesgue measure:

  $$\mathbb{Q}, \quad \mathbb{R} \backslash \mathbb{Q}, \quad \bigcap_{n \geqslant 2}\left[\frac{1}{n}, n\right] .$$

  (d) State the definition of a Borel measurable function $f: \mathbb{R} \rightarrow \mathbb{R}$.

  (e) Let $f$ be a Borel measurable function $f: \mathbb{R} \rightarrow \mathbb{R}$. Is it true that the subset of all $x \in \mathbb{R}$ where $f$ is continuous at $x$ is a Borel subset? Justify your answer.

  (f) Let $E \subseteq[0,1]$ be a Borel subset with $m(E)=1 / 2+\alpha, \alpha>0$. Show that

  $$E-E:=\{x-y: x, y \in E\}$$

  contains the interval $(-2 \alpha, 2 \alpha)$.

  (g) Let $E \subseteq \mathbb{R}$ be a Borel subset such that $m(E)>0$. Show that for every $\varepsilon>0$, there exists $a<b$ in $\mathbb{R}$ such that

  $$m(E \cap(a, b))>(1-\varepsilon) m((a, b)) .$$

  Deduce that $E-E$ contains an open interval around 0 .

  comment

• Paper 4, Section II, J

  Probability and Measure | Part II, 2018

  Let $(X, \mathcal{A})$ be a measurable space. Let $T: X \rightarrow X$ be a measurable map, and $\mu$ a probability measure on $(X, \mathcal{A})$.

  (a) State the definition of the following properties of the system $(X, \mathcal{A}, \mu, T)$ :

  (i) $\mu$ is T-invariant.

  (ii) $T$ is ergodic with respect to $\mu$.

  (b) State the pointwise ergodic theorem.

  (c) Give an example of a probability measure preserving system $(X, \mathcal{A}, \mu, T)$ in which $\operatorname{Card}\left(T^{-1}\{x\}\right)>1$ for $\mu$-a.e. $x$.

  (d) Assume $X$ is finite and $\mathcal{A}$ is the boolean algebra of all subsets of $X$. Suppose that $\mu$ is a $T$-invariant probability measure on $X$ such that $\mu(\{x\})>0$ for all $x \in X$. Show that $T$ is a bijection.

  (e) Let $X=\mathbb{N}$, the set of positive integers, and $\mathcal{A}$ be the $\sigma$-algebra of all subsets of $X$. Suppose that $\mu$ is a $T$-invariant ergodic probability measure on $X$. Show that there is a finite subset $Y \subseteq X$ with $\mu(Y)=1$.

  comment

Quantum Information and Computation

• Paper 1, Section I, D

  Quantum Information and Computation | Part II, 2018

  (a) Define what it means for a 2-qubit state $|\psi\rangle_{A B}$ of a composite quantum system $A B$ to be entangled.

  Consider the 2-qubit state

  $$|\alpha\rangle=\frac{1}{\sqrt{3}}(2|00\rangle-H \otimes H|11\rangle)$$

  where $H$ is the Hadamard gate. From the definition of entanglement, show that $|\alpha\rangle$ is an entangled state.

  (b) Alice and Bob are distantly separated in space. Initially they each hold one qubit of the 2-qubit entangled state

  $$\left|\phi^{+}\right\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$$

  They are able to perform local quantum operations (unitary gates and measurements) on quantum systems they hold. Alice wants to communicate two classical bits of information to Bob. Explain how she can achieve this (within their restricted operational resources) by sending him a single qubit.

  comment

• Paper 2, Section I, $10 D$

  Quantum Information and Computation | Part II, 2018

  (a) The classical controlled- $N O T$ operation applied to the 2-bit string $b 0$ (for $b=0$ or 1 ) achieves the cloning of $b$, i.e. the result is $b b$. Let $C X$ denote the quantum controlled$X$ (or controlled-NOT) operation on two qubits. For which qubit states $|\psi\rangle=a|0\rangle+b|1\rangle$ will the application of $C X$ to $|\psi\rangle|0\rangle$ (with the first qubit being the control qubit) achieve the cloning of $|\psi\rangle$ ? Justify your answer.

  (b) Let $\left|\alpha_{0}\right\rangle$ and $\left|\alpha_{1}\right\rangle$ be two distinct non-orthogonal quantum states. State and prove the quantum no-cloning theorem for unitary processes.

  comment

• Paper 2, Section II, D

  Quantum Information and Computation | Part II, 2018

  (a) Suppose that Alice and Bob are distantly separated in space and each has one qubit of the 2-qubit state $\left|\phi^{+}\right\rangle=\frac{1}{\sqrt{2}}(|00\rangle+|11\rangle)$. They also have the ability to perform local unitary quantum operations and local computational basis measurements, and to communicate only classically. Alice has a 1-qubit state $|\alpha\rangle$ (whose identity is unknown to her) which she wants to communicate to Bob. Show how this can be achieved using only the operational resources, listed above, that they have available.

  Suppose now that a third party, called Charlie, joins Alice and Bob. They are all mutually distantly separated in space and each holds one qubit of the 3-qubit state

  $$|\gamma\rangle=\frac{1}{\sqrt{2}}(|000\rangle+|111\rangle) .$$

  As previously with Alice and Bob, they are able to communicate with each other only classically, e.g. by telephone, and they can each also perform only local unitary operations and local computational basis measurements. Alice and Bob phone Charlie to say that they want to do some quantum teleportation and they need a shared $\left|\phi^{+}\right\rangle$state (as defined above). Show how Charlie can grant them their wish (with certainty), given their joint possession of $|\gamma\rangle$ and using only their allowed operational resources. [Hint: It may be useful to consider application of an appropriate Hadamard gate action.]

  (b) State the quantum no-signalling principle for a bipartite state $|\psi\rangle_{A B}$ of the composite system $A B$.

  Suppose we are given an unknown one of the two states

  $$\begin{aligned} &\left|\phi^{+}\right\rangle_{A B}=\frac{1}{\sqrt{2}}\left(|00\rangle_{A B}+|11\rangle_{A B}\right) \\ &\left|\phi^{-}\right\rangle_{A B}=\frac{1}{\sqrt{2}}\left(|00\rangle_{A B}-|11\rangle_{A B}\right) \end{aligned}$$

  and we wish to identify which state we have. Show that the minimum error probability for this state discrimination task is zero.

  Suppose now that we have access only to qubit $B$ of the received state. Show that we can now do no better in the state discrimination task than just making a random guess as to which state we have.

  comment

• Paper 3, Section I, 10D

  Quantum Information and Computation | Part II, 2018

  Let $B_{n}$ denote the set of all $n$-bit strings. For any Boolean function on 2 bits $f: B_{2} \rightarrow B_{1}$ consider the linear operation on 3 qubits defined by

  $$U_{f}|x\rangle|y\rangle=|x\rangle|y \oplus f(x)\rangle$$

  for all $x \in B_{2}, y \in B_{1}$ and $\oplus$ denoting addition of bits modulo 2 . Here the first register is a 2-qubit register and the second is a 1-qubit register. We are able to apply only the 1-qubit Pauli $X$ and Hadamard $H$ gates to any desired qubits, as well as the 3 -qubit gate $U_{f}$ to any three qubits. We can also perform measurements in the computational basis.

  (a) Describe how we can construct the state

  $$|f\rangle=\frac{1}{2} \sum_{x \in B_{2}}(-1)^{f(x)}|x\rangle$$

  starting from the standard 3-qubit state $|0\rangle|0\rangle|0\rangle$.

  (b) Suppose now that the gate $U_{f}$ is given to us but $f$ is not specified. However $f$ is promised to be one of two following cases:

  (i) $f$ is a constant function (i.e. $f(x)=0$ for all $x$, or $f(x)=1$ for all $x$ ),

  (ii) for any 2-bit string $x=b_{1} b_{2}$ we have $f\left(b_{1} b_{2}\right)=b_{1} \oplus b_{2}$ (with $\oplus$ as above).

  Show how we may determine with certainty which of the two cases (i) or (ii) applies, using only a single application of $U_{f}$.

  comment

• Paper 3, Section II, $15 \mathrm{D}$

  Quantum Information and Computation | Part II, 2018

  In this question you may assume the following fact about the quantum Fourier transform $Q F T \bmod N:$ if $N=A r$ and $0 \leqslant x_{0}<r$, where $A, r, x_{0} \in \mathbb{Z}$, then

  $$Q F T \frac{1}{\sqrt{A}} \sum_{k=0}^{A-1}\left|x_{0}+k r\right\rangle=\frac{1}{\sqrt{r}} \sum_{l=0}^{r-1} \omega^{x_{0} l A}|l A\rangle$$

  where $\omega=e^{2 \pi i / N}$.

  (a) Let $\mathbb{Z}_{N}$ denote the integers modulo $N$. Let $f: \mathbb{Z}_{N} \rightarrow \mathbb{Z}$ be a periodic function with period $r$ and with the property that $f$ is one-to-one within each period. We have one instance of the quantum state

  $$|f\rangle=\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1}|x\rangle|f(x)\rangle$$

  and the ability to calculate the function $f$ on at most two $x$ values of our choice.

  Describe a procedure that may be used to determine the period $r$ with success probability $O(1 / \log \log N)$. As a further requirement, at the end of the procedure we should know if it has been successful, or not, in outputting the correct period value. [You may assume that the number of integers less than $N$ that are coprime to $N$ is $O(N / \log \log N)]$.

  (b) Consider the function $f: \mathbb{Z}_{12} \rightarrow \mathbb{Z}_{10}$ defined by $f(x)=3^{x} \bmod 10$.

  (i) Show that $f$ is periodic and find the period.

  (ii) Suppose we are given the state $|f\rangle=\frac{1}{\sqrt{12}} \sum_{x=0}^{11}|x\rangle|f(x)\rangle$ and we measure the second register. What are the possible resulting measurement values $y$ and their probabilities?

  (iii) Suppose the measurement result was $y=3$. Find the resulting state $|\alpha\rangle$ of the first register after the measurement.

  (iv) Suppose we measure the state $Q F T|\alpha\rangle$ (with $|\alpha\rangle$ from part (iii)). What is the probability of each outcome $0 \leqslant c \leqslant 11$ ?

  comment

• Paper 4, Section I, 10D

  Quantum Information and Computation | Part II, 2018

  Let $B_{n}$ denote the set of all $n$-bit strings. Suppose we are given a 2-qubit quantum gate $I_{x_{0}}$ which is promised to be of the form

  $$I_{x_{0}}|x\rangle=\left\{\begin{array}{rr} |x\rangle & x \neq x_{0} \\ -|x\rangle & x=x_{0} \end{array}\right.$$

  but the 2-bit string $x_{0}$ is unknown to us. We wish to determine $x_{0}$ with the least number of queries to $I_{x_{0}}$. Define $A=I-2|\psi\rangle\langle\psi|$, where $I$ is the identity operator and $|\psi\rangle=\frac{1}{2} \sum_{x \in B_{2}}|x\rangle$.

  (a) Is $A$ unitary? Justify your answer.

  (b) Compute the action of $I_{x_{0}}$ on $|\psi\rangle$, and the action of $|\psi\rangle\langle\psi|$ on $\left|x_{0}\right\rangle$, in each case expressing your answer in terms of $|\psi\rangle$ and $\left|x_{0}\right\rangle$. Hence or otherwise show that $x_{0}$ may be determined with certainty using only one application of the gate $I_{x_{0}}$, together with any other gates that are independent of $x_{0}$.

  (c) Let $f_{x_{0}}: B_{2} \rightarrow B_{1}$ be the function having value 0 for all $x \neq x_{0}$ and having value 1 for $x=x_{0}$. It is known that a single use of $I_{x_{0}}$ can be implemented with a single query to a quantum oracle for the function $f_{x_{0}}$. But suppose instead that we have a classical oracle for $f_{x_{0}}$, i.e. a black box which, on input $x$, outputs the value of $f_{x_{0}}(x)$. Can we determine $x_{0}$ with certainty using a single query to the classical oracle? Justify your answer.

  comment

Representation Theory

• Paper 1, Section II, I

  Representation Theory | Part II, 2018

  (a) Define the derived subgroup, $G^{\prime}$, of a finite group $G$. Show that if $\chi$ is a linear character of $G$, then $G^{\prime} \leqslant$ ker $\chi$. Prove that the linear characters of $G$ are precisely the lifts to $G$ of the irreducible characters of $G / G^{\prime}$. [You should state clearly any additional results that you require.]

  (b) For $n \geqslant 1$, you may take as given that the group

  $$G_{6 n}:=\left\langle a, b: a^{2 n}=b^{3}=1, a^{-1} b a=b^{-1}\right\rangle$$

  has order $6 n$.

  (i) Let $\omega=e^{2 \pi i / 3}$. Show that if $\varepsilon$ is any $(2 n)$-th root of unity in $\mathbb{C}$, then there is a representation of $G_{6 n}$ over $\mathbb{C}$ which sends

  $$a \mapsto\left(\begin{array}{ll} 0 & \varepsilon \\ \varepsilon & 0 \end{array}\right), \quad b \mapsto\left(\begin{array}{cc} \omega & 0 \\ 0 & \omega^{2} \end{array}\right)$$

  (ii) Find all the irreducible representations of $G_{6 n}$.

  (iii) Find the character table of $G_{6 n}$.

  comment

• Paper 2, Section II, I

  Representation Theory | Part II, 2018

  (a) Suppose $H$ is a subgroup of a finite group $G, \chi$ is an irreducible character of $G$ and $\varphi_{1}, \ldots, \varphi_{r}$ are the irreducible characters of $H$. Show that in the restriction $\chi \downarrow_{H}=a_{1} \varphi_{1}+\cdots+a_{r} \varphi_{r}$, the multiplicities $a_{1}, \ldots, a_{r}$ satisfy

  $$\sum_{i=1}^{r} a_{i}^{2} \leqslant|G: H|$$

  Determine necessary and sufficient conditions under which the inequality in ( $\uparrow$ ) is actually an equality.

  (b) Henceforth suppose that $H$ is a (normal) subgroup of index 2 in $G$, and that $\chi$ is an irreducible character of $G$.

  Lift the non-trivial linear character of $G / H$ to obtain a linear character of $G$ which satisfies

  $$\lambda(g)= \begin{cases}1 & \text { if } g \in H \\ -1 & \text { if } g \notin H\end{cases}$$

  (i) Show that the following are equivalent:

  (1) $\chi \downarrow_{H}$ is irreducible;

  (2) $\chi(g) \neq 0$ for some $g \in G$ with $g \notin H$;

  (3) the characters $\chi$ and $\chi \lambda$ of $G$ are not equal.

  (ii) Suppose now that $\chi \downarrow_{H}$ is irreducible. Show that if $\psi$ is an irreducible character of $G$ which satisfies

  $$\psi \downarrow_{H}=\chi \downarrow_{H}$$

  then either $\psi=\chi$ or $\psi=\chi \lambda .$

  (iii) Suppose that $\chi \downarrow_{H}$ is the sum of two irreducible characters of $H$, say $\chi \downarrow_{H}=\psi_{1}+\psi_{2}$. If $\phi$ is an irreducible character of $G$ such that $\phi \downarrow_{H}$ has $\psi_{1}$ or $\psi_{2}$ as a constituent, show that $\phi=\chi$.

  (c) Suppose that $G$ is a finite group with a subgroup $K$ of index 3 , and let $\chi$ be an irreducible character of $G$. Prove that

  $$\left\langle\chi \downarrow_{K}, \chi \downarrow_{K}\right\rangle_{K}=1,2 \text { or } 3$$

  Give examples to show that each possibility can occur, giving brief justification in each case.

  comment

• Paper 3, Section II, I

  Representation Theory | Part II, 2018

  State the row orthogonality relations. Prove that if $\chi$ is an irreducible character of the finite group $G$, then $\chi(1)$ divides the order of $G$.

  Stating clearly any additional results you use, deduce the following statements:

  (i) Groups of order $p^{2}$, where $p$ is prime, are abelian.

  (ii) If $G$ is a group of order $2 p$, where $p$ is prime, then either the degrees of the irreducible characters of $G$ are all 1 , or they are

  $$1,1,2, \ldots, 2(\text { with }(p-1) / 2 \text { of degree } 2)$$

  (iii) No simple group has an irreducible character of degree 2 .

  (iv) Let $p$ and $q$ be prime numbers with $p>q$, and let $G$ be a non-abelian group of order $p q$. Then $q$ divides $p-1$ and $G$ has $q+((p-1) / q)$ conjugacy classes.

  comment

• Paper 4, Section II, I

  Representation Theory | Part II, 2018

  Define $G=\mathrm{SU}(2)$ and write down a complete list

  $$\left\{V_{n}: n=0,1,2, \ldots\right\}$$

  of its continuous finite-dimensional irreducible representations. You should define all the terms you use but proofs are not required. Find the character $\chi_{V_{n}}$ of $V_{n}$. State the Clebsch-Gordan formula.

  (a) Stating clearly any properties of symmetric powers that you need, decompose the following spaces into irreducible representations of $G$ :

  (i) $V_{4} \otimes V_{3}, V_{3} \otimes V_{3}, S^{2} V_{3}$;

  (ii) $V_{1} \otimes \cdots \otimes V_{1}$ (with $n$ multiplicands);

  (iii) $S^{3} V_{2}$.

  (b) Let $G$ act on the space $M_{3}(\mathbb{C})$ of $3 \times 3$ complex matrices by

  $$A: X \mapsto A_{1} X A_{1}^{-1}$$

  where $A_{1}$ is the block matrix $\left(\begin{array}{cc}A & 0 \\ 0 & 1\end{array}\right)$. Show that this gives a representation of $G$ and decompose it into irreducible summands.

  comment

Riemann Surfaces

• Paper 1, Section II, F

  Riemann Surfaces | Part II, 2018

  Given a complete analytic function $\mathcal{F}$ on a domain $G \subset \mathbb{C}$, define the germ of a function element $(f, D)$ of $\mathcal{F}$ at $z \in D$. Let $\mathcal{G}$ be the set of all germs of function elements in $G$. Describe without proofs the topology and complex structure on $\mathcal{G}$ and the natural covering map $\pi: \mathcal{G} \rightarrow G$. Prove that the evaluation map $\mathcal{E}: \mathcal{G} \rightarrow \mathbb{C}$ defined by

  $$\mathcal{E}\left([f]_{z}\right)=f(z)$$

  is analytic on each component of $\mathcal{G}$.

  Suppose $f: R \rightarrow S$ is an analytic map of compact Riemann surfaces with $B \subset S$ the set of branch points. Show that $f: R \backslash f^{-1}(B) \rightarrow S \backslash B$ is a regular covering map.

  Given $P \in S \backslash B$, explain how any closed curve in $S \backslash B$ with initial and final points $P$ yields a permutation of the set $f^{-1}(P)$. Show that the group $H$ obtained from all such closed curves is a transitive subgroup of the group of permutations of $f^{-1}(P)$.

  Find the group $H$ for the analytic map $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ where $f(z)=z^{2}+z^{-2}$.

  comment

• Paper 2, Section II, F

  Riemann Surfaces | Part II, 2018

  State the uniformisation theorem. List without proof the Riemann surfaces which are uniformised by $\mathbb{C}_{\infty}$ and those uniformised by $\mathbb{C}$.

  Let $U$ be a domain in $\mathbb{C}$ whose complement consists of more than one point. Deduce that $U$ is uniformised by the open unit disk.

  Let $R$ be a compact Riemann surface of genus $g$ and $P_{1}, \ldots, P_{n}$ be distinct points of $R$. Show that $R \backslash\left\{P_{1}, \ldots, P_{n}\right\}$ is uniformised by the open unit disk if and only if $2 g-2+n>0$, and by $\mathbb{C}$ if and only if $2 g-2+n=0$ or $-1$.

  Let $\Lambda$ be a lattice and $X=\mathbb{C} / \Lambda$ a complex torus. Show that an analytic map $f: \mathbb{C} \rightarrow X$ is either surjective or constant.

  Give with proof an example of a pair of Riemann surfaces which are homeomorphic but not conformally equivalent.

  comment

• Paper 3, Section II, F

  Riemann Surfaces | Part II, 2018

  Define the degree of an analytic map of compact Riemann surfaces, and state the Riemann-Hurwitz formula.

  Let $\Lambda$ be a lattice in $\mathbb{C}$ and $E=\mathbb{C} / \Lambda$ the associated complex torus. Show that the $\operatorname{map}$

  $$\psi: z+\Lambda \mapsto-z+\Lambda$$

  is biholomorphic with four fixed points in $E$.

  Let $S=E / \sim$ be the quotient surface (the topological surface obtained by identifying $z+\Lambda$ and $\psi(z+\Lambda)$ ), and let $p: E \rightarrow S$ be the associated projection map. Denote by $E^{\prime}$ the complement of the four fixed points of $\psi$, and let $S^{\prime}=p\left(E^{\prime}\right)$. Describe briefly a family of charts making $S^{\prime}$ into a Riemann surface, so that $p: E^{\prime} \rightarrow S^{\prime}$ is a holomorphic map.

  Now assume that, by adding finitely many points, it is possible to compactify $S^{\prime}$ to a Riemann surface $S$ so that $p$ extends to a regular map $E \rightarrow S$. Find the genus of $S$.

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2018

  The data frame Ambulance contains data on the number of ambulance requests from a Cambridgeshire hospital on different days. In addition to the number of ambulance requests on each day, the dataset records whether each day fell in the winter season, on a weekend, or on a bank holiday, as well as the pollution level on each day.

  A health researcher fitted two models to the dataset above using $R$. Consider the following code and its output.

  

  $$\begin{aligned} & \text { > head (Ambulance) } \\ & \text { Winter Weekend Bank. holiday Pollution. level Ambulance.requests } \\ & 1 \text { Yes Yes No High } 16 \end{aligned}$$

  

  $$\begin{aligned} & 3 \text { No No No High } 22 \\ & 4 \text { No } \quad \text { Yes } \quad \text { No } \quad \text { Medium } \quad 11 \end{aligned}$$

  

  

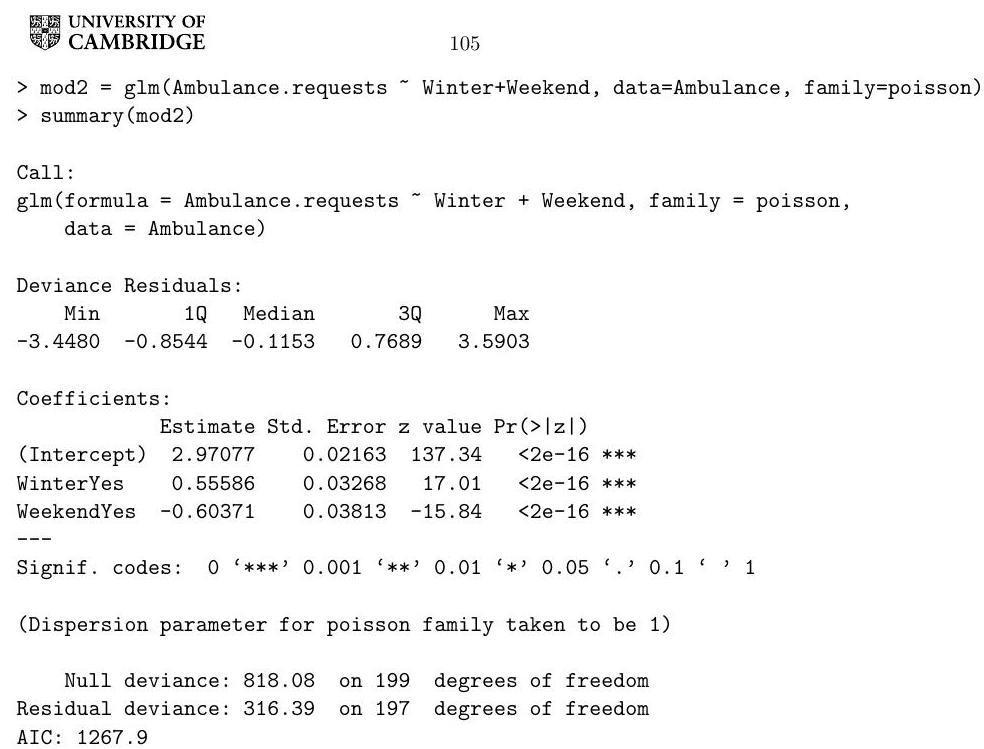
  Define the two models fitted by this code and perform a hypothesis test with level $1 \%$ in which one of the models is the null hypothesis and the other is the alternative. State the theorem used in this hypothesis test. You may use the information generated by the following commands.

  

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2018

  A clinical study follows a number of patients with an illness. Let $Y_{i} \in[0, \infty)$ be the length of time that patient $i$ lives and $x_{i} \in \mathbb{R}^{p}$ a vector of predictors, for $i \in\{1, \ldots, n\}$. We shall assume that $Y_{1}, \ldots, Y_{n}$ are independent. Let $f_{i}$ and $F_{i}$ be the probability density function and cumulative distribution function, respectively, of $Y_{i}$. The hazard function $h_{i}$ is defined as

  $$h_{i}(t)=\frac{f_{i}(t)}{1-F_{i}(t)} \quad \text { for } t \geqslant 0 .$$

  We shall assume that $h_{i}(t)=\lambda(t) \exp \left(\beta^{\top} x_{i}\right)$, where $\beta \in \mathbb{R}^{p}$ is a vector of coefficients and $\lambda(t)$ is some fixed hazard function.

  (a) Prove that $F_{i}(t)=1-\exp \left(-\int_{0}^{t} h_{i}(s) d s\right)$.

  (b) Using the equation in part (a), write the log-likelihood function for $\beta$ in terms of $\lambda, \beta, x_{i}$ and $Y_{i}$ only.

  (c) Show that the maximum likelihood estimate of $\beta$ can be obtained through a surrogate Poisson generalised linear model with an offset.

  comment

• Paper 2, Section I, $\mathbf{5 J}$

  Statistical Modelling | Part II, 2018

  Consider a linear model $Y=X \beta+\sigma^{2} \varepsilon$ with $\varepsilon \sim N(0, I)$, where the design matrix $X$ is $n$ by $p$. Provide an expression for the $F$-statistic used to test the hypothesis $\beta_{p_{0}+1}=\beta_{p_{0}+2}=\cdots=\beta_{p}=0$ for $p_{0}<p$. Show that it is a monotone function of a log-likelihood ratio statistic.

  comment

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2018

  The data frame Cases. of .flu contains a list of cases of flu recorded in 3 London hospitals during each month of 2017 . Consider the following $R$ code and its output.

  table (Cases. of.flu)

  Month Hospital

  $\begin{array}{lrrr}\text { Month } & \text { A } & \text { B } & \text { C } \\ \text { April } & 10 & 40 & 27\end{array}$

  $\begin{array}{lrrr}\text { April } & 10 & 40 & 27 \\ \text { August } & 9 & 34 & 19\end{array}$

  $\begin{array}{lrrr}\text { August } & 9 & 34 & 19 \\ \text { December } & 24 & 129 & 81\end{array}$

  $\begin{array}{llll}\text { December } & 24 & 129 & 81 \\ \text { February } & 49 & 134 & 74\end{array}$

  $\begin{array}{llll}\text { February } & 49 & 134 & 74 \\ \text { January } & 45 & 138 & 78\end{array}$

  $\begin{array}{lrrr}\text { July } & 5 & 138 & 78 \\ & 11 & 36 & 35\end{array}$

  $\begin{array}{llll}\text { June } & 11 & 36 & 22\end{array}$

  $\begin{array}{llll}\text { March } & 20 & 82 & 41\end{array}$

  May $5 \quad 43 \quad 23$

  November $17 \quad 82 \quad 62$

  October $6 \quad 26 \quad 19$

  September $640 \quad 21$

  Cases. of.flu.table = as.data.frame (table (Cases. of .flu))

  $>$ head (Cases. of .flu.table)

  Month Hospital Freq

  1 April A 10

  2 August A 9

  3 December A 24

  4 February A 49

  5 January A 45

  6 July A 5

  $>\bmod 1=$ glm (Freq ., data=Cases. of .flu.table, family=poisson)

  $>\bmod 1 \$ \mathrm{dev}$

  [1] $28.51836$

  levels (Cases. of.flu$Month)

  

  Describe a test for the null hypothesis of independence between the variables Month and Hospital using the deviance statistic. State the assumptions of the test.

  Perform the test at the $1 \%$ level for each of the two different models shown above. You may use the table below showing 99 th percentiles of the $\chi_{p}^{2}$ distribution with a range of degrees of freedom $p$. How would you explain the discrepancy between their conclusions?

  

  comment

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2018

  A scientist is studying the effects of a drug on the weight of mice. Forty mice are divided into two groups, control and treatment. The mice in the treatment group are given the drug, and those in the control group are given water instead. The mice are kept in 8 different cages. The weight of each mouse is monitored for 10 days, and the results of the experiment are recorded in the data frame Weight.data. Consider the following $R$ code and its output.

  head (Weight.data)

  Time Group Cage Mouse Weight

  11 Control 1 1 $24.77578$

  $2 \quad 2$ Control 1 1 $24.68766$

  $3 \quad 3$ Control $1 \quad 124.79008$

  44 Control $1 \quad 124.77005$

  $5 \quad 5$ Control 1 1 $24.65092$

  $6 \quad 6$ Control $1 \quad 124.38436$

  $>\bmod 1=\operatorname{lm}$ (Weight $\sim$ Time*Group $+$ Cage, data=Weight. data)

  $>\operatorname{summary}(\bmod 1)$

  Call:

  $\operatorname{lm}$ (formula $=$ Weight $~$Time $*$ Group $+$ Cage, data $=$ Weight. data)

  Residuals:

  Min $1 Q$ Median $3 Q$ Max

  $-1.36903-0.33527-0.01719 \quad 0.38807 \quad 1.24368$

  Coefficients:

  Estimate Std. Error t value $\operatorname{Pr}(>|t|)$

  $\begin{array}{lllll}\text { Time } & -0.006023 & 0.012616 & -0.477 & 0.63334\end{array}$

  GroupTreatment $\quad 0.321837 \quad 0.121993 \quad 2.638 \quad 0.00867 *$

  Cage2 $\quad-0.400228 \quad 0.095875-4.1743 .68 \mathrm{e}-05 * * *$

  $\begin{array}{lllll}\text { Cage3 } & 0.286941 & 0.102494 & 2.800 & 0.00537 *\end{array}$

  $\begin{array}{lllll}\text { Cage4 } & 0.007535 & 0.095875 & 0.079 & 0.93740\end{array}$

  $\begin{array}{rrrrr}\text { Cage6 } & 0.124767 & 0.125530 & 0.994 & 0.32087\end{array}$

  $\begin{array}{lllll}\text { Cage8 } & -0.295168 & 0.125530 & -2.351 & 0.01920 * \\ \text { Time:GroupTreatment } & -0.173515 & 0.017842 & -9.725 & <2 e-16 * * *\end{array}$

  Time: GroupTreatment $-0.173515 \quad 0.017842-9.725<2 \mathrm{e}-16 * * *$

  Signif. codes: 0 '' $0.001$ '' $0.01$ '' $0.05$ '., $0.1$ ', 1

  Residual standard error: $0.5125$ on 391 degrees of freedom

  Multiple R-squared: $0.5591$, Adjusted R-squared: $0.55$

  F-statistic: $61.97$ on 8 and 391 DF, p-value: $<2.2 \mathrm{e}-16$

  Which parameters describe the rate of weight loss with time in each group? According to the $\mathrm{R}$ output, is there a statistically significant weight loss with time in the control group?

  Three diagnostic plots were generated using the following $R$ code.

  Weight.data$Time[mouse1]

  

  Weight.data$Time[mouse2]

  

  Based on these plots, should you trust the significance tests shown in the output of the command summary (mod1)? Explain.

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2018

  Bridge is a card game played by 2 teams of 2 players each. A bridge club records the outcomes of many games between teams formed by its $m$ members. The outcomes are modelled by

  $$\mathbb{P}(\text { team }\{i, j\} \text { wins against team }\{k, \ell\})=\frac{\exp \left(\beta_{i}+\beta_{j}+\beta_{\{i, j\}}-\beta_{k}-\beta_{\ell}-\beta_{\{k, \ell\}}\right)}{1+\exp \left(\beta_{i}+\beta_{j}+\beta_{\{i, j\}}-\beta_{k}-\beta_{\ell}-\beta_{\{k, \ell\}}\right)},$$

  where $\beta_{i} \in \mathbb{R}$ is a parameter representing the skill of player $i$, and $\beta_{\{i, j\}} \in \mathbb{R}$ is a parameter representing how well-matched the team formed by $i$ and $j$ is.

  (a) Would it make sense to include an intercept in this logistic regression model? Explain your answer.

  (b) Suppose that players 1 and 2 always play together as a team. Is there a unique maximum likelihood estimate for the parameters $\beta_{1}, \beta_{2}$ and $\beta_{\{1,2\}}$ ? Explain your answer.

  (c) Under the model defined above, derive the asymptotic distribution (including the values of all relevant parameters) for the maximum likelihood estimate of the probability that team $\{i, j\}$ wins a game against team $\{k, \ell\}$. You can state it as a function of the true vector of parameters $\beta$, and the Fisher information matrix $i_{N}(\beta)$ with $N$ games. You may assume that $i_{N}(\beta) / N \rightarrow I(\beta)$ as $N \rightarrow \infty$, and that $\beta$ has a unique maximum likelihood estimate for $N$ large enough.

  comment

Statistical Physics

• Paper 1, Section II, A

  Statistical Physics | Part II, 2018

  (a) A macroscopic system has volume $V$ and contains $N$ particles. Let $\Omega(E, V, N ; \delta E)$ denote the number of states of the system which have energy in the range $(E, E+\delta E)$ where $\delta E \ll E$ represents experimental uncertainty. Define the entropy $S$ of the system and explain why the dependence of $S$ on $\delta E$ is usually negligible. Define the temperature and pressure of the system and hence obtain the fundamental thermodynamic relation.

  (b) A one-dimensional model of rubber consists of a chain of $N$ links, each of length a. The chain lies along the $x$-axis with one end fixed at $x=0$ and the other at $x=L$ where $L<N a$. The chain can "fold back" on itself so $x$ may not increase monotonically along the chain. Let $N_{\rightarrow}$ and $N_{\leftarrow}$ denote the number of links along which $x$ increases and decreases, respectively. All links have the same energy.

  (i) Show that $N_{\rightarrow}$ and $N_{\leftarrow}$ are uniquely determined by $L$ and $N$. Determine $\Omega(L, N)$, the number of different arrangements of the chain, as a function of $N_{\rightarrow}$ and $N_{\leftarrow}$. Hence show that, if $N_{\rightarrow} \gg 1$ and $N_{\leftarrow} \gg 1$ then the entropy of the chain is

  $$\begin{aligned} S(L, N)=k N & {\left[\log 2-\frac{1}{2}\left(1+\frac{L}{N a}\right) \log \left(1+\frac{L}{N a}\right)\right.} \\ &\left.-\frac{1}{2}\left(1-\frac{L}{N a}\right) \log \left(1-\frac{L}{N a}\right)\right] \end{aligned}$$

  where $k$ is Boltzmann's constant. [You may use Stirling's approximation: $n$ ! $\approx$ $\sqrt{2 \pi} n^{n+1 / 2} e^{-n}$ for $\left.n \gg 1 .\right]$

  (ii) Let $f$ denote the force required to hold the end of the chain fixed at $x=L$. This force does work $f d L$ on the chain if the length is increased by $d L$. Write down the fundamental thermodynamic relation for this system and hence calculate $f$ as a function of $L$ and the temperature $T$.

  Assume that $N a \gg L$. Show that the chain satisfies Hooke's law $f \propto L$. What happens if $f$ is held constant and $T$ is increased?

  comment

• Paper 2, Section II, A

  Statistical Physics | Part II, 2018

  (a) Starting from the canonical ensemble, derive the Maxwell-Boltzmann distribution for the velocities of particles in a classical gas of atoms of mass $m$. Derive also the distribution of speeds $v$ of the particles. Calculate the most probable speed.

  (b) A certain atom emits photons of frequency $\omega_{0}$. A gas of these atoms is contained in a box. A small hole is cut in a wall of the box so that photons can escape in the positive $x$-direction where they are received by a detector. The frequency of the photons received is Doppler shifted according to the formula

  $$\omega=\omega_{0}\left(1+\frac{v_{x}}{c}\right)$$

  where $v_{x}$ is the $x$-component of the velocity of the atom that emits the photon and $c$ is the speed of light. Let $T$ be the temperature of the gas.

  (i) Calculate the mean value $\langle\omega\rangle$ of $\omega$.

  (ii) Calculate the standard deviation $\sqrt{\left\langle(\omega-\langle\omega\rangle)^{2}\right\rangle}$.

  (iii) Show that the relative number of photons received with frequency between $\omega$ and $\omega+d \omega$ is $I(\omega) d \omega$ where

  $$I(\omega) \propto \exp \left(-a\left(\omega-\omega_{0}\right)^{2}\right)$$

  for some coefficient $a$ to be determined. Hence explain how observations of the radiation emitted by the gas can be used to measure its temperature.

  comment

• Paper 3, Section II, A

  Statistical Physics | Part II, 2018

  (a) A system of non-interacting bosons has single particle states $|i\rangle$ with energies $\epsilon_{i} \geqslant 0$. Show that the grand canonical partition function is

  $$\log \mathcal{Z}=-\sum_{i} \log \left(1-e^{-\beta\left(\epsilon_{i}-\mu\right)}\right)$$

  where $\beta=1 /(k T), k$ is Boltzmann's constant, and $\mu$ is the chemical potential. What is the maximum possible value for $\mu$ ?

  (b) A system of $N \gg 1$ bosons has one energy level with zero energy and $M \gg 1$ energy levels with energy $\epsilon>0$. The number of particles with energies $0, \epsilon$ is $N_{0}, N_{\epsilon}$ respectively.

  (i) Write down expressions for $\left\langle N_{0}\right\rangle$ and $\left\langle N_{\epsilon}\right\rangle$ in terms of $\mu$ and $\beta$.

  (ii) At temperature $T$ what is the maximum possible number $N_{\epsilon}^{\max }$ of bosons in the state with energy $\epsilon ?$ What happens for $N>N_{\epsilon}^{\max } ?$

  (iii) Calculate the temperature $T_{B}$ at which Bose condensation occurs.

  (iv) For $T>T_{B}$, show that $\mu=\epsilon\left(T_{B}-T\right) / T_{B}$. For $T<T_{B}$ show that

  $$\mu \approx-\frac{k T}{N} \frac{e^{\epsilon /(k T)}-1}{e^{\epsilon /(k T)}-e^{\epsilon /\left(k T_{B}\right)}} .$$

  (v) Calculate the mean energy $\langle E\rangle$ for $T>T_{B}$ and for $T<T_{B}$. Hence show that the heat capacity of the system is

  $$C \approx \begin{cases}\frac{1}{k T^{2}} \frac{M \epsilon^{2}}{\left(e^{\beta \epsilon}-1\right)^{2}} & T<T_{B} \\ 0 & T>T_{B}\end{cases}$$

  comment

• Paper 4, Section II, A

  Statistical Physics | Part II, 2018

  The one-dimensional Ising model consists of a set of $N$ spins $s_{i}$ with Hamiltonian

  $$H=-J \sum_{i=1}^{N} s_{i} s_{i+1}-\frac{B}{2} \sum_{i=1}^{N}\left(s_{i}+s_{i+1}\right)$$

  where periodic boundary conditions are imposed so $s_{N+1}=s_{1}$. Here $J$ is a positive coupling constant and $B$ is an external magnetic field. Define a $2 \times 2$ matrix $M$ with elements

  $$M_{s t}=\exp \left[\beta J s t+\frac{\beta B}{2}(s+t)\right]$$

  where indices $s, t$ take values $\pm 1$ and $\beta=(k T)^{-1}$ with $k$ Boltzmann's constant and $T$ temperature.

  (a) Prove that the partition function of the Ising model can be written as

  $$Z=\operatorname{Tr}\left(M^{N}\right)$$

  Calculate the eigenvalues of $M$ and hence determine the free energy in the thermodynamic limit $N \rightarrow \infty$. Explain why the Ising model does not exhibit a phase transition in one dimension.

  (b) Consider the case of zero magnetic field $B=0$. The correlation function $\left\langle s_{i} s_{j}\right\rangle$ is defined by

  $$\left\langle s_{i} s_{j}\right\rangle=\frac{1}{Z} \sum_{\left\{s_{k}\right\}} s_{i} s_{j} e^{-\beta H}$$

  (i) Show that, for $i>1$,

  $$\left\langle s_{1} s_{i}\right\rangle=\frac{1}{Z} \sum_{s, t} s t\left(M^{i-1}\right)_{s t}\left(M^{N-i+1}\right)_{t s}$$

  (ii) By diagonalizing $M$, or otherwise, calculate $M^{p}$ for any positive integer $p$. Hence show that

  $$\left\langle s_{1} s_{i}\right\rangle=\frac{\tanh ^{i-1}(\beta J)+\tanh ^{N-i+1}(\beta J)}{1+\tanh ^{N}(\beta J)}$$

  comment

Stochastic Financial Models

• Paper 1, Section II, K

  Stochastic Financial Models | Part II, 2018

  (a) What does it mean to say that $\left(M_{n}, \mathcal{F}_{n}\right)_{n \geqslant 0}$ is a martingale?

  (b) Let $Y_{1}, Y_{2}, \ldots$ be independent random variables on $(\Omega, \mathcal{F}, \mathbb{P})$ with $Y_{i}>0 \mathbb{P}$-a.s. and $\mathbb{E}\left[Y_{i}\right]=1, i \geqslant 1$. Further, let

  $$M_{0}=1 \quad \text { and } \quad M_{n}=\prod_{i=1}^{n} Y_{i}, \quad n \geqslant 1$$

  Show that $\left(M_{n}\right)_{n \geqslant 0}$ is a martingale with respect to the filtration $\mathcal{F}_{n}=\sigma\left(Y_{1}, \ldots, Y_{n}\right)$.

  (c) Let $X=\left(X_{n}\right)_{n \geqslant 0}$ be an adapted process with respect to a filtration $\left(\mathcal{F}_{n}\right)_{n \geqslant 0}$ such that $\mathbb{E}\left[\left|X_{n}\right|\right]<\infty$ for every $n$. Show that $X$ admits a unique decomposition

  $$X_{n}=M_{n}+A_{n}, \quad n \geqslant 0,$$

  where $M=\left(M_{n}\right)_{n \geqslant 0}$ is a martingale and $A=\left(A_{n}\right)_{n \geqslant 0}$ is a previsible process with $A_{0}=0$, which can recursively be constructed from $X$ as follows,

  $$A_{0}:=0, \quad A_{n+1}-A_{n}:=\mathbb{E}\left[X_{n+1}-X_{n} \mid \mathcal{F}_{n}\right]$$

  (d) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a super-martingale. Show that the following are equivalent:

  (i) $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale.

  (ii) $\mathbb{E}\left[X_{n}\right]=\mathbb{E}\left[X_{0}\right]$ for all $n \in \mathbb{N}$.

  comment

• Paper 2, Section II, K

  Stochastic Financial Models | Part II, 2018

  Consider the Black-Scholes model, i.e. a market model with one risky asset with price $S_{t}$ at time $t$ given by

  $$S_{t}=S_{0} \exp \left(\sigma B_{t}+\mu t\right),$$

  where $\left(B_{t}\right)_{t \geqslant 0}$ denotes a Brownian motion on $(\Omega, \mathcal{F}, \mathbb{P}), \mu>0$ the constant growth rate, $\sigma>0$ the constant volatility and $S_{0}>0$ the initial price of the asset. Assume that the riskless rate of interest is $r \geqslant 0$.

  (a) Consider a European option $C=f\left(S_{T}\right)$ with expiry $T>0$ for any bounded, continuous function $f: \mathbb{R} \rightarrow \mathbb{R}$. Use the Cameron-Martin theorem to characterize the equivalent martingale measure and deduce the following formula for the price $\pi_{C}$ of $C$ at time 0 :

  $$\pi_{C}=e^{-r T} \int_{-\infty}^{\infty} f\left(S_{0} \exp \left(\sigma \sqrt{T} y+\left(r-\frac{1}{2} \sigma^{2}\right) T\right)\right) \frac{1}{\sqrt{2 \pi}} e^{-y^{2} / 2} d y$$

  (b) Find the price at time 0 of a European option with maturity $T>0$ and payoff $C=\left(S_{T}\right)^{\gamma}$ for some $\gamma>1$. What is the value of the option at any time $t \in[0, T] ?$ Determine a hedging strategy (you only need to specify how many units of the risky asset are held at any time $t$ ).

  comment

• Paper 3, Section II, $29 K$

  Stochastic Financial Models | Part II, 2018

  Consider a multi-period model with asset prices $\bar{S}_{t}=\left(S_{t}^{0}, \ldots, S_{t}^{d}\right), t \in\{0, \ldots, T\}$, modelled on a probability space $(\Omega, \mathcal{F}, \mathbb{P})$ and adapted to a filtration $\left(\mathcal{F}_{t}\right)_{t \in\{0, \ldots, T\}}$. Assume that $\mathcal{F}_{0}$ is $\mathbb{P}$-trivial, i.e. $\mathbb{P}[A] \in\{0,1\}$ for all $A \in \mathcal{F}_{0}$, and assume that $S^{0}$ is a $\mathbb{P}$-a.s. strictly positive numéraire, i.e. $S_{t}^{0}>0 \mathbb{P}$-a.s. for all $t \in\{0, \ldots, T\}$. Further, let $X_{t}=\left(X_{t}^{1}, \ldots, X_{t}^{d}\right)$ denote the discounted price process defined by $X_{t}^{i}:=S_{t}^{i} / S_{t}^{0}, t \in\{0, \ldots, T\}, i \in\{1, \ldots, d\}$.

  (a) What does it mean to say that a self-financing strategy $\bar{\theta}$ is an arbitrage?

  (b) State the fundamental theorem of asset pricing.

  (c) Let $\mathbb{Q}$ be a probability measure on $(\Omega, \mathcal{F})$ which is equivalent to $\mathbb{P}$ and for which $\mathbb{E}_{\mathbb{Q}}\left[\left|X_{t}\right|\right]<\infty$ for all $t$. Show that the following are equivalent:

  (i) $\mathbb{Q}$ is a martingale measure.

  (ii) If $\bar{\theta}=\left(\theta^{0}, \theta\right)$ is self-financing and $\theta$ is bounded, i.e. $\max _{t=1, \ldots, T}\left|\theta_{t}\right| \leqslant c<\infty$ for a suitable $c>0$, then the value process $V$ of $\bar{\theta}$ is a $\mathbb{Q}$-martingale.

  (iii) If $\bar{\theta}=\left(\theta^{0}, \theta\right)$ is self-financing and $\theta$ is bounded, then the value process $V$ of $\bar{\theta}$ satisfies

  $$\mathbb{E}_{\mathbb{Q}}\left[V_{T}\right]=V_{0}$$

  [Hint: To show that (iii) implies (i) you might find it useful to consider self-financing strategies $\bar{\theta}=\left(\theta^{0}, \theta\right)$ with $\theta$ of the form

  $$\theta_{s}:= \begin{cases}\mathbf{1}_{A} & \text { if } s=t \\ 0 & \text { otherwise }\end{cases}$$

  for any $A \in \mathcal{F}_{t-1}$ and any $t \in\{1, \ldots, T\}$.]

  (d) Prove that if there exists a martingale measure $\mathbb{Q}$ satisfying the conditions in (c) then there is no arbitrage.

  comment

• Paper 4, Section II, K

  Stochastic Financial Models | Part II, 2018

  Consider a utility function $U: \mathbb{R} \rightarrow \mathbb{R}$, which is assumed to be concave, strictly increasing and twice differentiable. Further, $U$ satisfies

  $$\left|U^{\prime}(x)\right| \leqslant c|x|^{\alpha}, \quad \forall x \in \mathbb{R},$$

  for some positive constants $c$ and $\alpha$. Let $X$ be an $\mathcal{N}\left(\mu, \sigma^{2}\right)$-distributed random variable and set $f(\mu, \sigma):=\mathbb{E}[U(X)]$.

  (a) Show that

  $$\mathbb{E}\left[U^{\prime}(X)(X-\mu)\right]=\sigma^{2} \mathbb{E}\left[U^{\prime \prime}(X)\right]$$

  (b) Show that $\frac{\partial f}{\partial \mu}>0$ and $\frac{\partial f}{\partial \sigma} \leqslant 0$. Discuss this result in the context of meanvariance analysis.

  (c) Show that $f$ is concave in $\mu$ and $\sigma$, i.e. check that the matrix of second derivatives is negative semi-definite. [You may use without proof the fact that if a $2 \times 2$ matrix has nonpositive diagonal entries and a non-negative determinant, then it is negative semi-definite.]

  comment

Topics in Analysis

• Paper 1, Section I, $2 F$

  Topics in Analysis | Part II, 2018

  State and prove Sperner's lemma concerning colourings of points in a triangular grid.

  Suppose that $\triangle$ is a non-degenerate closed triangle with closed edges $\alpha_{1}, \alpha_{2}$ and $\alpha_{3}$. Show that we cannot find closed sets $A_{j}$ with $A_{j} \supseteq \alpha_{j}$, for $j=1,2,3$, such that

  $$\bigcup_{j=1}^{3} A_{j}=\Delta, \text { but } \bigcap_{j=1}^{3} A_{j}=\emptyset$$

  comment

• Paper 2, Section I, $2 F$

  Topics in Analysis | Part II, 2018

  For $\mathbf{x} \in \mathbb{R}^{n}$ we write $\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$. Define

  $$P:=\left\{\mathbf{x} \in \mathbb{R}^{n}: x_{j} \geqslant 0 \text { for } 1 \leqslant j \leqslant n\right\} .$$

  (a) Suppose that $L$ is a convex subset of $P$, that $(1,1, \ldots, 1) \in L$ and that $\prod_{j=1}^{n} x_{j} \leqslant 1$ for all $\mathbf{x} \in L$. Show that $\sum_{j=1}^{n} x_{j} \leqslant n$ for all $\mathbf{x} \in L$.

  (b) Suppose that $K$ is a non-empty closed bounded convex subset of $P$. Show that there is a $\mathbf{u} \in K$ such that $\prod_{j=1}^{n} x_{j} \leqslant \prod_{j=1}^{n} u_{j}$ for all $\mathbf{x} \in K$. If $u_{j} \neq 0$ for each $j$ with $1 \leqslant j \leqslant n$, show that

  $$\sum_{j=1}^{n} \frac{x_{j}}{u_{j}} \leqslant n$$

  for all $\mathbf{x} \in K$, and that $\mathbf{u}$ is unique.

  comment

• Paper 2, Section II, F

  Topics in Analysis | Part II, 2018

  (a) Give Bernstein's probabilistic proof of Weierstrass's theorem.

  (b) Are the following statements true or false? Justify your answer in each case.

  (i) If $f: \mathbb{R} \rightarrow \mathbb{R}$ is continuous, then there exists a sequence of polynomials $P_{n}$ converging pointwise to $f$ on $\mathbb{R}$.

  (ii) If $f: \mathbb{R} \rightarrow \mathbb{R}$ is continuous, then there exists a sequence of polynomials $P_{n}$ converging uniformly to $f$ on $\mathbb{R}$.

  (iii) If $f:(0,1] \rightarrow \mathbb{R}$ is continuous and bounded, then there exists a sequence of polynomials $P_{n}$ converging uniformly to $f$ on $(0,1]$.

  (iv) If $f:[0,1] \rightarrow \mathbb{R}$ is continuous and $x_{1}, x_{2}, \ldots, x_{m}$ are distinct points in $[0,1]$, then there exists a sequence of polynomials $P_{n}$ with $P_{n}\left(x_{j}\right)=f\left(x_{j}\right)$, for $j=1, \ldots, m$, converging uniformly to $f$ on $[0,1]$.

  (v) If $f:[0,1] \rightarrow \mathbb{R}$ is $m$ times continuously differentiable, then there exists a sequence of polynomials $P_{n}$ such that $P_{n}^{(r)} \rightarrow f^{(r)}$ uniformly on $[0,1]$ for each $r=0, \ldots, m$.

  comment

• Paper 3, Section I, $2 F$

  Topics in Analysis | Part II, 2018

  State a version of the Baire category theorem and use it to prove the following result:

  If $f: \mathbb{C} \rightarrow \mathbb{C}$ is analytic, but not a polynomial, then there exists a point $z_{0} \in \mathbb{C}$ such that each coefficient of the Taylor series of $f$ at $z_{0}$ is non-zero.

  comment

• Paper 4, Section I, $2 F$

  Topics in Analysis | Part II, 2018

  Let $0 \leqslant \alpha<1$ and $A>0$. If we have an infinite sequence of integers $m_{n}$ with $1 \leqslant m_{n} \leqslant A n^{\alpha}$, show that

  $$\sum_{n=1}^{\infty} \frac{m_{n}}{n !}$$

  is irrational.

  Does the result remain true if the $m_{n}$ are not restricted to integer values? Justify your answer.

  comment

• Paper 4, Section II, F

  Topics in Analysis | Part II, 2018

  We work in $\mathbb{C}$. Consider

  $$K=\{z:|z-2| \leqslant 1\} \cup\{z:|z+2| \leqslant 1\}$$

  and

  $$\Omega=\{z:|z-2|<3 / 2\} \cup\{z:|z+2|<3 / 2\}$$

  Show that if $f: \Omega \rightarrow \mathbb{C}$ is analytic, then there is a sequence of polynomials $p_{n}$ such that $p_{n}(z) \rightarrow f(z)$ uniformly on $K$.

  Show that there is a sequence of polynomials $P_{n}$ such that $P_{n}(z) \rightarrow 0$ uniformly for $|z-2| \leqslant 1$ and $P_{n}(z) \rightarrow 1$ uniformly for $|z+2| \leqslant 1$.

  Give two disjoint non-empty bounded closed sets $K_{1}$ and $K_{2}$ such that there does not exist a sequence of polynomials $Q_{n}$ with $Q_{n}(z) \rightarrow 0$ uniformly on $K_{1}$ and $Q_{n}(z) \rightarrow 1$ uniformly on $K_{2}$. Justify your answer.

  comment

Waves

• Paper 1, Section II, 39C

  Waves | Part II, 2018

  Derive the wave equation governing the velocity potential for linearised sound waves in a perfect gas. How is the pressure disturbance related to the velocity potential?

  A high pressure gas with unperturbed density $\rho_{0}$ is contained within a thin metal spherical shell which makes small amplitude spherically symmetric vibrations. Let the metal shell have radius $a$, mass $m$ per unit surface area, and an elastic stiffness which tries to restore the radius to its equilibrium value $a_{0}$ with a force $\kappa\left(a-a_{0}\right)$ per unit surface area. Assume that there is a vacuum outside the spherical shell. Show that the frequencies $\omega$ of vibration satisfy

  $$\theta^{2}\left(1+\frac{\alpha}{\theta \cot \theta-1}\right)=\frac{\kappa a_{0}^{2}}{m c_{0}^{2}}$$

  where $\theta=\omega a_{0} / c_{0}, \alpha=\rho_{0} a_{0} / m$, and $c_{0}$ is the speed of sound in the undisturbed gas. Briefly comment on the existence of solutions.

  [Hint: In terms of spherical polar coordinates you may assume that for a function $\psi \equiv \psi(r)$,

  $$\nabla^{2} \psi=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r \psi)$$

  comment

• Paper 2, Section II, C

  Waves | Part II, 2018

  A perfect gas occupies the region $x>0$ of a tube that lies parallel to the $x$-axis. The gas is initially at rest, with density $\rho_{1}$, pressure $p_{1}$, speed of sound $c_{1}$ and specific heat ratio $\gamma$. For times $t>0$ a piston, initially at $x=0$, is pushed into the gas at a constant speed $V$. A shock wave propagates at constant speed $U$ into the undisturbed gas ahead of the piston. Show that the excess pressure in the gas next to the piston, $p_{2}-p_{1} \equiv \beta p_{1}$, is given implicitly by the expression

  $$V^{2}=\frac{2 \beta^{2}}{2 \gamma+(\gamma+1) \beta} \frac{p_{1}}{\rho_{1}}$$

  Show also that

  $$\frac{U^{2}}{c_{1}^{2}}=1+\frac{\gamma+1}{2 \gamma} \beta$$

  and interpret this result.

  [Hint: You may assume for a perfect gas that the speed of sound is given by

  $$c^{2}=\frac{\gamma p}{\rho}$$

  and that the internal energy per unit mass is given by

  $$e=\frac{1}{\gamma-1} \frac{p}{\rho}$$

  comment

• Paper 3, Section II, 40C

  Waves | Part II, 2018

  Derive the ray-tracing equations

  $$\frac{d x_{i}}{d t}=\frac{\partial \Omega}{\partial k_{i}}, \quad \frac{d k_{i}}{d t}=-\frac{\partial \Omega}{\partial x_{i}}, \quad \frac{d \omega}{d t}=\frac{\partial \Omega}{\partial t}$$

  for wave propagation through a slowly-varying medium with local dispersion relation $\omega=\Omega(\mathbf{k} ; \mathbf{x}, t)$, where $\omega$ and $\mathbf{k}$ are the frequency and wavevector respectively, $t$ is time and $\mathbf{x}=(x, y, z)$ are spatial coordinates. The meaning of the notation $d / d t$ should be carefully explained.

  A slowly-varying medium has a dispersion relation $\Omega(\mathbf{k} ; \mathbf{x}, t)=k c(z)$, where $k=|\mathbf{k}|$. State and prove Snell's law relating the angle $\psi$ between a ray and the $z$-axis to $c$.

  Consider the case of a medium with wavespeed $c=c_{0}\left(1+\beta^{2} z^{2}\right)$, where $\beta$ and $c_{0}$ are positive constants. Show that a ray that passes through the origin with wavevector $k(\cos \phi, 0, \sin \phi)$, remains in the region

  $$|z| \leqslant z_{m} \equiv \frac{1}{\beta}\left[\frac{1}{|\cos \phi|}-1\right]^{1 / 2}$$

  By considering an approximation to the equation for a ray in the region $\left|z_{m}-z\right| \ll \beta^{-1}$, or otherwise, determine the path of a ray near $z_{m}$, and hence sketch rays passing through the origin for a few sample values of $\phi$ in the range $0<\phi<\pi / 2$.

  comment

• Paper 4, Section II, C

  Waves | Part II, 2018

  A physical system permits one-dimensional wave propagation in the $x$-direction according to the equation

  $$\left(1-2 \frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{4}}{\partial x^{4}}\right) \frac{\partial^{2} \varphi}{\partial t^{2}}+\frac{\partial^{4} \varphi}{\partial x^{4}}=0$$

  Derive the corresponding dispersion relation and sketch graphs of frequency, phase velocity and group velocity as functions of the wavenumber. Waves of what wavenumber are at the front of a dispersing wave train arising from a localised initial disturbance? For waves of what wavenumbers do wave crests move faster or slower than a packet of waves?

  Find the solution of the above equation for the initial disturbance given by

  $$\varphi(x, 0)=\int_{-\infty}^{\infty} 2 A(k) e^{i k x} d k, \quad \frac{\partial \varphi}{\partial t}(x, 0)=0$$

  where $A^{*}(-k)=A(k)$, and $A^{*}$ is the complex conjugate of $A$. Let $V=x / t$ be held fixed. Use the method of stationary phase to obtain a leading-order approximation to this solution for large $t$ when $0<V<V_{m}=(3 \sqrt{3}) / 8$, where the solutions for the stationary points should be left in implicit form.

  Very briefly discuss the nature of the solutions for $-V_{m}<V<0$ and $|V|>V_{m}$.

  [Hint: You may quote the result that the large time behaviour of

  $$\Phi(x, t)=\int_{-\infty}^{\infty} A(k) e^{i k x-i \omega(k) t} d k$$

  due to a stationary point $k=\alpha$, is given by

  $$\Phi(x, t) \sim\left(\frac{2 \pi}{\left|\omega^{\prime \prime}(\alpha)\right| t}\right)^{\frac{1}{2}} A(\alpha) e^{i \alpha x-i \omega(\alpha) t+i \sigma \pi / 4}$$

  where $\left.\sigma=-\operatorname{sgn}\left(\omega^{\prime \prime}(\alpha)\right) .\right]$

  comment