Part II, 2004

Algebraic Curves

• B2.10

  Algebraic Curves | Part II, 2004

  For each of the following curves $C$

  (i) $C=\left\{(x, y) \in \mathbb{A}^{2} \mid x^{3}-x=y^{2}\right\} \quad$ (ii) $C=\left\{(x, y) \in \mathbb{A}^{2} \mid x^{2} y+x y^{2}=x^{4}+y^{4}\right\}$

  compute the points at infinity of $\bar{C} \subset \mathbb{P}^{2}$ (i.e. describe $\bar{C} \backslash C$ ), and find the singular points of the projective curve $\bar{C}$.

  At which points of $\bar{C}$ is the rational map $\bar{C} \rightarrow \mathbb{P}^{1}$, given by $(X: Y: Z) \mapsto(X: Y)$, not defined? Justify your answer.

  comment

• B3.10

  Algebraic Curves | Part II, 2004

  (i) Let $f: X \rightarrow Y$ be a morphism of smooth projective curves. Define the divisor $f^{*}(D)$ if $D$ is a divisor on $Y$, and state the "finiteness theorem".

  (ii) Suppose $f: X \rightarrow \mathbb{P}^{1}$ is a morphism of degree 2 , that $X$ is smooth projective, and that $X \neq \mathbb{P}^{1}$. Let $P, Q \in X$ be distinct ramification points for $f$. Show that, as elements of $c l(X)$, we have $[P] \neq[Q]$, but $2[P]=2[Q]$.

  comment

• B4.9

  Algebraic Curves | Part II, 2004

  Let $F(X, Y, Z)$ be an irreducible homogeneous polynomial of degree $n$, and write $C=\left\{p \in \mathbb{P}^{2} \mid F(p)=0\right\}$ for the curve it defines in $\mathbb{P}^{2}$. Suppose $C$ is smooth. Show that the degree of its canonical class is $n(n-3)$.

  Hence, or otherwise, show that a smooth curve of genus 2 does not embed in $\mathbb{P}^{2}$.

  comment

Algebraic Topology

• B2.8

  Algebraic Topology | Part II, 2004

  Let $K$ and $L$ be finite simplicial complexes. Define the $n$-th chain group $C_{n}(K)$ and the boundary homomorphism $d_{n}: C_{n}(K) \rightarrow C_{n-1}(K)$. Prove that $d_{n-1} d_{n}=0$ and define the homology groups of $K$. Explain briefly how a simplicial map $f: K \rightarrow L$ induces a homomorphism $f_{\star}$ of homology groups.

  Suppose now that $K$ consists of the proper faces of a 3-dimensional simplex. Calculate from first principles the homology groups of $K$. If a simplicial map $f: K \rightarrow K$ gives a homeomorphism of the underlying polyhedron $|K|$, is the induced homology map $f_{\star}$ necessarily the identity?

  comment

• B3.7

  Algebraic Topology | Part II, 2004

  A finite simplicial complex $K$ is the union of subcomplexes $L$ and $M$. Describe the Mayer-Vietoris exact sequence that relates the homology groups of $K$ to those of $L$, $M$ and $L \cap M$. Define all the homomorphisms in the sequence, proving that they are well-defined (a proof of exactness is not required).

  A surface $X$ is constructed by identifying together (by means of a homeomorphism) the boundaries of two Möbius strips $Y$ and $Z$. Assuming relevant triangulations exist, determine the homology groups of $X$.

  comment

• B4.5

  Algebraic Topology | Part II, 2004

  Write down the definition of a covering space and a covering map. State and prove the path lifting property for covering spaces and state, without proof, the homotopy lifting property.

  Suppose that a group $G$ is a group of homeomorphisms of a space $X$. Prove that, under conditions to be stated, the quotient map $X \rightarrow X / G$ is a covering map and that $\pi_{1}(X / G)$ is isomorphic to $G$. Give two examples in which this last result can be used to determine the fundamental group of a space.

  comment

Algorithms and Networks

• A2.10

  Algorithms and Networks | Part II, 2004

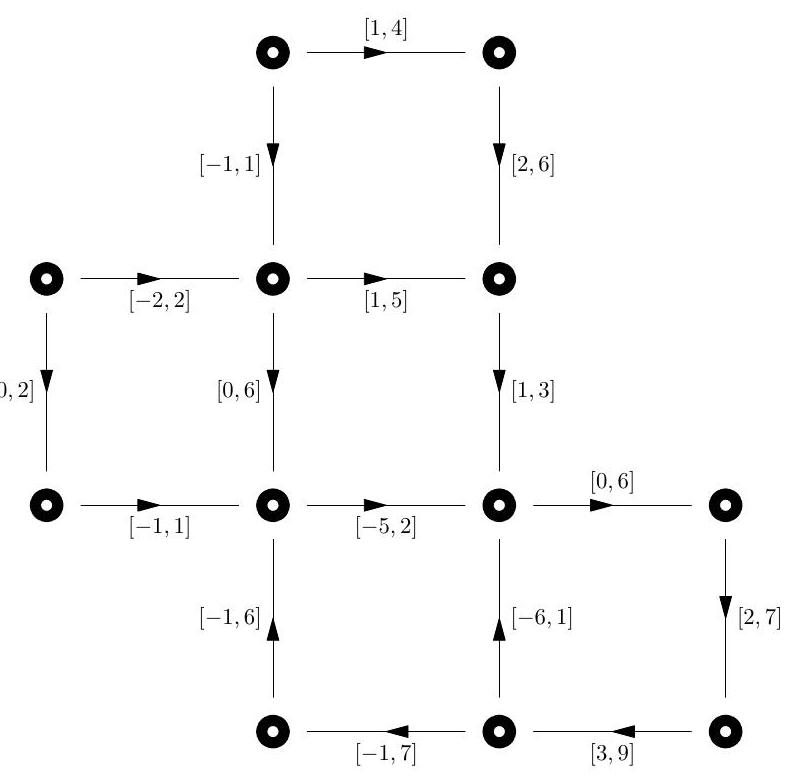
  (i) Define the minimum path and the maximum tension problems for a network with span intervals specified for each arc. State without proof the connection between the two problems, and describe the Max Tension Min Path algorithm of solving them.

  (ii) Find the minimum path between nodes $\mathbf{S}$ and $\mathbf{S}^{\prime}$ in the network below. The span intervals are displayed alongside the arcs.

  

  Part II 2004

  comment

• A3.10

  Algorithms and Networks | Part II, 2004

  (i) Consider the problem

  $$\begin{aligned} \text { minimise } & f(x) \\ \text { subject to } & g(x)=b, x \in X, \end{aligned}$$

  where $f: \mathbb{R}^{n} \longrightarrow \mathbb{R}, g: \mathbb{R}^{n} \longrightarrow \mathbb{R}^{m}, X \subseteq \mathbb{R}^{n}, x \in \mathbb{R}^{n}$ and $b \in \mathbb{R}^{m}$. State the Lagrange Sufficiency Theorem for problem $(*)$. What is meant by saying that this problem is strong Lagrangian? How is this related to the Lagrange Sufficiency Theorem? Define a supporting hyperplane and state a condition guaranteeing that problem $(*)$ is strong Lagrangian.

  (ii) Define the terms flow, divergence, circulation, potential and differential for a network with nodes $N$ and $\operatorname{arcs} A$.

  State the feasible differential problem for a network with span intervals $D(j)=$ $\left[d^{-}(j), d^{+}(j)\right], j \in A .$

  State, without proof, the Feasible Differential Theorem.

  [You must carefully define all quantities used in your statements.]

  Show that the network below does not support a feasible differential.

  

  Part II 2004

  comment

• A4.11

  Algorithms and Networks | Part II, 2004

  (i) Consider an unrestricted geometric programming problem

  $$\min g(t), \quad t=\left(t_{1}, \ldots, t_{m}\right)>0,$$

  where $g(t)$ is given by

  $$g(t)=\sum_{i=1}^{n} c_{i} t_{1}^{a_{i 1}} \ldots t_{m}^{a_{i m}}$$

  with $n \geq m$ and positive coefficients $c_{1} \ldots, c_{n}$. State the dual problem of $(*)$ and show that if $\lambda^{*}=\left(\lambda_{1}^{*}, \ldots, \lambda_{n}^{*}\right)$ is a dual optimum then any positive solution to the system

  $$t_{1}^{a_{i 1}} \ldots t_{m}^{a_{i m}}=\frac{1}{c_{i}} \lambda_{i}^{*} v\left(\lambda^{*}\right), \quad i=1, \ldots, n,$$

  gives an optimum for primal problem $(*)$. Here $v(\lambda)$ is the dual objective function.

  (ii) An amount of ore has to be moved from a pit in an open rectangular skip which is to be ordered from a supplier.

  The skip cost is $£ 36$ per $1 \mathrm{~m}^{2}$ for the bottom and two side walls and $£ 18$ per $1 \mathrm{~m}^{2}$ for the front and the back walls. The cost of loading ore into the skip is $£ 3$ per $1 \mathrm{~m}^{3}$, the cost of lifting is $£ 2$ per $1 \mathrm{~m}^{3}$, and the cost of unloading is $£ 1$ per $1 \mathrm{~m}^{3}$. The cost of moving an empty skip is negligible.

  Write down an unconstrained geometric programming problem for the optimal size (length, width, height) of skip minimizing the cost of moving $48 \mathrm{~m}^{3}$ of ore. By considering the dual problem, or otherwise, find the optimal cost and the optimal size of the skip.

  comment

Applications of Quantum Mechanics

• B1.23

  Applications of Quantum Mechanics | Part II, 2004

  The operator corresponding to a rotation through an angle $\theta$ about an axis $\mathbf{n}$, where $\mathbf{n}$ is a unit vector, is

  $$U(\mathbf{n}, \theta)=e^{i \theta \mathbf{n} \cdot \mathbf{J} / \hbar}$$

  If $U$ is unitary show that $\mathbf{J}$ must be hermitian. Let $\mathbf{V}=\left(V_{1}, V_{2}, V_{3}\right)$ be a vector operator such that

  $$U(\mathbf{n}, \delta \theta) \mathbf{V} U(\mathbf{n}, \delta \theta)^{-1}=\mathbf{V}+\delta \theta \mathbf{n} \times \mathbf{V} .$$

  Work out the commutators $\left[J_{i}, V_{j}\right]$. Calculate

  $$U(\hat{\mathbf{z}}, \theta) \mathbf{V U}(\hat{\mathbf{z}}, \theta)^{-1}$$

  for each component of $\mathbf{V}$.

  If $|j m\rangle$ are standard angular momentum states determine $\left\langle j m^{\prime}|U(\hat{\mathbf{z}}, \theta)| j m\right\rangle$ for any $j, m, m^{\prime}$ and also determine $\left\langle\frac{1}{2} m^{\prime}|U(\hat{\mathbf{y}}, \theta)| \frac{1}{2} m\right\rangle$.

  $\left[\right.$ Hint $\left.: J_{3}|j m\rangle=m \hbar|j m\rangle, J_{+}\left|\frac{1}{2}-\frac{1}{2}\right\rangle=\hbar\left|\frac{1}{2} \frac{1}{2}\right\rangle, J_{-}\left|\frac{1}{2} \frac{1}{2}\right\rangle=\hbar\left|\frac{1}{2}-\frac{1}{2}\right\rangle \cdot\right]$

  comment

• B2.23

  Applications of Quantum Mechanics | Part II, 2004

  The wave function for a single particle with a potential $V(r)$ has the asymptotic form for large $r$

  $$\psi(r, \theta) \sim e^{i k r \cos \theta}+f(\theta) \frac{e^{i k r}}{r} .$$

  How is $f(\theta)$ related to observable quantities? Show how $f(\theta)$ can be expressed in terms of phase shifts $\delta_{\ell}(k)$ for $\ell=0,1,2, \ldots$..

  Assume that $V(r)=0$ for $r \geq a$, and let $R_{\ell}(r)$ denote the solution of the radial Schrödinger equation, regular at $r=0$, with energy $\hbar^{2} k^{2} / 2 m$ and angular momentum $\ell$. Let $N_{\ell}(k)=a R_{\ell}^{\prime}(a) / R_{\ell}(a)$. Show that

  $$\tan \delta_{\ell}(k)=\frac{N_{\ell}(k) j_{\ell}(k a)-k a j_{\ell}^{\prime}(k a)}{N_{\ell}(k) n_{\ell}(k a)-k a n_{\ell}^{\prime}(k a)} .$$

  Assuming that $N_{\ell}(k)$ is a smooth function for $k \approx 0$, determine the expected behaviour of $\delta_{\ell}(k)$ as $k \rightarrow 0$. Show that for $k \rightarrow 0$ then $f(\theta) \rightarrow c$, with $c$ a constant, and determine $c$ in terms of $N_{0}(0)$.

  [For $V=0$ the two independent solutions of the radial Schrödinger equation are $j_{\ell}(k r)$ and $n_{\ell}(k r)$ with

  $$\begin{aligned} j_{\ell}(\rho) & \sim \frac{1}{\rho} \sin \left(\rho-\frac{1}{2} \ell \pi\right), n_{\ell}(\rho) \sim-\frac{1}{\rho} \cos \left(\rho-\frac{1}{2} \ell \pi\right) \text { as } \rho \rightarrow \\ j_{\ell}(\rho) & \propto \rho^{\ell}, n_{\ell}(\rho) \propto \rho^{-\ell-1} \text { as } \rho \rightarrow 0 \\ e^{i \rho \cos \theta} &=\sum_{\ell=0}^{\infty}(2 \ell+1) i^{\ell} j_{\ell}(\rho) P_{\ell}(\cos \theta), \\ j_{0}(\rho) &=\frac{\sin \rho}{\rho}, \quad n_{0}(\rho)=-\frac{\cos \rho}{\rho} \end{aligned}$$

  comment

• B3.23

  Applications of Quantum Mechanics | Part II, 2004

  For a periodic potential $V(\mathbf{r})=V(\mathbf{r}+\ell)$, where $\ell$ is a lattice vector, show that we may write

  $$V(\mathbf{r})=\sum_{\mathbf{g}} a_{\mathbf{g}} e^{i \mathbf{g} \cdot \mathbf{r}}, \quad a_{\mathbf{g}}^{*}=a_{-\mathbf{g}}$$

  where the set of $g$ should be defined.

  Show how to construct general wave functions satisfying $\psi(\mathbf{r}+\boldsymbol{\ell})=e^{i \mathbf{k} \cdot \boldsymbol{\ell}} \psi(\mathbf{r})$ in terms of free plane-wave wave-functions.

  Show that the nearly free electron model gives an energy gap $2\left|a_{\mathbf{g}}\right|$ when $\mathbf{k}=\frac{1}{2} \mathbf{g}$.

  Explain why, for a periodic potential, the allowed energies form bands $E_{n}(\mathbf{k})$ where $\mathbf{k}$ may be restricted to a single Brillouin zone. Show that $E_{n}(\mathbf{k})=E_{n}(\mathbf{k}+\mathbf{g})$ if $\mathbf{k}$ and $\mathbf{k}+\mathbf{g}$ belong to the Brillouin zone.

  How are bands related to whether a material is a conductor or an insulator?

  comment

• B4.24

  Applications of Quantum Mechanics | Part II, 2004

  Describe briefly the variational approach to determining approximate energy eigenvalues for a Hamiltonian $H$.

  Consider a Hamiltonian $H$ and two states $\left|\psi_{1}\right\rangle,\left|\psi_{2}\right\rangle$ such that

  $$\begin{array}{cl} \left\langle\psi_{1}|H| \psi_{1}\right\rangle=\left\langle\psi_{2}|H| \psi_{2}\right\rangle=\mathcal{E}, & \left\langle\psi_{2}|H| \psi_{1}\right\rangle=\left\langle\psi_{1}|H| \psi_{2}\right\rangle=\varepsilon \\ \left\langle\psi_{1} \mid \psi_{1}\right\rangle=\left\langle\psi_{2} \mid \psi_{2}\right\rangle=1, & \left\langle\psi_{2} \mid \psi_{1}\right\rangle=\left\langle\psi_{1} \mid \psi_{2}\right\rangle=s \end{array}$$

  Show that, by considering a linear combination $\alpha\left|\psi_{1}\right\rangle+\beta\left|\psi_{2}\right\rangle$, the variational method gives

  $$\frac{\mathcal{E}-\varepsilon}{1-s}, \quad \frac{\mathcal{E}+\varepsilon}{1+s}$$

  as approximate energy eigenvalues.

  Consider the Hamiltonian for an electron in the presence of two protons at $\mathbf{0}$ and $\mathbf{R}$,

  $$H=\frac{\mathbf{p}^{2}}{2 m}+\frac{e^{2}}{4 \pi \epsilon_{0}}\left(\frac{1}{R}-\frac{1}{|\mathbf{r}|}-\frac{1}{|\mathbf{r}-\mathbf{R}|}\right), \quad R=|\mathbf{R}|$$

  Let $\psi_{0}(\mathbf{r})=e^{-r / a} /\left(\pi a^{3}\right)^{\frac{1}{2}}$ be the ground state hydrogen atom wave function which satisfies

  $$\left(\frac{\mathbf{p}^{2}}{2 m}-\frac{e^{2}}{4 \pi \epsilon_{0}|\mathbf{r}|}\right) \psi_{0}(\mathbf{r})=E_{0} \psi_{0}(\mathbf{r}) .$$

  It is given that

  $$\begin{aligned} &S=\int \mathrm{d}^{3} r \psi_{0}(\mathbf{r}) \psi_{0}(\mathbf{r}-\mathbf{R})=\left(1+\frac{R}{a}+\frac{R^{2}}{3 a^{2}}\right) e^{-R / a} \\ &U=\int \mathrm{d}^{3} r \frac{1}{|\mathbf{r}|} \psi_{0}(\mathbf{r}) \psi_{0}(\mathbf{r}-\mathbf{R})=\frac{1}{a}\left(1+\frac{R}{a}\right) e^{-R / a} \end{aligned}$$

  and, for large $R$, that

  $$\int \mathrm{d}^{3} r \frac{1}{|\mathbf{r}-\mathbf{R}|} \psi_{0}(\mathbf{r})^{2}-\frac{1}{R}=\mathrm{O}\left(e^{-2 R / a}\right)$$

  Consider the trial wave function $\alpha \psi_{0}(\mathbf{r})+\beta \psi_{0}(\mathbf{r}-\mathbf{R})$. Show that the variational estimate for the ground state energy for large $R$ is

  $$E(R)=E_{0}+\frac{e^{2}}{4 \pi \epsilon_{0} R}(S-R U)+\mathrm{O}\left(e^{-2 R / a}\right) .$$

  Explain why there is an attractive force between the two protons for large $R$.

  comment

Applied Probability

• B2.13

  Applied Probability | Part II, 2004

  Let $M$ be a Poisson random measure of intensity $\lambda$ on the plane $\mathbb{R}^{2}$. Denote by $C(r)$ the circle $\left\{x \in \mathbb{R}^{2}:\|x\|<r\right\}$ of radius $r$ in $\mathbb{R}^{2}$ centred at the origin and let $R_{k}$ be the largest radius such that $C\left(R_{k}\right)$ contains precisely $k$ points of $M$. [Thus $C\left(R_{0}\right)$ is the largest circle about the origin containing no points of $M, C\left(R_{1}\right)$ is the largest circle about the origin containing a single point of $M$, and so on.] Calculate $\mathbb{E} R_{0}, \mathbb{E} R_{1}$ and $\mathbb{E} R_{2}$.

  Now let $N$ be a Poisson random measure of intensity $\lambda$ on the line $\mathbb{R}^{1}$. Let $L_{k}$ be the length of the largest open interval that covers the origin and contains precisely $k$ points of $N$. [Thus $L_{0}$ gives the length of the largest interval containing the origin but no points of $N, L_{1}$ gives the length of the largest interval containing the origin and a single point of $N$, and so on.] Calculate $\mathbb{E} L_{0}, \mathbb{E} L_{1}$ and $\mathbb{E} L_{2}$.

  comment

• B3.13

  Applied Probability | Part II, 2004

  Let $\left(X_{t}, t \geq 0\right)$ be a renewal process with holding times $\left(S_{n}, n=1,2, \ldots\right)$ and $\left(Y_{t}, t \geq 0\right)$ be a renewal-reward process over $\left(X_{t}\right)$ with a sequence of rewards $\left(W_{n}, n=1,2, \ldots\right)$. Under assumptions on $\left(S_{n}\right)$ and $\left(W_{n}\right)$ which you should state clearly, prove that the ratios

  $$X_{t} / t \text { and } Y_{t} / t$$

  converge as $t \rightarrow \infty$. You should specify the form of convergence guaranteed by your assumptions. The law of large numbers, in the appropriate form, for sums $S_{1}+\ldots+S_{n}$ and $W_{1}+\ldots+W_{n}$ can be used without proof.

  In a mountain resort, when you rent skiing equipment you are given two options. (1) You buy an insurance waiver that costs $C / 4$ where $C$ is the daily equipment rent. Under this option, the shop will immediately replace, at no cost to you, any piece of equipment you break during the day, no matter how many breaks you had. (2) If you don't buy the waiver, you'll pay $3 C$ in the case of any break.

  To find out which option is better for me, I decided to set up two models of renewalreward process $\left(Y_{t}\right)$. In the first model, (Option 1), all of the holding times $S_{n}$ are equal to 6 . In the second model, given that there is no break on day $n$ (an event of probability $4 / 5)$, we have $S_{n}=6, W_{n}=C$, but given that there is a break on day $n$, we have that $S_{n}$ is uniformly distributed on $(0,6)$, and $W_{n}=4 C$. (In the second model, I would not continue skiing after a break, whereas in the first I would.)

  Calculate in each of these models the limit

  $$\lim _{t \rightarrow \infty} Y_{t} / t$$

  representing the long-term average cost of a unit of my skiing time.

  comment

• B4.12

  Applied Probability | Part II, 2004

  Consider an $M / G / 1$ queue with $\rho=\lambda \mathbb{E} S<1$. Here $\lambda$ is the arrival rate and $\mathbb{E} S$ is the mean service time. Prove that in equilibrium, the customer's waiting time $W$ has the moment-generating function $M_{W}(t)=\mathbb{E} e^{t W}$ given by

  $$M_{W}(t)=\frac{(1-\rho) t}{t+\lambda\left(1-M_{S}(t)\right)}$$

  where $M_{S}(t)=\mathbb{E} e^{t S}$ is the moment-generating function of service time $S$.

  [You may assume that in equilibrium, the $M / G / 1$ queue size $X$ at the time immediately after the customer's departure has the probability generating function

  $$\left.\mathbb{E} z^{X}=\frac{(1-\rho)(1-z) M_{S}(\lambda(z-1))}{M_{S}(\lambda(z-1))-z}, \quad 0 \leqslant z<1 .\right]$$

  Deduce that when the service times are exponential of rate $\mu$ then

  $$M_{W}(t)=1-\rho+\frac{\lambda(1-\rho)}{\mu-\lambda-t}, \quad-\infty<t<\mu-\lambda .$$

  Further, deduce that $W$ takes value 0 with probability $1-\rho$ and that

  $$\mathbb{P}(W>x \mid W>0)=e^{-(\mu-\lambda) x}, \quad x>0 .$$

  Sketch the graph of $\mathbb{P}(W>x)$ as a function of $x$.

  Now consider the $M / G / 1$ queue in the heavy traffic approximation, when the service-time distribution is kept fixed and the arrival rate $\lambda \rightarrow 1 / \mathbb{E} S$, so that $\rho \rightarrow 1$. Assuming that the second moment $\mathbb{E} S^{2}<\infty$, check that the limiting distribution of the re-scaled waiting time $\tilde{W}_{\lambda}=(1-\lambda \mathbb{E} S) W$ is exponential, with rate $2 \mathbb{E} S / \mathbb{E} S^{2}$.

  comment

Coding and Cryptography

• A1.10

  Coding and Cryptography | Part II, 2004

  (i) What is a linear code? What does it mean to say that a linear code has length $n$ and minimum weight $d$ ? When is a linear code perfect? Show that, if $n=2^{r}-1$, there exists a perfect linear code of length $n$ and minimum weight 3 .

  (ii) Describe the construction of a Reed-Muller code. Establish its information rate and minimum weight.

  comment

• A2.9

  Coding and Cryptography | Part II, 2004

  (i) Describe how a stream cypher operates. What is a one-time pad?

  A one-time pad is used to send the message $x_{1} x_{2} x_{3} x_{4} x_{5} x_{6} y_{7}$ which is encoded as 0101011. By mistake, it is reused to send the message $y_{0} x_{1} x_{2} x_{3} x_{4} x_{5} x_{6}$ which is encoded as 0100010. Show that $x_{1} x_{2} x_{3} x_{4} x_{5} x_{6}$ is one of two possible messages, and find the two possibilities.

  (ii) Describe the RSA system associated with a public key $e$, a private key $d$ and the product $N$ of two large primes.

  Give a simple example of how the system is vulnerable to a homomorphism attack. Explain how a signature system prevents such an attack. [You are not asked to give an explicit signature system.]

  Explain how to factorise $N$ when $e, d$ and $N$ are known.

  comment

Combinatorics

• B1.5

  Combinatorics | Part II, 2004

  State and prove Menger's theorem (vertex form).

  Let $G$ be a graph of connectivity $\kappa(G) \geq k$ and let $S, T$ be disjoint subsets of $V(G)$ with $|S|,|T| \geq k$. Show that there exist $k$ vertex disjoint paths from $S$ to $T$.

  The graph $H$ is said to be $k$-linked if, for every sequence $s_{1}, \ldots, s_{k}, t_{1}, \ldots, t_{k}$ of $2 k$ distinct vertices, there exist $s_{i}-t_{i}$ paths, $1 \leq i \leq k$, that are vertex disjoint. By removing an edge from $K_{2 k}$, or otherwise, show that, for $k \geqslant 2$, $H$ need not be $k$-linked even if $\kappa(H) \geq 2 k-2$.

  Prove that if $|H|=n$ and $\delta(H) \geq \frac{1}{2}(n+3 k)-2$ then $H$ is $k$-linked.

  comment

• B2.5

  Combinatorics | Part II, 2004

  State and prove Sperner's lemma on antichains.

  The family $\mathcal{A} \subset \mathcal{P}[n]$ is said to split $[n]$ if, for all distinct $i, j \in[n]$, there exists $A \in \mathcal{A}$ with $i \in A$ but $j \notin A$. Prove that if $\mathcal{A}$ splits $[n]$ then $n \leq\left(\begin{array}{c}a \\ \lfloor a / 2\rfloor\end{array}\right)$, where $a=|\mathcal{A}|$.

  Show moreover that, if $\mathcal{A}$ splits $[n]$ and no element of $[n]$ is in more than $k<\lfloor a / 2\rfloor$ members of $\mathcal{A}$, then $n \leq\left(\begin{array}{l}a \\ k\end{array}\right)$.

  comment

• B4.1

  Combinatorics | Part II, 2004

  Write an essay on Ramsey's theorem. You should include the finite and infinite versions, together with some discussion of bounds in the finite case, and give at least one application.

  comment

Computational Statistics and Statistical Modelling

• A1.13

  Computational Statistics and Statistical Modelling | Part II, 2004

  (i) Assume that the $n$-dimensional vector $Y$ may be written as $Y=X \beta+\epsilon$, where $X$ is a given $n \times p$ matrix of $\operatorname{rank} p, \beta$ is an unknown vector, and

  $$\epsilon \sim N_{n}\left(0, \sigma^{2} I\right)$$

  Let $Q(\beta)=(Y-X \beta)^{T}(Y-X \beta)$. Find $\hat{\beta}$, the least-squares estimator of $\beta$, and state without proof the joint distribution of $\hat{\beta}$ and $Q(\hat{\beta})$.

  (ii) Now suppose that we have observations $\left(Y_{i j}, 1 \leqslant i \leqslant I, 1 \leqslant j \leqslant J\right)$ and consider the model

  $$\Omega: Y_{i j}=\mu+\alpha_{i}+\beta_{j}+\epsilon_{i j},$$

  where $\left(\alpha_{i}\right),\left(\beta_{j}\right)$ are fixed parameters with $\Sigma \alpha_{i}=0, \Sigma \beta_{j}=0$, and $\left(\epsilon_{i j}\right)$ may be assumed independent normal variables, with $\epsilon_{i j} \sim N\left(0, \sigma^{2}\right)$, where $\sigma^{2}$ is unknown.

  (a) Find $\left(\hat{\alpha}_{i}\right),\left(\hat{\beta}_{j}\right)$, the least-squares estimators of $\left(\alpha_{i}\right),\left(\beta_{j}\right)$.

  (b) Find the least-squares estimators of $\left(\alpha_{i}\right)$ under the hypothesis $H_{0}: \beta_{j}=0$ for all $j$.

  (c) Quoting any general theorems required, explain carefully how to test $H_{0}$, assuming $\Omega$ is true.

  (d) What would be the effect of fitting the model $\Omega_{1}: Y_{i j}=\mu+\alpha_{i}+\beta_{j}+\gamma_{i j}+\epsilon_{i j}$, where now $\left(\alpha_{i}\right),\left(\beta_{j}\right),\left(\gamma_{i j}\right)$ are all fixed unknown parameters, and $\left(\epsilon_{i j}\right)$ has the distribution given above?

  comment

• A2.12

  Computational Statistics and Statistical Modelling | Part II, 2004

  (i) Suppose we have independent observations $Y_{1}, \ldots, Y_{n}$, and we assume that for $i=1, \ldots, n, Y_{i}$ is Poisson with mean $\mu_{i}$, and $\log \left(\mu_{i}\right)=\beta^{T} x_{i}$, where $x_{1}, \ldots, x_{n}$ are given covariate vectors each of dimension $p$, where $\beta$ is an unknown vector of dimension $p$, and $p<n$. Assuming that $\left\{x_{1}, \ldots, x_{n}\right\}$ span $\mathbb{R}^{p}$, find the equation for $\hat{\beta}$, the maximum likelihood estimator of $\beta$, and write down the large-sample distribution of $\hat{\beta}$.

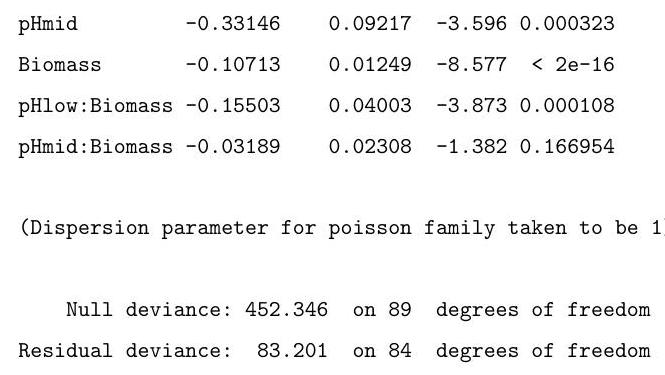
  (ii) A long-term agricultural experiment had 90 grassland plots, each $25 \mathrm{~m} \times 25 \mathrm{~m}$, differing in biomass, soil pH, and species richness (the count of species in the whole plot). While it was well-known that species richness declines with increasing biomass, it was not known how this relationship depends on soil pH, which for the given study has possible values "low", "medium" or "high", each taken 30 times. Explain the commands input, and interpret the resulting output in the (slightly edited) $R$ output below, in which "species" represents the species count.

  (The first and last 2 lines of the data are reproduced here as an aid. You may assume that the factor pH has been correctly set up.)

  

  

  comment

• A4.14

  Computational Statistics and Statistical Modelling | Part II, 2004

  Suppose that $Y_{1}, \ldots, Y_{n}$ are independent observations, with $Y_{i}$ having probability density function of the following form

  $$f\left(y_{i} \mid \theta_{i}, \phi\right)=\exp \left[\frac{y_{i} \theta_{i}-b\left(\theta_{i}\right)}{\phi}+c\left(y_{i}, \phi\right)\right]$$

  where $\mathbb{E}\left(Y_{i}\right)=\mu_{i}$ and $g\left(\mu_{i}\right)=\beta^{T} x_{i}$. You should assume that $g()$ is a known function, and $\beta, \phi$ are unknown parameters, with $\phi>0$, and also $x_{1}, \ldots, x_{n}$ are given linearly independent covariate vectors. Show that

  $$\frac{\partial \ell}{\partial \beta}=\sum \frac{\left(y_{i}-\beta_{i}\right)}{g^{\prime}\left(\mu_{i}\right) V_{i}} x_{i}$$

  where $\ell$ is the log-likelihood and $V_{i}=\operatorname{var}\left(Y_{i}\right)=\phi b^{\prime \prime}\left(\theta_{i}\right)$.

  Discuss carefully the (slightly edited) $\mathrm{R}$ output given below, and briefly suggest another possible method of analysis using the function $\mathrm{glm}$ ( ).

  $>s<-\operatorname{scan}()$

  1: $\begin{array}{llllll}33 & 63 & 157 & 38 & 108 & 159\end{array}$

  7:

  Read 6 items

  $>r<-\operatorname{scan}()$

  1: 327172565065248688773520

  $7:$

  Read 6 items

  $>$ gender <- $\operatorname{scan}(, " \|)$

  1: b b b g g g

  $7:$

  Read 6 items

  $>$ age <- $\operatorname{scan}(, " \prime)$

  1: 13&under 14-18 19&over

  4: 13&under 14-18 19&over

  7 :

  Read 6 items

  $>$ gender <- factor (gender) ; age <- factor (age)

  $>\operatorname{summary}(\mathrm{glm}(\mathrm{s} / \mathrm{r} \sim$ gender $+$ age, binomial, weights $=\mathrm{r}))$

  Coefficients:

  

  Null deviance: $221.797542$ on 5 degrees of freedom

  Residual deviance: $0.098749$ on 2 degrees of freedom

  Number of Fisher Scoring iterations: 3

  comment

Differentiable Manifolds

• B1.8

  Differentiable Manifolds | Part II, 2004

  What is a smooth vector bundle over a manifold $M$ ?

  Assuming the existence of "bump functions", prove that every compact manifold embeds in some Euclidean space $\mathbb{R}^{n}$.

  By choosing an inner product on $\mathbb{R}^{n}$, or otherwise, deduce that for any compact manifold $M$ there exists some vector bundle $\eta \rightarrow M$ such that the direct sum $T M \oplus \eta$ is isomorphic to a trivial vector bundle.

  comment

• B2 7

  Differentiable Manifolds | Part II, 2004

  For each of the following assertions, either provide a proof or give and justify a counterexample.

  [You may use, without proof, your knowledge of the de Rham cohomology of surfaces.]

  (a) A smooth map $f: S^{2} \rightarrow T^{2}$ must have degree zero.

  (b) An embedding $\varphi: S^{1} \rightarrow \Sigma_{g}$ extends to an embedding $\bar{\varphi}: D^{2} \rightarrow \Sigma_{g}$ if and only if the map

  $$\int_{\varphi\left(S^{1}\right)}: H^{1}\left(\Sigma_{g}\right) \rightarrow \mathbb{R}$$

  is the zero map.

  (c) $\mathbb{R} \mathbb{P}^{1} \times \mathbb{R P}^{2}$ is orientable.

  (d) The surface $\Sigma_{g}$ admits the structure of a Lie group if and only if $g=1$.

  comment

• B4.4

  Differentiable Manifolds | Part II, 2004

  Define what it means for a manifold to be oriented, and define a volume form on an oriented manifold.

  Prove carefully that, for a closed connected oriented manifold of dimension $n$, $H^{n}(M)=\mathbb{R}$.

  [You may assume the existence of volume forms on an oriented manifold.]

  If $M$ and $N$ are closed, connected, oriented manifolds of the same dimension, define the degree of a map $f: M \rightarrow N$.

  If $f$ has degree $d>1$ and $y \in N$, can $f^{-1}(y)$ be

  (i) infinite? (ii) a single point? (iii) empty?

  Briefly justify your answers.

  comment

Dynamics of Differential Equations

• B2.4

  Dynamics of Differential Equations | Part II, 2004

  (i) Define carefully what is meant by a Hopf bifurcation in a two-dimensional dynamical system. Write down the normal form for this bifurcation, correct to cubic order, and distinguish between bifurcations of supercritical and subcritical type. Describe, without detailed calculations, how a general two-dimensional system with a Hopf bifurcation at the origin can be reduced to normal form by a near-identity transformation.

  (ii) A Takens-Bogdanov bifurcation of a fixed point of a two-dimensional system is characterised by a Jacobian with the canonical form

  $$A=\left(\begin{array}{ll} 0 & 1 \\ 0 & 0 \end{array}\right)$$

  at the bifurcation point. Consider the system

  $$\begin{aligned} &\dot{x}=y+\alpha_{1} x^{2}+\beta_{1} x y+\gamma_{1} y^{2} \\ &\dot{y}=\alpha_{2} x^{2}+\beta_{2} x y+\gamma_{2} y^{2} \end{aligned}$$

  Show that a near-identity transformation of the form

  $$\begin{aligned} &\xi=x+a_{1} x^{2}+b_{1} x y+c_{1} y^{2} \\ &\eta=y+a_{2} x^{2}+b_{2} x y+c_{2} y^{2} \end{aligned}$$

  exists that reduces the system to the normal (canonical) form, correct up to quadratic terms,

  $$\dot{\xi}=\eta, \quad \dot{\eta}=\alpha_{2} \xi^{2}+\left(\beta_{2}+2 \alpha_{1}\right) \xi \eta .$$

  It is known that the general form of the equations near the bifurcation point can be written (setting $p=\alpha_{2}, q=\beta_{2}+2 \alpha_{1}$ )

  $$\dot{\xi}=\eta, \quad \dot{\eta}=\lambda \xi+\mu \eta+p \xi^{2}+q \xi \eta .$$

  Find all the fixed points of this system, and the values of $\lambda, \mu$ for which these fixed points have (a) steady state bifurcations and (b) Hopf bifurcations.

  comment

• B3.4

  Dynamics of Differential Equations | Part II, 2004

  (i) Describe the use of the stroboscopic method for obtaining approximate solutions to the second order equation

  $$\ddot{x}+x=\epsilon f(x, \dot{x}, t)$$

  when $|\epsilon| \ll 1$. In particular, by writing $x=R \cos (t+\phi), \dot{x}=-R \sin (t+\phi)$, obtain expressions in terms of $f$ for the rate of change of $R$ and $\phi$. Evaluate these expressions when $f=x^{2} \cos t$.

  (ii) In planetary orbit theory a crude model of an orbit subject to perturbation from a distant body is given by the equation

  $$\frac{d^{2} u}{d \theta^{2}}+u=\lambda-\delta^{2} u^{-2}-2 \delta^{3} u^{-3} \cos \theta$$

  where $0<\delta \ll 1,\left(u^{-1}, \theta\right)$ are polar coordinates in the plane, and $\lambda$ is a positive constant.

  (a) Show that when $\delta=0$ all bounded orbits are closed.

  (b) Now suppose $\delta \neq 0$, and look for almost circular orbits with $u=\lambda+\delta w(\theta)+a \delta^{2}$, where $a$ is a constant. By writing $w=R(\theta) \cos (\theta+\phi(\theta))$, and by making a suitable choice of the constant $a$, use the stroboscopic method to find equations for $d w / d \theta$ and $d \phi / d \theta$. By writing $z=R \exp (i \phi)$ and considering $d z / d \theta$, or otherwise, determine $R(\theta)$ and $\phi(\theta)$ in the case $R(0)=R_{0}, \phi(0)=0$. Hence describe the orbits of the system.

  comment

Electrodynamics

• B1.21

  Electrodynamics | Part II, 2004

  The Maxwell field tensor is

  $$F^{a b}=\left(\begin{array}{cccc} 0 & -E_{x} & -E_{y} & -E_{z} \\ E_{x} & 0 & -B_{z} & B_{y} \\ E_{y} & B_{z} & 0 & -B_{x} \\ E_{z} & -B_{y} & B_{x} & 0 \end{array}\right)$$

  and the 4-current density is $J^{a}=(\rho, \mathbf{j})$. Write down the 3-vector form of Maxwell's equations and the continuity equation, and obtain the equivalent 4-vector equations.

  Consider a Lorentz transformation from a frame $\mathcal{F}$ to a frame $\mathcal{F}^{\prime}$ moving with relative (coordinate) velocity $v$ in the $x$-direction

  $$L_{b}^{a}=\left(\begin{array}{cccc} \gamma & \gamma v & 0 & 0 \\ \gamma v & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  where $\gamma=1 / \sqrt{1-v^{2}}$. Obtain the transformation laws for $\mathbf{E}$ and $\mathbf{B}$. Which quantities, quadratic in $\mathbf{E}$ and $\mathbf{B}$, are Lorentz scalars?

  comment

• B2.21

  Electrodynamics | Part II, 2004

  A particle of rest mass $m$ and charge $q$ moves along a path $x^{a}(s)$, where $s$ is the particle's proper time. The equation of motion is

  $$m \ddot{x}^{a}=q F^{a b} \eta_{b c} \dot{x}^{c}$$

  where $\dot{x}^{a}=d x^{a} / d s$ etc., $F^{a b}$ is the Maxwell field tensor $\left(F^{01}=-E_{x}, F^{23}=-B_{x}\right.$, where $E_{x}$ and $B_{x}$ are the $x$-components of the electric and magnetic fields) and $\eta_{b c}$ is the Minkowski metric tensor. Show that $\dot{x}_{a} \ddot{x}^{a}=0$ and interpret both the equation of motion and this equation in the classical limit.

  The electromagnetic field is given in cartesian coordinates by $\mathbf{E}=(0, E, 0)$ and $\mathbf{B}=(0,0, E)$, where $E$ is constant and uniform. The particle starts from rest at the origin. Show that the orbit is given by

  $$9 x^{2}=2 \alpha y^{3}, \quad z=0$$

  where $\alpha=q E / m$.

  comment

• B4.21

  Electrodynamics | Part II, 2004

  Using Lorentz gauge, $A_{, a}^{a}=0$, Maxwell's equations for a current distribution $J^{a}$ can be reduced to $\square A^{a}(x)=\mu_{0} J^{a}(x)$. The retarded solution is

  $$A^{a}(x)=\frac{\mu_{0}}{2 \pi} \int d^{4} y \theta\left(z^{0}\right) \delta\left(z_{c} z^{c}\right) J^{a}(y)$$

  where $z^{a}=x^{a}-y^{a}$. Explain, heuristically, the rôle of the $\delta$-function and Heaviside step function $\theta$ in this formula.

  The current distribution is produced by a point particle of charge $q$ moving on a world line $r^{a}(s)$, where $s$ is the particle's proper time, so that

  $$J^{a}(y)=q \int d s V^{a}(s) \delta^{(4)}(y-r(s))$$

  where $V^{a}=\dot{r}^{a}(s)=d r^{a} / d s$. Show that

  $$A^{a}(x)=\frac{\mu_{0} q}{2 \pi} \int d s \theta\left(X^{0}\right) \delta\left(X_{c} X^{c}\right) V^{a}(s),$$

  where $X^{a}=x^{a}-r^{a}(s)$, and further that, setting $\alpha=X_{c} V^{c}$,

  $$A^{a}(x)=\frac{\mu_{0} q}{4 \pi}\left[\frac{V^{a}}{\alpha}\right]_{s=s^{*}}$$

  where $s^{*}$ should be defined. Verify that

  $$s^{*}, a=\left[\frac{X_{a}}{\alpha}\right]_{s=s^{*}} .$$

  Evaluating quantities at $s=s^{*}$ show that

  $$\left[\frac{V^{a}}{\alpha}\right]_{, b}=\frac{1}{\alpha^{2}}\left[-V^{a} V_{b}+S^{a} X_{b}\right]$$

  where $S^{a}=\dot{V}^{a}+V^{a}\left(1-X_{c} \dot{V}^{c}\right) / \alpha$. Hence verify that $A^{a}{ }_{, a}(x)=0$ and

  $$F_{a b}=\frac{\mu_{0} q}{4 \pi \alpha^{2}}\left(S_{a} X_{b}-S_{b} X_{a}\right) .$$

  Verify this formula for a stationary point charge at the origin.

  [Hint: If $f(s)$ has simple zeros at $s_{i}, i=1,2, \ldots$ then

  $$\delta(f(s))=\sum_{i} \frac{\delta\left(s_{i}\right)}{\left|f^{\prime}\left(s_{i}\right)\right|}$$

  comment

Electromagnetism

• A $1 . 5 \quad$ B $1 . 4 \quad$

  Electromagnetism | Part II, 2004

  (i) Show that the work done in assembling a localised charge distribution $\rho(\mathbf{r})$ in a region $V$ with an associated potential $\phi(\mathbf{r})$ is

  $$W=\frac{1}{2} \int_{V} \rho(\mathbf{r}) \phi(\mathbf{r}) d \tau$$

  and that this can be written as an integral over all space

  $$W=\frac{1}{2} \epsilon_{0} \int|\mathbf{E}|^{2} d \tau$$

  where the electric field $\mathbf{E}=-\nabla \phi$.

  (ii) What is the force per unit area on an infinite plane conducting sheet with a charge density $\sigma$ per unit area (a) if it is isolated in space and (b) if the electric field vanishes on one side of the sheet?

  An infinite cylindrical capacitor consists of two concentric cylindrical conductors with radii $a, b(a<b)$, carrying charges $\pm q$ per unit length respectively. Calculate the capacitance per unit length and the energy per unit length. Next determine the total force on each conductor, and calculate the rate of change of energy of the inner and outer conductors if they are moved radially inwards and outwards respectively with speed $v$. What is the corresponding rate of change of the capacitance?

  comment

• A2.5

  Electromagnetism | Part II, 2004

  (i) Write down the general solution of Poisson's equation. Derive from Maxwell's equations the Biot-Savart law for the magnetic field of a steady localised current distribution.

  (ii) A plane rectangular loop with sides of length $a$ and $b$ lies in the plane $z=0$ and is centred on the origin. Show that when $r=|\mathbf{r}| \gg a, b$, the vector potential $\mathbf{A}(\mathbf{r})$ is given approximately by

  $$\mathbf{A}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \frac{\mathbf{m} \wedge \mathbf{r}}{r^{3}}$$

  where $\mathbf{m}=I a b \hat{\mathbf{z}}$ is the magnetic moment of the loop.

  Hence show that the magnetic field $\mathbf{B}(\mathbf{r})$ at a great distance from an arbitrary small plane loop of area $A$, situated in the $x y$-plane near the origin and carrying a current $I$, is given by

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0} I A}{4 \pi r^{5}}\left(3 x z, 3 y z, 2 r^{2}-3 x^{2}-3 y^{2}\right)$$

  comment

• A3.5 B3.3

  Electromagnetism | Part II, 2004

  (i) State Maxwell's equations and show that the electric field $\mathbf{E}$ and the magnetic field $\mathbf{B}$ can be expressed in terms of a scalar potential $\phi$ and a vector potential $\mathbf{A}$. Hence derive the inhomogeneous wave equations that are satisfied by $\phi$ and $\mathbf{A}$ respectively.

  (ii) The plane $x=0$ separates a vacuum in the half-space $x<0$ from a perfectly conducting medium occupying the half-space $x>0$. Derive the boundary conditions on $\mathbf{E}$ and $\mathbf{B}$ at $x=0$.

  A plane electromagnetic wave with a magnetic field $\mathbf{B}=B(t, x, z) \hat{\mathbf{y}}$, travelling in the $x z$-plane at an angle $\theta$ to the $x$-direction, is incident on the interface at $x=0$. If the wave has frequency $\omega$ show that the total magnetic field is given by

  $$\mathbf{B}=B_{0} \cos \left(\frac{\omega x}{c} \cos \theta\right) \exp \left[i\left(\frac{\omega z}{c} \sin \theta-\omega t\right)\right] \hat{\mathbf{y}}$$

  where $B_{0}$ is a constant. Hence find the corresponding electric field $\mathbf{E}$, and obtain the surface charge density and the surface current at the interface.

  comment

• A4.5

  Electromagnetism | Part II, 2004

  Consider a frame $S^{\prime}$ moving with velocity v relative to the laboratory frame $S$ where $|\mathbf{v}|^{2} \ll c^{2}$. The electric and magnetic fields in $S$ are $\mathbf{E}$ and $\mathbf{B}$, while those measured in $S^{\prime}$ are $\mathbf{E}^{\prime}$ and $\mathbf{B}^{\prime}$. Given that $\mathbf{B}^{\prime}=\mathbf{B}$, show that

  $$\oint_{\Gamma} \mathbf{E}^{\prime} \cdot d \mathbf{l}=\oint_{\Gamma}(\mathbf{E}+\mathbf{v} \wedge \mathbf{B}) \cdot d \mathbf{l},$$

  for any closed circuit $\Gamma$ and hence that $\mathbf{E}^{\prime}=\mathbf{E}+\mathbf{v} \wedge \mathbf{B}$.

  Now consider a fluid with electrical conductivity $\sigma$ and moving with velocity $\mathbf{v}(\mathbf{r})$. Use Ohm's law in the moving frame to relate the current density $\mathbf{j}$ to the electric field $\mathbf{E}$ in the laboratory frame, and show that if $\mathbf{j}$ remains finite in the limit $\sigma \rightarrow \infty$ then

  $$\frac{\partial \mathbf{B}}{\partial t}=\nabla \wedge(\mathbf{v} \wedge \mathbf{B})$$

  The magnetic helicity $H$ in a volume $V$ is given by $\int_{V} \mathbf{A} \cdot \mathbf{B} d \tau$ where $\mathbf{A}$ is the vector potential. Show that if the normal components of $\mathbf{v}$ and $\mathbf{B}$ both vanish on the surface bounding $V$ then $d H / d t=0$.

  comment

Fluid Dynamics II

• B1.25

  Fluid Dynamics II | Part II, 2004

  Consider a uniform stream of inviscid incompressible fluid incident onto a twodimensional body (such as a circular cylinder). Sketch the flow in the region close to the stagnation point, $S$, at the front of the body.

  Let the fluid now have a small but non-zero viscosity. Using local co-ordinates $x$ along the boundary and $y$ normal to it, with the stagnation point as origin and $y>0$ in the fluid, explain why the local outer, inviscid flow is approximately of the form

  $$\mathbf{u}=(E x,-E y)$$

  for some positive constant $E$.

  Use scaling arguments to find the thickness $\delta$ of the boundary layer on the body near $S$. Hence show that there is a solution of the boundary layer equations of the form

  $$u(x, y)=E x f^{\prime}(\eta)$$

  where $\eta$ is a suitable similarity variable and $f$ satisfies

  $$f^{\prime \prime \prime}+f f^{\prime \prime}-f^{\prime^{2}}=-1 .$$

  What are the appropriate boundary conditions for $(*)$ and why? Explain briefly how you would obtain a numerical solution to $(*)$ subject to the appropriate boundary conditions.

  Explain why it is neither possible nor appropriate to perform a similar analysis near the rear stagnation point of the inviscid flow.

  comment

• B2.25

  Fluid Dynamics II | Part II, 2004

  An incompressible fluid with density $\rho$ and viscosity $\mu$ is forced by a pressure difference $\Delta p$ through the narrow gap between two parallel circular cylinders of radius $a$ with axes $2 a+b$ apart. Explaining any approximations made, show that, provided $b \ll a$ and $\rho b^{3} \Delta p \ll \mu^{2} a$, the volume flux (per unit length of cylinder) is

  $$\frac{2 b^{5 / 2} \Delta p}{9 \pi a^{1 / 2} \mu}$$

  when the cylinders are stationary.

  Show also that when the two cylinders rotate with angular velocities $\Omega$ and $-\Omega$ respectively, the change in the volume flux is

  $$\frac{4}{3} b a \Omega .$$

  For the case $\Delta p=0$, find and sketch the function $f(x)=u_{0}(x) /(a \Omega)$, where $u_{0}$ is the centreline velocity at position $x$ along the gap in the direction of flow. Comment on the values taken by $f$.

  comment

• B3.24

  Fluid Dynamics II | Part II, 2004

  Using the Milne-Thompson circle theorem, or otherwise, write down the complex potential $w$ describing inviscid incompressible two-dimensional flow past a circular cylinder of radius $a$ centred on the origin, with circulation $\kappa$ and uniform velocity $(U, V)$ in the far field.

  Hence, or otherwise, find an expression for the velocity field if the cylinder is replaced by a flat plate of length $4 a$, centred on the origin and aligned with the $x$-axis. Evaluate the velocity field on the two sides of the plate and confirm that the normal velocity is zero.

  Explain the significance of the Kutta condition, and determine the value of the circulation that satisfies the Kutta condition when $U>0$.

  With this value of the circulation, calculate the difference in pressure between the upper and lower sides of the plate at position $x(-2 a \leq x \leq 2 a)$. Comment briefly on the value of the pressure at the leading edge and the force that this would produce if the plate had a small non-zero thickness.

  Determine the force on the plate, explaining carefully the direction in which it acts.

  [The Blasius formula $F_{x}-i F_{y}=\frac{i \rho}{2} \oint_{C}\left(\frac{d w}{d z}\right)^{2} d z$, where $C$ is a closed contour lying just outside the body, may be used without proof.]

  comment

• B4.26

  Fluid Dynamics II | Part II, 2004

  Write an essay on the Kelvin-Helmholtz instability of a vortex sheet. Your essay should include a detailed linearised analysis, a physical interpretation of the instability, and an informal discussion of nonlinear effects and of the effects of viscosity.

  comment

Foundations of Quantum Mechanics

• A2.13 B2.22

  Foundations of Quantum Mechanics | Part II, 2004

  (i) The creation and annihilation operators for a harmonic oscillator of angular frequency $\omega$ satisfy the commutation relation $\left[a, a^{\dagger}\right]=1$. Write down an expression for the Hamiltonian $H$ in terms of $a$ and $a^{\dagger}$.

  There exists a unique ground state $|0\rangle$ of $H$ such that $a|0\rangle=0$. Explain how the space of eigenstates $|n\rangle, n=0,1,2, \ldots$ of $H$ is formed, and deduce the eigenenergies for these states. Show that

  $$a|n\rangle=\sqrt{n}|n-1\rangle, \quad a^{\dagger}|n\rangle=\sqrt{n+1}|n+1\rangle$$

  (ii) Write down the number operator $N$ of the harmonic oscillator in terms of $a$ and $a^{\dagger}$. Show that

  $$N|n\rangle=n|n\rangle$$

  The operator $K_{r}$ is defined to be

  $$K_{r}=\frac{a^{\dagger r} a^{r}}{r !}, \quad r=0,1,2, \ldots$$

  Show that $K_{r}$ commutes with $N$. Show also that

  $$K_{r}|n\rangle= \begin{cases}\frac{n !}{(n-r) ! r !}|n\rangle & r \leq n \\ 0 & r>n\end{cases}$$

  By considering the action of $K_{r}$ on the state $|n\rangle$ show that

  $$\sum_{r=0}^{\infty}(-1)^{r} K_{r}=|0\rangle\langle 0|$$

  comment

• A3.13 B3.21

  Foundations of Quantum Mechanics | Part II, 2004

  (i) A quantum mechanical system consists of two identical non-interacting particles with associated single-particle wave functions $\psi_{i}(x)$ and energies $E_{i}, i=1,2, \ldots$, where $E_{1}<E_{2}<\ldots$ Show how the states for the two lowest energy levels of the system are constructed and discuss their degeneracy when the particles have (a) spin 0 , (b) spin $1 / 2$.

  (ii) The Pauli matrices are defined to be

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  State how the spin operators $s_{1}, s_{2}, s_{3}$ may be expressed in terms of the Pauli matrices, and show that they describe states with total angular momentum $\frac{1}{2} \hbar$.

  An electron is at rest in the presence of a magnetic field $\mathbf{B}=(B, 0,0)$, and experiences an interaction potential $-\mu \boldsymbol{\sigma} \cdot \mathbf{B}$. At $t=0$ the state of the electron is the eigenstate of $s_{3}$ with eigenvalue $\frac{1}{2} \hbar$. Calculate the probability that at later time $t$ the electron will be measured to be in the eigenstate of $s_{3}$ with eigenvalue $\frac{1}{2} \hbar$.

  Part II 2004

  comment

• A4.15 B4.22

  Foundations of Quantum Mechanics | Part II, 2004

  The states of the hydrogen atom are denoted by $|n l m\rangle$ with $l<n,-l \leq m \leq l$ and associated energy eigenvalue $E_{n}$, where

  $$E_{n}=-\frac{e^{2}}{8 \pi \epsilon_{0} a_{0} n^{2}} .$$

  A hydrogen atom is placed in a weak electric field with interaction Hamiltonian

  $$H_{1}=-e \mathcal{E} z$$

  a) Derive the necessary perturbation theory to show that to $O\left(\mathcal{E}^{2}\right)$ the change in the energy associated with the state $|100\rangle$ is given by

  $$\Delta E_{1}=e^{2} \mathcal{E}^{2} \sum_{n=2}^{\infty} \sum_{l=0}^{n-1} \sum_{m=-l}^{l} \frac{|\langle 100|z| n l m\rangle|^{2}}{E_{1}-E_{n}}$$

  The wavefunction of the ground state $|100\rangle$ is

  $$\psi_{n=1}(\mathbf{r})=\frac{1}{\left(\pi a_{0}^{3}\right)^{1 / 2}} e^{-r / a_{0}}$$

  By replacing $E_{n}, \forall n>1$, in the denominator of $(*)$ by $E_{2}$ show that

  $$\left|\Delta E_{1}\right|<\frac{32 \pi}{3} \epsilon_{0} \mathcal{E}^{2} a_{0}^{3}$$

  b) Find a matrix whose eigenvalues are the perturbed energies to $O(\mathcal{E})$ for the states $|200\rangle$ and $|210\rangle$. Hence, determine these perturbed energies to $O(\mathcal{E})$ in terms of the matrix elements of $z$ between these states.

  [Hint:

  $$\begin{aligned} \langle n l m|z| n l m\rangle &=0 & & \forall n, l, m \\ \left\langle n l m|z| n l^{\prime} m^{\prime}\right\rangle &=0 & & \forall n, l, l^{\prime}, m, m^{\prime}, \quad m \neq m^{\prime} \end{aligned}$$

  comment

Functional Analysis

• A1.3

  Functional Analysis | Part II, 2004

  (i) Let $H$ be a Hilbert space, and let $M$ be a non-zero closed vector subspace of $H$. For $x \in H$, show that there is a unique closest point $P_{M}(x)$ to $x$ in $M$.

  (ii) (a) Let $x \in H$. Show that $x-P_{M}(x) \in M^{\perp}$. Show also that if $y \in M$ and $x-y \in M^{\perp}$ then $y=P_{M}(x)$.

  (b) Deduce that $H=M \bigoplus M^{\perp}$.

  (c) Show that the map $P_{M}$ from $H$ to $M$ is a continuous linear map, with $\left\|P_{M}\right\|=1$.

  (d) Show that $P_{M}$ is the projection onto $M$ along $M^{\perp}$.

  Now suppose that $A$ is a subspace of $H$ that is not necessarily closed. Explain why $A^{\perp}=\{0\}$ implies that $A$ is dense in $H .$

  Give an example of a subspace of $l^{2}$ that is dense in $l^{2}$ but is not equal to $l^{2}$.

  comment

• A2.3 B2.2

  Functional Analysis | Part II, 2004

  (i) Prove Riesz's Lemma, that if $V$ is a normed space and $A$ is a vector subspace of $V$ such that for some $0 \leqslant k<1$ we have $d(x, A) \leqslant k$ for all $x \in V$ with $\|x\|=1$, then $A$ is dense in $V$. [Here $d(x, A)$ denotes the distance from $x$ to $A$.]

  Deduce that any normed space whose unit ball is compact is finite-dimensional. [You may assume that every finite-dimensional normed space is complete.]

  Give an example of a sequence $f_{1}, f_{2}, \ldots$ in an infinite-dimensional normed space such that $\left\|f_{n}\right\| \leqslant 1$ for all $n$, but $f_{1}, f_{2}, \ldots$ has no convergent subsequence.

  (ii) Let $V$ be a vector space, and let $\|\cdot\|_{1}$ and $\|.\|_{2}$ be two norms on $V$. What does it mean to say that $\|\cdot\|_{1}$ and $\|.\|_{2}$ are equivalent?

  Show that on a finite-dimensional vector space all norms are equivalent. Deduce that every finite-dimensional normed space is complete.

  Exhibit two norms on the vector space $l^{1}$ that are not equivalent.

  In addition, exhibit two norms on the vector space $l^{\infty}$ that are not equivalent.

  comment

• A3.3 B3.2

  Functional Analysis | Part II, 2004

  (i) Let $H$ be an infinite-dimensional Hilbert space. Show that $H$ has a (countable) orthonormal basis if and only if $H$ has a countable dense subset. [You may assume familiarity with the Gram-Schmidt process.]

  State and prove Bessel's inequality.

  (ii) State Parseval's equation. Using this, prove that if $H$ has a countable dense subset then there is a surjective isometry from $H$ to $l^{2}$.

  Explain carefully why the functions $e^{i n \theta}, n \in \mathbb{Z}$, form an orthonormal basis for $L^{2}(\mathbb{T})$

  comment

• A4.3

  Functional Analysis | Part II, 2004

  State and prove the Dominated Convergence Theorem. [You may assume the Monotone Convergence Theorem.]

  Let $a$ and $p$ be real numbers, with $a>0$. Prove carefully that

  $$\int_{0}^{\infty} e^{-a x} \sin p x d x=\frac{p}{a^{2}+p^{2}}$$

  [Any standard results that you use should be stated precisely.]

  comment

Galois Theory

• B1.7

  Galois Theory | Part II, 2004

  Let $L / K$ be a finite extension of fields. Define the trace $\operatorname{Tr}_{L / K}(x)$ and norm $N_{L / K}(x)$ of an element $x \in L$.

  Assume now that the extension $L / K$ is Galois, with cyclic Galois group of prime order $p$, generated by $\sigma$.

  i) Show that $\operatorname{Tr}_{L / K}(x)=\sum_{n=0}^{p-1} \sigma^{n}(x)$.

  ii) Show that $\{\sigma(x)-x \mid x \in L\}$ is a $K$-vector subspace of $L$ of dimension $p-1$. Deduce that if $y \in L$, then $\operatorname{Tr}_{L / K}(y)=0$ if and only if $y=\sigma(x)-x$ for some $x \in L$. [You may assume without proof that $\operatorname{Tr}_{L / K}$ is surjective for any finite separable extension $L / K$.]

  iii) Suppose that $L$ has characteristic $p$. Deduce from (i) that every element of $K$ can be written as $\sigma(x)-x$ for some $x \in L$. Show also that if $\sigma(x)=x+1$, then $x^{p}-x$ belongs to $K$. Deduce that $L$ is the splitting field over $K$ of $X^{p}-X-a$ for some $a \in K$.

  comment

• B3.6

  Galois Theory | Part II, 2004

  Let $K$ be a field, and $G$ a finite subgroup of $K^{*}$. Show that $G$ is cyclic.

  Define the cyclotomic polynomials $\Phi_{m}$, and show from your definition that

  $$X^{m}-1=\prod_{d \mid m} \Phi_{d}(X)$$

  Deduce that $\Phi_{m}$ is a polynomial with integer coefficients.

  Let $p$ be a prime with $(m, p)=1$. Let $\Phi_{m} \equiv f_{1} \ldots f_{r} \quad(\bmod p)$, where $f_{i} \in \mathbb{F}_{p}[X]$ are irreducible. Show that for each $i$ the degree of $f_{i}$ is equal to the order of $p$ in the group $(\mathbb{Z} / m \mathbb{Z})^{*}$.

  Use this to write down an irreducible polynomial of degree 10 over $\mathbb{F}_{2}$.

  comment

• B4.3

  Galois Theory | Part II, 2004

  Let $M / K$ be a finite Galois extension of fields. Explain what is meant by the Galois correspondence between subfields of $M$ containing $K$ and subgroups of $\operatorname{Gal}(M / K)$. Show that if $K \subset L \subset M$ then $\operatorname{Gal}(M / L)$ is a normal subgroup of $\operatorname{Gal}(M / K)$ if and only if $L / K$ is normal. What is $\operatorname{Gal}(L / K)$ in this case?

  Let $M$ be the splitting field of $X^{4}-3$ over $\mathbb{Q}$. Prove that $\operatorname{Gal}(M / \mathbb{Q})$ is isomorphic to the dihedral group of order 8. Hence determine all subfields of $M$, expressing each in the form $\mathbb{Q}(x)$ for suitable $x \in M$.

  comment

General Relativity

• A1.15 B1.24

  General Relativity | Part II, 2004

  (i) What is an affine parameter $\lambda$ of a timelike or null geodesic? Prove that for a timelike geodesic one may take $\lambda$ to be proper time $\tau$. The metric

  $$d s^{2}=-d t^{2}+a^{2}(t) d \mathbf{x}^{2}$$

  with $\dot{a}(t)>0$ represents an expanding universe. Calculate the Christoffel symbols.

  (ii) Obtain the law of spatial momentum conservation for a particle of rest mass $m$ in the form

  $$m a^{2} \frac{d \mathbf{x}}{d \tau}=\mathbf{p}=\text { constant }$$

  Assuming that the energy $E=m d t / d \tau$, derive an expression for $E$ in terms of $m, \mathbf{p}$ and $a(t)$ and show that the energy is not conserved but rather that it decreases with time. In particular, show that if the particle is moving extremely relativistically then the energy decreases as $a^{-1}(t)$, and if it is moving non-relativistically then the kinetic energy, $E-m$, decreases as $a^{-2}(t)$.

  Show that the frequency $\omega_{e}$ of a photon emitted at time $t_{e}$ will be observed at time $t_{o}$ to have frequency

  $$\omega_{o}=\omega_{e} \frac{a\left(t_{e}\right)}{a\left(t_{o}\right)}$$

  comment

• A2.15 B2.24

  General Relativity | Part II, 2004

  (i) State and prove Birkhoff's theorem.

  (ii) Derive the Schwarzschild metric and discuss its relevance to the problem of gravitational collapse and the formation of black holes.

  [Hint: You may assume that the metric takes the form

  $$d s^{2}=-e^{\nu(r, t)} d t^{2}+e^{\lambda(r, t)} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  and that the non-vanishing components of the Einstein tensor are given by

  $$\begin{aligned} & G_{t t}=\frac{e^{2 \nu+\lambda}}{r^{2}}\left(-1+e^{\lambda}+r \lambda^{\prime}\right), \quad G_{r t}=e^{(\nu+\lambda) / 2} \frac{\dot{\lambda}}{r}, \quad G_{r r}=\frac{e^{\lambda}}{r^{2}}\left(1-e^{-\lambda}+r \nu^{\prime}\right), \\ & G_{\theta \theta}=\frac{1}{4} r^{2} e^{-\lambda}\left[2 \nu^{\prime \prime}+\left(\nu^{\prime}\right)^{2}+\frac{2}{r}\left(\nu^{\prime}-\lambda^{\prime}\right)-\nu^{\prime} \lambda^{\prime}\right]-\frac{1}{4} r^{2} e^{-\nu}\left[2 \ddot{\lambda}+(\dot{\lambda})^{2}-\dot{\lambda} \dot{\nu}\right] \\ =&\left.G_{r t} \text { and } G_{\phi \phi}=\sin ^{2} \theta G_{\theta \theta} .\right] \end{aligned}$$

  comment

• A4.17 B4.25

  General Relativity | Part II, 2004

  Starting from the Ricci identity

  $$V_{a ; b ; c}-V_{a ; c ; b}=V_{e} R_{a b c}^{e}$$

  give an expression for the curvature tensor $R_{a b c}^{e}$ of the Levi-Civita connection in terms of the Christoffel symbols and their partial derivatives. Using local inertial coordinates, or otherwise, establish that

  $$R_{a b c}^{e}+R_{b c a}^{e}+R_{c a b}^{e}=0 .$$

  A vector field with components $V^{a}$ satisfies

  $$V_{a ; b}+V_{b ; a}=0$$

  Show, using equation $(*)$ that

  $$V_{a ; b ; c}=V_{e} R_{c b a}^{e}$$

  and hence that

  $$V_{a ; b} ; b+R_{a}{ }^{c} V_{c}=0,$$

  where $R_{a b}$ is the Ricci tensor. Show that equation $(* *)$ may be written as

  $$\left(\partial_{c} g_{a b}\right) V^{c}+g_{c b} \partial_{a} V^{c}+g_{a c} \partial_{b} V^{c}=0$$

  If the metric is taken to be the Schwarzschild metric

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  show that $V^{a}=\delta^{a}{ }_{0}$ is a solution of $(* * *)$. Calculate $V^{a} ; a$.

  Electromagnetism can be described by a vector potential $A_{a}$ and a Maxwell field tensor $F_{a b}$ satisfying

  $$F_{a b}=A_{b ; a}-A_{a ; b} \quad \text { and } \quad F_{a b} ; b=0 .$$

  The divergence of $A_{a}$ is arbitrary and we may choose $A_{a} ; a=0$. With this choice show that in a general spacetime

  $$A_{a ; b}{ }^{; b}-R_{a}{ }^{c} A_{c}=0 .$$

  Hence show that in the Schwarzschild spacetime a tensor field whose only non-trivial components are $F_{t r}=-F_{r t}=Q / r^{2}$, where $Q$ is a constant, satisfies the field equations $(* * * *)$.

  comment

Geometry of Surfaces

• A2.7

  Geometry of Surfaces | Part II, 2004

  (i) What is a geodesic on a surface $M$ with Riemannian metric, and what are geodesic polar co-ordinates centred at a point $P$ on $M$ ? State, without proof, formulae for the Riemannian metric and the Gaussian curvature in terms of geodesic polar co-ordinates.

  (ii) Show that a surface with constant Gaussian curvature 0 is locally isometric to the Euclidean plane.

  comment

• A3.7

  Geometry of Surfaces | Part II, 2004

  (i) The catenoid is the surface $C$ in Euclidean $\mathbb{R}^{3}$, with co-ordinates $x, y, z$ and Riemannian metric $d s^{2}=d x^{2}+d y^{2}+d z^{2}$ obtained by rotating the curve $y=\cosh x$ about the $x$-axis, while the helicoid is the surface $H$ swept out by a line which lies along the $x$-axis at time $t=0$, and at time $t=t_{0}$ is perpendicular to the $z$-axis, passes through the point $\left(0,0, t_{0}\right)$ and makes an angle $t_{0}$ with the $x$-axis.

  Find co-ordinates on each of $C$ and $H$ and write $x, y, z$ in terms of these co-ordinates.

  (ii) Compute the induced Riemannian metrics on $C$ and $H$ in terms of suitable coordinates. Show that $H$ and $C$ are locally isometric. By considering the $x$-axis in $H$, show that this local isometry cannot be extended to a rigid motion of any open subset of Euclidean $\mathbb{R}^{3}$.

  comment

• A4.7

  Geometry of Surfaces | Part II, 2004

  Write an essay on the Gauss-Bonnet theorem and its proof.

  comment

Graph Theory

• A1.8

  Graph Theory | Part II, 2004

  (i) Let $G$ be a connected graph of order $n \geq 3$ such that for any two vertices $x$ and $y$,

  $$d(x)+d(y) \geq k$$

  Show that if $k<n$ then $G$ has a path of length $k$, and if $k=n$ then $G$ is Hamiltonian.

  (ii) State and prove Hall's theorem.

  [If you use any form of Menger's theorem, you must state it clearly.]

  Let $G$ be a graph with directed edges. For $S \subset V(G)$, let

  $$\Gamma_{+}(S)=\{y \in V(G): x y \in E(G) \text { for some } x \in S\}$$

  Find a necessary and sufficient condition, in terms of the sizes of the sets $\Gamma_{+}(S)$, for the existence of a set $F \subset E(G)$ such that at every vertex there is exactly one incoming edge and exactly one outgoing edge belonging to $F$.

  comment

• A2.8

  Graph Theory | Part II, 2004

  (i) State a result of Euler, relating the number of vertices, edges and faces of a plane graph. Show that if $G$ is a plane graph then $\chi(G) \leq 5$.

  (ii) Define the chromatic polynomial $p_{G}(t)$ of a graph $G$. Show that

  $$p_{G}(t)=t^{n}-a_{1} t^{n-1}+a_{2} t^{n-2}+\ldots+(-1)^{n} a_{n}$$

  where $a_{1}, \ldots, a_{n}$ are non-negative integers. Explain, with proof, how the chromatic polynomial is related to the number of vertices, edges and triangles in $G$. Show that if $C_{n}$ is a cycle of length $n \geq 3$, then

  $$p_{C_{n}}(t)=(t-1)^{n}+(-1)^{n}(t-1) .$$

  comment

• A4.9

  Graph Theory | Part II, 2004

  Write an essay on trees. You should include a proof of Cayley's result on the number of labelled trees of order $n$.

  Let $G$ be a graph of order $n \geq 2$. Which of the following statements are equivalent to the statement that $G$ is a tree? Give a proof or counterexample in each case.

  (a) $G$ is acyclic and $e(G) \geq n-1$.

  (b) $G$ is connected and $e(G) \leq n-1$.

  (c) $G$ is connected, triangle-free and has at least two leaves.

  (d) $G$ has the same degree sequence as $T$, for some tree $T$.

  comment

Groups, Rings and Fields

• A1.4 B1.3

  Groups, Rings and Fields | Part II, 2004

  (i) Let $R$ be a commutative ring. Define the terms prime ideal and maximal ideal, and show that if an ideal $M$ in $R$ is maximal then $M$ is also prime.

  (ii) Let $P$ be a non-trivial prime ideal in the commutative ring $R$ ('non-trivial' meaning that $P \neq\{0\}$ and $P \neq R$ ). If $P$ has finite index as a subgroup of $R$, show that $P$ is also maximal. Give an example to show that this may fail, if the assumption of finite index is omitted. Finally, show that if $R$ is a principal ideal domain, then every non-trivial prime ideal in $R$ is maximal.

  comment

• A2.4 B2.3

  Groups, Rings and Fields | Part II, 2004

  (i) State Gauss' Lemma on polynomial irreducibility. State and prove Eisenstein's criterion.

  (ii) Which of the following polynomials are irreducible over $\mathbb{Q}$ ? Justify your answers.

  (a) $x^{7}-3 x^{3}+18 x+12$

  (b) $x^{4}-4 x^{3}+11 x^{2}-3 x-5$

  (c) $1+x+x^{2}+\ldots+x^{p-1}$ with $p$ prime

  [Hint: consider substituting $y=x-1$.]

  (d) $x^{n}+p x+p^{2}$ with $p$ prime.

  [Hint: show any factor has degree at least two, and consider powers of $p$ dividing coefficients.]

  comment

• A3.4

  Groups, Rings and Fields | Part II, 2004

  (i) Let $K \leqslant \mathbb{C}$ be a field and $L \leqslant \mathbb{C}$ a finite normal extension of $K$. If $H$ is a finite subgroup of order $m$ in the Galois group $G(L \mid K)$, show that $L$ is a normal extension of the $H$-invariant subfield $I(H)$ of degree $m$ and that $G(L \mid I(H))=H$. [You may assume the theorem of the primitive element.]

  (ii) Show that the splitting field over $\mathbb{Q}$ of the polynomial $x^{4}+2$ is $\mathbb{Q}[\sqrt[4]{2}, i]$ and deduce that its Galois group has order 8. Exhibit a subgroup of order 4 of the Galois group, and determine the corresponding invariant subfield.

  comment

• A4.4

  Groups, Rings and Fields | Part II, 2004

  (a) Let $t$ be the maximal power of the prime $p$ dividing the order of the finite group $G$, and let $N\left(p^{t}\right)$ denote the number of subgroups of $G$ of order $p^{t}$. State clearly the numerical restrictions on $N\left(p^{t}\right)$ given by the Sylow theorems.

  If $H$ and $K$ are subgroups of $G$ of orders $r$ and $s$ respectively, and their intersection $H \cap K$ has order $t$, show the set $H K=\{h k: h \in H, k \in K\}$ contains $r s / t$ elements.

  (b) The finite group $G$ has 48 elements. By computing the possible values of $N(16)$, show that $G$ cannot be simple.

  comment

Hilbert Spaces

• B1.10

  Hilbert Spaces | Part II, 2004

  Suppose that $\left(e_{n}\right)$ and $\left(f_{m}\right)$ are orthonormal bases of a Hilbert space $H$ and that $T \in L(H)$.

  (a) Show that $\sum_{n=1}^{\infty}\left\|T\left(e_{n}\right)\right\|^{2}=\sum_{m=1}^{\infty}\left\|T^{*}\left(f_{m}\right)\right\|^{2}$.

  (b) Show that $\sum_{n=1}^{\infty}\left\|T\left(e_{n}\right)\right\|^{2}=\sum_{m=1}^{\infty}\left\|T\left(f_{m}\right)\right\|^{2}$.

  $T \in L(H)$ is a Hilbert-Schmidt operator if $\sum_{n=1}^{\infty}\left\|T\left(e_{n}\right)\right\|^{2}<\infty$ for some (and hence every) orthonormal basis $\left(e_{n}\right)$.

  (c) Show that the set HS of Hilbert-Schmidt operators forms a linear subspace of $L(H)$, and that $\langle T, S\rangle=\sum_{n=1}^{\infty}\left\langle T\left(e_{n}\right), S\left(e_{n}\right)\right\rangle$ is an inner product on $H S$; show that this inner product does not depend on the choice of the orthonormal basis $\left(e_{n}\right)$.

  (d) Let $\|T\|_{H S}$ be the corresponding norm. Show that $\|T\| \leqslant\|T\|_{H S}$, and show that a Hilbert-Schmidt operator is compact.

  comment

• B3.8

  Hilbert Spaces | Part II, 2004

  Let $H$ be a Hilbert space. An operator $T$ in $L(H)$ is normal if $T T^{*}=T^{*} T$. Suppose that $T$ is normal and that $\sigma(T) \subseteq \mathbb{R}$. Let $U=(T+i I)(T-i I)^{-1}$.

  (a) Suppose that $A$ is invertible and $A T=T A$. Show that $A^{-1} T=T A^{-1}$.

  (b) Show that $U$ is normal, and that $\sigma(U) \subseteq\{\lambda:|\lambda|=1\}$.

  (c) Show that $U^{-1}$ is normal.

  (d) Show that $U$ is unitary.

  (e) Show that $T$ is Hermitian.

  [You may use the fact that, if $S$ is normal, the spectral radius of $S$ is equal to $\|S\| .$ ]

  comment

• B4.7

  Hilbert Spaces | Part II, 2004

  Suppose that $T$ is a bounded linear operator on an infinite-dimensional Hilbert space $H$, and that $\langle T(x), x\rangle$ is real and non-negative for each $x \in H$.

  (a) Show that $T$ is Hermitian.

  (b) Let $w(T)=\sup \{\langle T(x), x\rangle:\|x\|=1\}$. Show that

  $$\|T(x)\|^{2} \leqslant w(T)\langle T(x), x\rangle \quad \text { for each } x \in H$$

  (c) Show that $\|T\|$ is an approximate eigenvalue for $T$.

  Suppose in addition that $T$ is compact and injective.

  (d) Show that $\|T\|$ is an eigenvalue for $T$, with finite-dimensional eigenspace.

  Explain how this result can be used to diagonalise $T$.

  comment

Information Theory

• B1.14

  Information Theory | Part II, 2004

  State the formula for the capacity of a memoryless channel.

  (a) Consider a memoryless channel where there are two input symbols, $A$ and $B$, and three output symbols, $A, B$, *. Suppose each input symbol is left intact with probability $1 / 2$, and transformed into a $*$ with probability $1 / 2$. Write down the channel matrix, and calculate the capacity.

  (b) Now suppose the output is further processed by someone who cannot distinguish $A$ and $*$, so that the matrix becomes

  $$\left(\begin{array}{cc} 1 & 0 \\ 1 / 2 & 1 / 2 \end{array}\right)$$

  Calculate the new capacity.

  comment

• B2.14

  Information Theory | Part II, 2004

  For integer-valued random variables $X$ and $Y$, define the relative entropy $h_{Y}(X)$ of $X$ relative to $Y$.

  Prove that $h_{Y}(X) \geqslant 0$, with equality if and only if $\mathbb{P}(X=x)=\mathbb{P}(Y=x)$ for all $x$.

  By considering $Y$, a geometric random variable with parameter chosen appropriately, show that if the mean $\mathbb{E} X=\mu<\infty$, then

  $$h(X) \leqslant(\mu+1) \log (\mu+1)-\mu \log \mu,$$

  with equality if $X$ is geometric.

  comment

• B4.13

  Information Theory | Part II, 2004

  Define a cyclic code of length $N$.

  Show how codewords can be identified with polynomials in such a way that cyclic codes correspond to ideals in the polynomial ring with a suitably chosen multiplication rule.

  Prove that any cyclic code $\mathcal{X}$ has a unique generator, i.e. a polynomial $c(X)$ of minimum degree, such that the code consists of the multiples of this polynomial. Prove that the rank of the code equals $N-\operatorname{deg} c(X)$, and show that $c(X)$ divides $X^{N}+1$.

  Let $\mathcal{X}$ be a cyclic code. Set

  $$\mathcal{X}^{\perp}=\left\{y=y_{1} \ldots y_{N}: \sum_{i=1}^{N} x_{i} y_{i}=0 \text { for all } x=x_{1} \ldots x_{N} \in \mathcal{X}\right\}$$

  (the dual code). Prove that $\mathcal{X}^{\perp}$ is cyclic and establish how the generators of $\mathcal{X}$ and $\mathcal{X}^{\perp}$ are related to each other.

  Show that the repetition and parity codes are cyclic, and determine their generators.

  comment

Logic, Computation and Set Theory

• A $1 . 7 \quad$ B1.12

  Logic, Computation and Set Theory | Part II, 2004

  (i) State and prove the Knaster-Tarski Fixed-Point Theorem.

  (ii) A subset $S$ of a poset $X$ is called an up-set if whenever $x, y \in X$ satisfy $x \in S$ and $x \leqslant y$ then also $y \in S$. Show that the set of up-sets of $X$ (ordered by inclusion) is a complete poset.

  Let $X$ and $Y$ be totally ordered sets, such that $X$ is isomorphic to an up-set in $Y$ and $Y$ is isomorphic to the complement of an up-set in $X$. Prove that $X$ is isomorphic to $Y$. Indicate clearly where in your argument you have made use of the fact that $X$ and $Y$ are total orders, rather than just partial orders.

  [Recall that posets $X$ and $Y$ are called isomorphic if there exists a bijection $f$ from $X$ to $Y$ such that, for any $x, y \in X$, we have $f(x) \leqslant f(y)$ if and only if $x \leqslant y$.]

  comment

• A3.8 B3.11

  Logic, Computation and Set Theory | Part II, 2004

  (i) State and prove the Compactness Theorem for first-order predicate logic.

  State and prove the Upward Löwenheim-Skolem Theorem.

  [You may use the Completeness Theorem for first-order predicate logic.]

  (ii) For each of the following theories, either give axioms (in the language of posets) for the theory or prove carefully that the theory is not axiomatisable.

  (a) The theory of posets having no maximal element.

  (b) The theory of posets having a unique maximal element.

  (c) The theory of posets having infinitely many maximal elements.

  (d) The theory of posets having finitely many maximal elements.

  (e) The theory of countable posets having a unique maximal element.

  comment

• A4.8 B4.10

  Logic, Computation and Set Theory | Part II, 2004

  Write an essay on recursive functions. Your essay should include a sketch of why every computable function is recursive, and an explanation of the existence of a universal recursive function, as well as brief discussions of the Halting Problem and of the relationship between recursive sets and recursively enumerable sets.

  [You may assume that every recursive function is computable. You do not need to give proofs that particular functions to do with prime-power decompositions are recursive.]

  comment

• B2.11

  Logic, Computation and Set Theory | Part II, 2004

  Define the sets $V_{\alpha}, \alpha \in O N$. Show that each $V_{\alpha}$ is transitive, and explain why $V_{\alpha} \subseteq V_{\beta}$ whenever $\alpha \leqslant \beta$. Prove that every set $x$ is a member of some $V_{\alpha}$.

  Which of the following are true and which are false? Give proofs or counterexamples as appropriate. You may assume standard properties of rank.

  (a) If the rank of a set $x$ is a (non-zero) limit then $x$ is infinite.

  (b) If the rank of a set $x$ is a successor then $x$ is finite.

  (c) If the rank of a set $x$ is countable then $x$ is countable.

  comment

Markov Chains

• A1.1 B1.1

  Markov Chains | Part II, 2004

  (i) Give the definitions of a recurrent and a null recurrent irreducible Markov chain.

  Let $\left(X_{n}\right)$ be a recurrent Markov chain with state space $I$ and irreducible transition matrix $P=\left(p_{i j}\right)$. Prove that the vectors $\gamma^{k}=\left(\gamma_{j}^{k}, j \in I\right), k \in I$, with entries $\gamma_{k}^{k}=1$ and

  $$\gamma_{i}^{k}=\mathbb{E}_{k}(\# \text { of visits to } i \text { before returning to } k), \quad i \neq k,$$

  are $P$-invariant:

  $$\gamma_{j}^{k}=\sum_{i \in I} \gamma_{i}^{k} p_{i j}$$

  (ii) Let $\left(W_{n}\right)$ be the birth and death process on $\mathbb{Z}_{+}=\{0,1,2, \ldots\}$ with the following transition probabilities:

  $$\begin{aligned} &p_{i, i+1}=p_{i, i-1}=\frac{1}{2}, i \geq 1 \\ &p_{01}=1 \end{aligned}$$

  By relating $\left(W_{n}\right)$ to the symmetric simple random walk $\left(Y_{n}\right)$ on $\mathbb{Z}$, or otherwise, prove that $\left(W_{n}\right)$ is a recurrent Markov chain. By considering invariant measures, or otherwise, prove that $\left(W_{n}\right)$ is null recurrent.

  Calculate the vectors $\gamma^{k}=\left(\gamma_{i}^{k}, i \in \mathbb{Z}_{+}\right)$for the chain $\left(W_{n}\right), k \in \mathbb{Z}_{+}$.

  Finally, let $W_{0}=0$ and let $N$ be the number of visits to 1 before returning to 0 . Show that $\mathbb{P}_{0}(N=n)=(1 / 2)^{n}, n \geq 1$.

  [You may use properties of the random walk $\left(Y_{n}\right)$ or general facts about Markov chains without proof but should clearly state them.]

  comment

• A2.1

  Markov Chains | Part II, 2004

  (i) Let $J$ be a proper subset of the finite state space $I$ of an irreducible Markov chain $\left(X_{n}\right)$, whose transition matrix $P$ is partitioned as

  $$P=J^{J}\left(\begin{array}{ll} A & J^{c} \\ C & D \end{array}\right)$$

  If only visits to states in $J$ are recorded, we see a $J$-valued Markov chain $\left(\tilde{X}_{n}\right)$; show that its transition matrix is

  $$\tilde{P}=A+B \sum_{n \geqslant 0} D^{n} C=A+B(I-D)^{-1} C$$

  (ii) Local MP Phil Anderer spends his time in London in the Commons $(C)$, in his flat $(F)$, in the bar $(B)$ or with his girlfriend $(G)$. Each hour, he moves from one to another according to the transition matrix $P$, though his wife (who knows nothing of his girlfriend) believes that his movements are governed by transition matrix $P^{W}$ :

  

  The public only sees Phil when he is in $J=\{C, F, B\}$; calculate the transition matrix $\tilde{P}$ which they believe controls his movements.

  Each time the public Phil moves to a new location, he phones his wife; write down the transition matrix which governs the sequence of locations from which the public Phil phones, and calculate its invariant distribution.

  Phil's wife notes down the location of each of his calls, and is getting suspicious - he is not at his flat often enough. Confronted, Phil swears his fidelity and resolves to dump his troublesome transition matrix, choosing instead

  

  Will this deal with his wife's suspicions? Explain your answer.

  comment

• A3.1 B3.1

  Markov Chains | Part II, 2004

  (i) Give the definition of the time-reversal of a discrete-time Markov chain $\left(X_{n}\right)$. Define a reversible Markov chain and check that every probability distribution satisfying the detailed balance equations is invariant.

  (ii) Customers arrive in a hairdresser's shop according to a Poisson process of rate $\lambda>0$. The shop has $s$ hairstylists and $N$ waiting places; each stylist is working (on a single customer) provided that there is a customer to serve, and any customer arriving when the shop is full (i.e. the numbers of customers present is $N+s$ ) is not admitted and never returns. Every admitted customer waits in the queue and then is served, in the first-come-first-served order (say), the service taking an exponential time of rate $\mu>0$; the service times of admitted customers are independent. After completing his/her service, the customer leaves the shop and never returns.

  Set up a Markov chain model for the number $X_{t}$ of customers in the shop at time $t \geq 0$. Assuming $\lambda<s \mu$, calculate the equilibrium distribution $\pi$ of this chain and explain why it is unique. Show that $\left(X_{t}\right)$ in equilibrium is time-reversible, i.e. $\forall T>0,\left(X_{t}, 0 \leq t \leq T\right)$ has the same distribution as $\left(Y_{t}, 0 \leq t \leq T\right)$ where $Y_{t}=X_{T-t}$, and $X_{0} \sim \pi$.

  comment

• A4.1

  Markov Chains | Part II, 2004

  (a) Give three definitions of a continuous-time Markov chain with a given $Q$-matrix on a finite state space: (i) in terms of holding times and jump probabilities, (ii) in terms of transition probabilities over small time intervals, and (iii) in terms of finite-dimensional distributions.

  (b) A flea jumps clockwise on the vertices of a triangle; the holding times are independent exponential random variables of rate one. Find the eigenvalues of the corresponding $Q$-matrix and express transition probabilities $p_{x y}(t), t \geq 0, x, y=A, B, C$, in terms of these roots. Deduce the formulas for the sums

  $$S_{0}(t)=\sum_{n=0}^{\infty} \frac{t^{3 n}}{(3 n) !}, \quad S_{1}(t)=\sum_{n=0}^{\infty} \frac{t^{3 n+1}}{(3 n+1) !}, \quad S_{2}(t)=\sum_{n=0}^{\infty} \frac{t^{3 n+2}}{(3 n+2) !}$$

  in terms of the functions $e^{t}, e^{-t / 2}, \cos (\sqrt{3} t / 2)$ and $\sin (\sqrt{3} t / 2)$.

  Find the limits

  $$\lim _{t \rightarrow \infty} e^{-t} S_{j}(t), \quad j=0,1,2 .$$

  What is the connection between the decompositions $e^{t}=S_{0}(t)+S_{1}(t)+S_{2}(t)$ and $e^{t}=\cosh t+\sinh t ?$

  comment

Mathematical Methods

• A2.17

  Mathematical Methods | Part II, 2004

  (i) Consider the integral equation

  $$\phi(x)=-\lambda \int_{a}^{b} K(x, t) \phi(t) d t+g(x)$$

  for $\phi$ in the interval $a \leq x \leq b$, where $\lambda$ is a real parameter and $g(x)$ is given. Describe the method of successive approximations for solving ( $\dagger$ ).

  Suppose that

  $$|K(x, t)| \leq M, \quad \forall x, t \in[a, b]$$

  By using the Cauchy-Schwarz inequality, or otherwise, show that the successive-approximation series for $\phi(x)$ converges absolutely provided

  $$|\lambda|<\frac{1}{M(b-a)} .$$

  (ii) The real function $\psi(x)$ satisfies the differential equation

  $$-\psi^{\prime \prime}(x)+\lambda \psi(x)=h(x), \quad 0<x<1$$

  where $h(x)$ is a given smooth function on $[0,1]$, subject to the boundary conditions

  $$\psi^{\prime}(0)=\psi(0), \quad \psi(1)=0 .$$

  By integrating $(\star)$, or otherwise, show that $\psi(x)$ obeys

  $$\psi(0)=\frac{1}{2} \int_{0}^{1}(1-t) h(t) d t-\frac{1}{2} \lambda \int_{0}^{1}(1-t) \psi(t) d t$$

  Hence, or otherwise, deduce that $\psi(x)$ obeys an equation of the form ( $\dagger$ ), with

  $$\begin{gathered} K(x, t)= \begin{cases}\frac{1}{2}(1-x)(1+t), & 0 \leq t \leq x \leq 1 \\ \frac{1}{2}(1+x)(1-t), & 0 \leq x \leq t \leq 1\end{cases} \\ \text { and } g(x)=\int_{0}^{1} K(x, t) h(t) d t \end{gathered}$$

  Deduce that the series solution for $\psi(x)$ converges provided $|\lambda|<2$.

  comment

• A3.17

  Mathematical Methods | Part II, 2004

  (i) Give a brief description of the method of matched asymptotic expansions, as applied to a differential equation of the type

  $$\epsilon y^{\prime \prime}+K y^{\prime}+f(y)=0, \quad 0<x<1,$$

  where $0<\epsilon \ll 1, K$ is a non-zero constant, $f$ is a suitable smooth function and the boundary values $y(0), y(1)$ are specified. An outline of Van Dyke's asymptotic matching principle should be included.

  (ii) Consider the boundary-value problem

  $$\epsilon y^{\prime \prime}+y^{\prime}-(2 x+1) y=0, \quad y(0)=0, \quad y(1)=e^{2}$$

  with $0<\epsilon \ll 1$. Find the integrating factor for the leading-order outer problem. Hence obtain the first two terms in the outer expansion.

  Rewrite the problem using an appropriate stretched inner variable. Hence obtain the first two terms of the inner exansion.

  Use van Dyke's matching principle to determine all the constants. Hence show that $y^{\prime}(0)=\epsilon^{-1}+\frac{25}{3}+O(\epsilon) .$

  comment

• A4.21

  Mathematical Methods | Part II, 2004

  State Watson's lemma, describing the asymptotic behaviour of the integral

  $$I(\lambda)=\int_{0}^{A} e^{-\lambda t} f(t) d t, \quad A>0$$

  as $\lambda \rightarrow \infty$, given that $f(t)$ has the asymptotic expansion

  $$f(t) \sim \sum_{n=0}^{\infty} a_{n} t^{n \beta}$$

  as $t \rightarrow 0_{+}$, where $\beta>0$.

  Consider the integral

  $$J(\lambda)=\int_{a}^{b} e^{\lambda \phi(t)} F(t) d t,$$

  where $\lambda \gg 1$ and $\phi(t)$ has a unique maximum in the interval $[a, b]$ at $c$, with $a<c<b$, such that

  $$\phi^{\prime}(c)=0, \quad \phi^{\prime \prime}(c)<0 .$$

  By using the change of variable from $t$ to $\zeta$, defined by

  $$\phi(t)-\phi(c)=-\zeta^{2}$$

  deduce an asymptotic expansion for $J(\lambda)$ as $\lambda \rightarrow \infty$. Show that the leading-order term gives

  $$J(\lambda) \sim e^{\lambda \phi(c)} F(c)\left(\frac{2 \pi}{\lambda\left|\phi^{\prime \prime}(c)\right|}\right)^{\frac{1}{2}}$$

  The gamma function $\Gamma(x)$ is defined for $x>0$ by

  $$\Gamma(x)=\int_{0}^{\infty} e^{(x-1) \log t-t} d t$$

  By means of the substitution $t=(x-1) s$, or otherwise, deduce that

  $$\Gamma(x+1) \sim x^{\left(x+\frac{1}{2}\right)} e^{-x} \sqrt{2 \pi}\left(1+\frac{1}{12 x}+\ldots\right)$$

  as $x \rightarrow \infty$

  comment

Methods of Mathematical Physics

• B1.19

  Methods of Mathematical Physics | Part II, 2004

  State the convolution theorem for Laplace transforms.

  The temperature $T(x, t)$ in a semi-infinite rod satisfies the heat equation

  $$\frac{\partial^{2} T}{\partial x^{2}}=\frac{1}{k} \frac{\partial T}{\partial t}, \quad x \geq 0, t \geq 0$$

  and the conditions $T(x, 0)=0$ for $x \geq 0, T(0, t)=f(t)$ for $t \geq 0$ and $T(x, t) \rightarrow 0$ as $x \rightarrow \infty$. Show that

  $$T(x, t)=\int_{0}^{t} f(\tau) G(x, t-\tau) d \tau$$

  where

  $$G(x, t)=\sqrt{\frac{x^{2}}{4 \pi k t^{3}}} e^{-x^{2} / 4 k t}$$

  comment

• B2.19

  Methods of Mathematical Physics | Part II, 2004

  (a) The Beta function is defined by

  $$\mathrm{B}(p, q)=\int_{0}^{1} x^{p-1}(1-x)^{q-1} d x$$

  Show that

  $$\mathrm{B}(p, q)=\int_{1}^{\infty} x^{-p-q}(x-1)^{q-1} d x$$

  (b) The function $J(p, q)$ is defined by

  $$J(p, q)=\int_{\gamma} t^{p-1}(1-t)^{q-1} d t$$

  where the integrand has a branch cut along the positive real axis. Just above the cut, $\arg t=0$. For $t>1$ just above the cut, arg $(1-t)=-\pi$. The contour $\gamma$ runs from $t=\infty e^{2 \pi i}$, round the origin in the negative sense, to $t=\infty$ (i.e. the contour is a reflection of the usual Hankel contour). What restriction must be placed on $p$ and $q$ for the integral to converge?

  By evaluating $J(p, q)$ in two ways, show that

  $$\left(1-e^{2 \pi i p}\right) \mathrm{B}(p, q)+\left(e^{-\pi i(q-1)}-e^{\pi i(2 p+q-1)}\right) \mathrm{B}(1-p-q, q)=0,$$

  where $p$ and $q$ are any non-integer complex numbers.

  Using the identity

  $$B(p, q)=\frac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}$$

  deduce that

  $$\Gamma(p) \Gamma(1-p) \sin (\pi p)=\Gamma(p+q) \Gamma(1-p-q) \sin [\pi(1-p-q)]$$

  and hence that

  $$\pi=\Gamma(q) \Gamma(1-q) \sin [\pi(1-q)]$$

  comment

• B3.19

  Methods of Mathematical Physics | Part II, 2004

  The function $w(z)$ satisfies the third-order differential equation

  $$\frac{d^{3} w}{d z^{3}}-z w=0$$

  subject to the conditions $w(z) \rightarrow 0$ as $z \rightarrow \pm i \infty$ and $w(0)=1$. Obtain an integral representation for $w(z)$ of the form

  $$w(z)=\int_{\gamma} e^{z t} f(t) d t$$

  and determine the function $f(t)$ and the contour $\gamma$.

  Using the change of variable $t=z^{1 / 3} \tau$, or otherwise, compute the leading term in the asymptotic expansion of $w(z)$ as $z \rightarrow+\infty$.

  comment

• B4.19

  Methods of Mathematical Physics | Part II, 2004

  Let $h(t)=i\left(t+t^{2}\right)$. Sketch the path of $\operatorname{Im}(h(t))=$ const. through the point $t=0$, and the path of $\operatorname{Im}(h(t))=$ const. through the point $t=1$.

  By integrating along these paths, show that as $\lambda \rightarrow \infty$

  $$\int_{0}^{1} t^{-1 / 2} e^{i \lambda\left(t+t^{2}\right)} d t \sim \frac{c_{1}}{\lambda^{1 / 2}}+\frac{c_{2} e^{2 i \lambda}}{\lambda},$$

  where the constants $c_{1}$ and $c_{2}$ are to be computed.

  comment

Nonlinear Dynamical Systems

• A1.6 B1.17

  Nonlinear Dynamical Systems | Part II, 2004

  (i) State Liapunov's First Theorem and La Salle's Invariance Principle. Use these results to show that the system

  $$\ddot{x}+k \dot{x}+\sin x=0, \quad k>0$$

  has an asymptotically stable fixed point at the origin.

  (ii) Define the basin of attraction of an invariant set of a dynamical system.

  Consider the equations

  $$\dot{x}=-x+\beta x y^{2}+x^{3}, \quad \dot{y}=-y+\beta y x^{2}+y^{3}, \quad \beta>2$$

  (a) Find the fixed points of the system and determine their type.

  (b) Show that the basin of attraction of the origin includes the union over $\alpha$ of the regions

  $$x^{2}+\alpha^{2} y^{2}<\frac{4 \alpha^{2}\left(1+\alpha^{2}\right)(\beta-1)}{\beta^{2}\left(1+\alpha^{2}\right)^{2}-4 \alpha^{2}} .$$

  Sketch these regions for $\alpha^{2}=1,1 / 2,2$ in the case $\beta=3$.

  comment

• A2.6 B2.17

  Nonlinear Dynamical Systems | Part II, 2004

  (i) A linear system in $\mathbb{R}^{2}$ takes the form $\dot{\mathbf{x}}=\mathrm{Ax}$. Explain (without detailed calculation but by giving examples) how to classify the dynamics of the system in terms of the determinant and the trace of A. Show your classification graphically, and describe the dynamics that occurs on the boundaries of the different regions on your diagram.

  (ii) A nonlinear system in $\mathbb{R}^{2}$ has the form $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x}), \mathbf{f}(0)=0$. The Jacobian (linearization) $A$ of $\mathbf{f}$ at the origin is non-hyperbolic, with one eigenvalue of $A$ in the left-hand half-plane. Define the centre manifold for this system, and explain (stating carefully any results you use) how the dynamics near the origin may be reduced to a one-dimensional system on the centre manifold.

  A dynamical system of this type has the form

  $$\begin{aligned} &\dot{x}=a x^{3}+b x y+c x^{5}+d x^{3} y+e x y^{2}+f x^{7}+g x^{5} y \\ &\dot{y}=-y+x^{2}-x^{4} \end{aligned}$$

  Find the coefficients for the expansion of the centre manifold correct up to and including terms of order $x^{6}$, and write down in terms of these coefficients the equation for the dynamics on the centre manifold up to order $x^{7}$. Using this reduced equation, give a complete set of conditions on the coefficients $a, b, c, \ldots$ that guarantee that the origin is stable.

  comment

• A3.6 B3.17

  Nonlinear Dynamical Systems | Part II, 2004

  (i) Consider a system in $\mathbb{R}^{2}$ that is almost Hamiltonian:

  $$\dot{x}=\frac{\partial H}{\partial y}+\epsilon g_{1}(x, y), \quad \dot{y}=-\frac{\partial H}{\partial x}+\epsilon g_{2}(x, y)$$

  where $H=H(x, y)$ and $|\epsilon| \ll 1$. Show that if the system has a periodic orbit $\mathcal{C}$ then $\oint_{\mathcal{C}} g_{2} d x-g_{1} d y=0$, and explain how to evaluate this orbit approximately for small $\epsilon$. Illustrate your method by means of the system

  $$\dot{x}=y+\epsilon x\left(1-x^{2}\right), \quad \dot{y}=-x .$$

  (ii) Consider the system

  $$\dot{x}=y, \quad \dot{y}=x-x^{3}+\epsilon y\left(1-\alpha x^{2}\right)$$

  (a) Show that when $\epsilon=0$ the system is Hamiltonian, and find the Hamiltonian. Sketch the trajectories in the case $\epsilon=0$. Identify the value $H_{c}$ of $H$ for which there is a homoclinic orbit.

  (b) Suppose $\epsilon>0$. Show that the small change $\Delta H$ in $H$ around an orbit of the Hamiltonian system can be expressed to leading order as an integral of the form

  $$\int_{x_{1}}^{x_{2}} \mathcal{F}(x, H) d x$$

  where $x_{1}, x_{2}$ are the extrema of the $x$-coordinates of the orbits of the Hamiltonian system, distinguishing between the cases $H<H_{c}, H>H_{c}$.

  (c) Find the value of $\alpha$, correct to leading order in $\epsilon$, at which the system has a homoclinic orbit.

  (d) By examining the eigenvalues of the Jacobian at the origin, determine the stability of the homoclinic orbit, being careful to state clearly any standard results that you use.

  comment

• A4.6 B4.17

  Nonlinear Dynamical Systems | Part II, 2004

  (a) Consider the map $G_{1}(x)=f(x+a)$, defined on $0 \leqslant x<1$, where $f(x)=x[\bmod 1]$, $0 \leqslant f<1$, and the constant $a$ satisfies $0 \leqslant a<1$. Give, with reasons, the values of $a$ (if any) for which the map has (i) a fixed point, (ii) a cycle of least period $n$, (iii) an aperiodic orbit. Does the map exhibit sensitive dependence on initial conditions?

  Show (graphically if you wish) that if the map has an $n$-cycle then it has an infinite number of such cycles. Is this still true if $G_{1}$ is replaced by $f(c x+a), 0<c<1 ?$

  (b) Consider the map

  $$G_{2}(x)=f\left(x+a+\frac{b}{2 \pi} \sin 2 \pi x\right)$$

  where $f(x)$ and $a$ are defined as in Part (a), and $b>0$ is a parameter.

  Find the regions of the $(a, b)$ plane for which the map has (i) no fixed points, (ii) exactly two fixed points.

  Now consider the possible existence of a 2-cycle of the map $G_{2}$ when $b \ll 1$, and suppose the elements of the cycle are $X, Y$ with $X<\frac{1}{2}$. By expanding $X, Y, a$ in powers of $b$, so that $X=X_{0}+b X_{1}+b^{2} X_{2}+O\left(b^{3}\right)$, and similarly for $Y$ and $a$, show that

  $$a=\frac{1}{2}+\frac{b^{2}}{8 \pi} \sin 4 \pi X_{0}+O\left(b^{3}\right)$$

  Use this result to sketch the region of the $(a, b)$ plane in which 2-cycles exist. How many distinct cycles are there for each value of $a$ in this region?

  comment

Nonlinear Waves

• A2.18

  Nonlinear Waves | Part II, 2004

  (i) Let $u(x, t)$ satisfy the Burgers equation

  $$\frac{\partial u}{\partial t}+u \frac{\partial u}{\partial x}=\nu \frac{\partial^{2} u}{\partial x^{2}}$$

  where $\nu$ is a positive constant. Consider solutions of the form $u=u(X)$, where $X=x-U t$ and $U$ is a constant, such that

  $$u \rightarrow u_{2}, \quad \frac{\partial u}{\partial X} \rightarrow 0 \quad \text { as } \quad X \rightarrow-\infty ; \quad u \rightarrow u_{1}, \quad \frac{\partial u}{\partial X} \rightarrow 0 \quad \text { as } \quad X \rightarrow \infty$$

  with $u_{2}>u_{1}$.

  Show that $U$ satisfies the so-called shock condition

  $$U=\frac{1}{2}\left(u_{2}+u_{1}\right)$$

  By using the factorisation

  $$\frac{1}{2} u^{2}-U u+A=\frac{1}{2}\left(u-u_{1}\right)\left(u-u_{2}\right)$$

  where $A$ is the constant of integration, express $u$ in terms of $X, u_{1}, u_{2}$ and $\nu$.

  (ii) According to shallow-water theory, river waves are characterised by the PDEs

  $$\begin{gathered} \frac{\partial v}{\partial t}+v \frac{\partial v}{\partial x}+g \cos \alpha \frac{\partial h}{\partial x}=g \sin \alpha-C_{f} \frac{v^{2}}{h} \\ \frac{\partial h}{\partial t}+v \frac{\partial h}{\partial x}+h \frac{\partial v}{\partial x}=0 \end{gathered}$$

  where $h(x, t)$ denotes the depth of the river, $v(x, t)$ denotes the mean velocity, $\alpha$ is the constant angle of inclination, and $C_{f}$ is the constant friction coefficient.

  Find the characteristic velocities and the characteristic form of the equations. Find the Riemann variables and show that if $C_{f}=0$ then the Riemann variables vary linearly with $t$ on the characteristics.

  comment

• A3.18

  Nonlinear Waves | Part II, 2004

  (i) Let $\Phi^{+}(t)$ and $\Phi^{-}(t)$ denote the boundary values of functions which are analytic inside and outside the unit disc centred on the origin, respectively. Let $C$ denote the boundary of this disc. Suppose that $\Phi^{+}(t)$ and $\Phi^{-}(t)$ satisfy the jump condition

  $$\Phi^{+}(t)=t^{-2} \Phi^{-}(t)+t^{-1}+\alpha\left(t^{-1}+t-t^{-3}\right), \quad t \in C,$$

  where $\alpha$ is a constant.

  Find the canonical solution of the associated homogeneous Riemann-Hilbert problem. Write down the orthogonality conditions.

  (ii) Consider the linear singular integral equation

  $$\left(t+t^{-1}\right) \psi(t)+\frac{t-t^{-1}}{\pi i} \oint_{C} \frac{\psi(\tau)}{\tau-t} d \tau=2+2 \alpha\left(1+t^{2}-t^{-2}\right)$$

  where $\oint$ denotes the principal value integral.

  Show that the associated Riemann-Hilbert problem has the jump condition defined in Part (i) above. Using this fact, find the value of the constant $\alpha$ that allows equation $(*)$ to have a solution. For this particular value of $\alpha$ find the unique solution $\psi(t)$.

  comment

• A4.23

  Nonlinear Waves | Part II, 2004

  Let $\psi(k ; x, t)$ satisfy the linear integral equation

  $$\psi(k ; x, t)+i e^{i\left(k x+k^{3} t\right)} \int_{L} \frac{\psi(l ; x, t)}{l+k} d \lambda(l)=e^{i\left(k x+k^{3} t\right)}$$

  where the measure $d \lambda(k)$ and the contour $L$ are such that $\psi(k ; x, t)$ exists and is unique.

  Let $q(x, t)$ be defined in terms of $\psi(k ; x, t)$ by

  $$q(x, t)=-\frac{\partial}{\partial x} \int_{L} \psi(k ; x, t) d \lambda(k)$$

  (a) Show that

  $$(M \psi)+i e^{i\left(k x+k^{3} t\right)} \int_{L} \frac{(M \psi)(l ; x, t)}{l+k} d \lambda(l)=0$$

  where

  $$M \psi \equiv \frac{\partial^{2} \psi}{\partial x^{2}}-i k \frac{\partial \psi}{\partial x}+q \psi$$

  (b) Show that

  $(N \psi)+i e^{i\left(k x+k^{3} t\right)} \int_{L} \frac{(N \psi)(l ; x, t)}{l+k} d \lambda(l)=3 k e^{i\left(k x+k^{3} t\right)} \int_{L} \frac{(M \psi)(l ; x, t)}{l+k} d \lambda(l)$,

  where

  $$N \psi \equiv \frac{\partial \psi}{\partial t}+\frac{\partial^{3} \psi}{\partial x^{3}}+3 q \frac{\partial \psi}{\partial x}$$

  (c) By recalling that the $\mathrm{KdV}$ equation

  $$\frac{\partial q}{\partial t}+\frac{\partial^{3} q}{\partial x^{3}}+6 q \frac{\partial q}{\partial x}=0$$

  admits the Lax pair

  $$M \psi=0, \quad N \psi=0,$$

  write down an expression for $d \lambda(l)$ which gives rise to the one-soliton solution of the $\mathrm{KdV}$ equation. Write down an expression for $\psi(k ; x, t)$ and for $q(x, t)$.

  comment

Number Fields

• B1.9

  Number Fields | Part II, 2004

  Let $K=\mathbb{Q}(\theta)$, where $\theta$ is a root of $X^{3}-4 X+1$. Prove that $K$ has degree 3 over $\mathbb{Q}$, and admits three distinct embeddings in $\mathbb{R}$. Find the discriminant of $K$ and determine the ring of integers $\mathcal{O}$ of $K$. Factorise $2 \mathcal{O}$ and $3 \mathcal{O}$ into a product of prime ideals.

  Using Minkowski's bound, show that $K$ has class number 1 provided all prime ideals in $\mathcal{O}$ dividing 2 and 3 are principal. Hence prove that $K$ has class number $1 .$

  [You may assume that the discriminant of $X^{3}+a X+b$ is $-4 a^{3}-27 b^{2}$.]

  comment

• B2.9

  Number Fields | Part II, 2004

  Let $m$ be an integer greater than 1 and let $\zeta_{m}$ denote a primitive $m$-th root of unity in $\mathbb{C}$. Let $\mathcal{O}$ be the ring of integers of $\mathbb{Q}\left(\zeta_{m}\right)$. If $p$ is a prime number with $(p, m)=1$, outline the proof that

  $$p \mathcal{O}=\wp_{1} \cdots \wp_{r},$$

  where the $\wp_{i}$ are distinct prime ideals of $\mathcal{O}$, and $r=\varphi(m) / f$ with $f$ the least integer $\geqslant 1$ such that $p^{f} \equiv 1 \bmod m$. [Here $\varphi(m)$ is the Euler $\varphi$-function of $\left.m\right]$.

  Determine the factorisations of $2,3,5$ and 11 in $\mathbb{Q}\left(\zeta_{5}\right)$. For each integer $n \geqslant 1$, prove that, in the ring of integers of $\mathbb{Q}\left(\zeta_{5^{n}}\right)$, there is a unique prime ideal dividing 2 , and a unique prime ideal dividing 3 .

  comment

• B4.6

  Number Fields | Part II, 2004

  Let $K$ be a finite extension of $\mathbb{Q}$, and $\mathcal{O}$ the ring of integers of $K$. Write an essay outlining the proof that every non-zero ideal of $\mathcal{O}$ can be written as a product of non-zero prime ideals, and that this factorisation is unique up to the order of the factors.

  comment

Number Theory

• A1.9

  Number Theory | Part II, 2004

  (i) State the law of quadratic reciprocity. For $p \neq 5$ an odd prime, evaluate the Legendre symbol

  $$\left(\frac{5}{p}\right)$$

  (ii) (a) Let $p_{1}, \ldots, p_{m}$ and $q_{1}, \ldots, q_{n}$ be distinct odd primes. Show that there exists an integer $x$ that is a quadratic residue modulo each of $p_{1}, \ldots, p_{m}$ and a quadratic non-residue modulo each of $q_{1}, \ldots, q_{n}$.

  (b) Let $p$ be an odd prime. Show that

  $$\sum_{a=1}^{p-1}\left(\frac{a}{p}\right)=0$$

  (c) Let $p$ be an odd prime. Using (b) or otherwise, evaluate

  $$\sum_{a=1}^{p-2}\left(\frac{a}{p}\right)\left(\frac{a+1}{p}\right)$$

  $\left[\right.$ Hint for $(c)$ : Use the equality $\left(\frac{x^{2} y}{p}\right)=\left(\frac{y}{p}\right)$, valid when $p$ does not divide $\left.x .\right]$

  comment

• A3.9

  Number Theory | Part II, 2004

  (i) Find a solution in integers of the Pell equation $x^{2}-17 y^{2}=1$.

  (ii) Define the continued fraction expansion of a real number $\theta>1$ and show that it converges to $\theta$.

  Show that if $N>0$ is a nonsquare integer and $x$ and $y$ are integer solutions of $x^{2}-N y^{2}=1$, then $x / y$ is a convergent of $\sqrt{N}$.

  comment

• A4.10

  Number Theory | Part II, 2004

  Write an essay on pseudoprimes and their role in primality testing. You should discuss pseudoprimes, Carmichael numbers, and Euler and strong pseudoprimes. Where appropriate, your essay should include small examples to illustrate your statements.

  comment

Numerical Analysis

• A1.20 B1.20

  Numerical Analysis | Part II, 2004

  (i) Define the Backward Difference Formula (BDF) method for ordinary differential equations and derive its two-step version.

  (ii) Prove that the interval $(-\infty, 0)$ belongs to the linear stability domain of the twostep BDF method.

  comment

• A2.19 B2.20

  Numerical Analysis | Part II, 2004

  (i) The five-point equations, which are obtained when the Poisson equation $\nabla^{2} u=f$ (with Dirichlet boundary conditions) is discretized in a square, are

  $$-u_{m-1, n}-u_{m, n-1}-u_{m+1, n}-u_{m, n+1}+4 u_{m, n}=f_{m, n}, \quad m, n=1,2, \ldots, M,$$

  where $u_{0, n}, u_{M+1, n}, u_{m, 0}, u_{m, M+1}=0$ for all $m, n=1,2, \ldots, M$.

  Formulate the Gauss-Seidel method for the above linear system and prove its convergence. In the proof you should carefully state any theorems you use. [You may use Part (ii) of this question.]

  (ii) By arranging the two-dimensional arrays $\left\{u_{m, n}\right\}_{m, n=1, \ldots, M}$ and $\left\{b_{m, n}\right\}_{m, n=1, \ldots, M}$ into the column vectors $\mathbf{u} \in \mathbb{R}^{M^{2}}$ and $\mathbf{b} \in \mathbb{R}^{M^{2}}$ respectively, the linear system described in Part (i) takes the matrix form $A \mathbf{u}=\mathbf{b}$. Prove that, regardless of the ordering of the points on the grid, the matrix $A$ is symmetric and positive definite.

  comment

• A3.19 B3.20

  Numerical Analysis | Part II, 2004

  (i) The diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad 0 \leqslant x \leqslant 1, \quad t \geqslant 0$$

  with the initial condition $u(x, 0)=\phi(x), 0 \leqslant x \leqslant 1$, and with zero boundary conditions at $x=0$ and $x=1$, can be solved by the method

  $$u_{m}^{n+1}=u_{m}^{n}+\mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right), \quad m=1,2, \ldots, M, \quad n \geqslant 0,$$

  where $\Delta x=1 /(M+1), \mu=\Delta t /(\Delta x)^{2}$, and $u_{m}^{n} \approx u(m \Delta x, n \Delta t)$. Prove that $\mu \leqslant \frac{1}{2}$ implies convergence.

  (ii) By discretizing the same equation and employing the same notation as in Part (i), determine conditions on $\mu>0$ such that the method

  $$\begin{aligned} &\left(\frac{1}{12}-\frac{1}{2} \mu\right) u_{m-1}^{n+1}+\left(\frac{5}{6}+\mu\right) u_{m}^{n+1}+\left(\frac{1}{12}-\frac{1}{2} \mu\right) u_{m+1}^{n+1}= \\ &\left(\frac{1}{12}+\frac{1}{2} \mu\right) u_{m-1}^{n}+\left(\frac{5}{6}-\mu\right) u_{m}^{n}+\left(\frac{1}{12}+\frac{1}{2} \mu\right) u_{m+1}^{n} \end{aligned}$$

  is stable.

  comment

• A4.22 B4.20

  Numerical Analysis | Part II, 2004

  Write an essay on the method of conjugate gradients. You should define the method, list its main properties and sketch the relevant proof. You should also prove that (in exact arithmetic) the method terminates in a finite number of steps, briefly mention the connection with Krylov subspaces, and describe the approach of preconditioned conjugate gradients.

  comment

Optimization and Control

• B2.15

  Optimization and Control | Part II, 2004

  A gambler is presented with a sequence of $n \geqslant 6$ random numbers, $N_{1}, N_{2}, \ldots, N_{n}$, one at a time. The distribution of $N_{k}$ is

  $$P\left(N_{k}=k\right)=1-P\left(N_{k}=-k\right)=p,$$

  where $1 /(n-2)<p \leq 1 / 3$. The gambler must choose exactly one of the numbers, just after it has been presented and before any further numbers are presented, but must wait until all the numbers are presented before his payback can be decided. It costs $£ 1$ to play the game. The gambler receives payback as follows: nothing if he chooses the smallest of all the numbers, $£ 2$ if he chooses the largest of all the numbers, and $£ 1$ otherwise.

  Show that there is an optimal strategy of the form "Choose the first number $k$ such that either (i) $N_{k}>0$ and $k \geq n-r_{0}$, or (ii) $k=n-1$ ", where you should determine the constant $r_{0}$ as explicitly as you can.

  comment

• B3.14

  Optimization and Control | Part II, 2004

  The strength of the economy evolves according to the equation

  $$\ddot{x}_{t}=-\alpha^{2} x_{t}+u_{t},$$

  where $x_{0}=\dot{x}_{0}=0$ and $u_{t}$ is the effort that the government puts into reform at time $t, t \geq 0$. The government wishes to maximize its chance of re-election at a given future time $T$, where this chance is some monotone increasing function of

  $$x_{T}-\frac{1}{2} \int_{0}^{T} u_{t}^{2} d t$$

  Use Pontryagin's maximum principle to determine the government's optimal reform policy, and show that the optimal trajectory of $x_{t}$ is

  $$x_{t}=\frac{t}{2} \alpha^{-2} \cos (\alpha(T-t))-\frac{1}{2} \alpha^{-3} \cos (\alpha T) \sin (\alpha t) .$$

  comment

• B4.14

  Optimization and Control | Part II, 2004

  Consider the deterministic dynamical system

  $$\dot{x}_{t}=A x_{t}+B u_{t}$$

  where $A$ and $B$ are constant matrices, $x_{t} \in \mathbb{R}^{n}$, and $u_{t}$ is the control variable, $u_{t} \in \mathbb{R}^{m}$. What does it mean to say that the system is controllable?

  Let $y_{t}=e^{-t A} x_{t}-x_{0}$. Show that if $V_{t}$ is the set of possible values for $y_{t}$ as the control $\left\{u_{s}: 0 \leq x \leq t\right\}$ is allowed to vary, then $V_{t}$ is a vector space.

  Show that each of the following three conditions is equivalent to controllability of the system.

  (i) The set $\left\{v \in \mathbb{R}^{n}: v^{\top} y_{t}=0\right.$ for all $\left.y_{t} \in V_{t}\right\}=\{0\}$.

  (ii) The matrix $H(t)=\int_{0}^{t} e^{-s A} B B^{\top} e^{-s A^{\top}} d s$ is (strictly) positive definite.

  (iii) The matrix $M_{n}=\left[\begin{array}{lllll}B & A B & A^{2} B & \cdots & A^{n-1} B\end{array}\right]$ has rank $n$.

  Consider the scalar system

  $$\sum_{j=0}^{n} a_{j}\left(\frac{d}{d t}\right)^{n-j} \xi_{t}=u_{t}$$

  where $a_{0}=1$. Show that this system is controllable.

  comment

Partial Differential Equations

• B1.18

  Partial Differential Equations | Part II, 2004

  (a) State and prove the Mean Value Theorem for harmonic functions.

  (b) Let $u \geqslant 0$ be a harmonic function on an open set $\Omega \subset \mathbb{R}^{n}$. Let $B(x, a)=\{y \in$ $\left.\mathbb{R}^{n}:|x-y|<a\right\}$. For any $x \in \Omega$ and for any $r>0$ such that $B(x, 4 r) \subset \Omega$, show that

  $$\sup _{\{y \in B(x, r)\}} u(y) \leqslant 3^{n} \inf _{\{y \in B(x, r)\}} u(y) .$$

  comment

• B2.18

  Partial Differential Equations | Part II, 2004

  (a) State and prove the Duhamel principle for the wave equation.

  (b) Let $u \in C^{2}\left([0, T] \times \mathbb{R}^{n}\right)$ be a solution of

  $$u_{t t}+u_{t}-\Delta u+u=0$$

  where $\Delta$ is taken in the variables $x \in \mathbb{R}^{n}$ and $u_{t}=\partial_{t} u$ etc.

  Using an 'energy method', or otherwise, show that, if $u=u_{t}=0$ on the set $\left\{t=0,\left|x-x_{0}\right| \leqslant t_{0}\right\}$ for some $\left(t_{0}, x_{0}\right) \in[0, T] \times \mathbb{R}^{n}$, then $u$ vanishes on the region $K(t, x)=\left\{(t, x): 0 \leqslant t \leqslant t_{0},\left|x-x_{0}\right| \leqslant t_{0}-t\right\}$. Hence deduce uniqueness for the Cauchy problem for the above PDE with Schwartz initial data.

  comment

• B3.18

  Partial Differential Equations | Part II, 2004

  (i) Find $w:[0, \infty) \times \mathbb{R} \longrightarrow \mathbb{R}$ such that $w(t, \cdot)$ is a Schwartz function of $\xi$ for each $t$ and solves

  $$\begin{gathered} w_{t}(t, \xi)+\left(1+\xi^{2}\right) w(t, \xi)=g(\xi), \\ w(0, \xi)=w_{0}(\xi), \end{gathered}$$

  where $g$ and $w_{0}$ are given Schwartz functions and $w_{t}$ denotes $\partial_{t} w$. If $\mathcal{F}$ represents the Fourier transform operator in the $\xi$ variables only and $\mathcal{F}^{-1}$ represents its inverse, show that the solution $w$ satisfies

  $$\partial_{t}\left(\mathcal{F}^{-1}\right) w(t, x)=\mathcal{F}^{-1}\left(\partial_{t} w\right)(t, x)$$

  and calculate $\lim _{t \rightarrow \infty} w(t, \cdot)$ in Schwartz space.

  (ii) Using the results of Part (i), or otherwise, show that there exists a solution of the initial value problem

  $$\begin{gathered} u_{t}(t, x)-u_{x x}(t, x)+u(t, x)=f(x) \\ u(0, x)=u_{0} \end{gathered}$$

  with $f$ and $u_{0}$ given Schwartz functions, such that

  $$\|u(t, \cdot)-\phi\|_{L^{\infty}(\mathbb{R})} \longrightarrow 0$$

  as $t \rightarrow \infty$ in Schwartz space, where $\phi$ is the solution of

  $$-\phi^{\prime \prime}+\phi=f .$$

  comment

• B4.18

  Partial Differential Equations | Part II, 2004

  (a) State a theorem of local existence, uniqueness and $C^{1}$ dependence on the initial data for a solution for an ordinary differential equation. Assuming existence, prove that the solution depends continuously on the initial data.

  (b) State a theorem of local existence of a solution for a general quasilinear firstorder partial differential equation with data on a smooth non-characteristic hypersurface. Prove this theorem in the linear case assuming the validity of the theorem in part (a); explain in your proof the importance of the non-characteristic condition.

  comment

Principles of Dynamics

• A1.2 B1.2

  Principles of Dynamics | Part II, 2004

  (i) In Hamiltonian mechanics the action is written

  $$S=\int d t\left(p^{a} \dot{q}^{a}-H\left(q^{a}, p^{a}, t\right)\right)$$

  Starting from Maupertius' principle $\delta S=0$, derive Hamilton's equations

  $$\dot{q}^{a}=\frac{\partial H}{\partial p^{a}}, \quad \dot{p}^{a}=-\frac{\partial H}{\partial q^{a}} .$$

  Show that $H$ is a constant of the motion if $\partial H / \partial t=0$. When is $p^{a}$ a constant of the motion?

  (ii) Consider the action $S$ given in Part (i), evaluated on a classical path, as a function of the final coordinates $q_{f}^{a}$ and final time $t_{f}$, with the initial coordinates and the initial time held fixed. Show that $S\left(q_{f}^{a}, t_{f}\right)$ obeys

  $$\frac{\partial S}{\partial q_{f}^{a}}=p_{f}^{a}, \quad \frac{\partial S}{\partial t_{f}}=-H\left(q_{f}^{a}, p_{f}^{a}, t_{f}\right)$$

  Now consider a simple harmonic oscillator with $H=\frac{1}{2}\left(p^{2}+q^{2}\right)$. Setting the initial time and the initial coordinate to zero, find the classical solution for $p$ and $q$ with final coordinate $q=q_{f}$ at time $t=t_{f}$. Hence calculate $S\left(t_{f}, q_{f}\right)$, and explicitly verify (2) in this case.

  comment

• A2.2 B2.1

  Principles of Dynamics | Part II, 2004

  (i) Consider a light rigid circular wire of radius $a$ and centre $O$. The wire lies in a vertical plane, which rotates about the vertical axis through $O$. At time $t$ the plane containing the wire makes an angle $\phi(t)$ with a fixed vertical plane. A bead of mass $m$ is threaded onto the wire. The bead slides without friction along the wire, and its location is denoted by $A$. The angle between the line $O A$ and the downward vertical is $\theta(t)$.

  Show that the Lagrangian of the system is

  $$\frac{m a^{2}}{2} \dot{\theta}^{2}+\frac{m a^{2}}{2} \dot{\phi}^{2} \sin ^{2} \theta+m g a \cos \theta .$$

  Calculate two independent constants of the motion, and explain their physical significance.

  (ii) A dynamical system has Hamiltonian $H(q, p, \lambda)$, where $\lambda$ is a parameter. Consider an ensemble of identical systems chosen so that the number density of systems, $f(q, p, t)$, in the phase space element $d q d p$ is either zero or one. Prove Liouville's Theorem, namely that the total area of phase space occupied by the ensemble is time-independent.

  Now consider a single system undergoing periodic motion $q(t), p(t)$. Give a heuristic argument based on Liouville's Theorem to show that the area enclosed by the orbit,

  $$I=\oint p d q$$

  is approximately conserved as the parameter $\lambda$ is slowly varied (i.e. that $I$ is an adiabatic invariant).

  Consider $H(q, p, \lambda)=\frac{1}{2} p^{2}+\lambda q^{2 n}$, with $n$ a positive integer. Show that as $\lambda$ is slowly varied the energy of the system, $E$, varies as

  $$E \propto \lambda^{1 /(n+1)} .$$

  comment

• A3.2

  Principles of Dynamics | Part II, 2004

  (i) Explain the concept of a canonical transformation from coordinates $\left(q^{a}, p^{a}\right)$ to $\left(Q^{a}, P^{a}\right)$. Derive the transformations corresponding to generating functions $F_{1}\left(t, q^{a}, Q^{a}\right)$ and $F_{2}\left(t, q^{a}, P^{a}\right)$.

  (ii) A particle moving in an electromagnetic field is described by the Lagrangian

  $$L=\frac{1}{2} m \dot{\mathbf{x}}^{2}-e\left(\phi-\frac{\dot{\mathbf{x}} \cdot \mathbf{A}}{c}\right)$$

  where $c$ is constant

  (a) Derive the equations of motion in terms of the electric and magnetic fields $\mathbf{E}$ and $\mathbf{B}$.

  (b) Show that $\mathbf{E}$ and $\mathbf{B}$ are invariant under the gauge transformation

  $$\mathbf{A} \rightarrow \mathbf{A}+\nabla \Lambda, \quad \phi \rightarrow \phi-\frac{1}{c} \frac{\partial \Lambda}{\partial t}$$

  for $\operatorname{arbitrary} \Lambda(t, \mathbf{x})$.

  (c) Construct the Hamiltonian. Find the generating function $F_{2}$ for the canonical transformation which implements the gauge transformation (1).

  comment

• A4.2

  Principles of Dynamics | Part II, 2004

  Consider a system of coordinates rotating with angular velocity $\boldsymbol{\omega}$ relative to an inertial coordinate system.

  Show that if a vector $\mathbf{v}$ is changing at a rate $d \mathbf{v} / d t$ in the inertial system, then it is changing at a rate

  $$\left.\frac{d \mathbf{v}}{d t}\right|_{\text {rot }}=\frac{d \mathbf{v}}{d t}-\boldsymbol{\omega} \wedge \mathbf{v}$$

  with respect to the rotating system.

  A solid body rotates with angular velocity $\omega$ in the absence of external torque. Consider the rotating coordinate system aligned with the principal axes of the body.

  (a) Show that in this system the motion is described by the Euler equations

  $\left.I_{1} \frac{d \omega_{1}}{d t}\right|_{\text {rot }}=\omega_{2} \omega_{3}\left(I_{2}-I_{3}\right) \quad,\left.\quad I_{2} \frac{d \omega_{2}}{d t}\right|_{\text {rot }}=\omega_{3} \omega_{1}\left(I_{3}-I_{1}\right) \quad,\left.\quad I_{3} \frac{d \omega_{3}}{d t}\right|_{\text {rot }}=\omega_{1} \omega_{2}\left(I_{1}-I_{2}\right)$, where $\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$ are the components of the angular velocity in the rotating system and $I_{1,2,3}$ are the principal moments of inertia.

  (b) Consider a body with three unequal moments of inertia, $I_{3}<I_{2}<I_{1}$. Show that rotation about the 1 and 3 axes is stable to small perturbations, but rotation about the 2 axis is unstable.

  (c) Use the Euler equations to show that the kinetic energy, $T$, and the magnitude of the angular momentum, $L$, are constants of the motion. Show further that

  $$2 T I_{3} \leq L^{2} \leq 2 T I_{1} \text {. }$$

  comment

Principles of Statistics

• A1.12 B1.15

  Principles of Statistics | Part II, 2004

  (i) What does it mean to say that a family $\{f(\cdot \mid \theta): \theta \in \Theta\}$ of densities is an exponential family?

  Consider the family of densities on $(0, \infty)$ parametrised by the positive parameters $a, b$ and defined by

  $$f(x \mid a, b)=\frac{a \exp \left(-(a-b x)^{2} / 2 x\right)}{\sqrt{2 \pi x^{3}}} \quad(x>0)$$

  Prove that this family is an exponential family, and identify the natural parameters and the reference measure.

  (ii) Let $\left(X_{1}, \ldots, X_{n}\right)$ be a sample drawn from the above distribution. Find the maximum-likelihood estimators of the parameters $(a, b)$. Find the Fisher information matrix of the family (in terms of the natural parameters). Briefly explain the significance of the Fisher information matrix in relation to unbiased estimation. Compute the mean of $X_{1}$ and of $X_{1}^{-1}$.

  comment

• A2.11 B2.16

  Principles of Statistics | Part II, 2004

  (i) In the context of a decision-theoretic approach to statistics, what is a loss function? a decision rule? the risk function of a decision rule? the Bayes risk of a decision rule? the Bayes rule with respect to a given prior distribution?

  Show how the Bayes rule with respect to a given prior distribution is computed.

  (ii) A sample of $n$ people is to be tested for the presence of a certain condition. A single real-valued observation is made on each one; this observation comes from density $f_{0}$ if the condition is absent, and from density $f_{1}$ if the condition is present. Suppose $\theta_{i}=0$ if the $i^{\text {th }}$person does not have the condition, $\theta_{i}=1$ otherwise, and suppose that the prior distribution for the $\theta_{i}$ is that they are independent with common distribution $P\left(\theta_{i}=1\right)=p \in(0,1)$, where $p$ is known. If $X_{i}$ denotes the observation made on the $i^{\text {th }}$person, what is the posterior distribution of the $\theta_{i}$ ?

  Now suppose that the loss function is defined by

  $$L_{0}(\theta, a) \equiv \sum_{j=1}^{n}\left(\alpha a_{j}\left(1-\theta_{j}\right)+\beta\left(1-a_{j}\right) \theta_{j}\right)$$

  for action $a \in[0,1]^{n}$, where $\alpha, \beta$ are positive constants. If $\pi_{j}$ denotes the posterior probability that $\theta_{j}=1$ given the data, prove that the Bayes rule for this prior and this loss function is to take $a_{j}=1$ if $\pi_{j}$ exceeds the threshold value $\alpha /(\alpha+\beta)$, and otherwise to take $a_{j}=0$.

  In an attempt to control the proportion of false positives, it is proposed to use a different loss function, namely,

  $$L_{1}(\theta, a) \equiv L_{0}(\theta, a)+\gamma I_{\left\{\sum a_{j}>0\right\}}\left(1-\frac{\sum \theta_{j} a_{j}}{\sum a_{j}}\right)$$

  where $\gamma>0$. Prove that the Bayes rule is once again a threshold rule, that is, we take action $a_{j}=1$ if and only if $\pi_{j}>\lambda$, and determine $\lambda$ as fully as you can.

  comment

• A3.12 B3.15

  Principles of Statistics | Part II, 2004

  (i) What is a sufficient statistic? What is a minimal sufficient statistic? Explain the terms nuisance parameter and ancillary statistic.

  (ii) Let $U_{1}, \ldots, U_{n}$ be independent random variables with common uniform( $([0,1])$ distribution, and suppose you observe $X_{i} \equiv a U_{i}^{-\beta}, i=1, \ldots, n$, where the positive parameters $a, \beta$ are unknown. Write down the joint density of $X_{1}, \ldots, X_{n}$ and prove that the statistic

  $$(m, p) \equiv\left(\min _{1 \leqslant j \leqslant n}\left\{X_{j}\right\}, \prod_{j=1}^{n} X_{j}\right)$$

  is minimal sufficient for $(a, \beta)$. Find the maximum-likelihood estimator $(\hat{a}, \hat{\beta})$ of $(a, \beta)$.

  Regarding $\beta$ as the parameter of interest and $a$ as the nuisance parameter, is $m$ ancillary? Find the mean and variance of $\hat{\beta}$. Hence find an unbiased estimator of $\beta$.

  comment

• A4.13 B4.15

  Principles of Statistics | Part II, 2004

  Suppose that $\theta \in \mathbb{R}^{d}$ is the parameter of a non-degenerate exponential family. Derive the asymptotic distribution of the maximum-likelihood estimator $\hat{\theta}_{n}$ of $\theta$ based on a sample of size $n$. [You may assume that the density is infinitely differentiable with respect to the parameter, and that differentiation with respect to the parameter commutes with integration.]

  Part II 2004

  comment

Probability and Measure

• B1.13

  Probability and Measure | Part II, 2004

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space and let $\mathcal{A}=\left(A_{i}: i=1,2, \ldots\right)$ be a sequence of events.

  (a) What is meant by saying that $\mathcal{A}$ is a family of independent events?

  (b) Define the events $\left\{A_{n}\right.$ infinitely often $\}$ and $\left\{A_{n}\right.$ eventually $\}$. State and prove the two Borel-Cantelli lemmas for $\mathcal{A}$.

  (c) Let $X_{1}, X_{2}, \ldots$ be the outcomes of a sequence of independent flips of a fair coin,

  $$\mathbb{P}\left(X_{i}=0\right)=\mathbb{P}\left(X_{i}=1\right)=\frac{1}{2} \quad \text { for } i \geqslant 1$$

  Let $L_{n}$ be the length of the run beginning at the $n^{\text {th }}$flip. For example, if the first fourteen outcomes are 01110010000110 , then $L_{1}=1, L_{2}=3, L_{3}=2$, etc.

  Show that

  $$\mathbb{P}\left(\limsup _{n \rightarrow \infty} \frac{L_{n}}{\log _{2} n}>1\right)=0$$

  and furthermore that

  $$\mathbb{P}\left(\limsup _{n \rightarrow \infty} \frac{L_{n}}{\log _{2} n}=1\right)=1$$

  comment

• B2.12

  Probability and Measure | Part II, 2004

  Let $(\Omega, \mathcal{F}, \mu)$ be a measure space and let $1 \leqslant p \leqslant \infty$.

  (a) Define the $L^{p}$-norm $\|f\|_{p}$ of a measurable function $f: \Omega \rightarrow \mathbb{R}$, and define the space $L^{p}(\Omega, \mathcal{F}, \mu) .$

  (b) Prove Minkowski's inequality:

  $$\|f+g\|_{p} \leqslant\|f\|_{p}+\|g\|_{p} \text { for } f, g \in L^{p}(\Omega, \mathcal{F}, \mu), 1 \leqslant p \leqslant \infty$$

  [You may use Hölder's inequality without proof provided it is clearly stated.]

  (c) Explain what is meant by saying that $L^{p}(\Omega, \mathcal{F}, \mu)$ is complete. Show that $L^{\infty}(\Omega, \mathcal{F}, \mu)$ is complete.

  (d) Suppose that $\left\{f_{n}: n \geqslant 1\right\}$ is a sequence of measurable functions satisfying $\left\|f_{n}\right\|_{p} \rightarrow 0$ as $n \rightarrow \infty$.

  (i) Show that if $p=\infty$, then $f_{n} \rightarrow 0$ almost everywhere.

  (ii) When $1 \leqslant p<\infty$, give an example of a measure space $(\Omega, \mathcal{F}, \mu)$ and such a sequence $\left\{f_{n}\right\}$ such that, for all $\omega \in \Omega, f_{n}(\omega) \nrightarrow 0$ as $n \rightarrow \infty$.

  comment

• B3.12

  Probability and Measure | Part II, 2004

  (a) Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space and let $\theta: \Omega \rightarrow \Omega$ be measurable. What is meant by saying that $\theta$ is measure-preserving? Define an invariant event and an invariant random variable, and explain what is meant by saying that $\theta$ is ergodic.

  (b) Let $m$ be a probability measure on $(\mathbb{R}, \mathcal{B})$. Let

  $$\Omega=\mathbb{R}^{\mathbb{N}}=\left\{x=\left(x_{1}, x_{2}, \ldots\right): x_{i} \in \mathbb{R} \text { for } i \geqslant 1\right\}$$

  let $\mathcal{F}$ be the smallest $\sigma$-field of $\Omega$ with respect to which the coordinate maps $X_{n}(x)=x_{n}$, for $x \in \Omega, n \geqslant 1$, are measurable, and let $\mathbb{P}$ be the unique probability measure on $(\Omega, \mathcal{F})$ satisfying

  $$\mathbb{P}\left(X_{i} \in A_{i} \text { for } 1 \leqslant i \leqslant n\right)=\prod_{i=1}^{n} m\left(A_{i}\right)$$

  for all $A_{i} \in \mathcal{B}, n \geqslant 1$. Define $\theta: \Omega \rightarrow \Omega$ by $\theta(x)=\left(x_{2}, x_{3}, \ldots\right)$ for $x=\left(x_{1}, x_{2}, \ldots\right)$.

  (i) Show that $\theta$ is measurable and measure-preserving.

  (ii) Define the tail $\sigma$-field $\mathcal{T}$ of the coordinate maps $X_{1}, X_{2}, \ldots$, and show that the invariant $\sigma$-field $\mathcal{I}$ of $\theta$ satisfies $\mathcal{I} \subseteq \mathcal{T}$. Deduce that $\theta$ is ergodic. [Any general result used must be stated clearly but the proof may be omitted.]

  (c) State Birkhoff's ergodic theorem and explain how to deduce that, given independent identically-distributed integrable random variables $Y_{1}, Y_{2}, \ldots$, there exists $\nu \in \mathbb{R}$ such that

  $$\frac{1}{n}\left(Y_{1}+Y_{2}+\cdots+Y_{n}\right) \rightarrow \nu \quad \text { a.e. as } \quad n \rightarrow \infty .$$

  comment

• B4.11

  Probability and Measure | Part II, 2004

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space and let $X, X_{1}, X_{2}, \ldots$ be random variables. Write an essay in which you discuss the statement: if $X_{n} \rightarrow X$ almost everywhere, then $\mathbb{E}\left(X_{n}\right) \rightarrow \mathbb{E}(X)$. You should include accounts of monotone, dominated, and bounded convergence, and of Fatou's lemma.

  [You may assume without proof the following fact. Let $(\Omega, \mathcal{F}, \mu)$ be a measure space, and let $f: \Omega \rightarrow \mathbb{R}$ be non-negative with finite integral $\mu(f) .$ If $\left(f_{n}: n \geqslant 1\right)$ are non-negative measurable functions with $f_{n}(\omega) \uparrow f(\omega)$ for all $\omega \in \Omega$, then $\mu\left(f_{n}\right) \rightarrow \mu(f)$ as $n \rightarrow \infty$.]

  comment

Quantum Physics

• A1.14

  Quantum Physics | Part II, 2004

  (i) Each particle in a system of $N$ identical fermions has a set of energy levels $E_{i}$ with degeneracy $g_{i}$, where $i=1,2, \ldots$. Derive the expression

  $$\bar{N}_{i}=\frac{g_{i}}{e^{\beta\left(E_{i}-\mu\right)}+1},$$

  for the mean number of particles $\bar{N}_{i}$ with energy $E_{i}$. Explain the physical significance of the parameters $\beta$ and $\mu$.

  (ii) The spatial eigenfunctions of energy for an electron of mass $m$ moving in two dimensions and confined to a square box of side $L$ are

  $$\psi_{n_{1} n_{2}}(\mathbf{x})=\frac{2}{L} \sin \left(\frac{n_{1} \pi x}{L}\right) \sin \left(\frac{n_{2} \pi y}{L}\right)$$

  where $n_{i}=1,2, \ldots(i=1,2)$. Calculate the associated energies.

  Hence show that when $L$ is large the number of states in energy range $E \rightarrow E+d E$ is

  $$\frac{m L^{2}}{2 \pi \hbar^{2}} d E$$

  How is this formula modified when electron spin is taken into account?

  The box is filled with $N$ electrons in equilibrium at temperature $T$. Show that the chemical potential $\mu$ is given by

  $$\mu=\frac{1}{\beta} \log \left(e^{\beta \pi \hbar^{2} \rho / m}-1\right)$$

  where $\rho$ is the number of particles per unit area in the box.

  What is the value of $\mu$ in the limit $T \rightarrow 0$ ?

  Calculate the total energy of the lowest state of the system of particles as a function of $N$ and $L$.

  comment

• A2.14

  Quantum Physics | Part II, 2004

  (i) A simple model of a crystal consists of an infinite linear array of sites equally spaced with separation $b$. The probability amplitude for an electron to be at the $n$-th site is $c_{n}, n=0, \pm 1, \pm 2, \ldots$. The Schrödinger equation for the $\left\{c_{n}\right\}$ is

  $$E c_{n}=E_{0} c_{n}-A\left(c_{n-1}+c_{n+1}\right)$$

  where $A$ is real and positive. Show that the allowed energies $E$ of the electron must lie in a band $\left|E-E_{0}\right| \leq 2 A$, and that the dispersion relation for $E$ written in terms of a certain parameter $k$ is given by

  $$E=E_{0}-2 A \cos k b$$

  What is the physical interpretation of $E_{0}, A$ and $k$ ?

  (ii) Explain briefly the idea of group velocity and show that it is given by

  $$v=\frac{1}{\hbar} \frac{d E(k)}{d k},$$

  for an electron of momentum $\hbar k$ and energy $E(k)$.

  An electron of charge $q$ confined to one dimension moves in a periodic potential under the influence of an electric field $\mathcal{E}$. Show that the equation of motion for the electron is

  $$\dot{v}=\frac{q \mathcal{E}}{\hbar^{2}} \frac{d^{2} E}{d k^{2}},$$

  where $v(t)$ is the group velocity of the electron at time $t$. Explain why

  $$m^{*}=\hbar^{2}\left(\frac{d^{2} E}{d k^{2}}\right)^{-1}$$

  can be interpreted as an effective mass.

  Show briefly how the absence from a band of an electron of charge $q$ and effective mass $m^{*}<0$ can be interpreted as the presence of a 'hole' carrier of charge $-q$ and effective mass $-m^{*}$.

  In the model of Part (i) show that

  (a) for $k^{2} \ll 12 / b^{2}$ an electron behaves like a free particle of mass $\hbar^{2} /\left(2 A b^{2}\right)$;

  (b) for $(\pi / b-k)^{2} \ll 12 / b^{2}$ a hole behaves like a free particle of mass $\hbar^{2} /\left(2 A b^{2}\right)$.

  comment

• A4.16

  Quantum Physics | Part II, 2004

  Explain the operation of the $n p$ junction. Your account should include a discussion of the following topics:

  (a) the rôle of doping and the fermi-energy;

  (b) the rôle of majority and minority carriers;

  (c) the contact potential;

  (d) the relationship $I(V)$ between the current $I$ flowing through the junction and the external voltage $V$ applied across the junction;

  (e) the property of rectification.

  comment

Representation Theory

• B1.6

  Representation Theory | Part II, 2004

  (a) Show that every irreducible complex representation of an abelian group is onedimensional.

  (b) Show, by example, that the analogue of (a) fails for real representations.

  (c) Let the cyclic group of order $n$ act on $\mathbb{C}^{n}$ by cyclic permutation of the standard basis vectors. Decompose this representation explicitly into irreducibles.

  comment

• B2.6

  Representation Theory | Part II, 2004

  Let $H$ be a group with three generators $c, g, h$ and relations $c^{p}=g^{p}=h^{p}=1$, $c g=g c, c h=h c$ and $g h=c h g$ where $p$ is a prime number.

  (a) Show that $|H|=p^{3}$. Show that the conjugacy classes of $H$ are the singletons $\{1\},\{c\}, \ldots,\left\{c^{p-1}\right\}$ and the sets $\left\{g^{m} h^{n}, c g^{m} h^{n}, \ldots, c^{p-1} g^{m} h^{n}\right\}$, as $m, n$ range from 0 to $p-1$, but $(m, n) \neq(0,0)$.

  (b) Find $p^{2}$ 1-dimensional representations of $H$.

  (c) Let $\omega \neq 1$ be a $p$ th root of unity. Show that the following defines an irreducible representation of $H$ on $\mathbb{C}^{p}$ :

  $$\begin{gathered} \rho(c)=\omega \mathrm{Id}, \\ \rho(g) \mathbf{e}_{k}=\omega^{k} \mathbf{e}_{k}, \\ \rho(h) \mathbf{e}_{p}=\mathbf{e}_{1} \text { and } \rho(h) \mathbf{e}_{k}=\mathbf{e}_{k+1} \text { if } k<p \end{gathered}$$

  where the $\mathbf{e}_{k}$ are the standard basis vectors of $\mathbb{C}^{p}$.

  (d) Show that (b) and (c) cover all irreducible isomorphism classes.

  comment

• B3.5

  Representation Theory | Part II, 2004

  Compute the character table for the group $A_{5}$ of even permutations of five elements. You may wish to follow the steps below.

  (a) List the conjugacy classes in $A_{5}$ and their orders.

  (b) $A_{5}$ acts on $\mathbb{C}^{5}$ by permuting the standard basis vectors. Show that $\mathbb{C}^{5}$ splits as $\mathbb{C} \oplus V$, where $\mathbb{C}$ is the trivial 1-dimensional representation and $V$ is irreducible.

  (c) By using the formula for the character of the symmetric square $S^{2} V$,

  $$\chi_{S^{2} V}(g)=\frac{1}{2}\left[\chi_{V}(g)^{2}+\chi_{V}\left(g^{2}\right)\right]$$

  decompose $S^{2} V$ to produce a 5-dimensional, irreducible representation, and find its character.

  (d) Show that the exterior square $\Lambda^{2} V$ decomposes into two distinct irreducibles and compute their characters, to complete the character table of $A_{5}$.

  [Hint: You can save yourself some computational effort if you can explain why the automorphism of $A_{5}$, defined by conjugation by a transposition in $S_{5}$, must swap the two summands of $\Lambda^{2} V$.]

  comment

• B4.2

  Representation Theory | Part II, 2004

  Write an essay on the finite-dimensional representations of $S U_{2}$, including a proof of their complete reducibility, and a description of the irreducible representations and the decomposition of their tensor products.

  comment

Riemann Surfaces

• B1.11

  Riemann Surfaces | Part II, 2004

  Let $\tau$ be a fixed complex number with positive imaginary part. For $z \in \mathbb{C}$, define

  $$v(z)=\sum_{n=-\infty}^{\infty} \exp \left(\pi i \tau n^{2}+2 \pi i n\left(z+\frac{1}{2}\right)\right) .$$

  Prove the identities

  $$v(z+1)=v(z), \quad v(-z)=v(z), \quad v(z+\tau)=-\exp (-\pi i \tau-2 \pi i z) \cdot v(z)$$

  and deduce that $v(\tau / 2)=0$. Show further that $\tau / 2$ is the only zero of $v$ in the parallelogram $P$ with vertices $-1 / 2,1 / 2,1 / 2+\tau,-1 / 2+\tau$.

  [You may assume that $v$ is holomorphic on $\mathbb{C}$.]

  Now let $\left\{a_{1}, \ldots, a_{k}\right\}$ and $\left\{b_{1}, \ldots, b_{k}\right\}$ be two sets of complex numbers and

  $$f(z)=\prod_{j=1}^{k} \frac{v\left(z-a_{j}\right)}{v\left(z-b_{j}\right)}$$

  Prove that $f$ is a doubly-periodic meromorphic function, with periods 1 and $\tau$, if and only if $\sum_{j=1}^{k}\left(a_{j}-b_{j}\right)$ is an integer.

  comment

• B3.9

  Riemann Surfaces | Part II, 2004

  (a) Let $f: R \rightarrow S$ be a non-constant holomorphic map between compact connected Riemann surfaces $R$ and $S$.

  Define the branching order $v_{f}(p)$ at a point $p \in R$ and show that it is well-defined. Show further that if $h$ is a holomorphic map on $S$ then $v_{h \circ f}(p)=v_{h}(f(p)) v_{f}(p)$.

  Define the degree of $f$ and state the Riemann-Hurwitz formula. Show that if $R$ has Euler characteristic 0 then either $S$ is the 2 -sphere or $v_{p}(f)=1$ for all $p \in R$.

  (b) Let $P$ and $Q$ be complex polynomials of degree $m \geq 2$ with no common roots. Explain briefly how the rational function $P(z) / Q(z)$ induces a holomorphic map $F$ from the 2-sphere $S^{2} \cong \mathbb{C} \cup\{\infty\}$ to itself. What is the degree of $F$ ? Show that there is at least one and at most $2 m-2$ points $w \in S^{2}$ such that the number of distinct solutions $z \in S^{2}$ of the equation $F(z)=w$ is strictly less than $\operatorname{deg} F$.

  comment

• B4.8

  Riemann Surfaces | Part II, 2004

  Let $\Lambda$ be a lattice in $\mathbb{C}, \Lambda=\mathbb{Z} \omega_{1}+\mathbb{Z} \omega_{2}$, where $\omega_{1}, \omega_{2} \neq 0$ and $\omega_{1} / \omega_{2} \notin \mathbb{R}$. By constructing an appropriate family of charts, show that the torus $\mathbb{C} / \Lambda$ is a Riemann surface and that the natural projection $\pi: z \in \mathbb{C} \rightarrow z+\Lambda \in \mathbb{C} / \Lambda$ is a holomorphic map.

  [You may assume without proof any known topological properties of $\mathbb{C} / \Lambda$.]

  Let $\Lambda^{\prime}=\mathbb{Z} \omega_{1}^{\prime}+\mathbb{Z} \omega_{2}^{\prime}$ be another lattice in $\mathbb{C}$, with $\omega_{1}^{\prime}, \omega_{2}^{\prime} \neq 0$ and $\omega_{1}^{\prime} / \omega_{2}^{\prime} \notin \mathbb{R}$. By considering paths from 0 to an arbitrary $z \in \mathbb{C}$, show that if $f: \mathbb{C} / \Lambda \rightarrow \mathbb{C} / \Lambda^{\prime}$ is a conformal equivalence then

  $$f(z+\Lambda)=(a z+b)+\Lambda^{\prime} \quad \text { for some } a, b, \in \mathbb{C}, \text { with } a \neq 0$$

  [Any form of the Monodromy Theorem and basic results on the lifts of paths may be used without proof, provided that these are correctly stated. You may assume without proof that every injective holomorphic function $F: \mathbb{C} \rightarrow \mathbb{C}$ is of the form $F(z)=a z+b$, for some $a, b \in \mathbb{C}$.]

  Give an explicit example of a non-constant holomorphic map $\mathbb{C} / \Lambda \rightarrow \mathbb{C} / \Lambda$ that is not a conformal equivalence.

  Part II 2004

  comment

Statistical Physics

• B1.22

  Statistical Physics | Part II, 2004

  Define the notions of entropy $S$ and thermodynamic temperature $T$ for a gas of particles in a variable volume $V$. Derive the fundamental relation

  $$d E=T d S-P d V$$

  The free energy of the gas is defined as $F=E-T S$. Why is it convenient to regard $F$ as a function of $T$ and $V$ ? By considering $F$, or otherwise, show that

  $$\left.\frac{\partial S}{\partial V}\right|_{T}=\left.\frac{\partial P}{\partial T}\right|_{V}$$

  Deduce that the entropy of an ideal gas, whose equation of state is $P V=N T$ (using energy units), has the form

  $$S=N \log \left(\frac{V}{N}\right)+N c(T)$$

  where $c(T)$ is independent of $N$ and $V$.

  Show that if the gas is in contact with a heat bath at temperature $T$, then the probability of finding the gas in a particular quantum microstate of energy $E_{r}$ is

  $$P_{r}=e^{\left(F-E_{r}\right) / T}$$

  comment

• B3.22

  Statistical Physics | Part II, 2004

  Describe briefly why a low density gas can be investigated using classical statistical mechanics.

  Explain why, for a gas of $N$ structureless atoms, the measure on phase space is

  $$\frac{1}{N !} \frac{d^{3 N} q d^{3 N} p}{(2 \pi \hbar)^{3 N}}$$

  and the probability density in phase space is proportional to

  $$e^{-E(q, p) / T}$$

  where $T$ is the temperature in energy units.

  Derive the Maxwell probability distribution for atomic speeds $v$,

  $$\rho(v)=\left(\frac{m}{2 \pi T}\right)^{3 / 2} 4 \pi v^{2} e^{-m v^{2} / 2 T}$$

  Why is this valid even if the atoms interact?

  Find the mean value $\bar{v}$ of the speed of the atoms.

  Is $\frac{1}{2} m(\bar{v})^{2}$ the mean kinetic energy of the atoms?

  comment

• B4.23

  Statistical Physics | Part II, 2004

  Derive the Bose-Einstein expression for the mean number of Bose particles $\bar{n}$ occupying a particular single-particle quantum state of energy $\varepsilon$, when the chemical potential is $\mu$ and the temperature is $T$ in energy units.

  Why is the chemical potential for a gas of photons given by $\mu=0$ ?

  Show that, for black-body radiation in a cavity of volume $V$ at temperature $T$, the mean number of photons in the angular frequency range $(\omega, \omega+d \omega)$ is

  $$\frac{V}{\pi^{2} c^{3}} \frac{\omega^{2} d \omega}{e^{\hbar \omega / T}-1}$$

  Hence, show that the total energy $E$ of the radiation in the cavity is

  $$E=K V T^{4}$$

  where $K$ is a constant that need not be evaluated.

  Use thermodynamic reasoning to find the entropy $S$ and pressure $P$ of the radiation and verify that

  $$E-T S+P V=0$$

  Why is this last result to be expected for a gas of photons?

  comment

Statistical Physics and Cosmology

• A1.16

  Statistical Physics and Cosmology | Part II, 2004

  (i) Consider a homogeneous and isotropic universe with mass density $\rho(t)$, pressure $P(t)$ and scale factor $a(t)$. As the universe expands its energy $E$ decreases according to the thermodynamic relation $d E=-P d V$ where $V$ is the volume. Deduce the fluid conservation law

  $$\dot{\rho}=-3 \frac{\dot{a}}{a}\left(\rho+\frac{P}{c^{2}}\right) .$$

  Apply the conservation of total energy (kinetic plus gravitational potential) to a test particle on the edge of a spherical region in this universe to obtain the Friedmann equation

  $$\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G}{3} \rho-\frac{k c^{2}}{a^{2}}$$

  where $k$ is a constant. State clearly any assumptions you have made.

  (ii) Our universe is believed to be flat $(k=0)$ and filled with two major components: pressure-free matter $\left(P_{\mathrm{M}}=0\right)$ and dark energy with equation of state $P_{\mathrm{Q}}=-\rho_{\mathrm{Q}} c^{2}$ where the mass densities today $\left(t=t_{0}\right)$ are given respectively by $\rho_{\mathrm{M} 0}$ and $\rho_{\mathrm{Q} 0}$. Assume that each component independently satisfies the fluid conservation equation to show that the total mass density can be expressed as

  $$\rho(t)=\frac{\rho_{\mathrm{M} 0}}{a^{3}}+\rho_{\mathrm{Q} 0},$$

  where we have set $a\left(t_{0}\right)=1$.

  Now consider the substitution $b=a^{3 / 2}$ in the Friedmann equation to show that the solution for the scale factor can be written in the form

  $$a(t)=\alpha(\sinh \beta t)^{2 / 3}$$

  where $\alpha$ and $\beta$ are constants. Setting $a\left(t_{0}\right)=1$, specify $\alpha$ and $\beta$ in terms of $\rho_{\mathrm{M} 0}, \rho_{\mathrm{Q} 0}$ and $t_{0}$. Show that the scale factor $a(t)$ has the expected behaviour for an Einstein-de Sitter universe at early times $(t \rightarrow 0)$ and that the universe accelerates at late times $(t \rightarrow \infty)$.

  [Hint: Recall that $\int d x / \sqrt{x^{2}+1}=\sinh ^{-1} x$.]

  comment

• A3.14

  Statistical Physics and Cosmology | Part II, 2004

  (i) In equilibrium, the number density of a non-relativistic particle species is given by

  $$n=g_{\mathrm{s}}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} e^{\left(\mu-m c^{2}\right) / k T}$$

  where $m$ is the mass, $\mu$ is the chemical potential and $g_{\mathrm{s}}$ is the spin degeneracy. At around $t=100$ seconds, deuterium $D$ forms through the nuclear fusion of nonrelativistic protons $p$ and neutrons $n$ via the interaction:

  $$p+n \leftrightarrow D$$

  What is the relationship between the chemical potentials of the three species when they are in chemical equilibrium? Show that the ratio of their number densities can be expressed as

  $$\frac{n_{D}}{n_{n} n_{p}} \approx\left(\frac{h^{2}}{\pi m_{p} k T}\right)^{3 / 2} e^{B_{D} / k T},$$

  where the deuterium binding energy is $B_{D}=\left(m_{n}+m_{p}-m_{D}\right) c^{2}$ and you may take $g_{D}=4$. Now consider the fractional densities $X_{a}=n_{a} / n_{B}$, where $n_{B}$ is the baryon number of the universe, to re-express the ratio above in the form

  $$\frac{X_{D}}{X_{n} X_{p}}$$

  which incorporates the baryon-to-photon ratio $\eta$ of the universe. [You may assume that the photon density is $n_{\gamma}=\frac{16 \pi \zeta(3)}{(h c)^{3}}(k T)^{3}$.] From this expression, explain why deuterium does not form until well below the temperature $k T \approx B_{D}$.

  (ii) The number density $n=N / V$ for a photon gas in equilibrium is given by the formula

  $$n=\frac{8 \pi}{c^{3}} \int_{0}^{\infty} \frac{\nu^{2} d \nu}{e^{h \nu / k T}-1},$$

  where $\nu$ is the photon frequency. By considering the substitution $x=h \nu / k T$, show that the photon number density can be expressed in the form

  $$n=\alpha T^{3}$$

  where the constant $\alpha$ need not be evaluated explicitly.

  State the equation of state for a photon gas and explain why the chemical potential of the photon vanishes. Assuming that the photon energy density $\epsilon=E / V=(4 \sigma / c) T^{4}$, use the first law $d E=T d S-P d V+\mu d N$ to show that the entropy density is given by

  $$s=S / V=\frac{16 \sigma}{3 c} T^{3}$$

  Hence explain why, when photons are in equilibrium at early times in our universe, their temperature varies inversely with the scale factor: $T \propto a^{-1}$.

  comment

• A4.18

  Statistical Physics and Cosmology | Part II, 2004

  (a) Consider an ideal gas of Fermi particles obeying the Pauli exclusion principle with a set of one-particle energy eigenstates $E_{i}$. Given the probability $p_{i}\left(n_{i}\right)$ at temperature $T$ that there are $n_{i}$ particles in the eigenstate $E_{i}$ :

  $$p_{i}\left(n_{i}\right)=\frac{e^{\left(\mu-E_{i}\right) n_{i} / k T}}{Z_{i}},$$

  determine the appropriate normalization factor $Z_{i}$. Use this to find the average number $\bar{n}_{i}$ of Fermi particles in the eigenstate $E_{i}$.

  Explain briefly why in generalizing these discrete eigenstates to a continuum in momentum space (in the range $p$ to $p+d p$ ) we must multiply by the density of states

  $$g(p) d p=\frac{4 \pi g_{s} V}{h^{3}} p^{2} d p$$

  where $g_{s}$ is the degeneracy of the eigenstates and $V$ is the volume.

  (b) With the energy expressed as a momentum integral

  $$E=\int_{0}^{\infty} E(p) \bar{n}(p) d p$$

  consider the effect of changing the volume $V$ so slowly that the occupation numbers do not change (i.e. particle number $N$ and entropy $S$ remain fixed). Show that the momentum varies as $d p / d V=-p / 3 V$ and so deduce from the first law expression

  $$\left(\frac{\partial E}{\partial V}\right)_{N, S}=-P$$

  that the pressure is given by

  $$P=\frac{1}{3 V} \int_{0}^{\infty} p E^{\prime}(p) \bar{n}(p) d p .$$

  Show that in the non-relativistic limit $P=\frac{2}{3} U / V$ where $U$ is the internal energy, while for ultrarelativistic particles $P=\frac{1}{3} E / V$.

  (c) Now consider a Fermi gas in the limit $T \rightarrow 0$ with all momentum eigenstates filled up to the Fermi momentum $p_{\mathrm{F}}$. Explain why the number density can be written as

  $$n=\frac{4 \pi g_{s}}{h^{3}} \int_{0}^{p_{\mathrm{F}}} p^{2} d p \propto p_{\mathrm{F}}^{3}$$

  From similar expressions for the energy, deduce in both the non-relativistic and ultrarelativistic limits that the pressure may be written as

  $$P \propto n^{\gamma}$$

  where $\gamma$ should be specified in each case.

  (d) Examine the stability of an object of radius $R$ consisting of such a Fermi degenerate gas by comparing the gravitational binding energy with the total kinetic energy. Briefly point out the relevance of these results to white dwarfs and neutron stars.

  comment

Stochastic Financial Models

• A1.11 B1.16

  Stochastic Financial Models | Part II, 2004

  (i) What does it mean to say that $U$ is a utility function? What is a utility function with constant absolute risk aversion (CARA)?

  Let $S_{t} \equiv\left(S_{t}^{1}, \ldots, S_{t}^{d}\right)^{T}$ denote the prices at time $t=0,1$ of $d$ risky assets, and suppose that there is also a riskless zeroth asset, whose price at time 0 is 1 , and whose price at time 1 is $1+r$. Suppose that $S_{1}$ has a multivariate Gaussian distribution, with mean $\mu_{1}$ and non-singular covariance $V$. An agent chooses at time 0 a portfolio $\theta=\left(\theta^{1}, \ldots, \theta^{d}\right)^{T}$ of holdings of the $d$ risky assets, at total cost $\theta \cdot S_{0}$, and at time 1 realises his gain $X=\theta \cdot\left(S_{1}-(1+r) S_{0}\right)$. Given that he wishes the mean of $X$ to be equal to $m$, find the smallest value that the variance $v$ of $X$ can be. What is the portfolio that achieves this smallest variance? Hence sketch the region in the $(v, m)$ plane of pairs $(v, m)$ that can be achieved by some choice of $\theta$, and indicate the mean-variance efficient frontier.

  (ii) Suppose that the agent has a CARA utility with coefficient $\gamma$ of absolute risk aversion. What portfolio will he choose in order to maximise $E U(X)$ ? What then is the mean of $X$ ?

  Regulation requires that the agent's choice of portfolio $\theta$ has to satisfy the valueat-risk (VaR) constraint

  $$m \geqslant-L+a \sqrt{v},$$

  where $L>0$ and $a>0$ are determined by the regulatory authority. Show that this constraint has no effect on the agent's decision if $\kappa \equiv \sqrt{\mu \cdot V^{-1} \mu} \geqslant a$. If $\kappa<a$, will this constraint necessarily affect the agent's choice of portfolio?

  comment

• A3.11 B3.16

  Stochastic Financial Models | Part II, 2004

  (i) Consider a single-period binomial model of a riskless asset (asset 0 ), worth 1 at time 0 and $1+r$ at time 1 , and a risky asset (asset 1 ), worth 1 at time 0 and worth $u$ at time 1 if the period was good, otherwise worth $d$. Assuming that

  $$d<1+r<u$$

  show how any contingent claim $Y$ to be paid at time 1 can be priced and exactly replicated. Briefly explain the significance of the condition $(*)$, and indicate how the analysis of the single-period model extends to many periods.

  (ii) Now suppose that $u=5 / 3, d=2 / 3, r=1 / 3$, and that the risky asset is worth $S_{0}=864=2^{5} \times 3^{3}$ at time zero. Show that the time- 0 value of an American put option with strike $K=S_{0}$ and expiry at time $t=3$ is equal to 79 , and find the optimal exercise policy.

  comment

• A4.12 B4.16

  Stochastic Financial Models | Part II, 2004

  What is Brownian motion $\left(B_{t}\right)_{t \geqslant 0}$ ? Briefly explain how Brownian motion can be considered as a limit of simple random walks. State the Reflection Principle for Brownian motion, and use it to derive the distribution of the first passage time $\tau_{a} \equiv \inf \left\{t: B_{t}=a\right\}$ to some level $a>0$.

  Suppose that $X_{t}=B_{t}+c t$, where $c>0$ is constant. Stating clearly any results to which you appeal, derive the distribution of the first-passage time $\tau_{a}^{(c)} \equiv \inf \left\{t: X_{t}=a\right\}$ to $a>0$.

  Now let $\sigma_{a} \equiv \sup \left\{t: X_{t}=a\right\}$, where $a>0$. Find the density of $\sigma_{a}$.

  comment

Symmetries and Groups in Physics

• A1.19

  Symmetries and Groups in Physics | Part II, 2004

  (i) State and prove Maschke's theorem for finite-dimensional representations of finite groups.

  (ii) $S_{3}$ is the group of bijections on $\{1,2,3\}$. Find the irreducible representations of $S_{3}$, state their dimensions and give their character table.

  Let $T_{2}$ be the set of objects $T_{2}=\left\{a_{i_{1} i_{2}}: i_{1}, i_{2}=1,2,3\right\}$. The operation of the permutation group $S_{3}$ on $T_{2}$ is defined by the operation of the elements of $S_{3}$ separately on each index $i_{1}$ and $i_{2}$. For example,

  $$P_{12}: a_{13} \rightarrow a_{23}, \quad P_{231}: a_{23} \rightarrow a_{31}, \quad P_{13}: a_{33} \rightarrow a_{11}$$

  By considering a representative operator from each conjugacy class of $S_{3}$, find the table of group characters for the representation $\mathcal{T}_{2}$ of $S_{3}$ acting on $T_{2}$. Hence, deduce the irreducible representations into which $\mathcal{T}_{2}$ decomposes.

  comment

• A3.15

  Symmetries and Groups in Physics | Part II, 2004

  (i) Show that the character of an $S U(2)$ transformation in the $2 l+1$ dimensional irreducible representation $d_{l}$ is given by

  $$\chi_{l}(\theta)=\frac{\sin [(l+1 / 2) \theta]}{\sin [\theta / 2]}$$

  What are the characters of irreducible $S O(3)$ representations?

  (ii) The isospin representation of two-particle states of pions and nucleons is spanned by the basis $T=\left\{\left|\pi^{+} p\right\rangle,\left|\pi^{+} n\right\rangle,\left|\pi^{0} p\right\rangle,\left|\pi^{0} n\right\rangle,\left|\pi^{-} p\right\rangle,\left|\pi^{-} n\right\rangle\right\}$.

  Pions form an isospin triplet with $\pi^{+}=|1,1\rangle, \pi^{0}=|1,0\rangle, \pi^{-}=|1,-1\rangle$; and nucleons form an isospin doublet with $p=|1 / 2,1 / 2\rangle, n=|1 / 2,-1 / 2\rangle$. Find the values of the isospin for the irreducible representations into which $T$ will decompose.

  Using $I_{-}|j, m\rangle=\sqrt{(j-m+1)(j+m)}|j, m-1\rangle$, write the states of the basis $T$ in terms of isospin states.

  Consider the transitions

  $$\begin{array}{ll} \pi^{+} p & \rightarrow \pi^{+} p \\ \pi^{-} p & \rightarrow \pi^{-} p \\ \pi^{-} p & \rightarrow \pi^{0} n \end{array}$$

  and show that their amplitudes satisfy a linear relation.

  comment

Theoretical Geophysics

• A1.17

  Theoretical Geophysics | Part II, 2004

  (i) What is the polarisation $\mathbf{P}$ and slowness $\mathbf{s}$ of the time-harmonic plane elastic wave $\mathbf{u}=\mathbf{A} \exp [i(\mathbf{k} \cdot \mathbf{x}-\omega t)] ?$

  Use the equation of motion for an isotropic homogenous elastic medium,

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+2 \mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})-\mu \boldsymbol{\nabla} \wedge(\boldsymbol{\nabla} \wedge \mathbf{u})$$

  to show that $\mathbf{s} \cdot \mathbf{s}$ takes one of two values and obtain the corresponding conditions on $\mathbf{P}$. If $\mathbf{s}$ is complex show that $\operatorname{Re}(\mathbf{s}) \cdot \operatorname{Im}(\mathbf{s})=0$.

  (ii) A homogeneous elastic layer of uniform thickness $h, S$-wave speed $\beta_{1}$ and shear modulus $\mu_{1}$ has a stress-free surface $z=0$ and overlies a lower layer of infinite depth, $S$-wave speed $\beta_{2}\left(>\beta_{1}\right)$ and shear modulus $\mu_{2}$. Show that the horizontal phase speed $c$ of trapped Love waves satisfies $\beta_{1}<c<\beta_{2}$. Show further that

  $$\tan \left[\left(\frac{c^{2}}{\beta_{1}^{2}}-1\right)^{1 / 2} k h\right]=\frac{\mu_{2}}{\mu_{1}}\left(\frac{1-c^{2} / \beta_{2}^{2}}{c^{2} / \beta_{1}^{2}-1}\right)^{1 / 2}$$

  where $k$ is the horizontal wavenumber.

  Assuming that (1) can be solved to give $c(k)$, explain how to obtain the propagation speed of a pulse of Love waves with wavenumber $k$.

  comment

• A2.16

  Theoretical Geophysics | Part II, 2004

  (i) Sketch the rays in a small region near the relevant boundary produced by reflection and refraction of a $P$-wave incident (a) from the mantle on the core-mantle boundary, (b) from the outer core on the inner-core boundary, and (c) from the mantle on the Earth's surface. [In each case, the region should be sufficiently small that the boundary appears to be planar.]

  Describe the ray paths denoted by $S S, P c P, S K S$ and $P K I K P$.

  Sketch the travel-time $(T-\Delta)$ curves for $P$ and $P c P$ paths from a surface source.

  (ii) From the surface of a flat Earth, an explosive source emits $P$-waves downwards into a stratified sequence of homogeneous horizontal elastic layers of thicknesses $h_{1}, h_{2}, h_{3}, \ldots$ and $P$-wave speeds $\alpha_{1}<\alpha_{2}<\alpha_{3}<\ldots$. A line of seismometers on the surface records the travel times of the various arrivals as a function of the distance $x$ from the source. Calculate the travel times, $T_{d}(x)$ and $T_{r}(x)$, of the direct wave and the wave that reflects exactly once at the bottom of layer 1 .

  Show that the travel time for the head wave that refracts in layer $n$ is given by

  $$T_{n}=\frac{x}{\alpha_{n}}+\sum_{i=1}^{n-1} \frac{2 h_{i}}{\alpha_{i}}\left(1-\frac{\alpha_{i}^{2}}{\alpha_{n}^{2}}\right)^{1 / 2}$$

  Sketch the travel-time curves for $T_{r}, T_{d}$ and $T_{2}$ on a single diagram and show that $T_{2}$ is tangent to $T_{r}$.

  Explain how the $\alpha_{i}$ and $h_{i}$ can be constructed from the travel times of first arrivals provided that each head wave is the first arrival for some range of $x$.

  comment

• A4.20

  Theoretical Geophysics | Part II, 2004

  In a reference frame rotating about a vertical axis with angular velocity $f / 2$, the horizontal components of the momentum equation for a shallow layer of inviscid, incompressible, fluid of uniform density $\rho$ are

  $$\begin{aligned} &\frac{D u}{D t}-f v=-\frac{1}{\rho} \frac{\partial p}{\partial x} \\ &\frac{D v}{D t}+f u=-\frac{1}{\rho} \frac{\partial p}{\partial y} \end{aligned}$$

  where $u$ and $v$ are independent of the vertical coordinate $z$, and $p$ is given by hydrostatic balance. State the nonlinear equations for conservation of mass and of potential vorticity for such a flow in a layer occupying $0<z<h(x, y, t)$. Find the pressure $p$.

  By linearising the equations about a state of rest and uniform thickness $H$, show that small disturbances $\eta=h-H$, where $\eta \ll H$, to the height of the free surface obey

  $$\frac{\partial^{2} \eta}{\partial t^{2}}-g H\left(\frac{\partial^{2} \eta}{\partial x^{2}}+\frac{\partial^{2} \eta}{\partial y^{2}}\right)+f^{2} \eta=f^{2} \eta_{0}-f H \zeta_{0}$$

  where $\eta_{0}$ and $\zeta_{0}$ are the values of $\eta$ and the vorticity $\zeta$ at $t=0$.

  Obtain the dispersion relation for homogeneous solutions of the form $\eta \propto \exp [i(k x-$ $\omega t)$ ] and calculate the group velocity of these Poincaré waves. Comment on the form of these results when $a k \ll 1$ and $a k \gg 1$, where the lengthscale $a$ should be identified.

  Explain what is meant by geostrophic balance. Find the long-time geostrophically balanced solution, $\eta_{\infty}$ and $\left(u_{\infty}, v_{\infty}\right)$, that results from initial conditions $\eta_{0}=A \operatorname{sgn}(x)$ and $(u, v)=0$. Explain briefly, without detailed calculation, how the evolution from the initial conditions to geostrophic balance could be found.

  comment

Transport Processes

• A1.18

  Transport Processes | Part II, 2004

  (i) In an experiment, a finite amount $M$ of marker gas of diffusivity $D$ is released at time $t=0$ into an infinite tube in the neighbourhood of the origin $x=0$. Starting from the one-dimensional diffusion equation for the concentration $C(x, t)$ of marker gas,

  $$C_{t}=D C_{x x}$$

  use dimensional analysis to show that

  $$C=\frac{M}{(D t)^{1 / 2}} f(\xi)$$

  for some dimensionless function $f$ of the similarity variable $\xi=x /(D t)^{1 / 2}$.

  Write down the equation and boundary conditions satisfied by $f(\xi)$.

  (ii) Consider the experiment of Part (i). Find $f(\xi)$ and sketch your answer in the form of a plot of $C$ against $x$ at a few different times $t$.

  Calculate $C(x, t)$ for a second experiment in which the concentration of marker gas at $x=0$ is instead raised to the value $C_{0}$ at $t=0$ and maintained at that value thereafter. Show that the total amount of marker gas released in this case becomes greater than $M$ after a time

  $$t=\frac{\pi}{16 D}\left(\frac{M}{C_{0}}\right)^{2} .$$

  Show further that, at much larger times than this, the concentration in the first experiment still remains greater than that in the second experiment for positions $x$ with $|x|>$ ${ }_{4} C_{0} D t / M$.

  [Hint: $\operatorname{erfc}(z) \equiv \frac{2}{\sqrt{\pi}} \int_{z}^{\infty} e^{-u^{2}} d u \sim \frac{1}{\sqrt{\pi} z} e^{-z^{2}}$ as $\left.z \rightarrow \infty .\right]$

  comment

• A3.16

  Transport Processes | Part II, 2004

  (i) Viscous, incompressible fluid of viscosity $\mu$ flows steadily in the $x$-direction in a uniform channel $0<y<h$. The plane $y=0$ is fixed and the plane $y=h$ has constant $x$-velocity $U$. Neglecting gravity, derive from first principles the equations of motion of the fluid and show that the $x$-component of the fluid velocity is $u(y)$ and satisfies

  $$0=-P_{x}+\mu u_{y y},$$

  where $P(x)$ is the pressure in the fluid. Write down the boundary conditions on $u$. Hence show that the volume flow rate $Q=\int_{0}^{h} u d y$ is given by

  $$Q=\frac{U h}{2}-\frac{P_{x} h^{3}}{12 \mu}$$

  (ii) A heavy rectangular body of width $L$ and infinite length (in the $z$-direction) is pivoted about one edge at $(x, y)=(0,0)$ above a fixed rigid horizontal plane $y=0$. The body has weight $W$ per unit length in the $z$-direction, its centre of mass is distance $L / 2$ from the pivot, and it is falling under gravity towards the fixed plane through a viscous, incompressible fluid. Let $\alpha(t) \ll 1$ be the angle between the body and the plane. Explain the approximations of lubrication theory which permit equations (1) and (2) of Part (i) to apply to the flow in the gap between the two surfaces.

  Deduce that, in the gap,

  $$P_{x}=\frac{6 \mu \dot{\alpha}}{x \alpha^{3}},$$

  where $\dot{\alpha}=d \alpha / d t$. By taking moments about $(x, y)=(0,0)$, deduce that $\alpha(t)$ is given by

  $$\frac{1}{\alpha^{2}}-\frac{1}{\alpha_{0}^{2}}=\frac{2 W t}{3 \mu L}$$

  where $\alpha(0)=\alpha_{0}$.

  comment

• A4.19

  Transport Processes | Part II, 2004

  (a) Solute diffuses and is advected in a moving fluid. Derive the transport equation and deduce that the solute concentration $C(\mathbf{x}, t)$ satisfies the advection-diffusion equation

  $$C_{t}+\nabla \cdot(\mathbf{u} C)=\nabla \cdot(D \nabla C)$$

  where $\mathbf{u}$ is the velocity field and $D$ the diffusivity. Write down the form this equation takes when $\nabla \cdot \mathbf{u}=0$, both $\mathbf{u}$ and $\nabla C$ are unidirectional, in the $x$-direction, and $D$ is a constant.

  (b) A solution occupies the region $x \geqslant 0$, bounded by a semi-permeable membrane at $x=0$ across which fluid passes (by osmosis) with velocity

  $$u=-k\left(C_{1}-C(0, t)\right)$$

  where $k$ is a positive constant, $C_{1}$ is a fixed uniform solute concentration in the region $x<0$, and $C(x, t)$ is the solute concentration in the fluid. The membrane does not allow solute to pass across $x=0$, and the concentration at $x=L$ is a fixed value $C_{L}$ (where $\left.C_{1}>C_{L}>0\right)$.

  Write down the differential equation and boundary conditions to be satisfied by $C$ in a steady state. Make the equations non-dimensional by using the substitutions

  $$X=\frac{x k C_{1}}{D}, \quad \theta(X)=\frac{C(x)}{C_{1}}, \quad \theta_{L}=\frac{C_{L}}{C_{1}},$$

  and show that the concentration distribution is given by

  $$\theta(X)=\theta_{L} \exp \left[\left(1-\theta_{0}\right)(\Lambda-X)\right]$$

  where $\Lambda$ and $\theta_{0}$ should be defined, and $\theta_{0}$ is given by the transcendental equation

  $$\theta_{0}=\theta_{L} e^{\Lambda-\Lambda \theta_{0}}$$

  What is the dimensional fluid velocity $u$, in terms of $\theta_{0} ?$

  (c) Show that if, instead of taking a finite value of $L$, you had tried to take $L$ infinite, then you would have been unable to solve for $\theta$ unless $\theta_{L}=0$, but in that case there would be no way of determining $\theta_{0}$.

  (d) Find asymptotic expansions for $\theta_{0}$ from equation $(*)$ in the following limits:

  (i) For $\theta_{L} \rightarrow 0, \Lambda$ fixed, expand $\theta_{0}$ as a power series in $\theta_{L}$, and equate coefficients to show that

  $$\theta_{0} \sim e^{\Lambda} \theta_{L}-\Lambda e^{2 \Lambda} \theta_{L}^{2}+O\left(\theta_{L}^{3}\right) .$$

  (ii) For $\Lambda \rightarrow \infty, \theta_{L}$ fixed, take logarithms, expand $\theta_{0}$ as a power series in $1 / \Lambda$, and show that

  $$\theta_{0} \sim 1+\frac{\log \theta_{L}}{\Lambda}+O\left(\frac{1}{\Lambda^{2}}\right)$$

  What is the limiting value of $\theta_{0}$ in the limits (i) and (ii)?

  (e) Both the expansions in (d) break down when $\theta_{L}=O\left(e^{-\Lambda}\right)$. To investigate the double limit $\Lambda \rightarrow \infty, \theta_{L} \rightarrow 0$, show that $(*)$ can be written as

  $$\lambda=\phi e^{\phi}$$

  where $\phi=\Lambda \theta_{0}$ and $\lambda$ is to be determined. Show that $\phi \sim \lambda-\lambda^{2}+\ldots$ for $\lambda \ll 1$, and $\phi \sim \log \lambda-\log \log \lambda+\ldots$ for $\lambda \gg 1$.

  Briefly discuss the implication of your results for the problem raised in (c) above.

  comment

Waves in Fluid and Solid Media

• B1.26

  Waves in Fluid and Solid Media | Part II, 2004

  A physical system permits one-dimensional wave propagation in the $x$-direction according to the equation

  $$\frac{\partial^{2} \psi}{\partial t^{2}}-\alpha^{2} \frac{\partial^{6} \psi}{\partial x^{6}}=0$$

  where $\alpha$ is a real positive constant. Derive the corresponding dispersion relation and sketch graphs of frequency, phase velocity and group velocity as functions of the wave number. Is it the shortest or the longest waves that are at the front of a dispersing wave train arising from a localised initial disturbance? Do the wave crests move faster or slower than a packet of waves?

  Find the solution of the above equation for the initial disturbance given by

  $$\psi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k, \quad \frac{\partial \psi}{\partial t}(x, 0)=0$$

  where $A(k)$ is real and $A(-k)=A(k)$.

  Use the method of stationary phase to obtain a leading-order approximation to this solution for large $t$ when $V=x / t$ is held fixed.

  [Note that

  $$\int_{-\infty}^{\infty} e^{\pm i u^{2}} d u=\pi^{\frac{1}{2}} e^{\pm i \pi / 4}$$

  comment

• B2.26

  Waves in Fluid and Solid Media | Part II, 2004

  The linearised equation of motion governing small disturbances in a homogeneous elastic medium of density $\rho$ is

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+\mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})+\mu \nabla^{2} \mathbf{u}$$

  where $\mathbf{u}(\mathbf{x}, t)$ is the displacement, and $\lambda$ and $\mu$ are the Lamé constants. Derive solutions for plane longitudinal waves $P$ with wavespeed $c_{P}$, and plane shear waves $S$ with wavespeed $c_{S}$.

  The half-space $y<0$ is filled with the elastic solid described above, while the slab $0<y<h$ is filled with an elastic solid with shear modulus $\bar{\mu}$, and wavespeeds $\bar{c}_{P}$ and $\bar{c}_{S}$. There is a vacuum in $y>h$. A harmonic plane $S H$ wave of frequency $\omega$ and unit amplitude propagates from $y<0$ towards the interface $y=0$. The wavevector is in the $x y$-plane, and makes an angle $\theta$ with the $y$-axis. Derive the complex amplitude, $R$, of the reflected $S H$ wave in $y<0$. Evaluate $|R|$ for all possible values of $\bar{c}_{S} / c_{S}$, and explain your answer.

  comment

• B3.25

  Waves in Fluid and Solid Media | Part II, 2004

  The dispersion relation for sound waves of frequency $\omega$ in a stationary, homogeneous gas is $\omega=c|\mathbf{k}|$, where $c$ is the speed of sound and $\mathbf{k}$ is the wavevector. Derive the dispersion relation for sound waves of frequency $\omega$ in a uniform flow with velocity U.

  For a slowly-varying medium with a local dispersion relation $\omega=\Omega(\mathbf{k} ; \mathbf{x}, t)$, derive the ray-tracing equations

  $$\frac{d x_{i}}{d t}=\frac{\partial \Omega}{\partial k_{i}}, \quad \frac{d k_{i}}{d t}=-\frac{\partial \Omega}{\partial x_{i}}, \quad \frac{d \omega}{d t}=\frac{\partial \Omega}{\partial t}$$

  The meaning of the notation $d / d t$ should be carefully explained.

  Suppose that two-dimensional sound waves with initial wavevector $\left(k_{0}, l_{0}\right)$ are generated at the origin in a gas occupying the half-space $y>0$. The gas has a mean velocity $(\gamma y, 0)$, where $0<\gamma \ll\left(k_{0}^{2}+l_{0}^{2}\right)^{\frac{1}{2}}$. Show that

  (a) if $k_{0}>0$ and $l_{0}>0$ then an initially upward propagating wavepacket returns to the level $y=0$ within a finite time, after having reached a maximum height that should be identified;

  (b) if $k_{0}<0$ and $l_{0}>0$ then an initially upward propagating wavepacket continues to propagate upwards for all time.

  For the case of a fixed frequency disturbance comment briefly on whether or not there is a quiet zone.

  comment

• B4.27

  Waves in Fluid and Solid Media | Part II, 2004

  A plane shock is moving with speed $U$ into a perfect gas. Ahead of the shock the gas is at rest with pressure $p_{1}$ and density $\rho_{1}$, while behind the shock the velocity, pressure and density of the gas are $u_{2}, p_{2}$ and $\rho_{2}$ respectively. Derive the Rankine-Hugoniot relations across the shock. Show that

  $$\frac{\rho_{1}}{\rho_{2}}=\frac{2 c_{1}^{2}+(\gamma-1) U^{2}}{(\gamma+1) U^{2}}$$

  where $c_{1}^{2}=\gamma p_{1} / \rho_{1}$ and $\gamma$ is the ratio of the specific heats of the gas. Now consider a change of frame such that the shock is stationary and the gas has a component of velocity $V$ parallel to the shock. Deduce that the angle of deflection $\delta$ of the flow which is produced by a stationary shock inclined at an angle $\alpha=\tan ^{-1}(U / V)$ to an oncoming stream of Mach number $M=\left(U^{2}+V^{2}\right)^{\frac{1}{2}} / c_{1}$ is given by

  $$\tan \delta=\frac{2 \cot \alpha\left(M^{2} \sin \alpha^{2}-1\right)}{2+M^{2}(\gamma+\cos 2 \alpha)}$$

  [Note that

  $$\left.\tan (\theta+\phi)=\frac{\tan \theta+\tan \phi}{1-\tan \theta \tan \phi} . \quad\right]$$

  comment