Part II, 2007
Part II, 2007
Jump to course
Define what it means for a group to act on a topological space . Prove that, if acts freely, in a sense that you should specify, then the quotient map is a covering map and there is a surjective group homomorphism from the fundamental group of to .
1.II.21H
(i) Compute the fundamental group of the Klein bottle. Show that this group is not abelian, for example by defining a suitable homomorphism to the symmetric group .
(ii) Let be the closed orientable surface of genus 2 . How many (connected) double coverings does have? Show that the fundamental group of admits a homomorphism onto the free group on 2 generators.
2.II.21H
State the Mayer-Vietoris sequence for a simplicial complex which is a union of two subcomplexes and . Define the homomorphisms in the sequence (but do not check that they are well-defined). Prove exactness of the sequence at the term .
4.II
Compute the homology of the space obtained from the torus by identifying to a point and to a point, for two distinct points and in
1.II.33A
In a certain spherically symmetric potential, the radial wavefunction for particle scattering in the sector ( -wave), for wavenumber and , is
where
with and real, positive constants. Scattering in sectors with can be neglected. Deduce the formula for the -matrix in this case and show that it satisfies the expected symmetry and reality properties. Show that the phase shift is
What is the scattering length for this potential?
From the form of the radial wavefunction, deduce the energies of the bound states, if any, in this system. If you were given only the -matrix as a function of , and no other information, would you reach the same conclusion? Are there any resonances here?
[Hint: Recall that for real , where is the phase shift.]
2.II.33A
Describe the variational method for estimating the ground state energy of a quantum system. Prove that an error of order in the wavefunction leads to an error of order in the energy.
Explain how the variational method can be generalized to give an estimate of the energy of the first excited state of a quantum system.
Using the variational method, estimate the energy of the first excited state of the anharmonic oscillator with Hamiltonian
How might you improve your estimate?
[Hint: If then
3.II.33A
Consider the Hamiltonian
for a particle of spin fixed in space, in a rotating magnetic field, where
and
with and constant, and .
There is an exact solution of the time-dependent Schrödinger equation for this Hamiltonian,
where and
Show that, for , this exact solution simplifies to a form consistent with the adiabatic approximation. Find the dynamic phase and the geometric phase in the adiabatic regime. What is the Berry phase for one complete cycle of ?
The Berry phase can be calculated as an integral of the form
Evaluate for the adiabatic evolution described above.
4.II.33A
Consider a 1-dimensional chain of atoms of mass (with large and with periodic boundary conditions). The interactions between neighbouring atoms are modelled by springs with alternating spring constants and , with .

In equilibrium, the separation of the atoms is , the natural length of the springs.
Find the frequencies of the longitudinal modes of vibration for this system, and show that they are labelled by a wavenumber that is restricted to a Brillouin zone. Identify the acoustic and optical bands of the vibration spectrum, and determine approximations for the frequencies near the centre of the Brillouin zone. What is the frequency gap between the acoustic and optical bands at the zone boundary?
Describe briefly the properties of the phonons in this system.
1.II.26J
An open air rock concert is taking place in beautiful Pine Valley, and enthusiastic fans from the entire state of Alifornia are heading there long before the much anticipated event. The arriving cars have to be directed to one of three large (practically unlimited) parking lots, and situated near the valley entrance. The traffic cop at the entrance to the valley decides to direct every third car (in the order of their arrival) to a particular lot. Thus, cars and so on are directed to lot , cars to lot and cars to lot .
Suppose that the total arrival process , at the valley entrance is Poisson, of rate (the initial time is taken to be considerably ahead of the actual event). Consider the processes and where is the number of cars arrived in lot by time . Assume for simplicity that the time to reach a parking lot from the entrance is negligible so that the car enters its specified lot at the time it crosses the valley entrance.
(a) Give the probability density function of the time of the first arrival in each of the processes .
(b) Describe the distribution of the time between two subsequent arrivals in each of these processes. Are these times independent? Justify your answer.
(c) Which of these processes are delayed renewal processes (where the distribution of the first arrival time differs from that of the inter-arrival time)?
(d) What are the corresponding equilibrium renewal processes?
(e) Describe how the direction rule should be changed for and to become Poisson processes, of rate . Will these Poisson processes be independent? Justify your answer.
2.II.26J
In this question we work with a continuous-time Markov chain where the rate of jump may depend on but not on . A virus can be in one of strains , and it mutates to strain with rate from each strain . (Mutations are caused by the chemical environment.) Set .
(a) Write down the Q-matrix (the generator) of the chain in terms of and .
(b) If , that is, , what are the communicating classes of the chain ?
(c) From now on assume that . State and prove a necessary and sufficient condition, in terms of the numbers , for the chain to have a single communicating class (which therefore should be closed).
(d) In general, what is the number of closed communicating classes in the chain ? Describe all open communicating classes of .
(e) Find the equilibrium distribution of . Is the chain reversible? Justify your answer.
(f) Write down the transition matrix of the discrete-time jump chain for and identify its equilibrium distribution. Is the jump chain reversible? Justify your answer.
3.II.25J
For a discrete-time Markov chain, if the probability of transition does not depend on then the chain is reduced to a sequence of independent random variables (states). In this case, the chain forgets about its initial state and enters equilibrium after a single transition. In the continuous-time case, a Markov chain whose rates of transition depend on but not on still 'remembers' its initial state and reaches equilibrium only in the limit as the time grows indefinitely. This question is an illustration of this property.
A protean sea sponge may change its colour among varieties , under the influence of the environment. The rate of transition from colour to equals and does not depend on . Consider a Q-matrix with entries
where . Assume that and let be the continuous-time Markov chain with generator . Given , let be the matrix of transition probabilities in time in chain .
(a) State the exponential relation between the matrices and .
(b) Set . Check that are equilibrium probabilities for the chain . Is this a unique equilibrium distribution? What property of the vector with entries relative to the matrix is involved here?
(c) Let be a vector with components such that . Show that . Compute
(d) Now let denote the (column) vector whose entries are 0 except for the th one which equals 1. Observe that the th row of is . Prove that
(e) Deduce the expression for transition probabilities in terms of rates and their sum .
4.II.26J
A population of rare Monarch butterflies functions as follows. At the times of a Poisson process of rate a caterpillar is produced from an egg. After an exponential time, the caterpillar is transformed into a pupa which, after an exponential time, becomes a butterfly. The butterfly lives for another exponential time and then dies. (The Poissonian assumption reflects the fact that butterflies lay a huge number of eggs most of which do not develop.) Suppose that all lifetimes are independent (of the arrival process and of each other) and let their rate be . Assume that the population is in an equilibrium and let be the number of caterpillars, the number of pupae and the number of butterflies (so that the total number of insects, in any metamorphic form, equals . Let be the equilibrium probability where
(a) Specify the rates of transitions for the resulting continuous-time Markov chain with states . (The rates are non-zero only when or and similarly for other co-ordinates.) Check that the holding rate for state is where .
(b) Let be the Q-matrix from (a). Consider the invariance equation . Verify that the only solution is
(c) Derive the marginal equilibrium probabilities and the conditional equilibrium probabilities .
(d) Determine whether the chain is positive recurrent, null-recurrent or transient.
(e) Verify that the equilibrium probabilities are the same as in the corresponding system (with the correct specification of the arrival rate and the service-time distribution).
1.II.30B
State Watson's lemma, describing the asymptotic behaviour of the integral
as , given that has the asymptotic expansion
as , where and .
Give an account of Laplace's method for finding asymptotic expansions of integrals of the form
for large real , where is real for real .
Deduce the following asymptotic expansion of the contour integral
as .
3.II.30B
Explain the method of stationary phase for determining the behaviour of the integral
for large . Here, the function is real and differentiable, and and are all real.
Apply this method to show that the first term in the asymptotic behaviour of the function
where with and real, is
as
4.II.31B
Consider the time-independent Schrödinger equation
where denotes and denotes . Suppose that
and consider a bound state . Write down the possible Liouville-Green approximate solutions for in each region, given that as .
Assume that may be approximated by near , where , and by near , where . The Airy function satisfies
and has the asymptotic expansions
and
Deduce that the energies of bound states are given approximately by the WKB condition:
1.I.9C
The action for a system with generalized coordinates, , for a time interval is given by
where is the Lagrangian, and where the end point values and are fixed at specified values. Derive Lagrange's equations from the principle of least action by considering the variation of for all possible paths.
What is meant by the statement that a particular coordinate is ignorable? Show that there is an associated constant of the motion, to be specified in terms of .
A particle of mass is constrained to move on the surface of a sphere of radius under a potential, , for which the Lagrangian is given by
Identify an ignorable coordinate and find the associated constant of the motion, expressing it as a function of the generalized coordinates. Evaluate the quantity
in terms of the same generalized coordinates, for this case. Is also a constant of the motion? If so, why?
2.I.9C
The Lagrangian for a particle of mass and charge moving in a magnetic field with position vector is given by
where the vector potential , which does not depend on time explicitly, is related to the magnetic field through
Write down Lagrange's equations and use them to show that the equation of motion of the particle can be written in the form
Deduce that the kinetic energy, , is constant.
When the magnetic field is of the form for some specified function , show further that
where and are constants.
2.II.15C
(a) A Hamiltonian system with degrees of freedom is described by the phase space coordinates and momenta . Show that the phase-space volume element
is conserved under time evolution.
(b) The Hamiltonian, , for the system in part (a) is independent of time. Show that if is a constant of the motion, then the Poisson bracket vanishes. Evaluate when
and
where the potential depends on the only through quantities of the form for .
(c) For a system with one degree of freedom, state what is meant by the transformation
being canonical. Show that the transformation is canonical if and only if the Poisson bracket .
3.I.9C
A particle of mass is constrained to move in the horizontal plane, around a circle of fixed radius whose centre is at the origin of a Cartesian coordinate system . A second particle of mass is constrained to move around a circle of fixed radius that also lies in a horizontal plane, but whose centre is at . It is given that the Lagrangian of the system can be written as
using the particles' cylindrical polar angles and as generalized coordinates. Deduce the equations of motion and use them to show that is constant, and that obeys an equation of the form
where is a constant to be determined.
Find two values of corresponding to equilibria, and show that one of the two equilibria is stable. Find the period of small oscillations about the stable equilibrium.
4.I
(a) Show that the principal moments of inertia for the oblate spheroid of mass defined by
are given by . Here is the semi-major axis and is the eccentricity.
[You may assume that a sphere of radius a has principal moments of inertia .]
(b) The spheroid in part (a) rotates about an axis that is not a principal axis. Euler's equations governing the angular velocity as viewed in the body frame are
and
Show that is constant. Show further that the angular momentum vector precesses around the axis with period
4.II.15C
The Hamiltonian for an oscillating particle with one degree of freedom is
The mass is a constant, and is a function of time alone. Write down Hamilton's equations and use them to show that
Now consider a case in which is constant and the oscillation is exactly periodic. Denote the constant value of in that case by . Consider the quantity , where the integral is taken over a single oscillation cycle. For any given function show that can be expressed as a function of and alone, namely
where the sign of the integrand alternates between the two halves of the oscillation cycle. Let be the period of oscillation. Show that the function has partial derivatives
You may assume without proof that and may be taken inside the integral.
Now let change very slowly with time , by a negligible amount during an oscillation cycle. Assuming that, to sufficient approximation,
where is the average value of over an oscillation cycle, and that
deduce that , carefully explaining your reasoning.
When
with a positive integer and positive, deduce that
for slowly-varying , where is a constant.
[Do not try to solve Hamilton's equations. Rather, consider the form taken by . ]
Compute the rank and minimum distance of the cyclic code with generator polynomial and parity-check polynomial . Now let be a root of in the field with 8 elements. We receive the word . Verify that , and hence decode using minimum-distance decoding.
1.I.4G
Let and be alphabets of sizes and . What does it mean to say that is a decipherable code? State the inequalities of Kraft and Gibbs, and deduce that if letters are drawn from with probabilities then the expected word length is at least .
1.II.11G
Define the bar product of linear codes and , where is a subcode of . Relate the rank and minimum distance of to those of and . Show that if denotes the dual code of , then
Using the bar product construction, or otherwise, define the Reed-Muller code for . Show that if , then the dual of is again a Reed-Muller code.
2.I.4G
Briefly explain how and why a signature scheme is used. Describe the El Gamal scheme.
2.II.11G
Define the capacity of a discrete memoryless channel. State Shannon's second coding theorem and use it to show that the discrete memoryless channel with channel matrix
has capacity .
4.I.4G
What is a linear feedback shift register? Explain the Berlekamp-Massey method for recovering the feedback polynomial of a linear feedback shift register from its output. Illustrate in the case when we observe output
1.I.10A
Describe the motion of light rays in an expanding universe with scale factor , and derive the redshift formula
where the light is emitted at time and observed at time .
A galaxy at comoving position is observed to have a redshift . Given that the galaxy emits an amount of energy per unit time, show that the total energy per unit time crossing a sphere centred on the galaxy and intercepting the earth is . Hence, show that the energy per unit time per unit area passing the earth is
1.II.15A
In a homogeneous and isotropic universe, the scale factor obeys the Friedmann equation
where is the matter density, which, together with the pressure , satisfies
Here, is a constant curvature parameter. Use these equations to show that the rate of change of the Hubble parameter satisfies
Suppose that an expanding Friedmann universe is filled with radiation (density and pressure as well as a "dark energy" component (density and pressure . Given that the energy densities of these two components are measured today to be
show that the curvature parameter must satisfy . Hence derive the following relations for the Hubble parameter and its time derivative:
Show qualitatively that universes with will recollapse to a Big Crunch in the future. [Hint: Sketch and versus for representative values of .]
For , find an explicit solution for the scale factor satisfying . Find the limiting behaviours of this solution for large and small . Comment briefly on their significance.
2.I.10A
The number density of photons in thermal equilibrium at temperature takes the form
At time and temperature , photons decouple from thermal equilibrium. By considering how the photon frequency redshifts as the universe expands, show that the form of the equilibrium frequency distribution is preserved, with the temperature for defined by
Show that the photon number density and energy density can be expressed in the form
where the constants and need not be evaluated explicitly.
3.I.10A
The number density of a non-relativistic species in thermal equilibrium is given by
Suppose that thermal and chemical equilibrium is maintained between protons p (mass , degeneracy ), neutrons (mass , degeneracy ) and helium-4 nuclei mass , degeneracy ) via the interaction
where you may assume the photons have zero chemical potential . Given that the binding energy of helium-4 obeys , show that the ratio of the number densities can be written as
Explain briefly why the baryon-to-photon ratio remains constant during the expansion of the universe, where and .
By considering the fractional densities of the species , re-express the ratio ( ) in the form
Given that , verify (very approximately) that this ratio approaches unity when . In reality, helium-4 is not formed until after deuterium production at a considerably lower temperature. Explain briefly the reason for this delay.
3.II.15A
A spherically symmetric star with outer radius has mass density and pressure , where is the distance from the centre of the star. Show that hydrostatic equilibrium implies the pressure support equation,
where is the mass inside radius . State without proof any results you may need.
Write down an integral expression for the total gravitational potential energy of the star. Hence use to deduce the virial theorem
where is the average pressure and is the volume of the star.
Given that a non-relativistic ideal gas obeys and that an ultrarelativistic gas obeys , where is the kinetic energy, discuss briefly the gravitational stability of a star in these two limits.
At zero temperature, the number density of particles obeying the Pauli exclusion principle is given by
where is the Fermi momentum, is the degeneracy and is Planck's constant. Deduce that the non-relativistic internal energy of these particles is
where is the mass of a particle. Hence show that the non-relativistic Fermi degeneracy pressure satisfies
Use the virial theorem to estimate that the radius of a star supported by Fermi degeneracy pressure is approximately
where is the total mass of the star.
[Hint: Assume and note that
4.I.10A
The equation governing density perturbation modes in a matter-dominated universe (with ) is
where is the comoving wavevector. Find the general solution for the perturbation, showing that there is a growing mode such that
Show that the physical wavelength corresponding to the comoving wavenumber crosses the Hubble radius at a time given by
According to inflationary theory, the amplitude of the variance at horizon-crossing is constant, that is, where and (the volume) are constants. Given this amplitude and the results obtained above, deduce that the power spectrum today takes the form
1.II.24H
Let be a smooth map between manifolds without boundary. Recall that is a submersion if is surjective for all . The canonical submersion is the standard projection of onto for , given by
(i) Let be a submersion, and . Show that there exist local coordinates around and such that , in these coordinates, is the canonical submersion. [You may assume the inverse function theorem.]
(ii) Show that submersions map open sets to open sets.
(iii) If is compact and connected, show that every submersion is surjective. Are there submersions of compact manifolds into Euclidean spaces with ?
2.II.24H
(i) What is a minimal surface? Explain why minimal surfaces always have non-positive Gaussian curvature.
(ii) A smooth map between two surfaces in 3-space is said to be conformal if
for all and all , where is a number which depends only on .
Let be a surface without umbilical points. Prove that is a minimal surface if and only if the Gauss map is conformal.
(iii) Show that isothermal coordinates exist around a non-planar point in a minimal surface.
3.II.23H
(i) Let be a smooth map between manifolds without boundary. Define critical point, critical value and regular value. State Sard's theorem.
(ii) Explain how to define the degree modulo 2 of a smooth map , indicating clearly the hypotheses on and . Show that a smooth map with non-zero degree modulo 2 must be surjective.
(iii) Let be the torus of revolution obtained by rotating the circle in the -plane around the -axis. Describe the critical points and the critical values of the Gauss map of . Find the degree modulo 2 of . Justify your answer by means of a sketch or otherwise.
4.II.24H
(i) What is a geodesic? Show that geodesics are critical points of the energy functional.
(ii) Let be a surface which admits a parametrization defined on an open subset of such that and , where is a function of alone and is a function of alone. Let be a geodesic and write . Show that
is independent of .
1.I.7E
Given a non-autonomous th-order differential equation
with , explain how it may be written in the autonomous first-order form for suitably chosen vectors and .
Given an autonomous system in , define the corresponding flow . What is equal to? Define the orbit through and the limit set of . Define a homoclinic orbit.
2.I.7E
Find and classify the fixed points of the system
What are the values of their Poincaré indices? Prove that there are no periodic orbits. Sketch the phase plane.
3.I.7E
State the Poincaré-Bendixson Theorem for a system in .
Prove that if then the system
has a periodic orbit in the region .
3.II.14E
The Lorenz equations are
where and are positive constants and .
(i) Show that the origin is globally asymptotically stable for by considering a function with a suitable choice of constants and
(ii) State, without proof, the Centre Manifold Theorem.
Show that the fixed point at the origin is nonhyperbolic at . What are the dimensions of the linear stable and (non-extended) centre subspaces at this point?
(iii) Let from now on. Make the substitutions and and derive the resulting equations for and .
The extended centre manifold is given by
where and can be expanded as power series about . What is known about and from the Centre Manifold Theorem? Assuming that , determine correct to and to . Hence obtain the evolution equation on the extended centre manifold correct to , and identify the type of bifurcation.
4.I.7E
By considering the binary representation of the sawtooth for , show that:
(i) has sensitive dependence on initial conditions on .
(ii) has topological transitivity on .
(iii) Periodic points are dense in .
Find all the 4-cycles of and express them as fractions.
4.II.14E
Consider the one-dimensional map defined by
where and are constants, is a parameter and .
(i) Find the fixed points of and determine the linear stability of . Hence show that there are bifurcations at , at and, if , at .
Sketch the bifurcation diagram for each of the cases:
In each case show the locus and stability of the fixed points in the -plane, and state the type of each bifurcation. [Assume that there are no further bifurcations in the region sketched.]
(ii) For the case (i.e. , you may assume that
Show that there are at most three 2-cycles and determine when they exist. By considering , or otherwise, show further that one 2-cycle is always unstable when it exists and that the others are unstable when . Sketch the bifurcation diagram showing the locus and stability of the fixed points and 2 -cycles. State briefly what you would expect to occur in the region .
1.II.34E
Frame is moving with uniform speed in the -direction relative to a laboratory frame . Using Cartesian coordinates and units such that , the relevant Lorentz transformation is
where . A straight thin wire of infinite extent lies along the -axis and carries charge and current line densities and per unit length, as measured in . Stating carefully your assumptions show that the corresponding quantities in are given by
Using cylindrical polar coordinates, and the integral forms of the Maxwell equations and , derive the electric and magnetic fields outside the wire in both frames.
In a standard notation the Lorentz transformation for the electric and magnetic fields is
Is your result consistent with this?
3.II
Consider a particle of charge moving with 3 -velocity . If the particle is moving slowly then Larmor's formula asserts that the instantaneous radiated power is
Suppose, however, that the particle is moving relativistically. Give reasons why one should conclude that is a Lorentz invariant. Writing the 4-velocity as where and , show that
where and where is the particle's proper time. Show also that
Deduce the relativistic version of Larmor's formula.
Suppose the particle moves in a circular orbit perpendicular to a uniform magnetic field . Show that
where is the mass of the particle, and comment briefly on the slow motion limit.
4.II.35E
An action
is given, where is a scalar field. Explain heuristically how to compute the functional derivative .
Consider the action for electromagnetism,
Here is the 4-current density, is the 4-potential and is the Maxwell field tensor. Obtain Maxwell's equations in 4-vector form.
Another action that is sometimes suggested is
Under which additional assumption can Maxwell's equations be obtained using this action?
Using this additional assumption establish the relationship between the actions and .
1.II.36B
Discuss how the methods of lubrication theory may be used to find viscous fluid flows in thin layers or narrow gaps, explaining carefully what inequalities need to hold in order that the theory may apply.
Viscous fluid of kinematic viscosity flows under the influence of gravity , down an inclined plane making an angle with the horizontal. The fluid layer lies between and , where are distances measured down the plane and perpendicular to it, and is of the same order as . Give conditions involving and that ensure that lubrication theory can be used, and solve the lubrication equations, together with the equation of mass conservation, to obtain an equation for in the form
where are constants to be determined. Show that there is a steady solution with constant, and interpret this physically. Show also that a solution of this equation exists in the form of a front, with , where , and as . Determine in terms of , find the shape of the front implicitly in the form , and show that as from below.
2.II.36B
Viscous fluid is extracted through a small hole in the tip of the cone given by in spherical polar coordinates . The total volume flux through the hole takes the constant value . It is given that there is a steady solution of the Navier-Stokes equations for the fluid velocity . For small enough , the velocity is well approximated by , where except in thin boundary layers near .
(i) Verify that the volume flux through the hole is approximately .
(ii) Construct a Reynolds number (depending on ) in terms of and the kinematic viscosity , and thus give an estimate of the value of below which solutions of this type will appear.
(iii) Assuming that there is a boundary layer near , write down the boundary layer equations in the usual form, using local Cartesian coordinates and parallel and perpendicular to the boundary. Show that the boundary layer thickness is proportional to , and show that the component of the velocity may be written in the form
Derive the equation and boundary conditions satisfied by . Give an expression, in terms of , for the volume flux through the boundary layer, and use this to derive the dependence of the first correction to the flow outside the boundary layer.
3.II B
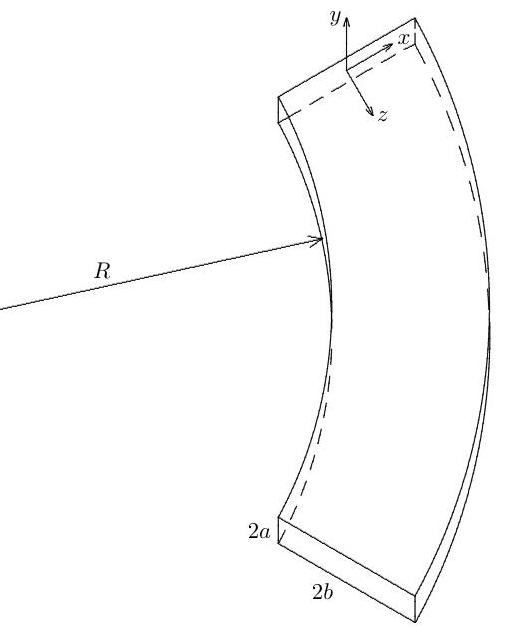
Viscous fluid of kinematic viscosity and density flows in a curved pipe of constant rectangular cross section and constant curvature. The cross-section has height and width (in the radial direction) with , and the radius of curvature of the inner wall is , with . A uniform pressure gradient is applied along the pipe.
(i) Assume to a first approximation that the pipe is straight, and ignore variation in the -direction, where are Cartesian coordinates referred to an origin at the centre of the section, with increasing radially and measured along the pipe. Find the flow field along the pipe in the form .
(ii) It is given that the largest component of the inertial acceleration due to the curvature of the pipe is in the direction. Consider the secondary flow induced in the plane, again ignoring variations in and any end effects (except for the requirement that there be zero total mass flux in the direction). Show that takes the form , where
and write down two equations determining the constants and . [It is not necessary to solve these equations.]
Give conditions on the parameters that ensure that .
4.II.37B
(i) Assuming that axisymmetric incompressible flow , with vorticity in spherical polar coordinates satisfies the equations
where
show that for Stokes flow satisfies the equation
(ii) A rigid sphere of radius moves at velocity through viscous fluid of density and dynamic viscosity which is at rest at infinity. Assuming Stokes flow and by applying the boundary conditions at and as , verify that is the appropriate solution to for this flow, where and are to be determined.
(iii) Hence find the velocity field outside the sphere. Without direct calculation, explain why the drag is in the direction and has magnitude proportional to .
(iv) A second identical sphere is introduced into the flow, at a distance from the first, and moving at the same velocity. Justify the assertion that, when the two spheres are at the same height, or when one is vertically above the other, the drag on each sphere is the same. Calculate the leading correction to the drag in each case, to leading order in .
[You may quote without proof the fact that, for an axisymmetric function ,
in spherical polar coordinates .]
1.I.8B
The coefficients and of the differential equation
are analytic in the punctured disc , and and are linearly independent solutions in the neighbourhood of the point in the disc. By considering the effect of analytically continuing and , show that the equation has a non-trivial solution of the form
1.II.14B
The function is defined by
where is a constant (which is not an integer). The path of integration, , is the Pochhammer contour, defined as follows. It starts at a point on the axis between 0 and 1 , then it circles the points 1 and 0 in the negative sense, then it circles the points 1 and 0 in the positive sense, returning to . At the start of the path, and the integrand is defined at other points on by analytic continuation along .
(i) For what values of is analytic? Give brief reasons for your answer.
(ii) Show that, in the case and ,
where is the Beta function.
(iii) Deduce that the only singularities of are simple poles. Explain carefully what happens if is a positive integer.
2.I.8B
The function is defined by
For what values of is analytic?
By considering , where is the Riemann zeta function which you may assume is given by
show that . Deduce from this result that the analytic continuation of is an entire function. [You may use properties of without proof.]
2.II.14B
Show that the equation
has solutions of the form , where
provided that is suitably chosen.
Hence find the general solution, evaluating the integrals explicitly. Show that the general solution is entire, but that there is no solution that satisfies and .
3.I.8B
Let and be any two linearly independent branches of the -function
where , and let be the Wronskian of and .
(i) How is related to the Wronskian of the principal branches of the -function at ?
(ii) Show that is an entire function.
(iii) Given that is bounded as , show that
where is a non-zero constant.
4.I.8B
The hypergeometric function is defined by
where and is a constant determined by the condition .
(i) Express in terms of Gamma functions.
(ii) By considering the th derivative , show that .
1.II.18F
Let be field extensions. Define the degree of the field extension , and state and prove the tower law.
Now let be a finite field. Show , for some prime and positive integer . Show also that contains a subfield of order if and only if .
If is an irreducible polynomial of degree over the finite field , determine its Galois group.
2.II.18F
Let , where is a primitive th root of unity and . Prove that there is an injective group homomorphism .
Show that, if is an intermediate subfield of , then is Galois. State carefully any results that you use.
Give an example where is non-trivial but is not surjective. Show that is surjective when and is a prime.
Determine all the intermediate subfields of and the automorphism groups . Write the quadratic subfield in the form for some .
3.II.18F
(i) Let be the splitting field of the polynomial over . Describe the field , the Galois group , and the action of on .
(ii) Let be the splitting field of the polynomial over . Describe the field and determine .
4.II.18F
Let be a monic polynomial, a splitting field for the roots of in . Let be the discriminant of . Explain why is a polynomial function in the coefficients of , and determine when .
Compute the Galois group of the polynomial .
1.II.35A
Starting from the Riemann tensor for a metric , define the Ricci tensor and the scalar curvature .
The Riemann tensor obeys
Deduce that
Write down Einstein's field equations in the presence of a matter source, with energymomentum tensor . How is the relation important for the consistency of Einstein's equations?
Show that, for a scalar function , one has
Assume that
for a scalar field . Show that the quantity
is then a constant.
2.II.35A
The symbol denotes the covariant derivative defined by the Christoffel connection for a metric . Explain briefly why
in general, where is a scalar field and is a covariant vector field.
A Killing vector field satisfies the equation
By considering the quantity , show that
Find all Killing vector fields in the case of flat Minkowski space-time.
For a metric of the form
where denotes the coordinates , show that and that . Deduce that the vector field is a Killing vector field.
[You may assume the standard symmetries of the Riemann tensor.]
4.II.36A
Consider a particle on a trajectory . Show that the geodesic equations, with affine parameter , coincide with the variational equations obtained by varying the integral
the end-points being fixed.
In the case that , show that the space-time metric is given in the form
for a certain function . Assuming the particle motion takes place in the plane show that
for constants. Writing , obtain the equation
where can be chosen to be 1 or 0 , according to whether the particle is massive or massless. In the case that , show that
In the massive case, show that there is an approximate solution of the form
where
What is the interpretation of this solution?
Show that there are two ways to embed a regular tetrahedron in a cube so that the vertices of the tetrahedron are also vertices of . Show that the symmetry group of permutes these tetrahedra and deduce that the symmetry group of is isomorphic to the Cartesian product of the symmetric group and the cyclic group .
1.II.12G
Define the Hausdorff -dimensional measure and the Hausdorff dimension of a subset of .
Set . Define the Cantor set and show that its Hausdorff -dimensional measure is at most
Let be independent Bernoulli random variables that take the values 0 and 2 , each with probability . Define
Show that is a random variable that takes values in the Cantor set .
Let be a subset of with . Show that and deduce that, for any set , we have
Hence, or otherwise, prove that and that the Cantor set has Hausdorff dimension .
2.I.3G
Explain what is meant by a lattice in the Euclidean plane . Prove that such a lattice is either for some vector or else for two linearly independent vectors in .
3.I.3G
Let be a 2-dimensional Euclidean crystallographic group. Define the lattice and point group corresponding to .
Prove that any non-trivial rotation in the point group of must have order or
4.I
Let be a circle on the Riemann sphere. Explain what it means to say that two points of the sphere are inverse points for the circle . Show that, for each point on the Riemann sphere, there is a unique point with inverse points. Define inversion in .
Prove that the composition of an even number of inversions is a Möbius transformation.
4.II.12G
Explain what it means to say that a group is a Kleinian group. What is the definition of the limit set for the group ? Prove that a fixed point of a parabolic element in must lie in the limit set.
Show that the matrix represents a parabolic transformation for any non-zero choice of the complex numbers and . Find its fixed point.
The Gaussian integers are . Let be the set of Möbius transformations with and . Prove that is a Kleinian group. For each point with non-zero integers, find a parabolic transformation that fixes . Deduce that the limit set for is all of the Riemann sphere.
1.II.17H
Let be a connected cubic graph drawn in the plane with each edge in the boundary of two distinct faces. Show that the associated map is 4 -colourable if and only if is 3 -edge colourable.
Is the above statement true if the plane is replaced by the torus and all faces are required to be simply connected? Give a proof or a counterexample.
2.II.17H
The Ramsey number of a graph is the smallest such that in any red/blue colouring of the edges of there is a monochromatic copy of .
Show that for every .
Let be the graph on four vertices obtained by adding an edge to a triangle. Show that .
3.II.17H
Let be a bipartite graph with vertex classes and , each of size . State and prove Hall's theorem giving a necessary and sufficient condition for to contain a perfect matching.
A vertex is flexible if every edge from is contained in a perfect matching. Show that if for every subset of with , then every is flexible.
Show that whenever contains a perfect matching, there is at least one flexible .
Give an example of such a where no of minimal degree is flexible.
4.II.17H
Let be a graph with vertices and edges. Show that if contains no , then .
Let denote the number of subgraphs of isomorphic to . Show that if , then contains at least paths of length 2 . By considering the numbers of vertices joined to each pair of vertices of , deduce that
Now let be the random graph on in which each pair of vertices is joined independently with probability . Find the expectation of . Deduce that if , then
1.II.31E
(i) Using the Cole-Hopf transformation
map the Burgers equation
to the heat equation
(ii) Given that the solution of the heat equation on the infinite line with initial condition is given by
show that the solution of the analogous problem for the Burgers equation with initial condition is given by
where the function is to be determined in terms of .
(iii) Determine the ODE characterising the scaling reduction of the spherical modified Korteweg-de Vries equation
2.II.31E
Solve the following linear singular equation
where denotes the unit circle, and denotes the principal value integral.
3.II.31E
Find a Lax pair formulation for the linearised NLS equation
Use this Lax pair formulation to show that the initial value problem on the infinite line of the linearised NLS equation is associated with the following Riemann-Hilbert problem
By deforming the above problem obtain the Riemann-Hilbert problem and hence the linear integral equation associated with the following system of nonlinear evolution PDEs
1.II.22G
Let be a normed vector space over . Define the dual space and show directly that is a Banach space. Show that the map defined by , for all , is a linear map. Using the Hahn-Banach theorem, show that is injective and .
Give an example of a Banach space for which is not surjective. Justify your answer.
2.II.22G
Let be a Banach space, a normed vector space, and a bounded linear map. Assume that is of second category in . Show that is surjective and is open whenever is open. Show that, if is also injective, then exists and is bounded.
Give an example of a continuous map such that is of second category in but is not surjective. Give an example of a continuous surjective map which does not take open sets to open sets.
3.II.21G
State and prove the Arzela-Ascoli theorem.
Let be a positive integer. Consider the subset consisting of all thrice differentiable solutions to the differential equation
with
Show that this set is totally bounded as a subset of .
[It may be helpful to consider interior maxima.]
4.II.22G
Let be a Banach space and a bounded linear map. Define the spectrum , point spectrum , resolvent , and resolvent set . Show that the spectrum is a closed and bounded subset of . Is the point spectrum always closed? Justify your answer.
Now suppose is a Hilbert space, and is self-adjoint. Show that the point spectrum is real.
A field contains seed-producing poppies in August of year . On average each poppy produces seeds, a number that is assumed not to vary from year to year. A fraction of seeds survive the winter and a fraction of those germinate in May of year . A fraction of those that survive the next winter germinate in year . Show that satisfies the following difference equation:
Write down the general solution of this equation, and show that the poppies in the field will eventually die out if
1.I.6B
A chemostat is a well-mixed tank of given volume that contains water in which lives a population of bacteria that consume nutrient whose concentration is per unit volume. An inflow pipe supplies a solution of nutrient at concentration and at a constant flow rate of units of volume per unit time. The mixture flows out at the same rate through an outflow pipe. The bacteria consume the nutrient at a rate , where
and the bacterial population grows at a rate , where .
Write down the differential equations for and show that they can be rescaled into the following form:
where are positive constants, to be found.
Show that this system of equations has a non-trivial steady state if and , and that it is stable.
2.II.13B
Show that the concentration of a diffusible chemical substance in a stationary medium satisfies the partial differential equation
where is the diffusivity and is the rate of supply of the chemical.
A finite amount of the chemical, , is supplied at the origin at time , and spreads out in a spherically symmetric manner, so that for , where is the radial coordinate. The diffusivity is given by , for constant . Show, by dimensional analysis or otherwise, that it is appropriate to seek a similarity solution in which
where are constants to be determined, and derive the ordinary differential equation satisfied by .
Solve this ordinary differential equation, subject to appropriate boundary conditions, and deduce that the chemical occupies a finite spherical region of radius
[Note: in spherical polar coordinates
3.I.6B
Consider a birth and death process in which births always give rise to two offspring, with rate , while the death rate per individual is .
Write down the master equation (or probability balance equation) for this system.
Show that the population mean is given by
where is the initial population mean, and that the population variance satisfies
3.II.13B
The number density of a population of cells is . The cells produce a chemical whose concentration is and respond to it chemotactically. The equations governing and are
(i) Give a biological interpretation of each term in these equations, where you may assume that and are all positive.
(ii) Show that there is a steady-state solution that is stable to spatially invariant disturbances.
(iii) Analyse small, spatially-varying perturbations to the steady state that satisfy for any variable , and show that a chemotactic instability is possible if
(iv) Find the critical value of at which the instability first appears as is increased.
4.I.6B
The non-dimensional equations for two competing populations are
Explain the meaning of each term in these equations.
Find all the fixed points of this system when and , and investigate their stability.
1.II.20H
Let .
(a) Show that and that the discriminant is equal to .
(b) Show that 2 ramifies in by showing that , and that is not a principal ideal. Show further that with . Deduce that neither nor is a principal ideal, but .
(c) Show that 5 splits in by showing that , and that
Deduce that has trivial class in the ideal class group of . Conclude that the ideal class group of is cyclic of order six.
[You may use the fact that
2.II.20H
Let and put .
(a) Show that 2,3 and are irreducible elements in . Deduce from the equation
that is not a principal ideal domain.
(b) Put and . Show that
Deduce that has class number 2 .
(c) Show that is the fundamental unit of . Hence prove that all solutions in integers of the equation are given by
4.II.20H
Let be a finite extension of and let be its ring of integers. We will assume that for some . The minimal polynomial of will be denoted by . For a prime number let
be the decomposition of into distinct irreducible monic factors . Let be a polynomial whose reduction modulo is . Show that
are the prime ideals of containing , that these are pairwise different, and
Determine the continued fraction of . Deduce two pairs of solutions in positive integers of the equation
1.I.1F
State the prime number theorem, and Bertrand's postulate.
Let be a finite set of prime numbers, and write for the number of positive integers no larger than , all of whose prime factors belong to . Prove that
where denotes the number of elements in . Deduce that, if is a strictly positive integer, we have
2.I.1F
Let be an odd prime number. Prove that 2 is a quadratic residue modulo when . Deduce that, if is a prime number strictly greater than 3 with such that is also a prime number, then is necessarily composite. Why does the argument break down for ?
3.II.11F
State the Chinese remainder theorem. Let be an odd positive integer. If is divisible by the square of a prime number , prove that there exists an integer such that but .
Define the Jacobi symbol
for any non-zero integer . Give a numerical example to show that
does not imply in general that is a square modulo . State and prove the law of quadratic reciprocity for the Jacobi symbol.
[You may assume the law of quadratic reciprocity for the Legendre symbol.]
Assume now that is divisible by the square of a prime number. Prove that there exists an integer with such that the congruence
does not hold. Show further that this congruence fails to hold for at least half of all relatively prime residue classes modulo .
4.I.1F
Prove Legendre's formula relating and for any positive real number . Use this formula to compute .
4.II.11F
Let be a prime number, and let be a polynomial with integer coefficients, whose leading coefficient is not divisible by . Prove that the congruence
has at most solutions, where is the degree of .
Deduce that all coefficients of the polynomial
must be divisible by , and prove that:
(i) ;
(ii) if is odd, the numerator of the fraction
is divisible by .
Assume now that . Show by example that (i) cannot be strengthened to .
1.II.38C
(a) For a numerical method to solve , define the linear stability domain and state when such a method is A-stable.
(b) Determine all values of the real parameter for which the Runge-Kutta method
is A-stable.
2.II.38C
(a) State the Householder-John theorem and explain how it can be used to design iterative methods for solving a system of linear equations .
(b) Let where is the diagonal part of , and and are, respectively, the strictly lower and strictly upper triangular parts of . Given a vector , consider the following iterative scheme:
Prove that if is a symmetric positive definite matrix, and , then the above iteration converges to the solution of the system .
3.II.38C
(a) Prove that all Toeplitz symmetric tridiagonal matrices
share the same eigenvectors with components , , and eigenvalues to be determined.
(b) The diffusion equation
is approximated by the Crank-Nicolson scheme
where , and is an approximation to . Assuming that show that the above scheme can be written in the form
where and the real matrices and should be found. Using matrix analysis, find the range of for which the scheme is stable. [Do not use Fourier analysis.]
4.II.39C
(a) Suppose that is a real matrix, and that and are given so that . Further, let be a non-singular matrix such that , where is the first coordinate vector and . Let . Prove that the eigenvalues of are together with the eigenvalues of the bottom right submatrix of
(b) Suppose again that is a real matrix, and that two linearly independent vectors are given such that the linear subspace spanned by and is invariant under the action of , i.e.,
Denote by an matrix whose two columns are the vectors and , and let be a non-singular matrix such that is upper triangular, that is,
Again let . Prove that the eigenvalues of are the eigenvalues of the top left submatrix of together with the eigenvalues of the bottom right submatrix of
2.II.29I
State Pontryagin's maximum principle in the case where both the terminal time and the terminal state are given.
Show that is the minimum value taken by the integral
subject to the constraints and , where
[You may find it useful to note the fact that the problem is rotationally symmetric about the -axis, so that the angle made by the initial velocity with the positive -axis may be chosen arbitrarily.]
3.II.28I
Let be a discrete-time controllable dynamical system (or Markov decision process) with countable state-space and action-space . Consider the -horizon dynamic optimization problem with instantaneous costs , on choosing action in state at time , with terminal cost , in state at time . Explain what is meant by a Markov control and how the choice of a control gives rise to a time-inhomogeneous Markov chain.
Suppose we can find a bounded function and a Markov control such that
with equality when , and such that for all . Here denotes the expected value of , given that we choose action in state at time . Show that is an optimal Markov control.
A well-shuffled pack of cards is placed face-down on the table. The cards are turned over one by one until none are left. Exactly once you may place a bet of on the event that the next two cards will be red. How should you choose the moment to bet? Justify your answer.
4.II.29I
Consider the scalar controllable linear system, whose state evolves by
with observations given by
Here, is the control variable, which is to be determined on the basis of the observations up to time , and are independent random variables. You wish to minimize the long-run average expected cost, where the instantaneous cost at time is . You may assume that the optimal control in equilibrium has the form , where is given by a recursion of the form
and where is chosen so that is independent of the observations up to time . Show that , and determine the minimal long-run average expected cost. You are not expected to simplify the arithmetic form of your answer but should show clearly how you have obtained it.
1.II.29A
(i) Consider the problem of solving the equation
for a function , with data specified on a hypersurface
Assume that are functions. Define the characteristic curves and explain what it means for the non-characteristic condition to hold at a point on . State a local existence and uniqueness theorem for the problem.
(ii) Consider the case and the equation
with data specified on the axis . Obtain a formula for the solution.
(iii) Consider next the case and the equation
with data specified on the hypersurface , which is given parametrically as where is defined by
Find the solution and show that it is a global solution. (Here "global" means is on all of .)
(iv) Consider next the equation
to be solved with the same data given on the same hypersurface as in (iii). Explain, with reference to the characteristic curves, why there is generally no global solution. Discuss the existence of local solutions defined in some neighbourhood of a given point for various . [You need not give formulae for the solutions.]
2.II.30A
Define (i) the Fourier transform of a tempered distribution , and (ii) the convolution of a tempered distribution and a Schwartz function . Give a formula for the Fourier transform of ("convolution theorem").
Let . Compute the Fourier transform of the tempered distribution defined by
and deduce the Kirchhoff formula for the solution of
Prove, by consideration of the quantities and , that any solution is also given by the Kirchhoff formula (uniqueness).
Prove a corresponding uniqueness statement for the initial value problem
where is a smooth positive real-valued function of only.
3.II.29A
Write down the formula for the solution for of the initial value problem for the heat equation in one space dimension
for a given smooth bounded function.
Define the distributional derivative of a tempered distribution . Define a fundamental solution of a constant-coefficient linear differential operator , and show that the distribution defined by the function is a fundamental solution for the operator .
For the equation
where , prove that there is a unique solution of the form with . Hence write down the solution of with general initial data and describe the large time behaviour.
4.II.30A
State and prove the mean value property for harmonic functions on .
Obtain a generalization of the mean value property for sub-harmonic functions on , i.e. functions for which
for all .
Let solve the equation
where is a real-valued continuous function. By considering the function show that, on any ball ,
1.II.32D
A particle in one dimension has position and momentum operators and whose eigenstates obey
Given a state , define the corresponding position-space and momentum-space wavefunctions and and show how each of these can be expressed in terms of the other. Derive the form taken in momentum space by the time-independent Schrödinger equation
for a general potential .
Now let with a positive constant. Show that the Schrödinger equation can be written
and verify that it has a solution for unique choices of and , to be determined (you need not find the normalisation constant, ). Check that this momentum space wavefunction can also be obtained from the position space solution .
2.II.32D
Let denote the combined spin eigenstates for a system of two particles, each with spin 1. Derive expressions for all states with in terms of product states.
Given that the particles are identical, and that the spatial wavefunction describing their relative position has definite orbital angular momentum , show that must be even. Suppose that this two-particle state is known to arise from the decay of a single particle, , also of spin 1. Assuming that total angular momentum and parity are conserved in this process, find the values of and that are allowed, depending on whether the intrinsic parity of is even or odd.
[You may set and use ]
3.II.32D
Let
be the position and momentum operators for a one-dimensional harmonic oscillator of mass and frequency . Write down the commutation relations obeyed by and and give an expression for the oscillator Hamiltonian in terms of them. Prove that the only energies allowed are with and give, without proof, a formula for a general normalised eigenstate in terms of .
A three-dimensional oscillator with charge is subjected to a weak electric field so that its total Hamiltonian is
where for and is a small, dimensionless parameter. Express the general eigenstate for the Hamiltonian with in terms of one-dimensional oscillator states, and give the corresponding energy eigenvalue. Use perturbation theory to compute the changes in energies of states in the lowest two levels when , working to the leading order at which non-vanishing corrections occur.
4.II.32D
The Hamiltonian for a particle of spin in a magnetic field is
and is a constant (the motion of the particle in space can be ignored). Consider a magnetic field which is independent of time. Writing , where is a unit vector, calculate the time evolution operator and show that if the particle is initially in a state the probability of measuring it to be in an orthogonal state after a time is
Evaluate this to find the probability for a transition from a state of spin up along the direction to one of spin down along the direction when .
Now consider a magnetic field whose and components are time-dependent but small:
Show that the probability for a transition from a spin-up state at time zero to a spin-down state at time (with spin measured along the direction, as before) is approximately
where you may assume . Comment on how this compares, when , with the result for a time-independent field.
[The first-order transition amplitude due to a perturbation is
where and are orthogonal eigenstates of the unperturbed Hamiltonian with eigenvalues and respectively.]
1.II.27I
Suppose that has density where . What does it mean to say that statistic is sufficient for ?
Suppose that , where is the parameter of interest, and is a nuisance parameter, and that the sufficient statistic has the form . What does it mean to say that the statistic is ancillary? If it is, how (according to the conditionality principle) do we test hypotheses on Assuming that the set of possible values for is discrete, show that is ancillary if and only if the density (probability mass function) factorises as
for some functions , and with the properties
for all , and .
Suppose now that are independent observations from a distribution, with density
Assuming that the criterion (*) holds also for observations which are not discrete, show that it is not possible to find sufficient for such that is ancillary when is regarded as a nuisance parameter, and is the parameter of interest.
2.II.27I
(i) State Wilks' likelihood ratio test of the null hypothesis against the alternative , where . Explain when this test may be used.
(ii) Independent identically-distributed observations take values in the set , with common distribution which under the null hypothesis is of the form
for some , where is an open subset of some Euclidean space , . Under the alternative hypothesis, the probability mass function of the is unrestricted.
Assuming sufficient regularity conditions on to guarantee the existence and uniqueness of a maximum-likelihood estimator of for each , show that for large the Wilks' likelihood ratio test statistic is approximately of the form
where , and . What is the asymptotic distribution of this statistic?
3.II.26I
(i) In the context of decision theory, what is a Bayes rule with respect to a given loss function and prior? What is an extended Bayes rule?
Characterise the Bayes rule with respect to a given prior in terms of the posterior distribution for the parameter given the observation. When for some , and the loss function is , what is the Bayes rule?
(ii) Suppose that , with loss function and suppose further that under .
Supposing that a prior is taken over , compute the Bayes risk of the decision rule . Find the posterior distribution of given , and confirm that its mean is of the form for some value of which you should identify. Hence show that the decision rule is an extended Bayes rule.
4.II.27I
Assuming sufficient regularity conditions on the likelihood for a univariate parameter , establish the Cramér-Rao lower bound for the variance of an unbiased estimator of .
If is an unbiased estimator of whose variance attains the Cramér-Rao lower bound for every value of , show that the likelihood function is an exponential family.
1.II.25J
Let be a set and be a set system.
(a) Explain what is meant by a -system, a -system and a -algebra.
(b) Show that is a -algebra if and only if is a -system and a -system.
(c) Which of the following set systems are -systems, -systems or -algebras? Justify your answers. ( denotes the number of elements in .)
and is even ,
and is even or ,
and
(d) State and prove the theorem on the uniqueness of extension of a measure.
[You may use standard results from the lectures without proof, provided they are clearly stated.]
2.II.25J
(a) State and prove the first Borel-Cantelli lemma. State the second Borel-Cantelli lemma.
(b) Let be a sequence of independent random variables that converges in probability to the limit . Show that is almost surely constant.
A sequence of random variables is said to be completely convergent to if
(c) Show that complete convergence implies almost sure convergence.
(d) Show that, for sequences of independent random variables, almost sure convergence also implies complete convergence.
(e) Find a sequence of (dependent) random variables that converges almost surely but does not converge completely.
3.II.24J
Let be a finite measure space, i.e. , and let .
(a) Define the -norm of a measurable function , define the space and define convergence in
In the following you may use inequalities from the lectures without proof, provided they are clearly stated.
(b) Let . Show that in implies .
(c) Let be a bounded measurable function with . Let
Show that and .
By using Jensen's inequality, or otherwise, show that
Prove that
Observe that
4.II.25J
Let be a measure space with and let be measurable.
(a) Define an invariant set and an invariant function .
What is meant by saying that is measure-preserving?
What is meant by saying that is ergodic?
(b) Which of the following functions to is ergodic? Justify your answer.
On the measure space with Lebesgue measure consider
On the discrete measure space consider
(c) State Birkhoff's almost everywhere ergodic theorem.
(d) Let be measure-preserving and let be bounded.
Prove that converges in for all .
1.II.19H
A finite group has seven conjugacy classes and the values of five of its irreducible characters are given in the following table.
Calculate the number of elements in the various conjugacy classes and complete the character table.
[You may not identify with any known group, unless you justify doing so.]
2.II.19H
Let be a finite group and let be its centre. Show that if is a complex irreducible representation of , assumed to be faithful (that is, the kernel of is trivial), then is cyclic.
Now assume that is a p-group (that is, the order of is a power of the prime , and assume that is cyclic. If is a faithful representation of , show that some irreducible component of is faithful.
[You may use without proof the fact that, since is a p-group, is non-trivial and any non-trivial normal subgroup of intersects non-trivially.]
Deduce that a finite -group has a faithful irreducible representation if and only if its centre is cyclic.
3.II.19H
Let be a finite group with a permutation action on the set . Describe the corresponding permutation character . Show that the multiplicity in of the principal character equals the number of orbits of on .
Assume that is transitive on , with . Show that contains an element which is fixed-point-free on , that is, for all in .
Assume that , with an irreducible character of , for some natural number . Show that .
[You may use without proof any facts about algebraic integers, provided you state them correctly.]
Explain how the action of on induces an action of on . Assume that has orbits on . If now
with distinct irreducible characters of , and natural numbers, show that . Deduce that, if , then and .
4.II.19H
Write an essay on the representation theory of .
Your answer should include a description of each irreducible representation and an explanation of how to decompose arbitrary representations into a direct sum of these.
1.II.23F
Define a complex structure on the unit sphere using stereographic projection charts . Let be an open set. Show that a continuous non-constant map is holomorphic if and only if is a meromorphic function. Deduce that a non-constant rational function determines a holomorphic map . Define what is meant by a rational function taking the value with multiplicity at infinity.
Define the degree of a rational function. Show that any rational function satisfies and give examples to show that the bounds are attained. Is it true that the product satisfies , for any non-constant rational functions and ? Justify your answer.
2.II.23F
A function is defined for by
where is a complex parameter with . Prove that this series converges uniformly on the subsets for and deduce that is holomorphic on .
You may assume without proof that
for all . Let be the logarithmic derivative . Show that
for all . Deduce that has only one zero in the parallelogram with vertices . Find all of the zeros of
Let be the lattice in generated by 1 and . Show that, for , the formula
gives a -periodic meromorphic function if and only if . Deduce that is -periodic.
3.II.22F
(i) Let and be compact connected Riemann surfaces and a non-constant holomorphic map. Define the branching order at showing that it is well defined. Prove that the set of ramification points is finite. State the Riemann-Hurwitz formula.
Now suppose that and have the same genus . Prove that, if , then is biholomorphic. In the case when , write down an example where is not biholomorphic.
[The inverse mapping theorem for holomorphic functions on domains in may be assumed without proof if accurately stated.]
(ii) Let be a non-singular algebraic curve in . Describe, without detailed proofs, a family of charts for , so that the restrictions to of the first and second projections are holomorphic maps. Show that the algebraic curve
is non-singular. Find all the ramification points of the .
4.II.23F
Let be a Riemann surface, a topological surface, and a continuous map. Suppose that every point admits a neighbourhood such that maps homeomorphically onto its image. Prove that has a complex structure such that is a holomorphic map.
A holomorphic map between Riemann surfaces is called a covering map if every has a neighbourhood with a disjoint union of open sets in , so that is biholomorphic for each . Suppose that a Riemann surface admits a holomorphic covering map from the unit . Prove that any holomorphic map is constant.
[You may assume any form of the monodromy theorem and basic results about the lifts of paths, provided that these are accurately stated.]
1.II.16G
By a directed set in a poset , we mean a nonempty subset such that any pair of elements of has an upper bound in . We say is directed-complete if each directed subset has a least upper bound in . Show that a poset is complete if and only if it is directed-complete and has joins for all its finite subsets. Show also that, for any two sets and , the set of partial functions from to , ordered by extension, is directed-complete.
Let be a directed-complete poset, and an order-preserving map which is inflationary, i.e. satisfies for all . We define a subset to be closed if it satisfies , and is also closed under joins of directed sets (i.e., and directed imply ). We write to mean that every closed set containing also contains . Show that is a partial order on , and that implies . Now consider the set of all functions which are order-preserving and satisfy for all . Show that is closed under composition of functions, and deduce that, for each , the set is directed. Defining for each , show that the function belongs to , and deduce that is the least fixed point of lying above , for each .
2.II.16G
Explain carefully what is meant by a deduction in the propositional calculus. State the completeness theorem for the propositional calculus, and deduce the compactness theorem.
Let be three pairwise-disjoint sets of primitive propositions, and suppose given compound propositions and such that holds. Let denote the set
If is any valuation making all the propositions in true, show that the set
is consistent. Deduce that is inconsistent, and hence show that there exists such that and both hold.
3.II.16G
Write down the recursive definitions of ordinal addition, multiplication and exponentiation. Prove carefully that for all , and hence show that for each non-zero ordinal there exists a unique such that
Deduce that any non-zero ordinal has a unique representation of the form
where and are non-zero natural numbers.
Two ordinals are said to be commensurable if we have neither nor . Show that and are commensurable if and only if there exists such that both and lie in the set
4.II.16G
Explain what is meant by a well-founded binary relation on a set.
Given a set , we say that a mapping is recursive if, given any set equipped with a mapping , there exists a unique such that , where denotes the mapping . Show that is recursive if and only if the relation is well-founded.
[If you need to use any form of the recursion theorem, you should prove it.]
1.I.5I
According to the Independent newspaper (London, 8 March 1994) the Metropolitan Police in London reported 30475 people as missing in the year ending March 1993. For those aged 18 or less, 96 of 10527 missing males and 146 of 11363 missing females were still missing a year later. For those aged 19 and above, the values were 157 of 5065 males and 159 of 3520 females. This data is summarised in the table below.
\begin{array}{rrrrr} & \multicolumn{3}{r}{\text { age }} \\ 1 & \text { Kender } & \text { M } & 96 & 10527 \\ 2 & \text { Kid } & \text { F } & 146 & 11363 \\ 3 & \text { Adult } & \text { M } & 157 & 5065 \\ 4 & \text { Adult } & \text { F } & 159 & 3520 \end{array}
Explain and interpret the commands and (slightly abbreviated) output below. You should describe the model being fitted, explain how the standard errors are calculated, and comment on the hypothesis tests being described in the summary. In particular, what is the worst of the four categories for the probability of remaining missing a year later?

For a person who was missing in the year ending in March 1993, find a formula, as a function of age and gender, for the estimated expected probability that they are still missing a year later.
1.II.13I
This problem deals with data collected as the number of each of two different strains of Ceriodaphnia organisms are counted in a controlled environment in which reproduction is occurring among the organisms. The experimenter places into the containers a varying concentration of a particular component of jet fuel that impairs reproduction. Hence it is anticipated that as the concentration of jet fuel grows, the mean number of organisms should decrease.
The table below gives a subset of the data. The full dataset has rows. The first column provides the number of organisms, the second the concentration of jet fuel (in grams per litre) and the third specifies the strain of the organism.
Explain and interpret the commands and (slightly abbreviated) output below. In particular, you should describe the model being fitted, explain how the standard errors are calculated, and comment on the hypothesis tests being described in the summary.
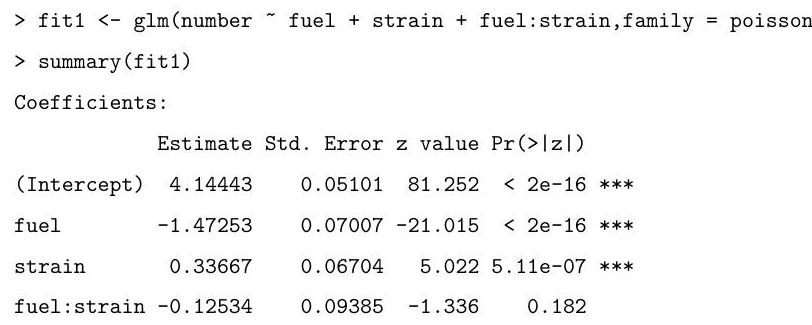
The following code fits two very similar models. Briefly explain the difference between these models and the one above. Motivate the fitting of these models in light of
Part II 2007 the summary from the fit of the one above.
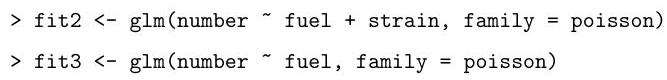
Denote by the three hypotheses being fitted in sequence above.
Explain the hypothesis tests, including an approximate test of the fit of , that can be performed using the output from the following code. Use these numbers to comment on the most appropriate model for the data.
, fit2$dev, fit3$dev)
[1]
[1]
2.I.5I
Consider the linear regression setting where the responses are assumed independent with means . Here is a vector of known explanatory variables and is a vector of unknown regression coefficients.
Show that if the response distribution is Laplace, i.e.,
then the maximum likelihood estimate of is obtained by minimising
Obtain the maximum likelihood estimate for in terms of .
Briefly comment on why the Laplace distribution cannot be written in exponential dispersion family form.
3.I.5I
Consider two possible experiments giving rise to observed data where
- The data are realizations of independent Poisson random variables, i.e.,
where , with an unknown (possibly vector) parameter. Write for the maximum likelihood estimator (m.l.e.) of and for the th fitted value under this model.
- The data are components of a realization of a multinomial random 'vector'
where the are non-negative integers with
Write for the m.l.e. of and for the th fitted value under this model.
Show that, if
then and for all . Explain the relevance of this result in the context of fitting multinomial models within a generalized linear model framework.
4.I.5I
Consider the normal linear model in vector notation, where
i.i.d. ,
where is known and is of full rank . Give expressions for maximum likelihood estimators and of and respectively, and state their joint distribution.
Suppose that there is a new pair , independent of , satisfying the relationship
We suppose that is known, and estimate by . State the distribution of
Find the form of a -level prediction interval for .
4.II.13I
Let have a Gamma distribution with density
Show that the Gamma distribution is of exponential dispersion family form. Deduce directly the corresponding expressions for and in terms of and . What is the canonical link function?
Let . Consider a generalised linear model (g.l.m.) for responses with random component defined by the Gamma distribution with canonical link , so that , where is the vector of unknown regression coefficients and is the vector of known values of the explanatory variables for the th observation, .
Obtain expressions for the score function and Fisher information matrix and explain how these can be used in order to approximate , the maximum likelihood estimator (m.l.e.) of .
[Use the canonical link function and assume that the dispersion parameter is known.]
Finally, obtain an expression for the deviance for a comparison of the full (saturated) model to the g.l.m. with canonical link using the m.l.e. (or estimated mean .
2.II.34D
Derive the Maxwell relation
The diagram below illustrates the Joule-Thomson throttling process for a porous barrier. A gas of volume , initially on the left-hand side of a thermally insulated pipe, is forced by a piston to go through the barrier using constant pressure . As a result the gas flows to the right-hand side, resisted by a piston which applies a constant pressure (with ). Eventually all of the gas occupies a volume on the right-hand side. Show that this process conserves enthalpy.
The Joule-Thomson coefficient is the change in temperature with respect to a change in pressure during a process that conserves enthalpy . Express the JouleThomson coefficient, , in terms of , the heat capacity at constant pressure , and the volume coefficient of expansion .
What is for an ideal gas?
If one wishes to use the Joule-Thomson process to cool a real (non-ideal) gas, what must the of be?

3.II.34D
For a 2-dimensional gas of nonrelativistic, non-interacting, spinless bosons, find the density of states in the neighbourhood of energy . [Hint: consider the gas in a box of size which has periodic boundary conditions. Work in the thermodynamic limit , with held finite.]
Calculate the number of particles per unit area at a given temperature and chemical potential.
Explain why Bose-Einstein condensation does not occur in this gas at any temperature.
[Recall that
4.II.34D
Consider a classical gas of diatomic molecules whose orientation is fixed by a strong magnetic field. The molecules are not free to rotate, but they are free to vibrate. Assuming that the vibrations are approximately harmonic, calculate the contribution to the partition function due to vibrations.
Evaluate the free energy , where is the total partition function for the gas, and hence calculate the entropy.
Note that and You may approximate ! by .]
1.II.28J
(i) What does it mean to say that a process is a martingale? What does the martingale convergence theorem tell us when applied to positive martingales?
(ii) What does it mean to say that a process is a Brownian motion? Show that with probability one.
(iii) Suppose that is a Brownian motion. Find such that
is a martingale. Discuss the limiting behaviour of and for this as .
2.II.28J
In the context of a single-period financial market with traded assets, what is an arbitrage? What is an equivalent martingale measure?
Fix and consider the following single-period market with 3 assets:
Asset 1 is a riskless bond and pays no interest.
Asset 2 is a stock with initial price per share; its possible final prices are with probability and with probability .
Asset 3 is another stock that behaves like an independent copy of asset 2 .
Find all equivalent martingale measures for the problem and characterise all contingent claims that can be replicated.
Consider a contingent claim that pays 1 if both risky assets move in the same direction and zero otherwise. Show that the lower arbitrage bound, simply obtained by calculating all possible prices as the pricing measure ranges over all equivalent martingale measures, is zero. Why might someone pay for such a contract?
3.II.27J
Suppose that over two periods a stock price moves on a binomial tree

(i) Determine for what values of the riskless rate there is no arbitrage. From here on, fix and determine the equivalent martingale measure.
(ii) Find the time-zero price and replicating portfolio for a European put option with strike 15 and expiry
(iii) Find the time-zero price and optimal exercise policy for an American put option with the same strike and expiry.
(iv) Deduce the corresponding (European and American) call option prices for the same strike and expiry.
4.II.28J
Briefly describe the Black-Scholes model. Consider a "cash-or-nothing" option with strike price , i.e. an option whose payoff at maturity is
It can be interpreted as a bet that the stock will be worth at least at time . Find a formula for its value at time , in terms of the spot price . Find a formula for its Delta (i.e. its hedge ratio). How does the Delta behave as ? Why is it difficult, in practice, to hedge such an instrument?
Write
Suppose that is a convex, compact subset of with . Show that there is a unique point such that
for all .
State a version of Runge's theorem and use it to prove the following theorem:
Let and define by the condition
for all and all . (We take to be the positive square root.) Then there exists a sequence of analytic functions such that for each as .
1.I.2F
Let be an integer with . Are the following statements true or false? Give proofs.
(i) There exists a real polynomial of degree such that
for all real .
(ii) There exists a real polynomial of degree such that
for all real .
(iii) There exists a real polynomial of degree such that
for all real .
2.II.12F
(i) Suppose that is continuous. Prove the theorem of Bernstein which states that, if we write
for , then uniformly as
(ii) Let and let be distinct points in . We write
for every continuous function . Show that, if
for all polynomials of degree or less, then for all and
(iii) If satisfies the conditions set out in (ii), show that
as whenever is continuous.
3.II.12F
(i) State and prove Liouville's theorem on approximation of algebraic numbers by rationals.
(ii) Consider the continued fraction
where the are strictly positive integers. You may assume the following algebraic facts about the th convergent .
Show that
Give explicit values for so that is transcendental and prove that you have done SO.
4.I.2F
State Brouwer's fixed point theorem for a triangle in two dimensions.
Let be a matrix with real positive entries and such that all its columns are non-zero vectors. Show that has an eigenvector with positive entries.
1.II.37C
A uniform elastic solid with density and Lamé moduli and occupies the region between rigid plane boundaries and . Show that SH waves can propagate in the direction within this layer, and find the dispersion relation for such waves.
Deduce for each mode (a) the cutoff frequency, (b) the phase velocity, and (c) the group velocity.
Show also that for each mode the kinetic energy and elastic energy are equal in an average sense to be made precise.
[You may assume that the elastic energy per unit volume .]
2.II.37C
Show that for a one-dimensional flow of a perfect gas at constant entropy the Riemann invariants are constant along characteristics .
Define a simple wave. Show that in a right-propagating simple wave
Now suppose instead that, owing to dissipative effects,
where is a positive constant. Suppose also that is prescribed at for all , say . Demonstrate that, unless a shock forms,
where, for each and is determined implicitly as the solution of the equation
Deduce that a shock will not form at any if
3.II.37C
Waves propagating in a slowly-varying medium satisfy the local dispersion relation
in the standard notation. Give a brief derivation of the ray-tracing equations for such waves; a formal justification is not required.
An ocean occupies the region . Water waves are incident on a beach near . The undisturbed water depth is
with a small positive constant and positive. The local dispersion relation is
and where are the wavenumber components in the directions. Far from the beach, the waves are planar with frequency and crests making an acute angle with the shoreline . Obtain a differential equation (in implicit form) for a ray , and show that near the shore the ray satisfies
where and should be found. Sketch the appearance of the wavecrests near the shoreline.
4.II
Show that, for a plane acoustic wave, the acoustic intensity may be written as in the standard notation.
Derive the general spherically-symmetric solution of the wave equation. Use it to find the velocity potential for waves radiated into an unbounded fluid by a pulsating sphere of radius
By considering the far field, or otherwise, find the time-average rate at which energy is radiated by the sphere.
You may assume that .]