Part II, 2021

Algebraic Geometry

• Paper 1, Section II, I

  Algebraic Geometry | Part II, 2021

  Let $k$ be an algebraically closed field and let $V \subset \mathbb{A}_{k}^{n}$ be a non-empty affine variety. Show that $V$ is a finite union of irreducible subvarieties.

  Let $V_{1}$ and $V_{2}$ be subvarieties of $\mathbb{A}_{k}^{n}$ given by the vanishing loci of ideals $I_{1}$ and $I_{2}$ respectively. Prove the following assertions.

  (i) The variety $V_{1} \cap V_{2}$ is equal to the vanishing locus of the ideal $I_{1}+I_{2}$.

  (ii) The variety $V_{1} \cup V_{2}$ is equal to the vanishing locus of the ideal $I_{1} \cap I_{2}$.

  Decompose the vanishing locus

  $$\mathbb{V}\left(X^{2}+Y^{2}-1, X^{2}-Z^{2}-1\right) \subset \mathbb{A}_{\mathbb{C}}^{3}$$

  into irreducible components.

  Let $V \subset \mathbb{A}_{k}^{3}$ be the union of the three coordinate axes. Let $W$ be the union of three distinct lines through the point $(0,0)$ in $\mathbb{A}_{k}^{2}$. Prove that $W$ is not isomorphic to $V$.

  comment

• Paper 2, Section II, I

  Algebraic Geometry | Part II, 2021

  Let $k$ be an algebraically closed field and $n \geqslant 1$. Exhibit $G L(n, k)$ as an open subset of affine space $\mathbb{A}_{k}^{n^{2}}$. Deduce that $G L(n, k)$ is smooth. Prove that it is also irreducible.

  Prove that $G L(n, k)$ is isomorphic to a closed subvariety in an affine space.

  Show that the matrix multiplication map

  $$G L(n, k) \times G L(n, k) \rightarrow G L(n, k)$$

  that sends a pair of matrices to their product is a morphism.

  Prove that any morphism from $\mathbb{A}_{k}^{n}$ to $\mathbb{A}_{k}^{1}\setminus\{0\}$ is constant.

  Prove that for $n \geqslant 2$ any morphism from $\mathbb{P}_{k}^{n}$ to $\mathbb{P}_{k}^{1}$ is constant.

  comment

• Paper 3, Section II, I

  Algebraic Geometry | Part II, 2021

  In this question, all varieties are over an algebraically closed field $k$ of characteristic zero.

  What does it mean for a projective variety to be smooth? Give an example of a smooth affine variety $X \subset \mathbb{A}_{k}^{n}$ whose projective closure $\bar{X} \subset \mathbb{P}_{k}^{n}$ is not smooth.

  What is the genus of a smooth projective curve? Let $X \subset \mathbb{P}_{k}^{4}$ be the hypersurface $V\left(X_{0}^{3}+X_{1}^{3}+X_{2}^{3}+X_{3}^{3}+X_{4}^{3}\right)$. Prove that $X$ contains a smooth curve of genus $1 .$

  Let $C \subset \mathbb{P}_{k}^{2}$ be an irreducible curve of degree 2 . Prove that $C$ is isomorphic to $\mathbb{P}_{k}^{1}$.

  We define a generalized conic in $\mathbb{P}_{k}^{2}$ to be the vanishing locus of a non-zero homogeneous quadratic polynomial in 3 variables. Show that there is a bijection between the set of generalized conics in $\mathbb{P}_{k}^{2}$ and the projective space $\mathbb{P}_{k}^{5}$, which maps the conic $V(f)$ to the point whose coordinates are the coefficients of $f$.

  (i) Let $R^{\circ} \subset \mathbb{P}_{k}^{5}$ be the subset of conics that consist of unions of two distinct lines. Prove that $R^{\circ}$ is not Zariski closed, and calculate its dimension.

  (ii) Let $I$ be the homogeneous ideal of polynomials vanishing on $R^{\circ}$. Determine generators for the ideal $I$.

  comment

• Paper 4, Section II, I

  Algebraic Geometry | Part II, 2021

  Let $C$ be a smooth irreducible projective algebraic curve over an algebraically closed field.

  Let $D$ be an effective divisor on $C$. Prove that the vector space $L(D)$ of rational functions with poles bounded by $D$ is finite dimensional.

  Let $D$ and $E$ be linearly equivalent divisors on $C$. Exhibit an isomorphism between the vector spaces $L(D)$ and $L(E)$.

  What is a canonical divisor on $C$ ? State the Riemann-Roch theorem and use it to calculate the degree of a canonical divisor in terms of the genus of $C$.

  Prove that the canonical divisor on a smooth cubic plane curve is linearly equivalent to the zero divisor.

  comment

Algebraic Topology

• Paper 1, Section II, 21F

  Algebraic Topology | Part II, 2021

  (a) What does it mean for two spaces $X$ and $Y$ to be homotopy equivalent?

  (b) What does it mean for a subspace $Y \subseteq X$ to be a retract of a space $X$ ? What does it mean for a space $X$ to be contractible? Show that a retract of a contractible space is contractible.

  (c) Let $X$ be a space and $A \subseteq X$ a subspace. We say the pair $(X, A)$ has the homotopy extension property if, for any pair of maps $f: X \times\{0\} \rightarrow Y$ and $H^{\prime}: A \times I \rightarrow Y$ with

  $$\left.f\right|_{A \times\{0\}}=\left.H^{\prime}\right|_{A \times\{0\}},$$

  there exists a map $H: X \times I \rightarrow Y$ with

  $$\left.H\right|_{X \times\{0\}}=f,\left.\quad H\right|_{A \times I}=H^{\prime}$$

  Now suppose that $A \subseteq X$ is contractible. Denote by $X / A$ the quotient of $X$ by the equivalence relation $x \sim x^{\prime}$ if and only if $x=x^{\prime}$ or $x, x^{\prime} \in A$. Show that, if $(X, A)$ satisfies the homotopy extension property, then $X$ and $X / A$ are homotopy equivalent.

  comment

• Paper 2, Section II, 21F

  Algebraic Topology | Part II, 2021

  (a) State a suitable version of the Seifert-van Kampen theorem and use it to calculate the fundamental groups of the torus $T^{2}:=S^{1} \times S^{1}$ and of the real projective plane $\mathbb{R P}^{2}$.

  (b) Show that there are no covering maps $T^{2} \rightarrow \mathbb{R} \mathbb{P}^{2}$ or $\mathbb{R P}^{2} \rightarrow T^{2}$.

  (c) Consider the following covering space of $S^{1} \vee S^{1}$ :

  

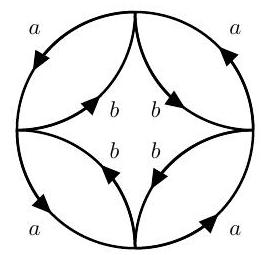
  Here the line segments labelled $a$ and $b$ are mapped to the two different copies of $S^{1}$ contained in $S^{1} \vee S^{1}$, with orientations as indicated.

  Using the Galois correspondence with basepoints, identify a subgroup of

  $$\pi_{1}\left(S^{1} \vee S^{1}, x_{0}\right)=F_{2}$$

  (where $x_{0}$ is the wedge point) that corresponds to this covering space.

  comment

• Paper 3, Section II, 20F

  Algebraic Topology | Part II, 2021

  Let $X$ be a space. We define the cone of $X$ to be

  $$C X:=(X \times I) / \sim$$

  where $\left(x_{1}, t_{1}\right) \sim\left(x_{2}, t_{2}\right)$ if and only if either $t_{1}=t_{2}=1$ or $\left(x_{1}, t_{1}\right)=\left(x_{2}, t_{2}\right)$.

  (a) Show that if $X$ is triangulable, so is $C X$. Calculate $H_{i}(C X)$. [You may use any results proved in the course.]

  (b) Let $K$ be a simplicial complex and $L \subseteq K$ a subcomplex. Let $X=|K|, A=|L|$, and let $X^{\prime}$ be the space obtained by identifying $|L| \subseteq|K|$ with $|L| \times\{0\} \subseteq C|L|$. Show that there is a long exact sequence

  $$\begin{aligned} \cdots \rightarrow & H_{i+1}\left(X^{\prime}\right) \rightarrow H_{i}(A) \rightarrow H_{i}(X) \rightarrow H_{i}\left(X^{\prime}\right) \rightarrow H_{i-1}(A) \rightarrow \cdots \\ & \cdots \rightarrow H_{1}\left(X^{\prime}\right) \rightarrow H_{0}(A) \rightarrow \mathbb{Z} \oplus H_{0}(X) \rightarrow H_{0}\left(X^{\prime}\right) \rightarrow 0 \end{aligned}$$

  (c) In part (b), suppose that $X=S^{1} \times S^{1}$ and $A=S^{1} \times\{x\} \subseteq X$ for some $x \in S^{1}$. Calculate $H_{i}\left(X^{\prime}\right)$ for all $i$.

  comment

• Paper 4, Section II, 21F

  Algebraic Topology | Part II, 2021

  (a) Define the Euler characteristic of a triangulable space $X$.

  (b) Let $\Sigma_{g}$ be an orientable surface of genus $g$. A $\operatorname{map} \pi: \Sigma_{g} \rightarrow S^{2}$ is a doublebranched cover if there is a set $Q=\left\{p_{1}, \ldots, p_{n}\right\} \subseteq S^{2}$ of branch points, such that the restriction $\pi: \Sigma_{g} \backslash \pi^{-1}(Q) \rightarrow S^{2} \backslash Q$ is a covering map of degree 2 , but for each $p \in Q$, $\pi^{-1}(p)$ consists of one point. By carefully choosing a triangulation of $S^{2}$, use the Euler characteristic to find a formula relating $g$ and $n$.

  comment

Analysis of Functions

• Paper 1, Section II, $23 \mathrm{H}$

  Analysis of Functions | Part II, 2021

  Below, $\mathcal{M}$ is the $\sigma$-algebra of Lebesgue measurable sets and $\lambda$ is Lebesgue measure.

  (a) State the Lebesgue differentiation theorem for an integrable function $f: \mathbb{R}^{n} \rightarrow \mathbb{C}$. Let $g: \mathbb{R} \rightarrow \mathbb{C}$ be integrable and define $G: \mathbb{R} \rightarrow \mathbb{C}$ by $G(x):=\int_{[a, x]} g d \lambda$ for some $a \in \mathbb{R}$. Show that $G$ is differentiable $\lambda$-almost everywhere.

  (b) Suppose $h: \mathbb{R} \rightarrow \mathbb{R}$ is strictly increasing, continuous, and maps sets of $\lambda$-measure zero to sets of $\lambda$-measure zero. Show that we can define a measure $\nu$ on $\mathcal{M}$ by setting $\nu(A):=\lambda(h(A))$ for $A \in \mathcal{M}$, and establish that $\nu \ll \lambda$. Deduce that $h$ is differentiable $\lambda$-almost everywhere. Does the result continue to hold if $h$ is assumed to be non-decreasing rather than strictly increasing?

  [You may assume without proof that a strictly increasing, continuous, function $w: \mathbb{R} \rightarrow \mathbb{R}$ is injective, and $w^{-1}: w(\mathbb{R}) \rightarrow \mathbb{R}$ is continuous.]

  comment

• Paper 2, Section II, H

  Analysis of Functions | Part II, 2021

  Define the Schwartz space, $\mathscr{S}\left(\mathbb{R}^{n}\right)$, and the space of tempered distributions, $\mathscr{S}^{\prime}\left(\mathbb{R}^{n}\right)$, stating what it means for a sequence to converge in each space.

  For a $C^{k}$ function $f: \mathbb{R}^{n} \rightarrow \mathbb{C}$, and non-negative integers $N, k$, we say $f \in X_{N, k}$ if

  $$\|f\|_{N, k}:=\sup _{x \in \mathbb{R}^{n} ;|\alpha| \leqslant k}\left|\left(1+|x|^{2}\right)^{\frac{N}{2}} D^{\alpha} f(x)\right|<\infty$$

  You may assume that $X_{N, k}$ equipped with $\|\cdot\|_{N, k}$ is a Banach space in which $\mathscr{S}\left(\mathbb{R}^{n}\right)$ is dense.

  (a) Show that if $u \in \mathscr{S}^{\prime}\left(\mathbb{R}^{n}\right)$ there exist $N, k \in \mathbb{Z}_{\geqslant 0}$ and $C>0$ such that

  $$|u[\phi]| \leqslant C\|\phi\|_{N, k} \text { for all } \phi \in \mathscr{S}\left(\mathbb{R}^{n}\right)$$

  Deduce that there exists a unique $\tilde{u} \in X_{N, k}^{\prime}$ such that $\tilde{u}[\phi]=u[\phi]$ for all $\phi \in \mathscr{S}\left(\mathbb{R}^{n}\right)$.

  (b) Recall that $v \in \mathscr{S}^{\prime}\left(\mathbb{R}^{n}\right)$ is positive if $v[\phi] \geqslant 0$ for all $\phi \in \mathscr{S}\left(\mathbb{R}^{n}\right)$ satisfying $\phi \geqslant 0$. Show that if $v \in \mathscr{S}^{\prime}\left(\mathbb{R}^{n}\right)$ is positive, then there exist $M \in \mathbb{Z}_{\geqslant 0}$ and $K>0$ such that

  $$|v[\phi]| \leqslant K\|\phi\|_{M, 0}, \quad \text { for all } \phi \in \mathscr{S}\left(\mathbb{R}^{n}\right)$$

  $\left[\right.$ Hint: Note that $\left.|\phi(x)| \leqslant\|\phi\|_{M, 0}\left(1+|x|^{2}\right)^{-\frac{M}{2}} \cdot\right]$

  comment

• Paper 3, Section II, H

  Analysis of Functions | Part II, 2021

  (a) State the Riemann-Lebesgue lemma. Show that the Fourier transform maps $\mathscr{S}\left(\mathbb{R}^{n}\right)$ to itself continuously.

  (b) For some $s \geqslant 0$, let $f \in L^{1}\left(\mathbb{R}^{3}\right) \cap H^{s}\left(\mathbb{R}^{3}\right)$. Consider the following system of equations for $\mathbf{B}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$

  $$\nabla \cdot \mathbf{B}=f, \quad \boldsymbol{\nabla} \times \mathbf{B}=\mathbf{0}$$

  Show that there exists a unique $\mathbf{B}=\left(B_{1}, B_{2}, B_{3}\right)$ solving the equations with $B_{j} \in$ $H^{s+1}\left(\mathbb{R}^{3}\right)$ for $j=1,2,3$. You need not find $\mathbf{B}$ explicitly, but should give an expression for the Fourier transform of $B_{j}$. Show that there exists a constant $C>0$ such that

  $$\left\|B_{j}\right\|_{H^{s+1}} \leqslant C\left(\|f\|_{L^{1}}+\|f\|_{H^{s}}\right), \quad j=1,2,3$$

  For what values of $s$ can we conclude that $B_{j} \in C^{1}\left(\mathbb{R}^{n}\right)$ ?

  comment

• Paper 4, Section II, $23 \mathrm{H}$

  Analysis of Functions | Part II, 2021

  Fix $1<p<\infty$ and let $q$ satisfy $p^{-1}+q^{-1}=1$

  (a) Let $\left(f_{j}\right)$ be a sequence of functions in $L^{p}\left(\mathbb{R}^{n}\right)$. For $f \in L^{p}\left(\mathbb{R}^{n}\right)$, what is meant by (i) $f_{j} \rightarrow f$ in $L^{p}\left(\mathbb{R}^{n}\right)$ and (ii) $f_{j} \rightarrow f$ in $L^{p}\left(\mathbb{R}^{n}\right)$ ? Show that if $f_{j} \rightarrow f$, then

  $$\|f\|_{L^{p}} \leqslant \liminf _{j \rightarrow \infty}\left\|f_{j}\right\|_{L^{p}}$$

  (b) Suppose that $\left(g_{j}\right)$ is a sequence with $g_{j} \in L^{p}\left(\mathbb{R}^{n}\right)$, and that there exists $K>0$ such that $\left\|g_{j}\right\|_{L^{p}} \leqslant K$ for all $j$. Show that there exists $g \in L^{p}\left(\mathbb{R}^{n}\right)$ and a subsequence $\left(g_{j_{k}}\right)_{k=1}^{\infty}$, such that for any sequence $\left(h_{k}\right)$ with $h_{k} \in L^{q}\left(\mathbb{R}^{n}\right)$ and $h_{k} \rightarrow h \in L^{q}\left(\mathbb{R}^{n}\right)$, we have

  $$\lim _{k \rightarrow \infty} \int_{\mathbb{R}^{n}} g_{j_{k}} h_{k} d x=\int_{\mathbb{R}^{n}} g h d x .$$

  Give an example to show that the result need not hold if the condition $h_{k} \rightarrow h$ is replaced by $h_{k} \rightarrow h$ in $L^{q}\left(\mathbb{R}^{n}\right)$.

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, B

  Applications of Quantum Mechanics | Part II, 2021

  (a) Discuss the variational principle that allows one to derive an upper bound on the energy $E_{0}$ of the ground state for a particle in one dimension subject to a potential $V(x)$.

  If $V(x)=V(-x)$, how could you adapt the variational principle to derive an upper bound on the energy $E_{1}$ of the first excited state?

  (b) Consider a particle of mass $2 m=\hbar^{2}$ (in certain units) subject to a potential

  $$V(x)=-V_{0} e^{-x^{2}} \quad \text { with } \quad V_{0}>0$$

  (i) Using the trial wavefunction

  $$\psi(x)=e^{-\frac{1}{2} x^{2} a}$$

  with $a>0$, derive the upper bound $E_{0} \leqslant E(a)$, where

  $$E(a)=\frac{1}{2} a-V_{0} \frac{\sqrt{a}}{\sqrt{1+a}}$$

  (ii) Find the zero of $E(a)$ in $a>0$ and show that any extremum must obey

  $$(1+a)^{3}=\frac{V_{0}^{2}}{a} .$$

  (iii) By sketching $E(a)$ or otherwise, deduce that there must always be a minimum in $a>0$. Hence deduce the existence of a bound state.

  (iv) Working perturbatively in $0<V_{0} \ll 1$, show that

  $$-V_{0}<E_{0} \leqslant-\frac{1}{2} V_{0}^{2}+\mathcal{O}\left(V_{0}^{3}\right)$$

  [Hint: You may use that $\int_{-\infty}^{\infty} e^{-b x^{2}} d x=\sqrt{\frac{\pi}{b}}$ for $\left.b>0 .\right]$

  comment

• Paper 2, Section II, 36B

  Applications of Quantum Mechanics | Part II, 2021

  (a) The $s$-wave solution $\psi_{0}$ for the scattering problem of a particle of mass $m$ and momentum $\hbar k$ has the asymptotic form

  $$\psi_{0}(r) \sim \frac{A}{r}[\sin (k r)+g(k) \cos (k r)]$$

  Define the phase shift $\delta_{0}$ and verify that $\tan \delta_{0}=g(k)$.

  (b) Define the scattering amplitude $f$. For a spherically symmetric potential of finite range, starting from $\sigma_{T}=\int|f|^{2} d \Omega$, derive the expression

  $$\sigma_{T}=\frac{4 \pi}{k^{2}} \sum_{l=0}^{\infty}(2 l+1) \sin ^{2} \delta_{l}$$

  giving the cross-section $\sigma_{T}$ in terms of the phase shifts $\delta_{l}$ of the partial waves.

  (c) For $g(k)=-k / K$ with $K>0$, show that a bound state exists and compute its energy. Neglecting the contributions from partial waves with $l>0$, show that

  $$\sigma_{T} \approx \frac{4 \pi}{K^{2}+k^{2}}$$

  (d) For $g(k)=\gamma /\left(K_{0}-k\right)$ with $K_{0}>0, \gamma>0$ compute the $s$-wave contribution to $\sigma_{T}$. Working to leading order in $\gamma \ll K_{0}$, show that $\sigma_{T}$ has a local maximum at $k=K_{0}$. Interpret this fact in terms of a resonance and compute its energy and decay width.

  comment

• Paper 3, Section II, 34B

  Applications of Quantum Mechanics | Part II, 2021

  (a) In three dimensions, define a Bravais lattice $\Lambda$ and its reciprocal lattice $\Lambda^{*}$.

  A particle is subject to a potential $V(\mathbf{x})$ with $V(\mathbf{x})=V(\mathbf{x}+\mathbf{r})$ for $\mathbf{x} \in \mathbb{R}^{3}$ and $\mathbf{r} \in \Lambda$. State and prove Bloch's theorem and specify how the Brillouin zone is related to the reciprocal lattice.

  (b) A body-centred cubic lattice $\Lambda_{B C C}$ consists of the union of the points of a cubic lattice $\Lambda_{1}$ and all the points $\Lambda_{2}$ at the centre of each cube:

  $$\begin{aligned} \Lambda_{B C C} & \equiv \Lambda_{1} \cup \Lambda_{2}, \\ \Lambda_{1} & \equiv\left\{\mathbf{r} \in \mathbb{R}^{3}: \mathbf{r}=n_{1} \hat{\mathbf{i}}+n_{2} \hat{\mathbf{j}}+n_{3} \hat{\mathbf{k}}, \text { with } n_{1,2,3} \in \mathbb{Z}\right\}, \\ \Lambda_{2} & \equiv\left\{\mathbf{r} \in \mathbb{R}^{3}: \mathbf{r}=\frac{1}{2}(\hat{\mathbf{i}}+\hat{\mathbf{j}}+\hat{\mathbf{k}})+\mathbf{r}^{\prime}, \text { with } \mathbf{r}^{\prime} \in \Lambda_{1}\right\}, \end{aligned}$$

  where $\hat{\mathbf{i}}, \hat{\mathbf{j}}$ and $\hat{\mathbf{k}}$ are unit vectors parallel to the Cartesian coordinates in $\mathbb{R}^{3}$. Show that $\Lambda_{B C C}$ is a Bravais lattice and determine the primitive vectors $\mathbf{a}_{1}, \mathbf{a}_{2}$ and $\mathbf{a}_{3}$.

  Find the reciprocal lattice $\Lambda_{B C C}^{*} .$ Briefly explain what sort of lattice it is.

  $\left[\right.$ Hint: The matrix $M=\frac{1}{2}\left(\begin{array}{ccc}-1 & 1 & 1 \\ 1 & -1 & 1 \\ 1 & 1 & -1\end{array}\right)$ has inverse $M^{-1}=\left(\begin{array}{lll}0 & 1 & 1 \\ 1 & 0 & 1 \\ 1 & 1 & 0\end{array}\right)$.

  comment

• Paper 4, Section II, B

  Applications of Quantum Mechanics | Part II, 2021

  (a) Consider the nearly free electron model in one dimension with mass $m$ and periodic potential $V(x)=\lambda U(x)$ with $0<\lambda \ll 1$ and

  $$U(x)=\sum_{l=-\infty}^{\infty} U_{l} \exp \left(\frac{2 \pi i}{a} l x\right)$$

  Ignoring degeneracies, the energy spectrum of Bloch states with wavenumber $k$ is

  $$E(k)=E_{0}(k)+\lambda\langle k|U| k\rangle+\lambda^{2} \sum_{k^{\prime} \neq k} \frac{\left\langle k|U| k^{\prime}\right\rangle\left\langle k^{\prime}|U| k\right\rangle}{E_{0}(k)-E_{0}\left(k^{\prime}\right)}+\mathcal{O}\left(\lambda^{3}\right)$$

  where $\{|k\rangle\}$ are normalized eigenstates of the free Hamiltonian with wavenumber $k$. What is $E_{0}$ in this formula?

  If we impose periodic boundary conditions on the wavefunctions, $\psi(x)=\psi(x+L)$ with $L=N a$ and $N$ a positive integer, what are the allowed values of $k$ and $k^{\prime}$ ? Determine $\left\langle k|U| k^{\prime}\right\rangle$ for these allowed values.

  (b) State when the above expression for $E(k)$ ceases to be a good approximation and explain why. Quoting any result you need from degenerate perturbation theory, calculate to $\mathcal{O}(\lambda)$ the location and width of the band gaps.

  (c) Determine the allowed energy bands for each of the potentials

  $$\begin{aligned} &\text { (i) } V(x)=2 \lambda \cos \left(\frac{2 \pi x}{a}\right) \text {, } \\ &\text { (ii) } V(x)=\lambda a \sum_{n=-\infty}^{\infty} \delta(x-n a) \text {. } \end{aligned}$$

  (d) Briefly discuss a macroscopic physical consequence of the existence of energy bands.

  comment

Applied Probability

• Paper 1, Section II, 28K

  Applied Probability | Part II, 2021

  The particles of an Ideal Gas form a spatial Poisson process on $\mathbb{R}^{3}$ with constant intensity $z>0$, called the activity of the gas.

  (a) Prove that the independent mixture of two Ideal Gases with activities $z_{1}$ and $z_{2}$ is again an Ideal Gas. What is its activity? [You must prove any results about Poisson processes that you use. The independent mixture of two gases with particles $\Pi_{1} \subset \mathbb{R}^{3}$ and $\Pi_{2} \subset \mathbb{R}^{3}$ is given by $\left.\Pi_{1} \cup \Pi_{2} .\right]$

  (b) For an Ideal Gas of activity $z>0$, find the limiting distribution of

  $$\frac{N\left(V_{i}\right)-\mathbb{E} N\left(V_{i}\right)}{\sqrt{\left|V_{i}\right|}}$$

  as $i \rightarrow \infty$ for a given sequence of subsets $V_{i} \subset \mathbb{R}^{3}$ with $\left|V_{i}\right| \rightarrow \infty$.

  (c) Let $g: \mathbb{R}^{3} \rightarrow \mathbb{R}$ be a smooth non-negative function vanishing outside a bounded subset of $\mathbb{R}^{3}$. Find the mean and variance of $\sum_{x} g(x)$, where the sum runs over the particles $x \in \mathbb{R}^{3}$ of an ideal gas of activity $z>0$. [You may use the properties of spatial Poisson processes established in the lectures.]

  [Hint: recall that the characteristic function of a Poisson random variable with mean $\lambda$ is $\left.e^{\left(e^{i t}-1\right) \lambda} \cdot\right]$

  comment

• Paper 2, Section II, $28 K$

  Applied Probability | Part II, 2021

  Let $X$ be an irreducible, non-explosive, continuous-time Markov process on the state space $\mathbb{Z}$ with generator $Q=\left(q_{x, y}\right)_{x, y \in \mathbb{Z}}$.

  (a) Define its jump chain $Y$ and prove that it is a discrete-time Markov chain.

  (b) Define what it means for $X$ to be recurrent and prove that $X$ is recurrent if and only if its jump chain $Y$ is recurrent. Prove also that this is the case if the transition semigroup $\left(p_{x, y}(t)\right)$ satisfies

  $$\int_{0}^{\infty} p_{0,0}(t) d t=\infty$$

  (c) Show that $X$ is recurrent for at least one of the following generators:

  $$\begin{array}{cc} q_{x, y}=(1+|x|)^{-2} e^{-|x-y|^{2}} & (x \neq y), \\ q_{x, y}=(1+|x-y|)^{-2} e^{-|x|^{2}} & (x \neq y) . \end{array}$$

  [Hint: You may use that the semigroup associated with a $Q$-matrix on $\mathbb{Z}$ such that $q_{x, y}$ depends only on $x-y$ (and has sufficient decay) can be written as

  $$p_{x, y}(t)=\frac{1}{2 \pi} \int_{-\pi}^{\pi} e^{-t \lambda(k)} e^{i k(x-y)} d k$$

  where $\lambda(k)=\sum_{y} q_{0, y}\left(1-e^{i k y}\right)$. You may also find the bound $1-\cos x \leqslant x^{2} / 2$ useful. $]$

  comment

• Paper 3, Section II, $27 \mathrm{~K}$

  Applied Probability | Part II, 2021

  (a) Customers arrive at a queue at the event times of a Poisson process of rate $\lambda$. The queue is served by two independent servers with exponential service times with parameter $\mu$ each. If the queue has length $n$, an arriving customer joins with probability $r^{n}$ and leaves otherwise (where $\left.r \in(0,1]\right)$. For which $\lambda>0, \mu>0$ and $r \in(0,1]$ is there a stationary distribution?

  (b) A supermarket allows a maximum of $N$ customers to shop at the same time. Customers arrive at the event times of a Poisson process of rate 1 , they enter the supermarket when possible, and they leave forever for another supermarket otherwise. Customers already in the supermarket pay and leave at the event times of an independent Poisson process of rate $\mu$. When is there a unique stationary distribution for the number of customers in the supermarket? If it exists, find it.

  (c) In the situation of part (b), started from equilibrium, show that the departure process is Poissonian.

  comment

• Paper 4, Section II, $27 \mathrm{~K}$

  Applied Probability | Part II, 2021

  Let $(X(t))_{t \geqslant 0}$ be a continuous-time Markov process with state space $I=\{1, \ldots, n\}$ and generator $Q=\left(q_{i j}\right)_{i, j \in I}$ satisfying $q_{i j}=q_{j i}$ for all $i, j \in I$. The local time up to time $t>0$ of $X$ is the random vector $L(t)=\left(L_{i}(t)\right)_{i \in I} \in \mathbb{R}^{n}$ defined by

  $$L_{i}(t)=\int_{0}^{t} 1_{X(s)=i} d s \quad(i \in I)$$

  (a) Let $f: I \times \mathbb{R}^{n} \rightarrow \mathbb{R}$ be any function that is differentiable with respect to its second argument, and set

  $$f_{t}(i, \ell)=\mathbb{E}_{i} f(X(t), \ell+L(t)), \quad\left(i \in I, \ell \in \mathbb{R}^{n}\right)$$

  Show that

  $$\frac{\partial}{\partial t} f_{t}(i, \ell)=M f_{t}(i, \ell)$$

  where

  $$M f(i, \ell)=\sum_{j \in I} q_{i j} f(j, \ell)+\frac{\partial}{\partial \ell_{i}} f(i, \ell)$$

  (b) For $y \in \mathbb{R}^{n}$, write $y^{2}=\left(y_{i}^{2}\right)_{i \in I} \in[0, \infty)^{n}$ for the vector of squares of the components of $y$. Let $f: I \times \mathbb{R}^{n} \rightarrow \mathbb{R}$ be a function such that $f(i, \ell)=0$ whenever $\sum_{j}\left|\ell_{j}\right| \geqslant T$ for some fixed $T$. Using integration by parts, or otherwise, show that for all $i$

  $$-\int_{\mathbb{R}^{n}} \exp \left(\frac{1}{2} y^{T} Q y\right) y_{i} \sum_{j=1}^{n} y_{j} M f\left(j, \frac{1}{2} y^{2}\right) d y=\int_{\mathbb{R}^{n}} \exp \left(\frac{1}{2} y^{T} Q y\right) f\left(i, \frac{1}{2} y^{2}\right) d y,$$

  where $y^{T} Q y$ denotes $\sum_{k, m \in I} y_{k} q_{k m} y_{m}$.

  (c) Let $g: \mathbb{R}^{n} \rightarrow \mathbb{R}$ be a function with $g(\ell)=0$ whenever $\sum_{j}\left|\ell_{j}\right| \geqslant T$ for some fixed $T$. Given $t>0, j \in I$, now let

  $$f(i, \ell)=\mathbb{E}_{i}\left[g(\ell+L(t)) 1_{X(t)=j}\right]$$

  in part (b) and deduce, using part (a), that

  $$\begin{aligned} \int_{\mathbb{R}^{n}} \exp \left(\frac{1}{2} y^{T} Q y\right) y_{i} y_{j} g\left(\frac{1}{2} y^{2}\right) d y \\ &=\int_{\mathbb{R}^{n}} \exp \left(\frac{1}{2} y^{T} Q y\right)\left(\int_{0}^{\infty} \mathbb{E}_{i}\left[1_{X(t)=j} g\left(\frac{1}{2} y^{2}+L(t)\right)\right] d t\right) d y \end{aligned}$$

  [You may exchange the order of integrals and derivatives without justification.]

  comment

Asymptotic Methods

• Paper 2, Section II, 32A

  Asymptotic Methods | Part II, 2021

  (a) Let $x(t)$ and $\phi_{n}(t)$, for $n=0,1,2, \ldots$, be real-valued functions on $\mathbb{R}$.

  (i) Define what it means for the sequence $\left\{\phi_{n}(t)\right\}_{n=0}^{\infty}$ to be an asymptotic sequence as $t \rightarrow \infty$.

  (ii) Define what it means for $x(t)$ to have the asymptotic expansion

  $$x(t) \sim \sum_{n=0}^{\infty} a_{n} \phi_{n}(t) \quad \text { as } \quad t \rightarrow \infty$$

  (b) Use the method of stationary phase to calculate the leading-order asymptotic approximation as $x \rightarrow \infty$ of

  $$I(x)=\int_{0}^{1} \sin \left(x\left(2 t^{4}-t^{2}\right)\right) d t$$

  [You may assume that $\int_{-\infty}^{\infty} e^{i u^{2}} d u=\sqrt{\pi} e^{i \pi / 4}$.]

  (c) Use Laplace's method to calculate the leading-order asymptotic approximation as $x \rightarrow \infty$ of

  $$J(x)=\int_{0}^{1} \sinh \left(x\left(2 t^{4}-t^{2}\right)\right) d t$$

  [In parts (b) and (c) you should include brief qualitative reasons for the origin of the leading-order contributions, but you do not need to give a formal justification.]

  comment

• Paper 3, Section II, 30A

  Asymptotic Methods | Part II, 2021

  (a) Carefully state Watson's lemma.

  (b) Use the method of steepest descent and Watson's lemma to obtain an infinite asymptotic expansion of the function

  $$I(x)=\int_{-\infty}^{\infty} \frac{e^{-x\left(z^{2}-2 i z\right)}}{1-i z} d z \quad \text { as } \quad x \rightarrow \infty$$

  comment

• Paper 4, Section II, A

  Asymptotic Methods | Part II, 2021

  (a) Classify the nature of the point at $\infty$ for the ordinary differential equation

  $$y^{\prime \prime}+\frac{2}{x} y^{\prime}+\left(\frac{1}{x}-\frac{1}{x^{2}}\right) y=0 .$$

  (b) Find a transformation from $(*)$ to an equation of the form

  $$u^{\prime \prime}+q(x) u=0$$

  and determine $q(x)$.

  (c) Given $u(x)$ satisfies ( $\dagger$, use the Liouville-Green method to find the first three terms in an asymptotic approximation as $x \rightarrow \infty$ for $u(x)$, verifying the consistency of any approximations made.

  (d) Hence obtain corresponding asymptotic approximations as $x \rightarrow \infty$ of two linearly independent solutions $y(x)$ of $(*)$.

  comment

Automata and Formal Languages

• Paper 1, Section I, F

  Automata and Formal Languages | Part II, 2021

  Let $f_{n, k}$ be the partial function on $k$ variables that is computed by the $n$th machine (or the empty function if $n$ does not encode a machine).

  Define the halting set $\mathbb{K}$.

  Given $A, B \subseteq \mathbb{N}$, what is a many-one reduction $A \leqslant_{m} B$ of $A$ to $B$ ?

  State the $s-m-n$ theorem and use it to show that a subset $X$ of $\mathbb{N}$ is recursively enumerable if and only if $X \leqslant_{m} \mathbb{K}$.

  Give an example of a set $S \subseteq \mathbb{N}$ with $\mathbb{K} \leqslant_{m} S$ but $\mathbb{K} \neq S$.

  [You may assume that $\mathbb{K}$ is recursively enumerable and that $0 \notin \mathbb{K}$.]

  comment

• Paper 1, Section II, F

  Automata and Formal Languages | Part II, 2021

  For $k \geqslant 1$ give the definition of a partial recursive function $f: \mathbb{N}^{k} \rightarrow \mathbb{N}$ in terms of basic functions, composition, recursion and minimisation.

  Show that the following partial functions from $\mathbb{N}$ to $\mathbb{N}$ are partial recursive: (i) $s(n)= \begin{cases}1 & n=0 \\ 0 & n \geqslant 1\end{cases}$ (ii) $r(n)= \begin{cases}1 & n \text { odd } \\ 0 & n \text { even } \text {, }\end{cases}$ (iii) $p(n)=\left\{\begin{array}{l}\text { undefined if } n \text { is odd } \\ 0 \text { if } n \text { is even }\end{array}\right.$

  Which of these can be defined without using minimisation?

  What is the class of functions $f: \mathbb{N}^{k} \rightarrow \mathbb{N}$ that can be defined using only basic functions and composition? [Hint: See which functions you can obtain and then show that these form a class that is closed with respect to the above.]

  Show directly that every function in this class is computable.

  comment

• Paper 2, Section I, F

  Automata and Formal Languages | Part II, 2021

  Assuming the definition of a deterministic finite-state automaton (DFA) $D=$ $\left(Q, \Sigma, \delta, q_{0}, F\right)$, what is the extended transition function $\hat{\delta}$ for $D$ ? Also assuming the definition of a nondeterministic finite-state automaton (NFA) $N$, what is $\hat{\delta}$ in this case?

  Define the languages accepted by $D$ and $N$, respectively, in terms of $\hat{\delta}$.

  Given an NFA $N$ as above, describe the subset construction and show that the resulting DFA $\bar{N}$ accepts the same language as $N$. If $N$ has one accept state then how many does $\bar{N}$ have?

  comment

• Paper 3, Section I, F

  Automata and Formal Languages | Part II, 2021

  Define a regular expression $R$ and explain how this gives rise to a language $\mathcal{L}(R)$.

  Define a deterministic finite-state automaton $D$ and the language $\mathcal{L}(D)$ that it accepts.

  State the relationship between languages obtained from regular expressions and languages accepted by deterministic finite-state automata.

  Let $L$ and $M$ be regular languages. Is $L \cup M$ always regular? What about $L \cap M$ ?

  Now suppose that $L_{1}, L_{2}, \ldots$ are regular languages. Is the countable union $\bigcup L_{i}$ always regular? What about the countable intersection $\bigcap L_{i}$ ?

  comment

• Paper 3, Section II, $12 F$

  Automata and Formal Languages | Part II, 2021

  Suppose that $G$ is a context-free grammar without $\epsilon$-productions. Given a derivation of some word $w$ in the language $L$ of $G$, describe a parse tree for this derivation.

  State and prove the pumping lemma for $L$. How would your proof differ if you did not assume that $G$ was in Chomsky normal form, but merely that $G$ has no $\epsilon$ - or unit productions?

  For the alphabet $\Sigma=\{a, b\}$ of terminal symbols, state whether the following languages over $\Sigma$ are context free, giving reasons for your answer. (i) $\left\{a^{i} b^{i} a^{i} \mid i \geqslant 0\right\}$, (ii) $\left\{a^{i} b^{j} \mid i \geqslant j \geqslant 0\right\}$, (iii) $\left\{w a b w \mid w \in\{a, b\}^{*}\right\}$.

  comment

• Paper 4, Section I, $4 \mathrm{~F}$

  Automata and Formal Languages | Part II, 2021

  State the pumping lemma for regular languages.

  Which of the following languages over the alphabet $\{0,1\}$ are regular?

  (i) $\left\{0^{i} 1^{i} 01 \mid i \geqslant 0\right\}$.

  (ii) $\left\{w \bar{w} \mid w \in\{0,1\}^{*}\right\}$ where $\bar{w}$ is the reverse of the word $w$.

  (iii) $\left\{w \in\{0,1\}^{*} \mid w\right.$ does not contain the subwords 01 or 10$\}$.

  comment

Classical Dynamics

• Paper 1, Section I, D

  Classical Dynamics | Part II, 2021

  Two equal masses $m$ move along a straight line between two stationary walls. The mass on the left is connected to the wall on its left by a spring of spring constant $k_{1}$, and the mass on the right is connected to the wall on its right by a spring of spring constant $k_{2}$. The two masses are connected by a third spring of spring constant $k_{3}$.

  (a) Show that the Lagrangian of the system can be written in the form

  $$L=\frac{1}{2} T_{i j} \dot{x}_{i} \dot{x}_{j}-\frac{1}{2} V_{i j} x_{i} x_{j}$$

  where $x_{i}(t)$, for $i=1,2$, are the displacements of the two masses from their equilibrium positions, and $T_{i j}$ and $V_{i j}$ are symmetric $2 \times 2$ matrices that should be determined.

  (b) Let

  $$k_{1}=k(1+\epsilon \delta), \quad k_{2}=k(1-\epsilon \delta), \quad k_{3}=k \epsilon,$$

  where $k>0, \epsilon>0$ and $|\epsilon \delta|<1$. Using Lagrange's equations of motion, show that the angular frequencies $\omega$ of the normal modes of the system are given by

  $$\omega^{2}=\lambda \frac{k}{m}$$

  where

  $$\lambda=1+\epsilon\left(1 \pm \sqrt{1+\delta^{2}}\right)$$

  comment

• Paper 2, Section I, D

  Classical Dynamics | Part II, 2021

  Show that, in a uniform gravitational field, the net gravitational torque on a system of particles, about its centre of mass, is zero.

  Let $S$ be an inertial frame of reference, and let $S^{\prime}$ be the frame of reference with the same origin and rotating with angular velocity $\boldsymbol{\omega}(t)$ with respect to $S$. You may assume that the rates of change of a vector $v$ observed in the two frames are related by

  $$\left(\frac{d \mathbf{v}}{d t}\right)_{S}=\left(\frac{d \mathbf{v}}{d t}\right)_{S^{\prime}}+\omega \times \mathbf{v} .$$

  Derive Euler's equations for the torque-free motion of a rigid body.

  Show that the general torque-free motion of a symmetric top involves precession of the angular-velocity vector about the symmetry axis of the body. Determine how the direction and rate of precession depend on the moments of inertia of the body and its angular velocity.

  comment

• Paper 2, Section II, D

  Classical Dynamics | Part II, 2021

  (a) Show that the Hamiltonian

  $$H=\frac{1}{2} p^{2}+\frac{1}{2} \omega^{2} q^{2},$$

  where $\omega$ is a positive constant, describes a simple harmonic oscillator with angular frequency $\omega$. Show that the energy $E$ and the action $I$ of the oscillator are related by $E=\omega I$.

  (b) Let $0<\epsilon<2$ be a constant. Verify that the differential equation

  $$\ddot{x}+\frac{x}{(\epsilon t)^{2}}=0 \quad \text { subject to } \quad x(1)=0, \quad \dot{x}(1)=1$$

  is solved by

  $$x(t)=\frac{\sqrt{t}}{k} \sin (k \log t)$$

  when $t>1$, where $k$ is a constant you should determine in terms of $\epsilon$.

  (c) Show that the solution in part (b) obeys

  $$\frac{1}{2} \dot{x}^{2}+\frac{1}{2} \frac{x^{2}}{(\epsilon t)^{2}}=\frac{1-\cos (2 k \log t)+2 k \sin (2 k \log t)+4 k^{2}}{8 k^{2} t}$$

  Hence show that the fractional variation of the action in the limit $\epsilon \ll 1$ is $O(\epsilon)$, but that these variations do not accumulate. Comment on this behaviour in relation to the theory of adiabatic invariance.

  comment

• Paper 3 , Section I, D

  Classical Dynamics | Part II, 2021

  The Lagrangian of a particle of mass $m$ and charge $q$ in an electromagnetic field takes the form

  $$L=\frac{1}{2} m|\dot{\mathbf{r}}|^{2}+q(-\phi+\dot{\mathbf{r}} \cdot \mathbf{A})$$

  Explain the meaning of $\phi$ and $\mathbf{A}$, and how they are related to the electric and magnetic fields.

  Obtain the canonical momentum $\mathbf{p}$ and the Hamiltonian $H(\mathbf{r}, \mathbf{p}, t)$.

  Suppose that the electric and magnetic fields have Cartesian components $(E, 0,0)$ and $(0,0, B)$, respectively, where $E$ and $B$ are positive constants. Explain why the Hamiltonian of the particle can be taken to be

  $$H=\frac{p_{x}^{2}}{2 m}+\frac{\left(p_{y}-q B x\right)^{2}}{2 m}+\frac{p_{z}^{2}}{2 m}-q E x$$

  State three independent integrals of motion in this case.

  comment

• Paper 4, Section I, D

  Classical Dynamics | Part II, 2021

  Briefly describe a physical object (a Lagrange top) whose Lagrangian is

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  Explain the meaning of the symbols in this equation.

  Write down three independent integrals of motion for this system, and show that the nutation of the top is governed by the equation

  $$\dot{u}^{2}=f(u),$$

  where $u=\cos \theta$ and $f(u)$ is a certain cubic function that you need not determine.

  comment

• Paper 4, Section II, 15D

  Classical Dynamics | Part II, 2021

  (a) Let $(\mathbf{q}, \mathbf{p})$ be a set of canonical phase-space variables for a Hamiltonian system with $n$ degrees of freedom. Define the Poisson bracket $\{f, g\}$ of two functions $f(\mathbf{q}, \mathbf{p})$ and $g(\mathbf{q}, \mathbf{p})$. Write down the canonical commutation relations that imply that a second set $(\mathbf{Q}, \mathbf{P})$ of phase-space variables is also canonical.

  (b) Consider the near-identity transformation

  $$\mathbf{Q}=\mathbf{q}+\delta \mathbf{q}, \quad \mathbf{P}=\mathbf{p}+\delta \mathbf{p}$$

  where $\delta \mathbf{q}(\mathbf{q}, \mathbf{p})$ and $\delta \mathbf{p}(\mathbf{q}, \mathbf{p})$ are small. Determine the approximate forms of the canonical commutation relations, accurate to first order in $\delta \mathbf{q}$ and $\delta \mathbf{p}$. Show that these are satisfied when

  $$\delta \mathbf{q}=\epsilon \frac{\partial F}{\partial \mathbf{p}}, \quad \delta \mathbf{p}=-\epsilon \frac{\partial F}{\partial \mathbf{q}}$$

  where $\epsilon$ is a small parameter and $F(\mathbf{q}, \mathbf{p})$ is some function of the phase-space variables.

  (c) In the limit $\epsilon \rightarrow 0$ this near-identity transformation is called the infinitesimal canonical transformation generated by $F$. Let $H(\mathbf{q}, \mathbf{p})$ be an autonomous Hamiltonian. Show that the change in the Hamiltonian induced by the infinitesimal canonical transformation is

  $$\delta H=-\epsilon\{F, H\} .$$

  Explain why $F$ is an integral of motion if and only if the Hamiltonian is invariant under the infinitesimal canonical transformation generated by $F$.

  (d) The Hamiltonian of the gravitational $N$-body problem in three-dimensional space is

  $$H=\frac{1}{2} \sum_{i=1}^{N} \frac{\left|\mathbf{p}_{i}\right|^{2}}{2 m_{i}}-\sum_{i=1}^{N-1} \sum_{j=i+1}^{N} \frac{G m_{i} m_{j}}{\left|\mathbf{r}_{i}-\mathbf{r}_{j}\right|}$$

  where $m_{i}, \mathbf{r}_{i}$ and $\mathbf{p}_{i}$ are the mass, position and momentum of body $i$. Determine the form of $F$ and the infinitesimal canonical transformation that correspond to the translational symmetry of the system.

  comment

Coding and Cryptography

• Paper 1, Section I, $3 K$

  Coding and Cryptography | Part II, 2021

  Let $C$ be an $[n, m, d]$ code. Define the parameters $n, m$ and $d$. In each of the following cases define the new code and give its parameters.

  (i) $C^{+}$is the parity extension of $C$.

  (ii) $C^{-}$is the punctured code (assume $n \geqslant 2$ ).

  (iii) $\bar{C}$ is the shortened code (assume $n \geqslant 2$ ).

  Let $C=\{000,100,010,001,110,101,011,111\}$. Suppose the parity extension of $C$ is transmitted through a binary symmetric channel where $p$ is the probability of a single-bit error in the channel. Calculate the probability that an error in the transmission of a single codeword is not noticed.

  comment

• Paper 1, Section II, $11 K$

  Coding and Cryptography | Part II, 2021

  Let $\Sigma_{1}=\left\{\mu_{1}, \ldots, \mu_{N}\right\}$ be a finite alphabet and $X$ a random variable that takes each value $\mu_{i}$ with probability $p_{i}$. Define the entropy $H(X)$ of $X$.

  Suppose $\Sigma_{2}=\{0,1\}$ and $c: \Sigma_{1} \rightarrow \Sigma_{2}^{*}$ is a decipherable code. Write down an expression for the expected word length $E(S)$ of $c$.

  Prove that the minimum expected word length $S^{*}$ of a decipherable code $c: \Sigma_{1} \rightarrow \Sigma_{2}^{*}$ satisfies

  $$H(X) \leqslant S^{*}<H(X)+1 .$$

  [You can use Kraft's and Gibbs' inequalities as long as they are clearly stated.]

  Suppose a decipherable binary code has word lengths $s_{1}, \ldots, s_{N}$. Show that

  $$N \log N \leqslant s_{1}+\cdots+s_{N} .$$

  Suppose $X$ is a source that emits $N$ sourcewords $a_{1}, \ldots, a_{N}$ and $p_{i}$ is the probability that $a_{i}$ is emitted, where $p_{1} \geqslant p_{2} \geqslant \cdots \geqslant p_{N}$. Let $b_{1}=0$ and $b_{i}=\sum_{j=1}^{i-1} p_{j}$ for $2 \leqslant i \leqslant N$. Let $s_{i}=\left\lceil-\log p_{i}\right\rceil$ for $1 \leqslant i \leqslant N$. Now define a code $c$ by $c\left(a_{i}\right)=b_{i}^{*}$ where $b_{i}^{*}$ is the (fractional part of the) binary expansion of $b_{i}$ to $s_{i}$ decimal places. Prove that this defines a decipherable code.

  What does it mean for a code to be optimal? Is the code $c$ defined in the previous paragraph in terms of the $b_{i}^{*}$ necessarily optimal? Justify your answer.

  comment

• Paper 2, Section I, K

  Coding and Cryptography | Part II, 2021

  State Shannon's noisy coding theorem for a binary symmetric channel, defining the terms involved.

  Suppose a channel matrix, with output alphabet of size $n$, is such that the entries in each row are the elements of the set $\left\{p_{1}, \ldots, p_{n}\right\}$ in some order. Further suppose that all columns are permutations of one another. Show that the channel's information capacity $C$ is given by

  $$C=\log n+\sum_{i=1}^{n} p_{i} \log p_{i}$$

  Show that the information capacity of the channel matrix

  $$\left(\begin{array}{cccc} \frac{1}{3} & \frac{1}{3} & \frac{1}{6} & \frac{1}{6} \\ \frac{1}{6} & \frac{1}{6} & \frac{1}{3} & \frac{1}{3} \end{array}\right)$$

  is given by $C=\frac{5}{3}-\log 3$.

  comment

• Paper 2, Section II, $12 K$

  Coding and Cryptography | Part II, 2021

  (a) Define what it means to say that $C$ is a binary cyclic code. Explain the bijection between the set of binary cyclic codes of length $n$ and the factors of $X^{n}-1$ in $\mathbb{F}_{2}[X]$.

  (b) What is a linear feedback shift register?

  Suppose that $M: \mathbb{F}_{2}^{d} \rightarrow \mathbb{F}_{2}^{d}$ is a linear feedback shift register. Further suppose $\mathbf{0} \neq \mathbf{x} \in \mathbb{F}_{2}^{d}$ and $k$ is a positive integer such that $M^{k} \mathbf{x}=\mathbf{x}$. Let $H$ be the $d \times k$ matrix $\left(\mathbf{x}, M \mathbf{x}, \ldots, M^{k-1} \mathbf{x}\right)$. Considering $H$ as a parity check matrix of a code $C$, show that $C$ is a binary cyclic code.

  (c) Suppose that $C$ is a binary cyclic code. Prove that, if $C$ does not contain the codeword $11 . . .1$, then all codewords in $C$ have even weight.

  comment

• Paper 3, Section I, K

  Coding and Cryptography | Part II, 2021

  Let $d \geqslant 2$. Define the Hamming code $C$ of length $2^{d}-1$. Explain what it means to be a perfect code and show that $C$ is a perfect code.

  Suppose you are using the Hamming code of length $2^{d}-1$ and you receive the message $111 \ldots 10$ of length $2^{d}-1$. How would you decode this message using minimum distance decoding? Explain why this leads to correct decoding if at most one channel error has occurred.

  comment

• Paper 4 , Section I, $3 K$

  Coding and Cryptography | Part II, 2021

  Describe the Rabin scheme for coding a message $x$ as $x^{2}$ modulo a certain integer $N$.

  Describe the RSA encryption scheme with public key $(N, e)$ and private key $d$.

  [In both cases you should explain how you encrypt and decrypt.]

  Give an advantage and a disadvantage that the Rabin scheme has over the RSA scheme.

  comment

Cosmology

• Paper 1, Section I, 9B

  Cosmology | Part II, 2021

  The continuity, Euler and Poisson equations governing how non-relativistic fluids with energy density $\rho$, pressure $P$ and velocity $\mathbf{v}$ propagate in an expanding universe take the form

  $$\begin{gathered} \frac{\partial \rho}{\partial t}+3 H \rho+\frac{1}{a} \boldsymbol{\nabla} \cdot(\rho \mathbf{v})=0 \\ \rho a\left(\frac{\partial}{\partial t}+\frac{\mathbf{v}}{a} \cdot \nabla\right) \mathbf{u}=-\frac{1}{c^{2}} \nabla P-\rho \boldsymbol{\nabla} \Phi \\ \nabla^{2} \Phi=\frac{4 \pi G}{c^{2}} \rho a^{2} \end{gathered}$$

  where $\mathbf{u}=\mathbf{v}+a H \mathbf{x}, H=\dot{a} / a$ and $a(t)$ is the scale factor.

  (a) Show that, for a homogeneous and isotropic flow with $P=\bar{P}(t), \rho=\bar{\rho}(t), \mathbf{v}=\mathbf{0}$ and $\Phi=\bar{\Phi}(t, \mathbf{x})$, consistency of the Euler equation with the Poisson equation implies Raychaudhuri's equation.

  (b) Explain why this derivation of Raychaudhuri's equation is an improvement over the derivation of the Friedmann equation using only Newtonian gravity.

  (c) Consider small perturbations about a homogeneous and isotropic flow,

  $$\rho=\bar{\rho}(t)+\epsilon \delta \rho, \quad \mathbf{v}=\epsilon \delta \mathbf{v}, \quad P=\bar{P}(t)+\epsilon \delta P \quad \text { and } \quad \Phi=\bar{\Phi}(t, \mathbf{x})+\epsilon \delta \Phi,$$

  with $\epsilon \ll 1$. Show that, to first order in $\epsilon$, the continuity equation can be written as

  $$\frac{\partial}{\partial t}\left(\frac{\delta \rho}{\bar{\rho}}\right)=-\frac{1}{a} \boldsymbol{\nabla} \cdot \delta \mathbf{v}$$

  comment

• Paper 1, Section II, 15B

  Cosmology | Part II, 2021

  (a) Consider the following action for the inflaton field $\phi$

  $$S=\int \mathrm{d}^{3} x \mathrm{~d} t a(t)^{3}\left[\frac{1}{2} \dot{\phi}^{2}-\frac{c^{2}}{2 a(t)^{2}} \nabla \phi \cdot \nabla \phi-V(\phi)\right]$$

  Use the principle of least action to derive the equation of motion for the inflaton $\phi$,

  $$\ddot{\phi}+3 H \dot{\phi}-\frac{c^{2}}{a(t)^{2}} \nabla^{2} \phi+\frac{\mathrm{d} V(\phi)}{\mathrm{d} \phi}=0$$

  where $H=\dot{a} / a$. [In the derivation you may discard boundary terms.]

  (b) Consider a regime where $V(\phi)$ is approximately constant so that the universe undergoes a period of exponential expansion during which $a=a_{0} e^{H_{\text {inf }} t}$. Show that $(*)$ can be written in terms of the spatial Fourier transform $\widehat{\phi}_{\mathbf{k}}(t)$ of $\phi(\mathbf{x}, t)$ as

  $$\ddot{\widehat{\phi}}_{\mathbf{k}}+3 H_{\mathrm{inf}} \dot{\hat{\phi}}_{\mathbf{k}}+\frac{c^{2} k^{2}}{a^{2}} \widehat{\phi}_{\mathbf{k}}=0 .$$

  (c) Define conformal time $\tau$ and determine the range of $\tau$ when $a=a_{0} e^{H_{\text {inf }} t}$. Show that $(* *)$ can be written in terms of the conformal time as

  $$\frac{\mathrm{d}^{2} \tilde{\phi}_{\mathbf{k}}}{\mathrm{d} \tau^{2}}+\left(c^{2} k^{2}-\frac{2}{\tau^{2}}\right) \widetilde{\phi}_{\mathbf{k}}=0, \quad \text { where } \quad \tilde{\phi}_{\mathbf{k}}=-\frac{1}{H_{\mathrm{inf}} \tau} \widehat{\phi}_{\mathbf{k}}$$

  (d) Let $|\mathrm{BD}\rangle$ denote the state that in the far past was in the ground state of the standard harmonic oscillator with frequency $\omega=c k$. Assuming that the quantum variance of $\widehat{\phi}_{\mathbf{k}}$ is given by

  $$P_{\mathbf{k}} \equiv\left\langle\mathrm{BD}\left|\widehat{\phi}_{\mathbf{k}} \widehat{\phi}_{\mathbf{k}}^{\dagger}\right| \mathrm{BD}\right\rangle=\frac{\hbar H_{\mathrm{inf}}^{2}}{2 c^{3} k^{3}}\left(1+\tau^{2} c^{2} k^{2}\right)$$

  explain in which sense inflation naturally generates a scale-invariant power spectrum. [You may use that $P_{\mathbf{k}}$ has dimensions of [length $\left.]^{3} .\right]$

  comment

• Paper 2, Section I, 9B

  Cosmology | Part II, 2021

  (a) The generalised Boltzmann distribution $P(\mathbf{p})$ is given by

  $$P(\mathbf{p})=\frac{e^{-\beta\left(E_{\mathbf{p}} n_{\mathbf{p}}-\mu n_{\mathbf{p}}\right)}}{\mathcal{Z}_{\mathbf{p}}}$$

  where $\beta=\left(k_{B} T\right)^{-1}, \mu$ is the chemical potential,

  $$\mathcal{Z}_{\mathbf{p}}=\sum_{n_{\mathbf{p}}} e^{-\beta\left(E_{\mathbf{p}} n_{\mathbf{p}}-\mu n_{\mathbf{p}}\right)}, \quad E_{\mathbf{p}}=\sqrt{m^{2} c^{4}+p^{2} c^{2}} \quad \text { and } \quad p=|\mathbf{p}|$$

  Find the average particle number $\langle N(\mathbf{p})\rangle$ with momentum $\mathbf{p}$, assuming that all particles have rest mass $m$ and are either

  (i) bosons, or

  (ii) fermions .

  (b) The photon total number density $n_{\gamma}$ is given by

  $$n_{\gamma}=\frac{2 \zeta(3)}{\pi^{2} \hbar^{3} c^{3}}\left(k_{B} T\right)^{3}$$

  where $\zeta(3) \approx 1.2$. Consider now the fractional ionisation of hydrogen

  $$X_{e}=\frac{n_{e}}{n_{e}+n_{H}}$$

  In our universe $n_{e}+n_{H}=n_{p}+n_{H} \approx \eta n_{\gamma}$, where $\eta \sim 10^{-9}$ is the baryon-to-photon number density. Find an expression for the ratio

  $$\frac{1-X_{e}}{X_{e}^{2}}$$

  in terms of $\eta,\left(k_{B} T\right)$, the electron mass $m_{e}$, the speed of light $c$ and the ionisation energy of hydrogen $I \approx 13.6 \mathrm{eV}$.

  One might expect neutral hydrogen to form at a temperature $k_{B} T \sim I$, but instead in our universe it happens at the much lower temperature $k_{B} T \approx 0.3 \mathrm{eV}$. Briefly explain why this happens.

  [You may use without proof the Saha equation

  $$\frac{n_{H}}{n_{e}^{2}}=\left(\frac{2 \pi \hbar^{2}}{m_{e} k_{B} T}\right)^{3 / 2} e^{\beta I}$$

  for chemical equilibrium in the reaction $\left.e^{-}+p^{+} \leftrightarrow H+\gamma .\right]$

  comment

• Paper 3, Section I, 9B

  Cosmology | Part II, 2021

  The expansion of the universe during inflation is governed by the Friedmann equation

  $$\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G}{3}\left[\frac{1}{2} \dot{\phi}^{2}+V(\phi)\right]$$

  and the equation of motion for the inflaton field $\phi$,

  $$\ddot{\phi}+3 \frac{\dot{a}}{a} \dot{\phi}+\frac{\mathrm{d} V}{\mathrm{~d} \phi}=0 .$$

  Consider the potential

  $$V=V_{0} e^{-\lambda \phi}$$

  with $V_{0}>0$ and $\lambda>0$.

  (a) Show that the inflationary equations have the exact solution

  $$a(t)=\left(\frac{t}{t_{0}}\right)^{\gamma} \quad \text { and } \quad \phi=\phi_{0}+\alpha \log t$$

  for arbitrary $t_{0}$ and appropriate choices of $\alpha, \gamma$ and $\phi_{0}$. Determine the range of $\lambda$ for which the solution exists. For what values of $\lambda$ does inflation occur?

  (b) Using the inflaton equation of motion and

  $$\rho=\frac{1}{2} \dot{\phi}^{2}+V$$

  together with the continuity equation

  $$\dot{\rho}+3 \frac{\dot{a}}{a}(\rho+P)=0,$$

  determine $P$.

  (c) What is the range of the pressure energy density ratio $\omega \equiv P / \rho$ for which inflation occurs?

  comment

• Paper 3, Section II, B

  Cosmology | Part II, 2021

  (a) Consider a closed universe endowed with cosmological constant $\Lambda>0$ and filled with radiation with pressure $P$ and energy density $\rho$. Using the equation of state $P=\frac{1}{3} \rho$ and the continuity equation

  $$\dot{\rho}+\frac{3 \dot{a}}{a}(\rho+P)=0,$$

  determine how $\rho$ depends on $a$. Give the physical interpretation of the scaling of $\rho$ with

  (b) For such a universe the Friedmann equation reads

  $$\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G}{3 c^{2}} \rho-\frac{c^{2}}{R^{2} a^{2}}+\frac{\Lambda}{3}$$

  What is the physical meaning of $R ?$

  (c) Making the substitution $a(t)=\alpha \tilde{a}(t)$, determine $\alpha$ and $\Gamma>0$ such that the Friedmann equation takes the form

  $$\left(\frac{\dot{\tilde{a}}}{\tilde{a}}\right)^{2}=\frac{\Gamma}{\tilde{a}^{4}}-\frac{1}{\tilde{a}^{2}}+\frac{\Lambda}{3} .$$

  Using the substitution $y(t)=\tilde{a}(t)^{2}$ and the boundary condition $y(0)=0$, deduce the boundary condition for $\dot{y}(0)$.

  Show that

  $$\ddot{y}=\frac{4 \Lambda}{3} y-2$$

  and hence that

  $$\tilde{a}^{2}(t)=\frac{3}{2 \Lambda}\left[1-\cosh \left(\sqrt{\frac{4 \Lambda}{3}} t\right)+\lambda \sinh \left(\sqrt{\frac{4 \Lambda}{3}} t\right)\right]$$

  Express the constant $\lambda$ in terms of $\Lambda$ and $\Gamma$.

  Sketch the graphs of $\tilde{a}(t)$ for the cases $\lambda>1, \lambda<1$ and $\lambda=1$.

  comment

• Paper 4, Section I, B

  Cosmology | Part II, 2021

  A collection of $N$ particles, with masses $m_{i}$ and positions $\mathbf{x}_{i}$, interact through a gravitational potential

  $$V=\sum_{i<j} V_{i j}=-\sum_{i<j} \frac{G m_{i} m_{j}}{\left|\mathbf{x}_{i}-\mathbf{x}_{j}\right|} .$$

  Assume that the system is gravitationally bound, and that the positions $\mathbf{x}_{i}$ and velocities $\dot{\mathbf{x}}_{i}$ are bounded for all time. Further, define the time average of a quantity $X$ by

  $$\bar{X}=\lim _{t \rightarrow \infty} \frac{1}{t} \int_{0}^{t} X\left(t^{\prime}\right) \mathrm{d} t^{\prime}$$

  (a) Assuming that the time average of the kinetic energy $T$ and potential energy $V$ are well defined, show that

  $$\bar{T}=-\frac{1}{2} \bar{V}$$

  [You should consider the quantity $I=\frac{1}{2} \sum_{i=1}^{N} m_{i} \mathbf{x}_{i} \cdot \mathbf{x}_{i}$, with all $\mathbf{x}_{i}$ measured relative to the centre of mass.]

  (b) Explain how part (a) can be used, together with observations, to provide evidence in favour of dark matter. [You may assume that time averaging may be replaced by an average over particles.]

  comment

Differential Geometry

• Paper 1, Section II, 26F

  Differential Geometry | Part II, 2021

  (a) Let $S \subset \mathbb{R}^{3}$ be a surface. Give a parametrisation-free definition of the first fundamental form of $S$. Use this definition to derive a description of it in terms of the partial derivatives of a local parametrisation $\phi: U \subset \mathbb{R}^{2} \rightarrow S$.

  (b) Let $a$ be a positive constant. Show that the half-cone

  $$\Sigma=\left\{(x, y, z) \mid z^{2}=a\left(x^{2}+y^{2}\right), z>0\right\}$$

  is locally isometric to the Euclidean plane. [Hint: Use polar coordinates on the plane.]

  (c) Define the second fundamental form and the Gaussian curvature of $S$. State Gauss' Theorema Egregium. Consider the set

  $$V=\left\{(x, y, z) \mid x^{2}+y^{2}+z^{2}-2 x y-2 y z=0\right\} \backslash\{(0,0,0)\} \subset \mathbb{R}^{3}$$

  (i) Show that $V$ is a surface.

  (ii) Calculate the Gaussian curvature of $V$ at each point. [Hint: Complete the square.]

  comment

• Paper 2, Section II, $26 \mathbf{F}$

  Differential Geometry | Part II, 2021

  Let $U$ be a domain in $\mathbb{R}^{2}$, and let $\phi: U \rightarrow \mathbb{R}^{3}$ be a smooth map. Define what it means for $\phi$ to be an immersion. What does it mean for an immersion to be isothermal?

  Write down a formula for the mean curvature of an immersion in terms of the first and second fundamental forms. What does it mean for an immersed surface to be minimal? Assume that $\phi(u, v)=(x(u, v), y(u, v), z(u, v))$ is an isothermal immersion. Prove that it is minimal if and only if $x, y, z$ are harmonic functions of $u, v$.

  For $u \in \mathbb{R}, v \in[0,2 \pi]$, and smooth functions $f, g: \mathbb{R} \rightarrow \mathbb{R}$, assume that

  $$\phi(u, v)=(f(u) \cos v, f(u) \sin v, g(u))$$

  is an isothermal immersion. Find all possible pairs $(f, g)$ such that this immersion is minimal.

  comment

• Paper 3, Section II, F

  Differential Geometry | Part II, 2021

  Let $X$ and $Y$ be smooth boundaryless manifolds. Suppose $f: X \rightarrow Y$ is a smooth map. What does it mean for $y \in Y$ to be a regular value of $f$ ? State Sard's theorem and the stack-of-records theorem.

  Suppose $g: X \rightarrow Y$ is another smooth map. What does it mean for $f$ and $g$ to be smoothly homotopic? Assume now that $X$ is compact, and has the same dimension as $Y$. Suppose that $y \in Y$ is a regular value for both $X$ and $Y$. Prove that

  $$\# f^{-1}(y)=\# g^{-1}(y)(\bmod 2)$$

  Let $U \subset S^{n}$ be a non-empty open subset of the sphere. Suppose that $h: S^{n} \rightarrow S^{n}$ is a smooth map such that $\# h^{-1}(y)=1(\bmod 2)$ for all $y \in U$. Show that there must exist a pair of antipodal points on $S^{n}$ which is mapped to another pair of antipodal points by $h$.

  [You may assume results about compact 1-manifolds provided they are accurately stated.]

  comment

• Paper 4, Section II, F

  Differential Geometry | Part II, 2021

  Let $I \subset \mathbb{R}$ be an interval, and $S \subset \mathbb{R}^{3}$ be a surface. Assume that $\alpha: I \rightarrow S$ is a regular curve parametrised by arc-length. Define the geodesic curvature of $\alpha$. What does it mean for $\alpha$ to be a geodesic curve?

  State the global Gauss-Bonnet theorem including boundary terms.

  Suppose that $S \subset \mathbb{R}^{3}$ is a surface diffeomorphic to a cylinder. How large can the number of simple closed geodesics on $S$ be in each of the following cases?

  (i) $S$ has Gaussian curvature everywhere zero;

  (ii) $S$ has Gaussian curvature everywhere positive;

  (iii) $S$ has Gaussian curvature everywhere negative.

  In cases where there can be two or more simple closed geodesics, must they always be disjoint? Justify your answer.

  [A formula for the Gaussian curvature of a surface of revolution may be used without proof if clearly stated. You may also use the fact that a piecewise smooth curve on a cylinder without self-intersections either bounds a domain homeomorphic to a disc or is homotopic to the waist-curve of the cylinder.]

  comment

Dynamical Systems

• Paper 1, Section II, A

  Dynamical Systems | Part II, 2021

  (a) State the properties defining a Lyapunov function for a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$. State Lyapunov's first theorem and La Salle's invariance principle.

  (b) Consider the system

  $$\begin{aligned} &\dot{x}=y \\ &\dot{y}=-\frac{2 x\left(1-x^{2}\right)}{\left(1+x^{2}\right)^{3}}-k y \end{aligned}$$

  Show that for $k>0$ the origin is asymptotically stable, stating clearly any arguments that you use.

  $$\left[\text { Hint: } \frac{d}{d x} \frac{x^{2}}{\left(1+x^{2}\right)^{2}}=\frac{2 x\left(1-x^{2}\right)}{\left(1+x^{2}\right)^{3}} \cdot\right]$$

  (c) Sketch the phase plane, (i) for $k=0$ and (ii) for $0<k \ll 1$, giving brief details of any reasoning and identifying the fixed points. Include the domain of stability of the origin in your sketch for case (ii).

  (d) For $k>0$ show that the trajectory $\mathbf{x}(t)$ with $\mathbf{x}(0)=\left(1, y_{0}\right)$, where $y_{0}>0$, satisfies $0<y(t)<\sqrt{y_{0}^{2}+\frac{1}{2}}$ for $t>0$. Show also that, for any $\epsilon>0$, the trajectory cannot remain outside the region $0<y<\epsilon$.

  comment

• Paper 2, Section II, A

  Dynamical Systems | Part II, 2021

  Consider a modified van der Pol system defined by

  $$\begin{aligned} &\dot{x}=y-\mu\left(\frac{1}{3} x^{3}-x\right) \\ &\dot{y}=-x+F \end{aligned}$$

  where $\mu>0$ and $F$ are constants.

  (a) A parallelogram PQRS of width $2 L$ is defined by

  $$\begin{array}{ll} P=(L, \mu f(L)), & Q=(L, 2 L-\mu f(L)) \\ R=(-L,-\mu f(L)), & S=(-L, \mu f(L)-2 L) \end{array}$$

  where $f(L)=\frac{1}{3} L^{3}-L$. Show that if $L$ is sufficiently large then trajectories never leave the region inside the parallelogram.

  Hence show that if $F^{2}<1$ there must be a periodic orbit. Explain your reasoning carefully.

  (b) Use the energy-balance method to analyse the behaviour of the system for $\mu \ll 1$, identifying the difference in behaviours between $F^{2}<1$ and $F^{2}>1$.

  (c) Describe the behaviour of the system for $\mu \gg 1$, using sketches of the phase plane to illustrate your arguments for the cases $0<F<1$ and $F>1$.

  comment

• Paper 3, Section II, A

  Dynamical Systems | Part II, 2021

  Consider the system

  $$\begin{aligned} &\dot{x}=\mu y+\beta x y+y^{2}, \\ &\dot{y}=x-y-x^{2} \end{aligned}$$

  where $\mu$ and $\beta$ are constants with $\beta>0$.

  (a) Find the fixed points, and classify those on $y=0$. State how the number of fixed points depends on $\mu$ and $\beta$. Hence, or otherwise, deduce the values of $\mu$ at which stationary bifurcations occur for fixed $\beta>0$.

  (b) Sketch bifurcation diagrams in the $(\mu, x)$-plane for the cases $0<\beta<1, \beta=1$ and $\beta>1$, indicating the stability of the fixed points and the type of the bifurcations in each case. [You are not required to prove that the stabilities or bifurcation types are as you indicate.]

  (c) For the case $\beta=1$, analyse the bifurcation at $\mu=-1$ using extended centre manifold theory and verify that the evolution equation on the centre manifold matches the behaviour you deduced from the bifurcation diagram in part (b).

  (d) For $0<\mu+1 \ll 1$, sketch the phase plane in the immediate neighbourhood of where the bifurcation of part (c) occurs.

  comment

• Paper 4, Section II, A

  Dynamical Systems | Part II, 2021

  (a) A continuous map $F$ of an interval into itself has a periodic orbit of period 3 . Prove that $F$ also has periodic orbits of period $n$ for all positive integers $n$.

  (b) What is the minimum number of distinct orbits of $F$ of periods 2,4 and 5 ? Explain your reasoning with a directed graph. [Formal proof is not required.]

  (c) Consider the piecewise linear map $F:[0,1] \rightarrow[0,1]$ defined by linear segments between $F(0)=\frac{1}{2}, F\left(\frac{1}{2}\right)=1$ and $F(1)=0$. Calculate the orbits of periods 2,4 and 5 that are obtained from the directed graph in part (b).

  [In part (a) you may assume without proof:

  (i) If $U$ and $V$ are non-empty closed bounded intervals such that $V \subseteq F(U)$ then there is a closed bounded interval $K \subseteq U$ such that $F(K)=V$.

  (ii) The Intermediate Value Theorem.]

  comment

Electrodynamics

• Paper 1, Section II, 37C

  Electrodynamics | Part II, 2021

  (a) An electromagnetic field is specified by a four-vector potential

  $$A^{\mu}(\mathbf{x}, t)=(\phi(\mathbf{x}, t) / c, \mathbf{A}(\mathbf{x}, t))$$

  Define the corresponding field-strength tensor $F^{\mu \nu}$ and state its transformation property under a general Lorentz transformation.

  (b) Write down two independent Lorentz scalars that are quadratic in the field strength and express them in terms of the electric and magnetic fields, $\mathbf{E}=-\boldsymbol{\nabla} \phi-\partial \mathbf{A} / \partial t$ and $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}$. Show that both these scalars vanish when evaluated on an electromagnetic plane-wave solution of Maxwell's equations of arbitrary wavevector and polarisation.

  (c) Find (non-zero) constant, homogeneous background fields $\mathbf{E}(\mathbf{x}, t)=\mathbf{E}_{0}$ and $\mathbf{B}(\mathbf{x}, t)=\mathbf{B}_{0}$ such that both the Lorentz scalars vanish. Show that, for any such background, the field-strength tensor obeys

  $$F_{\rho}^{\mu} F_{\sigma}^{\rho} F_{\nu}^{\sigma}=0$$

  (d) Hence find the trajectory of a relativistic particle of mass $m$ and charge $q$ in this background. You should work in an inertial frame where the particle is at rest at the origin at $t=0$ and in which $\mathbf{B}_{0}=\left(0,0, B_{0}\right)$.

  comment

• Paper 3, Section II, 36C

  Electrodynamics | Part II, 2021

  (a) Derive the Larmor formula for the total power $P$ emitted through a large sphere of radius $R$ by a non-relativistic particle of mass $m$ and charge $q$ with trajectory $\mathbf{x}(t)$. You may assume that the electric and magnetic fields describing radiation due to a source localised near the origin with electric dipole moment $\mathbf{p}(t)$ can be approximated as

  $$\begin{aligned} &\mathbf{B}_{\operatorname{Rad}}(\mathbf{x}, t)=-\frac{\mu_{0}}{4 \pi r c} \widehat{\mathbf{x}} \times \ddot{\mathbf{p}}(t-r / c) \\ &\mathbf{E}_{\mathrm{Rad}}(\mathbf{x}, t)=-c \widehat{\mathbf{x}} \times \mathbf{B}_{\operatorname{Rad}}(\mathbf{x}, t) \end{aligned}$$

  Here, the radial distance $r=|\mathbf{x}|$ is assumed to be much larger than the wavelength of emitted radiation which, in turn, is large compared to the spatial extent of the source.

  (b) A non-relativistic particle of mass $m$, moving at speed $v$ along the $x$-axis in the positive direction, encounters a step potential of width $L$ and height $V_{0}>0$ described by

  $$V(x)= \begin{cases}0, & x<0 \\ f(x), & 0 \leqslant x \leqslant L \\ V_{0}, & x>L\end{cases}$$

  where $f(x)$ is a monotonically increasing function with $f(0)=0$ and $f(L)=V_{0}$. The particle carries charge $q$ and loses energy by emitting electromagnetic radiation. Assume that the total energy loss through emission $\Delta E_{\text {Rad }}$ is negligible compared with the particle's initial kinetic energy $E=m v^{2} / 2$. For $E>V_{0}$, show that the total energy lost is

  $$\Delta E_{\mathrm{Rad}}=\frac{q^{2} \mu_{0}}{6 \pi m^{2} c} \sqrt{\frac{m}{2}} \int_{0}^{L} d x \frac{1}{\sqrt{E-f(x)}}\left(\frac{d f}{d x}\right)^{2}$$

  Find the total energy lost also for the case $E<V_{0}$.

  (c) Take $f(x)=V_{0} x / L$ and explicitly evaluate the particle energy loss $\Delta E_{\text {Rad }}$ in each of the cases $E>V_{0}$ and $E<V_{0}$. What is the maximum value attained by $\Delta E_{\text {Rad }}$ as $E$ is varied?

  comment

• Paper 4, Section II, 36C

  Electrodynamics | Part II, 2021

  (a) Define the electric displacement $\mathbf{D}(\mathbf{x}, t)$ for a medium which exhibits a linear response with polarisation constant $\epsilon$ to an applied electric field $\mathbf{E}(\mathbf{x}, t)$ with polarisation constant $\epsilon$. Write down the effective Maxwell equation obeyed by $\mathbf{D}(\mathbf{x})$ in the timeindependent case and in the absence of any additional mobile charges in the medium. Describe appropriate boundary conditions for the electric field at an interface between two regions with differing values of the polarisation constant. [You should discuss separately the components of the field normal to and tangential to the interface.]

  (b) Consider a sphere of radius $a$, centred at the origin, composed of dielectric material with polarisation constant $\epsilon$ placed in a vacuum and subjected to a constant, asymptotically homogeneous, electric field, $\mathbf{E}(\mathbf{x}, t)=\mathbf{E}(\mathbf{x})$ with $\mathbf{E}(\mathbf{x}) \rightarrow \mathbf{E}_{0}$ as $|\mathbf{x}| \rightarrow \infty$. Using the ansatz

  $$\mathbf{E}(\mathbf{x})= \begin{cases}\alpha \mathbf{E}_{0}, & |\mathbf{x}|<a \\ \mathbf{E}_{0}+\left(\beta\left(\widehat{\mathbf{x}} \cdot \mathbf{E}_{0}\right) \widehat{\mathbf{x}}+\delta \mathbf{E}_{0}\right) /|\mathbf{x}|^{3}, & |\mathbf{x}|>a\end{cases}$$

  with constants $\alpha, \beta$ and $\delta$ to be determined, find a solution to Maxwell's equations with appropriate boundary conditions at $|\mathbf{x}|=a$.

  (c) By comparing your solution with the long-range electric field due to a dipole consisting of electric charges $\pm q$ located at displacements $\pm \mathbf{d} / 2$ find the induced electric dipole moment of the dielectric sphere.

  comment

Fluid Dynamics II

• Paper 1, Section II, 39A

  Fluid Dynamics II | Part II, 2021

  (a) Write down the Stokes equations for the motion of an incompressible viscous fluid with negligible inertia (in the absence of body forces). What does it mean that Stokes flow is linear and reversible?

  (b) The region $a<r<b$ between two concentric rigid spheres of radii $a$ and $b$ is filled with fluid of large viscosity $\mu$. The outer sphere is held stationary, while the inner sphere is made to rotate with angular velocity $\boldsymbol{\Omega}$.

  (i) Use symmetry and the properties of Stokes flow to deduce that $p=0$, where $p$ is the pressure due to the flow.

  (ii) Verify that both solid-body rotation and $\mathbf{u}(\mathbf{x})=\boldsymbol{\Omega} \wedge \boldsymbol{\nabla}(1 / r)$ satisfy the Stokes equations with $p=0$. Hence determine the fluid velocity between the spheres.

  (iii) Calculate the stress tensor $\sigma_{i j}$ in the flow.

  (iv) Deduce that the couple $\mathbf{G}$ exerted by the fluid in $r<c$ on the fluid in $r>c$, where $a<c<b$, is given by

  $$\mathbf{G}=\frac{8 \pi \mu a^{3} b^{3} \mathbf{\Omega}}{b^{3}-a^{3}}$$

  independent of the value of $c$. [Hint: Do not substitute the form of $A$ and $B$ in $A+B r^{-3}$ until the end of the calculation.]

  Comment on the form of this result for $a \ll b$ and for $b-a \ll a$.

  $\left[Y o u\right.$ may use $\int_{r=R} n_{i} n_{j} d S=\frac{4}{3} \pi R^{2} \delta_{i j}$, where $\mathbf{n}$ is the normal to $\left.r=R .\right]$

  comment

• Paper 2, Section II, 39A

  Fluid Dynamics II | Part II, 2021

  (a) Incompressible fluid of viscosity $\mu$ fills the thin, slowly varying gap between rigid boundaries at $z=0$ and $z=h(x, y)>0$. The boundary at $z=0$ translates in its own plane with a constant velocity $\mathbf{U}=(U, 0,0)$, while the other boundary is stationary. If $h$ has typical magnitude $H$ and varies on a lengthscale $L$, state conditions for the lubrication approximation to be appropriate.

  Write down the lubrication equations for this problem and show that the horizontal volume flux $\mathbf{q}=\left(q_{x}, q_{y}, 0\right)$ is given by

  $$\mathbf{q}=\frac{\mathbf{U} h}{2}-\frac{h^{3}}{12 \mu} \nabla p$$

  where $p(x, y)$ is the pressure.

  Explain why $\mathbf{q}=\nabla \wedge(0,0, \psi)$ for some function $\psi(x, y)$. Deduce that $\psi$ satisfies the equation

  $$\nabla \cdot\left(\frac{1}{h^{3}} \nabla \psi\right)=-\frac{U}{h^{3}} \frac{\partial h}{\partial y}$$

  (b) Now consider the case $\mathbf{U}=\mathbf{0}, h=h_{0}$ for $r>a$ and $h=h_{1}$ for $r<a$, where $h_{0}, h_{1}$ and $a$ are constants, and $(r, \theta)$ are polar coordinates. A uniform pressure gradient $\nabla p=-G \mathbf{e}_{x}$ is applied at infinity. Show that $\psi \sim A r \sin \theta$ as $r \rightarrow \infty$, where the constant $A$ is to be determined.

  Given that $a \gg h_{0}, h_{1}$, you may assume that the equations of part (a) apply for $r<a$ and $r>a$, and are subject to conditions that the radial component $q_{r}$ of the volume flux and the pressure $p$ are both continuous across $r=a$. Show that these continuity conditions imply that

  $$\left[\frac{\partial \psi}{\partial \theta}\right]_{-}^{+}=0 \quad \text { and }\left[\frac{1}{h^{3}} \frac{\partial \psi}{\partial r}\right]_{-}^{+}=0$$

  respectively, where []$_{-}^{+}$denotes the jump across $r=a$.

  Hence determine $\psi(r, \theta)$ and deduce that the total flux through $r=a$ is given by

  $$\frac{4 A a h_{1}^{3}}{h_{0}^{3}+h_{1}^{3}}$$

  comment

• Paper 3, Section II, 38A

  Fluid Dynamics II | Part II, 2021

  Viscous fluid occupying $z>0$ is bounded by a rigid plane at $z=0$ and is extracted through a small hole at the origin at a constant flow rate $Q=2 \pi A$. Assume that for sufficiently small values of $R=|\mathbf{x}|$ the velocity $\mathbf{u}(\mathbf{x})$ is well-approximated by

  $$\mathbf{u}=-\frac{A \mathbf{x}}{R^{3}}$$

  except within a thin axisymmetric boundary layer near $z=0$.

  (a) Estimate the Reynolds number of the flow as a function of $R$, and thus give an estimate for how small $R$ needs to be for such a solution to be applicable. Show that the radial pressure gradient is proportional to $R^{-5}$.

  (b) In cylindrical polar coordinates $(r, \theta, z)$, the steady axisymmetric boundary-layer equations for the velocity components $(u, 0, w)$ can be written as

  $$u \frac{\partial u}{\partial r}+w \frac{\partial u}{\partial z}=-\frac{1}{\rho} \frac{d P}{d r}+\nu \frac{\partial^{2} u}{\partial z^{2}}, \quad \text { where } \quad u=-\frac{1}{r} \frac{\partial \Psi}{\partial z}, \quad w=\frac{1}{r} \frac{\partial \Psi}{\partial r}$$

  and $\Psi(r, z)$ is the Stokes streamfunction. Verify that the condition of incompressibility is satisfied by the use of $\Psi$.

  Use scaling arguments to estimate the thickness $\delta(r)$ of the boundary layer near $z=0$ and then to motivate seeking a similarity solution of the form

  $$\Psi=(A \nu r)^{1 / 2} F(\eta), \quad \text { where } \quad \eta=z / \delta(r)$$

  (c) Obtain the differential equation satisfied by $F$, and state the conditions that would determine its solution. [You are not required to find this solution.]

  By considering the flux in the boundary layer, explain why there should be a correction to the approximation $(*)$ of relative magnitude $(\nu R / A)^{1 / 2} \ll 1$.

  comment

• Paper 4, Section II, A

  Fluid Dynamics II | Part II, 2021

  Consider a steady axisymmetric flow with components $(-\alpha r, v(r), 2 \alpha z)$ in cylindrical polar coordinates $(r, \theta, z)$, where $\alpha$ is a positive constant. The fluid has density $\rho$ and kinematic viscosity $\nu$.

  (a) Briefly describe the flow and confirm that it is incompressible.

  (b) Show that the vorticity has one component $\omega(r)$, in the $z$ direction. Write down the corresponding vorticity equation and derive the solution

  $$\omega=\omega_{0} e^{-\alpha r^{2} /(2 \nu)}$$

  Hence find $v(r)$ and show that it has a maximum at some finite radius $r^{*}$, indicating how $r^{*}$ scales with $\nu$ and $\alpha$.

  (c) Find an expression for the net advection of angular momentum, prv, into the finite cylinder defined by $r \leqslant r_{0}$ and $-z_{0} \leqslant z \leqslant z_{0}$. Show that this is always positive and asymptotes to the value

  $$\frac{8 \pi \rho z_{0} \omega_{0} \nu^{2}}{\alpha}$$

  as $r_{0} \rightarrow \infty$

  (d) Show that the torque exerted on the cylinder of part (c) by the exterior flow is always negative and demonstrate that it exactly balances the net advection of angular momentum. Comment on why this has to be so.

  [You may assume that for a flow $(u, v, w)$ in cylindrical polar coordinates

  $$\begin{aligned} & e_{r \theta}=\frac{r}{2} \frac{\partial}{\partial r}\left(\frac{v}{r}\right)+\frac{1}{2 r} \frac{\partial u}{\partial \theta}, \quad e_{\theta z}=\frac{1}{2 r} \frac{\partial w}{\partial \theta}+\frac{1}{2} \frac{\partial v}{\partial z}, \quad e_{r z}=\frac{1}{2} \frac{\partial u}{\partial z}+\frac{1}{2} \frac{\partial w}{\partial r} \\ & \text { and } \left.\boldsymbol{\omega}=\frac{1}{r}\left|\begin{array}{ccc}\mathbf{e}_{r} & r \mathbf{e}_{\theta} & \mathbf{e}_{z} \\\partial / \partial r & \partial / \partial \theta & \partial / \partial z \\u & r v & w\end{array}\right| .\right] \end{aligned}$$

  comment

Further Complex Methods

• Paper 1, Section I, 7E

  Further Complex Methods | Part II, 2021

  Evaluate the integral

  $$\mathcal{P} \int_{0}^{\infty} \frac{\sin x}{x\left(x^{2}-1\right)} d x$$

  stating clearly any standard results involving contour integrals that you use.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2021

  (a) Functions $g_{1}(z)$ and $g_{2}(z)$ are analytic in a connected open set $\mathcal{D} \subseteq \mathbb{C}$ with $g_{1}=g_{2}$ in a non-empty open subset $\tilde{\mathcal{D}} \subset \mathcal{D}$. State the identity theorem.

  (b) Let $\mathcal{D}_{1}$ and $\mathcal{D}_{2}$ be connected open sets with $\mathcal{D}_{1} \cap \mathcal{D}_{2} \neq \emptyset$. Functions $f_{1}(z)$ and $f_{2}(z)$ are analytic on $\mathcal{D}_{1}$ and $\mathcal{D}_{2}$ respectively with $f_{1}=f_{2}$ on $\mathcal{D}_{1} \cap \mathcal{D}_{2}$. Explain briefly what is meant by analytic continuation of $f_{1}$ and use part (a) to prove that analytic continuation to $\mathcal{D}_{2}$ is unique.

  (c) The function $F(z)$ is defined by

  $$F(z)=\int_{-\infty}^{\infty} \frac{e^{i t}}{(t-z)^{n}} d t$$

  where $\operatorname{Im} z>0$ and $n$ is a positive integer. Use the method of contour deformation to construct the analytic continuation of $F(z)$ into $\operatorname{Im} z \leqslant 0$.

  (d) The function $G(z)$ is defined by

  $$G(z)=\int_{-\infty}^{\infty} \frac{e^{i t}}{(t-z)^{n}} d t$$

  where $\operatorname{Im} z \neq 0$ and $n$ is a positive integer. Prove that $G(z)$ experiences a discontinuity when $z$ crosses the real axis. Determine the value of this discontinuity. Hence, explain why $G(z)$ cannot be used as an analytic continuation of $F(z)$.

  comment

• Paper 2, Section I, 7E

  Further Complex Methods | Part II, 2021

  The function $w(z)$ satisfies the differential equation

  $$\tag{†} \frac{d^{2} w}{d z^{2}}+p(z) \frac{d w}{d z}+q(z) w=0$$

  where $p(z)$ and $q(z)$ are complex analytic functions except, possibly, for isolated singularities in $\overline{\mathbb{C}}=\mathbb{C} \cup\{\infty\}$ (the extended complex plane).

  (a) Given equation $(†)$, state the conditions for a point $z_{0} \in \mathbb{C}$ to be

  (i) an ordinary point,

  (ii) a regular singular point,

  (iii) an irregular singular point.

  (b) Now consider $z_{0}=\infty$ and use a suitable change of variables $z \rightarrow t$, with $y(t)=w(z)$, to rewrite $(†)$ as a differential equation that is satisfied by $y(t)$. Hence, deduce the conditions for $z_{0}=\infty$ to be

  (i) an ordinary point,

  (ii) a regular singular point,

  (iii) an irregular singular point.

  [In each case, you should express your answer in terms of the functions $p$ and $q$.]

  (c) Use the results above to prove that any equation of the form ( $\dagger$ ) must have at least one singular point in $\overline{\mathbb{C}}$.

  comment

• Paper 2, Section II, 13E

  Further Complex Methods | Part II, 2021

  The temperature $T(x, t)$ in a semi-infinite bar $(0 \leqslant x<\infty)$ satisfies the heat equation

  $$\frac{\partial T}{\partial t}=\kappa \frac{\partial^{2} T}{\partial x^{2}}, \quad \text { for } x>0 \text { and } t>0$$

  where $\kappa$ is a positive constant.

  For $t<0$, the bar is at zero temperature. For $t \geqslant 0$, the temperature is subject to the boundary conditions

  $$T(0, t)=a\left(1-e^{-b t}\right),$$

  where $a$ and $b$ are positive constants, and $T(x, t) \rightarrow 0$ as $x \rightarrow \infty$.

  (a) Show that the Laplace transform of $T(x, t)$ with respect to $t$ takes the form

  $$\hat{T}(x, p)=\hat{f}(p) e^{-x \sqrt{p / \kappa}}$$

  and find $\hat{f}(p)$. Hence write $\hat{T}(x, p)$ in terms of $a, b, \kappa, p$ and $x$.

  (b) By performing the inverse Laplace transform using contour integration, show that for $t \geqslant 0$

  $$T(x, t)=a\left[1-e^{-b t} \cos \left(\sqrt{\frac{b}{\kappa}} x\right)\right]+\frac{2 a b}{\pi} \mathcal{P} \int_{0}^{\infty} \frac{e^{-v^{2} t} \sin (x v / \sqrt{\kappa})}{v\left(v^{2}-b\right)} d v$$

  comment

• Paper 3 , Section I, 7E

  Further Complex Methods | Part II, 2021

  The Beta function is defined by

  $$B(p, q)=\int_{0}^{1} t^{p-1}(1-t)^{q-1} d t$$

  for $\operatorname{Re} p>0$ and $\operatorname{Re} q>0$.

  (a) Prove that $B(p, q)=B(q, p)$ and find $B(1, q)$.

  (b) Show that $(p+z) B(p, z+1)=z B(p, z)$.

  (c) For each fixed $p$ with $\operatorname{Re} p>0$, use part (b) to obtain the analytic continuation of $B(p, z)$ as an analytic function of $z \in \mathbb{C}$, with the exception of the points $z=$ $0,-1,-2,-3, \ldots$

  (d) Use part (c) to determine the type of singularity that the function $B(p, z)$ has at $z=0,-1,-2,-3, \ldots$, for fixed $p$ with $\operatorname{Re} p>0$.

  comment

• Paper 4 , Section I, 7E

  Further Complex Methods | Part II, 2021

  (a) Explain in general terms the meaning of the Papperitz symbol

  $$P\left\{\begin{array}{cccc} a & b & c & \\ \alpha & \beta & \gamma & z \\ \alpha^{\prime} & \beta^{\prime} & \gamma^{\prime} & \end{array}\right\}$$

  State a condition satisfied by $\alpha, \beta, \gamma, \alpha^{\prime}, \beta^{\prime}$ and $\gamma^{\prime}$. [You need not write down any differential equations explicitly, but should provide explicit explanation of the meaning of $a, b, c, \alpha, \beta, \gamma, \alpha^{\prime}, \beta^{\prime}$ and $\left.\gamma^{\prime} .\right]$

  (b) The Papperitz symbol

  $$P\left\{\begin{array}{cccc} 1 & -1 & \infty & \\ -m / 2 & m / 2 & n & z \\ m / 2 & -m / 2 & 1-n \end{array}\right\}$$

  where $n, m$ are constants, can be transformed into

  $$P\left\{\begin{array}{cccc} 0 & 1 & \infty & \\ 0 & 0 & n & \frac{1-z}{2} \\ m & -m & 1-n & \end{array}\right\}$$

  (i) Provide an explicit description of the transformations required to obtain ( $*)$ from $(t)$.

  (ii) One of the solutions to the $P$-equation that corresponds to $(*)$ is a hypergeometric function $F\left(a, b ; c ; z^{\prime}\right)$. Express $a, b, c$ and $z^{\prime}$ in terms of $n, m$ and $z$.

  comment

Galois Theory

• Paper 1, Section II, 18I

  Galois Theory | Part II, 2021

  (a) Let $K \subseteq L$ be fields, and $f(x) \in K[x]$ a polynomial.

  Define what it means for $L$ to be a splitting field for $f$ over $K$.

  Prove that splitting fields exist, and state precisely the theorem on uniqueness of splitting fields.

  Let $f(x)=x^{3}-2 \in \mathbb{Q}[x]$. Find a subfield of $\mathbb{C}$ which is a splitting field for $f$ over Q. Is this subfield unique? Justify your answer.

  (b) Let $L=\mathbb{Q}\left[\zeta_{7}\right]$, where $\zeta_{7}$ is a primitive 7 th root of unity.

  Show that the extension $L / \mathbb{Q}$ is Galois. Determine all subfields $M \subseteq L$.

  For each subfield $M$, find a primitive element for the extension $M / \mathbb{Q}$ explicitly in terms of $\zeta_{7}$, find its minimal polynomial, and write $\operatorname{down} \operatorname{Aut}(M / \mathbb{Q})$ and $\operatorname{Aut}(L / M)$.

  Which of these subfields $M$ are Galois over $\mathbb{Q}$ ?

  [You may assume the Galois correspondence, but should prove any results you need about cyclotomic extensions directly.]

  comment

• Paper 2, Section II, 18I

  Galois Theory | Part II, 2021

  (a) Let $f(x) \in \mathbb{F}_{q}[x]$ be a polynomial of degree $n$, and let $L$ be its splitting field.

  (i) Suppose that $f$ is irreducible. Compute $\operatorname{Gal}(f)$, carefully stating any theorems you use.

  (ii) Now suppose that $f(x)$ factors as $f=h_{1} \cdots h_{r}$ in $\mathbb{F}_{q}[x]$, with each $h_{i}$ irreducible, and $h_{i} \neq h_{j}$ if $i \neq j$. Compute $\operatorname{Gal}(f)$, carefully stating any theorems you use.

  (iii) Explain why $L / \mathbb{F}_{q}$ is a cyclotomic extension. Define the corresponding homomorphism $\operatorname{Gal}\left(L / \mathbb{F}_{q}\right) \hookrightarrow(\mathbb{Z} / m \mathbb{Z})^{*}$ for this extension (for a suitable integer $m$ ), and compute its image.

  (b) Compute $\operatorname{Gal}(f)$ for the polynomial $f=x^{4}+8 x+12 \in \mathbb{Q}[x]$. [You may assume that $f$ is irreducible and that its discriminant is $576^{2}$.]

  comment

• Paper 3, Section II, 18I

  Galois Theory | Part II, 2021

  Define the elementary symmetric functions in the variables $x_{1}, \ldots, x_{n}$. State the fundamental theorem of symmetric functions.

  Let $f(x)=x^{n}+a_{n-1} x^{n-1}+\cdots+a_{0} \in K[x]$, where $K$ is a field. Define the discriminant of $f$, and explain why it is a polynomial in $a_{0}, \ldots, a_{n-1}$.

  Compute the discriminant of $x^{5}+q$.

  Let $f(x)=x^{5}+p x^{2}+q$. When does the discriminant of $f(x)$ equal zero? Compute the discriminant of $f(x)$.

  comment

• Paper 4 , Section II, 18I

  Galois Theory | Part II, 2021

  Let $L$ be a field, and $G$ a group which acts on $L$ by field automorphisms.

  (a) Explain the meaning of the phrase in italics in the previous sentence.

  Show that the set $L^{G}$ of fixed points is a subfield of $L$.

  (b) Suppose that $G$ is finite, and set $K=L^{G}$. Let $\alpha \in L$. Show that $\alpha$ is algebraic and separable over $K$, and that the degree of $\alpha$ over $K$ divides the order of $G$.

  Assume that $\alpha$ is a primitive element for the extension $L / K$, and that $G$ is a subgroup of $\operatorname{Aut}(L)$. What is the degree of $\alpha$ over $K$ ? Justify your answer.

  (c) Let $L=\mathbb{C}(z)$, and let $\zeta_{n}$ be a primitive $n$th root of unity in $\mathbb{C}$ for some integer $n>1$. Show that the $\mathbb{C}$-automorphisms $\sigma, \tau$ of $L$ defined by

  $$\sigma(z)=\zeta_{n} z, \quad \tau(z)=1 / z$$

  generate a group $G$ isomorphic to the dihedral group of order $2 n$.

  Find an element $w \in L$ for which $L^{G}=\mathbb{C}(w)$.

  comment

General Relativity

• Paper 1, Section II, C

  General Relativity | Part II, 2021

  The Weyl tensor $C_{\alpha \beta \gamma \delta}$ may be defined (in $n=4$ spacetime dimensions) as

  $C_{\alpha \beta \gamma \delta}=R_{\alpha \beta \gamma \delta}-\frac{1}{2}\left(g_{\alpha \gamma} R_{\beta \delta}+g_{\beta \delta} R_{\alpha \gamma}-g_{\alpha \delta} R_{\beta \gamma}-g_{\beta \gamma} R_{\alpha \delta}\right)+\frac{1}{6}\left(g_{\alpha \gamma} g_{\beta \delta}-g_{\alpha \delta} g_{\beta \gamma}\right) R$

  where $R_{\alpha \beta \gamma \delta}$ is the Riemann tensor, $R_{\alpha \beta}$ is the Ricci tensor and $R$ is the Ricci scalar.

  (a) Show that $C_{\beta \alpha \delta}^{\alpha}=0$ and deduce that all other contractions vanish.

  (b) A conformally flat metric takes the form

  $$g_{\alpha \beta}=e^{2 \omega} \eta_{\alpha \beta},$$

  where $\eta_{\alpha \beta}$ is the Minkowski metric and $\omega$ is a scalar function. Calculate the Weyl tensor at a given point $p$. [You may assume that $\partial_{\alpha} \omega=0$ at $p$.]

  (c) The Schwarzschild metric outside a spherically symmetric mass (such as the Sun, Earth or Moon) is

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2} d \Omega^{2}$$

  (i) Calculate the leading-order contribution to the Weyl component $C_{t r t r}$ valid at large distances, $r \gg 2 M$, beyond the central spherical mass.

  (ii) What physical phenomenon, known from ancient times, can be attributed to this component of the Weyl tensor at the location of the Earth? [This is after subtracting off the Earth's own gravitational field, and neglecting the Earth's motion within the solar system.] Briefly explain why your answer is consistent with the Einstein equivalence principle.

  comment

• Paper 2, Section II, 38C

  General Relativity | Part II, 2021

  Consider the following metric for a 3-dimensional, static and rotationally symmetric Lorentzian manifold:

  $$d s^{2}=r^{-2}\left(-d t^{2}+d r^{2}\right)+r^{2} d \theta^{2}$$

  (a) Write down a Lagrangian $\mathcal{L}$ for arbitrary geodesics in this metric, if the geodesic is affinely parameterized with respect to $\lambda$. What condition may be imposed to distinguish spacelike, timelike, and null geodesics?

  (b) Find the three constants of motion for any geodesic.

  (c) Two observation stations are sitting at radii $r=R$ and $r=2 R$ respectively, and at the same angular coordinate. Each is accelerating so as to remain stationary with respect to time translations. At $t=0$ a photon is emitted from the naked singularity at $r=0$.

  (i) At what time $t_{1}$ does the photon reach the inner station?

  (ii) Express the frequency $\nu_{2}$ of the photon at the outer station in terms of the frequency $\nu_{1}$ at the inner station. Explain whether the photon is redshifted or blueshifted as it travels.

  (d) Consider a complete (i.e. infinite in both directions) spacelike geodesic on a constant- $t$ slice with impact parameter $b=r_{\min }>0$. What is the angle $\Delta \theta$ between the two asymptotes of the geodesic at $r=\infty$ ? [You need not be concerned with the sign of $\Delta \theta$ or the periodicity of the $\theta$ coordinate.]

  [Hint: You may find integration by substitution useful.]

  comment

• Paper 3, Section II, 37C

  General Relativity | Part II, 2021

  (a) Determine the signature of the metric tensor $g_{\mu \nu}$ given by

  $$g_{\mu \nu}=\left(\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & -1 & 0 \\ 0 & 0 & 0 & -1 \end{array}\right)$$

  Is it Riemannian, Lorentzian, or neither?

  (b) Consider a stationary black hole with the Schwarzschild metric:

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2} d \Omega^{2}$$

  These coordinates break down at the horizon $r=2 M$. By making a change of coordinates, show that this metric can be converted to infalling Eddington-Finkelstein coordinates.

  (c) A spherically symmetric, narrow pulse of radiation with total energy $E$ falls radially inwards at the speed of light from infinity, towards the origin of a spherically symmetric spacetime that is otherwise empty. Assume that the radial width $\lambda$ of the pulse is very small compared to the energy $(\lambda \ll E)$, and the pulse can therefore be treated as instantaneous.

  (i) Write down a metric for the region outside the pulse, which is free from coordinate singularities. Briefly justify your answer. For what range of coordinates is this metric valid?

  (ii) Write down a metric for the region inside the pulse. Briefly justify your answer. For what range of coordinates is this metric valid?

  (iii) What is the final state of the system?

  comment

• Paper 4 , Section II, $37 \mathrm{C}$

  General Relativity | Part II, 2021

  (a) A flat $(k=0)$, isotropic and homogeneous universe has metric $g_{\alpha \beta}$ given by

  $$d s^{2}=-d t^{2}+a^{2}(t)\left(d x^{2}+d y^{2}+d z^{2}\right)$$

  (i) Show that the non-vanishing Christoffel symbols and Ricci tensor components are

  $$\Gamma_{i i}^{0}=a \dot{a}, \quad \Gamma_{0 i}^{i}=\Gamma_{i 0}^{i}=\frac{\dot{a}}{a}, \quad R_{00}=-3 \frac{\ddot{a}}{a}, \quad R_{i i}=a \ddot{a}+2 \dot{a}^{2}$$

  where dots are time derivatives and $i \in\{1,2,3\}$ (no summation assumed).

  (ii) Derive the first-order Friedmann equation from the Einstein equations, $G_{\alpha \beta}+\Lambda g_{\alpha \beta}=8 \pi T_{\alpha \beta} .$

  (b) Consider a flat universe described by ( $\dagger$ ) with $\Lambda=0$ in which late-time acceleration is driven by "phantom" dark energy obeying an equation of state with pressure $P_{\mathrm{ph}}=w \rho_{\mathrm{ph}}$, where $w<-1$ and the energy density $\rho_{\mathrm{ph}}>0$. The remaining matter is dust, so we have $\rho=\rho_{\mathrm{ph}}+\rho_{\mathrm{dust}}$ with each component separately obeying $\dot{\rho}=-3 \frac{\dot{a}}{a}(\rho+P)$.

  (i) Calculate an approximate solution for the scale factor $a(t)$ that is valid at late times. Show that the asymptotic behaviour is given by a Big Rip, that is, a singularity in which $a \rightarrow \infty$ at some finite time $t^{*}$.

  (ii) Sketch a diagram of the scale factor $a$ as a function of $t$ for a convenient choice of $w$, ensuring that it includes (1) the Big Bang, (2) matter domination, (3) phantom-energy domination, and (4) the Big Rip. Label these epochs and mark them on the axes.

  (iii) Most reasonable classical matter fields obey the null energy condition, which states that the energy-momentum tensor everywhere satisfies $T_{\alpha \beta} V^{\alpha} V^{\beta} \geqslant 0$ for any null vector $V^{\alpha}$. Determine if this applies to phantom energy.

  [The energy-momentum tensor for a perfect fluid is $\left.T_{\alpha \beta}=(\rho+P) u_{\alpha} u_{\beta}+P g_{\alpha \beta}\right]$

  comment

Graph Theory

• Paper 1, Section II, 17G

  Graph Theory | Part II, 2021

  Define the binomial random graph $G(n, p)$, where $n \in \mathbb{N}$ and $p \in(0,1)$.

  (a) Let $G_{n} \sim G(n, p)$ and let $E_{t}$ be the event that $G_{n}$ contains a copy of the complete graph $K_{t}$. Show that if $p=p(n)$ is such that $p \cdot n^{2 /(t-1)} \rightarrow 0$ then $\mathbb{P}\left(E_{t}\right) \rightarrow 0$ as $n \rightarrow \infty$.

  (b) State Chebyshev's inequality. Show that if $p \cdot n \rightarrow \infty$ then $\mathbb{P}\left(E_{3}\right) \rightarrow 1$.

  (c) Let $H$ be a triangle with an added leaf vertex, that is

  $$H=\left(\left\{x_{1}, \ldots, x_{4}\right\},\left\{x_{1} x_{2}, x_{2} x_{3}, x_{3} x_{1}, x_{1} x_{4}\right\}\right),$$

  where $x_{1}, \ldots, x_{4}$ are distinct. Let $F$ be the event that $G_{n} \sim G(n, p)$ contains a copy of $H$. Show that if $p=n^{-0.9}$ then $\mathbb{P}(F) \rightarrow 1$.

  comment

• Paper 2, Section II, 17 G

  Graph Theory | Part II, 2021

  (a) Define a tree and what it means for a graph to be acyclic. Show that if $G$ is an acyclic graph on $n$ vertices then $e(G) \leqslant n-1$. [You may use the fact that a spanning tree on $n$ vertices has $n-1$ edges.]

  (b) Show that any 3-regular graph on $n$ vertices contains a cycle of length $\leqslant$ $100 \log n$. Hence show that there exists $n_{0}$ such that every 3-regular graph on more than $n_{0}$ vertices must contain two cycles $C_{1}, C_{2}$ with disjoint vertex sets.

  (c) An unfriendly partition of a graph $G=(V, E)$ is a partition $V=A \cup B$, where $A, B \neq \emptyset$, such that every vertex $v \in A$ has $|N(v) \cap B| \geqslant|N(v) \cap A|$ and every $v \in B$ has $|N(v) \cap A| \geqslant|N(v) \cap B|$. Show that every graph $G$ with $|G| \geqslant 2$ has an unfriendly partition.

  (d) A friendly partition of a graph $G=(V, E)$ is a partition $V=S \cup T$, where $S, T \neq \emptyset$, such that every vertex $v \in S$ has $|N(v) \cap S| \geqslant|N(v) \cap T|$ and every $v \in T$ has $|N(v) \cap T| \geqslant|N(v) \cap S|$. Give an example of a 3-regular graph (on at least 1 vertex) that does not have a friendly partition. Using part (b), show that for large enough $n_{0}$ every 3-regular graph $G$ with $|G| \geqslant n_{0}$ has a friendly partition.

  comment

• Paper 3, Section II, 17G

  Graph Theory | Part II, 2021

  (a) Define the Ramsey number $R(k)$ and show that $R(k) \leqslant 4^{k}$.

  Show that every 2-coloured complete graph $K_{n}$ with $n \geqslant 2$ contains a monochromatic spanning tree. Is the same true if $K_{n}$ is coloured with 3 colours? Give a proof or counterexample.

  (b) Let $G=(V, E)$ be a graph. Show that the number of paths of length 2 in $G$ is

  $$\sum_{x \in V} d(x)(d(x)-1) .$$

  Now consider a 2-coloured complete graph $K_{n}$ with $n \geqslant 3$. Show that the number of monochromatic triangles in $K_{n}$ is

  $$\frac{1}{2} \sum_{x}\left\{\left(\begin{array}{c} d_{r}(x) \\ 2 \end{array}\right)+\left(\begin{array}{c} d_{b}(x) \\ 2 \end{array}\right)\right\}-\frac{1}{2}\left(\begin{array}{l} n \\ 3 \end{array}\right)$$

  where $d_{r}(x)$ denotes the number of red edges incident with a vertex $x$ and $d_{b}(x)=$ $(n-1)-d_{r}(x)$ denotes the number of blue edges incident with $x$. [Hint: Count paths of length 2 in two different ways.]

  comment

• Paper 4, Section II, 17G

  Graph Theory | Part II, 2021

  State and prove Hall's theorem, giving any definitions required by the proof (e.g. of an $M$-alternating path).

  Let $G=(V, E)$ be a (not necessarily bipartite) graph, and let $\gamma(G)$ be the size of the largest matching in $G$. Let $\beta(G)$ be the smallest $k$ for which there exist $k$ vertices $v_{1}, \ldots, v_{k} \in V$ such that every edge in $G$ is incident with at least one of $v_{1}, \ldots, v_{k}$. Show that $\gamma(G) \leqslant \beta(G)$ and that $\beta(G) \leqslant 2 \gamma(G)$. For each positive integer $k$, find a graph $G$ with $\beta(G)=2 k$ and $\gamma(G)=k$. Determine $\beta(G)$ and $\gamma(G)$ when $G$ is the Turan graph $T_{3}(30)$ on 30 vertices.

  By using Hall's theorem, or otherwise, show that if $G$ is a bipartite graph then $\gamma(G)=\beta(G) .$

  Define the chromatic index $\chi^{\prime}(G)$ of a graph $G$. Prove that if $n=2^{r}$ with $r \geqslant 1$ then $\chi^{\prime}\left(K_{n}\right)=n-1$.

  comment

Integrable Systems

• Paper 1 , Section II, 33D

  Integrable Systems | Part II, 2021

  (a) Let $U(z, \bar{z}, \lambda)$ and $V(z, \bar{z}, \lambda)$ be matrix-valued functions, whilst $\psi(z, \bar{z}, \lambda)$ is a vector-valued function. Show that the linear system

  $$\partial_{z} \psi=U \psi, \quad \partial_{\bar{z}} \psi=V \psi$$

  is over-determined and derive a consistency condition on $U, V$ that is necessary for there to be non-trivial solutions.

  (b) Suppose that

  $$U=\frac{1}{2 \lambda}\left(\begin{array}{cc} \lambda \partial_{z} u & e^{-u} \\ e^{u} & -\lambda \partial_{z} u \end{array}\right) \quad \text { and } \quad V=\frac{1}{2}\left(\begin{array}{cc} -\partial_{\bar{z}} u & \lambda e^{u} \\ \lambda e^{-u} & \partial_{\bar{z}} u \end{array}\right)$$

  where $u(z, \bar{z})$ is a scalar function. Obtain a partial differential equation for $u$ that is equivalent to your consistency condition from part (a).

  (c) Now let $z=x+i y$ and suppose $u$ is independent of $y$. Show that the trace of $(U-V)^{n}$ is constant for all positive integers $n$. Hence, or otherwise, construct a non-trivial first integral of the equation

  $$\frac{d^{2} \phi}{d x^{2}}=4 \sinh \phi, \quad \text { where } \quad \phi=\phi(x)$$

  comment

• Paper 2, Section II, 34D

  Integrable Systems | Part II, 2021

  (a) Explain briefly how the linear operators $L=-\partial_{x}^{2}+u(x, t)$ and $A=4 \partial_{x}^{3}-3 u \partial_{x}-$ $3 \partial_{x} u$ can be used to give a Lax-pair formulation of the $\mathrm{KdV}$ equation $u_{t}+u_{x x x}-6 u u_{x}=0$.

  (b) Give a brief definition of the scattering data

  $$\mathcal{S}_{u(t)}=\left\{\{R(k, t)\}_{k \in \mathbb{R}},\left\{-\kappa_{n}(t)^{2}, c_{n}(t)\right\}_{n=1}^{N}\right\}$$

  attached to a smooth solution $u=u(x, t)$ of the KdV equation at time $t$. [You may assume $u(x, t)$ to be rapidly decreasing in $x$.] State the time dependence of $\kappa_{n}(t)$ and $c_{n}(t)$, and derive the time dependence of $R(k, t)$ from the Lax-pair formulation.

  (c) Show that

  $$F(x, t)=\sum_{n=1}^{N} c_{n}(t)^{2} e^{-\kappa_{n}(t) x}+\frac{1}{2 \pi} \int_{-\infty}^{\infty} R(k, t) e^{i k x} d k$$

  satisfies $\partial_{t} F+8 \partial_{x}^{3} F=0$. Now let $K(x, y, t)$ be the solution of the equation

  $$K(x, y, t)+F(x+y, t)+\int_{x}^{\infty} K(x, z, t) F(z+y, t) d z=0$$

  and let $u(x, t)=-2 \partial_{x} \phi(x, t)$, where $\phi(x, t)=K(x, x, t)$. Defining $G(x, y, t)$ by $G=$ $\left(\partial_{x}^{2}-\partial_{y}^{2}-u(x, t)\right) K(x, y, t)$, show that

  $$G(x, y, t)+\int_{x}^{\infty} G(x, z, t) F(z+y, t) d z=0$$

  (d) Given that $K(x, y, t)$ obeys the equations

  $$\begin{aligned} \left(\partial_{x}^{2}-\partial_{y}^{2}\right) K-u K &=0 \\ \left(\partial_{t}+4 \partial_{x}^{3}+4 \partial_{y}^{3}\right) K-3\left(\partial_{x} u\right) K-6 u \partial_{x} K &=0 \end{aligned}$$

  where $u=u(x, t)$, deduce that

  $$\partial_{t} K+\left(\partial_{x}+\partial_{y}\right)^{3} K-3 u\left(\partial_{x}+\partial_{y}\right) K=0$$

  and hence that $u$ solves the $\mathrm{KdV}$ equation.

  comment

• Paper 3, Section II, 32D

  Integrable Systems | Part II, 2021

  (a) Consider the group of transformations of $\mathbb{R}^{2}$ given by $g_{1}^{s}:(t, x) \mapsto(\tilde{t}, \tilde{x})=$ $(t, x+s t)$, where $s \in \mathbb{R}$. Show that this acts as a group of Lie symmetries for the equation $d^{2} x / d t^{2}=0$.

  (b) Let $\left(\psi_{1}, \psi_{2}\right) \in \mathbb{R}^{2}$ and define $\psi=\psi_{1}+i \psi_{2}$. Show that the vector field $\psi_{1} \partial_{\psi_{2}}-\psi_{2} \partial_{\psi_{1}}$ generates the group of phase rotations $g_{2}^{s}: \psi \rightarrow e^{i s} \psi$.

  (c) Show that the transformations of $\mathbb{R}^{2} \times \mathbb{C}$ defined by

  $$g^{s}:(t, x, \psi) \mapsto(\tilde{t}, \tilde{x}, \tilde{\psi})=\left(t, x+s t, \psi e^{i s x+i s^{2} t / 2}\right)$$

  form a one-parameter group generated by the vector field

  $$V=t \partial_{x}+x\left(\psi_{1} \partial_{\psi_{2}}-\psi_{2} \partial_{\psi_{1}}\right)=t \partial_{x}+i x\left(\psi \partial_{\psi}-\psi^{*} \partial_{\psi^{*}}\right)$$

  and find the second prolongation $\operatorname{Pr}^{(2)} g^{s}$ of the action of $\left\{g^{s}\right\}$. Hence find the coefficients $\eta^{0}$ and $\eta^{11}$ in the second prolongation of $V$,

  $\mathrm{pr}^{(2)} V=t \partial_{x}+\left(i x \psi \partial_{\psi}+\eta^{0} \partial_{\psi_{t}}+\eta^{1} \partial_{\psi_{x}}+\eta^{00} \partial_{\psi_{t t}}+\eta^{01} \partial_{\psi_{x t}}+\eta^{11} \partial_{\psi_{x x}}+\right.$ complex conjugate $)$.

  (d) Show that the group $\left\{g^{s}\right\}$ of transformations in part (c) acts as a group of Lie symmetries for the nonlinear Schrödinger equation $i \partial_{t} \psi+\frac{1}{2} \partial_{x}^{2} \psi+|\psi|^{2} \psi=0$. Given that $a e^{i a^{2} t / 2} \operatorname{sech}(a x)$ solves the nonlinear Schrödinger equation for any $a \in \mathbb{R}$, find a solution which describes a solitary wave travelling at arbitrary speed $s \in \mathbb{R}$.

  comment

Linear Analysis

• Paper 1, Section II, 22H

  Linear Analysis | Part II, 2021

  Let $H$ be a separable Hilbert space and $\left\{e_{i}\right\}$ be a Hilbertian (orthonormal) basis of $H$. Given a sequence $\left(x_{n}\right)$ of elements of $H$ and $x_{\infty} \in H$, we say that $x_{n}$ weakly converges to $x_{\infty}$, denoted $x_{n} \rightarrow x_{\infty}$, if $\forall h \in H, \lim _{n \rightarrow \infty}\left\langle x_{n}, h\right\rangle=\left\langle x_{\infty}, h\right\rangle$.

  (a) Given a sequence $\left(x_{n}\right)$ of elements of $H$, prove that the following two statements are equivalent:

  (i) $\exists x_{\infty} \in H$ such that $x_{n} \rightarrow x_{\infty}$;

  (ii) the sequence $\left(x_{n}\right)$ is bounded in $H$ and $\forall i \geqslant 1$, the sequence $\left(\left\langle x_{n}, e_{i}\right\rangle\right)$ is convergent.

  (b) Let $\left(x_{n}\right)$ be a bounded sequence of elements of $H$. Show that there exists $x_{\infty} \in H$ and a subsequence $\left(x_{\phi(n)}\right)$ such that $x_{\phi(n)} \rightarrow x_{\infty}$ in $H$.

  (c) Let $\left(x_{n}\right)$ be a sequence of elements of $H$ and $x_{\infty} \in H$ be such that $x_{n} \rightarrow x_{\infty}$. Show that the following three statements are equivalent:

  (i) $\lim _{n \rightarrow \infty}\left\|x_{n}-x_{\infty}\right\|=0$;

  (ii) $\lim _{n \rightarrow \infty}\left\|x_{n}\right\|=\left\|x_{\infty}\right\|$;

  (iii) $\forall \epsilon>0, \exists I(\epsilon)$ such that $\forall n \geqslant 1, \sum_{i \geqslant I(\epsilon)}\left|\left\langle x_{n}, e_{i}\right\rangle\right|^{2}<\epsilon$.

  comment

• Paper 2, Section II, 22H

  Linear Analysis | Part II, 2021

  (a) Let $V$ be a real normed vector space. Show that any proper subspace of $V$ has empty interior.

  Assuming $V$ to be infinite-dimensional and complete, prove that any algebraic basis of $V$ is uncountable. [The Baire category theorem can be used if stated properly.] Deduce that the vector space of polynomials with real coefficients cannot be equipped with a complete norm, i.e. a norm that makes it complete.

  (b) Suppose that $\|\cdot\|_{1}$ and $\|\cdot\|_{2}$ are norms on a vector space $V$ such that $\left(V,\|\cdot\|_{1}\right)$ and $\left(V,\|\cdot\|_{2}\right)$ are both complete. Prove that if there exists $C_{1}>0$ such that $\|x\|_{2} \leqslant C_{1}\|x\|_{1}$ for all $x \in V$, then there exists $C_{2}>0$ such that $\|x\|_{1} \leqslant C_{2}\|x\|_{2}$ for all $x \in V$. Is this still true without the assumption that $\left(V,\|\cdot\|_{1}\right)$ and $\left(V,\|\cdot\|_{2}\right)$ are both complete? Justify your answer.

  (c) Let $V$ be a real normed vector space (not necessarily complete) and $V^{*}$ be the set of linear continuous forms $f: V \rightarrow \mathbb{R}$. Let $\left(x_{n}\right)_{n \geqslant 1}$ be a sequence in $V$ such that $\sum_{n \geqslant 1}\left|f\left(x_{n}\right)\right|<\infty$ for all $f \in V^{*}$. Prove that

  $$\sup _{\|f\|_{V^{*} \leqslant 1}} \sum_{n \geqslant 1}\left|f\left(x_{n}\right)\right|<\infty .$$

  comment

• Paper 3, Section II, H

  Linear Analysis | Part II, 2021

  (a) State the Arzela-Ascoli theorem, including the definition of equicontinuity.

  (b) Consider a sequence $\left(f_{n}\right)$ of continuous real-valued functions on $\mathbb{R}$ such that for all $x \in \mathbb{R},\left(f_{n}(x)\right)$ is bounded and the sequence is equicontinuous at $x$. Prove that there exists $f \in C(\mathbb{R})$ and a subsequence $\left(f_{\varphi(n)}\right)$ such that $f_{\varphi(n)} \rightarrow f$ uniformly on any closed bounded interval.

  (c) Let $K$ be a Hausdorff compact topological space, and $C(K)$ the real-valued continuous functions on $K$. Let $\mathcal{K} \subset C(K)$ be a compact subset of $C(K)$. Prove that the collection of functions $\mathcal{K}$ is equicontinuous.

  (d) We say that a Hausdorff topological space $X$ is locally compact if every point has a compact neighbourhood. Let $X$ be such a space, $K \subset X$ compact and $U \subset X$ open such that $K \subset U$. Prove that there exists $f: X \rightarrow \mathbb{R}$ continuous with compact support contained in $U$ and equal to 1 on $K$. [Hint: Construct an open set $V$ such that $K \subset V \subset \bar{V} \subset U$ and $\bar{V}$ is compact, and use Urysohn's lemma to construct a function in $\bar{V}$ and then extend it by zero.]

  comment

• Paper 4, Section II, H

  Linear Analysis | Part II, 2021

  (a) Let $\left(H_{1},\langle\cdot, \cdot\rangle_{1}\right),\left(H_{2},\langle\cdot, \cdot\rangle_{2}\right)$ be two Hilbert spaces, and $T: H_{1} \rightarrow H_{2}$ be a bounded linear operator. Show that there exists a unique bounded linear operator $T^{*}: H_{2} \rightarrow H_{1}$ such that

  $$\left\langle T x_{1}, x_{2}\right\rangle_{2}=\left\langle x_{1}, T^{*} x_{2}\right\rangle_{1}, \quad \forall x_{1} \in H_{1}, x_{2} \in H_{2}$$

  (b) Let $H$ be a separable Hilbert space. We say that a sequence $\left(e_{i}\right)$ is a frame of $H$ if there exists $A, B>0$ such that

  $$\forall x \in H, \quad A\|x\|^{2} \leqslant \sum_{i \geqslant 1}\left|\left\langle x, e_{i}\right\rangle\right|^{2} \leqslant B\|x\|^{2}$$

  State briefly why such a frame exists. From now on, let $\left(e_{i}\right)$ be a frame of $H$. Show that $\operatorname{Span}\left\{e_{i}\right\}$ is dense in $H$.

  (c) Show that the linear map $U: H \rightarrow \ell^{2}$ given by $U(x)=\left(\left\langle x, e_{i}\right\rangle\right)_{i \geqslant 1}$ is bounded and compute its adjoint $U^{*}$.

  (d) Assume now that $\left(e_{i}\right)$ is a Hilbertian (orthonormal) basis of $H$ and let $a \in H$. Show that the Hilbert cube $\mathcal{C}_{a}=\left\{x \in H\right.$ such that $\left.\forall i \geqslant 1,\left|\left\langle x, e_{i}\right\rangle\right| \leqslant\left|\left\langle a, e_{i}\right\rangle\right|\right\}$ is a compact subset of $H$.

  comment

Logic and Set Theory

• Paper 1, Section II, 16G

  Logic and Set Theory | Part II, 2021

  Let $S$ and $T$ be sets of propositional formulae.

  (a) What does it mean to say that $S$ is deductively closed? What does it mean to say that $S$ is consistent? Explain briefly why if $S$ is inconsistent then some finite subset of $S$ is inconsistent.

  (b) We write $S \vdash T$ to mean $S \vdash t$ for all $t \in T$. If $S \vdash T$ and $T \vdash S$ we say $S$ and $T$ are equivalent. If $S$ is equivalent to a finite set $F$ of formulae we say that $S$ is finitary. Show that if $S$ is finitary then there is a finite set $R \subset S$ with $R \vdash S$.

  (c) Now let $T_{0}, T_{1}, T_{2}, \ldots$ be deductively closed sets of formulae with

  $$T_{0} \subset T_{1} \subset T_{2} \subset \cdots$$

  Show that each $T_{i}$ is consistent.

  Let $T=\bigcup_{i=0}^{\infty} T_{i}$. Show that $T$ is consistent and deductively closed, but that it is not finitary.

  comment

• Paper 2, Section II, G

  Logic and Set Theory | Part II, 2021

  Write down the inductive definition of ordinal exponentiation. Show that $\omega^{\alpha} \geqslant \alpha$ for every ordinal $\alpha$. Deduce that, for every ordinal $\alpha$, there is a least ordinal $\alpha^{*}$ with $\omega^{\alpha^{*}}>\alpha$. Show that, if $\alpha \neq 0$, then $\alpha^{*}$ must be a successor ordinal.

  Now let $\alpha$ be a non-zero ordinal. Show that there exist ordinals $\beta$ and $\gamma$, where $\gamma<\alpha$, and a positive integer $n$ such that $\alpha=\omega^{\beta} n+\gamma$. Hence, or otherwise, show that $\alpha$ can be written in the form

  $$\alpha=\omega^{\beta_{1}} n_{1}+\omega^{\beta_{2}} n_{2}+\cdots+\omega^{\beta_{k}} n_{k}$$

  where $k, n_{1}, n_{2}, \ldots, n_{k}$ are positive integers and $\beta_{1}>\beta_{2}>\cdots>\beta_{k}$ are ordinals. [We call this the Cantor normal form of $\alpha$, and you may henceforth assume that it is unique.]

  Given ordinals $\delta_{1}, \delta_{2}$ and positive integers $m_{1}, m_{2}$ find the Cantor normal form of $\omega^{\delta_{1}} m_{1}+\omega^{\delta_{2}} m_{2}$. Hence, or otherwise, given non-zero ordinals $\alpha$ and $\alpha^{\prime}$, find the Cantor normal form of $\alpha+\alpha^{\prime}$ in terms of the Cantor normal forms

  $$\alpha=\omega^{\beta_{1}} n_{1}+\omega^{\beta_{2}} n_{2}+\cdots+\omega^{\beta_{k}} n_{k}$$

  and

  $$\alpha^{\prime}=\omega^{\beta_{1}^{\prime}} n_{1}^{\prime}+\omega^{\beta_{2}^{\prime}} n_{2}^{\prime}+\cdots+\omega^{\beta_{k^{\prime}}^{\prime}} n_{k^{\prime}}^{\prime}$$

  of $\alpha$ and $\alpha^{\prime}$.

  comment

• Paper 3, Section II, 16G

  Logic and Set Theory | Part II, 2021

  (a) Let $\kappa$ and $\lambda$ be cardinals. What does it mean to say that $\kappa<\lambda$ ? Explain briefly why, assuming the Axiom of Choice, every infinite cardinal is of the form $\aleph_{\alpha}$ for some ordinal $\alpha$, and that for every ordinal $\alpha$ we have $\aleph_{\alpha+1}<2^{2^{\aleph_{\alpha}}}$.

  (b) Henceforth, you should not assume the Axiom of Choice.

  Show that, for any set $x$, there is an injection from $x$ to its power set $\mathcal{P} x$, but there is no bijection from $x$ to $\mathcal{P} x$. Deduce that if $\kappa$ is a cardinal then $\kappa<2^{\kappa}$.

  Let $x$ and $y$ be sets, and suppose that there exists a surjection $f: x \rightarrow y$. Show that there exists an injection $g: \mathcal{P} y \rightarrow \mathcal{P} x$.

  Let $\alpha$ be an ordinal. Prove that $\aleph_{\alpha} \aleph_{\alpha}=\aleph_{\alpha}$.

  By considering $\mathcal{P}\left(\omega_{\alpha} \times \omega_{\alpha}\right)$ as the set of relations on $\omega_{\alpha}$, or otherwise, show that there exists a surjection $f: \mathcal{P}\left(\omega_{\alpha} \times \omega_{\alpha}\right) \rightarrow \omega_{\alpha+1}$. Deduce that $\aleph_{\alpha+1}<2^{2^{\kappa_{\alpha}}}$.

  comment

• Paper 4, Section II, 16G

  Logic and Set Theory | Part II, 2021

  Write down the Axiom of Foundation.

  What is the transitive closure of a set $x$ ? Prove carefully that every set $x$ has a transitive closure. State and prove the principle of $\in$-induction.

  Let $(V, \in)$ be a model of $\mathrm{ZF}$. Let $F: V \rightarrow V$ be a surjective function class such that for all $x, y \in V$ we have $F(x) \in F(y)$ if and only if $x \in y$. Show, by $\in$-induction or otherwise, that $F$ is the identity.

  comment

Mathematical Biology

• Paper 1, Section I, 6E

  Mathematical Biology | Part II, 2021

  (a) Consider a population of size $N(t)$ whose per capita rates of birth and death are $b e^{-a N}$ and $d$, respectively, where $b>d$ and all parameters are positive constants.

  (i) Write down the equation for the rate of change of the population.

  (ii) Show that a population of size $N^{*}=\frac{1}{a} \log \frac{b}{d}$ is stationary and that it is asymptotically stable.

  (b) Consider now a disease introduced into this population, where the number of susceptibles and infectives, $S$ and $I$, respectively, satisfy the equations

  $$\begin{aligned} &\frac{d S}{d t}=b e^{-a S} S-\beta S I-d S \\ &\frac{d I}{d t}=\beta S I-(d+\delta) I \end{aligned}$$

  (i) Interpret the biological meaning of each term in the above equations and comment on the reproductive capacity of the susceptible and infected individuals.

  (ii) Show that the disease-free equilibrium, $S=N^{*}$ and $I=0$, is linearly unstable if

  $$N^{*}>\frac{d+\delta}{\beta}$$

  (iii) Show that when the disease-free equilibrium is unstable there exists an endemic equilibrium satisfying

  $$\beta I+d=b e^{-a S}$$

  and that this equilibrium is linearly stable.

  comment

• Paper 2, Section I, E

  Mathematical Biology | Part II, 2021

  Consider a stochastic birth-death process in a population of size $n(t)$, where deaths occur in pairs for $n \geqslant 2$. The probability per unit time of a birth, $n \rightarrow n+1$ for $n \geqslant 0$, is $b$, that of a pair of deaths, $n \rightarrow n-2$ for $n \geqslant 2$, is $d n$, and that of the death of a lonely singleton, $1 \rightarrow 0$, is $D$.

  (a) Write down the master equation for $p_{n}(t)$, the probability of a population of size $n$ at time $t$, distinguishing between the cases $n \geqslant 2, n=0$ and $n=1$.

  (b) For a function $f(n), n \geqslant 0$, show carefully that

  $$\frac{d}{d t}\langle f(n)\rangle=b \sum_{n=0}^{\infty}\left(f_{n+1}-f_{n}\right) p_{n}-d \sum_{n=2}^{\infty}\left(f_{n}-f_{n-2}\right) n p_{n}-D\left(f_{1}-f_{0}\right) p_{1}$$

  where $f_{n}=f(n)$.

  (c) Deduce the evolution equation for the mean $\mu(t)=\langle n\rangle$, and simplify it for the case $D=2 d$.

  (d) For the same value of $D$, show that

  $$\frac{d}{d t}\left\langle n^{2}\right\rangle=b(2 \mu+1)-4 d\left(\left\langle n^{2}\right\rangle-\mu\right)-2 d p_{1}$$

  Deduce that the variance $\sigma^{2}$ in the stationary state for $b, d>0$ satisfies

  $$\frac{3 b}{4 d}-\frac{1}{2}<\sigma^{2}<\frac{3 b}{4 d}$$

  comment

• Paper 3, Section I, E

  Mathematical Biology | Part II, 2021

  The population density $n(a, t)$ of individuals of age $a$ at time $t$ satisfies the partial differential equation

  $$\frac{\partial n}{\partial t}+\frac{\partial n}{\partial a}=-d(a) n(a, t)$$

  with the boundary condition

  $$n(0, t)=\int_{0}^{\infty} b(a) n(a, t) d a$$

  where $b(a)$ and $d(a)$ are, respectively, the per capita age-dependent birth and death rates.

  (a) What is the biological interpretation of the boundary condition?

  (b) Solve equation (1) assuming a separable form of solution, $n(a, t)=A(a) T(t)$.

  (c) Use equation (2) to obtain a necessary condition for the existence of a separable solution to the full problem.

  (d) For a birth rate $b(a)=\beta e^{-\lambda a}$ with $\lambda>0$ and an age-independent death rate $d$, show that a separable solution to the full problem exists and find the critical value of $\beta$ above which the population density grows with time.

  comment

• Paper 3, Section II, 13E

  Mathematical Biology | Part II, 2021

  Consider an epidemic spreading in a population that has been aggregated by age into groups numbered $i=1, \ldots, M$. The $i$ th age group has size $N_{i}$ and the numbers of susceptible, infective and recovered individuals in this group are, respectively, $S_{i}, I_{i}$ and $R_{i}$. The spread of the infection is governed by the equations

  $$\begin{aligned} \frac{d S_{i}}{d t} &=-\lambda_{i}(t) S_{i} \\ \frac{d I_{i}}{d t} &=\lambda_{i}(t) S_{i}-\gamma I_{i} \\ \frac{d R_{i}}{d t} &=\gamma I_{i} \end{aligned}$$

  where

  $$\lambda_{i}(t)=\beta \sum_{j=1}^{M} C_{i j} \frac{I_{j}}{N_{j}},$$

  and $C_{i j}$ is a matrix satisfying $N_{i} C_{i j}=N_{j} C_{j i}$, for $i, j=1, \ldots, M$.

  (a) Describe the biological meaning of the terms in equations (1) and (2), of the matrix $C_{i j}$ and the condition it satisfies, and of the lack of dependence of $\beta$ and $\gamma$ on $i$.

  State the condition on the matrix $C_{i j}$ that would ensure the absence of any transmission of infection between age groups.

  (b) In the early stages of an epidemic, $S_{i} \approx N_{i}$ and $I_{i} \ll N_{i}$. Use this information to linearise the dynamics appropriately, and show that the linearised system predicts

  $$\mathbf{I}(t)=\exp [\gamma(\mathbf{L}-\mathbf{1}) t] \mathbf{I}(0),$$

  where $\mathbf{I}(t)=\left[I_{1}(t), \ldots, I_{M}(t)\right]$ is the vector of infectives at time $t, \mathbf{1}$ is the $M \times M$ identity matrix and $\mathbf{L}$ is a matrix that should be determined.

  (c) Deduce a condition on the eigenvalues of the matrix $\mathbf{C}$ that allows the epidemic to grow.

  comment

• Paper 4, Section I, E

  Mathematical Biology | Part II, 2021

  A marine population grows logistically and disperses by diffusion. It is moderately predated on up to a distance $L$ from a straight coast. Beyond that distance, predation is sufficiently excessive to eliminate the population. The density $n(x, t)$ of the population at a distance $x<L$ from the coast satisfies

  $$\frac{\partial n}{\partial t}=r n\left(1-\frac{n}{K}\right)-\delta n+D \frac{\partial^{2} n}{\partial x^{2}}$$

  subject to the boundary conditions

  $$\frac{\partial n}{\partial x}=0 \text { at } x=0, \quad n=0 \text { at } x=L$$

  (a) Interpret the terms on the right-hand side of $(*)$, commenting on their dependence on $n$. Interpret the boundary conditions.

  (b) Show that a non-zero population is viable if $r>\delta$ and

  $$L>\frac{\pi}{2} \sqrt{\frac{D}{r-\delta}}$$

  Interpret these conditions.

  comment

• Paper 4, Section II, E

  Mathematical Biology | Part II, 2021

  The spatial density $n(x, t)$ of a population at location $x$ and time $t$ satisfies

  $$\frac{\partial n}{\partial t}=f(n)+D \frac{\partial^{2} n}{\partial x^{2}}$$

  where $f(n)=-n(n-r)(n-1), 0<r<1$ and $D>0$.

  (a) Give a biological example of the sort of phenomenon that this equation describes.

  (b) Show that there are three spatially homogeneous and stationary solutions to $(*)$, of which two are linearly stable to homogeneous perturbations and one is linearly unstable.

  (c) For $r=\frac{1}{2}$, find the stationary solution to $(*)$ subject to the conditions

  $$\lim _{x \rightarrow-\infty} n(x)=1, \quad \lim _{x \rightarrow \infty} n(x)=0 \quad \text { and } \quad n(0)=\frac{1}{2}$$

  (d) Write down the differential equation that is satisfied by a travelling-wave solution to $(*)$ of the form $n(x, t)=u(x-c t)$. Let $n_{0}(x)$ be the solution from part (c). Verify that $n_{0}(x-c t)$ satisfies this differential equation for $r \neq \frac{1}{2}$, provided the speed $c$ is chosen appropriately. [Hint: Consider the change to the equation from part (c).]

  (e) State how the sign of $c$ depends on $r$, and give a brief qualitative explanation for why this should be the case.

  comment

Mathematics of Machine Learning

• Paper 1, Section II, J

  Mathematics of Machine Learning | Part II, 2021

  Let $\mathcal{H}$ be a family of functions $h: \mathcal{X} \rightarrow\{0,1\}$ with $|\mathcal{H}| \geqslant 2$. Define the shattering coefficient $s(\mathcal{H}, n)$ and the $V C$ dimension $\mathrm{VC}(\mathcal{H})$ of $\mathcal{H}$.

  Briefly explain why if $\mathcal{H}^{\prime} \subseteq \mathcal{H}$ and $\left|\mathcal{H}^{\prime}\right| \geqslant 2$, then $\mathrm{VC}\left(\mathcal{H}^{\prime}\right) \leqslant \mathrm{VC}(\mathcal{H})$.

  Prove that if $\mathcal{F}$ is a vector space of functions $f: \mathcal{X} \rightarrow \mathbb{R}$ with $\mathcal{F}^{\prime} \subseteq \mathcal{F}$ and we define

  $$\mathcal{H}=\left\{\mathbf{1}_{\{u: f(u) \leqslant 0\}}: f \in \mathcal{F}^{\prime}\right\}$$

  then $\operatorname{VC}(\mathcal{H}) \leqslant \operatorname{dim}(\mathcal{F})$.

  Let $\mathcal{A}=\left\{\left\{x:\|x-c\|_{2}^{2} \leqslant r^{2}\right\}: c \in \mathbb{R}^{d}, r \in[0, \infty)\right\}$ be the set of all spheres in $\mathbb{R}^{d}$. Suppose $\mathcal{H}=\left\{\mathbf{1}_{A}: A \in \mathcal{A}\right\}$. Show that

  $$\mathrm{VC}(\mathcal{H}) \leqslant d+2$$

  $\left[\right.$ Hint: Consider the class of functions $\mathcal{F}^{\prime}=\left\{f_{c, r}: c \in \mathbb{R}^{d}, r \in[0, \infty)\right\}$, where

  $$f_{c, r}(x)=\|x\|_{2}^{2}-2 c^{T} x+\|c\|_{2}^{2}-r^{2}$$

  comment

• Paper 2, Section II, J

  Mathematics of Machine Learning | Part II, 2021

  (a) What is meant by the subdifferential $\partial f(x)$ of a convex function $f: \mathbb{R}^{d} \rightarrow \mathbb{R}$ at $x \in \mathbb{R}^{d}$ ? Write down the subdifferential $\partial f(x)$ of the function $f: \mathbb{R} \rightarrow \mathbb{R}$ given by $f(x)=\gamma|x|$, where $\gamma>0$.

  Show that $x$ minimises $f$ if and only if $0 \in \partial f(x)$.

  What does it mean for a function $f: \mathbb{R}^{d} \rightarrow \mathbb{R}$ to be strictly convex? Show that any minimiser of a strictly convex function must be unique.

  (b) Suppose we have input-output pairs $\left(x_{1}, y_{1}\right), \ldots,\left(x_{n}, y_{n}\right) \in\{-1,1\}^{p} \times\{-1,1\}$ with $p \geqslant 2$. Consider the objective function

  $$f(\beta)=\frac{1}{n} \sum_{i=1}^{n} \exp \left(-y_{i} x_{i}^{T} \beta\right)+\gamma\|\beta\|_{1}$$

  where $\beta=\left(\beta_{1}, \ldots, \beta_{p}\right)^{T}$ and $\gamma>0$. Assume that $\left(y_{i}\right)_{i=1}^{n} \neq\left(x_{i 1}\right)_{i=1}^{n}$. Fix $\beta_{2}, \ldots, \beta_{p}$ and define

  $$\kappa_{1}=\sum_{\substack{1 \leqslant i \leqslant n: \\ x_{i 1} \neq y_{i}}} \exp \left(-y_{i} \eta_{i}\right) \quad \text { and } \quad \kappa_{2}=\sum_{i=1}^{n} \exp \left(-y_{i} \eta_{i}\right)$$

  where $\eta_{i}=\sum_{j=2}^{p} x_{i j} \beta_{j}$ for $i=1, \ldots, n$. Show that if $\left|2 \kappa_{1}-\kappa_{2}\right| \leqslant \gamma$, then

  $$\operatorname{argmin}_{\beta_{1} \in \mathbb{R}} f\left(\beta_{1}, \beta_{2}, \ldots, \beta_{p}\right)=0 .$$

  [You may use any results from the course without proof, other than those whose proof is asked for directly.]

  comment

• Paper 4, Section II, J

  Mathematics of Machine Learning | Part II, 2021

  Let $D=\left(x_{i}, y_{i}\right)_{i=1}^{n}$ be a dataset of $n$ input-output pairs lying in $\mathbb{R}^{p} \times[-M, M]$ for $M \in \mathbb{R}$. Describe the random-forest algorithm as applied to $D$ using decision trees $\left(\hat{T}^{(b)}\right)_{b=1}^{B}$ to produce a fitted regression function $f_{\mathrm{rf}}$. [You need not explain in detail the construction of decision trees, but should describe any modifications specific to the random-forest algorithm.]

  Briefly explain why for each $x \in \mathbb{R}^{p}$ and $b=1, \ldots, B$, we have $\hat{T}^{(b)}(x) \in[-M, M]$.

  State the bounded-differences inequality.

  Treating $D$ as deterministic, show that with probability at least $1-\delta$,

  $$\sup _{x \in \mathbb{R}^{p}}\left|f_{\mathrm{rf}}(x)-\mu(x)\right| \leqslant M \sqrt{\frac{2 \log (1 / \delta)}{B}}+\mathbb{E}\left(\sup _{x \in \mathbb{R}^{p}}\left|f_{\mathrm{rf}}(x)-\mu(x)\right|\right),$$

  where $\mu(x):=\mathbb{E} f_{\mathrm{rf}}(x)$.

  $\left[\right.$ Hint: Treat each $\hat{T}^{(b)}$ as a random variable taking values in an appropriate space $\mathcal{Z}$ (of functions), and consider a function $G$ satisfying

  $$G\left(\hat{T}^{(1)}, \ldots, \hat{T}^{(B)}\right)=\sup _{x \in \mathbb{R}^{p}}\left|f_{\mathrm{rf}}(x)-\mu(x)\right|$$

  comment

Number Fields

• Paper 1, Section II, 20G

  Number Fields | Part II, 2021

  Let $K=\mathbb{Q}(\alpha)$, where $\alpha^{3}=5 \alpha-8$

  (a) Show that $[K: \mathbb{Q}]=3$.

  (b) Let $\beta=\left(\alpha+\alpha^{2}\right) / 2$. By considering the matrix of $\beta$ acting on $K$ by multiplication, or otherwise, show that $\beta$ is an algebraic integer, and that $(1, \alpha, \beta)$ is a $\mathbb{Z}$-basis for $\mathcal{O}_{K} \cdot$ [The discriminant of $T^{3}-5 T+8$ is $-4 \cdot 307$, and 307 is prime.]

  (c) Compute the prime factorisation of the ideal (3) in $\mathcal{O}_{K}$. Is (2) a prime ideal of $\mathcal{O}_{K} ?$ Justify your answer.

  comment

• Paper 2, Section II, 20G

  Number Fields | Part II, 2021

  Let $K$ be a field containing $\mathbb{Q}$. What does it mean to say that an element of $K$ is algebraic? Show that if $\alpha \in K$ is algebraic and non-zero, then there exists $\beta \in \mathbb{Z}[\alpha]$ such that $\alpha \beta$ is a non-zero (rational) integer.

  Now let $K$ be a number field, with ring of integers $\mathcal{O}_{K}$. Let $R$ be a subring of $\mathcal{O}_{K}$ whose field of fractions equals $K$. Show that every element of $K$ can be written as $r / m$, where $r \in R$ and $m$ is a positive integer.

  Prove that $R$ is a free abelian group of $\operatorname{rank}[K: \mathbb{Q}]$, and that $R$ has finite index in $\mathcal{O}_{K}$. Show also that for every nonzero ideal $I$ of $R$, the index $(R: I)$ of $I$ in $R$ is finite, and that for some positive integer $m, m \mathcal{O}_{K}$ is an ideal of $R$.

  Suppose that for every pair of non-zero ideals $I, J \subset R$, we have

  $$(R: I J)=(R: I)(R: J) .$$

  Show that $R=\mathcal{O}_{K}$.

  [You may assume without proof that $\mathcal{O}_{K}$ is a free abelian group of rank $[K: \mathbb{Q}]$ ] ]

  comment

• Paper 4 , Section II, 20G

  Number Fields | Part II, 2021

  (a) Compute the class group of $K=\mathbb{Q}(\sqrt{30})$. Find also the fundamental unit of $K$, stating clearly any general results you use.

  [The Minkowski bound for a real quadratic field is $\left|d_{K}\right|^{1 / 2} / 2 .$ ]

  (b) Let $K=\mathbb{Q}(\sqrt{d})$ be real quadratic, with embeddings $\sigma_{1}, \sigma_{2} \hookrightarrow \mathbb{R}$. An element $\alpha \in K$ is totally positive if $\sigma_{1}(\alpha)>0$ and $\sigma_{2}(\alpha)>0$. Show that the totally positive elements of $K$ form a subgroup of the multiplicative group $K^{*}$ of index 4 .

  Let $I, J \subset \mathcal{O}_{K}$ be non-zero ideals. We say that $I$ is narrowly equivalent to $J$ if there exists a totally positive element $\alpha$ of $K$ such that $I=\alpha J$. Show that this is an equivalence relation, and that the equivalence classes form a group under multiplication. Show also that the order of this group equals

  $$\begin{cases}\text { the class number } h_{K} \text { of } K & \text { if the fundamental unit of } K \text { has norm }-1 \\ 2 h_{K} & \text { otherwise. }\end{cases}$$

  comment

Number Theory

• Paper 1, Section I, 1I

  Number Theory | Part II, 2021

  State Euler's criterion.

  Let $p$ be an odd prime. Show that every primitive root modulo $p$ is a quadratic non-residue modulo $p$.

  Let $p$ be a Fermat prime, that is, a prime of the form $2^{2^{k}}+1$ for some $k \geqslant 1$. By evaluating $\phi(p-1)$, or otherwise, show that every quadratic non-residue modulo $p$ is a primitive root modulo $p$. Deduce that 3 is a primitive root modulo $p$ for every Fermat prime $p$.

  comment

• Paper 2, Section $I$, I

  Number Theory | Part II, 2021

  Define the Möbius function $\mu$, and explain what it means for it to be multiplicative.

  Show that for every positive integer $n$

  $$\sum_{d \mid n} \frac{\mu(d)^{2}}{\phi(d)}=\frac{n}{\phi(n)}$$

  where $\phi$ is the Euler totient function.

  Fix an integer $k \geqslant 1$. Use the Chinese remainder theorem to show that there are infinitely many positive integers $n$ for which

  $$\mu(n)=\mu(n+1)=\cdots=\mu(n+k)$$

  comment

• Paper 3, Section I, I

  Number Theory | Part II, 2021

  Define the continued fraction expansion of $\theta \in \mathbb{R}$, and show that this expansion terminates if and only if $\theta \in \mathbb{Q}$.

  Define the convergents $\left(p_{n} / q_{n}\right)_{n \geqslant-1}$ of the continued fraction expansion of $\theta$, and show that for all $n \geqslant 0$,

  $$p_{n} q_{n-1}-p_{n-1} q_{n}=(-1)^{n-1} .$$

  Deduce that if $\theta \in \mathbb{R} \backslash \mathbb{Q}$, then for all $n \geqslant 0$, at least one of

  $$\left|\theta-\frac{p_{n}}{q_{n}}\right|<\frac{1}{2 q_{n}^{2}} \quad \text { and } \quad\left|\theta-\frac{p_{n+1}}{q_{n+1}}\right|<\frac{1}{2 q_{n+1}^{2}}$$

  must hold.

  [You may assume that $\theta$ lies strictly between $p_{n} / q_{n}$ and $p_{n+1} / q_{n+1}$ for all $n \geqslant 0 .$ ]

  comment

• Paper 3, Section II, I

  Number Theory | Part II, 2021

  State what it means for two binary quadratic forms to be equivalent, and define the class number $h(d)$.

  Let $m$ be a positive integer, and let $f$ be a binary quadratic form. Show that $f$ properly represents $m$ if and only if $f$ is equivalent to a binary quadratic form

  $$m x^{2}+b x y+c y^{2}$$

  for some integers $b$ and $c$.

  Let $d<0$ be an integer such that $d \equiv 0$ or $1 \bmod 4$. Show that $m$ is properly represented by some binary quadratic form of discriminant $d$ if and only if $d$ is a square modulo $4 m$.

  Fix a positive integer $A \geqslant 2$. Show that $n^{2}+n+A$ is composite for some integer $n$ such that $0 \leqslant n \leqslant A-2$ if and only if $d=1-4 A$ is a square modulo $4 p$ for some prime $p<A$.

  Deduce that $h(1-4 A)=1$ if and only if $n^{2}+n+A$ is prime for all $n=0,1, \ldots, A-2$.

  comment

• Paper 4, Section I, I

  Number Theory | Part II, 2021

  Let $p$ be a prime, and let $N=\left(\begin{array}{c}2 n \\ n\end{array}\right)$ for some positive integer $n$.

  Show that if a prime power $p^{k}$ divides $N$ for some $k \geqslant 1$, then $p^{k} \leqslant 2 n$.

  Given a positive real $x$, define $\psi(x)=\sum_{n \leqslant x} \Lambda(n)$, where $\Lambda(n)$ is the von Mangoldt function, taking the value $\log p$ if $n=p^{k}$ for some prime $p$ and integer $k \geqslant 1$, and 0 otherwise. Show that

  $$\psi(x)=\sum_{p \leqslant x, p \text { prime }}\left\lfloor\frac{\log x}{\log p}\right\rfloor \log p$$

  Deduce that for all integers $n>1, \psi(2 n) \geqslant n \log 2$.

  comment

• Paper 4, Section II, I

  Number Theory | Part II, 2021

  (a) Let $N \geqslant 3$ be an odd integer and $b$ an integer with $(b, N)=1$. What does it mean to say that $N$ is a (Fermat) pseudoprime to base b?

  Let $b, k \geqslant 2$ be integers. Show that if $N \geqslant 3$ is an odd composite integer dividing $b^{k}-1$ and satisfying $N \equiv 1 \bmod k$, then $N$ is a pseudoprime to base $b$.

  (b) Fix $b \geqslant 2$. Let $p$ be an odd prime not dividing $b^{2}-1$, and let

  $$n=\frac{b^{p}-1}{b-1} \quad \text { and } \quad m=\frac{b^{p}+1}{b+1} .$$

  Use the conclusion of part (a) to show that $N=n m$ is a pseudoprime to base $b$. Deduce that there are infinitely many pseudoprimes to base $b$.

  (c) Let $b, k \geqslant 2$ be integers, and let $n=p_{1} \cdots p_{k}$, where $p_{1}, p_{2}, \ldots, p_{k}$ are distinct primes not dividing $2 b$. For each $j=1,2, \ldots, k$, let $r_{j}=n / p_{j}$. Show that $n$ is a pseudoprime to base $b$ if and only if for all $j=1,2, \ldots, k$, the order of $b$ modulo $p_{j}$ divides $r_{j}-1$.

  (d) By considering products of prime factors of $2^{k}-1$ and $2^{k}+1$ for primes $k \geqslant 5$, deduce that there are infinitely many pseudoprimes to base 2 with two prime factors.

  [Hint: You may assume that $\operatorname{gcd}(j, k)=1$ for $j, k \geqslant 1$ implies $\operatorname{gcd}\left(2^{j}-1,2^{k}-1\right)=1$, and that for $k>3,2^{k}+1$ is not a power of 3.]

  comment

Numerical Analysis

• Paper 1, Section II, E

  Numerical Analysis | Part II, 2021

  Let $A \in \mathbb{R}^{n \times n}$ with $n>2$ and define $\operatorname{Spec}(A)=\{\lambda \in \mathbb{C} \mid A-\lambda I$ is not invertible $\}$.

  The QR algorithm for computing $\operatorname{Spec}(A)$ is defined as follows. Set $A_{0}=A$. For $k=0,1, \ldots$ compute the $\mathrm{QR}$ factorization $A_{k}=Q_{k} R_{k}$ and set $A_{k+1}=R_{k} Q_{k}$. (Here $Q_{k}$ is an $n \times n$ orthogonal matrix and $R_{k}$ is an $n \times n$ upper triangular matrix.)

  (a) Show that $A_{k+1}$ is related to the original matrix $A$ by the similarity transformation $A_{k+1}=\bar{Q}_{k}^{T} A \bar{Q}_{k}$, where $\bar{Q}_{k}=Q_{0} Q_{1} \cdots Q_{k}$ is orthogonal and $\bar{Q}_{k} \bar{R}_{k}$ is the QR factorization of $A^{k+1}$ with $\bar{R}_{k}=R_{k} R_{k-1} \cdots R_{0}$.

  (b) Suppose that $A$ is symmetric and that its eigenvalues satisfy

  $$\left|\lambda_{1}\right|<\left|\lambda_{2}\right|<\cdots<\left|\lambda_{n-1}\right|=\left|\lambda_{n}\right|$$

  Suppose, in addition, that the first two canonical basis vectors are given by $\mathbf{e}_{1}=\sum_{i=1}^{n} b_{i} \mathbf{w}_{i}$, $\mathbf{e}_{2}=\sum_{i=1}^{n} c_{i} \mathbf{w}_{i}$, where $b_{i} \neq 0, c_{i} \neq 0$ for $i=1, \ldots, n$ and $\left\{\mathbf{w}_{i}\right\}_{i=1}^{n}$ are the normalised eigenvectors of $A$.

  Let $B_{k} \in \mathbb{R}^{2 \times 2}$ be the $2 \times 2$ upper left corner of $A_{k}$. Show that $d_{\mathrm{H}}\left(\operatorname{Spec}\left(B_{k}\right), S\right) \rightarrow 0$ as $k \rightarrow \infty$, where $S=\left\{\lambda_{n}\right\} \cup\left\{\lambda_{n-1}\right\}$ and $d_{\mathrm{H}}$ denotes the Hausdorff metric

  $$d_{\mathrm{H}}(X, Y)=\max \left\{\sup _{x \in X} \inf _{y \in Y}|x-y|, \sup _{y \in Y} \inf _{x \in X}|x-y|\right\}, \quad X, Y \subset \mathbb{C}$$

  [Hint: You may use the fact that for real symmetric matrices $U, V$ we have $\left.d_{\mathrm{H}}(\operatorname{Spec}(U), \operatorname{Spec}(V)) \leqslant\|U-V\|_{2} \cdot\right]$

  comment

• Paper 2, Section II, 41E

  Numerical Analysis | Part II, 2021

  (a) Let $\mathbf{x} \in \mathbb{R}^{N}$ and define $\mathbf{y} \in \mathbb{R}^{2 N}$ by

  $$y_{n}= \begin{cases}x_{n}, & 0 \leqslant n \leqslant N-1 \\ x_{2 N-n-1}, & N \leqslant n \leqslant 2 N-1\end{cases}$$

  Let $\mathbf{Y} \in \mathbb{C}^{2 N}$ be defined as the discrete Fourier transform (DFT) of $\mathbf{y}$, i.e.

  $$Y_{k}=\sum_{n=0}^{2 N-1} y_{n} \omega_{2 N}^{n k}, \quad \omega_{2 N}=\exp (-\pi i / N), \quad 0 \leqslant k \leqslant 2 N-1$$

  Show that

  $$Y_{k}=2 \omega_{2 N}^{-k / 2} \sum_{n=0}^{N-1} x_{n} \cos \left[\frac{\pi}{N}\left(n+\frac{1}{2}\right) k\right], \quad 0 \leqslant k \leqslant 2 N-1$$

  (b) Define the discrete cosine transform $(\mathrm{DCT}) \mathcal{C}_{N}: \mathbb{R}^{N} \rightarrow \mathbb{R}^{N}$ by

  $$\mathbf{z}=\mathcal{C}_{N} \mathbf{x}, \text { where } z_{k}=\sum_{n=0}^{N-1} x_{n} \cos \left[\frac{\pi}{N}\left(n+\frac{1}{2}\right) k\right], \quad k=0, \ldots, N-1$$

  For $N=2^{p}$ with $p \in \mathbb{N}$, show that, similar to the Fast Fourier Transform (FFT), there exists an algorithm that computes the DCT of a vector of length $N$, where the number of multiplications required is bounded by $C N \log N$, where $C$ is some constant independent of $N$.

  [You may not assume that the FFT algorithm requires $\mathcal{O}(N \log N)$ multiplications to compute the DFT of a vector of length $N$. If you use this, you must prove it.]

  comment

• Paper 3, Section II, 40E

  Numerical Analysis | Part II, 2021

  Consider discretisation of the diffusion equation

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad 0 \leqslant t \leqslant 1$$

  by the Crank-Nicholson method:

  $$u_{m}^{n+1}-\frac{1}{2} \mu\left(u_{m-1}^{n+1}-2 u_{m}^{n+1}+u_{m+1}^{n+1}\right)=u_{m}^{n}+\frac{1}{2} \mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right), \quad n=0, \ldots, N,$$

  where $\mu=\frac{k}{h^{2}}$ is the Courant number, $h$ is the step size in the space discretisation, $k=\frac{1}{N+1}$ is the step size in the time discretisation, and $u_{m}^{n} \approx u(m h, n k)$, where $u(x, t)$ is the solution of $(*)$. The initial condition $u(x, 0)=u_{0}(x)$ is given.

  (a) Consider the Cauchy problem for $(*)$ on the whole line, $x \in \mathbb{R}$ (thus $m \in \mathbb{Z}$ ), and derive the formula for the amplification factor of the Crank-Nicholson method ( $\dagger$ ). Use the amplification factor to show that the Crank-Nicholson method is stable for the Cauchy problem for all $\mu>0$.

  [You may quote basic properties of the Fourier transform mentioned in lectures, but not the theorem on sufficient and necessary conditions on the amplification factor to have stability.]

  (b) Consider $(*)$ on the interval $0 \leqslant x \leqslant 1$ (thus $m=1, \ldots, M$ and $h=\frac{1}{M+1}$ ) with Dirichlet boundary conditions $u(0, t)=\phi_{0}(t)$ and $u(1, t)=\phi_{1}(t)$, for some sufficiently smooth functions $\phi_{0}$ and $\phi_{1}$. Show directly (without using the Lax equivalence theorem) that, given sufficient smoothness of $u$, the Crank-Nicholson method is convergent, for any $\mu>0$, in the norm defined by $\|\boldsymbol{\eta}\|_{2, h}=\left(h \sum_{m=1}^{M}\left|\eta_{m}\right|^{2}\right)^{1 / 2}$ for $\boldsymbol{\eta} \in \mathbb{R}^{M}$.

  [You may assume that the Trapezoidal method has local order 3 , and that the standard three-point centred discretisation of the second derivative (as used in the CrankNicholson method) has local order 2.]

  comment

• Paper 4 , Section II, 40E

  Numerical Analysis | Part II, 2021

  (a) Show that if $A$ and $B$ are real matrices such that both $A$ and $A-B-B^{T}$ are symmetric positive definite, then the spectral radius of $H=-(A-B)^{-1} B$ is strictly less than $1 .$

  (b) Consider the Poisson equation $\nabla^{2} u=f$ (with zero Dirichlet boundary condition) on the unit square, where $f$ is some smooth function. Given $m \in \mathbb{N}$ and an equidistant grid on the unit square with stepsize $h=1 /(m+1)$, the standard five-point method is given by

  $$u_{i-1, j}+u_{i+1, j}+u_{i, j-1}+u_{i, j+1}-4 u_{i, j}=h^{2} f_{i, j}, \quad i, j=1, \ldots, m$$

  where $f_{i, j}=f(i h, j h)$ and $u_{0, j}=u_{m+1, j}=u_{i, 0}=u_{i, m+1}=0$. Equation $(*)$ can be written as a linear system $A x=b$, where $A \in \mathbb{R}^{m^{2} \times m^{2}}$ and $b \in \mathbb{R}^{m^{2}}$ both depend on the chosen ordering of the grid points.

  Use the result in part (a) to show that the Gauss-Seidel method converges for the linear system $A x=b$ described above, regardless of the choice of ordering of the grid points.

  [You may quote convergence results - based on the spectral radius of the iteration matrix - mentioned in the lecture notes.]

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, B

  Principles of Quantum Mechanics | Part II, 2021

  (a) A group $G$ of transformations acts on a quantum system. Briefly explain why the Born rule implies that these transformations may be represented by operators $U(g): \mathcal{H} \rightarrow \mathcal{H}$ obeying

  $$\begin{aligned} U(g)^{\dagger} U(g) &=1_{\mathcal{H}} \\ U\left(g_{1}\right) U\left(g_{2}\right) &=e^{i \phi\left(g_{1}, g_{2}\right)} U\left(g_{1} \cdot g_{2}\right) \end{aligned}$$

  for all $g_{1}, g_{2} \in G$, where $\phi\left(g_{1}, g_{2}\right) \in \mathbb{R}$.

  What additional property does $U(g)$ have when $G$ is a group of symmetries of the Hamiltonian? Show that symmetries correspond to conserved quantities.

  (b) The Coulomb Hamiltonian describing the gross structure of the hydrogen atom is invariant under time reversal, $t \mapsto-t$. Suppose we try to represent time reversal by a unitary operator $T$ obeying $U(t) T=T U(-t)$, where $U(t)$ is the time-evolution operator. Show that this would imply that hydrogen has no stable ground state.

  An operator $A: \mathcal{H} \rightarrow \mathcal{H}$ is antilinear if

  $$A(a|\alpha\rangle+b|\beta\rangle)=\bar{a} A|\alpha\rangle+\bar{b} A|\beta\rangle$$

  for all $|\alpha\rangle,|\beta\rangle \in \mathcal{H}$ and all $a, b \in \mathbb{C}$, and antiunitary if, in addition,

  $$\left\langle\beta^{\prime} \mid \alpha^{\prime}\right\rangle=\overline{\langle\beta \mid \alpha\rangle},$$

  where $\left|\alpha^{\prime}\right\rangle=A|\alpha\rangle$ and $\left|\beta^{\prime}\right\rangle=A|\beta\rangle$. Show that if time reversal is instead represented by an antiunitary operator then the above instability of hydrogen is avoided.

  comment

• Paper 2, Section II, B

  Principles of Quantum Mechanics | Part II, 2021

  (a) Let $\{|n\rangle\}$ be a basis of eigenstates of a non-degenerate Hamiltonian $H$, with corresponding eigenvalues $\left\{E_{n}\right\}$. Write down an expression for the energy levels of the perturbed Hamiltonian $H+\lambda \Delta H$, correct to second order in the dimensionless constant $\lambda \ll 1$.

  (b) A particle travels in one dimension under the influence of the potential

  $$V(X)=\frac{1}{2} m \omega^{2} X^{2}+\lambda \hbar \omega \frac{X^{3}}{L^{3}}$$

  where $m$ is the mass, $\omega$ a frequency and $L=\sqrt{\hbar / 2 m \omega}$ a length scale. Show that, to first order in $\lambda$, all energy levels coincide with those of the harmonic oscillator. Calculate the energy of the ground state to second order in $\lambda$.

  Does perturbation theory in $\lambda$ converge for this potential? Briefly explain your answer.

  comment

• Paper 3, Section II, B

  Principles of Quantum Mechanics | Part II, 2021

  (a) A quantum system with total angular momentum $j_{1}$ is combined with another of total angular momentum $j_{2}$. What are the possible values of the total angular momentum $j$ of the combined system? For given $j$, what are the possible values of the angular momentum along any axis?

  (b) Consider the case $j_{1}=j_{2}$. Explain why all the states with $j=2 j_{1}-1$ are antisymmetric under exchange of the angular momenta of the two subsystems, while all the states with $j=2 j_{1}-2$ are symmetric.

  (c) An exotic particle $X$ of spin 0 and negative intrinsic parity decays into a pair of indistinguishable particles $Y$. Assume each $Y$ particle has spin 1 and that the decay process conserves parity. Find the probability that the direction of travel of the $Y$ particles is observed to lie at an angle $\theta \in(\pi / 4,3 \pi / 4)$ from some axis along which their total spin is observed to be $+\hbar$ ?

  comment

• Paper 4, Section II, 33B

  Principles of Quantum Mechanics | Part II, 2021

  (a) A quantum system has Hamiltonian $H=H_{0}+V(t)$. Let $\{|n\rangle\}_{n \in \mathbb{N}_{0}}$ be an orthonormal basis of $H_{0}$ eigenstates, with corresponding energies $E_{n}=\hbar \omega_{n}$. For $t<0$, $V(t)=0$ and the system is in state $|0\rangle$. Calculate the probability that it is found to be in state $|1\rangle$ at time $t>0$, correct to lowest non-trivial order in $V$.

  (b) Now suppose $\{|0\rangle,|1\rangle\}$ form a basis of the Hilbert space, with respect to which

  $$\left(\begin{array}{cc} \langle 0|H| 0\rangle & \langle 0|H| 1\rangle \\ \langle 1|H| 0\rangle & \langle 1|H| 1\rangle \end{array}\right)=\left(\begin{array}{cc} \hbar \omega_{0} & \hbar v \Theta(t) e^{i \omega t} \\ \hbar v \Theta(t) e^{-i \omega t} & \hbar \omega_{1} \end{array}\right)$$

  where $\Theta(t)$ is the Heaviside step function and $v$ is a real constant. Calculate the exact probability that the system is in state $|1\rangle$ at time $t$. For which frequency $\omega$ is this probability maximized?

  comment

Principles of Statistics

• Paper 1, Section II, J

  Principles of Statistics | Part II, 2021

  Let $X_{1}, \ldots, X_{n}$ be random variables with joint probability density function in a statistical model $\left\{f_{\theta}: \theta \in \mathbb{R}\right\}$.

  (a) Define the Fisher information $I_{n}(\theta)$. What do we mean when we say that the Fisher information tensorises?

  (b) Derive the relationship between the Fisher information and the derivative of the score function in a regular model.

  (c) Consider the model defined by $X_{1}=\theta+\varepsilon_{1}$ and

  $$X_{i}=\theta(1-\sqrt{\gamma})+\sqrt{\gamma} X_{i-1}+\sqrt{1-\gamma} \varepsilon_{i} \quad \text { for } i=2, \ldots, n$$

  where $\varepsilon_{1}, \ldots, \varepsilon_{n}$ are i.i.d. $N(0,1)$ random variables, and $\gamma \in[0,1)$ is a known constant. Compute the Fisher information $I_{n}(\theta)$. For which values of $\gamma$ does the Fisher information tensorise? State a lower bound on the variance of an unbiased estimator $\hat{\theta}$ in this model.

  comment

• Paper 2, Section II, J

  Principles of Statistics | Part II, 2021

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. random observations taking values in $[0,1]$ with a continuous distribution function $F$. Let $\hat{F}_{n}(x)=n^{-1} \sum_{i=1}^{n} \mathbf{1}_{\left\{X_{i} \leqslant x\right\}}$ for each $x \in[0,1]$.

  (a) State the Kolmogorov-Smirnov theorem. Explain how this theorem may be used in a goodness-of-fit test for the null hypothesis $H_{0}: F=F_{0}$, with $F_{0}$ continuous.

  (b) Suppose you do not have access to the quantiles of the sampling distribution of the Kolmogorov-Smirnov test statistic. However, you are given i.i.d. samples $Z_{1}, \ldots, Z_{n m}$ with distribution function $F_{0}$. Describe a test of $H_{0}: F=F_{0}$ with size exactly $1 /(m+1)$.

  (c) Now suppose that $X_{1}, \ldots, X_{n}$ are i.i.d. taking values in $[0, \infty)$ with probability density function $f$, with $\sup _{x \geqslant 0}\left(|f(x)|+\left|f^{\prime}(x)\right|\right)<1$. Define the density estimator

  $$\left.\hat{f}_{n}(x)=n^{-2 / 3} \sum_{i=1}^{n} \mathbf{1}_{\left\{X_{i}\right.}-\frac{1}{2 n^{1 / 3}} \leqslant x \leqslant X_{i}+\frac{1}{2 n^{1 / 3}}\right\}, \quad x \geqslant 0 .$$

  Show that for all $x \geqslant 0$ and all $n \geqslant 1$,

  $$\mathbb{E}\left[\left(\hat{f}_{n}(x)-f(x)\right)^{2}\right] \leqslant \frac{2}{n^{2 / 3}} .$$

  comment

• Paper 3, Section II, J

  Principles of Statistics | Part II, 2021

  Let $X_{1}, \ldots, X_{n} \sim$ iid $\operatorname{Gamma}(\alpha, \beta)$ for some known $\alpha>0$ and some unknown $\beta>0$. [The gamma distribution has probability density function

  $$f(x)=\frac{\beta^{\alpha}}{\Gamma(\alpha)} x^{\alpha-1} e^{-\beta x}, \quad x>0$$

  and its mean and variance are $\alpha / \beta$ and $\alpha / \beta^{2}$, respectively.]

  (a) Find the maximum likelihood estimator $\hat{\beta}$ for $\beta$ and derive the distributional limit of $\sqrt{n}(\hat{\beta}-\beta)$. [You may not use the asymptotic normality of the maximum likelihood estimator proved in the course.]

  (b) Construct an asymptotic $(1-\gamma)$-level confidence interval for $\beta$ and show that it has the correct (asymptotic) coverage.

  (c) Write down all the steps needed to construct a candidate to an asymptotic $(1-\gamma)$-level confidence interval for $\beta$ using the nonparametric bootstrap.

  comment

• Paper 4, Section II, J

  Principles of Statistics | Part II, 2021

  Suppose that $X \mid \theta \sim \operatorname{Poisson}(\theta), \theta>0$, and suppose the prior $\pi$ on $\theta$ is a gamma distribution with parameters $\alpha>0$ and $\beta>0$. [Recall that $\pi$ has probability density function

  $$f(z)=\frac{\beta^{\alpha}}{\Gamma(\alpha)} z^{\alpha-1} e^{-\beta z}, \quad z>0$$

  and that its mean and variance are $\alpha / \beta$ and $\alpha / \beta^{2}$, respectively. ]

  (a) Find the $\pi$-Bayes estimator for $\theta$ for the quadratic loss, and derive its quadratic risk function.

  (b) Suppose we wish to estimate $\mu=e^{-\theta}=\mathbb{P}_{\theta}(X=0)$. Find the $\pi$-Bayes estimator for $\mu$ for the quadratic loss, and derive its quadratic risk function. [Hint: The moment generating function of a Poisson $(\theta)$ distribution is $M(t)=\exp \left(\theta\left(e^{t}-1\right)\right)$ for $t \in \mathbb{R}$, and that of a Gamma $(\alpha, \beta)$ distribution is $M(t)=(1-t / \beta)^{-\alpha}$ for $t<\beta$.]

  (c) State a sufficient condition for an admissible estimator to be minimax, and give a proof of this fact.

  (d) For each of the estimators in parts (a) and (b), is it possible to deduce using the condition in (c) that the estimator is minimax for some value of $\alpha$ and $\beta$ ? Justify your answer.

  comment

Probability and Measure

• Paper 1, Section II, H

  Probability and Measure | Part II, 2021

  (a) State and prove Fatou's lemma. [You may use the monotone convergence theorem without proof, provided it is clearly stated.]

  (b) Show that the inequality in Fatou's lemma can be strict.

  (c) Let $\left(X_{n}: n \in \mathbb{N}\right)$ and $X$ be non-negative random variables such that $X_{n} \rightarrow X$ almost surely as $n \rightarrow \infty$. Must we have $\mathbb{E} X \leqslant \sup _{n} \mathbb{E} X_{n}$ ?

  comment

• Paper 2, Section II, H

  Probability and Measure | Part II, 2021

  Let $(E, \mathcal{E}, \mu)$ be a measure space. A function $f$ is simple if it is of the form $f=\sum_{i=1}^{N} a_{i} 1_{A_{i}}$, where $a_{i} \in \mathbb{R}, N \in \mathbb{N}$ and $A_{i} \in \mathcal{E}$.

  Now let $f:(E, \mathcal{E}, \mu) \rightarrow[0, \infty]$ be a Borel-measurable map. Show that there exists a sequence $f_{n}$ of simple functions such that $f_{n}(x) \rightarrow f(x)$ for all $x \in E$ as $n \rightarrow \infty$.

  Next suppose $f$ is also $\mu$-integrable. Construct a sequence $f_{n}$ of simple $\mu$-integrable functions such that $\int_{E}\left|f_{n}-f\right| d \mu \rightarrow 0$ as $n \rightarrow \infty$.

  Finally, suppose $f$ is also bounded. Show that there exists a sequence $f_{n}$ of simple functions such that $f_{n} \rightarrow f$ uniformly on $E$ as $n \rightarrow \infty$.

  comment

• Paper 3, Section II, $26 \mathrm{H}$

  Probability and Measure | Part II, 2021

  Show that random variables $X_{1}, \ldots, X_{N}$ defined on some probability space $(\Omega, \mathcal{F}, \mathbb{P})$ are independent if and only if

  $$\mathbb{E}\left(\prod_{n=1}^{N} f_{n}\left(X_{n}\right)\right)=\prod_{n=1}^{N} \mathbb{E}\left(f_{n}\left(X_{n}\right)\right)$$

  for all bounded measurable functions $f_{n}: \mathbb{R} \rightarrow \mathbb{R}, n=1, \ldots, N$.

  Now let $\left(X_{n}: n \in \mathbb{N}\right)$ be an infinite sequence of independent Gaussian random variables with zero means, $\mathbb{E} X_{n}=0$, and finite variances, $\mathbb{E} X_{n}^{2}=\sigma_{n}^{2}>0$. Show that the series $\sum_{n=1}^{\infty} X_{n}$ converges in $L^{2}(\mathbb{P})$ if and only if $\sum_{n=1}^{\infty} \sigma_{n}^{2}<\infty$.

  [You may use without proof that $\mathbb{E}\left[e^{i u X_{n}}\right]=e^{-u^{2} \sigma_{n}^{2} / 2}$ for $u \in \mathbb{R}$.]

  comment

• Paper 4, Section II, 26H

  Probability and Measure | Part II, 2021

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space. Show that for any sequence $A_{n} \in \mathcal{F}$ satisfying $\sum_{n=1}^{\infty} \mathbb{P}\left(A_{n}\right)<\infty$ one necessarily has $\mathbb{P}\left(\limsup A_{n} A_{n}\right)=0 .$

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ and $X$ be random variables defined on $(\Omega, \mathcal{F}, \mathbb{P})$. Show that $X_{n} \rightarrow X$ almost surely as $n \rightarrow \infty$ implies that $X_{n} \rightarrow X$ in probability as $n \rightarrow \infty$.

  Show that $X_{n} \rightarrow X$ in probability as $n \rightarrow \infty$ if and only if for every subsequence $X_{n(k)}$ there exists a further subsequence $X_{n(k(r))}$ such that $X_{n(k(r))} \rightarrow X$ almost surely as $r \rightarrow \infty$.

  comment

Quantum Information and Computation

• Paper 1, Section I, $10 D$

  Quantum Information and Computation | Part II, 2021

  Alice wishes to communicate to Bob a 1-bit message $m=0$ or $m=1$ chosen by her with equal prior probabilities $1 / 2$. For $m=0$ (respectively $m=1$ ) she sends Bob the quantum state $\left|a_{0}\right\rangle$ (respectively $\left|a_{1}\right\rangle$ ). On receiving the state, Bob applies quantum operations to it, to try to determine Alice's message. The Helstrom-Holevo theorem asserts that the probability $P_{S}$ for Bob to correctly determine Alice's message is bounded by $P_{S} \leqslant \frac{1}{2}(1+\sin \theta)$, where $\theta=\cos ^{-1}\left|\left\langle a_{0} \mid a_{1}\right\rangle\right|$, and that this bound is achievable.

  (a) Suppose that $\left|a_{0}\right\rangle=|0\rangle$ and $\left|a_{1}\right\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$, and that Bob measures the received state in the basis $\left\{\left|b_{0}\right\rangle,\left|b_{1}\right\rangle\right\}$, where $\left|b_{0}\right\rangle=\cos \beta|0\rangle+\sin \beta|1\rangle$ and $\left|b_{1}\right\rangle=$ $-\sin \beta|0\rangle+\cos \beta|1\rangle$, to produce his output 0 or 1 , respectively. Calculate the probability $P_{S}$ that Bob correctly determines Alice's message, and show that the maximum value of $P_{S}$ over choices of $\beta \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right]$ achieves the Helstrom-Holevo bound.

  (b) State the no-cloning theorem as it applies to unitary processes and a set of two non-orthogonal states $\left\{\left|c_{0}\right\rangle,\left|c_{1}\right\rangle\right\}$. Show that the Helstrom-Holevo theorem implies the validity of the no-cloning theorem in this situation.

  comment

• Paper 2, Section I, 10D

  Quantum Information and Computation | Part II, 2021

  Let $\mathcal{B}_{n}$ denote the set of all $n$-bit strings and let $f: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$ be a Boolean function which obeys either

  (I) $f(x)=0$ for all $x \in \mathcal{B}_{n}$, or

  (II) $f(x)=0$ for exactly half of all $x \in \mathcal{B}_{n}$.

  Suppose we are given the $n$-qubit state

  $$|\xi\rangle=\frac{1}{\sqrt{2^{n}}} \sum_{x \in \mathcal{B}_{n}}(-1)^{f(x)}|x\rangle$$

  Show how we may determine with certainty whether $f$ is of case (I) or case (II).

  Suppose now that Alice and Bob are separated in space. Alice possesses a quantum oracle for a Boolean function $f_{A}: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$ and Bob similarly possess a quantum oracle for a Boolean function $f_{B}: \mathcal{B}_{n} \rightarrow \mathcal{B}_{1}$. These functions are arbitrary, except that either

  (1) $f_{A}(x)=f_{B}(x)$ for all $x \in \mathcal{B}_{n}$, or

  (2) $f_{A}(x)=f_{B}(x)$ for exactly half of all $x \in \mathcal{B}_{n}$.

  Alice and Bob each have available a supply of qubits in state $|0\rangle$ and each can apply local quantum operations (including their own function oracle) to any qubits in their possession. Additionally, they can send qubits to each other.

  Show how Bob may decide with certainty which case applies, after he has received $n$ qubits from Alice. [Hint: You may find it helpful to consider the function $h(x)=$ $f_{A}(x) \oplus f_{B}(x)$, where $\oplus$ denotes addition mod 2.]

  comment

• Paper 2, Section II, D

  Quantum Information and Computation | Part II, 2021

  Alice and Bob are separated in space and can communicate only over a noiseless public classical channel, i.e. they can exchange bit string messages perfectly, but the messages can be read by anyone. An eavesdropper Eve constantly monitors the channel, but cannot alter any passing messages. Alice wishes to communicate an $m$-bit string message to Bob whilst keeping it secret from Eve.

  (a) Explain how Alice can do this by the one-time pad method, specifying clearly any additional resource that Alice and Bob need. Explain why in this method, Alice's message does, in fact, remain secure against eavesdropping.

  (b) Suppose now that Alice and Bob do not possess the additional resource needed in part (a) for the one-time pad, but that they instead possess $n$ pairs of qubits, where $n \gg 1$, with each pair being in the state

  $$|\psi\rangle_{A B}=t|00\rangle_{A B}+s|11\rangle_{A B},$$

  where the real parameters $(t, s)$ are known to Alice and Bob and obey $t>s>0$ and $t^{2}+s^{2}=1$. For each qubit pair in state $|\psi\rangle_{A B}$, Alice possesses qubit $A$ and Bob possesses qubit $B$. They each also have available a supply of ancilla qubits, each in state $|0\rangle$, and they can each perform local quantum operations on qubits in their possession.

  Show how Alice, using only local quantum operations, can convert each $|\psi\rangle_{A B}$ state into $\left|\phi^{+}\right\rangle_{A B}=\frac{1}{\sqrt{2}}\left(|00\rangle_{A B}+|11\rangle_{A B}\right)$ by a process that succeeds with non-zero probability. [Hint: It may be useful for Alice to start by adjoining an ancilla qubit $|0\rangle_{A^{\prime}}$ and work locally on her two qubits in $\left.|0\rangle_{A^{\prime}}|\psi\rangle_{A B \cdot}\right]$

  Hence, or otherwise, show how Alice can communicate a bit string of expected length $\left(2 s^{2}\right) n$ to Bob in a way that keeps it secure against eavesdropping by Eve.

  comment

• Paper 3 , Section I, D

  Quantum Information and Computation | Part II, 2021

  Let $|\psi\rangle_{A B}$ be the joint state of a bipartite system $A B$ with subsystems $A$ and $B$ separated in space. Suppose that Alice and Bob have access only to subsystems $A$ and $B$ respectively, on which they can perform local quantum operations.

  Alice performs a unitary operation $U$ on $A$ and then a (generally incomplete) measurement on $A$, with projectors $\left\{\Pi_{a}\right\}$ labelled by her possible measurement outcomes $a$. Then Bob performs a complete measurement on $B$ relative to the orthonormal basis $\{|b\rangle\}$ labelled by his possible outcomes $b$.

  Show that the probability distribution of Bob's measurement outcomes is unaffected by whether or not Alice actually performs the local operations on $A$ described above.

  comment

• Paper 3, Section II, D

  Quantum Information and Computation | Part II, 2021

  Let $\mathcal{B}_{n}$ denote the set of all $n$-bit strings and let $\mathcal{H}_{n}$ denote the space of $n$ qubits.

  (a) Suppose $f: \mathcal{B}_{2} \rightarrow \mathcal{B}_{1}$ has the property that $f\left(x_{0}\right)=1$ for a unique $x_{0} \in \mathcal{B}_{2}$ and suppose we have a quantum oracle $U_{f}$.

  (i) Let $\left|\psi_{0}\right\rangle=\frac{1}{2} \sum_{x \in \mathcal{B}_{2}}|x\rangle$ and introduce the operators

  $$I_{x_{0}}=I_{2}-2\left|x_{0}\right\rangle\left\langle x_{0}\right| \quad \text { and } \quad J=I_{2}-2\left|\psi_{0}\right\rangle\left\langle\psi_{0}\right|$$

  on $\mathcal{H}_{2}$, where $I_{2}$ is the identity operator. Give a geometrical description of the actions of $-J, I_{x_{0}}$ and $Q=-J I_{x_{0}}$ on the 2-dimensional subspace of $\mathcal{H}_{2}$ given by the real span of $\left|x_{0}\right\rangle$ and $\left|\psi_{0}\right\rangle$. [You may assume without proof that the product of two reflections in $\mathbb{R}^{2}$ is a rotation through twice the angle between the mirror lines.]

  (ii) Using the results of part (i), or otherwise, show how we may determine $x_{0}$ with certainty, starting with a supply of qubits each in state $|0\rangle$ and using $U_{f}$ only once, together with other quantum operations that are independent of $f$.

  (b) Suppose $\mathcal{H}_{n}=A \oplus A^{\perp}$, where $A$ is a fixed linear subspace with orthogonal complement $A^{\perp}$. Let $\Pi_{A}$ denote the projection operator onto $A$ and let $I_{A}=I-2 \Pi_{A}$, where $I$ is the identity operator on $\mathcal{H}_{n}$.

  (i) Show that any $|\xi\rangle \in \mathcal{H}_{n}$ can be written as $|\xi\rangle=\sin \theta|\alpha\rangle+\cos \theta|\beta\rangle$, where $\theta \in[0, \pi / 2]$, and $|\alpha\rangle \in A$ and $|\beta\rangle \in A^{\perp}$ are normalised.

  (ii) Let $I_{\xi}=I-2|\xi\rangle\langle\xi|$ and $Q=-I_{\xi} I_{A}$. Show that $Q|\alpha\rangle=-\sin 2 \theta|\beta\rangle+\cos 2 \theta|\alpha\rangle$.

  (iii) Now assume, in addition, that $Q|\beta\rangle=\cos 2 \theta|\beta\rangle+\sin 2 \theta|\alpha\rangle$ and that $|\xi\rangle=$ $U|0 \ldots 0\rangle$ for some unitary operation $U$. Suppose we can implement the operators $U, U^{\dagger}, I_{A}$ as well as the operation $I-2|0 \ldots 0\rangle\langle 0 \ldots 0|$. In the case $\theta=\pi / 10$, show how the $n$-qubit state $|\alpha\rangle$ may be made exactly from $|0 \ldots 0\rangle$ by a process that succeeds with certainty.

  comment

• Paper 4, Section I, $10 D$

  Quantum Information and Computation | Part II, 2021

  Let $\mathcal{H}$ be a state space of dimension $N$ with standard orthonormal basis $\{|k\rangle\}$ labelled by $k \in \mathbb{Z}_{N}$. Let QFT denote the quantum Fourier transform $\bmod N$ and let $S$ denote the operation defined by $S|k\rangle=|k+1 \bmod N\rangle$.

  (a) Introduce the basis $\left\{\left|\chi_{k}\right\rangle\right\}$ defined by $\left|\chi_{k}\right\rangle=\mathrm{QFT}^{-1}|k\rangle$. Show that each $\left|\chi_{k}\right\rangle$ is an eigenstate of $S$ and determine the corresponding eigenvalue.

  (b) By expressing a generic state $|v\rangle \in \mathcal{H}$ in the $\left\{\left|\chi_{k}\right\rangle\right\}$ basis, show that QFT $|v\rangle$ and QFT $(S|v\rangle)$ have the same output distribution if measured in the standard basis.

  (c) Let $A, r$ be positive integers with $A r=N$, and let $x_{0}$ be an integer with $0 \leqslant x_{0}<r$. Suppose that we are given the state

  $$|\xi\rangle=\frac{1}{\sqrt{A}} \sum_{j=0}^{A-1}\left|x_{0}+j r \bmod N\right\rangle$$

  where $x_{0}$ and $r$ are unknown to us. Using part (b) or otherwise, show that a standard basis measurement on QFT $|\xi\rangle$ has an output distribution that is independent of $x_{0}$.

  comment

Representation Theory

• Paper 1, Section II, I

  Representation Theory | Part II, 2021

  (a) What does it mean to say that a representation of a group is completely reducible? State Maschke's theorem for representations of finite groups over fields of characteristic 0 . State and prove Schur's lemma. Deduce that if there exists a faithful irreducible complex representation of $G$, then $Z(G)$ is cyclic.

  (b) If $G$ is any finite group, show that the regular representation $\mathbb{C} G$ is faithful. Show further that for every finite simple group $G$, there exists a faithful irreducible complex representation of $G$.

  (c) Which of the following groups have a faithful irreducible representation? Give brief justification of your answers.

  (i) the cyclic groups $C_{n}(n$ a positive integer $)$;

  (ii) the dihedral group $D_{8}$;

  (iii) the direct product $C_{2} \times D_{8}$.

  comment

• Paper 2, Section II, I

  Representation Theory | Part II, 2021

  Let $G$ be a finite group and work over $\mathbb{C}$.

  (a) Let $\chi$ be a faithful character of $G$, and suppose that $\chi(g)$ takes precisely $r$ different values as $g$ varies over all the elements of $G$. Show that every irreducible character of $G$ is a constituent of one of the powers $\chi^{0}, \chi^{1}, \ldots, \chi^{r-1}$. [Standard properties of the Vandermonde matrix may be assumed if stated correctly.]

  (b) Assuming that the number of irreducible characters of $G$ is equal to the number of conjugacy classes of $G$, show that the irreducible characters of $G$ form a basis of the complex vector space of all class functions on $G$. Deduce that $g, h \in G$ are conjugate if and only if $\chi(g)=\chi(h)$ for all characters $\chi$ of $G$.

  (c) Let $\chi$ be a character of $G$ which is not faithful. Show that there is some irreducible character $\psi$ of $G$ such that $\left\langle\chi^{n}, \psi\right\rangle=0$ for all integers $n \geqslant 0$.

  comment

• Paper 3, Section II, I

  Representation Theory | Part II, 2021

  In this question we work over $\mathbb{C}$.

  (a) (i) Let $H$ be a subgroup of a finite group $G$. Given an $H$-space $W$, define the complex vector space $V=\operatorname{Ind}_{H}^{G}(W)$. Define, with justification, the $G$-action on $V$.

  (ii) Write $\mathcal{C}(g)$ for the conjugacy class of $g \in G$. Suppose that $H \cap \mathcal{C}(g)$ breaks up into $s$ conjugacy classes of $H$ with representatives $x_{1}, \ldots, x_{s}$. If $\psi$ is a character of $H$, write down, without proof, a formula for the induced character $\operatorname{Ind}_{H}^{G}(\psi)$ as a certain sum of character values $\psi\left(x_{i}\right)$.

  (b) Define permutations $a, b \in S_{7}$ by $a=\left(\begin{array}{llllll}1 & 2 & 3 & 4 & 5 & 6\end{array}\right), b=(235)(476)$ and let $G$ be the subgroup $\langle a, b\rangle$ of $S_{7}$. It is given that the elements of $G$ are all of the form $a^{i} b^{j}$ for $0 \leqslant i \leqslant 6,0 \leqslant j \leqslant 2$ and that $G$ has order 21 .

  (i) Find the orders of the centralisers $C_{G}(a)$ and $C_{G}(b)$. Hence show that there are five conjugacy classes of $G$.

  (ii) Find all characters of degree 1 of $G$ by lifting from a suitable quotient group.

  (iii) Let $H=\langle a\rangle$. By first inducing linear characters of $H$ using the formula stated in part (a)(ii), find the remaining irreducible characters of $G$.

  comment

• Paper 4, Section II, I

  Representation Theory | Part II, 2021

  (a) Define the group $S^{1}$. Sketch a proof of the classification of the irreducible continuous representations of $S^{1}$. Show directly that the characters obey an orthogonality relation.

  (b) Define the group $S U(2)$.

  (i) Show that there is a bijection between the conjugacy classes in $G=S U(2)$ and the subset $[-1,1]$ of the real line. [If you use facts about a maximal torus $T$, you should prove them.]

  (ii) Write $\mathcal{O}_{x}$ for the conjugacy class indexed by an element $x$, where $-1<x<1$. Show that $\mathcal{O}_{x}$ is homeomorphic to $S^{2}$. [Hint: First show that $\mathcal{O}_{x}$ is in bijection with $G / T$.

  (iii) Let $t: G \rightarrow[-1,1]$ be the parametrisation of conjugacy classes from part (i). Determine the representation of $G$ whose character is the function $g \mapsto 8 t(g)^{3}$.

  comment

Riemann Surfaces

• Paper 1, Section II, F

  Riemann Surfaces | Part II, 2021

  (a) Consider an open $\operatorname{disc} D \subseteq \mathbb{C}$. Prove that a real-valued function $u: D \rightarrow \mathbb{R}$ is harmonic if and only if

  $$u=\operatorname{Re}(f)$$

  for some analytic function $f$.

  (b) Give an example of a domain $D$ and a harmonic function $u: D \rightarrow \mathbb{R}$ that is not equal to the real part of an analytic function on $D$. Justify your answer carefully.

  (c) Let $u$ be a harmonic function on $\mathbb{C}_{*}$ such that $u(2 z)=u(z)$ for every $z \in \mathbb{C}_{*}$. Prove that $u$ is constant, justifying your answer carefully. Exhibit a countable subset $S \subseteq \mathbb{C}_{*}$ and a non-constant harmonic function $u$ on $\mathbb{C}_{*} \backslash S$ such that for all $z \in \mathbb{C}_{*} \backslash S$ we have $2 z \in \mathbb{C}_{*} \backslash S$ and $u(2 z)=u(z)$.

  (d) Prove that every non-constant harmonic function $u: \mathbb{C} \rightarrow \mathbb{R}$ is surjective.

  comment

• Paper 2, Section II, F

  Riemann Surfaces | Part II, 2021

  Let $D \subseteq \mathbb{C}$ be a domain, let $(f, U)$ be a function element in $D$, and let $\alpha:[0,1] \rightarrow D$ be a path with $\alpha(0) \in U$. Define what it means for a function element $(g, V)$ to be an analytic continuation of $(f, U)$ along $\alpha$.

  Suppose that $\beta:[0,1] \rightarrow D$ is a path homotopic to $\alpha$ and that $(h, V)$ is an analytic continuation of $(f, U)$ along $\beta$. Suppose, furthermore, that $(f, U)$ can be analytically continued along any path in $D$. Stating carefully any theorems that you use, prove that $g(\alpha(1))=h(\beta(1))$.

  Give an example of a function element $(f, U)$ that can be analytically continued to every point of $\mathbb{C}_{*}$ and a pair of homotopic paths $\alpha, \beta$ in $\mathbb{C}_{*}$ starting in $U$ such that the analytic continuations of $(f, U)$ along $\alpha$ and $\beta$ take different values at $\alpha(1)=\beta(1)$.

  comment

• Paper 3, Section II, F

  Riemann Surfaces | Part II, 2021

  (a) Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be a polynomial of degree $d>0$, and let $m_{1}, \ldots, m_{k}$ be the multiplicities of the ramification points of $f$. Prove that

  $$\sum_{i=1}^{k}\left(m_{i}-1\right)=d-1$$

  Show that, for any list of integers $m_{1}, \ldots, m_{k} \geqslant 2$ satisfying $(*)$, there is a polynomial $f$ of degree $d$ such that the $m_{i}$ are the multiplicities of the ramification points of $f$.

  (b) Let $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ be an analytic map, and let $B$ be the set of branch points. Prove that the restriction $f: \mathbb{C}_{\infty} \backslash f^{-1}(B) \rightarrow \mathbb{C}_{\infty} \backslash B$ is a regular covering map. Given $z_{0} \notin B$, explain how a closed loop $\gamma$ in $\mathbb{C}_{\infty} \backslash B$ gives rise to a permutation $\sigma_{\gamma}$ of $f^{-1}\left(z_{0}\right)$. Show that the group of all such permutations is transitive, and that the permutation $\sigma_{\gamma}$ only depends on $\gamma$ up to homotopy.

  (c) Prove that there is no meromorphic function $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ of degree 4 with branch points $B=\{0,1, \infty\}$ such that every preimage of 0 and 1 has ramification index 2 , while some preimage of $\infty$ has ramification index equal to 3. [Hint: You may use the fact that every non-trivial product of $(2,2)$-cycles in the symmetric group $S_{4}$ is a $(2,2)$-cycle.]

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2021

  Let $\mu>0$. The probability density function of the inverse Gaussian distribution (with the shape parameter equal to 1 ) is given by

  $$f(x ; \mu)=\frac{1}{\sqrt{2 \pi x^{3}}} \exp \left[-\frac{(x-\mu)^{2}}{2 \mu^{2} x}\right]$$

  Show that this is a one-parameter exponential family. What is its natural parameter? Show that this distribution has mean $\mu$ and variance $\mu^{3}$.

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2021

  The following data were obtained in a randomised controlled trial for a drug. Due to a manufacturing error, a subset of trial participants received a low dose (LD) instead of a standard dose (SD) of the drug.

  

  (a) Below we analyse the data using Poisson regression:

  

  (i) After introducing necessary notation, write down the Poisson models being fitted above.

  (ii) Write down the corresponding multinomial models, then state the key theoretical result (the "Poisson trick") that allows you to fit the multinomial models using Poisson regression. [You do not need to prove this theoretical result.]

  (iii) Explain why the number of degrees of freedom in the likelihood ratio test is 2 in the analysis of deviance table. What can you conclude about the drug?

  (b) Below is the summary table of the second model:

  

  (i) Drug efficacy is defined as one minus the ratio of the probability of worsening in the treated group to the probability of worsening in the control group. By using a more sophisticated method, a published analysis estimated that the drug efficacy is $90.0 \%$ for the LD treatment and $62.1 \%$ for the $\mathrm{SD}$ treatment. Are these numbers similar to what is obtained by Poisson regression? [Hint: $e^{-1} \approx 0.37, e^{-2} \approx 0.14$, and $e^{-3} \approx 0.05$, where $e$ is the base of the natural logarithm.]

  (ii) Explain why the information in the summary table is not enough to test the hypothesis that the LD drug and the SD drug have the same efficacy. Then describe how you can test this hypothesis using analysis of deviance in $R$.

  comment

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2021

  Define a generalised linear model for a sample $Y_{1}, \ldots, Y_{n}$ of independent random variables. Define further the concept of the link function. Define the binomial regression model (without the dispersion parameter) with logistic and probit link functions. Which of these is the canonical link function?

  comment

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2021

  Consider the normal linear model $Y \mid X \sim \mathrm{N}\left(X \beta, \sigma^{2} I\right)$, where $X$ is a $n \times p$ design matrix, $Y$ is a vector of responses, $I$ is the $n \times n$ identity matrix, and $\beta, \sigma^{2}$ are unknown parameters.

  Derive the maximum likelihood estimator of the pair $\beta$ and $\sigma^{2}$. What is the distribution of the estimator of $\sigma^{2}$ ? Use it to construct a $(1-\alpha)$-level confidence interval of $\sigma^{2}$. [You may use without proof the fact that the "hat matrix" $H=X\left(X^{T} X\right)^{-1} X^{T}$ is a projection matrix.]

  comment

• Paper 4 , Section I, J

  Statistical Modelling | Part II, 2021

  The data frame data contains the daily number of new avian influenza cases in a large poultry farm.

  

  Write down the model being fitted by the $R$ code below. Does the model seem to provide a satisfactory fit to the data? Justify your answer.

  The owner of the farm estimated that the size of the epidemic was initially doubling every 7 days. Is that estimate supported by the analysis below? [You may need $\log 2 \approx 0.69$.]

  

  

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2021

  Let $X$ be an $n \times p$ non-random design matrix and $Y$ be a $n$-vector of random responses. Suppose $Y \sim N\left(\mu, \sigma^{2} I\right)$, where $\mu$ is an unknown vector and $\sigma^{2}>0$ is known.

  (a) Let $\lambda \geqslant 0$ be a constant. Consider the ridge regression problem

  $$\hat{\beta}_{\lambda}=\arg \min _{\beta}\|Y-X \beta\|^{2}+\lambda\|\beta\|^{2} .$$

  Let $\hat{\mu}_{\lambda}=X \hat{\beta}_{\lambda}$ be the fitted values. Show that $\hat{\mu}_{\lambda}=H_{\lambda} Y$, where

  $$H_{\lambda}=X\left(X^{T} X+\lambda I\right)^{-1} X^{T}$$

  (b) Show that

  $$\mathbb{E}\left(\left\|Y-\hat{\mu}_{\lambda}\right\|^{2}\right)=\left\|\left(I-H_{\lambda}\right) \mu\right\|^{2}+\left\{n-2 \operatorname{trace}\left(H_{\lambda}\right)+\operatorname{trace}\left(H_{\lambda}^{2}\right)\right\} \sigma^{2}$$

  (c) Let $Y^{*}=\mu+\epsilon^{*}$, where $\epsilon^{*} \sim \mathrm{N}\left(0, \sigma^{2} I\right)$ is independent of $Y$. Show that $\left\|Y-\hat{\mu}_{\lambda}\right\|^{2}+2 \sigma^{2} \operatorname{trace}\left(H_{\lambda}\right)$ is an unbiased estimator of $\mathbb{E}\left(\left\|Y^{*}-\hat{\mu}_{\lambda}\right\|^{2}\right)$.

  (d) Describe the behaviour (monotonicity and limits) of $\mathbb{E}\left(\left\|Y^{*}-\hat{\mu}_{\lambda}\right\|^{2}\right)$ as a function of $\lambda$ when $p=n$ and $X=I$. What is the minimum value of $\mathbb{E}\left(\left\|Y^{*}-\hat{\mu}_{\lambda}\right\|^{2}\right)$ ?

  comment

Statistical Physics

• Paper 1, Section II, 36C

  Statistical Physics | Part II, 2021

  Throughout this question you should consider a classical gas and assume that the number of particles is fixed.

  (a) Write down the equation of state for an ideal gas. Write down an expression for the internal energy of an ideal gas in terms of the heat capacity at constant volume, $C_{V}$.

  (b) Starting from the first law of thermodynamics, find a relation between $C_{V}$ and the heat capacity at constant pressure, $C_{p}$, for an ideal gas. Hence give an expression for $\gamma=C_{p} / C_{V}$.

  (c) Describe the meaning of an adiabatic process. Using the first law of thermodynamics, derive the equation for an adiabatic process in the $(p, V)$-plane for an ideal gas.

  (d) Consider a simplified Otto cycle (an idealised petrol engine) involving an ideal gas and consisting of the following four reversible steps:

  $A \rightarrow B:$ Adiabatic compression from volume $V_{1}$ to volume $V_{2}<V_{1}$;

  $B \rightarrow C$ : Heat $Q_{1}$ injected at constant volume;

  $C \rightarrow D:$ Adiabatic expansion from volume $V_{2}$ to volume $V_{1}$;

  $D \rightarrow A:$ Heat $Q_{2}$ extracted at constant volume.

  Sketch the cycle in the $(p, V)$-plane and in the $(T, S)$-plane.

  Derive an expression for the efficiency, $\eta=W / Q_{1}$, where $W$ is the work out, in terms of the compression ratio $r=V_{1} / V_{2}$. How can the efficiency be maximized?

  comment

• Paper 2, Section II, $37 \mathrm{C}$

  Statistical Physics | Part II, 2021

  (a) What systems are described by microcanonical, canonical and grand canonical ensembles? Under what conditions is the choice of ensemble irrelevant?

  (b) In a simple model a meson consists of two quarks bound in a linear potential, $U(\mathbf{r})=\alpha|\mathbf{r}|$, where $\mathbf{r}$ is the relative displacement of the two quarks and $\alpha$ is a positive constant. You are given that the classical (non-relativistic) Hamiltonian for the meson is

  $$H(\mathbf{P}, \mathbf{R}, \mathbf{p}, \mathbf{r})=\frac{|\mathbf{P}|^{2}}{2 M}+\frac{|\mathbf{p}|^{2}}{2 \mu}+\alpha|\mathbf{r}|$$

  where $M=2 m$ is the total mass, $\mu=m / 2$ is the reduced mass, $\mathbf{P}$ is the total momentum, $\mathbf{p}=\mu d \mathbf{r} / d t$ is the internal momentum, and $\mathbf{R}$ is the centre of mass position.

  (i) Show that the partition function for a single meson in thermal equilibrium at temperature $T$ in a three-dimensional volume $V$ can be written as $Z_{1}=Z_{\text {trans }} Z_{\text {int }}$, where

  $$Z_{\text {trans }}=\frac{V}{(2 \pi \hbar)^{3}} \int d^{3} P e^{-\beta|\mathbf{P}|^{2} /(2 M)}, \quad Z_{\text {int }}=\frac{1}{(2 \pi \hbar)^{3}} \int d^{3} r d^{3} p e^{-\beta|\mathbf{p}|^{2} /(2 \mu)} e^{-\beta \alpha|\mathbf{r}|}$$

  and $\beta=1 /\left(k_{\mathrm{B}} T\right)$

  Evaluate $Z_{\text {trans }}$ and evaluate $Z_{\text {int }}$ in the large-volume limit $\left(\beta \alpha V^{1 / 3} \gg 1\right)$.

  What is the average separation of the quarks within the meson at temperature $T$ ?

  $\left[\right.$ You may assume that $\int_{-\infty}^{\infty} e^{-c x^{2}} d x=\sqrt{\pi / c}$ for $c>0$ ]

  (ii) Now consider an ideal gas of $N$ such mesons in a three-dimensional volume $V$.

  Calculate the total partition function of the gas.

  What is the heat capacity $C_{V} ?$

  comment

• Paper 3, Section II, C

  Statistical Physics | Part II, 2021

  (a) A gas of non-interacting particles with spin degeneracy $g_{s}$ has the energymomentum relationship $E=A(\hbar k)^{\alpha}$, for constants $A, \alpha>0$. Show that the density of states, $g(E) d E$, in a $d$-dimensional volume $V$ with $d \geqslant 2$ is given by

  $$g(E) d E=B V E^{(d-\alpha) / \alpha} d E$$

  where $B$ is a constant that you should determine. [You may denote the surface area of a unit $(d-1)$-dimensional sphere by $S_{d-1}$.]

  (b) Write down the Bose-Einstein distribution for the average number of identical bosons in a state with energy $E_{r} \geqslant 0$ in terms of $\beta=1 / k_{B} T$ and the chemical potential $\mu$. Explain why $\mu<0$.

  (c) Show that an ideal quantum Bose gas in a $d$-dimensional volume $V$, with $E=A(\hbar k)^{\alpha}$, as above, has

  $$p V=D E,$$

  where $p$ is the pressure and $D$ is a constant that you should determine.

  (d) For such a Bose gas, write down an expression for the number of particles that do not occupy the ground state. Use this to determine the values of $\alpha$ for which there exists a Bose-Einstein condensate at sufficiently low temperatures.

  comment

• Paper 4, Section II, 35C

  Statistical Physics | Part II, 2021

  (a) Explain what is meant by a first-order phase transition and a second-order phase transition.

  (b) Explain why the (Helmholtz) free energy is the appropriate thermodynamic potential to consider at fixed $T, V$ and $N$.

  (c) Consider a ferromagnet with free energy

  $$F(T, m)=F_{0}(T)+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}$$

  where $T$ is the temperature, $m$ is the magnetization, and $a, b, T_{c}>0$ are constants.

  Find the equilibrium value of $m$ at high and low temperatures. Hence, evaluate the equilibrium thermodynamic free energy as a function of $T$ and compute the entropy and heat capacity. Determine the jump in the heat capacity and identify the order of the phase transition.

  (d) Now consider a ferromagnet with free energy

  $$F(T, m)=F_{0}(T)+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}+\frac{c}{6} m^{6}$$

  where $a, b, c, T_{c}$ are constants with $a, c, T_{c}>0$, but $b \leqslant 0$.

  Find the equilibrium value of $m$ at high and low temperatures. What is the order of the phase transition?

  For $b=0$ determine the behaviour of the heat capacity at high and low temperatures.

  comment

Stochastic Financial Models

• Paper 1, Section II, 30K

  Stochastic Financial Models | Part II, 2021

  (a) What does it mean to say that a stochastic process $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale with respect to a filtration $\left(\mathcal{F}_{n}\right)_{n \geqslant 0}$ ?

  (b) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a martingale, and let $\xi_{n}=X_{n}-X_{n-1}$ for $n \geqslant 1$. Suppose $\xi_{n}$ takes values in the set $\{-1,+1\}$ almost surely for all $n \geqslant 1$. Show that $\left(X_{n}\right)_{n \geqslant 0}$ is a simple symmetric random walk, i.e. that the sequence $\left(\xi_{n}\right)_{n \geqslant 1}$ is $\operatorname{IID}$ with $\mathbb{P}\left(\xi_{1}=1\right)=1 / 2=$ $\mathbb{P}\left(\xi_{1}=-1\right) .$

  (c) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a martingale and let the bounded process $\left(H_{n}\right)_{n \geqslant 1}$ be previsible.

  Let $\hat{X}_{0}=0$ and

  $$\hat{X}_{n}=\sum_{k=1}^{n} H_{k}\left(X_{k}-X_{k-1}\right) \text { for } n \geqslant 1$$

  Show that $\left(\hat{X}_{n}\right)_{n \geqslant 0}$ is a martingale.

  (d) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk with $X_{0}=0$, and let

  $$T_{a}=\inf \left\{n \geqslant 0: X_{n}=a\right\}$$

  where $a$ is a positive integer. Let

  $$\hat{X}_{n}= \begin{cases}X_{n} & \text { if } n \leqslant T_{a} \\ 2 a-X_{n} & \text { if } n>T_{a}\end{cases}$$

  Show that $\left(\hat{X}_{n}\right)_{n \geqslant 0}$ is a simple symmetric random walk.

  (e) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk with $X_{0}=0$, and let $M_{n}=\max _{0 \leqslant k \leqslant n} X_{k}$. Compute $\mathbb{P}\left(M_{n}=a\right)$ for a positive integer $a$.

  comment

• Paper 2, Section II, 30K

  Stochastic Financial Models | Part II, 2021

  Consider a one-period market model with $d$ risky assets and one risk-free asset. Let $S_{t}$ denote the vector of prices of the risky assets at time $t \in\{0,1\}$ and let $r$ be the interest rate.

  (a) What does it mean to say a portfolio $\varphi \in \mathbb{R}^{d}$ is an arbitrage for this market?

  (b) An investor wishes to maximise their expected utility of time-1 wealth $X_{1}$ attainable by investing in the market with their time- 0 wealth $X_{0}=x$. The investor's utility function $U$ is increasing and concave. Show that, if there exists an optimal solution $X_{1}^{*}$ to the investor's expected utility maximisation problem, then the market has no arbitrage. [Assume that $U\left(X_{1}\right)$ is integrable for any attainable time-1 wealth $X_{1}$.]

  (c) Now introduce a contingent claim with time-1 bounded payout $Y$. How does the investor in part (b) calculate an indifference bid price $\pi(Y)$ for the claim? Assuming each such claim has a unique indifference price, show that the map $Y \mapsto \pi(Y)$ is concave. [Assume that any relevant utility maximisation problem that you consider has an optimal solution.]

  (d) Consider a contingent claim with time-1 bounded payout $Y$. Let $I \subseteq \mathbb{R}$ be the set of initial no-arbitrage prices for the claim; that is, the set $I$ consists of all $p$ such that the market augmented with the contingent claim with time- 0 price $p$ has no arbitrage. Show that $\pi(Y) \leqslant \sup \{p \in I\}$. [Assume that any relevant utility maximisation problem that you consider has an optimal solution. You may use results from lectures without proof, such as the fundamental theorem of asset pricing or the existence of marginal utility prices, as long as they are clearly stated.]

  comment

• Paper 3, Section II, 29K

  Stochastic Financial Models | Part II, 2021

  (a) Let $M=\left(M_{n}\right)_{n \geqslant 0}$ be a martingale and $\hat{M}=\left(\hat{M}_{n}\right)_{n \geqslant 0}$ a supermartingale. If $M_{0}=\hat{M}_{0}$, show that $\mathbb{E}\left(M_{T}\right) \geqslant \mathbb{E}\left(\hat{M}_{T}\right)$ for any bounded stopping time $T$. [If you use a general result about supermartingales, you must prove it.]

  (b) Consider a market with one stock with time- $n$ price $S_{n}$ and constant interest rate $r$. Explain why a self-financing investor's wealth process $\left(X_{n}\right)_{n \geqslant 0}$ satisfies

  $$X_{n}=(1+r) X_{n-1}+\theta_{n}\left[S_{n}-(1+r) S_{n-1}\right]$$

  where $\theta_{n}$ is the number of shares of the stock held during the $n$th period.

  (c) Given an initial wealth $X_{0}$, an investor seeks to maximize $\mathbb{E}\left[U\left(X_{N}\right)\right]$, where $U$ is a given utility function. Suppose the stock price is such that $S_{n}=S_{n-1} \xi_{n}$, where $\left(\xi_{n}\right)_{n \geqslant 1}$ is a sequence of independent copies of a random variable $\xi$. Let $V$ be defined inductively by

  $$V(n-1, x)=\sup _{t \in \mathbb{R}} \mathbb{E}[V(n,(1+r) x+t(1+r-\xi))]$$

  with terminal condition $V(N, x)=U(x)$ for all $x \in \mathbb{R}$.

  Show that the process $\left(V\left(n, X_{n}\right)\right)_{0 \leqslant n \leqslant N}$ is a supermartingale for any trading strategy $\left(\theta_{n}\right)_{1 \leqslant n \leqslant N}$. Suppose that the trading strategy $\left(\theta_{n}^{*}\right)_{1 \leqslant n \leqslant N}$ with corresponding wealth process $\left(X_{n}^{*}\right)_{0 \leqslant n \leqslant N}$ are such that the process $\left(V\left(n, X_{n}^{*}\right)\right)_{0 \leqslant n \leqslant N}$ is a martingale. Show that $\left(\theta_{n}^{*}\right)_{1 \leqslant n \leqslant N}$ is optimal.

  comment

• Paper 4, Section II, 29K

  Stochastic Financial Models | Part II, 2021

  (a) What does it mean to say that a stochastic process is a Brownian motion? Show that, if $\left(W_{t}\right)_{t \geqslant 0}$ is a continuous Gaussian process such that $\mathbb{E}\left(W_{t}\right)=0$ and $\mathbb{E}\left(W_{s} W_{t}\right)=s$ for all $0 \leqslant s \leqslant t$, then $\left(W_{t}\right)_{t \geqslant 0}$ is a Brownian motion.

  For the rest of the question, let $\left(W_{t}\right)_{t \geqslant 0}$ be a Brownian motion.

  (b) Let $\widehat{W}_{0}=0$ and $\widehat{W}_{t}=t W_{1 / t}$ for $t>0$. Show that $\left(\widehat{W}_{t}\right)_{t \geqslant 0}$ is a Brownian motion. [You may use without proof the Brownian strong law of large numbers: $W_{t} / t \rightarrow 0$ almost surely as $t \rightarrow \infty$.]

  (c) Fix constants $c \in \mathbb{R}$ and $T>0$. Show that

  $$\mathbb{E}\left[f\left(\left(W_{t}+c t\right)_{0 \leqslant t \leqslant T}\right)\right]=\mathbb{E}\left[\exp \left(c W_{T}-\frac{1}{2} c^{2} T\right) f\left(\left(W_{t}\right)_{0 \leqslant t \leqslant T}\right)\right]$$

  for any bounded function $f: C[0, T] \rightarrow \mathbb{R}$ of the form

  $$f(\omega)=g\left(\omega\left(t_{1}\right), \ldots, \omega\left(t_{n}\right)\right),$$

  for some fixed $g$ and fixed $0<t_{1}<\ldots<t_{n}=T$, where $C[0, T]$ is the space of continuous functions on $[0, T]$. [If you use a general theorem from the lectures, you should prove it.]

  (d) Fix constants $x \in \mathbb{R}$ and $T>0$. Show that

  $$\mathbb{E}\left[f\left(\left(W_{t}+x\right)_{t \geqslant T}\right)\right]=\mathbb{E}\left[\exp \left((x / T) W_{T}-\frac{1}{2}\left(x^{2} / T\right)\right) f\left(\left(W_{t}\right)_{t \geqslant T}\right)\right]$$

  for any bounded function $f: C[T, \infty) \rightarrow \mathbb{R}$. [In this part you may use the Cameron-Martin theorem without proof.]

  comment

Topics in Analysis

• Paper 1, Section I, 2H

  Topics in Analysis | Part II, 2021

  Write

  $$P=\left\{\mathbf{x} \in \mathbb{R}^{n}: x_{j} \geqslant 0 \text { for all } 1 \leqslant j \leqslant n\right\}$$

  and suppose that $K$ is a non-empty, closed, convex and bounded subset of $\mathbb{R}^{n}$ with $K \cap \operatorname{Int} P \neq \emptyset$. By taking logarithms, or otherwise, show that there is a unique $\mathbf{x}^{*} \in K \cap P$ such that

  $$\prod_{j=1}^{n} x_{j} \leqslant \prod_{j=1}^{n} x_{j}^{*}$$

  for all $\mathbf{x} \in K \cap P$.

  Show that $\sum_{j=1}^{n} \frac{x_{j}}{x_{j}^{*}} \leqslant n$ for all $\mathbf{x} \in K \cap P$.

  Identify the point $\mathbf{x}^{*}$ in the case that $K$ has the property

  $$\left(x_{1}, x_{2}, \ldots, x_{n-1}, x_{n}\right) \in K \Rightarrow\left(x_{2}, x_{3}, \ldots, x_{n}, x_{1}\right) \in K$$

  and justify your answer.

  Show that, given any $\mathbf{a} \in \operatorname{Int} P$, we can find a set $K$, as above, with $\mathbf{x}^{*}=\mathbf{a}$.

  comment

• Paper 2, Section I, $2 H$

  Topics in Analysis | Part II, 2021

  Let $\Omega$ be a non-empty bounded open set in $\mathbb{R}^{2}$ with closure $\bar{\Omega}$ and boundary $\partial \Omega$ and let $\phi: \bar{\Omega} \rightarrow \mathbb{R}$ be a continuous function. Give a proof or a counterexample for each of the following assertions.

  (i) If $\phi$ is twice differentiable on $\Omega$ with $\nabla^{2} \phi(\mathbf{x})>0$ for all $\mathbf{x} \in \Omega$, then there exists an $\mathbf{x}_{0} \in \partial \Omega$ with $\phi\left(\mathbf{x}_{0}\right) \geqslant \phi(\mathbf{x})$ for all $\mathbf{x} \in \bar{\Omega}$.

  (ii) If $\phi$ is twice differentiable on $\Omega$ with $\nabla^{2} \phi(\mathbf{x})<0$ for all $\mathbf{x} \in \Omega$, then there exists an $\mathbf{x}_{0} \in \partial \Omega$ with $\phi\left(\mathbf{x}_{0}\right) \geqslant \phi(\mathbf{x})$ for all $\mathbf{x} \in \bar{\Omega}$.

  (iii) If $\phi$ is four times differentiable on $\Omega$ with

  $$\frac{\partial^{4} \phi}{\partial x^{4}}(\mathbf{x})+\frac{\partial^{4} \phi}{\partial y^{4}}(\mathbf{x})>0$$

  for all $\mathbf{x} \in \Omega$, then there exists an $\mathbf{x}_{0} \in \partial \Omega$ with $\phi\left(\mathbf{x}_{0}\right) \geqslant \phi(\mathbf{x})$ for all $\mathbf{x} \in \bar{\Omega}$.

  (iv) If $\phi$ is twice differentiable on $\Omega$ with $\nabla^{2} \phi(\mathbf{x})=0$ for all $\mathbf{x} \in \Omega$, then there exists an $\mathbf{x}_{0} \in \partial \Omega$ with $\phi\left(\mathbf{x}_{0}\right) \geqslant \phi(\mathbf{x})$ for all $\mathbf{x} \in \bar{\Omega}$.

  comment

• Paper 2, Section II, H

  Topics in Analysis | Part II, 2021

  Let $r:[-1,1] \rightarrow \mathbb{R}$ be a continuous function with $r(x)>0$ for all but finitely many values of $x$.

  (a) Show that

  $$\langle u, v\rangle=\int_{-1}^{1} u(x) v(x) r(x) d x$$

  defines an inner product on $C([-1,1])$.

  (b) Show that for each $n$ there exists a polynomial $P_{n}$ of degree exactly $n$ which is orthogonal, with respect to the inner product $(*)$, to all polynomials of lower degree.

  (c) Show that $P_{n}$ has $n$ simple zeros $\omega_{1}(n), \omega_{2}(n), \ldots, \omega_{n}(n)$ on $[-1,1]$.

  (d) Show that for each $n$ there exist unique real numbers $A_{j}(n), 1 \leqslant j \leqslant n$, such that whenever $Q$ is a polynomial of degree at most $2 n-1$,

  $$\int_{-1}^{1} Q(x) r(x) d x=\sum_{j=1}^{n} A_{j}(n) Q\left(\omega_{j}(n)\right)$$

  (e) Show that

  $$\sum_{j=1}^{n} A_{j}(n) f\left(\omega_{j}(n)\right) \rightarrow \int_{-1}^{1} f(x) r(x) d x$$

  as $n \rightarrow \infty$ for all $f \in C([-1,1])$.

  (f) If $R>1, K>0, a_{m}$ is real with $\left|a_{m}\right| \leqslant K R^{-m}$ and $f(x)=\sum_{m=1}^{\infty} a_{m} x^{m}$, show that

  $$\left|\int_{-1}^{1} f(x) r(x) d x-\sum_{j=1}^{n} A_{j}(n) f\left(\omega_{j}(n)\right)\right| \leqslant \frac{2 K R^{-2 n+1}}{R-1} \int_{-1}^{1} r(x) d x$$

  (g) If $r(x)=\left(1-x^{2}\right)^{1 / 2}$ and $P_{n}(0)=1$, identify $P_{n}$ (giving brief reasons) and the $\omega_{j}(n)$. [Hint: A change of variable may be useful.]

  comment

• Paper 3 , Section I, $2 H$

  Topics in Analysis | Part II, 2021

  State Runge's theorem on the approximation of analytic functions by polynomials.

  Let $\Omega=\{z \in \mathbb{C}, \operatorname{Re} z>0, \operatorname{Im} z>0\}$. Establish whether the following statements are true or false by giving a proof or a counterexample in each case.

  (i) If $f: \Omega \rightarrow \mathbb{C}$ is the uniform limit of a sequence of polynomials $P_{n}$, then $f$ is a polynomial.

  (ii) If $f: \Omega \rightarrow \mathbb{C}$ is analytic, then there exists a sequence of polynomials $P_{n}$ such that for each integer $r \geqslant 0$ and each $z \in \Omega$ we have $P_{n}^{(r)}(z) \rightarrow f^{(r)}(z)$.

  comment

• Paper 4, Section I, 2H

  Topics in Analysis | Part II, 2021

  (a) State Brouwer's fixed-point theorem in 2 dimensions.

  (b) State an equivalent theorem on retraction and explain (without detailed calculations) why it is equivalent.

  (c) Suppose that $A$ is a $3 \times 3$ real matrix with strictly positive entries. By defining an appropriate function $f: \triangle \rightarrow \triangle$, where

  $$\triangle=\left\{\mathbf{x} \in \mathbb{R}^{3}: x_{1}+x_{2}+x_{3}=1, x_{1}, x_{2}, x_{3} \geqslant 0\right\}$$

  show that $A$ has a strictly positive eigenvalue.

  comment

• Paper 4, Section II, H

  Topics in Analysis | Part II, 2021

  Let $x$ be irrational with $n$th continued fraction convergent

  $$\frac{p_{n}}{q_{n}}=a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}+\frac{1}{a_{3}+\frac{1}{a_{n-1}+\frac{1}{a_{n}}}}}}$$

  Show that

  $$\left(\begin{array}{cc} p_{n} & p_{n-1} \\ q_{n} & q_{n-1} \end{array}\right)=\left(\begin{array}{cc} a_{0} & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{cc} a_{1} & 1 \\ 1 & 0 \end{array}\right) \cdots\left(\begin{array}{cc} a_{n-1} & 1 \\ 1 & 0 \end{array}\right)\left(\begin{array}{cc} a_{n} & 1 \\ 1 & 0 \end{array}\right)$$

  and deduce that

  $$\left|\frac{p_{n}}{q_{n}}-x\right| \leqslant \frac{1}{q_{n} q_{n+1}} .$$

  [You may quote the result that $x$ lies between $p_{n} / q_{n}$ and $p_{n+1} / q_{n+1} \cdot$ ]

  We say that $y$ is a quadratic irrational if it is an irrational root of a quadratic equation with integer coefficients. Show that if $y$ is a quadratic irrational, we can find an $M>0$ such that

  $$\left|\frac{p}{q}-y\right| \geqslant \frac{M}{q^{2}}$$

  for all integers $p$ and $q$ with $q>0$.

  Using the hypotheses and notation of the first paragraph, show that if the sequence $\left(a_{n}\right)$ is unbounded, $x$ cannot be a quadratic irrational.

  comment

Waves

• Paper 1, Section II, 40A

  Waves | Part II, 2021

  Compressible fluid of equilibrium density $\rho_{0}$, pressure $p_{0}$ and sound speed $c_{0}$ is contained in the region between an inner rigid sphere of radius $R$ and an outer elastic sphere of equilibrium radius $2 R$. The elastic sphere is made to oscillate radially in such a way that it exerts a spherically symmetric, perturbation pressure $\tilde{p}=\epsilon p_{0} \cos \omega t$ on the fluid at $r=2 R$, where $\epsilon \ll 1$ and the frequency $\omega$ is sufficiently small that

  $$\alpha \equiv \frac{\omega R}{c_{0}} \leqslant \frac{\pi}{2}$$

  You may assume that the acoustic velocity potential satisfies the wave equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}=c_{0}^{2} \nabla^{2} \phi$$

  (a) Derive an expression for $\phi(r, t)$.

  (b) Hence show that the net radial component of the acoustic intensity (wave-energy flux) $\mathbf{I}=\tilde{p} \mathbf{u}$ is zero when averaged appropriately in a way you should define. Interpret this result physically.

  (c) Briefly discuss the possible behaviour of the system if the forcing frequency $\omega$ is allowed to increase to larger values.

  $\left[\right.$ For a spherically symmetric variable $\left.\psi(r, t), \nabla^{2} \psi=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r \psi) .\right]$

  comment

• Paper 2, Section II, 40A

  Waves | Part II, 2021

  A semi-infinite elastic medium with shear modulus $\mu$ and shear-wave speed $c_{s}$ lies in $z \leqslant 0$. Above it, there is a layer $0 \leqslant z \leqslant h$ of a second elastic medium with shear modulus $\bar{\mu}$ and shear-wave speed $\bar{c}_{s}<c_{s}$. The top boundary is stress-free. Consider a monochromatic SH-wave propagating in the $x$-direction at speed $c$ with wavenumber $k>0$.

  (a) Derive the dispersion relation

  $$\tan \left[k h \sqrt{c^{2} / \bar{c}_{s}^{2}-1}\right]=\frac{\mu}{\bar{\mu}} \frac{\sqrt{1-c^{2} / c_{s}^{2}}}{\sqrt{c^{2} / \bar{c}_{s}^{2}-1}}$$

  for trapped modes with no disturbance as $z \rightarrow-\infty$.

  (b) Show graphically that there is always a zeroth mode, and show that the other modes have cut-off frequencies

  $$\omega_{c}^{(n)}=\frac{n \pi \bar{c}_{s} c_{s}}{h \sqrt{c_{s}^{2}-\bar{c}_{s}^{2}}}$$

  where $n$ is a positive integer. Sketch a graph of frequency $\omega$ against $k$ for the $n=1$ mode showing the behaviour near cut-off and for large $k$.

  comment

• Paper 3, Section II, 39A

  Waves | Part II, 2021

  Consider a two-dimensional stratified fluid of sufficiently slowly varying background density $\rho_{b}(z)$ that small-amplitude vertical-velocity perturbations $w(x, z, t)$ can be assumed to satisfy the linear equation

  $$\nabla^{2}\left(\frac{\partial^{2} w}{\partial t^{2}}\right)+N^{2}(z) \frac{\partial^{2} w}{\partial x^{2}}=0, \quad \text { where } N^{2}=\frac{-g}{\rho_{0}} \frac{d \rho_{b}}{d z}$$

  and $\rho_{0}$ is a constant. The background density profile is such that $N^{2}$ is piecewise constant with $N^{2}=N_{0}^{2}>0$ for $|z|>L$ and with $N^{2}=0$ in a layer $|z|<L$ of uniform density $\rho_{0}$.

  A monochromatic internal wave of amplitude $A_{I}$ is incident on the intermediate layer from $z=-\infty$, and produces velocity perturbations of the form

  $$w(x, z, t)=\widehat{w}(z) e^{i(k x-\omega t)}$$

  where $k>0$ and $0<\omega<N_{0}$.

  (a) Show that the vertical variations have the form

  $$\widehat{w}(z)= \begin{cases}A_{I} \exp [-i m(z+L)]+A_{R} \exp [i m(z+L)] \quad \text { for } z<-L \\ B_{C} \cosh k z+B_{S} \sinh k z & \text { for }|z|<L \\ A_{T} \exp [-i m(z-L)] & \text { for } z>L\end{cases}$$

  where $A_{R}, B_{C}, B_{S}$ and $A_{T}$ are (in general) complex amplitudes and

  $$m=k \sqrt{\frac{N_{0}^{2}}{\omega^{2}}-1}$$

  In particular, you should justify the choice of signs for the coefficients involving $m$.

  (b) What are the appropriate boundary conditions to impose on $\widehat{w}$at $z=\pm L$ to determine the unknown amplitudes?

  (c) Apply these boundary conditions to show that

  $$\frac{A_{T}}{A_{I}}=\frac{2 i m k}{2 i m k \cosh 2 \alpha+\left(k^{2}-m^{2}\right) \sinh 2 \alpha},$$

  where $\alpha=k L$.

  (d) Hence show that

  $$\left|\frac{A_{T}}{A_{I}}\right|^{2}=\left[1+\left(\frac{\sinh 2 \alpha}{\sin 2 \psi}\right)^{2}\right]^{-1}$$

  where $\psi$ is the angle between the incident wavevector and the downward vertical.

  comment

• Paper 4, Section II, 39A

  Waves | Part II, 2021

  A plane shock is moving with speed $U$ into a perfect gas. Ahead of the shock the gas is at rest with pressure $p_{1}$ and density $\rho_{1}$, while behind the shock the velocity, pressure and density of the gas are $u_{2}, p_{2}$ and $\rho_{2}$ respectively.

  (a) Write down the Rankine-Hugoniot relations across the shock, briefly explaining how they arise.

  (b) Show that

  $$\frac{\rho_{1}}{\rho_{2}}=\frac{2 c_{1}^{2}+(\gamma-1) U^{2}}{(\gamma+1) U^{2}}$$

  where $c_{1}^{2}=\gamma p_{1} / \rho_{1}$ and $\gamma$ is the ratio of the specific heats of the gas.

  (c) Now consider a change of frame such that the shock is stationary and the gas has a component of velocity $U$ parallel to the shock on both sides. Deduce that a stationary shock inclined at a 45 degree angle to an incoming stream of Mach number $M=\sqrt{2} U / c_{1}$ deflects the flow by an angle $\delta$ given by

  $$\tan \delta=\frac{M^{2}-2}{\gamma M^{2}+2}$$

  $\left[\right.$ Note that $\left.\tan (\alpha-\beta)=\frac{\tan \alpha-\tan \beta}{1+\tan \alpha \tan \beta} .\right]$

  comment