Part II, 2002

Algebraic Curves

• B2.10

  Algebraic Curves | Part II, 2002

  For $N \geq 1$, let $V_{N}$ be the (irreducible) projective plane curve $V_{N}: X^{N}+Y^{N}+Z^{N}=0$ over an algebraically closed field of characteristic zero.

  Show that $V_{N}$ is smooth (non-singular). For $m, n \geq 1$, let $\alpha_{m, n}: V_{m n} \rightarrow V_{m}$ be the morphism $\alpha_{m, n}(X: Y: Z)=\left(X^{n}: Y^{n}: Z^{n}\right)$. Determine the degree of $\alpha_{m, n}$, its points of ramification and the corresponding ramification indices.

  Applying the Riemann-Hurwitz formula to $\alpha_{1, n}$, determine the genus of $V_{n}$.

  comment

• B3.10

  Algebraic Curves | Part II, 2002

  Let $f=f(x, y)$ be an irreducible polynomial of degree $n \geq 2$ (over an algebraically closed field of characteristic zero) and $V_{0}=\{f=0\} \subset \mathbb{A}^{2}$ the corresponding affine plane curve. Assume that $V_{0}$ is smooth (non-singular) and that the projectivization $V \subset \mathbb{P}^{2}$ of $V_{0}$ intersects the line at infinity $\mathbb{P}^{2}-\mathbb{A}^{2}$ in $n$ distinct points. Show that $V$ is smooth and determine the divisor of the rational differential $\omega=\frac{d x}{f_{y}^{\prime}}$ on $V$. Deduce a formula for the genus of $V$.

  comment

• B4.9

  Algebraic Curves | Part II, 2002

  Write an essay on the Riemann-Roch theorem and some of its applications.

  comment

Algebraic Topology

• B2.8

  Algebraic Topology | Part II, 2002

  Show that the fundamental group $G$ of the Klein bottle is infinite. Show that $G$ contains an abelian subgroup of finite index. Show that $G$ is not abelian.

  comment

• B3.7

  Algebraic Topology | Part II, 2002

  For a finite simplicial complex $X$, let $b_{i}(X)$ denote the rank of the finitely generated abelian group $H_{i} X$. Define the Euler characteristic $\chi(X)$ by the formula

  $$\chi(X)=\sum_{i}(-1)^{i} b_{i}(X) .$$

  Let $a_{i}$ denote the number of $i$-simplices in $X$, for each $i \geqslant 0$. Show that

  $$\chi(X)=\sum_{i}(-1)^{i} a_{i}$$

  comment

• B4.5

  Algebraic Topology | Part II, 2002

  State the Mayer-Vietoris theorem for a finite simplicial complex $X$ which is the union of closed subcomplexes $A$ and $B$. Define all the maps in the long exact sequence. Prove that the sequence is exact at the term $H_{i} X$, for every $i \geqslant 0$.

  comment

Algorithms and Networks

• A2.10

  Algorithms and Networks | Part II, 2002

  (i) Let $G$ be a directed network with nodes $N$, arcs $A$ and capacities specified on each of the arcs. Define the terms feasible flow, divergence, cut, upper and lower cut capacities. Given two disjoint sets of nodes $N^{+}$and $N^{-}$, what does it mean to say that a cut $Q$ separates $N^{+}$from $N^{-}$? Prove that the flux of a feasible flow $x$ from $N^{+}$to $N^{-}$is bounded above by the upper capacity of $Q$, for any cut $Q$ separating $N^{+}$from $N^{-}$.

  (ii) Define the maximum-flow and minimum-cut problems. State the max-flow min-cut theorem and outline the main steps of the maximum-flow algorithm. Use the algorithm to find the maximum flow between the nodes 1 and 5 in a network whose node set is $\{1,2, \ldots, 5\}$, where the lower capacity of each arc is 0 and the upper capacity $c_{i j}$ of the directed arc joining node $i$ to node $j$ is given by the $(i, j)$-entry in the matrix

  $$\left(\begin{array}{ccccc} 0 & 7 & 9 & 8 & 0 \\ 0 & 0 & 6 & 8 & 4 \\ 0 & 9 & 0 & 2 & 10 \\ 0 & 3 & 7 & 0 & 6 \\ 0 & 0 & 0 & 0 & 0 \end{array}\right)$$

  [The painted-network theorem can be used without proof but should be stated clearly. You may assume in your description of the maximum-flow algorithm that you are given an initial feasible flow.]

  comment

• A3.10

  Algorithms and Networks | Part II, 2002

  (i) Consider the unconstrained geometric programme GP

  $$\text { minimise } g(t)=\sum_{i=1}^{n} c_{i} \prod_{j=1}^{m} t_{j}^{a_{i j}}$$

  subject to $t_{j}>0 \quad j=1, \ldots, m$.

  State the dual problem to GP. Give a careful statement of the AM-GM inequality, and use it to prove the primal-dual inequality for GP.

  (ii) Define min-path and max-tension problems. State and outline the proof of the max-tension min-path theorem.

  A company has branches in five cities $A, B, C, D$ and $E$. The fares for direct flights between these cities are as follows:

  \begin{tabular}{l|lllll} & $\mathrm{A}$ & $\mathrm{B}$ & $\mathrm{C}$ & $\mathrm{D}$ & $\mathrm{E}$ \ \hline $\mathrm{A}$ & $-$ & 50 & 40 & 25 & 10 \ $\mathrm{~B}$ & 50 & $-$ & 20 & 90 & 25 \ $\mathrm{C}$ & 40 & 20 & $-$ & 10 & 25 \ $\mathrm{D}$ & 25 & 90 & 10 & $-$ & 55 \ $\mathrm{E}$ & 10 & 25 & 25 & 55 & $-$ \end{tabular}

  Formulate this as a min-path problem. Illustrate the max-tension min-path algorithm by finding the cost of travelling by the cheapest routes between $D$ and each of the other cities.

  comment

• A4.11

  Algorithms and Networks | Part II, 2002

  Write an essay on Strong Lagrangian problems. You should give an account of duality and how it relates to the Strong Lagrangian property. In particular, establish carefully the relationship between the Strong Lagrangian property and supporting hyperplanes.

  Also, give an example of a class of problems that are Strong Lagrangian. [You should explain carefully why your example has the Strong Lagrangian property.]

  comment

Applications of Quantum Mechanics

• B1.23

  Applications of Quantum Mechanics | Part II, 2002

  A quantum system, with Hamiltonian $H_{0}$, has continuous energy eigenstates $|E\rangle$ for all $E \geq 0$, and also a discrete eigenstate $|0\rangle$, with $H_{0}|0\rangle=E_{0}|0\rangle,\langle 0 \mid 0\rangle=1, E_{0}>0$. A time-independent perturbation $H_{1}$, such that $\left\langle E\left|H_{1}\right| 0\right\rangle \neq 0$, is added to $H_{0}$. If the system is initially in the state $|0\rangle$ obtain the formula for the decay rate

  $$w=\frac{2 \pi}{\hbar} \rho\left(E_{0}\right)\left|\left\langle E_{0}\left|H_{1}\right| 0\right\rangle\right|^{2},$$

  where $\rho$ is the density of states.

  [You may assume that $\frac{1}{t}\left(\frac{\sin \frac{1}{2} \omega t}{\frac{1}{2} \omega}\right)^{2}$ behaves like $2 \pi \delta(\omega)$ for large $t$.]

  Assume that, for a particle moving in one dimension,

  $$H_{0}=E_{0}|0\rangle\left\langle 0\left|+\int_{-\infty}^{\infty} p^{2}\right| p\right\rangle\langle p| d p, \quad H_{1}=f \int_{-\infty}^{\infty}(|p\rangle\langle 0|+| 0\rangle\langle p|) d p$$

  where $\left\langle p^{\prime} \mid p\right\rangle=\delta\left(p^{\prime}-p\right)$, and $f$ is constant. Obtain $w$ in this case.

  comment

• B2.22

  Applications of Quantum Mechanics | Part II, 2002

  Define the reciprocal lattice for a lattice $L$ with lattice vectors $\ell$.

  A beam of electrons, with wave vector $\mathbf{k}$, is incident on a Bravais lattice $L$ with a large number of atoms, $N$. If the scattering amplitude for scattering on an individual atom in the direction $\hat{\mathbf{k}}^{\prime}$ is $f\left(\hat{\mathbf{k}}^{\prime}\right)$, show that the scattering amplitude for the whole lattice

  $$\sum_{\ell \in L} e^{i \mathbf{q} \cdot \ell} f\left(\hat{\mathbf{k}}^{\prime}\right), \quad \mathbf{q}=\mathbf{k}-|\mathbf{k}| \hat{\mathbf{k}}^{\prime}$$

  Derive the formula for the differential cross section

  $$\frac{\mathrm{d} \sigma}{\mathrm{d} \Omega}=N\left|f\left(\hat{\mathbf{k}}^{\prime}\right)\right|^{2} \Delta(\mathbf{q}),$$

  obtaining an explicit form for $\Delta(\mathbf{q})$. Show that $\Delta(\mathbf{q})$ is strongly peaked when $\mathbf{q}=\mathbf{g}$, a reciprocal lattice vector. Show that this leads to the Bragg formula $2 d \sin \frac{\theta}{2}=\lambda$, where $\theta$ is the scattering angle, $\lambda$ the electron wavelength and $d$ the separation between planes of atoms in the lattice.

  comment

• B3.23

  Applications of Quantum Mechanics | Part II, 2002

  A periodic potential is expressed as $V(\mathbf{x})=\sum_{\mathbf{g}} a_{\mathbf{g}} e^{i \mathbf{g} \cdot \mathbf{x}}$, where $\{\mathbf{g}\}$ are reciprocal lattice vectors and $a_{\mathbf{g}}{ }^{*}=a_{-\mathbf{g}}, a_{\mathbf{0}}=0$. In the nearly free electron model explain why it is appropriate, near the boundaries of energy bands, to consider a Bloch wave state

  $$\left|\psi_{\mathbf{k}}\right\rangle=\sum_{r} \alpha_{r}\left|\mathbf{k}_{r}\right\rangle, \quad \mathbf{k}_{r}=\mathbf{k}+\mathbf{g}_{r},$$

  where $|\mathbf{k}\rangle$ is a free electron state for wave vector $\mathbf{k},\left\langle\mathbf{k}^{\prime} \mid \mathbf{k}\right\rangle=\delta_{\mathbf{k}^{\prime} \mathbf{k}}$, and the sum is restricted to reciprocal lattice vectors $\mathbf{g}_{r}$ such that $\left|\mathbf{k}_{r}\right| \approx|\mathbf{k}|$. Obtain a determinantal formula for the possible energies $E(\mathbf{k})$ corresponding to Bloch wave states of this form.

  [You may take $\mathbf{g}_{1}=\mathbf{0}$ and assume $e^{i \mathbf{b} \cdot \mathbf{x}}|\mathbf{k}\rangle=|\mathbf{k}+\mathbf{b}\rangle$ for any $\mathbf{b}$.]

  Suppose the sum is restricted to just $\mathbf{k}$ and $\mathbf{k}+\mathbf{g}$. Show that there is a gap $2\left|a_{\mathbf{g}}\right|$ between energy bands. Setting $\mathbf{k}=-\frac{1}{2} \mathbf{g}+\mathbf{q}$, show that there are two Bloch wave states with energies near the boundaries of the energy bands

  $$E_{\pm}(\mathbf{k}) \approx \frac{\hbar^{2}|\mathbf{g}|^{2}}{8 m} \pm\left|a_{\mathbf{g}}\right|+\frac{\hbar^{2}|\mathbf{q}|^{2}}{2 m} \pm \frac{\hbar^{4}}{8 m^{2}\left|a_{\mathbf{g}}\right|}(\mathbf{q} \cdot \mathbf{g})^{2}$$

  What is meant by effective mass? Determine the value of the effective mass at the top and the bottom of the adjacent energy bands if $\mathbf{q}$ is parallel to $\mathrm{g}$.

  comment

• B4.24

  Applications of Quantum Mechanics | Part II, 2002

  Explain the variational method for computing the ground state energy for a quantum Hamiltonian.

  For the one-dimensional Hamiltonian

  $$H=\frac{1}{2} p^{2}+\lambda x^{4},$$

  obtain an approximate form for the ground state energy by considering as a trial state the state $|w\rangle$ defined by $a|w\rangle=0$, where $\langle w \mid w\rangle=1$ and $a=(w / 2 \hbar)^{\frac{1}{2}}(x+i p / w)$.

  [It is useful to note that $\left\langle w\left|\left(a+a^{\dagger}\right)^{4}\right| w\right\rangle=\left\langle w\left|\left(a^{2} a^{\dagger 2}+a a^{\dagger} a a^{\dagger}\right)\right| w\right\rangle$.]

  Explain why the states $a^{\dagger}|w\rangle$ may be used as trial states for calculating the first excited energy level.

  comment

Applied Probability

• B2.13

  Applied Probability | Part II, 2002

  Two enthusiastic probability students, Ros and Guil, sit an examination which starts at time 0 and ends at time $T$; they both decide to use the time to attempt a proof of a difficult theorem which carries a lot of extra marks.

  Ros' strategy is to write the proof continuously at a constant speed $\lambda$ lines per unit time. In a time interval of length $\delta t$ he has a probability $\mu \delta t+o(\delta t)$ of realising he has made a mistake. If that happens he instantly panics, erases everything he has written and starts all over again.

  Guil, on the other hand, keeps cool and thinks carefully about what he is doing. In a time interval of length $\delta t$, he has a probability $\lambda \delta t+o(\delta t)$ of writing the next line of proof and for each line he has written a probability $\mu \delta t+o(\delta t)$ of finding a mistake in that line, independently of all other lines he has written. When a mistake is found, he erases that line and carries on as usual, hoping for the best.

  Both Ros and Guil realise that, even if they manage to finish the proof, they will not recognise that they have done so and will carry on writing as much as they can.

  (a) Calculate $p_{l}(t)$, the probability that, for Ros, the length of his completed proof at time $t \geqslant l / \lambda$ is at least $l$.

  (b) Let $q_{n}(t)$ be the probability that Guil has $n$ lines of proof at time $t>0$. Show that

  $$\frac{\partial Q}{\partial t}=(s-1)\left(\lambda Q-\mu \frac{\partial Q}{\partial s}\right)$$

  where $Q(s, t)=\sum_{n=0}^{\infty} s^{n} q_{n}(t)$.

  (c) Suppose now that every time Ros starts all over again, the time until the next mistake has distribution $F$, independently of the past history. Write down a renewal-type integral equation satisfied by $l(t)$, the expected length of Ros' proof at time $t$. What is the expected length of proof produced by him at the end of the examination if $F$ is the exponential distribution with mean $1 / \mu$ ?

  (d) What is the expected length of proof produced by Guil at the end of the examination if each line that he writes survives for a length of time with distribution $F$, independently of all other lines?

  comment

• B3.13

  Applied Probability | Part II, 2002

  (a) Define a renewal process and a discrete renewal process.

  (b) State and prove the Discrete Renewal Theorem.

  (c) The sequence $\mathbf{u}=\left\{u_{n}: n \geqslant 0\right\}$ satisfies

  $$u_{0}=1, \quad u_{n}=\sum_{i=1}^{n} f_{i} u_{n-i}, \quad \text { for } n \geqslant 1$$

  for some collection of non-negative numbers $\left(f_{i}: i \in \mathbb{N}\right)$ summing to 1 . Let $U(s)=$ $\sum_{n=1}^{\infty} u_{n} s^{n}, F(s)=\sum_{n=1}^{\infty} f_{n} s^{n}$. Show that

  $$F(s)=\frac{U(s)}{1+U(s)} .$$

  Give a probabilistic interpretation of the numbers $u_{n}, f_{n}$ and $m_{n}=\sum_{i=1}^{n} u_{i}$.

  (d) Let the sequence $u_{n}$ be given by

  $$u_{2 n}=\left(\begin{array}{c} 2 n \\ n \end{array}\right)\left(\frac{1}{2}\right)^{2 n}, \quad u_{2 n+1}=0, \quad n \geqslant 1 .$$

  How is this related to the simple symmetric random walk on the integers $\mathbb{Z}$ starting from the origin, and its subsequent returns to the origin? Determine $F(s)$ in this case, either by calculating $U(s)$ or by showing that $F$ satisfies the quadratic equation

  $$F^{2}-2 F+s^{2}=0, \quad \text { for } \quad 0 \leqslant s<1 .$$

  comment

• B4.12

  Applied Probability | Part II, 2002

  Define a Poisson random measure. State and prove the Product Theorem for the jump times $J_{n}$ of a Poisson process with constant rate $\lambda$ and independent random variables $Y_{n}$ with law $\mu$. Write down the corresponding result for a Poisson process $\Pi$ in a space $E=\mathbb{R}^{d}$ with rate $\lambda(x)(x \in E)$ when we associate with each $X \in \Pi$ an independent random variable $m_{X}$ with density $\rho(X, d m)$.

  Prove Campbell's Theorem, i.e. show that if $M$ is a Poisson random measure on the space $E$ with intensity measure $\nu$ and $a: E \rightarrow \mathbb{R}$ is a bounded measurable function then

  $$\mathbf{E}\left[e^{\theta \Sigma}\right]=\exp \left(\int_{E}\left(e^{\theta a(y)}-1\right) \nu(d y)\right)$$

  where

  $$\Sigma=\int_{E} a(y) M(d y)=\sum_{X \in \Pi} a(X)$$

  Stars are scattered over three-dimensional space $\mathbb{R}^{3}$ in a Poisson process $\Pi$ with density $\nu(X)\left(X \in \mathbb{R}^{3}\right)$. Masses of the stars are independent random variables; the mass $m_{X}$ of a star at $X$ has the density $\rho(X, d m)$. The gravitational potential at the origin is given by

  $$F=\sum_{X \in \Pi} \frac{G m_{X}}{|X|}$$

  where $G$ is a constant. Find the moment generating function $\mathbf{E}\left[e^{\theta F}\right]$.

  A galaxy occupies a sphere of radius $R$ centred at the origin. The density of stars is $\nu(\mathbf{x})=1 /|\mathbf{x}|$ for points $\mathbf{x}$ inside the sphere; the mass of each star has the exponential distribution with mean $M$. Calculate the expected potential due to the galaxy at the origin. Let $C$ be a positive constant. Find the distribution of the distance from the origin to the nearest star whose contribution to the potential $F$ is at least $C$.

  comment

Coding and Cryptography

• A1.10

  Coding and Cryptography | Part II, 2002

  (i) Describe the original Hamming code of length 7 . Show how to encode a message word, and how to decode a received word involving at most one error. Explain why the procedure works.

  (ii) What is a linear binary code? What is its dual code? What is a cyclic binary code? Explain how cyclic binary codes of length $n$ correspond to polynomials in $\mathbb{F}_{2}[X]$ dividing $X^{n}+1$. Show that the dual of a cyclic code of length $n$ is cyclic of length $n$.

  Using the factorization

  $$X^{7}+1=(X+1)\left(X^{3}+X+1\right)\left(X^{3}+X^{2}+1\right)$$

  in $\mathbb{F}_{2}[X]$, find all cyclic binary codes of length 7 . Identify those which are Hamming codes and their duals. Justify your answer.

  comment

• A2.9

  Coding and Cryptography | Part II, 2002

  (i) Explain the idea of public key cryptography. Give an example of a public key system, explaining how it works.

  (ii) What is a general feedback register of length $d$ with initial fill $\left(X_{0}, \ldots, X_{d-1}\right)$ ? What is the maximal period of such a register, and why? What does it mean for such a register to be linear?

  Describe and justify the Berlekamp-Massey algorithm for breaking a cypher stream arising from a general linear feedback register of unknown length.

  Use the Berlekamp-Massey algorithm to find a linear recurrence in $\mathbb{F}_{2}$ with first eight terms $1,1,0,0,1,0,1,1$.

  comment

Combinatorics

• B1.5

  Combinatorics | Part II, 2002

  Prove that every graph $G$ on $n \geqslant 3$ vertices with minimal degree $\delta(G) \geqslant \frac{n}{2}$ is Hamiltonian. For each $n \geqslant 3$, give an example to show that this result does not remain true if we weaken the condition to $\delta(G) \geqslant \frac{n}{2}-1$ ( $n$ even) or $\delta(G) \geqslant \frac{n-1}{2}$ ( $n$ odd).

  Now let $G$ be a connected graph (with at least 2 vertices) without a cutvertex. Does $G$ Hamiltonian imply $G$ Eulerian? Does $G$ Eulerian imply $G$ Hamiltonian? Justify your answers.

  comment

• B2.5

  Combinatorics | Part II, 2002

  State and prove the local $L Y M$ inequality. Explain carefully when equality holds.

  Define the colex order and state the Kruskal-Katona theorem. Deduce that, if $n$ and $r$ are fixed positive integers with $1 \leqslant r \leqslant n-1$, then for every $1 \leqslant m \leqslant\left(\begin{array}{l}n \\ r\end{array}\right)$ we have

  $$\min \left\{|\partial \mathcal{A}|: \mathcal{A} \subset[n]^{(r)},|\mathcal{A}|=m\right\}=\min \left\{|\partial \mathcal{A}|: \mathcal{A} \subset[n+1]^{(r)},|\mathcal{A}|=m\right\}$$

  By a suitable choice of $n, r$ and $m$, show that this result does not remain true if we replace the lower shadow $\partial A$ with the upper shadow $\partial^{+} \mathcal{A}$.

  comment

• B4.1

  Combinatorics | Part II, 2002

  Write an essay on Ramsey theory. You should include the finite and infinite versions of Ramsey's theorem, together with a discussion of upper and lower bounds in the finite case.

  [You may restrict your attention to colourings by just 2 colours.]

  comment

Computational Statistics and Statistical Modelling

• A1.13

  Computational Statistics and Statistical Modelling | Part II, 2002

  (i) Suppose $Y_{1}, \ldots, Y_{n}$ are independent Poisson variables, and

  $$\mathbb{E}\left(Y_{i}\right)=\mu_{i}, \log \mu_{i}=\alpha+\beta^{T} x_{i}, 1 \leqslant i \leqslant n$$

  where $\alpha, \beta$ are unknown parameters, and $x_{1}, \ldots, x_{n}$ are given covariates, each of dimension $p$. Obtain the maximum-likelihood equations for $\alpha, \beta$, and explain briefly how you would check the validity of this model.

  (ii) The data below show $y_{1}, \ldots, y_{33}$, which are the monthly accident counts on a major US highway for each of the 12 months of 1970 , then for each of the 12 months of 1971 , and finally for the first 9 months of 1972 . The data-set is followed by the (slightly edited) $R$ output. You may assume that the factors 'Year' and 'month' have been set up in the appropriate fashion. Give a careful interpretation of this $R$ output, and explain (a) how you would derive the corresponding standardised residuals, and (b) how you would predict the number of accidents in October 1972 .

  $\begin{array}{llllllllllll}52 & 37 & 49 & 29 & 31 & 32 & 28 & 34 & 32 & 39 & 50 & 63 \\ 35 & 22 & 27 & 27 & 34 & 23 & 42 & 30 & 36 & 56 & 48 & 40 \\ 33 & 26 & 31 & 25 & 23 & 20 & 25 & 20 & 36 & & & \end{array}$

  $>$ first.glm $-\operatorname{glm}(\mathrm{y} \sim$ Year $+$ month, poisson $) ;$ summary(first.glm $)$

  Call:

  $\operatorname{glm}($ formula $=\mathrm{y} \sim$ Year $+$ month, family $=$ poisson $)$

  \begin{tabular}{lrlll} Coefficients: & & & & \ (Intercept) & Estimate & Std. Error & \multicolumn{1}{l}{ z value } & $\operatorname{Pr}(>|z|)$ \ Year1971 & $-0.81969$ & $0.09896$ & $38.600$ & $<2 e-16$ \ Year1972 & $-0.28794$ & $0.08267$ & $-3.483$ & $0.000496$ \ month2 & $-0.34484$ & $0.14176$ & $-2.433$ & $0.014994$ \ month3 & $-0.11466$ & $0.13296$ & $-0.862$ & $0.388459$ \ month4 & $-0.39304$ & $0.14380$ & $-2.733$ & $0.006271$ \ month5 & $-0.31015$ & $0.14034$ & $-2.210$ & $0.027108$ \ month6 & $-0.47000$ & $0.14719$ & $-3.193$ & $0.001408$ \ month7 & $-0.23361$ & $0.13732$ & $-1.701$ & $0.088889$ \ month8 & $-0.35667$ & $0.14226$ & $-2.507$ & $0.012168$ \ month9 & $-0.14310$ & $0.13397$ & $-1.068$ & $0.285444$ \ month10 & $0.10167$ & $0.13903$ & $0.731$ & $0.464628$ \ month11 & $0.13276$ & $0.13788$ & $0.963$ & $0.335639$ \ month12 & $0.18252$ & $0.13607$ & $1.341$ & $0.179812$ \end{tabular}

  Signif. codes: 0 (, $0.001$ (, $0.01$ (, $0.05$ '.

  (Dispersion parameter for poisson family taken to be 1 )

  $\begin{array}{rlll}\text { Null deviance: } & 101.143 & \text { on } 32 \text { degrees of freedom } \\ \text { Residual deviance: } & 27.273 & \text { on } 19 \text { degrees of freedom }\end{array}$

  Number of Fisher Scoring iterations: 3

  comment

• A2.12

  Computational Statistics and Statistical Modelling | Part II, 2002

  (i) Suppose that the random variable $Y$ has density function of the form

  $$f(y \mid \theta, \phi)=\exp \left[\frac{y \theta-b(\theta)}{\phi}+c(y, \phi)\right]$$

  where $\phi>0$. Show that $Y$ has expectation $b^{\prime}(\theta)$ and variance $\phi b^{\prime \prime}(\theta)$.

  (ii) Suppose now that $Y_{1}, \ldots, Y_{n}$ are independent negative exponential variables, with $Y_{i}$ having density function $f\left(y_{i} \mid \mu_{i}\right)=\frac{1}{\mu_{i}} e^{-y_{i} / \mu_{i}}$ for $y_{i}>0$. Suppose further that $g\left(\mu_{i}\right)=\beta^{T} x_{i}$ for $1 \leqslant i \leqslant n$, where $g(\cdot)$ is a known 'link' function, and $x_{1}, \ldots, x_{n}$ are given covariate vectors, each of dimension $p$. Discuss carefully the problem of finding $\hat{\beta}$, the maximum-likelihood estimator of $\beta$, firstly for the case $g\left(\mu_{i}\right)=1 / \mu_{i}$, and secondly for the case $g(\mu)=\log \mu_{i}$; in both cases you should state the large-sample distribution of $\hat{\beta}$.

  [Any standard theorems used need not be proved.]

  comment

• A4.14

  Computational Statistics and Statistical Modelling | Part II, 2002

  Assume that the $n$-dimensional observation vector $Y$ may be written as $Y=X \beta+\epsilon$, where $X$ is a given $n \times p$ matrix of rank $p, \beta$ is an unknown vector, with $\beta^{T}=\left(\beta_{1}, \ldots, \beta_{p}\right)$, and

  $$\epsilon \sim N_{n}\left(0, \sigma^{2} I\right)$$

  where $\sigma^{2}$ is unknown. Find $\hat{\beta}$, the least-squares estimator of $\beta$, and describe (without proof) how you would test

  $$H_{0}: \beta_{\nu}=0$$

  for a given $\nu$.

  Indicate briefly two plots that you could use as a check of the assumption $(*)$.

  Continued opposite Sulphur dioxide is one of the major air pollutants. A data-set presented by Sokal and Rohlf (1981) was collected on 41 US cities in 1969-71, corresponding to the following variables:

  $Y=$ sulphur dioxide content of air in micrograms per cubic metre

  $X 1=$ average annual temperature in degrees Fahrenheit

  $X 2$ = number of manufacturing enterprises employing 20 or more workers

  $X 3=$ population size (1970 census) in thousands

  $X 4=$ average annual wind speed in miles per hour

  $X 5=$ average annual precipitation in inches

  $X 6=$ average annual of days with precipitation per year $.$

  Interpret the $R$ output that follows below, quoting any standard theorems that you need to use.

  $$\begin{aligned} &>\text { next. } \operatorname{lm}-\operatorname{lm}(\log (\mathrm{Y}) \sim \mathrm{X} 1+\mathrm{X} 2+\mathrm{X} 3+\mathrm{X} 4+\mathrm{X} 5+\mathrm{X} 6) \\ &>\text { summary }(\text { next.lm }) \\ &\text { Call: } \operatorname{lm}(\text { formula }=\log (\mathrm{Y}) \sim \mathrm{X} 1+\mathrm{X} 2+\mathrm{X} 3+\mathrm{X} 4+\mathrm{X} 5+\mathrm{X} 6) \end{aligned}$$

  $$\begin{aligned} & \text { Call: } \operatorname{lm}(\text { formula }=\log (\mathrm{Y}) \sim \mathrm{X} 1+\mathrm{X} 2+\mathrm{X} 3+\mathrm{X} 4+\mathrm{X} 5+\mathrm{X} 6) \end{aligned}$$

  Residuals :

  $$\begin{array}{rrrrr} \text { Min } & 1 Q & \text { Median } & 3 Q & \text { Max } \\ \hline .79548 & -0.25538 & -0.01968 & 0.28328 & 0.98029 \end{array}$$

  $\begin{array}{lllll}-0.79548 & -0.25538 & -0.01968 & 0.28328 & 0.98029\end{array}$

  $\begin{array}{lrlcll}\text { Coefficients: } & & & & & \\ & \text { Estimate } & \text { Std. Error } & \text { t value } & \operatorname{Pr}(>|t|) & \\ \text { (Intercept) } & 7.2532456 & 1.4483686 & 5.008 & 1.68 \mathrm{e}-05 & * * * \\ \text { X1 } & -0.0599017 & 0.0190138 & -3.150 & 0.00339 & * * \\ \text { X2 } & 0.0012639 & 0.0004820 & 2.622 & 0.01298 & * \\ \text { X3 } & -0.0007077 & 0.0004632 & -1.528 & 0.13580 & \\ \text { X4 } & -0.1697171 & 0.0555563 & -3.055 & 0.00436 & * * \\ \text { X5 } & 0.0173723 & 0.0111036 & 1.565 & 0.12695 & \\ \text { X6 } & 0.0004347 & 0.0049591 & 0.088 & 0.93066\end{array}$

  Signif. codes: 0 ', $0.001$ ', $0.01$ ', $0.05$ ':

  Residual standard error: $0.448$ on 34 degrees of freedom

  Multiple R-Squared: $0.6541$

  F-statistic: $10.72$ on 6 and 34 degrees of freedom, p-value: $1.126 \mathrm{e}-06$

  comment

Differentiable Manifolds

• B1.8

  Differentiable Manifolds | Part II, 2002

  What is meant by a "bump function" on $\mathbb{R}^{n}$ ? If $U$ is an open subset of a manifold $M$, prove that there is a bump function on $M$ with support contained in $U$.

  Prove the following.

  (i) Given an open covering $\mathcal{U}$ of a compact manifold $M$, there is a partition of unity on $M$ subordinate to $\mathcal{U}$.

  (ii) Every compact manifold may be embedded in some Euclidean space.

  comment

• B2.7

  Differentiable Manifolds | Part II, 2002

  State, giving your reasons, whether the following are true or false.

  (a) Diffeomorphic connected manifolds must have the same dimension.

  (b) Every non-zero vector bundle has a nowhere-zero section.

  (c) Every projective space admits a volume form.

  (d) If a manifold $M$ has Euler characteristic zero, then $M$ is orientable.

  comment

• B4.4

  Differentiable Manifolds | Part II, 2002

  State and prove Stokes' Theorem for compact oriented manifolds-with-boundary.

  [You may assume results relating local forms on the manifold with those on its boundary provided you state them clearly.]

  Deduce that every differentiable map of the unit ball in $\mathbb{R}^{n}$ to itself has a fixed point.

  comment

Dynamical Systems

• B1.17

  Dynamical Systems | Part II, 2002

  Let $f_{c}$ be the map of the closed interval $[0,1]$ to itself given by

  $$f_{c}(x)=c x(1-x), \text { where } 0 \leqslant c \leqslant 4 .$$

  Sketch the graphs of $f_{c}$ and (without proof) of $f_{c}^{2}$, find their fixed points, and determine which of the fixed points of $f_{c}$ are attractors. Does your argument work for $c=3 ?$

  comment

• B3.17

  Dynamical Systems | Part II, 2002

  Let $\mathcal{A}$ be a finite alphabet of letters and $\Sigma$ either the semi-infinite space or the doubly infinite space of sequences whose elements are drawn from $\mathcal{A}$. Define the natural topology on $\Sigma$. If $W$ is a set of words, denote by $\Sigma_{W}$ the subspace of $\Sigma$ consisting of those sequences none of whose subsequences is in $W$. Prove that $\Sigma_{W}$ is a closed subspace of $\Sigma$; and state and prove a necessary and sufficient condition for a closed subspace of $\Sigma$ to have the form $\Sigma_{W}$ for some $W$.

  $$\begin{aligned} &\text { If } \mathcal{A}=\{0,1\} \text { and } \quad W=\{000,111,010,101\} \end{aligned}$$

  what is the space $\Sigma_{W}$ ?

  comment

• B4.17

  Dynamical Systems | Part II, 2002

  Let $\mathcal{S}$ be a metric space, $F$ a map of $\mathcal{S}$ to itself and $P$ a point of $\mathcal{S}$. Define an attractor for $F$ and an omega point of the orbit of $P$ under $F$.

  Let $f$ be the map of $\mathbb{R}$ to itself given by

  $$f(x)=x+\frac{1}{2}+c \sin ^{2} 2 \pi x$$

  where $c>0$ is so small that $f^{\prime}(x)>0$ for all $x$, and let $F$ be the map of $\mathbb{R} / \mathbb{Z}$ to itself induced by $f$. What points if any are

  (a) attractors for $F^{2}$,

  (b) omega points of the orbit of some point $P$ under $F$ ?

  Is the cycle $\left\{0, \frac{1}{2}\right\}$ an attractor?

  In the notation of the first two sentences, let $\mathcal{C}$ be a cycle of order $M$ and assume that $F$ is continuous. Prove that $\mathcal{C}$ is an attractor for $F$ if and only if each point of $\mathcal{C}$ is an attractor for $F^{M}$.

  comment

Dynamics of Differential Equations

• A1.6

  Dynamics of Differential Equations | Part II, 2002

  (i) A system in $\mathbb{R}^{2}$ obeys the equations:

  $$\begin{aligned} &\dot{x}=x-x^{5}-2 x y^{4}-2 y^{3}\left(a-x^{2}\right) \\ &\dot{y}=y-x^{4} y-2 y^{5}+x^{3}\left(a-x^{2}\right) \end{aligned}$$

  where $a$ is a positive constant.

  By considering the quantity $V=\alpha x^{4}+\beta y^{4}$, where $\alpha$ and $\beta$ are appropriately chosen, show that if $a>1$ then there is a unique fixed point and a unique limit cycle. How many fixed points are there when $a<1$ ?

  (ii) Consider the second order system

  $$\ddot{x}-\left(a-b x^{2}\right) \dot{x}+x-x^{3}=0,$$

  where $a, b$ are constants.

  (a) Find the fixed points and determine their stability.

  (b) Show that if the fixed point at the origin is unstable and $3 a>b$ then there are no limit cycles.

  [You may find it helpful to use the Liénard coordinate $z=\dot{x}-a x+\frac{1}{3} b x^{3}$.]

  comment

• A2.6 B2.4

  Dynamics of Differential Equations | Part II, 2002

  (i) Define the terms stable manifold and unstable manifold of a hyperbolic fixed point $\mathbf{x}_{0}$ of a dynamical system. State carefully the stable manifold theorem.

  Give an approximation, correct to fourth order in $|\mathbf{x}|$, for the stable and unstable manifolds of the origin for the system

  $$\left(\begin{array}{c} \dot{x} \\ \dot{y} \end{array}\right)=\left(\begin{array}{c} x+x^{2}-y^{2} \\ -y+x^{2} \end{array}\right) .$$

  (ii) State, without proof, the centre manifold theorem. Show that the fixed point at the origin of the system

  $$\begin{aligned} &\dot{x}=y-x+a x^{3}, \\ &\dot{y}=r x-y-z y \\ &\dot{z}=-z+x y \end{aligned}$$

  where $a$ is a constant, is non-hyperbolic at $r=1$.

  Using new coordinates $v=x+y, w=x-y$, find the centre manifold in the form

  $$w=\alpha v^{3}+\ldots, \quad z=\beta v^{2}+\gamma v^{4}+\ldots$$

  for constants $\alpha, \beta, \gamma$ to be determined. Hence find the evolution equation on the centre manifold in the form

  $$\dot{v}=\frac{1}{8}(a-1) v^{3}+\left(\frac{(3 a+1)(a+1)}{128}+\frac{(a-1)}{32}\right) v^{5}+\ldots$$

  Ignoring higher order terms, give conditions on $a$ that guarantee that the origin is asymptotically stable.

  comment

• A3.6 B3.4

  Dynamics of Differential Equations | Part II, 2002

  (i) Define the Floquet multiplier and Liapunov exponent for a periodic orbit $\hat{\mathbf{x}}(t)$ of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ in $\mathbb{R}^{2}$. Show that one multiplier is always unity, and that the other is given by

  $$\exp \left(\int_{0}^{T} \nabla \cdot \mathbf{f}(\hat{\mathbf{x}}(t)) d t\right)$$

  where $T$ is the period of the orbit.

  The Van der Pol oscillator $\ddot{x}+\epsilon \dot{x}\left(x^{2}-1\right)+x=0,0<\epsilon \ll 1$ has a limit cycle $\hat{x}(t) \approx 2 \sin t$. Show using $(*)$ that this orbit is stable.

  (ii) Show, by considering the normal form for a Hopf bifurcation from a fixed point $\mathbf{x}_{0}(\mu)$ of a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x}, \mu)$, that in some neighbourhood of the bifurcation the periodic orbit is stable when it exists in the range of $\mu$ for which $\mathbf{x}_{0}$ is unstable, and unstable in the opposite case.

  Now consider the system

  $$\left.\begin{array}{l} \dot{x}=x(1-y)+\mu x \\ \dot{y}=y(x-1)-\mu x \end{array}\right\} \quad x>0$$

  Show that the fixed point $(1+\mu, 1+\mu)$ has a Hopf bifurcation when $\mu=0$, and is unstable (stable) when $\mu>0(\mu<0)$.

  Suppose that a periodic orbit exists in $\mu>0$. Show without solving for the orbit that the result of part (i) shows that such an orbit is unstable. Define a similar result for $\mu<0$.

  What do you conclude about the existence of periodic orbits when $\mu \neq 0$ ? Check your answer by applying Dulac's criterion to the system, using the weighting $\rho=e^{-(x+y)}$.

  comment

• A4.6

  Dynamics of Differential Equations | Part II, 2002

  Define the terms homoclinic orbit, heteroclinic orbit and heteroclinic loop. In the case of a dynamical system that possesses a homoclinic orbit, explain, without detailed calculation, how to calculate its stability.

  A second order dynamical system depends on two parameters $\mu_{1}$ and $\mu_{2}$. When $\mu_{1}=\mu_{2}=0$ there is a heteroclinic loop between the points $P_{1}, P_{2}$ as in the diagram.

  

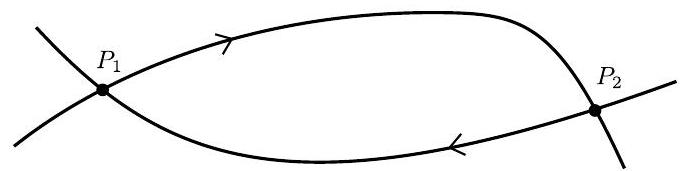
  When $\mu_{1}, \mu_{2}$ are small there are trajectories that pass close to the fixed points $P_{1}, P_{2}$ :

  By adapting the method used above for trajectories near homoclinic orbits, show that the distances $y_{n}, y_{n+1}$ to the stable manifold at $P_{1}$ on successive returns are related to $z_{n}$, $z_{n+1}$, the corresponding distances near $P_{2}$, by coupled equations of the form

  $$\left.\begin{array}{rl} z_{n} & =\left(y_{n}\right)^{\gamma_{1}}+\mu_{1}, \\ y_{n+1} & =\left(z_{n}\right)^{\gamma_{2}}+\mu_{2}, \end{array}\right\}$$

  where any arbitrary constants have been removed by rescaling, and $\gamma_{1}, \gamma_{2}$ depend on conditions near $P_{1}, P_{2}$. Show from these equations that there is a stable heteroclinic orbit $\left(\mu_{1}=\mu_{2}=0\right)$ if $\gamma_{1} \gamma_{2}>1$. Show also that in the marginal situation $\gamma_{1}=2, \gamma_{2}=\frac{1}{2}$ there can be a stable fixed point for small positive $y, z$ if $\mu_{2}<0, \mu_{2}^{2}<\mu_{1}$. Explain carefully the form of the orbit of the original dynamical system represented by the solution of the above map when $\mu_{2}^{2}=\mu_{1}$.

  comment

Electrodynamics

• B1.21

  Electrodynamics | Part II, 2002

  Explain how one can write Maxwell's equations in relativistic form by introducing an antisymmetric field strength tensor $F_{a b}$.

  In an inertial frame $S$, the electric and magnetic fields are $\mathbf{E}$ and $\mathbf{B}$. Suppose that there is a second inertial frame $S^{\prime}$ moving with velocity $v$ along the $x$-axis relative to $S$. Derive the rules for finding the electric and magnetic fields $\mathbf{E}^{\prime}$ and $\mathbf{B}^{\prime}$ in the frame $S^{\prime}$. Show that $|\mathbf{E}|^{2}-|\mathbf{B}|^{2}$ and $\mathbf{E} \cdot \mathbf{B}$ are invariant under Lorentz transformations.

  Suppose that $\mathbf{E}=E_{0}(0,1,0)$ and $\mathbf{B}=E_{0}(0, \cos \theta, \sin \theta)$, where $0 \leq \theta<\pi / 2$. At what velocity must an observer be moving in the frame $S$ for the electric and magnetic fields to appear to be parallel?

  Comment on the case $\theta=\pi / 2$.

  comment

• B2.20

  Electrodynamics | Part II, 2002

  A particle of rest mass $m$ and charge $q$ moves in an electromagnetic field given by a potential $A_{a}$ along a trajectory $x^{a}(\tau)$, where $\tau$ is the proper time along the particle's worldline. The action for such a particle is

  $$I=\int\left(m \sqrt{-\eta_{a b} \dot{x}^{a} \dot{x}^{b}}-q A_{a} \dot{x}^{a}\right) d \tau .$$

  Show that the Euler-Lagrange equations resulting from this action reproduce the relativistic equation of motion for the particle.

  Suppose that the particle is moving in the electrostatic field of a fixed point charge $Q$ with radial electric field $E_{r}$ given by

  $$E_{r}=\frac{Q}{4 \pi \epsilon_{0} r^{2}} .$$

  Show that one can choose a gauge such that $A_{i}=0$ and only $A_{0} \neq 0$. Find $A_{0}$.

  Assume that the particle executes planar motion, which in spherical polar coordinates $(r, \theta, \phi)$ can be taken to be in the plane $\theta=\pi / 2$. Derive the equations of motion for $t$ and $\phi$.

  By using the fact that $\eta_{a b} \dot{x}^{a} \dot{x}^{b}=-1$, find the equation of motion for $r$, and hence show that the shape of the orbit is described by

  $$\frac{d r}{d \phi}=\pm \frac{r^{2}}{\ell} \sqrt{\left(E+\frac{\gamma}{r}\right)^{2}-1-\frac{\ell^{2}}{r^{2}}}$$

  where $E(>1)$ and $\ell$ are constants of integration and $\gamma$ is to be determined.

  By putting $u=1 / r$ or otherwise, show that if $\gamma^{2}<\ell^{2}$ then the orbits are bounded and generally not closed, and show that the angle between successive minimal values of $r$ is $2 \pi\left(1-\gamma^{2} / \ell^{2}\right)^{-1 / 2}$.

  comment

• B4.21

  Electrodynamics | Part II, 2002

  Derive Larmor's formula for the rate at which radiation is produced by a particle of charge $q$ moving along a trajectory $\mathbf{x}(t)$.

  A non-relativistic particle of mass $m$, charge $q$ and energy $E$ is incident along a radial line in a central potential $V(r)$. The potential is vanishingly small for $r$ very large, but increases without bound as $r \rightarrow 0$. Show that the total amount of energy $\mathcal{E}$ radiated by the particle is

  $$\mathcal{E}=\frac{\mu_{0} q^{2}}{3 \pi m^{2}} \sqrt{\frac{m}{2}} \int_{r_{0}}^{\infty} \frac{1}{\sqrt{E-V(r)}}\left(\frac{d V}{d r}\right)^{2} d r$$

  where $V\left(r_{0}\right)=E$.

  Suppose that $V$ is the Coulomb potential $V(r)=A / r$. Evaluate $\mathcal{E}$.

  comment

Electromagnetism

• A $1 . 5 \quad$ B $1 . 4 \quad$

  Electromagnetism | Part II, 2002

  (i) Show that, in a region where there is no magnetic field and the charge density vanishes, the electric field can be expressed either as minus the gradient of a scalar potential $\phi$ or as the curl of a vector potential A. Verify that the electric field derived from

  $$\mathbf{A}=\frac{1}{4 \pi \epsilon_{0}} \frac{\mathbf{p} \wedge \mathbf{r}}{r^{3}}$$

  is that of an electrostatic dipole with dipole moment $\mathbf{p}$.

  [You may assume the following identities:

  $$\begin{gathered} \nabla(\mathbf{a} \cdot \mathbf{b})=\mathbf{a} \wedge(\nabla \wedge \mathbf{b})+\mathbf{b} \wedge(\nabla \wedge \mathbf{a})+(\mathbf{a} \cdot \nabla) \mathbf{b}+(\mathbf{b} \cdot \nabla) \mathbf{a} \\ \nabla \wedge(\mathbf{a} \wedge \mathbf{b})=(\mathbf{b} \cdot \nabla) \mathbf{a}-(\mathbf{a} \cdot \nabla) \mathbf{b}+\mathbf{a} \nabla \cdot \mathbf{b}-\mathbf{b} \nabla \cdot \mathbf{a} .] \end{gathered}$$

  (ii) An infinite conducting cylinder of radius $a$ is held at zero potential in the presence of a line charge parallel to the axis of the cylinder at distance $s_{0}>a$, with charge density $q$ per unit length. Show that the electric field outside the cylinder is equivalent to that produced by replacing the cylinder with suitably chosen image charges.

  comment

• A2.5

  Electromagnetism | Part II, 2002

  (i) Show that the Lorentz force corresponds to a curvature force and the gradient of a magnetic pressure, and that it can be written as the divergence of a second rank tensor, the Maxwell stress tensor.

  Consider the potential field $\mathbf{B}$ given by $\mathbf{B}=-\nabla \Phi$, where

  $$\Phi(x, y)=\left(\frac{B_{0}}{k}\right) \cos k x e^{-k y}$$

  referred to cartesian coordinates $(x, y, z)$. Obtain the Maxwell stress tensor and verify that its divergence vanishes.

  (ii) The magnetic field in a stellar atmosphere is maintained by steady currents and the Lorentz force vanishes. Show that there is a scalar field $\alpha$ such that $\nabla \wedge \mathbf{B}=\alpha \mathbf{B}$ and $\mathbf{B} \cdot \nabla \alpha=0$. Show further that if $\alpha$ is constant, then $\nabla^{2} \mathbf{B}+\alpha^{2} \mathbf{B}=0$. Obtain a solution in the form $\mathbf{B}=\left(B_{1}(z), B_{2}(z), 0\right)$; describe the structure of this field and sketch its variation in the $z$-direction.

  comment

• A3.5 B3.3

  Electromagnetism | Part II, 2002

  (i) A plane electromagnetic wave in a vacuum has an electric field

  $$\mathbf{E}=\left(E_{1}, E_{2}, 0\right) \cos (k z-\omega t),$$

  referred to cartesian axes $(x, y, z)$. Show that this wave is plane polarized and find the orientation of the plane of polarization. Obtain the corresponding plane polarized magnetic field and calculate the rate at which energy is transported by the wave.

  (ii) Suppose instead that

  $$\mathbf{E}=\left(E_{1} \cos (k z-\omega t), E_{2} \cos (k z-\omega t+\phi), 0\right),$$

  with $\phi$ a constant, $0<\phi<\pi$. Show that, if the axes are now rotated through an angle $\psi$ so as to obtain an elliptically polarized wave with an electric field

  $$\mathbf{E}^{\prime}=\left(F_{1} \cos (k z-\omega t+\chi), F_{2} \sin (k z-\omega t+\chi), 0\right),$$

  then

  $$\tan 2 \psi=\frac{2 E_{1} E_{2} \cos \phi}{E_{1}^{2}-E_{2}^{2}} .$$

  Show also that if $E_{1}=E_{2}=E$ there is an elliptically polarized wave with

  $$\mathbf{E}^{\prime}=\sqrt{2} E\left(\cos \left(k z-\omega t+\frac{1}{2} \phi\right) \cos \frac{1}{2} \phi, \sin \left(k z-\omega t+\frac{1}{2} \phi\right) \sin \frac{1}{2} \phi, 0\right) .$$

  comment

• A4.5

  Electromagnetism | Part II, 2002

  State the four integral relationships between the electric field $\mathbf{E}$ and the magnetic field $\mathbf{B}$ and explain their physical significance. Derive Maxwell's equations from these relationships and show that $\mathbf{E}$ and $\mathbf{B}$ can be described by a scalar potential $\phi$ and a vector potential A which satisfy the inhomogeneous wave equations

  $$\begin{gathered} \nabla^{2} \phi-\epsilon_{0} \mu_{0} \frac{\partial^{2} \phi}{\partial t^{2}}=-\frac{\rho}{\epsilon_{0}} \\ \nabla^{2} \mathbf{A}-\epsilon_{0} \mu_{0} \frac{\partial^{2} \mathbf{A}}{\partial t^{2}}=-\mu_{0} \mathbf{j} \end{gathered}$$

  If the current $\mathbf{j}$ satisfies Ohm's law and the charge density $\rho=0$, show that plane waves of the form

  $$\mathbf{A}=A(z, t) e^{i \omega t} \hat{\mathbf{x}},$$

  where $\hat{\mathbf{x}}$ is a unit vector in the $x$-direction of cartesian axes $(x, y, z)$, are damped. Find an approximate expression for $A(z, t)$ when $\omega \ll \sigma / \epsilon_{0}$, where $\sigma$ is the electrical conductivity.

  comment

Fluid Dynamics II

• B1.25

  Fluid Dynamics II | Part II, 2002

  State the minimum dissipation theorem for Stokes flow in a bounded domain.

  Fluid of density $\rho$ and viscosity $\mu$ fills an infinite cylindrical annulus $a \leq r \leq b$ between a fixed cylinder $r=a$ and a cylinder $r=b$ which rotates about its axis with constant angular velocity $\Omega$. In cylindrical polar coordinates $(r, \theta, z)$, the fluid velocity is $\mathbf{u}=(0, v(r), 0)$. The Reynolds number $\rho \Omega b^{2} / \mu$ is not necessarily small. Show that $v(r)=A r+B / r$, where $A$ and $B$ are constants to be determined.

  [You may assume that $\nabla^{2} \mathbf{u}=\left(0, \nabla^{2} v-v / r^{2}, 0\right)$ and $(\mathbf{u} \cdot \nabla) \mathbf{u}=\left(-v^{2} / r, 0,0\right) .$ ]

  Show that the outer cylinder exerts a couple $G_{0}$ per unit length on the fluid, where

  $$G_{0}=\frac{4 \pi \mu \Omega a^{2} b^{2}}{b^{2}-a^{2}} .$$

  [You may assume that, in standard notation, $e_{r \theta}=\frac{r}{2} \frac{d}{d r}\left(\frac{v}{r}\right)$.]

  Suppose now that $b \geq \sqrt{2} a$ and that the cylinder $r=a$ is replaced by a fixed cylinder whose cross-section is a square of side $2 a$ centred on $r=0$, all other conditions being unchanged. The flow may still be assumed steady. Explaining your argument carefully, show that the couple $G$ now required to maintain the motion of the outer cylinder is greater than $G_{0}$.

  comment

• B2.24

  Fluid Dynamics II | Part II, 2002

  A thin layer of liquid of kinematic viscosity $\nu$ flows under the influence of gravity down a plane inclined at an angle $\alpha$ to the horizontal $(0 \leq \alpha \leq \pi / 2)$. With origin $O$ on the plane, and axes $O x$ down the line of steepest slope and $O y$ normal to the plane, the free surface is given by $y=h(x, t)$, where $|\partial h / \partial x| \ll 1$. The pressure distribution in the liquid may be assumed to be hydrostatic. Using the approximations of lubrication theory, show that

  $$\frac{\partial h}{\partial t}=\frac{g}{3 \nu} \frac{\partial}{\partial x}\left\{h^{3}\left(\cos \alpha \frac{\partial h}{\partial x}-\sin \alpha\right)\right\} .$$

  Now suppose that

  $$h=h_{0}+\eta(x, t)$$

  where

  $$\eta(x, 0)=\eta_{0} e^{-x^{2} / a^{2}}$$

  and $h_{0}, \eta_{0}$ and $a$ are constants with $\eta_{0} \ll a, h_{0}$. Show that, to leading order,

  $$\eta(x, t)=\frac{a \eta_{0}}{\left(a^{2}+4 D t\right)^{1 / 2}} \exp \left\{-\frac{(x-U t)^{2}}{a^{2}+4 D t}\right\}$$

  where $U$ and $D$ are constants to be determined.

  Explain in physical terms the meaning of this solution.

  comment

• B3.24

  Fluid Dynamics II | Part II, 2002

  (i) Suppose that, with spherical polar coordinates, the Stokes streamfunction

  $$\Psi_{\lambda}(r, \theta)=r^{\lambda} \sin ^{2} \theta \cos \theta$$

  represents a Stokes flow and thus satisfies the equation $D^{2}\left(D^{2} \Psi_{\lambda}\right)=0$, where

  $$D^{2}=\frac{\partial^{2}}{\partial r^{2}}+\frac{\sin \theta}{r^{2}} \frac{\partial}{\partial \theta} \frac{1}{\sin \theta} \frac{\partial}{\partial \theta} .$$

  Show that the possible values of $\lambda$ are $5,3,0$ and $-2$. For which of these values is the corresponding flow irrotational? Sketch the streamlines of the flow for the case $\lambda=3$.

  (ii) A spherical drop of liquid of viscosity $\mu_{1}$, radius $a$ and centre at $r=0$, is suspended in another liquid of viscosity $\mu_{2}$ which flows with streamfunction

  $$\Psi \sim \Psi_{\infty}(r, \theta)=\alpha r^{3} \sin ^{2} \theta \cos \theta$$

  far from the drop. The two liquids are of equal densities, surface tension is sufficiently strong to keep the drop spherical, and inertia is negligible. Show that

  $$\Psi= \begin{cases}\left(A r^{5}+B r^{3}\right) \sin ^{2} \theta \cos \theta & (r<a), \\ \left(\alpha r^{3}+C+D / r^{2}\right) \sin ^{2} \theta \cos \theta & (r>a)\end{cases}$$

  and obtain four equations determining the constants $A, B, C$ and $D$. (You need not solve these equations.)

  [You may assume, with standard notation, that

  $$\left.u_{r}=\frac{1}{r^{2} \sin \theta} \frac{\partial \Psi}{\partial \theta} \quad, \quad u_{\theta}=-\frac{1}{r \sin \theta} \frac{\partial \Psi}{\partial r} \quad, \quad e_{r \theta}=\frac{1}{2}\left\{r \frac{\partial}{\partial r}\left(\frac{u_{\theta}}{r}\right)+\frac{1}{r} \frac{\partial u_{r}}{\partial \theta}\right\} .\right]$$

  comment

• B4.26

  Fluid Dynamics II | Part II, 2002

  Write an essay on boundary-layer theory and its application to the generation of lift in aerodynamics.

  You should include discussion of the derivation of the boundary-layer equation, the similarity transformation leading to the Falkner-Skan equation, the influence of an adverse pressure gradient, and the mechanism(s) by which circulation is generated in flow past bodies with a sharp trailing edge.

  comment

Foundations of Quantum Mechanics

• A2.13 B2.21

  Foundations of Quantum Mechanics | Part II, 2002

  (i) A Hamiltonian $H_{0}$ has energy eigenvalues $E_{r}$ and corresponding non-degenerate eigenstates $|r\rangle$. Show that under a small change in the Hamiltonian $\delta H$,

  $$\delta|r\rangle=\sum_{s \neq r} \frac{\langle s|\delta H| r\rangle}{E_{r}-E_{s}}|s\rangle,$$

  and derive the related formula for the change in the energy eigenvalue $E_{r}$ to first and second order in $\delta H$.

  (ii) The Hamiltonian for a particle moving in one dimension is $H=H_{0}+\lambda H^{\prime}$, where $H_{0}=p^{2} / 2 m+V(x), H^{\prime}=p / m$ and $\lambda$ is small. Show that

  $$\frac{i}{\hbar}\left[H_{0}, x\right]=H^{\prime}$$

  and hence that

  $$\delta E_{r}=-\lambda^{2} \frac{i}{\hbar}\left\langle r\left|H^{\prime} x\right| r\right\rangle=\lambda^{2} \frac{i}{\hbar}\left\langle r\left|x H^{\prime}\right| r\right\rangle$$

  to second order in $\lambda$.

  Deduce that $\delta E_{r}$ is independent of the particular state $|r\rangle$ and explain why this change in energy is exact to all orders in $\lambda$.

  comment

• A3.13 B3.21

  Foundations of Quantum Mechanics | Part II, 2002

  (i) Two particles with angular momenta $j_{1}, j_{2}$ and basis states $\left|j_{1} m_{1}\right\rangle,\left|j_{2} m_{2}\right\rangle$ are combined to give total angular momentum $j$ and basis states $|j m\rangle$. State the possible values of $j, m$ and show how a state with $j=m=j_{1}+j_{2}$ can be constructed. Briefly describe, for a general allowed value of $j$, what the Clebsch-Gordan coefficients are.

  (ii) If the angular momenta $j_{1}$ and $j_{2}$ are both 1 show that the combined state $|20\rangle$ is

  

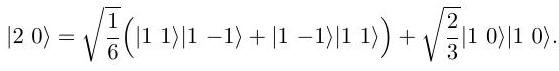
  Determine the corresponding expressions for the combined states $\left|\begin{array}{lll}1 & 0\rangle\end{array}\right\rangle$ and $|0 \quad 0\rangle$, assuming that they are respectively antisymmetric and symmetric under interchange of the two particles.

  If the combined system is in state $|0 \quad 0\rangle$ what is the probability that measurements of the $z$-component of angular momentum for either constituent particle will give the value of 1 ?

  $\left[\right.$ Hint: $\left.\quad J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle .\right]$

  comment

• A4.15 B4.22

  Foundations of Quantum Mechanics | Part II, 2002

  Discuss the consequences of indistinguishability for a quantum mechanical state consisting of two identical, non-interacting particles when the particles have (a) spin zero, (b) spin 1/2.

  The stationary Schrödinger equation for one particle in the potential

  $$-\frac{2 e^{2}}{4 \pi \epsilon_{0} r}$$

  has normalized, spherically symmetric, real wave functions $\psi_{n}(\mathbf{r})$ and energy eigenvalues $E_{n}$ with $E_{0}<E_{1}<E_{2}<\cdots$. What are the consequences of the Pauli exclusion principle for the ground state of the helium atom? Assuming that wavefunctions which are not spherically symmetric can be ignored, what are the states of the first excited energy level of the helium atom?

  [You may assume here that the electrons are non-interacting.]

  Show that, taking into account the interaction between the two electrons, the estimate for the energy of the ground state of the helium atom is

  $$2 E_{0}+\frac{e^{2}}{4 \pi \epsilon_{0}} \int \frac{d^{3} \mathbf{r}_{1} d^{3} \mathbf{r}_{2}}{\left|\mathbf{r}_{1}-\mathbf{r}_{2}\right|} \psi_{0}^{2}\left(\mathbf{r}_{1}\right) \psi_{0}^{2}\left(\mathbf{r}_{2}\right)$$

  comment

Functional Analysis

• A1.3

  Functional Analysis | Part II, 2002

  (i) Let $P_{r}\left(e^{i \theta}\right)$ be the real part of $\frac{1+r e^{i \theta}}{1-r e^{i \theta}}$. Establish the following properties of $P_{r}$ for $0 \leqslant r<1$ : (a) $0<P_{r}\left(e^{i \theta}\right)=P_{r}\left(e^{-i \theta}\right) \leqslant \frac{1+r}{1-r}$; (b) $P_{r}\left(e^{i \theta}\right) \leqslant P_{r}\left(e^{i \delta}\right)$ for $0<\delta \leqslant|\theta| \leqslant \pi$; (c) $P_{r}\left(e^{i \theta}\right) \rightarrow 0$, uniformly on $0<\delta \leqslant|\theta| \leqslant \pi$, as $r$ increases to 1 .

  (ii) Suppose that $f \in L^{1}(\mathbf{T})$, where $\mathbf{T}$ is the unit circle $\left\{e^{i \theta}:-\pi \leqslant \theta \leqslant \pi\right\}$. By definition, $\|f\|_{1}=\frac{1}{2 \pi} \int_{-\pi}^{\pi}\left|f\left(e^{i \theta}\right)\right| d \theta$. Let

  $$P_{r}(f)\left(e^{i \theta}\right)=\frac{1}{2 \pi} \int_{-\pi}^{\pi} P_{r}\left(e^{i(\theta-t)}\right) f\left(e^{i t}\right) d t$$

  Show that $P_{r}(f)$ is a continuous function on $\mathbf{T}$, and that $\left\|P_{r}(f)\right\|_{1} \leqslant\|f\|_{1}$.

  [You may assume without proof that $\frac{1}{2 \pi} \int_{-\pi}^{\pi} P_{r}\left(e^{i \theta}\right) d \theta=1$.]

  Show that $P_{r}(f) \rightarrow f$, uniformly on $\mathbf{T}$ as $r$ increases to 1 , if and only if $f$ is a continuous function on $\mathbf{T}$.

  Show that $\left\|P_{r}(f)-f\right\|_{1} \rightarrow 0$ as $r$ increases to 1 .

  comment

• A2.3 B2.2

  Functional Analysis | Part II, 2002

  (i) State and prove the parallelogram law for Hilbert spaces.

  Suppose that $K$ is a closed linear subspace of a Hilbert space $H$ and that $x \in H$. Show that $x$ is orthogonal to $K$ if and only if 0 is the nearest point to $x$ in $K$.

  (ii) Suppose that $H$ is a Hilbert space and that $\phi$ is a continuous linear functional on $H$ with $\|\phi\|=1$. Show that there is a sequence $\left(h_{n}\right)$ of unit vectors in $H$ with $\phi\left(h_{n}\right)$ real and $\phi\left(h_{n}\right)>1-1 / n$.

  Show that $h_{n}$ converges to a unit vector $h$, and that $\phi(h)=1$.

  Show that $h$ is orthogonal to $N$, the null space of $\phi$, and also that $H=N \oplus \operatorname{span}(h)$.

  Show that $\phi(k)=\langle k, h\rangle$, for all $k \in H$.

  comment

• A3.3 B3.2

  Functional Analysis | Part II, 2002

  (i) Suppose that $\left(f_{n}\right)$ is a decreasing sequence of continuous real-valued functions on a compact metric space $(X, d)$ which converges pointwise to 0 . By considering sets of the form $B_{n}=\left\{x: f_{n}(x)<\epsilon\right\}$, for $\epsilon>0$, or otherwise, show that $f_{n}$ converges uniformly to 0 .

  Can the condition that $\left(f_{n}\right)$ is decreasing be dropped? Can the condition that $(X, d)$ is compact be dropped? Justify your answers.

  (ii) Suppose that $k$ is a positive integer. Define polynomials $p_{n}$ recursively by

  $$p_{0}=0, \quad p_{n+1}(t)=p_{n}(t)+\left(t-p_{n}^{k}(t)\right) / k$$

  Show that $0 \leqslant p_{n}(t) \leqslant p_{n+1}(t) \leqslant t^{1 / k}$, for $t \in[0,1]$, and show that $p_{n}(t)$ converges to $t^{1 / k}$ uniformly on $[0,1]$.

  [You may wish to use the identity $a^{k}-b^{k}=(a-b)\left(a^{k-1}+a^{k-2} b+\ldots+b^{k-1}\right)$.]

  Suppose that $A$ is a closed subalgebra of the algebra $C(X)$ of continuous real-valued functions on a compact metric space $(X, d)$, equipped with the uniform norm, and suppose that $A$ has the property that for each $x \in X$ there exists $a \in A$ with $a(x) \neq 0$. Show that there exists $h \in A$ such that $0<h(x) \leqslant 1$ for all $x \in X$.

  Show that $h^{1 / k} \in A$ for each positive integer $k$, and show that $A$ contains the constant functions.

  comment

• A4.3

  Functional Analysis | Part II, 2002

  Define the distribution function $\Phi_{f}$ of a non-negative measurable function $f$ on the interval $I=[0,1]$. Show that $\Phi_{f}$ is a decreasing non-negative function on $[0, \infty]$ which is continuous on the right.

  Define the Lebesgue integral $\int_{I} f d m$. Show that $\int_{I} f d m=0$ if and only if $f=0$ almost everywhere.

  Suppose that $f$ is a non-negative Riemann integrable function on $[0,1]$. Show that there are an increasing sequence $\left(g_{n}\right)$ and a decreasing sequence $\left(h_{n}\right)$ of non-negative step functions with $g_{n} \leqslant f \leqslant h_{n}$ such that $\int_{0}^{1}\left(h_{n}(x)-g_{n}(x)\right) d x \rightarrow 0$.

  Show that the functions $g=\lim _{n} g_{n}$ and $h=\lim _{n} h_{n}$ are equal almost everywhere, that $f$ is measurable and that the Lebesgue integral $\int_{I} f d m$ is equal to the Riemann integral $\int_{0}^{1} f(x) d x$.

  Suppose that $j$ is a Riemann integrable function on $[0,1]$ and that $j(x)>0$ for all $x$. Show that $\int_{0}^{1} j(x) d x>0$.

  comment

Galois Theory

• B1.7

  Galois Theory | Part II, 2002

  Let $F \subset K$ be a finite extension of fields and let $G$ be the group of $F$-automorphisms of $K$. State a result relating the order of $G$ to the degree $[K: F]$.

  Now let $K=k\left(X_{1}, \ldots, X_{4}\right)$ be the field of rational functions in four variables over a field $k$ and let $F=k\left(s_{1}, \ldots, s_{4}\right)$ where $s_{1}, \ldots, s_{4}$ are the elementary symmetric polynomials in $k\left[X_{1}, \ldots, X_{4}\right]$. Show that the degree $[K: F] \leqslant 4$ ! and deduce that $F$ is the fixed field of the natural action of the symmetric group $S_{4}$ on $K$.

  Show that $X_{1} X_{3}+X_{2} X_{4}$ has a cubic minimum polynomial over $F$. Let $G=$ $\langle\sigma, \tau\rangle \subset S_{4}$ be the dihedral group generated by the permutations $\sigma=(1234)$ and $\tau=(13)$. Show that the fixed field of $G$ is $F\left(X_{1} X_{3}+X_{2} X_{4}\right)$. Find the fixed field of the subgroup $H=\left\langle\sigma^{2}, \tau\right\rangle$.

  comment

• B3.6

  Galois Theory | Part II, 2002

  Show that the polynomial $f(X)=X^{5}+27 X+16$ has no rational roots. Show that the splitting field of $f$ over the finite field $\mathbb{F}_{3}$ is an extension of degree 4 . Hence deduce that $f$ is irreducible over the rationals. Prove that $f$ has precisely two (non-multiple) roots over the finite field $\mathbb{F}_{7}$. Find the Galois group of $f$ over the rationals.

  [You may assume any general results you need including the fact that $A_{5}$ is the only index 2 subgroup of $S_{5}$.]

  comment

• B4.3

  Galois Theory | Part II, 2002

  Suppose $K, L$ are fields and $\sigma_{1}, \ldots, \sigma_{m}$ are distinct embeddings of $K$ into $L$. Prove that there do not exist elements $\lambda_{1}, \ldots, \lambda_{m}$ of $L$ (not all zero) such that $\lambda_{1} \sigma_{1}(x)+\ldots+$ $\lambda_{m} \sigma_{m}(x)=0$ for all $x \in K$. Deduce that if $K / k$ is a finite extension of fields, and $\sigma_{1}, \ldots, \sigma_{m}$ are distinct $k$-automorphisms of $K$, then $m \leqslant[K: k]$.

  Suppose now that $K$ is a Galois extension of $k$ with Galois group cyclic of order $n$, where $n$ is not divisible by the characteristic. If $k$ contains a primitive $n$th root of unity, prove that $K$ is a radical extension of $k$. Explain briefly the relevance of this result to the problem of solubility of cubics by radicals.

  comment

General Relativity

• A1.15 B1.24

  General Relativity | Part II, 2002

  (i) Given a covariant vector field $V_{a}$, define the curvature tensor $R_{b c d}^{a}$ by

  $$V_{a ; b c}-V_{a ; c b}=V_{e} R_{a b c}^{e}$$

  Express $R_{a b c}^{e}$ in terms of the Christoffel symbols and their derivatives. Show that

  $$R_{a b c}^{e}=-R_{a c b}^{e}$$

  Further, by setting $V_{a}=\partial \phi / \partial x^{a}$, deduce that

  $$R_{a b c}^{e}+R_{c a b}^{e}+R_{b c a}^{e}=0 .$$

  (ii) Write down an expression similar to (*) given in Part (i) for the quantity

  $$g_{a b ; c d}-g_{a b ; d c}$$

  and hence show that

  $$R_{e a b c}=-R_{a e b c} .$$

  Define the Ricci tensor, show that it is symmetric and write down the contracted Bianchi identities.

  In certain spacetimes of dimension $n \geq 2, R_{a b c d}$ takes the form

  $$R_{a b c d}=K\left(x^{e}\right)\left[g_{a c} g_{b d}-g_{a d} g_{b c}\right]$$

  Obtain the Ricci tensor and Ricci scalar. Deduce that $K$ is a constant in such spacetimes if the dimension $n$ is greater than 2 .

  comment

• A2.15 B2.23

  General Relativity | Part II, 2002

  (i) Consider the line element describing the interior of a star,

  $$d s^{2}=e^{2 \alpha(r)} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)-e^{2 \gamma(r)} d t^{2},$$

  defined for $0 \leq r \leq r_{0}$ by

  $$e^{-2 \alpha(r)}=1-A r^{2}$$

  and

  $$e^{\gamma(r)}=\frac{3}{2} e^{-\alpha_{0}}-\frac{1}{2} e^{-\alpha(r)}$$

  Here $A=2 M / r_{0}^{3}, M$ is the mass of the star, and $\alpha_{0}$ is defined to be $\alpha\left(r_{0}\right)$.

  The star is made of a perfect fluid with energy-momentum tensor

  $$T_{a b}=(p+\rho) u_{a} u_{b}+p g_{a b} .$$

  Here $u^{a}$ is the 4 -velocity of the fluid which is at rest, the density $\rho$ is constant throughout the star $\left(0 \leq r \leq r_{0}\right)$ and the pressure $p=p(r)$ depends only on the radial coordinate. Write down the Einstein field equations and show that (in geometrical units with $G=c=1$ ) they may equivalently be written as

  $$R_{a b}=8 \pi(p+\rho) u_{a} u_{b}+4 \pi(p-\rho) g_{a b} .$$

  (ii) Using the formulae below, or otherwise, show that for $0 \leq r \leq r_{0}$ one has

  $$\rho=\frac{3 A}{8 \pi}, \quad p(r)=\frac{3 A}{8 \pi}\left(\frac{e^{-\alpha(r)}-e^{-\alpha_{0}}}{3 e^{-\alpha_{0}}-e^{-\alpha(r)}}\right)$$

  [The non-zero components of the Ricci tensor are:

  $$\begin{gathered} R_{11}=-\gamma^{\prime \prime}+\alpha^{\prime} \gamma^{\prime}-\gamma^{\prime 2}+\frac{2 \alpha^{\prime}}{r}, \quad R_{22}=e^{-2 \alpha}\left[\left(\alpha^{\prime}-\gamma^{\prime}\right) r-1\right]+1 \\ R_{33}=\sin ^{2} \theta R_{22}, \quad R_{44}=e^{2 \gamma-2 \alpha}\left[\gamma^{\prime \prime}-\alpha^{\prime} \gamma^{\prime}+\gamma^{\prime 2}+\frac{2 \gamma^{\prime}}{r}\right] \end{gathered}$$

  Note that

  $$\alpha^{\prime}=A r e^{2 \alpha}, \quad \gamma^{\prime}=\frac{1}{2} A r e^{\alpha-\gamma}, \quad \gamma^{\prime \prime}=\frac{1}{2} A e^{\alpha-\gamma}+\frac{1}{2} A^{2} r^{2} e^{3 \alpha-\gamma}-\frac{1}{4} A^{2} r^{2} e^{2 \alpha-2 \gamma} \text { ] ] }$$

  comment

• A4.17 B4.25

  General Relativity | Part II, 2002

  With respect to the Schwarzschild coordinates $(r, \theta, \phi, t)$, the Schwarzschild geometry is given by

  $$d s^{2}=\left(1-\frac{r_{s}}{r}\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)-\left(1-\frac{r_{s}}{r}\right) d t^{2}$$

  where $r_{s}=2 M$ is the Schwarzschild radius and $M$ is the Schwarzschild mass. Show that, by a suitable choice of $(\theta, \phi)$, the general geodesic can regarded as moving in the equatorial plane $\theta=\pi / 2$. Obtain the equations governing timelike and null geodesics in terms of $u(\phi)$, where $u=1 / r$.

  Discuss light bending and perihelion precession in the solar system.

  comment

Geometry of Surfaces

• A $4 . 7 \quad$

  Geometry of Surfaces | Part II, 2002

  Write an essay on the Euler number of topological surfaces. Your essay should include a definition of subdivision, some examples of surfaces and their Euler numbers, and a discussion of the statement and significance of the Gauss-Bonnet theorem.

  comment

• A2.7

  Geometry of Surfaces | Part II, 2002

  (i)

  Consider the surface

  $$z=\frac{1}{2}\left(\lambda x^{2}+\mu y^{2}\right)+h(x, y)$$

  where $h(x, y)$ is a term of order at least 3 in $x, y$. Calculate the first fundamental form at $x=y=0$.

  (ii) Calculate the second fundamental form, at $x=y=0$, of the surface given in Part (i). Calculate the Gaussian curvature. Explain why your answer is consistent with Gauss' "Theorema Egregium".

  comment

• A3.7

  Geometry of Surfaces | Part II, 2002

  (i) State what it means for surfaces $f: U \rightarrow \mathbb{R}^{3}$ and $g: V \rightarrow \mathbb{R}^{3}$ to be isometric.

  Let $f: U \rightarrow \mathbb{R}^{3}$ be a surface, $\phi: V \rightarrow U$ a diffeomorphism, and let $g=f \circ \phi: V \rightarrow$ $\mathbb{R}^{3} .$

  State a formula comparing the first fundamental forms of $f$ and $g$.

  (ii) Give a proof of the formula referred to at the end of part (i). Deduce that "isometry" is an equivalence relation.

  The catenoid and the helicoid are the surfaces defined by

  $$(u, v) \rightarrow(u \cos v, u \sin v, v)$$

  and

  $$(\vartheta, z) \rightarrow(\cosh z \cos \vartheta, \cosh z \sin \vartheta, z)$$

  Show that the catenoid and the helicoid are isometric.

  comment

Graph Theory

• A1.8

  Graph Theory | Part II, 2002

  (i) State and prove a necessary and sufficient condition for a graph to be Eulerian (that is, to have an Eulerian circuit).

  Prove that, given any connected non-Eulerian graph $G$, there is an Eulerian graph $H$ and a vertex $v \in H$ such that $G=H-v$.

  (ii) Let $G$ be a connected plane graph with $n$ vertices, $e$ edges and $f$ faces. Prove that $n-e+f=2$. Deduce that $e \leq g(n-2) /(g-2)$, where $g$ is the smallest face size.

  The crossing number $c(G)$ of a non-planar graph $G$ is the minimum number of edgecrossings needed when drawing the graph in the plane. (The crossing of three edges at the same point is not allowed.) Show that if $G$ has $n$ vertices and $e$ edges then $c(G) \geq e-3 n+6$. Find $c\left(K_{6}\right)$.

  comment

• A2.8

  Graph Theory | Part II, 2002

  (i) Define the chromatic polynomial $p(G ; t)$ of the graph $G$, and establish the standard identity

  $$p(G ; t)=p(G-e ; t)-p(G / e ; t),$$

  where $e$ is an edge of $G$. Deduce that, if $G$ has $n$ vertices and $m$ edges, then

  $$p(G ; t)=a_{n} t^{n}-a_{n-1} t^{n-1}+a_{n-2} t^{n-2}+\ldots+(-1)^{n} a_{0},$$

  where $a_{n}=1, a_{n-1}=m$ and $a_{j} \geq 0$ for $0 \leq j \leq n$.

  (ii) Let $G$ and $p(G ; t)$ be as in Part (i). Show that if $G$ has $k$ components $G_{1}, \ldots, G_{k}$ then $p(G ; t)=\prod_{i=1}^{k} p\left(G_{i} ; t\right)$. Deduce that $a_{k}>0$ and $a_{j}=0$ for $0 \leq j<k$.

  Show that if $G$ is a tree then $p(G ; t)=t(t-1)^{n-1}$. Must the converse hold? Justify your answer.

  Show that if $p(G ; t)=p\left(T_{r}(n) ; t\right)$, where $T_{r}(n)$ is a Turán graph, then $G=T_{r}(n)$.

  comment

• A4.9

  Graph Theory | Part II, 2002

  Write an essay on connectivity in graphs.

  Your essay should include proofs of at least two major theorems, along with a discussion of one or two significant corollaries.

  comment

Groups, Rings and Fields

• A1.4

  Groups, Rings and Fields | Part II, 2002

  (i) What is a Sylow subgroup? State Sylow's Theorems.

  Show that any group of order 33 is cyclic.

  (ii) Prove the existence part of Sylow's Theorems.

  [You may use without proof any arithmetic results about binomial coefficients which you need.]

  Show that a group of order $p^{2} q$, where $p$ and $q$ are distinct primes, is not simple. Is it always abelian? Give a proof or a counterexample.

  comment

• A2.4 B2.3

  Groups, Rings and Fields | Part II, 2002

  (i) Show that the ring $\mathbb{Z}[i]$ is Euclidean.

  (ii) What are the units in $\mathbb{Z}[i]$ ? What are the primes in $\mathbb{Z}[i]$ ? Justify your answers. Factorize $11+7 i$ into primes in $\mathbb{Z}[i]$.

  comment

• A3.4

  Groups, Rings and Fields | Part II, 2002

  (i) What does it mean for a ring to be Noetherian? State Hilbert's Basis Theorem. Give an example of a Noetherian ring which is not a principal ideal domain.

  (ii) Prove Hilbert's Basis Theorem.

  Is it true that if the ring $R[X]$ is Noetherian, then so is $R ?$

  comment

• A4.4

  Groups, Rings and Fields | Part II, 2002

  Let $F$ be a finite field. Show that there is a unique prime $p$ for which $F$ contains the field $\mathbb{F}_{p}$ of $p$ elements. Prove that $F$ contains $p^{n}$ elements, for some $n \in \mathbb{N}$. Show that $x^{p^{n}}=x$ for all $x \in F$, and hence find a polynomial $f \in \mathbb{F}_{p}[X]$ such that $F$ is the splitting field of $f$. Show that, up to isomorphism, $F$ is the unique field $\mathbb{F}_{p^{n}}$ of size $p^{n}$.

  [Standard results about splitting fields may be assumed.]

  Prove that the mapping sending $x$ to $x^{p}$ is an automorphism of $\mathbb{F}_{p^{n}}$. Deduce that the Galois group Gal $\left(\mathbb{F}_{p^{n}} / \mathbb{F}_{p}\right)$ is cyclic of order $n$. For which $m$ is $\mathbb{F}_{p^{m}}$ a subfield of $\mathbb{F}_{p^{n}}$ ?

  comment

• B1.3

  Groups, Rings and Fields | Part II, 2002

  State Sylow's Theorems. Prove the existence part of Sylow's Theorems.

  Show that any group of order 33 is cyclic.

  Show that a group of order $p^{2} q$, where $p$ and $q$ are distinct primes, is not simple. Is it always abelian? Give a proof or a counterexample.

  comment

Hilbert Spaces

• B1.10

  Hilbert Spaces | Part II, 2002

  Let $H$ be a Hilbert space and let $T \in \mathcal{B}(H)$. Define what it means for $T$ to be bounded below. Prove that, if $L T=I$ for some $L \in \mathcal{B}(H)$, then $T$ is bounded below.

  Prove that an operator $T \in \mathcal{B}(H)$ is invertible if and only if both $T$ and $T^{*}$ are bounded below.

  Let $H$ be the sequence space $\ell^{2}$. Define the operators $S, R$ on $H$ by setting

  $$S(\xi)=\left(0, \xi_{1}, \xi_{2}, \xi_{3}, \ldots\right), \quad R(\xi)=\left(\xi_{2}, \xi_{3}, \xi_{4}, \ldots\right),$$

  for all $\xi=\left(\xi_{1}, \xi_{2}, \xi_{3}, \ldots\right) \in \ell^{2}$. Check that $R S=I$ but $S R \neq I$. Let $D=\{\lambda \in \mathbb{C}:|\lambda|<$ $1\}$. For each $\lambda \in D$, explain why $I-\lambda R$ is invertible, and define

  $$R(\lambda)=(I-\lambda R)^{-1} R$$

  Show that, for all $\lambda \in D$, we have $R(\lambda)(S-\lambda I)=I$, but $(S-\lambda I) R(\lambda) \neq I$. Deduce that, for all $\lambda \in D$, the operator $S-\lambda I$ is bounded below, but is not invertible. Deduce also that $\operatorname{Sp} S=\{\lambda \in \mathbb{C}:|\lambda| \leqslant 1\}$.

  Let $\lambda \in \mathbb{C}$ with $|\lambda|=1$, and for $n=1,2, \ldots$, define the element $x_{n}$ of $\ell^{2}$ by

  $$x_{n}=n^{-1 / 2}\left(\lambda^{-1}, \lambda^{-2}, \ldots, \lambda^{-n}, 0,0, \ldots\right) .$$

  Prove that $\left\|x_{n}\right\|=1$ but that $(S-\lambda I) x_{n} \rightarrow 0$ as $n \rightarrow \infty$. Deduce that, for $|\lambda|=1, S-\lambda I$ is not bounded below.

  comment

• B3.8

  Hilbert Spaces | Part II, 2002

  Let $H$ be an infinite-dimensional, separable Hilbert space. Let $T$ be a compact linear operator on $H$, and let $\lambda$ be a non-zero, approximate eigenvalue of $T$. Prove that $\lambda$ is an eigenvalue, and that the corresponding eigenspace $E_{\lambda}(T)=\{x \in H: T x=\lambda x\}$ is finite-dimensional.

  Let $S$ be a compact, self-adjoint operator on $H$. Prove that there is an orthonormal basis $\left(e_{n}\right)_{n \geqslant 0}$ of $H$, and a sequence $\left(\lambda_{n}\right)_{n \geqslant 0}$ in $\mathbb{C}$, such that (i) $S e_{n}=\lambda_{n} e_{n}(n \geqslant 0)$ and (ii) $\lambda_{n} \rightarrow 0$ as $n \rightarrow \infty$.

  Now let $S$ be compact, self-adjoint and injective. Let $R$ be a bounded self-adjoint operator on $H$ such that $R S=S R$. Prove that $H$ has an orthonormal basis $\left(e_{n}\right)_{n \geqslant 1}$, where, for every $n, e_{n}$ is an eigenvector, both of $S$ and of $R$.

  [You may assume, without proof, results about self-adjoint operators on finite-dimensional spaces.]

  comment

• B4.7

  Hilbert Spaces | Part II, 2002

  Throughout this question, $H$ is an infinite-dimensional, separable Hilbert space. You may use, without proof, any theorems about compact operators that you require.

  Define a Fredholm operator $T$, on a Hilbert space $H$, and define the index of $T$.

  (i) Prove that if $T$ is Fredholm then $\operatorname{im} T$ is closed.

  (ii) Let $F \in \mathcal{B}(H)$ and let $F$ have finite rank. Prove that $F^{*}$ also has finite rank.

  (iii) Let $T=I+F$, where $I$ is the identity operator on $H$ and $F$ has finite rank; let $E=\operatorname{im} F+\operatorname{im} F^{*}$. By considering $T \mid E$ and $T \mid E^{\perp}$ (or otherwise) prove that $T$ is Fredholm with ind $T=0$.

  (iv) Let $T \in \mathcal{B}(H)$ be Fredholm with ind $T=0$. Prove that $T=A+F$, where $A$ is invertible and $F$ has finite rank.

  [You may wish to note that $T$ effects an isomorphism from $(\operatorname{ker} T)^{\perp}$ onto $\operatorname{im} T$; also ker $T$ and $(\operatorname{im} T)^{\perp}$ have the same finite dimension.]

  (v) Deduce from (iii) and (iv) that $T \in \mathcal{B}(H)$ is Fredholm with ind $T=0$ if and only if $T=A+K$ with $A$ invertible and $K$ compact.

  (vi) Explain briefly, by considering suitable shift operators on $\ell^{2}$ (i.e. not using any theorems about Fredholm operators) that, for each $k \in \mathbb{Z}$, there is a Fredholm operator $S$ on $H$ with ind $S=k$.

  comment

Information Theory

• B1.14

  Information Theory | Part II, 2002

  (a) Define the entropy $h(X)$ and the mutual entropy $i(X, Y)$ of random variables $X$ and $Y$. Prove the inequality

  $$0 \leqslant i(X, Y) \leqslant \min \{h(X), h(Y)\}$$

  [You may assume the Gibbs inequality.]

  (b) Let $X$ be a random variable and let $\mathbf{Y}=\left(Y_{1}, \ldots, Y_{n}\right)$ be a random vector.

  (i) Prove or disprove by producing a counterexample the inequality

  $$i(X, \mathbf{Y}) \leqslant \sum_{j=1}^{n} i\left(X, Y_{j}\right)$$

  first under the assumption that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and then under the assumption that $Y_{1}, \ldots, Y_{n}$ are conditionally independent given $X$.

  (ii) Prove or disprove by producing a counterexample the inequality

  $$i(X, \mathbf{Y}) \geqslant \sum_{j=1}^{n} i\left(X, Y_{j}\right)$$

  first under the assumption that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and then under the assumption that $Y_{1}, \ldots, Y_{n}$ are conditionally independent given $X$.

  comment

• B2.14

  Information Theory | Part II, 2002

  Define the binary Hamming code of length $n=2^{\ell}-1$ and its dual. Prove that the Hamming code is perfect. Prove that in the dual code:

  (i) The weight of any non-zero codeword equals $2^{\ell-1}$;

  (ii) The distance between any pair of words equals $2^{\ell-1}$.

  [You may quote results from the course provided that they are carefully stated.]

  comment

• B4.13

  Information Theory | Part II, 2002

  Define the Huffman binary encoding procedure and prove its optimality among decipherable codes.

  comment

Logic, Computation and Set Theory

• A $1 . 7 \quad$ B1.12

  Logic, Computation and Set Theory | Part II, 2002

  (i) State the Knaster-Tarski fixed point theorem. Use it to prove the Cantor-Bernstein Theorem; that is, if there exist injections $A \rightarrow B$ and $B \rightarrow A$ for two sets $A$ and $B$ then there exists a bijection $A \rightarrow B$.

  (ii) Let $A$ be an arbitrary set and suppose given a subset $R$ of $P A \times A$. We define a subset $B \subseteq A$ to be $R$-closed just if whenever $(S, a) \in R$ and $S \subseteq B$ then $a \in B$. Show that the set of all $R$-closed subsets of $A$ is a complete poset in the inclusion ordering.

  Now assume that $A$ is itself equipped with a partial ordering $\leqslant$.

  (a) Suppose $R$ satisfies the condition that if $b \geqslant a \in A$ then $(\{b\}, a) \in R$.

  Show that if $B$ is $R$-closed then $c \leqslant b \in B$ implies $c \in B$.

  (b) Suppose that $R$ satisfies the following condition. Whenever $(S, a) \in R$ and $b \leqslant a$ then there exists $T \subseteq A$ such that $(T, b) \in R$, and for every $t \in T$ we have (i) $(\{b\}, t) \in R$, and (ii) $t \leqslant s$ for some $s \in S$. Let $B$ and $C$ be $R$-closed subsets of $A$. Show that the set

  $$[B \rightarrow C]=\{a \in A \mid \forall b \leqslant a(b \in B \Rightarrow b \in C)\}$$

  is $R$-closed.

  comment

• A3.8 B3.11

  Logic, Computation and Set Theory | Part II, 2002

  (i) Explain briefly what is meant by the terms register machine and computable function.

  Let $u$ be the universal computable function $u(m, n)=f_{m}(n)$ and $s$ a total computable function with $f_{s(m, n)}(k)=f_{m}(n, k)$. Here $f_{m}(n)$ and $f_{m}(n, k)$ are the unary and binary functions computed by the $m$-th register machine program $P_{m}$. Suppose $h: \mathbb{N} \rightarrow \mathbb{N}$ is a total computable function. By considering the function

  $$g(m, n)=u(h(s(m, m)), n)$$

  show that there is a number $a$ such that $f_{a}=f_{h(a)}$.

  (ii) Let $P$ be the set of all partial functions $\mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}$. Consider the mapping $\Phi: P \rightarrow P$ defined by

  $$\Phi(g)(m, n)= \begin{cases}n+1 & \text { if } m=0, \\ g(m-1,1) & \text { if } m>0, n=0 \text { and } g(m-1,1) \text { defined } \\ g(m-1, g(m, n-1)) & \text { if } m n>0 \text { and } g(m-1, g(m, n-1)) \text { defined }, \\ \text { undefined } & \text { otherwise. }\end{cases}$$

  (a) Show that any fixed point of $\Phi$ is a total function $\mathbb{N} \times \mathbb{N} \rightarrow \mathbb{N}$. Deduce that $\Phi$ has a unique fixed point.

  [The Bourbaki- Witt Theorem may be assumed if stated precisely.]

  (b) It follows from standard closure properties of the computable functions that there is a computable function $\psi$ such that

  $$\psi(p, m, n)=\Phi\left(f_{p}\right)(m, n) .$$

  Assuming this, show that there is a total computable function $h$ such that

  $$\Phi\left(f_{p}\right)=f_{h(p)} \text { for all } p .$$

  Deduce that the fixed point of $\Phi$ is computable.

  comment

• A4.8

  Logic, Computation and Set Theory | Part II, 2002

  Let $P$ be a set of primitive propositions. Let $L(P)$ denote the set of all compound propositions over $P$, and let $S$ be a subset of $L(P)$. Consider the relation $\preceq$ on $L(P)$ defined by

  $$s \preceq s t \text { if and only if } S \cup\{s\} \vdash t .$$

  Prove that $\preceq_{S}$ is reflexive and transitive. Deduce that if we define $\approx_{S}$ by $\left(s \approx_{S} t\right.$ if and only if $s \preceq_{S} t$ and $\left.t \preceq \preceq_{S} s\right)$, then $\approx_{S}$ is an equivalence relation and the quotient $B_{S}=L(P) / \approx_{S}$ is partially ordered by the relation $\leqslant_{S}$ induced by $\preccurlyeq_{S}$ (that is, $[s] \leqslant_{S}[t]$ if and only if $s \preccurlyeq_{S} t$, where square brackets denote equivalence classes).

  Assuming the result that $B_{S}$ is a Boolean algebra with lattice operations induced by the logical operations on $L(P)$ (that is, $[s] \wedge[t]=[s \wedge t]$, etc.), show that there is a bijection between the following two sets:

  (a) The set of lattice homomorphisms $B_{S} \rightarrow\{0,1\}$.

  (b) The set of models of the propositional theory $S$.

  Deduce that the completeness theorem for propositional logic is equivalent to the assertion that, for any Boolean algebra $B$ with more than one element, there exists a homomorphism $B \rightarrow\{0,1\}$.

  [You may assume the result that the completeness theorem implies the compactness theorem.]

  comment

• B2.11

  Logic, Computation and Set Theory | Part II, 2002

  Explain what is meant by a structure for a first-order language and by a model for a first-order theory. If $T$ is a first-order theory whose axioms are all universal sentences (that is, sentences of the form $\left(\forall x_{1} \ldots x_{n}\right) p$ where $p$ is quantifier-free), show that every substructure of a $T$-model is a $T$-model.

  Now let $T$ be an arbitrary first-order theory in a language $L$, and let $M$ be an $L$-structure satisfying all the universal sentences which are derivable from the axioms of $T$. If $p$ is a quantifier-free formula (with free variables $x_{1}, \ldots, x_{n}$ say) whose interpretation $[p]_{M}$ is a nonempty subset of $M^{n}$, show that $T \cup\left\{\left(\exists x_{1} \cdots x_{n}\right) p\right\}$ is consistent.

  Let $L^{\prime}$ be the language obtained from $L$ by adjoining a new constant $\widehat{a}$for each element $a$ of $M$, and let

  $$T^{\prime}=T \cup\left\{p\left[\widehat{a}_{1}, \ldots, \widehat{a}_{n} / x_{1}, \ldots, x_{n}\right] \mid p \text { is quantifier-free and }\left(a_{1}, \ldots, a_{n}\right) \in[p]_{M}\right\}$$

  Show that $T^{\prime}$ has a model. [You may use the Completeness and Compactness Theorems.] Explain briefly why any such model contains a substructure isomorphic to $M$.

  comment

• B4.10

  Logic, Computation and Set Theory | Part II, 2002

  Explain what is meant by a well-ordering of a set.

  Without assuming Zorn's Lemma, show that the power-set of any well-ordered set can be given a total (linear) ordering.

  By a selection function for a set $A$, we mean a function $f: P A \rightarrow P A$ such that $f(B) \subset B$ for all $B \subset A, f(B) \neq \emptyset$ for all $B \neq \emptyset$, and $f(B) \neq B$ if $B$ has more than one element. Suppose given a selection function $f$. Given a mapping $g: \alpha \rightarrow[0,1]$ for some ordinal $\alpha$, we define a subset $B(f, g) \subset A$ recursively as follows:

  $$\begin{aligned} &B(f, g)=A \quad \text { if } \alpha=0, \\ &B(f, g)=f\left(B\left(f,\left.g\right|_{\beta}\right)\right) \quad \text { if } \alpha=\beta^{+} \text {and } g(\beta)=1 \\ &B(f, g)=B\left(f,\left.g\right|_{\beta}\right) \backslash f\left(B\left(f,\left.g\right|_{\beta}\right)\right) \quad \text { if } \alpha=\beta^{+} \text {and } g(\beta)=0 \\ &B(f, g)=\bigcap\left\{B\left(f,\left.g\right|_{\beta}\right) \mid \beta<\alpha\right\} \quad \text { if } \alpha \text { is a limit ordinal. } \end{aligned}$$

  Show that, for any $x \in A$ and any ordinal $\alpha$, there exists a function $g$ with domain $\alpha$ such that $x \in B(f, g)$.

  [It may help to observe that $g$ is uniquely determined by $x$ and $\alpha$, though you need not show this explicitly.]

  Show also that there exists $\alpha$ such that, for every $g$ with domain $\alpha, B(f, g)$ is either empty or a singleton.

  Deduce that the assertion 'Every set has a selection function' implies that every set can be totally ordered.

  [Hartogs' Lemma may be assumed, provided you state it precisely.]

  comment

Markov Chains

• A1.1 B1.1

  Markov Chains | Part II, 2002

  (i) We are given a finite set of airports. Assume that between any two airports, $i$ and $j$, there are $a_{i j}=a_{j i}$ flights in each direction on every day. A confused traveller takes one flight per day, choosing at random from all available flights. Starting from $i$, how many days on average will pass until the traveller returns again to $i$ ? Be careful to allow for the case where there may be no flights at all between two given airports.

  (ii) Consider the infinite tree $T$ with root $R$, where, for all $m \geqslant 0$, all vertices at distance $2^{m}$ from $R$ have degree 3 , and where all other vertices (except $R$ ) have degree 2 . Show that the random walk on $T$ is recurrent.

  comment

• A2.1

  Markov Chains | Part II, 2002

  (i) In each of the following cases, the state-space $I$ and non-zero transition rates $q_{i j}$ $(i \neq j)$ of a continuous-time Markov chain are given. Determine in which cases the chain is explosive.

  (ii) Children arrive at a see-saw according to a Poisson process of rate 1 . Initially there are no children. The first child to arrive waits at the see-saw. When the second child arrives, they play on the see-saw. When the third child arrives, they all decide to go and play on the merry-go-round. The cycle then repeats. Show that the number of children at the see-saw evolves as a Markov Chain and determine its generator matrix. Find the probability that there are no children at the see-saw at time $t$.

  Hence obtain the identity

  $$\sum_{n=0}^{\infty} e^{-t} \frac{t^{3 n}}{(3 n) !}=\frac{1}{3}+\frac{2}{3} e^{-\frac{3}{2} t} \cos \frac{\sqrt{3}}{2} t$$

  $$\begin{aligned} & \text { (a) } I=\{1,2,3, \ldots\}, \quad q_{i, i+1}=i^{2}, \quad i \in I \text {, } \\ & \text { (b) } \quad I=\mathbb{Z}, \quad q_{i, i-1}=q_{i, i+1}=2^{i}, \quad i \in I \text {. } \end{aligned}$$

  comment

• A3.1 B3.1

  Markov Chains | Part II, 2002

  (i) Consider the continuous-time Markov chain $\left(X_{t}\right)_{t \geqslant 0}$ on $\{1,2,3,4,5,6,7\}$ with generator matrix

  $$Q=\left(\begin{array}{rrrrrrr} -6 & 2 & 0 & 0 & 0 & 4 & 0 \\ 2 & -3 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & -5 & 1 & 2 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 2 & 0 & -6 & 0 & 2 \\ 1 & 2 & 0 & 0 & 0 & -3 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & -2 \end{array}\right)$$

  Compute the probability, starting from state 3 , that $X_{t}$ hits state 2 eventually.

  Deduce that

  $$\lim _{t \rightarrow \infty} \mathbb{P}\left(X_{t}=2 \mid X_{0}=3\right)=\frac{4}{15}$$

  [Justification of standard arguments is not expected.]

  (ii) A colony of cells contains immature and mature cells. Each immature cell, after an exponential time of parameter 2, becomes a mature cell. Each mature cell, after an exponential time of parameter 3, divides into two immature cells. Suppose we begin with one immature cell and let $n(t)$ denote the expected number of immature cells at time $t$. Show that

  $$n(t)=\left(4 e^{t}+3 e^{-6 t}\right) / 7$$

  comment

• A4.1

  Markov Chains | Part II, 2002

  Write an essay on the long-time behaviour of discrete-time Markov chains on a finite state space. Your essay should include discussion of the convergence of probabilities as well as almost-sure behaviour. You should also explain what happens when the chain is not irreducible.

  comment

Mathematical Methods

• A2.17

  Mathematical Methods | Part II, 2002

  (i) Show that the equation

  $$\epsilon x^{4}-x^{2}+5 x-6=0, \quad|\epsilon| \ll 1$$

  has roots in the neighbourhood of $x=2$ and $x=3$. Find the first two terms of an expansion in $\epsilon$ for each of these roots.

  Find a suitable series expansion for the other two roots and calculate the first two terms in each case.

  (ii) Describe, giving reasons for the steps taken, how the leading-order approximation for $\lambda \gg 1$ to an integral of the form

  $$I(\lambda) \equiv \int_{A}^{B} f(t) e^{i \lambda g(t)} d t$$

  where $\lambda$ and $g$ are real, may be found by the method of stationary phase. Consider the cases where (a) $g^{\prime}(t)$ has one simple zero at $t=t_{0}$ with $A<t_{0}<B$; (b) $g^{\prime}(t)$ has more than one simple zero in $A<t<B$; and (c) $g^{\prime}(t)$ has only a simple zero at $t=B$. What is the order of magnitude of $I(\lambda)$ if $g^{\prime}(t)$ is non-zero for $A \leq t \leq B$ ?

  Use the method of stationary phase to find the leading-order approximation to

  $$J(\lambda) \equiv \int_{0}^{1} \sin \left[\lambda\left(2 t^{4}-t\right)\right] d t$$

  for $\lambda \gg 1$.

  [You may use the fact that $\int_{-\infty}^{\infty} e^{i u^{2}} d u=\sqrt{\pi} e^{i \pi / 4}$.]

  comment

• A3.17

  Mathematical Methods | Part II, 2002

  (i) State the Fredholm alternative for Fredholm integral equations of the second kind.

  Show that the integral equation

  $$\phi(x)-\lambda \int_{0}^{1}(x+t) \phi(t) d t=f(x), \quad 0 \leqslant x \leqslant 1$$

  where $f$ is a continuous function, has a unique solution for $\phi$ if $\lambda \neq-6 \pm 4 \sqrt{3}$. Derive this solution.

  (ii) Describe the WKB method for finding approximate solutions $f(x)$ of the equation

  $$\frac{d^{2} f(x)}{d x^{2}}+q(\epsilon x) f(x)=0$$

  where $q$ is an arbitrary non-zero, differentiable function and $\epsilon$ is a small parameter. Obtain these solutions in terms of an exponential with slowly varying exponent and slowly varying amplitude.

  Hence, by means of a suitable change of independent variable, find approximate solutions $w(t)$ of the equation

  $$\frac{d^{2} w}{d t^{2}}+\lambda^{2} t w=0$$

  in $t>0$, where $\lambda$ is a large parameter.

  comment

• A4.21

  Mathematical Methods | Part II, 2002

  State Watson's lemma giving an asymptotic expansion as $\lambda \rightarrow \infty$ for an integral of the form

  $$I_{1}=\int_{0}^{A} f(t) e^{-\lambda t} d t, \quad A>0$$

  Show how this result may be used to find an asymptotic expansion as $\lambda \rightarrow \infty$ for an integral of the form

  $$I_{2}=\int_{-A}^{B} f(t) e^{-\lambda t^{2}} d t, \quad A>0, B>0$$

  Hence derive Laplace's method for obtaining an asymptotic expansion as $\lambda \rightarrow \infty$ for an integral of the form

  $$I_{3}=\int_{a}^{b} f(t) e^{\lambda \phi(t)} d t$$

  where $\phi(t)$ is differentiable, for the cases: (i) $\phi^{\prime}(t)<0$ in $a \leq t \leq b$; and (ii) $\phi^{\prime}(t)$ has a simple zero at $t=c$ with $a<c<b$ and $\phi^{\prime \prime}(c)<0$.

  Find the first two terms in the asymptotic expansion as $x \rightarrow \infty$ of

  $$I_{4}=\int_{-\infty}^{\infty} \log \left(1+t^{2}\right) e^{-x t^{2}} d t$$

  [You may leave your answer expressed in terms of $\Gamma$-functions.]

  comment

Methods of Mathematical Physics

• B1.19

  Methods of Mathematical Physics | Part II, 2002

  State the Riemann-Lebesgue lemma as applied to the integral

  $$\int_{a}^{b} g(u) e^{i x u} d u$$

  where $g^{\prime}(u)$ is continuous and $a, b \in \mathbb{R}$.

  Use this lemma to show that, as $x \rightarrow+\infty$,

  $$\int_{a}^{b}(u-a)^{\lambda-1} f(u) e^{i x u} d u \sim f(a) e^{i x a} e^{i \pi \lambda / 2} \Gamma(\lambda) x^{-\lambda}$$

  where $f(u)$ is holomorphic, $f(a) \neq 0$ and $0<\lambda<1$. You should explain each step of your argument, but detailed analysis is not required.

  Hence find the leading order asymptotic behaviour as $x \rightarrow+\infty$ of

  $$\int_{0}^{1} \frac{e^{i x t^{2}}}{\left(1-t^{2}\right)^{\frac{1}{2}}} d t$$

  comment

• B2.18

  Methods of Mathematical Physics | Part II, 2002

  Show that

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{t^{z-1}}{t-a} d t=\pi i a^{z-1},$$

  where $a$ is real and positive, $0<\operatorname{Re}(z)<1$ and $\mathcal{P}$ denotes the Cauchy principal value; the principal branches of $t^{z}$ etc. are implied. Deduce that

  $$\int_{0}^{\infty} \frac{t^{z-1}}{t+a} d t=\pi a^{z-1} \operatorname{cosec} \pi z$$

  and that

  $$\mathcal{P} \int_{0}^{\infty} \frac{t^{z-1}}{t-a} d t=-\pi a^{z-1} \cot \pi z$$

  Use $(*)$ to show that, if $\operatorname{Im}(b)>0$, then

  $$\int_{0}^{\infty} \frac{t^{z-1}}{t-b} d t=-\pi b^{z-1}(\cot \pi z-i)$$

  What is the value of this integral if $\operatorname{Im}(b)<0$ ?

  comment

• B3.19

  Methods of Mathematical Physics | Part II, 2002

  Show that the equation

  $$z w^{\prime \prime}+w^{\prime}+(\lambda-z) w=0$$

  has solutions of the form

  $$w(z)=\int_{\gamma}(t-1)^{(\lambda-1) / 2}(t+1)^{-(\lambda+1) / 2} e^{z t} d t$$

  Give examples of possible choices of $\gamma$ to provide two independent solutions, assuming $\operatorname{Re}(z)>0$. Distinguish between the cases $\operatorname{Re} \lambda>-1$ and $\operatorname{Re} \lambda<1$. Comment on the case $-1<\operatorname{Re} \lambda<1$ and on the case that $\lambda$ is an odd integer.

  Show that, if $\operatorname{Re} \lambda<1$, there is a solution $w_{1}(z)$ that is bounded as $z \rightarrow+\infty$, and that, in this limit,

  $$w_{1}(z) \sim A e^{-z} z^{(\lambda-1) / 2}\left(1-\frac{(1-\lambda)^{2}}{8 z}\right),$$

  where $A$ is a constant.

  comment

• B4.19

  Methods of Mathematical Physics | Part II, 2002

  Let

  $$I(\lambda, a)=\int_{-i \infty}^{i \infty} \frac{e^{\lambda\left(t^{3}-3 t\right)}}{t^{2}-a^{2}} d t$$

  where $\lambda$ is real, $a$ is real and non-zero, and the path of integration runs up the imaginary axis. Show that, if $a^{2}>1$,

  $$I(\lambda, a) \sim \frac{i e^{-2 \lambda}}{1-a^{2}} \sqrt{\frac{\pi}{3 \lambda}}$$

  as $\lambda \rightarrow+\infty$ and sketch the relevant steepest descent path.

  What is the corresponding result if $a^{2}<1$ ?

  comment

Nonlinear Waves

• A2.18

  Nonlinear Waves | Part II, 2002

  (i) Find a travelling wave solution of unchanging shape for the modified Burgers equation (with $\alpha>0$ )

  $$\frac{\partial u}{\partial t}+u^{2} \frac{\partial u}{\partial x}=\alpha \frac{\partial^{2} u}{\partial x^{2}}$$

  with $u=0$ far ahead of the wave and $u=1$ far behind. What is the velocity of the wave? Sketch the shape of the wave.

  (ii) Explain why the method of characteristics, when applied to an equation of the type

  $$\frac{\partial u}{\partial t}+c(u) \frac{\partial u}{\partial x}=0$$

  with initial data $u(x, 0)=f(x)$, sometimes gives a multi-valued solution. State the shockfitting algorithm that gives a single-valued solution, and explain how it is justified.

  Consider the equation above, with $c(u)=u^{2}$. Suppose that

  $$u(x, 0)=\left\{\begin{array}{ll} 0 & x \geq 0 \\ 1 & x<0 \end{array} .\right.$$

  Sketch the characteristics in the $(x, t)$ plane. Show that a shock forms immediately, and calculate the velocity at which it moves.

  comment

• A3.18

  Nonlinear Waves | Part II, 2002

  (i) Show that the equation

  $$\frac{\partial \phi}{\partial t}-\frac{\partial^{2} \phi}{\partial x^{2}}+1-\phi^{2}=0$$

  has two solutions which are independent of both $x$ and $t$. Show that one of these is linearly stable. Show that the other solution is linearly unstable, and find the range of wavenumbers that exhibit the instability.

  Sketch the nonlinear evolution of the unstable solution after it receives a small, smooth, localized perturbation in the direction towards the stable solution.

  (ii) Show that the equations

  $$\begin{array}{r} \frac{\partial u}{\partial x}+\frac{\partial v}{\partial x}=e^{-u+v} \\ -\frac{\partial u}{\partial y}+\frac{\partial v}{\partial y}=e^{-u-v} \end{array}$$

  are a Bäcklund pair for the equations

  $$\frac{\partial^{2} u}{\partial x \partial y}=e^{-2 u}, \quad \frac{\partial^{2} v}{\partial x \partial y}=0$$

  By choosing $v$ to be a suitable constant, and using the Bäcklund pair, find a solution of the equation

  $$\frac{\partial^{2} u}{\partial x \partial y}=e^{-2 u}$$

  which is non-singular in the region $y<4 x$ of the $(x, y)$ plane and has the value $u=0$ at $x=\frac{1}{2}, y=0$.

  comment

Number Fields

• B1.9

  Number Fields | Part II, 2002

  Explain what is meant by an integral basis $\omega_{1}, \ldots, \omega_{n}$ of a number field $K$. Give an expression for the discriminant of $K$ in terms of the traces of the $\omega_{i} \omega_{j}$.

  Let $K=\mathbb{Q}(i, \sqrt{2})$. By computing the traces $T_{K / k}(\theta)$, where $k$ runs through the three quadratic subfields of $K$, show that the algebraic integers $\theta$ in $K$ have the form $\frac{1}{2}(\alpha+\beta \sqrt{2})$, where $\alpha=a+i b$ and $\beta=c+i d$ are Gaussian integers. By further computing the norm $N_{K / k}(\theta)$, where $k=\mathbb{Q}(\sqrt{2})$, show that $a$ and $b$ are even and that $c \equiv d(\bmod 2)$. Hence prove that an integral basis for $K$ is $1, i, \sqrt{2}, \frac{1}{2}(1+i) \sqrt{2}$.

  Calculate the discriminant of $K$.

  comment

• B2.9

  Number Fields | Part II, 2002

  Let $K=\mathbb{Q}(\sqrt{35})$. By Dedekind's theorem, or otherwise, show that the ideal equations

  $$2=[2, \omega]^{2}, \quad 5=[5, \omega]^{2}, \quad[\omega]=[2, \omega][5, \omega]$$

  hold in $K$, where $\omega=5+\sqrt{35}$. Deduce that $K$ has class number 2 .

  Verify that $1+\omega$ is the fundamental unit in $K$. Hence show that the complete solution in integers $x, y$ of the equation $x^{2}-35 y^{2}=-10$ is given by

  $$x+\sqrt{35} y=\pm \omega(1+\omega)^{n} \quad(n=0, \pm 1, \pm 2, \ldots) .$$

  Calculate the particular solution $x, y$ for $n=1$.

  [It can be assumed that the Minkowski constant for $K$ is $\frac{1}{2}$.]

  comment

• B4.6

  Number Fields | Part II, 2002

  Write an essay on one the following topics.

  (i) Dirichlet's unit theorem and the Pell equation.

  (ii) Ideals and the fundamental theorem of arithmetic.

  (iii) Dedekind's theorem and the factorisation of primes. (You should treat explicitly either the case of quadratic fields or that of the cyclotomic field.)

  comment

Number Theory

• A1.9

  Number Theory | Part II, 2002

  (i) Let $p$ be a prime number. Prove that the multiplicative group of the field with $p$ elements is cyclic.

  (ii) Let $p$ be an odd prime, and let $k \geqslant 1$ be an integer. Prove that we have $x^{2} \equiv 1 \bmod p^{k}$ if and only if either $x \equiv 1 \bmod p^{k}$ or $x \equiv-1 \bmod p^{k}$. Is this statement true when $p=2$ ?

  Let $m$ be an odd positive integer, and let $r$ be the number of distinct prime factors of $m$. Prove that there are precisely $2^{r}$ different integers $x$ satisfying $x^{2} \equiv 1 \bmod m$ and $0<x<m$.

  comment

• A3.9

  Number Theory | Part II, 2002

  (i) Let $\pi(x)$ denote the number of primes $\leqslant x$, where $x$ is a positive real number. State and prove Legendre's formula relating $\pi(x)$ to $\pi(\sqrt{x})$. Use this formula to compute $\pi(100)-\pi(10) .$

  (ii) Let $\zeta(s)=\sum_{n=1}^{\infty} n^{-s}$, where $s$ is a real number greater than 1 . Prove the following two assertions rigorously, assuming always that $s>1$. (a) $\zeta(s)=\prod_{p}\left(1-p^{-s}\right)^{-1}$, where the product is taken over all primes $p$; (b) $\zeta(s)=\frac{1}{1-2^{1-s}} \sum_{n=1}^{\infty} \frac{(-1)^{n-1}}{n^{s}}$.

  Explain why (b) enables us to define $\zeta(s)$ for $0<s<1$. Deduce from (b) that $\lim _{s \rightarrow 1}(s-1) \zeta(s)=1$.

  comment

• A4.10

  Number Theory | Part II, 2002

  Write an essay on quadratic reciprocity. Your essay should include (i) a proof of the law of quadratic reciprocity for the Legendre symbol, (ii) a proof of the law of quadratic reciprocity for the Jacobi symbol, and (iii) a comment on why this latter law is useful in primality testing.

  comment

Numerical Analysis

• A1.20 B1.20

  Numerical Analysis | Part II, 2002

  (i) Let $A$ be an $n \times n$ symmetric real matrix with distinct eigenvalues $\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}$ and corresponding eigenvectors $\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{n}$, where $\left\|\mathbf{v}_{l}\right\|=1$. Given $\mathbf{x}^{(0)} \in \mathbb{R}^{n},\left\|\mathbf{x}^{(0)}\right\|=1$, the sequence $\mathbf{x}^{(k)}$ is generated in the following manner. We set

  $$\begin{gathered} \mu=\mathbf{x}^{(k) T} A \mathbf{x}^{(k)} \\ \mathbf{y}=(A-\mu I)^{-1} \mathbf{x}^{(k)} \\ \mathbf{x}^{(k+1)}=\frac{\mathbf{y}}{\|\mathbf{y}\|} \end{gathered}$$

  Show that if

  $$\mathbf{x}^{(k)}=c^{-1}\left(\mathbf{v}_{1}+\alpha \sum_{l=2}^{n} d_{l} \mathbf{v}_{l}\right)$$

  where $\alpha$ is a real scalar and $c$ is chosen so that $\left\|\mathbf{x}^{(k)}\right\|=1$, then

  $$\mu=c^{-2}\left(\lambda_{1}+\alpha^{2} \sum_{j=2}^{n} \lambda_{j} d_{j}^{2}\right)$$

  Give an explicit expression for $c$.

  (ii) Use the above result to prove that, if $|\alpha|$ is small,

  $$\mathbf{x}^{(k+1)}=\tilde{c}^{-1}\left(\mathbf{v}_{1}+\alpha^{3} \sum_{l=2}^{n} \tilde{d}_{l} \mathbf{v}_{l}\right)+O\left(\alpha^{4}\right)$$

  and obtain the numbers $\tilde{c}$ and $\tilde{d}_{2}, \ldots, \tilde{d}_{n}$.

  comment

• A2.19 B2.19

  Numerical Analysis | Part II, 2002

  (i)

  Given the finite-difference method

  $$\sum_{k=-r}^{s} \alpha_{k} u_{m+k}^{n+1}=\sum_{k=-r}^{s} \beta_{k} u_{m+k}^{n}, \quad m, n \in \mathbb{Z}, n \geqslant 0$$

  define

  $$H(z)=\frac{\sum_{k=-r}^{s} \beta_{k} z^{k}}{\sum_{k=-r}^{s} \alpha_{k} z^{k}}$$

  Prove that this method is stable if and only if

  $$\left|H\left(e^{i \theta}\right)\right| \leqslant 1, \quad-\pi \leqslant \theta \leqslant \pi .$$

  [You may quote without proof known properties of the Fourier transform.]

  (ii) Find the range of the parameter $\mu$ such that the method

  $$(1-2 \mu) u_{m-1}^{n+1}+4 \mu u_{m}^{n+1}+(1-2 \mu) u_{m+1}^{n+1}=u_{m-1}^{n}+u_{m+1}^{n}$$

  is stable. Supposing that this method is used to solve the diffusion equation for $u(x, t)$, determine the order of magnitude of the local error as a power of $\Delta x$.

  comment

• A3.19 B3.20

  Numerical Analysis | Part II, 2002

  (i) Determine the order of the multistep method

  $$\mathbf{y}_{n+2}-(1+\alpha) \mathbf{y}_{n+1}+\alpha \mathbf{y}_{n}=h\left[\frac{1}{12}(5+\alpha) \mathbf{f}_{n+2}+\frac{2}{3}(1-\alpha) \mathbf{f}_{n+1}-\frac{1}{12}(1+5 \alpha) \mathbf{f}_{n}\right]$$

  for the solution of ordinary differential equations for different choices of $\alpha$ in the range $-1 \leqslant \alpha \leqslant 1$.

  (ii) Prove that no such choice of $\alpha$ results in a method whose linear stability domain includes the interval $(-\infty, 0)$.

  comment

• A4.22 B4.20

  Numerical Analysis | Part II, 2002

  Write an essay on the method of conjugate gradients. You should describe the algorithm, present an analysis of its properties and discuss its advantages.

  [Any theorems quoted should be stated precisely but need not be proved.]

  comment

Optimization and Control

• B2.15

  Optimization and Control | Part II, 2002

  State Pontryagin's maximum principle (PMP) for the problem of minimizing

  $$\int_{0}^{T} c(x(t), u(t)) d t+K(x(T))$$

  where $x(t) \in \mathbb{R}^{n}, u(t) \in \mathbb{R}^{m}, d x / d t=a(x(t), u(t))$; here, $x(0)$ and $T$ are given, and $x(T)$ is unconstrained.

  Consider the two-dimensional problem in which $d x_{1} / d t=x_{2}, d x_{2} / d t=u$, $c(x, u)=\frac{1}{2} u^{2}$ and $K(x(T))=\frac{1}{2} q x_{1}(T)^{2}, q>0$. Show that, by use of a variable $z(t)=x_{1}(t)+x_{2}(t)(T-t)$, one can rewrite this problem as an equivalent one-dimensional problem.

  Use PMP to solve this one-dimensional problem, showing that the optimal control can be expressed as $u(t)=-q z(T)(T-t)$, where $z(T)=z(0) /\left(1+\frac{1}{3} q T^{3}\right)$.

  Express $u(t)$ in a feedback form of $u(t)=k(t) z(t)$ for some $k(t)$.

  Suppose that the initial state $x(0)$ is perturbed by a small amount to $x(0)+\left(\epsilon_{1}, \epsilon_{2}\right)$. Give an expression (in terms of $\epsilon_{1}, \epsilon_{2}, x(0), q$ and $T$ ) for the increase in minimal cost.

  comment

• B3.14

  Optimization and Control | Part II, 2002

  Consider a scalar system with $x_{t+1}=\left(x_{t}+u_{t}\right) \xi_{t}$, where $\xi_{0}, \xi_{1}, \ldots$ is a sequence of independent random variables, uniform on the interval $[-a, a]$, with $a \leqslant 1$. We wish to choose $u_{0}, \ldots, u_{h-1}$ to minimize the expected value of

  $$\sum_{t=0}^{h-1}\left(c+x_{t}^{2}+u_{t}^{2}\right)+3 x_{h}^{2},$$

  where $u_{t}$ is chosen knowing $x_{t}$ but not $\xi_{t}$. Prove that the minimal expected cost can be written $V_{h}\left(x_{0}\right)=h c+x_{0}^{2} \Pi_{h}$ and derive a recurrence for calculating $\Pi_{1}, \ldots, \Pi_{h}$.

  How does your answer change if $u_{t}$ is constrained to lie in the set $\mathcal{U}\left(x_{t}\right)=\{u:$ $\left.\left|u+x_{t}\right|<\left|x_{t}\right|\right\} ?$

  Consider a stopping problem for which there are two options in state $x_{t}, t \geqslant 0$ :

  (1) stop: paying a terminal cost $3 x_{t}^{2}$; no further costs are incurred;

  (2) continue: choosing $u_{t} \in \mathcal{U}\left(x_{t}\right)$, paying $c+u_{t}^{2}+x_{t}^{2}$, and moving to state $x_{t+1}=\left(x_{t}+u_{t}\right) \xi_{t} .$

  Consider the problem of minimizing total expected cost subject to the constraint that no more than $h$ continuation steps are allowed. Suppose $a=1$. Show that an optimal policy stops if and only if either $h$ continuation steps have already been taken or $x^{2} \leqslant 2 c / 3$.

  [Hint: Use induction on $h$ to show that a one-step-look-ahead rule is optimal. You should not need to find the optimal $u_{t}$ for the continuation steps.]

  comment

• B4.14

  Optimization and Control | Part II, 2002

  A discrete-time decision process is defined on a finite set of states $I$ as follows. Upon entry to state $i_{t}$ at time $t$ the decision-maker observes a variable $\xi_{t}$. He then chooses the next state freely within $I$, at a cost of $c\left(i_{t}, \xi_{t}, i_{t+1}\right)$. Here $\left\{\xi_{0}, \xi_{1}, \ldots\right\}$ is a sequence of integer-valued, identically distributed random variables. Suppose there exist $\left\{\phi_{i}: i \in I\right\}$ and $\lambda$ such that for all $i \in I$

  $$\phi_{i}+\lambda=\sum_{k \in \mathbb{Z}} P\left(\xi_{t}=k\right) \min _{i^{\prime} \in I}\left[c\left(i, k, i^{\prime}\right)+\phi_{i^{\prime}}\right] .$$

  Let $\pi$ denote a policy. Show that

  $$\lambda=\inf _{\pi} \limsup _{t \rightarrow \infty} E_{\pi}\left[\frac{1}{t} \sum_{s=0}^{t-1} c\left(i_{s}, \xi_{s}, i_{s+1}\right)\right]$$

  At the start of each month a boat manufacturer receives orders for 1, 2 or 3 boats. These numbers are equally likely and independent from month to month. He can produce $j$ boats in a month at a cost of $6+3 j$ units. All orders are filled at the end of the month in which they are ordered. It is possible to make extra boats, ending the month with a stock of $i$ unsold boats, but $i$ cannot be more than 2 , and a holding cost of $c i$ is incurred during any month that starts with $i$ unsold boats in stock. Write down an optimality equation that can be used to find the long-run expected average-cost.

  Let $\pi$ be the policy of only ever producing sufficient boats to fill the present month's orders. Show that it is optimal if and only if $c \geqslant 2$.

  Suppose $c<2$. Starting from $\pi$, what policy is obtained after applying one step of the policy-improvement algorithm?

  comment

Partial Differential Equations

• B1.18

  Partial Differential Equations | Part II, 2002

  (a) Solve the equation, for a function $u(x, y)$,

  $$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0$$

  together with the boundary condition on the $x$-axis:

  $$u(x, 0)=x$$

  Find for which real numbers $a$ it is possible to solve $(*)$ with the following boundary condition specified on the line $y=a x$ :

  $$u(x, a x)=x$$

  Explain your answer in terms of the notion of characteristic hypersurface, which should be defined.

  (b) Solve the equation

  $$\frac{\partial u}{\partial x}+(1+u) \frac{\partial u}{\partial y}=0$$

  with the boundary condition on the $x$-axis

  $$u(x, 0)=x$$

  in the domain $\mathcal{D}=\left\{(x, y): 0<y<(x+1)^{2} / 4,-1<x<\infty\right\}$. Sketch the characteristics.

  comment

• B2.17

  Partial Differential Equations | Part II, 2002

  (a) Define the convolution $f * g$ of two functions. Write down a formula for a solution $u:[0, \infty) \times \mathbb{R}^{n} \rightarrow \mathbb{R}$ to the initial value problem

  $$\frac{\partial u}{\partial t}-\Delta u=0$$

  together with the boundary condition

  $$u(0, x)=f(x)$$

  for $f$ a bounded continuous function on $\mathbb{R}^{n}$. Comment briefly on the uniqueness of the solution.

  (b) State and prove the Duhamel principle giving the solution (for $t>0$ ) to the equation

  $$\frac{\partial u}{\partial t}-\Delta u=g$$

  together with the boundary condition

  $$u(0, x)=f(x)$$

  in terms of your answer to (a).

  (c) Show that if $v:[0, \infty) \times \mathbb{R}^{n} \rightarrow \mathbb{R}$ is the solution to

  $$\frac{\partial v}{\partial t}-\Delta v=G$$

  together with the boundary condition

  $$v(0, x)=f(x)$$

  with $G(t, x) \leq g(t, x)$ for all $(t, x)$ then $v(t, x) \leq u(t, x)$ for all $(t, x) \in(0, \infty) \times \mathbb{R}^{n}$.

  Finally show that if in addition there exists a point $\left(t_{0}, x_{0}\right)$ at which there is strict inequality in the assumption i.e.

  $$G\left(t_{0}, x_{0}\right)<g\left(t_{0}, x_{0}\right)$$

  then in fact

  $$v(t, x)<u(t, x)$$

  whenever $t>t_{0}$.

  comment

• B3.18

  Partial Differential Equations | Part II, 2002

  Define the Schwartz space $\mathcal{S}\left(\mathbb{R}^{n}\right)$ and the space of tempered distributions $\mathcal{S}^{\prime}\left(\mathbb{R}^{n}\right)$. State the Fourier inversion theorem for the Fourier transform of a Schwartz function.

  Consider the initial value problem:

  $$\begin{gathered} \frac{\partial^{2} u}{\partial t^{2}}-\Delta u+u=0, x \in \mathbb{R}^{n}, 0<t<\infty \\ u(0, x)=f(x), \quad \frac{\partial u}{\partial t}(0, x)=0 \end{gathered}$$

  for $f$ in the Schwartz space $\mathcal{S}\left(\mathbb{R}^{n}\right)$.

  Show that the solution can be written as

  $$u(t, x)=(2 \pi)^{-n / 2} \int_{\mathbb{R}^{n}} e^{i x \cdot \xi} \hat{u}(t, \xi) d \xi,$$

  where

  $$\hat{u}(t, \xi)=\cos \left(t \sqrt{1+|\xi|^{2}}\right) \hat{f}(\xi)$$

  and

  $$\hat{f}(\xi)=(2 \pi)^{-n / 2} \int_{\mathbb{R}^{n}} e^{-i x \cdot \xi} f(x) d x .$$

  State the Plancherel-Parseval theorem and hence deduce that

  $$\int_{\mathbb{R}^{n}}|u(t, x)|^{2} d x \leq \int_{\mathbb{R}^{n}}|f(x)|^{2} d x .$$

  comment

• B4.18

  Partial Differential Equations | Part II, 2002

  Discuss the notion of fundamental solution for a linear partial differential equation with constant coefficients.

  comment

Principles of Dynamics

• A1.2 B1.2

  Principles of Dynamics | Part II, 2002

  (i) Derive Hamilton's equations from Lagrange's equations. Show that the Hamiltonian $H$ is constant if the Lagrangian $L$ does not depend explicitly on time.

  (ii) A particle of mass $m$ is constrained to move under gravity, which acts in the negative $z$-direction, on the spheroidal surface $\epsilon^{-2}\left(x^{2}+y^{2}\right)+z^{2}=l^{2}$, with $0<\epsilon \leqslant 1$. If $\theta, \phi$ parametrize the surface so that

  $$x=\epsilon l \sin \theta \cos \phi, y=\epsilon l \sin \theta \sin \phi, z=l \cos \theta,$$

  find the Hamiltonian $H\left(\theta, \phi, p_{\theta}, p_{\phi}\right)$.

  Show that the energy

  $$E=\frac{p_{\theta}^{2}}{2 m l^{2}\left(\epsilon^{2} \cos ^{2} \theta+\sin ^{2} \theta\right)}+\frac{\alpha}{\sin ^{2} \theta}+m g l \cos \theta$$

  is a constant of the motion, where $\alpha$ is a non-negative constant.

  Rewrite this equation as

  $$\frac{1}{2} \dot{\theta}^{2}+V_{\mathrm{eff}}(\theta)=0$$

  and sketch $V_{\mathrm{eff}}(\theta)$ for $\epsilon=1$ and $\alpha>0$, identifying the maximal and minimal values of $\theta(t)$ for fixed $\alpha$ and $E$. If $\epsilon$ is now taken not to be unity, how do these values depend on $\epsilon$ ?

  comment

• A2.2 B2.1

  Principles of Dynamics | Part II, 2002

  (i) A number $N$ of non-interacting particles move in one dimension in a potential $V(x, t)$. Write down the Hamiltonian and Hamilton's equations for one particle.

  At time $t$, the number density of particles in phase space is $f(x, p, t)$. Write down the time derivative of $f$ along a particle's trajectory. By equating the rate of change of the number of particles in a fixed domain $V$ in phase space to the flux into $V$ across its boundary, deduce that $f$ is a constant along any particle's trajectory.

  (ii) Suppose that $V(x)=\frac{1}{2} m \omega^{2} x^{2}$, and particles are injected in such a manner that the phase space density is a constant $f_{1}$ at any point of phase space corresponding to a particle energy being smaller than $E_{1}$ and zero elsewhere. How many particles are present?

  Suppose now that the potential is very slowly altered to the square well form

  $$V(x)=\left\{\begin{array}{cc} 0, & -L<x<L \\ \infty & \text { elsewhere } \end{array}\right.$$

  Show that the greatest particle energy is now

  $$E_{2}=\frac{\pi^{2}}{8} \frac{E_{1}^{2}}{m L^{2} \omega^{2}} .$$

  comment

• A3.2

  Principles of Dynamics | Part II, 2002

  (i) Show that Hamilton's equations follow from the variational principle

  $$\delta \int_{t_{1}}^{t_{2}}[p \dot{q}-H(q, p, t)] d t=0$$

  under the restrictions $\delta q\left(t_{1}\right)=\delta q\left(t_{2}\right)=\delta p\left(t_{1}\right)=\delta p\left(t_{2}\right)=0$. Comment on the difference from the variational principle for Lagrange's equations.

  (ii) Suppose we transform from $p$ and $q$ to $p^{\prime}=p^{\prime}(q, p, t)$ and $q^{\prime}=q^{\prime}(q, p, t)$, with

  $$p^{\prime} \dot{q}^{\prime}-H^{\prime}=p \dot{q}-H+\frac{\mathrm{d}}{\mathrm{d} t} F\left(q, p, q^{\prime}, p^{\prime}, t\right)$$

  where $H^{\prime}$ is the new Hamiltonian. Show that $p^{\prime}$ and $q^{\prime}$ obey Hamilton's equations with Hamiltonian $H^{\prime}$.

  Show that the time independent generating function $F=F_{1}\left(q, q^{\prime}\right)=q^{\prime} / q$ takes the Hamiltonian

  $$H=\frac{1}{2 q^{2}}+\frac{1}{2} p^{2} q^{4}$$

  to harmonic oscillator form. Show that $q^{\prime}$ and $p^{\prime}$ obey the Poisson bracket relation

  $$\left\{q^{\prime}, p^{\prime}\right\}=1$$

  comment

• A4.2

  Principles of Dynamics | Part II, 2002

  Explain how the orientation of a rigid body can be specified by means of the three Eulerian angles, $\theta, \phi$ and $\psi$.

  An axisymmetric top of mass $M$ has principal moments of inertia $A, A$ and $C$, and is spinning with angular speed $n$ about its axis of symmetry. Its centre of mass lies a distance $h$ from the fixed point of support. Initially the axis of symmetry points vertically upwards. It then suffers a small disturbance. For what values of the spin is the initial configuration stable?

  If the spin is such that the initial configuration is unstable, what is the lowest angle reached by the symmetry axis in the nutation of the top? Find the maximum and minimum values of the precessional angular velocity $\dot{\phi}$.

  comment

Principles of Statistics

• A1.12 B1.15

  Principles of Statistics | Part II, 2002

  (i) Explain in detail the minimax and Bayes principles of decision theory.

  Show that if $d(X)$ is a Bayes decision rule for a prior density $\pi(\theta)$ and has constant risk function, then $d(X)$ is minimax.

  (ii) Let $X_{1}, \ldots, X_{p}$ be independent random variables, with $X_{i} \sim N\left(\mu_{i}, 1\right), i=1, \ldots, p$.

  Consider estimating $\mu=\left(\mu_{1}, \ldots, \mu_{p}\right)^{T}$ by $d=\left(d_{1}, \ldots, d_{p}\right)^{T}$, with loss function

  $$L(\mu, d)=\sum_{i=1}^{p}\left(\mu_{i}-d_{i}\right)^{2}$$

  What is the risk function of $X=\left(X_{1}, \ldots, X_{p}\right)^{T} ?$

  Consider the class of estimators of $\mu$ of the form

  $$d^{a}(X)=\left(1-\frac{a}{X^{T} X}\right) X$$

  indexed by $a \geqslant 0$. Find the risk function of $d^{a}(X)$ in terms of $E\left(1 / X^{T} X\right)$, which you should not attempt to evaluate, and deduce that $X$ is inadmissible. What is optimal value of $a$ ?

  [You may assume Stein's Lemma, that for suitably behaved real-valued functions $h$,

  $$\left.E\left\{\left(X_{i}-\mu_{i}\right) h(X)\right\}=E\left\{\frac{\partial h(X)}{\partial X_{i}}\right\} . \quad\right]$$

  comment

• A2.11 B2.16

  Principles of Statistics | Part II, 2002

  (i) Let $X$ be a random variable with density function $f(x ; \theta)$. Consider testing the simple null hypothesis $H_{0}: \theta=\theta_{0}$ against the simple alternative hypothesis $H_{1}: \theta=\theta_{1}$.

  What is the form of the optimal size $\alpha$ classical hypothesis test?

  Compare the form of the test with the Bayesian test based on the Bayes factor, and with the Bayes decision rule under the 0-1 loss function, under which a loss of 1 is incurred for an incorrect decision and a loss of 0 is incurred for a correct decision.

  (ii) What does it mean to say that a family of densities $\{f(x ; \theta), \theta \in \Theta\}$ with real scalar parameter $\theta$ is of monotone likelihood ratio?

  Suppose $X$ has a distribution from a family which is of monotone likelihood ratio with respect to a statistic $t(X)$ and that it is required to test $H_{0}: \theta \leqslant \theta_{0}$ against $H_{1}: \theta>\theta_{0}$.

  State, without proof, a theorem which establishes the existence of a uniformly most powerful test and describe in detail the form of the test.

  Let $X_{1}, \ldots, X_{n}$ be independent, identically distributed $U(0, \theta), \theta>0$. Find a uniformly most powerful size $\alpha$ test of $H_{0}: \theta \leqslant \theta_{0}$ against $H_{1}: \theta>\theta_{0}$, and find its power function. Show that we may construct a different, randomised, size $\alpha$ test with the same power function for $\theta \geqslant \theta_{0}$.

  comment

• A3.12 B3.15

  Principles of Statistics | Part II, 2002

  (i) Describe in detail how to perform the Wald, score and likelihood ratio tests of a simple null hypothesis $H_{0}: \theta=\theta_{0}$ given a random sample $X_{1}, \ldots, X_{n}$ from a regular oneparameter density $f(x ; \theta)$. In each case you should specify the asymptotic null distribution of the test statistic.

  (ii) Let $X_{1}, \ldots, X_{n}$ be an independent, identically distributed sample from a distribution $F$, and let $\hat{\theta}\left(X_{1}, \ldots, X_{n}\right)$ be an estimator of a parameter $\theta$ of $F$.

  Explain what is meant by: (a) the empirical distribution function of the sample; (b) the bootstrap estimator of the bias of $\hat{\theta}$, based on the empirical distribution function. Explain how a bootstrap estimator of the distribution function of $\hat{\theta}-\theta$ may be used to construct an approximate $1-\alpha$ confidence interval for $\theta$.

  Suppose the parameter of interest is $\theta=\mu^{2}$, where $\mu$ is the mean of $F$, and the estimator is $\hat{\theta}=\bar{X}^{2}$, where $\bar{X}=n^{-1} \sum_{i=1}^{n} X_{i}$ is the sample mean.

  Derive an explicit expression for the bootstrap estimator of the bias of $\hat{\theta}$ and show that it is biased as an estimator of the true bias of $\hat{\theta}$.

  Let $\hat{\theta}_{i}$ be the value of the estimator $\hat{\theta}\left(X_{1}, \ldots, X_{i-1}, X_{i+1}, \ldots, X_{n}\right)$ computed from the sample of size $n-1$ obtained by deleting $X_{i}$ and let $\hat{\theta} . n^{-1} \sum_{i=1}^{n} \hat{\theta}_{i}$. The jackknife estimator of the bias of $\hat{\theta}$ is

  $$b_{J}=(n-1)(\hat{\theta} .-\hat{\theta}) .$$

  Derive the jackknife estimator $b_{J}$ for the case $\hat{\theta}=\bar{X}^{2}$, and show that, as an estimator of the true bias of $\hat{\theta}$, it is unbiased.

  comment

• A4.13 B4.15

  Principles of Statistics | Part II, 2002

  (a) Let $X_{1}, \ldots, X_{n}$ be independent, identically distributed random variables from a one-parameter distribution with density function

  $$f(x ; \theta)=h(x) g(\theta) \exp \{\theta t(x)\}, x \in \mathbb{R} .$$

  Explain in detail how you would test

  $$H_{0}: \theta=\theta_{0} \text { against } H_{1}: \theta \neq \theta_{0} \text {. }$$

  What is the general form of a conjugate prior density for $\theta$ in a Bayesian analysis of this distribution?

  (b) Let $Y_{1}, Y_{2}$ be independent Poisson random variables, with means $(1-\psi) \lambda$ and $\psi \lambda$ respectively, with $\lambda$ known.

  Explain why the Conditionality Principle leads to inference about $\psi$ being drawn from the conditional distribution of $Y_{2}$, given $Y_{1}+Y_{2}$. What is this conditional distribution?

  (c) Suppose $Y_{1}, Y_{2}$ have distributions as in (b), but that $\lambda$ is now unknown.

  Explain in detail how you would test $H_{0}: \psi=\psi_{0}$ against $H_{1}: \psi \neq \psi_{0}$, and describe the optimality properties of your test.

  [Any general results you use should be stated clearly, but need not be proved.]

  comment

Probability and Measure

• B1.13

  Probability and Measure | Part II, 2002

  State and prove Dynkin's $\pi$-system lemma.

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space and let $\left(A_{n}\right)$ be a sequence of independent events such that $\lim _{n \rightarrow \infty} \mathbb{P}\left(A_{n}\right)=p$. Let $\mathcal{G}=\sigma\left(A_{1}, A_{2}, \ldots\right)$. Prove that

  $$\lim _{n \rightarrow \infty} \mathbb{P}\left(G \cap A_{n}\right)=p \mathbb{P}(G)$$

  for all $G \in \mathcal{G}$.

  comment

• B2.12

  Probability and Measure | Part II, 2002

  Let $\left(X_{n}\right)$ be a sequence of non-negative random variables on a common probability space with $\mathbb{E} X_{n} \leqslant 1$, such that $X_{n} \rightarrow 0$ almost surely. Determine which of the following statements are necessarily true, justifying your answers carefully: (a) $\mathbb{P}\left(X_{n} \geqslant 1\right) \rightarrow 0$ as $n \rightarrow \infty$; (b) $\mathbb{E} X_{n} \rightarrow 0$ as $n \rightarrow \infty$; (c) $\mathbb{E}\left(\sin \left(X_{n}\right)\right) \rightarrow 0$ as $n \rightarrow \infty$; (d) $\mathbb{E}\left(\sqrt{X_{n}}\right) \rightarrow 0$ as $n \rightarrow \infty$.

  [Standard limit theorems for integrals, and results about uniform integrability, may be used without proof provided that they are clearly stated.]

  comment

• B3.12

  Probability and Measure | Part II, 2002

  Derive the characteristic function of a real-valued random variable which is normally distributed with mean $\mu$ and variance $\sigma^{2}$. What does it mean to say that an $\mathbb{R}^{n}$-valued random variable has a multivariate Gaussian distribution? Prove that the distribution of such a random variable is determined by its $\left(\mathbb{R}^{n}\right.$-valued) mean and its covariance matrix.

  Let $X$ and $Y$ be random variables defined on the same probability space such that $(X, Y)$ has a Gaussian distribution. Show that $X$ and $Y$ are independent if and only if $\operatorname{cov}(X, Y)=0$. Show that, even if they are not independent, one may always write $X=a Y+Z$ for some constant $a$ and some random variable $Z$ independent of $Y$.

  [The inversion theorem for characteristic functions and standard results about independence may be assumed.]

  comment

• B4.11

  Probability and Measure | Part II, 2002

  State Birkhoff's Almost Everywhere Ergodic Theorem for measure-preserving transformations. Define what it means for a sequence of random variables to be stationary. Explain briefly how the stationarity of a sequence of random variables implies that a particular transformation is measure-preserving.

  A bag contains one white ball and one black ball. At each stage of a process one ball is picked from the bag (uniformly at random) and then returned to the bag together with another ball of the same colour. Let $X_{n}$ be a random variable which takes the value 0 if the $n$th ball added to the bag is white and 1 if it is black.

  (a) Show that the sequence $X_{1}, X_{2}, X_{3}, \ldots$ is stationary and hence that the proportion of black balls in the bag converges almost surely to some random variable $R$.

  (b) Find the distribution of $R$.

  [The fact that almost-sure convergence implies convergence in distribution may be used without proof.]

  comment

Quantum Physics

• A1.14

  Quantum Physics | Part II, 2002

  (i) A system of $N$ identical non-interacting bosons has energy levels $E_{i}$ with degeneracy $g_{i}, 1 \leq i<\infty$, for each particle. Show that in thermal equilibrium the number of particles $N_{i}$ with energy $E_{i}$ is given by

  $$N_{i}=\frac{g_{i}}{e^{\beta\left(E_{i}-\mu\right)}-1}$$

  where $\beta$ and $\mu$ are parameters whose physical significance should be briefly explained.

  (ii) A photon moves in a cubical box of side $L$. Assuming periodic boundary conditions, show that, for large $L$, the number of photon states lying in the frequency range $\omega \rightarrow \omega+d \omega$ is $\rho(\omega) d \omega$ where

  $$\rho(\omega)=L^{3}\left(\frac{\omega^{2}}{\pi^{2} c^{3}}\right)$$

  If the box is filled with thermal radiation at temperature $T$, show that the number of photons per unit volume in the frequency range $\omega \rightarrow \omega+d \omega$ is $n(\omega) d \omega$ where

  $$n(\omega)=\left(\frac{\omega^{2}}{\pi^{2} c^{3}}\right) \frac{1}{e^{\hbar \omega / k T}-1} .$$

  Calculate the energy density $W$ of the thermal radiation. Show that the pressure $P$ exerted on the surface of the box satisfies

  $$P=\frac{1}{3} W$$

  [You may use the result $\int_{0}^{\infty} \frac{x^{3} d x}{e^{x}-1}=\frac{\pi^{4}}{15}$.]

  comment

• A2.14

  Quantum Physics | Part II, 2002

  (i) A simple model of a one-dimensional crystal consists of an infinite array of sites equally spaced with separation $a$. An electron occupies the $n$th site with a probability amplitude $c_{n}$. The time-dependent Schrödinger equation governing these amplitudes is

  $$i \hbar \frac{d c_{n}}{d t}=E_{0} c_{n}-A\left(c_{n-1}+c_{n+1}\right)$$

  where $E_{0}$ is the energy of an electron at an isolated site and the amplitude for transition between neighbouring sites is $A>0$. By examining a solution of the form

  $$c_{n}=e^{i k a n-i E t / \hbar}$$

  show that $E$, the energy of the electron in the crystal, lies in a band

  $$E_{0}-2 A \leq E \leq E_{0}+2 A$$

  Identify the Brillouin zone for this model and explain its significance.

  (ii) In the above model the electron is now subject to an electric field $\mathcal{E}$ in the direction of increasing $n$. Given that the charge on the electron is $-e$ write down the norm of the time-dependent Schrödinger equation for the probability amplitudes. Show that it has a solution of the form

  $$c_{n}=\exp \left\{-\frac{i}{\hbar} \int_{0}^{t} \epsilon\left(t^{\prime}\right) d t^{\prime}+i\left(k-\frac{e \mathcal{E} t}{\hbar}\right) n a\right\}$$

  where

  $$\epsilon(t)=E_{0}-2 A \cos \left(\left(k-\frac{e \mathcal{E} t}{\hbar}\right) a\right)$$

  Explain briefly how to interpret this result and use it to show that the dynamical behaviour of an electron near the bottom of the energy band is the same as that for a free particle in the presence of an electric field with an effective mass $m^{*}=\hbar^{2} /\left(2 A a^{2}\right)$.

  comment

• A4.16

  Quantum Physics | Part II, 2002

  Explain how the energy band structure for electrons determines the conductivity properties of crystalline materials.

  A semiconductor has a conduction band with a lower edge $E_{c}$ and a valence band with an upper edge $E_{v}$. Assuming that the density of states for electrons in the conduction band is

  $$\rho_{c}(E)=B_{c}\left(E-E_{c}\right)^{\frac{1}{2}}, \quad E>E_{c}$$

  and in the valence band is

  $$\rho_{v}(E)=B_{v}\left(E_{v}-E\right)^{\frac{1}{2}}, \quad E<E_{v}$$

  where $B_{c}$ and $B_{v}$ are constants characteristic of the semiconductor, explain why at low temperatures the chemical potential for electrons lies close to the mid-point of the gap between the two bands.

  Describe what is meant by the doping of a semiconductor and explain the distinction between $n$-type and $p$-type semiconductors, and discuss the low temperature limit of the chemical potential in both cases. Show that, whatever the degree and type of doping,

  $$n_{e} n_{p}=B_{c} B_{v}[\Gamma(3 / 2)]^{2}(k T)^{3} e^{-\left(E_{c}-E_{v}\right) / k T}$$

  where $n_{e}$ is the density of electrons in the conduction band and $n_{p}$ is the density of holes in the valence band.

  comment

Representation Theory

• B1.6

  Representation Theory | Part II, 2002

  Construct the character table of the symmetric group $S_{5}$, explaining the steps in your construction.

  Use the character table to show that the alternating group $A_{5}$ is the only non-trivial normal subgroup of $S_{5}$.

  comment

• B2.6

  Representation Theory | Part II, 2002

  State and prove Schur's Lemma. Deduce that the centre of a finite group $G$ with a faithful irreducible complex representation $\rho$ is cyclic and that $Z(\rho(G))$ consists of scalar transformations.

  Let $G$ be the subgroup of order 18 of the symmetric group $S_{6}$ given by

  $$G=\langle(123),(456),(23)(56)\rangle$$

  Show that $G$ has a normal subgroup of order 9 and four normal subgroups of order 3 . By considering quotients, show that $G$ has two representations of dimension 1 and four inequivalent irreducible representations of degree 2 . Deduce that $G$ has no faithful irreducible complex representations.

  Show finally that if $G$ is a finite group with trivial centre and $H$ is a subgroup of $G$ with non-trivial centre, then any faithful representation of $G$ is reducible on restriction to $H$.

  comment

• B3.5

  Representation Theory | Part II, 2002

  Let $G$ be a finite group acting on a finite set $X$. Define the permutation representation $(\rho, \mathbb{C}[X])$ of $G$ and compute its character $\pi_{X}$. Prove that $\left\langle\pi_{X}, 1_{G}\right\rangle_{G}$ equals the number of orbits of $G$ on $X$. If $G$ acts also on the finite set $Y$, with character $\pi_{Y}$, show that $\left\langle\pi_{X}, \pi_{Y}\right\rangle_{G}$ equals the number of orbits of $G$ on $X \times Y$.

  Now let $G$ be the symmetric group $S_{n}$ acting naturally on the set $X=\{1, \ldots, n\}$, and let $X_{r}$ be the set of all $r$-element subsets of $X$. Let $\pi_{r}$ be the permutation character of $G$ on $X_{r}$. Prove that

  $$\left\langle\pi_{k}, \pi_{\ell}\right\rangle_{G}=\ell+1 \text { for } 0 \leqslant \ell \leqslant k \leqslant n / 2$$

  Deduce that the class functions

  $$\chi_{r}=\pi_{r}-\pi_{r-1}$$

  are irreducible characters of $S_{n}$, for $1 \leqslant r \leqslant n / 2$.

  comment

• B4.2

  Representation Theory | Part II, 2002

  Write an essay on the representation theory of $S U_{2}$.

  comment

Riemann Surfaces

• B1.11

  Riemann Surfaces | Part II, 2002

  (a) Define the notions of (abstract) Riemann surface, holomorphic map, and biholomorphic map between Riemann surfaces.

  (b) Prove the following theorem on the local form of a holomorphic map.

  For a holomorphic map $f: R \rightarrow S$ between Riemann surfaces, which is not constant near a point $r \in R$, there exist neighbourhoods $U$ of $r$ in $R$ and $V$ of $f(r)$ in $S$, together with biholomorphic identifications $\phi: U \rightarrow \Delta, \psi: V \rightarrow \Delta$, such that $(\psi \circ f)(x)=\phi(x)^{n}$, for all $x \in U$.

  (c) Prove further that a non-constant holomorphic map between compact, connected Riemann surfaces is surjective.

  (d) Deduce from (c) the fundamental theorem of algebra.

  comment

• B3.9

  Riemann Surfaces | Part II, 2002

  Let $\alpha_{1}, \alpha_{2}$ be two non-zero complex numbers with $\alpha_{1} / \alpha_{2} \notin \mathbb{R}$. Let $L$ be the lattice $\mathbb{Z} \alpha_{1} \oplus \mathbb{Z} \alpha_{2} \subset \mathbb{C}$. A meromorphic function $f$ on $\mathbb{C}$ is elliptic if $f(z+\lambda)=f(z)$, for all $z \in \mathbb{C}$ and $\lambda \in L$. The Weierstrass functions $\wp(z), \zeta(z), \sigma(z)$ are defined by the following properties:

  • $\wp(z)$ is elliptic, has double poles at the points of $L$ and no other poles, and $\wp(z)=$ $1 / z^{2}+O\left(z^{2}\right)$ near 0

  • $\zeta^{\prime}(z)=-\wp(z)$, and $\zeta(z)=1 / z+O\left(z^{3}\right)$ near 0 ;

  • $\sigma(z)$ is odd, and $\sigma^{\prime}(z) / \sigma(z)=\zeta(z)$, and $\sigma(z) / z \rightarrow 1$ as $z \rightarrow 0$.

  Prove the following

  (a) $\wp$, and hence $\zeta$ and $\sigma$, are uniquely determined by these properties. You are not expected to prove the existence of $\wp, \zeta, \sigma$, and you may use Liouville's theorem without proof.

  (b) $\zeta\left(z+\alpha_{i}\right)=\zeta(z)+2 \eta_{i}$, and $\sigma\left(z+\alpha_{i}\right)=k_{i} e^{2 \eta_{i} z} \sigma(z)$, for some constants $\eta_{i}, k_{i}(i=1,2)$.

  (c) $\sigma$ is holomorphic, has simple zeroes at the points of $L$, and has no other zeroes.

  (d) Given $a_{1}, \ldots, a_{n}$ and $b_{1}, \ldots, b_{n}$ in $\mathbb{C}$ with $a_{1}+\ldots+a_{n}=b_{1}+\ldots+b_{n}$, the function

  $$\frac{\sigma\left(z-a_{1}\right) \cdots \sigma\left(z-a_{n}\right)}{\sigma\left(z-b_{1}\right) \cdots \sigma\left(z-b_{n}\right)}$$

  is elliptic.

  (e) $\wp(u)-\wp(v)=-\frac{\sigma(u+v) \sigma(u-v)}{\sigma^{2}(u) \sigma^{2}(v)}$.

  (f) Deduce from (e), or otherwise, that $\frac{1}{2} \frac{\wp^{\prime}(u)-\wp^{\prime}(v)}{\wp(u)-\wp(v)}=\zeta(u+v)-\zeta(u)-\zeta(v)$.

  comment

• B4.8

  Riemann Surfaces | Part II, 2002

  A holomorphic map $p: S \rightarrow T$ between Riemann surfaces is called a covering map if every $t \in T$ has a neighbourhood $V$ for which $p^{-1}(V)$ breaks up as a disjoint union of open subsets $U_{\alpha}$ on which $p: U_{\alpha} \rightarrow V$ is biholomorphic.

  (a) Suppose that $f: R \rightarrow T$ is any holomorphic map of connected Riemann surfaces, $R$ is simply connected and $p: S \rightarrow T$ is a covering map. By considering the lifts of paths from $T$ to $S$, or otherwise, prove that $f$ lifts to a holomorphic map $\widetilde{f}: R \rightarrow S$, i.e. that there exists an $\widetilde{f}$ with $f=p \circ \widetilde{f}$.

  (b) Write down a biholomorphic map from the unit disk $\Delta=\{z \in \mathbb{C}:|z|<1\}$ onto a half-plane. Show that the unit disk $\Delta$ uniformizes the punctured unit disk $\Delta^{\times}=\Delta-\{0\}$ by constructing an explicit covering map $p: \Delta \rightarrow \Delta^{\times}$.

  (c) Using the uniformization theorem, or otherwise, prove that any holomorphic map from $\mathbb{C}$ to a compact Riemann surface of genus greater than one is constant.

  comment

Statistical Physics

• B1.22

  Statistical Physics | Part II, 2002

  A simple model for a rubber molecule consists of a one-dimensional chain of $n$ links each of fixed length $b$ and each of which is oriented in either the positive or negative direction. A unique state $i$ of the molecule is designated by giving the orientation $\pm 1$ of each link. If there are $n_{+}$links oriented in the positive direction and $n_{-}$links oriented in the negative direction then $n=n_{+}+n_{-}$and the length of the molecule is $l=\left(n_{+}-n_{-}\right) b$. The length of the molecule associated with state $i$ is $l_{i}$.

  What is the range of $l$ ?

  What is the number of states with $n, n_{+}, n_{-}$fixed?

  Consider an ensemble of $A$ copies of the molecule in which $a_{i}$ members are in state $i$ and write down the expression for the mean length $L$.

  By introducing a Lagrange multiplier $\tau$ for $L$ show that the most probable configuration for the $\left\{a_{i}\right\}$ with given length $L$ is found by maximizing

  $$\log \left(\frac{A !}{\prod_{i} a_{i} !}\right)+\tau \sum_{i} a_{i} l_{i}-\alpha \sum_{i} a_{i} .$$

  Hence show that the most probable configuration is given by

  $$p_{i}=\frac{e^{\tau l_{i}}}{Z},$$

  where $p_{i}$ is the probability for finding an ensemble member in the state $i$ and $Z$ is the partition function which should be defined.

  Show that $Z$ can be expressed as

  $$Z=\sum_{l} g(l) e^{\tau l}$$

  where the meaning of $g(l)$ should be explained.

  Hence show that $Z$ is given by

  $$Z=\sum_{n_{+}=0}^{n} \frac{n !}{n_{+} ! n_{-} !}\left(e^{\tau b}\right)^{n_{+}}\left(e^{-\tau b}\right)^{n_{-}}, \quad n_{+}+n_{-}=n$$

  and therefore that the free energy $G$ for the system is

  $$G=-n k T \log (2 \cosh \tau b) .$$

  Show that $\tau$ is determined by

  $$L=-\frac{1}{k T}\left(\frac{\partial G}{\partial \tau}\right)_{n}$$

  and hence that the equation of state is

  $$\tanh \tau b=\frac{L}{n b} .$$

  What are the independent variables on which $G$ depends?

  Explain why the tension in the rubber molecule is $k T \tau$.

  comment

• B3.22

  Statistical Physics | Part II, 2002

  A system consisting of non-interacting bosons has single-particle levels uniquely labelled by $r$ with energies $\epsilon_{r}, \epsilon_{r} \geq 0$. Show that the free energy in the grand canonical ensemble is

  $$F=k T \sum_{r} \log \left(1-e^{-\beta\left(\epsilon_{r}-\mu\right)}\right) .$$

  What is the maximum value for $\mu$ ?

  A system of $N$ bosons in a large volume $V$ has one energy level of energy zero and a large number $M \gg 1$ of energy levels of the same energy $\epsilon$, where $M$ takes the form $M=A V$ with $A$ a positive constant. What are the dimensions of $A ?$

  Show that the free energy is

  $$F=k T\left(\log \left(1-e^{\beta \mu}\right)+A V \log \left(1-e^{-\beta(\epsilon-\mu)}\right)\right)$$

  The numbers of particles with energies $0, \epsilon$ are respectively $N_{0}, N_{\epsilon}$. Write down expressions for $N_{0}, N_{\epsilon}$ in terms of $\mu$.

  At temperature $T$ what is the maximum number of bosons $N_{\epsilon}^{\max }$ in the normal phase (the state with energy $\epsilon$ )? Explain what happens when $N>N_{\epsilon}^{\max }$.

  Given $N$ and $T$ calculate the transition temperature $T_{B}$ at which Bose condensation occurs.

  For $T>T_{B}$ show that $\mu=\epsilon\left(T_{B}-T\right) / T_{B}$. What is the value of $\mu$ for $T<T_{B}$ ?

  Calculate the mean energy $E$ for (a) $T>T_{B}$ (b) $T<T_{B}$, and show that the heat capacity of the system at constant volume is

  $$C_{V}=\left\{\begin{array}{cl} \frac{1}{k T^{2}} \frac{A V \epsilon^{2}}{\left(e^{\beta \epsilon}-1\right)^{2}} & T<T_{B} \\ 0 & T>T_{B} \end{array}\right.$$

  comment

• B4.23

  Statistical Physics | Part II, 2002

  A perfect gas in equilibrium in a volume $V$ has quantum stationary states $|i\rangle$ with energies $E_{i}$. In a Boltzmann distribution, the probability that the system is in state $|i\rangle$ is $\rho_{i}=Z^{-1} e^{-E_{i} / k T}$. The entropy is defined to be $S=-k \sum_{i} \rho_{i} \log \rho_{i}$.

  For two nearby states establish the equation

  $$d E=T d S-P d V$$

  where $E$ and $P$ should be defined.

  For reversible changes show that

  $$d S=\frac{\delta Q}{T}$$

  where $\delta Q$ is the amount of heat transferred in the exchange.

  Define $C_{V}$, the heat capacity at constant volume.

  A system with constant heat capacity $C_{V}$ initially at temperature $T$ is heated at constant volume to a temperature $\Theta$. Show that the change in entropy is $\Delta S=$ $C_{V} \log (\Theta / T)$.

  Explain what is meant by isothermal and adiabatic transitions.

  Briefly, describe the Carnot cycle and define its efficiency. Explain briefly why no heat engine can be more efficient than one whose operation is based on a Carnot cycle.

  Three identical bodies with constant heat capacity at fixed volume $C_{V}$, are initially at temperatures $T_{1}, T_{2}, T_{3}$, respectively. Heat engines operate between the bodies with no input of work or heat from the outside and the respective temperatures are changed to $\Theta_{1}, \Theta_{2}, \Theta_{3}$, the volume of the bodies remaining constant. Show that, if the heat engines operate on a Carnot cycle, then

  $$\Theta_{1} \Theta_{2} \Theta_{3}=A, \quad \Theta_{1}+\Theta_{2}+\Theta_{3}=B$$

  where $A=T_{1} T_{2} T_{3}$ and $B=T_{1}+T_{2}+T_{3}$.

  Hence show that the maximum temperature to which any one of the bodies can be raised is $\Theta$ where

  $$\Theta+2\left(\frac{A}{\Theta}\right)^{1 / 2}=B$$

  Show that a solution is $\Theta=T$ if initially $T_{1}=T_{2}=T_{3}=T$. Do you expect there to be any other solutions?

  Find $\Theta$ if initially $T_{1}=300 \mathrm{~K}, T_{2}=300 \mathrm{~K}, T_{3}=100 \mathrm{~K}$.

  [Hint: Choose to maximize one temperature and impose the constraints above using Lagrange multipliers. ]

  comment

Statistical Physics and Cosmology

• A1.16

  Statistical Physics and Cosmology | Part II, 2002

  (i) Consider a one-dimensional model universe with "stars" distributed at random on the $x$-axis, and choose the origin to coincide with one of the stars; call this star the "homestar." Home-star astronomers have discovered that all other stars are receding from them with a velocity $v(x)$, that depends on the position $x$ of the star. Assuming non-relativistic addition of velocities, show how the assumption of homogeneity implies that $v(x)=H_{0} x$ for some constant $H_{0}$.

  In attempting to understand the history of their one-dimensional universe, homestar astronomers seek to determine the velocity $v(t)$ at time $t$ of a star at position $x(t)$. Assuming homogeneity, show how $x(t)$ is determined in terms of a scale factor $a(t)$ and hence deduce that $v(t)=H(t) x(t)$ for some function $H(t)$. What is the relation between $H(t)$ and $H_{0}$ ?

  (ii) Consider a three-dimensional homogeneous and isotropic universe with mass density $\rho(t)$, pressure $p(t)$ and scale factor $a(t)$. Given that $E(t)$ is the energy in volume $V(t)$, show how the relation $d E=-p d V$ yields the "fluid" equation

  $$\dot{\rho}=-3\left(\rho+\frac{p}{c^{2}}\right) H$$

  where $H=\dot{a} / a$.

  Show how conservation of energy applied to a test particle at the boundary of a spherical fluid element yields the Friedmann equation

  $$\dot{a}^{2}-\frac{8 \pi G}{3} \rho a^{2}=-k c^{2}$$

  for constant $k$. Hence obtain an equation for the acceleration $\ddot{a}$ in terms of $\rho, p$ and $a$.

  A model universe has mass density and pressure

  $$\rho=\frac{\rho_{0}}{a^{3}}+\rho_{1}, \quad p=-\rho_{1} c^{2},$$

  where $\rho_{0}$ is constant. What does the fluid equation imply about $\rho_{1}$ ? Show that the acceleration $\ddot{a}$ vanishes if

  $$a=\left(\frac{\rho_{0}}{2 \rho_{1}}\right)^{\frac{1}{3}}$$

  Hence show that this universe is static and determine the sign of the constant $k$.

  comment

• A3.14

  Statistical Physics and Cosmology | Part II, 2002

  (i) Write down the first law of thermodynamics for the change $d U$ in the internal energy $U(N, V, S)$ of a gas of $N$ particles in a volume $V$ with entropy $S$.

  Given that

  $$P V=(\gamma-1) U,$$

  where $P$ is the pressure, use the first law to show that $P V^{\gamma}$ is constant at constant $N$ and

  Write down the Boyle-Charles law for a non-relativistic ideal gas and hence deduce that the temperature $T$ is proportional to $V^{1-\gamma}$ at constant $N$ and $S$.

  State the principle of equipartition of energy and use it to deduce that

  $$U=\frac{3}{2} N k T$$

  Hence deduce the value of $\gamma$. Show that this value of $\gamma$ is such that the ratio $E_{i} / k T$ is unchanged by a change of volume at constant $N$ and $S$, where $E_{i}$ is the energy of the $i$-th one particle eigenstate of a non-relativistic ideal gas.

  (ii) A classical gas of non-relativistic particles of mass $m$ at absolute temperature $T$ and number density $n$ has a chemical potential

  $$\mu=m c^{2}-k T \ln \left(\frac{g_{s}}{n}\left(\frac{m k T}{2 \pi \hbar^{2}}\right)^{\frac{3}{2}}\right)$$

  where $g_{s}$ is the particle's spin degeneracy factor. What condition on $n$ is needed for the validity of this formula and why?

  Thermal and chemical equilibrium between two species of non-relativistic particles $a$ and $b$ is maintained by the reaction

  $$a+\alpha \leftrightarrow b+\beta$$

  where $\alpha$ and $\beta$ are massless particles with zero chemical potential. Given that particles $a$ and $b$ have masses $m_{a}$ and $m_{b}$ respectively, but equal spin degeneracy factors, find the number density ratio $n_{a} / n_{b}$ as a function of $m_{a}, m_{b}$ and $T$. Given that $m_{a}>m_{b}$ but $m_{a}-m_{b} \ll m_{b}$ show that

  $$\frac{n_{a}}{n_{b}} \approx f\left(\frac{\left(m_{a}-m_{b}\right) c^{2}}{k T}\right)$$

  for some function $f$ which you should determine.

  Explain how a reaction of the above type is relevant to a determination of the neutron to proton ratio in the early universe and why this ratio does not fall rapidly to zero as the universe cools. Explain briefly the process of primordial nucleosynthesis by which neutrons are converted into stable helium nuclei. Let

  $$Y_{H e}=\frac{\rho_{H e}}{\rho}$$

  be the fraction of the universe that ends up in helium. Compute $Y_{H e}$ as a function of the ratio $r=n_{a} / n_{b}$ at the time of nucleosynthesis.

  comment

• A4.18

  Statistical Physics and Cosmology | Part II, 2002

  What is an ideal gas? Explain how the microstates of an ideal gas of indistinguishable particles can be labelled by a set of integers. What range of values do these integers take for (a) a boson gas and (b) a Fermi gas?

  Let $E_{i}$ be the energy of the $i$-th one-particle energy eigenstate of an ideal gas in thermal equilibrium at temperature $T$ and let $p_{i}\left(n_{i}\right)$ be the probability that there are $n_{i}$ particles of the gas in this state. Given that

  $$p_{i}\left(n_{i}\right)=e^{-\beta E_{i} n_{i}} / Z_{i} \quad\left(\beta=\frac{1}{k T}\right)$$

  determine the normalization factor $Z_{i}$ for (a) a boson gas and (b) a Fermi gas. Hence obtain an expression for $\bar{n}_{i}$, the average number of particles in the $i$-th one-particle energy eigenstate for both cases (a) and (b).

  In the case of a Fermi gas, write down (without proof) the generalization of your formula for $\bar{n}_{i}$ to a gas at non-zero chemical potential $\mu$. Show how it leads to the concept of a Fermi energy $\epsilon_{F}$ for a gas at zero temperature. How is $\epsilon_{F}$ related to the Fermi momentum $p_{F}$ for (a) a non-relativistic gas and (b) an ultra-relativistic gas?

  In an approximation in which the discrete set of energies $E_{i}$ is replaced with a continuous set with momentum $p$, the density of one-particle states with momentum in the range $p$ to $p+d p$ is $g(p) d p$. Explain briefly why

  $$g(p) \propto p^{2} V$$

  where $V$ is the volume of the gas. Using this formula, obtain an expression for the total energy $E$ of an ultra-relativistic gas at zero chemical potential as an integral over $p$. Hence show that

  $$\frac{E}{V} \propto T^{\alpha},$$

  where $\alpha$ is a number that you should compute. Why does this result apply to a photon gas?

  Using the formula $(*)$ for a non-relativistic Fermi gas at zero temperature, obtain an expression for the particle number density $n$ in terms of the Fermi momentum and provide a physical interpretation of this formula in terms of the typical de Broglie wavelength. Obtain an analogous formula for the (internal) energy density and hence show that the pressure $P$ behaves as

  $$P \propto n^{\gamma}$$

  where $\gamma$ is a number that you should compute. [You need not prove any relation between the pressure and the energy density you use.] What is the origin of this pressure given that $T=0$ by assumption? Explain briefly and qualitatively how it is relevant to the stability of white dwarf stars.

  comment

Stochastic Financial Models

• A1.11 B1.16

  Stochastic Financial Models | Part II, 2002

  (i) The prices, $S_{i}$, of a stock in a binomial model at times $i=0,1,2$ are represented by the following binomial tree.

  

  The fixed interest rate per period is $1 / 5$ and the probability that the stock price increases in a period is $1 / 3$. Find the price at time 0 of a European call option with strike price 78 and expiry time $2 .$

  Explain briefly the ideas underlying your calculations.

  (ii) Consider an investor in a one-period model who may invest in $s$ assets, all of which are risky, with a random return vector $\boldsymbol{R}$ having mean $\mathbb{E} \boldsymbol{R}=\boldsymbol{r}$ and positivedefinite covariance matrix $\boldsymbol{V}$; assume that not all the assets have the same expected return. Show that any minimum-variance portfolio is equivalent to the investor dividing his wealth between two portfolios, the global minimum-variance portfolio and the diversified portfolio, both of which should be specified clearly in terms of $\boldsymbol{r}$ and $\boldsymbol{V}$.

  Now suppose that $\boldsymbol{R}=\left(R_{1}, R_{2}, \ldots, R_{s}\right)^{\top}$ where $R_{1}, R_{2}, \ldots, R_{s}$ are independent random variables with $R_{i}$ having the exponential distribution with probability density function $\lambda_{i} e^{-\lambda_{i} x}, x \geqslant 0$, where $\lambda_{i}>0,1 \leqslant i \leqslant s$. Determine the global minimum-variance portfolio and the diversified portfolio explicitly.

  Consider further the situation when the investor has the utility function $u(x)=$ $1-e^{-x}$, where $x$ denotes his wealth. Suppose that he acts to maximize the expected utility of his final wealth, and that his initial wealth is $w>0$. Show that he now divides his wealth between the diversified portfolio and the uniform portfolio, in which wealth is apportioned equally between the assets, and determine the amounts that he invests in each.

  comment

• A3.11 B3.16

  Stochastic Financial Models | Part II, 2002

  (i) Explain briefly what it means to say that a stochastic process $\left\{W_{t}, t \geqslant 0\right\}$ is a standard Brownian motion.

  Let $\left\{W_{t}, t \geqslant 0\right\}$ be a standard Brownian motion and let $a, b$ be real numbers. What condition must $a$ and $b$ satisfy to ensure that the process $e^{a W_{t}+b t}$ is a martingale? Justify your answer carefully.

  (ii) At the beginning of each of the years $r=0,1, \ldots, n-1$ an investor has income $X_{r}$, of which he invests a proportion $\rho_{r}, 0 \leqslant \rho_{r} \leqslant 1$, and consumes the rest during the year. His income at the beginning of the next year is

  $$X_{r+1}=X_{r}+\rho_{r} X_{r} W_{r}$$

  where $W_{0}, \ldots, W_{n-1}$ are independent positive random variables with finite means and $X_{0} \geqslant 0$ is a constant. He decides on $\rho_{r}$ after he has observed both $X_{r}$ and $W_{r}$ at the beginning of year $r$, but at that time he does not have any knowledge of the value of $W_{s}$, for any $s>r$. The investor retires in year $n$ and consumes his entire income during that year. He wishes to determine the investment policy that maximizes his expected total consumption

  $$\mathbb{E}\left[\sum_{r=0}^{n-1}\left(1-\rho_{r}\right) X_{r}+X_{n}\right]$$

  Prove that the optimal policy may be expressed in terms of the numbers $b_{0}, b_{1}, \ldots$, $b_{n}$ where $b_{n}=1, b_{r}=b_{r+1}+\mathbb{E} \max \left(b_{r+1} W_{r}, 1\right)$, for $r<n$, and determine the optimal expected total consumption.

  comment

• A4.12 B4.16

  Stochastic Financial Models | Part II, 2002

  Write an essay on the Black-Scholes formula for the price of a European call option on a stock. Your account should include a derivation of the formula and a careful analysis of its dependence on the parameters of the model.

  comment

Symmetries and Groups in Physics

• A1.17

  Symmetries and Groups in Physics | Part II, 2002

  (i) Let $H$ be a normal subgroup of the group $G$. Let $G / H$ denote the group of cosets $\tilde{g}=g H$ for $g \in G$. If $D: G \rightarrow G L\left(\mathbb{C}^{n}\right)$ is a representation of $G$ with $D\left(h_{1}\right)=D\left(h_{2}\right)$ for all $h_{1}, h_{2} \in H$ show that $\tilde{D}(\tilde{g})=D(g)$ is well-defined and that it is a representation of $G / H$. Show further that $\tilde{D}(\tilde{g})$ is irreducible if and only if $D(g)$ is irreducible.

  (ii) For a matrix $U \in S U(2)$ define the linear map $\Phi_{U}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ by $\Phi_{U}(\mathbf{x}) \cdot \boldsymbol{\sigma}=$ $U \mathbf{x} . \boldsymbol{\sigma} U^{\dagger}$ with $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)^{T}$ as the vector of the Pauli spin matrices

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  Show that $\left\|\Phi_{U}(\mathbf{x})\right\|=\|\mathbf{x}\|$. Because of the linearity of $\Phi_{U}$ there exists a matrix $R(U)$ such that $\Phi_{U}(\mathbf{x})=R(U) \mathbf{x}$. Given that any $S U(2)$ matrix can be written as

  $$U=\cos \alpha I-i \sin \alpha \mathbf{n} \cdot \boldsymbol{\sigma}$$

  where $\alpha \in[0, \pi]$ and $\mathbf{n}$ is a unit vector, deduce that $R(U) \in S O(3)$ for all $U \in S U(2)$. Compute $R(U) \mathbf{n}$ and $R(U) \mathbf{x}$ in the case that $\mathbf{x} \cdot \mathbf{n}=0$ and deduce that $R(U)$ is the matrix of a rotation about $\mathbf{n}$ with angle $2 \alpha$.

  [Hint: $\mathbf{m} . \boldsymbol{\sigma} \mathbf{n} . \boldsymbol{\sigma}=\mathbf{m} . \mathbf{n} I+i(\mathbf{m} \times \mathbf{n}) . \boldsymbol{\sigma} .]$

  Show that $R(U)$ defines a surjective homomorphism $\Theta: S U(2) \rightarrow S O(3)$ and find the kernel of $\Theta$.

  comment

• A3.15

  Symmetries and Groups in Physics | Part II, 2002

  (i) Let $D_{6}$ denote the symmetry group of rotations and reflections of a regular hexagon. The elements of $D_{6}$ are given by $\left\{e, c, c^{2}, c^{3}, c^{4}, c^{5}, b, b c, b c^{2}, b c^{3}, b c^{4}, b c^{5}\right\}$ with $c^{6}=b^{2}=e$ and $c b=b c^{5}$. The conjugacy classes of $D_{6}$ are $\{e\},\left\{c, c^{5}\right\},\left\{c^{2}, c^{4}\right\},\left\{c^{3}\right\},\left\{b, b c^{2}, b c^{4}\right\}$ and $\left\{b c, b c^{3}, b c^{5}\right\}$.

  Show that the character table of $D_{6}$ is

  \begin{tabular}{l|rrrrrr} $D_{6}$ & $e$ & $\left\{c, c^{5}\right\}$ & $\left\{c^{2}, c^{4}\right\}$ & $\left\{c^{3}\right\}$ & $\left\{b, b c^{2}, b c^{4}\right\}$ & $\left\{b c, b c^{3}, b c^{5}\right\}$ \ \hline$\chi_{1}$ & 1 & 1 & 1 & 1 & 1 & 1 \ $\chi_{2}$ & 1 & 1 & 1 & 1 & $-1$ & $-1$ \ $\chi_{3}$ & 1 & $-1$ & 1 & $-1$ & 1 & $-1$ \ $\chi_{4}$ & 1 & $-1$ & 1 & $-1$ & $-1$ & 1 \ $\chi_{5}$ & 2 & 1 & $-1$ & $-2$ & 0 & 0 \ $\chi_{6}$ & 2 & $-1$ & $-1$ & 2 & 0 & 0 \end{tabular}

  (ii) Show that the character of an $S O(3)$ rotation with angle $\theta$ in the $2 l+1$ dimensional irreducible representation of $S O(3)$ is given by

  $$\chi_{l}(\theta)=1+2 \cos \theta+2 \cos (2 \theta)+\ldots+2 \cos ((l-1) \theta)+2 \cos (l \theta)$$

  For a hexagonal crystal of atoms find how the degeneracy of the D-wave orbital states $(l=2)$ in the atomic central potential is split by the crystal potential with $D_{6}$ symmetry and give the new degeneracies.

  By using the fact that $D_{3}$ is isomorphic to $D_{6} /\left\{e, c^{3}\right\}$, or otherwise, find the degeneracies of eigenstates if the hexagonal symmetry is broken to the subgroup $D_{3}$ by a deformation. The introduction of a magnetic field further reduces the symmetry to $C_{3}$. What will the degeneracies of the energy eigenstates be now?

  comment

Theoretical Geophysics

• A1.19

  Theoretical Geophysics | Part II, 2002

  (i) In a reference frame rotating about a vertical axis with constant angular velocity $f / 2$ the horizontal components of the momentum equation for a shallow layer of inviscid, incompressible fluid of constant density $\rho$ are

  $$\begin{aligned} &\frac{D u}{D t}-f v=-\frac{1}{\rho} \frac{\partial P}{\partial x} \\ &\frac{D v}{D t}+f u=-\frac{1}{\rho} \frac{\partial P}{\partial y} \end{aligned}$$

  where $u, v$ and $P$ are independent of the vertical coordinate $z$.

  Define the Rossby number $R o$ for a flow with typical velocity $U$ and lengthscale $L$. What is the approximate form of the above equations when $R o \ll 1$ ?

  Show that the solution to the approximate equations is given by a streamfunction $\psi$ proportional to $P$.

  Conservation of potential vorticity for such a flow is represented by

  $$\frac{D}{D t} \frac{\zeta+f}{h}=0$$

  where $\zeta$ is the vertical component of relative vorticity and $h(x, y)$ is the thickness of the layer. Explain briefly why the potential vorticity of a column of fluid should be conserved.

  (ii) Suppose that the thickness of the rotating, shallow-layer flow in Part (i) is $h(y)=H_{0} \exp (-\alpha y)$ where $H_{0}$ and $\alpha$ are constants. By linearising the equation of conservation of potential vorticity about $u=v=\zeta=0$, show that the stream function for small disturbances to the state of rest obeys

  $$\frac{\partial}{\partial t}\left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\right) \psi+\beta \frac{\partial \psi}{\partial x}=0$$

  where $\beta$ is a constant that should be found.

  Obtain the dispersion relationship for plane-wave solutions of the form $\psi \propto$ $\exp [i(k x+l y-\omega t)]$. Hence calculate the group velocity.

  Show that if $\beta>0$ then the phase of these waves always propagates to the left (negative $x$ direction) but that the energy may propagate to either left or right.

  comment

• A2.16

  Theoretical Geophysics | Part II, 2002

  (i) State the equations that relate strain to displacement and stress to strain in a linear, isotropic elastic solid.

  In the absence of body forces, the Euler equation for infinitesimal deformations of a solid of density $\rho$ is

  $$\rho \frac{\partial^{2} u_{i}}{\partial t^{2}}=\frac{\partial \sigma_{i j}}{\partial x_{j}}$$

  Derive an equation for $\mathbf{u}(\mathbf{x}, t)$ in a linear, isotropic, homogeneous elastic solid. Hence show that both the dilatation $\theta=\boldsymbol{\nabla} \cdot \mathbf{u}$ and the rotation $\boldsymbol{\omega}=\nabla \wedge \mathbf{u}$ satisfy wave equations and find the corresponding wave speeds $\alpha$ and $\beta$.

  (ii) The ray parameter $p=r \sin i / v$ is constant along seismic rays in a spherically symmetric Earth, where $v(r)$ is the relevant wave speed $(\alpha$ or $\beta)$ and $i(r)$ is the angle between the ray and the local radial direction.

  Express $\tan i$ and sec $i$ in terms of $p$ and the variable $\eta(r)=r / v$. Hence show that the angular distance and travel time between a surface source and receiver, both at radius $R$, are given by

  $$\Delta(p)=2 \int_{r_{m}}^{R} \frac{p}{r} \frac{d r}{\left(\eta^{2}-p^{2}\right)^{1 / 2}} \quad, \quad T(p)=2 \int_{r_{m}}^{R} \frac{\eta^{2}}{r} \frac{d r}{\left(\eta^{2}-p^{2}\right)^{1 / 2}}$$

  where $r_{m}$ is the minimum radius attained by the ray. What is $\eta\left(r_{m}\right)$ ?

  A simple Earth model has a solid mantle in $R / 2<r<R$ and a liquid core in $r<R / 2$. If $\alpha(r)=A / r$ in the mantle, where $A$ is a constant, find $\Delta(p)$ and $T(p)$ for $\mathrm{P}$-arrivals (direct paths lying entirely in the mantle), and show that

  $$T=\frac{R^{2} \sin \Delta}{A}$$

  [You may assume that $\int \frac{d u}{u \sqrt{u-1}}=2 \cos ^{-1}\left(\frac{1}{\sqrt{u}}\right)$.]

  Sketch the $T-\Delta$ curves for $\mathrm{P}$ and $\mathrm{PcP}$ arrivals on the same diagram and explain briefly why they terminate at $\Delta=\cos ^{-1} \frac{1}{4}$.

  comment

• A4.20

  Theoretical Geophysics | Part II, 2002

  The equation of motion for small displacements $\mathbf{u}$ in a homogeneous, isotropic, elastic material is

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+2 \mu) \nabla(\boldsymbol{\nabla} \cdot \mathbf{u})-\mu \boldsymbol{\nabla} \wedge(\boldsymbol{\nabla} \wedge \mathbf{u})$$

  where $\lambda$ and $\mu$ are the Lamé constants. Derive the conditions satisfied by the polarisation $\mathbf{P}$ and (real) vector slowness s of plane-wave solutions $\mathbf{u}=\mathbf{P} f(\mathbf{s} \cdot \mathbf{x}-t)$, where $f$ is an arbitrary scalar function. Describe the division of these waves into $P$-waves, $S H$-waves and $S V$-waves.

  A plane harmonic $S V$-wave of the form

  $$\mathbf{u}=\left(s_{3}, 0,-s_{1}\right) \exp \left[i \omega\left(s_{1} x_{1}+s_{3} x_{3}-t\right)\right]$$

  travelling through homogeneous elastic material of $P$-wave speed $\alpha$ and $S$-wave speed $\beta$ is incident from $x_{3}<0$ on the boundary $x_{3}=0$ of rigid material in $x_{3}>0$ in which the displacement is identically zero.

  Write down the form of the reflected wavefield in $x_{3}<0$. Calculate the amplitudes of the reflected waves in terms of the components of the slowness vectors.

  Derive expressions for the components of the incident and reflected slowness vectors, in terms of the wavespeeds and the angle of incidence $\theta_{0}$. Hence show that there is no reflected $S V$-wave if

  $$\sin ^{2} \theta_{0}=\frac{\beta^{2}}{\alpha^{2}+\beta^{2}}$$

  Sketch the rays produced if the region $x_{3}>0$ is fluid instead of rigid.

  comment

Transport Processes

• A1.18

  Transport Processes | Part II, 2002

  (i) Material of thermal diffusivity $D$ occupies the semi-infinite region $x>0$ and is initially at uniform temperature $T_{0}$. For time $t>0$ the temperature at $x=0$ is held at a constant value $T_{1}>T_{0}$. Given that the temperature $T(x, t)$ in $x>0$ satisfies the diffusion equation $T_{t}=D T_{x x}$, write down the equation and the boundary and initial conditions satisfied by the dimensionless temperature $\theta=\left(T-T_{0}\right) /\left(T_{1}-T_{0}\right)$.

  Use dimensional analysis to show that the lengthscale of the region in which $T$ is significantly different from $T_{0}$ is proportional to $(D t)^{1 / 2}$. Hence show that this problem has a similarity solution

  $$\theta=\operatorname{erfc}(\xi / 2) \equiv \frac{2}{\sqrt{\pi}} \int_{\xi / 2}^{\infty} e^{-u^{2}} d u$$

  where $\xi=x /(D t)^{1 / 2}$.

  What is the rate of heat input, $-D T_{x}$, across the plane $x=0 ?$

  (ii) Consider the same problem as in Part (i) except that the boundary condition at $x=0$ is replaced by one of constant rate of heat input $Q$. Show that $\theta(\xi, t)$ satisfies the partial differential equation

  $$\theta_{\xi \xi}+\frac{\xi}{2} \theta_{\xi}=t \theta_{t}$$

  and write down the boundary conditions on $\theta(\xi, t)$. Deduce that the problem has a similarity solution of the form

  $$\theta=\frac{Q(t / D)^{1 / 2}}{T_{1}-T_{0}} f(\xi)$$

  Derive the ordinary differential equation and boundary conditions satisfied by $f(\xi)$.

  Differentiate this equation once to obtain

  $$f^{\prime \prime \prime}+\frac{\xi}{2} f^{\prime \prime}=0$$

  and solve for $f^{\prime}(\xi)$. Hence show that

  $$f(\xi)=\frac{2}{\sqrt{\pi}} e^{-\xi^{2} / 4}-\xi \operatorname{erfc}(\xi / 2)$$

  Sketch the temperature distribution $T(x, t)$ for various times $t$, and calculate $T(0, t)$ explicitly.

  comment

• A3.16

  Transport Processes | Part II, 2002

  (i) A layer of fluid of depth $h(x, t)$, density $\rho$ and viscosity $\mu$ sits on top of a rigid horizontal plane at $y=0$. Gravity $g$ acts vertically and surface tension is negligible.

  Assuming that the horizontal velocity component $u$ and pressure $p$ satisfy the lubrication equations

  $$\begin{aligned} &0=-p_{x}+\mu u_{y y} \\ &0=-p_{y}-\rho g, \end{aligned}$$

  together with appropriate boundary conditions at $y=0$ and $y=h$ (which should be stated), show that $h$ satisfies the partial differential equation

  $$h_{t}=\frac{g}{3 \nu}\left(h^{3} h_{x}\right)_{x},$$

  where $\nu=\mu / \rho$.

  (ii) A two-dimensional blob of the above fluid has fixed area $A$ and time-varying width $2 X(t)$, such that

  $$A=\int_{-X(t)}^{X(t)} h(x, t) d x$$

  The blob spreads under gravity.

  Use scaling arguments to show that, after an initial transient, $X(t)$ is proportional to $t^{1 / 5}$ and $h(0, t)$ is proportional to $t^{-1 / 5}$. Hence show that equation $(*)$ of Part (i) has a similarity solution of the form

  $$h(x, t)=\left(\frac{A^{2} \nu}{g t}\right)^{1 / 5} H(\xi), \quad \text { where } \quad \xi=\frac{x}{\left(A^{3} g t / \nu\right)^{1 / 5}}$$

  and find the differential equation satisfied by $H(\xi)$.

  Deduce that

  $$H= \begin{cases}{\left[\frac{9}{10}\left(\xi_{0}^{2}-\xi^{2}\right)\right]^{1 / 3}} & \text { in }-\xi_{0}<\xi<\xi_{0} \\ 0 & \text { in }|\xi|>\xi_{0}\end{cases}$$

  where

  $$X(t)=\xi_{0}\left(\frac{A^{3} g t}{\nu}\right)^{1 / 5}$$

  Express $\xi_{0}$ in terms of the integral

  $$I=\int_{-1}^{1}\left(1-u^{2}\right)^{1 / 3} d u$$

  comment

• A4.19

  Transport Processes | Part II, 2002

  (a) A biological vessel is modelled two-dimensionally as a fluid-filled channel bounded by parallel plane walls $y=\pm a$, embedded in an infinite region of fluid-saturated tissue. In the tissue a solute has concentration $C^{o u t}(y, t)$, diffuses with diffusivity $D$ and is consumed by biological activity at a rate $k C^{o u t}$ per unit volume, where $D$ and $k$ are constants. By considering the solute balance in a slice of tissue of infinitesimal thickness, show that

  $$C_{t}^{o u t}=D C_{y y}^{o u t}-k C^{\text {out }} .$$

  A steady concentration profile $C^{o u t}(y)$ results from a flux $\beta\left(C^{i n}-C_{a}^{o u t}\right)$, per unit area of wall, of solute from the channel into the tissue, where $C^{i n}$ is a constant concentration of solute that is maintained in the channel and $C_{a}^{\text {out }}=C^{\text {out }}(a)$. Write down the boundary conditions satisfied by $C^{\text {out }}(y)$. Solve for $C^{\text {out }}(y)$ and show that

  $$C_{a}^{o u t}=\frac{\gamma}{\gamma+1} C^{i n}$$

  where $\gamma=\beta / \sqrt{k D}$.

  (b) Now let the solute be supplied by steady flow down the channel from one end, $x=0$, with the channel taken to be semi-infinite in the $x$-direction. The cross-sectionally averaged velocity in the channel $u(x)$ varies due to a flux of fluid from the tissue to the channel (by osmosis) equal to $\lambda\left(C^{i n}-C_{a}^{\text {out }}\right)$ per unit area. Neglect both the variation of $C^{i n}(x)$ across the channel and diffusion in the $x$-direction.

  By considering conservation of fluid, show that

  $$a u_{x}=\lambda\left(C^{i n}-C_{a}^{o u t}\right)$$

  and write down the corresponding equation derived from conservation of solute. Deduce that

  $$u\left(\lambda C^{i n}+\beta\right)=u_{0}\left(\lambda C_{0}^{i n}+\beta\right),$$

  where $u_{0}=u(0)$ and $C_{0}^{i n}=C^{i n}(0)$.

  Assuming that equation $(*)$ still holds, even though $C^{\text {out }}$is now a function of $x$ as well as $y$, show that $u(x)$ satisfies the ordinary differential equation

  $$(\gamma+1) a u u_{x}+\beta u=u_{0}\left(\lambda C_{0}^{i n}+\beta\right)$$

  Find scales $\hat{x}$ and $\hat{u}$ such that the dimensionless variables $U=u / \hat{u}$ and $X=x / \hat{x}$ satisfy

  $$U U_{X}+U=1$$

  Derive the solution $(1-U) e^{U}=A e^{-X}$ and find the constant $A$.

  To what values do $u$ and $C_{i n}$ tend as $x \rightarrow \infty$ ?

  comment

Waves in Fluid and Solid Media

• B1.26

  Waves in Fluid and Solid Media | Part II, 2002

  Starting from the equations governing sound waves linearized about a state with density $\rho_{0}$ and sound speed $c_{0}$, derive the acoustic energy equation, giving expressions for the local energy density $E$ and energy flux $\mathbf{I}$.

  A sphere executes small-amplitude vibrations, with its radius varying according to

  $$r(t)=a+\operatorname{Re}\left(\epsilon e^{i \omega t}\right)$$

  with $0<\epsilon \ll a$. Find an expression for the velocity potential of the sound, $\tilde{\phi}(r, t)$. Show that the time-averaged rate of working by the surface of the sphere is

  $$2 \pi a^{2} \rho_{0} \omega^{2} \epsilon^{2} c_{0} \frac{\omega^{2} a^{2}}{c_{0}^{2}+\omega^{2} a^{2}}$$

  Calculate the value at $r=a$ of the dimensionless ratio $c_{0} \bar{E} /|\overline{\mathbf{I}}|$, where the overbars denote time-averaged values, and comment briefly on the limits $c_{0} \ll \omega a$ and $c_{0} \gg \omega a$.

  comment

• B2 25

  Waves in Fluid and Solid Media | Part II, 2002

  Starting from the equations for one-dimensional unsteady flow of a perfect gas of uniform entropy, show that the Riemann invariants,

  $$R_{\pm}=u \pm \frac{2}{\gamma-1}\left(c-c_{0}\right)$$

  are constant on characteristics $C_{\pm}$given by $\frac{d x}{d t}=u \pm c$, where $u(x, t)$ is the velocity of the gas, $c(x, t)$ is the local speed of sound and $\gamma$ is the specific heat ratio.

  Such a gas initially occupies the region $x>0$ to the right of a piston in an infinitely long tube. The gas and the piston are initially at rest. At time $t=0$ the piston starts moving to the left at a constant speed $V$. Find $u(x, t)$ and $c(x, t)$ in the three regions

  $$\begin{aligned} \text { (i) } \quad & c_{0} t \leq x \\ \text { (ii) } \quad a t & \leq x<c_{0} t \\ \text { (iii) }-V t & \leq x<a t \end{aligned}$$

  where $a=c_{0}-\frac{1}{2}(\gamma+1) V$. What is the largest value of $V$ for which $c$ is positive throughout region (iii)? What happens if $V$ exceeds this value?

  comment

• B3.25

  Waves in Fluid and Solid Media | Part II, 2002

  Consider the equation

  $$\frac{\partial \phi}{\partial t}+\frac{\partial \phi}{\partial x}-\frac{\partial^{3} \phi}{\partial x^{3}}=0$$

  Find the dispersion relation for waves of frequency $\omega$ and wavenumber $k$. Do the wave crests move faster or slower than a packet of waves?

  Write down the solution with initial value

  $$\phi(x, 0)=\int_{-\infty}^{\infty} A(k) e^{i k x} d k$$

  where $A(k)$ is real and $A(-k)=A(k)$.

  Use the method of stationary phase to obtain an approximation to $\phi(x, t)$ for large $t$, with $x / t$ having the constant value $V$. Explain, using the notion of group velocity, the constraint that must be placed on $V$.

  comment

• B4.27

  Waves in Fluid and Solid Media | Part II, 2002

  Write down the equation governing linearized displacements $\mathbf{u}(\mathbf{x}, t)$ in a uniform elastic medium of density $\rho$ and Lamé constants $\lambda$ and $\mu$. Derive solutions for monochromatic plane $P$ and $S$ waves, and find the corresponding wave speeds $c_{P}$ and $c_{S}$.

  Such an elastic solid occupies the half-space $z>0$, and the boundary $z=0$ is clamped rigidly so that $\mathbf{u}(x, y, 0, t)=\mathbf{0}$. A plane $S V$-wave with frequency $\omega$ and wavenumber $(k, 0,-m)$ is incident on the boundary. At some angles of incidence, there results both a reflected $S V$-wave with frequency $\omega^{\prime}$ and wavenumber $\left(k^{\prime}, 0, m^{\prime}\right)$ and a reflected $P$-wave with frequency $\omega^{\prime \prime}$ and wavenumber $\left(k^{\prime \prime}, 0, m^{\prime \prime}\right)$. Relate the frequencies and wavenumbers of the reflected waves to those of the incident wave. At what angles of incidence will there be a reflected $P$-wave?

  Find the amplitudes of the reflected waves as multiples of the amplitude of the incident wave. Confirm that these amplitudes give the sum of the time-averaged vertical fluxes of energy of the reflected waves equal to the time-averaged vertical flux of energy of the incident wave.

  [Results concerning the energy flux, energy density and kinetic energy density in a plane elastic wave may be quoted without proof.]

  comment