Part II, 2009

Algebraic Geometry

• Paper 1, Section II, G

  Algebraic Geometry | Part II, 2009

  Define what is meant by a rational map from a projective variety $V \subset \mathbb{P}^{n}$ to $\mathbb{P}^{m}$. What is a regular point of a rational map?

  Consider the rational map $\phi: \mathbb{P}^{2}-\rightarrow \mathbb{P}^{2}$ given by

  $$\left(X_{0}: X_{1}: X_{2}\right) \mapsto\left(X_{1} X_{2}: X_{0} X_{2}: X_{0} X_{1}\right)$$

  Show that $\phi$ is not regular at the points $(1: 0: 0),(0: 1: 0),(0: 0: 1)$ and that it is regular elsewhere, and that it is a birational map from $\mathbb{P}^{2}$ to itself.

  Let $V \subset \mathbb{P}^{2}$ be the plane curve given by the vanishing of the polynomial $X_{0}^{2} X_{1}^{3}+X_{1}^{2} X_{2}^{3}+X_{2}^{2} X_{0}^{3}$ over a field of characteristic zero. Show that $V$ is irreducible, and that $\phi$ determines a birational equivalence between $V$ and a nonsingular plane quartic.

  comment

• Paper 2, Section II, G

  Algebraic Geometry | Part II, 2009

  Let $V$ be an irreducible variety over an algebraically closed field $k$. Define the tangent space of $V$ at a point $P$. Show that for any integer $r \geqslant 0$, the set $\left\{P \in V \mid \operatorname{dim} T_{V, P} \geqslant r\right\}$ is a closed subvariety of $V$.

  Assume that $k$ has characteristic different from 2. Let $V=V(I) \subset \mathbb{P}^{4}$ be the variety given by the ideal $I=(F, G) \subset k\left[X_{0}, \ldots, X_{4}\right]$, where

  $$F=X_{1} X_{2}+X_{3} X_{4}, \quad G=X_{0} X_{1}+X_{3}^{2}+X_{4}^{2}$$

  Determine the singular subvariety of $V$, and compute $\operatorname{dim} T_{V, P}$ at each singular point $P$. [You may assume that $V$ is irreducible.]

  comment

• Paper 3, Section II, G

  Algebraic Geometry | Part II, 2009

  Let $V$ be a smooth projective curve, and let $D$ be an effective divisor on $V$. Explain how $D$ defines a morphism $\phi_{D}$ from $V$ to some projective space. State the necessary and sufficient conditions for $\phi_{D}$ to be finite. State the necessary and sufficient conditions for $\phi_{D}$ to be an isomorphism onto its image.

  Let $V$ have genus 2 , and let $K$ be an effective canonical divisor. Show that the morphism $\phi_{K}$ is a morphism of degree 2 from $V$ to $\mathbb{P}^{1}$.

  By considering the divisor $K+P_{1}+P_{2}$ for points $P_{i}$ with $P_{1}+P_{2} \nsim K$, show that there exists a birational morphism from $V$ to a singular plane quartic.

  [You may assume the Riemann-Roch Theorem.]

  comment

• Paper 4, Section II, G

  Algebraic Geometry | Part II, 2009

  State the Riemann-Roch theorem for a smooth projective curve $V$, and use it to outline a proof of the Riemann-Hurwitz formula for a non-constant morphism between projective nonsingular curves in characteristic zero.

  Let $V \subset \mathbb{P}^{2}$ be a smooth projective plane cubic over an algebraically closed field $k$ of characteristic zero, written in normal form $X_{0} X_{2}^{2}=F\left(X_{0}, X_{1}\right)$ for a homogeneous cubic polynomial $F$, and let $P_{0}=(0: 0: 1)$ be the point at infinity. Taking the group law on $V$ for which $P_{0}$ is the identity element, let $P \in V$ be a point of order 3 . Show that there exists a linear form $H \in k\left[X_{0}, X_{1}, X_{2}\right]$ such that $V \cap V(H)=\{P\}$.

  Let $H_{1}, H_{2} \in k\left[X_{0}, X_{1}, X_{2}\right]$ be nonzero linear forms. Suppose the lines $\left\{H_{i}=0\right\}$ are distinct, do not meet at a point of $V$, and are nowhere tangent to $V$. Let $W \subset \mathbb{P}^{3}$ be given by the vanishing of the polynomials

  $$X_{0} X_{2}^{2}-F\left(X_{0}, X_{1}\right), \quad X_{3}^{2}-H_{1}\left(X_{0}, X_{1}, X_{2}\right) H_{2}\left(X_{0}, X_{1}, X_{2}\right)$$

  Show that $W$ has genus 4 . [You may assume without proof that $W$ is an irreducible smooth curve.]

  comment

Algebraic Topology

• Paper 1, Section II, G

  Algebraic Topology | Part II, 2009

  Let $X$ be the space obtained by identifying two copies of the Möbius strip along their boundary. Use the Seifert-Van Kampen theorem to find a presentation of the fundamental group $\pi_{1}(X)$. Show that $\pi_{1}(X)$ is an infinite non-abelian group.

  comment

• Paper 2, Section II, $21 G$

  Algebraic Topology | Part II, 2009

  Let $p: X \rightarrow Y$ be a connected covering map. Define the notion of a deck transformation (also known as covering transformation) for $p$. What does it mean for $p$ to be a regular (normal) covering map?

  If $p^{-1}(y)$ contains $n$ points for each $y \in Y$, we say $p$ is $n$-to-1. Show that $p$ is regular under either of the following hypotheses:

  (1) $p$ is 2-to-1,

  (2) $\pi_{1}(Y)$ is abelian.

  Give an example of a 3 -to-1 cover of $S^{1} \vee S^{1}$ which is regular, and one which is not regular.

  comment

• Paper 3, Section II, G

  Algebraic Topology | Part II, 2009

  (i) Suppose that $(C, d)$ and $\left(C^{\prime}, d^{\prime}\right)$ are chain complexes, and $f, g: C \rightarrow C^{\prime}$ are chain maps. Define what it means for $f$ and $g$ to be chain homotopic.

  Show that if $f$ and $g$ are chain homotopic, and $f_{*}, g_{*}: H_{*}(C) \rightarrow H_{*}\left(C^{\prime}\right)$ are the induced maps, then $f_{*}=g_{*}$.

  (ii) Define the Euler characteristic of a finite chain complex.

  Given that one of the sequences below is exact and the others are not, which is the exact one?

  $$\begin{aligned} &0 \rightarrow \mathbb{Z}^{11} \rightarrow \mathbb{Z}^{24} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{13} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{25} \rightarrow \mathbb{Z}^{11} \rightarrow 0 \\ &0 \rightarrow \mathbb{Z}^{11} \rightarrow \mathbb{Z}^{24} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{13} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{24} \rightarrow \mathbb{Z}^{11} \rightarrow 0 \\ &0 \rightarrow \mathbb{Z}^{11} \rightarrow \mathbb{Z}^{24} \rightarrow \mathbb{Z}^{19} \rightarrow \mathbb{Z}^{13} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{23} \rightarrow \mathbb{Z}^{11} \rightarrow 0 \end{aligned}$$

  Justify your choice.

  comment

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2009

  Let $X$ be the subset of $\mathbb{R}^{4}$ given by $X=A \cup B \cup C \subset \mathbb{R}^{4}$, where $A, B$ and $C$ are defined as follows:

  $$\begin{aligned} &A=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=1\right\} \\ &B=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{1}=x_{2}=0, x_{3}^{2}+x_{4}^{2} \leqslant 1\right\} \\ &C=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{3}=x_{4}=0, x_{1}^{2}+x_{2}^{2} \leqslant 1\right\} \end{aligned}$$

  Compute $H_{*}(X)$

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, $34 \mathrm{D}$

  Applications of Quantum Mechanics | Part II, 2009

  Consider the scaled one-dimensional Schrödinger equation with a potential $V(x)$ such that there is a complete set of real, normalized bound states $\psi_{n}(x), n=0,1,2, \ldots$, with discrete energies $E_{0}<E_{1}<E_{2}<\ldots$, satisfying

  $$-\frac{d^{2} \psi_{n}}{d x^{2}}+V(x) \psi_{n}=E_{n} \psi_{n}$$

  Show that the quantity

  $$\langle E\rangle=\int_{-\infty}^{\infty}\left(\left(\frac{d \psi}{d x}\right)^{2}+V(x) \psi^{2}\right) d x$$

  where $\psi(x)$ is a real, normalized trial function depending on one or more parameters $\alpha$, can be used to estimate $E_{0}$, and show that $\langle E\rangle \geqslant E_{0}$.

  Let the potential be $V(x)=|x|$. Using a suitable one-parameter family of either Gaussian or piecewise polynomial trial functions, find a good estimate for $E_{0}$ in this case.

  How could you obtain a good estimate for $E_{1}$ ? [ You should suggest suitable trial functions, but DO NOT carry out any further integration.]

  comment

• Paper 2, Section II, D

  Applications of Quantum Mechanics | Part II, 2009

  A particle scatters quantum mechanically off a spherically symmetric potential $V(r)$. In the $l=0$ sector, and assuming $\hbar^{2} / 2 m=1$, the radial wavefunction $u(r)$ satisfies

  $$-\frac{d^{2} u}{d r^{2}}+V(r) u=k^{2} u$$

  and $u(0)=0$. The asymptotic behaviour of $u$, for large $r$, is

  $$u(r) \sim C\left(S(k) e^{i k r}-e^{-i k r}\right)$$

  where $C$ is a constant. Show that if $S(k)$ is analytically continued to complex $k$, then

  $$S(k) S(-k)=1 \quad \text { and } \quad S(k)^{*} S\left(k^{*}\right)=1$$

  Deduce that for real $k, S(k)=e^{2 i \delta_{0}(k)}$ for some real function $\delta_{0}(k)$, and that $\delta_{0}(k)=-\delta_{0}(-k) .$

  For a certain potential,

  $$S(k)=\frac{(k+i \lambda)(k+3 i \lambda)}{(k-i \lambda)(k-3 i \lambda)}$$

  where $\lambda$ is a real, positive constant. Evaluate the scattering length $a$ and the total cross section $4 \pi a^{2}$.

  Briefly explain the significance of the zeros of $S(k)$.

  comment

• Paper 3, Section II, D

  Applications of Quantum Mechanics | Part II, 2009

  An electron of charge $-e$ and mass $m$ is subject to a magnetic field of the form $\mathbf{B}=(0,0, B(y))$, where $B(y)$ is everywhere greater than some positive constant $B_{0}$. In a stationary state of energy $E$, the electron's wavefunction $\Psi$ satisfies

  $$-\frac{\hbar^{2}}{2 m}\left(\boldsymbol{\nabla}+\frac{i e}{\hbar} \mathbf{A}\right)^{2} \Psi+\frac{e \hbar}{2 m} \mathbf{B} \cdot \boldsymbol{\sigma} \Psi=E \Psi,$$

  where $\mathbf{A}$ is the vector potential and $\sigma_{1}, \sigma_{2}$ and $\sigma_{3}$ are the Pauli matrices.

  Assume that the electron is in a spin down state and has no momentum along the $z$-axis. Show that with a suitable choice of gauge, and after separating variables, equation (*) can be reduced to

  $$-\frac{d^{2} \chi}{d y^{2}}+(k+a(y))^{2} \chi-b(y) \chi=\epsilon \chi,$$

  where $\chi$ depends only on $y, \epsilon$ is a rescaled energy, and $b(y)$ a rescaled magnetic field strength. What is the relationship between $a(y)$ and $b(y)$ ?

  Show that $(* *)$ can be factorized in the form $M^{\dagger} M \chi=\epsilon \chi$ where

  $$M=\frac{d}{d y}+W(y)$$

  for some function $W(y)$, and deduce that $\epsilon$ is non-negative.

  Show that zero energy states exist for all $k$ and are therefore infinitely degenerate.

  comment

• Paper 4, Section II, D

  Applications of Quantum Mechanics | Part II, 2009

  What are meant by Bloch states and the Brillouin zone for a quantum mechanical particle moving in a one-dimensional periodic potential?

  Derive an approximate value for the lowest-lying energy gap for the Schrödinger equation

  $$-\frac{d^{2} \psi}{d x^{2}}-V_{0}(\cos x+\cos 2 x) \psi=E \psi$$

  when $V_{0}$ is small and positive.

  Estimate the width of this gap in the case that $V_{0}$ is large and positive.

  comment

Applied Probability

• Paper 1, Section II, J

  Applied Probability | Part II, 2009

  (a) Let $\left(X_{t}, t \geqslant 0\right)$ be a continuous-time Markov chain on a countable state space I. Explain what is meant by a stopping time for the chain $\left(X_{t}, t \geqslant 0\right)$. State the strong Markov property. What does it mean to say that $X$ is irreducible?

  (b) Let $\left(X_{t}, t \geqslant 0\right)$ be a Markov chain on $I=\{0,1, \ldots\}$ with $Q$-matrix given by $Q=\left(q_{i, j}\right)_{i, j \in I}$ such that:

  (1) $q_{i, 0}>0$ for all $i \geqslant 1$, but $q_{0, j}=0$ for all $j \in I$, and

  (2) $q_{i, i+1}>0$ for all $i \geqslant 1$, but $q_{i, j}=0$ if $j>i+1$.

  Is $\left(X_{t}, t \geqslant 0\right)$ irreducible? Fix $M \geqslant 1$, and assume that $X_{0}=i$, where $1 \leqslant i \leqslant M$. Show that if $J_{1}=\inf \left\{t \geqslant 0: X_{t} \neq X_{0}\right\}$ is the first jump time, then there exists $\delta>0$ such that $\mathbb{P}_{i}\left(X_{J_{1}}=0\right) \geqslant \delta$, uniformly over $1 \leqslant i \leqslant M$. Let $T_{0}=0$ and define recursively for $m \geqslant 0$,

  $$T_{m+1}=\inf \left\{t \geqslant T_{m}: X_{t} \neq X_{T_{m}} \text { and } 1 \leqslant X_{t} \leqslant M\right\}$$

  Let $A_{m}$ be the event $A_{m}=\left\{T_{m}<\infty\right\}$. Show that $\mathbb{P}_{i}\left(A_{m}\right) \leqslant(1-\delta)^{m}$, for $1 \leqslant i \leqslant M$.

  (c) Let $\left(X_{t}, t \geqslant 0\right)$ be the Markov chain from (b). Define two events $E$ and $F$ by

  $$E=\left\{X_{t}=0 \text { for all } t \text { large enough }\right\}, \quad F=\left\{\lim _{t \rightarrow \infty} X_{t}=+\infty\right\}$$

  Show that $\mathbb{P}_{i}(E \cup F)=1$ for all $i \in I$.

  comment

• Paper 2, Section II, J

  Applied Probability | Part II, 2009

  Let $X_{1}, X_{2}, \ldots$, be a sequence of independent, identically distributed positive random variables, with a common probability density function $f(x), x>0$. Call $X_{n}$ a record value if $X_{n}>\max \left\{X_{1}, \ldots, X_{n-1}\right\}$. Consider the sequence of record values

  $$V_{0}=0, V_{1}=X_{1}, \ldots, V_{n}=X_{i_{n}},$$

  where

  $$i_{n}=\min \left\{i \geqslant 1: X_{i}>V_{n-1}\right\}, n>1 .$$

  Define the record process $\left(R_{t}\right)_{t \geqslant 0}$ by $R_{0}=0$ and

  $$R_{t}=\max \left\{n \geqslant 1: V_{n}<t\right\}, \quad t>0$$

  (a) By induction on $n$, or otherwise, show that the joint probability density function of the random variables $V_{1}, \ldots, V_{n}$ is given by:

  $$f_{V_{1}, \ldots, V_{n}}\left(x_{1}, \ldots, x_{n}\right)=f\left(x_{1}\right) \frac{f\left(x_{2}\right)}{1-F\left(x_{1}\right)} \times \ldots \times \frac{f\left(x_{n}\right)}{1-F\left(x_{n-1}\right)},$$

  where $F(x)=\int_{0}^{x} f(y) \mathrm{d} y$ is the cumulative distribution function for $f(x)$.

  (b) Prove that the random variable $R_{t}$ has a Poisson distribution with parameter $\Lambda(t)$ of the form

  $$\Lambda(t)=\int_{0}^{t} \lambda(s) \mathrm{d} s,$$

  and determine the 'instantaneous rate' $\lambda(s)$.

  [Hint: You may use the formula

  $$\begin{aligned} &\mathbb{P}\left(R_{t}=k\right)=\mathbb{P}\left(V_{k} \leqslant t<V_{k+1}\right) \\ &=\int_{0}^{t} \ldots \int_{0}^{t} \mathbf{1}_{\left\{t_{1}<\ldots<t_{k}\right\}} f_{V_{1}, \ldots, V_{k}}\left(t_{1}, \ldots, t_{k}\right) \\ &\quad \times \mathbb{P}\left(V_{k+1}>t \mid V_{1}=t_{1}, \ldots, V_{k}=t_{k}\right) \prod_{j=1}^{k} \mathrm{~d} t_{j}, \end{aligned}$$

  for any $k \geqslant 1 .]$

  comment

• Paper 3, Section II, J

  Applied Probability | Part II, 2009

  (a) Define the Poisson process $\left(N_{t}, t \geqslant 0\right)$ with rate $\lambda>0$, in terms of its holding times. Show that for all times $t \geqslant 0, N_{t}$ has a Poisson distribution, with a parameter which you should specify.

  (b) Let $X$ be a random variable with probability density function

  $$f(x)=\frac{1}{2} \lambda^{3} x^{2} e^{-\lambda x} \mathbf{1}_{\{x>0\}} .$$

  Prove that $X$ is distributed as the sum $Y_{1}+Y_{2}+Y_{3}$ of three independent exponential random variables of rate $\lambda$. Calculate the expectation, variance and moment generating function of $X$.

  Consider a renewal process $\left(X_{t}, t \geqslant 0\right)$ with holding times having density $(*)$. Prove that the renewal function $m(t)=\mathbb{E}\left(X_{t}\right)$ has the form

  $$m(t)=\frac{\lambda t}{3}-\frac{1}{3} p_{1}(t)-\frac{2}{3} p_{2}(t)$$

  where $p_{1}(t)=\mathbb{P}\left(N_{t}=1 \bmod 3\right), p_{2}(t)=\mathbb{P}\left(N_{t}=2 \bmod 3\right)$ and $\left(N_{t}, t \geqslant 0\right)$ is the Poisson process of rate $\lambda$.

  (c) Consider the delayed renewal process $\left(X_{t}^{\mathrm{D}}, t \geqslant 0\right)$ with holding times $S_{1}^{\mathrm{D}}, S_{2}, S_{3}, \ldots$ where $\left(S_{n}, n \geqslant 1\right)$, are the holding times of $\left(X_{t}, t \geqslant 0\right)$ from (b). Specify the distribution of $S_{1}^{\mathrm{D}}$ for which the delayed process becomes the renewal process in equilibrium.

  [You may use theorems from the course provided that you state them clearly.]

  comment

• Paper 4, Section II, J

  Applied Probability | Part II, 2009

  A flea jumps on the vertices of a triangle $A B C$; its position is described by a continuous time Markov chain with a $Q$-matrix

  $$Q=\left(\begin{array}{ccc} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 1 & 0 & -1 \end{array}\right) \quad \begin{aligned} &A \\ &B \\ &C \end{aligned}$$

  (a) Draw a diagram representing the possible transitions of the flea together with the rates of each of these transitions. Find the eigenvalues of $Q$ and express the transition probabilities $p_{x y}(t), x, y=A, B, C$, in terms of these eigenvalues.

  [Hint: $\operatorname{det}(Q-\mu \mathbf{I})=(-1-\mu)^{3}+1$. Specifying the equilibrium distribution may help.]

  Hence specify the probabilities $\mathbb{P}\left(N_{t}=i \bmod 3\right)$ where $\left(N_{t}, t \geqslant 0\right)$ is a Poisson process of rate $1 .$

  (b) A second flea jumps on the vertices of the triangle $A B C$ as a Markov chain with Q-matrix

  $$Q^{\prime}=\left(\begin{array}{ccc} -\rho & 0 & \rho \\ \rho & -\rho & 0 \\ 0 & \rho & -\rho \end{array}\right) \quad \begin{aligned} &A \\ &B \\ &C \end{aligned}$$

  where $\rho>0$ is a given real number. Let the position of the second flea at time $t$ be denoted by $Y_{t}$. We assume that $\left(Y_{t}, t \geqslant 0\right)$ is independent of $\left(X_{t}, t \geqslant 0\right)$. Let $p(t)=\mathbb{P}\left(X_{t}=Y_{t}\right)$. Show that $\lim _{t \rightarrow \infty} p(t)$ exists and is independent of the starting points of $X$ and $Y$. Compute this limit.

  comment

Asymptotic Methods

• Paper 1, Section II, A

  Asymptotic Methods | Part II, 2009

  Consider the integral

  $$I(\lambda)=\int_{0}^{A} \mathrm{e}^{-\lambda t} f(t) d t, \quad A>0$$

  in the limit $\lambda \rightarrow \infty$, given that $f(t)$ has the asymptotic expansion

  $$f(t) \sim \sum_{n=0}^{\infty} a_{n} t^{n \beta}$$

  as $t \rightarrow 0_{+}$, where $\beta>0$. State Watson's lemma.

  Now consider the integral

  $$J(\lambda)=\int_{a}^{b} \mathrm{e}^{\lambda \phi(t)} F(t) d t$$

  where $\lambda \gg 1$ and the real function $\phi(t)$ has a unique maximum in the interval $[a, b]$ at $c$, with $a<c<b$, such that

  $$\phi^{\prime}(c)=0, \phi^{\prime \prime}(c)<0$$

  By making a monotonic change of variable from $t$ to a suitable variable $\zeta$ (Laplace's method), or otherwise, deduce the existence of an asymptotic expansion for $J(\lambda)$ as $\lambda \rightarrow \infty$. Derive the leading term

  $$J(\lambda) \sim \mathrm{e}^{\lambda \phi(c)} F(c)\left(\frac{2 \pi}{\lambda\left|\phi^{\prime \prime}(c)\right|}\right)^{\frac{1}{2}}$$

  The gamma function is defined for $x>0$ by

  $$\Gamma(x+1)=\int_{0}^{\infty} \exp (x \log t-t) d t$$

  By means of the substitution $t=x s$, or otherwise, deduce Stirling's formula

  $$\Gamma(x+1) \sim x^{\left(x+\frac{1}{2}\right)} \mathrm{e}^{-x} \sqrt{2 \pi}\left(1+\frac{1}{12 x}+\cdots\right)$$

  as $x \rightarrow \infty$

  comment

• Paper 3, Section II, A

  Asymptotic Methods | Part II, 2009

  Consider the contour-integral representation

  $$J_{0}(x)=\operatorname{Re} \frac{1}{i \pi} \int_{C} e^{i x \cosh t} d t$$

  of the Bessel function $J_{0}$ for real $x$, where $C$ is any contour from $-\infty-\frac{i \pi}{2}$ to $+\infty+\frac{i \pi}{2}$.

  Writing $t=u+i v$, give in terms of the real quantities $u, v$ the equation of the steepest-descent contour from $-\infty-\frac{i \pi}{2}$ to $+\infty+\frac{i \pi}{2}$ which passes through $t=0$.

  Deduce the leading term in the asymptotic expansion of $J_{0}(x)$, valid as $x \rightarrow \infty$

  $$J_{0}(x) \sim \sqrt{\frac{2}{\pi x}} \cos \left(x-\frac{\pi}{4}\right)$$

  comment

• Paper 4, Section II, A

  Asymptotic Methods | Part II, 2009

  The differential equation

  $$f^{\prime \prime}=Q(x) f$$

  has a singular point at $x=\infty$. Assuming that $Q(x)>0$, write down the Liouville Green lowest approximations $f_{\pm}(x)$ for $x \rightarrow \infty$, with $f_{-}(x) \rightarrow 0$.

  The Airy function $\operatorname{Ai}(x)$ satisfies $(*)$ with

  $$Q(x)=x$$

  and $\operatorname{Ai}(x) \rightarrow 0$ as $x \rightarrow \infty$. Writing

  $$\operatorname{Ai}(x)=w(x) f_{-}(x)$$

  show that $w(x)$ obeys

  $$x^{2} w^{\prime \prime}-\left(2 x^{5 / 2}+\frac{1}{2} x\right) w^{\prime}+\frac{5}{16} w=0$$

  Derive the expansion

  $$w \sim c\left(1-\frac{5}{48} x^{-3 / 2}\right) \quad \text { as } \quad x \rightarrow \infty$$

  where $c$ is a constant.

  comment

Classical Dynamics

• Paper 1, Section I, E

  Classical Dynamics | Part II, 2009

  Lagrange's equations for a system with generalized coordinates $q_{i}(t)$ are given by

  $$\frac{d}{d t}\left(\frac{\partial L}{\partial \dot{q}_{i}}\right)-\frac{\partial L}{\partial q_{i}}=0$$

  where $L$ is the Lagrangian. The Hamiltonian is given by

  $$H=\sum_{j} p_{j} \dot{q}_{j}-L,$$

  where the momentum conjugate to $q_{j}$ is

  $$p_{j}=\frac{\partial L}{\partial \dot{q}_{j}}$$

  Derive Hamilton's equations in the form

  $$\dot{q}_{i}=\frac{\partial H}{\partial p_{i}}, \quad \dot{p}_{i}=-\frac{\partial H}{\partial q_{i}}$$

  Explain what is meant by the statement that $q_{k}$ is an ignorable coordinate and give an associated constant of the motion in this case.

  The Hamiltonian for a particle of mass $m$ moving on the surface of a sphere of radius $a$ under a potential $V(\theta)$ is given by

  $$H=\frac{1}{2 m a^{2}}\left(p_{\theta}^{2}+\frac{p_{\phi}^{2}}{\sin ^{2} \theta}\right)+V(\theta)$$

  where the generalized coordinates are the spherical polar angles $(\theta, \phi)$. Write down two constants of the motion and show that it is possible for the particle to move with constant $\theta$ provided that

  $$p_{\phi}^{2}=\left(\frac{m a^{2} \sin ^{3} \theta}{\cos \theta}\right) \frac{d V}{d \theta} .$$

  comment

• Paper 2, Section $\mathbf{I}$, E

  Classical Dynamics | Part II, 2009

  A system of three particles of equal mass $m$ moves along the $x$ axis with $x_{i}$ denoting the $x$ coordinate of particle $i$. There is an equilibrium configuration for which $x_{1}=0$, $x_{2}=a$ and $x_{3}=2 a$.

  Particles 1 and 2, and particles 2 and 3, are connected by springs with spring constant $\mu$ that provide restoring forces when the respective particle separations deviate from their equilibrium values. In addition, particle 1 is connected to the origin by a spring with spring constant $16 \mu / 3$. The Lagrangian for the system is

  $$L=\frac{m}{2}\left(\dot{x}_{1}^{2}+\dot{\eta}_{1}^{2}+\dot{\eta}_{2}^{2}\right)-\frac{\mu}{2}\left(\frac{16}{3} x_{1}^{2}+\left(\eta_{1}-x_{1}\right)^{2}+\left(\eta_{2}-\eta_{1}\right)^{2}\right)$$

  where the generalized coordinates are $x_{1}, \eta_{1}=x_{2}-a$ and $\eta_{2}=x_{3}-2 a$.

  Write down the equations of motion. Show that the generalized coordinates can oscillate with a period $P=2 \pi / \omega$, where

  $$\omega^{2}=\frac{\mu}{3 m}$$

  and find the form of the corresponding normal mode in this case.

  comment

• Paper 2, Section II, E

  Classical Dynamics | Part II, 2009

  A symmetric top of unit mass moves under the action of gravity. The Lagrangian is given by

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-g l \cos \theta$$

  where the generalized coordinates are the Euler angles $(\theta, \phi, \psi)$, the principal moments of inertia are $I_{1}$ and $I_{3}$ and the distance from the centre of gravity of the top to the origin is $l$.

  Show that $\omega_{3}=\dot{\psi}+\dot{\phi} \cos \theta$ and $p_{\phi}=I_{1} \dot{\phi} \sin ^{2} \theta+I_{3} \omega_{3} \cos \theta$ are constants of the motion. Show further that, when $p_{\phi}=I_{3} \omega_{3}$, with $\omega_{3}>0$, the equation of motion for $\theta$ is

  $$\frac{d^{2} \theta}{d t^{2}}=\frac{g l \sin \theta}{I_{1}}\left(1-\frac{I_{3}^{2} \omega_{3}^{2}}{4 I_{1} g l \cos ^{4}(\theta / 2)}\right)$$

  Find the possible equilibrium values of $\theta$ in the two cases:

  (i) $I_{3}^{2} \omega_{3}^{2}>4 I_{1} g l$,

  (ii) $I_{3}^{2} \omega_{3}^{2}<4 I_{1} g l$.

  By considering linear perturbations in the neighbourhoods of the equilibria in each case, find which are unstable and give expressions for the periods of small oscillations about the stable equilibria.

  comment

• Paper 3, Section I, E

  Classical Dynamics | Part II, 2009

  (a) Show that the principal moments of inertia of a uniform circular cylinder of radius $a$, length $h$ and mass $M$ about its centre of mass are $I_{1}=I_{2}=M\left(a^{2} / 4+h^{2} / 12\right)$ and $I_{3}=M a^{2} / 2$, with the $x_{3}$ axis being directed along the length of the cylinder.

  (b) Euler's equations governing the angular velocity $\left(\omega_{1}, \omega_{2}, \omega_{3}\right)$ of an arbitrary rigid body as viewed in the body frame are

  $$\begin{aligned} &I_{1} \frac{d \omega_{1}}{d t}=\left(I_{2}-I_{3}\right) \omega_{2} \omega_{3} \\ &I_{2} \frac{d \omega_{2}}{d t}=\left(I_{3}-I_{1}\right) \omega_{3} \omega_{1} \end{aligned}$$

  and

  $$I_{3} \frac{d \omega_{3}}{d t}=\left(I_{1}-I_{2}\right) \omega_{1} \omega_{2}$$

  Show that, for the cylinder of part $(\mathrm{a}), \omega_{3}$ is constant. Show further that, when $\omega_{3} \neq 0$, the angular momentum vector precesses about the $x_{3}$ axis with angular velocity $\Omega$ given by

  $$\Omega=\left(\frac{3 a^{2}-h^{2}}{3 a^{2}+h^{2}}\right) \omega_{3}$$

  comment

• Paper 4, Section I, E

  Classical Dynamics | Part II, 2009

  (a) A Hamiltonian system with $n$ degrees of freedom has the Hamiltonian $H(\mathbf{p}, \mathbf{q})$, where $\mathbf{q}=\left(q_{1}, q_{2}, q_{3}, \ldots, q_{n}\right)$ are the coordinates and $\mathbf{p}=\left(p_{1}, p_{2}, p_{3}, \ldots, p_{n}\right)$ are the momenta.

  A second Hamiltonian system has the Hamiltonian $G=G(\mathbf{p}, \mathbf{q})$. Neither $H$ nor $G$ contains the time explicitly. Show that the condition for $H(\mathbf{p}, \mathbf{q})$ to be invariant under the evolution of the coordinates and momenta generated by the Hamiltonian $G(\mathbf{p}, \mathbf{q})$ is that the Poisson bracket $[H, G]$ vanishes. Deduce that $G$ is a constant of the motion for evolution under $H$.

  Show that, when $G=\alpha \sum_{k=1}^{n} p_{k}$, where $\alpha$ is constant, the motion it generates is a translation of each $q_{k}$ by an amount $\alpha t$, while the corresponding $p_{k}$ remains fixed. What do you infer is conserved when $H$ is invariant under this transformation?

  (b) When $n=3$ and $H$ is a function of $p_{1}^{2}+p_{2}^{2}+p_{3}^{2}$ and $q_{1}^{2}+q_{2}^{2}+q_{3}^{2}$ only, find $\left[H, L_{i}\right]$ when

  $$L_{i}=\epsilon_{i j k} q_{j} p_{k}$$

  comment

• Paper 4, Section II, E

  Classical Dynamics | Part II, 2009

  The Hamiltonian for a particle of mass $m$, charge $e$ and position vector $\mathbf{q}=(x, y, z)$, moving in an electromagnetic field, is given by

  $$H(\mathbf{p}, \mathbf{q}, t)=\frac{1}{2 m}\left(\mathbf{p}-\frac{e \mathbf{A}}{c}\right)^{2}$$

  where $\mathbf{A}(\mathbf{q}, t)$ is the vector potential. Write down Hamilton's equations and use them to derive the equations of motion for the charged particle.

  Show that, when $\mathbf{A}=\left(-y B_{0}(z, t), 0,0\right)$, there are solutions for which $p_{x}=0$ and for which the particle motion is such that

  $$\frac{d^{2} y}{d t^{2}}=-\Omega^{2} y$$

  where $\Omega=e B_{0} /(m c)$. Show in addition that the Hamiltonian may be written as

  $$H=\frac{m}{2}\left(\frac{d z}{d t}\right)^{2}+E^{\prime}$$

  where

  $$E^{\prime}=\frac{m}{2}\left(\left(\frac{d y}{d t}\right)^{2}+\Omega^{2} y^{2}\right)$$

  Assuming that $B_{0}$ is constant, find the action

  $$I\left(E^{\prime}, B_{0}\right)=\frac{1}{2 \pi} \oint m\left(\frac{d y}{d t}\right) d y$$

  associated with the $y$ motion.

  It is now supposed that $B_{0}$ varies on a time-scale much longer than $\Omega^{-1}$ and thus is slowly varying. Show by applying the theory of adiabatic invariance that the motion in the $z$ direction takes place under an effective potential and give an expression for it.

  comment

Coding and Cryptography

• Paper 1, Section I, H

  Coding and Cryptography | Part II, 2009

  I am putting up my Christmas lights. If I plug in a set of bulbs and one is defective, none will light up. A badly written note left over from the previous year tells me that exactly one of my 10 bulbs is defective and that the probability that the $k$ th bulb is defective is $k / 55$.

  (i) Find an explicit procedure for identifying the defective bulb in the least expected number of steps.

  [You should explain your method but no proof is required.]

  (ii) Is there a different procedure from the one you gave in (i) with the same expected number of steps? Either write down another procedure and explain briefly why it gives the same expected number or explain briefly why no such procedure exists.

  (iii) Because I make such a fuss about each test, my wife wishes me to tell her the maximum number $N$ of trials that might be required. Will the procedure in (i) give the minimum $N$ ? Either write down another procedure and explain briefly why it gives a smaller $N$ or explain briefly why no such procedure exists.

  comment

• Paper 1, Section II, H

  Coding and Cryptography | Part II, 2009

  (i) State and prove Gibbs' inequality.

  (ii) A casino offers me the following game: I choose strictly positive numbers $a_{1}, \ldots, a_{n}$ with $\sum_{j=1}^{n} a_{j}=1$. I give the casino my entire fortune $f$ and roll an $n$-sided die. With probability $p_{j}$ the casino returns $u_{j}^{-1} a_{j} f$ for $j=1,2, \ldots, n$. If I intend to play the game many times (staking my entire fortune each time) explain carefully why I should choose $a_{1}, \ldots, a_{n}$ to maximise $\sum_{j=1}^{n} p_{j} \log \left(u_{j}^{-1} a_{j}\right)$.

  [You should assume $n \geqslant 2$ and $u_{j}, p_{j}>0$ for each $j .$ ]

  (iii) Determine the appropriate $a_{1}, \ldots, a_{n}$. Let $\sum_{i=1}^{n} u_{i}=U$. Show that, if $U<1$, then, in the long run with high probability, my fortune increases. Show that, if $U>1$, the casino can choose $u_{1}, \ldots, u_{n}$ in such a way that, in the long run with high probability, my fortune decreases. Is it true that, if $U>1$, any choice of $u_{1}, \ldots, u_{n}$ will ensure that, in the long run with high probability, my fortune decreases? Why?

  comment

• Paper 2, Section I, $4 \mathrm{H}$

  Coding and Cryptography | Part II, 2009

  Knowing that

  $$25 \equiv 2886^{2} \quad \bmod 3953$$

  and that 3953 is the product of two primes $p$ and $q$, find $p$ and $q$.

  [You should explain your method in sufficient detail to show that it is reasonably general.]

  comment

• Paper 2, Section II, H

  Coding and Cryptography | Part II, 2009

  Describe the construction of the Reed-Miller code $R M(m, d)$. Establish its information rate and minimum weight.

  Show that every codeword in $R M(d, d-1)$ has even weight. By considering $\mathbf{x} \wedge \mathbf{y}$ with $\mathbf{x} \in R M(m, r)$ and $\mathbf{y} \in R M(m, m-r-1)$, or otherwise, show that $R M(m, m-r-1) \subseteq R M(m, r)^{\perp}$. Show that, in fact, $R M(m, m-r-1)=R M(m, r)^{\perp} .$

  comment

• Paper 3, Section I, $4 \mathrm{H}$

  Coding and Cryptography | Part II, 2009

  Define a binary code of length 15 with information rate $11 / 15$ which will correct single errors. Show that it has the rate stated and give an explicit procedure for identifying the error. Show that the procedure works.

  [Hint: You may wish to imitate the corresponding discussion for a code of length 7 .]

  comment

• Paper 4, Section I, H

  Coding and Cryptography | Part II, 2009

  What is a general feedback register? What is a linear feedback register? Give an example of a general feedback register which is not a linear feedback register and prove that it has the stated property.

  By giving proofs or counterexamples, establish which, if any, of the following statements are true and which, if any, are false.

  (i) Given two linear feedback registers, there always exist non-zero initial fills for which the outputs are identical.

  (ii) If two linear feedback registers have different lengths, there do not exist non-zero initial fills for which the outputs are identical.

  (iii) If two linear feedback registers have different lengths, there exist non-zero initial fills for which the outputs are not identical.

  (iv) There exist two linear feedback registers of different lengths and non-zero initial fills for which the outputs are identical.

  comment

Cosmology

• Paper 1, Section I, D

  Cosmology | Part II, 2009

  Prior to a time $t \sim 100,000$ years, the Universe was filled with a gas of photons and non-relativistic free electrons and protons maintained in equilibrium by Thomson scattering. At around $t \sim 400,000$ years, the protons and electrons began combining to form neutral hydrogen,

  $$p+e^{-} \leftrightarrow H+\gamma$$

  [You may assume that the equilibrium number density of a non-relativistic species $\left(k T \ll m c^{2}\right)$ is given by

  $$n=g_{s}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} \exp \left(\left(\mu-m c^{2}\right) / k T\right)$$

  while the photon number density is

  $$n_{\gamma}=16 \pi \zeta(3)\left(\frac{k T}{h c}\right)^{3}, \quad(\zeta(3) \approx 1.20 \ldots)$$

  Deduce Saha's equation for the recombination process $(*)$ stating clearly your assumptions and the steps made in the calculation,

  $$\frac{n_{e}^{2}}{n_{H}}=\left(\frac{2 \pi m_{e} k T}{h^{2}}\right)^{3 / 2} \exp (-I / k T)$$

  where $I$ is the ionization energy of hydrogen.

  Consider now the fractional ionization $X_{e}=n_{e} / n_{B}$ where $n_{B}=n_{p}+n_{H}=\eta n_{\gamma}$ is the baryon number of the Universe and $\eta$ is the baryon to photon ratio. Find an expression for the ratio

  $$\left(1-X_{e}\right) / X_{e}^{2}$$

  in terms only of $k T$ and constants such as $\eta$ and $I$.

  Suggest a reason why neutral hydrogen forms at a temperature $k T \approx 0.3 \mathrm{eV}$ which is much lower than the hydrogen ionization temperature $k T=I \approx 13 \mathrm{eV}$.

  comment

• Paper 1, Section II, D

  Cosmology | Part II, 2009

  (i) In a homogeneous and isotropic universe, the scalefactor $a(t)$ obeys the Friedmann equation

  $$\left(\frac{\dot{a}}{a}\right)^{2}+\frac{k c^{2}}{a^{2}}=\frac{8 \pi G}{3} \rho,$$

  where $\rho(t)$ is the matter density which, together with the pressure $P(t)$, satisfies

  $$\dot{\rho}=-3 \frac{\dot{a}}{a}\left(\rho+P / c^{2}\right)$$

  Use these two equations to derive the Raychaudhuri equation,

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3}\left(\rho+3 P / c^{2}\right)$$

  (ii) Conformal time $\tau$ is defined by taking $d t / d \tau=a$, so that $\dot{a}=a^{\prime} / a \equiv \mathcal{H}$ where primes denote derivatives with respect to $\tau$. For matter obeying the equation of state $P=w \rho c^{2}$, show that the Friedmann and energy conservation equations imply

  $$\mathcal{H}^{2}+k c^{2}=\frac{8 \pi G}{3} \rho_{0} a^{-(1+3 w)}$$

  where $\rho_{0}=\rho\left(t_{0}\right)$ and we take $a\left(t_{0}\right)=1$ today. Use the Raychaudhuri equation to derive the expression

  $$\mathcal{H}^{\prime}+\frac{1}{2}(1+3 w)\left[\mathcal{H}^{2}+k c^{2}\right]=0$$

  For a $k c^{2}=1$ closed universe, by solving first for $\mathcal{H}$ (or otherwise), show that the scale factor satisfies

  $$a=\alpha(\sin \beta \tau)^{2 /(1+3 w)}$$

  where $\alpha, \beta$ are constants. [Hint: You may assume that $\int d x /\left(1+x^{2}\right)=-\cot ^{-1} x+$ const.]

  For a closed universe dominated by pressure-free matter $(P=0)$, find the complete parametric solution

  $$a=\frac{1}{2} \alpha(1-\cos 2 \beta \tau), \quad t=\frac{\alpha}{4 \beta}(2 \beta \tau-\sin 2 \beta \tau)$$

  comment

• Paper 2, Section I, D

  Cosmology | Part II, 2009

  (a) The equilibrium distribution for the energy density of a massless neutrino takes the form

  $$\epsilon=\frac{4 \pi c}{h^{3}} \int_{0}^{\infty} \frac{p^{3} d p}{\exp (p c / k T)+1} .$$

  Show that this can be expressed in the form $\epsilon=\alpha T^{4}$, where the constant $\alpha$ need not be evaluated explicitly.

  (b) In the early universe, the entropy density $s$ at a temperature $T$ is $s=$ $(8 \sigma / 3 c) \mathcal{N}_{S} T^{3}$ where $\mathcal{N}_{S}$ is the total effective spin degrees of freedom. Briefly explain why $\mathcal{N}_{S}=\mathcal{N}_{*}+\mathcal{N}_{S D}$, each term of which consists of two separate components as follows: the contribution from each massless species in equilibrium $\left(T_{i}=T\right)$ is

  $$\mathcal{N}_{*}=\sum_{\text {bosons }} g_{i}+\frac{7}{8} \sum_{\text {fermions }} g_{i}$$

  and a similar sum for massless species which have decoupled,

  $$\mathcal{N}_{S D}=\sum_{\text {bosons }} g_{i}\left(\frac{T_{i}}{T}\right)^{3}+\frac{7}{8} \sum_{\text {fermions }} g_{i}\left(\frac{T_{i}}{T}\right)^{3}$$

  where in each case $g_{i}$ is the degeneracy and $T_{i}$ is the temperature of the species $i$.

  The three species of neutrinos and antineutrinos decouple from equilibrium at a temperature $T \approx 1 \mathrm{MeV}$, after which positrons and electrons annihilate at $T \approx 0.5 \mathrm{MeV}$, leaving photons in equilibrium with a small excess population of electrons. Using entropy considerations, explain why the ratio of the neutrino and photon temperatures today is given by

  $$\frac{T_{\nu}}{T_{\gamma}}=\left(\frac{4}{11}\right)^{1 / 3}$$

  comment

• Paper 3, Section I, D

  Cosmology | Part II, 2009

  (a) Write down an expression for the total gravitational potential energy $E_{\text {grav }}$ of a spherically symmetric star of outer radius $R$ in terms of its mass density $\rho(r)$ and the total mass $m(r)$ inside a radius $r$, satisfying the relation $d m / d r=4 \pi r^{2} \rho(r)$.

  An isotropic mass distribution obeys the pressure-support equation,

  $$\frac{d P}{d r}=-\frac{G m \rho}{r^{2}}$$

  where $P(r)$ is the pressure. Multiply this expression by $4 \pi r^{3}$ and integrate with respect to $r$ to derive the virial theorem relating the kinetic and gravitational energy of the star

  $$E_{\mathrm{kin}}=-\frac{1}{2} E_{\mathrm{grav}}$$

  where you may assume for a non-relativistic ideal gas that $E_{\mathrm{kin}}=\frac{3}{2}\langle P\rangle V$, with $\langle P\rangle$ the average pressure.

  (b) Consider a white dwarf supported by electron Fermi degeneracy pressure $P \approx h^{2} n^{5 / 3} / m_{\mathrm{e}}$, where $m_{\mathrm{e}}$ is the electron mass and $n$ is the number density. Assume a uniform density $\rho(r)=m_{\mathrm{p}} n(r) \approx m_{\mathrm{p}}\langle n\rangle$, so the total mass of the star is given by $M=(4 \pi / 3)\langle n\rangle m_{\mathrm{p}} R^{3}$ where $m_{\mathrm{p}}$ is the proton mass. Show that the total energy of the white dwarf can be written in the form

  $$E_{\mathrm{total}}=E_{\mathrm{kin}}+E_{\mathrm{grav}}=\frac{\alpha}{R^{2}}-\frac{\beta}{R},$$

  where $\alpha, \beta$ are positive constants which you should specify. Deduce that the white dwarf has a stable radius $R_{\mathrm{WD}}$ at which the energy is minimized, that is,

  $$R_{\mathrm{WD}} \sim \frac{h^{2} M^{-1 / 3}}{G m_{\mathrm{e}} m_{\mathrm{p}}^{5 / 3}} .$$

  comment

• Paper 3, Section II, D

  Cosmology | Part II, 2009

  In the Zel'dovich approximation, particle trajectories in a flat expanding universe are described by $\mathbf{r}(\mathbf{q}, t)=a(t)[\mathbf{q}+\mathbf{\Psi}(\mathbf{q}, t)]$, where $a(t)$ is the scale factor of the universe, $\mathbf{q}$ is the unperturbed comoving trajectory and $\boldsymbol{\Psi}$ is the comoving displacement. The particle equation of motion is

  $$\ddot{\mathbf{r}}=-\nabla \Phi-\frac{1}{\rho} \nabla P$$

  where $\rho$ is the mass density, $P$ is the pressure $\left(P \ll \rho c^{2}\right)$ and $\Phi$ is the Newtonian potential which satisfies the Poisson equation $\nabla^{2} \Phi=4 \pi G \rho$.

  (i) Show that the fractional density perturbation and the pressure gradient are given by

  $$\delta \equiv \frac{\rho-\bar{\rho}}{\bar{\rho}} \approx-\nabla_{\mathbf{q}} \cdot \boldsymbol{\Psi}, \quad \nabla P \approx-\bar{\rho} \frac{c_{s}^{2}}{a} \nabla_{\mathbf{q}}^{2} \boldsymbol{\Psi}$$

  where $\nabla_{\mathbf{q}}$ has components $\partial / \partial q_{i}, \bar{\rho}=\bar{\rho}(t)$ is the homogeneous background density and $c_{s}^{2} \equiv \partial P / \partial \rho$ is the sound speed. [You may assume that the Jacobian $\left|\partial r_{i} / \partial q_{j}\right|^{-1}=$ $\left|a \delta_{i j}+a \partial \psi_{i} / \partial q_{j}\right|^{-1} \approx a^{-3}\left(1-\nabla_{\mathbf{q}} \cdot \boldsymbol{\Psi}\right)$ for $\left.|\boldsymbol{\Psi}| \ll|\mathbf{q}| .\right]$

  Use this result to integrate the Poisson equation once and obtain then the evolution equation for the comoving displacement:

  $$\ddot{\boldsymbol{\Psi}}+2 \frac{\dot{a}}{a} \dot{\boldsymbol{\Psi}}-4 \pi G \bar{\rho} \boldsymbol{\Psi}-\frac{c_{s}^{2}}{a^{2}} \nabla_{\mathbf{q}}^{2} \boldsymbol{\Psi}=0$$

  [You may assume that the integral of $\nabla^{2} \Phi=4 \pi G \bar{\rho}$ is $\nabla \Phi=4 \pi G \bar{\rho} \mathbf{r} / 3$, that $\boldsymbol{\Psi}$ is irrotational and that the Raychaudhuri equation is $\ddot{a} / a \approx-4 \pi G \bar{\rho} / 3$ for $P \ll \rho c^{2}$.]

  Consider the Fourier expansion $\delta(\mathbf{x}, t)=\sum_{\mathbf{k}} \delta_{\mathbf{k}} \exp (i \mathbf{k} \cdot \mathbf{x})$ of the density perturbation using the comoving wavenumber $\mathbf{k}(k=|\mathbf{k}|)$ and obtain the evolution equation for the mode $\delta_{\mathbf{k}}$ :

  $$\ddot{\delta}_{\mathbf{k}}+2 \frac{\dot{a}}{a} \dot{\delta}_{\mathbf{k}}-\left(4 \pi G \bar{\rho}-c_{s}^{2} k^{2} / a^{2}\right) \delta_{\mathbf{k}}=0$$

  (ii) Consider a flat matter-dominated universe with $a(t)=\left(t / t_{0}\right)^{2 / 3}$ (background density $\left.\bar{\rho}=1 /\left(6 \pi G t^{2}\right)\right)$ and with an equation of state $P=\beta \rho^{4 / 3}$ to show that $(*)$ becomes

  $$\ddot{\delta}_{\mathbf{k}}+\frac{4}{3 t} \dot{\delta}_{\mathbf{k}}-\frac{1}{t^{2}}\left(\frac{2}{3}-\bar{v}_{s}^{2} k^{2}\right) \delta_{\mathbf{k}}=0$$

  where the constant $\bar{v}_{s}^{2} \equiv(4 \beta / 3)(6 \pi G)^{-1 / 3} t_{0}^{4 / 3}$. Seek power law solutions of the form $\delta_{\mathbf{k}} \propto t^{\alpha}$ to find the growing and decaying modes

  $$\delta_{\mathbf{k}}=A_{\mathbf{k}} t^{n+}+B_{\mathbf{k}} t^{n-} \quad \text { where } \quad n_{\pm}=-\frac{1}{6} \pm\left[\left(\frac{5}{6}\right)^{2}-\bar{v}_{s}^{2} k^{2}\right]^{1 / 2} .$$

  comment

• Paper 4, Section I, D

  Cosmology | Part II, 2009

  (a) Consider the motion of three galaxies $O, A, B$ at positions $\mathbf{r}_{O}, \mathbf{r}_{A}, \mathbf{r}_{B}$ in an isotropic and homogeneous universe. Assuming non-relativistic velocities $\mathbf{v}(\mathbf{r})$, show that spatial homogeneity implies

  $$\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{A}\right)=\mathbf{v}\left(\mathbf{r}_{B}-\mathbf{r}_{O}\right)-\mathbf{v}\left(\mathbf{r}_{A}-\mathbf{r}_{O}\right)$$

  that is, that the velocity field $\mathbf{v}$ is linearly related to $\mathbf{r}$ by

  $$v_{i}=\sum_{j} H_{i j} r_{j},$$

  where the matrix coefficients $H_{i j}$ are independent of $\mathbf{r}$. Further show that isotropy implies Hubble's law,

  $$\mathbf{v}=H \mathbf{r} \text {, }$$

  where the Hubble parameter $H$ is independent of $\mathbf{r}$. Presuming $H$ to be a function of time $t$, show that Hubble's law can be integrated to obtain the solution

  $$\mathbf{r}(t)=a(t) \mathbf{x}$$

  where $\mathbf{x}$ is a constant (comoving) position and the scalefactor $a(t)$ satisfies $H=\dot{a} / a$.

  (b) Define the cosmological horizon $d_{H}(t)$. For models with $a(t)=t^{\alpha}$ where $0<\alpha<1$, show that the cosmological horizon $d_{H}(t)=c t /(1-\alpha)$ is finite. Briefly explain the horizon problem.

  comment

Differential Geometry

• Paper 1, Section II, H

  Differential Geometry | Part II, 2009

  (i) Define manifold and manifold with boundary for subsets $X \subset \mathbb{R}^{N}$.

  (ii) Let $X$ and $Y$ be manifolds and $f: X \rightarrow Y$ a smooth map. Define what it means for $y \in Y$ to be a regular value of $f$.

  (iii) Let $n \geqslant 0$ and let $\mathbb{S}^{n}$ denote the set $\left\{\left(x^{1}, \ldots, x^{n+1}\right) \in \mathbb{R}^{n+1}: \sum_{i=1}^{n+1}\left(x^{i}\right)^{2}=1\right\}$. Let $B^{n+1}$ denote the set $\left\{\left(x^{1}, \ldots, x^{n+1}\right) \in \mathbb{R}^{n+1}: \sum_{i=1}^{n+1}\left(x^{i}\right)^{2} \leqslant 1\right\}$. Show that $\mathbb{S}^{n}$ is an $n$-dimensional manifold and $B^{n+1}$ is an $(n+1)$-dimensional manifold with boundary, with $\partial B^{n+1}=\mathbb{S}^{n}$.

  [You may use standard theorems involving regular values of smooth functions provided that you state them clearly.]

  (iv) For $n \geqslant 0$, consider the map $h: \mathbb{S}^{n} \rightarrow \mathbb{S}^{n}$ taking $\mathbf{x}$ to $-\mathbf{x}$. Show that $h$ is smooth. Now let $f$ be a smooth map $f: \mathbb{S}^{n} \rightarrow \mathbb{S}^{n}$ such that $f \circ h=f$. Show that $f$ is not smoothly homotopic to the identity map.

  comment

• Paper 2, Section II, H

  Differential Geometry | Part II, 2009

  (a) Let $\alpha: I \rightarrow \mathbb{R}^{3}$ be a smooth regular curve, parametrized by arc length, such that $\alpha^{\prime \prime}(s) \neq 0$ for all $s \in I$. Define the Frenet frame associated to $\alpha$ and derive the Frenet formulae, identifying curvature and torsion.

  (b) Let $\alpha, \tilde{\alpha}: I \rightarrow \mathbb{R}^{3}$ be as above such that $\tilde{k}(s)=k(s), \tilde{\tau}(s)=-\tau(s)$, where $k, \tilde{k}$ denote the curvature of $\alpha, \tilde{\alpha}$, respectively, and $\tau, \tilde{\tau}$ denote the torsion. Show that there exists a $T \in \mathrm{O}_{3}$ and $v \in \mathbb{R}^{3}$ such that

  $$\alpha=T \circ \tilde{\alpha}+v$$

  [You may appeal to standard facts about ordinary differential equations provided that they are clearly stated.]

  (c) Let $\alpha: I \rightarrow \mathbb{R}^{2}$ be a closed regular plane curve, bounding a region $K$. Let $A(K)$ denote the area of $K$, and let $k(s)$ denote the signed curvature at $\alpha(s)$.

  Show that there exists a point $s_{0} \in I$ such that

  $$k\left(s_{0}\right) \leqslant \sqrt{\pi / A(K)}$$

  [You may appeal to any standard theorem provided that it is clearly stated.]

  comment

• Paper 3, Section II, H

  Differential Geometry | Part II, 2009

  (a) State and prove the Theorema Egregium.

  (b) Let $X$ be a minimal surface without boundary in $\mathbb{R}^{3}$ which is closed as a subset of $\mathbb{R}^{3}$, and assume that $X$ is not contained in a closed ball. Let $\Pi$ be a plane in $\mathbb{R}^{3}$ with the property that $D_{n} \rightarrow \infty$ as $n \rightarrow \infty$, where for $n=0,1, \ldots$,

  $$D_{n}=\inf _{x \in X, d(x, 0) \geqslant n} d(x, \Pi)$$

  Here $d(x, y)$ denotes the Euclidean distance between $x$ and $y$ and $d(x, \Pi)=\inf _{y \in \Pi} d(x, y)$. Assume moreover that $X$ contains no planar points. Show that $X$ intersects $\Pi$.

  comment

• Paper 4, Section II, H

  Differential Geometry | Part II, 2009

  (a) Let $X$ be a compact surface (without boundary) in $\mathbb{R}^{3}$. State the global GaussBonnet formula for $X$, identifying all terms in the formula.

  (b) Let $X \subset \mathbb{R}^{3}$ be a surface. Define what it means for a curve $\gamma: I \rightarrow X$ to be a geodesic. State a theorem concerning the existence of geodesics and define the exponential map.

  (c) Let $\psi: X \rightarrow Y$ be an isometry and let $\gamma$ be a geodesic. Show that $\psi \circ \gamma$ is a geodesic. If $K_{X}$ denotes the Gaussian curvature of $X$, and $K_{Y}$ denotes the Gaussian curvature of $Y$, show that $K_{Y} \circ \psi=K_{X}$.

  Now suppose $\psi: X \rightarrow Y$ is a smooth map such that $\psi \circ \gamma$ is a geodesic for all $\gamma$ a geodesic. Is $\psi$ necessarily an isometry? Give a proof or counterexample.

  Similarly, suppose $\psi: X \rightarrow Y$ is a smooth map such that $K_{Y} \circ \psi=K_{X}$. Is $\psi$ necessarily an isometry? Give a proof or counterexample.

  comment

Dynamical Systems

• Paper 1, Section I, E

  Dynamical Systems | Part II, 2009

  Let $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ be a two-dimensional dynamical system with a fixed point at $\mathbf{x}=\mathbf{0}$. Define a Lyapunov function $V(\mathbf{x})$ and explain what it means for $\mathbf{x}=\mathbf{0}$ to be Lyapunov stable.

  Determine the values of $\beta$ for which $V=x^{2}+\beta y^{2}$ is a Lyapunov function in a sufficiently small neighbourhood of the origin for the system

  $$\begin{aligned} &\dot{x}=-x+2 y+2 x y-x^{2}-4 y^{2}, \\ &\dot{y}=-y+x y . \end{aligned}$$

  What can be deduced about the basin of attraction of the origin using $V$ when $\beta=2 ?$

  comment

• Paper 2, Section I, E

  Dynamical Systems | Part II, 2009

  For each of the one-dimensional systems

  (i) $\dot{x}=\mu^{2}-a^{2}+2 a x^{2}-x^{4}$,

  (ii) $\dot{x}=x\left(\mu^{2}-a^{2}+2 a x^{2}-x^{4}\right)$,

  determine the location and stability of all the fixed points. For each system sketch bifurcation diagrams in the $(\mu, x)$ plane in each of the two cases $a>0$ and $a<0$. Identify and carefully describe all the bifurcation points that occur.

  [Detailed calculations are not required, but bifurcation diagrams must be clearly labelled, and the locations of bifurcation points should be given.]

  comment

• Paper 3, Section I, E

  Dynamical Systems | Part II, 2009

  Consider the one-dimensional real map $x_{n+1}=F\left(x_{n}\right)=r x_{n}^{2}\left(1-x_{n}\right)$, where $r>0$. Locate the fixed points and explain for what ranges of the parameter $r$ each fixed point exists. For what range of $r$ does $F$ map the open interval $(0,1)$ into itself?

  Determine the location and type of all the bifurcations from the fixed points which occur. Sketch the location of the fixed points in the $(r, x)$ plane, indicating stability.

  comment

• Paper 3, Section II, E

  Dynamical Systems | Part II, 2009

  Consider the dynamical system

  $$\begin{aligned} &\dot{x}=-a x-2 x y, \\ &\dot{y}=x^{2}+y^{2}-b, \end{aligned}$$

  where $a \geqslant 0$ and $b>0$.

  (i) Find and classify the fixed points. Show that a bifurcation occurs when $4 b=a^{2}>0$.

  (ii) After shifting coordinates to move the relevant fixed point to the origin, and setting $a=2 \sqrt{b}-\mu$, carry out an extended centre manifold calculation to reduce the two-dimensional system to one of the canonical forms, and hence determine the type of bifurcation that occurs when $4 b=a^{2}>0$. Sketch phase portraits in the cases $0<a^{2}<4 b$ and $0<4 b<a^{2}$.

  (iii) Sketch the phase portrait in the case $a=0$. Prove that periodic orbits exist if and only if $a=0$.

  comment

• Paper 4, Section I, $7 \mathbf{E}$

  Dynamical Systems | Part II, 2009

  Consider the two-dimensional dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ given in polar coordinates by

  $$\begin{aligned} &\dot{r}=\left(r-r^{2}\right)(r-g(\theta)), \\ &\dot{\theta}=r, \end{aligned}$$

  $$\begin{aligned} & \dot{\theta}=r, \end{aligned}$$

  where $g(\theta)$ is continuously differentiable and $2 \pi$-periodic. Find a periodic orbit $\gamma$ for $(*)$ and, using the hint or otherwise, compute the Floquet multipliers of $\gamma$ in terms of $g(\theta)$. Explain why one of the Floquet multipliers is independent of $g(\theta)$. Give a sufficient condition for $\gamma$ to be asymptotically stable.

  Investigate the stability of $\gamma$ and the dynamics of $(*)$ in the case $g(\theta)=2 \sin \theta$.

  [Hint: The determinant of the fundamental matrix $\Phi(t)$ satisfies

  $$\frac{d}{d t} \operatorname{det} \Phi=(\nabla \cdot \mathbf{f}) \operatorname{det} \Phi$$

  comment

• Paper 4, Section II, E

  Dynamical Systems | Part II, 2009

  Let $I, J$ be closed bounded intervals in $\mathbb{R}$, and let $F: \mathbb{R} \rightarrow \mathbb{R}$ be a continuous map.

  Explain what is meant by the statement that ' $I F$-covers $J$ ' (written $I \rightarrow J)$. For a collection of intervals $I_{0}, \ldots, I_{k}$ define the associated directed graph $\Gamma$ and transition matrix $A$. Derive an expression for the number of (not necessarily least) period- $n$ points of $F$ in terms of $A$.

  Let $F$ have a 5 -cycle

  $$x_{0}<x_{1}<x_{2}<x_{3}<x_{4}$$

  such that $x_{i+1}=F\left(x_{i}\right)$ for $i=0, \ldots, 4$ where indices are taken modulo 5 . Write down the directed graph $\Gamma$ and transition matrix $A$ for the $F$-covering relations between the intervals $\left[x_{i}, x_{i+1}\right]$. Compute the number of $n$-cycles which are guaranteed to exist for $F$, for each integer $1 \leqslant n \leqslant 4$, and the intervals the points move between.

  Explain carefully whether or not $F$ is guaranteed to have a horseshoe. Must $F$ be chaotic? Could $F$ be a unimodal map? Justify your answers.

  Similarly, a continuous map $G: \mathbb{R} \rightarrow \mathbb{R}$ has a 5 -cycle

  $$x_{3}<x_{1}<x_{0}<x_{2}<x_{4}$$

  For what integer values of $n, 1 \leqslant n \leqslant 4$, is $G$ guaranteed to have an $n$-cycle?

  Is $G$ guaranteed to have a horseshoe? Must $G$ be chaotic? Justify your answers.

  comment

Electrodynamics

• Paper 1, Section II, C

  Electrodynamics | Part II, 2009

  The action for a modified version of electrodynamics is given by

  $$I=\int d^{4} x\left(-\frac{1}{4} F_{a b} F^{a b}-\frac{1}{2} m^{2} A_{a} A^{a}+\mu_{0} J^{a} A_{a}\right)$$

  where $m$ is an arbitrary constant, $F_{a b}=\partial_{a} A_{b}-\partial_{b} A_{a}$ and $J^{a}$ is a conserved current.

  (i) By varying $A_{a}$, derive the field equations analogous to Maxwell's equations by demanding that $\delta I=0$ for an arbitrary variation $\delta A_{a}$.

  (ii) Show that $\partial_{a} A^{a}=0$.

  (iii) Suppose that the current $J^{a}(x)$ is a function of position only. Show that

  $$A^{a}(\mathbf{x})=\frac{\mu_{0}}{4 \pi} \int d^{3} x^{\prime} \frac{J^{a}\left(\mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|} e^{-m\left|\mathbf{x}-\mathbf{x}^{\prime}\right|}$$

  comment

• Paper 3, Section II, C

  Electrodynamics | Part II, 2009

  A particle of charge of $q$ moves along a trajectory $y^{a}(s)$ in spacetime where $s$ is the proper time on the particle's world-line.

  Explain briefly why, in the gauge $\partial_{a} A^{a}=0$, the potential at the spacetime point $x$ is given by

  $$A^{a}(x)=\frac{\mu_{0} q}{2 \pi} \int d s \frac{d y^{a}}{d s} \theta\left(x^{0}-y^{0}(s)\right) \delta\left(\left(x^{c}-y^{c}(s)\right)\left(x^{d}-y^{d}(s)\right) \eta_{c d}\right)$$

  Evaluate this integral for a point charge moving relativistically along the $z$-axis, $x=y=0$, at constant velocity $v$ so that $z=v t .$

  Check your result by starting from the potential of a point charge at rest

  $$\begin{aligned} \mathbf{A} &=0 \\ \phi &=\frac{\mu_{0} q}{4 \pi\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2}} \end{aligned}$$

  and making an appropriate Lorentz transformation.

  comment

• Paper 4, Section II, C

  Electrodynamics | Part II, 2009

  In a superconductor, the charge carriers have a charge $q$, mass $m$ and number density $n$. Describe how to construct the superconducting current in terms of the vector potential A and the wavefunction of the charge carriers.

  Show that the current is gauge invariant.

  Derive the Helmholtz equation

  $$\nabla^{2} \mathbf{B}=\mathbf{B} / \ell^{2}$$

  for a time-independent magnetic field and evaluate the length scale $\ell$ in terms of $n, q$ and $m$.

  Why does this imply that magnetic flux cannot exist in a superconductor?

  comment

Fluid Dynamics II

• Paper 1, Section II, E

  Fluid Dynamics II | Part II, 2009

  Explain the assumptions of lubrication theory and its use in determining the flow in thin films.

  A cylindrical roller of radius a rotates at angular velocity $\Omega$ below the free surface at $y=0$ of a fluid of density $\rho$ and dynamic viscosity $\mu$. The gravitational acceleration is $g$, and the pressure above the free surface is $p_{0}$. The minimum distance of the roller below the fluid surface is $b$, where $b \ll a$. The depth of the roller $d(x)$ below the free surface may be approximated by $d(x) \approx b+x^{2} / 2 a$, where $x$ is the horizontal distance.

  (i) State the conditions for lubrication theory to be applicable to this problem. On the further assumption that the free surface may be taken to be flat, find the flow above the roller and calculate the horizontal volume flux $Q$ (per unit length in the third dimension) and the horizontal pressure gradient.

  (ii) Use the pressure gradient you have found to estimate the order of magnitude of the departure $h(x)$ of the free surface from $y=0$, and give conditions on the parameters that ensure that $|h| \ll b$, as required for part (i).

  [Hint: Integrals of the form

  $$I_{n}=\int_{-\infty}^{\infty}\left(1+t^{2}\right)^{-n} d t$$

  satisfy $I_{1}=\pi$ and

  $$I_{n+1}=\left(\frac{2 n-1}{2 n}\right) I_{n}$$

  for $n \geqslant 1 .]$

  comment

• Paper 2, Section II, E

  Fluid Dynamics II | Part II, 2009

  Show that two-dimensional Stokes flow $\mathbf{u}=(u(r, \phi), v(r, \phi), 0)$ in cylindrical polar coordinates $(r, \phi, z)$ has a stream function $\psi(r, \phi)$, with $u=r^{-1} \partial \psi / \partial \phi, v=-\partial \psi / \partial r$, that satisfies the biharmonic equation

  $$\nabla^{4} \psi=0$$

  Give, in terms of $\psi$ and/or its derivatives, the boundary conditions satisfied by $\psi$ on an impermeable plane of constant $\phi$ which is either (a) rigid or (b) stress-free.

  A rigid plane passes through the origin and lies along $\phi=-\alpha$. Fluid with viscosity $\mu$ is confined in the region $-\alpha<\phi<0$. A uniform tangential stress $S$ is applied on $\phi=0$. Show that the resulting flow may be described by a stream function $\psi$ of the form $\psi(r, \phi)=S r^{2} f(\phi)$, where $f(\phi)$ is to be found. Hence show that the radial flow $U(r)=u(r, 0)$ on $\phi=0$ is given by

  $$U(r)=\frac{S r}{\mu}\left(\frac{1-\cos 2 \alpha-\alpha \sin 2 \alpha}{\sin 2 \alpha-2 \alpha \cos 2 \alpha}\right)$$

  By expanding this expression for small $\alpha$ show that $U$ and $S$ have the same sign, provided that $\alpha$ is not too large. Discuss the situation when $\alpha>\alpha_{c}$, where tan $2 \alpha_{c}=2 \alpha_{c}$.

  [Hint: In plane polar coordinates

  $$\nabla^{2}=\frac{\partial^{2}}{\partial r^{2}}+\frac{1}{r} \frac{\partial}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial \phi^{2}}$$

  and the component $\sigma_{r \phi}$ of the stress tensor takes the form

  $$\sigma_{r \phi}=\mu\left(r \frac{\partial(v / r)}{\partial r}+\frac{1}{r} \frac{\partial u}{\partial \phi}\right)$$

  comment

• Paper 3, Section II, E

  Fluid Dynamics II | Part II, 2009

  An axisymmetric incompressible Stokes flow has the Stokes stream function $\Psi(R, \theta)$ in spherical polar coordinates $(R, \theta, \phi)$. Give expressions for the components $u_{R}$ and $u_{\theta}$ of the flow field in terms of $\Psi$, and show that

  $$\nabla \times \mathbf{u}=\left(0,0,-\frac{D^{2} \Psi}{R \sin \theta}\right)$$

  where

  $$D^{2} \Psi=\frac{\partial^{2} \Psi}{\partial R^{2}}+\frac{\sin \theta}{R^{2}} \frac{\partial}{\partial \theta}\left(\frac{1}{\sin \theta} \frac{\partial \Psi}{\partial \theta}\right)$$

  Write down the equation satisfied by $\Psi$.

  Verify that the Stokes stream function

  $$\Psi(R, \theta)=\frac{1}{2} U \sin ^{2} \theta\left(R^{2}-\frac{3}{2} a R+\frac{1}{2} \frac{a^{3}}{R}\right)$$

  represents the Stokes flow past a stationary sphere of radius $a$, when the fluid at large distance from the sphere moves at speed $U$ along the axis of symmetry.

  A sphere of radius a moves vertically upwards in the $z$ direction at speed $U$ through fluid of density $\rho$ and dynamic viscosity $\mu$, towards a free surface at $z=0$. Its distance $d$ from the surface is much greater than $a$. Assuming that the surface remains flat, show that the conditions of zero vertical velocity and zero tangential stress at $z=0$ can be approximately met for large $d / a$ by combining the Stokes flow for the sphere with that of an image sphere of the same radius located symmetrically above the free surface. Hence determine the leading-order behaviour of the horizontal flow on the free surface as a function of $r$, the horizontal distance from the sphere's centre line.

  What is the size of the next correction to your answer as a power of $a / d ?$ [Detailed calculation is not required.]

  [Hint: For an axisymmetric vector field $\mathbf{u}$,

  $$\nabla \times \mathbf{u}=\left(\frac{1}{R \sin \theta} \frac{\partial}{\partial \theta}\left(u_{\phi} \sin \theta\right),-\frac{1}{R} \frac{\partial}{\partial R}\left(R u_{\phi}\right), \frac{1}{R} \frac{\partial}{\partial R}\left(R u_{\theta}\right)-\frac{1}{R} \frac{\partial u_{R}}{\partial \theta}\right)$$

  comment

• Paper 4 , Section II, E

  Fluid Dynamics II | Part II, 2009

  Two regions of inviscid fluid with the same density are separated by a thin membrane at $y=0$. The fluid in $y>0$ has the uniform velocity $(U, 0,0)$ in Cartesian coordinates, while the fluid in $y<0$ is at rest.

  The membrane is now slightly perturbed to $y=\eta(x, t)$. The dynamical effect of the membrane is to induce a pressure difference across it equal to $\beta \partial^{4} \eta / \partial x^{4}$, where $\beta$ is a constant and the sign is such that the pressure is higher below the interface when $\partial^{4} \eta / \partial x^{4}>0$.

  On the assumption that the flow remains irrotational and all perturbations are small, derive the relation between $\sigma$ and $k$ for disturbances of the form $\eta(x, t)=\operatorname{Re}\left(C e^{i k x+\sigma t}\right)$, where $k$ is real but $\sigma$ may be complex. Show that there is instability only for $|k|<k_{\max }$, where $k_{\max }$ is to be determined. Find the maximum growth rate and the value of $|k|$ for which this is obtained.

  comment

Further Complex Methods

• Paper 1, Section I, B

  Further Complex Methods | Part II, 2009

  Find all second order linear ordinary homogenous differential equations which have a regular singular point at $z=0$, a regular singular point at $z=\infty$, and for which every other point in the complex $z$-plane is an analytic point.

  [You may use without proof Liouville's theorem.]

  comment

• Paper 1, Section II, B

  Further Complex Methods | Part II, 2009

  Let $F(z)$ be defined by

  $$F(z)=\int_{0}^{\infty} \frac{e^{-2 z t}}{1+t^{3}} d t, \quad|\arg z|<\frac{\pi}{2}$$

  Let $\tilde{F}(z)$ be defined by

  $$\tilde{F}(z)=\int_{0}^{-i \infty} \frac{e^{-2 z \zeta}}{1+\zeta^{3}} d \zeta, \quad \alpha<\arg z<\beta$$

  where the above integral is along the negative imaginary axis of the complex $\zeta$-plane and the real constants $\alpha$ and $\beta$ are to be determined.

  Using Cauchy's theorem, or otherwise, compute $F(z)-\tilde{F}(z)$ and hence find a formula for the analytic continuation of $F(z)$ for $\frac{\pi}{2} \leqslant \arg z<\pi$.

  comment

• Paper 2, Section I, B

  Further Complex Methods | Part II, 2009

  The Hilbert transform $\hat{f}$ of a function $f$ is defined by

  $$\hat{f}(x)=\frac{1}{\pi} P \int_{-\infty}^{\infty} \frac{f(y)}{y-x} d y$$

  where $P$ denotes the Cauchy principal value.

  (i) Compute the Hilbert transform of $(1-\cos t) / t$.

  (ii) Solve the following Riemann-Hilbert problem: Find $f^{+}(z)$ and $f^{-}(z)$, which are analytic functions in the upper and lower half $z$-planes respectively, such that

  $$\begin{aligned} &f^{+}(x)-f^{-}(x)=\frac{1-\cos x}{x}, \quad x \in \mathbb{R} \\ &f^{\pm}(z)=O\left(\frac{1}{z}\right), \quad z \rightarrow \infty, \quad \operatorname{Im} z \neq 0 \end{aligned}$$

  comment

• Paper 2, Section II, C

  Further Complex Methods | Part II, 2009

  Consider the initial-boundary value problem

  $$\begin{gathered} \frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad 0<x<\infty, \quad t>0 \\ u(x, 0)=x e^{-x}, \quad 0 \leqslant x<\infty \\ u(0, t)=\sin t, \quad t \geqslant 0 \end{gathered}$$

  where $u$ vanishes sufficiently fast for all $t$ as $x \rightarrow \infty$.

  (i) Express the solution as an integral (which you should not evaluate) in the complex $k$-plane

  (ii) Explain how to use appropriate contour deformation so that the relevant integrand decays exponentially as $|k| \rightarrow \infty$.

  comment

• Paper 3, Section $\mathbf{I}$, B

  Further Complex Methods | Part II, 2009

  Suppose that the real function $u(x, y)$ satisfies Laplace's equation in the upper half complex $z$-plane, $z=x+i y, x \in \mathbb{R}, y>0$, where

  $$u(x, y) \rightarrow 0 \quad \text { as } \quad \sqrt{x^{2}+y^{2}} \rightarrow \infty, \quad u(x, 0)=g(x), \quad x \in \mathbb{R} .$$

  The function $u(x, y)$ can then be expressed in terms of the Poisson integral

  $$u(x, y)=\frac{1}{\pi} \int_{-\infty}^{\infty} \frac{y g(\xi)}{(x-\xi)^{2}+y^{2}} d \xi, \quad x \in \mathbb{R}, y>0$$

  By employing the formula

  $$f(z)=2 u\left(\frac{z+\bar{a}}{2}, \frac{z-\bar{a}}{2 i}\right)-\overline{f(a)}$$

  where $a$ is a complex constant with $\operatorname{Im} a>0$, show that the analytic function whose real part is $u(x, y)$ is given by

  $$f(z)=\frac{1}{i \pi} \int_{-\infty}^{\infty} \frac{g(\xi)}{\xi-z} d \xi+i c, \quad \operatorname{Im} z>0$$

  where $c$ is a real constant.

  comment

• Paper 4, Section I, D

  Further Complex Methods | Part II, 2009

  Show that

  $$\Gamma(\alpha) \Gamma(\beta)=\Gamma(\alpha+\beta) \int_{0}^{1} t^{\alpha-1}(1-t)^{\beta-1} d t, \quad \operatorname{Re} \alpha>0, \quad \operatorname{Re} \beta>0$$

  where $\Gamma(z)$ denotes the Gamma function

  $$\Gamma(z)=\int_{0}^{\infty} x^{z-1} e^{-x} d x, \quad \operatorname{Re} z>0$$

  comment

Galois Theory

• Paper 1, Section II, H

  Galois Theory | Part II, 2009

  Define a $K$-isomorphism, $\varphi: L \rightarrow L^{\prime}$, where $L, L^{\prime}$ are fields containing a field $K$, and define $\operatorname{Aut}_{K}(L)$.

  Suppose $\alpha$ and $\beta$ are algebraic over $K$. Show that $K(\alpha)$ and $K(\beta)$ are $K$-isomorphic via an isomorphism mapping $\alpha$ to $\beta$ if and only if $\alpha$ and $\beta$ have the same minimal polynomial.

  Show that $\operatorname{Aut}_{K} K(\alpha)$ is finite, and a subgroup of the symmetric group $S_{d}$, where $d$ is the degree of $\alpha$.

  Give an example of a field $K$ of characteristic $p>0$ and $\alpha$ and $\beta$ of the same degree, such that $K(\alpha)$ is not isomorphic to $K(\beta)$. Does such an example exist if $K$ is finite? Justify your answer.

  comment

• Paper 2, Section II, H

  Galois Theory | Part II, 2009

  For each of the following polynomials over $\mathbb{Q}$, determine the splitting field $K$ and the Galois group $G$. (1) $x^{4}-2 x^{2}-25$. (2) $x^{4}-2 x^{2}+25$.

  comment

• Paper 3, Section II, H

  Galois Theory | Part II, 2009

  Let $K=\mathbb{F}_{p}(x)$, the function field in one variable, and let $G=\mathbb{F}_{p}$. The group $G$ acts as automorphisms of $K$ by $\sigma_{a}(x)=x+a$. Show that $K^{G}=\mathbb{F}_{p}(y)$, where $y=x^{p}-x$.

  [State clearly any theorems you use.]

  Is $K / K^{G}$ a separable extension?

  Now let

  $$H=\left\{\left(\begin{array}{ll} d & a \\ 0 & 1 \end{array}\right): a \in \mathbb{F}_{p}, d \in \mathbb{F}_{p}^{*}\right\}$$

  and let $H$ act on $K$ by $\left(\begin{array}{ll}d & a \\ 0 & 1\end{array}\right) x=d x+a$. (The group structure on $H$ is given by matrix multiplication.) Compute $K^{H}$. Describe your answer in the form $\mathbb{F}_{p}(z)$ for an explicit $z \in K$.

  Is $K^{G} / K^{H}$ a Galois extension? Find the minimum polynomial for $y$ over the field $K^{H}$.

  comment

• Paper 4, Section II, H

  Galois Theory | Part II, 2009

  (a) Let $K$ be a field. State what it means for $\xi_{n} \in K$ to be a primitive $n$th root of unity.

  Show that if $\xi_{n}$ is a primitive $n$th root of unity, then the characteristic of $K$ does not divide $n$. Prove any theorems you use.

  (b) Determine the minimum polynomial of a primitive 10 th root of unity $\xi_{10}$ over $\mathbb{Q}$.

  Show that $\sqrt{5} \in \mathbb{Q}\left(\xi_{10}\right)$.

  (c) Determine $\mathbb{F}_{3}\left(\xi_{10}\right), \mathbb{F}_{11}\left(\xi_{10}\right), \mathbb{F}_{19}\left(\xi_{10}\right)$.

  [Hint: Write a necessary and sufficient condition on $q$ for a finite field $\mathbb{F}_{q}$ to contain a primitive 10 th root of unity.]

  comment

General Relativity

• Paper 1, Section II, D

  General Relativity | Part II, 2009

  Write down the differential equations governing geodesic curves $x^{a}(\lambda)$ both when $\lambda$ is an affine parameter and when it is a general one.

  A conformal transformation of a spacetime is given by

  $$g_{a b} \rightarrow \tilde{g}_{a b}=\Omega^{2}(x) g_{a b}$$

  Obtain a formula for the new Christoffel symbols $\tilde{\Gamma}_{b c}^{a}$ in terms of the old ones and the derivatives of $\Omega$. Hence show that null geodesics in the metric $g_{a b}$ are also geodesic in the metric $\tilde{g}_{a b}$.

  Show that the Riemann tensor has only one independent component in two dimensions, and hence derive

  $$R=2 \operatorname{det}\left(g^{a b}\right) R_{0101}$$

  where $R$ is the Ricci scalar.

  It is given that in a 2-dimensional spacetime $M, R$ transforms as

  $$R \rightarrow \tilde{R}=\Omega^{-2}(R-2 \square \log \Omega)$$

  where $\square \phi=g^{a b} \nabla_{a} \nabla_{b} \phi$. Assuming that the equation $\square \phi=\rho(x)$ can always be solved, show that $\Omega$ can be chosen to set $\tilde{g}$ to be the metric of 2-dimensional Minkowski spacetime. Hence show that all null curves in $M$ are geodesic.

  Discuss the null geodesics if the line element of $M$ is

  $$d s^{2}=-t^{-1} d t^{2}+t d \theta^{2}$$

  where $t \in(-\infty, 0)$ or $(0, \infty)$ and $\theta \in[0,2 \pi]$.

  comment

• Paper 2, Section II, D

  General Relativity | Part II, 2009

  A spacetime has line element

  $$d s^{2}=-d t^{2}+t^{2 p_{1}} d x_{1}^{2}+t^{2 p_{2}} d x_{2}^{2}+t^{2 p_{3}} d x_{3}^{2},$$

  where $p_{1}, p_{2}$ and $p_{3}$ are constants. Calculate the Christoffel symbols.

  Find the constraints on $p_{1}, p_{2}$ and $p_{3}$ for this spacetime to be a solution of the vacuum Einstein equations with zero cosmological constant. For which values is the spacetime flat?

  Show that it is not possible to have all of $p_{1}, p_{2}$ and $p_{3}$ strictly positive, so that if they are all non-zero, the spacetime expands in at least one direction and contracts in at least one direction.

  [The Riemann tensor is given in terms of the Christoffel symbols by

  $$\left.R_{b c d}^{a}=\Gamma_{d b, c}^{a}-\Gamma_{c b, d}^{a}+\Gamma_{c f}^{a} \Gamma_{d b}^{f}-\Gamma_{d f}^{a} \Gamma_{c b}^{f}\right]$$

  comment

• Paper 4, Section II, D

  General Relativity | Part II, 2009

  The Schwarzschild metric is given by

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2}\left(d \theta^{2}+\sin ^{2} \theta d \phi^{2}\right)$$

  where $M$ is the mass in gravitational units. By using the radial component of the geodesic equations, or otherwise, show for a particle moving on a geodesic in the equatorial plane $\theta=\pi / 2$ with $r$ constant that

  $$\left(\frac{d \phi}{d t}\right)^{2}=\frac{M}{r^{3}}$$

  Show that such an orbit is stable for $r>6 M$.

  An astronaut circles the Earth freely for a long time on a circular orbit of radius $R$, while the astronaut's twin remains motionless on Earth, which is assumed to be spherical, with radius $R_{0}$, and non-rotating. Show that, on returning to Earth, the astronaut will be younger than the twin only if $2 R<3 R_{0}$.

  comment

Geometry of Group Actions

• Paper 1, Section I, F

  Geometry of Group Actions | Part II, 2009

  Explain what is meant by stereographic projection from the 2-dimensional sphere to the complex plane.

  Prove that $u$ and $v$ are the images under stereographic projection of antipodal points on the sphere if and only if $u \bar{v}=-1$.

  comment

• Paper 1, Section II, F

  Geometry of Group Actions | Part II, 2009

  Define frieze group and crystallographic group and give three examples of each, identifying them as abstract groups as well as geometrically.

  Let $G$ be a discrete group of isometries of the Euclidean plane which contains a translation. Prove that $G$ contains no element of order 5 .

  comment

• Paper 2, Section $\mathbf{I}$, F

  Geometry of Group Actions | Part II, 2009

  Describe the geodesics in the hyperbolic plane (in a model of your choice).

  Let $l_{1}$ and $l_{2}$ be geodesics in the hyperbolic plane which do not meet either in the plane or at infinity. By considering the action on a suitable third geodesic, or otherwise, prove that the composite $R_{l_{1}} \circ R_{l_{2}}$ of the reflections in the two geodesics has infinite order.

  comment

• Paper 3, Section I, F

  Geometry of Group Actions | Part II, 2009

  Explain why there are discrete subgroups of the Möbius group $\mathbb{P} S L_{2}(\mathbb{C})$ which abstractly are free groups of rank 2 .

  comment

• Paper 4, Section I, F

  Geometry of Group Actions | Part II, 2009

  For every $k \in \mathbb{R}$, show that there is a closed bounded totally disconnected subset $X$ of some Euclidean space, such that $X$ has Hausdorff dimension at least $k$. [Standard properties of Hausdorff dimension may be quoted without proof if carefully stated.]

  comment

• Paper 4, Section II, F

  Geometry of Group Actions | Part II, 2009

  Define three-dimensional hyperbolic space, the translation length of an isometry of hyperbolic 3 -space, and the axis of a hyperbolic isometry. Briefly explain how and why the latter two concepts are related.

  Find the translation length of the isometries defined by (i) $z \mapsto k z, k \in \mathbb{C} \backslash\{0\}$ and (ii) $z \mapsto \frac{3 z+2}{7 z+5}$.

  comment

Graph Theory

• Paper 1, Section II, $17 \mathrm{~F}$

  Graph Theory | Part II, 2009

  (i) State and prove Hall's theorem concerning matchings in bipartite graphs.

  (ii) The matching number of a graph $G$ is the maximum size of a family of independent edges (edges without shared vertices) in $G$. Deduce from Hall's theorem that if $G$ is a $k$-regular bipartite graph on $n$ vertices (some $k>0$ ) then $G$ has matching number $n / 2$.

  (iii) Now suppose that $G$ is an arbitrary $k$-regular graph on $n$ vertices (some $k>0)$. Show that $G$ has a matching number at least $\frac{k}{4 k-2} n$. [Hint: Let $S$ be the set of vertices in a maximal set of independent edges. Consider the edges of $G$ with exactly one endpoint in $S$.]

  For $k=2$, show that there are infinitely many graphs $G$ for which equality holds.

  comment

• Paper 2, Section II, F

  Graph Theory | Part II, 2009

  (i) Define the Turán graph $T_{r}(n)$. State and prove Turán's theorem.

  (ii) For each value of $n$ and $r$ with $n>r$, exhibit a graph $G$ on $n$ vertices that has fewer edges than $T_{r-1}(n)$ and yet is maximal $K_{r}$-free (meaning that $G$ contains no $K_{r}$ but the addition of any edge to $G$ produces a $K_{r}$ ). In the case $r=3$, determine the smallest number of edges that such a $G$ can have.

  comment

• Paper 3, Section II, F

  Graph Theory | Part II, 2009

  (a) State Brooks' theorem concerning the chromatic number $\chi(G)$ of a graph $G$. Prove it in the case when $G$ is 3-connected.

  [If you wish to assume that $G$ is regular, you should explain why this assumption is justified.]

  (b) State Vizing's theorem concerning the edge-chromatic number $\chi^{\prime}(G)$ of a graph $G$.

  (c) Are the following statements true or false? Justify your answers.

  (1) If $G$ is a connected graph on more than two vertices then $\chi(G) \leqslant \chi^{\prime}(G)$.

  (2) For every ordering of the vertices of a graph $G$, if we colour $G$ using the greedy algorithm (on this ordering) then the number of colours we use is at most $2 \chi(G)$.

  (3) For every ordering of the edges of a graph $G$, if we edge-colour $G$ using the greedy algorithm (on this ordering) then the number of colours we use is at most $2 \chi^{\prime}(G)$.

  comment

• Paper 4, Section II, F

  Graph Theory | Part II, 2009

  Let $X$ denote the number of triangles in a random graph $G$ chosen from $G(n, p)$. Find the mean and variance of $X$. Hence show that $p=n^{-1}$ is a threshold for the existence of a triangle, in the sense that if $p n \rightarrow 0$ then almost surely $G$ does not contain a triangle, while if $p n \rightarrow \infty$ then almost surely $G$ does contain a triangle.

  Now let $p=n^{-1 / 2}$, and let $Y$ denote the number of edges of $G$ (chosen as before from $G(n, p))$. By considering the mean of $Y-X$, show that for each $n \geqslant 3$ there exists a graph on $n$ vertices with at least $\frac{1}{6} n^{3 / 2}$ edges that is triangle-free. Is this within a constant factor of the best-possible answer (meaning the greatest number of edges that a triangle-free graph on $n$ vertices can have)?

  comment

Integrable Systems

• Paper 1, Section II, B

  Integrable Systems | Part II, 2009

  Let $H$ be a smooth function on a $2 n$-dimensional phase space with local coordinates $\left(p_{j}, q_{j}\right)$. Write down the Hamilton equations with the Hamiltonian given by $H$ and state the Arnold-Liouville theorem.

  By establishing the existence of sufficiently many first integrals demonstrate that the system of $n$ coupled harmonic oscillators with the Hamiltonian

  $$H=\frac{1}{2} \sum_{k=1}^{n}\left(p_{k}^{2}+\omega_{k}^{2} q_{k}^{2}\right)$$

  where $\omega_{1}, \ldots, \omega_{n}$ are constants, is completely integrable. Find the action variables for this system.

  comment

• Paper 2, Section II, B

  Integrable Systems | Part II, 2009

  Let $L=-\partial_{x}^{2}+u(x, t)$ be a Schrödinger operator and let $A$ be another differential operator which does not contain derivatives with respect to $t$ and such that

  $$L_{t}=[L, A] .$$

  Show that the eigenvalues of $L$ are independent of $t$, and deduce that if $f$ is an eigenfunction of $L$ then so is $f_{t}+A f$. [You may assume that $L$ is self-adjoint.]

  Let $f$ be an eigenfunction of $L$ corresponding to an eigenvalue $\lambda$ which is nondegenerate. Show that there exists a function $\hat{f}=\hat{f}(x, t, \lambda)$ such that

  $$L \hat{f}=\lambda \hat{f}, \quad \hat{f}_{t}+A \hat{f}=0 .$$

  Assume

  $$A=\partial_{x}^{3}+a_{1} \partial_{x}+a_{0},$$

  where $a_{k}=a_{k}(x, t), k=0,1$ are functions. Show that the system $(*)$ is equivalent to a pair of first order matrix PDEs

  $$\partial_{x} F=U F, \quad \partial_{t} F=V F$$

  where $F=\left(\hat{f}, \partial_{x} \hat{f}\right)^{T}$ and $U, V$ are $2 \times 2$ matrices which should be determined.

  comment

• Paper 3, Section II, B

  Integrable Systems | Part II, 2009

  Consider the partial differential equation

  $$\frac{\partial u}{\partial t}=u^{n} \frac{\partial u}{\partial x}+\frac{\partial^{2 k+1} u}{\partial x^{2 k+1}}$$

  where $u=u(x, t)$ and $k, n$ are non-negative integers.

  (i) Find a Lie point symmetry of $(*)$ of the form

  $$(x, t, u) \longrightarrow(\alpha x, \beta t, \gamma u),$$

  where $(\alpha, \beta, \gamma)$ are non-zero constants, and find a vector field generating this symmetry. Find two more vector fields generating Lie point symmetries of (*) which are not of the form $(* *)$ and verify that the three vector fields you have found form a Lie algebra.

  (ii) Put $(*)$ in a Hamiltonian form.

  comment

Linear Analysis

• Paper 1, Section II, H

  Linear Analysis | Part II, 2009

  (a) State and prove the Baire category theorem.

  (b) Let $X$ be a normed space. Show that every proper linear subspace $V \subset X$ has empty interior.

  (c) Let $\mathcal{P}$ be the vector space of all real polynomials in one variable. Using the Baire category theorem and the result from (b), prove that for any norm $\|\cdot\|$ on $\mathcal{P}$, the normed space $(\mathcal{P},\|\cdot\|)$ is not a Banach space.

  comment

• Paper 2, Section II, H

  Linear Analysis | Part II, 2009

  For $1 \leqslant p<\infty$ and a sequence $x=\left(x_{1}, x_{2}, \ldots\right)$, where $x_{j} \in \mathbb{C}$ for all $j \geqslant 1$, let $\|x\|_{p}=\left(\sum_{j=1}^{\infty}\left|x_{j}\right|^{p}\right)^{1 / p} .$

  Let $\ell^{p}=\left\{x=\left(x_{1}, x_{2}, \ldots\right): x_{j} \in \mathbb{C}\right.$ for all $j \geqslant 1$ and $\left.\|x\|_{p}<\infty\right\}$.

  (a) Let $p, q>1$ with $1 / p+1 / q=1, x=\left(x_{1}, x_{2}, \ldots\right) \in \ell^{p}$ and $y=\left(y_{1}, y_{2}, \ldots\right) \in \ell^{q}$. Prove Hölder's inequality:

  $$\sum_{j=1}^{\infty}\left|x_{j}\left\|y_{j} \mid \leqslant\right\| x\left\|_{p}\right\| y \|_{q}\right.$$

  (b) Use Hölder's inequality to prove the triangle inequality (known, in this case, as the Minkowski inequality):

  $$\|x+y\|_{p} \leqslant\|x\|_{p}+\|y\|_{p} \quad \text { for every } x, y \in \ell^{p} \quad \text { and every } 1<p<\infty$$

  (c) Let $2 \leqslant p<\infty$ and let $K$ be a closed, convex subset of $\ell^{p}$. Let $x \in \ell^{p}$ with $x \notin K$. Prove that there exists $y \in K$ such that

  $$\|x-y\|=\inf _{z \in K}\|x-z\| .$$

  [You may use without proof the fact that for every $2 \leqslant p<\infty$ and for every $x, y \in \ell^{p}$,

  $$\left.\|x+y\|_{p}^{p}+\|x-y\|_{p}^{p} \leqslant 2^{p-1}\left(\|x\|_{p}^{p}+\|y\|_{p}^{p}\right) .\right]$$

  comment

• Paper 3, Section II, H

  Linear Analysis | Part II, 2009

  (a) State the Arzela-Ascoli theorem, explaining the meaning of all concepts involved.

  (b) Prove the Arzela-Ascoli theorem.

  (c) Let $K$ be a compact topological space. Let $\left(f_{n}\right)_{n \in \mathbb{N}}$ be a sequence in the Banach space $C(K)$ of real-valued continuous functions over $K$ equipped with the supremum norm $\|\cdot\|$. Assume that for every $x \in K$, the sequence $f_{n}(x)$ is monotone increasing and that $f_{n}(x) \rightarrow f(x)$ for some $f \in C(K)$. Show that $\left\|f_{n}-f\right\| \rightarrow 0$ as $n \rightarrow \infty$.

  comment

• Paper 4, Section II, H

  Linear Analysis | Part II, 2009

  Let $X$ be a Banach space and let $T: X \rightarrow X$ be a bounded linear map.

  (a) Define the spectrum $\sigma(T)$, the resolvent set $\rho(T)$ and the point spectrum $\sigma_{p}(T)$ of $T$.

  (b) What does it mean for $T$ to be a compact operator?

  (c) Show that if $T$ is a compact operator on $X$ and $a>0$, then $T$ has at most finitely many linearly independent eigenvectors with eigenvalues having modulus larger than $a$.

  [You may use without proof the fact that for any finite dimensional proper subspace $Y$ of a Banach space $Z$, there exists $x \in Z$ with $\|x\|=1$ and $\operatorname{dist}(x, Y)=\inf _{y \in Y}\|x-y\|=1$.]

  (d) For a sequence $\left(\lambda_{n}\right)_{n \geqslant 1}$ of complex numbers, let $T: \ell^{2} \rightarrow \ell^{2}$ be defined by

  $$T\left(x_{1}, x_{2}, \ldots\right)=\left(\lambda_{1} x_{1}, \lambda_{2} x_{2}, \ldots\right) .$$

  Give necessary and sufficient conditions on the sequence $\left(\lambda_{n}\right)_{n} \geqslant 1$ for $T$ to be compact, and prove your assertion.

  comment

Logic and Set Theory

• Paper 1, Section II, G

  Logic and Set Theory | Part II, 2009

  Prove that if $G:$ On $\times V \rightarrow V$ is a definable function, then there is a definable function $F:$ On $\rightarrow V$ satisfying

  $$F(\alpha)=G(\alpha,\{F(\beta): \beta<\alpha\})$$

  Define the notion of an initial ordinal, and explain its significance for cardinal arithmetic. State Hartogs' lemma. Using the recursion theorem define, giving justification, a function $\omega:$ On $\rightarrow$ On which enumerates the infinite initial ordinals.

  Is there an ordinal $\alpha$ with $\alpha=\omega_{\alpha} ?$ Justify your answer.

  comment

• Paper 2, Section II, G

  Logic and Set Theory | Part II, 2009

  (i) Give an axiom system and rules of inference for the classical propositional calculus, and explain the notion of syntactic entailment. What does it mean to say that a set of propositions is consistent? Let $P$ be a set of primitive propositions and let $\Phi$ be a maximal consistent set of propositional formulae in the language based on $P$. Show that there is a valuation $v: P \rightarrow\{T, F\}$ with respect to which all members of $\Phi$ are true.

  [You should state clearly but need not prove those properties of syntactic entailment which you use.]

  (ii) Exhibit a theory $T$ which axiomatizes the collection of groups all of whose nonunit elements have infinite order. Is this theory finitely axiomatizable? Is the theory of groups all of whose elements are of finite order axiomatizable? Justify your answers.

  comment

• Paper 3, Section II, G

  Logic and Set Theory | Part II, 2009

  Let $x \subseteq \alpha$ be a subset of a (von Neumann) ordinal $\alpha$ taken with the induced ordering. Using the recursion theorem or otherwise show that $x$ is order isomorphic to a unique ordinal $\mu(x)$. Suppose that $x \subseteq y \subseteq \alpha$. Show that $\mu(x) \leqslant \mu(y) \leqslant \alpha$.

  Suppose that $x_{0} \subseteq x_{1} \subseteq x_{2} \subseteq \cdots$ is an increasing sequence of subsets of $\alpha$, with $x_{i}$ an initial segment of $x_{j}$ whenever $i<j$. Show that $\mu\left(\bigcup_{n} x_{n}\right)=\bigcup_{n} \mu\left(x_{n}\right)$. Does this result still hold if the condition on initial segments is omitted? Justify your answer.

  Suppose that $x_{0} \supseteq x_{1} \supseteq x_{2} \supseteq \cdots$ is a decreasing sequence of subsets of $\alpha$. Why is the sequence $\mu\left(x_{n}\right)$ eventually constant? Is it the case that $\mu\left(\bigcap_{n} x_{n}\right)=\bigcap_{n} \mu\left(x_{n}\right)$ ? Justify your answer.

  comment

• Paper 4, Section II, G

  Logic and Set Theory | Part II, 2009

  What is a transitive class? What is the significance of this notion for models of set theory?

  Prove that for any set $x$ there is a least transitive set $\mathrm{TC}(x)$, the transitive closure of $x$, with $x \subseteq \mathrm{TC}(x)$. Show that for any set $x$, one has $\mathrm{TC}(x)=x \cup \mathrm{TC}(\bigcup x)$, and deduce that $\mathrm{TC}(\{x\})=\{x\} \cup \operatorname{TC}(x)$.

  A set $x$ is hereditarily countable when every member of $\mathrm{TC}(\{x\})$ is countable. Let $(\mathrm{HC}, \in)$ be the collection of hereditarily countable sets with the usual membership relation. Is HC transitive? Show that $(\mathrm{HC}, \in)$ satisfies the axiom of unions. Show that $(\mathrm{HC}, \in)$ satisfies the axiom of separation. What other axioms of ZF set theory are satisfied in $(\mathrm{HC}, \in) ?$

  comment

Mathematical Biology

• Paper 1, Section I, A

  Mathematical Biology | Part II, 2009

  A discrete model for a population $N_{t}$ consists of

  $$N_{t+1}=\frac{r N_{t}}{\left(1+b N_{t}\right)^{2}},$$

  where $t$ is discrete time and $r, b>0$. What do $r$ and $b$ represent in this model? Show that for $r>1$ there is a stable fixed point.

  Suppose the initial condition is $N_{1}=1 / b$, and that $r>4$. Show, with the help of a cobweb, that the population $N_{t}$ is bounded by

  $$\frac{4 r^{2}}{(4+r)^{2} b} \leqslant N_{t} \leqslant \frac{r}{4 b}$$

  and attains those bounds.

  comment

• Paper 2, Section $I$, A

  Mathematical Biology | Part II, 2009

  Consider the reaction system

  $$A \stackrel{k_{1}}{\longrightarrow} X, \quad B+X \stackrel{k_{2}}{\longrightarrow} Y, \quad 2 X+Y \stackrel{k_{3}}{\longrightarrow} 3 X, \quad X \stackrel{k_{4}}{\longrightarrow} E,$$

  where the $k$ s are the rate constants, and the reactant concentrations of $A$ and $B$ are kept constant. Write down the governing differential equation system for the concentrations of $X$ and $Y$ and nondimensionalise the equations by setting $u=\alpha X$ and $v=\alpha Y, \tau=k_{4} t$ so that they become

  $$\frac{d u}{d \tau}=1-(b+1) u+a u^{2} v, \quad \frac{d v}{d \tau}=b u-a u^{2} v$$

  by suitable choice of $\alpha$. Thus find $a$ and $b$. Determine the positive steady state and show that there is a bifurcation value $b=b_{c}=1+a$ at which the steady state becomes unstable to a Hopf bifurcation. Find the period of the oscillations in the neighbourhood of $b_{c}$.

  comment

• Paper 2, Section II, A

  Mathematical Biology | Part II, 2009

  Travelling bands of microorganisms, chemotactically directed, move into a food source, consuming it as they go. A model for this is given by

  $$b_{t}=\frac{\partial}{\partial x}\left[D b_{x}-\frac{b \chi}{a} a_{x}\right], \quad a_{t}=-k b$$

  where $b(x, t)$ and $a(x, t)$ are the bacteria and nutrient respectively and $D, \chi$, and $k$ are positive constants. Look for travelling wave solutions, as functions of $z=x-c t$ where $c$ is the wave speed, with the boundary conditions $b \rightarrow 0$ as $|z| \rightarrow \infty, a \rightarrow 0$ as $z \rightarrow-\infty$, $a \rightarrow 1$ as $z \rightarrow \infty$. Hence show that $b(z)$ and $a(z)$ satisfy

  $$b^{\prime}=\frac{b}{c D}\left[\frac{k b \chi}{a}-c^{2}\right], \quad a^{\prime}=\frac{k b}{c}$$

  where the prime denotes differentiation with respect to $z$. Integrating $d b / d a$, find an algebraic relationship between $b(z)$ and $a(z)$.

  In the special case where $\chi=2 D$ show that

  $$a(z)=\left[1+K e^{-c z / D}\right]^{-1}, \quad b(z)=\frac{c^{2}}{k D} e^{-c z / D}\left[1+K e^{-c z / D}\right]^{-2}$$

  where $K$ is an arbitrary positive constant which is equivalent to a linear translation; it may be set to 1 . Sketch the wave solutions and explain the biological interpretation.

  comment

• Paper 3, Section I, A

  Mathematical Biology | Part II, 2009

  Consider an organism moving on a one-dimensional lattice of spacing $a$, taking steps either to the right or the left at regular time intervals $\tau$. In this random walk there is a slight bias to the right, that is the probabilities of moving to the right and left, $\alpha$ and $\beta$, are such that $\alpha-\beta=\epsilon$, where $0<\epsilon \ll 1$. Write down the appropriate master equation for this process. Show by taking the continuum limit in space and time that $p(x, t)$, the probability that an organism initially at $x=0$ is at $x$ after time $t$, obeys

  $$\frac{\partial p}{\partial t}+V \frac{\partial p}{\partial x}=D \frac{\partial^{2} p}{\partial x^{2}}$$

  Express the constants $V$ and $D$ in terms of $a, \tau, \alpha$ and $\beta$.

  comment

• Paper 3, Section II, A

  Mathematical Biology | Part II, 2009

  An activator-inhibitor reaction diffusion system in dimensionless form is given by

  $$u_{t}=u_{x x}+\frac{u^{2}}{v}-b u, \quad v_{t}=d v_{x x}+u^{2}-v$$

  where $b$ and $d$ are positive constants. Which is the activitor and which the inhibitor? Determine the positive steady states and show, by an examination of the eigenvalues in a linear stability analysis of the spatially uniform situation, that the reaction kinetics is stable if $b<1$.

  Determine the conditions for the steady state to be driven unstable by diffusion. Show that the parameter domain for diffusion-driven instability is given by $0<b<1$, $b d>3+2 \sqrt{2}$, and sketch the $(b, d)$ parameter space in which diffusion-driven instability occurs. Further show that at the bifurcation to such an instability the critical wave number $k_{c}$ is given by $k_{c}^{2}=(1+\sqrt{2}) / d$.

  comment

• Paper 4, Section I, A

  Mathematical Biology | Part II, 2009

  The diffusion equation for a chemical concentration $C(r, t)$ in three dimensions which depends only on the radial coordinate $r$ is

  $$C_{t}=D \frac{1}{r^{2}}\left(r^{2} C_{r}\right)_{r}$$

  The general similarity solution of this equation takes the form

  $$C(r, t)=t^{\alpha} F(\xi), \quad \xi=\frac{r}{t^{\beta}},$$

  where $\alpha$ and $\beta$ are to be determined. By direct substitution into $(*)$ and the requirement of a valid similarity solution, find one relation involving the exponents. Use the conservation of the total number of molecules to determine a second relation. Comment on the relationship between these exponents and the ones appropriate to the similarity solution of the one-dimensional diffusion equation. Show that $F$ obeys

  $$D\left(F^{\prime \prime}+\frac{2}{\xi} F^{\prime}\right)+\frac{1}{2} \xi F^{\prime}+\frac{3}{2} F=0$$

  and that the relevant solution describing the spreading of a delta-function initial condition is $F(\xi)=A \exp \left(-\xi^{2} / 4 D\right)$, where $A$ is a suitable normalisation that need not be found.

  comment

Number Fields

• Paper 1, Section II, H

  Number Fields | Part II, 2009

  Suppose that $K$ is a number field with ring of integers $\mathcal{O}_{K}$.

  (i) Suppose that $M$ is a sub- $\mathbb{Z}$-module of $\mathcal{O}_{K}$ of finite index $r$ and that $M$ is closed under multiplication. Define the discriminant of $M$ and of $\mathcal{O}_{K}$, and show that $\operatorname{disc}(M)=r^{2} \operatorname{disc}\left(\mathcal{O}_{K}\right) .$

  (ii) Describe $\mathcal{O}_{K}$ when $K=\mathbb{Q}[X] /\left(X^{3}+2 X+1\right)$.

  [You may assume that the polynomial $X^{3}+p X+q$ has discriminant $-4 p^{3}-27 q^{2}$.]

  (iii) Suppose that $f, g \in \mathbb{Z}[X]$ are monic quadratic polynomials with equal discriminant $d$, and that $d \notin\{0,1\}$ is square-free. Show that $\mathbb{Z}[X] /(f)$ is isomorphic to $\mathbb{Z}[X] /(g)$.

  [Hint: Classify quadratic fields in terms of discriminants.]

  comment

• Paper 2, Section II, H

  Number Fields | Part II, 2009

  Suppose that $K$ is a number field of degree $n=r+2 s$, where $K$ has exactly real embeddings.

  (i) Taking for granted the fact that there is a constant $C_{K}$ such that every integral ideal $I$ of $\mathcal{O}_{K}$ has a non-zero element $x$ such that $|N(x)| \leqslant C_{K} N(I)$, deduce that the class group of $K$ is finite.

  (ii) Compute the class group of $\mathbb{Q}(\sqrt{-21})$, given that you can take

  $$C_{K}=\left(\frac{4}{\pi}\right)^{s} \frac{n !}{n^{n}}\left|D_{K}\right|^{1 / 2}$$

  where $D_{K}$ is the discriminant of $K$.

  (iii) Find all integer solutions of $y^{2}=x^{3}-21$.

  comment

• Paper 4, Section II, H

  Number Fields | Part II, 2009

  Suppose that $K$ is a number field of degree $n=r+2 s$, where $K$ has exactly real embeddings.

  Show that the group of units in $\mathcal{O}_{K}$ is a finitely generated abelian group of rank at most $r+s-1$. Identify the torsion subgroup in terms of roots of unity.

  [General results about discrete subgroups of a Euclidean real vector space may be used without proof, provided that they are stated clearly.]

  Find all the roots of unity in $\mathbb{Q}(\sqrt{11})$.

  comment

Number Theory

• Paper 1, Section I, G

  Number Theory | Part II, 2009

  State the Chinese Remainder Theorem.

  Determine all integers $x$ satisfying the congruences $x \equiv 2 \bmod 3, x \equiv 2 \bmod 5$, $x \equiv 6 \bmod 7 .$

  comment

• Paper 2, Section $\mathbf{I}$, $1 \mathrm{G}$

  Number Theory | Part II, 2009

  State the law of quadratic reciprocity for the Jacobi symbol $\left(\frac{m}{n}\right)$, where $m, n$ are odd positive integers, and prove this law using the reciprocity law for the Legendre symbol.

  Compute the Jacobi symbol $\left(\frac{261}{317}\right)$.

  comment

• Paper 3, Section I, G

  Number Theory | Part II, 2009

  For any integer $x \geqslant 2$, define $\theta(x)=\sum_{p \leqslant x} \log p$, where the sum is taken over all primes $p \leqslant x$. Put $\theta(1)=0$. By studying the integer

  $$\left(\begin{array}{c} 2 n \\ n \end{array}\right)$$

  where $n \geqslant 1$ is an integer, prove that

  $$\theta(2 n)-\theta(n)<2 n \log 2$$

  Deduce that

  $$\theta(x)<(4 \log 2) x$$

  for all $x \geqslant 1$.

  comment

• Paper 3, Section II, G

  Number Theory | Part II, 2009

  Let $p$ be an odd prime. Prove that there is an equal number of quadratic residues and non-residues in the set $\{1, \ldots, p-1\}$.

  If $n$ is an integer prime to $p$, let $m_{n}$ be an integer such that $n m_{n} \equiv 1 \bmod p$. Prove that

  $$n(n+1) \equiv n^{2}\left(1+m_{n}\right) \bmod p$$

  and deduce that

  $$\sum_{n=1}^{p-1}\left(\frac{n(n+1)}{p}\right)=-1$$

  comment

• Paper 4, Section I, G

  Number Theory | Part II, 2009

  Let $W$ denote the set of all positive definite binary quadratic forms, with integer coefficients, and having discriminant $-67$. Let $S L_{2}(\mathbb{Z})$ be the group of all $2 \times 2$ matrices with integer entries and determinant 1. Prove that $W$ is infinite, but that all elements of $W$ are equivalent under the action of the group $S L_{2}(\mathbb{Z})$

  comment

• Paper 4, Section II, G

  Number Theory | Part II, 2009

  Let $s=\sigma+i t$, where $\sigma$ and $t$ are real, and for $\sigma>1$ let

  $$\zeta(s)=\sum_{n=1}^{\infty} \frac{1}{n^{s}}$$

  Prove that $\zeta(s)$ has no zeros in the half plane $\sigma>1$. Show also that for $\sigma>1$,

  $$\frac{1}{\zeta(s)}=\sum_{n=1}^{\infty} \frac{\mu(n)}{n^{s}}$$

  where $\mu$ denotes the Möbius function. Assuming that $\zeta(s)-\frac{1}{s-1}$ has an analytic continuation to the half plane $\sigma>0$, show that if $s=1+i t$, with $t \neq 0$, and $\zeta(s)=0$ then $s$ is at most a simple zero of $\zeta$.

  comment

Numerical Analysis

• Paper 1, Section II, B

  Numerical Analysis | Part II, 2009

  (i) Define the Jacobi method with relaxation for solving the linear system $A \boldsymbol{x}=\boldsymbol{b}$.

  (ii) For $\boldsymbol{x}^{*}$ and $\boldsymbol{x}^{(\nu)}$ being the exact and the iterated solution, respectively, let $e^{(\nu)}:=\boldsymbol{x}^{(\nu)}-\boldsymbol{x}^{*}$ be the error and $H_{\omega}$ the iteration matrix, so that

  $$e^{(\nu+1)}=H_{\omega} e^{(\nu)}$$

  Express $H_{\omega}$ in terms of the matrix $A$, its diagonal part $D$ and the relaxation parameter $\omega$, and find the eigenvectors $\boldsymbol{v}_{k}$ and the eigenvalues $\lambda_{k}(\omega)$ of $H_{\omega}$ for the $n \times n$ tridiagonal matrix

  $$A=\left[\begin{array}{rrrrr} 2 & -1 & & & \\ -1 & 2 & -1 & & \\ & \ddots & \ddots & \ddots & \\ & & -1 & 2 & -1 \\ & & & -1 & 2 \end{array}\right]$$

  [Hint: The eigenvectors and eigenvalues of $A$ are

  $$\left.\left(\boldsymbol{u}_{k}\right)_{i}=\sin \frac{k i \pi}{n+1}, \quad i=1, \ldots, n, \quad \lambda_{k}(A)=4 \sin ^{2} \frac{k \pi}{2(n+1)}, \quad k=1, \ldots, n .\right]$$

  (iii) For $A$ as above, let

  $$\boldsymbol{e}^{(\nu)}=\sum_{k=1}^{n} a_{k}^{(\nu)} \boldsymbol{v}_{k}$$

  be the expansion of the error with respect to the eigenvectors $\left(\boldsymbol{v}_{k}\right)$ of $H_{\omega}$.

  Find the range of parameter $\omega$ which provides convergence of the method for any $n$, and prove that, for any such $\omega$, the rate of convergence $e^{(\nu)} \rightarrow 0$ is not faster than $\left(1-c / n^{2}\right)^{\nu}$.

  (iv) Show that, for some $\omega$, the high frequency components $\left(\frac{n+1}{2} \leqslant k \leqslant n\right)$ of the error $e^{(\nu)}$ tend to zero much faster. Determine the optimal parameter $\omega_{*}$ which provides the largest suppression of the high frequency components per iteration, and find the corresponding attenuation factor $\mu_{*}$ (i.e. the least $\mu_{\omega}$ such that $\left|a_{k}^{(\nu+1)}\right| \leqslant \mu_{\omega}\left|a_{k}^{(\nu)}\right|$ for $\left.\frac{n+1}{2} \leqslant k \leqslant n\right)$.

  comment

• Paper 2, Section II, B

  Numerical Analysis | Part II, 2009

  The Poisson equation $\nabla^{2} u=f$ in the unit square $\Omega=[0,1] \times[0,1]$, equipped with appropriate boundary conditions on $\partial \Omega$, is discretized with the nine-point formula:

  $$\begin{aligned} \Gamma_{9}\left[u_{m, n}\right] &:=-\frac{10}{3} u_{m, n}+\frac{2}{3}\left(u_{m+1, n}+u_{m-1, n}+u_{m, n+1}+u_{m, n-1}\right) \\ &+\frac{1}{6}\left(u_{m+1, n+1}+u_{m+1, n-1}+u_{m-1, n+1}+u_{m-1, n-1}\right)=h^{2} f_{m, n} \end{aligned}$$

  where $1 \leqslant m, n \leqslant M, u_{m, n} \approx u(m h, n h)$, and $(m h, n h)$ are grid points.

  (i) Find the local error of approximation.

  (ii) Prove that the error is smaller if $f$ happens to satisfy the Laplace equation $\nabla^{2} f=0 .$

  (iii) Hence show that the modified nine-point scheme

  $$\begin{aligned} \Gamma_{9}\left[u_{m, n}\right] &=h^{2} f_{m, n}+\frac{1}{12} h^{2} \Gamma_{5}\left[f_{m, n}\right] \\ &:=h^{2} f_{m, n}+\frac{1}{12} h^{2}\left(f_{m+1, n}+f_{m-1, n}+f_{m, n+1}+f_{m, n-1}-4 f_{m, n}\right) \end{aligned}$$

  has the same smaller error as in (ii).

  [Hint. The nine-point discretization of $\nabla^{2} u$ can be written as

  $$\Gamma_{9}[u]=\left(\Gamma_{5}+\frac{1}{6} \Delta_{x}^{2} \Delta_{y}^{2}\right) u=\left(\Delta_{x}^{2}+\Delta_{y}^{2}+\frac{1}{6} \Delta_{x}^{2} \Delta_{y}^{2}\right) u$$

  where $\Gamma_{5}[u]=\left(\Delta_{x}^{2}+\Delta_{y}^{2}\right) u$ is the five-point discretization and

  $$\begin{aligned} &\Delta_{x}^{2} u(x, y):=u(x-h, y)-2 u(x, y)+u(x+h, y) \\ &\Delta_{y}^{2} u(x, y):=u(x, y-h)-2 u(x, y)+u(x, y+h) \end{aligned}$$

  comment

• Paper 3, Section II, B

  Numerical Analysis | Part II, 2009

  Prove that all Toeplitz tridiagonal $M \times M$ matrices $A$ of the form

  $$A=\left[\begin{array}{rrrrr} a & b & & & \\ -b & a & b & & \\ & \ddots & \ddots & \ddots & \\ & & -b & a & b \\ & & & -b & a \end{array}\right]$$

  share the same eigenvectors $\left(\boldsymbol{v}^{(k)}\right)_{k=1}^{M}$, with the components $\boldsymbol{v}_{m}^{(k)}=i^{m} \sin \frac{k m \pi}{M+1}, m=$ $1, \ldots, M$, where $i=\sqrt{-1}$, and find their eigenvalues.

  The advection equation

  $$\frac{\partial u}{\partial t}=\frac{\partial u}{\partial x}, \quad 0 \leqslant x \leqslant 1, \quad 0 \leqslant t \leqslant T,$$

  is approximated by the Crank-Nicolson scheme

  $$u_{m}^{n+1}-u_{m}^{n}=\frac{1}{4} \mu\left(u_{m+1}^{n+1}-u_{m-1}^{n+1}\right)+\frac{1}{4} \mu\left(u_{m+1}^{n}-u_{m-1}^{n}\right)$$

  where $\mu=\frac{\Delta t}{(\Delta x)^{2}}, \Delta x=\frac{1}{M+1}$, and $u_{m}^{n}$ is an approximation to $u(m \Delta x, n \Delta t)$. Assuming that $u(0, t)=u(1, t)=0$, show that the above scheme can be written in the form

  $$B \boldsymbol{u}^{n+1}=C \boldsymbol{u}^{n}, \quad 0 \leqslant n \leqslant T / \Delta t-1$$

  where $\boldsymbol{u}^{n}=\left[u_{1}^{n}, \ldots, u_{M}^{n}\right]^{T}$ and the real matrices $B$ and $C$ should be found. Using matrix analysis, find the range of $\mu$ for which the scheme is stable. [Fourier analysis is not acceptable.]

  comment

• Paper 4, Section II, B

  Numerical Analysis | Part II, 2009

  (a) For the $s$-step $s$-order Backward Differentiation Formula (BDF) for ordinary differential equations,

  $$\sum_{m=0}^{s} a_{m} y_{n+m}=h f_{n+s}$$

  express the polynomial $\rho(w)=\sum_{m=0}^{s} a_{m} w^{m}$ in a convenient explicit form.

  (b) Prove that the interval $(-\infty, 0)$ belongs to the linear stability domain of the 2-step BDF method.

  comment

Optimization and Control

• Paper 2, Section II, I

  Optimization and Control | Part II, 2009

  In the context of stochastic dynamic programming, explain what is meant by an average-reward optimal policy.

  A player has a fair coin and a six-sided die. At each epoch he may choose either to toss the coin or to roll the die. If he tosses the coin and it shows heads then he adds 1 to his total score, and if it shows tails then he adds 0 . If he rolls the die then he adds the number showing. He wins a reward of $£ 1$ whenever his total score is divisible by 3 .

  Suppose the player always tosses the coin. Find his average reward per toss.

  Still using the above policy, and given that he starts with a total score of $x$, let $F_{s}(x)$ be the expected total reward over the next $s$ epochs. Find the value of

  $$\lim _{s \rightarrow \infty}\left[F_{s}(x)-F_{s}(0)\right] .$$

  Use the policy improvement algorithm to find a policy that produces a greater average reward than the policy of only tossing the coin.

  Find the average-reward optimal policy.

  comment

• Paper 3, Section II, I

  Optimization and Control | Part II, 2009

  Two scalar systems have dynamics

  $$x_{t+1}=x_{t}+u_{t}+\epsilon_{t}, \quad y_{t+1}=y_{t}+w_{t}+\eta_{t},$$

  where $\left\{\epsilon_{t}\right\}$ and $\left\{\eta_{t}\right\}$ are independent sequences of independent and identically distributed random variables of mean 0 and variance 1 . Let

  $$F(x)=\inf _{\pi} \mathbb{E}\left[\sum_{t=0}^{\infty}\left(x_{t}^{2}+u_{t}^{2}\right)(2 / 3)^{t} \mid x_{0}=x\right]$$

  where $\pi$ is a policy in which $u_{t}$ depends on only $x_{0}, \ldots, x_{t}$.

  Show that $G(x)=P x^{2}+d$ is a solution to the optimality equation satisfied by $F(x)$, for some $P$ and $d$ which you should find.

  Find the optimal controls.

  State a theorem that justifies $F(x)=G(x)$.

  For each of the two cases (a) $\lambda=0$ and (b) $\lambda=1$, find controls $\left\{u_{t}, w_{t}\right\}$ which minimize

  $$\mathbb{E}\left[\sum_{t=0}^{\infty}\left(x_{t}^{2}+2 \lambda x_{t} y_{t}+y_{t}^{2}+u_{t}^{2}+w_{t}^{2}\right)(2 / 3+\lambda / 12)^{t} \mid x_{0}=x, y_{0}=y\right]$$

  comment

• Paper 4, Section II, I

  Optimization and Control | Part II, 2009

  Explain how transversality conditions can be helpful when employing Pontryagin's Maximum Principle to solve an optimal control problem.

  A particle in $\mathbb{R}^{2}$ starts at $(0,0.5)$ and follows the dynamics

  $$\dot{x}=u \sqrt{|y|}, \quad \dot{y}=v \sqrt{|y|}, \quad t \in[0, T],$$

  where controls $u(t)$ and $v(t)$ are to be chosen subject to $u^{2}(t)+v^{2}(t)=1$.

  Using Pontryagin's maximum principle do the following:

  (a) Find controls that minimize $-y(1)$;

  (b) Suppose we wish to choose $T$ and the controls $u, v$ to minimize $-y(T)+T$ under a constraint $(x(T), y(T))=(1,1)$. By expressing both $d y / d x$ and $d^{2} y / d x^{2}$ in terms of the adjoint variables, show that on an optimal trajectory,

  $$1+\left(\frac{d y}{d x}\right)^{2}+2 y \frac{d^{2} y}{d x^{2}}=0$$

  comment

Partial Differential Equations

• Paper 1, Section II, B

  Partial Differential Equations | Part II, 2009

  Consider the initial value problem for the so-called Liouville equation

  $$\begin{gathered} f_{t}+v \cdot \nabla_{x} f-\nabla V(x) \cdot \nabla_{v} f=0,(x, v) \in \mathbb{R}^{2 d}, t \in \mathbb{R} \\ f(x, v, t=0)=f_{I}(x, v) \end{gathered}$$

  for the function $f=f(x, v, t)$ on $\mathbb{R}^{2 d} \times \mathbb{R}$. Assume that $V=V(x)$ is a given function with $V, \nabla_{x} V$ Lipschitz continuous on $\mathbb{R}^{d}$.

  (i) Let $f_{I}(x, v)=\delta\left(x-x_{0}, v-v_{0}\right)$, for $x_{0}, v_{0} \in \mathbb{R}^{d}$ given. Show that a solution $f$ is given by

  $$f(x, v, t)=\delta\left(x-\hat{x}\left(t, x_{0}, v_{0}\right), v-\hat{v}\left(t, x_{0}, v_{0}\right)\right)$$

  where $(\hat{x}, \hat{v})$ solve the Newtonian system

  $$\begin{array}{ll} \dot{\hat{x}}=\hat{v}, & \hat{x}(t=0)=x_{0} \\ \dot{\hat{v}}=-\nabla V(\hat{x}), & \hat{v}(t=0)=v_{0} \end{array}$$

  (ii) Let $f_{I} \in L_{l o c}^{1}\left(\mathbb{R}^{2 d}\right), f_{I} \geqslant 0$. Prove (by using characteristics) that $f$ remains nonnegative (as long as it exists).

  (iii) Let $f_{I} \in L^{p}\left(\mathbb{R}^{2 d}\right), f_{I} \geqslant 0$ on $\mathbb{R}^{2 d}$. Show (by a formal argument) that

  $$\|f(\cdot, \cdot, t)\|_{L^{p}\left(\mathbb{R}^{2 d}\right)}=\left\|f_{I}\right\|_{L^{p}\left(\mathbb{R}^{2 d}\right)}$$

  for all $t \in \mathbb{R}, 1 \leqslant p<\infty$.

  (iv) Let $V(x)=\frac{1}{2}|x|^{2}$. Use the method of characteristics to solve the initial value problem for general initial data.

  comment

• Paper 2, Section II, B

  Partial Differential Equations | Part II, 2009

  (a) Solve the initial value problem for the Burgers equation

  $$\begin{gathered} u_{t}+\frac{1}{2}\left(u^{2}\right)_{x}=0, \quad x \in \mathbb{R}, t>0 \\ u(x, t=0)=u_{I}(x) \end{gathered}$$

  where

  $$u_{I}(x)= \begin{cases}1, & x<0 \\ 1-x, & 0<x<1 \\ 0, & x>1\end{cases}$$

  Use the method of characteristics. What is the maximal time interval in which this (weak) solution is well defined? What is the regularity of this solution?

  (b) Apply the method of characteristics to the Burgers equation subject to the initial condition

  $$u_{I}(x)= \begin{cases}1, & x>0 \\ 0, & x<0\end{cases}$$

  In $\{(x, t) \mid 0<x<t\}$ use the ansatz $u(x, t)=f\left(\frac{x}{t}\right)$ and determine $f$.

  (c) Using the method of characteristics show that the initial value problem for the Burgers equation has a classical solution defined for all $t>0$ if $u_{I}$ is continuously differentiable and

  $$\frac{d u_{I}}{d x}(x)>0$$

  for all $x \in \mathbb{R}$.

  comment

• Paper 3, Section II, B

  Partial Differential Equations | Part II, 2009

  (a) Consider the nonlinear elliptic problem

  $$\begin{cases}\Delta u=f(u, x), & x \in \Omega \subseteq \mathbb{R}^{d} \\ u=u_{D}, & x \in \partial \Omega\end{cases}$$

  Let $\frac{\partial f}{\partial u}(y, x) \geqslant 0$ for all $y \in \mathbb{R}, x \in \Omega$. Prove that there exists at most one classical solution.

  [Hint: Use the weak maximum principle.]

  (b) Let $\varphi \in \mathcal{C}_{0}^{\infty}\left(\mathbb{R}^{n}\right)$ be a radial function. Prove that the Fourier transform of $\varphi$ is radial too.

  (c) Let $\varphi \in \mathcal{C}_{0}^{\infty}\left(\mathbb{R}^{n}\right)$ be a radial function. Solve

  $$-\Delta u+u=\varphi(x), \quad x \in \mathbb{R}^{n}$$

  by Fourier transformation and prove that $u$ is a radial function.

  (d) State the Lax-Milgram lemma and explain its use in proving the existence and uniqueness of a weak solution of

  $$\begin{gathered} -\Delta u+a(x) u=f(x), x \in \Omega \\ u=0 \text { on } \partial \Omega \end{gathered}$$

  where $\Omega \subseteq \mathbb{R}^{d}$ bounded, $0 \leqslant \underline{a} \leqslant a(x) \leqslant \bar{a}<\infty$ for all $x \in \Omega$ and $f \in L^{2}(\Omega)$.

  comment

• Paper 4, Section II, B

  Partial Differential Equations | Part II, 2009

  Consider the two-dimensional domain

  $$G=\left\{(x, y) \mid R_{1}^{2}<x^{2}+y^{2}<R_{2}^{2}\right\}$$

  where $0<R_{1}<R_{2}<\infty$. Solve the Dirichlet boundary value problem for the Laplace equation

  $$\begin{gathered} \Delta u=0 \text { in } G, \\ u=u_{1}(\varphi), r=R_{1}, \\ u=u_{2}(\varphi), r=R_{2}, \end{gathered}$$

  where $(r, \varphi)$ are polar coordinates. Assume that $u_{1}, u_{2}$ are $2 \pi$-periodic functions on the real line and $u_{1}, u_{2} \in L_{l o c}^{2}(\mathbb{R})$.

  [Hint: Use separation of variables in polar coordinates, $u=R(r) \Phi(\varphi)$, with periodic boundary conditions for the function $\Phi$ of the angle variable. Use an ansatz of the form $R(r)=r^{\alpha}$ for the radial function.]

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, C

  Principles of Quantum Mechanics | Part II, 2009

  The position and momentum for a harmonic oscillator can be written

  $$\hat{x}=\left(\frac{\hbar}{2 m \omega}\right)^{1 / 2}\left(a+a^{\dagger}\right), \quad \hat{p}=\left(\frac{\hbar m \omega}{2}\right)^{1 / 2} i\left(a^{\dagger}-a\right)$$

  where $m$ is the mass, $\omega$ is the frequency, and the Hamiltonian is

  $$H=\frac{1}{2 m} \hat{p}^{2}+\frac{1}{2} m \omega^{2} \hat{x}^{2}=\hbar \omega\left(a^{\dagger} a+\frac{1}{2}\right)$$

  Starting from the commutation relations for $a$ and $a^{\dagger}$, determine the energy levels of the oscillator. Assuming a unique ground state, explain how all other energy eigenstates can be constructed from it.

  Consider a modified Hamiltonian

  $$H^{\prime}=H+\lambda \hbar \omega\left(a^{2}+a^{\dagger 2}\right)$$

  where $\lambda$ is a dimensionless parameter. Calculate the modified energy levels to second order in $\lambda$, quoting any standard formulas which you require. Show that the modified Hamiltonian can be written as

  $$H^{\prime}=\frac{1}{2 m} \alpha \hat{p}^{2}+\frac{1}{2} m \omega^{2} \beta \hat{x}^{2}$$

  where $\alpha$ and $\beta$ depend on $\lambda$. Hence find the modified energies exactly, assuming $|\lambda|<\frac{1}{2}$, and show that the results are compatible with those obtained from perturbation theory.

  comment

• Paper 2, Section II, C

  Principles of Quantum Mechanics | Part II, 2009

  Let $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)$ be a set of Hermitian operators obeying

  $$\left[\sigma_{i}, \sigma_{j}\right]=2 i \epsilon_{i j k} \sigma_{k} \quad \text { and } \quad(\mathbf{n} \cdot \boldsymbol{\sigma})^{2}=1$$

  where $\mathbf{n}$ is any unit vector. Show that $(*)$ implies

  $$(\mathbf{a} \cdot \boldsymbol{\sigma})(\mathbf{b} \cdot \boldsymbol{\sigma})=\mathbf{a} \cdot \mathbf{b}+i(\mathbf{a} \times \mathbf{b}) \cdot \boldsymbol{\sigma}$$

  for any vectors a and b. Explain, with reference to the properties $(*)$, how $\boldsymbol{\sigma}$ can be related to the intrinsic angular momentum $\mathbf{S}$ for a particle of spin $\frac{1}{2}$.

  Show that the operators $P_{\pm}=\frac{1}{2}(1 \pm \mathbf{n} \cdot \boldsymbol{\sigma})$ are Hermitian and obey

  $$P_{\pm}^{2}=P_{\pm}, \quad P_{+} P_{-}=P_{-} P_{+}=0$$

  Show also how $P_{\pm}$can be used to write any state $|\chi\rangle$ as a linear combination of eigenstates of $\mathbf{n} \cdot \boldsymbol{\sigma}$. Use this to deduce that if the system is in a normalised state $|\chi\rangle$ when $\mathbf{n} \cdot \boldsymbol{\sigma}$ is measured, then the results $\pm 1$ will be obtained with probabilities

  $$\| P_{\pm}|\chi\rangle \|^{2}=\frac{1}{2}(1 \pm\langle\chi|\mathbf{n} \cdot \boldsymbol{\sigma}| \chi\rangle)$$

  If $|\chi\rangle$ is a state corresponding to the system having spin up along a direction defined by a unit vector $\mathbf{m}$, show that a measurement will find the system to have spin up along $\mathbf{n}$ with probability $\frac{1}{2}(1+\mathbf{n} \cdot \mathbf{m})$.

  comment

• Paper 3, Section II, C

  Principles of Quantum Mechanics | Part II, 2009

  (i) Consider two quantum systems with angular momentum states $|j m\rangle$ and $|1 q\rangle$. The eigenstates corresponding to their combined angular momentum can be written as

  $$|J M\rangle=\sum_{q m} C_{q m}^{J M}|1 q\rangle|j m\rangle,$$

  where $C_{q m}^{J M}$ are Clebsch-Gordan coefficients for addition of angular momenta one and $j$. What are the possible values of $J$ and how must $q, m$ and $M$ be related for $C_{q m}^{J} M \neq 0$ ?

  Construct all states $|J M\rangle$ in terms of product states in the case $j=\frac{1}{2}$.

  (ii) A general stationary state for an electron in a hydrogen atom $|n \ell m\rangle$ is specified by the principal quantum number $n$ in addition to the labels $\ell$ and $m$ corresponding to the total orbital angular momentum and its component in the 3-direction (electron spin is ignored). An oscillating electromagnetic field can induce a transition to a new state $\left|n^{\prime} \ell^{\prime} m^{\prime}\right\rangle$ and, in a suitable approximation, the amplitude for this to occur is proportional to

  $$\left\langle n^{\prime} \ell^{\prime} m^{\prime}\left|\hat{x}_{i}\right| n \ell m\right\rangle,$$

  where $\hat{x}_{i}(i=1,2,3)$ are components of the electron's position. Give clear but concise arguments based on angular momentum which lead to conditions on $\ell, m, \ell^{\prime}, m^{\prime}$ and $i$ for the amplitude to be non-zero.

  Explain briefly how parity can be used to obtain an additional selection rule.

  [Standard angular momentum states $|j m\rangle$ are joint eigenstates of $\mathbf{J}^{2}$ and $J_{3}$, obeying

  $$J_{\pm}|j m\rangle=\sqrt{(j \mp m)(j \pm m+1)}|j m \pm 1\rangle, \quad J_{3}|j m\rangle=m|j m\rangle .$$

  You may also assume that $X_{\pm 1}=\frac{1}{\sqrt{2}}\left(\mp \hat{x}_{1}-i \hat{x}_{2}\right)$ and $X_{0}=\hat{x}_{3}$ have commutation relations with orbital angular momentum $\mathbf{L}$ given by

  $$\left[L_{3}, X_{q}\right]=q X_{q}, \quad\left[L_{\pm}, X_{q}\right]=\sqrt{(1 \mp q)(2 \pm q)} X_{q \pm 1}$$

  Units in which $\hbar=1$ are to be used throughout. ]

  comment

• Paper 4, Section II, C

  Principles of Quantum Mechanics | Part II, 2009

  For any given operators $A$ and $B$, show that $F(\lambda)=e^{\lambda A} B e^{-\lambda A}$ has derivative $F^{\prime}(\lambda)=e^{\lambda A}[A, B] e^{-\lambda A}$ and deduce an analogous formula for the $n$th derivative. Hence, by considering $F(\lambda)$ as a power series in $\lambda$, show that

  $$e^{A} B e^{-A}=B+[A, B]+\frac{1}{2 !}[A,[A, B]]+\ldots+\frac{1}{n !}[A,[A, \ldots[A, B] \ldots]]+\ldots$$

  A particle of unit mass in one dimension has position $\hat{x}$ and momentum $\hat{p}$ in the Schrödinger picture, and Hamiltonian

  $$H=\frac{1}{2} \hat{p}^{2}-\alpha \hat{x},$$

  where $\alpha$ is a constant. Apply $(*)$ to find the Heisenberg picture operators $\hat{x}(t)$ and $\hat{p}(t)$ in terms of $\hat{x}$ and $\hat{p}$, and check explicitly that $H(\hat{x}(t), \hat{p}(t))=H(\hat{x}, \hat{p})$.

  A particle of unit mass in two dimensions has position $\hat{x}_{i}$ and momentum $\hat{p}_{i}$ in the Schrödinger picture, and Hamiltonian

  $$H=\frac{1}{2}\left(\hat{p}_{1}^{2}+\hat{p}_{2}^{2}\right)-\beta\left(\hat{x}_{1} \hat{p}_{2}-\hat{x}_{2} \hat{p}_{1}\right)$$

  where $\beta$ is a constant. Calculate the Heisenberg picture momentum components $\hat{p}_{i}(t)$ in terms of $\hat{p}_{i}$ and verify that $\hat{p}_{1}(t)^{2}+\hat{p}_{2}(t)^{2}$ is independent of time. Now consider the interaction picture corresponding to $H=H_{0}+V$ : show that if $H_{0}=\frac{1}{2}\left(\hat{p}_{1}^{2}+\hat{p}_{2}^{2}\right)$ then the interaction picture position operators are $\hat{x}_{i}+t \hat{p}_{i}$, and use this to find the Heisenberg picture position operators $\hat{x}_{i}(t)$ in terms of $\hat{x}_{i}$ and $\hat{p}_{i}$.

  [Hint: If $\left[H_{0}, V\right]=0$ and $\bar{Q}(t)$ is an operator in the interaction picture, then the corresponding operator in the Heisenberg picture is $\left.Q(t)=e^{i t V / \hbar} \bar{Q}(t) e^{-i t V / \hbar} \cdot\right]$

  comment

Principles of Statistics

• Paper 1, Section II, I

  Principles of Statistics | Part II, 2009

  (i) Let $X_{1}, \ldots, X_{n}$ be independent and identically distributed random variables, having the exponential distribution $\mathcal{E}(\lambda)$ with density $p(x \mid \lambda)=\lambda \exp (-\lambda x)$ for $x, \lambda>0$. Show that $T_{n}=\sum_{i=1}^{n} X_{i}$ is minimal sufficient and complete for $\lambda$.

  [You may assume uniqueness of Laplace transforms.]

  (ii) For given $x>0$, it is desired to estimate the quantity $\phi=\operatorname{Prob}\left(X_{1}>x \mid \lambda\right)$. Compute the Fisher information for $\phi$.

  (iii) State the Lehmann-Scheffé theorem. Show that the estimator $\tilde{\phi}_{n}$ of $\phi$ defined by

  $$\tilde{\phi}_{n}= \begin{cases}0, & \text { if } T_{n}<x, \\ \left(1-\frac{x}{T_{n}}\right)^{n-1}, & \text { if } T_{n} \geqslant x\end{cases}$$

  is the minimum variance unbiased estimator of $\phi$ based on $\left(X_{1}, \ldots, X_{n}\right)$. Without doing any computations, state whether or not the variance of $\tilde{\phi}_{n}$ achieves the Cramér-Rao lower bound, justifying your answer briefly.

  Let $k \leqslant n$. Show that $\mathbb{E}\left(\tilde{\phi}_{k} \mid T_{n}, \lambda\right)=\tilde{\phi}_{n}$.

  comment

• Paper 2, Section II, I

  Principles of Statistics | Part II, 2009

  Suppose that the random vector $\mathbf{X}=\left(X_{1}, \ldots, X_{n}\right)$ has a distribution over $\mathbb{R}^{n}$ depending on a real parameter $\theta$, with everywhere positive density function $p(\mathbf{x} \mid \theta)$. Define the maximum likelihood estimator $\hat{\theta}$, the score variable $U$, the observed information $\hat{j}$ and the expected (Fisher) information $I$ for the problem of estimating $\theta$ from $\mathbf{X}$.

  For the case where the $\left(X_{i}\right)$ are independent and identically distributed, show that, as $n \rightarrow \infty, I^{-1 / 2} U \stackrel{d}{\rightarrow} \mathcal{N}(0,1)$. [You may assume sufficient conditions to allow interchange of integration over the sample space and differentiation with respect to the parameter.] State the asymptotic distribution of $\hat{\theta}$.

  The random vector $\mathbf{X}=\left(X_{1}, \ldots, X_{n}\right)$ is generated according to the rule

  $$X_{i+1}=\theta X_{i}+E_{i}$$

  where $X_{0}=1$ and the $\left(E_{i}\right)$ are independent and identically distributed from the standard normal distribution $\mathcal{N}(0,1)$. Write down the likelihood function for $\theta$ based on data $\mathbf{x}=\left(x_{1}, \ldots, x_{n}\right)$, find $\hat{\theta}$ and $\hat{j}$ and show that the pair $(\hat{\theta}, \hat{j})$ forms a minimal sufficient statistic.

  A Bayesian uses the improper prior density $\pi(\theta) \propto 1$. Show that, in the posterior, $S(\theta-\hat{\theta})$ (where $S$ is a statistic that you should identify) has the same distribution as $E_{1}$.

  comment

• Paper 3, Section II, I

  Principles of Statistics | Part II, 2009

  What is meant by an equaliser decision rule? What is meant by an extended Bayes rule? Show that a decision rule that is both an equaliser rule and extended Bayes is minimax.

  Let $X_{1}, \ldots, X_{n}$ be independent and identically distributed random variables with the normal distribution $\mathcal{N}\left(\theta, h^{-1}\right)$, and let $k>0$. It is desired to estimate $\theta$ with loss function $L(\theta, a)=1-\exp \left\{-\frac{1}{2} k(a-\theta)^{2}\right\}$.

  Suppose the prior distribution is $\theta \sim \mathcal{N}\left(m_{0}, h_{0}^{-1}\right)$. Find the Bayes act and the Bayes loss posterior to observing $X_{1}=x_{1}, \ldots, X_{n}=x_{n}$. What is the Bayes risk of the Bayes rule with respect to this prior distribution?

  Show that the rule that estimates $\theta$ by $\bar{X}=n^{-1} \sum_{i=1}^{n} X_{i}$ is minimax.

  comment

• Paper 4, Section II, I

  Principles of Statistics | Part II, 2009

  Consider the double dichotomy, where the loss is 0 for a correct decision and 1 for an incorrect decision. Describe the form of a Bayes decision rule. Assuming the equivalence of normal and extensive form analyses, deduce the Neyman-Pearson lemma.

  For a problem with random variable $X$ and real parameter $\theta$, define monotone likelihood ratio (MLR) and monotone test.

  Suppose the problem has MLR in a real statistic $T=t(X)$. Let $\phi$ be a monotone test, with power function $\gamma(\cdot)$, and let $\phi^{\prime}$ be any other test, with power function $\gamma^{\prime}(\cdot)$. Show that if $\theta_{1}>\theta_{0}$ and $\gamma\left(\theta_{0}\right)>\gamma^{\prime}\left(\theta_{0}\right)$, then $\gamma\left(\theta_{1}\right)>\gamma^{\prime}\left(\theta_{1}\right)$. Deduce that there exists $\theta^{*} \in[-\infty, \infty]$ such that $\gamma(\theta) \leqslant \gamma^{\prime}(\theta)$ for $\theta<\theta^{*}$, and $\gamma(\theta) \geqslant \gamma^{\prime}(\theta)$ for $\theta>\theta^{*}$.

  For an arbitrary prior distribution $\Pi$ with density $\pi(\cdot)$, and an arbitrary value $\theta^{*}$, show that the posterior odds

  $$\frac{\Pi\left(\theta>\theta^{*} \mid X=x\right)}{\Pi\left(\theta \leqslant \theta^{*} \mid X=x\right)}$$

  is a non-decreasing function of $t(x)$.

  comment

Probability and Measure

• Paper 1, Section II, J

  Probability and Measure | Part II, 2009

  Let $(E, \mathcal{E}, \mu)$ be a measure space. Explain what is meant by a simple function on $(E, \mathcal{E}, \mu)$ and state the definition of the integral of a simple function with respect to $\mu$.

  Explain what is meant by an integrable function on $(E, \mathcal{E}, \mu)$ and explain how the integral of such a function is defined.

  State the monotone convergence theorem.

  Show that the following map is linear

  $$f \mapsto \mu(f): L^{1}(E, \mathcal{E}, \mu) \rightarrow \mathbb{R}$$

  where $\mu(f)$ denotes the integral of $f$ with respect to $\mu$.

  [You may assume without proof any fact concerning simple functions and their integrals. You are not expected to prove the monotone convergence theorem.]

  comment

• Paper 2, Section II, J

  Probability and Measure | Part II, 2009

  State Kolmogorov's zero-one law.

  State Birkhoff's almost everywhere ergodic theorem and von Neumann's $L^{p}$-ergodic theorem.

  State the strong law of large numbers for independent and identically distributed integrable random variables, and use the results above to prove it.

  comment

• Paper 3, Section II, J

  Probability and Measure | Part II, 2009

  State and prove the first and second Borel-Cantelli lemmas.

  Let $\left(X_{n}: n \in \mathbb{N}\right)$ be a sequence of independent Cauchy random variables. Thus, each $X_{n}$ is real-valued, with density function

  $$f(x)=\frac{1}{\pi\left(1+x^{2}\right)} .$$

  Show that

  $$\limsup _{n \rightarrow \infty} \frac{\log X_{n}}{\log n}=c, \quad \text { almost surely, }$$

  for some constant $c$, to be determined.

  comment

• Paper 4, Section II, J

  Probability and Measure | Part II, 2009

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space and let $\mathcal{G}$ be a sub- $\sigma$-algebra of $\mathcal{F}$. Show that, for any random variable $X \in L^{2}(\mathbb{P})$, there exists a $\mathcal{G}$-measurable random variable $Y \in L^{2}(\mathbb{P})$ such that $\mathbb{E}((X-Y) Z)=0$ for all $\mathcal{G}$-measurable random variables $Z \in L^{2}(\mathbb{P})$.

  [You may assume without proof the completeness of $L^{2}(\mathbb{P}) .$ ]

  Let $(G, X)$ be a Gaussian random variable in $\mathbb{R}^{2}$, with mean $(\mu, \nu)$ and covariance $\operatorname{matrix}\left(\begin{array}{cc}u & v \\ v & w\end{array}\right)$. Assume that $\mathcal{F}=\sigma(G, X)$ and $\mathcal{G}=\sigma(G)$. Find the random variable $Y$ explicitly in this case.

  comment

Representation Theory

• Paper 1, Section II, F

  Representation Theory | Part II, 2009

  Let $G$ be a finite group, and suppose $G$ acts on the finite sets $X_{1}, X_{2}$. Define the permutation representation $\rho_{X_{1}}$ corresponding to the action of $G$ on $X_{1}$, and compute its character $\pi_{X_{1}}$. State and prove "Burnside's Lemma".

  Let $G$ act on $X_{1} \times X_{2}$ via the usual diagonal action. Prove that the character inner product $\left\langle\pi_{X_{1}}, \pi_{X_{2}}\right\rangle$ is equal to the number of $G$-orbits on $X_{1} \times X_{2}$.

  Hence, or otherwise, show that the general linear group $\mathrm{GL}_{2}(q)$ of invertible $2 \times 2$ matrices over the finite field of $q$ elements has an irreducible complex representation of dimension equal to $q$.

  Let $S_{n}$ be the symmetric group acting on the set $X=\{1,2, \ldots, n\}$. Denote by $Z$ the set of all 2-element subsets $\{i, j\}(i \neq j)$ of elements of $X$, with the natural action of $S_{n}$. If $n \geqslant 4$, decompose $\pi_{Z}$ into irreducible complex representations, and determine the dimension of each irreducible constituent. What can you say when $n=3$ ?

  comment

• Paper 2, Section II, 19F

  Representation Theory | Part II, 2009

  (i) Let $G$ be a finite group. Show that

  (1) If $\chi$ is an irreducible character of $G$ then so is its conjugate $\bar{\chi}$.

  (2) The product of any two characters of $G$ is again a character of $G$.

  (3) If $\chi$ and $\psi$ are irreducible characters of $G$ then

  $$\left\langle\chi \psi, 1_{G}\right\rangle= \begin{cases}1, & \text { if } \chi=\bar{\psi}, \\ 0, & \text { if } \chi \neq \bar{\psi} .\end{cases}$$

  (ii) If $\chi$ is a character of the finite group $G$, define $\chi_{S}$ and $\chi_{A}$. For $g \in G$ prove that

  $$\chi_{S}(g)=\frac{1}{2}\left(\chi^{2}(g)+\chi\left(g^{2}\right)\right) \quad \text { and } \chi_{A}(g)=\frac{1}{2}\left(\chi^{2}(g)-\chi\left(g^{2}\right)\right)$$

  (iii) A certain group of order 24 has precisely seven conjugacy classes with representatives $g_{1}, \ldots, g_{7}$; further, $G$ has a character $\chi$ with values as follows:

  $$\begin{array}{cccccccc} g_{i} & g_{1} & g_{2} & g_{3} & g_{4} & g_{5} & g_{6} & g_{7} \\ \left|C_{G}\left(g_{i}\right)\right| & 24 & 24 & 4 & 6 & 6 & 6 & 6 \\ \chi & 2 & -2 & 0 & -\omega^{2} & -\omega & \omega & \omega^{2} \end{array}$$

  where $\omega=e^{2 \pi i / 3}$.

  It is given that $g_{1}^{2}, g_{2}^{2}, g_{3}^{2}, g_{4}^{2}, g_{5}^{2}, g_{6}^{2}, g_{7}^{2}$ are conjugate to $g_{1}, g_{1}, g_{2}, g_{5}, g_{4}, g_{4}, g_{5}$ respectively.

  Determine $\chi_{S}$ and $\chi_{A}$, and show that both are irreducible.

  comment

• Paper 3, Section II, F

  Representation Theory | Part II, 2009

  Let $G=\mathrm{SU}(2)$. Let $V_{n}$ be the complex vector space of homogeneous polynomials of degree $n$ in two variables $z_{1}, z_{2}$. Define the usual left action of $G$ on $V_{n}$ and denote by $\rho_{n}: G \rightarrow \operatorname{GL}\left(V_{n}\right)$ the representation induced by this action. Describe the character $\chi_{n}$ afforded by $\rho_{n}$.

  Quoting carefully any results you need, show that

  (i) The representation $\rho_{n}$ has dimension $n+1$ and is irreducible for $n \in \mathbb{Z}_{\geqslant 0}$;

  (ii) Every finite-dimensional continuous irreducible representation of $G$ is one of the $\rho_{n}$;

  (iii) $V_{n}$ is isomorphic to its dual $V_{n}^{*}$.

  comment

• Paper 4, Section II, F

  Representation Theory | Part II, 2009

  Let $H \leqslant G$ be finite groups.

  (a) Let $\rho$ be a representation of $G$ affording the character $\chi$. Define the restriction, $\operatorname{Res}_{H}^{G} \rho$ of $\rho$ to $H$.

  Suppose $\chi$ is irreducible and suppose $\operatorname{Res}_{H}^{G} \rho$ affords the character $\chi_{H}$. Let $\psi_{1}, \ldots, \psi_{r}$ be the irreducible characters of $H$. Prove that $\chi_{H}=d_{1} \psi_{1}+\cdots+d_{r} \psi_{r}$, where the nonnegative integers $d_{1}, \ldots, d_{r}$ satisfy the inequality

  $$\sum_{i=1}^{r} d_{i}^{2} \leqslant|G: H|$$

  Prove that there is equality in (1) if and only if $\chi(g)=0$ for all elements $g$ of $G$ which lie outside $H$.

  (b) Let $\psi$ be a class function of $H$. Define the induced class function, $\operatorname{Ind}_{H}^{G} \psi$.

  State the Frobenius reciprocity theorem for class functions and deduce that if $\psi$ is a character of $H$ then $\operatorname{Ind}_{H}^{G} \psi$ is a character of $G$.

  Assuming $\psi$ is a character, identify a $G$-space affording the character $\operatorname{Ind}_{H}^{G} \psi$. Briefly justify your answer.

  (c) Let $\chi_{1}, \ldots, \chi_{k}$ be the irreducible characters of $G$ and let $\psi$ be an irreducible character of $H$. Show that the integers $e_{1}, \ldots, e_{k}$, which are given by $\operatorname{Ind}_{H}^{G}(\psi)=$ $e_{1} \chi_{1}+\cdots+e_{k} \chi_{k}$, satisfy

  $$\sum_{i=1}^{k} e_{i}^{2} \leqslant|G: H|$$

  comment

Riemann Surfaces

• Paper 1, Section II, G

  Riemann Surfaces | Part II, 2009

  (a) Let $X=\mathbb{C} \cup\{\infty\}$ be the Riemann sphere. Define the notion of a rational function $r$ and describe the function $f: X \rightarrow X$ determined by $r$. Assuming that $f$ is holomorphic and non-constant, define the degree of $r$ as a rational function and the degree of $f$ as a holomorphic map, and prove that the two degrees coincide. [You are not required to prove that the degree of $f$ is well-defined.]

  Let $A=\left\{a_{1}, a_{2}, a_{3}\right\}$ and $B=\left\{b_{1}, b_{2}, b_{3}\right\}$ be two subsets of $X$ each containing three distinct elements. Prove that $X \backslash A$ is biholomorphic to $X \backslash B$.

  (b) Let $Z \subset \mathbb{C}^{2}$ be the algebraic curve defined by the vanishing of the polynomial $p(z, w)=w^{2}-z^{3}+z^{2}+z$. Prove that $Z$ is smooth at every point. State the implicit function theorem and define a complex structure on $Z$, so that the maps $g, h: Z \rightarrow \mathbb{C}$ given by $g(z, w)=w, h(z, w)=z$ are holomorphic.

  Define what is meant by a ramification point of a holomorphic map between Riemann surfaces. Give an example of a ramification point of $g$ and calculate the branching order of $g$ at that point.

  comment

• Paper 2, Section II, G

  Riemann Surfaces | Part II, 2009

  (a) Let $\Lambda=\mathbb{Z}+\mathbb{Z} \tau$ be a lattice in $\mathbb{C}$, where the imaginary part of $\tau$ is positive. Define the terms elliptic function with respect to $\Lambda$ and order of an elliptic function.

  Suppose that $f$ is an elliptic function with respect to $\Lambda$ of order $m>0$. Show that the derivative $f^{\prime}$ is also an elliptic function with respect to $\Lambda$ and that its order $n$ satisfies $m+1 \leqslant n \leqslant 2 m$. Give an example of an elliptic function $f$ with $m=5$ and $n=6$, and an example of an elliptic function $f$ with $m=5$ and $n=9$.

  [Basic results about holomorphic maps may be used without proof, provided these are accurately stated.]

  (b) State the monodromy theorem. Using the monodromy theorem, or otherwise, prove that if two tori $\mathbb{C} / \Lambda_{1}$ and $\mathbb{C} / \Lambda_{2}$ are conformally equivalent then the lattices satisfy $\Lambda_{2}=a \Lambda_{1}$, for some $a \in \mathbb{C} \backslash\{0\}$.

  [You may assume that $\mathbb{C}$ is simply connected and every biholomorphic map of $\mathbb{C}$ onto itself is of the form $z \mapsto c z+d$, for some $c, d \in \mathbb{C}, c \neq 0$.]

  comment

• Paper 3, Section II, G

  Riemann Surfaces | Part II, 2009

  (i) Let $f(z)=\sum_{n=1}^{\infty} z^{2^{n}}$. Show that the unit circle is the natural boundary of the function element $(D(0,1), f)$, where $D(0,1)=\{z \in \mathbb{C}:|z|<1\}$.

  (ii) Let $X$ be a connected Riemann surface and $(D, h)$ a function element on $X$ into $\mathbb{C}$. Define a germ of $(D, h)$ at a point $p \in D$. Let $\mathcal{G}$ be the set of all the germs of function elements on $X$ into $\mathbb{C}$. Describe the topology and the complex structure on $\mathcal{G}$, and show that $\mathcal{G}$ is a covering of $X$ (in the sense of complex analysis). Show that there is a oneto-one correspondence between complete holomorphic functions on $X$ into $\mathbb{C}$ and the connected components of $\mathcal{G}$. [You are not required to prove that the topology on $\mathcal{G}$ is secondcountable.]

  comment

Statistical Modelling

• Paper 1, Section I, I

  Statistical Modelling | Part II, 2009

  Consider a binomial generalised linear model for data $y_{1}, \ldots, y_{n}$, modelled as realisations of independent $Y_{i} \sim \operatorname{Bin}\left(1, \mu_{i}\right)$ and $\operatorname{logit} \operatorname{link}$, i.e. $\log \frac{\mu_{i}}{1-\mu_{i}}=\beta x_{i}$, for some known constants $x_{1}, \ldots, x_{n}$, and an unknown parameter $\beta$. Find the log-likelihood for $\beta$, and the likelihood equations that must be solved to find the maximum likelihood estimator $\hat{\beta}$ of $\beta$.

  Compute the first and second derivatives of the log-likelihood for $\beta$, and explain the algorithm you would use to find $\hat{\beta}$.

  comment

• Paper 1, Section II, I

  Statistical Modelling | Part II, 2009

  A three-year study was conducted on the survival status of patients suffering from cancer. The age of the patients at the start of the study was recorded, as well as whether or not the initial tumour was malignant. The data are tabulated in $\mathrm{R}$ as follows:

  $$\begin{array}{rrrrr} > & \text { cancer } & & & \\ & & \text { age malignant } & \text { survive } & \text { die } \\ 1 & <50 & \text { no } & 77 & 10 \\ 2 & <50 & \text { yes } & 51 & 13 \\ 3 & 50-69 & \text { no } & 51 & 11 \\ 4 & 50-69 & \text { yes } & 38 & 20 \\ 5 & 70+ & \text { no } & 7 & 3 \\ 6 & 70+ & \text { yes } & 6 & 3 \end{array}$$

  Describe the model that is being fitted by the following $\mathrm{R}$ commands:

  

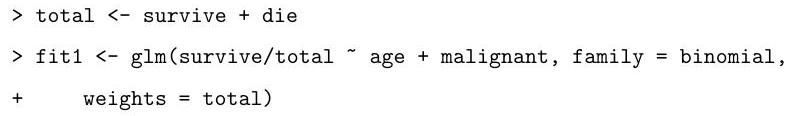
  Explain the (slightly abbreviated) output from the code below, describing how the hypothesis tests are performed and your conclusions based on their results.

  

  Based on the summary above, motivate and describe the following alternative model:

  

  Based on the output of the code that follows, which of the two models do you prefer? Why?

  

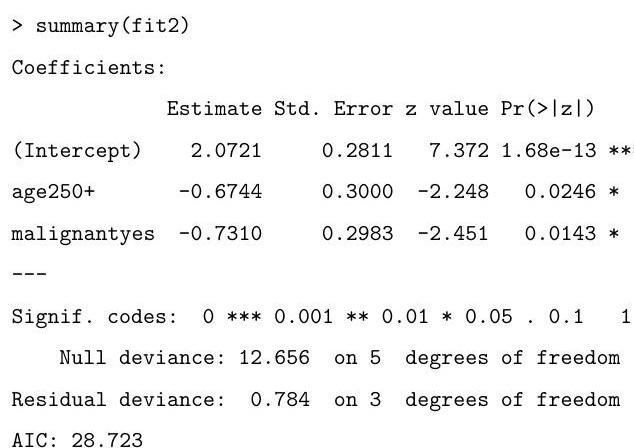
  What is the final value obtained by the following commands?

  

  comment

• Paper 2, Section I, I

  Statistical Modelling | Part II, 2009

  What is meant by an exponential dispersion family? Show that the family of Poisson distributions with parameter $\lambda$ is an exponential dispersion family by explicitly identifying the terms in the definition.

  Find the corresponding variance function and deduce directly from your calculations expressions for $\mathbb{E}(Y)$ and $\operatorname{Var}(Y)$ when $Y \sim \operatorname{Pois}(\lambda)$.

  What is the canonical link function in this case?

  comment

• Paper 3, Section $I$, I

  Statistical Modelling | Part II, 2009

  Consider the linear model $Y=X \beta+\varepsilon$, where $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$ and $X$ is an $n \times p$ matrix of full rank $p<n$. Suppose that the parameter $\beta$ is partitioned into $k$ sets as follows: $\beta^{\top}=\left(\beta_{1}^{\top} \cdots \beta_{k}^{\top}\right)$. What does it mean for a pair of sets $\beta_{i}, \beta_{j}, i \neq j$, to be orthogonal? What does it mean for all $k$ sets to be mutually orthogonal?

  In the model

  $$Y_{i}=\beta_{0}+\beta_{1} x_{i 1}+\beta_{2} x_{i 2}+\varepsilon_{i}$$

  where $\varepsilon_{i} \sim N\left(0, \sigma^{2}\right)$ are independent and identically distributed, find necessary and sufficient conditions on $x_{11}, \ldots, x_{n 1}, x_{12}, \ldots, x_{n 2}$ for $\beta_{0}, \beta_{1}$ and $\beta_{2}$ to be mutually orthogonal.

  If $\beta_{0}, \beta_{1}$ and $\beta_{2}$ are mutually orthogonal, what consequence does this have for the joint distribution of the corresponding maximum likelihood estimators $\hat{\beta}_{0}, \hat{\beta}_{1}$ and $\hat{\beta}_{2}$ ?

  comment

• Paper 4, Section I, $5 I$

  Statistical Modelling | Part II, 2009

  Sulphur dioxide is one of the major air pollutants. A dataset by Sokal and Rohlf (1981) was collected on 41 US cities/regions in 1969-1971. The annual measurements obtained for each region include (average) sulphur dioxide content, temperature, number of manufacturing enterprises employing more than 20 workers, population size in thousands, wind speed, precipitation, and the number of days with precipitation. The data are displayed in $R$ as follows (abbreviated):

  

  Describe the model being fitted by the following $R$ commands.

  $>$ fit $<-\operatorname{lm}(\log (\mathrm{so} 2) \sim$ temp $+$ manuf $+$ pop $+$ wind $+$ precip $+$ days $)$

  Explain the (slightly abbreviated) output below, describing in particular how the hypothesis tests are performed and your conclusions based on their results:

  

  Based on the summary above, suggest an alternative model.

  Finally, what is the value obtained by the following command?

  $>\operatorname{sqrt}\left(\operatorname{sum}\left(\operatorname{resid}(f i t)^{\sim} 2\right) / \mathrm{fit} \$ \mathrm{df}\right)$

  comment

• Paper 4, Section II, I

  Statistical Modelling | Part II, 2009

  Consider the linear model $Y=X \beta+\varepsilon$, where $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$ and $X$ is an $n \times p$ matrix of full rank $p<n$. Find the form of the maximum likelihood estimator $\hat{\beta}$ of $\beta$, and derive its distribution assuming that $\sigma^{2}$ is known.

  Assuming the prior $\pi\left(\beta, \sigma^{2}\right) \propto \sigma^{-2}$ find the joint posterior of $\left(\beta, \sigma^{2}\right)$ up to a normalising constant. Derive the posterior conditional distribution $\pi\left(\beta \mid \sigma^{2}, X, Y\right)$.

  Comment on the distribution of $\hat{\beta}$ found above and the posterior conditional $\pi\left(\beta \mid \sigma^{2}, X, Y\right)$. Comment further on the predictive distribution of $y^{*}$ at input $x^{*}$ under both the maximum likelihood and Bayesian approaches.

  comment

Statistical Physics

• Paper 2, Section II, D

  Statistical Physics | Part II, 2009

  The Van der Waals equation of state for a non-ideal gas is

  $$\left(p+\frac{a N^{2}}{V^{2}}\right)(V-b N)=N k T,$$

  where $a$ and $b$ are constants.

  (i) Briefly explain the physical motivation for differences between the Van der Waals and ideal gas equations of state.

  (ii) Find the volume dependence (at constant temperature) of the internal energy $E$ and the heat capacity $C_{V}$ of a Van der Waals gas.

  (iii) A Van der Waals gas is initially at temperature $T_{1}$ in an insulated container with volume $V_{1}$. A small opening is then made so that the gas can expand freely into an empty container, occupying both the old and new containers. The final result is that the gas now occupies a volume $V_{2}>V_{1}$. Calculate the final temperature $T_{2}$ assuming $C_{V}$ is temperature independent. You may assume the process happens quasistatically.

  comment

• Paper 3, Section II, D

  Statistical Physics | Part II, 2009

  Consider an ideal Bose gas in an external potential such that the resulting density of single particle states is given by

  $$g(\varepsilon)=B \varepsilon^{7 / 2}$$

  where $B$ is a positive constant.

  (i) Derive an expression for the critical temperature for Bose-Einstein condensation of a gas of $N$ of these atoms.

  [Recall

  $$\left.\frac{1}{\Gamma(n)} \int_{0}^{\infty} \frac{x^{n-1} \mathrm{~d} x}{z^{-1} e^{x}-1}=\sum_{\ell=1}^{\infty} \frac{z^{\ell}}{\ell^{n}}\right]$$

  (ii) What is the internal energy $E$ of the gas in the condensed state as a function of $N$ and $T$ ?

  (iii) Now consider the high temperature, classical limit instead. How does the internal energy $E$ depend on $N$ and $T$ ?

  comment

• Paper 4, Section II, D

  Statistical Physics | Part II, 2009

  Briefly state the ergodic hypothesis and explain its importance.

  Consider an ideal, classical, monatomic gas in the presence of a uniform gravitational field in the negative $z$-direction. For convenience, assume the gas is in an arbitrarily large cubic box.

  (i) Compute the internal energy $E$ of the gas.

  (ii) Explain your result for $E$ in relation to the equipartition theorem.

  (iii) What is the probability that an atom is located at a height between $z$ and $z+d z ?$

  (iv) What is the most probable speed of an atom of this gas?

  comment

Stochastic Financial Models

• Paper 1, Section II, J

  Stochastic Financial Models | Part II, 2009

  An investor must decide how to invest his initial wealth $w_{0}$ in $n$ assets for the coming year. At the end of the year, one unit of asset $i$ will be worth $X_{i}, i=1, \ldots, n$, where $X=\left(X_{1}, \ldots, X_{n}\right)^{T}$ has a multivariate normal distribution with mean $\mu$ and non-singular covariance matrix $V$. At the beginning of the year, one unit of asset $i$ costs $p_{i}$. In addition, he may invest in a riskless bank account; an initial investment of 1 in the bank account will have grown to $1+r>1$ at the end of the year.

  (a) The investor chooses to hold $\theta_{i}$ units of asset $i$, with the remaining $\varphi=w_{0}-\theta \cdot p$ in the bank account. His objective is to minimise the variance of his wealth $w_{1}=\varphi(1+r)+\theta \cdot X$ at the end of the year, subject to a required mean value $m$ for $w_{1}$. Derive the optimal portfolio $\theta^{*}$, and the minimised variance.

  (b) Describe the set $A \subseteq \mathbb{R}^{2}$ of achievable pairs $\left(\mathbb{E}\left[w_{1}\right], \operatorname{var}\left(w_{1}\right)\right)$ of mean and variance of the terminal wealth. Explain what is meant by the mean-variance efficient frontier as you do so.

  (c) Suppose that the investor requires expected mean wealth at time 1 to be $m$. He wishes to minimise the expected shortfall $\mathbb{E}\left[\left(w_{1}-(1+r) w_{0}\right)^{-}\right]$subject to this requirement. Show that he will choose a portfolio corresponding to a point on the mean-variance efficient frontier.

  comment

• Paper 2, Section II, J

  Stochastic Financial Models | Part II, 2009

  What is a martingale? What is a stopping time? State and prove the optional sampling theorem.

  Suppose that $\xi_{i}$ are independent random variables with values in $\{-1,1\}$ and common distribution $\mathbb{P}(\xi=1)=p=1-q$. Assume that $p>q$. Let $S_{n}$ be the random walk such that $S_{0}=0, S_{n}=S_{n-1}+\xi_{n}$ for $n \geqslant 1$. For $z \in(0,1)$, determine the set of values of $\theta$ for which the process $M_{n}=\theta^{S_{n}} z^{n}$ is a martingale. Hence derive the probability generating function of the random time

  $$\tau_{k}=\inf \left\{t: S_{t}=k\right\}$$

  where $k$ is a positive integer. Hence find the mean of $\tau_{k}$.

  Let $\tau_{k}^{\prime}=\inf \left\{t>\tau_{k}: S_{t}=k\right\}$. Clearly the mean of $\tau_{k}^{\prime}$ is greater than the mean of $\tau_{k}$; identify the point in your derivation of the mean of $\tau_{k}$ where the argument fails if $\tau_{k}$ is replaced by $\tau_{k}^{\prime}$.

  comment

• Paper 3, Section II, J

  Stochastic Financial Models | Part II, 2009

  What is a Brownian motion? State the assumptions of the Black-Scholes model of an asset price, and derive the time- 0 price of a European call option struck at $K$, and expiring at $T$.

  Find the time- 0 price of a European call option expiring at $T$, but struck at $S_{t}$, where $t \in(0, T)$, and $S_{t}$ is the price of the underlying asset at time $t$.

  comment

• Paper 4, Section II, J

  Stochastic Financial Models | Part II, 2009

  An agent with utility $U(x)=-\exp (-\gamma x)$, where $\gamma>0$ is a constant, may select at time 0 a portfolio of $n$ assets, which he then holds to time 1 . The values $X=\left(X_{1}, \ldots, X_{n}\right)^{T}$ of the assets at time 1 have a multivariate normal distribution with mean $\mu$ and nonsingular covariance matrix $V$. Prove that the agent will prefer portfolio $\psi \in \mathbb{R}^{n}$ to portfolio $\theta \in \mathbb{R}^{n}$ if and only if $q(\psi)>q(\theta)$, where

  $$q(x)=x \cdot \mu-\frac{\gamma}{2} x \cdot V x$$

  Determine his optimal portfolio.

  The agent initially holds portfolio $\theta$, which he may change to portfolio $\theta+z$ at cost $\varepsilon \sum_{i=1}^{n}\left|z_{i}\right|$, where $\varepsilon$ is some positive transaction cost. By considering the function $t \mapsto q(\theta+t z)$ for $0 \leqslant t \leqslant 1$, or otherwise, prove that the agent will have no reason to change his initial portfolio $\theta$ if and only if, for every $i=1, \ldots, n$,

  $$\left|\mu_{i}-\gamma(V \theta)_{i}\right| \leqslant \varepsilon$$

  comment

Topics in Analysis

• Paper 1, Section I, $2 F$

  Topics in Analysis | Part II, 2009

  (i) Let $n \geqslant 1$ and let $x_{1}, \ldots, x_{n}$ be distinct points in $[-1,1]$. Show that there exist numbers $A_{1}, \ldots, A_{n}$ such that

  $$\int_{-1}^{1} P(x) d x=\sum_{j=1}^{n} A_{j} P\left(x_{j}\right)$$

  for every polynomial $P$ of degree $\leqslant n-1$.

  (ii) Explain, without proof, how one can choose the points $x_{1}, \ldots, x_{n}$ and the numbers $A_{1}, \ldots, A_{n}$ such that $(*)$ holds for all polynomials $P$ of degree $\leqslant 2 n-1$.

  comment

• Paper 2, Section I, $2 F$

  Topics in Analysis | Part II, 2009

  (a) State Chebychev's Equal Ripple Criterion.

  (b) Let $n$ be a positive integer, $a_{0}, a_{1}, \ldots, a_{n-1} \in \mathbb{R}$ and

  $$p(x)=x^{n}+a_{n-1} x^{n-1}+\ldots+a_{1} x+a_{0} .$$

  Use Chebychev's Equal Ripple Criterion to prove that

  $$\sup _{x \in[-1,1]}|p(x)| \geqslant 2^{1-n}$$

  [You may use without proof that there is a polynomial $T_{n}(x)$ in $x$ of degree $n$, with the coefficient of $x^{n}$ equal to $2^{n-1}$, such that $T_{n}(\cos \theta)=\cos n \theta$ for all $\theta \in \mathbb{R}$.]

  comment

• Paper 2, Section II, F

  Topics in Analysis | Part II, 2009

  (a) State Brouwer's fixed point theorem in the plane.

  (b) Let $\mathbf{a}, \mathbf{b}, \mathbf{c}$ be unit vectors in $\mathbb{R}^{2}$ making $120^{\circ}$ angles with one another. Let $T$ be the triangle with vertices given by the points $\mathbf{a}, \mathbf{b}$ and $\mathbf{c}$ and let $I, J, K$ be the three sides of $T$. Prove that the following two statements are equivalent:

  (1) There exists no continuous function $f: T \rightarrow \partial T$ with $f(I) \subseteq I, f(J) \subseteq J$ and $f(K) \subseteq K$.

  (2) If $A, B, C$ are closed subsets of $\mathbb{R}^{2}$ such that $T \subseteq A \cup B \cup C, I \subseteq A, J \subseteq B$ and $K \subseteq C$, then $A \cap B \cap C \neq \emptyset$.

  (c) Let $f, g: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be continuous positive functions. Show that the system of equations

  $$\begin{aligned} &\left(1-x^{2}\right) f^{2}(x, y)-x^{2} g^{2}(x, y)=0 \\ &\left(1-y^{2}\right) g^{2}(x, y)-y^{2} f^{2}(x, y)=0 \end{aligned}$$

  has four distinct solutions on the unit circle $\mathbb{S}^{1}=\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2}=1\right\}$.

  comment

• Paper 3, Section I, $2 F$

  Topics in Analysis | Part II, 2009

  (a) If $f:(0,1) \rightarrow \mathbb{R}$ is continuous, prove that there exists a sequence of polynomials $P_{n}$ such that $P_{n} \rightarrow f$ uniformly on compact subsets of $(0,1)$.

  (b) If $f:(0,1) \rightarrow \mathbb{R}$ is continuous and bounded, prove that there exists a sequence of polynomials $Q_{n}$ such that $Q_{n}$ are uniformly bounded on $(0,1)$ and $Q_{n} \rightarrow f$ uniformly on compact subsets of $(0,1)$.

  comment

• Paper 3, Section II, F

  Topics in Analysis | Part II, 2009

  (a) State Runge's theorem on uniform approximation of analytic functions by polynomials.

  (b) Let $\Omega$ be an unbounded, connected, proper open subset of $\mathbb{C}$. For any given compact set $K \subset \mathbb{C} \backslash \Omega$ and any $\zeta \in \Omega$, show that there exists a sequence of complex polynomials converging uniformly on $K$ to the function $f(z)=(z-\zeta)^{-1}$.

  (c) Give an example, with justification, of a connected open subset $\Omega$ of $\mathbb{C}$, a compact subset $K$ of $\mathbb{C} \backslash \Omega$ and a point $\zeta \in \Omega$ such that there is no sequence of complex polynomials converging uniformly on $K$ to the function $f(z)=(z-\zeta)^{-1}$.

  comment

• Paper 4, Section I, $2 F$

  Topics in Analysis | Part II, 2009

  State Liouville's theorem on approximation of algebraic numbers by rationals, and use it to prove that the number

  $$\sum_{n=0}^{\infty} \frac{1}{10^{n !}}$$

  is transcendental.

  comment

Waves

• Paper 1, Section II, 38A

  Waves | Part II, 2009

  The wave equation with spherical symmetry may be written

  $$\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r \tilde{p})-\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}} \tilde{p}=0$$

  Find the solution for the pressure disturbance $\tilde{p}$ in an outgoing wave, driven by a timevarying source with mass outflow rate $q(t)$ at the origin, in an infinite fluid.

  A semi-infinite fluid of density $\rho$ and sound speed $c$ occupies the half space $x>0$. The plane $x=0$ is occupied by a rigid wall, apart from a small square element of side $h$ that is centred on the point $\left(0, y^{\prime}, z^{\prime}\right)$ and oscillates in and out with displacement $f_{0} e^{i \omega t}$. By modelling this element as a point source, show that the pressure field in $x>0$ is given by

  $$\tilde{p}(t, x, y, z)=-\frac{2 \rho \omega^{2} f_{0} h^{2}}{4 \pi R} e^{i \omega\left(t-\frac{R}{c}\right)}$$

  where $R=\left[x^{2}+\left(y-y^{\prime}\right)^{2}+\left(z-z^{\prime}\right)^{2}\right]^{1 / 2}$, on the assumption that $R \gg c / \omega \gg f_{0}, h$. Explain the factor 2 in the above formula.

  Now suppose that the plane $x=0$ is occupied by a loudspeaker whose displacement is given by

  $$x=f(y, z) e^{i \omega t},$$

  where $f(y, z)=0$ for $|y|,|z|>L$. Write down an integral expression for the pressure in $x>0$. In the far field where $r=\left(x^{2}+y^{2}+z^{2}\right)^{1 / 2} \gg L, \omega L^{2} / c, c / \omega$, show that

  $$\tilde{p}(t, x, y, z) \approx-\frac{\rho \omega^{2}}{2 \pi r} e^{i \omega(t-r / c)} \hat{f}(m, n)$$

  where $m=-\frac{\omega y}{r c}, n=-\frac{\omega z}{r c}$ and

  $$\hat{f}(m, n)=\int_{-\infty}^{\infty} \int_{-\infty}^{\infty} f\left(y^{\prime}, z^{\prime}\right) e^{-i\left(m y^{\prime}+n z^{\prime}\right)} d y^{\prime} d z^{\prime}$$

  Evaluate this integral when $f$ is given by

  $$f(y, z)= \begin{cases}1, & -a<y<a,-b<z<b \\ 0, & \text { otherwise }\end{cases}$$

  and discuss the result in the case $\omega b / c$ is small but $\omega a / c$ is of order unity.

  comment

• Paper 2, Section II, A

  Waves | Part II, 2009

  An elastic solid of density $\rho$ has Lamé moduli $\lambda$ and $\mu$. From the dynamic equation for the displacement vector $\mathbf{u}$, derive equations satisfied by the dilatational and shear potentials $\phi$ and $\psi$. Show that two types of plane harmonic wave can propagate in the solid, and explain the relationship between the displacement vector and the propagation direction in each case.

  A semi-infinite solid occupies the half-space $y<0$ and is bounded by a traction-free surface at $y=0$. A plane $P$-wave is incident on the plane $y=0$ with angle of incidence $\theta$. Describe the system of reflected waves, calculate the angles at which they propagate, and show that there is no reflected $P$-wave if

  $$4 \sigma(1-\sigma)^{1 / 2}(\beta-\sigma)^{1 / 2}=(1-2 \sigma)^{2}$$

  where

  $$\sigma=\beta \sin ^{2} \theta \quad \text { and } \quad \beta=\frac{\mu}{\lambda+2 \mu}$$

  comment

• Paper 3, Section II, A

  Waves | Part II, 2009

  Starting from the equations of motion for an inviscid, incompressible, stratified fluid of density $\rho_{0}(z)$, where $z$ is the vertical coordinate, derive the dispersion relation

  $$\omega^{2}=\frac{N^{2}\left(k^{2}+\ell^{2}\right)}{\left(k^{2}+\ell^{2}+m^{2}\right)}$$

  for small amplitude internal waves of wavenumber $(k, \ell, m)$, where $N$ is the constant Brunt-Väisälä frequency (which should be defined), explaining any approximations you make. Describe the wave pattern that would be generated by a small body oscillating about the origin with small amplitude and frequency $\omega$, the fluid being otherwise at rest.

  The body continues to oscillate when the fluid has a slowly-varying velocity $[U(z), 0,0]$, where $U^{\prime}(z)>0$. Show that a ray which has wavenumber $\left(k_{0}, 0, m_{0}\right)$ with $m_{0}<0$ at $z=0$ will propagate upwards, but cannot go higher than $z=z_{c}$, where

  $$U\left(z_{c}\right)-U(0)=N\left(k_{0}^{2}+m_{0}^{2}\right)^{-1 / 2}$$

  Explain what happens to the disturbance as $z$ approaches $z_{c}$.

  comment

• Paper 4, Section II, A

  Waves | Part II, 2009

  A perfect gas occupies a tube that lies parallel to the $x$-axis. The gas is initially at rest, with density $\rho_{1}$, pressure $p_{1}$ and specific heat ratio $\gamma$, and occupies the region $x>0$. For times $t>0$ a piston, initially at $x=0$, is pushed into the gas at a constant speed $V$. A shock wave propagates at constant speed $U$ into the undisturbed gas ahead of the piston. Show that the pressure in the gas next to the piston, $p_{2}$, is given by the expression

  $$V^{2}=\frac{\left(p_{2}-p_{1}\right)^{2}}{\rho_{1}\left(\frac{\gamma+1}{2} p_{2}+\frac{\gamma-1}{2} p_{1}\right)} .$$

  [You may assume that the internal energy per unit mass of perfect gas is given by

  $$E=\frac{1}{\gamma-1} \frac{p}{\rho}$$

  comment