Fluid Dynamics Ii
Fluid Dynamics Ii
Jump to year
Paper 1, Section II, 39A
(a) Write down the Stokes equations for the motion of an incompressible viscous fluid with negligible inertia (in the absence of body forces). What does it mean that Stokes flow is linear and reversible?
(b) The region between two concentric rigid spheres of radii and is filled with fluid of large viscosity . The outer sphere is held stationary, while the inner sphere is made to rotate with angular velocity .
(i) Use symmetry and the properties of Stokes flow to deduce that , where is the pressure due to the flow.
(ii) Verify that both solid-body rotation and satisfy the Stokes equations with . Hence determine the fluid velocity between the spheres.
(iii) Calculate the stress tensor in the flow.
(iv) Deduce that the couple exerted by the fluid in on the fluid in , where , is given by
independent of the value of . [Hint: Do not substitute the form of and in until the end of the calculation.]
Comment on the form of this result for and for .
may use , where is the normal to
Paper 2, Section II, 39A
(a) Incompressible fluid of viscosity fills the thin, slowly varying gap between rigid boundaries at and . The boundary at translates in its own plane with a constant velocity , while the other boundary is stationary. If has typical magnitude and varies on a lengthscale , state conditions for the lubrication approximation to be appropriate.
Write down the lubrication equations for this problem and show that the horizontal volume flux is given by
where is the pressure.
Explain why for some function . Deduce that satisfies the equation
(b) Now consider the case for and for , where and are constants, and are polar coordinates. A uniform pressure gradient is applied at infinity. Show that as , where the constant is to be determined.
Given that , you may assume that the equations of part (a) apply for and , and are subject to conditions that the radial component of the volume flux and the pressure are both continuous across . Show that these continuity conditions imply that
respectively, where []denotes the jump across .
Hence determine and deduce that the total flux through is given by
Paper 3, Section II, 38A
Viscous fluid occupying is bounded by a rigid plane at and is extracted through a small hole at the origin at a constant flow rate . Assume that for sufficiently small values of the velocity is well-approximated by
except within a thin axisymmetric boundary layer near .
(a) Estimate the Reynolds number of the flow as a function of , and thus give an estimate for how small needs to be for such a solution to be applicable. Show that the radial pressure gradient is proportional to .
(b) In cylindrical polar coordinates , the steady axisymmetric boundary-layer equations for the velocity components can be written as
and is the Stokes streamfunction. Verify that the condition of incompressibility is satisfied by the use of .
Use scaling arguments to estimate the thickness of the boundary layer near and then to motivate seeking a similarity solution of the form
(c) Obtain the differential equation satisfied by , and state the conditions that would determine its solution. [You are not required to find this solution.]
By considering the flux in the boundary layer, explain why there should be a correction to the approximation of relative magnitude .
Paper 4, Section II, A
Consider a steady axisymmetric flow with components in cylindrical polar coordinates , where is a positive constant. The fluid has density and kinematic viscosity .
(a) Briefly describe the flow and confirm that it is incompressible.
(b) Show that the vorticity has one component , in the direction. Write down the corresponding vorticity equation and derive the solution
Hence find and show that it has a maximum at some finite radius , indicating how scales with and .
(c) Find an expression for the net advection of angular momentum, prv, into the finite cylinder defined by and . Show that this is always positive and asymptotes to the value
as
(d) Show that the torque exerted on the cylinder of part (c) by the exterior flow is always negative and demonstrate that it exactly balances the net advection of angular momentum. Comment on why this has to be so.
[You may assume that for a flow in cylindrical polar coordinates
Paper 1, Section II, 39B
A viscous fluid is confined between an inner, impermeable cylinder of radius with centre at and another outer, impermeable cylinder of radius with centre at (so they touch at the origin and both have their axes in the direction). The inner cylinder rotates about its axis with angular velocity and the outer cylinder rotates about its axis with angular velocity . The fluid motion is two-dimensional and slow enough that the Stokes approximation is appropriate.
(i) Show that the boundary of the inner cylinder is described by the relationship
where are the usual polar coordinates centred on . Show also that on this cylinder the boundary condition on the tangential velocity can be written as
where and are the components of the velocity in the and directions respectively. Explain why the boundary condition (where is the streamfunction such that and can be imposed.
(ii) Write down the boundary conditions to be satisfied on the outer cylinder , explaining carefully why can also be imposed on this cylinder as well.
(iii) It is given that the streamfunction is of the form
where and are constants, which satisfies . Using the fact that due to the symmetry of the problem, show that the streamfunction is
where the constant is to be found.
(iv) Sketch the streamline pattern between the cylinders and determine the coordinates of the stagnation point in the flow.
Paper 2, Section II, 38B
Consider a two-dimensional flow of a viscous fluid down a plane inclined at an angle to the horizontal. Initially, the fluid, which has a volume , occupies a region with increasing down the slope. At large times the flow becomes thin-layer flow.
(i) Write down the two-dimensional Navier-Stokes equations and simplify them using the lubrication approximation. Show that the governing equation for the height of the film, , is
where is the kinematic viscosity of the fluid and is the acceleration due to gravity, being careful to justify why the streamwise pressure gradient has been ignored compared to the gravitational body force.
(ii) Develop a similarity solution to and, using the fact that the volume of fluid is conserved over time, derive an expression for the position and height of the head of the current downstream.
(iii) Fluid is now continuously supplied at . By using scaling analysis, estimate the rate at which fluid would have to be supplied for the head height to asymptote to a constant value at large times.
Paper 3, Section II, 38B
(a) Briefly outline the derivation of the boundary layer equation
explaining the significance of the symbols used and what sets the -direction.
(b) Viscous fluid occupies the sector in cylindrical coordinates which is bounded by rigid walls and there is a line sink at the origin of strength with . Assume that vorticity is confined to boundary layers along the rigid walls and .
(i) Find the flow outside the boundary layers and clarify why boundary layers exist at all.
(ii) Show that the boundary layer thickness along the wall is proportional to
(iii) Show that the boundary layer equation admits a similarity solution for the streamfunction of the form
where . You should find the equation and boundary conditions satisfied by .
(iv) Verify that
yields a solution provided the constant has one of two possible values. Which is the likely physical choice?
Paper 4 , Section II, 38B
Consider a two-dimensional horizontal vortex sheet of strength in a homogeneous inviscid fluid at height above a horizontal rigid boundary at so that the fluid velocity is
(i) Investigate the linear instability of the sheet by determining the relevant dispersion relation for small, inviscid, irrotational perturbations. For what wavelengths is the sheet unstable?
(ii) Evaluate the temporal growth rate and the wave propagation speed in the limits of both short and long waves. Using these results, sketch how the growth rate varies with the wavenumber.
(iii) Comment briefly on how the introduction of a stable density difference (fluid in is less dense than that in ) and surface tension at the interface would affect the growth rates.
Paper 1, Section II, A
A disc of radius and weight hovers at a height on a cushion of air above a horizontal air table - a fine porous plate through which air of density and dynamic viscosity is pumped upward at constant speed . You may assume that the air flow is axisymmetric with no flow in the azimuthal direction, and that the effect of gravity on the air may be ignored.
(a) Write down the relevant components of the Navier-Stokes equations. By estimating the size of the individual terms, simplify these equations when and .
(b) Explain briefly why it is reasonable to expect that the vertical velocity of the air below the disc is a function of distance above the air table alone, and thus find the steady pressure distribution below the disc. Hence show that
Paper 2, Section II, A
A viscous fluid is contained in a channel between rigid planes and . The fluid in the upper region (with ) has dynamic viscosity while the fluid in the lower region has dynamic viscosity . The plane at moves with velocity and the plane at moves with velocity , both in the direction. You may ignore the effect of gravity.
(a) Find the steady, unidirectional solution of the Navier-Stokes equations in which the interface between the two fluids remains at .
(b) Using the solution from part (a):
(i) calculate the stress exerted by the fluids on the two boundaries;
(ii) calculate the total viscous dissipation rate in the fluids;
(iii) demonstrate that the rate of working by boundaries balances the viscous dissipation rate in the fluids.
(c) Consider the situation where . Defining the volume flux in the upper region as and the volume flux in the lower region as , show that their ratio is independent of and satisfies
Paper 3, Section II, A
For a fluid with kinematic viscosity , the steady axisymmetric boundary-layer equations for flow primarily in the -direction are
where is the fluid velocity in the -direction and is the fluid velocity in the -direction. A thin, steady, axisymmetric jet emerges from a point at the origin and flows along the -axis in a fluid which is at rest far from the -axis.
(a) Show that the momentum flux
is independent of the position along the jet. Deduce that the thickness of the jet increases linearly with . Determine the scaling dependence on of the centre-line velocity . Hence show that the jet entrains fluid.
(b) A similarity solution for the streamfunction,
exists if satisfies the second order differential equation
Using appropriate boundary and normalisation conditions (which you should state clearly) to solve this equation, show that
Paper 4, Section II, A
(a) Show that the Stokes flow around a rigid moving sphere has the minimum viscous dissipation rate of all incompressible flows which satisfy the no-slip boundary conditions on the sphere.
(b) Let , where and are solutions of Laplace's equation, i.e. and .
(i) Show that is incompressible.
(ii) Show that satisfies Stokes equation if the pressure .
(c) Consider a rigid sphere moving with velocity . The Stokes flow around the sphere is given by
where the origin is chosen to be at the centre of the sphere. Find the values for and which ensure no-slip conditions are satisfied on the sphere.
Paper 1, Section II, C
A two-dimensional layer of very viscous fluid of uniform thickness sits on a stationary, rigid surface . It is impacted by a stream of air (which can be assumed inviscid) such that the air pressure at is , where and are constants, is the density of the air, and is the coordinate parallel to the surface.
What boundary conditions apply to the velocity and stress tensor of the viscous fluid at and ?
By assuming the form for the stream function of the flow, or otherwise, solve the Stokes equations for the velocity and pressure fields. Show that the layer thins at a rate
Paper 2, Section II, C
An initially unperturbed two-dimensional inviscid jet in has uniform speed in the direction, while the surrounding fluid is stationary. The unperturbed velocity field is therefore given by
Consider separately disturbances in which the layer occupies varicose disturbances) and disturbances in which the layer occupies sinuous disturbances , where , and determine the dispersion relation in each case.
Find asymptotic expressions for the real part of in the limits and and draw sketches of in each case.
Compare the rates of growth of the two types of disturbance.
Paper 3, Section II, C
For two Stokes flows and inside the same volume with different boundary conditions on its boundary , prove the reciprocal theorem
where and are the stress tensors associated with the flows.
Stating clearly any properties of Stokes flow that you require, use the reciprocal theorem to prove that the drag on a body translating with uniform velocity is given by
where is a symmetric second-rank tensor that depends only on the geometry of the body.
A slender rod falls slowly through very viscous fluid with its axis inclined to the vertical. Explain why the rod does not rotate, stating any properties of Stokes flow that you use.
When the axis of the rod is inclined at an angle to the vertical, the centre of mass of the rod travels at an angle to the vertical. Given that the rod falls twice as quickly when its axis is vertical as when its axis is horizontal, show that
Paper 4, Section II, C
A cylinder of radius rotates about its axis with angular velocity while its axis is fixed parallel to and at a distance from a rigid plane, where . Fluid of kinematic viscosity fills the space between the cylinder and the plane. Determine the gap width between the cylinder and the plane as a function of a coordinate parallel to the surface of the wall and orthogonal to the axis of the cylinder. What is the characteristic length scale, in the direction, for changes in the gap width? Taking an appropriate approximation for , valid in the region where the gap width is small, use lubrication theory to determine that the volume flux between the wall and the cylinder (per unit length along the axis) has magnitude , and state its direction.
Evaluate the tangential shear stress on the surface of the cylinder. Approximating the torque on the cylinder (per unit length along the axis) in the form of an integral , find the torque to leading order in .
Explain the restriction for the theory to be valid.
[You may use the facts that and
Paper 1, Section II, B
Fluid of density and dynamic viscosity occupies the region in Cartesian coordinates . A semi-infinite, dense array of cilia occupy the half plane , and apply a stress in the -direction on the adjacent fluid, working at a constant and uniform rate per unit area, which causes the fluid to move with steady velocity . Give a careful physical explanation of the boundary condition
paying particular attention to signs, where is the kinematic viscosity of the fluid. Why would you expect the fluid motion to be confined to a thin region near for sufficiently large values of ?
Write down the viscous-boundary-layer equations governing the thin region of fluid motion. Show that the flow can be approximated by a stream function
Determine the functions and . Show that the dimensionless function satisfies
What boundary conditions must be satisfied by ? By considering how the volume flux varies with downstream location , or otherwise, determine (with justification) the sign of the transverse flow .
Paper 2, Section II, B
A cylinder of radius falls at speed without rotating through viscous fluid adjacent to a vertical plane wall, with its axis horizontal and parallel to the wall. The distance between the cylinder and the wall is . Use lubrication theory in a frame of reference moving with the cylinder to determine that the two-dimensional volume flux between the cylinder and the wall is
upwards, relative to the cylinder.
Determine an expression for the viscous shear stress on the cylinder. Use this to calculate the viscous force and hence the torque on the cylinder. If the cylinder is free to rotate, what does your result say about the sense of rotation of the cylinder?
[Hint: You may quote the following integrals:
Paper 3, Section II, B
A spherical bubble of radius a moves with velocity through a viscous fluid that is at rest far from the bubble. The pressure and velocity fields outside the bubble are given by
respectively, where is the dynamic viscosity of the fluid, is the position vector from the centre of the bubble and . Using suffix notation, or otherwise, show that these fields satisfy the Stokes equations.
Obtain an expression for the stress tensor for the fluid outside the bubble and show that the velocity field above also satisfies all the appropriate boundary conditions.
Compute the drag force on the bubble.
[Hint: You may use
where the integral is taken over the surface of a sphere of radius a and is the outward unit normal to the surface.]
Paper 4, Section II, B
A horizontal layer of inviscid fluid of density occupying flows with velocity above a horizontal layer of inviscid fluid of density occupying and flowing with velocity , in Cartesian coordinates . There are rigid boundaries at . The interface between the two layers is perturbed to position .
Write down the full set of equations and boundary conditions governing this flow. Derive the linearised boundary conditions appropriate in the limit . Solve the linearised equations to show that the perturbation to the interface grows exponentially in time if
Sketch the right-hand side of this inequality as a function of . Thereby deduce the minimum value of that makes the system unstable for all wavelengths.
Paper 1, Section II, B
State the vorticity equation and interpret the meaning of each term.
A planar vortex sheet is diffusing in the presence of a perpendicular straining flow. The flow is everywhere of the form , where as , and and are constants. Show that the vorticity has the form , and obtain a scalar equation describing the evolution of .
Explain physically why the solution approaches a steady state in which the vorticity is concentrated near . Use scaling to estimate the thickness of the steady vorticity layer as a function of and the kinematic viscosity .
Determine the steady vorticity profile, , and the steady velocity profile, .
Hint:
State, with a brief physical justification, why you might expect this steady flow to be unstable to long-wavelength perturbations, defining what you mean by long.
Paper 2, Section II, B
For a two-dimensional flow in plane polar coordinates , state the relationship between the streamfunction and the flow components and . Show that the vorticity is given by , and deduce that the streamfunction for a steady two-dimensional Stokes flow satisfies the biharmonic equation
A rigid stationary circular disk of radius occupies the region . The flow far from the disk tends to a steady straining flow , where is a constant. Inertial forces may be neglected. Calculate the streamfunction, , for the far-field flow.
By making an appropriate assumption about its dependence on , find the streamfunction for the flow around the disk, and deduce the flow components, and .
Calculate the tangential surface stress, , acting on the boundary of the disk.
Hints: In plane polar coordinates ,
Paper 3, Section II, B
A cylindrical pipe of radius and length contains two viscous fluids arranged axisymmetrically with fluid 1 of viscosity occupying the central region , where , and fluid 2 of viscosity occupying the surrounding annular region . The flow in each fluid is assumed to be steady and unidirectional, with velocities and respectively, with respect to cylindrical coordinates aligned with the pipe. A fixed pressure drop is applied between the ends of the pipe.
Starting from the Navier-Stokes equations, derive the equations satisfied by and , and state all the boundary conditions. Show that the pressure gradient is constant.
Solve for the velocity profile in each fluid and calculate the corresponding flow rates, and .
Derive the relationship between and that yields the same flow rate in each fluid. Comment on the behaviour of in the limits and , illustrating your comment by sketching the flow profiles.
Hint: In cylindrical coordinates ,
Paper 4 , Section II, B
A thin layer of fluid of viscosity occupies the gap between a rigid flat plate at and a flexible no-slip boundary at . The flat plate moves with constant velocity and the flexible boundary moves with no component of velocity in the -direction.
State the two-dimensional lubrication equations governing the dynamics of the thin layer of fluid. Given a pressure gradient , solve for the velocity profile in the fluid and calculate the flux . Deduce that the pressure gradient satisfies
The shape of the flexible boundary is a periodic travelling wave, i.e. and , where and are constants. There is no applied average pressure gradient, so the pressure is also periodic with . Show that
where denotes the average over a period. Calculate the shear stress on the plate.
The speed is such that there is no need to apply an external tangential force to the plate in order to maintain its motion. Show that
Paper 1, Section II, E
(i) In a Newtonian fluid, the deviatoric stress tensor is linearly related to the velocity gradient so that the total stress tensor is
Show that for an incompressible isotropic fluid with a symmetric stress tensor we necessarily have
where is a constant which we call the dynamic viscosity and is the symmetric part of .
(ii) Consider Stokes flow due to the translation of a rigid sphere of radius so that the sphere exerts a force on the fluid. At distances much larger than the radius of the sphere, the instantaneous velocity and pressure fields are
where is measured with respect to an origin located at the centre of the sphere, and .
Consider a sphere of radius instantaneously concentric with . By explicitly computing the tractions and integrating them, show that the force exerted by the fluid located in on is constant and independent of , and evaluate it.
(iii) Explain why the Stokes equations in the absence of body forces can be written
Show that by integrating this equation in the fluid volume located instantaneously between and , you can recover the result in (ii) directly.
Paper 2, Section II, E
Consider an infinite rigid cylinder of radius a parallel to a horizontal rigid stationary surface. Let be the direction along the surface perpendicular to the cylinder axis, the direction normal to the surface (the surface is at ) and the direction along the axis of the cylinder. The cylinder moves with constant velocity . The minimum separation between the cylinder and the surface is denoted by .
(i) What are the conditions for the flow in the thin gap between the cylinder and the surface to be described by the lubrication equations? State carefully the relevant length scale in the direction.
(ii) Without doing any calculation, explain carefully why, in the lubrication limit, the net fluid force acting on the stationary surface at has no component in the direction.
(iii) Using the lubrication approximation, calculate the component of the velocity field in the gap between the cylinder and the surface, and determine the pressure gradient as a function of the gap thickness .
(iv) Compute the tangential component of the force, , acting on the bottom surface per unit length in the direction.
[You may quote the following integrals:
Paper 3, Section II, E
Consider a three-dimensional high-Reynolds number jet without swirl induced by a force imposed at the origin in a fluid at rest. The velocity in the jet, described using cylindrical coordinates , is assumed to remain steady and axisymmetric, and described by a boundary layer analysis.
(i) Explain briefly why the flow in the jet can be described by the boundary layer equations
(ii) Show that the momentum flux in the jet, , where is an infinite surface perpendicular to , is not a function of . Combining this result with scalings from the boundary layer equations, derive the scalings for the unknown width and typical velocity of the jet as functions of and the other parameters of the problem .
(iii) Solving for the flow using a self-similar Stokes streamfunction
show that satisfies the differential equation
What boundary conditions should be applied to this equation? Give physical reasons for them.
[Hint: In cylindrical coordinates for axisymmetric incompressible flow you are given the incompressibility condition as
the -component of the Navier-Stokes equation as
and the relationship between the Stokes streamfunction, , and the velocity components as
Paper 4, Section II, E
A stationary inviscid fluid of thickness and density is located below a free surface at and above a deep layer of inviscid fluid of the same density in flowing with uniform velocity in the direction. The base velocity profile is thus
while the free surface at is maintained flat by gravity.
By considering small perturbations of the vortex sheet at of the form , calculate the dispersion relationship between and in the irrotational limit. By explicitly deriving that
deduce that the vortex sheet is unstable at all wavelengths. Show that the growth rates of the unstable modes are approximately when and when .
Paper 1, Section II, B
A particle of arbitrary shape and volume moves at velocity through an unbounded incompressible fluid of density and viscosity . The Reynolds number of the flow is very small so that the inertia of the fluid can be neglected. Show that the particle experiences a force due to the surface stresses given by
where is a dimensionless second-rank tensor determined solely by the shape and orientation of the particle. State the reason why must be positive definite.
Show further that, if the particle has the same reflectional symmetries as a cube, then
Let be the radius of the smallest sphere that contains the particle (still assuming cubic symmetry). By considering the Stokes flow associated with this sphere, suitably extended, and using the minimum dissipation theorem (which should be stated carefully), show that
[You may assume the expression for the Stokes drag on a sphere.]
Paper 2, Section II, B
Air is blown over the surface of a large, deep reservoir of water in such a way as to exert a tangential stress in the -direction of magnitude for , with . The water is otherwise at rest and occupies the region . The surface remains flat.
Find order-of-magnitude estimates for the boundary-layer thickness and tangential surface velocity in terms of the relevant physical parameters.
Using the boundary-layer equations, find the ordinary differential equation governing the dimensionless function defined in the streamfunction
What are the boundary conditions on ?
Does as ? Why, or why not?
The total horizontal momentum flux across the vertical line is proportional to for . Find the exponent . By considering the steadiness of the momentum balance in the region , explain why the value of is consistent with the form of the stress exerted on the boundary.
Paper 3, Section II, B
A rigid sphere of radius falls under gravity through an incompressible fluid of density and viscosity towards a rigid horizontal plane. The minimum gap between the sphere and the plane satisfies . Find an approximation for the gap thickness between the sphere and the plane in the region , where is the distance from the axis of symmetry.
For a prescribed value of , use lubrication theory to find the radial velocity and the fluid pressure in the region . Explain why the approximations of lubrication theory require and .
Calculate the total vertical force due to the motion that is exerted by the fluid on the sphere. Deduce that if the sphere is settling under its own weight (corrected for buoyancy) then decreases exponentially. What is the exponential decay rate for a solid sphere of density in a fluid of density ?
Paper 4, Section II, B
An incompressible fluid of density and kinematic viscosity is confined in a channel with rigid stationary walls at . A spatially uniform pressure gradient is applied in the -direction. What is the physical significance of the dimensionless number
Assuming that the flow is unidirectional and time-harmonic, obtain expressions for the velocity profile and the total flux. [You may leave your answers as the real parts of complex functions.]
In each of the limits and , find and sketch the flow profiles, find leading-order asymptotic expressions for the total flux, and give a physical interpretation.
Suppose now that and that the channel walls oscillate in their own plane with velocity in the -direction. Without explicit calculation of the solution, sketch the flow profile in each of the limits and .
Paper 1, Section II, A
The velocity field and stress tensor satisfy the Stokes equations in a volume bounded by a surface . Let be another solenoidal velocity field. Show that
where and are the strain-rates corresponding to the velocity fields and respectively, and is the unit normal vector out of . Hence, or otherwise, prove the minimum dissipation theorem for Stokes flow.
A particle moves at velocity through a highly viscous fluid of viscosity contained in a stationary vessel. As the particle moves, the fluid exerts a drag force on it. Show that
Consider now the case when the particle is a small cube, with sides of length , moving in a very large vessel. You may assume that
for some constant . Use the minimum dissipation theorem, being careful to declare the domain(s) involved, to show that
[You may assume Stokes' result for the drag on a sphere of radius .]
Paper 2, Section II, A
Write down the boundary-layer equations for steady two-dimensional flow of a viscous incompressible fluid with velocity outside the boundary layer. Find the boundary layer thickness when , a constant. Show that the boundarylayer equations can be satisfied in this case by a streamfunction with suitable scaling function and similarity variable . Find the equation satisfied by and the associated boundary conditions.
Find the drag on a thin two-dimensional flat plate of finite length placed parallel to a uniform flow. Why does the drag not increase in proportion to the length of the plate? [You may assume that the boundary-layer solution is applicable except in negligibly small regions near the leading and trailing edges. You may also assume that .]
Paper 3, Section II, A
A disk hovers on a cushion of air above an air-table - a fine porous plate through which a constant flux of air is pumped. Let the disk have a radius and a weight and hover at a low height above the air-table. Let the volume flux of air, which has density and viscosity , be per unit surface area. The conditions are such that . Explain the significance of this restriction.
Find the pressure distribution in the air under the disk. Show that this pressure balances the weight of the disk if
Paper 4, Section II, A
Consider the flow of an incompressible fluid of uniform density and dynamic viscosity . Show that the rate of viscous dissipation per unit volume is given by
where is the strain rate.
Determine expressions for and when the flow is irrotational with velocity potential .
In deep water a linearised wave with a surface displacement has a velocity potential . Hence determine the rate of the viscous dissipation, averaged over a wave period , for an irrotational surface wave of wavenumber and small amplitude in a fluid with very small viscosity and great depth .
Calculate the depth-integrated kinetic energy per unit wavelength. Assuming that the average potential energy is equal to the average kinetic energy, show that the total wave energy decreases to leading order as , where should be found.
Paper 1, Section II, C
Define the strain-rate tensor in terms of the velocity components . Write down the relation between , the pressure and the stress in an incompressible Newtonian fluid of viscosity . Show that the local rate of stress-working is equal to the local rate of dissipation .
An incompressible fluid of density and viscosity occupies the semi-infinite region above a rigid plane boundary which oscillates with velocity . The fluid is at rest at infinity. Determine the velocity field produced by the boundary motion after any transients have decayed.
Show that the time-averaged rate of dissipation is
per unit area of the boundary. Verify that this is equal to the time average of the rate of working by the boundary on the fluid per unit area.
Paper 2, Section II, C
An incompressible viscous liquid occupies the long thin region for , where with and . The top boundary at is rigid and stationary. The bottom boundary at is rigid and moving at velocity . Fluid can move in and out of the ends and , where the pressure is the same, namely .
Explaining the approximations of lubrication theory as you use them, find the velocity profile in the long thin region, and show that the volume flux (per unit width in the -direction) is
Find also the value of (i) where the pressure is maximum, (ii) where the tangential viscous stress on the bottom vanishes, and (iii) where the tangential viscous stress on the top vanishes.
Paper 3, Section II, C
For two Stokes flows and inside the same volume with different boundary conditions on its boundary , prove the reciprocal theorem
where and are the stress fields associated with the flows.
When a rigid sphere of radius translates with velocity through unbounded fluid at rest at infinity, it may be shown that the traction per unit area, , exerted by the sphere on the fluid has the uniform value over the sphere surface. Find the drag on the sphere.
Suppose that the same sphere is now free of external forces and is placed with its centre at the origin in an unbounded Stokes flow given in the absence of the sphere as . By applying the reciprocal theorem to the perturbation to the flow generated by the presence of the sphere, and assuming this tends to zero sufficiently rapidly at infinity, show that the instantaneous velocity of the centre of the sphere is
where the integral is taken over the sphere of radius .
Paper 4, Section II, C
A steady, two-dimensional flow in the region takes the form at large , where is a positive constant. The boundary at is rigid and no-slip. Consider the velocity field with stream function , where and and is the kinematic viscosity. Show that this velocity field satisfies the Navier-Stokes equations provided that satisfies
What are the conditions on at and as ?
Paper 1, Section II, B
The steady two-dimensional boundary-layer equations for flow primarily in the direction are
A thin, steady, two-dimensional jet emerges from a point at the origin and flows along the -axis in a fluid at rest far from the -axis. Show that the momentum flux
is independent of position along the jet. Deduce that the thickness of the jet increases along the jet as , while the centre-line velocity decreases as .
A similarity solution for the jet is sought with a streamfunction of the form
Derive the nonlinear third-order non-dimensional differential equation governing , and write down the boundary and normalisation conditions which must be applied.
Paper 2, Section II, B
The energy equation for the motion of a viscous, incompressible fluid states that
Interpret each term in this equation and explain the meaning of the symbols used.
Consider steady rectilinear flow in a (not necessarily circular) pipe having rigid stationary walls. Deduce a relation between the viscous dissipation per unit length of the pipe, the pressure gradient , and the volume flux .
Starting from the Navier-Stokes equations, calculate the velocity field for steady rectilinear flow in a circular pipe of radius . Using the relationship derived above, or otherwise, find the viscous dissipation per unit length of this flow in terms of .
[Hint: In cylindrical polar coordinates,
Paper 3, Section II, B
If is harmonic, i.e. if , show that
satisfies the incompressibility condition and the Stokes equation. Show that the stress tensor is
Consider the Stokes flow corresponding to
where are the components of a constant vector . Show that on the sphere the normal component of velocity vanishes and the surface traction is in the normal direction. Hence deduce that the drag force on the sphere is given by
Paper 4, Section II, B
A viscous fluid flows along a slowly varying thin channel between no-slip surfaces at and under the action of a pressure gradient . After explaining the approximations and assumptions of lubrication theory, including a comment on the reduced Reynolds number, derive the expression for the volume flux
as well as the equation
In peristaltic pumping, the surface has a periodic form in space which propagates at a constant speed , i.e. , and no net pressure gradient is applied, i.e. the pressure gradient averaged over a period vanishes. Show that the average flux along the channel is given by
where denotes an average over one period.
Paper 1, Section II, A
Write down the Navier-Stokes equation for the velocity of an incompressible viscous fluid of density and kinematic viscosity . Cast the equation into dimensionless form. Define rectilinear flow, and explain why the spatial form of any steady rectilinear flow is independent of the Reynolds number.
(i) Such a fluid is contained between two infinitely long plates at . The lower plate is at rest while the upper plate moves at constant speed in the direction. There is an applied pressure gradient in the direction. Determine the flow field.
(ii) Now there is no applied pressure gradient, but baffles are attached to the lower plate at a distance from each other , lying between the plates so as to prevent any net volume flux in the direction. Assuming that far from the baffles the flow is essentially rectilinear, determine the flow field and the pressure gradient in the fluid.
Paper 2, Section II, A
What is lubrication theory? Explain the assumptions that go into the theory.
Viscous fluid with dynamic viscosity and density is contained between two flat plates, which approach each other at uniform speed . The first is fixed at . The second has its ends at , where . There is no flow in the direction, and all variation in may be neglected. There is no applied pressure gradient in the direction.
Assuming that is so small that lubrication theory applies, derive an expression for the horizontal volume flux at , in terms of the pressure gradient. Show that mass conservation implies that , so that . Derive another relation between and by setting the pressures at to be equal, and hence show that
Show that lubrication theory applies if .
Paper 3, Section II, A
The equation for the vorticity in two-dimensional incompressible flow takes the form
where
and is the stream function.
Show that this equation has a time-dependent similarity solution of the form
if and satisfies the equation
and is the effective Reynolds number.
Show that this solution is appropriate for the problem of two-dimensional flow between the rigid planes , and determine the boundary conditions on in that case.
Verify that has exact solutions, satisfying the boundary conditions, of the form
when . Sketch this solution when is large, and discuss whether such solutions are likely to be realised in practice.
Paper 4, Section II, A
An axisymmetric incompressible Stokes flow has the Stokes stream function in spherical polar coordinates . Give expressions for the components of the flow field in terms of . Show that the equation satisfied by is
Fluid is contained between the two spheres , with . The fluid velocity vanishes on the outer sphere, while on the inner sphere . It is assumed that Stokes flow applies.
(i) Show that the Stokes stream function,
is the general solution of proportional to and write down the conditions on that allow all the boundary conditions to be satisfied.
(ii) Now let , with as . Show that with .
(iii) Show that when is very large but finite, then the coefficients have the approximate form
Paper 1, Section II, E
Explain the assumptions of lubrication theory and its use in determining the flow in thin films.
A cylindrical roller of radius a rotates at angular velocity below the free surface at of a fluid of density and dynamic viscosity . The gravitational acceleration is , and the pressure above the free surface is . The minimum distance of the roller below the fluid surface is , where . The depth of the roller below the free surface may be approximated by , where is the horizontal distance.
(i) State the conditions for lubrication theory to be applicable to this problem. On the further assumption that the free surface may be taken to be flat, find the flow above the roller and calculate the horizontal volume flux (per unit length in the third dimension) and the horizontal pressure gradient.
(ii) Use the pressure gradient you have found to estimate the order of magnitude of the departure of the free surface from , and give conditions on the parameters that ensure that , as required for part (i).
[Hint: Integrals of the form
satisfy and
for
Paper 2, Section II, E
Show that two-dimensional Stokes flow in cylindrical polar coordinates has a stream function , with , that satisfies the biharmonic equation
Give, in terms of and/or its derivatives, the boundary conditions satisfied by on an impermeable plane of constant which is either (a) rigid or (b) stress-free.
A rigid plane passes through the origin and lies along . Fluid with viscosity is confined in the region . A uniform tangential stress is applied on . Show that the resulting flow may be described by a stream function of the form , where is to be found. Hence show that the radial flow on is given by
By expanding this expression for small show that and have the same sign, provided that is not too large. Discuss the situation when , where tan .
[Hint: In plane polar coordinates
and the component of the stress tensor takes the form
Paper 3, Section II, E
An axisymmetric incompressible Stokes flow has the Stokes stream function in spherical polar coordinates . Give expressions for the components and of the flow field in terms of , and show that
where
Write down the equation satisfied by .
Verify that the Stokes stream function
represents the Stokes flow past a stationary sphere of radius , when the fluid at large distance from the sphere moves at speed along the axis of symmetry.
A sphere of radius a moves vertically upwards in the direction at speed through fluid of density and dynamic viscosity , towards a free surface at . Its distance from the surface is much greater than . Assuming that the surface remains flat, show that the conditions of zero vertical velocity and zero tangential stress at can be approximately met for large by combining the Stokes flow for the sphere with that of an image sphere of the same radius located symmetrically above the free surface. Hence determine the leading-order behaviour of the horizontal flow on the free surface as a function of , the horizontal distance from the sphere's centre line.
What is the size of the next correction to your answer as a power of [Detailed calculation is not required.]
[Hint: For an axisymmetric vector field ,
Paper 4 , Section II, E
Two regions of inviscid fluid with the same density are separated by a thin membrane at . The fluid in has the uniform velocity in Cartesian coordinates, while the fluid in is at rest.
The membrane is now slightly perturbed to . The dynamical effect of the membrane is to induce a pressure difference across it equal to , where is a constant and the sign is such that the pressure is higher below the interface when .
On the assumption that the flow remains irrotational and all perturbations are small, derive the relation between and for disturbances of the form , where is real but may be complex. Show that there is instability only for , where is to be determined. Find the maximum growth rate and the value of for which this is obtained.
1.II.36A
Derive the relation between the stress tensor and the rate-of-strain tensor in an incompressible Newtonian fluid, using the result that there is a linear dependence between the components of and those of that is the same in all frames. Write down the boundary conditions that hold at an interface between two viscous fluids.
Viscous fluid is contained in a channel between the rigid planes and . The fluid in has dynamic viscosity , while that in has dynamic viscosity . Gravity may be neglected. The fluids move through the channel in the -direction under the influence of a pressure gradient applied at the ends of the channel. It may be assumed that the velocity has no -components, and all quantities are independent of .
Find a steady solution of the Navier-Stokes equation in which the interface between the two fluids remains at , the fluid velocity is everywhere independent of , and the pressure gradient is uniform. Use it to calculate the following:
(a) the viscous tangential stress at and at ; and
(b) the ratio of the volume fluxes of the two different fluids.
Comment on the limits of each of the results in (a) and (b) as , and as
2.II.36A
Viscous fluid with dynamic viscosity flows with velocity (in cartesian coordinates in a shallow container with a free surface at . The base of the container is rigid, and is at . A horizontal stress is applied at the free surface. Gravity may be neglected.
Using lubrication theory (conditions for the validity of which should be clearly stated), show that the horizontal volume flux satisfies the equations
where is the pressure. Find also an expression for the surface velocity in terms of and .
Now suppose that the container is cylindrical with boundary at , where , and that the surface stress is uniform and in the -direction, so with constant. It can be assumed that the correct boundary condition to apply at is , where is the unit normal.
Write , and show that satisfies the equation
Deduce that if (constant) then . Find in this case.
Now suppose that , where . Verify that to leading order in for some constant to be determined. Hence determine up to and including terms of order .
[Hint: for any vector field
3.II.36A
Show that, in cylindrical polar co-ordinates, the streamfunction for the velocity and vorticity of two-dimensional Stokes flow of incompressible fluid satisfies the equations
Show also that the pressure satisfies .
A stationary rigid circular cylinder of radius occupies the region . The flow around the cylinder tends at large distances to a simple shear flow, with velocity given in cartesian coordinates by . Inertial forces may be neglected.
By solving the equation for in cylindrical polars, determine the flow field everywhere. Determine the torque on the cylinder per unit length in .
[Hint: in cylindrical polars
The off-diagonal component of the rate-of-strain tensor is given by
4.II.37A
Viscous incompressible fluid of uniform density is extruded axisymmetrically from a thin circular slit of small radius centred at the origin and lying in the plane in cylindrical polar coordinates . There is no external radial pressure gradient. It is assumed that the fluid forms a thin boundary layer, close to and symmetric about the plane . The layer has thickness . The -component of the steady Navier-Stokes equations may be approximated by
(i) Prove that the quantity (proportional to the flux of radial momentum)
is independent of .
(ii) Show, by balancing terms in the momentum equation and assuming constancy of , that there is a similarity solution of the form
where are constants. Show that for suitable choices of and the equation for takes the form
(iii) Give an inequality connecting and that ensures that the boundary layer approximation is valid. Solve the equation to give a complete solution to the problem for when this inequality holds.
[Hint:
1.II.36B
Discuss how the methods of lubrication theory may be used to find viscous fluid flows in thin layers or narrow gaps, explaining carefully what inequalities need to hold in order that the theory may apply.
Viscous fluid of kinematic viscosity flows under the influence of gravity , down an inclined plane making an angle with the horizontal. The fluid layer lies between and , where are distances measured down the plane and perpendicular to it, and is of the same order as . Give conditions involving and that ensure that lubrication theory can be used, and solve the lubrication equations, together with the equation of mass conservation, to obtain an equation for in the form
where are constants to be determined. Show that there is a steady solution with constant, and interpret this physically. Show also that a solution of this equation exists in the form of a front, with , where , and as . Determine in terms of , find the shape of the front implicitly in the form , and show that as from below.
2.II.36B
Viscous fluid is extracted through a small hole in the tip of the cone given by in spherical polar coordinates . The total volume flux through the hole takes the constant value . It is given that there is a steady solution of the Navier-Stokes equations for the fluid velocity . For small enough , the velocity is well approximated by , where except in thin boundary layers near .
(i) Verify that the volume flux through the hole is approximately .
(ii) Construct a Reynolds number (depending on ) in terms of and the kinematic viscosity , and thus give an estimate of the value of below which solutions of this type will appear.
(iii) Assuming that there is a boundary layer near , write down the boundary layer equations in the usual form, using local Cartesian coordinates and parallel and perpendicular to the boundary. Show that the boundary layer thickness is proportional to , and show that the component of the velocity may be written in the form
Derive the equation and boundary conditions satisfied by . Give an expression, in terms of , for the volume flux through the boundary layer, and use this to derive the dependence of the first correction to the flow outside the boundary layer.
3.II B
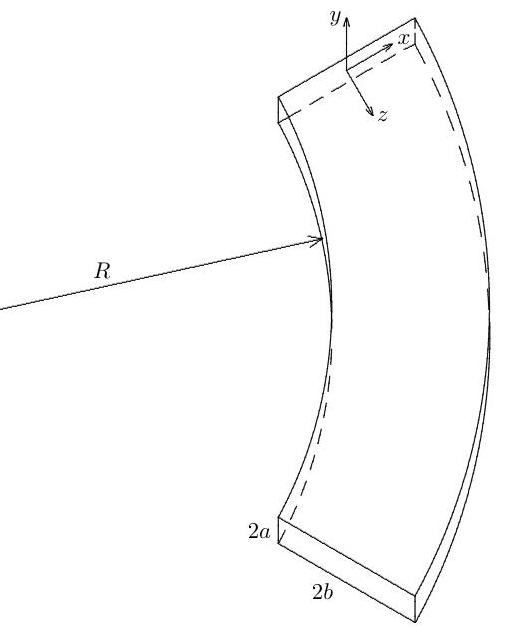
Viscous fluid of kinematic viscosity and density flows in a curved pipe of constant rectangular cross section and constant curvature. The cross-section has height and width (in the radial direction) with , and the radius of curvature of the inner wall is , with . A uniform pressure gradient is applied along the pipe.
(i) Assume to a first approximation that the pipe is straight, and ignore variation in the -direction, where are Cartesian coordinates referred to an origin at the centre of the section, with increasing radially and measured along the pipe. Find the flow field along the pipe in the form .
(ii) It is given that the largest component of the inertial acceleration due to the curvature of the pipe is in the direction. Consider the secondary flow induced in the plane, again ignoring variations in and any end effects (except for the requirement that there be zero total mass flux in the direction). Show that takes the form , where
and write down two equations determining the constants and . [It is not necessary to solve these equations.]
Give conditions on the parameters that ensure that .
4.II.37B
(i) Assuming that axisymmetric incompressible flow , with vorticity in spherical polar coordinates satisfies the equations
where
show that for Stokes flow satisfies the equation
(ii) A rigid sphere of radius moves at velocity through viscous fluid of density and dynamic viscosity which is at rest at infinity. Assuming Stokes flow and by applying the boundary conditions at and as , verify that is the appropriate solution to for this flow, where and are to be determined.
(iii) Hence find the velocity field outside the sphere. Without direct calculation, explain why the drag is in the direction and has magnitude proportional to .
(iv) A second identical sphere is introduced into the flow, at a distance from the first, and moving at the same velocity. Justify the assertion that, when the two spheres are at the same height, or when one is vertically above the other, the drag on each sphere is the same. Calculate the leading correction to the drag in each case, to leading order in .
[You may quote without proof the fact that, for an axisymmetric function ,
in spherical polar coordinates .]
1.II.36B
Write down the boundary conditions that are satisfied at the interface between two viscous fluids in motion. Briefly discuss the physical meaning of these boundary conditions.
A layer of incompressible fluid of density and viscosity flows steadily down a plane inclined at an angle to the horizontal. The layer is of uniform thickness measured perpendicular to the plane and the viscosity of the overlying air can be neglected. Using co-ordinates parallel and perpendicular to the plane, write down the equations of motion, and the boundary conditions on the plane and on the free top surface. Determine the pressure and velocity fields. Show that the volume flux down the plane is per unit cross-slope width.
Consider now the case where a second layer of fluid, of uniform thickness , viscosity , and density flows steadily on top of the first layer. Determine the pressure and velocity fields in each layer. Why does the velocity profile in the bottom layer depend on but not on ?
2.II.36B
A very long cylinder of radius a translates steadily at speed in a direction perpendicular to its axis and parallel to a plane boundary. The centre of the cylinder remains a distance above the plane, where , and the motion takes place through an incompressible fluid of viscosity .
Consider the force per unit length parallel to the plane that must be applied to the cylinder to maintain the motion. Explain why scales according to .
Approximating the lower cylindrical surface by a parabola, or otherwise, determine the velocity and pressure gradient fields in the space between the cylinder and the plane. Hence, by considering the shear stress on the plane, or otherwise, calculate explicitly.
[You may use
3.II.36B
Define the rate of strain tensor in terms of the velocity components .
Write down the relation between , the pressure and the stress tensor in an incompressible Newtonian fluid of viscosity .
Prove that is the local rate of dissipation per unit volume in the fluid.
Incompressible fluid of density and viscosity occupies the semi-infinite domain above a rigid plane boundary that oscillates with velocity , where and are constants. The fluid is at rest at . Determine the velocity field produced by the boundary motion after any transients have decayed.
Evaluate the time-averaged rate of dissipation in the fluid, per unit area of boundary.
4.II.37B
A line force of magnitude is applied in the positive -direction to an unbounded fluid, generating a thin two-dimensional jet along the positive -axis. The fluid is at rest at and there is negligible motion in . Write down the pressure gradient within the boundary layer. Deduce that the function defined by
is independent of for . Interpret this result, and explain why . Use scaling arguments to deduce that there is a similarity solution having stream function
Hence show that satisfies
Show that a solution of is
where is a constant to be determined by requiring that is independent of . Find the volume flux, , in the jet. Briefly indicate why increases as increases.
[Hint: You may use
Write down the Navier-Stokes equations for an incompressible fluid.
Explain the concepts of the Euler and Prandtl limits applied to the Navier-Stokes equations near a rigid boundary.
A steady two-dimensional flow given by far upstream flows past a semi-infinite flat plate, held at . Derive the boundary layer equation
for the stream-function near the plate, explaining any approximations made.
Show that the appropriate solution must be of the form
and determine the dimensionless variable .
Derive the equation and boundary conditions satisfied by . [You need not solve them.]
Suppose now that the plate has a finite length in the direction of the flow. Show that the force on the plate (per unit width perpendicular to the flow) is given by
1.II.36E
Consider a unidirectional flow with dynamic viscosity along a straight rigid-walled channel of uniform cross-sectional shape driven by a uniform applied pressure gradient . Write down the differential equation and boundary conditions governing the velocity along the channel.
Consider the situation when the boundary includes a sharp corner of angle . Explain why one might expect that, sufficiently close to the corner, the solution should be of the form
where and are polar co-ordinates with origin at the vertex and describing the two planes emanating from the corner. Determine .
If is the sector bounded by the lines and the circular arc , show that the flow is given by
where and are to be determined.
[Note that .]
Considering the values of and , comment briefly on the cases: (i) ;
(ii) ; and (iii) .
2.II.36E
A volume of very viscous fluid of density and dynamic viscosity is released at the origin on a rigid horizontal boundary at time . Using lubrication theory, determine the velocity profile in the gravity current once it has spread sufficiently that the axisymmetric thickness of the current is much less than the radius of the front.
Derive the differential equation
where is to be determined.
Write down the other equations that are needed to determine the appropriate similarity solution for this problem.
Determine the similarity solution and calculate .
4.II.37E
Consider flow of an incompressible fluid of uniform density and dynamic viscosity . Show that the rate of viscous dissipation per unit volume is given by
where is the strain rate.
Determine expressions for and when the flow is irrotational with velocity potential . Hence determine the rate of viscous dissipation, averaged over a wave period , for an irrotational two-dimensional surface wave of wavenumber and small amplitude in a fluid of very small viscosity and great depth .
[You may use without derivation that in deep water a linearised wave with surface displacement has velocity potential .]
Calculate the depth-integrated time-averaged kinetic energy per wavelength. Assuming that the average potential energy is equal to the average kinetic energy, show that the total wave energy decreases to leading order like , where
B1.25
Consider a uniform stream of inviscid incompressible fluid incident onto a twodimensional body (such as a circular cylinder). Sketch the flow in the region close to the stagnation point, , at the front of the body.
Let the fluid now have a small but non-zero viscosity. Using local co-ordinates along the boundary and normal to it, with the stagnation point as origin and in the fluid, explain why the local outer, inviscid flow is approximately of the form
for some positive constant .
Use scaling arguments to find the thickness of the boundary layer on the body near . Hence show that there is a solution of the boundary layer equations of the form
where is a suitable similarity variable and satisfies
What are the appropriate boundary conditions for and why? Explain briefly how you would obtain a numerical solution to subject to the appropriate boundary conditions.
Explain why it is neither possible nor appropriate to perform a similar analysis near the rear stagnation point of the inviscid flow.
B2.25
An incompressible fluid with density and viscosity is forced by a pressure difference through the narrow gap between two parallel circular cylinders of radius with axes apart. Explaining any approximations made, show that, provided and , the volume flux (per unit length of cylinder) is
when the cylinders are stationary.
Show also that when the two cylinders rotate with angular velocities and respectively, the change in the volume flux is
For the case , find and sketch the function , where is the centreline velocity at position along the gap in the direction of flow. Comment on the values taken by .
B3.24
Using the Milne-Thompson circle theorem, or otherwise, write down the complex potential describing inviscid incompressible two-dimensional flow past a circular cylinder of radius centred on the origin, with circulation and uniform velocity in the far field.
Hence, or otherwise, find an expression for the velocity field if the cylinder is replaced by a flat plate of length , centred on the origin and aligned with the -axis. Evaluate the velocity field on the two sides of the plate and confirm that the normal velocity is zero.
Explain the significance of the Kutta condition, and determine the value of the circulation that satisfies the Kutta condition when .
With this value of the circulation, calculate the difference in pressure between the upper and lower sides of the plate at position . Comment briefly on the value of the pressure at the leading edge and the force that this would produce if the plate had a small non-zero thickness.
Determine the force on the plate, explaining carefully the direction in which it acts.
[The Blasius formula , where is a closed contour lying just outside the body, may be used without proof.]
B4.26
Write an essay on the Kelvin-Helmholtz instability of a vortex sheet. Your essay should include a detailed linearised analysis, a physical interpretation of the instability, and an informal discussion of nonlinear effects and of the effects of viscosity.
B1.25
Consider a two-dimensional horizontal vortex sheet of strength at height above a horizontal rigid boundary at , so that the inviscid fluid velocity is
Examine the temporal linear instabililty of the sheet and determine the relevant dispersion relationship.
For what wavelengths is the sheet unstable?
Evaluate the temporal growth rate and the wave propagation speed in the limit of both short and long waves. Comment briefly on the significance of your results.
B2 24
A plate is drawn vertically out of a bath and the resultant liquid drains off the plate as a thin film. Using lubrication theory, show that the governing equation for the thickness of the film, is
where is time and is the distance down the plate measured from the top.
Verify that
satisfies and identify the function . Using this relationship or otherwise, determine an explicit expression for the thickness of the film assuming that it was initially of uniform thickness .
B3.24
A steady two-dimensional jet is generated in an infinite, incompressible fluid of density and kinematic viscosity by a point source of momentum with momentum flux in the direction per unit length located at the origin.
Using boundary layer theory, analyse the motion in the jet and show that the -component of the velocity is given by
where
Show that satisfies the differential equation
Write down the appropriate boundary conditions for this equation. [You need not solve the equation.]
B4.26
Show that the complex potential in the complex plane,
describes irrotational, inviscid flow past the rigid cylinder , placed in a uniform flow with circulation .
Show that the transformation
maps the circle in the plane onto the flat plate airfoil in the plane . Hence, write down an expression for the complex potential, , of uniform flow past the flat plate, with circulation . Indicate very briefly how the value of might be chosen to yield a physical solution.
Calculate the turning moment, , exerted on the flat plate by the flow.
(You are given that
where is the fluid density and the integral is to be completed around a contour enclosing the circle ).
B1.25
State the minimum dissipation theorem for Stokes flow in a bounded domain.
Fluid of density and viscosity fills an infinite cylindrical annulus between a fixed cylinder and a cylinder which rotates about its axis with constant angular velocity . In cylindrical polar coordinates , the fluid velocity is . The Reynolds number is not necessarily small. Show that , where and are constants to be determined.
[You may assume that and ]
Show that the outer cylinder exerts a couple per unit length on the fluid, where
[You may assume that, in standard notation, .]
Suppose now that and that the cylinder is replaced by a fixed cylinder whose cross-section is a square of side centred on , all other conditions being unchanged. The flow may still be assumed steady. Explaining your argument carefully, show that the couple now required to maintain the motion of the outer cylinder is greater than .
B2.24
A thin layer of liquid of kinematic viscosity flows under the influence of gravity down a plane inclined at an angle to the horizontal . With origin on the plane, and axes down the line of steepest slope and normal to the plane, the free surface is given by , where . The pressure distribution in the liquid may be assumed to be hydrostatic. Using the approximations of lubrication theory, show that
Now suppose that
where
and and are constants with . Show that, to leading order,
where and are constants to be determined.
Explain in physical terms the meaning of this solution.
B3.24
(i) Suppose that, with spherical polar coordinates, the Stokes streamfunction
represents a Stokes flow and thus satisfies the equation , where
Show that the possible values of are and . For which of these values is the corresponding flow irrotational? Sketch the streamlines of the flow for the case .
(ii) A spherical drop of liquid of viscosity , radius and centre at , is suspended in another liquid of viscosity which flows with streamfunction
far from the drop. The two liquids are of equal densities, surface tension is sufficiently strong to keep the drop spherical, and inertia is negligible. Show that
and obtain four equations determining the constants and . (You need not solve these equations.)
[You may assume, with standard notation, that
B4.26
Write an essay on boundary-layer theory and its application to the generation of lift in aerodynamics.
You should include discussion of the derivation of the boundary-layer equation, the similarity transformation leading to the Falkner-Skan equation, the influence of an adverse pressure gradient, and the mechanism(s) by which circulation is generated in flow past bodies with a sharp trailing edge.
B1.25
The energy equation for the motion of a viscous, incompressible fluid states that
Interpret each term in this equation and explain the meaning of the symbols used.
For steady rectilinear flow in a (not necessarily circular) pipe having rigid stationary walls, deduce a relation between the viscous dissipation per unit length of the pipe, the pressure gradient , and the volume flux .
Starting from the Navier-Stokes equations, calculate the velocity field for steady rectilinear flow in a circular pipe of radius . Using the relationship derived above, or otherwise, find in terms of the viscous dissipation per unit length for this flow.
[In cylindrical polar coordinates,
B2.24
Explain what is meant by a Stokes flow and show that, in such a flow, in the absence of body forces, , where is the stress tensor.
State and prove the reciprocal theorem for Stokes flow.
When a rigid sphere of radius translates with velocity through unbounded fluid at rest at infinity, it may be shown that the traction per unit area, , exerted by the sphere on the fluid, has the uniform value over the sphere surface. Find the drag on the sphere.
Suppose that the same sphere is free of external forces and is placed with its centre at the origin in an unbounded Stokes flow given in the absence of the sphere as . By applying the reciprocal theorem to the perturbation to the flow generated by the presence of the sphere, and assuming this to tend to zero sufficiently rapidly at infinity, show that the instantaneous velocity of the centre of the sphere is
Part II
B3.24
A planar flow of an inviscid, incompressible fluid is everywhere in the -direction and has velocity profile
By examining linear perturbations to the vortex sheet at that have the form , show that
and deduce the temporal stability of the sheet to disturbances of wave number .
Use this result to determine also the spatial growth rate and propagation speed of disturbances of frequency introduced at a fixed spatial position.
B4.26
Starting from the steady planar vorticity equation
outline briefly the derivation of the boundary layer equation
explaining the significance of the symbols used.
Viscous fluid occupies the region with rigid stationary walls along for and . There is a line sink at the origin of strength , with . Assuming that vorticity is confined to boundary layers along the rigid walls:
(a) Find the flow outside the boundary layers.
(b) Explain why the boundary layer thickness along the wall is proportional to , and deduce that
(c) Show that the boundary layer equation admits a solution having stream function
Find the equation and boundary conditions satisfied by .
(d) Verify that a solution is
provided that has one of two values to be determined. Should the positive or negative value be chosen?