Electromagnetism

2021

• Paper 1, Section II, 15D

  Electromagnetism | Part IB, 2021

  (a) Show that the magnetic flux passing through a simple, closed curve $C$ can be written as

  $$\Phi=\oint_{C} \mathbf{A} \cdot \mathbf{d} \mathbf{x},$$

  where $\mathbf{A}$ is the magnetic vector potential. Explain why this integral is independent of the choice of gauge.

  (b) Show that the magnetic vector potential due to a static electric current density $\mathbf{J}$, in the Coulomb gauge, satisfies Poisson's equation

  $$-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{J}$$

  Hence obtain an expression for the magnetic vector potential due to a static, thin wire, in the form of a simple, closed curve $C$, that carries an electric current $I$. [You may assume that the electric current density of the wire can be written as

  $$\mathbf{J}(\mathbf{x})=I \int_{C} \delta^{(3)}\left(\mathbf{x}-\mathbf{x}^{\prime}\right) \mathbf{d} \mathbf{x}^{\prime}$$

  where $\delta^{(3)}$ is the three-dimensional Dirac delta function.]

  (c) Consider two thin wires, in the form of simple, closed curves $C_{1}$ and $C_{2}$, that carry electric currents $I_{1}$ and $I_{2}$, respectively. Let $\Phi_{i j}$ (where $i, j \in\{1,2\}$ ) be the magnetic flux passing through the curve $C_{i}$ due to the current $I_{j}$ flowing around $C_{j}$. The inductances are defined by $L_{i j}=\Phi_{i j} / I_{j}$. By combining the results of parts (a) and (b), or otherwise, derive Neumann's formula for the mutual inductance,

  $$L_{12}=L_{21}=\frac{\mu_{0}}{4 \pi} \oint_{C_{1}} \oint_{C_{2}} \frac{\mathbf{d} \mathbf{x}_{1} \cdot \mathbf{d} \mathbf{x}_{2}}{\left|\mathbf{x}_{1}-\mathbf{x}_{2}\right|} .$$

  Suppose that $C_{1}$ is a circular loop of radius $a$, centred at $(0,0,0)$ and lying in the plane $z=0$, and that $C_{2}$ is a different circular loop of radius $b$, centred at $(0,0, c)$ and lying in the plane $z=c$. Show that the mutual inductance of the two loops is

  $$\frac{\mu_{0}}{4} \sqrt{a^{2}+b^{2}+c^{2}} f(q)$$

  where

  $$q=\frac{2 a b}{a^{2}+b^{2}+c^{2}}$$

  and the function $f(q)$ is defined, for $0<q<1$, by the integral

  $$f(q)=\int_{0}^{2 \pi} \frac{q \cos \theta d \theta}{\sqrt{1-q \cos \theta}}$$

  comment

• Paper 2, Section I, $4 \mathrm{D}$

  Electromagnetism | Part IB, 2021

  State Gauss's Law in the context of electrostatics.

  A simple coaxial cable consists of an inner conductor in the form of a perfectly conducting, solid cylinder of radius $a$, surrounded by an outer conductor in the form of a perfectly conducting, cylindrical shell of inner radius $b>a$ and outer radius $c>b$. The cylinders are coaxial and the gap between them is filled with a perfectly insulating material. The cable may be assumed to be straight and arbitrarily long.

  In a steady state, the inner conductor carries an electric charge $+Q$ per unit length, and the outer conductor carries an electric charge $-Q$ per unit length. The charges are distributed in a cylindrically symmetric way and no current flows through the cable.

  Determine the electrostatic potential and the electric field as functions of the cylindrical radius $r$, for $0<r<\infty$. Calculate the capacitance $C$ of the cable per unit length and the electrostatic energy $U$ per unit length, and verify that these are related by

  $$U=\frac{Q^{2}}{2 C}$$

  comment

• Paper 2, Section II, $16 \mathrm{D}$

  Electromagnetism | Part IB, 2021

  (a) Show that, for $|\mathbf{x}| \gg|\mathbf{y}|$,

  $$\frac{1}{|\mathbf{x}-\mathbf{y}|}=\frac{1}{|\mathbf{x}|}\left[1+\frac{\mathbf{x} \cdot \mathbf{y}}{|\mathbf{x}|^{2}}+\frac{3(\mathbf{x} \cdot \mathbf{y})^{2}-|\mathbf{x}|^{2}|\mathbf{y}|^{2}}{2|\mathbf{x}|^{4}}+O\left(\frac{|\mathbf{y}|^{3}}{|\mathbf{x}|^{3}}\right)\right]$$

  (b) A particle with electric charge $q>0$ has position vector $(a, 0,0)$, where $a>0$. An earthed conductor (held at zero potential) occupies the plane $x=0$. Explain why the boundary conditions can be satisfied by introducing a fictitious 'image' particle of appropriate charge and position. Hence determine the electrostatic potential and the electric field in the region $x>0$. Find the leading-order approximation to the potential for $|\mathbf{x}| \gg a$ and compare with that of an electric dipole. Directly calculate the total flux of the electric field through the plane $x=0$ and comment on the result. Find the induced charge distribution on the surface of the conductor, and the total induced surface charge. Sketch the electric field lines in the plane $z=0$.

  (c) Now consider instead a particle with charge $q$ at position $(a, b, 0)$, where $a>0$ and $b>0$, with earthed conductors occupying the planes $x=0$ and $y=0$. Find the leading-order approximation to the potential in the region $x, y>0$ for $|\mathbf{x}| \gg a, b$ and state what type of multipole potential this is.

  comment

• Paper 3, Section II, 15D

  Electromagnetism | Part IB, 2021

  (a) The energy density stored in the electric and magnetic fields $\mathbf{E}$ and $\mathbf{B}$ is given by

  $$w=\frac{\epsilon_{0}}{2} \mathbf{E} \cdot \mathbf{E}+\frac{1}{2 \mu_{0}} \mathbf{B} \cdot \mathbf{B}$$

  Show that, in regions where no electric current flows,

  $$\frac{\partial w}{\partial t}+\boldsymbol{\nabla} \cdot \mathbf{S}=0$$

  for some vector field $\mathbf{S}$ that you should determine.

  (b) The coordinates $x^{\prime \mu}=\left(c t^{\prime}, \mathbf{x}^{\prime}\right)$ in an inertial frame $\mathcal{S}^{\prime}$ are related to the coordinates $x^{\mu}=(c t, \mathbf{x})$ in an inertial frame $\mathcal{S}$ by a Lorentz transformation $x^{\prime \mu}=\Lambda_{\nu}^{\mu} x^{\nu}$, where

  $$\Lambda_{\nu}^{\mu}=\left(\begin{array}{cccc} \gamma & -\gamma v / c & 0 & 0 \\ -\gamma v / c & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  with $\gamma=\left(1-v^{2} / c^{2}\right)^{-1 / 2}$. Here $v$ is the relative velocity of $\mathcal{S}^{\prime}$ with respect to $\mathcal{S}$ in the x-direction.

  In frame $\mathcal{S}^{\prime}$, there is a static electric field $\mathbf{E}^{\prime}\left(\mathbf{x}^{\prime}\right)$ with $\partial \mathbf{E}^{\prime} / \partial t^{\prime}=0$, and no magnetic field. Calculate the electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$ in frame $\mathcal{S}$. Show that the energy density in frame $\mathcal{S}$ is given in terms of the components of $\mathbf{E}^{\prime}$ by

  $$w=\frac{\epsilon_{0}}{2}\left[E_{x}^{\prime 2}+\left(\frac{c^{2}+v^{2}}{c^{2}-v^{2}}\right)\left(E_{y}^{\prime 2}+E_{z}^{\prime 2}\right)\right]$$

  Use the fact that $\partial w / \partial t^{\prime}=0$ to show that

  $$\frac{\partial w}{\partial t}+\nabla \cdot\left(w v \mathbf{e}_{x}\right)=0$$

  where $\mathbf{e}_{x}$ is the unit vector in the $x$-direction.

  comment

• Paper 4, Section I, $5 \mathrm{D}$

  Electromagnetism | Part IB, 2021

  Write down Maxwell's equations in a vacuum. Show that they admit wave solutions with

  $$\mathbf{B}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{B}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right]$$

  where $\mathbf{B}_{0}, \mathbf{k}$ and $\omega$ must obey certain conditions that you should determine. Find the corresponding electric field $\mathbf{E}(\mathbf{x}, t)$.

  A light wave, travelling in the $x$-direction and linearly polarised so that the magnetic field points in the $z$-direction, is incident upon a conductor that occupies the half-space $x>0$. The electric and magnetic fields obey the boundary conditions $\mathbf{E} \times \mathbf{n}=\mathbf{0}$ and $\mathbf{B} \cdot \mathbf{n}=0$ on the surface of the conductor, where $\mathbf{n}$ is the unit normal vector. Determine the contributions to the magnetic field from the incident and reflected waves in the region $x \leqslant 0$. Compute the magnetic field tangential to the surface of the conductor.

  comment

2020

• Paper 1, Section II, D

  Electromagnetism | Part IB, 2020

  Write down the electric potential due to a point charge $Q$ at the origin.

  A dipole consists of a charge $Q$ at the origin, and a charge $-Q$ at position $-\mathbf{d}$. Show that, at large distances, the electric potential due to such a dipole is given by

  $$\Phi(\mathbf{x})=\frac{1}{4 \pi \epsilon_{0}} \frac{\mathbf{p} \cdot \mathbf{x}}{|\mathbf{x}|^{3}}$$

  where $\mathbf{p}=Q \mathbf{d}$ is the dipole moment. Hence show that the potential energy between two dipoles $\mathbf{p}_{1}$ and $\mathbf{p}_{2}$, with separation $\mathbf{r}$, where $|\mathbf{r}| \gg|\mathbf{d}|$, is

  $$U=\frac{1}{8 \pi \epsilon_{0}}\left(\frac{\mathbf{p}_{1} \cdot \mathbf{p}_{2}}{r^{3}}-\frac{3\left(\mathbf{p}_{1} \cdot \mathbf{r}\right)\left(\mathbf{p}_{2} \cdot \mathbf{r}\right)}{r^{5}}\right)$$

  Dipoles are arranged on an infinite chessboard so that they make an angle $\theta$ with the horizontal in an alternating pattern as shown in the figure. Compute the energy between a given dipole and its four nearest neighbours, and show that this is independent of $\theta$.

  

  comment

• Paper 2, Section I, D

  Electromagnetism | Part IB, 2020

  Two concentric spherical shells with radii $R$ and $2 R$ carry fixed, uniformly distributed charges $Q_{1}$ and $Q_{2}$ respectively. Find the electric field and electric potential at all points in space. Calculate the total energy of the electric field.

  comment

• Paper 2, Section II, D

  Electromagnetism | Part IB, 2020

  (a) A surface current $\mathbf{K}=K \mathbf{e}_{x}$, with $K$ a constant and $\mathbf{e}_{x}$ the unit vector in the $x$-direction, lies in the plane $z=0$. Use Ampère's law to determine the magnetic field above and below the plane. Confirm that the magnetic field is discontinuous across the surface, with the discontinuity given by

  $$\lim _{z \rightarrow 0^{+}} \mathbf{e}_{z} \times \mathbf{B}-\lim _{z \rightarrow 0^{-}} \mathbf{e}_{z} \times \mathbf{B}=\mu_{0} \mathbf{K}$$

  where $\mathbf{e}_{z}$ is the unit vector in the $z$-direction.

  (b) A surface current $\mathbf{K}$ flows radially in the $z=0$ plane, resulting in a pile-up of charge $Q$ at the origin, with $d Q / d t=I$, where $I$ is a constant.

  Write down the electric field $\mathbf{E}$ due to the charge at the origin, and hence the displacement current $\epsilon_{0} \partial \mathbf{E} / \partial t$.

  Confirm that, away from the plane and for $\theta<\pi / 2$, the magnetic field due to the displacement current is given by

  $$\mathbf{B}(r, \theta)=\frac{\mu_{0} I}{4 \pi r} \tan \left(\frac{\theta}{2}\right) \mathbf{e}_{\phi}$$

  where $(r, \theta, \phi)$ are the usual spherical polar coordinates. [Hint: Use Stokes' theorem applied to a spherical cap that subtends an angle $\theta$.]

  comment

2019

• Paper 1, Section II, A

  Electromagnetism | Part IB, 2019

  Let $\mathbf{E}(\mathbf{x})$ be the electric field and $\varphi(\mathbf{x})$ the scalar potential due to a static charge density $\rho(\mathbf{x})$, with all quantities vanishing as $r=|\mathbf{x}|$ becomes large. The electrostatic energy of the configuration is given by

  $$U=\frac{\varepsilon_{0}}{2} \int|\mathbf{E}|^{2} d V=\frac{1}{2} \int \rho \varphi d V$$

  with the integrals taken over all space. Verify that these integral expressions agree.

  Suppose that a total charge $Q$ is distributed uniformly in the region $a \leqslant r \leqslant b$ and that $\rho=0$ otherwise. Use the integral form of Gauss's Law to determine $\mathbf{E}(\mathbf{x})$ at all points in space and, without further calculation, sketch graphs to indicate how $|\mathbf{E}|$ and $\varphi$ depend on position.

  Consider the limit $b \rightarrow a$ with $Q$ fixed. Comment on the continuity of $\mathbf{E}$ and $\varphi$. Verify directly from each of the integrals in $(*)$ that $U=Q \varphi(a) / 2$ in this limit.

  Now consider a small change $\delta Q$ in the total charge $Q$. Show that the first-order change in the energy is $\delta U=\delta Q \varphi(a)$ and interpret this result.

  comment

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2019

  Write down the solution for the scalar potential $\varphi(\mathbf{x})$ that satisfies

  $$\nabla^{2} \varphi=-\frac{1}{\varepsilon_{0}} \rho,$$

  with $\varphi(\mathbf{x}) \rightarrow 0$ as $r=|\mathbf{x}| \rightarrow \infty$. You may assume that the charge distribution $\rho(\mathbf{x})$ vanishes for $r>R$, for some constant $R$. In an expansion of $\varphi(\mathbf{x})$ for $r \gg R$, show that the terms of order $1 / r$ and $1 / r^{2}$ can be expressed in terms of the total charge $Q$ and the electric dipole moment $\mathbf{p}$, which you should define.

  Write down the analogous solution for the vector potential $\mathbf{A}(\mathbf{x})$ that satisfies

  $$\nabla^{2} \mathbf{A}=-\mu_{0} \mathbf{J}$$

  with $\mathbf{A}(\mathbf{x}) \rightarrow \mathbf{0}$ as $r \rightarrow \infty$. You may assume that the current $\mathbf{J}(\mathbf{x})$ vanishes for $r>R$ and that it obeys $\nabla \cdot \mathbf{J}=0$ everywhere. In an expansion of $\mathbf{A}(\mathbf{x})$ for $r \gg R$, show that the term of order $1 / r$ vanishes.

  $\left[\right.$ Hint: $\left.\frac{\partial}{\partial x_{j}}\left(x_{i} J_{j}\right)=J_{i}+x_{i} \frac{\partial J_{j}}{\partial x_{j}} .\right]$

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2019

  Consider a conductor in the shape of a closed curve $C$ moving in the presence of a magnetic field B. State Faraday's Law of Induction, defining any quantities that you introduce.

  Suppose $C$ is a square horizontal loop that is allowed to move only vertically. The location of the loop is specified by a coordinate $z$, measured vertically upwards, and the edges of the loop are defined by $x=\pm a,-a \leqslant y \leqslant a$ and $y=\pm a,-a \leqslant x \leqslant a$. If the magnetic field is

  $$\mathbf{B}=b(x, y,-2 z),$$

  where $b$ is a constant, find the induced current $I$, given that the total resistance of the loop is $R$.

  Calculate the resulting electromagnetic force on the edge of the loop $x=a$, and show that this force acts at an angle $\tan ^{-1}(2 z / a)$ to the vertical. Find the total electromagnetic force on the loop and comment on its direction.

  Now suppose that the loop has mass $m$ and that gravity is the only other force acting on it. Show that it is possible for the loop to fall with a constant downward velocity $R m g /\left(8 b a^{2}\right)^{2}$.

  comment

• Paper 3, Section II, A

  Electromagnetism | Part IB, 2019

  The electric and magnetic fields $\mathbf{E}, \mathbf{B}$ in an inertial frame $\mathcal{S}$ are related to the fields $\mathbf{E}^{\prime}, \mathbf{B}^{\prime}$ in a frame $\mathcal{S}^{\prime}$ by a Lorentz transformation. Given that $\mathcal{S}^{\prime}$ moves in the $x$-direction with speed $v$ relative to $\mathcal{S}$, and that

  $$E_{y}^{\prime}=\gamma\left(E_{y}-v B_{z}\right), \quad B_{z}^{\prime}=\gamma\left(B_{z}-\left(v / c^{2}\right) E_{y}\right),$$

  write down equations relating the remaining field components and define $\gamma$. Use your answers to show directly that $\mathbf{E}^{\prime} \cdot \mathbf{B}^{\prime}=\mathbf{E} \cdot \mathbf{B}$.

  Give an expression for an additional, independent, Lorentz-invariant function of the fields, and check that it is invariant for the special case when $E_{y}=E$ and $B_{y}=B$ are the only non-zero components in the frame $\mathcal{S}$.

  Now suppose in addition that $c B=\lambda E$ with $\lambda$ a non-zero constant. Show that the angle $\theta$ between the electric and magnetic fields in $\mathcal{S}^{\prime}$ is given by

  $$\cos \theta=f(\beta)=\frac{\lambda\left(1-\beta^{2}\right)}{\left\{\left(1+\lambda^{2} \beta^{2}\right)\left(\lambda^{2}+\beta^{2}\right)\right\}^{1 / 2}}$$

  where $\beta=v / c$. By considering the behaviour of $f(\beta)$ as $\beta$ approaches its limiting values, show that the relative velocity of the frames can be chosen so that the angle takes any value in one of the ranges $0 \leqslant \theta<\pi / 2$ or $\pi / 2<\theta \leqslant \pi$, depending on the sign of $\lambda$.

  comment

• Paper 4, Section I, A

  Electromagnetism | Part IB, 2019

  Write down Maxwell's Equations for electric and magnetic fields $\mathbf{E}(\mathbf{x}, t)$ and $\mathbf{B}(\mathbf{x}, t)$ in the absence of charges and currents. Show that there are solutions of the form

  $$\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left\{\mathbf{E}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right\}, \quad \mathbf{B}(\mathbf{x}, t)=\operatorname{Re}\left\{\mathbf{B}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right\}$$

  if $\mathbf{E}_{0}$ and $\mathbf{k}$ satisfy a constraint and if $\mathbf{B}_{0}$ and $\omega$ are then chosen appropriately.

  Find the solution with $\mathbf{E}_{0}=E(1, i, 0)$, where $E$ is real, and $\mathbf{k}=k(0,0,1)$. Compute the Poynting vector and state its physical significance.

  comment

2018

• Paper 1, Section II, C

  Electromagnetism | Part IB, 2018

  Starting from the Lorentz force law acting on a current distribution $\mathbf{J}$ obeying $\boldsymbol{\nabla} \cdot \mathbf{J}=0$, show that the energy of a magnetic dipole $\mathbf{m}$ in the presence of a time independent magnetic field $\mathbf{B}$ is

  $$U=-\mathbf{m} \cdot \mathbf{B}$$

  State clearly any approximations you make.

  [You may use without proof the fact that

  $$\int(\mathbf{a} \cdot \mathbf{r}) \mathbf{J}(\mathbf{r}) \mathrm{d} V=-\frac{1}{2} \mathbf{a} \times \int(\mathbf{r} \times \mathbf{J}(\mathbf{r})) \mathrm{d} V$$

  for any constant vector $\mathbf{a}$, and the identity

  $$(\mathbf{b} \times \boldsymbol{\nabla}) \times \mathbf{c}=\boldsymbol{\nabla}(\mathbf{b} \cdot \mathbf{c})-\mathbf{b}(\boldsymbol{\nabla} \cdot \mathbf{c})$$

  which holds when $\mathbf{b}$ is constant.]

  A beam of slowly moving, randomly oriented magnetic dipoles enters a region where the magnetic field is

  $$\mathbf{B}=\hat{\mathbf{z}} B_{0}+(y \hat{\mathbf{x}}+x \hat{\mathbf{y}}) B_{1},$$

  with $B_{0}$ and $B_{1}$ constants. By considering their energy, briefly describe what happens to those dipoles that are parallel to, and those that are anti-parallel to the direction of $\mathbf{B}$.

  comment

• Paper 2, Section I, $\mathbf{6 C}$

  Electromagnetism | Part IB, 2018

  Derive the Biot-Savart law

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int_{V} \frac{\mathbf{j}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} \mathrm{~d} V$$

  from Maxwell's equations, where the time-independent current $\mathbf{j}(\mathbf{r})$ vanishes outside $V$. [You may assume that the vector potential can be chosen to be divergence-free.]

  comment

• Paper 2, Section II, C

  Electromagnetism | Part IB, 2018

  A plane with unit normal $\mathbf{n}$ supports a charge density and a current density that are each time-independent. Show that the tangential components of the electric field and the normal component of the magnetic field are continuous across the plane.

  Albert moves with constant velocity $\mathbf{v}=v \mathbf{n}$ relative to the plane. Find the boundary conditions at the plane on the normal component of the magnetic field and the tangential components of the electric field as seen in Albert's frame.

  comment

• Paper 3, Section II, C

  Electromagnetism | Part IB, 2018

  Use Maxwell's equations to show that

  $$\frac{d}{d t} \int_{\Omega}\left(\frac{\epsilon_{0}}{2} \mathbf{E} \cdot \mathbf{E}+\frac{1}{2 \mu_{0}} \mathbf{B} \cdot \mathbf{B}\right) d V+\int_{\Omega} \mathbf{J} \cdot \mathbf{E} d V=-\frac{1}{\mu_{0}} \int_{\partial \Omega}(\mathbf{E} \times \mathbf{B}) \cdot \mathbf{n} d S$$

  where $\Omega \subset \mathbb{R}^{3}$ is a bounded region, $\partial \Omega$ its boundary and $\mathbf{n}$ its outward-pointing normal. Give an interpretation for each of the terms in this equation.

  A certain capacitor consists of two conducting, circular discs, each of large area $A$, separated by a small distance along their common axis. Initially, the plates carry charges $q_{0}$ and $-q_{0}$. At time $t=0$ the plates are connected by a resistive wire, causing the charge on the plates to decay slowly as $q(t)=q_{0} \mathrm{e}^{-\lambda t}$ for some constant $\lambda$. Construct the Poynting vector and show that energy flows radially out of the capacitor as it discharges.

  comment

• Paper 4, Section I, $7 \mathrm{C}$

  Electromagnetism | Part IB, 2018

  Show that Maxwell's equations imply the conservation of charge.

  A conducting medium has $\mathbf{J}=\sigma \mathbf{E}$ where $\sigma$ is a constant. Show that any charge density decays exponentially in time, at a rate to be determined.

  comment

2017

• Paper 1, Section II, C

  Electromagnetism | Part IB, 2017

  Write down Maxwell's equations for the electric field $\mathbf{E}(\mathbf{x}, t)$ and the magnetic field $\mathbf{B}(\mathbf{x}, t)$ in a vacuum. Deduce that both $\mathbf{E}$ and $\mathbf{B}$ satisfy a wave equation, and relate the wave speed $c$ to the physical constants $\epsilon_{0}$ and $\mu_{0}$.

  Verify that there exist plane-wave solutions of the form

  $$\begin{aligned} &\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{e} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right] \\ &\mathbf{B}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{b} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right] \end{aligned}$$

  where $\mathbf{e}$ and $\mathbf{b}$ are constant complex vectors, $\mathbf{k}$ is a constant real vector and $\omega$ is a real constant. Derive the dispersion relation that relates the angular frequency $\omega$ of the wave to the wavevector $\mathbf{k}$, and give the algebraic relations between the vectors $\mathbf{e}, \mathbf{b}$ and $\mathbf{k}$ implied by Maxwell's equations.

  Let $\mathbf{n}$ be a constant real unit vector. Suppose that a perfect conductor occupies the region $\mathbf{n} \cdot \mathbf{x}<0$ with a plane boundary $\mathbf{n} \cdot \mathbf{x}=0$. In the vacuum region $\mathbf{n} \cdot \mathbf{x}>0$, a plane electromagnetic wave of the above form, with $\mathbf{k} \cdot \mathbf{n}<0$, is incident on the plane boundary. Write down the boundary conditions on $\mathbf{E}$ and $\mathbf{B}$ at the surface of the conductor. Show that Maxwell's equations and the boundary conditions are satisfied if the solution in the vacuum region is the sum of the incident wave given above and a reflected wave of the form

  $$\begin{aligned} &\mathbf{E}^{\prime}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{e}^{\prime} e^{i\left(\mathbf{k}^{\prime} \cdot \mathbf{x}-\omega t\right)}\right] \\ &\mathbf{B}^{\prime}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{b}^{\prime} e^{i\left(\mathbf{k}^{\prime} \cdot \mathbf{x}-\omega t\right)}\right] \end{aligned}$$

  where

  $$\begin{aligned} &\mathbf{e}^{\prime}=-\mathbf{e}+2(\mathbf{n} \cdot \mathbf{e}) \mathbf{n} \\ &\mathbf{b}^{\prime}=\mathbf{b}-2(\mathbf{n} \cdot \mathbf{b}) \mathbf{n} \\ &\mathbf{k}^{\prime}=\mathbf{k}-2(\mathbf{n} \cdot \mathbf{k}) \mathbf{n} \end{aligned}$$

  comment

• Paper 2, Section I, $\mathbf{6 C}$

  Electromagnetism | Part IB, 2017

  State Gauss's Law in the context of electrostatics.

  A spherically symmetric capacitor consists of two conductors in the form of concentric spherical shells of radii $a$ and $b$, with $b>a$. The inner sphere carries a charge $Q$ and the outer sphere carries a charge $-Q$. Determine the electric field $\mathbf{E}$ and the electrostatic potential $\phi$ in the regions $r<a, a<r<b$ and $r>b$. Show that the capacitance is

  $$C=\frac{4 \pi \epsilon_{0} a b}{b-a}$$

  and calculate the electrostatic energy of the system in terms of $Q$ and $C$.

  comment

• Paper 2, Section II, C

  Electromagnetism | Part IB, 2017

  In special relativity, the electromagnetic fields can be derived from a 4-vector potential $A^{\mu}=(\phi / c, \mathbf{A})$. Using the Minkowski metric tensor $\eta_{\mu \nu}$ and its inverse $\eta^{\mu \nu}$, state how the electromagnetic tensor $F_{\mu \nu}$ is related to the 4-potential, and write out explicitly the components of both $F_{\mu \nu}$ and $F^{\mu \nu}$ in terms of those of $\mathbf{E}$ and $\mathbf{B}$.

  If $x^{\prime \mu}=\Lambda_{\nu}^{\mu} x^{\nu}$ is a Lorentz transformation of the spacetime coordinates from one inertial frame $\mathcal{S}$ to another inertial frame $\mathcal{S}^{\prime}$, state how $F^{\prime \mu \nu}$ is related to $F^{\mu \nu}$.

  Write down the Lorentz transformation matrix for a boost in standard configuration, such that frame $\mathcal{S}^{\prime}$ moves relative to frame $\mathcal{S}$ with speed $v$ in the $+x$ direction. Deduce the transformation laws

  $$\begin{aligned} E_{x}^{\prime} &=E_{x} \\ E_{y}^{\prime} &=\gamma\left(E_{y}-v B_{z}\right) \\ E_{z}^{\prime} &=\gamma\left(E_{z}+v B_{y}\right) \\ B_{x}^{\prime} &=B_{x} \\ B_{y}^{\prime} &=\gamma\left(B_{y}+\frac{v}{c^{2}} E_{z}\right) \\ B_{z}^{\prime} &=\gamma\left(B_{z}-\frac{v}{c^{2}} E_{y}\right) \end{aligned}$$

  where $\gamma=\left(1-\frac{v^{2}}{c^{2}}\right)^{-1 / 2}$

  In frame $\mathcal{S}$, an infinitely long wire of negligible thickness lies along the $x$ axis. The wire carries $n$ positive charges $+q$ per unit length, which travel at speed $u$ in the $+x$ direction, and $n$ negative charges $-q$ per unit length, which travel at speed $u$ in the $-x$ direction. There are no other sources of the electromagnetic field. Write down the electric and magnetic fields in $\mathcal{S}$ in terms of Cartesian coordinates. Calculate the electric field in frame $\mathcal{S}^{\prime}$, which is related to $\mathcal{S}$ by a boost by speed $v$ as described above. Give an explanation of the physical origin of your expression.

  comment

• Paper 3, Section II, C

  Electromagnetism | Part IB, 2017

  (i) Two point charges, of opposite sign and unequal magnitude, are placed at two different locations. Show that the combined electrostatic potential vanishes on a sphere that encloses only the charge of smaller magnitude.

  (ii) A grounded, conducting sphere of radius $a$ is centred at the origin. A point charge $q$ is located outside the sphere at position vector $\mathbf{p}$. Formulate the differential equation and boundary conditions for the electrostatic potential outside the sphere. Using the result of part (i) or otherwise, show that the electric field outside the sphere is identical to that generated (in the absence of any conductors) by the point charge $q$ and an image charge $q^{\prime}$ located inside the sphere at position vector $\mathbf{p}^{\prime}$, provided that $\mathbf{p}^{\prime}$ and $q^{\prime}$ are chosen correctly.

  Calculate the magnitude and direction of the force experienced by the charge $q$.

  comment

• Paper 4 , Section I, $7 \mathrm{C}$

  Electromagnetism | Part IB, 2017

  A thin wire, in the form of a closed curve $C$, carries a constant current $I$. Using either the Biot-Savart law or the magnetic vector potential, show that the magnetic field far from the loop is of the approximate form

  $$\mathbf{B}(\mathbf{r}) \approx \frac{\mu_{0}}{4 \pi}\left[\frac{3(\mathbf{m} \cdot \mathbf{r}) \mathbf{r}-\mathbf{m}|\mathbf{r}|^{2}}{|\mathbf{r}|^{5}}\right]$$

  where $\mathbf{m}$ is the magnetic dipole moment of the loop. Derive an expression for $\mathbf{m}$ in terms of $I$ and the vector area spanned by the curve $C$.

  comment

2016

• Paper 1, Section II, D

  Electromagnetism | Part IB, 2016

  (a) From the differential form of Maxwell's equations with $\mathbf{J}=\mathbf{0}, \mathbf{B}=\mathbf{0}$ and a time-independent electric field, derive the integral form of Gauss's law.

  (b) Derive an expression for the electric field $\mathbf{E}$ around an infinitely long line charge lying along the $z$-axis with charge per unit length $\mu$. Find the electrostatic potential $\phi$ up to an arbitrary constant.

  (c) Now consider the line charge with an ideal earthed conductor filling the region $x>d$. State the boundary conditions satisfied by $\phi$ and $\mathbf{E}$ on the surface of the conductor.

  (d) Show that the same boundary conditions at $x=d$ are satisfied if the conductor is replaced by a second line charge at $x=2 d, y=0$ with charge per unit length $-\mu$.

  (e) Hence or otherwise, returning to the setup in (c), calculate the force per unit length acting on the line charge.

  (f) What is the charge per unit area $\sigma(y, z)$ on the surface of the conductor?

  comment

• Paper 2, Section I, $6 \mathrm{D}$

  Electromagnetism | Part IB, 2016

  (a) Derive the integral form of Ampère's law from the differential form of Maxwell's equations with a time-independent magnetic field, $\rho=0$ and $\mathbf{E}=\mathbf{0}$.

  (b) Consider two perfectly-conducting concentric thin cylindrical shells of infinite length with axes along the $z$-axis and radii $a$ and $b(a<b)$. Current $I$ flows in the positive $z$-direction in each shell. Use Ampère's law to calculate the magnetic field in the three regions: (i) $r<a$, (ii) $a<r<b$ and (iii) $r>b$, where $r=\sqrt{x^{2}+y^{2}}$.

  (c) If current $I$ now flows in the positive $z$-direction in the inner shell and in the negative $z$-direction in the outer shell, calculate the magnetic field in the same three regions.

  comment

• Paper 2, Section II, D

  Electromagnetism | Part IB, 2016

  (a) State the covariant form of Maxwell's equations and define all the quantities that appear in these expressions.

  (b) Show that $\mathbf{E} \cdot \mathbf{B}$ is a Lorentz scalar (invariant under Lorentz transformations) and find another Lorentz scalar involving $\mathbf{E}$ and $\mathbf{B}$.

  (c) In some inertial frame $S$ the electric and magnetic fields are respectively $\mathbf{E}=\left(0, E_{y}, E_{z}\right)$ and $\mathbf{B}=\left(0, B_{y}, B_{z}\right)$. Find the electric and magnetic fields, $\mathbf{E}^{\prime}=\left(0, E_{y}^{\prime}, E_{z}^{\prime}\right)$ and $\mathbf{B}^{\prime}=\left(0, B_{y}^{\prime}, B_{z}^{\prime}\right)$, in another inertial frame $S^{\prime}$ that is related to $S$ by the Lorentz transformation,

  $$\Lambda_{\nu}^{\mu}=\left(\begin{array}{cccc} \gamma & -\gamma v / c & 0 & 0 \\ -\gamma v / c & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  where $v$ is the velocity of $S^{\prime}$ in $S$ and $\gamma=\left(1-v^{2} / c^{2}\right)^{-1 / 2}$.

  (d) Suppose that $\mathbf{E}=E_{0}(0,1,0)$ and $\mathbf{B}=\frac{E_{0}}{c}(0, \cos \theta, \sin \theta)$ where $0 \leqslant \theta \leqslant \pi / 2$, and $E_{0}$ is a real constant. An observer is moving in $S$ with velocity $v$ parallel to the $x$-axis. What must $v$ be for the electric and magnetic fields to appear to the observer to be parallel? Comment on the case $\theta=\pi / 2$.

  comment

• Paper 3, Section II, D

  Electromagnetism | Part IB, 2016

  (a) State Faraday's law of induction for a moving circuit in a time-dependent magnetic field and define all the terms that appear.

  (b) Consider a rectangular circuit DEFG in the $z=0$ plane as shown in the diagram below. There are two rails parallel to the $x$-axis for $x>0$ starting at $\mathrm{D}$ at $(x, y)=(0,0)$ and $G$ at $(0, L)$. A battery provides an electromotive force $\mathcal{E}_{0}$ between $D$ and $G$ driving current in a positive sense around DEFG. The circuit is completed with a bar resistor of resistance $R$, length $L$ and mass $m$ that slides without friction on the rails; it connects $E$ at $(s(t), 0)$ and $F$ at $(s(t), L)$. The rest of the circuit has no resistance. The circuit is in a constant uniform magnetic field $B_{0}$ parallel to the $z$-axis.

  [In parts (i)-(iv) you can neglect any magnetic field due to current flow.]

  

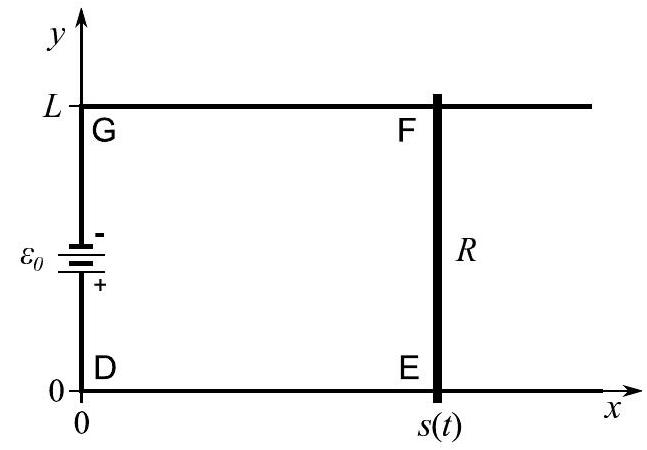
  (i) Calculate the current in the bar and indicate its direction on a diagram of the circuit.

  (ii) Find the force acting on the bar.

  (iii) If the initial velocity and position of the bar are respectively $\dot{s}(0)=v_{0}>0$ and $s(0)=s_{0}>0$, calculate $\dot{s}(t)$ and $s(t)$ for $t>0$.

  (iv) If $\mathcal{E}_{0}=0$, find the total energy dissipated in the circuit after $t=0$ and verify that total energy is conserved.

  (v) Describe qualitatively the effect of the magnetic field caused by the induced current flowing in the circuit when $\mathcal{E}_{0}=0$.

  comment

• Paper 4, Section I, D

  Electromagnetism | Part IB, 2016

  (a) Starting from Maxwell's equations, show that in a vacuum,

  $$\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}-\nabla^{2} \mathbf{E}=\mathbf{0} \quad \text { and } \quad \boldsymbol{\nabla} \cdot \mathbf{E}=0 \quad \text { where } \quad c=\sqrt{\frac{1}{\epsilon_{0} \mu_{0}}} .$$

  (b) Suppose that $\mathbf{E}=\frac{E_{0}}{\sqrt{2}}(1,1,0) \cos (k z-\omega t)$ where $E_{0}, k$ and $\omega$ are real constants.

  (i) What are the wavevector and the polarisation? How is $\omega$ related to $k$ ?

  (ii) Find the magnetic field $\mathbf{B}$.

  (iii) Compute and interpret the time-averaged value of the Poynting vector, $\mathbf{S}=\frac{1}{\mu_{0}} \mathbf{E} \times \mathbf{B}$.

  comment

2015

• Paper 1, Section II, A

  Electromagnetism | Part IB, 2015

  (i) Write down the Lorentz force law for $d \mathbf{p} / d t$ due to an electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$ acting on a particle of charge $q$ moving with velocity $\dot{\mathbf{x}}$.

  (ii) Write down Maxwell's equations in terms of $c$ (the speed of light in a vacuum), in the absence of charges and currents.

  (iii) Show that they can be manipulated into a wave equation for each component of $\mathbf{E}$.

  (iv) Show that Maxwell's equations admit solutions of the form

  $$\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left(\mathbf{E}_{0} e^{i(\omega t-\mathbf{k} \cdot \mathbf{x})}\right)$$

  where $\mathbf{E}_{\mathbf{0}}$ and $\mathbf{k}$ are constant vectors and $\omega$ is a constant (all real). Derive a condition on $\mathbf{k} \cdot \mathbf{E}_{\mathbf{0}}$ and relate $\omega$ and $\mathbf{k}$.

  (v) Suppose that a perfect conductor occupies the region $z<0$ and that a plane wave with $\mathbf{k}=(0,0,-k), \mathbf{E}_{0}=\left(E_{0}, 0,0\right)$ is incident from the vacuum region $z>0$. Write down boundary conditions for the $\mathbf{E}$ and $\mathbf{B}$ fields. Show that they can be satisfied if a suitable reflected wave is present, and determine the total $\mathbf{E}$ and $\mathbf{B}$ fields in real form.

  (vi) At time $t=\pi /(4 \omega)$, a particle of charge $q$ and mass $m$ is at $(0,0, \pi /(4 k))$ moving with velocity $(c / 2,0,0)$. You may assume that the particle is far enough away from the conductor so that we can ignore its effect upon the conductor and that $q E_{0}>0$. Give a unit vector for the direction of the Lorentz force on the particle at time $t=\pi /(4 \omega)$.

  (vii) Ignoring relativistic effects, find the magnitude of the particle's rate of change of velocity in terms of $E_{0}, q$ and $m$ at time $t=\pi /(4 \omega)$. Why is this answer inaccurate?

  comment

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2015

  In a constant electric field $\mathbf{E}=(E, 0,0)$ a particle of rest mass $m$ and charge $q>0$ has position $\mathbf{x}$ and velocity $\dot{\mathbf{x}}$. At time $t=0$, the particle is at rest at the origin. Including relativistic effects, calculate $\dot{\mathbf{x}}(t)$.

  Sketch a graph of $|\dot{\mathbf{x}}(t)|$ versus $t$, commenting on the $t \rightarrow \infty$ limit.

  Calculate $|\mathbf{x}(t)|$ as an explicit function of $t$ and find the non-relativistic limit at small times $t$.

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2015

  Consider the magnetic field

  $$\mathbf{B}=b[\mathbf{r}+(k \hat{\mathbf{z}}+l \hat{\mathbf{y}}) \hat{\mathbf{z}} \cdot \mathbf{r}+p \hat{\mathbf{x}}(\hat{\mathbf{y}} \cdot \mathbf{r})+n \hat{\mathbf{z}}(\hat{\mathbf{x}} \cdot \mathbf{r})],$$

  where $b \neq 0, \mathbf{r}=(x, y, z)$ and $\hat{\mathbf{x}}, \hat{\mathbf{y}}, \hat{\mathbf{z}}$ are unit vectors in the $x, y$ and $z$ directions, respectively. Imposing that this satisfies the expected equations for a static magnetic field in a vacuum, find $k, l, n$ and $p$.

  A circular wire loop of radius $a$, mass $m$ and resistance $R$ lies in the $(x, y)$ plane with its centre on the $z$-axis at $z$ and a magnetic field as given above. Calculate the magnetic flux through the loop arising from this magnetic field and also the force acting on the loop when a current $I$ is flowing around the loop in a clockwise direction about the $z$-axis.

  At $t=0$, the centre of the loop is at the origin, travelling with velocity $(0,0, v(t=0))$, where $v(0)>0$. Ignoring gravity and relativistic effects, and assuming that $I$ is only the induced current, find the time taken for the speed to halve in terms of $a, b, R$ and $m$. By what factor does the rate of heat generation change in this time?

  Where is the loop as $t \rightarrow \infty$ as a function of $a, b, R, v(0) ?$

  comment

• Paper 3, Section II, A

  Electromagnetism | Part IB, 2015

  A charge density $\rho=\lambda / r$ fills the region of 3-dimensional space $a<r<b$, where $r$ is the radial distance from the origin and $\lambda$ is a constant. Compute the electric field in all regions of space in terms of $Q$, the total charge of the region. Sketch a graph of the magnitude of the electric field versus $r$ (assuming that $Q>0$ ).

  Now let $\Delta=b-a \rightarrow 0$. Derive the surface charge density $\sigma$ in terms of $\Delta, a$ and $\lambda$ and explain how a finite surface charge density may be obtained in this limit. Sketch the magnitude of the electric field versus $r$ in this limit. Comment on any discontinuities, checking a standard result involving $\sigma$ for this particular case.

  A second shell of equal and opposite total charge is centred on the origin and has a radius $c<a$. Sketch the electric potential of this system, assuming that it tends to 0 as $r \rightarrow \infty$.

  comment

• Paper 4, Section I, A

  Electromagnetism | Part IB, 2015

  From Maxwell's equations, derive the Biot-Savart law

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int_{V} \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d^{3} \mathbf{r}^{\prime}$$

  giving the magnetic field $\mathbf{B}(\mathbf{r})$ produced by a steady current density $\mathbf{J}(\mathbf{r})$ that vanishes outside a bounded region $V$.

  [You may assume that you can choose a gauge such that the divergence of the magnetic vector potential is zero.]

  comment

2014

• Paper 1, Section II, A

  Electromagnetism | Part IB, 2014

  The region $z<0$ is occupied by an ideal earthed conductor and a point charge $q$ with mass $m$ is held above it at $(0,0, d)$.

  (i) What are the boundary conditions satisfied by the electric field $\mathbf{E}$ on the surface of the conductor?

  (ii) Consider now a system without the conductor mentioned above. A point charge $q$ with mass $m$ is held at $(0,0, d)$, and one of charge $-q$ is held at $(0,0,-d)$. Show that the boundary condition on $\mathbf{E}$ at $z=0$ is identical to the answer to (i). Explain why this represents the electric field due to the charge at $(0,0, d)$ under the influence of the conducting boundary.

  (iii) The original point charge in (i) is released with zero initial velocity. Find the time taken for the point charge to reach the plane (ignoring gravity).

  [You may assume that the force on the point charge is equal to $m d^{2} \mathbf{x} / d t^{2}$, where $\mathbf{x}$ is the position vector of the charge, and $t$ is time.]

  comment

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2014

  Starting from Maxwell's equations, deduce that

  $$\frac{d \Phi}{d t}=-\mathcal{E}$$

  for a moving circuit $C$, where $\Phi$ is the flux of $\mathbf{B}$ through the circuit and where the electromotive force $\mathcal{E}$ is defined to be

  $$\mathcal{E}=\oint_{\mathcal{C}}(\mathbf{E}+\mathbf{v} \times \mathbf{B}) \cdot \mathbf{d} \mathbf{r}$$

  where $\mathbf{v}=\mathbf{v}(\mathbf{r})$ denotes the velocity of a point $\mathbf{r}$ on $C$.

  [Hint: Consider the closed surface consisting of the surface $S(t)$ bounded by $C(t)$, the surface $S(t+\delta t)$ bounded by $C(t+\delta t)$ and the surface $S^{\prime}$ stretching from $C(t)$ to $C(t+\delta t)$. Show that the flux of $\mathbf{B}$ through $S^{\prime}$ is $-\delta t \oint_{C} \mathbf{B} \cdot(\mathbf{v} \times \mathbf{d r})$.]

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2014

  What is the relationship between the electric field $\mathbf{E}$ and the charge per unit area $\sigma$ on the surface of a perfect conductor?

  Consider a charge distribution $\rho(\mathbf{r})$ distributed with potential $\phi(\mathbf{r})$ over a finite volume $V$ within which there is a set of perfect conductors with charges $Q_{i}$, each at a potential $\phi_{i}$ (normalised such that the potential at infinity is zero). Using Maxwell's equations and the divergence theorem, derive a relationship between the electrostatic energy $W$ and a volume integral of an explicit function of the electric field $\mathbf{E}$, where

  $$W=\frac{1}{2} \int_{V} \rho \phi d \tau+\frac{1}{2} \sum_{i} Q_{i} \phi_{i}$$

  Consider $N$ concentric perfectly conducting spherical shells. Shell $n$ has radius $r_{n}$ (where $r_{n}>r_{n-1}$ ) and charge $q$ for $n=1$, and charge $2(-1)^{(n+1)} q$ for $n>1$. Show that

  $$W \propto \frac{1}{r_{1}},$$

  and determine the constant of proportionality.

  comment

• Paper 3, Section II, A

  Electromagnetism | Part IB, 2014

  (i) Consider charges $-q$ at $\pm \mathbf{d}$ and $2 q$ at $(0,0,0)$. Write down the electric potential.

  (ii) Take $\mathbf{d}=(0,0, d)$. A quadrupole is defined in the limit that $q \rightarrow \infty, d \rightarrow 0$ such that $q d^{2}$ tends to a constant $p$. Find the quadrupole's potential, showing that it is of the form

  $$\phi(\mathbf{r})=A \frac{\left(r^{2}+C z^{D}\right)}{r^{B}}$$

  where $r=|\mathbf{r}|$. Determine the constants $A, B, C$ and $D$.

  (iii) The quadrupole is fixed at the origin. At time $t=0$ a particle of charge $-Q(Q$ has the same sign as $q)$ and mass $m$ is at $(1,0,0)$ travelling with velocity $d \mathbf{r} / d t=(-\kappa, 0,0)$, where

  $$\kappa=\sqrt{\frac{Q p}{2 \pi \epsilon_{0} m}} .$$

  Neglecting gravity, find the time taken for the particle to reach the quadrupole in terms of $\kappa$, given that the force on the particle is equal to $m d^{2} \mathbf{r} / d t^{2}$.

  comment

• Paper 4, Section I, A

  Electromagnetism | Part IB, 2014

  A continuous wire of resistance $R$ is wound around a very long right circular cylinder of radius $a$, and length $l$ (long enough so that end effects can be ignored). There are $N \gg 1$ turns of wire per unit length, wound in a spiral of very small pitch. Initially, the magnetic field $\mathbf{B}$ is $\mathbf{0}$.

  Both ends of the coil are attached to a battery of electromotance $\mathcal{E}_{0}$ at $t=0$, which induces a current $I(t)$. Use Ampère's law to derive $\mathbf{B}$ inside and outside the cylinder when the displacement current may be neglected. Write the self-inductance of the coil $L$ in terms of the quantities given above. Using Ohm's law and Faraday's law of induction, find $I(t)$ explicitly in terms of $\mathcal{E}_{0}, R, L$ and $t$.

  comment

2013

• Paper 1, Section II, $16 \mathrm{D}$

  Electromagnetism | Part IB, 2013

  Briefly explain the main assumptions leading to Drude's theory of conductivity. Show that these assumptions lead to the following equation for the average drift velocity $\langle\mathbf{v}(t)\rangle$ of the conducting electrons:

  $$\frac{d\langle\mathbf{v}\rangle}{d t}=-\tau^{-1}\langle\mathbf{v}\rangle+(e / m) \mathbf{E}$$

  where $m$ and $e$ are the mass and charge of each conducting electron, $\tau^{-1}$ is the probability that a given electron collides with an ion in unit time, and $\mathbf{E}$ is the applied electric field.

  Given that $\langle\mathbf{v}\rangle=\mathbf{v}_{0} e^{-i \omega t}$ and $\mathbf{E}=\mathbf{E}_{0} e^{-i \omega t}$, where $\mathbf{v}_{0}$ and $\mathbf{E}_{0}$ are independent of $t$, show that

  $$\mathbf{J}=\sigma \mathbf{E}$$

  Here, $\sigma=\sigma_{s} /(1-i \omega \tau), \sigma_{s}=n e^{2} \tau / m$ and $n$ is the number of conducting electrons per unit volume.

  Now let $\mathbf{v}_{0}=\widetilde{\mathbf{v}}_{0} e^{i \mathbf{k} \cdot \mathbf{x}}$ and $\mathbf{E}_{0}=\widetilde{\mathbf{E}}_{0} e^{i \mathbf{k} \cdot \mathbf{x}}$, where $\widetilde{\mathbf{v}}_{0}$ and $\widetilde{\mathbf{E}}_{0}$ are constant. Assuming that $(*)$ remains valid, use Maxwell's equations (taking the charge density to be everywhere zero but allowing for a non-zero current density) to show that

  $$k^{2}=\frac{\omega^{2}}{c^{2}} \epsilon_{r}$$

  where the relative permittivity $\epsilon_{r}=1+i \sigma /\left(\omega \epsilon_{0}\right)$ and $k=|\mathbf{k}|$.

  In the case $\omega \tau \gg 1$ and $\omega<\omega_{p}$, where $\omega_{p}^{2}=\sigma_{s} / \tau \epsilon_{0}$, show that the wave decays exponentially with distance inside the conductor.

  comment

• Paper 2, Section I, D

  Electromagnetism | Part IB, 2013

  Use Maxwell's equations to obtain the equation of continuity

  $$\frac{\partial \rho}{\partial t}+\nabla \cdot \mathbf{J}=0$$

  Show that, for a body made from material of uniform conductivity $\sigma$, the charge density at any fixed internal point decays exponentially in time. If the body is finite and isolated, explain how this result can be consistent with overall charge conservation.

  comment

• Paper 2, Section II, D

  Electromagnetism | Part IB, 2013

  Starting with the expression

  $$\mathbf{A}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right) d V^{\prime}}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|}$$

  for the magnetic vector potential at the point $r$ due to a current distribution of density $\mathbf{J}(\mathbf{r})$, obtain the Biot-Savart law for the magnetic field due to a current $I$ flowing in a simple loop $C$ :

  $$\mathbf{B}(\mathbf{r})=-\frac{\mu_{0} I}{4 \pi} \oint_{C} \frac{d \mathbf{r}^{\prime} \times\left(\mathbf{r}^{\prime}-\mathbf{r}\right)}{\left|\mathbf{r}^{\prime}-\mathbf{r}\right|^{3}} \quad(\mathbf{r} \notin C) .$$

  Verify by direct differentiation that this satisfies $\boldsymbol{\nabla} \times \mathbf{B}=\mathbf{0}$. You may use without proof the identity $\boldsymbol{\nabla} \times(\mathbf{a} \times \mathbf{v})=\mathbf{a}(\boldsymbol{\nabla} \cdot \mathbf{v})-(\mathbf{a} \cdot \boldsymbol{\nabla}) \mathbf{v}$, where $\mathbf{a}$ is a constant vector and $\mathbf{v}$ is a vector field.

  Given that $C$ is planar, and is described in cylindrical polar coordinates by $z=0$, $r=f(\theta)$, show that the magnetic field at the origin is

  $$\widehat{\mathbf{z}} \frac{\mu_{0} I}{4 \pi} \oint \frac{d \theta}{f(\theta)}$$

  If $C$ is the ellipse $r(1-e \cos \theta)=\ell$, find the magnetic field at the focus due to a current $I$.

  comment

• Paper 3, Section II, D

  Electromagnetism | Part IB, 2013

  Three sides of a closed rectangular circuit $C$ are fixed and one is moving. The circuit lies in the plane $z=0$ and the sides are $x=0, y=0, x=a(t), y=b$, where $a(t)$ is a given function of time. A magnetic field $\mathbf{B}=\left(0,0, \frac{\partial f}{\partial x}\right)$ is applied, where $f(x, t)$ is a given function of $x$ and $t$ only. Find the magnetic flux $\Phi$ of $\mathbf{B}$ through the surface $S$ bounded by $C$.

  Find an electric field $\mathbf{E}_{\mathbf{0}}$ that satisfies the Maxwell equation

  $$\boldsymbol{\nabla} \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$$

  and then write down the most general solution $\mathbf{E}$ in terms of $\mathbf{E}_{0}$ and an undetermined scalar function independent of $f$.

  Verify that

  $$\oint_{C}(\mathbf{E}+\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{r}=-\frac{d \Phi}{d t},$$

  where $\mathbf{v}$ is the velocity of the relevant side of $C$. Interpret the left hand side of this equation.

  If a unit current flows round $C$, what is the rate of work required to maintain the motion of the moving side of the rectangle? You should ignore any electromagnetic fields produced by the current.

  comment

• Paper 4, Section I, D

  Electromagnetism | Part IB, 2013

  The infinite plane $z=0$ is earthed and the infinite plane $z=d$ carries a charge of $\sigma$ per unit area. Find the electrostatic potential between the planes.

  Show that the electrostatic energy per unit area (of the planes $z=$ constant) between the planes can be written as either $\frac{1}{2} \sigma^{2} d / \epsilon_{0}$ or $\frac{1}{2} \epsilon_{0} V^{2} / d$, where $V$ is the potential at $z=d$.

  The distance between the planes is now increased by $\alpha d$, where $\alpha$ is small. Show that the change in the energy per unit area is $\frac{1}{2} \sigma V \alpha$ if the upper plane $(z=d)$ is electrically isolated, and is approximately $-\frac{1}{2} \sigma V \alpha$ if instead the potential on the upper plane is maintained at $V$. Explain briefly how this difference can be accounted for.

  comment

2012

• Paper 1, Section II, B

  Electromagnetism | Part IB, 2012

  A sphere of radius a carries an electric charge $Q$ uniformly distributed over its surface. Calculate the electric field outside and inside the sphere. Also calculate the electrostatic potential outside and inside the sphere, assuming it vanishes at infinity. State the integral formula for the energy $U$ of the electric field and use it to evaluate $U$ as a function of $Q$

  Relate $\frac{d U}{d Q}$ to the potential on the surface of the sphere and explain briefly the physical interpretation of the relation.

  comment

• Paper 2, Section I, B

  Electromagnetism | Part IB, 2012

  Write down the expressions for a general, time-dependent electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$ in terms of a vector potential $\mathbf{A}$ and scalar potential $\phi$. What is meant by a gauge transformation of $\mathbf{A}$ and $\phi$ ? Show that $\mathbf{E}$ and $\mathbf{B}$ are unchanged under a gauge transformation.

  A plane electromagnetic wave has vector and scalar potentials

  $$\begin{aligned} \mathbf{A}(\mathbf{x}, t) &=\mathbf{A}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)} \\ \phi(\mathbf{x}, t) &=\phi_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)} \end{aligned}$$

  where $\mathbf{A}_{0}$ and $\phi_{0}$ are constants. Show that $\left(\mathbf{A}_{0}, \phi_{0}\right)$ can be modified to $\left(\mathbf{A}_{0}+\mu \mathbf{k}, \phi_{0}+\mu \omega\right)$ by a gauge transformation. What choice of $\mu$ leads to the modified $\mathbf{A}(\mathbf{x}, t)$ satisfying the Coulomb gauge condition $\boldsymbol{\nabla} \cdot \mathbf{A}=0$ ?

  comment

• Paper 2, Section II, B

  Electromagnetism | Part IB, 2012

  A straight wire has $n$ mobile, charged particles per unit length, each of charge $q$. Assuming the charges all move with velocity $v$ along the wire, show that the current is $I=n q v$.

  Using the Lorentz force law, show that if such a current-carrying wire is placed in a uniform magnetic field of strength $B$ perpendicular to the wire, then the force on the wire, per unit length, is $B I$.

  Consider two infinite parallel wires, with separation $L$, carrying (in the same sense of direction) positive currents $I_{1}$ and $I_{2}$, respectively. Find the force per unit length on each wire, determining both its magnitude and direction.

  comment

• Paper 3, Section II, B

  Electromagnetism | Part IB, 2012

  Using the Maxwell equations

  $$\begin{gathered} \nabla \cdot \mathbf{E}=\frac{\rho}{\epsilon_{0}}, \quad \nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t} \\ \nabla \cdot \mathbf{B}=0, \quad \boldsymbol{\nabla} \times \mathbf{B}-\epsilon_{0} \mu_{0} \frac{\partial \mathbf{E}}{\partial t}=\mu_{0} \mathbf{j} \end{gathered}$$

  show that in vacuum, E satisfies the wave equation

  $$\frac{1}{c^{2}} \frac{\partial^{2} \mathbf{E}}{\partial t^{2}}-\nabla^{2} \mathbf{E}=0$$

  where $c^{2}=\left(\epsilon_{0} \mu_{0}\right)^{-1}$, as well as $\nabla \cdot \mathbf{E}=0$. Also show that at a planar boundary between two media, $\mathbf{E}_{t}$ (the tangential component of $\mathbf{E}$ ) is continuous. Deduce that if one medium is of negligible resistance, $\mathbf{E}_{t}=0$.

  Consider an empty cubic box with walls of negligible resistance on the planes $x=0$, $x=a, y=0, y=a, z=0, z=a$, where $a>0$. Show that an electric field in the interior of the form

  $$\begin{aligned} &E_{x}=f(x) \sin \left(\frac{m \pi y}{a}\right) \sin \left(\frac{n \pi z}{a}\right) e^{-i \omega t} \\ &E_{y}=g(y) \sin \left(\frac{l \pi x}{a}\right) \sin \left(\frac{n \pi z}{a}\right) e^{-i \omega t} \\ &E_{z}=h(z) \sin \left(\frac{l \pi x}{a}\right) \sin \left(\frac{m \pi y}{a}\right) e^{-i \omega t} \end{aligned}$$

  with $l, m$ and $n$ positive integers, satisfies the boundary conditions on all six walls. Now suppose that

  $$f(x)=f_{0} \cos \left(\frac{l \pi x}{a}\right), \quad g(y)=g_{0} \cos \left(\frac{m \pi y}{a}\right), \quad h(z)=h_{0} \cos \left(\frac{n \pi z}{a}\right)$$

  where $f_{0}, g_{0}$ and $h_{0}$ are constants. Show that the wave equation $(*)$ is satisfied, and determine the frequency $\omega$. Find the further constraint on $f_{0}, g_{0}$ and $h_{0}$ ?

  comment

• Paper 4, Section I, B

  Electromagnetism | Part IB, 2012

  Define the notions of magnetic flux, electromotive force and resistance, in the context of a single closed loop of wire. Use the Maxwell equation

  $$\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$$

  to derive Faraday's law of induction for the loop, assuming the loop is at rest.

  Suppose now that the magnetic field is $\mathbf{B}=(0,0, B \tanh t)$ where $B$ is a constant, and that the loop of wire, with resistance $R$, is a circle of radius a lying in the $(x, y)$ plane. Calculate the current in the wire as a function of time.

  Explain briefly why, even in a time-independent magnetic field, an electromotive force may be produced in a loop of wire that moves through the field, and state the law of induction in this situation.

  comment

2011

• Paper 1, Section II, D

  Electromagnetism | Part IB, 2011

  Starting from the relevant Maxwell equation, derive Gauss's law in integral form.

  Use Gauss's law to obtain the potential at a distance $r$ from an infinite straight wire with charge $\lambda$ per unit length.

  Write down the potential due to two infinite wires parallel to the $z$-axis, one at $x=y=0$ with charge $\lambda$ per unit length and the other at $x=0, y=d$ with charge $-\lambda$ per unit length.

  Find the potential and the electric field in the limit $d \rightarrow 0$ with $\lambda d=p$ where $p$ is fixed. Sketch the equipotentials and the electric field lines.

  comment

• Paper 2, Section I, $\mathbf{6 C}$

  Electromagnetism | Part IB, 2011

  Maxwell's equations are

  $$\begin{gathered} \boldsymbol{\nabla} \cdot \mathbf{E}=\frac{\rho}{\epsilon_{0}}, \quad \boldsymbol{\nabla} \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t} \\ \nabla \cdot \mathbf{B}=0, \quad \nabla \times \mathbf{B}=\mu_{0} \mathbf{J}+\epsilon_{0} \mu_{0} \frac{\partial \mathbf{E}}{\partial t} \end{gathered}$$

  Find the equation relating $\rho$ and $\mathbf{J}$ that must be satisfied for consistency, and give the interpretation of this equation.

  Now consider the "magnetic limit" where $\rho=0$ and the term $\epsilon_{0} \mu_{0} \frac{\partial \mathbf{E}}{\partial t}$ is neglected. Let $\mathbf{A}$ be a vector potential satisfying the gauge condition $\boldsymbol{\nabla} \cdot \mathbf{A}=0$, and assume the scalar potential vanishes. Find expressions for $\mathbf{E}$ and $\mathbf{B}$ in terms of $\mathbf{A}$ and show that Maxwell's equations are all satisfied provided $\mathbf{A}$ satisfies the appropriate Poisson equation.

  comment

• Paper 2, Section II, C

  Electromagnetism | Part IB, 2011

  (i) Consider an infinitely long solenoid parallel to the $z$-axis whose cross section is a simple closed curve of arbitrary shape. A current $I$, per unit length of the solenoid, flows around the solenoid parallel to the $x-y$ plane. Show using the relevant Maxwell equation that the magnetic field $\mathbf{B}$ inside the solenoid is uniform, and calculate its magnitude.

  (ii) A wire loop in the shape of a regular hexagon of side length $a$ carries a current $I$. Use the Biot-Savart law to calculate $\mathbf{B}$ at the centre of the loop.

  comment

• Paper 3, Section II, C

  Electromagnetism | Part IB, 2011

  Show, using the vacuum Maxwell equations, that for any volume $V$ with surface $S$,

  $$\frac{d}{d t} \int_{V}\left(\frac{\epsilon_{0}}{2} \mathbf{E} \cdot \mathbf{E}+\frac{1}{2 \mu_{0}} \mathbf{B} \cdot \mathbf{B}\right) d V=\int_{S}\left(-\frac{1}{\mu_{0}} \mathbf{E} \times \mathbf{B}\right) \cdot \mathbf{d} \mathbf{S}$$

  What is the interpretation of this equation?

  A uniform straight wire, with a circular cross section of radius $r$, has conductivity $\sigma$ and carries a current $I$. Calculate $\frac{1}{\mu_{0}} \mathbf{E} \times \mathbf{B}$ at the surface of the wire, and hence find the flux of $\frac{1}{\mu_{0}} \mathbf{E} \times \mathbf{B}$ into unit length of the wire. Relate your result to the resistance of the wire, and the rate of energy dissipation.

  comment

• Paper 4, Section I, C

  Electromagnetism | Part IB, 2011

  A plane electromagnetic wave in a vacuum has electric field

  $$\mathbf{E}=\left(E_{0} \sin k(z-c t), 0,0\right)$$

  What are the wavevector, polarization vector and speed of the wave? Using Maxwell's equations, find the magnetic field B. Assuming the scalar potential vanishes, find a possible vector potential $\mathbf{A}$ for this wave, and verify that it gives the correct $\mathbf{E}$ and $\mathbf{B}$.

  comment

2010

• Paper 1, Section II, C

  Electromagnetism | Part IB, 2010

  A capacitor consists of three perfectly conducting coaxial cylinders of radii $a, b$ and $c$ where $0<a<b<c$, and length $L$ where $L \gg c$ so that end effects may be ignored. The inner and outer cylinders are maintained at zero potential, while the middle cylinder is held at potential $V$. Assuming its cylindrical symmetry, compute the electrostatic potential within the capacitor, the charge per unit length on the middle cylinder, the capacitance and the electrostatic energy, both per unit length.

  Next assume that the radii $a$ and $c$ are fixed, as is the potential $V$, while the radius $b$ is allowed to vary. Show that the energy achieves a minimum when $b$ is the geometric mean of $a$ and $c$.

  comment

• Paper 2, Section I, $\mathbf{6 C}$

  Electromagnetism | Part IB, 2010

  Write down Maxwell's equations for electromagnetic fields in a non-polarisable and non-magnetisable medium.

  Show that the homogenous equations (those not involving charge or current densities) can be solved in terms of vector and scalar potentials $\mathbf{A}$ and $\phi$.

  Then re-express the inhomogeneous equations in terms of $\mathbf{A}, \phi$ and $f=\nabla \cdot \mathbf{A}+c^{-2} \dot{\phi}$. Show that the potentials can be chosen so as to set $f=0$ and hence rewrite the inhomogeneous equations as wave equations for the potentials. [You may assume that the inhomogeneous wave equation $\nabla^{2} \psi-c^{-2} \ddot{\psi}=\sigma(\mathbf{x}, t)$ always has a solution $\psi(\mathbf{x}, t)$ for any given $\sigma(\mathbf{x}, t)$.]

  comment

• Paper 2, Section II, C

  Electromagnetism | Part IB, 2010

  A steady current $I_{2}$ flows around a loop $\mathcal{C}_{2}$ of a perfectly conducting narrow wire. Assuming that the gauge condition $\nabla \cdot \mathbf{A}=0$ holds, the vector potential at points away from the loop may be taken to be

  $$\mathbf{A}(\mathbf{r})=\frac{\mu_{0} I_{2}}{4 \pi} \oint_{\mathcal{C}_{2}} \frac{d \mathbf{r}_{2}}{\left|\mathbf{r}-\mathbf{r}_{2}\right|}$$

  First verify that the gauge condition is satisfied here. Then obtain the Biot-Savart formula for the magnetic field

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0} I_{2}}{4 \pi} \oint_{\mathcal{C}_{2}} \frac{d \mathbf{r}_{2} \times\left(\mathbf{r}-\mathbf{r}_{2}\right)}{\left|\mathbf{r}-\mathbf{r}_{2}\right|^{3}}$$

  Next suppose there is a similar but separate loop $\mathcal{C}_{1}$ with current $I_{1}$. Show that the magnetic force exerted on loop $\mathcal{C}_{1}$ by loop $\mathcal{C}_{2}$ is

  $$\mathbf{F}_{12}=\frac{\mu_{0} I_{1} I_{2}}{4 \pi} \oint_{\mathcal{C}_{1}} \oint_{\mathcal{C}_{2}} d \mathbf{r}_{1} \times\left(d \mathbf{r}_{2} \times \frac{\mathbf{r}_{1}-\mathbf{r}_{2}}{\left|\mathbf{r}_{1}-\mathbf{r}_{2}\right|^{3}}\right)$$

  Is this consistent with Newton's third law? Justify your answer.

  comment

• Paper 3, Section II, C

  Electromagnetism | Part IB, 2010

  Write down Maxwell's equations in a region with no charges and no currents. Show that if $\mathbf{E}(\mathbf{x}, t)$ and $\mathbf{B}(\mathbf{x}, t)$ is a solution then so is $\widetilde{\mathbf{E}}(\mathbf{x}, t)=c \mathbf{B}(\mathbf{x}, t)$ and $\widetilde{\mathbf{B}}(\mathbf{x}, t)=-\mathbf{E}(\mathbf{x}, t) / c$. Write down the boundary conditions on $\mathbf{E}$ and $\mathbf{B}$ at the boundary with unit normal $\mathbf{n}$ between a perfect conductor and a vacuum.

  Electromagnetic waves propagate inside a tube of perfectly conducting material. The tube's axis is in the $z$-direction, and it is surrounded by a vacuum. The fields may be taken to be the real parts of

  $$\mathbf{E}(\mathbf{x}, t)=\mathbf{e}(x, y) e^{i(k z-\omega t)}, \quad \mathbf{B}(\mathbf{x}, t)=\mathbf{b}(x, y) e^{i(k z-\omega t)}$$

  Write down Maxwell's equations in terms of $\mathbf{e}, \mathbf{b}, k$ and $\omega$.

  Suppose first that $b_{z}(x, y)=0$. Show that the solution is determined by

  $$\mathbf{e}=\left(\frac{\partial \psi}{\partial x}, \frac{\partial \psi}{\partial y}, i k\left[1-\frac{\omega^{2}}{k^{2} c^{2}}\right] \psi\right)$$

  where the function $\psi(x, y)$ satisfies

  $$\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}+\gamma^{2} \psi=0$$

  and $\psi$ vanishes on the boundary of the tube. Here $\gamma^{2}$ is a constant whose value should be determined.

  Obtain a similar condition for the case where $e_{z}(x, y)=0$. [You may find it useful to use a result from the first paragraph.] What is the corresponding boundary condition?

  comment

• Paper 4, Section I, B

  Electromagnetism | Part IB, 2010

  Give an expression for the force $\mathbf{F}$ on a charge $q$ moving at velocity $\mathbf{v}$ in electric and magnetic fields $\mathbf{E}$ and $\mathbf{B}$. Consider a stationary electric circuit $C$, and let $S$ be a stationary surface bounded by $C$. Derive from Maxwell's equations the result

  $$\mathcal{E}=-\frac{d \Phi}{d t}$$

  where the electromotive force $\mathcal{E}=\oint_{C} q^{-1} \mathbf{F} \cdot d \mathbf{r}$ and the flux $\Phi=\int_{S} \mathbf{B} \cdot d \mathbf{S}$.

  Now assume that $(*)$ also holds for a moving circuit. A circular loop of wire of radius $a$ and total resistance $R$, whose normal is in the $z$-direction, moves at constant speed $v$ in the $x$-direction in the presence of a magnetic field $\mathbf{B}=\left(0,0, B_{0} x / d\right)$. Find the current in the wire.

  comment

2009

• Paper 1, Section II, A

  Electromagnetism | Part IB, 2009

  Suppose the region $z<0$ is occupied by an earthed ideal conductor.

  (a) Derive the boundary conditions on the tangential electric field $\mathbf{E}$ that hold on the surface $z=0$.

  (b) A point charge $q$, with mass $m$, is held above the conductor at $(0,0, d)$. Show that the boundary conditions on the electric field are satisfied if we remove the conductor and instead place a second charge $-q$ at $(0,0,-d)$.

  (c) The original point charge is now released with zero initial velocity. Ignoring gravity, determine how long it will take for the charge to hit the plane.

  comment

• Paper 2, Section I, A

  Electromagnetism | Part IB, 2009

  For a volume $V$ with surface $S$, state Gauss's Law relating the flux of $\mathbf{E}$ across $S$ to the total charge within $V$.

  A uniformly charged sphere of radius $R$ has total charge $Q$.

  (a) Find the electric field inside the sphere.

  (b) Using the differential relation $d \mathbf{F}=\mathbf{E} d q$ between the force $d \mathbf{F}$ on a small charge $d q$ in an electric field $\mathbf{E}$, find the force on the top half of the sphere due to its bottom half. Express your answer in terms of $R$ and $Q$.

  comment

• Paper 2, Section II, A

  Electromagnetism | Part IB, 2009

  Starting from Maxwell's equations in vacuo, show that the cartesian components of $\mathbf{E}$ and $\mathbf{B}$ each satisfy

  $$\nabla^{2} f=\frac{1}{c^{2}} \frac{\partial^{2} f}{\partial t^{2}}$$

  Consider now a rectangular waveguide with its axis along $z$, width $a$ along $x$ and $b$ along $y$, with $a \geqslant b$. State and explain the boundary conditions on the fields $\mathbf{E}$ and $\mathbf{B}$ at the interior waveguide surfaces.

  One particular type of propagating wave has

  $$\mathbf{B}(x, y, z, t)=B_{0}(x, y) \hat{\mathbf{z}} e^{i(k z-\omega t)}$$

  Show that

  $$B_{x}=\frac{i}{(\omega / c)^{2}-k^{2}}\left(k \frac{\partial B_{z}}{\partial x}-\frac{\omega}{c^{2}} \frac{\partial E_{z}}{\partial y}\right)$$

  and derive an equivalent expression for $B_{y}$.

  Assume now that $E_{z}=0$. Write down the equation satisfied by $B_{z}$, find separable solutions, and show that the above implies Neumann boundary conditions on $B_{z}$. Find the "cutoff frequency" below which travelling waves do not propagate. For higher frequencies, find the wave velocity and the group velocity and explain the significance of your results.

  comment

• Paper 3, Section II, A

  Electromagnetism | Part IB, 2009

  Two long thin concentric perfectly conducting cylindrical shells of radii $a$ and $b$ $(a<b)$ are connected together at one end by a resistor of resistance $R$, and at the other by a battery that establishes a potential difference $V$. Thus, a current $I=V / R$ flows in opposite directions along each of the cylinders.

  (a) Using Ampère's law, find the magnetic field $\mathbf{B}$ in between the cylinders.

  (b) Using Gauss's law and the integral relationship between the potential and the electric field, or otherwise, show that the charge per unit length on the inner cylinder is

  $$\lambda=\frac{2 \pi \epsilon_{0} V}{\ln (b / a)}$$

  and also calculate the radial electric field.

  (c) Calculate the Poynting vector and by suitable integration verify that the power delivered by the system is $V^{2} / R$.

  comment

• Paper 4, Section I, A

  Electromagnetism | Part IB, 2009

  State the relationship between the induced EMF $V$ in a loop and the flux $\Phi$ through it. State the force law for a current-carrying wire in a magnetic field $\mathbf{B}$.

  A rectangular loop of wire with mass $m$, width $w$, vertical length $l$, and resistance $R$ falls out of a magnetic field under the influence of gravity. The magnetic field is $\mathbf{B}=B \hat{\mathbf{x}}$ for $z \geqslant 0$ and $\mathbf{B}=0$ for $z<0$, where $B$ is constant. Suppose the loop lies in the $(y, z)$ plane, with its top initially at $z=z_{0}<l$. Find the equation of motion for the loop and its terminal velocity, assuming that the loop continues to intersect the plane $z=0$.

  comment

2008

• 1.II.16B

  Electromagnetism | Part IB, 2008

  Suppose that the current density $\mathbf{J}(\mathbf{r})$ is constant in time but the charge density $\rho(\mathbf{r}, t)$ is not.

  (i) Show that $\rho$ is a linear function of time:

  $$\rho(\mathbf{r}, t)=\rho(\mathbf{r}, 0)+\dot{\rho}(\mathbf{r}, 0) t$$

  where $\dot{\rho}(\mathbf{r}, 0)$ is the time derivative of $\rho$ at time $t=0$.

  (ii) The magnetic induction due to a current density $\mathbf{J}(\mathbf{r})$ can be written as

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d V^{\prime}$$

  Show that this can also be written as

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \nabla \times \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d V^{\prime}$$

  (iii) Assuming that $\mathbf{J}$ vanishes at infinity, show that the curl of the magnetic field in (1) can be written as

  $$\nabla \times \mathbf{B}(\mathbf{r})=\mu_{0} \mathbf{J}(\mathbf{r})+\frac{\mu_{0}}{4 \pi} \nabla \int \frac{\nabla^{\prime} \cdot \mathbf{J}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d V^{\prime}$$

  [You may find useful the identities $\nabla \times(\nabla \times \mathbf{A})=\nabla(\nabla \cdot \mathbf{A})-\nabla^{2} \mathbf{A}$ and also $\left.\nabla^{2}\left(1 /\left|\mathbf{r}-\mathbf{r}^{\prime}\right|\right)=-4 \pi \delta\left(\mathbf{r}-\mathbf{r}^{\prime}\right) .\right]$

  (iv) Show that the second term on the right hand side of (2) can be expressed in terms of the time derivative of the electric field in such a way that $\mathbf{B}$ itself obeys Ampère's law with Maxwell's displacement current term, i.e. $\nabla \times \mathbf{B}=\mu_{0} \mathbf{J}+\mu_{0} \epsilon_{0} \partial \mathbf{E} / \partial t$.

  comment

• 2.I.6B

  Electromagnetism | Part IB, 2008

  Given the electric potential of a dipole

  $$\phi(r, \theta)=\frac{p \cos \theta}{4 \pi \epsilon_{0} r^{2}},$$

  where $p$ is the magnitude of the dipole moment, calculate the corresponding electric field and show that it can be written as

  $$\mathbf{E}(\mathbf{r})=\frac{1}{4 \pi \epsilon_{0}} \frac{1}{r^{3}}\left[3\left(\mathbf{p} \cdot \hat{\mathbf{e}}_{r}\right) \hat{\mathbf{e}}_{r}-\mathbf{p}\right]$$

  where $\hat{\mathbf{e}}_{r}$ is the unit vector in the radial direction.

  comment

• 2.II.17B

  Electromagnetism | Part IB, 2008

  Two perfectly conducting rails are placed on the $x y$-plane, one coincident with the $x$-axis, starting at $(0,0)$, the other parallel to the first rail a distance $\ell$ apart, starting at $(0, \ell)$. A resistor $R$ is connected across the rails between $(0,0)$ and $(0, \ell)$, and a uniform magnetic field $\mathbf{B}=B \hat{\mathbf{e}}_{z}$, where $\hat{\mathbf{e}}_{z}$ is the unit vector along the $z$-axis and $B>0$, fills the entire region of space. A metal bar of negligible resistance and mass $m$ slides without friction on the two rails, lying perpendicular to both of them in such a way that it closes the circuit formed by the rails and the resistor. The bar moves with speed $v$ to the right such that the area of the loop becomes larger with time.

  (i) Calculate the current in the resistor and indicate its direction of flow in a diagram of the system.

  (ii) Show that the magnetic force on the bar is

  $$\mathbf{F}=-\frac{B^{2} \ell^{2} v}{R} \hat{\mathbf{e}}_{x}$$

  (iii) Assume that the bar starts moving with initial speed $v_{0}$ at time $t=0$, and is then left to slide freely. Using your result from part (ii) and Newton's laws show that its velocity at the time $t$ is

  $$v(t)=v_{0} e^{-\left(B^{2} \ell^{2} / m R\right) t} .$$

  (iv) By calculating the total energy delivered to the resistor, verify that energy is conserved.

  comment

• 3.II.17B

  Electromagnetism | Part IB, 2008

  (i) From Maxwell's equations in vacuum,

  $$\begin{array}{ll} \nabla \cdot \mathbf{E}=0 & \nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t} \\ \nabla \cdot \mathbf{B}=0 & \nabla \times \mathbf{B}=\mu_{0} \epsilon_{0} \frac{\partial \mathbf{E}}{\partial t} \end{array}$$

  obtain the wave equation for the electric field E. [You may find the following identity useful: $\left.\nabla \times(\nabla \times \mathbf{A})=\nabla(\nabla \cdot \mathbf{A})-\nabla^{2} \mathbf{A} .\right]$

  (ii) If the electric and magnetic fields of a monochromatic plane wave in vacuum are

  $$\mathbf{E}(z, t)=\mathbf{E}_{0} \mathrm{e}^{i(k z-\omega t)} \text { and } \mathbf{B}(z, t)=\mathbf{B}_{0} \mathrm{e}^{i(k z-\omega t)}$$

  show that the corresponding electromagnetic waves are transverse (that is, both fields have no component in the direction of propagation).

  (iii) Use Faraday's law for these fields to show that

  $$\mathbf{B}_{0}=\frac{k}{\omega}\left(\hat{\mathbf{e}}_{z} \times \mathbf{E}_{0}\right)$$

  (iv) Explain with symmetry arguments how these results generalise to

  $$\mathbf{E}(\mathbf{r}, t)=E_{0} \mathrm{e}^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)} \hat{\mathbf{n}} \quad \text { and } \quad \mathbf{B}(\mathbf{r}, t)=\frac{1}{c} E_{0} \mathrm{e}^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}(\hat{\mathbf{k}} \times \hat{\mathbf{n}})$$

  where $\hat{\mathbf{n}}$ is the polarisation vector, i.e., the unit vector perpendicular to the direction of motion and along the direction of the electric field, and $\hat{\mathbf{k}}$ is the unit vector in the direction of propagation of the wave.

  (v) Using Maxwell's equations in vacuum prove that:

  $$\oint_{\mathcal{A}}\left(1 / \mu_{0}\right)(\mathbf{E} \times \mathbf{B}) \cdot d \mathcal{A}=-\frac{\partial}{\partial t} \int_{\mathcal{V}}\left(\frac{\epsilon_{0} E^{2}}{2}+\frac{B^{2}}{2 \mu_{0}}\right) d V$$

  where $\mathcal{V}$ is the closed volume and $\mathcal{A}$ is the bounding surface. Comment on the differing time dependencies of the left-hand-side of (1) for the case of (a) linearly-polarized and (b) circularly-polarized monochromatic plane waves.

  comment

• 4.I.7B

  Electromagnetism | Part IB, 2008

  The energy stored in a static electric field $\mathbf{E}$ is

  $$U=\frac{1}{2} \int \rho \phi d V,$$

  where $\phi$ is the associated electric potential, $\mathbf{E}=-\nabla \phi$, and $\rho$ is the volume charge density.

  (i) Assuming that the energy is calculated over all space and that $\mathbf{E}$ vanishes at infinity, show that the energy can be written as

  $$U=\frac{\epsilon_{0}}{2} \int|\mathbf{E}|^{2} d V$$

  (ii) Find the electric field produced by a spherical shell with total charge $Q$ and radius $R$, assuming it to vanish inside the shell. Find the energy stored in the electric field.

  comment

2007

• $2 . \mathrm{I} . 6 \mathrm{E} \quad$

  Electromagnetism | Part IB, 2007

  A metal has uniform conductivity $\sigma$. A cylindrical wire with radius $a$ and length $l$ is manufactured from the metal. Show, using Maxwell's equations, that when a steady current $I$ flows along the wire the current density within the wire is uniform.

  Deduce the electrical resistance of the wire and the rate of Ohmic dissipation within it.

  Indicate briefly, and without detailed calculation, whether your results would be affected if the wire was not straight.

  comment

• 1.II.16E

  Electromagnetism | Part IB, 2007

  A steady magnetic field $\mathbf{B}(\mathbf{x})$ is generated by a current distribution $\mathbf{j}(\mathbf{x})$ that vanishes outside a bounded region $V$. Use the divergence theorem to show that

  $$\int_{V} \mathbf{j} d V=0 \quad \text { and } \quad \int_{V} x_{i} j_{k} d V=-\int_{V} x_{k} j_{i} d V$$

  Define the magnetic vector potential $\mathbf{A}(\mathbf{x})$. Use Maxwell's equations to obtain a differential equation for $\mathbf{A}(\mathbf{x})$ in terms of $\mathbf{j}(\mathbf{x})$.

  It may be shown that for an unbounded domain the equation for $\mathbf{A}(\mathbf{x})$ has solution

  $$\mathbf{A}(\mathbf{x})=\frac{\mu_{0}}{4 \pi} \int_{V} \frac{\mathbf{j}\left(\mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|} d V^{\prime}$$

  Deduce that in general the leading order approximation for $\mathbf{A}(\mathbf{x})$ as $|\mathbf{x}| \rightarrow \infty$ is

  $$\mathbf{A}=\frac{\mu_{0}}{4 \pi} \frac{\mathbf{m} \times \mathbf{x}}{|\mathbf{x}|^{3}} \quad \text { where } \quad \mathbf{m}=\frac{1}{2} \int_{V} \mathbf{x}^{\prime} \times \mathbf{j}\left(\mathbf{x}^{\prime}\right) d V^{\prime}$$

  Find the corresponding far-field expression for $\mathbf{B}(\mathbf{x})$.

  comment

• 2.II.17E

  Electromagnetism | Part IB, 2007

  If $S$ is a fixed surface enclosing a volume $V$, use Maxwell's equations to show that

  $$\frac{d}{d t} \int_{V}\left(\frac{1}{2} \epsilon_{0} E^{2}+\frac{1}{2 \mu_{0}} B^{2}\right) d V+\int_{S} \mathbf{P} \cdot \mathbf{n} d S=-\int_{V} \mathbf{j} \cdot \mathbf{E} d V$$

  where $\mathbf{P}=(\mathbf{E} \times \mathbf{B}) / \mu_{0}$. Give a physical interpretation of each term in this equation.

  Show that Maxwell's equations for a vacuum permit plane wave solutions with $\mathbf{E}=E_{0}(0,1,0) \cos (k x-\omega t)$ with $E_{0}, k$ and $\omega$ constants, and determine the relationship between $k$ and $\omega$.

  Find also the corresponding $\mathbf{B}(\mathbf{x}, t)$ and hence the time average $<\mathbf{P}>$. What does $<\mathbf{P}>$ represent in this case?

  comment

• 3.II.17E

  Electromagnetism | Part IB, 2007

  A capacitor consists of three long concentric cylinders of radii $a, \lambda a$ and $2 a$ respectively, where $1<\lambda<2$. The inner and outer cylinders are earthed (i.e. held at zero potential); the cylinder of radius $\lambda a$ is raised to a potential $V$. Find the electrostatic potential in the regions between the cylinders and deduce the capacitance, $C(\lambda)$ per unit length, of the system.

  For $\lambda=1+\delta$ with $0<\delta \ll 1$ find $C(\lambda)$ correct to leading order in $\delta$ and comment on your result.

  Find also the value of $\lambda$ at which $C(\lambda)$ has an extremum. Is the extremum a maximum or a minimum? Justify your answer.

  comment

• 4.I $7 \mathrm{E} \quad$

  Electromagnetism | Part IB, 2007

  Write down Faraday's law of electromagnetic induction for a moving circuit $C(t)$ in a magnetic field $\mathbf{B}(\mathbf{x}, t)$. Explain carefully the meaning of each term in the equation.

  A thin wire is bent into a circular loop of radius $a$. The loop lies in the $(x, z)$-plane at time $t=0$. It spins steadily with angular velocity $\Omega \mathbf{k}$, where $\Omega$ is a constant and $\mathbf{k}$ is a unit vector in the $z$-direction. A spatially uniform magnetic field $\mathbf{B}=B_{0}(\cos \omega t, \sin \omega t, 0)$ is applied, with $B_{0}$ and $\omega$ both constant. If the resistance of the wire is $R$, find the current in the wire at time $t$.

  comment

2006

• 1.II.16G

  Electromagnetism | Part IB, 2006

  Three concentric conducting spherical shells of radii $a, b$ and $c(a<b<c)$ carry charges $q,-2 q$ and $3 q$ respectively. Find the electric field and electric potential at all points of space.

  Calculate the total energy of the electric field.

  comment

• 2.I.6G

  Electromagnetism | Part IB, 2006

  Given that the electric field $\mathbf{E}$ and the current density $\mathbf{j}$ within a conducting medium of uniform conductivity $\sigma$ are related by $j=\sigma \mathbf{E}$, use Maxwell's equations to show that the charge density $\rho$ in the medium obeys the equation

  $$\frac{\partial \rho}{\partial t}=-\frac{\sigma}{\epsilon_{0}} \rho .$$

  An infinitely long conducting cylinder of uniform conductivity $\sigma$ is set up with a uniform electric charge density $\rho_{0}$ throughout its interior. The region outside the cylinder is a vacuum. Obtain $\rho$ within the cylinder at subsequent times and hence obtain $\mathbf{E}$ and $\mathbf{j}$ within the cylinder as functions of time and radius. Calculate the value of $\mathbf{E}$ outside the cylinder.

  comment

• 2.II.17G

  Electromagnetism | Part IB, 2006

  Derive from Maxwell's equations the Biot-Savart law

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int_{V} \frac{\mathbf{j}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d V^{\prime}$$

  giving the magnetic field $\mathbf{B}(\mathbf{r})$ produced by a steady current density $\mathbf{j}(\mathbf{r})$ that vanishes outside a bounded region $V$.

  [You may assume that the divergence of the magnetic vector potential is zero.]

  A steady current density $\mathbf{j}(\mathbf{r})$ has the form $\mathbf{j}=\left(0, j_{\phi}(\mathbf{r}), 0\right)$ in cylindrical polar coordinates $(r, \phi, z)$ where

  $$j_{\phi}(\mathbf{r})= \begin{cases}k r & 0 \leqslant r \leqslant b, \quad-h \leqslant z \leqslant h \\ 0 & \text { otherwise },\end{cases}$$

  and $k$ is a constant. Find the magnitude and direction of the magnetic field at the origin.

  $$\left[\text { Hint }: \quad \int_{-h}^{h} \frac{d z}{\left(r^{2}+z^{2}\right)^{3 / 2}}=\frac{2 h}{r^{2}\left(h^{2}+r^{2}\right)^{1 / 2}}\right]$$

  comment

• 3.II.17G

  Electromagnetism | Part IB, 2006

  Write down Maxwell's equations in vacuo and show that they admit plane wave solutions in which

  $$\mathbf{E}(\mathbf{x}, t)=\operatorname{Re}\left(\mathbf{E}_{0} e^{i(\omega t-\mathbf{k} \cdot \mathbf{x})}\right), \quad \mathbf{k} \cdot \mathbf{E}_{0}=0,$$

  where $\mathbf{E}_{0}$ and $\mathbf{k}$ are constant vectors. Find the corresponding magnetic field $\mathbf{B}(\mathbf{x}, t)$ and the relationship between $\omega$ and $\mathbf{k}$.

  Write down the relations giving the discontinuities (if any) in the normal and tangential components of $\mathbf{E}$ and $\mathbf{B}$ across a surface $z=0$ which carries surface charge density $\sigma$ and surface current density $\mathbf{j}$.

  Suppose that a perfect conductor occupies the region $z<0$, and that a plane wave with $\mathbf{k}=(0,0,-k), \mathbf{E}_{0}=\left(E_{0}, 0,0\right)$ is incident from the vacuum region $z>0$. Show that the boundary conditions at $z=0$ can be satisfied if a suitable reflected wave is present, and find the induced surface charge and surface current densities.

  comment

• 4.I.7G

  Electromagnetism | Part IB, 2006

  Starting from Maxwell's equations, deduce Faraday's law of induction

  $$\frac{d \Phi}{d t}=-\varepsilon$$

  for a moving circuit $C$, where $\Phi$ is the flux of $\mathbf{B}$ through the circuit and where the EMF $\varepsilon$ is defined to be

  $$\varepsilon=\oint_{C}(\mathbf{E}+\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{r}$$

  with $\mathbf{v}(\mathbf{r})$ denoting the velocity of a point $\mathbf{r}$ of $C$.

  [Hint: consider the closed surface consisting of the surface $S(t)$ bounded by $C(t)$, the surface $S(t+\delta t)$ bounded by $C(t+\delta t)$ and the surface $S^{\prime}$ stretching from $C(t)$ to $C(t+\delta t)$. Show that the flux of $\mathbf{B}$ through $S^{\prime}$ is $-\oint_{C} \mathbf{B} \cdot(\mathbf{v} \times d \mathbf{r}) \delta t$.]

  comment

2005

• 1.II.16H

  Electromagnetism | Part IB, 2005

  For a static charge density $\rho(\mathbf{x})$ show that the energy may be expressed as

  $$E=\frac{1}{2} \int \rho \phi \mathrm{d}^{3} x=\frac{\epsilon_{0}}{2} \int \mathbf{E}^{2} \mathrm{~d}^{3} x,$$

  where $\phi(\mathbf{x})$ is the electrostatic potential and $\mathbf{E}(\mathbf{x})$ is the electric field.

  Determine the scalar potential and electric field for a sphere of radius $R$ with a constant charge density $\rho$. Also determine the total electrostatic energy.

  In a nucleus with $Z$ protons the volume is proportional to $Z$. Show that we may expect the electric contribution to energy to be proportional to $Z^{\frac{5}{3}}$.

  comment

• 2.I.6H

  Electromagnetism | Part IB, 2005

  Write down Maxwell's equations in the presence of a charge density $\rho$ and current density $\mathbf{J}$. Show that it is necessary that $\rho, \mathbf{J}$ satisfy a conservation equation.

  If $\rho, \mathbf{J}$ are zero outside a fixed region $V$ show that the total charge inside $V$ is a constant and also that

  $$\frac{\mathrm{d}}{\mathrm{d} t} \int_{V} \mathbf{x} \rho \mathrm{d}^{3} x=\int_{V} \mathbf{J ~}^{3} x .$$

  comment

• 2.II.17H

  Electromagnetism | Part IB, 2005

  Assume the magnetic field

  $$\mathbf{B}(\mathbf{x})=b(\mathbf{x}-3 \hat{\mathbf{z}} \hat{\mathbf{z}} \cdot \mathbf{x}),$$

  where $\hat{\mathbf{z}}$ is a unit vector in the vertical direction. Show that this satisfies the expected equations for a static magnetic field in vacuum.

  A circular wire loop, of radius $a$, mass $m$ and resistance $R$, lies in a horizontal plane with its centre on the $z$-axis at a height $z$ and there is a magnetic field given by $(*)$. Calculate the magnetic flux arising from this magnetic field through the loop and also the force acting on the loop when a current $I$ is flowing around the loop in a clockwise direction about the $z$-axis.

  Obtain an equation of motion for the height $z(t)$ when the wire loop is falling under gravity. Show that there is a solution in which the loop falls with constant speed $v$ which should be determined. Verify that in this situation the rate at which heat is generated by the current flowing in the loop is equal to the rate of loss of gravitational potential energy. What happens when $R \rightarrow 0$ ?

  comment

• 3.II.17H

  Electromagnetism | Part IB, 2005

  If $\mathbf{E}(\mathbf{x}, t), \mathbf{B}(\mathbf{x}, t)$ are solutions of Maxwell's equations in a region without any charges or currents show that $\mathbf{E}^{\prime}(\mathbf{x}, t)=c \mathbf{B}(\mathbf{x}, t), \mathbf{B}^{\prime}(\mathbf{x}, t)=-\mathbf{E}(\mathbf{x}, t) / c$ are also solutions.

  At the boundary of a perfect conductor with normal $\mathbf{n}$ briefly explain why

  $$\mathbf{n} \cdot \mathbf{B}=0, \quad \mathbf{n} \times \mathbf{E}=0$$

  Electromagnetic waves inside a perfectly conducting tube with axis along the $z$-axis are given by the real parts of complex solutions of Maxwell's equations of the form

  $$\mathbf{E}(\mathbf{x}, t)=\mathbf{e}(x, y) e^{i(k z-\omega t)}, \quad \mathbf{B}(\mathbf{x}, t)=\mathbf{b}(x, y) e^{i(k z-\omega t)} .$$

  Suppose $b_{z}=0$. Show that we can find a solution in this case in terms of a function $\psi(x, y)$ where

  $$\left(e_{x}, e_{y}\right)=\left(\frac{\partial}{\partial x} \psi, \frac{\partial}{\partial y} \psi\right), \quad e_{z}=i\left(k-\frac{\omega^{2}}{k c^{2}}\right) \psi,$$

  so long as $\psi$ satisfies

  $$\left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\gamma^{2}\right) \psi=0$$

  for suitable $\gamma$. Show that the boundary conditions are satisfied if $\psi=0$ on the surface of the tube.

  Obtain a similar solution with $e_{z}=0$ but show that the boundary conditions are now satisfied if the normal derivative $\partial \psi / \partial n=0$ on the surface of the tube.

  comment

• 4.I.7H

  Electromagnetism | Part IB, 2005

  For a static current density $\mathbf{J}(\mathbf{x})$ show that we may choose the vector potential $\mathbf{A}(\mathbf{x})$ so that

  $$-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{J} .$$

  For a loop $L$, centred at the origin, carrying a current $I$ show that

  $$\mathbf{A}(\mathbf{x})=\frac{\mu_{0} I}{4 \pi} \oint_{L} \frac{1}{|\mathbf{x}-\mathbf{r}|} \mathrm{d} \mathbf{r} \sim-\frac{\mu_{0} I}{4 \pi} \frac{1}{|\mathbf{x}|^{3}} \oint_{L} \frac{1}{2} \mathbf{x} \times(\mathbf{r} \times \mathrm{d} \mathbf{r}) \quad \text { as } \quad|\mathbf{x}| \rightarrow \infty$$

  [You may assume

  $$-\nabla^{2} \frac{1}{4 \pi|\mathbf{x}|}=\delta^{3}(\mathbf{x})$$

  and for fixed vectors $\mathbf{a}, \mathbf{b}$

  $$\left.\oint_{L} \mathbf{a} \cdot \mathrm{d} \mathbf{r}=0, \quad \oint_{L}(\mathbf{a} \cdot \mathbf{r} \mathbf{b} \cdot \mathrm{d} \mathbf{r}+\mathbf{b} \cdot \mathbf{r} \mathbf{a} \cdot \mathrm{d} \mathbf{r})=0 .\right]$$

  comment

2004

• 1.I.7B

  Electromagnetism | Part IB, 2004

  Write down Maxwell's equations and show that they imply the conservation of charge.

  In a conducting medium of conductivity $\sigma$, where $\mathbf{J}=\sigma \mathbf{E}$, show that any charge density decays in time exponentially at a rate to be determined.

  comment

• 1.II.18B

  Electromagnetism | Part IB, 2004

  Inside a volume $D$ there is an electrostatic charge density $\rho(\mathbf{r})$, which induces an electric field $\mathbf{E}(\mathbf{r})$ with associated electrostatic potential $\phi(\mathbf{r})$. The potential vanishes on the boundary of $D$. The electrostatic energy is

  $$W=\frac{1}{2} \int_{D} \rho \phi d^{3} \mathbf{r}$$

  Derive the alternative form

  $$W=\frac{\epsilon_{0}}{2} \int_{D} E^{2} d^{3} \mathbf{r}$$

  A capacitor consists of three identical and parallel thin metal circular plates of area $A$ positioned in the planes $z=-H, z=a$ and $z=H$, with $-H<a<H$, with centres on the $z$ axis, and at potentials $0, V$ and 0 respectively. Find the electrostatic energy stored, verifying that expressions (1) and (2) give the same results. Why is the energy minimal when $a=0$ ?

  comment

• 2.I.7B

  Electromagnetism | Part IB, 2004

  Write down the two Maxwell equations that govern steady magnetic fields. Show that the boundary conditions satisfied by the magnetic field on either side of a sheet carrying a surface current of density $\mathbf{s}$, with normal $\mathbf{n}$ to the sheet, are

  $$\mathbf{n} \times \mathbf{B}_{+}-\mathbf{n} \times \mathbf{B}_{-}=\mu_{0} \mathbf{s}$$

  Write down the force per unit area on the surface current.

  comment

• 2.II.18B

  Electromagnetism | Part IB, 2004

  The vector potential due to a steady current density $\mathbf{J}$ is given by

  $$\mathbf{A}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d^{3} \mathbf{r}^{\prime}$$

  where you may assume that $\mathbf{J}$ extends only over a finite region of space. Use $(*)$ to derive the Biot-Savart law

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d^{3} \mathbf{r}^{\prime}$$

  A circular loop of wire of radius $a$ carries a current $I$. Take Cartesian coordinates with the origin at the centre of the loop and the $z$-axis normal to the loop. Use the BiotSavart law to show that on the $z$-axis the magnetic field is in the axial direction and of magnitude

  $$B=\frac{\mu_{0} I a^{2}}{2\left(z^{2}+a^{2}\right)^{3 / 2}}$$

  comment

• 3.I.7B

  Electromagnetism | Part IB, 2004

  A wire is bent into the shape of three sides of a rectangle and is held fixed in the $z=0$ plane, with base $x=0$ and $-\ell<y<\ell$, and with arms $y=\pm \ell$ and $0<x<\ell$. A second wire moves smoothly along the arms: $x=X(t)$ and $-\ell<y<\ell$ with $0<X<\ell$. The two wires have resistance $R$ per unit length and mass $M$ per unit length. There is a time-varying magnetic field $B(t)$ in the $z$-direction.

  Using the law of induction, find the electromotive force around the circuit made by the two wires.

  Using the Lorentz force, derive the equation

  $$M \ddot{X}=-\frac{B}{R(X+2 \ell)} \frac{d}{d t}(X \ell B)$$

  comment

• 3.II.19B

  Electromagnetism | Part IB, 2004

  Starting from Maxwell's equations, derive the law of energy conservation in the form

  $$\frac{\partial W}{\partial t}+\nabla \cdot \mathbf{S}+\mathbf{J} \cdot \mathbf{E}=0$$

  where $W=\frac{\epsilon_{0}}{2} E^{2}+\frac{1}{2 \mu_{0}} B^{2}$ and $\mathbf{S}=\frac{1}{\mu_{0}} \mathbf{E} \times \mathbf{B}$.

  Evaluate $W$ and $\mathbf{S}$ for the plane electromagnetic wave in vacuum

  $$\mathbf{E}=\left(E_{0} \cos (k z-\omega t), 0,0\right) \quad \mathbf{B}=\left(0, B_{0} \cos (k z-\omega t), 0\right),$$

  where the relationships between $E_{0}, B_{0}, \omega$ and $k$ should be determined. Show that the electromagnetic energy propagates at speed $c^{2}=1 /\left(\epsilon_{0} \mu_{0}\right)$, i.e. show that $S=W c$.

  comment

• A $1 . 5 \quad$ B $1 . 4 \quad$

  Electromagnetism | Part II, 2004

  (i) Show that the work done in assembling a localised charge distribution $\rho(\mathbf{r})$ in a region $V$ with an associated potential $\phi(\mathbf{r})$ is

  $$W=\frac{1}{2} \int_{V} \rho(\mathbf{r}) \phi(\mathbf{r}) d \tau$$

  and that this can be written as an integral over all space

  $$W=\frac{1}{2} \epsilon_{0} \int|\mathbf{E}|^{2} d \tau$$

  where the electric field $\mathbf{E}=-\nabla \phi$.

  (ii) What is the force per unit area on an infinite plane conducting sheet with a charge density $\sigma$ per unit area (a) if it is isolated in space and (b) if the electric field vanishes on one side of the sheet?

  An infinite cylindrical capacitor consists of two concentric cylindrical conductors with radii $a, b(a<b)$, carrying charges $\pm q$ per unit length respectively. Calculate the capacitance per unit length and the energy per unit length. Next determine the total force on each conductor, and calculate the rate of change of energy of the inner and outer conductors if they are moved radially inwards and outwards respectively with speed $v$. What is the corresponding rate of change of the capacitance?

  comment

• A2.5

  Electromagnetism | Part II, 2004

  (i) Write down the general solution of Poisson's equation. Derive from Maxwell's equations the Biot-Savart law for the magnetic field of a steady localised current distribution.

  (ii) A plane rectangular loop with sides of length $a$ and $b$ lies in the plane $z=0$ and is centred on the origin. Show that when $r=|\mathbf{r}| \gg a, b$, the vector potential $\mathbf{A}(\mathbf{r})$ is given approximately by

  $$\mathbf{A}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \frac{\mathbf{m} \wedge \mathbf{r}}{r^{3}}$$

  where $\mathbf{m}=I a b \hat{\mathbf{z}}$ is the magnetic moment of the loop.

  Hence show that the magnetic field $\mathbf{B}(\mathbf{r})$ at a great distance from an arbitrary small plane loop of area $A$, situated in the $x y$-plane near the origin and carrying a current $I$, is given by

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0} I A}{4 \pi r^{5}}\left(3 x z, 3 y z, 2 r^{2}-3 x^{2}-3 y^{2}\right)$$

  comment

• A3.5 B3.3

  Electromagnetism | Part II, 2004

  (i) State Maxwell's equations and show that the electric field $\mathbf{E}$ and the magnetic field $\mathbf{B}$ can be expressed in terms of a scalar potential $\phi$ and a vector potential $\mathbf{A}$. Hence derive the inhomogeneous wave equations that are satisfied by $\phi$ and $\mathbf{A}$ respectively.

  (ii) The plane $x=0$ separates a vacuum in the half-space $x<0$ from a perfectly conducting medium occupying the half-space $x>0$. Derive the boundary conditions on $\mathbf{E}$ and $\mathbf{B}$ at $x=0$.

  A plane electromagnetic wave with a magnetic field $\mathbf{B}=B(t, x, z) \hat{\mathbf{y}}$, travelling in the $x z$-plane at an angle $\theta$ to the $x$-direction, is incident on the interface at $x=0$. If the wave has frequency $\omega$ show that the total magnetic field is given by

  $$\mathbf{B}=B_{0} \cos \left(\frac{\omega x}{c} \cos \theta\right) \exp \left[i\left(\frac{\omega z}{c} \sin \theta-\omega t\right)\right] \hat{\mathbf{y}}$$

  where $B_{0}$ is a constant. Hence find the corresponding electric field $\mathbf{E}$, and obtain the surface charge density and the surface current at the interface.

  comment

• A4.5

  Electromagnetism | Part II, 2004

  Consider a frame $S^{\prime}$ moving with velocity v relative to the laboratory frame $S$ where $|\mathbf{v}|^{2} \ll c^{2}$. The electric and magnetic fields in $S$ are $\mathbf{E}$ and $\mathbf{B}$, while those measured in $S^{\prime}$ are $\mathbf{E}^{\prime}$ and $\mathbf{B}^{\prime}$. Given that $\mathbf{B}^{\prime}=\mathbf{B}$, show that

  $$\oint_{\Gamma} \mathbf{E}^{\prime} \cdot d \mathbf{l}=\oint_{\Gamma}(\mathbf{E}+\mathbf{v} \wedge \mathbf{B}) \cdot d \mathbf{l},$$

  for any closed circuit $\Gamma$ and hence that $\mathbf{E}^{\prime}=\mathbf{E}+\mathbf{v} \wedge \mathbf{B}$.

  Now consider a fluid with electrical conductivity $\sigma$ and moving with velocity $\mathbf{v}(\mathbf{r})$. Use Ohm's law in the moving frame to relate the current density $\mathbf{j}$ to the electric field $\mathbf{E}$ in the laboratory frame, and show that if $\mathbf{j}$ remains finite in the limit $\sigma \rightarrow \infty$ then

  $$\frac{\partial \mathbf{B}}{\partial t}=\nabla \wedge(\mathbf{v} \wedge \mathbf{B})$$

  The magnetic helicity $H$ in a volume $V$ is given by $\int_{V} \mathbf{A} \cdot \mathbf{B} d \tau$ where $\mathbf{A}$ is the vector potential. Show that if the normal components of $\mathbf{v}$ and $\mathbf{B}$ both vanish on the surface bounding $V$ then $d H / d t=0$.

  comment

2003

• A $1 . 5 \quad$ B $1 . 4 \quad$

  Electromagnetism | Part II, 2003

  (i) Using Maxwell's equations as they apply to magnetostatics, show that the magnetic field $\mathbf{B}$ can be described in terms of a vector potential $\mathbf{A}$ on which the condition $\nabla \cdot \mathbf{A}=0$ may be imposed. Hence derive an expression, valid at any point in space, for the vector potential due to a steady current distribution of density $\mathbf{j}$ that is non-zero only within a finite domain.

  (ii) Verify that the vector potential $\mathbf{A}$ that you found in Part (i) satisfies $\nabla \cdot \mathbf{A}=0$, and use it to obtain the Biot-Savart law expression for $\mathbf{B}$. What is the corresponding result for a steady surface current distribution of density $\mathbf{s}$ ?

  In cylindrical polar coordinates $(\rho, \phi, z)$ (oriented so that $\mathbf{e}_{\rho} \times \mathbf{e}_{\phi}=\mathbf{e}_{z}$ ) a surface current

  $$\mathbf{s}=s(\rho) \mathbf{e}_{\phi}$$

  flows in the plane $z=0$. Given that

  $$s(\rho)= \begin{cases}4 I\left(1+\frac{a^{2}}{\rho^{2}}\right)^{\frac{1}{2}} & a \leqslant \rho \leqslant 3 a \\ 0 & \text { otherwise }\end{cases}$$

  show that the magnetic field at the point $\mathbf{r}=a \mathbf{e}_{z}$ has $z$-component

  $$B_{z}=\mu_{0} I \log 5 .$$

  State, with justification, the full result for $\mathbf{B}$ at the point $\mathbf{r}=a \mathbf{e}_{z}$.

  comment

• A2 $. 5 \quad$

  Electromagnetism | Part II, 2003

  (i) A plane electromagnetic wave has electric and magnetic fields

  $$\mathbf{E}=\mathbf{E}_{0} e^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}, \quad \mathbf{B}=\mathbf{B}_{0} e^{i(\mathbf{k} \cdot \mathbf{r}-\omega t)}$$

  for constant vectors $\mathbf{E}_{0}, \mathbf{B}_{0}$, constant positive angular frequency $\omega$ and constant wavevector $\mathbf{k}$. Write down the vacuum Maxwell equations and show that they imply

  $$\mathbf{k} \cdot \mathbf{E}_{0}=0, \quad \mathbf{k} \cdot \mathbf{B}_{0}=0, \quad \omega \mathbf{B}_{0}=\mathbf{k} \times \mathbf{E}_{0}$$

  Show also that $|\mathbf{k}|=\omega / c$, where $c$ is the speed of light.

  (ii) State the boundary conditions on $\mathbf{E}$ and $\mathbf{B}$ at the surface $S$ of a perfect conductor. Let $\sigma$ be the surface charge density and s the surface current density on $S$. How are $\sigma$ and $\mathbf{s}$ related to $\mathbf{E}$ and $\mathbf{B}$ ?

  A plane electromagnetic wave is incident from the half-space $x<0$ upon the surface $x=0$ of a perfectly conducting medium in $x>0$. Given that the electric and magnetic fields of the incident wave take the form $(*)$ with

  $$\mathbf{k}=k(\cos \theta, \sin \theta, 0) \quad(0<\theta<\pi / 2)$$

  and

  $$\mathbf{E}_{0}=\lambda(-\sin \theta, \cos \theta, 0),$$

  find $\mathbf{B}_{0}$.

  Reflection of the incident wave at $x=0$ produces a reflected wave with electric field

  $$\mathbf{E}_{0}^{\prime} e^{i\left(\mathbf{k}^{\prime} \cdot \mathbf{r}-\omega t\right)}$$

  with

  $$\mathbf{k}^{\prime}=k(-\cos \theta, \sin \theta, 0)$$

  By considering the boundary conditions at $x=0$ on the total electric field, show that

  $$\mathbf{E}_{0}^{\prime}=-\lambda(\sin \theta, \cos \theta, 0)$$

  Show further that the electric charge density on the surface $x=0$ takes the form

  $$\sigma=\sigma_{0} e^{i k(y \sin \theta-c t)}$$

  for a constant $\sigma_{0}$ that you should determine. Find the magnetic field of the reflected wave and hence the surface current density $\mathbf{s}$ on the surface $x=0$.

  comment

• A3.5 B3.3

  Electromagnetism | Part II, 2003

  (i) Given the electric field (in cartesian components)

  $$\mathbf{E}(\mathbf{r}, t)=\left(0, x / t^{2}, 0\right)$$

  use the Maxwell equation

  $$\nabla \times \mathbf{E}=-\frac{\partial \mathbf{B}}{\partial t}$$

  to find $\mathbf{B}$ subject to the boundary condition that $|\mathbf{B}| \rightarrow 0$ as $t \rightarrow \infty$.

  Let $S$ be the planar rectangular surface in the $x y$-plane with corners at

  $$(0,0,0), \quad(L, 0,0), \quad(L, a, 0), \quad(0, a, 0)$$

  where $a$ is a constant and $L=L(t)$ is some function of time. The magnetic flux through $S$ is given by the surface integral

  $$\Phi=\int_{S} \mathbf{B} \cdot d \mathbf{S}$$

  Compute $\Phi$ as a function of $t$.

  Let $\mathcal{C}$ be the closed rectangular curve that bounds the surface $S$, taken anticlockwise in the $x y$-plane, and let $\mathbf{v}$ be its velocity (which depends, in this case, on the segment of $\mathcal{C}$ being considered). Compute the line integral

  $$\oint_{\mathcal{C}}(\mathbf{E}+\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{r}$$

  Hence verify that

  $$\oint_{\mathcal{C}}(\mathbf{E}+\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{r}=-\frac{d \Phi}{d t}$$

  (ii) A surface $S$ is bounded by a time-dependent closed curve $\mathcal{C}(t)$ such that in time $\delta t$ it sweeps out a volume $\delta V$. By considering the volume integral

  $$\int_{\delta V} \nabla \cdot \mathbf{B} d \tau$$

  and using the divergence theorem, show that the Maxwell equation $\nabla \cdot \mathbf{B}=0$ implies that

  $$\frac{d \Phi}{d t}=\int_{S} \frac{\partial \mathbf{B}}{\partial t} \cdot d \mathbf{S}-\oint_{\mathcal{C}}(\mathbf{v} \times \mathbf{B}) \cdot d \mathbf{r}$$

  where $\Phi$ is the magnetic flux through $S$ as given in Part (i). Hence show, using (1) and Stokes' theorem, that (2) is a consequence of Maxwell's equations.

  comment

• A4.5

  Electromagnetism | Part II, 2003

  Let $\mathbf{E}(\mathbf{r})$ be the electric field due to a continuous static charge distribution $\rho(\mathbf{r})$ for which $|\mathbf{E}| \rightarrow 0$ as $|\mathbf{r}| \rightarrow \infty$. Starting from consideration of a finite system of point charges, deduce that the electrostatic energy of the charge distribution $\rho$ is

  $$W=\frac{1}{2} \varepsilon_{0} \int|\mathbf{E}|^{2} d \tau$$

  where the volume integral is taken over all space.

  A sheet of perfectly conducting material in the form of a surface $S$, with unit normal $\mathbf{n}$, carries a surface charge density $\sigma$. Let $E_{\pm}=\mathbf{n} \cdot \mathbf{E}_{\pm}$denote the normal components of the electric field $\mathbf{E}$ on either side of $S$. Show that

  $$\frac{1}{\varepsilon_{0}} \sigma=E_{+}-E_{-} .$$

  Three concentric spherical shells of perfectly conducting material have radii $a, b, c$ with $a<b<c$. The innermost and outermost shells are held at zero electric potential. The other shell is held at potential $V$. Find the potentials $\phi_{1}(r)$ in $a<r<b$ and $\phi_{2}(r)$ in $b<r<c$. Compute the surface charge density $\sigma$ on the shell of radius $b$. Use the formula $(*)$ to compute the electrostatic energy of the system.

  comment

2002

• A $1 . 5 \quad$ B $1 . 4 \quad$

  Electromagnetism | Part II, 2002

  (i) Show that, in a region where there is no magnetic field and the charge density vanishes, the electric field can be expressed either as minus the gradient of a scalar potential $\phi$ or as the curl of a vector potential A. Verify that the electric field derived from

  $$\mathbf{A}=\frac{1}{4 \pi \epsilon_{0}} \frac{\mathbf{p} \wedge \mathbf{r}}{r^{3}}$$

  is that of an electrostatic dipole with dipole moment $\mathbf{p}$.

  [You may assume the following identities:

  $$\begin{gathered} \nabla(\mathbf{a} \cdot \mathbf{b})=\mathbf{a} \wedge(\nabla \wedge \mathbf{b})+\mathbf{b} \wedge(\nabla \wedge \mathbf{a})+(\mathbf{a} \cdot \nabla) \mathbf{b}+(\mathbf{b} \cdot \nabla) \mathbf{a} \\ \nabla \wedge(\mathbf{a} \wedge \mathbf{b})=(\mathbf{b} \cdot \nabla) \mathbf{a}-(\mathbf{a} \cdot \nabla) \mathbf{b}+\mathbf{a} \nabla \cdot \mathbf{b}-\mathbf{b} \nabla \cdot \mathbf{a} .] \end{gathered}$$

  (ii) An infinite conducting cylinder of radius $a$ is held at zero potential in the presence of a line charge parallel to the axis of the cylinder at distance $s_{0}>a$, with charge density $q$ per unit length. Show that the electric field outside the cylinder is equivalent to that produced by replacing the cylinder with suitably chosen image charges.

  comment

• A2.5

  Electromagnetism | Part II, 2002

  (i) Show that the Lorentz force corresponds to a curvature force and the gradient of a magnetic pressure, and that it can be written as the divergence of a second rank tensor, the Maxwell stress tensor.

  Consider the potential field $\mathbf{B}$ given by $\mathbf{B}=-\nabla \Phi$, where

  $$\Phi(x, y)=\left(\frac{B_{0}}{k}\right) \cos k x e^{-k y}$$

  referred to cartesian coordinates $(x, y, z)$. Obtain the Maxwell stress tensor and verify that its divergence vanishes.

  (ii) The magnetic field in a stellar atmosphere is maintained by steady currents and the Lorentz force vanishes. Show that there is a scalar field $\alpha$ such that $\nabla \wedge \mathbf{B}=\alpha \mathbf{B}$ and $\mathbf{B} \cdot \nabla \alpha=0$. Show further that if $\alpha$ is constant, then $\nabla^{2} \mathbf{B}+\alpha^{2} \mathbf{B}=0$. Obtain a solution in the form $\mathbf{B}=\left(B_{1}(z), B_{2}(z), 0\right)$; describe the structure of this field and sketch its variation in the $z$-direction.

  comment

• A3.5 B3.3

  Electromagnetism | Part II, 2002

  (i) A plane electromagnetic wave in a vacuum has an electric field

  $$\mathbf{E}=\left(E_{1}, E_{2}, 0\right) \cos (k z-\omega t),$$

  referred to cartesian axes $(x, y, z)$. Show that this wave is plane polarized and find the orientation of the plane of polarization. Obtain the corresponding plane polarized magnetic field and calculate the rate at which energy is transported by the wave.

  (ii) Suppose instead that

  $$\mathbf{E}=\left(E_{1} \cos (k z-\omega t), E_{2} \cos (k z-\omega t+\phi), 0\right),$$

  with $\phi$ a constant, $0<\phi<\pi$. Show that, if the axes are now rotated through an angle $\psi$ so as to obtain an elliptically polarized wave with an electric field

  $$\mathbf{E}^{\prime}=\left(F_{1} \cos (k z-\omega t+\chi), F_{2} \sin (k z-\omega t+\chi), 0\right),$$

  then

  $$\tan 2 \psi=\frac{2 E_{1} E_{2} \cos \phi}{E_{1}^{2}-E_{2}^{2}} .$$

  Show also that if $E_{1}=E_{2}=E$ there is an elliptically polarized wave with

  $$\mathbf{E}^{\prime}=\sqrt{2} E\left(\cos \left(k z-\omega t+\frac{1}{2} \phi\right) \cos \frac{1}{2} \phi, \sin \left(k z-\omega t+\frac{1}{2} \phi\right) \sin \frac{1}{2} \phi, 0\right) .$$

  comment

• A4.5

  Electromagnetism | Part II, 2002

  State the four integral relationships between the electric field $\mathbf{E}$ and the magnetic field $\mathbf{B}$ and explain their physical significance. Derive Maxwell's equations from these relationships and show that $\mathbf{E}$ and $\mathbf{B}$ can be described by a scalar potential $\phi$ and a vector potential A which satisfy the inhomogeneous wave equations

  $$\begin{gathered} \nabla^{2} \phi-\epsilon_{0} \mu_{0} \frac{\partial^{2} \phi}{\partial t^{2}}=-\frac{\rho}{\epsilon_{0}} \\ \nabla^{2} \mathbf{A}-\epsilon_{0} \mu_{0} \frac{\partial^{2} \mathbf{A}}{\partial t^{2}}=-\mu_{0} \mathbf{j} \end{gathered}$$

  If the current $\mathbf{j}$ satisfies Ohm's law and the charge density $\rho=0$, show that plane waves of the form

  $$\mathbf{A}=A(z, t) e^{i \omega t} \hat{\mathbf{x}},$$

  where $\hat{\mathbf{x}}$ is a unit vector in the $x$-direction of cartesian axes $(x, y, z)$, are damped. Find an approximate expression for $A(z, t)$ when $\omega \ll \sigma / \epsilon_{0}$, where $\sigma$ is the electrical conductivity.

  comment

2001

• A $1 . 5 \quad$ B $1 . 4 \quad$

  Electromagnetism | Part II, 2001

  (i) Write down the two Maxwell equations that govern steady magnetic fields. Show that the boundary conditions satisfied by the magnetic field on either side of a current sheet, $\mathbf{J}$, with unit normal to the sheet $\mathbf{n}$, are

  $$\mathbf{n} \wedge \mathbf{B}_{2}-\mathbf{n} \wedge \mathbf{B}_{1}=\mu_{0} \mathbf{J}$$

  State without proof the force per unit area on $\mathbf{J}$.

  (ii) Conducting gas occupies the infinite slab $0 \leqslant x \leqslant a$. It carries a steady current $\mathbf{j}=(0,0, j)$ and a magnetic field $\mathbf{B}=(0, B, 0)$ where $\mathbf{j}$, $\mathbf{B}$ depend only on $x$. The pressure is $p(x)$. The equation of hydrostatic equilibrium is $\nabla p=\mathbf{j} \wedge \mathbf{B}$. Write down the equations to be solved in this case. Show that $p+\left(1 / 2 \mu_{0}\right) B^{2}$ is independent of $x$. Using the suffixes 1,2 to denote values at $x=0, a$, respectively, verify that your results are in agreement with those of Part (i) in the case of $a \rightarrow 0$.

  Suppose that

  $$j(x)=\frac{\pi j_{0}}{2 a} \sin \left(\frac{\pi x}{a}\right), \quad B_{1}=0, \quad p_{2}=0$$

  Find $B(x)$ everywhere in the slab.

  comment

• A2.5

  Electromagnetism | Part II, 2001

  (i) Write down the expression for the electrostatic potential $\phi(\mathbf{r})$ due to a distribution of charge $\rho(\mathbf{r})$ contained in a volume $V$. Perform the multipole expansion of $\phi(\mathbf{r})$ taken only as far as the dipole term.

  (ii) If the volume $V$ is the sphere $|\mathbf{r}| \leqslant a$ and the charge distribution is given by

  $$\rho(\mathbf{r})= \begin{cases}r^{2} \cos \theta & r \leqslant a \\ 0 & r>a\end{cases}$$

  where $r, \theta$ are spherical polar coordinates, calculate the charge and dipole moment. Hence deduce $\phi$ as far as the dipole term.

  Obtain an exact solution for $r>a$ by solving the boundary value problem using trial solutions of the forms

  $$\phi=\frac{A \cos \theta}{r^{2}} \text { for } r>a,$$

  and

  $$\phi=B r \cos \theta+C r^{4} \cos \theta \text { for } r<a .$$

  Show that the solution obtained from the multipole expansion is in fact exact for $r>a$.

  [You may use without proof the result

  $$\left.\nabla^{2}\left(r^{k} \cos \theta\right)=(k+2)(k-1) r^{k-2} \cos \theta, \quad k \in \mathbb{N} .\right]$$

  comment

• A3.5 B3.3

  Electromagnetism | Part II, 2001

  (i) Develop the theory of electromagnetic waves starting from Maxwell equations in vacuum. You should relate the wave-speed $c$ to $\epsilon_{0}$ and $\mu_{0}$ and establish the existence of plane, plane-polarized waves in which $\mathbf{E}$ takes the form

  $$\mathbf{E}=\left(E_{0} \cos (k z-\omega t), 0,0\right) .$$

  You should give the form of the magnetic field $\mathbf{B}$ in this case.

  (ii) Starting from Maxwell's equation, establish Poynting's theorem.

  $$-\mathbf{j} \cdot \mathbf{E}=\frac{\partial W}{\partial t}+\nabla \cdot \mathbf{S},$$

  where $W=\frac{\epsilon_{0}}{2} \mathbf{E}^{2}+\frac{1}{2 \mu_{0}} \mathbf{B}^{2}$ and $\mathbf{S}=\frac{1}{\mu_{0}} \mathbf{E} \wedge \mathbf{B}$. Give physical interpretations of $W, S$ and the theorem.

  Compute the averages over space and time of $W$ and $\mathbf{S}$ for the plane wave described in (i) and relate them. Comment on the result.

  comment

• A4.5 $\quad$

  Electromagnetism | Part II, 2001

  Write down the form of Ohm's Law that applies to a conductor if at a point $\mathbf{r}$ it is moving with velocity $\mathbf{v}(\mathbf{r})$.

  Use two of Maxwell's equations to prove that

  $$\int_{C}(\mathbf{E}+\mathbf{v} \wedge \mathbf{B}) \cdot d \mathbf{r}=-\frac{d}{d t} \int_{S} \mathbf{B} \cdot d \mathbf{S}$$

  where $C(t)$ is a moving closed loop, $\mathbf{v}$ is the velocity at the point $\mathbf{r}$ on $C$, and $S$ is a surface spanning $C$. The time derivative on the right hand side accounts for changes in both $C$ and B. Explain briefly the physical importance of this result.

  Find and sketch the magnetic field $\mathbf{B}$ described in the vector potential

  $$\mathbf{A}(r, \theta, z)=\left(0, \frac{1}{2} b r z, 0\right)$$

  in cylindrical polar coordinates $(r, \theta, z)$, where $b>0$ is constant.

  A conducting circular loop of radius $a$ and resistance $R$ lies in the plane $z=h(t)$ with its centre on the $z$-axis.

  Find the magnitude and direction of the current induced in the loop as $h(t)$ changes with time, neglecting self-inductance.

  At time $t=0$ the loop is at rest at $z=0$. For time $t>0$ the loop moves with constant velocity $d h / d t=v>0$. Ignoring the inertia of the loop, use energy considerations to find the force $F(t)$ necessary to maintain this motion.

  [ In cylindrical polar coordinates

  $$\left.\operatorname{curl} \mathbf{A}=\left(\frac{1}{r} \frac{\partial A_{z}}{\partial \theta}-\frac{\partial A_{\theta}}{\partial z}, \frac{\partial A_{r}}{\partial z}-\frac{\partial A_{z}}{\partial r}, \frac{1}{r} \frac{\partial}{\partial r}\left(r A_{\theta}\right)-\frac{1}{r} \frac{\partial A_{r}}{\partial \theta}\right)\right]$$

  Part II

  comment