Statistical Physics
Statistical Physics
Jump to year
Paper 1, Section II, 36C
Throughout this question you should consider a classical gas and assume that the number of particles is fixed.
(a) Write down the equation of state for an ideal gas. Write down an expression for the internal energy of an ideal gas in terms of the heat capacity at constant volume, .
(b) Starting from the first law of thermodynamics, find a relation between and the heat capacity at constant pressure, , for an ideal gas. Hence give an expression for .
(c) Describe the meaning of an adiabatic process. Using the first law of thermodynamics, derive the equation for an adiabatic process in the -plane for an ideal gas.
(d) Consider a simplified Otto cycle (an idealised petrol engine) involving an ideal gas and consisting of the following four reversible steps:
Adiabatic compression from volume to volume ;
: Heat injected at constant volume;
Adiabatic expansion from volume to volume ;
Heat extracted at constant volume.
Sketch the cycle in the -plane and in the -plane.
Derive an expression for the efficiency, , where is the work out, in terms of the compression ratio . How can the efficiency be maximized?
Paper 2, Section II,
(a) What systems are described by microcanonical, canonical and grand canonical ensembles? Under what conditions is the choice of ensemble irrelevant?
(b) In a simple model a meson consists of two quarks bound in a linear potential, , where is the relative displacement of the two quarks and is a positive constant. You are given that the classical (non-relativistic) Hamiltonian for the meson is
where is the total mass, is the reduced mass, is the total momentum, is the internal momentum, and is the centre of mass position.
(i) Show that the partition function for a single meson in thermal equilibrium at temperature in a three-dimensional volume can be written as , where
and
Evaluate and evaluate in the large-volume limit .
What is the average separation of the quarks within the meson at temperature ?
You may assume that for ]
(ii) Now consider an ideal gas of such mesons in a three-dimensional volume .
Calculate the total partition function of the gas.
What is the heat capacity
Paper 3, Section II, C
(a) A gas of non-interacting particles with spin degeneracy has the energymomentum relationship , for constants . Show that the density of states, , in a -dimensional volume with is given by
where is a constant that you should determine. [You may denote the surface area of a unit -dimensional sphere by .]
(b) Write down the Bose-Einstein distribution for the average number of identical bosons in a state with energy in terms of and the chemical potential . Explain why .
(c) Show that an ideal quantum Bose gas in a -dimensional volume , with , as above, has
where is the pressure and is a constant that you should determine.
(d) For such a Bose gas, write down an expression for the number of particles that do not occupy the ground state. Use this to determine the values of for which there exists a Bose-Einstein condensate at sufficiently low temperatures.
Paper 4, Section II, 35C
(a) Explain what is meant by a first-order phase transition and a second-order phase transition.
(b) Explain why the (Helmholtz) free energy is the appropriate thermodynamic potential to consider at fixed and .
(c) Consider a ferromagnet with free energy
where is the temperature, is the magnetization, and are constants.
Find the equilibrium value of at high and low temperatures. Hence, evaluate the equilibrium thermodynamic free energy as a function of and compute the entropy and heat capacity. Determine the jump in the heat capacity and identify the order of the phase transition.
(d) Now consider a ferromagnet with free energy
where are constants with , but .
Find the equilibrium value of at high and low temperatures. What is the order of the phase transition?
For determine the behaviour of the heat capacity at high and low temperatures.
Paper 1, Section II, A
Using the notion of entropy, show that two systems that can freely exchange energy reach the same temperature. Show that the energy of a system increases with temperature.
A system consists of distinguishable, non-interacting spin atoms in a magnetic field, where is large. The energy of an atom is if the spin is up and if the spin is down. Find the entropy and energy if a fraction of the atoms have spin up. Determine as a function of temperature, and deduce the allowed range of . Verify that the energy of the system increases with temperature in this range.
Paper 2, Section II, A
Using the Gibbs free energy , derive the Maxwell relation
Define the notions of heat capacity at constant volume, , and heat capacity at constant pressure, . Show that
Derive the Clausius-Clapeyron relation for along the first-order phase transition curve between a liquid and a gas. Find the simplified form of this relation, assuming the gas has much larger volume than the liquid and that the gas is ideal. Assuming further that the latent heat is a constant, determine the form of as a function of along the phase transition curve. [You may assume there is no discontinuity in the Gibbs free energy across the phase transition curve.]
Paper 3, Section II, A
Starting with the density of electromagnetic radiation modes in -space, determine the energy of black-body radiation in a box of volume at temperature .
Using the first law of thermodynamics show that
By using this relation determine the pressure of the black-body radiation.
[You are given the following:
(i) The mean number of photons in a radiation mode of frequency is ,
(ii) ,
(iii) You may assume vanishes with more rapidly than linearly, as . ]
Paper 4, Section II, A
Consider a classical gas of particles in volume , where the total energy is the standard kinetic energy plus a potential depending on the relative locations of the particles .
(i) Starting from the partition function, show that the free energy of the gas is
where is the free energy when .
(ii) Suppose now that the gas is fairly dilute and that the integral in is small compared to and is dominated by two-particle interactions. Show that the free energy simplifies to the form
and find an integral expression for . Using ( ) find the equation of state of the gas, and verify that is the second virial coefficient.
(iii) The equation of state for a Clausius gas is
for some constant . Find the second virial coefficient for this gas. Evaluate for a gas of hard sphere atoms of radius .
Paper 1, Section II, D
(a) Explain, from a macroscopic and microscopic point of view, what is meant by an adiabatic change. A system has access to heat baths at temperatures and , with . Show that the most effective method for repeatedly converting heat to work, using this system, is by combining isothermal and adiabatic changes. Define the efficiency and calculate it in terms of and .
(b) A thermal system (of constant volume) undergoes a phase transition at temperature . The heat capacity of the system is measured to be
where are constants. A theoretical calculation of the entropy for leads to
How can the value of the theoretically-obtained constant be verified using macroscopically measurable quantities?
Paper 2, Section II, D
Using the classical statistical mechanics of a gas of molecules with negligible interactions, derive the ideal gas law. Explain briefly to what extent this law is independent of the molecule's internal structure.
Calculate the entropy of a monatomic gas of low density, with negligible interactions. Deduce the equation relating the pressure and volume of the gas on a curve in the -plane along which is constant.
[You may use for
Paper 3, Section II, D
What is meant by the chemical potential of a thermodynamic system? Derive the Gibbs distribution for a system at temperature and chemical potential (and fixed volume) with variable particle number .
Consider a non-interacting, two-dimensional gas of fermionic particles in a region of fixed area, at temperature and chemical potential . Using the Gibbs distribution, find the mean occupation number of a one-particle quantum state of energy . Show that the density of states is independent of and deduce that the mean number of particles between energies and is very well approximated for by
where is the Fermi energy. Show that, for small, the heat capacity of the gas has a power-law dependence on , and find the power.
Paper 4, Section II, D
Give an outline of the Landau theory of phase transitions for a system with one real order parameter . Describe the phase transitions that can be modelled by the Landau potentials (i) , (ii) ,
where and are control parameters that depend on the temperature and pressure.
In case (ii), find the curve of first-order phase transitions in the plane. Find the region where it is possible for superheating to occur. Find also the region where it is possible for supercooling to occur.
Paper 1, Section II, A
(a) A macroscopic system has volume and contains particles. Let denote the number of states of the system which have energy in the range where represents experimental uncertainty. Define the entropy of the system and explain why the dependence of on is usually negligible. Define the temperature and pressure of the system and hence obtain the fundamental thermodynamic relation.
(b) A one-dimensional model of rubber consists of a chain of links, each of length a. The chain lies along the -axis with one end fixed at and the other at where . The chain can "fold back" on itself so may not increase monotonically along the chain. Let and denote the number of links along which increases and decreases, respectively. All links have the same energy.
(i) Show that and are uniquely determined by and . Determine , the number of different arrangements of the chain, as a function of and . Hence show that, if and then the entropy of the chain is
where is Boltzmann's constant. [You may use Stirling's approximation: ! for
(ii) Let denote the force required to hold the end of the chain fixed at . This force does work on the chain if the length is increased by . Write down the fundamental thermodynamic relation for this system and hence calculate as a function of and the temperature .
Assume that . Show that the chain satisfies Hooke's law . What happens if is held constant and is increased?
Paper 2, Section II, A
(a) Starting from the canonical ensemble, derive the Maxwell-Boltzmann distribution for the velocities of particles in a classical gas of atoms of mass . Derive also the distribution of speeds of the particles. Calculate the most probable speed.
(b) A certain atom emits photons of frequency . A gas of these atoms is contained in a box. A small hole is cut in a wall of the box so that photons can escape in the positive -direction where they are received by a detector. The frequency of the photons received is Doppler shifted according to the formula
where is the -component of the velocity of the atom that emits the photon and is the speed of light. Let be the temperature of the gas.
(i) Calculate the mean value of .
(ii) Calculate the standard deviation .
(iii) Show that the relative number of photons received with frequency between and is where
for some coefficient to be determined. Hence explain how observations of the radiation emitted by the gas can be used to measure its temperature.
Paper 3, Section II, A
(a) A system of non-interacting bosons has single particle states with energies . Show that the grand canonical partition function is
where is Boltzmann's constant, and is the chemical potential. What is the maximum possible value for ?
(b) A system of bosons has one energy level with zero energy and energy levels with energy . The number of particles with energies is respectively.
(i) Write down expressions for and in terms of and .
(ii) At temperature what is the maximum possible number of bosons in the state with energy What happens for
(iii) Calculate the temperature at which Bose condensation occurs.
(iv) For , show that . For show that
(v) Calculate the mean energy for and for . Hence show that the heat capacity of the system is
Paper 4, Section II, A
The one-dimensional Ising model consists of a set of spins with Hamiltonian
where periodic boundary conditions are imposed so . Here is a positive coupling constant and is an external magnetic field. Define a matrix with elements
where indices take values and with Boltzmann's constant and temperature.
(a) Prove that the partition function of the Ising model can be written as
Calculate the eigenvalues of and hence determine the free energy in the thermodynamic limit . Explain why the Ising model does not exhibit a phase transition in one dimension.
(b) Consider the case of zero magnetic field . The correlation function is defined by
(i) Show that, for ,
(ii) By diagonalizing , or otherwise, calculate for any positive integer . Hence show that
Paper 1, Section II, D
Explain what is meant by the microcanonical ensemble for a quantum system. Sketch how to derive the probability distribution for the canonical ensemble from the microcanonical ensemble. Under what physical conditions should each type of ensemble be used?
A paramagnetic solid contains atoms with magnetic moment , where is a positive constant and is the intrinsic angular momentum of the atom. In an applied magnetic field , the energy of an atom is . Consider . Each atom has total angular momentum , so the possible values of are .
Show that the partition function for a single atom is
where .
Compute the average magnetic moment of the atom. Sketch for , and on the same graph.
The total magnetization is , where is the number of atoms. The magnetic susceptibility is defined by
Show that the solid obeys Curie's law at high temperatures. Compute the susceptibility at low temperatures and give a physical explanation for the result.
Paper 2, Section II, 34D
(a) The entropy of a thermodynamic ensemble is defined by the formula
where is the Boltzmann constant. Explain what is meant by in this formula. Write down an expression for in the grand canonical ensemble, defining any variables you need. Hence show that the entropy is related to the grand canonical partition function by
(b) Consider a gas of non-interacting fermions with single-particle energy levels .
(i) Show that the grand canonical partition function is given by
(ii) Assume that the energy levels are continuous with density of states , where and are positive constants. Prove that
and give expressions for the constant and the function .
(iii) The gas is isolated and undergoes a reversible adiabatic change. By considering the ratio , prove that remains constant. Deduce that and remain constant in this process, where and are constants whose values you should determine.
Paper 3, Section II, D
(a) Describe the Carnot cycle using plots in the -plane and the -plane. In which steps of the cycle is heat absorbed or emitted by the gas? In which steps is work done on, or by, the gas?
(b) An ideal monatomic gas undergoes a reversible cycle described by a triangle in the -plane with vertices at the points with coordinates and respectively. The cycle is traversed in the order .
(i) Write down the equation of state and an expression for the internal energy of the gas.
(ii) Derive an expression relating to and . Use your expression to calculate the heat supplied to, or emitted by, the gas along and .
(iii) Show that heat is supplied to the gas along part of the line , and is emitted by the gas along the other part of the line.
(iv) Calculate the efficiency where is the total work done by the cycle and is the total heat supplied.
Paper 4, Section II, D
The van der Waals equation of state is
where is the pressure, is the volume divided by the number of particles, is the temperature, is Boltzmann's constant and are positive constants.
(i) Prove that the Gibbs free energy satisfies . Hence obtain an expression for and use it to explain the Maxwell construction for determining the pressure at which the gas and liquid phases can coexist at a given temperature.
(ii) Explain what is meant by the critical point and determine the values corresponding to this point.
(iii) By defining and , derive the law of corresponding states:
(iv) To investigate the behaviour near the critical point, let and , where and are small. Expand to cubic order in and hence show that
At fixed small , let and be the values of corresponding to the liquid and gas phases on the co-existence curve. By changing the integration variable from to , use the Maxwell construction to show that . Deduce that, as the critical point is approached along the co-existence curve,
Paper 1, Section II, C
Consider an ideal quantum gas with one-particle states of energy . Let denote the probability that state is occupied by particles. Here, can take the values 0 or 1 for fermions and any non-negative integer for bosons. The entropy of the gas is given by
(a) Write down the constraints that must be satisfied by the probabilities if the average energy and average particle number are kept at fixed values.
Show that if is maximised then
where and are Lagrange multipliers. What is ?
(b) Insert these probabilities into the expression for , and combine the result with the first law of thermodynamics to find the meaning of and .
(c) Calculate the average occupation number for a gas of fermions.
Paper 2, Section II, C
(a) What is meant by the canonical ensemble? Consider a system in the canonical ensemble that can be in states with energies . Write down the partition function for this system and the probability that the system is in state . Derive an expression for the average energy in terms of the partition function.
(b) Consider an anharmonic oscillator with energy levels
where is a positive constant and is a small constant. Let the oscillator be in contact with a reservoir at temperature . Show that, to linear order in , the partition function for the oscillator is given by
where and are constants to be determined. Also show that, to linear order in , the average energy of a system of uncoupled oscillators of this type is given by
where are constants to be determined.
Paper 3, Section II, C
(a) Consider an ideal gas consisting of identical classical particles of mass moving freely in a volume with Hamiltonian . Show that the partition function of the gas has the form
and find as a function of the temperature .
[You may assume that for .]
(b) A monatomic gas of interacting particles is a modification of an ideal gas where any pair of particles with separation interact through a potential energy . The partition function for this gas can be written as
where . The virial expansion of the equation of state for small densities is
Using the free energy, show that
(c) The Lennard-Jones potential is
where and are positive constants. Find the separation where and the separation where has its minimum. Sketch the graph of . Calculate for this potential using the approximations
Paper 4, Section II, 33C
(a) State the first law of thermodynamics. Derive the Maxwell relation
(b) Consider a thermodynamic system whose energy at constant temperature is volume independent, i.e.
Show that this implies that the pressure has the form for some function .
(c) For a photon gas inside a cavity of volume , the energy and pressure are given in terms of the energy density , which depends only on the temperature , by
Show that this implies where is a constant. Show that the entropy is
and calculate the energy and free energy in terms of their respective fundamental variables.
Paper 1, Section II, C
(a) Define the canonical partition function for a system with energy levels , where labels states, given that the system is in contact with a heat reservoir at temperature . What is the probability that the system occupies state ? Starting from an expression for the entropy , deduce that
(b) Consider an ensemble consisting of copies of the system in part (a) with very large, so that there are members of the ensemble in state . Starting from an expression for the number of ways in which this can occur, find the entropy of the ensemble and hence re-derive the expression . [You may assume Stirling's formula for large.
(c) Consider a system of non-interacting particles at temperature . Each particle has internal states with energies
Assuming that the internal states are the only relevant degrees of freedom, calculate the total entropy of the system. Find the limiting values of the entropy as and and comment briefly on your answers.
Paper 2, Section II, C
(a) State the Bose-Einstein distribution formula for the mean occupation numbers of discrete single-particle states with energies in a gas of bosons. Write down expressions for the total particle number and the total energy when the singleparticle states can be treated as continuous, with energies and density of states .
(b) Blackbody radiation at temperature is equivalent to a gas of photons with
where is the volume and is a constant. What value of the chemical potential is required when applying the Bose-Einstein distribution to photons? Show that the heat capacity at constant volume satisfies for some constant , to be determined.
(c) Consider a system of bosonic particles of fixed total number . The particles are trapped in a potential which has ground state energy zero and which gives rise to a density of states , where is a constant. Explain, for this system, what is meant by Bose-Einstein condensation and show that the critical temperature satisfies . If is the number of particles in the ground state, show that for just below
for some constant , to be determined.
(d) Would you expect photons to exhibit Bose-Einstein condensation? Explain your answer very briefly.
Paper 3, Section II, C
(a) A sample of gas has pressure , volume , temperature and entropy .
(i) Use the first law of thermodynamics to derive the Maxwell relation
(ii) Define the heat capacity at constant pressure and the enthalpy and show that .
(b) Consider a perfectly insulated pipe with a throttle valve, as shown.
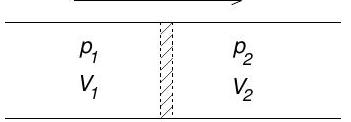
Gas initially occupying volume on the left is forced slowly through the valve at constant pressure . A constant pressure is maintained on the right and the final volume occupied by the gas after passing through the valve is .
(i) Show that the enthalpy of the gas is unchanged by this process.
(ii) The Joule-Thomson coefficient is defined to be . Show that
[You may assume the identity ]
(iii) Suppose that the gas obeys an equation of state
where is the number of particles. Calculate to first order in and hence derive a condition on for obtaining a positive Joule-Thomson coefficient.
Paper 4, Section II, C
The Ising model consists of particles, labelled by , arranged on a -dimensional Euclidean lattice with periodic boundary conditions. Each particle has spin up , or down , and the energy in the presence of a magnetic field is
where is a constant and indicates that the second sum is over each pair of nearest neighbours (every particle has nearest neighbours). Let , where is the temperature.
(i) Express the average spin per particle, , in terms of the canonical partition function .
(ii) Show that in the mean-field approximation
where is a single-particle partition function, is an effective magnetic field which you should find in terms of and , and is a prefactor which you should also evaluate.
(iii) Deduce an equation that determines for general values of and temperature . Without attempting to solve for explicitly, discuss how the behaviour of the system depends on temperature when , deriving an expression for the critical temperature and explaining its significance.
(iv) Comment briefly on whether the results obtained using the mean-field approximation for are consistent with an expression for the free energy of the form
where and are positive constants.
Paper 1, Section II, E
Write down the equation of state and the internal energy of a monatomic ideal gas.
Describe the meaning of an adiabatic process. Derive the equation for an adiabatic process in the pressure-volume plane for a monatomic ideal gas.
Briefly describe the Carnot cycle. Sketch the Carnot cycle in the plane and in the temperature entropy plane.
The Diesel cycle is an idealised version of the process realised in the Diesel engine. It consists of the following four reversible steps:

Sketch the Diesel cycle for a monatomic gas in the plane and the plane. Determine the equations for the curves and in the plane.
The efficiency of the cycle is defined as
where is the heat entering the gas in step and is the heat leaving the gas in step . Calculate as a function of the temperatures at points and .
Paper 2, Section II, E
Briefly describe the microcanonical, canonical and grand canonical ensembles. Why do they agree in the thermodynamic limit?
A harmonic oscillator in one spatial dimension has Hamiltonian
Here and are the momentum and position of the oscillator, is its mass and its frequency. The harmonic oscillator is placed in contact with a heat bath at temperature . What is the relevant ensemble?
Treating the harmonic oscillator classically, compute the mean energy , the energy fluctuation and the heat capacity .
Treating the harmonic oscillator quantum mechanically, compute the mean energy , the energy fluctuation and the heat capacity .
In what limit of temperature do the classical and quantum results agree? Explain why they differ away from this limit. Describe an experiment for which this difference has implications.
Paper 3, Section II, E
In the grand canonical ensemble, at temperature and chemical potential , what is the probability of finding a system in a state with energy and particle number ?
A particle with spin degeneracy and mass moves in spatial dimensions with dispersion relation . Compute the density of states . [You may denote the area of a unit -dimensional sphere as .]
Treating the particles as non-interacting fermions, determine the energy of a gas in terms of the pressure and volume .
Derive an expression for the Fermi energy in terms of the number density of particles. Compute the degeneracy pressure at zero temperature in terms of the number of particles and the Fermi energy.
Show that at high temperatures the gas obeys the ideal gas law (up to small corrections which you need not compute).
Paper 4, Section II, E
The Dieterici equation of state of a gas is
where is the pressure, is the volume divided by the number of particles, is the temperature, and is the Boltzmann constant. Provide a physical interpretation for the constants and .
Briefly explain how the Dieterici equation captures the liquid-gas phase transition. What is the maximum temperature at which such a phase transition can occur?
The Gibbs free energy is given by
where is the energy and is the entropy. Explain why the Gibbs free energy is proportional to the number of particles in the system.
On either side of a first-order phase transition the Gibbs free energies are equal. Use this fact to derive the Clausius-Clapeyron equation for a line along which there is a first-order liquid-gas phase transition,
where is the latent heat which you should define.
Assume that the volume of liquid is negligible compared to the volume of gas and that the latent heat is constant. Further assume that the gas can be well approximated by the ideal gas law. Solve to obtain an equation for the phase-transition line in the plane.
Paper 1, Section II, 35A
(i) What is the occupation number of a state with energy according to the Fermi-Dirac statistics for a given chemical potential ?
(ii) Assuming that the energy is spin independent, what is the number of electrons which can occupy an energy level?
(iii) Consider a semi-infinite metal slab occupying (and idealized to have infinite extent in the plane) and a vacuum environment at . An electron with momentum inside the slab will escape the metal in the direction if it has a sufficiently large momentum to overcome a potential barrier relative to the Fermi energy , i.e. if
where is the electron mass.
At fixed temperature , some fraction of electrons will satisfy this condition, which results in a current density in the direction (an electron having escaped the metal once is considered lost, never to return). Each electron escaping provides a contribution to this current density, where is the velocity and the elementary charge.
(a) Briefly describe the Fermi-Dirac distribution as a function of energy in the limit , where is the Boltzmann constant. What is the chemical potential in this limit?
(b) Assume that the electrons behave like an ideal, non-relativistic Fermi gas and that and . Calculate the current density associated with the electrons escaping the metal in the direction. How could we easily increase the strength of the current?
Paper 2, Section II, 35A
(i) The first law of thermodynamics is , where is the chemical potential. Briefly describe its meaning.
(ii) What is equipartition of energy? Under which conditions is it valid? Write down the heat capacity at constant volume for a monatomic ideal gas.
(iii) Starting from the first law of thermodynamics, and using the fact that for an ideal gas , show that the entropy of an ideal gas containing particles can be written as
where and are temperature and volume of the gas, is the Boltzmann constant, and we define the heat capacity per particle as .
(iv) The Gibbs free energy is defined as . Verify that it is a function of temperature , pressure and particle number . Explain why depends on the particle number through .
(v) Calculate the chemical potential for an ideal gas with heat capacity per particle . Calculate for the special case of a monatomic gas.
Paper 3, Section II, 35A
(i) Briefly describe the microcanonical ensemble.
(ii) For quantum mechanical systems the energy levels are discrete. Explain why we can write the probability distribution in this case as
What assumption do we make for the energy interval ?
Consider independent linear harmonic oscillators of equal frequency . Their total energy is given by
Here is the excitation number of oscillator .
(iii) Show that, for fixed and , the number of possibilities to distribute the excitations over oscillators (i.e. the number of different choices consistent with ) is given by
[Hint: You may wish to consider the set of oscillators plus "additional" excitations and what it means to choose objects from this set.]
(iv) Using the probability distribution of part (ii), calculate the probability distribution for the "first" oscillator as a function of its energy .
(v) If then exactly one value of will correspond to a total energy inside the interval . In this case, show that
Approximate this result in the limit .
Paper 4, Section II, A
A classical particle of mass moving non-relativistically in two-dimensional space is enclosed inside a circle of radius and attached by a spring with constant to the centre of the circle. The particle thus moves in a potential
where . Let the particle be coupled to a heat reservoir at temperature .
(i) Which of the ensembles of statistical physics should be used to model the system?
(ii) Calculate the partition function for the particle.
(iii) Calculate the average energy and the average potential energy of the particle.
(iv) What is the average energy in:
(a) the limit (strong coupling)?
(b) the limit (weak coupling)?
Compare the two results with the values expected from equipartition of energy.
Paper 1, Section II, C
A meson consists of two quarks, attracted by a linear potential energy
where is the separation between the quarks and is a constant. Treating the quarks classically, compute the vibrational partition function that arises from the separation of quarks. What is the average separation of the quarks at temperature ?
Consider an ideal gas of these mesons that have the orientation of the quarks fixed so the mesons do not rotate. Compute the total partition function of the gas. What is its heat capacity ?
[Note: ]
Paper 2, Section II, C
Explain what is meant by an isothermal expansion and an adiabatic expansion of a gas.
By first establishing a suitable Maxwell relation, show that
and
The energy in a gas of blackbody radiation is given by , where is a constant. Derive an expression for the pressure .
Show that if the radiation expands adiabatically, is constant.
Paper 3, Section II, C
A ferromagnet has magnetization order parameter and is at temperature . The free energy is given by
where and are positive constants. Find the equilibrium value of the magnetization at both high and low temperatures.
Evaluate the free energy of the ground state as a function of temperature. Hence compute the entropy and heat capacity. Determine the jump in the heat capacity and identify the order of the phase transition.
After imposing a background magnetic field , the free energy becomes
Explain graphically why the system undergoes a first-order phase transition at low temperatures as changes sign.
The spinodal point occurs when the meta-stable vacuum ceases to exist. Determine the temperature of the spinodal point as a function of and .
Paper 4, Section II, C
Non-relativistic electrons of mass are confined to move in a two-dimensional plane of area . Each electron has two spin states. Compute the density of states and show that it is constant.
Write down expressions for the number of particles and the average energy of a gas of fermions in terms of the temperature and chemical potential . Find an expression for the Fermi Energy in terms of .
For , you may assume that the chemical potential does not change with temperature. Compute the low temperature heat capacity of a gas of fermions. [You may use the approximation that, for large ,
Paper 1, Section II, D
Describe the physical relevance of the microcanonical, canonical and grand canonical ensembles. Explain briefly the circumstances under which all ensembles are equivalent.
The Gibbs entropy for a probability distribution over states is
By imposing suitable constraints on , show how maximising the entropy gives rise to the probability distributions for the microcanonical and canonical ensembles.
A system consists of non-interacting particles fixed at points in a lattice. Each particle has three states with energies . If the system is at a fixed temperature , determine the average energy and the heat capacity . Evaluate each in the limits and .
Describe a configuration of the system that would have negative temperature. Does this system obey the third law of thermodynamics?
Paper 2, Section II, D
Write down the partition function for a single classical non-relativistic particle of mass moving in three dimensions in a potential and in equilibrium with a heat bath at temperature .
A system of non-interacting classical non-relativistic particles, in equilibrium at temperature , is placed in a potential
where is a positive integer. Using the partition function, show that the free energy is
where
Explain the physical relevance of the constant term in the expression .
Viewing as an external parameter, akin to volume, compute the conjugate pressure and show that the equation of state coincides with that of an ideal gas.
Compute the energy , heat capacity and entropy of the gas. Determine the local particle number density as a function of .
Paper 3, Section II, D
A gas of non-interacting particles has energy-momentum relationship for some constants and . Determine the density of states in a threedimensional volume .
Explain why the chemical potential satisfies for the Bose-Einstein distribution.
Show that an ideal quantum Bose gas with the energy-momentum relationship above has
If the particles are bosons at fixed temperature and chemical potential , write down an expression for the number of particles that do not occupy the ground state. Use this to determine the values of for which there exists a Bose-Einstein condensate at sufficiently low temperatures.
Discuss whether a gas of photons can undergo Bose-Einstein condensation.
Paper 4, Section II, D
(i) Define the Gibbs free energy for a gas of particles with pressure at a temperature . Explain why it is necessarily proportional to the number of particles in the system. Given volume and chemical potential , prove that
(ii) The van der Waals equation of state is
Explain the physical significance of the terms with constants and . Sketch the isotherms of the van der Waals equation. Show that the critical point lies at
(iii) Describe the Maxwell construction to determine the condition for phase equilibrium. Hence sketch the regions of the van der Waals isotherm at that correspond to metastable and unstable states. Sketch those regions that correspond to stable liquids and stable gases.
(iv) Show that, as the critical point is approached along the co-existence curve,
Show that, as the critical point is approached along an isotherm,
Paper 2, Section II, C
Consider a 3-dimensional gas of non-interacting particles in a box of size where the allowed momenta are . Assuming the particles have an energy , calculate the density of states as .
Treating the particles as classical explain why the partition function is
Obtain an expression for the total energy .
Why is By considering the dependence of the energies on the volume show that the pressure is given by
What are the results for the pressure for non-relativistic particles and also for relativistic particles when their mass can be neglected?
What is the thermal wavelength for non-relativistic particles? Why are the classical results correct if the thermal wavelength is much smaller than the mean particle separation?
Paper 3, Section II, C
(i) Given the following density of states for a particle in 3 dimensions
write down the partition function for a gas of such non-interacting particles, assuming they can be treated classically. From this expression, calculate the energy of the system and the heat capacities and . You may take it as given that .
[Hint: The formula may be useful.]
(ii) Using thermodynamic relations obtain the relation between heat capacities and compressibilities
where the isothermal and adiabatic compressibilities are given by
derivatives taken at constant temperature and entropy, respectively.
(iii) Find and for the ideal gas considered above.
Paper 4, Section II, C
(i) Let be the probability that a system is in a state labelled by with particles and energy . Define
has a maximum, consistent with a fixed mean total number of particles , mean total energy and , when . Let and show that
where may be identified with the temperature and with the chemical potential.
(ii) For two weakly coupled systems 1,2 then and , . Show that where, if is stationary under variations in and for fixed, we must have .
(iii) Define the grand partition function for the system in (i) and show that
(iv) For a system with single particle energy levels the possible states are labelled by , where and . Show that
Calculate . How is this related to a free fermion gas?
Paper 2, Section II, D
The Van der Waals equation of state for a non-ideal gas is
where and are constants.
(i) Briefly explain the physical motivation for differences between the Van der Waals and ideal gas equations of state.
(ii) Find the volume dependence (at constant temperature) of the internal energy and the heat capacity of a Van der Waals gas.
(iii) A Van der Waals gas is initially at temperature in an insulated container with volume . A small opening is then made so that the gas can expand freely into an empty container, occupying both the old and new containers. The final result is that the gas now occupies a volume . Calculate the final temperature assuming is temperature independent. You may assume the process happens quasistatically.
Paper 3, Section II, D
Consider an ideal Bose gas in an external potential such that the resulting density of single particle states is given by
where is a positive constant.
(i) Derive an expression for the critical temperature for Bose-Einstein condensation of a gas of of these atoms.
[Recall
(ii) What is the internal energy of the gas in the condensed state as a function of and ?
(iii) Now consider the high temperature, classical limit instead. How does the internal energy depend on and ?
Paper 4, Section II, D
Briefly state the ergodic hypothesis and explain its importance.
Consider an ideal, classical, monatomic gas in the presence of a uniform gravitational field in the negative -direction. For convenience, assume the gas is in an arbitrarily large cubic box.
(i) Compute the internal energy of the gas.
(ii) Explain your result for in relation to the equipartition theorem.
(iii) What is the probability that an atom is located at a height between and
(iv) What is the most probable speed of an atom of this gas?
Prove that energy fluctuations in a canonical distribution are given by
where is the absolute temperature, is the heat capacity at constant volume, and is Boltzmann's constant.
Prove the following relation in a similar manner:
Show that, for an ideal gas of monatomic molecules where , these equations can be reduced to
3.II.34E
Derive the following two relations:
and
[You may use any standard Maxwell relation without proving it.]
Experimentalists very seldom measure directly; they measure and use thermodynamics to extract . Use your results from the first part of this question to find a formula for in terms of the easily measured quantities
(the volume coefficient of expansion) and
(the isothermal compressibility).
4.II.34D
Show that the Fermi momentum of a gas of non-interacting electrons in volume is
Consider the electrons to be effectively massless, so that an electron of momentum has (relativistic) energy . Show that the mean energy per electron at zero temperature is .
When a constant external magnetic field of strength is applied to the electron gas, each electron gets an energy contribution depending on whether its spin is parallel or antiparallel to the field. Here is the magnitude of the magnetic moment of an electron. Calculate the total magnetic moment of the electron gas at zero temperature, assuming is much less than .
2.II.34D
Derive the Maxwell relation
The diagram below illustrates the Joule-Thomson throttling process for a porous barrier. A gas of volume , initially on the left-hand side of a thermally insulated pipe, is forced by a piston to go through the barrier using constant pressure . As a result the gas flows to the right-hand side, resisted by a piston which applies a constant pressure (with ). Eventually all of the gas occupies a volume on the right-hand side. Show that this process conserves enthalpy.
The Joule-Thomson coefficient is the change in temperature with respect to a change in pressure during a process that conserves enthalpy . Express the JouleThomson coefficient, , in terms of , the heat capacity at constant pressure , and the volume coefficient of expansion .
What is for an ideal gas?
If one wishes to use the Joule-Thomson process to cool a real (non-ideal) gas, what must the of be?

3.II.34D
For a 2-dimensional gas of nonrelativistic, non-interacting, spinless bosons, find the density of states in the neighbourhood of energy . [Hint: consider the gas in a box of size which has periodic boundary conditions. Work in the thermodynamic limit , with held finite.]
Calculate the number of particles per unit area at a given temperature and chemical potential.
Explain why Bose-Einstein condensation does not occur in this gas at any temperature.
[Recall that
4.II.34D
Consider a classical gas of diatomic molecules whose orientation is fixed by a strong magnetic field. The molecules are not free to rotate, but they are free to vibrate. Assuming that the vibrations are approximately harmonic, calculate the contribution to the partition function due to vibrations.
Evaluate the free energy , where is the total partition function for the gas, and hence calculate the entropy.
Note that and You may approximate ! by .]
2.II.34D
What is meant by the heat capacity of a thermodynamic system? By establishing a suitable Maxwell identity, show that
In a certain model of interacting particles in a volume and at temperature , the partition function is
where and are constants. Find the equation of state and the entropy for this gas of particles. Find the energy and hence the heat capacity of the gas, and verify that the relation is satisfied.
3.II.34D
What is meant by the chemical potential of a thermodynamic system? Derive the Gibbs distribution with variable particle number , for a system at temperature and chemical potential . (You may assume that the volume does not vary.)
Consider a non-interacting gas of fermions in a box of fixed volume, at temperature and chemical potential . Use the Gibbs distribution to find the mean occupation number of a one-particle quantum state of energy . Assuming that the density of states is , for some constant , deduce that the mean number of particles with energies between and is
Why can be identified with the Fermi energy when ? Estimate the number of particles with energies greater than when is small but non-zero.
4.II.34D
Two examples of phenomenological temperature measurements are (i) the mark reached along the length of a liquid-in-glass thermometer; and (ii) the wavelength of the brightest colour of electromagnetic radiation emitted by a hot body (used, for example, to measure the surface temperature of a star).
Give the definition of temperature in statistical physics, and explain how the analysis of ideal gases and black body radiation is used to calibrate and improve phenomenological temperature measurements like those mentioned above. You should give brief derivations of any key results that you use.
2.II.34D
Write down the first law of thermodynamics in differential form applied to an infinitesimal reversible change.
Explain what is meant by an adiabatic change.
Starting with the first law in differential form, derive the Maxwell relation
Hence show that
For radiation in thermal equilibrium at temperature in volume , it is given that and . Hence deduce Stefan's Law,
where is a constant.
The radiation is allowed to expand adiabatically. Show that is constant during the expansion.
3.II.34D
A free spinless particle moving in two dimensions is confined to a square box of side . By imposing periodic boundary conditions show that the number of states in the energy range is , where
If, instead, the particle is an electron with magnetic moment moving in a constant external magnetic field , show that
Let there be electrons in the box. Explain briefly how to construct the ground state of the system. Let be the Fermi energy. Show that when
Show also that the magnetic moment of the system in its ground state is given by
and that the ground state energy is
4.II.34D
Write down an expression for the partition function of a classical particle of mass moving in three dimensions in a potential and in equilibrium with a heat bath at temperature .
A system of non-interacting classical particles is placed in the potential
where is a positive integer. The gas is in equilibrium at temperature . Using a suitable rescaling of variables, show that the free energy is given by
where
Regarding as an external parameter, find the thermodynamic force , conjugate to , exerted by this system. Find the equation of state and compare with that of an ideal gas confined in a volume .
Derive expressions for the entropy , the internal energy and the total heat capacity at constant .
Show that for all the total heat capacity at constant is given by
[Note that
B1.22
Define the notions of entropy and thermodynamic temperature for a gas of particles in a variable volume . Derive the fundamental relation
The free energy of the gas is defined as . Why is it convenient to regard as a function of and ? By considering , or otherwise, show that
Deduce that the entropy of an ideal gas, whose equation of state is (using energy units), has the form
where is independent of and .
Show that if the gas is in contact with a heat bath at temperature , then the probability of finding the gas in a particular quantum microstate of energy is
B3.22
Describe briefly why a low density gas can be investigated using classical statistical mechanics.
Explain why, for a gas of structureless atoms, the measure on phase space is
and the probability density in phase space is proportional to
where is the temperature in energy units.
Derive the Maxwell probability distribution for atomic speeds ,
Why is this valid even if the atoms interact?
Find the mean value of the speed of the atoms.
Is the mean kinetic energy of the atoms?
B4.23
Derive the Bose-Einstein expression for the mean number of Bose particles occupying a particular single-particle quantum state of energy , when the chemical potential is and the temperature is in energy units.
Why is the chemical potential for a gas of photons given by ?
Show that, for black-body radiation in a cavity of volume at temperature , the mean number of photons in the angular frequency range is
Hence, show that the total energy of the radiation in the cavity is
where is a constant that need not be evaluated.
Use thermodynamic reasoning to find the entropy and pressure of the radiation and verify that
Why is this last result to be expected for a gas of photons?
B1.22
A gas in equilibrium at temperature and pressure has quantum stationary states with energies in volume . What does it mean to say that a change in volume from to is reversible?
Write down an expression for the probability that the gas is in state . How is the entropy defined in terms of these probabilities? Write down an expression for the energy of the gas, and establish the relation
for reversible changes.
By considering the quantity , derive the Maxwell relation
A gas obeys the equation of state
where is a constant and is a function of only. The gas is expanded isothermally, at temperature , from volume to volume . Find the work done on the gas. Show that the heat absorbed by the gas is given by
B3.22
A diatomic molecule, free to move in two space dimensions, has classical Hamiltonian
where is the particle's momentum and is its angular momentum. Write down the classical partition function for an ideal gas of such molecules in thermal equilibrium at temperature . Show that it can be written in the form
where and are the one-molecule partition functions associated with the translational and rotational degrees of freedom, respectively. Compute and and hence show that the energy of the gas is given by
where is Boltzmann's constant. How does this result illustrate the principle of equipartition of energy?
In an improved model of the two-dimensional gas of diatomic molecules, the angular momentum is quantized in integer multiples of :
Write down an expression for in this case. Given that , obtain an expression for the energy in the form
where and are constants that should be computed. How is this result compatible with the principle of equipartition of energy? Find , the specific heat at constant volume, for .
Why can the sum over in be approximated by an integral when ? Deduce that in this limit.
B4.23
A gas of non-interacting identical bosons in volume , with one-particle energy levels , is in equilibrium at temperature and chemical potential . Let be the number of particles in the th one-particle state. Write down an expression for the grand partition function . Write down an expression for the probability of finding a given set of occupation numbers of the one-particle states. Hence determine the mean occupation numbers (the Bose-Einstein distribution). Write down expressions, in terms of the mean occupation numbers, for the total energy and total number of particles .
Write down an expression for the grand potential in terms of . Given that
show that can be written in the form
for some function , which you should determine. Hence show that for any change of the gas that leaves the mean occupation numbers unchanged. Consider a (quasi-static) change of with this property. Using the formula
and given that for each , show that
What is the value of for photons?
Let , so that is a function only of and . Why does the energy density depend only on Using the Maxwell relation
and the first law of thermodynamics for reversible changes, show that
and hence that
for some power that you should determine. Show further that
Hence verify, given , that is left unchanged by a change of at constant .
B1.22
A simple model for a rubber molecule consists of a one-dimensional chain of links each of fixed length and each of which is oriented in either the positive or negative direction. A unique state of the molecule is designated by giving the orientation of each link. If there are links oriented in the positive direction and links oriented in the negative direction then and the length of the molecule is . The length of the molecule associated with state is .
What is the range of ?
What is the number of states with fixed?
Consider an ensemble of copies of the molecule in which members are in state and write down the expression for the mean length .
By introducing a Lagrange multiplier for show that the most probable configuration for the with given length is found by maximizing
Hence show that the most probable configuration is given by
where is the probability for finding an ensemble member in the state and is the partition function which should be defined.
Show that can be expressed as
where the meaning of should be explained.
Hence show that is given by
and therefore that the free energy for the system is
Show that is determined by
and hence that the equation of state is
What are the independent variables on which depends?
Explain why the tension in the rubber molecule is .
B3.22
A system consisting of non-interacting bosons has single-particle levels uniquely labelled by with energies . Show that the free energy in the grand canonical ensemble is
What is the maximum value for ?
A system of bosons in a large volume has one energy level of energy zero and a large number of energy levels of the same energy , where takes the form with a positive constant. What are the dimensions of
Show that the free energy is
The numbers of particles with energies are respectively . Write down expressions for in terms of .
At temperature what is the maximum number of bosons in the normal phase (the state with energy )? Explain what happens when .
Given and calculate the transition temperature at which Bose condensation occurs.
For show that . What is the value of for ?
Calculate the mean energy for (a) (b) , and show that the heat capacity of the system at constant volume is
B4.23
A perfect gas in equilibrium in a volume has quantum stationary states with energies . In a Boltzmann distribution, the probability that the system is in state is . The entropy is defined to be .
For two nearby states establish the equation
where and should be defined.
For reversible changes show that
where is the amount of heat transferred in the exchange.
Define , the heat capacity at constant volume.
A system with constant heat capacity initially at temperature is heated at constant volume to a temperature . Show that the change in entropy is .
Explain what is meant by isothermal and adiabatic transitions.
Briefly, describe the Carnot cycle and define its efficiency. Explain briefly why no heat engine can be more efficient than one whose operation is based on a Carnot cycle.
Three identical bodies with constant heat capacity at fixed volume , are initially at temperatures , respectively. Heat engines operate between the bodies with no input of work or heat from the outside and the respective temperatures are changed to , the volume of the bodies remaining constant. Show that, if the heat engines operate on a Carnot cycle, then
where and .
Hence show that the maximum temperature to which any one of the bodies can be raised is where
Show that a solution is if initially . Do you expect there to be any other solutions?
Find if initially .
[Hint: Choose to maximize one temperature and impose the constraints above using Lagrange multipliers. ]
B1.22
Write down the first law of thermodynamics in differential form for an infinitesimal reversible change in terms of the increments and , where and are to be defined. Briefly give an interpretation of each term and deduce that
Define the specific heat at constant volume and show that for an adiabatic change
Derive the Maxwell relation
where is temperature and hence show that
An imperfect gas of volume obeys the van der Waals equation of state
where and are non-negative constants. Show that
and deduce that is a function of only. It can further be shown that in this case is independent of . Hence show that
is constant on adiabatic curves.
B3.22
A system consists of weakly interacting non-relativistic fermions, each of mass , in a three-dimensional volume, . Derive the Fermi-Dirac distribution
where is the number of particles with energy in and . Explain the physical significance of .
Explain how the constant is determined by the number of particles and write down expressions for and the internal energy in terms of .
Show that, in the limit ,
where .
Show also that in this limit
Deduce that the condition implies that . Discuss briefly whether or not this latter condition is satisfied in a white dwarf star and in a dilute electron gas at room temperature.
Note that .
B4.23
Given that the free energy can be written in terms of the partition function as show that the entropy and internal energy are given by
A system of particles has Hamiltonian where is the set of particle momenta and the set of particle coordinates. Write down the expression for the classical partition function for this system in equilibrium at temperature . In a particular case is given by
Let be a homogeneous function in all the , and in a subset of the . Derive the principle of equipartition for this system.
A system consists of weakly interacting harmonic oscillators each with Hamiltonian
Using equipartition calculate the classical specific heat of the system, . Also calculate the classical entropy .
Write down the expression for the quantum partition function of the system and derive expressions for the specific heat and the entropy in terms of and the parameter . Show for that
where should be calculated. Comment briefly on the physical significance of the constant and why it is non-zero.