Statistical Physics

2021

• Paper 1, Section II, 36C

  Statistical Physics | Part II, 2021

  Throughout this question you should consider a classical gas and assume that the number of particles is fixed.

  (a) Write down the equation of state for an ideal gas. Write down an expression for the internal energy of an ideal gas in terms of the heat capacity at constant volume, $C_{V}$.

  (b) Starting from the first law of thermodynamics, find a relation between $C_{V}$ and the heat capacity at constant pressure, $C_{p}$, for an ideal gas. Hence give an expression for $\gamma=C_{p} / C_{V}$.

  (c) Describe the meaning of an adiabatic process. Using the first law of thermodynamics, derive the equation for an adiabatic process in the $(p, V)$-plane for an ideal gas.

  (d) Consider a simplified Otto cycle (an idealised petrol engine) involving an ideal gas and consisting of the following four reversible steps:

  $A \rightarrow B:$ Adiabatic compression from volume $V_{1}$ to volume $V_{2}<V_{1}$;

  $B \rightarrow C$ : Heat $Q_{1}$ injected at constant volume;

  $C \rightarrow D:$ Adiabatic expansion from volume $V_{2}$ to volume $V_{1}$;

  $D \rightarrow A:$ Heat $Q_{2}$ extracted at constant volume.

  Sketch the cycle in the $(p, V)$-plane and in the $(T, S)$-plane.

  Derive an expression for the efficiency, $\eta=W / Q_{1}$, where $W$ is the work out, in terms of the compression ratio $r=V_{1} / V_{2}$. How can the efficiency be maximized?

  comment

• Paper 2, Section II, $37 \mathrm{C}$

  Statistical Physics | Part II, 2021

  (a) What systems are described by microcanonical, canonical and grand canonical ensembles? Under what conditions is the choice of ensemble irrelevant?

  (b) In a simple model a meson consists of two quarks bound in a linear potential, $U(\mathbf{r})=\alpha|\mathbf{r}|$, where $\mathbf{r}$ is the relative displacement of the two quarks and $\alpha$ is a positive constant. You are given that the classical (non-relativistic) Hamiltonian for the meson is

  $$H(\mathbf{P}, \mathbf{R}, \mathbf{p}, \mathbf{r})=\frac{|\mathbf{P}|^{2}}{2 M}+\frac{|\mathbf{p}|^{2}}{2 \mu}+\alpha|\mathbf{r}|$$

  where $M=2 m$ is the total mass, $\mu=m / 2$ is the reduced mass, $\mathbf{P}$ is the total momentum, $\mathbf{p}=\mu d \mathbf{r} / d t$ is the internal momentum, and $\mathbf{R}$ is the centre of mass position.

  (i) Show that the partition function for a single meson in thermal equilibrium at temperature $T$ in a three-dimensional volume $V$ can be written as $Z_{1}=Z_{\text {trans }} Z_{\text {int }}$, where

  $$Z_{\text {trans }}=\frac{V}{(2 \pi \hbar)^{3}} \int d^{3} P e^{-\beta|\mathbf{P}|^{2} /(2 M)}, \quad Z_{\text {int }}=\frac{1}{(2 \pi \hbar)^{3}} \int d^{3} r d^{3} p e^{-\beta|\mathbf{p}|^{2} /(2 \mu)} e^{-\beta \alpha|\mathbf{r}|}$$

  and $\beta=1 /\left(k_{\mathrm{B}} T\right)$

  Evaluate $Z_{\text {trans }}$ and evaluate $Z_{\text {int }}$ in the large-volume limit $\left(\beta \alpha V^{1 / 3} \gg 1\right)$.

  What is the average separation of the quarks within the meson at temperature $T$ ?

  $\left[\right.$ You may assume that $\int_{-\infty}^{\infty} e^{-c x^{2}} d x=\sqrt{\pi / c}$ for $c>0$ ]

  (ii) Now consider an ideal gas of $N$ such mesons in a three-dimensional volume $V$.

  Calculate the total partition function of the gas.

  What is the heat capacity $C_{V} ?$

  comment

• Paper 3, Section II, C

  Statistical Physics | Part II, 2021

  (a) A gas of non-interacting particles with spin degeneracy $g_{s}$ has the energymomentum relationship $E=A(\hbar k)^{\alpha}$, for constants $A, \alpha>0$. Show that the density of states, $g(E) d E$, in a $d$-dimensional volume $V$ with $d \geqslant 2$ is given by

  $$g(E) d E=B V E^{(d-\alpha) / \alpha} d E$$

  where $B$ is a constant that you should determine. [You may denote the surface area of a unit $(d-1)$-dimensional sphere by $S_{d-1}$.]

  (b) Write down the Bose-Einstein distribution for the average number of identical bosons in a state with energy $E_{r} \geqslant 0$ in terms of $\beta=1 / k_{B} T$ and the chemical potential $\mu$. Explain why $\mu<0$.

  (c) Show that an ideal quantum Bose gas in a $d$-dimensional volume $V$, with $E=A(\hbar k)^{\alpha}$, as above, has

  $$p V=D E,$$

  where $p$ is the pressure and $D$ is a constant that you should determine.

  (d) For such a Bose gas, write down an expression for the number of particles that do not occupy the ground state. Use this to determine the values of $\alpha$ for which there exists a Bose-Einstein condensate at sufficiently low temperatures.

  comment

• Paper 4, Section II, 35C

  Statistical Physics | Part II, 2021

  (a) Explain what is meant by a first-order phase transition and a second-order phase transition.

  (b) Explain why the (Helmholtz) free energy is the appropriate thermodynamic potential to consider at fixed $T, V$ and $N$.

  (c) Consider a ferromagnet with free energy

  $$F(T, m)=F_{0}(T)+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}$$

  where $T$ is the temperature, $m$ is the magnetization, and $a, b, T_{c}>0$ are constants.

  Find the equilibrium value of $m$ at high and low temperatures. Hence, evaluate the equilibrium thermodynamic free energy as a function of $T$ and compute the entropy and heat capacity. Determine the jump in the heat capacity and identify the order of the phase transition.

  (d) Now consider a ferromagnet with free energy

  $$F(T, m)=F_{0}(T)+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}+\frac{c}{6} m^{6}$$

  where $a, b, c, T_{c}$ are constants with $a, c, T_{c}>0$, but $b \leqslant 0$.

  Find the equilibrium value of $m$ at high and low temperatures. What is the order of the phase transition?

  For $b=0$ determine the behaviour of the heat capacity at high and low temperatures.

  comment

2020

• Paper 1, Section II, A

  Statistical Physics | Part II, 2020

  Using the notion of entropy, show that two systems that can freely exchange energy reach the same temperature. Show that the energy of a system increases with temperature.

  A system consists of $N$ distinguishable, non-interacting spin $\frac{1}{2}$ atoms in a magnetic field, where $N$ is large. The energy of an atom is $\varepsilon>0$ if the spin is up and $-\varepsilon$ if the spin is down. Find the entropy and energy if a fraction $\alpha$ of the atoms have spin up. Determine $\alpha$ as a function of temperature, and deduce the allowed range of $\alpha$. Verify that the energy of the system increases with temperature in this range.

  comment

• Paper 2, Section II, A

  Statistical Physics | Part II, 2020

  Using the Gibbs free energy $G(T, P)=E-T S+P V$, derive the Maxwell relation

  $$\left.\frac{\partial S}{\partial P}\right|_{T}=-\left.\frac{\partial V}{\partial T}\right|_{P}$$

  Define the notions of heat capacity at constant volume, $C_{V}$, and heat capacity at constant pressure, $C_{P}$. Show that

  $$C_{P}-C_{V}=\left.\left.T \frac{\partial V}{\partial T}\right|_{P} \frac{\partial P}{\partial T}\right|_{V}$$

  Derive the Clausius-Clapeyron relation for $\frac{d P}{d T}$ along the first-order phase transition curve between a liquid and a gas. Find the simplified form of this relation, assuming the gas has much larger volume than the liquid and that the gas is ideal. Assuming further that the latent heat is a constant, determine the form of $P$ as a function of $T$ along the phase transition curve. [You may assume there is no discontinuity in the Gibbs free energy across the phase transition curve.]

  comment

• Paper 3, Section II, A

  Statistical Physics | Part II, 2020

  Starting with the density of electromagnetic radiation modes in $\mathbf{k}$-space, determine the energy $E$ of black-body radiation in a box of volume $V$ at temperature $T$.

  Using the first law of thermodynamics show that

  $$\left.\frac{\partial E}{\partial V}\right|_{T}=\left.T \frac{\partial P}{\partial T}\right|_{V}-P$$

  By using this relation determine the pressure $P$ of the black-body radiation.

  [You are given the following:

  (i) The mean number of photons in a radiation mode of frequency $\omega$ is $\frac{1}{e^{\hbar \omega / T}-1}$,

  (ii) $1+\frac{1}{2^{4}}+\frac{1}{3^{4}}+\cdots=\frac{\pi^{4}}{90}$,

  (iii) You may assume $P$ vanishes with $T$ more rapidly than linearly, as $T \rightarrow 0$. ]

  comment

• Paper 4, Section II, A

  Statistical Physics | Part II, 2020

  Consider a classical gas of $N$ particles in volume $V$, where the total energy is the standard kinetic energy plus a potential $U\left(\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{N}\right)$ depending on the relative locations of the particles $\left\{\mathbf{x}_{i}: 1 \leqslant i \leqslant N\right\}$.

  (i) Starting from the partition function, show that the free energy of the gas is

  $$F=F_{\text {ideal }}-T \log \left\{1+\frac{1}{V^{N}} \int\left(e^{-U / T}-1\right) d^{3 N} x\right\}$$

  where $F_{\text {ideal }}$ is the free energy when $U \equiv 0$.

  (ii) Suppose now that the gas is fairly dilute and that the integral in $(*)$ is small compared to $V^{N}$ and is dominated by two-particle interactions. Show that the free energy simplifies to the form

  $$F=F_{\text {ideal }}+\frac{N^{2} T}{V} B(T)$$

  and find an integral expression for $B(T)$. Using ( $\dagger$ ) find the equation of state of the gas, and verify that $B(T)$ is the second virial coefficient.

  (iii) The equation of state for a Clausius gas is

  $$P(V-N b)=N T$$

  for some constant $b$. Find the second virial coefficient for this gas. Evaluate $b$ for a gas of hard sphere atoms of radius $r_{0}$.

  comment

2019

• Paper 1, Section II, D

  Statistical Physics | Part II, 2019

  (a) Explain, from a macroscopic and microscopic point of view, what is meant by an adiabatic change. A system has access to heat baths at temperatures $T_{1}$ and $T_{2}$, with $T_{2}>T_{1}$. Show that the most effective method for repeatedly converting heat to work, using this system, is by combining isothermal and adiabatic changes. Define the efficiency and calculate it in terms of $T_{1}$ and $T_{2}$.

  (b) A thermal system (of constant volume) undergoes a phase transition at temperature $T_{\mathrm{c}}$. The heat capacity of the system is measured to be

  $$C= \begin{cases}\alpha T & \text { for } T<T_{\mathrm{c}} \\ \beta & \text { for } T>T_{\mathrm{c}}\end{cases}$$

  where $\alpha, \beta$ are constants. A theoretical calculation of the entropy $S$ for $T>T_{\mathrm{c}}$ leads to

  $$S=\beta \log T+\gamma$$

  How can the value of the theoretically-obtained constant $\gamma$ be verified using macroscopically measurable quantities?

  comment

• Paper 2, Section II, D

  Statistical Physics | Part II, 2019

  Using the classical statistical mechanics of a gas of molecules with negligible interactions, derive the ideal gas law. Explain briefly to what extent this law is independent of the molecule's internal structure.

  Calculate the entropy $S$ of a monatomic gas of low density, with negligible interactions. Deduce the equation relating the pressure $P$ and volume $V$ of the gas on a curve in the $PV$-plane along which $S$ is constant.

  [You may use $\int_{-\infty}^{\infty} e^{-\alpha x^{2}} d x=\left(\frac{\pi}{\alpha}\right)^{\frac{1}{2}}$ for $\left.\alpha>0 .\right]$

  comment

• Paper 3, Section II, D

  Statistical Physics | Part II, 2019

  What is meant by the chemical potential $\mu$ of a thermodynamic system? Derive the Gibbs distribution for a system at temperature $T$ and chemical potential $\mu$ (and fixed volume) with variable particle number $N$.

  Consider a non-interacting, two-dimensional gas of $N$ fermionic particles in a region of fixed area, at temperature $T$ and chemical potential $\mu$. Using the Gibbs distribution, find the mean occupation number $n_{F}(\varepsilon)$ of a one-particle quantum state of energy $\varepsilon$. Show that the density of states $g(\varepsilon)$ is independent of $\varepsilon$ and deduce that the mean number of particles between energies $\varepsilon$ and $\varepsilon+d \varepsilon$ is very well approximated for $T \ll \varepsilon_{F}$ by

  $$\frac{N}{\varepsilon_{F}} \frac{d \varepsilon}{e^{\left(\varepsilon-\varepsilon_{F}\right) / T+1}}$$

  where $\varepsilon_{F}$ is the Fermi energy. Show that, for $T$ small, the heat capacity of the gas has a power-law dependence on $T$, and find the power.

  comment

• Paper 4, Section II, D

  Statistical Physics | Part II, 2019

  Give an outline of the Landau theory of phase transitions for a system with one real order parameter $\phi$. Describe the phase transitions that can be modelled by the Landau potentials (i) $G=\frac{1}{4} \phi^{4}+\frac{1}{2} \varepsilon \phi^{2}$, (ii) $G=\frac{1}{6} \phi^{6}+\frac{1}{4} g \phi^{4}+\frac{1}{2} \varepsilon \phi^{2}$,

  where $\varepsilon$ and $g$ are control parameters that depend on the temperature and pressure.

  In case (ii), find the curve of first-order phase transitions in the $(g, \varepsilon)$ plane. Find the region where it is possible for superheating to occur. Find also the region where it is possible for supercooling to occur.

  comment

2018

• Paper 1, Section II, A

  Statistical Physics | Part II, 2018

  (a) A macroscopic system has volume $V$ and contains $N$ particles. Let $\Omega(E, V, N ; \delta E)$ denote the number of states of the system which have energy in the range $(E, E+\delta E)$ where $\delta E \ll E$ represents experimental uncertainty. Define the entropy $S$ of the system and explain why the dependence of $S$ on $\delta E$ is usually negligible. Define the temperature and pressure of the system and hence obtain the fundamental thermodynamic relation.

  (b) A one-dimensional model of rubber consists of a chain of $N$ links, each of length a. The chain lies along the $x$-axis with one end fixed at $x=0$ and the other at $x=L$ where $L<N a$. The chain can "fold back" on itself so $x$ may not increase monotonically along the chain. Let $N_{\rightarrow}$ and $N_{\leftarrow}$ denote the number of links along which $x$ increases and decreases, respectively. All links have the same energy.

  (i) Show that $N_{\rightarrow}$ and $N_{\leftarrow}$ are uniquely determined by $L$ and $N$. Determine $\Omega(L, N)$, the number of different arrangements of the chain, as a function of $N_{\rightarrow}$ and $N_{\leftarrow}$. Hence show that, if $N_{\rightarrow} \gg 1$ and $N_{\leftarrow} \gg 1$ then the entropy of the chain is

  $$\begin{aligned} S(L, N)=k N & {\left[\log 2-\frac{1}{2}\left(1+\frac{L}{N a}\right) \log \left(1+\frac{L}{N a}\right)\right.} \\ &\left.-\frac{1}{2}\left(1-\frac{L}{N a}\right) \log \left(1-\frac{L}{N a}\right)\right] \end{aligned}$$

  where $k$ is Boltzmann's constant. [You may use Stirling's approximation: $n$ ! $\approx$ $\sqrt{2 \pi} n^{n+1 / 2} e^{-n}$ for $\left.n \gg 1 .\right]$

  (ii) Let $f$ denote the force required to hold the end of the chain fixed at $x=L$. This force does work $f d L$ on the chain if the length is increased by $d L$. Write down the fundamental thermodynamic relation for this system and hence calculate $f$ as a function of $L$ and the temperature $T$.

  Assume that $N a \gg L$. Show that the chain satisfies Hooke's law $f \propto L$. What happens if $f$ is held constant and $T$ is increased?

  comment

• Paper 2, Section II, A

  Statistical Physics | Part II, 2018

  (a) Starting from the canonical ensemble, derive the Maxwell-Boltzmann distribution for the velocities of particles in a classical gas of atoms of mass $m$. Derive also the distribution of speeds $v$ of the particles. Calculate the most probable speed.

  (b) A certain atom emits photons of frequency $\omega_{0}$. A gas of these atoms is contained in a box. A small hole is cut in a wall of the box so that photons can escape in the positive $x$-direction where they are received by a detector. The frequency of the photons received is Doppler shifted according to the formula

  $$\omega=\omega_{0}\left(1+\frac{v_{x}}{c}\right)$$

  where $v_{x}$ is the $x$-component of the velocity of the atom that emits the photon and $c$ is the speed of light. Let $T$ be the temperature of the gas.

  (i) Calculate the mean value $\langle\omega\rangle$ of $\omega$.

  (ii) Calculate the standard deviation $\sqrt{\left\langle(\omega-\langle\omega\rangle)^{2}\right\rangle}$.

  (iii) Show that the relative number of photons received with frequency between $\omega$ and $\omega+d \omega$ is $I(\omega) d \omega$ where

  $$I(\omega) \propto \exp \left(-a\left(\omega-\omega_{0}\right)^{2}\right)$$

  for some coefficient $a$ to be determined. Hence explain how observations of the radiation emitted by the gas can be used to measure its temperature.

  comment

• Paper 3, Section II, A

  Statistical Physics | Part II, 2018

  (a) A system of non-interacting bosons has single particle states $|i\rangle$ with energies $\epsilon_{i} \geqslant 0$. Show that the grand canonical partition function is

  $$\log \mathcal{Z}=-\sum_{i} \log \left(1-e^{-\beta\left(\epsilon_{i}-\mu\right)}\right)$$

  where $\beta=1 /(k T), k$ is Boltzmann's constant, and $\mu$ is the chemical potential. What is the maximum possible value for $\mu$ ?

  (b) A system of $N \gg 1$ bosons has one energy level with zero energy and $M \gg 1$ energy levels with energy $\epsilon>0$. The number of particles with energies $0, \epsilon$ is $N_{0}, N_{\epsilon}$ respectively.

  (i) Write down expressions for $\left\langle N_{0}\right\rangle$ and $\left\langle N_{\epsilon}\right\rangle$ in terms of $\mu$ and $\beta$.

  (ii) At temperature $T$ what is the maximum possible number $N_{\epsilon}^{\max }$ of bosons in the state with energy $\epsilon ?$ What happens for $N>N_{\epsilon}^{\max } ?$

  (iii) Calculate the temperature $T_{B}$ at which Bose condensation occurs.

  (iv) For $T>T_{B}$, show that $\mu=\epsilon\left(T_{B}-T\right) / T_{B}$. For $T<T_{B}$ show that

  $$\mu \approx-\frac{k T}{N} \frac{e^{\epsilon /(k T)}-1}{e^{\epsilon /(k T)}-e^{\epsilon /\left(k T_{B}\right)}} .$$

  (v) Calculate the mean energy $\langle E\rangle$ for $T>T_{B}$ and for $T<T_{B}$. Hence show that the heat capacity of the system is

  $$C \approx \begin{cases}\frac{1}{k T^{2}} \frac{M \epsilon^{2}}{\left(e^{\beta \epsilon}-1\right)^{2}} & T<T_{B} \\ 0 & T>T_{B}\end{cases}$$

  comment

• Paper 4, Section II, A

  Statistical Physics | Part II, 2018

  The one-dimensional Ising model consists of a set of $N$ spins $s_{i}$ with Hamiltonian

  $$H=-J \sum_{i=1}^{N} s_{i} s_{i+1}-\frac{B}{2} \sum_{i=1}^{N}\left(s_{i}+s_{i+1}\right)$$

  where periodic boundary conditions are imposed so $s_{N+1}=s_{1}$. Here $J$ is a positive coupling constant and $B$ is an external magnetic field. Define a $2 \times 2$ matrix $M$ with elements

  $$M_{s t}=\exp \left[\beta J s t+\frac{\beta B}{2}(s+t)\right]$$

  where indices $s, t$ take values $\pm 1$ and $\beta=(k T)^{-1}$ with $k$ Boltzmann's constant and $T$ temperature.

  (a) Prove that the partition function of the Ising model can be written as

  $$Z=\operatorname{Tr}\left(M^{N}\right)$$

  Calculate the eigenvalues of $M$ and hence determine the free energy in the thermodynamic limit $N \rightarrow \infty$. Explain why the Ising model does not exhibit a phase transition in one dimension.

  (b) Consider the case of zero magnetic field $B=0$. The correlation function $\left\langle s_{i} s_{j}\right\rangle$ is defined by

  $$\left\langle s_{i} s_{j}\right\rangle=\frac{1}{Z} \sum_{\left\{s_{k}\right\}} s_{i} s_{j} e^{-\beta H}$$

  (i) Show that, for $i>1$,

  $$\left\langle s_{1} s_{i}\right\rangle=\frac{1}{Z} \sum_{s, t} s t\left(M^{i-1}\right)_{s t}\left(M^{N-i+1}\right)_{t s}$$

  (ii) By diagonalizing $M$, or otherwise, calculate $M^{p}$ for any positive integer $p$. Hence show that

  $$\left\langle s_{1} s_{i}\right\rangle=\frac{\tanh ^{i-1}(\beta J)+\tanh ^{N-i+1}(\beta J)}{1+\tanh ^{N}(\beta J)}$$

  comment

2017

• Paper 1, Section II, D

  Statistical Physics | Part II, 2017

  Explain what is meant by the microcanonical ensemble for a quantum system. Sketch how to derive the probability distribution for the canonical ensemble from the microcanonical ensemble. Under what physical conditions should each type of ensemble be used?

  A paramagnetic solid contains atoms with magnetic moment $\boldsymbol{\mu}=\mu_{B} \mathbf{J}$, where $\mu_{B}$ is a positive constant and $\mathbf{J}$ is the intrinsic angular momentum of the atom. In an applied magnetic field $\mathbf{B}$, the energy of an atom is $-\boldsymbol{\mu} \cdot \mathbf{B}$. Consider $\mathbf{B}=(0,0, B)$. Each atom has total angular momentum $J \in \mathbb{Z}$, so the possible values of $J_{z}=m \in \mathbb{Z}$ are $-J \leqslant m \leqslant J$.

  Show that the partition function for a single atom is

  $$Z_{1}(T, B)=\frac{\sinh \left(x\left(J+\frac{1}{2}\right)\right)}{\sinh (x / 2)}$$

  where $x=\mu_{B} B / k T$.

  Compute the average magnetic moment $\left\langle\mu_{z}\right\rangle$ of the atom. Sketch $\left\langle\mu_{z}\right\rangle / J$ for $J=1$, $J=2$ and $J=3$ on the same graph.

  The total magnetization is $M_{z}=N\left\langle\mu_{z}\right\rangle$, where $N$ is the number of atoms. The magnetic susceptibility is defined by

  $$\chi=\left(\frac{\partial M_{z}}{\partial B}\right)_{T}$$

  Show that the solid obeys Curie's law at high temperatures. Compute the susceptibility at low temperatures and give a physical explanation for the result.

  comment

• Paper 2, Section II, 34D

  Statistical Physics | Part II, 2017

  (a) The entropy of a thermodynamic ensemble is defined by the formula

  $$S=-k \sum_{n} p(n) \log p(n)$$

  where $k$ is the Boltzmann constant. Explain what is meant by $p(n)$ in this formula. Write down an expression for $p(n)$ in the grand canonical ensemble, defining any variables you need. Hence show that the entropy $S$ is related to the grand canonical partition function $\mathcal{Z}(T, \mu, V)$ by

  $$S=k\left[\frac{\partial}{\partial T}(T \log \mathcal{Z})\right]_{\mu, V}$$

  (b) Consider a gas of non-interacting fermions with single-particle energy levels $\epsilon_{i}$.

  (i) Show that the grand canonical partition function $\mathcal{Z}$ is given by

  $$\log \mathcal{Z}=\sum_{i} \log \left(1+e^{-\left(\epsilon_{i}-\mu\right) /(k T)}\right)$$

  (ii) Assume that the energy levels are continuous with density of states $g(\epsilon)=A V \epsilon^{a}$, where $A$ and $a$ are positive constants. Prove that

  $$\log \mathcal{Z}=V T^{b} f(\mu / T)$$

  and give expressions for the constant $b$ and the function $f$.

  (iii) The gas is isolated and undergoes a reversible adiabatic change. By considering the ratio $S / N$, prove that $\mu / T$ remains constant. Deduce that $V T^{c}$ and $p V^{d}$ remain constant in this process, where $c$ and $d$ are constants whose values you should determine.

  comment

• Paper 3, Section II, D

  Statistical Physics | Part II, 2017

  (a) Describe the Carnot cycle using plots in the $(p, V)$-plane and the $(T, S)$-plane. In which steps of the cycle is heat absorbed or emitted by the gas? In which steps is work done on, or by, the gas?

  (b) An ideal monatomic gas undergoes a reversible cycle described by a triangle in the $(p, V)$-plane with vertices at the points $A, B, C$ with coordinates $\left(p_{0}, V_{0}\right),\left(2 p_{0}, V_{0}\right)$ and $\left(p_{0}, 2 V_{0}\right)$ respectively. The cycle is traversed in the order $A B C A$.

  (i) Write down the equation of state and an expression for the internal energy of the gas.

  (ii) Derive an expression relating $T d S$ to $d p$ and $d V$. Use your expression to calculate the heat supplied to, or emitted by, the gas along $A B$ and $C A$.

  (iii) Show that heat is supplied to the gas along part of the line $B C$, and is emitted by the gas along the other part of the line.

  (iv) Calculate the efficiency $\eta=W / Q$ where $W$ is the total work done by the cycle and $Q$ is the total heat supplied.

  comment

• Paper 4, Section II, D

  Statistical Physics | Part II, 2017

  The van der Waals equation of state is

  $$p=\frac{k T}{v-b}-\frac{a}{v^{2}}$$

  where $p$ is the pressure, $v=V / N$ is the volume divided by the number of particles, $T$ is the temperature, $k$ is Boltzmann's constant and $a, b$ are positive constants.

  (i) Prove that the Gibbs free energy $G=E+p V-T S$ satisfies $G=\mu N$. Hence obtain an expression for $(\partial \mu / \partial p)_{T, N}$ and use it to explain the Maxwell construction for determining the pressure at which the gas and liquid phases can coexist at a given temperature.

  (ii) Explain what is meant by the critical point and determine the values $p_{c}, v_{c}, T_{c}$ corresponding to this point.

  (iii) By defining $\bar{p}=p / p_{c}, \bar{v}=v / v_{c}$ and $\bar{T}=T / T_{c}$, derive the law of corresponding states:

  $$\bar{p}=\frac{8 \bar{T}}{3 \bar{v}-1}-\frac{3}{\bar{v}^{2}} .$$

  (iv) To investigate the behaviour near the critical point, let $\bar{T}=1+t$ and $\bar{v}=1+\phi$, where $t$ and $\phi$ are small. Expand $\bar{p}$ to cubic order in $\phi$ and hence show that

  $$\left(\frac{\partial \bar{p}}{\partial \phi}\right)_{t}=-\frac{9}{2} \phi^{2}+\mathcal{O}\left(\phi^{3}\right)+t[-6+\mathcal{O}(\phi)] .$$

  At fixed small $t$, let $\phi_{l}(t)$ and $\phi_{g}(t)$ be the values of $\phi$ corresponding to the liquid and gas phases on the co-existence curve. By changing the integration variable from $p$ to $\phi$, use the Maxwell construction to show that $\phi_{l}(t)=-\phi_{g}(t)$. Deduce that, as the critical point is approached along the co-existence curve,

  $$\bar{v}_{\text {gas }}-\bar{v}_{\text {liquid }} \sim\left(T_{c}-T\right)^{1 / 2}$$

  comment

2016

• Paper 1, Section II, C

  Statistical Physics | Part II, 2016

  Consider an ideal quantum gas with one-particle states $|i\rangle$ of energy $\epsilon_{i}$. Let $p_{i}^{\left(n_{i}\right)}$ denote the probability that state $|i\rangle$ is occupied by $n_{i}$ particles. Here, $n_{i}$ can take the values 0 or 1 for fermions and any non-negative integer for bosons. The entropy of the gas is given by

  $$S=-k_{B} \sum_{i} \sum_{n_{i}} p_{i}^{\left(n_{i}\right)} \ln p_{i}^{\left(n_{i}\right)}$$

  (a) Write down the constraints that must be satisfied by the probabilities if the average energy $\langle E\rangle$ and average particle number $\langle N\rangle$ are kept at fixed values.

  Show that if $S$ is maximised then

  $$p_{i}^{\left(n_{i}\right)}=\frac{1}{\mathcal{Z}_{i}} e^{-\left(\beta \epsilon_{i}+\gamma\right) n_{i}}$$

  where $\beta$ and $\gamma$ are Lagrange multipliers. What is $\mathcal{Z}_{i}$ ?

  (b) Insert these probabilities $p_{i}^{\left(n_{i}\right)}$ into the expression for $S$, and combine the result with the first law of thermodynamics to find the meaning of $\beta$ and $\gamma$.

  (c) Calculate the average occupation number $\left\langle n_{i}\right\rangle=\sum_{n_{i}} n_{i} p_{i}^{\left(n_{i}\right)}$ for a gas of fermions.

  comment

• Paper 2, Section II, C

  Statistical Physics | Part II, 2016

  (a) What is meant by the canonical ensemble? Consider a system in the canonical ensemble that can be in states $|n\rangle, n=0,1,2, \ldots$ with energies $E_{n}$. Write down the partition function for this system and the probability $p(n)$ that the system is in state $|n\rangle$. Derive an expression for the average energy $\langle E\rangle$ in terms of the partition function.

  (b) Consider an anharmonic oscillator with energy levels

  $$\hbar \omega\left[\left(n+\frac{1}{2}\right)+\delta\left(n+\frac{1}{2}\right)^{2}\right], \quad n=0,1,2, \ldots$$

  where $\omega$ is a positive constant and $0<\delta \ll 1$ is a small constant. Let the oscillator be in contact with a reservoir at temperature $T$. Show that, to linear order in $\delta$, the partition function $Z_{1}$ for the oscillator is given by

  $$Z_{1}=\frac{c_{1}}{\sinh \frac{x}{2}}\left[1+\delta c_{2} x\left(1+\frac{2}{\sinh ^{2} \frac{x}{2}}\right)\right], \quad x=\frac{\hbar \omega}{k_{B} T}$$

  where $c_{1}$ and $c_{2}$ are constants to be determined. Also show that, to linear order in $\delta$, the average energy of a system of $N$ uncoupled oscillators of this type is given by

  $$\langle E\rangle=\frac{N \hbar \omega}{2}\left\{c_{3} \operatorname{coth} \frac{x}{2}+\delta\left[c_{4}+\frac{c_{5}}{\sinh ^{2} \frac{x}{2}}\left(1-x \operatorname{coth} \frac{x}{2}\right)\right]\right\}$$

  where $c_{3}, c_{4}, c_{5}$ are constants to be determined.

  comment

• Paper 3, Section II, C

  Statistical Physics | Part II, 2016

  (a) Consider an ideal gas consisting of $N$ identical classical particles of mass $m$ moving freely in a volume $V$ with Hamiltonian $H=|\mathbf{p}|^{2} / 2 m$. Show that the partition function of the gas has the form

  $$Z_{\text {ideal }}=\frac{V^{N}}{\lambda^{3 N} N !}$$

  and find $\lambda$ as a function of the temperature $T$.

  [You may assume that $\int_{-\infty}^{\infty} e^{-a x^{2}} d x=\sqrt{\pi / a}$ for $a>0$.]

  (b) A monatomic gas of interacting particles is a modification of an ideal gas where any pair of particles with separation $r$ interact through a potential energy $U(r)$. The partition function for this gas can be written as

  $$Z=Z_{\text {ideal }}\left[1+\frac{2 \pi N}{V} \int_{0}^{\infty} f(r) r^{2} d r\right]^{N}$$

  where $f(r)=e^{-\beta U(r)}-1, \quad \beta=1 /\left(k_{B} T\right)$. The virial expansion of the equation of state for small densities $N / V$ is

  $$\frac{p}{k_{B} T}=\frac{N}{V}+B_{2}(T) \frac{N^{2}}{V^{2}}+\mathcal{O}\left(\frac{N^{3}}{V^{3}}\right)$$

  Using the free energy, show that

  $$B_{2}(T)=-2 \pi \int_{0}^{\infty} f(r) r^{2} d r$$

  (c) The Lennard-Jones potential is

  $$U(r)=\epsilon\left(\frac{r_{0}^{12}}{r^{12}}-2 \frac{r_{0}^{6}}{r^{6}}\right)$$

  where $\epsilon$ and $r_{0}$ are positive constants. Find the separation $\sigma$ where $U(\sigma)=0$ and the separation $r_{\min }$ where $U(r)$ has its minimum. Sketch the graph of $U(r)$. Calculate $B_{2}(T)$ for this potential using the approximations

  $$f(r)=e^{-\beta U(r)}-1 \simeq \begin{cases}-1 & \text { for } \quad r<\sigma \\ -\beta U(r) & \text { for } r \geqslant \sigma\end{cases}$$

  comment

• Paper 4, Section II, 33C

  Statistical Physics | Part II, 2016

  (a) State the first law of thermodynamics. Derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial p}{\partial T}\right)_{V}$$

  (b) Consider a thermodynamic system whose energy $E$ at constant temperature $T$ is volume independent, i.e.

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=0$$

  Show that this implies that the pressure has the form $p(T, V)=T f(V)$ for some function $f$.

  (c) For a photon gas inside a cavity of volume $V$, the energy $E$ and pressure $p$ are given in terms of the energy density $U$, which depends only on the temperature $T$, by

  $$E(T, V)=U(T) V, \quad p(T, V)=\frac{1}{3} U(T)$$

  Show that this implies $U(T)=\sigma T^{4}$ where $\sigma$ is a constant. Show that the entropy is

  $$S=\frac{4}{3} \sigma T^{3} V$$

  and calculate the energy $E(S, V)$ and free energy $F(T, V)$ in terms of their respective fundamental variables.

  comment

2015

• Paper 1, Section II, C

  Statistical Physics | Part II, 2015

  (a) Define the canonical partition function $Z$ for a system with energy levels $E_{n}$, where $n$ labels states, given that the system is in contact with a heat reservoir at temperature $T$. What is the probability $p(n)$ that the system occupies state $n$ ? Starting from an expression for the entropy $S=k_{B} \partial(T \ln Z) / \partial T$, deduce that

  $$S=-k_{B} \sum_{n} p(n) \ln p(n)$$

  (b) Consider an ensemble consisting of $W$ copies of the system in part (a) with $W$ very large, so that there are $W p(n)$ members of the ensemble in state $n$. Starting from an expression for the number of ways in which this can occur, find the entropy $S_{W}$ of the ensemble and hence re-derive the expression $(*)$. [You may assume Stirling's formula $\ln X ! \approx X \ln X-X$ for $X$ large. $]$

  (c) Consider a system of $N$ non-interacting particles at temperature $T$. Each particle has $q$ internal states with energies

  $$0, \mathcal{E}, 2 \mathcal{E}, \ldots,(q-1) \mathcal{E}$$

  Assuming that the internal states are the only relevant degrees of freedom, calculate the total entropy of the system. Find the limiting values of the entropy as $T \rightarrow 0$ and $T \rightarrow \infty$ and comment briefly on your answers.

  comment

• Paper 2, Section II, C

  Statistical Physics | Part II, 2015

  (a) State the Bose-Einstein distribution formula for the mean occupation numbers $n_{i}$ of discrete single-particle states $i$ with energies $E_{i}$ in a gas of bosons. Write down expressions for the total particle number $N$ and the total energy $U$ when the singleparticle states can be treated as continuous, with energies $E \geqslant 0$ and density of states $g(E)$.

  (b) Blackbody radiation at temperature $T$ is equivalent to a gas of photons with

  $$g(E)=A V E^{2}$$

  where $V$ is the volume and $A$ is a constant. What value of the chemical potential is required when applying the Bose-Einstein distribution to photons? Show that the heat capacity at constant volume satisfies $C_{V} \propto T^{\alpha}$ for some constant $\alpha$, to be determined.

  (c) Consider a system of bosonic particles of fixed total number $N \gg 1$. The particles are trapped in a potential which has ground state energy zero and which gives rise to a density of states $g(E)=B E^{2}$, where $B$ is a constant. Explain, for this system, what is meant by Bose-Einstein condensation and show that the critical temperature satisfies $T_{c} \propto N^{1 / 3}$. If $N_{0}$ is the number of particles in the ground state, show that for $T$ just below $T_{c}$

  $$N_{0} / N \approx 1-\left(T / T_{c}\right)^{\gamma}$$

  for some constant $\gamma$, to be determined.

  (d) Would you expect photons to exhibit Bose-Einstein condensation? Explain your answer very briefly.

  comment

• Paper 3, Section II, C

  Statistical Physics | Part II, 2015

  (a) A sample of gas has pressure $p$, volume $V$, temperature $T$ and entropy $S$.

  (i) Use the first law of thermodynamics to derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial p}\right)_{T}=-\left(\frac{\partial V}{\partial T}\right)_{p} .$$

  (ii) Define the heat capacity at constant pressure $C_{p}$ and the enthalpy $H$ and show that $C_{p}=(\partial H / \partial T)_{p}$.

  (b) Consider a perfectly insulated pipe with a throttle valve, as shown.

  

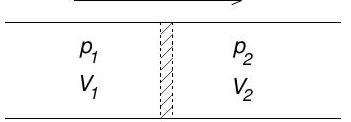
  Gas initially occupying volume $V_{1}$ on the left is forced slowly through the valve at constant pressure $p_{1}$. A constant pressure $p_{2}$ is maintained on the right and the final volume occupied by the gas after passing through the valve is $V_{2}$.

  (i) Show that the enthalpy $H$ of the gas is unchanged by this process.

  (ii) The Joule-Thomson coefficient is defined to be $\mu=(\partial T / \partial p)_{H}$. Show that

  $$\mu=\frac{V}{C_{p}}\left[\frac{T}{V}\left(\frac{\partial V}{\partial T}\right)_{p}-1\right]$$

  [You may assume the identity $(\partial y / \partial x)_{u}=-(\partial u / \partial x)_{y} /(\partial u / \partial y)_{x} \cdot$ ]

  (iii) Suppose that the gas obeys an equation of state

  $$p=k_{B} T\left[\frac{N}{V}+B_{2}(T) \frac{N^{2}}{V^{2}}\right]$$

  where $N$ is the number of particles. Calculate $\mu$ to first order in $N / V$ and hence derive a condition on $\frac{d}{d T}\left(\frac{B_{2}(T)}{T}\right)$ for obtaining a positive Joule-Thomson coefficient.

  comment

• Paper 4, Section II, C

  Statistical Physics | Part II, 2015

  The Ising model consists of $N$ particles, labelled by $i$, arranged on a $D$-dimensional Euclidean lattice with periodic boundary conditions. Each particle has spin up $s_{i}=+1$, or down $s_{i}=-1$, and the energy in the presence of a magnetic field $B$ is

  $$E=-B \sum_{i} s_{i}-J \sum_{\langle i, j\rangle} s_{i} s_{j}$$

  where $J>0$ is a constant and $\langle i, j\rangle$ indicates that the second sum is over each pair of nearest neighbours (every particle has $2 D$ nearest neighbours). Let $\beta=1 / k_{B} T$, where $T$ is the temperature.

  (i) Express the average spin per particle, $m=\left(\sum_{i}\left\langle s_{i}\right\rangle\right) / N$, in terms of the canonical partition function $Z$.

  (ii) Show that in the mean-field approximation

  $$Z=C\left[Z_{1}\left(\beta B_{\mathrm{eff}}\right)\right]^{N}$$

  where $Z_{1}$ is a single-particle partition function, $B_{\text {eff }}$ is an effective magnetic field which you should find in terms of $B, J, D$ and $m$, and $C$ is a prefactor which you should also evaluate.

  (iii) Deduce an equation that determines $m$ for general values of $B, J$ and temperature $T$. Without attempting to solve for $m$ explicitly, discuss how the behaviour of the system depends on temperature when $B=0$, deriving an expression for the critical temperature $T_{c}$ and explaining its significance.

  (iv) Comment briefly on whether the results obtained using the mean-field approximation for $B=0$ are consistent with an expression for the free energy of the form

  $$F(m, T)=F_{0}(T)+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}$$

  where $a$ and $b$ are positive constants.

  comment

2014

• Paper 1, Section II, E

  Statistical Physics | Part II, 2014

  Write down the equation of state and the internal energy of a monatomic ideal gas.

  Describe the meaning of an adiabatic process. Derive the equation for an adiabatic process in the pressure-volume $(P, V)$ plane for a monatomic ideal gas.

  Briefly describe the Carnot cycle. Sketch the Carnot cycle in the $(P, V)$ plane and in the temperature entropy $(T, S)$ plane.

  The Diesel cycle is an idealised version of the process realised in the Diesel engine. It consists of the following four reversible steps:

  

  Sketch the Diesel cycle for a monatomic gas in the $(P, V)$ plane and the $(T, S)$ plane. Determine the equations for the curves $B \rightarrow C$ and $D \rightarrow A$ in the $(T, S)$ plane.

  The efficiency $\eta$ of the cycle is defined as

  $$\eta=1-\frac{Q_{\text {out }}}{Q_{\text {in }}}$$

  where $Q_{\text {in }}$ is the heat entering the gas in step $B \rightarrow C$ and $Q_{\text {out }}$ is the heat leaving the gas in step $D \rightarrow A$. Calculate $\eta$ as a function of the temperatures at points $A, B, C$ and $D$.

  comment

• Paper 2, Section II, E

  Statistical Physics | Part II, 2014

  Briefly describe the microcanonical, canonical and grand canonical ensembles. Why do they agree in the thermodynamic limit?

  A harmonic oscillator in one spatial dimension has Hamiltonian

  $$H=\frac{p^{2}}{2 m}+\frac{m}{2} \omega^{2} x^{2}$$

  Here $p$ and $x$ are the momentum and position of the oscillator, $m$ is its mass and $\omega$ its frequency. The harmonic oscillator is placed in contact with a heat bath at temperature $T$. What is the relevant ensemble?

  Treating the harmonic oscillator classically, compute the mean energy $\langle E\rangle$, the energy fluctuation $\Delta E^{2}$ and the heat capacity $C$.

  Treating the harmonic oscillator quantum mechanically, compute the mean energy $\langle E\rangle$, the energy fluctuation $\Delta E^{2}$ and the heat capacity $C$.

  In what limit of temperature do the classical and quantum results agree? Explain why they differ away from this limit. Describe an experiment for which this difference has implications.

  comment

• Paper 3, Section II, E

  Statistical Physics | Part II, 2014

  In the grand canonical ensemble, at temperature $T$ and chemical potential $\mu$, what is the probability of finding a system in a state with energy $E$ and particle number $N$ ?

  A particle with spin degeneracy $g_{s}$ and mass $m$ moves in $d \geqslant 2$ spatial dimensions with dispersion relation $E=\hbar^{2} k^{2} / 2 m$. Compute the density of states $g(E)$. [You may denote the area of a unit $(d-1)$-dimensional sphere as $S_{d-1}$.]

  Treating the particles as non-interacting fermions, determine the energy $E$ of a gas in terms of the pressure $P$ and volume $V$.

  Derive an expression for the Fermi energy in terms of the number density of particles. Compute the degeneracy pressure at zero temperature in terms of the number of particles and the Fermi energy.

  Show that at high temperatures the gas obeys the ideal gas law (up to small corrections which you need not compute).

  comment

• Paper 4, Section II, E

  Statistical Physics | Part II, 2014

  The Dieterici equation of state of a gas is

  $$P=\frac{k_{B} T}{v-b} \exp \left(-\frac{a}{k_{B} T v}\right)$$

  where $P$ is the pressure, $v=V / N$ is the volume divided by the number of particles, $T$ is the temperature, and $k_{B}$ is the Boltzmann constant. Provide a physical interpretation for the constants $a$ and $b$.

  Briefly explain how the Dieterici equation captures the liquid-gas phase transition. What is the maximum temperature at which such a phase transition can occur?

  The Gibbs free energy is given by

  $$G=E+P V-T S$$

  where $E$ is the energy and $S$ is the entropy. Explain why the Gibbs free energy is proportional to the number of particles in the system.

  On either side of a first-order phase transition the Gibbs free energies are equal. Use this fact to derive the Clausius-Clapeyron equation for a line along which there is a first-order liquid-gas phase transition,

  $$\frac{d P}{d T}=\frac{L}{T\left(V_{\text {gas }}-V_{\text {liquid }}\right)}$$

  where $L$ is the latent heat which you should define.

  Assume that the volume of liquid is negligible compared to the volume of gas and that the latent heat is constant. Further assume that the gas can be well approximated by the ideal gas law. Solve $(*)$ to obtain an equation for the phase-transition line in the $(P, T)$ plane.

  comment

2013

• Paper 1, Section II, 35A

  Statistical Physics | Part II, 2013

  (i) What is the occupation number of a state $i$ with energy $E_{i}$ according to the Fermi-Dirac statistics for a given chemical potential $\mu$ ?

  (ii) Assuming that the energy $E$ is spin independent, what is the number $g_{s}$ of electrons which can occupy an energy level?

  (iii) Consider a semi-infinite metal slab occupying $z \leqslant 0$ (and idealized to have infinite extent in the $x y$ plane) and a vacuum environment at $z>0$. An electron with momentum $\left(p_{x}, p_{y}, p_{z}\right)$ inside the slab will escape the metal in the $+z$ direction if it has a sufficiently large momentum $p_{z}$ to overcome a potential barrier $V_{0}$ relative to the Fermi energy $\epsilon_{\mathrm{F}}$, i.e. if

  $$\frac{p_{z}^{2}}{2 m} \geqslant \epsilon_{\mathrm{F}}+V_{0}$$

  where $m$ is the electron mass.

  At fixed temperature $T$, some fraction of electrons will satisfy this condition, which results in a current density $j_{z}$ in the $+z$ direction (an electron having escaped the metal once is considered lost, never to return). Each electron escaping provides a contribution $\delta j_{z}=-e v_{z}$ to this current density, where $v_{z}$ is the velocity and $e$ the elementary charge.

  (a) Briefly describe the Fermi-Dirac distribution as a function of energy in the limit $k_{\mathrm{B}} T \ll \epsilon_{\mathrm{F}}$, where $k_{\mathrm{B}}$ is the Boltzmann constant. What is the chemical potential $\mu$ in this limit?

  (b) Assume that the electrons behave like an ideal, non-relativistic Fermi gas and that $k_{\mathrm{B}} T \ll V_{0}$ and $k_{\mathrm{B}} T \ll \epsilon_{\mathrm{F}}$. Calculate the current density $j_{z}$ associated with the electrons escaping the metal in the $+z$ direction. How could we easily increase the strength of the current?

  comment

• Paper 2, Section II, 35A

  Statistical Physics | Part II, 2013

  (i) The first law of thermodynamics is $d E=T d S-p d V+\mu d N$, where $\mu$ is the chemical potential. Briefly describe its meaning.

  (ii) What is equipartition of energy? Under which conditions is it valid? Write down the heat capacity $C_{V}$ at constant volume for a monatomic ideal gas.

  (iii) Starting from the first law of thermodynamics, and using the fact that for an ideal gas $(\partial E / \partial V)_{T}=0$, show that the entropy of an ideal gas containing $N$ particles can be written as

  $$S(T, V)=N\left(\int \frac{c_{V}(T)}{T} d T+k_{\mathrm{B}} \ln \frac{V}{N}+\mathrm{const}\right)$$

  where $T$ and $V$ are temperature and volume of the gas, $k_{\mathrm{B}}$ is the Boltzmann constant, and we define the heat capacity per particle as $c_{V}=C_{V} / N$.

  (iv) The Gibbs free energy $G$ is defined as $G=E+p V-T S$. Verify that it is a function of temperature $T$, pressure $p$ and particle number $N$. Explain why $G$ depends on the particle number $N$ through $G=\mu(T, p) N$.

  (v) Calculate the chemical potential $\mu$ for an ideal gas with heat capacity per particle $c_{V}(T)$. Calculate $\mu$ for the special case of a monatomic gas.

  comment

• Paper 3, Section II, 35A

  Statistical Physics | Part II, 2013

  (i) Briefly describe the microcanonical ensemble.

  (ii) For quantum mechanical systems the energy levels are discrete. Explain why we can write the probability distribution in this case as

  $$p\left(\left\{n_{i}\right\}\right)= \begin{cases}\text { const }>0 & \text { for } E \leqslant E\left(\left\{n_{i}\right\}\right)<E+\Delta E \\ 0 & \text { otherwise }\end{cases}$$

  What assumption do we make for the energy interval $\Delta E$ ?

  Consider $N$ independent linear harmonic oscillators of equal frequency $\omega$. Their total energy is given by

  $$E\left(\left\{n_{i}\right\}\right)=\sum_{i=1}^{N} \hbar \omega\left(n_{i}+\frac{1}{2}\right)=M \hbar \omega+\frac{N}{2} \hbar \omega \quad \text { with } \quad M=\sum_{i=1}^{N} n_{i}$$

  Here $n_{i}=0,1,2, \ldots$ is the excitation number of oscillator $i$.

  (iii) Show that, for fixed $N$ and $M$, the number $g_{N}(M)$ of possibilities to distribute the $M$ excitations over $N$ oscillators (i.e. the number of different choices $\left\{n_{i}\right\}$ consistent with $M$ ) is given by

  $$g_{N}(M)=\frac{(M+N-1) !}{M !(N-1) !}$$

  [Hint: You may wish to consider the set of $N$ oscillators plus $M-1$ "additional" excitations and what it means to choose $M$ objects from this set.]

  (iv) Using the probability distribution of part (ii), calculate the probability distribution $p\left(E_{1}\right)$ for the "first" oscillator as a function of its energy $E_{1}=n_{1} \hbar \omega+\frac{1}{2} \hbar \omega$.

  (v) If $\Delta E=\hbar \omega \ll E$ then exactly one value of $M$ will correspond to a total energy inside the interval $(E, E+\Delta E)$. In this case, show that

  $$p\left(E_{1}\right) \approx \frac{g_{N-1}\left(M-n_{1}\right)}{g_{N}(M)} .$$

  Approximate this result in the limit $N \gg 1, M \gg n_{1}$.

  comment

• Paper 4, Section II, A

  Statistical Physics | Part II, 2013

  A classical particle of mass $m$ moving non-relativistically in two-dimensional space is enclosed inside a circle of radius $R$ and attached by a spring with constant $\kappa$ to the centre of the circle. The particle thus moves in a potential

  $$V(r)= \begin{cases}\frac{1}{2} \kappa r^{2} & \text { for } r<R \\ \infty & \text { for } r \geqslant R\end{cases}$$

  where $r^{2}=x^{2}+y^{2}$. Let the particle be coupled to a heat reservoir at temperature $T$.

  (i) Which of the ensembles of statistical physics should be used to model the system?

  (ii) Calculate the partition function for the particle.

  (iii) Calculate the average energy $\langle E\rangle$ and the average potential energy $\langle V\rangle$ of the particle.

  (iv) What is the average energy in:

  (a) the limit $\frac{1}{2} \kappa R^{2} \gg k_{\mathrm{B}} T$ (strong coupling)?

  (b) the limit $\frac{1}{2} \kappa R^{2} \ll k_{\mathrm{B}} T$ (weak coupling)?

  Compare the two results with the values expected from equipartition of energy.

  comment

2012

• Paper 1, Section II, C

  Statistical Physics | Part II, 2012

  A meson consists of two quarks, attracted by a linear potential energy

  $$V=\alpha x$$

  where $x$ is the separation between the quarks and $\alpha$ is a constant. Treating the quarks classically, compute the vibrational partition function that arises from the separation of quarks. What is the average separation of the quarks at temperature $T$ ?

  Consider an ideal gas of these mesons that have the orientation of the quarks fixed so the mesons do not rotate. Compute the total partition function of the gas. What is its heat capacity $C_{V}$ ?

  [Note: $\int_{-\infty}^{+\infty} d x e^{-a x^{2}}=\sqrt{\pi / a} .$ ]

  comment

• Paper 2, Section II, C

  Statistical Physics | Part II, 2012

  Explain what is meant by an isothermal expansion and an adiabatic expansion of a gas.

  By first establishing a suitable Maxwell relation, show that

  $$\left.\frac{\partial E}{\partial V}\right|_{T}=\left.T \frac{\partial p}{\partial T}\right|_{V}-p$$

  and

  $$\left.\frac{\partial C_{V}}{\partial V}\right|_{T}=\left.T \frac{\partial^{2} p}{\partial T^{2}}\right|_{V}$$

  The energy in a gas of blackbody radiation is given by $E=a V T^{4}$, where $a$ is a constant. Derive an expression for the pressure $p(V, T)$.

  Show that if the radiation expands adiabatically, $V T^{3}$ is constant.

  comment

• Paper 3, Section II, C

  Statistical Physics | Part II, 2012

  A ferromagnet has magnetization order parameter $m$ and is at temperature $T$. The free energy is given by

  $$F(T ; m)=F_{0}(T)+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}$$

  where $a, b$ and $T_{c}$ are positive constants. Find the equilibrium value of the magnetization at both high and low temperatures.

  Evaluate the free energy of the ground state as a function of temperature. Hence compute the entropy and heat capacity. Determine the jump in the heat capacity and identify the order of the phase transition.

  After imposing a background magnetic field $B$, the free energy becomes

  $$F(T ; m)=F_{0}(T)+B m+\frac{a}{2}\left(T-T_{c}\right) m^{2}+\frac{b}{4} m^{4}$$

  Explain graphically why the system undergoes a first-order phase transition at low temperatures as $B$ changes sign.

  The spinodal point occurs when the meta-stable vacuum ceases to exist. Determine the temperature $T$ of the spinodal point as a function of $T_{c}, a, b$ and $B$.

  comment

• Paper 4, Section II, C

  Statistical Physics | Part II, 2012

  Non-relativistic electrons of mass $m$ are confined to move in a two-dimensional plane of area $A$. Each electron has two spin states. Compute the density of states $g(E)$ and show that it is constant.

  Write down expressions for the number of particles $N$ and the average energy $\langle E\rangle$ of a gas of fermions in terms of the temperature $T$ and chemical potential $\mu$. Find an expression for the Fermi Energy $E_{F}$ in terms of $N$.

  For $k_{B} T \ll E_{F}$, you may assume that the chemical potential does not change with temperature. Compute the low temperature heat capacity of a gas of fermions. [You may use the approximation that, for large $z$,

  $$\left.\int_{0}^{\infty} \frac{x^{n} d x}{z^{-1} e^{x}+1} \approx \frac{1}{n+1}(\log z)^{n+1}+\frac{\pi^{2} n}{6}(\log z)^{n-1} .\right]$$

  comment

2011

• Paper 1, Section II, D

  Statistical Physics | Part II, 2011

  Describe the physical relevance of the microcanonical, canonical and grand canonical ensembles. Explain briefly the circumstances under which all ensembles are equivalent.

  The Gibbs entropy for a probability distribution $p(n)$ over states is

  $$S=-k_{B} \sum_{n} p(n) \log p(n) .$$

  By imposing suitable constraints on $p(n)$, show how maximising the entropy gives rise to the probability distributions for the microcanonical and canonical ensembles.

  A system consists of $N$ non-interacting particles fixed at points in a lattice. Each particle has three states with energies $E=-\epsilon, 0,+\epsilon$. If the system is at a fixed temperature $T$, determine the average energy $E$ and the heat capacity $C$. Evaluate each in the limits $T \rightarrow \infty$ and $T \rightarrow 0$.

  Describe a configuration of the system that would have negative temperature. Does this system obey the third law of thermodynamics?

  comment

• Paper 2, Section II, D

  Statistical Physics | Part II, 2011

  Write down the partition function for a single classical non-relativistic particle of mass $m$ moving in three dimensions in a potential $U(\mathbf{x})$ and in equilibrium with a heat bath at temperature $T$.

  A system of $N$ non-interacting classical non-relativistic particles, in equilibrium at temperature $T$, is placed in a potential

  $$U(\mathbf{x})=\frac{\left(x^{2}+y^{2}+z^{2}\right)^{n}}{V^{2 n / 3}}$$

  where $n$ is a positive integer. Using the partition function, show that the free energy is

  $$F=-N k_{B} T\left(\log V+\frac{3}{2} \frac{n+1}{n} \log k_{B} T+\log I_{n}+\text { const }\right)$$

  where

  $$I_{n}=\left(\frac{m}{2 \pi \hbar^{2}}\right)^{3 / 2} \int_{0}^{\infty} 4 \pi u^{2} \exp \left(-u^{2 n}\right) d u$$

  Explain the physical relevance of the constant term in the expression $(*)$.

  Viewing $V$ as an external parameter, akin to volume, compute the conjugate pressure $p$ and show that the equation of state coincides with that of an ideal gas.

  Compute the energy $E$, heat capacity $C_{V}$ and entropy $S$ of the gas. Determine the local particle number density as a function of $|\mathbf{x}|$.

  comment

• Paper 3, Section II, D

  Statistical Physics | Part II, 2011

  A gas of non-interacting particles has energy-momentum relationship $E=A(\hbar k)^{\alpha}$ for some constants $A$ and $\alpha$. Determine the density of states $g(E) d E$ in a threedimensional volume $V$.

  Explain why the chemical potential $\mu$ satisfies $\mu<0$ for the Bose-Einstein distribution.

  Show that an ideal quantum Bose gas with the energy-momentum relationship above has

  $$p V=\frac{\alpha E}{3} .$$

  If the particles are bosons at fixed temperature $T$ and chemical potential $\mu$, write down an expression for the number of particles that do not occupy the ground state. Use this to determine the values of $\alpha$ for which there exists a Bose-Einstein condensate at sufficiently low temperatures.

  Discuss whether a gas of photons can undergo Bose-Einstein condensation.

  comment

• Paper 4, Section II, D

  Statistical Physics | Part II, 2011

  (i) Define the Gibbs free energy for a gas of $N$ particles with pressure $p$ at a temperature $T$. Explain why it is necessarily proportional to the number of particles $N$ in the system. Given volume $V$ and chemical potential $\mu$, prove that

  $$\left.\frac{\partial \mu}{\partial p}\right|_{T}=\frac{V}{N} .$$

  (ii) The van der Waals equation of state is

  $$\left(p+\frac{a N^{2}}{V^{2}}\right)(V-N b)=N k_{B} T$$

  Explain the physical significance of the terms with constants $a$ and $b$. Sketch the isotherms of the van der Waals equation. Show that the critical point lies at

  $$k_{B} T_{c}=\frac{8 a}{27 b}, \quad V_{c}=3 b N, \quad p_{c}=\frac{a}{27 b^{2}} .$$

  (iii) Describe the Maxwell construction to determine the condition for phase equilibrium. Hence sketch the regions of the van der Waals isotherm at $T<T_{c}$ that correspond to metastable and unstable states. Sketch those regions that correspond to stable liquids and stable gases.

  (iv) Show that, as the critical point is approached along the co-existence curve,

  $$V_{\text {gas }}-V_{\text {liquid }} \sim\left(T_{c}-T\right)^{1 / 2} .$$

  Show that, as the critical point is approached along an isotherm,

  $$p-p_{c} \sim\left(V-V_{c}\right)^{3} .$$

  comment

2010

• Paper 2, Section II, C

  Statistical Physics | Part II, 2010

  Consider a 3-dimensional gas of $N$ non-interacting particles in a box of size $L$ where the allowed momenta are $\left\{\mathbf{p}_{i}\right\}$. Assuming the particles have an energy $\epsilon(|\mathbf{p}|), \epsilon^{\prime}(p)>0$, calculate the density of states $g(\epsilon) d \epsilon$ as $L \rightarrow \infty$.

  Treating the particles as classical explain why the partition function is

  $$Z=\frac{z^{N}}{N !}, \quad z=\int_{0}^{\infty} d \epsilon g(\epsilon) e^{-\epsilon / k T}$$

  Obtain an expression for the total energy $E$.

  Why is $\mathbf{p}_{i} \propto 1 / L ?$ By considering the dependence of the energies on the volume $V$ show that the pressure $P$ is given by

  $$P V=\frac{N}{3 z} \int_{0}^{\infty} d \epsilon g(\epsilon) p \epsilon^{\prime}(p) e^{-\epsilon / k T}$$

  What are the results for the pressure for non-relativistic particles and also for relativistic particles when their mass can be neglected?

  What is the thermal wavelength for non-relativistic particles? Why are the classical results correct if the thermal wavelength is much smaller than the mean particle separation?

  comment

• Paper 3, Section II, C

  Statistical Physics | Part II, 2010

  (i) Given the following density of states for a particle in 3 dimensions

  $$g(\varepsilon)=K V \varepsilon^{1 / 2}$$

  write down the partition function for a gas of $N$ such non-interacting particles, assuming they can be treated classically. From this expression, calculate the energy $E$ of the system and the heat capacities $C_{V}$ and $C_{P}$. You may take it as given that $P V=\frac{2}{3} E$.

  [Hint: The formula $\int_{0}^{\infty} d y y^{2} e^{-y^{2}}=\sqrt{\pi} / 4$ may be useful.]

  (ii) Using thermodynamic relations obtain the relation between heat capacities and compressibilities

  $$\frac{C_{P}}{C_{V}}=\frac{\kappa_{T}}{\kappa_{S}}$$

  where the isothermal and adiabatic compressibilities are given by

  $$\kappa=-\frac{1}{V} \frac{\partial V}{\partial P},$$

  derivatives taken at constant temperature and entropy, respectively.

  (iii) Find $\kappa_{T}$ and $\kappa_{S}$ for the ideal gas considered above.

  comment

• Paper 4, Section II, C

  Statistical Physics | Part II, 2010

  (i) Let $\rho_{i}$ be the probability that a system is in a state labelled by $i$ with $N_{i}$ particles and energy $E_{i}$. Define

  $$s\left(\rho_{i}\right)=-k \sum_{i} \rho_{i} \log \rho_{i} .$$

  $s\left(\rho_{i}\right)$ has a maximum, consistent with a fixed mean total number of particles $N$, mean total energy $E$ and $\sum_{i} \rho_{i}=1$, when $\rho_{i}=\bar{\rho}_{i}$. Let $S(E, N)=s\left(\bar{\rho}_{i}\right)$ and show that

  $$\frac{\partial S}{\partial E}=\frac{1}{T}, \quad \frac{\partial S}{\partial N}=-\frac{\mu}{T},$$

  where $T$ may be identified with the temperature and $\mu$ with the chemical potential.

  (ii) For two weakly coupled systems 1,2 then $\rho_{i, j}=\rho_{1, i} \rho_{2, j}$ and $E_{i, j}=E_{1, i}+E_{2, j}$, $N_{i, j}=N_{1, i}+N_{2, j}$. Show that $S(E, N)=S_{1}\left(E_{1}, N_{1}\right)+S_{2}\left(E_{2}, N_{2}\right)$ where, if $S(E, N)$ is stationary under variations in $E_{1}, E_{2}$ and $N_{1}, N_{2}$ for $E=E_{1}+E_{2}, N=N_{1}+N_{2}$ fixed, we must have $T_{1}=T_{2}, \mu_{1}=\mu_{2}$.

  (iii) Define the grand partition function $\mathcal{Z}(T, \mu)$ for the system in (i) and show that

  $$k \log \mathcal{Z}=S-\frac{1}{T} E+\frac{\mu}{T} N, \quad S=\frac{\partial}{\partial T}(k T \log \mathcal{Z})$$

  (iv) For a system with single particle energy levels $\epsilon_{r}$ the possible states are labelled by $i=\left\{n_{r}: n_{r}=0,1\right\}$, where $N_{i}=\sum_{r} n_{r}, E_{i}=\sum_{r} n_{r} \epsilon_{r}$ and $\sum_{i}=\prod_{r} \sum_{n_{r}=0,1}$. Show that

  $$\bar{\rho}_{i}=\prod_{r} \frac{e^{-n_{r}\left(\epsilon_{r}-\mu\right) / k T}}{1+e^{-\left(\epsilon_{r}-\mu\right) / k T}} .$$

  Calculate $\bar{n}_{r}$. How is this related to a free fermion gas?

  comment

2009

• Paper 2, Section II, D

  Statistical Physics | Part II, 2009

  The Van der Waals equation of state for a non-ideal gas is

  $$\left(p+\frac{a N^{2}}{V^{2}}\right)(V-b N)=N k T,$$

  where $a$ and $b$ are constants.

  (i) Briefly explain the physical motivation for differences between the Van der Waals and ideal gas equations of state.

  (ii) Find the volume dependence (at constant temperature) of the internal energy $E$ and the heat capacity $C_{V}$ of a Van der Waals gas.

  (iii) A Van der Waals gas is initially at temperature $T_{1}$ in an insulated container with volume $V_{1}$. A small opening is then made so that the gas can expand freely into an empty container, occupying both the old and new containers. The final result is that the gas now occupies a volume $V_{2}>V_{1}$. Calculate the final temperature $T_{2}$ assuming $C_{V}$ is temperature independent. You may assume the process happens quasistatically.

  comment

• Paper 3, Section II, D

  Statistical Physics | Part II, 2009

  Consider an ideal Bose gas in an external potential such that the resulting density of single particle states is given by

  $$g(\varepsilon)=B \varepsilon^{7 / 2}$$

  where $B$ is a positive constant.

  (i) Derive an expression for the critical temperature for Bose-Einstein condensation of a gas of $N$ of these atoms.

  [Recall

  $$\left.\frac{1}{\Gamma(n)} \int_{0}^{\infty} \frac{x^{n-1} \mathrm{~d} x}{z^{-1} e^{x}-1}=\sum_{\ell=1}^{\infty} \frac{z^{\ell}}{\ell^{n}}\right]$$

  (ii) What is the internal energy $E$ of the gas in the condensed state as a function of $N$ and $T$ ?

  (iii) Now consider the high temperature, classical limit instead. How does the internal energy $E$ depend on $N$ and $T$ ?

  comment

• Paper 4, Section II, D

  Statistical Physics | Part II, 2009

  Briefly state the ergodic hypothesis and explain its importance.

  Consider an ideal, classical, monatomic gas in the presence of a uniform gravitational field in the negative $z$-direction. For convenience, assume the gas is in an arbitrarily large cubic box.

  (i) Compute the internal energy $E$ of the gas.

  (ii) Explain your result for $E$ in relation to the equipartition theorem.

  (iii) What is the probability that an atom is located at a height between $z$ and $z+d z ?$

  (iv) What is the most probable speed of an atom of this gas?

  comment

2008

• $2 . \mathrm{II} . 34 \mathrm{E} \quad$

  Statistical Physics | Part II, 2008

  Prove that energy fluctuations in a canonical distribution are given by

  $$\left\langle(E-\langle E\rangle)^{2}\right\rangle=k_{B} T^{2} C_{V}$$

  where $T$ is the absolute temperature, $C_{V}=\left.\frac{\partial\langle E\rangle}{\partial T}\right|_{V}$ is the heat capacity at constant volume, and $k_{B}$ is Boltzmann's constant.

  Prove the following relation in a similar manner:

  $$\left\langle(E-\langle E\rangle)^{3}\right\rangle=k_{B}^{2}\left[\left.T^{4} \frac{\partial C_{V}}{\partial T}\right|_{V}+2 T^{3} C_{V}\right]$$

  Show that, for an ideal gas of $N$ monatomic molecules where $\langle E\rangle=\frac{3}{2} N k_{B} T$, these equations can be reduced to

  $$\frac{1}{\langle E\rangle^{2}}\left\langle(E-\langle E\rangle)^{2}\right\rangle=\frac{2}{3 N} \quad \text { and } \quad \frac{1}{\langle E\rangle^{3}}\left\langle(E-\langle E\rangle)^{3}\right\rangle=\frac{8}{9 N^{2}}$$

  comment

• 3.II.34E

  Statistical Physics | Part II, 2008

  Derive the following two relations:

  $$T d S=C_{p} d T-\left.T \frac{\partial V}{\partial T}\right|_{p} d p$$

  and

  $$T d S=C_{V} d T+\left.T \frac{\partial p}{\partial T}\right|_{V} d V$$

  [You may use any standard Maxwell relation without proving it.]

  Experimentalists very seldom measure $C_{V}$ directly; they measure $C_{p}$ and use thermodynamics to extract $C_{V}$. Use your results from the first part of this question to find a formula for $C_{p}-C_{V}$ in terms of the easily measured quantities

  $$\alpha=\left.\frac{1}{V} \frac{\partial V}{\partial T}\right|_{p}$$

  (the volume coefficient of expansion) and

  $$\kappa=-\left.\frac{1}{V} \frac{\partial V}{\partial p}\right|_{T}$$

  (the isothermal compressibility).

  comment

• 4.II.34D

  Statistical Physics | Part II, 2008

  Show that the Fermi momentum $p_{F}$ of a gas of $N$ non-interacting electrons in volume $V$ is

  $$p_{F}=\left(3 \pi^{2} \hbar^{3} \frac{N}{V}\right)^{1 / 3}$$

  Consider the electrons to be effectively massless, so that an electron of momentum $p$ has (relativistic) energy $c p$. Show that the mean energy per electron at zero temperature is $3 c p_{F} / 4$.

  When a constant external magnetic field of strength $B$ is applied to the electron gas, each electron gets an energy contribution $\pm \mu B$ depending on whether its spin is parallel or antiparallel to the field. Here $\mu$ is the magnitude of the magnetic moment of an electron. Calculate the total magnetic moment of the electron gas at zero temperature, assuming $\mu B$ is much less than $c p_{F}$.

  comment

2007

• 2.II.34D

  Statistical Physics | Part II, 2007

  Derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial p}\right)_{T}=-\left(\frac{\partial V}{\partial T}\right)_{p}$$

  The diagram below illustrates the Joule-Thomson throttling process for a porous barrier. A gas of volume $V_{1}$, initially on the left-hand side of a thermally insulated pipe, is forced by a piston to go through the barrier using constant pressure $p_{1}$. As a result the gas flows to the right-hand side, resisted by a piston which applies a constant pressure $p_{2}$ (with $p_{2}<p_{1}$ ). Eventually all of the gas occupies a volume $V_{2}$ on the right-hand side. Show that this process conserves enthalpy.

  The Joule-Thomson coefficient $\mu_{\mathrm{JT}}$ is the change in temperature with respect to a change in pressure during a process that conserves enthalpy $H$. Express the JouleThomson coefficient, $\mu_{\mathrm{JT}} \equiv\left(\frac{\partial T}{\partial p}\right)_{H}$, in terms of $T, V$, the heat capacity at constant pressure $C_{p}$, and the volume coefficient of expansion $\alpha \equiv \frac{1}{V}\left(\frac{\partial V}{\partial T}\right)_{p}$.

  What is $\mu_{\mathrm{JT}}$ for an ideal gas?

  If one wishes to use the Joule-Thomson process to cool a real (non-ideal) gas, what must the $\operatorname{sign}$ of $\mu_{\mathrm{JT}}$ be?

  

  comment

• 3.II.34D

  Statistical Physics | Part II, 2007

  For a 2-dimensional gas of $N$ nonrelativistic, non-interacting, spinless bosons, find the density of states $g(\varepsilon)$ in the neighbourhood of energy $\varepsilon$. [Hint: consider the gas in a box of size $L \times L$ which has periodic boundary conditions. Work in the thermodynamic limit $N \rightarrow \infty, L \rightarrow \infty$, with $N / L^{2}$ held finite.]

  Calculate the number of particles per unit area at a given temperature and chemical potential.

  Explain why Bose-Einstein condensation does not occur in this gas at any temperature.

  [Recall that

  $$\left.\frac{1}{\Gamma(n)} \int_{0}^{\infty} \frac{x^{n-1} d x}{z^{-1} e^{x}-1}=\sum_{\ell=1}^{\infty} \frac{z^{\ell}}{\ell^{n}}\right]$$

  comment

• 4.II.34D

  Statistical Physics | Part II, 2007

  Consider a classical gas of diatomic molecules whose orientation is fixed by a strong magnetic field. The molecules are not free to rotate, but they are free to vibrate. Assuming that the vibrations are approximately harmonic, calculate the contribution to the partition function due to vibrations.

  Evaluate the free energy $F=-k T \ln Z$, where $Z$ is the total partition function for the gas, and hence calculate the entropy.

  $\left[\right.$ Note that $\int_{-\infty}^{\infty} \exp \left(-a u^{2}\right) d u=\sqrt{\pi / a}$ and $\int_{0}^{\infty} u^{2} \exp \left(-a u^{2}\right) d u=\sqrt{\pi} / 4 a^{3 / 2} . \quad$ You may approximate $\ln N$ ! by $N \ln N-N$.]

  comment

2006

• 2.II.34D

  Statistical Physics | Part II, 2006

  What is meant by the heat capacity $C_{V}$ of a thermodynamic system? By establishing a suitable Maxwell identity, show that

  $$\left.\frac{\partial C_{V}}{\partial V}\right|_{T}=\left.T \frac{\partial^{2} P}{\partial T^{2}}\right|_{V} .$$

  In a certain model of $N$ interacting particles in a volume $V$ and at temperature $T$, the partition function is

  $$Z=\frac{1}{N !}(V-a N)^{N}(b T)^{3 N / 2}$$

  where $a$ and $b$ are constants. Find the equation of state and the entropy for this gas of particles. Find the energy and hence the heat capacity $C_{V}$ of the gas, and verify that the relation $(*)$ is satisfied.

  comment

• 3.II.34D

  Statistical Physics | Part II, 2006

  What is meant by the chemical potential of a thermodynamic system? Derive the Gibbs distribution with variable particle number $N$, for a system at temperature $T$ and chemical potential $\mu$. (You may assume that the volume does not vary.)

  Consider a non-interacting gas of fermions in a box of fixed volume, at temperature $T$ and chemical potential $\mu$. Use the Gibbs distribution to find the mean occupation number of a one-particle quantum state of energy $\varepsilon$. Assuming that the density of states is $C \varepsilon^{1 / 2}$, for some constant $C$, deduce that the mean number of particles with energies between $\varepsilon$ and $\varepsilon+d \varepsilon$ is

  $$\frac{C \varepsilon^{\frac{1}{2}} d \varepsilon}{e^{(\varepsilon-\mu) / T}+1} .$$

  Why can $\mu$ be identified with the Fermi energy $\varepsilon_{F}$ when $T=0$ ? Estimate the number of particles with energies greater than $\varepsilon_{F}$ when $T$ is small but non-zero.

  comment

• 4.II.34D

  Statistical Physics | Part II, 2006

  Two examples of phenomenological temperature measurements are (i) the mark reached along the length of a liquid-in-glass thermometer; and (ii) the wavelength of the brightest colour of electromagnetic radiation emitted by a hot body (used, for example, to measure the surface temperature of a star).

  Give the definition of temperature in statistical physics, and explain how the analysis of ideal gases and black body radiation is used to calibrate and improve phenomenological temperature measurements like those mentioned above. You should give brief derivations of any key results that you use.

  comment

2005

• 2.II.34D

  Statistical Physics | Part II, 2005

  Write down the first law of thermodynamics in differential form applied to an infinitesimal reversible change.

  Explain what is meant by an adiabatic change.

  Starting with the first law in differential form, derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  Hence show that

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=T\left(\frac{\partial P}{\partial T}\right)_{V}-P$$

  For radiation in thermal equilibrium at temperature $T$ in volume $V$, it is given that $E=V e(T)$ and $P=e(T) / 3$. Hence deduce Stefan's Law,

  $$E=a V T^{4}$$

  where $a$ is a constant.

  The radiation is allowed to expand adiabatically. Show that $V T^{3}$ is constant during the expansion.

  comment

• 3.II.34D

  Statistical Physics | Part II, 2005

  A free spinless particle moving in two dimensions is confined to a square box of side $L$. By imposing periodic boundary conditions show that the number of states in the energy range $\epsilon \rightarrow \epsilon+d \epsilon$ is $g(\epsilon) d \epsilon$, where

  $$g(\epsilon)=\frac{m L^{2}}{2 \pi \hbar^{2}}$$

  If, instead, the particle is an electron with magnetic moment $\mu$ moving in a constant external magnetic field $H$, show that

  $$g(\epsilon)= \begin{cases}\frac{m L^{2}}{2 \pi \hbar^{2}}, & -\mu H<\epsilon<\mu H \\ \frac{m L^{2}}{\pi \hbar^{2}}, & \mu H<\epsilon\end{cases}$$

  Let there be $N$ electrons in the box. Explain briefly how to construct the ground state of the system. Let $\epsilon$ be the Fermi energy. Show that when $\epsilon>\mu H$

  $$N=\frac{m L^{2}}{\pi \hbar^{2}} \epsilon .$$

  Show also that the magnetic moment $M$ of the system in its ground state is given by

  $$M=\frac{\mu^{2} m L^{2}}{\pi \hbar^{2}} H$$

  and that the ground state energy is

  $$\frac{1}{2} \frac{\pi \hbar^{2}}{m L^{2}} N^{2}-\frac{1}{2} M H$$

  comment

• 4.II.34D

  Statistical Physics | Part II, 2005

  Write down an expression for the partition function of a classical particle of mass $m$ moving in three dimensions in a potential $U(\mathbf{x})$ and in equilibrium with a heat bath at temperature $T$.

  A system of $N$ non-interacting classical particles is placed in the potential

  $$U(\mathbf{x})=\frac{\left(x^{2}+y^{2}+z^{2}\right)^{n}}{V^{2 n / 3}}$$

  where $n$ is a positive integer. The gas is in equilibrium at temperature $T$. Using a suitable rescaling of variables, show that the free energy $F$ is given by

  $$\frac{F}{N}=-k T\left(\log V+\frac{3}{2} \frac{n+1}{n} \log k T+\log I_{n}\right)$$

  where

  $$I_{n}=\left(\frac{2 m \pi}{h^{2}}\right)^{3 / 2} \int_{0}^{\infty} 4 \pi u^{2} e^{-u^{2 n}} d u$$

  Regarding $V$ as an external parameter, find the thermodynamic force $P$, conjugate to $V$, exerted by this system. Find the equation of state and compare with that of an ideal gas confined in a volume $V$.

  Derive expressions for the entropy $S$, the internal energy $E$ and the total heat capacity $C_{V}$ at constant $V$.

  Show that for all $n$ the total heat capacity at constant $P$ is given by

  $$C_{P}=C_{V}+N k$$

  [Note that $\left.\int_{0}^{\infty} u^{2} e^{-u^{2} / 2} d u=\sqrt{\frac{\pi}{2}} .\right]$

  comment

2004

• B1.22

  Statistical Physics | Part II, 2004

  Define the notions of entropy $S$ and thermodynamic temperature $T$ for a gas of particles in a variable volume $V$. Derive the fundamental relation

  $$d E=T d S-P d V$$

  The free energy of the gas is defined as $F=E-T S$. Why is it convenient to regard $F$ as a function of $T$ and $V$ ? By considering $F$, or otherwise, show that

  $$\left.\frac{\partial S}{\partial V}\right|_{T}=\left.\frac{\partial P}{\partial T}\right|_{V}$$

  Deduce that the entropy of an ideal gas, whose equation of state is $P V=N T$ (using energy units), has the form

  $$S=N \log \left(\frac{V}{N}\right)+N c(T)$$

  where $c(T)$ is independent of $N$ and $V$.

  Show that if the gas is in contact with a heat bath at temperature $T$, then the probability of finding the gas in a particular quantum microstate of energy $E_{r}$ is

  $$P_{r}=e^{\left(F-E_{r}\right) / T}$$

  comment

• B3.22

  Statistical Physics | Part II, 2004

  Describe briefly why a low density gas can be investigated using classical statistical mechanics.

  Explain why, for a gas of $N$ structureless atoms, the measure on phase space is

  $$\frac{1}{N !} \frac{d^{3 N} q d^{3 N} p}{(2 \pi \hbar)^{3 N}}$$

  and the probability density in phase space is proportional to

  $$e^{-E(q, p) / T}$$

  where $T$ is the temperature in energy units.

  Derive the Maxwell probability distribution for atomic speeds $v$,

  $$\rho(v)=\left(\frac{m}{2 \pi T}\right)^{3 / 2} 4 \pi v^{2} e^{-m v^{2} / 2 T}$$

  Why is this valid even if the atoms interact?

  Find the mean value $\bar{v}$ of the speed of the atoms.

  Is $\frac{1}{2} m(\bar{v})^{2}$ the mean kinetic energy of the atoms?

  comment

• B4.23

  Statistical Physics | Part II, 2004

  Derive the Bose-Einstein expression for the mean number of Bose particles $\bar{n}$ occupying a particular single-particle quantum state of energy $\varepsilon$, when the chemical potential is $\mu$ and the temperature is $T$ in energy units.

  Why is the chemical potential for a gas of photons given by $\mu=0$ ?

  Show that, for black-body radiation in a cavity of volume $V$ at temperature $T$, the mean number of photons in the angular frequency range $(\omega, \omega+d \omega)$ is

  $$\frac{V}{\pi^{2} c^{3}} \frac{\omega^{2} d \omega}{e^{\hbar \omega / T}-1}$$

  Hence, show that the total energy $E$ of the radiation in the cavity is

  $$E=K V T^{4}$$

  where $K$ is a constant that need not be evaluated.

  Use thermodynamic reasoning to find the entropy $S$ and pressure $P$ of the radiation and verify that

  $$E-T S+P V=0$$

  Why is this last result to be expected for a gas of photons?

  comment

2003

• B1.22

  Statistical Physics | Part II, 2003

  A gas in equilibrium at temperature $T$ and pressure $P$ has quantum stationary states $i$ with energies $E_{i}(V)$ in volume $V$. What does it mean to say that a change in volume from $V$ to $V+d V$ is reversible?

  Write down an expression for the probability that the gas is in state $i$. How is the entropy $S$ defined in terms of these probabilities? Write down an expression for the energy $E$ of the gas, and establish the relation

  $$d E=T d S-P d V$$

  for reversible changes.

  By considering the quantity $F=E-T S$, derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  A gas obeys the equation of state

  $$P V=R T+\frac{B(T)}{V}$$

  where $R$ is a constant and $B(T)$ is a function of $T$ only. The gas is expanded isothermally, at temperature $T$, from volume $V_{0}$ to volume $2 V_{0}$. Find the work $\Delta W$ done on the gas. Show that the heat $\Delta Q$ absorbed by the gas is given by

  $$\Delta Q=R T \log 2+\frac{T}{2 V_{0}} \frac{d B}{d T}$$

  comment

• B3.22

  Statistical Physics | Part II, 2003

  A diatomic molecule, free to move in two space dimensions, has classical Hamiltonian

  $$H=\frac{1}{2 m}|\mathbf{p}|^{2}+\frac{1}{2 I} J^{2}$$

  where $\mathbf{p}=\left(p_{1}, p_{2}\right)$ is the particle's momentum and $J$ is its angular momentum. Write down the classical partition function $Z$ for an ideal gas of $N$ such molecules in thermal equilibrium at temperature $T$. Show that it can be written in the form

  $$Z=\left(z_{t} z_{r o t}\right)^{N}$$

  where $z_{t}$ and $z_{\text {rot }}$ are the one-molecule partition functions associated with the translational and rotational degrees of freedom, respectively. Compute $z_{t}$ and $z_{r o t}$ and hence show that the energy $E$ of the gas is given by

  $$E=\frac{3}{2} N k T$$

  where $k$ is Boltzmann's constant. How does this result illustrate the principle of equipartition of energy?

  In an improved model of the two-dimensional gas of diatomic molecules, the angular momentum $J$ is quantized in integer multiples of $\hbar$ :

  $$J=j \hbar, \quad j=0, \pm 1, \pm 2, \ldots$$

  Write down an expression for $z_{\text {rot }}$ in this case. Given that $k T \ll\left(\hbar^{2} / 2 I\right)$, obtain an expression for the energy $E$ in the form

  $$E \approx A T+B e^{-\hbar^{2} / 2 I k T}$$

  where $A$ and $B$ are constants that should be computed. How is this result compatible with the principle of equipartition of energy? Find $C_{v}$, the specific heat at constant volume, for $k T \ll\left(\hbar^{2} / 2 I\right)$.

  Why can the sum over $j$ in $z_{\text {rot }}$ be approximated by an integral when $k T \gg\left(\hbar^{2} / 2 I\right)$ ? Deduce that $E \approx \frac{3}{2} N k T$ in this limit.

  comment

• B4.23

  Statistical Physics | Part II, 2003

  A gas of non-interacting identical bosons in volume $V$, with one-particle energy levels $\epsilon_{r}, r=1,2, \ldots, \infty$, is in equilibrium at temperature $T$ and chemical potential $\mu$. Let $n_{r}$ be the number of particles in the $r$ th one-particle state. Write down an expression for the grand partition function $\mathcal{Z}$. Write down an expression for the probability of finding a given set of occupation numbers $n_{r}$ of the one-particle states. Hence determine the mean occupation numbers $\bar{n}_{r}$ (the Bose-Einstein distribution). Write down expressions, in terms of the mean occupation numbers, for the total energy $E$ and total number of particles $N$.

  Write down an expression for the grand potential $\Omega$ in terms of $\mathcal{Z}$. Given that

  $$S=-\left(\frac{\partial \Omega}{\partial T}\right)_{V, \mu}$$

  show that $S$ can be written in the form

  $$S=k \sum_{r} f\left(\bar{n}_{r}\right)$$

  for some function $f$, which you should determine. Hence show that $d S=0$ for any change of the gas that leaves the mean occupation numbers unchanged. Consider a (quasi-static) change of $V$ with this property. Using the formula

  $$P=-\left(\frac{\partial E}{\partial V}\right)_{N, S}$$

  and given that $\epsilon_{r} \propto V^{-\sigma}(\sigma>0)$ for each $r$, show that

  $$P=\sigma(E / V)$$

  What is the value of $\sigma$ for photons?

  Let $\mu=0$, so that $E$ is a function only of $T$ and $V$. Why does the energy density $\varepsilon=E / V$ depend only on $T ?$ Using the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  and the first law of thermodynamics for reversible changes, show that

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=T\left(\frac{\partial P}{\partial T}\right)_{V}-P$$

  and hence that

  $$\varepsilon(T) \propto T^{\gamma}$$

  for some power $\gamma$ that you should determine. Show further that

  $$S \propto\left(T V^{\sigma}\right)^{\frac{1}{\sigma}} .$$

  Hence verify, given $\mu=0$, that $\bar{n}_{r}$ is left unchanged by a change of $V$ at constant $S$.

  comment

2002

• B1.22

  Statistical Physics | Part II, 2002

  A simple model for a rubber molecule consists of a one-dimensional chain of $n$ links each of fixed length $b$ and each of which is oriented in either the positive or negative direction. A unique state $i$ of the molecule is designated by giving the orientation $\pm 1$ of each link. If there are $n_{+}$links oriented in the positive direction and $n_{-}$links oriented in the negative direction then $n=n_{+}+n_{-}$and the length of the molecule is $l=\left(n_{+}-n_{-}\right) b$. The length of the molecule associated with state $i$ is $l_{i}$.

  What is the range of $l$ ?

  What is the number of states with $n, n_{+}, n_{-}$fixed?

  Consider an ensemble of $A$ copies of the molecule in which $a_{i}$ members are in state $i$ and write down the expression for the mean length $L$.

  By introducing a Lagrange multiplier $\tau$ for $L$ show that the most probable configuration for the $\left\{a_{i}\right\}$ with given length $L$ is found by maximizing

  $$\log \left(\frac{A !}{\prod_{i} a_{i} !}\right)+\tau \sum_{i} a_{i} l_{i}-\alpha \sum_{i} a_{i} .$$

  Hence show that the most probable configuration is given by

  $$p_{i}=\frac{e^{\tau l_{i}}}{Z},$$

  where $p_{i}$ is the probability for finding an ensemble member in the state $i$ and $Z$ is the partition function which should be defined.

  Show that $Z$ can be expressed as

  $$Z=\sum_{l} g(l) e^{\tau l}$$

  where the meaning of $g(l)$ should be explained.

  Hence show that $Z$ is given by

  $$Z=\sum_{n_{+}=0}^{n} \frac{n !}{n_{+} ! n_{-} !}\left(e^{\tau b}\right)^{n_{+}}\left(e^{-\tau b}\right)^{n_{-}}, \quad n_{+}+n_{-}=n$$

  and therefore that the free energy $G$ for the system is

  $$G=-n k T \log (2 \cosh \tau b) .$$

  Show that $\tau$ is determined by

  $$L=-\frac{1}{k T}\left(\frac{\partial G}{\partial \tau}\right)_{n}$$

  and hence that the equation of state is

  $$\tanh \tau b=\frac{L}{n b} .$$

  What are the independent variables on which $G$ depends?

  Explain why the tension in the rubber molecule is $k T \tau$.

  comment

• B3.22

  Statistical Physics | Part II, 2002

  A system consisting of non-interacting bosons has single-particle levels uniquely labelled by $r$ with energies $\epsilon_{r}, \epsilon_{r} \geq 0$. Show that the free energy in the grand canonical ensemble is

  $$F=k T \sum_{r} \log \left(1-e^{-\beta\left(\epsilon_{r}-\mu\right)}\right) .$$

  What is the maximum value for $\mu$ ?

  A system of $N$ bosons in a large volume $V$ has one energy level of energy zero and a large number $M \gg 1$ of energy levels of the same energy $\epsilon$, where $M$ takes the form $M=A V$ with $A$ a positive constant. What are the dimensions of $A ?$

  Show that the free energy is

  $$F=k T\left(\log \left(1-e^{\beta \mu}\right)+A V \log \left(1-e^{-\beta(\epsilon-\mu)}\right)\right)$$

  The numbers of particles with energies $0, \epsilon$ are respectively $N_{0}, N_{\epsilon}$. Write down expressions for $N_{0}, N_{\epsilon}$ in terms of $\mu$.

  At temperature $T$ what is the maximum number of bosons $N_{\epsilon}^{\max }$ in the normal phase (the state with energy $\epsilon$ )? Explain what happens when $N>N_{\epsilon}^{\max }$.

  Given $N$ and $T$ calculate the transition temperature $T_{B}$ at which Bose condensation occurs.

  For $T>T_{B}$ show that $\mu=\epsilon\left(T_{B}-T\right) / T_{B}$. What is the value of $\mu$ for $T<T_{B}$ ?

  Calculate the mean energy $E$ for (a) $T>T_{B}$ (b) $T<T_{B}$, and show that the heat capacity of the system at constant volume is

  $$C_{V}=\left\{\begin{array}{cl} \frac{1}{k T^{2}} \frac{A V \epsilon^{2}}{\left(e^{\beta \epsilon}-1\right)^{2}} & T<T_{B} \\ 0 & T>T_{B} \end{array}\right.$$

  comment

• B4.23

  Statistical Physics | Part II, 2002

  A perfect gas in equilibrium in a volume $V$ has quantum stationary states $|i\rangle$ with energies $E_{i}$. In a Boltzmann distribution, the probability that the system is in state $|i\rangle$ is $\rho_{i}=Z^{-1} e^{-E_{i} / k T}$. The entropy is defined to be $S=-k \sum_{i} \rho_{i} \log \rho_{i}$.

  For two nearby states establish the equation

  $$d E=T d S-P d V$$

  where $E$ and $P$ should be defined.

  For reversible changes show that

  $$d S=\frac{\delta Q}{T}$$

  where $\delta Q$ is the amount of heat transferred in the exchange.

  Define $C_{V}$, the heat capacity at constant volume.

  A system with constant heat capacity $C_{V}$ initially at temperature $T$ is heated at constant volume to a temperature $\Theta$. Show that the change in entropy is $\Delta S=$ $C_{V} \log (\Theta / T)$.

  Explain what is meant by isothermal and adiabatic transitions.

  Briefly, describe the Carnot cycle and define its efficiency. Explain briefly why no heat engine can be more efficient than one whose operation is based on a Carnot cycle.

  Three identical bodies with constant heat capacity at fixed volume $C_{V}$, are initially at temperatures $T_{1}, T_{2}, T_{3}$, respectively. Heat engines operate between the bodies with no input of work or heat from the outside and the respective temperatures are changed to $\Theta_{1}, \Theta_{2}, \Theta_{3}$, the volume of the bodies remaining constant. Show that, if the heat engines operate on a Carnot cycle, then

  $$\Theta_{1} \Theta_{2} \Theta_{3}=A, \quad \Theta_{1}+\Theta_{2}+\Theta_{3}=B$$

  where $A=T_{1} T_{2} T_{3}$ and $B=T_{1}+T_{2}+T_{3}$.

  Hence show that the maximum temperature to which any one of the bodies can be raised is $\Theta$ where

  $$\Theta+2\left(\frac{A}{\Theta}\right)^{1 / 2}=B$$

  Show that a solution is $\Theta=T$ if initially $T_{1}=T_{2}=T_{3}=T$. Do you expect there to be any other solutions?

  Find $\Theta$ if initially $T_{1}=300 \mathrm{~K}, T_{2}=300 \mathrm{~K}, T_{3}=100 \mathrm{~K}$.

  [Hint: Choose to maximize one temperature and impose the constraints above using Lagrange multipliers. ]

  comment

2001

• B1.22

  Statistical Physics | Part II, 2001

  Write down the first law of thermodynamics in differential form for an infinitesimal reversible change in terms of the increments $d E, d S$ and $d V$, where $E, S$ and $V$ are to be defined. Briefly give an interpretation of each term and deduce that

  $$P=-\left(\frac{\partial E}{\partial V}\right)_{S}, \quad T=\left(\frac{\partial E}{\partial S}\right)_{V}$$

  Define the specific heat at constant volume $C_{V}$ and show that for an adiabatic change

  $$C_{V} d T+\left(\left(\frac{\partial E}{\partial V}\right)_{T}+P\right) d V=0$$

  Derive the Maxwell relation

  $$\left(\frac{\partial S}{\partial V}\right)_{T}=\left(\frac{\partial P}{\partial T}\right)_{V}$$

  where $T$ is temperature and hence show that

  $$\left(\frac{\partial E}{\partial V}\right)_{T}=-P+T\left(\frac{\partial P}{\partial T}\right)_{V}$$

  An imperfect gas of volume $V$ obeys the van der Waals equation of state

  $$\left(P+\frac{a}{V^{2}}\right)(V-b)=R T$$

  where $a$ and $b$ are non-negative constants. Show that

  $$\left(\frac{\partial C_{V}}{\partial V}\right)_{T}=0,$$

  and deduce that $C_{V}$ is a function of $T$ only. It can further be shown that in this case $C_{V}$ is independent of $T$. Hence show that

  $$T(V-b)^{R / C_{V}}$$

  is constant on adiabatic curves.

  comment

• B3.22

  Statistical Physics | Part II, 2001

  A system consists of $N$ weakly interacting non-relativistic fermions, each of mass $m$, in a three-dimensional volume, $V$. Derive the Fermi-Dirac distribution

  $$n(\epsilon)=K V g \frac{\epsilon^{1 / 2}}{\exp ((\epsilon-\mu) / k T)+1}$$

  where $n(\epsilon) d \epsilon$ is the number of particles with energy in $(\epsilon, \epsilon+d \epsilon)$ and $K=2 \pi(2 m)^{3 / 2} / h^{3}$. Explain the physical significance of $g$.

  Explain how the constant $\mu$ is determined by the number of particles $N$ and write down expressions for $N$ and the internal energy $E$ in terms of $n(\epsilon)$.

  Show that, in the limit $\kappa \equiv e^{-\mu / k T} \gg 1$,

  $$N=\frac{V}{A \kappa}\left(1-\frac{1}{2 \sqrt{2} \kappa}+O\left(\frac{1}{\kappa^{2}}\right)\right)$$

  where $A=h^{3} / g(2 \pi m k T)^{3 / 2}$.

  Show also that in this limit

  $$E=\frac{3}{2} N k T\left(1+\frac{1}{4 \sqrt{2} \kappa}+O\left(\frac{1}{\kappa^{2}}\right)\right) \text {. }$$

  Deduce that the condition $\kappa \gg 1$ implies that $A N / V \ll 1$. Discuss briefly whether or not this latter condition is satisfied in a white dwarf star and in a dilute electron gas at room temperature.

  $\left[\right.$ Note that $\left.\int_{0}^{\infty} d u e^{-u^{2} a}=\frac{1}{2} \sqrt{\frac{\pi}{a}}\right]$.

  comment

• B4.23

  Statistical Physics | Part II, 2001

  Given that the free energy $F$ can be written in terms of the partition function $Z$ as $F=-k T \log Z$ show that the entropy $S$ and internal energy $E$ are given by

  $$S=k \frac{\partial(T \log Z)}{\partial T}, \quad E=k T^{2} \frac{\partial \log Z}{\partial T}$$

  A system of particles has Hamiltonian $H(\mathbf{p}, \mathbf{q})$ where $\mathbf{p}$ is the set of particle momenta and $\mathbf{q}$ the set of particle coordinates. Write down the expression for the classical partition function $Z_{C}$ for this system in equilibrium at temperature $T$. In a particular case $H$ is given by

  $$H(\mathbf{p}, \mathbf{q})=p_{\alpha} A_{\alpha \beta}(\mathbf{q}) p_{\beta}+q_{\alpha} B_{\alpha \beta}(\mathbf{q}) q_{\beta}$$

  Let $H$ be a homogeneous function in all the $p_{\alpha}, 1 \leq \alpha \leq N$, and in a subset of the $q_{\alpha}, 1 \leq \alpha \leq M(M \leq N)$. Derive the principle of equipartition for this system.

  A system consists of $N$ weakly interacting harmonic oscillators each with Hamiltonian

  $$h(p, q)=\frac{1}{2} p^{2}+\frac{1}{2} \omega^{2} q^{2} .$$

  Using equipartition calculate the classical specific heat of the system, $C_{C}(T)$. Also calculate the classical entropy $S_{C}(T)$.

  Write down the expression for the quantum partition function of the system and derive expressions for the specific heat $C(T)$ and the entropy $S(T)$ in terms of $N$ and the parameter $\theta=\hbar \omega / k T$. Show for $\theta \ll 1$ that

  $$C(T)=C_{C}(T)+O(\theta), \quad S(T)=S_{C}(T)+S_{0}+O(\theta)$$

  where $S_{0}$ should be calculated. Comment briefly on the physical significance of the constant $S_{0}$ and why it is non-zero.

  comment