Algebraic Topology

2021

• Paper 1, Section II, 21F

  Algebraic Topology | Part II, 2021

  (a) What does it mean for two spaces $X$ and $Y$ to be homotopy equivalent?

  (b) What does it mean for a subspace $Y \subseteq X$ to be a retract of a space $X$ ? What does it mean for a space $X$ to be contractible? Show that a retract of a contractible space is contractible.

  (c) Let $X$ be a space and $A \subseteq X$ a subspace. We say the pair $(X, A)$ has the homotopy extension property if, for any pair of maps $f: X \times\{0\} \rightarrow Y$ and $H^{\prime}: A \times I \rightarrow Y$ with

  $$\left.f\right|_{A \times\{0\}}=\left.H^{\prime}\right|_{A \times\{0\}},$$

  there exists a map $H: X \times I \rightarrow Y$ with

  $$\left.H\right|_{X \times\{0\}}=f,\left.\quad H\right|_{A \times I}=H^{\prime}$$

  Now suppose that $A \subseteq X$ is contractible. Denote by $X / A$ the quotient of $X$ by the equivalence relation $x \sim x^{\prime}$ if and only if $x=x^{\prime}$ or $x, x^{\prime} \in A$. Show that, if $(X, A)$ satisfies the homotopy extension property, then $X$ and $X / A$ are homotopy equivalent.

  comment

• Paper 2, Section II, 21F

  Algebraic Topology | Part II, 2021

  (a) State a suitable version of the Seifert-van Kampen theorem and use it to calculate the fundamental groups of the torus $T^{2}:=S^{1} \times S^{1}$ and of the real projective plane $\mathbb{R P}^{2}$.

  (b) Show that there are no covering maps $T^{2} \rightarrow \mathbb{R} \mathbb{P}^{2}$ or $\mathbb{R P}^{2} \rightarrow T^{2}$.

  (c) Consider the following covering space of $S^{1} \vee S^{1}$ :

  

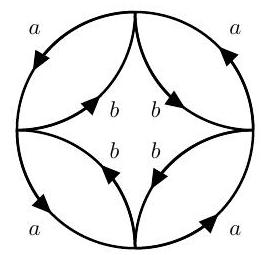
  Here the line segments labelled $a$ and $b$ are mapped to the two different copies of $S^{1}$ contained in $S^{1} \vee S^{1}$, with orientations as indicated.

  Using the Galois correspondence with basepoints, identify a subgroup of

  $$\pi_{1}\left(S^{1} \vee S^{1}, x_{0}\right)=F_{2}$$

  (where $x_{0}$ is the wedge point) that corresponds to this covering space.

  comment

• Paper 3, Section II, 20F

  Algebraic Topology | Part II, 2021

  Let $X$ be a space. We define the cone of $X$ to be

  $$C X:=(X \times I) / \sim$$

  where $\left(x_{1}, t_{1}\right) \sim\left(x_{2}, t_{2}\right)$ if and only if either $t_{1}=t_{2}=1$ or $\left(x_{1}, t_{1}\right)=\left(x_{2}, t_{2}\right)$.

  (a) Show that if $X$ is triangulable, so is $C X$. Calculate $H_{i}(C X)$. [You may use any results proved in the course.]

  (b) Let $K$ be a simplicial complex and $L \subseteq K$ a subcomplex. Let $X=|K|, A=|L|$, and let $X^{\prime}$ be the space obtained by identifying $|L| \subseteq|K|$ with $|L| \times\{0\} \subseteq C|L|$. Show that there is a long exact sequence

  $$\begin{aligned} \cdots \rightarrow & H_{i+1}\left(X^{\prime}\right) \rightarrow H_{i}(A) \rightarrow H_{i}(X) \rightarrow H_{i}\left(X^{\prime}\right) \rightarrow H_{i-1}(A) \rightarrow \cdots \\ & \cdots \rightarrow H_{1}\left(X^{\prime}\right) \rightarrow H_{0}(A) \rightarrow \mathbb{Z} \oplus H_{0}(X) \rightarrow H_{0}\left(X^{\prime}\right) \rightarrow 0 \end{aligned}$$

  (c) In part (b), suppose that $X=S^{1} \times S^{1}$ and $A=S^{1} \times\{x\} \subseteq X$ for some $x \in S^{1}$. Calculate $H_{i}\left(X^{\prime}\right)$ for all $i$.

  comment

• Paper 4, Section II, 21F

  Algebraic Topology | Part II, 2021

  (a) Define the Euler characteristic of a triangulable space $X$.

  (b) Let $\Sigma_{g}$ be an orientable surface of genus $g$. A $\operatorname{map} \pi: \Sigma_{g} \rightarrow S^{2}$ is a doublebranched cover if there is a set $Q=\left\{p_{1}, \ldots, p_{n}\right\} \subseteq S^{2}$ of branch points, such that the restriction $\pi: \Sigma_{g} \backslash \pi^{-1}(Q) \rightarrow S^{2} \backslash Q$ is a covering map of degree 2 , but for each $p \in Q$, $\pi^{-1}(p)$ consists of one point. By carefully choosing a triangulation of $S^{2}$, use the Euler characteristic to find a formula relating $g$ and $n$.

  comment

2020

• Paper 1, Section II, $21 \mathbf{F}$

  Algebraic Topology | Part II, 2020

  Let $p: \mathbb{R}^{2} \rightarrow S^{1} \times S^{1}=: X$ be the map given by

  $$p\left(r_{1}, r_{2}\right)=\left(e^{2 \pi i r_{1}}, e^{2 \pi i r_{2}}\right)$$

  where $S^{1}$ is identified with the unit circle in $\mathbb{C}$. [You may take as given that $p$ is a covering map.]

  (a) Using the covering map $p$, show that $\pi_{1}\left(X, x_{0}\right)$ is isomorphic to $\mathbb{Z}^{2}$ as a group, where $x_{0}=(1,1) \in X$.

  (b) Let $\mathrm{GL}_{2}(\mathbb{Z})$ denote the group of $2 \times 2$ matrices $A$ with integer entries such that $\operatorname{det} A=\pm 1$. If $A \in \mathrm{GL}_{2}(\mathbb{Z})$, we obtain a linear transformation $A: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$. Show that this linear transformation induces a homeomorphism $f_{A}: X \rightarrow X$ with $f_{A}\left(x_{0}\right)=x_{0}$ and such that $f_{A *}: \pi_{1}\left(X, x_{0}\right) \rightarrow \pi_{1}\left(X, x_{0}\right)$ agrees with $A$ as a map $\mathbb{Z}^{2} \rightarrow \mathbb{Z}^{2}$.

  (c) Let $p_{i}: \widehat{X}_{i} \rightarrow X$ for $i=1,2$ be connected covering maps of degree 2 . Show that there exist homeomorphisms $\phi: \widehat{X}_{1} \rightarrow \widehat{X}_{2}$ and $\psi: X \rightarrow X$ so that the diagram

  

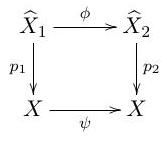
  is commutative.

  comment

• Paper 2, Section II, F

  Algebraic Topology | Part II, 2020

  (a) Let $f: X \rightarrow Y$ be a map of spaces. We define the mapping cylinder $M_{f}$ of $f$ to be the space

  $$(([0,1] \times X) \sqcup Y) / \sim$$

  with $(0, x) \sim f(x)$. Show carefully that the canonical inclusion $Y \hookrightarrow M_{f}$ is a homotopy equivalence.

  (b) Using the Seifert-van Kampen theorem, show that if $X$ is path-connected and $\alpha: S^{1} \rightarrow X$ is a map, and $x_{0}=\alpha\left(\theta_{0}\right)$ for some point $\theta_{0} \in S^{1}$, then

  $$\pi_{1}\left(X \cup_{\alpha} D^{2}, x_{0}\right) \cong \pi_{1}\left(X, x_{0}\right) /\langle\langle[\alpha]\rangle\rangle$$

  Use this fact to construct a connected space $X$ with

  $$\pi_{1}(X) \cong\left\langle a, b \mid a^{3}=b^{7}\right\rangle$$

  (c) Using a covering space of $S^{1} \vee S^{1}$, give explicit generators of a subgroup of $F_{2}$ isomorphic to $F_{3}$. Here $F_{n}$ denotes the free group on $n$ generators.

  comment

• Paper 3, Section II, 20F

  Algebraic Topology | Part II, 2020

  Let $K$ be a simplicial complex with four vertices $v_{1}, \ldots, v_{4}$ with simplices $\left\langle v_{1}, v_{2}, v_{3}\right\rangle$, $\left\langle v_{1}, v_{4}\right\rangle$ and $\left\langle v_{2}, v_{4}\right\rangle$ and their faces.

  (a) Draw a picture of $|K|$, labelling the vertices.

  (b) Using the definition of homology, calculate $H_{n}(K)$ for all $n$.

  (c) Let $L$ be the subcomplex of $K$ consisting of the vertices $v_{1}, v_{2}, v_{4}$ and the 1 simplices $\left\langle v_{1}, v_{2}\right\rangle,\left\langle v_{1}, v_{4}\right\rangle,\left\langle v_{2}, v_{4}\right\rangle$. Let $i: L \rightarrow K$ be the inclusion. Construct a simplicial $\operatorname{map} j: K \rightarrow L$ such that the topological realisation $|j|$ of $j$ is a homotopy inverse to $|i|$. Construct an explicit chain homotopy $h: C_{\bullet}(K) \rightarrow C_{\bullet}(K)$ between $i_{\bullet} \circ j_{\bullet}$ and $\mathrm{id}_{C_{\bullet}(K)}$, and verify that $h$ is a chain homotopy.

  comment

• Paper 4 , Section II, 21F

  Algebraic Topology | Part II, 2020

  In this question, you may assume all spaces involved are triangulable.

  (a) (i) State and prove the Mayer-Vietoris theorem. [You may assume the theorem that states that a short exact sequence of chain complexes gives rise to a long exact sequence of homology groups.]

  (ii) Use Mayer-Vietoris to calculate the homology groups of an oriented surface of genus $g$.

  (b) Let $S$ be an oriented surface of genus $g$, and let $D_{1}, \ldots, D_{n}$ be a collection of mutually disjoint closed subsets of $S$ with each $D_{i}$ homeomorphic to a two-dimensional disk. Let $D_{i}^{\circ}$ denote the interior of $D_{i}$, homeomorphic to an open two-dimensional disk, and let

  $$T:=S \backslash\left(D_{1}^{\circ} \cup \cdots \cup D_{n}^{\circ}\right)$$

  Show that

  $$H_{i}(T)= \begin{cases}\mathbb{Z} & i=0 \\ \mathbb{Z}^{2 g+n-1} & i=1 \\ 0 & \text { otherwise }\end{cases}$$

  (c) Let $T$ be the surface given in (b) when $S=S^{2}$ and $n=3$. Let $f: T \rightarrow S^{1} \times S^{1}$ be a map. Does there exist a map $g: S^{1} \times S^{1} \rightarrow T$ such that $f \circ g$ is homotopic to the identity map? Justify your answer.

  comment

2019

• Paper 1, Section II, F

  Algebraic Topology | Part II, 2019

  In this question, $X$ and $Y$ are path-connected, locally simply connected spaces.

  (a) Let $f: Y \rightarrow X$ be a continuous map, and $\widehat{X}$a path-connected covering space of $X$. State and prove a uniqueness statement for lifts of $f$ to $\widehat{X}$.

  (b) Let $p: \widehat{X} \rightarrow X$ be a covering map. A covering transformation of $p$ is a homeomorphism $\phi: \widehat{X} \rightarrow \widehat{X}$such that $p \circ \phi=p$. For each integer $n \geqslant 3$, give an example of a space $X$ and an $n$-sheeted covering map $p_{n}: \widehat{X}_{n} \rightarrow X$ such that the only covering transformation of $p_{n}$ is the identity map. Justify your answer. [Hint: Take $X$ to be a wedge of two circles.]

  (c) Is there a space $X$ and a 2-sheeted covering map $p_{2}: \widehat{X}_{2} \rightarrow X$ for which the only covering transformation of $p_{2}$ is the identity? Justify your answer briefly.

  comment

• Paper 2, Section II, F

  Algebraic Topology | Part II, 2019

  Let $T=S^{1} \times S^{1}, U=S^{1} \times D^{2}$ and $V=D^{2} \times S^{1}$. Let $i: T \rightarrow U, j: T \rightarrow V$ be the natural inclusion maps. Consider the space $S:=U \cup_{T} V$; that is,

  $$S:=(U \sqcup V) / \sim$$

  where $\sim$ is the smallest equivalence relation such that $i(x) \sim j(x)$ for all $x \in T$.

  (a) Prove that $S$ is homeomorphic to the 3 -sphere $S^{3}$.

  [Hint: It may help to think of $S^{3}$ as contained in $\mathbb{C}^{2}$.]

  (b) Identify $T$ as a quotient of the square $I \times I$ in the usual way. Let $K$ be the circle in $T$ given by the equation $y=\frac{2}{3} x \bmod 1 . K$ is illustrated in the figure below.

  

  Compute a presentation for $\pi_{1}(S-K)$, where $S-K$ is the complement of $K$ in $S$, and deduce that $\pi_{1}(S-K)$ is non-abelian.

  comment

• Paper 3, Section II, F

  Algebraic Topology | Part II, 2019

  Let $K$ be a simplicial complex, and $L$ a subcomplex. As usual, $C_{k}(K)$ denotes the group of $k$-chains of $K$, and $C_{k}(L)$ denotes the group of $k$-chains of $L$.

  (a) Let

  $$C_{k}(K, L)=C_{k}(K) / C_{k}(L)$$

  for each integer $k$. Prove that the boundary map of $K$ descends to give $C_{\bullet}(K, L)$ the structure of a chain complex.

  (b) The homology groups of $K$ relative to $L$, denoted by $H_{k}(K, L)$, are defined to be the homology groups of the chain complex $C_{\bullet}(K, L)$. Prove that there is a long exact sequence that relates the homology groups of $K$ relative to $L$ to the homology groups of $K$ and the homology groups of $L$.

  (c) Let $D_{n}$ be the closed $n$-dimensional disc, and $S^{n-1}$ be the $(n-1)$-dimensional sphere. Exhibit simplicial complexes $K_{n}$ and subcomplexes $L_{n-1}$ such that $D_{n} \cong\left|K_{n}\right|$ in such a way that $\left|L_{n-1}\right|$ is identified with $S^{n-1}$.

  (d) Compute the relative homology groups $H_{k}\left(K_{n}, L_{n-1}\right)$, for all integers $k \geqslant 0$ and $n \geqslant 2$ where $K_{n}$ and $L_{n-1}$ are as in (c).

  comment

• Paper 4, Section II, F

  Algebraic Topology | Part II, 2019

  State the Lefschetz fixed point theorem.

  Let $n \geqslant 2$ be an integer, and $x_{0} \in S^{2}$ a choice of base point. Define a space

  $$X:=\left(S^{2} \times \mathbb{Z} / n \mathbb{Z}\right) / \sim$$

  where $\mathbb{Z} / n \mathbb{Z}$ is discrete and $\sim$ is the smallest equivalence relation such that $\left(x_{0}, i\right) \sim$ $\left(-x_{0}, i+1\right)$ for all $i \in \mathbb{Z} / n \mathbb{Z}$. Let $\phi: X \rightarrow X$ be a homeomorphism without fixed points. Use the Lefschetz fixed point theorem to prove the following facts.

  (i) If $\phi^{3}=\mathrm{Id}_{X}$ then $n$ is divisible by 3 .

  (ii) If $\phi^{2}=\operatorname{Id}_{X}$ then $n$ is even.

  comment

2018

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2018

  (a) Let $V$ be the vector space of 3-dimensional upper-triangular matrices with real entries:

  $$V=\left\{\left(\begin{array}{ccc} 1 & x & y \\ 0 & 1 & z \\ 0 & 0 & 1 \end{array}\right) \mid x, y, z \in \mathbb{R}\right\}$$

  Let $\Gamma$ be the set of elements of $V$ for which $x, y, z$ are integers. Notice that $\Gamma$ is a subgroup of $G L_{3}(\mathbb{R})$; let $\Gamma$ act on $V$ by left-multiplication and let $N=\Gamma \backslash V$. Show that the quotient $\operatorname{map} V \rightarrow N$ is a covering map.

  (b) Consider the unit circle $S^{1} \subseteq \mathbb{C}$, and let $T=S^{1} \times S^{1}$. Show that the map $f: T \rightarrow T$ defined by

  $$f(z, w)=(z w, w)$$

  is a homeomorphism.

  (c) Let $M=[0,1] \times T / \sim$, where $\sim$ is the smallest equivalence relation satisfying

  $$(1, x) \sim(0, f(x))$$

  for all $x \in T$. Prove that $N$ and $M$ are homeomorphic by exhibiting a homeomorphism $M \rightarrow N$. [You may assume without proof that $N$ is Hausdorff.]

  (d) Prove that $\pi_{1}(M) \cong \Gamma$.

  comment

• Paper 2, Section II, H

  Algebraic Topology | Part II, 2018

  (a) Define the first barycentric subdivision $K^{\prime}$ of a simplicial complex $K$. Hence define the $r^{t h}$ barycentric subdivision $K^{(r)}$. [You do not need to prove that $K^{\prime}$ is a simplicial complex.]

  (b) Define the mesh $\mu(K)$ of a simplicial complex $K$. State a result that describes the behaviour of $\mu\left(K^{(r)}\right)$ as $r \rightarrow \infty$.

  (c) Define a simplicial approximation to a continuous map of polyhedra

  $$f:|K| \rightarrow|L|$$

  Prove that, if $g$ is a simplicial approximation to $f$, then the realisation $|g|:|K| \rightarrow|L|$ is homotopic to $f$.

  (d) State and prove the simplicial approximation theorem. [You may use the Lebesgue number lemma without proof, as long as you state it clearly.]

  (e) Prove that every continuous map of spheres $S^{n} \rightarrow S^{m}$ is homotopic to a constant map when $n<m$.

  comment

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2018

  (a) State a version of the Seifert-van Kampen theorem for a cell complex $X$ written as the union of two subcomplexes $Y, Z$.

  (b) Let

  $$X_{n}=\underbrace{S^{1} \vee \ldots \vee S^{1}}_{n} \vee \mathbb{R} P^{2}$$

  for $n \geqslant 1$, and take any $x_{0} \in X_{n}$. Write down a presentation for $\pi_{1}\left(X_{n}, x_{0}\right)$.

  (c) By computing a homology group of a suitable four-sheeted covering space of $X_{n}$, prove that $X_{n}$ is not homotopy equivalent to a compact, connected surface whenever $n \geqslant 1$.

  comment

• Paper 4, Section II, H

  Algebraic Topology | Part II, 2018

  (a) State the Mayer-Vietoris theorem for a union of simplicial complexes

  $$K=M \cup N$$

  with $L=M \cap N$.

  (b) Construct the map $\partial_{*}: H_{k}(K) \rightarrow H_{k-1}(L)$ that appears in the statement of the theorem. [You do not need to prove that the map is well defined, or a homomorphism.]

  (c) Let $K$ be a simplicial complex with $|K|$ homeomorphic to the $n$-dimensional sphere $S^{n}$, for $n \geqslant 2$. Let $M \subseteq K$ be a subcomplex with $|M|$ homeomorphic to $S^{n-1} \times[-1,1]$. Suppose that $K=M \cup N$, such that $L=M \cap N$ has polyhedron $|L|$ identified with $S^{n-1} \times\{-1,1\} \subseteq S^{n-1} \times[-1,1]$. Prove that $|N|$ has two path components.

  comment

2017

• Paper 1, Section II, I

  Algebraic Topology | Part II, 2017

  Let $X$ be a topological space and let $x_{0}$ and $x_{1}$ be points of $X$.

  (a) Explain how a path $u:[0,1] \rightarrow X$ from $x_{0}$ to $x_{1}$ defines a map $u_{\sharp}: \pi_{1}\left(X, x_{0}\right) \rightarrow$ $\pi_{1}\left(X, x_{1}\right)$.

  (b) Prove that $u_{\sharp}$ is an isomorphism of groups.

  (c) Let $\alpha, \beta:\left(S^{1}, 1\right) \rightarrow\left(X, x_{0}\right)$ be based loops in $X$. Suppose that $\alpha, \beta$ are homotopic as unbased maps, i.e. the homotopy is not assumed to respect basepoints. Show that the corresponding elements of $\pi_{1}\left(X, x_{0}\right)$ are conjugate.

  (d) Take $X$ to be the 2-torus $S^{1} \times S^{1}$. If $\alpha, \beta$ are homotopic as unbased loops as in part (c), then exhibit a based homotopy between them. Interpret this fact algebraically.

  (e) Exhibit a pair of elements in the fundamental group of $S^{1} \vee S^{1}$ which are homotopic as unbased loops but not as based loops. Justify your answer.

  comment

• Paper 2, Section II, I

  Algebraic Topology | Part II, 2017

  (a) (i) Define the push-out of the following diagram of groups.

  

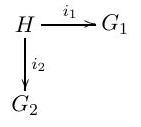
  When is a push-out a free product with amalgamation?

  (ii) State the Seifert-van Kampen theorem.

  (b) Let $X=\mathbb{R} P^{2} \vee S^{1}$ (recalling that $\mathbb{R} P^{2}$ is the real projective plane), and let $x \in X$.

  (i) Compute the fundamental group $\pi_{1}(X, x)$ of the space $X$.

  (ii) Show that there is a surjective homomorphism $\phi: \pi_{1}(X, x) \rightarrow S_{3}$, where $S_{3}$ is the symmetric group on three elements.

  (c) Let $\widehat{X} \rightarrow X$ be the covering space corresponding to the kernel of $\phi$.

  (i) Draw $\widehat{X}$and justify your answer carefully.

  (ii) Does $\widehat{X}$retract to a graph? Justify your answer briefly.

  (iii) Does $\widehat{X}$deformation retract to a graph? Justify your answer briefly.

  comment

• Paper 3, Section II, I

  Algebraic Topology | Part II, 2017

  The $n$-torus is the product of $n$ circles:

  $$T^{n}=\underbrace{S^{1} \times \ldots \times S^{1}}_{n \text { times }} .$$

  For all $n \geqslant 1$ and $0 \leqslant k \leqslant n$, compute $H_{k}\left(T^{n}\right)$.

  [You may assume that relevant spaces are triangulable, but you should state carefully any version of any theorem that you use.]

  comment

• Paper 4, Section II, I

  Algebraic Topology | Part II, 2017

  Recall that $\mathbb{R} P^{n}$ is real projective $n$-space, the quotient of $S^{n}$ obtained by identifying antipodal points. Consider the standard embedding of $S^{n}$ as the unit sphere in $\mathbb{R}^{n+1}$.

  (a) For $n$ odd, show that there exists a continuous map $f: S^{n} \rightarrow S^{n}$ such that $f(x)$ is orthogonal to $x$, for all $x \in S^{n}$.

  (b) Exhibit a triangulation of $\mathbb{R} P^{n}$.

  (c) Describe the map $H_{n}\left(S^{n}\right) \rightarrow H_{n}\left(S^{n}\right)$ induced by the antipodal map, justifying your answer.

  (d) Show that, for $n$ even, there is no continuous map $f: S^{n} \rightarrow S^{n}$ such that $f(x)$ is orthogonal to $x$ for all $x \in S^{n}$.

  comment

2016

• Paper 1, Section II, G

  Algebraic Topology | Part II, 2016

  Let $T=S^{1} \times S^{1}$ be the 2-dimensional torus. Let $\alpha: S^{1} \rightarrow T$ be the inclusion of the coordinate circle $S^{1} \times\{1\}$, and let $X$ be the result of attaching a 2-cell along $\alpha$.

  (a) Write down a presentation for the fundamental group of $X$ (with respect to some basepoint), and identify it with a well-known group.

  (b) Compute the simplicial homology of any triangulation of $X$.

  (c) Show that $X$ is not homotopy equivalent to any compact surface.

  comment

• Paper 2, Section II, G

  Algebraic Topology | Part II, 2016

  (a) Let $K, L$ be simplicial complexes, and $f:|K| \rightarrow|L|$ a continuous map. What does it mean to say that $g: K \rightarrow L$ is a simplicial approximation to $f ?$

  (b) Define the barycentric subdivision of a simplicial complex $K$, and state the Simplicial Approximation Theorem.

  (c) Show that if $g$ is a simplicial approximation to $f$ then $f \simeq|g|$.

  (d) Show that the natural inclusion $\left|K^{(1)}\right| \rightarrow|K|$ induces a surjective map on fundamental groups.

  comment

• Paper 3, Section II, G

  Algebraic Topology | Part II, 2016

  Construct a space $X$ as follows. Let $Z_{1}, Z_{2}, Z_{3}$ each be homeomorphic to the standard 2-sphere $S^{2} \subseteq \mathbb{R}^{3}$. For each $i$, let $x_{i} \in Z_{i}$ be the North pole $(1,0,0)$ and let $y_{i} \in Z_{i}$ be the South pole $(-1,0,0)$. Then

  $$X=\left(Z_{1} \sqcup Z_{2} \sqcup Z_{3}\right) / \sim$$

  where $x_{i+1} \sim y_{i}$ for each $i$ (and indices are taken modulo 3 ).

  (a) Describe the universal cover of $X$.

  (b) Compute the fundamental group of $X$ (giving your answer as a well-known group).

  (c) Show that $X$ is not homotopy equivalent to the circle $S^{1}$.

  comment

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2016

  Let $T=S^{1} \times S^{1}$ be the 2-dimensional torus, and let $X$ be constructed from $T$ by removing a small open disc.

  (a) Show that $X$ is homotopy equivalent to $S^{1} \vee S^{1}$.

  (b) Show that the universal cover of $X$ is homotopy equivalent to a tree.

  (c) Exhibit (finite) cell complexes $X, Y$, such that $X$ and $Y$ are not homotopy equivalent but their universal covers $\widetilde{X}, \widetilde{Y}$are.

  [State carefully any results from the course that you use.]

  comment

2015

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2015

  State carefully a version of the Seifert-van Kampen theorem for a cover of a space by two closed sets.

  Let $X$ be the space obtained by gluing together a Möbius band $M$ and a torus $T=S^{1} \times S^{1}$ along a homeomorphism of the boundary of $M$ with $S^{1} \times\{1\} \subset T$. Find a presentation for the fundamental group of $X$, and hence show that it is infinite and non-abelian.

  comment

• Paper 2, Section II, H

  Algebraic Topology | Part II, 2015

  Define what it means for $p: \widetilde{X} \rightarrow X$ to be a covering map, and what it means to say that $p$ is a universal cover.

  Let $p: \tilde{X} \rightarrow X$ be a universal cover, $A \subset X$ be a locally path connected subspace, and $\tilde{A} \subset p^{-1}(A)$ be a path component containing a point $\tilde{a}_{0}$ with $p\left(\tilde{a}_{0}\right)=a_{0}$. Show that the restriction $\left.p\right|_{\tilde{A}}: \widetilde{A} \rightarrow A$ is a covering map, and that under the Galois correspondence it corresponds to the subgroup

  $$\operatorname{Ker}\left(\pi_{1}\left(A, a_{0}\right) \rightarrow \pi_{1}\left(X, a_{0}\right)\right)$$

  of $\pi_{1}\left(A, a_{0}\right)$.

  comment

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2015

  Let $K$ and $L$ be simplicial complexes. Explain what is meant by a simplicial approximation to a continuous map $f:|K| \rightarrow|L|$. State the simplicial approximation theorem, and define the homomorphism induced on homology by a continuous map between triangulable spaces. [You do not need to show that the homomorphism is welldefined.]

  Let $h: S^{1} \rightarrow S^{1}$ be given by $z \mapsto z^{n}$ for a positive integer $n$, where $S^{1}$ is considered as the unit complex numbers. Compute the map induced by $h$ on homology.

  comment

• Paper 4, Section II, H

  Algebraic Topology | Part II, 2015

  State the Mayer-Vietoris theorem for a simplicial complex $K$ which is the union of two subcomplexes $M$ and $N$. Explain briefly how the connecting homomorphism $\partial_{n}: H_{n}(K) \rightarrow H_{n-1}(M \cap N)$ is defined.

  If $K$ is the union of subcomplexes $M_{1}, M_{2}, \ldots, M_{n}$, with $n \geqslant 2$, such that each intersection

  $$M_{i_{1}} \cap M_{i_{2}} \cap \cdots \cap M_{i_{k}}, \quad 1 \leqslant k \leqslant n,$$

  is either empty or has the homology of a point, then show that

  $$H_{i}(K)=0 \quad \text { for } \quad i \geqslant n-1 .$$

  Construct examples for each $n \geqslant 2$ showing that this is sharp.

  comment

2014

• Paper 1, Section II, F

  Algebraic Topology | Part II, 2014

  Define what it means for a map $p: \widetilde{X} \rightarrow X$ to be a covering space. State the homotopy lifting lemma.

  Let $p:\left(\tilde{X}, \tilde{x}_{0}\right) \rightarrow\left(X, x_{0}\right)$ be a based covering space and let $f:\left(Y, y_{0}\right) \rightarrow\left(X, x_{0}\right)$ be a based map from a path-connected and locally path-connected space. Show that there is a based lift $\tilde{f}:\left(Y, y_{0}\right) \rightarrow\left(\tilde{X}, \tilde{x}_{0}\right)$ of $f$ if and only if $f_{*}\left(\pi_{1}\left(Y, y_{0}\right)\right) \subseteq p_{*}\left(\pi_{1}\left(\widetilde{X}, \tilde{x}_{0}\right)\right)$.

  comment

• Paper 2, Section II, F

  Algebraic Topology | Part II, 2014

  Let $A=\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ be a matrix with integer entries. Considering $S^{1}$ as the quotient space $\mathbb{R} / \mathbb{Z}$, show that the function

  $$\begin{aligned} \varphi_{A}: S^{1} \times S^{1} & \longrightarrow S^{1} \times S^{1} \\ ([x],[y]) & \longmapsto([a x+b y],[c x+d y]) \end{aligned}$$

  is well-defined and continuous. If in addition $\operatorname{det}(A)=\pm 1$, show that $\varphi_{A}$ is a homeomorphism.

  State the Seifert-van Kampen theorem. Let $X_{A}$ be the space obtained by gluing together two copies of $S^{1} \times D^{2}$ along their boundaries using the homeomorphism $\varphi_{A}$. Show that the fundamental group of $X_{A}$ is cyclic and determine its order.

  comment

• Paper 3, Section II, F

  Algebraic Topology | Part II, 2014

  Let $K$ be a simplicial complex in $\mathbb{R}^{N}$, which we may also consider as lying in $\mathbb{R}^{N+1}$ using the first $N$ coordinates. Write $c=(0,0, \ldots, 0,1) \in \mathbb{R}^{N+1}$. Show that if $\left\langle v_{0}, v_{1}, \ldots, v_{n}\right\rangle$ is a simplex of $K$ then $\left\langle v_{0}, v_{1}, \ldots, v_{n}, c\right\rangle$ is a simplex in $\mathbb{R}^{N+1}$.

  Let $L \leqslant K$ be a subcomplex and let $\bar{K}$ be the collection

  $$K \cup\left\{\left\langle v_{0}, v_{1}, \ldots, v_{n}, c\right\rangle \mid\left\langle v_{0}, v_{1}, \ldots, v_{n}\right\rangle \in L\right\} \cup\{\langle c\rangle\}$$

  of simplices in $\mathbb{R}^{N+1}$. Show that $\bar{K}$ is a simplicial complex.

  If $|K|$ is a Möbius band, and $|L|$ is its boundary, show that

  $$H_{i}(\bar{K}) \cong \begin{cases}\mathbb{Z} & \text { if } i=0 \\ \mathbb{Z} / 2 & \text { if } i=1 \\ 0 & \text { if } i \geqslant 2\end{cases}$$

  comment

• Paper 4, Section II, F

  Algebraic Topology | Part II, 2014

  State the Lefschetz fixed point theorem.

  Let $X$ be an orientable surface of genus $g$ (which you may suppose has a triangulation), and let $f: X \rightarrow X$ be a continuous map such that

  1. $f^{3}=\operatorname{Id}_{X}$,

  2. $f$ has no fixed points.

  By considering the eigenvalues of the linear map $f_{*}: H_{1}(X ; \mathbb{Q}) \rightarrow H_{1}(X ; \mathbb{Q})$, and their multiplicities, show that $g$ must be congruent to 1 modulo 3 .

  comment

2013

• Paper 1, Section II, 21G

  Algebraic Topology | Part II, 2013

  (i) Define the notion of the fundamental group $\pi_{1}\left(X, x_{0}\right)$ of a path-connected space $X$ with base point $x_{0}$.

  (ii) Prove that if a group $G$ acts freely and properly discontinuously on a simply connected space $Z$, then $\pi_{1}\left(G \backslash Z, x_{0}\right)$ is isomorphic to $G$. [You may assume the homotopy lifting property, provided that you state it clearly.]

  (iii) Suppose that $p, q$ are distinct points on the 2 -sphere $S^{2}$ and that $X=S^{2} /(p \sim q)$. Exhibit a simply connected space $Z$ with an action of a group $G$ as in (ii) such that $X=G \backslash Z$, and calculate $\pi_{1}\left(X, x_{0}\right)$.

  comment

• Paper 2, Section II, G

  Algebraic Topology | Part II, 2013

  (i) State the Seifert-van Kampen theorem.

  (ii) Assuming any standard results about the fundamental group of a circle that you wish, calculate the fundamental group of the $n$-sphere, for every $n \geqslant 2$.

  (iii) Suppose that $n \geqslant 3$ and that $X$ is a path-connected topological $n$-manifold. Show that $\pi_{1}\left(X, x_{0}\right)$ is isomorphic to $\pi_{1}\left(X-\{P\}, x_{0}\right)$ for any $P \in X-\left\{x_{0}\right\}$.

  comment

• Paper 3, Section II, G

  Algebraic Topology | Part II, 2013

  (i) State, but do not prove, the Mayer-Vietoris theorem for the homology groups of polyhedra.

  (ii) Calculate the homology groups of the $n$-sphere, for every $n \geqslant 0$.

  (iii) Suppose that $a \geqslant 1$ and $b \geqslant 0$. Calculate the homology groups of the subspace $X$ of $\mathbb{R}^{a+b}$ defined by $\sum_{i=1}^{a} x_{i}^{2}-\sum_{j=a+1}^{a+b} x_{j}^{2}=1$.

  comment

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2013

  (i) State, but do not prove, the Lefschetz fixed point theorem.

  (ii) Show that if $n$ is even, then for every map $f: S^{n} \rightarrow S^{n}$ there is a point $x \in S^{n}$ such that $f(x)=\pm x$. Is this true if $n$ is odd? [Standard results on the homology groups for the $n$-sphere may be assumed without proof, provided they are stated clearly.]

  comment

2012

• Paper 1, Section II, G

  Algebraic Topology | Part II, 2012

  Define the notions of covering projection and of locally path-connected space. Show that a locally path-connected space is path-connected if it is connected.

  Suppose $f: Y \rightarrow X$ and $g: Z \rightarrow X$ are continuous maps, the space $Y$ is connected and locally path-connected and that $g$ is a covering projection. Suppose also that we are given base-points $x_{0}, y_{0}, z_{0}$ satisfying $f\left(y_{0}\right)=x_{0}=g\left(z_{0}\right)$. Show that there is a continuous $\tilde{f}: Y \rightarrow Z$ satisfying $\tilde{f}\left(y_{0}\right)=z_{0}$ and $g \tilde{f}=f$ if and only if the image of $f_{*}: \Pi_{1}\left(Y, y_{0}\right) \rightarrow \Pi_{1}\left(X, x_{0}\right)$ is contained in that of $g_{*}: \Pi_{1}\left(Z, z_{0}\right) \rightarrow \Pi_{1}\left(X, x_{0}\right)$. [You may assume the path-lifting and homotopy-lifting properties of covering projections.]

  Now suppose $X$ is locally path-connected, and both $f: Y \rightarrow X$ and $g: Z \rightarrow X$ are covering projections with connected domains. Show that $Y$ and $Z$ are homeomorphic as spaces over $X$ if and only if the images of their fundamental groups under $f_{*}$ and $g_{*}$ are conjugate subgroups of $\Pi_{1}\left(X, x_{0}\right)$.

  comment

• Paper 2, Section II, G

  Algebraic Topology | Part II, 2012

  State the Seifert-Van Kampen Theorem. Deduce that if $f: S^{1} \rightarrow X$ is a continuous map, where $X$ is path-connected, and $Y=X \cup_{f} B^{2}$ is the space obtained by adjoining a disc to $X$ via $f$, then $\Pi_{1}(Y)$ is isomorphic to the quotient of $\Pi_{1}(X)$ by the smallest normal subgroup containing the image of $f_{*}: \Pi_{1}\left(S^{1}\right) \rightarrow \Pi_{1}(X)$.

  State the classification theorem for connected triangulable 2-manifolds. Use the result of the previous paragraph to obtain a presentation of $\Pi_{1}\left(M_{g}\right)$, where $M_{g}$ denotes the compact orientable 2 -manifold of genus $g>0$.

  comment

• Paper 3, Section II, G

  Algebraic Topology | Part II, 2012

  State the Mayer-Vietoris Theorem for a simplicial complex $K$ expressed as the union of two subcomplexes $L$ and $M$. Explain briefly how the connecting homomorphism $\delta_{*}: H_{n}(K) \rightarrow H_{n-1}(L \cap M)$, which appears in the theorem, is defined. [You should include a proof that $\delta_{*}$ is well-defined, but need not verify that it is a homomorphism.]

  Now suppose that $|K| \cong S^{3}$, that $|L|$ is a solid torus $S^{1} \times B^{2}$, and that $|L \cap M|$ is the boundary torus of $|L|$. Show that $\delta_{*}: H_{3}(K) \rightarrow H_{2}(L \cap M)$ is an isomorphism, and hence calculate the homology groups of $M$. [You may assume that a generator of $H_{3}(K)$ may be represented by a 3 -cycle which is the sum of all the 3 -simplices of $K$, with 'matching' orientations.]

  comment

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2012

  State and prove the Lefschetz fixed-point theorem. Hence show that the $n$-sphere $S^{n}$ does not admit a topological group structure for any even $n>0$. [The existence and basic properties of simplicial homology with rational coefficients may be assumed.]

  comment

2011

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2011

  Are the following statements true or false? Justify your answers.

  (i) If $x$ and $y$ lie in the same path-component of $X$, then $\Pi_{1}(X, x) \cong \Pi_{1}(X, y)$.

  (ii) If $x$ and $y$ are two points of the Klein bottle $K$, and $u$ and $v$ are two paths from $x$ to $y$, then $u$ and $v$ induce the same isomorphism from $\Pi_{1}(K, x)$ to $\Pi_{1}(K, y)$.

  (iii) $\Pi_{1}(X \times Y,(x, y))$ is isomorphic to $\Pi_{1}(X, x) \times \Pi_{1}(Y, y)$ for any two spaces $X$ and $Y$.

  (iv) If $X$ and $Y$ are connected polyhedra and $H_{1}(X) \cong H_{1}(Y)$, then $\Pi_{1}(X) \cong \Pi_{1}(Y)$.

  comment

• Paper 2, Section II, H

  Algebraic Topology | Part II, 2011

  Explain what is meant by a covering projection. State and prove the pathlifting property for covering projections, and indicate briefly how it generalizes to a lifting property for homotopies between paths. [You may assume the Lebesgue Covering Theorem.]

  Let $X$ be a simply connected space, and let $G$ be a subgroup of the group of all homeomorphisms $X \rightarrow X$. Suppose that, for each $x \in X$, there exists an open neighbourhood $U$ of $x$ such that $U \cap g[U]=\emptyset$ for each $g \in G$ other than the identity. Show that the projection $p: X \rightarrow X / G$ is a covering projection, and deduce that $\Pi_{1}(X / G) \cong G$.

  By regarding $S^{3}$ as the set of all quaternions of modulus 1 , or otherwise, show that there is a quotient space of $S^{3}$ whose fundamental group is a non-abelian group of order $8 .$

  comment

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2011

  Let $K$ and $L$ be (finite) simplicial complexes. Explain carefully what is meant by a simplicial approximation to a continuous map $f:|K| \rightarrow|L|$. Indicate briefly how the cartesian product $|K| \times|L|$ may be triangulated.

  Two simplicial maps $g, h: K \rightarrow L$ are said to be contiguous if, for each simplex $\sigma$ of $K$, there exists a simplex $\sigma *$ of $L$ such that both $g(\sigma)$ and $h(\sigma)$ are faces of $\sigma *$. Show that:

  (i) any two simplicial approximations to a given map $f:|K| \rightarrow|L|$ are contiguous;

  (ii) if $g$ and $h$ are contiguous, then they induce homotopic maps $|K| \rightarrow|L|$;

  (iii) if $f$ and $g$ are homotopic maps $|K| \rightarrow|L|$, then for some subdivision $K^{(n)}$ of $K$ there exists a sequence $\left(h_{1}, h_{2}, \ldots, h_{m}\right)$ of simplicial maps $K^{(n)} \rightarrow L$ such that $h_{1}$ is a simplicial approximation to $f, h_{m}$ is a simplicial approximation to $g$ and each pair $\left(h_{i}, h_{i+1}\right)$ is contiguous.

  comment

• Paper 4, Section II, H

  Algebraic Topology | Part II, 2011

  State the Mayer-Vietoris theorem, and use it to calculate, for each integer $q>1$, the homology group of the space $X_{q}$ obtained from the unit disc $B^{2} \subseteq \mathbb{C}$ by identifying pairs of points $\left(z_{1}, z_{2}\right)$ on its boundary whenever $z_{1}^{q}=z_{2}^{q}$. [You should construct an explicit triangulation of $X_{q}$.]

  Show also how the theorem may be used to calculate the homology groups of the suspension $S K$ of a connected simplicial complex $K$ in terms of the homology groups of $K$, and of the wedge union $X \vee Y$ of two connected polyhedra. Hence show that, for any finite sequence $\left(G_{1}, G_{2}, \ldots, G_{n}\right)$ of finitely-generated abelian groups, there exists a polyhedron $X$ such that $H_{0}(X) \cong \mathbb{Z}, H_{i}(X) \cong G_{i}$ for $1 \leqslant i \leqslant n$ and $H_{i}(X)=0$ for $i>n$. [You may assume the structure theorem which asserts that any finitely-generated abelian group is isomorphic to a finite direct sum of (finite or infinite) cyclic groups.]

  comment

2010

• Paper 1, Section II, H

  Algebraic Topology | Part II, 2010

  State the path lifting and homotopy lifting lemmas for covering maps. Suppose that $X$ is path connected and locally path connected, that $p_{1}: Y_{1} \rightarrow X$ and $p_{2}: Y_{2} \rightarrow X$ are covering maps, and that $Y_{1}$ and $Y_{2}$ are simply connected. Using the lemmas you have stated, but without assuming the correspondence between covering spaces and subgroups of $\pi_{1}$, prove that $Y_{1}$ is homeomorphic to $Y_{2}$.

  comment

• Paper 2, Section II, $\mathbf{2 1 H}$

  Algebraic Topology | Part II, 2010

  Let $G$ be the finitely presented group $G=\left\langle a, b \mid a^{2} b^{3} a^{3} b^{2}=1\right\rangle$. Construct a path connected space $X$ with $\pi_{1}(X, x) \cong G$. Show that $X$ has a unique connected double cover $\pi: Y \rightarrow X$, and give a presentation for $\pi_{1}(Y, y)$.

  comment

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2010

  Suppose $X$ is a finite simplicial complex and that $H_{*}(X)$ is a free abelian group for each value of $*$. Using the Mayer-Vietoris sequence or otherwise, compute $H_{*}\left(S^{1} \times X\right)$ in terms of $H_{*}(X)$. Use your result to compute $H_{*}\left(T^{n}\right)$.

  [Note that $T^{n}=S^{1} \times \ldots \times S^{1}$, where there are $n$ factors in the product.]

  comment

• Paper 4, Section II, $\mathbf{2 1 H}$

  Algebraic Topology | Part II, 2010

  State the Snake Lemma. Explain how to define the boundary map which appears in it, and check that it is well-defined. Derive the Mayer-Vietoris sequence from the Snake Lemma.

  Given a chain complex $C$, let $A \subset C$ be the span of all elements in $C$ with grading greater than or equal to $n$, and let $B \subset C$ be the span of all elements in $C$ with grading less than $n$. Give a short exact sequence of chain complexes relating $A, B$, and $C$. What is the boundary map in the corresponding long exact sequence?

  comment

2009

• Paper 1, Section II, G

  Algebraic Topology | Part II, 2009

  Let $X$ be the space obtained by identifying two copies of the Möbius strip along their boundary. Use the Seifert-Van Kampen theorem to find a presentation of the fundamental group $\pi_{1}(X)$. Show that $\pi_{1}(X)$ is an infinite non-abelian group.

  comment

• Paper 2, Section II, $21 G$

  Algebraic Topology | Part II, 2009

  Let $p: X \rightarrow Y$ be a connected covering map. Define the notion of a deck transformation (also known as covering transformation) for $p$. What does it mean for $p$ to be a regular (normal) covering map?

  If $p^{-1}(y)$ contains $n$ points for each $y \in Y$, we say $p$ is $n$-to-1. Show that $p$ is regular under either of the following hypotheses:

  (1) $p$ is 2-to-1,

  (2) $\pi_{1}(Y)$ is abelian.

  Give an example of a 3 -to-1 cover of $S^{1} \vee S^{1}$ which is regular, and one which is not regular.

  comment

• Paper 3, Section II, G

  Algebraic Topology | Part II, 2009

  (i) Suppose that $(C, d)$ and $\left(C^{\prime}, d^{\prime}\right)$ are chain complexes, and $f, g: C \rightarrow C^{\prime}$ are chain maps. Define what it means for $f$ and $g$ to be chain homotopic.

  Show that if $f$ and $g$ are chain homotopic, and $f_{*}, g_{*}: H_{*}(C) \rightarrow H_{*}\left(C^{\prime}\right)$ are the induced maps, then $f_{*}=g_{*}$.

  (ii) Define the Euler characteristic of a finite chain complex.

  Given that one of the sequences below is exact and the others are not, which is the exact one?

  $$\begin{aligned} &0 \rightarrow \mathbb{Z}^{11} \rightarrow \mathbb{Z}^{24} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{13} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{25} \rightarrow \mathbb{Z}^{11} \rightarrow 0 \\ &0 \rightarrow \mathbb{Z}^{11} \rightarrow \mathbb{Z}^{24} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{13} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{24} \rightarrow \mathbb{Z}^{11} \rightarrow 0 \\ &0 \rightarrow \mathbb{Z}^{11} \rightarrow \mathbb{Z}^{24} \rightarrow \mathbb{Z}^{19} \rightarrow \mathbb{Z}^{13} \rightarrow \mathbb{Z}^{20} \rightarrow \mathbb{Z}^{23} \rightarrow \mathbb{Z}^{11} \rightarrow 0 \end{aligned}$$

  Justify your choice.

  comment

• Paper 4, Section II, G

  Algebraic Topology | Part II, 2009

  Let $X$ be the subset of $\mathbb{R}^{4}$ given by $X=A \cup B \cup C \subset \mathbb{R}^{4}$, where $A, B$ and $C$ are defined as follows:

  $$\begin{aligned} &A=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{1}^{2}+x_{2}^{2}+x_{3}^{2}+x_{4}^{2}=1\right\} \\ &B=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{1}=x_{2}=0, x_{3}^{2}+x_{4}^{2} \leqslant 1\right\} \\ &C=\left\{\left(x_{1}, x_{2}, x_{3}, x_{4}\right) \in \mathbb{R}^{4}: x_{3}=x_{4}=0, x_{1}^{2}+x_{2}^{2} \leqslant 1\right\} \end{aligned}$$

  Compute $H_{*}(X)$

  comment

2008

• 1.II.21F

  Algebraic Topology | Part II, 2008

  (i) State the van Kampen theorem.

  (ii) Calculate the fundamental group of the wedge $S^{2} \vee S^{1}$.

  (iii) Let $X=\mathbb{R}^{3} \backslash A$ where $A$ is a circle. Calculate the fundamental group of $X$.

  comment

• 2.II.21F

  Algebraic Topology | Part II, 2008

  Prove the Borsuk-Ulam theorem in dimension 2: there is no map $f: S^{2} \rightarrow S^{1}$ such that $f(-x)=-f(x)$ for every $x \in S^{2}$. Deduce that $S^{2}$ is not homeomorphic to any subset of $\mathbb{R}^{2}$.

  comment

• 3.II.20F

  Algebraic Topology | Part II, 2008

  Let $X$ be the quotient space obtained by identifying one pair of antipodal points on $S^{2}$. Using the Mayer-Vietoris exact sequence, calculate the homology groups and the Betti numbers of $X$.

  comment

• 4.II.21F

  Algebraic Topology | Part II, 2008

  Let $X$ and $Y$ be topological spaces.

  (i) Show that a map $f: X \rightarrow Y$ is a homotopy equivalence if there exist maps $g, h: Y \rightarrow X$ such that $f g \simeq 1_{Y}$ and $h f \simeq 1_{X}$. More generally, show that a map $f: X \rightarrow Y$ is a homotopy equivalence if there exist maps $g, h: Y \rightarrow X$ such that $f g$ and $h f$ are homotopy equivalences.

  (ii) Suppose that $\tilde{X}$ and $\tilde{Y}$ are universal covering spaces of the path-connected, locally path-connected spaces $X$ and $Y$. Using path-lifting properties, show that if $X \simeq Y$ then $\tilde{X} \simeq \tilde{Y}$.

  comment

2007

• $3 . \mathrm{II} . 20 \mathrm{H}$

  Algebraic Topology | Part II, 2007

  Define what it means for a group $G$ to act on a topological space $X$. Prove that, if $G$ acts freely, in a sense that you should specify, then the quotient map $X \rightarrow X / G$ is a covering map and there is a surjective group homomorphism from the fundamental group of $X / G$ to $G$.

  comment

• 1.II.21H

  Algebraic Topology | Part II, 2007

  (i) Compute the fundamental group of the Klein bottle. Show that this group is not abelian, for example by defining a suitable homomorphism to the symmetric group $S_{3}$.

  (ii) Let $X$ be the closed orientable surface of genus 2 . How many (connected) double coverings does $X$ have? Show that the fundamental group of $X$ admits a homomorphism onto the free group on 2 generators.

  comment

• 2.II.21H

  Algebraic Topology | Part II, 2007

  State the Mayer-Vietoris sequence for a simplicial complex $X$ which is a union of two subcomplexes $A$ and $B$. Define the homomorphisms in the sequence (but do not check that they are well-defined). Prove exactness of the sequence at the term $H_{i}(A \cap B)$.

  comment

• 4.II $. 21 \mathrm{H}$

  Algebraic Topology | Part II, 2007

  Compute the homology of the space obtained from the torus $S^{1} \times S^{1}$ by identifying $S^{1} \times\{p\}$ to a point and $S^{1} \times\{q\}$ to a point, for two distinct points $p$ and $q$ in $S^{1} .$

  comment

2006

• 1.II.21H

  Algebraic Topology | Part II, 2006

  Compute the homology groups of the "pinched torus" obtained by identifying a meridian circle $S^{1} \times\{p\}$ on the torus $S^{1} \times S^{1}$ to a point, for some point $p \in S^{1}$.

  comment

• 2.II.21H

  Algebraic Topology | Part II, 2006

  State the simplicial approximation theorem. Compute the number of 0 -simplices (vertices) in the barycentric subdivision of an $n$-simplex and also compute the number of $n$-simplices. Finally, show that there are at most countably many homotopy classes of continuous maps from the 2-sphere to itself.

  comment

• 3.II.20H

  Algebraic Topology | Part II, 2006

  Let $X$ be the union of two circles identified at a point: the "figure eight". Classify all the connected double covering spaces of $X$. If we view these double coverings just as topological spaces, determine which of them are homeomorphic to each other and which are not.

  comment

• 4.II.21H

  Algebraic Topology | Part II, 2006

  Fix a point $p$ in the torus $S^{1} \times S^{1}$. Let $G$ be the group of homeomorphisms $f$ from the torus $S^{1} \times S^{1}$ to itself such that $f(p)=p$. Determine a non-trivial homomorphism $\phi$ from $G$ to the group $\operatorname{GL}(2, \mathbb{Z})$.

  [The group $\mathrm{GL}(2, \mathbb{Z})$ consists of $2 \times 2$ matrices with integer coefficients that have an inverse which also has integer coefficients.]

  Establish whether each $f$ in the kernel of $\phi$ is homotopic to the identity map.

  comment

2005

• 1.II.21H

  Algebraic Topology | Part II, 2005

  (i) Show that if $E \rightarrow T$ is a covering map for the torus $T=S^{1} \times S^{1}$, then $E$ is homeomorphic to one of the following: the plane $\mathbb{R}^{2}$, the cylinder $\mathbb{R} \times S^{1}$, or the torus $T$.

  (ii) Show that any continuous map from a sphere $S^{n}(n \geqslant 2)$ to the torus $T$ is homotopic to a constant map.

  [General theorems from the course may be used without proof, provided that they are clearly stated.]

  comment

• 2.II.21H

  Algebraic Topology | Part II, 2005

  State the Van Kampen Theorem. Use this theorem and the fact that $\pi_{1} S^{1}=\mathbb{Z}$ to compute the fundamental groups of the torus $T=S^{1} \times S^{1}$, the punctured torus $T \backslash\{p\}$, for some point $p \in T$, and the connected sum $T \# T$ of two copies of $T$.

  comment

• 3.II.20H

  Algebraic Topology | Part II, 2005

  Let $X$ be a space that is triangulable as a simplicial complex with no $n$-simplices. Show that any continuous map from $X$ to $S^{n}$ is homotopic to a constant map.

  [General theorems from the course may be used without proof, provided they are clearly stated.]

  comment

• 4.II.21H

  Algebraic Topology | Part II, 2005

  Let $X$ be a simplicial complex. Suppose $X=B \cup C$ for subcomplexes $B$ and $C$, and let $A=B \cap C$. Show that the inclusion of $A$ in $B$ induces an isomorphism $H_{*} A \rightarrow H_{*} B$ if and only if the inclusion of $C$ in $X$ induces an isomorphism $H_{*} C \rightarrow H_{*} X$.

  comment

2004

• B2.8

  Algebraic Topology | Part II, 2004

  Let $K$ and $L$ be finite simplicial complexes. Define the $n$-th chain group $C_{n}(K)$ and the boundary homomorphism $d_{n}: C_{n}(K) \rightarrow C_{n-1}(K)$. Prove that $d_{n-1} d_{n}=0$ and define the homology groups of $K$. Explain briefly how a simplicial map $f: K \rightarrow L$ induces a homomorphism $f_{\star}$ of homology groups.

  Suppose now that $K$ consists of the proper faces of a 3-dimensional simplex. Calculate from first principles the homology groups of $K$. If a simplicial map $f: K \rightarrow K$ gives a homeomorphism of the underlying polyhedron $|K|$, is the induced homology map $f_{\star}$ necessarily the identity?

  comment

• B3.7

  Algebraic Topology | Part II, 2004

  A finite simplicial complex $K$ is the union of subcomplexes $L$ and $M$. Describe the Mayer-Vietoris exact sequence that relates the homology groups of $K$ to those of $L$, $M$ and $L \cap M$. Define all the homomorphisms in the sequence, proving that they are well-defined (a proof of exactness is not required).

  A surface $X$ is constructed by identifying together (by means of a homeomorphism) the boundaries of two Möbius strips $Y$ and $Z$. Assuming relevant triangulations exist, determine the homology groups of $X$.

  comment

• B4.5

  Algebraic Topology | Part II, 2004

  Write down the definition of a covering space and a covering map. State and prove the path lifting property for covering spaces and state, without proof, the homotopy lifting property.

  Suppose that a group $G$ is a group of homeomorphisms of a space $X$. Prove that, under conditions to be stated, the quotient map $X \rightarrow X / G$ is a covering map and that $\pi_{1}(X / G)$ is isomorphic to $G$. Give two examples in which this last result can be used to determine the fundamental group of a space.

  comment

2003

• B2.8

  Algebraic Topology | Part II, 2003

  Define the fundamental group of a topological space and explain briefly why a continuous map gives rise to a homomorphism between fundamental groups.

  Let $X$ be a subspace of the Euclidean space $\mathbb{R}^{3}$ which contains all of the points $(x, y, 0)$ with $(x, y) \neq(0,0)$, and which does not contain any of the points $(0,0, z)$. Show that $X$ has an infinite fundamental group.

  comment

• B3.7

  Algebraic Topology | Part II, 2003

  Define a covering map. Prove that any covering map induces an injective homomorphisms of fundamental groups.

  Show that there is a non-trivial covering map of the real projective plane. Explain how to use this to find the fundamental group of the real projective plane.

  comment

• B4.5

  Algebraic Topology | Part II, 2003

  State the Mayer-Vietoris theorem. You should give the definition of all the homomorphisms involved.

  Compute the homology groups of the union of the 2 -sphere with the line segment from the North pole to the South pole.

  comment

2002

• B2.8

  Algebraic Topology | Part II, 2002

  Show that the fundamental group $G$ of the Klein bottle is infinite. Show that $G$ contains an abelian subgroup of finite index. Show that $G$ is not abelian.

  comment

• B3.7

  Algebraic Topology | Part II, 2002

  For a finite simplicial complex $X$, let $b_{i}(X)$ denote the rank of the finitely generated abelian group $H_{i} X$. Define the Euler characteristic $\chi(X)$ by the formula

  $$\chi(X)=\sum_{i}(-1)^{i} b_{i}(X) .$$

  Let $a_{i}$ denote the number of $i$-simplices in $X$, for each $i \geqslant 0$. Show that

  $$\chi(X)=\sum_{i}(-1)^{i} a_{i}$$

  comment

• B4.5

  Algebraic Topology | Part II, 2002

  State the Mayer-Vietoris theorem for a finite simplicial complex $X$ which is the union of closed subcomplexes $A$ and $B$. Define all the maps in the long exact sequence. Prove that the sequence is exact at the term $H_{i} X$, for every $i \geqslant 0$.

  comment

2001

• B2.8

  Algebraic Topology | Part II, 2001

  Show that the fundamental group of the 2-torus $S^{1} \times S^{1}$ is isomorphic to $\mathbf{Z} \times \mathbf{Z}$.

  Show that an injective continuous map from the circle $S^{1}$ to itself induces multiplication by $\pm 1$ on the fundamental group.

  Show that there is no retraction from the solid torus $S^{1} \times D^{2}$ to its boundary.

  comment

• B3.7

  Algebraic Topology | Part II, 2001

  Write down the Mayer-Vietoris sequence and describe all the maps involved.

  Use the Mayer-Vietoris sequence to compute the homology of the $n$-sphere $S^{n}$ for all $n$.

  comment

• B4.5

  Algebraic Topology | Part II, 2001

  Write an essay on the definition of simplicial homology groups. The essay should include a discussion of orientations, of the action of a simplicial map and a proof of $\partial^{2}=0$.

  comment