Stochastic Financial Models
Stochastic Financial Models
Jump to year
Paper 1, Section II, 30K
(a) What does it mean to say that a stochastic process is a martingale with respect to a filtration ?
(b) Let be a martingale, and let for . Suppose takes values in the set almost surely for all . Show that is a simple symmetric random walk, i.e. that the sequence is with
(c) Let be a martingale and let the bounded process be previsible.
Let and
Show that is a martingale.
(d) Let be a simple symmetric random walk with , and let
where is a positive integer. Let
Show that is a simple symmetric random walk.
(e) Let be a simple symmetric random walk with , and let . Compute for a positive integer .
Paper 2, Section II, 30K
Consider a one-period market model with risky assets and one risk-free asset. Let denote the vector of prices of the risky assets at time and let be the interest rate.
(a) What does it mean to say a portfolio is an arbitrage for this market?
(b) An investor wishes to maximise their expected utility of time-1 wealth attainable by investing in the market with their time- 0 wealth . The investor's utility function is increasing and concave. Show that, if there exists an optimal solution to the investor's expected utility maximisation problem, then the market has no arbitrage. [Assume that is integrable for any attainable time-1 wealth .]
(c) Now introduce a contingent claim with time-1 bounded payout . How does the investor in part (b) calculate an indifference bid price for the claim? Assuming each such claim has a unique indifference price, show that the map is concave. [Assume that any relevant utility maximisation problem that you consider has an optimal solution.]
(d) Consider a contingent claim with time-1 bounded payout . Let be the set of initial no-arbitrage prices for the claim; that is, the set consists of all such that the market augmented with the contingent claim with time- 0 price has no arbitrage. Show that . [Assume that any relevant utility maximisation problem that you consider has an optimal solution. You may use results from lectures without proof, such as the fundamental theorem of asset pricing or the existence of marginal utility prices, as long as they are clearly stated.]
Paper 3, Section II, 29K
(a) Let be a martingale and a supermartingale. If , show that for any bounded stopping time . [If you use a general result about supermartingales, you must prove it.]
(b) Consider a market with one stock with time- price and constant interest rate . Explain why a self-financing investor's wealth process satisfies
where is the number of shares of the stock held during the th period.
(c) Given an initial wealth , an investor seeks to maximize , where is a given utility function. Suppose the stock price is such that , where is a sequence of independent copies of a random variable . Let be defined inductively by
with terminal condition for all .
Show that the process is a supermartingale for any trading strategy . Suppose that the trading strategy with corresponding wealth process are such that the process is a martingale. Show that is optimal.
Paper 4, Section II, 29K
(a) What does it mean to say that a stochastic process is a Brownian motion? Show that, if is a continuous Gaussian process such that and for all , then is a Brownian motion.
For the rest of the question, let be a Brownian motion.
(b) Let and for . Show that is a Brownian motion. [You may use without proof the Brownian strong law of large numbers: almost surely as .]
(c) Fix constants and . Show that
for any bounded function of the form
for some fixed and fixed , where is the space of continuous functions on . [If you use a general theorem from the lectures, you should prove it.]
(d) Fix constants and . Show that
for any bounded function . [In this part you may use the Cameron-Martin theorem without proof.]
Paper 1, Section II, 30K
Consider a single-period asset price model in where, for ,
with a non-random vector in and
Assume that is invertible. An investor has initial wealth which is invested in the market at time 0 , to hold units of the riskless asset and units of risky asset , for .
(a) Show that in order to minimize the variance of the wealth held at time 1 , subject to the constraint
with given, the investor should choose a portfolio of the form
where is to be determined.
(b) Show that the same portfolio is optimal for a utility-maximizing investor with CARA utility function
for a unique choice of , also to be determined.
Paper 2, Section II, 29K
Let be a discrete-time asset price model in with numéraire.
(i) What is meant by an arbitrage for such a model?
(ii) What does it mean to say that the model is complete?
Consider now the case where and where
for some and some independent positive random variables with for all .
(iii) Find an equivalent probability measure such that the discounted asset price is a martingale.
(iv) Does this model have an arbitrage? Justify your answer.
(v) By considering the contingent claim or otherwise, show that this model is not complete.
Paper 3, Section II, 29K
(a) Let be a real-valued random process.
(i) What does it mean to say that is a Brownian motion?
(ii) State the reflection principle for Brownian motion.
(b) Suppose that is a Brownian motion and set and .
(i) Find the joint distribution function of and .
(ii) Show that has a joint density function on given by
(iii) You are given that two of the three processes and have the same distribution. Identify which two, justifying your answer.
Paper 4, Section II, K
(i) What does it mean to say that is a Black-Scholes model with interest rate , drift and volatility ?
(ii) Write down the Black-Scholes pricing formula for the time- 0 value of a time- contingent claim .
(iii) Show that if is a European call of strike and maturity then
(iv) For the European call, derive the Black-Scholes pricing formula
where is the standard normal distribution function and and are to be determined.
(v) Fix and consider a modified contract which gives the investor the right but not the obligation to buy one unit of the risky asset at price , either at time or time but not both, where the choice of exercise time is to be made by the investor at time . Determine whether the investor should exercise the contract at time .
Paper 1, Section II, 30K
(a) What does it mean to say that is a martingale? (b) Let be a Markov chain defined by and
and
for . Show that is a martingale with respect to the filtration where is trivial and for .
(c) Let be adapted with respect to a filtration with for all . Show that the following are equivalent:
(i) is a martingale.
(ii) For every stopping time , the stopped process defined by , , is a martingale.
(iii) for all and every stopping time .
[Hint: To show that (iii) implies (i) you might find it useful to consider the stopping time
for any
Paper 2, Section II,
(a) In the context of a multi-period model in discrete time, what does it mean to say that a probability measure is an equivalent martingale measure?
(b) State the fundamental theorem of asset pricing.
(c) Consider a single-period model with one risky asset having initial price . At time 1 its value is a random variable on of the form
where . Assume that there is a riskless numéraire with . Show that there is no arbitrage in this model.
[Hint: You may find it useful to consider a density of the form and find suitable and . You may use without proof that if is a normal random variable then .]
(d) Now consider a multi-period model with one risky asset having a non-random initial price and a price process of the form
where are i.i.d. -distributed random variables on . Assume that there is a constant riskless numéraire with for all . Show that there exists no arbitrage in this model.
Paper 3, Section II, K
In the Black-Scholes model the price at time 0 for a European option of the form with maturity is given by
(a) Find the price at time 0 of a European call option with maturity and strike price in terms of the standard normal distribution function. Derive the put-call parity to find the price of the corresponding European put option.
(b) The digital call option with maturity and strike price has payoff given by
What is the value of the option at any time ? Determine the number of units of the risky asset that are held in the hedging strategy at time .
(c) The digital put option with maturity and strike price has payoff
Find the put-call parity for digital options and deduce the Black-Scholes price at time 0 for a digital put.
Paper 4, Section II, K
(a) Describe the (Cox-Ross-Rubinstein) binomial model. What are the necessary and sufficient conditions on the model parameters for it to be arbitrage-free? How is the equivalent martingale measure characterised in this case?
(b) Consider a discounted claim of the form for some function . Show that the value process of is of the form
for , where the function is given by
You may use any property of conditional expectations without proof.
(c) Suppose that only depends on the terminal value of the stock price. Derive an explicit formula for the value of at time .
(d) Suppose that is of the form , where . Show that the value process of is of the form
for , where the function is given by
for a function to be determined.
Paper 1, Section II, K
(a) What does it mean to say that is a martingale?
(b) Let be independent random variables on with -a.s. and . Further, let
Show that is a martingale with respect to the filtration .
(c) Let be an adapted process with respect to a filtration such that for every . Show that admits a unique decomposition
where is a martingale and is a previsible process with , which can recursively be constructed from as follows,
(d) Let be a super-martingale. Show that the following are equivalent:
(i) is a martingale.
(ii) for all .
Paper 2, Section II, K
Consider the Black-Scholes model, i.e. a market model with one risky asset with price at time given by
where denotes a Brownian motion on the constant growth rate, the constant volatility and the initial price of the asset. Assume that the riskless rate of interest is .
(a) Consider a European option with expiry for any bounded, continuous function . Use the Cameron-Martin theorem to characterize the equivalent martingale measure and deduce the following formula for the price of at time 0 :
(b) Find the price at time 0 of a European option with maturity and payoff for some . What is the value of the option at any time Determine a hedging strategy (you only need to specify how many units of the risky asset are held at any time ).
Paper 3, Section II,
Consider a multi-period model with asset prices , modelled on a probability space and adapted to a filtration . Assume that is -trivial, i.e. for all , and assume that is a -a.s. strictly positive numéraire, i.e. -a.s. for all . Further, let denote the discounted price process defined by .
(a) What does it mean to say that a self-financing strategy is an arbitrage?
(b) State the fundamental theorem of asset pricing.
(c) Let be a probability measure on which is equivalent to and for which for all . Show that the following are equivalent:
(i) is a martingale measure.
(ii) If is self-financing and is bounded, i.e. for a suitable , then the value process of is a -martingale.
(iii) If is self-financing and is bounded, then the value process of satisfies
[Hint: To show that (iii) implies (i) you might find it useful to consider self-financing strategies with of the form
for any and any .]
(d) Prove that if there exists a martingale measure satisfying the conditions in (c) then there is no arbitrage.
Paper 4, Section II, K
Consider a utility function , which is assumed to be concave, strictly increasing and twice differentiable. Further, satisfies
for some positive constants and . Let be an -distributed random variable and set .
(a) Show that
(b) Show that and . Discuss this result in the context of meanvariance analysis.
(c) Show that is concave in and , i.e. check that the matrix of second derivatives is negative semi-definite. [You may use without proof the fact that if a matrix has nonpositive diagonal entries and a non-negative determinant, then it is negative semi-definite.]
Paper 1, Section II, J
(a) What does it mean to say that is a martingale?
(b) Let be independent random variables on with and . Further, let
where
Show that is a martingale with respect to the natural filtration .
(c) State and prove the optional stopping theorem for a bounded stopping time .
Paper 2, Section II,
(a) What is a Brownian motion?
(b) Let be a Brownian motion. Show that the process , , is also a Brownian motion.
(c) Let . Show that for all (i.e. and have the same laws). Conclude that a.s.
(d) Show that .
Paper 3, Section II, J
(a) State the fundamental theorem of asset pricing for a multi-period model.
Consider a market model in which there is no arbitrage, the prices for all European put and call options are already known and there is a riskless asset with for some . The holder of a so-called 'chooser option' has the right to choose at a preassigned time between a European call and a European put option on the same asset , both with the same strike price and the same maturity . [We assume that at time the holder will take the option having the higher price at that time.]
(b) Show that the payoff function of the chooser option is given by
(c) Show that the price of the chooser option is given by
where and denote the price of a European call and put option, respectively, with strike and maturity .
Paper 4, Section II, J
(a) Describe the (Cox-Ross-Rubinstein) binomial model. When is the model arbitragefree? How is the equivalent martingale measure characterised in this case?
(b) What is the price and the hedging strategy for any given contingent claim in the binomial model?
(c) For any fixed and , the payoff function of a forward-start-option is given by
Find a formula for the price of the forward-start-option in the binomial model.
Paper 1, Section II, 28K
(a) What is a Brownian motion?
(b) State the Brownian reflection principle. State the Cameron-Martin theorem for Brownian motion with constant drift.
(c) Let be a Brownian motion. Show that
where is the standard normal distribution function.
(d) Find
Paper 2, Section II, K
In the context of the Black-Scholes model, let be the initial price of the stock, and let be its volatility. Assume that the risk-free interest rate is zero and the stock pays no dividends. Let denote the initial price of a European call option with strike and maturity date .
(a) Show that the Black-Scholes formula can be written in the form
where and depend on and , and is the standard normal distribution function.
(b) Let be the initial price of a put option with strike and maturity . Show that
(c) Show that
(d) Consider a European contingent claim with maturity and payout
Assuming , show that its initial price can be written as for a volatility parameter which you should express in terms of and .
Paper 3, Section II, K
Consider the following two-period market model. There is a risk-free asset which pays interest at rate . There is also a risky stock with prices given by
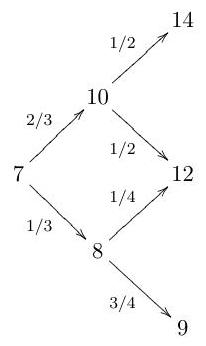
The above diagram should be read as
and so forth.
(a) Find the risk-neutral probabilities.
(b) Consider a European put option with strike expiring at time . What is the initial no-arbitrage price of the option? How many shares should be held in each period to replicate the payout?
(c) Now consider an American put option with the same strike and expiration date. Find the optimal exercise policy, assuming immediate exercise is not allowed. Would your answer change if you were allowed to exercise the option at time 0 ?
Paper 4, Section II, K
Let be concave and strictly increasing, and let be a vector space of random variables. For every random variable let
and suppose there exists a random variable such that
For a random variable , let be such that .
(a) Show that for every constant we have , and that if , then . Hence show that if for constants , then
(b) Show that is concave, and hence show is decreasing for .
(c) Assuming is continuously differentiable, show that converges as , and that there exists a random variable such that
Paper 1, Section II,
(i) What does it mean to say that is a martingale?
(ii) If is an integrable random variable and , prove that is a martingale. [Standard facts about conditional expectation may be used without proof provided they are clearly stated.] When is it the case that the limit exists almost surely?
(iii) An urn contains initially one red ball and one blue ball. A ball is drawn at random and then returned to the urn with a new ball of the other colour. This process is repeated, adding one ball at each stage to the urn. If the number of red balls after draws and replacements is , and the number of blue balls is , show that is a martingale, where
Does this martingale converge almost surely?
Paper 2, Section II,
(i) What is Brownian motion?
(ii) Suppose that is Brownian motion, and the price at time of a risky asset is given by
where is the constant growth rate, and is the constant volatility of the asset. Assuming that the riskless rate of interest is , derive an expression for the price at time 0 of a European call option with strike and expiry , explaining briefly the basis for your calculation.
(iii) With the same notation, derive the time-0 price of a European option with expiry which at expiry pays
Paper 3, Section II,
A single-period market consists of assets whose prices at time are denoted by , and a riskless bank account bearing interest rate . The value of is given, and . An investor with utility wishes to choose a portfolio of the available assets so as to maximize the expected utility of her wealth at time 1. Find her optimal investment.
What is the market portfolio for this problem? What is the beta of asset ? Derive the Capital Asset Pricing Model, that
Excess return of asset Excess return of market portfolio .
The Sharpe ratio of a portfolio is defined to be the excess return of the portfolio divided by the standard deviation of the portfolio . If is the correlation of the return on asset with the return on the market portfolio, prove that
Sharpe ratio of asset Sharpe ratio of market portfolio .
Paper 4, Section II,
(i) An investor in a single-period market with time- 0 wealth may generate any time-1 wealth of the form , where is any element of a vector space of random variables. The investor's objective is to maximize , where is strictly increasing, concave and . Define the utility indifference price of a random variable .
Prove that the map is concave. [You may assume that any supremum is attained.]
(ii) Agent has utility . The agents may buy for time- 0 price a risky asset which will be worth at time 1 , where is random and has density
Assuming zero interest, prove that agent will optimally choose to buy
units of the risky asset at time 0 .
If the asset is in unit net supply, if , and if , prove that the market for the risky asset will clear at price
What happens if
Paper 1, Section II, K
Suppose that denotes the vector of prices of assets at times , and that denotes the vector of the numbers of the different assets held by an investor from time to time . Assuming that asset 0 is a bank account paying zero interest, that is, for all , explain what is meant by the statement that the portfolio process is self-financing. If the portfolio process is self-financing, prove that for any
where , and .
Suppose now that the are independent with common distribution. Let
where and the infimum is taken over all self-financing portfolio processes with . Explain why should satisfy the equation
If is a positive-definite symmetric matrix satisfying the equation
show that has a solution of the form .
Paper 2, Section II, K
An agent has expected-utility preferences over his possible wealth at time 1 ; that is, the wealth is preferred to wealth if and only if , where the function is strictly concave and twice continuously differentiable. The agent can trade in a market, with the time-1 value of his portfolio lying in an affine space of random variables. Assuming cash can be held between time 0 and time 1 , define the agent's time-0 utility indifference price for a contingent claim with time-1 value . Assuming any regularity conditions you may require, prove that the map is concave.
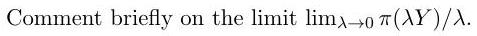
Consider a market with two claims with time-1 values and . Their joint distribution is
At time 0 , arbitrary quantities of the claim can be bought at price , but is not marketed. Derive an explicit expression for in the case where
where is a given constant.
Paper 3, Section II,
Derive the Black-Scholes formula for the time- 0 price of a European call option with expiry and strike written on an asset with volatility and time-0 price , and where is the riskless rate of interest. Explain what is meant by the delta hedge for this option, and determine it explicitly.
In terms of the Black-Scholes call option price formula , find the time- 0 price of a forward-starting option, which pays at time , where and are given. Find the price of an option which pays at time . How would this option be hedged?
Paper 4, Section II, K
Write down the Black-Scholes partial differential equation (PDE), and explain briefly its relevance to option pricing.
Show how a change of variables reduces the Black-Scholes PDE to the heat equation:
where is a given boundary function.
Consider the following numerical scheme for solving the heat equation on the equally spaced grid where and and , and . We approximate by where
and is a constant and the operator is the matrix with non-zero entries and . By considering what happens when , show that the finite-difference scheme is stable if and only if
where . For what values of is the scheme unconditionally stable?
Paper 1, Section II, 29J
(i) Suppose that the price of an asset at time is given by
where is a Brownian motion, and are positive constants, and is the riskless rate of interest, assumed constant. In this model, explain briefly why the time-0 price of a derivative which delivers a bounded random variable at time should be given by . What feature of this model ensures that the price is unique?
Derive an expression for the time- 0 price of a European call option with strike and expiry . Explain the italicized terms.
(ii) Suppose now that the price of an asset at time is given by
where the and are positive constants, and the other notation is as in part (i) above. Show that the time-0 price of a European call option with strike and expiry written on this asset can be expressed as
where the are constants. Explain how the are characterized.
Paper 2, Section II, J
What does it mean to say that is a supermartingale?
State and prove Doob's Upcrossing Inequality for a supermartingale.
Let be a martingale indexed by negative time, that is, for each , and . Using Doob's Upcrossing Inequality, prove that the limit exists almost surely.
Paper 3, Section II, J
Suppose that is a sequence of independent and identically distributed random variables such that for all . Each day, an agent receives an income, the income on day being . After receiving this income, his wealth is . From this wealth, he chooses to consume , and invests the remainder in a bank account which pays a daily interest rate of . Write down the equation for the evolution of .
Suppose we are given constants , and define the functions
where . The agent's objective is to attain
where the supremum is taken over all adapted sequences . If the value function is defined for by
with , explain briefly why you expect the to satisfy
Show that the solution to has the form
for constants to be identified. What is the form of the consumption choices that achieve the supremum in ?
Paper 4, Section II, J
Let denote the time- prices of risky assets in which an agent may invest, . He may also invest his money in a bank account, which will return interest at rate . At time 0 , he knows and , and he knows that . If he chooses at time 0 to invest cash value in risky asset , express his wealth at time 1 in terms of his initial wealth , the choices , the value of , and .
Suppose that his goal is to minimize the variance of subject to the requirement that the mean should be at least , where is given. What portfolio should he choose to achieve this?
Suppose instead that his goal is to minimize subject to the same constraint. Show that his optimal portfolio is unchanged.
Paper 1, Section II, J
Consider a multi-period binomial model with a risky asset and a riskless asset . In each period, the value of the risky asset is multiplied by if the period was good, and by otherwise. The riskless asset is worth at time , where .
(i) Assuming that and that
show how any contingent claim to be paid at time 1 can be priced and exactly replicated. Briefly explain the significance of the condition (1), and indicate how the analysis of the single-period model extends to many periods.
(ii) Now suppose that . We assume that , and that the risky asset is worth at time zero. Find the time- 0 value of an American put option with strike price and expiry at time , and find the optimal exercise policy. (Assume that the option cannot be exercised immediately at time zero.)
Paper 2, Section II, J
(i) Give the definition of Brownian motion.
(ii) The price of an asset evolving in continuous time is represented as
where is a standard Brownian motion and and are constants. If riskless investment in a bank account returns a continuously compounded rate of interest , derive the Black-Scholes formula for the time-0 price of a European call option on asset with strike price and expiry . [Standard results from the course may be used without proof but must be stated clearly.]
(iii) In the same financial market, a certain contingent claim pays at time , where . Find the closed-form expression for the time- 0 value of this contingent claim.
Show that for every and ,
Using this identity, how would you replicate (at least approximately) the contingent claim with a portfolio consisting only of European calls?
Paper 3, Section II, J
(i) Let be a filtration. Give the definition of a martingale and a stopping time with respect to the filtration .
(ii) State Doob's optional stopping theorem. Give an example of a martingale and a stopping time such that .
(iii) Let be a standard random walk on , that is, , where are i.i.d. and or with probability .
Let where is a positive integer. Show that for all ,
Carefully justify all steps in your derivation.
[Hint. For all find such that is a martingale. You may assume that is almost surely finite.]
Let . By introducing a suitable martingale, compute .
Paper 4, Section II, J
In a one-period market, there are risky assets whose returns at time 1 are given by a column vector . The return vector has a multivariate Gaussian distribution with expectation and non-singular covariance matrix . In addition, there is a bank account giving interest , so that one unit of cash invested at time 0 in the bank account will be worth units of cash at time 1 .
An agent with the initial wealth invests in risky assets and keeps the remainder in the bank account. The return on the agent's portfolio is
The agent's utility function is , where is a parameter. His objective is to maximize .
(i) Find the agent's optimal portfolio and its expected return.
[Hint. Relate to and
(ii) Under which conditions does the optimal portfolio that you found in (i) require borrowing from the bank account?
(iii) Find the optimal portfolio if it is required that all of the agent's wealth be invested in risky assets.
Paper 1, Section II, J
In a one-period market, there are assets whose prices at time are given by . The prices of the assets at time 1 have a distribution, with non-singular covariance , and the prices at time 0 are known constants. In addition, there is a bank account giving interest , so that one unit of cash invested at time 0 will be worth units of cash at time 1 .
An agent with initial wealth chooses a portfolio of the assets to hold, leaving him with in the bank account. His objective is to maximize his expected utility
Find his optimal portfolio in each of the following three situations:
(i) is unrestricted;
(ii) no investment in the bank account is allowed: ;
(iii) the initial holdings of cash must be non-negative.
For the third problem, show that the optimal initial holdings of cash will be zero if and only if
Paper 2, Section II, J
Consider a symmetric simple random walk taking values in statespace , where an integer . Writing , the transition probabilities are given by
where .
What does it mean to say that is a martingale? Find a condition on and such that
is a martingale. If for some real , show that is a martingale if
Suppose that the random walk starts at position at time 0 , and suppose that
Stating fully any results to which you appeal, prove that
where is as given at . Deduce that as
and comment briefly on this result.
Paper 3, Section II, J
First, what is a Brownian motion?
(i) The price of an asset evolving in continuous time is represented as
where is a standard Brownian motion, and and are constants. If riskless investment in a bank account returns a continuously-compounded rate of interest , derive a formula for the time-0 price of a European call option on the asset with strike and expiry . You may use any general results, but should state them clearly.
(ii) In the same financial market, consider now a derivative which pays
at time . Find the time-0 price for this derivative. Show that it is less than the price of the European call option which you derived in (i).
Paper 4, Section II, J
In a two-period model, two agents enter a negotiation at time 0 . Agent knows that he will receive a random payment at time , where the joint distribution of is known to both agents, and . At the outcome of the negotiation, there will be an agreed risk transfer random variable which agent 1 will pay to agent 2 at time 1 . The objective of agent 1 is to maximize , and the objective of agent 2 is to maximize , where the functions are strictly increasing, strictly concave, , and have the properties that
Show that, unless there exists some such that
the risk transfer could be altered to the benefit of both agents, and so would not be the conclusion of the negotiation.
Show that, for given , the relation determines a unique risk transfer , and that is a function of .
Paper 1, Section II, I
What is a Brownian motion? State the reflection principle for Brownian motion.
Let be a Brownian motion. Let . Prove
for all . Hence, show that the random variables and have the same distribution.
Find the density function of the random variable .
Paper 2, Section II, I
What is a martingale? What is a supermartingale? What is a stopping time?
Let be a martingale and a supermartingale with respect to a common filtration. If , show that for any bounded stopping time .
[If you use a general result about supermartingales, you must prove it.]
Consider a market with one stock with prices and constant interest rate . Explain why an investor's wealth satisfies
where is the number of shares of the stock held during the th period.
Given an initial wealth , an investor seeks to maximize where is a given utility function. Suppose the stock price is such that where is a sequence of independent and identically distributed random variables. Let be defined inductively by
with terminal condition for all .
Show that the process is a supermartingale for any trading strategy .
Suppose is a trading strategy such that the corresponding wealth process makes a martingale. Show that is optimal.
Paper 3, Section II, I
Consider a market with two assets, a riskless bond and a risky stock, both of whose initial (time-0) prices are . At time 1 , the price of the bond is a constant and the price of the stock is uniformly distributed on the interval where is a constant.
Describe the set of state price densities.
Consider a contingent claim whose payout at time 1 is given by . Use the fundamental theorem of asset pricing to show that, if there is no arbitrage, the initial price of the claim is larger than and smaller than .
Now consider an investor with initial wealth , and assume . The investor's goal is to maximize his expected utility of time-1 wealth , where . Show that the optimal number of shares of stock to hold is .
What would be the investor's marginal utility price of the contingent claim described above?
Paper 4, Section II, I
Consider a market with no riskless asset and risky stocks where the price of stock at time is denoted . We assume the vector is not random, and we let and . Assume is not singular.
Suppose an investor has initial wealth , which he invests in the stocks so that his wealth at time 1 is for some . He seeks to minimize the subject to his budget constraint and the condition that for a given constant .
Illustrate this investor's problem by drawing a diagram of the mean-variance efficient frontier. Write down the Lagrangian for the problem. Show that there are two vectors and (which do not depend on the constants and ) such that the investor's optimal portfolio is a linear combination of and .
Another investor with initial wealth seeks to maximize his expected utility of time 1 wealth, subject to his budget constraint. Assuming that is Gaussian and for a constant , show that the optimal portfolio in this case is also a linear combination of and .
[You may use the moment generating function of the Gaussian distribution without derivation.]
Continue to assume is Gaussian, but now assume that is increasing, concave, and twice differentiable, and that and are of exponential growth but not necessarily of the form . (Recall that a function is of exponential growth if for some constants positive constants .) Prove that the utility maximizing investor still holds a linear combination of and .
[You may use the Gaussian integration by parts formula
where is a vector of independent standard normal random variables, and is differentiable and of exponential growth. You may also interchange integration and differentiation without justification.]
Paper 1, Section II, J
An investor must decide how to invest his initial wealth in assets for the coming year. At the end of the year, one unit of asset will be worth , where has a multivariate normal distribution with mean and non-singular covariance matrix . At the beginning of the year, one unit of asset costs . In addition, he may invest in a riskless bank account; an initial investment of 1 in the bank account will have grown to at the end of the year.
(a) The investor chooses to hold units of asset , with the remaining in the bank account. His objective is to minimise the variance of his wealth at the end of the year, subject to a required mean value for . Derive the optimal portfolio , and the minimised variance.
(b) Describe the set of achievable pairs of mean and variance of the terminal wealth. Explain what is meant by the mean-variance efficient frontier as you do so.
(c) Suppose that the investor requires expected mean wealth at time 1 to be . He wishes to minimise the expected shortfall subject to this requirement. Show that he will choose a portfolio corresponding to a point on the mean-variance efficient frontier.
Paper 2, Section II, J
What is a martingale? What is a stopping time? State and prove the optional sampling theorem.
Suppose that are independent random variables with values in and common distribution . Assume that . Let be the random walk such that for . For , determine the set of values of for which the process is a martingale. Hence derive the probability generating function of the random time
where is a positive integer. Hence find the mean of .
Let . Clearly the mean of is greater than the mean of ; identify the point in your derivation of the mean of where the argument fails if is replaced by .
Paper 3, Section II, J
What is a Brownian motion? State the assumptions of the Black-Scholes model of an asset price, and derive the time- 0 price of a European call option struck at , and expiring at .
Find the time- 0 price of a European call option expiring at , but struck at , where , and is the price of the underlying asset at time .
Paper 4, Section II, J
An agent with utility , where is a constant, may select at time 0 a portfolio of assets, which he then holds to time 1 . The values of the assets at time 1 have a multivariate normal distribution with mean and nonsingular covariance matrix . Prove that the agent will prefer portfolio to portfolio if and only if , where
Determine his optimal portfolio.
The agent initially holds portfolio , which he may change to portfolio at cost , where is some positive transaction cost. By considering the function for , or otherwise, prove that the agent will have no reason to change his initial portfolio if and only if, for every ,
1.II.28J
(a) In the context of the Black-Scholes formula, let be the time- 0 spot price, be the strike price, be the time to maturity, and let be the volatility. Assume that the interest rate is constant and assume absence of dividends. Write for the time- 0 price of a standard European call. The Black-Scholes formula can be written in the following form
State how the quantities and depend on and .
Assume that you sell this option at time 0 . What is your replicating portfolio at time 0 ?
[No proofs are required.]
(b) Compute the limit of as . Construct an explicit arbitrage under the assumption that European calls are traded above this limiting price.
(c) Compute the limit of as . Construct an explicit arbitrage under the assumption that European calls are traded below this limiting price.
(d) Express in terms of and the derivative
[Hint: you may find it useful to express in terms of .]
[You may use without proof the formula .]
(e) Say what is meant by implied volatility and explain why the previous results make it well-defined.
2.II.28J
(a) Let be a Brownian motion and consider the process
for deterministic. For which values of is a supermartingale? For which values of is a martingale? For which values of is a martingale? Justify your answers.
(b) Assume that the riskless rates of return for Dollar investors and Euro investors are and respectively. Thus, 1 Dollar at time 0 in the bank account of a Dollar investor will grow to Dollars at time . For a Euro investor, the Dollar is a risky, tradable asset. Let be his equivalent martingale measure and assume that the EUR/USD exchange rate at time , that is, the number of Euros that one Dollar will buy at time , is given by
where is a Brownian motion under . Determine as function of and . Verify that is a martingale if .
(c) Let be as in part (b). Let now be an equivalent martingale measure for a Dollar investor and assume that the EUR/USD exchange rate at time is given by
where now is a Brownian motion under . Determine as function of and . Given , check, under , that is is not a martingale but that is a martingale.
(d) Assuming still that , rederive the final conclusion of part (c), namely the martingale property of , directly from part (b).
3.II.27J
Consider a vector of asset prices evolving over time . The asset price is assumed constant over time. In this context, explain what is an arbitrage and prove that the existence of an equivalent martingale measure implies noarbitrage.
Suppose that over two periods a stock price moves on a binomial tree
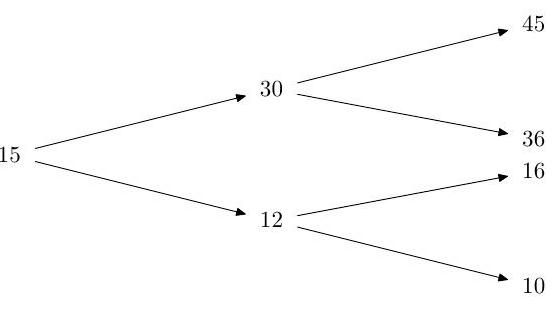
Assume riskless rate . Determine the equivalent martingale measure. [No proof is required.]
Sell an American put with strike 15 and expiry 2 at its no-arbitrage price, which you should determine.
Verify that the buyer of the option should use his early exercise right if the first period is bad.
Assume that the first period is bad, and that the buyer forgets to exercise. How much risk-free profit can you lock in?
4.II.28J
(a) Consider a family of independent, identically distributed, positive random variables and fix . Define inductively
Compute, for , the conditional expectation .
(b) Fix . In the setting of part (a), compute also , where
(c) Let be as in part (b). An investor with wealth at time 0 wishes to invest it in such a way as to maximise where is the wealth at the start of day . Let be fixed. On day , he chooses the proportion of his wealth to invest in a single risky asset, so that his wealth at the start of day will be
Here, is as in part (a) and is the per-period riskless rate of interest. If denotes the value function of this optimization problem, show that and give a formula for . Verify that, in the case , your answer is in agreement with part (b).
1.II.28J
(i) What does it mean to say that a process is a martingale? What does the martingale convergence theorem tell us when applied to positive martingales?
(ii) What does it mean to say that a process is a Brownian motion? Show that with probability one.
(iii) Suppose that is a Brownian motion. Find such that
is a martingale. Discuss the limiting behaviour of and for this as .
2.II.28J
In the context of a single-period financial market with traded assets, what is an arbitrage? What is an equivalent martingale measure?
Fix and consider the following single-period market with 3 assets:
Asset 1 is a riskless bond and pays no interest.
Asset 2 is a stock with initial price per share; its possible final prices are with probability and with probability .
Asset 3 is another stock that behaves like an independent copy of asset 2 .
Find all equivalent martingale measures for the problem and characterise all contingent claims that can be replicated.
Consider a contingent claim that pays 1 if both risky assets move in the same direction and zero otherwise. Show that the lower arbitrage bound, simply obtained by calculating all possible prices as the pricing measure ranges over all equivalent martingale measures, is zero. Why might someone pay for such a contract?
3.II.27J
Suppose that over two periods a stock price moves on a binomial tree

(i) Determine for what values of the riskless rate there is no arbitrage. From here on, fix and determine the equivalent martingale measure.
(ii) Find the time-zero price and replicating portfolio for a European put option with strike 15 and expiry
(iii) Find the time-zero price and optimal exercise policy for an American put option with the same strike and expiry.
(iv) Deduce the corresponding (European and American) call option prices for the same strike and expiry.
4.II.28J
Briefly describe the Black-Scholes model. Consider a "cash-or-nothing" option with strike price , i.e. an option whose payoff at maturity is
It can be interpreted as a bet that the stock will be worth at least at time . Find a formula for its value at time , in terms of the spot price . Find a formula for its Delta (i.e. its hedge ratio). How does the Delta behave as ? Why is it difficult, in practice, to hedge such an instrument?
1.II.28I
Over two periods a stock price moves on a binomial tree.
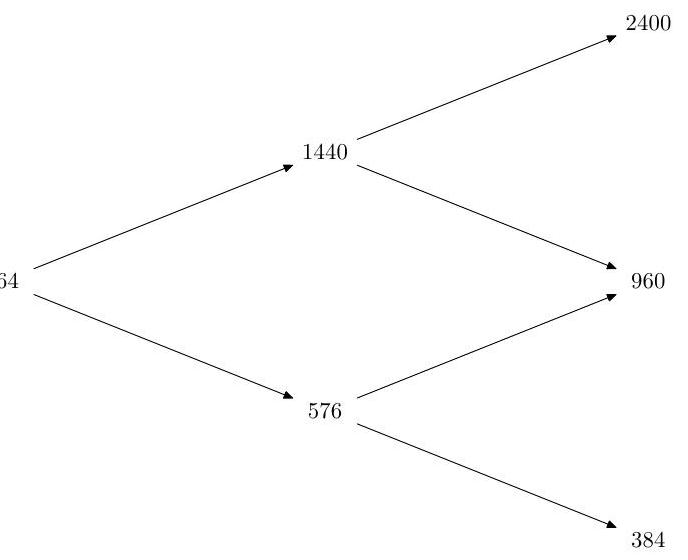
Assuming that the riskless rate is constant at , verify that all risk-neutral up-probabilities are given by one value . Find the time- 0 value of the following three put options all struck at , with expiry 2 :
(a) a European put;
(b) an American put;
(c) a European put modified by raising the strike to at time 1 if the stock went down in the first period.
2.II.28I
(a) In the context of a single-period financial market with traded assets and a single riskless asset earning interest at rate , what is an arbitrage? What is an equivalent martingale measure? Explain marginal utility pricing, and how it leads to an equivalent martingale measure.
(b) Consider the following single-period market with two assets. The first is a riskless bond, worth 1 at time 0 , and 1 at time 1 . The second is a share, worth 1 at time 0 and worth at time 1 , where is uniformly distributed on the interval , where . Under what condition on is this model arbitrage free? When it is, characterise the set of equivalent martingale measures.
An agent with utility and with wealth at time 0 aims to pick the number of shares to hold so as to maximise his expected utility of wealth at time 1 . Show that he will choose to be positive if and only if .
An option pays at time 1 . Assuming that , deduce that the agent's price for this option will be , and show that the range of possible prices for this option as the pricing measure varies in is the interval .
3.II.27I
Let denote the riskless rate and let be a fixed volatility parameter.
(a) Let be a Black-Scholes asset with zero dividends:
where is standard Brownian motion. Derive the Black-Scholes partial differential equation for the price of a European option on with bounded payoff at expiry :
[You may use the fact that for functions satisfying exponential growth conditions, and standard Brownian motion , the process
is a martingale.]
(b) Indicate the changes in your argument when the asset pays dividends continuously at rate . Find the corresponding Black-Scholes partial differential equation.
(c) Assume . Find a closed form solution for the time-0 price of a European power option with payoff .
4.II.28I
State the definitions of a martingale and a stopping time.
State and prove the optional sampling theorem.
If is a martingale, under what conditions is it true that converges with probability 1 as ? Show by an example that some condition is necessary.
A market consists of agents, each of whom is either optimistic or pessimistic. At each time , one of the agents is selected at random, and chooses to talk to one of the other agents (again selected at random), whose type he then adopts. If choices in different periods are independent, show that the proportion of pessimists is a martingale. What can you say about the limiting behaviour of the proportion of pessimists as time tends to infinity?
1.II.28J
Let be a zero-mean Gaussian vector, with covariance matrix . In a simple single-period economy with agents, agent will receive at time . If is a contingent claim to be paid at time 1 , define agent 's reservation bid price for , assuming his preferences are given by for any contingent claim .
Assuming that for each , where , show that agent 's reservation bid price for units of is
As , find the limit of agent 's per-unit reservation bid price for , and comment on the expression you obtain.
The agents bargain, and reach an equilibrium. Assuming that the contingent claim is in zero net supply, show that the equilibrium price of will be
where and . Show that at that price agent will choose to buy
units of .
By computing the improvement in agent 's expected utility, show that the value to agent of access to this market is equal to a fixed payment of
2.II.28J
(i) At the beginning of year , an investor makes decisions about his investment and consumption for the coming year. He first takes out an amount from his current wealth , and sets this aside for consumption. He splits his remaining wealth between a bank account (unit wealth invested at the start of the year will have grown to a sure amount by the end of the year), and the stock market. Unit wealth invested in the stock market will have become the random amount by the end of the year.
The investor's objective is to invest and consume so as to maximise the expected value of , where is strictly increasing and strictly convex. Consider the dynamic programming equation (Bellman equation) for his problem,
Explain all undefined notation, and explain briefly why the equation holds.
(ii) Supposing that the are independent and identically distributed, and that , where is different from 1 , find as explicitly as you can the form of the agent's optimal policy.
(iii) Return to the general problem of (i). Assuming that the sample space is finite, and that all suprema are attained, show that
where denotes the optimal consumption and wealth process for the problem. Explain the significance of each of these equalities.
3.II.27J
Suppose that over two periods a stock price moves on a binomial tree:

(a) Find an arbitrage opportunity when the riskless rate equals . Give precise details of when and how much you buy, borrow and sell.
(b) From here on, assume instead that the riskless rate equals . Determine the equivalent martingale measure. [No proof is required.]
(c) Determine the time-zero price of an American put with strike 15 and expiry 2 . Assume you sell it at this price. Which hedge do you put on at time zero? Consider the scenario of two bad periods. How does your hedge work?
(d) The buyer of the American put turns out to be an unsophisticated investor who fails to use his early exercise right when he should. Assume the first period was bad. How much profit can you make out of this? You should detail your exact strategy.
4.II.28J
(a) In the context of the Black-Scholes formula, let be spot price, be strike price, be time to maturity, and assume constant interest rate , volatility and absence of dividends. Write down explicitly the prices of a European call and put,
Use for the normal distribution function. [No proof is required.]
(b) From here on assume . Keeping fixed, we shorten the notation to and similarly for . Show that put-call symmetry holds:
Check homogeneity: for every real
(c) Show that the price of a down-and-out European call with strike and barrier is given by
(d)
(i) Specialize the last expression to and simplify.
(ii) Answer a popular interview question in investment banks: What is the fair value of a down-and-out call given that ? Identify the corresponding hedge. [It may be helpful to compute Delta first.]
(iii) Does this hedge work beyond the Black-Scholes model? When does it fail?
A1.11 B1.16
(i) What does it mean to say that is a utility function? What is a utility function with constant absolute risk aversion (CARA)?
Let denote the prices at time of risky assets, and suppose that there is also a riskless zeroth asset, whose price at time 0 is 1 , and whose price at time 1 is . Suppose that has a multivariate Gaussian distribution, with mean and non-singular covariance . An agent chooses at time 0 a portfolio of holdings of the risky assets, at total cost , and at time 1 realises his gain . Given that he wishes the mean of to be equal to , find the smallest value that the variance of can be. What is the portfolio that achieves this smallest variance? Hence sketch the region in the plane of pairs that can be achieved by some choice of , and indicate the mean-variance efficient frontier.
(ii) Suppose that the agent has a CARA utility with coefficient of absolute risk aversion. What portfolio will he choose in order to maximise ? What then is the mean of ?
Regulation requires that the agent's choice of portfolio has to satisfy the valueat-risk (VaR) constraint
where and are determined by the regulatory authority. Show that this constraint has no effect on the agent's decision if . If , will this constraint necessarily affect the agent's choice of portfolio?
A3.11 B3.16
(i) Consider a single-period binomial model of a riskless asset (asset 0 ), worth 1 at time 0 and at time 1 , and a risky asset (asset 1 ), worth 1 at time 0 and worth at time 1 if the period was good, otherwise worth . Assuming that
show how any contingent claim to be paid at time 1 can be priced and exactly replicated. Briefly explain the significance of the condition , and indicate how the analysis of the single-period model extends to many periods.
(ii) Now suppose that , and that the risky asset is worth at time zero. Show that the time- 0 value of an American put option with strike and expiry at time is equal to 79 , and find the optimal exercise policy.
A4.12 B4.16
What is Brownian motion ? Briefly explain how Brownian motion can be considered as a limit of simple random walks. State the Reflection Principle for Brownian motion, and use it to derive the distribution of the first passage time to some level .
Suppose that , where is constant. Stating clearly any results to which you appeal, derive the distribution of the first-passage time to .
Now let , where . Find the density of .
A1.11 B1.16
(i) In the context of a single-period financial market with traded assets, what is an arbitrage? What is an equivalent martingale measure?
A simple single-period financial market contains two assets, (a bond), and (a share). The period can be good, bad, or indifferent, with probabilities each. At the beginning of the period, time 0 , both assets are worth 1 , i.e.
and at the end of the period, time 1 , the share is worth
where . The bond is always worth 1 at the end of the period. Show that there is no arbitrage in this market if and only if .
(ii) An agent with strictly increasing strictly concave utility has wealth at time 0 , and wishes to invest his wealth in shares and bonds so as to maximise his expected utility of wealth at time 1 . Explain how the solution to his optimisation problem generates an equivalent martingale measure.
Assume now that , and . Characterise all equivalent martingale measures for this problem. Characterise all equivalent martingale measures which arise as solutions of an agent's optimisation problem.
Calculate the largest and smallest possible prices for a European call option with strike 1 and expiry 1, as the pricing measure ranges over all equivalent martingale measures. Calculate the corresponding bounds when the pricing measure is restricted to the set arising from expected-utility-maximising agents' optimisation problems.
A3.11 B3.16
(i) What does it mean to say that the process is a Brownian motion? What does it mean to say that the process is a martingale?
Suppose that is a Brownian motion and the process is given in terms of as
for constants . For what values of is the process
a martingale? (Here, is a positive constant.)
(ii) In a standard Black-Scholes model, the price at time of a share is represented as . You hold a perpetual American put option on this share, with strike ; you may exercise at any stopping time , and upon exercise you receive . Let . Suppose you plan to use the exercise policy: 'Exercise as soon as the price falls to or lower.' Calculate what the option would be worth if you were to follow this policy. (Assume that the riskless rate of interest is constant and equal to .) For what choice of is this value maximised?
A4.12 B4.16
A single-period market contains risky assets, , initially worth , and at time 1 worth random amounts whose first two moments are given by
An agent with given initial wealth is considering how to invest in the available assets, and has asked for your advice. Develop the theory of the mean-variance efficient frontier far enough to exhibit explicitly the minimum-variance portfolio achieving a required mean return, assuming that is non-singular. How does your analysis change if a riskless asset is added to the market? Under what (sufficient) conditions would an agent maximising expected utility actually choose a portfolio on the mean-variance efficient frontier?
A1.11 B1.16
(i) The prices, , of a stock in a binomial model at times are represented by the following binomial tree.
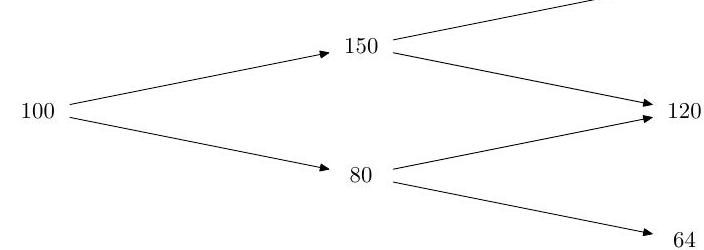
The fixed interest rate per period is and the probability that the stock price increases in a period is . Find the price at time 0 of a European call option with strike price 78 and expiry time
Explain briefly the ideas underlying your calculations.
(ii) Consider an investor in a one-period model who may invest in assets, all of which are risky, with a random return vector having mean and positivedefinite covariance matrix ; assume that not all the assets have the same expected return. Show that any minimum-variance portfolio is equivalent to the investor dividing his wealth between two portfolios, the global minimum-variance portfolio and the diversified portfolio, both of which should be specified clearly in terms of and .
Now suppose that where are independent random variables with having the exponential distribution with probability density function , where . Determine the global minimum-variance portfolio and the diversified portfolio explicitly.
Consider further the situation when the investor has the utility function , where denotes his wealth. Suppose that he acts to maximize the expected utility of his final wealth, and that his initial wealth is . Show that he now divides his wealth between the diversified portfolio and the uniform portfolio, in which wealth is apportioned equally between the assets, and determine the amounts that he invests in each.
A3.11 B3.16
(i) Explain briefly what it means to say that a stochastic process is a standard Brownian motion.
Let be a standard Brownian motion and let be real numbers. What condition must and satisfy to ensure that the process is a martingale? Justify your answer carefully.
(ii) At the beginning of each of the years an investor has income , of which he invests a proportion , and consumes the rest during the year. His income at the beginning of the next year is
where are independent positive random variables with finite means and is a constant. He decides on after he has observed both and at the beginning of year , but at that time he does not have any knowledge of the value of , for any . The investor retires in year and consumes his entire income during that year. He wishes to determine the investment policy that maximizes his expected total consumption
Prove that the optimal policy may be expressed in terms of the numbers , where , for , and determine the optimal expected total consumption.
A4.12 B4.16
Write an essay on the Black-Scholes formula for the price of a European call option on a stock. Your account should include a derivation of the formula and a careful analysis of its dependence on the parameters of the model.
A1.11 B1.16
(i) The price of the stock in the binomial model at time , is , where are independent, identically-distributed random variables with and the initial price is a constant. Denote the fixed interest rate on the bank account by , where , and let the discount factor . Determine the unique value for which the sequence is a martingale.
Explain briefly the significance of for the pricing of contingent claims in the model.
(ii) Let denote the first time that a standard Brownian motion reaches the level . Prove that for ,
where is the standard normal distribution function.
Suppose that and represent the prices at time of two different stocks with initial prices 1 and 2 , respectively; the prices evolve so that they may be represented as and , respectively, where and are independent standard Brownian motions and and are constants. Let denote the first time, if ever, that the prices of the two stocks are the same. Determine , for .
A3.11 B3.16
(i) Suppose that is a random variable having the normal distribution with and .
For positive constants show that
where is the standard normal distribution function.
In the context of the Black-Scholes model, derive the formula for the price at time 0 of a European call option on the stock at strike price and maturity time when the interest rate is and the volatility of the stock is .
(ii) Let denote the price of the call option in the Black-Scholes model specified in (i). Show that and sketch carefully the dependence of on the volatility (when the other parameters in the model are held fixed).
Now suppose that it is observed that the interest rate lies in the range and when it changes it is linked to the volatility by the formula . Consider a call option at strike price , where is the stock price at time 0 . There is a small increase in the interest rate; will the price of the option increase or decrease (assuming that the stock price is unaffected)? Justify your answer carefully.
[You may assume that the function is decreasing in , and increases to as , where is the standard-normal distribution function and .]
A4.12 B4.16
Write an essay on the mean-variance approach to portfolio selection in a one-period model. Your essay should contrast the solution in the case when all the assets are risky with that for the case when there is a riskless asset.