Applied Probability
Applied Probability
Jump to year
Paper 1, Section II, 28K
The particles of an Ideal Gas form a spatial Poisson process on with constant intensity , called the activity of the gas.
(a) Prove that the independent mixture of two Ideal Gases with activities and is again an Ideal Gas. What is its activity? [You must prove any results about Poisson processes that you use. The independent mixture of two gases with particles and is given by
(b) For an Ideal Gas of activity , find the limiting distribution of
as for a given sequence of subsets with .
(c) Let be a smooth non-negative function vanishing outside a bounded subset of . Find the mean and variance of , where the sum runs over the particles of an ideal gas of activity . [You may use the properties of spatial Poisson processes established in the lectures.]
[Hint: recall that the characteristic function of a Poisson random variable with mean is
Paper 2, Section II,
Let be an irreducible, non-explosive, continuous-time Markov process on the state space with generator .
(a) Define its jump chain and prove that it is a discrete-time Markov chain.
(b) Define what it means for to be recurrent and prove that is recurrent if and only if its jump chain is recurrent. Prove also that this is the case if the transition semigroup satisfies
(c) Show that is recurrent for at least one of the following generators:
[Hint: You may use that the semigroup associated with a -matrix on such that depends only on (and has sufficient decay) can be written as
where . You may also find the bound useful.
Paper 3, Section II,
(a) Customers arrive at a queue at the event times of a Poisson process of rate . The queue is served by two independent servers with exponential service times with parameter each. If the queue has length , an arriving customer joins with probability and leaves otherwise (where . For which and is there a stationary distribution?
(b) A supermarket allows a maximum of customers to shop at the same time. Customers arrive at the event times of a Poisson process of rate 1 , they enter the supermarket when possible, and they leave forever for another supermarket otherwise. Customers already in the supermarket pay and leave at the event times of an independent Poisson process of rate . When is there a unique stationary distribution for the number of customers in the supermarket? If it exists, find it.
(c) In the situation of part (b), started from equilibrium, show that the departure process is Poissonian.
Paper 4, Section II,
Let be a continuous-time Markov process with state space and generator satisfying for all . The local time up to time of is the random vector defined by
(a) Let be any function that is differentiable with respect to its second argument, and set
Show that
where
(b) For , write for the vector of squares of the components of . Let be a function such that whenever for some fixed . Using integration by parts, or otherwise, show that for all
where denotes .
(c) Let be a function with whenever for some fixed . Given , now let
in part (b) and deduce, using part (a), that
[You may exchange the order of integrals and derivatives without justification.]
Paper 1, Section II, 28K
(a) What is meant by a birth process with strictly positive rates Explain what is meant by saying that is non-explosive.
(b) Show that is non-explosive if and only if
(c) Suppose , and where . Show that
Paper 2, Section II, 27K
(i) Let be a Markov chain in continuous time on the integers with generator . Define the corresponding jump chain .
Define the terms irreducibility and recurrence for . If is irreducible, show that is recurrent if and only if is recurrent.
(ii) Suppose
Show that is transient, find an invariant distribution, and show that is explosive. [Any general results may be used without proof but should be stated clearly.]
Paper 3, Section II, 27K
Define a renewal-reward process, and state the renewal-reward theorem.
A machine is repaired at time . After any repair, it functions without intervention for a time that is exponentially distributed with parameter , at which point it breaks down (assume the usual independence). Following any repair at time , say, it is inspected at times , and instantly repaired if found to be broken (the inspection schedule is then restarted). Find the long run proportion of time that is working. [You may express your answer in terms of an integral.]
Paper 4, Section II, K
(i) Explain the notation in the context of queueing theory. [In the following, you may use without proof the fact that is the invariant distribution of such a queue when .
(ii) In a shop queue, some customers rejoin the queue after having been served. Let and . Consider a queue subject to the modification that, on completion of service, each customer leaves the shop with probability , or rejoins the shop queue with probability . Different customers behave independently of one another, and all service times are independent random variables.
Find the distribution of the total time a given customer spends being served by the server. Hence show that equilibrium is possible if , and find the invariant distribution of the queue-length in this case.
(iii) Show that, in equilibrium, the departure process is Poissonian, whereas, assuming the rejoining customers go to the end of the queue, the process of customers arriving at the queue (including the rejoining ones) is not Poissonian.
Paper 1, Section II, K
Let be a countable set, and let be a Markov transition matrix with for all . Let be a discrete-time Markov chain on the state space with transition matrix .
The continuous-time process is constructed as follows. Let be independent, identically distributed random variables having the exponential distribution with mean 1. Let be a function on such that for all and some constant . Let for . Let and for . Finally, let for .
(a) Explain briefly why is a continuous-time Markov chain on , and write down its generator in terms of and the vector .
(b) What does it mean to say that the chain is irreducible? What does it mean to say a state is (i) recurrent and (ii) positive recurrent?
(c) Show that
(i) is irreducible if and only if is irreducible;
(ii) is recurrent if and only if is recurrent.
(d) Suppose is irreducible and positive recurrent with invariant distribution . Express the invariant distribution of in terms of and .
Paper 2, Section II, K
Let be a Markov chain on the non-negative integers with generator given by
for a given collection of positive numbers .
(a) State the transition matrix of the jump chain of .
(b) Why is not reversible?
(c) Prove that is transient if and only if .
(d) Assume that . Derive a necessary and sufficient condition on the parameters for to be explosive.
(e) Derive a necessary and sufficient condition on the parameters for the existence of an invariant measure for .
[You may use any general results from the course concerning Markov chains and pure birth processes so long as they are clearly stated.]
Paper 3, Section II, K
(a) What does it mean to say that a continuous-time Markov chain ) with state space is reversible in equilibrium? State the detailed balance equations, and show that any probability distribution on satisfying them is invariant for the chain.
(b) Customers arrive in a shop in the manner of a Poisson process with rate . There are servers, and capacity for up to people waiting for service. Any customer arriving when the shop is full (in that the total number of customers present is ) is not admitted and never returns. Service times are exponentially distributed with parameter , and they are independent of one another and of the arrivals process. Describe the number of customers in the shop at time as a Markov chain.
Calculate the invariant distribution of , and explain why is the unique invariant distribution. Show that is reversible in equilibrium.
[Any general result from the course may be used without proof, but must be stated clearly.]
Paper 4, Section II, K
(a) Let be such that is finite for any bounded measurable set . State the properties which define a (non-homogeneous) Poisson process on with intensity function .
(b) Let be a Poisson process on with intensity function , and let be a given function. Give a clear statement of the necessary conditions on the pair subject to which is a Poisson process on . When these conditions hold, express the mean measure of in terms of and .
(c) Let be a homogeneous Poisson process on with constant intensity 1 , and let be given by . Show that is a homogeneous Poisson process on with constant intensity .
Let be an increasing sequence of positive random variables such that the points of are Show that has density function
Paper 1, Section II, J
Let be a continuous function. Explain what is meant by an inhomogeneous Poisson process with intensity function .
Let be such an inhomogeneous Poisson process, and let where is strictly increasing, differentiable and satisfies . Show that is a homogeneous Poisson process with intensity 1 if for all , where . Deduce that has the Poisson distribution with mean .
Bicycles arrive at the start of a long road in the manner of a Poisson process with constant intensity . The th bicycle has constant velocity , where are independent, identically distributed random variables, which are independent of . Cyclists can overtake one another freely. Show that the number of bicycles on the first miles of the road at time has the Poisson distribution with parameter .
Paper 2, Section II, J
Let be a continuous-time Markov chain on the finite state space . Define the terms generator (or Q-matrix) and invariant distribution, and derive an equation that links the generator and any invariant distribution . Comment on the possible non-uniqueness of invariant distributions.
Suppose is irreducible, and let be a Poisson process with intensity , that is independent of . Let be the value of immediately after the th arrival-time of (and . Show that is a discrete-time Markov chain, state its transition matrix and prove that it has the same invariant distribution as .
Paper 3, Section II, J
Individuals arrive in a shop in the manner of a Poisson process with intensity , and they await service in the order of their arrival. Their service times are independent, identically distributed random variables . For , let be the number remaining in the shop immediately after the th departure. Show that
where is the number of arrivals during the th service period, and .
Show that
where is a typical service period, and is the traffic intensity of the queue.
Suppose , and the queue is in equilibrium in the sense that and have the same distribution for all . Express in terms of . Deduce that the mean waiting time (prior to service) of a typical individual is .
Paper 4, Section II, J
Let be independent, identically distributed random variables with finite mean . Explain what is meant by saying that the random variable is a stopping time with respect to the sequence .
Let be a stopping time with finite mean . Prove Wald's equation:
[Here and in the following, you may use any standard theorem about integration.]
Suppose the are strictly positive, and let be the renewal process with interarrival times . Prove that satisfies the elementary renewal theorem:
A computer keyboard contains 100 different keys, including the lower and upper case letters, the usual symbols, and the space bar. A monkey taps the keys uniformly at random. Find the mean number of keys tapped until the first appearance of the sequence 'lava' as a sequence of 4 consecutive characters.
Find the mean number of keys tapped until the first appearance of the sequence 'aa' as a sequence of 2 consecutive characters.
Paper 1, Section II,
(a) Define a continuous time Markov chain with infinitesimal generator and jump chain .
(b) Let be a transient state of a continuous-time Markov chain with . Show that the time spent in state has an exponential distribution and explicitly state its parameter.
[You may use the fact that if , then for .]
(c) Let be an asymmetric random walk in continuous time on the non-negative integers with reflection at 0 , so that
Suppose that and . Show that for all , the total time spent in state is exponentially distributed with parameter .
Assume now that has some general distribution with probability generating function . Find the expected amount of time spent at 0 in terms of .
Paper 2, Section II, K
(a) Give the definition of a Poisson process on . Let be a Poisson process on . Show that conditional on , the jump times have joint density function
where is the indicator of the set .
(b) Let be a Poisson process on with intensity and jump times . If is a real function, we define for all
Show that for all the following is true
Paper 3, Section II, K
(a) Define the Moran model and Kingman's -coalescent. Define Kingman's infinite coalescent.
Show that Kingman's infinite coalescent comes down from infinity. In other words, with probability one, the number of blocks of is finite at any time .
(b) Give the definition of a renewal process.
Let denote the sequence of inter-arrival times of the renewal process . Suppose that .
Prove that as .
Prove that for some strictly positive .
[Hint: Consider the renewal process with inter-arrival times for some suitable .]
Paper 4, Section II,
(a) Give the definition of an queue. Prove that if is the arrival rate and the service rate and , then the length of the queue is a positive recurrent Markov chain. What is the equilibrium distribution?
If the queue is in equilibrium and a customer arrives at some time , what is the distribution of the waiting time (time spent waiting in the queue plus service time)?
(b) We now modify the above queue: on completion of service a customer leaves with probability , or goes to the back of the queue with probability . Find the distribution of the total time a customer spends being served.
Hence show that equilibrium is possible if and find the stationary distribution.
Show that, in equilibrium, the departure process is Poisson.
[You may use relevant theorems provided you state them clearly.]
Paper 1, Section II, J
(a) Define a continuous-time Markov chain with infinitesimal generator and jump chain .
(b) Prove that if a state is transient for , then it is transient for .
(c) Prove or provide a counterexample to the following: if is positive recurrent for , then it is positive recurrent for .
(d) Consider the continuous-time Markov chain on with non-zero transition rates given by
Determine whether is transient or recurrent. Let , where is the first jump time. Does have an invariant distribution? Justify your answer. Calculate .
(e) Let be a continuous-time random walk on with and for all with . Determine for which values of the walk is transient and for which it is recurrent. In the recurrent case, determine the range of for which it is also positive recurrent. [Here denotes the Euclidean norm of .]
Paper 2, Section II, J
(a) Define an queue and write without proof its stationary distribution. State Burke's theorem for an queue.
(b) Let be an queue with arrival rate and service rate started from the stationary distribution. For each , denote by the last time before that a customer departed the queue and the first time after that a customer departed the queue. If there is no arrival before time , then we set . What is the limit as of ? Explain.
(c) Consider a system of queues serving a finite number of customers in the following way: at station , customers are served immediately and the service times are independent exponentially distributed with parameter ; after service, each customer goes to station with probability . We assume here that the system is closed, i.e., for all .
Let be the state space of the Markov chain. Write down its -matrix. Also write down the -matrix corresponding to the position in the network of one customer (that is, when ). Show that there is a unique distribution such that . Show that
defines an invariant measure for the chain. Are the queue lengths independent at equilibrium?
Paper 3, Section II, J
(a) State the thinning and superposition properties of a Poisson process on . Prove the superposition property.
(b) A bi-infinite Poisson process with is a process with independent and stationary increments over . Moreover, for all , the increment has the Poisson distribution with parameter . Prove that such a process exists.
(c) Let be a bi-infinite Poisson process on of intensity . We identify it with the set of points of discontinuity of , i.e., . Show that if we shift all the points of by the same constant , then the resulting process is also a Poisson process of intensity .
Now suppose we shift every point of by or with equal probability. Show that the final collection of points is still a Poisson process of intensity . [You may assume the thinning and superposition properties for the bi-infinite Poisson process.]
Paper 4, Section II, J
(a) Give the definition of a renewal process. Let be a renewal process associated with with . Show that almost surely
(b) Give the definition of Kingman's -coalescent. Let be the first time that all blocks have coalesced. Find an expression for . Let be the total length of the branches of the tree, i.e., if is the first time there are lineages, then . Show that as . Show also that for all , where is a positive constant, and that in probability
Paper 1, Section II, K
(a) Give the definition of a birth and death chain in terms of its generator. Show that a measure is invariant for a birth and death chain if and only if it solves the detailed balance equations.
(b) There are servers in a post office and a single queue. Customers arrive as a Poisson process of rate and the service times at each server are independent and exponentially distributed with parameter . Let denote the number of customers in the post office at time . Find conditions on and for to be positive recurrent, null recurrent and transient, justifying your answers.
Paper 2, Section II,
(i) Defne a Poisson process on with rate . Let and be two independent Poisson processes on of rates and respectively. Prove that is also a Poisson process and find its rate.
(ii) Let be a discrete time Markov chain with transition matrix on the finite state space . Find the generator of the continuous time Markov chain in terms of and . Show that if is an invariant distribution for , then it is also invariant for .
Suppose that has an absorbing state . If and are the absorption times for and respectively, write an equation that relates and , where .
[Hint: You may want to prove that if are i.i.d. non-negative random variables with and is an independent non-negative random variable, then
Paper 3, Section II, K
(i) Let be a Poisson process of parameter . Let be obtained by taking each point of and, independently of the other points, keeping it with probability . Show that is another Poisson process and find its intensity. Show that for every fixed the random variables and are independent.
(ii) Suppose we have bins, and balls arrive according to a Poisson process of rate 1 . Upon arrival we choose a bin uniformly at random and place the ball in it. We let be the maximum number of balls in any bin at time . Show that
[You may use the fact that if is a Poisson random variable of mean 1 , then
Paper 4, Section II, K
(i) Let be a Markov chain on and . Let be the hitting time of and denote the total time spent at by the chain before hitting . Show that if , then
(ii) Define the Moran model and show that if is the number of individuals carrying allele at time and is the fixation time of allele , then
Show that conditionally on fixation of an allele being present initially in individuals,
Paper 1, Section II, J
(i) Explain what a -matrix is. Let be a -matrix. Define the notion of a Markov chain in continuous time with -matrix given by , and give a construction of . [You are not required to justify this construction.]
(ii) A population consists of individuals at time . We assume that each individual gives birth to a new individual at constant rate . As the population is competing for resources, we assume that for each , if , then any individual in the population at time dies in the time interval with probability , where is a given sequence satisfying for . Formulate a Markov chain model for and write down the -matrix explicitly. Then find a necessary and sufficient condition on so that the Markov chain has an invariant distribution. Compute the invariant distribution in the case where and .
Paper 2, Section II, J
(i) Explain what the Moran model and the infinite alleles model are. State Ewens' sampling formula for the distribution of the allelic frequency spectrum in terms of where with denoting the mutation rate per individual and the population size.
Let be the number of allelic types in a sample of size . Give, without justification, an expression for in terms of .
(ii) Let and be as above. Show that for we have that
for some constant that does not depend on .
Show that, given , the distribution of the allelic frequency spectrum does not depend on .
Show that the value of which maximises is the one for which .
Paper 3, Section II, J
(i) Define a Poisson process with intensity . Specify without justification the distribution of . Let denote the jump times of . Derive the joint distribution of given .
(ii) Let be a Poisson process with intensity and let be a sequence of i.i.d. random variables, independent of , all having the same distribution as a random variable . Show that if is a real-valued function of real variables , and are the jump times of then
for all . [Hint: Condition on and , using (i).]
(iii) A university library is open from 9 am to . Students arrive at times of a Poisson process with intensity . Each student spends a random amount of time in the library, independently of the other students. These times are identically distributed for all students and have the same distribution as a random variable . Show that the number of students in the library at is a Poisson random variable with a mean that you should specify.
Paper 4, Section II, J
(i) Define the queue with arrival rate and service rate . Find conditions on the parameters and for the queue to be transient, null recurrent, and positive recurrent, briefly justifying your answers. In the last case give with justification the invariant distribution explicitly. Answer the same questions for an queue.
(ii) At a taxi station, customers arrive at a rate of 3 per minute, and taxis at a rate of 2 per minute. Suppose that a taxi will wait no matter how many other taxis are present. However, if a person arriving does not find a taxi waiting he or she leaves to find alternative transportation.
Find the long-run proportion of arriving customers who get taxis, and find the average number of taxis waiting in the long run.
An agent helps to assign customers to taxis, and so long as there are taxis waiting he is unable to have his coffee. Once a taxi arrives, how long will it take on average before he can have another sip of his coffee?
Paper 1, Section II, J
Let be a Markov chain on with -matrix given by
where .
(i) Show that is transient if and only if . [You may assume without proof that for all and all sufficiently small positive .]
(ii) Assume that . Find a necessary and sufficient condition for to be almost surely explosive. [You may assume without proof standard results about pure birth processes, provided that they are stated clearly.]
(iii) Find a stationary measure for . For the case and , show that is positive recurrent if and only if .
Paper 2, Section II, J
(i) Define a Poisson process as a Markov chain on the non-negative integers and state three other characterisations.
(ii) Let be a continuous positive function. Let be a right-continuous process with independent increments, such that
where the terms are uniform in . Show that is a Poisson random variable with parameter .
(iii) Let be a sequence of independent and identically distributed positive random variables with continuous density function . We define the sequence of successive records, , by and, for ,
The record process,, is then defined by
Explain why the increments of are independent. Show that is a Poisson random variable with parameter where .
[You may assume the following without proof: For fixed , let (respectively, ) be the subsequence of obtained by retaining only those elements that are greater than (respectively, smaller than) . Then (respectively, ) is a sequence of independent variables each having the distribution of conditioned on (respectively, ); and and are independent.]
Paper 3, Section II, J
Define the Moran model. Describe briefly the infinite sites model of mutations.
We henceforth consider a population with individuals evolving according to the rules of the Moran model. In addition we assume:
the allelic type of any individual at any time lies in a given countable state space ;
individuals are subject to mutations at constant rate , independently of the population dynamics;
each time a mutation occurs, if the allelic type of the individual was , it changes to with probability , where is a given Markovian transition matrix on that is symmetric:
(i) Show that, if two individuals are sampled at random from the population at some time , then the time to their most recent common ancestor has an exponential distribution, with a parameter that you should specify.
(ii) Let be the total number of mutations that accumulate on the two branches separating these individuals from their most recent common ancestor. Show that is a geometric random variable, and specify its probability parameter .
(iii) The first individual is observed to be of type . Explain why the probability that the second individual is also of type is
where is a Markov chain on with transition matrix and is independent of .
Paper 4, Section II, J
(i) Define an queue. Justifying briefly your answer, specify when this queue has a stationary distribution, and identify that distribution. State and prove Burke's theorem for this queue.
(ii) Let denote a Jackson network of queues, where the entrance and service rates for queue are respectively and , and each customer leaving queue moves to queue with probability after service. We assume for each ; with probability a customer leaving queue departs from the system. State Jackson's theorem for this network. [You are not required to prove it.] Are the processes independent at equilibrium? Justify your answer.
(iii) Let be the process of final departures from queue . Show that, at equilibrium, is independent of . Show that, for each fixed is a Poisson process, and specify its rate.
Paper 1, Section II,
(a) Give the definition of a Poisson process with rate , using its transition rates. Show that for each , the distribution of is Poisson with a parameter to be specified.
Let and let denote the jump times of . What is the distribution of (You do not need to justify your answer.)
(b) Let . Compute the joint probability density function of given . Deduce that, given has the same distribution as the nondecreasing rearrangement of independent uniform random variables on .
(c) Starting from time 0, passengers arrive on platform at King's Cross station, with constant rate , in order to catch a train due to depart at time . Using the above results, or otherwise, find the expected total time waited by all passengers (the sum of all passengers' waiting times).
Paper 2, Section II, K
(a) A colony of bacteria evolves as follows. Let be a random variable with values in the positive integers. Each bacterium splits into copies of itself after an exponentially distributed time of parameter . Each of the daughters then splits in the same way but independently of everything else. This process keeps going forever. Let denote the number of bacteria at time . Specify the -matrix of the Markov chain . [It will be helpful to introduce , and you may assume for simplicity that
(b) Using the Kolmogorov forward equation, or otherwise, show that if , then for some to be explicitly determined in terms of . Assuming that , deduce the value of for all , and show that does not explode. [You may differentiate series term by term and exchange the order of summation without justification.]
(c) We now assume that with probability 1 . Fix and let . Show that satisfies
By making the change of variables , show that . Deduce that for all where .
Paper 3, Section II, K
We consider a system of two queues in tandem, as follows. Customers arrive in the first queue at rate . Each arriving customer is immediately served by one of infinitely many servers at rate . Immediately after service, customers join a single-server second queue which operates on a first-come, first-served basis, and has a service rate . After service in this second queue, each customer returns to the first queue with probability , and otherwise leaves the system forever. A schematic representation is given below:

(a) Let and denote the number of customers at time in queues number 1 and 2 respectively, including those currently in service at time . Give the transition rates of the Markov chain .
(b) Write down an equation satisfied by any invariant measure for this Markov chain. Let and . Define a measure by
Show that it is possible to find so that is an invariant measure of , if and only if . Give the values of and in this case.
(c) Assume now that . Show that the number of customers is not positive recurrent.
[Hint. One way to solve the problem is as follows. Assume it is positive recurrent. Observe that is greater than a queue with arrival rate . Deduce that is greater than a queue with arrival rate and service rate . You may use without proof the fact that the departure process from the first queue is then, at equilibrium, a Poisson process with rate , and you may use without proof properties of thinned Poisson processes.]
Paper 4, Section II,
(a) Define the Moran model and Kingman's -coalescent. State and prove a theorem which describes the relationship between them. [You may use without proof a construction of the Moran model for all .]
(b) Let . Suppose that a population of individuals evolves according to the rules of the Moran model. Assume also that each individual in the population undergoes a mutation at constant rate . Each time a mutation occurs, we assume that the allelic type of the corresponding individual changes to an entirely new type, never seen before in the population. Let be the homozygosity probability, i.e., the probability that two individuals sampled without replacement from the population have the same genetic type. Give an expression for .
(c) Let denote the probability that a sample of size consists of one allelic type (monomorphic population). Show that , where denotes the sum of all the branch lengths in the genealogical tree of the sample - that is, , where is the first time that the genealogical tree of the sample has lineages. Deduce that
Paper 1, Section II, J
(i) Let be a Markov chain with finitely many states. Define a stopping time and state the strong Markov property.
(ii) Let be a Markov chain with state-space and Q-matrix
Consider the integral , the signed difference between the times spent by the chain at states and by time , and let
Derive the equation
(iii) Obtain another equation relating to .
(iv) Assuming that , where is a non-negative constant, calculate .
(v) Give an intuitive explanation why the function must have the exponential form for some .
Paper 2, Section II, J
(i) Explain briefly what is meant by saying that a continuous-time Markov chain is a birth-and-death process with birth rates , and death rates , .
(ii) In the case where is recurrent, find a sufficient condition on the birth and death parameters to ensure that
and express in terms of these parameters. State the reversibility property of .
Jobs arrive according to a Poisson process of rate . They are processed individually, by a single server, the processing times being independent random variables, each with the exponential distribution of rate . After processing, the job either leaves the system, with probability , or, with probability , it splits into two separate jobs which are both sent to join the queue for processing again. Let denote the number of jobs in the system at time .
(iii) In the case , evaluate , and find the expected time that the processor is busy between two successive idle periods.
(iv) What happens if ?
Paper 3, Section II, J
(i) Define an inhomogeneous Poisson process with rate function .
(ii) Show that the number of arrivals in an inhomogeneous Poisson process during the interval has the Poisson distribution with mean
(iii) Suppose that is a non-negative real-valued random process. Conditional on , let be an inhomogeneous Poisson process with rate function . Such a process is called a doubly-stochastic Poisson process. Show that the variance of cannot be less than its mean.
(iv) Now consider the process obtained by deleting every odd-numbered point in an ordinary Poisson process of rate . Check that
Deduce that is not a doubly-stochastic Poisson process.
Paper 4, Section II, J
At an queue, the arrival times form a Poisson process of rate while service times are independent of each other and of the arrival times and have a common distribution with mean .
(i) Show that the random variables giving the number of customers left in the queue at departure times form a Markov chain.
(ii) Specify the transition probabilities of this chain as integrals in involving parameter . [No proofs are needed.]
(iii) Assuming that and the chain is positive recurrent, show that its stationary distribution has the generating function given by
for an appropriate function , to be specified.
(iv) Deduce that, in equilibrium, has the mean value
Paper 1, Section II, I
(a) Define what it means to say that is an equilibrium distribution for a Markov chain on a countable state space with Q-matrix , and give an equation which is satisfied by any equilibrium distribution. Comment on the possible non-uniqueness of equilibrium distributions.
(b) State a theorem on convergence to an equilibrium distribution for a continuoustime Markov chain.
A continuous-time Markov chain has three states and the Qmatrix is of the form
where the rates are not all zero.
[Note that some of the may be zero, and those cases may need special treatment.]
(c) Find the equilibrium distributions of the Markov chain in question. Specify the cases of uniqueness and non-uniqueness.
(d) Find the limit of the transition matrix when .
(e) Describe the jump chain and its equilibrium distributions. If is the jump probability matrix, find the limit of as .
Paper 2, Section II, I
(a) Let be the sum of independent exponential random variables of rate . Compute the moment generating function of . Show that, as , functions converge to a limit. Describe the random variable for which the limiting function coincides with .
(b) Define the queue with infinite capacity (sometimes written ). Introduce the embedded discrete-time Markov chain and write down the recursive relation between and .
Consider, for each fixed and for , an queue with arrival rate and with service times distributed as . Assume that the queue is empty at time 0 . Let be the earliest time at which a customer departs leaving the queue empty. Let be the first arrival time and the length of the busy period.
(c) Prove that the moment generating functions and are related by the equation
(d) Prove that the moment generating functions and are related by the equation
(e) Assume that, for all ,
for some random variables and . Calculate and . What service time distribution do these values correspond to?
Paper 3, Section II, I
Cars looking for a parking space are directed to one of three unlimited parking lots A, B and C. First, immediately after the entrance, the road forks: one direction is to lot A, the other to B and C. Shortly afterwards, the latter forks again, between B and C. See the diagram below.
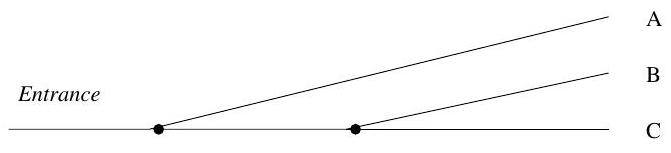
The policeman at the first road fork directs an entering car with probability to A and with probability to the second fork. The policeman at the second fork sends the passing cars to or alternately: cars approaching the second fork go to and cars to .
Assuming that the total arrival process of cars is Poisson of rate , consider the processes and , where is the number of cars directed to lot by time , for . The times for a car to travel from the first to the second fork, or from a fork to the parking lot, are all negligible.
(a) Characterise each of the processes and , by specifying if it is (i) Poisson, (ii) renewal or (iii) delayed renewal. Correspondingly, specify the rate, the holding-time distribution and the distribution of the delay.
(b) In the case of a renewal process, determine the equilibrium delay distribution.
(c) Given , write down explicit expressions for the probability that the interval is free of points in the corresponding process, .
Paper 4, Section II, I
(a) Let be an irreducible continuous-time Markov chain on a finite or countable state space. What does it mean to say that the chain is (i) transient, (ii) recurrent, (iii) positive recurrent, (iv) null recurrent? What is the relation between equilibrium distributions and properties (iii) and (iv)?
A population of microorganisms develops in continuous time; the size of the population is a Markov chain with states Suppose . It is known that after a short time , the probability that increased by one is and (if ) the probability that the population was exterminated between times and and never revived by time is . Here and are given positive constants. All other changes in the value of have a combined probability .
(b) Write down the Q-matrix of Markov chain and determine if is irreducible. Show that is non-explosive. Determine the jump chain.
(c) Now assume that
Determine whether the chain is transient or recurrent, and in the latter case whether it is positive or null recurrent. Answer the same questions for the jump chain. Justify your answers.
Paper 1, Section II, J
(a) Let be a continuous-time Markov chain on a countable state space I. Explain what is meant by a stopping time for the chain . State the strong Markov property. What does it mean to say that is irreducible?
(b) Let be a Markov chain on with -matrix given by such that:
(1) for all , but for all , and
(2) for all , but if .
Is irreducible? Fix , and assume that , where . Show that if is the first jump time, then there exists such that , uniformly over . Let and define recursively for ,
Let be the event . Show that , for .
(c) Let be the Markov chain from (b). Define two events and by
Show that for all .
Paper 2, Section II, J
Let , be a sequence of independent, identically distributed positive random variables, with a common probability density function . Call a record value if . Consider the sequence of record values
where
Define the record process by and
(a) By induction on , or otherwise, show that the joint probability density function of the random variables is given by:
where is the cumulative distribution function for .
(b) Prove that the random variable has a Poisson distribution with parameter of the form
and determine the 'instantaneous rate' .
[Hint: You may use the formula
for any
Paper 3, Section II, J
(a) Define the Poisson process with rate , in terms of its holding times. Show that for all times has a Poisson distribution, with a parameter which you should specify.
(b) Let be a random variable with probability density function
Prove that is distributed as the sum of three independent exponential random variables of rate . Calculate the expectation, variance and moment generating function of .
Consider a renewal process with holding times having density . Prove that the renewal function has the form
where and is the Poisson process of rate .
(c) Consider the delayed renewal process with holding times where , are the holding times of from (b). Specify the distribution of for which the delayed process becomes the renewal process in equilibrium.
[You may use theorems from the course provided that you state them clearly.]
Paper 4, Section II, J
A flea jumps on the vertices of a triangle ; its position is described by a continuous time Markov chain with a -matrix
(a) Draw a diagram representing the possible transitions of the flea together with the rates of each of these transitions. Find the eigenvalues of and express the transition probabilities , in terms of these eigenvalues.
[Hint: . Specifying the equilibrium distribution may help.]
Hence specify the probabilities where is a Poisson process of rate
(b) A second flea jumps on the vertices of the triangle as a Markov chain with Q-matrix
where is a given real number. Let the position of the second flea at time be denoted by . We assume that is independent of . Let . Show that exists and is independent of the starting points of and . Compute this limit.
1.II.26I
Let be an irreducible continuous-time Markov chain with initial probability distribution and Q-matrix (for short: a CTMC), on a finite state space .
(i) Define the terms reversible CTMC and detailed balance equations (DBEs) and explain, without proof, the relation between them.
(ii) Prove that any solution of the DBEs is an equilibrium distribution (ED) for .
Let be an irreducible discrete-time Markov chain with initial probability distribution and transition probability matrix (for short: a DTMC), on the state space .
(iii) Repeat the two definitions from (i) in the context of the DTMC . State also in this context the relation between them, and prove a statement analogous to (ii).
(iv) What does it mean to say that is the jump chain for ? State and prove a relation between the ED for the and the ED for its jump chain .
(v) Prove that is reversible (in equilibrium) if and only if its jump chain is reversible (in equilibrium).
(vi) Consider now a continuous time random walk on a graph. More precisely, consider a CTMC on an undirected graph, where some pairs of states are joined by one or more non-oriented 'links' . Here is the number of links between and . Assume that the jump rate is proportional to . Can the chain be reversible? Identify the corresponding jump chain (which determines a discrete-time random walk on the graph) and comment on its reversibility.
2.II.26I
Consider a continuous-time Markov chain given by the diagram below.

We will assume that the rates and are all positive.
(a) Is the chain irreducible?
(b) Write down the standard equations for the hitting probabilities
and
Explain how to identify the probabilities and among the solutions to these equations.
[You should state the theorem you use but its proof is not required.]
(c) Set and find a matrix such that
The recursion matrix has a 'standard' eigenvalue and a 'standard' eigenvector that do not depend on the transition rates: what are they and why are they always present?
(d) Calculate the second eigenvalue of the matrix , and the corresponding eigenvector, in the form , where .
(e) Suppose the second eigenvalue is . What can you say about and ? Is the chain transient or recurrent? Justify your answer.
(f) Now assume the opposite: the second eigenvalue is . Check that in this case . Is the chain transient or recurrent under this condition?
(g) Finally, specify, by means of inequalities between the parameters and , when the chain is recurrent and when it is transient.
3.II.25I
Let be an irreducible continuous-time Markov chain with countably many states. What does it mean to say the chain is (i) positive recurrent, (ii) null recurrent? Consider the chain with the arrow diagram below.
In this question we analyse the existence of equilibrium probabilities and of the chain being in state or , and the impact of this fact on positive and null recurrence of the chain.
(a) Write down the invariance equations and check that they have the form
where is a recursion matrix:
(b) Verify that the row vector is an eigenvector of with the eigenvalue where
Hence, specify the form of equilibrium probabilities and and conclude that the chain is positive recurrent if and only if .
4.II.26I
On a hot summer night, opening my window brings some relief. This attracts hordes of mosquitoes who manage to negotiate a dense window net. But, luckily, I have a mosquito trapping device in my room.
Assume the mosquitoes arrive in a Poisson process at rate ; afterwards they wander around for independent and identically distributed random times with a finite mean , where denotes the random wandering time of a mosquito, and finally are trapped by the device.
(a) Identify a mathematical model, which was introduced in the course, for the number of mosquitoes present in the room at times .
(b) Calculate the distribution of in terms of and the tail probabilities of the wandering time , where is the number of mosquitoes in the room at time (assuming that at the initial time, ).
(c) Write down the distribution for , the number of mosquitoes in the room in equilibrium, in terms of and .
(d) Instead of waiting for the number of mosquitoes to reach equilibrium, I close the window at time . For let be the number of mosquitoes left at time , i.e. time units after closing the window. Calculate the distribution of .
(e) Let be the time needed to trap all mosquitoes in the room after closing the window at time . By considering the event , or otherwise, compute .
(f) Now suppose that the time at which I shut the window is very large, so that I can assume that the number of mosquitoes in the room has the distribution of . Let be the further time needed to trap all mosquitoes in the room. Show that
where .
1.II.26J
An open air rock concert is taking place in beautiful Pine Valley, and enthusiastic fans from the entire state of Alifornia are heading there long before the much anticipated event. The arriving cars have to be directed to one of three large (practically unlimited) parking lots, and situated near the valley entrance. The traffic cop at the entrance to the valley decides to direct every third car (in the order of their arrival) to a particular lot. Thus, cars and so on are directed to lot , cars to lot and cars to lot .
Suppose that the total arrival process , at the valley entrance is Poisson, of rate (the initial time is taken to be considerably ahead of the actual event). Consider the processes and where is the number of cars arrived in lot by time . Assume for simplicity that the time to reach a parking lot from the entrance is negligible so that the car enters its specified lot at the time it crosses the valley entrance.
(a) Give the probability density function of the time of the first arrival in each of the processes .
(b) Describe the distribution of the time between two subsequent arrivals in each of these processes. Are these times independent? Justify your answer.
(c) Which of these processes are delayed renewal processes (where the distribution of the first arrival time differs from that of the inter-arrival time)?
(d) What are the corresponding equilibrium renewal processes?
(e) Describe how the direction rule should be changed for and to become Poisson processes, of rate . Will these Poisson processes be independent? Justify your answer.
2.II.26J
In this question we work with a continuous-time Markov chain where the rate of jump may depend on but not on . A virus can be in one of strains , and it mutates to strain with rate from each strain . (Mutations are caused by the chemical environment.) Set .
(a) Write down the Q-matrix (the generator) of the chain in terms of and .
(b) If , that is, , what are the communicating classes of the chain ?
(c) From now on assume that . State and prove a necessary and sufficient condition, in terms of the numbers , for the chain to have a single communicating class (which therefore should be closed).
(d) In general, what is the number of closed communicating classes in the chain ? Describe all open communicating classes of .
(e) Find the equilibrium distribution of . Is the chain reversible? Justify your answer.
(f) Write down the transition matrix of the discrete-time jump chain for and identify its equilibrium distribution. Is the jump chain reversible? Justify your answer.
3.II.25J
For a discrete-time Markov chain, if the probability of transition does not depend on then the chain is reduced to a sequence of independent random variables (states). In this case, the chain forgets about its initial state and enters equilibrium after a single transition. In the continuous-time case, a Markov chain whose rates of transition depend on but not on still 'remembers' its initial state and reaches equilibrium only in the limit as the time grows indefinitely. This question is an illustration of this property.
A protean sea sponge may change its colour among varieties , under the influence of the environment. The rate of transition from colour to equals and does not depend on . Consider a Q-matrix with entries
where . Assume that and let be the continuous-time Markov chain with generator . Given , let be the matrix of transition probabilities in time in chain .
(a) State the exponential relation between the matrices and .
(b) Set . Check that are equilibrium probabilities for the chain . Is this a unique equilibrium distribution? What property of the vector with entries relative to the matrix is involved here?
(c) Let be a vector with components such that . Show that . Compute
(d) Now let denote the (column) vector whose entries are 0 except for the th one which equals 1. Observe that the th row of is . Prove that
(e) Deduce the expression for transition probabilities in terms of rates and their sum .
4.II.26J
A population of rare Monarch butterflies functions as follows. At the times of a Poisson process of rate a caterpillar is produced from an egg. After an exponential time, the caterpillar is transformed into a pupa which, after an exponential time, becomes a butterfly. The butterfly lives for another exponential time and then dies. (The Poissonian assumption reflects the fact that butterflies lay a huge number of eggs most of which do not develop.) Suppose that all lifetimes are independent (of the arrival process and of each other) and let their rate be . Assume that the population is in an equilibrium and let be the number of caterpillars, the number of pupae and the number of butterflies (so that the total number of insects, in any metamorphic form, equals . Let be the equilibrium probability where
(a) Specify the rates of transitions for the resulting continuous-time Markov chain with states . (The rates are non-zero only when or and similarly for other co-ordinates.) Check that the holding rate for state is where .
(b) Let be the Q-matrix from (a). Consider the invariance equation . Verify that the only solution is
(c) Derive the marginal equilibrium probabilities and the conditional equilibrium probabilities .
(d) Determine whether the chain is positive recurrent, null-recurrent or transient.
(e) Verify that the equilibrium probabilities are the same as in the corresponding system (with the correct specification of the arrival rate and the service-time distribution).
1.II.26J
(a) What is a -matrix? What is the relationship between the transition matrix of a continuous time Markov process and its generator ?
(b) A pond has three lily pads, labelled 1, 2, and 3. The pond is also the home of a frog that hops from pad to pad in a random fashion. The position of the frog is a continuous time Markov process on with generator
Sketch an arrow diagram corresponding to and determine the communicating classes. Find the probability that the frog is on pad 2 in equilibrium. Find the probability that the frog is on pad 2 at time given that the frog is on pad 1 at time 0 .
2.II.26J
(a) Define a renewal process with independent, identically-distributed holding times State without proof the strong law of large numbers for . State without proof the elementary renewal theorem for the mean value .
(b) A circular bus route consists of ten bus stops. At exactly 5am, the bus starts letting passengers in at the main bus station (stop 1). It then proceeds to stop 2 where it stops to let passengers in and out. It continues in this fashion, stopping at stops 3 to 10 in sequence. After leaving stop 10, the bus heads to stop 1 and the cycle repeats. The travel times between stops are exponentially distributed with mean 4 minutes, and the time required to let passengers in and out at each stop are exponentially distributed with mean 1 minute. Calculate approximately the average number of times the bus has gone round its route by .
When the driver's shift finishes, at exactly , he immediately throws all the passengers off the bus if the bus is already stopped, or otherwise, he drives to the next stop and then throws the passengers off. He then drives as fast as he can round the rest of the route to the main bus station. Giving reasons but not proofs, calculate approximately the average number of stops he will drive past at the end of his shift while on his way back to the main bus station, not including either the stop at which he throws off the passengers or the station itself.
3.II.25J
A passenger plane with numbered seats is about to take off; seats have already been taken, and now the last passenger enters the cabin. The first passengers were advised by the crew, rather imprudently, to take their seats completely at random, but the last passenger is determined to sit in the place indicated on his ticket. If his place is free, he takes it, and the plane is ready to fly. However, if his seat is taken, he insists that the occupier vacates it. In this case the occupier decides to follow the same rule: if the free seat is his, he takes it, otherwise he insists on his place being vacated. The same policy is then adopted by the next unfortunate passenger, and so on. Each move takes a random time which is exponentially distributed with mean . What is the expected duration of the plane delay caused by these displacements?
4.II.26J
(a) Let be a Poisson process of rate . Let be a number between 0 and 1 and suppose that each jump in is counted as type one with probability and type two with probability , independently for different jumps and independently of the Poisson process. Let be the number of type-one jumps and the number of type-two jumps by time . What can you say about the pair of processes and ? What if we fix probabilities with and consider types instead of two?
(b) A person collects coupons one at a time, at jump times of a Poisson process of rate . There are types of coupons, and each time a coupon of type is obtained with probability , independently of the previously collected coupons and independently of the Poisson process. Let be the first time when a complete set of coupon types is collected. Show that
Let be the total number of coupons collected by the time the complete set of coupon types is obtained. Show that . Hence, or otherwise, deduce that does not depend on .
1.II.26I
A cell has been placed in a biological solution at time . After an exponential time of rate , it is divided, producing cells with probability , with the mean value means that the cell dies . The same mechanism is applied to each of the living cells, independently.
(a) Let be the number of living cells in the solution by time . Prove that . [You may use without proof, if you wish, the fact that, if a positive function satisfies for and is differentiable at zero, then , for some
Let be the probability generating function of . Prove that it satisfies the following differential equation
(b) Now consider the case where each cell is divided in two cells . Let be the number of cells produced in the solution by time .
Calculate the distribution of . Is an inhomogeneous Poisson process? If so, what is its rate ? Justify your answer.
2.II.26I
What does it mean to say that is a renewal process?
Let be a renewal process with holding times and let . For , set . Show that
for all , with equality if .
Consider now the case where are exponential random variables. Show that
and that, as ,
3.II.25I
Consider an loss system with arrival rate and service-time distribution . Thus, arrivals form a Poisson process of rate , service times are independent with common distribution , there are servers and there is no space for waiting. Use Little's Lemma to obtain a relation between the long-run average occupancy and the stationary probability that the system is full.
Cafe-Bar Duo has 23 serving tables. Each table can be occupied either by one person or two. Customers arrive either singly or in a pair; if a table is empty they are seated and served immediately, otherwise, they leave. The times between arrivals are independent exponential random variables of mean . Each arrival is twice as likely to be a single person as a pair. A single customer stays for an exponential time of mean 20 , whereas a pair stays for an exponential time of mean 30 ; all these times are independent of each other and of the process of arrivals. The value of orders taken at each table is a constant multiple of the time that it is occupied.
Express the long-run rate of revenue of the cafe as a function of the probability that an arriving customer or pair of customers finds the cafe full.
By imagining a cafe with infinitely many tables, show that where is a Poisson random variable of parameter . Deduce that is very small. [Credit will be given for any useful numerical estimate, an upper bound of being sufficient for full credit.]
4.II.26I
A particle performs a continuous-time nearest neighbour random walk on a regular triangular lattice inside an angle , starting from the corner. See the diagram below. The jump rates are from the corner and in each of the six directions if the particle is inside the angle. However, if the particle is on the edge of the angle, the rate is along the edge away from the corner and to each of three other neighbouring sites in the angle. See the diagram below, where a typical trajectory is also shown.
The particle position at time is determined by its vertical level and its horizontal position . For , if then . Here are positions inside, and 0 and positions on the edge of the angle, at vertical level .
Let be the times of subsequent jumps of process and consider the embedded discrete-time Markov chains
where is the vertical level immediately after time is the horizontal position immediately after time , and is the horizontal position immediately before time . (a) Assume that is a Markov chain with transition probabilities
and that is a continuous-time Markov chain with rates
[You will be asked to justify these assumptions in part (b) of the question.] Determine whether the chains and are transient, positive recurrent or null recurrent.
(b) Now assume that, conditional on and previously passed vertical levels, the horizontal positions and are uniformly distributed on . In other words, for all attainable values and for all ,
Deduce that and are indeed Markov chains with transition probabilities and rates as in (a).
(c) Finally, prove property .
B2.13
Let be a Poisson random measure of intensity on the plane . Denote by the circle of radius in centred at the origin and let be the largest radius such that contains precisely points of . [Thus is the largest circle about the origin containing no points of is the largest circle about the origin containing a single point of , and so on.] Calculate and .
Now let be a Poisson random measure of intensity on the line . Let be the length of the largest open interval that covers the origin and contains precisely points of . [Thus gives the length of the largest interval containing the origin but no points of gives the length of the largest interval containing the origin and a single point of , and so on.] Calculate and .
B3.13
Let be a renewal process with holding times and be a renewal-reward process over with a sequence of rewards . Under assumptions on and which you should state clearly, prove that the ratios
converge as . You should specify the form of convergence guaranteed by your assumptions. The law of large numbers, in the appropriate form, for sums and can be used without proof.
In a mountain resort, when you rent skiing equipment you are given two options. (1) You buy an insurance waiver that costs where is the daily equipment rent. Under this option, the shop will immediately replace, at no cost to you, any piece of equipment you break during the day, no matter how many breaks you had. (2) If you don't buy the waiver, you'll pay in the case of any break.
To find out which option is better for me, I decided to set up two models of renewalreward process . In the first model, (Option 1), all of the holding times are equal to 6 . In the second model, given that there is no break on day (an event of probability , we have , but given that there is a break on day , we have that is uniformly distributed on , and . (In the second model, I would not continue skiing after a break, whereas in the first I would.)
Calculate in each of these models the limit
representing the long-term average cost of a unit of my skiing time.
B4.12
Consider an queue with . Here is the arrival rate and is the mean service time. Prove that in equilibrium, the customer's waiting time has the moment-generating function given by
where is the moment-generating function of service time .
[You may assume that in equilibrium, the queue size at the time immediately after the customer's departure has the probability generating function
Deduce that when the service times are exponential of rate then
Further, deduce that takes value 0 with probability and that
Sketch the graph of as a function of .
Now consider the queue in the heavy traffic approximation, when the service-time distribution is kept fixed and the arrival rate , so that . Assuming that the second moment , check that the limiting distribution of the re-scaled waiting time is exponential, with rate .
B2.13
Let be the sum of independent exponential random variables of rate . Compute the moment generating function of .
Consider, for each fixed and for , an queue with arrival rate and with service times distributed as . Assume that the queue is empty at time 0 and write for the earliest time at which a customer departs leaving the queue empty. Show that, as converges in distribution to a random variable whose moment generating function satisfies
Hence obtain the mean value of .
For what service-time distribution would the empty-to-empty time correspond exactly to ?
B3.13
State the product theorem for Poisson random measures.
Consider a system of queues, each with infinitely many servers, in which, for , customers leaving the th queue immediately arrive at the th queue. Arrivals to the first queue form a Poisson process of rate . Service times at the th queue are all independent with distribution , and independent of service times at other queues, for all . Assume that initially the system is empty and write for the number of customers at queue at time . Show that are independent Poisson random variables.
In the case show that
where is a Poisson process of rate .
Suppose now that arrivals to the first queue stop at time . Determine the mean number of customers at the th queue at each time .
B4.12
Explain what is meant by a renewal process and by a renewal-reward process.
State and prove the law of large numbers for renewal-reward processes.
A component used in a manufacturing process has a maximum lifetime of 2 years and is equally likely to fail at any time during that period. If the component fails whilst in use, it is replaced immediately by a similar component, at a cost of . The factory owner may alternatively replace the component before failure, at a time of his choosing, at a cost of . What should the factory owner do?
B2.13
Two enthusiastic probability students, Ros and Guil, sit an examination which starts at time 0 and ends at time ; they both decide to use the time to attempt a proof of a difficult theorem which carries a lot of extra marks.
Ros' strategy is to write the proof continuously at a constant speed lines per unit time. In a time interval of length he has a probability of realising he has made a mistake. If that happens he instantly panics, erases everything he has written and starts all over again.
Guil, on the other hand, keeps cool and thinks carefully about what he is doing. In a time interval of length , he has a probability of writing the next line of proof and for each line he has written a probability of finding a mistake in that line, independently of all other lines he has written. When a mistake is found, he erases that line and carries on as usual, hoping for the best.
Both Ros and Guil realise that, even if they manage to finish the proof, they will not recognise that they have done so and will carry on writing as much as they can.
(a) Calculate , the probability that, for Ros, the length of his completed proof at time is at least .
(b) Let be the probability that Guil has lines of proof at time . Show that
where .
(c) Suppose now that every time Ros starts all over again, the time until the next mistake has distribution , independently of the past history. Write down a renewal-type integral equation satisfied by , the expected length of Ros' proof at time . What is the expected length of proof produced by him at the end of the examination if is the exponential distribution with mean ?
(d) What is the expected length of proof produced by Guil at the end of the examination if each line that he writes survives for a length of time with distribution , independently of all other lines?
B3.13
(a) Define a renewal process and a discrete renewal process.
(b) State and prove the Discrete Renewal Theorem.
(c) The sequence satisfies
for some collection of non-negative numbers summing to 1 . Let . Show that
Give a probabilistic interpretation of the numbers and .
(d) Let the sequence be given by
How is this related to the simple symmetric random walk on the integers starting from the origin, and its subsequent returns to the origin? Determine in this case, either by calculating or by showing that satisfies the quadratic equation
B4.12
Define a Poisson random measure. State and prove the Product Theorem for the jump times of a Poisson process with constant rate and independent random variables with law . Write down the corresponding result for a Poisson process in a space with rate when we associate with each an independent random variable with density .
Prove Campbell's Theorem, i.e. show that if is a Poisson random measure on the space with intensity measure and is a bounded measurable function then
where
Stars are scattered over three-dimensional space in a Poisson process with density . Masses of the stars are independent random variables; the mass of a star at has the density . The gravitational potential at the origin is given by
where is a constant. Find the moment generating function .
A galaxy occupies a sphere of radius centred at the origin. The density of stars is for points inside the sphere; the mass of each star has the exponential distribution with mean . Calculate the expected potential due to the galaxy at the origin. Let be a positive constant. Find the distribution of the distance from the origin to the nearest star whose contribution to the potential is at least .
B2.13
Let be a Poisson random measure on with constant intensity . For , denote by the line in obtained by rotating the line through an angle about the origin.
Consider the line process .
(i) What is the distribution of the number of lines intersecting the disc ?
(ii) What is the distribution of the distance from the origin to the nearest line?
(iii) What is the distribution of the distance from the origin to the th nearest line?
B3.13
Consider an queue with arrival rate and traffic intensity less
than 1. Prove that the moment-generating function of a typical busy period, , satisfies
where is the moment-generating function of a typical service time.
If service times are exponentially distributed with parameter , show that
for all sufficiently small but positive values of .
B4.12
Define a renewal process and a renewal reward process.
State and prove the strong law of large numbers for these processes.
[You may assume the strong law of large numbers for independent, identically-distributed random variables.
State and prove Little's formula.
Customers arrive according to a Poisson process with rate at a single server, but a restricted waiting room causes those who arrive when customers are already present to be lost. Accepted customers have service times which are independent and identicallydistributed with mean and independent of the arrival process. Let be the equilibrium probability that an arriving customer finds customers already present.
Using Little's formula, or otherwise, determine a relationship between and
Part II