Further Complex Methods

2021

• Paper 1, Section I, 7E

  Further Complex Methods | Part II, 2021

  Evaluate the integral

  $$\mathcal{P} \int_{0}^{\infty} \frac{\sin x}{x\left(x^{2}-1\right)} d x$$

  stating clearly any standard results involving contour integrals that you use.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2021

  (a) Functions $g_{1}(z)$ and $g_{2}(z)$ are analytic in a connected open set $\mathcal{D} \subseteq \mathbb{C}$ with $g_{1}=g_{2}$ in a non-empty open subset $\tilde{\mathcal{D}} \subset \mathcal{D}$. State the identity theorem.

  (b) Let $\mathcal{D}_{1}$ and $\mathcal{D}_{2}$ be connected open sets with $\mathcal{D}_{1} \cap \mathcal{D}_{2} \neq \emptyset$. Functions $f_{1}(z)$ and $f_{2}(z)$ are analytic on $\mathcal{D}_{1}$ and $\mathcal{D}_{2}$ respectively with $f_{1}=f_{2}$ on $\mathcal{D}_{1} \cap \mathcal{D}_{2}$. Explain briefly what is meant by analytic continuation of $f_{1}$ and use part (a) to prove that analytic continuation to $\mathcal{D}_{2}$ is unique.

  (c) The function $F(z)$ is defined by

  $$F(z)=\int_{-\infty}^{\infty} \frac{e^{i t}}{(t-z)^{n}} d t$$

  where $\operatorname{Im} z>0$ and $n$ is a positive integer. Use the method of contour deformation to construct the analytic continuation of $F(z)$ into $\operatorname{Im} z \leqslant 0$.

  (d) The function $G(z)$ is defined by

  $$G(z)=\int_{-\infty}^{\infty} \frac{e^{i t}}{(t-z)^{n}} d t$$

  where $\operatorname{Im} z \neq 0$ and $n$ is a positive integer. Prove that $G(z)$ experiences a discontinuity when $z$ crosses the real axis. Determine the value of this discontinuity. Hence, explain why $G(z)$ cannot be used as an analytic continuation of $F(z)$.

  comment

• Paper 2, Section I, 7E

  Further Complex Methods | Part II, 2021

  The function $w(z)$ satisfies the differential equation

  $$\tag{†} \frac{d^{2} w}{d z^{2}}+p(z) \frac{d w}{d z}+q(z) w=0$$

  where $p(z)$ and $q(z)$ are complex analytic functions except, possibly, for isolated singularities in $\overline{\mathbb{C}}=\mathbb{C} \cup\{\infty\}$ (the extended complex plane).

  (a) Given equation $(†)$, state the conditions for a point $z_{0} \in \mathbb{C}$ to be

  (i) an ordinary point,

  (ii) a regular singular point,

  (iii) an irregular singular point.

  (b) Now consider $z_{0}=\infty$ and use a suitable change of variables $z \rightarrow t$, with $y(t)=w(z)$, to rewrite $(†)$ as a differential equation that is satisfied by $y(t)$. Hence, deduce the conditions for $z_{0}=\infty$ to be

  (i) an ordinary point,

  (ii) a regular singular point,

  (iii) an irregular singular point.

  [In each case, you should express your answer in terms of the functions $p$ and $q$.]

  (c) Use the results above to prove that any equation of the form ( $\dagger$ ) must have at least one singular point in $\overline{\mathbb{C}}$.

  comment

• Paper 2, Section II, 13E

  Further Complex Methods | Part II, 2021

  The temperature $T(x, t)$ in a semi-infinite bar $(0 \leqslant x<\infty)$ satisfies the heat equation

  $$\frac{\partial T}{\partial t}=\kappa \frac{\partial^{2} T}{\partial x^{2}}, \quad \text { for } x>0 \text { and } t>0$$

  where $\kappa$ is a positive constant.

  For $t<0$, the bar is at zero temperature. For $t \geqslant 0$, the temperature is subject to the boundary conditions

  $$T(0, t)=a\left(1-e^{-b t}\right),$$

  where $a$ and $b$ are positive constants, and $T(x, t) \rightarrow 0$ as $x \rightarrow \infty$.

  (a) Show that the Laplace transform of $T(x, t)$ with respect to $t$ takes the form

  $$\hat{T}(x, p)=\hat{f}(p) e^{-x \sqrt{p / \kappa}}$$

  and find $\hat{f}(p)$. Hence write $\hat{T}(x, p)$ in terms of $a, b, \kappa, p$ and $x$.

  (b) By performing the inverse Laplace transform using contour integration, show that for $t \geqslant 0$

  $$T(x, t)=a\left[1-e^{-b t} \cos \left(\sqrt{\frac{b}{\kappa}} x\right)\right]+\frac{2 a b}{\pi} \mathcal{P} \int_{0}^{\infty} \frac{e^{-v^{2} t} \sin (x v / \sqrt{\kappa})}{v\left(v^{2}-b\right)} d v$$

  comment

• Paper 3 , Section I, 7E

  Further Complex Methods | Part II, 2021

  The Beta function is defined by

  $$B(p, q)=\int_{0}^{1} t^{p-1}(1-t)^{q-1} d t$$

  for $\operatorname{Re} p>0$ and $\operatorname{Re} q>0$.

  (a) Prove that $B(p, q)=B(q, p)$ and find $B(1, q)$.

  (b) Show that $(p+z) B(p, z+1)=z B(p, z)$.

  (c) For each fixed $p$ with $\operatorname{Re} p>0$, use part (b) to obtain the analytic continuation of $B(p, z)$ as an analytic function of $z \in \mathbb{C}$, with the exception of the points $z=$ $0,-1,-2,-3, \ldots$

  (d) Use part (c) to determine the type of singularity that the function $B(p, z)$ has at $z=0,-1,-2,-3, \ldots$, for fixed $p$ with $\operatorname{Re} p>0$.

  comment

• Paper 4 , Section I, 7E

  Further Complex Methods | Part II, 2021

  (a) Explain in general terms the meaning of the Papperitz symbol

  $$P\left\{\begin{array}{cccc} a & b & c & \\ \alpha & \beta & \gamma & z \\ \alpha^{\prime} & \beta^{\prime} & \gamma^{\prime} & \end{array}\right\}$$

  State a condition satisfied by $\alpha, \beta, \gamma, \alpha^{\prime}, \beta^{\prime}$ and $\gamma^{\prime}$. [You need not write down any differential equations explicitly, but should provide explicit explanation of the meaning of $a, b, c, \alpha, \beta, \gamma, \alpha^{\prime}, \beta^{\prime}$ and $\left.\gamma^{\prime} .\right]$

  (b) The Papperitz symbol

  $$P\left\{\begin{array}{cccc} 1 & -1 & \infty & \\ -m / 2 & m / 2 & n & z \\ m / 2 & -m / 2 & 1-n \end{array}\right\}$$

  where $n, m$ are constants, can be transformed into

  $$P\left\{\begin{array}{cccc} 0 & 1 & \infty & \\ 0 & 0 & n & \frac{1-z}{2} \\ m & -m & 1-n & \end{array}\right\}$$

  (i) Provide an explicit description of the transformations required to obtain ( $*)$ from $(t)$.

  (ii) One of the solutions to the $P$-equation that corresponds to $(*)$ is a hypergeometric function $F\left(a, b ; c ; z^{\prime}\right)$. Express $a, b, c$ and $z^{\prime}$ in terms of $n, m$ and $z$.

  comment

2020

• Paper 1, Section I, 7 E

  Further Complex Methods | Part II, 2020

  The function $I(z)$, defined by

  $$I(z)=\int_{0}^{\infty} t^{z-1} e^{-t} d t$$

  is analytic for $\operatorname{Re} z>0$.

  (i) Show that $I(z+1)=z I(z)$.

  (ii) Use part (i) to construct an analytic continuation of $I(z)$ into Re $z \leqslant 0$, except at isolated singular points, which you need to identify.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2020

  Use the change of variable $z=\sin ^{2} x$, to rewrite the equation

  $$\frac{d^{2} y}{d x^{2}}+k^{2} y=0$$

  where $k$ is a real non-zero number, as the hypergeometric equation

  $$\frac{d^{2} w}{d z^{2}}+\left(\frac{C}{z}+\frac{1+A+B-C}{z-1}\right) \frac{d w}{d z}+\frac{A B}{z(z-1)} w=0$$

  where $y(x)=w(z)$, and $A, B$ and $C$ should be determined explicitly.

  (i) Show that ( $\$)$ is a Papperitz equation, with 0,1 and $\infty$ as its regular singular points. Hence, write the corresponding Papperitz symbol,

  $$P\left\{\begin{array}{cccc} 0 & 1 & \infty \\ 0 & 0 & A \\ 1-C & C-A-B & B \end{array}\right\}$$

  in terms of $k$.

  (ii) By solving ( $\dagger$ ) directly or otherwise, find the hypergeometric function $F(A, B ; C ; z)$ that is the solution to $(\ddagger)$ and is analytic at $z=0$ corresponding to the exponent 0 at $z=0$, and satisfies $F(A, B ; C ; 0)=1$; moreover, write it in terms of $k$ and

  (iii) By performing a suitable exponential shifting find the second solution, independent of $F(A, B ; C ; z)$, which corresponds to the exponent $1-C$, and hence write $F\left(\frac{1+k}{2}, \frac{1-k}{2} ; \frac{3}{2} ; z\right)$ in terms of $k$ and $x$.

  comment

• Paper 2, Section $I$, E

  Further Complex Methods | Part II, 2020

  Evaluate

  $$\int_{C} \frac{d z}{\sin ^{3} z}$$

  where $C$ is the circle $|z|=4$ traversed in the counter-clockwise direction.

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2020

  A semi-infinite elastic string is initially at rest on the $x$-axis with $0 \leqslant x<\infty$. The transverse displacement of the string, $y(x, t)$, is governed by the partial differential equation

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}$$

  where $c$ is a positive real constant. For $t \geqslant 0$ the string is subject to the boundary conditions $y(0, t)=f(t)$ and $y(x, t) \rightarrow 0$ as $x \rightarrow \infty$.

  (i) Show that the Laplace transform of $y(x, t)$ takes the form

  $$\hat{y}(x, p)=\hat{f}(p) e^{-p x / c}$$

  (ii) For $f(t)=\sin \omega t$, with $\omega \in \mathbb{R}^{+}$, find $\hat{f}(p)$ and hence write $\hat{y}(x, p)$ in terms of $\omega, c, p$ and $x$. Obtain $y(x, t)$ by performing the inverse Laplace transform using contour integration. Provide a physical interpretation of the result.

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2020

  The Weierstrass elliptic function is defined by

  $$\mathcal{P}(z)=\frac{1}{z^{2}}+\sum_{m, n}\left[\frac{1}{\left(z-\omega_{m, n}\right)^{2}}-\frac{1}{\omega_{m, n^{2}}}\right]$$

  where $\omega_{m, n}=m \omega_{1}+n \omega_{2}$, with non-zero periods $\left(\omega_{1}, \omega_{2}\right)$ such that $\omega_{1} / \omega_{2}$ is not real, and where $(m, n)$ are integers not both zero.

  (i) Show that, in a neighbourhood of $z=0$,

  $$\mathcal{P}(z)=\frac{1}{z^{2}}+\frac{1}{20} g_{2} z^{2}+\frac{1}{28} g_{3} z^{4}+O\left(z^{6}\right)$$

  where

  $$g_{2}=60 \sum_{m, n}\left(\omega_{m, n}\right)^{-4}, \quad g_{3}=140 \sum_{m, n}\left(\omega_{m, n}\right)^{-6}$$

  (ii) Deduce that $\mathcal{P}$ satisfies

  $$\left(\frac{d \mathcal{P}}{d z}\right)^{2}=4 \mathcal{P}^{3}-g_{2} \mathcal{P}-g_{3}$$

  comment

• Paper 4, Section I, E

  Further Complex Methods | Part II, 2020

  The Hilbert transform of a function $f(x)$ is defined by

  $$\mathcal{H}(f)(y):=\frac{1}{\pi} \mathcal{P} \int_{-\infty}^{+\infty} \frac{f(x)}{y-x} d x$$

  Calculate the Hilbert transform of $f(x)=\cos \omega x$, where $\omega$ is a non-zero real constant.

  comment

2019

• Paper 1, Section I, A

  Further Complex Methods | Part II, 2019

  The Beta function is defined by

  $$B(p, q):=\int_{0}^{1} t^{p-1}(1-t)^{q-1} d t=\frac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}$$

  where $\operatorname{Re} p>0, \operatorname{Re} q>0$, and $\Gamma$ is the Gamma function.

  (a) By using a suitable substitution and properties of Beta and Gamma functions, show that

  $$\int_{0}^{1} \frac{d x}{\sqrt{1-x^{4}}}=\frac{[\Gamma(1 / 4)]^{2}}{\sqrt{32 \pi}}$$

  (b) Deduce that

  $$K(1 / \sqrt{2})=\frac{4[\Gamma(5 / 4)]^{2}}{\sqrt{\pi}}$$

  where $K(k)$ is the complete elliptic integral, defined as

  $$K(k):=\int_{0}^{1} \frac{d t}{\sqrt{\left(1-t^{2}\right)\left(1-k^{2} t^{2}\right)}}$$

  [Hint: You might find the change of variable $x=t\left(2-t^{2}\right)^{-1 / 2}$ helpful in part (b).]

  comment

• Paper 1, Section II, A

  Further Complex Methods | Part II, 2019

  (a) Consider the Papperitz symbol (or P-symbol):

  $$\tag{†} P\left\{\begin{array}{cccc} a & b & c & \\ \alpha & \beta & \gamma & z \\ \alpha^{\prime} & \beta^{\prime} & \gamma^{\prime} & \end{array}\right\}$$

  Explain in general terms what this $P$-symbol represents.

  [You need not write down any differential equations explicitly, but should provide an explanation of the meaning of $a, b, c, \alpha, \beta, \gamma, \alpha^{\prime}, \beta^{\prime}$ and $\left.\gamma^{\prime} .\right]$

  (b) Prove that the action of $[(z-a) /(z-b)]^{\delta}$ on $(†)$ results in the exponential shifting,

  $$\tag{‡} P\left\{\begin{array}{cccc} a & b & c \\ \alpha+\delta & \beta-\delta & \gamma & z \\ \alpha^{\prime}+\delta & \beta^{\prime}-\delta & \gamma^{\prime} \end{array}\right\}$$

  [Hint: It may prove useful to start by considering the relationship between two solutions, $\omega$ and $\omega_{1}$, which satisfy the $P$-equations described by the respective $P$-symbols ($†$) and $‡$]

  (c) Explain what is meant by a Möbius transformation of a second order differential equation. By using suitable transformations acting on $(†)$, show how to obtain the $P$ symbol

  $$\tag{*} P\left\{\begin{array}{cccc} 0 & 1 & \infty \\ 0 & 0 & a & z \\ 1-c & c-a-b & b \end{array}\right\}$$

  which corresponds to the hypergeometric equation.

  (d) The hypergeometric function $F(a, b, c ; z)$ is defined to be the solution of the differential equation corresponding to $(\star)$ that is analytic at $z=0$ with $F(a, b, c ; 0)=1$, which corresponds to the exponent zero. Use exponential shifting to show that the second solution, which corresponds to the exponent $1-c$, is

  $$z^{1-c} F(a-c+1, b-c+1,2-c ; z) .$$

  comment

• Paper 2, Section I, A

  Further Complex Methods | Part II, 2019

  Assume that $|f(z) / z| \rightarrow 0$ as $|z| \rightarrow \infty$ and that $f(z)$ is analytic in the upper half-plane (including the real axis). Evaluate

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x\left(x^{2}+a^{2}\right)} d x$$

  where $a$ is a positive real number.

  [You must state clearly any standard results involving contour integrals that you use.]

  comment

• Paper 2, Section II, A

  Further Complex Methods | Part II, 2019

  The Riemann zeta function is defined as

  $$\zeta(z):=\sum_{n=1}^{\infty} \frac{1}{n^{z}}$$

  for $R e(z)>1$, and by analytic continuation to the rest of $\mathbb{C}$ except at singular points. The integral representation of ( $\dagger$ ) for $\operatorname{Re}(z)>1$ is given by

  $$\zeta(z)=\frac{1}{\Gamma(z)} \int_{0}^{\infty} \frac{t^{z-1}}{e^{t}-1} d t$$

  where $\Gamma$ is the Gamma function.

  (a) The Hankel representation is defined as

  $$\zeta(z)=\frac{\Gamma(1-z)}{2 \pi i} \int_{-\infty}^{\left(0^{+}\right)} \frac{t^{z-1}}{e^{-t}-1} d t$$

  Explain briefly why this representation gives an analytic continuation of $\zeta(z)$ as defined in ( $\ddagger$ ) to all $z$ other than $z=1$, using a diagram to illustrate what is meant by the upper limit of the integral in $(\star)$.

  [You may assume $\Gamma(z) \Gamma(1-z)=\pi / \sin (\pi z)$.]

  (b) Find

  $$\operatorname{Res}\left(\frac{t^{-z}}{e^{-t}-1}, t=2 \pi i n\right)$$

  where $n$ is an integer and the poles are simple.

  (c) By considering

  $$\int_{\gamma} \frac{t^{-z}}{e^{-t}-1} d t$$

  where $\gamma$ is a suitably modified Hankel contour and using the result of part (b), derive the reflection formula:

  $$\zeta(1-z)=2^{1-z} \pi^{-z} \cos \left(\frac{1}{2} \pi z\right) \Gamma(z) \zeta(z)$$

  comment

• Paper 3, Section I, A

  Further Complex Methods | Part II, 2019

  The equation

  $$z w^{\prime \prime}+w=0$$

  has solutions of the form

  $$w(z)=\int_{\gamma} e^{z t} f(t) d t$$

  for suitably chosen contours $\gamma$ and some suitable function $f(t)$.

  (a) Find $f(t)$ and determine the required condition on $\gamma$, which you should express in terms of $z$ and $t$.

  (b) Use the result of part (a) to specify a possible contour with the help of a clearly labelled diagram.

  comment

• Paper 4, Section I, A

  Further Complex Methods | Part II, 2019

  A single-valued function $\operatorname{Arcsin}(z)$ can be defined, for $0 \leqslant \arg z<2 \pi$, by means of an integral as:

  $$\operatorname{Arcsin}(z)=\int_{0}^{z} \frac{d t}{\left(1-t^{2}\right)^{1 / 2}}$$

  (a) Choose a suitable branch-cut with the integrand taking a value $+1$ at the origin on the upper side of the cut, i.e. at $t=0^{+}$, and describe suitable paths of integration in the two cases $0 \leqslant \arg z \leqslant \pi$ and $\pi<\arg z<2 \pi$.

  (b) Construct the multivalued function $\arcsin (z)$ by analytic continuation.

  (c) Express arcsin $\left(e^{2 \pi i} z\right)$ in terms of $\operatorname{Arcsin}(z)$ and deduce the periodicity property of $\sin (z)$.

  comment

2018

• Paper 1, Section I, B

  Further Complex Methods | Part II, 2018

  The Beta and Gamma functions are defined by

  $$\begin{aligned} B(p, q) &=\int_{0}^{1} t^{p-1}(1-t)^{q-1} d t \\ \Gamma(p) &=\int_{0}^{\infty} e^{-t} t^{p-1} d t \end{aligned}$$

  where $\operatorname{Re} p>0, \operatorname{Re} q>0$.

  (a) By using a suitable substitution, or otherwise, prove that

  $$B(z, z)=2^{1-2 z} B\left(z, \frac{1}{2}\right)$$

  for $\operatorname{Re} z>0$. Extending $B$ by analytic continuation, for which values of $z \in \mathbb{C}$ does this result hold?

  (b) Prove that

  $$B(p, q)=\frac{\Gamma(p) \Gamma(q)}{\Gamma(p+q)}$$

  for $\operatorname{Re} p>0, \operatorname{Re} q>0$

  comment

• Paper 1, Section II, B

  Further Complex Methods | Part II, 2018

  The equation

  $$\tag{†} z w^{\prime \prime}+2 a w^{\prime}+z w=0,$$

  where $a$ is a constant with $\operatorname{Re} a>0$, has solutions of the form

  $$w(z)=\int_{\gamma} e^{z t} f(t) d t$$

  for suitably chosen contours $\gamma$ and some suitable function $f(t)$.

  (a) Find $f(t)$ and determine the condition on $\gamma$, which you should express in terms of $z, t$ and $a$.

  (b) Use the results of part (a) to show that $\gamma$ can be a finite contour and specify two possible finite contours with the help of a clearly labelled diagram. Hence, find the corresponding solution of the equation $(†)$ in the case $a=1$.

  (c) In the case $a=1$ and real $z$, show that $\gamma$ can be an infinite contour and specify two possible infinite contours with the help of a clearly labelled diagram. [Hint: Consider separately the cases $z>0$ and $z<0$.] Hence, find a second, linearly independent solution of the equation ( $\dagger$ ) in this case.

  comment

• Paper 2, Section $I$, $7 \mathrm{~B}$

  Further Complex Methods | Part II, 2018

  Show that

  $$\int_{-\infty}^{\infty} \frac{\cos n x-\cos m x}{x^{2}} d x=\pi(m-n),$$

  in the sense of Cauchy principal value, where $n$ and $m$ are positive integers. [State clearly any standard results involving contour integrals that you use.]

  comment

• Paper 2, Section II, B

  Further Complex Methods | Part II, 2018

  Consider a multi-valued function $w(z)$.

  (a) Explain what is meant by a branch point and a branch cut.

  (b) Consider $z=e^{w}$.

  (i) By writing $z=r e^{i \theta}$, where $0 \leqslant \theta<2 \pi$, and $w=u+i v$, deduce the expression for $w(z)$ in terms of $r$ and $\theta$. Hence, show that $w$ is infinitely valued and state its principal value.

  (ii) Show that $z=0$ and $z=\infty$ are the branch points of $w$. Deduce that the line $\operatorname{Im} z=0, \operatorname{Re} z>0$ is a possible choice of branch cut.

  (iii) Use the Cauchy-Riemann conditions to show that $w$ is analytic in the cut plane. Show that $\frac{d w}{d z}=\frac{1}{z}$.

  comment

• Paper 3, Section I, B

  Further Complex Methods | Part II, 2018

  Using a suitable branch cut, show that

  $$\int_{-a}^{a}\left(a^{2}-x^{2}\right)^{1 / 2} d x=\frac{a^{2} \pi}{2},$$

  where $a>0$.

  comment

• Paper 4, Section I, B

  Further Complex Methods | Part II, 2018

  State the conditions for a point $z=z_{0}$ to be a regular singular point of a linear second-order homogeneous ordinary differential equation in the complex plane.

  Find all singular points of the Bessel equation

  $$z^{2} y^{\prime \prime}(z)+z y^{\prime}(z)+\left(z^{2}-\frac{1}{4}\right) y(z)=0$$

  and determine whether they are regular or irregular.

  By writing $y(z)=f(z) / \sqrt{z}$, find two linearly independent solutions of $(*)$. Comment on the relationship of your solutions to the nature of the singular points.

  comment

2017

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2017

  Calculate the value of the integral

  $$P \int_{-\infty}^{\infty} \frac{e^{-i x}}{x^{n}} d x$$

  where $P$ stands for Principal Value and $n$ is a positive integer.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2017

  The Riemann zeta function is defined by

  $$\zeta_{R}(s)=\sum_{n=1}^{\infty} n^{-s}$$

  for $\operatorname{Re}(s)>1$.

  Show that

  $$\zeta_{R}(s)=\frac{1}{\Gamma(s)} \int_{0}^{\infty} \frac{t^{s-1}}{e^{t}-1} d t$$

  Let $I(s)$ be defined by

  $$I(s)=\frac{\Gamma(1-s)}{2 \pi i} \int_{C} \frac{t^{s-1}}{e^{-t}-1} d t$$

  where $C$ is the Hankel contour.

  Show that $I(s)$ provides an analytic continuation of $\zeta_{R}(s)$ for a range of $s$ which should be determined.

  Hence evaluate $\zeta_{R}(-1)$.

  comment

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2017

  Euler's formula for the Gamma function is

  $$\Gamma(z)=\frac{1}{z} \prod_{n=1}^{\infty}\left(1+\frac{1}{n}\right)^{z}\left(1+\frac{z}{n}\right)^{-1}$$

  Use Euler's formula to show

  $$\frac{\Gamma(2 z)}{2^{2 z} \Gamma(z) \Gamma\left(z+\frac{1}{2}\right)}=C$$

  where $C$ is a constant.

  Evaluate $C$.

  [Hint: You may use $\Gamma(z) \Gamma(1-z)=\pi / \sin (\pi z) .]$

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2017

  The hypergeometric equation is represented by the Papperitz symbol

  $$P\left\{\begin{array}{ccc} 0 & 1 & \infty \\ 0 & 0 & a \\ 1-c & c-a-b & b \end{array}\right\}$$

  and has solution $y_{0}(z)=F(a, b, c ; z)$.

  Functions $y_{1}(z)$ and $y_{2}(z)$ are defined by

  $$y_{1}(z)=F(a, b, a+b+1-c ; 1-z)$$

  and

  $$y_{2}(z)=(1-z)^{c-a-b} F(c-a, c-b, c-a-b+1 ; 1-z),$$

  where $c-a-b$ is not an integer.

  Show that $y_{1}(z)$ and $y_{2}(z)$ obey the hypergeometric equation $(*)$.

  Explain why $y_{0}(z)$ can be written in the form

  $$y_{0}(z)=A y_{1}(z)+B y_{2}(z)$$

  where $A$ and $B$ are independent of $z$ but depend on $a, b$ and $c$.

  Suppose that

  $$F(a, b, c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  with $\operatorname{Re}(c)>\operatorname{Re}(b)>0$ and $|\arg (1-z)|<\pi$. Find expressions for $A$ and $B$.

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2017

  Find all the singular points of the differential equation

  $$z \frac{d^{2} y}{d z^{2}}+(2-z) \frac{d y}{d z}-y=0$$

  and determine whether they are regular or irregular singular points.

  By writing $y(z)=f(z) / z$, find two linearly independent solutions to this equation.

  Comment on the relationship of your solutions to the nature of the singular points of the original differential equation.

  comment

• Paper 4, Section I, $7 \mathbf{E} \quad$

  Further Complex Methods | Part II, 2017

  Consider the differential equation

  $$z \frac{d^{2} y}{d z^{2}}-2 \frac{d y}{d z}+z y=0$$

  Laplace's method finds a solution of this differential equation by writing $y(z)$ in the form

  $$y(z)=\int_{C} e^{z t} f(t) d t$$

  where $C$ is a closed contour.

  Determine $f(t)$. Hence find two linearly independent real solutions of $(\star)$ for $z$ real.

  comment

2016

• Paper 1, Section I, A

  Further Complex Methods | Part II, 2016

  Evaluate the integral

  $$f(p)=\mathcal{P} \int_{-\infty}^{\infty} d x \frac{e^{i p x}}{x^{4}-1}$$

  where $p$ is a real number, for (i) $p>0$ and (ii) $p<0$.

  comment

• Paper 1, Section II, A

  Further Complex Methods | Part II, 2016

  (a) Legendre's equation for $w(z)$ is

  $$\left(z^{2}-1\right) w^{\prime \prime}+2 z w^{\prime}-\ell(\ell+1) w=0, \quad \text { where } \quad \ell=0,1,2, \ldots$$

  Let $\mathcal{C}$ be a closed contour. Show by direct substitution that for $z$ within $\mathcal{C}$

  $$\int_{\mathcal{C}} d t \frac{\left(t^{2}-1\right)^{\ell}}{(t-z)^{\ell+1}}$$

  is a non-trivial solution of Legendre's equation.

  (b) Now consider

  $$Q_{\nu}(z)=\frac{1}{4 i \sin \nu \pi} \int_{\mathcal{C}^{\prime}} d t \frac{\left(t^{2}-1\right)^{\nu}}{(t-z)^{\nu+1}}$$

  for real $\nu>-1$ and $\nu \neq 0,1,2, \ldots$. The closed contour $\mathcal{C}^{\prime}$ is defined to start at the origin, wind around $t=1$ in a counter-clockwise direction, then wind around $t=-1$ in a clockwise direction, then return to the origin, without encircling the point $z$. Assuming that $z$ does not lie on the real interval $-1 \leqslant x \leqslant 1$, show by deforming $\mathcal{C}^{\prime}$ onto this interval that functions $Q_{\ell}(z)$ may be defined as limits of $Q_{\nu}(z)$ with $\nu \rightarrow \ell=0,1,2, \ldots$.

  Find an explicit expression for $Q_{0}(z)$ and verify that it satisfies Legendre's equation with $\ell=0$.

  comment

• Paper 2, Section I, A

  Further Complex Methods | Part II, 2016

  The Euler product formula for the Gamma function is

  $$\Gamma(z)=\lim _{n \rightarrow \infty} \frac{n ! n^{z}}{z(z+1) \ldots(z+n)}$$

  Use this to show that

  $$\frac{\Gamma(2 z)}{2^{2 z} \Gamma(z) \Gamma\left(z+\frac{1}{2}\right)}=c,$$

  where $c$ is a constant, independent of $z$. Find the value of $c$.

  comment

• Paper 2, Section II, A

  Further Complex Methods | Part II, 2016

  The Hurwitz zeta function $\zeta_{\mathrm{H}}(s, q)$ is defined for $\operatorname{Re}(q)>0$ by

  $$\zeta_{\mathrm{H}}(s, q)=\sum_{n=0}^{\infty} \frac{1}{(q+n)^{s}}$$

  State without proof the complex values of $s$ for which this series converges.

  Consider the integral

  $$I(s, q)=\frac{\Gamma(1-s)}{2 \pi i} \int_{\mathcal{C}} d z \frac{z^{s-1} e^{q z}}{1-e^{z}}$$

  where $\mathcal{C}$ is the Hankel contour. Show that $I(s, q)$ provides an analytic continuation of the Hurwitz zeta function for all $s \neq 1$. Include in your account a careful discussion of removable singularities. [Hint: $\Gamma(s) \Gamma(1-s)=\pi / \sin (\pi s)$.]

  Show that $I(s, q)$ has a simple pole at $s=1$ and find its residue.

  comment

• Paper 3, Section I, A

  Further Complex Methods | Part II, 2016

  The functions $f(x)$ and $g(x)$ have Laplace transforms $F(p)$ and $G(p)$ respectively, and $f(x)=g(x)=0$ for $x \leqslant 0$. The convolution $h(x)$ of $f(x)$ and $g(x)$ is defined by

  $$h(x)=\int_{0}^{x} f(y) g(x-y) d y \quad \text { for } \quad x>0 \quad \text { and } \quad h(x)=0 \quad \text { for } \quad x \leqslant 0$$

  Express the Laplace transform $H(p)$ of $h(x)$ in terms of $F(p)$ and $G(p)$.

  Now suppose that $f(x)=x^{\alpha}$ and $g(x)=x^{\beta}$ for $x>0$, where $\alpha, \beta>-1$. Find expressions for $F(p)$ and $G(p)$ by using a standard integral formula for the Gamma function. Find an expression for $h(x)$ by using a standard integral formula for the Beta function. Hence deduce that

  $$\frac{\Gamma(z) \Gamma(w)}{\Gamma(z+w)}=\mathrm{B}(z, w)$$

  for all $\operatorname{Re}(z)>0, \operatorname{Re}(w)>0$.

  comment

• Paper 4, Section I, 7A

  Further Complex Methods | Part II, 2016

  Consider the equation for $w(z)$ :

  $$w^{\prime \prime}+p(z) w^{\prime}+q(z) w=0 .$$

  State necessary and sufficient conditions on $p(z)$ and $q(z)$ for $z=0$ to be (i) an ordinary point or (ii) a regular singular point. Derive the corresponding conditions for the point $z=\infty$.

  Determine the most general equation of the form $(*)$ that has regular singular points at $z=0$ and $z=\infty$, with all other points being ordinary.

  comment

2015

• Paper 1, Section $I$, B

  Further Complex Methods | Part II, 2015

  Evaluate the real integral

  $$\int_{0}^{\infty} \frac{x^{1 / 2} \ln x}{1+x^{2}} d x$$

  where $x^{1 / 2}$ is taken to be the positive square root.

  What is the value of

  $$\int_{0}^{\infty} \frac{x^{1 / 2}}{1+x^{2}} d x ?$$

  comment

• Paper 1, Section II, B

  Further Complex Methods | Part II, 2015

  Consider the differential equation

  $$x y^{\prime \prime}+(a-x) y^{\prime}-b y=0$$

  where $a$ and $b$ are constants with $\operatorname{Re}(b)>0$ and $\operatorname{Re}(a-b)>0$. Laplace's method for finding solutions involves writing

  $$y(x)=\int_{C} e^{x t} f(t) d t$$

  for some suitable contour $C$ and some suitable function $f(t)$. Determine $f(t)$ for the equation $(*)$ and use a clearly labelled diagram to specify contours $C$ giving two independent solutions when $x$ is real in each of the cases $x>0$ and $x<0$.

  Now let $a=3$ and $b=1$. Find explicit expressions for two independent solutions to $(*)$. Find, in addition, a solution $y(x)$ with $y(0)=1$.

  comment

• Paper 2, Section I, B

  Further Complex Methods | Part II, 2015

  Give a brief description of what is meant by analytic continuation.

  The dilogarithm function is defined by

  $$\mathrm{Li}_{2}(z)=\sum_{n=1}^{\infty} \frac{z^{n}}{n^{2}}, \quad|z|<1$$

  Let

  $$f(z)=-\int_{C} \frac{1}{u} \ln (1-u) d u$$

  where $C$ is a contour that runs from the origin to the point $z$. Show that $f(z)$ provides an analytic continuation of $\mathrm{Li}_{2}(z)$ and describe its domain of definition in the complex plane, given a suitable branch cut.

  comment

• Paper 2, Section II, B

  Further Complex Methods | Part II, 2015

  The Riemann zeta function is defined by the sum

  $$\zeta(s)=\sum_{n=1}^{\infty} n^{-s}$$

  which converges for $\operatorname{Re} s>1$. Show that

  $$\zeta(s)=\frac{1}{\Gamma(s)} \int_{0}^{\infty} \frac{t^{s-1}}{e^{t}-1} d t, \quad \operatorname{Re} s>1$$

  The analytic continuation of $\zeta(s)$ is given by the Hankel contour integral

  $$\zeta(s)=\frac{\Gamma(1-s)}{2 \pi i} \int_{-\infty}^{0+} \frac{t^{s-1}}{e^{-t}-1} d t$$

  Verify that this agrees with the integral $(*)$ above when Re $s>1$ and $s$ is not an integer. [You may assume $\Gamma(s) \Gamma(1-s)=\pi / \sin \pi s$.] What happens when $s=2,3,4, \ldots$ ?

  Evaluate $\zeta(0)$. Show that $\left(e^{-t}-1\right)^{-1}+\frac{1}{2}$ is an odd function of $t$ and hence, or otherwise, show that $\zeta(-2 n)=0$ for any positive integer $n$.

  comment

• Paper 3, Section $I$, B

  Further Complex Methods | Part II, 2015

  Define what is meant by the Cauchy principal value in the particular case

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{\cos x}{x^{2}-a^{2}} d x$$

  where the constant $a$ is real and strictly positive. Evaluate this expression explicitly, stating clearly any standard results involving contour integrals that you use.

  comment

• Paper 4, Section I, B

  Further Complex Methods | Part II, 2015

  Explain how the Papperitz symbol

  $$P\left\{\begin{array}{cccc} z_{1} & z_{2} & z_{3} & \\ \alpha_{1} & \beta_{1} & \gamma_{1} & z \\ \alpha_{2} & \beta_{2} & \gamma_{2} & \end{array}\right\}$$

  represents a differential equation with certain properties. [You need not write down the differential equation explicitly.]

  The hypergeometric function $F(a, b, c ; z)$ is defined to be the solution of the equation given by the Papperitz symbol

  

  that is analytic at $z=0$ and such that $F(a, b, c ; 0)=1$. Show that

  $$F(a, b, c ; z)=(1-z)^{-a} F\left(a, c-b, c ; \frac{z}{z-1}\right) \text {, }$$

  indicating clearly any general results for manipulating Papperitz symbols that you use.

  comment

2014

• Paper 1, Section $I$, B

  Further Complex Methods | Part II, 2014

  Show that the Cauchy-Riemann equations for $f: \mathbb{C} \rightarrow \mathbb{C}$ are equivalent to

  $$\frac{\partial f}{\partial \bar{z}}=0 \text {, }$$

  where $z=x+i y$, and $\partial / \partial \bar{z}$ should be defined in terms of $\partial / \partial x$ and $\partial / \partial y$. Use Green's theorem, together with the formula $d z d \bar{z}=-2 i d x d y$, to establish the generalised Cauchy formula

  $$\oint_{\gamma} f(z, \bar{z}) d z=-\iint_{D} \frac{\partial f}{\partial \bar{z}} d z d \bar{z}$$

  where $\gamma$ is a contour in the complex plane enclosing the region $D$ and $f$ is sufficiently differentiable.

  comment

• Paper 1, Section II, 14B

  Further Complex Methods | Part II, 2014

  Obtain solutions of the second-order ordinary differential equation

  $$z w^{\prime \prime}-w=0$$

  in the form

  $$w(z)=\int_{\gamma} f(t) e^{-z t} d t$$

  where the function $f$ and the choice of contour $\gamma$ should be determined from the differential equation.

  Show that a non-trivial solution can be obtained by choosing $\gamma$ to be a suitable closed contour, and find the resulting solution in this case, expressing your answer in the form of a power series.

  Describe a contour $\gamma$ that would provide a second linearly independent solution for the case $\operatorname{Re}(z)>0$.

  comment

• Paper 2, Section I, B

  Further Complex Methods | Part II, 2014

  Suppose $z=0$ is a regular singular point of a linear second-order homogeneous ordinary differential equation in the complex plane. Define the monodromy matrix $M$ around $z=0$.

  Demonstrate that if

  $$M=\left(\begin{array}{ll} 1 & 1 \\ 0 & 1 \end{array}\right)$$

  then the differential equation admits a solution of the form $a(z)+b(z) \log z$, where $a(z)$ and $b(z)$ are single-valued functions.

  comment

• Paper 2, Section II, 14B

  Further Complex Methods | Part II, 2014

  Use the Euler product formula

  $$\Gamma(z)=\lim _{n \rightarrow \infty} \frac{n ! n^{z}}{z(z+1) \ldots(z+n)}$$

  to show that:

  (i) $\Gamma(z+1)=z \Gamma(z)$;

  (ii) $\frac{1}{\Gamma(z)}=z e^{\gamma z} \prod_{k=1}^{\infty}\left(1+\frac{z}{k}\right) e^{-z / k}$, where $\gamma=\lim _{n \rightarrow \infty}\left(1+\frac{1}{2}+\cdots+\frac{1}{n}-\log n\right)$.

  Deduce that

  $$\frac{d}{d z} \log (\Gamma(z))=-\gamma-\frac{1}{z}+z \sum_{k=1}^{\infty} \frac{1}{k(z+k)}$$

  comment

• Paper 3, Section I, B

  Further Complex Methods | Part II, 2014

  State the conditions for a point $z=z_{0}$ to be a regular singular point of a linear second-order homogeneous ordinary differential equation in the complex plane.

  Find all singular points of the Airy equation

  $$w^{\prime \prime}(z)-z w(z)=0$$

  and determine whether they are regular or irregular.

  comment

• Paper 4, Section I, B

  Further Complex Methods | Part II, 2014

  Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be a function such that

  $$f\left(z+\omega_{1}\right)=f(z), \quad f\left(z+\omega_{2}\right)=f(z)$$

  where $\omega_{1}, \omega_{2} \in \mathbb{C} \backslash\{0\}$ and $\omega_{1} / \omega_{2}$ is not real. Show that if $f$ is analytic on $\mathbb{C}$ then it is a constant. [Liouville's theorem may be used if stated.] Give an example of a non-constant meromorphic function which satisfies (1).

  comment

2013

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2013

  Prove that there are no second order linear ordinary homogeneous differential equations for which all points in the extended complex plane are analytic.

  Find all such equations which have one regular singular point at $z=0$.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2013

  Show that the equation

  $$(z-1) w^{\prime \prime}-z w^{\prime}+(4-2 z) w=0$$

  has solutions of the form $w(z)=\int_{\gamma} \exp (z t) f(t) d t$, where

  $$f(t)=\frac{\exp (-t)}{(t-a)(t-b)^{2}}$$

  and the contour $\gamma$ is any closed curve in the complex plane, where $a$ and $b$ are real constants which should be determined.

  Use this to find the general solution, evaluating the integrals explicitly.

  comment

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2013

  (i) Find all branch points of $\left(z^{3}-1\right)^{1 / 4}$ on an extended complex plane.

  (ii) Use a branch cut to evaluate the integral

  $$\int_{-2}^{2}\left(4-x^{2}\right)^{1 / 2} d x$$

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2013

  The Beta function is defined for $\operatorname{Re}(z)>0$ as

  $$B(z, q)=\int_{0}^{1} t^{q-1}(1-t)^{z-1} d t, \quad(\operatorname{Re}(q)>0)$$

  and by analytic continuation elsewhere in the complex $z$-plane.

  Show that:

  (i) $(z+q) B(z+1, q)=z B(z, q)$;

  (ii) $\Gamma(z)^{2}=B(z, z) \Gamma(2 z)$.

  By considering $\Gamma\left(z / 2^{m}\right)$ for all positive integers $m$, deduce that $\Gamma(z) \neq 0$ for all $z$ with $\operatorname{Re}(z)>0$.

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2013

  Let a real-valued function $u=u(x, y)$ be the real part of a complex-valued function $f=f(z)$ which is analytic in the neighbourhood of a point $z=0$, where $z=x+i y .$ Derive a formula for $f$ in terms of $u$ and use it to find an analytic function $f$ whose real part is

  $$\frac{x^{3}+x^{2}-y^{2}+x y^{2}}{(x+1)^{2}+y^{2}}$$

  and such that $f(0)=0$.

  comment

• Paper 4, Section I, E

  Further Complex Methods | Part II, 2013

  Let the function $f(z)$ be analytic in the upper half-plane and such that $|f(z)| \rightarrow 0$ as $|z| \rightarrow \infty$. Show that

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{f(x)}{x} d x=i \pi f(0),$$

  where $\mathcal{P}$ denotes the Cauchy principal value.

  Use the Cauchy integral theorem to show that

  $$\mathcal{P} \int_{-\infty}^{\infty} \frac{u(x, 0)}{x-t} d x=-\pi v(t, 0), \quad \mathcal{P} \int_{-\infty}^{\infty} \frac{v(x, 0)}{x-t} d x=\pi u(t, 0),$$

  where $u(x, y)$ and $v(x, y)$ are the real and imaginary parts of $f(z)$.

  comment

2012

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2012

  Recall that if $f(z)$ is analytic in a neighbourhood of $z_{0} \neq 0$, then

  $$f(z)+\overline{f\left(z_{0}\right)}=2 u\left(\frac{z+\overline{z_{0}}}{2}, \frac{z-\overline{z_{0}}}{2 i}\right)$$

  where $u(x, y)$ is the real part of $f(z)$. Use this fact to construct the imaginary part of an analytic function whose real part is given by

  $$u(x, y)=y \int_{-\infty}^{\infty} \frac{g(t) d t}{(t-x)^{2}+y^{2}}, \quad x, y \in \mathbb{R}, y \neq 0$$

  where $g(t)$ is real and has sufficient smoothness and decay.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2012

  (a) Suppose that $F(z), z=x+i y, x, y \in \mathbb{R}$, is analytic in the upper-half complex $z$-plane and $O(1 / z)$ as $z \rightarrow \infty, y \geqslant 0$. Show that the real and imaginary parts of $F(x)$, denoted by $U(x)$ and $V(x)$ respectively, satisfy the so-called Kramers-Kronig formulae:

  $$U(x)=H V(x), \quad V(x)=-H U(x), \quad x \in \mathbb{R} .$$

  Here, $H$ denotes the Hilbert transform, i.e.,

  $$(H f)(x)=\frac{1}{\pi} \mathrm{PV} \int_{-\infty}^{\infty} \frac{f(\xi)}{\xi-x} d \xi$$

  where $\mathrm{PV}$ denotes the principal value integral.

  (b) Let the real function $u(x, y)$ satisfy the Laplace equation in the upper-half complex z-plane, i.e.,

  $$\frac{\partial^{2} u(x, y)}{\partial x^{2}}+\frac{\partial^{2} u(x, y)}{\partial y^{2}}=0, \quad-\infty<x<\infty, \quad y>0$$

  Assuming that $u(x, y)$ decays for large $|x|$ and for large $y$, show that $F=u_{z}$ is an analytic function for $\operatorname{Im} z>0, z=x+i y$. Then, find an expression for $u_{y}(x, 0)$ in terms of $u_{x}(x, 0)$.

  comment

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2012

  The hypergeometric function $F(a, b ; c ; z)$ is defined as the particular solution of the second order linear ODE characterised by the Papperitz symbol

  $$\mathrm{P}\left\{\begin{array}{cccc} 0 & 1 & \infty \\ 0 & 0 & a & z \\ 1-c & c-a-b & b \end{array}\right\}$$

  that is analytic at $z=0$ and satisfies $F(a, b ; c ; 0)=1$.

  Using the fact that a second solution $w(z)$ of the above ODE is of the form

  $$w(z)=z^{1-c} u(z)$$

  where $u(z)$ is analytic in the neighbourhood of the origin, express $w(z)$ in terms of $F$.

  comment

• Paper 2, Section II, $14 \mathrm{E}$

  Further Complex Methods | Part II, 2012

  Let the complex function $q(x, t)$ satisfy

  $$i \frac{\partial q(x, t)}{\partial t}+\frac{\partial^{2} q(x, t)}{\partial x^{2}}=0, \quad 0<x<\infty, 0<t<T$$

  where $T$ is a positive constant. The unified transform method implies that the solution of any well-posed problem for the above equation is given by

  $$\begin{aligned} q(x, t) &=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i k x-i k^{2} t} \hat{q}_{0}(k) d k \\ &-\frac{1}{2 \pi} \int_{L} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(i k^{2}, t\right)-i \tilde{g}_{1}\left(i k^{2}, t\right)\right] d k \end{aligned}$$

  where $L$ is the union of the rays $(i \infty, 0)$ and $(0, \infty), \hat{q}_{0}(k)$ denotes the Fourier transform of the initial condition $q_{0}(x)$, and $\tilde{g}_{0}, \tilde{g}_{1}$ denote the $t$-transforms of the boundary values $q(0, t), q_{x}(0, t)$ :

  $$\begin{gathered} \hat{q}_{0}(k)=\int_{0}^{\infty} e^{-i k x} q_{0}(x) d x, \quad \operatorname{Im} k \leqslant 0, \\ =\int_{0}^{t} e^{k s} q(0, s) d s, \quad \tilde{g}_{1}(k, t)=\int_{0}^{t} e^{k s} q_{x}(0, s) d s, \quad k \in \mathbb{C}, \quad 0<t<T . \end{gathered}$$

  Furthermore, $q_{0}(x), q(0, t)$ and $q_{x}(0, t)$ are related via the so-called global relation

  $$e^{i k^{2} t} \hat{q}(k, t)=\hat{q}_{0}(k)+k \tilde{g}_{0}\left(i k^{2}, t\right)-i \tilde{g}_{1}\left(i k^{2}, t\right), \quad \operatorname{Im} k \leqslant 0$$

  where $\hat{q}(k, t)$ denotes the Fourier transform of $q(x, t)$.

  (a) Assuming the validity of (1) and (2), use the global relation to eliminate $\tilde{g}_{1}$ from equation (1).

  (b) For the particular case that

  $$q_{0}(x)=e^{-a^{2} x}, \quad 0<x<\infty ; \quad q(0, t)=\cos b t, \quad 0<t<T,$$

  where $a$ and $b$ are real numbers, use the representation obtained in (a) to express the solution in terms of an integral along the real axis and an integral along $L$ (you should not attempt to evaluate these integrals). Show that it is possible to deform these two integrals to a single integral along a new contour $\tilde{L}$, which you should sketch.

  [You may assume the validity of Jordan's lemma.]

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2012

  The Beta function, denoted by $B\left(z_{1}, z_{2}\right)$, is defined by

  $$B\left(z_{1}, z_{2}\right)=\frac{\Gamma\left(z_{1}\right) \Gamma\left(z_{2}\right)}{\Gamma\left(z_{1}+z_{2}\right)}, \quad z_{1}, z_{2} \in \mathbb{C}$$

  where $\Gamma(z)$ denotes the Gamma function. It can be shown that

  $$B\left(z_{1}, z_{2}\right)=\int_{0}^{\infty} \frac{v^{z_{2}-1} d v}{(1+v)^{z_{1}+z_{2}}}, \quad \operatorname{Re} z_{1}>0, \operatorname{Re} z_{2}>0$$

  By computing this integral for the particular case of $z_{1}+z_{2}=1$, and by employing analytic continuation, deduce that $\Gamma(z)$ satisfies the functional equation

  $$\Gamma(z) \Gamma(1-z)=\frac{\pi}{\sin \pi z}, \quad z \in \mathbb{C} .$$

  comment

• Paper 4, Section I, E

  Further Complex Methods | Part II, 2012

  Use the Laplace kernel method to write integral representations in the complex $t$-plane for two linearly independent solutions of the confluent hypergeometric equation

  $$z \frac{d^{2} w(z)}{d z^{2}}+(c-z) \frac{d w(z)}{d z}-a w(z)=0$$

  in the case that $\operatorname{Re}(z)>0, \operatorname{Re}(c)>\operatorname{Re}(a)>0, a$ and $c-a$ are not integers.

  comment

2011

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2011

  Show that the following integral is well defined:

  $$I(a, b)=\int_{0}^{\infty}\left(\frac{e^{-b x}}{e^{i a} e^{x}-1}-\frac{e^{b x}}{e^{-i a} e^{x}-1}\right) d x, \quad 0<a<\infty, a \neq 2 n \pi, n \in \mathbb{Z}, 0<b<1$$

  Express $I(a, b)$ in terms of a combination of hypergeometric functions.

  [You may assume without proof that the hypergeometric function $F(a, b ; c ; z)$ can be expressed in the form

  $$F(a, b ; c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  for appropriate restrictions on $c, b, z$. Furthermore,

  $$\Gamma(z+1)=z \Gamma(z) \cdot]$$

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2011

  (i) By assuming the validity of the Fourier transform pair, prove the validity of the following transform pair:

  $$\begin{gathered} \hat{q}(k)=\int_{0}^{\infty} e^{-i k x} q(x) d x, \quad \operatorname{Im} k \leqslant 0, \\ q(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} e^{i k x} \hat{q}(k) d k+\frac{c}{2 \pi} \int_{L} e^{i k x} \hat{q}(-k) d k, \quad 0<x<\infty, \end{gathered}$$

  where $c$ is an arbitrary complex constant and $L$ is the union of the two rays arg $k=\frac{\pi}{2}$ and $\arg k=0$ with the orientation shown in the figure below:

  

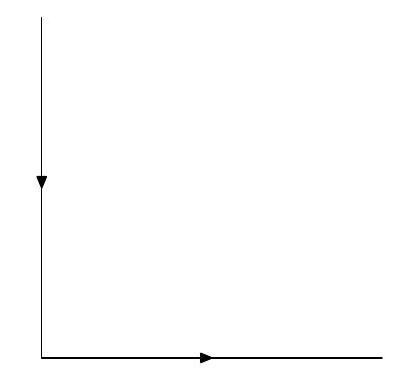
  The contour $L$.

  (ii) Verify that the partial differential equation

  $$i q_{t}+q_{x x}=0, \quad 0<x<\infty, t>0,$$

  can be rewritten in the following form:

  $$\left(e^{-i k x+i k^{2} t} q\right)_{t}-\left[e^{-i k x+i k^{2} t}\left(-k q+i q_{x}\right)\right]_{x}=0, \quad k \in \mathbb{C} .$$

  Consider equation (2) supplemented with the conditions

  $$\begin{aligned} &q(x, 0)=q_{0}(x), \quad 0<x<\infty \\ &q(x, t) \text { vanishes sufficiently fast for all } t \text { as } x \rightarrow \infty \end{aligned}$$

  By using equations (1a) and (3), show that

  $$\hat{q}(k, t)=e^{-i k^{2} t} \hat{q}_{0}(k)+e^{-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)-i \tilde{g}_{1}\left(k^{2}, t\right)\right], \operatorname{Im} k \leqslant 0$$

  where

  $$\hat{q}_{0}(k)=\int_{0}^{\infty} e^{-i k x} q_{0}(x) d x, \quad \operatorname{Im} k \leqslant 0$$

  Part II, $2011 \quad$ List of Questions

  [TURN OVER

  $$\tilde{g}_{0}(k, t)=\int_{0}^{t} e^{i k \tau} q(0, \tau) d \tau, \quad \tilde{g}_{1}(k, t)=\int_{0}^{t} e^{i k \tau} q_{x}(0, \tau) d \tau, k \in \mathbb{C}, t>0 .$$

  Use (1b) to invert equation (5) and furthermore show that

  $$\int_{-\infty}^{\infty} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)+i \tilde{g}_{1}\left(k^{2}, t\right)\right] d k=\int_{L} e^{i k x-i k^{2} t}\left[k \tilde{g}_{0}\left(k^{2}, t\right)+i \tilde{g}_{1}\left(k^{2}, t\right)\right] d k, t>0, x>0$$

  Hence determine the constant $c$ so that the solution of equation (2), with the conditions (4) and with the condition that either $q(0, t)$ or $q_{x}(0, t)$ is given, can be expressed in terms of an integral involving $\hat{q}_{0}(k)$ and either $\tilde{g}_{0}$ or $\tilde{g}_{1}$.

  comment

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2011

  Find the two complex-valued functions $F^{+}(z)$ and $F^{-}(z)$ such that all of the following hold:

  (i) $F^{+}(z)$ and $F^{-}(z)$ are analytic for $\operatorname{Im} z>0$ and $\operatorname{Im} z<0$ respectively, where $z=x+i y, x, y \in \mathbb{R}$.

  (ii) $F^{+}(x)-F^{-}(x)=\frac{1}{x^{4}+1}, \quad x \in \mathbb{R}$.

  (iii) $F^{\pm}(z)=O\left(\frac{1}{z}\right), \quad z \rightarrow \infty, \quad \operatorname{Im} z \neq 0$.

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2011

  Consider the following sum related to Riemann's zeta function:

  $$S:=\sum_{m=1}^{\left[\frac{a}{2 \pi}\right]} m^{s-1}, \quad s=\sigma+i t, \sigma, t \in \mathbb{R}, \quad a>2 \pi, a \neq 2 \pi N, N \in \mathbb{Z}^{+},$$

  where $[a / 2 \pi]$ denotes the integer part of $a / 2 \pi$.

  (i) By using an appropriate branch cut, show that

  $$S=\frac{e^{-\frac{i \pi s}{2}}}{(2 \pi)^{s}} \int_{L} f(z, s) d z, \quad f(z, s)=\frac{e^{-z}}{1-e^{-z}} z^{s-1}$$

  where $L$ is the circle in the complex $z$-plane centred at $i(a+b) / 2$ with radius $(a-b) / 2$, $0<b<2 \pi$.

  (ii) Use the above representation to show that, for $a>2 \pi$ and $0<b<2 \pi$,

  $$\sum_{m=1}^{\left[\frac{a}{2 \pi}\right]} m^{s-1}=\frac{1}{(2 \pi)^{s}}\left[e^{-\frac{i \pi s}{2}} \int_{C_{b}^{a}} f(z, s) d z-e^{\frac{i \pi s}{2}} \int_{C_{-a}^{-b}} f(z, s) d z+\frac{a^{s}}{s}-\frac{b^{s}}{s}\right]$$

  where $f(z, s)$ is defined in (i) and the curves $C_{b}^{a}, C_{-a}^{-b}$ are the following semi-circles in the right half complex $z$-plane:

  

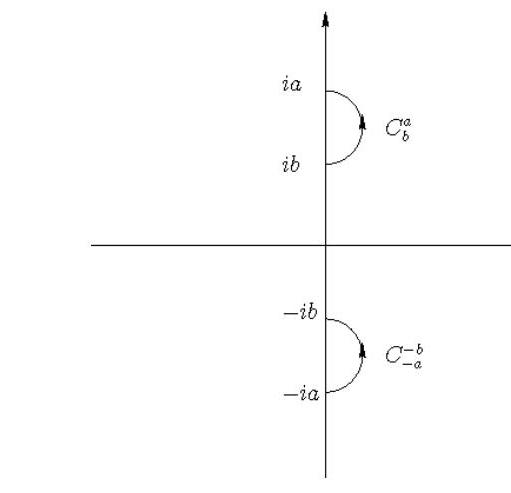
  The curves $C_{b}^{a}$ and $C_{-a}^{-b}$.

  $$\begin{aligned} C_{b}^{a} &=\left\{\frac{i(a+b)}{2}+\frac{(a-b)}{2} e^{i \theta}, \quad-\frac{\pi}{2}<\theta<\frac{\pi}{2}\right\} \\ C_{-a}^{-b} &=\left\{\frac{-i(a+b)}{2}+\frac{(a-b)}{2} e^{i \theta}, \quad-\frac{\pi}{2}<\theta<\frac{\pi}{2}\right\} \end{aligned}$$

  Part II, 2011 List of Questions

  [TURN OVER

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2011

  Explain the meaning of $z_{j}$ in the Weierstrass canonical product formula

  $$f(z)=f(0) \exp \left[\frac{f^{\prime}(0)}{f(0)} z\right] \prod_{j=1}^{\infty}\left\{\left(1-\frac{z}{z_{j}}\right) e^{\frac{z}{z_{j}}}\right\}$$

  Show that

  $$\frac{\sin (\pi z)}{\pi z}=\prod_{n=1}^{\infty}\left(1-\frac{z^{2}}{n^{2}}\right)$$

  Deduce that

  $$\pi \cot (\pi z)=\frac{1}{z}+2 \sum_{n=1}^{\infty} \frac{z}{z^{2}-n^{2}}$$

  comment

• Paper 4, Section $I$, E

  Further Complex Methods | Part II, 2011

  Let $F(z)$ be defined by

  $$F(z)=\int_{0}^{\infty} \frac{e^{-z t}}{1+t^{2}} d t, \quad|\arg z|<\frac{\pi}{2}$$

  Let $\tilde{F}(z)$ be defined by

  $$\tilde{F}(z)=\mathcal{P} \int_{0}^{\infty e^{-\frac{i \pi}{2}}} \frac{e^{-z \zeta}}{1+\zeta^{2}} d \zeta, \quad 0<\arg z<\pi$$

  where $\mathcal{P}$ denotes principal value integral and the contour is the negative imaginary axis.

  By computing $F(z)-\tilde{F}(z)$, obtain a formula for the analytic continuation of $F(z)$ for $\frac{\pi}{2} \leqslant \arg z<\pi$.

  comment

2010

• Paper 1, Section I, E

  Further Complex Methods | Part II, 2010

  Let the complex-valued function $f(z)$ be analytic in the neighbourhood of the point $z_{0}$ and let $u(x, y)$ be the real part of $f(z)$. Show that

  $$f(z)=2 u\left(\frac{z+\bar{z}_{0}}{2}, \frac{z-\bar{z}_{0}}{2 i}\right)-\overline{f\left(z_{0}\right)}, \quad z=x+i y$$

  Hence find the analytic function whose real part is

  $$e^{-y}[x \cos x-y \sin x]$$

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2010

  Consider the partial differential equation for $u(x, t)$,

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}+\beta \frac{\partial u}{\partial x}, \quad \beta>0, \quad 0<x<\infty, \quad t>0$$

  where $u(x, t)$ is required to vanish rapidly for all $t$ as $x \rightarrow \infty$.

  (i) Verify that the PDE $(*)$ can be written in the following form

  $$\left(e^{-i k x+\left(k^{2}-i \beta k\right) t} u\right)_{t}=\left(e^{-i k x+\left(k^{2}-i \beta k\right) t}\left[(i k+\beta) u+u_{x}\right]\right)_{x}$$

  (ii) Define $\hat{u}(k, t)=\int_{0}^{\infty} e^{-i k x} u(x, t) d x$, which is analytic for $\operatorname{Im} k \leqslant 0$. Determine $\hat{u}(k, t)$ in terms of $\hat{u}(k, 0)$ and also the functions $f_{0}, f_{1}$ defined by

  $$f_{0}(\omega, t)=\int_{0}^{t} e^{-\omega\left(t-t^{\prime}\right)} u\left(0, t^{\prime}\right) d t^{\prime}, \quad f_{1}(\omega, t)=\int_{0}^{t} e^{-\omega\left(t-t^{\prime}\right)} u_{x}\left(0, t^{\prime}\right) d t^{\prime}$$

  (iii) Show that in the inverse transform expression for $u(x, t)$ the integrals involving $f_{0}, f_{1}$ may be transformed to the contour

  $$L=\left\{k \in \mathbb{C}: \operatorname{Re}\left(k^{2}-i \beta k\right)=0, \operatorname{Im} k \geqslant \beta\right\}$$

  By considering $\hat{u}\left(k^{\prime}, t\right)$ where $k^{\prime}=-k+i \beta$ and $k \in L$, show that it is possible to obtain an equation which allows $f_{1}$ to be eliminated.

  (iv) Obtain an integral expression for the solution of $(*)$ subject to the the initialboundary value conditions of given $u(x, 0), u(0, t)$.

  [You need to show that

  $$\int_{L} e^{i k x} \hat{u}\left(k^{\prime}, t\right) d k=0, \quad x>0,$$

  by an appropriate closure of the contour which should be justified.]

  comment

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2010

  Define

  $$F^{\pm}(x)=\lim _{\epsilon \rightarrow 0} \frac{1}{2 \pi i} \int_{-\infty}^{\infty} \frac{f(t)}{t-(x \pm i \epsilon)} d t, \quad x \in \mathbb{R}$$

  Using the fact that

  $$F^{\pm}(x)=\pm \frac{f(x)}{2}+\frac{1}{2 \pi i} P \int_{-\infty}^{\infty} \frac{f(t)}{t-x} d t, \quad x \in \mathbb{R}$$

  where $P$ denotes the Cauchy principal value, find two complex-valued functions $F^{+}(z)$ and $F^{-}(z)$ which satisfy the following conditions

  1. $F^{+}(z)$ and $F^{-}(z)$ are analytic for $\operatorname{Im} z>0$ and $\operatorname{Im} z<0$ respectively, $z=x+i y$;

  2. $F^{+}(x)-F^{-}(x)=\frac{\sin x}{x}, \quad x \in \mathbb{R}$;

  3. $F^{\pm}(z)=\mathrm{O}\left(\frac{1}{z}\right), \quad z \rightarrow \infty, \quad \operatorname{Im} z \neq 0$.

  comment

• Paper 2, Section II, 14E

  Further Complex Methods | Part II, 2010

  Let

  $$I(z)=i \oint_{C} \frac{u^{z-1}}{u^{2}-4 u+1} d u$$

  where $C$ is a closed anti-clockwise contour which consists of the unit circle joined to a loop around a branch cut along the negative axis between $-1$ and 0 . Show that

  $$I(z)=F(z)+G(z)$$

  where

  $$F(z)=2 \sin (\pi z) \int_{0}^{1} \frac{x^{z-1}}{x^{2}+4 x+1} d x, \quad \operatorname{Re} z>0$$

  and

  $$G(z)=\frac{1}{2} \int_{-\pi}^{\pi} \frac{e^{i(z-1) \theta}}{1+2 \sin ^{2} \frac{\theta}{2}} d \theta, \quad z \in \mathbb{C}$$

  Evaluate $I(z)$ using Cauchy's theorem. Explain how this may be used to obtain an analytic continuation of $F(z)$ valid for all $z \in \mathbb{C}$.

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2010

  Let $\Gamma(z)$ and $\zeta(z)$ denote the gamma and the zeta functions respectively, namely

  $$\begin{aligned} &\Gamma(z)=\int_{0}^{\infty} x^{z-1} e^{-x} d x, \quad \operatorname{Re} z>0 \\ &\zeta(z)=\sum_{m=1}^{\infty} \frac{1}{m^{z}}, \quad \operatorname{Re} z>1 \end{aligned}$$

  By employing a series expansion of $\left(1-e^{-x}\right)^{-2}$, prove the following identity

  $$\int_{0}^{\infty} \frac{x^{z}}{\left(e^{x}-1\right)^{2}} d x=\Gamma(z+1)[\zeta(z)-\zeta(z+1)], \quad \operatorname{Re} z>1$$

  comment

• Paper 4, Section $I$, E

  Further Complex Methods | Part II, 2010

  The hypergeometric function $F(a, b ; c ; z)$ can be expressed in the form

  $$F(a, b ; c ; z)=\frac{\Gamma(c)}{\Gamma(b) \Gamma(c-b)} \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  for appropriate restrictions on $c, b, z$.

  Express the following integral in terms of a combination of hypergeometric functions

  $$I(u, A)=\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}} \frac{e^{i t(u+1)}}{e^{i t}+i A} d t, \quad|A|>1$$

  [You may use without proof that $\Gamma(z+1)=z \Gamma(z) .$ ]

  comment

2009

• Paper 1, Section I, B

  Further Complex Methods | Part II, 2009

  Find all second order linear ordinary homogenous differential equations which have a regular singular point at $z=0$, a regular singular point at $z=\infty$, and for which every other point in the complex $z$-plane is an analytic point.

  [You may use without proof Liouville's theorem.]

  comment

• Paper 1, Section II, B

  Further Complex Methods | Part II, 2009

  Let $F(z)$ be defined by

  $$F(z)=\int_{0}^{\infty} \frac{e^{-2 z t}}{1+t^{3}} d t, \quad|\arg z|<\frac{\pi}{2}$$

  Let $\tilde{F}(z)$ be defined by

  $$\tilde{F}(z)=\int_{0}^{-i \infty} \frac{e^{-2 z \zeta}}{1+\zeta^{3}} d \zeta, \quad \alpha<\arg z<\beta$$

  where the above integral is along the negative imaginary axis of the complex $\zeta$-plane and the real constants $\alpha$ and $\beta$ are to be determined.

  Using Cauchy's theorem, or otherwise, compute $F(z)-\tilde{F}(z)$ and hence find a formula for the analytic continuation of $F(z)$ for $\frac{\pi}{2} \leqslant \arg z<\pi$.

  comment

• Paper 2, Section I, B

  Further Complex Methods | Part II, 2009

  The Hilbert transform $\hat{f}$ of a function $f$ is defined by

  $$\hat{f}(x)=\frac{1}{\pi} P \int_{-\infty}^{\infty} \frac{f(y)}{y-x} d y$$

  where $P$ denotes the Cauchy principal value.

  (i) Compute the Hilbert transform of $(1-\cos t) / t$.

  (ii) Solve the following Riemann-Hilbert problem: Find $f^{+}(z)$ and $f^{-}(z)$, which are analytic functions in the upper and lower half $z$-planes respectively, such that

  $$\begin{aligned} &f^{+}(x)-f^{-}(x)=\frac{1-\cos x}{x}, \quad x \in \mathbb{R} \\ &f^{\pm}(z)=O\left(\frac{1}{z}\right), \quad z \rightarrow \infty, \quad \operatorname{Im} z \neq 0 \end{aligned}$$

  comment

• Paper 2, Section II, C

  Further Complex Methods | Part II, 2009

  Consider the initial-boundary value problem

  $$\begin{gathered} \frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad 0<x<\infty, \quad t>0 \\ u(x, 0)=x e^{-x}, \quad 0 \leqslant x<\infty \\ u(0, t)=\sin t, \quad t \geqslant 0 \end{gathered}$$

  where $u$ vanishes sufficiently fast for all $t$ as $x \rightarrow \infty$.

  (i) Express the solution as an integral (which you should not evaluate) in the complex $k$-plane

  (ii) Explain how to use appropriate contour deformation so that the relevant integrand decays exponentially as $|k| \rightarrow \infty$.

  comment

• Paper 3, Section $\mathbf{I}$, B

  Further Complex Methods | Part II, 2009

  Suppose that the real function $u(x, y)$ satisfies Laplace's equation in the upper half complex $z$-plane, $z=x+i y, x \in \mathbb{R}, y>0$, where

  $$u(x, y) \rightarrow 0 \quad \text { as } \quad \sqrt{x^{2}+y^{2}} \rightarrow \infty, \quad u(x, 0)=g(x), \quad x \in \mathbb{R} .$$

  The function $u(x, y)$ can then be expressed in terms of the Poisson integral

  $$u(x, y)=\frac{1}{\pi} \int_{-\infty}^{\infty} \frac{y g(\xi)}{(x-\xi)^{2}+y^{2}} d \xi, \quad x \in \mathbb{R}, y>0$$

  By employing the formula

  $$f(z)=2 u\left(\frac{z+\bar{a}}{2}, \frac{z-\bar{a}}{2 i}\right)-\overline{f(a)}$$

  where $a$ is a complex constant with $\operatorname{Im} a>0$, show that the analytic function whose real part is $u(x, y)$ is given by

  $$f(z)=\frac{1}{i \pi} \int_{-\infty}^{\infty} \frac{g(\xi)}{\xi-z} d \xi+i c, \quad \operatorname{Im} z>0$$

  where $c$ is a real constant.

  comment

• Paper 4, Section I, D

  Further Complex Methods | Part II, 2009

  Show that

  $$\Gamma(\alpha) \Gamma(\beta)=\Gamma(\alpha+\beta) \int_{0}^{1} t^{\alpha-1}(1-t)^{\beta-1} d t, \quad \operatorname{Re} \alpha>0, \quad \operatorname{Re} \beta>0$$

  where $\Gamma(z)$ denotes the Gamma function

  $$\Gamma(z)=\int_{0}^{\infty} x^{z-1} e^{-x} d x, \quad \operatorname{Re} z>0$$

  comment

2008

• 1.I.8C

  Further Complex Methods | Part II, 2008

  The function $F$ is defined by

  $$F(z)=\int_{0}^{\infty} \frac{t^{z-1}}{(t+1)^{2}} d t$$

  For which values of $z$ does the integral converge?

  Show that, for these values,

  $$F(z)=\frac{\pi(1-z)}{\sin (\pi z)} .$$

  comment

• 1.II.14C

  Further Complex Methods | Part II, 2008

  Show that under the change of variable $z=\sin ^{2} x$ the equation

  $$\frac{d^{2} w}{d x^{2}}+n^{2} w=0$$

  becomes

  $$\frac{d^{2} w}{d z^{2}}+\frac{2 z-1}{2 z(z-1)} \frac{d w}{d z}-\frac{n^{2}}{4(z-1) z} w=0$$

  Show that this is a Papperitz equation and that the corresponding $P$-function is

  $$P\left\{\begin{array}{rrrr} 0 & \infty & 1 & \\ 0 & \frac{1}{2} n & 0 & z \\ \frac{1}{2} & -\frac{1}{2} n & \frac{1}{2} & \end{array}\right\}$$

  Deduce that $F\left(\frac{1}{2} n,-\frac{1}{2} n ; \frac{1}{2} ; \sin ^{2} x\right)=\cos n x$.

  comment

• 2.I.8C

  Further Complex Methods | Part II, 2008

  The Beta function is defined for $\operatorname{Re} z>0$ by

  $$\mathrm{B}(z, q)=\int_{0}^{1} t^{q-1}(1-t)^{z-1} d t \quad(\operatorname{Re} q>0)$$

  and by analytic continuation elsewhere in the complex $z$-plane.

  Show that

  $$\left(\frac{z+q}{z}\right) \mathrm{B}(z+1, q)=\mathrm{B}(z, q)$$

  and explain how this result can be used to obtain the analytic continuation of $\mathrm{B}(z, q)$. Hence show that $\mathrm{B}(z, q)$ is analytic except for simple poles and find the residues at the poles.

  comment

• 2.II.14C

  Further Complex Methods | Part II, 2008

  (i) The function $f$ is defined by

  $$f(z)=\int_{C} t^{z-1} d t$$

  where $C$ is the circle $|t|=r$, described anti-clockwise starting on the positive real axis and where the value of $t^{z-1}$ at each point on $C$ is determined by analytic continuation along $C$ with $\arg t=0$ at the starting point. Verify by direct integration that $f$ is an entire function, the values of which depend on $r$.

  (ii) The function $J$ is defined by

  $$J(z)=\int_{\gamma} e^{t}\left(t^{2}-1\right)^{z} d t$$

  where $\gamma$ is a figure of eight, starting at $t=0$, looping anti-clockwise round $t=1$ and returning to $t=0$, then looping clockwise round $t=-1$ and returning again to $t=0$. The value of $\left(t^{2}-1\right)^{z}$ is determined by analytic continuation along $\gamma$ with $\arg \left(t^{2}-1\right)=-\pi$ at the start. Show that, for $\operatorname{Re} z>-1$,

  $$J(z)=-2 i \sin \pi z I(z),$$

  where

  $$I(z)=\int_{-1}^{1} e^{t}\left(t^{2}-1\right)^{z} d t$$

  Explain how this provides the analytic continuation of $I(z)$. Classify the singular points of the analytically continued function, commenting on the points $z=0,1, \ldots$.

  Explain briefly why the analytic continuation could not be obtained by this method if $\gamma$ were replaced by the circle $|t|=2$.

  comment

• 3.I.8C

  Further Complex Methods | Part II, 2008

  What is the effect of the Möbius transformation $z \rightarrow \frac{z}{z-1}$ on the points $z=0$, $z=\infty$ and $z=1$ ?

  By considering

  $$(z-1)^{-a} P\left\{\begin{array}{cccc} 0 & \infty & 1 & \\ 0 & a & 0 & z(z-1)^{-1} \\ 1-c & c-b & b-a & \end{array}\right\}$$

  or otherwise, show that $(z-1)^{-a} F\left(a, c-b ; c ; z(z-1)^{-1}\right)$ is a branch of the $P$-function

  

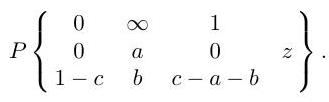
  Give a linearly independent branch.

  comment

• 4.I.8C

  Further Complex Methods | Part II, 2008

  The Hilbert transform $\hat{f}$ of a function $f$ is defined by

  $$\hat{f}(t)=\frac{1}{\pi} \mathcal{P} \int_{-\infty}^{\infty} \frac{f(\tau)}{t-\tau} d \tau,$$

  where $\mathcal{P}$ denotes the Cauchy principal value.

  Show that the Hilbert transform of $\frac{\sin t}{t}$ is $\frac{1-\cos t}{t} .$

  comment

2007

• 1.I.8B

  Further Complex Methods | Part II, 2007

  The coefficients $p(z)$ and $q(z)$ of the differential equation

  $$w^{\prime \prime}(z)+p(z) w^{\prime}(z)+q(z) w(z)=0$$

  are analytic in the punctured disc $0<|z|<R$, and $w_{1}(z)$ and $w_{2}(z)$ are linearly independent solutions in the neighbourhood of the point $z_{0}$ in the disc. By considering the effect of analytically continuing $w_{1}$ and $w_{2}$, show that the equation $(*)$ has a non-trivial solution of the form

  $$w(z)=z^{\sigma} \sum_{n=-\infty}^{\infty} c_{n} z^{n}$$

  comment

• 1.II.14B

  Further Complex Methods | Part II, 2007

  The function $J(z)$ is defined by

  $$J(z)=\int_{\mathcal{P}} t^{z-1}(1-t)^{b-1} d t$$

  where $b$ is a constant (which is not an integer). The path of integration, $\mathcal{P}$, is the Pochhammer contour, defined as follows. It starts at a point $A$ on the axis between 0 and 1 , then it circles the points 1 and 0 in the negative sense, then it circles the points 1 and 0 in the positive sense, returning to $A$. At the start of the path, $\arg (t)=\arg (1-t)=0$ and the integrand is defined at other points on $\mathcal{P}$ by analytic continuation along $\mathcal{P}$.

  (i) For what values of $z$ is $J(z)$ analytic? Give brief reasons for your answer.

  (ii) Show that, in the case $\operatorname{Re} z>0$ and $\operatorname{Re} b>0$,

  $$J(z)=-4 e^{-\pi i(z+b)} \sin (\pi z) \sin (\pi b) \mathrm{B}(z, b)$$

  where $\mathrm{B}(z, b)$ is the Beta function.

  (iii) Deduce that the only singularities of $\mathrm{B}(z, b)$ are simple poles. Explain carefully what happens if $z$ is a positive integer.

  comment

• 2.I.8B

  Further Complex Methods | Part II, 2007

  The function $I(z)$ is defined by

  $$I(z)=\frac{1}{\Gamma(z)} \int_{0}^{\infty} \frac{t^{z-1}}{e^{t}+1} d t$$

  For what values of $z$ is $I(z)$ analytic?

  By considering $I(z)-\zeta(z)$, where $\zeta(z)$ is the Riemann zeta function which you may assume is given by

  $$\zeta(z)=\frac{1}{\Gamma(z)} \int_{0}^{\infty} \frac{t^{z-1}}{e^{t}-1} d t \quad(\operatorname{Re} z>1)$$

  show that $I(z)=\left(1-2^{1-z}\right) \zeta(z)$. Deduce from this result that the analytic continuation of $I(z)$ is an entire function. [You may use properties of $\zeta(z)$ without proof.]

  comment

• 2.II.14B

  Further Complex Methods | Part II, 2007

  Show that the equation

  $$z w^{\prime \prime}-(1+z) w^{\prime}+2(1-z) w=0$$

  has solutions of the form $w(z)=\int_{\gamma} e^{z t} f(t) d t$, where

  $$f(t)=\frac{1}{(t-2)(t+1)^{2}}$$

  provided that $\gamma$ is suitably chosen.

  Hence find the general solution, evaluating the integrals explicitly. Show that the general solution is entire, but that there is no solution that satisfies $w(0)=0$ and $w^{\prime}(0) \neq 0$.

  comment

• 3.I.8B

  Further Complex Methods | Part II, 2007

  Let $w_{1}(z)$ and $w_{2}(z)$ be any two linearly independent branches of the $P$-function

  $$\left\{\begin{array}{cccc} 0 & \infty & 1 & \\ \alpha & \beta & \gamma & z \\ \alpha^{\prime} & \beta^{\prime} & \gamma^{\prime} & \end{array}\right\}$$

  where $\alpha+\alpha^{\prime}+\beta+\beta^{\prime}+\gamma+\gamma^{\prime}=1$, and let $W(z)$ be the Wronskian of $w_{1}(z)$ and $w_{2}(z)$.

  (i) How is $W(z)$ related to the Wronskian of the principal branches of the $P$-function at $z=0$ ?

  (ii) Show that $z^{-\alpha-\alpha^{\prime}+1}(1-z)^{-\gamma-\gamma^{\prime}+1} W(z)$ is an entire function.

  (iii) Given that $z^{\beta+\beta^{\prime}+1} W(z)$ is bounded as $z \rightarrow \infty$, show that

  $$W(z)=A z^{\alpha+\alpha^{\prime}-1}(1-z)^{\gamma+\gamma^{\prime}-1}$$

  where $A$ is a non-zero constant.

  comment

• 4.I.8B

  Further Complex Methods | Part II, 2007

  The hypergeometric function $F(a, b ; c ; z)$ is defined by

  $$F(a, b ; c ; z)=K \int_{0}^{1} t^{b-1}(1-t)^{c-b-1}(1-t z)^{-a} d t$$

  where $|\arg (1-t z)|<\pi$ and $K$ is a constant determined by the condition $F(a, b ; c ; 0)=1$.

  (i) Express $K$ in terms of Gamma functions.

  (ii) By considering the $n$th derivative $F^{(n)}(a, b ; c ; 0)$, show that $F(a, b ; c ; z)=F(b, a ; c ; z)$.

  comment

2006

• 1.I.8E

  Further Complex Methods | Part II, 2006

  The function $f(t)$ satisfies $f(t)=0$ for $t<1$ and

  $$f(t+1)-\frac{1}{2} f(t)=H(t),$$

  where $H(t)$ is the Heaviside step function. By taking Laplace transforms, show that, for $t \geqslant 1$,

  $$f(t)=2+2^{1-t} \sum_{n=-\infty}^{\infty} \frac{e^{2 \pi n i t}}{2 \pi n i-\log 2}$$

  and verify directly from the inversion integral that your solution satisfies $f(t)=0$ for $t<1$.

  comment

• 2.I.8E

  Further Complex Methods | Part II, 2006

  The function $F(t)$ is defined, for $\operatorname{Re} t>-1$, by

  $$F(t)=\int_{0}^{\infty} \frac{u^{t} e^{-u}}{1+u} d u$$

  and by analytic continuation elsewhere in the complex $t$-plane. By considering the integral of a suitable function round a Hankel contour, obtain the analytic continuation of $F(t)$ and hence show that singularities of $F(t)$ can occur only at $z=-1,-2,-3, \ldots$.

  comment

• 3.I.8E

  Further Complex Methods | Part II, 2006

  Show that, for $b \neq 0$,

  $$\mathcal{P} \int_{0}^{\infty} \frac{\cos u}{u^{2}-b^{2}} d u=-\frac{\pi}{2 b} \sin b$$

  where $\mathcal{P}$ denotes the Cauchy principal value.

  comment

• 3.II.14E

  Further Complex Methods | Part II, 2006

  It is given that the hypergeometric function $F(a, b ; c ; z)$ is the solution of the hypergeometric equation determined by the Papperitz symbol

  $$P\left\{\begin{array}{ccc} 0 & \infty & 1 \\ 0 & a & 0 \\ 1-c & b & c-a-b \end{array}\right\}$$

  that is analytic at $z=0$ and satisfies $F(a, b ; c ; 0)=1$, and that for $\operatorname{Re}(c-a-b)>0$

  $$F(a, b ; c ; 1)=\frac{\Gamma(c) \Gamma(c-a-b)}{\Gamma(c-a) \Gamma(c-b)} .$$

  [You may assume that $a, b, c$ are such that $F(a, b ; c ; 1)$ exists.]

  (a) Show, by manipulating Papperitz symbols, that

  $$F(a, b ; c ; z)=(1-z)^{-a} F\left(a, c-b ; c ; \frac{z}{z-1}\right) \quad(|\arg (1-z)|<\pi) .$$

  (b) Let $w_{1}(z)=(-z)^{-a} F\left(a, 1+a-c ; 1+a-b ; \frac{1}{z}\right)$, where $|\arg (-z)|<\pi$. Show that $w_{1}(z)$ satisfies the hypergeometric equation determined by $(*)$.

  (c) By considering the limit $z \rightarrow \infty$ in parts (a) and (b) above, deduce that, for $|\arg (-z)|<\pi$,

  $$F(a, b ; c ; z)=\frac{\Gamma(c) \Gamma(b-a)}{\Gamma(b) \Gamma(c-a)} w_{1}(z)+(\text { a similar term with } a \text { and } b \text { interchanged })$$

  comment

• 4.I.8E

  Further Complex Methods | Part II, 2006

  By means of the change of variable $u=r s, v=r(1-s)$ in a suitable double integral, or otherwise, show that for $\operatorname{Re} z>0$

  $$\left[\Gamma\left(\frac{1}{2} z\right)\right]^{2}=B\left(\frac{1}{2} z, \frac{1}{2} z\right) \Gamma(z)$$

  Deduce that, if $\Gamma(z)=0$ for some $z$ with $\operatorname{Re} z>0$, then $\Gamma\left(z / 2^{m}\right)=0$ for any positive integer $m$.

  Prove that $\Gamma(z) \neq 0$ for any $z$.

  comment

• 4.II.14E

  Further Complex Methods | Part II, 2006

  Let $I=\int_{0}^{1}\left[x\left(1-x^{2}\right)\right]^{1 / 3} d x$

  (a) Express $I$ in terms of an integral of the form $\oint\left(z^{3}-z\right)^{1 / 3} d z$, where the path of integration is a large circle. You should explain carefully which branch of $\left(z^{3}-z\right)^{1 / 3}$ you choose, by using polar co-ordinates with respect to the branch points. Hence show that $I=\frac{1}{6} \pi \operatorname{cosec} \frac{1}{3} \pi$.

  (b) Give an alternative method of evaluating $I$, by making a suitable change of variable and expressing $I$ in terms of a beta function.

  comment

2005

• 1.I.8A

  Further Complex Methods | Part II, 2005

  Explain what is meant by the Papperitz symbol

  $$P\left\{\begin{array}{cccc} z_{1} & z_{2} & z_{3} & \\ \alpha & \beta & \gamma & z \\ \alpha^{\prime} & \beta^{\prime} & \gamma^{\prime} & \end{array}\right\}$$

  The hypergeometric function $F(a, b ; c ; z)$ is defined as the solution of the equation determined by the Papperitz symbol

  $$P\left\{\begin{array}{ccc} 0 & \infty & 1 \\ 0 & a & 0 \\ 1-c & b & c-a-b \end{array}\right\}$$

  that is analytic at $z=0$ and satisfies $F(a, b ; c ; 0)=1$.

  Show, explaining each step, that

  $$F(a, b ; c ; z)=(1-z)^{c-a-b} F(c-a, c-b ; c ; z)$$

  comment

• 2.I.8A

  Further Complex Methods | Part II, 2005

  The Hankel representation of the gamma function is

  $$\Gamma(z)=\frac{1}{2 i \sin (\pi z)} \int_{-\infty}^{\left(0^{+}\right)} t^{z-1} e^{t} d t$$

  where the path of integration is the Hankel contour.

  Use this representation to find the residue of $\Gamma(z)$ at $z=-n$, where $n$ is a nonnegative integer.

  Is there a pole at $z=n$, where $n$ is a positive integer? Justify your answer carefully, working only from the above representation of $\Gamma(z)$.

  comment

• 3.I.8A

  Further Complex Methods | Part II, 2005

  The functions $f$ and $g$ have Laplace transforms $\widehat{f}$ and $\widehat{g}$, and satisfy $f(t)=0=g(t)$ for $t<0$. The convolution $h$ of $f$ and $g$ is defined by

  $$h(u)=\int_{0}^{u} f(u-v) g(v) d v$$

  and has Laplace transform $\widehat{h}$. Prove (the convolution theorem) that $\widehat{h}(p)=\widehat{f}(p) \widehat{g}(p)$.

  Given that $\int_{0}^{t}(t-s)^{-1 / 2} s^{-1 / 2} d s=\pi \quad(t>0)$, deduce the Laplace transform of the function $f(t)$, where

  $$f(t)=\left\{\begin{array}{l} t^{-1 / 2}, \quad t>0 \\ 0, \quad t \leqslant 0 \end{array}\right.$$

  comment

• 3.II.14A

  Further Complex Methods | Part II, 2005

  Show that the equation

  $$z w^{\prime \prime}+2 k w^{\prime}+z w=0,$$

  where $k$ is constant, has solutions of the form

  $$w(z)=\int_{\gamma}\left(t^{2}+1\right)^{k-1} e^{z t} d t$$

  provided that the path $\gamma$ is chosen so that $\left[\left(t^{2}+1\right)^{k} e^{z t}\right]_{\gamma}=0$.

  (i) In the case Re $k>0$, show that there is a choice of $\gamma$ for which $w(0)=i B\left(k, \frac{1}{2}\right)$.

  (ii) In the case $k=n / 2$, where $n$ is any integer, show that $\gamma$ can be a finite contour and that the corresponding solution satisfies $w(0)=0$ if $n \leqslant-1$.

  comment

• 4.I.8A

  Further Complex Methods | Part II, 2005

  Write down necessary and sufficient conditions on the functions $p(z)$ and $q(z)$ for the point $z=0$ to be (i) an ordinary point and (ii) a regular singular point of the equation

  $$w^{\prime \prime}+p(z) w^{\prime}+q(z) w=0 .$$

  Show that the point $z=\infty$ is an ordinary point if and only if

  $$p(z)=2 z^{-1}+z^{-2} P\left(z^{-1}\right), \quad q(z)=z^{-4} Q\left(z^{-1}\right),$$

  where $P$ and $Q$ are analytic in a neighbourhood of the origin.

  Find the most general equation of the form $(*)$ that has a regular singular point at $z=0$ but no other singular points.

  comment

• 4.II.14A

  Further Complex Methods | Part II, 2005

  Two representations of the zeta function are

  $$\zeta(z)=\frac{\Gamma(1-z)}{2 \pi i} \int_{-\infty}^{\left(0^{+}\right)} \frac{t^{z-1}}{e^{-t}-1} d t \quad \text { and } \quad \zeta(z)=\sum_{1}^{\infty} n^{-z}$$

  where, in the integral representation, the path is the Hankel contour and the principal branch of $t^{z-1}$, for which $|\arg z|<\pi$, is to be used. State the range of $z$ for which each representation is valid.

  Evaluate the integral

  $$\int_{\gamma} \frac{t^{z-1}}{e^{-t}-1} d t$$

  where $\gamma$ is a closed path consisting of the straight line $z=\pi i+x$, with $|x|<2 N \pi$, and the semicircle $|z-\pi i|=2 N \pi$, with $\operatorname{Im} z>\pi$, where $N$ is a positive integer.

  Making use of this result and assuming, when necessary, that the integral along the curved part of $\gamma$ is negligible when $N$ is large, derive the functional equation

  $$\zeta(z)=2^{z} \pi^{z-1} \sin (\pi z / 2) \Gamma(1-z) \zeta(1-z)$$

  for $z \neq 1$.

  comment