Principles Of Quantum Mechanics
Principles Of Quantum Mechanics
Jump to year
Paper 1, Section II, B
(a) A group of transformations acts on a quantum system. Briefly explain why the Born rule implies that these transformations may be represented by operators obeying
for all , where .
What additional property does have when is a group of symmetries of the Hamiltonian? Show that symmetries correspond to conserved quantities.
(b) The Coulomb Hamiltonian describing the gross structure of the hydrogen atom is invariant under time reversal, . Suppose we try to represent time reversal by a unitary operator obeying , where is the time-evolution operator. Show that this would imply that hydrogen has no stable ground state.
An operator is antilinear if
for all and all , and antiunitary if, in addition,
where and . Show that if time reversal is instead represented by an antiunitary operator then the above instability of hydrogen is avoided.
Paper 2, Section II, B
(a) Let be a basis of eigenstates of a non-degenerate Hamiltonian , with corresponding eigenvalues . Write down an expression for the energy levels of the perturbed Hamiltonian , correct to second order in the dimensionless constant .
(b) A particle travels in one dimension under the influence of the potential
where is the mass, a frequency and a length scale. Show that, to first order in , all energy levels coincide with those of the harmonic oscillator. Calculate the energy of the ground state to second order in .
Does perturbation theory in converge for this potential? Briefly explain your answer.
Paper 3, Section II, B
(a) A quantum system with total angular momentum is combined with another of total angular momentum . What are the possible values of the total angular momentum of the combined system? For given , what are the possible values of the angular momentum along any axis?
(b) Consider the case . Explain why all the states with are antisymmetric under exchange of the angular momenta of the two subsystems, while all the states with are symmetric.
(c) An exotic particle of spin 0 and negative intrinsic parity decays into a pair of indistinguishable particles . Assume each particle has spin 1 and that the decay process conserves parity. Find the probability that the direction of travel of the particles is observed to lie at an angle from some axis along which their total spin is observed to be ?
Paper 4, Section II, 33B
(a) A quantum system has Hamiltonian . Let be an orthonormal basis of eigenstates, with corresponding energies . For , and the system is in state . Calculate the probability that it is found to be in state at time , correct to lowest non-trivial order in .
(b) Now suppose form a basis of the Hilbert space, with respect to which
where is the Heaviside step function and is a real constant. Calculate the exact probability that the system is in state at time . For which frequency is this probability maximized?
Paper 1, Section II, A
Let be the lowering operator of a one dimensional quantum harmonic oscillator of mass and frequency , and let be the ground state defined by .
a) Evaluate the commutator .
b) For , let be the unitary operator and define . By differentiating with respect to or otherwise, show that
c) The ground state of the harmonic oscillator saturates the uncertainty relation . Compute when the oscillator is in the state .
Paper 2, Section II, A
(a) Consider the Hamiltonian , where is time-independent and non-degenerate. The system is prepared to be in some state at time , where is an orthonormal basis of eigenstates of . Derive an expression for the state at time , correct to first order in , giving your answer in the interaction picture.
(b) An atom is modelled as a two-state system, where the excited state has energy above that of the ground state . The atom interacts with an electromagnetic field, modelled as a harmonic oscillator of frequency . The Hamiltonian is , where
is the Hamiltonian in the absence of interactions and
describes the coupling between the atom and the field.
(i) Interpret each of the two terms in . What value must the constant take for time evolution to be unitary?
(ii) At the atom is in state while the field is described by the (normalized) state of the oscillator. Calculate the probability that at time the atom will be in its excited state and the field will be described by the excited state of the oscillator. Give your answer to first non-trivial order in perturbation theory. Show that this probability vanishes when .
Paper 3, Section II, 33A
Explain what is meant by the terms boson and fermion.
Three distinguishable spin-1 particles are governed by the Hamiltonian
where is the spin operator of particle and is a positive constant. How many spin states are possible altogether? By considering the total spin operator, determine the eigenvalues and corresponding degeneracies of the Hamiltonian.
Now consider the case that all three particles are indistinguishable and all have the same spatial wavefunction. What are the degeneracies of the Hamiltonian in this case?
Paper 4, Section II,
Briefly explain why the density operator obeys and . What is meant by a pure state and a mixed state?
A two-state system evolves under the Hamiltonian , where is a constant vector and are the Pauli matrices. At time the system is described by a density operator
where is the identity operator. Initially, the vector obeys and . Find in terms of a and . At what time, if any, is the system definitely in the state that obeys
Paper 1, Section II, B
A isotropic harmonic oscillator of mass and frequency has lowering operators
where and are the position and momentum operators. Assuming the standard commutation relations for and , evaluate the commutators and , for , among the components of the raising and lowering operators.
How is the ground state of the oscillator defined? How are normalised higher excited states obtained from ? [You should determine the appropriate normalisation constant for each energy eigenstate.]
By expressing the orbital angular momentum operator in terms of the raising and lowering operators, show that each first excited state of the isotropic oscillator has total orbital angular momentum quantum number , and find a linear combination of these first excited states obeying and .
Paper 2, Section II, B
(a) Let and be two eigenstates of a time-independent Hamiltonian , separated in energy by . At time the system is perturbed by a small, time independent operator . The perturbation is turned off at time . Show that if the system is initially in state , the probability of a transition to state is approximately
(b) An uncharged particle with spin one-half and magnetic moment travels at speed through a region of uniform magnetic field . Over a length of its path, an additional perpendicular magnetic field is applied. The spin-dependent part of the Hamiltonian is
where and are Pauli matrices. The particle initially has its spin aligned along the direction of . Find the probability that it makes a transition to the state with opposite spin
(i) by assuming and using your result from part (a),
(ii) by finding the exact evolution of the state.
[Hint: for any 3-vector , where is the unit matrix, and
Paper 3, Section II, B
Consider the Hamiltonian , where is a small perturbation. If , write down an expression for the eigenvalues of , correct to second order in the perturbation, assuming the energy levels of are non-degenerate.
In a certain three-state system, and take the form
with and real, positive constants and .
(a) Consider first the case and . Use the results of degenerate perturbation theory to obtain the energy eigenvalues correct to order .
(b) Now consider the different case and . Use the results of non-degenerate perturbation theory to obtain the energy eigenvalues correct to order . Why is it not necessary to use degenerate perturbation theory in this case?
(c) Obtain the exact energy eigenvalues in case (b), and compare these to your perturbative results by expanding to second order in .
Paper 4, Section II, B
Define the spin raising and spin lowering operators and . Show that
where and .
Two spin- particles, with spin operators and , have a Hamiltonian
where and are constants. Express in terms of the two particles' spin raising and spin lowering operators and the corresponding -components , . Hence find the eigenvalues of . Show that there is a unique groundstate in the limit and that the first excited state is triply degenerate in this limit. Explain this degeneracy by considering the action of the combined spin operator on the energy eigenstates.
Paper 1, Section II, D
A one-dimensional harmonic oscillator has Hamiltonian
where . Show that , where and .
This oscillator is perturbed by adding a new term to the Hamiltonian. Given that
show that the ground state of the perturbed system is
to first order in . [You may use the fact that, in non-degenerate perturbation theory, a perturbation causes the first-order shift
in the energy level.]
Paper 2, Section II, D
Explain what is meant by the intrinsic parity of a particle.
In each of the decay processes below, parity is conserved.
A deuteron has intrinsic parity and spin . A negatively charged pion has spin . The ground state of a hydrogenic 'atom' formed from a deuteron and a pion decays to two identical neutrons , each of spin and parity . Deduce the intrinsic parity of the pion.
The particle has spin and decays as
What are the allowed values of the orbital angular momentum? In the centre of mass frame, the vector joining the pion to the neutron makes an angle to the -axis. The final state is an eigenstate of and the spatial probability distribution is proportional to . Deduce the intrinsic parity of the .
[Hint: You may use the fact that the first three Legendre polynomials are given by
Paper 3, Section II, D
A quantum system is prepared in the ground state at time . It is subjected to a time-varying Hamiltonian . Show that, to first order in , the system evolves as
where and
A large number of hydrogen atoms, each in the ground state, are subjected to an electric field
where is a constant. Show that the fraction of atoms found in the state is, after a long time and to lowest non-trivial order in ,
where is the energy difference between the and states, and is the electron charge and the Bohr radius. What fraction of atoms lie in the state?
[Hint: You may assume the hydrogenic wavefunctions
and the integral
for a positive integer.]
Paper 4, Section II, D
The spin operators obey the commutation relations . Let be an eigenstate of the spin operators and , with and . Show that
where . When , use this to derive the explicit matrix representation
in a basis in which is diagonal.
A beam of atoms, each with spin 1 , is polarised to have spin along the direction . This beam enters a Stern-Gerlach filter that splits the atoms according to their spin along the -axis. Show that , where (respectively, ) is the number of atoms emerging from the filter with spins parallel (respectively, anti-parallel) to .
Paper 1, Section II, C
The position and momentum operators of the harmonic oscillator can be written as
where is the mass, is the frequency and the Hamiltonian is
Assuming that
derive the commutation relations for and . Construct the Hamiltonian in terms of and . Assuming that there is a unique ground state, explain how all other energy eigenstates can be constructed from it. Determine the energy of each of these eigenstates.
Consider the modified Hamiltonian
where is a dimensionless parameter. Use perturbation theory to calculate the modified energy levels to second order in , quoting any standard formulae that you require. Show that the modified Hamiltonian can be written as
Assuming , calculate the modified energies exactly. Show that the results are compatible with those obtained from perturbation theory.
Paper 2, Section II, C
Let be a set of Hermitian operators obeying
where is any unit vector. Show that implies that
for any vectors a and . Explain, with reference to the properties , how can be related to the intrinsic angular momentum for a particle of spin .
Show that the operators are Hermitian and obey
Show how can be used to write any state as a linear combination of eigenstates of . Use this to deduce that if the system is in a normalised state when is measured, then the results will be obtained with probabilities
If is a state corresponding to the system having spin up along a direction defined by a unit vector , show that a measurement will find the system to have spin up along with probability .
Paper 3, Section II, C
The angular momentum operators obey the commutation relations
where .
A quantum mechanical system involves the operators and such that
Define and . Show that and obey the same commutation relations as and .
Suppose that the system is in the state such that . Show that is an eigenstate of . Let . Show that is an eigenstate of and find the eigenvalue. How many other states do you expect to find with same value of ? Find them.
Paper 4, Section II, C
The Hamiltonian for a quantum system in the Schrödinger picture is
where is independent of time and the parameter is small. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.
Let and be eigenstates of with distinct eigenvalues and respectively. Show that if the system was in the state in the remote past, then the probability of measuring it to be in a different state at a time is
Let the system be a simple harmonic oscillator with , where . Let be the ground state which obeys . Suppose
with . In the remote past the system was in the ground state. Find the probability, to lowest non-trivial order in , for the system to be in the first excited state in the far future.
Paper 1, Section II, A
A particle in one dimension has position and momentum operators and whose eigenstates obey
For a state , define the position-space and momentum-space wavefunctions and and show how each of these can be expressed in terms of the other.
Write down the translation operator and check that your expression is consistent with the property . For a state , relate the position-space and momentum-space wavefunctions for to and respectively.
Now consider a harmonic oscillator with mass , frequency , and annihilation and creation operators
Let and be the wavefunctions corresponding to the normalised energy eigenstates , where .
(i) Express explicitly in terms of the wavefunctions .
(ii) Given that , where the are polynomials and , show that
[You may quote standard results for a harmonic oscillator. You may also use, without proof, for operators and which each commute with
Paper 2, Section II, A
(a) Let be standard, normalised angular momentum eigenstates with labels specifying eigenvalues for and . Taking units in which ,
Check the coefficients above by computing norms of states, quoting any angular momentum commutation relations that you require.
(b) Two particles, each of spin , have combined spin states . Find expressions for all such states with in terms of product states.
(c) Suppose that the particles in part (b) move about their centre of mass with a spatial wavefunction that is a spherically symmetric function of relative position. If the particles are identical, what spin states are allowed? Justify your answer.
(d) Now consider two particles of spin 1 that are not identical and are both at rest. If the 3-component of the spin of each particle is zero, what is the probability that their total, combined spin is zero?
Paper 3, Section II, 31 A
A three-dimensional oscillator has Hamiltonian
where the constants are real and positive. Assuming a unique ground state, construct the general normalised eigenstate of and give a formula for its energy eigenvalue. [You may quote without proof results for a one-dimensional harmonic oscillator of mass and frequency that follow from writing and
List all states in the four lowest energy levels of in the cases:
(i) ;
(ii) and , where .
Now consider with subject to a perturbation
where is small. Compute the changes in energies for the ground state and the states at the first excited level of the original Hamiltonian, working to the leading order at which nonzero corrections occur. [You may quote without proof results from perturbation theory.]
Explain briefly why some energy levels of the perturbed Hamiltonian will be exactly degenerate. [Hint: Compare with (ii) above.]
Paper 4, Section II, A
(a) Consider a quantum system with Hamiltonian , where is independent of time. Define the interaction picture corresponding to this Hamiltonian and derive an expression for the time derivative of an operator in the interaction picture, assuming it is independent of time in the Schrödinger picture.
(b) The Pauli matrices satisfy
Explain briefly how these properties allow to be used to describe a quantum system with spin .
(c) A particle with spin has position and momentum operators and . The unitary operator corresponding to a rotation through an angle about an axis is where is the total angular momentum. Check this statement by considering the effect of an infinitesimal rotation on and .
(d) Suppose that the particle in part (c) has Hamiltonian with
where is the orbital angular momentum and are constants. Show that all components of are independent of time in the interaction picture. Is this true in the Heisenberg picture?
[You may quote commutation relations of with and .]
Paper 1, Section II, A
If and are operators which each commute with their commutator , show that
By solving this differential equation for , deduce that
The annihilation and creation operators for a harmonic oscillator of mass and frequency are defined by
Write down an expression for the general normalised eigenstate of the oscillator Hamiltonian in terms of the ground state . What is the energy eigenvalue of the state
Suppose the oscillator is now subject to a small perturbation so that it is described by the modified Hamiltonian with . Show that
where is a constant, to be determined. Hence show that to the shift in the ground state energy as a result of the perturbation is
[Standard results of perturbation theory may be quoted without proof.]
Paper 2, Section II, A
Express the spin operator for a particle of spin in terms of the Pauli matrices where
Show that for any unit vector and deduce that
The space of states for a particle of spin has basis states which are eigenstates of with eigenvalues and respectively. If the Hamiltonian for the particle is , find
as linear combinations of the basis states.
The space of states for a system of two spin particles is . Write down explicit expressions for the joint eigenstates of and , where is the sum of the spin operators for the particles.
Suppose that the two-particle system has Hamiltonian and that at time the system is in the state with eigenvalue . Calculate the probability that at time the system will be measured to be in the state with eigenvalue zero.
Paper 3, Section II, A
Let denote the normalised joint eigenstates of and , where is the angular momentum operator for a quantum system. State clearly the possible values of the quantum numbers and and write down the corresponding eigenvalues in units with .
Consider two quantum systems with angular momentum states and . The eigenstates corresponding to their combined angular momentum can be written as
where are Clebsch-Gordan coefficients for addition of angular momenta and . What are the possible values of and what is a necessary condition relating and in order that ?
Calculate the values of for and for all . Use the sign convention that when takes its maximum value.
A particle with spin and intrinsic parity is at rest. It decays into two particles and with spin and spin 0 , respectively. Both and have intrinsic parity . The relative orbital angular momentum quantum number for the two particle system is . What are the possible values of for the cases and ?
Suppose particle is prepared in the state before it decays. Calculate the probability for particle to be found in the state , given that .
What is the probability if instead ?
[Units with should be used throughout. You may also use without proof
Paper 4, Section II, A
The Hamiltonian for a quantum system in the Schrödinger picture is , where is independent of time and the parameter is small. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.
Suppose that and are eigenstates of with distinct eigenvalues and , respectively. Show that if the system is in state at time zero then the probability of measuring it to be in state at time is
Let be the Hamiltonian for an isotropic three-dimensional harmonic oscillator of mass and frequency , with being the ground state wavefunction (where ) and being wavefunctions for the states at the first excited energy level . The oscillator is in its ground state at when a perturbation
is applied, with , and is then measured after a very large time has elapsed. Show that to first order in perturbation theory the oscillator will be found in one particular state at the first excited energy level with probability
but that the probability that it will be found in either of the other excited states is zero (to this order).
You may use the fact that
Paper 1, Section II, A
Let and be the position operator, momentum operator and Hamiltonian for a particle moving in one dimension. Let be the state vector for the particle. The position and momentum eigenstates have inner products
Show that
where and are the wavefunctions in the position representation and momentum representation, respectively. Show how and may be expressed in terms of each other.
For general , express in terms of , and hence write down the time-independent Schrödinger equation in the momentum representation satisfied by .
Consider now the case . Show that there is a bound state with energy , with wavefunction satisfying
Hence show that there is a unique value for and determine this value.
Paper 2, Section II, A
(i) Let and be the annihilation and creation operators, respectively, for a simple harmonic oscillator whose Hamiltonian is
with . Explain how the set of eigenstates of is obtained and deduce the corresponding eigenvalues. Show that
(ii) Consider a system whose unperturbed Hamiltonian is
where and all other commutators are zero. Find the degeneracies of the eigenvalues of with energies and .
The system is perturbed so that it is now described by the Hamiltonian
where . Using degenerate perturbation theory, calculate to the energies of the eigenstates associated with the level .
Write down the eigenstates, to , associated with these perturbed energies. By explicit evaluation show that they are in fact exact eigenstates of with these energies as eigenvalues.
Paper 3, Section II, A
Let and denote the standard angular-momentum operators and states so that, in units where ,
Show that is unitary. Define
and
Find expressions for and as linear combinations of and . Briefly explain why represents a rotation of through angle about the 2-axis.
Show that
Express as a linear combination of the states . By expressing in terms of , use to determine the coefficients in this expansion.
A particle of spin 1 is in the state at time . It is subject to the Hamiltonian
where . At time the value of is measured and found to be . At time the value of is measured again and found to be . Show that the joint probability for these two values to be measured is
[The following result may be quoted:
Paper 4, Section II, A
Define the interaction picture for a quantum mechanical system with Schrödinger picture Hamiltonian and explain why the interaction and Schrödinger pictures give the same physical predictions for transition rates between eigenstates of . Derive the equation of motion for the interaction picture states .
A system consists of just two states and , with respect to which
Writing the interaction picture state as , show that the interaction picture equation of motion can be written as
where and . Hence show that satisfies
Given that , show that the solution takes the form
where is a frequency to be determined and is a complex constant of integration.
Substitute this solution for into to determine and, by imposing the normalization condition at , show that .
At time the system is in the state . Write down the probability of finding the system in the state at time .
Paper 1, Section II, E
Consider a composite system of several identical particles. Describe how the multiparticle state is constructed from single-particle states. For the case of two identical particles, describe how considering the interchange symmetry leads to the definition of bosons and fermions.
Consider two non-interacting, identical particles, each with spin 1 . The singleparticle, spin-independent Hamiltonian has non-degenerate eigenvalues and wavefunctions where labels the particle and In terms of these single-particle wavefunctions and single-particle spin states and , write down all of the two-particle states and energies for:
(i) the ground state;
(ii) the first excited state.
Assume now that is a linear function of . Find the degeneracy of the energy level of the two-particle system for:
(iii) even;
(iv) odd.
Paper 2, Section II, 33E
(i) In units where , angular momentum states obey
Use the algebra of angular momentum to derive the following in terms of and : (a) ; (b) ; (c) .
(ii) Find in terms of and . Thus calculate the quantum numbers of the state in terms of and . Derive the normalisation of the state . Therefore, show that
finding in terms of .
(iii) Consider the combination of a spinless particle with an electron of spin and orbital angular momentum 1. Calculate the probability that the electron has a spin of in the -direction if the combined system has an angular momentum of in the -direction and a total angular momentum of . Repeat the calculation for a total angular momentum of .
Paper 3, Section II, E
A particle moves in one dimension in an infinite square-well potential for and for . Find the energy eigenstates. Show that the energy eigenvalues are given by for integer , where is a constant which you should find.
The system is perturbed by the potential . Show that the energy of the level remains unchanged to first order in . Show that the ground-state wavefunction is
where and are numerical constants which you should find. Briefly comment on the conservation of parity in the unperturbed and perturbed systems.
Paper 4, Section II, E
(i) The creation and annihilation operators for a harmonic oscillator of angular frequency satisfy the commutation relation . Write down an expression for the Hamiltonian and number operator in terms of and . Explain how the space of eigenstates , of is formed, and deduce the eigenenergies for these states. Show that
(ii) The operator is defined to be
for Show that commutes with . Show that if , then
and otherwise. By considering the action of on the state , deduce that
Paper 1, Section II, A
Let and be the simple harmonic oscillator annihilation and creation operators, respectively. Write down the commutator .
Consider a new operator , where with a real constant. Show that
Consider the Hamiltonian
where and are real and such that . Assuming that and , with a real constant, show that
Thus, calculate the energy of in terms of and , where is an eigenvalue of .
Assuming that , calculate in terms of and . Find the possible values of . Finally, show that the energy eigenvalues of the system are
Paper 2, Section II, A
(a) Define the Heisenberg picture of quantum mechanics in relation to the Schrödinger picture. Explain how the two pictures provide equivalent descriptions of physical results.
(b) Derive the equation of motion for an operator in the Heisenberg picture.
For a particle of mass moving in one dimension, the Hamiltonian is
where and are the position and momentum operators, and the state vector is . The eigenstates of and satisfy
Use standard methods in the Dirac formalism to show that
Calculate and express in terms of the position space wavefunction .
Write down the momentum space Hamiltonian for the potential
Paper 3, Section II, A
Discuss the consequences of indistinguishability for a quantum mechanical state consisting of two identical, non-interacting particles when the particles have (a) spin zero, (b) spin 1/2.
The stationary Schrödinger equation for one particle in the potential
has normalised, spherically-symmetric real wavefunctions and energy eigenvalues with . The helium atom can be modelled by considering two non-interacting spin 1/2 particles in the above potential. What are the consequences of the Pauli exclusion principle for the ground state? Write down the two-electron state for this model in the form of a spatial wavefunction times a spin state. Assuming that wavefunctions are spherically-symmetric, find the states of the first excited energy level of the helium atom. What combined angular momentum quantum numbers does each state have?
Assuming standard perturbation theory results, arrive at a multi-dimensional integral in terms of the one-particle wavefunctions for the first-order correction to the helium ground state energy, arising from the electron-electron interaction.
Paper 4, Section II, A
Setting , the raising and lowering operators for angular momentum satisfy
where . Find the matrix representation for in the basis
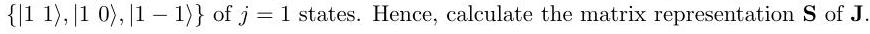
Suppose that the angular momentum of the state is measured in the direction to be . Find the components of , expressing each component by a single term consisting of products of powers of and multiplied by constants.
Suppose that two measurements of a total angular momentum 1 system are made. The first is made in the third direction with value , and the second measurement is subsequently immediately made in direction . What is the probability that the second measurement is also ?
Paper 1, Section II, D
Two individual angular momentum states , acted on by and respectively, can be combined to form a combined state . What is the combined angular momentum operator in terms of and ? [Units in which are to be used throughout.]
Defining raising and lowering operators , where , find an expression for in terms of and . Show that this implies
Write down the state with and with eigenvalue in terms of the individual angular momentum states. From this starting point, calculate the combined state with eigenvalues and in terms of the individual angular momentum states.
If and and the combined system is in the state , what is the probability of measuring the eigenvalues of individual angular momentum states to be and 0 , respectively?
[You may assume without proof that standard angular momentum states are joint eigenstates of and , obeying
and that
Paper 2, Section II, D
A quantum system has energy eigenstates with eigenvalues . An observable is such that .
(a) What is the commutator of with the Hamiltonian ?
(b) Given , consider the state
Determine:
(i) The probability of measuring to be .
(ii) The probability of measuring energy followed by another immediate measurement of energy .
(iii) The average of many separate measurements of , each measurement being on a state , as .
(c) Given and for , consider the state
where .
(i) Show that the probability of measuring an eigenvalue of is
where and are integers that you should find.
(ii) Show that is , where and are integers that you should find.
(iii) Given that is measured to be at time , write down the state after a time has passed. What is then the subsequent probability at time of measuring the energy to be ?
Paper 3, Section II, D
The Pauli matrices , with
are used to represent angular momentum operators with respect to basis states and corresponding to spin up and spin down along the -axis. They satisfy
(i) How are and represented? How is the spin operator s related to and ? Check that the commutation relations between the spin operators are as desired. Check that acting on a spin one-half state has the correct eigenvalue.
What are the states obtained by applying to the eigenstates and of ?
(ii) Let be the space of states for a spin one-half system. Consider a combination of three such systems with states belonging to and spin operators acting on each subsystem denoted by with . Find the eigenvalues of the operators
of the state
(iii) Consider now whether these outcomes for measurements of particular combinations of the operators in the state could be reproduced by replacing the spin operators with classical variables which take values according to some probabilities. Assume that these variables are identical to the quantum measurements of on . Show that classically this implies a unique possibility for
and find its value.
State briefly how this result could be used to experimentally test quantum mechanics.
Paper 4, Section II, D
The quantum-mechanical observable has just two orthonormal eigenstates and with eigenvalues and 1 , respectively. The operator is defined by , where
Defining orthonormal eigenstates of to be and with eigenvalues , , respectively, consider a perturbation to first order in for the states
where are complex coefficients. The real eigenvalues are also expanded to first order in :
From first principles, find .
Working exactly to all orders, find the real eigenvalues directly. Show that the exact eigenvectors of may be taken to be of the form
finding and the real numerical coefficient in the process.
By expanding the exact expressions, again find , verifying the perturbation theory results above.
Paper 1, Section II, C
Two states , with angular momenta , are combined to form states with total angular momentum
Write down the state with in terms of the original angular momentum states. Briefly describe how the other combined angular momentum states may be found in terms of the original angular momentum states.
If , explain why the state with must be of the form
By considering , determine a relation between and , hence find .
If the system is in the state what is the probability, written in terms of , of measuring the combined total angular momentum to bero?
[Standard angular momentum states are joint eigenstates of and , obeying
Units in which have been used throughout.]
Paper 2, Section II, C
Consider a joint eigenstate of and . Write down a unitary operator for rotation of the state by an angle about an axis with direction , where is a unit vector. How would a state with zero orbital angular momentum transform under such a rotation?
What is the relation between the angular momentum operator and the Pauli matrices when ? Explicitly calculate , for an arbitrary real vector , in this case. What are the eigenvalues of the operator ? Show that the unitary rotation operator for can be expressed as
Starting with a state the component of angular momentum along a direction , making and angle with the -axis, is susequently measured to be . Immediately after this measurement the state is . Write down an eigenvalue equation for in terms of . Show that the probability for measuring an angular momentum of along the direction is, assuming is in the plane,
where is a unit vector in the -direction. Using show that the probability that is of the form
determining the integers and in the process.
[Assume . The Pauli matrices are
Paper 3, Section II, C
What are the commutation relations between the position operator and momentum operator ? Show that this is consistent with being hermitian.
The annihilation operator for a harmonic oscillator is
in units where the mass and frequency of the oscillator are 1 . Derive the relation . Write down an expression for the Hamiltonian
in terms of the operator .
Assume there exists a unique ground state of such that . Explain how the space of eigenstates , is formed, and deduce the energy eigenvalues for these states. Show that
finding and in terms of .
Calculate the energy eigenvalues of the Hamiltonian for two harmonic oscillators
What is the degeneracy of the energy level? Suppose that the two oscillators are then coupled by adding the extra term
to , where . Calculate the energies for the states of the unperturbed system with the three lowest energy eigenvalues to first order in using perturbation theory.
[You may assume standard perturbation theory results.]
Paper 4, Section II, C
The Hamiltonian for a quantum system in the Schrödinger picture is
where is independent of time. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.
Let and be orthonormal eigenstates of with eigenvalues and respectively. Assume for . Show that if the system is initially, at , in the state then the probability of measuring it to be the state after a time is
to order .
Suppose a system has a basis of just two orthonormal states and , with respect to which
where
Use to calculate the probability of a transition from state to state after a time to order .
Show that the time dependent Schrödinger equation has a solution
Calculate the transition probability exactly. Hence find the condition for the order approximation to be valid.
Paper 1, Section II, C
The position and momentum for a harmonic oscillator can be written
where is the mass, is the frequency, and the Hamiltonian is
Starting from the commutation relations for and , determine the energy levels of the oscillator. Assuming a unique ground state, explain how all other energy eigenstates can be constructed from it.
Consider a modified Hamiltonian
where is a dimensionless parameter. Calculate the modified energy levels to second order in , quoting any standard formulas which you require. Show that the modified Hamiltonian can be written as
where and depend on . Hence find the modified energies exactly, assuming , and show that the results are compatible with those obtained from perturbation theory.
Paper 2, Section II, C
Let be a set of Hermitian operators obeying
where is any unit vector. Show that implies
for any vectors a and b. Explain, with reference to the properties , how can be related to the intrinsic angular momentum for a particle of spin .
Show that the operators are Hermitian and obey
Show also how can be used to write any state as a linear combination of eigenstates of . Use this to deduce that if the system is in a normalised state when is measured, then the results will be obtained with probabilities
If is a state corresponding to the system having spin up along a direction defined by a unit vector , show that a measurement will find the system to have spin up along with probability .
Paper 3, Section II, C
(i) Consider two quantum systems with angular momentum states and . The eigenstates corresponding to their combined angular momentum can be written as
where are Clebsch-Gordan coefficients for addition of angular momenta one and . What are the possible values of and how must and be related for ?
Construct all states in terms of product states in the case .
(ii) A general stationary state for an electron in a hydrogen atom is specified by the principal quantum number in addition to the labels and corresponding to the total orbital angular momentum and its component in the 3-direction (electron spin is ignored). An oscillating electromagnetic field can induce a transition to a new state and, in a suitable approximation, the amplitude for this to occur is proportional to
where are components of the electron's position. Give clear but concise arguments based on angular momentum which lead to conditions on and for the amplitude to be non-zero.
Explain briefly how parity can be used to obtain an additional selection rule.
[Standard angular momentum states are joint eigenstates of and , obeying
You may also assume that and have commutation relations with orbital angular momentum given by
Units in which are to be used throughout. ]
Paper 4, Section II, C
For any given operators and , show that has derivative and deduce an analogous formula for the th derivative. Hence, by considering as a power series in , show that
A particle of unit mass in one dimension has position and momentum in the Schrödinger picture, and Hamiltonian
where is a constant. Apply to find the Heisenberg picture operators and in terms of and , and check explicitly that .
A particle of unit mass in two dimensions has position and momentum in the Schrödinger picture, and Hamiltonian
where is a constant. Calculate the Heisenberg picture momentum components in terms of and verify that is independent of time. Now consider the interaction picture corresponding to : show that if then the interaction picture position operators are , and use this to find the Heisenberg picture position operators in terms of and .
[Hint: If and is an operator in the interaction picture, then the corresponding operator in the Heisenberg picture is
1.II.32D
(a) If and are operators which each commute with their commutator , show that . By considering
and differentiating with respect to the parameter , show also that
where .
(b) Consider a one-dimensional quantum system with position and momentum . Write down a formula for the operator corresponding to translation through , calculate , and show that your answer is consistent with the assumption that position eigenstates obey . Given this assumption, express the wavefunction for in terms of the wavefunction for .
Now suppose the one-dimensional system is a harmonic oscillator of mass and frequency . Show that
where are normalised wavefunctions with energies .
[Standard results for constructing normalised energy eigenstates in terms of annihilation and creation operators
may be quoted without proof.]
2.II.32D
Derive approximate expressions for the eigenvalues of a Hamiltonian , working to second order in the parameter and assuming the eigenstates and eigenvalues of are known and non-degenerate.
Let be angular momentum operators with joint eigenstates of and . What are the possible values of the labels and and what are the corresponding eigenvalues of the operators?
A particle with spin is trapped in space (its position and momentum can be ignored) but is subject to a magnetic field of the form , resulting in a Hamiltonian . Starting from the eigenstates and eigenvalues of this Hamiltonian when , use perturbation theory to compute the leading order corrections to the energies when is non-zero but much smaller than . Compare with the exact result.
[You may set and use ]
3.II
Explain, in a few lines, how the Pauli matrices with
are used to represent angular momentum operators with respect to basis states and corresponding to spin up and spin down along the 3 -axis. You should state clearly which properties of the matrices correspond to general features of angular momentum and which are specific to spin half.
Consider two spin-half particles labelled A and B, each with its spin operators and spin eigenstates. Find the matrix representation of
with respect to a basis of two-particle states . Show that the eigenvalues of the matrix are and find the eigenvectors.
What is the behaviour of each eigenvector under interchange of and ? If the particles are identical, and there are no other relevant degrees of freedom, which of the two-particle states are allowed?
By relating to the operator discussed above, show that your findings are consistent with standard results for addition of angular momentum.
4.II.32D
Define the interaction picture for a quantum mechanical system with Schrödinger picture Hamiltonian and explain why either picture gives the same physical predictions. Derive an equation of motion for interaction picture states and use this to show that the probability of a transition from a state at time zero to a state at time is
correct to second order in , where the initial and final states are orthogonal eigenstates of with eigenvalues and .
Consider a perturbed harmonic oscillator:
with and annihilation and creation operators (all usual properties may be assumed). Working to order , find the probability for a transition from an initial state with to a final state with after time .
Suppose becomes large and perturbation theory still applies. Explain why the rate for each allowed transition is sharply peaked, as a function of , around .
1.II.32D
A particle in one dimension has position and momentum operators and whose eigenstates obey
Given a state , define the corresponding position-space and momentum-space wavefunctions and and show how each of these can be expressed in terms of the other. Derive the form taken in momentum space by the time-independent Schrödinger equation
for a general potential .
Now let with a positive constant. Show that the Schrödinger equation can be written
and verify that it has a solution for unique choices of and , to be determined (you need not find the normalisation constant, ). Check that this momentum space wavefunction can also be obtained from the position space solution .
2.II.32D
Let denote the combined spin eigenstates for a system of two particles, each with spin 1. Derive expressions for all states with in terms of product states.
Given that the particles are identical, and that the spatial wavefunction describing their relative position has definite orbital angular momentum , show that must be even. Suppose that this two-particle state is known to arise from the decay of a single particle, , also of spin 1. Assuming that total angular momentum and parity are conserved in this process, find the values of and that are allowed, depending on whether the intrinsic parity of is even or odd.
[You may set and use ]
3.II.32D
Let
be the position and momentum operators for a one-dimensional harmonic oscillator of mass and frequency . Write down the commutation relations obeyed by and and give an expression for the oscillator Hamiltonian in terms of them. Prove that the only energies allowed are with and give, without proof, a formula for a general normalised eigenstate in terms of .
A three-dimensional oscillator with charge is subjected to a weak electric field so that its total Hamiltonian is
where for and is a small, dimensionless parameter. Express the general eigenstate for the Hamiltonian with in terms of one-dimensional oscillator states, and give the corresponding energy eigenvalue. Use perturbation theory to compute the changes in energies of states in the lowest two levels when , working to the leading order at which non-vanishing corrections occur.
4.II.32D
The Hamiltonian for a particle of spin in a magnetic field is
and is a constant (the motion of the particle in space can be ignored). Consider a magnetic field which is independent of time. Writing , where is a unit vector, calculate the time evolution operator and show that if the particle is initially in a state the probability of measuring it to be in an orthogonal state after a time is
Evaluate this to find the probability for a transition from a state of spin up along the direction to one of spin down along the direction when .
Now consider a magnetic field whose and components are time-dependent but small:
Show that the probability for a transition from a spin-up state at time zero to a spin-down state at time (with spin measured along the direction, as before) is approximately
where you may assume . Comment on how this compares, when , with the result for a time-independent field.
[The first-order transition amplitude due to a perturbation is
where and are orthogonal eigenstates of the unperturbed Hamiltonian with eigenvalues and respectively.]
1.II.32D
A particle in one dimension has position and momentum operators and . Explain how to introduce the position-space wavefunction for a quantum state and use this to derive a formula for . Find the wavefunctions for and in terms of , stating clearly any standard properties of position and momentum eigenstates which you require.
Define annihilation and creation operators and for a harmonic oscillator of unit mass and frequency and write the Hamiltonian
in terms of them. Let be a normalized eigenstate of with eigenvalue , a complex number. Show that cannot be an eigenstate of unless , and that is an eigenstate of with the lowest possible energy. Find a normalized wavefunction for for any . Do there exist normalizable eigenstates of ? Justify your answer.
2.II.32A
Let and denote the eigenstates of for a particle of spin . Show that
are eigenstates of for any . Show also that the composite state
for two spin- particles, is unchanged under a transformation
applied to all one-particle states. Hence, by considering the action of certain components of the spin operator for the composite system, show that is a state of total spin zero.
Two spin- particles A and B have combined spin zero (as in the state above) but are widely separated in space. A magnetic field is applied to particle B in such a way that its spin states are transformed according to , for a certain value of , while the spin states of particle A are unaffected. Once this has been done, a measurement is made of for particle A, followed by a measurement of for particle B. List the possible results for this pair of measurements and find the total probability, in terms of , for each pair of outcomes to occur. For which outcomes is the two-particle system left in an eigenstate of the combined total spin operator, , and what is the eigenvalue for each such outcome?
3.II.32D
Consider a Hamiltonian with known eigenstates and eigenvalues (possibly degenerate). Derive a general method for calculating the energies of a new Hamiltonian to first order in the parameter . Apply this method to find approximate expressions for the new energies close to an eigenvalue of , given that there are just two orthonormal eigenstates and corresponding to and that
A charged particle of mass moves in two-dimensional space but is confined to a square box . In the absence of any potential within this region the allowed wavefunctions are
inside the box, and zero outside. A weak electric field is now applied, modifying the Hamiltonian by a term , where is small. Show that the three lowest new energy levels for the particle are approximately
[It may help to recall that .]
4.II.32A
Define the Heisenberg picture of quantum mechanics in relation to the Schrödinger picture and explain how these formulations give rise to identical physical predictions. Derive an equation of motion for an operator in the Heisenberg picture, assuming the operator is independent of time in the Schrödinger picture.
State clearly the form of the unitary operator corresponding to a rotation through an angle about an axis (a unit vector) for a general quantum system. Verify your statement for the case in which the system is a single particle by considering the effect of an infinitesimal rotation on the particle's position and on its spin .
Show that if the Hamiltonian for a particle is of the form
then all components of the total angular momentum are independent of time in the Heisenberg picture. Is the same true for either orbital or spin angular momentum?
[You may quote commutation relations involving components of and .]
1.II.32D
A one-dimensional harmonic oscillator has Hamiltonian
where
Assuming the existence of a normalised state with , verify that
are eigenstates of with energies , to be determined, and that these states all have unit norm.
The Hamiltonian is now modified by a term
where is a positive integer. Use perturbation theory to find the change in the lowest energy level to order for any . [You may quote any standard formula you need.]
Compute by perturbation theory, again to order , the change in the first excited energy level when . Show that in this special case, , the exact change in all energy levels as a result of the perturbation is .
2.II.32D
The components of are hermitian matrices obeying
for any unit vector . Show that these properties imply
for any constant vectors a and . Assuming that is real, explain why the matrix is unitary, and show that
Hence deduce that
where is any unit vector orthogonal to .
Write down an equation relating the matrices and the angular momentum operator for a particle of spin one half, and explain briefly the significance of the conditions . Show that if is a state with spin 'up' measured along the direction then, for a certain choice of is a state with spin 'up' measured along the direction .
3.II.32D
The angular momentum operators and refer to independent systems, each with total angular momentum one. The combination of these systems has a basis of states which are of product form where and are the eigenvalues of and respectively. Let denote the alternative basis states which are simultaneous eigenstates of and , where is the combined angular momentum. What are the possible values of and ? Find expressions for all states with in terms of product states. How do these states behave when the constituent systems are interchanged?
Two spin-one particles and have no mutual interaction but they each move in a potential which is independent of spin. The single-particle energy levels and the corresponding wavefunctions are the same for either or . Given that , explain how to construct the two-particle states of lowest energy and combined total spin for the cases that (i) and are identical, and (ii) and are not identical.
[You may assume and use the result
4.II.32D
The Hamiltonian for a quantum system in the Schrödinger picture is
where is independent of time and the parameter is small. Define the interaction picture corresponding to this Hamiltonian and derive a time evolution equation for interaction picture states.
Let and be eigenstates of with distinct eigenvalues and respectively. Show that if the system is initially in state then the probability of measuring it to be in state after a time is
Deduce that if , where is a time-independent operator and is a positive constant, then the probability for such a transition to have occurred after a very long time is approximately