Classical Dynamics
Classical Dynamics
Jump to year
Paper 1, Section I, D
Two equal masses move along a straight line between two stationary walls. The mass on the left is connected to the wall on its left by a spring of spring constant , and the mass on the right is connected to the wall on its right by a spring of spring constant . The two masses are connected by a third spring of spring constant .
(a) Show that the Lagrangian of the system can be written in the form
where , for , are the displacements of the two masses from their equilibrium positions, and and are symmetric matrices that should be determined.
(b) Let
where and . Using Lagrange's equations of motion, show that the angular frequencies of the normal modes of the system are given by
where
Paper 2, Section I, D
Show that, in a uniform gravitational field, the net gravitational torque on a system of particles, about its centre of mass, is zero.
Let be an inertial frame of reference, and let be the frame of reference with the same origin and rotating with angular velocity with respect to . You may assume that the rates of change of a vector observed in the two frames are related by
Derive Euler's equations for the torque-free motion of a rigid body.
Show that the general torque-free motion of a symmetric top involves precession of the angular-velocity vector about the symmetry axis of the body. Determine how the direction and rate of precession depend on the moments of inertia of the body and its angular velocity.
Paper 2, Section II, D
(a) Show that the Hamiltonian
where is a positive constant, describes a simple harmonic oscillator with angular frequency . Show that the energy and the action of the oscillator are related by .
(b) Let be a constant. Verify that the differential equation
is solved by
when , where is a constant you should determine in terms of .
(c) Show that the solution in part (b) obeys
Hence show that the fractional variation of the action in the limit is , but that these variations do not accumulate. Comment on this behaviour in relation to the theory of adiabatic invariance.
Paper 3 , Section I, D
The Lagrangian of a particle of mass and charge in an electromagnetic field takes the form
Explain the meaning of and , and how they are related to the electric and magnetic fields.
Obtain the canonical momentum and the Hamiltonian .
Suppose that the electric and magnetic fields have Cartesian components and , respectively, where and are positive constants. Explain why the Hamiltonian of the particle can be taken to be
State three independent integrals of motion in this case.
Paper 4, Section I, D
Briefly describe a physical object (a Lagrange top) whose Lagrangian is
Explain the meaning of the symbols in this equation.
Write down three independent integrals of motion for this system, and show that the nutation of the top is governed by the equation
where and is a certain cubic function that you need not determine.
Paper 4, Section II, 15D
(a) Let be a set of canonical phase-space variables for a Hamiltonian system with degrees of freedom. Define the Poisson bracket of two functions and . Write down the canonical commutation relations that imply that a second set of phase-space variables is also canonical.
(b) Consider the near-identity transformation
where and are small. Determine the approximate forms of the canonical commutation relations, accurate to first order in and . Show that these are satisfied when
where is a small parameter and is some function of the phase-space variables.
(c) In the limit this near-identity transformation is called the infinitesimal canonical transformation generated by . Let be an autonomous Hamiltonian. Show that the change in the Hamiltonian induced by the infinitesimal canonical transformation is
Explain why is an integral of motion if and only if the Hamiltonian is invariant under the infinitesimal canonical transformation generated by .
(d) The Hamiltonian of the gravitational -body problem in three-dimensional space is
where and are the mass, position and momentum of body . Determine the form of and the infinitesimal canonical transformation that correspond to the translational symmetry of the system.
Paper 1, Section I, B
A linear molecule is modelled as four equal masses connected by three equal springs. Using the Cartesian coordinates of the centres of the four masses, and neglecting any forces other than those due to the springs, write down the Lagrangian of the system describing longitudinal motions of the molecule.
Rewrite and simplify the Lagrangian in terms of the generalized coordinates
Deduce Lagrange's equations for . Hence find the normal modes of the system and their angular frequencies, treating separately the symmetric and antisymmetric modes of oscillation.
Paper 2, Section I, B
A particle of mass has position vector in a frame of reference that rotates with angular velocity . The particle moves under the gravitational influence of masses that are fixed in the rotating frame. Explain why the Lagrangian of the particle is of the form
Show that Lagrange's equations of motion are equivalent to
Identify the canonical momentum conjugate to . Obtain the Hamiltonian and Hamilton's equations for this system.
Paper 2, Section II, B
A symmetric top of mass rotates about a fixed point that is a distance from the centre of mass along the axis of symmetry; its principal moments of inertia about the fixed point are and . The Lagrangian of the top is
(i) Draw a diagram explaining the meaning of the Euler angles and .
(ii) Derive expressions for the three integrals of motion and .
(iii) Show that the nutational motion is governed by the equation
and derive expressions for the effective potential and the modified energy in terms of and .
(iv) Suppose that
where is a small positive number. By expanding to second order in and , show that there is a stable equilibrium solution with , provided that . Determine the equilibrium value of and the precession rate , to the same level of approximation.
Paper 3, Section I, B
A particle of mass experiences a repulsive central force of magnitude , where is its distance from the origin. Write down the Hamiltonian of the system.
The Laplace-Runge-Lenz vector for this system is defined by
where is the angular momentum and is the radial unit vector. Show that
where is the Poisson bracket. What are the integrals of motion of the system? Show that the polar equation of the orbit can be written as
where and are non-negative constants.
Paper 4, Section I, B
Derive expressions for the angular momentum and kinetic energy of a rigid body in terms of its mass , the position of its centre of mass, its inertia tensor (which should be defined) about its centre of mass, and its angular velocity .
A spherical planet of mass and radius has density proportional to . Given that and , evaluate the inertia tensor of the planet in terms of and .
Paper 4, Section II, B
(a) Explain how the Hamiltonian of a system can be obtained from its Lagrangian . Deduce that the action can be written as
Show that Hamilton's equations are obtained if the action, computed between fixed initial and final configurations and , is minimized with respect to independent variations of and .
(b) Let be a new set of coordinates on the same phase space. If the old and new coordinates are related by a type-2 generating function such that
deduce that the canonical form of Hamilton's equations applies in the new coordinates, but with a new Hamiltonian given by
(c) For each of the Hamiltonians (i) , (ii) ,
express the general solution at time in terms of the initial values given by at time . In each case, show that the transformation from to is canonical for all values of , and find the corresponding generating function explicitly.
Paper 1, Section I, E
(a) A mechanical system with degrees of freedom has the Lagrangian , where are the generalized coordinates and .
Suppose that is invariant under the continuous symmetry transformation , where is a real parameter and . State and prove Noether's theorem for this system.
(b) A particle of mass moves in a conservative force field with potential energy , where is the position vector in three-dimensional space.
Let be cylindrical polar coordinates. is said to have helical symmetry if it is of the form
for some constant . Show that a particle moving in a potential with helical symmetry has a conserved quantity that is a linear combination of angular and linear momenta.
Paper 2, Section I, E
(a) State Hamilton's equations for a system with degrees of freedom and Hamilto, where are canonical phase-space variables.
(b) Define the Poisson bracket of two functions and .
(c) State the canonical commutation relations of the variables and .
(d) Show that the time-evolution of any function is given by
(e) Show further that the Poisson bracket of any two conserved quantities is also a conserved quantity.
[You may assume the Jacobi identity,
Paper 2, Section II, E
The Lagrangian of a particle of mass and charge moving in an electromagnetic field described by scalar and vector potentials and is
where is the position vector of the particle and .
(a) Show that Lagrange's equations are equivalent to the equation of motion
where
are the electric and magnetic fields.
(b) Show that the related Hamiltonian is
where . Obtain Hamilton's equations for this system.
(c) Verify that the electric and magnetic fields remain unchanged if the scalar and vector potentials are transformed according to
where is a scalar field. Show that the transformed Lagrangian differs from by the total time-derivative of a certain quantity. Why does this leave the form of Lagrange's equations invariant? Show that the transformed Hamiltonian and phase-space variables are related to and by a canonical transformation.
[Hint: In standard notation, the canonical transformation associated with the type-2 generating function is given by
Paper 3, Section I, E
A simple harmonic oscillator of mass and spring constant has the equation of motion
(a) Describe the orbits of the system in phase space. State how the action of the oscillator is related to a geometrical property of the orbits in phase space. Derive the action-angle variables and give the form of the Hamiltonian of the oscillator in action-angle variables.
(b) Suppose now that the spring constant varies in time. Under what conditions does the theory of adiabatic invariance apply? Assuming that these conditions hold, identify an adiabatic invariant and determine how the energy and amplitude of the oscillator vary with in this approximation.
Paper 4, Section I, E
(a) The angular momentum of a rigid body about its centre of mass is conserved.
Derive Euler's equations,
explaining the meaning of the quantities appearing in the equations.
(b) Show that there are two independent conserved quantities that are quadratic functions of , and give a physical interpretation of them.
(c) Derive a linear approximation to Euler's equations that applies when and . Use this to determine the stability of rotation about each of the three principal axes of an asymmetric top.
Paper 4, Section II, E
(a) Explain what is meant by a Lagrange top. You may assume that such a top has the Lagrangian
in terms of the Euler angles . State the meaning of the quantities and appearing in this expression.
Explain why the quantity
is conserved, and give two other independent integrals of motion.
Show that steady precession, with a constant value of , is possible if
(b) A rigid body of mass is of uniform density and its surface is defined by
where is a positive constant and are Cartesian coordinates in the body frame.
Calculate the values of and for this symmetric top, when it rotates about the sharp point at the origin of this coordinate system.
Paper 1, Section I, B
Derive Hamilton's equations from an action principle.
Consider a two-dimensional phase space with the Hamiltonian . Show that is the first integral for some constant which should be determined. By considering the surfaces of constant in the extended phase space, solve Hamilton's equations, and sketch the orbits in the phase space.
Paper 2, Section I, B
Let . Consider a Lagrangian
of a particle constrained to move on a sphere of radius . Use Lagrange multipliers to show that
Now, consider the system with , and find the particle trajectories.
Paper 2, Section II, B
Define a body frame of a rotating rigid body, and show that there exists a vector such that
Let be the angular momentum of a free rigid body expressed in the body frame. Derive the Euler equations from the conservation of angular momentum.
Verify that the kinetic energy , and the total angular momentum are conserved. Hence show that
where is a quartic polynomial which should be explicitly determined in terms of and .
Paper 3, Section I, B
Three particles of unit mass move along a line in a potential
where is the coordinate of the th particle, .
Write the Lagrangian in the form
and specify the matrices and .
Find the normal frequencies and normal modes for this system.
Paper 4, Section I, B
State and prove Noether's theorem in Lagrangian mechanics.
Consider a Lagrangian
for a particle moving in the upper half-plane in a potential which only depends on . Find two independent first integrals.
Paper 4, Section II, B
Given a Lagrangian with degrees of freedom , define the Hamiltonian and show how Hamilton's equations arise from the Lagrange equations and the Legendre transform.
Consider the Lagrangian for a symmetric top moving in constant gravity:
where and are constants. Construct the corresponding Hamiltonian, and find three independent Poisson-commuting first integrals of Hamilton's equations.
Paper 1, Section I, E
Consider a Lagrangian system with Lagrangian , where , and constraints
Use the method of Lagrange multipliers to show that this is equivalent to a system with Lagrangian , where , and are coordinates on the surface of constraints.
Consider a bead of unit mass in constrained to move (with no potential) on a wire given by an equation , where are Cartesian coordinates. Show that the Euler-Lagrange equations take the form
for some which should be specified. Find one first integral of the EulerLagrange equations, and thus show that
where should be given in the form of an integral.
[Hint: You may assume that the Euler-Lagrange equations hold in all coordinate systems.]
Paper 2, Section I, E
Derive the Lagrange equations from the principle of stationary action
where the end points and are fixed.
Let and be a scalar and a vector, respectively, depending on . Consider the Lagrangian
and show that the resulting Euler-Lagrange equations are invariant under the transformations
where is an arbitrary function, and is a constant which should be determined.
Paper 2, Section II, E
Show that an object's inertia tensor about a point displaced from the centre of mass by a vector is given by
where is the total mass of the object, and is the inertia tensor about the centre of mass.
Find the inertia tensor of a cube of uniform density, with edge of length , about one of its vertices.
Paper 3, Section I, E
Define an integrable system with -dimensional phase space. Define angle-action variables.
Consider a two-dimensional phase space with the Hamiltonian
where is a positive integer and the mass changes slowly in time. Use the fact that the action is an adiabatic invariant to show that the energy varies in time as , where is a constant which should be found.
Paper 4, Section I, E
Consider the Poisson bracket structure on given by
and show that , where and is any polynomial function on .
Let , where are positive constants. Find the explicit form of Hamilton's equations
Find a condition on such that the oscillation described by
is linearly unstable, where are small.
Paper 4, Section II,
Explain how geodesics of a Riemannian metric
arise from the kinetic Lagrangian
where .
Find geodesics of the metric on the upper half plane
with the metric
and sketch the geodesic containing the points and .
[Hint: Consider
Paper 1, Section I, E
Consider a one-parameter family of transformations such that for all time , and
where is a Lagrangian and a dot denotes differentiation with respect to . State and prove Noether's theorem.
Consider the Lagrangian
where the potential is a function of two variables. Find a continuous symmetry of this Lagrangian and construct the corresponding conserved quantity. Use the Euler-Lagrange equations to explicitly verify that the function you have constructed is independent of .
Paper 2, Section I, E
Consider the Lagrangian
where are positive constants and is a positive integer. Find three conserved quantities and show that satisfies
where is a polynomial of degree which should be determined.
Paper 2, Section II, E
Define what it means for the transformation given by
to be canonical. Show that a transformation is canonical if and only if
Show that the transformation given by
is canonical for any real constant . Find the corresponding generating function.
Paper 3, Section I, E
Consider a six-dimensional phase space with coordinates for . Compute the Poisson brackets , where .
Consider the Hamiltonian
and show that the resulting Hamiltonian system admits three Poisson-commuting independent first integrals.
Paper 4, Section I, E
Using conservation of angular momentum in the body frame, derive the Euler equations for a rigid body:
[You may use the formula without proof.]
Assume that the principal moments of inertia satisfy . Determine whether a rotation about the principal 3-axis leads to stable or unstable perturbations.
Paper 4, Section II,
A particle of unit mass is attached to one end of a light, stiff rod of length . The other end of the rod is held at a fixed position, such that the rod is free to swing in any direction. Write down the Lagrangian for the system giving a clear definition of any angular variables you introduce. [You should assume the acceleration is constant.]
Find two independent constants of the motion.
The particle is projected horizontally with speed from a point where the rod lies at an angle to the downward vertical, with . In terms of and , find the critical speed such that the particle always remains at its initial height.
The particle is now projected horizontally with speed but from a point at angle to the vertical, where . Show that the height of the particle oscillates, and find the period of oscillation in terms of and .
Paper 1, Section I, D
(a) The action for a one-dimensional dynamical system with a generalized coordinate and Lagrangian is given by
State the principle of least action and derive the Euler-Lagrange equation.
(b) A planar spring-pendulum consists of a light rod of length and a bead of mass , which is able to slide along the rod without friction and is attached to the ends of the rod by two identical springs of force constant as shown in the figure. The rod is pivoted at one end and is free to swing in a vertical plane under the influence of gravity.
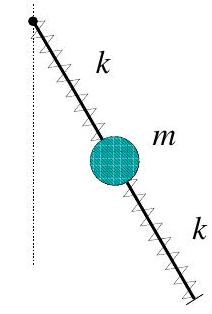
(i) Identify suitable generalized coordinates and write down the Lagrangian of the system.
(ii) Derive the equations of motion.
Paper 2, Section I, D
The Lagrangian for a heavy symmetric top of mass , pinned at a point that is a distance from the centre of mass, is
(a) Find all conserved quantities. In particular, show that , the spin of the top, is constant.
(b) Show that obeys the equation of motion
where the explicit form of should be determined.
(c) Determine the condition for uniform precession with no nutation, that is and const. For what values of does such uniform precession occur?
Paper 2, Section II, C
(a) Consider a Lagrangian dynamical system with one degree of freedom. Write down the expression for the Hamiltonian of the system in terms of the generalized velocity , momentum , and the Lagrangian . By considering the differential of the Hamiltonian, or otherwise, derive Hamilton's equations.
Show that if is ignorable (cyclic) with respect to the Lagrangian, i.e. , then it is also ignorable with respect to the Hamiltonian.
(b) A particle of charge and mass moves in the presence of electric and magnetic fields such that the scalar and vector potentials are and , where are Cartesian coordinates and are constants. The Lagrangian of the particle is
Starting with the Lagrangian, derive an explicit expression for the Hamiltonian and use Hamilton's equations to determine the motion of the particle.
Paper 3, Section I,
(a) Consider a particle of mass that undergoes periodic motion in a one-dimensional potential . Write down the Hamiltonian for the system. Explain what is meant by the angle-action variables of the system and write down the integral expression for the action variable .
(b) For and fixed total energy , describe the shape of the trajectories in phase-space. By using the expression for the area enclosed by the trajectory, or otherwise, find the action variable in terms of and . Hence describe how changes with if varies slowly with time. Justify your answer.
Paper 4, Section I, D
A triatomic molecule is modelled by three masses moving in a line while connected to each other by two identical springs of force constant as shown in the figure.

(a) Write down the Lagrangian and derive the equations describing the motion of the atoms.
(b) Find the normal modes and their frequencies. What motion does the lowest frequency represent?
Paper 4, Section II, C
Consider a rigid body with angular velocity , angular momentum and position vector , in its body frame.
(a) Use the expression for the kinetic energy of the body,
to derive an expression for the tensor of inertia of the body, I. Write down the relationship between and .
(b) Euler's equations of torque-free motion of a rigid body are
Working in the frame of the principal axes of inertia, use Euler's equations to show that the energy and the squared angular momentum are conserved.
(c) Consider a cuboid with sides and , and with mass distributed uniformly.
(i) Use the expression for the tensor of inertia derived in (a) to calculate the principal moments of inertia of the body.
(ii) Assume and , and suppose that the initial conditions are such that
with the initial angular velocity perpendicular to the intermediate principal axis . Derive the first order differential equation for in terms of and and hence determine the long-term behaviour of .
Paper 1, Section I, A
Consider a one-dimensional dynamical system with generalized coordinate and momentum .
(a) Define the Poisson bracket of two functions and .
(b) Verify the Leibniz rule
(c) Explain what is meant by a canonical transformation .
(d) State the condition for a transformation to be canonical in terms of the Poisson bracket . Use this to determine whether or not the following transformations are canonical:
(i) ,
(ii) ,
(iii) .
Paper 2, Section I, A
The components of the angular velocity of a rigid body and of the position vector are given in a body frame.
(a) The kinetic energy of the rigid body is defined as
Given that the centre of mass is at rest, show that can be written in the form
where the explicit form of the tensor should be determined.
(b) Explain what is meant by the principal moments of inertia.
(c) Consider a rigid body with principal moments of inertia and , which are all unequal. Derive Euler's equations of torque-free motion
(d) The body rotates about the principal axis with moment of inertia . Derive the condition for stable rotation.
Paper 2, Section II, A
A planar pendulum consists of a mass at the end of a light rod of length . The pivot of the pendulum is attached to a bead of mass , which slides along a horizontal rod without friction. The bead is connected to the ends of the horizontal rod by two identical springs of force constant . The pivot constrains the pendulum to swing in the vertical plane through the horizontal rod. The horizontal rod is mounted on a bracket, so the system could rotate about the vertical axis which goes through its centre as shown in the figure.
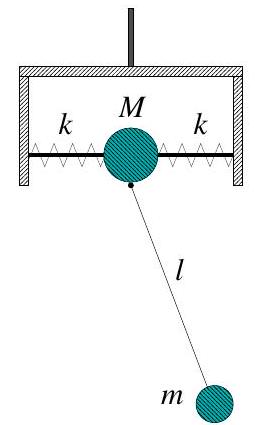
(a) Initially, the system is not allowed to rotate about the vertical axis.
(i) Identify suitable generalized coordinates and write down the Lagrangian of the system.
(ii) Write down expression(s) for any conserved quantities. Justify your answer.
(iii) Derive the equations of motion.
(iv) For and , find the frequencies of small oscillations around the stable equilibrium and the corresponding normal modes. Describe the respective motions of the system.
(b) Assume now that the system is free to rotate about the vertical axis without friction. Write down the Lagrangian of the system. Identify and calculate the additional conserved quantity.
Paper 3, Section I, A
(a) The action for a one-dimensional dynamical system with a generalized coordinate and Lagrangian is given by
State the principle of least action. Write the expression for the Hamiltonian in terms of the generalized velocity , the generalized momentum and the Lagrangian . Use it to derive Hamilton's equations from the principle of least action.
(b) The motion of a particle of charge and mass in an electromagnetic field with scalar potential and vector potential is characterized by the Lagrangian
(i) Write down the Hamiltonian of the particle.
(ii) Consider a particle which moves in three dimensions in a magnetic field with , where is a constant. There is no electric field. Obtain Hamilton's equations for the particle.
Paper 4, Section I, A
Consider a heavy symmetric top of mass with principal moments of inertia , and , where . The top is pinned at point , which is at a distance from the centre of mass, , as shown in the figure.
Its angular velocity in a body frame is given by
where and are the Euler angles.
(a) Assuming that , are chosen to be the principal axes, write down the Lagrangian of the top in terms of and the principal moments of inertia. Hence find the Lagrangian in terms of the Euler angles.
(b) Find all conserved quantities. Show that , the spin of the top, is constant.
(c) By eliminating and , derive a second-order differential equation for .
Paper 4, Section II, A
(a) Consider a system with one degree of freedom, which undergoes periodic motion in the potential . The system's Hamiltonian is
(i) Explain what is meant by the angle and action variables, and , of the system and write down the integral expression for the action variable . Is conserved? Is conserved?
(ii) Consider , where is a positive constant. Find in terms of , the total energy , the mass , and a dimensionless constant factor (which you need not compute explicitly).
(iii) Hence describe how changes with if varies slowly with time. Justify your answer.
(b) Consider now a particle which moves in a plane subject to a central force-field .
(i) Working in plane polar coordinates , write down the Hamiltonian of the system. Hence deduce two conserved quantities. Prove that the system is integrable and state the number of action variables.
(ii) For a particle which moves on an elliptic orbit find the action variables associated with radial and tangential motions. Can the relationship between the frequencies of the two motions be deduced from this result? Justify your answer.
(iii) Describe how changes with and if one or both of them vary slowly with time.
[You may use
where .]
Paper 1, Section I, B
Consider an -dimensional dynamical system with generalized coordinates and momenta .
(a) Define the Poisson bracket of two functions and .
(b) Assuming Hamilton's equations of motion, prove that if a function Poisson commutes with the Hamiltonian, that is , then is a constant of the motion.
(c) Assume that is an ignorable coordinate, that is the Hamiltonian does not depend on it explicitly. Using the formalism of Poisson brackets prove that the conjugate momentum is conserved.
Paper 2, Section I, B
(i) Consider a rigid body with principal moments of inertia . Derive Euler's equations of torque-free motion,
with components of the angular velocity given in the body frame.
(ii) Use Euler's equations to show that the energy and the square of the total angular momentum of the body are conserved.
(iii) Consider a torque-free motion of a symmetric top with . Show that in the body frame the vector of angular velocity precesses about the body-fixed axis with constant angular frequency equal to .
Paper 2, Section II, B
(i) The action for a system with a generalized coordinate is given by
(a) State the Principle of Least Action and derive the Euler-Lagrange equation.
(b) Consider an arbitrary function . Show that leads to the same equation of motion.
(ii) A wire frame in a shape of an equilateral triangle with side rotates in a horizontal plane with constant angular frequency about a vertical axis through . A bead of mass is threaded on and moves without friction. The bead is connected to and by two identical light springs of force constant and equilibrium length .
(a) Introducing the displacement of the particle from the mid point of , determine the Lagrangian .
(b) Derive the equation of motion. Identify the integral of the motion.
(c) Describe the motion of the bead. Find the condition for there to be a stable equilibrium and find the frequency of small oscillations about it when it exists.
Paper 3, Section I, B
Two equal masses are connected to each other and to fixed points by three springs of force constant and as shown in the figure.
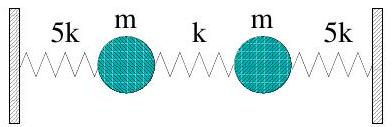
(i) Write down the Lagrangian and derive the equations describing the motion of the system in the direction parallel to the springs.
(ii) Find the normal modes and their frequencies. Comment on your results.
Paper 4, Section I, B
The Lagrangian for a heavy symmetric top of mass , pinned at point which is a distance from the centre of mass, is
(i) Starting with the fixed space frame and choosing at its origin, sketch the top with embedded body frame axis being the symmetry axis. Clearly identify the Euler angles .
(ii) Obtain the momenta and and the Hamiltonian . Derive Hamilton's equations. Identify the three conserved quantities.
Paper 4, Section II, B
The motion of a particle of charge and mass in an electromagnetic field with scalar potential and vector potential is characterized by the Lagrangian
(i) Write down the Hamiltonian of the particle.
(ii) Write down Hamilton's equations of motion for the particle.
(iii) Show that Hamilton's equations are invariant under the gauge transformation
for an arbitrary function .
(iv) The particle moves in the presence of a field such that and , where are Cartesian coordinates and is a constant.
(a) Find a gauge transformation such that only one component of remains non-zero.
(b) Determine the motion of the particle.
(v) Now assume that varies very slowly with time on a time-scale much longer than . Find the quantity which remains approximately constant throughout the motion.
[You may use the expression for the action variable .]
Paper 1, Section I, A
Consider a heavy symmetric top of mass , pinned at point , which is a distance from the centre of mass.
(a) Working in the body frame (where is the symmetry axis of the top) define the Euler angles and show that the components of the angular velocity can be expressed in terms of the Euler angles as
(b) Write down the Lagrangian of the top in terms of the Euler angles and the principal moments of inertia .
(c) Find the three constants of motion.
Paper 2, Section I, A
(a) The action for a system with a generalized coordinate is given by
State the Principle of Least Action and state the Euler-Lagrange equation.
(b) Consider a light rigid circular wire of radius and centre . The wire lies in a vertical plane, which rotates about the vertical axis through . At time the plane containing the wire makes an angle with a fixed vertical plane. A bead of mass is threaded onto the wire. The bead slides without friction along the wire, and its location is denoted by . The angle between the line and the downward vertical is .
Show that the Lagrangian of this system is
Calculate two independent constants of the motion, and explain their physical significance.
Paper 2, Section II, A
Consider a rigid body with principal moments of inertia .
(a) Derive Euler's equations of torque-free motion
with components of the angular velocity given in the body frame.
(b) Show that rotation about the second principal axis is unstable if .
(c) The principal moments of inertia of a uniform cylinder of radius , height and mass about its centre of mass are
The cylinder has two identical cylindrical holes of radius drilled along its length. The axes of symmetry of the holes are at a distance from the axis of symmetry of the cylinder such that and . All three axes lie in a single plane. Compute the principal moments of inertia of the body.
Paper 3, Section I, A
The motion of a particle of charge and mass in an electromagnetic field with scalar potential and vector potential is characterized by the Lagrangian
(a) Show that the Euler-Lagrange equation is invariant under the gauge transformation
for an arbitrary function .
(b) Derive the equations of motion in terms of the electric and magnetic fields and .
[Recall that and .]
Paper 4, Section I, A
Consider a one-dimensional dynamical system with generalized coordinate and momentum .
(a) Define the Poisson bracket of two functions and .
(b) Find the Poisson brackets and .
(c) Assuming Hamilton's equations of motion prove that
(d) State the condition for a transformation to be canonical in terms of the Poisson brackets found in (b). Use this to determine whether or not the following transformations are canonical:
(i) ,
(ii) ,
where is constant.
Paper 4, Section II, A
A homogenous thin rod of mass and length is constrained to rotate in a horizontal plane about its centre . A bead of mass is set to slide along the rod without friction. The bead is attracted to by a force resulting in a potential , where is the distance from .
(a) Identify suitable generalized coordinates and write down the Lagrangian of the system.
(b) Identify all conserved quantities.
(c) Derive the equations of motion and show that one of them can be written as
where the form of the effective potential should be found explicitly.
(d) Sketch the effective potential. Find and characterize all points of equilibrium.
(e) Find the frequencies of small oscillations around the stable equilibria.
Paper 1, Section I, C
(i) A particle of mass and charge , at position , moves in an electromagnetic field with scalar potential and vector potential . Verify that the Lagrangian
gives the correct equations of motion.
[Note that and .]
(ii) Consider the case of a constant uniform magnetic field, with , given by , , where are Cartesian coordinates and is a constant. Find the motion of the particle, and describe it carefully.
Paper 2, Section I, C
Three particles, each of mass , move along a straight line. Their positions on the line containing the origin, , are and . They are subject to forces derived from the potential energy function
Obtain Lagrange's equations for the system, and show that the frequency, , of a normal mode satisfies
where . Find a complete set of normal modes for the system, and draw a diagram indicating the nature of the corresponding motions.
Paper 2, Section II, C
Derive Euler's equations governing the torque-free and force-free motion of a rigid body with principal moments of inertia and , where . Identify two constants of the motion. Hence, or otherwise, find the equilibrium configurations such that the angular-momentum vector, as measured with respect to axes fixed in the body, remains constant. Discuss the stability of these configurations.
A spacecraft may be regarded as moving in a torque-free and force-free environment. Nevertheless, flexing of various parts of the frame can cause significant dissipation of energy. How does the angular-momentum vector ultimately align itself within the body?
Paper 3, Section I,
The Lagrangian for a heavy symmetric top is
State Noether's Theorem. Hence, or otherwise, find two conserved quantities linear in momenta, and a third conserved quantity quadratic in momenta.
Writing , deduce that obeys an equation of the form
where is cubic in . [You need not determine the explicit form of ]
Paper 4, Section I, C
(i) A dynamical system is described by the Hamiltonian . Define the Poisson bracket of two functions . Assuming the Hamiltonian equations of motion, find an expression for in terms of the Poisson bracket.
(ii) A one-dimensional system has the Hamiltonian
Show that is a constant of the motion. Deduce the form of along a classical path, in terms of the constants and .
Paper 4, Section II, C
Given a Hamiltonian system with variables , state the definition of a canonical transformation
where and . Write down a matrix equation that is equivalent to the condition that the transformation is canonical.
Consider a harmonic oscillator of unit mass, with Hamiltonian
Write down the Hamilton-Jacobi equation for Hamilton's principal function , and deduce the Hamilton-Jacobi equation
for Hamilton's characteristic function .
Solve (1) to obtain an integral expression for , and deduce that, at energy ,
Let , and define the angular coordinate
You may assume that (2) implies
Deduce that
from which
Hence, or otherwise, show that the transformation from variables to is canonical.
Paper 1, Section I, D
A system with coordinates , has the Lagrangian . Define the energy .
Consider a charged particle, of mass and charge , moving with velocity in the presence of a magnetic field . The usual vector equation of motion can be derived from the Lagrangian
where is the vector potential.
The particle moves in the presence of a field such that
referred to cylindrical polar coordinates . Obtain two constants of the motion, and write down the Lagrangian equations of motion obtained by variation of and .
Show that, if the particle is projected from the point with velocity , it will describe a circular orbit provided that .
Paper 2, Section I, D
Given the form
for the kinetic energy and potential energy of a mechanical system, deduce Lagrange's equations of motion.
A light elastic string of length , fixed at both ends, has three particles, each of mass , attached at distances from one end. Gravity can be neglected. The particles vibrate with small oscillations transversely to the string, the tension in the string providing the restoring force. Take the displacements of the particles, , to be the generalized coordinates. Take units such that and show that
Find the normal-mode frequencies for this system.
Paper 2, Section II, D
An axially-symmetric top of mass is free to rotate about a fixed point on its axis. The principal moments of inertia about are , and the centre of gravity is at a distance from . Define Euler angles and which specify the orientation of the top, where is the inclination of to the upward vertical. Show that there are three conserved quantities for the motion, and give their physical meaning.
Initially, the top is spinning with angular velocity about , with vertically above , before being disturbed slightly. Show that, in the subsequent motion, will remain close to zero provided , but that if , then will attain a maximum value given by
Paper 3, Section I, D
Euler's equations for the angular velocity of a rigid body, viewed in the body frame, are
and cyclic permutations, where the principal moments of inertia are assumed to obey .
Write down two quadratic first integrals of the motion.
There is a family of solutions , unique up to time-translations , which obey the boundary conditions as and as , for a given positive constant . Show that, for such a solution, one has
where is the angular momentum and is the kinetic energy.
By eliminating and in favour of , or otherwise, show that, in this case, the second Euler equation reduces to
where and . Find the general solution .
[You are not expected to calculate or
Paper 4, Section I, D
A system with one degree of freedom has Lagrangian . Define the canonical momentum and the energy . Show that is constant along any classical path.
Consider a classical path with the boundary-value data
Define the action of the path. Show that the total derivative along the classical path obeys
Using Lagrange's equations, or otherwise, deduce that
where is the final momentum.
Paper 4, Section II, D
A system is described by the Hamiltonian . Define the Poisson bracket of two functions , and show from Hamilton's equations that
Consider the Hamiltonian
and define
where . Evaluate and , and show that and . Show further that, when is regarded as a function of the independent complex variables and of , one has
Deduce that both and are constant during the motion.
Paper 1, Section I, E
Lagrange's equations for a system with generalized coordinates are given by
where is the Lagrangian. The Hamiltonian is given by
where the momentum conjugate to is
Derive Hamilton's equations in the form
Explain what is meant by the statement that is an ignorable coordinate and give an associated constant of the motion in this case.
The Hamiltonian for a particle of mass moving on the surface of a sphere of radius under a potential is given by
where the generalized coordinates are the spherical polar angles . Write down two constants of the motion and show that it is possible for the particle to move with constant provided that
Paper 2, Section , E
A system of three particles of equal mass moves along the axis with denoting the coordinate of particle . There is an equilibrium configuration for which , and .
Particles 1 and 2, and particles 2 and 3, are connected by springs with spring constant that provide restoring forces when the respective particle separations deviate from their equilibrium values. In addition, particle 1 is connected to the origin by a spring with spring constant . The Lagrangian for the system is
where the generalized coordinates are and .
Write down the equations of motion. Show that the generalized coordinates can oscillate with a period , where
and find the form of the corresponding normal mode in this case.
Paper 2, Section II, E
A symmetric top of unit mass moves under the action of gravity. The Lagrangian is given by
where the generalized coordinates are the Euler angles , the principal moments of inertia are and and the distance from the centre of gravity of the top to the origin is .
Show that and are constants of the motion. Show further that, when , with , the equation of motion for is
Find the possible equilibrium values of in the two cases:
(i) ,
(ii) .
By considering linear perturbations in the neighbourhoods of the equilibria in each case, find which are unstable and give expressions for the periods of small oscillations about the stable equilibria.
Paper 3, Section I, E
(a) Show that the principal moments of inertia of a uniform circular cylinder of radius , length and mass about its centre of mass are and , with the axis being directed along the length of the cylinder.
(b) Euler's equations governing the angular velocity of an arbitrary rigid body as viewed in the body frame are
and
Show that, for the cylinder of part is constant. Show further that, when , the angular momentum vector precesses about the axis with angular velocity given by
Paper 4, Section I, E
(a) A Hamiltonian system with degrees of freedom has the Hamiltonian , where are the coordinates and are the momenta.
A second Hamiltonian system has the Hamiltonian . Neither nor contains the time explicitly. Show that the condition for to be invariant under the evolution of the coordinates and momenta generated by the Hamiltonian is that the Poisson bracket vanishes. Deduce that is a constant of the motion for evolution under .
Show that, when , where is constant, the motion it generates is a translation of each by an amount , while the corresponding remains fixed. What do you infer is conserved when is invariant under this transformation?
(b) When and is a function of and only, find when
Paper 4, Section II, E
The Hamiltonian for a particle of mass , charge and position vector , moving in an electromagnetic field, is given by
where is the vector potential. Write down Hamilton's equations and use them to derive the equations of motion for the charged particle.
Show that, when , there are solutions for which and for which the particle motion is such that
where . Show in addition that the Hamiltonian may be written as
where
Assuming that is constant, find the action
associated with the motion.
It is now supposed that varies on a time-scale much longer than and thus is slowly varying. Show by applying the theory of adiabatic invariance that the motion in the direction takes place under an effective potential and give an expression for it.
1.I.9A
The action for a system with generalized coordinates for a time interval is given by
where is the Lagrangian. The end point values and are fixed.
Derive Lagrange's equations from the principle of least action by considering the variation of for all possible paths.
Define the momentum conjugate to . Derive a condition for to be a constant of the motion.
A symmetric top moves under the action of a potential . The Lagrangian is given by
where the generalized coordinates are the Euler angles and the principal moments of inertia are and .
Show that is a constant of the motion and give expressions for two others. Show further that it is possible for the top to move with both and constant provided these satisfy the condition
2.I.9A
A system of particles , with mass , moves around a circle of radius . The angle between the radius to particle and a fixed reference radius is . The interaction potential for the system is
where is a constant and .
The Lagrangian for the system is
Write down the equation of motion for particle and show that the system is in equilibrium when the particles are equally spaced around the circle.
Show further that the system always has a normal mode of oscillation with zero frequency. What is the form of the motion associated with this?
Find all the frequencies and modes of oscillation when and , where is a constant.
2.II.15B
A particle of mass , charge and position vector moves in a magnetic field whose vector potential is A. Its Hamiltonian is given by
Write down Hamilton's equations and use them to derive the equations of motion for the charged particle.
Define the Poisson bracket for general and . Show that for motion governed by the above Hamiltonian
Consider the vector potential to be given by , where . Use Hamilton's equations to show that is constant and that circular motion at radius with angular frequency is possible provided that
3.I.9E
Writing , Hamilton's equations may be written in the form
where the matrix
and and 0 denote the unit and zero matrices respectively.
Explain what is meant by the statement that the transformation ,
is canonical, and show that the condition for this is that
where is the Jacobian matrix with elements
Use this condition to show that for a system with the transformation given by
is canonical.
4.I.9B
(a) Show that the principal moments of inertia for an infinitesimally thin uniform rectangular sheet of mass with sides of length and (with ) about its centre of mass are and .
(b) Euler's equations governing the angular velocity of the sheet as viewed in the body frame are
and
A possible solution of these equations is such that the sheet rotates with , and constant.
By linearizing, find the equations governing small motions in the neighbourhood of this solution that have . Use these to show that there are solutions corresponding to instability such that and are both proportional to exp , with
4.II.15B
(a) A Hamiltonian system with degrees of freedom has Hamiltonian , where the coordinates and the momenta respectively.
Show from Hamilton's equations that when does not depend on time explicitly, for any function ,
where denotes the Poisson bracket.
For a system of interacting vortices
where is a constant. Show that the quantity defined by
is a constant of the motion.
(b) The action for a Hamiltonian system with one degree of freedom with for which the motion is periodic is
Show without assuming any specific form for that the period of the motion is given by
Suppose now that the system has a parameter that is allowed to vary slowly with time. Explain briefly what is meant by the statement that the action is an adiabatic invariant. Suppose that when this parameter is fixed, when . Deduce that, if decreases on an orbit with any when the parameter is slowly varied, then increases.
1.I.9C
The action for a system with generalized coordinates, , for a time interval is given by
where is the Lagrangian, and where the end point values and are fixed at specified values. Derive Lagrange's equations from the principle of least action by considering the variation of for all possible paths.
What is meant by the statement that a particular coordinate is ignorable? Show that there is an associated constant of the motion, to be specified in terms of .
A particle of mass is constrained to move on the surface of a sphere of radius under a potential, , for which the Lagrangian is given by
Identify an ignorable coordinate and find the associated constant of the motion, expressing it as a function of the generalized coordinates. Evaluate the quantity
in terms of the same generalized coordinates, for this case. Is also a constant of the motion? If so, why?
2.I.9C
The Lagrangian for a particle of mass and charge moving in a magnetic field with position vector is given by
where the vector potential , which does not depend on time explicitly, is related to the magnetic field through
Write down Lagrange's equations and use them to show that the equation of motion of the particle can be written in the form
Deduce that the kinetic energy, , is constant.
When the magnetic field is of the form for some specified function , show further that
where and are constants.
2.II.15C
(a) A Hamiltonian system with degrees of freedom is described by the phase space coordinates and momenta . Show that the phase-space volume element
is conserved under time evolution.
(b) The Hamiltonian, , for the system in part (a) is independent of time. Show that if is a constant of the motion, then the Poisson bracket vanishes. Evaluate when
and
where the potential depends on the only through quantities of the form for .
(c) For a system with one degree of freedom, state what is meant by the transformation
being canonical. Show that the transformation is canonical if and only if the Poisson bracket .
3.I.9C
A particle of mass is constrained to move in the horizontal plane, around a circle of fixed radius whose centre is at the origin of a Cartesian coordinate system . A second particle of mass is constrained to move around a circle of fixed radius that also lies in a horizontal plane, but whose centre is at . It is given that the Lagrangian of the system can be written as
using the particles' cylindrical polar angles and as generalized coordinates. Deduce the equations of motion and use them to show that is constant, and that obeys an equation of the form
where is a constant to be determined.
Find two values of corresponding to equilibria, and show that one of the two equilibria is stable. Find the period of small oscillations about the stable equilibrium.
4.I
(a) Show that the principal moments of inertia for the oblate spheroid of mass defined by
are given by . Here is the semi-major axis and is the eccentricity.
[You may assume that a sphere of radius a has principal moments of inertia .]
(b) The spheroid in part (a) rotates about an axis that is not a principal axis. Euler's equations governing the angular velocity as viewed in the body frame are
and
Show that is constant. Show further that the angular momentum vector precesses around the axis with period
4.II.15C
The Hamiltonian for an oscillating particle with one degree of freedom is
The mass is a constant, and is a function of time alone. Write down Hamilton's equations and use them to show that
Now consider a case in which is constant and the oscillation is exactly periodic. Denote the constant value of in that case by . Consider the quantity , where the integral is taken over a single oscillation cycle. For any given function show that can be expressed as a function of and alone, namely
where the sign of the integrand alternates between the two halves of the oscillation cycle. Let be the period of oscillation. Show that the function has partial derivatives
You may assume without proof that and may be taken inside the integral.
Now let change very slowly with time , by a negligible amount during an oscillation cycle. Assuming that, to sufficient approximation,
where is the average value of over an oscillation cycle, and that
deduce that , carefully explaining your reasoning.
When
with a positive integer and positive, deduce that
for slowly-varying , where is a constant.
[Do not try to solve Hamilton's equations. Rather, consider the form taken by . ]
1.I.9C
Hamilton's equations for a system with degrees of freedom can be written in vector form as
where is a -vector and the matrix takes the form
where 1 is the identity matrix. Derive the condition for a transformation of the form to be canonical. For a system with a single degree of freedom, show that the following transformation is canonical for all nonzero values of :
1.II.15C
(a) In the Hamiltonian framework, the action is defined as
Derive Hamilton's equations from the principle of least action. Briefly explain how the functional variations in this derivation differ from those in the derivation of Lagrange's equations from the principle of least action. Show that is a constant of the motion whenever .
(b) What is the invariant quantity arising in Liouville's theorem? Does the theorem depend on assuming ? State and prove Liouville's theorem for a system with a single degree of freedom.
(c) A particle of mass bounces elastically along a perpendicular between two parallel walls a distance apart. Sketch the path of a single cycle in phase space, assuming that the velocity changes discontinuously at the wall. Compute the action as a function of the energy and the constants . Verify that the period of oscillation is given by . Suppose now that the distance changes slowly. What is the relevant adiabatic invariant? How does change as a function of ?
2.I.9C
Two point masses, each of mass , are constrained to lie on a straight line and are connected to each other by a spring of force constant . The left-hand mass is also connected to a wall on the left by a spring of force constant . The right-hand mass is similarly connected to a wall on the right, by a spring of force constant , so that the potential energy is
where is the distance from equilibrium of the mass. Derive the equations of motion. Find the frequencies of the normal modes.
3.I.9C
A pendulum of length oscillates in the plane, making an angle with the vertical axis. The pivot is attached to a moving lift that descends with constant acceleration , so that the position of the bob is
Given that the Lagrangian for an unconstrained particle is
determine the Lagrangian for the pendulum in terms of the generalized coordinate . Derive the equation of motion in terms of . What is the motion when ?
Find the equilibrium configurations for arbitrary . Determine which configuration is stable when
and when
3.II.15C
A particle of mass is constrained to move on the surface of a sphere of radius .
The Lagrangian is given in spherical polar coordinates by
where gravity is constant. Find the two constants of the motion.
The particle is projected horizontally with velocity from a point whose depth below the centre is . Find such that the particle trajectory
(i) just grazes the horizontal equatorial plane ;
(ii) remains at depth for all time .
4.I.9C
Calculate the principal moments of inertia for a uniform cylinder, of mass , radius and height , about its centre of mass. For what height-to-radius ratio does the cylinder spin like a sphere?
1.I.9C
A particle of mass is constrained to move on a circle of radius , centre in a horizontal plane . A second particle of mass moves on a circle of radius , centre in a horizontal plane . The two particles are connected by a spring whose potential energy is
where is the distance between the particles. How many degrees of freedom are there? Identify suitable generalized coordinates and write down the Lagrangian of the system in terms of them.
1.II.15C
(i) The action for a system with generalized coordinates is given by
Derive Lagrange's equations from the principle of least action by considering all paths with fixed endpoints, .
(ii) A pendulum consists of a point mass at the end of a light rod of length . The pivot of the pendulum is attached to a mass which is free to slide without friction along a horizontal rail. Choose as generalized coordinates the position of the pivot and the angle that the pendulum makes with the vertical.
Write down the Lagrangian and derive the equations of motion.
Find the frequency of small oscillations around the stable equilibrium.
Now suppose that a force acts on the pivot causing it to travel with constant acceleration in the -direction. Find the equilibrium angle of the pendulum.
2.I.9C
A rigid body has principal moments of inertia and and is moving under the action of no forces with angular velocity components . Its motion is described by Euler's equations
Are the components of the angular momentum to be evaluated in the body frame or the space frame?
Now suppose that an asymmetric body is moving with constant angular velocity . Show that this motion is stable if and only if is the largest or smallest principal moment.
3.I.9C
Define the Poisson bracket between two functions and on phase space. If has no explicit time dependence, and there is a Hamiltonian , show that Hamilton's equations imply
A particle with position vector and momentum has angular momentum . Compute and .
3.II.15C
(i) A point mass with position and momentum undergoes one-dimensional periodic motion. Define the action variable in terms of and . Prove that an orbit of energy has period
(ii) Such a system has Hamiltonian
where is a positive constant and during the motion. Sketch the orbits in phase space both for energies and . Show that the action variable is given in terms of the energy by
Hence show that for the period of the orbit is , where is the greatest value of the momentum during the orbit.
4.I.9C
Define a canonical transformation for a one-dimensional system with coordinates . Show that if the transformation is canonical then .
Find the values of constants and such that the following transformations are canonical: (i) . (ii) .