Markov Chains

2021

• Paper 1, Section II, 19H

  Markov Chains | Part IB, 2021

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain with transition matrix $P$. What is a stopping time of $\left(X_{n}\right)_{n \geqslant 0}$ ? What is the strong Markov property?

  The exciting game of 'Unopoly' is played by a single player on a board of 4 squares. The player starts with $£ m$ (where $m \in \mathbb{N}$ ). During each turn, the player tosses a fair coin and moves one or two places in a clockwise direction $(1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1)$ according to whether the coin lands heads or tails respectively. The player collects $£ 2$ each time they pass (or land on) square 1. If the player lands on square 3 however, they immediately lose $£ 1$ and go back to square 2. The game continues indefinitely unless the player is on square 2 with $£ 0$, in which case the player loses the game and the game ends.

  

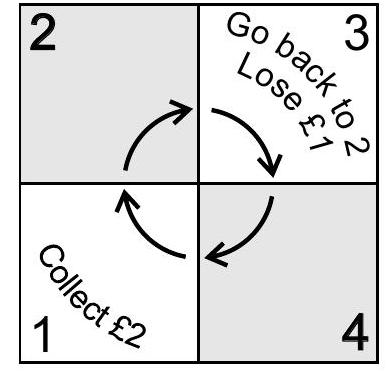
  (a) By setting up an appropriate Markov chain, show that if the player is at square 2 with $£ m$, where $m \geqslant 1$, the probability that they are ever at square 2 with $£(m-1)$ is $2 / 3 .$

  (b) Find the probability of losing the game when the player starts on square 1 with $£ m$, where $m \geqslant 1$.

  [Hint: Take the state space of your Markov chain to be $\{1,2,4\} \times\{0,1, \ldots\}$.]

  comment

• Paper 2, Section II, 18H

  Markov Chains | Part IB, 2021

  Let $P$ be a transition matrix on state space $I$. What does it mean for a distribution $\pi$ to be an invariant distribution? What does it mean for $\pi$ and $P$ to be in detailed balance? Show that if $\pi$ and $P$ are in detailed balance, then $\pi$ is an invariant distribution.

  (a) Assuming that an invariant distribution exists, state the relationship between this and

  (i) the expected return time to a state $i$;

  (ii) the expected time spent in a state $i$ between visits to a state $k$.

  (b) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain with transition matrix $P=\left(p_{i j}\right)_{i, j \in I}$ where $I=\{0,1,2, \ldots\}$. The transition probabilities are given for $i \geqslant 1$ by

  $$p_{i j}= \begin{cases}q^{-(i+2)} & \text { if } j=i+1, \\ q^{-i} & \text { if } j=i-1 \\ 1-q^{-(i+2)}-q^{-i} & \text { if } j=i\end{cases}$$

  where $q \geqslant 2$. For $p \in(0,1]$ let $p_{01}=p=1-p_{00}$. Compute the following, justifying your answers:

  (i) The expected time spent in states $\{2,4,6, \ldots\}$ between visits to state 1 ;

  (ii) The expected time taken to return to state 1 , starting from 1 ;

  (iii) The expected time taken to hit state 0 starting from $1 .$

  comment

• Paper 3 , Section I, H

  Markov Chains | Part IB, 2021

  Consider a Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ on a state space $I$.

  (a) Define the notion of a communicating class. What does it mean for a communicating class to be closed?

  (b) Taking $I=\{1, \ldots, 6\}$, find the communicating classes associated with the transition matrix $P$ given by

  $$P=\left(\begin{array}{cccccc} 0 & 0 & 0 & 0 & \frac{1}{4} & \frac{3}{4} \\ \frac{1}{4} & 0 & 0 & 0 & \frac{1}{2} & \frac{1}{4} \\ 0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 & 0 \\ 0 & \frac{1}{2} & 0 & 0 & \frac{1}{2} & 0 \\ \frac{1}{4} & \frac{1}{2} & 0 & 0 & 0 & \frac{1}{4} \\ 1 & 0 & 0 & 0 & 0 & 0 \end{array}\right)$$

  and identify which are closed.

  (c) Find the expected time for the Markov chain with transition matrix $P$ above to reach 6 starting from 1 .

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2021

  Show that the simple symmetric random walk on $\mathbb{Z}$ is recurrent.

  Three particles perform independent simple symmetric random walks on $\mathbb{Z}$. What is the probability that they are all simultaneously at 0 infinitely often? Justify your answer.

  [You may assume without proof that there exist constants $A, B>0$ such that $A \sqrt{n}(n / e)^{n} \leqslant n ! \leqslant B \sqrt{n}(n / e)^{n}$ for all positive integers $\left.n .\right]$

  comment

2020

• Paper 1, Section II, H

  Markov Chains | Part IB, 2020

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain with transition matrix $P$. What is a stopping time of $\left(X_{n}\right)_{n \geqslant 0}$ ? What is the strong Markov property?

  A porter is trying to apprehend a student who is walking along a long narrow path at night. Being unaware of the porter, the student's location $Y_{n}$ at time $n \geqslant 0$ evolves as a simple symmetric random walk on $\mathbb{Z}$. The porter's initial location $Z_{0}$ is $2 m$ units to the right of the student, so $Z_{0}-Y_{0}=2 m$ where $m \geqslant 1$. The future locations $Z_{n+1}$ of the porter evolve as follows: The porter moves to the left (so $Z_{n+1}=Z_{n}-1$ ) with probability $q \in\left(\frac{1}{2}, 1\right)$, and to the right with probability $1-q$ whenever $Z_{n}-Y_{n}>2$. When $Z_{n}-Y_{n}=2$, the porter's probability of moving left changes to $r \in(0,1)$, and the probability of moving right is $1-r$.

  (a) By setting up an appropriate Markov chain, show that for $m \geqslant 2$, the expected time for the porter to be a distance $2(m-1)$ away from the student is $2 /(2 q-1)$.

  (b) Show that the expected time for the porter to catch the student, i.e. for their locations to coincide, is

  $$\frac{2}{r}+\left(m+\frac{1}{r}-2\right) \frac{2}{2 q-1} .$$

  [You may use without proof the fact that the time for the porter to catch the student is finite with probability 1 for any $m \geqslant 1$.]

  comment

• Paper 2, Section I, H

  Markov Chains | Part IB, 2020

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain with state space $\{1,2\}$ and transition matrix

  $$P=\left(\begin{array}{cc} 1-\alpha & \alpha \\ \beta & 1-\beta \end{array}\right)$$

  where $\alpha, \beta \in(0,1]$. Compute $\mathbb{P}\left(X_{n}=1 \mid X_{0}=1\right)$. Find the value of $\mathbb{P}\left(X_{n}=1 \mid X_{0}=2\right)$.

  comment

2019

• Paper 1, Section II, H

  Markov Chains | Part IB, 2019

  Let $P$ be a transition matrix for a Markov chain $\left(X_{n}\right)$ on a state space with $N$ elements with $N<\infty$. Assume that the Markov chain is aperiodic and irreducible and let $\pi$ be its unique invariant distribution. Assume that $X_{0} \sim \pi$.

  (a) Let $P^{*}(x, y)=\mathbb{P}\left[X_{0}=y \mid X_{1}=x\right]$. Show that $P^{*}(x, y)=\pi(y) P(y, x) / \pi(x)$.

  (b) Let $T=\min \left\{n \geqslant 1: X_{n}=X_{0}\right\}$. Compute $\mathbb{E}[T]$ in terms of an explicit function of $N$.

  (c) Suppose that a cop and a robber start from a common state chosen from $\pi$. The robber then takes one step according to $P^{*}$ and stops. The cop then moves according to $P$ independently of the robber until the cop catches the robber (i.e., the cop visits the state occupied by the robber). Compute the expected amount of time for the cop to catch the robber.

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2019

  Fix $n \geqslant 1$ and let $G$ be the graph consisting of a copy of $\{0, \ldots, n\}$ joining vertices $A$ and $B$, a copy of $\{0, \ldots, n\}$ joining vertices $B$ and $C$, and a copy of $\{0, \ldots, n\}$ joining vertices $B$ and $D$. Let $E$ be the vertex adjacent to $B$ on the segment from $B$ to $C$. Shown below is an illustration of $G$ in the case $n=5$. The vertices are solid squares and edges are indicated by straight lines.

  

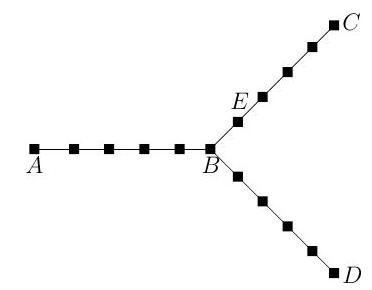
  Let $\left(X_{k}\right)$ be a simple random walk on $G$. In other words, in each time step, $X$ moves to one of its neighbours with equal probability. Assume that $X_{0}=A$.

  (a) Compute the expected amount of time for $X$ to hit $B$.

  (b) Compute the expected amount of time for $X$ to hit $E$. [Hint: first show that the expected amount of time $x$ for $X$ to go from $B$ to $E$ satisfies $x=\frac{1}{3}+\frac{2}{3}(L+x)$ where $L$ is the expected return time of $X$ to $B$ when starting from $B$.]

  (c) Compute the expected amount of time for $X$ to hit $C$. [Hint: for each $i$, let $v_{i}$ be the vertex which is $i$ places to the right of $B$ on the segment from $B$ to $C$. Derive an equation for the expected amount of time $x_{i}$ for $X$ to go from $v_{i}$ to $v_{i+1}$.]

  Justify all of your answers.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2019

  Suppose that $\left(X_{n}\right)$ is a Markov chain with state space $S$.

  (a) Give the definition of a communicating class.

  (b) Give the definition of the period of a state $a \in S$.

  (c) Show that if two states communicate then they have the same period.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2019

  For a Markov chain $X$ on a state space $S$ with $u, v \in S$, we let $p_{u v}(n)$ for $n \in\{0,1, \ldots\}$ be the probability that $X_{n}=v$ when $X_{0}=u$.

  (a) Let $X$ be a Markov chain. Prove that if $X$ is recurrent at a state $v$, then $\sum_{n=0}^{\infty} p_{v v}(n)=\infty$. [You may use without proof that the number of returns of a Markov chain to a state $v$ when starting from $v$ has the geometric distribution.]

  (b) Let $X$ and $Y$ be independent simple symmetric random walks on $\mathbb{Z}^{2}$ starting from the origin 0 . Let $Z=\sum_{n=0}^{\infty} \mathbf{1}_{\left\{X_{n}=Y_{n}\right\}}$. Prove that $\mathbb{E}[Z]=\sum_{n=0}^{\infty} p_{00}(2 n)$ and deduce that $\mathbb{E}[Z]=\infty$. [You may use without proof that $p_{x y}(n)=p_{y x}(n)$ for all $x, y \in \mathbb{Z}^{2}$ and $n \in \mathbb{N}$, and that $X$ is recurrent at 0.]

  comment

2018

• Paper 1, Section II, H

  Markov Chains | Part IB, 2018

  A coin-tossing game is played by two players, $A_{1}$ and $A_{2}$. Each player has a coin and the probability that the coin tossed by player $A_{i}$ comes up heads is $p_{i}$, where $0<p_{i}<1, i=1,2$. The players toss their coins according to the following scheme: $A_{1}$ tosses first and then after each head, $A_{2}$ pays $A_{1}$ one pound and $A_{1}$ has the next toss, while after each tail, $A_{1}$ pays $A_{2}$ one pound and $A_{2}$ has the next toss.

  Define a Markov chain to describe the state of the game. Find the probability that the game ever returns to a state where neither player has lost money.

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2018

  For a finite irreducible Markov chain, what is the relationship between the invariant probability distribution and the mean recurrence times of states?

  A particle moves on the $2^{n}$ vertices of the hypercube, $\{0,1\}^{n}$, in the following way: at each step the particle is equally likely to move to each of the $n$ adjacent vertices, independently of its past motion. (Two vertices are adjacent if the Euclidean distance between them is one.) The initial vertex occupied by the particle is $(0,0, \ldots, 0)$. Calculate the expected number of steps until the particle

  (i) first returns to $(0,0, \ldots, 0)$,

  (ii) first visits $(0,0, \ldots, 0,1)$,

  (iii) first visits $(0,0, \ldots, 0,1,1)$.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2018

  The mathematics course at the University of Barchester is a three-year one. After the end-of-year examinations there are three possibilities:

  (i) failing and leaving (probability $p$ );

  (ii) taking that year again (probability $q$ );

  (iii) going on to the next year (or graduating, if the current year is the third one) (probability $r$ ).

  Thus there are five states for a student $\left(1^{\text {st }}\right.$ year, $2^{\text {nd }}$year, $3^{\text {rd }}$year, left without a degree, graduated).

  Write down the $5 \times 5$ transition matrix. Classify the states, assuming $p, q, r \in(0,1)$. Find the probability that a student will eventually graduate.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2018

  Let $P=\left(p_{i j}\right)_{i, j \in S}$ be the transition matrix for an irreducible Markov chain on the finite state space $S$.

  (a) What does it mean to say that a distribution $\pi$ is the invariant distribution for the chain?

  (b) What does it mean to say that the chain is in detailed balance with respect to a distribution $\pi$ ? Show that if the chain is in detailed balance with respect to a distribution $\pi$ then $\pi$ is the invariant distribution for the chain.

  (c) A symmetric random walk on a connected finite graph is the Markov chain whose state space is the set of vertices of the graph and whose transition probabilities are

  $$p_{i j}= \begin{cases}1 / D_{i} & \text { if } j \text { is adjacent to } i \\ 0 & \text { otherwise }\end{cases}$$

  where $D_{i}$ is the number of vertices adjacent to vertex $i$. Show that the random walk is in detailed balance with respect to its invariant distribution.

  comment

2017

• Paper 1, Section II, H

  Markov Chains | Part IB, 2017

  A rich and generous man possesses $n$ pounds. Some poor cousins arrive at his mansion. Being generous he decides to give them money. On day 1 , he chooses uniformly at random an integer between $n-1$ and 1 inclusive and gives it to the first cousin. Then he is left with $x$ pounds. On day 2 , he chooses uniformly at random an integer between $x-1$ and 1 inclusive and gives it to the second cousin and so on. If $x=1$ then he does not give the next cousin any money. His choices of the uniform numbers are independent. Let $X_{i}$ be his fortune at the end of day $i$.

  Show that $X$ is a Markov chain and find its transition probabilities.

  Let $\tau$ be the first time he has 1 pound left, i.e. $\tau=\min \left\{i \geqslant 1: X_{i}=1\right\}$. Show that

  $$\mathbb{E}[\tau]=\sum_{i=1}^{n-1} \frac{1}{i}$$

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2017

  Let $Y_{1}, Y_{2}, \ldots$ be i.i.d. random variables with values in $\{1,2, \ldots\}$ and $\mathbb{E}\left[Y_{1}\right]=\mu<\infty$. Moreover, suppose that the greatest common divisor of $\left\{n: \mathbb{P}\left(Y_{1}=n\right)>0\right\}$ is 1 . Consider the following process

  $$X_{n}=\inf \left\{m \geqslant n: Y_{1}+\ldots+Y_{k}=m, \text { for some } k \geqslant 0\right\}-n .$$

  (a) Show that $X$ is a Markov chain and find its transition probabilities.

  (b) Let $T_{0}=\inf \left\{n \geqslant 1: X_{n}=0\right\}$. Find $\mathbb{E}_{0}\left[T_{0}\right]$.

  (c) Find the limit as $n \rightarrow \infty$ of $\mathbb{P}\left(X_{n}=0\right)$. State carefully any theorems from the course that you are using.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2017

  (a) What does it mean to say that a Markov chain is reversible?

  (b) Let $G$ be a finite connected graph on $n$ vertices. What does it mean to say that $X$ is a simple random walk on $G$ ?

  Find the unique invariant distribution $\pi$ of $X$.

  Show that $X$ is reversible when $X_{0} \sim \pi$.

  [You may use, without proof, results about detailed balance equations, but you should state them clearly.]

  comment

• Paper 4, Section I, $\mathbf{9 H}$

  Markov Chains | Part IB, 2017

  Prove that the simple symmetric random walk on $\mathbb{Z}^{3}$ is transient.

  [Any combinatorial inequality can be used without proof.]

  comment

2016

• Paper 1, Section II, H

  Markov Chains | Part IB, 2016

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk on the integers, starting at $X_{0}=0$.

  (a) What does it mean to say that a Markov chain is irreducible? What does it mean to say that an irreducible Markov chain is recurrent? Show that $\left(X_{n}\right)_{n} \geqslant 0$ is irreducible and recurrent.

  [Hint: You may find it helpful to use the limit

  $$\lim _{k \rightarrow \infty} \sqrt{k} 2^{-2 k}\left(\begin{array}{c} 2 k \\ k \end{array}\right)=\sqrt{\pi}$$

  You may also use without proof standard necessary and sufficient conditions for recurrence.]

  (b) What does it mean to say that an irreducible Markov chain is positive recurrent? Determine, with proof, whether $\left(X_{n}\right)_{n \geqslant 0}$ is positive recurrent.

  (c) Let

  $$T=\inf \left\{n \geqslant 1: X_{n}=0\right\}$$

  be the first time the chain returns to the origin. Compute $\mathbb{E}\left[s^{T}\right]$ for a fixed number $0<s<1$.

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2016

  (a) Prove that every open communicating class of a Markov chain is transient. Prove that every finite transient communicating class is open. Give an example of a Markov chain with an infinite transient closed communicating class.

  (b) Consider a Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ with state space $\{a, b, c, d\}$ and transition probabilities given by the matrix

  $$P=\left(\begin{array}{cccc} 1 / 3 & 0 & 1 / 3 & 1 / 3 \\ 0 & 1 / 4 & 0 & 3 / 4 \\ 1 / 2 & 1 / 2 & 0 & 0 \\ 0 & 2 / 3 & 0 & 1 / 3 \end{array}\right)$$

  (i) Compute $\mathbb{P}\left(X_{n}=b \mid X_{0}=d\right)$ for a fixed $n \geqslant 0$.

  (ii) Compute $\mathbb{P}\left(X_{n}=c\right.$ for some $\left.n \geqslant 1 \mid X_{0}=a\right)$.

  (iii) Show that $P^{n}$ converges as $n \rightarrow \infty$, and determine the limit.

  [Results from lectures can be used without proof if stated carefully.]

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2016

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain such that $X_{0}=i$. Prove that

  $$\sum_{n=0}^{\infty} \mathbb{P}_{i}\left(X_{n}=i\right)=\frac{1}{\mathbb{P}_{i}\left(X_{n} \neq i \text { for all } n \geqslant 1\right)}$$

  where $1 / 0=+\infty$. [You may use the strong Markov property without proof.]

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2016

  Consider two boxes, labelled $\mathrm{A}$ and B. Initially, there are no balls in box $\mathrm{A}$ and $k$ balls in box B. Each minute later, one of the $k$ balls is chosen uniformly at random and is moved to the opposite box. Let $X_{n}$ denote the number of balls in box A at time $n$, so that $X_{0}=0$.

  (a) Find the transition probabilities of the Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ and show that it is reversible in equilibrium.

  (b) Find $\mathbb{E}(T)$, where $T=\inf \left\{n \geqslant 1: X_{n}=0\right\}$ is the next time that all $k$ balls are again in box $B$.

  comment

2015

• Paper 1, Section II, H

  Markov Chains | Part IB, 2015

  Consider a particle moving between the vertices of the graph below, taking steps along the edges. Let $X_{n}$ be the position of the particle at time $n$. At time $n+1$ the particle moves to one of the vertices adjoining $X_{n}$, with each of the adjoining vertices being equally likely, independently of previous moves. Explain briefly why $\left(X_{n} ; n \geqslant 0\right)$ is a Markov chain on the vertices. Is this chain irreducible? Find an invariant distribution for this chain.

  

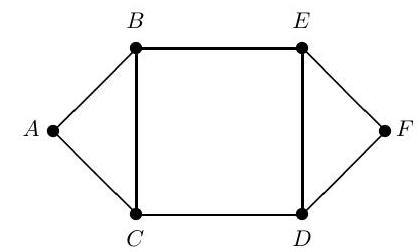
  Suppose that the particle starts at $B$. By adapting the transition matrix, or otherwise, find the probability that the particle hits vertex $A$ before vertex $F$.

  Find the expected first passage time from $B$ to $F$ given no intermediate visit to $A$.

  [Results from the course may be used without proof provided that they are clearly stated.]

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2015

  (a) What does it mean for a transition matrix $P$ and a distribution $\lambda$ to be in detailed balance? Show that if $P$ and $\lambda$ are in detailed balance then $\lambda=\lambda P$.

  (b) A mathematician owns $r$ bicycles, which she sometimes uses for her journey from the station to College in the morning and for the return journey in the evening. If it is fine weather when she starts a journey, and if there is a bicycle available at the current location, then she cycles; otherwise she takes the bus. Assume that with probability $p$, $0<p<1$, it is fine when she starts a journey, independently of all other journeys. Let $X_{n}$ denote the number of bicycles at the current location, just before the mathematician starts the $n$th journey.

  (i) Show that $\left(X_{n} ; n \geqslant 0\right)$ is a Markov chain and write down its transition matrix.

  (ii) Find the invariant distribution of the Markov chain.

  (iii) Show that the Markov chain satisfies the necessary conditions for the convergence theorem for Markov chains and find the limiting probability that the mathematician's $n$th journey is by bicycle.

  [Results from the course may be used without proof provided that they are clearly stated.]

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2015

  Define what is meant by a communicating class and a closed class in a Markov chain.

  A Markov chain $\left(X_{n}: n \geqslant 0\right)$ with state space $\{1,2,3,4\}$ has transition matrix

  $$P=\left(\begin{array}{cccc} \frac{1}{2} & 0 & \frac{1}{2} & 0 \\ 0 & \frac{1}{2} & 0 & \frac{1}{2} \\ \frac{1}{2} & 0 & \frac{1}{2} & 0 \\ \frac{1}{2} & 0 & 0 & \frac{1}{2} \end{array}\right)$$

  Write down the communicating classes for this Markov chain and state whether or not each class is closed.

  If $X_{0}=2$, let $N$ be the smallest $n$ such that $X_{n} \neq 2$. Find $\mathbb{P}(N=n)$ for $n=1,2, \ldots$ and $\mathbb{E}(N)$. Describe the evolution of the chain if $X_{0}=2$.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2015

  Let $X_{0}, X_{1}, X_{2}, \ldots$ be independent identically distributed random variables with $\mathbb{P}\left(X_{i}=1\right)=1-\mathbb{P}\left(X_{i}=0\right)=p, 0<p<1$. Let $Z_{n}=X_{n-1}+c X_{n}, n=1,2, \ldots$, where $c$ is a constant. For each of the following cases, determine whether or not $\left(Z_{n}: n \geqslant 1\right)$ is a Markov chain: (a) $c=0$; (b) $c=1$; (c) $c=2$.

  In each case, if $\left(Z_{n}: n \geqslant 1\right)$ is a Markov chain, explain why, and give its state space and transition matrix; if it is not a Markov chain, give an example to demonstrate that it is not.

  comment

2014

• Paper 1, Section II, 20H

  Markov Chains | Part IB, 2014

  Consider a homogeneous Markov chain $\left(X_{n}: n \geqslant 0\right)$ with state space $S$ and transition $\operatorname{matrix} P=\left(p_{i, j}: i, j \in S\right)$. For a state $i$, define the terms aperiodic, positive recurrent and ergodic.

  Let $S=\{0,1,2, \ldots\}$ and suppose that for $i \geqslant 1$ we have $p_{i, i-1}=1$ and

  $$p_{0,0}=0, p_{0, j}=p q^{j-1}, j=1,2, \ldots,$$

  where $p=1-q \in(0,1)$. Show that this Markov chain is irreducible.

  Let $T_{0}=\inf \left\{n \geqslant 1: X_{n}=0\right\}$ be the first passage time to 0 . Find $\mathbb{P}\left(T_{0}=n \mid X_{0}=0\right)$ and show that state 0 is ergodic.

  Find the invariant distribution $\pi$ for this Markov chain. Write down:

  (i) the mean recurrence time for state $i, i \geqslant 1$;

  (ii) $\lim _{n \rightarrow \infty} \mathbb{P}\left(X_{n} \neq 0 \mid X_{0}=0\right)$.

  [Results from the course may be quoted without proof, provided they are clearly stated.]

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2014

  Let $\left(X_{n}: n \geqslant 0\right)$ be a homogeneous Markov chain with state space $\mathrm{S}$ and transition matrix $P=\left(p_{i, j}: i, j \in S\right)$. For $A \subseteq S$, let

  $$H^{A}=\inf \left\{n \geqslant 0: X_{n} \in A\right\} \text { and } h_{i}^{A}=\mathbb{P}\left(H^{A}<\infty \mid X_{0}=i\right), i \in S$$

  Prove that $h^{A}=\left(h_{i}^{A}: i \in S\right)$ is the minimal non-negative solution to the equations

  $$h_{i}^{A}= \begin{cases}1 & \text { for } i \in A \\ \sum_{j \in S} p_{i, j} h_{j}^{A} & \text { otherwise. }\end{cases}$$

  Three people $A, B$ and $C$ play a series of two-player games. In the first game, two people play and the third person sits out. Any subsequent game is played between the winner of the previous game and the person sitting out the previous game. The overall winner of the series is the first person to win two consecutive games. The players are evenly matched so that in any game each of the two players has probability $\frac{1}{2}$ of winning the game, independently of all other games. For $n=1,2, \ldots$, let $X_{n}$ be the ordered pair consisting of the winners of games $n$ and $n+1$. Thus the state space is $\{A A, A B, A C, B A, B B, B C, C A, C B, C C\}$, and, for example, $X_{1}=A C$ if $A$ wins the first game and $C$ wins the second.

  The first game is between $A$ and $B$. Treating $A A, B B$ and $C C$ as absorbing states, or otherwise, find the probability of winning the series for each of the three players.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2014

  Let $\left(X_{n}: n \geqslant 0\right)$ be a homogeneous Markov chain with state space $S$. For $i, j$ in $S$ let $p_{i, j}(n)$ denote the $n$-step transition probability $\mathbb{P}\left(X_{n}=j \mid X_{0}=i\right)$.

  (i) Express the $(m+n)$-step transition probability $p_{i, j}(m+n)$ in terms of the $n$-step and $m$-step transition probabilities.

  (ii) Write $i \rightarrow j$ if there exists $n \geqslant 0$ such that $p_{i, j}(n)>0$, and $i \leftrightarrow j$ if $i \rightarrow j$ and $j \rightarrow i$. Prove that if $i \leftrightarrow j$ and $i \neq j$ then either both $i$ and $j$ are recurrent or both $i$ and $j$ are transient. [You may assume that a state $i$ is recurrent if and only if $\sum_{n=0}^{\infty} p_{i, i}(n)=\infty$, and otherwise $i$ is transient.]

  (iii) A Markov chain has state space $\{0,1,2,3\}$ and transition matrix

  $$\left(\begin{array}{cccc} \frac{1}{2} & \frac{1}{3} & 0 & \frac{1}{6} \\ 0 & \frac{3}{4} & 0 & \frac{1}{4} \\ \frac{1}{2} & \frac{1}{2} & 0 & 0 \\ \frac{1}{2} & 0 & 0 & \frac{1}{2} \end{array}\right)$$

  For each state $i$, determine whether $i$ is recurrent or transient. [Results from the course may be quoted without proof, provided they are clearly stated.]

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2014

  Let $\left(X_{n}: n \geqslant 0\right)$ be a homogeneous Markov chain with state space $S$ and transition $\operatorname{matrix} P=\left(p_{i, j}: i, j \in S\right)$.

  (a) Let $W_{n}=X_{2 n}, n=0,1,2, \ldots$ Show that $\left(W_{n}: n \geqslant 0\right)$ is a Markov chain and give its transition matrix. If $\lambda_{i}=\mathbb{P}\left(X_{0}=i\right), i \in S$, find $\mathbb{P}\left(W_{1}=0\right)$ in terms of the $\lambda_{i}$ and the $p_{i, j}$.

  [Results from the course may be quoted without proof, provided they are clearly stated.]

  (b) Suppose that $S=\{-1,0,1\}, p_{0,1}=p_{-1,-1}=0$ and $p_{-1,0} \neq p_{1,0}$. Let $Y_{n}=\left|X_{n}\right|$, $n=0,1,2, \ldots$ In terms of the $p_{i, j}$, find

  (i) $\mathbb{P}\left(Y_{n+1}=0 \mid Y_{n}=1, Y_{n-1}=0\right)$ and

  (ii) $\mathbb{P}\left(Y_{n+1}=0 \mid Y_{n}=1, Y_{n-1}=1, Y_{n-2}=0\right)$.

  What can you conclude about whether or not $\left(Y_{n}: n \geqslant 0\right)$ is a Markov chain?

  comment

2013

• Paper 1, Section II, 20H

  Markov Chains | Part IB, 2013

  A Markov chain has state space $\{a, b, c\}$ and transition matrix

  $$P=\left(\begin{array}{ccc} 0 & 3 / 5 & 2 / 5 \\ 3 / 4 & 0 & 1 / 4 \\ 2 / 3 & 1 / 3 & 0 \end{array}\right)$$

  where the rows $1,2,3$ correspond to $a, b, c$, respectively. Show that this Markov chain is equivalent to a random walk on some graph with 6 edges.

  Let $k(i, j)$ denote the mean first passage time from $i$ to $j$.

  (i) Find $k(a, a)$ and $k(a, b)$.

  (ii) Given $X_{0}=a$, find the expected number of steps until the walk first completes a step from $b$ to $c$.

  (iii) Suppose the distribution of $X_{0}$ is $\left(\pi_{1}, \pi_{2}, \pi_{3}\right)=(5,4,3) / 12$. Let $\tau(a, b)$ be the least $m$ such that $\{a, b\}$ appears as a subsequence of $\left\{X_{0}, X_{1}, \ldots, X_{m}\right\}$. By comparing the distributions of $\left\{X_{0}, X_{1}, \ldots, X_{m}\right\}$ and $\left\{X_{m}, \ldots, X_{1}, X_{0}\right\}$ show that $E \tau(a, b)=E \tau(b, a)$ and that

  $$k(b, a)-k(a, b)=\sum_{i \in\{a, b, c\}} \pi_{i}[k(i, a)-k(i, b)]$$

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2013

  (i) Suppose $\left(X_{n}\right)_{n \geqslant 0}$ is an irreducible Markov chain and $f_{i j}=P\left(X_{n}=j\right.$ for some $\left.n \geqslant 1 \mid X_{0}=i\right)$. Prove that $f_{i i} \geqslant f_{i j} f_{j i}$ and that

  $$\sum_{n=0}^{\infty} P_{i}\left(X_{n}=i\right)=\sum_{n=1}^{\infty} f_{i i}^{n-1}$$

  (ii) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a symmetric random walk on the $\mathbb{Z}^{2}$ lattice. Prove that $\left(X_{n}\right)_{n \geqslant 0}$ is recurrent. You may assume, for $n \geqslant 1$,

  $$1 / 2<2^{-2 n} \sqrt{n}\left(\begin{array}{c} 2 n \\ n \end{array}\right)<1$$

  (iii) A princess and monster perform independent random walks on the $\mathbb{Z}^{2}$ lattice. The trajectory of the princess is the symmetric random walk $\left(X_{n}\right)_{n \geqslant 0}$. The monster's trajectory, denoted $\left(Z_{n}\right)_{n \geqslant 0}$, is a sleepy version of an independent symmetric random walk $\left(Y_{n}\right)_{n \geqslant 0}$. Specifically, given an infinite sequence of integers $0=n_{0}<n_{1}<\cdots$, the monster sleeps between these times, so $Z_{n_{i}+1}=\cdots=Z_{n_{i+1}}=Y_{i+1}$. Initially, $X_{0}=(100,0)$ and $Z_{0}=Y_{0}=(0,100)$. The princess is captured if and only if at some future time she and the monster are simultaneously at $(0,0)$.

  Compare the capture probabilities for an active monster, who takes $n_{i+1}=n_{i}+1$ for all $i$, and a sleepy monster, who takes $n_{i}$ spaced sufficiently widely so that

  $$P\left(X_{k}=(0,0) \text { for some } k \in\left\{n_{i}+1, \ldots, n_{i+1}\right\}\right)>1 / 2$$

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2013

  Prove that if a distribution $\pi$ is in detailed balance with a transition matrix $P$ then it is an invariant distribution for $P$.

  Consider the following model with 2 urns. At each time, $t=0,1, \ldots$ one of the following happens:

  • with probability $\beta$ a ball is chosen at random and moved to the other urn (but nothing happens if both urns are empty);

  • with probability $\gamma$ a ball is chosen at random and removed (but nothing happens if both urns are empty);

  • with probability $\alpha$ a new ball is added to a randomly chosen urn,

  where $\alpha+\beta+\gamma=1$ and $\alpha<\gamma$. State $(i, j)$ denotes that urns 1,2 contain $i$ and $j$ balls respectively. Prove that there is an invariant measure

  $$\lambda_{i, j}=\frac{(i+j) !}{i ! j !}(\alpha / 2 \gamma)^{i+j}$$

  Find the proportion of time for which there are $n$ balls in the system.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2013

  Suppose $P$ is the transition matrix of an irreducible recurrent Markov chain with state space $I$. Show that if $x$ is an invariant measure and $x_{k}>0$ for some $k \in I$, then $x_{j}>0$ for all $j \in I$.

  Let

  $$\gamma_{j}^{k}=p_{k j}+\sum_{t=1}^{\infty} \sum_{i_{1} \neq k, \ldots, i_{t} \neq k} p_{k i_{t}} p_{i_{t} i_{t-1}} \cdots p_{i_{1} j}$$

  Give a meaning to $\gamma_{j}^{k}$ and explain why $\gamma_{k}^{k}=1$.

  Suppose $x$ is an invariant measure with $x_{k}=1$. Prove that $x_{j} \geqslant \gamma_{j}^{k}$ for all $j$.

  comment

2012

• Paper 1, Section II, 20H

  Markov Chains | Part IB, 2012

  A Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ has as its state space the integers, with

  $$p_{i, i+1}=p, \quad p_{i, i-1}=q=1-p$$

  and $p_{i j}=0$ otherwise. Assume $p>q$.

  Let $T_{j}=\inf \left\{n \geqslant 1: X_{n}=j\right\}$ if this is finite, and $T_{j}=\infty$ otherwise. Let $V_{0}$ be the total number of hits on 0 , and let $V_{0}(n)$ be the total number of hits on 0 within times $0, \ldots, n-1$. Let

  $$\begin{aligned} h_{i} &=P\left(V_{0}>0 \mid X_{0}=i\right) \\ r_{i}(n) &=E\left[V_{0}(n) \mid X_{0}=i\right] \\ r_{i} &=E\left[V_{0} \mid X_{0}=i\right] \end{aligned}$$

  (i) Quoting an appropriate theorem, find, for every $i$, the value of $h_{i}$.

  (ii) Show that if $\left(x_{i}, i \in \mathbb{Z}\right)$ is any non-negative solution to the system of equations

  $$\begin{aligned} x_{0} &=1+q x_{1}+p x_{-1}, \\ x_{i} &=q x_{i-1}+p x_{i+1}, \quad \text { for all } i \neq 0 \end{aligned}$$

  then $x_{i} \geqslant r_{i}(n)$ for all $i$ and $n$.

  (iii) Show that $P\left(V_{0}\left(T_{1}\right) \geqslant k \mid X_{0}=1\right)=q^{k}$ and $E\left[V_{0}\left(T_{1}\right) \mid X_{0}=1\right]=q / p$.

  (iv) Explain why $r_{i+1}=(q / p) r_{i}$ for $i>0$.

  (v) Find $r_{i}$ for all $i$.

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2012

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be the symmetric random walk on vertices of a connected graph. At each step this walk jumps from the current vertex to a neighbouring vertex, choosing uniformly amongst them. Let $T_{i}=\inf \left\{n \geqslant 1: X_{n}=i\right\}$. For each $i \neq j$ let $q_{i j}=P\left(T_{j}<T_{i} \mid X_{0}=i\right)$ and $m_{i j}=E\left(T_{j} \mid X_{0}=i\right)$. Stating any theorems that you use:

  (i) Prove that the invariant distribution $\pi$ satisfies detailed balance.

  (ii) Use reversibility to explain why $\pi_{i} q_{i j}=\pi_{j} q_{j i}$ for all $i, j$.

  Consider a symmetric random walk on the graph shown below.

  

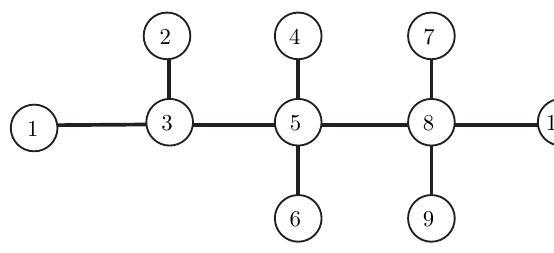
  (iii) Find $m_{33}$.

  (iv) The removal of any edge $(i, j)$ leaves two disjoint components, one which includes $i$ and one which includes $j$. Prove that $m_{i j}=1+2 e_{i j}(i)$, where $e_{i j}(i)$ is the number of edges in the component that contains $i$.

  (v) Show that $m_{i j}+m_{j i} \in\{18,36,54,72\}$ for all $i \neq j$.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2012

  A runner owns $k$ pairs of running shoes and runs twice a day. In the morning she leaves her house by the front door, and in the evening she leaves by the back door. On starting each run she looks for shoes by the door through which she exits, and runs barefoot if none are there. At the end of each run she is equally likely to return through the front or back doors. She removes her shoes (if any) and places them by the door. In the morning of day 1 all shoes are by the back door so she must run barefoot.

  Let $p_{00}^{(n)}$ be the probability that she runs barefoot on the morning of day $n+1$. What conditions are satisfied in this problem which ensure $\lim _{n \rightarrow \infty} p_{00}^{(n)}$ exists? Show that its value is $1 / 2 k$.

  Find the expected number of days that will pass until the first morning that she finds all $k$ pairs of shoes at her front door.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2012

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be an irreducible Markov chain with $p_{i j}^{(n)}=P\left(X_{n}=j \mid X_{0}=i\right)$. Define the meaning of the statements:

  (i) state $i$ is transient,

  (ii) state $i$ is aperiodic.

  Give a criterion for transience that can be expressed in terms of the probabilities $\left(p_{i i}^{(n)}, n=0,1, \ldots\right)$.

  Prove that if a state $i$ is transient then all states are transient.

  Prove that if a state $i$ is aperiodic then all states are aperiodic.

  Suppose that $p_{i i}^{(n)}=0$ unless $n$ is divisible by 3 . Given any other state $j$, prove that $p_{j j}^{(n)}=0$ unless $n$ is divisible by 3 .

  comment

2011

• Paper 1, Section II, H

  Markov Chains | Part IB, 2011

  Let $P=\left(p_{i j}\right)_{i, j \in S}$ be the transition matrix for an irreducible Markov chain on the finite state space $S$.

  (i) What does it mean to say $\pi$ is the invariant distribution for the chain?

  (ii) What does it mean to say the chain is in detailed balance with respect to $\pi$ ?

  (iii) A symmetric random walk on a connected finite graph is the Markov chain whose state space is the set of vertices of the graph and whose transition probabilities are

  $$p_{i j}= \begin{cases}1 / D_{i} & \text { if } j \text { is adjacent to } i \\ 0 & \text { otherwise }\end{cases}$$

  where $D_{i}$ is the number of vertices adjacent to vertex $i$. Show that the random walk is in detailed balance with respect to its invariant distribution.

  (iv) Let $\pi$ be the invariant distribution for the transition matrix $P$, and define an inner product for vectors $x, y \in \mathbb{R}^{S}$ by the formula

  $$\langle x, y\rangle=\sum_{i \in S} x_{i} \pi_{i} y_{i}$$

  Show that the equation

  $$\langle x, P y\rangle=\langle P x, y\rangle$$

  holds for all vectors $x, y \in \mathbb{R}^{S}$ if and only if the chain is in detailed balance with respect to $\pi$. [Here $z \in \mathbb{R}^{S}$ means $z=\left(z_{i}\right)_{i \in S}$.]

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2011

  (i) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain on the finite state space $S$ with transition matrix $P$. Fix a subset $A \subseteq S$, and let

  $$H=\inf \left\{n \geqslant 0: X_{n} \in A\right\} .$$

  Fix a function $g$ on $S$ such that $0<g(i) \leqslant 1$ for all $i \in S$, and let

  $$V_{i}=\mathbb{E}\left[\prod_{n=0}^{H-1} g\left(X_{n}\right) \mid X_{0}=i\right]$$

  where $\prod_{n=0}^{-1} a_{n}=1$ by convention. Show that

  $$V_{i}= \begin{cases}1 & \text { if } i \in A \\ g(i) \sum_{j \in S} P_{i j} V_{j} & \text { otherwise. }\end{cases}$$

  (ii) A flea lives on a polyhedron with $N$ vertices, labelled $1, \ldots, N$. It hops from vertex to vertex in the following manner: if one day it is on vertex $i>1$, the next day it hops to one of the vertices labelled $1, \ldots, i-1$ with equal probability, and it dies upon reaching vertex 1. Let $X_{n}$ be the position of the flea on day $n$. What are the transition probabilities for the Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ ?

  (iii) Let $H$ be the number of days the flea is alive, and let

  $$V_{i}=\mathbb{E}\left(s^{H} \mid X_{0}=i\right)$$

  where $s$ is a real number such that $0<s \leqslant 1$. Show that $V_{1}=1$ and

  $$\frac{i}{s} V_{i+1}=V_{i}+\frac{i-1}{s} V_{i}$$

  for $i \geqslant 1$. Conclude that

  $$\mathbb{E}\left(s^{H} \mid X_{0}=N\right)=\prod_{i=1}^{N-1}\left(1+\frac{s-1}{i}\right)$$

  [Hint. Use part (i) with $A=\{1\}$ and a well-chosen function $g$. ]

  (iv) Show that

  $$\mathbb{E}\left(H \mid X_{0}=N\right)=\sum_{i=1}^{N-1} \frac{1}{i}$$

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2011

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain with state space $S$.

  (i) What does it mean to say that $\left(X_{n}\right)_{n} \geqslant 0$ has the strong Markov property? Your answer should include the definition of the term stopping time.

  (ii) Show that

  $$\mathbb{P}\left(X_{n}=i \text { at least } k \text { times } \mid X_{0}=i\right)=\left[\mathbb{P}\left(X_{n}=i \text { at least once } \mid X_{0}=i\right)\right]^{k}$$

  for a state $i \in S$. You may use without proof the fact that $\left(X_{n}\right)_{n \geqslant 0}$ has the strong Markov property.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2011

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain on a state space $S$, and let $p_{i j}(n)=\mathbb{P}\left(X_{n}=j \mid X_{0}=i\right)$.

  (i) What does the term communicating class mean in terms of this chain?

  (ii) Show that $p_{i i}(m+n) \geqslant p_{i j}(m) p_{j i}(n)$.

  (iii) The period $d_{i}$ of a state $i$ is defined to be

  $$d_{i}=\operatorname{gcd}\left\{n \geqslant 1: p_{i i}(n)>0\right\}$$

  Show that if $i$ and $j$ are in the same communicating class and $p_{j j}(r)>0$, then $d_{i}$ divides $r$.

  comment

2010

• Paper 1, Section II, E

  Markov Chains | Part IB, 2010

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain.

  (a) What does it mean to say that a state $i$ is positive recurrent? How is this property related to the equilibrium probability $\pi_{i}$ ? You do not need to give a full proof, but you should carefully state any theorems you use.

  (b) What is a communicating class? Prove that if states $i$ and $j$ are in the same communicating class and $i$ is positive recurrent then $j$ is positive recurrent also.

  A frog is in a pond with an infinite number of lily pads, numbered $1,2,3, \ldots$ She hops from pad to pad in the following manner: if she happens to be on pad $i$ at a given time, she hops to one of pads $(1,2, \ldots, i, i+1)$ with equal probability.

  (c) Find the equilibrium distribution of the corresponding Markov chain.

  (d) Now suppose the frog starts on pad $k$ and stops when she returns to it. Show that the expected number of times the frog hops is $e(k-1)$ ! where $e=2.718 \ldots$ What is the expected number of times she will visit the lily pad $k+1$ ?

  comment

• Paper 2, Section II, E

  Markov Chains | Part IB, 2010

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple, symmetric random walk on the integers $\{\ldots,-1,0,1, \ldots\}$, with $X_{0}=0$ and $\mathbb{P}\left(X_{n+1}=i \pm 1 \mid X_{n}=i\right)=1 / 2$. For each integer $a \geqslant 1$, let $T_{a}=\inf \left\{n \geqslant 0: X_{n}=a\right\}$. Show that $T_{a}$ is a stopping time.

  Define a random variable $Y_{n}$ by the rule

  $$Y_{n}= \begin{cases}X_{n} & \text { if } n<T_{a} \\ 2 a-X_{n} & \text { if } n \geqslant T_{a}\end{cases}$$

  Show that $\left(Y_{n}\right)_{n} \geqslant 0$ is also a simple, symmetric random walk.

  Let $M_{n}=\max _{0 \leqslant i \leqslant n} X_{n}$. Explain why $\left\{M_{n} \geqslant a\right\}=\left\{T_{a} \leqslant n\right\}$ for $a \geqslant 0$. By using the process $\left(Y_{n}\right)_{n \geqslant 0}$ constructed above, show that, for $a \geqslant 0$,

  $$\mathbb{P}\left(M_{n} \geqslant a, X_{n} \leqslant a-1\right)=\mathbb{P}\left(X_{n} \geqslant a+1\right),$$

  and thus

  $$\mathbb{P}\left(M_{n} \geqslant a\right)=\mathbb{P}\left(X_{n} \geqslant a\right)+\mathbb{P}\left(X_{n} \geqslant a+1\right)$$

  Hence compute

  $$\mathbb{P}\left(M_{n}=a\right)$$

  when $a$ and $n$ are positive integers with $n \geqslant a$. [Hint: if $n$ is even, then $X_{n}$ must be even, and if $n$ is odd, then $X_{n}$ must be odd.]

  comment

• Paper 3, Section I, E

  Markov Chains | Part IB, 2010

  An intrepid tourist tries to ascend Springfield's famous infinite staircase on an icy day. When he takes a step with his right foot, he reaches the next stair with probability $1 / 2$, otherwise he falls down and instantly slides back to the bottom with probability $1 / 2$. Similarly, when he steps with his left foot, he reaches the next stair with probability $1 / 3$, or slides to the bottom with probability $2 / 3$. Assume that he always steps first with his right foot when he is at the bottom, and alternates feet as he ascends. Let $X_{n}$ be his position after his $n$th step, so that $X_{n}=i$ when he is on the stair $i, i=0,1,2, \ldots$, where 0 is the bottom stair.

  (a) Specify the transition probabilities $p_{i j}$ for the Markov chain $\left(X_{n}\right)_{n} \geqslant 0$ for any $i, j \geqslant 0$.

  (b) Find the equilibrium probabilities $\pi_{i}$, for $i \geqslant 0$. [Hint: $\left.\pi_{0}=5 / 9 .\right]$

  (c) Argue that the chain is irreducible and aperiodic and evaluate the limit

  $$\lim _{n \rightarrow \infty} \mathbb{P}\left(X_{n}=i\right)$$

  for each $i \geqslant 0$.

  comment

• Paper 4, Section I, E

  Markov Chains | Part IB, 2010

  Consider a Markov chain $\left(X_{n}\right)_{n} \geqslant 0$ with state space $\{a, b, c, d\}$ and transition probabilities given by the following table.

  \begin{tabular}{c|cccc} & $a$ & $b$ & $c$ & $d$ \ \hline$a$ & $1 / 4$ & $1 / 4$ & $1 / 2$ & 0 \ $b$ & 0 & $1 / 4$ & 0 & $3 / 4$ \ $c$ & $1 / 2$ & 0 & $1 / 4$ & $1 / 4$ \ $d$ & 0 & $1 / 2$ & 0 & $1 / 2$ \end{tabular}

  By drawing an appropriate diagram, determine the communicating classes of the chain, and classify them as either open or closed. Compute the following transition and hitting probabilities:

  • $\mathbb{P}\left(X_{n}=b \mid X_{0}=d\right)$ for a fixed $n \geqslant 0$

  • $\mathbb{P}\left(X_{n}=c\right.$ for some $\left.n \geqslant 1 \mid X_{0}=a\right)$.

  comment

2009

• Paper 1, Section II, H

  Markov Chains | Part IB, 2009

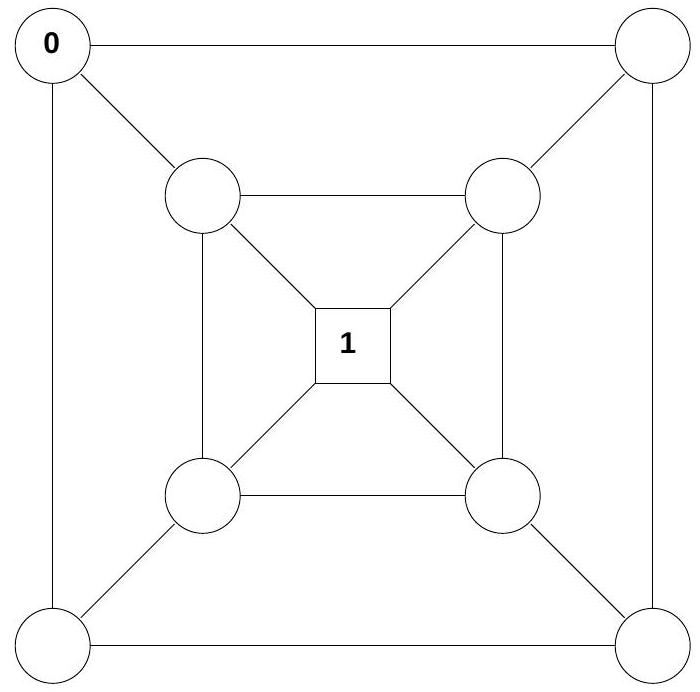
  A gerbil is introduced into a maze at the node labelled 0 in the diagram. It roams at random through the maze until it reaches the node labelled 1. At each vertex, it chooses to move to one of the neighbouring nodes with equal probability, independently of all other choices. Find the mean number of moves required for the gerbil to reach node 1 .

  Suppose now that the gerbil is intelligent, in that when it reaches a node it will not immediately return to the node from which it has just come, choosing with equal probability from all other neighbouring nodes. Express the movement of the gerbil in terms of a Markov chain whose states and transition probabilities you should specify. Find the mean number of moves until the intelligent gerbil reaches node 1 . Compare with your answer to the first part, and comment briefly.

  

  comment

• Paper 2, Section II, H

  Markov Chains | Part IB, 2009

  Suppose that $B$ is a non-empty subset of the statespace $I$ of a Markov chain $X$ with transition matrix $P$, and let $\tau \equiv \inf \left\{n \geqslant 0: X_{n} \in B\right\}$, with the convention that inf $\emptyset=\infty$. If $h_{i}=P\left(\tau<\infty \mid X_{0}=i\right)$, show that the equations

  (a)

  $$g_{i} \geqslant(P g)_{i} \equiv \sum_{j \in I} p_{i j} g_{j} \geqslant 0 \quad \forall i$$

  $$g_{i}=1 \quad \forall i \in B$$

  are satisfied by $g=h$.

  If $g$ satisfies (a), prove that $g$ also satisfies

  $(c)$

  $$g_{i} \geqslant(\tilde{P} g)_{i} \quad \forall i,$$

  where

  $$\tilde{p}_{i j}=\left\{\begin{array}{cl} p_{i j} & (i \notin B), \\ \delta_{i j} & (i \in B) \end{array}\right.$$

  By interpreting the transition matrix $\tilde{P}$, prove that $h$ is the minimal solution to the equations (a), (b).

  Now suppose that $P$ is irreducible. Prove that $P$ is recurrent if and only if the only solutions to (a) are constant functions.

  comment

• Paper 3, Section I, H

  Markov Chains | Part IB, 2009

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple random walk on the integers: the random variables $\xi_{n} \equiv X_{n}-X_{n-1}$ are independent, with distribution

  $$P(\xi=1)=p, \quad P(\xi=-1)=q$$

  where $0<p<1$, and $q=1-p$. Consider the hitting time $\tau=\inf \left\{n: X_{n}=0\right.$ or $\left.X_{n}=N\right\}$, where $N>1$ is a given integer. For fixed $s \in(0,1)$ define $\xi_{k}=E\left[s^{\tau}: X_{\tau}=0 \mid X_{0}=k\right]$ for $k=0, \ldots, N$. Show that the $\xi_{k}$ satisfy a second-order difference equation, and hence find them.

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2009

  In chess, a bishop is allowed to move only in straight diagonal lines. Thus if the bishop stands on the square marked $\mathrm{A}$ in the diagram, it is able in one move to reach any of the squares marked with an asterisk. Suppose that the bishop moves at random around the chess board, choosing at each move with equal probability from the squares it can reach, the square chosen being independent of all previous choices. The bishop starts at the bottom left-hand corner of the board.

  If $X_{n}$ is the position of the bishop at time $n$, show that $\left(X_{n}\right)_{n \geqslant 0}$ is a reversible Markov chain, whose statespace you should specify. Find the invariant distribution of this Markov chain.

  What is the expected number of moves the bishop will make before first returning to its starting square?

  

  comment

2008

• 1.II.19H

  Markov Chains | Part IB, 2008

  The village green is ringed by a fence with $N$ fenceposts, labelled $0,1, \ldots, N-1$. The village idiot is given a pot of paint and a brush, and started at post 0 with instructions to paint all the posts. He paints post 0 , and then chooses one of the two nearest neighbours, 1 or $N-1$, with equal probability, moving to the chosen post and painting it. After painting a post, he chooses with equal probability one of the two nearest neighbours, moves there and paints it (regardless of whether it is already painted). Find the distribution of the last post unpainted.

  comment

• 2.II.20H

  Markov Chains | Part IB, 2008

  A Markov chain with state-space $I=\mathbb{Z}^{+}$has non-zero transition probabilities $p_{00}=q_{0}$ and

  $$p_{i, i+1}=p_{i}, \quad p_{i+1, i}=q_{i+1} \quad(i \in I) .$$

  Prove that this chain is recurrent if and only if

  $$\sum_{n \geqslant 1} \prod_{r=1}^{n} \frac{q_{r}}{p_{r}}=\infty$$

  Prove that this chain is positive-recurrent if and only if

  $$\sum_{n \geqslant 1} \prod_{r=1}^{n} \frac{p_{r-1}}{q_{r}}<\infty$$

  comment

• 3.I.9H

  Markov Chains | Part IB, 2008

  What does it mean to say that a Markov chain is recurrent?

  Stating clearly any general results to which you appeal, prove that the symmetric simple random walk on $\mathbb{Z}$ is recurrent.

  comment

• 4.I.9H

  Markov Chains | Part IB, 2008

  A Markov chain on the state-space $I=\{1,2,3,4,5,6,7\}$ has transition matrix

  $$P=\left(\begin{array}{ccccccc} 0 & 1 / 2 & 1 / 4 & 0 & 1 / 4 & 0 & 0 \\ 1 / 3 & 0 & 1 / 2 & 0 & 0 & 1 / 6 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 1 / 2 & 0 & 1 / 2 \end{array}\right)$$

  Classify the chain into its communicating classes, deciding for each what the period is, and whether the class is recurrent.

  For each $i, j \in I$ say whether the $\operatorname{limit}^{-1} \lim _{n \rightarrow \infty} p_{i j}^{(n)}$ exists, and evaluate the limit when it does exist.

  comment

2007

• 1.II.19C

  Markov Chains | Part IB, 2007

  Consider a Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ on states $\{0,1, \ldots, r\}$ with transition matrix $\left(P_{i j}\right)$, where $P_{0,0}=1=P_{r, r}$, so that 0 and $r$ are absorbing states. Let

  $$A=\left(X_{n}=0, \text { for some } n \geqslant 0\right) \text {, }$$

  be the event that the chain is absorbed in 0 . Assume that $h_{i}=\mathbb{P}\left(A \mid X_{0}=i\right)>0$ for $1 \leqslant i<r$.

  Show carefully that, conditional on the event $A,\left(X_{n}\right)_{n \geqslant 0}$ is a Markov chain and determine its transition matrix.

  Now consider the case where $P_{i, i+1}=\frac{1}{2}=P_{i, i-1}$, for $1 \leqslant i<r$. Suppose that $X_{0}=i, 1 \leqslant i<r$, and that the event $A$ occurs; calculate the expected number of transitions until the chain is first in the state 0 .

  comment

• 2.II.20C

  Markov Chains | Part IB, 2007

  Consider a Markov chain with state space $S=\{0,1,2, \ldots\}$ and transition matrix given by

  $$P_{i, j}= \begin{cases}q p^{j-i+1} & \text { for } i \geqslant 1 \text { and } j \geqslant i-1 \\ q p^{j} & \text { for } i=0 \text { and } j \geqslant 0\end{cases}$$

  and $P_{i, j}=0$ otherwise, where $0<p=1-q<1$.

  For each value of $p, 0<p<1$, determine whether the chain is transient, null recurrent or positive recurrent, and in the last case find the invariant distribution.

  comment

• 3.I.9C

  Markov Chains | Part IB, 2007

  Consider a Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ with state space $S=\{0,1\}$ and transition matrix

  $$P=\left(\begin{array}{cc} \alpha & 1-\alpha \\ 1-\beta & \beta \end{array}\right)$$

  where $0<\alpha<1$ and $0<\beta<1$.

  Calculate $\mathbb{P}\left(X_{n}=0 \mid X_{0}=0\right)$ for each $n \geqslant 0$.

  comment

• 4.I.9C

  Markov Chains | Part IB, 2007

  For a Markov chain with state space $S$, define what is meant by the following:

  (i) states $i, j \in S$ communicate;

  (ii) state $i \in S$ is recurrent.

  Prove that communication is an equivalence relation on $S$ and that if two states $i, j$ communicate and $i$ is recurrent then $j$ is recurrent.

  comment

2006

• 1.II.19C

  Markov Chains | Part IB, 2006

  Explain what is meant by a stopping time of a Markov chain $\left(X_{n}\right)_{n \geq 0}$. State the strong Markov property.

  Show that, for any state $i$, the probability, starting from $i$, that $\left(X_{n}\right)_{n \geq 0}$ makes infinitely many visits to $i$ can take only the values 0 or 1 .

  Show moreover that, if

  $$\sum_{n=0}^{\infty} \mathbb{P}_{i}\left(X_{n}=i\right)=\infty$$

  then $\left(X_{n}\right)_{n \geq 0}$ makes infinitely many visits to $i$ with probability $1 .$

  comment

• 2.II.20C

  Markov Chains | Part IB, 2006

  Consider the Markov chain $\left(X_{n}\right)_{n \geq 0}$ on the integers $\mathbb{Z}$ whose non-zero transition probabilities are given by $p_{0,1}=p_{0,-1}=1 / 2$ and

  $$\begin{gathered} p_{n, n-1}=1 / 3, \quad p_{n, n+1}=2 / 3, \quad \text { for } n \geq 1 \\ p_{n, n-1}=3 / 4, \quad p_{n, n+1}=1 / 4, \quad \text { for } n \leqslant-1 \end{gathered}$$

  (a) Show that, if $X_{0}=1$, then $\left(X_{n}\right)_{n \geq 0}$ hits 0 with probability $1 / 2$.

  (b) Suppose now that $X_{0}=0$. Show that, with probability 1 , as $n \rightarrow \infty$ either $X_{n} \rightarrow \infty$ or $X_{n} \rightarrow-\infty$.

  (c) In the case $X_{0}=0$ compute $\mathbb{P}\left(X_{n} \rightarrow \infty\right.$ as $\left.n \rightarrow \infty\right)$.

  comment

• 3.I.9C

  Markov Chains | Part IB, 2006

  A hungry student always chooses one of three places to get his lunch, basing his choice for one day on his gastronomic experience the day before. He sometimes tries a sandwich from Natasha's Patisserie: with probability $1 / 2$ this is delicious so he returns the next day; if the sandwich is less than delicious, he chooses with equal probability $1 / 4$ either to eat in Hall or to cook for himself. Food in Hall leaves no strong impression, so he chooses the next day each of the options with equal probability $1 / 3$. However, since he is a hopeless cook, he never tries his own cooking two days running, always preferring to buy a sandwich the next day. On the first day of term the student has lunch in Hall. What is the probability that 60 days later he is again having lunch in Hall?

  [ Note $0^{0}=1$.]

  comment

• 4.I.9C

  Markov Chains | Part IB, 2006

  A game of chance is played as follows. At each turn the player tosses a coin, which lands heads or tails with equal probability $1 / 2$. The outcome determines a score for that turn, which depends also on the cumulative score so far. Write $S_{n}$ for the cumulative score after $n$ turns. In particular $S_{0}=0$. When $S_{n}$ is odd, a head scores 1 but a tail scores 0 . When $S_{n}$ is a multiple of 4 , a head scores 4 and a tail scores 1 . When $S_{n}$ is even but is not a multiple of 4 , a head scores 2 and a tail scores 1 . By considering a suitable four-state Markov chain, determine the long run proportion of turns for which $S_{n}$ is a multiple of 4 . State clearly any general theorems to which you appeal.

  comment

2005

• 1.II.19D

  Markov Chains | Part IB, 2005

  Every night Lancelot and Guinevere sit down with four guests for a meal at a circular dining table. The six diners are equally spaced around the table and just before each meal two individuals are chosen at random and they exchange places from the previous night while the other four diners stay in the same places they occupied at the last meal; the choices on successive nights are made independently. On the first night Lancelot and Guinevere are seated next to each other.

  Find the probability that they are seated diametrically opposite each other on the $(n+1)$ th night at the round table, $n \geqslant 1$.

  comment

• 2.II.20D

  Markov Chains | Part IB, 2005

  Consider a Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ with state space $\{0,1,2, \ldots\}$ and transition probabilities given by

  $$P_{i, j}=p q^{i-j+1}, \quad 0<j \leqslant i+1, \quad \text { and } \quad P_{i, 0}=q^{i+1} \quad \text { for } \quad i \geqslant 0$$

  with $P_{i, j}=0$, otherwise, where $0<p<1$ and $q=1-p$.

  For each $i \geqslant 1$, let

  $$h_{i}=\mathbb{P}\left(X_{n}=0, \text { for some } n \geqslant 0 \mid X_{0}=i\right),$$

  that is, the probability that the chain ever hits the state 0 given that it starts in state $i$. Write down the equations satisfied by the probabilities $\left\{h_{i}, i \geqslant 1\right\}$ and hence, or otherwise, show that they satisfy a second-order recurrence relation with constant coefficients. Calculate $h_{i}$ for each $i \geqslant 1$.

  Determine for each value of $p, 0<p<1$, whether the chain is transient, null recurrent or positive recurrent and in the last case calculate the stationary distribution.

  [Hint: When the chain is positive recurrent, the stationary distribution is geometric.]

  comment

• 3.I.9D

  Markov Chains | Part IB, 2005

  Prove that if two states of a Markov chain communicate then they have the same period.

  Consider a Markov chain with state space $\{1,2, \ldots, 7\}$ and transition probabilities determined by the matrix

  $$\left(\begin{array}{ccccccc} 0 & \frac{1}{4} & \frac{1}{4} & 0 & 0 & \frac{1}{4} & \frac{1}{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{2} & 0 & 0 & 0 & 0 & \frac{1}{2} & 0 \\ \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & 0 & \frac{1}{6} & \frac{1}{6} \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \end{array}\right)$$

  Identify the communicating classes of the chain and for each class state whether it is open or closed and determine its period.

  comment

• 4.I.9D

  Markov Chains | Part IB, 2005

  Prove that the simple symmetric random walk in three dimensions is transient.

  [You may wish to recall Stirling's formula: $n ! \sim(2 \pi)^{\frac{1}{2}} n^{n+\frac{1}{2}} e^{-n} .$ ]

  comment

2004

• 1.I.11H

  Markov Chains | Part IB, 2004

  Let $P=\left(P_{i j}\right)$ be a transition matrix. What does it mean to say that $P$ is (a) irreducible, $(b)$ recurrent?

  Suppose that $P$ is irreducible and recurrent and that the state space contains at least two states. Define a new transition matrix $\tilde{P}$ by

  $$\tilde{P}_{i j}=\left\{\begin{array}{lll} 0 & \text { if } & i=j \\ \left(1-P_{i i}\right)^{-1} P_{i j} & \text { if } & i \neq j \end{array}\right.$$

  Prove that $\tilde{P}$ is also irreducible and recurrent.

  comment

• 1.II.22H

  Markov Chains | Part IB, 2004

  Consider the Markov chain with state space $\{1,2,3,4,5,6\}$ and transition matrix

  $$\left(\begin{array}{cccccc} 0 & 0 & \frac{1}{2} & 0 & 0 & \frac{1}{2} \\ \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & 0 \\ \frac{1}{3} & 0 & \frac{1}{3} & 0 & 0 & \frac{1}{3} \\ \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} \\ 0 & 0 & 0 & 0 & 1 & 0 \\ \frac{1}{4} & 0 & \frac{1}{2} & 0 & 0 & \frac{1}{4} \end{array}\right) \text {. }$$

  Determine the communicating classes of the chain, and for each class indicate whether it is open or closed.

  Suppose that the chain starts in state 2 ; determine the probability that it ever reaches state 6 .

  Suppose that the chain starts in state 3 ; determine the probability that it is in state 6 after exactly $n$ transitions, $n \geqslant 1$.

  comment

• 2.I.11H

  Markov Chains | Part IB, 2004

  Let $\left(X_{r}\right)_{r \geqslant 0}$ be an irreducible, positive-recurrent Markov chain on the state space $S$ with transition matrix $\left(P_{i j}\right)$ and initial distribution $P\left(X_{0}=i\right)=\pi_{i}, i \in S$, where $\left(\pi_{i}\right)$ is the unique invariant distribution. What does it mean to say that the Markov chain is reversible?

  Prove that the Markov chain is reversible if and only if $\pi_{i} P_{i j}=\pi_{j} P_{j i}$ for all $i, j \in S$.

  comment

• 2.II.22H

  Markov Chains | Part IB, 2004

  Consider a Markov chain on the state space $S=\{0,1,2, \ldots\} \cup\left\{1^{\prime}, 2^{\prime}, 3^{\prime}, \ldots\right\}$ with transition probabilities as illustrated in the diagram below, where $0<q<1$ and $p=1-q$.

  

  For each value of $q, 0<q<1$, determine whether the chain is transient, null recurrent or positive recurrent.

  When the chain is positive recurrent, calculate the invariant distribution.

  comment

• A1.1 B1.1

  Markov Chains | Part II, 2004

  (i) Give the definitions of a recurrent and a null recurrent irreducible Markov chain.

  Let $\left(X_{n}\right)$ be a recurrent Markov chain with state space $I$ and irreducible transition matrix $P=\left(p_{i j}\right)$. Prove that the vectors $\gamma^{k}=\left(\gamma_{j}^{k}, j \in I\right), k \in I$, with entries $\gamma_{k}^{k}=1$ and

  $$\gamma_{i}^{k}=\mathbb{E}_{k}(\# \text { of visits to } i \text { before returning to } k), \quad i \neq k,$$

  are $P$-invariant:

  $$\gamma_{j}^{k}=\sum_{i \in I} \gamma_{i}^{k} p_{i j}$$

  (ii) Let $\left(W_{n}\right)$ be the birth and death process on $\mathbb{Z}_{+}=\{0,1,2, \ldots\}$ with the following transition probabilities:

  $$\begin{aligned} &p_{i, i+1}=p_{i, i-1}=\frac{1}{2}, i \geq 1 \\ &p_{01}=1 \end{aligned}$$

  By relating $\left(W_{n}\right)$ to the symmetric simple random walk $\left(Y_{n}\right)$ on $\mathbb{Z}$, or otherwise, prove that $\left(W_{n}\right)$ is a recurrent Markov chain. By considering invariant measures, or otherwise, prove that $\left(W_{n}\right)$ is null recurrent.

  Calculate the vectors $\gamma^{k}=\left(\gamma_{i}^{k}, i \in \mathbb{Z}_{+}\right)$for the chain $\left(W_{n}\right), k \in \mathbb{Z}_{+}$.

  Finally, let $W_{0}=0$ and let $N$ be the number of visits to 1 before returning to 0 . Show that $\mathbb{P}_{0}(N=n)=(1 / 2)^{n}, n \geq 1$.

  [You may use properties of the random walk $\left(Y_{n}\right)$ or general facts about Markov chains without proof but should clearly state them.]

  comment

• A2.1

  Markov Chains | Part II, 2004

  (i) Let $J$ be a proper subset of the finite state space $I$ of an irreducible Markov chain $\left(X_{n}\right)$, whose transition matrix $P$ is partitioned as

  $$P=J^{J}\left(\begin{array}{ll} A & J^{c} \\ C & D \end{array}\right)$$

  If only visits to states in $J$ are recorded, we see a $J$-valued Markov chain $\left(\tilde{X}_{n}\right)$; show that its transition matrix is

  $$\tilde{P}=A+B \sum_{n \geqslant 0} D^{n} C=A+B(I-D)^{-1} C$$

  (ii) Local MP Phil Anderer spends his time in London in the Commons $(C)$, in his flat $(F)$, in the bar $(B)$ or with his girlfriend $(G)$. Each hour, he moves from one to another according to the transition matrix $P$, though his wife (who knows nothing of his girlfriend) believes that his movements are governed by transition matrix $P^{W}$ :

  

  The public only sees Phil when he is in $J=\{C, F, B\}$; calculate the transition matrix $\tilde{P}$ which they believe controls his movements.

  Each time the public Phil moves to a new location, he phones his wife; write down the transition matrix which governs the sequence of locations from which the public Phil phones, and calculate its invariant distribution.

  Phil's wife notes down the location of each of his calls, and is getting suspicious - he is not at his flat often enough. Confronted, Phil swears his fidelity and resolves to dump his troublesome transition matrix, choosing instead

  

  Will this deal with his wife's suspicions? Explain your answer.

  comment

• A3.1 B3.1

  Markov Chains | Part II, 2004

  (i) Give the definition of the time-reversal of a discrete-time Markov chain $\left(X_{n}\right)$. Define a reversible Markov chain and check that every probability distribution satisfying the detailed balance equations is invariant.

  (ii) Customers arrive in a hairdresser's shop according to a Poisson process of rate $\lambda>0$. The shop has $s$ hairstylists and $N$ waiting places; each stylist is working (on a single customer) provided that there is a customer to serve, and any customer arriving when the shop is full (i.e. the numbers of customers present is $N+s$ ) is not admitted and never returns. Every admitted customer waits in the queue and then is served, in the first-come-first-served order (say), the service taking an exponential time of rate $\mu>0$; the service times of admitted customers are independent. After completing his/her service, the customer leaves the shop and never returns.

  Set up a Markov chain model for the number $X_{t}$ of customers in the shop at time $t \geq 0$. Assuming $\lambda<s \mu$, calculate the equilibrium distribution $\pi$ of this chain and explain why it is unique. Show that $\left(X_{t}\right)$ in equilibrium is time-reversible, i.e. $\forall T>0,\left(X_{t}, 0 \leq t \leq T\right)$ has the same distribution as $\left(Y_{t}, 0 \leq t \leq T\right)$ where $Y_{t}=X_{T-t}$, and $X_{0} \sim \pi$.

  comment

• A4.1

  Markov Chains | Part II, 2004

  (a) Give three definitions of a continuous-time Markov chain with a given $Q$-matrix on a finite state space: (i) in terms of holding times and jump probabilities, (ii) in terms of transition probabilities over small time intervals, and (iii) in terms of finite-dimensional distributions.

  (b) A flea jumps clockwise on the vertices of a triangle; the holding times are independent exponential random variables of rate one. Find the eigenvalues of the corresponding $Q$-matrix and express transition probabilities $p_{x y}(t), t \geq 0, x, y=A, B, C$, in terms of these roots. Deduce the formulas for the sums

  $$S_{0}(t)=\sum_{n=0}^{\infty} \frac{t^{3 n}}{(3 n) !}, \quad S_{1}(t)=\sum_{n=0}^{\infty} \frac{t^{3 n+1}}{(3 n+1) !}, \quad S_{2}(t)=\sum_{n=0}^{\infty} \frac{t^{3 n+2}}{(3 n+2) !}$$

  in terms of the functions $e^{t}, e^{-t / 2}, \cos (\sqrt{3} t / 2)$ and $\sin (\sqrt{3} t / 2)$.

  Find the limits

  $$\lim _{t \rightarrow \infty} e^{-t} S_{j}(t), \quad j=0,1,2 .$$

  What is the connection between the decompositions $e^{t}=S_{0}(t)+S_{1}(t)+S_{2}(t)$ and $e^{t}=\cosh t+\sinh t ?$

  comment

2003

• A1.1 B1.1

  Markov Chains | Part II, 2003

  (i) Let $\left(X_{n}, Y_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk in $\mathbb{Z}^{2}$, starting from $(0,0)$, and set $T=\inf \left\{n \geqslant 0: \max \left\{\left|X_{n}\right|,\left|Y_{n}\right|\right\}=2\right\}$. Determine the quantities $\mathbb{E}(T)$ and $\mathbb{P}\left(X_{T}=2\right.$ and $\left.Y_{T}=0\right)$.

  (ii) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a discrete-time Markov chain with state-space $I$ and transition matrix $P$. What does it mean to say that a state $i \in I$ is recurrent? Prove that $i$ is recurrent if and only if $\sum_{n=0}^{\infty} p_{i i}^{(n)}=\infty$, where $p_{i i}^{(n)}$ denotes the $(i, i)$ entry in $P^{n}$.

  Show that the simple symmetric random walk in $\mathbb{Z}^{2}$ is recurrent.

  comment

• A2.1

  Markov Chains | Part II, 2003

  (i) What is meant by a Poisson process of rate $\lambda$ ? Show that if $\left(X_{t}\right)_{t \geqslant 0}$ and $\left(Y_{t}\right)_{t \geqslant 0}$ are independent Poisson processes of rates $\lambda$ and $\mu$ respectively, then $\left(X_{t}+Y_{t}\right)_{t \geqslant 0}$ is also a Poisson process, and determine its rate.

  (ii) A Poisson process of rate $\lambda$ is observed by someone who believes that the first holding time is longer than all subsequent holding times. How long on average will it take before the observer is proved wrong?

  comment

• A3.1 B3.1

  Markov Chains | Part II, 2003

  (i) Consider the continuous-time Markov chain $\left(X_{t}\right)_{t \geqslant 0}$ with state-space $\{1,2,3,4\}$ and $Q$-matrix

  $$Q=\left(\begin{array}{rrrr} -2 & 0 & 0 & 2 \\ 1 & -3 & 2 & 0 \\ 0 & 2 & -2 & 0 \\ 1 & 5 & 2 & -8 \end{array}\right)$$

  Set

  $$Y_{t}= \begin{cases}X_{t} & \text { if } X_{t} \in\{1,2,3\} \\ 2 & \text { if } X_{t}=4\end{cases}$$

  and

  $$Z_{t}= \begin{cases}X_{t} & \text { if } X_{t} \in\{1,2,3\} \\ 1 & \text { if } X_{t}=4\end{cases}$$

  Determine which, if any, of the processes $\left(Y_{t}\right)_{t \geqslant 0}$ and $\left(Z_{t}\right)_{t \geqslant 0}$ are Markov chains.

  (ii) Find an invariant distribution for the chain $\left(X_{t}\right)_{t \geqslant 0}$ given in Part (i). Suppose $X_{0}=1$. Find, for all $t \geqslant 0$, the probability that $X_{t}=1$.

  comment

• A4.1

  Markov Chains | Part II, 2003

  Consider a pack of cards labelled $1, \ldots, 52$. We repeatedly take the top card and insert it uniformly at random in one of the 52 possible places, that is, either on the top or on the bottom or in one of the 50 places inside the pack. How long on average will it take for the bottom card to reach the top?

  Let $p_{n}$ denote the probability that after $n$ iterations the cards are found in increasing order. Show that, irrespective of the initial ordering, $p_{n}$ converges as $n \rightarrow \infty$, and determine the limit $p$. You should give precise statements of any general results to which you appeal.

  Show that, at least until the bottom card reaches the top, the ordering of cards inserted beneath it is uniformly random. Hence or otherwise show that, for all $n$,

  $$\left|p_{n}-p\right| \leqslant 52(1+\log 52) / n$$

  comment

2002

• A1.1 B1.1

  Markov Chains | Part II, 2002

  (i) We are given a finite set of airports. Assume that between any two airports, $i$ and $j$, there are $a_{i j}=a_{j i}$ flights in each direction on every day. A confused traveller takes one flight per day, choosing at random from all available flights. Starting from $i$, how many days on average will pass until the traveller returns again to $i$ ? Be careful to allow for the case where there may be no flights at all between two given airports.

  (ii) Consider the infinite tree $T$ with root $R$, where, for all $m \geqslant 0$, all vertices at distance $2^{m}$ from $R$ have degree 3 , and where all other vertices (except $R$ ) have degree 2 . Show that the random walk on $T$ is recurrent.

  comment

• A2.1

  Markov Chains | Part II, 2002

  (i) In each of the following cases, the state-space $I$ and non-zero transition rates $q_{i j}$ $(i \neq j)$ of a continuous-time Markov chain are given. Determine in which cases the chain is explosive.

  (ii) Children arrive at a see-saw according to a Poisson process of rate 1 . Initially there are no children. The first child to arrive waits at the see-saw. When the second child arrives, they play on the see-saw. When the third child arrives, they all decide to go and play on the merry-go-round. The cycle then repeats. Show that the number of children at the see-saw evolves as a Markov Chain and determine its generator matrix. Find the probability that there are no children at the see-saw at time $t$.

  Hence obtain the identity

  $$\sum_{n=0}^{\infty} e^{-t} \frac{t^{3 n}}{(3 n) !}=\frac{1}{3}+\frac{2}{3} e^{-\frac{3}{2} t} \cos \frac{\sqrt{3}}{2} t$$

  $$\begin{aligned} & \text { (a) } I=\{1,2,3, \ldots\}, \quad q_{i, i+1}=i^{2}, \quad i \in I \text {, } \\ & \text { (b) } \quad I=\mathbb{Z}, \quad q_{i, i-1}=q_{i, i+1}=2^{i}, \quad i \in I \text {. } \end{aligned}$$

  comment

• A3.1 B3.1

  Markov Chains | Part II, 2002

  (i) Consider the continuous-time Markov chain $\left(X_{t}\right)_{t \geqslant 0}$ on $\{1,2,3,4,5,6,7\}$ with generator matrix

  $$Q=\left(\begin{array}{rrrrrrr} -6 & 2 & 0 & 0 & 0 & 4 & 0 \\ 2 & -3 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & -5 & 1 & 2 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 2 & 2 & 0 & -6 & 0 & 2 \\ 1 & 2 & 0 & 0 & 0 & -3 & 0 \\ 0 & 0 & 1 & 0 & 1 & 0 & -2 \end{array}\right)$$

  Compute the probability, starting from state 3 , that $X_{t}$ hits state 2 eventually.

  Deduce that

  $$\lim _{t \rightarrow \infty} \mathbb{P}\left(X_{t}=2 \mid X_{0}=3\right)=\frac{4}{15}$$

  [Justification of standard arguments is not expected.]

  (ii) A colony of cells contains immature and mature cells. Each immature cell, after an exponential time of parameter 2, becomes a mature cell. Each mature cell, after an exponential time of parameter 3, divides into two immature cells. Suppose we begin with one immature cell and let $n(t)$ denote the expected number of immature cells at time $t$. Show that

  $$n(t)=\left(4 e^{t}+3 e^{-6 t}\right) / 7$$

  comment

• A4.1

  Markov Chains | Part II, 2002

  Write an essay on the long-time behaviour of discrete-time Markov chains on a finite state space. Your essay should include discussion of the convergence of probabilities as well as almost-sure behaviour. You should also explain what happens when the chain is not irreducible.

  comment

2001

• A1.1 B1.1

  Markov Chains | Part II, 2001

  (i) Let $X=\left(X_{n}: 0 \leqslant n \leqslant N\right)$ be an irreducible Markov chain on the finite state space $S$ with transition matrix $P=\left(p_{i j}\right)$ and invariant distribution $\pi$. What does it mean to say that $X$ is reversible in equilibrium?

  Show that $X$ is reversible in equilibrium if and only if $\pi_{i} p_{i j}=\pi_{j} p_{j i}$ for all $i, j \in S$.

  (ii) A finite connected graph $G$ has vertex set $V$ and edge set $E$, and has neither loops nor multiple edges. A particle performs a random walk on $V$, moving at each step to a randomly chosen neighbour of the current position, each such neighbour being picked with equal probability, independently of all previous moves. Show that the unique invariant distribution is given by $\pi_{v}=d_{v} /(2|E|)$ where $d_{v}$ is the degree of vertex $v$.

  A rook performs a random walk on a chessboard; at each step, it is equally likely to make any of the moves which are legal for a rook. What is the mean recurrence time of a corner square. (You should give a clear statement of any general theorem used.)

  [A chessboard is an $8 \times 8$ square grid. A legal move is one of any length parallel to the axes.]

  comment

• A2.1

  Markov Chains | Part II, 2001

  (i) The fire alarm in Mill Lane is set off at random times. The probability of an alarm during the time-interval $(u, u+h)$ is $\lambda(u) h+o(h)$ where the 'intensity function' $\lambda(u)$ may vary with the time $u$. Let $N(t)$ be the number of alarms by time $t$, and set $N(0)=0$. Show, subject to reasonable extra assumptions to be stated clearly, that $p_{i}(t)=P(N(t)=i)$ satisfies

  $$p_{0}^{\prime}(t)=-\lambda(t) p_{0}(t), \quad p_{i}^{\prime}(t)=\lambda(t)\left\{p_{i-1}(t)-p_{i}(t)\right\}, \quad i \geqslant 1 .$$

  Deduce that $N(t)$ has the Poisson distribution with parameter $\Lambda(t)=\int_{0}^{t} \lambda(u) d u$.

  (ii) The fire alarm in Clarkson Road is different. The number $M(t)$ of alarms by time $t$ is such that

  $$P(M(t+h)=m+1 \mid M(t)=m)=\lambda_{m} h+o(h),$$

  where $\lambda_{m}=\alpha m+\beta, m \geqslant 0$, and $\alpha, \beta>0$. Show, subject to suitable extra conditions, that $p_{m}(t)=P(M(t)=m)$ satisfies a set of differential-difference equations to be specified. Deduce without solving these equations in their entirety that $M(t)$ has mean $\beta\left(e^{\alpha t}-1\right) / \alpha$, and find the variance of $M(t)$.

  comment

• A3.1 B3.1

  Markov Chains | Part II, 2001

  (i) Explain what is meant by the transition semigroup $\left\{P_{t}\right\}$ of a Markov chain $X$ in continuous time. If the state space is finite, show under assumptions to be stated clearly, that $P_{t}^{\prime}=G P_{t}$ for some matrix $G$. Show that a distribution $\pi$ satisfies $\pi G=0$ if and only if $\pi P_{t}=\pi$ for all $t \geqslant 0$, and explain the importance of such $\pi$.

  (ii) Let $X$ be a continuous-time Markov chain on the state space $S=\{1,2\}$ with generator

  $$G=\left(\begin{array}{cc} -\beta & \beta \\ \gamma & -\gamma \end{array}\right), \quad \text { where } \beta, \gamma>0 .$$

  Show that the transition semigroup $P_{t}=\exp (t G)$ is given by

  $$(\beta+\gamma) P_{t}=\left(\begin{array}{cc} \gamma+\beta h(t) & \beta(1-h(t)) \\ \gamma(1-h(t)) & \beta+\gamma h(t) \end{array}\right),$$

  where $h(t)=e^{-t(\beta+\gamma)}$.

  For $0<\alpha<1$, let

  $$H(\alpha)=\left(\begin{array}{cc} \alpha & 1-\alpha \\ 1-\alpha & \alpha \end{array}\right)$$

  For a continuous-time chain $X$, let $M$ be a matrix with $(i, j)$ entry

  $P(X(1)=j \mid X(0)=i)$, for $i, j \in S$. Show that there is a chain $X$ with $M=H(\alpha)$ if and only if $\alpha>\frac{1}{2}$.

  comment

• A4.1

  Markov Chains | Part II, 2001

  Write an essay on the convergence to equilibrium of a discrete-time Markov chain on a countable state-space. You should include a discussion of the existence of invariant distributions, and of the limit theorem in the non-null recurrent case.

  comment