Optimization

2021

• Paper 1, Section I, $\mathbf{7 H}$

  Optimization | Part IB, 2021

  (a) Let $f_{i}: \mathbb{R}^{d} \rightarrow \mathbb{R}$ be a convex function for each $i=1, \ldots, m$. Show that

  $$x \mapsto \max _{i=1, \ldots, m} f_{i}(x) \quad \text { and } \quad x \mapsto \sum_{i=1}^{m} f_{i}(x)$$

  are both convex functions.

  (b) Fix $c \in \mathbb{R}^{d}$. Show that if $f: \mathbb{R} \rightarrow \mathbb{R}$ is convex, then $g: \mathbb{R}^{d} \rightarrow \mathbb{R}$ given by $g(x)=f\left(c^{T} x\right)$ is convex.

  (c) Fix vectors $a_{1}, \ldots, a_{n} \in \mathbb{R}^{d}$. Let $Q: \mathbb{R}^{d} \rightarrow \mathbb{R}$ be given by

  $$Q(\beta)=\sum_{i=1}^{n} \log \left(1+e^{a_{i}^{T} \beta}\right)+\sum_{j=1}^{d}\left|\beta_{j}\right|$$

  Show that $Q$ is convex. [You may use any result from the course provided you state it.]

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2021

  Find the solution to the following Optimization problem using the simplex algorithm:

  Write down the dual problem and give its solution.

  $$\begin{aligned} & \text { maximise } 3 x_{1}+6 x_{2}+4 x_{3} \\ & \text { subject to } 2 x_{1}+3 x_{2}+x_{3} \leqslant 7 \text {, } \\ & 4 x_{1}+2 x_{2}+2 x_{3} \leqslant 5, \\ & x_{1}+x_{2}+2 x_{3} \leqslant 2, \quad x_{1}, x_{2}, x_{3} \geqslant 0 . \end{aligned}$$

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2021

  Explain what is meant by a two-person zero-sum game with $m \times n$ payoff matrix $A$, and define what is meant by an optimal strategy for each player. What are the relationships between the optimal strategies and the value of the game?

  Suppose now that

  $$A=\left(\begin{array}{cccc} 0 & 1 & 1 & -4 \\ -1 & 0 & 2 & 2 \\ -1 & -2 & 0 & 3 \\ 4 & -2 & -3 & 0 \end{array}\right)$$

  Show that if strategy $p=\left(p_{1}, p_{2}, p_{3}, p_{4}\right)^{T}$ is optimal for player I, it must also be optimal for player II. What is the value of the game in this case? Justify your answer.

  Explain why we must have $(A p)_{i} \leqslant 0$ for all $i$. Hence or otherwise, find the optimal strategy $p$ and prove that it is unique.

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2021

  (a) Consider the linear program

  $$\begin{aligned} P: \quad \text { maximise over } x \geqslant 0, & c^{T} x \\ \text { subject to } & A x=b \end{aligned}$$

  where $A \in \mathbb{R}^{m \times n}, c \in \mathbb{R}^{n}$ and $b \in \mathbb{R}^{m}$. What is meant by a basic feasible solution?

  (b) Prove that if $P$ has a finite maximum, then there exists a solution that is a basic feasible solution.

  (c) Now consider the optimization problem

  $$Q: \quad \text { maximise over } x \geqslant 0, \quad \frac{c^{T} x}{d^{T} x}$$

  subject to $A x=b$,

  $$d^{T} x>0,$$

  where matrix $A$ and vectors $c, b$ are as in the problem $P$, and $d \in \mathbb{R}^{n}$. Suppose there exists a solution $x^{*}$ to $Q$. Further consider the linear program

  $$\begin{aligned} R: \quad \text { maximise over } y \geqslant 0, t \geqslant 0, & c^{T} y \\ & A y=b t \\ & d^{T} y=1 \end{aligned}$$

  (i) Suppose $d_{i}>0$ for all $i=1, \ldots, n$. Show that the maximum of $R$ is finite and at least as large as that of $Q$.

  (ii) Suppose, in addition to the condition in part (i), that the entries of $A$ are strictly positive. Show that the maximum of $R$ is equal to that of $Q$.

  (iii) Let $\mathcal{B}$ be the set of basic feasible solutions of the linear program $P$. Assuming the conditions in parts (i) and (ii) above, show that

  $$\frac{c^{T} x^{*}}{d^{T} x^{*}}=\max _{x \in \mathcal{B}} \frac{c^{T} x}{d^{T} x}$$

  [Hint: Argue that if $(y, t)$ is in the set $\mathcal{A}$ of basic feasible solutions to $R$, then $y / t \in \mathcal{B} .]$

  comment

2020

• Paper 1, Section I, H

  Optimization | Part IB, 2020

  Solve the following Optimization problem using the simplex algorithm:

  $$\begin{array}{rr} \operatorname{maximise} & x_{1}+x_{2} \\ \text { subject to } & \left|x_{1}-2 x_{2}\right| \leqslant 2 \\ & 4 x_{1}+x_{2} \leqslant 4, \quad x_{1}, x_{2} \geqslant 0 \end{array}$$

  Suppose the constraints above are now replaced by $\left|x_{1}-2 x_{2}\right| \leqslant 2+\epsilon_{1}$ and $4 x_{1}+x_{2} \leqslant 4+\epsilon_{2}$. Give an expression for the maximum objective value that is valid for all sufficiently small non-zero $\epsilon_{1}$ and $\epsilon_{2}$.

  comment

• Paper 2, Section II, H

  Optimization | Part IB, 2020

  State and prove the Lagrangian sufficiency theorem.

  Solve, using the Lagrangian method, the optimization problem

  $$\begin{array}{ll} \operatorname{maximise} & x+y+2 a \sqrt{1+z} \\ \text { subject to } & x+\frac{1}{2} y^{2}+z=b \\ & x, z \geqslant 0 \end{array}$$

  where the constants $a$ and $b$ satisfy $a \geqslant 1$ and $b \geqslant 1 / 2$.

  [You need not prove that your solution is unique.]

  comment

2019

• Paper 1, Section I, H

  Optimization | Part IB, 2019

  Suppose that $f$ is an infinitely differentiable function on $\mathbb{R}$. Assume that there exist constants $0<C_{1}, C_{2}<\infty$ so that $\left|f^{\prime \prime}(x)\right| \geqslant C_{1}$ and $\left|f^{\prime \prime \prime}(x)\right| \leqslant C_{2}$ for all $x \in \mathbb{R}$. Fix $x_{0} \in \mathbb{R}$ and for each $n \in \mathbb{N}$ set

  $$x_{n}=x_{n-1}-\frac{f^{\prime}\left(x_{n-1}\right)}{f^{\prime \prime}\left(x_{n-1}\right)} .$$

  Let $x^{*}$ be the unique value of $x$ where $f$ attains its minimum. Prove that

  $$\left|x^{*}-x_{n+1}\right| \leqslant \frac{C_{2}}{2 C_{1}}\left|x^{*}-x_{n}\right|^{2} \quad \text { for all } n \in \mathbb{N} .$$

  [Hint: Express $f^{\prime}\left(x^{*}\right)$ in terms of the Taylor series for $f^{\prime}$ at $x_{n}$ using the Lagrange form of the remainder: $f^{\prime}\left(x^{*}\right)=f^{\prime}\left(x_{n}\right)+f^{\prime \prime}\left(x_{n}\right)\left(x^{*}-x_{n}\right)+\frac{1}{2} f^{\prime \prime \prime}\left(y_{n}\right)\left(x^{*}-x_{n}\right)^{2}$ where $y_{n}$ is between $x_{n}$ and $\left.x^{*} .\right]$

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2019

  State the Lagrange sufficiency theorem.

  Find the maximum of $\log (x y z)$ over $x, y, z>0$ subject to the constraint

  $$x^{2}+y^{2}+z^{2}=1$$

  using Lagrange multipliers. Carefully justify why your solution is in fact the maximum.

  Find the maximum of $\log (x y z)$ over $x, y, z>0$ subject to the constraint

  $$x^{2}+y^{2}+z^{2} \leqslant 1$$

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2019

  (a) Suppose that $A \in \mathbb{R}^{m \times n}$ and $b \in \mathbb{R}^{m}$, with $n \geqslant m$. What does it mean for $x \in \mathbb{R}^{n}$ to be a basic feasible solution of the equation $A x=b ?$

  Assume that the $m$ rows of $A$ are linearly independent, every set of $m$ columns is linearly independent, and every basic solution has exactly $m$ non-zero entries. Prove that the extreme points of $\mathcal{X}(b)=\{x \geqslant 0: A x=b\}$ are the basic feasible solutions of $A x=b$. [Here, $x \geqslant 0$ means that each of the coordinates of $x$ are at least 0 .]

  (b) Use the simplex method to solve the linear program

  $$\begin{array}{cl} \max & 4 x_{1}+3 x_{2}+7 x_{3} \\ \text { s.t. } & x_{1}+3 x_{2}+x_{3} \leqslant 14 \\ & 4 x_{1}+3 x_{2}+2 x_{3} \leqslant 5 \\ & -x_{1}+x_{2}-x_{3} \geqslant-2 \\ & x_{1}, x_{2}, x_{3} \geqslant 0 \end{array}$$

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2019

  (a) State and prove the max-flow min-cut theorem.

  (b) (i) Apply the Ford-Fulkerson algorithm to find the maximum flow of the network illustrated below, where $S$ is the source and $T$ is the sink.

  

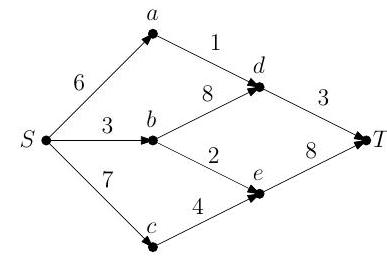
  (ii) Verify the optimality of your solution using the max-flow min-cut theorem.

  (iii) Is there a unique flow which attains the maximum? Explain your answer.

  (c) Prove that the Ford-Fulkerson algorithm always terminates when the network is finite, the capacities are integers, and the algorithm is initialised where the initial flow is 0 across all edges. Prove also in this case that the flow across each edge is an integer.

  comment

2018

• Paper 1, Section I, 8H

  Optimization | Part IB, 2018

  What is meant by a transportation problem? Illustrate the transportation algorithm by solving the problem with three sources and three destinations described by the table

  

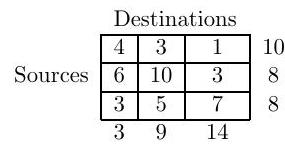
  where the figures in the boxes denote transportation costs, the right-hand column denotes supplies, and the bottom row denotes requirements.

  comment

• Paper 2, Section $I$, H

  Optimization | Part IB, 2018

  What does it mean to state that $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$ is a convex function?

  Suppose that $f, g: \mathbb{R}^{n} \rightarrow \mathbb{R}$ are convex functions, and for $b \in \mathbb{R}$ let

  $$\phi(b)=\inf \{f(x): g(x) \leqslant b\}$$

  Assuming $\phi(b)$ is finite for all $b \in \mathbb{R}$, prove that the function $\phi$ is convex.

  comment

• Paper 3, Section II, 21H

  Optimization | Part IB, 2018

  State and prove the Lagrangian Sufficiency Theorem.

  The manufacturers, $A$ and $B$, of two competing soap powders must plan how to allocate their advertising resources ( $X$ and $Y$ pounds respectively) among $n$ distinct geographical regions. If $x_{i} \geqslant 0$ and $y_{i} \geqslant 0$ denote, respectively, the resources allocated to area $i$ by $A$ and $B$ then the number of packets sold by $A$ and $B$ in area $i$ are

  $$\frac{x_{i} u_{i}}{x_{i}+y_{i}}, \quad \frac{y_{i} u_{i}}{x_{i}+y_{i}}$$

  respectively, where $u_{i}$ is the total market in area $i$, and $u_{1}, u_{2}, \ldots, u_{n}$ are known constants. The difference between the amount sold by $A$ and $B$ is then

  $$\sum_{i=1}^{n} \frac{x_{i}-y_{i}}{x_{i}+y_{i}} u_{i}$$

  $A$ seeks to maximize this quantity, while $B$ seeks to minimize it.

  (i) If $A$ knows $B$ 's allocation, how should $A$ choose $x=\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ ?

  (ii) Determine the best strategies for $A$ and $B$ if each assumes the other will know its strategy and react optimally.

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2018

  Given a network with a source $A$, a sink $B$, and capacities on directed edges, define a cut. What is meant by the capacity of a cut? State the max-flow min-cut theorem. If the capacities of edges are integral, what can be said about the maximum flow?

  Consider an $m \times n$ matrix $A$ in which each entry is either 0 or 1 . We say that a set of lines (rows or columns of the matrix) covers the matrix if each 1 belongs to some line of the set. We say that a set of 1 's is independent if no pair of 1 's of the set lie in the same line. Use the max-flow min-cut theorem to show that the maximal number of independent 1's equals the minimum number of lines that cover the matrix.

  comment

2017

• Paper 1, Section I, H

  Optimization | Part IB, 2017

  Solve the following linear programming problem using the simplex method:

  $$\begin{array}{r} \max \left(x_{1}+2 x_{2}+x_{3}\right) \\ \text { subject to } \quad x_{1}, x_{2}, x_{3} \geqslant 0 \\ x_{1}+x_{2}+2 x_{3} \leqslant 10 \\ 2 x_{1}+x_{2}+3 x_{3} \leqslant 15 \end{array}$$

  Suppose we now subtract $\Delta \in[0,10]$ from the right hand side of the last two constraints. Find the new optimal value.

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2017

  Consider the following optimization problem

  $$\mathrm{P}: \quad \min f(x) \quad \text { subject to } \quad g(x)=b, x \in X .$$

  (a) Write down the Lagrangian for this problem. State the Lagrange sufficiency theorem.

  (b) Formulate the dual problem. State and prove the weak duality property.

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2017

  (a) Explain what is meant by a two-person zero-sum game with payoff matrix $A=\left(a_{i j}: 1 \leqslant i \leqslant m, 1 \leqslant j \leqslant n\right)$ and define what is an optimal strategy (also known as a maximin strategy) for each player.

  (b) Suppose the payoff matrix $A$ is antisymmetric, i.e. $m=n$ and $a_{i j}=-a_{j i}$ for all $i, j$. What is the value of the game? Justify your answer.

  (c) Consider the following two-person zero-sum game. Let $n \geqslant 3$. Both players simultaneously call out one of the numbers $\{1, \ldots, n\}$. If the numbers differ by one, the player with the higher number wins $£ 1$ from the other player. If the players' choices differ by 2 or more, the player with the higher number pays $£ 2$ to the other player. In the event of a tie, no money changes hands.

  Write down the payoff matrix.

  For the case when $n=3$ find the value of the game and an optimal strategy for each player.

  Find the value of the game and an optimal strategy for each player for all $n$.

  [You may use results from the course provided you state them clearly.]

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2017

  (a) Let $G$ be a flow network with capacities $c_{i j}$ on the edges. Explain the maximum flow problem on this network defining all the notation you need.

  (b) Describe the Ford-Fulkerson algorithm for finding a maximum flow and state the max-flow min-cut theorem.

  (c) Apply the Ford-Fulkerson algorithm to find a maximum flow and a minimum cut of the following network:

  

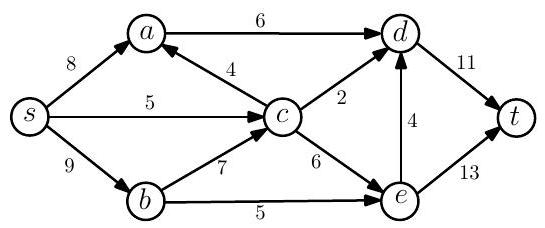
  (d) Suppose that we add $\varepsilon>0$ to each capacity of a flow network. Is it true that the maximum flow will always increase by $\varepsilon$ ? Justify your answer.

  comment

2016

• Paper 1, Section I, H

  Optimization | Part IB, 2016

  $$A=\left(\begin{array}{rrr} 5 & -2 & -5 \\ -2 & 3 & 2 \\ -3 & 6 & 2 \\ 4 & -8 & -6 \end{array}\right)$$

  be the payoff of a two-person zero-sum game, where player I (randomly) picks a row to maximise the expected payoff and player II picks a column to minimise the expected payoff. Find each player's optimal strategy and the value of the game.

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2016

  Use the simplex algorithm to find the optimal solution to the linear program:

  $$\operatorname{maximise} 3 x+5 y \text { subject to } \begin{aligned} 8 x+3 y+10 z & \leqslant 9, \quad x, y, z \geqslant 0 \\ 5 x+2 y+4 z & \leqslant 8 \\ 2 x+y+3 z & \leqslant 2 \end{aligned}$$

  Write down the dual problem and find its solution.

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2016

  (a) State and prove the Lagrangian sufficiency theorem.

  (b) Let $n \geqslant 1$ be a given constant, and consider the problem:

  $$\operatorname{minimise} \sum_{i=1}^{n}\left(2 y_{i}^{2}+x_{i}^{2}\right) \text { subject to } x_{i}=1+\sum_{k=1}^{i} y_{k} \text { for all } i=1, \ldots, n$$

  Find, with proof, constants $a, b, A, B$ such that the optimal solution is given by

  $$x_{i}=a 2^{i}+b 2^{-i} \text { and } y_{i}=A 2^{i}+B 2^{-i} \text {, for all } i=1, \ldots, n .$$

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2016

  (a) What is the maximal flow problem in a network? Explain the Ford-Fulkerson algorithm. Prove that this algorithm terminates if the initial flow is set to zero and all arc capacities are rational numbers.

  (b) Let $A=\left(a_{i, j}\right)_{i, j}$ be an $n \times n$ matrix. We say that $A$ is doubly stochastic if $0 \leqslant a_{i, j} \leqslant 1$ for $i, j$ and

  $$\begin{aligned} &\sum_{i=1}^{n} a_{i, j}=1 \text { for all } j \\ &\sum_{j=1}^{n} a_{i, j}=1 \text { for all } i \end{aligned}$$

  We say that $A$ is a permutation matrix if $a_{i, j} \in\{0,1\}$ for all $i, j$ and

  for all $j$ there exists a unique $i$ such that $a_{i, j}=1$,

  for all $i$ there exists a unique $j$ such that $a_{i, j}=1$.

  Let $\mathcal{C}$ be the set of all $n \times n$ doubly stochastic matrices. Show that a matrix $A$ is an extreme point of $\mathcal{C}$ if and only if $A$ is a permutation matrix.

  comment

2015

• Paper 1, Section I, H

  Optimization | Part IB, 2015

  (a) Consider a network with vertices in $V=\{1, \ldots, n\}$ and directed edges $(i, j)$ in $E \subseteq V \times V$. Suppose that 1 is the source and $n$ is the sink. Let $C_{i j}, 0<C_{i j}<\infty$, be the capacity of the edge from vertex $i$ to vertex $j$ for $(i, j) \in E$. Let a cut be a partition of $V=\{1, \ldots, n\}$ into $S$ and $V \backslash S$ with $1 \in S$ and $n \in V \backslash S$. Define the capacity of the cut $S$. Write down the maximum flow problem. Prove that the maximum flow is bounded above by the minimum cut capacity.

  (b) Find the maximum flow from the source to the sink in the network below, where the directions and capacities of the edges are shown. Explain your reasoning.

  

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2015

  Define what it means to say that a set $S \subseteq \mathbb{R}^{n}$ is convex. What is meant by an extreme point of a convex set $S$ ?

  Consider the set $S \subseteq \mathbb{R}^{2}$ given by

  $$S=\left\{\left(x_{1}, x_{2}\right): x_{1}+4 x_{2} \leqslant 30,3 x_{1}+7 x_{2} \leqslant 60, x_{1} \geqslant 0, x_{2} \geqslant 0\right\}$$

  Show that $S$ is convex, and give the coordinates of all extreme points of $S$.

  For all possible choices of $c_{1}>0$ and $c_{2}>0$, find the maximum value of $c_{1} x_{1}+c_{2} x_{2}$ subject to $\left(x_{1}, x_{2}\right) \in S$.

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2015

  Consider the linear programming problem $P$ :

  $$\text { minimise } c^{T} x \text { subject to } A x \geqslant b, x \geqslant 0,$$

  where $x$ and $c$ are in $\mathbb{R}^{n}, A$ is a real $m \times n$ matrix, $b$ is in $\mathbb{R}^{m}$ and ${ }^{T}$ denotes transpose. Derive the dual linear programming problem $D$. Show from first principles that the dual of $D$ is $P$.

  Suppose that $c^{T}=(6,10,11), b^{T}=(1,1,3)$ and $A=\left(\begin{array}{lll}1 & 3 & 8 \\ 1 & 1 & 2 \\ 2 & 4 & 4\end{array}\right)$. Write down the dual $D$ and find the optimal solution of the dual using the simplex algorithm. Hence, or otherwise, find the optimal solution $x^{*}=\left(x_{1}^{*}, x_{2}^{*}, x_{3}^{*}\right)$ of $P$.

  Suppose that $c$ is changed to $\tilde{c}=\left(6+\varepsilon_{1}, 10+\varepsilon_{2}, 11+\varepsilon_{3}\right)$. Give necessary and sufficient conditions for $x^{*}$ still to be the optimal solution of $P$. If $\varepsilon_{1}=\varepsilon_{2}=0$, find the range of values for $\varepsilon_{3}$ for which $x^{*}$ is still the optimal solution of $P$.

  comment

• Paper 4, Section II, 20H

  Optimization | Part IB, 2015

  Suppose the recycling manager in a particular region is responsible for allocating all the recyclable waste that is collected in $n$ towns in the region to the $m$ recycling centres in the region. Town $i$ produces $s_{i}$ lorry loads of recyclable waste each day, and recycling centre $j$ needs to handle $d_{j}$ lorry loads of waste a day in order to be viable. Suppose that $\sum_{i} s_{i}=\sum_{j} d_{j}$. Suppose further that $c_{i j}$ is the cost of transporting a lorry load of waste from town $i$ to recycling centre $j$. The manager wishes to decide the number $x_{i j}$ of lorry loads of recyclable waste that should go from town $i$ to recycling centre $j$, $i=1, \ldots, n, j=1, \ldots, m$, in such a way that all the recyclable waste produced by each town is transported to recycling centres each day, and each recycling centre works exactly at the viable level each day. Use the Lagrangian sufficiency theorem, which you should quote carefully, to derive necessary and sufficient conditions for $\left(x_{i j}\right)$ to minimise the total cost under the above constraints.

  Suppose that there are three recycling centres $A, B$ and $C$, needing 5,20 and 20 lorry loads of waste each day, respectively, and suppose there are three towns $a, b$ and $c$ producing 20,15 and 10 lorry loads of waste each day, respectively. The costs of transporting a lorry load of waste from town $a$ to recycling centres $A, B$ and $C$ are $£ 90, £ 100$ and $£ 100$, respectively. The corresponding costs for town $b$ are $£ 130, £ 140$ and $£ 100$, while for town $c$ they are $£ 110, £ 80$ and $£ 80$. Recycling centre $A$ has reported that it currently receives 5 lorry loads of waste per day from town $a$, and recycling centre $C$ has reported that it currently receives 10 lorry loads of waste per day from each of towns $b$ and c. Recycling centre $B$ has failed to report. What is the cost of the current arrangement for transporting waste from the towns to the recycling centres? Starting with the current arrangement as an initial solution, use the transportation algorithm (explaining each step carefully) in order to advise the recycling manager how many lorry loads of waste should go from each town to each of the recycling centres in order to minimise the cost. What is the minimum cost?

  comment

2014

• Paper 1, Section I, 8H

  Optimization | Part IB, 2014

  State and prove the Lagrangian sufficiency theorem.

  Use the Lagrangian sufficiency theorem to find the minimum of $2 x_{1}^{2}+2 x_{2}^{2}+x_{3}^{2}$ subject to $x_{1}+x_{2}+x_{3}=1$ (where $x_{1}, x_{2}$ and $x_{3}$ are real).

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2014

  Explain what is meant by a two-player zero-sum game with $m \times n$ pay-off matrix $P=\left(p_{i j}\right)$, and state the optimal strategies for each player.

  Find these optimal strategies when

  $$P=\left(\begin{array}{rr} -4 & 2 \\ 2 & -4 \end{array}\right)$$

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2014

  Use the two-phase simplex method to maximise $2 x_{1}+x_{2}+x_{3}$ subject to the constraints

  $$x_{1}+x_{2} \geqslant 1, \quad x_{1}+x_{2}+2 x_{3} \leqslant 4, \quad x_{i} \geqslant 0 \text { for } i=1,2,3$$

  Derive the dual of this linear programming problem and find the optimal solution of the dual.

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2014

  Consider a network with a single source and a single sink, where all the edge capacities are finite. Write down the maximum flow problem, and state the max-flow min-cut theorem.

  Describe the Ford-Fulkerson algorithm. If all edge capacities are integers, explain why, starting from a suitable initial flow, the algorithm is guaranteed to end after a finite number of iterations.

  The graph in the diagram below represents a one-way road network taking traffic from point $A$ to point $B$ via five roundabouts $R_{i}, i=1, \ldots, 5$. The capacity of each road is shown on the diagram in terms of vehicles per minute. Assuming that all roundabouts can deal with arbitrary amounts of flow of traffic, find the maximum flow of traffic (in vehicles per minute) through this network of roads. Show that this flow is indeed optimal.

  After a heavy storm, roundabout $R_{2}$ is flooded and only able to deal with at most 20 vehicles per minute. Find a suitable new network for the situation after the storm. Apply the Ford-Fulkerson algorithm to the new network, starting with the zero flow and explaining each step, to determine the maximum flow and the associated flows on each road.

  

  comment

2013

• Paper 1, Section I, $8 \mathrm{H}$

  Optimization | Part IB, 2013

  State sufficient conditions for $p$ and $q$ to be optimal mixed strategies for the row and column players in a zero-sum game with payoff matrix $A$ and value $v$.

  Rowena and Colin play a hide-and-seek game. Rowena hides in one of 3 locations, and then Colin searches them in some order. If he searches in order $i, j, k$ then his search cost is $c_{i}, c_{i}+c_{j}$ or $c_{i}+c_{j}+c_{k}$, depending upon whether Rowena hides in $i, j$ or $k$, respectively, and where $c_{1}, c_{2}, c_{3}$ are all positive. Rowena (Colin) wishes to maximize (minimize) the expected search cost.

  Formulate the payoff matrix for this game.

  Let $c=c_{1}+c_{2}+c_{3}$. Suppose that Colin starts his search in location $i$ with probability $c_{i} / c$, and then, if he does not find Rowena, he searches the remaining two locations in random order. What bound does this strategy place on the value of the game?

  Guess Rowena's optimal hiding strategy, show that it is optimal and find the value of the game.

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2013

  Given a network with a source $A$, a sink $B$, and capacities on directed arcs, define what is meant by a minimum cut.

  The $m$ streets and $n$ intersections of a town are represented by sets of edges $E$ and vertices $V$ of a connected graph. A city planner wishes to make all streets one-way while ensuring it possible to drive away from each intersection along at least $k$ different streets.

  Use a theorem about min-cut and max-flow to prove that the city planner can achieve his goal provided that the following is true:

  $$d(U) \geqslant k|U| \text { for all } U \subseteq V,$$

  where $|U|$ is the size of $U$ and $d(U)$ is the number edges with at least one end in $U$. How could the planner find street directions that achieve his goal?

  [Hint: Consider a network having nodes $A, B$, nodes $a_{1}, \ldots, a_{m}$ for the streets and nodes $b_{1}, \ldots, b_{n}$ for the intersections. There are directed arcs from $A$ to each and from each $b_{i}$ to $B$. From each $a_{i}$ there are two further arcs, directed towards $b_{j}$ and $b_{j^{\prime}}$ that correspond to endpoints of street $i .]$

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2013

  Use the two phase method to find all optimal solutions to the problem

  $$\begin{aligned} \operatorname{maximize} 2 x_{1}+3 x_{2}+x_{3} \\ \text { subject to } x_{1}+x_{2}+x_{3} & \leqslant 40 \\ 2 x_{1}+x_{2}-x_{3} & \geqslant 10 \\ -x_{2}+x_{3} & \geqslant 10 \\ x_{1}, x_{2}, x_{3} & \geqslant 0 \end{aligned}$$

  Suppose that the values $(40,10,10)$ are perturbed to $(40,10,10)+\left(\epsilon_{1}, \epsilon_{2}, \epsilon_{3}\right)$. Find an expression for the change in the optimal value, which is valid for all sufficiently small values of $\epsilon_{1}, \epsilon_{2}, \epsilon_{3}$.

  Suppose that $\left(\epsilon_{1}, \epsilon_{2}, \epsilon_{3}\right)=(\theta,-2 \theta, 0)$. For what values of $\theta$ is your expression valid?

  comment

• Paper 4, Section II, 20H

  Optimization | Part IB, 2013

  Given real numbers $a$ and $b$, consider the problem $\mathrm{P}$ of minimizing

  $$f(x)=a x_{11}+2 x_{12}+3 x_{13}+b x_{21}+4 x_{22}+x_{23}$$

  subject to $x_{i j} \geqslant 0$ and

  $$\begin{array}{r} x_{11}+x_{12}+x_{13}=5 \\ x_{21}+x_{22}+x_{23}=5 \\ x_{11}+x_{21}=3 \\ x_{12}+x_{22}=3 \\ x_{13}+x_{23}=4 \end{array}$$

  List all the basic feasible solutions, writing them as $2 \times 3$ matrices $\left(x_{i j}\right)$.

  Let $f(x)=\sum_{i j} c_{i j} x_{i j}$. Suppose there exist $\lambda_{i}, \mu_{j}$ such that

  $$\lambda_{i}+\mu_{j} \leqslant c_{i j} \text { for all } i \in\{1,2\}, j \in\{1,2,3\}$$

  Prove that if $x$ and $x^{\prime}$ are both feasible for $\mathrm{P}$ and $\lambda_{i}+\mu_{j}=c_{i j}$ whenever $x_{i j}>0$, then $f(x) \leqslant f\left(x^{\prime}\right) .$

  Let $x^{*}$ be the initial feasible solution that is obtained by formulating $\mathrm{P}$ as a transportation problem and using a greedy method that starts in the upper left of the matrix $\left(x_{i j}\right)$. Show that if $a+2 \leqslant b$ then $x^{*}$ minimizes $f$.

  For what values of $a$ and $b$ is one step of the transportation algorithm sufficient to pivot from $x^{*}$ to a solution that maximizes $f$ ?

  comment

2012

• Paper 1, Section I, 8H

  Optimization | Part IB, 2012

  State the Lagrangian sufficiency theorem.

  Use Lagrange multipliers to find the optimal values of $x_{1}$ and $x_{2}$ in the problem: maximize $x_{1}^{2}+x_{2} \quad$ subject to $\quad x_{1}^{2}+\frac{1}{2} x_{2}^{2} \leqslant b_{1}, \quad x_{1} \geqslant b_{2}$ and $x_{1}, x_{2} \geqslant 0$ for all values of $b_{1}, b_{2}$ such that $b_{1}-b_{2}^{2} \geqslant 0$.

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2012

  Consider the two-player zero-sum game with payoff matrix

  $$A=\left(\begin{array}{rrr} 2 & 0 & -2 \\ 3 & 4 & 5 \\ 6 & 0 & 6 \end{array}\right)$$

  Express the problem of finding the column player's optimal strategy as a linear programming problem in which $x_{1}+x_{2}+x_{3}$ is to be maximized subject to some constraints.

  Solve this problem using the simplex algorithm and find the optimal strategy for the column player.

  Find also, from the final tableau you obtain, both the value of the game and the row player's optimal strategy.

  comment

• Paper 3, Section II, 21H

  Optimization | Part IB, 2012

  For given positive real numbers $\left(c_{i j}: i, j \in\{1,2,3\}\right)$, consider the linear program

  $$P: \operatorname{minimize} \sum_{i=1}^{3} \sum_{j=1}^{3} c_{i j} x_{i j},$$

  subject to $\sum_{i=1}^{3} x_{i j} \leqslant 1$ for all $j, \quad \sum_{j=1}^{3} x_{i j} \geqslant 1$ for all $i$,

  and $x_{i j} \geqslant 0$ for all $i, j$.

  (i) Consider the feasible solution $x$ in which $x_{11}=x_{12}=x_{22}=x_{23}=x_{31}=x_{33}=1 / 2$ and $x_{i j}=0$ otherwise. Write down two basic feasible solutions of $P$, one of which you can be sure is at least as good as $x$. Are either of these basic feasible solutions of $P$ degenerate?

  (ii) Starting from a general definition of a Lagrangian dual problem show that the dual of $P$ can be written as

  $$D: \operatorname{maximize}_{\lambda_{i} \geqslant 0, \mu_{i} \geqslant 0} \sum_{i=1}^{3}\left(\lambda_{i}-\mu_{i}\right) \quad \text { subject to } \lambda_{i}-\mu_{j} \leqslant c_{i j} \text { for all } i, j .$$

  What happens to the optimal value of this problem if the constraints $\lambda_{i} \geqslant 0$ and $\mu_{i} \geqslant 0$ are removed?

  Prove that $x_{11}=x_{22}=x_{33}=1$ is an optimal solution to $P$ if and only if there exist $\lambda_{1}, \lambda_{2}, \lambda_{3}$ such that

  $$\lambda_{i}-\lambda_{j} \leqslant c_{i j}-c_{j j}, \quad \text { for all } i, j$$

  [You may use any facts that you know from the general theory of linear programming provided that you state them.]

  comment

• Paper 4, Section II, 20H

  Optimization | Part IB, 2012

  Describe the Ford-Fulkerson algorithm.

  State conditions under which the algorithm is guaranteed to terminate in a finite number of steps. Explain why it does so, and show that it finds a maximum flow. [You may assume that the value of a flow never exceeds the value of any cut.]

  In a football league of $n$ teams the season is partly finished. Team $i$ has already won $w_{i}$ matches. Teams $i$ and $j$ are to meet in $m_{i j}$ further matches. Thus the total number of remaining matches is $M=\sum_{i<j} m_{i j}$. Assume there will be no drawn matches. We wish to determine whether it is possible for the outcomes of the remaining matches to occur in such a way that at the end of the season the numbers of wins by the teams are $\left(x_{1}, \ldots, x_{n}\right)$.

  Invent a network flow problem in which the maximum flow from source to sink equals $M$ if and only if $\left(x_{1}, \ldots, x_{n}\right)$ is a feasible vector of final wins.

  Illustrate your idea by answering the question of whether or not $x=(7,5,6,6)$ is a possible profile of total end-of-season wins when $n=4, w=(1,2,3,4)$, and $M=14$ with

  $$\left(m_{i j}\right)=\left(\begin{array}{cccc} - & 2 & 2 & 2 \\ 2 & - & 1 & 1 \\ 2 & 1 & - & 6 \\ 2 & 1 & 6 & - \end{array}\right)$$

  comment

2011

• Paper 1, Section I, H

  Optimization | Part IB, 2011

  Suppose that $A x \leqslant b$ and $x \geqslant 0$ and $A^{T} y \geqslant c$ and $y \geqslant 0$ where $x$ and $c$ are $n$-dimensional column vectors, $y$ and $b$ are $m$-dimensional column vectors, and $A$ is an $m \times n$ matrix. Here, the vector inequalities are interpreted component-wise.

  (i) Show that $c^{T} x \leqslant b^{T} y$.

  (ii) Find the maximum value of

  $$\begin{aligned} 6 x_{1}+8 x_{2}+3 x_{3} \quad \text { subject to } & 2 x_{1}+4 x_{2}+x_{3} \leqslant 10 \\ & 3 x_{1}+4 x_{2}+3 x_{3} \leqslant 6 \\ & x_{1}, x_{2}, x_{3} \geqslant 0 \end{aligned}$$

  You should state any results from the course used in your solution.

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2011

  Let $N=\{1, \ldots, n\}$ be the set of nodes of a network, where 1 is the source and $n$ is the $\operatorname{sink}$. Let $c_{i j}$ denote the capacity of the arc from node $i$ to node $j$.

  (i) In the context of maximising the flow through this network, define the following terms: feasible flow, flow value, cut, cut capacity.

  (ii) State and prove the max-flow min-cut theorem for network flows.

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2011

  (i) What does it mean to say a set $C \subseteq \mathbb{R}^{n}$ is convex?

  (ii) What does it mean to say $z$ is an extreme point of a convex set $C ?$

  Let $A$ be an $m \times n$ matrix, where $n>m$. Let $b$ be an $m \times 1$ vector, and let

  $$C=\left\{x \in \mathbb{R}^{n}: A x=b, x \geqslant 0\right\}$$

  where the inequality is interpreted component-wise.

  (iii) Show that $C$ is convex.

  (iv) Let $z=\left(z_{1}, \ldots, z_{n}\right)^{T}$ be a point in $C$ with the property that at least $m+1$ indices $i$ are such that $z_{i}>0$. Show that $z$ is not an extreme point of $C$. [Hint: If $r>m$, then any set of $r$ vectors in $\mathbb{R}^{m}$ is linearly dependent.]

  (v) Now suppose that every set of $m$ columns of $A$ is linearly independent. Let $z=\left(z_{1}, \ldots, z_{n}\right)^{T}$ be a point in $C$ with the property that at most $m$ indices $i$ are such that $z_{i}>0$. Show that $z$ is an extreme point of $C$.

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2011

  A company must ship coal from four mines, labelled $A, B, C, D$, to supply three factories, labelled $a, b, c$. The per unit transport cost, the outputs of the mines, and the requirements of the factories are given below.

  \begin{tabular}{c|c|c|c|c|c} & $A$ & $B$ & $C$ & $D$ & \ \hline$a$ & 12 & 3 & 5 & 2 & 34 \ \hline$b$ & 4 & 11 & 2 & 6 & 21 \ \hline$c$ & 3 & 9 & 7 & 4 & 23 \ \hline & 20 & 32 & 15 & 11 & \end{tabular}

  For instance, mine $B$ can produce 32 units of coal, factory a requires 34 units of coal, and it costs 3 units of money to ship one unit of coal from $B$ to $a$. What is the minimal cost of transporting coal from the mines to the factories?

  Now suppose increased efficiency allows factory $b$ to reduce its requirement to $20.8$ units of coal, and as a consequence, mine $B$ reduces its output to $31.8$ units. By how much does the transport cost decrease?

  comment

2010

• Paper 1, Section I, 8E

  Optimization | Part IB, 2010

  What is the maximal flow problem in a network?

  Explain the Ford-Fulkerson algorithm. Why must this algorithm terminate if the initial flow is set to zero and all arc capacities are rational numbers?

  comment

• Paper 2, Section I, E

  Optimization | Part IB, 2010

  Consider the function $\phi$ defined by

  $$\phi(b)=\inf \left\{x^{2}+y^{4}: x+2 y=b\right\}$$

  Use the Lagrangian sufficiency theorem to evaluate $\phi(3)$. Compute the derivative $\phi^{\prime}(3)$.

  comment

• Paper 3 , Section II, E

  Optimization | Part IB, 2010

  Let $A$ be the $m \times n$ payoff matrix of a two-person, zero-sum game. What is Player I's optimization problem?

  Write down a sufficient condition that a vector $p \in \mathbb{R}^{m}$ is an optimal mixed strategy for Player I in terms of the optimal mixed strategy of Player II and the value of the game. If $m=n$ and $A$ is an invertible, symmetric matrix such that $A^{-1} e \geqslant 0$, where $e=(1, \ldots, 1)^{T} \in \mathbb{R}^{m}$, show that the value of the game is $\left(e^{T} A^{-1} e\right)^{-1}$

  Consider the following game: Players I and II each have three cards labelled 1,2 , and 3. Each player chooses one of her cards, independently of the other, and places it in the same envelope. If the sum of the numbers in the envelope is smaller than or equal to 4, then Player II pays Player I the sum (in $£$ ), and otherwise Player I pays Player II the sum. (For instance, if Player I chooses card 3 and Player II choose card 2, then Player I pays Player II £5.) What is the optimal strategy for each player?

  comment

• Paper 4, Section II, E

  Optimization | Part IB, 2010

  A factory produces three types of sugar, types $X$, $Y$, and $Z$, from three types of syrup, labelled $A, B$, and C. The following table contains the number of litres of syrup necessary to make each kilogram of sugar.

  \begin{tabular}{c|ccc} & $\mathrm{X}$ & $\mathrm{Y}$ & $\mathrm{Z}$ \ \hline $\mathrm{A}$ & 3 & 2 & 1 \ $\mathrm{~B}$ & 2 & 3 & 2 \ $\mathrm{C}$ & 4 & 1 & 2 \end{tabular}

  For instance, one kilogram of type $\mathrm{X}$ sugar requires 3 litres of $\mathrm{A}, 2$ litres of $\mathrm{B}$, and 4 litres of C. The factory can sell each type of sugar for one pound per kilogram. Assume that the factory owner can use no more than 44 litres of $\mathrm{A}$ and 51 litres of $\mathrm{B}$, but is required by law to use at least 12 litres of C. If her goal is to maximize profit, how many kilograms of each type of sugar should the factory produce?

  comment

2009

• Paper 1, Section I, H

  Optimization | Part IB, 2009

  Find an optimal solution to the linear programming problem

  $$\max 3 x_{1}+2 x_{2}+2 x_{3}$$

  in $x \geqslant 0$ subject to

  $$\begin{gathered} 7 x_{1}+3 x_{2}+5 x_{3} \leqslant 44 \\ x_{1}+2 x_{2}+x_{3} \leqslant 10 \\ x_{1}+x_{2}+x_{3} \geqslant 8 \end{gathered}$$

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2009

  The diagram shows a network of sewage treatment plants, shown as circles, connected by pipes. Some pipes (indicated by a line with an arrowhead at one end only) allow sewage to flow in one direction only, others (indicated by a line with an arrowhead at both ends) allow sewage to flow in either direction. The capacities of the pipes are shown. The system serves three towns, shown in the diagram as squares.

  Each sewage treatment plant can treat a limited amount of sewage, indicated by the number in the circle, and this may not be exceeded for fear of environmental damage. Treated sewage is pumped into the sea, but at any treatment plant incoming untreated sewage may be immediately pumped to another plant for treatment there.

  Find the maximum amount of sewage which can be handled by the system, and how this is assigned to each of the three towns.

  

  comment

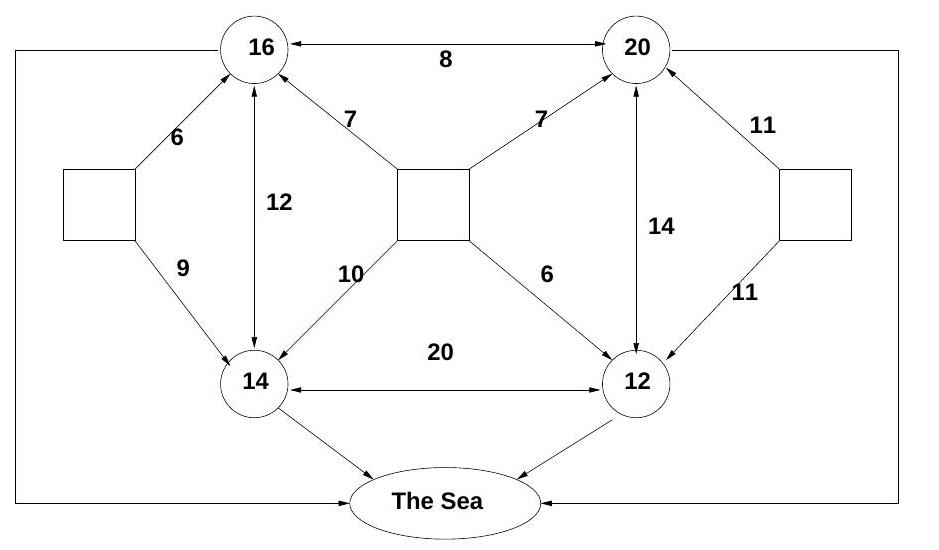
• Paper 3, Section II, H

  Optimization | Part IB, 2009

  Four factories supply stuff to four shops. The production capacities of the factories are $7,12,8$ and 9 units per week, and the requirements of the shops are 8 units per week each. If the costs of transporting a unit of stuff from factory $i$ to shop $j$ is the $(i, j)$ th element in the matrix

  $$\left(\begin{array}{cccc} 6 & 10 & 3 & 5 \\ 4 & 8 & 6 & 12 \\ 3 & 4 & 9 & 2 \\ 5 & 7 & 2 & 6 \end{array}\right)$$

  find a minimal-cost allocation of the outputs of the factories to the shops.

  Suppose that the cost of producing one unit of stuff varies across the factories, being $3,2,4,5$ respectively. Explain how you would modify the original problem to minimise the total cost of production and of transportation, and find an optimal solution for the modified problem.

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2009

  In a pure exchange economy, there are $J$ agents, and $d$ goods. Agent $j$ initially holds an endowment $x_{j} \in \mathbb{R}^{d}$ of the $d$ different goods, $j=1, \ldots, J$. Agent $j$ has preferences given by a concave utility function $U_{j}: \mathbb{R}^{d} \rightarrow \mathbb{R}$ which is strictly increasing in each of its arguments, and is twice continuously differentiable. Thus agent $j$ prefers $y \in \mathbb{R}^{d}$ to $x \in \mathbb{R}^{d}$ if and only if $U_{j}(y) \geqslant U_{j}(x)$.

  The agents meet and engage in mutually beneficial trades. Thus if agent $i$ holding $z_{i}$ meets agent $j$ holding $z_{j}$, then the amounts $z_{i}^{\prime}$ held by agent $i$ and $z_{j}^{\prime}$ held by agent $j$ after trading must satisfy $U_{i}\left(z_{i}^{\prime}\right) \geqslant U_{i}\left(z_{i}\right), U_{j}\left(z_{j}^{\prime}\right) \geqslant U_{j}\left(z_{j}\right)$, and $z_{i}^{\prime}+z_{j}^{\prime}=z_{i}+z_{j}$. Meeting and trading continues until, finally, agent $j$ holds $y_{j} \in \mathbb{R}^{d}$, where

  $$\sum_{j} x_{j}=\sum_{j} y_{j}$$

  and there are no further mutually beneficial trades available to any pair of agents. Prove that there must exist a vector $v \in \mathbb{R}^{d}$ and positive scalars $\lambda_{1}, \ldots, \lambda_{J}$ such that

  $$\nabla U_{j}\left(y_{j}\right)=\lambda_{j} v$$

  for all $j$. Show that for some positive $a_{1}, \ldots, a_{J}$ the final allocations $y_{j}$ are what would be achieved by a social planner, whose objective is to obtain

  $$\max \sum_{j} a_{j} U_{j}\left(y_{j}\right) \quad \text { subject to } \sum_{j} y_{j}=\sum_{j} x_{j}$$

  comment

2008

• 1.I.8H

  Optimization | Part IB, 2008

  State the Lagrangian Sufficiency Theorem for the maximization over $x$ of $f(x)$ subject to the constraint $g(x)=b$.

  For each $p>0$, solve

  $$\max \sum_{i=1}^{d} x_{i}^{p} \quad \text { subject to } \sum_{i=1}^{d} x_{i}=1, \quad x_{i} \geqslant 0 .$$

  comment

• 2.I.9H

  Optimization | Part IB, 2008

  Goods from three warehouses have to be delivered to five shops, the cost of transporting one unit of good from warehouse $i$ to shop $j$ being $c_{i j}$, where

  $$C=\left(\begin{array}{ccccc} 2 & 3 & 6 & 6 & 4 \\ 7 & 6 & 1 & 1 & 5 \\ 3 & 6 & 6 & 2 & 1 \end{array}\right)$$

  The requirements of the five shops are respectively $9,6,12,5$ and 10 units of the good, and each warehouse holds a stock of 15 units. Find a minimal-cost allocation of goods from warehouses to shops and its associated cost.

  comment

• 3.II.20H

  Optimization | Part IB, 2008

  Use the simplex algorithm to solve the problem

  $$\max x_{1}+2 x_{2}-6 x_{3}$$

  subject to $x_{1}, x_{2} \geqslant 0,\left|x_{3}\right| \leqslant 5$, and

  $$\begin{array}{r} x_{1}+x_{2}+x_{3} \leqslant 7 \\ 2 x_{2}+x_{3} \geqslant 1 \end{array}$$

  comment

• 4.II.20H

  Optimization | Part IB, 2008

  (i) Suppose that $f: \mathbb{R}^{n} \rightarrow \mathbb{R}$, and $g: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ are continuously differentiable. Suppose that the problem

  $\max f(x)$ subject to $g(x)=b$

  is solved by a unique $\bar{x}=\bar{x}(b)$ for each $b \in \mathbb{R}^{m}$, and that there exists a unique $\lambda(b) \in \mathbb{R}^{m}$ such that

  $$\varphi(b) \equiv f(\bar{x}(b))=\sup _{x}\left\{f(x)+\lambda(b)^{T}(b-g(x))\right\}$$

  Assuming that $\bar{x}$ and $\lambda$ are continuously differentiable, prove that

  $$\frac{\partial \varphi}{\partial b_{i}}(b)=\lambda_{i}(b)$$

  (ii) The output of a firm is a function of the capital $K$ deployed, and the amount $L$ of labour employed, given by

  $$f(K, L)=K^{\alpha} L^{\beta}$$

  where $\alpha, \beta \in(0,1)$. The firm's manager has to optimize the output subject to the budget constraint

  $$K+w L=b,$$

  where $w>0$ is the wage rate and $b>0$ is the available budget. By casting the problem in Lagrangian form, find the optimal solution and verify the relation $(*)$.

  comment

2007

• $3 . \mathrm{II} . 20 \mathrm{C}$

  Optimization | Part IB, 2007

  State and prove the Lagrangian sufficiency theorem.

  Solve the problem

  $$\begin{array}{ll} \text { maximize } & x_{1}+3 \ln \left(1+x_{2}\right) \\ \text { subject to } \quad & 2 x_{1}+3 x_{2} \leqslant c_{1} \\ & \ln \left(1+x_{1}\right) \geqslant c_{2}, \quad x_{1} \geqslant 0, x_{2} \geqslant 0 \end{array}$$

  where $c_{1}$ and $c_{2}$ are non-negative constants satisfying $c_{1}+2 \geqslant 2 e^{c_{2}}$.

  comment

• 1.I.8C

  Optimization | Part IB, 2007

  State and prove the max-flow min-cut theorem for network flows.

  comment

• 2.I.9C

  Optimization | Part IB, 2007

  Consider the game with payoff matrix

  $$\left(\begin{array}{lll} 2 & 5 & 4 \\ 3 & 2 & 2 \\ 2 & 1 & 3 \end{array}\right)$$

  where the $(i, j)$ entry is the payoff to the row player if the row player chooses row $i$ and the column player chooses column $j$.

  Find the value of the game and the optimal strategies for each player.

  comment

• 4.II $20 \mathrm{C}$

  Optimization | Part IB, 2007

  Consider the linear programming problem

  $$\begin{aligned} \operatorname{minimize} \quad & 2 x_{1}-3 x_{2}-2 x_{3} \\ \text { subject to } \quad-& 2 x_{1}+2 x_{2}+4 x_{3} \leqslant 5 \\ & 4 x_{1}+2 x_{2}-5 x_{3} \leqslant 8 \\ & 5 x_{1}-4 x_{2}+\frac{1}{2} x_{3} \leqslant 5, \quad x_{i} \geqslant 0, \quad i=1,2,3 . \end{aligned}$$

  (i) After adding slack variables $z_{1}, z_{2}$ and $z_{3}$ and performing one iteration of the simplex algorithm, the following tableau is obtained.

  \begin{tabular}{c|rrrrrr|c} & $x_{1}$ & $x_{2}$ & $x_{3}$ & $z_{1}$ & $z_{2}$ & $z_{3}$ & \ \hline$x_{2}$ & $-1$ & 1 & 2 & $1 / 2$ & 0 & 0 & $5 / 2$ \ $z_{2}$ & 6 & 0 & $-9$ & $-1$ & 1 & 0 & 3 \ $z_{3}$ & 1 & 0 & $17 / 2$ & 2 & 0 & 1 & 15 \ \hline Payoff & $-1$ & 0 & 4 & $3 / 2$ & 0 & 0 & $15 / 2$ \end{tabular}

  Complete the solution of the problem.

  (ii) Now suppose that the problem is amended so that the objective function becomes

  $$2 x_{1}-3 x_{2}-5 x_{3}$$

  Find the solution of this new problem.

  (iii) Formulate the dual of the problem in (ii) and identify the optimal solution to the dual.

  comment

2006

• $2 . \mathrm{I} . 9 \mathrm{C} \quad$

  Optimization | Part IB, 2006

  Consider the maximal flow problem on a finite set $N$, with source $A$, sink $B$ and capacity constraints $c_{i j}$ for $i, j \in N$. Explain what is meant by a cut and by the capacity of a cut.

  Show that the maximal flow value cannot exceed the minimal cut capacity.

  Take $N=\{0,1,2,3,4\}^{2}$ and suppose that, for $i=\left(i_{1}, i_{2}\right)$ and $j=\left(j_{1}, j_{2}\right)$,

  $$c_{i j}=\max \left\{\left|i_{1}-i_{2}\right|,\left|j_{1}-j_{2}\right|\right\} \quad \text { if } \quad\left|i_{1}-j_{1}\right|+\left|i_{2}-j_{2}\right|=1,$$

  and $c_{i j}=0$ otherwise. Thus the node set is a square grid of 25 points, with positive flow capacity only between nearest neighbours, and where the capacity of an edge in the grid equals the larger of the distances of its two endpoints from the diagonal. Find a maximal flow from $(0,3)$ to $(3,0)$. Justify your answer.

  comment

• 1.I.8C

  Optimization | Part IB, 2006

  State the Lagrangian sufficiency theorem.

  Let $p \in(1, \infty)$ and let $a_{1}, \ldots, a_{n} \in \mathbb{R}$. Maximize

  $$\sum_{i=1}^{n} a_{i} x_{i}$$

  subject to

  $$\sum_{i=1}^{n}\left|x_{i}\right|^{p} \leqslant 1, \quad x_{1}, \ldots, x_{n} \in \mathbb{R}$$

  comment

• 3.II.20C

  Optimization | Part IB, 2006

  Explain what is meant by a two-person zero-sum game with payoff matrix $A=\left(a_{i j}: 1 \leqslant i \leqslant m, \quad 1 \leqslant j \leqslant n\right)$ and what is meant by an optimal strategy $p=\left(p_{i}: 1 \leqslant i \leqslant m\right)$.

  Consider the following betting game between two players: each player bets an amount $1,2,3$ or 4 ; if both bets are the same, then the game is void; a bet of 1 beats a bet of 4 but otherwise the larger bet wins; the winning player collects both bets. Write down the payoff matrix $A$ and explain why the optimal strategy $p=\left(p_{1}, p_{2}, p_{3}, p_{4}\right)^{T}$ must satisfy $(A p)_{i} \leqslant 0$ for all $i$. Hence find $p$.

  comment

• 4.II.20C

  Optimization | Part IB, 2006

  Use a suitable version of the simplex algorithm to solve the following linear programming problem:

  $\begin{array}{lrrrrr}\operatorname{maximize} & 50 x_{1} & - & 30 x_{2}+x_{3} & \\ \text { subject to } & x_{1}+ & x_{2}+x_{3} & \leq 30 \\ & 2 x_{1} & - & x_{2} & & \leq 35 \\ & x_{1} & + & 2 x_{2} & -x_{3} & \geq 40 \\ \text { and } & & & x_{1}, x_{2}, x_{3} & \geq 0\end{array}$

  comment

2005

• 1.I.8D

  Optimization | Part IB, 2005

  Consider the problem:

  $$\begin{array}{ll} \text { Minimize } & \sum_{i=1}^{m} \sum_{j=1}^{n} c_{i j} x_{i j} \\ \text { subject to } & \sum_{j=1}^{n} x_{i j}=a_{i}, \quad i=1, \ldots, m, \\ & \sum_{i=1}^{m} x_{i j}=b_{j}, \quad j=1, \ldots, n \\ & x_{i j} \geqslant 0, \quad \text { for all } i, j \end{array}$$

  where $a_{i} \geqslant 0, b_{j} \geqslant 0$ satisfy $\sum_{i=1}^{m} a_{i}=\sum_{j=1}^{n} b_{j}$.

  Formulate the dual of this problem and state necessary and sufficient conditions for optimality.

  comment

• 2.I.9D

  Optimization | Part IB, 2005

  Explain what is meant by a two-person zero-sum game with payoff matrix $A=\left(a_{i j}\right)$.

  Show that the problems of the two players may be expressed as a dual pair of linear programming problems. State without proof a set of sufficient conditions for a pair of strategies for the two players to be optimal.

  comment

• 3.II.20D

  Optimization | Part IB, 2005

  Consider the linear programming problem

  $$\begin{aligned} \operatorname{maximize} \quad 4 x_{1}+x_{2}-9 x_{3} & \\ \text { subject to } \quad x_{2}-11 x_{3} & \leqslant 11 \\ -3 x_{1}+2 x_{2}-7 x_{3} & \leqslant 16 \\ 9 x_{1}-2 x_{2}+10 x_{3} & \leqslant 29, \quad x_{i} \geqslant 0, \quad i=1,2,3 . \end{aligned}$$

  (a) After adding slack variables $z_{1}, z_{2}$ and $z_{3}$ and performing one pivot in the simplex algorithm the following tableau is obtained:

  \begin{tabular}{c|rrrrrr|r} & $x_{1}$ & $x_{2}$ & $x_{3}$ & $z_{1}$ & $z_{2}$ & $z_{3}$ & \ \hline$z_{1}$ & 0 & 1 & $-11$ & 1 & 0 & 0 & 11 \ $z_{2}$ & 0 & $\frac{4}{3}$ & $-\frac{11}{3}$ & 0 & 1 & $\frac{1}{3}$ & $\frac{77}{3}$ \ $x_{1}$ & 1 & $-\frac{2}{9}$ & $\frac{10}{9}$ & 0 & 0 & $\frac{1}{9}$ & $\frac{29}{9}$ \ \hline Payoff & 0 & $\frac{17}{9}$ & $-\frac{121}{9}$ & 0 & 0 & $-\frac{4}{9}$ & $-\frac{116}{9}$ \end{tabular}

  Complete the solution of the problem using the simplex algorithm.

  (b) Obtain the dual problem and identify its optimal solution from the optimal tableau in (a).

  (c) Suppose that the right-hand sides in the constraints to the original problem are changed from $(11,16,29)$ to $\left(11+\epsilon_{1}, 16+\epsilon_{2}, 29+\epsilon_{3}\right)$. Give necessary and sufficient conditions on $\left(\epsilon_{1}, \epsilon_{2}, \epsilon_{3}\right)$ which ensure that the optimal solution to the dual obtained in (b) remains optimal for the dual for the amended problem.

  comment

• 4.II.20D

  Optimization | Part IB, 2005

  Describe the Ford-Fulkerson algorithm for finding a maximal flow from a source to a sink in a directed network with capacity constraints on the arcs. Explain why the algorithm terminates at an optimal flow when the initial flow and the capacity constraints are rational.

  Illustrate the algorithm by applying it to the problem of finding a maximal flow from $S$ to $T$ in the network below.

  

  comment

2004

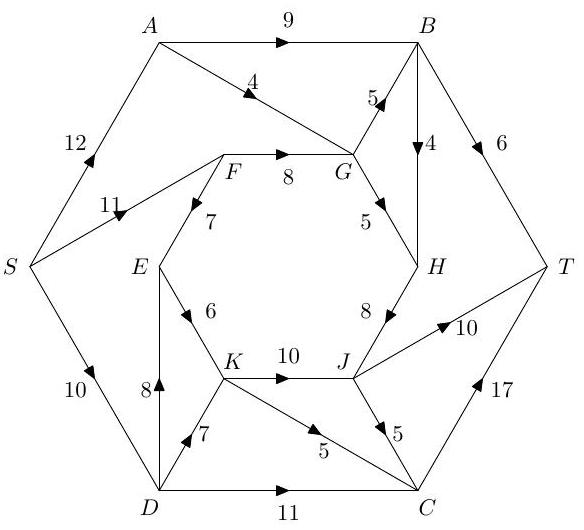
• 3.I.12G

  Optimization | Part IB, 2004

  Consider the two-person zero-sum game Rock, Scissors, Paper. That is, a player gets 1 point by playing Rock when the other player chooses Scissors, or by playing Scissors against Paper, or Paper against Rock; the losing player gets $-1$ point. Zero points are received if both players make the same move.

  Suppose player one chooses Rock and Scissors (but never Paper) with probabilities $p$ and $1-p, 0 \leqslant p \leqslant 1$. Write down the maximization problem for player two's optimal strategy. Determine the optimal strategy for each value of $p$.

  comment

• 3.II.23G

  Optimization | Part IB, 2004

  Consider the following linear programming problem:

  $$\begin{aligned} \text { maximize }-x_{1}+3 x_{2} \\ \text { subject to } \quad x_{1}+x_{2} & \geqslant 3 \\ -x_{1}+2 x_{2} & \geqslant 6 \\ -x_{1}+x_{2} & \leqslant 2, \\ x_{2} & \leqslant 5, \\ x_{i} & \geqslant 0, \quad i=1,2 . \end{aligned}$$

  Write down the Phase One problem in this case, and solve it.

  By using the solution of the Phase One problem as an initial basic feasible solution for the Phase Two simplex algorithm, solve the above maximization problem. That is, find the optimal tableau and read the optimal solution $\left(x_{1}, x_{2}\right)$ and optimal value from it.

  comment

• 4.I.10G

  Optimization | Part IB, 2004

  State and prove the max flow/min cut theorem. In your answer you should define clearly the following terms: flow; maximal flow; cut; capacity.

  comment

• 4.II.20G

  Optimization | Part IB, 2004

  For any number $c \in(0,1)$, find the minimum and maximum values of

  $$\sum_{i=1}^{n} x_{i}^{c}$$

  subject to $\sum_{i=1}^{n} x_{i}=1, x_{1}, \ldots, x_{n} \geqslant 0$. Find all the points $\left(x_{1}, \ldots, x_{n}\right)$ at which the minimum and maximum are attained. Justify your answer.

  comment

2003

• $3 . \mathrm{I} . 5 \mathrm{H} \quad$

  Optimization | Part IB, 2003

  Two players A and B play a zero-sum game with the pay-off matrix

  \begin{tabular}{r|rrr} & $B_{1}$ & $B_{2}$ & $B_{3}$ \ \hline$A_{1}$ & 4 & $-2$ & $-5$ \ $A_{2}$ & $-2$ & 4 & 3 \ $A_{3}$ & $-3$ & 6 & 2 \ $A_{4}$ & 3 & $-8$ & $-6$ \end{tabular}

  Here, the $(i, j)$ entry of the matrix indicates the pay-off to player A if he chooses move $A_{i}$ and player $\mathrm{B}$ chooses move $B_{j}$. Show that the game can be reduced to a zero-sum game with $2 \times 2$ pay-off matrix.

  Determine the value of the game and the optimal strategy for player A.

  comment

• 3.II.15H

  Optimization | Part IB, 2003

  Explain what is meant by a transportation problem where the total demand equals the total supply. Write the Lagrangian and describe an algorithm for solving such a problem. Starting from the north-west initial assignment, solve the problem with three sources and three destinations described by the table

  \begin{tabular}{|rrr|r|} \hline 5 & 9 & 1 & 36 \ 3 & 10 & 6 & 84 \ 7 & 2 & 5 & 40 \ \hline 14 & 68 & 78 & \ \hline \end{tabular}

  where the figures in the $3 \times 3$ box denote the transportation costs (per unit), the right-hand column denotes supplies, and the bottom row demands.

  comment

• 4.I.5H

  Optimization | Part IB, 2003

  State and prove the Lagrangian sufficiency theorem for a general optimization problem with constraints.

  comment

• 4.II.14H

  Optimization | Part IB, 2003

  Use the two-phase simplex method to solve the problem

  $$\begin{array}{llllll} \operatorname{minimize} & 5 x_{1}-12 x_{2}+13 x_{3} & & \\ \text { subject to } & 4 x_{1}+5 x_{2} & & \leq & 9 \\ & 6 x_{1}+4 x_{2}+ & x_{3} & \geq & 12 \\ & 3 x_{1}+2 x_{2}-x_{3} & \leq & 3 \\ & x_{i} \geq 0, & i=1,2,3 \end{array}$$

  comment

2002

• $3 . \mathrm{I} . 5 \mathrm{H} \quad$

  Optimization | Part IB, 2002

  Consider a two-person zero-sum game with a payoff matrix

  $$\left(\begin{array}{ll} 3 & b \\ 5 & 2 \end{array}\right)$$

  where $0<b<\infty$. Here, the $(i, j)$ entry of the matrix indicates the payoff to player one if he chooses move $i$ and player two move $j$. Suppose player one chooses moves 1 and 2 with probabilities $p$ and $1-p, 0 \leq p \leq 1$. Write down the maximization problem for the optimal strategy and solve it for each value of $b$.

  comment

• 3.II.15H

  Optimization | Part IB, 2002

  Consider the following linear programming problem

  $$\begin{array}{ll} \text { maximise } & -2 x_{1}+3 x_{2} \\ \text { subject to } & x_{1}-x_{2} \geq 1 \\ & 4 x_{1}-x_{2} \geq 10 \\ & x_{2} \leq 6 \\ & x_{i} \geq 0, i=1,2 \end{array}$$

  Write down the Phase One problem for (1) and solve it.

  By using the solution of the Phase One problem as an initial basic feasible solution for the Phase Two simplex algorithm, solve (1), i.e., find the optimal tableau and read the optimal solution $\left(x_{1}, x_{2}\right)$ and optimal value from it.

  comment

• 4.I.5H

  Optimization | Part IB, 2002

  State and prove the max flow/min cut theorem. In your answer you should define clearly the following terms: flow, maximal flow, cut, capacity.

  comment

• 4.II.14H

  Optimization | Part IB, 2002

  A gambler at a horse race has an amount $b>0$ to bet. The gambler assesses $p_{i}$, the probability that horse $i$ will win, and knows that $s_{i} \geq 0$ has been bet on horse $i$ by others, for $i=1,2, \ldots, n$. The total amount bet on the race is shared out in proportion to the bets on the winning horse, and so the gambler's optimal strategy is to choose $\left(x_{1}, x_{2}, \ldots, x_{n}\right)$ so that it maximizes

  $$\sum_{i=1}^{n} \frac{p_{i} x_{i}}{s_{i}+x_{i}} \quad \text { subject to } \sum_{i=1}^{n} x_{i}=b, \quad x_{1}, \ldots, x_{n} \geq 0$$

  where $x_{i}$ is the amount the gambler bets on horse $i$. Show that the optimal solution to (1) also solves the following problem:

  $$\text { minimize } \sum_{i=1}^{n} \frac{p_{i} s_{i}}{s_{i}+x_{i}} \quad \text { subject to } \sum_{i=1}^{n} x_{i}=b, \quad x_{1}, \ldots, x_{n} \geq 0$$

  Assume that $p_{1} / s_{1} \geq p_{2} / s_{2} \geq \ldots \geq p_{n} / s_{n}$. Applying the Lagrangian sufficiency theorem, prove that the optimal solution to (1) satisfies

  $$\frac{p_{1} s_{1}}{\left(s_{1}+x_{1}\right)^{2}}=\ldots=\frac{p_{k} s_{k}}{\left(s_{k}+x_{k}\right)^{2}}, \quad x_{k+1}=\ldots=x_{n}=0$$

  with maximal possible $k \in\{1,2, \ldots, n\}$.

  [You may use the fact that for all $\lambda<0$, the minimum of the function $x \mapsto \frac{p s}{s+x}-\lambda x$ on the non-negative axis $0 \leq x<\infty$ is attained at

  $$\left.x(\lambda)=\left(\sqrt{\frac{p s}{-\lambda}}-s\right)^{+} \equiv \max \left(\sqrt{\frac{p s}{-\lambda}}-s, 0\right) .\right]$$

  Deduce that if $b$ is small enough, the gambler's optimal strategy is to bet on the horses for which the ratio $p_{i} / s_{i}$ is maximal. What is his expected gain in this case?

  comment

2001

• $3 . \mathrm{I} . 5 \mathrm{D} \quad$

  Optimization | Part IB, 2001

  Let $a_{1}, \ldots, a_{n}$ be given constants, not all equal.

  Use the Lagrangian sufficiency theorem, which you should state clearly, without proof, to minimize $\sum_{i=1}^{n} x_{i}^{2}$ subject to the two constraints $\sum_{i=1}^{n} x_{i}=1, \sum_{i=1}^{n} a_{i} x_{i}=0 .$

  comment

• 3.II.15D

  Optimization | Part IB, 2001

  Consider the following linear programming problem,

  $$\begin{array}{lrl} \operatorname{minimize} \quad(3-p) x_{1}+p x_{2} & \\ \text { subject to } & 2 x_{1}+x_{2} & \geqslant 8 \\ x_{1}+3 x_{2} & \geqslant 9 \\ x_{1} & \leqslant 6 \\ x_{1}, x_{2} & \geqslant 0 \end{array}$$

  Formulate the problem in a suitable way for solution by the two-phase simplex method.

  Using the two-phase simplex method, show that if $2 \leqslant p \leqslant \frac{9}{4}$ then the optimal solution has objective function value $9-p$, while if $\frac{9}{4}<p \leqslant 3$ the optimal objective function value is $18-5 p$.

  comment

• 4.I.5D

  Optimization | Part IB, 2001

  Explain what is meant by a two-person zero-sum game with payoff matrix $A=\left[a_{i j}\right]$. Write down a set of sufficient conditions for a pair of strategies to be optimal for such a game.

  A fair coin is tossed and the result is shown to player I, who must then decide to 'pass' or 'bet'. If he passes, he must pay player II $£ 1$. If he bets, player II, who does not know the result of the coin toss, may either 'fold' or 'call the bet'. If player II folds, she pays player I $£ 1$. If she calls the bet and the toss was a head, she pays player I $£ 2$; if she calls the bet and the toss was a tail, player I must pay her $£ 2$.

  Formulate this as a two-person zero-sum game and find optimal strategies for the two players. Show that the game has value $\frac{1}{3}$.

  [Hint: Player I has four possible moves and player II two.]

  comment

• 4.II.14D

  Optimization | Part IB, 2001

  Dumbledore Publishers must decide how many copies of the best-selling "History of Hogwarts" to print in the next two months to meet demand. It is known that the demands will be for 40 thousand and 60 thousand copies in the first and second months respectively, and these demands must be met on time. At the beginning of the first month, a supply of 10 thousand copies is available, from existing stock. During each month, Dumbledore can produce up to 40 thousand copies, at a cost of 400 galleons per thousand copies. By having employees work overtime, up to 150 thousand additional copies can be printed each month, at a cost of 450 galleons per thousand copies. At the end of each month, after production and the current month's demand has been satisfied, a holding cost of 20 galleons per thousand copies is incurred.

  Formulate a transportation problem, with 5 supply points and 3 demand points, to minimize the sum of production and holding costs during the two month period, and solve it.

  [You may assume that copies produced during a month can be used to meet demand in that month.]

  comment