Part II, 2020

Algebraic Geometry

• Paper 1, Section II, F

  Algebraic Geometry | Part II, 2020

  Let $k$ be an algebraically closed field of characteristic zero. Prove that an affine variety $V \subset \mathbb{A}_{k}^{n}$ is irreducible if and only if the associated ideal $I(V)$ of polynomials that vanish on $V$ is prime.

  Prove that the variety $\mathbb{V}\left(y^{2}-x^{3}\right) \subset \mathbb{A}_{k}^{2}$ is irreducible.

  State what it means for an affine variety over $k$ to be smooth and determine whether or not $\mathbb{V}\left(y^{2}-x^{3}\right)$ is smooth.

  comment

• Paper 2, Section II, F

  Algebraic Geometry | Part II, 2020

  Let $k$ be an algebraically closed field of characteristic not equal to 2 and let $V \subset \mathbb{P}_{k}^{3}$ be a nonsingular quadric surface.

  (a) Prove that $V$ is birational to $\mathbb{P}_{k}^{2}$.

  (b) Prove that there exists a pair of disjoint lines on $V$.

  (c) Prove that the affine variety $W=\mathbb{V}(x y z-1) \subset \mathbb{A}_{k}^{3}$ does not contain any lines.

  comment

• Paper 3, Section II, F

  Algebraic Geometry | Part II, 2020

  (i) Suppose $f(x, y)=0$ is an affine equation whose projective completion is a smooth projective curve. Give a basis for the vector space of holomorphic differential forms on this curve. [You are not required to prove your assertion.]

  Let $C \subset \mathbb{P}^{2}$ be the plane curve given by the vanishing of the polynomial

  $$X_{0}^{4}-X_{1}^{4}-X_{2}^{4}=0$$

  over the complex numbers.

  (ii) Prove that $C$ is nonsingular.

  (iii) Let $\ell$ be a line in $\mathbb{P}^{2}$ and define $D$ to be the divisor $\ell \cap C$. Prove that $D$ is a canonical divisor on $C$.

  (iv) Calculate the minimum degree $d$ such that there exists a non-constant map

  $$C \rightarrow \mathbb{P}^{1}$$

  of degree $d$.

  [You may use any results from the lectures provided that they are stated clearly.]

  comment

• Paper 4, Section II, F

  Algebraic Geometry | Part II, 2020

  Let $P_{0}, \ldots, P_{n}$ be a basis for the homogeneous polynomials of degree $n$ in variables $Z_{0}$ and $Z_{1}$. Then the image of the $\operatorname{map} \mathbb{P}^{1} \rightarrow \mathbb{P}^{n}$ given by

  $$\left[Z_{0}, Z_{1}\right] \mapsto\left[P_{0}\left(Z_{0}, Z_{1}\right), \ldots, P_{n}\left(Z_{0}, Z_{1}\right)\right]$$

  is called a rational normal curve.

  Let $p_{1}, \ldots, p_{n+3}$ be a collection of points in general linear position in $\mathbb{P}^{n}$. Prove that there exists a unique rational normal curve in $\mathbb{P}^{n}$ passing through these points.

  Choose a basis of homogeneous polynomials of degree 3 as above, and give generators for the homogeneous ideal of the corresponding rational normal curve.

  comment

Algebraic Topology

• Paper 1, Section II, $21 \mathbf{F}$

  Algebraic Topology | Part II, 2020

  Let $p: \mathbb{R}^{2} \rightarrow S^{1} \times S^{1}=: X$ be the map given by

  $$p\left(r_{1}, r_{2}\right)=\left(e^{2 \pi i r_{1}}, e^{2 \pi i r_{2}}\right)$$

  where $S^{1}$ is identified with the unit circle in $\mathbb{C}$. [You may take as given that $p$ is a covering map.]

  (a) Using the covering map $p$, show that $\pi_{1}\left(X, x_{0}\right)$ is isomorphic to $\mathbb{Z}^{2}$ as a group, where $x_{0}=(1,1) \in X$.

  (b) Let $\mathrm{GL}_{2}(\mathbb{Z})$ denote the group of $2 \times 2$ matrices $A$ with integer entries such that $\operatorname{det} A=\pm 1$. If $A \in \mathrm{GL}_{2}(\mathbb{Z})$, we obtain a linear transformation $A: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$. Show that this linear transformation induces a homeomorphism $f_{A}: X \rightarrow X$ with $f_{A}\left(x_{0}\right)=x_{0}$ and such that $f_{A *}: \pi_{1}\left(X, x_{0}\right) \rightarrow \pi_{1}\left(X, x_{0}\right)$ agrees with $A$ as a map $\mathbb{Z}^{2} \rightarrow \mathbb{Z}^{2}$.

  (c) Let $p_{i}: \widehat{X}_{i} \rightarrow X$ for $i=1,2$ be connected covering maps of degree 2 . Show that there exist homeomorphisms $\phi: \widehat{X}_{1} \rightarrow \widehat{X}_{2}$ and $\psi: X \rightarrow X$ so that the diagram

  

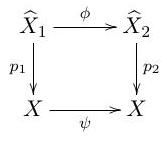
  is commutative.

  comment

• Paper 2, Section II, F

  Algebraic Topology | Part II, 2020

  (a) Let $f: X \rightarrow Y$ be a map of spaces. We define the mapping cylinder $M_{f}$ of $f$ to be the space

  $$(([0,1] \times X) \sqcup Y) / \sim$$

  with $(0, x) \sim f(x)$. Show carefully that the canonical inclusion $Y \hookrightarrow M_{f}$ is a homotopy equivalence.

  (b) Using the Seifert-van Kampen theorem, show that if $X$ is path-connected and $\alpha: S^{1} \rightarrow X$ is a map, and $x_{0}=\alpha\left(\theta_{0}\right)$ for some point $\theta_{0} \in S^{1}$, then

  $$\pi_{1}\left(X \cup_{\alpha} D^{2}, x_{0}\right) \cong \pi_{1}\left(X, x_{0}\right) /\langle\langle[\alpha]\rangle\rangle$$

  Use this fact to construct a connected space $X$ with

  $$\pi_{1}(X) \cong\left\langle a, b \mid a^{3}=b^{7}\right\rangle$$

  (c) Using a covering space of $S^{1} \vee S^{1}$, give explicit generators of a subgroup of $F_{2}$ isomorphic to $F_{3}$. Here $F_{n}$ denotes the free group on $n$ generators.

  comment

• Paper 3, Section II, 20F

  Algebraic Topology | Part II, 2020

  Let $K$ be a simplicial complex with four vertices $v_{1}, \ldots, v_{4}$ with simplices $\left\langle v_{1}, v_{2}, v_{3}\right\rangle$, $\left\langle v_{1}, v_{4}\right\rangle$ and $\left\langle v_{2}, v_{4}\right\rangle$ and their faces.

  (a) Draw a picture of $|K|$, labelling the vertices.

  (b) Using the definition of homology, calculate $H_{n}(K)$ for all $n$.

  (c) Let $L$ be the subcomplex of $K$ consisting of the vertices $v_{1}, v_{2}, v_{4}$ and the 1 simplices $\left\langle v_{1}, v_{2}\right\rangle,\left\langle v_{1}, v_{4}\right\rangle,\left\langle v_{2}, v_{4}\right\rangle$. Let $i: L \rightarrow K$ be the inclusion. Construct a simplicial $\operatorname{map} j: K \rightarrow L$ such that the topological realisation $|j|$ of $j$ is a homotopy inverse to $|i|$. Construct an explicit chain homotopy $h: C_{\bullet}(K) \rightarrow C_{\bullet}(K)$ between $i_{\bullet} \circ j_{\bullet}$ and $\mathrm{id}_{C_{\bullet}(K)}$, and verify that $h$ is a chain homotopy.

  comment

• Paper 4 , Section II, 21F

  Algebraic Topology | Part II, 2020

  In this question, you may assume all spaces involved are triangulable.

  (a) (i) State and prove the Mayer-Vietoris theorem. [You may assume the theorem that states that a short exact sequence of chain complexes gives rise to a long exact sequence of homology groups.]

  (ii) Use Mayer-Vietoris to calculate the homology groups of an oriented surface of genus $g$.

  (b) Let $S$ be an oriented surface of genus $g$, and let $D_{1}, \ldots, D_{n}$ be a collection of mutually disjoint closed subsets of $S$ with each $D_{i}$ homeomorphic to a two-dimensional disk. Let $D_{i}^{\circ}$ denote the interior of $D_{i}$, homeomorphic to an open two-dimensional disk, and let

  $$T:=S \backslash\left(D_{1}^{\circ} \cup \cdots \cup D_{n}^{\circ}\right)$$

  Show that

  $$H_{i}(T)= \begin{cases}\mathbb{Z} & i=0 \\ \mathbb{Z}^{2 g+n-1} & i=1 \\ 0 & \text { otherwise }\end{cases}$$

  (c) Let $T$ be the surface given in (b) when $S=S^{2}$ and $n=3$. Let $f: T \rightarrow S^{1} \times S^{1}$ be a map. Does there exist a map $g: S^{1} \times S^{1} \rightarrow T$ such that $f \circ g$ is homotopic to the identity map? Justify your answer.

  comment

Analysis of Functions

• Paper 1, Section II, I

  Analysis of Functions | Part II, 2020

  Let $\mathbb{R}^{n}$ be equipped with the $\sigma$-algebra of Lebesgue measurable sets, and Lebesgue measure.

  (a) Given $f \in L^{\infty}\left(\mathbb{R}^{n}\right), g \in L^{1}\left(\mathbb{R}^{n}\right)$, define the convolution $f \star g$, and show that it is a bounded, continuous function. [You may use without proof continuity of translation on $L^{p}\left(\mathbb{R}^{n}\right)$ for $\left.1 \leqslant p<\infty .\right]$

  Suppose $A \subset \mathbb{R}^{n}$ is a measurable set with $0<|A|<\infty$ where $|A|$ denotes the Lebesgue measure of $A$. By considering the convolution of $f(x)=\mathbb{1}_{A}(x)$ and $g(x)=\mathbb{1}_{A}(-x)$, or otherwise, show that the set $A-A=\{x-y: x, y \in A\}$ contains an open neighbourhood of 0 . Does this still hold if $|A|=\infty$ ?

  (b) Suppose that $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ is a measurable function satisfying

  $$f(x+y)=f(x)+f(y), \quad \text { for all } x, y \in \mathbb{R}^{n}$$

  Let $B_{r}=\left\{y \in \mathbb{R}^{m}:|y|<r\right\}$. Show that for any $\epsilon>0$ :

  (i) $f^{-1}\left(B_{\epsilon}\right)-f^{-1}\left(B_{\epsilon}\right) \subset f^{-1}\left(B_{2 \epsilon}\right)$,

  (ii) $f^{-1}\left(B_{k \epsilon}\right)=k f^{-1}\left(B_{\epsilon}\right)$ for all $k \in \mathbb{N}$, where for $\lambda>0$ and $A \subset \mathbb{R}^{n}, \lambda A$ denotes the set $\{\lambda x: x \in A\}$.

  Show that $f$ is continuous at 0 and hence deduce that $f$ is continuous everywhere.

  comment

• Paper 3, Section II, 22I

  Analysis of Functions | Part II, 2020

  Let $X$ be a Banach space.

  (a) Define the dual space $X^{\prime}$, giving an expression for $\|\Lambda\|_{X^{\prime}}$ for $\Lambda \in X^{\prime}$. If $Y=L^{p}\left(\mathbb{R}^{n}\right)$ for some $1 \leqslant p<\infty$, identify $Y^{\prime}$ giving an expression for a general element of $Y^{\prime}$. [You need not prove your assertion.]

  (b) For a sequence $\left(\Lambda_{i}\right)_{i=1}^{\infty}$ with $\Lambda_{i} \in X^{\prime}$, what is meant by: (i) $\Lambda_{i} \rightarrow \Lambda$, (ii) $\Lambda_{i} \rightarrow \Lambda$ (iii) $\Lambda_{i} \stackrel{*}{\rightarrow} \Lambda$ ? Show that (i) $\Longrightarrow$ (ii) $\Longrightarrow$ (iii). Find a sequence $\left(f_{i}\right)_{i=1}^{\infty}$ with $f_{i} \in$ $L^{\infty}(\mathbb{R})=\left(L^{1}(\mathbb{R})\right)^{\prime}$ such that, for some $f, g \in L^{\infty}\left(\mathbb{R}^{n}\right)$ :

  $$f_{i} \stackrel{*}{\rightarrow} f, \quad f_{i}^{2} \stackrel{*}{\rightarrow} g, \quad g \neq f^{2} .$$

  (c) For $f \in C_{c}^{0}\left(\mathbb{R}^{n}\right)$, let $\Lambda: C_{c}^{0}\left(\mathbb{R}^{n}\right) \rightarrow \mathbb{C}$ be the map $\Lambda f=f(0)$. Show that $\Lambda$ may be extended to a continuous linear map $\tilde{\Lambda}: L^{\infty}\left(\mathbb{R}^{n}\right) \rightarrow \mathbb{C}$, and deduce that $\left(L^{\infty}\left(\mathbb{R}^{n}\right)\right)^{\prime} \neq L^{1}\left(\mathbb{R}^{n}\right)$. For which $1 \leqslant p \leqslant \infty$ is $L^{p}\left(\mathbb{R}^{n}\right)$ reflexive? [You may use without proof the Hahn-Banach theorem].

  comment

• Paper 4, Section II, 23I

  Analysis of Functions | Part II, 2020

  (a) Define the Sobolev space $H^{s}\left(\mathbb{R}^{n}\right)$ for $s \in \mathbb{R}$.

  (b) Let $k$ be a non-negative integer and let $s>k+\frac{n}{2}$. Show that if $u \in H^{s}\left(\mathbb{R}^{n}\right)$ then there exists $u^{*} \in C^{k}\left(\mathbb{R}^{n}\right)$ with $u=u^{*}$ almost everywhere.

  (c) Show that if $f \in H^{s}\left(\mathbb{R}^{n}\right)$ for some $s \in \mathbb{R}$, there exists a unique $u \in H^{s+4}\left(\mathbb{R}^{n}\right)$ which solves:

  $$\Delta \Delta u+\Delta u+u=f$$

  in a distributional sense. Prove that there exists a constant $C>0$, independent of $f$, such that:

  $$\|u\|_{H^{s+4}} \leqslant C\|f\|_{H^{s}}$$

  For which $s$ will $u$ be a classical solution?

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, C

  Applications of Quantum Mechanics | Part II, 2020

  Consider the quantum mechanical scattering of a particle of mass $m$ in one dimension off a parity-symmetric potential, $V(x)=V(-x)$. State the constraints imposed by parity, unitarity and their combination on the components of the $S$-matrix in the parity basis,

  $$S=\left(\begin{array}{cc} S_{++} & S_{+-} \\ S_{-+} & S_{--} \end{array}\right)$$

  For the specific potential

  $$V=\hbar^{2} \frac{U_{0}}{2 m}\left[\delta_{D}(x+a)+\delta_{D}(x-a)\right]$$

  show that

  $$S_{--}=e^{-i 2 k a}\left[\frac{\left(2 k-i U_{0}\right) e^{i k a}+i U_{0} e^{-i k a}}{\left(2 k+i U_{0}\right) e^{-i k a}-i U_{0} e^{i k a}}\right]$$

  For $U_{0}<0$, derive the condition for the existence of an odd-parity bound state. For $U_{0}>0$ and to leading order in $U_{0} a \gg 1$, show that an odd-parity resonance exists and discuss how it evolves in time.

  comment

• Paper 2, Section II, $35 \mathrm{C}$

  Applications of Quantum Mechanics | Part II, 2020

  a) Consider a particle moving in one dimension subject to a periodic potential, $V(x)=V(x+a)$. Define the Brillouin zone. State and prove Bloch's theorem.

  b) Consider now the following periodic potential

  $$V=V_{0}(\cos (x)-\cos (2 x))$$

  with positive constant $V_{0}$.

  i) For very small $V_{0}$, use the nearly-free electron model to compute explicitly the lowest-energy band gap to leading order in degenerate perturbation theory.

  ii) For very large $V_{0}$, the electron is localised very close to a minimum of the potential. Estimate the two lowest energies for such localised eigenstates and use the tight-binding model to estimate the lowest-energy band gap.

  comment

• Paper 3, Section II, C

  Applications of Quantum Mechanics | Part II, 2020

  (a) For the quantum scattering of a beam of particles in three dimensions off a spherically symmetric potential $V(r)$ that vanishes at large $r$, discuss the boundary conditions satisfied by the wavefunction $\psi$ and define the scattering amplitude $f(\theta)$. Assuming the asymptotic form

  $$\psi=\sum_{l=0}^{\infty} \frac{2 l+1}{2 i k}\left[(-1)^{l+1} \frac{e^{-i k r}}{r}+\left(1+2 i f_{l}\right) \frac{e^{i k r}}{r}\right] P_{l}(\cos \theta),$$

  state the constraints on $f_{l}$ imposed by the unitarity of the $S$-matrix and define the phase shifts $\delta_{l}$.

  (b) For $V_{0}>0$, consider the specific potential

  $$V(r)=\left\{\begin{array}{lc} \infty, & r \leqslant a \\ -V_{0}, & a<r \leqslant 2 a \\ 0, & r>2 a \end{array}\right.$$

  (i) Show that the s-wave phase shift $\delta_{0}$ obeys

  $$\tan \left(\delta_{0}\right)=\frac{k \cos (2 k a)-\kappa \cot (\kappa a) \sin (2 k a)}{k \sin (2 k a)+\kappa \cot (\kappa a) \cos (2 k a)},$$

  where $\kappa^{2}=k^{2}+2 m V_{0} / \hbar^{2}$.

  (ii) Compute the scattering length $a_{s}$ and find for which values of $\kappa$ it diverges. Discuss briefly the physical interpretation of the divergences. [Hint: you may find this trigonometric identity useful

  $$\left.\tan (A+B)=\frac{\tan A+\tan B}{1-\tan A \tan B} .\right]$$

  comment

• Paper 4, Section II, $34 C$

  Applications of Quantum Mechanics | Part II, 2020

  (a) For a particle of charge $q$ moving in an electromagnetic field with vector potential $\boldsymbol{A}$ and scalar potential $\phi$, write down the classical Hamiltonian and the equations of motion.

  (b) Consider the vector and scalar potentials

  $$\boldsymbol{A}=\frac{B}{2}(-y, x, 0), \quad \phi=0$$

  (i) Solve the equations of motion. Define and compute the cyclotron frequency $\omega_{B}$.

  (ii) Write down the quantum Hamiltonian of the system in terms of the angular momentum operator

  $$L_{z}=x p_{y}-y p_{x}$$

  Show that the states

  $$\psi(x, y)=f(x+i y) e^{-\left(x^{2}+y^{2}\right) q B / 4 \hbar}$$

  for any function $f$, are energy eigenstates and compute their energy. Define Landau levels and discuss this result in relation to them.

  (iii) Show that for $f(w)=w^{M}$, the wavefunctions in ( $\dagger$ ) are eigenstates of angular momentum and compute the corresponding eigenvalue. These wavefunctions peak in a ring around the origin. Estimate its radius. Using these two facts or otherwise, estimate the degeneracy of Landau levels.

  comment

Applied Probability

• Paper 1, Section II, 28K

  Applied Probability | Part II, 2020

  (a) What is meant by a birth process $N=(N(t): t \geqslant 0)$ with strictly positive rates $\lambda_{0}, \lambda_{1}, \ldots ?$ Explain what is meant by saying that $N$ is non-explosive.

  (b) Show that $N$ is non-explosive if and only if

  $$\sum_{n=0}^{\infty} \frac{1}{\lambda_{n}}=\infty$$

  (c) Suppose $N(0)=0$, and $\lambda_{n}=\alpha n+\beta$ where $\alpha, \beta>0$. Show that

  $$\mathbb{E}(N(t))=\frac{\beta}{\alpha}\left(e^{\alpha t}-1\right) .$$

  comment

• Paper 2, Section II, 27K

  Applied Probability | Part II, 2020

  (i) Let $X$ be a Markov chain in continuous time on the integers $\mathbb{Z}$ with generator $\mathbf{G}=\left(g_{i, j}\right)$. Define the corresponding jump chain $Y$.

  Define the terms irreducibility and recurrence for $X$. If $X$ is irreducible, show that $X$ is recurrent if and only if $Y$ is recurrent.

  (ii) Suppose

  $$g_{i, i-1}=3^{|i|}, \quad g_{i, i}=-3^{|i|+1}, \quad g_{i, i+1}=2 \cdot 3^{|i|}, \quad i \in \mathbb{Z} .$$

  Show that $X$ is transient, find an invariant distribution, and show that $X$ is explosive. [Any general results may be used without proof but should be stated clearly.]

  comment

• Paper 3, Section II, 27K

  Applied Probability | Part II, 2020

  Define a renewal-reward process, and state the renewal-reward theorem.

  A machine $M$ is repaired at time $t=0$. After any repair, it functions without intervention for a time that is exponentially distributed with parameter $\lambda$, at which point it breaks down (assume the usual independence). Following any repair at time $T$, say, it is inspected at times $T, T+m, T+2 m, \ldots$, and instantly repaired if found to be broken (the inspection schedule is then restarted). Find the long run proportion of time that $M$ is working. [You may express your answer in terms of an integral.]

  comment

• Paper 4, Section II, K

  Applied Probability | Part II, 2020

  (i) Explain the notation $\mathrm{M}(\lambda) / \mathrm{M}(\mu) / 1$ in the context of queueing theory. [In the following, you may use without proof the fact that $\pi_{n}=(\lambda / \mu)^{n}$ is the invariant distribution of such a queue when $0<\lambda<\mu$.

  (ii) In a shop queue, some customers rejoin the queue after having been served. Let $\lambda, \beta \in(0, \infty)$ and $\delta \in(0,1)$. Consider a $\mathrm{M}(\lambda) / \mathrm{M}(\mu) / 1$ queue subject to the modification that, on completion of service, each customer leaves the shop with probability $\delta$, or rejoins the shop queue with probability $1-\delta$. Different customers behave independently of one another, and all service times are independent random variables.

  Find the distribution of the total time a given customer spends being served by the server. Hence show that equilibrium is possible if $\lambda<\delta \mu$, and find the invariant distribution of the queue-length in this case.

  (iii) Show that, in equilibrium, the departure process is Poissonian, whereas, assuming the rejoining customers go to the end of the queue, the process of customers arriving at the queue (including the rejoining ones) is not Poissonian.

  comment

Asymptotic Methods

• Paper 2, Section II, D

  Asymptotic Methods | Part II, 2020

  (a) Let $\delta>0$ and $x_{0} \in \mathbb{R}$. Let $\left\{\phi_{n}(x)\right\}_{n=0}^{\infty}$ be a sequence of (real) functions that are nonzero for all $x$ with $0<\left|x-x_{0}\right|<\delta$, and let $\left\{a_{n}\right\}_{n=0}^{\infty}$ be a sequence of nonzero real numbers. For every $N=0,1,2, \ldots$, the function $f(x)$ satisfies

  $$f(x)-\sum_{n=0}^{N} a_{n} \phi_{n}(x)=o\left(\phi_{N}(x)\right), \quad \text { as } \quad x \rightarrow x_{0}$$

  (i) Show that $\phi_{n+1}(x)=o\left(\phi_{n}(x)\right)$, for all $n=0,1,2, \ldots$; i.e., $\left\{\phi_{n}(x)\right\}_{n=0}^{\infty}$ is an asymptotic sequence.

  (ii) Show that for any $N=0,1,2, \ldots$, the functions $\phi_{0}(x), \phi_{1}(x), \ldots, \phi_{N}(x)$ are linearly independent on their domain of definition.

  (b) Let

  $$I(\varepsilon)=\int_{0}^{\infty}(1+\varepsilon t)^{-2} e^{-(1+\varepsilon) t} d t, \quad \text { for } \varepsilon>0$$

  (i) Find an asymptotic expansion (not necessarily a power series) of $I(\varepsilon)$, as $\varepsilon \rightarrow 0^{+}$.

  (ii) Find the first four terms of the expansion of $I(\varepsilon)$ into an asymptotic power series of $\varepsilon$, that is, with error $o\left(\varepsilon^{3}\right)$ as $\varepsilon \rightarrow 0^{+}$.

  comment

• Paper 3, Section II, D

  Asymptotic Methods | Part II, 2020

  (a) Find the leading order term of the asymptotic expansion, as $x \rightarrow \infty$, of the integral

  $$I(x)=\int_{0}^{3 \pi} e^{(t+x \cos t)} d t$$

  (b) Find the first two leading nonzero terms of the asymptotic expansion, as $x \rightarrow \infty$, of the integral

  $$J(x)=\int_{0}^{\pi}(1-\cos t) e^{-x \ln (1+t)} d t$$

  comment

• Paper 4, Section II, A

  Asymptotic Methods | Part II, 2020

  Consider the differential equation

  $$\tag{†} y^{\prime \prime}-y^{\prime}-\frac{2(x+1)}{x^{2}} y=0$$

  (i) Classify what type of regularity/singularity equation $(†)$ has at $x=\infty$.

  (ii) Find a transformation that maps equation ($†$) to an equation of the form

  $$u^{\prime \prime}+q(x) u=0$$

  (iii) Find the leading-order term of the asymptotic expansions of the solutions of equation $(*)$, as $x \rightarrow \infty$, using the Liouville-Green method.

  (iv) Derive the leading-order term of the asymptotic expansion of the solutions $y$ of ($†$). Check that one of them is an exact solution for $(†)$.

  comment

Automata and Formal Languages

• Paper 1, Section I, $4 \mathbf{F}$

  Automata and Formal Languages | Part II, 2020

  Define an alphabet $\Sigma$, a word over $\Sigma$ and a language over $\Sigma$.

  What is a regular expression $R$ and how does this give rise to a language $\mathcal{L}(R) ?$

  Given any alphabet $\Sigma$, show that there exist languages $L$ over $\Sigma$ which are not equal to $\mathcal{L}(R)$ for any regular expression $R$. [You are not required to exhibit a specific $L$.]

  comment

• Paper 1, Section II, F

  Automata and Formal Languages | Part II, 2020

  (a) Define a register machine, a sequence of instructions for a register machine and a partial computable function. How do we encode a register machine?

  (b) What is a partial recursive function? Show that a partial computable function is partial recursive. [You may assume that for a given machine with a given number of inputs, the function outputting its state in terms of the inputs and the time $t$ is recursive.]

  (c) (i) Let $g: \mathbb{N} \rightarrow \mathbb{N}$ be the partial function defined as follows: if $n$ codes a register machine and the ensuing partial function $f_{n, 1}$ is defined at $n$, set $g(n)=f_{n, 1}(n)+1$. Otherwise set $g(n)=0$. Is $g$ a partial computable function?

  (ii) Let $h: \mathbb{N} \rightarrow \mathbb{N}$ be the partial function defined as follows: if $n$ codes a register machine and the ensuing partial function $f_{n, 1}$ is defined at $n$, set $h(n)=f_{n, 1}(n)+1$. Otherwise, set $h(n)=0$ if $n$ is odd and let $h(n)$ be undefined if $n$ is even. Is $h$ a partial computable function?

  comment

• Paper 2, Section I, F

  Automata and Formal Languages | Part II, 2020

  Assuming the definition of a partial recursive function from $\mathbb{N}$ to $\mathbb{N}$, what is a recursive subset of $\mathbb{N}$ ? What is a recursively enumerable subset of $\mathbb{N}$ ?

  Show that a subset $E \subseteq \mathbb{N}$ is recursive if and only if $E$ and $\mathbb{N} \backslash E$ are recursively enumerable.

  Are the following subsets of $\mathbb{N}$ recursive?

  (i) $\mathbb{K}:=\left\{n \mid n\right.$ codes a program and $f_{n, 1}(n)$ halts at some stage $\}$.

  (ii) $\mathbb{K}_{100}:=\left\{n \mid n\right.$ codes a program and $f_{n, 1}(n)$ halts within 100 steps $\}$.

  comment

• Paper 3, Section I, F

  Automata and Formal Languages | Part II, 2020

  Define a context-free grammar $G$, a sentence of $G$ and the language $\mathcal{L}(G)$ generated by $G$.

  For the alphabet $\Sigma=\{a, b\}$, which of the following languages over $\Sigma$ are contextfree? (i) $\left\{a^{2 m} b^{2 m} \mid m \geqslant 0\right\}$,

  (ii) $\left\{a^{m^{2}} b^{m^{2}} \mid m \geqslant 0\right\}$.

  [You may assume standard results without proof if clearly stated.]

  comment

• Paper 3, Section II, F

  Automata and Formal Languages | Part II, 2020

  Give the definition of a deterministic finite state automaton and of a regular language.

  State and prove the pumping lemma for regular languages.

  Let $S=\left\{2^{n} \mid n=0,1,2, \ldots\right\}$ be the subset of $\mathbb{N}$ consisting of the powers of 2 .

  If we write the elements of $S$ in base 2 (with no preceding zeros), is $S$ a regular language over $\{0,1\}$ ?

  Now suppose we write the elements of $S$ in base 10 (again with no preceding zeros). Show that $S$ is not a regular language over $\{0,1,2,3,4,5,6,7,8,9\}$. [Hint: Give a proof by contradiction; use the above lemma to obtain a sequence $a_{1}, a_{2}, \ldots$ of powers of 2, then consider $a_{i+1}-10^{d} a_{i}$ for $i=1,2,3, \ldots$ and a suitable fixed d.]

  comment

• Paper 4, Section I, $4 F$

  Automata and Formal Languages | Part II, 2020

  Define what it means for a context-free grammar (CFG) to be in Chomsky normal form $(\mathrm{CNF})$.

  Describe without proof each stage in the process of converting a CFG $G=$ $(N, \Sigma, P, S)$ into an equivalent CFG $\bar{G}$ which is in CNF. For each of these stages, when are the nonterminals $N$ left unchanged? What about the terminals $\Sigma$ and the generated language $\mathcal{L}(G)$ ?

  Give an example of a CFG $G$ whose generated language $\mathcal{L}(G)$ is infinite and equal to $\mathcal{L}(\bar{G})$.

  comment

Classical Dynamics

• Paper 1, Section I, B

  Classical Dynamics | Part II, 2020

  A linear molecule is modelled as four equal masses connected by three equal springs. Using the Cartesian coordinates $x_{1}, x_{2}, x_{3}, x_{4}$ of the centres of the four masses, and neglecting any forces other than those due to the springs, write down the Lagrangian of the system describing longitudinal motions of the molecule.

  Rewrite and simplify the Lagrangian in terms of the generalized coordinates

  $$q_{1}=\frac{x_{1}+x_{4}}{2}, \quad q_{2}=\frac{x_{2}+x_{3}}{2}, \quad q_{3}=\frac{x_{1}-x_{4}}{2}, \quad q_{4}=\frac{x_{2}-x_{3}}{2}$$

  Deduce Lagrange's equations for $q_{1}, q_{2}, q_{3}, q_{4}$. Hence find the normal modes of the system and their angular frequencies, treating separately the symmetric and antisymmetric modes of oscillation.

  comment

• Paper 2, Section I, B

  Classical Dynamics | Part II, 2020

  A particle of mass $m$ has position vector $\mathbf{r}(t)$ in a frame of reference that rotates with angular velocity $\boldsymbol{\omega}(t)$. The particle moves under the gravitational influence of masses that are fixed in the rotating frame. Explain why the Lagrangian of the particle is of the form

  $$L=\frac{1}{2} m(\dot{\mathbf{r}}+\boldsymbol{\omega} \times \mathbf{r})^{2}-V(\mathbf{r}) .$$

  Show that Lagrange's equations of motion are equivalent to

  $$m(\ddot{\mathbf{r}}+2 \boldsymbol{\omega} \times \dot{\mathbf{r}}+\dot{\boldsymbol{\omega}} \times \mathbf{r}+\boldsymbol{\omega} \times(\boldsymbol{\omega} \times \mathbf{r}))=-\boldsymbol{\nabla} V$$

  Identify the canonical momentum $\mathbf{p}$ conjugate to $\mathbf{r}$. Obtain the Hamiltonian $H(\mathbf{r}, \mathbf{p})$ and Hamilton's equations for this system.

  comment

• Paper 2, Section II, B

  Classical Dynamics | Part II, 2020

  A symmetric top of mass $M$ rotates about a fixed point that is a distance $l$ from the centre of mass along the axis of symmetry; its principal moments of inertia about the fixed point are $I_{1}=I_{2}$ and $I_{3}$. The Lagrangian of the top is

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-M g l \cos \theta$$

  (i) Draw a diagram explaining the meaning of the Euler angles $\theta, \phi$ and $\psi$.

  (ii) Derive expressions for the three integrals of motion $E, L_{3}$ and $L_{z}$.

  (iii) Show that the nutational motion is governed by the equation

  $$\frac{1}{2} I_{1} \dot{\theta}^{2}+V_{\text {eff }}(\theta)=E^{\prime}$$

  and derive expressions for the effective potential $V_{\mathrm{eff}}(\theta)$ and the modified energy $E^{\prime}$ in terms of $E, L_{3}$ and $L_{z}$.

  (iv) Suppose that

  $$L_{z}=L_{3}\left(1-\frac{\epsilon^{2}}{2}\right)$$

  where $\epsilon$ is a small positive number. By expanding $V_{\text {eff }}$ to second order in $\epsilon$ and $\theta$, show that there is a stable equilibrium solution with $\theta=O(\epsilon)$, provided that $L_{3}^{2}>4 M g l I_{1}$. Determine the equilibrium value of $\theta$ and the precession rate $\dot{\phi}$, to the same level of approximation.

  comment

• Paper 3, Section I, B

  Classical Dynamics | Part II, 2020

  A particle of mass $m$ experiences a repulsive central force of magnitude $k / r^{2}$, where $r=|\mathbf{r}|$ is its distance from the origin. Write down the Hamiltonian of the system.

  The Laplace-Runge-Lenz vector for this system is defined by

  $$\mathbf{A}=\mathbf{p} \times \mathbf{L}+m k \hat{\mathbf{r}}$$

  where $\mathbf{L}=\mathbf{r} \times \mathbf{p}$ is the angular momentum and $\hat{\mathbf{r}}=\mathbf{r} / r$ is the radial unit vector. Show that

  $$\{\mathbf{L}, H\}=\{\mathbf{A}, H\}=\mathbf{0},$$

  where $\{\cdot, \cdot\}$ is the Poisson bracket. What are the integrals of motion of the system? Show that the polar equation of the orbit can be written as

  $$r=\frac{\lambda}{e \cos \theta-1},$$

  where $\lambda$ and $e$ are non-negative constants.

  comment

• Paper 4, Section I, B

  Classical Dynamics | Part II, 2020

  Derive expressions for the angular momentum and kinetic energy of a rigid body in terms of its mass $M$, the position $\mathbf{X}(t)$ of its centre of mass, its inertia tensor $I$ (which should be defined) about its centre of mass, and its angular velocity $\boldsymbol{\omega}$.

  A spherical planet of mass $M$ and radius $R$ has density proportional to $r^{-1} \sin (\pi r / R)$. Given that $\int_{0}^{\pi} x \sin x d x=\pi$ and $\int_{0}^{\pi} x^{3} \sin x d x=\pi\left(\pi^{2}-6\right)$, evaluate the inertia tensor of the planet in terms of $M$ and $R$.

  comment

• Paper 4, Section II, B

  Classical Dynamics | Part II, 2020

  (a) Explain how the Hamiltonian $H(\mathbf{q}, \mathbf{p}, t)$ of a system can be obtained from its Lagrangian $L(\mathbf{q}, \dot{\mathbf{q}}, t)$. Deduce that the action can be written as

  $$S=\int(\mathbf{p} \cdot d \mathbf{q}-H d t)$$

  Show that Hamilton's equations are obtained if the action, computed between fixed initial and final configurations $\mathbf{q}\left(t_{1}\right)$ and $\mathbf{q}\left(t_{2}\right)$, is minimized with respect to independent variations of $\mathbf{q}$ and $\mathbf{p}$.

  (b) Let $(\mathbf{Q}, \mathbf{P})$ be a new set of coordinates on the same phase space. If the old and new coordinates are related by a type-2 generating function $F_{2}(\mathbf{q}, \mathbf{P}, t)$ such that

  $$\mathbf{p}=\frac{\partial F_{2}}{\partial \mathbf{q}}, \quad \mathbf{Q}=\frac{\partial F_{2}}{\partial \mathbf{P}}$$

  deduce that the canonical form of Hamilton's equations applies in the new coordinates, but with a new Hamiltonian given by

  $$K=H+\frac{\partial F_{2}}{\partial t}$$

  (c) For each of the Hamiltonians (i) $H=H(p)$, (ii) $H=\frac{1}{2}\left(q^{2}+p^{2}\right)$,

  express the general solution $(q(t), p(t))$ at time $t$ in terms of the initial values given by $(Q, P)=(q(0), p(0))$ at time $t=0$. In each case, show that the transformation from $(q, p)$ to $(Q, P)$ is canonical for all values of $t$, and find the corresponding generating function $F_{2}(q, P, t)$ explicitly.

  comment

Coding and Cryptography

• Paper 1, Section I, I

  Coding and Cryptography | Part II, 2020

  (a) Briefly describe the methods of Shannon-Fano and of Huffman for the construction of prefix-free binary codes.

  (b) In this part you are given that $-\log _{2}(1 / 10) \approx 3.32,-\log _{2}(2 / 10) \approx 2.32$, $-\log _{2}(3 / 10) \approx 1.74$ and $-\log _{2}(4 / 10) \approx 1.32$.

  Let $\mathcal{A}=\{1,2,3,4\}$. For $k \in \mathcal{A}$, suppose that the probability of choosing $k$ is $k / 10$.

  (i) Find a Shannon-Fano code for this system and the expected word length.

  (ii) Find a Huffman code for this system and the expected word length.

  (iii) Verify that Shannon's noiseless coding theorem is satisfied in each case.

  comment

• Paper 1, Section II, I

  Coding and Cryptography | Part II, 2020

  (a) What does it mean to say that a binary code has length $n$, size $M$ and minimum distance d?

  Let $A(n, d)$ be the largest value of $M$ for which there exists a binary $[n, M, d]$-code.

  (i) Show that $A(n, 1)=2^{n}$.

  (ii) Suppose that $n, d>1$. Show that if a binary $[n, M, d]$-code exists, then a binary $[n-1, M, d-1]$-code exists. Deduce that $A(n, d) \leqslant A(n-1, d-1)$.

  (iii) Suppose that $n, d \geqslant 1$. Show that $A(n, d) \leqslant 2^{n-d+1}$.

  (b) (i) For integers $M$ and $N$ with $0 \leqslant N \leqslant M$, show that

  $$N(M-N) \leqslant\left\{\begin{array}{cl} M^{2} / 4, & \text { if } M \text { is even }, \\ \left(M^{2}-1\right) / 4, & \text { if } M \text { is odd } \end{array}\right.$$

  For the remainder of this question, suppose that $C$ is a binary $[n, M, d]$-code. For codewords $x=\left(x_{1} \ldots x_{n}\right), y=\left(y_{1} \ldots y_{n}\right) \in C$ of length $n$, we define $x+y$ to be the word $\left(\left(x_{1}+y_{1}\right) \ldots\left(x_{n}+y_{n}\right)\right)$ with addition modulo $2 .$

  (ii) Explain why the Hamming distance $d(x, y)$ is the number of 1 s in $x+y$.

  (iii) Now we construct an $\left(\begin{array}{c}M \\ 2\end{array}\right) \times n$ array $A$ whose rows are all the words $x+y$ for pairs of distinct codewords $x, y$. Show that the number of $1 \mathrm{~s}$ in $A$ is at most

  $$\begin{cases}n M^{2} / 4, & \text { if } M \text { is even } \\ n\left(M^{2}-1\right) / 4, & \text { if } M \text { is odd }\end{cases}$$

  Show also that the number of $1 \mathrm{~s}$ in $A$ is at least $d\left(\begin{array}{c}M \\ 2\end{array}\right)$.

  (iv) Using the inequalities derived in part(b) (iii), deduce that if $d$ is even and $n<2 d$ then

  $$A(n, d) \leqslant 2\left\lfloor\frac{d}{2 d-n}\right\rfloor$$

  comment

• Paper 2, Section I, I

  Coding and Cryptography | Part II, 2020

  (a) Define the information capacity of a discrete memoryless channel (DMC).

  (b) Consider a DMC where there are two input symbols, $A$ and $B$, and three output symbols, $A, B$ and $\star$. Suppose each input symbol is left intact with probability $1 / 2$, and transformed into a $\star$ with probability $1 / 2$.

  (i) Write down the channel matrix, and calculate the information capacity.

  (ii) Now suppose the output is further processed by someone who cannot distinguish between $A$ and $\star$, so that the channel matrix becomes

  $$\left(\begin{array}{cc} 1 & 0 \\ 1 / 2 & 1 / 2 \end{array}\right)$$

  Calculate the new information capacity.

  comment

• Paper 2, Section II, I

  Coding and Cryptography | Part II, 2020

  Let $C$ be the Hamming $(n, n-d)$ code of weight 3 , where $n=2^{d}-1, d>1$. Let $H$ be the parity-check matrix of $C$. Let $\nu(j)$ be the number of codewords of weight $j$ in $C$.

  (i) Show that for any two columns $h_{1}$ and $h_{2}$ of $H$ there exists a unique third column $h_{3}$ such that $h_{3}=h_{2}+h_{1}$. Deduce that $\nu(3)=n(n-1) / 6$.

  (ii) Show that $C$ contains a codeword of weight $n$.

  (iii) Find formulae for $\nu(n-1), \nu(n-2)$ and $\nu(n-3)$. Justify your answer in each case.

  comment

• Paper 3, Section I, I

  Coding and Cryptography | Part II, 2020

  Let $N$ and $p$ be very large positive integers with $p$ a prime and $p>N$. The Chair of the Committee is able to inscribe pairs of very large integers on discs. The Chair wishes to inscribe a collection of discs in such a way that any Committee member who acquires $r$ of the discs and knows the prime $p$ can deduce the integer $N$, but owning $r-1$ discs will give no information whatsoever. What strategy should the Chair follow?

  [You may use without proof standard properties of the determinant of the $r \times r$ Vandermonde matrix.]

  comment

• Paper 4, Section I, I

  Coding and Cryptography | Part II, 2020

  (a) What does it mean to say that a cipher has perfect secrecy? Show that if a cipher has perfect secrecy then there must be at least as many possible keys as there are possible plaintext messages. What is a one-time pad? Show that a one-time pad has perfect secrecy.

  (b) I encrypt a binary sequence $a_{1}, a_{2}, \ldots, a_{N}$ using a one-time pad with key sequence $k_{1}, k_{2}, k_{3}, \ldots .$ I transmit $a_{1}+k_{1}, a_{2}+k_{2}, \ldots, a_{N}+k_{N}$ to you. Then, by mistake, I also transmit $a_{1}+k_{2}, a_{2}+k_{3}, \ldots, a_{N}+k_{N+1}$ to you. Assuming that you know I have made this error, and that my message makes sense, how would you go about finding my message? Can you now decipher other messages sent using the same part of the key sequence? Briefly justify your answer.

  comment

Cosmology

• Paper 1, Section I, D

  Cosmology | Part II, 2020

  The Friedmann equation is

  $$H^{2}=\frac{8 \pi G}{3 c^{2}}\left(\rho-\frac{k c^{2}}{R^{2} a^{2}}\right)$$

  Briefly explain the meaning of $H, \rho, k$ and $R$.

  Derive the Raychaudhuri equation,

  $$\frac{\ddot{a}}{a}=-\frac{4 \pi G}{3 c^{2}}(\rho+3 P),$$

  where $P$ is the pressure, stating clearly any results that are required.

  Assume that the strong energy condition $\rho+3 P \geqslant 0$ holds. Show that there was necessarily a Big Bang singularity at time $t_{B B}$ such that

  $$t_{0}-t_{B B} \leqslant H_{0}^{-1}$$

  where $H_{0}=H\left(t_{0}\right)$ and $t_{0}$ is the time today.

  comment

• Paper 1, Section II, D

  Cosmology | Part II, 2020

  A fluid with pressure $P$ sits in a volume $V$. The change in energy due to a change in volume is given by $d E=-P d V$. Use this in a cosmological context to derive the continuity equation,

  $$\dot{\rho}=-3 H(\rho+P),$$

  with $\rho$ the energy density, $H=\dot{a} / a$ the Hubble parameter, and $a$ the scale factor.

  In a flat universe, the Friedmann equation is given by

  $$H^{2}=\frac{8 \pi G}{3 c^{2}} \rho .$$

  Given a universe dominated by a fluid with equation of state $P=w \rho$, where $w$ is a constant, determine how the scale factor $a(t)$ evolves.

  Define conformal time $\tau$. Assume that the early universe consists of two fluids: radiation with $w=1 / 3$ and a network of cosmic strings with $w=-1 / 3$. Show that the Friedmann equation can be written as

  $$\left(\frac{d a}{d \tau}\right)^{2}=B \rho_{\mathrm{eq}}\left(a^{2}+a_{\mathrm{eq}}^{2}\right)$$

  where $\rho_{\mathrm{eq}}$ is the energy density in radiation, and $a_{\mathrm{eq}}$ is the scale factor, both evaluated at radiation-string equality. Here, $B$ is a constant that you should determine. Find the solution $a(\tau)$.

  comment

• Paper 2, Section I, D

  Cosmology | Part II, 2020

  During inflation, the expansion of the universe is governed by the Friedmann equation,

  $$H^{2}=\frac{8 \pi G}{3 c^{2}}\left(\frac{1}{2} \dot{\phi}^{2}+V(\phi)\right)$$

  and the equation of motion for the inflaton field $\phi$,

  $$\ddot{\phi}+3 H \dot{\phi}+\frac{\partial V}{\partial \phi}=0 \text {. }$$

  The slow-roll conditions are $\dot{\phi}^{2} \ll V(\phi)$ and $\ddot{\phi} \ll H \dot{\phi}$. Under these assumptions, solve for $\phi(t)$ and $a(t)$ for the potentials:

  (i) $V(\phi)=\frac{1}{2} m^{2} \phi^{2}$ and

  (ii) $V(\phi)=\frac{1}{4} \lambda \phi^{4}, \quad(\lambda>0)$.

  comment

• Paper 3, Section I, D

  Cosmology | Part II, 2020

  At temperature $T$, with $\beta=1 /\left(k_{B} T\right)$, the distribution of ultra-relativistic particles with momentum $\mathbf{p}$ is given by

  $$n(\mathbf{p})=\frac{1}{e^{\beta p c} \mp 1},$$

  where the minus sign is for bosons and the plus $\operatorname{sign}$ for fermions, and with $p=|\mathbf{p}|$.

  Show that the total number of fermions, $n_{\mathrm{f}}$, is related to the total number of bosons, $n_{\mathrm{b}}$, by $n_{\mathrm{f}}=\frac{3}{4} n_{\mathrm{b}}$.

  Show that the total energy density of fermions, $\rho_{\mathrm{f}}$, is related to the total energy density of bosons, $\rho_{\mathrm{b}}$, by $\rho_{\mathrm{f}}=\frac{7}{8} \rho_{\mathrm{b}}$.

  comment

• Paper 3, Section II, D

  Cosmology | Part II, 2020

  In an expanding spacetime, the density contrast $\delta(\mathbf{x}, t)$ satisfies the linearised equation

  $$\ddot{\delta}+2 H \dot{\delta}-c_{s}^{2}\left(\frac{1}{a^{2}} \nabla^{2}+k_{J}^{2}\right) \delta=0,$$

  where $a$ is the scale factor, $H$ is the Hubble parameter, $c_{s}$ is a constant, and $k_{J}$ is the Jeans wavenumber, defined by

  $$c_{s}^{2} k_{J}^{2}=\frac{4 \pi G}{c^{2}} \bar{\rho}(t)$$

  with $\bar{\rho}(t)$ the background, homogeneous energy density.

  (i) Solve for $\delta(\mathbf{x}, t)$ in a static universe, with $a=1$ and $H=0$ and $\bar{\rho}$ constant. Identify two regimes: one in which sound waves propagate, and one in which there is an instability.

  (ii) In a matter-dominated universe with $\bar{\rho} \sim 1 / a^{3}$, use the Friedmann equation $H^{2}=8 \pi G \bar{\rho} / 3 c^{2}$ to find the growing and decaying long-wavelength modes of $\delta$ as a function of $a$.

  (iii) Assuming $c_{s}^{2} \approx c_{s}^{2} k_{J}^{2} \approx 0$ in equation $(*)$, find the growth of matter perturbations in a radiation-dominated universe and find the growth of matter perturbations in a curvature-dominated universe.

  comment

• Paper 4 , Section I, D

  Cosmology | Part II, 2020

  At temperature $T$ and chemical potential $\mu$, the number density of a non-relativistic particle species with mass $m \gg k_{B} T / c^{2}$ is given by

  $$n=g\left(\frac{m k_{B} T}{2 \pi \hbar^{2}}\right)^{3 / 2} e^{-\left(m c^{2}-\mu\right) / k_{B} T},$$

  where $g$ is the number of degrees of freedom of this particle.

  At recombination, electrons and protons combine to form hydrogen. Use the result above to derive the Saha equation

  $$n_{H} \approx n_{e}^{2}\left(\frac{2 \pi \hbar^{2}}{m_{e} k_{B} T}\right)^{3 / 2} e^{E_{\mathrm{bind}} / k_{B} T}$$

  where $n_{H}$ is the number density of hydrogen atoms, $n_{e}$ the number density of electrons, $m_{e}$ the mass of the electron and $E_{\text {bind }}$ the binding energy of hydrogen. State any assumptions that you use in this derivation.

  comment

Differential Geometry

• Paper 1, Section II, I

  Differential Geometry | Part II, 2020

  (a) Let $X \subset \mathbb{R}^{N}$ be a manifold. Give the definition of the tangent space $T_{p} X$ of $X$ at a point $p \in X$.

  (b) Show that $X:=\left\{-x_{0}^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}=-1\right\} \cap\left\{x_{0}>0\right\}$ defines a submanifold of $\mathbb{R}^{4}$ and identify explicitly its tangent space $T_{\mathbf{x}} X$ for any $\mathbf{x} \in X$.

  (c) Consider the matrix group $O(1,3) \subset \mathbb{R}^{4^{2}}$ consisting of all $4 \times 4$ matrices $A$ satisfying

  $$A^{t} M A=M$$

  where $M$ is the diagonal $4 \times 4$ matrix $M=\operatorname{diag}(-1,1,1,1)$.

  (i) Show that $O(1,3)$ forms a group under matrix multiplication, i.e. it is closed under multiplication and every element in $O(1,3)$ has an inverse in $O(1,3)$.

  (ii) Show that $O(1,3)$ defines a 6-dimensional manifold. Identify the tangent space $T_{A} O(1,3)$ for any $A \in O(1,3)$ as a set $\{A Y\}_{Y \in \mathfrak{S}}$ where $Y$ ranges over a linear subspace $\mathfrak{S} \subset \mathbb{R}^{4^{2}}$ which you should identify explicitly.

  (iii) Let $X$ be as defined in (b) above. Show that $O^{+}(1,3) \subset O(1,3)$ defined as the set of all $A \in O(1,3)$ such that $A \mathbf{x} \in X$ for all $\mathbf{x} \in X$ is both a subgroup and a submanifold of full dimension.

  [You may use without proof standard theorems from the course concerning regular values and transversality.]

  comment

• Paper 2, Section II, I

  Differential Geometry | Part II, 2020

  (a) State the fundamental theorem for regular curves in $\mathbb{R}^{3}$.

  (b) Let $\alpha: \mathbb{R} \rightarrow \mathbb{R}^{3}$ be a regular curve, parameterised by arc length, such that its image $\alpha(\mathbb{R}) \subset \mathbb{R}^{3}$ is a one-dimensional submanifold. Suppose that the set $\alpha(\mathbb{R})$ is preserved by a nontrivial proper Euclidean motion $\phi: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$.

  Show that there exists $\sigma_{0} \in \mathbb{R}$ corresponding to $\phi$ such that $\phi(\alpha(s))=\alpha\left(\pm s+\sigma_{0}\right)$ for all $s \in \mathbb{R}$, where the choice of $\pm \operatorname{sign}$ is independent of $s$. Show also that the curvature $k(s)$ and torsion $\tau(s)$ of $\alpha$ satisfy

  $$\begin{gathered} k\left(\pm s+\sigma_{0}\right)=k(s) \text { and } \\ \tau\left(\pm s+\sigma_{0}\right)=\tau(s) \end{gathered}$$

  with equation (2) valid only for $s$ such that $k(s)>0$. In the case where the sign is $+$ and $\sigma_{0}=0$, show that $\alpha(\mathbb{R})$ is a straight line.

  (c) Give an explicit example of a curve $\alpha$ satisfying the requirements of (b) such that neither of $k(s)$ and $\tau(s)$ is a constant function, and such that the curve $\alpha$ is closed, i.e. such that $\alpha(s)=\alpha\left(s+s_{0}\right)$ for some $s_{0}>0$ and all $s$. [Here a drawing would suffice.]

  (d) Suppose now that $\alpha: \mathbb{R} \rightarrow \mathbb{R}^{3}$ is an embedded regular curve parameterised by arc length $s$. Suppose further that $k(s)>0$ for all $s$ and that $k(s)$ and $\tau(s)$ satisfy (1) and (2) for some $\sigma_{0}$, where the choice $\pm$ is independent of $s$, and where $\sigma_{0} \neq 0$ in the case of + sign. Show that there exists a nontrivial proper Euclidean motion $\phi$ such that the set $\alpha(\mathbb{R})$ is preserved by $\phi$. [You may use the theorem of part (a) without proof.]

  comment

• Paper 3, Section II, I

  Differential Geometry | Part II, 2020

  (a) Show that for a compact regular surface $S \subset \mathbb{R}^{3}$, there exists a point $p \in S$ such that $K(p)>0$, where $K$ denotes the Gaussian curvature. Show that if $S$ is contained in a closed ball of radius $R$ in $\mathbb{R}^{3}$, then there is a point $p$ such that $K(p) \geqslant R^{-2}$.

  (b) For a regular surface $S \subset \mathbb{R}^{3}$, give the definition of a geodesic polar coordinate system at a point $p \in S$. Show that in such a coordinate system, $\lim _{r \rightarrow 0} G(r, \theta)=0$, $\lim _{r \rightarrow 0}(\sqrt{G})_{r}(r, \theta)=1, E(r, \theta)=1$ and $F(r, \theta)=0$. [You may use without proof standard properties of the exponential map provided you state them clearly.]

  (c) Let $S \subset \mathbb{R}^{3}$ be a regular surface. Show that if $K \leqslant 0$, then any geodesic polar coordinate ball $B\left(p, \epsilon_{0}\right) \subset S$ of radius $\epsilon_{0}$ around $p$ has area satisfying

  $$\text { Area } B\left(p, \epsilon_{0}\right) \geqslant \pi \epsilon_{0}^{2}$$

  [You may use without proof the identity $(\sqrt{G})_{r r}(r, \theta)=-\sqrt{G} K$.]

  (d) Let $S \subset \mathbb{R}^{3}$ be a regular surface, and now suppose $-\infty<K \leqslant C$ for some constant $0<C<\infty$. Given any constant $0<\gamma<1$, show that there exists $\epsilon_{0}>0$, depending only on $C$ and $\gamma$, so that if $B(p, \epsilon) \subset S$ is any geodesic polar coordinate ball of radius $\epsilon \leqslant \epsilon_{0}$, then

  $$\text { Area } B(p, \epsilon) \geqslant \gamma \pi \epsilon^{2}$$

  [Hint: For any fixed $\theta_{0}$, consider the function $f(r):=\sqrt{G}\left(r, \theta_{0}\right)-\alpha \sin (\sqrt{C} r)$, for all $0<$ $\alpha<\frac{1}{\sqrt{C}}$. Derive the relation $f^{\prime \prime} \geqslant-C f$ and show $f(r)>0$ for an appropriate range of $r .$ The following variant of Wirtinger's inequality may be useful and can be assumed without proof: if $g$ is a $C^{1}$ function on $[0, L]$ vanishing at 0 , then $\int_{0}^{L}|g(x)|^{2} d x \leqslant \frac{L}{2 \pi} \int_{0}^{L}\left|g^{\prime}(x)\right|^{2} d x$.]

  comment

• Paper 4, Section II, I

  Differential Geometry | Part II, 2020

  (a) State the Gauss-Bonnet theorem for compact regular surfaces $S \subset \mathbb{R}^{3}$ without boundary. Identify all expressions occurring in any formulae.

  (b) Let $S \subset \mathbb{R}^{3}$ be a compact regular surface without boundary and suppose that its Gaussian curvature $K(x) \geqslant 0$ for all $x \in S$. Show that $S$ is diffeomorphic to the sphere.

  Let $S_{n}$ be a sequence of compact regular surfaces in $\mathbb{R}^{3}$ and let $K_{n}(x)$ denote the Gaussian curvature of $S_{n}$ at $x \in S_{n}$. Suppose that

  $$\limsup _{n \rightarrow \infty} \inf _{x \in S_{n}} K_{n}(x) \geqslant 0$$

  (c) Give an example to show that it does not follow that for all sufficiently large $n$ the surface $S_{n}$ is diffeomorphic to the sphere.

  (d) Now assume, in addition to $(\star)$, that all of the following conditions hold:

  (1) There exists a constant $R<\infty$ such that for all $n, S_{n}$ is contained in a ball of radius $R$ around the origin.

  (2) There exists a constant $M<\infty$ such that $\operatorname{Area}\left(S_{n}\right) \leqslant M$ for all $n$.

  (3) There exists a constant $\epsilon_{0}>0$ such that for all $n$, all points $p \in S_{n}$ admit a geodesic polar coordinate system centred at $p$ of radius at least $\epsilon_{0}$.

  (4) There exists a constant $C<\infty$ such that on all such geodesic polar neighbourhoods, $\left|\partial_{r} K_{n}\right| \leqslant C$ for all $n$, where $r$ denotes a geodesic polar coordinate.

  (i) Show that for all sufficiently large $n$, the surface $S_{n}$ is diffeomorphic to the sphere. [Hint: It may be useful to identify a geodesic polar ball $B\left(p_{n}, \epsilon_{0}\right)$ in each $S_{n}$ for which $\int_{B\left(p_{n}, \epsilon_{0}\right)} K_{n} d A$ is bounded below by a positive constant independent of $n$.]

  (ii) Explain how your example from (c) fails to satisfy one or more of these extra conditions (1)-(4).

  [You may use without proof the standard computations for geodesic polar coordinates: $E=1, F=0, \lim _{r \rightarrow 0} G(r, \theta)=0, \lim _{r \rightarrow 0}(\sqrt{G})_{r}(r, \theta)=1$, and $\left.(\sqrt{G})_{r r}=-K \sqrt{G} .\right]$

  comment

Dynamical Systems

• Paper 1, Section II, 32E

  Dynamical Systems | Part II, 2020

  (i) For the dynamical system

  $$\dot{x}=-x\left(x^{2}-2 \mu\right)\left(x^{2}-\mu+a\right),$$

  sketch the bifurcation diagram in the $(\mu, x)$ plane for the three cases $a<0, a=0$ and $a>0$. Describe the bifurcation points that occur in each case.

  (ii) For the case when $a<0$ only, confirm the types of bifurcation by finding the system to leading order near each of the bifurcations.

  (iii) Explore the structural stability of these bifurcations by adding a small positive constant $\epsilon$ to the right-hand side of $(\uparrow)$ and by sketching the bifurcation diagrams, for the three cases $a<0, a=0$ and $a>0$. Which of the original bifurcations are structurally stable?

  comment

• Paper 2, Section II, E

  Dynamical Systems | Part II, 2020

  (a) State and prove Dulac's criterion. State clearly the Poincaré-Bendixson theorem.

  (b) For $(x, y) \in \mathbb{R}^{2}$ and $k>0$, consider the dynamical system

  $$\begin{aligned} &\dot{x}=k x-5 y-(3 x+y)\left(5 x^{2}-6 x y+5 y^{2}\right) \\ &\dot{y}=5 x+(k-6) y-(x+3 y)\left(5 x^{2}-6 x y+5 y^{2}\right) \end{aligned}$$

  (i) Use Dulac's criterion to find a range of $k$ for which this system does not have any periodic orbit.

  (ii) Find a suitable $f(k)>0$ such that trajectories enter the disc $x^{2}+y^{2} \leqslant f(k)$ and do not leave it.

  (iii) Given that the system has no fixed points apart from the origin for $k<10$, give a range of $k$ for which there will exist at least one periodic orbit.

  comment

• Paper 3, Section II, E

  Dynamical Systems | Part II, 2020

  (a) A dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$ has a fixed point at the origin. Define the terms asymptotic stability, Lyapunov function and domain of stability of the fixed point $\mathbf{x}=\mathbf{0}$. State and prove Lyapunov's first theorem and state (without proof) La Salle's invariance principle.

  (b) Consider the system

  $$\begin{aligned} \dot{x} &=-2 x+x^{3}+\sin (2 y), \\ \dot{y} &=-x-y^{3} \end{aligned}$$

  (i) Show that trajectories cannot leave the square $S=\{(x, y):|x|<1,|y|<1\}$. Show also that there are no fixed points in $S$ other than the origin. Is this enough to deduce that $S$ is in the domain of stability of the origin?

  (ii) Construct a Lyapunov function of the form $V=x^{2} / 2+g(y)$. Deduce that the origin is asymptotically stable.

  (iii) Find the largest rectangle of the form $|x|<x_{0},|y|<y_{0}$ on which $V$ is a strict Lyapunov function. Is this enough to deduce that this region is in the domain of stability of the origin?

  (iv) Purely from using the Lyapunov function $V$, what is the most that can be deduced about the domain of stability of the origin?

  comment

• Paper 4, Section II, E

  Dynamical Systems | Part II, 2020

  (a) Let $F: I \rightarrow I$ be a continuous map defined on an interval $I \subset \mathbb{R}$. Define what it means (i) for $F$ to have a horseshoe and (ii) for $F$ to be chaotic. [Glendinning's definition should be used throughout this question.]

  (b) Consider the map defined on the interval $[-1,1]$ by

  $$F(x)=1-\mu|x|$$

  with $0<\mu \leqslant 2$.

  (i) Sketch $F(x)$ and $F^{2}(x)$ for a case when $0<\mu<1$ and a case when $1<\mu<2$.

  (ii) Describe fully the long term dynamics for $0<\mu<1$. What happens for $\mu=1$ ?

  (iii) When does $F$ have a horseshoe? When does $F^{2}$ have a horseshoe?

  (iv) For what values of $\mu$ is the map $F$ chaotic?

  comment

Electrodynamics

• Paper 1, Section II, 37D

  Electrodynamics | Part II, 2020

  A relativistic particle of rest mass $m$ and electric charge $q$ follows a worldline $x^{\mu}(\lambda)$ in Minkowski spacetime where $\lambda=\lambda(\tau)$ is an arbitrary parameter which increases monotonically with the proper time $\tau$. We consider the motion of the particle in a background electromagnetic field with four-vector potential $A^{\mu}(x)$ between initial and final values of the proper time denoted $\tau_{i}$ and $\tau_{f}$ respectively.

  (i) Write down an action for the particle's motion. Explain what is meant by a gauge transformation of the electromagnetic field. How does the action change under a gauge transformation?

  (ii) Derive an equation of motion for the particle by considering the variation of the action with respect to the worldline $x^{\mu}(\lambda)$. Setting $\lambda=\tau$ show that your equation of motion reduces to the Lorentz force law,

  $$m \frac{d u^{\mu}}{d \tau}=q F^{\mu \nu} u_{\nu}$$

  where $u^{\mu}=d x^{\mu} / d \tau$ is the particle's four-velocity and $F^{\mu \nu}=\partial^{\mu} A^{\nu}-\partial^{\nu} A^{\mu}$ is the Maxwell field-strength tensor.

  (iii) Working in an inertial frame with spacetime coordinates $x^{\mu}=(c t, x, y, z)$, consider the case of a constant, homogeneous magnetic field of magnitude $B$, pointing in the $z$-direction, and vanishing electric field. In a gauge where $A^{\mu}=(0,0, B x, 0)$, show that the equation of motion $(*)$ is solved by circular motion in the $x-y$ plane with proper angular frequency $\omega=q B / m$.

  (iv) Let $v$ denote the speed of the particle in this inertial frame with Lorentz factor $\gamma(v)=1 / \sqrt{1-v^{2} / c^{2}}$. Find the radius $R=R(v)$ of the circle as a function of $v$. Setting $\tau_{f}=\tau_{i}+2 \pi / \omega$, evaluate the action $S=S(v)$ for a single period of the particle's motion.

  comment

• Paper 3, Section II, D

  Electrodynamics | Part II, 2020

  The Maxwell stress tensor $\sigma$ of the electromagnetic fields is a two-index Cartesian tensor with components

  $$\sigma_{i j}=-\epsilon_{0}\left(E_{i} E_{j}-\frac{1}{2}|\mathbf{E}|^{2} \delta_{i j}\right)-\frac{1}{\mu_{0}}\left(B_{i} B_{j}-\frac{1}{2}|\mathbf{B}|^{2} \delta_{i j}\right)$$

  where $i, j=1,2,3$, and $E_{i}$ and $B_{i}$ denote the Cartesian components of the electric and magnetic fields $\mathbf{E}(\mathbf{x}, t)$ and $\mathbf{B}(\mathbf{x}, t)$ respectively.

  (i) Consider an electromagnetic field sourced by charge and current densities denoted by $\rho(\mathbf{x}, t)$ and $\mathbf{J}(\mathbf{x}, t)$ respectively. Using Maxwell's equations and the Lorentz force law, show that the components of $\sigma$ obey the equation

  $$\sum_{j=1}^{3} \frac{\partial \sigma_{i j}}{\partial x_{j}}+\frac{\partial g_{i}}{\partial t}=-(\rho \mathbf{E}+\mathbf{J} \times \mathbf{B})_{i}$$

  where $g_{i}$, for $i=1,2,3$, are the components of a vector field $\mathbf{g}(\mathbf{x}, t)$ which you should give explicitly in terms of $\mathbf{E}$ and $\mathbf{B}$. Explain the physical interpretation of this equation and of the quantities $\sigma$ and $\mathbf{g}$.

  (ii) A localised source near the origin, $\mathbf{x}=0$, emits electromagnetic radiation. Far from the source, the resulting electric and magnetic fields can be approximated as

  $$\mathbf{B}(\mathbf{x}, t) \simeq \mathbf{B}_{0}(\mathbf{x}) \sin (\omega t-\mathbf{k} \cdot \mathbf{x}), \quad \mathbf{E}(\mathbf{x}, t) \simeq \mathbf{E}_{0}(\mathbf{x}) \sin (\omega t-\mathbf{k} \cdot \mathbf{x})$$

  where $\mathbf{B}_{0}(\mathbf{x})=\frac{\mu_{0} \omega^{2}}{4 \pi r c} \hat{\mathbf{x}} \times \mathbf{p}_{0}$ and $\mathbf{E}_{0}(\mathbf{x})=-c \hat{\mathbf{x}} \times \mathbf{B}_{0}(\mathbf{x})$ with $r=|\mathbf{x}|$ and $\hat{\mathbf{x}}=\mathbf{x} / r$. Here, $\mathbf{k}=(\omega / c) \hat{\mathbf{x}}$ and $\mathbf{p}_{0}$ is a constant vector.

  Calculate the pressure exerted by these fields on a spherical shell of very large radius $R$ centred on the origin. [You may assume that $\mathbf{E}$ and $\mathbf{B}$ vanish for $r>R$ and that the shell material is absorbant, i.e. no reflected wave is generated.]

  comment

• Paper 4 , Section II, 36D

  Electrodynamics | Part II, 2020

  (a) A dielectric medium exhibits a linear response if the electric displacement $\mathbf{D}(\mathbf{x}, t)$ and magnetizing field $\mathbf{H}(\mathbf{x}, t)$ are related to the electric and magnetic fields, $\mathbf{E}(\mathbf{x}, t)$ and $\mathbf{B}(\mathbf{x}, t)$, as

  $$\mathbf{D}=\epsilon \mathbf{E}, \quad \mathbf{B}=\mu \mathbf{H}$$

  where $\epsilon$ and $\mu$ are constants characterising the electric and magnetic polarisability of the material respectively. Write down the Maxwell equations obeyed by the fields $\mathbf{D}, \mathbf{H}, \mathbf{B}$ and $\mathbf{E}$ in this medium in the absence of free charges or currents.

  (b) Two such media with constants $\epsilon_{-}$and $\epsilon_{+}$(but the same $\mu$ ) fill the regions $x<0$ and $x>0$ respectively in three-dimensions with Cartesian coordinates $(x, y, z)$.

  (i) Starting from Maxwell's equations, derive the appropriate boundary conditions at $x=0$ for a time-independent electric field $\mathbf{E}(\mathbf{x})$.

  (ii) Consider a candidate solution of Maxwell's equations describing the reflection and transmission of an incident electromagnetic wave of wave vector $\mathbf{k}_{I}$ and angular frequency $\omega_{I}$ off the interface at $x=0$. The electric field is given as,

  $$\mathbf{E}(\mathbf{x}, t)=\left\{\begin{array}{cc} \sum_{X=I, R} \operatorname{Im}\left[\mathbf{E}_{X} \exp \left(i \mathbf{k}_{X} \cdot \mathbf{x}-i \omega_{X} t\right)\right], & x<0 \\ \operatorname{Im}\left[\mathbf{E}_{T} \exp \left(i \mathbf{k}_{T} \cdot \mathbf{x}-i \omega_{T} t\right)\right], & x>0 \end{array}\right.$$

  where $\mathbf{E}_{I}, \mathbf{E}_{R}$ and $\mathbf{E}_{T}$ are constant real vectors and $\operatorname{Im}[z]$ denotes the imaginary part of a complex number $z$. Give conditions on the parameters $\mathbf{E}_{X}, \mathbf{k}_{X}, \omega_{X}$ for $X=I, R, T$, such that the above expression for the electric field $\mathbf{E}(\mathbf{x}, t)$ solves Maxwell's equations for all $x \neq 0$, together with an appropriate magnetic field $\mathbf{B}(\mathbf{x}, t)$ which you should determine.

  (iii) We now parametrize the incident wave vector as $\mathbf{k}_{I}=k_{I}\left(\cos \left(\theta_{I}\right) \hat{\mathbf{i}}_{x}+\sin \left(\theta_{I}\right) \hat{\mathbf{i}}_{z}\right)$, where $\hat{\mathbf{i}}_{x}$ and $\hat{\mathbf{i}}_{z}$ are unit vectors in the $x$ - and $z$-directions respectively, and choose the incident polarisation vector to satisfy $\mathbf{E}_{I} \cdot \hat{\mathbf{i}}_{x}=0$. By imposing appropriate boundary conditions for $\mathbf{E}(\mathbf{x}, t)$ at $x=0$, which you may assume to be the same as those for the time-independent case considered above, determine the Cartesian components of the wavevector $\mathbf{k}_{T}$ as functions of $k_{I}, \theta_{I}, \epsilon_{+}$and $\epsilon_{-}$.

  (iv) For $\epsilon_{+}<\epsilon_{-}$find a critical value $\theta_{I}^{\text {cr }}$ of the angle of incidence $\theta_{I}$ above which there is no real solution for the wavevector $\mathbf{k}_{T}$. Write down a solution for $\mathbf{E}(\mathbf{x}, t)$ when $\theta_{I}>\theta_{I}^{\mathrm{cr}}$ and comment on its form.

  comment

Fluid Dynamics II

• Paper 1, Section II, 39B

  Fluid Dynamics II | Part II, 2020

  A viscous fluid is confined between an inner, impermeable cylinder of radius $a$ with centre at $(x, y)=(0, a)$ and another outer, impermeable cylinder of radius $2 a$ with centre at $(0,2 a)$ (so they touch at the origin and both have their axes in the $z$ direction). The inner cylinder rotates about its axis with angular velocity $\Omega$ and the outer cylinder rotates about its axis with angular velocity $-\Omega / 4$. The fluid motion is two-dimensional and slow enough that the Stokes approximation is appropriate.

  (i) Show that the boundary of the inner cylinder is described by the relationship

  $$r=2 a \sin \theta,$$

  where $(r, \theta)$ are the usual polar coordinates centred on $(x, y)=(0,0)$. Show also that on this cylinder the boundary condition on the tangential velocity can be written as

  $$u_{r} \cos \theta+u_{\theta} \sin \theta=a \Omega,$$

  where $u_{r}$ and $u_{\theta}$ are the components of the velocity in the $r$ and $\theta$ directions respectively. Explain why the boundary condition $\psi=0$ (where $\psi$ is the streamfunction such that $u_{r}=\frac{1}{r} \frac{\partial \psi}{\partial \theta}$ and $\left.u_{\theta}=-\frac{\partial \psi}{\partial r}\right)$ can be imposed.

  (ii) Write down the boundary conditions to be satisfied on the outer cylinder $r=4 a \sin \theta$, explaining carefully why $\psi=0$ can also be imposed on this cylinder as well.

  (iii) It is given that the streamfunction is of the form

  $$\psi=A \sin ^{2} \theta+B r^{2}+C r \sin \theta+D \sin ^{3} \theta / r$$

  where $A, B, C$ and $D$ are constants, which satisfies $\nabla^{4} \psi=0$. Using the fact that $B=0$ due to the symmetry of the problem, show that the streamfunction is

  $$\psi=\frac{\alpha \sin \theta}{r}(r-2 a \sin \theta)(r-4 a \sin \theta)$$

  where the constant $\alpha$ is to be found.

  (iv) Sketch the streamline pattern between the cylinders and determine the $(x, y)$ coordinates of the stagnation point in the flow.

  comment

• Paper 2, Section II, 38B

  Fluid Dynamics II | Part II, 2020

  Consider a two-dimensional flow of a viscous fluid down a plane inclined at an angle $\alpha$ to the horizontal. Initially, the fluid, which has a volume $V$, occupies a region $0 \leqslant x \leqslant x^{*}$ with $x$ increasing down the slope. At large times the flow becomes thin-layer flow.

  (i) Write down the two-dimensional Navier-Stokes equations and simplify them using the lubrication approximation. Show that the governing equation for the height of the film, $h=h(x, t)$, is

  $$\tag{†} \frac{\partial h}{\partial t}+\frac{\partial}{\partial x}\left(\frac{g h^{3} \sin \alpha}{3 \nu}\right)=0$$

  where $\nu$ is the kinematic viscosity of the fluid and $g$ is the acceleration due to gravity, being careful to justify why the streamwise pressure gradient has been ignored compared to the gravitational body force.

  (ii) Develop a similarity solution to $(†)$ and, using the fact that the volume of fluid is conserved over time, derive an expression for the position and height of the head of the current downstream.

  (iii) Fluid is now continuously supplied at $x=0$. By using scaling analysis, estimate the rate at which fluid would have to be supplied for the head height to asymptote to a constant value at large times.

  comment

• Paper 3, Section II, 38B

  Fluid Dynamics II | Part II, 2020

  (a) Briefly outline the derivation of the boundary layer equation

  $$u u_{x}+v u_{y}=U d U / d x+\nu u_{y y}$$

  explaining the significance of the symbols used and what sets the $x$-direction.

  (b) Viscous fluid occupies the sector $0<\theta<\alpha$ in cylindrical coordinates which is bounded by rigid walls and there is a line sink at the origin of strength $\alpha Q$ with $Q / \nu \gg 1$. Assume that vorticity is confined to boundary layers along the rigid walls $\theta=0$ $(x>0, y=0)$ and $\theta=\alpha$.

  (i) Find the flow outside the boundary layers and clarify why boundary layers exist at all.

  (ii) Show that the boundary layer thickness along the wall $y=0$ is proportional to

  $$\delta:=\left(\frac{\nu}{Q}\right)^{1 / 2} x$$

  (iii) Show that the boundary layer equation admits a similarity solution for the streamfunction $\psi(x, y)$ of the form

  $$\psi=(\nu Q)^{1 / 2} f(\eta)$$

  where $\eta=y / \delta$. You should find the equation and boundary conditions satisfied by $f$.

  (iv) Verify that

  $$\frac{d f}{d \eta}=\frac{5-\cosh (\sqrt{2} \eta+c)}{1+\cosh (\sqrt{2} \eta+c)}$$

  yields a solution provided the constant $c$ has one of two possible values. Which is the likely physical choice?

  comment

• Paper 4 , Section II, 38B

  Fluid Dynamics II | Part II, 2020

  Consider a two-dimensional horizontal vortex sheet of strength $U$ in a homogeneous inviscid fluid at height $h$ above a horizontal rigid boundary at $y=0$ so that the fluid velocity is

  $$\boldsymbol{u}=\left\{\begin{array}{cr} U \hat{\boldsymbol{x}}, & 0<y<h \\ \mathbf{0}, & h<y \end{array}\right.$$

  (i) Investigate the linear instability of the sheet by determining the relevant dispersion relation for small, inviscid, irrotational perturbations. For what wavelengths is the sheet unstable?

  (ii) Evaluate the temporal growth rate and the wave propagation speed in the limits of both short and long waves. Using these results, sketch how the growth rate varies with the wavenumber.

  (iii) Comment briefly on how the introduction of a stable density difference (fluid in $y>h$ is less dense than that in $0<y<h$ ) and surface tension at the interface would affect the growth rates.

  comment

Further Complex Methods

• Paper 1, Section I, 7 E

  Further Complex Methods | Part II, 2020

  The function $I(z)$, defined by

  $$I(z)=\int_{0}^{\infty} t^{z-1} e^{-t} d t$$

  is analytic for $\operatorname{Re} z>0$.

  (i) Show that $I(z+1)=z I(z)$.

  (ii) Use part (i) to construct an analytic continuation of $I(z)$ into Re $z \leqslant 0$, except at isolated singular points, which you need to identify.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2020

  Use the change of variable $z=\sin ^{2} x$, to rewrite the equation

  $$\frac{d^{2} y}{d x^{2}}+k^{2} y=0$$

  where $k$ is a real non-zero number, as the hypergeometric equation

  $$\frac{d^{2} w}{d z^{2}}+\left(\frac{C}{z}+\frac{1+A+B-C}{z-1}\right) \frac{d w}{d z}+\frac{A B}{z(z-1)} w=0$$

  where $y(x)=w(z)$, and $A, B$ and $C$ should be determined explicitly.

  (i) Show that ( $\$)$ is a Papperitz equation, with 0,1 and $\infty$ as its regular singular points. Hence, write the corresponding Papperitz symbol,

  $$P\left\{\begin{array}{cccc} 0 & 1 & \infty \\ 0 & 0 & A \\ 1-C & C-A-B & B \end{array}\right\}$$

  in terms of $k$.

  (ii) By solving ( $\dagger$ ) directly or otherwise, find the hypergeometric function $F(A, B ; C ; z)$ that is the solution to $(\ddagger)$ and is analytic at $z=0$ corresponding to the exponent 0 at $z=0$, and satisfies $F(A, B ; C ; 0)=1$; moreover, write it in terms of $k$ and

  (iii) By performing a suitable exponential shifting find the second solution, independent of $F(A, B ; C ; z)$, which corresponds to the exponent $1-C$, and hence write $F\left(\frac{1+k}{2}, \frac{1-k}{2} ; \frac{3}{2} ; z\right)$ in terms of $k$ and $x$.

  comment

• Paper 2, Section $I$, E

  Further Complex Methods | Part II, 2020

  Evaluate

  $$\int_{C} \frac{d z}{\sin ^{3} z}$$

  where $C$ is the circle $|z|=4$ traversed in the counter-clockwise direction.

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2020

  A semi-infinite elastic string is initially at rest on the $x$-axis with $0 \leqslant x<\infty$. The transverse displacement of the string, $y(x, t)$, is governed by the partial differential equation

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}$$

  where $c$ is a positive real constant. For $t \geqslant 0$ the string is subject to the boundary conditions $y(0, t)=f(t)$ and $y(x, t) \rightarrow 0$ as $x \rightarrow \infty$.

  (i) Show that the Laplace transform of $y(x, t)$ takes the form

  $$\hat{y}(x, p)=\hat{f}(p) e^{-p x / c}$$

  (ii) For $f(t)=\sin \omega t$, with $\omega \in \mathbb{R}^{+}$, find $\hat{f}(p)$ and hence write $\hat{y}(x, p)$ in terms of $\omega, c, p$ and $x$. Obtain $y(x, t)$ by performing the inverse Laplace transform using contour integration. Provide a physical interpretation of the result.

  comment

• Paper 3, Section I, E

  Further Complex Methods | Part II, 2020

  The Weierstrass elliptic function is defined by

  $$\mathcal{P}(z)=\frac{1}{z^{2}}+\sum_{m, n}\left[\frac{1}{\left(z-\omega_{m, n}\right)^{2}}-\frac{1}{\omega_{m, n^{2}}}\right]$$

  where $\omega_{m, n}=m \omega_{1}+n \omega_{2}$, with non-zero periods $\left(\omega_{1}, \omega_{2}\right)$ such that $\omega_{1} / \omega_{2}$ is not real, and where $(m, n)$ are integers not both zero.

  (i) Show that, in a neighbourhood of $z=0$,

  $$\mathcal{P}(z)=\frac{1}{z^{2}}+\frac{1}{20} g_{2} z^{2}+\frac{1}{28} g_{3} z^{4}+O\left(z^{6}\right)$$

  where

  $$g_{2}=60 \sum_{m, n}\left(\omega_{m, n}\right)^{-4}, \quad g_{3}=140 \sum_{m, n}\left(\omega_{m, n}\right)^{-6}$$

  (ii) Deduce that $\mathcal{P}$ satisfies

  $$\left(\frac{d \mathcal{P}}{d z}\right)^{2}=4 \mathcal{P}^{3}-g_{2} \mathcal{P}-g_{3}$$

  comment

• Paper 4, Section I, E

  Further Complex Methods | Part II, 2020

  The Hilbert transform of a function $f(x)$ is defined by

  $$\mathcal{H}(f)(y):=\frac{1}{\pi} \mathcal{P} \int_{-\infty}^{+\infty} \frac{f(x)}{y-x} d x$$

  Calculate the Hilbert transform of $f(x)=\cos \omega x$, where $\omega$ is a non-zero real constant.

  comment

Galois Theory

• Paper 1, Section II, 18G

  Galois Theory | Part II, 2020

  (a) State and prove the tower law.

  (b) Let $K$ be a field and let $f(x) \in K[x]$.

  (i) Define what it means for an extension $L / K$ to be a splitting field for $f$.

  (ii) Suppose $f$ is irreducible in $K[x]$, and char $K=0$. Let $M / K$ be an extension of fields. Show that the roots of $f$ in $M$ are distinct.

  (iii) Let $h(x)=x^{q^{n}}-x \in K[x]$, where $K=F_{q}$ is the finite field with $q$ elements. Let $L$ be a splitting field for $h$. Show that the roots of $h$ in $L$ are distinct. Show that $[L: K]=n$. Show that if $f(x) \in K[x]$ is irreducible, and deg $f=n$, then $f$ divides $x^{q^{n}}-x$.

  (iv) For each prime $p$, give an example of a field $K$, and a polynomial $f(x) \in K[x]$ of degree $p$, so that $f$ has at most one root in any extension $L$ of $K$, with multiplicity $p$.

  comment

• Paper 2, Section II, 18G

  Galois Theory | Part II, 2020

  (a) Let $K$ be a field and let $L$ be the splitting field of a polynomial $f(x) \in K[x]$. Let $\xi_{N}$ be a primitive $N^{\text {th }}$root of unity. Show that $\operatorname{Aut}\left(L\left(\xi_{N}\right) / K\left(\xi_{N}\right)\right)$ is a subgroup of $\operatorname{Aut}(L / K)$.

  (b) Suppose that $L / K$ is a Galois extension of fields with cyclic Galois group generated by an element $\sigma$ of order $d$, and that $K$ contains a primitive $d^{\text {th }}$root of unity $\xi_{d}$. Show that an eigenvector $\alpha$ for $\sigma$ on $L$ with eigenvalue $\xi_{d}$ generates $L / K$, that is, $L=K(\alpha)$. Show that $\alpha^{d} \in K$.

  (c) Let $G$ be a finite group. Define what it means for $G$ to be solvable.

  Determine whether

  (i) $G=S_{4} ; \quad$ (ii) $G=S_{5}$

  are solvable.

  (d) Let $K=\mathbb{Q}\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right)$ be the field of fractions of the polynomial ring $\mathbb{Q}\left[a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right]$. Let $f(x)=x^{5}-a_{1} x^{4}+a_{2} x^{3}-a_{3} x^{2}+a_{4} x-a_{5} \in K[x]$. Show that $f$ is not solvable by radicals. [You may use results from the course provided that you state them clearly.]

  comment

• Paper 3, Section II, 18G

  Galois Theory | Part II, 2020

  (a) Let $L / K$ be a Galois extension of fields, with $\operatorname{Aut}(L / K)=A_{10}$, the alternating group on 10 elements. Find $[L: K]$.

  Let $f(x)=x^{2}+b x+c \in K[x]$ be an irreducible polynomial, char $K \neq 2$. Show that $f(x)$ remains irreducible in $L[x] .$

  (b) Let $L=\mathbb{Q}\left[\xi_{11}\right]$, where $\xi_{11}$ is a primitive $11^{\text {th }}$root of unity.

  Determine all subfields $M \subseteq L$. Which are Galois over $\mathbb{Q}$ ?

  For each proper subfield $M$, show that an element in $M$ which is not in $\mathbb{Q}$ must be primitive, and give an example of such an element explicitly in terms of $\xi_{11}$ for each $M$. [You do not need to justify that your examples are not in $\mathbb{Q}$.]

  Find a primitive element for the extension $L / \mathbb{Q}$.

  comment

• Paper 4, Section II, 18G

  Galois Theory | Part II, 2020

  (a) Let $K$ be a field. Define the discriminant $\Delta(f)$ of a polynomial $f(x) \in K[x]$, and explain why it is in $K$, carefully stating any theorems you use.

  Compute the discriminant of $x^{4}+r x+s$.

  (b) Let $K$ be a field and let $f(x) \in K[x]$ be a quartic polynomial with roots $\alpha_{1}, \ldots, \alpha_{4}$ such that $\alpha_{1}+\cdots+\alpha_{4}=0$.

  Define the resolvant cubic $g(x)$ of $f(x)$.

  Suppose that $\Delta(f)$ is a square in $K$. Prove that the resolvant cubic is irreducible if and only if $G a l(f)=A_{4}$. Determine the possible Galois groups Gal $(f)$ if $g(x)$ is reducible.

  The resolvant cubic of $x^{4}+r x+s$ is $x^{3}-4 s x-r^{2}$. Using this, or otherwise, determine $\operatorname{Gal}(f)$, where $f(x)=x^{4}+8 x+12 \in \mathbb{Q}[x]$. [You may use without proof that $f$ is irreducible.]

  comment

General Relativity

• Paper 1, Section II, 38D

  General Relativity | Part II, 2020

  Let $(\mathcal{M}, \boldsymbol{g})$ be a four-dimensional manifold with metric $g_{\alpha \beta}$ of Lorentzian signature.

  The Riemann tensor $\boldsymbol{R}$ is defined through its action on three vector fields $\boldsymbol{X}, \boldsymbol{V}, \boldsymbol{W}$ by

  $$\boldsymbol{R}(\boldsymbol{X}, \boldsymbol{V}) \boldsymbol{W}=\nabla_{\boldsymbol{X}} \nabla_{\boldsymbol{V}} \boldsymbol{W}-\nabla_{\boldsymbol{V}} \nabla_{\boldsymbol{X}} \boldsymbol{W}-\nabla_{[\boldsymbol{X}, \boldsymbol{V}]} \boldsymbol{W}$$

  and the Ricci identity is given by

  $$\nabla_{\alpha} \nabla_{\beta} V^{\gamma}-\nabla_{\beta} \nabla_{\alpha} V^{\gamma}=R_{\rho \alpha \beta}^{\gamma} V^{\rho} .$$

  (i) Show that for two arbitrary vector fields $\boldsymbol{V}, \boldsymbol{W}$, the commutator obeys

  $$[\boldsymbol{V}, \boldsymbol{W}]^{\alpha}=V^{\mu} \nabla_{\mu} W^{\alpha}-W^{\mu} \nabla_{\mu} V^{\alpha}$$

  (ii) Let $\gamma: I \times I^{\prime} \rightarrow \mathcal{M}, \quad I, I^{\prime} \subset \mathbb{R},(s, t) \mapsto \gamma(s, t)$ be a one-parameter family of affinely parametrized geodesics. Let $\boldsymbol{T}$ be the tangent vector to the geodesic $\gamma(s=$ const, $t)$ and $\boldsymbol{S}$ be the tangent vector to the curves $\gamma(s, t=$ const $)$. Derive the equation for geodesic deviation,

  $$\nabla_{T} \nabla_{T} \boldsymbol{S}=\boldsymbol{R}(\boldsymbol{T}, \boldsymbol{S}) \boldsymbol{T}$$

  (iii) Let $X^{\alpha}$ be a unit timelike vector field $\left(X^{\mu} X_{\mu}=-1\right)$ that satisfies the geodesic equation $\nabla_{\boldsymbol{X}} \boldsymbol{X}=0$ at every point of $\mathcal{M}$. Define

  $$\begin{array}{ll} B_{\alpha \beta}:=\nabla_{\beta} X_{\alpha}, & h_{\alpha \beta}:=g_{\alpha \beta}+X_{\alpha} X_{\beta}, \\ \Theta:=B^{\alpha \beta} h_{\alpha \beta}, \quad \sigma_{\alpha \beta}:=B_{(\alpha \beta)}-\frac{1}{3} \Theta h_{\alpha \beta}, & \omega_{\alpha \beta}:=B_{[\alpha \beta]} . \end{array}$$

  Show that

  $$\begin{gathered} B_{\alpha \beta} X^{\alpha}=B_{\alpha \beta} X^{\beta}=h_{\alpha \beta} X^{\alpha}=h_{\alpha \beta} X^{\beta}=0 \\ B_{\alpha \beta}=\frac{1}{3} \Theta h_{\alpha \beta}+\sigma_{\alpha \beta}+\omega_{\alpha \beta}, \quad g^{\alpha \beta} \sigma_{\alpha \beta}=0 \end{gathered}$$

  (iv) Let $\boldsymbol{S}$ denote the geodesic deviation vector, as defined in (ii), of the family of geodesics defined by the vector field $X^{\alpha}$. Show that $\boldsymbol{S}$ satisfies

  $$X^{\mu} \nabla_{\mu} S^{\alpha}=B_{\mu}^{\alpha} S^{\mu}$$

  (v) Show that

  $$X^{\mu} \nabla_{\mu} B_{\alpha \beta}=-B_{\beta}^{\mu} B_{\alpha \mu}+R_{\mu \beta \alpha}{ }^{\nu} X^{\mu} X_{\nu}$$

  comment

• Paper 2, Section II, $37 \mathrm{D}$

  General Relativity | Part II, 2020

  The Schwarzschild metric is given by

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2} d \theta^{2}+r^{2} \sin ^{2} \theta d \phi^{2}$$

  (i) Show that geodesics in the Schwarzschild spacetime obey the equation

  $$\frac{1}{2} \dot{r}^{2}+V(r)=\frac{1}{2} E^{2}, \quad \text { where } V(r)=\frac{1}{2}\left(1-\frac{2 M}{r}\right)\left(\frac{L^{2}}{r^{2}}-Q\right)$$

  where $E, L, Q$ are constants and the dot denotes differentiation with respect to a suitably chosen affine parameter $\lambda$.

  (ii) Consider the following three observers located in one and the same plane in the Schwarzschild spacetime which also passes through the centre of the black hole:

  • Observer $\mathcal{O}_{1}$ is on board a spacecraft (to be modeled as a pointlike object moving on a geodesic) on a circular orbit of radius $r>3 M$ around the central mass $M$.

  • Observer $\mathcal{O}_{2}$ starts at the same position as $\mathcal{O}_{1}$ but, instead of orbiting, stays fixed at the initial coordinate position by using rocket propulsion to counteract the gravitational pull.

  • Observer $\mathcal{O}_{3}$ is also located at a fixed position but at large distance $r \rightarrow \infty$ from the central mass and is assumed to be able to see $\mathcal{O}_{1}$ whenever the two are at the same azimuthal angle $\phi$.

  Show that the proper time intervals $\Delta \tau_{1}, \Delta \tau_{2}, \Delta \tau_{3}$, that are measured by the three observers during the completion of one full orbit of observer $\mathcal{O}_{1}$, are given by

  $$\Delta \tau_{i}=2 \pi \sqrt{\frac{r^{2}\left(r-\alpha_{i} M\right)}{M}}, \quad i=1,2,3$$

  where $\alpha_{1}, \alpha_{2}$ and $\alpha_{3}$ are numerical constants that you should determine.

  (iii) Briefly interpret the result by arranging the $\Delta \tau_{i}$ in ascending order.

  comment

• Paper 3, Section II, 37D

  General Relativity | Part II, 2020

  (a) Let $(\mathcal{M}, \boldsymbol{g})$ be a four-dimensional spacetime and let $\boldsymbol{T}$ denote the rank $\left(\begin{array}{l}1 \\ 1\end{array}\right)$ tensor defined by

  $$\boldsymbol{T}: \mathcal{T}_{p}^{*}(\mathcal{M}) \times \mathcal{T}_{p}(\mathcal{M}) \rightarrow \mathbb{R}, \quad(\boldsymbol{\eta}, \boldsymbol{V}) \mapsto \boldsymbol{\eta}(\boldsymbol{V}), \quad \forall \boldsymbol{\eta} \in \mathcal{T}_{p}^{*}(\mathcal{M}), \quad \boldsymbol{V} \in \mathcal{T}_{p}(\mathcal{M})$$

  Determine the components of the tensor $\boldsymbol{T}$ and use the general law for the transformation of tensor components under a change of coordinates to show that the components of $\boldsymbol{T}$ are the same in any coordinate system.

  (b) In Cartesian coordinates $(t, x, y, z)$ the Minkowski metric is given by

  $$d s^{2}=-d t^{2}+d x^{2}+d y^{2}+d z^{2} .$$

  Spheroidal coordinates $(r, \theta, \phi)$ are defined through

  $$\begin{aligned} x &=\sqrt{r^{2}+a^{2}} \sin \theta \cos \phi \\ y &=\sqrt{r^{2}+a^{2}} \sin \theta \sin \phi \\ z &=r \cos \theta \end{aligned}$$

  where $a \geqslant 0$ is a real constant.

  (i) Show that the Minkowski metric in coordinates $(t, r, \theta, \phi)$ is given by

  $$d s^{2}=-d t^{2}+\frac{r^{2}+a^{2} \cos ^{2} \theta}{r^{2}+a^{2}} d r^{2}+\left(r^{2}+a^{2} \cos ^{2} \theta\right) d \theta^{2}+\left(r^{2}+a^{2}\right) \sin ^{2} \theta d \phi^{2}$$

  (ii) Transform the metric ( $\dagger$ ) to null coordinates given by $u=t-r, R=r$ and show that $\partial / \partial R$ is not a null vector field for $a>0$.

  (iii) Determine a new azimuthal angle $\varphi=\phi-F(R)$ such that in the new coordinate system $(u, R, \theta, \varphi)$, the vector field $\partial / \partial R$ is null for any $a \geqslant 0$. Write down the Minkowski metric in this new coordinate system.

  comment

• Paper 4 , Section II, 37D

  General Relativity | Part II, 2020

  In linearized general relativity, we consider spacetime metrics that are perturbatively close to Minkowski, $g_{\mu \nu}=\eta_{\mu \nu}+h_{\mu \nu}$, where $\eta_{\mu \nu}=\operatorname{diag}(-1,1,1,1)$ and $h_{\mu \nu}=\mathcal{O}(\epsilon) \ll 1$. In the Lorenz gauge, the Einstein tensor, at linear order, is given by

  $$\tag{†} G_{\mu \nu}=-\frac{1}{2} \square \bar{h}_{\mu \nu}, \quad \bar{h}_{\mu \nu}=h_{\mu \nu}-\frac{1}{2} \eta_{\mu \nu} h$$

  where $\square=\eta^{\mu \nu} \partial_{\mu} \partial_{\nu}$ and $h=\eta^{\mu \nu} h_{\mu \nu}$.

  (i) Show that the (fully nonlinear) Einstein equations $G_{\alpha \beta}=8 \pi T_{\alpha \beta}$ can be equivalently written in terms of the Ricci tensor $R_{\alpha \beta}$ as

  $$R_{\alpha \beta}=8 \pi\left(T_{\alpha \beta}-\frac{1}{2} g_{\alpha \beta} T\right), \quad T=g^{\mu \nu} T_{\mu \nu}$$

  Show likewise that equation $(†)$ can be written as

  $$\square h_{\mu \nu}=-16 \pi\left(T_{\mu \nu}-\frac{1}{2} \eta_{\mu \nu} T\right)$$

  (ii) In the Newtonian limit we consider matter sources with small velocities $v \ll 1$ such that time derivatives $\partial / \partial t \sim v \partial / \partial x^{i}$ can be neglected relative to spatial derivatives, and the only non-negligible component of the energy-momentum tensor is the energy density $T_{00}=\rho$. Show that in this limit, we recover from equation $(*)$ the Poisson equation $\vec{\nabla}^{2} \Phi=4 \pi \rho$ of Newtonian gravity if we identify $h_{00}=-2 \Phi$.

  (iii) A point particle of mass $M$ is modelled by the energy density $\rho=M \delta(r)$. Derive the Newtonian potential $\Phi$ for this point particle by solving the Poisson equation.

  [You can assume the solution of $\vec{\nabla}^{2} \varphi=f(\boldsymbol{r})$ is $\varphi(\boldsymbol{r})=-\int \frac{f\left(\boldsymbol{r}^{\prime}\right)}{4 \pi\left|\boldsymbol{r}-\boldsymbol{r}^{\prime}\right|} d^{3} r^{\prime} .$ ]

  (iv) Now consider the Einstein equations with a small positive cosmological constant, $G_{\alpha \beta}+\Lambda g_{\alpha \beta}=8 \pi T_{\alpha \beta}, \Lambda=\mathcal{O}(\epsilon)>0$. Repeat the steps of questions (i)-(iii), again identifying $h_{00}=-2 \Phi$, to show that the Newtonian limit is now described by the Poisson equation $\vec{\nabla}^{2} \Phi=4 \pi \rho-\Lambda$, and that a solution for the potential of a point particle is given by

  $$\Phi=-\frac{M}{r}-B r^{2}$$

  where $B$ is a constant you should determine. Briefly discuss the effect of the $B r^{2}$ term and determine for which range of the radius $r$ the weak-field limit is a justified approximation. [Hint: Absorb the term $\Lambda g_{\alpha \beta}$ as part of the energy-momentum tensor. Note also that in spherical symmetry $\vec{\nabla}^{2} f=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r f)$.]

  comment

Graph Theory

• Paper 1, Section II, 17G

  Graph Theory | Part II, 2020

  (a) The complement of a graph is defined as having the same vertex set as the graph, with vertices being adjacent in the complement if and only if they are not adjacent in the graph.

  Show that no planar graph of order greater than 10 has a planar complement.

  What is the maximum order of a bipartite graph that has a bipartite complement?

  (b) For the remainder of this question, let $G$ be a connected bridgeless planar graph with $n \geqslant 4$ vertices, $e$ edges, and containing no circuit of length 4 . Suppose that it is drawn with $f$ faces, of which $t$ are 3-sided.

  Show that $2 e \geqslant 3 t+5(f-t)$. Show further that $e \geqslant 3 t$, and hence $f \leqslant 8 e / 15$.

  Deduce that $e \leqslant 15(n-2) / 7$. Is there some $n$ and some $G$ for which equality holds? [Hint: consider "slicing the corners off" a dodecahedron.]

  comment

• Paper 2, Section II, 17G

  Graph Theory | Part II, 2020

  (i) Define the local connectivity $\kappa(a, b ; G)$ for two non-adjacent vertices $a$ and $b$ in a graph $G$. Prove Menger's theorem, that $G$ contains a set of $\kappa(a, b ; G)$ vertex-disjoint $a-b$ paths.

  (ii) Recall that a subdivision $T K_{r}$ of $K_{r}$ is any graph obtained from $K_{r}$ by replacing its edges by vertex-disjoint paths. Let $G$ be a 3 -connected graph. Show that $G$ contains a $T K_{3}$. Show further that $G$ contains a $T K_{4}$. Must $G$ contain a $T K_{5}$?

  comment

• Paper 3, Section II, $17 \mathrm{G}$

  Graph Theory | Part II, 2020

  (i) State and prove Turán's theorem.

  (ii) Let $G$ be a graph of order $2 n \geqslant 4$ with $n^{2}+1$ edges. Show that $G$ must contain a triangle, and that if $n=2$ then $G$ contains two triangles.

  (iii) Show that if every edge of $G$ lies in a triangle then $G$ contains at least $\left(n^{2}+1\right) / 3$ triangles.

  (iv) Suppose that $G$ has some edge $u v$ contained in no triangles. Show that $\Gamma(u) \cap \Gamma(v)=\emptyset$, and that if $|\Gamma(u)|+|\Gamma(v)|=2 n$ then $\Gamma(u)$ and $\Gamma(v)$ are not both independent sets.

  By induction on $n$, or otherwise, show that every graph of order $2 n \geqslant 4$ with $n^{2}+1$ edges contains at least $n$ triangles. [Hint: If uv is an edge that is contained in no triangles, consider $G-u-v$.]

  comment

• Paper 4 , Section II, $17 G$

  Graph Theory | Part II, 2020

  State and prove Vizing's theorem about the chromatic index $\chi^{\prime}(G)$ of a graph $G$.

  Let $K_{m, n}$ be the complete bipartite graph with class sizes $m$ and $n$. By first considering $\chi^{\prime}\left(K_{n, n}\right)$, find $\chi^{\prime}\left(K_{m, n}\right)$ for all $m$ and $n$.

  Let $G$ be the graph of order $2 n+1$ obtained by subdividing a single edge of $K_{n, n}$ by a new vertex. Show that $\chi^{\prime}(G)=\Delta(G)+1$, where $\Delta(G)$ is the maximum degree of $G$.

  comment

Integrable Systems

• Paper 1, Section II, 33C

  Integrable Systems | Part II, 2020

  (a) Show that if $L$ is a symmetric matrix $\left(L=L^{T}\right)$ and $B$ is skew-symmetric $\left(B=-B^{T}\right)$ then $[B, L]=B L-L B$ is symmetric.

  (b) Consider the real $n \times n$ symmetric matrix

  $$L=\left(\begin{array}{cccccccc} 0 & a_{1} & 0 & 0 & \cdots & \cdots & \cdots & 0 \\ a_{1} & 0 & a_{2} & 0 & \cdots & \cdots & \cdots & 0 \\ 0 & a_{2} & 0 & a_{3} & \cdots & \cdots & \cdots & 0 \\ 0 & 0 & a_{3} & \cdots & \cdots & \cdots & \cdots & 0 \\ \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots & \cdots \\ 0 & \cdots & \cdots & \cdots & \cdots & \cdots & a_{n-2} & 0 \\ 0 & \cdots & \cdots & \cdots & \cdots & a_{n-2} & 0 & a_{n-1} \\ 0 & \cdots & \cdots & \cdots & \cdots & 0 & a_{n-1} & 0 \end{array}\right)$$

  (i.e. $L_{i, i+1}=L_{i+1, i}=a_{i}$ for $1 \leqslant i \leqslant n-1$, all other entries being zero) and the real $n \times n$ skew-symmetric matrix

  $$B=\left(\begin{array}{cccccccc} 0 & 0 & a_{1} a_{2} & 0 & \cdots & \cdots & \cdots & 0 \\ 0 & 0 & 0 & a_{2} a_{3} & \cdots & \ldots & \ldots & 0 \\ -a_{1} a_{2} & 0 & 0 & 0 & \ldots & \ldots & \ldots & 0 \\ 0 & -a_{2} a_{3} & 0 & \ldots & \cdots & \ldots & \ldots & 0 \\ \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots & \ldots \\ 0 & \ldots & \ldots & \ldots & \ldots & \ldots & 0 & a_{n-2} a_{n-1} \\ 0 & \ldots & \cdots & \cdots & \cdots & 0 & 0 & 0 \\ 0 & \ldots & \cdots & \cdots & \ldots & -a_{n-2} a_{n-1} & 0 & 0 \end{array}\right)$$

  (i.e. $B_{i, i+2}=-B_{i+2, i}=a_{i} a_{i+1}$ for $1 \leqslant i \leqslant n-2$, all other entries being zero).

  (i) Compute $[B, L]$.

  (ii) Assume that the $a_{j}$ are smooth functions of time $t$ so the matrix $L=L(t)$ also depends smoothly on $t$. Show that the equation $\frac{d L}{d t}=[B, L]$ implies that

  $$\frac{d a_{j}}{d t}=f\left(a_{j-1}, a_{j}, a_{j+1}\right)$$

  for some function $f$ which you should find explicitly.

  (iii) Using the transformation $a_{j}=\frac{1}{2} \exp \left[\frac{1}{2} u_{j}\right]$ show that

  $$\frac{d u_{j}}{d t}=\frac{1}{2}\left(e^{u_{j+1}}-e^{u_{j-1}}\right)$$

  for $j=1, \ldots n-1$. [Use the convention $u_{0}=-\infty, a_{0}=0, u_{n}=-\infty, a_{n}=0 .$ ]

  (iv) Deduce that given a solution of equation ( $\dagger$, there exist matrices $\{U(t)\}_{t \in \mathbb{R}}$ depending on time such that $L(t)=U(t) L(0) U(t)^{-1}$, and explain how to obtain first integrals for $(t)$ from this.

  comment

• Paper 2, Section II, 33C

  Integrable Systems | Part II, 2020

  (i) Explain how the inverse scattering method can be used to solve the initial value problem for the $\mathrm{KdV}$ equation

  $$u_{t}+u_{x x x}-6 u u_{x}=0, \quad u(x, 0)=u_{0}(x)$$

  including a description of the scattering data associated to the operator $L_{u}=-\partial_{x}^{2}+u(x, t)$, its time dependence, and the reconstruction of $u$ via the inverse scattering problem.

  (ii) Solve the inverse scattering problem for the reflectionless case, in which the reflection coefficient $R(k)$ is identically zero and the discrete scattering data consists of a single bound state, and hence derive the 1-soliton solution of $\mathrm{KdV}$.

  (iii) Consider the direct and inverse scattering problems in the case of a small potential $u(x)=\epsilon q(x)$, with $\epsilon$ arbitrarily small: $0<\epsilon \ll 1$. Show that the reflection coefficient is given by

  $$R(k)=\epsilon \int_{-\infty}^{\infty} \frac{e^{-2 i k z}}{2 i k} q(z) d z+O\left(\epsilon^{2}\right)$$

  and verify that the solution of the inverse scattering problem applied to this reflection coefficient does indeed lead back to the potential $u=\epsilon q$ when calculated to first order in

  

  comment

• Paper 3, Section II, 32C

  Integrable Systems | Part II, 2020

  (a) Given a smooth vector field

  $$V=V_{1}(x, u) \frac{\partial}{\partial x}+\phi(x, u) \frac{\partial}{\partial u}$$

  on $\mathbb{R}^{2}$ define the prolongation of $V$ of arbitrary order $N$.

  Calculate the prolongation of order two for the group $S O(2)$ of transformations of $\mathbb{R}^{2}$ given for $s \in \mathbb{R}$ by

  $$g^{s}\left(\begin{array}{l} u \\ x \end{array}\right)=\left(\begin{array}{l} u \cos s-x \sin s \\ u \sin s+x \cos s \end{array}\right)$$

  and hence, or otherwise, calculate the prolongation of order two of the vector field $V=-x \partial_{u}+u \partial_{x}$. Show that both of the equations $u_{x x}=0$ and $u_{x x}=\left(1+u_{x}^{2}\right)^{\frac{3}{2}}$ are invariant under this action of $S O(2)$, and interpret this geometrically.

  (b) Show that the sine-Gordon equation

  $$\frac{\partial^{2} u}{\partial X \partial T}=\sin u$$

  admits the group $\left\{g^{s}\right\}_{s \in \mathbb{R}}$, where

  $$g^{s}:\left(\begin{array}{c} X \\ T \\ u \end{array}\right) \mapsto\left(\begin{array}{c} e^{s} X \\ e^{-s} T \\ u \end{array}\right)$$

  as a group of Lie point symmetries. Show that there is a group invariant solution of the form $u(X, T)=F(z)$ where $z$ is an invariant formed from the independent variables, and hence obtain a second order equation for $w=w(z)$ where $\exp [i F]=w$.

  comment

Linear Analysis

• Paper 1, Section II, I

  Linear Analysis | Part II, 2020

  (a) Define the dual space $X^{*}$ of a (real) normed space $(X,\|\cdot\|)$. Define what it means for two normed spaces to be isometrically isomorphic. Prove that $\left(l_{1}\right)^{*}$ is isometrically isomorphic to $l_{\infty}$.

  (b) Let $p \in(1, \infty)$. [In this question, you may use without proof the fact that $\left(l_{p}\right)^{*}$ is isometrically isomorphic to $l_{q}$ where $\frac{1}{p}+\frac{1}{q}=1$.]

  (i) Show that if $\left\{\phi_{m}\right\}_{m=1}^{\infty}$ is a countable dense subset of $\left(l_{p}\right)^{*}$, then the function

  $$d(x, y):=\sum_{m=1}^{\infty} 2^{-m} \frac{\left|\phi_{m}(x-y)\right|}{1+\left|\phi_{m}(x-y)\right|}$$

  defines a metric on the closed unit ball $B \subset l_{p}$. Show further that for a sequence $\left\{x^{(n)}\right\}_{n=1}^{\infty}$ of elements $x^{(n)} \in B$, we have

  $$\phi\left(x^{(n)}\right) \rightarrow \phi(x) \quad \forall \phi \in\left(l_{p}\right)^{*} \quad \Leftrightarrow \quad d\left(x^{(n)}, x\right) \rightarrow 0$$

  Deduce that $(B, d)$ is a compact metric space.

  (ii) Give an example to show that for a sequence $\left\{x^{(n)}\right\}_{n=1}^{\infty}$ of elements $x^{(n)} \in B$ and $x \in B$,

  $$\phi\left(x^{(n)}\right) \rightarrow \phi(x) \quad \forall \phi \in\left(l_{p}\right)^{*} \quad \Rightarrow \quad\left\|x^{(n)}-x\right\|_{l_{p}} \rightarrow 0$$

  comment

• Paper 2, Section II, I

  Linear Analysis | Part II, 2020

  (a) State and prove the Baire Category theorem.

  Let $p>1$. Apply the Baire Category theorem to show that $\bigcup_{1 \leqslant q<p} l_{q} \neq l_{p}$. Give an explicit element of $l_{p} \backslash \bigcup_{1 \leqslant q<p} l_{q}$.

  (b) Use the Baire Category theorem to prove that $C([0,1])$ contains a function which is nowhere differentiable.

  (c) Let $(X,\|\cdot\|)$ be a real Banach space. Verify that the map sending $x$ to the function $e_{x}: \phi \mapsto \phi(x)$ is a continuous linear map of $X$ into $\left(X^{*}\right)^{*}$ where $X^{*}$ denotes the dual space of $(X,\|\cdot\|)$. Taking for granted the fact that this map is an isometry regardless of the norm on $X$, prove that if $\|\cdot\|^{\prime}$ is another norm on the vector space $X$ which is not equivalent to $\|\cdot\|$, then there is a linear function $\psi: X \rightarrow \mathbb{R}$ which is continuous with respect to one of the two norms $\|\cdot\|,\|\cdot\|^{\prime}$ and not continuous with respect to the other.

  comment

• Paper 3, Section II, I

  Linear Analysis | Part II, 2020

  Let $H$ be a separable complex Hilbert space.

  (a) For an operator $T: H \rightarrow H$, define the spectrum and point spectrum. Define what it means for $T$ to be: (i) a compact operator; (ii) a self-adjoint operator and (iii) a finite rank operator.

  (b) Suppose $T: H \rightarrow H$ is compact. Prove that given any $\delta>0$, there exists a finite-dimensional subspace $E \subset H$ such that $\left\|T\left(e_{n}\right)-P_{E} T\left(e_{n}\right)\right\|<\delta$ for each $n$, where $\left\{e_{1}, e_{2}, e_{3}, \ldots\right\}$ is an orthonormal basis for $H$ and $P_{E}$ denotes the orthogonal projection onto $E$. Deduce that a compact operator is the operator norm limit of finite rank operators.

  (c) Suppose that $S: H \rightarrow H$ has finite rank and $\lambda \in \mathbb{C} \backslash\{0\}$ is not an eigenvalue of $S$. Prove that $S-\lambda I$ is surjective. [You may wish to consider the action of $S(S-\lambda I)$ on $\left.\operatorname{ker}(S)^{\perp} .\right]$

  (d) Suppose $T: H \rightarrow H$ is compact and $\lambda \in \mathbb{C} \backslash\{0\}$ is not an eigenvalue of $T$. Prove that the image of $T-\lambda I$ is dense in $H$.

  Prove also that $T-\lambda I$ is bounded below, i.e. prove also that there exists a constant $c>0$ such that $\|(T-\lambda I) x\| \geqslant c\|x\|$ for all $x \in H$. Deduce that $T-\lambda I$ is surjective.

  comment

• Paper 4, Section II, I

  Linear Analysis | Part II, 2020

  (a) For $K$ a compact Hausdorff space, what does it mean to say that a set $S \subset C(K)$ is equicontinuous. State and prove the Arzelà-Ascoli theorem.

  (b) Suppose $K$ is a compact Hausdorff space for which $C(K)$ is a countable union of equicontinuous sets. Prove that $K$ is finite.

  (c) Let $F: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ be a bounded, continuous function and let $x_{0} \in \mathbb{R}^{n}$. Consider the problem of finding a differentiable function $x:[0,1] \rightarrow \mathbb{R}^{n}$ with

  $$x(0)=x_{0} \quad \text { and } \quad x^{\prime}(t)=F(x(t))$$

  for all $t \in[0,1]$. For each $k=1,2,3, \ldots$, let $x_{k}:[0,1] \rightarrow \mathbb{R}^{n}$ be defined by setting $x_{k}(0)=x_{0}$ and

  $$x_{k}(t)=x_{0}+\int_{0}^{t} F\left(y_{k}(s)\right) d s$$

  for $t \in[0,1]$, where

  $$y_{k}(t)=x_{k}\left(\frac{j}{k}\right)$$

  for $t \in\left(\frac{j}{k}, \frac{j+1}{k}\right]$ and $j \in\{0,1, \ldots, k-1\}$.

  (i) Verify that $x_{k}$ is well-defined and continuous on $[0,1]$ for each $k$.

  (ii) Prove that there exists a differentiable function $x:[0,1] \rightarrow \mathbb{R}^{n}$ solving (*) for $t \in[0,1]$.

  comment

Logic and Set Theory

• Paper 1, Section II, H

  Logic and Set Theory | Part II, 2020

  [Throughout this question, assume the axiom of choice.]

  Let $\kappa, \lambda$ and $\mu$ be cardinals. Define $\kappa+\lambda, \kappa \lambda$ and $\kappa^{\lambda}$. What does it mean to say $\kappa \leqslant \lambda$ ? Show that $\left(\kappa^{\lambda}\right)^{\mu}=\kappa^{\lambda \mu}$. Show also that $2^{\kappa}>\kappa$.

  Assume now that $\kappa$ and $\lambda$ are infinite. Show that $\kappa \kappa=\kappa$. Deduce that $\kappa+\lambda=\kappa \lambda=\max \{\kappa, \lambda\}$. Which of the following are always true and which can be false? Give proofs or counterexamples as appropriate. (i) $\kappa^{\lambda}=2^{\lambda}$; (ii) $\kappa \leqslant \lambda \Longrightarrow \kappa^{\lambda}=2^{\lambda}$; (iii) $\kappa^{\lambda}=\lambda^{\kappa}$.

  comment

• Paper 2, Section II, H

  Logic and Set Theory | Part II, 2020

  (a) This part of the question is concerned with propositional logic.

  Let $P$ be a set of primitive propositions. Let $S \subset L(P)$ be a consistent, deductively closed set such that for every $t \in L(P)$ either $t \in S$ or $\neg t \in S$. Show that $S$ has a model.

  (b) This part of the question is concerned with predicate logic.

  (i) State Gödel's completeness theorem for first-order logic. Deduce the compactness theorem, which you should state precisely.

  (ii) Let $X$ be an infinite set. For each $x \in X$, let $L_{x}$ be a subset of $X$. Suppose that for any finite $Y \subseteq X$ there exists a function $f_{Y}: Y \rightarrow\{1, \ldots, 100\}$ such that for all $x \in Y$ and all $y \in Y \cap L_{x}, f_{Y}(x) \neq f_{Y}(y)$. Show that there exists a function $F: X \rightarrow\{1, \ldots, 100\}$ such that for all $x \in X$ and all $y \in L_{x}, F(x) \neq F(y)$.

  comment

• Paper 3, Section II, $16 \mathrm{H}$

  Logic and Set Theory | Part II, 2020

  Let $(V, \in)$ be a model of ZF. Give the definition of a class and a function class in $V$. Use the concept of function class to give a short, informal statement of the Axiom of Replacement.

  Let $z_{0}=\omega$ and, for each $n \in \omega$, let $z_{n+1}=\mathcal{P} z_{n}$. Show that $y=\left\{z_{n} \mid n \in \omega\right\}$ is a set.

  We say that a set $x$ is small if there is an injection from $x$ to $z_{n}$ for some $n \in \omega$. Let HS be the class of sets $x$ such that every member of $\mathrm{TC}(\{x\})$ is small, where $\mathrm{TC}(\{x\})$ is the transitive closure of $\{x\}$. Show that $n \in \mathbf{H S}$ for all $n \in \omega$ and deduce that $\omega \in \mathbf{H S}$. Show further that $z_{n} \in \mathbf{H S}$ for all $n \in \omega$. Deduce that $y \in \mathbf{H S}$.

  Is $(\mathbf{H S}, \in)$ a model of ZF? Justify your answer.

  $[$ Recall that $0=\emptyset$ and that $n+1=n \cup\{n\}$ for all $n \in \omega .]$

  comment

• Paper 4, Section II, 16H

  Logic and Set Theory | Part II, 2020

  (a) State Zorn's lemma.

  [Throughout the remainder of this question, assume Zorn's lemma.]

  (b) Let $P$ be a poset in which every non-empty chain has an upper bound and let $x \in P$. By considering the poset $P_{x}=\{y \in P \mid x \leqslant y\}$, show that $P$ has a maximal element $\sigma$ with $x \leqslant \sigma$.

  (c) A filter is a non-empty subset $\mathcal{F} \subset \mathcal{P}(\mathbb{N})$ satisfying the following three conditions:

  • if $A, B \in \mathcal{F}$ then $A \cap B \in \mathcal{F}$

  • if $A \in \mathcal{F}$ and $A \subset B$ then $B \in \mathcal{F}$

  • $\emptyset \notin \mathcal{F} .$

  An ultrafilter is a filter $\mathcal{U}$ such that for all $A \subset \mathbb{N}$ we have either $A \in \mathcal{U}$ or $A^{c} \in \mathcal{U}$, where $A^{c}=\mathbb{N} \backslash A$.

  (i) For each $n \in \mathbb{N}$, show that $\mathcal{U}_{n}=\{A \subset \mathbb{N} \mid n \in A\}$ is an ultrafilter.

  (ii) Show that $\mathcal{F}=\left\{A \subset \mathbb{N} \mid A^{c}\right.$ is finite $\}$ is a filter but not an ultrafilter, and that for all $n \in \mathbb{N}$ we have $\mathcal{F} \not \subset \mathcal{U}_{n}$.

  (iii) Does there exist an ultrafilter $\mathcal{U}$ such that $\mathcal{U} \neq \mathcal{U}_{n}$ for any $n \in \mathbb{N}$ ? Justify your answer.

  comment

Mathematical Biology

• Paper 1, Section I, 6B

  Mathematical Biology | Part II, 2020

  Consider a bivariate diffusion process with drift vector $A_{i}(\mathbf{x})=a_{i j} x_{j}$ and diffusion matrix $b_{i j}$ where

  $$a_{i j}=\left(\begin{array}{cc} -1 & 1 \\ -2 & -1 \end{array}\right), \quad b_{i j}=\left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right)$$

  $\mathbf{x}=\left(x_{1}, x_{2}\right)$ and $i, j=1,2$.

  (i) Write down the Fokker-Planck equation for the probability $P\left(x_{1}, x_{2}, t\right)$.

  (ii) Plot the drift vector as a vector field around the origin in the region $\left|x_{1}\right|<1$, $\left|x_{2}\right|<1$.

  (iii) Obtain the stationary covariances $C_{i j}=\left\langle x_{i} x_{j}\right\rangle$ in terms of the matrices $a_{i j}$ and $b_{i j}$ and hence compute their explicit values.

  comment

• Paper 2, Section I, 6B

  Mathematical Biology | Part II, 2020

  Consider the system of predator-prey equations

  $$\begin{aligned} &\frac{d N_{1}}{d t}=-\epsilon_{1} N_{1}+\alpha N_{1} N_{2} \\ &\frac{d N_{2}}{d t}=\epsilon_{2} N_{2}-\alpha N_{1} N_{2} \end{aligned}$$

  where $\epsilon_{1}, \epsilon_{2}$ and $\alpha$ are positive constants.

  (i) Determine the non-zero fixed point $\left(N_{1}^{*}, N_{2}^{*}\right)$ of this system.

  (ii) Show that the system can be written in the form

  $$\frac{d x_{i}}{d t}=\sum_{j=1}^{2} K_{i j} \frac{\partial H}{\partial x_{j}}, \quad i=1,2$$

  where $x_{i}=\log \left(N_{i} / N_{i}^{*}\right)$ and a suitable $2 \times 2$ antisymmetric matrix $K_{i j}$ and scalar function $H\left(x_{1}, x_{2}\right)$ are to be identified.

  (iii) Hence, or otherwise, show that $H$ is constant on solutions of the predator-prey equations.

  comment

• Paper 3, Section I, B

  Mathematical Biology | Part II, 2020

  Consider a model for the common cold in which the population is partitioned into susceptible $(S)$, infective $(I)$, and recovered $(R)$ categories, which satisfy

  $$\begin{aligned} \frac{d S}{d t} &=\alpha R-\beta S I \\ \frac{d I}{d t} &=\beta S I-\gamma I \\ \frac{d R}{d t} &=\gamma I-\alpha R \end{aligned}$$

  where $\alpha, \beta$ and $\gamma$ are positive constants.

  (i) Show that the sum $N \equiv S+I+R$ does not change in time.

  (ii) Determine the condition, in terms of $\beta, \gamma$ and $N$, for an endemic steady state to exist, that is, a time-independent state with a non-zero number of infectives.

  (iii) By considering a reduced set of equations for $S$ and $I$ only, show that the endemic steady state identified in (ii) above, if it exists, is stable.

  comment

• Paper 3, Section II, 13B

  Mathematical Biology | Part II, 2020

  The larva of a parasitic worm disperses in one dimension while laying eggs at rate $\lambda>0$. The larvae die at rate $\mu$ and have diffusivity $D$, so that their density, $n(x, t)$, obeys

  $$\frac{\partial n}{\partial t}=D \frac{\partial^{2} n}{\partial x^{2}}-\mu n, \quad(D>0, \mu>0)$$

  The eggs do not diffuse, so that their density, $e(x, t)$, obeys

  $$\frac{\partial e}{\partial t}=\lambda n$$

  At $t=0$ there are no eggs and $N$ larvae concentrated at $x=0$, so that $n(x, 0)=N \delta(x)$.

  (i) Determine $n(x, t)$ for $t>0$. Show that $n(x, t) \rightarrow 0$ as $t \rightarrow \infty$.

  (ii) Determine the limit of $e(x, t)$ as $t \rightarrow \infty$.

  (iii) Provide a physical explanation for the remnant density of the eggs identified in part (ii).

  [You may quote without proof the results

  $$\begin{aligned} \int_{-\infty}^{\infty} \exp \left(-x^{2}\right) d x &=\sqrt{\pi} \\ \int_{-\infty}^{\infty} \frac{\exp (i k x)}{k^{2}+\alpha^{2}} d k &=\pi \exp (-\alpha|x|) / \alpha, \quad \alpha>0 \end{aligned}$$

  comment

• Paper 4, Section I, B

  Mathematical Biology | Part II, 2020

  Consider a population process in which the probability of transition from a state with $n$ individuals to a state with $n+1$ individuals in the interval $(t, t+\Delta t)$ is $\lambda n \Delta t$ for small $\Delta t$.

  (i) Write down the master equation for the probability, $P_{n}(t)$, of the state $n$ at time $t$ for $n \geqslant 1$

  (ii) Assuming an initial distribution

  $$P_{n}(0)= \begin{cases}1, & \text { if } n=1 \\ 0, & \text { if } n>1\end{cases}$$

  show that

  $$P_{n}(t)=\exp (-\lambda t)(1-\exp (-\lambda t))^{n-1}$$

  (iii) Hence, determine the mean of $n$ for $t>0$.

  comment

• Paper 4, Section II, 14B

  Mathematical Biology | Part II, 2020

  Consider the stochastic catalytic reaction

  $$E \leftrightharpoons E S, \quad E S \rightarrow E+P$$

  in which a single enzyme $E$ complexes reversibly to $E S$ (at forward rate $k_{1}$ and reverse rate $k_{1}^{\prime}$ ) and decomposes into product $P$ (at forward rate $k_{2}$ ), regenerating enzyme $E$. Assume there is sufficient substrate $S$ so that this catalytic cycle can continue indefinitely. Let $P(E, n)$ be the probability of the state with enzyme $E$ and $n$ products and $P(E S, n)$ the probability of the state with complex $E S$ and $n$ products, these states being mutually exclusive.

  (i) Write down the master equation for the probabilities $P(E, n)$ and $P(E S, n)$ for $n \geqslant 0$

  (ii) Assuming an initial state with zero products, solve the master equation for $P(E, 0)$ and $P(E S, 0)$.

  (iii) Hence find the probability distribution $f(\tau)$ of the time $\tau$ taken to form the first product.

  (iv) Obtain the mean of $\tau$.

  comment

Mathematics of Machine Learning

• Paper 1, Section II, J

  Mathematics of Machine Learning | Part II, 2020

  (a) Let $Z_{1}, \ldots, Z_{n}$ be i.i.d. random elements taking values in a set $\mathcal{Z}$ and let $\mathcal{F}$ be a class of functions $f: \mathcal{Z} \rightarrow \mathbb{R}$. Define the Rademacher complexity $\mathcal{R}_{n}(\mathcal{F})$. Write down an inequality relating the Rademacher complexity and

  $$\mathbb{E}\left(\sup _{f \in \mathcal{F}} \frac{1}{n} \sum_{i=1}^{n}\left(f\left(Z_{i}\right)-\mathbb{E} f\left(Z_{i}\right)\right)\right)$$

  State the bounded differences inequality.

  (b) Now given i.i.d. input-output pairs $\left(X_{1}, Y_{1}\right), \ldots,\left(X_{n}, Y_{n}\right) \in \mathcal{X} \times\{-1,1\}$ consider performing empirical risk minimisation with misclassification loss over the class $\mathcal{H}$ of classifiers $h: \mathcal{X} \rightarrow\{-1,1\}$. Denote by $\hat{h}$ the empirical risk minimiser [which you may assume exists]. For any classifier $h$, let $R(h)$ be its misclassification risk and suppose this is minimised over $\mathcal{H}$ by $h^{*} \in \mathcal{H}$. Prove that with probability at least $1-\delta$,

  $$R(\hat{h})-R\left(h^{*}\right) \leqslant 2 \mathcal{R}_{n}(\mathcal{F})+\sqrt{\frac{2 \log (2 / \delta)}{n}}$$

  for $\delta \in(0,1]$, where $\mathcal{F}$ is a class of functions $f: \mathcal{X} \times\{-1,1\} \rightarrow\{0,1\}$ related to $\mathcal{H}$ that you should specify.

  (c) Let $Z_{i}=\left(X_{i}, Y_{i}\right)$ for $i=1, \ldots, n$. Define the empirical Rademacher complexity $\hat{\mathcal{R}}\left(\mathcal{F}\left(Z_{1: n}\right)\right)$. Show that with probability at least $1-\delta$,

  $$R(\hat{h})-R\left(h^{*}\right) \leqslant 2 \hat{\mathcal{R}}\left(\mathcal{F}\left(Z_{1: n}\right)\right)+2 \sqrt{\frac{2 \log (3 / \delta)}{n}}$$

  comment

• Paper 2, Section II, J

  Mathematics of Machine Learning | Part II, 2020

  (a) Let $\mathcal{F}$ be a family of functions $f: \mathcal{X} \rightarrow\{0,1\}$. What does it mean for $x_{1: n} \in \mathcal{X}^{n}$ to be shattered by $\mathcal{F}$ ? Define the shattering coefficient $s(\mathcal{F}, n)$ and the $V C$ dimension $\operatorname{VC}(\mathcal{F})$ of $\mathcal{F}$

  Let

  $$\mathcal{A}=\left\{\prod_{j=1}^{d}\left(-\infty, a_{j}\right]: a_{1}, \ldots, a_{d} \in \mathbb{R}\right\}$$

  and set $\mathcal{F}=\left\{\mathbf{1}_{A}: A \in \mathcal{A}\right\}$. Compute $\operatorname{VC}(\mathcal{F})$.

  (b) State the Sauer-Shelah lemma.

  (c) Let $\mathcal{F}_{1}, \ldots, \mathcal{F}_{r}$ be families of functions $f: \mathcal{X} \rightarrow\{0,1\}$ with finite VC dimension $v \geqslant 1$. Now suppose $x_{1: n}$ is shattered by $\cup_{k=1}^{r} \mathcal{F}_{k}$. Show that

  $$2^{n} \leqslant r(n+1)^{v} .$$

  Conclude that for $v \geqslant 3$,

  $$\mathrm{VC}\left(\cup_{k=1}^{r} \mathcal{F}_{k}\right) \leqslant 4 v \log _{2}(2 v)+2 \log _{2}(r)$$

  [You may use without proof the fact that if $x \leqslant \alpha+\beta \log _{2}(x+1)$ with $\alpha>0$ and $\beta \geqslant 3$, then $x \leqslant 4 \beta \log _{2}(2 \beta)+2 \alpha$ for $x \geqslant 1$.]

  (d) Now let $\mathcal{B}$ be the collection of subsets of $\mathbb{R}^{p}$ of the form of a product $\prod_{j=1}^{p} A_{j}$ of intervals $A_{j}$, where exactly $d \in\{1, \ldots, p\}$ of the $A_{j}$ are of the form $\left(-\infty, a_{j}\right]$ for $a_{j} \in \mathbb{R}$ and the remaining $p-d$ intervals are $\mathbb{R}$. Set $\mathcal{G}=\left\{\mathbf{1}_{B}: B \in \mathcal{B}\right\}$. Show that when $d \geqslant 3$,

  $$\mathrm{VC}(\mathcal{G}) \leqslant 2 d\left[2 \log _{2}(2 d)+\log _{2}(p)\right]$$

  comment

• Paper 4, Section II, J

  Mathematics of Machine Learning | Part II, 2020

  Suppose we have input-output pairs $\left(x_{1}, y_{1}\right), \ldots,\left(x_{n}, y_{n}\right) \in \mathbb{R}^{p} \times\{-1,1\}$. Consider the empirical risk minimisation problem with hypothesis class

  $$\mathcal{H}=\left\{x \mapsto x^{T} \beta: \beta \in C\right\}$$

  where $C$ is a non-empty closed convex subset of $\mathbb{R}^{p}$, and logistic loss

  $$\ell(h(x), y)=\log _{2}\left(1+e^{-y h(x)}\right),$$

  for $h \in \mathcal{H}$ and $(x, y) \in \mathbb{R}^{p} \times\{-1,1\}$.

  (i) Show that the objective function $f$ of the optimisation problem is convex.

  (ii) Let $\pi_{C}(x)$ denote the projection of $x$ onto $C$. Describe the procedure of stochastic gradient descent (SGD) for minimisation of $f$ above, giving explicit forms for any gradients used in the algorithm.

  (iii) Suppose $\hat{\beta}$ minimises $f(\beta)$ over $\beta \in C$. Suppose $\max _{i=1, \ldots, n}\left\|x_{i}\right\|_{2} \leqslant M$ and $\sup _{\beta \in C}\|\beta\|_{2} \leqslant R$. Prove that the output $\bar{\beta}$ of $k$ iterations of the SGD algorithm with some fixed step size $\eta$ (which you should specify), satisfies

  $$\mathbb{E} f(\bar{\beta})-f(\hat{\beta}) \leqslant \frac{2 M R}{\log (2) \sqrt{k}}$$

  (iv) Now suppose that the step size at iteration $s$ is $\eta_{s}>0$ for each $s=1, \ldots, k$. Show that, writing $\beta_{s}$ for the $s$ th iterate of SGD, we have

  $$\mathbb{E} f(\tilde{\beta})-f(\hat{\beta}) \leqslant \frac{A_{2} M^{2}}{2 A_{1}\{\log (2)\}^{2}}+\frac{2 R^{2}}{A_{1}}$$

  where

  $$\tilde{\beta}=\frac{1}{A_{1}} \sum_{s=1}^{k} \eta_{s} \beta_{s}, \quad A_{1}=\sum_{s=1}^{k} \eta_{s} \quad \text { and } \quad A_{2}=\sum_{s=1}^{k} \eta_{s}^{2}$$

  [You may use standard properties of convex functions and projections onto closed convex sets without proof provided you state them.]

  comment

Number Fields

• Paper 1, Section II, 20G

  Number Fields | Part II, 2020

  State Minkowski's theorem.

  Let $K=\mathbb{Q}(\sqrt{-d})$, where $d$ is a square-free positive integer, not congruent to 3 $(\bmod 4) .$ Show that every nonzero ideal $I \subset \mathcal{O}_{K}$ contains an element $\alpha$ with

  $$0<\left|N_{K / \mathbb{Q}}(\alpha)\right| \leqslant \frac{4 \sqrt{d}}{\pi} N(I)$$

  Deduce the finiteness of the class group of $K$.

  Compute the class group of $\mathbb{Q}(\sqrt{-22})$. Hence show that the equation $y^{3}=x^{2}+22$ has no integer solutions.

  comment

• Paper 2, Section II, 20G

  Number Fields | Part II, 2020

  (a) Let $K$ be a number field of degree $n$. Define the discriminant $\operatorname{disc}\left(\alpha_{1}, \ldots, \alpha_{n}\right)$ of an $n$-tuple of elements $\alpha_{i}$ of $K$, and show that it is nonzero if and only if $\alpha_{1}, \ldots, \alpha_{n}$ is a $\mathbb{Q}$-basis for $K$.

  (b) Let $K=\mathbb{Q}(\alpha)$ where $\alpha$ has minimal polynomial

  $$T^{n}+\sum_{j=0}^{n-1} a_{j} T^{j}, \quad a_{j} \in \mathbb{Z}$$

  and assume that $p$ is a prime such that, for every $j, a_{j} \equiv 0(\bmod p)$, but $a_{0} \not \equiv 0\left(\bmod p^{2}\right)$.

  (i) Show that $P=(p, \alpha)$ is a prime ideal, that $P^{n}=(p)$ and that $\alpha \notin P^{2}$. [Do not assume that $\mathcal{O}_{K}=\mathbb{Z}[\alpha]$.]

  (ii) Show that the index of $\mathbb{Z}[\alpha]$ in $\mathcal{O}_{K}$ is prime to $p$.

  (iii) If $K=\mathbb{Q}(\alpha)$ with $\alpha^{3}+3 \alpha+3=0$, show that $\mathcal{O}_{K}=\mathbb{Z}[\alpha]$. [You may assume without proof that the discriminant of $T^{3}+a T+b$ is $-4 a^{3}-27 b^{2}$.]

  comment

• Paper 4, Section II, 20G

  Number Fields | Part II, 2020

  Let $K$ be a number field of degree $n$, and let $\left\{\sigma_{i}: K \hookrightarrow \mathbb{C}\right\}$ be the set of complex embeddings of $K$. Show that if $\alpha \in \mathcal{O}_{K}$ satisfies $\left|\sigma_{i}(\alpha)\right|=1$ for every $i$, then $\alpha$ is a root of unity. Prove also that there exists $c>1$ such that if $\alpha \in \mathcal{O}_{K}$ and $\left|\sigma_{i}(\alpha)\right|<c$ for all $i$, then $\alpha$ is a root of unity.

  State Dirichlet's Unit theorem.

  Let $K \subset \mathbb{R}$ be a real quadratic field. Assuming Dirichlet's Unit theorem, show that the set of units of $K$ which are greater than 1 has a smallest element $\epsilon$, and that the group of units of $K$ is then $\left\{\pm \epsilon^{n} \mid n \in \mathbb{Z}\right\}$. Determine $\epsilon$ for $\mathbb{Q}(\sqrt{11})$, justifying your result. [If you use the continued fraction algorithm, you must prove it in full.]

  comment

Number Theory

• Paper 1, Section I, H

  Number Theory | Part II, 2020

  What does it mean to say that a positive definite binary quadratic form is reduced?

  Find all reduced binary quadratic forms of discriminant $-20$.

  Prove that if a prime $p \neq 5$ is represented by $x^{2}+5 y^{2}$, then $p \equiv 1,3,7$ or $9 \bmod 20$.

  comment

• Paper 2, Section I, $1 \mathbf{H}$

  Number Theory | Part II, 2020

  Let $\theta \in \mathbb{R}$.

  For each integer $n \geqslant-1$, define the convergents $p_{n} / q_{n}$ of the continued fraction expansion of $\theta$. Show that for all $n \geqslant 0, p_{n} q_{n-1}-p_{n-1} q_{n}=(-1)^{n-1}$. Deduce that if $q \in \mathbb{N}$ and $p \in \mathbb{Z}$ satisfy

  $$\left|\theta-\frac{p}{q}\right|<\left|\theta-\frac{p_{n}}{q_{n}}\right|$$

  then $q>q_{n}$.

  Compute the continued fraction expansion of $\sqrt{12}$. Hence or otherwise find a solution in positive integers $x$ and $y$ to the equation $x^{2}-12 y^{2}=1$.

  comment

• Paper 3, Section I, $1 \mathrm{H}$

  Number Theory | Part II, 2020

  Let $N \geqslant 3$ be an odd integer and $b$ an integer with $(b, N)=1$. What does it mean to say that $N$ is an Euler pseudoprime to base $b$ ?

  Show that if $N$ is not an Euler pseudoprime to some base $b_{0}$, then it is not an Euler pseudoprime to at least half the bases $\{1 \leqslant b<N:(b, N)=1\}$.

  Show that if $N$ is odd and composite, then there exists an integer $b$ such that $N$ is not an Euler pseudoprime to base $b$.

  comment

• Paper 3, Section II, 11H

  Number Theory | Part II, 2020

  Let $p$ be an odd prime.

  (i) Define the Legendre symbol $\left(\frac{x}{p}\right)$, and show that when $(x, p)=1$, then $\left(\frac{x^{-1}}{p}\right)=\left(\frac{x}{p}\right)$.

  (ii) State and prove Gauss's lemma, and use it to evaluate $\left(\frac{-1}{p}\right)$. [You may assume Euler's criterion.]

  (iii) Prove that

  $$\sum_{x=1}^{p}\left(\frac{x}{p}\right)=0$$

  and deduce that

  $$\sum_{x=1}^{p}\left(\frac{x(x+1)}{p}\right)=-1$$

  Hence or otherwise determine the number of pairs of consecutive integers $z, z+1$ such that $1 \leqslant z, z+1 \leqslant p-1$ and both $z$ and $z+1$ are quadratic residues $\bmod p$.

  comment

• Paper 4 , Section II, 11H

  Number Theory | Part II, 2020

  (a) What does it mean to say that a function $f: \mathbb{N} \rightarrow \mathbb{C}$ is multiplicative? Show that if $f, g: \mathbb{N} \rightarrow \mathbb{C}$ are both multiplicative, then so is $f \star g: \mathbb{N} \rightarrow \mathbb{C}$, defined for all $n \in \mathbb{N}$ by

  $$f \star g(n)=\sum_{d \mid n} f(d) g\left(\frac{n}{d}\right)$$

  Show that if $f=\mu \star g$, where $\mu$ is the Möbius function, then $g=f \star 1$, where 1 denotes the constant function 1 .

  (b) Let $\tau(n)$ denote the number of positive divisors of $n$. Find $f, g: \mathbb{N} \rightarrow \mathbb{C}$ such that $\tau=f \star g$, and deduce that $\tau$ is multiplicative. Hence or otherwise show that for all $s \in \mathbb{C}$ with $\operatorname{Re}(s)>1$,

  $$\sum_{n=1}^{\infty} \frac{\tau(n)}{n^{s}}=\zeta(s)^{2}$$

  where $\zeta$ is the Riemann zeta function.

  (c) Fix $k \in \mathbb{N}$. By considering suitable powers of the product of the first $k+1$ primes, show that

  $$\tau(n) \geqslant(\log n)^{k}$$

  for infinitely many $n \in \mathbb{N}$.

  (d) Fix $\epsilon>0$. Show that

  $$\frac{\tau(n)}{n^{\epsilon}}=\prod_{p \text { prime, } p^{\alpha}|| n} \frac{(\alpha+1)}{p^{\alpha \epsilon}}$$

  where $p^{\alpha} \| n$ denotes the fact that $\alpha \in \mathbb{N}$ is such that $p^{\alpha} \mid n$ but $p^{\alpha+1} \nmid n$. Deduce that there exists a positive constant $C(\epsilon)$ depending only on $\epsilon$ such that for all $n \in \mathbb{N}, \tau(n) \leqslant C(\epsilon) n^{\epsilon} .$

  comment

• Paper 4, Section I, H

  Number Theory | Part II, 2020

  Let $p$ be a prime.

  State and prove Lagrange's theorem on the number of solutions of a polynomial congruence modulo $p$. Deduce that $(p-1) ! \equiv-1 \bmod p$.

  Let $k$ be a positive integer such that $k \mid(p-1)$. Show that the congruence

  $$x^{k} \equiv 1 \quad \bmod p$$

  has precisely $k$ solutions modulo $p$.

  comment

Numerical Analysis

• Paper 1, Section II, E

  Numerical Analysis | Part II, 2020

  Let $A \in \mathbb{R}^{n \times n}$ be a real symmetric matrix with distinct eigenvalues $\lambda_{1}<\lambda_{2}<\cdots<$ $\lambda_{n}$ and a corresponding orthonormal basis of real eigenvectors $\left\{\boldsymbol{w}_{i}\right\}_{i=1}^{n}$. Given a unit norm vector $\boldsymbol{x}^{(0)} \in \mathbb{R}^{n}$, and a set of parameters $s_{k} \in \mathbb{R}$, consider the inverse iteration algorithm

  $$\left(A-s_{k} I\right) \boldsymbol{y}=\boldsymbol{x}^{(k)}, \quad \boldsymbol{x}^{(k+1)}=\boldsymbol{y} /\|\boldsymbol{y}\|, \quad k \geqslant 0 .$$

  (a) Let $s_{k}=s=$ const for all $k$. Assuming that $\boldsymbol{x}^{(0)}=\sum_{i=1}^{n} c_{i} \boldsymbol{w}_{i}$ with all $c_{i} \neq 0$, prove that

  $$s<\lambda_{1} \Rightarrow \boldsymbol{x}^{(k)} \rightarrow \boldsymbol{w}_{1} \quad \text { or } \quad \boldsymbol{x}^{(k)} \rightarrow-\boldsymbol{w}_{1} \quad(k \rightarrow \infty) .$$

  Explain briefly what happens to $\boldsymbol{x}^{(k)}$ when $\lambda_{m}<s<\lambda_{m+1}$ for some $m \in\{1,2, \ldots, n-1\}$, and when $\lambda_{n}<s$.

  (b) Let $s_{k}=\left(A \boldsymbol{x}^{(k)}, \boldsymbol{x}^{(k)}\right)$ for $k \geqslant 0$. Assuming that, for some $k$, some $a_{i} \in \mathbb{R}$ and for a small $\epsilon$,

  $$\boldsymbol{x}^{(k)}=c^{-1}\left(\boldsymbol{w}_{1}+\epsilon \sum_{i \geqslant 2} a_{i} \boldsymbol{w}_{i}\right)$$

  where $c$ is the appropriate normalising constant. Show that $s_{k}=\lambda_{1}-K \epsilon^{2}+\mathcal{O}\left(\epsilon^{4}\right)$ and determine the value of $K$. Hence show that

  $$\boldsymbol{x}^{(k+1)}=c_{1}^{-1}\left(\boldsymbol{w}_{1}+\epsilon^{3} \sum_{i \geqslant 2} b_{i} \boldsymbol{w}_{i}+\mathcal{O}\left(\epsilon^{5}\right)\right)$$

  where $c_{1}$ is the appropriate normalising constant, and find expressions for $b_{i}$.

  comment

• Paper 2, Section II, 40E

  Numerical Analysis | Part II, 2020

  (a) For $A \in \mathbb{R}^{n \times n}$ and nonzero $\boldsymbol{v} \in \mathbb{R}^{n}$, define the $m$-th Krylov subspace $K_{m}(A, \boldsymbol{v})$ of $\mathbb{R}^{n}$. Prove that if $A$ has $n$ linearly independent eigenvectors with at most $s$ distinct eigenvalues, then

  $$\operatorname{dim} K_{m}(A, \boldsymbol{v}) \leqslant s \quad \forall m$$

  (b) Define the term residual in the conjugate gradient (CG) method for solving a system $A \boldsymbol{x}=\boldsymbol{b}$ with a symmetric positive definite $A$. State two properties of the method regarding residuals and their connection to certain Krylov subspaces, and hence show that, for any right-hand side $\boldsymbol{b}$, the method finds the exact solution after at most $s$ iterations, where $s$ is the number of distinct eigenvalues of $A$.

  (c) The preconditioned CG-method $P A P^{T} \widehat{\boldsymbol{x}}=P \boldsymbol{b}$ is applied for solving $A \boldsymbol{x}=\boldsymbol{b}$, with

  

  Prove that the method finds the exact solution after two iterations at most.

  (d) Prove that, for any symmetric positive definite $A$, we can find a preconditioner $P$ such that the preconditioned CG-method for solving $A \boldsymbol{x}=\boldsymbol{b}$ would require only one step. Explain why this preconditioning is of hardly any use.

  comment

• Paper 3, Section II, 40E

  Numerical Analysis | Part II, 2020

  (a) Give the definition of a normal matrix. Prove that if $A$ is normal, then the (Euclidean) matrix $\ell_{2}$-norm of $A$ is equal to its spectral radius, i.e., $\|A\|_{2}=\rho(A)$.

  (b) The advection equation

  $$u_{t}=u_{x}, \quad 0 \leqslant x \leqslant 1, \quad 0 \leqslant t<\infty$$

  is discretized by the Crank-Nicolson scheme

  $$u_{m}^{n+1}-u_{m}^{n}=\frac{1}{4} \mu\left(u_{m+1}^{n+1}-u_{m-1}^{n+1}\right)+\frac{1}{4} \mu\left(u_{m+1}^{n}-u_{m-1}^{n}\right), \quad m=1,2, \ldots, M, \quad n \in \mathbb{Z}_{+}$$

  Here, $\mu=\frac{k}{h}$ is the Courant number, with $k=\Delta t, h=\Delta x=\frac{1}{M+1}$, and $u_{m}^{n}$ is an approximation to $u(m h, n k)$.

  Using the eigenvalue analysis and carefully justifying each step, determine conditions on $\mu>0$ for which the method is stable. [Hint: All M $\times M$ Toeplitz anti-symmetric tridiagonal (TAT) matrices have the same set of orthogonal eigenvectors, and a TAT matrix with the elements $a_{j, j}=a$ and $a_{j, j+1}=-a_{j, j-1}=b$ has the eigenvalues $\lambda_{k}=a+2 \mathrm{i} b \cos \frac{\pi k}{M+1}$ where $\mathrm{i}=\sqrt{-1}$. ]

  (c) Consider the same advection equation for the Cauchy problem $(x \in \mathbb{R}, 0 \leqslant t \leqslant$ $T)$. Now it is discretized by the two-step leapfrog scheme

  $$u_{m}^{n+1}=\mu\left(u_{m+1}^{n}-u_{m-1}^{n}\right)+u_{m}^{n-1} .$$

  Applying the Fourier technique, find the range of $\mu>0$ for which the method is stable.

  comment

• Paper 4 , Section II, 40E

  Numerical Analysis | Part II, 2020

  (a) For a function $f=f(x, y)$ which is real analytic in $\mathbb{R}^{2}$ and 2-periodic in each variable, its Fourier expansion is given by the formula

  $$f(x, y)=\sum_{m, n \in \mathbb{Z}} \widehat{f}_{m, n} e^{i \pi m x+i \pi n y}, \quad \widehat{f}_{m, n}=\frac{1}{4} \int_{-1}^{1} \int_{-1}^{1} f(t, \theta) e^{-i \pi m t-i \pi n \theta} d t d \theta$$

  Derive expressions for the Fourier coefficients of partial derivatives $f_{x}, f_{y}$ and those of the product $h(x, y)=f(x, y) g(x, y)$ in terms of $\widehat{f}_{m, n}$ and $\widehat{g}_{m, n}$.

  (b) Let $u(x, y)$ be the 2-periodic solution in $\mathbb{R}^{2}$ of the general second-order elliptic PDE

  $$\left(a u_{x}\right)_{x}+\left(a u_{y}\right)_{y}=f$$

  where $a$ and $f$ are both real analytic and 2-periodic, and $a(x, y)>0$. We impose the normalisation condition $\int_{-1}^{1} \int_{-1}^{1} u d x d y=0$ and note from the PDE $\int_{-1}^{1} \int_{-1}^{1} f d x d y=0$.

  Construct explicitly the infinite-dimensional linear algebraic system that arises from the application of the Fourier spectral method to the above equation, and explain how to truncate this system to a finite-dimensional one.

  (c) Specify the truncated system for the unknowns $\left\{\widehat{u}_{m, n}\right\}$ for the case

  $$a(x, y)=5+2 \cos \pi x+2 \cos \pi y$$

  and prove that, for any ordering of the Fourier coefficients $\left\{\widehat{u}_{m, n}\right\}$ into one-dimensional array, the resulting system is symmetric and positive definite. [You may use the Gershgorin theorem without proof.]

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, A

  Principles of Quantum Mechanics | Part II, 2020

  Let $A=(m \omega X+i P) / \sqrt{2 m \hbar \omega}$ be the lowering operator of a one dimensional quantum harmonic oscillator of mass $m$ and frequency $\omega$, and let $|0\rangle$ be the ground state defined by $A|0\rangle=0$.

  a) Evaluate the commutator $\left[A, A^{\dagger}\right]$.

  b) For $\gamma \in \mathbb{R}$, let $S(\gamma)$ be the unitary operator $S(\gamma)=\exp \left(-\frac{\gamma}{2}\left(A^{\dagger} A^{\dagger}-A A\right)\right)$ and define $A(\gamma)=S^{\dagger}(\gamma) A S(\gamma)$. By differentiating with respect to $\gamma$ or otherwise, show that

  $$A(\gamma)=A \cosh \gamma-A^{\dagger} \sinh \gamma$$

  c) The ground state of the harmonic oscillator saturates the uncertainty relation $\Delta X \Delta P \geqslant \hbar / 2$. Compute $\Delta X \Delta P$ when the oscillator is in the state $|\gamma\rangle=S(\gamma)|0\rangle$.

  comment

• Paper 2, Section II, A

  Principles of Quantum Mechanics | Part II, 2020

  (a) Consider the Hamiltonian $H(t)=H_{0}+\delta H(t)$, where $H_{0}$ is time-independent and non-degenerate. The system is prepared to be in some state $|\psi\rangle=\sum_{r} a_{r}|r\rangle$ at time $t=0$, where $\{|r\rangle\}$ is an orthonormal basis of eigenstates of $H_{0}$. Derive an expression for the state at time $t$, correct to first order in $\delta H(t)$, giving your answer in the interaction picture.

  (b) An atom is modelled as a two-state system, where the excited state $|e\rangle$ has energy $\hbar \Omega$ above that of the ground state $|g\rangle$. The atom interacts with an electromagnetic field, modelled as a harmonic oscillator of frequency $\omega$. The Hamiltonian is $H(t)=H_{0}+\delta H(t)$, where

  $$H_{0}=\frac{\hbar \Omega}{2}(|e\rangle\langle e|-| g\rangle\langle g|) \otimes 1_{\text {field }}+1_{\text {atom }} \otimes \hbar \omega\left(A^{\dagger} A+\frac{1}{2}\right)$$

  is the Hamiltonian in the absence of interactions and

  $$\delta H(t)= \begin{cases}0, & t \leqslant 0 \\ \frac{1}{2} \hbar(\Omega-\omega)\left(|e\rangle\langle g|\otimes A+\beta| g\rangle\langle e| \otimes A^{\dagger}\right), & t>0\end{cases}$$

  describes the coupling between the atom and the field.

  (i) Interpret each of the two terms in $\delta H(t)$. What value must the constant $\beta$ take for time evolution to be unitary?

  (ii) At $t=0$ the atom is in state $(|e\rangle+|g\rangle) / \sqrt{2}$ while the field is described by the (normalized) state $e^{-1 / 2} e^{-A^{\dagger}}|0\rangle$ of the oscillator. Calculate the probability that at time $t$ the atom will be in its excited state and the field will be described by the $n^{\text {th }}$excited state of the oscillator. Give your answer to first non-trivial order in perturbation theory. Show that this probability vanishes when $t=\pi /(\Omega-\omega)$.

  comment

• Paper 3, Section II, 33A

  Principles of Quantum Mechanics | Part II, 2020

  Explain what is meant by the terms boson and fermion.

  Three distinguishable spin-1 particles are governed by the Hamiltonian

  $$H=\frac{2 \lambda}{\hbar^{2}}\left(\mathbf{S}_{1} \cdot \mathbf{S}_{2}+\mathbf{S}_{2} \cdot \mathbf{S}_{3}+\mathbf{S}_{3} \cdot \mathbf{S}_{1}\right)$$

  where $\mathbf{S}_{i}$ is the spin operator of particle $i$ and $\lambda$ is a positive constant. How many spin states are possible altogether? By considering the total spin operator, determine the eigenvalues and corresponding degeneracies of the Hamiltonian.

  Now consider the case that all three particles are indistinguishable and all have the same spatial wavefunction. What are the degeneracies of the Hamiltonian in this case?

  comment

• Paper 4, Section II,

  Principles of Quantum Mechanics | Part II, 2020

  Briefly explain why the density operator $\rho$ obeys $\rho \geqslant 0$ and $\operatorname{Tr}(\rho)=1$. What is meant by a pure state and a mixed state?

  A two-state system evolves under the Hamiltonian $H=\hbar \boldsymbol{\omega} \cdot \boldsymbol{\sigma}$, where $\boldsymbol{\omega}$ is a constant vector and $\sigma$ are the Pauli matrices. At time $t$ the system is described by a density operator

  $$\rho(t)=\frac{1}{2}\left(1_{\mathcal{H}}+\mathbf{a}(t) \cdot \boldsymbol{\sigma}\right)$$

  where $1_{\mathcal{H}}$ is the identity operator. Initially, the vector $\mathbf{a}(0)=\mathbf{a}$ obeys $|\mathbf{a}|<1$ and $\mathbf{a} \cdot \boldsymbol{\omega}=0$. Find $\rho(t)$ in terms of a and $\boldsymbol{\omega}$. At what time, if any, is the system definitely in the state $\left|\uparrow_{x}\right\rangle$ that obeys $\sigma_{x}\left|\uparrow_{x}\right\rangle=+\left|\uparrow_{x}\right\rangle ?$

  comment

Principles of Statistics

• Paper 1, Section II, J

  Principles of Statistics | Part II, 2020

  State and prove the Cramér-Rao inequality for a real-valued parameter $\theta$. [Necessary regularity conditions need not be stated.]

  In a general decision problem, define what it means for a decision rule to be minimax.

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. from a $N(\theta, 1)$ distribution, where $\theta \in \Theta=[0, \infty)$. Prove carefully that $\bar{X}_{n}=\frac{1}{n} \sum_{i=1}^{n} X_{i}$ is minimax for quadratic risk on $\Theta$.

  comment

• Paper 2, Section II, J

  Principles of Statistics | Part II, 2020

  Consider $X_{1}, \ldots, X_{n}$ from a $N\left(\mu, \sigma^{2}\right)$ distribution with parameter $\theta=\left(\mu, \sigma^{2}\right) \in$ $\Theta=\mathbb{R} \times(0, \infty)$. Derive the likelihood ratio test statistic $\Lambda_{n}\left(\Theta, \Theta_{0}\right)$ for the composite hypothesis

  $$H_{0}: \sigma^{2}=1 \text { vs. } H_{1}: \sigma^{2} \neq 1$$

  where $\Theta_{0}=\{(\mu, 1): \mu \in \mathbb{R}\}$ is the parameter space constrained by $H_{0}$.

  Prove carefully that

  $$\Lambda_{n}\left(\Theta, \Theta_{0}\right) \rightarrow^{d} \chi_{1}^{2} \quad \text { as } n \rightarrow \infty$$

  where $\chi_{1}^{2}$ is a Chi-Square distribution with one degree of freedom.

  comment

• Paper 3, Section II, J

  Principles of Statistics | Part II, 2020

  Let $\Theta=\mathbb{R}^{p}$, let $\mu>0$ be a probability density function on $\Theta$ and suppose we are given a further auxiliary conditional probability density function $q(\cdot \mid t)>0, t \in \Theta$, on $\Theta$ from which we can generate random draws. Consider a sequence of random variables $\left\{\vartheta_{m}: m \in \mathbb{N}\right\}$ generated as follows:

  • For $m \in \mathbb{N}$ and given $\vartheta_{m}$, generate a new draw $s_{m} \sim q\left(\cdot \mid \vartheta_{m}\right)$.

  • Define

  $$\vartheta_{m+1}= \begin{cases}s_{m}, & \text { with probability } \rho\left(\vartheta_{m}, s_{m}\right) \\ \vartheta_{m}, & \text { with probability } 1-\rho\left(\vartheta_{m}, s_{m}\right)\end{cases}$$

  where $\rho(t, s)=\min \left\{\frac{\mu(s)}{\mu(t)} \frac{q(t \mid s)}{q(s \mid t)}, 1\right\}$.

  (i) Show that the Markov chain $\left(\vartheta_{m}\right)$ has invariant measure $\mu$, that is, show that for all (measurable) subsets $B \subset \Theta$ and all $m \in \mathbb{N}$ we have

  $$\int_{\Theta} \operatorname{Pr}\left(\vartheta_{m+1} \in B \mid \vartheta_{m}=t\right) \mu(t) d t=\int_{B} \mu(\theta) d \theta$$

  (ii) Now suppose that $\mu$ is the posterior probability density function arising in a statistical model $\{f(\cdot, \theta): \theta \in \Theta\}$ with observations $x$ and a $N\left(0, I_{p}\right)$ prior distribution on $\theta$. Derive a family $\{q(\cdot \mid t): t \in \Theta\}$ such that in the above algorithm the acceptance probability $\rho(t, s)$ is a function of the likelihood ratio $f(x, s) / f(x, t)$, and for which the probability density function $q(\cdot \mid t)$ has covariance matrix $2 \delta I_{p}$ for all $t \in \Theta$.

  comment

• Paper 4 , Section II, J

  Principles of Statistics | Part II, 2020

  Consider $X_{1}, \ldots, X_{n}$ drawn from a statistical model $\{f(\cdot, \theta): \theta \in \Theta\}, \Theta=\mathbb{R}^{p}$, with non-singular Fisher information matrix $I(\theta)$. For $\theta_{0} \in \Theta, h \in \mathbb{R}^{p}$, define likelihood ratios

  $$Z_{n}(h)=\log \frac{\prod_{i=1}^{n} f\left(X_{i}, \theta_{0}+h / \sqrt{n}\right)}{\prod_{i=1}^{n} f\left(X_{i}, \theta_{0}\right)}, \quad X_{i} \sim^{i . i . d .} f\left(\cdot, \theta_{0}\right)$$

  Next consider the probability density functions $\left(p_{h}: h \in \mathbb{R}^{p}\right)$ of normal distributions $N\left(h, I\left(\theta_{0}\right)^{-1}\right)$ with corresponding likelihood ratios given by

  $$Z(h)=\log \frac{p_{h}(X)}{p_{0}(X)}, \quad X \sim p_{0} .$$

  Show that for every fixed $h \in \mathbb{R}^{p}$, the random variables $Z_{n}(h)$ converge in distribution as $n \rightarrow \infty$ to $Z(h) .$

  [You may assume suitable regularity conditions of the model $\{f(\cdot, \theta): \theta \in \Theta\}$ without specification, and results on uniform laws of large numbers from lectures can be used without proof.]

  comment

Probability and Measure

• Paper 1, Section II, 27K

  Probability and Measure | Part II, 2020

  (a) Let $(X, \mathcal{F}, \nu)$ be a probability space. State the definition of the space $\mathbb{L}^{2}(X, \mathcal{F}, \nu)$. Show that it is a Hilbert space.

  (b) Give an example of two real random variables $Z_{1}, Z_{2}$ that are not independent and yet have the same law.

  (c) Let $Z_{1}, \ldots, Z_{n}$ be $n$ random variables distributed uniformly on $[0,1]$. Let $\lambda$ be the Lebesgue measure on the interval $[0,1]$, and let $\mathcal{B}$ be the Borel $\sigma$-algebra. Consider the expression

  $$D(f):=\operatorname{Var}\left[\frac{1}{n}\left(f\left(Z_{1}\right)+\ldots+f\left(Z_{n}\right)\right)-\int_{[0,1]} f d \lambda\right]$$

  where Var denotes the variance and $f \in \mathbb{L}^{2}([0,1], \mathcal{B}, \lambda)$.

  Assume that $Z_{1}, \ldots, Z_{n}$ are pairwise independent. Compute $D(f)$ in terms of the variance $\operatorname{Var}(f):=\operatorname{Var}\left(f\left(Z_{1}\right)\right)$.

  (d) Now we no longer assume that $Z_{1}, \ldots, Z_{n}$ are pairwise independent. Show that

  $$\sup D(f) \geqslant \frac{1}{n},$$

  where the supremum ranges over functions $f \in \mathbb{L}^{2}([0,1], \mathcal{B}, \lambda)$ such that $\|f\|_{2}=1$ and $\int_{[0,1]} f d \lambda=0$.

  [Hint: you may wish to compute $D\left(f_{p, q}\right)$ for the family of functions $f_{p, q}=\sqrt{\frac{k}{2}}\left(1_{I_{p}}-1_{I_{q}}\right)$ where $1 \leqslant p, q \leqslant k, I_{j}=\left[\frac{j}{k}, \frac{j+1}{k}\right)$ and $1_{A}$ denotes the indicator function of the subset $\left.A .\right]$

  comment

• Paper 2, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2020

  Let $X$ be a set. Recall that a Boolean algebra $\mathcal{B}$ of subsets of $X$ is a family of subsets containing the empty set, which is stable under finite union and under taking complements. As usual, let $\sigma(\mathcal{B})$ be the $\sigma$-algebra generated by $\mathcal{B}$.

  (a) State the definitions of a $\sigma$-algebra, that of a measure on a measurable space, as well as the definition of a probability measure.

  (b) State Carathéodory's extension theorem.

  (c) Let $(X, \mathcal{F}, \mu)$ be a probability measure space. Let $\mathcal{B} \subset \mathcal{F}$ be a Boolean algebra of subsets of $X$. Let $\mathcal{C}$ be the family of all $A \in \mathcal{F}$ with the property that for every $\epsilon>0$, there is $B \in \mathcal{B}$ such that

  $$\mu(A \triangle B)<\epsilon,$$

  where $A \triangle B$ denotes the symmetric difference of $A$ and $B$, i.e., $A \triangle B=(A \cup B) \backslash(A \cap B)$.

  (i) Show that $\sigma(\mathcal{B})$ is contained in $\mathcal{C}$. Show by example that this may fail if $\mu(X)=+\infty$.

  (ii) Now assume that $(X, \mathcal{F}, \mu)=\left([0,1], \mathcal{L}_{[0,1]}, m\right)$, where $\mathcal{L}_{[0,1]}$ is the $\sigma$-algebra of Lebesgue measurable subsets of $[0,1]$ and $m$ is the Lebesgue measure. Let $\mathcal{B}$ be the family of all finite unions of sub-intervals. Is it true that $\mathcal{C}$ is equal to $\mathcal{L}_{[0,1]}$ in this case? Justify your answer.

  comment

• Paper 3, Section II, 26K

  Probability and Measure | Part II, 2020

  Let $(X, \mathcal{A}, m, T)$ be a probability measure preserving system.

  (a) State what it means for $(X, \mathcal{A}, m, T)$ to be ergodic.

  (b) State Kolmogorov's 0-1 law for a sequence of independent random variables. What does it imply for the canonical model associated with an i.i.d. random process?

  (c) Consider the special case when $X=[0,1], \mathcal{A}$ is the $\sigma$-algebra of Borel subsets, and $T$ is the map defined as

  $$T x=\left\{\begin{array}{l} 2 x, \quad \text { if } x \in\left[0, \frac{1}{2}\right] \\ 2-2 x, \quad \text { if } x \in\left[\frac{1}{2}, 1\right] \end{array}\right.$$

  (i) Check that the Lebesgue measure $m$ on $[0,1]$ is indeed an invariant probability measure for $T$.

  (ii) Let $X_{0}:=1_{\left(0, \frac{1}{2}\right)}$ and $X_{n}:=X_{0} \circ T^{n}$ for $n \geqslant 1$. Show that $\left(X_{n}\right)_{n \geqslant 0}$ forms a sequence of i.i.d. random variables on $(X, \mathcal{A}, m)$, and that the $\sigma$-algebra $\sigma\left(X_{0}, X_{1}, \ldots\right)$ is all of $\mathcal{A}$. [Hint: check first that for any integer $n \geqslant 0, T^{-n}\left(0, \frac{1}{2}\right)$ is a disjoint union of $2^{n}$ intervals of length $1 / 2^{n+1}$.]

  (iii) Is $(X, \mathcal{A}, m, T)$ ergodic? Justify your answer.

  comment

• Paper 4, Section II, K

  Probability and Measure | Part II, 2020

  (a) State and prove the strong law of large numbers for sequences of i.i.d. random variables with a finite moment of order 4 .

  (b) Let $\left(X_{k}\right)_{k \geqslant 1}$ be a sequence of independent random variables such that

  $$\mathbb{P}\left(X_{k}=1\right)=\mathbb{P}\left(X_{k}=-1\right)=\frac{1}{2}$$

  Let $\left(a_{k}\right)_{k \geqslant 1}$ be a sequence of real numbers such that

  $$\sum_{k \geqslant 1} a_{k}^{2}<\infty$$

  Set

  $$S_{n}:=\sum_{k=1}^{n} a_{k} X_{k}$$

  (i) Show that $S_{n}$ converges in $\mathbb{L}^{2}$ to a random variable $S$ as $n \rightarrow \infty$. Does it converge in $\mathbb{L}^{1}$ ? Does it converge in law?

  (ii) Show that $\|S\|_{4} \leqslant 3^{1 / 4}\|S\|_{2}$.

  (iii) Let $\left(Y_{k}\right)_{k \geqslant 1}$ be a sequence of i.i.d. standard Gaussian random variables, i.e. each $Y_{k}$ is distributed as $\mathcal{N}(0,1)$. Show that then $\sum_{k=1}^{n} a_{k} Y_{k}$ converges in law as $n \rightarrow \infty$ to a random variable and determine the law of the limit.

  comment

Quantum Information and Computation

• Paper 1, Section I, 10C

  Quantum Information and Computation | Part II, 2020

  Suppose we measure an observable $A=\hat{n} \cdot \vec{\sigma}$on a qubit, where $\hat{n}=\left(n_{x}, n_{y}, n_{z}\right) \in \mathbb{R}^{3}$ is a unit vector and $\vec{\sigma}=\left(\sigma_{x}, \sigma_{y}, \sigma_{z}\right)$ is the vector of Pauli operators.

  (i) Express $A$ as a $2 \times 2$ matrix in terms of the components of $\hat{n}$.

  (ii) Representing $\hat{n}$ in terms of spherical polar coordinates as $\hat{n}=(1, \theta, \phi)$, rewrite the above matrix in terms of the angles $\theta$ and $\phi$.

  (iii) What are the possible outcomes of the above measurement?

  (iv) Suppose the qubit is initially in a state $|1\rangle$. What is the probability of getting an outcome 1?

  (v) Consider the three-qubit state

  $$|\psi\rangle=a|000\rangle+b|010\rangle+c|110\rangle+d|111\rangle+e|100\rangle$$

  Suppose the second qubit is measured relative to the computational basis. What is the probability of getting an outcome 1? State the rule that you are using.

  comment

• Paper 2, Section I, 10C

  Quantum Information and Computation | Part II, 2020

  Consider the set of states

  $$\left|\beta_{z x}\right\rangle:=\frac{1}{\sqrt{2}}\left[|0 x\rangle+(-1)^{z}|1 \bar{x}\rangle\right],$$

  where $x, z \in\{0,1\}$ and $\bar{x}=x \oplus 1$ (addition modulo 2 ).

  (i) Show that

  $$(H \otimes \mathbb{I}) \circ \mathrm{CX}\left|\beta_{z x}\right\rangle=|z x\rangle \quad \forall z, x \in\{0,1\},$$

  where $H$ denotes the Hadamard gate and CX denotes the controlled- $X$ gate.

  (ii) Show that for any $z, x \in\{0,1\}$,

  $$\tag{*} \left(Z^{z} X^{x} \otimes \mathbb{I}\right)\left|\beta_{00}\right\rangle=\left|\beta_{z x}\right\rangle .$$

  [Hint: For any unitary operator $U$, we have $(U \otimes \mathbb{I})\left|\beta_{00}\right\rangle=\left(\mathbb{I} \otimes U^{T}\right)\left|\beta_{00}\right\rangle$, where $U^{T}$ denotes the transpose of $U$ with respect to the computational basis.]

  (iii) Suppose Alice and Bob initially share the state $\left|\beta_{00}\right\rangle$. Show using (*) how Alice can communicate two classical bits to Bob by sending him only a single qubit.

  comment

• Paper 2, Section II, 15C

  Quantum Information and Computation | Part II, 2020

  (a) Show how the $n$-qubit state

  $$\left|\psi_{n}\right\rangle:=\frac{1}{\sqrt{2^{n}}} \sum_{x \in B_{n}}|x\rangle$$

  can be generated from a computational basis state of $\mathbb{C}^{n}$ by the action of Hadamard gates.

  (b) Prove that $C Z=(I \otimes H) C N O T_{12}(I \otimes H)$, where $C Z$ denotes the controlled- $Z$ gate. Justify (without any explicit calculations) the following identity:

  $$C N O T_{12}=(I \otimes H) C Z(I \otimes H)$$

  (c) Consider the following two-qubit circuit:

  

  What is its action on an arbitrary 2-qubit state $|\psi\rangle \otimes|\phi\rangle ?$ In particular, for two given states $|\psi\rangle$ and $|\phi\rangle$, find the states $|\alpha\rangle$ and $|\beta\rangle$ such that

  $$U(|\psi\rangle \otimes|\phi\rangle)=|\alpha\rangle \otimes|\beta\rangle .$$

  (d) Consider the following quantum circuit diagram

  

  where the measurement is relative to the computational basis and $U$ is the quantum gate from part (c). Note that the second gate in the circuit performs the following controlled operation:

  $$|0\rangle|\psi\rangle|\phi\rangle \mapsto|0\rangle|\psi\rangle|\phi\rangle ;|1\rangle|\psi\rangle|\phi\rangle \mapsto|1\rangle U(|\psi\rangle|\phi\rangle) .$$

  (i) Give expressions for the joint state of the three qubits after the action of the first Hadamard gate; after the action of the quantum gate $U$; and after the action of the second Hadamard gate.

  (ii) Compute the probabilities $p_{0}$ and $p_{1}$ of getting outcome 0 and 1 , respectively, in the measurement.

  (iii) How can the above circuit be used to determine (with high probability) whether the two states $|\psi\rangle$ and $|\phi\rangle$ are identical or not? [Assume that you are given arbitrarily many copies of the three input states and that the quantum circuit can be used arbitrarily many times.]

  comment

• Paper 3, Section I, $10 C$

  Quantum Information and Computation | Part II, 2020

  For $\phi \in[0,2 \pi)$ and $|\psi\rangle \in \mathbb{C}^{4}$ consider the operator

  $$R_{\psi}^{\phi}=\mathbb{I}-\left(1-e^{i \phi}\right)|\psi\rangle\langle\psi|$$

  Let $U$ be a unitary operator on $\mathbb{C}^{4}=\mathbb{C}^{2} \otimes \mathbb{C}^{2}$ with action on $|00\rangle$ given as follows

  $$\tag{†} U|00\rangle=\sqrt{p}|g\rangle+\sqrt{1-p}|b\rangle=:\left|\psi_{\mathrm{in}}\right\rangle$$

  where $p$ is a constant in $[0,1]$ and $|g\rangle,|b\rangle \in \mathbb{C}^{4}$ are orthonormal states.

  (i) Give an explicit expression of the state $R_{g}^{\phi} U|00\rangle$.

  (ii) Find a $|\psi\rangle \in \mathbb{C}^{4}$ for which $R_{\psi}^{\pi}=U R_{00}^{\pi} U^{\dagger}$.

  (iii) Choosing $p=1 / 4$ in equation ($\dagger$), calculate the state $U R_{00}^{\pi} U^{\dagger} R_{g}^{\phi} U|00\rangle$. For what choice of $\phi \in[0,2 \pi)$ is this state proportional to $|g\rangle$ ?

  (iv) Describe how the above considerations can be used to find a marked element $g$ in a list of four items $\left\{g, b_{1}, b_{2}, b_{3}\right\}$. Assume that you have the state $|00\rangle$ and can act on it with a unitary operator that prepares the uniform superposition of four orthonormal basis states $|g\rangle,\left|b_{1}\right\rangle,\left|b_{2}\right\rangle,\left|b_{3}\right\rangle$ of $\mathbb{C}^{4}$. [You may use the operators $U$ (defined in (†)), $U^{\dagger}$ and $R_{\psi}^{\phi}$ for any choice of $\phi \in[0,2 \pi)$ and any $|\psi\rangle \in \mathbb{C}^{4}$.]

  comment

• Paper 3, Section II, C

  Quantum Information and Computation | Part II, 2020

  Consider the quantum oracle $U_{f}$ for a function $f: B_{n} \rightarrow B_{n}$ which acts on the state $|x\rangle|y\rangle$ of $2 n$ qubits as follows:

  $$U_{f}|x\rangle|y\rangle=|x\rangle|y \oplus f(x)\rangle$$

  The function $f$ is promised to have the following property: there exists a $z \in B_{n}$ such that for any $x, y \in B_{n}$,

  $$[f(x)=f(y)] \text { if and only if } x \oplus y \in\left\{0^{n}, z\right\}$$

  where $0^{n} \equiv(0,0, \ldots, 0) \in B_{n}$.

  (a) What is the nature of the function $f$ for the case in which $z=0^{n}$, and for the case in which $z \neq 0^{n}$ ?

  (b) Suppose initially each of the $2 n$ qubits are in the state $|0\rangle$. They are then subject to the following operations:

  1. Each of the first $n$ qubits forming an input register are acted on by Hadamard gates;

  2. The $2 n$ qubits are then acted on by the quantum oracle $U_{f}$;

  3. Next, the qubits in the input register are individually acted on by Hadamard gates.

  (i) List the states of the $2 n$ qubits after each of the above operations; the expression for the final state should involve the $n$-bit "dot product" which is defined as follows:

  $$a \cdot b=\left(a_{1} b_{1}+a_{2} b_{2}+\ldots+a_{n} b_{n}\right) \bmod 2$$

  where $a, b \in B_{n}$ with $a=\left(a_{1}, \ldots, a_{n}\right)$ and $b=\left(b_{1}, \ldots, b_{n}\right)$.

  (ii) Justify that if $z=0^{n}$ then for any $y \in B_{n}$ and any $\varphi(x, y) \in\{-1$, $+1\}$, the following identity holds:

  $$\| \sum_{x \in B_{n}} \varphi(x, y)|f(x)\rangle\left\|^{2}=\right\| \sum_{x \in B_{n}} \varphi(x, y)|x\rangle \|^{2}$$

  (iii) For the case $z=0^{n}$, what is the probability that a measurement of the input register, relative to the computational basis of $\mathbb{C}^{n}$ results in a string $y \in B_{n}$ ?

  (iv) For the case $z \neq 0^{n}$, show that the probability that the above-mentioned measurement of the input register results in a string $y \in B_{n}$, is equal to the following:

  zero for all strings $y \in B_{n}$ satisfying $y \cdot z=1$, and $2^{-(n-1)}$ for any fixed string $y \in B_{n}$ satisfying $y \cdot z=0$.

  [State any identity you may employ. You may use $(x \oplus z) \cdot y=(x \cdot y) \oplus(z \cdot y), \forall x, y, z \in B_{n}$.]

  comment

• Paper 4, Section I, C

  Quantum Information and Computation | Part II, 2020

  (i) What is the action of $\mathrm{QFT}_{N}$ on a state $|x\rangle$, where $x \in\{0,1,2, \ldots, N-1\}$ and $\mathrm{QFT}_{N}$ denotes the Quantum Fourier Transform modulo $N$ ?

  (ii) For the case $N=4$ write $0,1,2,3$ respectively in binary as $00,01,10,11$ thereby identifying the four-dimensional space as that of two qubits. Show that $\mathrm{QFT}_{N}|10\rangle$ is an unentangled state of the two qubits.

  (iii) Prove that $\left(\mathrm{QFT}_{N}\right)^{2}|x\rangle=|N-x\rangle$, where $\left(\mathrm{QFT}_{N}\right)^{2} \equiv \mathrm{QFT}_{N} \circ \mathrm{QFT}_{N}$.

  [Hint: For $\omega=e^{2 \pi i / N}, \sum_{m=0}^{N-1} \omega^{m K}=0$ if $K$ is not a multiple of $N$.]

  (iv) What is the action of $\left(\mathrm{QFT}_{N}\right)^{4}$ on a state $|x\rangle$, for any $x \in\{0,1,2, \ldots, N-1\}$ ? Use the above to determine what the eigenvalues of $\mathrm{QFT}_{N}$ are.

  comment

Representation Theory

• Paper 1, Section II, F

  Representation Theory | Part II, 2020

  State and prove Maschke's theorem.

  Let $G$ be the group of isometries of $\mathbb{Z}$. Recall that $G$ is generated by the elements $t, s$ where $t(n)=n+1$ and $s(n)=-n$ for $n \in \mathbb{Z}$.

  Show that every non-faithful finite-dimensional complex representation of $G$ is a direct sum of subrepresentations of dimension at most two.

  Write down a finite-dimensional complex representation of the group $(\mathbb{Z},+)$ that is not a direct sum of one-dimensional subrepresentations. Hence, or otherwise, find a finitedimensional complex representation of $G$ that is not a direct sum of subrepresentations of dimension at most two. Briefly justify your answer.

  [Hint: You may assume that any non-trivial normal subgroup of $G$ contains an element of the form $t^{m}$ for some $m>0$.]

  comment

• Paper 2, Section II, F

  Representation Theory | Part II, 2020

  Let $G$ be the unique non-abelian group of order 21 up to isomorphism. Compute the character table of $G$.

  [You may find it helpful to think of $G$ as the group of $2 \times 2$ matrices of the form $\left(\begin{array}{cc}a & b \\ 0 & a^{-1}\end{array}\right)$ with $a, b \in \mathbb{F}_{7}$ and $a^{3}=1$. You may use any standard results from the course provided you state them clearly.]

  comment

• Paper 3, Section II, F

  Representation Theory | Part II, 2020

  State Mackey's restriction formula and Frobenius reciprocity for characters. Deduce Mackey's irreducibility criterion for an induced representation.

  For $n \geqslant 2$ show that if $S_{n-1}$ is the subgroup of $S_{n}$ consisting of the elements that fix $n$, and $W$ is a complex representation of $S_{n-1}$, then $\operatorname{Ind}_{S_{n-1}}^{S_{n}} W$ is not irreducible.

  comment

• Paper 4, Section II, F

  Representation Theory | Part II, 2020

  (a) State and prove Burnside's lemma. Deduce that if a finite group $G$ acts 2transitively on a set $X$ then the corresponding permutation character has precisely two (distinct) irreducible summands.

  (b) Suppose that $\mathbb{F}_{q}$ is a field with $q$ elements. Write down a list of conjugacy class representatives for $G L_{2}\left(\mathbb{F}_{q}\right)$. Consider the natural action of $G L_{2}\left(\mathbb{F}_{q}\right)$ on the set of lines through the origin in $\mathbb{F}_{q}^{2}$. What values does the corresponding permutation character take on each conjugacy class representative in your list? Decompose this permutation character into irreducible characters.

  comment

Riemann Surfaces

• Paper 1, Section II, 24F

  Riemann Surfaces | Part II, 2020

  Assuming any facts about triangulations that you need, prove the Riemann-Hurwitz theorem.

  Use the Riemann-Hurwitz theorem to prove that, for any cubic polynomial $f: \mathbb{C} \rightarrow \mathbb{C}$, there are affine transformations $g(z)=a z+b$ and $h(z)=c z+d$ such that $k(z)=g \circ f \circ h(z)$ is of one of the following two forms:

  $$k(z)=z^{3} \text { or } k(z)=z\left(z^{2} / 3-1\right)$$

  comment

• Paper 2, Section II, 23F

  Riemann Surfaces | Part II, 2020

  Let $f: \mathbb{C}_{\infty} \rightarrow \mathbb{C}_{\infty}$ be a rational function. What does it mean for $p \in \mathbb{C}_{\infty}$ to be a ramification point? What does it mean for $p \in \mathbb{C}_{\infty}$ to be a branch point?

  Let $B$ be the set of branch points of $f$, and let $R$ be the set of ramification points. Show that

  $$f: \mathbb{C}_{\infty} \backslash R \rightarrow \mathbb{C}_{\infty} \backslash B$$

  is a regular covering map.

  State the monodromy theorem. For $w \in \mathbb{C}_{\infty} \backslash B$, explain how a closed curve based at $w$ defines a permutation of $f^{-1}(w)$.

  For the rational function

  $$f(z)=\frac{z(2-z)}{(1-z)^{4}}$$

  identify the group of all such permutations.

  comment

• Paper 3, Section II, F

  Riemann Surfaces | Part II, 2020

  Let $\Lambda=\langle\lambda, \mu\rangle \subseteq \mathbb{C}$ be a lattice. Give the definition of the associated Weierstrass $\wp$-function as an infinite sum, and prove that it converges. [You may use without proof the fact that

  $$\sum_{w \in \Lambda \backslash\{0\}} \frac{1}{|w|^{t}}$$

  converges if and only if $t>2$.]

  Consider the half-lattice points

  $$z_{1}=\lambda / 2, \quad z_{2}=\mu / 2, \quad z_{3}=(\lambda+\mu) / 2,$$

  and let $e_{i}=\wp\left(z_{i}\right)$. Using basic properties of $\wp$, explain why the values $e_{1}, e_{2}, e_{3}$ are distinct

  Give an example of a lattice $\Lambda$ and a conformal equivalence $\theta: \mathbb{C} / \Lambda \rightarrow \mathbb{C} / \Lambda$ such that $\theta$ acts transitively on the images of the half-lattice points $z_{1}, z_{2}, z_{3}$.

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2020

  Consider a generalised linear model with full column rank design matrix $X \in \mathbb{R}^{n \times p}$, output variables $Y=\left(Y_{1}, \ldots, Y_{n}\right) \in \mathbb{R}^{n}$, link function $g$, mean parameters $\mu=\left(\mu_{1}, \ldots, \mu_{n}\right)$ and known dispersion parameters $\sigma_{i}^{2}=a_{i} \sigma^{2}, i=1, \ldots, n$. Denote its variance function by $V$ and recall that $g\left(\mu_{i}\right)=x_{i}^{T} \beta, i=1, \ldots, n$, where $\beta \in \mathbb{R}^{p}$ and $x_{i}^{T}$ is the $i^{\text {th }}$row of $X$.

  (a) Define the score function in terms of the log-likelihood function and the Fisher information matrix, and define the update of the Fisher scoring algorithm.

  (b) Let $W \in \mathbb{R}^{n \times n}$ be a diagonal matrix with positive entries. Note that $X^{T} W X$ is invertible. Show that

  $$\operatorname{argmin}_{b \in \mathbb{R}^{p}}\left\{\sum_{i=1}^{n} W_{i i}\left(Y_{i}-x_{i}^{T} b\right)^{2}\right\}=\left(X^{T} W X\right)^{-1} X^{T} W Y$$

  [Hint: you may use that $\left.\operatorname{argmin}_{b \in \mathbb{R}^{p}}\left\{\left\|Y-X^{T} b\right\|^{2}\right\}=\left(X^{T} X\right)^{-1} X^{T} Y .\right]$

  (c) Recall that the score function and the Fisher information matrix have entries

  $$\begin{aligned} &U_{j}(\beta)=\sum_{i=1}^{n} \frac{\left(Y_{i}-\mu_{i}\right) X_{i j}}{a_{i} \sigma^{2} V\left(\mu_{i}\right) g^{\prime}\left(\mu_{i}\right)} \quad j=1, \ldots, p \\ &i_{j k}(\beta)=\sum_{i=1}^{n} \frac{X_{i j} X_{i k}}{a_{i} \sigma^{2} V\left(\mu_{i}\right)\left\{g^{\prime}\left(\mu_{i}\right)\right\}^{2}} \quad j, k=1, \ldots, p \end{aligned}$$

  Justify, performing the necessary calculations and using part (b), why the Fisher scoring algorithm is also known as the iterative reweighted least squares algorithm.

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2020

  We consider a subset of the data on car insurance claims from Hallin and Ingenbleek (1983). For each customer, the dataset includes total payments made per policy-year, the amount of kilometres driven, the bonus from not having made previous claims, and the brand of the car. The amount of kilometres driven is a factor taking values $1,2,3,4$, or 5 , where a car in level $i+1$ has driven a larger number of kilometres than a car in level $i$ for any $i=1,2,3,4$. A statistician from an insurance company fits the following model on $R$.

  $>$ model1 <- Im(Paymentperpolicyyr as numeric(Kilometres) $+$ Brand $+$ Bonus)

  (i) Why do you think the statistician transformed variable Kilometres from a factor to a numerical variable?

  (ii) To check the quality of the model, the statistician applies a function to model1 which returns the following figure:

  

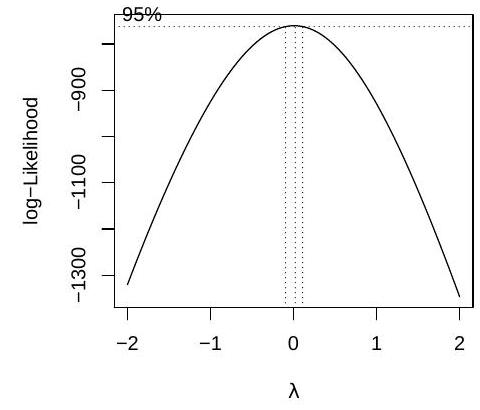
  What does the plot represent? Does it suggest that model1 is a good model? Explain. If not, write down a model which the plot suggests could be better.

  (iii) The statistician fits the model suggested by the graph and calls it model2. Consider the following abbreviated output:

  $>\operatorname{summary}(\operatorname{model2})$

  $\cdots$

  Coefficients:

  $\begin{array}{lrrrr}\text { (Intercept) } & 6.514035 & 0.186339 & 34.958 & <2 \mathrm{e}-16 * * * \\ \text { as.numeric(Kilometres) } & 0.057132 & 0.032654 & 1.750 & 0.08126 . \\ \text { Brand2 } & 0.363869 & 0.186857 & 1.947 & 0.05248 .\end{array}$

  Brand2

  $\cdots$

  Brand9

  $\begin{array}{lllll}0.125446 & 0.186857 & 0.671 & 0.50254\end{array}$

  Bonus

  

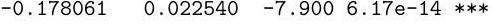
  Signif. codes: 0 '' $0.001$ '' $0.01$ '' $0.05$ '.' $0.1$ ' 1

  Residual standard error: $0.7817$ on 284 degrees of freedom ..

  Using the output, write down a $95 \%$ prediction interval for the ratio between the total payments per policy year for two cars of the same brand and with the same value of Bonus, one of which has a Kilometres value one higher than the other. You may express your answer as a function of quantiles of a common distribution, which you should specify.

  (iv) Write down a generalised linear model for Paymentperpolicyyr which may be a better model than model1 and give two reasons. You must specify the link function.

  comment

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2020

  The data frame WCG contains data from a study started in 1960 about heart disease. The study used 3154 adult men, all free of heart disease at the start, and eight and a half years later it recorded into variable chd whether they suffered from heart disease (1 if the respective man did and 0 otherwise) along with their height and average number of cigarettes smoked per day. Consider the $\mathrm{R}$ code below and its abbreviated output.

  

  (a) Write down the model fitted by the code above.

  (b) Interpret the effect on heart disease of a man smoking an average of two packs of cigarettes per day if each pack contains 20 cigarettes.

  (c) Give an alternative latent logistic-variable representation of the model. [Hint: if $F$ is the cumulative distribution function of a logistic random variable, its inverse function is the logit function.]

  comment

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2020

  Suppose we have data $\left(Y_{1}, x_{1}^{T}\right), \ldots,\left(Y_{n}, x_{n}^{T}\right)$, where the $Y_{i}$ are independent conditional on the design matrix $X$ whose rows are the $x_{i}^{T}, i=1, \ldots, n$. Suppose that given $x_{i}$, the true probability density function of $Y_{i}$ is $f_{x_{i}}$, so that the data is generated from an element of a model $\mathcal{F}:=\left\{\left(f_{x_{i}}(\cdot ; \theta)\right)_{i=1}^{n}, \theta \in \Theta\right\}$ for some $\Theta \subseteq \mathbb{R}^{q}$ and $q \in \mathbb{N}$.

  (a) Define the log-likelihood function for $\mathcal{F}$, the maximum likelihood estimator of $\theta$ and Akaike's Information Criterion (AIC) for $\mathcal{F}$.

  From now on let $\mathcal{F}$ be the normal linear model, i.e. $Y:=\left(Y_{1}, \ldots, Y_{n}\right)^{T}=X \beta+\varepsilon$, where $X \in \mathbb{R}^{n \times p}$ has full column rank and $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$.

  (b) Let $\hat{\sigma}^{2}$ denote the maximum likelihood estimator of $\sigma^{2}$. Show that the AIC of $\mathcal{F}$ is

  $$n\left(1+\log \left(2 \pi \hat{\sigma}^{2}\right)\right)+2(p+1)$$

  (c) Let $\chi_{n-p}^{2}$ be a chi-squared distribution on $n-p$ degrees of freedom. Using any results from the course, show that the distribution of the AIC of $\mathcal{F}$ is

  $$n \log \left(\chi_{n-p}^{2}\right)+n\left(\log \left(2 \pi \sigma^{2} / n\right)+1\right)+2(p+1)$$

  $\left[\right.$ Hint: $\hat{\sigma}^{2}:=n^{-1}\|Y-X \hat{\beta}\|^{2}=n^{-1}\|(I-P) \varepsilon\|^{2}$, where $\hat{\beta}$ is the maximum likelihood estimator of $\beta$ and $P$ is the projection matrix onto the column space of $X$.]

  comment

• Paper 4, Section I, J

  Statistical Modelling | Part II, 2020

  Suppose you have a data frame with variables response, covar1, and covar2. You run the following commands on $R$.

  

  $\begin{array}{llllll}\text { covar2 } & 0.3755 & 2.5978 & 0.145 & 0.886\end{array}$

  ...

  (a) Consider the following three scenarios:

  (i) All the output you have is the abbreviated output of summary (model) above.

  (ii) You have the abbreviated output of summary (model) above together with

  Residual standard error: $0.8097$ on 47 degrees of freedom

  Multiple R-squared: $0.8126$, Adjusted R-squared: $0.8046$

  F-statistic: $101.9$ on 2 and 47 DF, p-value: < $2.2 e-16$

  (iii) You have the abbreviated output of summary (model) above together with

  Residual standard error: $0.9184$ on 47 degrees of freedom

  Multiple R-squared: $0.000712$, Adjusted R-squared: $-0.04181$

  F-statistic: $0.01674$ on 2 and 47 DF, p-value: $0.9834$

  What conclusion can you draw about which variables explain the response in each of the three scenarios? Explain.

  (b) Assume now that you have the abbreviated output of summary (model) above together with

  anova(lm(response $~ 1), \operatorname{lm}($ response $\sim \operatorname{covar} 1)$, model $)$

  

  What are the values of the entries with a question mark? [You may express your answers as arithmetic expressions if necessary].

  comment

• Paper 4, Section II, J

  Statistical Modelling | Part II, 2020

  (a) Define a generalised linear model $(\mathrm{GLM})$ with design matrix $X \in \mathbb{R}^{n \times p}$, output variables $Y:=\left(Y_{1}, \ldots, Y_{n}\right)^{T}$ and parameters $\mu:=\left(\mu_{1}, \ldots, \mu_{n}\right)^{T}, \beta \in \mathbb{R}^{p}$ and $\sigma_{i}^{2}:=a_{i} \sigma^{2} \in(0, \infty), i=1, \ldots, n$. Derive the moment generating function of $Y$, i.e. give an expression for $\mathbb{E}\left[\exp \left(t^{T} Y\right)\right], t \in \mathbb{R}^{n}$, wherever it is well-defined.

  Assume from now on that the GLM satisfies the usual regularity assumptions, $X$ has full column rank, and $\sigma^{2}$ is known and satisfies $1 / \sigma^{2} \in \mathbb{N}$.

  (b) Let $\tilde{Y}:=\left(\tilde{Y}_{1}, \ldots, \tilde{Y}_{n / \sigma^{2}}\right)^{T}$ be the output variables of a GLM from the same family as that of part (a) and parameters $\tilde{\mu}:=\left(\tilde{\mu}_{1}, \ldots, \tilde{\mu}_{n / \sigma^{2}}\right)^{T}$ and $\tilde{\sigma}^{2}:=\left(\tilde{\sigma}_{1}^{2}, \ldots, \tilde{\sigma}_{n / \sigma^{2}}^{2}\right)$. Suppose the output variables may be split into $n$ blocks of size $1 / \sigma^{2}$ with constant parameters. To be precise, for each block $i=1, \ldots, n$, if $j \in\left\{(i-1) / \sigma^{2}+1, \ldots, i / \sigma^{2}\right\}$ then

  $$\tilde{\mu}_{j}=\mu_{i} \quad \text { and } \quad \tilde{\sigma}_{j}^{2}=a_{i}$$

  with $\mu_{i}=\mu_{i}(\beta)$ and $a_{i}$ defined as in part $($ a $)$. Let $\bar{Y}:=\left(\bar{Y}_{1}, \ldots, \bar{Y}_{n}\right)^{T}$, where $\bar{Y}_{i}:=$ $\sigma^{2} \sum_{k=1}^{1 / \sigma^{2}} \tilde{Y}_{(i-1) / \sigma^{2}+k}$.

  (i) Show that $\bar{Y}$ is equal to $Y$ in distribution. [Hint: you may use without proof that moment generating functions uniquely determine distributions from exponential dispersion families.]

  (ii) For any $\tilde{y} \in \mathbb{R}^{n / \sigma^{2}}$, let $\bar{y}=\left(\bar{y}_{1}, \ldots, \bar{y}_{n}\right)^{T}$, where $\bar{y}_{i}:=\sigma^{2} \sum_{k=1}^{1 / \sigma^{2}} \tilde{y}_{(i-1) / \sigma^{2}+k}$. Show that the model function of $\tilde{Y}$ satisfies

  $$f\left(\tilde{y} ; \tilde{\mu}, \tilde{\sigma}^{2}\right)=g_{1}\left(\bar{y} ; \tilde{\mu}, \tilde{\sigma}^{2}\right) \times g_{2}\left(\tilde{y} ; \tilde{\sigma}^{2}\right)$$

  for some functions $g_{1}, g_{2}$, and conclude that $\bar{Y}$ is a sufficient statistic for $\beta$ from $\tilde{Y}$.

  (iii) For the model and data from part (a), let $\hat{\mu}$ be the maximum likelihood estimator for $\mu$ and let $D(Y ; \mu)$ be the deviance at $\mu$. Using (i) and (ii), show that

  $$\frac{D(Y ; \hat{\mu})}{\sigma^{2}}={ }^{d} 2 \log \left\{\frac{\sup _{\tilde{\mu}^{\prime} \in \widetilde{\mathcal{M}}_{1}} f\left(\tilde{Y} ; \tilde{\mu}^{\prime}, \tilde{\sigma}^{2}\right)}{\sup _{\tilde{\mu}^{\prime} \in \widetilde{\mathcal{M}}_{0}} f\left(\tilde{Y} ; \tilde{\mu}^{\prime}, \tilde{\sigma}^{2}\right)}\right\}$$

  where $=^{d}$ means equality in distribution and $\widetilde{\mathcal{M}}_{0}$ and $\widetilde{\mathcal{M}}_{1}$ are nested subspaces of $\mathbb{R}^{n / \sigma^{2}}$ which you should specify. Argue that $\operatorname{dim}\left(\widetilde{\mathcal{M}}_{1}\right)=n$ and $\operatorname{dim}\left(\widetilde{\mathcal{M}}_{0}\right)=p$, and, assuming the usual regularity assumptions, conclude that

  $$\frac{D(Y ; \hat{\mu})}{\sigma^{2}} \rightarrow^{d} \chi_{n-p}^{2} \quad \text { as } \sigma^{2} \rightarrow 0$$

  stating the name of the result from class that you use.

  comment

Statistical Physics

• Paper 1, Section II, A

  Statistical Physics | Part II, 2020

  Using the notion of entropy, show that two systems that can freely exchange energy reach the same temperature. Show that the energy of a system increases with temperature.

  A system consists of $N$ distinguishable, non-interacting spin $\frac{1}{2}$ atoms in a magnetic field, where $N$ is large. The energy of an atom is $\varepsilon>0$ if the spin is up and $-\varepsilon$ if the spin is down. Find the entropy and energy if a fraction $\alpha$ of the atoms have spin up. Determine $\alpha$ as a function of temperature, and deduce the allowed range of $\alpha$. Verify that the energy of the system increases with temperature in this range.

  comment

• Paper 2, Section II, A

  Statistical Physics | Part II, 2020

  Using the Gibbs free energy $G(T, P)=E-T S+P V$, derive the Maxwell relation

  $$\left.\frac{\partial S}{\partial P}\right|_{T}=-\left.\frac{\partial V}{\partial T}\right|_{P}$$

  Define the notions of heat capacity at constant volume, $C_{V}$, and heat capacity at constant pressure, $C_{P}$. Show that

  $$C_{P}-C_{V}=\left.\left.T \frac{\partial V}{\partial T}\right|_{P} \frac{\partial P}{\partial T}\right|_{V}$$

  Derive the Clausius-Clapeyron relation for $\frac{d P}{d T}$ along the first-order phase transition curve between a liquid and a gas. Find the simplified form of this relation, assuming the gas has much larger volume than the liquid and that the gas is ideal. Assuming further that the latent heat is a constant, determine the form of $P$ as a function of $T$ along the phase transition curve. [You may assume there is no discontinuity in the Gibbs free energy across the phase transition curve.]

  comment

• Paper 3, Section II, A

  Statistical Physics | Part II, 2020

  Starting with the density of electromagnetic radiation modes in $\mathbf{k}$-space, determine the energy $E$ of black-body radiation in a box of volume $V$ at temperature $T$.

  Using the first law of thermodynamics show that

  $$\left.\frac{\partial E}{\partial V}\right|_{T}=\left.T \frac{\partial P}{\partial T}\right|_{V}-P$$

  By using this relation determine the pressure $P$ of the black-body radiation.

  [You are given the following:

  (i) The mean number of photons in a radiation mode of frequency $\omega$ is $\frac{1}{e^{\hbar \omega / T}-1}$,

  (ii) $1+\frac{1}{2^{4}}+\frac{1}{3^{4}}+\cdots=\frac{\pi^{4}}{90}$,

  (iii) You may assume $P$ vanishes with $T$ more rapidly than linearly, as $T \rightarrow 0$. ]

  comment

• Paper 4, Section II, A

  Statistical Physics | Part II, 2020

  Consider a classical gas of $N$ particles in volume $V$, where the total energy is the standard kinetic energy plus a potential $U\left(\mathbf{x}_{1}, \mathbf{x}_{2}, \ldots, \mathbf{x}_{N}\right)$ depending on the relative locations of the particles $\left\{\mathbf{x}_{i}: 1 \leqslant i \leqslant N\right\}$.

  (i) Starting from the partition function, show that the free energy of the gas is

  $$F=F_{\text {ideal }}-T \log \left\{1+\frac{1}{V^{N}} \int\left(e^{-U / T}-1\right) d^{3 N} x\right\}$$

  where $F_{\text {ideal }}$ is the free energy when $U \equiv 0$.

  (ii) Suppose now that the gas is fairly dilute and that the integral in $(*)$ is small compared to $V^{N}$ and is dominated by two-particle interactions. Show that the free energy simplifies to the form

  $$F=F_{\text {ideal }}+\frac{N^{2} T}{V} B(T)$$

  and find an integral expression for $B(T)$. Using ( $\dagger$ ) find the equation of state of the gas, and verify that $B(T)$ is the second virial coefficient.

  (iii) The equation of state for a Clausius gas is

  $$P(V-N b)=N T$$

  for some constant $b$. Find the second virial coefficient for this gas. Evaluate $b$ for a gas of hard sphere atoms of radius $r_{0}$.

  comment

Stochastic Financial Models

• Paper 1, Section II, 30K

  Stochastic Financial Models | Part II, 2020

  Consider a single-period asset price model $\left(\bar{S}_{0}, \bar{S}_{1}\right)$ in $\mathbb{R}^{d+1}$ where, for $n=0,1$,

  $$\bar{S}_{n}=\left(S_{n}^{0}, S_{n}\right)=\left(S_{n}^{0}, S_{n}^{1}, \ldots, S_{n}^{d}\right)$$

  with $S_{0}$ a non-random vector in $\mathbb{R}^{d}$ and

  $$S_{0}^{0}=1, \quad S_{1}^{0}=1+r, \quad S_{1} \sim N(\mu, V) .$$

  Assume that $V$ is invertible. An investor has initial wealth $w_{0}$ which is invested in the market at time 0 , to hold $\theta^{0}$ units of the riskless asset $S^{0}$ and $\theta^{i}$ units of risky asset $i$, for $i=1, \ldots, d$.

  (a) Show that in order to minimize the variance of the wealth $\bar{\theta} \cdot \bar{S}_{1}$ held at time 1 , subject to the constraint

  $$\mathbb{E}\left(\bar{\theta} \cdot \bar{S}_{1}\right)=w_{1}$$

  with $w_{1}$ given, the investor should choose a portfolio of the form

  $$\theta=\lambda \theta_{m}, \quad \theta_{m}=V^{-1}\left(\mu-(1+r) S_{0}\right)$$

  where $\lambda$ is to be determined.

  (b) Show that the same portfolio is optimal for a utility-maximizing investor with CARA utility function

  $$U(x)=-\exp \{-\gamma x\}$$

  for a unique choice of $\gamma$, also to be determined.

  comment

• Paper 2, Section II, 29K

  Stochastic Financial Models | Part II, 2020

  Let $\left(S_{n}^{0}, S_{n}\right)_{0 \leqslant n \leqslant T}$ be a discrete-time asset price model in $\mathbb{R}^{d+1}$ with numéraire.

  (i) What is meant by an arbitrage for such a model?

  (ii) What does it mean to say that the model is complete?

  Consider now the case where $d=1$ and where

  $$S_{n}^{0}=(1+r)^{n}, \quad S_{n}=S_{0} \prod_{k=1}^{n} Z_{k}$$

  for some $r>0$ and some independent positive random variables $Z_{1}, \ldots, Z_{T}$ with $\log Z_{n} \sim N\left(\mu, \sigma^{2}\right)$ for all $n$.

  (iii) Find an equivalent probability measure $\mathbb{P}^{*}$ such that the discounted asset price $\left(S_{n} / S_{n}^{0}\right)_{0 \leqslant n \leqslant T}$ is a martingale.

  (iv) Does this model have an arbitrage? Justify your answer.

  (v) By considering the contingent claim $\left(S_{1}\right)^{2}$ or otherwise, show that this model is not complete.

  comment

• Paper 3, Section II, 29K

  Stochastic Financial Models | Part II, 2020

  (a) Let $\left(B_{t}\right)_{t \geqslant 0}$ be a real-valued random process.

  (i) What does it mean to say that $\left(B_{t}\right)_{t \geqslant 0}$ is a Brownian motion?

  (ii) State the reflection principle for Brownian motion.

  (b) Suppose that $\left(B_{t}\right)_{t \geqslant 0}$ is a Brownian motion and set $M_{t}=\sup _{s \leqslant t} B_{s}$ and $Z_{t}=M_{t}-B_{t}$.

  (i) Find the joint distribution function of $B_{t}$ and $M_{t}$.

  (ii) Show that $\left(M_{t}, Z_{t}\right)$ has a joint density function on $[0, \infty)^{2}$ given by

  $$\mathbb{P}\left(M_{t} \in d y \text { and } Z_{t} \in d z\right)=\frac{2}{\sqrt{2 \pi t}} \frac{(y+z)}{t} e^{-(y+z)^{2} /(2 t)} d y d z$$

  (iii) You are given that two of the three processes $\left(\left|B_{t}\right|\right)_{t \geqslant 0},\left(M_{t}\right)_{t \geqslant 0}$ and $\left(Z_{t}\right)_{t \geqslant 0}$ have the same distribution. Identify which two, justifying your answer.

  comment

• Paper 4, Section II, K

  Stochastic Financial Models | Part II, 2020

  (i) What does it mean to say that $\left(S_{t}^{0}, S_{t}\right)_{0 \leqslant t \leqslant T}$ is a Black-Scholes model with interest rate $r$, drift $\mu$ and volatility $\sigma$ ?

  (ii) Write down the Black-Scholes pricing formula for the time- 0 value $V_{0}$ of a time- $T$ contingent claim $C$.

  (iii) Show that if $C$ is a European call of strike $K$ and maturity $T$ then

  $$V_{0} \geqslant S_{0}-e^{-r T} K$$

  (iv) For the European call, derive the Black-Scholes pricing formula

  $$V_{0}=S_{0} \Phi\left(d^{+}\right)-e^{-r T} K \Phi\left(d^{-}\right)$$

  where $\Phi$ is the standard normal distribution function and $d^{+}$and $d^{-}$are to be determined.

  (v) Fix $t \in(0, T)$ and consider a modified contract which gives the investor the right but not the obligation to buy one unit of the risky asset at price $K$, either at time $t$ or time $T$ but not both, where the choice of exercise time is to be made by the investor at time $t$. Determine whether the investor should exercise the contract at time $t$.

  comment

Topics in Analysis

• Paper 1, Section I, $\mathbf{2 H}$

  Topics in Analysis | Part II, 2020

  Let $\gamma:[0,1] \rightarrow \mathbb{C}$ be a continuous map never taking the value 0 and satisfying $\gamma(0)=\gamma(1)$. Define the degree (or winding number) $w(\gamma ; 0)$ of $\gamma$ about 0 . Prove the following.

  (i) If $\delta:[0,1] \rightarrow \mathbb{C} \backslash\{0\}$ is a continuous map satisfying $\delta(0)=\delta(1)$, then the winding number of the product $\gamma \delta$ is given by $w(\gamma \delta ; 0)=w(\gamma ; 0)+w(\delta ; 0)$.

  (ii) If $\sigma:[0,1] \rightarrow \mathbb{C}$ is continuous, $\sigma(0)=\sigma(1)$ and $|\sigma(t)|<|\gamma(t)|$ for each $0 \leqslant t \leqslant 1$, then $w(\gamma+\sigma ; 0)=w(\gamma ; 0)$.

  (iii) Let $D=\{z \in \mathbb{C}:|z| \leqslant 1\}$ and let $f: D \rightarrow \mathbb{C}$ be a continuous function with $f(z) \neq 0$ whenever $|z|=1$. Define $\alpha:[0,1] \rightarrow \mathbb{C}$ by $\alpha(t)=f\left(e^{2 \pi i t}\right)$. Then if $w(\alpha ; 0) \neq 0$, there must exist some $z \in D$, such that $f(z)=0$. [It may help to define $F(s, t):=f\left(s e^{2 \pi i t}\right)$. Homotopy invariance of the winding number may be assumed.]

  comment

• Paper 2, Section I, $2 \mathrm{H}$

  Topics in Analysis | Part II, 2020

  Show that every Legendre polynomial $p_{n}$ has $n$ distinct roots in $[-1,1]$, where $n$ is the degree of $p_{n}$.

  Let $x_{1}, \ldots, x_{n}$ be distinct numbers in $[-1,1]$. Show that there are unique real numbers $A_{1}, \ldots, A_{n}$ such that the formula

  $$\int_{-1}^{1} P(t) d t=\sum_{i=1}^{n} A_{i} P\left(x_{i}\right)$$

  holds for every polynomial $P$ of degree less than $n$.

  Now suppose that the above formula in fact holds for every polynomial $P$ of degree less than $2 n$. Show that then $x_{1}, \ldots, x_{n}$ are the roots of $p_{n}$. Show also that $\sum_{i=1}^{n} A_{i}=2$ and that all $A_{i}$ are positive.

  comment

• Paper 2, Section II, H

  Topics in Analysis | Part II, 2020

  Let $T$ be a (closed) triangle in $\mathbb{R}^{2}$ with edges $I, J, K$. Let $A, B, C$, be closed subsets of $T$, such that $I \subset A, J \subset B, K \subset C$ and $T=A \cup B \cup C$. Prove that $A \cap B \cap C$ is non-empty.

  Deduce that there is no continuous map $f: D \rightarrow \partial D$ such that $f(p)=p$ for all $p \in \partial D$, where $D=\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2} \leqslant 1\right\}$ is the closed unit disc and $\partial D=\left\{(x, y) \in \mathbb{R}^{2}: x^{2}+y^{2}=1\right\}$ is its boundary.

  Let now $\alpha, \beta, \gamma \subset \partial D$ be three closed arcs, each arc making an angle of $2 \pi / 3$ (in radians) in $\partial D$ and $\alpha \cup \beta \cup \gamma=\partial D$. Let $P, Q$ and $R$ be open subsets of $D$, such that $\alpha \subset P$, $\beta \subset Q$ and $\gamma \subset R$. Suppose that $P \cup Q \cup R=D$. Show that $P \cap Q \cap R$ is non-empty. [You may assume that for each closed bounded subset $K \subset \mathbb{R}^{2}, d(x, K)=\min \{\|x-y\|: y \in K\}$ defines a continuous function on $\mathbb{R}^{2}$.]

  comment

• Paper 3, Section I, H

  Topics in Analysis | Part II, 2020

  State Runge's theorem about the uniform approximation of holomorphic functions by polynomials.

  Explicitly construct, with a brief justification, a sequence of polynomials which converges uniformly to $1 / z$ on the semicircle $\{z:|z|=1, \operatorname{Re}(z) \leqslant 0\}$.

  Does there exist a sequence of polynomials converging uniformly to $1 / z$ on $\{z:|z|=1, z \neq 1\}$ ? Give a justification.

  comment

• Paper 4, Section I, $2 \mathrm{H}$

  Topics in Analysis | Part II, 2020

  Define what is meant by a nowhere dense set in a metric space. State a version of the Baire Category theorem.

  Let $f:[1, \infty) \rightarrow \mathbb{R}$ be a continuous function such that $f(n x) \rightarrow 0$ as $n \rightarrow \infty$ for every fixed $x \geqslant 1$. Show that $f(t) \rightarrow 0$ as $t \rightarrow \infty$.

  comment

• Paper 4, Section II, H

  Topics in Analysis | Part II, 2020

  (a) State Liouville's theorem on the approximation of algebraic numbers by rationals.

  (b) Let $\left(a_{n}\right)_{n=0}^{\infty}$ be a sequence of positive integers and let

  $$\alpha=a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2}+\frac{1}{a_{3}+\ldots}}}$$

  be the value of the associated continued fraction.

  (i) Prove that the $n$th convergent $p_{n} / q_{n}$ satisfies

  $$\left|\alpha-\frac{p_{n}}{q_{n}}\right| \leqslant\left|\alpha-\frac{p}{q}\right|$$

  for all the rational numbers $\frac{p}{q}$ such that $0<q \leqslant q_{n}$.

  (ii) Show that if the sequence $\left(a_{n}\right)$ is bounded, then one can choose $c>0$ (depending only on $\alpha$ ), so that for every rational number $\frac{a}{b}$,

  $$\left|\alpha-\frac{a}{b}\right|>\frac{c}{b^{2}}$$

  (iii) Show that if the sequence $\left(a_{n}\right)$ is unbounded, then for each $c>0$ there exist infinitely many rational numbers $\frac{a}{b}$ such that

  $$\left|\alpha-\frac{a}{b}\right|<\frac{c}{b^{2}}$$

  [You may assume without proof the relation

  $$\left.\left(\begin{array}{ll} p_{n+1} & p_{n} \\ q_{n+1} & q_{n} \end{array}\right)=\left(\begin{array}{cc} p_{n} & p_{n-1} \\ q_{n} & q_{n+1} \end{array}\right)\left(\begin{array}{cc} a_{n+1} & 1 \\ 1 & 0 \end{array}\right), \quad n=1,2, \ldots .\right]$$

  comment

Waves

• Paper 1, Section II, B

  Waves | Part II, 2020

  (a) Write down the linearised equations governing motion of an inviscid compressible fluid at uniform entropy. Assuming that the velocity is irrotational, show that the velocity potential $\phi(\mathbf{x}, t)$ satisfies the wave equation and identify the wave speed $c_{0}$. Obtain from these linearised equations the energy-conservation equation

  $$\frac{\partial E}{\partial t}+\nabla \cdot \mathbf{I}=0$$

  and give expressions for the acoustic-energy density $E$ and the acoustic-energy flux, or intensity, I.

  (b) Inviscid compressible fluid with density $\rho_{0}$ and sound speed $c_{0}$ occupies the regions $y<0$ and $y>0$, which are separated by a thin elastic membrane at an undisturbed position $y=0$. The membrane has mass per unit area $m$ and is under a constant tension $T$. Small displacements of the membrane to $y=\eta(x, t)$ are coupled to small acoustic disturbances in the fluid with velocity potential $\phi(x, y, t)$.

  (i) Write down the (linearised) kinematic and dynamic boundary conditions at the membrane. [Hint: The elastic restoring force on the membrane is like that on a stretched string.]

  (ii) Show that the dispersion relation for waves proportional to $\cos (k x-\omega t)$ propagating along the membrane with $|\phi| \rightarrow 0$ as $y \rightarrow \pm \infty$ is given by

  $$\left\{m+\frac{2 \rho_{0}}{\left(k^{2}-\omega^{2} / c_{0}^{2}\right)^{1 / 2}}\right\} \omega^{2}=T k^{2}$$

  Interpret this equation by explaining physically why all disturbances propagate with phase speed $c$ less than $(T / m)^{1 / 2}$ and why $c(k) \rightarrow 0$ as $k \rightarrow 0$.

  (iii) Show that in such a wave the component $\left\langle I_{y}\right\rangle$ of mean acoustic intensity perpendicular to the membrane is zero.

  comment

• Paper 2, Section II, 39B

  Waves | Part II, 2020

  Small displacements $\mathbf{u}(\mathbf{x}, t)$ in a homogeneous elastic medium are governed by the equation

  $$\rho \frac{\partial^{2} \mathbf{u}}{\partial t^{2}}=(\lambda+2 \mu) \boldsymbol{\nabla}(\boldsymbol{\nabla} \cdot \mathbf{u})-\mu \boldsymbol{\nabla} \wedge(\boldsymbol{\nabla} \wedge \mathbf{u})$$

  where $\rho$ is the density, and $\lambda$ and $\mu$ are the Lamé constants.

  (a) Show that the equation supports two types of harmonic plane-wave solutions, $\mathbf{u}=\mathbf{A} \exp [i(\mathbf{k} \cdot \mathbf{x}-\omega t)]$, with distinct wavespeeds, $c_{P}$ and $c_{S}$, and distinct polarizations. Write down the direction of the displacement vector A for a $P$-wave, an $S V$-wave and an $S H$-wave, in each case for the wavevector $(k, 0, m)$.

  (b) Given $k$ and $c$, with $c>c_{P}\left(>c_{S}\right)$, explain how to construct a superposition of $P$-waves with wavenumbers $\left(k, 0, m_{P}\right)$ and $\left(k, 0,-m_{P}\right)$, such that

  $$\mathbf{u}(x, z, t)=e^{i k(x-c t)}\left(f_{1}(z), 0, i f_{3}(z)\right)$$

  where $f_{1}(z)$ is an even function, and $f_{1}$ and $f_{3}$ are both real functions, to be determined. Similarly, find a superposition of $S V$-waves with $\mathbf{u}$ again in the form $(*)$.

  (c) An elastic waveguide consists of an elastic medium in $-H<z<H$ with rigid boundaries at $z=\pm H$. Using your answers to part (b), show that the waveguide supports propagating eigenmodes that are a mixture of $P$ - and $S V$-waves, and have dispersion relation $c(k)$ given by

  $$a \tan (a k H)=-\frac{\tan (b k H)}{b}, \quad \text { where } \quad a=\left(\frac{c^{2}}{c_{P}^{2}}-1\right)^{1 / 2} \quad \text { and } \quad b=\left(\frac{c^{2}}{c_{S}^{2}}-1\right)^{1 / 2}$$

  Sketch the two sides of the dispersion relationship as functions of $c$. Explain briefly why there are infinitely many solutions.

  comment

• Paper 3, Section II, B

  Waves | Part II, 2020

  The dispersion relation for capillary waves on the surface of deep water is

  $$\omega^{2}=S^{2}|k|^{3}$$

  where $S=(T / \rho)^{1 / 2}, \rho$ is the density and $T$ is the coefficient of surface tension. The free surface $z=\eta(x, t)$ is undisturbed for $t<0$, when it is suddenly impacted by an object, giving the initial conditions at time $t=0$ :

  $$\eta=0 \quad \text { and } \quad \frac{\partial \eta}{\partial t}= \begin{cases}-W, & |x|<\epsilon \\ 0, & |x|>\epsilon\end{cases}$$

  where $W$ is a constant.

  (i) Use Fourier analysis to find an integral expression for $\eta(x, t)$ when $t>0$.

  (ii) Use the method of stationary phase to find the asymptotic behaviour of $\eta(V t, t)$ for fixed $V>0$ as $t \rightarrow \infty$, for the case $V \ll \epsilon^{-1 / 2} S$. Show that the result can be written in the form

  $$\eta(x, t) \sim \frac{W \epsilon S t^{2}}{x^{5 / 2}} F\left(\frac{x^{3}}{S^{2} t^{2}}\right)$$

  and determine the function $F$.

  (iii) Give a brief physical interpretation of the link between the condition $\epsilon V^{2} / S^{2} \ll$ 1 and the simple dependence on the product $W \epsilon$.

  [You are given that $\int_{-\infty}^{\infty} e^{\pm i a u^{2}} d u=(\pi / a)^{1 / 2} e^{\pm i \pi / 4} \quad$ for $a>0 .$ ]

  comment

• Paper 4, Section II, B

  Waves | Part II, 2020

  (a) Show that the equations for one-dimensional unsteady flow of an inviscid compressible fluid at constant entropy can be put in the form

  $$\left(\frac{\partial}{\partial t}+(u \pm c) \frac{\partial}{\partial x}\right) R_{\pm}=0$$

  where $u$ and $c$ are the fluid velocity and the local sound speed, respectively, and the Riemann invariants $R_{\pm}$are to be defined.

  Such a fluid occupies a long narrow tube along the $x$-axis. For times $t<0$ it is at rest with uniform pressure $p_{0}$, density $\rho_{0}$ and sound speed $c_{0}$. At $t=0$ a finite segment, $0 \leqslant x \leqslant L$, is disturbed so that $u=U(x)$ and $c=c_{0}+C(x)$, with $U=C=0$ for $x \leqslant 0$ and $x \geqslant L$. Explain, with the aid of a carefully labelled sketch, how two independent simple waves emerge after some time. You may assume that no shock waves form.

  (b) A fluid has the adiabatic equation of state

  $$p(\rho)=A-\frac{B^{2}}{\rho}$$

  where $A$ and $B$ are positive constants and $\rho>B^{2} / A$.

  (i) Calculate the Riemann invariants for this fluid, and express $u \pm c$ in terms of $R_{\pm}$ and $c_{0}$. Deduce that in a simple wave with $R_{-}=0$ the velocity field translates, without any nonlinear distortion, at the equilibrium sound speed $c_{0}$.

  (ii) At $t=0$ this fluid occupies $x>0$ and is at rest with uniform pressure, density and sound speed. For $t>0$ a piston initially at $x=0$ executes simple harmonic motion with position $x(t)=a \sin \omega t$, where $a \omega<c_{0}$. Show that $u(x, t)=U(\phi)$, where $\phi=\omega\left(t-x / c_{0}\right)$, for some function $U$ that is zero for $\phi<0$ and is $2 \pi$-periodic, but not simple harmonic, for $\phi>0$. By approximately inverting the relationship between $\phi$ and the time $\tau$ that a characteristic leaves the piston for the case $\epsilon=a \omega / c_{0} \ll 1$, show that

  $$U(\phi)=a \omega\left(\cos \phi-\epsilon \sin ^{2} \phi-\frac{3}{2} \epsilon^{2} \sin ^{2} \phi \cos \phi+O\left(\epsilon^{3}\right)\right) \quad \text { for } \quad \phi>0$$

  comment