Part II, 2008, Paper 1

Algebraic Topology

• 1.II.21F

  Algebraic Topology | Part II, 2008

  (i) State the van Kampen theorem.

  (ii) Calculate the fundamental group of the wedge $S^{2} \vee S^{1}$.

  (iii) Let $X=\mathbb{R}^{3} \backslash A$ where $A$ is a circle. Calculate the fundamental group of $X$.

  comment

Applications of Quantum Mechanics

• 1.II.33E

  Applications of Quantum Mechanics | Part II, 2008

  A beam of particles each of mass $m$ and energy $\hbar^{2} k^{2} /(2 m)$ scatters off an axisymmetric potential $V$. In the first Born approximation the scattering amplitude is

  $$f(\theta)=-\frac{m}{2 \pi \hbar^{2}} \int e^{-i\left(\mathbf{k}-\mathbf{k}_{0}\right) \cdot \mathbf{x}^{\prime}} V\left(\mathbf{x}^{\prime}\right) d^{3} x^{\prime}$$

  where $\mathbf{k}_{0}=(0,0, k)$ is the wave vector of the incident particles and $\mathbf{k}=(k \sin \theta, 0, k \cos \theta)$ is the wave vector of the outgoing particles at scattering angle $\theta$ (and $\phi=0$ ). Let $\mathbf{q}=\mathbf{k}-\mathbf{k}_{0}$ and $q=|\mathbf{q}|$. Show that when the scattering potential $V$ is spherically symmetric the expression $(*)$ simplifies to

  $$f(\theta)=-\frac{2 m}{\hbar^{2} q} \int_{0}^{\infty} r^{\prime} V\left(r^{\prime}\right) \sin \left(q r^{\prime}\right) d r^{\prime}$$

  and find the relation between $q$ and $\theta$.

  Calculate this scattering amplitude for the potential $V(r)=V_{0} e^{-r}$ where $V_{0}$ is a constant, and show that at high energies the particles emerge predominantly in a narrow cone around the forward beam direction. Estimate the angular width of the cone.

  comment

Applied Probability

• 1.II.26I

  Applied Probability | Part II, 2008

  Let $\left(X_{t}, t \geqslant 0\right)$ be an irreducible continuous-time Markov chain with initial probability distribution $\pi$ and Q-matrix $Q$ (for short: a $(\pi, Q)$ CTMC), on a finite state space $I$.

  (i) Define the terms reversible CTMC and detailed balance equations (DBEs) and explain, without proof, the relation between them.

  (ii) Prove that any solution of the DBEs is an equilibrium distribution (ED) for $\left(X_{t}\right)$.

  Let $\left(Y_{n}, n=0,1, \ldots\right)$ be an irreducible discrete-time Markov chain with initial probability distribution $\widehat{\pi}$and transition probability matrix $\widehat{P}$(for short: a $(\widehat{\pi}, \widehat{P})$ DTMC), on the state space $I$.

  (iii) Repeat the two definitions from (i) in the context of the DTMC $\left(Y_{n}\right)$. State also in this context the relation between them, and prove a statement analogous to (ii).

  (iv) What does it mean to say that $\left(Y_{n}\right)$ is the jump chain for $\left(X_{t}\right)$ ? State and prove a relation between the ED $\pi$ for the $\operatorname{CTMC}\left(X_{t}\right)$ and the ED $\widehat{\pi}$for its jump chain $\left(Y_{n}\right)$.

  (v) Prove that $\left(X_{t}\right)$ is reversible (in equilibrium) if and only if its jump chain $\left(Y_{n}\right)$ is reversible (in equilibrium).

  (vi) Consider now a continuous time random walk on a graph. More precisely, consider a CTMC $\left(X_{t}\right)$ on an undirected graph, where some pairs of states $i, j \in I$ are joined by one or more non-oriented 'links' $e_{i j}(1), \ldots, e_{i j}\left(m_{i j}\right)$. Here $m_{i j}=m_{j i}$ is the number of links between $i$ and $j$. Assume that the jump rate $q_{i j}$ is proportional to $m_{i j}$. Can the chain $\left(X_{t}\right)$ be reversible? Identify the corresponding jump chain $\left(Y_{n}\right)$ (which determines a discrete-time random walk on the graph) and comment on its reversibility.

  comment

Asymptotic Methods

• 1.II $. 30 \mathrm{~A}$

  Asymptotic Methods | Part II, 2008

  Obtain an expression for the $n$th term of an asymptotic expansion, valid as $\lambda \rightarrow \infty$, for the integral

  $$I(\lambda)=\int_{0}^{1} t^{2 \alpha} e^{-\lambda\left(t^{2}+t^{3}\right)} d t \quad(\alpha>-1 / 2) .$$

  Estimate the value of $n$ for the term of least magnitude.

  Obtain the first two terms of an asymptotic expansion, valid as $\lambda \rightarrow \infty$, for the integral

  $$J(\lambda)=\int_{0}^{1} t^{2 \alpha} e^{-\lambda\left(t^{2}-t^{3}\right)} d t \quad(-1 / 2<\alpha<0)$$

  [Hint:

  $$\left.\Gamma(z)=\int_{0}^{\infty} t^{z-1} e^{-t} d t .\right]$$

  [Stirling's formula may be quoted.]

  comment

Classical Dynamics

• 1.I.9A

  Classical Dynamics | Part II, 2008

  The action for a system with generalized coordinates $q_{i}(t)$ for a time interval $\left[t_{1}, t_{2}\right]$ is given by

  $$S=\int_{t_{1}}^{t_{2}} L\left(q_{i}, \dot{q}_{i}, t\right) d t$$

  where $L$ is the Lagrangian. The end point values $q_{i}\left(t_{1}\right)$ and $q_{i}\left(t_{2}\right)$ are fixed.

  Derive Lagrange's equations from the principle of least action by considering the variation of $S$ for all possible paths.

  Define the momentum $p_{i}$ conjugate to $q_{i}$. Derive a condition for $p_{i}$ to be a constant of the motion.

  A symmetric top moves under the action of a potential $V(\theta)$. The Lagrangian is given by

  $$L=\frac{1}{2} I_{1}\left(\dot{\theta}^{2}+\dot{\phi}^{2} \sin ^{2} \theta\right)+\frac{1}{2} I_{3}(\dot{\psi}+\dot{\phi} \cos \theta)^{2}-V$$

  where the generalized coordinates are the Euler angles $(\theta, \phi, \psi)$ and the principal moments of inertia are $I_{1}$ and $I_{3}$.

  Show that $\omega_{3}=\dot{\psi}+\dot{\phi} \cos \theta$ is a constant of the motion and give expressions for two others. Show further that it is possible for the top to move with both $\theta$ and $\dot{\phi}$ constant provided these satisfy the condition

  $$I_{1} \dot{\phi}^{2} \sin \theta \cos \theta-I_{3} \omega_{3} \dot{\phi} \sin \theta=\frac{d V}{d \theta}$$

  comment

Coding and Cryptography

• 1.I.4G

  Coding and Cryptography | Part II, 2008

  Define the entropy $H(X)$ of a random variable $X$ that takes no more than $N$ different values. What are the maximum and the minimum values for the entropy for a fixed value of $N$ ? Explain when the maximum and minimum are attained. You should prove any inequalities that you use.

  comment

• 1.II.12G

  Coding and Cryptography | Part II, 2008

  State Shannon's Noisy Coding Theorem for a binary symmetric channel.

  Define the mutual information of two discrete random variables $X$ and $Y$. Prove that the mutual information is symmetric and non-negative. Define also the information capacity of a channel.

  A channel transmits numbers chosen from the alphabet $\mathcal{A}=\{0,1,2\}$ and has transition matrix

  $$\left(\begin{array}{ccc} 1-2 \beta & \beta & \beta \\ \beta & 1-2 \beta & \beta \\ \beta & \beta & 1-2 \beta \end{array}\right)$$

  for a number $\beta$ with $0 \leqslant \beta \leqslant \frac{1}{3}$. Calculate the information capacity of the channel.

  comment

Cosmology

• 1.I.10E

  Cosmology | Part II, 2008

  The number density of particles of mass $m$ at equilibrium in the early universe is given by the integral

  $$n=\frac{4 \pi g_{\mathrm{s}}}{h^{3}} \int_{0}^{\infty} \frac{p^{2} d p}{\exp [(E(p)-\mu) / k T] \mp 1}, \quad \begin{cases}- & \text { bosons } \\ + & \text { fermions }\end{cases}$$

  where $E(p)=c \sqrt{p^{2}+m^{2} c^{2}}, \mu$ is the chemical potential, and $g_{\mathrm{s}}$ is the spin degeneracy. Assuming that the particles remain in equilibrium when they become non-relativistic $\left(k T, \mu \ll m c^{2}\right)$, show that the number density can be expressed as

  $$n=g_{\mathrm{s}}\left(\frac{2 \pi m k T}{h^{2}}\right)^{3 / 2} e^{\left(\mu-m c^{2}\right) / k T} .$$

  [Hint: Recall that $\left.\int_{0}^{\infty} d x e^{-\sigma^{2} x^{2}}=\sqrt{\pi} /(2 \sigma), \quad(\sigma>0) .\right]$

  At around $t=100$ seconds, deuterium $D$ forms through the nuclear fusion of nonrelativistic protons $p$ and neutrons $n$ via the interaction $p+n \leftrightarrow D$. In equilibrium, what is the relationship between the chemical potentials of the three species? Show that the ratio of their number densities can be expressed as

  $$\frac{n_{D}}{n_{n} n_{p}} \approx\left(\frac{\pi m_{p} k T}{h^{2}}\right)^{-3 / 2} e^{B_{D} / k T}$$

  where the deuterium binding energy is $B_{D}=\left(m_{n}+m_{p}-m_{D}\right) c^{2}$ and you may take $g_{D}=4$. Now consider the fractional densities $X_{a}=n_{a} / n_{B}$, where $n_{B}$ is the baryon density of the universe, to re-express the ratio above in the form $X_{D} /\left(X_{n} X_{p}\right)$, which incorporates the baryon-to-photon ratio $\eta$ of the universe.

  [You may assume that the photon density is $n_{\gamma}=\left(16 \pi \zeta(3) /(h c)^{3}\right)(k T)^{3}$.]

  Why does deuterium form only at temperatures much lower than that given by $k T \approx B_{D}$ ?

  comment

• 1.II.15E

  Cosmology | Part II, 2008

  (i) A homogeneous and isotropic universe has mass density $\rho(t)$ and scale factor $a(t)$. Show how the conservation of total energy (kinetic plus gravitational potential) when applied to a test particle on the edge of a spherical region in this universe can be used to obtain the Friedmann equation

  $$H^{2} \equiv\left(\frac{\dot{a}}{a}\right)^{2}=\frac{8 \pi G}{3} \rho-\frac{k c^{2}}{a^{2}},$$

  where $k$ is a constant. State clearly any assumptions you have made.

  (ii) Assume that the universe is flat $(k=0)$ and filled with two major components: pressure-free matter $\left(P_{\mathrm{M}}=0\right)$ and dark energy with equation of state $P_{\Lambda}=-\rho_{\Lambda} c^{2}$ where their mass densities today $\left(t=t_{0}\right)$ are given respectively by $\rho_{\mathrm{M} 0}$ and $\rho_{\Lambda 0}$. Assuming that each component independently satisfies the fluid conservation equation, $\dot{\rho}=-3 H\left(\rho+P / c^{2}\right)$, show that the total mass density can be expressed as

  $$\rho(t)=\frac{\rho_{\mathrm{M} 0}}{a^{3}}+\rho_{\Lambda 0}$$

  where we have set $a\left(t_{0}\right)=1$.

  Hence, solve the Friedmann equation and show that the scale factor can be expressed in the form

  $$a(t)=\alpha(\sinh \beta t)^{2 / 3},$$

  where $\alpha$ and $\beta$ are constants which you should specify in terms of $\rho_{\mathrm{M} 0}, \rho_{\Lambda 0}$ and $t_{0}$.

  [Hint: try the substitution $b=a^{3 / 2}$.]

  Show that the scale factor $a(t)$ has the expected behaviour for a matter-dominated universe at early times $(t \rightarrow 0)$ and that the universe accelerates at late times $(t \rightarrow \infty)$.

  comment

Differential Geometry

• 1.II.24H

  Differential Geometry | Part II, 2008

  Let $n \geqslant 1$ be an integer, and let $M(n)$ denote the set of $n \times n$ real-valued matrices. We make $M(n)$ into an $n^{2}$-dimensional smooth manifold via the obvious identification $M(n)=\mathbb{R}^{n^{2}}$.

  (a) Let $G L(n)$ denote the subset

  $$G L(n)=\left\{A \in M(n): A^{-1} \text { exists }\right\}$$

  Show that $G L(n)$ is a submanifold of $M(n)$. What is $\operatorname{dim} G L(n)$ ?

  (b) Now let $S L(n) \subset G L(n)$ denote the subset

  $$S L(n)=\{A \in G L(n): \operatorname{det} A=1\}$$

  Show that for $A \in G L(n)$,

  $$(d \text { det })_{A} B=\operatorname{tr}\left(A^{-1} B\right) \operatorname{det} A .$$

  Show that $S L(n)$ is a submanifold of $G L(n)$. What is the dimension of $S L(n) ?$

  (c) Now consider the set $X=M(n) \backslash G L(n)$. For what values of $n \geqslant 1$ is $X$ a submanifold of $M(n)$ ?

  comment

Dynamical Systems

• 1.I.7A

  Dynamical Systems | Part II, 2008

  Sketch the phase plane of the system

  $$\begin{aligned} &\dot{x}=y \\ &\dot{y}=-x+x^{2}-k y \end{aligned}$$

  (i) for $k=0$ and (ii) for $k=1 / 10$. Include in your sketches any trajectories that are the separatrices of a saddle point. In case (ii) shade the domain of stability of the origin.

  comment

Electrodynamics

• 1.II $. 34 \mathrm{D} \quad$

  Electrodynamics | Part II, 2008

  Frame $\mathcal{S}^{\prime}$ is moving with uniform speed $v$ in the $x$-direction relative to a laboratory frame $\mathcal{S}$. The components of the electric and magnetic fields $\mathbf{E}$ and $\mathbf{B}$ in the two frames are related by the Lorentz transformation

  where $\gamma=1 / \sqrt{1-v^{2}}$ and units are chosen so that $c=1$. How do the components of the spatial vector $\mathbf{F}=\mathbf{E}+i \mathbf{B}$ (where $i=\sqrt{-1}$ ) transform?

  Show that $\mathbf{F}^{\prime}$ is obtained from $\mathbf{F}$ by a rotation through $\theta$ about a spatial axis $\mathbf{n}$, where $\mathbf{n}$ and $\theta$ should be determined. Hence, or otherwise, show that there are precisely two independent scalars associated with $\mathbf{F}$ which are preserved by the Lorentz transformation, and obtain them.

  [Hint: since $|v|<1$ there exists a unique real $\psi$ such that $v=\tanh \psi$.]

  comment

Fluid Dynamics II

• 1.II.36A

  Fluid Dynamics II | Part II, 2008

  Derive the relation between the stress tensor $\sigma_{i j}$ and the rate-of-strain tensor $e_{i j}$ in an incompressible Newtonian fluid, using the result that there is a linear dependence between the components of $\sigma_{i j}$ and those of $e_{i j}$ that is the same in all frames. Write down the boundary conditions that hold at an interface between two viscous fluids.

  Viscous fluid is contained in a channel between the rigid planes $y=-a$ and $y=a$. The fluid in $y<0$ has dynamic viscosity $\mu_{-}$, while that in $y>0$ has dynamic viscosity $\mu_{+}$. Gravity may be neglected. The fluids move through the channel in the $x$-direction under the influence of a pressure gradient applied at the ends of the channel. It may be assumed that the velocity has no $z$-components, and all quantities are independent of $z$.

  Find a steady solution of the Navier-Stokes equation in which the interface between the two fluids remains at $y=0$, the fluid velocity is everywhere independent of $x$, and the pressure gradient is uniform. Use it to calculate the following:

  (a) the viscous tangential stress at $y=-a$ and at $y=a$; and

  (b) the ratio of the volume fluxes of the two different fluids.

  Comment on the limits of each of the results in (a) and (b) as $\mu_{+} / \mu_{-} \rightarrow 1$, and as $\mu_{+} / \mu_{-} \rightarrow \infty$

  comment

Further Complex Methods

• 1.I.8C

  Further Complex Methods | Part II, 2008

  The function $F$ is defined by

  $$F(z)=\int_{0}^{\infty} \frac{t^{z-1}}{(t+1)^{2}} d t$$

  For which values of $z$ does the integral converge?

  Show that, for these values,

  $$F(z)=\frac{\pi(1-z)}{\sin (\pi z)} .$$

  comment

• 1.II.14C

  Further Complex Methods | Part II, 2008

  Show that under the change of variable $z=\sin ^{2} x$ the equation

  $$\frac{d^{2} w}{d x^{2}}+n^{2} w=0$$

  becomes

  $$\frac{d^{2} w}{d z^{2}}+\frac{2 z-1}{2 z(z-1)} \frac{d w}{d z}-\frac{n^{2}}{4(z-1) z} w=0$$

  Show that this is a Papperitz equation and that the corresponding $P$-function is

  $$P\left\{\begin{array}{rrrr} 0 & \infty & 1 & \\ 0 & \frac{1}{2} n & 0 & z \\ \frac{1}{2} & -\frac{1}{2} n & \frac{1}{2} & \end{array}\right\}$$

  Deduce that $F\left(\frac{1}{2} n,-\frac{1}{2} n ; \frac{1}{2} ; \sin ^{2} x\right)=\cos n x$.

  comment

Galois Theory

• 1.II.18H

  Galois Theory | Part II, 2008

  Find the Galois group of the polynomial $f(x)=x^{4}+x^{3}+1$ over (i) the finite field $\mathbf{F}_{2}$, (ii) the finite field $\mathbf{F}_{3}$, (iii) the finite field $\mathbf{F}_{4}$, (iv) the field $\mathbf{Q}$ of rational numbers.

  [Results from the course which you use should be stated precisely.]

  comment

General Relativity

• 1.II.35E

  General Relativity | Part II, 2008

  For the metric

  $$\mathrm{d} s^{2}=\frac{1}{r^{2}}\left(-\mathrm{d} t^{2}+\mathrm{d} r^{2}\right), \quad r \geqslant 0,$$

  obtain the geodesic equations of motion. For a massive particle show that

  $$\left(\frac{\mathrm{d} r}{\mathrm{~d} t}\right)^{2}=1-\frac{1}{k^{2} r^{2}}$$

  for some constant $k$. Show that the particle moves on trajectories

  $$r^{2}-t^{2}=\frac{1}{k^{2}}, \quad k r=\sec \tau, \quad k t=\tan \tau$$

  where $\tau$ is the proper time, if the origins of $t, \tau$ are chosen appropriately.

  comment

Geometry of Group Actions

• 1.I.3G

  Geometry of Group Actions | Part II, 2008

  Prove that an isometry of Euclidean space $\mathbb{R}^{3}$ is an affine transformation.

  Deduce that a finite group of isometries of $\mathbb{R}^{3}$ has a common fixed point.

  comment

• 1.II.11G

  Geometry of Group Actions | Part II, 2008

  What is meant by an inversion in a circle in $\mathbb{C} \cup\{\infty\}$ ? Show that a composition of two inversions is a Möbius transformation.

  Hence, or otherwise, show that if $C^{+}$and $C^{-}$are two disjoint circles in $\mathbb{C}$, then the composition of the inversions in $C^{+}$and $C^{-}$has two fixed points.

  comment

Graph Theory

• 1.II .17F

  Graph Theory | Part II, 2008

  State a result of Euler concerning the number of vertices, edges and faces of a connected plane graph. Deduce that if $G$ is a planar graph then $\delta(G) \leqslant 5$. Show that if $G$ is a planar graph then $\chi(G) \leqslant 5$.

  Are the following statements true or false? Justify your answers.

  [You may quote standard facts about planar and non-planar graphs, provided that they are clearly stated.]

  (i) If $G$ is a graph with $\chi(G) \leqslant 4$ then $G$ is planar.

  (ii) If $G$ is a connected graph with average degree at most $2.01$ then $G$ is planar.

  (iii) If $G$ is a connected graph with average degree at most 2 then $G$ is planar.

  comment

Integrable Systems

• 1.II.31C

  Integrable Systems | Part II, 2008

  Define an integrable system in the context of Hamiltonian mechanics with a finite number of degrees of freedom and state the Arnold-Liouville theorem.

  Consider a six-dimensional phase space with its canonical coordinates $\left(p_{j}, q_{j}\right)$, $j=1,2,3$, and the Hamiltonian

  $$\frac{1}{2} \sum_{j=1}^{3} p_{j}^{2}+F(r)$$

  where $r=\sqrt{q_{1}^{2}+q_{2}^{2}+q_{3}^{2}}$ and where $F$ is an arbitrary function. Show that both $M_{1}=q_{2} p_{3}-q_{3} p_{2}$ and $M_{2}=q_{3} p_{1}-q_{1} p_{3}$ are first integrals.

  State the Jacobi identity and deduce that the Poisson bracket

  $$M_{3}=\left\{M_{1}, M_{2}\right\}$$

  is also a first integral. Construct a suitable expression out of $M_{1}, M_{2}, M_{3}$ to demonstrate that the system admits three first integrals in involution and thus satisfies the hypothesis of the Arnold-Liouville theorem.

  comment

Linear Analysis

• 1.II.22F

  Linear Analysis | Part II, 2008

  Suppose $p$ and $q$ are real numbers with $p^{-1}+q^{-1}=1$ and $p, q>1$. Show, quoting any results on convexity that you need, that

  $$a^{1 / p} b^{1 / q} \leqslant \frac{a}{p}+\frac{b}{q}$$

  for all real positive $a$ and $b$.

  Define the space $l^{p}$ and show that it is a complete normed vector space.

  comment

Logic and Set Theory

• 1.II.16G

  Logic and Set Theory | Part II, 2008

  What is a well-ordered set? Show that given any two well-ordered sets there is a unique order isomorphism between one and an initial segment of the other.

  Show that for any ordinal $\alpha$ and for any non-zero ordinal $\beta$ there are unique ordinals $\gamma$ and $\delta$ with $\alpha=\beta \cdot \gamma+\delta$ and $\delta<\beta$.

  Show that a non-zero ordinal $\lambda$ is a limit ordinal if and only if $\lambda=\omega \cdot \gamma$ for some non-zero ordinal $\gamma$.

  [You may assume standard properties of ordinal addition, multiplication and subtraction.]

  comment

Mathematical Biology

• 1.I.6B

  Mathematical Biology | Part II, 2008

  A gene product with concentration $g$ is produced by a chemical $S$ of concentration $s$, is autocatalysed and degrades linearly according to the kinetic equation

  $$\frac{d g}{d t}=f(g, s)=s+k \frac{g^{2}}{1+g^{2}}-g$$

  where $k>0$ is a constant.

  First consider the case $s=0$. Show that if $k>2$ there are two positive steady states, and determine their stability. Sketch the reaction rate $f(g, 0)$.

  Now consider $s>0$. Show that there is a single steady state if $s$ exceeds a critical value. If the system starts in the steady state $g=0$ with $s=0$ and then $s$ is increased sufficiently before decreasing back to zero, show that a biochemical switch can be achieved to a state $g=g_{2}$, whose value you should determine.

  comment

Number Fields

• 1.II.20G

  Number Fields | Part II, 2008

  (a) Define the ideal class group of an algebraic number field $K$. State a result involving the discriminant of $K$ that implies that the ideal class group is finite.

  (b) Put $K=\mathbb{Q}(\omega)$, where $\omega=\frac{1}{2}(1+\sqrt{-23})$, and let $\mathcal{O}_{K}$ be the ring of integers of $K$. Show that $\mathcal{O}_{K}=\mathbb{Z}+\mathbb{Z} \omega$. Factorise the ideals [2] and [3] in $\mathcal{O}_{K}$ into prime ideals. Verify that the equation of ideals

  $$[2, \omega][3, \omega]=[\omega]$$

  holds. Hence prove that $K$ has class number 3 .

  comment

Number Theory

• 1.I.1H

  Number Theory | Part II, 2008

  Define the continued fraction of a real number $\alpha$.

  Compute the continued fraction of $\sqrt{19}$.

  comment

Numerical Analysis

• 1.II.38C

  Numerical Analysis | Part II, 2008

  The Poisson equation $\nabla^{2} u=f$ in the unit square $\Omega=[0,1] \times[0,1]$, with zero boundary conditions on $\partial \Omega$, is discretized with the nine-point formula

  $$\begin{aligned} \frac{10}{3} u_{m, n} &-\frac{2}{3}\left(u_{m+1, n}+u_{m-1, n}+u_{m, n+1}+u_{m, n-1}\right) \\ &-\frac{1}{6}\left(u_{m+1, n+1}+u_{m+1, n-1}+u_{m-1, n+1}+u_{m-1, n-1}\right)=-h^{2} f_{m, n}, \end{aligned}$$

  where $1 \leqslant m, n \leqslant M, u_{m, n} \approx u(m h, n h)$, and $(m h, n h)$ are grid points.

  (a) Prove that, for any ordering of the grid points, the method can be written as $A \mathbf{u}=\mathbf{b}$ with a symmetric positive-definite matrix $A$.

  (b) Describe the Jacobi method for solving a linear system of equations, and prove that it converges for the above system.

  [You may quote without proof the corollary of the Householder-John theorem regarding convergence of the Jacobi method.]

  comment

Partial Differential Equations

• 1.II.29C

  Partial Differential Equations | Part II, 2008

  (i) State the local existence theorem for the first order quasi-linear partial differential equation

  $$\sum_{j=1}^{n} a_{j}(x, u) \frac{\partial u}{\partial x_{j}}=b(x, u)$$

  which is to be solved for a real-valued function with data specified on a hypersurface $S$. Include a definition of "non-characteristic" in your answer.

  (ii) Consider the linear constant-coefficient case (that is, when all the functions $a_{1}, \ldots, a_{n}$ are real constants and $b(x, u)=c x+d$ for some $c=\left(c_{1}, \ldots, c_{n}\right)$ with $c_{1}, \ldots, c_{n}$ real and $d$ real) and with the hypersurface $S$ taken to be the hyperplane $\mathbf{x} \cdot \mathbf{n}=0$. Explain carefully the relevance of the non-characteristic condition in obtaining a solution via the method of characteristics.

  (iii) Solve the equation

  $$\frac{\partial u}{\partial y}+u \frac{\partial u}{\partial x}=0$$

  with initial data $u(0, y)=-y$ prescribed on $x=0$, for a real-valued function $u(x, y)$. Describe the domain on which your solution is $C^{1}$ and comment on this in relation to the theorem stated in (i).

  comment

Principles of Quantum Mechanics

• 1.II.32D

  Principles of Quantum Mechanics | Part II, 2008

  (a) If $A$ and $B$ are operators which each commute with their commutator $[A, B]$, show that $\left[A, e^{B}\right]=[A, B] e^{B}$. By considering

  $$F(\lambda)=e^{\lambda A} e^{\lambda B} e^{-\lambda(A+B)}$$

  and differentiating with respect to the parameter $\lambda$, show also that

  $$e^{A} e^{B}=C e^{A+B}=e^{A+B} C$$

  where $C=e^{\frac{1}{2}[A, B]}$.

  (b) Consider a one-dimensional quantum system with position $\hat{x}$ and momentum $\hat{p}$. Write down a formula for the operator $U(\alpha)$ corresponding to translation through $\alpha$, calculate $[\hat{x}, U(\alpha)]$, and show that your answer is consistent with the assumption that position eigenstates obey $|x+\alpha\rangle=U(\alpha)|x\rangle$. Given this assumption, express the wavefunction for $U(\alpha)|\psi\rangle$ in terms of the wavefunction $\psi(x)$ for $|\psi\rangle$.

  Now suppose the one-dimensional system is a harmonic oscillator of mass $m$ and frequency $\omega$. Show that

  $$\psi_{0}(x-\alpha)=e^{-m \omega \alpha^{2} / 4 \hbar} \sum_{n=0}^{\infty}\left(\frac{m \omega}{2 \hbar}\right)^{n / 2} \frac{\alpha^{n}}{\sqrt{n !}} \psi_{n}(x),$$

  where $\psi_{n}(x)$ are normalised wavefunctions with energies $E_{n}=\hbar \omega\left(n+\frac{1}{2}\right)$.

  [Standard results for constructing normalised energy eigenstates in terms of annihilation and creation operators

  $$a=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}+\frac{i}{m \omega} \hat{p}\right), \quad a^{\dagger}=\left(\frac{m \omega}{2 \hbar}\right)^{1 / 2}\left(\hat{x}-\frac{i}{m \omega} \hat{p}\right)$$

  may be quoted without proof.]

  comment

Principles of Statistics

• 1.II.27I

  Principles of Statistics | Part II, 2008

  An angler starts fishing at time 0. Fish bite in a Poisson Process of rate $\Lambda$ per hour, so that, if $\Lambda=\lambda$, the number $N_{t}$ of fish he catches in the first $t$ hours has the Poisson distribution $\mathcal{P}(\lambda t)$, while $T_{n}$, the time in hours until his $n$th bite, has the Gamma distribution $\Gamma(n, \lambda)$, with density function

  $$p(t \mid \lambda)=\frac{\lambda^{n}}{(n-1) !} t^{n-1} e^{-\lambda t} \quad(t>0) .$$

  Bystander $B_{1}$ plans to watch for 3 hours, and to record the number $N_{3}$ of fish caught. Bystander $B_{2}$ plans to observe until the 10 th bite, and to record $T_{10}$, the number of hours until this occurs.

  For $B_{1}$, show that $\widetilde{\Lambda}_{1}:=N_{3} / 3$ is an unbiased estimator of $\Lambda$ whose variance function achieves the Cramér-Rao lower bound

  Find an unbiased estimator of $\Lambda$ for $B_{2}$, of the form $\widetilde{\Lambda}_{2}=k / T_{10}$. Does it achieve the Cramér-Rao lower bound? Is it minimum-variance-unbiased? Justify your answers.

  In fact, the 10 th fish bites after exactly 3 hours. For each of $B_{1}$ and $B_{2}$, write down the likelihood function for $\Lambda$ based their observations. What does the Likelihood Principle have to say about the inferences to be drawn by $B_{1}$ and $B_{2}$, and why? Compute the estimates $\tilde{\lambda}_{1}$ and $\widetilde{\lambda}_{2}$ produced by applying $\widetilde{\Lambda}_{1}$ and $\widetilde{\Lambda}_{2}$ to the observed data. Does the method of minimum-variance-unbiased estimation respect the Likelihood Principle?

  comment

Probability and Measure

• 1.II $. 25 \mathrm{~J} \quad$

  Probability and Measure | Part II, 2008

  State the Dominated Convergence Theorem.

  Hence or otherwise prove Kronecker's Lemma: if $\left(a_{j}\right)$ is a sequence of non-negative reals such that

  $$\sum_{j=1}^{\infty} \frac{a_{j}}{j}<\infty$$

  then

  $$n^{-1} \sum_{j=1}^{n} a_{j} \rightarrow 0 \quad(n \rightarrow \infty)$$

  Let $\xi_{1}, \xi_{2}, \ldots$ be independent $N(0,1)$ random variables and set $S_{n}=\xi_{1}+\ldots+\xi_{n}$. Let $\mathcal{F}_{0}$ be the collection of all finite unions of intervals of the form $(a, b)$, where $a$ and $b$ are rational, together with the whole line $\mathbb{R}$. Prove that with probability 1 the limit

  $$m(B) \equiv \lim _{n \rightarrow \infty} \frac{1}{n} \sum_{j=1}^{n} I_{B}\left(S_{j}\right)$$

  exists for all $B \in \mathcal{F}_{0}$, and identify it. Is it possible to extend $m$ defined on $\mathcal{F}_{0}$ to a measure on the Borel $\sigma$-algebra of $\mathbb{R}$ ? Justify your answer.

  comment

Representation Theory

• 1.II.19G

  Representation Theory | Part II, 2008

  For a complex representation $V$ of a finite group $G$, define the action of $G$ on the dual representation $V^{*}$. If $\alpha$ denotes the character of $V$, compute the character $\beta$ of $V^{*}$.

  [Your formula should express $\beta(g)$ just in terms of the character $\alpha$.]

  Using your formula, how can you tell from the character whether a given representation is self-dual, that is, isomorphic to the dual representation?

  Let $V$ be an irreducible representation of $G$. Show that the trivial representation occurs as a summand of $V \otimes V$ with multiplicity either 0 or 1 . Show that it occurs once if and only if $V$ is self-dual.

  For a self-dual irreducible representation $V$, show that $V$ either has a nondegenerate $G$-invariant symmetric bilinear form or a nondegenerate $G$-invariant alternating bilinear form, but not both.

  If $V$ is an irreducible self-dual representation of odd dimension $n$, show that the corresponding homomorphism $G \rightarrow G L(n, \mathbf{C})$ is conjugate to a homomorphism into the orthogonal group $O(n, \mathbf{C})$. Here $O(n, \mathbf{C})$ means the subgroup of $G L(n, \mathbf{C})$ that preserves a nondegenerate symmetric bilinear form on $\mathbf{C}^{n}$.

  comment

Riemann Surfaces

• 1.II.23H

  Riemann Surfaces | Part II, 2008

  Define the terms Riemann surface, holomorphic map between Riemann surfaces and biholomorphic map.

  Show, without using the notion of degree, that a non-constant holomorphic map between compact connected Riemann surfaces must be surjective.

  Let $\phi$ be a biholomorphic map of the punctured unit disc $\Delta^{*}=\{0<|z|<1\} \subset \mathbb{C}$ onto itself. Show that $\phi$ extends to a biholomorphic map of the open unit disc $\Delta$ to itself such that $\phi(0)=0$.

  Suppose that $f: R \rightarrow S$ is a continuous holomorphic map between Riemann surfaces and $f$ is holomorphic on $R \backslash\{p\}$, where $p$ is a point in $R$. Show that $f$ is then holomorphic on all of $R$.

  [The Open Mapping Theorem may be used without proof if clearly stated.]

  comment

Statistical Modelling

• 1.I.5J

  Statistical Modelling | Part II, 2008

  Consider the following Binomial generalized linear model for data $y_{1}, \ldots, y_{n}$, with logit link function. The data $y_{1}, \ldots, y_{n}$ are regarded as observed values of independent random variables $Y_{1}, \ldots, Y_{n}$, where

  $$Y_{i} \sim \operatorname{Bin}\left(1, \mu_{i}\right), \quad \log \frac{\mu_{i}}{1-\mu_{i}}=\beta^{\top} x_{i}, \quad i=1, \ldots, n,$$

  where $\beta$ is an unknown $p$-dimensional parameter, and where $x_{1}, \ldots, x_{n}$ are known $p$ dimensional explanatory variables. Write down the likelihood function for $y=\left(y_{1}, \ldots, y_{n}\right)$ under this model.

  Show that the maximum likelihood estimate $\hat{\beta}$ satisfies an equation of the form $X^{\top} y=X^{\top} \hat{\mu}$, where $X$ is the $p \times n$ matrix with rows $x_{1}^{\top}, \ldots, x_{n}^{\top}$, and where $\hat{\mu}=$ $\left(\hat{\mu}_{1}, \ldots, \hat{\mu}_{n}\right)$, with $\hat{\mu}_{i}$ a function of $x_{i}$ and $\hat{\beta}$, which you should specify.

  Define the deviance $D(y ; \hat{\mu})$ and find an explicit expression for $D(y ; \hat{\mu})$ in terms of $y$ and $\hat{\mu}$ in the case of the model above.

  comment

• 1.II.13J

  Statistical Modelling | Part II, 2008

  Consider performing a two-way analysis of variance (ANOVA) on the following data: $>\mathrm{Y}[,, 1]$ $\mathrm{Y}[,, 2]$ $\mathrm{Y}[,, 3]$ $[, 1] \quad[, 2]$ $[, 1] \quad[, 2]$ $[, 1] \quad[, 2]$

  

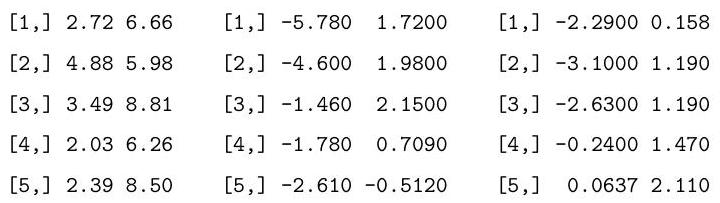
  Explain and interpret the R commands and (slightly abbreviated) output below. In particular, you should describe the model being fitted, and comment on the hypothesis tests which are performed under the summary and anova commands. $>\mathrm{K}<-\operatorname{dim}(\mathrm{Y})[1]$ $>I<-\operatorname{dim}(Y)[2]$ $>\mathrm{J}<-\operatorname{dim}(\mathrm{Y})[3]$ $>\mathrm{C}(\mathrm{I}, \mathrm{J}, \mathrm{K})$

  [1] $2 \quad 3 \quad 10$

  $>y<-$ as.vector $(Y)$

  $>\mathrm{a}<-\mathrm{gl}(\mathrm{I}, \mathrm{K}$, length $(\mathrm{y}))$

  $>\mathrm{b}<-\operatorname{gl}(\mathrm{J}, \mathrm{K} * \mathrm{I}$, length $(\mathrm{y}))$

  $>f i t 1<-\operatorname{lm}(\mathrm{y} \sim \mathrm{a}+\mathrm{b})$

  $>\operatorname{summary}(f i t 1)$

  Coefficients:

  Estimate Std. Error t value $\operatorname{Pr}(>|t|)$

  (Intercept) $3.7673 \quad 0.3032 \quad 12.43<2 \mathrm{e}-16 * * *$

  $\mathrm{a} 2 \quad 3.4542 \quad 0.3032 \quad 11.393 .27 \mathrm{e}-16 * * *$

  b2 $-6.3215<0.3713-17.03<2 \mathrm{e}-16 * * *$

  b3 $-5.8268<0.3713-15.69<2 \mathrm{e}-16 * * *$

  $>\operatorname{anova}(\mathrm{fit1})$

  

  The following $\mathrm{R}$ code fits a similar model. Briefly explain the difference between this model and the one above. Based on the output of the anova call below, say whether you prefer this model over the one above, and explain your preference.

  

  Finally, explain what is being calculated in the code below and give the value that would be obtained by the final line of code.

  

  comment

Stochastic Financial Models

• 1.II.28J

  Stochastic Financial Models | Part II, 2008

  (a) In the context of the Black-Scholes formula, let $S_{0}$ be the time- 0 spot price, $K$ be the strike price, $T$ be the time to maturity, and let $\sigma$ be the volatility. Assume that the interest rate $r$ is constant and assume absence of dividends. Write $\mathrm{EC}\left(S_{0}, K, \sigma, r, T\right)$ for the time- 0 price of a standard European call. The Black-Scholes formula can be written in the following form

  $$\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)=S_{0} \Phi\left(d_{1}\right)-e^{-r T} K \Phi\left(d_{2}\right)$$

  State how the quantities $d_{1}$ and $d_{2}$ depend on $S_{0}, K, \sigma, r$ and $T$.

  Assume that you sell this option at time 0 . What is your replicating portfolio at time 0 ?

  [No proofs are required.]

  (b) Compute the limit of $\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$ as $\sigma \rightarrow \infty$. Construct an explicit arbitrage under the assumption that European calls are traded above this limiting price.

  (c) Compute the limit of $\operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$ as $\sigma \rightarrow 0$. Construct an explicit arbitrage under the assumption that European calls are traded below this limiting price.

  (d) Express in terms of $S_{0}, d_{1}$ and $T$ the derivative

  $$\frac{\partial}{\partial \sigma} \operatorname{EC}\left(S_{0}, K, \sigma, r, T\right)$$

  [Hint: you may find it useful to express $\frac{\partial}{\partial \sigma} d_{1}$ in terms of $\frac{\partial}{\partial \sigma} d_{2}$.]

  [You may use without proof the formula $S_{0} \Phi^{\prime}\left(d_{1}\right)-e^{-r T} K \Phi^{\prime}\left(d_{2}\right)=0$.]

  (e) Say what is meant by implied volatility and explain why the previous results make it well-defined.

  comment

Topics in Analysis

• 1.I.2F

  Topics in Analysis | Part II, 2008

  Let $P_{0}, P_{1}, P_{2}, \ldots$ be non-zero orthogonal polynomials on an interval $[a, b]$ such that the degree of $P_{j}$ is equal to $j$ for every $j=0,1,2, \ldots$, where the orthogonality is with respect to the inner product $<f, g>=\int_{a}^{b} f g$. If $f$ is any continuous function on $[a, b]$ orthogonal to $P_{0}, P_{1}, \ldots, P_{n-1}$ and not identically zero, prove that $f$ must have at least $n$ distinct zeros in $(a, b)$.

  comment

Waves

• 1.II $. 37 \mathrm{~B}$

  Waves | Part II, 2008

  Show that in an acoustic plane wave the velocity and perturbation pressure are everywhere proportional and find the constant of proportionality.

  Gas occupies a tube lying parallel to the $x$-axis. In the regions $x<0$ and $x>L$ the gas has uniform density $\rho_{0}$ and sound speed $c_{0}$. For $0<x<L$ the gas is cooled so that it has uniform density $\rho_{1}$ and sound speed $c_{1}$. A harmonic plane wave with frequency $\omega$ is incident from $x=-\infty$. Show that the amplitude of the wave transmitted into $x>L$ relative to that of the incident wave is

  $$|T|=\left[\cos ^{2} k_{1} L+\frac{1}{4}\left(\lambda+\lambda^{-1}\right)^{2} \sin ^{2} k_{1} L\right]^{-1 / 2}$$

  where $\lambda=\rho_{1} c_{1} / \rho_{0} c_{0}$ and $k_{1}=\omega / c_{1}$.

  What are the implications of this result if $\lambda \gg 1$ ?

  comment