Part IB, 2003

Analysis II

• $3 . \mathrm{II} . 11 \mathrm{~F} \quad$

  Analysis II | Part IB, 2003

  State and prove the Contraction Mapping Theorem.

  Let $(X, d)$ be a bounded metric space, and let $F$ denote the set of all continuous maps $X \rightarrow X$. Let $\rho: F \times F \rightarrow \mathbb{R}$ be the function

  $$\rho(f, g)=\sup \{d(f(x), g(x)): x \in X\}$$

  Show that $\rho$ is a metric on $F$, and that $(F, \rho)$ is complete if $(X, d)$ is complete. [You may assume that a uniform limit of continuous functions is continuous.]

  Now suppose that $(X, d)$ is complete. Let $C \subseteq F$ be the set of contraction mappings, and let $\theta: C \rightarrow X$ be the function which sends a contraction mapping to its unique fixed point. Show that $\theta$ is continuous. [Hint: fix $f \in C$ and consider $d(\theta(g), f(\theta(g)))$, where $g \in C$ is close to $f$.]

  comment

• 1.I.1F

  Analysis II | Part IB, 2003

  Let $E$ be a subset of $\mathbb{R}^{n}$. Prove that the following conditions on $E$ are equivalent:

  (i) $E$ is closed and bounded.

  (ii) $E$ has the Bolzano-Weierstrass property (i.e., every sequence in $E$ has a subsequence convergent to a point of $E$ ).

  (iii) Every continuous real-valued function on $E$ is bounded.

  [The Bolzano-Weierstrass property for bounded closed intervals in $\mathbb{R}^{1}$ may be assumed.]

  comment

• 1.II.10F

  Analysis II | Part IB, 2003

  Explain briefly what is meant by a metric space, and by a Cauchy sequence in a metric space.

  A function $d: X \times X \rightarrow \mathbb{R}$ is called a pseudometric on $X$ if it satisfies all the conditions for a metric except the requirement that $d(x, y)=0$ implies $x=y$. If $d$ is a pseudometric on $X$, show that the binary relation $R$ on $X$ defined by $x R y \Leftrightarrow d(x, y)=0$ is an equivalence relation, and that the function $d$ induces a metric on the set $X / R$ of equivalence classes.

  Now let $(X, d)$ be a metric space. If $\left(x_{n}\right)$ and $\left(y_{n}\right)$ are Cauchy sequences in $X$, show that the sequence whose $n$th term is $d\left(x_{n}, y_{n}\right)$ is a Cauchy sequence of real numbers. Deduce that the function $\bar{d}$ defined by

  $$\bar{d}\left(\left(x_{n}\right),\left(y_{n}\right)\right)=\lim _{n \rightarrow \infty} d\left(x_{n}, y_{n}\right)$$

  is a pseudometric on the set $C$ of all Cauchy sequences in $X$. Show also that there is an isometric embedding (that is, a distance-preserving mapping) $X \rightarrow C / R$, where $R$ is the equivalence relation on $C$ induced by the pseudometric $\bar{d}$ as in the previous paragraph. Under what conditions on $X$ is $X \rightarrow C / R$ bijective? Justify your answer.

  comment

• 2.I.1F

  Analysis II | Part IB, 2003

  Explain what it means for a function $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{1}$ to be differentiable at a point $(a, b)$. Show that if the partial derivatives $\partial f / \partial x$ and $\partial f / \partial y$ exist in a neighbourhood of $(a, b)$ and are continuous at $(a, b)$ then $f$ is differentiable at $(a, b)$.

  Let

  $$f(x, y)=\frac{x y}{x^{2}+y^{2}} \quad((x, y) \neq(0,0))$$

  and $f(0,0)=0$. Do the partial derivatives of $f$ exist at $(0,0) ?$ Is $f$ differentiable at $(0,0) ?$ Justify your answers.

  comment

• 2.II.10F

  Analysis II | Part IB, 2003

  Let $V$ be the space of $n \times n$ real matrices. Show that the function

  $$N(A)=\sup \left\{\|A \mathbf{x}\|: \mathbf{x} \in \mathbb{R}^{n},\|\mathbf{x}\|=1\right\}$$

  (where $\|-\|$ denotes the usual Euclidean norm on $\mathbb{R}^{n}$ ) defines a norm on $V$. Show also that this norm satisfies $N(A B) \leqslant N(A) N(B)$ for all $A$ and $B$, and that if $N(A)<\epsilon$ then all entries of $A$ have absolute value less than $\epsilon$. Deduce that any function $f: V \rightarrow \mathbb{R}$ such that $f(A)$ is a polynomial in the entries of $A$ is continuously differentiable.

  Now let $d: V \rightarrow \mathbb{R}$ be the mapping sending a matrix to its determinant. By considering $d(I+H)$ as a polynomial in the entries of $H$, show that the derivative $d^{\prime}(I)$ is the function $H \mapsto \operatorname{tr} H$. Deduce that, for any $A, d^{\prime}(A)$ is the mapping $H \mapsto \operatorname{tr}((\operatorname{adj} A) H)$, where $\operatorname{adj} A$ is the adjugate of $A$, i.e. the matrix of its cofactors.

  [Hint: consider first the case when $A$ is invertible. You may assume the results that the set $U$ of invertible matrices is open in $V$ and that its closure is the whole of $V$, and the identity $(\operatorname{adj} A) A=\operatorname{det} A . I$.]

  comment

• 3.I.1F

  Analysis II | Part IB, 2003

  Let $V$ be the vector space of continuous real-valued functions on $[-1,1]$. Show that the function

  $$\|f\|=\int_{-1}^{1}|f(x)| d x$$

  defines a norm on $V$.

  Let $f_{n}(x)=x^{n}$. Show that $\left(f_{n}\right)$ is a Cauchy sequence in $V$. Is $\left(f_{n}\right)$ convergent? Justify your answer.

  comment

• 4.I.1F

  Analysis II | Part IB, 2003

  Explain what it means for a sequence of functions $\left(f_{n}\right)$ to converge uniformly to a function $f$ on an interval. If $\left(f_{n}\right)$ is a sequence of continuous functions converging uniformly to $f$ on a finite interval $[a, b]$, show that

  $$\int_{a}^{b} f_{n}(x) d x \longrightarrow \int_{a}^{b} f(x) d x \quad \text { as } n \rightarrow \infty$$

  Let $f_{n}(x)=x \exp (-x / n) / n^{2}, x \geqslant 0$. Does $f_{n} \rightarrow 0$ uniformly on $[0, \infty) ?$ Does $\int_{0}^{\infty} f_{n}(x) d x \rightarrow 0$ ? Justify your answers.

  comment

• 4.II.10F

  Analysis II | Part IB, 2003

  Let $\left(f_{n}\right)_{n \geqslant 1}$ be a sequence of continuous complex-valued functions defined on a set $E \subseteq \mathbb{C}$, and converging uniformly on $E$ to a function $f$. Prove that $f$ is continuous on $E$.

  State the Weierstrass $M$-test for uniform convergence of a series $\sum_{n=1}^{\infty} u_{n}(z)$ of complex-valued functions on a set $E$.

  Now let $f(z)=\sum_{n=1}^{\infty} u_{n}(z)$, where

  $$u_{n}(z)=n^{-2} \sec (\pi z / 2 n) .$$

  Prove carefully that $f$ is continuous on $\mathbb{C} \backslash \mathbb{Z}$.

  [You may assume the inequality $|\cos z| \geqslant|\cos (\operatorname{Re} z)| \cdot]$

  comment

Complex Methods

• 1.I.7B

  Complex Methods | Part IB, 2003

  Let $u(x, y)$ and $v(x, y)$ be a pair of conjugate harmonic functions in a domain $D$.

  Prove that

  $$U(x, y)=e^{-2 u v} \cos \left(u^{2}-v^{2}\right) \quad \text { and } \quad V(x, y)=e^{-2 u v} \sin \left(u^{2}-v^{2}\right)$$

  also form a pair of conjugate harmonic functions in $D$.

  comment

• 1.II.16B

  Complex Methods | Part IB, 2003

  Sketch the region $A$ which is the intersection of the discs

  $$D_{0}=\{z \in \mathbb{C}:|z|<1\} \quad \text { and } \quad D_{1}=\{z \in \mathbb{C}:|z-(1+i)|<1\} .$$

  Find a conformal mapping that maps $A$ onto the right half-plane $H=\{z \in \mathbb{C}: \operatorname{Re} z>0\}$. Also find a conformal mapping that maps $A$ onto $D_{0}$.

  [Hint: You may find it useful to consider maps of the form $w(z)=\frac{a z+b}{c z+d}$.]

  comment

• 2.I.7B

  Complex Methods | Part IB, 2003

  (a) Using the residue theorem, evaluate

  $$\int_{|z|=1}\left(z-\frac{1}{z}\right)^{2 n} \frac{d z}{z}$$

  (b) Deduce that

  $$\int_{0}^{2 \pi} \sin ^{2 n} t d t=\frac{\pi}{2^{2 n-1}} \frac{(2 n) !}{(n !)^{2}}$$

  comment

• 2.II.16B

  Complex Methods | Part IB, 2003

  (a) Show that if $f$ satisfies the equation

  $$f^{\prime \prime}(x)-x^{2} f(x)=\mu f(x), \quad x \in \mathbb{R},$$

  where $\mu$ is a constant, then its Fourier transform $\widehat{f}$ satisfies the same equation, i.e.

  $$\widehat{f}^{\prime \prime}(\lambda)-\lambda^{2} \widehat{f}(\lambda)=\mu \widehat{f}(\lambda) .$$

  (b) Prove that, for each $n \geq 0$, there is a polynomial $p_{n}(x)$ of degree $n$, unique up to multiplication by a constant, such that

  $$f_{n}(x)=p_{n}(x) e^{-x^{2} / 2}$$

  is a solution of $(*)$ for some $\mu=\mu_{n}$.

  (c) Using the fact that $g(x)=e^{-x^{2} / 2}$ satisfies $\widehat{g}=c g$ for some constant $c$, show that the Fourier transform of $f_{n}$ has the form

  $$\widehat{f_{n}}(\lambda)=q_{n}(\lambda) e^{-\lambda^{2} / 2}$$

  where $q_{n}$ is also a polynomial of degree $n$.

  (d) Deduce that the $f_{n}$ are eigenfunctions of the Fourier transform operator, i.e. $\widehat{f_{n}}(x)=c_{n} f_{n}(x)$ for some constants $c_{n} .$

  comment

• 4.I.8B

  Complex Methods | Part IB, 2003

  Find the Laurent series centred on 0 for the function

  $$f(z)=\frac{1}{(z-1)(z-2)}$$

  in each of the domains (a) $|z|<1$, (b) $1<|z|<2$, (c) $|z|>2$.

  comment

• 4.II.17B

  Complex Methods | Part IB, 2003

  Let

  $$f(z)=\frac{z^{m}}{1+z^{n}}, \quad n>m+1, \quad m, n \in \mathbb{N},$$

  and let $C_{R}$ be the boundary of the domain

  $$D_{R}=\left\{z=r e^{i \theta}: 0<r<R, \quad 0<\theta<\frac{2 \pi}{n}\right\}, \quad R>1 .$$

  (a) Using the residue theorem, determine

  $$\int_{C_{R}} f(z) d z$$

  (b) Show that the integral of $f(z)$ along the circular part $\gamma_{R}$ of $C_{R}$ tends to 0 as $R \rightarrow \infty$.

  (c) Deduce that

  $$\int_{0}^{\infty} \frac{x^{m}}{1+x^{n}} d x=\frac{\pi}{n \sin \frac{\pi(m+1)}{n}}$$

  comment

Fluid Dynamics

• 1.I.6C

  Fluid Dynamics | Part IB, 2003

  An unsteady fluid flow has velocity field given in Cartesian coordinates $(x, y, z)$ by $\mathbf{u}=(1, x t, 0)$, where $t$ denotes time. Dye is released into the fluid from the origin continuously. Find the position at time $t$ of the dye particle that was released at time $s$ and hence show that the dye streak lies along the curve

  $$y=\frac{1}{2} t x^{2}-\frac{1}{6} x^{3}$$

  comment

• 1.II.15C

  Fluid Dynamics | Part IB, 2003

  Starting from the Euler equations for incompressible, inviscid flow

  $$\rho \frac{D \mathbf{u}}{D t}=-\nabla p, \quad \nabla \cdot \mathbf{u}=0$$

  derive the vorticity equation governing the evolution of the vorticity $\boldsymbol{\omega}=\nabla \times \mathbf{u}$.

  Consider the flow

  $$\mathbf{u}=\beta(-x,-y, 2 z)+\Omega(t)(-y, x, 0)$$

  in Cartesian coordinates $(x, y, z)$, where $t$ is time and $\beta$ is a constant. Compute the vorticity and show that it evolves in time according to

  $$\boldsymbol{\omega}=\omega_{0} \mathrm{e}^{2 \beta t} \mathbf{k}$$

  where $\omega_{0}$ is the initial magnitude of the vorticity and $\mathbf{k}$ is a unit vector in the $z$-direction.

  Show that the material curve $C(t)$ that takes the form

  $$x^{2}+y^{2}=1 \quad \text { and } \quad z=1$$

  at $t=0$ is given later by

  $$x^{2}+y^{2}=a^{2}(t) \quad \text { and } \quad z=\frac{1}{a^{2}(t)},$$

  where the function $a(t)$ is to be determined.

  Calculate the circulation of $\mathbf{u}$ around $C$ and state how this illustrates Kelvin's circulation theorem.

  comment

• 3.I.8C

  Fluid Dynamics | Part IB, 2003

  Show that the velocity field

  $$\mathbf{u}=\mathbf{U}+\frac{\boldsymbol{\Gamma} \times \mathbf{r}}{2 \pi r^{2}},$$

  where $\mathbf{U}=(U, 0,0), \mathbf{\Gamma}=(0,0, \Gamma)$ and $\mathbf{r}=(x, y, 0)$ in Cartesian coordinates $(x, y, z)$, represents the combination of a uniform flow and the flow due to a line vortex. Define and evaluate the circulation of the vortex.

  Show that

  $$\oint_{C_{R}}(\mathbf{u} \cdot \mathbf{n}) \mathbf{u} d l \rightarrow \frac{1}{2} \boldsymbol{\Gamma} \times \mathbf{U} \quad \text { as } \quad R \rightarrow \infty$$

  where $C_{R}$ is a circle $x^{2}+y^{2}=R^{2}, z=$ const. Explain how this result is related to the lift force on a two-dimensional aerofoil or other obstacle.

  comment

• 3.II.18C

  Fluid Dynamics | Part IB, 2003

  State the form of Bernoulli's theorem appropriate for an unsteady irrotational motion of an inviscid incompressible fluid in the absence of gravity.

  Water of density $\rho$ is driven through a tube of length $L$ and internal radius $a$ by the pressure exerted by a spherical, water-filled balloon of radius $R(t)$ attached to one end of the tube. The balloon maintains the pressure of the water entering the tube at $2 \gamma / R$ in excess of atmospheric pressure, where $\gamma$ is a constant. It may be assumed that the water exits the tube at atmospheric pressure. Show that

  $$R^{3} \ddot{R}+2 R^{2} \dot{R}^{2}=-\frac{\gamma a^{2}}{2 \rho L} .$$

  Solve equation ( $\dagger$ ), by multiplying through by $2 R \dot{R}$ or otherwise, to obtain

  $$t=R_{0}^{2}\left(\frac{2 \rho L}{\gamma a^{2}}\right)^{1 / 2}\left[\frac{\pi}{4}-\frac{\theta}{2}+\frac{1}{4} \sin 2 \theta\right]$$

  where $\theta=\sin ^{-1}\left(R / R_{0}\right)$ and $R_{0}$ is the initial radius of the balloon. Hence find the time when $R=0$.

  comment

• 4.I.7C

  Fluid Dynamics | Part IB, 2003

  Inviscid fluid issues vertically downwards at speed $u_{0}$ from a circular tube of radius a. The fluid falls onto a horizontal plate a distance $H$ below the end of the tube, where it spreads out axisymmetrically.

  Show that while the fluid is falling freely it has speed

  $$u=u_{0}\left[1+\frac{2 g}{u_{0}^{2}}(H-z)\right]^{1 / 2}$$

  and occupies a circular jet of radius

  $$R=a\left[1+\frac{2 g}{u_{0}^{2}}(H-z)\right]^{-1 / 4},$$

  where $z$ is the height above the plate and $g$ is the acceleration due to gravity.

  Show further that along the plate, at radial distances $r \gg a$ (i.e. far from the falling jet), where the fluid is flowing almost horizontally, it does so as a film of height $h(r)$, where

  $$\frac{a^{4}}{4 r^{2} h^{2}}=1+\frac{2 g}{u_{0}^{2}}(H-h)$$

  comment

• 4.II.16C

  Fluid Dynamics | Part IB, 2003

  Define the terms irrotational flow and incompressible flow. The two-dimensional flow of an incompressible fluid is given in terms of a streamfunction $\psi(x, y)$ as

  $$\mathbf{u}=(u, v)=\left(\frac{\partial \psi}{\partial y},-\frac{\partial \psi}{\partial x}\right)$$

  in Cartesian coordinates $(x, y)$. Show that the line integral

  $$\int_{\mathbf{x}_{1}}^{\mathbf{x}_{\mathbf{2}}} \mathbf{u} \cdot \mathbf{n} d l=\psi\left(\mathbf{x}_{\mathbf{2}}\right)-\psi\left(\mathbf{x}_{\mathbf{1}}\right)$$

  along any path joining the points $\mathbf{x}_{\mathbf{1}}$ and $\mathbf{x}_{\mathbf{2}}$, where $\mathbf{n}$ is the unit normal to the path. Describe how this result is related to the concept of mass conservation.

  Inviscid, incompressible fluid is contained in the semi-infinite channel $x>0$, $0<y<1$, which has rigid walls at $x=0$ and at $y=0,1$, apart from a small opening at the origin through which the fluid is withdrawn with volume flux $m$ per unit distance in the third dimension. Show that the streamfunction for irrotational flow in the channel can be chosen (up to an additive constant) to satisfy the equation

  $$\frac{\partial^{2} \psi}{\partial x^{2}}+\frac{\partial^{2} \psi}{\partial y^{2}}=0$$

  and boundary conditions

  if it is assumed that the flow at infinity is uniform. Solve the boundary-value problem above using separation of variables to obtain

  $$\psi=-m y+\frac{2 m}{\pi} \sum_{n=1}^{\infty} \frac{1}{n} \sin n \pi y e^{-n \pi x}$$

  $$\begin{aligned} & \psi=0 \quad \text { on } y=0, x>0, \\ & \psi=-m \quad \text { on } x=0,0<y<1, \\ & \psi=-m \quad \text { on } y=1, x>0, \\ & \psi \rightarrow-m y \quad \text { as } x \rightarrow \infty, \end{aligned}$$

  comment

Further Analysis

• $2 . \mathrm{I} . 4 \mathrm{E} \quad$

  Further Analysis | Part IB, 2003

  Let $\tau_{1}$ be the collection of all subsets $A \subset \mathbb{N}$ such that $A=\emptyset$ or $\mathbb{N} \backslash A$ is finite. Let $\tau_{2}$ be the collection of all subsets of $\mathbb{N}$ of the form $I_{n}=\{n, n+1, n+2, \ldots\}$, together with the empty set. Prove that $\tau_{1}$ and $\tau_{2}$ are both topologies on $\mathbb{N}$.

  Show that a function $f$ from the topological space $\left(\mathbb{N}, \tau_{1}\right)$ to the topological space $\left(\mathbb{N}, \tau_{2}\right)$ is continuous if and only if one of the following alternatives holds:

  (i) $f(n) \rightarrow \infty$ as $n \rightarrow \infty$;

  (ii) there exists $N \in \mathbb{N}$ such that $f(n)=N$ for all but finitely many $n$ and $f(n) \leqslant N$ for all $n$.

  comment

• $3 . \mathrm{I} . 3 \mathrm{E} \quad$

  Further Analysis | Part IB, 2003

  (a) Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be an analytic function such that $|f(z)| \leqslant 1+|z|^{1 / 2}$ for every $z$. Prove that $f$ is constant.

  (b) Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be an analytic function such that $\operatorname{Re}(f(z)) \geqslant 0$ for every $z$. Prove that $f$ is constant.

  comment

• 2.II.13E

  Further Analysis | Part IB, 2003

  (a) Let $f:[1, \infty) \rightarrow \mathbb{C}$ be defined by $f(t)=t^{-1} e^{2 \pi i t}$ and let $X$ be the image of $f$. Prove that $X \cup\{0\}$ is compact and path-connected. [Hint: you may find it helpful to set $\left.s=t^{-1} .\right]$

  (b) Let $g:[1, \infty) \rightarrow \mathbb{C}$ be defined by $g(t)=\left(1+t^{-1}\right) e^{2 \pi i t}$, let $Y$ be the image of $g$ and let $\bar{D}$ be the closed unit $\operatorname{disc}\{z \in \mathbb{C}:|z| \leq 1\}$. Prove that $Y \cup \bar{D}$ is connected. Explain briefly why it is not path-connected.

  comment

• 3.II.13E

  Further Analysis | Part IB, 2003

  (a) State Taylor's Theorem.

  (b) Let $f(z)=\sum_{n=0}^{\infty} a_{n}\left(z-z_{0}\right)^{n}$ and $g(z)=\sum_{n=0}^{\infty} b_{n}\left(z-z_{0}\right)^{n}$ be defined whenever $\left|z-z_{0}\right|<r$. Suppose that $z_{k} \rightarrow z_{0}$ as $k \rightarrow \infty$, that no $z_{k}$ equals $z_{0}$ and that $f\left(z_{k}\right)=g\left(z_{k}\right)$ for every $k$. Prove that $a_{n}=b_{n}$ for every $n \geqslant 0$.

  (c) Let $D$ be a domain, let $z_{0} \in D$ and let $\left(z_{k}\right)$ be a sequence of points in $D$ that converges to $z_{0}$, but such that no $z_{k}$ equals $z_{0}$. Let $f: D \rightarrow \mathbb{C}$ and $g: D \rightarrow \mathbb{C}$ be analytic functions such that $f\left(z_{k}\right)=g\left(z_{k}\right)$ for every $k$. Prove that $f(z)=g(z)$ for every $z \in D$.

  (d) Let $D$ be the domain $\mathbb{C} \backslash\{0\}$. Give an example of an analytic function $f: D \rightarrow \mathbb{C}$ such that $f\left(n^{-1}\right)=0$ for every positive integer $n$ but $f$ is not identically 0 .

  (e) Show that any function with the property described in (d) must have an essential singularity at the origin.

  comment

• 4.I.4E

  Further Analysis | Part IB, 2003

  (a) State and prove Morera's Theorem.

  (b) Let $D$ be a domain and for each $n \in \mathbb{N}$ let $f_{n}: D \rightarrow \mathbb{C}$ be an analytic function. Suppose that $f: D \rightarrow \mathbb{C}$ is another function and that $f_{n} \rightarrow f$ uniformly on $D$. Prove that $f$ is analytic.

  comment

• 4.II.13E

  Further Analysis | Part IB, 2003

  (a) State the residue theorem and use it to deduce the principle of the argument, in a form that involves winding numbers.

  (b) Let $p(z)=z^{5}+z$. Find all $z$ such that $|z|=1$ and $\operatorname{Im}(p(z))=0$. Calculate $\operatorname{Re}(p(z))$ for each such $z$. [It will be helpful to set $z=e^{i \theta}$. You may use the addition formulae $\sin \alpha+\sin \beta=2 \sin \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)$ and $\cos \alpha+\cos \beta=2 \cos \left(\frac{\alpha+\beta}{2}\right) \cos \left(\frac{\alpha-\beta}{2}\right)$.]

  (c) Let $\gamma:[0,2 \pi] \rightarrow \mathbb{C}$ be the closed path $\theta \mapsto e^{i \theta}$. Use your answer to (b) to give a rough sketch of the path $p \circ \gamma$, paying particular attention to where it crosses the real axis.

  (d) Hence, or otherwise, determine for every real $t$ the number of $z$ (counted with multiplicity) such that $|z|<1$ and $p(z)=t$. (You need not give rigorous justifications for your calculations.)

  comment

Geometry

• 1.I.4F

  Geometry | Part IB, 2003

  Describe the geodesics (that is, hyperbolic straight lines) in either the disc model or the half-plane model of the hyperbolic plane. Explain what is meant by the statements that two hyperbolic lines are parallel, and that they are ultraparallel.

  Show that two hyperbolic lines $l$ and $l^{\prime}$ have a unique common perpendicular if and only if they are ultraparallel.

  [You may assume standard results about the group of isometries of whichever model of the hyperbolic plane you use.]

  comment

• 1.II.13F

  Geometry | Part IB, 2003

  Write down the Riemannian metric in the half-plane model of the hyperbolic plane. Show that Möbius transformations mapping the upper half-plane to itself are isometries of this model.

  Calculate the hyperbolic distance from $i b$ to $i c$, where $b$ and $c$ are positive real numbers. Assuming that the hyperbolic circle with centre $i b$ and radius $r$ is a Euclidean circle, find its Euclidean centre and radius.

  Suppose that $a$ and $b$ are positive real numbers for which the points $i b$ and $a+i b$ of the upper half-plane are such that the hyperbolic distance between them coincides with the Euclidean distance. Obtain an expression for $b$ as a function of $a$. Hence show that, for any $b$ with $0<b<1$, there is a unique positive value of $a$ such that the hyperbolic distance between $i b$ and $a+i b$ coincides with the Euclidean distance.

  comment

• 3.I.4F

  Geometry | Part IB, 2003

  Show that any isometry of Euclidean 3 -space which fixes the origin can be written as a composite of at most three reflections in planes through the origin, and give (with justification) an example of an isometry for which three reflections are necessary.

  comment

• 3.II.14F

  Geometry | Part IB, 2003

  State and prove the Gauss-Bonnet formula for the area of a spherical triangle. Deduce a formula for the area of a spherical $n$-gon with angles $\alpha_{1}, \alpha_{2}, \ldots, \alpha_{n}$. For what range of values of $\alpha$ does there exist a (convex) regular spherical $n$-gon with angle $\alpha$ ?

  Let $\Delta$ be a spherical triangle with angles $\pi / p, \pi / q$ and $\pi / r$ where $p, q, r$ are integers, and let $G$ be the group of isometries of the sphere generated by reflections in the three sides of $\Delta$. List the possible values of $(p, q, r)$, and in each case calculate the order of the corresponding group $G$. If $(p, q, r)=(2,3,5)$, show how to construct a regular dodecahedron whose group of symmetries is $G$.

  [You may assume that the images of $\Delta$ under the elements of $G$ form a tessellation of the sphere.]

  comment

Linear Mathematics

• 1.I $. 5 \mathrm{E} \quad$

  Linear Mathematics | Part IB, 2003

  Let $V$ be the subset of $\mathbb{R}^{5}$ consisting of all quintuples $\left(a_{1}, a_{2}, a_{3}, a_{4}, a_{5}\right)$ such that

  $$a_{1}+a_{2}+a_{3}+a_{4}+a_{5}=0$$

  and

  $$a_{1}+2 a_{2}+3 a_{3}+4 a_{4}+5 a_{5}=0$$

  Prove that $V$ is a subspace of $\mathbb{R}^{5}$. Solve the above equations for $a_{1}$ and $a_{2}$ in terms of $a_{3}, a_{4}$ and $a_{5}$. Hence, exhibit a basis for $V$, explaining carefully why the vectors you give form a basis.

  comment

• 1.II.14E

  Linear Mathematics | Part IB, 2003

  (a) Let $U, U^{\prime}$ be subspaces of a finite-dimensional vector space $V$. Prove that $\operatorname{dim}\left(U+U^{\prime}\right)=\operatorname{dim} U+\operatorname{dim} U^{\prime}-\operatorname{dim}\left(U \cap U^{\prime}\right) .$

  (b) Let $V$ and $W$ be finite-dimensional vector spaces and let $\alpha$ and $\beta$ be linear maps from $V$ to $W$. Prove that

  $$\operatorname{rank}(\alpha+\beta) \leqslant \operatorname{rank} \alpha+\operatorname{rank} \beta$$

  (c) Deduce from this result that

  $$\operatorname{rank}(\alpha+\beta) \geqslant|\operatorname{rank} \alpha-\operatorname{rank} \beta|$$

  (d) Let $V=W=\mathbb{R}^{n}$ and suppose that $1 \leqslant r \leqslant s \leqslant n$. Exhibit linear maps $\alpha, \beta: V \rightarrow W$ such that $\operatorname{rank} \alpha=r, \operatorname{rank} \beta=s$ and $\operatorname{rank}(\alpha+\beta)=s-r$. Suppose that $r+s \geqslant n$. Exhibit linear maps $\alpha, \beta: V \rightarrow W$ such that $\operatorname{rank} \alpha=r, \operatorname{rank} \beta=s$ and $\operatorname{rank}(\alpha+\beta)=n$.

  comment

• 2.I.6E

  Linear Mathematics | Part IB, 2003

  Let $a_{1}, a_{2}, \ldots, a_{n}$ be distinct real numbers. For each $i$ let $\mathbf{v}_{i}$ be the vector $\left(1, a_{i}, a_{i}^{2}, \ldots, a_{i}^{n-1}\right)$. Let $A$ be the $n \times n$ matrix with rows $\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{n}$ and let $\mathbf{c}$ be a column vector of size $n$. Prove that $A \mathbf{c}=\mathbf{0}$ if and only if $\mathbf{c}=\mathbf{0}$. Deduce that the vectors $\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{n} \operatorname{span} \mathbb{R}^{n}$.

  [You may use general facts about matrices if you state them clearly.]

  comment

• 2.II.15E

  Linear Mathematics | Part IB, 2003

  (a) Let $A=\left(a_{i j}\right)$ be an $m \times n$ matrix and for each $k \leqslant n$ let $A_{k}$ be the $m \times k$ matrix formed by the first $k$ columns of $A$. Suppose that $n>m$. Explain why the nullity of $A$ is non-zero. Prove that if $k$ is minimal such that $A_{k}$ has non-zero nullity, then the nullity of $A_{k}$ is 1 .

  (b) Suppose that no column of $A$ consists entirely of zeros. Deduce from (a) that there exist scalars $b_{1}, \ldots, b_{k}$ (where $k$ is defined as in (a)) such that $\sum_{j=1}^{k} a_{i j} b_{j}=0$ for every $i \leqslant m$, but whenever $\lambda_{1}, \ldots, \lambda_{k}$ are distinct real numbers there is some $i \leqslant m$ such that $\sum_{j=1}^{k} a_{i j} \lambda_{j} b_{j} \neq 0$.

  (c) Now let $\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{m}$ and $\mathbf{w}_{1}, \mathbf{w}_{2}, \ldots, \mathbf{w}_{m}$ be bases for the same real $m$ dimensional vector space. Let $\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}$ be distinct real numbers such that for every $j$ the vectors $\mathbf{v}_{1}+\lambda_{j} \mathbf{w}_{1}, \ldots, \mathbf{v}_{m}+\lambda_{j} \mathbf{w}_{m}$ are linearly dependent. For each $j$, let $a_{1 j}, \ldots, a_{m j}$ be scalars, not all zero, such that $\sum_{i=1}^{m} a_{i j}\left(\mathbf{v}_{i}+\lambda_{j} \mathbf{w}_{i}\right)=\mathbf{0}$. By applying the result of (b) to the matrix $\left(a_{i j}\right)$, deduce that $n \leqslant m$.

  (d) It follows that the vectors $\mathbf{v}_{1}+\lambda \mathbf{w}_{1}, \ldots, \mathbf{v}_{m}+\lambda \mathbf{w}_{m}$ are linearly dependent for at most $m$ values of $\lambda$. Explain briefly how this result can also be proved using determinants.

  comment

• 3.I.7G

  Linear Mathematics | Part IB, 2003

  Let $\alpha$ be an endomorphism of a finite-dimensional real vector space $U$ and let $\beta$ be another endomorphism of $U$ that commutes with $\alpha$. If $\lambda$ is an eigenvalue of $\alpha$, show that $\beta$ maps the kernel of $\alpha-\lambda \iota$ into itself, where $\iota$ is the identity map. Suppose now that $\alpha$ is diagonalizable with $n$ distinct real eigenvalues where $n=\operatorname{dim} U$. Prove that if there exists an endomorphism $\beta$ of $U$ such that $\alpha=\beta^{2}$, then $\lambda \geqslant 0$ for all eigenvalues $\lambda$ of $\alpha$.

  comment

• 3.II.17G

  Linear Mathematics | Part IB, 2003

  Define the determinant $\operatorname{det}(A)$ of an $n \times n$ complex matrix A. Let $A_{1}, \ldots, A_{n}$ be the columns of $A$, let $\sigma$ be a permutation of $\{1, \ldots, n\}$ and let $A^{\sigma}$ be the matrix whose columns are $A_{\sigma(1)}, \ldots, A_{\sigma(n)}$. Prove from your definition of determinant that $\operatorname{det}\left(A^{\sigma}\right)=\epsilon(\sigma) \operatorname{det}(A)$, where $\epsilon(\sigma)$ is the sign of the permutation $\sigma$. Prove also that $\operatorname{det}(A)=\operatorname{det}\left(A^{t}\right) .$

  Define the adjugate matrix $\operatorname{adj}(A)$ and prove from your $\operatorname{definitions}$ that $A \operatorname{adj}(A)=$ $\operatorname{adj}(A) A=\operatorname{det}(A) I$, where $I$ is the identity matrix. Hence or otherwise, prove that if $\operatorname{det}(A) \neq 0$, then $A$ is invertible.

  Let $C$ and $D$ be real $n \times n$ matrices such that the complex matrix $C+i D$ is invertible. By considering $\operatorname{det}(C+\lambda D)$ as a function of $\lambda$ or otherwise, prove that there exists a real number $\lambda$ such that $C+\lambda D$ is invertible. [You may assume that if a matrix $A$ is invertible, then $\operatorname{det}(A) \neq 0$.]

  Deduce that if two real matrices $A$ and $B$ are such that there exists an invertible complex matrix $P$ with $P^{-1} A P=B$, then there exists an invertible real matrix $Q$ such that $Q^{-1} A Q=B$.

  comment

• 4.I.6G

  Linear Mathematics | Part IB, 2003

  Let $\alpha$ be an endomorphism of a finite-dimensional real vector space $U$ such that $\alpha^{2}=\alpha$. Show that $U$ can be written as the direct sum of the kernel of $\alpha$ and the image of $\alpha$. Hence or otherwise, find the characteristic polynomial of $\alpha$ in terms of the dimension of $U$ and the rank of $\alpha$. Is $\alpha$ diagonalizable? Justify your answer.

  comment

• 4.II.15G

  Linear Mathematics | Part IB, 2003

  Let $\alpha \in L(U, V)$ be a linear map between finite-dimensional vector spaces. Let

  $$\begin{gathered} M^{l}(\alpha)=\{\beta \in L(V, U): \beta \alpha=0\} \quad \text { and } \\ M^{r}(\alpha)=\{\beta \in L(V, U): \alpha \beta=0\} . \end{gathered}$$

  (a) Prove that $M^{l}(\alpha)$ and $M^{r}(\alpha)$ are subspaces of $L(V, U)$ of dimensions

  $$\begin{gathered} \operatorname{dim} M^{l}(\alpha)=(\operatorname{dim} V-\operatorname{rank} \alpha) \operatorname{dim} U \quad \text { and } \\ \operatorname{dim} M^{r}(\alpha)=\operatorname{dim} \operatorname{ker}(\alpha) \operatorname{dim} V \end{gathered}$$

  [You may use the result that there exist bases in $U$ and $V$ so that $\alpha$ is represented by

  $$\left(\begin{array}{cc} I_{r} & 0 \\ 0 & 0 \end{array}\right)$$

  where $I_{r}$ is the $r \times r$ identity matrix and $r$ is the rank of $\left.\alpha .\right]$

  (b) Let $\Phi: L(U, V) \rightarrow L\left(V^{*}, U^{*}\right)$ be given by $\Phi(\alpha)=\alpha^{*}$, where $\alpha^{*}$ is the dual map induced by $\alpha$. Prove that $\Phi$ is an isomorphism. [You may assume that $\Phi$ is linear, and you may use the result that a finite-dimensional vector space and its dual have the same dimension.]

  (c) Prove that

  $$\Phi\left(M^{l}(\alpha)\right)=M^{r}\left(\alpha^{*}\right) \quad \text { and } \quad \Phi\left(M^{r}(\alpha)\right)=M^{l}\left(\alpha^{*}\right)$$

  [You may use the results that $(\beta \alpha)^{*}=\alpha^{*} \beta^{*}$ and that $\beta^{* *}$ can be identified with $\beta$ under the canonical isomorphism between a vector space and its double dual.]

  (d) Conclude that $\operatorname{rank}(\alpha)=\operatorname{rank}\left(\alpha^{*}\right)$.

  comment

Methods

• 1.I.2D

  Methods | Part IB, 2003

  Fermat's principle of optics states that the path of a light ray connecting two points will be such that the travel time $t$ is a minimum. If the speed of light varies continuously in a medium and is a function $c(y)$ of the distance from the boundary $y=0$, show that the path of a light ray is given by the solution to

  $$c(y) y^{\prime \prime}+c^{\prime}(y)\left(1+y^{\prime 2}\right)=0$$

  where $y^{\prime}=\frac{d y}{d x}$, etc. Show that the path of a light ray in a medium where the speed of light $c$ is a constant is a straight line. Also find the path from $(0,0)$ to $(1,0)$ if $c(y)=y$, and sketch it.

  comment

• 1.II.11D

  Methods | Part IB, 2003

  (a) Determine the Green's function $G(x, \xi)$ for the operator $\frac{d^{2}}{d x^{2}}+k^{2}$ on $[0, \pi]$ with Dirichlet boundary conditions by solving the boundary value problem

  $$\frac{d^{2} G}{d x^{2}}+k^{2} G=\delta(x-\xi), \quad G(0)=0, G(\pi)=0$$

  when $k$ is not an integer.

  (b) Use the method of Green's functions to solve the boundary value problem

  $$\frac{d^{2} y}{d x^{2}}+k^{2} y=f(x), \quad y(0)=a, y(\pi)=b$$

  when $k$ is not an integer.

  comment

• 2.I.2C

  Methods | Part IB, 2003

  Explain briefly why the second-rank tensor

  $$\int_{S} x_{i} x_{j} d S(\mathbf{x})$$

  is isotropic, where $S$ is the surface of the unit sphere centred on the origin.

  A second-rank tensor is defined by

  $$T_{i j}(\mathbf{y})=\int_{S}\left(y_{i}-x_{i}\right)\left(y_{j}-x_{j}\right) d S(\mathbf{x})$$

  where $S$ is the surface of the unit sphere centred on the origin. Calculate $T(\mathbf{y})$ in the form

  $$T_{i j}=\lambda \delta_{i j}+\mu y_{i} y_{j}$$

  where $\lambda$ and $\mu$ are to be determined.

  By considering the action of $T$ on $\mathbf{y}$ and on vectors perpendicular to $\mathbf{y}$, determine the eigenvalues and associated eigenvectors of $T$.

  comment

• 2.II.11C

  Methods | Part IB, 2003

  State the transformation law for an $n$ th-rank tensor $T_{i j \cdots k}$.

  Show that the fourth-rank tensor

  $$c_{i j k l}=\alpha \delta_{i j} \delta_{k l}+\beta \delta_{i k} \delta_{j l}+\gamma \delta_{i l} \delta_{j k}$$

  is isotropic for arbitrary scalars $\alpha, \beta$ and $\gamma$.

  The stress $\sigma_{i j}$ and strain $e_{i j}$ in a linear elastic medium are related by

  $$\sigma_{i j}=c_{i j k l} e_{k l} .$$

  Given that $e_{i j}$ is symmetric and that the medium is isotropic, show that the stress-strain relationship can be written in the form

  $$\sigma_{i j}=\lambda e_{k k} \delta_{i j}+2 \mu e_{i j}$$

  Show that $e_{i j}$ can be written in the form $e_{i j}=p \delta_{i j}+d_{i j}$, where $d_{i j}$ is a traceless tensor and $p$ is a scalar to be determined. Show also that necessary and sufficient conditions for the stored elastic energy density $E=\frac{1}{2} \sigma_{i j} e_{i j}$ to be non-negative for any deformation of the solid are that

  $$\mu \geq 0 \quad \text { and } \quad \lambda \geq-\frac{2}{3} \mu .$$

  comment

• 3.I.2D

  Methods | Part IB, 2003

  Consider the path between two arbitrary points on a cone of interior angle $2 \alpha$. Show that the arc-length of the path $r(\theta)$ is given by

  $$\int\left(r^{2}+r^{\prime 2} \operatorname{cosec}^{2} \alpha\right)^{1 / 2} d \theta$$

  where $r^{\prime}=\frac{d r}{d \theta}$. By minimizing the total arc-length between the points, determine the equation for the shortest path connecting them.

  comment

• 3.II.12D

  Methods | Part IB, 2003

  The transverse displacement $y(x, t)$ of a stretched string clamped at its ends $x=0, l$ satisfies the equation

  $$\frac{\partial^{2} y}{\partial t^{2}}=c^{2} \frac{\partial^{2} y}{\partial x^{2}}-2 k \frac{\partial y}{\partial t}, \quad y(x, 0)=0, \frac{\partial y}{\partial t}(x, 0)=\delta(x-a)$$

  where $c>0$ is the wave velocity, and $k>0$ is the damping coefficient. The initial conditions correspond to a sharp blow at $x=a$ at time $t=0$.

  (a) Show that the subsequent motion of the string is given by

  $$y(x, t)=\frac{1}{\sqrt{\alpha_{n}^{2}-k^{2}}} \sum_{n} 2 e^{-k t} \sin \frac{\alpha_{n} a}{c} \sin \frac{\alpha_{n} x}{c} \sin /\left(\sqrt{\alpha_{n}^{2}-k^{2}} t\right)$$

  where $\alpha_{n}=\pi c n / l$.

  (b) Describe what happens in the limits of small and large damping. What critical parameter separates the two cases?

  comment

• 4.I.2D

  Methods | Part IB, 2003

  Consider the wave equation in a spherically symmetric coordinate system

  $$\frac{\partial^{2} u(r, t)}{\partial t^{2}}=c^{2} \Delta u(r, t)$$

  where $\Delta u=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r u)$ is the spherically symmetric Laplacian operator.

  (a) Show that the general solution to the equation above is

  $$u(r, t)=\frac{1}{r}[f(r+c t)+g(r-c t)]$$

  where $f(x), g(x)$ are arbitrary functions.

  (b) Using separation of variables, determine the wave field $u(r, t)$ in response to a pulsating source at the origin $u(0, t)=A \sin \omega t$.

  comment

• 4.II.11D

  Methods | Part IB, 2003

  The velocity potential $\phi(r, \theta)$ for inviscid flow in two dimensions satisfies the Laplace equation

  $$\Delta \phi=\left[\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial \theta^{2}}\right] \phi(r, \theta)=0$$

  (a) Using separation of variables, derive the general solution to the equation above that is single-valued and finite in each of the domains (i) $0 \leqslant r \leqslant a$; (ii) $a \leqslant r<\infty$.

  (b) Assuming $\phi$ is single-valued, solve the Laplace equation subject to the boundary conditions $\frac{\partial \phi}{\partial r}=0$ at $r=a$, and $\frac{\partial \phi}{\partial r} \rightarrow U \cos \theta$ as $r \rightarrow \infty$. Sketch the lines of constant potential.

  comment

Numerical Analysis

• 2.I.5B

  Numerical Analysis | Part IB, 2003

  Let

  $$A=\left(\begin{array}{cccc} 1 & a & a^{2} & a^{3} \\ a^{3} & 1 & a & a^{2} \\ a^{2} & a^{3} & 1 & a \\ a & a^{2} & a^{3} & 1 \end{array}\right), \quad b=\left(\begin{array}{c} \gamma \\ 0 \\ 0 \\ \gamma a \end{array}\right), \quad \gamma=1-a^{4} \neq 0$$

  Find the LU factorization of the matrix $A$ and use it to solve the system $A x=b$.

  comment

• 2.II.14B

  Numerical Analysis | Part IB, 2003

  Let

  $$f^{\prime \prime}(0) \approx a_{0} f(-1)+a_{1} f(0)+a_{2} f(1)=\mu(f)$$

  be an approximation of the second derivative which is exact for $f \in \mathcal{P}_{2}$, the set of polynomials of degree $\leq 2$, and let

  $$e(f)=f^{\prime \prime}(0)-\mu(f)$$

  be its error.

  (a) Determine the coefficients $a_{0}, a_{1}, a_{2}$.

  (b) Using the Peano kernel theorem prove that, for $f \in C^{3}[-1,1]$, the set of threetimes continuously differentiable functions, the error satisfies the inequality

  $$|e(f)| \leq \frac{1}{3} \max _{x \in[-1,1]}\left|f^{\prime \prime \prime}(x)\right| .$$

  comment

• 3.I.6B

  Numerical Analysis | Part IB, 2003

  Given $(n+1)$ distinct points $x_{0}, x_{1}, \ldots, x_{n}$, let

  $$\ell_{i}(x)=\prod_{\substack{k=0 \\ k \neq i}}^{n} \frac{x-x_{k}}{x_{i}-x_{k}}$$

  be the fundamental Lagrange polynomials of degree $n$, let

  $$\omega(x)=\prod_{i=0}^{n}\left(x-x_{i}\right)$$

  and let $p$ be any polynomial of degree $\leq n$.

  (a) Prove that $\sum_{i=0}^{n} p\left(x_{i}\right) \ell_{i}(x) \equiv p(x)$.

  (b) Hence or otherwise derive the formula

  $$\frac{p(x)}{\omega(x)}=\sum_{i=0}^{n} \frac{A_{i}}{x-x_{i}}, \quad A_{i}=\frac{p\left(x_{i}\right)}{\omega^{\prime}\left(x_{i}\right)}$$

  which is the decomposition of $p(x) / \omega(x)$ into partial fractions.

  comment

• 3.II.16B

  Numerical Analysis | Part IB, 2003

  The functions $H_{0}, H_{1}, \ldots$ are generated by the Rodrigues formula:

  $$H_{n}(x)=(-1)^{n} e^{x^{2}} \frac{d^{n}}{d x^{n}} e^{-x^{2}}$$

  (a) Show that $H_{n}$ is a polynomial of degree $n$, and that the $H_{n}$ are orthogonal with respect to the scalar product

  $$(f, g)=\int_{-\infty}^{\infty} f(x) g(x) e^{-x^{2}} d x$$

  (b) By induction or otherwise, prove that the $H_{n}$ satisfy the three-term recurrence relation

  $$H_{n+1}(x)=2 x H_{n}(x)-2 n H_{n-1}(x) .$$

  [Hint: you may need to prove the equality $H_{n}^{\prime}(x)=2 n H_{n-1}(x)$ as well.]

  comment

Optimization

• $3 . \mathrm{I} . 5 \mathrm{H} \quad$

  Optimization | Part IB, 2003

  Two players A and B play a zero-sum game with the pay-off matrix

  \begin{tabular}{r|rrr} & $B_{1}$ & $B_{2}$ & $B_{3}$ \ \hline$A_{1}$ & 4 & $-2$ & $-5$ \ $A_{2}$ & $-2$ & 4 & 3 \ $A_{3}$ & $-3$ & 6 & 2 \ $A_{4}$ & 3 & $-8$ & $-6$ \end{tabular}

  Here, the $(i, j)$ entry of the matrix indicates the pay-off to player A if he chooses move $A_{i}$ and player $\mathrm{B}$ chooses move $B_{j}$. Show that the game can be reduced to a zero-sum game with $2 \times 2$ pay-off matrix.

  Determine the value of the game and the optimal strategy for player A.

  comment

• 3.II.15H

  Optimization | Part IB, 2003

  Explain what is meant by a transportation problem where the total demand equals the total supply. Write the Lagrangian and describe an algorithm for solving such a problem. Starting from the north-west initial assignment, solve the problem with three sources and three destinations described by the table

  \begin{tabular}{|rrr|r|} \hline 5 & 9 & 1 & 36 \ 3 & 10 & 6 & 84 \ 7 & 2 & 5 & 40 \ \hline 14 & 68 & 78 & \ \hline \end{tabular}

  where the figures in the $3 \times 3$ box denote the transportation costs (per unit), the right-hand column denotes supplies, and the bottom row demands.

  comment

• 4.I.5H

  Optimization | Part IB, 2003

  State and prove the Lagrangian sufficiency theorem for a general optimization problem with constraints.

  comment

• 4.II.14H

  Optimization | Part IB, 2003

  Use the two-phase simplex method to solve the problem

  $$\begin{array}{llllll} \operatorname{minimize} & 5 x_{1}-12 x_{2}+13 x_{3} & & \\ \text { subject to } & 4 x_{1}+5 x_{2} & & \leq & 9 \\ & 6 x_{1}+4 x_{2}+ & x_{3} & \geq & 12 \\ & 3 x_{1}+2 x_{2}-x_{3} & \leq & 3 \\ & x_{i} \geq 0, & i=1,2,3 \end{array}$$

  comment

Quadratic Mathematics

• 1.I.8G

  Quadratic Mathematics | Part IB, 2003

  Let $U$ and $V$ be finite-dimensional vector spaces. Suppose that $b$ and $c$ are bilinear forms on $U \times V$ and that $b$ is non-degenerate. Show that there exist linear endomorphisms $S$ of $U$ and $T$ of $V$ such that $c(x, y)=b(S(x), y)=b(x, T(y))$ for all $(x, y) \in U \times V$.

  comment

• 1.II.17G

  Quadratic Mathematics | Part IB, 2003

  (a) Suppose $p$ is an odd prime and $a$ an integer coprime to $p$. Define the Legendre symbol $\left(\frac{a}{p}\right)$ and state Euler's criterion.

  (b) Compute $\left(\frac{-1}{p}\right)$ and prove that

  $$\left(\frac{a b}{p}\right)=\left(\frac{a}{p}\right)\left(\frac{b}{p}\right)$$

  whenever $a$ and $b$ are coprime to $p$.

  (c) Let $n$ be any integer such that $1 \leqslant n \leqslant p-2$. Let $m$ be the unique integer such that $1 \leqslant m \leqslant p-2$ and $m n \equiv 1(\bmod p)$. Prove that

  $$\left(\frac{n(n+1)}{p}\right)=\left(\frac{1+m}{p}\right)$$

  (d) Find

  $$\sum_{n=1}^{p-2}\left(\frac{n(n+1)}{p}\right)$$

  comment

• 2.I.8G

  Quadratic Mathematics | Part IB, 2003

  Let $U$ be a finite-dimensional real vector space and $b$ a positive definite symmetric bilinear form on $U \times U$. Let $\psi: U \rightarrow U$ be a linear map such that $b(\psi(x), y)+b(x, \psi(y))=0$ for all $x$ and $y$ in $U$. Prove that if $\psi$ is invertible, then the dimension of $U$ must be even. By considering the restriction of $\psi$ to its image or otherwise, prove that the rank of $\psi$ is always even.

  comment

• 2.II.17G

  Quadratic Mathematics | Part IB, 2003

  Let $S$ be the set of all $2 \times 2$ complex matrices $A$ which are hermitian, that is, $A^{*}=A$, where $A^{*}=\bar{A}^{t}$.

  (a) Show that $S$ is a real 4-dimensional vector space. Consider the real symmetric bilinear form $b$ on this space defined by

  $$b(A, B)=\frac{1}{2}(\operatorname{tr}(A B)-\operatorname{tr}(A) \operatorname{tr}(B)) .$$

  Prove that $b(A, A)=-\operatorname{det} A$ and $b(A, I)=-\frac{1}{2} \operatorname{tr}(A)$, where $I$ denotes the identity matrix.

  (b) Consider the three matrices

  $$A_{1}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right), \quad A_{2}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right) \quad \text { and } \quad A_{3}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right)$$

  Prove that the basis $I, A_{1}, A_{2}, A_{3}$ of $S$ diagonalizes $b$. Hence or otherwise find the rank and signature of $b$.

  (c) Let $Q$ be the set of all $2 \times 2$ complex matrices $C$ which satisfy $C+C^{*}=\operatorname{tr}(C) I$. Show that $Q$ is a real 4-dimensional vector space. Given $C \in Q$, put

  $$\Phi(C)=\frac{1-i}{2} \operatorname{tr}(C) I+i C .$$

  Show that $\Phi$ takes values in $S$ and is a linear isomorphism between $Q$ and $S$.

  (d) Define a real symmetric bilinear form on $Q$ by setting $c(C, D)=-\frac{1}{2} \operatorname{tr}(C D)$, $C, D \in Q$. Show that $b(\Phi(C), \Phi(D))=c(C, D)$ for all $C, D \in Q$. Find the rank and signature of the symmetric bilinear form $c$ defined on $Q$.

  comment

• 3.I.9G

  Quadratic Mathematics | Part IB, 2003

  Let $f(x, y)=a x^{2}+b x y+c y^{2}$ be a binary quadratic form with integer coefficients. Explain what is meant by the discriminant $d$ of $f$. State a necessary and sufficient condition for some form of discriminant $d$ to represent an odd prime number $p$. Using this result or otherwise, find the primes $p$ which can be represented by the form $x^{2}+3 y^{2}$.

  comment

• 3.II.19G

  Quadratic Mathematics | Part IB, 2003

  Let $U$ be a finite-dimensional real vector space endowed with a positive definite inner product. A linear map $\tau: U \rightarrow U$ is said to be an orthogonal projection if $\tau$ is self-adjoint and $\tau^{2}=\tau$.

  (a) Prove that for every orthogonal projection $\tau$ there is an orthogonal decomposition

  $$U=\operatorname{ker}(\tau) \oplus \operatorname{im}(\tau)$$

  (b) Let $\phi: U \rightarrow U$ be a linear map. Show that if $\phi^{2}=\phi$ and $\phi \phi^{*}=\phi^{*} \phi$, where $\phi^{*}$ is the adjoint of $\phi$, then $\phi$ is an orthogonal projection. [You may find it useful to prove first that if $\phi \phi^{*}=\phi^{*} \phi$, then $\phi$ and $\phi^{*}$ have the same kernel.]

  (c) Show that given a subspace $W$ of $U$ there exists a unique orthogonal projection $\tau$ such that $\operatorname{im}(\tau)=W$. If $W_{1}$ and $W_{2}$ are two subspaces with corresponding orthogonal projections $\tau_{1}$ and $\tau_{2}$, show that $\tau_{2} \circ \tau_{1}=0$ if and only if $W_{1}$ is orthogonal to $W_{2}$.

  (d) Let $\phi: U \rightarrow U$ be a linear map satisfying $\phi^{2}=\phi$. Prove that one can define a positive definite inner product on $U$ such that $\phi$ becomes an orthogonal projection.

  comment

Quantum Mechanics

• 1.I $. 9 \mathrm{~A} \quad$

  Quantum Mechanics | Part IB, 2003

  A particle of mass $m$ is confined inside a one-dimensional box of length $a$. Determine the possible energy eigenvalues.

  comment

• 1.II.18A

  Quantum Mechanics | Part IB, 2003

  What is the significance of the expectation value

  $$\langle Q\rangle=\int \psi^{*}(x) Q \psi(x) d x$$

  of an observable $Q$ in the normalized state $\psi(x)$ ? Let $Q$ and $P$ be two observables. By considering the norm of $(Q+i \lambda P) \psi$ for real values of $\lambda$, show that

  $$\left\langle Q^{2}\right\rangle\left\langle P^{2}\right\rangle \geqslant \frac{1}{4}|\langle[Q, P]\rangle|^{2}$$

  The uncertainty $\Delta Q$ of $Q$ in the state $\psi(x)$ is defined as

  $$(\Delta Q)^{2}=\left\langle(Q-\langle Q\rangle)^{2}\right\rangle .$$

  Deduce the generalized uncertainty relation,

  $$\Delta Q \Delta P \geqslant \frac{1}{2}|\langle[Q, P]\rangle| .$$

  A particle of mass $m$ moves in one dimension under the influence of the potential $\frac{1}{2} m \omega^{2} x^{2}$. By considering the commutator $[x, p]$, show that the expectation value of the Hamiltonian satisfies

  $$\langle H\rangle \geqslant \frac{1}{2} \hbar \omega .$$

  comment

• 2.I.9A

  Quantum Mechanics | Part IB, 2003

  What is meant by the statement than an operator is hermitian?

  A particle of mass $m$ moves in the real potential $V(x)$ in one dimension. Show that the Hamiltonian of the system is hermitian.

  Show that

  $$\begin{aligned} \frac{d}{d t}\langle x\rangle &=\frac{1}{m}\langle p\rangle \\ \frac{d}{d t}\langle p\rangle &=\left\langle-V^{\prime}(x)\right\rangle \end{aligned}$$

  where $p$ is the momentum operator and $\langle A\rangle$ denotes the expectation value of the operator $A$.

  comment

• 2.II.18A

  Quantum Mechanics | Part IB, 2003

  A particle of mass $m$ and energy $E$ moving in one dimension is incident from the left on a potential barrier $V(x)$ given by

  $$V(x)= \begin{cases}V_{0} & 0 \leqslant x \leqslant a \\ 0 & \text { otherwise }\end{cases}$$

  with $V_{0}>0$.

  In the limit $V_{0} \rightarrow \infty, a \rightarrow 0$ with $V_{0} a=U$ held fixed, show that the transmission probability is

  $$T=\left(1+\frac{m U^{2}}{2 E \hbar^{2}}\right)^{-1}$$

  comment

• 3.II.20A

  Quantum Mechanics | Part IB, 2003

  The radial wavefunction for the hydrogen atom satisfies the equation

  $$\frac{-\hbar^{2}}{2 m} \frac{1}{r^{2}} \frac{d}{d r}\left(r^{2} \frac{d}{d r} R(r)\right)+\frac{\hbar^{2}}{2 m r^{2}} \ell(\ell+1) R(r)-\frac{e^{2}}{4 \pi \epsilon_{0} r} R(r)=E R(r) .$$

  Explain the origin of each term in this equation.

  The wavefunctions for the ground state and first radially excited state, both with $\ell=0$, can be written as

  $$\begin{aligned} &R_{1}(r)=N_{1} \exp (-\alpha r) \\ &R_{2}(r)=N_{2}(r+b) \exp (-\beta r) \end{aligned}$$

  respectively, where $N_{1}$ and $N_{2}$ are normalization constants. Determine $\alpha, \beta, b$ and the corresponding energy eigenvalues $E_{1}$ and $E_{2}$.

  A hydrogen atom is in the first radially excited state. It makes the transition to the ground state, emitting a photon. What is the frequency of the emitted photon?

  comment

Special Relativity

• 3.I.10A

  Special Relativity | Part IB, 2003

  What are the momentum and energy of a photon of wavelength $\lambda$ ?

  A photon of wavelength $\lambda$ is incident on an electron. After the collision, the photon has wavelength $\lambda^{\prime}$. Show that

  $$\lambda^{\prime}-\lambda=\frac{h}{m c}(1-\cos \theta),$$

  where $\theta$ is the scattering angle and $m$ is the electron rest mass.

  comment

• 4.I.9A

  Special Relativity | Part IB, 2003

  Prove that the two-dimensional Lorentz transformation can be written in the form

  $$\begin{aligned} x^{\prime} &=x \cosh \phi-c t \sinh \phi \\ c t^{\prime} &=-x \sinh \phi+c t \cosh \phi \end{aligned}$$

  where $\tanh \phi=v / c$. Hence, show that

  $$\begin{aligned} &x^{\prime}+c t^{\prime}=e^{-\phi}(x+c t) \\ &x^{\prime}-c t^{\prime}=e^{\phi}(x-c t) \end{aligned}$$

  Given that frame $S^{\prime}$ has speed $v$ with respect to $S$ and $S^{\prime \prime}$ has speed $v^{\prime}$ with respect to $S^{\prime}$, use this formalism to find the speed $v^{\prime \prime}$ of $S^{\prime \prime}$ with respect to $S$.

  [Hint: rotation through a hyperbolic angle $\phi$, followed by rotation through $\phi^{\prime}$, is equivalent to rotation through $\phi+\phi^{\prime}$.]

  comment

• 4.II.18A

  Special Relativity | Part IB, 2003

  A pion of rest mass $M$ decays at rest into a muon of rest mass $m<M$ and a neutrino of zero rest mass. What is the speed $u$ of the muon?

  In the pion rest frame $S$, the muon moves in the $y$-direction. A moving observer, in a frame $S^{\prime}$ with axes parallel to those in the pion rest frame, wishes to take measurements of the decay along the $x$-axis, and notes that the pion has speed $v$ with respect to the $x$-axis. Write down the four-dimensional Lorentz transformation relating $S^{\prime}$ to $S$ and determine the momentum of the muon in $S^{\prime}$. Hence show that in $S^{\prime}$ the direction of motion of the muon makes an angle $\theta$ with respect to the $y$-axis, where

  $$\tan \theta=\frac{M^{2}+m^{2}}{M^{2}-m^{2}} \frac{v}{\left(c^{2}-v^{2}\right)^{1 / 2}} .$$

  comment

Statistics

• $1 . \mathrm{I} . 3 \mathrm{H} \quad$

  Statistics | Part IB, 2003

  Derive the least squares estimators $\hat{\alpha}$ and $\hat{\beta}$ for the coefficients of the simple linear regression model

  $$Y_{i}=\alpha+\beta\left(x_{i}-\bar{x}\right)+\varepsilon_{i}, \quad i=1, \ldots, n,$$

  where $x_{1}, \ldots, x_{n}$ are given constants, $\bar{x}=n^{-1} \sum_{i=1}^{n} x_{i}$, and $\varepsilon_{i}$ are independent with $\mathrm{E} \varepsilon_{i}=0, \operatorname{Var} \varepsilon_{i}=\sigma^{2}, i=1, \ldots, n$.

  A manufacturer of optical equipment has the following data on the unit cost (in pounds) of certain custom-made lenses and the number of units made in each order:

  \begin{tabular}{l|ccccc} No. of units, $x_{i}$ & 1 & 3 & 5 & 10 & 12 \ \hline Cost per unit, $y_{i}$ & 58 & 55 & 40 & 37 & 22 \end{tabular}

  Assuming that the conditions underlying simple linear regression analysis are met, estimate the regression coefficients and use the estimated regression equation to predict the unit cost in an order for 8 of these lenses.

  [Hint: for the data above, $S_{x y}=\sum_{i=1}^{n}\left(x_{i}-\bar{x}\right) y_{i}=-257.4$.]

  comment

• 1.II.12H

  Statistics | Part IB, 2003

  Suppose that six observations $X_{1}, \ldots, X_{6}$ are selected at random from a normal distribution for which both the mean $\mu_{X}$ and the variance $\sigma_{X}^{2}$ are unknown, and it is found that $S_{X X}=\sum_{i=1}^{6}\left(x_{i}-\bar{x}\right)^{2}=30$, where $\bar{x}=\frac{1}{6} \sum_{i=1}^{6} x_{i}$. Suppose also that 21 observations $Y_{1}, \ldots, Y_{21}$ are selected at random from another normal distribution for which both the mean $\mu_{Y}$ and the variance $\sigma_{Y}^{2}$ are unknown, and it is found that $S_{Y Y}=40$. Derive carefully the likelihood ratio test of the hypothesis $H_{0}: \sigma_{X}^{2}=\sigma_{Y}^{2}$ against $H_{1}: \sigma_{X}^{2}>\sigma_{Y}^{2}$ and apply it to the data above at the $0.05$ level.

  

  comment

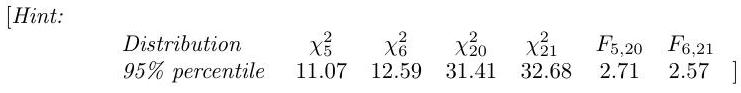
• 2.I.3H

  Statistics | Part IB, 2003

  Let $X_{1}, \ldots, X_{n}$ be a random sample from the $N\left(\theta, \sigma^{2}\right)$ distribution, and suppose that the prior distribution for $\theta$ is $N\left(\mu, \tau^{2}\right)$, where $\sigma^{2}, \mu, \tau^{2}$ are known. Determine the posterior distribution for $\theta$, given $X_{1}, \ldots, X_{n}$, and the best point estimate of $\theta$ under both quadratic and absolute error loss.

  comment

• 2.II.12H

  Statistics | Part IB, 2003

  An examination was given to 500 high-school students in each of two large cities, and their grades were recorded as low, medium, or high. The results are given in the table below.

  \begin{tabular}{l|ccc} & Low & Medium & High \ \hline City A & 103 & 145 & 252 \ City B & 140 & 136 & 224 \end{tabular}

  Derive carefully the test of homogeneity and test the hypothesis that the distributions of scores among students in the two cities are the same.

  

  comment

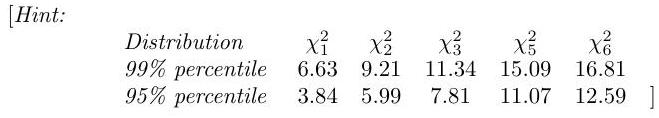
• 4.I.3H

  Statistics | Part IB, 2003

  The following table contains a distribution obtained in 320 tosses of 6 coins and the corresponding expected frequencies calculated with the formula for the binomial distribution for $p=0.5$ and $n=6$.

  \begin{tabular}{l|rrrrrrr} No. heads & 0 & 1 & 2 & 3 & 4 & 5 & 6 \ \hline Observed frequencies & 3 & 21 & 85 & 110 & 62 & 32 & 7 \ Expected frequencies & 5 & 30 & 75 & 100 & 75 & 30 & 5 \end{tabular}

  Conduct a goodness-of-fit test at the $0.05$ level for the null hypothesis that the coins are all fair.

  [Hint:

  $\left.\begin{array}{lcccc}\text { Distribution } & \chi_{5}^{2} & \chi_{6}^{2} & \chi_{7}^{2} \\ 95 \% \text { percentile } & 11.07 & 12.59 & 14.07 & \end{array}\right]$

  comment

• 4.II.12H $\quad$

  Statistics | Part IB, 2003

  State and prove the Rao-Blackwell theorem.

  Suppose that $X_{1}, \ldots, X_{n}$ are independent random variables uniformly distributed over $(\theta, 3 \theta)$. Find a two-dimensional sufficient statistic $T(X)$ for $\theta$. Show that an unbiased estimator of $\theta$ is $\hat{\theta}=X_{1} / 2$.

  Find an unbiased estimator of $\theta$ which is a function of $T(X)$ and whose mean square error is no more than that of $\hat{\theta}$.

  comment