1.II.12H
Suppose that six observations are selected at random from a normal distribution for which both the mean and the variance are unknown, and it is found that , where . Suppose also that 21 observations are selected at random from another normal distribution for which both the mean and the variance are unknown, and it is found that . Derive carefully the likelihood ratio test of the hypothesis against and apply it to the data above at the level.
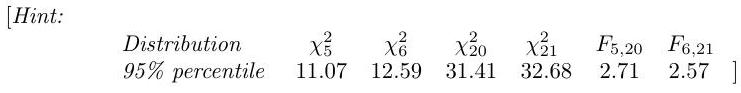
Typos? Please submit corrections to this page on GitHub.