Part IB, 2021

Analysis and Topology

• Paper 1, Section II, F

  Analysis and Topology | Part IB, 2021

  Let $f: X \rightarrow Y$ be a map between metric spaces. Prove that the following two statements are equivalent:

  (i) $f^{-1}(A) \subset X$ is open whenever $A \subset Y$ is open.

  (ii) $f\left(x_{n}\right) \rightarrow f(a)$ for any sequence $x_{n} \rightarrow a$.

  For $f: X \rightarrow Y$ as above, determine which of the following statements are always true and which may be false, giving a proof or a counterexample as appropriate.

  (a) If $X$ is compact and $f$ is continuous, then $f$ is uniformly continuous.

  (b) If $X$ is compact and $f$ is continuous, then $Y$ is compact.

  (c) If $X$ is connected, $f$ is continuous and $f(X)$ is dense in $Y$, then $Y$ is connected.

  (d) If the set $\{(x, y) \in X \times Y: y=f(x)\}$ is closed in $X \times Y$ and $Y$ is compact, then $f$ is continuous.

  comment

• Paper 2, Section I, $2 F$

  Analysis and Topology | Part IB, 2021

  Let $K:[0,1] \times[0,1] \rightarrow \mathbb{R}$ be a continuous function and let $C([0,1])$ denote the set of continuous real-valued functions on $[0,1]$. Given $f \in C([0,1])$, define the function $T f$ by the expression

  $$T f(x)=\int_{0}^{1} K(x, y) f(y) d y$$

  (a) Prove that $T$ is a continuous map $C([0,1]) \rightarrow C([0,1])$ with the uniform metric on $C([0,1])$.

  (b) Let $d_{1}$ be the metric on $C([0,1])$ given by

  $$d_{1}(f, g)=\int_{0}^{1}|f(x)-g(x)| d x$$

  Is $T$ continuous with respect to $d_{1} ?$

  comment

• Paper 2, Section II, F

  Analysis and Topology | Part IB, 2021

  Let $k_{n}: \mathbb{R} \rightarrow \mathbb{R}$ be a sequence of functions satisfying the following properties:

  1. $k_{n}(x) \geqslant 0$ for all $n$ and $x \in \mathbb{R}$ and there is $R>0$ such that $k_{n}$ vanishes outside $[-R, R]$ for all $n$

  2. each $k_{n}$ is continuous and

  $$\int_{-\infty}^{\infty} k_{n}(t) d t=1$$

  3. given $\varepsilon>0$ and $\delta>0$, there exists a positive integer $N$ such that if $n \geqslant N$, then

  $$\int_{-\infty}^{-\delta} k_{n}(t) d t+\int_{\delta}^{\infty} k_{n}(t) d t<\varepsilon$$

  Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a bounded continuous function and set

  $$f_{n}(x):=\int_{-\infty}^{\infty} k_{n}(t) f(x-t) d t$$

  Show that $f_{n}$ converges uniformly to $f$ on any compact subset of $\mathbb{R}$.

  Let $g:[0,1] \rightarrow \mathbb{R}$ be a continuous function with $g(0)=g(1)=0$. Show that there is a sequence of polynomials $p_{n}$ such that $p_{n}$ converges uniformly to $g$ on $[0,1]$. $[$ Hint: consider the functions

  $$k_{n}(t)= \begin{cases}\left(1-t^{2}\right)^{n} / c_{n} & t \in[-1,1] \\ 0 & \text { otherwise }\end{cases}$$

  where $c_{n}$ is a suitably chosen constant.]

  comment

• Paper 3, Section II, F

  Analysis and Topology | Part IB, 2021

  Define the terms connected and path-connected for a topological space. Prove that the interval $[0,1]$ is connected and that if a topological space is path-connected, then it is connected.

  Let $X$ be an open subset of Euclidean space $\mathbb{R}^{n}$. Show that $X$ is connected if and only if $X$ is path-connected.

  Let $X$ be a topological space with the property that every point has a neighbourhood homeomorphic to an open set in $\mathbb{R}^{n}$. Assume $X$ is connected; must $X$ be also pathconnected? Briefly justify your answer.

  Consider the following subsets of $\mathbb{R}^{2}$ :

  $$\begin{gathered} A=\{(x, 0): x \in(0,1]\}, \quad B=\{(0, y): y \in[1 / 2,1]\}, \text { and } \\ C_{n}=\{(1 / n, y): y \in[0,1]\} \text { for } n \geqslant 1 \end{gathered}$$

  Let

  $$X=A \cup B \cup \bigcup_{n \geqslant 1} C_{n}$$

  with the subspace topology. Is $X$ path-connected? Is $X$ connected? Justify your answers.

  comment

• Paper 4, Section I, $2 F$

  Analysis and Topology | Part IB, 2021

  Let $X$ be a topological space with an equivalence relation, $\tilde{X}$ the set of equivalence classes, $\pi: X \rightarrow \tilde{X}$, the quotient map taking a point in $X$ to its equivalence class.

  (a) Define the quotient topology on $\tilde{X}$ and check it is a topology.

  (b) Prove that if $Y$ is a topological space, a map $f: \tilde{X} \rightarrow Y$ is continuous if and only if $f \circ \pi$ is continuous.

  (c) If $X$ is Hausdorff, is it true that $\tilde{X}$ is also Hausdorff? Justify your answer.

  comment

• Paper 4, Section II, F

  Analysis and Topology | Part IB, 2021

  (a) Let $g:[0,1] \times \mathbb{R}^{n} \rightarrow \mathbb{R}$ be a continuous function such that for each $t \in[0,1]$, the partial derivatives $D_{i} g(t, x)(i=1, \ldots, n)$ of $x \mapsto g(t, x)$ exist and are continuous on $[0,1] \times \mathbb{R}^{n}$. Define $G: \mathbb{R}^{n} \rightarrow \mathbb{R}$ by

  $$G(x)=\int_{0}^{1} g(t, x) d t$$

  Show that $G$ has continuous partial derivatives $D_{i} G$ given by

  $$D_{i} G(x)=\int_{0}^{1} D_{i} g(t, x) d t$$

  for $i=1, \ldots, n$.

  (b) Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be an infinitely differentiable function, that is, partial derivatives $D_{i_{1}} D_{i_{2}} \cdots D_{i_{k}} f$ exist and are continuous for all $k \in \mathbb{N}$ and $i_{1}, \ldots, i_{k} \in\{1,2\}$. Show that for any $\left(x_{1}, x_{2}\right) \in \mathbb{R}^{2}$,

  $$f\left(x_{1}, x_{2}\right)=f\left(x_{1}, 0\right)+x_{2} D_{2} f\left(x_{1}, 0\right)+x_{2}^{2} h\left(x_{1}, x_{2}\right)$$

  where $h: \mathbb{R}^{2} \rightarrow \mathbb{R}$ is an infinitely differentiable function.

  [Hint: You may use the fact that if $u: \mathbb{R} \rightarrow \mathbb{R}$ is infinitely differentiable, then

  $$\left.u(1)=u(0)+u^{\prime}(0)+\int_{0}^{1}(1-t) u^{\prime \prime}(t) d t .\right]$$

  comment

Complex Analysis

• Paper 3, Section II, G

  Complex Analysis | Part IB, 2021

  Let $\gamma$ be a curve (not necessarily closed) in $\mathbb{C}$ and let $[\gamma]$ denote the image of $\gamma$. Let $\phi:[\gamma] \rightarrow \mathbb{C}$ be a continuous function and define

  $$f(z)=\int_{\gamma} \frac{\phi(\lambda)}{\lambda-z} d \lambda$$

  for $z \in \mathbb{C} \backslash[\gamma]$. Show that $f$ has a power series expansion about every $a \notin[\gamma]$.

  Using Cauchy's Integral Formula, show that a holomorphic function has complex derivatives of all orders. [Properties of power series may be assumed without proof.] Let $f$ be a holomorphic function on an open set $U$ that contains the closed disc $\bar{D}(a, r)$. Obtain an integral formula for the derivative of $f$ on the open disc $D(a, r)$ in terms of the values of $f$ on the boundary of the disc.

  Show that if holomorphic functions $f_{n}$ on an open set $U$ converge locally uniformly to a holomorphic function $f$ on $U$, then $f_{n}^{\prime}$ converges locally uniformly to $f^{\prime}$.

  Let $D_{1}$ and $D_{2}$ be two overlapping closed discs. Let $f$ be a holomorphic function on some open neighbourhood of $D=D_{1} \cap D_{2}$. Show that there exist open neighbourhoods $U_{j}$ of $D_{j}$ and holomorphic functions $f_{j}$ on $U_{j}, j=1,2$, such that $f(z)=f_{1}(z)+f_{2}(z)$ on $U_{1} \cap U_{2}$.

  comment

• Paper 4, Section I, $3 G$

  Complex Analysis | Part IB, 2021

  Let $f$ be a holomorphic function on a neighbourhood of $a \in \mathbb{C}$. Assume that $f$ has a zero of order $k$ at $a$ with $k \geqslant 1$. Show that there exist $\varepsilon>0$ and $\delta>0$ such that for any $b$ with $0<|b|<\varepsilon$ there are exactly $k$ distinct values of $z \in D(a, \delta)$ with $f(z)=b$.

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, B

  Complex Analysis or Complex Methods | Part IB, 2021

  Let $x>0, x \neq 2$, and let $C_{x}$ denote the positively oriented circle of radius $x$ centred at the origin. Define

  $$g(x)=\oint_{C_{x}} \frac{z^{2}+e^{z}}{z^{2}(z-2)} d z$$

  Evaluate $g(x)$ for $x \in(0, \infty) \backslash\{2\}$.

  comment

• Paper 1, Section II, G

  Complex Analysis or Complex Methods | Part IB, 2021

  (a) State a theorem establishing Laurent series of analytic functions on suitable domains. Give a formula for the $n^{\text {th }}$Laurent coefficient.

  Define the notion of isolated singularity. State the classification of an isolated singularity in terms of Laurent coefficients.

  Compute the Laurent series of

  $$f(z)=\frac{1}{z(z-1)}$$

  on the annuli $A_{1}=\{z: 0<|z|<1\}$ and $A_{2}=\{z: 1<|z|\}$. Using this example, comment on the statement that Laurent coefficients are unique. Classify the singularity of $f$ at 0 .

  (b) Let $U$ be an open subset of the complex plane, let $a \in U$ and let $U^{\prime}=U \backslash\{a\}$. Assume that $f$ is an analytic function on $U^{\prime}$ with $|f(z)| \rightarrow \infty$ as $z \rightarrow a$. By considering the Laurent series of $g(z)=\frac{1}{f(z)}$ at $a$, classify the singularity of $f$ at $a$ in terms of the Laurent coefficients. [You may assume that a continuous function on $U$ that is analytic on $U^{\prime}$ is analytic on $U$.]

  Now let $f: \mathbb{C} \rightarrow \mathbb{C}$ be an entire function with $|f(z)| \rightarrow \infty$ as $z \rightarrow \infty$. By considering Laurent series at 0 of $f(z)$ and of $h(z)=f\left(\frac{1}{z}\right)$, show that $f$ is a polynomial.

  (c) Classify, giving reasons, the singularity at the origin of each of the following functions and in each case compute the residue:

  $$g(z)=\frac{\exp (z)-1}{z \log (z+1)} \quad \text { and } \quad h(z)=\sin (z) \sin (1 / z)$$

  comment

• Paper 2, Section II, B

  Complex Analysis or Complex Methods | Part IB, 2021

  (a) Let $f: \mathbb{C} \rightarrow \mathbb{C}$ be an entire function and let $a>0, b>0$ be constants. Show that if

  $$|f(z)| \leqslant a|z|^{n / 2}+b$$

  for all $z \in \mathbb{C}$, where $n$ is a positive odd integer, then $f$ must be a polynomial with degree not exceeding $\lfloor n / 2\rfloor$ (closest integer part rounding down).

  Does there exist a function $f$, analytic in $\mathbb{C} \backslash\{0\}$, such that $|f(z)| \geqslant 1 / \sqrt{|z|}$ for all nonzero $z ?$ Justify your answer.

  (b) State Liouville's Theorem and use it to show the following.

  (i) If $u$ is a positive harmonic function on $\mathbb{R}^{2}$, then $u$ is a constant function.

  (ii) Let $L=\{z \mid z=a x+b, x \in \mathbb{R}\}$ be a line in $\mathbb{C}$ where $a, b \in \mathbb{C}, a \neq 0$. If $f: \mathbb{C} \rightarrow \mathbb{C}$ is an entire function such that $f(\mathbb{C}) \cap L=\emptyset$, then $f$ is a constant function.

  comment

Complex Methods

• Paper 3, Section I, B

  Complex Methods | Part IB, 2021

  Find the value of $A$ for which the function

  $$\phi(x, y)=x \cosh y \sin x+A y \sinh y \cos x$$

  satisfies Laplace's equation. For this value of $A$, find a complex analytic function of which $\phi$ is the real part.

  comment

• Paper 4, Section II, B

  Complex Methods | Part IB, 2021

  Let $f(t)$ be defined for $t \geqslant 0$. Define the Laplace transform $\widehat{f}(s)$ of $f$. Find an expression for the Laplace transform of $\frac{d f}{d t}$ in terms of $\widehat{f}$.

  Three radioactive nuclei decay sequentially, so that the numbers $N_{i}(t)$ of the three types obey the equations

  $$\begin{aligned} \frac{d N_{1}}{d t} &=-\lambda_{1} N_{1} \\ \frac{d N_{2}}{d t} &=\lambda_{1} N_{1}-\lambda_{2} N_{2} \\ \frac{d N_{3}}{d t} &=\lambda_{2} N_{2}-\lambda_{3} N_{3} \end{aligned}$$

  where $\lambda_{3}>\lambda_{2}>\lambda_{1}>0$ are constants. Initially, at $t=0, N_{1}=N, N_{2}=0$ and $N_{3}=n$. Using Laplace transforms, find $N_{3}(t)$.

  By taking an appropriate limit, find $N_{3}(t)$ when $\lambda_{2}=\lambda_{1}=\lambda>0$ and $\lambda_{3}>\lambda$.

  comment

Electromagnetism

• Paper 1, Section II, 15D

  Electromagnetism | Part IB, 2021

  (a) Show that the magnetic flux passing through a simple, closed curve $C$ can be written as

  $$\Phi=\oint_{C} \mathbf{A} \cdot \mathbf{d} \mathbf{x},$$

  where $\mathbf{A}$ is the magnetic vector potential. Explain why this integral is independent of the choice of gauge.

  (b) Show that the magnetic vector potential due to a static electric current density $\mathbf{J}$, in the Coulomb gauge, satisfies Poisson's equation

  $$-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{J}$$

  Hence obtain an expression for the magnetic vector potential due to a static, thin wire, in the form of a simple, closed curve $C$, that carries an electric current $I$. [You may assume that the electric current density of the wire can be written as

  $$\mathbf{J}(\mathbf{x})=I \int_{C} \delta^{(3)}\left(\mathbf{x}-\mathbf{x}^{\prime}\right) \mathbf{d} \mathbf{x}^{\prime}$$

  where $\delta^{(3)}$ is the three-dimensional Dirac delta function.]

  (c) Consider two thin wires, in the form of simple, closed curves $C_{1}$ and $C_{2}$, that carry electric currents $I_{1}$ and $I_{2}$, respectively. Let $\Phi_{i j}$ (where $i, j \in\{1,2\}$ ) be the magnetic flux passing through the curve $C_{i}$ due to the current $I_{j}$ flowing around $C_{j}$. The inductances are defined by $L_{i j}=\Phi_{i j} / I_{j}$. By combining the results of parts (a) and (b), or otherwise, derive Neumann's formula for the mutual inductance,

  $$L_{12}=L_{21}=\frac{\mu_{0}}{4 \pi} \oint_{C_{1}} \oint_{C_{2}} \frac{\mathbf{d} \mathbf{x}_{1} \cdot \mathbf{d} \mathbf{x}_{2}}{\left|\mathbf{x}_{1}-\mathbf{x}_{2}\right|} .$$

  Suppose that $C_{1}$ is a circular loop of radius $a$, centred at $(0,0,0)$ and lying in the plane $z=0$, and that $C_{2}$ is a different circular loop of radius $b$, centred at $(0,0, c)$ and lying in the plane $z=c$. Show that the mutual inductance of the two loops is

  $$\frac{\mu_{0}}{4} \sqrt{a^{2}+b^{2}+c^{2}} f(q)$$

  where

  $$q=\frac{2 a b}{a^{2}+b^{2}+c^{2}}$$

  and the function $f(q)$ is defined, for $0<q<1$, by the integral

  $$f(q)=\int_{0}^{2 \pi} \frac{q \cos \theta d \theta}{\sqrt{1-q \cos \theta}}$$

  comment

• Paper 2, Section I, $4 \mathrm{D}$

  Electromagnetism | Part IB, 2021

  State Gauss's Law in the context of electrostatics.

  A simple coaxial cable consists of an inner conductor in the form of a perfectly conducting, solid cylinder of radius $a$, surrounded by an outer conductor in the form of a perfectly conducting, cylindrical shell of inner radius $b>a$ and outer radius $c>b$. The cylinders are coaxial and the gap between them is filled with a perfectly insulating material. The cable may be assumed to be straight and arbitrarily long.

  In a steady state, the inner conductor carries an electric charge $+Q$ per unit length, and the outer conductor carries an electric charge $-Q$ per unit length. The charges are distributed in a cylindrically symmetric way and no current flows through the cable.

  Determine the electrostatic potential and the electric field as functions of the cylindrical radius $r$, for $0<r<\infty$. Calculate the capacitance $C$ of the cable per unit length and the electrostatic energy $U$ per unit length, and verify that these are related by

  $$U=\frac{Q^{2}}{2 C}$$

  comment

• Paper 2, Section II, $16 \mathrm{D}$

  Electromagnetism | Part IB, 2021

  (a) Show that, for $|\mathbf{x}| \gg|\mathbf{y}|$,

  $$\frac{1}{|\mathbf{x}-\mathbf{y}|}=\frac{1}{|\mathbf{x}|}\left[1+\frac{\mathbf{x} \cdot \mathbf{y}}{|\mathbf{x}|^{2}}+\frac{3(\mathbf{x} \cdot \mathbf{y})^{2}-|\mathbf{x}|^{2}|\mathbf{y}|^{2}}{2|\mathbf{x}|^{4}}+O\left(\frac{|\mathbf{y}|^{3}}{|\mathbf{x}|^{3}}\right)\right]$$

  (b) A particle with electric charge $q>0$ has position vector $(a, 0,0)$, where $a>0$. An earthed conductor (held at zero potential) occupies the plane $x=0$. Explain why the boundary conditions can be satisfied by introducing a fictitious 'image' particle of appropriate charge and position. Hence determine the electrostatic potential and the electric field in the region $x>0$. Find the leading-order approximation to the potential for $|\mathbf{x}| \gg a$ and compare with that of an electric dipole. Directly calculate the total flux of the electric field through the plane $x=0$ and comment on the result. Find the induced charge distribution on the surface of the conductor, and the total induced surface charge. Sketch the electric field lines in the plane $z=0$.

  (c) Now consider instead a particle with charge $q$ at position $(a, b, 0)$, where $a>0$ and $b>0$, with earthed conductors occupying the planes $x=0$ and $y=0$. Find the leading-order approximation to the potential in the region $x, y>0$ for $|\mathbf{x}| \gg a, b$ and state what type of multipole potential this is.

  comment

• Paper 3, Section II, 15D

  Electromagnetism | Part IB, 2021

  (a) The energy density stored in the electric and magnetic fields $\mathbf{E}$ and $\mathbf{B}$ is given by

  $$w=\frac{\epsilon_{0}}{2} \mathbf{E} \cdot \mathbf{E}+\frac{1}{2 \mu_{0}} \mathbf{B} \cdot \mathbf{B}$$

  Show that, in regions where no electric current flows,

  $$\frac{\partial w}{\partial t}+\boldsymbol{\nabla} \cdot \mathbf{S}=0$$

  for some vector field $\mathbf{S}$ that you should determine.

  (b) The coordinates $x^{\prime \mu}=\left(c t^{\prime}, \mathbf{x}^{\prime}\right)$ in an inertial frame $\mathcal{S}^{\prime}$ are related to the coordinates $x^{\mu}=(c t, \mathbf{x})$ in an inertial frame $\mathcal{S}$ by a Lorentz transformation $x^{\prime \mu}=\Lambda_{\nu}^{\mu} x^{\nu}$, where

  $$\Lambda_{\nu}^{\mu}=\left(\begin{array}{cccc} \gamma & -\gamma v / c & 0 & 0 \\ -\gamma v / c & \gamma & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{array}\right)$$

  with $\gamma=\left(1-v^{2} / c^{2}\right)^{-1 / 2}$. Here $v$ is the relative velocity of $\mathcal{S}^{\prime}$ with respect to $\mathcal{S}$ in the x-direction.

  In frame $\mathcal{S}^{\prime}$, there is a static electric field $\mathbf{E}^{\prime}\left(\mathbf{x}^{\prime}\right)$ with $\partial \mathbf{E}^{\prime} / \partial t^{\prime}=0$, and no magnetic field. Calculate the electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$ in frame $\mathcal{S}$. Show that the energy density in frame $\mathcal{S}$ is given in terms of the components of $\mathbf{E}^{\prime}$ by

  $$w=\frac{\epsilon_{0}}{2}\left[E_{x}^{\prime 2}+\left(\frac{c^{2}+v^{2}}{c^{2}-v^{2}}\right)\left(E_{y}^{\prime 2}+E_{z}^{\prime 2}\right)\right]$$

  Use the fact that $\partial w / \partial t^{\prime}=0$ to show that

  $$\frac{\partial w}{\partial t}+\nabla \cdot\left(w v \mathbf{e}_{x}\right)=0$$

  where $\mathbf{e}_{x}$ is the unit vector in the $x$-direction.

  comment

• Paper 4, Section I, $5 \mathrm{D}$

  Electromagnetism | Part IB, 2021

  Write down Maxwell's equations in a vacuum. Show that they admit wave solutions with

  $$\mathbf{B}(\mathbf{x}, t)=\operatorname{Re}\left[\mathbf{B}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)}\right]$$

  where $\mathbf{B}_{0}, \mathbf{k}$ and $\omega$ must obey certain conditions that you should determine. Find the corresponding electric field $\mathbf{E}(\mathbf{x}, t)$.

  A light wave, travelling in the $x$-direction and linearly polarised so that the magnetic field points in the $z$-direction, is incident upon a conductor that occupies the half-space $x>0$. The electric and magnetic fields obey the boundary conditions $\mathbf{E} \times \mathbf{n}=\mathbf{0}$ and $\mathbf{B} \cdot \mathbf{n}=0$ on the surface of the conductor, where $\mathbf{n}$ is the unit normal vector. Determine the contributions to the magnetic field from the incident and reflected waves in the region $x \leqslant 0$. Compute the magnetic field tangential to the surface of the conductor.

  comment

Fluid Dynamics

• Paper 1, Section II, A

  Fluid Dynamics | Part IB, 2021

  A two-dimensional flow is given by a velocity potential

  $$\phi(x, y, t)=\epsilon y \sin (x-t)$$

  where $\epsilon$ is a constant.

  (a) Find the corresponding velocity field $\mathbf{u}(x, y, t)$. Determine $\boldsymbol{\nabla} \cdot \mathbf{u}$.

  (b) The time-average $\langle\psi\rangle(x, y)$ of a quantity $\psi(x, y, t)$ is defined as

  $$\langle\psi\rangle(x, y)=\frac{1}{2 \pi} \int_{0}^{2 \pi} \psi(x, y, t) d t .$$

  Show that the time-average of this velocity field is zero everywhere. Write down an expression for the acceleration of fluid particles, and find the time-average of this expression at a fixed point $(x, y)$.

  (c) Now assume that $|\epsilon| \ll 1$. The material particle at $(0,0)$ at $t=0$ is marked with dye. Write down equations for its subsequent motion. Verify that its position $(x, y)$ for $t>0$ is given (correct to terms of order $\epsilon^{2}$ ) by

  $$\begin{aligned} x &=\epsilon^{2}\left(\frac{1}{4} \sin 2 t+\frac{t}{2}-\sin t\right) \\ y &=\epsilon(\cos t-1) \end{aligned}$$

  Deduce the time-average velocity of the dyed particle correct to this order.

  comment

• Paper 2, Section I, A

  Fluid Dynamics | Part IB, 2021

  Consider an axisymmetric container, initially filled with water to a depth $h_{I}$. A small circular hole of radius $r_{0}$ is opened in the base of the container at $z=0$.

  (a) Determine how the radius $r$ of the container should vary with $z<h_{I}$ so that the depth of the water will decrease at a constant rate.

  (b) For such a container, determine how the cross-sectional area $A$ of the free surface should decrease with time.

  [You may assume that the flow rate through the opening is sufficiently small that Bernoulli's theorem for steady flows can be applied.]

  comment

• Paper 3, Section I, A

  Fluid Dynamics | Part IB, 2021

  A two-dimensional flow $\mathbf{u}=(u, v)$ has a velocity field given by

  $$u=\frac{x^{2}-y^{2}}{\left(x^{2}+y^{2}\right)^{2}} \quad \text { and } \quad v=\frac{2 x y}{\left(x^{2}+y^{2}\right)^{2}}$$

  (a) Show explicitly that this flow is incompressible and irrotational away from the origin.

  (b) Find the stream function for this flow.

  (c) Find the velocity potential for this flow.

  comment

• Paper 3, Section II, A

  Fluid Dynamics | Part IB, 2021

  A two-dimensional layer of viscous fluid lies between two rigid boundaries at $y=\pm L_{0}$. The boundary at $y=L_{0}$ oscillates in its own plane with velocity $\left(U_{0} \cos \omega t, 0\right)$, while the boundary at $y=-L_{0}$ oscillates in its own plane with velocity $\left(-U_{0} \cos \omega t, 0\right)$. Assume that there is no pressure gradient and that the fluid flows parallel to the boundary with velocity $(u(y, t), 0)$, where $u(y, t)$ can be written as $u(y, t)=\operatorname{Re}\left[U_{0} f(y) \exp (i \omega t)\right]$.

  (a) By exploiting the symmetry of the system or otherwise, show that

  $$f(y)=\frac{\sinh [(1+i) \Delta \hat{y}]}{\sinh [(1+i) \Delta]}, \text { where } \hat{y}=\frac{y}{L_{0}} \text { and } \Delta=\left(\frac{\omega L_{0}^{2}}{2 \nu}\right)^{1 / 2}$$

  (b) Hence or otherwise, show that

  where $\Delta_{\pm}=\Delta(1 \pm \hat{y})$.

  (c) Show that, for $\Delta \ll 1$,

  $$u(y, t) \simeq \frac{U_{0} y}{L_{0}} \cos \omega t$$

  and briefly interpret this result physically.

  $$\begin{aligned} & \frac{u(y, t)}{U_{0}}=\frac{\cos \omega t\left[\cosh \Delta_{+} \cos \Delta_{-}-\cosh \Delta_{-} \cos \Delta_{+}\right]}{(\cosh 2 \Delta-\cos 2 \Delta)} \\ & +\frac{\sin \omega t\left[\sinh \Delta_{+} \sin \Delta_{-}-\sinh \Delta_{-} \sin \Delta_{+}\right]}{(\cosh 2 \Delta-\cos 2 \Delta)}, \end{aligned}$$

  comment

• Paper 4, Section II, A

  Fluid Dynamics | Part IB, 2021

  Consider the spherically symmetric motion induced by the collapse of a spherical cavity of radius $a(t)$, centred on the origin. For $r<a$, there is a vacuum, while for $r>a$, there is an inviscid incompressible fluid with constant density $\rho$. At time $t=0, a=a_{0}$, and the fluid is at rest and at constant pressure $p_{0}$.

  (a) Consider the radial volume transport in the fluid $Q(R, t)$, defined as

  $$Q(R, t)=\int_{r=R} u d S$$

  where $u$ is the radial velocity, and $d S$ is an infinitesimal element of the surface of a sphere of radius $R \geqslant a$. Use the incompressibility condition to establish that $Q$ is a function of time alone.

  (b) Using the expression for pressure in potential flow or otherwise, establish that

  $$\frac{1}{4 \pi a} \frac{d Q}{d t}-\frac{(\dot{a})^{2}}{2}=-\frac{p_{0}}{\rho}$$

  where $\dot{a}(t)$ is the radial velocity of the cavity boundary.

  (c) By expressing $Q(t)$ in terms of $a$ and $\dot{a}$, show that

  $$\dot{a}=-\sqrt{\frac{2 p_{0}}{3 \rho}\left(\frac{a_{0}^{3}}{a^{3}}-1\right)}$$

  [Hint: You may find it useful to assume $\dot{a}(t)$ is an explicit function of a from the outset.]

  (d) Hence write down an integral expression for the implosion time $\tau$, i.e. the time for the radius of the cavity $a \rightarrow 0$. [Do not attempt to evaluate the integral.]

  comment

Geometry

• Paper 1, Section I, F

  Geometry | Part IB, 2021

  Let $f: \mathbb{R}^{3} \rightarrow \mathbb{R}$ be a smooth function and let $\Sigma=f^{-1}(0)$ (assumed not empty). Show that if the differential $D f_{p} \neq 0$ for all $p \in \Sigma$, then $\Sigma$ is a smooth surface in $\mathbb{R}^{3}$.

  Is $\left\{(x, y, z) \in \mathbb{R}^{3}: x^{2}+y^{2}=\cosh \left(z^{2}\right)\right\}$ a smooth surface? Is every surface $\Sigma \subset \mathbb{R}^{3}$ of the form $f^{-1}(0)$ for some smooth $f: \mathbb{R}^{3} \rightarrow \mathbb{R}$ ? Justify your answers.

  comment

• Paper 1, Section II, F

  Geometry | Part IB, 2021

  Let $S \subset \mathbb{R}^{3}$ be an oriented surface. Define the Gauss map $N$ and show that the differential $D N_{p}$ of the Gauss map at any point $p \in S$ is a self-adjoint linear map. Define the Gauss curvature $\kappa$ and compute $\kappa$ in a given parametrisation.

  A point $p \in S$ is called umbilic if $D N_{p}$ has a repeated eigenvalue. Let $S \subset \mathbb{R}^{3}$ be a surface such that every point is umbilic and there is a parametrisation $\phi: \mathbb{R}^{2} \rightarrow S$ such that $S=\phi\left(\mathbb{R}^{2}\right)$. Prove that $S$ is part of a plane or part of a sphere. $[$ Hint: consider the symmetry of the mixed partial derivatives $n_{u v}=n_{v u}$, where $n(u, v)=N(\phi(u, v))$ for $\left.(u, v) \in \mathbb{R}^{2} .\right]$

  comment

• Paper 2, Section II, E

  Geometry | Part IB, 2021

  Define $\mathbb{H}$, the upper half plane model for the hyperbolic plane, and show that $\operatorname{PSL}_{2}(\mathbb{R})$ acts on $\mathbb{H}$ by isometries, and that these isometries preserve the orientation of $\mathbb{H}$.

  Show that every orientation preserving isometry of $\mathbb{H}$ is in $P S L_{2}(\mathbb{R})$, and hence the full group of isometries of $\mathbb{H}$ is $G=P S L_{2}(\mathbb{R}) \cup P S L_{2}(\mathbb{R}) \tau$, where $\tau z=-\bar{z}$.

  Let $\ell$ be a hyperbolic line. Define the reflection $\sigma_{\ell}$ in $\ell$. Now let $\ell, \ell^{\prime}$ be two hyperbolic lines which meet at a point $A \in \mathbb{H}$ at an angle $\theta$. What are the possibilities for the group $G$ generated by $\sigma_{\ell}$ and $\sigma_{\ell^{\prime}}$ ? Carefully justify your answer.

  comment

• Paper 3, Section I, E

  Geometry | Part IB, 2021

  State the local Gauss-Bonnet theorem for geodesic triangles on a surface. Deduce the Gauss-Bonnet theorem for closed surfaces. [Existence of a geodesic triangulation can be assumed.]

  Let $S_{r} \subset \mathbb{R}^{3}$ denote the sphere with radius $r$ centred at the origin. Show that the Gauss curvature of $S_{r}$ is $1 / r^{2}$. An octant is any of the eight regions in $S_{r}$ bounded by arcs of great circles arising from the planes $x=0, y=0, z=0$. Verify directly that the local Gauss-Bonnet theorem holds for an octant. [You may assume that the great circles on $S_{r}$ are geodesics.]

  comment

• Paper 3, Section II, E

  Geometry | Part IB, 2021

  Let $S \subset \mathbb{R}^{3}$ be an embedded smooth surface and $\gamma:[0,1] \rightarrow S$ a parameterised smooth curve on $S$. What is the energy of $\gamma$ ? By applying the Euler-Lagrange equations for stationary curves to the energy function, determine the differential equations for geodesics on $S$ explicitly in terms of a parameterisation of $S$.

  If $S$ contains a straight line $\ell$, prove from first principles that each segment $[P, Q] \subset \ell$ (with some parameterisation) is a geodesic on $S$.

  Let $H \subset \mathbb{R}^{3}$ be the hyperboloid defined by the equation $x^{2}+y^{2}-z^{2}=1$ and let $P=\left(x_{0}, y_{0}, z_{0}\right) \in H$. By considering appropriate isometries, or otherwise, display explicitly three distinct (as subsets of $H$ ) geodesics $\gamma: \mathbb{R} \rightarrow H$ through $P$ in the case when $z_{0} \neq 0$ and four distinct geodesics through $P$ in the case when $z_{0}=0$. Justify your answer.

  Let $\gamma: \mathbb{R} \rightarrow H$ be a geodesic, with coordinates $\gamma(t)=(x(t), y(t), z(t))$. Clairaut's relation asserts $\rho(t) \sin \psi(t)$ is constant, where $\rho(t)=\sqrt{x(t)^{2}+y(t)^{2}}$ and $\psi(t)$ is the angle between $\dot{\gamma}(t)$ and the plane through the point $\gamma(t)$ and the $z$-axis. Deduce from Clairaut's relation that there exist infinitely many geodesics $\gamma(t)$ on $H$ which stay in the half-space $\{z>0\}$ for all $t \in \mathbb{R}$.

  [You may assume that if $\gamma(t)$ satisfies the geodesic equations on $H$ then $\gamma$ is defined for all $t \in \mathbb{R}$ and the Euclidean norm $\|\dot{\gamma}(t)\|$ is constant. If you use a version of the geodesic equations for a surface of revolution, then that should be proved.]

  comment

• Paper 4, Section II, F

  Geometry | Part IB, 2021

  Define an abstract smooth surface and explain what it means for the surface to be orientable. Given two smooth surfaces $S_{1}$ and $S_{2}$ and a map $f: S_{1} \rightarrow S_{2}$, explain what it means for $f$ to be smooth

  For the cylinder

  $$C=\left\{(x, y, z) \in \mathbb{R}^{3}: x^{2}+y^{2}=1\right\},$$

  let $a: C \rightarrow C$ be the orientation reversing diffeomorphism $a(x, y, z)=(-x,-y,-z)$. Let $S$ be the quotient of $C$ by the equivalence relation $p \sim a(p)$ and let $\pi: C \rightarrow S$ be the canonical projection map. Show that $S$ can be made into an abstract smooth surface so that $\pi$ is smooth. Is $S$ orientable? Justify your answer.

  comment

Groups, Rings and Modules

• Paper 1, Section II, G

  Groups, Rings and Modules | Part IB, 2021

  Show that a ring $R$ is Noetherian if and only if every ideal of $R$ is finitely generated. Show that if $\phi: R \rightarrow S$ is a surjective ring homomorphism and $R$ is Noetherian, then $S$ is Noetherian.

  State and prove Hilbert's Basis Theorem.

  Let $\alpha \in \mathbb{C}$. Is $\mathbb{Z}[\alpha]$ Noetherian? Justify your answer.

  Give, with proof, an example of a Unique Factorization Domain that is not Noetherian.

  Let $R$ be the ring of continuous functions $\mathbb{R} \rightarrow \mathbb{R}$. Is $R$ Noetherian? Justify your answer.

  comment

• Paper 2, Section I, $1 G$

  Groups, Rings and Modules | Part IB, 2021

  Let $M$ be a module over a Principal Ideal Domain $R$ and let $N$ be a submodule of $M$. Show that $M$ is finitely generated if and only if $N$ and $M / N$ are finitely generated.

  comment

• Paper 2, Section II, G

  Groups, Rings and Modules | Part IB, 2021

  Let $M$ be a module over a ring $R$ and let $S \subset M$. Define what it means that $S$ freely generates $M$. Show that this happens if and only if for every $R$-module $N$, every function $f: S \rightarrow N$ extends uniquely to a homomorphism $\phi: M \rightarrow N$.

  Let $M$ be a free module over a (non-trivial) ring $R$ that is generated (not necessarily freely) by a subset $T \subset M$ of size $m$. Show that if $S$ is a basis of $M$, then $S$ is finite with $|S| \leqslant m$. Hence, or otherwise, deduce that any two bases of $M$ have the same number of elements. Denoting this number $\operatorname{rk} M$ and by quoting any result you need, show that if $R$ is a Euclidean Domain and $N$ is a submodule of $M$, then $N$ is free with $\operatorname{rk} N \leqslant \operatorname{rk} M$.

  State the Primary Decomposition Theorem for a finitely generated module $M$ over a Euclidean Domain $R$. Deduce that any finite subgroup of the multiplicative group of a field is cyclic.

  comment

• Paper 3, Section I, G

  Groups, Rings and Modules | Part IB, 2021

  Let $G$ be a finite group, and let $H$ be a proper subgroup of $G$ of index $n$.

  Show that there is a normal subgroup $K$ of $G$ such that $|G / K|$ divides $n$ ! and $|G / K| \geqslant n$.

  Show that if $G$ is non-abelian and simple, then $G$ is isomorphic to a subgroup of $A_{n}$.

  comment

• Paper 3, Section II, 10G

  Groups, Rings and Modules | Part IB, 2021

  Let $p$ be a non-zero element of a Principal Ideal Domain $R$. Show that the following are equivalent:

  (i) $p$ is prime;

  (ii) $p$ is irreducible;

  (iii) $(p)$ is a maximal ideal of $R$;

  (iv) $R /(p)$ is a field;

  (v) $R /(p)$ is an Integral Domain.

  Let $R$ be a Principal Ideal Domain, $S$ an Integral Domain and $\phi: R \rightarrow S$ a surjective ring homomorphism. Show that either $\phi$ is an isomorphism or $S$ is a field.

  Show that if $R$ is a commutative ring and $R[X]$ is a Principal Ideal Domain, then $R$ is a field.

  Let $R$ be an Integral Domain in which every two non-zero elements have a highest common factor. Show that in $R$ every irreducible element is prime.

  comment

• Paper 4, Section II, G

  Groups, Rings and Modules | Part IB, 2021

  Let $H$ and $P$ be subgroups of a finite group $G$. Show that the sets $H x P, x \in G$, partition $G$. By considering the action of $H$ on the set of left cosets of $P$ in $G$ by left multiplication, or otherwise, show that

  $$\frac{|H x P|}{|P|}=\frac{|H|}{\left|H \cap x P x^{-1}\right|}$$

  for any $x \in G$. Deduce that if $G$ has a Sylow $p$-subgroup, then so does $H$.

  Let $p, n \in \mathbb{N}$ with $p$ a prime. Write down the order of the group $G L_{n}(\mathbb{Z} / p \mathbb{Z})$. Identify in $G L_{n}(\mathbb{Z} / p \mathbb{Z})$ a Sylow $p$-subgroup and a subgroup isomorphic to the symmetric group $S_{n}$. Deduce that every finite group has a Sylow $p$-subgroup.

  State Sylow's theorem on the number of Sylow $p$-subgroups of a finite group.

  Let $G$ be a group of order $p q$, where $p>q$ are prime numbers. Show that if $G$ is non-abelian, then $q \mid p-1$.

  comment

Linear Algebra

• Paper 1, Section I, $1 \mathrm{E}$

  Linear Algebra | Part IB, 2021

  Let $V$ be a vector space over $\mathbb{R}, \operatorname{dim} V=n$, and let $\langle,$,$rangle be a non-degenerate anti-$ symmetric bilinear form on $V$.

  Let $v \in V, v \neq 0$. Show that $v^{\perp}$ is of dimension $n-1$ and $v \in v^{\perp}$. Show that if $W \subseteq v^{\perp}$ is a subspace with $W \oplus \mathbb{R} v=v^{\perp}$, then the restriction of $\langle,$,$rangle to W$ is nondegenerate.

  Conclude that the dimension of $V$ is even.

  comment

• Paper 1, Section II, E

  Linear Algebra | Part IB, 2021

  Let $d \geqslant 1$, and let $J_{d}=\left(\begin{array}{ccccc}0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \cdots & 0 \\ & & \cdots & \cdots & \\ 0 & 0 & \cdots & 0 & 1 \\ 0 & 0 & \ldots & 0 & 0\end{array}\right) \in \operatorname{Mat}_{d}(\mathbb{C})$.

  (a) (i) Compute $J_{d}^{n}$, for all $n \geqslant 0$.

  (ii) Hence, or otherwise, compute $\left(\lambda I+J_{d}\right)^{n}$, for all $n \geqslant 0$.

  (b) Let $V$ be a finite-dimensional vector space over $\mathbb{C}$, and let $\varphi \in \operatorname{End}(V)$. Suppose $\varphi^{n}=0$ for some $n>1$.

  (i) Determine the possible eigenvalues of $\varphi$.

  (ii) What are the possible Jordan blocks of $\varphi$ ?

  (iii) Show that if $\varphi^{2}=0$, there exists a decomposition

  $$V=U \oplus W_{1} \oplus W_{2}$$

  where $\varphi(U)=\varphi\left(W_{1}\right)=0, \varphi\left(W_{2}\right)=W_{1}$, and $\operatorname{dim} W_{2}=\operatorname{dim} W_{1}$.

  comment

• Paper 2, Section II, E

  Linear Algebra | Part IB, 2021

  (a) Compute the characteristic polynomial and minimal polynomial of

  $$A=\left(\begin{array}{ccc} -2 & -6 & -9 \\ 3 & 7 & 9 \\ -1 & -2 & -2 \end{array}\right)$$

  Write down the Jordan normal form for $A$.

  (b) Let $V$ be a finite-dimensional vector space over $\mathbb{C}, f: V \rightarrow V$ be a linear map, and for $\alpha \in \mathbb{C}, n \geqslant 1$, write

  $$W_{\alpha, n}:=\left\{v \in V \mid(f-\alpha I)^{n} v=0\right\}$$

  (i) Given $v \in W_{\alpha, n}, v \neq 0$, construct a non-zero eigenvector for $f$ in terms of $v$.

  (ii) Show that if $w_{1}, \ldots, w_{d}$ are non-zero eigenvectors for $f$ with eigenvalues $\alpha_{1}, \ldots, \alpha_{d}$, and $\alpha_{i} \neq \alpha_{j}$ for all $i \neq j$, then $w_{1}, \ldots, w_{d}$ are linearly independent.

  (iii) Show that if $v_{1} \in W_{\alpha_{1}, n}, \ldots, v_{d} \in W_{\alpha_{d}, n}$ are all non-zero, and $\alpha_{i} \neq \alpha_{j}$ for all $i \neq j$, then $v_{1}, \ldots, v_{d}$ are linearly independent.

  comment

• Paper 3, Section II, 9E

  Linear Algebra | Part IB, 2021

  (a) (i) State the rank-nullity theorem.

  Let $U$ and $W$ be vector spaces. Write down the definition of their direct sum $U \oplus W$ and the inclusions $i: U \rightarrow U \oplus W, j: W \rightarrow U \oplus W$.

  Now let $U$ and $W$ be subspaces of a vector space $V$. Define $l: U \cap W \rightarrow U \oplus W$ by $l(x)=i x-j x .$

  Describe the quotient space $(U \oplus W) / \operatorname{Im}(l)$ as a subspace of $V$.

  (ii) Let $V=\mathbb{R}^{5}$, and let $U$ be the subspace of $V$ spanned by the vectors

  $$\left(\begin{array}{c} 1 \\ 2 \\ -1 \\ 1 \\ 1 \end{array}\right),\left(\begin{array}{l} 1 \\ 0 \\ 0 \\ 1 \\ 0 \end{array}\right),\left(\begin{array}{c} -2 \\ 2 \\ 2 \\ 1 \\ -2 \end{array}\right)$$

  and $W$ the subspace of $V$ spanned by the vectors

  $$\left(\begin{array}{c} 3 \\ 2 \\ -3 \\ 1 \\ 3 \end{array}\right),\left(\begin{array}{l} 1 \\ 1 \\ 0 \\ 0 \\ 0 \end{array}\right),\left(\begin{array}{c} 1 \\ -4 \\ -1 \\ -2 \\ 1 \end{array}\right)$$

  Determine the dimension of $U \cap W$.

  (b) Let $A, B$ be complex $n$ by $n$ matrices with $\operatorname{rank}(B)=k$.

  Show that $\operatorname{det}(A+t B)$ is a polynomial in $t$ of degree at most $k$.

  Show that if $k=n$ the polynomial is of degree precisely $n$.

  Give an example where $k \geqslant 1$ but this polynomial is zero.

  comment

• Paper 4, Section I, $1 \mathbf{E}$

  Linear Algebra | Part IB, 2021

  Let $\operatorname{Mat}_{n}(\mathbb{C})$ be the vector space of $n$ by $n$ complex matrices.

  Given $A \in \operatorname{Mat}_{n}(\mathbb{C})$, define the linear $\operatorname{map}_{A}: \operatorname{Mat}_{n}(\mathbb{C}) \rightarrow \operatorname{Mat}_{n}(\mathbb{C})$,

  $$X \mapsto A X-X A$$

  (i) Compute a basis of eigenvectors, and their associated eigenvalues, when $A$ is the diagonal matrix

  $$A=\left(\begin{array}{llll} 1 & & & \\ & 2 & & \\ & & \ddots & \\ & & & n \end{array}\right)$$

  What is the rank of $\varphi_{A}$ ?

  (ii) Now let $A=\left(\begin{array}{ll}0 & 1 \\ 0 & 0\end{array}\right)$. Write down the matrix of the linear transformation $\varphi_{A}$ with respect to the standard basis of $\operatorname{Mat}_{2}(\mathbb{C})$.

  What is its Jordan normal form?

  comment

• Paper 4, Section II, E

  Linear Algebra | Part IB, 2021

  (a) Let $V$ be a complex vector space of dimension $n$.

  What is a Hermitian form on $V$ ?

  Given a Hermitian form, define the matrix $A$ of the form with respect to the basis $v_{1}, \ldots, v_{n}$ of $V$, and describe in terms of $A$ the value of the Hermitian form on two elements of $V$.

  Now let $w_{1}, \ldots, w_{n}$ be another basis of $V$. Suppose $w_{i}=\sum_{j} p_{i j} v_{j}$, and let $P=\left(p_{i j}\right)$. Write down the matrix of the form with respect to this new basis in terms of $A$ and $P$.

  Let $N=V^{\perp}$. Describe the dimension of $N$ in terms of the matrix $A$.

  (b) Write down the matrix of the real quadratic form

  $$x^{2}+y^{2}+2 z^{2}+2 x y+2 x z-2 y z .$$

  Using the Gram-Schmidt algorithm, find a basis which diagonalises the form. What are its rank and signature?

  (c) Let $V$ be a real vector space, and $\langle,$,$rangle a symmetric bilinear form on it. Let A$ be the matrix of this form in some basis.

  Prove that the signature of $\langle,$,$rangle is the number of positive eigenvalues of A$ minus the number of negative eigenvalues.

  Explain, using an example, why the eigenvalues themselves depend on the choice of a basis.

  comment

Markov Chains

• Paper 1, Section II, 19H

  Markov Chains | Part IB, 2021

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain with transition matrix $P$. What is a stopping time of $\left(X_{n}\right)_{n \geqslant 0}$ ? What is the strong Markov property?

  The exciting game of 'Unopoly' is played by a single player on a board of 4 squares. The player starts with $£ m$ (where $m \in \mathbb{N}$ ). During each turn, the player tosses a fair coin and moves one or two places in a clockwise direction $(1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1)$ according to whether the coin lands heads or tails respectively. The player collects $£ 2$ each time they pass (or land on) square 1. If the player lands on square 3 however, they immediately lose $£ 1$ and go back to square 2. The game continues indefinitely unless the player is on square 2 with $£ 0$, in which case the player loses the game and the game ends.

  

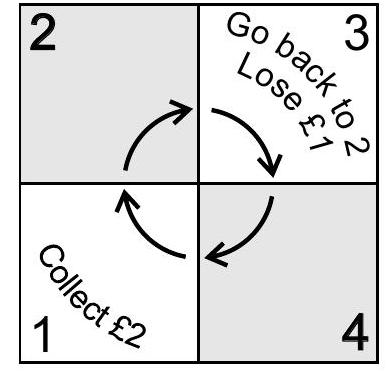
  (a) By setting up an appropriate Markov chain, show that if the player is at square 2 with $£ m$, where $m \geqslant 1$, the probability that they are ever at square 2 with $£(m-1)$ is $2 / 3 .$

  (b) Find the probability of losing the game when the player starts on square 1 with $£ m$, where $m \geqslant 1$.

  [Hint: Take the state space of your Markov chain to be $\{1,2,4\} \times\{0,1, \ldots\}$.]

  comment

• Paper 2, Section II, 18H

  Markov Chains | Part IB, 2021

  Let $P$ be a transition matrix on state space $I$. What does it mean for a distribution $\pi$ to be an invariant distribution? What does it mean for $\pi$ and $P$ to be in detailed balance? Show that if $\pi$ and $P$ are in detailed balance, then $\pi$ is an invariant distribution.

  (a) Assuming that an invariant distribution exists, state the relationship between this and

  (i) the expected return time to a state $i$;

  (ii) the expected time spent in a state $i$ between visits to a state $k$.

  (b) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a Markov chain with transition matrix $P=\left(p_{i j}\right)_{i, j \in I}$ where $I=\{0,1,2, \ldots\}$. The transition probabilities are given for $i \geqslant 1$ by

  $$p_{i j}= \begin{cases}q^{-(i+2)} & \text { if } j=i+1, \\ q^{-i} & \text { if } j=i-1 \\ 1-q^{-(i+2)}-q^{-i} & \text { if } j=i\end{cases}$$

  where $q \geqslant 2$. For $p \in(0,1]$ let $p_{01}=p=1-p_{00}$. Compute the following, justifying your answers:

  (i) The expected time spent in states $\{2,4,6, \ldots\}$ between visits to state 1 ;

  (ii) The expected time taken to return to state 1 , starting from 1 ;

  (iii) The expected time taken to hit state 0 starting from $1 .$

  comment

• Paper 3 , Section I, H

  Markov Chains | Part IB, 2021

  Consider a Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ on a state space $I$.

  (a) Define the notion of a communicating class. What does it mean for a communicating class to be closed?

  (b) Taking $I=\{1, \ldots, 6\}$, find the communicating classes associated with the transition matrix $P$ given by

  $$P=\left(\begin{array}{cccccc} 0 & 0 & 0 & 0 & \frac{1}{4} & \frac{3}{4} \\ \frac{1}{4} & 0 & 0 & 0 & \frac{1}{2} & \frac{1}{4} \\ 0 & \frac{1}{2} & 0 & \frac{1}{2} & 0 & 0 \\ 0 & \frac{1}{2} & 0 & 0 & \frac{1}{2} & 0 \\ \frac{1}{4} & \frac{1}{2} & 0 & 0 & 0 & \frac{1}{4} \\ 1 & 0 & 0 & 0 & 0 & 0 \end{array}\right)$$

  and identify which are closed.

  (c) Find the expected time for the Markov chain with transition matrix $P$ above to reach 6 starting from 1 .

  comment

• Paper 4, Section I, H

  Markov Chains | Part IB, 2021

  Show that the simple symmetric random walk on $\mathbb{Z}$ is recurrent.

  Three particles perform independent simple symmetric random walks on $\mathbb{Z}$. What is the probability that they are all simultaneously at 0 infinitely often? Justify your answer.

  [You may assume without proof that there exist constants $A, B>0$ such that $A \sqrt{n}(n / e)^{n} \leqslant n ! \leqslant B \sqrt{n}(n / e)^{n}$ for all positive integers $\left.n .\right]$

  comment

Methods

• Paper 1, Section II, C

  Methods | Part IB, 2021

  (a) By introducing the variables $\xi=x+c t$ and $\eta=x-c t$ (where $c$ is a constant), derive d'Alembert's solution of the initial value problem for the wave equation:

  $$u_{t t}-c^{2} u_{x x}=0, \quad u(x, 0)=\phi(x), \quad u_{t}(x, 0)=\psi(x)$$

  where $-\infty<x<\infty, t \geqslant 0$ and $\phi$ and $\psi$ are given functions (and subscripts denote partial derivatives).

  (b) Consider the forced wave equation with homogeneous initial conditions:

  $$u_{t t}-c^{2} u_{x x}=f(x, t), \quad u(x, 0)=0, \quad u_{t}(x, 0)=0$$

  where $-\infty<x<\infty, t \geqslant 0$ and $f$ is a given function. You may assume that the solution is given by

  $$u(x, t)=\frac{1}{2 c} \int_{0}^{t} \int_{x-c(t-s)}^{x+c(t-s)} f(y, s) d y d s$$

  For the forced wave equation $u_{t t}-c^{2} u_{x x}=f(x, t)$, now in the half space $x \geqslant 0$ (and with $t \geqslant 0$ as before), find (in terms of $f$ ) the solution for $u(x, t)$ that satisfies the (inhomogeneous) initial conditions

  $$u(x, 0)=\sin x, \quad u_{t}(x, 0)=0, \quad \text { for } x \geqslant 0$$

  and the boundary condition $u(0, t)=0$ for $t \geqslant 0$.

  comment

• Paper 2, Section I, C

  Methods | Part IB, 2021

  Consider the differential operator

  $$\mathcal{L} y=\frac{d^{2} y}{d x^{2}}+2 \frac{d y}{d x}$$

  acting on real functions $y(x)$ with $0 \leqslant x \leqslant 1$.

  (i) Recast the eigenvalue equation $\mathcal{L} y=-\lambda y$ in Sturm-Liouville form $\tilde{\mathcal{L}} y=-\lambda w y$, identifying $\tilde{\mathcal{L}}$ and $w$.

  (ii) If boundary conditions $y(0)=y(1)=0$ are imposed, show that the eigenvalues form an infinite discrete set $\lambda_{1}<\lambda_{2}<\ldots$ and find the corresponding eigenfunctions $y_{n}(x)$ for $n=1,2, \ldots$. If $f(x)=x-x^{2}$ on $0 \leqslant x \leqslant 1$ is expanded in terms of your eigenfunctions i.e. $f(x)=\sum_{n=1}^{\infty} A_{n} y_{n}(x)$, give an expression for $A_{n}$. The expression can be given in terms of integrals that you need not evaluate.

  comment

• Paper 2, Section II, A

  Methods | Part IB, 2021

  The Fourier transform $\tilde{f}(k)$ of a function $f(x)$ and its inverse are given by

  $$\tilde{f}(k)=\int_{-\infty}^{\infty} f(x) e^{-i k x} d x, \quad f(x)=\frac{1}{2 \pi} \int_{-\infty}^{\infty} \tilde{f}(k) e^{i k x} d k$$

  (a) Calculate the Fourier transform of the function $f(x)$ defined by:

  $$f(x)= \begin{cases}1 & \text { for } 0<x<1 \\ -1 & \text { for }-1<x<0 \\ 0 & \text { otherwise }\end{cases}$$

  (b) Show that the inverse Fourier transform of $\tilde{g}(k)=e^{-\lambda|k|}$, for $\lambda$ a positive real constant, is given by

  $$g(x)=\frac{\lambda}{\pi\left(x^{2}+\lambda^{2}\right)}$$

  (c) Consider the problem in the quarter plane $0 \leqslant x, 0 \leqslant y$ :

  $$\begin{aligned} \frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}} &=0 ; \\ u(x, 0) &= \begin{cases}1 & \text { for } 0<x<1, \\ 0 & \text { otherwise; }\end{cases} \\ u(0, y)=\lim _{x \rightarrow \infty} u(x, y)=\lim _{y \rightarrow \infty} u(x, y) &=0 . \end{aligned}$$

  Use the answers from parts (a) and (b) to show that

  $$u(x, y)=\frac{4 x y}{\pi} \int_{0}^{1} \frac{v d v}{\left[(x-v)^{2}+y^{2}\right]\left[(x+v)^{2}+y^{2}\right]}$$

  (d) Hence solve the problem in the quarter plane $0 \leqslant x, 0 \leqslant y$ :

  $$\begin{aligned} \frac{\partial^{2} w}{\partial x^{2}}+\frac{\partial^{2} w}{\partial y^{2}} &=0 ; \\ w(x, 0) &= \begin{cases}1 & \text { for } 0<x<1 \\ 0 & \text { otherwise }\end{cases} \\ w(0, y) &= \begin{cases}1 & \text { for } 0<y<1 \\ 0 & \text { otherwise }\end{cases} \\ \lim _{x \rightarrow \infty} w(x, y)=\lim _{y \rightarrow \infty} w(x, y) &=0 \end{aligned}$$

  [You may quote without proof any property of Fourier transforms.]

  comment

• Paper 3, Section I, A

  Methods | Part IB, 2021

  Let $f(\theta)$ be a $2 \pi$-periodic function with Fourier expansion

  $$f(\theta)=\frac{1}{2} a_{0}+\sum_{n=1}^{\infty}\left(a_{n} \cos n \theta+b_{n} \sin n \theta\right)$$

  Find the Fourier coefficients $a_{n}$ and $b_{n}$ for

  $$f(\theta)=\left\{\begin{aligned} 1, & 0<\theta<\pi \\ -1, & \pi<\theta<2 \pi \end{aligned}\right.$$

  Hence, or otherwise, find the Fourier coefficients $A_{n}$ and $B_{n}$ for the $2 \pi$-periodic function $F$ defined by

  $$F(\theta)=\left\{\begin{array}{cc} \theta, & 0<\theta<\pi \\ 2 \pi-\theta, & \pi<\theta<2 \pi \end{array}\right.$$

  Use your answers to evaluate

  $$\sum_{r=0}^{\infty} \frac{(-1)^{r}}{2 r+1} \quad \text { and } \quad \sum_{r=0}^{\infty} \frac{1}{(2 r+1)^{2}}$$

  comment

• Paper 3, Section II, A

  Methods | Part IB, 2021

  Let $P(x)$ be a solution of Legendre's equation with eigenvalue $\lambda$,

  $$\left(1-x^{2}\right) \frac{d^{2} P}{d x^{2}}-2 x \frac{d P}{d x}+\lambda P=0$$

  such that $P$ and its derivatives $P^{(k)}(x)=d^{k} P / d x^{k}, k=0,1,2, \ldots$, are regular at all points $x$ with $-1 \leqslant x \leqslant 1$.

  (a) Show by induction that

  $$\left(1-x^{2}\right) \frac{d^{2}}{d x^{2}}\left[P^{(k)}\right]-2(k+1) x \frac{d}{d x}\left[P^{(k)}\right]+\lambda_{k} P^{(k)}=0$$

  for some constant $\lambda_{k}$. Find $\lambda_{k}$ explicitly and show that its value is negative when $k$ is sufficiently large, for a fixed value of $\lambda$.

  (b) Write the equation for $P^{(k)}(x)$ in part (a) in self-adjoint form. Hence deduce that if $P^{(k)}(x)$ is not identically zero, then $\lambda_{k} \geqslant 0$.

  [Hint: Establish a relation between integrals of the form $\int_{-1}^{1}\left[P^{(k+1)}(x)\right]^{2} f(x) d x$ and $\int_{-1}^{1}\left[P^{(k)}(x)\right]^{2} g(x) d x$ for certain functions $f(x)$ and $\left.g(x) .\right]$

  (c) Use the results of parts (a) and (b) to show that if $P(x)$ is a non-zero, regular solution of Legendre's equation on $-1 \leqslant x \leqslant 1$, then $P(x)$ is a polynomial of degree $n$ and $\lambda=n(n+1)$ for some integer $n=0,1,2, \ldots$

  comment

• Paper 4, Section II, C

  Methods | Part IB, 2021

  The function $\theta(x, t)$ obeys the diffusion equation

  $$\frac{\partial \theta}{\partial t}=D \frac{\partial^{2} \theta}{\partial x^{2}}$$

  Verify that

  $$\theta(x, t)=\frac{1}{\sqrt{t}} e^{-x^{2} / 4 D t}$$

  is a solution of $(*)$, and by considering $\int_{-\infty}^{\infty} \theta(x, t) d x$, find the solution having the initial form $\theta(x, 0)=\delta(x)$ at $t=0$.

  Find, in terms of the error function, the solution of $(*)$ having the initial form

  $$\theta(x, 0)= \begin{cases}1, & |x| \leqslant 1 \\ 0, & |x|>1\end{cases}$$

  Sketch a graph of this solution at various times $t \geqslant 0$.

  [The error function is

  $$\left.\operatorname{Erf}(x)=\frac{2}{\sqrt{\pi}} \int_{0}^{x} e^{-y^{2}} d y .\right]$$

  comment

Numerical Analysis

• Paper 1, Section I, B

  Numerical Analysis | Part IB, 2021

  Prove, from first principles, that there is an algorithm that can determine whether any real symmetric matrix $A \in \mathbb{R}^{n \times n}$ is positive definite or not, with the computational cost (number of arithmetic operations) bounded by $\mathcal{O}\left(n^{3}\right)$.

  [Hint: Consider the LDL decomposition.]

  comment

• Paper 1, Section II, B

  Numerical Analysis | Part IB, 2021

  For the ordinary differential equation

  $$\boldsymbol{y}^{\prime}=\boldsymbol{f}(t, \boldsymbol{y}), \quad \boldsymbol{y}(0)=\tilde{\boldsymbol{y}}_{0}, \quad t \geqslant 0$$

  where $\boldsymbol{y}(t) \in \mathbb{R}^{N}$ and the function $\boldsymbol{f}: \mathbb{R} \times \mathbb{R}^{N} \rightarrow \mathbb{R}^{N}$ is analytic, consider an explicit one-step method described as the mapping

  $$\boldsymbol{y}_{n+1}=\boldsymbol{y}_{n}+h \varphi\left(t_{n}, \boldsymbol{y}_{n}, h\right)$$

  Here $\varphi: \mathbb{R}_{+} \times \mathbb{R}^{N} \times \mathbb{R}_{+} \rightarrow \mathbb{R}^{N}, n=0,1, \ldots$ and $t_{n}=n h$ with time step $h>0$, producing numerical approximations $\boldsymbol{y}_{n}$ to the exact solution $\boldsymbol{y}\left(t_{n}\right)$ of equation $(*)$, with $\boldsymbol{y}_{0}$ being the initial value of the numerical solution.

  (i) Define the local error of a one-step method.

  (ii) Let $\|\cdot\|$ be a norm on $\mathbb{R}^{N}$ and suppose that

  $$\|\boldsymbol{\varphi}(t, \boldsymbol{u}, h)-\boldsymbol{\varphi}(t, \boldsymbol{v}, h)\| \leqslant L\|\boldsymbol{u}-\boldsymbol{v}\|,$$

  for all $h>0, t \in \mathbb{R}, \boldsymbol{u}, \boldsymbol{v} \in \mathbb{R}^{N}$, where $L$ is some positive constant. Let $t^{*}>0$ be given and $\boldsymbol{e}_{0}=\boldsymbol{y}_{0}-\boldsymbol{y}(0)$ denote the initial error (potentially non-zero). Show that if the local error of the one-step method ( $\uparrow$ ) is $\mathcal{O}\left(h^{p+1}\right)$, then

  $$\max _{n=0, \ldots,\left\lfloor t^{*} / h\right\rfloor}\left\|\boldsymbol{y}_{n}-\boldsymbol{y}(n h)\right\| \leqslant e^{t^{*} L}\left\|\boldsymbol{e}_{0}\right\|+\mathcal{O}\left(h^{p}\right), \quad h \rightarrow 0$$

  (iii) Let $N=1$ and consider equation $(*)$ where $f$ is time-independent satisfying $|f(u)-f(v)| \leqslant K|u-v|$ for all $u, v \in \mathbb{R}$, where $K$ is a positive constant. Consider the one-step method given by

  $$y_{n+1}=y_{n}+\frac{1}{4} h\left(k_{1}+3 k_{2}\right), \quad k_{1}=f\left(y_{n}\right), \quad k_{2}=f\left(y_{n}+\frac{2}{3} h k_{1}\right) .$$

  Use part (ii) to show that for this method we have that equation (††) holds (with a potentially different constant $L$ ) for $p=2$.

  comment

• Paper 2, Section II, 17B

  Numerical Analysis | Part IB, 2021

  (a) Define Householder reflections and show that a real Householder reflection is symmetric and orthogonal. Moreover, show that if $H, A \in \mathbb{R}^{n \times n}$, where $H$ is a Householder reflection and $A$ is a full matrix, then the computational cost (number of arithmetic operations) of computing $H A H^{-1}$ can be $\mathcal{O}\left(n^{2}\right)$ operations, as opposed to $\mathcal{O}\left(n^{3}\right)$ for standard matrix products.

  (b) Show that for any $A \in \mathbb{R}^{n \times n}$ there exists an orthogonal matrix $Q \in \mathbb{R}^{n \times n}$ such that

  $$Q A Q^{T}=T=\left[\begin{array}{ccccc} t_{1,1} & t_{1,2} & t_{1,3} & \cdots & t_{1, n} \\ t_{2,1} & t_{2,2} & t_{2,3} & \cdots & t_{2, n} \\ 0 & t_{3,2} & t_{3,3} & \cdots & t_{3, n} \\ \vdots & \ddots & \ddots & \ddots & \vdots \\ 0 & \cdots & 0 & t_{n, n-1} & t_{n, n} \end{array}\right]$$

  In particular, $T$ has zero entries below the first subdiagonal. Show that one can compute such a $T$ and $Q$ (they may not be unique) using $\mathcal{O}\left(n^{3}\right)$ arithmetic operations.

  [Hint: Multiply A from the left and right with Householder reflections.]

  comment

• Paper 3, Section II, B

  Numerical Analysis | Part IB, 2021

  The functions $p_{0}, p_{1}, p_{2}, \ldots$ are generated by the formula

  $$p_{n}(x)=(-1)^{n} x^{-1 / 2} e^{x} \frac{d^{n}}{d x^{n}}\left(x^{n+1 / 2} e^{-x}\right), \quad 0 \leqslant x<\infty$$

  (a) Show that $p_{n}(x)$ is a monic polynomial of degree $n$. Write down the explicit forms of $p_{0}(x), p_{1}(x), p_{2}(x)$.

  (b) Demonstrate the orthogonality of these polynomials with respect to the scalar product

  $$\langle f, g\rangle=\int_{0}^{\infty} x^{1 / 2} e^{-x} f(x) g(x) d x$$

  i.e. that $\left\langle p_{n}, p_{m}\right\rangle=0$ for $m \neq n$, and show that

  $$\left\langle p_{n}, p_{n}\right\rangle=n ! \Gamma\left(n+\frac{3}{2}\right)$$

  where $\Gamma(y)=\int_{0}^{\infty} x^{y-1} e^{-x} d x$.

  (c) Assuming that a three-term recurrence relation in the form

  $$p_{n+1}(x)=\left(x-\alpha_{n}\right) p_{n}(x)-\beta_{n} p_{n-1}(x), \quad n=1,2, \ldots$$

  holds, find the explicit expressions for $\alpha_{n}$ and $\beta_{n}$ as functions of $n$.

  [Hint: you may use the fact that $\Gamma(y+1)=y \Gamma(y) .]$

  comment

• Paper 4, Section I, B

  Numerical Analysis | Part IB, 2021

  (a) Given the data $f(0)=0, f(1)=4, f(2)=2, f(3)=8$, find the interpolating cubic polynomial $p_{3} \in \mathbb{P}_{3}[x]$ in the Newton form.

  (b) We add to the data one more value, $f(-2)=10$. Find the interpolating quartic polynomial $p_{4} \in \mathbb{P}_{4}[x]$ for the extended data in the Newton form.

  comment

Optimization

• Paper 1, Section I, $\mathbf{7 H}$

  Optimization | Part IB, 2021

  (a) Let $f_{i}: \mathbb{R}^{d} \rightarrow \mathbb{R}$ be a convex function for each $i=1, \ldots, m$. Show that

  $$x \mapsto \max _{i=1, \ldots, m} f_{i}(x) \quad \text { and } \quad x \mapsto \sum_{i=1}^{m} f_{i}(x)$$

  are both convex functions.

  (b) Fix $c \in \mathbb{R}^{d}$. Show that if $f: \mathbb{R} \rightarrow \mathbb{R}$ is convex, then $g: \mathbb{R}^{d} \rightarrow \mathbb{R}$ given by $g(x)=f\left(c^{T} x\right)$ is convex.

  (c) Fix vectors $a_{1}, \ldots, a_{n} \in \mathbb{R}^{d}$. Let $Q: \mathbb{R}^{d} \rightarrow \mathbb{R}$ be given by

  $$Q(\beta)=\sum_{i=1}^{n} \log \left(1+e^{a_{i}^{T} \beta}\right)+\sum_{j=1}^{d}\left|\beta_{j}\right|$$

  Show that $Q$ is convex. [You may use any result from the course provided you state it.]

  comment

• Paper 2, Section I, H

  Optimization | Part IB, 2021

  Find the solution to the following Optimization problem using the simplex algorithm:

  Write down the dual problem and give its solution.

  $$\begin{aligned} & \text { maximise } 3 x_{1}+6 x_{2}+4 x_{3} \\ & \text { subject to } 2 x_{1}+3 x_{2}+x_{3} \leqslant 7 \text {, } \\ & 4 x_{1}+2 x_{2}+2 x_{3} \leqslant 5, \\ & x_{1}+x_{2}+2 x_{3} \leqslant 2, \quad x_{1}, x_{2}, x_{3} \geqslant 0 . \end{aligned}$$

  comment

• Paper 3, Section II, H

  Optimization | Part IB, 2021

  Explain what is meant by a two-person zero-sum game with $m \times n$ payoff matrix $A$, and define what is meant by an optimal strategy for each player. What are the relationships between the optimal strategies and the value of the game?

  Suppose now that

  $$A=\left(\begin{array}{cccc} 0 & 1 & 1 & -4 \\ -1 & 0 & 2 & 2 \\ -1 & -2 & 0 & 3 \\ 4 & -2 & -3 & 0 \end{array}\right)$$

  Show that if strategy $p=\left(p_{1}, p_{2}, p_{3}, p_{4}\right)^{T}$ is optimal for player I, it must also be optimal for player II. What is the value of the game in this case? Justify your answer.

  Explain why we must have $(A p)_{i} \leqslant 0$ for all $i$. Hence or otherwise, find the optimal strategy $p$ and prove that it is unique.

  comment

• Paper 4, Section II, H

  Optimization | Part IB, 2021

  (a) Consider the linear program

  $$\begin{aligned} P: \quad \text { maximise over } x \geqslant 0, & c^{T} x \\ \text { subject to } & A x=b \end{aligned}$$

  where $A \in \mathbb{R}^{m \times n}, c \in \mathbb{R}^{n}$ and $b \in \mathbb{R}^{m}$. What is meant by a basic feasible solution?

  (b) Prove that if $P$ has a finite maximum, then there exists a solution that is a basic feasible solution.

  (c) Now consider the optimization problem

  $$Q: \quad \text { maximise over } x \geqslant 0, \quad \frac{c^{T} x}{d^{T} x}$$

  subject to $A x=b$,

  $$d^{T} x>0,$$

  where matrix $A$ and vectors $c, b$ are as in the problem $P$, and $d \in \mathbb{R}^{n}$. Suppose there exists a solution $x^{*}$ to $Q$. Further consider the linear program

  $$\begin{aligned} R: \quad \text { maximise over } y \geqslant 0, t \geqslant 0, & c^{T} y \\ & A y=b t \\ & d^{T} y=1 \end{aligned}$$

  (i) Suppose $d_{i}>0$ for all $i=1, \ldots, n$. Show that the maximum of $R$ is finite and at least as large as that of $Q$.

  (ii) Suppose, in addition to the condition in part (i), that the entries of $A$ are strictly positive. Show that the maximum of $R$ is equal to that of $Q$.

  (iii) Let $\mathcal{B}$ be the set of basic feasible solutions of the linear program $P$. Assuming the conditions in parts (i) and (ii) above, show that

  $$\frac{c^{T} x^{*}}{d^{T} x^{*}}=\max _{x \in \mathcal{B}} \frac{c^{T} x}{d^{T} x}$$

  [Hint: Argue that if $(y, t)$ is in the set $\mathcal{A}$ of basic feasible solutions to $R$, then $y / t \in \mathcal{B} .]$

  comment

Quantum Mechanics

• Paper 1, Section II, C

  Quantum Mechanics | Part IB, 2021

  Consider a quantum mechanical particle of mass $m$ in a one-dimensional stepped potential well $U(x)$ given by:

  $$U(x)= \begin{cases}\infty & \text { for } x<0 \text { and } x>a \\ 0 & \text { for } 0 \leqslant x \leqslant a / 2 \\ U_{0} & \text { for } a / 2<x \leqslant a\end{cases}$$

  where $a>0$ and $U_{0} \geqslant 0$ are constants.

  (i) Show that all energy levels $E$ of the particle are non-negative. Show that any level $E$ with $0<E<U_{0}$ satisfies

  $$\frac{1}{k} \tan \frac{k a}{2}=-\frac{1}{l} \tanh \frac{l a}{2}$$

  where

  $$k=\sqrt{\frac{2 m E}{\hbar^{2}}}>0 \quad \text { and } \quad l=\sqrt{\frac{2 m\left(U_{0}-E\right)}{\hbar^{2}}}>0$$

  (ii) Suppose that initially $U_{0}=0$ and the particle is in the ground state of the potential well. $U_{0}$ is then changed to a value $U_{0}>0$ (while the particle's wavefunction stays the same) and the energy of the particle is measured. For $0<E<U_{0}$, give an expression in terms of $E$ for prob $(E)$, the probability that the energy measurement will find the particle having energy $E$. The expression may be left in terms of integrals that you need not evaluate.

  comment

• Paper 2, Section II, C

  Quantum Mechanics | Part IB, 2021

  (a) Write down the expressions for the probability density $\rho$ and associated current density $j$ of a quantum particle in one dimension with wavefunction $\psi(x, t)$. Show that if $\psi$ is a stationary state then the function $j$ is constant.

  For the non-normalisable free particle wavefunction $\psi(x, t)=A e^{i k x-i E t / \hbar}$ (where $E$ and $k$ are real constants and $A$ is a complex constant) compute the functions $\rho$ and $j$, and briefly give a physical interpretation of the functions $\psi, \rho$ and $j$ in this case.

  (b) A quantum particle of mass $m$ and energy $E>0$ moving in one dimension is incident from the left in the potential $V(x)$ given by

  $$V(x)=\left\{\begin{array}{cl} -V_{0} & 0 \leqslant x \leqslant a \\ 0 & x<0 \text { or } x>a \end{array}\right.$$

  where $a$ and $V_{0}$ are positive constants. Write down the form of the wavefunction in the regions $x<0,0 \leqslant x \leqslant a$ and $x>a$.

  Suppose now that $V_{0}=3 E$. Show that the probability $T$ of transmission of the particle into the region $x>a$ is given by

  $$T=\frac{16}{16+9 \sin ^{2}\left(\frac{a \sqrt{8 m E}}{\hbar}\right)}$$

  comment

• Paper 3, Section I, C

  Quantum Mechanics | Part IB, 2021

  The electron in a hydrogen-like atom moves in a spherically symmetric potential $V(r)=-K / r$ where $K$ is a positive constant and $r$ is the radial coordinate of spherical polar coordinates. The two lowest energy spherically symmetric normalised states of the electron are given by

  $$\chi_{1}(r)=\frac{1}{\sqrt{\pi} a^{3 / 2}} e^{-r / a} \quad \text { and } \quad \chi_{2}(r)=\frac{1}{4 \sqrt{2 \pi} a^{3 / 2}}\left(2-\frac{r}{a}\right) e^{-r / 2 a}$$

  where $a=\hbar^{2} / m K$ and $m$ is the mass of the electron. For any spherically symmetric function $f(r)$, the Laplacian is given by $\nabla^{2} f=\frac{d^{2} f}{d r^{2}}+\frac{2}{r} \frac{d f}{d r}$.

  (i) Suppose that the electron is in the state $\chi(r)=\frac{1}{2} \chi_{1}(r)+\frac{\sqrt{3}}{2} \chi_{2}(r)$ and its energy is measured. Find the expectation value of the result.

  (ii) Suppose now that the electron is in state $\chi(r)$ (as above) at time $t=0$. Let $R(t)$ be the expectation value of a measurement of the electron's radial position $r$ at time $t$. Show that the value of $R(t)$ oscillates sinusoidally about a constant level and determine the frequency of the oscillation.

  comment

• Paper 4, Section I, C

  Quantum Mechanics | Part IB, 2021

  Let $\Psi(x, t)$ be the wavefunction for a particle of mass $m$ moving in one dimension in a potential $U(x)$. Show that, with suitable boundary conditions as $x \rightarrow \pm \infty$,

  $$\frac{d}{d t} \int_{-\infty}^{\infty}|\Psi(x, t)|^{2} d x=0$$

  Why is this important for the interpretation of quantum mechanics?

  Verify the result above by first calculating $|\Psi(x, t)|^{2}$ for the free particle solution

  $$\Psi(x, t)=C f(t)^{1 / 2} \exp \left(-\frac{1}{2} f(t) x^{2}\right) \quad \text { with } \quad f(t)=\left(\alpha+\frac{i \hbar}{m} t\right)^{-1}$$

  where $C$ and $\alpha>0$ are real constants, and then considering the resulting integral.

  comment

• Paper 4, Section II, C

  Quantum Mechanics | Part IB, 2021

  (a) Consider the angular momentum operators $\hat{L}_{x}, \hat{L}_{y}, \hat{L}_{z}$ and $\hat{\mathbf{L}}^{2}=\hat{L}_{x}^{2}+\hat{L}_{y}^{2}+\hat{L}_{z}^{2}$ where

  $$\hat{L}_{z}=\hat{x} \hat{p}_{y}-\hat{y} \hat{p}_{x}, \quad \hat{L}_{x}=\hat{y} \hat{p}_{z}-\hat{z} \hat{p}_{y} \text { and } \hat{L}_{y}=\hat{z} \hat{p}_{x}-\hat{x} \hat{p}_{z} .$$

  Use the standard commutation relations for these operators to show that

  $$\hat{L}_{\pm}=\hat{L}_{x} \pm i \hat{L}_{y} \quad \text { obeys } \quad\left[\hat{L}_{z}, \hat{L}_{\pm}\right]=\pm \hbar \hat{L}_{\pm} \quad \text { and } \quad\left[\hat{\mathbf{L}}^{2}, \hat{L}_{\pm}\right]=0$$

  Deduce that if $\varphi$ is a joint eigenstate of $\hat{L}_{z}$ and $\hat{\mathbf{L}}^{2}$ with angular momentum quantum numbers $m$ and $\ell$ respectively, then $\hat{L}_{\pm} \varphi$ are also joint eigenstates, provided they are non-zero, with quantum numbers $m \pm 1$ and $\ell$.

  (b) A harmonic oscillator of mass $M$ in three dimensions has Hamiltonian

  $$\hat{H}=\frac{1}{2 M}\left(\hat{p}_{x}^{2}+\hat{p}_{y}^{2}+\hat{p}_{z}^{2}\right)+\frac{1}{2} M \omega^{2}\left(\hat{x}^{2}+\hat{y}^{2}+\hat{z}^{2}\right) .$$

  Find eigenstates of $\hat{H}$ in terms of eigenstates $\psi_{n}$ for an oscillator in one dimension with $n=0,1,2, \ldots$ and eigenvalues $\hbar \omega\left(n+\frac{1}{2}\right)$; hence determine the eigenvalues $E$ of $\hat{H}$.

  Verify that the ground state for $\hat{H}$ is a joint eigenstate of $\hat{L}_{z}$ and $\hat{\mathbf{L}}^{2}$ with $\ell=m=0$. At the first excited energy level, find an eigenstate of $\hat{L}_{z}$ with $m=0$ and construct from this two eigenstates of $\hat{L}_{z}$ with $m=\pm 1$.

  Why should you expect to find joint eigenstates of $\hat{L}_{z}, \hat{\mathbf{L}}^{2}$ and $\hat{H}$ ?

  [ The first two eigenstates for an oscillator in one dimension are $\psi_{0}(x)=$ $C_{0} \exp \left(-M \omega x^{2} / 2 \hbar\right)$ and $\psi_{1}(x)=C_{1} x \exp \left(-M \omega x^{2} / 2 \hbar\right)$, where $C_{0}$ and $C_{1}$ are normalisation constants. ]

  comment

Statistics

• Paper 1, Section I, H

  Statistics | Part IB, 2021

  Let $X_{1}, \ldots, X_{n}$ be i.i.d. Bernoulli $(p)$ random variables, where $n \geqslant 3$ and $p \in(0,1)$ is unknown.

  (a) What does it mean for a statistic $T$ to be sufficient for $p$ ? Find such a sufficient statistic $T$.

  (b) State and prove the Rao-Blackwell theorem.

  (c) By considering the estimator $X_{1} X_{2}$ of $p^{2}$, find an unbiased estimator of $p^{2}$ that is a function of the statistic $T$ found in part (a), and has variance strictly smaller than that of $X_{1} X_{2}$.

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2021

  (a) Show that if $W_{1}, \ldots, W_{n}$ are independent random variables with common $\operatorname{Exp}(1)$ distribution, then $\sum_{i=1}^{n} W_{i} \sim \Gamma(n, 1)$. [Hint: If $W \sim \Gamma(\alpha, \lambda)$ then $\mathbb{E} e^{t W}=\{\lambda /(\lambda-t)\}^{\alpha}$ if $t<\lambda$ and $\infty$ otherwise.]

  (b) Show that if $X \sim U(0,1)$ then $-\log X \sim \operatorname{Exp}(1)$.

  (c) State the Neyman-Pearson lemma.

  (d) Let $X_{1}, \ldots, X_{n}$ be independent random variables with common density proportional to $x^{\theta} \mathbf{1}_{(0,1)}(x)$ for $\theta \geqslant 0$. Find a most powerful test of size $\alpha$ of $H_{0}: \theta=0$ against $H_{1}: \theta=1$, giving the critical region in terms of a quantile of an appropriate gamma distribution. Find a uniformly most powerful test of size $\alpha$ of $H_{0}: \theta=0$ against $H_{1}: \theta>0$.

  comment

• Paper 2, Section I, $\mathbf{6 H}$

  Statistics | Part IB, 2021

  The efficacy of a new drug was tested as follows. Fifty patients were given the drug, and another fifty patients were given a placebo. A week later, the numbers of patients whose symptoms had gone entirely, improved, stayed the same and got worse were recorded, as summarised in the following table.

  \begin{tabular}{|c|c|c|} \hline & Drug & Placebo \ \hline symptoms gone & 14 & 6 \ improved & 21 & 19 \ same & 10 & 10 \ worse & 5 & 15 \ \hline \end{tabular}

  Conduct a $5 \%$ significance level test of the null hypothesis that the medicine and placebo have the same effect, against the alternative that their effects differ.

  [Hint: You may find some of the following values relevant:

  \begin{tabular}{|c|cccccc|} \hline Distribution & $\chi_{1}^{2}$ & $\chi_{2}^{2}$ & $\chi_{3}^{2}$ & $\chi_{4}^{2}$ & $\chi_{6}^{2}$ & $\chi_{8}^{2}$ \ \hline 95 th percentile & $3.84$ & $5.99$ & $7.81$ & $9.48$ & $12.59$ & $15.51$ \ \hline \end{tabular}

  comment

• Paper 3, Section II, $18 \mathrm{H}$

  Statistics | Part IB, 2021

  Consider the normal linear model $Y=X \beta+\varepsilon$ where $X$ is a known $n \times p$ design matrix with $n-2>p \geqslant 1, \beta \in \mathbb{R}^{p}$ is an unknown vector of parameters, and $\varepsilon \sim N_{n}\left(0, \sigma^{2} I\right)$ is a vector of normal errors with each component having variance $\sigma^{2}>0$. Suppose $X$ has full column rank.

  (i) Write down the maximum likelihood estimators, $\hat{\beta}$ and $\hat{\sigma}^{2}$, for $\beta$ and $\sigma^{2}$ respectively. [You need not derive these.]

  (ii) Show that $\hat{\beta}$ is independent of $\hat{\sigma}^{2}$.

  (iii) Find the distributions of $\hat{\beta}$ and $n \hat{\sigma}^{2} / \sigma^{2}$.

  (iv) Consider the following test statistic for testing the null hypothesis $H_{0}: \beta=0$ against the alternative $\beta \neq 0$ :

  $$T:=\frac{\|\hat{\beta}\|^{2}}{n \hat{\sigma}^{2}} .$$

  Let $\lambda_{1} \geqslant \lambda_{2} \geqslant \cdots \geqslant \lambda_{p}>0$ be the eigenvalues of $X^{T} X$. Show that under $H_{0}, T$ has the same distribution as

  $$\frac{\sum_{j=1}^{p} \lambda_{j}^{-1} W_{j}}{Z}$$

  where $Z \sim \chi_{n-p}^{2}$ and $W_{1}, \ldots, W_{p}$ are independent $\chi_{1}^{2}$ random variables, independent of $Z$.

  [Hint: You may use the fact that $X=U D V^{T}$ where $U \in \mathbb{R}^{n \times p}$ has orthonormal columns, $V \in \mathbb{R}^{p \times p}$ is an orthogonal matrix and $D \in \mathbb{R}^{p \times p}$ is a diagonal matrix with $\left.D_{i i}=\sqrt{\lambda_{i}} .\right]$

  (v) Find $\mathbb{E} T$ when $\beta \neq 0$. [Hint: If $R \sim \chi_{\nu}^{2}$ with $\nu>2$, then $\mathbb{E}(1 / R)=1 /(\nu-2)$.]

  comment

• Paper 4, Section II, $\mathbf{1 7 H}$

  Statistics | Part IB, 2021

  Suppose we wish to estimate the probability $\theta \in(0,1)$ that a potentially biased coin lands heads up when tossed. After $n$ independent tosses, we observe $X$ heads.

  (a) Write down the maximum likelihood estimator $\hat{\theta}$ of $\theta$.

  (b) Find the mean squared error $f(\theta)$ of $\hat{\theta}$ as a function of $\theta$. Compute $\sup _{\theta \in(0,1)} f(\theta)$.

  (c) Suppose a uniform prior is placed on $\theta$. Find the Bayes estimator of $\theta$ under squared error loss $L(\theta, a)=(\theta-a)^{2}$.

  (d) Now find the Bayes estimator $\tilde{\theta}$ under the $\operatorname{loss} L(\theta, a)=\theta^{\alpha-1}(1-\theta)^{\beta-1}(\theta-a)^{2}$, where $\alpha, \beta \geqslant 1$. Show that

  $$\tilde{\theta}=w \hat{\theta}+(1-w) \theta_{0},$$

  where $w$ and $\theta_{0}$ depend on $n, \alpha$ and $\beta$.

  (e) Determine the mean squared error $g_{w, \theta_{0}}(\theta)$ of $\tilde{\theta}$ as defined by $(*)$.

  (f) For what range of values of $w$ do we have $\sup _{\theta \in(0,1)} g_{w, 1 / 2}(\theta) \leqslant \sup _{\theta \in(0,1)} f(\theta)$ ?

  [Hint: The mean of a Beta $(a, b)$ distribution is $a /(a+b)$ and its density $p(u)$ at $u \in[0,1]$ is $c_{a, b} u^{a-1}(1-u)^{b-1}$, where $c_{a, b}$ is a normalising constant.]

  comment

Variational Principles

• Paper 1, Section I, D

  Variational Principles | Part IB, 2021

  Let $D$ be a bounded region of $\mathbb{R}^{2}$, with boundary $\partial D$. Let $u(x, y)$ be a smooth function defined on $D$, subject to the boundary condition that $u=0$ on $\partial D$ and the normalization condition that

  $$\int_{D} u^{2} d x d y=1$$

  Let $I[u]$ be the functional

  $$I[u]=\int_{D}|\nabla u|^{2} d x d y$$

  Show that $I[u]$ has a stationary value, subject to the stated boundary and normalization conditions, when $u$ satisfies a partial differential equation of the form

  $$\nabla^{2} u+\lambda u=0$$

  in $D$, where $\lambda$ is a constant.

  Determine how $\lambda$ is related to the stationary value of the functional $I[u]$. $[$ Hint: Consider $\boldsymbol{\nabla} \cdot(u \boldsymbol{\nabla} u)$.]

  comment

• Paper 2, Section II, D

  Variational Principles | Part IB, 2021

  A particle of unit mass moves in a smooth one-dimensional potential $V(x)$. Its path $x(t)$ is such that the action integral

  $$S[x]=\int_{a}^{b} L(x, \dot{x}) d t$$

  has a stationary value, where $a$ and $b>a$ are constants, a dot denotes differentiation with respect to time $t$

  $$L(x, \dot{x})=\frac{1}{2} \dot{x}^{2}-V(x)$$

  is the Lagrangian function and the initial and final positions $x(a)$ and $x(b)$ are fixed.

  By considering $S[x+\epsilon \xi]$ for suitably restricted functions $\xi(t)$, derive the differential equation governing the motion of the particle and obtain an integral expression for the second variation $\delta^{2} S$.

  If $x(t)$ is a solution of the equation of motion and $x(t)+\epsilon u(t)+O\left(\epsilon^{2}\right)$ is also a solution of the equation of motion in the limit $\epsilon \rightarrow 0$, show that $u(t)$ satisfies the equation

  $$\ddot{u}+V^{\prime \prime}(x) u=0$$

  If $u(t)$ satisfies this equation and is non-vanishing for $a \leqslant t \leqslant b$, show that

  $$\delta^{2} S=\frac{1}{2} \int_{a}^{b}\left(\dot{\xi}-\frac{\dot{u} \xi}{u}\right)^{2} d t$$

  Consider the simple harmonic oscillator, for which

  $$V(x)=\frac{1}{2} \omega^{2} x^{2}$$

  where $2 \pi / \omega$ is the oscillation period. Show that the solution of the equation of motion is a local minimum of the action integral, provided that the time difference $b-a$ is less than half an oscillation period.

  comment

• Paper 3, Section I, D

  Variational Principles | Part IB, 2021

  Find the function $y(x)$ that gives a stationary value of the functional

  $$I[y]=\int_{0}^{1}\left(y^{\prime 2}+y y^{\prime}+y^{\prime}+y^{2}+y x^{2}\right) d x$$

  subject to the boundary conditions $y(0)=-1$ and $y(1)=e-e^{-1}-\frac{3}{2}$.

  comment

• Paper 4 , Section II, 13D

  Variational Principles | Part IB, 2021

  (a) Consider the functional

  $$I[y]=\int_{a}^{b} L\left(y, y^{\prime} ; x\right) d x$$

  where $0<a<b$, and $y(x)$ is subject to the requirement that $y(a)$ and $y(b)$ are some fixed constants. Derive the equation satisfied by $y(x)$ when $\delta I=0$ for all variations $\delta y$ that respect the boundary conditions.

  (b) Consider the function

  $$L\left(y, y^{\prime} ; x\right)=\frac{\sqrt{1+y^{\prime 2}}}{x} .$$

  Verify that, if $y(x)$ describes an arc of a circle, with centre on the $y$-axis, then $\delta I=0$.

  (c) Consider the function

  $$L\left(y, y^{\prime} ; x\right)=\frac{\sqrt{1+y^{\prime 2}}}{y}$$

  Find $y(x)$ such that $\delta I=0$ subject to the requirement that $y(a)=a$ and $y(b)=\sqrt{2 a b-b^{2}}$, with $b<2 a$. Sketch the curve $y(x)$.

  comment