Part IB, 2005

Analysis II

• 1.II.11B

  Analysis II | Part IB, 2005

  Let $\left(f_{n}\right)_{n \geqslant 1}$ be a sequence of continuous real-valued functions defined on a set $E \subset \mathbf{R}$. Suppose that the functions $f_{n}$ converge uniformly to a function $f$. Prove that $f$ is continuous on $E$.

  Show that the series $\sum_{n=1}^{\infty} 1 / n^{1+x}$ defines a continuous function on the half-open interval $(0,1]$.

  [Hint: You may assume the convergence of standard series.]

  comment

• 2.I.3B

  Analysis II | Part IB, 2005

  Define uniform continuity for a real-valued function defined on an interval in $\mathbf{R}$.

  Is a uniformly continuous function on the interval $(0,1)$ necessarily bounded?

  Is $1 / x$ uniformly continuous on $(0,1)$ ?

  Is $\sin (1 / x)$ uniformly continuous on $(0,1)$ ?

  Justify your answers.

  comment

• 2.II.13B

  Analysis II | Part IB, 2005

  Use the standard metric on $\mathbf{R}^{n}$ in this question.

  (i) Let $A$ be a nonempty closed subset of $\mathbf{R}^{n}$ and $y$ a point in $\mathbf{R}^{n}$. Show that there is a point $x \in A$ which minimizes the distance to $y$, in the sense that $d(x, y) \leqslant d(a, y)$ for all $a \in A$.

  (ii) Suppose that the set $A$ in part (i) is convex, meaning that $A$ contains the line segment between any two of its points. Show that point $x \in A$ described in part (i) is unique.

  comment

• 3.I.3B

  Analysis II | Part IB, 2005

  Let $f: \mathbf{R}^{2} \rightarrow \mathbf{R}$ be a function. What does it mean to say that $f$ is differentiable at a point $(a, b)$ in $\mathbf{R}^{2}$ ? Show that if $f$ is differentiable at $(a, b)$, then $f$ is continuous at $(a, b)$.

  For each of the following functions, determine whether or not it is differentiable at $(0,0)$. Justify your answers.

  (i)

  $$f(x, y)= \begin{cases}x^{2} y^{2}\left(x^{2}+y^{2}\right)^{-1} & \text { if }(x, y) \neq(0,0) \\ 0 & \text { if }(x, y)=(0,0)\end{cases}$$

  (ii)

  $$f(x, y)= \begin{cases}x^{2}\left(x^{2}+y^{2}\right)^{-1} & \text { if }(x, y) \neq(0,0) \\ 0 & \text { if }(x, y)=(0,0)\end{cases}$$

  comment

• 3.II.13B

  Analysis II | Part IB, 2005

  Let $f$ be a real-valued differentiable function on an open subset $U$ of $\mathbf{R}^{n}$. Assume that $0 \notin U$ and that for all $x \in U$ and $\lambda>0, \lambda x$ is also in $U$. Suppose that $f$ is homogeneous of degree $c \in \mathbf{R}$, in the sense that $f(\lambda x)=\lambda^{c} f(x)$ for all $x \in U$ and $\lambda>0$. By means of the Chain Rule or otherwise, show that

  $$\left.D f\right|_{x}(x)=c f(x)$$

  for all $x \in U$. (Here $\left.D f\right|_{x}$ denotes the derivative of $f$ at $x$, viewed as a linear map $\mathbf{R}^{n} \rightarrow \mathbf{R}$.)

  Conversely, show that any differentiable function $f$ on $U$ with $\left.D f\right|_{x}(x)=c f(x)$ for all $x \in U$ must be homogeneous of degree $c$.

  comment

• 4.I 3 B

  Analysis II | Part IB, 2005

  Let $V$ be the vector space of continuous real-valued functions on $[0,1]$. Show that the function

  $$\|f\|=\int_{0}^{1}|f(x)| d x$$

  defines a norm on $V$.

  For $n=1,2, \ldots$, let $f_{n}(x)=e^{-n x}$. Is $f_{n}$ a convergent sequence in the space $V$ with this norm? Justify your answer.

  comment

• 4.II.13B

  Analysis II | Part IB, 2005

  Let $F:[-a, a] \times\left[x_{0}-r, x_{0}+r\right] \rightarrow \mathbf{R}$ be a continuous function. Let $C$ be the maximum value of $|F(t, x)|$. Suppose there is a constant $K$ such that

  $$|F(t, x)-F(t, y)| \leqslant K|x-y|$$

  for all $t \in[-a, a]$ and $x, y \in\left[x_{0}-r, x_{0}+r\right]$. Let $b<\min (a, r / C, 1 / K)$. Show that there is a unique $C^{1}$ function $x:[-b, b] \rightarrow\left[x_{0}-r, x_{0}+r\right]$ such that

  $$x(0)=x_{0}$$

  and

  $$\frac{d x}{d t}=F(t, x(t)) .$$

  [Hint: First show that the differential equation with its initial condition is equivalent to the integral equation

  $$\left.x(t)=x_{0}+\int_{0}^{t} F(s, x(s)) d s .\right]$$

  comment

Complex Analysis

• 3.II.14A

  Complex Analysis | Part IB, 2005

  State the Cauchy integral formula, and use it to deduce Liouville's theorem.

  Let $f$ be a meromorphic function on the complex plane such that $\left|f(z) / z^{n}\right|$ is bounded outside some disc (for some fixed integer $n$ ). By considering Laurent expansions, or otherwise, show that $f$ is a rational function in $z$.

  comment

• 4.I.4A

  Complex Analysis | Part IB, 2005

  Let $\gamma:[0,1] \rightarrow \mathbf{C}$ be a closed path, where all paths are assumed to be piecewise continuously differentiable, and let $a$ be a complex number not in the image of $\gamma$. Write down an expression for the winding number $n(\gamma, a)$ in terms of a contour integral. From this characterization of the winding number, prove the following properties:

  (a) If $\gamma_{1}$ and $\gamma_{2}$ are closed paths not passing through zero, and if $\gamma:[0,1] \rightarrow \mathbf{C}$ is defined by $\gamma(t)=\gamma_{1}(t) \gamma_{2}(t)$ for all $t$, then

  $$n(\gamma, 0)=n\left(\gamma_{1}, 0\right)+n\left(\gamma_{2}, 0\right)$$

  (b) If $\eta:[0,1] \rightarrow \mathbf{C}$ is a closed path whose image is contained in $\{\operatorname{Re}(z)>0\}$, then $n(\eta, 0)=0$.

  (c) If $\gamma_{1}$ and $\gamma_{2}$ are closed paths and $a$ is a complex number, not in the image of either path, such that

  $$\left|\gamma_{1}(t)-\gamma_{2}(t)\right|<\left|\gamma_{1}(t)-a\right|$$

  for all $t$, then $n\left(\gamma_{1}, a\right)=n\left(\gamma_{2}, a\right)$.

  [You may wish here to consider the path defined by $\eta(t)=1-\left(\gamma_{1}(t)-\gamma_{2}(t)\right) /\left(\gamma_{1}(t)-a\right)$.]

  comment

Complex Analysis or Complex Methods

• 1.I.3F

  Complex Analysis or Complex Methods | Part IB, 2005

  State the Cauchy integral formula.

  Using the Cauchy integral formula, evaluate

  $$\int_{|z|=2} \frac{z^{3}}{z^{2}+1} d z$$

  comment

• 1.II.13F

  Complex Analysis or Complex Methods | Part IB, 2005

  Determine a conformal mapping from $\Omega_{0}=\mathbf{C} \backslash[-1,1]$ to the complex unit disc $\Omega_{1}=\{z \in \mathbf{C}:|z|<1\} .$

  [Hint: A standard method is first to map $\Omega_{0}$ to $\mathbf{C} \backslash(-\infty, 0]$, then to the complex right half-plane $\{z \in \mathbf{C}: \operatorname{Re} z>0\}$ and, finally, to $\left.\Omega_{1} .\right]$

  comment

• 2.II.14F

  Complex Analysis or Complex Methods | Part IB, 2005

  Let $F=P / Q$ be a rational function, where $\operatorname{deg} Q \geqslant \operatorname{deg} P+2$ and $Q$ has no real zeros. Using the calculus of residues, write a general expression for

  $$\int_{-\infty}^{\infty} F(x) e^{i x} d x$$

  in terms of residues and briefly sketch its proof.

  Evaluate explicitly the integral

  $$\int_{-\infty}^{\infty} \frac{\cos x}{4+x^{4}} d x$$

  comment

Complex Methods

• 3.I.5F

  Complex Methods | Part IB, 2005

  Define a harmonic function and state when the harmonic functions $f$ and $g$ are conjugate

  Let $\{u, v\}$ and $\{p, q\}$ be two pairs of harmonic conjugate functions. Prove that $\{p(u, v), q(u, v)\}$ are also harmonic conjugate.

  comment

• 4.II.15F

  Complex Methods | Part IB, 2005

  Determine the Fourier expansion of the function $f(x)=\sin \lambda x$, where $-\pi \leqslant x \leqslant \pi$, in the two cases where $\lambda$ is an integer and $\lambda$ is a real non-integer.

  Using the Parseval identity in the case $\lambda=\frac{1}{2}$, find an explicit expression for the sum

  $$\sum_{n=1}^{\infty} \frac{n^{2}}{\left(4 n^{2}-1\right)^{2}}$$

  comment

Electromagnetism

• 1.II.16H

  Electromagnetism | Part IB, 2005

  For a static charge density $\rho(\mathbf{x})$ show that the energy may be expressed as

  $$E=\frac{1}{2} \int \rho \phi \mathrm{d}^{3} x=\frac{\epsilon_{0}}{2} \int \mathbf{E}^{2} \mathrm{~d}^{3} x,$$

  where $\phi(\mathbf{x})$ is the electrostatic potential and $\mathbf{E}(\mathbf{x})$ is the electric field.

  Determine the scalar potential and electric field for a sphere of radius $R$ with a constant charge density $\rho$. Also determine the total electrostatic energy.

  In a nucleus with $Z$ protons the volume is proportional to $Z$. Show that we may expect the electric contribution to energy to be proportional to $Z^{\frac{5}{3}}$.

  comment

• 2.I.6H

  Electromagnetism | Part IB, 2005

  Write down Maxwell's equations in the presence of a charge density $\rho$ and current density $\mathbf{J}$. Show that it is necessary that $\rho, \mathbf{J}$ satisfy a conservation equation.

  If $\rho, \mathbf{J}$ are zero outside a fixed region $V$ show that the total charge inside $V$ is a constant and also that

  $$\frac{\mathrm{d}}{\mathrm{d} t} \int_{V} \mathbf{x} \rho \mathrm{d}^{3} x=\int_{V} \mathbf{J ~}^{3} x .$$

  comment

• 2.II.17H

  Electromagnetism | Part IB, 2005

  Assume the magnetic field

  $$\mathbf{B}(\mathbf{x})=b(\mathbf{x}-3 \hat{\mathbf{z}} \hat{\mathbf{z}} \cdot \mathbf{x}),$$

  where $\hat{\mathbf{z}}$ is a unit vector in the vertical direction. Show that this satisfies the expected equations for a static magnetic field in vacuum.

  A circular wire loop, of radius $a$, mass $m$ and resistance $R$, lies in a horizontal plane with its centre on the $z$-axis at a height $z$ and there is a magnetic field given by $(*)$. Calculate the magnetic flux arising from this magnetic field through the loop and also the force acting on the loop when a current $I$ is flowing around the loop in a clockwise direction about the $z$-axis.

  Obtain an equation of motion for the height $z(t)$ when the wire loop is falling under gravity. Show that there is a solution in which the loop falls with constant speed $v$ which should be determined. Verify that in this situation the rate at which heat is generated by the current flowing in the loop is equal to the rate of loss of gravitational potential energy. What happens when $R \rightarrow 0$ ?

  comment

• 3.II.17H

  Electromagnetism | Part IB, 2005

  If $\mathbf{E}(\mathbf{x}, t), \mathbf{B}(\mathbf{x}, t)$ are solutions of Maxwell's equations in a region without any charges or currents show that $\mathbf{E}^{\prime}(\mathbf{x}, t)=c \mathbf{B}(\mathbf{x}, t), \mathbf{B}^{\prime}(\mathbf{x}, t)=-\mathbf{E}(\mathbf{x}, t) / c$ are also solutions.

  At the boundary of a perfect conductor with normal $\mathbf{n}$ briefly explain why

  $$\mathbf{n} \cdot \mathbf{B}=0, \quad \mathbf{n} \times \mathbf{E}=0$$

  Electromagnetic waves inside a perfectly conducting tube with axis along the $z$-axis are given by the real parts of complex solutions of Maxwell's equations of the form

  $$\mathbf{E}(\mathbf{x}, t)=\mathbf{e}(x, y) e^{i(k z-\omega t)}, \quad \mathbf{B}(\mathbf{x}, t)=\mathbf{b}(x, y) e^{i(k z-\omega t)} .$$

  Suppose $b_{z}=0$. Show that we can find a solution in this case in terms of a function $\psi(x, y)$ where

  $$\left(e_{x}, e_{y}\right)=\left(\frac{\partial}{\partial x} \psi, \frac{\partial}{\partial y} \psi\right), \quad e_{z}=i\left(k-\frac{\omega^{2}}{k c^{2}}\right) \psi,$$

  so long as $\psi$ satisfies

  $$\left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}+\gamma^{2}\right) \psi=0$$

  for suitable $\gamma$. Show that the boundary conditions are satisfied if $\psi=0$ on the surface of the tube.

  Obtain a similar solution with $e_{z}=0$ but show that the boundary conditions are now satisfied if the normal derivative $\partial \psi / \partial n=0$ on the surface of the tube.

  comment

• 4.I.7H

  Electromagnetism | Part IB, 2005

  For a static current density $\mathbf{J}(\mathbf{x})$ show that we may choose the vector potential $\mathbf{A}(\mathbf{x})$ so that

  $$-\nabla^{2} \mathbf{A}=\mu_{0} \mathbf{J} .$$

  For a loop $L$, centred at the origin, carrying a current $I$ show that

  $$\mathbf{A}(\mathbf{x})=\frac{\mu_{0} I}{4 \pi} \oint_{L} \frac{1}{|\mathbf{x}-\mathbf{r}|} \mathrm{d} \mathbf{r} \sim-\frac{\mu_{0} I}{4 \pi} \frac{1}{|\mathbf{x}|^{3}} \oint_{L} \frac{1}{2} \mathbf{x} \times(\mathbf{r} \times \mathrm{d} \mathbf{r}) \quad \text { as } \quad|\mathbf{x}| \rightarrow \infty$$

  [You may assume

  $$-\nabla^{2} \frac{1}{4 \pi|\mathbf{x}|}=\delta^{3}(\mathbf{x})$$

  and for fixed vectors $\mathbf{a}, \mathbf{b}$

  $$\left.\oint_{L} \mathbf{a} \cdot \mathrm{d} \mathbf{r}=0, \quad \oint_{L}(\mathbf{a} \cdot \mathbf{r} \mathbf{b} \cdot \mathrm{d} \mathbf{r}+\mathbf{b} \cdot \mathbf{r} \mathbf{a} \cdot \mathrm{d} \mathbf{r})=0 .\right]$$

  comment

Fluid Dynamics

• 1.I.5E

  Fluid Dynamics | Part IB, 2005

  Explain how a streamfunction $\psi$ can be used to represent in Cartesian Coordinates an incompressible flow in two dimensions. Show that the streamlines are given by $\psi=$ const.

  Consider the two-dimensional incompressible flow

  $$\mathbf{u}(x, y, t)=(x+\sin t,-y)$$

  (a) Find the streamfunction, and hence the streamlines at $t=\frac{\pi}{2}$.

  (b) Find the path of a fluid particle released at $t=0$ from $\left(x_{0}, 1\right)$. For what value of $x_{0}$ does the particle not tend to infinity?

  comment

• 1.II.17E

  Fluid Dynamics | Part IB, 2005

  State Bernoulli's expression for the pressure in an unsteady potential flow with conservative force $-\nabla \chi$.

  A spherical bubble in an incompressible liquid of density $\rho$ has radius $R(t)$. If the pressure far from the bubble is $p_{\infty}$ and inside the bubble is $p_{b}$, show that

  $$p_{b}-p_{\infty}=\rho\left(\frac{3}{2} \dot{R}^{2}+R \ddot{R}\right)$$

  Calculate the kinetic energy $K(t)$ in the flow outside the bubble, and hence show that

  $$\dot{K}=\left(p_{b}-p_{\infty}\right) \dot{V}$$

  where $V(t)$ is the volume of the bubble.

  If $p_{b}(t)=p_{\infty} V_{0} / V$, show that

  $$K=K_{0}+p_{\infty}\left(V_{0} \ln \frac{V}{V_{0}}-V+V_{0}\right)$$

  where $K=K_{0}$ when $V=V_{0}$.

  comment

• 2.I.8E

  Fluid Dynamics | Part IB, 2005

  For a steady flow of an incompressible fluid of density $\rho$, show that

  $$\mathbf{u} \times \boldsymbol{\omega}=\nabla H,$$

  where $\boldsymbol{\omega}=\nabla \times \mathbf{u}$ is the vorticity and $H$ is to be found. Deduce that $H$ is constant along streamlines.

  Now consider a flow in the $x y$-plane described by a streamfunction $\psi(x, y)$. Evaluate $\mathbf{u} \times \boldsymbol{\omega}$ and deduce from $H=H(\psi)$ that

  $$\frac{d H}{d \psi}+\omega=0$$

  comment

• 3.II.18E

  Fluid Dynamics | Part IB, 2005

  Consider the velocity potential in plane polar coordinates

  $$\phi(r, \theta)=U\left(r+\frac{a^{2}}{r}\right) \cos \theta+\frac{\kappa \theta}{2 \pi}$$

  Find the velocity field and show that it corresponds to flow past a cylinder $r=a$ with circulation $\kappa$ and uniform flow $U$ at large distances.

  Find the distribution of pressure $p$ over the surface of the cylinder. Hence find the $x$ and $y$ components of the force on the cylinder

  $$\left(F_{x}, F_{y}\right)=\int(\cos \theta, \sin \theta) p a d \theta .$$

  comment

• 4.II.18E

  Fluid Dynamics | Part IB, 2005

  A fluid of density $\rho_{1}$ occupies the region $z>0$ and a second fluid of density $\rho_{2}$ occupies the region $z<0$. State the equations and boundary conditions that are satisfied by the corresponding velocity potentials $\phi_{1}$ and $\phi_{2}$ and pressures $p_{1}$ and $p_{2}$ when the system is perturbed so that the interface is at $z=\zeta(x, t)$ and the motion is irrotational.

  Seek a set of linearised equations and boundary conditions when the disturbances are proportional to $e^{i(k x-\omega t)}$, and derive the dispersion relation

  $$\omega^{2}=\frac{\rho_{2}-\rho_{1}}{\rho_{2}+\rho_{1}} g k,$$

  where $g$ is the gravitational acceleration.

  comment

Geometry

• 1.I $2 \mathrm{~A} \quad$

  Geometry | Part IB, 2005

  Let $\sigma: \mathbf{R}^{2} \rightarrow \mathbf{R}^{3}$ be the map defined by

  $$\sigma(u, v)=((a+b \cos u) \cos v,(a+b \cos u) \sin v, b \sin u)$$

  where $0<b<a$. Describe briefly the image $T=\sigma\left(\mathbf{R}^{2}\right) \subset \mathbf{R}^{3}$. Let $V$ denote the open subset of $\mathbf{R}^{2}$ given by $0<u<2 \pi, 0<v<2 \pi$; prove that the restriction $\sigma_{V}$ defines a smooth parametrization of a certain open subset (which you should specify) of $T$. Hence, or otherwise, prove that $T$ is a smooth embedded surface in $\mathbf{R}^{3}$.

  [You may assume that the image under $\sigma$ of any open set $B \subset \mathbf{R}^{2}$ is open in $T$.]

  comment

• 2.II.12A

  Geometry | Part IB, 2005

  Let $U$ be an open subset of $\mathbf{R}^{2}$ equipped with a Riemannian metric. For $\gamma:[0,1] \rightarrow U$ a smooth curve, define what is meant by its length and energy. Prove that length $(\gamma)^{2} \leq \operatorname{energy}(\gamma)$, with equality if and only if $\dot{\gamma}$ has constant norm with respect to the metric.

  Suppose now $U$ is the upper half plane model of the hyperbolic plane, and $P, Q$ are points on the positive imaginary axis. Show that a smooth curve $\gamma$ joining $P$ and $Q$ represents an absolute minimum of the length of such curves if and only if $\gamma(t)=i v(t)$, with $v$ a smooth monotonic real function.

  Suppose that a smooth curve $\gamma$ joining the above points $P$ and $Q$ represents a stationary point for the energy under proper variations; deduce from an appropriate form of the Euler-Lagrange equations that $\gamma$ must be of the above form, with $\dot{v} / v$ constant.

  comment

• 3.I.2A

  Geometry | Part IB, 2005

  Write down the Riemannian metric on the disc model $\Delta$ of the hyperbolic plane. Given that the length minimizing curves passing through the origin correspond to diameters, show that the hyperbolic circle of radius $\rho$ centred on the origin is just the Euclidean circle centred on the origin with Euclidean $\operatorname{radius~} \tanh (\rho / 2)$. Prove that the hyperbolic area is $2 \pi(\cosh \rho-1)$.

  State the Gauss-Bonnet theorem for the area of a hyperbolic triangle. Given a hyperbolic triangle and an interior point $P$, show that the distance from $P$ to the nearest side is at most $\cosh ^{-1}(3 / 2)$.

  comment

• 3.II.12A

  Geometry | Part IB, 2005

  Describe geometrically the stereographic projection map $\pi$ from the unit sphere $S^{2}$ to the extended complex plane $\mathbf{C}_{\infty}=\mathbf{C} \cup\{\infty\}$, positioned equatorially, and find a formula for $\pi$.

  Show that any Möbius transformation $T \neq 1$ on $\mathbf{C}_{\infty}$ has one or two fixed points. Show that the Möbius transformation corresponding (under the stereographic projection map) to a rotation of $S^{2}$ through a non-zero angle has exactly two fixed points $z_{1}$ and $z_{2}$, where $z_{2}=-1 / \bar{z}_{1}$. If now $T$ is a Möbius transformation with two fixed points $z_{1}$ and $z_{2}$ satisfying $z_{2}=-1 / \bar{z}_{1}$, prove that either $T$ corresponds to a rotation of $S^{2}$, or one of the fixed points, say $z_{1}$, is an attractive fixed point, i.e. for $z \neq z_{2}, T^{n} z \rightarrow z_{1}$ as $n \rightarrow \infty$.

  [You may assume the fact that any rotation of $S^{2}$ corresponds to some Möbius transformation of $\mathbf{C}_{\infty}$ under the stereographic projection map.]

  comment

• 4.II.12A

  Geometry | Part IB, 2005

  Given a parametrized smooth embedded surface $\sigma: V \rightarrow U \subset \mathbf{R}^{3}$, where $V$ is an open subset of $\mathbf{R}^{2}$ with coordinates $(u, v)$, and a point $P \in U$, define what is meant by the tangent space at $P$, the unit normal $\mathbf{N}$ at $P$, and the first fundamental form

  $$E d u^{2}+2 F d u d v+G d v^{2} .$$

  [You need not show that your definitions are independent of the parametrization.]

  The second fundamental form is defined to be

  $$L d u^{2}+2 M d u d v+N d v^{2},$$

  where $L=\sigma_{u u} \cdot \mathbf{N}, M=\sigma_{u v} \cdot \mathbf{N}$ and $N=\sigma_{v v} \cdot \mathbf{N}$. Prove that the partial derivatives of $\mathbf{N}$ (considered as a vector-valued function of $u, v$ ) are of the form $\mathbf{N}_{u}=a \sigma_{u}+b \sigma_{v}$, $\mathbf{N}_{v}=c \sigma_{u}+d \sigma_{v}$, where

  $$-\left(\begin{array}{cc} L & M \\ M & N \end{array}\right)=\left(\begin{array}{ll} a & b \\ c & d \end{array}\right)\left(\begin{array}{ll} E & F \\ F & G \end{array}\right)$$

  Explain briefly the significance of the determinant $a d-b c$.

  comment

Groups, Rings and Modules

• $3 . \mathrm{II} . 11 \mathrm{C}$

  Groups, Rings and Modules | Part IB, 2005

  (i) Define a primitive polynomial in $\mathbb{Z}[x]$, and prove that the product of two primitive polynomials is primitive. Deduce that $\mathbb{Z}[x]$ is a unique factorization domain.

  (ii) Prove that

  $$\mathbb{Q}[x] /\left(x^{5}-4 x+2\right)$$

  is a field. Show, on the other hand, that

  $$\mathbb{Z}[x] /\left(x^{5}-4 x+2\right)$$

  is an integral domain, but is not a field.

  comment

• 1.II.10C

  Groups, Rings and Modules | Part IB, 2005

  Let $G$ be a group, and $H$ a subgroup of finite index. By considering an appropriate action of $G$ on the set of left cosets of $H$, prove that $H$ always contains a normal subgroup $K$ of $G$ such that the index of $K$ in $G$ is finite and divides $n$ !, where $n$ is the index of $H$ in $G$.

  Now assume that $G$ is a finite group of order $p q$, where $p$ and $q$ are prime numbers with $p<q$. Prove that the subgroup of $G$ generated by any element of order $q$ is necessarily normal.

  comment

• 2.I.2C

  Groups, Rings and Modules | Part IB, 2005

  Define an automorphism of a group $G$, and the natural group law on the set $\operatorname{Aut}(G)$ of all automorphisms of $G$. For each fixed $h$ in $G$, put $\psi(h)(g)=h g h^{-1}$ for all $g$ in $G$. Prove that $\psi(h)$ is an automorphism of $G$, and that $\psi$ defines a homomorphism from $G$ into $\operatorname{Aut}(G)$.

  comment

• 2.II.11C

  Groups, Rings and Modules | Part IB, 2005

  Let $A$ be the abelian group generated by two elements $x, y$, subject to the relation $6 x+9 y=0$. Give a rigorous explanation of this statement by defining $A$ as an appropriate quotient of a free abelian group of rank 2. Prove that $A$ itself is not a free abelian group, and determine the exact structure of $A$.

  comment

• 3.I.1C

  Groups, Rings and Modules | Part IB, 2005

  Define what is meant by two elements of a group $G$ being conjugate, and prove that this defines an equivalence relation on $G$. If $G$ is finite, sketch the proof that the cardinality of each conjugacy class divides the order of $G$.

  comment

• 4.I.2C

  Groups, Rings and Modules | Part IB, 2005

  State Eisenstein's irreducibility criterion. Let $n$ be an integer $>1$. Prove that $1+x+\ldots+x^{n-1}$ is irreducible in $\mathbb{Z}[x]$ if and only if $n$ is a prime number.

  comment

• 4.II.11C

  Groups, Rings and Modules | Part IB, 2005

  Let $R$ be the ring of Gaussian integers $\mathbb{Z}[i]$, where $i^{2}=-1$, which you may assume to be a unique factorization domain. Prove that every prime element of $R$ divides precisely one positive prime number in $\mathbb{Z}$. List, without proof, the prime elements of $R$, up to associates.

  Let $p$ be a prime number in $\mathbb{Z}$. Prove that $R / p R$ has cardinality $p^{2}$. Prove that $R / 2 R$ is not a field. If $p \equiv 3 \bmod 4$, show that $R / p R$ is a field. If $p \equiv 1 \bmod 4$, decide whether $R / p R$ is a field or not, justifying your answer.

  comment

Linear Algebra

• 1.I.1C

  Linear Algebra | Part IB, 2005

  Let $V$ be an $n$-dimensional vector space over $\mathbf{R}$, and let $\beta: V \rightarrow V$ be a linear map. Define the minimal polynomial of $\beta$. Prove that $\beta$ is invertible if and only if the constant term of the minimal polynomial of $\beta$ is non-zero.

  comment

• 1.II.9C

  Linear Algebra | Part IB, 2005

  Let $V$ be a finite dimensional vector space over $\mathbf{R}$, and $V^{*}$ be the dual space of $V$.

  If $W$ is a subspace of $V$, we define the subspace $\alpha(W)$ of $V^{*}$ by

  $$\alpha(W)=\left\{f \in V^{*}: f(w)=0 \text { for all } w \text { in } W\right\}$$

  Prove that $\operatorname{dim}(\alpha(W))=\operatorname{dim}(V)-\operatorname{dim}(W)$. Deduce that, if $A=\left(a_{i j}\right)$ is any real $m \times n$-matrix of rank $r$, the equations

  $$\sum_{j=1}^{n} a_{i j} x_{j}=0 \quad(i=1, \ldots, m)$$

  have $n-r$ linearly independent solutions in $\mathbf{R}^{n}$.

  comment

• 2.I.1C

  Linear Algebra | Part IB, 2005

  Let $\Omega$ be the set of all $2 \times 2$ matrices of the form $\alpha=a I+b J+c K+d L$, where $a, b, c, d$ are in $\mathbf{R}$, and

  $$I=\left(\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right), J=\left(\begin{array}{cc} i & 0 \\ 0 & -i \end{array}\right), K=\left(\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right), L=\left(\begin{array}{cc} 0 & i \\ i & 0 \end{array}\right) \quad\left(i^{2}=-1\right) .$$

  Prove that $\Omega$ is closed under multiplication and determine its dimension as a vector space over $\mathbf{R}$. Prove that

  $$(a I+b J+c K+d L)(a I-b J-c K-d L)=\left(a^{2}+b^{2}+c^{2}+d^{2}\right) I$$

  and deduce that each non-zero element of $\Omega$ is invertible.

  comment

• 2.II.10C

  Linear Algebra | Part IB, 2005

  (i) Let $A=\left(a_{i j}\right)$ be an $n \times n$ matrix with entries in C. Define the determinant of $A$, the cofactor of each $a_{i j}$, and the adjugate matrix $\operatorname{adj}(A)$. Assuming the expansion of the determinant of a matrix in terms of its cofactors, prove that

  $$\operatorname{adj}(A) A=\operatorname{det}(A) I_{n}$$

  where $I_{n}$ is the $n \times n$ identity matrix.

  (ii) Let

  $$A=\left(\begin{array}{llll} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 \end{array}\right)$$

  Show the eigenvalues of $A$ are $\pm 1, \pm i$, where $i^{2}=-1$, and determine the diagonal matrix to which $A$ is similar. For each eigenvalue, determine a non-zero eigenvector.

  comment

• 3.II.10B

  Linear Algebra | Part IB, 2005

  Let $S$ be the vector space of functions $f: \mathbf{R} \rightarrow \mathbf{R}$ such that the $n$th derivative of $f$ is defined and continuous for every $n \geqslant 0$. Define linear maps $A, B: S \rightarrow S$ by $A(f)=d f / d x$ and $B(f)(x)=x f(x)$. Show that

  $$[A, B]=1_{S},$$

  where in this question $[A, B]$ means $A B-B A$ and $1_{S}$ is the identity map on $S$.

  Now let $V$ be any real vector space with linear maps $A, B: V \rightarrow V$ such that $[A, B]=1_{V}$. Suppose that there is a nonzero element $y \in V$ with $A y=0$. Let $W$ be the subspace of $V$ spanned by $y, B y, B^{2} y$, and so on. Show that $A(B y)$ is in $W$ and give a formula for it. More generally, show that $A\left(B^{i} y\right)$ is in $W$ for each $i \geqslant 0$, and give a formula for it.

  Show, using your formula or otherwise, that $\left\{y, B y, B^{2} y, \ldots\right\}$ are linearly independent. (Or, equivalently: show that $y, B y, B^{2} y, \ldots, B^{n} y$ are linearly independent for every $n \geqslant 0$.)

  comment

• 4.I.1B

  Linear Algebra | Part IB, 2005

  Define what it means for an $n \times n$ complex matrix to be unitary or Hermitian. Show that every eigenvalue of a Hermitian matrix is real. Show that every eigenvalue of a unitary matrix has absolute value 1 .

  Show that two eigenvectors of a Hermitian matrix that correspond to different eigenvalues are orthogonal, using the standard inner product on $\mathbf{C}^{n}$.

  comment

• 4.II.10B

  Linear Algebra | Part IB, 2005

  (i) Let $V$ be a finite-dimensional real vector space with an inner product. Let $e_{1}, \ldots, e_{n}$ be a basis for $V$. Prove by an explicit construction that there is an orthonormal basis $f_{1}, \ldots, f_{n}$ for $V$ such that the span of $e_{1}, \ldots, e_{i}$ is equal to the span of $f_{1}, \ldots, f_{i}$ for every $1 \leqslant i \leqslant n$.

  (ii) For any real number $a$, consider the quadratic form

  $$q_{a}(x, y, z)=x y+y z+z x+a x^{2}$$

  on $\mathbf{R}^{3}$. For which values of $a$ is $q_{a}$ nondegenerate? When $q_{a}$ is nondegenerate, compute its signature in terms of $a$.

  comment

Markov Chains

• 1.II.19D

  Markov Chains | Part IB, 2005

  Every night Lancelot and Guinevere sit down with four guests for a meal at a circular dining table. The six diners are equally spaced around the table and just before each meal two individuals are chosen at random and they exchange places from the previous night while the other four diners stay in the same places they occupied at the last meal; the choices on successive nights are made independently. On the first night Lancelot and Guinevere are seated next to each other.

  Find the probability that they are seated diametrically opposite each other on the $(n+1)$ th night at the round table, $n \geqslant 1$.

  comment

• 2.II.20D

  Markov Chains | Part IB, 2005

  Consider a Markov chain $\left(X_{n}\right)_{n \geqslant 0}$ with state space $\{0,1,2, \ldots\}$ and transition probabilities given by

  $$P_{i, j}=p q^{i-j+1}, \quad 0<j \leqslant i+1, \quad \text { and } \quad P_{i, 0}=q^{i+1} \quad \text { for } \quad i \geqslant 0$$

  with $P_{i, j}=0$, otherwise, where $0<p<1$ and $q=1-p$.

  For each $i \geqslant 1$, let

  $$h_{i}=\mathbb{P}\left(X_{n}=0, \text { for some } n \geqslant 0 \mid X_{0}=i\right),$$

  that is, the probability that the chain ever hits the state 0 given that it starts in state $i$. Write down the equations satisfied by the probabilities $\left\{h_{i}, i \geqslant 1\right\}$ and hence, or otherwise, show that they satisfy a second-order recurrence relation with constant coefficients. Calculate $h_{i}$ for each $i \geqslant 1$.

  Determine for each value of $p, 0<p<1$, whether the chain is transient, null recurrent or positive recurrent and in the last case calculate the stationary distribution.

  [Hint: When the chain is positive recurrent, the stationary distribution is geometric.]

  comment

• 3.I.9D

  Markov Chains | Part IB, 2005

  Prove that if two states of a Markov chain communicate then they have the same period.

  Consider a Markov chain with state space $\{1,2, \ldots, 7\}$ and transition probabilities determined by the matrix

  $$\left(\begin{array}{ccccccc} 0 & \frac{1}{4} & \frac{1}{4} & 0 & 0 & \frac{1}{4} & \frac{1}{4} \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & \frac{1}{3} & 0 & \frac{1}{3} & \frac{1}{3} \\ \frac{1}{2} & 0 & 0 & 0 & 0 & \frac{1}{2} & 0 \\ \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & 0 & \frac{1}{6} & \frac{1}{6} \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 \end{array}\right)$$

  Identify the communicating classes of the chain and for each class state whether it is open or closed and determine its period.

  comment

• 4.I.9D

  Markov Chains | Part IB, 2005

  Prove that the simple symmetric random walk in three dimensions is transient.

  [You may wish to recall Stirling's formula: $n ! \sim(2 \pi)^{\frac{1}{2}} n^{n+\frac{1}{2}} e^{-n} .$ ]

  comment

Methods

• 1.II.14E

  Methods | Part IB, 2005

  Find the Fourier Series of the function

  $$f(\theta)= \begin{cases}1 & 0 \leq \theta<\pi \\ -1 & \pi \leq \theta<2 \pi\end{cases}$$

  Find the solution $\phi(r, \theta)$ of the Poisson equation in two dimensions inside the unit disk $r \leq 1$

  $$\nabla^{2} \phi=\frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \phi}{\partial r}\right)+\frac{1}{r^{2}} \frac{\partial^{2} \phi}{\partial \theta^{2}}=f(\theta)$$

  subject to the boundary condition $\phi(1, \theta)=0$.

  [Hint: The general solution of $r^{2} R^{\prime \prime}+r R^{\prime}-n^{2} R=r^{2}$ is $R=a r^{n}+b r^{-n}-r^{2} /\left(n^{2}-4\right) .$ ]

  From the solution, show that

  $$\int_{r \leq 1} f \phi d A=-\frac{4}{\pi} \sum_{n \text { odd }} \frac{1}{n^{2}(n+2)^{2}}$$

  comment

• 2.I.5E

  Methods | Part IB, 2005

  Consider the differential equation for $x(t)$ in $t>0$

  $$\ddot{x}-k^{2} x=f(t),$$

  subject to boundary conditions $x(0)=0$, and $\dot{x}(0)=0$. Find the Green function $G\left(t, t^{\prime}\right)$ such that the solution for $x(t)$ is given by

  $$x(t)=\int_{0}^{t} G\left(t, t^{\prime}\right) f\left(t^{\prime}\right) d t^{\prime} .$$

  comment

• 2.II.15E

  Methods | Part IB, 2005

  Write down the Euler-Lagrange equation for the variational problem for $r(z)$

  $$\delta \int_{-h}^{h} F\left(z, r, r^{\prime}\right) d z=0$$

  with boundary conditions $r(-h)=r(h)=R$, where $R$ is a given positive constant. Show that if $F$ does not depend explicitly on $z$, i.e. $F=F\left(r, r^{\prime}\right)$, then the equation has a first integral

  $$F-r^{\prime} \frac{\partial F}{\partial r^{\prime}}=\frac{1}{k},$$

  where $k$ is a constant.

  An axisymmetric soap film $r(z)$ is formed between two circular rings $r=R$ at $z=\pm H$. Find the equation governing the shape which minimizes the surface area. Show that the shape takes the form

  $$r(z)=k^{-1} \cosh k z .$$

  Show that there exist no solution if $R / H<\sinh A$, where $A$ is the unique positive solution of $A=\operatorname{coth} A$.

  comment

• 3.I.6E

  Methods | Part IB, 2005

  Describe briefly the method of Lagrangian multipliers for finding the stationary points of a function $f(x, y)$ subject to a constraint $g(x, y)=0$.

  Use the method to find the stationary values of $x y$ subject to the constraint $\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 .$

  comment

• 3.II.15H

  Methods | Part IB, 2005

  Obtain the power series solution about $t=0$ of

  $$\left(1-t^{2}\right) \frac{\mathrm{d}^{2}}{\mathrm{~d} t^{2}} y-2 t \frac{\mathrm{d}}{\mathrm{d} t} y+\lambda y=0$$

  and show that regular solutions $y(t)=P_{n}(t)$, which are polynomials of degree $n$, are obtained only if $\lambda=n(n+1), n=0,1,2, \ldots$ Show that the polynomial must be even or odd according to the value of $n$.

  Show that

  $$\int_{-1}^{1} P_{n}(t) P_{m}(t) \mathrm{d} t=k_{n} \delta_{n m}$$

  for some $k_{n}>0$.

  Using the identity

  $$\left(x \frac{\partial^{2}}{\partial x^{2}} x+\frac{\partial}{\partial t}\left(1-t^{2}\right) \frac{\partial}{\partial t}\right) \frac{1}{\left(1-2 x t+x^{2}\right)^{\frac{1}{2}}}=0,$$

  and considering an expansion $\sum_{n} a_{n}(x) P_{n}(t)$ show that

  $$\frac{1}{\left(1-2 x t+x^{2}\right)^{\frac{1}{2}}}=\sum_{n=0}^{\infty} x^{n} P_{n}(t), \quad 0<x<1$$

  if we assume $P_{n}(1)=1$.

  By considering

  $$\int_{-1}^{1} \frac{1}{1-2 x t+x^{2}} d t$$

  determine the coefficient $k_{n}$.

  comment

• 4.I.5H

  Methods | Part IB, 2005

  Show how the general solution of the wave equation for $y(x, t)$,

  $$\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}} y(x, t)-\frac{\partial^{2}}{\partial x^{2}} y(x, t)=0$$

  can be expressed as

  $$y(x, t)=f(c t-x)+g(c t+x) .$$

  Show that the boundary conditions $y(0, t)=y(L, t)=0$ relate the functions $f$ and $g$ and require them to be periodic with period $2 L$.

  Show that, with these boundary conditions,

  $$\frac{1}{2} \int_{0}^{L}\left(\frac{1}{c^{2}}\left(\frac{\partial y}{\partial t}\right)^{2}+\left(\frac{\partial y}{\partial x}\right)^{2}\right) \mathrm{d} x=\int_{-L}^{L} g^{\prime}(c t+x)^{2} \mathrm{~d} x$$

  and that this is a constant independent of $t$.

  comment

• 4.II.16H

  Methods | Part IB, 2005

  Define an isotropic tensor and show that $\delta_{i j}, \epsilon_{i j k}$ are isotropic tensors.

  For $\hat{\mathbf{x}}$ a unit vector and $\mathrm{d} S(\hat{\mathbf{x}})$ the area element on the unit sphere show that

  $$\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i_{1}} \ldots \hat{x}_{i_{n}}$$

  is an isotropic tensor for any $n$. Hence show that

  $$\begin{aligned} &\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j}=a \delta_{i j}, \quad \int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j} \hat{x}_{k}=0 \\ &\int \mathrm{d} S(\hat{\mathbf{x}}) \hat{x}_{i} \hat{x}_{j} \hat{x}_{k} \hat{x}_{l}=b\left(\delta_{i j} \delta_{k l}+\delta_{i k} \delta_{j l}+\delta_{i l} \delta_{j k}\right) \end{aligned}$$

  for some $a, b$ which should be determined.

  Explain why

  $$\int_{V} \mathrm{~d}^{3} x\left(x_{1}+\sqrt{-1} x_{2}\right)^{n} f(|\mathbf{x}|)=0, \quad n=2,3,4$$

  where $V$ is the region inside the unit sphere.

  [The general isotropic tensor of rank 4 has the form $a \delta_{i j} \delta_{k l}+b \delta_{i k} \delta_{j l}+c \delta_{i l} \delta_{j k} .$ ]

  comment

Metric and Topological Spaces

• 1.II.12A

  Metric and Topological Spaces | Part IB, 2005

  Suppose that $\left(X, d_{X}\right)$ and $\left(Y, d_{Y}\right)$ are metric spaces. Show that the definition

  $$d\left(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)\right)=d_{X}\left(x_{1}, x_{2}\right)+d_{Y}\left(y_{1}, y_{2}\right)$$

  defines a metric on the product $X \times Y$, under which the projection map $\pi: X \times Y \rightarrow Y$ is continuous.

  If $\left(X, d_{X}\right)$ is compact, show that every sequence in $X$ has a subsequence converging to a point of $X$. Deduce that the projection map $\pi$ then has the property that, for any closed subset $F \subset X \times Y$, the image $\pi(F)$ is closed in $Y$. Give an example to show that this fails if $\left(X, d_{X}\right)$ is not assumed compact.

  comment

• 2.I.4A

  Metric and Topological Spaces | Part IB, 2005

  Let $X$ be a topological space. Suppose that $U_{1}, U_{2}, \ldots$ are connected subsets of $X$ with $U_{j} \cap U_{1}$ non-empty for all $j>0$. Prove that

  $$W=\bigcup_{j>0} U_{j}$$

  is connected. If each $U_{j}$ is path-connected, prove that $W$ is path-connected.

  comment

• 3.I.4A

  Metric and Topological Spaces | Part IB, 2005

  Show that a topology $\tau_{1}$ is determined on the real line $\mathbf{R}$ by specifying that a nonempty subset is open if and only if it is a union of half-open intervals $\{a \leq x<b\}$, where $a<b$ are real numbers. Determine whether $\left(\mathbf{R}, \tau_{1}\right)$ is Hausdorff.

  Let $\tau_{2}$ denote the cofinite topology on $\mathbf{R}$ (that is, a non-empty subset is open if and only if its complement is finite). Prove that the identity map induces a continuous $\operatorname{map}\left(\mathbf{R}, \tau_{1}\right) \rightarrow\left(\mathbf{R}, \tau_{2}\right)$.

  comment

• 4.II.14A

  Metric and Topological Spaces | Part IB, 2005

  Let $(M, d)$ be a metric space, and $F$ a non-empty closed subset of $M$. For $x \in M$, set

  $$d(x, F)=\inf _{z \in F} d(x, z)$$

  Prove that $d(x, F)$ is a continuous function of $x$, and that it is strictly positive for $x \notin F$.

  A topological space is called normal if for any pair of disjoint closed subsets $F_{1}, F_{2}$, there exist disjoint open subsets $U_{1} \supset F_{1}, U_{2} \supset F_{2}$. By considering the function

  $$d\left(x, F_{1}\right)-d\left(x, F_{2}\right)$$

  or otherwise, deduce that any metric space is normal.

  Suppose now that $X$ is a normal topological space, and that $F_{1}, F_{2}$ are disjoint closed subsets in $X$. Prove that there exist open subsets $W_{1} \supset F_{1}, W_{2} \supset F_{2}$, whose closures are disjoint. In the case when $X=\mathbf{R}^{2}$ with the standard metric topology, $F_{1}=\{(x,-1 / x): x<0\}$ and $F_{2}=\{(x, 1 / x): x>0\}$, find explicit open subsets $W_{1}, W_{2}$ with the above property.

  comment

Numerical Analysis

• 1.I.6F

  Numerical Analysis | Part IB, 2005

  Determine the Cholesky factorization (without pivoting) of the matrix

  $$A=\left[\begin{array}{ccc} 2 & -4 & 2 \\ -4 & 10+\lambda & 2+3 \lambda \\ 2 & 2+3 \lambda & 23+9 \lambda \end{array}\right]$$

  where $\lambda$ is a real parameter. Hence, find the range of values of $\lambda$ for which the matrix $A$ is positive definite.

  comment

• 2.II.18F

  Numerical Analysis | Part IB, 2005

  (a) Let $\left\{Q_{n}\right\}_{n \geqslant 0}$ be a set of polynomials orthogonal with respect to some inner product $(\cdot, \cdot)$ in the interval $[a, b]$. Write explicitly the least-squares approximation to $f \in C[a, b]$ by an $n$ th-degree polynomial in terms of the polynomials $\left\{Q_{n}\right\}_{n \geqslant 0}$.

  (b) Let an inner product be defined by the formula

  $$(g, h)=\int_{-1}^{1}\left(1-x^{2}\right)^{-\frac{1}{2}} g(x) h(x) d x$$

  Determine the $n$th degree polynomial approximation of $f(x)=\left(1-x^{2}\right)^{\frac{1}{2}}$ with respect to this inner product as a linear combination of the underlying orthogonal polynomials.

  comment

• 3.II.19F

  Numerical Analysis | Part IB, 2005

  Given real $\mu \neq 0$, we consider the matrix

  $$A=\left[\begin{array}{cccc} \frac{1}{\mu} & 1 & 0 & 0 \\ -1 & \frac{1}{\mu} & 1 & 0 \\ 0 & -1 & \frac{1}{\mu} & 1 \\ 0 & 0 & -1 & \frac{1}{\mu} \end{array}\right]$$

  Construct the Jacobi and Gauss-Seidel iteration matrices originating in the solution of the linear system $A x=b$.

  Determine the range of real $\mu \neq 0$ for which each iterative procedure converges.

  comment

• 4.I.8F

  Numerical Analysis | Part IB, 2005

  Define Gaussian quadrature.

  Evaluate the coefficients of the Gaussian quadrature of the integral

  $$\int_{-1}^{1}\left(1-x^{2}\right) f(x) d x$$

  which uses two function evaluations.

  comment

Optimization

• 1.I.8D

  Optimization | Part IB, 2005

  Consider the problem:

  $$\begin{array}{ll} \text { Minimize } & \sum_{i=1}^{m} \sum_{j=1}^{n} c_{i j} x_{i j} \\ \text { subject to } & \sum_{j=1}^{n} x_{i j}=a_{i}, \quad i=1, \ldots, m, \\ & \sum_{i=1}^{m} x_{i j}=b_{j}, \quad j=1, \ldots, n \\ & x_{i j} \geqslant 0, \quad \text { for all } i, j \end{array}$$

  where $a_{i} \geqslant 0, b_{j} \geqslant 0$ satisfy $\sum_{i=1}^{m} a_{i}=\sum_{j=1}^{n} b_{j}$.

  Formulate the dual of this problem and state necessary and sufficient conditions for optimality.

  comment

• 2.I.9D

  Optimization | Part IB, 2005

  Explain what is meant by a two-person zero-sum game with payoff matrix $A=\left(a_{i j}\right)$.

  Show that the problems of the two players may be expressed as a dual pair of linear programming problems. State without proof a set of sufficient conditions for a pair of strategies for the two players to be optimal.

  comment

• 3.II.20D

  Optimization | Part IB, 2005

  Consider the linear programming problem

  $$\begin{aligned} \operatorname{maximize} \quad 4 x_{1}+x_{2}-9 x_{3} & \\ \text { subject to } \quad x_{2}-11 x_{3} & \leqslant 11 \\ -3 x_{1}+2 x_{2}-7 x_{3} & \leqslant 16 \\ 9 x_{1}-2 x_{2}+10 x_{3} & \leqslant 29, \quad x_{i} \geqslant 0, \quad i=1,2,3 . \end{aligned}$$

  (a) After adding slack variables $z_{1}, z_{2}$ and $z_{3}$ and performing one pivot in the simplex algorithm the following tableau is obtained:

  \begin{tabular}{c|rrrrrr|r} & $x_{1}$ & $x_{2}$ & $x_{3}$ & $z_{1}$ & $z_{2}$ & $z_{3}$ & \ \hline$z_{1}$ & 0 & 1 & $-11$ & 1 & 0 & 0 & 11 \ $z_{2}$ & 0 & $\frac{4}{3}$ & $-\frac{11}{3}$ & 0 & 1 & $\frac{1}{3}$ & $\frac{77}{3}$ \ $x_{1}$ & 1 & $-\frac{2}{9}$ & $\frac{10}{9}$ & 0 & 0 & $\frac{1}{9}$ & $\frac{29}{9}$ \ \hline Payoff & 0 & $\frac{17}{9}$ & $-\frac{121}{9}$ & 0 & 0 & $-\frac{4}{9}$ & $-\frac{116}{9}$ \end{tabular}

  Complete the solution of the problem using the simplex algorithm.

  (b) Obtain the dual problem and identify its optimal solution from the optimal tableau in (a).

  (c) Suppose that the right-hand sides in the constraints to the original problem are changed from $(11,16,29)$ to $\left(11+\epsilon_{1}, 16+\epsilon_{2}, 29+\epsilon_{3}\right)$. Give necessary and sufficient conditions on $\left(\epsilon_{1}, \epsilon_{2}, \epsilon_{3}\right)$ which ensure that the optimal solution to the dual obtained in (b) remains optimal for the dual for the amended problem.

  comment

• 4.II.20D

  Optimization | Part IB, 2005

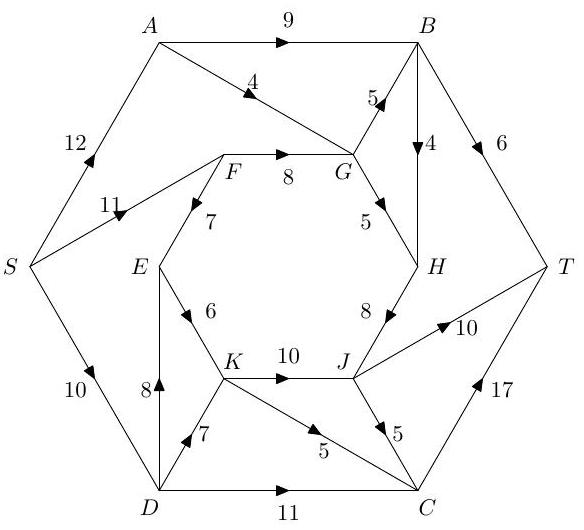
  Describe the Ford-Fulkerson algorithm for finding a maximal flow from a source to a sink in a directed network with capacity constraints on the arcs. Explain why the algorithm terminates at an optimal flow when the initial flow and the capacity constraints are rational.

  Illustrate the algorithm by applying it to the problem of finding a maximal flow from $S$ to $T$ in the network below.

  

  comment

Quantum Mechanics

• 1.II.15G

  Quantum Mechanics | Part IB, 2005

  The wave function of a particle of mass $m$ that moves in a one-dimensional potential well satisfies the Schrödinger equation with a potential that is zero in the region $-a \leq x \leq a$ and infinite elsewhere,

  $$V(x)=0 \quad \text { for } \quad|x| \leq a, \quad V(x)=\infty \quad \text { for } \quad|x|>a$$

  Determine the complete set of normalised energy eigenfunctions for the particle and show that the energy eigenvalues are

  $$E=\frac{\hbar^{2} \pi^{2} n^{2}}{8 m a^{2}}$$

  where $n$ is a positive integer.

  At time $t=0$ the wave function is

  $$\psi(x)=\frac{1}{\sqrt{5 a}} \cos \left(\frac{\pi x}{2 a}\right)+\frac{2}{\sqrt{5 a}} \sin \left(\frac{\pi x}{a}\right)$$

  in the region $-a \leq x \leq a$, and zero otherwise. Determine the possible results for a measurement of the energy of the system and the relative probabilities of obtaining these energies.

  In an experiment the system is measured to be in its lowest possible energy eigenstate. The width of the well is then doubled while the wave function is unaltered. Calculate the probability that a later measurement will find the particle to be in the lowest energy state of the new potential well.

  comment

• 2.II.16G

  Quantum Mechanics | Part IB, 2005

  A particle of mass $m$ moving in a one-dimensional harmonic oscillator potential satisfies the Schrödinger equation

  $$H \Psi(x, t)=i \hbar \frac{\partial}{\partial t} \Psi(x, t),$$

  where the Hamiltonian is given by

  $$H=-\frac{\hbar^{2}}{2 m} \frac{d^{2}}{d x^{2}}+\frac{1}{2} m \omega^{2} x^{2}$$

  The operators $a$ and $a^{\dagger}$ are defined by

  $$a=\frac{1}{\sqrt{2}}\left(\beta x+\frac{i}{\beta \hbar} p\right), \quad a^{\dagger}=\frac{1}{\sqrt{2}}\left(\beta x-\frac{i}{\beta \hbar} p\right)$$

  where $\beta=\sqrt{m \omega / \hbar}$ and $p=-i \hbar \partial / \partial x$ is the usual momentum operator. Show that $\left[a, a^{\dagger}\right]=1$.

  Express $x$ and $p$ in terms of $a$ and $a^{\dagger}$ and, hence or otherwise, show that $H$ can be written in the form

  $$H=\left(a^{\dagger} a+\frac{1}{2}\right) \hbar \omega$$

  Show, for an arbitrary wave function $\Psi$, that $\int d x \Psi^{*} H \Psi \geq \frac{1}{2} \hbar \omega$ and hence that the energy of any state satisfies the bound

  $$E \geq \frac{1}{2} \hbar \omega$$

  Hence, or otherwise, show that the ground state wave function satisfies $a \Psi_{0}=0$ and that its energy is given by

  $$E_{0}=\frac{1}{2} \hbar \omega$$

  By considering $H$ acting on $a^{\dagger} \Psi_{0},\left(a^{\dagger}\right)^{2} \Psi_{0}$, and so on, show that states of the form

  $$\left(a^{\dagger}\right)^{n} \Psi_{0}$$

  $(n>0)$ are also eigenstates and that their energies are given by $E_{n}=\left(n+\frac{1}{2}\right) \hbar \omega .$

  comment

• 3.I.7G

  Quantum Mechanics | Part IB, 2005

  The wave function $\Psi(x, t)$ is a solution of the time-dependent Schrödinger equation for a particle of mass $m$ in a potential $V(x)$,

  $$H \Psi(x, t)=i \hbar \frac{\partial}{\partial t} \Psi(x, t),$$

  where $H$ is the Hamiltonian. Define the expectation value, $\langle\mathcal{O}\rangle$, of any operator $\mathcal{O}$.

  At time $t=0, \Psi(x, t)$ can be written as a sum of the form

  $$\Psi(x, 0)=\sum_{n} a_{n} u_{n}(x),$$

  where $u_{n}$ is a complete set of normalized eigenfunctions of the Hamiltonian with energy eigenvalues $E_{n}$ and $a_{n}$ are complex coefficients that satisfy $\sum_{n} a_{n}^{*} a_{n}=1$. Find $\Psi(x, t)$ for $t>0$. What is the probability of finding the system in a state with energy $E_{p}$ at time $t$ ?

  Show that the expectation value of the energy is independent of time.

  comment

• 3.II.16G

  Quantum Mechanics | Part IB, 2005

  A particle of mass $\mu$ moves in two dimensions in an axisymmetric potential. Show that the time-independent Schrödinger equation can be separated in polar coordinates. Show that the angular part of the wave function has the form $e^{i m \phi}$, where $\phi$ is the angular coordinate and $m$ is an integer. Suppose that the potential is zero for $r<a$, where $r$ is the radial coordinate, and infinite otherwise. Show that the radial part of the wave function satisfies

  $$\frac{d^{2} R}{d \rho^{2}}+\frac{1}{\rho} \frac{d R}{d \rho}+\left(1-\frac{m^{2}}{\rho^{2}}\right) R=0$$

  where $\rho=r\left(2 \mu E / \hbar^{2}\right)^{1 / 2}$. What conditions must $R$ satisfy at $r=0$ and $R=a$ ?

  Show that, when $m=0$, the equation has the solution $R(\rho)=\sum_{k=0}^{\infty} A_{k} \rho^{k}$, where $A_{k}=0$ if $k$ is odd and

  $$A_{k+2}=-\frac{A_{k}}{(k+2)^{2}}$$

  if $k$ is even

  Deduce the coefficients $A_{2}$ and $A_{4}$ in terms of $A_{0}$. By truncating the series expansion at order $\rho^{4}$, estimate the smallest value of $\rho$ at which the $R$ is zero. Hence give an estimate of the ground state energy.

  [You may use the fact that the Laplace operator is given in polar coordinates by the expression

  $$\left.\nabla^{2}=\frac{\partial^{2}}{\partial r^{2}}+\frac{1}{r} \frac{\partial}{\partial r}+\frac{1}{r^{2}} \frac{\partial^{2}}{\partial \phi^{2}}\right]$$

  comment

• 4.I.6G

  Quantum Mechanics | Part IB, 2005

  Define the commutator $[A, B]$ of two operators, $A$ and $B$. In three dimensions angular momentum is defined by a vector operator $\mathbf{L}$ with components

  $$L_{x}=y p_{z}-z p_{y} \quad L_{y}=z p_{x}-x p_{z} \quad L_{z}=x p_{y}-y p_{x}$$

  Show that $\left[L_{x}, L_{y}\right]=i \hbar L_{z}$ and use this, together with permutations, to show that $\left[\mathbf{L}^{2}, L_{w}\right]=0$, where $w$ denotes any of the directions $x, y, z$.

  At a given time the wave function of a particle is given by

  $$\psi=(x+y+z) \exp \left(-\sqrt{x^{2}+y^{2}+z^{2}}\right)$$

  Show that this is an eigenstate of $\mathbf{L}^{2}$ with eigenvalue equal to $2 \hbar^{2}$.

  comment

Special Relativity

• 1.I.4G

  Special Relativity | Part IB, 2005

  The four-velocity $U_{\mu}$ of a particle of rest mass $m$ is defined by $U_{\mu}=d x_{\mu} / d \tau$, where $\tau$ is the proper time (the time as measured in the particle's rest frame). Derive the expression for each of the four components of $U_{\mu}$ in terms of the components of the three-velocity and the speed of light, $c$.

  Show that $U \cdot U=c^{2}$ for an appropriately defined scalar product.

  The four-momentum, $p_{\mu}=m U_{\mu}$, of a particle of rest mass $m$ defines a relativistic generalisation of energy and momentum. Show that the standard non-relativistic expressions for the momentum and kinetic energy of a particle with mass $m$ travelling with velocity $v$ are obtained in the limit $v / c \ll 1$. Show also how the concept of a rest energy equal to $m c^{2}$ emerges.

  comment

• 2.I.7G

  Special Relativity | Part IB, 2005

  Bob and Alice are twins. Bob accelerates rapidly away from Earth in a rocket that travels in a straight line until it reaches a velocity $v$ relative to the Earth. It then travels with constant $v$ for a long time before reversing its engines and decelerating rapidly until it is travelling at a velocity $-v$ relative to the Earth. After a further long period of time the rocket returns to Earth, decelerating rapidly until it is at rest. Alice remains on Earth throughout. Sketch the space-time diagram that describes Bob's world-line in Alice's rest frame, assuming that the periods of acceleration and deceleration are negligibly small compared to the total time, explain carefully why Bob ages less than Alice between his departure and his return and show that

  $$\Delta t_{B}=\left(1-\frac{v^{2}}{c^{2}}\right)^{1 / 2} \Delta t_{A}$$

  where $\Delta t_{B}$ is the time by which Bob has aged and $\Delta t_{A}$ is the time by which Alice has aged.

  Indicate on your diagram how Bob sees Alice aging during his voyage.

  comment

• 4.II.17G

  Special Relativity | Part IB, 2005

  Obtain the Lorentz transformations that relate the coordinates of an event measured in one inertial frame $(t, x, y, z)$ to those in another inertial frame moving with velocity $v$ along the $x$ axis. Take care to state the assumptions that lead to your result.

  A star is at rest in a three-dimensional coordinate frame $\mathcal{S}^{\prime}$ that is moving at constant velocity $v$ along the $x$ axis of a second coordinate frame $\mathcal{S}$. The star emits light of frequency $\nu^{\prime}$, which may considered to be a beam of photons. A light ray from the star to the origin in $\mathcal{S}^{\prime}$ is a straight line that makes an angle $\theta^{\prime}$ with the $x^{\prime}$ axis. Write down the components of the four-momentum of a photon in this light ray.

  The star is seen by an observer at rest at the origin of $\mathcal{S}$ at time $t=t^{\prime}=0$, when the origins of the coordinate frames $\mathcal{S}$ and $\mathcal{S}^{\prime}$ coincide. The light that reaches the observer moves along a line through the origin that makes an angle $\theta$ to the $x$ axis and has frequency $\nu$. Make use of the Lorentz transformations between the four-momenta of a photon in these two frames to determine the relation

  $$\lambda=\lambda^{\prime}\left(1-\frac{v^{2}}{c^{2}}\right)^{-1 / 2}\left(1+\frac{v}{c} \cos \theta\right)$$

  where $\lambda$ is the observed wavelength of the photon and $\lambda^{\prime}$ is the wavelength in the star's rest frame.

  Comment on the form of this result in the special cases with $\cos \theta=1, \cos \theta=-1$ and $\cos \theta=0$.

  [You may assume that the energy of a photon of frequency $\nu \mathrm{~ i s ~ h}$ momentum is a three-vector of magnitude $h \nu / c .]$

  comment

Statistics

• $1 . \mathrm{I} . 7 \mathrm{D} \quad$

  Statistics | Part IB, 2005

  The fast-food chain McGonagles have three sizes of their takeaway haggis, Large, Jumbo and Soopersize. A survey of 300 randomly selected customers at one branch choose 92 Large, 89 Jumbo and 119 Soopersize haggises.

  Is there sufficient evidence to reject the hypothesis that all three sizes are equally popular? Explain your answer carefully.

  $$\left[\begin{array}{ccccccccc} \text { Distribution } & t_{1} & t_{2} & t_{3} & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & F_{1,2} & F_{2,3} \\ \text { 95\% percentile } & 6 \cdot 31 & 2.92 & 2 \cdot 35 & 3.84 & 5.99 & 7 \cdot 82 & 18 \cdot 51 & 9.55 \end{array}\right]$$

  comment

• 1.II.18D

  Statistics | Part IB, 2005

  In the context of hypothesis testing define the following terms: (i) simple hypothesis; (ii) critical region; (iii) size; (iv) power; and (v) type II error probability.

  State, without proof, the Neyman-Pearson lemma.

  Let $X$ be a single observation from a probability density function $f$. It is desired to test the hypothesis

  $$H_{0}: f=f_{0} \quad \text { against } \quad H_{1}: f=f_{1},$$

  with $f_{0}(x)=\frac{1}{2}|x| e^{-x^{2} / 2}$ and $f_{1}(x)=\Phi^{\prime}(x),-\infty<x<\infty$, where $\Phi(x)$ is the distribution function of the standard normal, $N(0,1)$.

  Determine the best test of size $\alpha$, where $0<\alpha<1$, and express its power in terms of $\Phi$ and $\alpha$.

  Find the size of the test that minimizes the sum of the error probabilities. Explain your reasoning carefully.

  comment

• 2.II.19D

  Statistics | Part IB, 2005

  Let $X_{1}, \ldots, X_{n}$ be a random sample from a probability density function $f(x \mid \theta)$, where $\theta$ is an unknown real-valued parameter which is assumed to have a prior density $\pi(\theta)$. Determine the optimal Bayes point estimate $a\left(X_{1}, \ldots, X_{n}\right)$ of $\theta$, in terms of the posterior distribution of $\theta$ given $X_{1}, \ldots, X_{n}$, when the loss function is

  $$L(\theta, a)= \begin{cases}\gamma(\theta-a) & \text { when } \theta \geqslant a \\ \delta(a-\theta) & \text { when } \theta \leqslant a\end{cases}$$

  where $\gamma$ and $\delta$ are given positive constants.

  Calculate the estimate explicitly in the case when $f(x \mid \theta)$ is the density of the uniform distribution on $(0, \theta)$ and $\pi(\theta)=e^{-\theta} \theta^{n} / n !, \theta>0$.

  comment

• 3.I.8D

  Statistics | Part IB, 2005

  Let $X_{1}, \ldots, X_{n}$ be a random sample from a normal distribution with mean $\mu$ and variance $\sigma^{2}$, where $\mu$ and $\sigma^{2}$ are unknown. Derive the form of the size- $\alpha$ generalized likelihood-ratio test of the hypothesis $H_{0}: \mu=\mu_{0}$ against $H_{1}: \mu \neq \mu_{0}$, and show that it is equivalent to the standard $t$-test of size $\alpha$.

  [You should state, but need not derive, the distribution of the test statistic.]

  comment

• 4.II.19D

  Statistics | Part IB, 2005

  Let $Y_{1}, \ldots, Y_{n}$ be observations satisfying

  $$Y_{i}=\beta x_{i}+\epsilon_{i}, \quad 1 \leqslant i \leqslant n$$

  where $\epsilon_{1}, \ldots, \epsilon_{n}$ are independent random variables each with the $N\left(0, \sigma^{2}\right)$ distribution. Here $x_{1}, \ldots, x_{n}$ are known but $\beta$ and $\sigma^{2}$ are unknown.

  (i) Determine the maximum-likelihood estimates $\left(\widehat{\beta}, \widehat{\sigma}^{2}\right)$ of $\left(\beta, \sigma^{2}\right)$.

  (ii) Find the distribution of $\widehat{\beta}$.

  (iii) By showing that $Y_{i}-\widehat{\beta} x_{i}$ and $\widehat{\beta}$ are independent, or otherwise, determine the joint distribution of $\widehat{\beta}$ and $\widehat{\sigma}^{2}$.

  (iv) Explain carefully how you would test the hypothesis $H_{0}: \beta=\beta_{0}$ against $H_{1}: \beta \neq \beta_{0}$.

  comment