Part IB, 2004

Analysis II

• $3 . \mathrm{II} . 16 \mathrm{~F} \quad$

  Analysis II | Part IB, 2004

  State and prove the contraction mapping theorem.

  Let $a$ be a positive real number, and take $X=\left[\sqrt{\frac{a}{2}}, \infty\right)$. Prove that the function

  $$f(x)=\frac{1}{2}\left(x+\frac{a}{x}\right)$$

  is a contraction from $X$ to $X$. Find the unique fixed point of $f$.

  comment

• 1.I.4G

  Analysis II | Part IB, 2004

  Define what it means for a sequence of functions $F_{n}:(0,1) \rightarrow \mathbb{R}$, where $n=1,2, \ldots$, to converge uniformly to a function $F$.

  For each of the following sequences of functions on $(0,1)$, find the pointwise limit function. Which of these sequences converge uniformly? Justify your answers.

  (i) $F_{n}(x)=\frac{1}{n} e^{x}$

  (ii) $F_{n}(x)=e^{-n x^{2}}$

  (iii) $F_{n}(x)=\sum_{i=0}^{n} x^{i}$

  comment

• 1.II.15G

  Analysis II | Part IB, 2004

  State the axioms for a norm on a vector space. Show that the usual Euclidean norm on $\mathbb{R}^{n}$,

  $$\|x\|=\left(x_{1}^{2}+x_{2}^{2}+\ldots+x_{n}^{2}\right)^{1 / 2}$$

  satisfies these axioms.

  Let $U$ be any bounded convex open subset of $\mathbb{R}^{n}$ that contains 0 and such that if $x \in U$ then $-x \in U$. Show that there is a norm on $\mathbb{R}^{n}$, satisfying the axioms, for which $U$ is the set of points in $\mathbb{R}^{n}$ of norm less than 1 .

  comment

• 2.I.3G

  Analysis II | Part IB, 2004

  Consider a sequence of continuous functions $F_{n}:[-1,1] \rightarrow \mathbb{R}$. Suppose that the functions $F_{n}$ converge uniformly to some continuous function $F$. Show that the integrals $\int_{-1}^{1} F_{n}(x) d x$ converge to $\int_{-1}^{1} F(x) d x$.

  Give an example to show that, even if the functions $F_{n}(x)$ and $F(x)$ are differentiable, the derivatives $F_{n}^{\prime}(0)$ need not converge to $F^{\prime}(0)$.

  comment

• 2.II.14G

  Analysis II | Part IB, 2004

  Let $X$ be a non-empty complete metric space. Give an example to show that the intersection of a descending sequence of non-empty closed subsets of $X, A_{1} \supset A_{2} \supset \cdots$, can be empty. Show that if we also assume that

  $$\lim _{n \rightarrow \infty} \operatorname{diam}\left(A_{n}\right)=0$$

  then the intersection is not empty. Here the diameter $\operatorname{diam}(A)$ is defined as the supremum of the distances between any two points of a set $A$.

  We say that a subset $A$ of $X$ is dense if it has nonempty intersection with every nonempty open subset of $X$. Let $U_{1}, U_{2}, \ldots$ be any sequence of dense open subsets of $X$. Show that the intersection $\bigcap_{n=1}^{\infty} U_{n}$ is not empty.

  [Hint: Look for a descending sequence of subsets $A_{1} \supset A_{2} \supset \cdots$, with $A_{i} \subset U_{i}$, such that the previous part of this problem applies.]

  comment

• 3.I.4F

  Analysis II | Part IB, 2004

  Let $X$ and $X^{\prime}$ be metric spaces with metrics $d$ and $d^{\prime}$. If $u=\left(x, x^{\prime}\right)$ and $v=\left(y, y^{\prime}\right)$ are any two points of $X \times X^{\prime}$, prove that the formula

  $$D(u, v)=\max \left\{d(x, y), d^{\prime}\left(x^{\prime}, y^{\prime}\right)\right\}$$

  defines a metric on $X \times X^{\prime}$. If $X=X^{\prime}$, prove that the diagonal $\Delta$ of $X \times X$ is closed in $X \times X$.

  comment

• 4.I.3F

  Analysis II | Part IB, 2004

  Let $U, V$ be open sets in $\mathbb{R}^{n}, \mathbb{R}^{m}$, respectively, and let $f: U \rightarrow V$ be a map. What does it mean for $f$ to be differentiable at a point $u$ of $U$ ?

  Let $g: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be the map given by

  $$g(x, y)=|x|+|y|$$

  Prove that $g$ is differentiable at all points $(a, b)$ with $a b \neq 0$.

  comment

• 4.II.13F

  Analysis II | Part IB, 2004

  State the inverse function theorem for maps $f: U \rightarrow \mathbb{R}^{2}$, where $U$ is a non-empty open subset of $\mathbb{R}^{2}$.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ be the function defined by

  $$f(x, y)=\left(x, x^{3}+y^{3}-3 x y\right) .$$

  Find a non-empty open subset $U$ of $\mathbb{R}^{2}$ such that $f$ is locally invertible on $U$, and compute the derivative of the local inverse.

  Let $C$ be the set of all points $(x, y)$ in $\mathbb{R}^{2}$ satisfying

  $$x^{3}+y^{3}-3 x y=0$$

  Prove that $f$ is locally invertible at all points of $C$ except $(0,0)$ and $\left(2^{2 / 3}, 2^{1 / 3}\right)$. Deduce that, for each point $(a, b)$ in $C$ except $(0,0)$ and $\left(2^{2 / 3}, 2^{1 / 3}\right)$, there exist open intervals $I, J$ containing $a, b$, respectively, such that for each $x$ in $I$, there is a unique point $y$ in $J$ with $(x, y)$ in $C$.

  comment

Complex Methods

• 1.I.5A

  Complex Methods | Part IB, 2004

  Determine the poles of the following functions and calculate their residues there. (i) $\frac{1}{z^{2}+z^{4}}$, (ii) $\frac{e^{1 / z^{2}}}{z-1}$, (iii) $\frac{1}{\sin \left(e^{z}\right)}$.

  comment

• 1.II.16A

  Complex Methods | Part IB, 2004

  Let $p$ and $q$ be two polynomials such that

  $$q(z)=\prod_{l=1}^{m}\left(z-\alpha_{l}\right)$$

  where $\alpha_{1}, \ldots, \alpha_{m}$ are distinct non-real complex numbers and $\operatorname{deg} p \leqslant m-1$. Using contour integration, determine

  $$\int_{-\infty}^{\infty} \frac{p(x)}{q(x)} e^{i x} d x$$

  carefully justifying all steps.

  comment

• 2.I.5A

  Complex Methods | Part IB, 2004

  Let the functions $f$ and $g$ be analytic in an open, nonempty domain $\Omega$ and assume that $g \neq 0$ there. Prove that if $|f(z)| \equiv|g(z)|$ in $\Omega$ then there exists $\alpha \in \mathbb{R}$ such that $f(z) \equiv e^{i \alpha} g(z)$.

  comment

• 2.II.16A

  Complex Methods | Part IB, 2004

  Prove by using the Cauchy theorem that if $f$ is analytic in the open disc $\Omega=\{z \in \mathbb{C}:|z|<1\}$ then there exists a function $g$, analytic in $\Omega$, such that $g^{\prime}(z)=f(z)$, $z \in \Omega$.

  comment

• 4.I.5A

  Complex Methods | Part IB, 2004

  State and prove the Parseval formula.

  [You may use without proof properties of convolution, as long as they are precisely stated.]

  comment

• 4.II.15A

  Complex Methods | Part IB, 2004

  (i) Show that the inverse Fourier transform of the function

  $$\hat{g}(s)= \begin{cases}e^{s}-e^{-s}, & |s| \leqslant 1 \\ 0, & |s| \geqslant 1\end{cases}$$

  is

  $$g(x)=\frac{2 i}{\pi} \frac{1}{1+x^{2}}(x \sinh 1 \cos x-\cosh 1 \sin x)$$

  (ii) Determine, by using Fourier transforms, the solution of the Laplace equation

  $$\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}=0$$

  given in the strip $-\infty<x<\infty, 0<y<1$, together with the boundary conditions

  $$u(x, 0)=g(x), \quad u(x, 1) \equiv 0, \quad-\infty<x<\infty$$

  where $g$ has been given above.

  [You may use without proof properties of Fourier transforms.]

  comment

Electromagnetism

• 1.I.7B

  Electromagnetism | Part IB, 2004

  Write down Maxwell's equations and show that they imply the conservation of charge.

  In a conducting medium of conductivity $\sigma$, where $\mathbf{J}=\sigma \mathbf{E}$, show that any charge density decays in time exponentially at a rate to be determined.

  comment

• 1.II.18B

  Electromagnetism | Part IB, 2004

  Inside a volume $D$ there is an electrostatic charge density $\rho(\mathbf{r})$, which induces an electric field $\mathbf{E}(\mathbf{r})$ with associated electrostatic potential $\phi(\mathbf{r})$. The potential vanishes on the boundary of $D$. The electrostatic energy is

  $$W=\frac{1}{2} \int_{D} \rho \phi d^{3} \mathbf{r}$$

  Derive the alternative form

  $$W=\frac{\epsilon_{0}}{2} \int_{D} E^{2} d^{3} \mathbf{r}$$

  A capacitor consists of three identical and parallel thin metal circular plates of area $A$ positioned in the planes $z=-H, z=a$ and $z=H$, with $-H<a<H$, with centres on the $z$ axis, and at potentials $0, V$ and 0 respectively. Find the electrostatic energy stored, verifying that expressions (1) and (2) give the same results. Why is the energy minimal when $a=0$ ?

  comment

• 2.I.7B

  Electromagnetism | Part IB, 2004

  Write down the two Maxwell equations that govern steady magnetic fields. Show that the boundary conditions satisfied by the magnetic field on either side of a sheet carrying a surface current of density $\mathbf{s}$, with normal $\mathbf{n}$ to the sheet, are

  $$\mathbf{n} \times \mathbf{B}_{+}-\mathbf{n} \times \mathbf{B}_{-}=\mu_{0} \mathbf{s}$$

  Write down the force per unit area on the surface current.

  comment

• 2.II.18B

  Electromagnetism | Part IB, 2004

  The vector potential due to a steady current density $\mathbf{J}$ is given by

  $$\mathbf{A}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|} d^{3} \mathbf{r}^{\prime}$$

  where you may assume that $\mathbf{J}$ extends only over a finite region of space. Use $(*)$ to derive the Biot-Savart law

  $$\mathbf{B}(\mathbf{r})=\frac{\mu_{0}}{4 \pi} \int \frac{\mathbf{J}\left(\mathbf{r}^{\prime}\right) \times\left(\mathbf{r}-\mathbf{r}^{\prime}\right)}{\left|\mathbf{r}-\mathbf{r}^{\prime}\right|^{3}} d^{3} \mathbf{r}^{\prime}$$

  A circular loop of wire of radius $a$ carries a current $I$. Take Cartesian coordinates with the origin at the centre of the loop and the $z$-axis normal to the loop. Use the BiotSavart law to show that on the $z$-axis the magnetic field is in the axial direction and of magnitude

  $$B=\frac{\mu_{0} I a^{2}}{2\left(z^{2}+a^{2}\right)^{3 / 2}}$$

  comment

• 3.I.7B

  Electromagnetism | Part IB, 2004

  A wire is bent into the shape of three sides of a rectangle and is held fixed in the $z=0$ plane, with base $x=0$ and $-\ell<y<\ell$, and with arms $y=\pm \ell$ and $0<x<\ell$. A second wire moves smoothly along the arms: $x=X(t)$ and $-\ell<y<\ell$ with $0<X<\ell$. The two wires have resistance $R$ per unit length and mass $M$ per unit length. There is a time-varying magnetic field $B(t)$ in the $z$-direction.

  Using the law of induction, find the electromotive force around the circuit made by the two wires.

  Using the Lorentz force, derive the equation

  $$M \ddot{X}=-\frac{B}{R(X+2 \ell)} \frac{d}{d t}(X \ell B)$$

  comment

• 3.II.19B

  Electromagnetism | Part IB, 2004

  Starting from Maxwell's equations, derive the law of energy conservation in the form

  $$\frac{\partial W}{\partial t}+\nabla \cdot \mathbf{S}+\mathbf{J} \cdot \mathbf{E}=0$$

  where $W=\frac{\epsilon_{0}}{2} E^{2}+\frac{1}{2 \mu_{0}} B^{2}$ and $\mathbf{S}=\frac{1}{\mu_{0}} \mathbf{E} \times \mathbf{B}$.

  Evaluate $W$ and $\mathbf{S}$ for the plane electromagnetic wave in vacuum

  $$\mathbf{E}=\left(E_{0} \cos (k z-\omega t), 0,0\right) \quad \mathbf{B}=\left(0, B_{0} \cos (k z-\omega t), 0\right),$$

  where the relationships between $E_{0}, B_{0}, \omega$ and $k$ should be determined. Show that the electromagnetic energy propagates at speed $c^{2}=1 /\left(\epsilon_{0} \mu_{0}\right)$, i.e. show that $S=W c$.

  comment

Fluid Dynamics

• 1.I.9C

  Fluid Dynamics | Part IB, 2004

  From the general mass-conservation equation, show that the velocity field $\mathbf{u}(\mathbf{x})$ of an incompressible fluid is solenoidal, i.e. that $\nabla \cdot \mathbf{u}=0$.

  Verify that the two-dimensional flow

  $$\mathbf{u}=\left(\frac{y}{x^{2}+y^{2}}, \frac{-x}{x^{2}+y^{2}}\right)$$

  is solenoidal and find a streamfunction $\psi(x, y)$ such that $\mathbf{u}=(\partial \psi / \partial y,-\partial \psi / \partial x)$.

  comment

• 1.II.20C

  Fluid Dynamics | Part IB, 2004

  A layer of water of depth $h$ flows along a wide channel with uniform velocity $(U, 0)$, in Cartesian coordinates $(x, y)$, with $x$ measured downstream. The bottom of the channel is at $y=-h$, and the free surface of the water is at $y=0$. Waves are generated on the free surface so that it has the new position $y=\eta(x, t)=a e^{i(\omega t-k x)}$.

  Write down the equation and the full nonlinear boundary conditions for the velocity potential $\phi$ (for the perturbation velocity) and the motion of the free surface.

  By linearizing these equations about the state of uniform flow, show that

  where $g$ is the acceleration due to gravity.

  Hence, determine the dispersion relation for small-amplitude surface waves

  $$(\omega-k U)^{2}=g k \tanh k h .$$

  comment

• 3.I.10C

  Fluid Dynamics | Part IB, 2004

  State Bernoulli's equation for unsteady motion of an irrotational, incompressible, inviscid fluid subject to a conservative body force $-\nabla \chi$.

  A long vertical U-tube of uniform cross section contains an inviscid, incompressible fluid whose surface, in equilibrium, is at height $h$ above the base. Derive the equation

  $$h \frac{d^{2} \zeta}{d t^{2}}+g \zeta=0$$

  governing the displacement $\zeta$ of the surface on one side of the U-tube, where $t$ is time and $g$ is the acceleration due to gravity.

  $$\begin{aligned} & \frac{\partial \eta}{\partial t}+U \frac{\partial \eta}{\partial x}=\frac{\partial \phi}{\partial y}, \quad \frac{\partial \phi}{\partial t}+U \frac{\partial \phi}{\partial x}+g \eta=0 \quad \text { on } \quad y=0 \\ & \frac{\partial \phi}{\partial y}=0 \quad \text { on } \quad y=-h, \end{aligned}$$

  comment

• 3.II.21C

  Fluid Dynamics | Part IB, 2004

  Use separation of variables to determine the irrotational, incompressible flow

  $$\mathbf{u}=U \frac{a^{3}}{r^{3}}\left(\cos \theta \mathbf{e}_{r}+\frac{1}{2} \sin \theta \mathbf{e}_{\theta}\right)$$

  around a solid sphere of radius $a$ translating at velocity $U$ along the direction $\theta=0$ in spherical polar coordinates $r$ and $\theta$.

  Show that the total kinetic energy of the fluid is

  $$K=\frac{1}{4} M_{f} U^{2},$$

  where $M_{f}$ is the mass of fluid displaced by the sphere.

  A heavy sphere of mass $M$ is released from rest in an inviscid fluid. Determine its speed after it has fallen through a distance $h$ in terms of $M, M_{f}, g$ and $h$.

  comment

• 4.I.8C

  Fluid Dynamics | Part IB, 2004

  Write down the vorticity equation for the unsteady flow of an incompressible, inviscid fluid with no body forces acting.

  Show that the flow field

  $$\mathbf{u}=(-x, x \omega(t), z-1)$$

  has uniform vorticity of magnitude $\omega(t)=\omega_{0} e^{t}$ for some constant $\omega_{0}$.

  comment

• 4.II.18C

  Fluid Dynamics | Part IB, 2004

  Use Euler's equation to derive the momentum integral

  $$\int_{S}\left(p n_{i}+\rho n_{j} u_{j} u_{i}\right) d S=0$$

  for the steady flow $\mathbf{u}=\left(u_{1}, u_{2}, u_{3}\right)$ and pressure $p$ of an inviscid,incompressible fluid of density $\rho$, where $S$ is a closed surface with normal $\mathbf{n}$.

  A cylindrical jet of water of area $A$ and speed $u$ impinges axisymmetrically on a stationary sphere of radius $a$ and is deflected into a conical sheet of vertex angle $\alpha$ as shown. Gravity is being ignored.

  

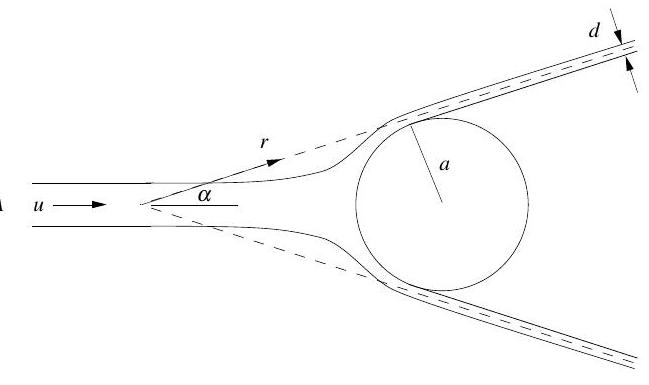
  Use a suitable form of Bernoulli's equation to determine the speed of the water in the conical sheet, being careful to state how the equation is being applied.

  Use conservation of mass to show that the width $d(r)$ of the sheet far from the point of impact is given by

  $$d=\frac{A}{2 \pi r \sin \alpha},$$

  where $r$ is the distance along the sheet measured from the vertex of the cone.

  Finally, use the momentum integral to determine the net force on the sphere in terms of $\rho, u, A$ and $\alpha$.

  comment

Further Analysis

• $2 . \mathrm{I} . 4 \mathrm{E} \quad$

  Further Analysis | Part IB, 2004

  Let $\tau$ be the topology on $\mathbb{N}$ consisting of the empty set and all sets $X \subset \mathbb{N}$ such that $\mathbb{N} \backslash X$ is finite. Let $\sigma$ be the usual topology on $\mathbb{R}$, and let $\rho$ be the topology on $\mathbb{R}$ consisting of the empty set and all sets of the form $(x, \infty)$ for some real $x$.

  (i) Prove that all continuous functions $f:(\mathbb{N}, \tau) \rightarrow(\mathbb{R}, \sigma)$ are constant.

  (ii) Give an example with proof of a non-constant function $f:(\mathbb{N}, \tau) \rightarrow(\mathbb{R}, \rho)$ that is continuous.

  comment

• $3 . \mathrm{II} . 17 \mathrm{E} \quad$

  Further Analysis | Part IB, 2004

  (i) Explain why the formula

  $$f(z)=\sum_{n=-\infty}^{\infty} \frac{1}{(z-n)^{2}}$$

  defines a function that is analytic on the domain $\mathbb{C} \backslash \mathbb{Z}$. [You need not give full details, but should indicate what results are used.]

  Show also that $f(z+1)=f(z)$ for every $z$ such that $f(z)$ is defined.

  (ii) Write $\log z$ for $\log r+i \theta$ whenever $z=r e^{i \theta}$ with $r>0$ and $-\pi<\theta \leqslant \pi$. Let $g$ be defined by the formula

  $$g(z)=f\left(\frac{1}{2 \pi i} \log z\right)$$

  Prove that $g$ is analytic on $\mathbb{C} \backslash\{0,1\}$.

  [Hint: What would be the effect of redefining $\log z$ to be $\log r+i \theta$ when $z=r e^{i \theta}$, $r>0$ and $0 \leqslant \theta<2 \pi$ ?]

  (iii) Determine the nature of the singularity of $g$ at $z=1$.

  comment

• 2.II.15E

  Further Analysis | Part IB, 2004

  (i) Let $X$ be the set of all infinite sequences $\left(\epsilon_{1}, \epsilon_{2}, \ldots\right)$ such that $\epsilon_{i} \in\{0,1\}$ for all $i$. Let $\tau$ be the collection of all subsets $Y \subset X$ such that, for every $\left(\epsilon_{1}, \epsilon_{2}, \ldots\right) \in Y$ there exists $n$ such that $\left(\eta_{1}, \eta_{2}, \ldots\right) \in Y$ whenever $\eta_{1}=\epsilon_{1}, \eta_{2}=\epsilon_{2}, \ldots, \eta_{n}=\epsilon_{n}$. Prove that $\tau$ is a topology on $X$.

  (ii) Let a distance $d$ be defined on $X$ by

  $$d\left(\left(\epsilon_{1}, \epsilon_{2}, \ldots\right),\left(\eta_{1}, \eta_{2}, \ldots\right)\right)=\sum_{n=1}^{\infty} 2^{-n}\left|\epsilon_{n}-\eta_{n}\right|$$

  Prove that $d$ is a metric and that the topology arising from $d$ is the same as $\tau$.

  comment

• 3.I.5E

  Further Analysis | Part IB, 2004

  Let $C$ be the contour that goes once round the boundary of the square

  $$\{z:-1 \leqslant \operatorname{Re} z \leqslant 1,-1 \leqslant \operatorname{Im} z \leqslant 1\}$$

  in an anticlockwise direction. What is $\int_{C} \frac{d z}{z}$ ? Briefly justify your answer.

  Explain why the integrals along each of the four edges of the square are equal.

  Deduce that $\int_{-1}^{1} \frac{d t}{1+t^{2}}=\frac{\pi}{2}$.

  comment

• 4.I.4E

  Further Analysis | Part IB, 2004

  (i) Let $D$ be the open unit disc of radius 1 about the point $3+3 i$. Prove that there is an analytic function $f: D \rightarrow \mathbb{C}$ such that $f(z)^{2}=z$ for every $z \in D$.

  (ii) Let $D^{\prime}=\mathbb{C} \backslash\{z \in \mathbb{C}: \operatorname{Im} z=0$, Re $z \leqslant 0\}$. Explain briefly why there is at most one extension of $f$ to a function that is analytic on $D^{\prime}$.

  (iii) Deduce that $f$ cannot be extended to an analytic function on $\mathbb{C} \backslash\{0\}$.

  comment

• 4.II.14E

  Further Analysis | Part IB, 2004

  (i) State and prove Rouché's theorem.

  [You may assume the principle of the argument.]

  (ii) Let $0<c<1$. Prove that the polynomial $p(z)=z^{3}+i c z+8$ has three roots with modulus less than 3. Prove that one root $\alpha$ satisfies $\operatorname{Re} \alpha>0, \operatorname{Im} \alpha>0$; another, $\beta$, satisfies $\operatorname{Re} \beta>0$, Im $\beta<0$; and the third, $\gamma$, has $\operatorname{Re} \gamma<0$.

  (iii) For sufficiently small $c$, prove that $\operatorname{Im} \gamma>0$.

  [You may use results from the course if you state them precisely.]

  comment

Geometry

• 1.I.3G

  Geometry | Part IB, 2004

  Using the Riemannian metric

  $$d s^{2}=\frac{d x^{2}+d y^{2}}{y^{2}}$$

  define the length of a curve and the area of a region in the upper half-plane $H=\{x+i y: y>0\}$.

  Find the hyperbolic area of the region $\{(x, y) \in H: 0<x<1, y>1\}$.

  comment

• 1.II.14G

  Geometry | Part IB, 2004

  Show that for every hyperbolic line $L$ in the hyperbolic plane $H$ there is an isometry of $H$ which is the identity on $L$ but not on all of $H$. Call it the reflection $R_{L}$.

  Show that every isometry of $H$ is a composition of reflections.

  comment

• 3.I.3G

  Geometry | Part IB, 2004

  State Euler's formula for a convex polyhedron with $F$ faces, $E$ edges, and $V$ vertices.

  Show that any regular polyhedron whose faces are pentagons has the same number of vertices, edges and faces as the dodecahedron.

  comment

• 3.II.15G

  Geometry | Part IB, 2004

  Let $a, b, c$ be the lengths of a right-angled triangle in spherical geometry, where $c$ is the hypotenuse. Prove the Pythagorean theorem for spherical geometry in the form

  $$\cos c=\cos a \cos b$$

  Now consider such a spherical triangle with the sides $a, b$ replaced by $\lambda a, \lambda b$ for a positive number $\lambda$. Show that the above formula approaches the usual Pythagorean theorem as $\lambda$ approaches zero.

  comment

Groups, Rings and Modules

• $1 . \mathrm{I} . 2 \mathrm{~F} \quad$

  Groups, Rings and Modules | Part IB, 2004

  Let $G$ be a finite group of order $n$. Let $H$ be a subgroup of $G$. Define the normalizer $N(H)$ of $H$, and prove that the number of distinct conjugates of $H$ is equal to the index of $N(H)$ in $G$. If $p$ is a prime dividing $n$, deduce that the number of Sylow $p$-subgroups of $G$ must divide $n$.

  [You may assume the existence and conjugacy of Sylow subgroups.]

  Prove that any group of order 72 must have either 1 or 4 Sylow 3-subgroups.

  comment

• $3 . \mathrm{II} . 14 \mathrm{~F} \quad$

  Groups, Rings and Modules | Part IB, 2004

  Let $L$ be the group $\mathbb{Z}^{3}$ consisting of 3-dimensional row vectors with integer components. Let $M$ be the subgroup of $L$ generated by the three vectors

  $$u=(1,2,3), v=(2,3,1), w=(3,1,2) \text {. }$$

  (i) What is the index of $M$ in $L$ ?

  (ii) Prove that $M$ is not a direct summand of $L$.

  (iii) Is the subgroup $N$ generated by $u$ and $v$ a direct summand of $L$ ?

  (iv) What is the structure of the quotient group $L / M$ ?

  comment

• $3 . \mathrm{I} . 2 \mathrm{~F} \quad$

  Groups, Rings and Modules | Part IB, 2004

  Let $R$ be the subring of all $z$ in $\mathbb{C}$ of the form

  $$z=\frac{a+b \sqrt{-3}}{2}$$

  where $a$ and $b$ are in $\mathbb{Z}$ and $a \equiv b(\bmod 2)$. Prove that $N(z)=z \bar{z}$ is a non-negative element of $\mathbb{Z}$, for all $z$ in $R$. Prove that the multiplicative group of units of $R$ has order 6 . Prove that $7 R$ is the intersection of two prime ideals of $R$.

  [You may assume that $R$ is a unique factorization domain.]

  comment

• 1.II.13F

  Groups, Rings and Modules | Part IB, 2004

  State the structure theorem for finitely generated abelian groups. Prove that a finitely generated abelian group $A$ is finite if and only if there exists a prime $p$ such that $A / p A=0$.

  Show that there exist abelian groups $A \neq 0$ such that $A / p A=0$ for all primes $p$. Prove directly that your example of such an $A$ is not finitely generated.

  comment

• 2.I.2F

  Groups, Rings and Modules | Part IB, 2004

  Prove that the alternating group $A_{5}$ is simple.

  comment

• 2.II.13F

  Groups, Rings and Modules | Part IB, 2004

  Let $K$ be a subgroup of a group $G$. Prove that $K$ is normal if and only if there is a group $H$ and a homomorphism $\phi: G \rightarrow H$ such that

  $$K=\{g \in G: \phi(g)=1\}$$

  Let $G$ be the group of all $2 \times 2$ matrices $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ with $a, b, c, d$ in $\mathbb{Z}$ and $a d-b c=1$. Let $p$ be a prime number, and take $K$ to be the subset of $G$ consisting of all $\left(\begin{array}{ll}a & b \\ c & d\end{array}\right)$ with $a \equiv d \equiv 1(\bmod p)$ and $c \equiv b \equiv 0(\bmod p) .$ Prove that $K$ is a normal subgroup of $G .$

  comment

• 4.I.2F

  Groups, Rings and Modules | Part IB, 2004

  State Gauss's lemma and Eisenstein's irreducibility criterion. Prove that the following polynomials are irreducible in $\mathbb{Q}[x]$ :

  (i) $x^{5}+5 x+5$;

  (ii) $x^{3}-4 x+1$;

  (iii) $x^{p-1}+x^{p-2}+\ldots+x+1$, where $p$ is any prime number.

  comment

• 4.II.12F

  Groups, Rings and Modules | Part IB, 2004

  Answer the following questions, fully justifying your answer in each case.

  (i) Give an example of a ring in which some non-zero prime ideal is not maximal.

  (ii) Prove that $\mathbb{Z}[x]$ is not a principal ideal domain.

  (iii) Does there exist a field $K$ such that the polynomial $f(x)=1+x+x^{3}+x^{4}$ is irreducible in $K[x]$ ?

  (iv) Is the ring $\mathbb{Q}[x] /\left(x^{3}-1\right)$ an integral domain?

  (v) Determine all ring homomorphisms $\phi: \mathbb{Q}[x] /\left(x^{3}-1\right) \rightarrow \mathbb{C}$.

  comment

Linear Algebra

• 1.I.1H

  Linear Algebra | Part IB, 2004

  Suppose that $\left\{\mathbf{e}_{1}, \ldots, \mathbf{e}_{r+1}\right\}$ is a linearly independent set of distinct elements of a vector space $V$ and $\left\{\mathbf{e}_{1}, \ldots, \mathbf{e}_{r}, \mathbf{f}_{r+1}, \ldots, \mathbf{f}_{m}\right\}$ spans $V$. Prove that $\mathbf{f}_{r+1}, \ldots, \mathbf{f}_{m}$ may be reordered, as necessary, so that $\left\{\mathbf{e}_{1}, \ldots \mathbf{e}_{r+1}, \mathbf{f}_{r+2}, \ldots, \mathbf{f}_{m}\right\}$ spans $V$.

  Suppose that $\left\{\mathbf{e}_{1}, \ldots, \mathbf{e}_{n}\right\}$ is a linearly independent set of distinct elements of $V$ and that $\left\{\mathbf{f}_{1}, \ldots, \mathbf{f}_{m}\right\}$ spans $V$. Show that $n \leqslant m$.

  comment

• 1.II.12H

  Linear Algebra | Part IB, 2004

  Let $U$ and $W$ be subspaces of the finite-dimensional vector space $V$. Prove that both the sum $U+W$ and the intersection $U \cap W$ are subspaces of $V$. Prove further that

  $$\operatorname{dim} U+\operatorname{dim} W=\operatorname{dim}(U+W)+\operatorname{dim}(U \cap W)$$

  Let $U, W$ be the kernels of the maps $A, B: \mathbb{R}^{4} \rightarrow \mathbb{R}^{2}$ given by the matrices $A$ and $B$ respectively, where

  $$A=\left(\begin{array}{rrrr} 1 & 2 & -1 & -3 \\ -1 & 1 & 2 & -4 \end{array}\right), \quad B=\left(\begin{array}{rrrr} 1 & -1 & 2 & 0 \\ 0 & 1 & 2 & -4 \end{array}\right)$$

  Find a basis for the intersection $U \cap W$, and extend this first to a basis of $U$, and then to a basis of $U+W$.

  comment

• 2.I.1E

  Linear Algebra | Part IB, 2004

  For each $n$ let $A_{n}$ be the $n \times n$ matrix defined by

  $$\left(A_{n}\right)_{i j}= \begin{cases}i & i \leqslant j \\ j & i>j\end{cases}$$

  What is $\operatorname{det} A_{n} ?$ Justify your answer.

  [It may be helpful to look at the cases $n=1,2,3$ before tackling the general case.]

  comment

• 2.II.12E

  Linear Algebra | Part IB, 2004

  Let $Q$ be a quadratic form on a real vector space $V$ of dimension $n$. Prove that there is a basis $\mathbf{e}_{1}, \ldots, \mathbf{e}_{n}$ with respect to which $Q$ is given by the formula

  $$Q\left(\sum_{i=1}^{n} x_{i} \mathbf{e}_{i}\right)=x_{1}^{2}+\ldots+x_{p}^{2}-x_{p+1}^{2}-\ldots-x_{p+q}^{2}$$

  Prove that the numbers $p$ and $q$ are uniquely determined by the form $Q$. By means of an example, show that the subspaces $\left\langle\mathbf{e}_{1}, \ldots, \mathbf{e}_{p}\right\rangle$ and $\left\langle\mathbf{e}_{p+1}, \ldots, \mathbf{e}_{p+q}\right\rangle$ need not be uniquely determined by $Q$.

  comment

• 3.I.1E

  Linear Algebra | Part IB, 2004

  Let $V$ be a finite-dimensional vector space over $\mathbb{R}$. What is the dual space of $V$ ? Prove that the dimension of the dual space is the same as that of $V$.

  comment

• 3.II.13E

  Linear Algebra | Part IB, 2004

  (i) Let $V$ be an $n$-dimensional vector space over $\mathbb{C}$ and let $\alpha: V \rightarrow V$ be an endomorphism. Suppose that the characteristic polynomial of $\alpha$ is $\Pi_{i=1}^{k}\left(x-\lambda_{i}\right)^{n_{i}}$, where the $\lambda_{i}$ are distinct and $n_{i}>0$ for every $i$.

  Describe all possibilities for the minimal polynomial and prove that there are no further ones.

  (ii) Give an example of a matrix for which both the characteristic and the minimal polynomial are $(x-1)^{3}(x-3)$.

  (iii) Give an example of two matrices $A, B$ with the same rank and the same minimal and characteristic polynomials such that there is no invertible matrix $P$ with $P A P^{-1}=B$.

  comment

• 4.I.1E

  Linear Algebra | Part IB, 2004

  Let $V$ be a real $n$-dimensional inner-product space and let $W \subset V$ be a $k$ dimensional subspace. Let $\mathbf{e}_{1}, \ldots, \mathbf{e}_{k}$ be an orthonormal basis for $W$. In terms of this basis, give a formula for the orthogonal projection $\pi: V \rightarrow W$.

  Let $v \in V$. Prove that $\pi v$ is the closest point in $W$ to $v$.

  [You may assume that the sequence $\mathbf{e}_{1}, \ldots, \mathbf{e}_{k}$ can be extended to an orthonormal basis $\mathbf{e}_{1}, \ldots, \mathbf{e}_{n}$ of $V$.]

  comment

• 4.II.11E

  Linear Algebra | Part IB, 2004

  (i) Let $V$ be an $n$-dimensional inner-product space over $\mathbb{C}$ and let $\alpha: V \rightarrow V$ be a Hermitian linear map. Prove that $V$ has an orthonormal basis consisting of eigenvectors of $\alpha$.

  (ii) Let $\beta: V \rightarrow V$ be another Hermitian map. Prove that $\alpha \beta$ is Hermitian if and only if $\alpha \beta=\beta \alpha$.

  (iii) A Hermitian map $\alpha$ is positive-definite if $\langle\alpha v, v\rangle>0$ for every non-zero vector $v$. If $\alpha$ is a positive-definite Hermitian map, prove that there is a unique positivedefinite Hermitian map $\beta$ such that $\beta^{2}=\alpha$.

  comment

Markov Chains

• 1.I.11H

  Markov Chains | Part IB, 2004

  Let $P=\left(P_{i j}\right)$ be a transition matrix. What does it mean to say that $P$ is (a) irreducible, $(b)$ recurrent?

  Suppose that $P$ is irreducible and recurrent and that the state space contains at least two states. Define a new transition matrix $\tilde{P}$ by

  $$\tilde{P}_{i j}=\left\{\begin{array}{lll} 0 & \text { if } & i=j \\ \left(1-P_{i i}\right)^{-1} P_{i j} & \text { if } & i \neq j \end{array}\right.$$

  Prove that $\tilde{P}$ is also irreducible and recurrent.

  comment

• 1.II.22H

  Markov Chains | Part IB, 2004

  Consider the Markov chain with state space $\{1,2,3,4,5,6\}$ and transition matrix

  $$\left(\begin{array}{cccccc} 0 & 0 & \frac{1}{2} & 0 & 0 & \frac{1}{2} \\ \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & \frac{1}{5} & 0 \\ \frac{1}{3} & 0 & \frac{1}{3} & 0 & 0 & \frac{1}{3} \\ \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} & \frac{1}{6} \\ 0 & 0 & 0 & 0 & 1 & 0 \\ \frac{1}{4} & 0 & \frac{1}{2} & 0 & 0 & \frac{1}{4} \end{array}\right) \text {. }$$

  Determine the communicating classes of the chain, and for each class indicate whether it is open or closed.

  Suppose that the chain starts in state 2 ; determine the probability that it ever reaches state 6 .

  Suppose that the chain starts in state 3 ; determine the probability that it is in state 6 after exactly $n$ transitions, $n \geqslant 1$.

  comment

• 2.I.11H

  Markov Chains | Part IB, 2004

  Let $\left(X_{r}\right)_{r \geqslant 0}$ be an irreducible, positive-recurrent Markov chain on the state space $S$ with transition matrix $\left(P_{i j}\right)$ and initial distribution $P\left(X_{0}=i\right)=\pi_{i}, i \in S$, where $\left(\pi_{i}\right)$ is the unique invariant distribution. What does it mean to say that the Markov chain is reversible?

  Prove that the Markov chain is reversible if and only if $\pi_{i} P_{i j}=\pi_{j} P_{j i}$ for all $i, j \in S$.

  comment

• 2.II.22H

  Markov Chains | Part IB, 2004

  Consider a Markov chain on the state space $S=\{0,1,2, \ldots\} \cup\left\{1^{\prime}, 2^{\prime}, 3^{\prime}, \ldots\right\}$ with transition probabilities as illustrated in the diagram below, where $0<q<1$ and $p=1-q$.

  

  For each value of $q, 0<q<1$, determine whether the chain is transient, null recurrent or positive recurrent.

  When the chain is positive recurrent, calculate the invariant distribution.

  comment

Methods

• 1.I.6B

  Methods | Part IB, 2004

  Write down the general isotropic tensors of rank 2 and 3 .

  According to a theory of magnetostriction, the mechanical stress described by a second-rank symmetric tensor $\sigma_{i j}$ is induced by the magnetic field vector $B_{i}$. The stress is linear in the magnetic field,

  $$\sigma_{i j}=A_{i j k} B_{k},$$

  where $A_{i j k}$ is a third-rank tensor which depends only on the material. Show that $\sigma_{i j}$ can be non-zero only in anisotropic materials.

  comment

• 1.II.17B

  Methods | Part IB, 2004

  The equation governing small amplitude waves on a string can be written as

  $$\frac{\partial^{2} y}{\partial t^{2}}=\frac{\partial^{2} y}{\partial x^{2}}$$

  The end points $x=0$ and $x=1$ are fixed at $y=0$. At $t=0$, the string is held stationary in the waveform,

  $$y(x, 0)=x(1-x) \quad \text { in } \quad 0 \leq x \leq 1 .$$

  The string is then released. Find $y(x, t)$ in the subsequent motion.

  Given that the energy

  $$\int_{0}^{1}\left[\left(\frac{\partial y}{\partial t}\right)^{2}+\left(\frac{\partial y}{\partial x}\right)^{2}\right] d x$$

  is constant in time, show that

  $$\sum_{\substack{n \text { odd } \\ n \geqslant 1}} \frac{1}{n^{4}}=\frac{\pi^{4}}{96}$$

  comment

• 2.I.6B

  Methods | Part IB, 2004

  Write down the general form of the solution in polar coordinates $(r, \theta)$ to Laplace's equation in two dimensions.

  Solve Laplace's equation for $\phi(r, \theta)$ in $0<r<1$ and in $1<r<\infty$, subject to the conditions

  $$\begin{gathered} \phi \rightarrow 0 \quad \text { as } \quad r \rightarrow 0 \text { and } r \rightarrow \infty \\ \left.\phi\right|_{r=1+}=\left.\phi\right|_{r=1-} \quad \text { and }\left.\quad \frac{\partial \phi}{\partial r}\right|_{r=1+}-\left.\frac{\partial \phi}{\partial r}\right|_{r=1-}=\cos 2 \theta+\cos 4 \theta . \end{gathered}$$

  comment

• 2.II.17B

  Methods | Part IB, 2004

  Let $I_{i j}(P)$ be the moment-of-inertia tensor of a rigid body relative to the point $P$. If $G$ is the centre of mass of the body and the vector $G P$ has components $X_{i}$, show that

  $$I_{i j}(P)=I_{i j}(G)+M\left(X_{k} X_{k} \delta_{i j}-X_{i} X_{j}\right),$$

  where $M$ is the mass of the body.

  Consider a cube of uniform density and side $2 a$, with centre at the origin. Find the inertia tensor about the centre of mass, and thence about the corner $P=(a, a, a)$.

  Find the eigenvectors and eigenvalues of $I_{i j}(P)$.

  comment

• 3.I.6D

  Methods | Part IB, 2004

  Let

  $$S[x]=\int_{0}^{T} \frac{1}{2}\left(\dot{x}^{2}-\omega^{2} x^{2}\right) \mathrm{d} t, \quad x(0)=a, \quad x(T)=b .$$

  For any variation $\delta x(t)$ with $\delta x(0)=\delta x(T)=0$, show that $\delta S=0$ when $x=x_{c}$ with

  $$x_{c}(t)=\frac{1}{\sin \omega T}[a \sin \omega(T-t)+b \sin \omega t] .$$

  By using integration by parts, show that

  $$S\left[x_{c}\right]=\left[\frac{1}{2} x_{c} \dot{x}_{c}\right]_{0}^{T}=\frac{\omega}{2 \sin \omega T}\left[\left(a^{2}+b^{2}\right) \cos \omega T-2 a b\right]$$

  comment

• 3.II.18D

  Methods | Part IB, 2004

  Starting from the Euler-Lagrange equations, show that the condition for the variation of the integral $\int I\left(y, y^{\prime}\right) \mathrm{d} x$ to be stationary is

  $$I-y^{\prime} \frac{\partial I}{\partial y^{\prime}}=\text { constant }$$

  In a medium with speed of light $c(y)$ the ray path taken by a light signal between two points satisfies the condition that the time taken is stationary. Consider the region $0<y<\infty$ and suppose $c(y)=e^{\lambda y}$. Derive the equation for the light ray path $y(x)$. Obtain the solution of this equation and show that the light ray between $(-a, 0)$ and $(a, 0)$ is given by

  $$e^{\lambda y}=\frac{\cos \lambda x}{\cos \lambda a},$$

  if $\lambda a<\frac{\pi}{2}$.

  Sketch the path for $\lambda a$ close to $\frac{\pi}{2}$ and evaluate the time taken for a light signal between these points.

  [The substitution $u=k e^{\lambda y}$, for some constant $k$, should prove useful in solving the differential equation.]

  comment

• 4.I.6C

  Methods | Part IB, 2004

  Chebyshev polynomials $T_{n}(x)$ satisfy the differential equation

  $$\left(1-x^{2}\right) y^{\prime \prime}-x y^{\prime}+n^{2} y=0 \quad \text { on } \quad[-1,1],$$

  where $n$ is an integer.

  Recast this equation into Sturm-Liouville form and hence write down the orthogonality relationship between $T_{n}(x)$ and $T_{m}(x)$ for $n \neq m$.

  By writing $x=\cos \theta$, or otherwise, show that the polynomial solutions of ( $\dagger$ ) are proportional to $\cos \left(n \cos ^{-1} x\right)$.

  comment

• 4.II.16C

  Methods | Part IB, 2004

  Obtain the Green function $G(x, \xi)$ satisfying

  $$G^{\prime \prime}+\frac{2}{x} G^{\prime}+k^{2} G=\delta(x-\xi),$$

  where $k$ is real, subject to the boundary conditions

  $$\begin{array}{rll} G \text { is finite } & \text { at } & x=0, \\ G=0 & \text { at } & x=1 . \end{array}$$

  [Hint: You may find the substitution $G=H / x$ helpful.]

  Use the Green function to determine that the solution of the differential equation

  $$y^{\prime \prime}+\frac{2}{x} y^{\prime}+k^{2} y=1,$$

  subject to the boundary conditions

  $$\begin{array}{rll} y \text { is finite } & \text { at } & x=0, \\ y=0 & \text { at } & x=1, \end{array}$$

  is

  $$y=\frac{1}{k^{2}}\left[1-\frac{\sin k x}{x \sin k}\right]$$

  comment

Numerical Analysis

• 2.I.9A

  Numerical Analysis | Part IB, 2004

  Determine the coefficients of Gaussian quadrature for the evaluation of the integral

  $$\int_{0}^{1} f(x) x d x$$

  that uses two function evaluations.

  comment

• 2.II.20A

  Numerical Analysis | Part IB, 2004

  Given an $m \times n$ matrix $A$ and $\mathbf{b} \in \mathbb{R}^{m}$, prove that the vector $\mathbf{x} \in \mathbb{R}^{n}$ is the solution of the least-squares problem for $A \mathbf{x} \approx \mathbf{b}$ if and only if $A^{T}(A \mathbf{x}-\mathbf{b})=\mathbf{0}$. Let

  $$A=\left[\begin{array}{cc} 1 & 2 \\ -3 & 1 \\ 1 & 3 \\ 4 & 1 \end{array}\right], \quad \mathbf{b}=\left[\begin{array}{c} 3 \\ 0 \\ -1 \\ 2 \end{array}\right]$$

  Determine the solution of the least-squares problem for $A \mathbf{x} \approx \mathbf{b}$.

  comment

• 3.I.11A

  Numerical Analysis | Part IB, 2004

  The linear system

  $$\left[\begin{array}{lll} \alpha & 2 & 1 \\ 1 & \alpha & 2 \\ 2 & 1 & \alpha \end{array}\right] \mathbf{x}=\mathbf{b}$$

  where real $\alpha \neq 0$ and $\mathbf{b} \in \mathbb{R}^{3}$ are given, is solved by the iterative procedure

  $$\mathbf{x}^{(k+1)}=-\frac{1}{\alpha}\left[\begin{array}{lll} 0 & 2 & 1 \\ 1 & 0 & 2 \\ 2 & 1 & 0 \end{array}\right] \mathbf{x}^{(k)}+\frac{1}{\alpha} \mathbf{b}, \quad k \geqslant 0$$

  Determine the conditions on $\alpha$ that guarantee convergence.

  comment

• 3.II.22A

  Numerical Analysis | Part IB, 2004

  Given $f \in C^{3}[0,1]$, we approximate $f^{\prime}\left(\frac{1}{3}\right)$ by the linear combination

  $$\mathcal{T}[f]=-\frac{5}{3} f(0)+\frac{4}{3} f\left(\frac{1}{2}\right)+\frac{1}{3} f(1)$$

  By finding the Peano kernel, determine the least constant $c$ such that

  $$\left|\mathcal{T}[f]-f^{\prime}\left(\frac{1}{3}\right)\right| \leq c\left\|f^{\prime \prime \prime}\right\|_{\infty} .$$

  comment

Optimization

• 3.I.12G

  Optimization | Part IB, 2004

  Consider the two-person zero-sum game Rock, Scissors, Paper. That is, a player gets 1 point by playing Rock when the other player chooses Scissors, or by playing Scissors against Paper, or Paper against Rock; the losing player gets $-1$ point. Zero points are received if both players make the same move.

  Suppose player one chooses Rock and Scissors (but never Paper) with probabilities $p$ and $1-p, 0 \leqslant p \leqslant 1$. Write down the maximization problem for player two's optimal strategy. Determine the optimal strategy for each value of $p$.

  comment

• 3.II.23G

  Optimization | Part IB, 2004

  Consider the following linear programming problem:

  $$\begin{aligned} \text { maximize }-x_{1}+3 x_{2} \\ \text { subject to } \quad x_{1}+x_{2} & \geqslant 3 \\ -x_{1}+2 x_{2} & \geqslant 6 \\ -x_{1}+x_{2} & \leqslant 2, \\ x_{2} & \leqslant 5, \\ x_{i} & \geqslant 0, \quad i=1,2 . \end{aligned}$$

  Write down the Phase One problem in this case, and solve it.

  By using the solution of the Phase One problem as an initial basic feasible solution for the Phase Two simplex algorithm, solve the above maximization problem. That is, find the optimal tableau and read the optimal solution $\left(x_{1}, x_{2}\right)$ and optimal value from it.

  comment

• 4.I.10G

  Optimization | Part IB, 2004

  State and prove the max flow/min cut theorem. In your answer you should define clearly the following terms: flow; maximal flow; cut; capacity.

  comment

• 4.II.20G

  Optimization | Part IB, 2004

  For any number $c \in(0,1)$, find the minimum and maximum values of

  $$\sum_{i=1}^{n} x_{i}^{c}$$

  subject to $\sum_{i=1}^{n} x_{i}=1, x_{1}, \ldots, x_{n} \geqslant 0$. Find all the points $\left(x_{1}, \ldots, x_{n}\right)$ at which the minimum and maximum are attained. Justify your answer.

  comment

Quantum Mechanics

• 1.I.8D

  Quantum Mechanics | Part IB, 2004

  From the time-dependent Schrödinger equation for $\psi(x, t)$, derive the equation

  $$\frac{\partial \rho}{\partial t}+\frac{\partial j}{\partial x}=0$$

  for $\rho(x, t)=\psi^{*}(x, t) \psi(x, t)$ and some suitable $j(x, t)$.

  Show that $\psi(x, t)=e^{i(k x-\omega t)}$ is a solution of the time-dependent Schrödinger equation with zero potential for suitable $\omega(k)$ and calculate $\rho$ and $j$. What is the interpretation of this solution?

  comment

• 1.II.19D

  Quantum Mechanics | Part IB, 2004

  The angular momentum operators are $\mathbf{L}=\left(L_{1}, L_{2}, L_{3}\right)$. Write down their commutation relations and show that $\left[L_{i}, \mathbf{L}^{2}\right]=0$. Let

  $$L_{\pm}=L_{1} \pm i L_{2},$$

  and show that

  $$\mathbf{L}^{2}=L_{-} L_{+}+L_{3}^{2}+\hbar L_{3} .$$

  Verify that $\mathbf{L} f(r)=0$, where $r^{2}=x_{i} x_{i}$, for any function $f$. Show that

  $$L_{3}\left(x_{1}+i x_{2}\right)^{n} f(r)=n \hbar\left(x_{1}+i x_{2}\right)^{n} f(r), \quad L_{+}\left(x_{1}+i x_{2}\right)^{n} f(r)=0$$

  for any integer $n$. Show that $\left(x_{1}+i x_{2}\right)^{n} f(r)$ is an eigenfunction of $\mathbf{L}^{2}$ and determine its eigenvalue. Why must $L_{-}\left(x_{1}+i x_{2}\right)^{n} f(r)$ be an eigenfunction of $\mathbf{L}^{2}$ ? What is its eigenvalue?

  comment

• 2.I.8D

  Quantum Mechanics | Part IB, 2004

  A quantum mechanical system is described by vectors $\psi=\left(\begin{array}{l}a \\ b\end{array}\right)$. The energy eigenvectors are

  $$\psi_{0}=\left(\begin{array}{c} \cos \theta \\ \sin \theta \end{array}\right), \quad \psi_{1}=\left(\begin{array}{c} -\sin \theta \\ \cos \theta \end{array}\right)$$

  with energies $E_{0}, E_{1}$ respectively. The system is in the state $\left(\begin{array}{l}1 \\ 0\end{array}\right)$ at time $t=0$. What is the probability of finding it in the state $\left(\begin{array}{l}0 \\ 1\end{array}\right)$ at a later time $t ?$

  comment

• 2.II.19D

  Quantum Mechanics | Part IB, 2004

  Consider a Hamiltonian of the form

  $$H=\frac{1}{2 m}(p+i f(x))(p-i f(x)), \quad-\infty<x<\infty,$$

  where $f(x)$ is a real function. Show that this can be written in the form $H=p^{2} /(2 m)+V(x)$, for some real $V(x)$ to be determined. Show that there is a wave function $\psi_{0}(x)$, satisfying a first-order equation, such that $H \psi_{0}=0$. If $f$ is a polynomial of degree $n$, show that $n$ must be odd in order for $\psi_{0}$ to be normalisable. By considering $\int \mathrm{d} x \psi^{*} H \psi$ show that all energy eigenvalues other than that for $\psi_{0}$ must be positive.

  For $f(x)=k x$, use these results to find the lowest energy and corresponding wave function for the harmonic oscillator Hamiltonian

  $$H_{\text {oscillator }}=\frac{p^{2}}{2 m}+\frac{1}{2} m \omega^{2} x^{2} .$$

  comment

• 3.I $9 \mathrm{D} \quad$

  Quantum Mechanics | Part IB, 2004

  Write down the expressions for the classical energy and angular momentum for an electron in a hydrogen atom. In the Bohr model the angular momentum $L$ is quantised so that

  $$L=n \hbar,$$

  for integer $n$. Assuming circular orbits, show that the radius of the $n$ 'th orbit is

  $$r_{n}=n^{2} a$$

  and determine $a$. Show that the corresponding energy is then

  $$E_{n}=-\frac{e^{2}}{8 \pi \epsilon_{0} r_{n}}$$

  comment

• 3.II.20D

  Quantum Mechanics | Part IB, 2004

  A one-dimensional system has the potential

  $$V(x)= \begin{cases}0 & x<0 \\ \frac{\hbar^{2} U}{2 m} & 0<x<L \\ 0 & x>L\end{cases}$$

  For energy $E=\hbar^{2} \epsilon /(2 m), \epsilon<U$, the wave function has the form

  $$\psi(x)= \begin{cases}a e^{i k x}+c e^{-i k x} & x<0 \\ e \cosh K x+f \sinh K x & 0<x<L \\ d e^{i k(x-L)}+b e^{-i k(x-L)} & x>L\end{cases}$$

  By considering the relation between incoming and outgoing waves explain why we should expect

  $$|c|^{2}+|d|^{2}=|a|^{2}+|b|^{2}$$

  Find four linear relations between $a, b, c, d, e, f$. Eliminate $d, e, f$ and show that

  $$c=\frac{1}{D}\left[b+\frac{1}{2}\left(\lambda-\frac{1}{\lambda}\right) \sinh K L a\right]$$

  where $D=\cosh K L-\frac{1}{2}\left(\lambda+\frac{1}{\lambda}\right) \sinh K L$ and $\lambda=K /(i k)$. By using the result for $c$, or otherwise, explain why the solution for $d$ is

  $$d=\frac{1}{D}\left[a+\frac{1}{2}\left(\lambda-\frac{1}{\lambda}\right) \sinh K L b\right]$$

  For $b=0$ define the transmission coefficient $T$ and show that, for large $L$,

  $$T \approx 16 \frac{\epsilon(U-\epsilon)}{U^{2}} e^{-2 \sqrt{U-\epsilon} L}$$

  comment

Special Relativity

• 3.I $. 8 \mathrm{~B} \quad$

  Special Relativity | Part IB, 2004

  Write down the Lorentz transformation with one space dimension between two inertial frames $S$ and $S^{\prime}$ moving relatively to one another at speed $V$.

  A particle moves at velocity $u$ in frame $S$. Find its velocity $u^{\prime}$ in frame $S^{\prime}$ and show that $u^{\prime}$ is always less than $c$.

  comment

• 4.I.7D

  Special Relativity | Part IB, 2004

  For a particle with energy $E$ and momentum $(p \cos \theta, p \sin \theta, 0)$, explain why an observer moving in the $x$-direction with velocity $v$ would find

  $$E^{\prime}=\gamma(E-p \cos \theta v), \quad p^{\prime} \cos \theta^{\prime}=\gamma\left(p \cos \theta-E \frac{v}{c^{2}}\right), \quad p^{\prime} \sin \theta^{\prime}=p \sin \theta,$$

  where $\gamma=\left(1-v^{2} / c^{2}\right)^{-\frac{1}{2}}$. What is the relation between $E$ and $p$ for a photon? Show that the same relation holds for $E^{\prime}$ and $p^{\prime}$ and that

  $$\cos \theta^{\prime}=\frac{\cos \theta-\frac{v}{c}}{1-\frac{v}{c} \cos \theta}$$

  What happens for $v \rightarrow c$ ?

  comment

• 4.II.17D

  Special Relativity | Part IB, 2004

  State how the 4 -momentum $p_{\mu}$ of a particle is related to its energy and 3momentum. How is $p_{\mu}$ related to the particle mass? For two particles with 4 -momenta $p_{1 \mu}$ and $p_{2 \mu}$ find a Lorentz-invariant expression that gives the total energy in their centre of mass frame.

  A photon strikes an electron at rest. What is the minimum energy it must have in order for it to create an electron and positron, of the same mass $m_{e}$ as the electron, in addition to the original electron? Express the result in units of $m_{e} c^{2}$.

  [It may be helpful to consider the minimum necessary energy in the centre of mass frame.]

  comment

Statistics

• 1.I.10H

  Statistics | Part IB, 2004

  Use the generalized likelihood-ratio test to derive Student's $t$-test for the equality of the means of two populations. You should explain carefully the assumptions underlying the test.

  comment

• 1.II.21H

  Statistics | Part IB, 2004

  State and prove the Rao-Blackwell Theorem.

  Suppose that $X_{1}, X_{2}, \ldots, X_{n}$ are independent, identically-distributed random variables with distribution

  $$P\left(X_{1}=r\right)=p^{r-1}(1-p), \quad r=1,2, \ldots$$

  where $p, 0<p<1$, is an unknown parameter. Determine a one-dimensional sufficient statistic, $T$, for $p$.

  By first finding a simple unbiased estimate for $p$, or otherwise, determine an unbiased estimate for $p$ which is a function of $T$.

  comment

• 2.I.10H

  Statistics | Part IB, 2004

  A study of 60 men and 90 women classified each individual according to eye colour to produce the figures below.

  \begin{tabular}{|c|c|c|c|} \cline { 2 - 4 } \multicolumn{1}{c|}{} & Blue & Brown & Green \ \hline Men & 20 & 20 & 20 \ \hline Women & 20 & 50 & 20 \ \hline \end{tabular}

  Explain how you would analyse these results. You should indicate carefully any underlying assumptions that you are making.

  A further study took 150 individuals and classified them both by eye colour and by whether they were left or right handed to produce the following table.

  \begin{tabular}{|c|c|c|c|} \cline { 2 - 4 } \multicolumn{1}{c|}{} & Blue & Brown & Green \ \hline Left Handed & 20 & 20 & 20 \ \hline Right Handed & 20 & 50 & 20 \ \hline \end{tabular}

  How would your analysis change? You should again set out your underlying assumptions carefully.

  [You may wish to note the following percentiles of the $\chi^{2}$ distribution.

  $\left.\begin{array}{ccccccc} & \chi_{1}^{2} & \chi_{2}^{2} & \chi_{3}^{2} & \chi_{4}^{2} & \chi_{5}^{2} & \chi_{6}^{2} \\ 95 \% \text { percentile } & 3.84 & 5.99 & 7.81 & 9.49 & 11.07 & 12.59 \\ 99 \% \text { percentile } & 6.64 & 9.21 & 11.34 & 13.28 & 15.09 & 16.81\end{array}\right]$

  comment

• 2.II.21H

  Statistics | Part IB, 2004

  Defining carefully the terminology that you use, state and prove the NeymanPearson Lemma.

  Let $X$ be a single observation from the distribution with density function

  $$f(x \mid \theta)=\frac{1}{2} e^{-|x-\theta|}, \quad-\infty<x<\infty$$

  for an unknown real parameter $\theta$. Find the best test of size $\alpha, 0<\alpha<1$, of the hypothesis $H_{0}: \theta=\theta_{0}$ against $H_{1}: \theta=\theta_{1}$, where $\theta_{1}>\theta_{0}$.

  When $\alpha=0.05$, for which values of $\theta_{0}$ and $\theta_{1}$ will the power of the best test be at least $0.95$ ?

  comment

• 4.I $9 \mathrm{H} \quad$

  Statistics | Part IB, 2004

  Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, with $Y_{i}$ having the normal distribution with mean $\beta x_{i}$ and variance $\sigma^{2}$; here $\beta, \sigma^{2}$ are unknown and $x_{1}, \ldots, x_{n}$ are known constants.

  Derive the least-squares estimate of $\beta$.

  Explain carefully how to test the hypothesis $H_{0}: \beta=0$ against $H_{1}: \beta \neq 0$.

  comment

• 4.II.19H

  Statistics | Part IB, 2004

  It is required to estimate the unknown parameter $\theta$ after observing $X$, a single random variable with probability density function $f(x \mid \theta)$; the parameter $\theta$ has the prior distribution with density $\pi(\theta)$ and the loss function is $L(\theta, a)$. Show that the optimal Bayesian point estimate minimizes the posterior expected loss.

  Suppose now that $f(x \mid \theta)=\theta e^{-\theta x}, x>0$ and $\pi(\theta)=\mu e^{-\mu \theta}, \theta>0$, where $\mu>0$ is known. Determine the posterior distribution of $\theta$ given $X$.

  Determine the optimal Bayesian point estimate of $\theta$ in the cases when

  (i) $L(\theta, a)=(\theta-a)^{2}$, and

  (ii) $L(\theta, a)=|(\theta-a) / \theta|$.

  comment