Use Euler's equation to derive the momentum integral

$$\int_{S}\left(p n_{i}+\rho n_{j} u_{j} u_{i}\right) d S=0$$

for the steady flow $\mathbf{u}=\left(u_{1}, u_{2}, u_{3}\right)$ and pressure $p$ of an inviscid,incompressible fluid of density $\rho$, where $S$ is a closed surface with normal $\mathbf{n}$.

A cylindrical jet of water of area $A$ and speed $u$ impinges axisymmetrically on a stationary sphere of radius $a$ and is deflected into a conical sheet of vertex angle $\alpha$ as shown. Gravity is being ignored.

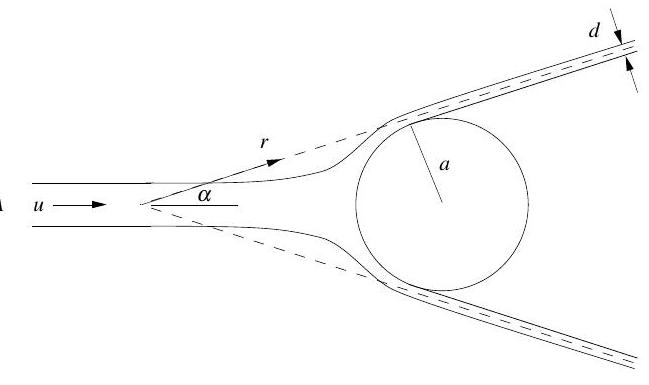
Use a suitable form of Bernoulli's equation to determine the speed of the water in the conical sheet, being careful to state how the equation is being applied.

Use conservation of mass to show that the width $d(r)$ of the sheet far from the point of impact is given by

$$d=\frac{A}{2 \pi r \sin \alpha},$$

where $r$ is the distance along the sheet measured from the vertex of the cone.

Finally, use the momentum integral to determine the net force on the sphere in terms of $\rho, u, A$ and $\alpha$.