Foundations Of Quantum Mechanics
Foundations Of Quantum Mechanics
Jump to year
A2.13 B2.22
(i) The creation and annihilation operators for a harmonic oscillator of angular frequency satisfy the commutation relation . Write down an expression for the Hamiltonian in terms of and .
There exists a unique ground state of such that . Explain how the space of eigenstates of is formed, and deduce the eigenenergies for these states. Show that
(ii) Write down the number operator of the harmonic oscillator in terms of and . Show that
The operator is defined to be
Show that commutes with . Show also that
By considering the action of on the state show that
A3.13 B3.21
(i) A quantum mechanical system consists of two identical non-interacting particles with associated single-particle wave functions and energies , where Show how the states for the two lowest energy levels of the system are constructed and discuss their degeneracy when the particles have (a) spin 0 , (b) spin .
(ii) The Pauli matrices are defined to be
State how the spin operators may be expressed in terms of the Pauli matrices, and show that they describe states with total angular momentum .
An electron is at rest in the presence of a magnetic field , and experiences an interaction potential . At the state of the electron is the eigenstate of with eigenvalue . Calculate the probability that at later time the electron will be measured to be in the eigenstate of with eigenvalue .
Part II 2004
A4.15 B4.22
The states of the hydrogen atom are denoted by with and associated energy eigenvalue , where
A hydrogen atom is placed in a weak electric field with interaction Hamiltonian
a) Derive the necessary perturbation theory to show that to the change in the energy associated with the state is given by
The wavefunction of the ground state is
By replacing , in the denominator of by show that
b) Find a matrix whose eigenvalues are the perturbed energies to for the states and . Hence, determine these perturbed energies to in terms of the matrix elements of between these states.
[Hint:
A2.13 B2.21
(i) Define the Heisenberg picture of quantum mechanics in relation to the Schrödinger picture. Explain how the two pictures provide equivalent descriptions of observable results.
Derive the equation of motion for an operator in the Heisenberg picture.
(ii) For a particle moving in one dimension, the Hamiltonian is
where and are the position and momentum operators, and the state vector is .
Eigenstates of and satisfy
Use standard methods in the Dirac formalism to show that
Calculate and express in terms of the position space wave function .
Compute the momentum space Hamiltonian for the harmonic oscillator with potential .
A3.13 B3.21
(i) What are the commutation relations satisfied by the components of an angular momentum vector ? State the possible eigenvalues of the component when has eigenvalue .
Describe how the Pauli matrices
are used to construct the components of the angular momentum vector for a spin system. Show that they obey the required commutation relations.
Show that and each have eigenvalues . Verify that has eigenvalue
(ii) Let and denote the standard operators and state vectors of angular momentum theory. Assume units where . Consider the operator
Show that
Show that the state vectors are eigenvectors of . Suppose that is measured for a system in the state ; show that the probability that the result is equals
Consider the case . Evaluate the probability that the measurement of will result in .
A4.15 B4.22
Discuss the quantum mechanics of the one-dimensional harmonic oscillator using creation and annihilation operators, showing how the energy levels are calculated.
A quantum mechanical system consists of two interacting harmonic oscillators and has the Hamiltonian
For , what are the degeneracies of the three lowest energy levels? For compute, to lowest non-trivial order in perturbation theory, the energies of the ground state and first excited state.
[Standard results for perturbation theory may be stated without proof.]
A2.13 B2.21
(i) A Hamiltonian has energy eigenvalues and corresponding non-degenerate eigenstates . Show that under a small change in the Hamiltonian ,
and derive the related formula for the change in the energy eigenvalue to first and second order in .
(ii) The Hamiltonian for a particle moving in one dimension is , where and is small. Show that
and hence that
to second order in .
Deduce that is independent of the particular state and explain why this change in energy is exact to all orders in .
A3.13 B3.21
(i) Two particles with angular momenta and basis states are combined to give total angular momentum and basis states . State the possible values of and show how a state with can be constructed. Briefly describe, for a general allowed value of , what the Clebsch-Gordan coefficients are.
(ii) If the angular momenta and are both 1 show that the combined state is
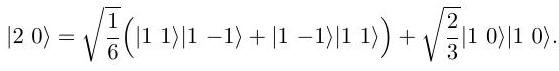
Determine the corresponding expressions for the combined states and , assuming that they are respectively antisymmetric and symmetric under interchange of the two particles.
If the combined system is in state what is the probability that measurements of the -component of angular momentum for either constituent particle will give the value of 1 ?
Hint:
A4.15 B4.22
Discuss the consequences of indistinguishability for a quantum mechanical state consisting of two identical, non-interacting particles when the particles have (a) spin zero, (b) spin 1/2.
The stationary Schrödinger equation for one particle in the potential
has normalized, spherically symmetric, real wave functions and energy eigenvalues with . What are the consequences of the Pauli exclusion principle for the ground state of the helium atom? Assuming that wavefunctions which are not spherically symmetric can be ignored, what are the states of the first excited energy level of the helium atom?
[You may assume here that the electrons are non-interacting.]
Show that, taking into account the interaction between the two electrons, the estimate for the energy of the ground state of the helium atom is
A2.13 B2.21
(i) Hermitian operators , satisfy . The eigenvectors , satisfy and . By differentiating with respect to verify that
and hence show that
Show that
and
(ii) A quantum system has Hamiltonian , where is a small perturbation. The eigenvalues of are . Give (without derivation) the formulae for the first order and second order perturbations in the energy level of a non-degenerate state. Suppose that the th energy level of has degenerate states. Explain how to determine the eigenvalues of corresponding to these states to first order in .
In a particular quantum system an orthonormal basis of states is given by , where are integers. The Hamiltonian is given by
where and unless and are both even.
Obtain an expression for the ground state energy to second order in the perturbation, . Find the energy eigenvalues of the first excited state to first order in the perturbation. Determine a matrix (which depends on two independent parameters) whose eigenvalues give the first order energy shift of the second excited state.
A3.13 B3.21
(i) Write the Hamiltonian for the harmonic oscillator,
in terms of creation and annihilation operators, defined by
Obtain an expression for by using the usual commutation relation between and . Deduce the quantized energy levels for this system.
(ii) Define the number operator, , in terms of creation and annihilation operators, and . The normalized eigenvector of with eigenvalue is . Show that .
Determine and in the basis defined by .
Show that
Verify the relation
by considering the action of both sides of the equation on an arbitrary basis vector.
A4.15 B4.22
(i) The two states of a spin- particle corresponding to spin pointing along the axis are denoted by and . Explain why the states
correspond to the spins being aligned along a direction at an angle to the direction.
The spin- 0 state of two spin- particles is
Show that this is independent of the direction chosen to define . If the spin of particle 1 along some direction is measured to be show that the spin of particle 2 along the same direction is determined, giving its value.
[The Pauli matrices are given by
(ii) Starting from the commutation relation for angular momentum in the form
obtain the possible values of , where are the eigenvalues of and are the eigenvalues of . Show that the corresponding normalized eigenvectors, , satisfy
and that
The state is defined by
for any complex . By expanding the exponential show that . Verify that
and hence show that
If verify that is a solution of the time-dependent Schrödinger equation.