Part II, 2002, Paper 1

Applications of Quantum Mechanics

• B1.23

  Applications of Quantum Mechanics | Part II, 2002

  A quantum system, with Hamiltonian $H_{0}$, has continuous energy eigenstates $|E\rangle$ for all $E \geq 0$, and also a discrete eigenstate $|0\rangle$, with $H_{0}|0\rangle=E_{0}|0\rangle,\langle 0 \mid 0\rangle=1, E_{0}>0$. A time-independent perturbation $H_{1}$, such that $\left\langle E\left|H_{1}\right| 0\right\rangle \neq 0$, is added to $H_{0}$. If the system is initially in the state $|0\rangle$ obtain the formula for the decay rate

  $$w=\frac{2 \pi}{\hbar} \rho\left(E_{0}\right)\left|\left\langle E_{0}\left|H_{1}\right| 0\right\rangle\right|^{2},$$

  where $\rho$ is the density of states.

  [You may assume that $\frac{1}{t}\left(\frac{\sin \frac{1}{2} \omega t}{\frac{1}{2} \omega}\right)^{2}$ behaves like $2 \pi \delta(\omega)$ for large $t$.]

  Assume that, for a particle moving in one dimension,

  $$H_{0}=E_{0}|0\rangle\left\langle 0\left|+\int_{-\infty}^{\infty} p^{2}\right| p\right\rangle\langle p| d p, \quad H_{1}=f \int_{-\infty}^{\infty}(|p\rangle\langle 0|+| 0\rangle\langle p|) d p$$

  where $\left\langle p^{\prime} \mid p\right\rangle=\delta\left(p^{\prime}-p\right)$, and $f$ is constant. Obtain $w$ in this case.

  comment

Coding and Cryptography

• A1.10

  Coding and Cryptography | Part II, 2002

  (i) Describe the original Hamming code of length 7 . Show how to encode a message word, and how to decode a received word involving at most one error. Explain why the procedure works.

  (ii) What is a linear binary code? What is its dual code? What is a cyclic binary code? Explain how cyclic binary codes of length $n$ correspond to polynomials in $\mathbb{F}_{2}[X]$ dividing $X^{n}+1$. Show that the dual of a cyclic code of length $n$ is cyclic of length $n$.

  Using the factorization

  $$X^{7}+1=(X+1)\left(X^{3}+X+1\right)\left(X^{3}+X^{2}+1\right)$$

  in $\mathbb{F}_{2}[X]$, find all cyclic binary codes of length 7 . Identify those which are Hamming codes and their duals. Justify your answer.

  comment

Combinatorics

• B1.5

  Combinatorics | Part II, 2002

  Prove that every graph $G$ on $n \geqslant 3$ vertices with minimal degree $\delta(G) \geqslant \frac{n}{2}$ is Hamiltonian. For each $n \geqslant 3$, give an example to show that this result does not remain true if we weaken the condition to $\delta(G) \geqslant \frac{n}{2}-1$ ( $n$ even) or $\delta(G) \geqslant \frac{n-1}{2}$ ( $n$ odd).

  Now let $G$ be a connected graph (with at least 2 vertices) without a cutvertex. Does $G$ Hamiltonian imply $G$ Eulerian? Does $G$ Eulerian imply $G$ Hamiltonian? Justify your answers.

  comment

Computational Statistics and Statistical Modelling

• A1.13

  Computational Statistics and Statistical Modelling | Part II, 2002

  (i) Suppose $Y_{1}, \ldots, Y_{n}$ are independent Poisson variables, and

  $$\mathbb{E}\left(Y_{i}\right)=\mu_{i}, \log \mu_{i}=\alpha+\beta^{T} x_{i}, 1 \leqslant i \leqslant n$$

  where $\alpha, \beta$ are unknown parameters, and $x_{1}, \ldots, x_{n}$ are given covariates, each of dimension $p$. Obtain the maximum-likelihood equations for $\alpha, \beta$, and explain briefly how you would check the validity of this model.

  (ii) The data below show $y_{1}, \ldots, y_{33}$, which are the monthly accident counts on a major US highway for each of the 12 months of 1970 , then for each of the 12 months of 1971 , and finally for the first 9 months of 1972 . The data-set is followed by the (slightly edited) $R$ output. You may assume that the factors 'Year' and 'month' have been set up in the appropriate fashion. Give a careful interpretation of this $R$ output, and explain (a) how you would derive the corresponding standardised residuals, and (b) how you would predict the number of accidents in October 1972 .

  $\begin{array}{llllllllllll}52 & 37 & 49 & 29 & 31 & 32 & 28 & 34 & 32 & 39 & 50 & 63 \\ 35 & 22 & 27 & 27 & 34 & 23 & 42 & 30 & 36 & 56 & 48 & 40 \\ 33 & 26 & 31 & 25 & 23 & 20 & 25 & 20 & 36 & & & \end{array}$

  $>$ first.glm $-\operatorname{glm}(\mathrm{y} \sim$ Year $+$ month, poisson $) ;$ summary(first.glm $)$

  Call:

  $\operatorname{glm}($ formula $=\mathrm{y} \sim$ Year $+$ month, family $=$ poisson $)$

  \begin{tabular}{lrlll} Coefficients: & & & & \ (Intercept) & Estimate & Std. Error & \multicolumn{1}{l}{ z value } & $\operatorname{Pr}(>|z|)$ \ Year1971 & $-0.81969$ & $0.09896$ & $38.600$ & $<2 e-16$ \ Year1972 & $-0.28794$ & $0.08267$ & $-3.483$ & $0.000496$ \ month2 & $-0.34484$ & $0.14176$ & $-2.433$ & $0.014994$ \ month3 & $-0.11466$ & $0.13296$ & $-0.862$ & $0.388459$ \ month4 & $-0.39304$ & $0.14380$ & $-2.733$ & $0.006271$ \ month5 & $-0.31015$ & $0.14034$ & $-2.210$ & $0.027108$ \ month6 & $-0.47000$ & $0.14719$ & $-3.193$ & $0.001408$ \ month7 & $-0.23361$ & $0.13732$ & $-1.701$ & $0.088889$ \ month8 & $-0.35667$ & $0.14226$ & $-2.507$ & $0.012168$ \ month9 & $-0.14310$ & $0.13397$ & $-1.068$ & $0.285444$ \ month10 & $0.10167$ & $0.13903$ & $0.731$ & $0.464628$ \ month11 & $0.13276$ & $0.13788$ & $0.963$ & $0.335639$ \ month12 & $0.18252$ & $0.13607$ & $1.341$ & $0.179812$ \end{tabular}

  Signif. codes: 0 (, $0.001$ (, $0.01$ (, $0.05$ '.

  (Dispersion parameter for poisson family taken to be 1 )

  $\begin{array}{rlll}\text { Null deviance: } & 101.143 & \text { on } 32 \text { degrees of freedom } \\ \text { Residual deviance: } & 27.273 & \text { on } 19 \text { degrees of freedom }\end{array}$

  Number of Fisher Scoring iterations: 3

  comment

Differentiable Manifolds

• B1.8

  Differentiable Manifolds | Part II, 2002

  What is meant by a "bump function" on $\mathbb{R}^{n}$ ? If $U$ is an open subset of a manifold $M$, prove that there is a bump function on $M$ with support contained in $U$.

  Prove the following.

  (i) Given an open covering $\mathcal{U}$ of a compact manifold $M$, there is a partition of unity on $M$ subordinate to $\mathcal{U}$.

  (ii) Every compact manifold may be embedded in some Euclidean space.

  comment

Dynamical Systems

• B1.17

  Dynamical Systems | Part II, 2002

  Let $f_{c}$ be the map of the closed interval $[0,1]$ to itself given by

  $$f_{c}(x)=c x(1-x), \text { where } 0 \leqslant c \leqslant 4 .$$

  Sketch the graphs of $f_{c}$ and (without proof) of $f_{c}^{2}$, find their fixed points, and determine which of the fixed points of $f_{c}$ are attractors. Does your argument work for $c=3 ?$

  comment

Dynamics of Differential Equations

• A1.6

  Dynamics of Differential Equations | Part II, 2002

  (i) A system in $\mathbb{R}^{2}$ obeys the equations:

  $$\begin{aligned} &\dot{x}=x-x^{5}-2 x y^{4}-2 y^{3}\left(a-x^{2}\right) \\ &\dot{y}=y-x^{4} y-2 y^{5}+x^{3}\left(a-x^{2}\right) \end{aligned}$$

  where $a$ is a positive constant.

  By considering the quantity $V=\alpha x^{4}+\beta y^{4}$, where $\alpha$ and $\beta$ are appropriately chosen, show that if $a>1$ then there is a unique fixed point and a unique limit cycle. How many fixed points are there when $a<1$ ?

  (ii) Consider the second order system

  $$\ddot{x}-\left(a-b x^{2}\right) \dot{x}+x-x^{3}=0,$$

  where $a, b$ are constants.

  (a) Find the fixed points and determine their stability.

  (b) Show that if the fixed point at the origin is unstable and $3 a>b$ then there are no limit cycles.

  [You may find it helpful to use the Liénard coordinate $z=\dot{x}-a x+\frac{1}{3} b x^{3}$.]

  comment

Electrodynamics

• B1.21

  Electrodynamics | Part II, 2002

  Explain how one can write Maxwell's equations in relativistic form by introducing an antisymmetric field strength tensor $F_{a b}$.

  In an inertial frame $S$, the electric and magnetic fields are $\mathbf{E}$ and $\mathbf{B}$. Suppose that there is a second inertial frame $S^{\prime}$ moving with velocity $v$ along the $x$-axis relative to $S$. Derive the rules for finding the electric and magnetic fields $\mathbf{E}^{\prime}$ and $\mathbf{B}^{\prime}$ in the frame $S^{\prime}$. Show that $|\mathbf{E}|^{2}-|\mathbf{B}|^{2}$ and $\mathbf{E} \cdot \mathbf{B}$ are invariant under Lorentz transformations.

  Suppose that $\mathbf{E}=E_{0}(0,1,0)$ and $\mathbf{B}=E_{0}(0, \cos \theta, \sin \theta)$, where $0 \leq \theta<\pi / 2$. At what velocity must an observer be moving in the frame $S$ for the electric and magnetic fields to appear to be parallel?

  Comment on the case $\theta=\pi / 2$.

  comment

Fluid Dynamics II

• B1.25

  Fluid Dynamics II | Part II, 2002

  State the minimum dissipation theorem for Stokes flow in a bounded domain.

  Fluid of density $\rho$ and viscosity $\mu$ fills an infinite cylindrical annulus $a \leq r \leq b$ between a fixed cylinder $r=a$ and a cylinder $r=b$ which rotates about its axis with constant angular velocity $\Omega$. In cylindrical polar coordinates $(r, \theta, z)$, the fluid velocity is $\mathbf{u}=(0, v(r), 0)$. The Reynolds number $\rho \Omega b^{2} / \mu$ is not necessarily small. Show that $v(r)=A r+B / r$, where $A$ and $B$ are constants to be determined.

  [You may assume that $\nabla^{2} \mathbf{u}=\left(0, \nabla^{2} v-v / r^{2}, 0\right)$ and $(\mathbf{u} \cdot \nabla) \mathbf{u}=\left(-v^{2} / r, 0,0\right) .$ ]

  Show that the outer cylinder exerts a couple $G_{0}$ per unit length on the fluid, where

  $$G_{0}=\frac{4 \pi \mu \Omega a^{2} b^{2}}{b^{2}-a^{2}} .$$

  [You may assume that, in standard notation, $e_{r \theta}=\frac{r}{2} \frac{d}{d r}\left(\frac{v}{r}\right)$.]

  Suppose now that $b \geq \sqrt{2} a$ and that the cylinder $r=a$ is replaced by a fixed cylinder whose cross-section is a square of side $2 a$ centred on $r=0$, all other conditions being unchanged. The flow may still be assumed steady. Explaining your argument carefully, show that the couple $G$ now required to maintain the motion of the outer cylinder is greater than $G_{0}$.

  comment

Functional Analysis

• A1.3

  Functional Analysis | Part II, 2002

  (i) Let $P_{r}\left(e^{i \theta}\right)$ be the real part of $\frac{1+r e^{i \theta}}{1-r e^{i \theta}}$. Establish the following properties of $P_{r}$ for $0 \leqslant r<1$ : (a) $0<P_{r}\left(e^{i \theta}\right)=P_{r}\left(e^{-i \theta}\right) \leqslant \frac{1+r}{1-r}$; (b) $P_{r}\left(e^{i \theta}\right) \leqslant P_{r}\left(e^{i \delta}\right)$ for $0<\delta \leqslant|\theta| \leqslant \pi$; (c) $P_{r}\left(e^{i \theta}\right) \rightarrow 0$, uniformly on $0<\delta \leqslant|\theta| \leqslant \pi$, as $r$ increases to 1 .

  (ii) Suppose that $f \in L^{1}(\mathbf{T})$, where $\mathbf{T}$ is the unit circle $\left\{e^{i \theta}:-\pi \leqslant \theta \leqslant \pi\right\}$. By definition, $\|f\|_{1}=\frac{1}{2 \pi} \int_{-\pi}^{\pi}\left|f\left(e^{i \theta}\right)\right| d \theta$. Let

  $$P_{r}(f)\left(e^{i \theta}\right)=\frac{1}{2 \pi} \int_{-\pi}^{\pi} P_{r}\left(e^{i(\theta-t)}\right) f\left(e^{i t}\right) d t$$

  Show that $P_{r}(f)$ is a continuous function on $\mathbf{T}$, and that $\left\|P_{r}(f)\right\|_{1} \leqslant\|f\|_{1}$.

  [You may assume without proof that $\frac{1}{2 \pi} \int_{-\pi}^{\pi} P_{r}\left(e^{i \theta}\right) d \theta=1$.]

  Show that $P_{r}(f) \rightarrow f$, uniformly on $\mathbf{T}$ as $r$ increases to 1 , if and only if $f$ is a continuous function on $\mathbf{T}$.

  Show that $\left\|P_{r}(f)-f\right\|_{1} \rightarrow 0$ as $r$ increases to 1 .

  comment

Galois Theory

• B1.7

  Galois Theory | Part II, 2002

  Let $F \subset K$ be a finite extension of fields and let $G$ be the group of $F$-automorphisms of $K$. State a result relating the order of $G$ to the degree $[K: F]$.

  Now let $K=k\left(X_{1}, \ldots, X_{4}\right)$ be the field of rational functions in four variables over a field $k$ and let $F=k\left(s_{1}, \ldots, s_{4}\right)$ where $s_{1}, \ldots, s_{4}$ are the elementary symmetric polynomials in $k\left[X_{1}, \ldots, X_{4}\right]$. Show that the degree $[K: F] \leqslant 4$ ! and deduce that $F$ is the fixed field of the natural action of the symmetric group $S_{4}$ on $K$.

  Show that $X_{1} X_{3}+X_{2} X_{4}$ has a cubic minimum polynomial over $F$. Let $G=$ $\langle\sigma, \tau\rangle \subset S_{4}$ be the dihedral group generated by the permutations $\sigma=(1234)$ and $\tau=(13)$. Show that the fixed field of $G$ is $F\left(X_{1} X_{3}+X_{2} X_{4}\right)$. Find the fixed field of the subgroup $H=\left\langle\sigma^{2}, \tau\right\rangle$.

  comment

General Relativity

• A1.15 B1.24

  General Relativity | Part II, 2002

  (i) Given a covariant vector field $V_{a}$, define the curvature tensor $R_{b c d}^{a}$ by

  $$V_{a ; b c}-V_{a ; c b}=V_{e} R_{a b c}^{e}$$

  Express $R_{a b c}^{e}$ in terms of the Christoffel symbols and their derivatives. Show that

  $$R_{a b c}^{e}=-R_{a c b}^{e}$$

  Further, by setting $V_{a}=\partial \phi / \partial x^{a}$, deduce that

  $$R_{a b c}^{e}+R_{c a b}^{e}+R_{b c a}^{e}=0 .$$

  (ii) Write down an expression similar to (*) given in Part (i) for the quantity

  $$g_{a b ; c d}-g_{a b ; d c}$$

  and hence show that

  $$R_{e a b c}=-R_{a e b c} .$$

  Define the Ricci tensor, show that it is symmetric and write down the contracted Bianchi identities.

  In certain spacetimes of dimension $n \geq 2, R_{a b c d}$ takes the form

  $$R_{a b c d}=K\left(x^{e}\right)\left[g_{a c} g_{b d}-g_{a d} g_{b c}\right]$$

  Obtain the Ricci tensor and Ricci scalar. Deduce that $K$ is a constant in such spacetimes if the dimension $n$ is greater than 2 .

  comment

Graph Theory

• A1.8

  Graph Theory | Part II, 2002

  (i) State and prove a necessary and sufficient condition for a graph to be Eulerian (that is, to have an Eulerian circuit).

  Prove that, given any connected non-Eulerian graph $G$, there is an Eulerian graph $H$ and a vertex $v \in H$ such that $G=H-v$.

  (ii) Let $G$ be a connected plane graph with $n$ vertices, $e$ edges and $f$ faces. Prove that $n-e+f=2$. Deduce that $e \leq g(n-2) /(g-2)$, where $g$ is the smallest face size.

  The crossing number $c(G)$ of a non-planar graph $G$ is the minimum number of edgecrossings needed when drawing the graph in the plane. (The crossing of three edges at the same point is not allowed.) Show that if $G$ has $n$ vertices and $e$ edges then $c(G) \geq e-3 n+6$. Find $c\left(K_{6}\right)$.

  comment

Groups, Rings and Fields

• A1.4

  Groups, Rings and Fields | Part II, 2002

  (i) What is a Sylow subgroup? State Sylow's Theorems.

  Show that any group of order 33 is cyclic.

  (ii) Prove the existence part of Sylow's Theorems.

  [You may use without proof any arithmetic results about binomial coefficients which you need.]

  Show that a group of order $p^{2} q$, where $p$ and $q$ are distinct primes, is not simple. Is it always abelian? Give a proof or a counterexample.

  comment

• B1.3

  Groups, Rings and Fields | Part II, 2002

  State Sylow's Theorems. Prove the existence part of Sylow's Theorems.

  Show that any group of order 33 is cyclic.

  Show that a group of order $p^{2} q$, where $p$ and $q$ are distinct primes, is not simple. Is it always abelian? Give a proof or a counterexample.

  comment

Hilbert Spaces

• B1.10

  Hilbert Spaces | Part II, 2002

  Let $H$ be a Hilbert space and let $T \in \mathcal{B}(H)$. Define what it means for $T$ to be bounded below. Prove that, if $L T=I$ for some $L \in \mathcal{B}(H)$, then $T$ is bounded below.

  Prove that an operator $T \in \mathcal{B}(H)$ is invertible if and only if both $T$ and $T^{*}$ are bounded below.

  Let $H$ be the sequence space $\ell^{2}$. Define the operators $S, R$ on $H$ by setting

  $$S(\xi)=\left(0, \xi_{1}, \xi_{2}, \xi_{3}, \ldots\right), \quad R(\xi)=\left(\xi_{2}, \xi_{3}, \xi_{4}, \ldots\right),$$

  for all $\xi=\left(\xi_{1}, \xi_{2}, \xi_{3}, \ldots\right) \in \ell^{2}$. Check that $R S=I$ but $S R \neq I$. Let $D=\{\lambda \in \mathbb{C}:|\lambda|<$ $1\}$. For each $\lambda \in D$, explain why $I-\lambda R$ is invertible, and define

  $$R(\lambda)=(I-\lambda R)^{-1} R$$

  Show that, for all $\lambda \in D$, we have $R(\lambda)(S-\lambda I)=I$, but $(S-\lambda I) R(\lambda) \neq I$. Deduce that, for all $\lambda \in D$, the operator $S-\lambda I$ is bounded below, but is not invertible. Deduce also that $\operatorname{Sp} S=\{\lambda \in \mathbb{C}:|\lambda| \leqslant 1\}$.

  Let $\lambda \in \mathbb{C}$ with $|\lambda|=1$, and for $n=1,2, \ldots$, define the element $x_{n}$ of $\ell^{2}$ by

  $$x_{n}=n^{-1 / 2}\left(\lambda^{-1}, \lambda^{-2}, \ldots, \lambda^{-n}, 0,0, \ldots\right) .$$

  Prove that $\left\|x_{n}\right\|=1$ but that $(S-\lambda I) x_{n} \rightarrow 0$ as $n \rightarrow \infty$. Deduce that, for $|\lambda|=1, S-\lambda I$ is not bounded below.

  comment

Information Theory

• B1.14

  Information Theory | Part II, 2002

  (a) Define the entropy $h(X)$ and the mutual entropy $i(X, Y)$ of random variables $X$ and $Y$. Prove the inequality

  $$0 \leqslant i(X, Y) \leqslant \min \{h(X), h(Y)\}$$

  [You may assume the Gibbs inequality.]

  (b) Let $X$ be a random variable and let $\mathbf{Y}=\left(Y_{1}, \ldots, Y_{n}\right)$ be a random vector.

  (i) Prove or disprove by producing a counterexample the inequality

  $$i(X, \mathbf{Y}) \leqslant \sum_{j=1}^{n} i\left(X, Y_{j}\right)$$

  first under the assumption that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and then under the assumption that $Y_{1}, \ldots, Y_{n}$ are conditionally independent given $X$.

  (ii) Prove or disprove by producing a counterexample the inequality

  $$i(X, \mathbf{Y}) \geqslant \sum_{j=1}^{n} i\left(X, Y_{j}\right)$$

  first under the assumption that $Y_{1}, \ldots, Y_{n}$ are independent random variables, and then under the assumption that $Y_{1}, \ldots, Y_{n}$ are conditionally independent given $X$.

  comment

Logic, Computation and Set Theory

• A $1 . 7 \quad$ B1.12

  Logic, Computation and Set Theory | Part II, 2002

  (i) State the Knaster-Tarski fixed point theorem. Use it to prove the Cantor-Bernstein Theorem; that is, if there exist injections $A \rightarrow B$ and $B \rightarrow A$ for two sets $A$ and $B$ then there exists a bijection $A \rightarrow B$.

  (ii) Let $A$ be an arbitrary set and suppose given a subset $R$ of $P A \times A$. We define a subset $B \subseteq A$ to be $R$-closed just if whenever $(S, a) \in R$ and $S \subseteq B$ then $a \in B$. Show that the set of all $R$-closed subsets of $A$ is a complete poset in the inclusion ordering.

  Now assume that $A$ is itself equipped with a partial ordering $\leqslant$.

  (a) Suppose $R$ satisfies the condition that if $b \geqslant a \in A$ then $(\{b\}, a) \in R$.

  Show that if $B$ is $R$-closed then $c \leqslant b \in B$ implies $c \in B$.

  (b) Suppose that $R$ satisfies the following condition. Whenever $(S, a) \in R$ and $b \leqslant a$ then there exists $T \subseteq A$ such that $(T, b) \in R$, and for every $t \in T$ we have (i) $(\{b\}, t) \in R$, and (ii) $t \leqslant s$ for some $s \in S$. Let $B$ and $C$ be $R$-closed subsets of $A$. Show that the set

  $$[B \rightarrow C]=\{a \in A \mid \forall b \leqslant a(b \in B \Rightarrow b \in C)\}$$

  is $R$-closed.

  comment

Markov Chains

• A1.1 B1.1

  Markov Chains | Part II, 2002

  (i) We are given a finite set of airports. Assume that between any two airports, $i$ and $j$, there are $a_{i j}=a_{j i}$ flights in each direction on every day. A confused traveller takes one flight per day, choosing at random from all available flights. Starting from $i$, how many days on average will pass until the traveller returns again to $i$ ? Be careful to allow for the case where there may be no flights at all between two given airports.

  (ii) Consider the infinite tree $T$ with root $R$, where, for all $m \geqslant 0$, all vertices at distance $2^{m}$ from $R$ have degree 3 , and where all other vertices (except $R$ ) have degree 2 . Show that the random walk on $T$ is recurrent.

  comment

Methods of Mathematical Physics

• B1.19

  Methods of Mathematical Physics | Part II, 2002

  State the Riemann-Lebesgue lemma as applied to the integral

  $$\int_{a}^{b} g(u) e^{i x u} d u$$

  where $g^{\prime}(u)$ is continuous and $a, b \in \mathbb{R}$.

  Use this lemma to show that, as $x \rightarrow+\infty$,

  $$\int_{a}^{b}(u-a)^{\lambda-1} f(u) e^{i x u} d u \sim f(a) e^{i x a} e^{i \pi \lambda / 2} \Gamma(\lambda) x^{-\lambda}$$

  where $f(u)$ is holomorphic, $f(a) \neq 0$ and $0<\lambda<1$. You should explain each step of your argument, but detailed analysis is not required.

  Hence find the leading order asymptotic behaviour as $x \rightarrow+\infty$ of

  $$\int_{0}^{1} \frac{e^{i x t^{2}}}{\left(1-t^{2}\right)^{\frac{1}{2}}} d t$$

  comment

Number Fields

• B1.9

  Number Fields | Part II, 2002

  Explain what is meant by an integral basis $\omega_{1}, \ldots, \omega_{n}$ of a number field $K$. Give an expression for the discriminant of $K$ in terms of the traces of the $\omega_{i} \omega_{j}$.

  Let $K=\mathbb{Q}(i, \sqrt{2})$. By computing the traces $T_{K / k}(\theta)$, where $k$ runs through the three quadratic subfields of $K$, show that the algebraic integers $\theta$ in $K$ have the form $\frac{1}{2}(\alpha+\beta \sqrt{2})$, where $\alpha=a+i b$ and $\beta=c+i d$ are Gaussian integers. By further computing the norm $N_{K / k}(\theta)$, where $k=\mathbb{Q}(\sqrt{2})$, show that $a$ and $b$ are even and that $c \equiv d(\bmod 2)$. Hence prove that an integral basis for $K$ is $1, i, \sqrt{2}, \frac{1}{2}(1+i) \sqrt{2}$.

  Calculate the discriminant of $K$.

  comment

Number Theory

• A1.9

  Number Theory | Part II, 2002

  (i) Let $p$ be a prime number. Prove that the multiplicative group of the field with $p$ elements is cyclic.

  (ii) Let $p$ be an odd prime, and let $k \geqslant 1$ be an integer. Prove that we have $x^{2} \equiv 1 \bmod p^{k}$ if and only if either $x \equiv 1 \bmod p^{k}$ or $x \equiv-1 \bmod p^{k}$. Is this statement true when $p=2$ ?

  Let $m$ be an odd positive integer, and let $r$ be the number of distinct prime factors of $m$. Prove that there are precisely $2^{r}$ different integers $x$ satisfying $x^{2} \equiv 1 \bmod m$ and $0<x<m$.

  comment

Numerical Analysis

• A1.20 B1.20

  Numerical Analysis | Part II, 2002

  (i) Let $A$ be an $n \times n$ symmetric real matrix with distinct eigenvalues $\lambda_{1}, \lambda_{2}, \ldots, \lambda_{n}$ and corresponding eigenvectors $\mathbf{v}_{1}, \mathbf{v}_{2}, \ldots, \mathbf{v}_{n}$, where $\left\|\mathbf{v}_{l}\right\|=1$. Given $\mathbf{x}^{(0)} \in \mathbb{R}^{n},\left\|\mathbf{x}^{(0)}\right\|=1$, the sequence $\mathbf{x}^{(k)}$ is generated in the following manner. We set

  $$\begin{gathered} \mu=\mathbf{x}^{(k) T} A \mathbf{x}^{(k)} \\ \mathbf{y}=(A-\mu I)^{-1} \mathbf{x}^{(k)} \\ \mathbf{x}^{(k+1)}=\frac{\mathbf{y}}{\|\mathbf{y}\|} \end{gathered}$$

  Show that if

  $$\mathbf{x}^{(k)}=c^{-1}\left(\mathbf{v}_{1}+\alpha \sum_{l=2}^{n} d_{l} \mathbf{v}_{l}\right)$$

  where $\alpha$ is a real scalar and $c$ is chosen so that $\left\|\mathbf{x}^{(k)}\right\|=1$, then

  $$\mu=c^{-2}\left(\lambda_{1}+\alpha^{2} \sum_{j=2}^{n} \lambda_{j} d_{j}^{2}\right)$$

  Give an explicit expression for $c$.

  (ii) Use the above result to prove that, if $|\alpha|$ is small,

  $$\mathbf{x}^{(k+1)}=\tilde{c}^{-1}\left(\mathbf{v}_{1}+\alpha^{3} \sum_{l=2}^{n} \tilde{d}_{l} \mathbf{v}_{l}\right)+O\left(\alpha^{4}\right)$$

  and obtain the numbers $\tilde{c}$ and $\tilde{d}_{2}, \ldots, \tilde{d}_{n}$.

  comment

Partial Differential Equations

• B1.18

  Partial Differential Equations | Part II, 2002

  (a) Solve the equation, for a function $u(x, y)$,

  $$\frac{\partial u}{\partial x}+\frac{\partial u}{\partial y}=0$$

  together with the boundary condition on the $x$-axis:

  $$u(x, 0)=x$$

  Find for which real numbers $a$ it is possible to solve $(*)$ with the following boundary condition specified on the line $y=a x$ :

  $$u(x, a x)=x$$

  Explain your answer in terms of the notion of characteristic hypersurface, which should be defined.

  (b) Solve the equation

  $$\frac{\partial u}{\partial x}+(1+u) \frac{\partial u}{\partial y}=0$$

  with the boundary condition on the $x$-axis

  $$u(x, 0)=x$$

  in the domain $\mathcal{D}=\left\{(x, y): 0<y<(x+1)^{2} / 4,-1<x<\infty\right\}$. Sketch the characteristics.

  comment

Principles of Dynamics

• A1.2 B1.2

  Principles of Dynamics | Part II, 2002

  (i) Derive Hamilton's equations from Lagrange's equations. Show that the Hamiltonian $H$ is constant if the Lagrangian $L$ does not depend explicitly on time.

  (ii) A particle of mass $m$ is constrained to move under gravity, which acts in the negative $z$-direction, on the spheroidal surface $\epsilon^{-2}\left(x^{2}+y^{2}\right)+z^{2}=l^{2}$, with $0<\epsilon \leqslant 1$. If $\theta, \phi$ parametrize the surface so that

  $$x=\epsilon l \sin \theta \cos \phi, y=\epsilon l \sin \theta \sin \phi, z=l \cos \theta,$$

  find the Hamiltonian $H\left(\theta, \phi, p_{\theta}, p_{\phi}\right)$.

  Show that the energy

  $$E=\frac{p_{\theta}^{2}}{2 m l^{2}\left(\epsilon^{2} \cos ^{2} \theta+\sin ^{2} \theta\right)}+\frac{\alpha}{\sin ^{2} \theta}+m g l \cos \theta$$

  is a constant of the motion, where $\alpha$ is a non-negative constant.

  Rewrite this equation as

  $$\frac{1}{2} \dot{\theta}^{2}+V_{\mathrm{eff}}(\theta)=0$$

  and sketch $V_{\mathrm{eff}}(\theta)$ for $\epsilon=1$ and $\alpha>0$, identifying the maximal and minimal values of $\theta(t)$ for fixed $\alpha$ and $E$. If $\epsilon$ is now taken not to be unity, how do these values depend on $\epsilon$ ?

  comment

Principles of Statistics

• A1.12 B1.15

  Principles of Statistics | Part II, 2002

  (i) Explain in detail the minimax and Bayes principles of decision theory.

  Show that if $d(X)$ is a Bayes decision rule for a prior density $\pi(\theta)$ and has constant risk function, then $d(X)$ is minimax.

  (ii) Let $X_{1}, \ldots, X_{p}$ be independent random variables, with $X_{i} \sim N\left(\mu_{i}, 1\right), i=1, \ldots, p$.

  Consider estimating $\mu=\left(\mu_{1}, \ldots, \mu_{p}\right)^{T}$ by $d=\left(d_{1}, \ldots, d_{p}\right)^{T}$, with loss function

  $$L(\mu, d)=\sum_{i=1}^{p}\left(\mu_{i}-d_{i}\right)^{2}$$

  What is the risk function of $X=\left(X_{1}, \ldots, X_{p}\right)^{T} ?$

  Consider the class of estimators of $\mu$ of the form

  $$d^{a}(X)=\left(1-\frac{a}{X^{T} X}\right) X$$

  indexed by $a \geqslant 0$. Find the risk function of $d^{a}(X)$ in terms of $E\left(1 / X^{T} X\right)$, which you should not attempt to evaluate, and deduce that $X$ is inadmissible. What is optimal value of $a$ ?

  [You may assume Stein's Lemma, that for suitably behaved real-valued functions $h$,

  $$\left.E\left\{\left(X_{i}-\mu_{i}\right) h(X)\right\}=E\left\{\frac{\partial h(X)}{\partial X_{i}}\right\} . \quad\right]$$

  comment

Probability and Measure

• B1.13

  Probability and Measure | Part II, 2002

  State and prove Dynkin's $\pi$-system lemma.

  Let $(\Omega, \mathcal{F}, \mathbb{P})$ be a probability space and let $\left(A_{n}\right)$ be a sequence of independent events such that $\lim _{n \rightarrow \infty} \mathbb{P}\left(A_{n}\right)=p$. Let $\mathcal{G}=\sigma\left(A_{1}, A_{2}, \ldots\right)$. Prove that

  $$\lim _{n \rightarrow \infty} \mathbb{P}\left(G \cap A_{n}\right)=p \mathbb{P}(G)$$

  for all $G \in \mathcal{G}$.

  comment

Quantum Physics

• A1.14

  Quantum Physics | Part II, 2002

  (i) A system of $N$ identical non-interacting bosons has energy levels $E_{i}$ with degeneracy $g_{i}, 1 \leq i<\infty$, for each particle. Show that in thermal equilibrium the number of particles $N_{i}$ with energy $E_{i}$ is given by

  $$N_{i}=\frac{g_{i}}{e^{\beta\left(E_{i}-\mu\right)}-1}$$

  where $\beta$ and $\mu$ are parameters whose physical significance should be briefly explained.

  (ii) A photon moves in a cubical box of side $L$. Assuming periodic boundary conditions, show that, for large $L$, the number of photon states lying in the frequency range $\omega \rightarrow \omega+d \omega$ is $\rho(\omega) d \omega$ where

  $$\rho(\omega)=L^{3}\left(\frac{\omega^{2}}{\pi^{2} c^{3}}\right)$$

  If the box is filled with thermal radiation at temperature $T$, show that the number of photons per unit volume in the frequency range $\omega \rightarrow \omega+d \omega$ is $n(\omega) d \omega$ where

  $$n(\omega)=\left(\frac{\omega^{2}}{\pi^{2} c^{3}}\right) \frac{1}{e^{\hbar \omega / k T}-1} .$$

  Calculate the energy density $W$ of the thermal radiation. Show that the pressure $P$ exerted on the surface of the box satisfies

  $$P=\frac{1}{3} W$$

  [You may use the result $\int_{0}^{\infty} \frac{x^{3} d x}{e^{x}-1}=\frac{\pi^{4}}{15}$.]

  comment

Representation Theory

• B1.6

  Representation Theory | Part II, 2002

  Construct the character table of the symmetric group $S_{5}$, explaining the steps in your construction.

  Use the character table to show that the alternating group $A_{5}$ is the only non-trivial normal subgroup of $S_{5}$.

  comment

Riemann Surfaces

• B1.11

  Riemann Surfaces | Part II, 2002

  (a) Define the notions of (abstract) Riemann surface, holomorphic map, and biholomorphic map between Riemann surfaces.

  (b) Prove the following theorem on the local form of a holomorphic map.

  For a holomorphic map $f: R \rightarrow S$ between Riemann surfaces, which is not constant near a point $r \in R$, there exist neighbourhoods $U$ of $r$ in $R$ and $V$ of $f(r)$ in $S$, together with biholomorphic identifications $\phi: U \rightarrow \Delta, \psi: V \rightarrow \Delta$, such that $(\psi \circ f)(x)=\phi(x)^{n}$, for all $x \in U$.

  (c) Prove further that a non-constant holomorphic map between compact, connected Riemann surfaces is surjective.

  (d) Deduce from (c) the fundamental theorem of algebra.

  comment

Statistical Physics

• B1.22

  Statistical Physics | Part II, 2002

  A simple model for a rubber molecule consists of a one-dimensional chain of $n$ links each of fixed length $b$ and each of which is oriented in either the positive or negative direction. A unique state $i$ of the molecule is designated by giving the orientation $\pm 1$ of each link. If there are $n_{+}$links oriented in the positive direction and $n_{-}$links oriented in the negative direction then $n=n_{+}+n_{-}$and the length of the molecule is $l=\left(n_{+}-n_{-}\right) b$. The length of the molecule associated with state $i$ is $l_{i}$.

  What is the range of $l$ ?

  What is the number of states with $n, n_{+}, n_{-}$fixed?

  Consider an ensemble of $A$ copies of the molecule in which $a_{i}$ members are in state $i$ and write down the expression for the mean length $L$.

  By introducing a Lagrange multiplier $\tau$ for $L$ show that the most probable configuration for the $\left\{a_{i}\right\}$ with given length $L$ is found by maximizing

  $$\log \left(\frac{A !}{\prod_{i} a_{i} !}\right)+\tau \sum_{i} a_{i} l_{i}-\alpha \sum_{i} a_{i} .$$

  Hence show that the most probable configuration is given by

  $$p_{i}=\frac{e^{\tau l_{i}}}{Z},$$

  where $p_{i}$ is the probability for finding an ensemble member in the state $i$ and $Z$ is the partition function which should be defined.

  Show that $Z$ can be expressed as

  $$Z=\sum_{l} g(l) e^{\tau l}$$

  where the meaning of $g(l)$ should be explained.

  Hence show that $Z$ is given by

  $$Z=\sum_{n_{+}=0}^{n} \frac{n !}{n_{+} ! n_{-} !}\left(e^{\tau b}\right)^{n_{+}}\left(e^{-\tau b}\right)^{n_{-}}, \quad n_{+}+n_{-}=n$$

  and therefore that the free energy $G$ for the system is

  $$G=-n k T \log (2 \cosh \tau b) .$$

  Show that $\tau$ is determined by

  $$L=-\frac{1}{k T}\left(\frac{\partial G}{\partial \tau}\right)_{n}$$

  and hence that the equation of state is

  $$\tanh \tau b=\frac{L}{n b} .$$

  What are the independent variables on which $G$ depends?

  Explain why the tension in the rubber molecule is $k T \tau$.

  comment

Statistical Physics and Cosmology

• A1.16

  Statistical Physics and Cosmology | Part II, 2002

  (i) Consider a one-dimensional model universe with "stars" distributed at random on the $x$-axis, and choose the origin to coincide with one of the stars; call this star the "homestar." Home-star astronomers have discovered that all other stars are receding from them with a velocity $v(x)$, that depends on the position $x$ of the star. Assuming non-relativistic addition of velocities, show how the assumption of homogeneity implies that $v(x)=H_{0} x$ for some constant $H_{0}$.

  In attempting to understand the history of their one-dimensional universe, homestar astronomers seek to determine the velocity $v(t)$ at time $t$ of a star at position $x(t)$. Assuming homogeneity, show how $x(t)$ is determined in terms of a scale factor $a(t)$ and hence deduce that $v(t)=H(t) x(t)$ for some function $H(t)$. What is the relation between $H(t)$ and $H_{0}$ ?

  (ii) Consider a three-dimensional homogeneous and isotropic universe with mass density $\rho(t)$, pressure $p(t)$ and scale factor $a(t)$. Given that $E(t)$ is the energy in volume $V(t)$, show how the relation $d E=-p d V$ yields the "fluid" equation

  $$\dot{\rho}=-3\left(\rho+\frac{p}{c^{2}}\right) H$$

  where $H=\dot{a} / a$.

  Show how conservation of energy applied to a test particle at the boundary of a spherical fluid element yields the Friedmann equation

  $$\dot{a}^{2}-\frac{8 \pi G}{3} \rho a^{2}=-k c^{2}$$

  for constant $k$. Hence obtain an equation for the acceleration $\ddot{a}$ in terms of $\rho, p$ and $a$.

  A model universe has mass density and pressure

  $$\rho=\frac{\rho_{0}}{a^{3}}+\rho_{1}, \quad p=-\rho_{1} c^{2},$$

  where $\rho_{0}$ is constant. What does the fluid equation imply about $\rho_{1}$ ? Show that the acceleration $\ddot{a}$ vanishes if

  $$a=\left(\frac{\rho_{0}}{2 \rho_{1}}\right)^{\frac{1}{3}}$$

  Hence show that this universe is static and determine the sign of the constant $k$.

  comment

Stochastic Financial Models

• A1.11 B1.16

  Stochastic Financial Models | Part II, 2002

  (i) The prices, $S_{i}$, of a stock in a binomial model at times $i=0,1,2$ are represented by the following binomial tree.

  

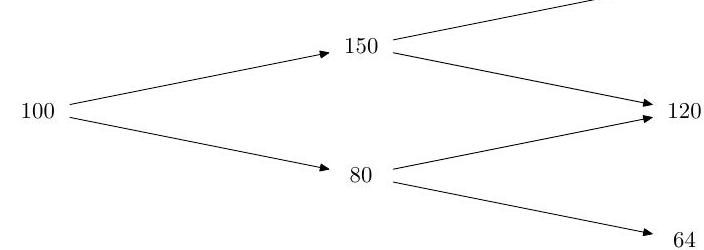
  The fixed interest rate per period is $1 / 5$ and the probability that the stock price increases in a period is $1 / 3$. Find the price at time 0 of a European call option with strike price 78 and expiry time $2 .$

  Explain briefly the ideas underlying your calculations.

  (ii) Consider an investor in a one-period model who may invest in $s$ assets, all of which are risky, with a random return vector $\boldsymbol{R}$ having mean $\mathbb{E} \boldsymbol{R}=\boldsymbol{r}$ and positivedefinite covariance matrix $\boldsymbol{V}$; assume that not all the assets have the same expected return. Show that any minimum-variance portfolio is equivalent to the investor dividing his wealth between two portfolios, the global minimum-variance portfolio and the diversified portfolio, both of which should be specified clearly in terms of $\boldsymbol{r}$ and $\boldsymbol{V}$.

  Now suppose that $\boldsymbol{R}=\left(R_{1}, R_{2}, \ldots, R_{s}\right)^{\top}$ where $R_{1}, R_{2}, \ldots, R_{s}$ are independent random variables with $R_{i}$ having the exponential distribution with probability density function $\lambda_{i} e^{-\lambda_{i} x}, x \geqslant 0$, where $\lambda_{i}>0,1 \leqslant i \leqslant s$. Determine the global minimum-variance portfolio and the diversified portfolio explicitly.

  Consider further the situation when the investor has the utility function $u(x)=$ $1-e^{-x}$, where $x$ denotes his wealth. Suppose that he acts to maximize the expected utility of his final wealth, and that his initial wealth is $w>0$. Show that he now divides his wealth between the diversified portfolio and the uniform portfolio, in which wealth is apportioned equally between the assets, and determine the amounts that he invests in each.

  comment

Symmetries and Groups in Physics

• A1.17

  Symmetries and Groups in Physics | Part II, 2002

  (i) Let $H$ be a normal subgroup of the group $G$. Let $G / H$ denote the group of cosets $\tilde{g}=g H$ for $g \in G$. If $D: G \rightarrow G L\left(\mathbb{C}^{n}\right)$ is a representation of $G$ with $D\left(h_{1}\right)=D\left(h_{2}\right)$ for all $h_{1}, h_{2} \in H$ show that $\tilde{D}(\tilde{g})=D(g)$ is well-defined and that it is a representation of $G / H$. Show further that $\tilde{D}(\tilde{g})$ is irreducible if and only if $D(g)$ is irreducible.

  (ii) For a matrix $U \in S U(2)$ define the linear map $\Phi_{U}: \mathbb{R}^{3} \rightarrow \mathbb{R}^{3}$ by $\Phi_{U}(\mathbf{x}) \cdot \boldsymbol{\sigma}=$ $U \mathbf{x} . \boldsymbol{\sigma} U^{\dagger}$ with $\boldsymbol{\sigma}=\left(\sigma_{1}, \sigma_{2}, \sigma_{3}\right)^{T}$ as the vector of the Pauli spin matrices

  $$\sigma_{1}=\left(\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right), \quad \sigma_{2}=\left(\begin{array}{cc} 0 & -i \\ i & 0 \end{array}\right), \quad \sigma_{3}=\left(\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array}\right)$$

  Show that $\left\|\Phi_{U}(\mathbf{x})\right\|=\|\mathbf{x}\|$. Because of the linearity of $\Phi_{U}$ there exists a matrix $R(U)$ such that $\Phi_{U}(\mathbf{x})=R(U) \mathbf{x}$. Given that any $S U(2)$ matrix can be written as

  $$U=\cos \alpha I-i \sin \alpha \mathbf{n} \cdot \boldsymbol{\sigma}$$

  where $\alpha \in[0, \pi]$ and $\mathbf{n}$ is a unit vector, deduce that $R(U) \in S O(3)$ for all $U \in S U(2)$. Compute $R(U) \mathbf{n}$ and $R(U) \mathbf{x}$ in the case that $\mathbf{x} \cdot \mathbf{n}=0$ and deduce that $R(U)$ is the matrix of a rotation about $\mathbf{n}$ with angle $2 \alpha$.

  [Hint: $\mathbf{m} . \boldsymbol{\sigma} \mathbf{n} . \boldsymbol{\sigma}=\mathbf{m} . \mathbf{n} I+i(\mathbf{m} \times \mathbf{n}) . \boldsymbol{\sigma} .]$

  Show that $R(U)$ defines a surjective homomorphism $\Theta: S U(2) \rightarrow S O(3)$ and find the kernel of $\Theta$.

  comment

Theoretical Geophysics

• A1.19

  Theoretical Geophysics | Part II, 2002

  (i) In a reference frame rotating about a vertical axis with constant angular velocity $f / 2$ the horizontal components of the momentum equation for a shallow layer of inviscid, incompressible fluid of constant density $\rho$ are

  $$\begin{aligned} &\frac{D u}{D t}-f v=-\frac{1}{\rho} \frac{\partial P}{\partial x} \\ &\frac{D v}{D t}+f u=-\frac{1}{\rho} \frac{\partial P}{\partial y} \end{aligned}$$

  where $u, v$ and $P$ are independent of the vertical coordinate $z$.

  Define the Rossby number $R o$ for a flow with typical velocity $U$ and lengthscale $L$. What is the approximate form of the above equations when $R o \ll 1$ ?

  Show that the solution to the approximate equations is given by a streamfunction $\psi$ proportional to $P$.

  Conservation of potential vorticity for such a flow is represented by

  $$\frac{D}{D t} \frac{\zeta+f}{h}=0$$

  where $\zeta$ is the vertical component of relative vorticity and $h(x, y)$ is the thickness of the layer. Explain briefly why the potential vorticity of a column of fluid should be conserved.

  (ii) Suppose that the thickness of the rotating, shallow-layer flow in Part (i) is $h(y)=H_{0} \exp (-\alpha y)$ where $H_{0}$ and $\alpha$ are constants. By linearising the equation of conservation of potential vorticity about $u=v=\zeta=0$, show that the stream function for small disturbances to the state of rest obeys

  $$\frac{\partial}{\partial t}\left(\frac{\partial^{2}}{\partial x^{2}}+\frac{\partial^{2}}{\partial y^{2}}\right) \psi+\beta \frac{\partial \psi}{\partial x}=0$$

  where $\beta$ is a constant that should be found.

  Obtain the dispersion relationship for plane-wave solutions of the form $\psi \propto$ $\exp [i(k x+l y-\omega t)]$. Hence calculate the group velocity.

  Show that if $\beta>0$ then the phase of these waves always propagates to the left (negative $x$ direction) but that the energy may propagate to either left or right.

  comment

Transport Processes

• A1.18

  Transport Processes | Part II, 2002

  (i) Material of thermal diffusivity $D$ occupies the semi-infinite region $x>0$ and is initially at uniform temperature $T_{0}$. For time $t>0$ the temperature at $x=0$ is held at a constant value $T_{1}>T_{0}$. Given that the temperature $T(x, t)$ in $x>0$ satisfies the diffusion equation $T_{t}=D T_{x x}$, write down the equation and the boundary and initial conditions satisfied by the dimensionless temperature $\theta=\left(T-T_{0}\right) /\left(T_{1}-T_{0}\right)$.

  Use dimensional analysis to show that the lengthscale of the region in which $T$ is significantly different from $T_{0}$ is proportional to $(D t)^{1 / 2}$. Hence show that this problem has a similarity solution

  $$\theta=\operatorname{erfc}(\xi / 2) \equiv \frac{2}{\sqrt{\pi}} \int_{\xi / 2}^{\infty} e^{-u^{2}} d u$$

  where $\xi=x /(D t)^{1 / 2}$.

  What is the rate of heat input, $-D T_{x}$, across the plane $x=0 ?$

  (ii) Consider the same problem as in Part (i) except that the boundary condition at $x=0$ is replaced by one of constant rate of heat input $Q$. Show that $\theta(\xi, t)$ satisfies the partial differential equation

  $$\theta_{\xi \xi}+\frac{\xi}{2} \theta_{\xi}=t \theta_{t}$$

  and write down the boundary conditions on $\theta(\xi, t)$. Deduce that the problem has a similarity solution of the form

  $$\theta=\frac{Q(t / D)^{1 / 2}}{T_{1}-T_{0}} f(\xi)$$

  Derive the ordinary differential equation and boundary conditions satisfied by $f(\xi)$.

  Differentiate this equation once to obtain

  $$f^{\prime \prime \prime}+\frac{\xi}{2} f^{\prime \prime}=0$$

  and solve for $f^{\prime}(\xi)$. Hence show that

  $$f(\xi)=\frac{2}{\sqrt{\pi}} e^{-\xi^{2} / 4}-\xi \operatorname{erfc}(\xi / 2)$$

  Sketch the temperature distribution $T(x, t)$ for various times $t$, and calculate $T(0, t)$ explicitly.

  comment

Waves in Fluid and Solid Media

• B1.26

  Waves in Fluid and Solid Media | Part II, 2002

  Starting from the equations governing sound waves linearized about a state with density $\rho_{0}$ and sound speed $c_{0}$, derive the acoustic energy equation, giving expressions for the local energy density $E$ and energy flux $\mathbf{I}$.

  A sphere executes small-amplitude vibrations, with its radius varying according to

  $$r(t)=a+\operatorname{Re}\left(\epsilon e^{i \omega t}\right)$$

  with $0<\epsilon \ll a$. Find an expression for the velocity potential of the sound, $\tilde{\phi}(r, t)$. Show that the time-averaged rate of working by the surface of the sphere is

  $$2 \pi a^{2} \rho_{0} \omega^{2} \epsilon^{2} c_{0} \frac{\omega^{2} a^{2}}{c_{0}^{2}+\omega^{2} a^{2}}$$

  Calculate the value at $r=a$ of the dimensionless ratio $c_{0} \bar{E} /|\overline{\mathbf{I}}|$, where the overbars denote time-averaged values, and comment briefly on the limits $c_{0} \ll \omega a$ and $c_{0} \gg \omega a$.

  comment