Part IB, 2012, Paper 2

Analysis II

• Paper 2, Section I, E

  Analysis II | Part IB, 2012

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be a function. What does it mean to say that $f$ is differentiable at a point $(x, y) \in \mathbb{R}^{2} ?$ Prove directly from this definition, that if $f$ is differentiable at $(x, y)$, then $f$ is continuous at $(x, y)$.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be the function:

  $$f(x, y)= \begin{cases}x^{2}+y^{2} & \text { if } x \text { and } y \text { are rational } \\ 0 & \text { otherwise. }\end{cases}$$

  For which points $(x, y) \in \mathbb{R}^{2}$ is $f$ differentiable? Justify your answer.

  comment

• Paper 2, Section II, E

  Analysis II | Part IB, 2012

  Let $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ be a mapping. Fix $a \in \mathbb{R}^{n}$ and prove that the following two statements are equivalent:

  (i) Given $\varepsilon>0$ there is $\delta>0$ such that $\|f(x)-f(a)\|<\varepsilon$ whenever $\|x-a\|<\delta$ (we use the standard norm in Euclidean space).

  (ii) $f\left(x_{n}\right) \rightarrow f(a)$ for any sequence $x_{n} \rightarrow a$.

  We say that $f$ is continuous if (i) (or equivalently (ii)) holds for every $a \in \mathbb{R}^{n}$.

  Let $E$ and $F$ be subsets of $\mathbb{R}^{n}$ and $\mathbb{R}^{m}$ respectively. For $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ as above, determine which of the following statements are always true and which may be false, giving a proof or a counterexample as appropriate.

  (a) If $f^{-1}(F)$ is closed whenever $F$ is closed, then $f$ is continuous.

  (b) If $f$ is continuous, then $f^{-1}(F)$ is closed whenever $F$ is closed.

  (c) If $f$ is continuous, then $f(E)$ is open whenever $E$ is open.

  (d) If $f$ is continuous, then $f(E)$ is bounded whenever $E$ is bounded.

  (e) If $f$ is continuous and $f^{-1}(F)$ is bounded whenever $F$ is bounded, then $f(E)$ is closed whenever $E$ is closed.

  comment

Complex Analysis or Complex Methods

• Paper 2, Section II, A

  Complex Analysis or Complex Methods | Part IB, 2012

  By a suitable choice of contour show that, for $-1<\alpha<1$,

  $$\int_{0}^{\infty} \frac{x^{\alpha}}{1+x^{2}} \mathrm{~d} x=\frac{\pi}{2 \cos (\alpha \pi / 2)}$$

  comment

Electromagnetism

• Paper 2, Section I, B

  Electromagnetism | Part IB, 2012

  Write down the expressions for a general, time-dependent electric field $\mathbf{E}$ and magnetic field $\mathbf{B}$ in terms of a vector potential $\mathbf{A}$ and scalar potential $\phi$. What is meant by a gauge transformation of $\mathbf{A}$ and $\phi$ ? Show that $\mathbf{E}$ and $\mathbf{B}$ are unchanged under a gauge transformation.

  A plane electromagnetic wave has vector and scalar potentials

  $$\begin{aligned} \mathbf{A}(\mathbf{x}, t) &=\mathbf{A}_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)} \\ \phi(\mathbf{x}, t) &=\phi_{0} e^{i(\mathbf{k} \cdot \mathbf{x}-\omega t)} \end{aligned}$$

  where $\mathbf{A}_{0}$ and $\phi_{0}$ are constants. Show that $\left(\mathbf{A}_{0}, \phi_{0}\right)$ can be modified to $\left(\mathbf{A}_{0}+\mu \mathbf{k}, \phi_{0}+\mu \omega\right)$ by a gauge transformation. What choice of $\mu$ leads to the modified $\mathbf{A}(\mathbf{x}, t)$ satisfying the Coulomb gauge condition $\boldsymbol{\nabla} \cdot \mathbf{A}=0$ ?

  comment

• Paper 2, Section II, B

  Electromagnetism | Part IB, 2012

  A straight wire has $n$ mobile, charged particles per unit length, each of charge $q$. Assuming the charges all move with velocity $v$ along the wire, show that the current is $I=n q v$.

  Using the Lorentz force law, show that if such a current-carrying wire is placed in a uniform magnetic field of strength $B$ perpendicular to the wire, then the force on the wire, per unit length, is $B I$.

  Consider two infinite parallel wires, with separation $L$, carrying (in the same sense of direction) positive currents $I_{1}$ and $I_{2}$, respectively. Find the force per unit length on each wire, determining both its magnitude and direction.

  comment

Fluid Dynamics

• Paper 2, Section I, A

  Fluid Dynamics | Part IB, 2012

  Starting from Euler's equation for the motion of an inviscid fluid, derive the vorticity equation in the form

  $$\frac{D \boldsymbol{\omega}}{D t}=\boldsymbol{\omega} \cdot \nabla \boldsymbol{u}$$

  Deduce that an initially irrotational flow remains irrotational.

  Consider a plane flow that at time $t=0$ is described by the streamfunction

  $$\psi=x^{2}+y^{2} .$$

  Calculate the vorticity everywhere at times $t>0$.

  comment

Geometry

• Paper 2, Section II, G

  Geometry | Part IB, 2012

  Let $S$ be a closed surface, equipped with a triangulation. Define the Euler characteristic $\chi(S)$ of $S$. How does $\chi(S)$ depend on the triangulation?

  Let $V, E$ and $F$ denote the number of vertices, edges and faces of the triangulation. Show that $2 E=3 F$.

  Suppose now the triangulation is tidy, meaning that it has the property that no two vertices are joined by more than one edge. Deduce that $V$ satisfies

  $$V \geqslant \frac{7+\sqrt{49-24 \chi(S)}}{2} .$$

  Hence compute the minimal number of vertices of a tidy triangulation of the real projective plane. [Hint: it may be helpful to consider the icosahedron as a triangulation of the sphere $\left.S^{2} .\right]$

  comment

Groups, Rings and Modules

• Paper 2, Section I, $2 G$

  Groups, Rings and Modules | Part IB, 2012

  What does it mean to say that the finite group $G$ acts on the set $\Omega$ ?

  By considering an action of the symmetry group of a regular tetrahedron on a set of pairs of edges, show there is a surjective homomorphism $S_{4} \rightarrow S_{3}$.

  [You may assume that the symmetric group $S_{n}$ is generated by transpositions.]

  comment

• Paper 2, Section II, G

  Groups, Rings and Modules | Part IB, 2012

  State Gauss's Lemma. State Eisenstein's irreducibility criterion.

  (i) By considering a suitable substitution, show that the polynomial $1+X^{3}+X^{6}$ is irreducible over $\mathbb{Q}$.

  (ii) By working in $\mathbb{Z}_{2}[X]$, show that the polynomial $1-X^{2}+X^{5}$ is irreducible over $\mathbb{Q}$.

  comment

Linear Algebra

• Paper 2, Section I, $1 F$

  Linear Algebra | Part IB, 2012

  Define the determinant $\operatorname{det} A$ of an $n \times n$ real matrix $A$. Suppose that $X$ is a matrix with block form

  $$X=\left(\begin{array}{cc} A & B \\ 0 & C \end{array}\right) \text {, }$$

  where $A, B$ and $C$ are matrices of dimensions $n \times n, n \times m$ and $m \times m$ respectively. Show that $\operatorname{det} X=(\operatorname{det} A)(\operatorname{det} C)$.

  comment

• Paper 2, Section II, F

  Linear Algebra | Part IB, 2012

  (i) Define the transpose of a matrix. If $V$ and $W$ are finite-dimensional real vector spaces, define the dual of a linear map $T: V \rightarrow W$. How are these two notions related?

  Now suppose $V$ and $W$ are finite-dimensional inner product spaces. Use the inner product on $V$ to define a linear map $V \rightarrow V^{*}$ and show that it is an isomorphism. Define the adjoint of a linear map $T: V \rightarrow W$. How are the adjoint of $T$ and its dual related? If $A$ is a matrix representing $T$, under what conditions is the adjoint of $T$ represented by the transpose of $A$ ?

  (ii) Let $V=C[0,1]$ be the vector space of continuous real-valued functions on $[0,1]$, equipped with the inner product

  $$\langle f, g\rangle=\int_{0}^{1} f(t) g(t) d t$$

  Let $T: V \rightarrow V$ be the linear map

  $$T f(t)=\int_{0}^{t} f(s) d s$$

  What is the adjoint of $T ?$

  comment

Markov Chains

• Paper 2, Section II, H

  Markov Chains | Part IB, 2012

  Let $\left(X_{n}\right)_{n \geqslant 0}$ be the symmetric random walk on vertices of a connected graph. At each step this walk jumps from the current vertex to a neighbouring vertex, choosing uniformly amongst them. Let $T_{i}=\inf \left\{n \geqslant 1: X_{n}=i\right\}$. For each $i \neq j$ let $q_{i j}=P\left(T_{j}<T_{i} \mid X_{0}=i\right)$ and $m_{i j}=E\left(T_{j} \mid X_{0}=i\right)$. Stating any theorems that you use:

  (i) Prove that the invariant distribution $\pi$ satisfies detailed balance.

  (ii) Use reversibility to explain why $\pi_{i} q_{i j}=\pi_{j} q_{j i}$ for all $i, j$.

  Consider a symmetric random walk on the graph shown below.

  

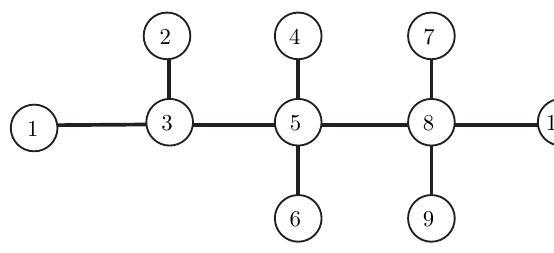
  (iii) Find $m_{33}$.

  (iv) The removal of any edge $(i, j)$ leaves two disjoint components, one which includes $i$ and one which includes $j$. Prove that $m_{i j}=1+2 e_{i j}(i)$, where $e_{i j}(i)$ is the number of edges in the component that contains $i$.

  (v) Show that $m_{i j}+m_{j i} \in\{18,36,54,72\}$ for all $i \neq j$.

  comment

Methods

• Paper 2, Section I, C

  Methods | Part IB, 2012

  Using the method of characteristics, obtain a solution to the equation

  $$u_{x}+2 x u_{y}=y$$

  subject to the Cauchy data $u(0, y)=1+y^{2}$ for $-\frac{1}{2}<y<\frac{1}{2}$.

  Sketch the characteristics and specify the greatest region of the plane in which a unique solution exists.

  comment

• Paper 2, Section II, C

  Methods | Part IB, 2012

  Consider the linear differential operator $\mathcal{L}$ defined by

  $$\mathcal{L} y:=-\frac{d^{2} y}{d x^{2}}+y$$

  on the interval $0 \leqslant x<\infty$. Given the boundary conditions $y(0)=0$ and $\lim _{x \rightarrow \infty} y(x)=0$, find the Green's function $G(x, \xi)$ for $\mathcal{L}$ with these boundary conditions. Hence, or otherwise, obtain the solution of

  $$\mathcal{L} y= \begin{cases}1, & 0 \leqslant x \leqslant \mu \\ 0, & \mu<x<\infty\end{cases}$$

  subject to the above boundary conditions, where $\mu$ is a positive constant. Show that your piecewise solution is continuous at $x=\mu$ and has the value

  $$y(\mu)=\frac{1}{2}\left(1+e^{-2 \mu}-2 e^{-\mu}\right) .$$

  comment

Metric and Topological Spaces

• Paper 2, Section I,

  Metric and Topological Spaces | Part IB, 2012

  For each case below, determine whether the given metrics $d_{1}$ and $d_{2}$ induce the same topology on $X$. Justify your answers.

  $$\begin{gathered} \text { (i) } X=\mathbb{R}^{2}, d_{1}\left(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)\right)=\sup \left\{\left|x_{1}-x_{2}\right|,\left|y_{1}-y_{2}\right|\right\} \\ d_{2}\left(\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right)\right)=\left|x_{1}-x_{2}\right|+\left|y_{1}-y_{2}\right| . \\ \text { (ii) } X=C[0,1], d_{1}(f, g)=\sup _{t \in[0,1]}|f(t)-g(t)| \\ d_{2}(f, g)=\int_{0}^{1}|f(t)-g(t)| d t . \end{gathered}$$

  comment

Numerical Analysis

• Paper 2, Section II, D

  Numerical Analysis | Part IB, 2012

  Let $\left\{P_{n}\right\}_{n=0}^{\infty}$ be the sequence of monic polynomials of degree $n$ orthogonal on the interval $[-1,1]$ with respect to the weight function $w$.

  Prove that each $P_{n}$ has $n$ distinct zeros in the interval $(-1,1)$.

  Let $P_{0}(x)=1, P_{1}(x)=x-a_{1}$, and let $P_{n}$ satisfy the following three-term recurrence relation:

  $$P_{n}(x)=\left(x-a_{n}\right) P_{n-1}(x)-b_{n}^{2} P_{n-2}(x), \quad n \geqslant 2$$

  Set

  $$A_{n}=\left[\begin{array}{ccccc} a_{1} & b_{2} & 0 & \cdots & 0 \\ b_{2} & a_{2} & b_{3} & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & 0 \\ \vdots & \ddots & b_{n-1} & a_{n-1} & b_{n} \\ 0 & \cdots & 0 & b_{n} & a_{n} \end{array}\right]$$

  Prove that $P_{n}(x)=\operatorname{det}\left(x I-A_{n}\right), n \geqslant 1$, and deduce that all the eigenvalues of $A_{n}$ are distinct and reside in $(-1,1)$.

  comment

Optimization

• Paper 2, Section I, H

  Optimization | Part IB, 2012

  Consider the two-player zero-sum game with payoff matrix

  $$A=\left(\begin{array}{rrr} 2 & 0 & -2 \\ 3 & 4 & 5 \\ 6 & 0 & 6 \end{array}\right)$$

  Express the problem of finding the column player's optimal strategy as a linear programming problem in which $x_{1}+x_{2}+x_{3}$ is to be maximized subject to some constraints.

  Solve this problem using the simplex algorithm and find the optimal strategy for the column player.

  Find also, from the final tableau you obtain, both the value of the game and the row player's optimal strategy.

  comment

Quantum Mechanics

• Paper 2, Section II, C

  Quantum Mechanics | Part IB, 2012

  Consider a quantum mechanical particle in a one-dimensional potential $V(x)$, for which $V(x)=V(-x)$. Prove that when the energy eigenvalue $E$ is non-degenerate, the energy eigenfunction $\chi(x)$ has definite parity.

  Now assume the particle is in the double potential well

  $$V(x)= \begin{cases}U, & 0 \leqslant|x| \leqslant l_{1} \\ 0, & l_{1}<|x| \leqslant l_{2} \\ \infty, & l_{2}<|x|\end{cases}$$

  where $0<l_{1}<l_{2}$ and $0<E<U$ (U being large and positive). Obtain general expressions for the even parity energy eigenfunctions $\chi^{+}(x)$ in terms of trigonometric and hyperbolic functions. Show that

  $$-\tan \left[k\left(l_{2}-l_{1}\right)\right]=\frac{k}{\kappa} \operatorname{coth}\left(\kappa l_{1}\right)$$

  where $k^{2}=\frac{2 m E}{\hbar^{2}}$ and $\kappa^{2}=\frac{2 m(U-E)}{\hbar^{2}}$.

  comment

Statistics

• Paper 2, Section I, H

  Statistics | Part IB, 2012

  Let the sample $x=\left(x_{1}, \ldots, x_{n}\right)$ have likelihood function $f(x ; \theta)$. What does it mean to say $T(x)$ is a sufficient statistic for $\theta$ ?

  Show that if a certain factorization criterion is satisfied then $T$ is sufficient for $\theta$.

  Suppose that $T$ is sufficient for $\theta$ and there exist two samples, $x$ and $y$, for which $T(x) \neq T(y)$ and $f(x ; \theta) / f(y ; \theta)$ does not depend on $\theta$. Let

  $$T_{1}(z)= \begin{cases}T(z) & z \neq y \\ T(x) & z=y\end{cases}$$

  Show that $T_{1}$ is also sufficient for $\theta$.

  Explain why $T$ is not minimally sufficient for $\theta$.

  comment

Variational Principles

• Paper 2, Section II, B

  Variational Principles | Part IB, 2012

  (i) A two-dimensional oscillator has action

  $$S=\int_{t_{0}}^{t_{1}}\left\{\frac{1}{2} \dot{x}^{2}+\frac{1}{2} \dot{y}^{2}-\frac{1}{2} \omega^{2} x^{2}-\frac{1}{2} \omega^{2} y^{2}\right\} d t$$

  Find the equations of motion as the Euler-Lagrange equations associated to $S$, and use them to show that

  $$J=\dot{x} y-\dot{y} x$$

  is conserved. Write down the general solution of the equations of motion in terms of sin $\omega t$ and $\cos \omega t$, and evaluate $J$ in terms of the coefficients which arise in the general solution.

  (ii) Another kind of oscillator has action

  $$\widetilde{S}=\int_{t_{0}}^{t_{1}}\left\{\frac{1}{2} \dot{x}^{2}+\frac{1}{2} \dot{y}^{2}-\frac{1}{4} \alpha x^{4}-\frac{1}{2} \beta x^{2} y^{2}-\frac{1}{4} \alpha y^{4}\right\} d t$$

  where $\alpha$ and $\beta$ are real constants. Find the equations of motion and use these to show that in general $J=\dot{x} y-\dot{y} x$ is not conserved. Find the special value of the ratio $\beta / \alpha$ for which $J$ is conserved. Explain what is special about the action $\widetilde{S}$in this case, and state the interpretation of $J$.

  comment