Part IB, 2009, Paper 1

Analysis II

• Paper 1, Section II, E

  Analysis II | Part IB, 2009

  Define a function $f: \mathbb{R} \rightarrow \mathbb{R}$ by

  $$f(x)=\sum_{n=1}^{\infty} 2^{-n}\left\|2^{n} x\right\|$$

  where $\|t\|$ is the distance from $t$ to the nearest integer. Prove that $f$ is continuous. [Results about uniform convergence may not be used unless they are clearly stated and proved.]

  Suppose now that $g: \mathbb{R} \rightarrow \mathbb{R}$ is a function which is differentiable at some point $x$, and let $\left(u_{n}\right)_{n=1}^{\infty},\left(v_{n}\right)_{n=1}^{\infty}$ be two sequences of real numbers with $u_{n} \leqslant x \leqslant v_{n}$ for all $n$, $u_{n} \neq v_{n}$ and $u_{n}, v_{n} \rightarrow x$ as $n \rightarrow \infty$. Prove that

  $$\lim _{n \rightarrow \infty} \frac{g\left(v_{n}\right)-g\left(u_{n}\right)}{v_{n}-u_{n}}$$

  exists.

  By considering appropriate sequences of rationals with denominator $2^{-n}$, or otherwise, show that $f$ is nowhere differentiable.

  comment

Complex Analysis or Complex Methods

• Paper 1, Section I, D

  Complex Analysis or Complex Methods | Part IB, 2009

  Let $f(z)=u(x, y)+i v(x, y)$, where $z=x+i y$, be an analytic function of $z$ in a domain $D$ of the complex plane. Derive the Cauchy-Riemann equations relating the partial derivatives of $u$ and $v$.

  For $u=e^{-x} \cos y$, find $v$ and hence $f(z)$.

  comment

• Paper 1, Section II, D

  Complex Analysis or Complex Methods | Part IB, 2009

  Consider the real function $f(t)$ of a real variable $t$ defined by the following contour integral in the complex $s$-plane:

  $$f(t)=\frac{1}{2 \pi i} \int_{\Gamma} \frac{e^{s t}}{\left(s^{2}+1\right) s^{1 / 2}} d s,$$

  where the contour $\Gamma$ is the line $s=\gamma+i y,-\infty<y<\infty$, for constant $\gamma>0$. By closing the contour appropriately, show that

  $$f(t)=\sin (t-\pi / 4)+\frac{1}{\pi} \int_{0}^{\infty} \frac{e^{-r t} d r}{\left(r^{2}+1\right) r^{1 / 2}}$$

  when $t>0$ and is zero when $t<0$. You should justify your evaluation of the inversion integral over all parts of the contour.

  By expanding $\left(r^{2}+1\right)^{-1} r^{-1 / 2}$ as a power series in $r$, and assuming that you may integrate the series term by term, show that the two leading terms, as $t \rightarrow \infty$, are

  $$f(t) \sim \sin (t-\pi / 4)+\frac{1}{(\pi t)^{1 / 2}}+\cdots$$

  [You may assume that $\int_{0}^{\infty} x^{-1 / 2} e^{-x} d x=\pi^{1 / 2}$.]

  comment

Electromagnetism

• Paper 1, Section II, A

  Electromagnetism | Part IB, 2009

  Suppose the region $z<0$ is occupied by an earthed ideal conductor.

  (a) Derive the boundary conditions on the tangential electric field $\mathbf{E}$ that hold on the surface $z=0$.

  (b) A point charge $q$, with mass $m$, is held above the conductor at $(0,0, d)$. Show that the boundary conditions on the electric field are satisfied if we remove the conductor and instead place a second charge $-q$ at $(0,0,-d)$.

  (c) The original point charge is now released with zero initial velocity. Ignoring gravity, determine how long it will take for the charge to hit the plane.

  comment

Fluid Dynamics

• Paper 1, Section I, D

  Fluid Dynamics | Part IB, 2009

  A steady velocity field $\mathbf{u}=\left(u_{r}, u_{\theta}, u_{z}\right)$ is given in cylindrical polar coordinates $(r, \theta, z)$ by

  $$u_{r}=-\alpha r, \quad u_{\theta}=\frac{\gamma}{r}\left(1-e^{-\beta r^{2}}\right), \quad u_{z}=2 \alpha z$$

  where $\alpha, \beta, \gamma$ are positive constants.

  Show that this represents a possible flow of an incompressible fluid, and find the vorticity $\omega$.

  Show further that

  $$\operatorname{curl}(\mathbf{u} \wedge \boldsymbol{\omega})=-\nu \nabla^{2} \boldsymbol{\omega}$$

  for a constant $\nu$ which should be calculated.

  [The divergence and curl operators in cylindrical polars are given by

  $$\begin{aligned} \operatorname{div} \mathbf{u} &=\frac{1}{r} \frac{\partial}{\partial r}\left(r u_{r}\right)+\frac{1}{r} \frac{\partial u_{\theta}}{\partial \theta}+\frac{\partial u_{z}}{\partial z} \\ \operatorname{curl} \mathbf{u} &=\left(\frac{1}{r} \frac{\partial u_{z}}{\partial \theta}-\frac{\partial u_{\theta}}{\partial z}, \frac{\partial u_{r}}{\partial z}-\frac{\partial u_{z}}{\partial r}, \frac{1}{r} \frac{\partial}{\partial r}\left(r u_{\theta}\right)-\frac{1}{r} \frac{\partial u_{r}}{\partial \theta}\right) \\ \text { and ,when } \boldsymbol{\omega} &=[0,0, \omega(r, z)], \\ \nabla^{2} \boldsymbol{\omega} &\left.=\left[0,0, \frac{1}{r} \frac{\partial}{\partial r}\left(r \frac{\partial \omega}{\partial r}\right)+\frac{\partial^{2} \omega}{\partial z^{2}}\right] .\right] \end{aligned}$$

  comment

• Paper 1, Section II, D

  Fluid Dynamics | Part IB, 2009

  A canal has uniform width and a bottom that is horizontal apart from a localised slowly-varying hump of height $D(x)$ whose maximum value is $D_{\text {max }}$. Far upstream the water has depth $h_{1}$ and velocity $u_{1}$. Show that the depth $h(x)$ of the water satisfies the following equation:

  $$\frac{D(x)}{h_{1}}=1-\frac{h}{h_{1}}-\frac{F}{2}\left(\frac{h_{1}^{2}}{h^{2}}-1\right)$$

  where $F=u_{1}^{2} / g h_{1}$.

  Describe qualitatively how $h(x)$ varies as the flow passes over the hump in the three cases

  $$\begin{array}{ll} \text { (i) } F<1 & \text { and } D_{\max }<D^{*} \\ \text { (ii) } F>1 & \text { and } D_{\max }<D^{*} \\ \text { (iii) } \quad D_{\max } & =D^{*}, \end{array}$$

  where $D^{*}=h_{1}\left(1-\frac{3}{2} F^{1 / 3}+\frac{1}{2} F\right)$.

  Calculate the water depth far downstream in case (iii) when $F<1$.

  comment

Geometry

• Paper 1, Section I, G

  Geometry | Part IB, 2009

  What is an ideal hyperbolic triangle? State a formula for its area.

  Compute the area of a hyperbolic disk of hyperbolic radius $\rho$. Hence, or otherwise, show that no hyperbolic triangle completely contains a hyperbolic circle of hyperbolic radius $2 .$

  comment

Groups, Rings and Modules

• Paper 1, Section II, F

  Groups, Rings and Modules | Part IB, 2009

  Prove that a principal ideal domain is a unique factorization domain.

  Give, with justification, an example of an element of $\mathbb{Z}[\sqrt{-3}]$ which does not have a unique factorization as a product of irreducibles. Show how $\mathbb{Z}[\sqrt{-3}]$ may be embedded as a subring of index 2 in a ring $R$ (that is, such that the additive quotient group $R / \mathbb{Z}[\sqrt{-3}]$ has order 2) which is a principal ideal domain. [You should explain why $R$ is a principal ideal domain, but detailed proofs are not required.]

  comment

Linear Algebra

• Paper 1, Section I, G

  Linear Algebra | Part IB, 2009

  (1) Let $V$ be a finite-dimensional vector space and let $T: V \rightarrow V$ be a non-zero endomorphism of $V$. If $\operatorname{ker}(T)=\operatorname{im}(T)$ show that the dimension of $V$ is an even integer. Find the minimal polynomial of $T$. [You may assume the rank-nullity theorem.]

  (2) Let $A_{i}, 1 \leqslant i \leqslant 3$, be non-zero subspaces of a vector space $V$ with the property that

  $$V=A_{1} \oplus A_{2}=A_{2} \oplus A_{3}=A_{1} \oplus A_{3} .$$

  Show that there is a 2-dimensional subspace $W \subset V$ for which all the $W \cap A_{i}$ are one-dimensional.

  comment

• Paper 1, Section II, G

  Linear Algebra | Part IB, 2009

  Define the dual of a vector space $V$. State and prove a formula for its dimension.

  Let $V$ be the vector space of real polynomials of degree at most $n$. If $\left\{a_{0}, \ldots, a_{n}\right\}$ are distinct real numbers, prove that there are unique real numbers $\left\{\lambda_{0}, \ldots, \lambda_{n}\right\}$ with

  $$\frac{d p}{d x}(0)=\sum_{j=0}^{n} \lambda_{j} p\left(a_{j}\right)$$

  for every $p(x) \in V$.

  comment

Markov Chains

• Paper 1, Section II, H

  Markov Chains | Part IB, 2009

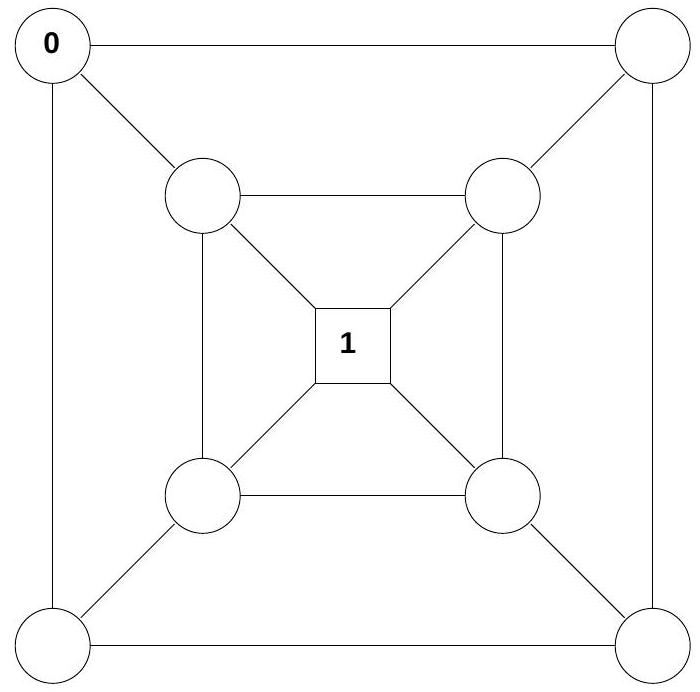
  A gerbil is introduced into a maze at the node labelled 0 in the diagram. It roams at random through the maze until it reaches the node labelled 1. At each vertex, it chooses to move to one of the neighbouring nodes with equal probability, independently of all other choices. Find the mean number of moves required for the gerbil to reach node 1 .

  Suppose now that the gerbil is intelligent, in that when it reaches a node it will not immediately return to the node from which it has just come, choosing with equal probability from all other neighbouring nodes. Express the movement of the gerbil in terms of a Markov chain whose states and transition probabilities you should specify. Find the mean number of moves until the intelligent gerbil reaches node 1 . Compare with your answer to the first part, and comment briefly.

  

  comment

Methods

• Paper 1, Section II, B

  Methods | Part IB, 2009

  Find a power series solution about $x=0$ of the equation

  $$x y^{\prime \prime}+(1-x) y^{\prime}+\lambda y=0,$$

  with $y(0)=1$, and show that $y$ is a polynomial if and only if $\lambda$ is a non-negative integer $n$. Let $y_{n}$ be the solution for $\lambda=n$. Establish an orthogonality relation between $y_{m}$ and $y_{n}(m \neq n)$.

  Show that $y_{m} y_{n}$ is a polynomial of degree $m+n$, and hence that

  $$y_{m} y_{n}=\sum_{p=0}^{m+n} a_{p} y_{p}$$

  for appropriate choices of the coefficients $a_{p}$ and with $a_{m+n} \neq 0$.

  For given $n>0$, show that the functions

  $$\left\{y_{m}, y_{m} y_{n}: m=0,1,2, \ldots, n-1\right\}$$

  are linearly independent.

  Let $f(x)$ be a polynomial of degree 3. Explain why the expansion

  $$f(x)=a_{0} y_{0}(x)+a_{1} y_{1}(x)+a_{2} y_{2}(x)+a_{3} y_{1}(x) y_{2}(x)$$

  holds for appropriate choices of $a_{p}, p=0,1,2,3$. Hence show that

  $$\int_{0}^{\infty} e^{-x} f(x) d x=w_{1} f\left(\alpha_{1}\right)+w_{2} f\left(\alpha_{2}\right)$$

  where

  $$w_{1}=\frac{y_{1}\left(\alpha_{2}\right)}{y_{1}\left(\alpha_{2}\right)-y_{1}\left(\alpha_{1}\right)}, \quad w_{2}=\frac{-y_{1}\left(\alpha_{1}\right)}{y_{1}\left(\alpha_{2}\right)-y_{1}\left(\alpha_{1}\right)},$$

  and $\alpha_{1}, \alpha_{2}$ are the zeros of $y_{2}$. You need not construct the polynomials $y_{1}(x), y_{2}(x)$ explicitly.

  comment

Metric and Topological Spaces

• Paper 1, Section II, F

  Metric and Topological Spaces | Part IB, 2009

  Given a function $f: X \rightarrow Y$ between metric spaces, we write $\Gamma_{f}$ for the subset $\{(x, f(x)) \mid x \in X\}$ of $X \times Y .$

  (i) If $f$ is continuous, show that $\Gamma_{f}$ is closed in $X \times Y$.

  (ii) If $Y$ is compact and $\Gamma_{f}$ is closed in $X \times Y$, show that $f$ is continuous.

  (iii) Give an example of a function $f: \mathbb{R} \rightarrow \mathbb{R}$ such that $\Gamma_{f}$ is closed but $f$ is not continuous.

  comment

Numerical Analysis

• Paper 1, Section I, C

  Numerical Analysis | Part IB, 2009

  The real non-singular matrix $A \in \mathbb{R}^{m \times m}$ is written in the form $A=A_{D}+A_{U}+A_{L}$, where the matrices $A_{D}, A_{U}, A_{L} \in \mathbb{R}^{m \times m}$ are diagonal and non-singular, strictly uppertriangular and strictly lower-triangular respectively.

  Given $b \in \mathbb{R}^{m}$, the Jacobi iteration for solving $A x=b$ is

  $$A_{D} x_{n}=-\left(A_{U}+A_{L}\right) x_{n-1}+b, \quad n=1,2 \ldots$$

  where the $n$th iterate is $x_{n} \in \mathbb{R}^{m}$. Show that the iteration converges to the solution $x$ of $A x=b$, independent of the starting choice $x_{0}$, if and only if the spectral radius $\rho(H)$ of the matrix $H=-A_{D}^{-1}\left(A_{U}+A_{L}\right)$ is less than 1 .

  Hence find the range of values of the real number $\mu$ for which the iteration will converge when

  $$A=\left[\begin{array}{rrr} 1 & 0 & -\mu \\ -\mu & 3 & -\mu \\ -4 \mu & 0 & 4 \end{array}\right]$$

  comment

Optimization

• Paper 1, Section I, H

  Optimization | Part IB, 2009

  Find an optimal solution to the linear programming problem

  $$\max 3 x_{1}+2 x_{2}+2 x_{3}$$

  in $x \geqslant 0$ subject to

  $$\begin{gathered} 7 x_{1}+3 x_{2}+5 x_{3} \leqslant 44 \\ x_{1}+2 x_{2}+x_{3} \leqslant 10 \\ x_{1}+x_{2}+x_{3} \geqslant 8 \end{gathered}$$

  comment

Quantum Mechanics

• Paper 1, Section II, B

  Quantum Mechanics | Part IB, 2009

  A particle of mass $m$ moves in one dimension in a potential $V(x)$ which satisfies $V(x)=V(-x)$. Show that the eigenstates of the Hamiltonian $H$ can be chosen so that they are also eigenstates of the parity operator $P$. For eigenstates with odd parity $\psi^{\text {odd }}(x)$, show that $\psi^{o d d}(0)=0$.

  A potential $V(x)$ is given by

  $$V(x)= \begin{cases}\kappa \delta(x) & |x|<a \\ \infty & |x|>a\end{cases}$$

  State the boundary conditions satisfied by $\psi(x)$ at $|x|=a$, and show also that

  $$\frac{\hbar^{2}}{2 m} \lim _{\epsilon \rightarrow 0}\left[\left.\frac{d \psi}{d x}\right|_{\epsilon}-\left.\frac{d \psi}{d x}\right|_{-\epsilon}\right]=\kappa \psi(0)$$

  Let the energy eigenstates of even parity be given by

  $$\psi^{\text {even }}(x)=\left\{\begin{array}{lc} A \cos \lambda x+B \sin \lambda x & -a<x<0 \\ A \cos \lambda x-B \sin \lambda x & 0<x<a \\ 0 & \text { otherwise } \end{array}\right.$$

  Verify that $\psi^{\text {even }}(x)$ satisfies

  $$P \psi^{\text {even }}(x)=\psi^{\text {even }}(x)$$

  By demanding that $\psi^{e v e n}(x)$ satisfy the relevant boundary conditions show that

  $$\tan \lambda a=-\frac{\hbar^{2}}{m} \frac{\lambda}{\kappa}$$

  For $\kappa>0$ show that the energy eigenvalues $E_{n}^{\text {even }}, n=0,1,2, \ldots$, with $E_{n}^{\text {even }}<E_{n+1}^{\text {even }}$, satisfy

  $$\eta_{n}=E_{n}^{e v e n}-\frac{1}{2 m}\left[\frac{(2 n+1) \hbar \pi}{2 a}\right]^{2}>0$$

  Show also that

  $$\lim _{n \rightarrow \infty} \eta_{n}=0,$$

  and give a physical explanation of this result.

  Show that the energy eigenstates with odd parity and their energy eigenvalues do not depend on $\kappa$.

  comment

Special Relativity

• Paper 1, Section I, C

  Special Relativity | Part IB, 2009

  Write down the components of the position four-vector $x_{\mu}$. Hence find the components of the four-momentum $p_{\mu}=M U_{\mu}$ of a particle of mass $M$, where $U_{\mu}=d x_{\mu} / d \tau$, with $\tau$ being the proper time.

  The particle, viewed in a frame in which it is initially at rest, disintegrates leaving a particle of mass $m$ moving with constant velocity together with other remnants which have a total three-momentum $\mathbf{p}$ and energy $E$. Show that

  $$m=\sqrt{\left(M-\frac{E}{c^{2}}\right)^{2}-\frac{|\mathbf{p}|^{2}}{c^{2}}}$$

  comment

Statistics

• Paper 1, Section I, $\mathbf{7 H} \quad$

  Statistics | Part IB, 2009

  What does it mean to say that an estimator $\hat{\theta}$ of a parameter $\theta$ is unbiased?

  An $n$-vector $Y$ of observations is believed to be explained by the model

  $$Y=X \beta+\varepsilon$$

  where $X$ is a known $n \times p$ matrix, $\beta$ is an unknown $p$-vector of parameters, $p<n$, and $\varepsilon$ is an $n$-vector of independent $N\left(0, \sigma^{2}\right)$ random variables. Find the maximum-likelihood estimator $\hat{\beta}$ of $\beta$, and show that it is unbiased.

  comment

• Paper 1, Section II, H

  Statistics | Part IB, 2009

  What is the critical region $C$ of a test of the null hypothesis $H_{0}: \theta \in \Theta_{0}$ against the alternative $H_{1}: \theta \in \Theta_{1}$ ? What is the size of a test with critical region $C ?$ What is the power function of a test with critical region $C$ ?

  State and prove the Neyman-Pearson Lemma.

  If $X_{1}, \ldots, X_{n}$ are independent with $\operatorname{common} \operatorname{Exp}(\lambda)$ distribution, and $0<\lambda_{0}<\lambda_{1}$, find the form of the most powerful size- $\alpha$ test of $H_{0}: \lambda=\lambda_{0}$ against $H_{1}: \lambda=\lambda_{1}$. Find the power function as explicitly as you can, and prove that it is increasing in $\lambda$. Deduce that the test you have constructed is a size- $\alpha$ test of $H_{0}: \lambda \leqslant \lambda_{0}$ against $H_{1}: \lambda=\lambda_{1}$.

  comment