Dynamics Of Differential Equations
Dynamics Of Differential Equations
Jump to year
B2.4
(i) Define carefully what is meant by a Hopf bifurcation in a two-dimensional dynamical system. Write down the normal form for this bifurcation, correct to cubic order, and distinguish between bifurcations of supercritical and subcritical type. Describe, without detailed calculations, how a general two-dimensional system with a Hopf bifurcation at the origin can be reduced to normal form by a near-identity transformation.
(ii) A Takens-Bogdanov bifurcation of a fixed point of a two-dimensional system is characterised by a Jacobian with the canonical form
at the bifurcation point. Consider the system
Show that a near-identity transformation of the form
exists that reduces the system to the normal (canonical) form, correct up to quadratic terms,
It is known that the general form of the equations near the bifurcation point can be written (setting )
Find all the fixed points of this system, and the values of for which these fixed points have (a) steady state bifurcations and (b) Hopf bifurcations.
B3.4
(i) Describe the use of the stroboscopic method for obtaining approximate solutions to the second order equation
when . In particular, by writing , obtain expressions in terms of for the rate of change of and . Evaluate these expressions when .
(ii) In planetary orbit theory a crude model of an orbit subject to perturbation from a distant body is given by the equation
where are polar coordinates in the plane, and is a positive constant.
(a) Show that when all bounded orbits are closed.
(b) Now suppose , and look for almost circular orbits with , where is a constant. By writing , and by making a suitable choice of the constant , use the stroboscopic method to find equations for and . By writing and considering , or otherwise, determine and in the case . Hence describe the orbits of the system.
A1.6
(i) State and prove Dulac's Criterion for the non-existence of periodic orbits in . Hence show (choosing a weighting factor of the form ) that there are no periodic orbits of the equations
(ii) State the Poincaré-Bendixson Theorem. A model of a chemical reaction (the Brusselator) is defined by the second order system
where are positive parameters. Show that there is a unique fixed point. Show that, for a suitable choice of , trajectories enter the closed region bounded by , and . Deduce that when , the system has a periodic orbit.
A2.6 B2.4
(i) What is a Liapunov function?
Consider the second order ODE
By finding a suitable Liapunov function of the form , where and are to be determined, show that the origin is asymptotically stable. Using your form of , find the greatest value of such that a trajectory through is guaranteed to tend to the origin as .
[Any theorems you use need not be proved but should be clearly stated.]
(ii) Explain the use of the stroboscopic method for investigating the dynamics of equations of the form , when . In particular, for , derive the equations, correct to order ,
where the brackets denote an average over the period of the unperturbed oscillator.
Find the form of the right hand sides of these equations explicitly when , where . Show that apart from the origin there is another fixed point of , and determine its stability. Sketch the trajectories in space in the case . What do you deduce about the dynamics of the full equation?
[You may assume that .]
A3.6 B3.4
(i) Define the Poincaré index of a curve for a vector field . Explain why the index is uniquely given by the sum of the indices for small curves around each fixed point within . Write down the indices for a saddle point and for a focus (spiral) or node, and show that the index of a periodic solution of has index unity.
A particular system has a periodic orbit containing five fixed points, and two further periodic orbits. Sketch the possible arrangements of these orbits, assuming there are no degeneracies.
(ii) A dynamical system in depending on a parameter has a homoclinic orbit when . Explain how to determine the stability of this orbit, and sketch the different behaviours for and in the case that the orbit is stable.
Now consider the system
where are constants. Show that the origin is a saddle point, and that if there is an orbit homoclinic to the origin then are related by
where the integral is taken round the orbit. Evaluate this integral for small by approximating by its form when . Hence give conditions on (small) that lead to a stable homoclinic orbit at the origin. [Note that .]
A4.6
Explain what is meant by a steady-state bifurcation of a fixed point of an ODE , in , where is a real parameter. Give examples for of equations exhibiting saddle-node, transcritical and pitchfork bifurcations.
Consider the system in , with ,
Show that the fixed point has a bifurcation when , while the fixed points have a bifurcation when . By finding the first approximation to the extended centre manifold, construct the normal form at the bifurcation point in each case, and determine the respective bifurcation types. Deduce that for just greater than , and for just less than 1 , there is a stable pair of "mixed-mode" solutions with .
A1.6
(i) A system in obeys the equations:
where is a positive constant.
By considering the quantity , where and are appropriately chosen, show that if then there is a unique fixed point and a unique limit cycle. How many fixed points are there when ?
(ii) Consider the second order system
where are constants.
(a) Find the fixed points and determine their stability.
(b) Show that if the fixed point at the origin is unstable and then there are no limit cycles.
[You may find it helpful to use the Liénard coordinate .]
A2.6 B2.4
(i) Define the terms stable manifold and unstable manifold of a hyperbolic fixed point of a dynamical system. State carefully the stable manifold theorem.
Give an approximation, correct to fourth order in , for the stable and unstable manifolds of the origin for the system
(ii) State, without proof, the centre manifold theorem. Show that the fixed point at the origin of the system
where is a constant, is non-hyperbolic at .
Using new coordinates , find the centre manifold in the form
for constants to be determined. Hence find the evolution equation on the centre manifold in the form
Ignoring higher order terms, give conditions on that guarantee that the origin is asymptotically stable.
A3.6 B3.4
(i) Define the Floquet multiplier and Liapunov exponent for a periodic orbit of a dynamical system in . Show that one multiplier is always unity, and that the other is given by
where is the period of the orbit.
The Van der Pol oscillator has a limit cycle . Show using that this orbit is stable.
(ii) Show, by considering the normal form for a Hopf bifurcation from a fixed point of a dynamical system , that in some neighbourhood of the bifurcation the periodic orbit is stable when it exists in the range of for which is unstable, and unstable in the opposite case.
Now consider the system
Show that the fixed point has a Hopf bifurcation when , and is unstable (stable) when .
Suppose that a periodic orbit exists in . Show without solving for the orbit that the result of part (i) shows that such an orbit is unstable. Define a similar result for .
What do you conclude about the existence of periodic orbits when ? Check your answer by applying Dulac's criterion to the system, using the weighting .
A4.6
Define the terms homoclinic orbit, heteroclinic orbit and heteroclinic loop. In the case of a dynamical system that possesses a homoclinic orbit, explain, without detailed calculation, how to calculate its stability.
A second order dynamical system depends on two parameters and . When there is a heteroclinic loop between the points as in the diagram.
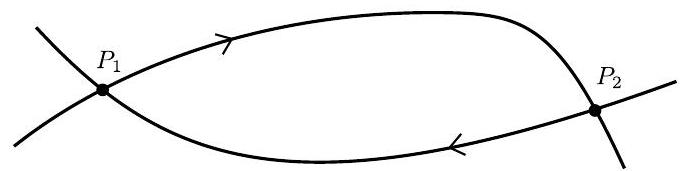
When are small there are trajectories that pass close to the fixed points :

By adapting the method used above for trajectories near homoclinic orbits, show that the distances to the stable manifold at on successive returns are related to , , the corresponding distances near , by coupled equations of the form
where any arbitrary constants have been removed by rescaling, and depend on conditions near . Show from these equations that there is a stable heteroclinic orbit if . Show also that in the marginal situation there can be a stable fixed point for small positive if . Explain carefully the form of the orbit of the original dynamical system represented by the solution of the above map when .
A1.6
(i) Given a differential equation for , explain what it means to say that the solution is given by a flow . Define the orbit, , through a point and the -limit set, , of . Define also a homoclinic orbit to a fixed point . Sketch a flow in with a homoclinic orbit, and identify (without detailed justification) the -limit sets for each point in your diagram.
(ii) Consider the differential equations
Transform the equations to polar coordinates in the plane. Solve the equation for to find , and hence find . Hence, or otherwise, determine (with justification) the -limit set for all points .
A2.6 B2.4
(i) Define a Liapounov function for a flow on . Explain what it means for a fixed point of the flow to be Liapounov stable. State and prove Liapounov's first stability theorem.
(ii) Consider the damped pendulum
where . Show that there are just two fixed points (considering the phase space as an infinite cylinder), and that one of these is the origin and is Liapounov stable. Show further that the origin is asymptotically stable, and that the the -limit set of each point in the phase space is one or other of the two fixed points, justifying your answer carefully.
[You should state carefully any theorems you use in your answer, but you need not prove them.]
A3.6 B3.4
(i) Define a hyperbolic fixed point of a flow determined by a differential equation where and is (i.e. differentiable). State the Hartman-Grobman Theorem for flow near a hyperbolic fixed point. For nonlinear flows in with a hyperbolic fixed point , does the theorem necessarily allow us to distinguish, on the basis of the linearized flow near between (a) a stable focus and a stable node; and (b) a saddle and a stable node? Justify your answers briefly.
(ii) Show that the system:
has a fixed point on the -axis. Show that there is a bifurcation at and determine the stability of the fixed point for and for .
Make a linear change of variables of the form , where and are constants to be determined, to bring the system into the form:
and hence determine whether the periodic orbit produced in the bifurcation is stable or unstable, and whether it exists in or .
A4.6
Write a short essay about periodic orbits in flows in two dimensions. Your essay should include criteria for the existence and non-existence of periodic orbits, and should mention (with sketches) at least two bifurcations that create or destroy periodic orbits in flows as a parameter is altered (though a detailed analysis of any bifurcation is not required).