Geometry Of Group Actions

Jump to year

2010

Paper 1, Section I, F
Geometry of Group Actions | Part II, 2010
Explain what it means to say that $G$ is a crystallographic group of isometries of the Euclidean plane and that $\bar{G}$ is its point group. Prove the crystallographic restriction: a rotation in such a point group $\bar{G}$ must have order $1,2,3,4$ or 6 .
comment
Paper 1, Section II, F
Geometry of Group Actions | Part II, 2010
For which circles $\Gamma$ does inversion in $\Gamma$ interchange 0 and $\infty$ ?
Let $\Gamma$ be a circle that lies entirely within the unit $\operatorname{disc} \mathbb{D}=\{z \in \mathbb{C}:|z|<1\} .$ Let $K$ be inversion in this circle $\Gamma$ , let $J$ be inversion in the unit circle, and let $T$ be the Möbius transformation $K \circ J$ . Show that, if $z_{0}$ is a fixed point of $T$ , then
$J\left(z_{0}\right)=K\left(z_{0}\right)$
and this point is another fixed point of $T$ .
By applying a suitable isometry of the hyperbolic plane $\mathbb{D}$ , or otherwise, show that $\Gamma$ is the set of points at a fixed hyperbolic distance from some point of $\mathbb{D}$ .
comment
Paper 2, Section I, F
Geometry of Group Actions | Part II, 2010
Show that a map $T: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ is an isometry for the Euclidean metric on the plane $\mathbb{R}^{2}$ if and only if there is a vector $\boldsymbol{v} \in \mathbb{R}^{2}$ and an orthogonal linear map $B \in \mathrm{O}(2)$ with
$T(\boldsymbol{x})=B(\boldsymbol{x})+\boldsymbol{v} \quad \text { for all } \boldsymbol{x} \in \mathbb{R}^{2}$
When $T$ is an isometry with $\operatorname{det} B=-1$ , show that $T$ is either a reflection or a glide reflection.
comment
Paper 3, Section I, F
Geometry of Group Actions | Part II, 2010
Let $U$ be a "triangular" region in the unit disc $\mathbb{D}$ bounded by three hyperbolic geodesics $\gamma_{1}, \gamma_{2}, \gamma_{3}$ that do not meet in $\mathbb{D}$ nor on its boundary. Let $J_{k}$ be inversion in $\gamma_{k}$ and set
$A=J_{2} \circ J_{1} ; \quad B=J_{3} \circ J_{2} .$
Let $G$ be the group generated by the Möbius transformations $A$ and $B$ . Describe briefly a fundamental set for the group $G$ acting on $\mathbb{D}$ .
Prove that $G$ is a free group on the two generators $A$ and $B$ . Describe the quotient surface $\mathbb{D} / G$ .
comment
Paper 4, Section I, F
Geometry of Group Actions | Part II, 2010
Define loxodromic transformations and explain how to determine when a Möbius transformation
$T: z \mapsto \frac{a z+b}{c z+d} \quad \text { with } \quad a d-b c=1$
is loxodromic.
Show that any Möbius transformation that maps a disc $\Delta$ onto itself cannot be loxodromic.
comment
Paper 4, Section II, F
Geometry of Group Actions | Part II, 2010
Explain briefly how Möbius transformations of the Riemann sphere are extended to give isometries of the unit ball $B^{3} \subset \mathbb{R}^{3}$ for the hyperbolic metric.
Which Möbius transformations have extensions that fix the origin in $B^{3}$ ?
For which Möbius transformations $T$ can we find a hyperbolic line in $B^{3}$ that $T$ maps onto itself? For which of these Möbius transformations is there only one such hyperbolic line?
comment

2009

Paper 1, Section I, F
Geometry of Group Actions | Part II, 2009
Explain what is meant by stereographic projection from the 2-dimensional sphere to the complex plane.
Prove that $u$ and $v$ are the images under stereographic projection of antipodal points on the sphere if and only if $u \bar{v}=-1$ .
comment
Paper 1, Section II, F
Geometry of Group Actions | Part II, 2009
Define frieze group and crystallographic group and give three examples of each, identifying them as abstract groups as well as geometrically.
Let $G$ be a discrete group of isometries of the Euclidean plane which contains a translation. Prove that $G$ contains no element of order 5 .
comment
Paper 2, Section $\mathbf{I}$ , F
Geometry of Group Actions | Part II, 2009
Describe the geodesics in the hyperbolic plane (in a model of your choice).
Let $l_{1}$ and $l_{2}$ be geodesics in the hyperbolic plane which do not meet either in the plane or at infinity. By considering the action on a suitable third geodesic, or otherwise, prove that the composite $R_{l_{1}} \circ R_{l_{2}}$ of the reflections in the two geodesics has infinite order.
comment
Paper 3, Section I, F
Geometry of Group Actions | Part II, 2009
Explain why there are discrete subgroups of the Möbius group $\mathbb{P} S L_{2}(\mathbb{C})$ which abstractly are free groups of rank 2 .
comment
Paper 4, Section I, F
Geometry of Group Actions | Part II, 2009
For every $k \in \mathbb{R}$ , show that there is a closed bounded totally disconnected subset $X$ of some Euclidean space, such that $X$ has Hausdorff dimension at least $k$ . [Standard properties of Hausdorff dimension may be quoted without proof if carefully stated.]
comment
Paper 4, Section II, F
Geometry of Group Actions | Part II, 2009
Define three-dimensional hyperbolic space, the translation length of an isometry of hyperbolic 3 -space, and the axis of a hyperbolic isometry. Briefly explain how and why the latter two concepts are related.
Find the translation length of the isometries defined by (i) $z \mapsto k z, k \in \mathbb{C} \backslash\{0\}$ and (ii) $z \mapsto \frac{3 z+2}{7 z+5}$ .
comment

2008

1.I.3G
Geometry of Group Actions | Part II, 2008
Prove that an isometry of Euclidean space $\mathbb{R}^{3}$ is an affine transformation.
Deduce that a finite group of isometries of $\mathbb{R}^{3}$ has a common fixed point.
comment
1.II.11G
Geometry of Group Actions | Part II, 2008
What is meant by an inversion in a circle in $\mathbb{C} \cup\{\infty\}$ ? Show that a composition of two inversions is a Möbius transformation.
Hence, or otherwise, show that if $C^{+}$ and $C^{-}$ are two disjoint circles in $\mathbb{C}$ , then the composition of the inversions in $C^{+}$ and $C^{-}$ has two fixed points.
comment
2.I.3G
Geometry of Group Actions | Part II, 2008
State a theorem classifying lattices in $\mathbb{R}^{2}$ . Define a frieze group.
Show there is a frieze group which is isomorphic to $\mathbb{Z}$ but is not generated by a translation, and draw a picture whose symmetries are this group.
comment
3.I.3G
Geometry of Group Actions | Part II, 2008
Let $\operatorname{dim}_{H}$ denote the Hausdorff dimension of a set in $\mathbb{R}^{n}$ . Prove that if $\operatorname{dim}_{H}(F)<1$ then $F$ is totally disconnected.
[You may assume that if $f: \mathbb{R}^{n} \rightarrow \mathbb{R}^{m}$ is a Lipschitz map then
$\left.\operatorname{dim}_{H}(f(F)) \leqslant \operatorname{dim}_{H}(F) .\right]$
comment
4.I $3 \mathrm{G}$
Geometry of Group Actions | Part II, 2008
Define the hyperbolic metric (in the sense of metric spaces) on the 3 -ball.
Given a finite set in hyperbolic 3 -space, show there is at least one closed ball of minimal radius containing that set.
comment
4.II.12G
Geometry of Group Actions | Part II, 2008
What does it mean for a subgroup $G$ of the Möbius group to be discrete?
Show that a discrete group necessarily acts properly discontinuously in hyperbolic 3-space.
[You may assume that a discrete subgroup of a matrix group is a closed subset.]
comment

2007

$1 . \mathrm{I} . 3 \mathrm{G}$
Geometry of Group Actions | Part II, 2007
Show that there are two ways to embed a regular tetrahedron in a cube $C$ so that the vertices of the tetrahedron are also vertices of $C$ . Show that the symmetry group of $C$ permutes these tetrahedra and deduce that the symmetry group of $C$ is isomorphic to the Cartesian product $S_{4} \times C_{2}$ of the symmetric group $S_{4}$ and the cyclic group $C_{2}$ .
comment
1.II.12G
Geometry of Group Actions | Part II, 2007
Define the Hausdorff $d$ -dimensional measure $\mathcal{H}^{d}(C)$ and the Hausdorff dimension of a subset $C$ of $\mathbb{R}$ .
Set $s=\log 2 / \log 3$ . Define the Cantor set $C$ and show that its Hausdorff $s$ -dimensional measure is at most $1 .$
Let $\left(X_{n}\right)$ be independent Bernoulli random variables that take the values 0 and 2 , each with probability $\frac{1}{2}$ . Define
$\xi=\sum_{n=1}^{\infty} \frac{X_{n}}{3^{n}}$
Show that $\xi$ is a random variable that takes values in the Cantor set $C$ .
Let $U$ be a subset of $\mathbb{R}$ with $3^{-(k+1)} \leqslant \operatorname{diam}(U)<3^{-k}$ . Show that $\mathbb{P}(\xi \in U) \leqslant 2^{-k}$ and deduce that, for any set $U \subset \mathbb{R}$ , we have
$\mathbb{P}(\xi \in U) \leqslant 2(\operatorname{diam}(U))^{s}$
Hence, or otherwise, prove that $\mathcal{H}^{s}(C) \geqslant \frac{1}{2}$ and that the Cantor set has Hausdorff dimension $s$ .
comment
2.I.3G
Geometry of Group Actions | Part II, 2007
Explain what is meant by a lattice in the Euclidean plane $\mathbb{R}^{2}$ . Prove that such a lattice is either $\mathbb{Z} \boldsymbol{w}$ for some vector $\boldsymbol{w} \in \mathbb{R}^{2}$ or else $\mathbb{Z} \boldsymbol{w}_{1}+\mathbb{Z} \boldsymbol{w}_{2}$ for two linearly independent vectors $\boldsymbol{w}_{1}, \boldsymbol{w}_{2}$ in $\mathbb{R}^{2}$ .
comment
3.I.3G
Geometry of Group Actions | Part II, 2007
Let $G$ be a 2-dimensional Euclidean crystallographic group. Define the lattice and point group corresponding to $G$ .
Prove that any non-trivial rotation in the point group of $G$ must have order $2,3,4$ or $6 .$
comment
4.I $. 3 \mathrm{G}$
Geometry of Group Actions | Part II, 2007
Let $\Gamma$ be a circle on the Riemann sphere. Explain what it means to say that two points of the sphere are inverse points for the circle $\Gamma$ . Show that, for each point $z$ on the Riemann sphere, there is a unique point $z^{\prime}$ with $z, z^{\prime}$ inverse points. Define inversion in $\Gamma$ .
Prove that the composition of an even number of inversions is a Möbius transformation.
comment
4.II.12G
Geometry of Group Actions | Part II, 2007
Explain what it means to say that a group $G$ is a Kleinian group. What is the definition of the limit set for the group $G$ ? Prove that a fixed point of a parabolic element in $G$ must lie in the limit set.
Show that the matrix $\left(\begin{array}{cc}1+a w & -a w^{2} \\ a & 1-a w\end{array}\right)$ represents a parabolic transformation for any non-zero choice of the complex numbers $a$ and $w$ . Find its fixed point.
The Gaussian integers are $\mathbb{Z}[i]=\{m+i n: m, n \in \mathbb{Z}\}$ . Let $G$ be the set of Möbius transformations $z \mapsto \frac{a z+b}{c z+d}$ with $a, b, c, d \in \mathbb{Z}[i]$ and $a d-b c=1$ . Prove that $G$ is a Kleinian group. For each point $w=\frac{p+i q}{r}$ with $p, q, r$ non-zero integers, find a parabolic transformation $T \in G$ that fixes $w$ . Deduce that the limit set for $G$ is all of the Riemann sphere.
comment

2005

1.I.3G
Geometry of Group Actions | Part II, 2005
Let $G$ be a subgroup of the group of isometries $\operatorname{Isom}\left(\mathbb{R}^{2}\right)$ of the Euclidean plane. What does it mean to say that $G$ is discrete?
Supposing that $G$ is discrete, show that the subgroup $G_{T}$ of $G$ consisting of all translations in $G$ is generated by translations in at most two linearly independent vectors in $\mathbb{R}^{2}$ . Show that there is a homomorphism $G \rightarrow O(2)$ with kernel $G_{T}$ .
Draw, and briefly explain, pictures which illustrate two different possibilities for $G$ when $G_{T}$ is isomorphic to the additive group $\mathbb{Z}$ .
comment
1.II.12G
Geometry of Group Actions | Part II, 2005
What is the limit set of a subgroup $G$ of Möbius transformations?
Suppose that $G$ is complicated and has no finite orbit in $\mathbb{C} \cup\{\infty\}$ . Prove that the limit set of $G$ is infinite. Can the limit set be countable?
State Jørgensen's inequality, and deduce that not every two-generator subgroup $G=\langle A, B\rangle$ of Möbius transformations is discrete. Briefly describe two examples of discrete two-generator subgroups, one for which the limit set is connected and one for which it is disconnected.
comment
2.I.3G
Geometry of Group Actions | Part II, 2005
Describe the geodesics in the disc model of the hyperbolic plane $\mathbb{H}^{2}$ .
Define the area of a region in $\mathbb{H}^{2}$ . Compute the area $A(r)$ of a hyperbolic circle of radius $r$ from the definition just given. Compute the circumference $C(r)$ of a hyperbolic circle of radius $r$ , and check explicitly that $d A(r) / d r=C(r)$ .
How could you define $\pi$ geometrically if you lived in $\mathbb{H}^{2}$ ? Briefly justify your answer.
comment
3.I.3G
Geometry of Group Actions | Part II, 2005
By considering fixed points in $\mathbb{C} \cup\{\infty\}$ , prove that any complex Möbius transformation is conjugate either to a map of the form $z \mapsto k z$ for some $k \in \mathbb{C}$ or to $z \mapsto z+1$ . Deduce that two Möbius transformations $g, h$ (neither the identity) are conjugate if and only if $\operatorname{tr}^{2}(g)=\operatorname{tr}^{2}(h)$ .
Does every Möbius transformation $g$ also have a fixed point in $\mathbb{H}^{3}$ ? Briefly justify your answer.
comment
4.I.3G
Geometry of Group Actions | Part II, 2005
Show that a set $F \subset \mathbb{R}^{n}$ with Hausdorff dimension strictly less than one is totally disconnected.
What does it mean for a Möbius transformation to pair two discs? By considering a pair of disjoint discs and a pair of tangent discs, or otherwise, explain in words why there is a 2-generator Schottky group with limit set $\Lambda \subset \mathbb{S}^{2}$ which has Hausdorff dimension at least 1 but which is not homeomorphic to a circle.
comment
4.II.12G
Geometry of Group Actions | Part II, 2005
For real $s \geqslant 0$ and $F \subset \mathbb{R}^{n}$ , give a careful definition of the $s$ -dimensional Hausdorff measure of $F$ and of the Hausdorff dimension $\operatorname{dim}_{H}(F)$ of $F$ .
For $1 \leqslant i \leqslant k$ , suppose $S_{i}: \mathbb{R}^{n} \rightarrow \mathbb{R}^{n}$ is a similarity with contraction factor $c_{i} \in(0,1)$ . Prove there is a unique non-empty compact invariant set $I$ for the $\left\{S_{i}\right\}$ . State a formula for the Hausdorff dimension of $I$ , under an assumption on the $S_{i}$ you should state.
Hence show the Hausdorff dimension of the fractal $F$ given by iterating the scheme below (at each stage replacing each edge by a new copy of the generating template) is $\operatorname{dim}_{H}(F)=3 / 2$ .
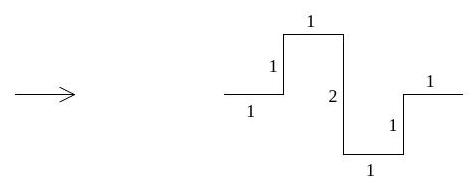
[Numbers denote lengths]
comment