Algorithms And Networks
Algorithms And Networks
Jump to year
A2.10
(i) Define the minimum path and the maximum tension problems for a network with span intervals specified for each arc. State without proof the connection between the two problems, and describe the Max Tension Min Path algorithm of solving them.
(ii) Find the minimum path between nodes and in the network below. The span intervals are displayed alongside the arcs.

Part II 2004
A3.10
(i) Consider the problem
where and . State the Lagrange Sufficiency Theorem for problem . What is meant by saying that this problem is strong Lagrangian? How is this related to the Lagrange Sufficiency Theorem? Define a supporting hyperplane and state a condition guaranteeing that problem is strong Lagrangian.
(ii) Define the terms flow, divergence, circulation, potential and differential for a network with nodes and .
State the feasible differential problem for a network with span intervals
State, without proof, the Feasible Differential Theorem.
[You must carefully define all quantities used in your statements.]
Show that the network below does not support a feasible differential.
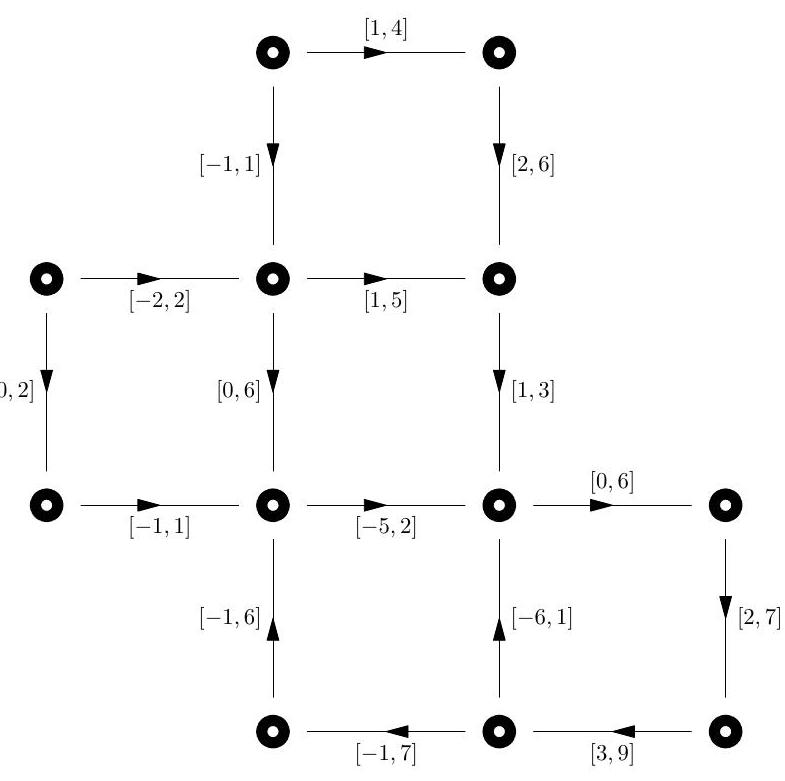
Part II 2004
A4.11
(i) Consider an unrestricted geometric programming problem
where is given by
with and positive coefficients . State the dual problem of and show that if is a dual optimum then any positive solution to the system
gives an optimum for primal problem . Here is the dual objective function.
(ii) An amount of ore has to be moved from a pit in an open rectangular skip which is to be ordered from a supplier.
The skip cost is per for the bottom and two side walls and per for the front and the back walls. The cost of loading ore into the skip is per , the cost of lifting is per , and the cost of unloading is per . The cost of moving an empty skip is negligible.
Write down an unconstrained geometric programming problem for the optimal size (length, width, height) of skip minimizing the cost of moving of ore. By considering the dual problem, or otherwise, find the optimal cost and the optimal size of the skip.
A2.10
(i) Consider a network with node set and set of directed arcs equipped with functions and with . Given we define the differential by for . We say that is a feasible differential if
Write down a necessary and sufficient condition on for the existence of a feasible differential and prove its necessity.
Assuming Minty's Lemma, describe an algorithm to construct a feasible differential and outline how this algorithm establishes the sufficiency of the condition you have given.
(ii) Let , where are finite sets. A matching in is a subset such that, for all and ,
A matching is maximal if for any other matching with we must have . Formulate the problem of finding a maximal matching in in terms of an optimal distribution problem on a suitably defined network, and hence in terms of a standard linear optimization problem.
[You may assume that the optimal distribution subject to integer constraints is integervalued.]
A3.10
(i) Consider the problem
where and . State and prove the Lagrangian sufficiency theorem.
In each of the following cases, where and , determine whether the Lagrangian sufficiency theorem can be applied to solve the problem:
(ii) Consider the problem in
where is a positive-definite symmetric matrix, is an matrix, and . Explain how to reduce this problem to the solution of simultaneous linear equations.
Consider now the problem
Describe the active set method for its solution.
Consider the problem
where . Draw a diagram partitioning the -plane into regions according to which constraints are active at the minimum.
A4.11
Define the optimal distribution problem. State what it means for a circuit to be flow-augmenting, and what it means for to be unbalanced. State the optimality theorem for flows. Describe the simplex-on-a-graph algorithm, giving a brief justification of its stopping rules.
Consider the problem of finding, in the network shown below, a minimum-cost flow from to of value 2 . Here the circled numbers are the upper arc capacities, the lower arc capacities all being zero, and the uncircled numbers are costs. Apply the simplex-on-agraph algorithm to solve this problem, taking as initial flow the superposition of a unit flow along the path and a unit flow along the path .
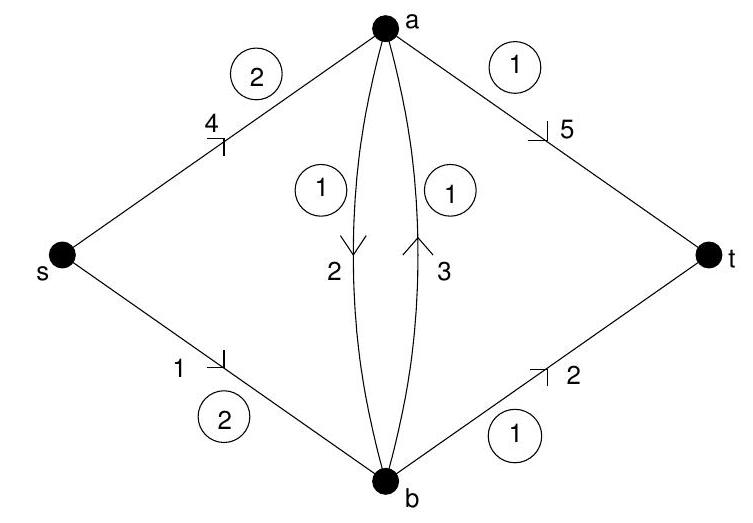
Part II 2003
A2.10
(i) Let be a directed network with nodes , arcs and capacities specified on each of the arcs. Define the terms feasible flow, divergence, cut, upper and lower cut capacities. Given two disjoint sets of nodes and , what does it mean to say that a cut separates from ? Prove that the flux of a feasible flow from to is bounded above by the upper capacity of , for any cut separating from .
(ii) Define the maximum-flow and minimum-cut problems. State the max-flow min-cut theorem and outline the main steps of the maximum-flow algorithm. Use the algorithm to find the maximum flow between the nodes 1 and 5 in a network whose node set is , where the lower capacity of each arc is 0 and the upper capacity of the directed arc joining node to node is given by the -entry in the matrix
[The painted-network theorem can be used without proof but should be stated clearly. You may assume in your description of the maximum-flow algorithm that you are given an initial feasible flow.]
A3.10
(i) Consider the unconstrained geometric programme GP
subject to .
State the dual problem to GP. Give a careful statement of the AM-GM inequality, and use it to prove the primal-dual inequality for GP.
(ii) Define min-path and max-tension problems. State and outline the proof of the max-tension min-path theorem.
A company has branches in five cities and . The fares for direct flights between these cities are as follows:
\begin{tabular}{l|lllll} & & & & & \ \hline & & 50 & 40 & 25 & 10 \ & 50 & & 20 & 90 & 25 \ & 40 & 20 & & 10 & 25 \ & 25 & 90 & 10 & & 55 \ & 10 & 25 & 25 & 55 & \end{tabular}
Formulate this as a min-path problem. Illustrate the max-tension min-path algorithm by finding the cost of travelling by the cheapest routes between and each of the other cities.
A4.11
Write an essay on Strong Lagrangian problems. You should give an account of duality and how it relates to the Strong Lagrangian property. In particular, establish carefully the relationship between the Strong Lagrangian property and supporting hyperplanes.
Also, give an example of a class of problems that are Strong Lagrangian. [You should explain carefully why your example has the Strong Lagrangian property.]
A2.10
(i) Let be a directed network with nodes and . Let be a subset of the nodes, be a flow on , and be the divergence of . Describe carefully what is meant by a cut . Define the arc-cut incidence , and the flux of across . Define also the divergence of . Show that .
Now suppose that capacity constraints are specified on each of the arcs. Define the upper cut capacity of . State the feasible distribution problem for a specified divergence , and show that the problem only has a solution if and for all cuts .
(ii) Describe an algorithm to find a feasible distribution given a specified divergence and capacity constraints on each arc. Explain what happens when no feasible distribution exists.
Illustrate the algorithm by either finding a feasible circulation, or demonstrating that one does not exist, in the network given below. Arcs are labelled with capacity constraint intervals.
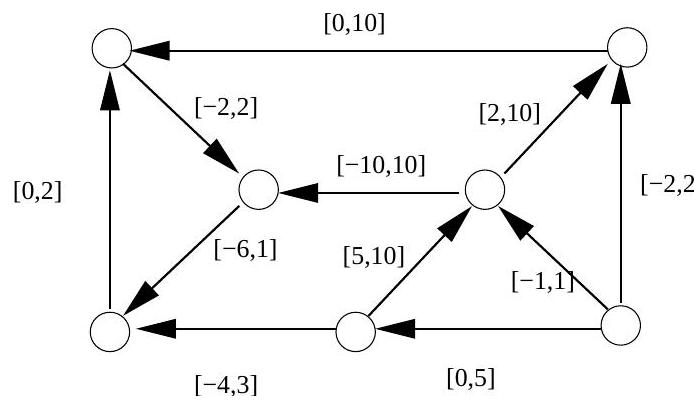
Part II
A3.10
(i) Let be the problem
Explain carefully what it means for the problem to be Strong Lagrangian.
Outline the main steps in a proof that a quadratic programming problem
where is a symmetric positive semi-definite matrix, is Strong Lagrangian.
[You should carefully state the results you need, but should not prove them.]
(ii) Consider the quadratic programming problem:
State necessary and sufficient conditions for to be optimal, and use the activeset algorithm (explaining your steps briefly) to solve the problem starting with initial condition . Demonstrate that the solution you have found is optimal by showing that it satisfies the necessary and sufficient conditions stated previously.
A4.11
State the optimal distribution problem. Carefully describe the simplex-on-a-graph algorithm for solving optimal distribution problems when the flow in each arc in the network is constrained to lie in the interval . Explain how the algorithm can be initialised if there is no obvious feasible solution with which to begin. Describe the adjustments that are needed for the algorithm to cope with more general capacity constraints for each arc (where may be finite or infinite).
Part II