Part II, 2021, Paper 1

Algebraic Geometry

• Paper 1, Section II, I

  Algebraic Geometry | Part II, 2021

  Let $k$ be an algebraically closed field and let $V \subset \mathbb{A}_{k}^{n}$ be a non-empty affine variety. Show that $V$ is a finite union of irreducible subvarieties.

  Let $V_{1}$ and $V_{2}$ be subvarieties of $\mathbb{A}_{k}^{n}$ given by the vanishing loci of ideals $I_{1}$ and $I_{2}$ respectively. Prove the following assertions.

  (i) The variety $V_{1} \cap V_{2}$ is equal to the vanishing locus of the ideal $I_{1}+I_{2}$.

  (ii) The variety $V_{1} \cup V_{2}$ is equal to the vanishing locus of the ideal $I_{1} \cap I_{2}$.

  Decompose the vanishing locus

  $$\mathbb{V}\left(X^{2}+Y^{2}-1, X^{2}-Z^{2}-1\right) \subset \mathbb{A}_{\mathbb{C}}^{3}$$

  into irreducible components.

  Let $V \subset \mathbb{A}_{k}^{3}$ be the union of the three coordinate axes. Let $W$ be the union of three distinct lines through the point $(0,0)$ in $\mathbb{A}_{k}^{2}$. Prove that $W$ is not isomorphic to $V$.

  comment

Algebraic Topology

• Paper 1, Section II, 21F

  Algebraic Topology | Part II, 2021

  (a) What does it mean for two spaces $X$ and $Y$ to be homotopy equivalent?

  (b) What does it mean for a subspace $Y \subseteq X$ to be a retract of a space $X$ ? What does it mean for a space $X$ to be contractible? Show that a retract of a contractible space is contractible.

  (c) Let $X$ be a space and $A \subseteq X$ a subspace. We say the pair $(X, A)$ has the homotopy extension property if, for any pair of maps $f: X \times\{0\} \rightarrow Y$ and $H^{\prime}: A \times I \rightarrow Y$ with

  $$\left.f\right|_{A \times\{0\}}=\left.H^{\prime}\right|_{A \times\{0\}},$$

  there exists a map $H: X \times I \rightarrow Y$ with

  $$\left.H\right|_{X \times\{0\}}=f,\left.\quad H\right|_{A \times I}=H^{\prime}$$

  Now suppose that $A \subseteq X$ is contractible. Denote by $X / A$ the quotient of $X$ by the equivalence relation $x \sim x^{\prime}$ if and only if $x=x^{\prime}$ or $x, x^{\prime} \in A$. Show that, if $(X, A)$ satisfies the homotopy extension property, then $X$ and $X / A$ are homotopy equivalent.

  comment

Analysis of Functions

• Paper 1, Section II, $23 \mathrm{H}$

  Analysis of Functions | Part II, 2021

  Below, $\mathcal{M}$ is the $\sigma$-algebra of Lebesgue measurable sets and $\lambda$ is Lebesgue measure.

  (a) State the Lebesgue differentiation theorem for an integrable function $f: \mathbb{R}^{n} \rightarrow \mathbb{C}$. Let $g: \mathbb{R} \rightarrow \mathbb{C}$ be integrable and define $G: \mathbb{R} \rightarrow \mathbb{C}$ by $G(x):=\int_{[a, x]} g d \lambda$ for some $a \in \mathbb{R}$. Show that $G$ is differentiable $\lambda$-almost everywhere.

  (b) Suppose $h: \mathbb{R} \rightarrow \mathbb{R}$ is strictly increasing, continuous, and maps sets of $\lambda$-measure zero to sets of $\lambda$-measure zero. Show that we can define a measure $\nu$ on $\mathcal{M}$ by setting $\nu(A):=\lambda(h(A))$ for $A \in \mathcal{M}$, and establish that $\nu \ll \lambda$. Deduce that $h$ is differentiable $\lambda$-almost everywhere. Does the result continue to hold if $h$ is assumed to be non-decreasing rather than strictly increasing?

  [You may assume without proof that a strictly increasing, continuous, function $w: \mathbb{R} \rightarrow \mathbb{R}$ is injective, and $w^{-1}: w(\mathbb{R}) \rightarrow \mathbb{R}$ is continuous.]

  comment

Applications of Quantum Mechanics

• Paper 1, Section II, B

  Applications of Quantum Mechanics | Part II, 2021

  (a) Discuss the variational principle that allows one to derive an upper bound on the energy $E_{0}$ of the ground state for a particle in one dimension subject to a potential $V(x)$.

  If $V(x)=V(-x)$, how could you adapt the variational principle to derive an upper bound on the energy $E_{1}$ of the first excited state?

  (b) Consider a particle of mass $2 m=\hbar^{2}$ (in certain units) subject to a potential

  $$V(x)=-V_{0} e^{-x^{2}} \quad \text { with } \quad V_{0}>0$$

  (i) Using the trial wavefunction

  $$\psi(x)=e^{-\frac{1}{2} x^{2} a}$$

  with $a>0$, derive the upper bound $E_{0} \leqslant E(a)$, where

  $$E(a)=\frac{1}{2} a-V_{0} \frac{\sqrt{a}}{\sqrt{1+a}}$$

  (ii) Find the zero of $E(a)$ in $a>0$ and show that any extremum must obey

  $$(1+a)^{3}=\frac{V_{0}^{2}}{a} .$$

  (iii) By sketching $E(a)$ or otherwise, deduce that there must always be a minimum in $a>0$. Hence deduce the existence of a bound state.

  (iv) Working perturbatively in $0<V_{0} \ll 1$, show that

  $$-V_{0}<E_{0} \leqslant-\frac{1}{2} V_{0}^{2}+\mathcal{O}\left(V_{0}^{3}\right)$$

  [Hint: You may use that $\int_{-\infty}^{\infty} e^{-b x^{2}} d x=\sqrt{\frac{\pi}{b}}$ for $\left.b>0 .\right]$

  comment

Applied Probability

• Paper 1, Section II, 28K

  Applied Probability | Part II, 2021

  The particles of an Ideal Gas form a spatial Poisson process on $\mathbb{R}^{3}$ with constant intensity $z>0$, called the activity of the gas.

  (a) Prove that the independent mixture of two Ideal Gases with activities $z_{1}$ and $z_{2}$ is again an Ideal Gas. What is its activity? [You must prove any results about Poisson processes that you use. The independent mixture of two gases with particles $\Pi_{1} \subset \mathbb{R}^{3}$ and $\Pi_{2} \subset \mathbb{R}^{3}$ is given by $\left.\Pi_{1} \cup \Pi_{2} .\right]$

  (b) For an Ideal Gas of activity $z>0$, find the limiting distribution of

  $$\frac{N\left(V_{i}\right)-\mathbb{E} N\left(V_{i}\right)}{\sqrt{\left|V_{i}\right|}}$$

  as $i \rightarrow \infty$ for a given sequence of subsets $V_{i} \subset \mathbb{R}^{3}$ with $\left|V_{i}\right| \rightarrow \infty$.

  (c) Let $g: \mathbb{R}^{3} \rightarrow \mathbb{R}$ be a smooth non-negative function vanishing outside a bounded subset of $\mathbb{R}^{3}$. Find the mean and variance of $\sum_{x} g(x)$, where the sum runs over the particles $x \in \mathbb{R}^{3}$ of an ideal gas of activity $z>0$. [You may use the properties of spatial Poisson processes established in the lectures.]

  [Hint: recall that the characteristic function of a Poisson random variable with mean $\lambda$ is $\left.e^{\left(e^{i t}-1\right) \lambda} \cdot\right]$

  comment

Automata and Formal Languages

• Paper 1, Section I, F

  Automata and Formal Languages | Part II, 2021

  Let $f_{n, k}$ be the partial function on $k$ variables that is computed by the $n$th machine (or the empty function if $n$ does not encode a machine).

  Define the halting set $\mathbb{K}$.

  Given $A, B \subseteq \mathbb{N}$, what is a many-one reduction $A \leqslant_{m} B$ of $A$ to $B$ ?

  State the $s-m-n$ theorem and use it to show that a subset $X$ of $\mathbb{N}$ is recursively enumerable if and only if $X \leqslant_{m} \mathbb{K}$.

  Give an example of a set $S \subseteq \mathbb{N}$ with $\mathbb{K} \leqslant_{m} S$ but $\mathbb{K} \neq S$.

  [You may assume that $\mathbb{K}$ is recursively enumerable and that $0 \notin \mathbb{K}$.]

  comment

• Paper 1, Section II, F

  Automata and Formal Languages | Part II, 2021

  For $k \geqslant 1$ give the definition of a partial recursive function $f: \mathbb{N}^{k} \rightarrow \mathbb{N}$ in terms of basic functions, composition, recursion and minimisation.

  Show that the following partial functions from $\mathbb{N}$ to $\mathbb{N}$ are partial recursive: (i) $s(n)= \begin{cases}1 & n=0 \\ 0 & n \geqslant 1\end{cases}$ (ii) $r(n)= \begin{cases}1 & n \text { odd } \\ 0 & n \text { even } \text {, }\end{cases}$ (iii) $p(n)=\left\{\begin{array}{l}\text { undefined if } n \text { is odd } \\ 0 \text { if } n \text { is even }\end{array}\right.$

  Which of these can be defined without using minimisation?

  What is the class of functions $f: \mathbb{N}^{k} \rightarrow \mathbb{N}$ that can be defined using only basic functions and composition? [Hint: See which functions you can obtain and then show that these form a class that is closed with respect to the above.]

  Show directly that every function in this class is computable.

  comment

Classical Dynamics

• Paper 1, Section I, D

  Classical Dynamics | Part II, 2021

  Two equal masses $m$ move along a straight line between two stationary walls. The mass on the left is connected to the wall on its left by a spring of spring constant $k_{1}$, and the mass on the right is connected to the wall on its right by a spring of spring constant $k_{2}$. The two masses are connected by a third spring of spring constant $k_{3}$.

  (a) Show that the Lagrangian of the system can be written in the form

  $$L=\frac{1}{2} T_{i j} \dot{x}_{i} \dot{x}_{j}-\frac{1}{2} V_{i j} x_{i} x_{j}$$

  where $x_{i}(t)$, for $i=1,2$, are the displacements of the two masses from their equilibrium positions, and $T_{i j}$ and $V_{i j}$ are symmetric $2 \times 2$ matrices that should be determined.

  (b) Let

  $$k_{1}=k(1+\epsilon \delta), \quad k_{2}=k(1-\epsilon \delta), \quad k_{3}=k \epsilon,$$

  where $k>0, \epsilon>0$ and $|\epsilon \delta|<1$. Using Lagrange's equations of motion, show that the angular frequencies $\omega$ of the normal modes of the system are given by

  $$\omega^{2}=\lambda \frac{k}{m}$$

  where

  $$\lambda=1+\epsilon\left(1 \pm \sqrt{1+\delta^{2}}\right)$$

  comment

Coding and Cryptography

• Paper 1, Section I, $3 K$

  Coding and Cryptography | Part II, 2021

  Let $C$ be an $[n, m, d]$ code. Define the parameters $n, m$ and $d$. In each of the following cases define the new code and give its parameters.

  (i) $C^{+}$is the parity extension of $C$.

  (ii) $C^{-}$is the punctured code (assume $n \geqslant 2$ ).

  (iii) $\bar{C}$ is the shortened code (assume $n \geqslant 2$ ).

  Let $C=\{000,100,010,001,110,101,011,111\}$. Suppose the parity extension of $C$ is transmitted through a binary symmetric channel where $p$ is the probability of a single-bit error in the channel. Calculate the probability that an error in the transmission of a single codeword is not noticed.

  comment

• Paper 1, Section II, $11 K$

  Coding and Cryptography | Part II, 2021

  Let $\Sigma_{1}=\left\{\mu_{1}, \ldots, \mu_{N}\right\}$ be a finite alphabet and $X$ a random variable that takes each value $\mu_{i}$ with probability $p_{i}$. Define the entropy $H(X)$ of $X$.

  Suppose $\Sigma_{2}=\{0,1\}$ and $c: \Sigma_{1} \rightarrow \Sigma_{2}^{*}$ is a decipherable code. Write down an expression for the expected word length $E(S)$ of $c$.

  Prove that the minimum expected word length $S^{*}$ of a decipherable code $c: \Sigma_{1} \rightarrow \Sigma_{2}^{*}$ satisfies

  $$H(X) \leqslant S^{*}<H(X)+1 .$$

  [You can use Kraft's and Gibbs' inequalities as long as they are clearly stated.]

  Suppose a decipherable binary code has word lengths $s_{1}, \ldots, s_{N}$. Show that

  $$N \log N \leqslant s_{1}+\cdots+s_{N} .$$

  Suppose $X$ is a source that emits $N$ sourcewords $a_{1}, \ldots, a_{N}$ and $p_{i}$ is the probability that $a_{i}$ is emitted, where $p_{1} \geqslant p_{2} \geqslant \cdots \geqslant p_{N}$. Let $b_{1}=0$ and $b_{i}=\sum_{j=1}^{i-1} p_{j}$ for $2 \leqslant i \leqslant N$. Let $s_{i}=\left\lceil-\log p_{i}\right\rceil$ for $1 \leqslant i \leqslant N$. Now define a code $c$ by $c\left(a_{i}\right)=b_{i}^{*}$ where $b_{i}^{*}$ is the (fractional part of the) binary expansion of $b_{i}$ to $s_{i}$ decimal places. Prove that this defines a decipherable code.

  What does it mean for a code to be optimal? Is the code $c$ defined in the previous paragraph in terms of the $b_{i}^{*}$ necessarily optimal? Justify your answer.

  comment

Cosmology

• Paper 1, Section I, 9B

  Cosmology | Part II, 2021

  The continuity, Euler and Poisson equations governing how non-relativistic fluids with energy density $\rho$, pressure $P$ and velocity $\mathbf{v}$ propagate in an expanding universe take the form

  $$\begin{gathered} \frac{\partial \rho}{\partial t}+3 H \rho+\frac{1}{a} \boldsymbol{\nabla} \cdot(\rho \mathbf{v})=0 \\ \rho a\left(\frac{\partial}{\partial t}+\frac{\mathbf{v}}{a} \cdot \nabla\right) \mathbf{u}=-\frac{1}{c^{2}} \nabla P-\rho \boldsymbol{\nabla} \Phi \\ \nabla^{2} \Phi=\frac{4 \pi G}{c^{2}} \rho a^{2} \end{gathered}$$

  where $\mathbf{u}=\mathbf{v}+a H \mathbf{x}, H=\dot{a} / a$ and $a(t)$ is the scale factor.

  (a) Show that, for a homogeneous and isotropic flow with $P=\bar{P}(t), \rho=\bar{\rho}(t), \mathbf{v}=\mathbf{0}$ and $\Phi=\bar{\Phi}(t, \mathbf{x})$, consistency of the Euler equation with the Poisson equation implies Raychaudhuri's equation.

  (b) Explain why this derivation of Raychaudhuri's equation is an improvement over the derivation of the Friedmann equation using only Newtonian gravity.

  (c) Consider small perturbations about a homogeneous and isotropic flow,

  $$\rho=\bar{\rho}(t)+\epsilon \delta \rho, \quad \mathbf{v}=\epsilon \delta \mathbf{v}, \quad P=\bar{P}(t)+\epsilon \delta P \quad \text { and } \quad \Phi=\bar{\Phi}(t, \mathbf{x})+\epsilon \delta \Phi,$$

  with $\epsilon \ll 1$. Show that, to first order in $\epsilon$, the continuity equation can be written as

  $$\frac{\partial}{\partial t}\left(\frac{\delta \rho}{\bar{\rho}}\right)=-\frac{1}{a} \boldsymbol{\nabla} \cdot \delta \mathbf{v}$$

  comment

• Paper 1, Section II, 15B

  Cosmology | Part II, 2021

  (a) Consider the following action for the inflaton field $\phi$

  $$S=\int \mathrm{d}^{3} x \mathrm{~d} t a(t)^{3}\left[\frac{1}{2} \dot{\phi}^{2}-\frac{c^{2}}{2 a(t)^{2}} \nabla \phi \cdot \nabla \phi-V(\phi)\right]$$

  Use the principle of least action to derive the equation of motion for the inflaton $\phi$,

  $$\ddot{\phi}+3 H \dot{\phi}-\frac{c^{2}}{a(t)^{2}} \nabla^{2} \phi+\frac{\mathrm{d} V(\phi)}{\mathrm{d} \phi}=0$$

  where $H=\dot{a} / a$. [In the derivation you may discard boundary terms.]

  (b) Consider a regime where $V(\phi)$ is approximately constant so that the universe undergoes a period of exponential expansion during which $a=a_{0} e^{H_{\text {inf }} t}$. Show that $(*)$ can be written in terms of the spatial Fourier transform $\widehat{\phi}_{\mathbf{k}}(t)$ of $\phi(\mathbf{x}, t)$ as

  $$\ddot{\widehat{\phi}}_{\mathbf{k}}+3 H_{\mathrm{inf}} \dot{\hat{\phi}}_{\mathbf{k}}+\frac{c^{2} k^{2}}{a^{2}} \widehat{\phi}_{\mathbf{k}}=0 .$$

  (c) Define conformal time $\tau$ and determine the range of $\tau$ when $a=a_{0} e^{H_{\text {inf }} t}$. Show that $(* *)$ can be written in terms of the conformal time as

  $$\frac{\mathrm{d}^{2} \tilde{\phi}_{\mathbf{k}}}{\mathrm{d} \tau^{2}}+\left(c^{2} k^{2}-\frac{2}{\tau^{2}}\right) \widetilde{\phi}_{\mathbf{k}}=0, \quad \text { where } \quad \tilde{\phi}_{\mathbf{k}}=-\frac{1}{H_{\mathrm{inf}} \tau} \widehat{\phi}_{\mathbf{k}}$$

  (d) Let $|\mathrm{BD}\rangle$ denote the state that in the far past was in the ground state of the standard harmonic oscillator with frequency $\omega=c k$. Assuming that the quantum variance of $\widehat{\phi}_{\mathbf{k}}$ is given by

  $$P_{\mathbf{k}} \equiv\left\langle\mathrm{BD}\left|\widehat{\phi}_{\mathbf{k}} \widehat{\phi}_{\mathbf{k}}^{\dagger}\right| \mathrm{BD}\right\rangle=\frac{\hbar H_{\mathrm{inf}}^{2}}{2 c^{3} k^{3}}\left(1+\tau^{2} c^{2} k^{2}\right)$$

  explain in which sense inflation naturally generates a scale-invariant power spectrum. [You may use that $P_{\mathbf{k}}$ has dimensions of [length $\left.]^{3} .\right]$

  comment

Differential Geometry

• Paper 1, Section II, 26F

  Differential Geometry | Part II, 2021

  (a) Let $S \subset \mathbb{R}^{3}$ be a surface. Give a parametrisation-free definition of the first fundamental form of $S$. Use this definition to derive a description of it in terms of the partial derivatives of a local parametrisation $\phi: U \subset \mathbb{R}^{2} \rightarrow S$.

  (b) Let $a$ be a positive constant. Show that the half-cone

  $$\Sigma=\left\{(x, y, z) \mid z^{2}=a\left(x^{2}+y^{2}\right), z>0\right\}$$

  is locally isometric to the Euclidean plane. [Hint: Use polar coordinates on the plane.]

  (c) Define the second fundamental form and the Gaussian curvature of $S$. State Gauss' Theorema Egregium. Consider the set

  $$V=\left\{(x, y, z) \mid x^{2}+y^{2}+z^{2}-2 x y-2 y z=0\right\} \backslash\{(0,0,0)\} \subset \mathbb{R}^{3}$$

  (i) Show that $V$ is a surface.

  (ii) Calculate the Gaussian curvature of $V$ at each point. [Hint: Complete the square.]

  comment

Dynamical Systems

• Paper 1, Section II, A

  Dynamical Systems | Part II, 2021

  (a) State the properties defining a Lyapunov function for a dynamical system $\dot{\mathbf{x}}=\mathbf{f}(\mathbf{x})$. State Lyapunov's first theorem and La Salle's invariance principle.

  (b) Consider the system

  $$\begin{aligned} &\dot{x}=y \\ &\dot{y}=-\frac{2 x\left(1-x^{2}\right)}{\left(1+x^{2}\right)^{3}}-k y \end{aligned}$$

  Show that for $k>0$ the origin is asymptotically stable, stating clearly any arguments that you use.

  $$\left[\text { Hint: } \frac{d}{d x} \frac{x^{2}}{\left(1+x^{2}\right)^{2}}=\frac{2 x\left(1-x^{2}\right)}{\left(1+x^{2}\right)^{3}} \cdot\right]$$

  (c) Sketch the phase plane, (i) for $k=0$ and (ii) for $0<k \ll 1$, giving brief details of any reasoning and identifying the fixed points. Include the domain of stability of the origin in your sketch for case (ii).

  (d) For $k>0$ show that the trajectory $\mathbf{x}(t)$ with $\mathbf{x}(0)=\left(1, y_{0}\right)$, where $y_{0}>0$, satisfies $0<y(t)<\sqrt{y_{0}^{2}+\frac{1}{2}}$ for $t>0$. Show also that, for any $\epsilon>0$, the trajectory cannot remain outside the region $0<y<\epsilon$.

  comment

Electrodynamics

• Paper 1, Section II, 37C

  Electrodynamics | Part II, 2021

  (a) An electromagnetic field is specified by a four-vector potential

  $$A^{\mu}(\mathbf{x}, t)=(\phi(\mathbf{x}, t) / c, \mathbf{A}(\mathbf{x}, t))$$

  Define the corresponding field-strength tensor $F^{\mu \nu}$ and state its transformation property under a general Lorentz transformation.

  (b) Write down two independent Lorentz scalars that are quadratic in the field strength and express them in terms of the electric and magnetic fields, $\mathbf{E}=-\boldsymbol{\nabla} \phi-\partial \mathbf{A} / \partial t$ and $\mathbf{B}=\boldsymbol{\nabla} \times \mathbf{A}$. Show that both these scalars vanish when evaluated on an electromagnetic plane-wave solution of Maxwell's equations of arbitrary wavevector and polarisation.

  (c) Find (non-zero) constant, homogeneous background fields $\mathbf{E}(\mathbf{x}, t)=\mathbf{E}_{0}$ and $\mathbf{B}(\mathbf{x}, t)=\mathbf{B}_{0}$ such that both the Lorentz scalars vanish. Show that, for any such background, the field-strength tensor obeys

  $$F_{\rho}^{\mu} F_{\sigma}^{\rho} F_{\nu}^{\sigma}=0$$

  (d) Hence find the trajectory of a relativistic particle of mass $m$ and charge $q$ in this background. You should work in an inertial frame where the particle is at rest at the origin at $t=0$ and in which $\mathbf{B}_{0}=\left(0,0, B_{0}\right)$.

  comment

Fluid Dynamics II

• Paper 1, Section II, 39A

  Fluid Dynamics II | Part II, 2021

  (a) Write down the Stokes equations for the motion of an incompressible viscous fluid with negligible inertia (in the absence of body forces). What does it mean that Stokes flow is linear and reversible?

  (b) The region $a<r<b$ between two concentric rigid spheres of radii $a$ and $b$ is filled with fluid of large viscosity $\mu$. The outer sphere is held stationary, while the inner sphere is made to rotate with angular velocity $\boldsymbol{\Omega}$.

  (i) Use symmetry and the properties of Stokes flow to deduce that $p=0$, where $p$ is the pressure due to the flow.

  (ii) Verify that both solid-body rotation and $\mathbf{u}(\mathbf{x})=\boldsymbol{\Omega} \wedge \boldsymbol{\nabla}(1 / r)$ satisfy the Stokes equations with $p=0$. Hence determine the fluid velocity between the spheres.

  (iii) Calculate the stress tensor $\sigma_{i j}$ in the flow.

  (iv) Deduce that the couple $\mathbf{G}$ exerted by the fluid in $r<c$ on the fluid in $r>c$, where $a<c<b$, is given by

  $$\mathbf{G}=\frac{8 \pi \mu a^{3} b^{3} \mathbf{\Omega}}{b^{3}-a^{3}}$$

  independent of the value of $c$. [Hint: Do not substitute the form of $A$ and $B$ in $A+B r^{-3}$ until the end of the calculation.]

  Comment on the form of this result for $a \ll b$ and for $b-a \ll a$.

  $\left[Y o u\right.$ may use $\int_{r=R} n_{i} n_{j} d S=\frac{4}{3} \pi R^{2} \delta_{i j}$, where $\mathbf{n}$ is the normal to $\left.r=R .\right]$

  comment

Further Complex Methods

• Paper 1, Section I, 7E

  Further Complex Methods | Part II, 2021

  Evaluate the integral

  $$\mathcal{P} \int_{0}^{\infty} \frac{\sin x}{x\left(x^{2}-1\right)} d x$$

  stating clearly any standard results involving contour integrals that you use.

  comment

• Paper 1, Section II, E

  Further Complex Methods | Part II, 2021

  (a) Functions $g_{1}(z)$ and $g_{2}(z)$ are analytic in a connected open set $\mathcal{D} \subseteq \mathbb{C}$ with $g_{1}=g_{2}$ in a non-empty open subset $\tilde{\mathcal{D}} \subset \mathcal{D}$. State the identity theorem.

  (b) Let $\mathcal{D}_{1}$ and $\mathcal{D}_{2}$ be connected open sets with $\mathcal{D}_{1} \cap \mathcal{D}_{2} \neq \emptyset$. Functions $f_{1}(z)$ and $f_{2}(z)$ are analytic on $\mathcal{D}_{1}$ and $\mathcal{D}_{2}$ respectively with $f_{1}=f_{2}$ on $\mathcal{D}_{1} \cap \mathcal{D}_{2}$. Explain briefly what is meant by analytic continuation of $f_{1}$ and use part (a) to prove that analytic continuation to $\mathcal{D}_{2}$ is unique.

  (c) The function $F(z)$ is defined by

  $$F(z)=\int_{-\infty}^{\infty} \frac{e^{i t}}{(t-z)^{n}} d t$$

  where $\operatorname{Im} z>0$ and $n$ is a positive integer. Use the method of contour deformation to construct the analytic continuation of $F(z)$ into $\operatorname{Im} z \leqslant 0$.

  (d) The function $G(z)$ is defined by

  $$G(z)=\int_{-\infty}^{\infty} \frac{e^{i t}}{(t-z)^{n}} d t$$

  where $\operatorname{Im} z \neq 0$ and $n$ is a positive integer. Prove that $G(z)$ experiences a discontinuity when $z$ crosses the real axis. Determine the value of this discontinuity. Hence, explain why $G(z)$ cannot be used as an analytic continuation of $F(z)$.

  comment

Galois Theory

• Paper 1, Section II, 18I

  Galois Theory | Part II, 2021

  (a) Let $K \subseteq L$ be fields, and $f(x) \in K[x]$ a polynomial.

  Define what it means for $L$ to be a splitting field for $f$ over $K$.

  Prove that splitting fields exist, and state precisely the theorem on uniqueness of splitting fields.

  Let $f(x)=x^{3}-2 \in \mathbb{Q}[x]$. Find a subfield of $\mathbb{C}$ which is a splitting field for $f$ over Q. Is this subfield unique? Justify your answer.

  (b) Let $L=\mathbb{Q}\left[\zeta_{7}\right]$, where $\zeta_{7}$ is a primitive 7 th root of unity.

  Show that the extension $L / \mathbb{Q}$ is Galois. Determine all subfields $M \subseteq L$.

  For each subfield $M$, find a primitive element for the extension $M / \mathbb{Q}$ explicitly in terms of $\zeta_{7}$, find its minimal polynomial, and write $\operatorname{down} \operatorname{Aut}(M / \mathbb{Q})$ and $\operatorname{Aut}(L / M)$.

  Which of these subfields $M$ are Galois over $\mathbb{Q}$ ?

  [You may assume the Galois correspondence, but should prove any results you need about cyclotomic extensions directly.]

  comment

General Relativity

• Paper 1, Section II, C

  General Relativity | Part II, 2021

  The Weyl tensor $C_{\alpha \beta \gamma \delta}$ may be defined (in $n=4$ spacetime dimensions) as

  $C_{\alpha \beta \gamma \delta}=R_{\alpha \beta \gamma \delta}-\frac{1}{2}\left(g_{\alpha \gamma} R_{\beta \delta}+g_{\beta \delta} R_{\alpha \gamma}-g_{\alpha \delta} R_{\beta \gamma}-g_{\beta \gamma} R_{\alpha \delta}\right)+\frac{1}{6}\left(g_{\alpha \gamma} g_{\beta \delta}-g_{\alpha \delta} g_{\beta \gamma}\right) R$

  where $R_{\alpha \beta \gamma \delta}$ is the Riemann tensor, $R_{\alpha \beta}$ is the Ricci tensor and $R$ is the Ricci scalar.

  (a) Show that $C_{\beta \alpha \delta}^{\alpha}=0$ and deduce that all other contractions vanish.

  (b) A conformally flat metric takes the form

  $$g_{\alpha \beta}=e^{2 \omega} \eta_{\alpha \beta},$$

  where $\eta_{\alpha \beta}$ is the Minkowski metric and $\omega$ is a scalar function. Calculate the Weyl tensor at a given point $p$. [You may assume that $\partial_{\alpha} \omega=0$ at $p$.]

  (c) The Schwarzschild metric outside a spherically symmetric mass (such as the Sun, Earth or Moon) is

  $$d s^{2}=-\left(1-\frac{2 M}{r}\right) d t^{2}+\left(1-\frac{2 M}{r}\right)^{-1} d r^{2}+r^{2} d \Omega^{2}$$

  (i) Calculate the leading-order contribution to the Weyl component $C_{t r t r}$ valid at large distances, $r \gg 2 M$, beyond the central spherical mass.

  (ii) What physical phenomenon, known from ancient times, can be attributed to this component of the Weyl tensor at the location of the Earth? [This is after subtracting off the Earth's own gravitational field, and neglecting the Earth's motion within the solar system.] Briefly explain why your answer is consistent with the Einstein equivalence principle.

  comment

Graph Theory

• Paper 1, Section II, 17G

  Graph Theory | Part II, 2021

  Define the binomial random graph $G(n, p)$, where $n \in \mathbb{N}$ and $p \in(0,1)$.

  (a) Let $G_{n} \sim G(n, p)$ and let $E_{t}$ be the event that $G_{n}$ contains a copy of the complete graph $K_{t}$. Show that if $p=p(n)$ is such that $p \cdot n^{2 /(t-1)} \rightarrow 0$ then $\mathbb{P}\left(E_{t}\right) \rightarrow 0$ as $n \rightarrow \infty$.

  (b) State Chebyshev's inequality. Show that if $p \cdot n \rightarrow \infty$ then $\mathbb{P}\left(E_{3}\right) \rightarrow 1$.

  (c) Let $H$ be a triangle with an added leaf vertex, that is

  $$H=\left(\left\{x_{1}, \ldots, x_{4}\right\},\left\{x_{1} x_{2}, x_{2} x_{3}, x_{3} x_{1}, x_{1} x_{4}\right\}\right),$$

  where $x_{1}, \ldots, x_{4}$ are distinct. Let $F$ be the event that $G_{n} \sim G(n, p)$ contains a copy of $H$. Show that if $p=n^{-0.9}$ then $\mathbb{P}(F) \rightarrow 1$.

  comment

Integrable Systems

• Paper 1 , Section II, 33D

  Integrable Systems | Part II, 2021

  (a) Let $U(z, \bar{z}, \lambda)$ and $V(z, \bar{z}, \lambda)$ be matrix-valued functions, whilst $\psi(z, \bar{z}, \lambda)$ is a vector-valued function. Show that the linear system

  $$\partial_{z} \psi=U \psi, \quad \partial_{\bar{z}} \psi=V \psi$$

  is over-determined and derive a consistency condition on $U, V$ that is necessary for there to be non-trivial solutions.

  (b) Suppose that

  $$U=\frac{1}{2 \lambda}\left(\begin{array}{cc} \lambda \partial_{z} u & e^{-u} \\ e^{u} & -\lambda \partial_{z} u \end{array}\right) \quad \text { and } \quad V=\frac{1}{2}\left(\begin{array}{cc} -\partial_{\bar{z}} u & \lambda e^{u} \\ \lambda e^{-u} & \partial_{\bar{z}} u \end{array}\right)$$

  where $u(z, \bar{z})$ is a scalar function. Obtain a partial differential equation for $u$ that is equivalent to your consistency condition from part (a).

  (c) Now let $z=x+i y$ and suppose $u$ is independent of $y$. Show that the trace of $(U-V)^{n}$ is constant for all positive integers $n$. Hence, or otherwise, construct a non-trivial first integral of the equation

  $$\frac{d^{2} \phi}{d x^{2}}=4 \sinh \phi, \quad \text { where } \quad \phi=\phi(x)$$

  comment

Linear Analysis

• Paper 1, Section II, 22H

  Linear Analysis | Part II, 2021

  Let $H$ be a separable Hilbert space and $\left\{e_{i}\right\}$ be a Hilbertian (orthonormal) basis of $H$. Given a sequence $\left(x_{n}\right)$ of elements of $H$ and $x_{\infty} \in H$, we say that $x_{n}$ weakly converges to $x_{\infty}$, denoted $x_{n} \rightarrow x_{\infty}$, if $\forall h \in H, \lim _{n \rightarrow \infty}\left\langle x_{n}, h\right\rangle=\left\langle x_{\infty}, h\right\rangle$.

  (a) Given a sequence $\left(x_{n}\right)$ of elements of $H$, prove that the following two statements are equivalent:

  (i) $\exists x_{\infty} \in H$ such that $x_{n} \rightarrow x_{\infty}$;

  (ii) the sequence $\left(x_{n}\right)$ is bounded in $H$ and $\forall i \geqslant 1$, the sequence $\left(\left\langle x_{n}, e_{i}\right\rangle\right)$ is convergent.

  (b) Let $\left(x_{n}\right)$ be a bounded sequence of elements of $H$. Show that there exists $x_{\infty} \in H$ and a subsequence $\left(x_{\phi(n)}\right)$ such that $x_{\phi(n)} \rightarrow x_{\infty}$ in $H$.

  (c) Let $\left(x_{n}\right)$ be a sequence of elements of $H$ and $x_{\infty} \in H$ be such that $x_{n} \rightarrow x_{\infty}$. Show that the following three statements are equivalent:

  (i) $\lim _{n \rightarrow \infty}\left\|x_{n}-x_{\infty}\right\|=0$;

  (ii) $\lim _{n \rightarrow \infty}\left\|x_{n}\right\|=\left\|x_{\infty}\right\|$;

  (iii) $\forall \epsilon>0, \exists I(\epsilon)$ such that $\forall n \geqslant 1, \sum_{i \geqslant I(\epsilon)}\left|\left\langle x_{n}, e_{i}\right\rangle\right|^{2}<\epsilon$.

  comment

Logic and Set Theory

• Paper 1, Section II, 16G

  Logic and Set Theory | Part II, 2021

  Let $S$ and $T$ be sets of propositional formulae.

  (a) What does it mean to say that $S$ is deductively closed? What does it mean to say that $S$ is consistent? Explain briefly why if $S$ is inconsistent then some finite subset of $S$ is inconsistent.

  (b) We write $S \vdash T$ to mean $S \vdash t$ for all $t \in T$. If $S \vdash T$ and $T \vdash S$ we say $S$ and $T$ are equivalent. If $S$ is equivalent to a finite set $F$ of formulae we say that $S$ is finitary. Show that if $S$ is finitary then there is a finite set $R \subset S$ with $R \vdash S$.

  (c) Now let $T_{0}, T_{1}, T_{2}, \ldots$ be deductively closed sets of formulae with

  $$T_{0} \subset T_{1} \subset T_{2} \subset \cdots$$

  Show that each $T_{i}$ is consistent.

  Let $T=\bigcup_{i=0}^{\infty} T_{i}$. Show that $T$ is consistent and deductively closed, but that it is not finitary.

  comment

Mathematical Biology

• Paper 1, Section I, 6E

  Mathematical Biology | Part II, 2021

  (a) Consider a population of size $N(t)$ whose per capita rates of birth and death are $b e^{-a N}$ and $d$, respectively, where $b>d$ and all parameters are positive constants.

  (i) Write down the equation for the rate of change of the population.

  (ii) Show that a population of size $N^{*}=\frac{1}{a} \log \frac{b}{d}$ is stationary and that it is asymptotically stable.

  (b) Consider now a disease introduced into this population, where the number of susceptibles and infectives, $S$ and $I$, respectively, satisfy the equations

  $$\begin{aligned} &\frac{d S}{d t}=b e^{-a S} S-\beta S I-d S \\ &\frac{d I}{d t}=\beta S I-(d+\delta) I \end{aligned}$$

  (i) Interpret the biological meaning of each term in the above equations and comment on the reproductive capacity of the susceptible and infected individuals.

  (ii) Show that the disease-free equilibrium, $S=N^{*}$ and $I=0$, is linearly unstable if

  $$N^{*}>\frac{d+\delta}{\beta}$$

  (iii) Show that when the disease-free equilibrium is unstable there exists an endemic equilibrium satisfying

  $$\beta I+d=b e^{-a S}$$

  and that this equilibrium is linearly stable.

  comment

Mathematics of Machine Learning

• Paper 1, Section II, J

  Mathematics of Machine Learning | Part II, 2021

  Let $\mathcal{H}$ be a family of functions $h: \mathcal{X} \rightarrow\{0,1\}$ with $|\mathcal{H}| \geqslant 2$. Define the shattering coefficient $s(\mathcal{H}, n)$ and the $V C$ dimension $\mathrm{VC}(\mathcal{H})$ of $\mathcal{H}$.

  Briefly explain why if $\mathcal{H}^{\prime} \subseteq \mathcal{H}$ and $\left|\mathcal{H}^{\prime}\right| \geqslant 2$, then $\mathrm{VC}\left(\mathcal{H}^{\prime}\right) \leqslant \mathrm{VC}(\mathcal{H})$.

  Prove that if $\mathcal{F}$ is a vector space of functions $f: \mathcal{X} \rightarrow \mathbb{R}$ with $\mathcal{F}^{\prime} \subseteq \mathcal{F}$ and we define

  $$\mathcal{H}=\left\{\mathbf{1}_{\{u: f(u) \leqslant 0\}}: f \in \mathcal{F}^{\prime}\right\}$$

  then $\operatorname{VC}(\mathcal{H}) \leqslant \operatorname{dim}(\mathcal{F})$.

  Let $\mathcal{A}=\left\{\left\{x:\|x-c\|_{2}^{2} \leqslant r^{2}\right\}: c \in \mathbb{R}^{d}, r \in[0, \infty)\right\}$ be the set of all spheres in $\mathbb{R}^{d}$. Suppose $\mathcal{H}=\left\{\mathbf{1}_{A}: A \in \mathcal{A}\right\}$. Show that

  $$\mathrm{VC}(\mathcal{H}) \leqslant d+2$$

  $\left[\right.$ Hint: Consider the class of functions $\mathcal{F}^{\prime}=\left\{f_{c, r}: c \in \mathbb{R}^{d}, r \in[0, \infty)\right\}$, where

  $$f_{c, r}(x)=\|x\|_{2}^{2}-2 c^{T} x+\|c\|_{2}^{2}-r^{2}$$

  comment

Number Fields

• Paper 1, Section II, 20G

  Number Fields | Part II, 2021

  Let $K=\mathbb{Q}(\alpha)$, where $\alpha^{3}=5 \alpha-8$

  (a) Show that $[K: \mathbb{Q}]=3$.

  (b) Let $\beta=\left(\alpha+\alpha^{2}\right) / 2$. By considering the matrix of $\beta$ acting on $K$ by multiplication, or otherwise, show that $\beta$ is an algebraic integer, and that $(1, \alpha, \beta)$ is a $\mathbb{Z}$-basis for $\mathcal{O}_{K} \cdot$ [The discriminant of $T^{3}-5 T+8$ is $-4 \cdot 307$, and 307 is prime.]

  (c) Compute the prime factorisation of the ideal (3) in $\mathcal{O}_{K}$. Is (2) a prime ideal of $\mathcal{O}_{K} ?$ Justify your answer.

  comment

Number Theory

• Paper 1, Section I, 1I

  Number Theory | Part II, 2021

  State Euler's criterion.

  Let $p$ be an odd prime. Show that every primitive root modulo $p$ is a quadratic non-residue modulo $p$.

  Let $p$ be a Fermat prime, that is, a prime of the form $2^{2^{k}}+1$ for some $k \geqslant 1$. By evaluating $\phi(p-1)$, or otherwise, show that every quadratic non-residue modulo $p$ is a primitive root modulo $p$. Deduce that 3 is a primitive root modulo $p$ for every Fermat prime $p$.

  comment

Numerical Analysis

• Paper 1, Section II, E

  Numerical Analysis | Part II, 2021

  Let $A \in \mathbb{R}^{n \times n}$ with $n>2$ and define $\operatorname{Spec}(A)=\{\lambda \in \mathbb{C} \mid A-\lambda I$ is not invertible $\}$.

  The QR algorithm for computing $\operatorname{Spec}(A)$ is defined as follows. Set $A_{0}=A$. For $k=0,1, \ldots$ compute the $\mathrm{QR}$ factorization $A_{k}=Q_{k} R_{k}$ and set $A_{k+1}=R_{k} Q_{k}$. (Here $Q_{k}$ is an $n \times n$ orthogonal matrix and $R_{k}$ is an $n \times n$ upper triangular matrix.)

  (a) Show that $A_{k+1}$ is related to the original matrix $A$ by the similarity transformation $A_{k+1}=\bar{Q}_{k}^{T} A \bar{Q}_{k}$, where $\bar{Q}_{k}=Q_{0} Q_{1} \cdots Q_{k}$ is orthogonal and $\bar{Q}_{k} \bar{R}_{k}$ is the QR factorization of $A^{k+1}$ with $\bar{R}_{k}=R_{k} R_{k-1} \cdots R_{0}$.

  (b) Suppose that $A$ is symmetric and that its eigenvalues satisfy

  $$\left|\lambda_{1}\right|<\left|\lambda_{2}\right|<\cdots<\left|\lambda_{n-1}\right|=\left|\lambda_{n}\right|$$

  Suppose, in addition, that the first two canonical basis vectors are given by $\mathbf{e}_{1}=\sum_{i=1}^{n} b_{i} \mathbf{w}_{i}$, $\mathbf{e}_{2}=\sum_{i=1}^{n} c_{i} \mathbf{w}_{i}$, where $b_{i} \neq 0, c_{i} \neq 0$ for $i=1, \ldots, n$ and $\left\{\mathbf{w}_{i}\right\}_{i=1}^{n}$ are the normalised eigenvectors of $A$.

  Let $B_{k} \in \mathbb{R}^{2 \times 2}$ be the $2 \times 2$ upper left corner of $A_{k}$. Show that $d_{\mathrm{H}}\left(\operatorname{Spec}\left(B_{k}\right), S\right) \rightarrow 0$ as $k \rightarrow \infty$, where $S=\left\{\lambda_{n}\right\} \cup\left\{\lambda_{n-1}\right\}$ and $d_{\mathrm{H}}$ denotes the Hausdorff metric

  $$d_{\mathrm{H}}(X, Y)=\max \left\{\sup _{x \in X} \inf _{y \in Y}|x-y|, \sup _{y \in Y} \inf _{x \in X}|x-y|\right\}, \quad X, Y \subset \mathbb{C}$$

  [Hint: You may use the fact that for real symmetric matrices $U, V$ we have $\left.d_{\mathrm{H}}(\operatorname{Spec}(U), \operatorname{Spec}(V)) \leqslant\|U-V\|_{2} \cdot\right]$

  comment

Principles of Quantum Mechanics

• Paper 1, Section II, B

  Principles of Quantum Mechanics | Part II, 2021

  (a) A group $G$ of transformations acts on a quantum system. Briefly explain why the Born rule implies that these transformations may be represented by operators $U(g): \mathcal{H} \rightarrow \mathcal{H}$ obeying

  $$\begin{aligned} U(g)^{\dagger} U(g) &=1_{\mathcal{H}} \\ U\left(g_{1}\right) U\left(g_{2}\right) &=e^{i \phi\left(g_{1}, g_{2}\right)} U\left(g_{1} \cdot g_{2}\right) \end{aligned}$$

  for all $g_{1}, g_{2} \in G$, where $\phi\left(g_{1}, g_{2}\right) \in \mathbb{R}$.

  What additional property does $U(g)$ have when $G$ is a group of symmetries of the Hamiltonian? Show that symmetries correspond to conserved quantities.

  (b) The Coulomb Hamiltonian describing the gross structure of the hydrogen atom is invariant under time reversal, $t \mapsto-t$. Suppose we try to represent time reversal by a unitary operator $T$ obeying $U(t) T=T U(-t)$, where $U(t)$ is the time-evolution operator. Show that this would imply that hydrogen has no stable ground state.

  An operator $A: \mathcal{H} \rightarrow \mathcal{H}$ is antilinear if

  $$A(a|\alpha\rangle+b|\beta\rangle)=\bar{a} A|\alpha\rangle+\bar{b} A|\beta\rangle$$

  for all $|\alpha\rangle,|\beta\rangle \in \mathcal{H}$ and all $a, b \in \mathbb{C}$, and antiunitary if, in addition,

  $$\left\langle\beta^{\prime} \mid \alpha^{\prime}\right\rangle=\overline{\langle\beta \mid \alpha\rangle},$$

  where $\left|\alpha^{\prime}\right\rangle=A|\alpha\rangle$ and $\left|\beta^{\prime}\right\rangle=A|\beta\rangle$. Show that if time reversal is instead represented by an antiunitary operator then the above instability of hydrogen is avoided.

  comment

Principles of Statistics

• Paper 1, Section II, J

  Principles of Statistics | Part II, 2021

  Let $X_{1}, \ldots, X_{n}$ be random variables with joint probability density function in a statistical model $\left\{f_{\theta}: \theta \in \mathbb{R}\right\}$.

  (a) Define the Fisher information $I_{n}(\theta)$. What do we mean when we say that the Fisher information tensorises?

  (b) Derive the relationship between the Fisher information and the derivative of the score function in a regular model.

  (c) Consider the model defined by $X_{1}=\theta+\varepsilon_{1}$ and

  $$X_{i}=\theta(1-\sqrt{\gamma})+\sqrt{\gamma} X_{i-1}+\sqrt{1-\gamma} \varepsilon_{i} \quad \text { for } i=2, \ldots, n$$

  where $\varepsilon_{1}, \ldots, \varepsilon_{n}$ are i.i.d. $N(0,1)$ random variables, and $\gamma \in[0,1)$ is a known constant. Compute the Fisher information $I_{n}(\theta)$. For which values of $\gamma$ does the Fisher information tensorise? State a lower bound on the variance of an unbiased estimator $\hat{\theta}$ in this model.

  comment

Probability and Measure

• Paper 1, Section II, H

  Probability and Measure | Part II, 2021

  (a) State and prove Fatou's lemma. [You may use the monotone convergence theorem without proof, provided it is clearly stated.]

  (b) Show that the inequality in Fatou's lemma can be strict.

  (c) Let $\left(X_{n}: n \in \mathbb{N}\right)$ and $X$ be non-negative random variables such that $X_{n} \rightarrow X$ almost surely as $n \rightarrow \infty$. Must we have $\mathbb{E} X \leqslant \sup _{n} \mathbb{E} X_{n}$ ?

  comment

Quantum Information and Computation

• Paper 1, Section I, $10 D$

  Quantum Information and Computation | Part II, 2021

  Alice wishes to communicate to Bob a 1-bit message $m=0$ or $m=1$ chosen by her with equal prior probabilities $1 / 2$. For $m=0$ (respectively $m=1$ ) she sends Bob the quantum state $\left|a_{0}\right\rangle$ (respectively $\left|a_{1}\right\rangle$ ). On receiving the state, Bob applies quantum operations to it, to try to determine Alice's message. The Helstrom-Holevo theorem asserts that the probability $P_{S}$ for Bob to correctly determine Alice's message is bounded by $P_{S} \leqslant \frac{1}{2}(1+\sin \theta)$, where $\theta=\cos ^{-1}\left|\left\langle a_{0} \mid a_{1}\right\rangle\right|$, and that this bound is achievable.

  (a) Suppose that $\left|a_{0}\right\rangle=|0\rangle$ and $\left|a_{1}\right\rangle=\frac{1}{\sqrt{2}}(|0\rangle+|1\rangle)$, and that Bob measures the received state in the basis $\left\{\left|b_{0}\right\rangle,\left|b_{1}\right\rangle\right\}$, where $\left|b_{0}\right\rangle=\cos \beta|0\rangle+\sin \beta|1\rangle$ and $\left|b_{1}\right\rangle=$ $-\sin \beta|0\rangle+\cos \beta|1\rangle$, to produce his output 0 or 1 , respectively. Calculate the probability $P_{S}$ that Bob correctly determines Alice's message, and show that the maximum value of $P_{S}$ over choices of $\beta \in\left(-\frac{\pi}{2}, \frac{\pi}{2}\right]$ achieves the Helstrom-Holevo bound.

  (b) State the no-cloning theorem as it applies to unitary processes and a set of two non-orthogonal states $\left\{\left|c_{0}\right\rangle,\left|c_{1}\right\rangle\right\}$. Show that the Helstrom-Holevo theorem implies the validity of the no-cloning theorem in this situation.

  comment

Representation Theory

• Paper 1, Section II, I

  Representation Theory | Part II, 2021

  (a) What does it mean to say that a representation of a group is completely reducible? State Maschke's theorem for representations of finite groups over fields of characteristic 0 . State and prove Schur's lemma. Deduce that if there exists a faithful irreducible complex representation of $G$, then $Z(G)$ is cyclic.

  (b) If $G$ is any finite group, show that the regular representation $\mathbb{C} G$ is faithful. Show further that for every finite simple group $G$, there exists a faithful irreducible complex representation of $G$.

  (c) Which of the following groups have a faithful irreducible representation? Give brief justification of your answers.

  (i) the cyclic groups $C_{n}(n$ a positive integer $)$;

  (ii) the dihedral group $D_{8}$;

  (iii) the direct product $C_{2} \times D_{8}$.

  comment

Riemann Surfaces

• Paper 1, Section II, F

  Riemann Surfaces | Part II, 2021

  (a) Consider an open $\operatorname{disc} D \subseteq \mathbb{C}$. Prove that a real-valued function $u: D \rightarrow \mathbb{R}$ is harmonic if and only if

  $$u=\operatorname{Re}(f)$$

  for some analytic function $f$.

  (b) Give an example of a domain $D$ and a harmonic function $u: D \rightarrow \mathbb{R}$ that is not equal to the real part of an analytic function on $D$. Justify your answer carefully.

  (c) Let $u$ be a harmonic function on $\mathbb{C}_{*}$ such that $u(2 z)=u(z)$ for every $z \in \mathbb{C}_{*}$. Prove that $u$ is constant, justifying your answer carefully. Exhibit a countable subset $S \subseteq \mathbb{C}_{*}$ and a non-constant harmonic function $u$ on $\mathbb{C}_{*} \backslash S$ such that for all $z \in \mathbb{C}_{*} \backslash S$ we have $2 z \in \mathbb{C}_{*} \backslash S$ and $u(2 z)=u(z)$.

  (d) Prove that every non-constant harmonic function $u: \mathbb{C} \rightarrow \mathbb{R}$ is surjective.

  comment

Statistical Modelling

• Paper 1, Section I, J

  Statistical Modelling | Part II, 2021

  Let $\mu>0$. The probability density function of the inverse Gaussian distribution (with the shape parameter equal to 1 ) is given by

  $$f(x ; \mu)=\frac{1}{\sqrt{2 \pi x^{3}}} \exp \left[-\frac{(x-\mu)^{2}}{2 \mu^{2} x}\right]$$

  Show that this is a one-parameter exponential family. What is its natural parameter? Show that this distribution has mean $\mu$ and variance $\mu^{3}$.

  comment

• Paper 1, Section II, J

  Statistical Modelling | Part II, 2021

  The following data were obtained in a randomised controlled trial for a drug. Due to a manufacturing error, a subset of trial participants received a low dose (LD) instead of a standard dose (SD) of the drug.

  

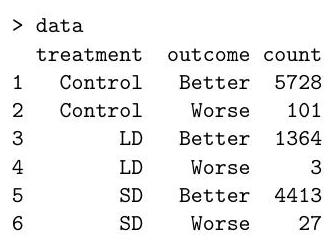
  (a) Below we analyse the data using Poisson regression:

  

  (i) After introducing necessary notation, write down the Poisson models being fitted above.

  (ii) Write down the corresponding multinomial models, then state the key theoretical result (the "Poisson trick") that allows you to fit the multinomial models using Poisson regression. [You do not need to prove this theoretical result.]

  (iii) Explain why the number of degrees of freedom in the likelihood ratio test is 2 in the analysis of deviance table. What can you conclude about the drug?

  (b) Below is the summary table of the second model:

  

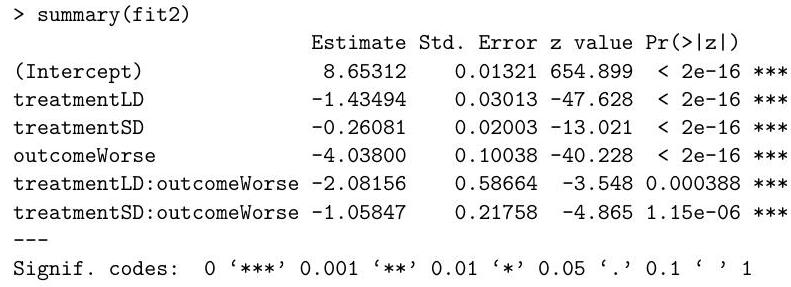
  (i) Drug efficacy is defined as one minus the ratio of the probability of worsening in the treated group to the probability of worsening in the control group. By using a more sophisticated method, a published analysis estimated that the drug efficacy is $90.0 \%$ for the LD treatment and $62.1 \%$ for the $\mathrm{SD}$ treatment. Are these numbers similar to what is obtained by Poisson regression? [Hint: $e^{-1} \approx 0.37, e^{-2} \approx 0.14$, and $e^{-3} \approx 0.05$, where $e$ is the base of the natural logarithm.]

  (ii) Explain why the information in the summary table is not enough to test the hypothesis that the LD drug and the SD drug have the same efficacy. Then describe how you can test this hypothesis using analysis of deviance in $R$.

  comment

Statistical Physics

• Paper 1, Section II, 36C

  Statistical Physics | Part II, 2021

  Throughout this question you should consider a classical gas and assume that the number of particles is fixed.

  (a) Write down the equation of state for an ideal gas. Write down an expression for the internal energy of an ideal gas in terms of the heat capacity at constant volume, $C_{V}$.

  (b) Starting from the first law of thermodynamics, find a relation between $C_{V}$ and the heat capacity at constant pressure, $C_{p}$, for an ideal gas. Hence give an expression for $\gamma=C_{p} / C_{V}$.

  (c) Describe the meaning of an adiabatic process. Using the first law of thermodynamics, derive the equation for an adiabatic process in the $(p, V)$-plane for an ideal gas.

  (d) Consider a simplified Otto cycle (an idealised petrol engine) involving an ideal gas and consisting of the following four reversible steps:

  $A \rightarrow B:$ Adiabatic compression from volume $V_{1}$ to volume $V_{2}<V_{1}$;

  $B \rightarrow C$ : Heat $Q_{1}$ injected at constant volume;

  $C \rightarrow D:$ Adiabatic expansion from volume $V_{2}$ to volume $V_{1}$;

  $D \rightarrow A:$ Heat $Q_{2}$ extracted at constant volume.

  Sketch the cycle in the $(p, V)$-plane and in the $(T, S)$-plane.

  Derive an expression for the efficiency, $\eta=W / Q_{1}$, where $W$ is the work out, in terms of the compression ratio $r=V_{1} / V_{2}$. How can the efficiency be maximized?

  comment

Stochastic Financial Models

• Paper 1, Section II, 30K

  Stochastic Financial Models | Part II, 2021

  (a) What does it mean to say that a stochastic process $\left(X_{n}\right)_{n \geqslant 0}$ is a martingale with respect to a filtration $\left(\mathcal{F}_{n}\right)_{n \geqslant 0}$ ?

  (b) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a martingale, and let $\xi_{n}=X_{n}-X_{n-1}$ for $n \geqslant 1$. Suppose $\xi_{n}$ takes values in the set $\{-1,+1\}$ almost surely for all $n \geqslant 1$. Show that $\left(X_{n}\right)_{n \geqslant 0}$ is a simple symmetric random walk, i.e. that the sequence $\left(\xi_{n}\right)_{n \geqslant 1}$ is $\operatorname{IID}$ with $\mathbb{P}\left(\xi_{1}=1\right)=1 / 2=$ $\mathbb{P}\left(\xi_{1}=-1\right) .$

  (c) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a martingale and let the bounded process $\left(H_{n}\right)_{n \geqslant 1}$ be previsible.

  Let $\hat{X}_{0}=0$ and

  $$\hat{X}_{n}=\sum_{k=1}^{n} H_{k}\left(X_{k}-X_{k-1}\right) \text { for } n \geqslant 1$$

  Show that $\left(\hat{X}_{n}\right)_{n \geqslant 0}$ is a martingale.

  (d) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk with $X_{0}=0$, and let

  $$T_{a}=\inf \left\{n \geqslant 0: X_{n}=a\right\}$$

  where $a$ is a positive integer. Let

  $$\hat{X}_{n}= \begin{cases}X_{n} & \text { if } n \leqslant T_{a} \\ 2 a-X_{n} & \text { if } n>T_{a}\end{cases}$$

  Show that $\left(\hat{X}_{n}\right)_{n \geqslant 0}$ is a simple symmetric random walk.

  (e) Let $\left(X_{n}\right)_{n \geqslant 0}$ be a simple symmetric random walk with $X_{0}=0$, and let $M_{n}=\max _{0 \leqslant k \leqslant n} X_{k}$. Compute $\mathbb{P}\left(M_{n}=a\right)$ for a positive integer $a$.

  comment

Topics in Analysis

• Paper 1, Section I, 2H

  Topics in Analysis | Part II, 2021

  Write

  $$P=\left\{\mathbf{x} \in \mathbb{R}^{n}: x_{j} \geqslant 0 \text { for all } 1 \leqslant j \leqslant n\right\}$$

  and suppose that $K$ is a non-empty, closed, convex and bounded subset of $\mathbb{R}^{n}$ with $K \cap \operatorname{Int} P \neq \emptyset$. By taking logarithms, or otherwise, show that there is a unique $\mathbf{x}^{*} \in K \cap P$ such that

  $$\prod_{j=1}^{n} x_{j} \leqslant \prod_{j=1}^{n} x_{j}^{*}$$

  for all $\mathbf{x} \in K \cap P$.

  Show that $\sum_{j=1}^{n} \frac{x_{j}}{x_{j}^{*}} \leqslant n$ for all $\mathbf{x} \in K \cap P$.

  Identify the point $\mathbf{x}^{*}$ in the case that $K$ has the property

  $$\left(x_{1}, x_{2}, \ldots, x_{n-1}, x_{n}\right) \in K \Rightarrow\left(x_{2}, x_{3}, \ldots, x_{n}, x_{1}\right) \in K$$

  and justify your answer.

  Show that, given any $\mathbf{a} \in \operatorname{Int} P$, we can find a set $K$, as above, with $\mathbf{x}^{*}=\mathbf{a}$.

  comment

Waves

• Paper 1, Section II, 40A

  Waves | Part II, 2021

  Compressible fluid of equilibrium density $\rho_{0}$, pressure $p_{0}$ and sound speed $c_{0}$ is contained in the region between an inner rigid sphere of radius $R$ and an outer elastic sphere of equilibrium radius $2 R$. The elastic sphere is made to oscillate radially in such a way that it exerts a spherically symmetric, perturbation pressure $\tilde{p}=\epsilon p_{0} \cos \omega t$ on the fluid at $r=2 R$, where $\epsilon \ll 1$ and the frequency $\omega$ is sufficiently small that

  $$\alpha \equiv \frac{\omega R}{c_{0}} \leqslant \frac{\pi}{2}$$

  You may assume that the acoustic velocity potential satisfies the wave equation

  $$\frac{\partial^{2} \phi}{\partial t^{2}}=c_{0}^{2} \nabla^{2} \phi$$

  (a) Derive an expression for $\phi(r, t)$.

  (b) Hence show that the net radial component of the acoustic intensity (wave-energy flux) $\mathbf{I}=\tilde{p} \mathbf{u}$ is zero when averaged appropriately in a way you should define. Interpret this result physically.

  (c) Briefly discuss the possible behaviour of the system if the forcing frequency $\omega$ is allowed to increase to larger values.

  $\left[\right.$ For a spherically symmetric variable $\left.\psi(r, t), \nabla^{2} \psi=\frac{1}{r} \frac{\partial^{2}}{\partial r^{2}}(r \psi) .\right]$

  comment