Part II, 2018, Paper 3

Algebraic Geometry

• Paper 3, Section II, I

  Algebraic Geometry | Part II, 2018

  (a) State the Riemann-Roch theorem.

  (b) Let $E$ be a smooth projective curve of genus 1 over an algebraically closed field $k$, with char $k \neq 2,3$. Show that there exists an isomorphism from $E$ to the plane cubic in $\mathbf{P}^{2}$ defined by the equation

  $$y^{2}=\left(x-\lambda_{1}\right)\left(x-\lambda_{2}\right)\left(x-\lambda_{3}\right)$$

  for some distinct $\lambda_{1}, \lambda_{2}, \lambda_{3} \in k$.

  (c) Let $Q$ be the point at infinity on $E$. Show that the map $E \rightarrow C l^{0}(E), P \mapsto[P-Q]$ is an isomorphism.

  Describe how this defines a group structure on $E$. Denote addition by $\boxplus$. Determine all the points $P \in E$ with $P \boxplus P=Q$ in terms of the equation of the plane curve in part (b).

  comment

Algebraic Topology

• Paper 3, Section II, H

  Algebraic Topology | Part II, 2018

  (a) State a version of the Seifert-van Kampen theorem for a cell complex $X$ written as the union of two subcomplexes $Y, Z$.

  (b) Let

  $$X_{n}=\underbrace{S^{1} \vee \ldots \vee S^{1}}_{n} \vee \mathbb{R} P^{2}$$

  for $n \geqslant 1$, and take any $x_{0} \in X_{n}$. Write down a presentation for $\pi_{1}\left(X_{n}, x_{0}\right)$.

  (c) By computing a homology group of a suitable four-sheeted covering space of $X_{n}$, prove that $X_{n}$ is not homotopy equivalent to a compact, connected surface whenever $n \geqslant 1$.

  comment

Analysis of Functions

• Paper 3, Section II, $22 F$

  Analysis of Functions | Part II, 2018

  (a) Let $(X, \mathcal{A}, \mu)$ be a measure space. Define the spaces $L^{p}(X)$ for $p \in[1, \infty]$. Prove that if $\mu(X)<\infty$ then $L^{q}(X) \subset L^{p}(X)$ for all $1 \leqslant p<q \leqslant \infty$.

  (b) Now let $X=\mathbb{R}^{n}$ endowed with Borel sets and Lebesgue measure. Describe the dual spaces of $L^{p}(X)$ for $p \in[1, \infty)$. Define reflexivity and say which $L^{p}(X)$ are reflexive. Prove that $L^{1}(X)$ is not the dual space of $L^{\infty}(X)$

  (c) Now let $X \subset \mathbb{R}^{n}$ be a Borel subset and consider the measure space $(X, \mathcal{A}, \mu)$ induced from Borel sets and Lebesgue measure on $\mathbb{R}^{n}$.

  (i) Given any $p \in[1, \infty]$, prove that any sequence $\left(f_{n}\right)$ in $L^{p}(X)$ converging in $L^{p}(X)$ to some $f \in L^{p}(X)$ admits a subsequence converging almost everywhere to $f$.

  (ii) Prove that if $L^{q}(X) \subset L^{p}(X)$ for $1 \leqslant p<q \leqslant \infty$ then $\mu(X)<\infty$. [Hint: You might want to prove first that the inclusion is continuous with the help of one of the corollaries of Baire's category theorem.]

  comment

Applications of Quantum Mechanics

• Paper 3, Section II, A

  Applications of Quantum Mechanics | Part II, 2018

  A beam of particles of mass $m$ and momentum $p=\hbar k$ is incident along the $z$-axis. The beam scatters off a spherically symmetric potential $V(r)$. Write down the asymptotic form of the wavefunction in terms of the scattering amplitude $f(\theta)$.

  The incoming plane wave and the scattering amplitude can be expanded in partial waves as,

  $$\begin{gathered} e^{i k r \cos \theta} \sim \frac{1}{2 i k r} \sum_{l=0}^{\infty}(2 l+1)\left(e^{i k r}-(-1)^{l} e^{-i k r}\right) P_{l}(\cos \theta) \\ f(\theta)=\sum_{l=0}^{\infty} \frac{2 l+1}{k} f_{l} P_{l}(\cos \theta) \end{gathered}$$

  where $P_{l}$ are Legendre polynomials. Define the $S$-matrix. Assuming that the S-matrix is unitary, explain why we can write

  $$f_{l}=e^{i \delta_{l}} \sin \delta_{l}$$

  for some real phase shifts $\delta_{l}$. Obtain an expression for the total cross-section $\sigma_{T}$ in terms of the phase shifts $\delta_{l}$.

  [Hint: You may use the orthogonality of Legendre polynomials:

  $$\left.\int_{-1}^{+1} d w P_{l}(w) P_{l^{\prime}}(w)=\frac{2}{2 l+1} \delta_{l l^{\prime}} .\right]$$

  Consider the repulsive, spherical potential

  $$V(r)=\left\{\begin{array}{cc} +V_{0} & r<a \\ 0 & r>a \end{array}\right.$$

  where $V_{0}=\hbar^{2} \gamma^{2} / 2 m$. By considering the s-wave solution to the Schrödinger equation, show that

  $$\frac{\tan \left(k a+\delta_{0}\right)}{k a}=\frac{\tanh \left(\sqrt{\gamma^{2}-k^{2}} a\right)}{\sqrt{\gamma^{2}-k^{2}} a}$$

  For low momenta, $k a \ll 1$, compute the s-wave contribution to the total cross-section. Comment on the physical interpretation of your result in the limit $\gamma a \rightarrow \infty$.

  comment

Applied Probability

• Paper 3, Section II, J

  Applied Probability | Part II, 2018

  Individuals arrive in a shop in the manner of a Poisson process with intensity $\lambda$, and they await service in the order of their arrival. Their service times are independent, identically distributed random variables $S_{1}, S_{2}, \ldots$. For $n \geqslant 1$, let $Q_{n}$ be the number remaining in the shop immediately after the $n$th departure. Show that

  $$Q_{n+1}=A_{n}+Q_{n}-h\left(Q_{n}\right)$$

  where $A_{n}$ is the number of arrivals during the $(n+1)$ th service period, and $h(x)=$ $\min \{1, x\}$.

  Show that

  $$\mathbb{E}\left(A_{n}\right)=\rho, \quad \mathbb{E}\left(A_{n}^{2}\right)=\rho+\lambda^{2} \mathbb{E}\left(S^{2}\right),$$

  where $S$ is a typical service period, and $\rho=\lambda \mathbb{E}(S)$ is the traffic intensity of the queue.

  Suppose $\rho<1$, and the queue is in equilibrium in the sense that $Q_{n}$ and $Q_{n+1}$ have the same distribution for all $n$. Express $\mathbb{E}\left(Q_{n}\right)$ in terms of $\lambda, \mathbb{E}(S), \mathbb{E}\left(S^{2}\right)$. Deduce that the mean waiting time (prior to service) of a typical individual is $\frac{1}{2} \lambda \mathbb{E}\left(S^{2}\right) /(1-\rho)$.

  comment

Asymptotic Methods

• Paper 3, Section II, B

  Asymptotic Methods | Part II, 2018

  (a) Find the curves of steepest descent emanating from $t=0$ for the integral

  $$J_{x}(x)=\frac{1}{2 \pi i} \int_{C} e^{x(\sinh t-t)} d t$$

  for $x>0$ and determine the angles at which they meet at $t=0$, and their asymptotes at infinity.

  (b) An integral representation for the Bessel function $K_{\nu}(x)$ for real $x>0$ is

  $$K_{\nu}(x)=\frac{1}{2} \int_{-\infty}^{+\infty} e^{\nu h(t)} d t \quad, \quad h(t)=t-\left(\frac{x}{\nu}\right) \cosh t$$

  Show that, as $\nu \rightarrow+\infty$, with $x$ fixed,

  $$K_{\nu}(x) \sim\left(\frac{\pi}{2 \nu}\right)^{\frac{1}{2}}\left(\frac{2 \nu}{e x}\right)^{\nu}$$

  comment

Automata and Formal Languages

• Paper 3, Section I, G

  Automata and Formal Languages | Part II, 2018

  (a) Define what it means for a context-free grammar (CFG) to be in Chomsky normal form ( $\mathrm{CNF})$.

  (b) Give an algorithm for converting a CFG $G$ into a corresponding CFG $G_{\text {Chom }}$ in CNF satisfying $\mathcal{L}\left(G_{\text {Chom }}\right)=\mathcal{L}(G)-\{\epsilon\}$. [You need only outline the steps, without proof.]

  (c) Convert the following $\mathrm{CFG}\ G$ :

  $$S \rightarrow A S c \mid B, \quad A \rightarrow a, \quad B \rightarrow b$$

  into a grammar in CNF.

  comment

• Paper 3, Section II, G

  Automata and Formal Languages | Part II, 2018

  (a) State and prove the pumping lemma for regular languages.

  (b) Let $D$ be a minimal deterministic finite-state automaton whose language $\mathcal{L}(D)$ is finite. Let $\Gamma_{D}$ be the transition diagram of $D$, and suppose there exists a non-empty closed path $\gamma$ in $\Gamma_{D}$ starting and ending at state $p$.

  (i) Show that there is no path in $\Gamma_{D}$ from $p$ to any accept state of $D$.

  (ii) Show that there is no path in $\Gamma_{D}$ from $p$ to any other state of $D$.

  comment

Classical Dynamics

• Paper 3, Section I, B

  Classical Dynamics | Part II, 2018

  Three particles of unit mass move along a line in a potential

  $$V=\frac{1}{2}\left(\left(x_{1}-x_{2}\right)^{2}+\left(x_{1}-x_{3}\right)^{2}+\left(x_{3}-x_{2}\right)^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right)$$

  where $x_{i}$ is the coordinate of the $i$ th particle, $i=1,2,3$.

  Write the Lagrangian in the form

  $$\mathcal{L}=\frac{1}{2} T_{i j} \dot{x}_{i} \dot{x}_{j}-\frac{1}{2} V_{i j} x_{i} x_{j}$$

  and specify the matrices $T_{i j}$ and $V_{i j}$.

  Find the normal frequencies and normal modes for this system.

  comment

Coding and Cryptography

• Paper 3, Section $I$, H

  Coding and Cryptography | Part II, 2018

  Compute the rank and minimum distance of the cyclic code with generator polynomial $g(X)=X^{3}+X^{2}+1$ and parity check polynomial $h(X)=X^{4}+X^{3}+X^{2}+1$. Now let $\alpha$ be a root of $g(X)$ in the field with 8 elements. We receive the word $r(X)=X^{2}+X+1$ $\left(\bmod X^{7}-1\right)$. Verify that $r(\alpha)=\alpha^{4}$, and hence decode $r(X)$ using minimum-distance decoding.

  comment

Cosmology

• Paper 3, Section I, B

  Cosmology | Part II, 2018

  The energy density of a particle species is defined by

  $$\epsilon=\int_{0}^{\infty} E(p) n(p) d p$$

  where $E(p)=c \sqrt{p^{2}+m^{2} c^{2}}$ is the energy, and $n(p)$ the distribution function, of a particle with momentum $p$. Here $c$ is the speed of light and $m$ is the rest mass of the particle. If the particle species is in thermal equilibrium then the distribution function takes the form

  $$n(p)=\frac{4 \pi}{h^{3}} g \frac{p^{2}}{\exp ((E(p)-\mu) / k T) \mp 1}$$

  where $g$ is the number of degrees of freedom of the particle, $T$ is the temperature, $h$ and $k$ are constants and $-$ is for bosons and $+$ is for fermions.

  (a) Stating any assumptions you require, show that in the very early universe the energy density of a given particle species $i$ is

  $$\epsilon_{i}=\frac{4 \pi g_{i}}{(h c)^{3}}(k T)^{4} \int_{0}^{\infty} \frac{y^{3}}{e^{y} \mp 1} d y$$

  (b) Show that the total energy density in the very early universe is

  $$\epsilon=\frac{4 \pi^{5}}{15(h c)^{3}} g^{*}(k T)^{4}$$

  where $g^{*}$ is defined by

  $$g^{*} \equiv \sum_{\text {Bosons }} g_{i}+\frac{7}{8} \sum_{\text {Fermions }} g_{i}$$

  [Hint: You may use the fact that $\left.\int_{0}^{\infty} y^{3}\left(e^{y}-1\right)^{-1} d y=\pi^{4} / 15 .\right]$

  comment

• Paper 3, Section II, B

  Cosmology | Part II, 2018

  The pressure support equation for stars is

  $$\frac{1}{r^{2}} \frac{d}{d r}\left[\frac{r^{2}}{\rho} \frac{d P}{d r}\right]=-4 \pi G \rho$$

  where $\rho$ is the density, $P$ is the pressure, $r$ is the radial distance, and $G$ is Newton's constant.

  (a) What two boundary conditions should we impose on the above equation for it to describe a star?

  (b) By assuming a polytropic equation of state,

  $$P(r)=K \rho^{1+\frac{1}{n}}(r)$$

  where $K$ is a constant, derive the Lane-Emden equation

  $$\frac{1}{\xi^{2}} \frac{d}{d \xi}\left[\xi^{2} \frac{d \theta}{d \xi}\right]=-\theta^{n}$$

  where $\rho=\rho_{c} \theta^{n}$, with $\rho_{c}$ the density at the centre of the star, and $r=a \xi$, for some $a$ that you should determine.

  (c) Show that the mass of a polytropic star is

  $$M=\frac{1}{2 \sqrt{\pi}}\left(\frac{(n+1) K}{G}\right)^{\frac{3}{2}} \rho_{c}^{\frac{3-n}{2 n}} Y_{n}$$

  where $Y_{n} \equiv-\left.\xi_{1}^{2} \frac{d \theta}{d \xi}\right|_{\xi=\xi_{1}}$ and $\xi_{1}$ is the value of $\xi$ at the surface of the star.

  (d) Derive the following relation between the mass, $M$, and radius, $R$, of a polytropic star

  $$M=A_{n} K^{\frac{n}{n-1}} R^{\frac{3-n}{1-n}}$$

  where you should determine the constant $A_{n}$. What type of star does the $n=3$ polytrope represent and what is the significance of the mass being constant for this star?

  comment

Differential Geometry

• Paper 3, Section II, I

  Differential Geometry | Part II, 2018

  Let $S \subset \mathbb{R}^{3}$ be a surface.

  (a) Define the Gaussian curvature $K$ of $S$ in terms of the coefficients of the first and second fundamental forms, computed with respect to a local parametrization $\phi(u, v)$ of $S$.

  Prove the Theorema Egregium, i.e. show that the Gaussian curvature can be expressed entirely in terms of the coefficients of the first fundamental form and their first and second derivatives with respect to $u$ and $v$.

  (b) State the global Gauss-Bonnet theorem for a compact orientable surface $S$.

  (c) Now assume that $S$ is non-compact and diffeomorphic to $\mathbb{S}^{2} \backslash\{(1,0,0)\}$ but that there is a point $p \in \mathbb{R}^{3}$ such that $S \cup\{p\}$ is a compact subset of $\mathbb{R}^{3}$. Is it necessarily the case that $\int_{S} K d A=4 / \pi ?$ Justify your answer.

  comment

Dynamical Systems

• Paper 3, Section II, 32E

  Dynamical Systems | Part II, 2018

  Consider the system

  $$\dot{x}=y, \quad \dot{y}=\mu_{1} x+\mu_{2} y-(x+y)^{3}$$

  where $\mu_{1}$ and $\mu_{2}$ are parameters.

  By considering a function of the form $V(x, y)=f(x+y)+\frac{1}{2} y^{2}$, show that when $\mu_{1}=\mu_{2}=0$ the origin is globally asymptotically stable. Sketch the phase plane for this case.

  Find the fixed points for the general case. Find the values of $\mu_{1}$ and $\mu_{2}$ for which the fixed points have (i) a stationary bifurcation and (ii) oscillatory (Hopf) bifurcations. Sketch these bifurcation values in the $\left(\mu_{1}, \mu_{2}\right)$-plane.

  For the case $\mu_{2}=-1$, find the leading-order approximation to the extended centre manifold of the bifurcation as $\mu_{1}$ varies, assuming that $\mu_{1}=O\left(x^{2}\right)$. Find also the evolution equation on the extended centre manifold to leading order. Deduce the type of bifurcation, and sketch the bifurcation diagram in the $\left(\mu_{1}, x\right)$-plane.

  comment

Electrodynamics

• Paper 3, Section II, D

  Electrodynamics | Part II, 2018

  Starting from the covariant form of the Maxwell equations and making a suitable choice of gauge which you should specify, show that the 4-vector potential due to an arbitrary 4-current $J^{\mu}(x)$ obeys the wave equation,

  $$\left(\nabla^{2}-\frac{1}{c^{2}} \frac{\partial^{2}}{\partial t^{2}}\right) A^{\mu}=-\mu_{0} J^{\mu}$$

  where $x^{\mu}=(c t, \mathbf{x})$.

  Use the method of Green's functions to show that, for a localised current distribution, this equation is solved by

  $$A^{\mu}(t, \mathbf{x})=\frac{\mu_{0}}{4 \pi} \int d^{3} x^{\prime} \frac{J^{\mu}\left(t_{\mathrm{ret}}, \mathbf{x}^{\prime}\right)}{\left|\mathbf{x}-\mathbf{x}^{\prime}\right|}$$

  for some $t_{\text {ret }}$ that you should specify.

  A point particle, of charge $q$, moving along a worldline $y^{\mu}(\tau)$ parameterised by proper time $\tau$, produces a 4 -vector potential

  $$A^{\mu}(x)=\frac{\mu_{0} q c}{4 \pi} \frac{\dot{y}^{\mu}\left(\tau_{\star}\right)}{\left|R^{\nu}\left(\tau_{\star}\right) \dot{y}_{\nu}\left(\tau_{\star}\right)\right|}$$

  where $R^{\mu}(\tau)=x^{\mu}-y^{\mu}(\tau)$. Define $\tau_{\star}(x)$ and draw a spacetime diagram to illustrate its physical significance.

  Suppose the particle follows a circular trajectory,

  $$\mathbf{y}(t)=(R \cos (\omega t), R \sin (\omega t), 0)$$

  (with $y^{0}=c t$ ), in some inertial frame with coordinates $(c t, x, y, z)$. Evaluate the resulting 4 -vector potential at a point on the $z$-axis as a function of $z$ and $t$.

  comment

Fluid Dynamics II

• Paper 3, Section II, C

  Fluid Dynamics II | Part II, 2018

  For two Stokes flows $\mathbf{u}^{(1)}(\mathbf{x})$ and $\mathbf{u}^{(2)}(\mathbf{x})$ inside the same volume $V$ with different boundary conditions on its boundary $S$, prove the reciprocal theorem

  $$\int_{S} u_{i}^{(1)} \sigma_{i j}^{(2)} n_{j} d S=\int_{S} u_{i}^{(2)} \sigma_{i j}^{(1)} n_{j} d S$$

  where $\sigma^{(1)}$ and $\sigma^{(2)}$ are the stress tensors associated with the flows.

  Stating clearly any properties of Stokes flow that you require, use the reciprocal theorem to prove that the drag $\mathbf{F}$ on a body translating with uniform velocity $\mathbf{U}$ is given by

  $$F_{i}=A_{i j} U_{j},$$

  where $\mathbf{A}$ is a symmetric second-rank tensor that depends only on the geometry of the body.

  A slender rod falls slowly through very viscous fluid with its axis inclined to the vertical. Explain why the rod does not rotate, stating any properties of Stokes flow that you use.

  When the axis of the rod is inclined at an angle $\theta$ to the vertical, the centre of mass of the rod travels at an angle $\phi$ to the vertical. Given that the rod falls twice as quickly when its axis is vertical as when its axis is horizontal, show that

  $$\tan \phi=\frac{\sin \theta \cos \theta}{1+\cos ^{2} \theta}$$

  comment

Further Complex Methods

• Paper 3, Section I, B

  Further Complex Methods | Part II, 2018

  Using a suitable branch cut, show that

  $$\int_{-a}^{a}\left(a^{2}-x^{2}\right)^{1 / 2} d x=\frac{a^{2} \pi}{2},$$

  where $a>0$.

  comment

Galois Theory

• Paper 3, Section II, I

  Galois Theory | Part II, 2018

  Let $L$ be a finite field extension of a field $K$, and let $G$ be a finite group of $K$ automorphisms of $L$. Denote by $L^{G}$ the field of elements of $L$ fixed by the action of $G$.

  (a) Prove that the degree of $L$ over $L^{G}$ is equal to the order of the group $G$.

  (b) For any $\alpha \in L$ write $f(t, \alpha)=\Pi_{g \in G}(t-g(\alpha))$.

  (i) Suppose that $L=K(\alpha)$. Prove that the coefficients of $f(t, \alpha)$ generate $L^{G}$ over $K$.

  (ii) Suppose that $L=K\left(\alpha_{1}, \alpha_{2}\right)$. Prove that the coefficients of $f\left(t, \alpha_{1}\right)$ and $f\left(t, \alpha_{2}\right)$ lie in $L^{G}$. By considering the case $L=K\left(a_{1}^{1 / 2}, a_{2}^{1 / 2}\right)$ with $a_{1}$ and $a_{2}$ in $K$, or otherwise, show that they need not generate $L^{G}$ over $K$.

  comment

General Relativity

• Paper 3, Section II, E

  General Relativity | Part II, 2018

  The Schwarzschild metric in isotropic coordinates $\bar{x}^{\bar{\alpha}}=(\bar{t}, \bar{x}, \bar{y}, \bar{z}), \bar{\alpha}=0, \ldots, 3$, is given by:

  $$d s^{2}=\bar{g}_{\bar{\alpha} \bar{\beta}} d \bar{x}^{\bar{\alpha}} d \bar{x}^{\bar{\beta}}=-\frac{(1-A)^{2}}{(1+A)^{2}} d \bar{t}^{2}+(1+A)^{4}\left(d \bar{x}^{2}+d \bar{y}^{2}+d \bar{z}^{2}\right)$$

  where

  $$A=\frac{m}{2 \bar{r}}, \quad \bar{r}=\sqrt{\bar{x}^{2}+\bar{y}^{2}+\bar{z}^{2}}$$

  and $m$ is the mass of the black hole.

  (a) Let $x^{\mu}=(t, x, y, z), \mu=0, \ldots, 3$, denote a coordinate system related to $\bar{x}^{\bar{\alpha}}$ by

  $$\bar{t}=\gamma(t-v x), \quad \bar{x}=\gamma(x-v t), \quad \bar{y}=y, \quad \bar{z}=z,$$

  where $\gamma=1 / \sqrt{1-v^{2}}$ and $-1<v<1$. Write down the transformation matrix $\partial \bar{x}^{\bar{\alpha}} / \partial x^{\mu}$, briefly explain its physical meaning and show that the inverse transformation is of the same form, but with $v \rightarrow-v$.

  (b) Using the coordinate transformation matrix of part (a), or otherwise, show that the components $g_{\mu \nu}$ of the metric in coordinates $x^{\mu}$ are given by

  $$d s^{2}=g_{\mu \nu} d x^{\mu} d x^{\nu}=f(A)\left(-d t^{2}+d x^{2}+d y^{2}+d z^{2}\right)+\gamma^{2} g(A)(d t-v d x)^{2}$$

  where $f$ and $g$ are functions of $A$ that you should determine. You should also express $A$ in terms of the coordinates $(t, x, y, z)$.

  (c) Consider the limit $v \rightarrow 1$ with $p=m \gamma$ held constant. Show that for points $x \neq t$ the function $A \rightarrow 0$, while $\gamma^{2} A$ tends to a finite value, which you should determine. Hence determine the metric components $g_{\mu \nu}$ at points $x \neq t$ in this limit.

  comment

Graph Theory

• Paper 3, Section II, I

  Graph Theory | Part II, 2018

  What does it mean to say that a graph $G$ has a $k$-colouring? What are the chromatic number $\chi(G)$ and the independence number $\alpha(G)$ of a graph $G$ ? For each $r \geqslant 3$, give an example of a graph $G$ such that $\chi(G)>r$ but $K_{r} \not \subset G$.

  Let $g, k \geqslant 3$. Show that there exists a graph $G$ containing no cycle of length $\leqslant g$ with $\chi(G) \geqslant k$.

  Show also that if $n$ is sufficiently large then there is a triangle-free $G$ of order $n$ with $\alpha(G)<n^{0.7}$.

  comment

Integrable Systems

• Paper 3, Section II, A

  Integrable Systems | Part II, 2018

  Suppose $\psi^{s}:(x, u) \mapsto(\tilde{x}, \tilde{u})$ is a smooth one-parameter group of transformations acting on $\mathbb{R}^{2}$.

  (a) Define the generator of the transformation,

  $$V=\xi(x, u) \frac{\partial}{\partial x}+\eta(x, u) \frac{\partial}{\partial u}$$

  where you should specify $\xi$ and $\eta$ in terms of $\psi^{s}$.

  (b) Define the $n^{\text {th }}$prolongation of $V, \operatorname{Pr}^{(n)} V$ and explicitly compute $\operatorname{Pr}^{(1)} V$ in terms of $\xi, \eta$.

  Recall that if $\psi^{s}$ is a Lie point symmetry of the ordinary differential equation:

  $$\Delta\left(x, u, \frac{d u}{d x}, \ldots, \frac{d^{n} u}{d x^{n}}\right)=0$$

  then it follows that $\operatorname{Pr}^{(n)} V[\Delta]=0$ whenever $\Delta=0$.

  (c) Consider the ordinary differential equation:

  $$\frac{d u}{d x}=F(x, u),$$

  for $F$ a smooth function. Show that if $V$ generates a Lie point symmetry of this equation, then:

  $$0=\eta_{x}+\left(\eta_{u}-\xi_{x}-F \xi_{u}\right) F-\xi F_{x}-\eta F_{u}$$

  (d) Find all the Lie point symmetries of the equation:

  $$\frac{d u}{d x}=x G\left(\frac{u}{x^{2}}\right)$$

  where $G$ is an arbitrary smooth function.

  comment

Linear Analysis

• Paper 3, Section II, F

  Linear Analysis | Part II, 2018

  (a) Let $X$ be a normed vector space and let $Y$ be a Banach space. Show that the space of bounded linear operators $\mathcal{B}(X, Y)$ is a Banach space.

  (b) Let $X$ and $Y$ be Banach spaces, and let $D \subset X$ be a dense linear subspace. Prove that a bounded linear map $T: D \rightarrow Y$ can be extended uniquely to a bounded linear map $T: X \rightarrow Y$ with the same operator norm. Is the claim also true if one of $X$ and $Y$ is not complete?

  (c) Let $X$ be a normed vector space. Let $\left(x_{n}\right)$ be a sequence in $X$ such that

  $$\sum_{n=1}^{\infty}\left|f\left(x_{n}\right)\right|<\infty \quad \forall f \in X^{*}$$

  Prove that there is a constant $C$ such that

  $$\sum_{n=1}^{\infty}\left|f\left(x_{n}\right)\right| \leqslant C\|f\| \quad \forall f \in X^{*}$$

  comment

Logic and Set Theory

• Paper 3, Section II, G

  Logic and Set Theory | Part II, 2018

  State and prove the Compactness Theorem for first-order predicate logic. State and prove the Upward Löwenheim-Skolem Theorem.

  [You may assume the Completeness Theorem for first-order predicate logic.]

  For each of the following theories, either give axioms (in the specified language) for the theory or prove that the theory is not axiomatisable.

  (i) The theory of finite groups (in the language of groups).

  (ii) The theory of groups in which every non-identity element has infinite order (in the language of groups).

  (iii) The theory of total orders (in the language of posets).

  (iv) The theory of well-orderings (in the language of posets).

  If a theory is axiomatisable by a set $S$ of sentences, and also by a finite set $T$ of sentences, does it follow that the theory is axiomatisable by some finite subset of $S$ ? Justify your answer.

  comment

Mathematical Biology

• Paper 3, Section I, $\mathbf{6 C}$

  Mathematical Biology | Part II, 2018

  Consider a nonlinear model for the axisymmetric dispersal of a population in two spatial dimensions whose density, $n(r, t)$, obeys

  $$\frac{\partial n}{\partial t}=D \boldsymbol{\nabla} \cdot(n \boldsymbol{\nabla} n)$$

  where $D$ is a positive constant, $r$ is a radial polar coordinate, and $t$ is time.

  Show that

  $$2 \pi \int_{0}^{\infty} n(r, t) r d r=N$$

  is constant. Interpret this condition.

  Show that a similarity solution of the form

  $$n(r, t)=\left(\frac{N}{D t}\right)^{1 / 2} f\left(\frac{r}{(N D t)^{1 / 4}}\right)$$

  is valid for $t>0$ provided that the scaling function $f(x)$ satisfies

  $$\frac{d}{d x}\left(x f \frac{d f}{d x}+\frac{1}{4} x^{2} f\right)=0 .$$

  Show that there exists a value $x_{0}$ (which need not be evaluated) such that $f(x)>0$ for $x<x_{0}$ but $f(x)=0$ for $x>x_{0}$. Determine the area within which $n(r, t)>0$ at time $t$ in terms of $x_{0}$.

  [Hint: The gradient and divergence operators in cylindrical polar coordinates act on radial functions $f$ and $g$ as

  $$\left.\boldsymbol{\nabla} f(r)=\frac{\partial f}{\partial r} \hat{\boldsymbol{r}} \quad, \quad \boldsymbol{\nabla} \cdot[g(r) \hat{\boldsymbol{r}}]=\frac{1}{r} \frac{\partial}{\partial r}(r g(r)) .\right]$$

  comment

• Paper 3, Section II, C

  Mathematical Biology | Part II, 2018

  Consider fluctuations of a population described by the vector $\mathbf{x}=\left(x_{1}, x_{2}, \ldots, x_{N}\right)$. The probability of the state $\mathbf{x}$ at time $t, P(\mathbf{x}, t)$, obeys the multivariate Fokker-Planck equation

  $$\frac{\partial P}{\partial t}=-\frac{\partial}{\partial x_{i}}\left(A_{i}(\mathbf{x}) P\right)+\frac{1}{2} \frac{\partial^{2}}{\partial x_{i} \partial x_{j}}\left(B_{i j}(\mathbf{x}) P\right),$$

  where $P=P(\mathbf{x}, t), A_{i}$ is a drift vector and $B_{i j}$ is a symmetric positive-definite diffusion matrix, and the summation convention is used throughout.

  (a) Show that the Fokker-Planck equation can be expressed as a continuity equation

  $$\frac{\partial P}{\partial t}+\nabla \cdot \mathbf{J}=0$$

  for some choice of probability flux $\mathbf{J}$ which you should determine explicitly. Here, $\nabla=\left(\frac{\partial}{\partial x_{1}}, \frac{\partial}{\partial x_{2}}, \ldots, \frac{\partial}{\partial x_{N}}\right)$ denotes the gradient operator.

  (b) Show that the above implies that an initially normalised probability distribution remains normalised,

  $$\int P(\mathbf{x}, t) d V=1$$

  at all times, where the volume element $d V=d x_{1} d x_{2} \ldots d x_{N}$.

  (c) Show that the first two moments of the probability distribution obey

  $$\begin{aligned} \frac{d}{d t}\left\langle x_{k}\right\rangle &=\left\langle A_{k}\right\rangle \\ \frac{d}{d t}\left\langle x_{k} x_{l}\right\rangle &=\left\langle x_{l} A_{k}+x_{k} A_{l}+B_{k l}\right\rangle \end{aligned}$$

  (d) Now consider small fluctuations with zero mean, and assume that it is possible to linearise the drift vector and the diffusion matrix as $A_{i}(\mathbf{x})=a_{i j} x_{j}$ and $B_{i j}(\mathbf{x})=b_{i j}$ where $a_{i j}$ has real negative eigenvalues and $b_{i j}$ is a symmetric positive-definite matrix. Express the probability flux in terms of the matrices $a_{i j}$ and $b_{i j}$ and assume that it vanishes in the stationary state.

  (e) Hence show that the multivariate normal distribution,

  $$P(\mathbf{x})=\frac{1}{Z} \exp \left(-\frac{1}{2} D_{i j} x_{i} x_{j}\right)$$

  where $Z$ is a normalisation and $D_{i j}$ is symmetric, is a solution of the linearised FokkerPlanck equation in the stationary state, and obtain an equation that relates $D_{i j}$ to the matrices $a_{i j}$ and $b_{i j}$.

  (f) Show that the inverse of the matrix $D_{i j}$ is the matrix of covariances $C_{i j}=\left\langle x_{i} x_{j}\right\rangle$ and obtain an equation relating $C_{i j}$ to the matrices $a_{i j}$ and $b_{i j}$.

  comment

Number Theory

• Paper 3, Section I, G

  Number Theory | Part II, 2018

  What is a multiplicative function? Show that if $f(n)$ is a multiplicative function, then so is $g(n)=\sum_{d \mid n} f(d)$.

  Define the Möbius function $\mu(n)$, and show that it is multiplicative. Deduce that

  $$\sum_{d \mid n} \mu(d)= \begin{cases}1 & \text { if } n=1 \\ 0 & \text { if } n>1\end{cases}$$

  and that

  $$f(n)=\sum_{e \mid n} \mu(e) g\left(\frac{n}{e}\right) .$$

  What is $g(n)$ if $f(n)=n ?$ What is $f(n)$ if $g(n)=n ?$

  comment

• Paper 3, Section II, G

  Number Theory | Part II, 2018

  What does it mean to say that a positive definite binary quadratic form is reduced? What does it mean to say that two binary quadratic forms are equivalent? Show that every positive definite binary quadratic form is equivalent to some reduced form.

  Show that the reduced positive definite binary quadratic forms of discriminant $-35$ are $f_{1}=x^{2}+x y+9 y^{2}$ and $f_{2}=3 x^{2}+x y+3 y^{2}$. Show also that a prime $p>7$ is represented by $f_{i}$ if and only if

  $$\left(\frac{p}{5}\right)=\left(\frac{p}{7}\right)= \begin{cases}+1 & (i=1) \\ -1 & (i=2)\end{cases}$$

  comment

Numerical Analysis

• Paper 3, Section II, E

  Numerical Analysis | Part II, 2018

  The diffusion equation for $u(x, t)$ :

  $$\frac{\partial u}{\partial t}=\frac{\partial^{2} u}{\partial x^{2}}, \quad x \in \mathbb{R}, \quad t \geqslant 0$$

  is solved numerically by the difference scheme

  $$u_{m}^{n+1}=u_{m}^{n}+\frac{3}{2} \mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right)-\frac{1}{2} \mu\left(u_{m-1}^{n-1}-2 u_{m}^{n-1}+u_{m+1}^{n-1}\right) .$$

  Here $\mu=\frac{k}{h^{2}}$ is the Courant number, with $k=\Delta t, h=\Delta x$, and $u_{m}^{n} \approx u(m h, n k)$.

  (a) Prove that, as $k \rightarrow 0$ with constant $\mu$, the local error of the method is $\mathcal{O}\left(k^{2}\right)$.

  (b) Applying the Fourier stability analysis, show that the method is stable if and only if $\mu \leqslant \frac{1}{4}$. [Hint: If a polynomial $p(x)=x^{2}-2 \alpha x+\beta$ has real roots, then those roots lie in $[a, b]$ if and only if $p(a) p(b) \geqslant 0$ and $\alpha \in[a, b]$.]

  (c) Prove that, for the same equation, the leapfrog scheme

  $$u_{m}^{n+1}=u_{m}^{n-1}+2 \mu\left(u_{m-1}^{n}-2 u_{m}^{n}+u_{m+1}^{n}\right)$$

  is unstable for any choice of $\mu>0$.

  comment

Optimisation and Control

• Paper 3, Section II, K

  Optimisation and Control | Part II, 2018

  The scalars $x_{t}, y_{t}, u_{t}$ are related by the equations

  $$x_{t}=x_{t-1}+u_{t-1}, \quad y_{t}=x_{t-1}+\eta_{t-1}, \quad t=1,2, \ldots, T,$$

  where the initial state $x_{0}$ is normally distributed with mean $\hat{x}_{0}$ and variance 1 and $\left\{\eta_{t}\right\}$ is a sequence of independent random variables each normally distributed with mean 0 and variance 1 . The control variable $u_{t}$ is to be chosen at time $t$ on the basis of information $W_{t}$, where $W_{0}=\left(\hat{x}_{0}\right)$ and

  $$W_{t}=\left(\hat{x}_{0}, u_{0}, \ldots, u_{t-1}, y_{1}, \ldots, y_{t}\right), \quad t=1,2, \ldots, T$$

  (a) Let $\hat{x}_{1}, \hat{x}_{2}, \ldots, \hat{x}_{T}$ be the Kalman filter estimates of $x_{1}, x_{2}, \ldots, x_{T}$, i.e.

  $$\hat{x}_{t}=\hat{x}_{t-1}+u_{t-1}+h_{t}\left(y_{t}-\hat{x}_{t-1}\right)$$

  where $h_{t}$ is chosen to minimise $\mathbb{E}\left(\left(\hat{x}_{t}-x_{t}\right)^{2} \mid W_{t}\right)$. Calculate $h_{t}$ and show that, conditional on $W_{t}, x_{t}$ is normally distributed with mean $\hat{x}_{t}$ and variance $V_{t}=1 /(1+t)$.

  (b) Define

  $$\begin{aligned} &F\left(W_{T}\right)=\mathbb{E}\left(x_{T}^{2} \mid W_{T}\right), \quad \text { and } \\ &F\left(W_{t}\right)=\inf _{u_{t}, \ldots, u_{T-1}} \mathbb{E}\left(x_{T}^{2}+\sum_{j=t}^{T-1} u_{j}^{2} \mid W_{t}\right), \quad t=0, \ldots, T-1 . \end{aligned}$$

  Show that $F\left(W_{t}\right)=\hat{x}_{t}^{2} P_{t}+d_{t}$, where $P_{t}=1 /(T-t+1), d_{T}=1 /(1+T)$ and $d_{t-1}=V_{t-1} V_{t} P_{t}+d_{t}$.

  (c) Show that the minimising control $u_{t}$ can be expressed in the form $u_{t}=-K_{t} \hat{x}_{t}$ and find $K_{t}$. How would the expression for $K_{t}$ be altered if $x_{0}$ or $\left\{\eta_{t}\right\}$ had variances other than 1?

  comment

Principles of Quantum Mechanics

• Paper 3, Section II, D

  Principles of Quantum Mechanics | Part II, 2018

  A quantum system is prepared in the ground state $|0\rangle$ at time $t=0$. It is subjected to a time-varying Hamiltonian $H=H_{0}+\Delta(t)$. Show that, to first order in $\Delta(t)$, the system evolves as

  $$|\psi(t)\rangle=\sum_{k} c_{k}(t) \mathrm{e}^{-i E_{k} t / \hbar}|k\rangle$$

  where $H_{0}|k\rangle=E_{k}|k\rangle$ and

  $$c_{k}(t)=\frac{1}{i \hbar} \int_{0}^{t}\left\langle k\left|\Delta\left(t^{\prime}\right)\right| 0\right\rangle \mathrm{e}^{i\left(E_{k}-E_{0}\right) t^{\prime} / \hbar} \mathrm{d} t^{\prime}$$

  A large number of hydrogen atoms, each in the ground state, are subjected to an electric field

  $$\mathbf{E}(t)=\left\{\begin{array}{lll} 0 & \text { for } & t<0 \\ \hat{\mathbf{z}} \mathcal{E}_{0} \exp (-t / \tau) & \text { for } & t>0 \end{array}\right.$$

  where $\mathcal{E}_{0}$ is a constant. Show that the fraction of atoms found in the state $|n, \ell, m\rangle=$ $|2,1,0\rangle$ is, after a long time and to lowest non-trivial order in $\mathcal{E}_{0}$,

  $$\frac{2^{15}}{3^{10}} \frac{a_{0}^{2} e^{2} \mathcal{E}_{0}^{2}}{\hbar^{2}\left(\omega^{2}+1 / \tau^{2}\right)}$$

  where $\hbar \omega$ is the energy difference between the $|2,1,0\rangle$ and $|1,0,0\rangle$ states, and $e$ is the electron charge and $a_{0}$ the Bohr radius. What fraction of atoms lie in the $|2,0,0\rangle$ state?

  [Hint: You may assume the hydrogenic wavefunctions

  $$\langle\mathbf{r} \mid 1,0,0\rangle=\frac{2}{\sqrt{4 \pi}} \frac{1}{a_{0}^{3 / 2}} \exp \left(-\frac{r}{a_{0}}\right) \quad \text { and } \quad\langle\mathbf{r} \mid 2,1,0\rangle=\frac{1}{\sqrt{4 \pi}} \frac{1}{\left(2 a_{0}\right)^{3 / 2}} \frac{r}{a_{0}} \cos \theta \exp \left(-\frac{r}{2 a_{0}}\right)$$

  and the integral

  $$\int_{0}^{\infty} r^{m} \mathrm{e}^{-\alpha r} \mathrm{~d} r=\frac{m !}{\alpha^{m+1}}$$

  for $m$ a positive integer.]

  comment

Principles of Statistics

• Paper 3, Section II, K

  Principles of Statistics | Part II, 2018

  In the model $\left\{\mathcal{N}\left(\theta, I_{p}\right), \theta \in \mathbb{R}^{p}\right\}$ of a Gaussian distribution in dimension $p$, with unknown mean $\theta$ and known identity covariance matrix $I_{p}$, we estimate $\theta$ based on a sample of i.i.d. observations $X_{1}, \ldots, X_{n}$ drawn from $\mathcal{N}\left(\theta_{0}, I_{p}\right)$.

  (a) Define the Fisher information $I\left(\theta_{0}\right)$, and compute it in this model.

  (b) We recall that the observed Fisher information $i_{n}(\theta)$ is given by

  $$i_{n}(\theta)=\frac{1}{n} \sum_{i=1}^{n} \nabla_{\theta} \log f\left(X_{i}, \theta\right) \nabla_{\theta} \log f\left(X_{i}, \theta\right)^{\top}$$

  Find the limit of $\hat{i}_{n}=i_{n}\left(\hat{\theta}_{M L E}\right)$, where $\hat{\theta}_{M L E}$ is the maximum likelihood estimator of $\theta$ in this model.

  (c) Define the Wald statistic $W_{n}(\theta)$ and compute it. Give the limiting distribution of $W_{n}\left(\theta_{0}\right)$ and explain how it can be used to design a confidence interval for $\theta_{0}$.

  [You may use results from the course provided that you state them clearly.]

  comment

Probability and Measure

• Paper 3, Section II, J

  Probability and Measure | Part II, 2018

  Let $m$ be the Lebesgue measure on the real line. Recall that if $E \subseteq \mathbb{R}$ is a Borel subset, then

  $$m(E)=\inf \left\{\sum_{n \geqslant 1}\left|I_{n}\right|, E \subseteq \bigcup_{n \geqslant 1} I_{n}\right\},$$

  where the infimum is taken over all covers of $E$ by countably many intervals, and $|I|$ denotes the length of an interval $I$.

  (a) State the definition of a Borel subset of $\mathbb{R}$.

  (b) State a definition of a Lebesgue measurable subset of $\mathbb{R}$.

  (c) Explain why the following sets are Borel and compute their Lebesgue measure:

  $$\mathbb{Q}, \quad \mathbb{R} \backslash \mathbb{Q}, \quad \bigcap_{n \geqslant 2}\left[\frac{1}{n}, n\right] .$$

  (d) State the definition of a Borel measurable function $f: \mathbb{R} \rightarrow \mathbb{R}$.

  (e) Let $f$ be a Borel measurable function $f: \mathbb{R} \rightarrow \mathbb{R}$. Is it true that the subset of all $x \in \mathbb{R}$ where $f$ is continuous at $x$ is a Borel subset? Justify your answer.

  (f) Let $E \subseteq[0,1]$ be a Borel subset with $m(E)=1 / 2+\alpha, \alpha>0$. Show that

  $$E-E:=\{x-y: x, y \in E\}$$

  contains the interval $(-2 \alpha, 2 \alpha)$.

  (g) Let $E \subseteq \mathbb{R}$ be a Borel subset such that $m(E)>0$. Show that for every $\varepsilon>0$, there exists $a<b$ in $\mathbb{R}$ such that

  $$m(E \cap(a, b))>(1-\varepsilon) m((a, b)) .$$

  Deduce that $E-E$ contains an open interval around 0 .

  comment

Quantum Information and Computation

• Paper 3, Section I, 10D

  Quantum Information and Computation | Part II, 2018

  Let $B_{n}$ denote the set of all $n$-bit strings. For any Boolean function on 2 bits $f: B_{2} \rightarrow B_{1}$ consider the linear operation on 3 qubits defined by

  $$U_{f}|x\rangle|y\rangle=|x\rangle|y \oplus f(x)\rangle$$

  for all $x \in B_{2}, y \in B_{1}$ and $\oplus$ denoting addition of bits modulo 2 . Here the first register is a 2-qubit register and the second is a 1-qubit register. We are able to apply only the 1-qubit Pauli $X$ and Hadamard $H$ gates to any desired qubits, as well as the 3 -qubit gate $U_{f}$ to any three qubits. We can also perform measurements in the computational basis.

  (a) Describe how we can construct the state

  $$|f\rangle=\frac{1}{2} \sum_{x \in B_{2}}(-1)^{f(x)}|x\rangle$$

  starting from the standard 3-qubit state $|0\rangle|0\rangle|0\rangle$.

  (b) Suppose now that the gate $U_{f}$ is given to us but $f$ is not specified. However $f$ is promised to be one of two following cases:

  (i) $f$ is a constant function (i.e. $f(x)=0$ for all $x$, or $f(x)=1$ for all $x$ ),

  (ii) for any 2-bit string $x=b_{1} b_{2}$ we have $f\left(b_{1} b_{2}\right)=b_{1} \oplus b_{2}$ (with $\oplus$ as above).

  Show how we may determine with certainty which of the two cases (i) or (ii) applies, using only a single application of $U_{f}$.

  comment

• Paper 3, Section II, $15 \mathrm{D}$

  Quantum Information and Computation | Part II, 2018

  In this question you may assume the following fact about the quantum Fourier transform $Q F T \bmod N:$ if $N=A r$ and $0 \leqslant x_{0}<r$, where $A, r, x_{0} \in \mathbb{Z}$, then

  $$Q F T \frac{1}{\sqrt{A}} \sum_{k=0}^{A-1}\left|x_{0}+k r\right\rangle=\frac{1}{\sqrt{r}} \sum_{l=0}^{r-1} \omega^{x_{0} l A}|l A\rangle$$

  where $\omega=e^{2 \pi i / N}$.

  (a) Let $\mathbb{Z}_{N}$ denote the integers modulo $N$. Let $f: \mathbb{Z}_{N} \rightarrow \mathbb{Z}$ be a periodic function with period $r$ and with the property that $f$ is one-to-one within each period. We have one instance of the quantum state

  $$|f\rangle=\frac{1}{\sqrt{N}} \sum_{x=0}^{N-1}|x\rangle|f(x)\rangle$$

  and the ability to calculate the function $f$ on at most two $x$ values of our choice.

  Describe a procedure that may be used to determine the period $r$ with success probability $O(1 / \log \log N)$. As a further requirement, at the end of the procedure we should know if it has been successful, or not, in outputting the correct period value. [You may assume that the number of integers less than $N$ that are coprime to $N$ is $O(N / \log \log N)]$.

  (b) Consider the function $f: \mathbb{Z}_{12} \rightarrow \mathbb{Z}_{10}$ defined by $f(x)=3^{x} \bmod 10$.

  (i) Show that $f$ is periodic and find the period.

  (ii) Suppose we are given the state $|f\rangle=\frac{1}{\sqrt{12}} \sum_{x=0}^{11}|x\rangle|f(x)\rangle$ and we measure the second register. What are the possible resulting measurement values $y$ and their probabilities?

  (iii) Suppose the measurement result was $y=3$. Find the resulting state $|\alpha\rangle$ of the first register after the measurement.

  (iv) Suppose we measure the state $Q F T|\alpha\rangle$ (with $|\alpha\rangle$ from part (iii)). What is the probability of each outcome $0 \leqslant c \leqslant 11$ ?

  comment

Representation Theory

• Paper 3, Section II, I

  Representation Theory | Part II, 2018

  State the row orthogonality relations. Prove that if $\chi$ is an irreducible character of the finite group $G$, then $\chi(1)$ divides the order of $G$.

  Stating clearly any additional results you use, deduce the following statements:

  (i) Groups of order $p^{2}$, where $p$ is prime, are abelian.

  (ii) If $G$ is a group of order $2 p$, where $p$ is prime, then either the degrees of the irreducible characters of $G$ are all 1 , or they are

  $$1,1,2, \ldots, 2(\text { with }(p-1) / 2 \text { of degree } 2)$$

  (iii) No simple group has an irreducible character of degree 2 .

  (iv) Let $p$ and $q$ be prime numbers with $p>q$, and let $G$ be a non-abelian group of order $p q$. Then $q$ divides $p-1$ and $G$ has $q+((p-1) / q)$ conjugacy classes.

  comment

Riemann Surfaces

• Paper 3, Section II, F

  Riemann Surfaces | Part II, 2018

  Define the degree of an analytic map of compact Riemann surfaces, and state the Riemann-Hurwitz formula.

  Let $\Lambda$ be a lattice in $\mathbb{C}$ and $E=\mathbb{C} / \Lambda$ the associated complex torus. Show that the $\operatorname{map}$

  $$\psi: z+\Lambda \mapsto-z+\Lambda$$

  is biholomorphic with four fixed points in $E$.

  Let $S=E / \sim$ be the quotient surface (the topological surface obtained by identifying $z+\Lambda$ and $\psi(z+\Lambda)$ ), and let $p: E \rightarrow S$ be the associated projection map. Denote by $E^{\prime}$ the complement of the four fixed points of $\psi$, and let $S^{\prime}=p\left(E^{\prime}\right)$. Describe briefly a family of charts making $S^{\prime}$ into a Riemann surface, so that $p: E^{\prime} \rightarrow S^{\prime}$ is a holomorphic map.

  Now assume that, by adding finitely many points, it is possible to compactify $S^{\prime}$ to a Riemann surface $S$ so that $p$ extends to a regular map $E \rightarrow S$. Find the genus of $S$.

  comment

Statistical Modelling

• Paper 3, Section I, J

  Statistical Modelling | Part II, 2018

  The data frame Cases. of .flu contains a list of cases of flu recorded in 3 London hospitals during each month of 2017 . Consider the following $R$ code and its output.

  table (Cases. of.flu)

  Month Hospital

  $\begin{array}{lrrr}\text { Month } & \text { A } & \text { B } & \text { C } \\ \text { April } & 10 & 40 & 27\end{array}$

  $\begin{array}{lrrr}\text { April } & 10 & 40 & 27 \\ \text { August } & 9 & 34 & 19\end{array}$

  $\begin{array}{lrrr}\text { August } & 9 & 34 & 19 \\ \text { December } & 24 & 129 & 81\end{array}$

  $\begin{array}{llll}\text { December } & 24 & 129 & 81 \\ \text { February } & 49 & 134 & 74\end{array}$

  $\begin{array}{llll}\text { February } & 49 & 134 & 74 \\ \text { January } & 45 & 138 & 78\end{array}$

  $\begin{array}{lrrr}\text { July } & 5 & 138 & 78 \\ & 11 & 36 & 35\end{array}$

  $\begin{array}{llll}\text { June } & 11 & 36 & 22\end{array}$

  $\begin{array}{llll}\text { March } & 20 & 82 & 41\end{array}$

  May $5 \quad 43 \quad 23$

  November $17 \quad 82 \quad 62$

  October $6 \quad 26 \quad 19$

  September $640 \quad 21$

  Cases. of.flu.table = as.data.frame (table (Cases. of .flu))

  $>$ head (Cases. of .flu.table)

  Month Hospital Freq

  1 April A 10

  2 August A 9

  3 December A 24

  4 February A 49

  5 January A 45

  6 July A 5

  $>\bmod 1=$ glm (Freq ., data=Cases. of .flu.table, family=poisson)

  $>\bmod 1 \$ \mathrm{dev}$

  [1] $28.51836$

  levels (Cases. of.flu$Month)

  

  Describe a test for the null hypothesis of independence between the variables Month and Hospital using the deviance statistic. State the assumptions of the test.

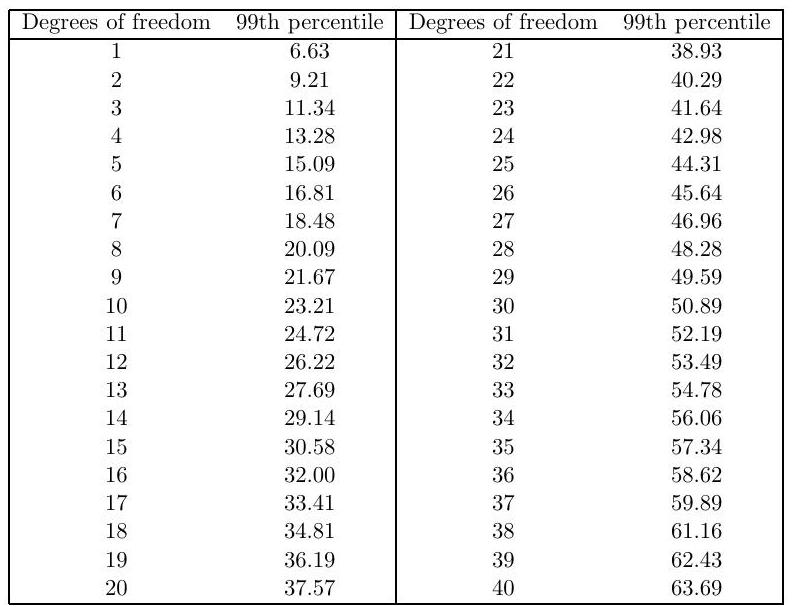
  Perform the test at the $1 \%$ level for each of the two different models shown above. You may use the table below showing 99 th percentiles of the $\chi_{p}^{2}$ distribution with a range of degrees of freedom $p$. How would you explain the discrepancy between their conclusions?

  

  comment

Statistical Physics

• Paper 3, Section II, A

  Statistical Physics | Part II, 2018

  (a) A system of non-interacting bosons has single particle states $|i\rangle$ with energies $\epsilon_{i} \geqslant 0$. Show that the grand canonical partition function is

  $$\log \mathcal{Z}=-\sum_{i} \log \left(1-e^{-\beta\left(\epsilon_{i}-\mu\right)}\right)$$

  where $\beta=1 /(k T), k$ is Boltzmann's constant, and $\mu$ is the chemical potential. What is the maximum possible value for $\mu$ ?

  (b) A system of $N \gg 1$ bosons has one energy level with zero energy and $M \gg 1$ energy levels with energy $\epsilon>0$. The number of particles with energies $0, \epsilon$ is $N_{0}, N_{\epsilon}$ respectively.

  (i) Write down expressions for $\left\langle N_{0}\right\rangle$ and $\left\langle N_{\epsilon}\right\rangle$ in terms of $\mu$ and $\beta$.

  (ii) At temperature $T$ what is the maximum possible number $N_{\epsilon}^{\max }$ of bosons in the state with energy $\epsilon ?$ What happens for $N>N_{\epsilon}^{\max } ?$

  (iii) Calculate the temperature $T_{B}$ at which Bose condensation occurs.

  (iv) For $T>T_{B}$, show that $\mu=\epsilon\left(T_{B}-T\right) / T_{B}$. For $T<T_{B}$ show that

  $$\mu \approx-\frac{k T}{N} \frac{e^{\epsilon /(k T)}-1}{e^{\epsilon /(k T)}-e^{\epsilon /\left(k T_{B}\right)}} .$$

  (v) Calculate the mean energy $\langle E\rangle$ for $T>T_{B}$ and for $T<T_{B}$. Hence show that the heat capacity of the system is

  $$C \approx \begin{cases}\frac{1}{k T^{2}} \frac{M \epsilon^{2}}{\left(e^{\beta \epsilon}-1\right)^{2}} & T<T_{B} \\ 0 & T>T_{B}\end{cases}$$

  comment

Stochastic Financial Models

• Paper 3, Section II, $29 K$

  Stochastic Financial Models | Part II, 2018

  Consider a multi-period model with asset prices $\bar{S}_{t}=\left(S_{t}^{0}, \ldots, S_{t}^{d}\right), t \in\{0, \ldots, T\}$, modelled on a probability space $(\Omega, \mathcal{F}, \mathbb{P})$ and adapted to a filtration $\left(\mathcal{F}_{t}\right)_{t \in\{0, \ldots, T\}}$. Assume that $\mathcal{F}_{0}$ is $\mathbb{P}$-trivial, i.e. $\mathbb{P}[A] \in\{0,1\}$ for all $A \in \mathcal{F}_{0}$, and assume that $S^{0}$ is a $\mathbb{P}$-a.s. strictly positive numéraire, i.e. $S_{t}^{0}>0 \mathbb{P}$-a.s. for all $t \in\{0, \ldots, T\}$. Further, let $X_{t}=\left(X_{t}^{1}, \ldots, X_{t}^{d}\right)$ denote the discounted price process defined by $X_{t}^{i}:=S_{t}^{i} / S_{t}^{0}, t \in\{0, \ldots, T\}, i \in\{1, \ldots, d\}$.

  (a) What does it mean to say that a self-financing strategy $\bar{\theta}$ is an arbitrage?

  (b) State the fundamental theorem of asset pricing.

  (c) Let $\mathbb{Q}$ be a probability measure on $(\Omega, \mathcal{F})$ which is equivalent to $\mathbb{P}$ and for which $\mathbb{E}_{\mathbb{Q}}\left[\left|X_{t}\right|\right]<\infty$ for all $t$. Show that the following are equivalent:

  (i) $\mathbb{Q}$ is a martingale measure.

  (ii) If $\bar{\theta}=\left(\theta^{0}, \theta\right)$ is self-financing and $\theta$ is bounded, i.e. $\max _{t=1, \ldots, T}\left|\theta_{t}\right| \leqslant c<\infty$ for a suitable $c>0$, then the value process $V$ of $\bar{\theta}$ is a $\mathbb{Q}$-martingale.

  (iii) If $\bar{\theta}=\left(\theta^{0}, \theta\right)$ is self-financing and $\theta$ is bounded, then the value process $V$ of $\bar{\theta}$ satisfies

  $$\mathbb{E}_{\mathbb{Q}}\left[V_{T}\right]=V_{0}$$

  [Hint: To show that (iii) implies (i) you might find it useful to consider self-financing strategies $\bar{\theta}=\left(\theta^{0}, \theta\right)$ with $\theta$ of the form

  $$\theta_{s}:= \begin{cases}\mathbf{1}_{A} & \text { if } s=t \\ 0 & \text { otherwise }\end{cases}$$

  for any $A \in \mathcal{F}_{t-1}$ and any $t \in\{1, \ldots, T\}$.]

  (d) Prove that if there exists a martingale measure $\mathbb{Q}$ satisfying the conditions in (c) then there is no arbitrage.

  comment

Topics in Analysis

• Paper 3, Section I, $2 F$

  Topics in Analysis | Part II, 2018

  State a version of the Baire category theorem and use it to prove the following result:

  If $f: \mathbb{C} \rightarrow \mathbb{C}$ is analytic, but not a polynomial, then there exists a point $z_{0} \in \mathbb{C}$ such that each coefficient of the Taylor series of $f$ at $z_{0}$ is non-zero.

  comment

Waves

• Paper 3, Section II, 40C

  Waves | Part II, 2018

  Derive the ray-tracing equations

  $$\frac{d x_{i}}{d t}=\frac{\partial \Omega}{\partial k_{i}}, \quad \frac{d k_{i}}{d t}=-\frac{\partial \Omega}{\partial x_{i}}, \quad \frac{d \omega}{d t}=\frac{\partial \Omega}{\partial t}$$

  for wave propagation through a slowly-varying medium with local dispersion relation $\omega=\Omega(\mathbf{k} ; \mathbf{x}, t)$, where $\omega$ and $\mathbf{k}$ are the frequency and wavevector respectively, $t$ is time and $\mathbf{x}=(x, y, z)$ are spatial coordinates. The meaning of the notation $d / d t$ should be carefully explained.

  A slowly-varying medium has a dispersion relation $\Omega(\mathbf{k} ; \mathbf{x}, t)=k c(z)$, where $k=|\mathbf{k}|$. State and prove Snell's law relating the angle $\psi$ between a ray and the $z$-axis to $c$.

  Consider the case of a medium with wavespeed $c=c_{0}\left(1+\beta^{2} z^{2}\right)$, where $\beta$ and $c_{0}$ are positive constants. Show that a ray that passes through the origin with wavevector $k(\cos \phi, 0, \sin \phi)$, remains in the region

  $$|z| \leqslant z_{m} \equiv \frac{1}{\beta}\left[\frac{1}{|\cos \phi|}-1\right]^{1 / 2}$$

  By considering an approximation to the equation for a ray in the region $\left|z_{m}-z\right| \ll \beta^{-1}$, or otherwise, determine the path of a ray near $z_{m}$, and hence sketch rays passing through the origin for a few sample values of $\phi$ in the range $0<\phi<\pi / 2$.

  comment