Part II, 2011, Paper 2

Algebraic Geometry

• Paper 2, Section II, H

  Algebraic Geometry | Part II, 2011

  (i) Let $k$ be an algebraically closed field, and let $I$ be an ideal in $k\left[x_{0}, \ldots, x_{n}\right]$. Define what it means for $I$ to be homogeneous.

  Now let $Z \subseteq \mathbb{A}^{n+1}$ be a Zariski closed subvariety invariant under $k^{*}=k-\{0\}$; that is, if $z \in Z$ and $\lambda \in k^{*}$, then $\lambda z \in Z$. Show that $I(Z)$ is a homogeneous ideal.

  (ii) Let $f \in k\left[x_{1}, \ldots, x_{n-1}\right]$, and let $\Gamma=\left\{(x, f(x)) \mid x \in \mathbb{A}^{n-1}\right\} \subseteq \mathbb{A}^{n}$ be the graph of $f$.

  Let $\bar{\Gamma}$ be the closure of $\Gamma$ in $\mathbb{P}^{n}$.

  Write, in terms of $f$, the homogeneous equations defining $\bar{\Gamma}$.

  Assume that $k$ is an algebraically closed field of characteristic zero. Now suppose $n=3$ and $f(x, y)=y^{3}-x^{2} \in k[x, y]$. Find the singular points of the projective surface $\bar{\Gamma}$.

  comment

Algebraic Topology

• Paper 2, Section II, H

  Algebraic Topology | Part II, 2011

  Explain what is meant by a covering projection. State and prove the pathlifting property for covering projections, and indicate briefly how it generalizes to a lifting property for homotopies between paths. [You may assume the Lebesgue Covering Theorem.]

  Let $X$ be a simply connected space, and let $G$ be a subgroup of the group of all homeomorphisms $X \rightarrow X$. Suppose that, for each $x \in X$, there exists an open neighbourhood $U$ of $x$ such that $U \cap g[U]=\emptyset$ for each $g \in G$ other than the identity. Show that the projection $p: X \rightarrow X / G$ is a covering projection, and deduce that $\Pi_{1}(X / G) \cong G$.

  By regarding $S^{3}$ as the set of all quaternions of modulus 1 , or otherwise, show that there is a quotient space of $S^{3}$ whose fundamental group is a non-abelian group of order $8 .$

  comment

Applications of Quantum Mechanics

• Paper 2, Section II, E

  Applications of Quantum Mechanics | Part II, 2011

  A beam of particles of mass $m$ and momentum $p=\hbar k$, incident along the $z$-axis, is scattered by a spherically symmetric potential $V(r)$, where $V(r)=0$ for large $r$. State the boundary conditions on the wavefunction as $r \rightarrow \infty$ and hence define the scattering amplitude $f(\theta)$, where $\theta$ is the scattering angle.

  Given that, for large $r$,

  $$e^{i k r \cos \theta}=\frac{1}{2 i k r} \sum_{l=0}^{\infty}(2 l+1)\left(e^{i k r}-(-1)^{l} e^{-i k r}\right) P_{l}(\cos \theta)$$

  explain how the partial-wave expansion can be used to define the phase shifts $\delta_{l}(k)(l=$ $0,1,2, \ldots)$. Furthermore, given that $d \sigma / d \Omega=|f(\theta)|^{2}$, derive expressions for $f(\theta)$ and the total cross-section $\sigma$ in terms of the $\delta_{l}$.

  In a particular case $V(r)$ is given by

  $$V(r)=\left\{\begin{array}{cl} \infty, & r<a \\ -V_{0}, & a<r<2 a \\ 0, & r>2 a \end{array}\right.$$

  where $V_{0}>0$. Show that the $\mathrm{S}$-wave phase shift $\delta_{0}$ satisfies

  $$\tan \left(\delta_{0}\right)=\frac{k \cos (2 k a)-\kappa \cot (\kappa a) \sin (2 k a)}{k \sin (2 k a)+\kappa \cot (\kappa a) \cos (2 k a)},$$

  where $\kappa^{2}=2 m V_{0} / \hbar^{2}+k^{2}$.

  Derive an expression for the scattering length $a_{s}$ in terms of $\kappa$. Find the values of $\kappa$ for which $\left|a_{s}\right|$ diverges and briefly explain their physical significance.

  comment

Applied Probability

• Paper 2, Section II, J

  Applied Probability | Part II, 2011

  (i) Explain briefly what is meant by saying that a continuous-time Markov chain $X(t)$ is a birth-and-death process with birth rates $\lambda_{i}>0, i \geqslant 0$, and death rates $\mu_{i}>0$, $i \geqslant 1$.

  (ii) In the case where $X(t)$ is recurrent, find a sufficient condition on the birth and death parameters to ensure that

  $$\lim _{t \rightarrow \infty} \mathbb{P}(X(t)=j)=\pi_{j}>0, \quad j \geqslant 0$$

  and express $\pi_{j}$ in terms of these parameters. State the reversibility property of $X(t)$.

  Jobs arrive according to a Poisson process of rate $\lambda>0$. They are processed individually, by a single server, the processing times being independent random variables, each with the exponential distribution of rate $\nu>0$. After processing, the job either leaves the system, with probability $p, 0<p<1$, or, with probability $1-p$, it splits into two separate jobs which are both sent to join the queue for processing again. Let $X(t)$ denote the number of jobs in the system at time $t$.

  (iii) In the case $1+\lambda / \nu<2 p$, evaluate $\lim _{t \rightarrow \infty} \mathbb{P}(X(t)=j), j=0,1, \ldots$, and find the expected time that the processor is busy between two successive idle periods.

  (iv) What happens if $1+\lambda / \nu \geqslant 2 p$ ?

  comment

Classical Dynamics

• Paper 2, Section I, C

  Classical Dynamics | Part II, 2011

  Three particles, each of mass $m$, move along a straight line. Their positions on the line containing the origin, $O$, are $x_{1}, x_{2}$ and $x_{3}$. They are subject to forces derived from the potential energy function

  $$V=\frac{1}{2} m \Omega^{2}\left[\left(x_{1}-x_{2}\right)^{2}+\left(x_{2}-x_{3}\right)^{2}+\left(x_{3}-x_{1}\right)^{2}+x_{1}^{2}+x_{2}^{2}+x_{3}^{2}\right]$$

  Obtain Lagrange's equations for the system, and show that the frequency, $\omega$, of a normal mode satisfies

  $$f^{3}-9 f^{2}+24 f-16=0$$

  where $f=\left(\omega^{2} / \Omega^{2}\right)$. Find a complete set of normal modes for the system, and draw a diagram indicating the nature of the corresponding motions.

  comment

• Paper 2, Section II, C

  Classical Dynamics | Part II, 2011

  Derive Euler's equations governing the torque-free and force-free motion of a rigid body with principal moments of inertia $I_{1}, I_{2}$ and $I_{3}$, where $I_{1}<I_{2}<I_{3}$. Identify two constants of the motion. Hence, or otherwise, find the equilibrium configurations such that the angular-momentum vector, as measured with respect to axes fixed in the body, remains constant. Discuss the stability of these configurations.

  A spacecraft may be regarded as moving in a torque-free and force-free environment. Nevertheless, flexing of various parts of the frame can cause significant dissipation of energy. How does the angular-momentum vector ultimately align itself within the body?

  comment

Coding and Cryptography

• Paper 2, Section I, G

  Coding and Cryptography | Part II, 2011

  I happen to know that an apparently fair coin actually has probability $p$ of heads with $1>p>1 / 2$. I play a very long sequence of games of heads and tails in which my opponent pays me back twice my stake if the coin comes down heads and takes my stake if the coin comes down tails. I decide to bet a proportion $\alpha$ of my fortune at the end of the $n$th game in the $(n+1)$ st game. Determine, giving justification, the value $\alpha_{0}$ maximizing the expected logarithm of my fortune in the long term, assuming I use the same $\alpha_{0}$ at each game. Can it be actually disadvantageous for me to choose an $\alpha<\alpha_{0}$ (in the sense that I would be better off not playing)? Can it be actually disadvantageous for me to choose an $\alpha>\alpha_{0}$ ?

  [Moral issues should be ignored.]

  comment

• Paper 2, Section II, G

  Coding and Cryptography | Part II, 2011

  Define a cyclic code. Show that there is a bijection between the cyclic codes of length $n$ and the factors of $X^{n}-1$ over the field $\mathbb{F}_{2}$ of order 2 .

  What is meant by saying that $\alpha$ is a primitive $n$th root of unity in a finite field extension $K$ of $\mathbb{F}_{2}$ ? What is meant by saying that $C$ is a BCH code of length $n$ with defining set $\left\{\alpha, \alpha^{2}, \ldots, \alpha^{\delta-1}\right\}$ ? Show that such a code has minimum distance at least $\delta$.

  Suppose that $K$ is a finite field extension of $\mathbb{F}_{2}$ in which $X^{7}-1$ factorises into linear factors. Show that if $\beta$ is a root of $X^{3}+X^{2}+1$ then $\beta$ is a primitive 7 th root of unity and $\beta^{2}$ is also a root of $X^{3}+X^{2}+1$. Quoting any further results that you need show that the $\mathrm{BCH}$ code of length 7 with defining set $\left\{\beta, \beta^{2}\right\}$ is the Hamming code.

  [Results on the Vandermonde determinant may be used without proof provided they are quoted correctly.]

  comment

Cosmology

• Paper 2, Section I, E

  Cosmology | Part II, 2011

  A spherically symmetric star in hydrostatic equilibrium has density $\rho(r)$ and pressure $P(r)$, which satisfy the pressure support equation,

  $$\frac{d P}{d r}=-\frac{G m \rho}{r^{2}}$$

  where $m(r)$ is the mass within a radius $r$. Show that this implies

  $$\frac{d}{d r}\left(\frac{r^{2}}{\rho} \frac{d P}{d r}\right)=-4 \pi G r^{2} \rho .$$

  Provide a justification for choosing the boundary conditions $d P / d r=0$ at the centre of the $\operatorname{star}(r=0)$ and $P=0$ at its outer radius $(r=R)$.

  Use the pressure support equation $(*)$ to derive the virial theorem for a star,

  $$\langle P\rangle V=-\frac{1}{3} E_{\mathrm{grav}}$$

  where $\langle P\rangle$ is the average pressure, $V$ is the total volume of the star and $E_{\text {grav }}$ is its total gravitational potential energy.

  comment

Differential Geometry

• Paper 2, Section II, I

  Differential Geometry | Part II, 2011

  Let $\alpha: I \rightarrow \mathbb{R}^{3}$ be a smooth curve parametrized by arc-length, with $\alpha^{\prime \prime}(s) \neq 0$ for all $s \in I$. Define what is meant by the Frenet frame $t(s), n(s), b(s)$, the curvature and torsion of $\alpha$. State and prove the Frenet formulae.

  By considering $\langle\alpha, t \times n\rangle$, or otherwise, show that, if for each $s \in I$ the vectors $\alpha(s)$, $t(s)$ and $n(s)$ are linearly dependent, then $\alpha(s)$ is a plane curve.

  State and prove the isoperimetric inequality for $C^{1}$ regular plane curves.

  [You may assume Wirtinger's inequality, provided you state it accurately.]

  comment

Dynamical Systems

• Paper 2, Section I, C

  Dynamical Systems | Part II, 2011

  State the Poincaré-Bendixson theorem for two-dimensional dynamical systems.

  A dynamical system can be written in polar coordinates $(r, \theta)$ as

  $$\begin{aligned} &\dot{r}=r-r^{3}(1+\alpha \cos \theta) \\ &\dot{\theta}=1-r^{2} \beta \cos \theta \end{aligned}$$

  where $\alpha$ and $\beta$ are constants with $0<\alpha<1$.

  Show that trajectories enter the annulus $(1+\alpha)^{-1 / 2}<r<(1-\alpha)^{-1 / 2}$.

  Show that if there is a fixed point $\left(r_{0}, \theta_{0}\right)$ inside the annulus then $r_{0}^{2}=(\beta-\alpha) / \beta$ and $\cos \theta_{0}=1 /(\beta-\alpha)$.

  Use the Poincaré-Bendixson theorem to derive conditions on $\beta$ that guarantee the existence of a periodic orbit.

  comment

Fluid Dynamics II

• Paper 2, Section II, B

  Fluid Dynamics II | Part II, 2011

  The energy equation for the motion of a viscous, incompressible fluid states that

  $$\frac{d}{d t} \int_{V} \frac{1}{2} \rho u^{2} d V+\int_{S} \frac{1}{2} \rho u^{2} u_{i} n_{i} d S=\int_{S} u_{i} \sigma_{i j} n_{j} d S-2 \mu \int_{V} e_{i j} e_{i j} d V$$

  Interpret each term in this equation and explain the meaning of the symbols used.

  Consider steady rectilinear flow in a (not necessarily circular) pipe having rigid stationary walls. Deduce a relation between the viscous dissipation per unit length of the pipe, the pressure gradient $G$, and the volume flux $Q$.

  Starting from the Navier-Stokes equations, calculate the velocity field for steady rectilinear flow in a circular pipe of radius $a$. Using the relationship derived above, or otherwise, find the viscous dissipation per unit length of this flow in terms of $G$.

  [Hint: In cylindrical polar coordinates,

  $$\nabla^{2} w(r)=\frac{1}{r} \frac{d}{d r}\left(r \frac{d w}{d r}\right)$$

  comment

Further Complex Methods

• Paper 2, Section I, E

  Further Complex Methods | Part II, 2011

  Find the two complex-valued functions $F^{+}(z)$ and $F^{-}(z)$ such that all of the following hold:

  (i) $F^{+}(z)$ and $F^{-}(z)$ are analytic for $\operatorname{Im} z>0$ and $\operatorname{Im} z<0$ respectively, where $z=x+i y, x, y \in \mathbb{R}$.

  (ii) $F^{+}(x)-F^{-}(x)=\frac{1}{x^{4}+1}, \quad x \in \mathbb{R}$.

  (iii) $F^{\pm}(z)=O\left(\frac{1}{z}\right), \quad z \rightarrow \infty, \quad \operatorname{Im} z \neq 0$.

  comment

• Paper 2, Section II, E

  Further Complex Methods | Part II, 2011

  Consider the following sum related to Riemann's zeta function:

  $$S:=\sum_{m=1}^{\left[\frac{a}{2 \pi}\right]} m^{s-1}, \quad s=\sigma+i t, \sigma, t \in \mathbb{R}, \quad a>2 \pi, a \neq 2 \pi N, N \in \mathbb{Z}^{+},$$

  where $[a / 2 \pi]$ denotes the integer part of $a / 2 \pi$.

  (i) By using an appropriate branch cut, show that

  $$S=\frac{e^{-\frac{i \pi s}{2}}}{(2 \pi)^{s}} \int_{L} f(z, s) d z, \quad f(z, s)=\frac{e^{-z}}{1-e^{-z}} z^{s-1}$$

  where $L$ is the circle in the complex $z$-plane centred at $i(a+b) / 2$ with radius $(a-b) / 2$, $0<b<2 \pi$.

  (ii) Use the above representation to show that, for $a>2 \pi$ and $0<b<2 \pi$,

  $$\sum_{m=1}^{\left[\frac{a}{2 \pi}\right]} m^{s-1}=\frac{1}{(2 \pi)^{s}}\left[e^{-\frac{i \pi s}{2}} \int_{C_{b}^{a}} f(z, s) d z-e^{\frac{i \pi s}{2}} \int_{C_{-a}^{-b}} f(z, s) d z+\frac{a^{s}}{s}-\frac{b^{s}}{s}\right]$$

  where $f(z, s)$ is defined in (i) and the curves $C_{b}^{a}, C_{-a}^{-b}$ are the following semi-circles in the right half complex $z$-plane:

  

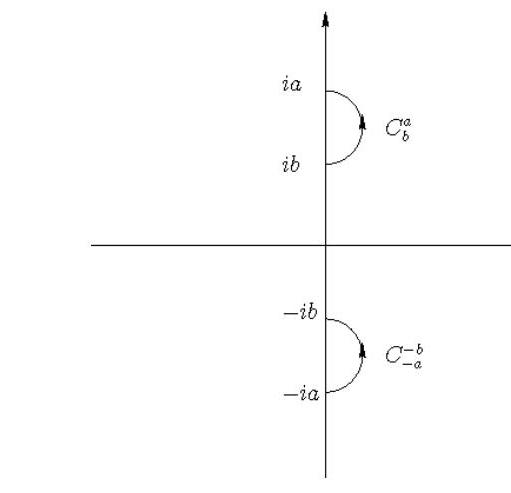
  The curves $C_{b}^{a}$ and $C_{-a}^{-b}$.

  $$\begin{aligned} C_{b}^{a} &=\left\{\frac{i(a+b)}{2}+\frac{(a-b)}{2} e^{i \theta}, \quad-\frac{\pi}{2}<\theta<\frac{\pi}{2}\right\} \\ C_{-a}^{-b} &=\left\{\frac{-i(a+b)}{2}+\frac{(a-b)}{2} e^{i \theta}, \quad-\frac{\pi}{2}<\theta<\frac{\pi}{2}\right\} \end{aligned}$$

  Part II, 2011 List of Questions

  [TURN OVER

  comment

Galois Theory

• Paper 2, Section II, H

  Galois Theory | Part II, 2011

  Let $F=\mathbb{C}(x, y)$ be the function field in two variables $x, y$. Let $n \geqslant 1$, and $K=\mathbb{C}\left(x^{n}+y^{n}, x y\right)$ be the subfield of $F$ of all rational functions in $x^{n}+y^{n}$ and $x y .$

  (i) Let $K^{\prime}=K\left(x^{n}\right)$, which is a subfield of $F$. Show that $K^{\prime} / K$ is a quadratic extension.

  (ii) Show that $F / K^{\prime}$ is cyclic of order $n$, and $F / K$ is Galois. Determine the Galois $\operatorname{group} \operatorname{Gal}(F / K)$.

  comment

General Relativity

• Paper 2, Section II, 36D

  General Relativity | Part II, 2011

  The curvature tensor $R_{b c d}^{a}$ satisfies

  $$V_{a ; b c}-V_{a ; c b}=V_{e} R_{a b c}^{e}$$

  for any covariant vector field $V_{a}$. Hence express $R_{a b c}^{e}$ in terms of the Christoffel symbols and their derivatives. Show that

  $$R_{a b c}^{e}=-R_{a c b}^{e}$$

  Further, by setting $V_{a}=\partial \phi / \partial x^{a}$, deduce that

  $$R_{a b c}^{e}+R_{c a b}^{e}+R_{b c a}^{e}=0 .$$

  Using local inertial coordinates or otherwise, obtain the Bianchi identities.

  Define the Ricci tensor in terms of the curvature tensor and show that it is symmetric. [You may assume that $R_{a b c d}=-R_{b a c d}$.] Write down the contracted Bianchi identities.

  In certain spacetimes of dimension $n \geqslant 2, R_{a b c d}$ takes the form

  $$R_{a b c d}=K\left(g_{a c} g_{b d}-g_{a d} g_{b c}\right)$$

  Obtain the Ricci tensor and curvature scalar. Deduce, under some restriction on $n$ which should be stated, that $K$ is a constant.

  comment

Geometry and Groups

• Paper 2, Section $I$, $3 \mathrm{G}$

  Geometry and Groups | Part II, 2011

  Let $A$ and $B$ be two rotations of the Euclidean plane $\mathbb{E}^{2}$ about centres $a$ and $b$ respectively. Show that the conjugate $A B A^{-1}$ is also a rotation and find its fixed point. When do $A$ and $B$ commute? Show that the commutator $A B A^{-1} B^{-1}$ is a translation.

  Deduce that any group of orientation-preserving isometries of the Euclidean plane either fixes a point or is infinite.

  comment

Graph Theory

• Paper 2, Section II, F

  Graph Theory | Part II, 2011

  What does it mean to say that a graph $G$ is $k$-colourable? Define the chromatic number $\chi(G)$ of a graph $G$, and the chromatic number $\chi(S)$ of a closed surface $S$.

  State the Euler-Poincaré formula relating the numbers of vertices, edges and faces in a drawing of a graph $G$ on a closed surface $S$ of Euler characteristic $E$. Show that if $E \leqslant 0$ then

  $$\chi(S) \leqslant\left[\frac{7+\sqrt{49-24 E}}{2}\right\rfloor$$

  Find, with justification, the chromatic number of the Klein bottle $N_{2}$. Show that if $G$ is a triangle-free graph which can be drawn on the Klein bottle then $\chi(G) \leqslant 4$.

  [You may assume that the Klein bottle has Euler characteristic 0 , and that $K_{6}$ can be drawn on the Klein bottle but $K_{7}$ cannot. You may use Brooks's theorem.]

  comment

Integrable Systems

• Paper 2, Section II, A

  Integrable Systems | Part II, 2011

  Consider the Poisson structure

  $$\{F, G\}=\int_{\mathbb{R}} \frac{\delta F}{\delta u(x)} \frac{\partial}{\partial x} \frac{\delta G}{\delta u(x)} d x$$

  where $F, G$ are polynomial functionals of $u, u_{x}, u_{x x}, \ldots$. Assume that $u, u_{x}, u_{x x}, \ldots$ tend to zero as $|x| \rightarrow \infty$.

  (i) Show that $\{F, G\}=-\{G, F\}$.

  (ii) Write down Hamilton's equations for $u=u(x, t)$ corresponding to the following Hamiltonians:

  $$H_{0}[u]=\int_{\mathbb{R}} \frac{1}{2} u^{2} d x, \quad H[u]=\int_{\mathbb{R}}\left(\frac{1}{2} u_{x}^{2}+u^{3}+u u_{x}\right) d x$$

  (iii) Calculate the Poisson bracket $\left\{H_{0}, H\right\}$, and hence or otherwise deduce that the following overdetermined system of partial differential equations for $u=u\left(x, t_{0}, t\right)$ is compatible:

  $$\begin{gathered} u_{t_{0}}=u_{x} \\ u_{t}=6 u u_{x}-u_{x x x} \end{gathered}$$

  [You may assume that the Jacobi identity holds for (1).]

  (iv) Find a symmetry of (3) generated by $X=\partial / \partial u+\alpha t \partial / \partial x$ for some constant $\alpha \in \mathbb{R}$ which should be determined. Construct a vector field $Y$ corresponding to the one parameter group

  $$x \rightarrow \beta x, \quad t \rightarrow \gamma t, \quad u \rightarrow \delta u,$$

  where $(\beta, \gamma, \delta)$ should be determined from the symmetry requirement. Find the Lie algebra generated by the vector fields $(X, Y)$.

  comment

Linear Analysis

• Paper 2, Section II, G

  Linear Analysis | Part II, 2011

  State and prove the Baire Category Theorem. Let $f: \mathbb{R} \rightarrow \mathbb{R}$ be a function. For $x \in \mathbb{R}$, define

  $$\omega_{f}(x)=\inf _{\delta>0} \sup _{\substack{|y-x| \leqslant \delta \\\left|y^{\prime}-x\right| \leqslant \delta}}\left|f(y)-f\left(y^{\prime}\right)\right|$$

  Show that $f$ is continuous at $x$ if and only if $\omega_{f}(x)=0$.

  Show that for any $\epsilon>0$ the set $\left\{x \in \mathbb{R}: \omega_{f}(x)<\epsilon\right\}$ is open.

  Hence show that the set of points at which $f$ is continuous cannot be precisely the set $\mathbb{Q}$ of rationals.

  comment

Logic and Set Theory

• Paper 2, Section II, H

  Logic and Set Theory | Part II, 2011

  State and prove Zorn's Lemma. [You may assume Hartogs' Lemma.] Where in your argument have you made use of the Axiom of Choice?

  Show that every real vector space has a basis.

  Let $V$ be a real vector space having a basis of cardinality $\aleph_{1}$. What is the cardinality of $V$ ? Justify your answer.

  comment

Mathematical Biology

• Paper 2, Section I, B

  Mathematical Biology | Part II, 2011

  A population with variable growth and harvesting is modelled by the equation

  $$u_{t+1}=\max \left(\frac{r u_{t}^{2}}{1+u_{t}^{2}}-E u_{t}, 0\right)$$

  where $r$ and $E$ are positive constants.

  Given that $r>1$, show that a non-zero steady state exists if $0<E<E_{m}(r)$, where $E_{m}(r)$ is to be determined.

  Show using a cobweb diagram that, if $E<E_{m}(r)$, a non-zero steady state may be attained only if the initial population $u_{0}$ satisfies $\alpha<u_{0}<\beta$, where $\alpha$ should be determined explicitly and $\beta$ should be specified as a root of an algebraic equation.

  With reference to the cobweb diagram, give an additional criterion that implies that $\alpha<u_{0}<\beta$ is a sufficient condition, as well as a necessary condition, for convergence to a non-zero steady state.

  comment

• Paper 2, Section II, B

  Mathematical Biology | Part II, 2011

  Consider a population subject to the following birth-death process. When the number of individuals in the population is $n$, the probability of an increase from $n$ to $n+1$ in unit time is $\beta n+\gamma$ and the probability of a decrease from $n$ to $n-1$ is $\alpha n(n-1)$, where $\alpha, \beta$ and $\gamma$ are constants.

  Show that the master equation for $P(n, t)$, the probability that at time $t$ the population has $n$ members, is

  $$\frac{\partial P}{\partial t}=\alpha n(n+1) P(n+1, t)-\alpha n(n-1) P(n, t)+(\beta n-\beta+\gamma) P(n-1, t)-(\beta n+\gamma) P(n, t) .$$

  Show that $\langle n\rangle$, the mean number of individuals in the population, satisfies

  $$\frac{d\langle n\rangle}{d t}=-\alpha\left\langle n^{2}\right\rangle+(\alpha+\beta)\langle n\rangle+\gamma$$

  Deduce that, in a steady state,

  $$\langle n\rangle=\frac{\alpha+\beta}{2 \alpha} \pm \sqrt{\frac{(\alpha+\beta)^{2}}{4 \alpha^{2}}+\frac{\gamma}{\alpha}-(\Delta n)^{2}}$$

  where $\Delta n$ is the standard deviation of $n$. When is the minus sign admissable?

  Show how a Fokker-Planck equation of the form

  $$\frac{\partial P}{\partial t}=\frac{\partial}{\partial n}[g(n) P(n, t)]+\frac{1}{2} \frac{\partial^{2}}{\partial n^{2}}[h(n) P(n, t)]$$

  may be derived under conditions to be explained, where the functions $g(n)$ and $h(n)$ should be evaluated.

  In the case $\alpha \ll \gamma$ and $\beta=0$, find the leading-order approximation to $n_{*}$ such that $g\left(n_{*}\right)=0$. Defining the new variable $x=n-n_{*}$, where $g\left(n_{*}\right)=0$, approximate $g(n)$ by $g^{\prime}\left(n_{*}\right) x$ and $h(n)$ by $h\left(n_{*}\right)$. Solve $(*)$ for $P(x)$ in the steady-state limit and deduce leading-order estimates for $\langle n\rangle$ and $(\Delta n)^{2}$.

  comment

Number Fields

• Paper 2, Section II, F

  Number Fields | Part II, 2011

  (i) Suppose that $d>1$ is a square-free integer. Describe, with justification, the ring of integers in the field $K=\mathbb{Q}(\sqrt{d})$.

  (ii) Show that $\mathbb{Q}\left(2^{1 / 3}\right)=\mathbb{Q}\left(4^{1 / 3}\right)$ and that $\mathbb{Z}\left[4^{1 / 3}\right]$ is not the ring of integers in this field.

  comment

Number Theory

• Paper 2, Section I, I

  Number Theory | Part II, 2011

  (i) Find a primitive root modulo $17 .$

  (ii) Let $p$ be a prime of the form $2^{m}+1$ for some integer $m \geqslant 1$. Prove that every quadratic non-residue modulo $p$ is a primitive root modulo $p$.

  comment

Numerical Analysis

• Paper 2, Section II, A

  Numerical Analysis | Part II, 2011

  Let $A \in \mathbb{R}^{n \times n}$ be a real matrix with $n$ linearly independent eigenvectors. The eigenvalues of $A$ can be calculated from the sequence $x^{(k)}, k=0,1, \ldots$, which is generated by the power method

  $$x^{(k+1)}=\frac{A x^{(k)}}{\left\|A x^{(k)}\right\|},$$

  where $x^{(0)}$ is a real nonzero vector.

  (i) Describe the asymptotic properties of the sequence $x^{(k)}$ in the case that the eigenvalues $\lambda_{i}$ of $A$ satisfy $\left|\lambda_{i}\right|<\left|\lambda_{n}\right|, i=1, \ldots, n-1$, and the eigenvectors are of unit length.

  (ii) Present the implementation details for the power method for the setting in (i) and define the Rayleigh quotient.

  (iii) Let $A$ be the $3 \times 3$ matrix

  $$A=\lambda I+P, \quad P=\left(\begin{array}{lll} 0 & 0 & 0 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right)$$

  where $\lambda$ is real and nonzero. Find an explicit expression for $A^{k}, k=1,2,3, \ldots$

  Let the sequence $x^{(k)}$ be generated by the power method as above. Deduce from your expression for $A^{k}$ that the first and second components of $x^{(k+1)}$ tend to zero as $k \rightarrow \infty$. Further show that this implies $A x^{(k+1)}-\lambda x^{(k+1)} \rightarrow 0$ as $k \rightarrow \infty$.

  comment

Optimization and Control

• Paper 2, Section II, K

  Optimization and Control | Part II, 2011

  Consider an optimal stopping problem in which the optimality equation takes the form

  $$F_{t}(x)=\max \left\{r(x), E\left[F_{t+1}\left(x_{t+1}\right)\right]\right\}, \quad t=1, \ldots, N-1,$$

  $F_{N}(x)=r(x)$, and where $r(x)>0$ for all $x$. Let $S$ denote the stopping set of the onestep-look-ahead rule. Show that if $S$ is closed (in a sense you should explain) then the one-step-look-ahead rule is optimal.

  $N$ biased coins are to be tossed successively. The probability that the $i$ th coin toss will show a head is known to be $p_{i}\left(0<p_{i}<1\right)$. At most once, after observing a head, and before tossing the next coin, you may guess that you have just seen the last head (i.e. that all subsequent tosses will show tails). If your guess turns out to be correct then you win $£ 1$.

  Suppose that you have not yet guessed 'last head', and the $i$ th toss is a head. Show that it cannot be optimal to guess that this is the last head if

  $$\frac{p_{i+1}}{q_{i+1}}+\cdots+\frac{p_{N}}{q_{N}}>1$$

  where $q_{j}=1-p_{j}$.

  Suppose that $p_{i}=1 / i$. Show that it is optimal to guess that the last head is the first head (if any) to occur after having tossed at least $i^{*}$ coins, where $i^{*} \approx N / e$ when $N$ is large.

  comment

Partial Differential Equations

• Paper 2, Section II, A

  Partial Differential Equations | Part II, 2011

  Consider the Schrödinger equation

  $$\begin{aligned} i \partial_{t} \psi(t, x) &=-\frac{1}{2} \Delta \psi(t, x)+V(x) \psi(t, x), \quad x \in \mathbb{R}^{n}, t>0 \\ \psi(t=0, x) &=\psi_{I}(x), \quad x \in \mathbb{R}^{n} \end{aligned}$$

  where $V$ is a smooth real-valued function.

  Prove that, for smooth solutions, the following equations are valid for all $t>0$ :

  (i)

  $$\int_{\mathbb{R}^{n}}|\psi(t, x)|^{2} d x=\int_{\mathbb{R}^{n}}\left|\psi_{I}(x)\right|^{2} d x$$

  (ii)

  $$\begin{aligned} &\int_{\mathbb{R}^{n}} \frac{1}{2}|\nabla \psi(t, x)|^{2} d x+\int_{\mathbb{R}^{n}} V(x)|\psi(t, x)|^{2} d x \\ &=\int_{\mathbb{R}^{n}} \frac{1}{2}\left|\nabla \psi_{I}(x)\right|^{2} d x+\int_{\mathbb{R}^{n}} V(x)\left|\psi_{I}(x)\right|^{2} d x \end{aligned}$$

  comment

Principles of Quantum Mechanics

• Paper 2, Section II, D

  Principles of Quantum Mechanics | Part II, 2011

  A quantum system has energy eigenstates $|n\rangle$ with eigenvalues $E_{n}=n \hbar, n \in$ $\{1,2,3, \ldots\}$. An observable $Q$ is such that $Q|n\rangle=q_{n}|n\rangle$.

  (a) What is the commutator of $Q$ with the Hamiltonian $H$ ?

  (b) Given $q_{n}=\frac{1}{n}$, consider the state

  $$|\psi\rangle \propto \sum_{n=1}^{N} \sqrt{n}|n\rangle$$

  Determine:

  (i) The probability of measuring $Q$ to be $1 / N$.

  (ii) The probability of measuring energy $\hbar$ followed by another immediate measurement of energy $2 \hbar$.

  (iii) The average of many separate measurements of $Q$, each measurement being on a state $|\psi\rangle$, as $N \rightarrow \infty$.

  (c) Given $q_{1}=1$ and $q_{n}=-1$ for $n>1$, consider the state

  $$|\psi\rangle \propto \sum_{n=1}^{\infty} \alpha^{n / 2}|n\rangle,$$

  where $0<\alpha<1$.

  (i) Show that the probability of measuring an eigenvalue $q=-1$ of $|\psi\rangle$ is

  $$A+B \alpha$$

  where $A$ and $B$ are integers that you should find.

  (ii) Show that $\langle Q\rangle_{\psi}$ is $C+D \alpha$, where $C$ and $D$ are integers that you should find.

  (iii) Given that $Q$ is measured to be $-1$ at time $t=0$, write down the state after a time $t$ has passed. What is then the subsequent probability at time $t$ of measuring the energy to be $2 \hbar$ ?

  comment

Principles of Statistics

• Paper 2, Section II, K

  Principles of Statistics | Part II, 2011

  Random variables $X_{1}, \ldots, X_{n}$ are independent and identically distributed from the normal distribution with unknown mean $\mathrm{M}$ and unknown precision (inverse variance) $H$. Show that the likelihood function, for data $X_{1}=x_{1}, \ldots, X_{n}=x_{n}$, is

  $$L_{n}(\mu, h) \propto h^{n / 2} \exp \left(-\frac{1}{2} h\left\{n(\bar{x}-\mu)^{2}+S\right\}\right)$$

  where $\bar{x}:=n^{-1} \sum_{i} x_{i}$ and $S:=\sum_{i}\left(x_{i}-\bar{x}\right)^{2}$.

  A bivariate prior distribution for $(\mathrm{M}, H)$ is specified, in terms of hyperparameters $\left(\alpha_{0}, \beta_{0}, m_{0}, \lambda_{0}\right)$, as follows. The marginal distribution of $H$ is $\Gamma\left(\alpha_{0}, \beta_{0}\right)$, with density

  $$\pi(h) \propto h^{\alpha_{0}-1} e^{-\beta_{0} h} \quad(h>0),$$

  and the conditional distribution of $\mathrm{M}$, given $H=h$, is normal with mean $m_{0}$ and precision $\lambda_{0} h$.

  Show that the conditional prior distribution of $H$, given $M=\mu$, is

  $$H \mid \mathrm{M}=\mu \quad \sim\left(\alpha_{0}+\frac{1}{2}, \beta_{0}+\frac{1}{2} \lambda_{0}\left(\mu-m_{0}\right)^{2}\right)$$

  Show that the posterior joint distribution of $(\mathrm{M}, H)$, given $X_{1}=x_{1}, \ldots, X_{n}=x_{n}$, has the same form as the prior, with updated hyperparameters $\left(\alpha_{n}, \beta_{n}, m_{n}, \lambda_{n}\right)$ which you should express in terms of the prior hyperparameters and the data.

  [You may use the identity

  $$p(t-a)^{2}+q(t-b)^{2}=(t-\delta)^{2}+p q(a-b)^{2}$$

  where $p+q=1$ and $\delta=p a+q b$.]

  Explain how you could implement Gibbs sampling to generate a random sample from the posterior joint distribution.

  comment

Probability and Measure

• Paper 2, Section II, $26 \mathrm{~K}$

  Probability and Measure | Part II, 2011

  (i) Define the notions of a $\pi$-system and a $d$-system. State and prove Dynkin's lemma.

  (ii) Let $\left(E_{1}, \mathcal{E}_{1}, \mu_{1}\right)$ and $\left(E_{2}, \mathcal{E}_{2}, \mu_{2}\right)$ denote two finite measure spaces. Define the $\sigma$ algebra $\mathcal{E}_{1} \otimes \mathcal{E}_{2}$ and the product measure $\mu_{1} \otimes \mu_{2}$. [You do not need to verify that such a measure exists.] State (without proof) Fubini's Theorem.

  (iii) Let $(E, \mathcal{E}, \mu)$ be a measure space, and let $f$ be a non-negative Borel-measurable function. Let $G$ be the subset of $E \times \mathbb{R}$ defined by

  $$G=\{(x, y) \in E \times \mathbb{R}: 0 \leqslant y \leqslant f(x)\}$$

  Show that $G \in \mathcal{E} \otimes \mathcal{B}(\mathbb{R})$, where $\mathcal{B}(\mathbb{R})$ denotes the Borel $\sigma$-algebra on $\mathbb{R}$. Show further that

  $$\int f d \mu=(\mu \otimes \lambda)(G)$$

  where $\lambda$ is Lebesgue measure.

  comment

Representation Theory

• Paper 2, Section II, I

  Representation Theory | Part II, 2011

  State Maschke's Theorem for finite-dimensional complex representations of the finite group $G$. Show by means of an example that the requirement that $G$ be finite is indispensable.

  Now let $G$ be a (possibly infinite) group and let $H$ be a normal subgroup of finite index $r$ in $G$. Let $g_{1}, \ldots, g_{r}$ be representatives of the cosets of $H$ in $G$. Suppose that $V$ is a finite-dimensional completely reducible $\mathbb{C} G$-module. Show that

  (i) if $U$ is a $\mathbb{C} H$-submodule of $V$ and $g \in G$, then the set $g U=\{g u: u \in U\}$ is a $\mathbb{C} H$-submodule of $V$;

  (ii) if $U$ is a $\mathbb{C} H$-submodule of $V$, then $\sum_{i=1}^{r} g_{i} U$ is a $\mathbb{C} G$-submodule of $V$;

  (iii) $V$ is completely reducible regarded as a $\mathbb{C} H$-module.

  Hence deduce that if $\chi$ is an irreducible character of the finite group $G$ then all the constituents of $\chi_{H}$ have the same degree.

  comment

Riemann Surfaces

• Paper 2, Section II, 23G

  Riemann Surfaces | Part II, 2011

  Let $\Lambda$ be a lattice in $\mathbb{C}$ generated by 1 and $\tau$, where $\tau$ is a fixed complex number with non-zero imaginary part. Suppose that $f$ is a meromorphic function on $\mathbb{C}$ for which the poles of $f$ are precisely the points in $\Lambda$, and for which $f(z)-1 / z^{2} \rightarrow 0$ as $z \rightarrow 0$. Assume moreover that $f^{\prime}(z)$ determines a doubly periodic function with respect to $\Lambda$ with $f^{\prime}(-z)=-f^{\prime}(z)$ for all $z \in \mathbb{C} \backslash \Lambda$. Prove that:

  (i) $f(-z)=f(z)$ for all $z \in \mathbb{C} \backslash \Lambda$.

  (ii) $f$ is doubly periodic with respect to $\Lambda$.

  (iii) If it exists, $f$ is uniquely determined by the above properties.

  (iv) For some complex number $A, f$ satisfies the differential equation $f^{\prime \prime}(z)=6 f(z)^{2}+A$.

  comment

Statistical Modelling

• Paper 2, Section I, J

  Statistical Modelling | Part II, 2011

  Let $f_{0}$ be a probability density function, with cumulant generating function $K$. Define what it means for a random variable $Y$ to have a model function of exponential dispersion family form, generated by $f_{0}$. Compute the cumulant generating function $K_{Y}$ of $Y$ and deduce expressions for the mean and variance of $Y$ that depend only on first and second derivatives of $K$.

  comment

Statistical Physics

• Paper 2, Section II, D

  Statistical Physics | Part II, 2011

  Write down the partition function for a single classical non-relativistic particle of mass $m$ moving in three dimensions in a potential $U(\mathbf{x})$ and in equilibrium with a heat bath at temperature $T$.

  A system of $N$ non-interacting classical non-relativistic particles, in equilibrium at temperature $T$, is placed in a potential

  $$U(\mathbf{x})=\frac{\left(x^{2}+y^{2}+z^{2}\right)^{n}}{V^{2 n / 3}}$$

  where $n$ is a positive integer. Using the partition function, show that the free energy is

  $$F=-N k_{B} T\left(\log V+\frac{3}{2} \frac{n+1}{n} \log k_{B} T+\log I_{n}+\text { const }\right)$$

  where

  $$I_{n}=\left(\frac{m}{2 \pi \hbar^{2}}\right)^{3 / 2} \int_{0}^{\infty} 4 \pi u^{2} \exp \left(-u^{2 n}\right) d u$$

  Explain the physical relevance of the constant term in the expression $(*)$.

  Viewing $V$ as an external parameter, akin to volume, compute the conjugate pressure $p$ and show that the equation of state coincides with that of an ideal gas.

  Compute the energy $E$, heat capacity $C_{V}$ and entropy $S$ of the gas. Determine the local particle number density as a function of $|\mathbf{x}|$.

  comment

Stochastic Financial Models

• Paper 2, Section II, J

  Stochastic Financial Models | Part II, 2011

  Consider a symmetric simple random walk $\left(Z_{n}\right)_{n \in \mathbb{Z}^{+}}$taking values in statespace $I=h \mathbb{Z}^{2} \equiv\{(i h, j h): i, j \in \mathbb{Z}\}$, where $h \equiv N^{-1}(N$ an integer $)$. Writing $Z_{n} \equiv\left(X_{n}, Y_{n}\right)$, the transition probabilities are given by

  $$P\left(\Delta Z_{n}=(h, 0)\right)=P\left(\Delta Z_{n}=(0, h)\right)=P\left(\Delta Z_{n}=(-h, 0)\right)=P\left(\Delta Z_{n}=(0,-h)\right)=\frac{1}{4},$$

  where $\Delta Z_{n} \equiv Z_{n}-Z_{n-1}$.

  What does it mean to say that $\left(M_{n}, \mathcal{F}_{n}\right)_{n \in \mathbb{Z}^{+}}$is a martingale? Find a condition on $\theta$ and $\lambda$ such that

  $$M_{n}=\exp \left(\theta X_{n}-\lambda Y_{n}\right)$$

  is a martingale. If $\theta=i \alpha$ for some real $\alpha$, show that $M$ is a martingale if

  $$e^{-\lambda h}=2-\cos (\alpha h)-\sqrt{(2-\cos (\alpha h))^{2}-1}$$

  Suppose that the random walk $Z$ starts at position $(0,1) \equiv(0, N h)$ at time 0 , and suppose that

  $$\tau=\inf \left\{n: Y_{n}=0\right\} .$$

  Stating fully any results to which you appeal, prove that

  $$E \exp \left(i \alpha X_{\tau}\right)=e^{-\lambda}$$

  where $\lambda$ is as given at $(*)$. Deduce that as $N \rightarrow \infty$

  $$E \exp \left(i \alpha X_{\tau}\right) \rightarrow e^{-|\alpha|}$$

  and comment briefly on this result.

  comment

Topics in Analysis

• Paper 2, Section I, F

  Topics in Analysis | Part II, 2011

  (i) Let $x_{1}, x_{2}, \ldots, x_{n} \in[-1,1]$ be any set of $n$ distinct numbers. Show that there exist numbers $A_{1}, A_{2}, \ldots, A_{n}$ such that the formula

  $$\int_{-1}^{1} p(x) d x=\sum_{j=1}^{n} A_{j} p\left(x_{j}\right)$$

  is valid for every polynomial $p$ of degree $\leqslant n-1$.

  (ii) For $n=0,1,2, \ldots$, let $p_{n}$ be the Legendre polynomial, over $[-1,1]$, of degree $n$. Suppose that $x_{1}, x_{2}, \ldots, x_{n} \in[-1,1]$ are the roots of $p_{n}$, and $A_{1}, A_{2}, \ldots, A_{n}$ are the numbers corresponding to $x_{1}, x_{2}, \ldots, x_{n}$ as in (i).

  [You may assume without proof that for $n \geqslant 1, p_{n}$ has $n$ distinct roots in $[-1,1] .$ ]

  Prove that the integration formula in (i) is now valid for any polynomial $p$ of degree $\leqslant 2 n-1$.

  (iii) Is it possible to choose $n$ distinct points $x_{1}, x_{2}, \ldots, x_{n} \in[-1,1]$ and corresponding numbers $A_{1}, A_{2}, \ldots, A_{n}$ such that the integration formula in (i) is valid for any polynomial $p$ of degree $\leqslant 2 n$ ? Justify your answer.

  comment

• Paper 2, Section II, F

  Topics in Analysis | Part II, 2011

  Let $C[0,1]$ be the space of real continuous functions on the interval $[0,1]$. A mapping $L: C[0,1] \rightarrow C[0,1]$ is said to be positive if $L(f) \geqslant 0$ for each $f \in C[0,1]$ with $f \geqslant 0$, and linear if $L(a f+b g)=a L(f)+b L(g)$ for all functions $f, g \in C[0,1]$ and constants $a, b \in \mathbb{R}$.

  (i) Let $L_{n}: C[0,1] \rightarrow C[0,1]$ be a sequence of positive, linear mappings such that $L_{n}(f) \rightarrow f$ uniformly on $[0,1]$ for the three functions $f(x)=1, x, x^{2}$. Prove that $L_{n}(f) \rightarrow f$ uniformly on $[0,1]$ for every $f \in C[0,1]$.

  (ii) Define $B_{n}: C[0,1] \rightarrow C[0,1]$ by

  $$B_{n}(f)(x)=\sum_{k=0}^{n}\left(\begin{array}{l} n \\ k \end{array}\right) f\left(\frac{k}{n}\right) x^{k}(1-x)^{n-k}$$

  where $\left(\begin{array}{l}n \\ k\end{array}\right)=\frac{n !}{k !(n-k) !}$. Using the result of part (i), or otherwise, prove that $B_{n}(f) \rightarrow f$ uniformly on $[0,1]$.

  (iii) Let $f \in C[0,1]$ and suppose that

  $$\int_{0}^{1} f(x) x^{4 n} d x=0$$

  for each $n=0,1, \ldots$ Prove that $f$ must be the zero function.

  [You should not use the Stone-Weierstrass theorem without proof.]

  comment

Waves

• Paper 2, Section II, 38B

  Waves | Part II, 2011

  A uniform elastic solid with wavespeeds $c_{P}$ and $c_{S}$ occupies the region $z<0$. An $S$-wave with displacement

  $$\mathbf{u}=(\cos \theta, 0,-\sin \theta) \mathrm{e}^{\mathrm{i} k(x \sin \theta+z \cos \theta)-\mathrm{i} \omega t}$$

  is incident from $z<0$ on a rigid boundary at $z=0$. Find the form and amplitudes of the reflected waves.

  When is the reflected $P$-wave evanescent? Show that if the $P$-wave is evanescent then the amplitude of the reflected $S$-wave has the same magnitude as the incident wave, and interpret this result physically.

  comment