Part IB, 2004, Paper 4

Analysis II

• 4.I.3F

  Analysis II | Part IB, 2004

  Let $U, V$ be open sets in $\mathbb{R}^{n}, \mathbb{R}^{m}$, respectively, and let $f: U \rightarrow V$ be a map. What does it mean for $f$ to be differentiable at a point $u$ of $U$ ?

  Let $g: \mathbb{R}^{2} \rightarrow \mathbb{R}$ be the map given by

  $$g(x, y)=|x|+|y|$$

  Prove that $g$ is differentiable at all points $(a, b)$ with $a b \neq 0$.

  comment

• 4.II.13F

  Analysis II | Part IB, 2004

  State the inverse function theorem for maps $f: U \rightarrow \mathbb{R}^{2}$, where $U$ is a non-empty open subset of $\mathbb{R}^{2}$.

  Let $f: \mathbb{R}^{2} \rightarrow \mathbb{R}^{2}$ be the function defined by

  $$f(x, y)=\left(x, x^{3}+y^{3}-3 x y\right) .$$

  Find a non-empty open subset $U$ of $\mathbb{R}^{2}$ such that $f$ is locally invertible on $U$, and compute the derivative of the local inverse.

  Let $C$ be the set of all points $(x, y)$ in $\mathbb{R}^{2}$ satisfying

  $$x^{3}+y^{3}-3 x y=0$$

  Prove that $f$ is locally invertible at all points of $C$ except $(0,0)$ and $\left(2^{2 / 3}, 2^{1 / 3}\right)$. Deduce that, for each point $(a, b)$ in $C$ except $(0,0)$ and $\left(2^{2 / 3}, 2^{1 / 3}\right)$, there exist open intervals $I, J$ containing $a, b$, respectively, such that for each $x$ in $I$, there is a unique point $y$ in $J$ with $(x, y)$ in $C$.

  comment

Complex Methods

• 4.I.5A

  Complex Methods | Part IB, 2004

  State and prove the Parseval formula.

  [You may use without proof properties of convolution, as long as they are precisely stated.]

  comment

• 4.II.15A

  Complex Methods | Part IB, 2004

  (i) Show that the inverse Fourier transform of the function

  $$\hat{g}(s)= \begin{cases}e^{s}-e^{-s}, & |s| \leqslant 1 \\ 0, & |s| \geqslant 1\end{cases}$$

  is

  $$g(x)=\frac{2 i}{\pi} \frac{1}{1+x^{2}}(x \sinh 1 \cos x-\cosh 1 \sin x)$$

  (ii) Determine, by using Fourier transforms, the solution of the Laplace equation

  $$\frac{\partial^{2} u}{\partial x^{2}}+\frac{\partial^{2} u}{\partial y^{2}}=0$$

  given in the strip $-\infty<x<\infty, 0<y<1$, together with the boundary conditions

  $$u(x, 0)=g(x), \quad u(x, 1) \equiv 0, \quad-\infty<x<\infty$$

  where $g$ has been given above.

  [You may use without proof properties of Fourier transforms.]

  comment

Fluid Dynamics

• 4.I.8C

  Fluid Dynamics | Part IB, 2004

  Write down the vorticity equation for the unsteady flow of an incompressible, inviscid fluid with no body forces acting.

  Show that the flow field

  $$\mathbf{u}=(-x, x \omega(t), z-1)$$

  has uniform vorticity of magnitude $\omega(t)=\omega_{0} e^{t}$ for some constant $\omega_{0}$.

  comment

• 4.II.18C

  Fluid Dynamics | Part IB, 2004

  Use Euler's equation to derive the momentum integral

  $$\int_{S}\left(p n_{i}+\rho n_{j} u_{j} u_{i}\right) d S=0$$

  for the steady flow $\mathbf{u}=\left(u_{1}, u_{2}, u_{3}\right)$ and pressure $p$ of an inviscid,incompressible fluid of density $\rho$, where $S$ is a closed surface with normal $\mathbf{n}$.

  A cylindrical jet of water of area $A$ and speed $u$ impinges axisymmetrically on a stationary sphere of radius $a$ and is deflected into a conical sheet of vertex angle $\alpha$ as shown. Gravity is being ignored.

  

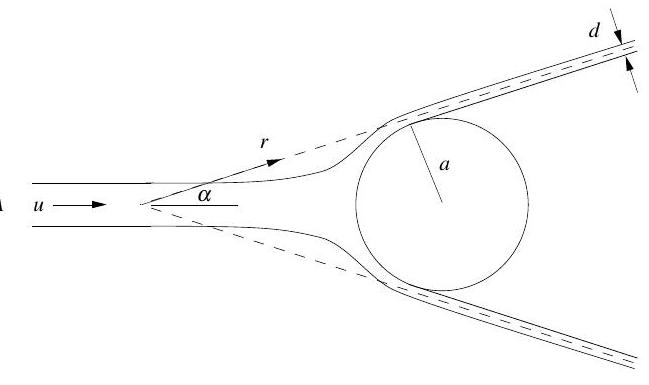
  Use a suitable form of Bernoulli's equation to determine the speed of the water in the conical sheet, being careful to state how the equation is being applied.

  Use conservation of mass to show that the width $d(r)$ of the sheet far from the point of impact is given by

  $$d=\frac{A}{2 \pi r \sin \alpha},$$

  where $r$ is the distance along the sheet measured from the vertex of the cone.

  Finally, use the momentum integral to determine the net force on the sphere in terms of $\rho, u, A$ and $\alpha$.

  comment

Further Analysis

• 4.I.4E

  Further Analysis | Part IB, 2004

  (i) Let $D$ be the open unit disc of radius 1 about the point $3+3 i$. Prove that there is an analytic function $f: D \rightarrow \mathbb{C}$ such that $f(z)^{2}=z$ for every $z \in D$.

  (ii) Let $D^{\prime}=\mathbb{C} \backslash\{z \in \mathbb{C}: \operatorname{Im} z=0$, Re $z \leqslant 0\}$. Explain briefly why there is at most one extension of $f$ to a function that is analytic on $D^{\prime}$.

  (iii) Deduce that $f$ cannot be extended to an analytic function on $\mathbb{C} \backslash\{0\}$.

  comment

• 4.II.14E

  Further Analysis | Part IB, 2004

  (i) State and prove Rouché's theorem.

  [You may assume the principle of the argument.]

  (ii) Let $0<c<1$. Prove that the polynomial $p(z)=z^{3}+i c z+8$ has three roots with modulus less than 3. Prove that one root $\alpha$ satisfies $\operatorname{Re} \alpha>0, \operatorname{Im} \alpha>0$; another, $\beta$, satisfies $\operatorname{Re} \beta>0$, Im $\beta<0$; and the third, $\gamma$, has $\operatorname{Re} \gamma<0$.

  (iii) For sufficiently small $c$, prove that $\operatorname{Im} \gamma>0$.

  [You may use results from the course if you state them precisely.]

  comment

Groups, Rings and Modules

• 4.I.2F

  Groups, Rings and Modules | Part IB, 2004

  State Gauss's lemma and Eisenstein's irreducibility criterion. Prove that the following polynomials are irreducible in $\mathbb{Q}[x]$ :

  (i) $x^{5}+5 x+5$;

  (ii) $x^{3}-4 x+1$;

  (iii) $x^{p-1}+x^{p-2}+\ldots+x+1$, where $p$ is any prime number.

  comment

• 4.II.12F

  Groups, Rings and Modules | Part IB, 2004

  Answer the following questions, fully justifying your answer in each case.

  (i) Give an example of a ring in which some non-zero prime ideal is not maximal.

  (ii) Prove that $\mathbb{Z}[x]$ is not a principal ideal domain.

  (iii) Does there exist a field $K$ such that the polynomial $f(x)=1+x+x^{3}+x^{4}$ is irreducible in $K[x]$ ?

  (iv) Is the ring $\mathbb{Q}[x] /\left(x^{3}-1\right)$ an integral domain?

  (v) Determine all ring homomorphisms $\phi: \mathbb{Q}[x] /\left(x^{3}-1\right) \rightarrow \mathbb{C}$.

  comment

Linear Algebra

• 4.I.1E

  Linear Algebra | Part IB, 2004

  Let $V$ be a real $n$-dimensional inner-product space and let $W \subset V$ be a $k$ dimensional subspace. Let $\mathbf{e}_{1}, \ldots, \mathbf{e}_{k}$ be an orthonormal basis for $W$. In terms of this basis, give a formula for the orthogonal projection $\pi: V \rightarrow W$.

  Let $v \in V$. Prove that $\pi v$ is the closest point in $W$ to $v$.

  [You may assume that the sequence $\mathbf{e}_{1}, \ldots, \mathbf{e}_{k}$ can be extended to an orthonormal basis $\mathbf{e}_{1}, \ldots, \mathbf{e}_{n}$ of $V$.]

  comment

• 4.II.11E

  Linear Algebra | Part IB, 2004

  (i) Let $V$ be an $n$-dimensional inner-product space over $\mathbb{C}$ and let $\alpha: V \rightarrow V$ be a Hermitian linear map. Prove that $V$ has an orthonormal basis consisting of eigenvectors of $\alpha$.

  (ii) Let $\beta: V \rightarrow V$ be another Hermitian map. Prove that $\alpha \beta$ is Hermitian if and only if $\alpha \beta=\beta \alpha$.

  (iii) A Hermitian map $\alpha$ is positive-definite if $\langle\alpha v, v\rangle>0$ for every non-zero vector $v$. If $\alpha$ is a positive-definite Hermitian map, prove that there is a unique positivedefinite Hermitian map $\beta$ such that $\beta^{2}=\alpha$.

  comment

Methods

• 4.I.6C

  Methods | Part IB, 2004

  Chebyshev polynomials $T_{n}(x)$ satisfy the differential equation

  $$\left(1-x^{2}\right) y^{\prime \prime}-x y^{\prime}+n^{2} y=0 \quad \text { on } \quad[-1,1],$$

  where $n$ is an integer.

  Recast this equation into Sturm-Liouville form and hence write down the orthogonality relationship between $T_{n}(x)$ and $T_{m}(x)$ for $n \neq m$.

  By writing $x=\cos \theta$, or otherwise, show that the polynomial solutions of ( $\dagger$ ) are proportional to $\cos \left(n \cos ^{-1} x\right)$.

  comment

• 4.II.16C

  Methods | Part IB, 2004

  Obtain the Green function $G(x, \xi)$ satisfying

  $$G^{\prime \prime}+\frac{2}{x} G^{\prime}+k^{2} G=\delta(x-\xi),$$

  where $k$ is real, subject to the boundary conditions

  $$\begin{array}{rll} G \text { is finite } & \text { at } & x=0, \\ G=0 & \text { at } & x=1 . \end{array}$$

  [Hint: You may find the substitution $G=H / x$ helpful.]

  Use the Green function to determine that the solution of the differential equation

  $$y^{\prime \prime}+\frac{2}{x} y^{\prime}+k^{2} y=1,$$

  subject to the boundary conditions

  $$\begin{array}{rll} y \text { is finite } & \text { at } & x=0, \\ y=0 & \text { at } & x=1, \end{array}$$

  is

  $$y=\frac{1}{k^{2}}\left[1-\frac{\sin k x}{x \sin k}\right]$$

  comment

Optimization

• 4.I.10G

  Optimization | Part IB, 2004

  State and prove the max flow/min cut theorem. In your answer you should define clearly the following terms: flow; maximal flow; cut; capacity.

  comment

• 4.II.20G

  Optimization | Part IB, 2004

  For any number $c \in(0,1)$, find the minimum and maximum values of

  $$\sum_{i=1}^{n} x_{i}^{c}$$

  subject to $\sum_{i=1}^{n} x_{i}=1, x_{1}, \ldots, x_{n} \geqslant 0$. Find all the points $\left(x_{1}, \ldots, x_{n}\right)$ at which the minimum and maximum are attained. Justify your answer.

  comment

Special Relativity

• 4.I.7D

  Special Relativity | Part IB, 2004

  For a particle with energy $E$ and momentum $(p \cos \theta, p \sin \theta, 0)$, explain why an observer moving in the $x$-direction with velocity $v$ would find

  $$E^{\prime}=\gamma(E-p \cos \theta v), \quad p^{\prime} \cos \theta^{\prime}=\gamma\left(p \cos \theta-E \frac{v}{c^{2}}\right), \quad p^{\prime} \sin \theta^{\prime}=p \sin \theta,$$

  where $\gamma=\left(1-v^{2} / c^{2}\right)^{-\frac{1}{2}}$. What is the relation between $E$ and $p$ for a photon? Show that the same relation holds for $E^{\prime}$ and $p^{\prime}$ and that

  $$\cos \theta^{\prime}=\frac{\cos \theta-\frac{v}{c}}{1-\frac{v}{c} \cos \theta}$$

  What happens for $v \rightarrow c$ ?

  comment

• 4.II.17D

  Special Relativity | Part IB, 2004

  State how the 4 -momentum $p_{\mu}$ of a particle is related to its energy and 3momentum. How is $p_{\mu}$ related to the particle mass? For two particles with 4 -momenta $p_{1 \mu}$ and $p_{2 \mu}$ find a Lorentz-invariant expression that gives the total energy in their centre of mass frame.

  A photon strikes an electron at rest. What is the minimum energy it must have in order for it to create an electron and positron, of the same mass $m_{e}$ as the electron, in addition to the original electron? Express the result in units of $m_{e} c^{2}$.

  [It may be helpful to consider the minimum necessary energy in the centre of mass frame.]

  comment

Statistics

• 4.I $9 \mathrm{H} \quad$

  Statistics | Part IB, 2004

  Suppose that $Y_{1}, \ldots, Y_{n}$ are independent random variables, with $Y_{i}$ having the normal distribution with mean $\beta x_{i}$ and variance $\sigma^{2}$; here $\beta, \sigma^{2}$ are unknown and $x_{1}, \ldots, x_{n}$ are known constants.

  Derive the least-squares estimate of $\beta$.

  Explain carefully how to test the hypothesis $H_{0}: \beta=0$ against $H_{1}: \beta \neq 0$.

  comment

• 4.II.19H

  Statistics | Part IB, 2004

  It is required to estimate the unknown parameter $\theta$ after observing $X$, a single random variable with probability density function $f(x \mid \theta)$; the parameter $\theta$ has the prior distribution with density $\pi(\theta)$ and the loss function is $L(\theta, a)$. Show that the optimal Bayesian point estimate minimizes the posterior expected loss.

  Suppose now that $f(x \mid \theta)=\theta e^{-\theta x}, x>0$ and $\pi(\theta)=\mu e^{-\mu \theta}, \theta>0$, where $\mu>0$ is known. Determine the posterior distribution of $\theta$ given $X$.

  Determine the optimal Bayesian point estimate of $\theta$ in the cases when

  (i) $L(\theta, a)=(\theta-a)^{2}$, and

  (ii) $L(\theta, a)=|(\theta-a) / \theta|$.

  comment